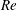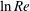1. Introduction
Our concern is with nonlinear equilibrium structures which develop in growing boundary layers. In a previous paper, Deguchi & Hall (Reference Deguchi and Hall2014a ), hereafter referred to as DH, described a class of nonlinear equilibrium structures generated in a layer at the edge of the asymptotic suction boundary layer (ASBL). The boundary layer thickness of this flow is unchanged in the streamwise direction and so there are no non-parallel effects, which we know from, for example, Hall (Reference Hall1983) to be crucial in the streamwise development of streamwise vortex disturbances. In the first instance we will investigate how the nonlinear interaction at the heart of the free-stream coherent states of DH is modified by non-parallel effects. Then we describe how the streaky structures stimulated by the nonlinear interaction at the edge of the boundary layer are accommodated by the rest of the flow; we will see that the effects are major and lead to flow structures completely different from the parallel case.
In turbulent boundary layers, coherent structures are observed both near to the wall and further out towards the edge of the boundary layer. Experimental observations of outer layer coherent structures show that the structures are typically characterized by
${\rm\Lambda}$
-shaped and hairpin-shaped vortices rather than the rolls and streaks seen in the near-wall region; see Head & Bandyopadhyay (Reference Head and Bandyopadhyay1981), Robinson (Reference Robinson1991), Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) and Adrian (Reference Adrian2007). The relationship between the inner and outer coherent structures has been of much interest in boundary layer studies. For example, Rao, Narasimha & Narayanan (Reference Rao, Narasimha and Narayanan1971) and Head & Bandyopadhyay (Reference Head and Bandyopadhyay1981) suggested that the vortical structure situated outside the boundary layer is coupled to the inner boundary layer structure. In contrast, Jimenez & Pinelli (Reference Jimenez and Pinelli1999) claimed that the inner and outer coherent structures are independent. A key property of the coherent structures in growing boundary layers is that these structures can exist only for a finite interval in the streamwise direction. Once generated they evolve over many boundary layer length scales before decaying to zero. The generation and annihilation of the structures occurs regularly at different positions and times in the flow.
The work reported in DH was partially motivated by many recent investigations of exact coherent structures in parallel internal shear flows, most notably plane Couette flow. The first numerical results for nonlinear equilibrium solutions in plane Couette flow are due to Nagata (Reference Nagata1990), while the terminology ‘exact coherent structures’ can be traced back to the work of Waleffe (Reference Waleffe1997), who interpreted the solutions and coherent structures in turbulent transition using dynamical systems theory. The interaction involving rolls, streaks and waves which drives the ‘self-sustained process’ uncovered numerically by Waleffe was shown by Hall & Sherwin (Reference Hall and Sherwin2010) to be exactly the vortex–wave interaction theory elucidated by Hall & Smith (Reference Hall and Smith1991) in the context of high-Reynolds-number flows.
Therefore, we shall now make a few remarks about why it is believed that the asymptotic theories of exact coherent structures are important to shear flow transition processes. The exact coherent structures found numerically are usually labelled as lower or upper branch states by tracing them back to the saddle-node bifurcation from which they emanate. For the lower branch plane Couette flow solution, Hall & Sherwin (Reference Hall and Sherwin2010) demonstrated that the asymptotic results of vortex–wave interaction theory are almost indistinguishable from the full numerical solutions even at Reynolds numbers of the order of
$10^{3}$
. Although the exact coherent structures have a relatively simple time dependence, a number of studies have revealed the importance of such structures in more complicated flow dynamics. Numerical investigations have shown that the lower branch states often act as edge states separating initial disturbances which eventually become turbulent or remain laminar, while the upper branch states often act as attractors for fully turbulent flows; see Itano & Toh (Reference Itano and Toh2001), Skufca, Yorke & Eckhardt (Reference Skufca, Yorke and Eckhardt2006), Gibson, Halcrow & Cvitanovic (Reference Gibson, Halcrow and Cvitanovic2008) and Kreilos & Eckhardt (Reference Kreilos and Eckhardt2012). Thus, it was believed that the states were of a fundamentally different nature. However, Deguchi & Hall (Reference Deguchi and Hall2014b
) recently showed that at high Reynolds numbers the upper and lower branch modes have the same vortex–wave interaction structure as first given by Hall & Smith (Reference Hall and Smith1991). Therefore, this means that at increasingly high Reynolds numbers of engineering interest vortex–wave interaction theory might sensibly be used to define both the edge states and at least some properties of turbulent attractors. The reader is referred to the article of Deguchi & Hall (Reference Deguchi and Hall2014c
) for a discussion of the key numerical and asymptotic results for plane Couette flow.
A further link between the asymptotic theory of exact coherent structures and turbulence simulations or experiments in channel flows was given by Deguchi, Hall & Walton (Reference Deguchi, Hall and Walton2013). In that paper, the long-streamwise-wavenumber limit of the vortex–wave interaction system was used as a starting point to describe equilibrium states where weak and strong localizations are found in the streamwise and spanwise directions. In Deguchi & Hall (Reference Deguchi and Hall2014b
), it was found by finite-Reynolds-number computations that the streamwise localization is sometimes enhanced when the convergence to the long-wavelength asymptotic state is prevented by the snaking of the solution branch. The origin of the snaking is the local contamination of the long-wavelength structure by the
$O(1)$
wavelength vortex–wave interaction state. The reader is referred to Deguchi & Hall (Reference Deguchi and Hall2014b
) and the papers referenced in that paper for more discussion of snaking. The localized states and mean-flow distortion described by these studies were found to be similar to turbulent spots found experimentally or numerically in, for example, Lundbladh & Johansson (Reference Lundbladh and Johansson1991), Tillmark & Alfredsson (Reference Tillmark and Alfredsson1992) and Duguet, Schlatter & Henningson (Reference Duguet, Schlatter and Henningson2009).
In view of the apparent importance of exact coherent structures in internal flows, DH investigated the development of such states when plane Couette flow is deformed via homotopy into the ASBL. The ASBL was chosen as a simple model of boundary layers because it is a parallel one so that it does not come with the complication of boundary layer growth. Recently, a relationship between exact coherent structures and edge states of this flow was investigated by Kreilos et al. (Reference Kreilos, Veble, Schneider and Eckhardt2013) and Khapko et al. (Reference Khapko, Kreilos, Schlatter, Duguet, Eckhardt and Henningson2012). DH found that some typical vortex–wave interaction states of plane Couette flow deform into equivalent states in the ASBL. The structure of such asymptotic states is concentrated in the near-wall boundary layer and captures features of the edge states.
However, solutions were also found where the roll–streak–wave interaction is localized in the free stream of the boundary layer while the interaction simultaneously generates large-amplitude near-wall streaks. At large values of the Reynolds number these free-stream coherent structures develop what we will show here to be a canonical form relevant to quite arbitrary boundary layers. The free-stream coherent structures found numerically and described asymptotically in DH are intrinsically associated with the boundary layer nature of the background state. DH refer to the region where the nonlinear interaction is localized as the production layer. Within the production layer the exponential correction of the streamwise velocity from its free-stream value is small and there is a nonlinear interaction involving rolls, waves and streaks described by a nonlinear eigenvalue problem associated with the unit-Reynolds-number Navier–Stokes equations. Below the layer the flow returns to its unperturbed state at leading order but the small correction of the mean streamwise velocity interacts with a decaying roll flow to produce an exponentially increasing streak flow. The growth of the streak was found to continue all the way down to the unperturbed boundary layer where the streak therefore attained its maximum size. This streak generation mechanism is a direct consequence of the unperturbed flow approaching its free-stream value through exponentially small terms. One of the main results of DH was to show that large-amplitude wall streaks can occur as a passive byproduct of the nonlinear interaction at the edge of the boundary layer. This result is of relevance to the debate in the turbulence community about the interplay, if any, between near-wall streaks and free-stream coherent structures. Here, we remark that a similar generation mechanism resulting in a large wall streak was observed earlier by Brandt, Henningson & Ponziani (Reference Brandt, Henningson and Ponziani2002), where an interaction of a pair of oblique linear disturbances was considered.
In these asymptotic or fully numerical studies of exact coherent structures in parallel flows, periodicity in the streamwise direction is assumed. However, for a growing boundary layer that approach is no longer viable, and moving downstream the local Reynolds number changes, so any coherent structure moving downstream must adjust to the local boundary layer length scale and Reynolds number. Thus, high-resolution calculations of exact coherent structures in developed flows are not easily extended to growing boundary layers. For example, in a Blasius boundary layer the local streamwise and spanwise wavenumbers increase like the square root of the distance along the wall, so the number of modes retained would need to change at the same rate. Obviously, without the periodic assumption a direct calculation of growing boundary layers requires massive computational power. Moreover, the transition process is not clear unless a specific upstream input is prescribed. In the case of shear flows which can support Tollmien–Schlichting waves much is known about the route to transition and there is excellent agreement between experiment and numerical simulations of transition following the excitation of the waves upstream. It is also widely known that the streaky field is then generated by secondary instability. However, if the upstream input is sufficiently strong the generation of the streaky field can be bypassed. Although details of the transition process cannot be discussed without reference to the receptivity problem, the work of Khapko et al. (Reference Khapko, Kreilos, Schlatter, Duguet, Eckhardt and Henningson2012) suggests the relevance of equilibrium states to bypass transition. To the best of our knowledge, the only equilibrium state calculations in growing boundary layers are due to Cherubini et al. (Reference Cherubini, De Palma, Robinet and Bottaro2011) and Duguet et al. (Reference Duguet, Schlatter, Henningson and Eckhardt2012), where edge states of Blasius flow were identified by imposing some initial conditions. However, such coherent structures must ultimately disappear when the boundary layer is unforced.
It is known from the asymptotic work by Hall (Reference Hall1983) that centrifugal instabilities in growing boundary layers are dominated by non-parallel effects, and we anticipate a similar complication here since the underlying roll–streak flow in exact coherent structures scales in the same way as the centrifugal instability problem. Crucially, in this asymptotic framework the equations become parabolic in the long spatial scale and we can march the equations spatially from some given upstream conditions. Therefore, it seems appropriate to use a high-Reynolds-number assumption to describe the generic mechanism of coherent structures in boundary layers; indeed, it is worth noting that without the high-Reynolds-number assumption the boundary layer itself would not exist. We also point out that, although the original formulation of vortex–wave interaction theory by Hall & Smith (Reference Hall and Smith1991) was for growing boundary layers and had a similar long-spatial-scale development, the asymptotically obtained interaction equations for that problem remain unsolved.
The free-stream coherent structures derived in DH owe their very existence to the fact that in the ASBL the difference of the streamwise velocity from its free-stream value is an exponentially decaying function of distance from the wall. For growing boundary layers the corresponding approach is more complex and the wave–roll–streak system at the heart of the interaction must adjust to local properties of the flow as the interaction moves downstream. We shall show that, surprisingly, the production layer problem for the ASBL is generic to almost all two-dimensional or weakly three-dimensional boundary layers. The streak induced at the production layer takes on a maximum beneath that layer and non-parallel effect restrict the streaks to exist only over finite distances in the downstream direction. Therefore, free-stream coherent structures can connect the near-wall behaviour to a nonlinear interaction in the free stream, and so, if our nonlinear states are relevant to turbulent flows, the interaction between wall streaks and the outer flow in turbulent boundary layers is not necessarily as one-sided as some authors believe.
In order to set the scene we shall in the next section recall the description in DH of the production layer problem for the ASBL. In § 3 we shall discuss the nature of the approach of a quite general boundary layer to its free-stream form; this issue was discussed at length by Brown & Stewartson (Reference Brown and Stewartson1965) and so we quote the key results from their work. In § 4 we will derive the production layer problem for arbitrary two-dimensional boundary layers. Section 5 concerns the roll–streak flow driven by the forcing in the production layer. Results are presented for Blasius flow in § 6, and in § 7 we give some conclusions. In appendix A some details of the structure described in § 5 are given, while in appendix B we discuss the extension of the work to infinite swept boundary layers.
2. Free-stream coherent structures in the parallel boundary layer
Now let us summarize the key features of the exact free-stream coherent structures described in DH for the ASBL. Consider the flow of a viscous fluid of kinematic viscosity
${\it\nu}$
past a plate defined by
$y^{\ast }=0$
with respect to Cartesian coordinates
$(x^{\ast },y^{\ast },z^{\ast })$
. If the corresponding velocity field is
$\boldsymbol{u}^{\ast }=(u^{\ast },v^{\ast },w^{\ast })$
, we impose the condition
$\boldsymbol{u}^{\ast }\rightarrow (U^{\ast },-V^{\ast },0)$
a long distance from the wall, while at the wall we require that
$\boldsymbol{u}^{\ast }=(0,-V^{\ast },0)$
. If we now use
${\it\nu}/V^{\ast }$
as a length scale, write
$(x,y,z)=(x^{\ast },y^{\ast },z^{\ast })/({\it\nu}/V^{\ast })$
and take
$U^{\ast }$
as a typical flow speed, then the basic ASBL velocity field satisfying the equations of motion and the boundary conditions is
$$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{u}_{b}=(1-\text{e}^{-y})\boldsymbol{i}-\frac{\boldsymbol{j}}{Re},\end{eqnarray}$$
where
$Re=U^{\ast }/V^{\ast }$
is the Reynolds number and
$\boldsymbol{i}$
and
$\boldsymbol{j}$
are unit vectors in the
$x$
and
$y$
directions respectively. The structure identified in DH sits in the free stream in a layer of depth
$O(1)$
a distance
$\ln Re$
from the wall. Within that layer the total velocity field differs from the free-stream speed by
$O(1/Re)$
. The structure moves downstream with a speed differing from the dimensionless free-stream speed of unity by an amount
$O(1/Re)$
. We take coordinates
$({\it\Phi},Y,Z)=(x-ct,y-\ln Re,z)$
so that the flow we are considering is located in a box a distance
$\ln Re$
from the wall with all sides of size
$O(1)$
. Since the nonlinear interaction that produces the new state occurs in this layer, DH referred to it as the production layer. We write
$$\begin{eqnarray}\displaystyle \boldsymbol{u} & = & \displaystyle (1,0,0)+Re^{-1}\boldsymbol{U}({\it\Phi},Y,Z)+\cdots \,,\nonumber\\ \displaystyle & & \displaystyle \quad p=Re^{-2}P({\it\Phi},Y,Z)+\cdots \,,\quad c=1-Re^{-1}c_{1}+\cdots \,,\phantom{\sum }\end{eqnarray}$$
and the nonlinear eigenvalue problem for the perturbed wavespeed
$c_{1}$
is then found to be
$$\begin{eqnarray}\displaystyle & ([\boldsymbol{U}+c_{1}\boldsymbol{i}]\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{U}=-\boldsymbol{{\rm\nabla}}P+{\rm\nabla}^{2}\boldsymbol{U}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{U}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{U}({\it\Phi},Y,Z) & = & \displaystyle \boldsymbol{U}({\it\Phi},Y,Z+2{\rm\pi}/{\it\beta})=\boldsymbol{U}({\it\Phi}+2{\rm\pi}/{\it\alpha},Y,Z),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P({\it\Phi},Y,Z) & = & \displaystyle P({\it\Phi},Y,Z+2{\rm\pi}/{\it\beta})=P({\it\Phi}+2{\rm\pi}/{\it\alpha},Y,Z)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (U,V,W)\rightarrow (0,-1,0)\quad \text{as }Y\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (U\text{e}^{Y},V,W)\rightarrow (-1,-1,0)\quad \text{as }Y\rightarrow -\infty . & \displaystyle\end{eqnarray}$$
$\boldsymbol{{\rm\nabla}}$
is defined by
$\boldsymbol{{\rm\nabla}}=(\partial _{{\it\Phi}},\partial _{Y},\partial _{Z})$
and
${\it\alpha},{\it\beta}$
are streamwise and spanwise wavenumbers respectively. The conditions in the vertical direction require that below the layer the flow returns to the ASBL at leading order and that above the layer it approaches the free-stream velocity field of the ASBL. What is crucial is the second of these conditions, which requires that
$U\backsim \text{e}^{-Y}$
for large negative
$Y$
and therefore does not preclude the possibility that higher-order terms in
$U$
also grow exponentially albeit at a lower rate. This higher-order growth can only occur for the part of
$U$
independent of
$x$
, and allows it to grow exponentially large compared with its value in the production layer. Thus, a viscous nonlinear wave–roll–streak interaction involving a small
$O(1/Re)$
velocity field in the production layer generates a much larger streak beneath that layer. A more detailed examination of the flow shows that exponential growth is possible only for spanwise wavenumbers
${\it\beta}<1/\sqrt{2}$
. The system (2.3)–(2.8) specifies a nonlinear eigenvalue problem for
$c_{1}=c_{1}({\it\alpha},{\it\beta})$
in terms of specified wavenumbers
${\it\alpha},{\it\beta}$
.
In order to analyse the possibility of the higher-order growth, it is convenient to decompose the total flow field into its mean flow, vortex and wave components. Here, the mean-flow component is the average in
${\it\Phi}$
,
$Z$
of the total flow, while the vortex component is the
${\it\Phi}$
average of the flow without the mean part. The vortex components of
$U$
and
$(V,W)$
are called the streak and roll respectively. The mechanism for the growth is found by looking at the roll and streak components as the production layer is exited in the negative
$Y$
direction. It should be noted that the roll field owes its existence to the Reynolds stresses associated with the wavefield because there are no external forces to sustain it. Since the self-sustained mechanism is not operational for large negative
$Y$
, the wave must quickly decay, and thus the roll must also decay exponentially. Then the streak is driven through the nonlinear term in the streamwise momentum equation involving the roll acting on the mean flow. The fact that the mean flow is growing exponentially for large negative
$Y$
in order to return to the basic ASBL enables the streak to also grow exponentially. Thus, a viscous nonlinear wave–roll–streak interaction of a small velocity field in the production layer generates a much larger streak below the layer; the roll–streak flow beneath the production layer is discussed in the more detailed asymptotic analysis below.
Due to the symmetry of the solution computed in DH, the roll–streak flow has one half of the spanwise wavelength of the wave. An analysis of the roll–streak equations below the production layer shows that the flow there behaves like
$$\begin{eqnarray}\displaystyle & U\rightarrow -\text{e}^{-Y}+J_{1}\text{e}^{({\it\omega}_{1}-1)Y}\cos (2{\it\beta}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & V\rightarrow K_{1}\text{e}^{{\it\omega}_{1}Y}\cos (2{\it\beta}z)+\cdots & \displaystyle\end{eqnarray}$$
$Y\rightarrow -\infty$
, where the constant
${\it\omega}_{1}$
is defined by 
$$\begin{eqnarray}{\it\omega}_{1}=\frac{\sqrt{1+16{\it\beta}^{2}}-1}{2}\geqslant 0\end{eqnarray}$$
and
$J_{1}=-K_{1}/(2{\it\omega}_{1})$
. It follows that the exponential growth of the streak is possible only for spanwise wavenumbers
${\it\beta}<1/\sqrt{2}$
. We further note that the higher harmonics in
$z$
and the mean-flow correction term can also grow for large negative
$Y$
, but more slowly than the term proportional to
$\cos (2{\it\beta}z)$
. The constant
$K_{1}=K_{1}({\it\alpha},{\it\beta})$
multiplying the least slowly exponentially decaying part of
$V$
is to be determined as a part of the numerical solution of the nonlinear eigenvalue problem for
$c_{1}$
.
If we now write the streak and roll flows exiting the production layer in terms of the variable describing the unperturbed boundary layer we find that
$$\begin{eqnarray}\displaystyle & u\rightarrow 1-\text{e}^{-y}+Re^{-{\it\omega}_{1}}J_{1}\text{e}^{({\it\omega}_{1}-1)y}\cos (2{\it\beta}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & v\rightarrow -Re^{-1}+Re^{-({\it\omega}_{1}+1)}K_{1}\text{e}^{{\it\omega}_{1}y}\cos (2{\it\beta}z)+\cdots & \displaystyle\end{eqnarray}$$
$Y\rightarrow -\infty$
. Thus, we see that the term proportional to
$\cos (2{\it\beta}z)$
in
$u$
is now of size
$Re^{-{\it\omega}_{1}}\gg Re^{-1}$
if
${\it\beta}<1/\sqrt{2}$
. The above forms for
$u,v$
are then reduced to zero within the main boundary layer, see DH, and it turns out that the maximum of the streamwise velocity component proportional to
$\cos (2{\it\beta}z)$
occurs within the unperturbed boundary layer. Therefore, the free-stream coherent structure has a fully nonlinear interaction involving tiny
$O(Re^{-1})$
wave, roll and streak fields in the production layer stimulating a passive streak of much larger size,
$O(Re^{-{\it\omega}_{1}})$
, concentrated in the wall layer.
The asymptotic structure described by DH was found to be in excellent agreement with numerical calculations of equilibrium solutions of the full equations of motion. That excellent agreement allows us to extract, for example,
$c_{1},K_{1}$
of the production layer structure from the high-Reynolds-number ASBL computation. DH gave solutions of the production layer eigenvalue problem for a range of vales of
${\it\beta}$
and
${\it\alpha}/{\it\beta}=0.5$
. Here, we give results for an extended range of values of
${\it\beta}$
for the same ratio of
${\it\alpha}/{\it\beta}$
, and we see in figure 1(a) that a closed loop of eigenvalues
$c_{1}$
beginning and ending in saddle-node bifurcations exists over a finite range of values of
${\it\beta}\in [0.2062,0.4633]$
. The corresponding values of the constant
$K_{1}$
, which plays a crucial role in the streak generation, can be extracted from the computations and are shown in figure 1(b). Along the bifurcation curve, the flow fields at
${\it\beta}=0.23,0.3$
and 0.44 are visualized in figures 2 and 3. Figure 3 shows that all of the flow fields are characterized by
${\rm\Lambda}$
-shaped counter-rotating vortex pairs. The corresponding roll–streak field in figure 2 shows that growing streak and decaying roll fields are indeed generated as a result of interaction.
Figure 1. The values of (a)
$c_{1}$
and (b)
$K_{1}$
of the production layer eigenvalue solution for
${\it\alpha}/{\it\beta}=0.5$
. The curves are computed from the ASBL solutions with finite height
$H$
and Reynolds number
$Re$
. It should be noted that the upper branch of (a) corresponds to that of (b). The convergence to the asymptotic state is confirmed by computing solutions for
$(Re,H)=(200\,000,24),(100\,000,32),(100\,000,48)$
and
$(100\,000,56)$
by using up to 180 Chebyshev modes, 14 streamwise modes and 26 spanwise modes.
Figure 2. The streamwise-averaged field of the production layer solutions along the bifurcation curve in figure 1 ((a,d)
${\it\beta}=0.23$
; (b,e)
${\it\beta}=0.3$
; (c,f)
${\it\beta}=0.44$
). The disturbance velocity
$U+\text{e}^{Y}$
(i.e. the streak) and vorticity
$\partial _{Z}V-\partial _{Y}W$
associated with the roll are plotted in the left and right halves of each figure. Here,
$C_{max}=3668.4$
(a), 2670.5 (b) and 1476.9 (c) for the streaks,
$C_{max}=94.5$
(a), 92.2 (b), 111.2 (c) for the rolls;
$C_{max}=3524.7$
(d), 2403.8 (e) and 1327.7 (f) for the streaks,
$C_{max}=75.3$
(d), 69.4 (e) and 99.9 (f) for the rolls.
Figure 3. Three-dimensional plots of the disturbance flow field of the production layer solutions along the bifurcation curve in figure 1 ((a,d)
${\it\beta}=0.23$
; (b,e)
${\it\beta}=0.3$
; (c,f)
${\it\beta}=0.44$
). The red/blue surfaces correspond to where the streamwise vorticity is 70 % of its maximum/minimum value. The colourmap corresponding to the streak contours shown in the figure is as given in figure 2.
3. The approach of a boundary layer flow to its free-stream form
The question of how an arbitrary two-dimensional boundary layer approaches its free-stream form was addressed, most notably, by Brown & Stewartson (Reference Brown and Stewartson1965) and Goldstein (Reference Goldstein1965). It was found that, apart from isolated singular cases where the approach to the free-stream speed is through algebraically decaying terms, the approach to the free stream is through exponentially decaying terms with the exponent proportional to the square of the distance from the wall. That is of course different from the case of the ASBL, so we might be apprehensive about applying the DH approach to growing boundary layers given that the whole nonlinear interaction described there hinges on the streamwise velocity being an exponential function of distance from the wall. However, what will become apparent in both this and the next sections is that non-parallelism mimics the effect of wall suction so as to force the decay in a localized region to be once again an exponential function of distance. Here, we will summarize the main results of Brown & Stewartson (Reference Brown and Stewartson1965) needed for our analysis. Using the notation of Brown & Stewartson (Reference Brown and Stewartson1965), we take the boundary layer equations in the form
$$\begin{eqnarray}\displaystyle & \displaystyle u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=U_{1}\frac{\partial U_{1}}{\partial x}+\frac{\partial ^{2}u}{\partial y^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0. & \displaystyle\end{eqnarray}$$
$x,y$
measure distance along and perpendicular to the wall and
$U_{1}(x)$
is the free-stream speed. The equations are to be solved subject to 
$$\begin{eqnarray}\displaystyle & u=v=0\quad \text{on }y=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & u\rightarrow U_{1}\quad \text{as }y\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$u$
as a function of
$y$
at some value of
$x$
, say
$x=x_{1}$
. Following the discussion given by Brown & Stewartson (Reference Brown and Stewartson1965), we seek a solution of the equations for large
$y$
of the form 
$$\begin{eqnarray}u=U_{1}(x)+A(x,y)\exp \left[-\frac{(y-k(x))^{2}}{2F(x)}\right]+\cdots \,,\quad v=-yU_{1}^{\prime }(x)+h^{\prime }(x)+\cdots \,,\end{eqnarray}$$
where the displacement thickness
$k$
and
$F,h^{\prime }$
are functions of
$x$
alone,
$A$
is algebraic in
$y$
and a prime denotes a derivative with respect to
$x$
. By substituting the above expression into the boundary layer equations then equating like powers of
$y^{2},y,1$
we obtain
$$\begin{eqnarray}U_{1}F^{\prime }+2U_{1}^{\prime }F=2,\end{eqnarray}$$
$$\begin{eqnarray}U_{1}k^{\prime }+U_{1}^{\prime }k=h^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{1}\frac{\partial A}{\partial x}+\left(\frac{2}{F}-U_{1}^{\prime }\right)y\frac{\partial A}{\partial y}+A\left(U_{1}^{\prime }+\frac{1}{F}\right)=0.\end{eqnarray}$$
Hence, it follows that
$$\begin{eqnarray}FU_{1}^{2}=2\int _{x_{1}}^{x}U_{1}(\widehat{x})\,\text{d}\widehat{x},\quad kU_{1}=(h+k_{1}).\end{eqnarray}$$
Here,
$x_{1},k_{1}$
are constants of integration and the equation for
$A$
can be integrated to give
$$\begin{eqnarray}A=-\widehat{A}(x)\left(\frac{y}{\sqrt{F}}\right)^{n},\end{eqnarray}$$
where
$n,\widehat{A}(x)$
are fixed by the upstream conditions. For example, for Blasius flow, which has
$U_{1}=1$
, we find that
$n=-1,k_{1}=x_{1}=0$
and
$h=h_{1}\sqrt{2x}$
. It follows that for Blasius flow
$F=2x,k(x)=h(x)$
and that for large
$y$
$$\begin{eqnarray}u\simeq 1-\frac{\widehat{A}\sqrt{2x}}{y}\exp \left[-\frac{(y-h_{1}\sqrt{2x})^{2}}{4x}\right],\end{eqnarray}$$
where 
.
Thus, the major difference between the ASBL and growing boundary layers is that the approach to the free-stream speed occurs through an exponential dependence on the square of the displaced distance from the wall rather than the first power. For the free-stream coherent structures in the ASBL it was the part of the mean flow decaying exponentially that produced the growing streaks beneath the production layer, and so it is not clear at this stage that growing boundary layers can support a related kind of free-stream coherent structure.
4. The production layer problem for free-stream coherent structures in any two-dimensional boundary layer
We consider the general boundary layer flow discussed in the previous section with speed
$U^{\ast }U_{1}(x^{\ast })$
a long way from the wall defined by
$y^{\ast }=0$
. We use boundary layer scalings and so take dimensionless variables
$(x,y,z)\!=\!((x^{\ast }/L),Re^{1/2}(y^{\ast }/L),Re^{1/2}(z^{\ast }/L))$
, where
$L$
is a typical streamwise length scale and
$Re=(U^{\ast }L/{\it\nu})$
is the Reynolds number. Throughout, we will assume that the Reynolds number is large. If we scale the corresponding velocity components on
$U^{\ast },Re^{-1/2}U^{\ast },Re^{-1/2}U^{\ast }$
, time on
$(U^{\ast }/L)$
and pressure on
${\it\rho}U^{\ast 2}$
, where
${\it\rho}$
is the fluid density, then the Navier–Stokes equations take the form
$$\begin{eqnarray}\displaystyle & (\partial _{t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}=-(\partial _{x}p,Re\,\partial _{y}p,Re\,\partial _{z}p)^{\text{T}}+(Re^{-1}\partial _{x}^{2}+\partial _{y}^{2}+\partial _{z}^{2})\boldsymbol{u}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & u=v=w=0\quad \text{on }y=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (u,v,w)\rightarrow (U_{1},-yU_{1}^{\prime },0)\quad \text{as }y\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$u,v,p$
satisfy the boundary layer equations (3.1) and (3.2) of the previous section with
$p=-(U_{1}^{2}/2)$
. The velocity field approaches its free-stream form through exponentially small terms as described in the previous section so that, for sufficiently large
$y$
, the basic flows
$u,v$
are given by (3.5) and
$w=0$
, with
$A,h,k,F$
as given in the previous section. We assume that, given some large as yet unspecified quantity
$K$
, the nonlinear interaction driving a free-stream coherent structure takes place in a box with all the sides of comparable dimensional length
$Re^{-1/2}K^{-1}L$
located a distance
$KL$
from the wall. In view of our scalings for
$x,y,z$
with respect to that coordinate system, the box should be taken to have respective sides of lengths
$Re^{-1/2}K^{-1},K^{-1},K^{-1}$
; the functional dependence of
$K$
on
$R$
can be fixed by the following argument.
First, we assume that the wave-like part of the flow in the production layer convects downstream with almost the free-stream speed. Next, we take the difference of the streamwise velocity component from its free-stream value to be comparable with
$A(x,y)\exp [-((y-k(x))^{2}/2F(x))]$
, the corresponding deviation of the unperturbed streamwise velocity component from its free-stream value. The production layer is viscous, so, based on the above assumptions, we can fix
$K$
by balancing convective and viscous terms. This requires
$$\begin{eqnarray}A(x,y)\exp \left[-\frac{(y-k(x))^{2}}{2F(x)}\right]\partial _{x}\sim Re^{-1}\partial _{x}^{2}.\end{eqnarray}$$
Noting that
$A(x,y)=-\widehat{A}(x)(y/\sqrt{F})^{n}$
, where
$n$
is fixed by the upstream conditions and
$\widehat{A}$
is a known function of
$x$
, within the production layer we write
$$\begin{eqnarray}\frac{(y-k(x))}{\sqrt{F(x)}}=K+\frac{\widetilde{Y}}{K\sqrt{F(x)}},\end{eqnarray}$$
so that
$$\begin{eqnarray}A(x,y)\exp \left[-\frac{(y-k(x))^{2}}{2F(x)}\right]\approx -\widehat{A}K^{n}\text{e}^{-(K^{2}/2)}\text{e}^{-(\widetilde{Y}/\sqrt{F})}.\end{eqnarray}$$
Since
$\partial _{x}$
is now
$O(KRe^{1/2})$
, the balance between convective and diffusion effects is achieved if
$$\begin{eqnarray}K^{n}\text{e}^{-K^{2}/2}=\frac{K}{\sqrt{Re}},\quad \rightarrow K=\sqrt{\ln Re}+(n-1)\frac{\ln (\sqrt{\ln Re})}{\sqrt{\ln Re}}+\cdots \,.\end{eqnarray}$$
The argument given above is essentially the same as that first given by Gulyaev et al. (Reference Gulyaev, Kozlov, Kuznetsov, Mineev and Sekundov1989) in the context of the penetration of free-stream disturbances into a boundary layer. More recently, Dong & Wu (Reference Dong and Wu2013) discussed the layer in the context of the continuous spectrum associated with linear instability. The minor difference between the scalings of the latter papers and here arises because the structures here have streamwise wavelength comparable with the depth of the layer. The fact that the boundary layer is growing also means that the wavespeed of the structure must change as it moves downstream. From the streamwise scaling, we can take care of this local requirement by expressing the wave dependence of the production layer structure, taken to be of fixed period
$(2{\rm\pi}/{\it\Omega})$
in time, by defining a phase variable
$\widetilde{{\it\Phi}}$
,
$$\begin{eqnarray}\widetilde{{\it\Phi}}=KRe^{1/2}\left(\int ^{x}\left[{\it\alpha}_{0}(x)+\frac{K}{\sqrt{Re}}{\it\alpha}_{1}(x)+\cdots \,\right]\,\text{d}x-{\it\Omega}t\right).\end{eqnarray}$$
Here, the difference in size between the first two terms inside the integral is fixed by the difference in size between the free-stream speed and the streamwise velocity in the production layer. Since the wave has fixed frequency
${\it\Omega}$
and convects downstream with the free-stream speed it follows immediately that
$$\begin{eqnarray}{\it\alpha}_{0}(x)U_{1}(x)={\it\Omega},\end{eqnarray}$$
which fixes the local leading-order streamwise wavenumber.
The production layer structure operates on the same length scale in all three directions, so we must introduce a short spanwise variable
$\widetilde{Z}=Kz$
. Given our choice of box size and the streamwise velocity scale, the scalings for the normal and spanwise velocity components in the production layer then follow from the equation of continuity (4.2). In the production layer we then write
$$\begin{eqnarray}\displaystyle \displaystyle u & = & \displaystyle U_{1}+\frac{K}{\sqrt{Re}}\widetilde{U}(x,\widetilde{{\it\Phi}},\widetilde{Y},\widetilde{Z})+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v & = & \displaystyle -KU_{1}^{\prime }\sqrt{F}+K\widetilde{V}(x,\widetilde{{\it\Phi}},\widetilde{Y},\widetilde{Z})+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w & = & \displaystyle K\widetilde{W}(x,\widetilde{{\it\Phi}},\widetilde{Y},\widetilde{Z})+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle p & = & \displaystyle \frac{1}{2}U_{1}^{2}+\frac{K^{2}}{Re}\widetilde{P}(x,\widetilde{{\it\Phi}},\widetilde{Y},\widetilde{Z})+\cdots \,.\end{eqnarray}$$
$\partial _{t}+u\partial _{x}+v\partial _{y}+w\partial _{z}$
is approximated by 
$$\begin{eqnarray}\displaystyle & & \displaystyle KRe^{1/2}({\it\alpha}_{0}U_{1}-{\it\Omega})\partial _{\widetilde{{\it\Phi}}}+K^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{{\it\alpha}_{1}U_{1}\partial _{\widetilde{{\it\Phi}}}-\!\left[U_{1}^{\prime }\sqrt{F}+\frac{U_{1}F^{\prime }}{2\sqrt{F}}\right]\!\partial _{\widetilde{Y}}+{\it\alpha}_{0}\widetilde{U}\partial _{\widetilde{{\it\Phi}}}+\widetilde{V}\partial _{\widetilde{Y}}+\widetilde{W}\partial _{\widetilde{Z}}\right\}+\cdots \,.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In view of (4.10), the leading-order term vanishes and using (3.6) the terms in the square bracket can be replaced by
$1/\sqrt{F}$
. Hence, we see that non-parallel effects produce an effective suction velocity
$1/\sqrt{F}$
, which plays an identical role to the constant suction driving an ASBL. This is the crucial result, which allows for non-parallel effects in the production layer to be taken care of in a quasi-parallel manner. The zeroth-order approximation to the production layer equations for a growing boundary layer therefore becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\left[\widetilde{\boldsymbol{U}}+\frac{U_{1}{\it\alpha}_{1}\boldsymbol{i}}{{\it\alpha}_{0}}-\frac{\boldsymbol{j}}{\sqrt{F}}\right]\boldsymbol{\cdot }\widetilde{\boldsymbol{{\rm\nabla}}}\right)\widetilde{\boldsymbol{U}}=-\widetilde{\boldsymbol{{\rm\nabla}}}\widetilde{P}+\widetilde{\boldsymbol{{\rm\nabla}}}^{2}\widetilde{\boldsymbol{U}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \widetilde{\boldsymbol{{\rm\nabla}}}\boldsymbol{\cdot }\widetilde{\boldsymbol{U}}=0, & \displaystyle\end{eqnarray}$$
$\widetilde{\boldsymbol{{\rm\nabla}}}=({\it\alpha}_{0}\partial _{\widetilde{{\it\Phi}}},\partial _{\widetilde{Y}},\partial _{\widetilde{Z}})$
. The velocity field
$\widetilde{\boldsymbol{U}}$
must return at leading order to its unperturbed value (
$-\widehat{A}\text{e}^{-\widetilde{Y}/\sqrt{F}},0,0$
) above and below the production layer, so that we must impose the conditions 
$$\begin{eqnarray}\displaystyle & (\widetilde{U},\widetilde{V},\widetilde{W})\rightarrow (0,0,0)\quad \text{as }\widetilde{Y}\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (\widetilde{U}\text{e}^{\widetilde{Y}/\sqrt{F}},\widetilde{V},\widetilde{W})\rightarrow (-\widehat{A},0,0)\quad \text{as }\widetilde{Y}\rightarrow -\infty . & \displaystyle\end{eqnarray}$$
$\widetilde{{\it\Phi}},\widetilde{Z}$
with periods
$2{\rm\pi},(2{\rm\pi}/{\it\beta}_{0})$
respectively. We see that, apart from various scaling factors, the production layer problem is identical to (2.3)–(2.8) first derived for the ASBL. In fact, if we write
$(U,V,W,P)=\sqrt{F}(\widetilde{U},\widetilde{V}-(1/\sqrt{F}),\widetilde{W},\sqrt{F}\widetilde{P})$
and make the transformations 
$$\begin{eqnarray}{\it\Phi}=\frac{\widetilde{{\it\Phi}}}{{\it\alpha}_{0}\sqrt{F}},\quad Y=\frac{\widetilde{Y}}{\sqrt{F}}-\ln (\sqrt{F}\widehat{A}),\quad Z=\frac{\widetilde{Z}}{\sqrt{F}},\quad c_{1}=\frac{U_{1}{\it\alpha}_{1}\sqrt{F}}{{\it\alpha}_{0}},\end{eqnarray}$$
then the leading-order equations in the production layer become (2.3)–(2.8) with local wavenumbers
${\it\alpha}={\it\alpha}_{0}\sqrt{F}={\it\Omega}\sqrt{F}/U_{1}$
and
${\it\beta}={\it\beta}_{0}\sqrt{F}$
. We have shown the rather remarkable result that the production layer problem for the ASBL is apparently generic in so far as it applies to all boundary layers approaching the free-stream speed through exponentially decaying terms. Thus, we conclude that as the interaction proceeds downstream, the solution can be determined from the ASBL problem with the appropriate local values of the streamwise and spanwise wavenumbers. The dependence of
$U_{1}$
on
$x$
fixes the functional form of the local wavenumbers. For Blasius flow the local wavenumbers
${\it\alpha},{\it\beta}$
are in a constant ratio as the structure evolves downstream. More generally, for a Falkner–Skan boundary layer with free-stream speed
$U_{1}$
proportional to
$x^{m}$
the local streamwise and spanwise wavenumbers
${\it\alpha},{\it\beta}$
are related by
${\it\beta}/{\it\alpha}^{(1-m)/(3-m)}=$
constant.
For the ASBL the solution beneath the production layer is relatively simple, with the decaying roll and growing streak continuing with the exponential behaviour fixed on exiting the production layer all the way to the unperturbed boundary layer where the roll and streak are reduced to zero. For a growing boundary layer we shall see that the picture is completely different, with non-parallel effects coming into play and indeed dominating the flow. Based on the asymptotic forms (2.9) and (2.10) for what we now refer to as the canonical production layer problem (2.3)–(2.8), and the description given above, we can write down the asymptotic forms for the streak and roll on exiting the production layer associated with a growing boundary layer. Using (2.9), (2.10) and (4.20) we find
$$\begin{eqnarray}\displaystyle & \displaystyle u\rightarrow U_{1}-\frac{K}{\sqrt{Re}}\widehat{A}\text{e}^{-(\widetilde{Y}/\sqrt{F})}+\frac{K}{\sqrt{Re}}\frac{J_{1}(\sqrt{F}\widehat{A})^{(1-{\it\omega}_{1})}}{\sqrt{F}}\text{e}^{({\it\omega}_{1}-1)(\widetilde{Y}/\sqrt{F})}\cos (2K{\it\beta}_{0}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v\rightarrow -KU_{1}^{\prime }\sqrt{F}+K\frac{K_{1}(\sqrt{F}\widehat{A})^{-{\it\omega}_{1}}}{\sqrt{F}}\text{e}^{{\it\omega}_{1}(\widetilde{Y}/\sqrt{F})}\cos (2K{\it\beta}_{0}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
$\widetilde{Y}\rightarrow -\infty$
. Here, we have retained only the leading-order
$z$
-independent part of the velocity since the leading-order exponentially growing term will dominate. It should be noted that
$J_{1},K_{1}$
are determined from the canonical production layer problem with wavenumbers
${\it\alpha}_{0}\sqrt{F}$
and
${\it\beta}_{0}\sqrt{F}$
.
We recall that the question in § 2 of whether the fundamental
$z$
-dependent terms generated in the production layer grow or decay exponentially as
$Y$
tends to
$-\infty$
depends on the size of the spanwise wavenumber. In the growing boundary layer case the behaviour is therefore fixed by
$\sqrt{F}{\it\beta}_{0}$
, so that for a fixed physical vortex spanwise wavelength the growth of a streak beneath the production layer will only occur for values of
$x$
satisfying
$\sqrt{F}{\it\beta}_{0}<(1/\sqrt{2})$
. It is important, however, to point out that the latter condition is only a necessary condition for the production layer problem to produce an exponentially growing streak.
5. The roll–streak flow beneath the production layer
We need to consider the flow below the production layer in order to see how the exponential growth of the streak exiting the production layer is accommodated by the rest of the flow. We shall now solve for the induced flow between the production layer and the wall and, following DH, we use the fact that here the disturbance is always small compared with the basic flow. The appropriate approximation to the equations of motion is valid all the way down to the wall and leads to the linear Görtler vortex equations of Hall (Reference Hall1983) with the Görtler number set equal to zero; more recently, these equations are elsewhere referred to as the boundary-region equations. If the unperturbed boundary layer is denoted by
$\boldsymbol{u}=(u_{b},v_{b},0)$
we perturb the flow by writing
$$\begin{eqnarray}u=u_{b}+u_{s}(x,y)\cos (2K{\it\beta}_{0}z),\quad v=v_{b}+v_{r}(x,y)\cos (2K{\it\beta}_{0}z),\end{eqnarray}$$
$$\begin{eqnarray}w=w_{r}(x,y)\sin (2K{\it\beta}_{0}z),\quad p=U_{1}^{2}/2+Re^{-1}p_{r}(x,y)\cos (2K{\it\beta}_{0}z),\end{eqnarray}$$
where, in view of (4.21) and (4.22), we have taken the spanwise wavenumber to be
$2K{\it\beta}_{0}$
. The component
$u_{s}$
represents the streak while
$(v_{r},w_{r})$
is the roll. The primitive form of the linearized system satisfied by the perturbation is found from (4.1) and (4.2) to be
$$\begin{eqnarray}(u_{b}\partial _{x}+v_{b}\partial _{y})\left[\begin{array}{@{}c@{}}u_{s}\\ v_{r}\\ w_{r}\end{array}\right]+(u_{s}\partial _{x}+v_{r}\partial _{y})\left[\begin{array}{@{}c@{}}u_{b}\\ v_{b}\\ 0\end{array}\right]=\left[\begin{array}{@{}c@{}}0\\ -\partial _{y}p_{r}\\ 2K{\it\beta}_{0}p_{r}\end{array}\right]+(\partial _{y}^{2}-4K^{2}{\it\beta}_{0}^{2})\left[\begin{array}{@{}c@{}}u_{s}\\ v_{r}\\ w_{r}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\partial _{x}u_{s}+\partial _{y}v_{r}+2K{\it\beta}_{0}w_{r}=0.\end{eqnarray}$$
The above equations are parabolic in
$x$
and can be integrated by marching in
$x$
subject to an initial velocity distribution imposed at some value of
$x$
and subject to the forcing conditions (4.21) and (4.22). Without any loss of generality we suppose that the production layer forcing begins at
$x=1$
. The forcing from the production layer is on a short,
$O(K^{-1})$
, spanwise length scale, so (5.3) and (5.4) develop what turns out to be a rich asymptotic structure as the roll–streak flow develops downstream.
Within the present asymptotic framework we cannot address the issue of how this initial velocity field is created, but since in the high-Reynolds-number limit the equations are parabolic in
$x$
, the problem is well posed. Likewise, we note in passing that the vortex–wave interaction solutions of, for example, Hall & Smith (Reference Hall and Smith1991) and Hall & Sherwin (Reference Hall and Sherwin2010) are yet to be connected formally to an imposed upstream velocity field, but nevertheless full direct Navier–Stokes simulations certainly reveal the relevance of these states to turbulent flows.
The production layer is located a distance
$O(K)$
from the wall and is of thickness
$O(K^{-1})$
, and so, not surprisingly, the most important region to consider is the layer where
$y\sim O(K)$
. Beneath the production layer the asymptotic form of the roll–streak flow will adjust to be compatible with the mean flow which no longer has a simple exponential form, and so henceforth we will refer to the region
$y\sim O(K)$
as the adjustment layer. In order to motivate the large-wavenumber solution of (5.3) and (5.4) in the adjustment layer we first write the forcing from the production layer in a slightly different form. We define the scaled similarity variable
${\it\xi}=(y-k(x))/(K\sqrt{F(x)})$
, so that
$(\widetilde{Y}/\sqrt{F})=K^{2}({\it\xi}-1)$
, and seek a solution where
${\it\xi}$
is
$O(1)$
. The appropriate form for the structure in this layer is indicated by expressing the roll and streak flows emanating from the production layer in terms of
$({\it\xi}-1)$
. A little manipulation shows that (4.21) and (4.22) become
$$\begin{eqnarray}\displaystyle & \displaystyle u\rightarrow U_{1}-\frac{K}{\sqrt{Re}}\widehat{A}\text{e}^{-K^{2}({\it\xi}-1)}+\frac{K}{\sqrt{Re}}\frac{J_{1}(\sqrt{F}\widehat{A})^{(1-{\it\omega}_{1})}}{\sqrt{F}}\text{e}^{K^{2}({\it\omega}_{1}-1)({\it\xi}-1)}\cos (2K{\it\beta}_{0}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v\rightarrow -KU_{1}^{\prime }\sqrt{F}+K\frac{K_{1}(\sqrt{F}\widehat{A})^{-{\it\omega}_{1}}}{\sqrt{F}}\text{e}^{K^{2}{\it\omega}_{1}({\it\xi}-1)}\cos (2K{\it\beta}_{0}z)+\cdots \,, & \displaystyle\end{eqnarray}$$
${\it\xi}\rightarrow 1_{-}$
. It is important to realize here that the quantities
${\it\omega}_{1},J_{1},K_{1}$
are functions of
$x$
because at each local station the canonical production layer problem (2.3)–(2.8) is to be solved with the local values of the wavenumbers. Based on the production layer solution, and the fact that
$x$
is
$O(1)$
, we might anticipate that the
$x$
dependence will be parametric, but we will see below that this is not the case. Suppose we now adopt the roll–streak scaling as in (4.21) and (4.22) and write 
$$\begin{eqnarray}u_{s}=KR^{-1/2}U_{s}(x,{\it\xi}),\quad v_{r}=KV_{r}(x,{\it\xi}),\quad w_{r}=KW_{r}(x,{\it\xi}),\quad p_{r}=K^{2}P_{r}(x,{\it\xi});\end{eqnarray}$$
then if the pressure and spanwise disturbance velocity are eliminated from (5.3) and (5.4) we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle K^{-2}\left(\frac{\partial _{{\it\xi}}^{2}}{K^{2}}+{\it\xi}\partial _{{\it\xi}}-F[\partial _{x}+4K^{2}{\it\beta}_{0}^{2}]\right)U_{s}-F^{1/2}\widehat{A}V_{r}{\it\xi}^{n+1}\text{e}^{-K^{2}({\it\xi}^{2}-1)/2}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\partial _{{\it\xi}}^{2}}{K^{2}}+{\it\xi}\partial _{{\it\xi}}+1-F[\partial _{x}+4K^{2}{\it\beta}_{0}^{2}]\right)\left(\frac{\partial _{{\it\xi}}^{2}}{K^{2}}-4K^{2}F{\it\beta}_{0}^{2}\right)\frac{V_{r}}{\sqrt{F}}=0, & \displaystyle\end{eqnarray}$$
${\it\xi}\sim O(1)$
the basic flow can be approximated as
$u_{b}\sim U_{1}-\widehat{A}{\it\xi}^{n}\text{e}^{-K^{2}({\it\xi}^{2}-1)/2}$
and
$v_{b}\sim -KU_{1}^{\prime }\sqrt{F}{\it\xi}+h^{\prime }$
. The form of the above equations and the boundary conditions at the edge of the production layer (5.5) and (5.6) suggest that the solution can be found using a Wentzel–Kramers–Brillouin (WKB) approach.
In order to solve for the roll it is first convenient to define the quantity
$\mathscr{V}_{r}(x,{\it\xi})$
, which satisfies
$$\begin{eqnarray}\left(\frac{\partial _{{\it\xi}}^{2}}{K^{2}}+{\it\xi}\partial _{{\it\xi}}+1-F[\partial _{x}+K^{2}4{\it\beta}_{0}^{2}]\right)\mathscr{V}_{r}=0.\end{eqnarray}$$
In fact,
$\mathscr{V}_{r}(x,{\it\xi})$
is proportional to the streamwise vorticity and can be used to determine the roll velocity
$V_{r}$
by solving
$$\begin{eqnarray}\left(\frac{\partial _{{\it\xi}}^{2}}{K^{2}}-4K^{2}F{\it\beta}_{0}^{2}\right)\frac{V_{r}}{\sqrt{F}}=\mathscr{V}_{r}.\end{eqnarray}$$
The streak can then be found using (5.8). The nature of the WKB solution for the streamwise vorticity will reveal the presence of a shock associated with the onset of forcing from the production layer. The ‘jumps’ across the shock which straddle a curve
$\mathscr{C}$
emanating from
$({\it\xi},x)=(1,1)$
are resolved by the introduction of a diffusion front; see figure 4. It follows from (5.11) that the solution for
$V_{r}$
will contain homogeneous (irrotational) and inhomogeneous terms with different WKB phase functions, and the exponential dependence driven by
$\mathscr{V}_{r}$
dominates that associated with the operator
$((\partial _{{\it\xi}}^{2}/K^{2})-K^{2}4F{\it\beta}_{0}^{2})$
everywhere above a second curve
$\mathscr{D}$
emanating from
$({\it\xi},x)=(1,1)$
; see figure 4. The curve
$\mathscr{D}$
acts like a classical WKB turning point across which the exponential dependence driven by
$\mathscr{V}_{r}$
becomes subdominant to that associated with the homogeneous part. In the region below
$\mathscr{D}$
the roll flow becomes irrotational at leading order and takes on a particularly simple form.
Figure 4. The different regions associated with the adjustment layer. Crossing the diffusion front corresponds to a switch between the upper/lower WKB solutions, while on crossing the lower curve the roll flow becomes irrotational. The thin lines represent the characteristic curves of the Charpit solutions of the eikonal equation.
We shall see that both the diffusion front and the WKB turning point layer are of thickness
$O(K^{-1})$
in
${\it\xi}$
. The three regions subdivided by the curves
$\mathscr{C}$
and
$\mathscr{D}$
are referred to as the upper region, lower region and irrotational region; see figure 4. In § 5.1 we begin by calculating the WKB solution for
$\mathscr{V}_{r}$
in the upper and lower adjustment layers. Having found
$\mathscr{V}_{r}$
in the adjustment layer we then solve for
$V_{r}$
,
$U_{s}$
in § 5.2. The solutions are used to construct a composite solution valid in the adjustment layer, the diffusion front and the WKB turning point layer described in appendix A.
5.1. The streamwise vorticity in the upper and lower adjustment layers
We begin by seeking a WKB solution of the form
$$\begin{eqnarray}\mathscr{V}_{r}=K^{2}\mathscr{V}(x,{\it\xi},K)\text{e}^{K^{2}{\it\Theta}(x,{\it\xi})},\end{eqnarray}$$
where, following the usual nomenclature, we refer to
${\it\Theta}$
as the phase function and
$\mathscr{V}$
as the amplitude. We shall see that
$\mathscr{V}\sim O(1)$
in the upper adjustment layer while
$\mathscr{V}\sim O(K^{-1})$
in the lower adjustment layer. The roll equation is satisfied exactly if
$$\begin{eqnarray}\displaystyle & & \displaystyle ({\it\Theta}_{{\it\xi}}^{2}+{\it\xi}{\it\Theta}_{{\it\xi}}-F(U_{1}{\it\Theta}_{x}+4{\it\beta}_{0}^{2}))\mathscr{V}\nonumber\\ \displaystyle & & \displaystyle \quad +\,[K^{-4}\mathscr{V}_{{\it\xi}{\it\xi}}+K^{-2}\{(2{\it\Theta}_{{\it\xi}}+{\it\xi})\mathscr{V}_{{\it\xi}}+({\it\Theta}_{{\it\xi}{\it\xi}}+1)\mathscr{V}-FU_{1}\mathscr{V}_{x}\}]=0,\end{eqnarray}$$
where the subscripts
$x,{\it\xi}$
represent partial differentiations. In the limit
$K\rightarrow \infty$
the terms in the square brackets in (5.13) are neglected to give the eikonal equation for
${\it\Theta}$
,
$$\begin{eqnarray}{\it\Theta}_{{\it\xi}}^{2}+{\it\xi}{\it\Theta}_{{\it\xi}}-F(U_{1}{\it\Theta}_{x}^{}+4{\it\beta}_{0}^{2})=0.\end{eqnarray}$$
At the next order the terms in the curly bracket in (5.13) produce an amplitude equation for the leading-order approximation to
$\mathscr{V}$
,
$$\begin{eqnarray}(2{\it\Theta}_{{\it\xi}}+{\it\xi})\mathscr{V}_{{\it\xi}}+({\it\Theta}_{{\it\xi}{\it\xi}}+1)\mathscr{V}-FU_{1}\mathscr{V}_{x}=0.\end{eqnarray}$$
The phase
${\it\Theta}$
is found by using Charpit’s method, which shows how information from the production layer for
$x\geqslant 1$
propagates down into the upper adjustment layer. Once the phase function
${\it\Theta}$
is known, (5.15) can be integrated to find the leading-order amplitude function.
5.1.1. The upper adjustment layer
Downstream of
$x=1$
the effect of the interaction will first diffuse into the upper adjustment layer through the phase function
${\it\Theta}$
. It follows from (5.5) and (5.6) that the appropriate conditions for
${\it\Theta}$
are
$$\begin{eqnarray}{\it\Theta}=0,\quad {\it\Theta}_{{\it\xi}}={\it\omega}_{1}(x)\quad \text{on }{\it\xi}=1\text{ for }x\geqslant 1,\end{eqnarray}$$
while
$\mathscr{V}$
must satisfy
$$\begin{eqnarray}\mathscr{V}=\frac{K_{1}(\sqrt{F}\widehat{A})^{-{\it\omega}_{1}}}{F}({\it\omega}_{1}^{2}-4F{\it\beta}_{0}^{2})\equiv \mathscr{V}_{0}(x)\quad \text{on }{\it\xi}=1\text{ for }x\geqslant 1.\end{eqnarray}$$
Here, it should be stressed that in these equations all the functions apart from
${\it\Theta}$
are fixed by the production layer problem at the location
$x$
. The eikonal equation is a first-order nonlinear partial differential equation and can be solved using Charpit’s method. We parameterize the characteristic curve on which the boundary conditions are to be specified by
$$\begin{eqnarray}x=s,\quad {\it\xi}=1,\quad s\geqslant 1.\end{eqnarray}$$
If we let
$\widehat{p}={\it\Theta}_{x}$
and
$\widehat{q}={\it\Theta}_{{\it\xi}}$
, then the Charpit equations associated with (5.14) are
$$\begin{eqnarray}\frac{\text{d}x}{FU_{1}}=\frac{\text{d}{\it\xi}}{-(2\widehat{q}+{\it\xi})}=\frac{\text{d}\widehat{p}}{-((FU_{1})^{\prime }\widehat{p}+4{\it\beta}_{0}^{2}F^{\prime })}=\frac{\text{d}\widehat{q}}{\widehat{q}}=\frac{\text{d}{\it\Theta}}{FU_{1}\widehat{p}-\widehat{q}(2\widehat{q}+{\it\xi})}=\text{d}{\it\tau},\end{eqnarray}$$
which must be solved subject to
$$\begin{eqnarray}{\it\tau}=0,\quad {\it\Theta}=\widehat{p}=0,\quad \widehat{q}={\it\omega}_{1}(s),\quad \mathscr{V}=\mathscr{V}_{0}(s)\quad \text{on }x=s,~{\it\xi}=1~\text{for}~s\geqslant 1.\end{eqnarray}$$
Along each characteristic curve
$x,{\it\xi},\widehat{p},\widehat{q},{\it\Theta}$
can be solved in terms of the variable
${\it\tau}$
. Thus, the phase function
${\it\Theta}$
satisfying the required boundary condition is given implicitly in terms of
${\it\xi},x$
by
$$\begin{eqnarray}\text{e}^{{\it\tau}}=\frac{U_{1}(x)\sqrt{F(x)}}{U_{1}(s)\sqrt{F(s)}},\quad {\it\xi}=(1+{\it\omega}_{1}(s))\text{e}^{-{\it\tau}}-{\it\omega}_{1}(s)\text{e}^{{\it\tau}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\Theta}=\left(\frac{1-\text{e}^{2{\it\tau}}}{2}\right){\it\omega}_{1}^{2}(s)-4{\it\beta}_{0}^{2}\int _{s}^{x}\frac{\text{d}\widehat{x}}{U_{1}(\widehat{x})},\quad {\it\Theta}_{{\it\xi}}={\it\omega}_{1}(s)\text{e}^{{\it\tau}},\quad {\it\Theta}_{{\it\xi}{\it\xi}}=\frac{-\text{e}^{2{\it\tau}}}{B(s)+\text{e}^{2{\it\tau}}},\phantom{\mathop{\sum }_{\mathop{\sum }_{\sum }}}\end{eqnarray}$$
where
$$\begin{eqnarray}B(x)=\frac{(2{\it\omega}_{1}+1)({\it\omega}_{1}+1)+4{\it\beta}_{0}^{2}U_{1}FF^{\prime }}{{\it\omega}_{1}(2{\it\omega}_{1}+1)-4{\it\beta}_{0}^{2}U_{1}FF^{\prime }}.\end{eqnarray}$$
We complete the solution in the upper diffusion layer by solving (5.15) for
$\mathscr{V}$
. Along a characteristic curve we have
$$\begin{eqnarray}({\it\Theta}_{{\it\xi}{\it\xi}}+1)\mathscr{V}-FU_{1}\mathscr{V}_{x}=0,\end{eqnarray}$$
so the solution for the amplitude is found by integrating to give
$$\begin{eqnarray}\mathscr{V}=\mathscr{V}_{0}(s)\exp \left\{\int _{0}^{{\it\tau}}[{\it\Theta}_{{\it\xi}{\it\xi}}+1]\,\text{d}\widehat{{\it\tau}}\right\}=\mathscr{V}_{0}(s)\text{e}^{{\it\tau}}\sqrt{\frac{B(s)+1}{B(s)+\text{e}^{2{\it\tau}}}}.\end{eqnarray}$$
The phase in (5.22) and the amplitude in (5.25) uniquely determine the solution in the adjustment layer above the curve
$\mathscr{C}$
. The limiting characteristic corresponds to
$s=1$
and so the curve
$\mathscr{C}$
is defined by
$$\begin{eqnarray}{\it\xi}=\overline{{\it\xi}}(x)=\frac{(1+{\it\omega}_{1}(1))}{I(x)}-{\it\omega}_{1}(1)I(x),\end{eqnarray}$$
where
$$\begin{eqnarray}I(x)=\frac{U_{1}(x)\sqrt{F(x)}}{U_{1}(1)\sqrt{F(1)}}.\end{eqnarray}$$
On the curve
$\mathscr{C}$
we deduce that
$$\begin{eqnarray}\mathscr{V}=\overline{\mathscr{V}}(x)=\mathscr{V}_{0}(1)I(x)\sqrt{\frac{B(1)+1}{B(1)+I^{2}(x)}}.\end{eqnarray}$$
It is easy to show that
$\overline{\mathscr{V}}(x)$
is regular in
$x$
for
${\it\xi}\in [0,1]$
. At the curve
$\mathscr{C}$
the quantity
$\mathscr{V}_{r}$
is reduced in size within the diffusion front. Thus, at large spanwise wavenumbers we anticipate that the effect of the forcing from the production layer beginning at
$x=1$
is most strongly felt in the upper adjustment layer which sits between
${\it\xi}=1$
and
${\it\xi}=\overline{{\it\xi}}(x)$
. However, we shall see that the maximum of the WKB streak phase occurs in the lower adjustment layer which sits beneath the curve
$\mathscr{C}$
.
5.1.2. The lower adjustment layer
The production layer forcing determines the adjustment layer solution only above
$\mathscr{C}$
. Beneath the curve
$\mathscr{C}$
we continue the WKB solution by stipulating that all characteristics now must pass through the singular point
$({\it\xi},x)=(1,1)$
. We retain the expression for
$\mathscr{V}_{r}$
given by (5.12), so the Charpit equations remain the same as (5.19) but with different boundary conditions. By using
$s\geqslant {\it\omega}_{1}(1)$
as a parameter, the Charpit solution satisfying
$$\begin{eqnarray}{\it\tau}=0,\quad {\it\Theta}=0,\quad {\it\Theta}_{{\it\xi}}=s\quad \text{for }s\geqslant {\it\omega}_{1}(1)\end{eqnarray}$$
is found to be
$$\begin{eqnarray}\text{e}^{{\it\tau}}=I(x),\quad {\it\xi}=\frac{(1+s)}{I}-sI,\end{eqnarray}$$
$$\begin{eqnarray}{\it\Theta}=\frac{1-I^{2}}{2}s^{2}-4{\it\beta}_{0}^{2}\int _{1}^{x}\frac{\text{d}\widehat{x}}{U_{1}(\widehat{x})},\quad {\it\Theta}_{{\it\xi}}=sI,\quad {\it\Theta}_{{\it\xi}{\it\xi}}=-\frac{I^{2}}{I^{2}-1}.\end{eqnarray}$$
Eliminating
$s$
from (5.30) and (5.31), we find an explicit expression for the phase function
${\it\Theta}$
. The amplitude function
$\mathscr{V}$
can again be found by integrating along a characteristic to give
$$\begin{eqnarray}\mathscr{V}=N(s)\frac{I(x)}{\sqrt{I^{2}(x)-1}},\end{eqnarray}$$
where
$N(s)$
is an arbitrary function of
$s=s(x,{\it\xi})$
. This arbitrariness is of course associated with the fact that, since all the characteristics pass through
$(x,{\it\xi})=(1,1)$
, there is no boundary condition to be imposed on
$\mathscr{V}$
at
${\it\tau}=0$
.
An examination of the upper and lower Charpit solutions (5.22) and (5.31) shows that, if
$[.]$
denotes the difference in a quantity just above or below
$\mathscr{C}$
, then
$$\begin{eqnarray}[{\it\Theta}]=0,\quad [{\it\Theta}_{{\it\xi}}]=0,\quad [{\it\Theta}_{{\it\xi}{\it\xi}}]\equiv J(x)\neq 0.\end{eqnarray}$$
Therefore, the two forms of the WKB solution do not have phases that connect smoothly at
$\mathscr{C}$
defined by
${\it\xi}=\overline{{\it\xi}}(x)$
. The jump points to the existence of a diffusion front or shock at the curve
$\mathscr{C}$
. The thickness of the diffusion front is fixed by observing that
$\text{e}^{K^{2}{\it\Theta}}$
changes by a factor
$\text{e}^{K^{2}({\it\xi}-\overline{{\it\xi}})^{2}J/2}$
across the shock, which means that the amplitude function must vary on an
$O(1)$
length scale
${\it\phi}$
proportional to
$K({\it\xi}-\overline{{\it\xi}})$
. Thus, the diffusion front is of thickness
$O(K^{-1})$
in
${\it\xi}$
and the jump is accommodated in this layer. The details of the solution within the diffusion front are given in appendix A.
By taking the limit of
$|{\it\phi}|$
large in the diffusion layer solution we find that the solution matches the upper form of the WKB solution, while a match with the lower form (5.32) requires
$$\begin{eqnarray}N(s)=\frac{\mathscr{V}_{0}(1)}{K\sqrt{2{\rm\pi}}(s-{\it\omega}_{1}(1))}.\end{eqnarray}$$
This means that the amplitude of the vorticity in the WKB solution falls by a factor of
$K^{-1}$
on passing through
$\mathscr{C}$
from above. Thus, to summarize, in the lower adjustment layer
$\mathscr{V}_{r}$
is given by (5.12) with the phase function
${\it\Theta}$
given by (5.31) and the amplitude
$$\begin{eqnarray}\mathscr{V}=\frac{-\mathscr{V}_{0}(1)I\sqrt{I^{2}-1}}{K\sqrt{2{\rm\pi}}[I{\it\xi}-1+{\it\omega}_{1}(1)(I^{2}-1)]}.\end{eqnarray}$$
Having found the streamwise vorticity induced below the production layer we now solve for the roll and streak.
5.2. The roll–streak flow generated beneath the production layer
Given
$\mathscr{V}_{r}$
we can solve (5.11) for the roll flow and then (5.8) for the streak flow. In this section we denote the upper/lower WKB solution by a
$+/-$
superscript. If we use the WKB form of
$\mathscr{V}_{r}$
(5.12) with the phase
${\it\Theta}$
given by
$$\begin{eqnarray}{\it\Theta}^{+}\quad \text{in (5.20)},\quad {\it\Theta}^{-}\quad \text{in (5.31)}\end{eqnarray}$$
and the amplitude
$\mathscr{V}$
given by
$$\begin{eqnarray}\mathscr{V}^{+}\quad \text{in (5.22)},\quad \mathscr{V}^{-}\quad \text{in (5.32)},\end{eqnarray}$$
then we find that
$$\begin{eqnarray}V_{r}=\frac{\sqrt{F}\mathscr{V}\text{e}^{K^{2}{\it\Theta}}}{{\it\Theta}_{{\it\xi}}^{2}-F4{\it\beta}_{0}^{2}},\quad U_{s}=-\frac{\sqrt{F}\widehat{A}{\it\xi}^{n}\text{e}^{-K^{2}(({\it\xi}^{2}-1)/2)}}{2{\it\Theta}_{{\it\xi}}}V_{r}.\end{eqnarray}$$
We recall that the upper and lower adjustment layers are separated at
${\it\xi}=\overline{{\it\xi}}(x)$
defined by (5.26). By using the scaled normal coordinate
${\it\phi}=K({\it\xi}-\overline{{\it\xi}}(x))/{\rm\Delta}(x)$
with
${\rm\Delta}(x)$
as defined in appendix A, it is shown there that the diffusion front solution
$\mathscr{V}_{r}$
takes the form
$$\begin{eqnarray}\mathscr{V}_{r}=K^{2}\mathscr{V}^{C}(x,{\it\phi})\text{e}^{K^{2}{\it\Theta}^{C}(x,{\it\phi},K)}.\end{eqnarray}$$
Here,
${\it\Theta}^{C}$
is the Taylor series expansion of
${\it\Theta}^{+}$
around
${\it\xi}=\bar{{\it\xi}}$
; see the appendix for more details. A careful examination shows that (5.38) become singular when
$({\it\Theta}_{{\it\xi}}^{2}-4F{\it\beta}_{0}^{2})$
vanishes, and this happens when the lower Charpit parameter
$s=\sqrt{F}2{\it\beta}_{0}/I$
. Thus, the curve
$\mathscr{D}$
alluded to earlier and which lies beneath
$\mathscr{C}$
is defined as
$$\begin{eqnarray}{\it\xi}=\underline{{\it\xi}}(x)=I^{-1}+\sqrt{F}2{\it\beta}_{0}(I^{-2}-1).\end{eqnarray}$$
The origin of this singular behaviour corresponds to the two possible phases in a WKB solution of (5.9) coalescing, and so we have a classical WKB turning point problem. The details of this layer can be found in appendix A. Taking
${\it\varphi}=K({\it\xi}-\underline{{\it\xi}}(x))/{\it\delta}(x)$
with
${\it\delta}(x)$
as defined in appendix A, it is shown that in the turning point layer the roll is given by
$$\begin{eqnarray}V_{r}=V^{D}(x,{\it\varphi})\text{e}^{K^{2}{\it\Theta}^{D}(x,{\it\varphi},K)}.\end{eqnarray}$$
Here,
${\it\Theta}^{D}$
is the Taylor series expansion of
${\it\Theta}^{-}$
around the curve
$\mathscr{D}$
; see the appendix for more details. Beneath the curve
$\mathscr{D}$
we have irrotational flow of the form
$$\begin{eqnarray}V_{r}=V^{i}(x)\text{e}^{{\it\Theta}^{i}(x,{\it\xi})},\quad U_{s}=-\frac{\sqrt{F}\widehat{A}{\it\xi}^{n+1}\text{e}^{-K^{2}(({\it\xi}^{2}-1)/2)}}{({\it\xi}+\underline{{\it\xi}}){\it\Theta}_{{\it\xi}}^{i}}V_{r},\end{eqnarray}$$
which matches with the WKB turning point layer solution. The functions
$V^{i}$
and
${\it\Theta}^{i}$
are given in appendix A. We recall that
$\mathscr{V}^{+}$
is
$O(1)$
and
$\mathscr{V}^{-}$
is
$O(K^{-1})$
. Thus, on crossing the curve
$\mathscr{D}$
from above the roll amplitude increases in size by a factor of
$K$
.
Now we complete the calculation of the induced roll–streak driven by the motion in the production layer. The results can be combined to produce a composite asymptotic approximation valid everywhere beneath the production layer. First, we define the WKB phase of the roll as
$$\begin{eqnarray}{\it\Theta}=\left\{\begin{array}{@{}ll@{}}{\it\Theta}^{+}\quad & \text{in (5.20)}\quad \text{if }{\it\xi}\geqslant \overline{{\it\xi}},\\ {\it\Theta}^{-}\quad & \text{in (5.31)}\quad \text{if }\overline{{\it\xi}}>{\it\xi}\geqslant \underline{{\it\xi}},\\ {\it\Theta}^{i}\quad & \text{in (A 18)}\quad \text{if }{\it\xi}<\underline{{\it\xi}}.\end{array}\right.\end{eqnarray}$$
Although this WKB phase function is continuous everywhere, there are singularities for the roll amplitude when crossing
$\mathscr{C}$
or
$\mathscr{D}$
. Thus, we consider the following composite roll solution so that the limiting forms of
$\mathscr{V}^{C}(x,{\it\phi})$
and
$V^{D}(x,{\it\varphi})$
cancel the singularities:
$$\begin{eqnarray}V_{r}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\mathscr{V}^{C}}{\mathscr{V}_{\infty }^{C}}\frac{V^{D}}{V_{\infty }^{D}}\frac{\sqrt{F}\mathscr{V}^{+}\text{e}^{K^{2}{\it\Theta}}}{{\it\Theta}_{{\it\xi}}^{2}-F4{\it\beta}_{0}^{2}}\quad & \text{if }{\it\xi}\geqslant \overline{{\it\xi}},\\ \displaystyle \frac{\mathscr{V}^{C}}{\mathscr{V}_{-\infty }^{C}}\frac{V^{D}}{V_{\infty }^{D}}\frac{\sqrt{F}\mathscr{V}^{-}\text{e}^{K^{2}{\it\Theta}}}{{\it\Theta}_{{\it\xi}}^{2}-F4{\it\beta}_{0}^{2}}\quad & \text{if }\overline{{\it\xi}}>{\it\xi}\geqslant \underline{{\it\xi}},\\ \displaystyle \frac{\mathscr{V}^{C}}{\mathscr{V}_{-\infty }^{C}}\frac{V^{D}}{V_{-\infty }^{D}}V^{i}\text{e}^{K^{2}{\it\Theta}}\quad & \text{if }{\it\xi}<\underline{{\it\xi}}.\end{array}\right.\end{eqnarray}$$
The limiting forms
$\mathscr{V}_{\infty }^{C}(x,{\it\phi}),\mathscr{V}_{-\infty }^{C}(x,{\it\phi}),V_{\infty }^{D}(x,{\it\varphi})$
and
$V_{-\infty }^{D}(x,{\it\varphi})$
are given in (A 8) and (A 18). It should be noted that by taking the logarithm we can show that the above expression becomes a standard composite solution of the form of (inner solution)
$+$
(outer solution)
$-$
(common part).
The composite roll solution also completes the description of the composite streak flow in the region
$x>1,1\geqslant {\it\xi}>0$
through the streak equations in (5.38b
) for
${\it\xi}\geqslant \underline{{\it\xi}}$
and (5.42b
) for
${\it\xi}<\underline{{\it\xi}}$
. We note that our asymptotic solution breaks down when
$x\rightarrow 1_{+}$
because the subdominant part of the roll solution becomes singular and is eventually comparable with the leading-order term. We shall see in the following section that the asymptotic solution already constructed agrees well with a full numerical calculation of the streak apart from near
$x=1$
. Moreover, the maximum streak amplitude occurs well downstream of that point and is well described by the asymptotic theory. Therefore, we do not consider the extra region separately. Because of the WKB form of the solution the size of the streak is primarily determined by the effective phase function
$$\begin{eqnarray}M(x,{\it\xi})={\it\Theta}(x,{\it\xi})-\frac{{\it\xi}^{2}-1}{2},\end{eqnarray}$$
with
${\it\Theta}$
given by (5.43). Of particular importance is the question of where the streak WKB phase takes on its maximum value. The necessary condition for a maximum,
$\partial _{x}M=\partial _{{\it\xi}}M=0$
, shows that the maximum occurs in the lower adjustment layer where
$$\begin{eqnarray}{\it\beta}_{0}\sqrt{2F}(2I^{2}-1)=I,\quad {\it\xi}={\it\beta}_{0}\sqrt{2F}.\end{eqnarray}$$
Thus, the maximum streak amplitude occurs well downstream of
$x=1$
and well away from
${\it\xi}=0$
. This means that the streak structure in the unperturbed main boundary layer, where
${\it\xi}\sim O(K^{-1})$
, is not dominant. However, we indicate briefly how the roll–streak flow is continued into the main boundary layer. The solution follows in much the same way as for the ASBL, see DH, and is closely linked to the WKB description of small-wavelength linear Taylor or Görtler vortex modes given by Hall (Reference Hall1982). For
${\it\eta}=y/\sqrt{F}\sim O(1)$
, the vertical structure of the roll–streak field must operate on the same length scale, and so the vertical structure for the roll will be proportional to
$\exp [K^{2}{\it\Theta}_{0}(x)+K{\it\theta}(x,y)]$
, where
${\it\Theta}_{0}(x)={\it\Theta}(x,0)$
is the
${\it\xi}\rightarrow 0$
limit of the WKB phase of the roll. Using (5.3) and (5.4) we see that the eikonal equation for
${\it\theta}$
will only involve
${\it\eta}$
derivatives of the phase function and there will be two positive and two negative roots. One of the positive values will match onto the incoming (decaying towards the wall) roll, and together with the corresponding solutions for the negative roots can be used to satisfy the no-slip condition at
${\it\eta}=0$
. Thus, within the boundary layer the roll–streak has the same size in terms of
$Re$
as the roll–streak at the bottom of the adjustment layer.
6. Results for free-stream coherent structures in Blasius flow
In this section we use the asymptotic description of the streak presented in the last section to make predictions for a Blasius boundary layer. In that case,
$U_{1}=1,F=2x$
and the basic flow can be approximated by (3.11) for large
$y$
. We suppose that the production layer interaction starts at
$x=1$
so that the flow field corresponds to the left saddle-node bifurcation point at
${\it\beta}\approx 0.2062$
in figure 1(a). This means that we must choose
${\it\beta}_{0}\approx 0.2062/\sqrt{2}\approx 0.1458$
and
${\it\Omega}={\it\beta}_{0}/2$
. Moving downstream, the larger
${\it\beta}=\sqrt{2x}{\it\beta}_{0}$
solution in figure 1(a) is taken and the interaction ends when
${\it\beta}$
reaches the right saddle node at
${\it\beta}\approx 0.4633$
, i.e.
$x\approx 5.05$
. Therefore, the interaction can only occur over a finite interval in the streamwise direction; this is consistent with experimental observations. In order to construct the adjustment layer roll–streak solution we need the value of
$K_{1}$
at each position
$x$
. Here, we use the upper branch solutions in figure 1(b) for this purpose.
Given the values of
$K_{1}$
and
$Re$
we can march the boundary region equations (5.3) and (5.4) downstream to produce numerical solutions beneath the production layer. The composite asymptotic solution (5.44) will then be used to predict the roll–streak structure and compare it with direct solutions of the linearized boundary-region equations. Following Hall (Reference Hall1983), equations (5.3) and (5.4) are most easily solved by eliminating the pressure and spanwise disturbance velocity to produce a fourth-order equation in
$y$
for
$v_{r}$
and a second-order equation in
$y$
for
$u_{s}$
. For computational purposes the equations are further rewritten in terms of
$x$
and the similarity variable
${\it\eta}=y/\sqrt{2x}$
; see for example (2.9) of Hall (Reference Hall1983). Here, second-order-accurate central difference is employed to approximate derivatives with respect to
${\it\eta}$
using 2000 grid points. At the end points of the grid, no-slip conditions are used at the wall and the production layer conditions (5.5) and (5.6) are specified at
${\it\eta}=K+h_{1}$
, i.e.
${\it\xi}=1$
. In order to march downstream the Crank–Nicolson method is used for the diffusion terms while the other terms are treated by the Adams–Bashforth method. We integrate (5.3) and (5.4) using the initial conditions
$u_{s}=v_{r}=0$
at
$x=1$
for all
${\it\eta}$
with the streamwise step size
$10^{-4}$
. It should be noted again that the asymptotic solution computed in § 5 is valid only a small distance beyond
$x=1$
and so does not satisfy the same initial conditions as those applied above. However, we expect that a short distance downstream the numerical solution will approach the asymptotic solution.
Before presenting the comparison of the asymptotic and boundary-region equation solutions we discuss the properties of the WKB phase function which is independent of
$Re$
and the value of
$K_{1}$
. The dominant asymptotic scales for the roll
$v_{r}$
and streak
$u_{s}$
are given approximately by
$Re^{{\it\Theta}}$
and
$Re^{M-1/2}$
respectively, so we can deduce from the values of
${\it\Theta}$
and
$M$
how the induced roll and streak vary in size in the adjustment layer. Figure 5 shows contour plots of
${\it\Theta}$
and
$M$
in the
$x{-}{\it\xi}$
plane. The locations of the diffusion front and the WKB turning point layer are shown as the solid curves. The thin curve represents the maximum in
${\it\xi}$
of
$M$
where
${\it\Theta}_{{\it\xi}}-{\it\xi}=0$
. If calculations are continued at higher values of
$x$
we find that the curve reaches
${\it\xi}=1$
at
$x=1/(4{\it\beta}_{0}^{2})\approx 11.8$
. Beyond this point there is no streak growth below the production layer; see the necessary condition for the streak growth given at the end of § 4. The variation of
$M$
along the thin curve is plotted in figure 6. We see that
$M$
attains its global maximum value in the lower adjustment layer. From (5.46), this maximum occurs at
$x=(1+2{\it\beta}_{0})/(4{\it\beta}_{0})\approx 2.22$
and
${\it\xi}=2{\it\beta}_{0}\sqrt{x}\approx 0.434$
, as indicated by the circle symbol in figure 5. The maximum value of
$M$
is approximately 0.25 and so the streak amplitude indeed increases in size by a maximum factor
$\simeq Re^{0.25}$
from the edge of the production layer. The variation of
$M$
is also plotted at
${\it\xi}=0$
in figure 6. We observe that, for Blasius flow,
$M$
is constant at
${\it\xi}=0$
in the irrotational adjustment layer, and that the constant is approximately
$0.5-\sqrt{8}{\it\beta}_{0}\approx 0.088$
, so that
$M$
has reduced from its maximum value but is still slightly increased from its value in the production layer.
Figure 5. The roll phase function
${\it\Theta}$
(a) and the streak phase function
$M$
(b) for Blasius flow. The thick lines are the curves
$\mathscr{C}$
and
$\mathscr{D}$
. The thin line in (b) shows the position where the maximum of
$M$
in
${\it\xi}$
occurs. The circle on the thin line denotes where
$M$
is a maximum in
$x,{\it\xi}$
.
Figure 6. The maximum in
${\it\xi}$
of
$M$
as a function of
$x$
, and
$M$
at the lower boundary.
Now let us compare the composite streak solution and the streak part of the solution of the boundary-region equations. The results are presented in figure 7 for
$Re=10^{4},10^{7}$
and 1010. It should be noted that we only plot the composite solutions up to
${\it\xi}=0.1$
. As shown by the black dashed line in (a,c,e), for Blasius flow the limiting curves
$\mathscr{C}$
and
$\mathscr{D}$
reduce at leading order to straight lines in the
$x{-}y$
plane. We see that as the Reynolds number increases the asymptotic and numerical approaches give increasingly consistent predictions of the streak field, including its maximum value the overall shape. It is worth bearing in mind that the agreement is very encouraging given that our ‘large’ expansion parameter
$K\simeq \sqrt{\ln Re}$
is only approximately 4 even for
$Re=10^{10}$
. We see in the figure that with increasing
$Re$
the maximum of the streak solution from the boundary-region equation calculation moves upstream, thereby approaching that predicted by the phase function
$M$
. The other small maximum of the composite solution appearing in the irrotational region is also captured in the slight expansion of the boundary-region equation solution near
$x=1$
.
Figure 7. Comparison of the composite solution (a,c,e) and the boundary-region equation solution (b,d,f). The streak field
$-u_{s}$
is shown for (a)
$Re=10^{4}$
, (b)
$Re=10^{7}$
and (c)
$Re=10^{10}$
. The white dashed line represents
${\it\xi}=1$
. The black dashed lines in (a,c,e) are the curves
$\mathscr{C}$
and
$\mathscr{D}$
.
In figure 8, a
$y{-}z$
slice of the disturbance streamwise velocity and vorticity is plotted at
$x=1.244,2.116$
and 4.552. The numerical solutions of the boundary-region equations for
$Re=10^{7}$
were used. The streamwise positions chosen correspond to
${\it\beta}=0.23,0.3$
and 0.44, and therefore the flow regimes shown in figure 8 match to the production layer solutions shown in figure 2(a–c) after some rescaling. The combined plot of the production layer solution and the boundary-region equation solution for
$Re=10^{4}$
is given in figure 9 to show the evolution of the structure. The overall flow structure is now clear. Even for the non-parallel flow a key result of DH does not change: large-amplitude wall streaks occur as a passive byproduct of the nonlinear interaction at the edge of the boundary layer. However, since solutions of the canonical production layer problem (2.3)–(2.8) only exist for a finite range of
$x$
, and there is a necessary condition for streak growth at a given streamwise location, the large streak induced in the adjustment layer must ultimately diminish for large
$x$
.
Figure 8. The
$y{-}z$
plot of the roll–streak field for
$Re=10^{7}$
. The boundary-region equation solutions at
$x=1.244$
, 2.116 and 4.552 are used. The disturbance streamwise velocity and vorticity are plotted in the left and right halves of each figure. Here,
$C_{max}=0.01$
(a), 0.03 (b) and 0.03 (c) for the streaks;
$C_{max}=8$
(a), 10 (b) and 25 (c) for the rolls. The horizontal white dashed lines represent
${\it\xi}=1$
.
Figure 9. Combined plot of the free-stream coherent structures for the Blasius boundary layer;
$Re=10^{4}$
. The green surface represents the isocontour of the streamwise vorticity computed by the upper branch ASBL solutions in figure 1. See § 4 for the rescaling used to map out the ASBL solutions to the production layer solution shown in this figure. The red/blue surfaces are positive/negative isocontours of the streak computed by the boundary layer solution shown in figure 7. The interval
$x\in [2,3]$
,
$z\in [0,2{\rm\pi}/{\it\beta}]$
is used. The transparent grey surface is the 99 % unperturbed boundary layer thickness.
7. Conclusion and discussion
Our asymptotic theory has uncovered a family of coherent structures for arbitrary growing boundary layer flow. The coherent structures are produced by a nonlinear interaction of waves, rolls and streaks in a layer at the edge of the boundary layer. In this ‘production layer’, the interaction problem found in DH turns out to be a generic kind of nonlinear interaction in the free stream. At the local streamwise position around
$x$
, the production layer solutions can be found from the ASBL results with ‘local’ wavenumbers. The local wavenumbers are functions of
$x$
, since the local wavelengths must be changed so that the wave has fixed frequency and fixed spanwise global wavenumber for all
$x$
. Thus, the streamwise distance
$x$
only affects the production layer problem parametrically. The distance to the production layer from the wall,
$K$
, is approximately scaled as
$\sqrt{\ln Re}$
. The production layer thickness of
$O(K^{-1})$
is found to be thinner than the main boundary layer; it should be noted that for the ASBL the thickness of the production layer was comparable to the main boundary layer. Moreover, we saw that free-stream coherent structures now cause the streaks to have wavelengths a factor of
$K$
smaller than those of the vortex–wave interaction states. For the ASBL the spanwise wavelengths of both modes were comparable; see DH. Between the production layer and the main boundary layer, there is an adjustment layer of thickness
$O(K)$
where a rich asymptotic structure has been found. The adjustment layer solution is found to take on a WKB form for large
$Re$
, with three different regions separated by a diffusion front and a WKB turning point layer. For Blasius flow, the composite asymptotic solution and the direct numerical solution beneath the production layer are compared for finite
$Re$
and excellent agreement is observed.
We believe that the equilibrium solutions we described provide a new mechanism through which nonlinear structures in the free stream communicate with structures near the wall. We have found, for the first time, what can be thought of as a self-sustaining structure that may persist over both long times and streamwise distances at the edge of the growing boundary layer. At the very least, our result suggests that in turbulent simulations the free-stream disturbances might not be as passive as some believe; it should be noted that whether the free-stream coherent structure describes a particular turbulent flow is not our main issue. The point is that we show that the edge of a boundary layer can support tiny nonlinear structures stimulating much larger passive motions lower down in the boundary layer. That makes the question of whether wall streaks drive structures in the free stream or vice versa perhaps more complicated than was thought to be the case.
In order to calculate the adjustment layer solution we used the forcing from the upper branch production layer solution found in DH; see figure 1. Since the solution exists for a finite local spanwise wavenumber range, the production layer forcing only exists for a finite streamwise interval; that result is consistent with experimental observations; see, for example, Adrian (Reference Adrian2007). However, in our asymptotic framework, we did not address how the production layer interaction starts and ends. In general, the mechanism by which the asymptotic states are created or destroyed as the flow evolves in experiments cannot be addressed within the asymptotic theory so far developed, but a great deal of evidence from Navier–Stokes simulations suggests the importance of exact coherent structures in flow dynamics; see § 1. Likewise, the asymptotic theory of the free-stream coherent structures which we derived for a growing boundary layer describes the spatial evolution of the states from an upstream disturbance consistent with their asymptotic structure.
Here, we shall comment briefly on this issue. First, if we use the phase variable
$\widetilde{{\it\Phi}}=KRe^{1/2}(\int ^{x}{\it\alpha}_{0}(\widehat{x})\,\text{d}\widehat{x}-{\it\Omega}t)$
instead of (4.9) and introduce a new short streamwise variable
${\it\zeta}=K^{2}\int _{x_{0}}^{x}U_{1}^{-1}\,\text{d}\widehat{x}$
around
$x=x_{0}$
, then we find an ‘unsteady’ form of the production layer problem where the phase speed term is replaced by the derivative with respect to the time-like variable
${\it\zeta}$
. Thus, if solutions of this unsteady canonical production layer problem exist, we can use them to describe the short-scale development of the growing boundary layer production layer problem. The scaling of
${\it\zeta}$
means that this phenomenon occurs at
$x-x_{0}\sim O(K^{-2})$
for arbitrary
$x_{0}$
; it should be noted that this streamwise scale is smaller than the non-parallel scale but much larger than that of the wave oscillation. It is now clear from this small-scale dynamical system that in order to sustain our equilibrium solutions we need to choose the upstream condition to be on the stable manifold of the production layer solution at
$x=1$
, which corresponds to the left saddle node in figure 1. Moreover, after the upper and lower branches of the production layer problem end at the right saddle node, it is reasonable to assume that the disturbance decays back to the unperturbed flow. In this case the forcing from the production layer diminishes in an
$O(K^{-2})$
streamwise length after the saddle node is reached. More generally, if there is a heteroclinic connection between two equilibrium solutions of the canonical production layer problem, which is similar to that observed in plane Couette flow by Halcrow et al. (Reference Halcrow, Gibson, Cvitanović and Viswavath2009), it is possible to consider a jump between the two distinct production layer solution branches in figure 1 at a certain streamwise position.
The production layer interaction for growing boundary layers is similar to that for the ASBL in that the interaction drives large-amplitude streaks near the wall and further out in the boundary layer, suggesting the possibility that some near-wall streaks are the passive signature of self-sustained free-stream coherent structures. However, for growing boundary layers the maximum of the streak occurs in the adjustment layer, unlike in the ASBL case, where the maximum of the streak occurs in the main boundary layer. This flow structure is entirely consistent with a number of boundary layer experiments and simulations summarized by Adrian (Reference Adrian2007), where a strong vortex signature in the free stream creates a large streamwise velocity distortion beneath the vortex. In experiments the streamwise velocity distortion has two peaks according to the schematic pictures in Adrian (Reference Adrian2007). The first peak, which occurs between the free-stream vortex and the main boundary layer, is reminiscent of the passive streaky field seen in the free-stream modes studied in this paper. We recall here that there is widespread belief that the vortex–wave interaction/self-sustaining process is the one sustaining wall streaks in turbulent flows. On that basis the vortex–wave interaction states found by DH for the ASBL are probably relevant to wall streaks in turbulent growing boundary layers, although direct evidence of the relevance cannot be addressed without the solution of the full vortex–wave interaction problem formulated by Hall & Smith (Reference Hall and Smith1991) for growing boundary layers. Therefore, the second peak in the main boundary layer is likely to be a consequence of a wall mode of vortex–wave interaction type. A comparison of these two distinct modes for the ASBL can be found in DH.
Nonlinear states involving both vortex–wave structures and the free-stream coherent structures are allowed by the Navier–Stokes equations. The two modes can coexist almost independently for growing boundary layers since the modes have different spanwise length scales. The presence of wall modes just influences the location of the production layer slightly via a mean-flow distortion in the free stream. It is an open question whether the streak induced by a free-stream mode can produce a wall mode. The interplay of the two structures could be determined from the properties of those solutions and upstream conditions. We do not attempt that problem here, but certainly the fact that wall streaks in the ASBL can be generated passively by nonlinear interactions in the free stream is at least suggestive that the motion in the free stream is not necessarily the result of interactions near the wall.
However, if we assume that the two structures coexist in turbulent boundary layers some characteristics of experimentally observed coherent structures can be elucidated. Consistent with the asymptotic theories here and in Hall & Sherwin (Reference Hall and Sherwin2010), in experiments streamwise roll–streak structures are found in the unperturbed boundary layer while there is more complicated vortex structure above them. A
${\rm\Lambda}$
-shaped vortex sitting at the top of the structure in the free stream has been observed in experiments and is similar to our production layer solution. It was pointed out by DH and Deguchi & Hall (Reference Deguchi and Hall2014c
) that our production layer solutions do not have the head part of the hairpin structure sometimes observed in experiments. However, we note that the production layer problem in the unit-Reynolds-number Navier–Stokes form does not preclude the possibility of hairpin-shaped solutions. This is of course another motivation to solve the unsteady version of the canonical production layer problem. The computation may be done by directly solving the unsteady version of (2.3)–(2.6) with asymptotic conditions (2.7) and (2.8), or alternatively by ASBL simulations with some minor modifications. It should be noticed that for any type of production layer solutions the streak, which is passively driven in the adjustment layer, exists only for a finite streamwise interval since there is a critical streamwise position where the streak growth beneath the production layer is prohibited; see figure 5.
The existence of the production layer interaction is only dependent on the basic flow profile approaching its free-stream form through exponentially decaying terms, and therefore the free-stream coherent structure theory presented in DH and here has quite a wide range of application. This type of exponential decay towards the free stream can be typically found in quite general boundary layers or jets. Indeed, Deguchi & Hall (Reference Deguchi and Hall2014c ) demonstrated that the free-stream coherent structures can be built into the Burgers vortex sheet problem where once again the flow approaches its free-stream form through exponentially small terms. In our boundary layer study the roll–streak flow is only forced by the production layer interaction. When the flow is also forced by an external body force, induced linear instability of the basic flow and the production layer can compete and resonate. Therefore, it is of interest to consider the production layer problem in curved flows where centrifugal instabilities are possible.
Finally, we remark that the discussion so far in this paper is valid for any two-dimensional boundary layer. For infinite swept boundary layers our analysis is readily modified to account for the three-dimensionality of the boundary layer. A discussion of that problem is given in appendix B. This flow is relevant to flows over swept wings, where the spanwise component is a ‘parasitic’ boundary layer decoupled from the flow in the
$x{-}y$
directions, which is itself identical to the flow in the case with zero spanwise flow. The spanwise velocity is then determined by an equation involving the
$x{-}y$
velocity field and is directly proportional to the free-stream spanwise velocity component. In aerodynamics, increasing the free-stream spanwise velocity corresponds to increasing the angle of sweep of the wing. It is easy to show that when the sweep is increased from zero there is at first little effect on the production layer problem, and thus there is a growth of the streak towards the adjustment layer. However, for larger values of the sweep the effect of the sweep gradually diminishes the penetration of the growing streak into the adjustment layer, and a new thin layer appears in the adjustment layer. With increasing sweep the position of the new layer moves up to the production layer, so that ultimately the sweep kills off the link to the near-wall streaks. This adjustment layer behaviour is similar to the Gortler vortex instability in three-dimensional boundary layers discussed by Hall (Reference Hall1985). For more general three-dimensional boundary layers the approach to the free-stream velocity is more complicated and so we cannot take our results over to a general three-dimensional boundary layer.
Acknowledgement
This work was supported by EPSRC grant EP/1037946/1. We wish to thank the referees for constructive comments on the first draft of this paper.
Appendix A. The diffusion front and the WKB turning point layer
(a) The diffusion front problem
The function
${\it\Theta}_{{\it\xi}{\it\xi}}$
is discontinuous at
$\mathscr{C}$
so that the two forms of the WKB solution do not connect smoothly there and a diffusion front must exist. The structure at the front leads to a failure of the WKB approach and is rectified by bringing higher derivatives back into play in a layer straddling the front. The thickness of the layer follows immediately from the condition that the second-order derivative in the square bracket of (5.13) must be comparable with the leading-order terms. This condition requires that the layer should be of thickness
$O(K^{-1})$
in
${\it\xi}$
, so we write
$$\begin{eqnarray}{\it\phi}=\frac{K({\it\xi}-\overline{{\it\xi}}(x))}{{\rm\Delta}(x)},\end{eqnarray}$$
with the function
${\rm\Delta}(x)$
to be determined in terms of the jump in the second derivative of the phase
$J(x)$
.
We denote a quantity evaluated on
$\mathscr{C}$
by an overbar and quantity defined by the upper/lower form of the WKB solution by a
$+/-$
superscript. The formal solution of the diffusion front problem then follows by writing
$$\begin{eqnarray}\mathscr{V}_{r}=K^{2}\mathscr{V}^{C}(x,{\it\phi})\text{e}^{K^{2}{\it\Theta}^{C}(x,{\it\phi},K)}.\end{eqnarray}$$
Here, we have taken
${\it\Theta}^{C}(x,{\it\phi},K)$
to be the truncated Taylor series expansion of
${\it\Theta}^{+}$
around
${\it\xi}=\overline{{\it\xi}}$
:
$$\begin{eqnarray}{\it\Theta}^{+}\approx \overline{{\it\Theta}}^{+}+\overline{{\it\Theta}}_{{\it\xi}}^{+}({\it\xi}-\overline{{\it\xi}})+\frac{\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}}{2}({\it\xi}-\overline{{\it\xi}})^{2}\equiv {\it\Theta}^{C},\end{eqnarray}$$
where we note that
$\overline{{\it\Theta}}^{+}$
,
$\overline{{\it\Theta}}_{{\it\xi}}^{+}$
and
$\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}$
are functions of
$x$
only. We can show from the Charpit equation (5.19) that
$$\begin{eqnarray}2\overline{{\it\Theta}}_{{\it\xi}}^{+}+\overline{{\it\xi}}+FU_{1}\overline{{\it\xi}}^{\prime }=0.\end{eqnarray}$$
Thus, from (5.13), (A 1) and (A 4) the function
$\mathscr{V}^{C}(x,{\it\phi})$
satisfies
$$\begin{eqnarray}\frac{1}{{\it\Delta}^{2}}\mathscr{V}_{{\it\phi}{\it\phi}}^{C}+\left[2\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}+1+FU_{1}\frac{{\it\Delta}^{\prime }}{{\it\Delta}}\right]{\it\phi}\mathscr{V}_{{\it\phi}}^{C}+(\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}+1)\mathscr{V}^{C}-FU_{1}\mathscr{V}_{x}^{C}=0,\end{eqnarray}$$
where a subscript
${\it\phi}$
represents a partial differentiation with respect to that variable. The jump
$J(x)$
is expressed as
$(\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}-\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{-})$
. The matching with the upper form of the WKB solution together with the condition that
$\mathscr{V}^{C}$
tends to zero below the diffusion front requires
$$\begin{eqnarray}\mathscr{V}^{C}\rightarrow \left\{\begin{array}{@{}l@{}}\overline{\mathscr{V}}(x)\quad \text{as }{\it\phi}\rightarrow \infty ,\\ 0\quad \text{as }{\it\phi}\rightarrow -\infty ,\end{array}\right.\end{eqnarray}$$
where
$\overline{\mathscr{V}}(x)$
is the limiting upper WKB amplitude defined in (5.28).
In order to solve the equation for
$\mathscr{V}^{C}$
we make some observations. First, we note that if
${\rm\Delta}(x)=\sqrt{2/J}$
then
$$\begin{eqnarray}\frac{2}{{\it\Delta}^{2}}=2\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{+}+1+FU_{1}\frac{{\it\Delta}^{\prime }}{{\it\Delta}},\end{eqnarray}$$
so that the terms in the square bracket of (A 5) simplify. Second, using the above result and (5.24) enables us to find a separable solution for
$\mathscr{V}^{C}$
of the form
$\mathscr{V}^{C}=\overline{\mathscr{V}}(x)\widehat{\mathscr{V}}^{C}({\it\phi})$
, where
$\widehat{\mathscr{V}}^{C}({\it\phi})$
satisfies the error function equation. Hence, it follows that
$$\begin{eqnarray}\mathscr{V}^{C}=\overline{\mathscr{V}}\frac{\text{erf}({\it\phi})+1}{2}\rightarrow \left\{\begin{array}{@{}ll@{}}\mathscr{V}_{\infty }^{C}\equiv \overline{\mathscr{V}}\quad & \text{as }{\it\phi}\rightarrow \infty ,\\ \displaystyle \mathscr{V}_{-\infty }^{C}\equiv -\frac{\overline{\mathscr{V}}}{2\sqrt{{\rm\pi}}{\it\phi}}\text{e}^{-{\it\phi}^{2}}\quad & \text{as }{\it\phi}\rightarrow -\infty ,\end{array}\right.\end{eqnarray}$$
where
$\text{erf}(x)=(2/\sqrt{{\rm\pi}})\int _{0}^{x}\text{e}^{-\widehat{x}^{2}}\,\text{d}\widehat{x}$
. Thus, it is clear that the exponential behaviour of
$\mathscr{V}^{C}$
in the large negative
${\it\phi}$
produces the required phase jump.
The large-
${\it\phi}$
form of the solution (A 8) ensures the required match with the upper adjustment layer solution, while the asymptotic form for large negative
${\it\phi}$
yields the unknown function of
$s$
appearing in the lower WKB amplitude (5.32). From (5.24) and (A 7) we can show that
$$\begin{eqnarray}FU_{1}\frac{\text{d}}{\text{d}x}[\ln (\overline{\mathscr{V}}{\it\Delta})]=\frac{I^{2}}{I^{2}-1},\end{eqnarray}$$
so that
$$\begin{eqnarray}\overline{\mathscr{V}}{\it\Delta}=\mathscr{V}_{0}(1)\sqrt{2}\sqrt{I^{2}-1}.\end{eqnarray}$$
Using (A 10) we deduce that as
${\it\phi}\rightarrow -\infty$
, (A 1) behaves like
$$\begin{eqnarray}\mathscr{V}_{r}\rightarrow K^{2}\left(\frac{-\mathscr{V}_{0}(1)\sqrt{I^{2}-1}}{K\sqrt{2{\rm\pi}}({\it\xi}-\overline{{\it\xi}})}\right)\exp \left[K^{2}\left\{\overline{{\it\Theta}}^{-}+\overline{{\it\Theta}}_{{\it\xi}}^{-}({\it\xi}-\overline{{\it\xi}})+\frac{\overline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{-}}{2}({\it\xi}-\overline{{\it\xi}})^{2}\right\}\right].\end{eqnarray}$$
We therefore obtain a match with the lower form of the WKB solution if we take
$N(s)$
to be defined by (5.34).
(b) The WKB turning point layer
Once the roll vorticity
$\mathscr{V}_{r}$
is known, we calculate the roll velocity field
$V_{r}$
by solving (5.11). In the lower adjustment layer the roll velocity is given by (5.38) with
${\it\Theta}={\it\Theta}^{-}$
given by (5.31), and the WKB turning point problem occurs when the phase function of the homogeneous WKB solution of this equation coincides with
${\it\Theta}$
. The difficulty arises on the curve
$\mathscr{D}$
defined by
${\it\xi}=\underline{{\it\xi}}(x)$
in (5.40). The remedy is to introduce a thin layer straddling
$\mathscr{D}$
in which a second-order term derivative of the amplitude function can enter. That consideration, similar to the last section, shows that the layer is of thickness
$O(K^{-1})$
, so that we write
$$\begin{eqnarray}{\it\varphi}=\frac{K({\it\xi}-\underline{{\it\xi}}(x))}{{\it\delta}(x)},\end{eqnarray}$$
where
${\it\delta}(x)$
is again determined in terms of the jump in the second derivative of the phase.
We write the formal solution of the WKB turning point layer as
$$\begin{eqnarray}V_{r}=V^{D}(x,{\it\varphi})\text{e}^{K^{2}{\it\Theta}^{D}(x,{\it\varphi},K)},\end{eqnarray}$$
where
${\it\Theta}^{D}(x,{\it\varphi},K)$
is the truncated Taylor series expansion of the lower Charpit phase around
${\it\varphi}=0$
,
$$\begin{eqnarray}{\it\Theta}^{-}\approx \underline{{\it\Theta}}^{-}+\underline{{\it\Theta}}_{{\it\xi}}^{-}({\it\xi}-\underline{{\it\xi}})+\frac{\underline{{\it\Theta}}_{\,{\it\xi}{\it\xi}}^{-}}{2}({\it\xi}-\underline{{\it\xi}})^{2}\equiv {\it\Theta}^{D},\end{eqnarray}$$
and we denote a quantity evaluated on
$\mathscr{D}$
by an underbar. Since beneath the curve
$\mathscr{D}$
the phase of the homogeneous part satisfies
${\it\Theta}_{{\it\xi}}=2\sqrt{2}F$
, the phase beneath
$\mathscr{D}$
does not have terms proportional to
${\it\xi}^{2}$
. Thus, we anticipate the jump
$[{\it\Theta}_{{\it\xi}{\it\xi}}]=-\underline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{-}$
$=I^{2}/(I^{2}-1)$
across the curve
$\mathscr{D}$
and write
$$\begin{eqnarray}{\it\delta}(x)=\sqrt{2/(-\underline{{\it\Theta}}_{{\it\xi}{\it\xi}}^{-})}.\end{eqnarray}$$
Using (5.11) we find that
$V^{D}$
satisfies
$$\begin{eqnarray}\frac{\partial V^{D}}{\partial {\it\varphi}}-2{\it\varphi}V^{D}=-\frac{V_{i}}{\sqrt{{\rm\pi}}},\end{eqnarray}$$
where we have defined
$V^{i}(x)$
as
$$\begin{eqnarray}V^{i}=\frac{-\mathscr{V}_{0}(1)I}{4{\it\beta}_{0}[2\sqrt{F}{\it\beta}_{0}-{\it\omega}_{1}(1)I]}.\end{eqnarray}$$
It follows that
$V^{D}$
can be solved as
$$\begin{eqnarray}V^{D}=-V^{i}\frac{\text{e}^{{\it\varphi}^{2}}(\text{erf}({\it\varphi})-1)}{2}\rightarrow \left\{\begin{array}{@{}l@{}}\displaystyle V_{\infty }^{D}=\frac{V^{i}}{2\sqrt{{\rm\pi}}{\it\varphi}}\quad \text{as }{\it\varphi}\rightarrow \infty ,\quad \\ V_{-\infty }^{D}=V^{i}\text{e}^{{\it\varphi}^{2}}\quad \text{as }{\it\varphi}\rightarrow -\infty .\quad \end{array}\right.\end{eqnarray}$$
The first of the above equations shows that moving upwards from
$\mathscr{D}$
the roll
$V_{r}$
matches to that of the lower WKB solution. On the other hand, when
${\it\varphi}\rightarrow -\infty$
we see that the exponential term exactly cancels the quadratic term in
${\it\Theta}^{D}$
, so that below
$\mathscr{D}$
the roll
$V_{r}$
is given by
$$\begin{eqnarray}V_{r}=V^{i}(x)\text{e}^{K^{2}{\it\Theta}^{i}(x,{\it\xi})},\end{eqnarray}$$
where the phase
$$\begin{eqnarray}{\it\Theta}^{i}(x,{\it\xi})=2{\it\beta}_{0}^{2}\left[F(I^{-2}-1)-2\int _{1}^{x}\frac{\text{d}\widehat{x}}{U_{1}(\widehat{x})}\right]+2\sqrt{F}{\it\beta}_{0}({\it\xi}-\underline{{\it\xi}});\end{eqnarray}$$
this ensures the leading-order irrotational property of the flow.
Appendix B. Free-stream coherent structures in three-dimensional flows: infinite swept boundary layers
Here, we generalize the discussion of free-stream coherent structures given in the main part of this paper to include the effect of a spanwise cross-flow. We retain the Navier–Stokes equations written in the form (4.1) and (4.2), but for the spanwise velocity we now impose the conditions
$$\begin{eqnarray}w=0\quad \text{on }y=0,\quad w\rightarrow {\it\Gamma}\quad \text{as }y\rightarrow \infty ,\end{eqnarray}$$
where
$Re^{-1/2}{\it\Gamma}\lesssim O(1)$
is the size of the cross-flow velocity at infinity.
The basic spanwise velocity is completely determined in terms of the unswept two-dimensional boundary layer. By using the basic flow
$(u_{b},v_{b})=(u,v)$
given in § 3, we can show that the basic spanwise velocity
$w_{b}$
satisfies
$$\begin{eqnarray}u_{b}\frac{\partial w_{b}}{\partial x}+v_{b}\frac{\partial w_{b}}{\partial y}=\frac{\partial ^{2}w_{b}}{\partial y^{2}}.\end{eqnarray}$$
For large
$y$
the asymptotic approach of the spanwise basic flow to its free-stream value is easily shown to be given by
$$\begin{eqnarray}w_{b}={\it\Gamma}\left(1+\text{d}(x)y^{-1}\exp \left[-\frac{(y-k(x))^{2}}{2F(x)}\right]+\cdots \!\right),\end{eqnarray}$$
where the exponent of the exponential term is the same as that in (3.5) and
$\text{d}(x)$
is a given
$O(1)$
function.
In the production layer scaling (4.11)–(4.14), we need to replace (4.13) by
$$\begin{eqnarray}w={\it\Gamma}+K\widetilde{W}(x,\widetilde{{\it\Phi}},\widetilde{Y},\widetilde{Z})+\cdots \,,\end{eqnarray}$$
where the first term in the expansion is the constant free-stream value of the spanwise mean flow. This difference produces an extra term in the production layer problem. However, since this extra term can be cancelled if we define a ‘drift’ variable
$\overrightarrow{Z}=\widetilde{Z}-{\it\Gamma}t$
so that
$\partial _{t}\rightarrow \partial _{t}-{\it\Gamma}\partial _{\overrightarrow{Z}}$
and
$\partial _{\widetilde{Z}}\rightarrow \partial _{\overrightarrow{Z}}$
, we get exactly the production layer problem for the two-dimensional problem. This is not an unexpected result since the change in the spanwise variable means moving in a frame of reference sliding in the spanwise direction with the constant free-stream velocity of the unperturbed spanwise flow. In other words, since the spanwise component of the boundary layer is constant across the production layer, we can recover the unswept production layer problem by sliding the coordinate frame in the spanwise direction with the appropriate speed. It should be noted that this is possible only because the unperturbed spanwise velocity is at leading order constant in the production layer and down to the edge of the unperturbed boundary layer.
Within the adjustment layer the spanwise velocity is constant at leading order, so initially sweeping the boundary layer there has essentially no effect; however, within the unperturbed boundary layer the forced structure will now differ from the two-dimensional case. In order to see how sweep eventually enters the adjustment layer problem consider the operator
$\partial _{t}+u\partial _{x}+v\partial _{y}+w\partial _{z}-{\rm\nabla}^{2}$
there. Once again the extra term from the time derivative associated with the drift coordinate can be used to cancel the leading-order term coming from the spanwise mean part of the flow multiplying the
$\partial _{z}$
term. However, the next-order exponential correction term of the spanwise mean part enters the equations at a layer around
$(y-k/\sqrt{F})=\overrightarrow{K}$
, where
$\overrightarrow{K}$
satisfies
$$\begin{eqnarray}{\it\Gamma}\overrightarrow{K}^{-1}\text{e}^{-\overrightarrow{K}^{2}/2}\partial _{z}\sim \partial _{z}^{2}.\end{eqnarray}$$
Since
$\partial _{z}\sim K$
, if we write
${\it\Gamma}=Re^{l}$
with
$0<l<1/2$
then we see that a balance occurs when
$$\begin{eqnarray}\overrightarrow{K}^{-1}\text{e}^{-\overrightarrow{K}^{2}/2}=KRe^{-l},\quad \overrightarrow{K}=\sqrt{2l\ln Re}+\cdots \,,\end{eqnarray}$$
and the upper and lower limits for
$l$
put the new layer in the main boundary layer and the production layer respectively. In this new layer we write
$$\begin{eqnarray}\frac{(y-k(x))}{\sqrt{F(x)}}=\overrightarrow{K}+\frac{\overrightarrow{Y}}{\overrightarrow{K}\sqrt{F(x)}}\end{eqnarray}$$
and
$$\begin{eqnarray}v=v_{b}+K\mathscr{V}(x,\overrightarrow{Y})\exp [\text{i}2{\it\beta}_{0}\overrightarrow{Z}+{\it\Theta}(x,\overrightarrow{Y})]+\text{c.c.}+\cdots\end{eqnarray}$$
to seek the roll solution of WKB form. Here, c.c. stands for complex conjugate. The eikonal equation associated with the roll problem is
$$\begin{eqnarray}\left(\frac{{\it\Phi}_{\overrightarrow{Y}}^{2}}{2l}-4{\it\beta}_{0}^{2}-2\text{i}{\it\beta}_{0}\text{e}^{-\overrightarrow{Y}}+\cdots \!\right)\left(\frac{{\it\Phi}_{\overrightarrow{Y}}^{2}}{2l}-4{\it\beta}_{0}^{2}\right)=0.\end{eqnarray}$$
No root crossing is possible, and the complex root from above connects with the root
${\it\Phi}_{\overrightarrow{Y}}\sim \text{e}^{-(\overrightarrow{Y}\!/2)}$
at large negative
$\overrightarrow{Y}$
, so we get super-exponential decay of the roll on exiting the new layer moving downwards. An examination of the streak equation shows that it also has super-exponential decay below the new layer, so the sweep basically kills off the induced streak at some position between the production layer and the wall.
Now we summarize the effect of sweep inferred from the above analysis. On increasing
${\it\Gamma}$
from zero, the first distinguished scaling of
${\it\Gamma}$
is achieved when the spanwise free-stream velocity is comparable with the spanwise velocity component of the free-stream coherent structure in the production layer. That occurs when
${\it\Gamma}\sim O(K)$
, and the production layer problem is unchanged from (4.16)–(4.19) except that the spanwise velocity must now approach its non-negligible constant free-stream value. In a frame of reference sliding in the spanwise direction with spanwise flow outside the boundary layer, the problem is reduced exactly to the two-dimensional case. Thus, for weak sweep the structures survive unscathed apart from now sliding in the spanwise direction. Within the adjustment layer the flow is found from the two-dimensional case again moving into a frame of reference sliding in the spanwise direction. However, at some stage as the spanwise mean flow increases the exponential correction to the unperturbed spanwise boundary layer from its free-stream form enters the leading-order equations determining the roll and streak fields. The effect is to destroy the roll and streak flows within a thin layer at some position in the adjustment layer with no penetration of the streak towards the wall. Thus, increasing the sweep moves the position of the thin layer up until it reaches the production layer, and no induced streak is generated beneath the production layer. The size of the spanwise free-stream speed needed to achieve this limit is
${\it\Gamma}\sim O(Re^{1/2})$
. Thus, we have a situation very similar to the Görtler vortex problem in three-dimensional boundary layers, see Hall (Reference Hall1985), where increasing the sweep basically destroys the Görtler vortex mechanism. Further increase of the sweep eventually modifies and destroys the canonical production layer structure given in two-dimensional boundary layers.
