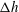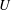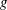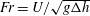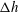1. Introduction
Free-surface flows around the hulls of moving ships exhibit a variety of wave patterns whose study covers a wide range of topics in the theory of water waves. Typical examples are the train of waves found in the far field, commonly known as Kelvin waves, which are well described by the linear theory of gravity waves (Whitham Reference Whitham1974). Coming to the near field and going from bow to stern, some distance upstream of the hull a bow wave develops that locally raises the water level, thus leading to an extra contribution to the total drag.
Large-amplitude breaking waves are also found around the ship. Indeed, at the bow two divergent waves originate which eventually turn into plunging or spilling breakers depending on the velocity of the ship and the geometry of the hull. These waves are not the only example of large-amplitude breakers found in naval hydrodynamics. In rough sea conditions, waves can break suddenly on hitting the hull, giving birth to high-speed jets that might damage other ship structures. A recent review on this problem, commonly known as slamming, was published by Faltinsen, Landrini & Greco (Reference Faltinsen, Landrini and Greco2004).
In high-speed vessels with transom sterns, the bluff end of the hull leads to a sudden expansion of the flow towards the centre of the wake. Depending on the shape of the transom, two plunging waves can form at its lower corners which move faster than the spilling flow that originates them. These waves, hereafter denoted as corner waves, are precisely the focus of the present study. The importance of these waves arises from the fact that, when they collide at the flow’s symmetry plane, a structure known as a rooster tail appears, which contributes significantly to aeration of the flow around the hull (see figure 1 a). Thus, an understanding of the mechanisms that lead to corner wave formation and evolution is instrumental to predict the dynamics of this flow pattern.
Figure 1. (a) Wake structure downstream from the stern of a dummy ship model for large
$\mathit{Fr}$
numbers (courtesy of Drazen et al.
Reference Drazen, Beale, Bhushan, Fullerton, O’Shea, Brucker, Dommermuth, Wyatt, Carrica, Fu and Stern2010). (b) Corner wave developing downstream from the corner of a plate in a finite-width recirculating water channel (see Martínez-Legazpi Reference Martínez-Legazpi2011 for experimental details). Interestingly, even though immediately downstream from the plate the flow does not correspond to our idealized model (which, strictly speaking, only applies to an infinitely long prismatic bar), still at intermediate distances the same wave pattern is observed. (c) Sketch of the flow configuration.
Apart from their interest in naval hydrodynamics, the formation of corner waves is relevant in some civil engineering problems such as sudden expansions in channels or spillways. Hager & Mazumder (Reference Hager and Mazumder1992) and Hager & Yasuda (Reference Hager and Yasuda1997) studied the flow downstream from a sudden expansion in a water channel using the shallow water approximation. However, although it provides an accurate description of the overall flow, this approach is unable to capture the formation of the kind of plunging corner waves considered here.
From a more fundamental point of view, it will be shown that using the two-dimensions-plus-time approximation the corner wave flow is a natural extension of the classical dam-break problem. In fact, the present study is closely related to that of Korobkin & Yilmaz (Reference Korobkin and Yilmaz2009) in which the authors studied, using asymptotic techniques, the evolution of the free surface near the contact point between the water mass and the basin, predicting the formation of a wall jet. Another variation of the dam-break problem much more similar to the topic of the present paper has been considered by several authors, namely the case when the discharge occurs over a wet basin. Stansby, Chegini & Barnes (Reference Stansby, Chegini and Barnes1998) performed an experimental and numerical investigation of the dam-break flow originated when the vertical plate separating two liquid masses with different depths is suddenly removed. They observed a mushroom-shaped planar jet that emerged from the lower corner of the free surface, which they related to the singularity appearing in the pressure field near that corner. However, they could not resolve properly the initial stages of its evolution, which are essential to investigate the possible self-similar structure of the wave at short times and, more importantly, to explain the mushroom-like shape of the jet. It is worth mentioning that the present problem is different from that studied by Stansby et al. (Reference Stansby, Chegini and Barnes1998), even though the initial configuration of the flow regions is similar. In the corner wave problem, there is no vertical dam separating liquid masses of different initial heights. Goater & Hogg (Reference Goater and Hogg2011) used the shallow water theory which, as already mentioned, is unable to capture the plunging-jet structure of the wave. In particular, in their approach the corner wave is seen as a discontinuity, a bore, that propagates as a front. Nevertheless, it is interesting to notice that this bore resembles the spilling corner wave observed in some high-Froude-number flow configurations when a plate is blocking part of the test section of a water channel (Martínez-Legazpi et al. Reference Martínez-Legazpi, Rodríguez-Rodríguez, Marugán-Cruz and Lasheras2013). More recently, Yilmaz, Korobkin & Iafrati (Reference Yilmaz, Korobkin and Iafrati2013) studied numerically and theoretically the dam-break problem with a wet basin when the two fluids that come into contact after removing the dam have different densities. They considered the nature of the singularity appearing at short times. To that end, the authors focused on the leading-order small-time solution. This approach, although key to understanding the nature of the solution, as will be shown below, does not allow us to describe the development of the jet.
The mechanisms governing the initial evolution of the corner wave, and similarly the initial jet in the dam-breaking problem, are not fully understood. This is precisely the focus of our present study. However, once the amplitude of the corner wave becomes of the order of the water height difference that originates the flow, say
${\rm\Delta}h$
, the behaviour of these waves should not differ from other plunging waves generated in two-dimensions-plus-time flows which are known to follow a ballistic trajectory (Shakeri et al.
Reference Shakeri, Maxeiner, Fu and Duncan2009a
; Shakeri, Tavakolinejad & Duncan Reference Shakeri, Tavakolinejad and Duncan2009b
; Martínez-Legazpi et al.
Reference Martínez-Legazpi, Rodríguez-Rodríguez, Marugán-Cruz and Lasheras2013, see figure 1
b).
With these ideas in mind, the paper is organized as follows. In § 2, the problem is formulated and the two-dimensions-plus-time approach is introduced. Section 3 is devoted to the analysis of the leading-order solution at short times, which will be shown to admit a self-similar formulation. In § 4, the numerical method used to solve the problem posed in § 3 is presented, while the physical mechanism behind the formation of the wave is discussed in § 5. Finally, § 6 summarizes the most important results of the study.
2. Problem formulation
Let us consider the steady motion of an inviscid liquid flowing downstream from the stern of a bluff body partially submerged in the flow. The velocity field far upstream of the stern is uniform with speed
$U$
. The rear end of the body is semi-infinite in both the horizontal and vertical directions, with a horizontal edge at a depth
${\rm\Delta}h$
underneath the free-surface level far upstream and a vertical edge that forms a square corner with the former. Let the corner be the origin of coordinates, with the
$\tilde{x}$
axis pointing downstream, the
$\tilde{z}$
axis pointing vertically upward and the
${\tilde{y}}$
axis forming a right-handed trihedron, as shown in figure 1(c). Thus, considering the body as a semi-infinite prismatic bar, it occupies the region
$\tilde{x}<0,{\tilde{y}}>0,\tilde{z}>0$
. Under these conditions, in the presence of gravity,
$g$
, the Froude number of the flow,
$\mathit{Fr}$
, arises naturally as
$$\begin{eqnarray}\mathit{Fr}=\frac{U}{\sqrt{g{\rm\Delta}h}}.\end{eqnarray}$$
In the present context, the Froude number can be interpreted as the ratio between the free stream velocity,
$U$
, and the characteristic velocity induced by the spilling of a water column of height
${\rm\Delta}h$
, namely
$\sqrt{g{\rm\Delta}h}$
. In what follows, the problem will be made dimensionless using
${\rm\Delta}h$
as the length scale and
$\sqrt{g{\rm\Delta}h}$
as the velocity scale. Thus, the dimensionless free stream velocity is
$U/\sqrt{g{\rm\Delta}h}$
, namely the Froude number
$\mathit{Fr}$
.
The flow is described by a velocity potential,
${\it\Phi}(x,y,z)$
(made dimensionless using
${\it\Phi}=\tilde{{\it\Phi}}/(g^{1/2}{\rm\Delta}h^{3/2})$
), which satisfies Laplace’s equation,
${\rm\nabla}^{2}{\it\Phi}=0$
, and by the equation of the free surface,
$\mathit{F}(x,y,z)=0$
. At this surface, the following boundary conditions apply: a kinematic condition imposing that the free surface is a material surface,
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}{\it\Phi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\mathit{F}=0,\end{eqnarray}$$
and a dynamic boundary condition which follows from the Bernoulli equation and the assumption that the atmospheric pressure is zero,
$$\begin{eqnarray}{\textstyle \frac{1}{2}}|\boldsymbol{{\rm\nabla}}{\it\Phi}|^{2}+z=C.\end{eqnarray}$$
The constant
$C$
is obtained by evaluating (2.3) at the free surface far away upstream,
$x\rightarrow -\infty$
, where the free surface is horizontal,
$z=1$
, and the stream is uniform with
$\boldsymbol{{\rm\nabla}}{\it\Phi}=\mathit{Fr}\,\boldsymbol{i}$
(where
$\boldsymbol{i}$
is the downstream unit vector), yielding
$$\begin{eqnarray}{\textstyle \frac{1}{2}}|\boldsymbol{{\rm\nabla}}{\it\Phi}|^{2}+z={\textstyle \frac{1}{2}}\mathit{Fr}^{2}+1.\end{eqnarray}$$
Finally, an impermeable bottom will be placed at the plane
$z=-H$
, thus yielding
$$\begin{eqnarray}\partial _{z}{\it\Phi}|_{z=-H}=0.\end{eqnarray}$$
Although not necessary to describe the evolution of the wave, the presence of the bottom is incorporated here to extend our results to flows of interest in hydraulics, where shallow depths are usually considered.
2.1. Two-dimensions-plus-time approach
We now simplify the problem for large Froude numbers,
$\mathit{Fr}\gg 1$
. As will be shown below, the key feature of the flow in this limit is the formation of a three-dimensional steady wave, anchored at the rear lower corner of the body, and whose profile grows downstream in a similar fashion to the profile of an unsteady plunging wave (see figure 1
b). Before introducing any simplification, it is convenient to express the velocity potential as
$$\begin{eqnarray}{\it\Phi}=x\mathit{Fr}+{\it\phi}(x,y,z,\mathit{Fr}).\end{eqnarray}$$
The first term in (2.6) represents the uniform free stream, whereas the second corresponds to gravity-induced perturbations to this uniform velocity field. Taking the gradient, and assuming that
${\it\phi}\rightarrow 0$
as
$x\rightarrow -\infty$
,
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}{\it\Phi}=\mathit{Fr}\,\boldsymbol{i}+\boldsymbol{{\rm\nabla}}{\it\phi}.\end{eqnarray}$$
Introducing expression (2.7) into the dynamic boundary condition (2.4), we may write
$$\begin{eqnarray}\mathit{Fr}\partial _{x}{\it\phi}+{\textstyle \frac{1}{2}}((\partial _{y}{\it\phi})^{2}+(\partial _{z}{\it\phi})^{2})=1-z-{\textstyle \frac{1}{2}}(\partial _{x}{\it\phi})^{2},\end{eqnarray}$$
and, proceeding likewise in the kinematic boundary condition (2.2),
$$\begin{eqnarray}\mathit{Fr}\partial _{x}\mathit{F}+\partial _{x}{\it\phi}\partial _{x}\mathit{F}+\partial _{y}{\it\phi}\partial _{y}\mathit{F}+\partial _{z}{\it\phi}\partial _{z}\mathit{F}=0.\end{eqnarray}$$
From (2.8) we can deduce that, to see velocities of order unity in the
$y$
–
$z$
plane, one has to move along
$x$
a distance of the order of
$x\sim O(\mathit{Fr})$
. In the next two subsections, we consider the structure of the solution at both small (
$x\sim O(1)$
) and large (
$x\sim O(Fr)$
) distances from the body.
2.1.1. Near-field region,
$x\sim O(1)$
Immediately downstream from the stern, the boundary conditions change abruptly, since part of the liquid is suddenly exposed to the ambient pressure. The flow in this region is three-dimensional with
$\partial _{x}{\it\phi},\partial _{y}{\it\phi}$
and
$\partial _{z}{\it\phi}$
being of the same order of magnitude.
Without gravity effects,
$\mathit{Fr}=\infty$
, the upper boundary of the flow is described by
$$\begin{eqnarray}\mathit{F}_{\infty }(y,z)\!:\left\{\begin{array}{@{}ll@{}}(z-1), & y<0,\\ y, & 0\leqslant z\leqslant 1,\\ z, & y>0,\end{array}\right.\end{eqnarray}$$
and is independent of the presence of the free surface in
$x>0$
. Accounting for gravity,
$\mathit{F}(x,y,z,\mathit{Fr})\rightarrow \mathit{F}_{\infty }(y,z)$
, for any value of
$\mathit{Fr}$
, as
$x\rightarrow -\infty$
.
In the limit
$\mathit{Fr}\rightarrow \infty$
, the dynamic boundary condition (2.8) becomes non-trivial only if
$\mathit{Fr}\partial _{x}{\it\phi}$
balances
$1-z$
, which provides the scaling
$$\begin{eqnarray}{\it\phi}=\frac{1}{\mathit{Fr}}{\it\phi}^{(0)}(x,y,z)\end{eqnarray}$$
for the velocity potential in the near-field region. Similarly, under the scaling (2.11), the kinematic boundary condition (2.9) is non-trivial, in the limit
$\mathit{Fr}\rightarrow \infty$
, only if
$$\begin{eqnarray}\mathit{F}(x,y,z,\mathit{Fr})=\mathit{F}_{\infty }(y,z)+\frac{1}{\mathit{Fr}^{2}}\mathit{F}^{(0)}(x,y,z),\end{eqnarray}$$
where the function
$\mathit{F}_{\infty }(y,z)$
is given by (2.10). Notice that both
${\it\phi}^{(0)}(x,y,z)$
and
$\mathit{F}^{(0)}(x,y,z)$
are of order
${\sim}O(1)$
as
$\mathit{Fr}\rightarrow \infty$
. Thus, if we substitute (2.11)–(2.12) in the original Laplace equation and boundary conditions (2.8)–(2.9) and take the limit
$\mathit{Fr}\rightarrow \infty$
, we arrive at a linear boundary-value problem for the potential
${\it\phi}^{(0)}(x,y,z)$
and the shape function
$\mathit{F}^{(0)}(x,y,z)$
. In this latter case, (2.12) enforces the application of the boundary conditions of the linear problem on the known surface
$\mathit{F}_{\infty }(y,z)=0$
for both
$x<0$
and
$x>0$
. Hence, to the leading order, the dynamic boundary condition (2.8), for both
$\mathit{Fr}\rightarrow \infty$
and
$x>0$
, yields
$$\begin{eqnarray}\partial _{x}{\it\phi}^{(0)}=1-z\quad (\text{on }\mathit{F}_{\infty }(y,z)=0).\end{eqnarray}$$
Likewise, the kinematic boundary condition (2.9) reads
$$\begin{eqnarray}\partial _{x}\mathit{F}^{(0)}+\partial _{y}{\it\phi}^{(0)}\partial _{y}\mathit{F}_{\infty }+\partial _{z}{\it\phi}^{(0)}\partial _{z}\mathit{F}_{\infty }=0\quad (\text{also on }\mathit{F}_{\infty }(y,z)=0).\end{eqnarray}$$
Additionally, the no-penetration condition at the bottom (2.5) becomes
$\partial _{z}{\it\phi}^{(0)}=0$
.
The formulated problem for the near-field region is complex because of its three-dimensionality and mixed boundary conditions. However, the problem is linear and can be readily solved by using the domain decomposition method, for example. The normal derivative of the potential,
$\partial _{n}{\it\phi}^{(0)}$
, is zero on the rigid parts of the liquid boundary and the streamwise velocity component,
$\partial _{x}{\it\phi}^{(0)}$
, is prescribed on the free surface both upstream and downstream from the stern. The potential
${\it\phi}^{(0)}$
decays as
$x\rightarrow -\infty$
while it grows linearly,
${\it\phi}^{(0)}\sim f(y,z)x$
, as
$x\rightarrow \infty$
, which follows from (2.13). The function
$f(y,z)$
was determined by Martínez-Legazpi (Reference Martínez-Legazpi2011), appendix C, by using the conformal mapping technique. In particular, the condition (2.13) provides that
$f(y,z)=1-z$
on the vertical branch of the free surface. This implies that the
$z$
-velocity component on this branch increases linearly in
$x$
,
$\partial _{z}{\it\phi}^{(0)}(x,0,z)\sim -x$
, as
$x\rightarrow \infty$
. This result provides that the gradient
$\boldsymbol{{\rm\nabla}}{\it\phi}^{(0)}\sim O(x)$
, as
$x\rightarrow \infty$
, and then
$\mathit{F}^{(0)}\sim O(x^{2})$
, which follows from (2.14).
Therefore, the near-field linear solution is not valid in the far field,
$x\rightarrow \infty$
, where
$x\sim O(\mathit{Fr})$
, as the shape function,
$\mathit{F}^{(0)}(x,y,z)$
, in (2.12) is of order
$O(x^{2})$
whereas its correction term,
$\mathit{Fr}^{-2}\mathit{F}^{(0)}(x,y,z)$
in (2.12), is of order
$O(1)$
. However, in the far field, the potential,
${\it\phi}^{(0)}(x,y,z)$
, is of order
$O(x)$
whereas
${\it\phi}$
is of order
$O(1)$
(from (2.11)). This means that, at the leading order, as
$\mathit{Fr}\rightarrow \infty$
, the flow in the near-field region is a uniform stream with the non-dimensional speed
$\mathit{Fr}$
(see figure 1
a). This provides the matching condition between the near-field region, of
$x\sim O(1)$
, and the far-field region, where
$x\sim O(\mathit{Fr})$
.
2.1.2. Far-field region,
$x\sim O(Fr)$
To describe the flow in the far-field region downstream from the stern, it is convenient to rescale the downstream coordinate as
$t=x/Fr$
, such that velocities in the
$y$
–
$z$
plane of order unity occur at
$t\sim O(1)$
. In terms of the new variable, the Laplace equation transforms into
$$\begin{eqnarray}\partial _{yy}^{2}{\it\phi}+\partial _{zz}^{2}{\it\phi}=-Fr^{-2}\partial _{tt}^{2}{\it\phi},\end{eqnarray}$$
whereas (2.8) becomes
$$\begin{eqnarray}\partial _{t}{\it\phi}+{\textstyle \frac{1}{2}}((\partial _{y}{\it\phi})^{2}+(\partial _{z}{\it\phi})^{2})=1-z-\mathit{Fr}^{-2}{\textstyle \frac{1}{2}}(\partial _{t}{\it\phi})^{2}.\end{eqnarray}$$
In the same way, the kinematic boundary condition (2.9) becomes
$$\begin{eqnarray}\partial _{t}\mathit{F}+\partial _{y}{\it\phi}\,\partial _{y}\mathit{F}+\partial _{z}{\it\phi}\,\partial _{z}\mathit{F}=-\mathit{Fr}^{-2}\partial _{t}{\it\phi}\,\partial _{t}\mathit{F}.\end{eqnarray}$$
It should be noted that (2.15)–(2.17) are exact equations valid for any
$\mathit{Fr}$
and written in the non-dimensional stretched variables,
$t,y,z$
. The two-dimensions-plus-time assumption enters in the formulation when we take the limit
$Fr\rightarrow \infty$
, which yields
$$\begin{eqnarray}\partial _{yy}^{2}{\it\phi}+\partial _{zz}^{2}{\it\phi}=0\end{eqnarray}$$
and turns the dynamic boundary condition (2.16) into
$$\begin{eqnarray}\partial _{t}{\it\phi}+{\textstyle \frac{1}{2}}((\partial _{y}{\it\phi})^{2}+(\partial _{z}{\it\phi})^{2})=1-z.\end{eqnarray}$$
Proceeding likewise, the kinematic boundary condition (2.17) becomes
$$\begin{eqnarray}\partial _{t}\mathit{F}+\partial _{y}{\it\phi}\,\partial _{y}\mathit{F}+\partial _{z}{\it\phi}\partial _{z}\mathit{F}=0.\end{eqnarray}$$
The new variable
$t$
is treated in this approximation as a time-like variable. The initial conditions for this system follow from matching the far-field solution of (2.18)–(2.20) in the limit
$t\rightarrow 0$
with the near-field linear solution of (2.13)–(2.14) in the limit
$x\rightarrow \infty$
. It should be noted that the near-field region shrinks to the section
$t=0$
in the approximation described here. The matching conditions, and the results of § 2.1.1 in terms of the behaviour of the near-field solution as
$x\rightarrow \infty$
, provide not only the initial conditions for (2.18)–(2.20),
$$\begin{eqnarray}{\it\phi}=0,\quad \mathit{F}(t,y,z)=\mathit{F}_{\infty }(y,z)\quad \text{at}~t=0,\end{eqnarray}$$
but also the orders of the unknown functions as
$t\rightarrow 0$
, namely
$$\begin{eqnarray}{\it\phi}\sim O(t),\quad \mathit{F}(t,y,z)\sim \mathit{F}_{\infty }(y,z)+O(t^{2}),\quad \text{as}~t\rightarrow 0.\end{eqnarray}$$
In summary, the problem is transformed approximately from the original three-dimensional steady problem to the unsteady two-dimensional problem (2.18)–(2.21a,b ). The latter problem is more amenable to being treated using numerical as well as analytical methods. The approach followed here, commonly known as the two-dimensions-plus-time approximation, is widely used in a variety of problems of interest in naval hydrodynamics (Shakeri et al. Reference Shakeri, Maxeiner, Fu and Duncan2009a ,Reference Shakeri, Tavakolinejad and Duncan b ) and hydraulics (Hager & Mazumder Reference Hager and Mazumder1992; Hager & Yasuda Reference Hager and Yasuda1997).
The initial conditions (2.21a,b
) imply that the far-field solution at the scale
$x\sim O(\mathit{Fr})$
can be obtained without knowing the near-field solution. The near-field solution here serves to match the three-dimensional flow just downstream from the stern with the quasi-two-dimensional flow in the far-field region. Notice that the far-field solution cannot be used in close proximity to the stern, where capillary effects and the viscous boundary layer, which develops as the fluid flows along the surface of the solid body, are important. An order-of-magnitude analysis of these effects is given at the end of the discussion, § 5.
3. Self-similar structure of the flow near the corner at short times
Near the corner of the stern of the body, where
$x/Fr\ll 1$
but
$x\gg 1$
, or equivalently at the initial stages of development of the flow,
$t\ll 1$
, the asymptotically small size of the wave compared with the height of the spilling water mass suggests the existence of a self-similar solution due to the absence of characteristic lengths. To investigate the structure of the flow close to the corner point, it is convenient to work in polar coordinates
$(r,{\it\theta})$
, where
$r\ll 1$
(see figure 2 for their definition). Thus, the free surface can be expressed locally as
$F(r,{\it\theta},t)\equiv r_{S}({\it\theta},t)-r=0$
. With this formulation, the similarity solution is sought in the form
$$\begin{eqnarray}{\it\Phi}(r,{\it\theta},t)=t+{\it\phi}(r,{\it\theta},t)=t+t^{{\it\alpha}}\,{\it\varphi}({\it\rho},{\it\theta})\end{eqnarray}$$
and
$$\begin{eqnarray}r_{S}({\it\theta},t)=t^{{\it\beta}}\,{\it\rho}_{S}({\it\theta}),\end{eqnarray}$$
where
${\it\rho}=r/t^{{\it\beta}}$
is the similarity variable and the positive constants
${\it\alpha}$
and
${\it\beta}$
are to be determined. After introducing these expressions into (2.18)–(2.20), the problem reduces to the Laplace equation for the potential
${\it\varphi}$
together with the following boundary conditions at the free surface:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}{\it\varphi}-{\it\beta}{\it\rho}_{S}\partial _{{\it\rho}}{\it\varphi}+\frac{1}{2}\left((\partial _{{\it\rho}}{\it\varphi})^{2}+\frac{1}{{\it\rho}_{S}^{2}}(\partial _{{\it\theta}}{\it\varphi})^{2}\right)+t^{{\it\beta}-{\it\alpha}+1}{\it\rho}_{S}\sin {\it\theta}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\beta}{\it\rho}_{S}+\frac{{\it\rho}_{S}^{\prime }}{{\it\rho}_{S}^{2}}\partial _{{\it\theta}}{\it\varphi}-\partial _{{\it\rho}}{\it\varphi}=0, & \displaystyle\end{eqnarray}$$
${\it\rho}_{S}^{\prime }=\text{d}{\it\rho}_{S}/\text{d}{\it\theta}$
. It should be pointed out that, for the unsteady and convective terms to be of the same order in the boundary conditions (3.3) and (3.4), the exponents
${\it\alpha}$
and
${\it\beta}$
have been assumed to satisfy 
$$\begin{eqnarray}2{\it\beta}-{\it\alpha}-1=0.\end{eqnarray}$$
The second condition needed to determine these exponents, and thus the structure of the similarity solution, is found by imposing that, in the limit
${\it\rho}\rightarrow \infty$
, the rescaled potential
${\it\varphi}$
matches the double limit
$r\rightarrow 0$
and
$t\rightarrow 0$
of the original potential
${\it\phi}$
.
To express this condition mathematically, the potential and the free surface at short times,
$t\ll 1$
(or
$x\ll Fr$
), are expanded in power series of
$t$
following the results of § 2.1.1. The asymptotic formulae (2.22a,b
) yield that at the early stage,
$t\ll 1$
, the velocity potential
${\it\phi}(t,r,{\it\theta})$
and the free surface function
$\mathit{F}(t,r,{\it\theta})$
, which describes the shape of the free surface, have the form
$$\begin{eqnarray}\displaystyle & {\it\phi}(t,r,{\it\theta})=t\,{\it\phi}^{(1)}(r,{\it\theta})+O(t^{3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathit{F}(t,r,{\it\theta})=\mathit{F}_{\infty }(y,z)+t^{2}\,\mathit{F}^{(2)}(r,{\it\theta})+O(t^{3}). & \displaystyle\end{eqnarray}$$
Introducing this ansatz into the original two-dimensions-plus-time problem (2.18)–(2.20), and retaining only the leading-order terms as
$t\rightarrow 0$
, the following boundary-value problem for
${\it\phi}^{(1)}$
is obtained:
$$\begin{eqnarray}\displaystyle & {\rm\nabla}^{2}{\it\phi}^{(1)}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\phi}^{(1)}=1-z & \displaystyle\end{eqnarray}$$
$\mathit{F}_{\infty }(y,z)=0$
, from (2.10), and 
$$\begin{eqnarray}\partial _{z}{\it\phi}^{(1)}|_{z=-H}=0\end{eqnarray}$$
at the bottom. A sketch of the boundary conditions (3.9)–(3.10) is depicted in figure 2.
This problem was solved analytically using conformal mapping (see Martínez-Legazpi Reference Martínez-Legazpi2011 for the details). In the limit
$r\rightarrow 0$
, it was found that
$$\begin{eqnarray}{\it\Phi}=t-Jtr^{2/3}\sin \left(\frac{2{\it\theta}}{3}\right)+tr\sin {\it\theta}+O(tr^{4/3}),\end{eqnarray}$$
where
$J=J(H)$
is a positive constant that is obtained by solving the full problem (3.8)–(3.10). Interestingly, its value is nearly constant,
$J\approx 1.125$
, for
$H\gtrsim 2$
(Martínez-Legazpi Reference Martínez-Legazpi2011).
Thus, on imposing the aforementioned matching condition between the leading-order term of
${\it\phi}$
(first term on the right-hand side of (3.11)) and
${\it\varphi}$
, and substituting
$r=t^{{\it\beta}}{\it\rho}$
, we obtain
$$\begin{eqnarray}{\it\Phi}\approx t-Jt^{1+2{\it\beta}/3}{\it\rho}^{2/3}\sin \left({\textstyle \frac{2}{3}}{\it\theta}\right)\sim t+t^{{\it\alpha}}{\it\varphi}\end{eqnarray}$$
for
${\it\rho}\rightarrow \infty$
, which gives the following relation between the exponents
${\it\alpha}$
and
${\it\beta}$
:
$-3{\it\alpha}+2{\it\beta}+3=0$
. Together with condition (3.5), this leads to
${\it\alpha}=2$
and
${\it\beta}=3/2$
. Notice that, if the potential and the similarity variable are rescaled in the following way:
$\tilde{{\it\varphi}}=J^{-3/2}{\it\varphi}$
and
$\tilde{{\it\rho}}=J^{-3/4}{\it\rho}$
, the boundary conditions (3.3) and (3.4) remain invariant, while the constant
$J$
disappears from the matching condition (3.12). The fact that
$J$
disappears from the formulation of the inner problem suggests that the structure of this inner solution is unaffected by the depth,
$H$
, which would only modulate the wave velocity. Thus, hereafter, for the sake of simplicity and without loss of generality, we let
$J=1$
and drop the tilde from the formulation.
It is interesting to notice that the last term of (3.3), the hydrostatic term in the Bernoulli equation near the corner, turns out to be negligible for
$t\ll 1$
, since it scales with the time raised to the exponent
${\it\beta}-{\it\alpha}+1=1/2$
. Order of magnitude analysis shows that gravity affects the flow near the corner only through the matching condition (3.12) as
${\it\rho}\rightarrow \infty$
. In fact, the velocity potential in the outer limit of the flow near the corner (3.11) is induced by a hydrostatic pressure gradient of order unity (
${\it\rho}g{\rm\Delta}h$
in dimensional variables), whereas the hydrostatic term in the Bernoulli equation (3.3) represents the hydrostatic pressure difference across distances of the order of the size of the wave, which is asymptotically small for
$t\ll 1$
. Therefore, at short times, the latter contribution is negligible compared with the former.
To summarize, the self-similar solution valid near the corner at short times can be obtained by solving Laplace’s equation for the rescaled self-similar potential,
${\rm\nabla}^{2}{\it\varphi}=0$
, subjected to the following boundary conditions on the free surface:
$$\begin{eqnarray}\displaystyle & \displaystyle 2{\it\varphi}-\frac{3}{2}{\it\rho}_{S}\partial _{{\it\rho}}{\it\varphi}+\frac{1}{2}\left((\partial _{{\it\rho}}{\it\varphi})^{2}+\frac{1}{{\it\rho}_{S}^{2}}(\partial _{{\it\theta}}{\it\varphi})^{2}\right)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{3}{2}{\it\rho}_{S}+\frac{{\it\rho}_{S}^{\prime }}{{\it\rho}_{S}^{2}}\partial _{{\it\theta}}{\it\varphi}-\partial _{{\it\rho}}{\it\varphi}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}\sim -{\it\rho}^{2/3}\sin \left({\textstyle \frac{2}{3}}{\it\theta}\right)\end{eqnarray}$$
for
${\it\rho}\rightarrow \infty$
, which follows from the matching condition (3.12). Correspondingly, the free surface should match with
${\it\rho}_{S}({\it\theta})(-\!\sin {\it\theta})^{3/4}\sim 3^{-3/4}$
as
${\it\theta}\rightarrow 0^{-}$
and
${\it\rho}_{S}({\it\theta})(\cos {\it\theta})^{3/4}\sim 3^{-3/4}$
as
${\it\theta}\rightarrow -({\rm\pi}/2)^{+}$
. We remark again that, although gravity is not explicitly present in the self-similar boundary conditions at the free surface (3.13)–(3.14), its contribution enters into the problem through the far-field condition (3.15), which comes from solving the gravity-driven flow described by (3.8)–(3.10).
4. Numerical method
In order to treat the problem
${\rm\nabla}^{2}{\it\varphi}=0$
with the boundary and far-field conditions (3.13)–(3.15) numerically, it is convenient to work with the original non-self-similar coordinates (
$y$
,
$z$
) or (
$r$
,
${\it\theta}$
) and potential
${\it\phi}(r,{\it\theta},t)=t^{2}{\it\varphi}(r/t^{3/2},{\it\theta})$
, so that a time-marching method can be used. The numerical procedure is as follows. Laplace’s equation is solved in a closed fluid domain bounded by the free surface,
$S_{FS}(t)$
, and a circle arc, the far-field boundary
$S_{FF}$
, centred at the origin with a radius
$R_{max}$
which, in the present problem, was chosen to be
$R_{max}=1000$
. At this boundary, both the potential,
${\it\phi}$
, and its normal derivative,
$\partial _{r}{\it\phi}$
, are evaluated using the far-field asymptotic expression
${\it\phi}=-tr^{2/3}\sin (2{\it\theta}/3)$
(second term of (3.11) with
$J=1$
). At the beginning of each time step, the potential at the free surface is known, so that the normal velocity at this surface,
$\partial _{n}{\it\phi}$
, can be calculated by using a boundary element method adapted from the open library BEMLIB (Pozrikidis Reference Pozrikidis2002). Once the normal velocity is known, it is used to evolve the free surface, whereas the dynamic boundary condition, simplified by neglecting the hydrostatic term,
$\partial _{t}{\it\phi}+1|\boldsymbol{{\rm\nabla}}{\it\phi}|^{2}/2=0$
, is used to evolve the free-surface potential. After each time step, the free surface is remeshed to prevent numerical instabilities by ensuring a minimum panel size, and to guarantee that more nodes are concentrated near the region where the wave forms. At the middle plane of the wave,
${\it\theta}=-{\rm\pi}/4$
, the minimum panel size
${\rm\Delta}s_{min}=0.01$
was used, with panel lengths increasing successively by 1 % as they were placed farther away from the central region. Finally, to perform the time marching, the third-order Runge–Kutta scheme proposed by A. Wray (Spalart, Moser & Rogers Reference Spalart, Moser and Rogers1991) was employed. The time step was adapted to ensure a minimum Courant–Friedrichs–Lewy condition of 0.25.
5. Results and discussion
A very remarkable result is that, before the numerical computation has fully converged everywhere to a final self-similar state, the jet adopts a mushroom shape with two lateral thin jets, hereafter denoted as jetlets, that overturn onto the free surface near the base of the main jet, as can be seen in the yellow curve (lighter curve in print) of figure 3(a). A key consequence of this is that, although the self-similar problem can be formulated mathematically, its solution is unphysical as it predicts the self-intersection of the free surface.
Figure 3. (a) Rescaled free surface near the corner at the time steps corresponding to the symbols in figure 4(a) (black curves). The yellow (online)/lighter (in print) curve denotes the last time step of the simulation before the lateral jets impact onto the free surface. In this figure,
$({\it\xi},{\it\eta})=(y,z)/t^{3/2}$
are rescaled Cartesian coordinates. (b) Snapshots of the jet at different time steps (with
${\rm\Delta}t\approx 0.03$
between them), with the uppermost one corresponding to the yellow/lighter curve in (a). Notice that the tips of the jetlets always move forward in a fixed reference frame, but backwards with respect to the base of the jet, which causes the overturning.
Nonetheless, outside the region where the jetlets overturn, the free surface converges to a self-similar profile when rescaled by the factor
$t^{3/2}$
. In figure 3(a), it can be observed how the branches
${\it\xi}\gtrsim 0.8$
and
${\it\eta}\gtrsim 0.8$
neatly collapse onto a single curve for all the time steps shown. In fact, although only the last time steps of the simulation are plotted for the sake of clarity, this convergence is achieved after a few simulation steps. On the other hand, although more slowly, the radial location of the tip of the main jet,
$r_{tip}=r_{S}({\it\theta}=-{\rm\pi}/4)$
, eventually tends to the law
$r_{tip}\sim A_{r}t^{3/2}$
, as can be observed in figure 4(a). This figure also shows how the potential at that location follows the self-similar scaling
${\it\phi}_{tip}\sim A_{p}t^{2}$
. The solid lines in the figure represent the asymptotic values for both rescaled magnitudes computed using the self-similar boundary conditions (3.13) and (3.14). The values of
$A_{r}$
and
$A_{p}$
are obtained as part of the numerical solution. However, it is possible to find a relation between these two coefficients by using only the aforementioned boundary conditions at the tip of the jet. It should be noted that the form of the jet and the flow are symmetric with respect to the centreline (
${\it\theta}=-{\rm\pi}/4$
). Thus, at the jet tip,
$\partial _{{\it\theta}}{\it\varphi}=0,{\it\rho}_{S}=A_{r}$
and
${\it\varphi}=A_{p}$
, which turns the system (3.13)–(3.14) into
$$\begin{eqnarray}\displaystyle & 2A_{p}-{\textstyle \frac{3}{2}}A_{r}D+{\textstyle \frac{1}{2}}D^{2}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\textstyle \frac{3}{2}}A_{r}-D=0, & \displaystyle\end{eqnarray}$$
$D=\partial _{{\it\rho}}{\it\varphi}$
at the jet tip. The system (5.2) provides the relationship between
$A_{p}$
and
$A_{r}$
, 
$$\begin{eqnarray}A_{p}={\textstyle \frac{9}{16}}A_{r}^{2}.\end{eqnarray}$$
The numerical solution of the problem returns
$A_{r}\simeq 1.115$
and
$A_{p}\simeq 0.697$
. Then, using (5.3),
$$\begin{eqnarray}\frac{16A_{p}}{9A_{r}^{2}}=0.9977.\end{eqnarray}$$
Theoretically, the right-hand side of (5.4) should be 1. It is seen that the numerical results are rather accurate in predicting the motion of the jet.
Figure 4. (a) Time-marching numerical evolution of the rescaled radial coordinate of the free surface,
$r_{tip}/t^{3/2}$
(black circles), and the rescaled potential,
${\it\phi}_{tip}/t^{2}$
(red squares), at the tip of the jet (
${\it\theta}=-{\rm\pi}/4$
). The solid lines correspond to the asymptotic values of these magnitudes computed using (3.14) (black) and (3.13) (yellow (online)/lighter (in print)) respectively. (b) Far-field behaviour of the numerical solution (yellow (online)/lighter (in print)) compared with the asymptotic solution of the self-similar problem (black dashed line),
${\it\eta}=(1/3){\it\xi}^{-1/3}$
. The yellow/lighter curve corresponds to the last time step of the simulation, shown also in red in figure 3(a). (c) Normal derivative of the modified velocity potential,
$S$
, at the free surface as a function of the arc-length parameter,
$s$
. The self-similar condition
$\partial _{n}S=0$
is fulfilled fairly well, except in the region dominated by the jetlet, corresponding to the range between
$s\approx 1$
and
$s\approx 5$
.
The good agreement between the numerical results and the predictions of these equations ensures the convergence of the solution close to the tip of the jet, where these boundary conditions are fulfilled with a relative error smaller than
$4\times 10^{-3}$
. As a further proof of the convergence of the solution, at least outside the region of the jetlets, it is illustrative to examine the evolution of the normal derivative of a modified velocity potential,
$S$
, defined as
$$\begin{eqnarray}S={\it\varphi}-{\textstyle \frac{3}{4}}{\it\rho}^{2},\end{eqnarray}$$
similar to the modified potential used, for instance, by Iafrati & Korobkin (Reference Iafrati and Korobkin2004). Indeed, introducing the definition (5.5) into the kinematic boundary condition (3.14), and relating the derivatives with respect to the coordinates
${\it\rho}$
and
${\it\theta}$
,
$\partial _{{\it\rho}}S$
and
$\partial _{{\it\theta}}S$
, to the derivatives along the directions normal and tangential to the free surface,
$\partial _{n}S$
and
$\partial _{s}S$
respectively, the kinematic boundary condition yields
$\partial _{n}S=0$
. Figure 4(c) shows the evolution of
$\partial _{n}S$
along the free surface as a function of the arc-length parameter,
$s$
. Notice that, except in the region dominated by the jetlet, corresponding to the range between
$s\approx 1$
and
$s\approx 5$
in figure 4(c), the normal derivative of the modified potential has nearly converged to
$\partial _{n}S=0$
. This means that the shape of the free surface is already the self-similar one outside that range. This includes not only the free surface outside the wave but also its leading edge.
Furthermore, to prove that the free surface converges to the self-similar solution in the far field, where an asymptotic expression can be obtained, figure 4(b) compares the last time step of the numerical simulation (yellow/lighter curve) with the far-field asymptotic solution (black dashed line). In the limit
$y\gg 1$
, where
$y\approx r$
, the free surface,
$z_{S}(y)$
, evolves as
$$\begin{eqnarray}\frac{\text{d}z_{S}}{\text{d}t}\approx -\frac{1}{r}\left.\frac{\partial {\it\phi}}{\partial {\it\theta}}\right|_{{\it\theta}=0}\approx \frac{2}{3}ty^{-1/3},\quad \text{thus}~z_{S}\approx \frac{1}{3}t^{2}y^{-1/3}~\text{and}~{\it\eta}_{S}\approx \frac{1}{3}{\it\xi}^{-1/3},\end{eqnarray}$$
with
$({\it\xi},{\it\eta})=(y,z)/t^{3/2}$
. Notice that use has been made of (3.11) to evaluate the derivative of the potential. It can be observed that the numerical and asymptotic solutions agree fairly well for
${\it\xi}\gtrsim 10$
. It should be pointed out that this comparison serves also to validate that the far-field boundary of the numerical domain,
$r=R_{max}$
, was sufficiently far away for the simulation to smoothly converge to the far-field solution. Indeed, the numerical free surface exhibits the asymptotic behaviour for more than a decade in the rescaled variables. It is worth pointing out that the numerical scheme proposed in § 4 to obtain the self-similar structure can also be applied to solve the full flow configuration. In the Appendix, the full unsteady two-dimensional problem described by the system (2.18)–(2.20) plus the impermeability condition at the bottom,
$\partial _{z}{\it\phi}|_{z=-H}=0$
, is solved, showing good agreement with the self-similar scaling (see figure 6). Interestingly, the solution of the full problem departs from this scaling when the size of the wave becomes of order unity, as the third term on the right-hand side of (3.11) becomes important.
The formation of the jetlets can be attributed to the local acceleration of the free surface near the corner. Indeed, the location of the tip of the main jet moves with a monotonically increasing velocity that grows as
$t^{1/2}$
, as predicted by the self-similar analysis. Thus, for a non-inertial observer moving with the jet’s tip, there exists an apparent gravity, i.e. an inertial force, pushing the jet back towards the origin. This purely kinematic mechanism is the same as that by which a liquid jet directed vertically upwards in the presence of gravity opens up radially and overspills after reaching its maximum height. Conversely, from the point of view of an inertial observer, the jetlets are formed by the increasing speed of the fluid velocity at the base of the main jet, which makes the head of the jet open up into the lateral structures. Once these jetlets are sent away from the main structure, their tips keep a constant velocity, thus the free surface eventually catches up with them. This process is illustrated in figure 3(b), where the free surface has been plotted in the original variables (
$y$
,
$z$
) for several time instants before the impact. Notice that the tips of the lateral jets always move forward, but more slowly than the main free surface, which causes the apparent overturn and thus the formation of a closed air cavity.
A similar overturning of the free surface in a self-preserving flow has recently been described by Semenov, Wu & Olivier (Reference Semenov, Wu and Olivier2013) in the head-on collision of two liquid wedges. These authors point out that, since the length scale of the flow, and thus the size of the entrapped air cavity, grows in time, the pressure inside the cavity must decrease, leading to the appearance of an inward pressure gradient that would eventually distort the splash jet. Similar jets, known as re-entrant jets, are also observed in the flow behind a fully submerged plate when a cavity forms downstream. Although these jets can be observed experimentally, they are unstable and appear intermittently (Bifkhoff & Zarantonello Reference Bifkhoff and Zarantonello1957). Such complex flow configurations cannot be described within the framework of the planar potential flow used here.
Nevertheless, in experiments, the jetlets would not form immediately, due to capillary effects. To explain this, let us define a local Bond number,
$\mathit{Bo}_{\ell }={\it\sigma}/{\it\rho}g\ell ^{2}$
, with
${\it\sigma}$
the surface tension,
${\it\rho}$
the liquid density and
$\ell /{\rm\Delta}h\sim t^{3/2}$
the length scale of the corner wave. It is clear that, at short times,
$\mathit{Bo}_{\ell }\sim \mathit{Bo}_{{\rm\Delta}h}t^{-3}$
, and hence the flow is due to surface tension which would preclude the formation of the jetlets. In summary, the self-similar formulation developed in this paper is only valid for
$\mathit{Bo}_{{\rm\Delta}h}^{1/3}\ll t\ll 1$
, with
$\mathit{Bo}_{{\rm\Delta}h}={\it\sigma}/{\it\rho}g{\rm\Delta}h^{2}$
. Interestingly, this could explain why in the experiments of Stansby et al. (Reference Stansby, Chegini and Barnes1998), the mushroom-shaped jet is only observed after some time. In a problem similar to the three-dimensional one considered in this paper, namely the flow downstream from a partially submerged plate, Martínez-Legazpi (Reference Martínez-Legazpi2011) did not observe the jetlets in his experiments, where the Bond number was of the order of
$\mathit{Bo}_{{\rm\Delta}h}\sim 10^{-4}$
. However, two divergent waves were observed which remained attached to the corner of the plate, as can be seen in figure 5: a strong wave, A, and a weak one, B. It is reasonable to attribute the formation of the divergent wave B to the upper jetlet of the corner wave, whose development into a separated jet would be hindered by gravity.
Figure 5. Top view of the flow downstream from a partially submerged plate, an experimental approximation to the studied problem. Two surface waves, A and B, remain attached to the corner of the plate (Martínez-Legazpi Reference Martínez-Legazpi2011).
Another effect that limits the applicability of the two-dimensions-plus-time approach very close to the body is the possible existence of a developed boundary layer of thickness
${\it\delta}\ll 1$
at the stern. Thus, the theory derived here is only applicable when the size of the corner wave is much larger than this initial thickness. This yields the condition
$t\gg {\it\delta}^{2/3}$
. Finally, in actual experiments, the exact location where the free streamline detaches from the body would be determined by its detailed geometry through the Villat–Brillouin condition (see Wu Reference Wu1972), whereas in the present study the detachment is assumed to occur at an infinitely sharp trailing edge.
To conclude this section, it is worth mentioning that the corner wave flow is connected to the flow set in motion by an accelerated plate inclined at an angle
${\it\alpha}=45^{\circ }$
with respect to the undisturbed free surface. Needham, Chamberlain & Billingham (Reference Needham, Chamberlain and Billingham2008) studied the self-similar structure of this flow near the contact point between the plate and the free surface for different values of the angle,
${\it\alpha}$
. Remarkably, although the formulation of the inner problem is identical to that described here, these authors found no numerical solution for values of
${\it\alpha}>{\it\alpha}_{c}=12.6^{\circ }$
. The self-intersection of the free surface found in the present work could be the reason why their numerical method did not converge for values of
${\it\alpha}$
larger than a critical value
${\it\alpha}_{c}<45^{\circ }$
.
Figure 6. (a) Free surface of the full problem computed numerically at a time when the corner jet has already developed. The inset shows a zoom of the jet region. (b) Logarithmic plot showing the evolution of the radius of the tip,
$r_{tip}$
(black circles), and the potential at that location,
${\it\phi}_{tip}$
(red squares). The black and red solid lines have slopes
$3/2$
and 2 respectively.
6. Conclusions
The flow near the lower corner of a partially submerged bluff body has been studied with the focus on the formation of the jet-like waves that develop there. This flow is a simplified model for other configurations commonly found in naval hydrodynamics and civil engineering. When the Froude number defined with the velocity of the body,
$U$
, and the deadrise height,
${\rm\Delta}h$
, is large, the flow is slender and can be described with the so-called two-dimensions-plus-time approximation. This approximation allows the transformation of a steady three-dimensional problem into an unsteady two-dimensional one, which is more amenable to being treated using both analytical and numerical techniques. In particular, the region near the corner of the three-dimensional problem converts into the limit at short times of the corresponding two-dimensional one. Interestingly, on applying this transformation the flow becomes analogous to the dam-break problem with a wet basin.
Using matched asymptotic expansions, the structure of the flow near the corner has been described at short times. The leading-order solution admits a self-similar formulation in which the free surface evolves as
$r_{S}\sim t^{3/2}$
. This solution is dominated by the hydrostatic pressure produced by the water column of height
${\rm\Delta}h$
, which can be considered as uniform at the length scale of the self-similar region. Since at short times this height is much larger than the size of the self-similar region itself, hydrostatic pressure variations within this region are negligible compared with the hydrostatic pressure due to the water column of height
${\rm\Delta}h$
. However, for times of order unity, the amplitude of the wave also becomes of order unity and the hydrostatic term in the Euler–Bernoulli equation becomes important, thus the free surface is no longer symmetric with respect to the line bisecting the corner. Instead, it follows a ballistic trajectory as described by several authors (for instance Shakeri et al. (Reference Shakeri, Maxeiner, Fu and Duncan2009a
,Reference Shakeri, Tavakolinejad and Duncan
b
) for a planar unsteady flow and Martínez-Legazpi et al. (Reference Martínez-Legazpi, Rodríguez-Rodríguez, Marugán-Cruz and Lasheras2013) for a fully three-dimensional flow).
Interestingly, numerical computations show that the self-similar solution exhibits a mushroom-shaped jet which gives birth to two thin lateral jets which eventually overturn onto the free surface, leading to a self-intersecting and thus unphysical solution. A similar structure was reported by Stansby et al. (Reference Stansby, Chegini and Barnes1998), although in their experiments surface tension precluded the formation of these jetlets. A kinematic effect, namely the continuous acceleration of the free surface that pushes the main jet, is responsible for this mushroom-like structure and for the formation of the lateral jets.
Acknowledgements
The authors wish to gratefully acknowledge the support and valuable comments made by Professors J. M. Gordillo, A. Sevilla and C. Martínez-Bazán during the development of this work. This research has been supported by the Spanish Secretaría de Estado de Investigación Desarrollo e Innovación and European Funds under project no. DPI2011-28356-C03-02 and by the Office of Naval Research of the USA through grant N00014-05-1-0121.
Appendix. Numerical solution of the full unsteady two-dimensional problem
We conclude with a discussion about the observability of the self-similar structure studied in § 3 in a real flow configuration. As an example, we have simulated numerically the full unsteady two-dimensional problem described by the system (2.18)–(2.20) plus the impermeability condition at the bottom,
$\partial _{z}{\it\phi}|_{z=-H}=0$
.
The numerical method coincides with that described in § 4, except for two differences. First, the computational domain is bounded laterally by two impermeable walls placed at
$y=\pm 3$
, and second, the corner of the initial condition has been rounded with an initial curvature radius
${\it\delta}=1.5\times 10^{-3}$
. Notice that, from the physical point of view, the effect of this corner is to delay the time one has to wait until the self-similar scaling is observed, as it introduces a characteristic length,
${\it\delta}$
, into the problem. In fact, examination of figure 6(b) reveals that, although the tip’s radius grows approximately as
$r_{tip}\sim t^{3/2}$
for a relatively long time span, the potential takes longer to converge to the asymptotic regime
${\it\phi}_{tip}\sim t^{2}$
. More importantly, at
$t\approx 0.3$
the numerical results depart from the predictions of the asymptotic solution. This is a consequence of the effect of the hydrostatic term neglected in the dynamic boundary condition (third term on the left-hand side of (3.3)), which becomes progressively more important as the size of the corner wave becomes of order unity.
Despite these effects, the message that we want to convey in this paper is that the analysis performed in §§ 2–4 is able to describe approximately the structure of the flow at short times, when the corner wave is formed. Indeed, a mushroom-shaped jet can be observed in figure 6(a), corresponding to the last time step shown in figure 6(b). It is interesting to notice how the jet is no longer symmetric, due to the effect of the hydrostatic term mentioned above.
