3.1. Problem description

3.1.1. Initial equilibrium state without flow

In the absence of fluid flow, a differential equation describing the buckled sheet can be written in terms of the local balance of moments:

(3.1)\begin{equation} B\frac{{\textrm{d}}^{2}\theta(s)}{{\textrm{d}}s^{2}}+P_0\sin\theta(s)=0,\end{equation}

where $s$ is the curvilinear coordinate, $\theta$ is the angle between the sheet and the $x$-axis (inset of figure 1) and $P_0$ is the compressive reaction force per unit height applied at the front end ($s = 0$) of the sheet in the positive $x$-direction. Note that $P_0$ is also applied at the rear end ($s = L$) of the sheet in the negative $x$-direction.

Because the sheet is clamped at both edges, Dirichlet boundary conditions are applied at both edges: $\theta (s=0) = \theta (s=L) = 0$. Moreover, for the fundamental buckling mode with the fore–aft symmetric shape and the two clamped ends on the same $y = 0$ line, the $y$-directional reaction force $F_y$ at both ends is zero. If a deviation in the $y$-direction exists between the positions of the two clamped ends or an asymmetric buckling mode of a higher order is considered as an initial shape, an additional term with a non-zero $F_y$ at the front end should be involved in (3.1). Because a length ratio in the range $L^{*} = 0.5$–$0.9$ can cause large deflection, the nonlinear equation from the elastica theory is adopted instead of the linear equation (Timoshenko & Gere Reference Timoshenko and Gere2009). For a flapping flag model in which one edge is free to move, the relative importance of compressive force (tensile force) depends on the model conditions and flow regime (Shelley, Vandenberghe & Zhang Reference Shelley, Vandenberghe and Zhang2005), and the compressive force is generally neglected. However, for the buckled sheet model, the compressive force should be balanced by the bending force, even in the absence of fluid flow, to achieve the post-buckling configuration imposed by end-shortening ($L_0<L$).

The buckled sheet without fluid flow is in four-fold symmetry, provided that both ends are on the same $y$-coordinate. The total shape of the sheet is composed of four identical pieces, and the total shape can be constructed by rotating and reflecting the pieces (Timoshenko & Gere Reference Timoshenko and Gere2009; Wagner & Vella Reference Wagner and Vella2013). Thus, we consider only a quarter of the sheet from $s=0$ to $s=L/4$ to solve (3.1). To obtain the shape of the sheet piece, the compressive force $P_0$ at $s = 0$ and the angle at the inflection point, $s = L/4$, with zero curvature value (${\textrm {d}} \theta /{\textrm {d}}s = 0$) are first calculated for given $L$ and $L_0$ (and thus $L^{*}$), using elliptical integrals in (3.2a,b) (Timoshenko & Gere Reference Timoshenko and Gere2009):

(3.2a,b)\begin{equation} \frac{1}{4}L_0=2\left(\frac{EI}{P_0}\right)^{{1}/{2}} \textrm{E}\left[\sin\frac{\theta_0}{2}\right]-\frac{1}{4}L \quad\textrm{and}\quad \frac{1}{4}L=4\left(\frac{EI}{P_0}\right)^{{1}/{2}} \textrm{K}\left[\sin\frac{\theta_0}{2}\right], \end{equation}

where $\textrm {K}[~]$ and $\textrm {E}[~]$ are the complete elliptical integrals of the first and second kinds, respectively. The shape of the sheet piece is then obtained numerically by solving (3.1) with the $P_0$ value and boundary conditions, ${\textrm {d}} \theta /{\textrm {d}}s = 0$ and $\theta = \theta _0$ at the inflection point ($s = L/4$). Additionally, for given $L$ and $L_0$, the maximum transverse displacement $w_0$ of the total sheet, which appears at $s = L/2$, can be calculated from

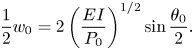(3.3)\begin{equation} \frac{1}{2}w_0=2\left(\frac{EI}{P_0}\right)^{{1}/{2}}\sin\frac{\theta_0}{2}. \end{equation}

The deformed shapes with no fluid flow, which are predicted by the nonlinear equation (3.1) and the linear Euler–Bernoulli equation, are compared in appendix A.

3.1.2. Equilibrium state with flow

On the other hand, with fluid flow, the fluid force $F_f$ normal to the surface of the sheet is exerted on the buckled sheet as a distributed load, and the reaction force $F_y$ in the $y$-direction is additionally imposed at the front end ($s = 0$) of the sheet (figure 2a); $F_y$ is zero without the fluid force. The fluid force on the sheet with a finite aspect ratio can be modelled with the combination of resistive force and reactive force (Lighthill Reference Lighthill1960; Buchak et al. Reference Buchak, Eloy and Reis2010; Michelin & Doaré Reference Michelin and Doaré2013; Tavallaeinejad et al. Reference Tavallaeinejad, Païdoussis and Legrand2018). The resistive force is expressed as the normal force experienced by a flat plate under fluid flow, and the reactive force is caused by an acceleration of the fluid flow that follows the shape of the sheet. Because the deformed sheet maintains an equilibrium state at each free-stream velocity before the sheet begins to snap at a critical velocity, the quasi-steady fluid force is assumed. Moreover, for a slender sheet at the equilibrium state, the magnitude of the reactive force, which scales with the square of sheet height, is much smaller than that of the resistive force, which scales with the sheet height. In this study, we use slender sheets with small aspect ratios in $H^{*} = [0.07\text {--}0.18]$ and thus consider only the resistive fluid force for simplicity. To establish an equilibrium equation in terms of moment balance at a given coordinate $s$, we first divide the quasi-steady resistive fluid force $F_f$ into two components, $F_{f,x}$ and $F_{f,y}$. Then, the fluid force components per infinitesimal segment ${\textrm {d}}s$ and per unit height are modelled as

(3.4a,b)\begin{equation} {\textrm{d}}F_{f,x} = \tfrac{1}{2}\rho_f U^{2} C_D(s)\, {\textrm{d}}s \quad\textrm{and}\quad {\textrm{d}}F_{f,y} = \tfrac{1}{2}\rho_f U^{2} C_L(s)\, {\textrm{d}}s. \end{equation}

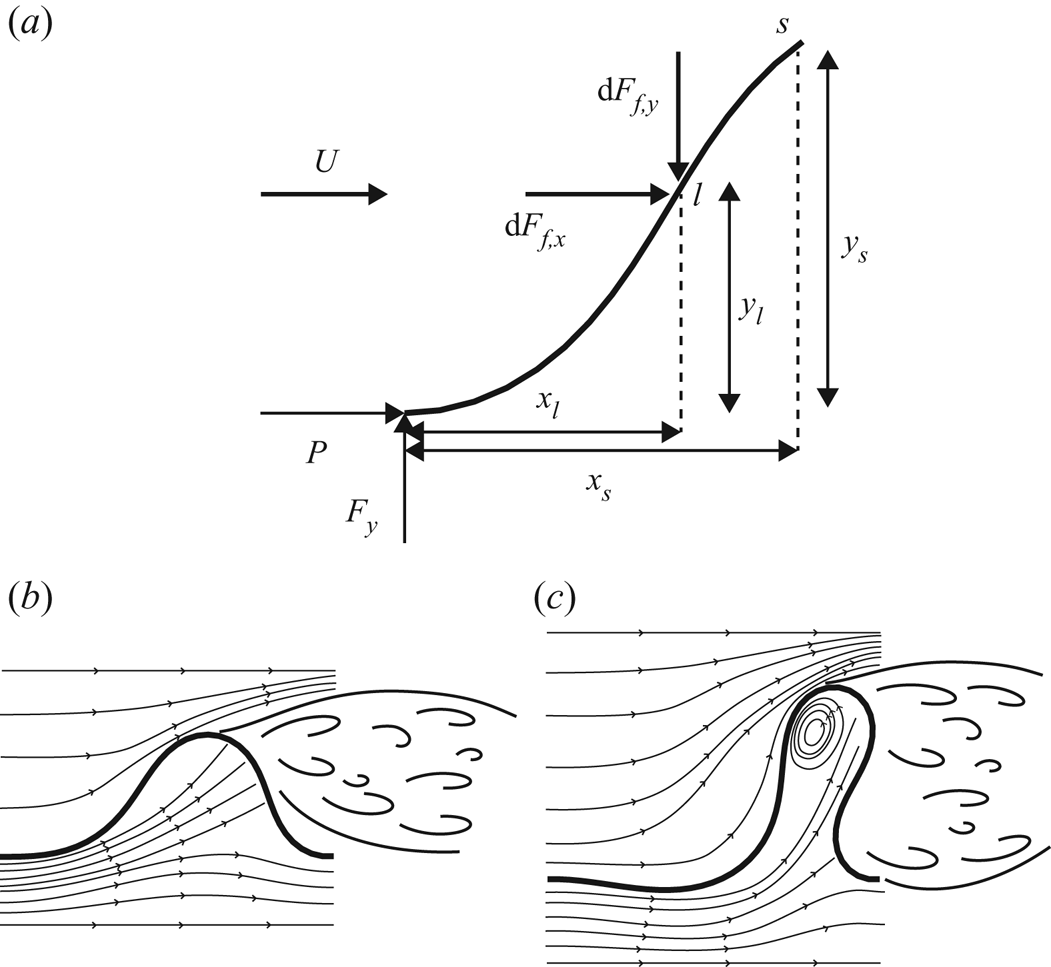
Figure 2. (a) Schematic diagram of the forces imposed on the sheet from the front end ($s = 0$) to a given coordinate $s$. (b,c) Illustration of streamlines around the sheet for (b) a large length ratio ($L^{*} = 0.75$) and (c) a small length ratio ($L^{*} = 0.50$).

For the quasi-steady fluid force model, Bollay (Reference Bollay1939) presented the normal force coefficient of a rectangular wing with a small aspect ratio, which was established by a nonlinear wing theory. Because the normal force coefficient in Bollay (Reference Bollay1939) did not have an explicit form, Polhamus (Reference Polhamus1966) proposed the explicit form of the normal force acting on an inclined rigid plate with an angle of attack of $\theta$, using leading-edge suction analogy. The normal coefficient $C_N$, drag coefficient $C_D\ (= C_N\sin \theta$) and lift coefficient $C_L\ (= C_N\cos \theta$) are expressed as follows:

(3.5a)\begin{gather} C_N(\theta) = K_p\sin\theta\cos\theta + K_v\sin^{2}\theta , \end{gather}

(3.5b)\begin{gather}C_D(\theta) = K_p\sin^{2}\theta\cos\theta + K_v\sin^{3}\theta , \end{gather}

(3.5c)\begin{gather}C_L(\theta) = K_p\sin\theta\cos^{2}\theta + K_v\sin^{2}\theta\cos\theta, \end{gather}

where $K_p$ and $K_v$ in (3.5) are associated with potential lift and vortex lift, respectively, and they are functions of the aspect ratio $H^{*}$ of the sheet only. Tavallaeinejad et al. (Reference Tavallaeinejad, Païdoussis and Legrand2018) obtained fitting curves for $K_p$ and $K_v$ in a wide range of $H^{*}$ based on the results of Bollay (Reference Bollay1939). In the present study, the fitting curves presented in Tavallaeinejad et al. (Reference Tavallaeinejad, Païdoussis and Legrand2018) are used to extract $K_p$ and $K_v$ values for a given $H^{*}$. The viscous shear stress exerted on the sheet roughly scales as $\mu U/\delta$, where $\mu$ is the dynamic viscosity of the fluid and $\delta$ is the representative boundary layer thickness. As the Reynolds number ${Re}\ (=UL/\nu )$ is $O(10^{4}$–$10^{5})$ in this study, the boundary layer is laminar, and accordingly $\delta \sim {Re}^{-{1}/{2}}L$. The relative magnitude of the tangential force per unit area (viscous shear stress), $\mu U/\delta$, over the normal resistive force per unit area, $\frac {1}{2}\rho _f U^{2} C_N$, scales as ${Re}^{-{1}/{2}}/C_N$. Because ${Re} = O(10^{4}$–$10^{5})$ and $C_N = O(10^{0})$, the force induced by the viscous stress can be neglected.

Using $F_{f,x}$, $F_{f,y}$ and the internal reaction forces ($P$ and $F_y$), the local balance of moments per unit length at $s$ is formulated as

(3.6)\begin{align} &B\frac{{\textrm{d}}^{2}\theta(s)}{{\textrm{d}}s^{2}}+\left[P+\frac{1}{2}\rho_fU^{2} \int_{0}^{s}{C_D(\theta(l))\, {\textrm{d}}l}\right]\sin\theta(s)\nonumber\\ &\quad -\left[F_y-\frac{1}{2}\rho_fU^{2}\int_{0}^{s}{C_L(\theta(l))\, {\textrm{d}}l}\right] \cos\theta(s)=0. \end{align}

Note that $F_{f,y}$ is positive along the negative $y$-direction (figure 2a). By combining the two integrals in (3.6), one obtains

(3.7)\begin{align} B\frac{{\textrm{d}}^{2}\theta(s)}{{\textrm{d}}s^{2}}+P\sin\theta(s)-F_y\cos\theta(s)+ \frac{1}{2}\rho_fU^{2}\int_{0}^{s}{C_N(\theta(l))\cos(\theta(l)-\theta(s))\, {\textrm{d}}l}=0. \end{align}

The left-hand side of (3.7) indicates the local balance of moments, which is caused by the bending shear force, internal forces and normal component of fluid force. For the prediction of the stability boundary where the transition appears, the inertial force term of the sheet can be omitted from the equation; this approach will be justified in § 4, where the effect of the mass ratio on the transition is discussed.

Equation (3.7) is only applicable for $0\leq s < s|_{y = y_{max}}$, because the free stream does not directly impose any force on the sheet for $s \geq s|_{y=y_{max}}$; $s|_{y=y_{max}}$ is the apex of the sheet (the point of maximum transverse displacement). As for the outer (positive $y$) side of the sheet, if the flow separation occurs at the apex of the sheet, the pressure on the outer side behind the apex can be roughly approximated to be constant because of the formation of the wake (figure 2b,c) (Alben et al. Reference Alben, Shelley and Zhang2002). For the sheet with a small aspect ratio $H^{*} = [0.07\text {--}0.18]$ considered in our study, the free stream is entrained into the area below the buckled sheet, and the entrained flow can exert a loading on the rear part of the sheet.

The pressure difference between the two surfaces of the rear part depends on the $L^{*}$ value, which determines the volume of space below the buckled part. For $L^{*}$ close to unity (small initial deflection), because of a small change in the direction for the entrained flow (figure 2b), the entrained flow can exert a great loading on the rear part of the sheet. The pressure difference between the two surfaces of the rear part is not negligible, and thus it should be considered to precisely predict the deformed shape. However, instead of the complicated modelling of the pressure difference for $L^{*}$ close to unity, we roughly assume that the effect of pressure difference in the rear part is relatively small and no net fluid-dynamic loading is applied on the rear part because the pressure difference in the front part is more critical to determine the overall shape of the sheet. In § 3.3, we will report that, despite this rough assumption, numerical simulation results for the deformed shape are in good agreement with experimental results for $L^{*}$ close to unity. On the other hand, for a small $L^{*}$ with large initial deflection, the entrained flow inside the buckled part veers greatly, as shown in figure 2(c), forming a circulating region, which eventually results in negligible pressure difference between the two surfaces on the rear part.

In summary, for all $L^{*}$ addressed in this study, we assume that no net fluid-dynamic loading is applied on the rear part, and the following two equations, (3.8a) and (3.8b), are used to predict the equilibrium shape of the sheet at each free-stream velocity before bifurcation and to find the critical velocity:

(3.8a)\begin{align} &B\frac{{\textrm{d}}^{2}\theta(s)}{{\textrm{d}}s^{2}}+P\sin\theta(s)-F_y\cos\theta(s)\nonumber\\ &\quad +\frac{1}{2}\rho_fU^{2}\int_{0}^{s}{C_N(\theta(l))\cos(\theta(l) -\theta(s))\, {\textrm{d}}l}=0, \quad s < s|_{y = y_{max}},\end{align}

(3.8b)\begin{align} &B\frac{{\textrm{d}}^{2}\theta(s)}{{\textrm{d}}s^{2}}+P\sin\theta(s)-F_y\cos\theta(s)\nonumber\\ &\quad +\frac{1}{2}\rho_fU^{2}\int_{0}^{s_{y_{max}}}{C_N(\theta(l))\cos(\theta(l) -\theta(s))\, {\textrm{d}}l}=0, \quad s \geq s|_{y = y_{max}}. \end{align}

The governing equations differ between the regions before and after the apex.

3.2. Numerical method

To solve nonlinear equations (3.8a) and (3.8b), numerical simulations are required. The solution of (3.1) corresponding to $U = 0$ is used as an initial guess for the given model. For the finite-difference method, the sheet is discretized into segments of constant length ${\rm \Delta} s = L/N$, where $N$ is the number of grids ($N = 61$). The discretized forms of (3.8a) and (3.8b) at each grid point $i$ are

(3.9a)\begin{align} &B\frac{\theta_{i+1}-2\theta_i+\theta_{i-1}}{({\rm \Delta} s)^{2}} +\left[P+\frac{1}{2}\rho_fU^{2}\int_{0}^{s_i}{C_D(\theta(l))\, {\textrm{d}}l}\right]\sin\theta_i \nonumber\\ &\quad -\left[F_y-\frac{1}{2}\rho_fU^{2}\int_{0}^{s_i}{C_L(\theta(l))\, {\textrm{d}}l}\right] \cos\theta_i=0, \quad i = 1,\ldots,m, \end{align}

(3.9b)\begin{align} &B\frac{\theta_{i+1}-2\theta_i+\theta_{i-1}}{({\rm \Delta} s)^{2}}+ \left[P+\frac{1}{2}\rho_fU^{2}\int_{0}^{s_m}{C_D(\theta(l))\, {\textrm{d}}l}\right]\sin\theta_i \nonumber\\ &\quad -\left[F_y-\frac{1}{2}\rho_fU^{2}\int_{0}^{s_m}{C_L(\theta(l))\, {\textrm{d}}l}\right] \cos\theta_i=0,\quad i = m+1,\ldots,N-1, \end{align}

where $\theta _i = \theta (i{\rm \Delta} s)$, ${\textrm {d}}^{2}\theta /{\textrm {d}}s^{2}$ is discretized using the standard second-order difference method and $m$ is the grid point immediately before $s|_{y=y_{max}}$. The integrals in (3.9a) and (3.9b) are evaluated with the extended trapezoidal rule. Starting from the initial solution for $U = 0$, the solution at each $U$ is obtained with intervals of ${\rm \Delta} U$ varying from 0.50 at low $U$ to 0.05 near $U = U_c$. The $\theta$ values of the previous step are used to compute $C_D$ and $C_L$ in the current step, and $s|_{y=y_{max}}$ from the previous step is used to determine which of (3.9a) and (3.9b) is used for each grid point. Because the sheet is clamped at both edges, boundary conditions are applied as

(3.10)\begin{equation} \theta_{{front} (i=1)} = \theta_{{rear} (i=N)}=0.\end{equation}

Equations (3.9a) and (3.9b) with (3.10) form a system of nonlinear equations that can be solved using Newton's method at each $U$. The $P$ and $F_y$ values are adjusted by the shooting method until the solution satisfies the following boundary conditions at the rear end: $x(L) = L_0$ and $y(L) = 0$. Iteration ceases when the total error at the rear end is $\epsilon = (\epsilon _x^{2} + \epsilon _y^{2})^{{1}/{2}} \leq L \times 10^{-4}$, where $\epsilon _x = |x_N - L_0|$ and $\epsilon _y = |y_N - 0|$. According to our numerical simulation, when $U$ reaches a certain velocity, there exists no solution that satisfies the error criterion at the rear end, which means that the equilibrium state is no longer possible. That velocity is defined as the critical flow velocity, beyond which an inertial effect of the sheet should be considered. The critical flow velocity and transition to limit-cycle oscillation are discussed in § 4. We also conducted two separate convergence tests with a smaller ${\rm \Delta} U$ and a larger $N$. For $L^{*} = 0.50$ and $0.86$, the differences in the shape deformation at each $U$ and the critical velocity were found to be negligible between the original result and the new result using the smaller ${\rm \Delta} U$ varying from $0.10$ at low $U$ to $0.025$ near $U = U_c$. Furthermore, the difference in the equilibrium shapes at each $U$ between the two cases using 61 and 201 grid points was negligible. For example, near $U = U_c$, the maximum difference in the $y$-coordinate between the two cases, $({\rm \Delta} y)_{max}/L_0$, was just $0.003$ at $L^{*} = 0.50$.

3.3. Shape of a sheet at equilibrium

For an equilibrium shape at each free-stream velocity and length ratio before bifurcation, the numerical solution of (3.9) and (3.10) is in excellent agreement with the experimental result, despite the simple modelling of the fluid force (figure 3a). Depending on the length ratio $L^{*}$, the sheets show different trends in deformation. For a large $L^{*}$ close to unity (smaller deflection), the apex of the sheet is mainly displaced in the streamwise direction as $U$ increases, and the transverse location of the apex remains similar (figure 3ai), which leads to an enhanced curvature at the rear part of the sheet. Until the free-stream velocity reaches the critical velocity, the streamwise shift of the apex is primarily observed, and the sheet does not cross the midline (straight line between the two clamped ends).

Figure 3. (a) Superimposed equilibrium shapes of the buckled sheet for several free-stream velocities before bifurcation: $[L^{*}, H^{*}, m^{*}] = [0.86, 0.14, 1.09]$ (i); $[0.75, 0.13, 0.95]$ (ii); $[0.60, 0.10, 0.76]$ (iii); and $[0.43, 0.07, 0.54]$ (iv). The black solid lines are obtained by our experimental measurements, and the red dotted lines are from our numerical simulations. (b,c) The $y$-coordinate ($y/w_0$) of the sheet at $x = L_0/2$ versus $U^{*}$ from (b) the numerical simulations and (c) the experimental measurements: $H^{*} = [0.08\text {--}0.14]$. In panels (b) and (c), the colour of the dot denotes the magnitude of $L^{*}\ (=0.50\text {--}0.86)$ as in the colour bar: the same colour for a given $L^{*}$. Each dot represents the case of a specific $U^{*}$ increasing from $U^{*} = 0$.

For a small $L^{*}$, the front part of the sheet undergoes significant streamwise movement as well as transverse movement as $U$ increases, and the front part can cross the midline when $U$ is close to the critical velocity (figure 3aii,aiii). For a smaller $L^{*}$, the buckled sheet continues to deform along the flow direction on one side (figure 3aiv). In this case, as the flow velocity increases, the part near the apex of the sheet bends backwards. Subsequently, two points of the sheet can contact each other to form a teardrop shape, and the snap-through does not appear, even for a higher $U$. This state cannot be obtained by the numerical simulations; in figure 3(aiv), the red dotted line corresponding to the numerical simulation is not provided for the most deformed shape.

The deformation of our snap-through model can be compared with that of another snap-through model under fluid flow studied by Gomez et al. (Reference Gomez, Moulton and Vella2017b). The deformations of both models are similar in that, for a smaller $L^{*}$, the displacement of the sheet becomes more notable with increasing flow velocity. However, the detailed deformed configurations vary slightly because a different type of fluid flow and different range of the length ratio were used in Gomez et al. (Reference Gomez, Moulton and Vella2017b). The range of the length ratio in Gomez et al. (Reference Gomez, Moulton and Vella2017b) is much closer to unity ($L^{*} > 0.96$) than that of our model, and thus, for each point on the sheet, the transverse displacement is dominant over the streamwise displacement. Because the model of Gomez et al. (Reference Gomez, Moulton and Vella2017b) is confined in a narrow flow channel with strong blockage effect at ${Re} = O(10^{-2})$, hydrodynamic pressure on the buckled sheet decreases monotonically along the streamwise direction, indicating that a large fluid loading is imposed on the front part of the sheet. Accordingly, the front part of the sheet can cross the midline even for $L^{*} > 0.96$; see supplementary figure 3 in Gomez et al. (Reference Gomez, Moulton and Vella2017b). On the other hand, because the initial deflection of our model is greater than that of Gomez et al. (Reference Gomez, Moulton and Vella2017b), both streamwise and transverse displacements are important in our model, in particular for a small $L^{*}$ (figure 3a). Moreover, for our model in unbounded flow, the fluid force (3.4a,b) is affected solely by the deflection angle $\theta$ at each point on the sheet, in contrast to the model confined in a narrow channel. For $L^{*}$ close to unity, because of a small deflection angle, the fluid force imposed on the front part of the sheet along the transverse direction is small, and the sheet does not cross the midline before snap-through instability occurs.

To quantitatively investigate the deformation of a sheet at the equilibrium state, we introduce a dimensionless free-stream velocity $U^{*}$ suitable for the snap-through model and use it instead of $U$ hereafter. The fluid inertial force exerted on the sheet per unit height scales simply as $F_f \sim \rho _f U^{2}w_0$, where $w_0$ indicates the maximum transverse displacement of the sheet in the absence of fluid flow: the frontal area of the sheet at $U = 0$ (figure 1). The bending force per unit height scales as $F_b \sim B/L^{2}$. Then, the dimensionless free-stream velocity, which represents the ratio of the fluid inertial force to the bending force, is defined as $U^{*} = U(\rho _fw_0L^{2}/B)^{{1}/{2}}$. As the definition of $U^{*}$ in this study includes $w_0$, it differs from the form generally used for flapping flag models, $U^{*}= U(\rho _f L^{3}/B)^{{1}/{2}}$ (e.g. Connell & Yue Reference Connell and Yue2007; Alben & Shelley Reference Alben and Shelley2008; Kim et al. Reference Kim, Cossé, Cerdeira and Gharib2013; Kim & Kim Reference Kim and Kim2019). For the flag models, the sheet length $L$ is the only length parameter to represent the geometrical feature of its two-dimensional profile. In contrast to the flag models, two length parameters, $L$ and $w_0$, are required together to represent the configuration of the buckled sheet. Thus, for the snap-through model, $U(\rho _fw_0L^{2}/B)^{{1}/{2}}$ is a more appropriate dimensionless velocity parameter to indicate the relative magnitude of the fluid inertial force and the bending force.

The deformation of the buckled sheet can be characterized by the transverse displacement $y/w_0$ of the sheet at $x = L_0/2$. The transverse displacements acquired from numerical simulations are plotted as a function of the dimensionless free-stream velocity $U^{*}$ in figure 3(b). The $y/w_0$ values tend to collapse onto a single curve, regardless of the $L^{*}$ values considered in this study. While the variation in $y/w_0$ is minor in the low-$U^{*}$ regime, $y/w_0$ drops sharply in the high-$U^{*}$ regime. However, for a small $L^{*}$, the deformation of the sheet becomes more significant near the critical velocity, and accordingly the $y_{x=L_0/2}/w_0$ values of the sheet near the critical velocity tend to deviate from the collapsed curve (rightmost dots in figure 3b). Experimental results for $y_{x=L_0/2}/w_0$ also show a similar trend to the results of the numerical simulations despite some deviations (figure 3c).

Generally, snap-through instability follows a saddle-node bifurcation where the stable equilibrium and unstable equilibrium are closer with increasing bifurcation parameter such as flow rate or inclined angle at the clamped ends, and the two equilibrium states encounter each other at a critical value in a vertical fold (Gomez et al. Reference Gomez, Moulton and Vella2017a,Reference Gomez, Moulton and Vellab). The snap-through instability of our model using $U^{*}$ as a bifurcation parameter seems to follow the saddle-node bifurcation, as can be inferred from figure 3(b,c). However, in figure 3(b,c), the $y_{x = L_0/2}/w_0$ values of all cases do not end at exactly vertical fold points. Even from our numerical simulation using a smaller step size of $U$ to examine the convergence of the results, the branches did not become more vertical at the critical velocity. The sheet could snap prematurely due to the presence of disturbance by the experimental set-up, and thus the vertical fold points may not be distinct, in contrast to the ideal saddle-node bifurcation diagram. In addition, our model may not exhibit a clear vertical fold due to the large deflection and streamwise shift of the sheet. More detailed theoretical examination on the bifurcation remains as a future study.

Moreover, the magnitudes of the two internal forces at the front end, the streamwise compressive force $P$ and the transverse supporting force $F_y$ depicted in figure 2(a), are strongly affected by the free-stream velocity $U^{*}$ (and consequently by the change in the deformed shape) for each $L^{*}$. Notably, $P$ and $F_y$ exhibit opposite trends in terms of $U^{*}$ (figure 4a,b). In figure 4(a,b), $P$ and $F_y$ are normalized by the compressive force $P_0$ in the absence of fluid flow; $P/P_0 = 1$ at $U^{*} = 0$ for all cases of $L^{*}$. See appendix A for a detailed explanation of $P_0$. Without fluid flow, the compressive force at the front end of the sheet is positive, which means that it acts along the positive $x$-axis to maintain the bucked shape. As $U^{*}$ increases, the compressive force tends to decrease to maintain the force balance with the external fluid force acting along the positive $x$-axis (figure 4a). In particular, for $L^{*} = 0.50$ and $0.55$, $P/P_0$ becomes negative for large values of $U^{*}$. This indicates that, for a sheet with large initial deflection at high $U^{*}$, the fluid-dynamic loading distributed on the sheet along the streamwise direction is so large that the reaction force on the front end of the sheet should be negative for force balance; i.e. a tension force along the negative $x$-axis should be applied at the clamped end to maintain the given $L^{*}$.

Figure 4. (a) Dimensionless streamwise compressive force $P/P_0$ and (b) transverse supporting force $F_y/P_0$ at the front end of the sheet for $L^{*} = 0.50$–$0.86$. The colour of the dot denotes the magnitude of $L^{*}$, as in the colour bar: the same colour for a given $L^{*}$. Each dot represents the case of a specific $U^{*}$ increasing from $U^{*} = 0$. The data in the two panels are from the numerical simulations with aspect ratio $H^{*} = [0.08\text {--}0.14]$. (c) Comparison of sheet deformations with increasing $U^{*}$ near $U_c^{*}$ between (i) $L^{*} = 0.86$ and (ii) $L^{*} = 0.50$.

Unlike $P/P_0$, the supporting force $F_y/P_0$ tends to increase monotonically with $U^{*}$, although its slope varies with $L^{*}$ (figure 4b). Notably, the sheet with a small $L^{*}$ exhibits a sudden jump of $F_y$ near the critical velocity, which is attributed to the change in a deformation trend. As $U^{*}$ increases, the sheet with a large $L^{*}$ ($L^{*} = 0.86$ in figure 4c) gradually deforms without any sudden change in the deformation trend even near the critical velocity. However, for a small $L^{*}$ ($L^{*} = 0.50$ in figure 4c), the transverse displacement becomes dominant with increasing free-stream velocity, and the front part of the sheet crosses the midline ($y = 0$ line) after a certain free-stream velocity even in the equilibrium state. This notable transverse displacement of the sheet at a high free-stream velocity close to the critical velocity leads to the sudden jump of $F_y/P_0$ in figure 4(b).

5.1. Kinematic characteristics of periodic snap-through

The clamping constraints at both ends of a buckled sheet yield some remarkable features in the post-equilibrium state of $U^{*} > U_c^{*}$. As the buckled sheet undergoes periodic snap-through oscillations, its kinematic response differs with location on the sheet (figure 7a,b). In figure 7(a,b), the central and rear parts of the sheet oscillate with a greater oscillation amplitude and a transverse velocity than the front part. Although the rear part has an amplitude comparable to that of the central part, the maximum transverse velocity of the rear part is approximately twice as large. Moreover, the amplitude and transverse velocity profiles are not smooth, but are rather abrupt with sharp peaks. Flow-induced snap-through in our study occurs through the asymmetric configuration between the front and rear parts of the sheet because of the flow direction. The fluid force imposed on the sheet displaces the sheet along the streamwise direction, and snapping occurs more distinctly in the rear part, as depicted in figure 5(a). Geometrically, the streamwise shift of the sheet by the fluid flow increases the curvature of the rear part before the sheet snaps to the opposite side, and a greater bending energy is stored and released in the rear part, which results in a sharp peak in the transverse velocity during the snapping motion.

Figure 7. (a) Dimensionless transverse displacement $y/w_0$ and (b) transverse velocity $v/U$ in the $y$-direction at three different streamwise locations: $x/L_0=0.2$ (blue), $x/L_0=0.5$ (red) and $x/L_0=0.8$ (yellow). Here $[L^{*}, H^{*}, m^{*}, U^{*}] = [0.75, 0.13, 0.95, 11.10]$ for panels (a) and (b). Time $t$ is non-dimensionalized by $U$ and $w_0$, thus: $t^{*}=tU/w_0$. (c) Dimensionless oscillation frequency $f^{*}\ (=f(2w_0)/U)$ for several cases of $L^{*}$. (d) Contours of vorticity $\omega _z w_0/U$ around the snapping sheet (black solid line) at two extreme phases. Vortex shedding, which is denoted by the dotted line, is observed behind the apex of the sheet. Here $[L^{*}, H^{*}, m^{*}, U^{*}] = [0.75, 0.13, 1.71\times 10^{-3}, 11.70]$ for panel (d).

To further understand the characteristics of periodic snap-through oscillations, the dimensionless oscillation frequency is examined. Generally, a peak-to-peak oscillation amplitude is widely used as a characteristic length for the dimensionless oscillation frequency in studies of oscillating thin structures such as the flapping propulsion of animals and flapping flags (e.g. Alexander Reference Alexander2003; Connell & Yue Reference Connell and Yue2007; Kim et al. Reference Kim, Cossé, Cerdeira and Gharib2013). The maximum oscillation amplitude of the buckled sheet is almost the same as the maximum transverse displacement $w_0$ of the sheet without fluid flow (figure 7a). Hence, $2w_0$, which represents the peak-to-peak amplitude, is adopted as a length parameter to define the dimensionless oscillation frequency: $f^{*} =f (2w_0)/U$. In a wide range of $U^{*} = 9.6$–$25.8$ and $L^{*} = 0.55$–$0.88$, $f^{*}$ is mostly distributed within a narrow range between $0.06$ and $0.12$ (figure 7c). As for the relation between the dimensional parameters, the dimensional oscillation frequency $f$ continuously increases with the dimensional velocity $U$ for a given $L^{*}$.

The oscillation frequency is correlated with the shedding frequency of the vortices generated by the oscillating sheet. According to flow visualization using particle image velocimetry in the water tunnel, flow separation and consequent vortex shedding occur periodically at the apex of the sheet when the sheet reaches two extreme phases having the maximum amplitude in the positive and negative $y$-directions (figure 7d). In contrast to a fixed bluff body (Williamson Reference Williamson1996), the periodic vortex shedding is not initiated and maintained by mutual interaction of counter-rotating vortices in the snap-through model. Instead, the vortex shedding is subjected to the periodic oscillation of the sheet, and the vortex shedding frequency becomes identical to the oscillation frequency of the sheet, which differs from the vortex shedding frequency of the fixed bluff body.

5.2. Modal analysis

To examine how the modal behaviour of the oscillating sheet is affected by its two clamped ends, proper orthogonal decomposition (POD) is conducted with the displacement data represented in curvilinear coordinates. The mean-subtracted dataset of the transverse displacement, $\hat {y} = y - \bar {y}$, is linearly decomposed in the following manner:

(5.1)\begin{equation} y(\boldsymbol{s},t)-\bar{y}(\boldsymbol{s}) = \sum_{j=1}^{m}a_j \phi_j(\boldsymbol{s},t), \end{equation}

where $y$ is the transverse displacement of the sheet, $\bar {y}$ is the time-averaged value of $y$, $m$ is the total number of modes considered for POD, $\phi _j$ is the orthogonal POD modal shape that corresponds to mode $j$, and $a_j(t)$ is the temporal displacement coefficient of mode $j$. The POD mode $\phi _j$ can be obtained from singular value decomposition (SVD) (Berkooz, Holmes & Lumley Reference Berkooz, Holmes and Lumley1993; Taira et al. Reference Taira, Brunton, Dawson, Rowley, Colonius, McKeon, Schmidt, Gordeyev, Theofilis and Ukeiley2017). In matrix form, the data of $\hat {y}$ expressed as ${\boldsymbol{\mathsf{Y}}}$ can be decomposed using SVD as

(5.2)\begin{equation} {\boldsymbol{\mathsf{Y}}}=\boldsymbol{\varPhi} \boldsymbol{\varSigma}\boldsymbol{\varPsi}^\textrm{T}, \end{equation}

where $\boldsymbol {\varPhi } = [\phi _1, \phi _2,\ldots ,\phi _m]$ and $\boldsymbol {\varSigma }$ takes singular values ($\sigma _1, \sigma _2,\ldots , \sigma _m$) along its diagonal. The singular value $\sigma _j^{2}$ indicates the energy level of mode $j$, and singular values are arranged from mode $1$ to mode $m$ in order of the amount of energy. The relative energy (energy fraction) captured by each mode can be computed as

(5.3)\begin{equation} \text{relative energy of mode }i= \frac{\sigma_i^{2}}{\sum_{j=1}^{m}\sigma_j^{2} } . \end{equation}

According to the POD results, for each $U^{*}$, the order of a modal shape corresponds to that of a harmonic mode with a clamped–clamped end condition (figure 8a–c). However, at each mode, the shape of the POD mode is displaced slightly in the streamwise direction from that of the harmonic mode due to fluid loading. While the first and second POD modes are dominant in terms of relative energy distribution, higher-order modes remain negligible in the entire $U^{*}$ range considered in this study (figure 8d). The relative energy level of the first mode at $U^{*} = 11.7$, $13.6$ and $16.6$ exceeds $0.4$, and that of the second mode is around $0.3$. The relative energy levels of higher-order modes are less than $0.1$. The dominance of the first and second modes in the snap-through oscillations seems to be different from the trend of a flapping flag with a fixed front end and a free rear end, which exhibits various vibrational modes depending on the dimensionless flow velocity and mass ratio (Tang & Païdoussis Reference Tang and Païdoussis2007; Eloy et al. Reference Eloy, Lagrange, Souilliez and Schouveiler2008; Michelin et al. Reference Michelin, Llewellyn Smith and Glover2008; Huang & Sung Reference Huang and Sung2010).

Figure 8. (a) First, (b) second and (c) third modal shapes at three flow velocities: $U^{*} = 11.7$ (dotted line), $13.6$ (dashed line) and $16.6$ (dash-dotted line). In panels (a)–(c), the harmonic mode with a clamped–clamped end condition is shown by the solid line for comparison. (d) Relative energy of POD modes for $U^{*} = 11.7$ (blue), $13.6$ (red) and $16.6$ (green). Here $[L^{*}, H^{*}, m^{*}] = [0.75, 0.13, 0.95]$.

5.3. Bending energy

Because of its initial buckled configuration and quick snapping process, the sheet exhibits salient features regarding the elastic strain energy stored during the periodic oscillations. The elastic strain energy consists of bending energy and compressive force energy along the sheet. Because the sheet is assumed to be inextensible, the compression energy arises from the imposed end-shortening condition ($L_0 < L$), and it is constant if $L^{*}$ is held fixed (Audoly & Pomeau Reference Audoly and Pomeau2010). Thus, only the bending energy of the sheet is considered in our examination of temporal variations in the strain energy. The bending energy per unit height is defined as $E_b(t)=\tfrac {1}{2}EI\int _0^{L} \kappa (s,t)^{2}\, {\textrm {d}}s$, where $\kappa \ (=({\textrm {d}}^{2}y/{\textrm {d}x}^{2})/[1+({\textrm {d}y}/{\textrm {d}x})^{2}]^{{3}/{2}})$ is the curvature. The curvature was calculated with the dataset of positions acquired from the captured images. The sheet was discretized into $240$–$250$ segments along its length, and the central-difference scheme was used to obtain ${\textrm {d}y}/{\textrm {d}x}$ and $\textrm {d}^{2}y/{\textrm {d} x}^{2}$ for each segment; because the segments had the same length $\textrm {d}s$, different values of ${\textrm {d}x}$ were considered for the segments when ${\textrm {d}y}/{\textrm {d}x}$ and $\textrm {d}^{2}y/{\textrm {d}x}^{2}$ were discretized.

In figure 9(a), at the instant just before rapid snapping to the opposite side, the dimensionless bending energy $E_b/E_{b,max}$ reaches its maximum value; $E_{b,max}$ is the maximum bending energy over 50 cycles in this study. Moreover, the phase just after the rapid snapping is complete corresponds to the minimum value of $E_b/E_{b,max}$. As shown by the light red and green regions, respectively, in figure 9(a), the time span required to release the bending energy generally becomes shorter than the time span required to store the bending energy, which results in a sawtooth waveform in the time history of the bending energy. The sharpness of the sawtooth waveform is found to be dependent on $L^{*}$. While the time history curve is sharp near the onset of snap-through for $L^{*} > 0.7$, the curve becomes blunt and exhibits plateaus for $L^{*} < 0.7$ (figure 11 in appendix B). Despite a change in the curve shape of the bending energy, rapid energy release during the snap-through process is consistently observed over a wide range of $L^{*}$.

Figure 9. (a) Dimensionless bending energy $E_b/E_{b,max}$ stored in the sheet during snap-through oscillations; $E_{b,max}$ is the maximum bending energy over 50 cycles. The red dashed line denotes the level of $E_b/E_{b,max}$ at $U^{*} = 0$. A curve fitted from the experimental data (black circles) is denoted as the blue solid line. The insets describe the shape of the sheet at the phase of maximum bending energy (left) and minimum bending energy (right) for $U^{*} = 11.1$ as well as the initial shape for $U^{*} = 0$ (centre). Here $[L^{*}, H^{*}, m^{*}] = [0.75, 0.13, 0.95]$. (b) Ratio of bending energy at each free-stream velocity to bending energy at $U^{*} =0$: $E_b/E_{b,0}$. Circles denote the value of $E_b/E_{b,0}$ before $U^{*} = U^{*}_c$, and squares and triangles denote the maximum and minimum $E_b/E_{b,0}$ over successive cycles after $U^{*} = U^{*}_c$, respectively. Here $[L^{*}, H^{*}, m^{*}] = [0.60\text {--}0.86, 0.10\text {--}0.14, 0.76\text {--}1.08]$.

As $U^{*}/U^{*}_c$ increases from zero up to unity in the equilibrium state ($U^{*}/U^{*}_c < 1$), the ratio of the bending energy at a given flow velocity to the bending energy at $U^{*} = 0$, $E_b/E_{b,0}$, gradually grows from $1.0$ to $1.6$ owing to enhanced deflection of the sheet along the flow direction. Regardless of the variations in $L^{*}$, the $E_b/E_{b,0}$ values are distributed narrowly at a given $U^{*}/U^{*}_c$ (figure 9b). In the post-equilibrium state ($U^{*}/U^{*}_c \geq 1$), the maximum and minimum values of $E_b/E_{b,0}$ over successive cycles form separate groups around $2.5$ and $1.0$, respectively. For a given $U^{*}/U^{*}_c$, the difference in the bending energy between the two extreme phases, ${\rm \Delta} E_b/E_{b,0}\ (=[E_{b,max} - E_{b,min}]/E_{b,0})$, increases slightly as $L^{*}$ increases, which implies that the energy release by the snapping is more effective as $L^{*}$ is closer to unity.

During the periodic oscillations, the instantaneous configurations of the sheet at the upper and lower energy limits remain similar to the second and first modal shapes, respectively (figure 9b), and this trend is universal for all $U^{*}$ values considered in this study; for example, see the insets of figure 9(a) and figure 11 in appendix B. The higher-order modes are not dominant at any phase of the oscillations. If the higher-order modal shape was dominant, the curvature of the sheet constrained by the clamped ends would be much greater than that of the second modal shape, resulting in a dramatic growth in the bending energy. Accordingly, although both maximum and minimum values of the bending energy tend to increase slightly with $U^{*}$ in limit-cycle oscillation, each of them is confined within a narrow range without a notable jump in energy level: the maximum $E_b/E_{b,0}$ ranges from $2.3$ to $3.0$ and the minimum $E_b/E_{b,0}$ ranges from $0.8$ to $1.2$.

The aforementioned characteristics of the bending energy are in stark contrast to those of the flag models, which experience smooth temporal variations in bending energy during periodic oscillations. Owing to the buckled configuration, the ratio of minimum bending energy to maximum bending energy remains at least $40\,\%$ in the snap-through model (figure 9a). Meanwhile, it is almost zero in the flag model (Gurugubelli & Jaiman Reference Gurugubelli and Jaiman2015) because the flapping flag becomes almost straight at some point. Furthermore, unlike the flag model, which exhibits similar time spans for energy storage and release, the snap-through model displays a shorter time span for energy release than for energy storage.