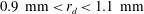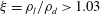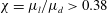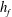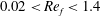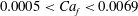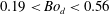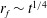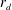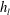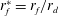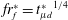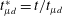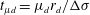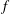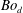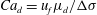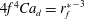1 Introduction
A lighter, miscible drop of lower surface tension on the surface of a deep horizontal fluid layer of higher surface tension shows a fascinating interplay of surface-tension-driven film spreading, instability of the spreading film, followed by its retraction and the eventual dissolution of the drop. In addition to the unclear physical processes behind these phenomena, these are also important in many applications like drug delivery (Grotberg Reference Grotberg1994), coating processes (La Due, Muller & Swangler Reference La Due, Muller and Swangler1996), ink-jet printing (Le Reference Le1998) and the removal of oil spills (Fay Reference Fay1969). The present study presents the various phenomena that occur in such a case and then proposes a scaling theory for the spreading of a film from a buoyant, miscible drop of lower surface tension but higher viscosity on a deep layer of higher-surface-tension liquid of lower viscosity. The observed scaling and its proposed explanation are different from the previous studies with very viscous drops (Bacri, Debregeas & Brochard-Wyart Reference Bacri, Debregeas and Brochard-Wyart1996) or with soluble or insoluble surfactant drops (Halpern & Grotberg Reference Halpern and Grotberg1992; Jensen & Grotberg Reference Jensen and Grotberg1993).
When an insoluble drop comes in contact with the horizontal surface of a liquid layer, when the surface tension of the liquid layer is larger than that of the drop (
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{l}-\unicode[STIX]{x1D70E}_{d}>0$
), often due to the drop being a surfactant drop, an outward horizontal force acts on the drop which spreads it. The spreading is found to occur in the form of a film (Joos & Pintens Reference Joos and Pintens1977), the film being assumed to be a monolayer for the spreading of surfactant drops. Here, as well as in all later notation, we use the subscript
$f$
to denote the spreading film,
$d$
to denote the drop and
$l$
to denote the liquid layer beneath the film that spreads from the drop. In such a situation, the monolayer is assumed to have no viscous dissipation in it and is expected to spread as a rigid sheet (Jensen & Grotberg Reference Jensen and Grotberg1993). The increase of film radius (
$r_{f}$
) with time is then determined by the nature of viscous dissipation in the underlying liquid layer, which differs for thin (
$\unicode[STIX]{x1D716}=h_{l}/r_{d}\ll 1$
) and deep (
$\unicode[STIX]{x1D716}\gg 1$
) layers, where
$h_{l}$
is the liquid layer thickness and
$r_{d}$
the initial drop radius. We focus on the previous deep-layer results below, since the present study is for deep layers; the reader is referred to the review of Grotberg & Gaver III (Reference Grotberg and Gaver1996) and the papers by Jensen & Halpern (Reference Jensen and Halpern1998) and Dussaud, Matar & Troian (Reference Dussaud, Matar and Troian2005) for the thin-layer results.
For the spreading of a low-viscosity insoluble surfactant drop on a deep liquid layer, Landt & Volmer (Reference Landt and Volmer1926), Fay (Reference Fay1969), Joos & Pintens (Reference Joos and Pintens1977) and Joos & Van Hunsel (Reference Joos and Van Hunsel1985) proposed that the balance of the viscous resistance in a boundary layer below the spreading surfactant monolayer with the driving interfacial tension force results in the dimensionless film radius,
$r_{f}^{\ast }=r_{f}(t)/r_{d}=(2/\sqrt{3}){t_{\unicode[STIX]{x1D707}l}^{\ast }}^{3/4}$
. Here
$t_{\unicode[STIX]{x1D707}l}^{\ast }=t/t_{\unicode[STIX]{x1D707}l}$
, with
$t_{\unicode[STIX]{x1D707}l}=(\unicode[STIX]{x1D70C}_{l}\unicode[STIX]{x1D707}_{l}r_{d}^{4}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}^{2})^{1/3}$
being the visco-capillary time scale for deep layers; and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
has to be replaced by the spreading parameter if the interfacial tension between the spreading and the underlying liquid is also important. The same scaling was written by Jensen (Reference Jensen1995) as
$r_{f}(t)\sim (A^{2}M^{2}t^{3}/\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}_{d})^{1/8}$
for the mass
$M$
of the surfactant drop and
$A=\text{d}\unicode[STIX]{x1D70E}/\text{d}\unicode[STIX]{x1D6E4}$
, with
$\unicode[STIX]{x1D6E4}$
being the local surfactant concentration; the latter expression reduces to the
$3/4$
power law when
$\unicode[STIX]{x1D6E4}\sim M/r_{f}^{2}$
and
$A\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D6E4}$
. The similarity solution for the spreading of a strip of viscous oil over water also shows the
$3/4$
power law when the underlying boundary layers dominate (Foda & Cox Reference Foda and Cox1980). The experimental evidence for this
$3/4$
power law is not conclusive. For the spreading of surfactants, the
$3/4$
power law has been observed for low-viscosity FC-129 (a fluorochemical surfactant) on CCl
$_{4}$
, but not for the low-viscosity CTAB/PFAC (cetyl trimethyl ammonium bromide/perfluoroalkyl carboxylate) mixture on benzene, which showed an exponent of 0.575 (Joos & Van Hunsel Reference Joos and Van Hunsel1985). Further, even when high-viscosity silicone oil (965 cP) spreading on water obeyed this law (Dussaud & Troian Reference Dussaud and Troian1998), 20 cP PDMS (polydimethylsiloxane) on 100 cP glycerine–water solution showed
$r_{f}\sim t^{0.4}$
while spreading of 1000 cP PDMS on the same substrate showed
$r_{f}\sim t^{0.5}$
(Fraaije & Cazabat Reference Fraaije and Cazabat1989).
When the spreading drop is very viscous, Bacri et al. (Reference Bacri, Debregeas and Brochard-Wyart1996), not considering the film around the drop, proposed that the dimensionless drop diameter,
$r_{d}^{\ast }=r_{d}(t)/r_{d}\sim {t_{\unicode[STIX]{x1D707}d}^{\ast }}^{1/4}$
, where
$t_{\unicode[STIX]{x1D707}d}^{\ast }=t/t_{\unicode[STIX]{x1D707}d}$
, with
$t_{\unicode[STIX]{x1D707}d}=\unicode[STIX]{x1D707}_{d}r_{d}/\unicode[STIX]{x1D70E}_{e}$
being the visco-capillary time scale for the drop and
$\unicode[STIX]{x1D70E}_{e}$
is the effective surface tension, defined as the harmonic mean of the interfacial tensions on drop–air and drop–liquid layer interfaces. This scaling was proposed to occur when the dominant viscous dissipation inside the spreading drop balanced the surface tension force at the triple line. The
$t^{1/4}$
scaling was observed by Bacri et al. (Reference Bacri, Debregeas and Brochard-Wyart1996) in extremely viscous PDMS (29 310–97 700 cP) spreading over glycerol–water mixture (5.97–934 cP) till
$r_{d}(t)/l_{c}<1$
, where the capillary length
$l_{c}=\sqrt{\unicode[STIX]{x1D70E}_{e}/\unicode[STIX]{x1D70C}_{e}g}$
with
$\unicode[STIX]{x1D70C}_{e}=\unicode[STIX]{x1D70C}_{d}(1-\unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{l})$
as the effective density. The dependence of
$r_{d}(t)$
on other fluid properties and the initial drop diameter
$r_{d}$
however was not verified.
If the spreading drop is also soluble in the underlying liquid layer, the geometry of spreading depends on the rate of adsorption of the drop fluid into the liquid layer; however, the spreading rate still remains largely unaffected, as was proposed by Jensen & Grotberg (Reference Jensen and Grotberg1992, Reference Jensen and Grotberg1993) and experimentally verified by Afsar-Siddiqui, Luckham & Matar (Reference Afsar-Siddiqui, Luckham and Matar2003) for very thin liquid layers. In the case of volatile, less viscous drops of various fluids, which spread on a more viscous, deep water layer, in which they are insoluble, Dussaud & Troian (Reference Dussaud and Troian1998) found that the radius of the film increases for all cases as
$t^{1/2}$
. The difference from the expected
$3/4$
power law was hypothesised to be due to the cooling of the film by evaporation, which would change the nature of the boundary layer below the film from a Blasius type. However, other reasons also give a
$t^{1/2}$
power law, as was found by Bacri et al. (Reference Bacri, Debregeas and Brochard-Wyart1996) for the spreading of viscous drops when the spreading drop radius becomes larger than
$l_{c}$
, in which case the viscous dissipation inside the drop balances the work done by gravitational forces.
As the above discussion has shown, the spreading of drops on deep fluid layers is complex and inadequately understood, with different scaling laws being proposed in different parameter regimes. These scalings also do not seem to be fully verified since most verification experiments study only the time dependence of the spreading radius, without studying the effect of the property ratios of the drop and the substrate fluid. Another consideration that has been unexplored is the role of the initial radius of the drop on its spreading rate, through its ability to influence the initial conditions as well as through its effect on the flux of drop fluid into the spreading film. A commonly encountered regime, namely, the film spreading of a slightly more viscous liquid on a less viscous deep layer, especially when the spreading liquid is not a surfactant so that significant viscous dissipation could occur in the spreading film, has not been explored. In such a case, when the drop fluid is also soluble and volatile, the scaling law for spreading is even less well known. Such a regime is important as it is commonly encountered in the spreading and eventual mixing of short-chain alcohols on solvents like water, which have many technological applications.
In this paper we study the film spreading from drops of ethanol–water mixture, of ethanol concentrations
$20\,\%\leqslant C_{e}\leqslant 100\,\%$
, and radii
$0.9~\text{mm}<r_{d}<1.1~\text{mm}$
, on the surface of a thick layer (
$h_{l}=5~\text{mm}$
) of water. The spreading occurs very fast, and is over within approximately 0.5 s since it is surface-tension-driven, as shown by the range of the film capillary numbers,
$Ca_{f}=\unicode[STIX]{x1D707}_{f}u_{f}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
,
$0.0005<Ca_{f}<0.0069$
. However, since the film Reynolds numbers (
$Re_{f}=u_{f}h_{f}/\unicode[STIX]{x1D708}_{f}$
) are in the range of
$0.02<Re_{f}<1.4$
, viscous forces are greater than inertial effects. Further, owing to high surface tension forces, the film Weber numbers are also small (
$We_{f}=\unicode[STIX]{x1D70C}_{f}u_{f}^{2}h_{f}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}<0.005$
); inertia in film spreading dynamics is negligible. The drop is also lighter than the underlying liquid, with the range of density ratios (
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D70C}_{l}/\unicode[STIX]{x1D70C}_{d}$
) being
$1.27>\unicode[STIX]{x1D709}>1.03$
so that it stays at the free surface while the film spreads; the drop remains an approximate ellipsoid form since the range of drop Bond numbers (
$Bo_{d}=\unicode[STIX]{x1D70C}_{d}gr_{d}^{2}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
) was
$0.19<Bo_{d}<0.56$
. Surface tension dominates over gravitational forces in the spreading process since the Bond number based on film thickness will be even smaller. Even though the drop is more viscous than the underlying layer, with the range of viscosity ratios (
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D707}_{l}/\unicode[STIX]{x1D707}_{d}$
) being
$0.81>\unicode[STIX]{x1D712}>0.4$
, since the film Ohnesorge number
$Oh_{f}=\unicode[STIX]{x1D707}_{f}/\sqrt{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}_{f}h_{f}}\sim 10^{-2}$
, surface tension dominates over viscous resistance in spreading. In such a situation, we show that, different from the earlier suggested regimes of film spreading, a balance of viscous resistance in the film with the driving surface tension force gives rise to a
$r_{f}\sim t^{1/4}$
scaling law. More importantly, by modelling the initial coalescence of the drop with the liquid layer, we estimate the initial fraction of the drop that forms the film. By including this fraction in the scaling analysis, we clarify the dependence of the spreading rate on the initial drop radius and the property ratios of the drop and the liquid layer. The paper is organised as follows. We describe the experimental set-up and procedure in § 2, followed by a qualitative description of the spreading phenomena in § 3. The proposed scaling law is developed and verified in detail in § 4, before concluding the paper by discussing the implications of the proposed scaling in § 5.
2 Experiments
The experiments were conducted by adding ethanol–water drops of varying concentrations of ethanol (
$C_{e}$
) and radii (
$r_{d}$
) to the surface of a water layer of height
$h_{l}=5~\text{mm}$
in a Petri dish of 100 mm diameter, as shown in the schematic of figure 1. Larger height experiments with
$h_{l}=75~\text{mm}$
were also conducted in a 85 mm diameter beaker. The drops were produced from capillaries of different sizes connected to a syringe pump. The flow rate of the syringe pump was fixed low (
$2.4~\text{ml}~\text{h}^{-1}$
) so that the liquid coming out from the capillary was in the dripping regime (Clanet & Lasheras Reference Clanet and Lasheras1999). The equivalent spherical radius of the drop (
$r_{d}$
) was determined from the number of drops required to fill a specific volume for each of the capillaries used; the values of
$r_{d}$
are shown in table 1. Care was taken to maintain the flow rate and the orientation of the capillary to be the same in all experiments with each capillary. The height of the capillary tip was adjusted so that the drops detached from the capillary very close to the free surface to avoid inertial effects due to the impingement of the drop on the water surface. The range of concentrations of the ethanol–water drops, the corresponding densities (
$\unicode[STIX]{x1D70C}_{d}$
), surface tension with air (
$\unicode[STIX]{x1D70E}_{d}$
) and kinematic viscosities (
$\unicode[STIX]{x1D707}_{d}$
) of the drop solutions are shown in table 1.
Figure 1. Schematic of the experimental set-up.
Table 1. Properties of the drop, the driving surface tension difference, the drop Bond number and the range of relevant dimensionless numbers of the film. The properties of the drop at different concentrations are at
$25\,^{\circ }$
C, obtained from Ernst, Watkins & Ruwe (Reference Ernst, Watkins and Ruwe1936), Blanchette, Messio & Bush (Reference Blanchette, Messio and Bush2009) and Khattab et al. (Reference Khattab, Bandarkar, Fakhree and Jouban2012). The properties of the underlying water layer are
$\unicode[STIX]{x1D70E}_{l}=54~\text{mN}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D707}_{l}=0.89~\text{cP}$
and
$\unicode[STIX]{x1D70C}_{l}=1000~\text{kg}~\text{m}^{-3}$
.
The top-view visualisation of the spreading dynamics, shown in figure 2, was done using aluminium particles, which, when mixed with water, form a thin layer of particles at the free surface. As determined by a particle size analyser (Microtrac Inc), the aluminium particles had a median diameter of
$14.65~\unicode[STIX]{x03BC}\text{m}$
, mean diameter of
$5.09~\unicode[STIX]{x03BC}\text{m}$
, with the particle diameters distributed in an asymmetric distribution between
$0.3~\unicode[STIX]{x03BC}\text{m}$
and
$100~\unicode[STIX]{x03BC}\text{m}$
. At the concentration of the particles used (163 ppm), the surface tension of water was measured as
$54~\text{mN}~\text{m}^{-1}$
, the details of which are given in appendix A. The top view of the spreading dynamics was captured by a high-speed camera (LaVision ProHS) at approximately 800 f.p.s. (frames per second) with light-emitting diode (LED) backlighting, as shown in figure 1. In some cases, 5 ppm of Rhodamine 5B was added to the drop in these top-view visualisations so as to distinguish the drop fluid from the underlying water layer. The surface tension reduction at 5 ppm dye concentration was measured to be 0.14 %, which has negligible effect on the dynamics. The spreading radius of the film
$r_{f}(t)$
was measured as the radius of the circular region devoid of tracer particles, as seen in figure 2(c), from such top-view images at increasing times
$t$
, the time calculated from the frame number of the image, knowing the frame rate (f.p.s.). The centre of measurement was fixed as the tip of the capillary seen in top-view images and zero time as the time of contact of the drop with the liquid surface. The film radius in each image was calculated as the mean from three measurements, taken at three azimuthal locations on the film where a minimum local radius of the film could be identified; the locations spanned the full circumference of the film. The velocities of expansion of the film front
$u_{f}$
were calculated by taking the time derivative of the power-law fit through the increasing part of
$r_{f}$
versus
$t$
. A sample fit for
$C_{e}=60\,\%$
and
$r_{d}=0.97~\text{mm}$
is shown in the inset of figure 4. The errors associated with the measurement of
$r_{f}$
,
$t$
and
$u_{f}$
are discussed in appendix B. In addition, to understand the coalescence of the drop with the water layer and the subsequent spreading of the film, high-speed shadowgraph visualisations of the side view were conducted in a
$5~\text{cm}\times 5~\text{cm}$
cross-section glass tank with
$h_{l}=5~\text{cm}$
, using a Photron SA5 camera at 2000 f.p.s. Hollow glass spheres of
$10~\unicode[STIX]{x03BC}\text{m}$
diameter were added in the water layer and backlighting was used to obtain shadowgraphs combined with particle visualisation; a typical image sequence obtained is shown in figure 3. Images with large exposure time, of laser-induced fluorescence of
$6~\unicode[STIX]{x03BC}\text{m}$
fluorescent particles in the drop and scattering from
$55~\unicode[STIX]{x03BC}\text{m}$
polyamide particles in water by a vertical laser sheet, was used to observe vortices, as shown in figure 3(i).
Figure 2. Top views of the sequence of spreading and eventual mixing of a 100 % ethanol drop of radius
$r_{d}=0.97~\text{mm}$
on the surface of a water layer of height
$h_{l}=5~\text{mm}$
. (a–c) Capillary wave propagation followed by the expanding circular film, seen as the white circular region. The dark circular region at the centre of the expanding film is the drop, dyed with Rhodamine 5B. (d–f) The expanding film becomes unstable at its outer periphery and then develops outward-propagating fingers. (g–i) The drop at the centre of the film develops holes and eventually mixes, while the film retracts. The size of each image is
$35~\text{mm}\times 22.5~\text{mm}$
. See movie 1 available in the supplementary movies at https://doi.org/10.1017/jfm.2017.562.
3 Description of the phenomena
3.1 Coalescence and spreading dynamics
Figure 3. (a–h) Side views of the sequence of coalescence and film spreading when an ethanol drop of radius
$r_{d}=1.1~\text{mm}$
and 100 % concentration mixes with a water layer of
$h_{l}=5~\text{cm}$
height. The point A shows the fraction of the drop being drawn apart by coalescence that forms the spreading film. The size of each image is
$16.88~\text{mm}\times 8.4~\text{mm}$
. (i) Side-view visualisation of film spreading from a drop of
$r_{d}=1.1~\text{mm}$
and
$C_{e}=100\,\%$
with
$55~\unicode[STIX]{x03BC}\text{m}$
polyamide particles in the substrate and
$6~\unicode[STIX]{x03BC}\text{m}$
fluorescent particles in the drop. The dashed circles show the tip vortices at the periphery of the spreading film. The image shown is the negative of the obtained image for clarity and is of size
$22.5~\text{mm}\times 9.08~\text{mm}$
. See supplementary movie 2.
Figure 4. Variation of the film radius with time for different drop radii, ethanol concentrations and layer height. The hollow symbols represent
$r_{d}=0.97~\text{mm}$
with varying ethanol concentrations in the drop: ○,
$C_{e}=100\,\%$
; ▫,
$C_{e}=80\,\%$
; ♢,
$C_{e}=60\,\%$
; ✩,
$C_{e}=40\,\%$
;
$+$
,
$C_{e}=20\,\%$
. The solid symbols represent experiments with 100 % concentration with varying
$r_{d}$
: ▼,
$r_{d}=0.9~\text{mm}$
; ▲,
$r_{d}=1.1~\text{mm}$
. The experiments with hollow and solid symbols had the water layer height
$h_{l}=5~\text{mm}$
. An experiment with a larger layer height
$h_{l}=75~\text{mm}$
,
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
is shown by
$\odot$
. The dashed line shows the
$1/4$
slope of the data. The inset shows the
$r_{f}$
versus
$t$
data for
$C_{e}=60\,\%$
and
$r_{d}=0.97~\text{mm}$
along with the curve fit
$r_{f}=11.89t^{0.232}$
, from which the velocity is calculated.
Figure 2 shows the top views of the sequence of spreading of an ethanol drop of
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
. The local depression in surface tension caused at the point of contact of the drop with water results in radially outward Marangoni forces, which cause a thin film of ethanol–water mixture to spread. The expanding white circular region that is free of particles, seen in figure 2(a–c), shows the spreading film. We also notice the initiation and propagation of capillary waves ahead of the expanding film in figure 2(a–c). After some time (90 ms), the outer front of the film develops instabilities resulting in outward-moving fingers or plumes as seen in figure 2(d–f). Even though there is an inward flow in between these outward-growing fingers, the radius of the continuous film region, as well as the circular region covering the outer tips of the growing fingers, go on increasing in time, but with decreasing velocities (see supplementary movie 1). The length of the fingers increase along with the radius of the continuous film region, until the velocity of expansion of the continuous film reduces to zero, after which the continuous film region begins to retract inwards (figure 2
g–i) while the outer tips of the fingers remain approximately stationary in time. The total time of film expansion is approximately 0.4 s. Most of the drop remains at the centre of the expanding film during the whole time of film expansion, seen as the dark circular region at the centre of the expanding film in figure 2(a–f). This remnant part of the drop also expands, but at a much slower rate than the film, thins and then develops holes in it. The remnant drop eventually gets mixed with water by a combination of convection and diffusion, after the continuous film has started retracting, as seen in figure 2(g–i); the total time from contact to dissolution being approximately 0.6 s.
The side views of the film spreading process for a similar concentration drop with
$r_{d}=1.1~\text{mm}$
, shown in figure 3, clarifies the critical role of the initial coalescence between the drop and the water layer in film formation. Regions marked as A in figure 3(a–f) show that a small fraction of the drop, from its bottom, gets pulled apart by the neck expansion during coalescence and becomes the source of the drop fluid in the film (see supplementary movie 2). As figure 3(a–f) shows, the major part of the drops goes down and then bounces back due to its buoyancy, while the initial bottom part of the drop gets pulled apart to form the spreading film. It could also be noticed that there is no substantial motion in the regions below the spreading film, except for a vertical redistribution of the particles at the interface seen as the dark region below the film in figure 3(g,h). Such a distribution of particles at the interface occurs because of the vertical momentum imparted to the interface as a result of the vertical oscillations of the drop due to the ligament retraction dynamics during pinch-off from the capillary. We now look at the quantitative variation of the radius of the expanding continuous circular film (
$r_{f}$
) as a function of time (
$t$
), measured as discussed in § 2, from images similar to that in figure 2.
3.2 Spreading radius and velocity
Figure 5. Variation of the film expansion velocity with time for different drop radii, ethanol concentrations and layer height. The symbols are the same as in figure 4.
Figure 4 shows the measured values of
$r_{f}(t)$
as a function of time
$t$
for different
$C_{e}$
(hollow symbols), with different
$r_{d}$
(solid symbols) and with different
$h_{l}$
(hollow circle with dot), the zero time being at the instant of contact of the drop with water. The horizontal error bars show the error in time measurement due to the uncertainty of the time of contact, discussed in appendix B. As discussed in appendix B,
$r_{f}$
is the mean of three azimuthal measurements; the range of these three measured radii is shown in figure 4 for
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
as the vertical bars. This range increases in the later measurements since the film develops azimuthal instabilities after expanding for some time to form fingers in its outer periphery, as we saw in figure 2(d). After this instability occurs,
$r_{f}(t)$
is measured as the radius of the continuous film, not including the region with fingers. The plot includes measurements after the instability at the edge of the film occurs; no change in the rate of expansion of
$r_{f}$
is seen after the instability occurs.
The radius
$r_{f}$
increases as the continuous film region expands with time (figure 2
a–g) and then starts to decrease with time once the film front starts to retract (figure 2
g–i). The inset in figure 4 shows the curve fit that is used to calculate the film expansion velocity (
$u_{f}$
) for one experiment, as discussed in § 2. The film expansion velocities (
$u_{f}$
) decrease with time, as shown in figure 5. The initial (
$t\approx 0.03$
s) expansion velocities of the film are high (
${>}10~\text{cm}~\text{s}^{-1}$
), which reduces to zero, beyond which the velocities reverse their direction due to film retraction. Retraction occurs over a shorter time than expansion; for example, for
$r_{d}=0.97~\text{mm}$
and
$C_{e}=100\,\%$
, shown with ○ in figure 4, film expansion occurs over 0.4 s while retraction occurs over 0.2 s.
Figure 4 shows that, at any time, a larger
$C_{e}$
in the drop results in a larger radius of the film. The slopes of
$r_{f}$
versus
$t$
for different ethanol concentrations are approximately the same, indicating the same power-law dependence of
$r_{f}$
on
$t$
for different ethanol concentrations; this power law is approximately
$t^{1/4}$
as shown by the dashed line in figure 4. For the same
$r_{d}$
, the higher the concentration of ethanol in the drop, the larger is the maximum
$r_{f}$
and the larger is the time of spreading. It could also be noticed that, at any specific time,
$r_{f}$
has a non-monotonic dependence on the initial radius of the drop
$r_{d}$
. The hollow circles and the hollow circles with a centre dot in figure 4 are identical experiments except that the water layer height (
$h_{l}$
) was 15 times larger in the latter. These two datasets fall on each other, implying that the radius
$r_{f}$
at any time, the exponent of the power law of
$r_{f}$
versus
$t$
, as well as the velocity of spreading are all independent of the height of the underlying liquid layer; this independence of
$h_{l}$
paves the way to our scaling analysis in § 4. We now proceed to find scaling relations for these dependences of
$r_{f}$
on time,
$r_{d}$
and the fluid properties. The scaling analysis presented in this paper is limited to the expanding radius of the spreading film, and does not include the retraction of the film.
4 Scaling analysis
As we saw in § 3.2, the spreading radius
$r_{f}$
and velocities
$u_{f}$
are independent of
$h_{l}$
, the underlying liquid layer height. Such would be the case if viscous dissipation in a boundary layer below the film was the dominant resistance for the spreading film, as discussed in § 1; this would however give
$r_{f}\sim t^{3/4}$
, quite different from the observed time dependence in figure 4. The ratio of viscous stress due to a Blasius boundary layer below the spreading film,
$\unicode[STIX]{x1D70F}_{bl}=\unicode[STIX]{x1D707}_{l}u_{f}/\unicode[STIX]{x1D6FF}_{bl}$
, to the viscous stress in the film,
$\unicode[STIX]{x1D70F}_{f}=\unicode[STIX]{x1D707}_{f}u_{f}/h_{f}$
, is
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70F}_{f}}{\unicode[STIX]{x1D70F}_{bl}}=\frac{\unicode[STIX]{x1D707}_{f}}{\unicode[STIX]{x1D707}_{l}}\frac{\unicode[STIX]{x1D6FF}_{bl}}{h_{f}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}_{bl}$
is the Blasius boundary layer thickness. When
$t=0.2~\text{s}$
and
$r_{f}=10~\text{mm}$
at the end of the expansion of the film for
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
, we have
$\unicode[STIX]{x1D6FF}_{bl}\sim \sqrt{\unicode[STIX]{x1D708}_{l}t}\approx 400~\unicode[STIX]{x03BC}\text{m}$
and
$h_{f}=4r_{d}^{3}G/3r_{f}^{2}\approx 5.33~\unicode[STIX]{x03BC}\text{m}$
(see (4.2) and (4.21) later), resulting in
$\unicode[STIX]{x1D70F}_{f}/\unicode[STIX]{x1D70F}_{bl}\approx 75$
. The film viscous stress is approximately two orders of magnitude higher than the stress due to a possible Blasius boundary layer in the present case. Similarly, the viscous extensional stress in the film is
$\unicode[STIX]{x1D70F}_{e}\sim \unicode[STIX]{x1D707}_{f}u_{f}/r_{f}$
. The ratio
$\unicode[STIX]{x1D70F}_{f}/\unicode[STIX]{x1D70F}_{e}\sim r_{f}/h_{f}\sim 1876$
, using the above values of
$r_{f}$
and
$h_{f}$
; the viscous shear stress in the film is hence three orders of magnitude higher than the viscous extensional stress in the film.
We hence consider the situation where the spreading dynamics is likely to be determined by the balance of viscous shear stresses within the film with the driving surface tension force; a similar assumption has been made by Hernández-Sánchez, Eddi & Snoeijer (Reference Hernández-Sánchez, Eddi and Snoeijer2015) for spreading due to a continuous supply of IPA (isopropyl alcohol). We also saw in § 3.1 that, during the period of spreading of the film, only a fraction of the volume of the drop is pulled apart by the neck expansion, which then spreads as the film. Based on these observations and on the assumption that the initial fraction of the drop mass remains well mixed while spreading as the film, we now develop a scaling analysis below. The analysis uses the balance of forces within the spreading film and an estimate of the initial fraction obtained from coalescence dynamics. The resultant scaling law captures the dependence of
$r_{f}$
and
$u_{f}$
on time, on the initial radius of the drop and on the initial concentration of ethanol in the drop, which as we saw in § 3.2 are the prime variables on which the spreading depends.
4.1 Mass and momentum balance
Figure 6. Schematic of film spreading from a lighter miscible drop on a deep liquid layer showing the symbols used.
We assume the spreading to be as shown in figure 6. As we saw in § 3.2, the film spreading is rapid, with the spreading being over in 0.4 s for the 100 % ethanol drop. Further, as could be seen from figure 2, only a small fraction of the drop spreads as the film during the time of film spreading. Owing to the small characteristic time of spreading (
$t_{\unicode[STIX]{x1D707}f}\sim r_{f}/u_{f}$
), we assume that the film is well mixed during its spreading so that the density of the film remains a constant over the short time of spreading. This assumption implies that the loss of ethanol from the film during spreading due to evaporation and mixing with the underlying water layer is small. As shown in appendix C, the evaporation velocities are of the order of
$10^{-5}~\text{m}~\text{s}^{-1}$
while
$u_{f}\sim 5\times 10^{-2}~\text{m}~\text{s}^{-1}$
; evaporative flux in
$t_{\unicode[STIX]{x1D707}f}$
will be negligible compared to the longitudinal flux in the film. Since convective mixing is absent (see figure 3), the downward mixing velocities, of the order of diffusive velocities
$D/h_{f}\sim 10^{-4}~\text{m}~\text{s}^{-1}$
, are also negligible in time
$t_{\unicode[STIX]{x1D707}f}$
. When fraction
$G$
of the volume of the drop spreads as a film of constant density
$\unicode[STIX]{x1D70C}_{f}$
, with a time-dependent film height
$h_{f}(t)$
, mass balance of the drop and the film implies that
$$\begin{eqnarray}G{\textstyle \frac{4}{3}}\unicode[STIX]{x03C0}r_{d}^{3}\unicode[STIX]{x1D70C}_{d}=\unicode[STIX]{x03C0}r_{f}^{2}h_{f}\unicode[STIX]{x1D70C}_{f}.\end{eqnarray}$$
The change in the radius of the drop fluid reservoir, seen as the dark centre region in figure 2(a–f), is small while the film spreads. Further, the value of
$t_{\unicode[STIX]{x1D707}f}$
is small. For these reasons, we assume the change in volume of the drop during
$t_{\unicode[STIX]{x1D707}f}$
to be negligible; the change in density of the drop is also then negligible in
$t_{\unicode[STIX]{x1D707}f}$
(
$\text{d}\unicode[STIX]{x1D70C}_{d}/\text{d}t\approx 0$
when
$t<t_{\unicode[STIX]{x1D707}f}$
). Since the mass and momentum changes of the drop reservoir over
$t_{\unicode[STIX]{x1D707}f}$
are then negligible, as shown in appendix D, the mass balance of the drop and the film reduces to
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}u_{f}h_{f}\unicode[STIX]{x1D70C}_{f}+\unicode[STIX]{x03C0}r_{f}^{2}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}h_{f}}{\text{d}t}=0.\end{eqnarray}$$
Similarly, as shown in appendix D, using (4.3) in the momentum balance for the drop and the film and neglecting terms involving change in mass and momentum of the drop reservoir implies that
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}(\unicode[STIX]{x1D70E}_{l}-\unicode[STIX]{x1D70E}_{f})-\unicode[STIX]{x1D707}_{f}\frac{u_{f}}{h_{f}}\unicode[STIX]{x03C0}r_{f}^{2}=\unicode[STIX]{x03C0}r_{f}^{2}h_{f}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}u_{f}}{\text{d}t}.\end{eqnarray}$$
4.2 Scaling of spreading radius and velocity
Figure 7. Variation of the dimensionless numbers of the film with time for an experiment with
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
: ○,
$Re_{f}$
; ▫,
$We_{f}$
; ♢,
$Oh_{f}$
;
$+$
,
$Ca_{f}$
.
We now estimate the range of dimensionless numbers of the film during its spreading so as to simplify (4.4). We assume that the spreading occurs fast enough to neglect the mixing of the film with the underlying water layer, so that the film properties are the same as the drop properties, implying
$\unicode[STIX]{x1D70C}_{f}=\unicode[STIX]{x1D70C}_{d}$
,
$\unicode[STIX]{x1D70E}_{f}=\unicode[STIX]{x1D70E}_{d}$
and
$\unicode[STIX]{x1D707}_{f}=\unicode[STIX]{x1D707}_{d}$
. Figure 7 shows the variation of the dimensionless numbers of the film as a function of time in a typical experiment of 100 % ethanol drop of
$r_{d}=0.97~\text{mm}$
. The Weber numbers based on film thickness (
$We_{f}=\unicode[STIX]{x1D70C}_{f}u_{f}^{2}h_{f}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
) are much less than one (
$0<We_{f}<0.005$
), implying that the surface tension effects are much more than the inertia effects in film spreading. Similarly, since the Reynolds numbers based on film thickness (
$Re_{f}=\unicode[STIX]{x1D70C}_{f}u_{f}h_{f}/\unicode[STIX]{x1D707}_{f}$
) are in the range
$0.06<Re_{f}<1.4$
, viscous effects are greater than inertia effects, except at the beginning of the film spreading when
$Re_{f}$
is of order one. The capillary numbers (
$Ca_{f}=\unicode[STIX]{x1D707}_{f}u_{f}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
) are very small (
$0.0006<Ca_{f}<0.0035$
); surface tension forces dominate over viscous resistance. The values of Ohnesorge numbers (
$Oh_{f}=\unicode[STIX]{x1D707}_{f}/\sqrt{\unicode[STIX]{x1D70C}_{f}h_{f}\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}$
) are in the range of
$0.049<Oh_{f}<0.099$
; surface tension is more predominant than viscous effects.
Based on the order of these dimensionless numbers, the momentum equation (4.4) can be simplified as follows. Since
$\text{d}u_{f}/\text{d}t\sim u_{f}/t_{\unicode[STIX]{x1D707}f}$
with
$t_{\unicode[STIX]{x1D707}f}\sim r_{f}/u_{f}$
, the ratio of the term on the right-hand side of (4.4) to the first term on the left-hand side is
$We_{f}$
; as seen in figure 7,
$We_{f}\ll 1$
. Similarly, the ratio of the term on the right-hand side of (4.4) to the second term on the left-hand side of (4.4) is
$Re_{f}(h_{f}/r_{f})$
. Since
$Re_{f}<1$
, as shown in figure 7, and
$h_{f}/r_{f}\ll 1$
, since the film thickness is much smaller than its radius, we have
$Re_{f}(h_{f}/r_{f})\ll 1$
. At the same time, the ratio of the terms on the left-hand side of (4.4) is
$h_{f}/Ca_{f}r_{f}$
, which is of order one, since
$Ca_{f}\ll 1$
(figure 7) and
$h_{f}/r_{f}\ll 1$
. Hence, to leading order, the term on the right-hand side of (4.4) can be neglected. Further, assuming the film properties are the same as the drop properties, the momentum balance reduces to
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D707}_{d}\frac{u_{f}}{h_{f}}\unicode[STIX]{x03C0}r_{f}^{2}.\end{eqnarray}$$
Eliminating
$h_{f}$
from (4.2) and (4.5) gives
$$\begin{eqnarray}r_{f}^{3}\dot{r_{f}}=\frac{8}{3}Gr_{d}^{3}\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}_{d}}.\end{eqnarray}$$
On integrating (4.6), we get
$$\begin{eqnarray}r_{f}^{\ast }=c_{1}(Gt_{\unicode[STIX]{x1D707}d}^{\ast })^{1/4}\end{eqnarray}$$
as the scaling of the dimensionless film radius
$r_{f}^{\ast }=r_{f}/r_{d}$
on the dimensionless time
$t_{\unicode[STIX]{x1D707}d}^{\ast }=t/t_{\unicode[STIX]{x1D707}d}$
, with the characteristic time of spreading,
$$\begin{eqnarray}t_{\unicode[STIX]{x1D707}d}=\frac{\unicode[STIX]{x1D707}_{d}r_{d}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}},\end{eqnarray}$$
and the constant of integration
$c_{1}=(32/3)^{1/4}$
. Since,
$\dot{r_{f}}=u_{f}$
, the radial velocity of film spreading, equation (4.6) can also be rewritten in dimensionless form as
$$\begin{eqnarray}Ca_{d}=c_{2}G{r_{f}^{\ast }}^{-3},\end{eqnarray}$$
where the capillary number
$Ca_{d}=u_{f}\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
is the dimensionless spreading velocity and
$c_{2}=8/3$
. In the scaling laws (4.7) and (4.9),
$G$
is the initial fraction of the drop that mixes to form the film, which is still unknown. We now obtain an expression for
$G$
based on the coalescence dynamics of the drop and the liquid layer.
4.3 Estimation of the initial spreading fraction G
Figure 8. Schematic of the initial stages of coalescence of a drop with a liquid layer.
Figure 8 shows the schematic of the initial stage of coalescence of the drop with the liquid layer, which is a schematic of the zoomed view close to the interface in figure 3(b). The fraction of the volume of the drop
$G$
that is pulled apart by the neck expansion in the coalescence time
$t_{co}$
is
$$\begin{eqnarray}G=\frac{2\unicode[STIX]{x03C0}r_{n}\unicode[STIX]{x1D6FF}u_{r}t_{co}}{{\textstyle \frac{4}{3}}\unicode[STIX]{x03C0}{r_{d}}^{3}},\end{eqnarray}$$
where, as shown in figure 8,
$\unicode[STIX]{x1D6FF}$
is the thickness of the neck region,
$r_{n}$
is the neck radius and
$u_{r}$
is the neck retraction velocity.
The coalescence time
$t_{co}$
in (4.10) depends on the Bond number of the drop,
$Bo_{d}=\unicode[STIX]{x1D70C}_{d}gr_{d}^{2}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
. For low
$Bo_{d}$
, the coalescence is purely capillary-driven with
$t_{co}$
equal to the capillary time scale
$t_{c}=\sqrt{\unicode[STIX]{x1D70C}_{d}r_{d}^{3}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}$
, while for large
$Bo_{d}$
,
$t_{co}$
is equal to the gravity time scale
$t_{g}=\sqrt{r_{d}/g}$
(Chen, Mandre & Feng Reference Chen, Mandre and Feng2006). As shown in table 1, the range of values of
$Bo_{d}$
for the present experiments is
$0.12<Bo_{d}<0.26$
; the present experiments fall in an intermediate
$Bo_{d}$
range. Chen et al. (Reference Chen, Mandre and Feng2006) have shown that, for such a capillary–gravity regime of drop coalescence,
$$\begin{eqnarray}t_{co}=0.77\sqrt{\frac{\unicode[STIX]{x1D70C}_{d}r_{d}^{3}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}(1+Bo_{d})}},\end{eqnarray}$$
which tends to
$t_{c}$
as
$Bo_{d}\rightarrow 0$
and to
$t_{g}$
as
$Bo_{d}$
becomes large.
The thickness of the neck
$\unicode[STIX]{x1D6FF}$
in (4.10) can be estimated in the following way. From the geometry of figure 8,
$$\begin{eqnarray}w=r_{d}(1-\cos \unicode[STIX]{x1D703}),\end{eqnarray}$$
which, on substitution of
$\cos \unicode[STIX]{x1D703}\approx 1-\unicode[STIX]{x1D703}^{2}/2$
for small
$\unicode[STIX]{x1D703}$
, becomes equal to
$$\begin{eqnarray}w=\frac{r_{d}\unicode[STIX]{x1D703}^{2}}{2}.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D703}\approx r_{n}/r_{d}$
for small
$\unicode[STIX]{x1D703}$
from figure 8, (4.13) becomes
$$\begin{eqnarray}w=\frac{r_{n}^{2}}{2r_{d}}.\end{eqnarray}$$
Mass balance of the retracting rim resulting in a bulge of diameter
$\unicode[STIX]{x1D6FF}$
at the tip of the rim would imply
$$\begin{eqnarray}\int _{0}^{r_{n}}2\unicode[STIX]{x03C0}r_{n}w\,\text{d}r_{n}=\unicode[STIX]{x03C0}\left(\frac{\unicode[STIX]{x1D6FF}}{2}\right)^{2}2\unicode[STIX]{x03C0}r_{n}.\end{eqnarray}$$
Evaluating the integral in (4.15), after substituting for
$w$
from (4.14), and simplifying, we get
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}=\sqrt{\frac{r_{n}^{3}}{2\unicode[STIX]{x03C0}r_{d}}}.\end{eqnarray}$$
From scaling arguments, Eggers, Lister & Stone (Reference Eggers, Lister and Stone1999) obtained the same relation, without the prefactor, for drop coalescence.
The neck retraction velocity
$u_{r}$
in (4.10) is a resultant of the balance of inertia
$\unicode[STIX]{x1D70C}_{d}u_{r}^{2}/2$
and surface tension force
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/r_{n}$
to give
$$\begin{eqnarray}u_{r}=c_{3}\sqrt{\frac{2\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70C}_{d}r_{n}}},\end{eqnarray}$$
where
$c_{3}$
is a constant prefactor, whose value is chosen later to obtain the limiting value of
$G$
as
$Bo_{d}\rightarrow 0$
. Substituting (4.11), (4.16) and (4.17) into (4.10) and noting that
$r_{n}/r_{d}\approx \unicode[STIX]{x1D703}$
for small
$\unicode[STIX]{x1D703}$
in figure 8, we get
$$\begin{eqnarray}G\approx c_{4}\sqrt{\frac{\unicode[STIX]{x1D703}^{4}}{1+Bo_{d}}},\end{eqnarray}$$
where
$c_{4}=0.65c_{3}$
. To eliminate
$\unicode[STIX]{x1D703}$
from (4.18), we need one more relation of
$G$
in terms of
$\unicode[STIX]{x1D703}$
, which can be obtained as follows. From the geometry of figure 8,
$$\begin{eqnarray}G\approx {\textstyle \frac{1}{2}}\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}r_{n}^{2}/{\textstyle \frac{4}{3}}\unicode[STIX]{x03C0}r_{d}^{3}.\end{eqnarray}$$
Replacing
$\unicode[STIX]{x1D6FF}$
in (4.19) from (4.16) and noting that
$r_{n}/r_{d}\approx \unicode[STIX]{x1D703}$
for small
$\unicode[STIX]{x1D703}$
, we get
$$\begin{eqnarray}G\approx {\textstyle \frac{3}{20}}\unicode[STIX]{x1D703}^{7/2}.\end{eqnarray}$$
Replacing
$\unicode[STIX]{x1D703}$
in (4.18) in terms of
$G$
from (4.20) results in
$$\begin{eqnarray}G\approx \frac{1}{2(1+Bo_{d})^{7/6}},\end{eqnarray}$$
where we have chosen the prefactor
$c_{3}=0.39$
so as to get
$G=0.5$
when
$Bo_{d}\rightarrow 0$
, as found by Chen et al. (Reference Chen, Mandre and Feng2006).
4.4
$Bo_{d}$
dependence and validation
The scaling of the dimensionless film radius (4.7) and the dimensionless film velocity (4.9) can now be expressed in terms of the drop Bond number (
$Bo_{d}$
) by writing
$G$
in these equations in terms of
$Bo_{d}$
using (4.21). By doing such a substitution, we obtain
$$\begin{eqnarray}fr_{f}^{\ast }={t_{\unicode[STIX]{x1D707}d}^{\ast }}^{1/4}\end{eqnarray}$$
and
$$\begin{eqnarray}4f^{4}Ca_{d}={r_{f}^{\ast }}^{-3},\end{eqnarray}$$
where the function
$$\begin{eqnarray}f(Bo_{d})=\frac{3^{1/4}}{2}(1+Bo_{d})^{7/24}.\end{eqnarray}$$
Since
$r_{f}^{\ast }$
in (4.23) is given by (4.22), (4.23) can also be rewritten in terms of
$t_{\unicode[STIX]{x1D707}d}^{\ast }$
, so as to obtain a decreasing dependence of dimensionless film velocity on time in the form
$4fCa_{d}={t_{\unicode[STIX]{x1D707}d}^{\ast }}^{-3/4}$
. Equations (4.22) and (4.23) are the proposed scalings that are expected to capture the dependence of spreading radii and velocities on time, property ratios between the drop and the liquid layer, and the initial drop radius; we now verify these relations with our experimental data shown in figure 4.
Figure 9. Variation of the dimensionless film radius with the dimensionless time. The symbols are as in figure 4.
Figure 10. Variation of the dimensionless film velocity with dimensionless film radius. The symbols are as in figure 4.
Figure 9 shows the variation of the dimensionless spreading radius
$r_{f}^{\ast }$
, scaled by the function
$f$
, with the dimensionless time
$t_{\unicode[STIX]{x1D707}d}^{\ast }$
, plotted using the data shown in figure 4 for different
$C_{e}$
,
$r_{d}$
and
$h_{l}$
. The part of the data that shows an increasing film radius collapses fairly well onto
$$\begin{eqnarray}fr_{f}^{\ast }=0.83{t_{\unicode[STIX]{x1D707}d}^{\ast }}^{1/4},\end{eqnarray}$$
shown by the dashed line in figure 9, the prefactor being close to the expected value of 1 from (4.22). The variation of the dimensionless film expansion velocity
$Ca_{d}$
, scaled by
$4f^{4}$
, with the dimensionless spreading radius
$r_{f}^{\ast }$
is shown in figure 10. Similar to that in figure 9, the data collapse fairly well onto
$$\begin{eqnarray}4f^{4}Ca_{d}=0.5{r_{f}^{\ast }}^{-3}.\end{eqnarray}$$
The data show a
$-3$
power-law exponent except for a slight deviation at small
$r_{f}^{\ast }$
. This deviation is expected to be due to the non-negligible inertial effects in film spreading for small
$r_{f}$
when the film spreads very fast (see figure 5) so that
$We_{f}$
becomes close to one, as seen in figure 7. The present analysis neglected the inertial effects in film spreading and is only valid when
$We_{f}<1$
. Further, the present analysis assumed that
$r_{d}\ll r_{f}$
; this assumption also breaks down at small
$r_{f}$
when the film radius is of the same size as the drop radius. The reason for the prefactors in (4.25) and (4.26) to be slightly less than 1 could be the slight inaccuracy of the prefactors assumed in the scaling relationships used in the derivation of (4.22) and (4.23).
5 Conclusions and discussion
The primary result of this paper is the scaling law developed for the spreading radius
$r_{f}$
of a film, spreading from a buoyant, miscible drop, when the viscous dissipation in the spreading film is the dominant resistance to surface-tension-driven spreading. The proposed scaling law is
$$\begin{eqnarray}r_{f}\sim \left(\frac{t\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}_{d}}r_{d}^{3}\right)^{1/4}\frac{1}{f},\end{eqnarray}$$
a function of two length scales
$t\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{d}$
and the initial drop radius
$r_{d}$
modified by a dimensionless function
$f(Bo_{d})$
, given by (4.24). The above scaling has the correct
$t^{1/4}$
time dependence shown by experiments in figure 4. The scaling law (5.1) also captures the dependence of
$r_{f}$
on drop properties as well as that on
$r_{d}$
since it collapses all the data with different ethanol concentrations in the drop (
$C_{e}$
) and
$r_{d}$
onto a single dimensionless curve
$fr_{f}^{\ast }=0.83\,{t_{\unicode[STIX]{x1D707}d}^{\ast }}^{1/4}$
(4.25), where the dimensionless time is
$t_{\unicode[STIX]{x1D707}d}^{\ast }=t/t_{\unicode[STIX]{x1D707}d}$
, with the characteristic time of spreading
$t_{\unicode[STIX]{x1D707}d}=\unicode[STIX]{x1D707}_{d}r_{d}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
, and the dimensionless film radius is
$r_{f}^{\ast }=r_{f}/r_{d}$
.
The dependence of
$r_{f}$
on drop properties and
$r_{d}$
is complex since
$f$
is a function of the drop Bond number
$Bo_{d}$
; however, the effects of property variations on
$r_{f}$
could be qualitatively understood by examining (5.1) and (4.24). As was shown in figure 4,
$r_{f}$
increases at any time
$t$
with increasing concentration of ethanol in the drop. Such an increase is captured by the positive power-law dependence of
$r_{f}$
on
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
in (5.1); increase in
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
increases the spreading force, resulting in larger
$r_{f}$
at any time. Increasing the concentration of ethanol in the drop shows a non-monotonic variation in the viscosity of the drop, with
$\unicode[STIX]{x1D707}_{d}$
increasing till 40 % concentration and then decreasing with further increase of concentration (see table 1). A decrease in the viscosity of the drop
$\unicode[STIX]{x1D707}_{d}$
, and hence that of the spreading film, should speed up the spreading since
$\unicode[STIX]{x1D707}_{d}$
appears with a negative power in (5.1); such an outcome is expected due to the reduced viscous dissipation in the film with reduced
$\unicode[STIX]{x1D707}_{d}$
. The novelty of (5.1) is that, by explicitly considering the coalescence dynamics, the dependence of
$r_{f}$
on
$r_{d}$
was included in the scaling law. This dependence of
$r_{f}$
on
$r_{d}$
is non-monotonic, as seen in figure 4. The scaling (5.1) captures this non-monotonic variation since the functional dependence of
$r_{f}$
on
$r_{d}$
shown by (5.1) is non-monotonic, thereby bringing all the different
$r_{d}$
data onto the line (4.25) in figure 9.
The velocity of the film spreading scaled as
$$\begin{eqnarray}u_{f}\sim \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}_{d}}\left(\frac{r_{d}}{r_{f}}\right)^{3}\frac{1}{4f^{4}},\end{eqnarray}$$
showing that the characteristic velocity of spreading is
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{d}$
, with the spreading velocity decreasing with increasing spreading radius as
$r_{f}^{-3}$
. This scaling also collapsed all the velocity data obtained with different drop concentrations and
$r_{d}$
onto a single line
$4f^{4}Ca_{d}=0.5{r_{f}^{\ast }}^{-3}$
(4.26), as shown in figure 10, implying that the dependence of
$u_{f}$
on drop properties and
$r_{d}$
was adequately captured by the scaling law (5.2). Owing to (5.2) and (5.1) it is also obvious that the spreading velocity showed a decrease with time as
$t^{-3/4}$
, before the film starts to retract at a specific value of
$r_{f}$
.
These conclusions were verified with measurements of spreading radii obtained by the top-view visualisations of ethanol–water drops spreading over a water layer, whose height was much larger than the drop radii. The visualisations showed that the spreading and eventual dissolution of the drop has many distinct stages. In the first stage, a capillary wave propagates from the point of contact of the drop with the water layer followed by an expanding circular film of ethanol–water mixture (figure 2 a–c). At some specific radius of spreading, the expanding, continuous film becomes unstable at its periphery, resulting in outward-propagating fingers, while the film continues its expansion (figure 2 d). The major part of the drop remains at the centre of the film, which expands with decreasing velocity. The film starts to retract after some time, the drop thins and develops holes in it and eventually mixes with water and disappears (figure 2 g–i). From the side-view visualisations, it became clear that the film originates from an initial fraction of the drop that is pulled apart in the neck expansion during coalescence of the drop with the water layer.
Based on these observations, the scaling law (5.1) was developed by combining the mass and momentum balance of the spreading film with the mass balance between the drop and the film, in which the initial fraction of the drop
$G$
appears. By calculating the flux of drop mass during the time of coalescence when the neck region retracts with capillary velocity, along with geometrical constraints,
$G\approx 1/(2(1+Bo_{d})^{7/6})$
was obtained as a function of the drop Bond number (4.21). The dependence of
$r_{f}$
on
$r_{d}$
, which, as we saw, had a non-monotonic dependence, was thus explicitly brought into the scaling law of
$r_{f}$
; the resulting scaling law (5.1) then captured the non-monotonic dependence of
$r_{f}$
on
$r_{d}$
. These results were obtained for the case of film Weber number less than one, so that inertial effects were neglected in the spreading of the film. The analysis was also restricted to the values of viscosity ratios
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D707}_{l}/\unicode[STIX]{x1D707}_{d}<1$
so that viscous dissipation inside the film dominates over that in the underlying liquid layer. Further, the value of density ratio
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D70C}_{l}/\unicode[STIX]{x1D70C}_{d}>1$
was also needed so that the drop remains at the free surface while the film spreads.
Even though the developed scaling law satisfactorily describes the dependence of film expansion on time, drop radius and drop properties, there are still many unresolved issues in the phenomena shown by the spreading and eventual mixing of a drop on a liquid surface. The physics behind the retraction process of the film is still not clear. The same is the case about the point of transition from spreading to retraction, which in the present scaling occurs at different values of
$t_{\unicode[STIX]{x1D707}d}^{\ast }$
(see figure 9). An effort to collapse the expansion, transition from expansion to retraction, and the retraction onto a single curve, even though difficult, needs to be attempted. The physics behind the instability and the development of fingers at the periphery of a surface-tension-driven expanding film over a deep liquid layer is not clear; the corresponding thin-layer case has been explored by many researchers (see Warner, Craster & Matar Reference Warner, Craster and Matar2004, and references therein), without yet achieving a complete understanding. The scaling in the large-Weber-number situation of the present case, which would presumably occur when the film viscosity is smaller than the liquid layer viscosity, with both the viscosities being low, is also still unexplored.
Acknowledgements
We gratefully acknowledge the help provided by Professor B. S. Murthy, Nanotechnology Lab, IIT Madras, for particle characterisation, Dr K. Anand, Flow Characterisation Lab, IIT Madras, for the surface tension measurements, and Professor M. Panchagnula, Multiphase flow physics lab, IIT Madras, for the use of high-speed photography. The equipment used in this study was funded by the grant SR/FST/ETII-017/2003 from DST, Government of India.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.562.
Appendix A. Effect of particle concentration on surface tension
Figure 11. Variation of surface tension of water with surface density of aluminium particles: ○, by Wilhelmy plate; ▫, by Du Nouy ring.
Aluminium particles are surface-active and hence they change the surface tension of water. The surface tension of water laden with aluminium particles was measured for different particle concentrations. The measurements were performed using a Sigma 700/701 force tensiometer (Biolin Scientific) using Wilhelmy plate and Du Nouy ring probes. We used particle surface densities from 0 to
$78~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
(i.e. 0–100 ppm) spanning the surface density of
$77~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
(i.e. 163 ppm) of particles used in the experiments. The relations between surface densities and ppm are different in visualisations and surface tension measurements since the volume-to-area ratio of the containers were different. Figure 11 shows that the mean surface tension, calculated from 10 repeated measurements, varies nonlinearly, with a decrease till
$15~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
followed by an increase till
$30~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
. The values again drop between
$30$
and
$45~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
and then stay approximately in the range
$50{-}55~\text{mN}~\text{m}^{-1}$
for
$45{-}80~\unicode[STIX]{x03BC}\text{g}~\text{cm}^{-2}$
. Similar decreasing and increasing values of surface tension with increasing particle concentrations of titanium oxide particles have been observed earlier by Dong & Johnson (Reference Dong and Johnson2003). The initial decrease is expected to be due to decrease in free energy and the later increase to be due to capillary forces between particles (Dong & Johnson Reference Dong and Johnson2003). Owing to this non-monotonic variation, we then measured the surface tension of water with Al particles at the concentration used in visualisations many times and have now used the measured mean value of
$54~\text{mN}~\text{m}^{-1}$
in all our calculations.
Appendix B. Error in
$r_{f}$
,
$t$
and
$u_{f}$
An estimate of the error in the measurement of
$r_{f}$
, based on the number of pixels needed to cover the interface between the particle and the particle-free regions, was 4 pixels. This number of pixels occupy a region of 0.3 mm at the resolution of our imaging. Hence the maximum error possible, corresponding to our lowest
$r_{f}$
, is 7 %.
In addition to these measurement errors of
$r_{f}$
, there is also the variation of
$r_{f}$
azimuthally due to the deviation of the film periphery from a circle. The range of this deviation increases as the film expands with time since instabilities start to develop at the periphery as the film expands. The range of this variation of
$r_{f}$
is now shown in figure 4 by showing the maximum and minimum values of
$r_{f}$
from the three measurements at the three azimuthal locations on the film. This range is less than the vertical shift in
$r_{f}$
due to the change in
$C_{e}$
and
$r_{d}$
.
The error in time measurements is due to (i) the error in frame rate as well as (ii) the error in the initial time of contact of the drop with the water surface. The error in the time of each image due to the error in f.p.s. is negligible compared to the error in the initial time estimation. The actual instance of initial contact of the drop with the substrate could be just after the previous frame or just before the subsequent frame, from the frame that we identify as the frame at which contact occurs. Therefore, the error in the initial time of contact is of the order of
$\pm 1/\text{f.p.s.}=\pm 0.025~\text{s}$
. This error in the initial time implies that the
$r_{f}$
versus
$t$
curves could shift by
$2/\text{f.p.s.}$
horizontally; we show this error in the initial time as the horizontal error bars in figure 4.
Since
$u_{f}$
is calculated from
$$\begin{eqnarray}u_{f}=ABt^{B-1},\end{eqnarray}$$
as the derivative of the power-law fit
$$\begin{eqnarray}r_{f}=At^{B},\end{eqnarray}$$
$\unicode[STIX]{x1D6FF}u_{f}$
, the error in
$u_{f}$
, is due to the error in the curve fit and that in
$t$
. The error in the curve fit is estimated by calculating the maximum and minimum values of
$A$
and
$B$
that will fit
$r_{f}\pm \unicode[STIX]{x1D6FF}r_{f}$
, where
$\unicode[STIX]{x1D6FF}r_{f}$
is the known error of 0.3 mm in
$r_{f}$
. From (B 1),
$$\begin{eqnarray}|\unicode[STIX]{x1D6FF}u_{f}|=\left|\frac{\text{d}u_{f}}{\text{d}A}\unicode[STIX]{x1D6FF}A\right|+\left|\frac{\text{d}u_{f}}{\text{d}B}\unicode[STIX]{x1D6FF}B\right|+\left|\frac{\text{d}u_{f}}{\text{d}t}\unicode[STIX]{x1D6FF}t\right|,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}A,\unicode[STIX]{x1D6FF}B$
and
$\unicode[STIX]{x1D6FF}t$
are the errors in
$A,B$
and
$t$
. By evaluating the derivatives in (B 3) from (B 1) and rewriting in terms of
$u_{f}$
, we get
$$\begin{eqnarray}\left|\frac{\unicode[STIX]{x1D6FF}u_{f}}{u_{f}}\right|=\left|\frac{\unicode[STIX]{x1D6FF}A}{A}\right|+\left|\frac{\unicode[STIX]{x1D6FF}B}{B}\right|+\left|(B-1)\frac{\unicode[STIX]{x1D6FF}t}{t}\right|+|\unicode[STIX]{x1D6FF}B\ln t|.\end{eqnarray}$$
For the case of
$C_{e}=100\,\%$
and
$r_{d}=0.97~\text{mm}$
, we have
$A=15.09$
,
$B=0.27$
,
$\unicode[STIX]{x1D6FF}A=0.09$
,
$\unicode[STIX]{x1D6FF}B=0.005$
and
$\unicode[STIX]{x1D6FF}t=0.025~\text{s}$
. Using these values in (B 4) at
$t=0.01~\text{s}$
and
$u_{f}=100~\text{mm}~\text{s}^{-1}$
, we obtain 12 % error in
$u_{f}$
. This value and the error values at two other later times are shown in figure 5.
Appendix C. Evaporation velocity
The horizontal velocity of evaporation from a horizontal film, as given by Lock (Reference Lock1996), is
$$\begin{eqnarray}U_{e}=\frac{\unicode[STIX]{x1D6FC}_{v}}{L}(Ra^{2}Ja^{3})^{1/5},\end{eqnarray}$$
where the Jacob number,
$Ja=c_{pv}\unicode[STIX]{x0394}T/\unicode[STIX]{x1D706}_{v}$
, is the ratio of sensible heat to latent heat, the Rayleigh number,
$Ra=g(\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{v})L^{3}/\unicode[STIX]{x1D708}_{v}\unicode[STIX]{x1D6FC}_{v}$
, is the ratio of buoyancy to dissipative effects, with the subscript
$v$
denoting property values of the vapour,
$L$
is the length of the film,
$\unicode[STIX]{x1D706}$
is the latent heat of vaporisation,
$\unicode[STIX]{x0394}T$
and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
are the temperature and density differences between the liquid surface and the ambient,
$c_{p}$
is the specific heat at constant pressure,
$\unicode[STIX]{x1D6FC}$
is the thermal diffusivity,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D70C}$
is the density. By continuity, the vertical evaporation velocity is then
$$\begin{eqnarray}V_{e}=U_{e}\left(\frac{Ja}{Ra}\right)^{1/4}=\frac{\unicode[STIX]{x1D6FC}_{v}}{L}(Ra^{3}Ja^{17})^{1/20}.\end{eqnarray}$$
Using the following properties of ethanol vapour,
$c_{pv}=1400~\text{J}~\text{kg}^{-1}~\text{K}^{-1}$
,
$\unicode[STIX]{x1D708}_{v}=0.835\times 10^{-5}~\text{N}~\text{s}~\text{m}^{-2}$
,
$\unicode[STIX]{x1D70C}_{v}=0.085~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D706}_{v}=1025\times 10^{3}~\text{J}~\text{kg}^{-1}$
,
$\unicode[STIX]{x1D6FD}=750\times 10^{-6}~\text{K}^{-1}$
,
$\unicode[STIX]{x0394}T\approx 1~\text{K}$
,
$\unicode[STIX]{x1D6FC}_{v}=0.00011~\text{m}^{2}~\text{s}^{-1}$
and the mean length of the film
$L=5~\text{mm}$
, we obtain
$$\begin{eqnarray}V_{e}\sim 4\times 10^{-5}~\text{m}~\text{s}^{-1},\end{eqnarray}$$
which is three orders smaller than
$u_{f}$
.
Appendix D. Mass and momentum balance
Consider a control volume, enclosing the drop and the expanding film shown in figure 6, which deforms and expands with the film. Mass balance implies that
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x03C0}(r_{f}^{2}-r_{d}^{2})h_{f}\unicode[STIX]{x1D70C}_{f})+\frac{\text{d}}{\text{d}t}\left(\frac{4}{3}\unicode[STIX]{x03C0}r_{d}^{3}\unicode[STIX]{x1D70C}_{d}\right)=0.\end{eqnarray}$$
Expanding the derivative, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x03C0}r_{f}^{2}h_{f}\frac{\text{d}\unicode[STIX]{x1D70C}_{f}}{\text{d}t}-\unicode[STIX]{x03C0}r_{d}^{2}h_{f}\frac{\text{d}\unicode[STIX]{x1D70C}_{f}}{\text{d}t}+2\unicode[STIX]{x03C0}r_{f}h_{f}\unicode[STIX]{x1D70C}_{f}u_{f}+\unicode[STIX]{x03C0}r_{f}^{2}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}h_{f}}{\text{d}t}-2\unicode[STIX]{x03C0}r_{d}h_{f}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}r_{d}}{\text{d}t}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x03C0}r_{d}^{2}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}h_{f}}{\text{d}t}+\frac{4}{3}\unicode[STIX]{x03C0}r_{d}^{3}\frac{\text{d}\unicode[STIX]{x1D70C}_{d}}{\text{d}t}+4\unicode[STIX]{x03C0}r_{d}^{2}\unicode[STIX]{x1D70C}_{d}\frac{\text{d}r_{d}}{\text{d}t}=0.\end{eqnarray}$$
When
$$\begin{eqnarray}\text{d}\unicode[STIX]{x1D70C}_{f}/\text{d}t\simeq 0,\quad \text{d}\unicode[STIX]{x1D70C}_{d}/\text{d}t\simeq 0,\quad \text{d}r_{d}/\text{d}t\simeq 0\quad \text{and}\quad r_{d}\ll r_{f},\end{eqnarray}$$
equation (D 2) reduces to
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}h_{f}\unicode[STIX]{x1D70C}_{f}u_{f}+\unicode[STIX]{x03C0}r_{f}^{2}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}h_{f}}{\text{d}t}=0.\end{eqnarray}$$
Similarly, momentum balance over the same control volume implies that
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x03C0}r_{f}^{2}h_{f}\unicode[STIX]{x1D70C}_{f}u_{f})+\frac{\text{d}}{\text{d}t}\left(\frac{4}{3}\unicode[STIX]{x03C0}r_{d}^{3}\unicode[STIX]{x1D70C}_{d}u_{d}\right)=2\unicode[STIX]{x03C0}r_{f}(\unicode[STIX]{x1D70E}_{l}-\unicode[STIX]{x1D70E}_{f})-\unicode[STIX]{x1D707}_{f}\frac{u_{f}}{h_{f}}\unicode[STIX]{x03C0}r_{f}^{2},\end{eqnarray}$$
where
$u_{d}$
is the velocity inside the drop. Expanding the derivatives in (D 5) and applying (D 3), along with
$\text{d}u_{d}/\text{d}t\simeq 0$
, we get
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}h_{f}u_{f}^{2}+\unicode[STIX]{x03C0}r_{f}^{2}h_{f}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}u_{f}}{\text{d}t}+\unicode[STIX]{x03C0}r_{f}^{2}u_{f}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}h_{f}}{\text{d}t}=2\unicode[STIX]{x03C0}r_{f}(\unicode[STIX]{x1D70E}_{l}-\unicode[STIX]{x1D70E}_{f})-\unicode[STIX]{x1D707}_{f}\frac{u_{f}}{h_{f}}\unicode[STIX]{x03C0}r_{f}^{2}.\end{eqnarray}$$
From (D 4), the sum of the first and third terms in (D 6) is zero, resulting in
$$\begin{eqnarray}2\unicode[STIX]{x03C0}r_{f}(\unicode[STIX]{x1D70E}_{l}-\unicode[STIX]{x1D70E}_{f})-\unicode[STIX]{x1D707}_{f}\frac{u_{f}}{h_{f}}\unicode[STIX]{x03C0}r_{f}^{2}=\unicode[STIX]{x03C0}r_{f}^{2}h_{f}\unicode[STIX]{x1D70C}_{f}\frac{\text{d}u_{f}}{\text{d}t}.\end{eqnarray}$$
