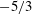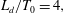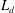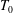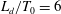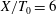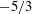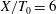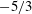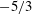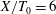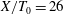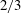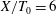1 Introduction
The flow past a slender cylinder (either circular or square one) is one of the most important free shear flows (Williamson Reference Williamson1996). It has long been known that Kármán’s vortex street can be generated if the Reynolds number is larger than a certain value. Compared with a single wake, the flows downstream of two or more slender bluff bodies are much more complicated (Kolář, Lyn & Rodi Reference Kolář, Lyn and Rodi1997; Zhou et al. Reference Zhou, Wang, Xu and Jin2001; Alam, Zhou & Wang Reference Alam, Zhou and Wang2011; Alam & Zhou Reference Alam and Zhou2013; Alam, Bai & Zhou Reference Alam, Bai and Zhou2016), in which the interactions of vortex streets are involved. Such flows can be encountered in a wide variety of practical engineering situations (e.g. heat exchangers, offshore platforms, bridge piers, wind farms). Therefore, the flow behind two side-by-side cylinders is a subject of great practical importance.
The flow behind two square cylinders is largely decided by the gap ratio
![]() $L_{d}/T_{0}$
, where
$L_{d}/T_{0}$
, where
![]() $L_{d}$
is the separation distance between two cylinders and
$L_{d}$
is the separation distance between two cylinders and
![]() $T_{0}$
is the cylinder thickness. Previous experimental studies (Alam et al.
Reference Alam, Zhou and Wang2011; Alam & Zhou Reference Alam and Zhou2013) suggested that for the dual-wake flows with different gap ratios
$T_{0}$
is the cylinder thickness. Previous experimental studies (Alam et al.
Reference Alam, Zhou and Wang2011; Alam & Zhou Reference Alam and Zhou2013) suggested that for the dual-wake flows with different gap ratios
![]() $L_{d}/T_{0}$
, different flow patterns can be identified. Grid-generated turbulence, in the upstream of which wake interactions occur, has been intensively investigated over the past several decades. By using the scaling law of a single wake (Townsend Reference Townsend1956), Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) introduced the wake-interaction length scale with
$L_{d}/T_{0}$
, different flow patterns can be identified. Grid-generated turbulence, in the upstream of which wake interactions occur, has been intensively investigated over the past several decades. By using the scaling law of a single wake (Townsend Reference Townsend1956), Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) introduced the wake-interaction length scale with
![]() $X_{\ast }=L_{d}^{2}/T_{0}$
to normalize the streamwise distance from the grid element
$X_{\ast }=L_{d}^{2}/T_{0}$
to normalize the streamwise distance from the grid element
![]() $X$
. It was demonstrated that when the downstream distance
$X$
. It was demonstrated that when the downstream distance
![]() $X$
is normalized by
$X$
is normalized by
![]() $X_{\ast }$
, various centreline statistics of the turbulence behind grid elements with different mesh sizes can be collapsed together (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Nagata et al.
Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013; Nagata et al.
Reference Nagata, Saiki, Sakai, Ito and Iwano2017). Note that immediately behind a grid element, four wakes are generated and they interact with their neighbouring wakes. Compared with the grid-generated turbulence, the turbulent flow behind two side-by-side cylinders is a more fundamental problem related to wake interactions. Therefore the simplest assessment of the wake-interaction length scale can be achieved by investigating the dual-wake flow behind two square cylinders.
$X_{\ast }$
, various centreline statistics of the turbulence behind grid elements with different mesh sizes can be collapsed together (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Nagata et al.
Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013; Nagata et al.
Reference Nagata, Saiki, Sakai, Ito and Iwano2017). Note that immediately behind a grid element, four wakes are generated and they interact with their neighbouring wakes. Compared with the grid-generated turbulence, the turbulent flow behind two side-by-side cylinders is a more fundamental problem related to wake interactions. Therefore the simplest assessment of the wake-interaction length scale can be achieved by investigating the dual-wake flow behind two square cylinders.
The turbulent flow in the immediate vicinity of a grid element has recently received considerable attention (Hurst & Vassilicos Reference Hurst and Vassilicos2007, Valente & Vassilicos Reference Valente and Vassilicos2011, Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2014; Zhou et al.
Reference Zhou, Nagata, Sakai, Ito and Hayase2015, Reference Zhou, Nagata, Sakai, Ito and Hayase2016a
). One interesting finding, which has been extensively reported (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010, Nagata et al.
Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013; Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
,Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase
b
, Reference Zhou, Nagata, Sakai, Ito and Hayase2016b
; Laizet, Nedić & Vassilicos Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
; Paul, Papadakis & Vassilicos Reference Paul, Papadakis and Vassilicos2017) is that turbulent flow in the lee of the grid can be highly intermittent with non-Gaussian distributions of the velocity fluctuations. The profile of the probability density function (PDF) of the streamwise velocity fluctuations
![]() $u^{\prime }$
is much wider than the corresponding Gaussian distribution, indicating a large probability of occurrence of the extreme events (in some papers (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
) also called intense events). Moreover, the skewness of
$u^{\prime }$
is much wider than the corresponding Gaussian distribution, indicating a large probability of occurrence of the extreme events (in some papers (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
) also called intense events). Moreover, the skewness of
![]() $u^{\prime }$
in the upstream region is negative, revealing that the PDF profiles are negatively skewed (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017). A less noticed observation (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Zhou et al.
Reference Zhou, Nagata, Sakai, Ito and Hayase2016b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017) is that the extreme events appear to be closely related to the formation of the
$u^{\prime }$
in the upstream region is negative, revealing that the PDF profiles are negatively skewed (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017). A less noticed observation (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Zhou et al.
Reference Zhou, Nagata, Sakai, Ito and Hayase2016b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017) is that the extreme events appear to be closely related to the formation of the
![]() $-5/3$
scaling power law.
$-5/3$
scaling power law.
It is well known that a class of flows called ‘free shear flows’ including turbulent jets and wakes share some important turbulence characteristics, for example, self-similarity of various one-point statistics and the existence of very thin/sharp layers separating the free shear flows from their surrounding non-turbulent ambient flows (da Silva et al. Reference da Silva, Hunt, Eames and Westerweel2014). Interestingly, a recent numerical study by Zhou et al. (Reference Zhou, Nagata, Sakai and Watanabe2018) demonstrated that the extreme events can also be found in the merging regions of dual-parallel jet flows. However, the extreme events found in the merging region are quite different from those in the grid-generated turbulence. The corresponding probability distribution in dual-plane jet flows is positively skewed, not the contrary.
In light of the above mentioned publications, the present paper tries to find answers to the following two questions:
(1) In both grid-generated turbulence and dual-plane jet flows, extreme events can be found. The first question that naturally arises is whether the extreme events can also be found in the flow behind two square cylinders with different gap ratios? If the answer is yes, then what physical mechanisms are responsible for the extreme events? Moreover, it is of equal importance to clarify the characteristics of the extreme events.
(2) Previous studies suggested that the extreme events appear to be closely related to the appearance of the
![]() $-5/3$
scaling power law. A question then arises concerning the intimate relationship between the occurrence of the extreme events and the well-defined
$-5/3$
scaling power law. A question then arises concerning the intimate relationship between the occurrence of the extreme events and the well-defined
![]() $-5/3$
energy spectra. More specifically, how do the extreme events contribute to the appearance of the
$-5/3$
energy spectra. More specifically, how do the extreme events contribute to the appearance of the
![]() $-5/3$
scaling law? The observation that the
$-5/3$
scaling law? The observation that the
![]() $-5/3$
scaling law can be found in the region where the extreme events occur is not in accord with Kolmogorov’s prediction. Note also that according to the Kolmogorov phenomenology, in the so-called ‘inertial subrange’ the second-order structure function in real space is expected to acquire a power law with an exponent close to
$-5/3$
scaling law can be found in the region where the extreme events occur is not in accord with Kolmogorov’s prediction. Note also that according to the Kolmogorov phenomenology, in the so-called ‘inertial subrange’ the second-order structure function in real space is expected to acquire a power law with an exponent close to
![]() $2/3$
when the corresponding
$2/3$
when the corresponding
![]() $-5/3$
energy spectrum can be identified. The characteristics of the second-order structure function in the flow region where the extreme events can be identified is consequently another interesting topic and is of particular importance.
$-5/3$
energy spectrum can be identified. The characteristics of the second-order structure function in the flow region where the extreme events can be identified is consequently another interesting topic and is of particular importance.
The organization of the rest of the paper is as follows. Section 2 presents the details about the simulation conditions and numerical method. In § 3, the discussion on the wake-interaction scale is given and the statistical results concerning the extreme events are presented. In § 4, the relationship between the extreme events and the
![]() $-5/3$
energy spectra is explored. The spatial evolution of the corresponding second-order structure function is also discussed. Finally, the main conclusions and remaining issues, which should be addressed in future, are listed in § 5.
$-5/3$
energy spectra is explored. The spatial evolution of the corresponding second-order structure function is also discussed. Finally, the main conclusions and remaining issues, which should be addressed in future, are listed in § 5.
2 Numerical details
We perform direct numerical simulations (DNSs) of the flow behind two side-by-side square cylinders with three different gap ratios, i.e.
![]() $L_{d}/T_{0}=4$
, 6 and 8. The details of the three cases are summarized in table 1. A schematic view of the computational domain is presented in figure 1 along with the coordinate system. Two identical parallel square cylinders are placed at the downstream streamwise location
$L_{d}/T_{0}=4$
, 6 and 8. The details of the three cases are summarized in table 1. A schematic view of the computational domain is presented in figure 1 along with the coordinate system. Two identical parallel square cylinders are placed at the downstream streamwise location
![]() $X_{bar}/T_{0}=8$
from the inlet. The inlet length
$X_{bar}/T_{0}=8$
from the inlet. The inlet length
![]() $X_{bar}$
is comparable to those in previous numerical investigations of grid-generated turbulence (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
; Paul, Papadakis & Vassilicos Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018). Note also that the blockage ratios are
$X_{bar}$
is comparable to those in previous numerical investigations of grid-generated turbulence (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
; Paul, Papadakis & Vassilicos Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018). Note also that the blockage ratios are
![]() $7.1\,\%$
,
$7.1\,\%$
,
![]() $6.7\,\%$
and
$6.7\,\%$
and
![]() $5.9\,\%$
, which are much smaller than those in previous studies (i.e.
$5.9\,\%$
, which are much smaller than those in previous studies (i.e.
![]() $19\,\%$
in Laizet et al. (Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
) and
$19\,\%$
in Laizet et al. (Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
) and
![]() $20\,\%$
in Paul et al. (Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018)). It might be worth mentioning that for the studies mentioned (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018), the numerical results are reported to be in good accord with the corresponding experimental results. Thus, our choice of
$20\,\%$
in Paul et al. (Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018)). It might be worth mentioning that for the studies mentioned (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015a
,Reference Laizet, Nedić and Vassilicos
b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017, Reference Paul, Papadakis and Vassilicos2018), the numerical results are reported to be in good accord with the corresponding experimental results. Thus, our choice of
![]() $X_{bar}$
is expected to be sufficiently large. The inlet Reynolds number
$X_{bar}$
is expected to be sufficiently large. The inlet Reynolds number
![]() $Re_{T_{0}}=U_{in}T_{0}/\unicode[STIX]{x1D708}$
, with
$Re_{T_{0}}=U_{in}T_{0}/\unicode[STIX]{x1D708}$
, with
![]() $\unicode[STIX]{x1D708}$
being viscosity, is 2500 for all three cases. A uniformly distributed velocity
$\unicode[STIX]{x1D708}$
being viscosity, is 2500 for all three cases. A uniformly distributed velocity
![]() $U_{in}$
is imposed at the inlet and a convective condition is applied at the outlet. The periodic boundary conditions are adopted in the
$U_{in}$
is imposed at the inlet and a convective condition is applied at the outlet. The periodic boundary conditions are adopted in the
![]() $Y$
and
$Y$
and
![]() $Z$
directions. The nodes are uniformly distributed in all three directions.
$Z$
directions. The nodes are uniformly distributed in all three directions.
Table 1. Geometric and numerical details.


Figure 1. (a) Schematic front view and (b) schematic side view of the computational domain.
The immersed boundary method (Parnaudeau et al.
Reference Parnaudeau, Carlier, Heitz and Lamballais2008) is adopted for the modelling of the two square cylinders. The massively parallel solver ‘Incompact3d’ (Laizet & Lamballais Reference Laizet and Lamballais2009; Laizet, Lamballais & Vassilicos Reference Laizet, Lamballais and Vassilicos2010; Laizet & Li Reference Laizet and Li2011), which is based on a Cartesian mesh, is used to solve the incompressible Navier–Stokes equations. The sixth-order central compact schemes proposed by Lele (Reference Lele1992) are used for the spatial discretion. Concerning the time advancement, the third-order Adams–Bashforth scheme is adopted with a time step
![]() $\unicode[STIX]{x0394}t=0.0045T_{0}/U_{in}$
and data are averaged over 200 000 time steps for all three cases. In the current DNS, the maximum Courant–Friedrichs–Levy number is 0.14. Refer to Laizet & Lamballais (Reference Laizet and Lamballais2009), Laizet et al. (Reference Laizet, Lamballais and Vassilicos2010) and Laizet & Li (Reference Laizet and Li2011) for a detailed description of the DNS code and the corresponding parallel strategy.
$\unicode[STIX]{x0394}t=0.0045T_{0}/U_{in}$
and data are averaged over 200 000 time steps for all three cases. In the current DNS, the maximum Courant–Friedrichs–Levy number is 0.14. Refer to Laizet & Lamballais (Reference Laizet and Lamballais2009), Laizet et al. (Reference Laizet, Lamballais and Vassilicos2010) and Laizet & Li (Reference Laizet and Li2011) for a detailed description of the DNS code and the corresponding parallel strategy.

Figure 2. (a) Vertical distribution of
![]() $U_{m}/U_{in}$
at a far downstream location (i.e.
$U_{m}/U_{in}$
at a far downstream location (i.e.
![]() $X/T_{0}=26$
) for all three cases. (b) Definition sketch of the quasi-half-width
$X/T_{0}=26$
) for all three cases. (b) Definition sketch of the quasi-half-width
![]() $b(x)$
. The red dashed line presents the centreline of the square cylinder. The mean streamwise velocity
$b(x)$
. The red dashed line presents the centreline of the square cylinder. The mean streamwise velocity
![]() $U_{min}$
and velocity deficit
$U_{min}$
and velocity deficit
![]() $U-U_{min}$
are marked in red. Only the top half of the whole domain is shown.
$U-U_{min}$
are marked in red. Only the top half of the whole domain is shown.
Redford, Castro & Coleman (Reference Redford, Castro and Coleman2012) demonstrated that to avoid significant contamination on the wake growth imposed by the boundary conditions, the smallest lateral domain size (
![]() $L_{Y}$
in our current study) is
$L_{Y}$
in our current study) is
![]() $L_{Y}\simeq 5.9\unicode[STIX]{x1D6FF}$
, where
$L_{Y}\simeq 5.9\unicode[STIX]{x1D6FF}$
, where
![]() $\unicode[STIX]{x1D6FF}$
is the wake half-width. As shown in figure 2(a), the two wakes have not yet fully merged together even at the most downstream location for all three cases. Thus, we could not directly use this criterion in our current study. Instead, we propose a quasi-half-width
$\unicode[STIX]{x1D6FF}$
is the wake half-width. As shown in figure 2(a), the two wakes have not yet fully merged together even at the most downstream location for all three cases. Thus, we could not directly use this criterion in our current study. Instead, we propose a quasi-half-width
![]() $b$
which is defined as the vertical distance from the centreline to the location where
$b$
which is defined as the vertical distance from the centreline to the location where
![]() $(U-U_{min})/U_{0}=1/2$
with
$(U-U_{min})/U_{0}=1/2$
with
![]() $U_{0}=(U_{c}-U_{min})$
being the quasi-velocity deficit (see figure 2
b). The ratios
$U_{0}=(U_{c}-U_{min})$
being the quasi-velocity deficit (see figure 2
b). The ratios
![]() $L_{Y}/b$
for the cases with
$L_{Y}/b$
for the cases with
![]() $L_{d}/T_{0}=4$
, 6 and 8 are 8.6, 6.7 and 5.9, respectively, at the furthest downstream location considered (i.e.
$L_{d}/T_{0}=4$
, 6 and 8 are 8.6, 6.7 and 5.9, respectively, at the furthest downstream location considered (i.e.
![]() $X/T_{0}=26$
). Even for the case with the largest separation distance, the lateral domain size satisfies the criterion proposed by Redford et al. (Reference Redford, Castro and Coleman2012) at the most downstream location. Therefore, the vertical size of our simulation domain is sufficiently large.
$X/T_{0}=26$
). Even for the case with the largest separation distance, the lateral domain size satisfies the criterion proposed by Redford et al. (Reference Redford, Castro and Coleman2012) at the most downstream location. Therefore, the vertical size of our simulation domain is sufficiently large.
The spatial resolutions
![]() $(\unicode[STIX]{x0394}X\unicode[STIX]{x0394}Y\unicode[STIX]{x0394}Z)^{1/3}$
with respect to the Kolmogorov microscale
$(\unicode[STIX]{x0394}X\unicode[STIX]{x0394}Y\unicode[STIX]{x0394}Z)^{1/3}$
with respect to the Kolmogorov microscale
![]() $\unicode[STIX]{x1D702}$
along the centreline are explored (not shown herein), where
$\unicode[STIX]{x1D702}$
along the centreline are explored (not shown herein), where
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
. Here,
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
. Here,
![]() $\unicode[STIX]{x1D700}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D634}_{ij}\unicode[STIX]{x1D634}_{ij}\rangle$
with the strain rate
$\unicode[STIX]{x1D700}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D634}_{ij}\unicode[STIX]{x1D634}_{ij}\rangle$
with the strain rate
![]() $\unicode[STIX]{x1D634}_{ij}$
being
$\unicode[STIX]{x1D634}_{ij}$
being
![]() $(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}^{\prime }/\unicode[STIX]{x2202}x_{i})/2$
, where the angled brackets
$(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}^{\prime }/\unicode[STIX]{x2202}x_{i})/2$
, where the angled brackets
![]() $\langle \rangle$
refer to an average over time
$\langle \rangle$
refer to an average over time
![]() $t$
and
$t$
and
![]() $Z$
. Laizet et al. (Reference Laizet, Nedić and Vassilicos2015a
) investigated the influence of the spatial resolution on the turbulent flow generated by a single square grid and demonstrated that a resolution of
$Z$
. Laizet et al. (Reference Laizet, Nedić and Vassilicos2015a
) investigated the influence of the spatial resolution on the turbulent flow generated by a single square grid and demonstrated that a resolution of
![]() $\unicode[STIX]{x1D6E5}\simeq 7\unicode[STIX]{x1D702}$
is fine enough to reproduce the first-, second-, third- and fourth-order momentums of one point velocities within an error of less than 10 %, whereas a higher resolution
$\unicode[STIX]{x1D6E5}\simeq 7\unicode[STIX]{x1D702}$
is fine enough to reproduce the first-, second-, third- and fourth-order momentums of one point velocities within an error of less than 10 %, whereas a higher resolution
![]() $\unicode[STIX]{x1D6E5}\simeq 5\unicode[STIX]{x1D702}$
is enough to guarantee the numerical results of the first- and second-order momentums to within an error of 5 %. We confirmed the lowest spatial resolution is found in the case with
$\unicode[STIX]{x1D6E5}\simeq 5\unicode[STIX]{x1D702}$
is enough to guarantee the numerical results of the first- and second-order momentums to within an error of 5 %. We confirmed the lowest spatial resolution is found in the case with
![]() $L_{d}/T_{0}=4$
. Even for this case, the worst resolution is still below
$L_{d}/T_{0}=4$
. Even for this case, the worst resolution is still below
![]() $5\unicode[STIX]{x1D702}$
. For the other two cases, the spatial resolution is always smaller than
$5\unicode[STIX]{x1D702}$
. For the other two cases, the spatial resolution is always smaller than
![]() $3.4\unicode[STIX]{x1D702}$
. Therefore, the current mesh setting is fine enough to capture the turbulence behaviour. Further evaluations of numerical strategies and parameters are presented in supplementary appendices A, B and C; supplementary materials are available online at https://doi.org/10.1017/jfm.2019.456.
$3.4\unicode[STIX]{x1D702}$
. Therefore, the current mesh setting is fine enough to capture the turbulence behaviour. Further evaluations of numerical strategies and parameters are presented in supplementary appendices A, B and C; supplementary materials are available online at https://doi.org/10.1017/jfm.2019.456.
3 Wake interaction and extreme events
This work is devoted to the study of the extreme events and the energy spectra (also the second-order structure function) in turbulent flows behind two side-by-side square cylinders. Before delving deep into the relationship between the extreme events and the
![]() $-5/3$
spectra, in this section we explored some related fundamental aspects of dual-wake flows (e.g. wake-interaction pattern, wake-interaction length scale, spatial evolution of various turbulence characteristics and formation mechanisms of the extreme events), which represent actually the first important objective of this work.
$-5/3$
spectra, in this section we explored some related fundamental aspects of dual-wake flows (e.g. wake-interaction pattern, wake-interaction length scale, spatial evolution of various turbulence characteristics and formation mechanisms of the extreme events), which represent actually the first important objective of this work.
3.1 Flow visualizations
In figure 3, the magnitudes of the normalized instantaneous vorticity
![]() $\unicode[STIX]{x1D6FA}/(U_{in}/T_{0})$
, where
$\unicode[STIX]{x1D6FA}/(U_{in}/T_{0})$
, where
![]() $\unicode[STIX]{x1D6FA}=(\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6FA}_{i})^{1/2}$
with
$\unicode[STIX]{x1D6FA}=(\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6FA}_{i})^{1/2}$
with
![]() $\unicode[STIX]{x1D6FA}_{i}=\unicode[STIX]{x1D700}_{ijk}\unicode[STIX]{x2202}u_{k}/\unicode[STIX]{x2202}x_{j}$
and
$\unicode[STIX]{x1D6FA}_{i}=\unicode[STIX]{x1D700}_{ijk}\unicode[STIX]{x2202}u_{k}/\unicode[STIX]{x2202}x_{j}$
and
![]() $\unicode[STIX]{x1D700}_{ijk}$
being the Levi-Civita symbol, are plotted for all three cases in the
$\unicode[STIX]{x1D700}_{ijk}$
being the Levi-Civita symbol, are plotted for all three cases in the
![]() $X{-}Y$
plane, which certainly provides insights into the wake-interaction patterns, at least to some extent. Figure 3 shows that perceptible oscillations can be found upstream of the cylinders. A similar spike-like behaviour was also reported in the DNSs of turbulent flow in Trias, Gorobets & Oliva (Reference Trias, Gorobets and Oliva2015), although in their paper a contour plot of the Kolmogorov length scale
$X{-}Y$
plane, which certainly provides insights into the wake-interaction patterns, at least to some extent. Figure 3 shows that perceptible oscillations can be found upstream of the cylinders. A similar spike-like behaviour was also reported in the DNSs of turbulent flow in Trias, Gorobets & Oliva (Reference Trias, Gorobets and Oliva2015), although in their paper a contour plot of the Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}$
is presented. Obviously, the Kolmogorov length scale is closely related to the velocity gradients. Thus, the existence of the oscillations is related to the fact that streamlines can be distorted upstream of the cylinders.
$\unicode[STIX]{x1D702}$
is presented. Obviously, the Kolmogorov length scale is closely related to the velocity gradients. Thus, the existence of the oscillations is related to the fact that streamlines can be distorted upstream of the cylinders.

Figure 3. Visualizations of the magnitude of instantaneous vorticity
![]() $\unicode[STIX]{x1D6FA}/(U_{in}/T_{0})$
in the
$\unicode[STIX]{x1D6FA}/(U_{in}/T_{0})$
in the
![]() $X{-}Y$
plane. (a,b)
$X{-}Y$
plane. (a,b)
![]() $L_{d}/T_{0}=4$
; (c,d)
$L_{d}/T_{0}=4$
; (c,d)
![]() $L_{d}/T_{0}=6$
; (e,f)
$L_{d}/T_{0}=6$
; (e,f)
![]() $L_{d}/T_{0}=8$
. All maps cover only part of the simulation domain and are shown on a linear scale. Note that to visualize the wake-interaction pattern, for each of the cases considered two randomly selected instantaneous flow fields are plotted.
$L_{d}/T_{0}=8$
. All maps cover only part of the simulation domain and are shown on a linear scale. Note that to visualize the wake-interaction pattern, for each of the cases considered two randomly selected instantaneous flow fields are plotted.
By and large, two different flow patterns can be observed depending on the separation distance between the cylinders. For the case with
![]() $L_{d}/T_{0}=4$
, the gap flow is weak and beyond
$L_{d}/T_{0}=4$
, the gap flow is weak and beyond
![]() $X/T_{0}=8$
only one large wake can be observed. For the cases with large gap ratios (
$X/T_{0}=8$
only one large wake can be observed. For the cases with large gap ratios (
![]() $L_{d}/T_{0}=6$
and
$L_{d}/T_{0}=6$
and
![]() $8$
), the gap flow is straight and the two vortex streets persist longer downstream. Thus, depending on the strength of the gap flow, the three simulation cases can be simply divided into two regimes: weak gap flow regime and robust gap flow regime. In the weak gap flow regime, two vortex streets merge into one, whilst in the robust gap flow regime with a large separation between the square cylinders, the two vortex streets do not merge. One could reasonably expect that the two vortex streets in the robust gap flow regime will finally merge in the further downstream region. However, in this study, owing to the limited streamwise length, the combination of the two wakes is not significant, as suggested by figure 2.
$8$
), the gap flow is straight and the two vortex streets persist longer downstream. Thus, depending on the strength of the gap flow, the three simulation cases can be simply divided into two regimes: weak gap flow regime and robust gap flow regime. In the weak gap flow regime, two vortex streets merge into one, whilst in the robust gap flow regime with a large separation between the square cylinders, the two vortex streets do not merge. One could reasonably expect that the two vortex streets in the robust gap flow regime will finally merge in the further downstream region. However, in this study, owing to the limited streamwise length, the combination of the two wakes is not significant, as suggested by figure 2.
3.2 Wake-interaction length scale
In the preceding subsection, two different flow patterns can be identified. In this subsection, we shall demonstrate that the turbulence characteristics in different regimes are quite different based on the wake-interaction length scale. As suggested by Townsend (Reference Townsend1956), the growth of the width of a plane turbulent wake follows
![]() $\unicode[STIX]{x1D6FF}\propto \sqrt{T_{0}X}$
. It is tempting to study the wake interactions behind two side-by-side square cylinders by using this scaling law, as has been done by Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010). For a given separation distance
$\unicode[STIX]{x1D6FF}\propto \sqrt{T_{0}X}$
. It is tempting to study the wake interactions behind two side-by-side square cylinders by using this scaling law, as has been done by Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010). For a given separation distance
![]() $L_{d}$
, the two wakes are expected to meet at a downstream streamwise location
$L_{d}$
, the two wakes are expected to meet at a downstream streamwise location
![]() $X_{\ast }$
where
$X_{\ast }$
where
![]() $\unicode[STIX]{x1D6FF}(X_{\ast })\propto \sqrt{T_{0}X}$
. Consequently, we can now derive the wake-interaction length scale as
$\unicode[STIX]{x1D6FF}(X_{\ast })\propto \sqrt{T_{0}X}$
. Consequently, we can now derive the wake-interaction length scale as
![]() $X_{\ast }=L_{d}^{2}/T_{0}$
. The original formula for the wake-interaction scale by Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) has been improved by Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) to assess the drag coefficient of the wake generators.
$X_{\ast }=L_{d}^{2}/T_{0}$
. The original formula for the wake-interaction scale by Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) has been improved by Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) to assess the drag coefficient of the wake generators.
The wake-interaction length scale
![]() $X_{\ast }$
indeed has been successfully applied to fractal-generated turbulence (see, for example, Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Nagata et al.
Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013). In fractal-generated turbulence, the interactions of four wakes are involved, which significantly increase the complexities. Recall that the wake-interaction length scale is based on the interactions of two wakes. To fully investigate the wake interactions with different gap ratios
$X_{\ast }$
indeed has been successfully applied to fractal-generated turbulence (see, for example, Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Nagata et al.
Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013). In fractal-generated turbulence, the interactions of four wakes are involved, which significantly increase the complexities. Recall that the wake-interaction length scale is based on the interactions of two wakes. To fully investigate the wake interactions with different gap ratios
![]() $L_{d}/T_{0}$
and assess whether the evolution of turbulent flow scales with the wake-interaction length scale, various centreline statistics are considered.
$L_{d}/T_{0}$
and assess whether the evolution of turbulent flow scales with the wake-interaction length scale, various centreline statistics are considered.

Figure 4. Streamwise evolution of the mean velocity
![]() $U_{c}$
along the centreline. (a) As a function of
$U_{c}$
along the centreline. (a) As a function of
![]() $X/T_{0}$
; (b) as a function of
$X/T_{0}$
; (b) as a function of
![]() $X/X_{\ast }$
.
$X/X_{\ast }$
.
In figure 4, we plot the streamwise evolution of the mean centreline velocity
![]() $U_{c}/U_{in}$
versus
$U_{c}/U_{in}$
versus
![]() $X/T_{0}$
(a) and
$X/T_{0}$
(a) and
![]() $X/X_{\ast }$
(b). Note that in previous studies concerning wake interactions (Zhou et al.
Reference Zhou, Wang, Xu and Jin2001; Alam et al.
Reference Alam, Zhou and Wang2011; Alam & Zhou Reference Alam and Zhou2013; Alam et al.
Reference Alam, Bai and Zhou2016; Zheng & Alam Reference Zheng and Alam2017), the size of the square cylinder, i.e.
$X/X_{\ast }$
(b). Note that in previous studies concerning wake interactions (Zhou et al.
Reference Zhou, Wang, Xu and Jin2001; Alam et al.
Reference Alam, Zhou and Wang2011; Alam & Zhou Reference Alam and Zhou2013; Alam et al.
Reference Alam, Bai and Zhou2016; Zheng & Alam Reference Zheng and Alam2017), the size of the square cylinder, i.e.
![]() $T_{0}$
, was extensively used as a scaling parameter for no particular reason. Thus, in this work, in addition to the wake-interaction length scale
$T_{0}$
, was extensively used as a scaling parameter for no particular reason. Thus, in this work, in addition to the wake-interaction length scale
![]() $X_{\ast }$
, the streamwise distance is also normalized by
$X_{\ast }$
, the streamwise distance is also normalized by
![]() $T_{0}$
. As one might expect, the value of
$T_{0}$
. As one might expect, the value of
![]() $U_{c}$
at
$U_{c}$
at
![]() $X/T_{0}=0$
decreases with the increase of the separation distance
$X/T_{0}=0$
decreases with the increase of the separation distance
![]() $L_{d}/T_{0}$
. However, at
$L_{d}/T_{0}$
. However, at
![]() $X/T_{0}=26$
, which is the most downstream location considered,
$X/T_{0}=26$
, which is the most downstream location considered,
![]() $U_{c}/U_{in}$
in the case with
$U_{c}/U_{in}$
in the case with
![]() $L_{d}/T_{0}=8$
becomes largest. When the streamwise distance
$L_{d}/T_{0}=8$
becomes largest. When the streamwise distance
![]() $X$
is normalized by
$X$
is normalized by
![]() $X_{\ast }$
, the two profiles corresponding to the cases with
$X_{\ast }$
, the two profiles corresponding to the cases with
![]() $L_{d}/T_{0}=6$
and 8 collapse onto a single curve at
$L_{d}/T_{0}=6$
and 8 collapse onto a single curve at
![]() $X/X_{\ast }>0.2$
. Thus, the largest
$X/X_{\ast }>0.2$
. Thus, the largest
![]() $U_{c}$
found in the case with
$U_{c}$
found in the case with
![]() $L_{d}/T_{0}=8$
at
$L_{d}/T_{0}=8$
at
![]() $X/T_{0}=26$
is attributed to its slower spatial evolution with respect to the coordinate distance
$X/T_{0}=26$
is attributed to its slower spatial evolution with respect to the coordinate distance
![]() $X$
. It is not surprising that the wake-interaction length scale cannot be applied to the case with
$X$
. It is not surprising that the wake-interaction length scale cannot be applied to the case with
![]() $L_{d}/T_{0}=4$
, since only one large vortex street can be identified in the downstream region, as shown in figure 3. The evolution of the streamwise root mean square (r.m.s.) velocity
$L_{d}/T_{0}=4$
, since only one large vortex street can be identified in the downstream region, as shown in figure 3. The evolution of the streamwise root mean square (r.m.s.) velocity
![]() $U_{rms}$
along the centreline is given in figure 5. It is clear that the profile of the case with
$U_{rms}$
along the centreline is given in figure 5. It is clear that the profile of the case with
![]() $L_{d}/T_{0}=4$
is fundamentally different from the other two profiles. However, due to the limited streamwise length, the decay region is missing for the case with
$L_{d}/T_{0}=4$
is fundamentally different from the other two profiles. However, due to the limited streamwise length, the decay region is missing for the case with
![]() $L_{d}/T_{0}=8$
. Thus, we could not draw a solid conclusion concerning the wake-interaction scale.
$L_{d}/T_{0}=8$
. Thus, we could not draw a solid conclusion concerning the wake-interaction scale.

Figure 5. Streamwise evolution of the r.m.s. velocity
![]() $U_{rms}$
along the centreline. (a) As a function of
$U_{rms}$
along the centreline. (a) As a function of
![]() $X/T_{0}$
; (b) as a function of
$X/T_{0}$
; (b) as a function of
![]() $X/X_{\ast }$
.
$X/X_{\ast }$
.

Figure 6. Streamwise evolution of the skewness of fluctuating streamwise velocity
![]() $S_{u}$
along the centreline. (a) As a function of
$S_{u}$
along the centreline. (a) As a function of
![]() $X/T_{0}$
; (b) as a function of
$X/T_{0}$
; (b) as a function of
![]() $X/X_{\ast }$
. The horizontal dashed line indicates
$X/X_{\ast }$
. The horizontal dashed line indicates
![]() $S_{u}=0$
.
$S_{u}=0$
.

Figure 7. Streamwise evolution of the flatness of fluctuating streamwise velocity
![]() $F_{u}$
along the centreline. (a) As a function of
$F_{u}$
along the centreline. (a) As a function of
![]() $X/T_{0}$
; (b) as a function of
$X/T_{0}$
; (b) as a function of
![]() $X/X_{\ast }$
. The horizontal dashed line indicates
$X/X_{\ast }$
. The horizontal dashed line indicates
![]() $F_{u}=3$
.
$F_{u}=3$
.
Figures 6 and 7 show the evolution of the centreline skewness
![]() $S_{u}$
and flatness
$S_{u}$
and flatness
![]() $F_{u}$
, where
$F_{u}$
, where
![]() $S_{u}=\langle u^{\prime 3}\rangle /\langle u^{\prime 2}\rangle ^{3/2}$
and
$S_{u}=\langle u^{\prime 3}\rangle /\langle u^{\prime 2}\rangle ^{3/2}$
and
![]() $F_{u}=\langle {u^{\prime }}^{4}\rangle /\langle u^{\prime 2}\rangle ^{2}$
. Extreme events with negative
$F_{u}=\langle {u^{\prime }}^{4}\rangle /\langle u^{\prime 2}\rangle ^{2}$
. Extreme events with negative
![]() $S_{u}$
and large
$S_{u}$
and large
![]() $F_{u}$
can only be found in the cases with larger gap ratios (
$F_{u}$
can only be found in the cases with larger gap ratios (
![]() $L_{d}/T_{0}=6$
and 8). In contrast, the profiles of
$L_{d}/T_{0}=6$
and 8). In contrast, the profiles of
![]() $S_{u}$
and
$S_{u}$
and
![]() $F_{u}$
for the case with
$F_{u}$
for the case with
![]() $L_{d}/T_{0}=4$
are more or less flat. The most intense events occur at
$L_{d}/T_{0}=4$
are more or less flat. The most intense events occur at
![]() $X/X_{\ast }\simeq 0.2$
and with downstream distance,
$X/X_{\ast }\simeq 0.2$
and with downstream distance,
![]() $S_{u}$
and
$S_{u}$
and
![]() $F_{u}$
gradually acquire the corresponding values of a Gaussian distribution. Note that the location with the largest negative value of
$F_{u}$
gradually acquire the corresponding values of a Gaussian distribution. Note that the location with the largest negative value of
![]() $S_{u}$
, i.e.
$S_{u}$
, i.e.
![]() $X/X_{\ast }\simeq 0.2$
, is close to the corresponding location in the turbulence generated by a single square grid (Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
). It is worth mentioning that in a previous study of the turbulence generated by a single square grid (Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
), the corresponding gap ratio was 9.1, which is close to the cases with
$X/X_{\ast }\simeq 0.2$
, is close to the corresponding location in the turbulence generated by a single square grid (Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
). It is worth mentioning that in a previous study of the turbulence generated by a single square grid (Zhou et al.
Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
), the corresponding gap ratio was 9.1, which is close to the cases with
![]() $L_{d}/T_{0}=8$
. It is therefore clear from figure 6 that only for the cases with larger
$L_{d}/T_{0}=8$
. It is therefore clear from figure 6 that only for the cases with larger
![]() $L_{d}$
, can the extreme events be found and the distribution of the velocity fluctuations in the upstream region is highly non-Gaussian. As shown in figures 6 and 7, for the case with larger gap ratios (
$L_{d}$
, can the extreme events be found and the distribution of the velocity fluctuations in the upstream region is highly non-Gaussian. As shown in figures 6 and 7, for the case with larger gap ratios (
![]() $L_{d}/T_{0}=6$
and 8) the use of the wake-interaction length scale
$L_{d}/T_{0}=6$
and 8) the use of the wake-interaction length scale
![]() $X_{\ast }$
does return a better description of the streamwise evolution of
$X_{\ast }$
does return a better description of the streamwise evolution of
![]() $S_{u}$
and
$S_{u}$
and
![]() $F_{u}$
, albeit that the two profiles do not completely collapse and the profiles for the case with
$F_{u}$
, albeit that the two profiles do not completely collapse and the profiles for the case with
![]() $L_{d}/T_{0}=8$
are not well converged.
$L_{d}/T_{0}=8$
are not well converged.
In this subsection, we test the wake-interaction length scale
![]() $X_{\ast }$
and reveal that for the case with
$X_{\ast }$
and reveal that for the case with
![]() $L_{d}/T_{0}=4$
, the streamwise evolution of various centreline statistics does not scale with
$L_{d}/T_{0}=4$
, the streamwise evolution of various centreline statistics does not scale with
![]() $X_{\ast }$
. Recall that the derivation of
$X_{\ast }$
. Recall that the derivation of
![]() $X_{\ast }$
is based on the interactions of two independent wakes. And it is demonstrated that for the case with
$X_{\ast }$
is based on the interactions of two independent wakes. And it is demonstrated that for the case with
![]() $L_{d}/T_{0}=4$
the two wakes merge into one in the downstream region (i.e.
$L_{d}/T_{0}=4$
the two wakes merge into one in the downstream region (i.e.
![]() $X/T_{0}>8$
). As a result, it is not surprising that the wake-interaction length scale cannot be applied. However, for the case with larger separation distance (i.e.
$X/T_{0}>8$
). As a result, it is not surprising that the wake-interaction length scale cannot be applied. However, for the case with larger separation distance (i.e.
![]() $L_{d}/T_{0}=6$
and 8), some of the turbulence characteristics more or less scale with
$L_{d}/T_{0}=6$
and 8), some of the turbulence characteristics more or less scale with
![]() $X_{\ast }$
, as happens in the case of the grid-generated turbulence, rather than simply
$X_{\ast }$
, as happens in the case of the grid-generated turbulence, rather than simply
![]() $X/T_{0}$
. Note that for a typical low-blockage space-filling grid, the corresponding
$X/T_{0}$
. Note that for a typical low-blockage space-filling grid, the corresponding
![]() $L_{d}/T_{0}$
is much larger. For example, as shown in Nagata et al. (Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013) the ratios of the largest mesh size to the thickness of the largest bars considered are 12.4, 13.8 and 14.0, respectively. Thus, the separation distances considered (i.e.
$L_{d}/T_{0}$
is much larger. For example, as shown in Nagata et al. (Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013) the ratios of the largest mesh size to the thickness of the largest bars considered are 12.4, 13.8 and 14.0, respectively. Thus, the separation distances considered (i.e.
![]() $L_{d}/T_{0}=4,6$
and 8) may not well represent the two wake problem when the wakes are far enough from each other.
$L_{d}/T_{0}=4,6$
and 8) may not well represent the two wake problem when the wakes are far enough from each other.
3.3 Extreme events
As mentioned in the introduction, extreme events can be closely related to the appearance of the
![]() $-5/3$
spectra. In this subsection, the characteristics along with the formation mechanism of the extreme events shall be discussed. It can be seen that extreme events are found in the cases with relatively larger gap ratios, namely,
$-5/3$
spectra. In this subsection, the characteristics along with the formation mechanism of the extreme events shall be discussed. It can be seen that extreme events are found in the cases with relatively larger gap ratios, namely,
![]() $L_{d}/T_{0}=6$
and 8. For the case with the largest gap ratio
$L_{d}/T_{0}=6$
and 8. For the case with the largest gap ratio
![]() $L_{d}/T_{0}=8$
, however, the dual-wake flow still undergoes transition at the furthest downstream location at which the numerical data are available and the corresponding skewness
$L_{d}/T_{0}=8$
, however, the dual-wake flow still undergoes transition at the furthest downstream location at which the numerical data are available and the corresponding skewness
![]() $S_{u}$
takes a large negative value. From now on we therefore concentrate attention on the case with
$S_{u}$
takes a large negative value. From now on we therefore concentrate attention on the case with
![]() $L_{d}/T_{0}=6$
, which allows us to perform a complete investigation of the extreme events.
$L_{d}/T_{0}=6$
, which allows us to perform a complete investigation of the extreme events.

Figure 8. PDF distributions of (a)
![]() $u^{\prime }$
and (b)
$u^{\prime }$
and (b)
![]() $\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
![]() $X/T_{0}=6$
and 26. The corresponding Gaussian fits at
$X/T_{0}=6$
and 26. The corresponding Gaussian fits at
![]() $X/T_{0}=26$
(represented by red open circles) are also plotted for comparison.
$X/T_{0}=26$
(represented by red open circles) are also plotted for comparison.

Figure 9. Time traces of (a)
![]() $u^{\prime }/U_{rms}$
and
$u^{\prime }/U_{rms}$
and
![]() $v^{\prime }/V_{rms}$
and (b) time traces of
$v^{\prime }/V_{rms}$
and (b) time traces of
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $u^{\prime }/U_{rms}$
at
$u^{\prime }/U_{rms}$
at
![]() $X/T_{0}=6$
and
$X/T_{0}=6$
and
![]() $Y/T_{0}=0$
. The origin of time for all lines is the same. Two different time frames (TF1 and TF2) with the appearance of extreme events can be identified.
$Y/T_{0}=0$
. The origin of time for all lines is the same. Two different time frames (TF1 and TF2) with the appearance of extreme events can be identified.
Figure 8 shows the PDFs of the streamwise velocity fluctuations
![]() $u^{\prime }$
and their time derivative
$u^{\prime }$
and their time derivative
![]() $\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
![]() $X/T_{0}=6$
and 26. Note that at
$X/T_{0}=6$
and 26. Note that at
![]() $X/T_{0}=6$
the most intense events occur, whereas the turbulent flow is almost Gaussian distributed at
$X/T_{0}=6$
the most intense events occur, whereas the turbulent flow is almost Gaussian distributed at
![]() $X/T_{0}=26$
(i.e.
$X/T_{0}=26$
(i.e.
![]() $S_{u}\simeq 0$
and
$S_{u}\simeq 0$
and
![]() $F_{u}\simeq 3$
). The distributions of
$F_{u}\simeq 3$
). The distributions of
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
at
![]() $X/T_{0}=6$
have significant fat tails compared with those at
$X/T_{0}=6$
have significant fat tails compared with those at
![]() $X/T_{0}=26$
, suggesting the probability of the rare events (i.e. intense value of
$X/T_{0}=26$
, suggesting the probability of the rare events (i.e. intense value of
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
) at
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}t$
) at
![]() $X/T_{0}=6$
is considerably larger.
$X/T_{0}=6$
is considerably larger.
To provide deeper insight into the extreme events, figure 9(a) presents the time traces of the centreline velocity fluctuation
![]() $u^{\prime }/U_{rms}$
and
$u^{\prime }/U_{rms}$
and
![]() $v^{\prime }/V_{rms}$
at
$v^{\prime }/V_{rms}$
at
![]() $X/T_{0}=6$
, where
$X/T_{0}=6$
, where
![]() $v^{\prime }$
and
$v^{\prime }$
and
![]() $V_{rms}$
are the vertical velocity fluctuations and the corresponding r.m.s. velocity, respectively. The variations of
$V_{rms}$
are the vertical velocity fluctuations and the corresponding r.m.s. velocity, respectively. The variations of
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
are relatively smooth and exhibit quasi-periodic (regular) oscillations except for the TF1 and TF2. Figure 9(b) shows the time evolution of the magnitude of vorticity
$v^{\prime }$
are relatively smooth and exhibit quasi-periodic (regular) oscillations except for the TF1 and TF2. Figure 9(b) shows the time evolution of the magnitude of vorticity
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $u^{\prime }$
at
$u^{\prime }$
at
![]() $X/T_{0}=6$
, which suggests that non-turbulent regions (i.e. quiescent regions with negligibly small magnitude of vorticity) are dominant. The occurrences of the extreme events are only found in the turbulent region (i.e. fluctuating region with high vorticity). Note that in the case of the dual-wake flow, the most intense events occur at a location where the flow is not always in the turbulent region, as in the turbulence generated by a single square grid (see figures 5 and 8 in Zhou et al. (Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
); figures 9 and 10 in Laizet et al. (Reference Laizet, Nedić and Vassilicos2015b
)). Another finding from figure 9 concerning the occurrence of the extreme events is that
$X/T_{0}=6$
, which suggests that non-turbulent regions (i.e. quiescent regions with negligibly small magnitude of vorticity) are dominant. The occurrences of the extreme events are only found in the turbulent region (i.e. fluctuating region with high vorticity). Note that in the case of the dual-wake flow, the most intense events occur at a location where the flow is not always in the turbulent region, as in the turbulence generated by a single square grid (see figures 5 and 8 in Zhou et al. (Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014a
); figures 9 and 10 in Laizet et al. (Reference Laizet, Nedić and Vassilicos2015b
)). Another finding from figure 9 concerning the occurrence of the extreme events is that
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
are closely correlated (i.e. in phase within TF1 and anti-phased within TF2). More quantitatively, the joint PDFs of
$v^{\prime }$
are closely correlated (i.e. in phase within TF1 and anti-phased within TF2). More quantitatively, the joint PDFs of
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
at
$v^{\prime }$
at
![]() $X/T_{0}=6$
are shown in figure 10. The joint PDFs at a further downstream location
$X/T_{0}=6$
are shown in figure 10. The joint PDFs at a further downstream location
![]() $X/T_{0}=26$
are also presented for comparison. Figure 10(a) suggests that the flow particles with either high positive or high negative
$X/T_{0}=26$
are also presented for comparison. Figure 10(a) suggests that the flow particles with either high positive or high negative
![]() $v^{\prime }$
tend to possess large negative
$v^{\prime }$
tend to possess large negative
![]() $u^{\prime }$
. This observation is therefore in accord with the assumption that the large magnitude of
$u^{\prime }$
. This observation is therefore in accord with the assumption that the large magnitude of
![]() $v^{\prime }$
is more likely to be associated with a large negative
$v^{\prime }$
is more likely to be associated with a large negative
![]() $u^{\prime }$
. The contour lines corresponding to rare events are approximately symmetrical with respect to the horizontal line, i.e.
$u^{\prime }$
. The contour lines corresponding to rare events are approximately symmetrical with respect to the horizontal line, i.e.
![]() $v^{\prime }/V_{rms}=0$
, confirming that
$v^{\prime }/V_{rms}=0$
, confirming that
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
can be either in phase or out of phase with each other. At
$v^{\prime }$
can be either in phase or out of phase with each other. At
![]() $X/T_{0}=26$
, however, all contour lines acquire a ‘pancake’ shape instead, suggesting that
$X/T_{0}=26$
, however, all contour lines acquire a ‘pancake’ shape instead, suggesting that
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
are essentially statistically uncorrelated.
$v^{\prime }$
are essentially statistically uncorrelated.

Figure 10. Joint PDFs of
![]() $u^{\prime }/U_{rms}$
and
$u^{\prime }/U_{rms}$
and
![]() $v^{\prime }/V_{rms}$
. (a) At
$v^{\prime }/V_{rms}$
. (a) At
![]() $X/T_{0}=6$
; (b) at
$X/T_{0}=6$
; (b) at
![]() $X/T_{0}=26$
. A total of six contour levels (i.e. 0.1, 0.05,
$X/T_{0}=26$
. A total of six contour levels (i.e. 0.1, 0.05,
![]() $0.01$
,
$0.01$
,
![]() $0.005$
,
$0.005$
,
![]() $0.001$
and
$0.001$
and
![]() $0.0005$
) are shown.
$0.0005$
) are shown.
The formation of the extreme events can be explained by using a Lagrangian description. One can imagine that the local fluid particles along the centreline with large magnitude of
![]() $v^{\prime }$
have a better chance of being from a location with a larger vertical distance from the centreline. In the near field of a square cylinder, the turbulent wake consists of vortex tube clusters, which are usually characterized by a large magnitude of vorticity, and the velocity deficit is still significant. These slower vortex tube clusters serve as obstacles and can easily slow down the local turbulent flow, resulting in the extreme events with negative
$v^{\prime }$
have a better chance of being from a location with a larger vertical distance from the centreline. In the near field of a square cylinder, the turbulent wake consists of vortex tube clusters, which are usually characterized by a large magnitude of vorticity, and the velocity deficit is still significant. These slower vortex tube clusters serve as obstacles and can easily slow down the local turbulent flow, resulting in the extreme events with negative
![]() $S_{u}$
. Relying on the direction of the vertical movement,
$S_{u}$
. Relying on the direction of the vertical movement,
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
can be either in phase or out of phase with each other along the centreline as shown in figures 9 and 10.
$v^{\prime }$
can be either in phase or out of phase with each other along the centreline as shown in figures 9 and 10.
4 Energy spectra and structure functions
In this section, we shall answer the two important remaining questions: the relationship between the occurrence of the extreme events and the well-defined
![]() $-5/3$
energy spectra and also the characteristics of the second-order structure function at the location where the extreme events occur and the flow is highly intermittent.
$-5/3$
energy spectra and also the characteristics of the second-order structure function at the location where the extreme events occur and the flow is highly intermittent.
4.1 One-dimensional energy spectra
Before investigating the relationship between the extreme events and the energy spectra, we need to obtain the shape of the one-dimensional energy spectra first. The one-dimensional energy spectra of the streamwise velocity fluctuation
![]() $u^{\prime }$
at
$u^{\prime }$
at
![]() $X/T_{0}=6$
and 26 along the centreline for the case with
$X/T_{0}=6$
and 26 along the centreline for the case with
![]() $L_{d}/T_{0}=6$
are given in figure 11. Note that at the upstream location (i.e.
$L_{d}/T_{0}=6$
are given in figure 11. Note that at the upstream location (i.e.
![]() $X/T_{0}=6$
) the turbulent flows are highly non-Gaussian distributed and highly intermittent, whereas at the far downstream location (i.e.
$X/T_{0}=6$
) the turbulent flows are highly non-Gaussian distributed and highly intermittent, whereas at the far downstream location (i.e.
![]() $X/T_{0}=26$
) the flow field becomes approximately Gaussian distributed and approximately fully turbulent. The spectra at the two chosen locations display pronounced peaks at the normalized frequency
$X/T_{0}=26$
) the flow field becomes approximately Gaussian distributed and approximately fully turbulent. The spectra at the two chosen locations display pronounced peaks at the normalized frequency
![]() $St=fT_{0}/U_{in}=0.142$
corresponding to the vortex shedding frequency (more specifically, the regular and slow oscillation of
$St=fT_{0}/U_{in}=0.142$
corresponding to the vortex shedding frequency (more specifically, the regular and slow oscillation of
![]() $u^{\prime }$
at
$u^{\prime }$
at
![]() $X/T_{0}=6$
as shown in figure 9). The dominant frequency
$X/T_{0}=6$
as shown in figure 9). The dominant frequency
![]() $fT_{0}/U_{in}=0.142$
is approximately half the value found in the flow behind a single square cylinder. For example, as presented in Portela, Papadakis & Vassilicos (Reference Portela, Papadakis and Vassilicos2017) when the inlet Reynolds number is
$fT_{0}/U_{in}=0.142$
is approximately half the value found in the flow behind a single square cylinder. For example, as presented in Portela, Papadakis & Vassilicos (Reference Portela, Papadakis and Vassilicos2017) when the inlet Reynolds number is
![]() $Re_{T_{0}}=3900$
, the corresponding
$Re_{T_{0}}=3900$
, the corresponding
![]() $fT_{0}/U_{in}$
is 0.267. In a previous experiment of dual-wake flows with a slightly smaller gap ratio
$fT_{0}/U_{in}$
is 0.267. In a previous experiment of dual-wake flows with a slightly smaller gap ratio
![]() $L_{d}/T_{0}=5$
and much larger inlet Reynolds number
$L_{d}/T_{0}=5$
and much larger inlet Reynolds number
![]() $Re_{T_{0}}=47\,000$
, the returned
$Re_{T_{0}}=47\,000$
, the returned
![]() $St$
is 0.128, which is close to our simulation result (Alam & Zhou Reference Alam and Zhou2013).
$St$
is 0.128, which is close to our simulation result (Alam & Zhou Reference Alam and Zhou2013).

Figure 11. (a) Energy spectra of
![]() $u^{\prime }$
at
$u^{\prime }$
at
![]() $X/T_{0}=6$
and 26 for the case with
$X/T_{0}=6$
and 26 for the case with
![]() $L_{d}/T_{0}=6$
. The vertical dashed line indicates
$L_{d}/T_{0}=6$
. The vertical dashed line indicates
![]() $St=fT_{0}/U_{in}=0.142$
; (b) the corresponding compensated energy spectra
$St=fT_{0}/U_{in}=0.142$
; (b) the corresponding compensated energy spectra
![]() $E_{uu}(fT_{0}/U_{in})^{5/3}$
. The horizontal (i.e. frequency) axis is linear.
$E_{uu}(fT_{0}/U_{in})^{5/3}$
. The horizontal (i.e. frequency) axis is linear.
Compared with
![]() $X/T_{0}=26$
, at
$X/T_{0}=26$
, at
![]() $X/T_{0}=6$
the vortex shedding contains more energy; that is the peak value of
$X/T_{0}=6$
the vortex shedding contains more energy; that is the peak value of
![]() $E_{uu}$
is much larger at
$E_{uu}$
is much larger at
![]() $X/T_{0}=6$
. However, except for the narrow frequency range corresponding to vortex shedding, the energy spectrum at
$X/T_{0}=6$
. However, except for the narrow frequency range corresponding to vortex shedding, the energy spectrum at
![]() $X/T_{0}=6$
is always much smaller than that at
$X/T_{0}=6$
is always much smaller than that at
![]() $X/T_{0}=26$
. This is due to the smooth evolution of
$X/T_{0}=26$
. This is due to the smooth evolution of
![]() $u^{\prime }$
as shown in figure 9, albeit the extreme events bearing large fluctuating energy (see figure 9). Note that even the velocity fluctuations at
$u^{\prime }$
as shown in figure 9, albeit the extreme events bearing large fluctuating energy (see figure 9). Note that even the velocity fluctuations at
![]() $X/T_{0}$
= 6 and 26 appear to have more or less identical strengths (magnitudes of
$X/T_{0}$
= 6 and 26 appear to have more or less identical strengths (magnitudes of
![]() $U_{rms}$
) (see figure 5), their intrinsic properties are actually quite different as already shown in figures 8 and 11.
$U_{rms}$
) (see figure 5), their intrinsic properties are actually quite different as already shown in figures 8 and 11.
The energy spectrum at
![]() $X/T_{0}=6$
exhibits a well-defined
$X/T_{0}=6$
exhibits a well-defined
![]() $-5/3$
power law with a range for more than a decade. With downstream distance, however, the range of the
$-5/3$
power law with a range for more than a decade. With downstream distance, however, the range of the
![]() $-5/3$
power law is eroded, albeit the corresponding r.m.s. velocity is even slightly larger (see figure 5) and the local Reynolds numbers based on the Taylor microscale remains approximately unchanged, that is,
$-5/3$
power law is eroded, albeit the corresponding r.m.s. velocity is even slightly larger (see figure 5) and the local Reynolds numbers based on the Taylor microscale remains approximately unchanged, that is,
![]() $Re_{\unicode[STIX]{x1D706}}\simeq 100$
(not shown herein). Another interesting finding is that for both locations, the shedding frequency
$Re_{\unicode[STIX]{x1D706}}\simeq 100$
(not shown herein). Another interesting finding is that for both locations, the shedding frequency
![]() $St=0.142$
defines the beginning of the
$St=0.142$
defines the beginning of the
![]() $-5/3$
power-law energy spectra.
$-5/3$
power-law energy spectra.
Similar observations have already been reported in various kinds of turbulent flows. For instance, in the near field of grid-generated turbulence (single square grid (Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017), regular grid (Isaza, Salazar & Warhaft Reference Isaza, Salazar and Warhaft2014), fractal grid (Laizet, Vassilicos & Cambon Reference Laizet, Vassilicos and Cambon2013; Hearst & Lavoie Reference Hearst and Lavoie2014)), the power spectrum exhibits a well-defined power law with an exponent close to
![]() $-5/3$
and the range of the
$-5/3$
and the range of the
![]() $-5/3$
scaling narrows with downstream distance. Zhou et al. (Reference Zhou, Nagata, Sakai and Watanabe2018) demonstrated in a dual-plane jet flow, the range of the
$-5/3$
scaling narrows with downstream distance. Zhou et al. (Reference Zhou, Nagata, Sakai and Watanabe2018) demonstrated in a dual-plane jet flow, the range of the
![]() $-5/3$
power law also decreases further downstream. Even downstream of a single square prism, a similar observation can also be found (Portela et al.
Reference Portela, Papadakis and Vassilicos2017).
$-5/3$
power law also decreases further downstream. Even downstream of a single square prism, a similar observation can also be found (Portela et al.
Reference Portela, Papadakis and Vassilicos2017).
4.2 Filtered fluctuating velocity fields
To take the observation in the preceding subsection (i.e. well-defined
![]() $-5/3$
spectra can be found at both streamwise locations considered) one step further, the relationship between the energy spectra and the extreme events will be discussed here. At
$-5/3$
spectra can be found at both streamwise locations considered) one step further, the relationship between the energy spectra and the extreme events will be discussed here. At
![]() $X/T_{0}=6$
, the flow field is not fully turbulent; there are alternations between laminar large-scale oscillations and strong turbulent fluctuations (e.g. TF1 and TF2). To shed light on the physical mechanism responsible for the wider range of the
$X/T_{0}=6$
, the flow field is not fully turbulent; there are alternations between laminar large-scale oscillations and strong turbulent fluctuations (e.g. TF1 and TF2). To shed light on the physical mechanism responsible for the wider range of the
![]() $-5/3$
power law at
$-5/3$
power law at
![]() $X/T_{0}=6$
in the high-frequency range, we first attempt to subtract the signal in the low-frequency range. The velocity fluctuating signals are passed through a highpass filter with the low cutoff frequency
$X/T_{0}=6$
in the high-frequency range, we first attempt to subtract the signal in the low-frequency range. The velocity fluctuating signals are passed through a highpass filter with the low cutoff frequency
![]() $fT_{0}/U_{in}$
being 2.0. Thus, the filter data are expected to contain signals with frequency
$fT_{0}/U_{in}$
being 2.0. Thus, the filter data are expected to contain signals with frequency
![]() $fT_{0}/U_{in}$
larger than 2.0, where the
$fT_{0}/U_{in}$
larger than 2.0, where the
![]() $-5/3$
power law is absent. Throughout this paper, the velocity data are filtered using eighth-order zero-lag (i.e. bidirectional) Butterworth filters (e.g. highpass, bandpass and lowpass filters). And the scripts
$-5/3$
power law is absent. Throughout this paper, the velocity data are filtered using eighth-order zero-lag (i.e. bidirectional) Butterworth filters (e.g. highpass, bandpass and lowpass filters). And the scripts
![]() ${<}$
,
${<}$
,
![]() ${\sim}$
and
${\sim}$
and
![]() ${>}$
stand for statistics associated with high-, intermediate- and low-frequency components, respectively. For instance, the velocity fluctuation can be decomposed as
${>}$
stand for statistics associated with high-, intermediate- and low-frequency components, respectively. For instance, the velocity fluctuation can be decomposed as
![]() $u^{\prime }=u_{{>}}^{\prime }+u_{{\sim}}^{\prime }+u_{{<}}^{\prime }$
. The use of high-order filters allows us to efficiently remove the unwanted components. Considering the fact that filters chosen are bidirectional, the filtered signals can be expected to be delay compensated. A further validation of the involved filtering processes is given in supplementary appendix D.
$u^{\prime }=u_{{>}}^{\prime }+u_{{\sim}}^{\prime }+u_{{<}}^{\prime }$
. The use of high-order filters allows us to efficiently remove the unwanted components. Considering the fact that filters chosen are bidirectional, the filtered signals can be expected to be delay compensated. A further validation of the involved filtering processes is given in supplementary appendix D.

Figure 12. (a) Energy spectrum of the filtered velocity signal
![]() $u_{{<}}^{\prime }/U_{in}$
subject to a highpass filter with a cutoff frequency of 2.0. Energy spectrum of the original velocity signal (i.e. entire signal)
$u_{{<}}^{\prime }/U_{in}$
subject to a highpass filter with a cutoff frequency of 2.0. Energy spectrum of the original velocity signal (i.e. entire signal)
![]() $u^{\prime }$
is also shown for comparison. The vertical dashed line indicates
$u^{\prime }$
is also shown for comparison. The vertical dashed line indicates
![]() $fT_{0}/U_{in}=2$
. (b) Time traces of the filtered signals
$fT_{0}/U_{in}=2$
. (b) Time traces of the filtered signals
![]() $u_{{<}}^{\prime }/U_{in}$
. The time evolution of the original velocity signals
$u_{{<}}^{\prime }/U_{in}$
. The time evolution of the original velocity signals
![]() $u^{\prime }$
shown in figure 9 is also plotted as a comparison.
$u^{\prime }$
shown in figure 9 is also plotted as a comparison.
Figure 12(a) shows the spectrum of filtered velocity fluctuations
![]() $u_{{<}}^{\prime }$
corresponding to the high-frequency range
$u_{{<}}^{\prime }$
corresponding to the high-frequency range
![]() $fT_{0}/U_{in}>2.0$
. For comparison, the spectrum of the entire fluctuating signal
$fT_{0}/U_{in}>2.0$
. For comparison, the spectrum of the entire fluctuating signal
![]() $u^{\prime }$
already shown in figure 11 is also included. The profile corresponding to
$u^{\prime }$
already shown in figure 11 is also included. The profile corresponding to
![]() $u_{{<}}^{\prime }$
in the high-frequency range remains virtually intact and unaffected. In contrast, the fluctuating signals within the low-frequency range are efficiently subtracted. We now apply the chosen highpass filter to the time traces of
$u_{{<}}^{\prime }$
in the high-frequency range remains virtually intact and unaffected. In contrast, the fluctuating signals within the low-frequency range are efficiently subtracted. We now apply the chosen highpass filter to the time traces of
![]() $u^{\prime }$
shown in figure 9. As can be seen in figure 12(b), except for the fluctuating signals in the TF1 and TF2, the filtered signals are in a relatively quiescent state with negligible magnitude. This observation suggests that the high-frequency signals contribute to the extreme events.
$u^{\prime }$
shown in figure 9. As can be seen in figure 12(b), except for the fluctuating signals in the TF1 and TF2, the filtered signals are in a relatively quiescent state with negligible magnitude. This observation suggests that the high-frequency signals contribute to the extreme events.
We further divide the intermediate range (i.e.
![]() $0.2<fT_{0}/U_{in}<2.0$
), where the
$0.2<fT_{0}/U_{in}<2.0$
), where the
![]() $-5/3$
spectrum can be found, into two subranges (
$-5/3$
spectrum can be found, into two subranges (
![]() $u_{{\sim}}^{\prime }=u_{{\sim},l}^{\prime }+u_{{\sim},h}^{\prime }$
) to explore the erosion of the
$u_{{\sim}}^{\prime }=u_{{\sim},l}^{\prime }+u_{{\sim},h}^{\prime }$
) to explore the erosion of the
![]() $-5/3$
scaling. Figures 13(a) and 13(b) show the energy spectrum and the velocity signal in the high-frequency zone of the
$-5/3$
scaling. Figures 13(a) and 13(b) show the energy spectrum and the velocity signal in the high-frequency zone of the
![]() $-5/3$
scaling range (i.e.
$-5/3$
scaling range (i.e.
![]() $0.8<fT_{0}/U_{in}<2.0$
). The fact that the non-zero fluctuations are mainly found in TF1 and TF2 indicates an intimate relationship between intermittent events and the extended
$0.8<fT_{0}/U_{in}<2.0$
). The fact that the non-zero fluctuations are mainly found in TF1 and TF2 indicates an intimate relationship between intermittent events and the extended
![]() $-5/3$
power law. In other words, we could safely draw the conclusion that the occurrences of the extreme events (TF1 and TF2) contribute to the formation of the
$-5/3$
power law. In other words, we could safely draw the conclusion that the occurrences of the extreme events (TF1 and TF2) contribute to the formation of the
![]() $-5/3$
power law in the high-frequency range (i.e.
$-5/3$
power law in the high-frequency range (i.e.
![]() $fT_{0}/U_{in}\gtrsim 0.8$
in figure 12
b). The range over which the
$fT_{0}/U_{in}\gtrsim 0.8$
in figure 12
b). The range over which the
![]() $-5/3$
power law can be found therefore is determined by two turbulence behaviours, one being the large-scale vortex shedding and the other being the occurrence of the extreme events. With increasing downstream distance, the strength of the extreme events becomes weaker (see figure 6
a), which results in the deterioration of the range of the
$-5/3$
power law can be found therefore is determined by two turbulence behaviours, one being the large-scale vortex shedding and the other being the occurrence of the extreme events. With increasing downstream distance, the strength of the extreme events becomes weaker (see figure 6
a), which results in the deterioration of the range of the
![]() $-5/3$
power law.
$-5/3$
power law.

Figure 13. (a) Energy spectrum of the filtered velocity signal
![]() $u_{{\sim},h}^{\prime }/U_{in}$
subject to a band-pass filter with a lower cutoff frequency of 0.8 and a higher cutoff frequency of 2.0. Energy spectrum of the original velocity signal (i.e. entire signal)
$u_{{\sim},h}^{\prime }/U_{in}$
subject to a band-pass filter with a lower cutoff frequency of 0.8 and a higher cutoff frequency of 2.0. Energy spectrum of the original velocity signal (i.e. entire signal)
![]() $u^{\prime }$
is also shown for comparison. The vertical dashed lines indicate
$u^{\prime }$
is also shown for comparison. The vertical dashed lines indicate
![]() $fT_{0}/U_{in}=0.8$
and 2.0. (b) Time traces of the filtered signal
$fT_{0}/U_{in}=0.8$
and 2.0. (b) Time traces of the filtered signal
![]() $u_{{\sim},h}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
$u_{{\sim},h}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
![]() $u^{\prime }$
shown in figure 9 is also plotted as a comparison.
$u^{\prime }$
shown in figure 9 is also plotted as a comparison.

Figure 14. (a) Energy spectrum of the filtered velocity signal
![]() $u_{{\sim},l}^{\prime }/U_{in}$
subject to a band-pass filter with a lower cutoff frequency of 0.2 and a higher cutoff frequency of 0.8. Energy spectrum of the original velocity signal (i.e. entire signal)
$u_{{\sim},l}^{\prime }/U_{in}$
subject to a band-pass filter with a lower cutoff frequency of 0.2 and a higher cutoff frequency of 0.8. Energy spectrum of the original velocity signal (i.e. entire signal)
![]() $u^{\prime }$
is also shown for comparison. The vertical dashed lines indicate
$u^{\prime }$
is also shown for comparison. The vertical dashed lines indicate
![]() $fT_{0}/U_{in}=0.2$
and 0.8. (b) Time traces of the filtered signal
$fT_{0}/U_{in}=0.2$
and 0.8. (b) Time traces of the filtered signal
![]() $u_{{\sim},l}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
$u_{{\sim},l}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
![]() $u^{\prime }$
shown in figure 9 is also plotted as a comparison.
$u^{\prime }$
shown in figure 9 is also plotted as a comparison.
It must, however, be pointed out that there is a large part of the
![]() $-5/3$
power law which is not in the highpass filtered field, that is, the intermediate-frequency range
$-5/3$
power law which is not in the highpass filtered field, that is, the intermediate-frequency range
![]() $0.2\lesssim t/(T_{0}/U_{in})\lesssim 0.8$
. To investigate what is responsible for this part of the spectrum, we use a bandpass filter to extract the velocity signals within this range. And the higher and lower cutoff frequencies are set to
$0.2\lesssim t/(T_{0}/U_{in})\lesssim 0.8$
. To investigate what is responsible for this part of the spectrum, we use a bandpass filter to extract the velocity signals within this range. And the higher and lower cutoff frequencies are set to
![]() $fT_{0}/U_{in}=0.8$
and 0.2, respectively (see figures 14
a and 14
b). The time-traces of the filtered signals
$fT_{0}/U_{in}=0.8$
and 0.2, respectively (see figures 14
a and 14
b). The time-traces of the filtered signals
![]() $u_{{\sim}}^{\prime }$
demonstrate that the strength of the filtered velocity
$u_{{\sim}}^{\prime }$
demonstrate that the strength of the filtered velocity
![]() $u_{{\sim}}^{\prime }$
is weak and as expected the oscillation behaviour possesses smaller periods. In contrast to the formation of the
$u_{{\sim}}^{\prime }$
is weak and as expected the oscillation behaviour possesses smaller periods. In contrast to the formation of the
![]() $-5/3$
scaling in the high-frequency range where the turbulent motions are dominant, in the intermediate-frequency range both laminar and turbulent motions contribute to the appearance of the
$-5/3$
scaling in the high-frequency range where the turbulent motions are dominant, in the intermediate-frequency range both laminar and turbulent motions contribute to the appearance of the
![]() $-5/3$
scaling.
$-5/3$
scaling.

Figure 15. (a) Energy spectrum of the filtered velocity signal
![]() $u_{{>}}^{\prime }/U_{in}$
subject to a lowpass filter with a lower cutoff frequency of 0.2. Energy spectrum of the original velocity signal (i.e. entire signal)
$u_{{>}}^{\prime }/U_{in}$
subject to a lowpass filter with a lower cutoff frequency of 0.2. Energy spectrum of the original velocity signal (i.e. entire signal)
![]() $u^{\prime }$
is also shown for comparison. The vertical dashed line indicates
$u^{\prime }$
is also shown for comparison. The vertical dashed line indicates
![]() $fT_{0}/U_{in}=0.2$
. (b) Time traces of the filtered signal
$fT_{0}/U_{in}=0.2$
. (b) Time traces of the filtered signal
![]() $u_{{>}}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
$u_{{>}}^{\prime }/U_{in}$
. The time evolution of the original velocity signal
![]() $u^{\prime }$
shown in figure 9 is also plotted as a comparison.
$u^{\prime }$
shown in figure 9 is also plotted as a comparison.
Let us finally consider the behaviour in the low-frequency range (i.e.
![]() $fT_{0}/U_{in}\lesssim 0.2$
), which stems from large-scale vortex shedding. A lowpass filter with the cutoff frequency of
$fT_{0}/U_{in}\lesssim 0.2$
), which stems from large-scale vortex shedding. A lowpass filter with the cutoff frequency of
![]() $fT_{0}/U_{in}=0.2$
is used. Expect for TF1 and TF2, as shown in figure 15(b) the large-scale periodic oscillations of
$fT_{0}/U_{in}=0.2$
is used. Expect for TF1 and TF2, as shown in figure 15(b) the large-scale periodic oscillations of
![]() $u_{{>}}^{\prime }$
corresponding to the energy containing range hold most of the energy.
$u_{{>}}^{\prime }$
corresponding to the energy containing range hold most of the energy.
Figure 16 shows the PDFs of the normalized velocity components
![]() $u_{{>}}^{\prime }/U_{rms}^{{>}}$
,
$u_{{>}}^{\prime }/U_{rms}^{{>}}$
,
![]() $u_{{\sim}}^{\prime }/U_{rms}^{{\sim}}$
and
$u_{{\sim}}^{\prime }/U_{rms}^{{\sim}}$
and
![]() $u_{{<}}^{\prime }/U_{rms}^{{<}}$
at
$u_{{<}}^{\prime }/U_{rms}^{{<}}$
at
![]() $X/T_{0}=6$
. The probability distribution of
$X/T_{0}=6$
. The probability distribution of
![]() $u^{\prime }/U_{rms}$
is shown for comparison. Except for the profile corresponding to
$u^{\prime }/U_{rms}$
is shown for comparison. Except for the profile corresponding to
![]() $u_{{<}}^{\prime }$
, all other probability distributions are negatively skewed and the profiles of
$u_{{<}}^{\prime }$
, all other probability distributions are negatively skewed and the profiles of
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
exhibit pronounced fatter tails. The statistical characteristics of
$u_{{<}}^{\prime }$
exhibit pronounced fatter tails. The statistical characteristics of
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $u_{{>}}^{\prime }$
,
$u_{{>}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
(e.g. r.m.s., skewness and flatness) at
$u_{{<}}^{\prime }$
(e.g. r.m.s., skewness and flatness) at
![]() $X/T_{0}=6$
and 26 are listed in table 2. For instance, the skewness of
$X/T_{0}=6$
and 26 are listed in table 2. For instance, the skewness of
![]() $u_{{>}}^{\prime }$
is obtained as
$u_{{>}}^{\prime }$
is obtained as
![]() $S(u_{{>}}^{\prime })=\langle u_{{>}}^{\prime 3}\rangle /\langle u_{{>}}^{\prime 2}\rangle ^{3/2}$
. At the downstream location
$S(u_{{>}}^{\prime })=\langle u_{{>}}^{\prime 3}\rangle /\langle u_{{>}}^{\prime 2}\rangle ^{3/2}$
. At the downstream location
![]() $X/T_{0}=26$
, the definitions of the components
$X/T_{0}=26$
, the definitions of the components
![]() $u_{{>}}^{\prime }$
,
$u_{{>}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
are the same as those at
$u_{{<}}^{\prime }$
are the same as those at
![]() $X/T_{0}=6$
. The negative values of
$X/T_{0}=6$
. The negative values of
![]() $S(u_{{>}}^{\prime })$
and
$S(u_{{>}}^{\prime })$
and
![]() $S(u_{{\sim}}^{\prime })$
at
$S(u_{{\sim}}^{\prime })$
at
![]() $X/T_{0}=6$
imply that the probability distributions within different frequency ranges are negatively skewed, whereas
$X/T_{0}=6$
imply that the probability distributions within different frequency ranges are negatively skewed, whereas
![]() $S(u_{{<}}^{\prime })\simeq 0$
suggests a symmetrical shape. And the velocity signals in the intermediate- and high-frequency ranges are significantly intermittent for
$S(u_{{<}}^{\prime })\simeq 0$
suggests a symmetrical shape. And the velocity signals in the intermediate- and high-frequency ranges are significantly intermittent for
![]() $F(u_{{\sim}}^{\prime })=33$
and
$F(u_{{\sim}}^{\prime })=33$
and
![]() $F(u_{{<}}^{\prime })=79$
. These findings are in accord with the corresponding probability distributions shown in figure 16. With downstream distance at
$F(u_{{<}}^{\prime })=79$
. These findings are in accord with the corresponding probability distributions shown in figure 16. With downstream distance at
![]() $X/T_{0}=26$
, the magnitudes of the flatness are close to that of a Gaussian distribution.
$X/T_{0}=26$
, the magnitudes of the flatness are close to that of a Gaussian distribution.
The intermittent features found at
![]() $X/T_{0}=6$
in the intermediate- and low-frequency ranges are distinctly different from the so-called ‘dissipation-range intermittency’, which is believed to be only associated with scales that are comparable to or smaller than the Kolmogorov dissipation scale (see, for example, Frisch (Reference Frisch1995) and references therein). It has been suggested that the concept of ‘dissipation-range intermittency’ does not necessarily violate the self-similarity in the inertial subrange, which is not the case for our study.
$X/T_{0}=6$
in the intermediate- and low-frequency ranges are distinctly different from the so-called ‘dissipation-range intermittency’, which is believed to be only associated with scales that are comparable to or smaller than the Kolmogorov dissipation scale (see, for example, Frisch (Reference Frisch1995) and references therein). It has been suggested that the concept of ‘dissipation-range intermittency’ does not necessarily violate the self-similarity in the inertial subrange, which is not the case for our study.

Figure 16. Probability distributions of
![]() $u_{{>}}^{\prime }/U_{rms}^{{>}}$
,
$u_{{>}}^{\prime }/U_{rms}^{{>}}$
,
![]() $u_{{\sim}}^{\prime }/U_{rms}^{{\sim}}$
and
$u_{{\sim}}^{\prime }/U_{rms}^{{\sim}}$
and
![]() $u_{{<}}^{\prime }/U_{rms}^{{<}}$
at
$u_{{<}}^{\prime }/U_{rms}^{{<}}$
at
![]() $X/T_{0}=6$
. The profile of
$X/T_{0}=6$
. The profile of
![]() $P(u^{\prime }/U_{rms})$
is also shown for comparison.
$P(u^{\prime }/U_{rms})$
is also shown for comparison.
Table 2. Strength (i.e. r.m.s.), skewness and flatness of
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $u_{{>}}^{\prime }$
,
$u_{{>}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
at
$u_{{<}}^{\prime }$
at
![]() $X/T_{0}=6$
and 26.
$X/T_{0}=6$
and 26.
We close this subsection with a short remark concerning the appearance of a well-defined
![]() $-5/3$
power-law spectrum in the near field, where the turbulent flow is still developing and suffers a subsequent deterioration in the
$-5/3$
power-law spectrum in the near field, where the turbulent flow is still developing and suffers a subsequent deterioration in the
![]() $-5/3$
range. First, the corresponding velocity fluctuations are highly intermittent, which can be roughly resolved into two parts, one being the large-scale vortex shedding and the other being the occurrence of the extreme events. As has already been confirmed in § 3, the formation of the extreme events is not necessarily directly related to the local Reynolds number. This suggestion is in accord with the previous findings that a well-defined
$-5/3$
range. First, the corresponding velocity fluctuations are highly intermittent, which can be roughly resolved into two parts, one being the large-scale vortex shedding and the other being the occurrence of the extreme events. As has already been confirmed in § 3, the formation of the extreme events is not necessarily directly related to the local Reynolds number. This suggestion is in accord with the previous findings that a well-defined
![]() $-5/3$
power law can be found at the location where the local Reynolds number is very small. Similar conclusions have been drawn by previous researchers. It was pointed out by Kraichnan (Reference Kraichnan1974) that ‘Kolmogorov’s 1941 theory has achieved an embarrassment of success. The
$-5/3$
power law can be found at the location where the local Reynolds number is very small. Similar conclusions have been drawn by previous researchers. It was pointed out by Kraichnan (Reference Kraichnan1974) that ‘Kolmogorov’s 1941 theory has achieved an embarrassment of success. The
![]() $-5/3$
-spectrum has been found not only where it reasonably could be expected but also at Reynolds numbers too small for a distinct inertial range to exist and in boundary layers and shear flows…’. A similar but more recent statement is as follows: ‘Conditions for the occurrence of a
$-5/3$
-spectrum has been found not only where it reasonably could be expected but also at Reynolds numbers too small for a distinct inertial range to exist and in boundary layers and shear flows…’. A similar but more recent statement is as follows: ‘Conditions for the occurrence of a
![]() $-5/3$
spectrum appear to be more “forgiving” than those initially outlined by Kolmogorov’ (Isaza et al.
Reference Isaza, Salazar and Warhaft2014).
$-5/3$
spectrum appear to be more “forgiving” than those initially outlined by Kolmogorov’ (Isaza et al.
Reference Isaza, Salazar and Warhaft2014).
It is the large-scale vortex shedding and the occurrence of the intermittent fluctuations instead of the local Reynolds number
![]() $Re_{\unicode[STIX]{x1D706}}$
that actually determine the range of the
$Re_{\unicode[STIX]{x1D706}}$
that actually determine the range of the
![]() $-5/3$
power law. Our current work contributes to the understanding of the appearance of the
$-5/3$
power law. Our current work contributes to the understanding of the appearance of the
![]() $-5/3$
power-law scaling in the near field of a spatially developing turbulent flow (see, for example, Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2014; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017; Portela et al.
Reference Portela, Papadakis and Vassilicos2017). Finally, it should be stressed that the frequency range over which the spectrum has an exponent close to
$-5/3$
power-law scaling in the near field of a spatially developing turbulent flow (see, for example, Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2014; Laizet et al.
Reference Laizet, Nedić and Vassilicos2015b
; Paul et al.
Reference Paul, Papadakis and Vassilicos2017; Portela et al.
Reference Portela, Papadakis and Vassilicos2017). Finally, it should be stressed that the frequency range over which the spectrum has an exponent close to
![]() $-5/3$
is defined by two distinctly different behaviours corresponding to large-scale vortex shedding and occurrence of the extreme events. This finding obviously disobeys the predictions given by Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
,Reference Kolmogorov
c
). It must be pointed out that in this work, we confirm that the extreme events and the
$-5/3$
is defined by two distinctly different behaviours corresponding to large-scale vortex shedding and occurrence of the extreme events. This finding obviously disobeys the predictions given by Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
,Reference Kolmogorov
c
). It must be pointed out that in this work, we confirm that the extreme events and the
![]() $-5/3$
energy spectrum at
$-5/3$
energy spectrum at
![]() $X/T_{0}=6$
are closely related. One cannot claim that it is the extreme events that are causing the
$X/T_{0}=6$
are closely related. One cannot claim that it is the extreme events that are causing the
![]() $-5/3$
energy spectrum.
$-5/3$
energy spectrum.
4.3 Second-order structure function
In this subsection, we address the final question raised in the introduction section, that is, the shape of the second-order structure function in the flow region where the extreme events can be identified. Thus, we explore the second-order structure function
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
with
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
with
![]() $\unicode[STIX]{x1D6FF}u^{\prime }(\unicode[STIX]{x0394}t)$
being
$\unicode[STIX]{x1D6FF}u^{\prime }(\unicode[STIX]{x0394}t)$
being
![]() $u^{\prime }(t+\unicode[STIX]{x0394}t)-u^{\prime }(t)$
at the two extensively investigated locations (i.e.
$u^{\prime }(t+\unicode[STIX]{x0394}t)-u^{\prime }(t)$
at the two extensively investigated locations (i.e.
![]() $X/T_{0}=6$
and 26). According to our definition, the second-order structure function
$X/T_{0}=6$
and 26). According to our definition, the second-order structure function
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
depends on the streamwise location
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
depends on the streamwise location
![]() $X$
and time difference
$X$
and time difference
![]() $\unicode[STIX]{x0394}t$
. According to the Kolmogorov phenomenology, in the so-called ‘inertial subrange’ we have the well-known
$\unicode[STIX]{x0394}t$
. According to the Kolmogorov phenomenology, in the so-called ‘inertial subrange’ we have the well-known
![]() $2/3$
power law (i.e. equivalent to the
$2/3$
power law (i.e. equivalent to the
![]() $-5/3$
energy spectrum in frequency space) albeit the range of the
$-5/3$
energy spectrum in frequency space) albeit the range of the
![]() $2/3$
power law in real space is always much smaller than the frequency range over which the
$2/3$
power law in real space is always much smaller than the frequency range over which the
![]() $-5/3$
power law can be found (see, for example, Tennekes & Lumley Reference Tennekes and Lumley1972; Frisch Reference Frisch1995; Pope Reference Pope2000). It is worth mentioning that structure functions considered here are actually averaged structure functions.
$-5/3$
power law can be found (see, for example, Tennekes & Lumley Reference Tennekes and Lumley1972; Frisch Reference Frisch1995; Pope Reference Pope2000). It is worth mentioning that structure functions considered here are actually averaged structure functions.

Figure 17. Second-order structure functions
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
at
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
at
![]() $X/T_{0}=6$
and 26 along the centreline. The vertical dashed line corresponds to half-vortex shedding cycle (i.e. the phase difference between
$X/T_{0}=6$
and 26 along the centreline. The vertical dashed line corresponds to half-vortex shedding cycle (i.e. the phase difference between
![]() $u^{\prime }(\unicode[STIX]{x0394}t)$
and
$u^{\prime }(\unicode[STIX]{x0394}t)$
and
![]() $u^{\prime }(t+\unicode[STIX]{x0394}t)$
is
$u^{\prime }(t+\unicode[STIX]{x0394}t)$
is
![]() $\unicode[STIX]{x03C0}$
).
$\unicode[STIX]{x03C0}$
).
Figure 17 shows
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
versus
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
versus
![]() $\unicode[STIX]{x0394}tU_{in}/T_{0}$
at
$\unicode[STIX]{x0394}tU_{in}/T_{0}$
at
![]() $X/T_{0}=6$
and 26 along the centreline. At
$X/T_{0}=6$
and 26 along the centreline. At
![]() $X/T_{0}=6$
the expected
$X/T_{0}=6$
the expected
![]() $2/3$
power law is absent and the turbulent flow exhibits a substantial power-law range with a large exponent close to
$2/3$
power law is absent and the turbulent flow exhibits a substantial power-law range with a large exponent close to
![]() $1$
in the intermediate range
$1$
in the intermediate range
![]() $0.1\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
instead. In contrast, at the downstream location
$0.1\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
instead. In contrast, at the downstream location
![]() $X/T_{0}=26$
the second-order structure function acquires an approximate
$X/T_{0}=26$
the second-order structure function acquires an approximate
![]() $2/3$
scaling law within the intermediate range
$2/3$
scaling law within the intermediate range
![]() $0.3\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
, which is in accord with Kolmogorov’s prediction. Compared with the upstream location
$0.3\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
, which is in accord with Kolmogorov’s prediction. Compared with the upstream location
![]() $X/T_{0}=6$
, at
$X/T_{0}=6$
, at
![]() $X/T_{0}=26$
the
$X/T_{0}=26$
the
![]() $-5/3$
frequency range is smaller but still a discernible
$-5/3$
frequency range is smaller but still a discernible
![]() $2/3$
power law can be identified. Thus, the absence of the
$2/3$
power law can be identified. Thus, the absence of the
![]() $2/3$
scaling law at
$2/3$
scaling law at
![]() $X/T_{0}=6$
is unlikely to be associated with the squeezing effect introduced by the Fourier transform.
$X/T_{0}=6$
is unlikely to be associated with the squeezing effect introduced by the Fourier transform.

Figure 18. Second-order structure functions of
![]() $u_{{<}}^{\prime }$
,
$u_{{<}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{>}}^{\prime }$
at (a)
$u_{{>}}^{\prime }$
at (a)
![]() $X/T_{0}=6$
and (b)
$X/T_{0}=6$
and (b)
![]() $X/T_{0}=26$
along the centreline. For comparison, the corresponding profile of
$X/T_{0}=26$
along the centreline. For comparison, the corresponding profile of
![]() $u^{\prime }$
is also plotted. From bottom to top, the three horizontal dashed lines indicate
$u^{\prime }$
is also plotted. From bottom to top, the three horizontal dashed lines indicate
![]() $2(U_{rms}^{{<}})^{2}$
,
$2(U_{rms}^{{<}})^{2}$
,
![]() $2(U_{rms}^{{\sim}})^{2}$
and
$2(U_{rms}^{{\sim}})^{2}$
and
![]() $2(U_{rms}^{{>}})^{2}$
. The vertical dashed lines correspond to half-vortex shedding cycle.
$2(U_{rms}^{{>}})^{2}$
. The vertical dashed lines correspond to half-vortex shedding cycle.
For sufficiently small
![]() $\unicode[STIX]{x0394}t$
, the Taylor expansion of the velocity difference is
$\unicode[STIX]{x0394}t$
, the Taylor expansion of the velocity difference is
![]() $u^{\prime }(t+\unicode[STIX]{x0394}t)-u^{\prime }(t)=(\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)\unicode[STIX]{x0394}t+O(\unicode[STIX]{x0394}t^{2})$
. The second-order structure is therefore
$u^{\prime }(t+\unicode[STIX]{x0394}t)-u^{\prime }(t)=(\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)\unicode[STIX]{x0394}t+O(\unicode[STIX]{x0394}t^{2})$
. The second-order structure is therefore
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =\langle (\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)^{2}\rangle \unicode[STIX]{x0394}t^{2}+O(\unicode[STIX]{x0394}t^{3})$
. Figure 17 further shows that for small
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =\langle (\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)^{2}\rangle \unicode[STIX]{x0394}t^{2}+O(\unicode[STIX]{x0394}t^{3})$
. Figure 17 further shows that for small
![]() $\unicode[STIX]{x0394}t$
, the second-order structure functions at
$\unicode[STIX]{x0394}t$
, the second-order structure functions at
![]() $X/T_{0}=6$
and 26 indeed acquire a well-defined power law with an exponent close to 2, implying that in current DNSs the small dissipation scales are well resolved in time.
$X/T_{0}=6$
and 26 indeed acquire a well-defined power law with an exponent close to 2, implying that in current DNSs the small dissipation scales are well resolved in time.
To shed light on the formation mechanism of the substantial
![]() $1$
power law at
$1$
power law at
![]() $X/T_{0}=6$
, the second-order structure functions of the filtered flow fields (i.e.
$X/T_{0}=6$
, the second-order structure functions of the filtered flow fields (i.e.
![]() $u_{{>}}^{\prime }$
,
$u_{{>}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
) are computed (see figure 18
a). The second-order structure functions at
$u_{{<}}^{\prime }$
) are computed (see figure 18
a). The second-order structure functions at
![]() $X/T_{0}=26$
are shown in figure 18(b) as a further comparison. Obviously, at sufficiently large
$X/T_{0}=26$
are shown in figure 18(b) as a further comparison. Obviously, at sufficiently large
![]() $\unicode[STIX]{x0394}t$
, we have
$\unicode[STIX]{x0394}t$
, we have
![]() $\langle \unicode[STIX]{x1D6FF}u_{{<}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{<}})^{2}$
,
$\langle \unicode[STIX]{x1D6FF}u_{{<}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{<}})^{2}$
,
![]() $\langle \unicode[STIX]{x1D6FF}u_{{\sim}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{\sim}})^{2}$
and
$\langle \unicode[STIX]{x1D6FF}u_{{\sim}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{\sim}})^{2}$
and
![]() $\langle \unicode[STIX]{x1D6FF}u_{{>}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{>}})^{2}$
, which is indeed the case as shown in both figures 18(a) and 18(b).
$\langle \unicode[STIX]{x1D6FF}u_{{>}}^{\prime 2}(\unicode[STIX]{x0394}t)\rangle =2(U_{rms}^{{>}})^{2}$
, which is indeed the case as shown in both figures 18(a) and 18(b).
From Parseval’s theorem, we can derive the following relations:
and
A brief justification of the two equations can be found in supplementary appendix D. These two equations allow us to quantify the contribution of each velocity components,
![]() $u_{{>}}^{\prime }$
,
$u_{{>}}^{\prime }$
,
![]() $u_{{\sim}}^{\prime }$
and
$u_{{\sim}}^{\prime }$
and
![]() $u_{{<}}^{\prime }$
, on the profile shape of
$u_{{<}}^{\prime }$
, on the profile shape of
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
. Figure 18(a) implies that the discrepancy from the
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
. Figure 18(a) implies that the discrepancy from the
![]() $2/3$
scaling is probably associated with the strong vortex shedding. More specifically, for the time difference
$2/3$
scaling is probably associated with the strong vortex shedding. More specifically, for the time difference
![]() $\unicode[STIX]{x0394}tU_{in}/T_{0}\simeq 3$
, which defines the end of the
$\unicode[STIX]{x0394}tU_{in}/T_{0}\simeq 3$
, which defines the end of the
![]() $1$
slope, the large-scale velocity components
$1$
slope, the large-scale velocity components
![]() $u_{{>}}^{\prime }$
make an overwhelming contribution to
$u_{{>}}^{\prime }$
make an overwhelming contribution to
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
.
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
.
At
![]() $X/T_{0}=6$
and 26, the second-order structure function of
$X/T_{0}=6$
and 26, the second-order structure function of
![]() $u_{{>}}^{\prime }$
acquire a well-defined 2 power-law scaling in the range
$u_{{>}}^{\prime }$
acquire a well-defined 2 power-law scaling in the range
![]() $\unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
. Moreover, the vortex shedding periods are more or less the same (see figures 11 and 17). That is, the time scales of
$\unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
. Moreover, the vortex shedding periods are more or less the same (see figures 11 and 17). That is, the time scales of
![]() $u_{{>}}^{\prime }$
at
$u_{{>}}^{\prime }$
at
![]() $X/T_{0}=6$
and 26 are close to each other. Therefore, the stronger vortex shedding at
$X/T_{0}=6$
and 26 are close to each other. Therefore, the stronger vortex shedding at
![]() $X/T_{0}=6$
, as can be seen from the height of the oscillations in figure 18 and peak values of the spectra in figure 11, corresponds to a large coefficient
$X/T_{0}=6$
, as can be seen from the height of the oscillations in figure 18 and peak values of the spectra in figure 11, corresponds to a large coefficient
![]() $\langle (\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)^{2}\rangle$
, which can significantly contaminate the profile of
$\langle (\unicode[STIX]{x2202}u^{\prime }(t)/\unicode[STIX]{x2202}t)^{2}\rangle$
, which can significantly contaminate the profile of
![]() $\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
within the range
$\langle \unicode[STIX]{x1D6FF}u^{\prime 2}(\unicode[STIX]{x0394}t)\rangle$
within the range
![]() $0.3\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
(see figure 18
a). In other words, fluid motions within this intermediate range are not sufficiently separated from large-scale motions and can directly ‘feel’ the large-scale vortex shedding. This observation violates Kolmogorov’s universal equilibrium hypothesis. In the range
$0.3\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 3$
(see figure 18
a). In other words, fluid motions within this intermediate range are not sufficiently separated from large-scale motions and can directly ‘feel’ the large-scale vortex shedding. This observation violates Kolmogorov’s universal equilibrium hypothesis. In the range
![]() $0.1\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 0.3$
, however, the interpretation of the appearance of the approximate
$0.1\lesssim \unicode[STIX]{x0394}tU_{in}/T_{0}\lesssim 0.3$
, however, the interpretation of the appearance of the approximate
![]() $1$
power law should not be pushed too far since this exponent lies between the scaling law of
$1$
power law should not be pushed too far since this exponent lies between the scaling law of
![]() $2/3$
and 2. It is difficult to accurately compute the scaling law in the transition region between the
$2/3$
and 2. It is difficult to accurately compute the scaling law in the transition region between the
![]() $2/3$
power-law range and the dissipation range with an exponent close 2. We again demonstrate that the
$2/3$
power-law range and the dissipation range with an exponent close 2. We again demonstrate that the
![]() $-5/3$
energy spectrum found at
$-5/3$
energy spectrum found at
![]() $X/T_{0}=6$
is not the well-known Kolmogorov
$X/T_{0}=6$
is not the well-known Kolmogorov
![]() $-5/3$
spectrum. On the other hand, at
$-5/3$
spectrum. On the other hand, at
![]() $X/T_{0}=26$
, the occurrence of the
$X/T_{0}=26$
, the occurrence of the
![]() $2/3$
scaling of the second-order structure function along with the
$2/3$
scaling of the second-order structure function along with the
![]() $-5/3$
energy spectrum appear to be in accord with the Kolmogorov phenomenology.
$-5/3$
energy spectrum appear to be in accord with the Kolmogorov phenomenology.
5 Conclusion
The streamwise evolutions of the statistical characteristics of turbulent flows behind two side-by-side square cylinders with different gap ratios (i.e.
![]() $L_{d}/T_{0}=4$
, 6 and 8) are investigated by using DNSs. The wake-interaction length scale
$L_{d}/T_{0}=4$
, 6 and 8) are investigated by using DNSs. The wake-interaction length scale
![]() $X_{\ast }$
, which is widely used to normalize the streamwise distance in the grid-generated turbulence, is explored in this paper. It is demonstrated that for the case with large gap ratios, in which two vortex streets are more persist,
$X_{\ast }$
, which is widely used to normalize the streamwise distance in the grid-generated turbulence, is explored in this paper. It is demonstrated that for the case with large gap ratios, in which two vortex streets are more persist,
![]() $X_{\ast }$
can be used to describe the evolution of some important turbulence characteristics, at least to some extent.
$X_{\ast }$
can be used to describe the evolution of some important turbulence characteristics, at least to some extent.
To shed light on the formation mechanism of the extreme events, the turbulent flows at
![]() $X/T_{0}=6$
and 26 in the case with
$X/T_{0}=6$
and 26 in the case with
![]() $L_{d}/T_{0}=6$
are extensively investigated. Our study confirms that the occurrences of the extreme events are associated with the large magnitude of
$L_{d}/T_{0}=6$
are extensively investigated. Our study confirms that the occurrences of the extreme events are associated with the large magnitude of
![]() $v^{\prime }$
. The energy spectrum at
$v^{\prime }$
. The energy spectrum at
![]() $X/T_{0}=6$
, where turbulent flow is highly intermittent with the occurrence of the extreme events and undergoes transition to a fully turbulent state, acquires a well-defined
$X/T_{0}=6$
, where turbulent flow is highly intermittent with the occurrence of the extreme events and undergoes transition to a fully turbulent state, acquires a well-defined
![]() $-5/3$
power law with a range for almost a decade. By extracting the velocity signals in the high-frequency region, we provide the first direct evidence that the occurrence of the well-known
$-5/3$
power law with a range for almost a decade. By extracting the velocity signals in the high-frequency region, we provide the first direct evidence that the occurrence of the well-known
![]() $-5/3$
power spectrum is directly attributed to the extreme events. In the intermediate-frequency range, both laminar and turbulent behaviours contribute to the formation of the
$-5/3$
power spectrum is directly attributed to the extreme events. In the intermediate-frequency range, both laminar and turbulent behaviours contribute to the formation of the
![]() $-5/3$
scaling law. In the downstream region
$-5/3$
scaling law. In the downstream region
![]() $X/T_{0}=26$
, however, the strength of the extreme events becomes weaker. Consequently, the range of the
$X/T_{0}=26$
, however, the strength of the extreme events becomes weaker. Consequently, the range of the
![]() $-5/3$
energy spectrum narrows. The absence of the
$-5/3$
energy spectrum narrows. The absence of the
![]() $2/3$
power law of the second-order structure function at
$2/3$
power law of the second-order structure function at
![]() $X/T_{0}=6$
finds its roots in the strong large-scale vortex shedding and the motions in the intermediate range can directly ‘feel’ the large-scale vortex shedding, which violates Kolmogorov’s universal equilibrium hypothesis.
$X/T_{0}=6$
finds its roots in the strong large-scale vortex shedding and the motions in the intermediate range can directly ‘feel’ the large-scale vortex shedding, which violates Kolmogorov’s universal equilibrium hypothesis.
In this work, we prove that the extreme events and the
![]() $-5/3$
power-law scaling are closely related. Not limited to the dual-wake flow presented in this study, the appearance of the non-Kolmogorov
$-5/3$
power-law scaling are closely related. Not limited to the dual-wake flow presented in this study, the appearance of the non-Kolmogorov
![]() $-5/3$
power-law scaling can also be found in the near field of various kinds of turbulent flows, as has already been reported. This work may open an avenue for understanding this phenomenon.
$-5/3$
power-law scaling can also be found in the near field of various kinds of turbulent flows, as has already been reported. This work may open an avenue for understanding this phenomenon.
To investigate what physical mechanisms are responsible for the emergence of the
![]() $-5/3$
spectrum at
$-5/3$
spectrum at
![]() $X/T_{0}=6$
, we need to explore the corresponding scale-by-scale energy budget by resorting to the Kármán–Howarth–Monin–Hill equation, which is directly derived from the Navier–Stokes equations without making any assumptions and consequently can be used to study the energy transfer process in any kind of turbulence. Also, how the strong vortex shedding in the upstream region affects the energy cascade is another important topic, which should be pursued in future works.
$X/T_{0}=6$
, we need to explore the corresponding scale-by-scale energy budget by resorting to the Kármán–Howarth–Monin–Hill equation, which is directly derived from the Navier–Stokes equations without making any assumptions and consequently can be used to study the energy transfer process in any kind of turbulence. Also, how the strong vortex shedding in the upstream region affects the energy cascade is another important topic, which should be pursued in future works.
Acknowledgements
This work was in part supported by the National Natural Science Foundation of China (no. 11802133), the Natural Science Foundation of Jiangsu Province (no. BK20180454) and the Fundamental Research Funds for the Central Universities (no. 30918011325). Part of this study was also supported by MEXT KAKENHI (nos 18H01367 and 18H01369). Parts of the numerical simulations were carried out on the supercomputer at Tokoku University (no. J18I078: Institute of Fluid Science, Tohoku University and no. CP02APR18: Advanced Fluid Information Research Center, Institute of Fluid Science, Tohoku University) and the assistance of Professor T. Hayase at Tohoku University in performing the verification simulations is greatly appreciated.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2019.456.