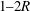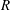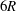1. Introduction
In turbulent pipe flows, we generally recognize four distinct types of coherent motion (Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011). The first is the near-wall streaks, which are regions of low momentum located in the viscous sublayer with a spanwise spacing of
$100{\it\nu}/u_{{\it\tau}}$
, where
$u_{{\it\tau}}$
is the friction velocity and
${\it\nu}$
is the fluid kinematic viscosity. The second is the hairpin or horseshoe vortices (Theodorsen Reference Theodorsen1952), which display a variety of scales with a minimum height of approximately
$100{\it\nu}/u_{{\it\tau}}$
. The third and fourth are the large-scale and very-large-scale motions (LSMs and VLSMs respectively).
The LSMs are believed to be the result of an alignment of hairpin vortices (sometimes referred to as ‘hairpin packets’), travelling at a common convective velocity and characterized by a region of low-momentum fluid between the hairpin legs (Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000; Ganapathisubramani, Longmire & Marusic Reference Ganapathisubramani, Longmire and Marusic2003; Tomkins & Adrian Reference Tomkins and Adrian2003). Measurements using multiple-plane particle image velocimetry (PIV) show the streamwise and wall-normal extent of these structures (Hambleton, Hutchins & Marusic Reference Hambleton, Hutchins and Marusic2006), and there is now an emerging consensus that the LSMs are initiated at the wall, grow upwards in the streamwise direction at a mean angle of approximately
$12^{\circ }$
to form a ramp-like structure with a streamwise extent of
$2{-}3R$
in pipes (
$R$
is the pipe radius), and then finally detach from the wall while initiating a new attached structure at the wall (Adrian Reference Adrian2007).
The VLSMs are structures of uncertain origin, marked by long meandering regions of low- and high-speed momentum in the outer layer of wall-bounded turbulence. They have been characterized primarily by using spatio-temporal two-point correlations, or point measurements in combination with Taylor’s hypothesis. Kim & Adrian (Reference Kim and Adrian1999) were the first to identify their presence by the occurrence of low-frequency peaks in the premultiplied energy spectra of streamwise velocity fluctuations in a turbulent pipe flow. Later work (del Álamo & Jiménez Reference del Álamo and Jiménez2003; del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004; Guala, Hommema & Adrian Reference Guala, Hommema and Adrian2006; Monty et al.
Reference Monty, Stewart, Williams and Chong2007; Bailey et al.
Reference Bailey, Hultmark, Smits and Schultz2008) confirmed the presence of these large-scale structures in pipe and channel flows over a very wide range of Reynolds numbers, with a streamwise extent of as much as
$30R$
. Hutchins & Marusic (Reference Hutchins and Marusic2007) found that these structures also exist in boundary layers, where they are called ‘superstructures’, extending to more than
$10{\it\delta}$
even in atmospheric surface layers (where
${\it\delta}$
is the boundary layer thickness). Balakumar & Adrian (Reference Balakumar and Adrian2007) showed that 40–65 % of the turbulence kinetic energy was carried by wavelengths larger than
$3{\it\delta}$
, and Bailey & Smits (Reference Bailey and Smits2010) found that these structures spanned a third of the circumference of the pipe. In supersonic boundary layers, Ganapathisubramani, Clemens & Dolling (Reference Ganapathisubramani, Clemens and Dolling2006) found the spatial extent of the superstructures to be over
$8{\it\delta}$
(the limit of their PIV field of view), while Ganapathisubramani, Clemens & Dolling (Reference Ganapathisubramani, Clemens and Dolling2009) combined wide-field high-speed PIV with Taylor’s hypothesis and discovered even longer structures.
Hellström, Sinha & Smits (Reference Hellström, Sinha and Smits2011) analysed time-resolved stereo PIV data in the cross-stream plane of pipe flow for a Reynolds number of
$Re_{D}=$
12 500 using snapshot proper orthogonal decomposition (POD). Here,
$Re_{D}=2RU_{b}/{\it\nu}$
, where
$U_{b}$
is the bulk velocity. They showed that the velocity fields constructed using only the lower-order modes display many characteristics common to the VLSMs, such as long radially and azimuthally meandering behaviour. However, the convergence of the POD modes in that work was limited by the short time interval, corresponding to a convective displacement of
$22R$
.
Baltzer, Adrian & Wu (Reference Baltzer, Adrian and Wu2013) investigated a direct numerical simulation of a turbulent pipe flow for
$Re_{D}=24\,580$
, and found the presence of LSM-like structures pseudo-aligning in a helical pattern with an azimuthal angle of
$4{-}5^{\circ }$
, which they suggested as the basis for VLSM formation. Proper orthogonal decomposition analysis indicated that the most energetic modes contained two or three azimuthal structures
$(m=\{2,3\})$
with a streamwise wavelength of
$15{-}30R$
, limited to an integer fraction of their computational domain.
Hellström & Smits (Reference Hellström and Smits2014) addressed the modal convergence in Hellström et al. (Reference Hellström, Sinha and Smits2011) by obtaining a much larger data set, for
$Re_{D}=$
50 000 and 100 000. The low-order modes were similar to those found by Bailey & Smits (Reference Bailey and Smits2010) using cross-correlation techniques, spanning from the wall well in to the wake region. The dominant motion consisted of three azimuthal structures, which were only weakly dependent on the Reynolds number. These energetic modes were identified as significant contributors to the shear stress; for instance, the first 10 modes contribute 15 % of the turbulence kinetic energy and 43 % of the integrated shear stress. The modes with one radial and two, three or four azimuthal structures
$(m=\{2,3,4\})$
exhibited a characteristic frequency corresponding to a convective length of
$20{-}40R$
, similar to that seen for the VLSM.
Figure 1. The dual-plane PIV experimental set-up, where the two PIV planes are orthogonally polarized.
Despite this earlier work, the spatial extent and therefore the origin of VLSMs has been much debated. In particular, Kim & Adrian (Reference Kim and Adrian1999) suggested that the VLSMs are a consequence of an alignment of the LSMs, and this point was also reiterated by Dennis & Nickels (Reference Dennis and Nickels2011) using 3D PIV data, whereas del Álamo & Jiménez (Reference del Álamo and Jiménez2006) proposed that the VLSMs could be formed by linear or nonlinear processes. Here, we address this question by examining the spatial structure and evolution of the VLSMs, and the spatio-temporal transitions between successive VLSMs using dual-plane PIV in turbulent pipe flow. We will analyse the data using POD, since Hellström et al. (Reference Hellström, Sinha and Smits2011) demonstrated that these modes capture well the large-scale structures. Our primary focus will be on the modes previously associated with the VLSM, that is,
$m=\{2,3,4\}$
. We build on this POD approach and use conditional analysis to identify the origin of the VLSMs and determine their relationship to the LSMs.
2. Experimental set-up
The experiment was conducted in the same pipe flow facility as described by Hellström & Smits (Reference Hellström and Smits2014). The pipe is made of seven glass sections each 1.2 m long with an inner diameter of
$D=38.1\pm 0.025~\text{mm}$
, resulting in a development length of
$200D$
. The results presented here were obtained at a single Reynolds number,
$Re_{D}=U_{b}D/{\it\nu}=$
104 000, and the working fluid was water at room temperature. The corresponding friction Reynolds number
$Re_{{\it\tau}}=u_{{\it\tau}}R/{\it\nu}=2460$
.
The flow was simultaneously investigated in two planes using dual-plane PIV, similar to that used by Ganapathisubramani et al. (Reference Ganapathisubramani, Longmire, Marusic and Pothos2005); see figure 1. The first plane was a cross-sectional plane and was interrogated using stereoscopic PIV (2D–3C). The second plane was a streamwise plane along the pipe centreline, spanning
$4.8R$
in the streamwise direction, centred on the cross-plane, and it was investigated using planar PIV (2D–2C). The laser sheets were generated by a Nd:YAG dual-cavity pulsed laser with
$50~\text{mJ}~\text{pulse}^{-1}$
, equipped with an adjustable beam splitter such that the intensities could be independently balanced. The two 1 mm thick light sheets were orthogonally polarized using a pair of half-wave plates, allowing particles in each plane to be distinguished using a pair of linear polarizers placed in front of each camera. The cross-sectional plane was vertically polarized to minimize the scatter in the vertical direction and thereby reduce the contamination of the planar PIV image (Adrian & Westerweel Reference Adrian and Westerweel2011). Similarly, the streamwise plane was horizontally polarized.
The three 5.5 Megapixel LaVision Imager sCMOS cameras were operated at 30 Hz with an interframe time of
$40~{\rm\mu}\text{s}$
, so that at
$Re_{D}=$
104 000 there was a bulk convective displacement of
$0.96R$
between two consecutive data planes. The flow was seeded using
$10~{\rm\mu}\text{m}$
hollow glass spheres, and although the scattered light lost some of its polarization, the polarization was sufficient to separate the two orthogonal images with little cross-talk.
The test section was enclosed by an acrylic box, filled with water to minimize the optical distortion due to refraction through the pipe wall. The pipe wall thickness (
$1.27\pm 0.064~\text{mm}$
) was minimized to further reduce the reflection and distortion caused by the mismatch between the refractive index of water and that of glass. The PIV calibration method was similar to that presented by van Doorne & Westerweel (Reference van Doorne and Westerweel2007) and Hellström et al. (Reference Hellström, Sinha and Smits2011). An access port was located immediately downstream of the test section in order to insert the planar and stereo PIV calibration targets while the pipe was filled with water. The stereo PIV target was a 1.6 mm thick plate with 272 dots set in a rectangular grid. The target was traversed 2 mm in each direction of the laser sheet, resulting in three calibration images for each stereo PIV camera. The planar target was a 150 mm long D-shaped cylinder having circular ends, with 189 dots arranged in a rectangular grid. The target was attached to a micrometer stage for streamwise alignment of the streamwise plane with the cross-plane.
The data consisted of ten blocks, each containing 2200 image pairs. The images were processed using DaVis 8.1.6, and the resulting velocity field for the cross-plane consisted of 20 vectors
$\text{mm}^{-2}$
on a square mesh. The velocity components were interpolated onto a new mesh with polar coordinates
$[r,{\it\theta},x]$
, having 132 radial mesh points spaced a distance
${\rm\Delta}r$
, and 834 azimuthal mesh points, matching the vector density at the wall while oversampling at the pipe centre. The streamwise plane resulted in 15 vectors
$\text{mm}^{-2}$
, and these data were interpolated onto a mesh with radial grid points that matched the cross-plane. The singularity point at
$r=0$
, when performing POD, was avoided by offsetting the inner mesh points by
${\rm\Delta}r/2$
.
In the streamwise plane approximately 100 vectors, corresponding to 0.3 % of the total vector count, were corrupted by the depolarized scatter off the pipe wall from the cross-plane light sheet. These vectors were estimated by performing snapshot POD on the streamwise plane, while excluding the corrupt vectors. The excluded vectors were then interpolated for each snapshot POD mode, where the fields are smoother than in the instantaneous velocity realizations. The complete velocity field was subsequently obtained by reconstructing the interpolated POD modes.
The data analysis was performed in three steps: snapshot POD analysis on the three-component fluctuating velocity data in the cross-plane, a temporal analysis of the most energetic mode and its transitional modes, and a conditional mode analysis to simultaneously visualize the average mode shapes in the cross-plane and the streamwise plane.
3. Snapshot POD
We begin with snapshot POD analysis of the three-component fluctuating velocity data in the cross-plane. The procedure is similar to that followed by Hellström & Smits (Reference Hellström and Smits2014), who simultaneously performed classical and snapshot POD on a cross-stream plane in the same pipe as used here. They found that snapshot POD may suffer from mode mixing, resulting in some non-optimal modes composed of parts of optimal modes. The effect of mode mixing can be reduced by decomposing the azimuthal direction using a Fourier series expansion, as proposed by Duggleby & Paul (Reference Duggleby and Paul2010). The POD equation in pipe coordinates can be written as
$$\begin{eqnarray}\int _{r^{\prime }}\unicode[STIX]{x1D64E}(m;r,r^{\prime }){\it\Phi}_{n}(m;r^{\prime })\,\text{d}r^{\prime }={\it\lambda}_{n}(m){\it\Phi}_{n}(m;r),\end{eqnarray}$$
where
$n$
represents the POD mode number,
${\it\Phi}_{n}$
are the eigenfunctions with the corresponding eigenvalues
${\it\lambda}_{n}$
, and
$m$
represents the azimuthally decomposed mode number. Here,
$r$
from the polar integration is absorbed into the eigenfunctions and the cross-correlation tensor (Glauser & George Reference Glauser and George1987; Citriniti & George Reference Citriniti and George2000; Tutkun, Johansson & George Reference Tutkun, Johansson and George2008). The time-averaged cross-correlation tensor becomes
$$\begin{eqnarray}\unicode[STIX]{x1D64E}(m;r,r^{\prime })=\lim _{{\it\tau}\rightarrow \infty }\frac{1}{{\it\tau}}\int _{0}^{{\it\tau}}r^{1/2}\boldsymbol{u}(m;r,t)\boldsymbol{u}^{\ast }(m;r^{\prime },t)r^{\prime 1/2}\,\text{d}t,\end{eqnarray}$$
with
$^{\ast }$
denoting the complex conjugate. The method of snapshots assumes that the flow is separable in time and space functions, which can be written in pipe coordinates as
$$\begin{eqnarray}{\it\alpha}_{n}(m;t)=\int _{r}\boldsymbol{u}(m;r,t)r^{1/2}{\it\Phi}_{n}^{\ast }(m;r)\,\text{d}r.\end{eqnarray}$$
The eigenvalue problem can then be rewritten to yield the POD coefficients,
${\it\alpha}_{n}$
, as in
$$\begin{eqnarray}\lim _{{\it\tau}\rightarrow \infty }\frac{1}{{\it\tau}}\int _{0}^{{\it\tau}}\left(r^{1/2}\boldsymbol{u}(m;r,t),r^{1/2}\boldsymbol{u}(m;r,t^{\prime })\right){\it\alpha}_{n}(m;t)\,\text{d}t^{\prime }={\it\lambda}_{n}(m){\it\alpha}_{n}(m;t),\end{eqnarray}$$
where
$(\cdot \,,\cdot )$
is the inner product over
$r$
. Due to the azimuthal decomposition, the eigenfunctions are reduced to one complex radial mode for each
$m$
and
$n$
, which can be found according to
$$\begin{eqnarray}\lim _{{\it\tau}\rightarrow \infty }\frac{1}{{\it\tau}}\int _{0}^{{\it\tau}}r^{1/2}\boldsymbol{u}(m;r,t){\it\alpha}_{n}^{\ast }(m;t)\,\text{d}t={\it\Phi}_{n}(m;r){\it\lambda}^{n}(m).\end{eqnarray}$$
The relative turbulence kinetic energy of the first 15 azimuthal modes
$m$
and five POD modes
$n$
is seen in figure 2. The five most energetic modes,
$(m,n)=(1{-}5,1)$
, corresponding to the first five modal pairs reported by Hellström & Smits (Reference Hellström and Smits2014), contribute 16 % of the total energy. The cumulative energy for
$(m,n)=(1{-}5,1{-}5)$
contributes 28 % of the total energy.
Figure 2. The columns show the scaled energy content of the first five POD modes
$n$
and first 15 azimuthal modes
$m$
(scaled mode energy
${\it\xi}_{n}(m)$
), and the dashed curve shows the cumulative energy content of first five POD modes.
Thus, the POD modes are reduced to a set of complex radial profiles, one for each POD mode number and azimuthal mode number combination. The mode shapes are illustrated in figure 3. The pipe centreline is located at
$y/R=1$
, around which the POD mode is revolved with a magnitude corresponding to a sine wave having the appropriate azimuthal wavelength set by
$m$
. Here, we have applied a phase shift to each mode, to ensure that they are real, and so only the real component is shown. The shapes of the five most energetic POD modes,
$(m,n)=(1{-}5,1)$
, are shown in figure 3(a), and the behaviour of the higher-order POD modes,
$(m,n)=(3,1{-}5)$
, is shown in figure 3(b); the higher-order POD modes have an increasing number of radial structures. Higher-order POD modes do not necessarily correspond to more radial structures; for instance, the second and fourth POD modes exhibit similar profiles while the fourth mode contains wall-detached structures, whereas the second mode does not. It can be seen that the most energetic structure is composed of three azimuthal structures
$(m=3)$
with a radial profile containing one structure, similar to the structures identified by Bailey & Smits (Reference Bailey and Smits2010) and those associated with the VLSMs by Hellström & Smits (Reference Hellström and Smits2014). It should be noted how the structures approach the wall as the azimuthal mode number increases.
Figure 3. (a) The first POD mode for the first–fifth azimuthal modes,
$(m,n)=(1{-}5,1)$
; (b) the first five POD modes for the third azimuthal mode,
$(m,n)=(3,1{-}5)$
.
We now examine the temporal occurrence/intensity of each mode by using the POD coefficients,
${\it\alpha}_{n}(m;t)$
. We assume on the basis of our previous work (Hellström et al.
Reference Hellström, Sinha and Smits2011; Hellström & Smits Reference Hellström and Smits2014) that the basic features of the VLSMs, especially their meandering behaviour and azimuthal extent, are well captured by the behaviour of the first few POD modes, and we propose that the evolution of the VLSMs can be determined by identifying the transitions that lead to these lower-order modes. Although the convective displacement between two snapshots is large in the current experiment (
$0.96R$
), it is smaller than the typical length of the LSM, and at least an order of magnitude smaller than the reported length of the VLSM, and therefore we expect to be able to track the meandering behaviour of the VLSM and its connection to the LSM using this approach.
Figure 4 shows the magnitude of the correlation
${\it\rho}$
of the POD coefficient
${\it\alpha}_{1}(3,t)$
and all other coefficients
$(m,n)=(1{-}15,1{-}5)$
, for positive and negative time shifts
$\pm {\it\tau}$
, where
${\it\tau}=1$
corresponds to the convective displacement of
$0.96R$
based on
$U_{b}$
. Here, the normalized cross-correlation is defined as
$$\begin{eqnarray}{\it\rho}(m_{1},m_{2},n_{1},n_{2},{\it\tau})=\frac{({\it\alpha}_{n_{1}}(m_{1},t),{\it\alpha}_{n_{2}}(m_{2},t+{\it\tau}))}{\Vert {\it\alpha}_{n_{1}}(m_{1},t)\Vert \Vert {\it\alpha}_{n_{2}}(m_{2},t)\Vert },\end{eqnarray}$$
where
$\left(\cdot \,,\cdot \right)$
is the sliding inner product with respect to time and
$\Vert \cdot \Vert$
represents its
$L^{2}$
norm. The highest correlations are all within the same azimuthal mode number,
$m=3$
, indicating that within
$\pm {\it\tau}$
the structures either remain the same or they transition to a higher-order POD mode with the same azimuthal mode number. The results therefore suggest that the transition of the structures is associated with a change in radial behaviour rather than with a change in azimuthal mode number, and so these higher-order radial modes describe the transition in and out of these large energetic motions. The mode shapes associated with the transition of
${\it\Phi}_{1}(3;r)$
are shown in figure 3(b).
Figure 4. The magnitude of the cross-correlation of the POD coefficient
${\it\alpha}_{1}(3,t)$
and all other coefficients up to
$(m,n)=(5,15)$
using one time step offset,
${\it\tau}=1$
. (a) Correlation for
${\it\tau}=-1$
, showing the likelihood of a mode to temporally precede
${\it\Phi}_{1}(3;r)$
; (b) correlation for
${\it\tau}=+1$
, showing the likelihood of a mode to temporally follow
${\it\Phi}_{1}(3;r)$
.
Figure 5. Autocorrelation of
${\it\alpha}_{n}(3,t)$
, revealing the temporal extent of
${\it\Phi}_{n}(3;r)$
before a modal transition occurs, indicating the likely length of the meandering coherent structure. Autocorrelation for POD mode (a)
$n=1$
, (b)
$n=3$
.
A similar procedure was performed for
${\it\Phi}_{1}(2;r)$
and
${\it\Phi}_{1}(4;r)$
. These modal combinations show a similar evolution to that of
${\it\Phi}_{1}(3;r)$
, where the low-order mode is first preceded and then followed by transitional modes with higher-order radial behaviour, again suggesting a radial evolution of the structure. The data from this analysis are not shown here for brevity.
The correlation analysis revealed the likely structure of the transition in and out of the energetic motions. To examine the spatio-temporal extent of the structures themselves, as well as their meandering behaviour, we use the autocorrelation of
${\it\alpha}_{n}(3,t)$
. The results are shown in figure 5. Because
${\it\alpha}_{1}(3;t)$
is azimuthally decomposed into Fourier modes, it will resolve an azimuthally meandering structure. We see that the autocorrelation of
${\it\alpha}_{1}(3,t)$
decays after one time step, after which it has transitioned to a higher-order POD mode, suggesting that the structure contained in
${\it\Phi}_{1}(3;r)$
has a spatio-temporal extent of
$1{-}2R$
, similar to that ascribed to the LSMs and much smaller than the wavelength of
$6{-}20R$
previously ascribed to the VLSMs. The autocorrelations for the higher-order POD modes, or the transitional modes, have a length scale shorter than the
$0.96R$
resolved by the cross-plane, indicating rapid modal transitions, see figure 5(b). This disconnect between the wavelengths associated with these energetic modes suggests that the structural components of the VLSM persist, on average, for only approximately one pipe diameter. The VLSMs appear to represent either the alignment of these shorter structures, as indicated by Kim & Adrian (Reference Kim and Adrian1999) in pipes and Dennis & Nickels (Reference Dennis and Nickels2011) in boundary layers, or the recurrence of a specific mode.
4. Temporal comparison
The link between the LSM and VLSM structures can be further explored by combining the POD analysis presented here with the time-resolved data obtained by Hellström et al. (Reference Hellström, Sinha and Smits2011) at
$Re_{D}=$
12 500. We intend to identify the flow structures associated with the low-order POD mode and its transitional modes. However, the time-resolved data were acquired over a rather short time interval, and we cannot expect to use the POD modes as they are not well converged. Instead, as the evolution of the structures is resolved within each azimuthal mode number, we azimuthally decompose the velocity field into a Fourier series expansion and in that way investigate the flow for each azimuthal mode number.
Figure 6(a) shows a carpet plot of the streamwise velocity fluctuations at a wall-normal location of
$y/R=0.2$
, where Taylor’s hypothesis was used to convert time to streamwise distance,
$x/R$
, and where
$s/R$
represents the scaled azimuthal arclength. Figure 6(b) shows the reconstructed velocity field using only the azimuthal mode
$m=3$
at the same wall-normal location. By inspection, there appear to be coherent structures of
$O(6R)$
spanning
$x/R=[0,6]$
, and shorter structures at
$x/R=10,14$
and 18. Figure 6(c) shows the streamwise velocity field for
$m=4$
at
$y/R=0.1$
. These structures are similar to those extracted using the first snapshot POD mode by Hellström et al. (Reference Hellström, Sinha and Smits2011). Again, there exist coherent azimuthally steady structures with an estimated length of
$O(6R)$
and a repetition rate of approximately
$10R$
. These structures span from
$x/R=[0,5],[7,13]$
and [16, 21].
Figure 6. Carpet plots of the streamwise velocity fluctuations at
$Re_{D}=$
12 500, constructed using Taylor’s hypothesis. (a) Instantaneous streamwise velocity fluctuations at a wall-normal distance of
$y/R=0.2$
(taken from Hellström et al.
Reference Hellström, Sinha and Smits2011). (b) Reconstructed velocity field using the azimuthal mode number
$m=3$
at
$y/R=0.2$
. (c) Reconstructed velocity field for
$m=4$
at
$y/R=0.1$
. Flow is from left to right.
The structures with a length scale of
$O(6R)$
seem to be broken into shorter blocks of approximately
$2R$
. The alignment of shorter structures is more apparent in figure 7, where the streamwise radial behaviour of the structures is visualized at
$s/R=0$
. It can be seen that the coherent structures in figure 6(c) at
$x/R=[16,21]$
in fact consist of an alignment of shorter structures, figure 7(b)
$x/R=[16,21]$
. A similar behaviour can be seen at
$x/R=[2,6]$
for the carpet plots representing
$m=3$
.
Figure 7. Carpet plots of the streamwise velocity fluctuations at
$Re_{D}=$
12 500, constructed using Taylor’s hypothesis. (a) Reconstructed velocity field using the azimuthal mode number
$m=3$
at
$s/R=0$
. (b) Reconstructed velocity field for
$m=4$
at
$s/R=0$
. Flow is from left to right.
The results suggest that a typical alignment of approximately 2–3 energetic structures (as in figure 7(b) at
$x/R=[14,21]$
) repeated at a spacing of approximately
$10R$
. It is also apparent that the azimuthal meandering of the longer structures is a consequence of the superposition of modes with different azimuthal mode numbers, rather than the meandering of a structure described by a specific modal pair.
5. Conditional dual-plane modes
The previous analysis has relied on a temporal interpretation of the velocity field, using either time correlations or Taylor’s hypothesis. The spatial extent of the transition between modes will now be examined by analysing the dual-plane PIV data.
We introduce a conditionally time-averaged mode,
${\it\Psi}_{(m,n)}$
, as a method to simultaneously visualize the mode shape in both planes. These modes are subject to the condition that the magnitude of the real part of the POD coefficient in the cross-stream plane is larger than its root-mean-square (r.m.s.), which is a measure of how active a mode is while aligned with the streamwise plane. That is, we define
$$\begin{eqnarray}{\it\Psi}_{(m,n)}(x,r,{\it\theta})=\left.\left\langle u_{i}(x,r,{\it\theta},t)\frac{\text{Re}\{{\it\alpha}_{n}(m;t)\}}{|\text{Re}\{{\it\alpha}_{n}(m;t)\}|}\right||\text{Re}\{{\it\alpha}_{n}(m;t)\}|>{\it\alpha}_{n}^{rms}(m)\right\rangle ,\end{eqnarray}$$
where
$u_{i}$
is the dual-plane fluctuating velocity field and
$$\begin{eqnarray}{\it\alpha}_{n}^{rms}(m)=\left<{\it\alpha}_{n}(m;t){\it\alpha}_{n}^{\ast }(m;t)\right>^{1/2}.\end{eqnarray}$$
A consequence of the phase shift applied to each mode to force them to be real and the alignment of the two planes is that the POD coefficient is real when a structure is aligned with the streamwise plane. The modes were largely insensitive to the threshold limit, and so the r.m.s. value (
${\it\alpha}_{n}^{rms}(m)$
) was chosen due to its convenience. The set of instantaneous velocity snapshots satisfying the condition is doubled in number by allowing both positive and negative values of
${\it\alpha}_{n}(m;t)$
, as long as its magnitude is larger than the threshold. In the case of negative
${\it\alpha}_{n}(m;t)$
, the instantaneous fluctuating velocity field was rectified by multiplying the velocity field with
$-1$
, indicated by the second term in (5.1). Typically 3500 of the 22 000 snapshots available satisfied the condition for each mode number. Therefore, the conditional averages presented in this section are well converged.
The process is illustrated in figure 8, where we compare an instantaneous velocity field for which
$|\text{Re}\{{\it\alpha}_{1}(3;t)\}|>{\it\alpha}_{1}^{rms}(3)$
with the corresponding conditionally averaged mode. We see that the principal effect of the conditional average is to remove the jitter caused by the other modes that are present in the instantaneous velocity field. The streamwise extent of the structures in the conditional modes is sensitive to any azimuthal rotation; the rotation results in a weaker correlation and a prematurely decaying structure. However, as shown earlier, the azimuthal rotation is weak and is not expected to significantly affect the streamwise extent of the conditional modes. The energy associated with each structure is identified through the cross-plane POD, and the limited field of view of the streamwise plane is not expected to provide any bias or to have any influence on the visualized structures. It can, however, be seen that the structure in figure 8(b) is truncated by the domain, and the transition between structures is inspected by the transitional modes.
Figure 8. Visualization of the conditional mode process for
$(m,n)=(3,1)$
. (a) Instantaneous snapshot of the
$|\text{Re}\{{\it\alpha}_{1}(3;t)\}|>{\it\alpha}_{1}^{rms}(3)$
event. (b) Conditional mode acquired by averaging the subset of snapshots satisfying the
$|\text{Re}\{{\it\alpha}_{1}(3;t)\}|>{\it\alpha}_{1}^{rms}(3)$
condition. Red and blue correspond to positive and negative values of the streamwise velocity fluctuations respectively. Flow goes from left to right.
Figure 9. Conditional modes showing the evolution of
$(m,n)=(3,1{-}3)$
in (a–c) and
$(4,1{-}3)$
in (d–f): (a)
${\it\Psi}_{(3,1)}$
, (b)
${\it\Psi}_{(3,2)}$
, (c)
${\it\Psi}_{(3,3)}$
, (d)
${\it\Psi}_{(4,1)}$
, (e)
${\it\Psi}_{(4,2)}$
, (f)
${\it\Psi}_{(4,3)}$
. Here, (a) shows the initial structures for
$m=3$
, while (b,c) show the transitional modes. Similarly, (d) shows the initial structures for
$m=4$
and (e,f) its transitional modes. Red and blue correspond to positive and negative values of the streamwise velocity fluctuations respectively. Flow goes from left to right.
Figure 9 shows the conditional modes for azimuthal modes
$m=3$
and 4, and the first three POD modes
$n=1{-}3$
. The evolution of structures with
$m=3$
is seen in (a–c) and for
$m=4$
in (d–f), with the initial structure in (a,d) and its transitional modes in (b,c,e,f). While the transitional modes are active upstream and downstream of the initial structure, we show the downstream counterparts, where we have adjusted the sign of the mode such that we only receive correlations with zero phase.
We can now examine the POD modes and the accompanying spatial evolution in the cross-stream plane. In figure 9(a,d) we see the initial structure, which remains attached while growing in size, extending from the wall well into the central part of the pipe. As seen in the autocorrelation in figure 5, the streamwise extent of the structures is approximately
$2{-}4R$
. This behaviour may be seen in the first conditional modes, at
$x/R=2$
, where the structures start to detach from the wall and the intensity of the conditional mode weakens as a consequence of modal transition. A transition from the initial structure can occur through one of the transitional modes, with a higher radial behaviour. The transitional modes show the detachment of the previous structure and the start of a new structure. The upstream structures show a ramp-like behaviour with a detached downstream end, under which a new structure of either the same, (c,f), or opposite, (b,e), sign is initiated at the wall. This evolution is very similar to the growth of the LSMs described by Adrian et al. (Reference Adrian, Meinhart and Tomkins2000). The transition between these structures is rapid and occurs over a distance of one radius. It can also be seen that the structures near the wall shown in the transitional modes (c,f) blend together, appearing as one coherent structure. A similar feature was seen in figure 6, where the carpet plots closer to the wall exhibit longer and more coherent structures.
Therefore, the conditional mode analysis confirms that the modes associated with the VLSM, that is
$m=\{2,3,4\}$
, are much shorter than expected, more of the scale associated with LSM rather than VLSM.
6. Discussion and conclusions
We found that the most energetic POD modes, previously shown to be associated with the VLSMs, are instead characterized by a streamwise and temporal extent of
${\approx}2R$
, after which a transition to a new structure occurs which is characterized by the detachment and decay of an old structure and the initiation of a new structure at the wall. Our observations are consistent with the view that these modes describe basic building blocks with streamwise extent similar to that of the LSM, and that these blocks line up to create a longer structure with a characteristic length estimated to be approximately
$6R$
. It was also shown that the structure described by a specific azimuthal mode number,
$m$
, was azimuthally steady. The meandering is instead a consequence of the interaction between structures with different azimuthal mode numbers.
Our observations seemingly contradict previous studies that indicated that the VLSM can extend up to
$30R$
in length. However, it must be recognized that all previous works that show elongated structures use multipoint temporal measurements and interpret them as spatial data. For example, Hellström & Smits (Reference Hellström and Smits2014) presented the frequency spectra associated with the same POD modes as presented here, and found that the frequency peak corresponded to a convective bulk velocity displacement of
$20{-}40R$
; they concluded that VLSMs can extend up to this length. However, based on the findings of the current study, we propose that the coherence of the long meandering structures visualized by multipoint measurements is actually the consequence of a pseudo-alignment of shorter modes/structures, combined with the reccurrence of a specific mode/structure at regular time intervals. The shorter structures appear to have characteristics very similar to LSM, and our observations are in broad agreement with the suggestion by Kim & Adrian (Reference Kim and Adrian1999) and Dennis & Nickels (Reference Dennis and Nickels2011) that the VLSMs are in fact not spatial structures but a temporal manifestation of repeating LSMs.
Acknowledgement
This work was supported under ONR grant no. N00014-13-1-0174 (Program Manager R. Joslin) and ERC grant no. 277472.
