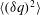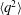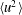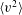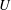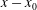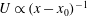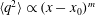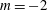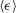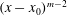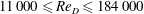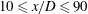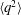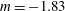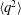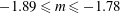1. Introduction
The concept of similarity, or self-preservation, which assumes that the flow scales with single velocity and length scales, has been an important tool for analysis in turbulence research. One major benefit of this concept is the reduction of the number of equations that may be used to describe turbulent flows. The similarity of the mean momentum and turbulent energy equations for jet flows has been discussed extensively in many papers (e.g. Panchapakesan & Lumley Reference Panchapakesan and Lumley1993; Burattini, Antonia & Danaila Reference Burattini, Antonia and Danaila2005b
) and textbooks (e.g. Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000). For turbulent round jets, an empirical observation is that the profiles of
$U_{m}/U(x)$
and
$\langle u_{i}u_{j}\rangle /U(x)^{2}$
become self-similar (i.e. independent of the downstream location of the jet,
$x$
) when expressed in terms of
${\it\xi}\equiv y/y_{0.5}(x)$
; here
$U_{m}$
is the mean streamwise velocity,
$U(x)$
is the axial velocity along the jet centreline, and
$\langle u_{i}u_{j}\rangle$
is the Reynolds shear stress. The parameter
${\it\xi}\equiv y/y_{0.5}(x)$
is the similarity variable, where
$y$
is the radial coordinate and
$y_{0.5}$
is the jet half-width radius, which is defined as the radial location at which the mean jet velocity is equal to half the local maximum mean velocity relative to the centreline. Experimental evidence has shown that
$y_{0.5}=S(x-x_{0})$
, where
$S$
is the spread rate of the jet and
$x_{0}$
is the virtual origin, which depends on the initial conditions (George Reference George, George and Arndt1989; Malmstrom et al.
Reference Malmstrom, Kirkpatrick, Christensen and Knappmiller1997; Fellouah, Ball & Pollard Reference Fellouah, Ball and Pollard2009). Based on the classical self-similarity concept in round jets, the outer turbulent length scale grows approximately linearly along the centreline (e.g.
$\ell \propto (x-x_{0})$
, where
$\ell$
is a typical outer length scale), and the mean velocity is inversely proportional to distance (
$U\propto (x-x_{0})^{-1}$
). Assuming that the normalised mean kinetic energy dissipation rate parameter is constant (
$C_{{\it\epsilon}}=\langle {\it\epsilon}\rangle \ell /u_{0}^{3/2}$
, with
$u_{0}$
being a typical turbulent velocity scale and assumed to vary as
$(x-x_{0})^{-2}$
), it can be obtained that the mean kinetic energy dissipation rate,
$\langle {\it\epsilon}\rangle$
, varies as
$(x-x_{0})^{-4}$
(e.g. Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980). It has also been documented for some time that the turbulence intensity (
$\langle u^{2}\rangle ^{0.5}/U$
) reaches a plateau when the jet is self-similar. Given the fact that
$U$
is inversely proportional to distance,
$\langle u^{2}\rangle$
therefore has to follow a power law along the centreline with an exponent equal to
$-2$
. In Tennekes & Lumley (Reference Tennekes and Lumley1972), it was noted that turbulence intensities are about half an order of magnitude smaller than the jet velocity if
$Re$
is infinite and
$y_{0.5}/x\rightarrow 0$
. However, these assumptions are not realised in turbulent flows encountered in laboratory conditions, where both
$Re$
and
$x$
are finite. In addition, the effect of initial conditions on the power-law behaviour of turbulent kinetic energy was ignored. A key aim of this paper is to demonstrate that these assumptions can be relaxed significantly and that the form of the streamwise evolution of the velocity fluctuations and dissipation, as well as their decay, can be obtained directly from the governing equations.
The concept of similarity has been not only applied to the mean momentum and turbulent energy equations but also investigated for all scales of motion. George (Reference George1992) (referred to as G92 hereafter) applied his analysis (known as equilibrium similarity) to the decay of homogeneous, isotropic turbulence by considering the spectral energy equation
$$\begin{eqnarray}\frac{\partial E(k)}{\partial t}=T(k)-2{\it\nu}k^{2}E(k),\end{eqnarray}$$
where
$E(k)$
is the three-dimensional kinetic energy spectrum and
$T(k)$
is the nonlinear spectral transfer function. G92 showed that all terms in (1.1) evolve in exactly the same manner, with the mean turbulent kinetic energy
$\langle q^{2}\rangle =\langle u^{2}\rangle +\langle v^{2}\rangle +\langle w^{2}\rangle$
and the Taylor microscale
${\it\lambda}$
used as appropriate scaling parameters to normalise all scales of motion. In addition, it was shown that
$\langle q^{2}\rangle$
decays as a power law in time, and that
${\it\lambda}$
grows as the square root of time. The coefficient and decay rate in the power-law equation of
$\langle q^{2}\rangle$
were shown to be dependent on initial conditions.
In addition to the spectral energy equation, the transport equation for the second-order structure function has received particular attention. Burattini, Antonia & Danaila (Reference Burattini, Antonia and Danaila2005a
) derived a transport equation for the total turbulent energy structure function
$\langle ({\it\delta}q)^{2}\rangle \;(=\langle ({\it\delta}u)^{2}\rangle +\langle ({\it\delta}v)^{2}\rangle +\langle ({\it\delta}w)^{2}\rangle )$
from the incompressible Navier–Stokes equations along the centreline of a turbulent round jet using the same procedure as in Danaila et al. (Reference Danaila, Anselmet, Zhou and Antonia2001) and Danaila, Anselmet & Antonia (Reference Danaila, Anselmet and Antonia2002), viz.
$$\begin{eqnarray}\displaystyle & & \displaystyle -\langle ({\it\delta}u)({\it\delta}q)^{2}\rangle +2{\it\nu}\frac{\text{d}}{\text{d}r}\langle ({\it\delta}q)^{2}\rangle -\frac{U}{r^{2}}\int _{0}^{r}s^{2}\frac{\partial }{\partial x}\langle ({\it\delta}q)^{2}\rangle \,\text{d}s\nonumber\\ \displaystyle & & \displaystyle \quad -2\frac{\partial U}{\partial x}\frac{1}{r^{2}}\int _{0}^{r}s^{2}(\langle ({\it\delta}u)^{2}\rangle -\langle ({\it\delta}v)^{2}\rangle )\,\text{d}s=\frac{4}{3}\langle {\it\epsilon}\rangle r.\end{eqnarray}$$
In this equation,
${\it\delta}u\equiv u(x+r)-u(x)$
is the longitudinal velocity increment (for the streamwise velocity component
$u$
),
$r$
is the distance between two points considered along the
$x$
direction,
$U$
is the mean streamwise velocity along the centreline,
$s$
is a dummy separation variable, and
$\langle ({\it\delta}u)^{2}\rangle$
,
$\langle ({\it\delta}v)^{2}\rangle$
and
$\langle ({\it\delta}w)^{2}\rangle$
are the second-order structure functions of
$u$
,
$v$
and
$w$
, respectively. The first term on the left-hand side of (1.2) is the third-order structure function that represents advection, while the second term is diffusion, which represents viscous effects. The third term quantifies the role of the streamwise inhomogeneity. The fourth term represents the role of the energy production. The right-hand side of (1.2) is proportional to the mean dissipation rate of turbulent kinetic energy and balances the sum of the terms on the left-hand side. In Burattini et al. (Reference Burattini, Antonia and Danaila2005a
), (1.2) was satisfied along the centreline of a round jet (
$35\leqslant x/D\leqslant 90$
) by the hot-wire data to an acceptable approximation. It was shown that although the sum of the advection and diffusion terms balances dissipation at small scales, inclusion of the production and streamwise inhomogeneity terms leads to a satisfactory balance for the whole range of scales. However, computation of the streamwise inhomogeneity term requires
$\langle ({\it\delta}q)^{2}\rangle$
to be known at different streamwise locations, which involves significant uncertainties associated with numerical differentiation of the data. This may lead to an imbalance between the dissipation and the terms on the left-hand side of (1.2). As will be discussed later, this issue can be resolved significantly by using a similarity approach such as the one proposed here. Burattini et al. (Reference Burattini, Antonia and Danaila2005a
,Reference Burattini, Antonia and Danaila
b
) were the first to consider a similarity analysis of the transport equation for the centreline of a round jet. Burattini et al. (Reference Burattini, Antonia and Danaila2005b
) suggested that self-similar forms can exist for each term of (1.2) independent of the Reynolds number and the choice of similarity variables. They also showed experimentally that the energy structure functions, measured at a number of locations along the axis of the jet, collapse over a significant range of scales when normalised by
${\it\lambda}$
(as well as the Kolmogorov scale,
${\it\eta}$
, and the integral scale,
$L$
) and
$\langle q^{2}\rangle$
.
In the present work, we extend the equilibrium similarity analysis of G92 to the turbulent energy structure function in a round turbulent jet, i.e. (1.2). Based on our analysis, the similarity variables are formally obtained from the governing equations. One major consequence of the current analysis is that new forms of the decay law of velocity fluctuations and dissipation are obtained with no further assumptions (or empirical observations) on the characteristic length and velocity scales. Finally, a novel self-similar form of (1.2) is derived. A particularly useful feature of the current analysis is that it can alleviate some of the difficulties involved in calculating the
$\partial /\partial x$
terms (production and decay terms). As will be demonstrated, the terms in the energy scale budget equation can be studied if
$\langle ({\it\delta}q)^{2}\rangle$
and the mean velocity are measured at a single point. This avoids the necessity of measuring the structure functions at different axial locations and the related uncertainties associated with the numerical differentiation (Lavoie et al.
Reference Lavoie, Burattini, Djenidi and Antonia2005; Antonia & Burattini Reference Antonia and Burattini2006). It should be mentioned that the present equilibrium similarity solution does not require the Reynolds number to be large for a specified set of initial conditions (George Reference George1992). The suggested similarity solutions are tested against new experimental data and previously reported data, which were all taken along the centreline of a round jet.
2. Theoretical considerations
In order to bring (1.2) into a self-similar form, following Antonia et al. (Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003), Burattini et al. (Reference Burattini, Antonia and Danaila2005b ) and G92, we assume that
$$\begin{eqnarray}\displaystyle & \langle ({\it\delta}q)^{2}\rangle =Q(x)f(\tilde{r}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \langle ({\it\delta}u)^{2}\rangle =M(x)e(\tilde{r}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \langle ({\it\delta}v)^{2}\rangle =R(x)h(\tilde{r}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & -\langle ({\it\delta}u)({\it\delta}q)^{2}\rangle =T(x)g(\tilde{r}), & \displaystyle\end{eqnarray}$$
$Q(x)$
,
$M(x)$
and
$R(x)$
are velocity scales that characterise the second-order structure functions of
$q$
,
$u$
and
$v$
, and
$T(x)$
characterises the third-order structure function
$-\langle ({\it\delta}u)({\it\delta}q)^{2}\rangle$
. Here
$\tilde{r}=r/\ell$
, where
$r$
is the streamwise separation and
$\ell$
is a characteristic length scale which is to be determined.
Upon substituting (2.1)–(2.4) into (1.2), differentiating, rearranging terms by separating terms that depend on
$x$
from those that depend on
$r/\ell$
and multiplying by
$\ell /({\it\nu}Q(x))$
, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{T(x)\ell }{{\it\nu}Q(x)}\right]g+[2]\frac{\text{d}f}{\text{d}\tilde{r}}+\left[\frac{U\ell }{{\it\nu}}\frac{\text{d}\ell }{\text{d}x}\right]\frac{{\it\Gamma}_{1}}{\tilde{r}^{2}}-\left[\frac{U\ell ^{2}}{{\it\nu}Q(x)}\frac{\text{d}Q(x)}{\text{d}x}\right]\frac{{\it\Gamma}_{2}}{\tilde{r}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\left[2\frac{\text{d}U}{\text{d}x}\frac{M(x)}{{\it\nu}Q(x)}\ell ^{2}\right]\frac{{\it\Gamma}_{3}}{\tilde{r}^{2}}+\left[2\frac{\text{d}U}{\text{d}x}\frac{R(x)}{{\it\nu}Q(x)}\ell ^{2}\right]\frac{{\it\Gamma}_{4}}{\tilde{r}^{2}}=\frac{4}{3}\left[\frac{\langle {\it\epsilon}\rangle \ell ^{2}}{{\it\nu}Q(x)}\right]\tilde{r},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\Gamma}_{1}=\int _{0}^{r/\ell }\left(\frac{s}{\ell }\right)^{3}\frac{\text{d}f}{\text{d}\tilde{r}}\,\text{d}\!\left(\frac{s}{\ell }\right),\quad {\it\Gamma}_{2}=\int _{0}^{r/\ell }\left(\frac{s}{\ell }\right)^{2}f\,\text{d}\!\left(\frac{s}{\ell }\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\Gamma}_{3}=\int _{0}^{r/\ell }\left(\frac{s}{\ell }\right)^{2}e\,\text{d}\!\left(\frac{s}{\ell }\right),\quad {\it\Gamma}_{4}=\int _{0}^{r/\ell }\left(\frac{s}{\ell }\right)^{2}h\,\text{d}\!\left(\frac{s}{\ell }\right). & \displaystyle\end{eqnarray}$$
Since the multiplier in the second term of (2.5) is constant, all the other terms must also be constant for similarity to hold. They can be rewritten as
$$\begin{eqnarray}\displaystyle & \displaystyle \left[\frac{T(x)\ell }{{\it\nu}Q(x)}\right]=\text{constant}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[\frac{U\ell }{{\it\nu}}\frac{\text{d}\ell }{\text{d}x}\right]=a, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[\frac{U\ell ^{2}}{{\it\nu}Q(x)}\frac{\text{d}Q(x)}{\text{d}x}\right]=b, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[2\frac{\text{d}U}{\text{d}x}\frac{M(x)}{{\it\nu}Q(x)}\ell ^{2}\right]=c, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[2\frac{\text{d}U}{\text{d}x}\frac{R(x)}{{\it\nu}Q(x)}\ell ^{2}\right]=d, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[\frac{\langle {\it\epsilon}\rangle \ell ^{2}}{{\it\nu}Q(x)}\right]=\text{constant}. & \displaystyle\end{eqnarray}$$
In order to calculate all the constants, some additional information is required. As the momentum flux is constant, the velocity along the centreline of a round jet can be obtained as (see Pope Reference Pope2000)
$$\begin{eqnarray}U=C/(x-x_{0}),\end{eqnarray}$$
where
$C$
is a constant and
$x_{0}$
is the virtual origin. For the region near the axisymmetric jet centreline, the kinetic energy budget equation can be approximated as (see Burattini et al.
Reference Burattini, Antonia and Danaila2005a
)
$$\begin{eqnarray}\langle {\it\epsilon}\rangle =-\frac{U}{2}\frac{\text{d}\langle q^{2}\rangle }{\text{d}x}-(\langle u^{2}\rangle -\langle v^{2}\rangle )\frac{\text{d}U}{\text{d}x},\end{eqnarray}$$
where
$$\begin{eqnarray}\langle q^{2}\rangle =\langle u^{2}\rangle +2\langle v^{2}\rangle .\end{eqnarray}$$
Substituting (2.15) into (2.13) and multiplying by a factor of
$-2$
gives
$$\begin{eqnarray}\left[\frac{U}{{\it\nu}Q(x)}\frac{\text{d}\langle q^{2}\rangle }{\text{d}x}\ell ^{2}\right]+\left[2\frac{\text{d}U}{\text{d}x}\frac{(\langle u^{2}\rangle -\langle v^{2}\rangle )}{{\it\nu}Q(x)}\ell ^{2}\right]=\text{constant}.\end{eqnarray}$$
Subtracting (2.12) from (2.11) yields
$$\begin{eqnarray}\left[2\frac{\text{d}U}{\text{d}x}\frac{M(x)-R(x)}{{\it\nu}Q(x)}\ell ^{2}\right]=\text{constant}.\end{eqnarray}$$
If (2.10) is added to (2.18), then
$$\begin{eqnarray}\left[\frac{U}{{\it\nu}Q(x)}\frac{\text{d}Q(x)}{\text{d}x}\ell ^{2}\right]+\left[2\frac{\text{d}U}{\text{d}x}\frac{M(x)-R(x)}{{\it\nu}Q(x)}\ell ^{2}\right]=\text{constant}.\end{eqnarray}$$
Comparing (2.19) with (2.17), it follows that
$Q(x)\sim \langle q^{2}\rangle$
and
$M(x)-R(x)\sim \langle u^{2}\rangle -\langle v^{2}\rangle$
. Here,
$M(x)$
and
$R(x)$
may be related to the velocity fluctuations
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
, respectively.
Integration of (2.9) yields
$$\begin{eqnarray}\ell ^{2}=\frac{a}{C}{\it\nu}(x-x_{0})^{2},\end{eqnarray}$$
which indicates that the characteristic length scales linearly with
$(x-x_{0})$
. Using (2.14) and the fact that
$Q(x)\sim \langle q^{2}\rangle$
, (2.10) can be written as
$$\begin{eqnarray}\left[\frac{C\ell ^{2}}{{\it\nu}(x-x_{0})}\frac{\text{d}\langle q^{2}\rangle }{\langle q^{2}\rangle }\frac{1}{\text{d}x}\right]=b.\end{eqnarray}$$
Upon substituting (2.20) into (2.21) and performing some simplifications, it emerges that
$$\begin{eqnarray}\frac{\text{d}\langle q^{2}\rangle }{\langle q^{2}\rangle }=\frac{b}{a}\frac{\text{d}x}{(x-x_{0})}.\end{eqnarray}$$
The solution of (2.22) takes the form
$$\begin{eqnarray}\langle q^{2}\rangle =A(x-x_{0})^{m},\end{eqnarray}$$
where
$m=b/a$
. This equation indicates that the characteristic velocity scale should follow a power law along the jet centreline. Comparing (2.11) and (2.12) suggests that
$$\begin{eqnarray}\frac{M(x)}{R(x)}=\frac{\langle u^{2}\rangle }{\langle v^{2}\rangle }\end{eqnarray}$$
remains constant. Therefore, by considering (2.16) and (2.23), it follows that
$$\begin{eqnarray}\displaystyle \langle u^{2}\rangle & = & \displaystyle A_{1}(x-x_{0})^{m},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle v^{2}\rangle & = & \displaystyle A_{2}(x-x_{0})^{m}\end{eqnarray}$$
$A=A_{1}+2A_{2}$
. Substituting (2.14), (2.23), (2.25) and (2.26) into (2.15) gives 
$$\begin{eqnarray}\langle {\it\epsilon}\rangle =C\left[\frac{-(A_{1}+2A_{2})m}{2}+(A_{1}-A_{2})\right](x-x_{0})^{m-2}.\end{eqnarray}$$
From (2.27) it immediately follows that the dissipation
$\langle {\it\epsilon}\rangle$
decays with an exponent of
$m-2$
along the centreline. Substituting (2.23) and (2.27) into the general equation for the Taylor microscale (Antonia et al.
Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003), viz.
$$\begin{eqnarray}{\it\lambda}^{2}=5{\it\nu}\frac{\langle q^{2}\rangle }{\langle {\it\epsilon}\rangle },\end{eqnarray}$$
gives
$$\begin{eqnarray}{\it\lambda}^{2}=5{\it\nu}\frac{2(A_{1}+2A_{2})}{-C(A_{1}+2A_{2})m+2C(A_{1}-A_{2})}(x-x_{0})^{2}.\end{eqnarray}$$
Comparing (2.20) and (2.29) confirms that
${\it\lambda}$
is the relevant characteristic length scale (i.e.
$\ell ={\it\lambda}$
). With
$\ell ={\it\lambda}$
and
$Q(x)\sim \langle q^{2}\rangle$
, (2.8) implies that
$$\begin{eqnarray}T(x)\sim {\it\nu}\frac{\langle q^{2}\rangle }{{\it\lambda}},\end{eqnarray}$$
or
$$\begin{eqnarray}T(x)\sim \mathit{Re}_{{\it\lambda}}^{-1}\langle q^{2}\rangle ^{3/2},\end{eqnarray}$$
where the corresponding turbulence Reynolds number is defined here as (cf. Antonia et al. Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003)
$$\begin{eqnarray}\mathit{Re}_{{\it\lambda}}=\frac{\langle q^{2}\rangle ^{1/2}{\it\lambda}}{3^{1/2}\,{\it\nu}}.\end{eqnarray}$$
By considering
$Q(x)\equiv \langle q^{2}\rangle$
and
$T(x)\equiv 3^{-1/2}\mathit{Re}_{{\it\lambda}}^{-1}\langle q^{2}\rangle ^{3/2}$
and performing some manipulations, (2.5) can be written as
$$\begin{eqnarray}g+2\frac{\text{d}f}{\text{d}\tilde{r}}+10(c_{1}+2c_{2})\frac{{\it\Gamma}_{1}}{\tilde{r}^{2}}-10m(c_{1}+2c_{2})\frac{{\it\Gamma}_{2}}{\tilde{r}^{2}}+20c_{1}\frac{{\it\Gamma}_{3}}{\tilde{r}^{2}}-20c_{2}\frac{{\it\Gamma}_{4}}{\tilde{r}^{2}}=\frac{20}{3}\tilde{r},\end{eqnarray}$$
where
$$\begin{eqnarray}c_{1}=\frac{A_{1}}{-(A_{1}+2A_{2})m+2(A_{1}-A_{2})},\quad c_{2}=\frac{A_{2}}{-(A_{1}+2A_{2})m+2(A_{1}-A_{2})}.\end{eqnarray}$$
The normalised form of the third-order structure function
$g$
can be determined when the normalised second-order structure function
$f$
, the power-law exponent
$m$
of
$\langle q^{2}\rangle$
and the decay rate constants
$A_{1}$
and
$A_{2}$
are known. A particularly useful feature of this self-similar equation is that it avoids the difficulties involved in calculating the
$\partial /\partial x$
terms (production and decay terms) in (1.2).
For simplicity, (2.33) can be rewritten as
$$\begin{eqnarray}A+B+D+P=C,\end{eqnarray}$$
where
$A$
is the turbulent advection term (the generalised third-order structure function or the first term on the left-hand side of (2.33)),
$B$
is the diffusion term (second term on the left-hand side of (2.33)),
$D$
is the inhomogeneous decay term along the streamwise direction
$x$
(the sum of the third and fourth terms on the left-hand side of (2.33)),
$P$
is the production term (the sum of the fifth and sixth terms on the left-hand side of (2.33)) and
$C$
is the dissipation term and the balance of all the other terms (the right-hand side term in (2.33)).
3. Experimental details
Experimental measurements were performed to test the similarity solutions obtained in the previous section. An air jet was generated using a fan mounted on antivibration pads. The air then exits a settling chamber via a round duct to the inlet of a smoothly contracting axisymmetric nozzle. The experiments were carried out at the exit Reynolds number of
$\mathit{Re}_{D}=50\,000$
, where
$\mathit{Re}_{D}$
is calculated based on the jet exit mean velocity (
$U_{j}=10.65~\text{m}~\text{s}^{-1}$
) and the nozzle exit diameter
$D=0.0736~\text{m}$
. The jet has a top-hat velocity profile at the exit. The axial turbulence intensity in the potential core of the flow near the jet exit was less than 0.7 % (see Sadeghi & Pollard Reference Sadeghi and Pollard2012 and Sadeghi, Lavoie & Pollard Reference Sadeghi, Lavoie and Pollard2014 for further details about the exit conditions of the jet). The measurements were performed for
$10\leqslant x/D\leqslant 25$
. Measurements of the turbulence statistics were obtained using a stationary cross-wire probe. The wires were made of
$2.5~{\rm\mu}\text{m}$
diameter tungsten wire with a 0.5 mm sensing length. The hot-wires were calibrated in the jet core before and after each experiment. Similar to the scheme described in Burattini & Antonia (Reference Burattini and Antonia2005), the cross-wire was calibrated using a look-up table, with calibration angles within the range
$\pm 40^{\circ }$
, in intervals of
$10^{\circ }$
. The signals were low-pass filtered at a cutoff frequency
$f_{c}$
, which was selected based on the onset of electronic noise and close to the Kolmogorov frequency,
$f_{k}\equiv U/2{\rm\pi}{\it\eta}$
, where
${\it\eta}\equiv {\it\nu}^{3/4}/\langle {\it\epsilon}\rangle ^{1/4}$
. The measurements were taken with a sampling frequency of
$f_{s}\geqslant 2f_{c}$
. The sampling time was selected to ensure that enough data would be taken to achieve statistical convergence of
$\langle q^{2}\rangle$
(at least within
$\pm 2\,\%$
) and in the peak value of the generalised normalised third-order structure function
$\langle ({\it\delta}u)^{2}({\it\delta}q)\rangle$
(at least within
$\pm 4\,\%$
, which typically required 10 min of sampling time). In the present work, the modified Taylor hypothesis based on the models developed by Lumley (Reference Lumley1965) was used to convert time into a spatial series. In addition, data were corrected for the effect of high-frequency noise and finite spatial resolution (Hearst et al.
Reference Hearst, Buxton, Ganapathisubramani and Lavoie2012; Xu et al.
Reference Xu, Pollard, Mi, Secretain and Sadeghi2013; Sadeghi et al.
Reference Sadeghi, Lavoie and Pollard2014).
Characterisation of the small-scale motions in turbulent flows has been a challenging problem in turbulence research, especially in turbulent shear flows. One of the primary experimental concerns has been the determination of the mean-square gradients of the fluctuating velocity field to estimate the rate of dissipation of turbulence kinetic energy, viz.
$$\begin{eqnarray}\langle {\it\epsilon}\rangle =\frac{1}{2}{\it\nu}\left\langle \left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)^{2}\right\rangle .\end{eqnarray}$$
Twelve separate derivative correlations must be determined before the dissipation can be truly calculated. Since it is difficult to calculate all velocity derivatives accurately from experimental measurements, it has been common to use alternative assumptions to estimate the dissipation rate. The most well-known assumption is local isotropy. The dissipation for isotropic turbulence reduces to
$$\begin{eqnarray}\langle {\it\epsilon}\rangle _{iso}=15{\it\nu}\left\langle \left(\frac{\partial u}{\partial x}\right)^{2}\right\rangle .\end{eqnarray}$$
This is the simplest definition of the dissipation, which has been extensively used to estimate the dissipation rate in experimental studies, even when the flow was not exactly locally isotropic. The failure of local isotropy in turbulent jet flows has long been documented in the literature (e.g. Wygnanski & Fiedler Reference Wygnanski and Fiedler1969; Champagne Reference Champagne1978; Burattini & Antonia Reference Burattini and Antonia2005; Burattini et al. Reference Burattini, Antonia and Danaila2005b ). Using homogeneity and incompressibility, another estimate for the dissipation can be obtained as (see e.g. Hinze 1975; George & Hussein Reference George and Hussein1991)
$$\begin{eqnarray}\langle {\it\epsilon}\rangle _{hom}={\it\nu}\left\langle \left(\frac{\partial u_{i}}{\partial x_{j}}\right)^{2}\right\rangle .\end{eqnarray}$$
By assuming axisymmetry, a relatively crude approximation for this equation can be obtained as (e.g. Danaila et al. Reference Danaila, Anselmet and Antonia2002; Burattini et al. Reference Burattini, Antonia and Danaila2005a ,Reference Burattini, Antonia and Danaila b )
$$\begin{eqnarray}\langle {\it\epsilon}\rangle _{hom}=3{\it\nu}\left[\left\langle \left(\frac{\partial u}{\partial x}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial v}{\partial x}\right)^{2}\right\rangle \right].\end{eqnarray}$$
The components for estimating the dissipation from (3.4) can be obtained with a cross-wire. Following previous studies in jet flows (e.g. Burattini et al.
Reference Burattini, Antonia and Danaila2005a
,Reference Burattini, Antonia and Danaila
b
),
$\langle {\it\epsilon}\rangle _{hom}$
is used here as the dissipation since the assumptions employed for its estimate are less restrictive than the alternative assumption of local isotropy along the jet centreline.
Table 1 provides estimates of several parameters measured downstream of the current jet, including the dissipation estimated with the aforementioned techniques. Using the dissipation and longitudinal integral scale (
$L_{u}$
), the non-dimensional energy dissipation rate,
$C_{{\it\epsilon}}$
, along the centreline of the jet is also listed in table 1. Here,
$C_{{\it\epsilon}}$
is defined as
$$\begin{eqnarray}C_{{\it\epsilon}}\equiv L_{u}\langle {\it\epsilon}\rangle \langle u^{2}\rangle ^{-3/2},\end{eqnarray}$$
where
$$\begin{eqnarray}L_{u}=\frac{1}{\langle u^{2}\rangle }\int _{0}^{r_{0}}B_{u,u}(r)\,\text{d}r,\end{eqnarray}$$
with
$B_{u,u}$
being the correlation of
$\langle {\it\alpha}(x+r){\it\alpha}(x)\rangle$
.
Table 1. Turbulent flow properties at four downstream locations along the jet centreline.
The dissipation (or the mean-square gradients of the fluctuating velocity field) can be used to estimate other important turbulent length scales (i.e. the Taylor microscale,
${\it\lambda}$
, and the Kolmogorov length scale,
${\it\eta}$
). The Taylor microscale and the Taylor Reynolds number have been extensively estimated in the literature using the isotropic relations of
$$\begin{eqnarray}{\it\lambda}_{iso}=\frac{\langle u^{2}\rangle ^{1/2}}{\displaystyle \left\langle \left(\frac{\partial u}{\partial x}\right)^{2}\right\rangle ^{1/2}}\end{eqnarray}$$
and
$$\begin{eqnarray}\mathit{Re}_{{\it\lambda}_{iso}}=\frac{\langle u^{2}\rangle ^{1/2}{\it\lambda}_{iso}}{{\it\nu}},\end{eqnarray}$$
respectively. However, in the current work, more general definitions of Taylor microscale, (2.28), and Taylor microscale Reynolds number, (2.32), which avoid the directional ambiguity of the turbulence statistics, are used (Corrsin Reference Corrsin, Flügge and Truesdell1963; Fulachier & Antonia Reference Fulachier and Antonia1983; Antonia et al.
Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003). In table 1,
${\it\lambda}_{hom}$
and
$\mathit{Re}_{{\it\lambda}_{hom}}$
are estimated by using
$\langle {\it\epsilon}\rangle _{hom}$
in (2.28) and (2.32). The Kolmogorov length scale of
${\it\eta}_{hom}$
is obtained by substituting
$\langle {\it\epsilon}\rangle _{hom}$
into
$$\begin{eqnarray}{\it\eta}\equiv {\it\nu}^{3/4}/\langle {\it\epsilon}\rangle ^{1/4}.\end{eqnarray}$$
The values for
${\it\lambda}_{iso}$
,
$\mathit{Re}_{{\it\lambda}_{iso}}$
and
${\it\eta}_{iso}$
are also provided for reference as they are the most common parameters cited in many other works.
4. Presentation and discussion of the experimental results
The similarity of the mean momentum equations is investigated over the present range of measurements. For this purpose, the radial profiles of the mean velocity and Reynolds shear stress are presented for four locations (
$x/D=10$
, 15, 20 and 25) in figure 1. The profiles are normalised by the jet half-velocity radius (
$y_{0.5}$
) and the mean centreline velocity (
$U_{c}$
), which are the relevant scales for the self-similarity of mean momentum equations in jet flows (see e.g. Pope Reference Pope2000; Burattini et al.
Reference Burattini, Antonia and Danaila2005b
). The profiles of the mean velocity and Reynolds shear stress exhibit satisfactory collapse over the present range of measurements.
Figure 1. Radial profiles of (a) mean velocity and (b) Reynolds shear stress at four axial locations: ○,
$x/D=10$
; ▫,
$x/D=15$
; ▿,
$x/D=20$
;
$\times$
,
$x/D=25$
.
The axial mean velocity along the jet centreline is displayed in figure 2. As expected, it decays almost linearly with axial distance. For a self-similar jet, the centreline velocity variation can be written as
$$\begin{eqnarray}\frac{U_{j}}{U_{c}}=\frac{1}{B}\left(\frac{x-x_{0}}{D}\right),\end{eqnarray}$$
which is the inverted normalised form of (2.14). A least-squares fit to the data gives a mean velocity decay constant of
$B=6.6$
(or
$C=B\ast D\ast U_{j}=5.17$
) and a virtual origin of
$x_{0}=-1.68D$
. Here,
$B$
is very similar to the values obtained by Weisgraber & Liepman (Reference Weisgraber and Liepman1998) and Ferdman, Otugen & Kim (Reference Ferdman, Otugen and Kim2000) (
$B\sim 6.7$
) and is in good agreement with the results of Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993) and Burattini et al. (Reference Burattini, Antonia and Danaila2005b
) (
$B\sim 6.1$
). It is generally accepted that there will be some variability in the mean velocity decay constant and virtual origin (see e.g. table 1 in Fellouah et al.
Reference Fellouah, Ball and Pollard2009) for different experiments, which is typically related to differences in the measurement region, exit Reynolds number, experimental technique and initial conditions (Malmstrom et al.
Reference Malmstrom, Kirkpatrick, Christensen and Knappmiller1997; Xu & Antonia Reference Xu and Antonia2002; Pollard & Uddin Reference Pollard and Uddin2007).
Figure 2. Axial decay of the mean velocity along the centreline; the solid line is the least-squares fit to the data.
The streamwise variations of
$\langle q^{2}\rangle$
,
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
, measured along the jet centreline and normalised by
$U_{j}^{2}$
, are shown in figure 3(a). A curve fit was applied to the data using the virtual origin of
$x_{0}=-1.68D$
. It was found that
$\langle q^{2}\rangle$
,
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
follow closely a power law with exponent
$m=-1.83$
, in agreement with (2.23)–(2.26). The decay rate constants for
$\langle q^{2}\rangle$
,
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
are estimated to be
$A=3.29$
,
$A_{1}=1.43$
and
$A_{2}=0.93$
, respectively. In order to investigate the validity of the solution over an extended streamwise range, we have tested the equilibrium similarity solution using three previously published experimental datasets, where data have been taken over a longer streamwise distance. The evolution of
$\langle q^{2}\rangle ~(\equiv \langle u^{2}\rangle +2\langle v^{2}\rangle )$
along the centreline of axisymmetric turbulent jets from previous studies is illustrated in figure 3(b). The experimental conditions for these studies are summarised in table 2. Curve fits were applied to the data using the corresponding virtual origins listed in table 2. It was found that in the aforementioned experiments,
$\langle q^{2}\rangle$
follows a power law with
$-1.89\leqslant m\leqslant -1.78$
, consistent with the present data. As both downstream distance and Reynolds number are finite in previous experiments as well as in the current work, it is not unexpected to observe that the exponent for
$\langle q^{2}\rangle$
(or
$\langle u^{2}\rangle$
) is not the traditional value of
$-2$
but rather a slightly greater value. In addition, the influence on
$m$
of measurement uncertainties and slight differences in initial conditions cannot be ignored. Assuming
$\langle u^{2}\rangle \sim (x-x_{0})^{m}$
and
$U_{c}\sim (x-x_{0})^{-1}$
, we have that
$\langle u^{2}\rangle /(U_{c})^{2}\sim (x-x_{0})^{m+2}$
. Therefore, if
$m$
is slightly greater than
$-2$
,
$\langle u^{2}\rangle /(U_{c})^{2}$
(or
$(\langle u^{2}\rangle ^{0.5}/U_{c})$
) should grow slowly. For example, the streamwise variation of
$\langle u^{2}\rangle ^{0.5}/U_{c}$
for the present experiment is shown in figure 4. A power-law fit was applied to the data using
$x_{0}=-1.68D$
, which gives a power-law exponent of 0.085 (
$(m+2)/2$
). This case can be observed in previous experimental data, although the reason has never been discussed in detail (perhaps due to a very slow growth). Apart from the experiments specified herein, this slow growth in turbulence intensities
$(\langle u^{2}\rangle ^{0.5}/U_{c})$
along the jet axis has been noted by other authors, such as Ruffin et al. (Reference Ruffin, Schiestel, Anselmet, Amielh and Fulachier1994), Tong & Warhaft (Reference Tong and Warhaft1994), Amielh et al. (Reference Amielh, Djeridane, Anselmet and Fulachier1996), Abdel-Rahman, Chakroun & Al-Fahed (Reference Abdel-Rahman, Chakroun and Al-Fahed1997), Xu & Antonia (Reference Xu and Antonia2002), Fellouah et al. (Reference Fellouah, Ball and Pollard2009), Mi, Xu & Zhou (Reference Mi, Xu and Zhou2013) and Taub et al. (Reference Taub, Lee, Balachandar and Sherif2013). It should be pointed out that in the aforementioned experiments (similar to the present work), the streamwise extent is limited.
Figure 3. (a) Streamwise variation of normalised
$\langle q^{2}\rangle$
(▫),
$\langle u^{2}\rangle$
(○) and
$\langle v^{2}\rangle$
(▵) along the centreline of the current jet. (b) Streamwise variation of normalised
$\langle q^{2}\rangle$
along the centreline of round jets: ▿, from Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993); ○, from Burattini et al. (Reference Burattini, Antonia and Danaila2005b
); ▵, from Quinn (Reference Quinn2006); ▫, from the current work. The solid lines represent least-squares fits to the data.
Table 2. Experimental conditions on the jet centreline for different round jets.
Figure 4. Evolution of the turbulence intensity along the centreline; the solid line is the least-squares fit to the data.
The axial profile of the ratio
$\langle u^{2}\rangle /\langle v^{2}\rangle$
is plotted as a function of
$x/D$
in figure 5. This ratio is approximately constant as a function of
$x/D$
with a value of 1.53. The fact that this ratio must be constant in the self-similar region was suggested previously in § 2. It is interesting to note that
$\langle u^{2}\rangle /\langle v^{2}\rangle \approx 1.56$
was obtained by Hussein, Capp & George (Reference Hussein, Capp and George1994) and Burattini et al. (Reference Burattini, Antonia and Danaila2005b
) in the self-similar region along the centreline of round jets at
$\mathit{Re}_{D}=95\,500$
and 140 000, respectively. This may suggest that the ratio
$\langle u^{2}\rangle /\langle v^{2}\rangle$
(and equivalently
$\langle q^{2}\rangle /\langle u^{2}\rangle$
and
$\langle q^{2}\rangle /\langle v^{2}\rangle$
) is not affected by the jet exit Reynolds number, at least for
$\mathit{Re}_{D}\gtrsim 20\,000$
, which corresponds to the onset of the mixing transition in round jets (Dimotakis Reference Dimotakis2000; Fellouah & Pollard Reference Fellouah and Pollard2010).
Figure 5. Axial profile of the ratio
$\langle u^{2}\rangle /\langle v^{2}\rangle$
along the axis; the solid line is the average of the data.
As discussed in § 2, the turbulent kinetic energy
$\langle q^{2}\rangle$
and the Taylor microscale
${\it\lambda}$
were shown to be the relevant scales for the similarity of all scales of flow along the jet centreline. Therefore, (2.1) and (2.4) can be rewritten as
$$\begin{eqnarray}f(r/{\it\lambda})=\langle ({\it\delta}q)^{2}\rangle /\langle q^{2}\rangle\end{eqnarray}$$
and
$$\begin{eqnarray}g(r/{\it\lambda})=-\langle ({\it\delta}u)({\it\delta}q)^{2}\rangle /(3^{-1/2}\mathit{Re}_{{\it\lambda}}^{-1}\langle q^{2}\rangle ^{3/2}),\end{eqnarray}$$
respectively. In addition, it was suggested that
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
, together with
${\it\lambda}$
, are relevant scales for
$\langle ({\it\delta}u)^{2}\rangle$
and
$\langle ({\it\delta}v)^{2}\rangle$
, viz.
$$\begin{eqnarray}\displaystyle & e(r/{\it\lambda})=\langle ({\it\delta}u)^{2}\rangle /\langle u^{2}\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & h(r/{\it\lambda})=\langle ({\it\delta}v)^{2}\rangle /\langle v^{2}\rangle . & \displaystyle\end{eqnarray}$$
$f(r/{\it\lambda})$
measured at the four locations considered here (
$x/D=10$
, 15, 20 and 25) are shown in figure 6. The second-order structure functions of
$q$
are found to collapse approximately at each streamwise location, which suggests that the similarity parameters found in the analysis are justified. The distributions of
$e(r/{\it\lambda})$
and
$h(r/{\it\lambda})$
are also shown in figure 6. The second-order structure functions of
$u$
and
$v$
are also found to collapse approximately using the normalisation parameters. Therefore, it can be confirmed that the suggestion that
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
are the relevant velocity scales for self-similarity of
$\langle ({\it\delta}u)^{2}\rangle$
and
$\langle ({\it\delta}v)^{2}\rangle$
, respectively, is accurate.
Figure 6. Distributions of
$f$
,
$e$
and
$h$
as functions of
$r/{\it\lambda}_{hom}$
at four axial locations
$x/D=10,15,20$
and 25. The structure functions have been shifted successively with respect to the lower one; each horizontal dashed line represents an offset of 2.
The normalised third-order structure function,
$g(r/{\it\lambda})$
, at locations
$x/D=10$
, 15, 20 and 25 is plotted in figure 7. The collapse of
$g(r/{\it\lambda})$
is reasonable, with departures from similarity isolated to
$r/{\it\lambda}\gtrsim 8$
.
Figure 7. Distributions of
$g(r/{\it\lambda}_{hom})$
at four axial locations
$x/D=10,15,20$
and 25.
We now turn our attention to (2.33), which was derived as the similarity form of (1.2). The scale-by-scale budget measured at
$x/D=15$
in terms of
$r/{\it\lambda}$
is plotted in figure 8. The Taylor microscale
${\it\lambda}$
was used to normalise
$r$
, as it was theoretically obtained to be the relevant turbulence length scale for self-preservation at all scales (§ 2). This figure demonstrates that (2.33) is adequately satisfied by the experimental data (i.e.
$A+B+D+P\approx C$
). Similar to Burattini et al. (Reference Burattini, Antonia and Danaila2005a
), at small
$r/{\it\lambda}$
the diffusion term
$B$
dominates, while at large
$r/{\it\lambda}$
the decay term
$D$
and the production term
$P$
are the dominant terms. A very good balance of all terms at very large scales confirms that the similarity forms of the production term
$P$
and inhomogeneous decay term
$D$
are measured accurately. The advection term
$A$
goes to zero at both small and large separations, while its maximum is located at
$r\simeq 0.8{\it\lambda}$
, similar to previous observations from grid turbulence experiments and along the jet centreline (Burattini et al.
Reference Burattini, Antonia and Danaila2005a
). The peak value of the advection term
$A$
occurs at a value of
$r/{\it\lambda}$
in the vicinity of
$B=D$
. The production term
$P$
becomes important for
$r/{\it\lambda}\gtrsim 8$
, where the value of the diffusion term
$B$
begins to decrease at a higher rate with increasing
$r/{\it\lambda}$
. This point is very close to the value of
$r/{\it\lambda}$
where
$A=D$
.
Figure 8. The terms in (2.35) at
$x/D=15$
: ▴, the advection term
$A$
; ▫, the diffusion term
$B$
; ▿, the decay term
$D$
; ▾, the production term
$P$
; ○, the sum
$A+B+D+P$
. The solid black line is the dissipation term
$C$
.
5. Conclusion
Using an equilibrium similarity analysis, the similarity form of the transport equation of the second-order structure function was obtained along the centreline of a turbulent round jet. An important consequence of the current analysis is the derivation of forms for the decay law directly from the governing equations, rather than from classical empirical observations. It is shown that the self-similar form of the equations yields a solution such that the turbulent kinetic energy and the mean kinetic energy dissipation rate decay following power laws of the form
$\langle q^{2}\rangle \propto (x-x_{0})^{m}$
and
$\langle {\it\epsilon}\rangle \propto (x-x_{0})^{m-2}$
, respectively, along the centreline. In addition, the characteristic length scale, which was shown to be the Taylor microscale, grows as
$(x-x_{0})$
. It is also suggested that the normalised third-order structure function can be estimated from the normalised second-order structure functions, the power-law exponent
$m$
and the decay rate constants of
$\langle u^{2}\rangle$
and
$\langle v^{2}\rangle$
.
Experimental measurements were conducted at
$\mathit{Re}_{D}=50\,000$
over the range
$10\leqslant x/D\leqslant 25$
along the centreline of a round jet to validate the theoretical analysis. It was found that a power-law decay region does exist over the present range of measurements for
$\langle q^{2}\rangle$
with
$m=-1.83$
. The accuracy of this solution was confirmed using previously published data for round jets at
$11\,000\leqslant \mathit{Re}_{D}\leqslant 184\,000$
over the range
$20\leqslant x/D\leqslant 90$
(
$-1.89\leqslant m\leqslant -1.78$
). Finally, the balance of all terms in (2.33), derived as a new self-similar equation for round jets, was investigated. The experimental data satisfied the relation to a very close approximation.
Acknowledgements
The authors acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada under the Discovery and RTI grant programmes. H.S. would like to thank R. J. Hearst for useful discussions.
