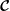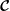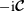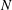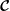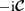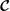1. Introduction
We consider the flow of a fluid, which fills a volume
![]() $V$
with a rigid closed boundary
$V$
with a rigid closed boundary
![]() $\partial V$
and outward normal
$\partial V$
and outward normal
![]() $\boldsymbol{n}$
. If the fluid is non-rotating, homogeneous and inviscid, it cannot support incompressible wave motions, even in a gravitational field. For, if the velocity
$\boldsymbol{n}$
. If the fluid is non-rotating, homogeneous and inviscid, it cannot support incompressible wave motions, even in a gravitational field. For, if the velocity
![]() $\boldsymbol{v}$
is irrotational, then there is a potential
$\boldsymbol{v}$
is irrotational, then there is a potential
![]() ${\it\Phi}$
such that
${\it\Phi}$
such that
![]() $\boldsymbol{v}=\boldsymbol{{\rm\nabla}}{\it\Phi}$
and
$\boldsymbol{v}=\boldsymbol{{\rm\nabla}}{\it\Phi}$
and
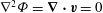 ${\rm\nabla}^{2}{\it\Phi}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
${\rm\nabla}^{2}{\it\Phi}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V$
with
$V$
with
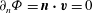 $\partial _{n}{\it\Phi}=\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\partial _{n}{\it\Phi}=\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V$
. These equations imply that
$\partial V$
. These equations imply that
![]() ${\it\Phi}$
is constant and
${\it\Phi}$
is constant and
![]() $\boldsymbol{v}=\mathbf{0}$
. However, if the fluid is rotating, it can support wave motions. Thomson (Reference Thomson1877, p. 297) rotated a spherical shell filled with liquid and mounted on gimbals. The spherical copper shell ran smoothly even at high rotation rates. An oblate spheroid also ran smoothly, but a prolate spheroid reacted violently, destroying the gimbal mounting through resonance of the container with internal waves in the fluid. Such free oscillations, which depend on the dynamically dominant rotation and are almost rigid rotations, are usually referred to as inertial waves, but other terms including Poincaré waves, Rossby waves or gyroscopic waves are also used. There may also be steady geostrophic modes. Our general interest is in the spatial modes of free oscillations and in the effects of forcing, when rotation is dynamically dominant. The specific aim of the present paper is to enumerate the spatial modes of inertial waves and the geostrophic modes if
$\boldsymbol{v}=\mathbf{0}$
. However, if the fluid is rotating, it can support wave motions. Thomson (Reference Thomson1877, p. 297) rotated a spherical shell filled with liquid and mounted on gimbals. The spherical copper shell ran smoothly even at high rotation rates. An oblate spheroid also ran smoothly, but a prolate spheroid reacted violently, destroying the gimbal mounting through resonance of the container with internal waves in the fluid. Such free oscillations, which depend on the dynamically dominant rotation and are almost rigid rotations, are usually referred to as inertial waves, but other terms including Poincaré waves, Rossby waves or gyroscopic waves are also used. There may also be steady geostrophic modes. Our general interest is in the spatial modes of free oscillations and in the effects of forcing, when rotation is dynamically dominant. The specific aim of the present paper is to enumerate the spatial modes of inertial waves and the geostrophic modes if
![]() $V$
is a sphere, and to establish their orthogonality and completeness.
$V$
is a sphere, and to establish their orthogonality and completeness.
Let
![]() $\boldsymbol{v}^{\prime }$
be the fluid velocity in an inertial reference frame
$\boldsymbol{v}^{\prime }$
be the fluid velocity in an inertial reference frame
![]() $O^{\prime }$
. The velocity
$O^{\prime }$
. The velocity
![]() $\boldsymbol{v}^{\prime }$
is an almost rigid rotation if there exists an angular velocity
$\boldsymbol{v}^{\prime }$
is an almost rigid rotation if there exists an angular velocity
![]() ${\it\bf\Omega}$
such that
${\it\bf\Omega}$
such that
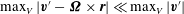 $\max _{V}|\boldsymbol{v}^{\prime }-{\it\bf\Omega}\times \boldsymbol{r}|\ll \max _{V}|\boldsymbol{v}^{\prime }|$
. There is no unique method to determine
$\max _{V}|\boldsymbol{v}^{\prime }-{\it\bf\Omega}\times \boldsymbol{r}|\ll \max _{V}|\boldsymbol{v}^{\prime }|$
. There is no unique method to determine
![]() ${\it\bf\Omega}$
from
${\it\bf\Omega}$
from
![]() $\boldsymbol{v}^{\prime }$
. Let
$\boldsymbol{v}^{\prime }$
. Let
![]() $O$
be a reference frame rotating with the undetermined angular velocity
$O$
be a reference frame rotating with the undetermined angular velocity
![]() ${\it\bf\Omega}$
, with
${\it\bf\Omega}$
, with
![]() $O^{\prime }$
and
$O^{\prime }$
and
![]() $O$
sharing a common origin so that
$O$
sharing a common origin so that
![]() $\boldsymbol{r}^{\prime }=\boldsymbol{r}$
. Let
$\boldsymbol{r}^{\prime }=\boldsymbol{r}$
. Let
![]() $R_{1}^{2}$
be the ratio of the kinetic energies of the flow in the two frames
$R_{1}^{2}$
be the ratio of the kinetic energies of the flow in the two frames
![]() $O$
and
$O$
and
![]() $O^{\prime }$
, i.e.
$O^{\prime }$
, i.e.
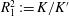 $R_{1}^{2}:=K/K^{\prime }$
, where
$R_{1}^{2}:=K/K^{\prime }$
, where
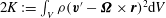 $2K:=\int _{V}{\it\rho}(\boldsymbol{v}^{\prime }-{\it\bf\Omega}\times \boldsymbol{r})^{2}\text{d}V$
and
$2K:=\int _{V}{\it\rho}(\boldsymbol{v}^{\prime }-{\it\bf\Omega}\times \boldsymbol{r})^{2}\text{d}V$
and
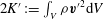 $2K^{\prime }:=\int _{V}{\it\rho}{\boldsymbol{v}^{\prime }}^{2}\text{d}V$
. Minimisation of
$2K^{\prime }:=\int _{V}{\it\rho}{\boldsymbol{v}^{\prime }}^{2}\text{d}V$
. Minimisation of
![]() $R_{1}^{2}$
yields the angular velocity
$R_{1}^{2}$
yields the angular velocity
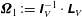 ${\it\bf\Omega}_{1}:=\unicode[STIX]{x1D644}_{V}^{-1}\cdot \unicode[STIX]{x1D647}_{V}$
, where
${\it\bf\Omega}_{1}:=\unicode[STIX]{x1D644}_{V}^{-1}\cdot \unicode[STIX]{x1D647}_{V}$
, where
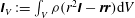 $\unicode[STIX]{x1D644}_{V}:=\int _{V}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V$
and
$\unicode[STIX]{x1D644}_{V}:=\int _{V}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V$
and
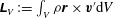 $\unicode[STIX]{x1D647}_{V}:=\int _{V}{\it\rho}\boldsymbol{r}\times \boldsymbol{v}^{\prime }\text{d}V$
are the inertia tensor and the angular momentum of the fluid in
$\unicode[STIX]{x1D647}_{V}:=\int _{V}{\it\rho}\boldsymbol{r}\times \boldsymbol{v}^{\prime }\text{d}V$
are the inertia tensor and the angular momentum of the fluid in
![]() $O^{\prime }$
. Minimisation of
$O^{\prime }$
. Minimisation of
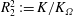 $R_{2}^{2}:=K/K_{{\it\Omega}}$
, where
$R_{2}^{2}:=K/K_{{\it\Omega}}$
, where
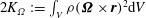 $2K_{{\it\Omega}}:=\int _{V}{\it\rho}({\it\bf\Omega}\times \boldsymbol{r})^{2}\text{d}V$
, yields the alternative angular velocity,
$2K_{{\it\Omega}}:=\int _{V}{\it\rho}({\it\bf\Omega}\times \boldsymbol{r})^{2}\text{d}V$
, yields the alternative angular velocity,
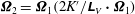 ${\it\bf\Omega}_{2}={\it\bf\Omega}_{1}(2K^{\prime }/\unicode[STIX]{x1D647}_{V}\boldsymbol{\cdot }{\it\bf\Omega}_{1})$
. The two values
${\it\bf\Omega}_{2}={\it\bf\Omega}_{1}(2K^{\prime }/\unicode[STIX]{x1D647}_{V}\boldsymbol{\cdot }{\it\bf\Omega}_{1})$
. The two values
![]() ${\it\bf\Omega}_{1}$
and
${\it\bf\Omega}_{1}$
and
![]() ${\it\bf\Omega}_{2}$
differ only slightly, if
${\it\bf\Omega}_{2}$
differ only slightly, if
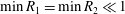 $\min R_{1}=\min R_{2}\ll 1$
. We will consider flows with the same rigidly rotating base.
$\min R_{1}=\min R_{2}\ll 1$
. We will consider flows with the same rigidly rotating base.
We non-dimensionalise
![]() $t$
,
$t$
,
![]() ${\it\bf\Omega}$
,
${\it\bf\Omega}$
,
![]() $\boldsymbol{r}$
,
$\boldsymbol{r}$
,
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() ${\it\rho}$
on the rotation time scale
${\it\rho}$
on the rotation time scale
![]() $(2{\it\Omega}_{\star })^{-1}$
with a typical length
$(2{\it\Omega}_{\star })^{-1}$
with a typical length
![]() $L_{\star }$
, rotation rate
$L_{\star }$
, rotation rate
![]() ${\it\Omega}_{\star }$
, speed
${\it\Omega}_{\star }$
, speed
![]() $v_{\star }$
and density
$v_{\star }$
and density
![]() ${\it\rho}_{\star }$
. Thus the velocities are related by
${\it\rho}_{\star }$
. Thus the velocities are related by
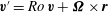 $\boldsymbol{v}^{\prime }=\mathit{Ro}\,\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{r}$
, scaling
$\boldsymbol{v}^{\prime }=\mathit{Ro}\,\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{r}$
, scaling
![]() $\boldsymbol{v}^{\prime }$
with a typical speed
$\boldsymbol{v}^{\prime }$
with a typical speed
![]() ${\it\Omega}_{\star }L_{\star }$
relative to
${\it\Omega}_{\star }L_{\star }$
relative to
![]() $O^{\prime }$
and introducing the Rossby number
$O^{\prime }$
and introducing the Rossby number
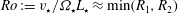 $\mathit{Ro}:=v_{\star }/{\it\Omega}_{\star }L_{\star }\approx \min (R_{1},R_{2})$
. The description in the rotating frame is simpler than the inertial frame
$\mathit{Ro}:=v_{\star }/{\it\Omega}_{\star }L_{\star }\approx \min (R_{1},R_{2})$
. The description in the rotating frame is simpler than the inertial frame
![]() $O^{\prime }$
for flows that are almost rigid rotations. Under the transformation from
$O^{\prime }$
for flows that are almost rigid rotations. Under the transformation from
![]() $O^{\prime }$
to
$O^{\prime }$
to
![]() $O$
, a vector field
$O$
, a vector field
![]() $\boldsymbol{F}^{\prime }$
defined independently of the reference frame maps to
$\boldsymbol{F}^{\prime }$
defined independently of the reference frame maps to
![]() $\boldsymbol{F}=\boldsymbol{F}^{\prime }$
and the spatial gradient is invariant,
$\boldsymbol{F}=\boldsymbol{F}^{\prime }$
and the spatial gradient is invariant,
 $\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{F}^{\prime }=\boldsymbol{{\rm\nabla}}\boldsymbol{F}$
. This is false for frame-dependent (relative) fields such as the velocity, thus
$\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{F}^{\prime }=\boldsymbol{{\rm\nabla}}\boldsymbol{F}$
. This is false for frame-dependent (relative) fields such as the velocity, thus
 $$\begin{eqnarray}\mathit{Ro}^{-1}\,\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }=\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+\mathit{Ro}^{-1}\,{\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r})+{\it\bf\Omega}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{Ro}^{-1}\,\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }=\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+\mathit{Ro}^{-1}\,{\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r})+{\it\bf\Omega}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}.\end{eqnarray}$$
Thus
![]() $\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }$
in the inertial frame cannot be neglected. Combined with
$\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }$
in the inertial frame cannot be neglected. Combined with
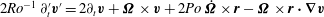 $2\mathit{Ro}^{-1}\,\partial _{t}^{\prime }\boldsymbol{v}^{\prime }=2\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+2\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}-{\it\bf\Omega}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}$
, this gives the transformation for the convective derivative,
$2\mathit{Ro}^{-1}\,\partial _{t}^{\prime }\boldsymbol{v}^{\prime }=2\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+2\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}-{\it\bf\Omega}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}$
, this gives the transformation for the convective derivative,
 $$\begin{eqnarray}\mathit{Ro}^{-1}\,D_{t}^{\prime }\boldsymbol{v}^{\prime }=D_{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}+{\textstyle \frac{1}{2}}\mathit{Ro}^{-1}\,{\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r}),\end{eqnarray}$$
$$\begin{eqnarray}\mathit{Ro}^{-1}\,D_{t}^{\prime }\boldsymbol{v}^{\prime }=D_{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}+{\textstyle \frac{1}{2}}\mathit{Ro}^{-1}\,{\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r}),\end{eqnarray}$$
where
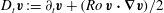 $D_{t}\boldsymbol{v}:=\partial _{t}\boldsymbol{v}+(\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v})/2$
,
$D_{t}\boldsymbol{v}:=\partial _{t}\boldsymbol{v}+(\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v})/2$
,
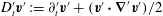 $D_{t}^{\prime }\boldsymbol{v}^{\prime }:=\partial _{t}^{\prime }\boldsymbol{v}^{\prime }+(\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime })/2$
and
$D_{t}^{\prime }\boldsymbol{v}^{\prime }:=\partial _{t}^{\prime }\boldsymbol{v}^{\prime }+(\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime })/2$
and
![]() $\mathit{Po}$
is the Poincaré number. Thus
$\mathit{Po}$
is the Poincaré number. Thus
![]() $\mathit{Ro}\rightarrow 0$
does not remove the advective term in the inertial frame.
$\mathit{Ro}\rightarrow 0$
does not remove the advective term in the inertial frame.
Thus the effects of steady rotation can be characterised mathematically by the Coriolis force in a rotating reference frame. In a frame
![]() $O$
rotating with angular velocity
$O$
rotating with angular velocity
![]() ${\it\bf\Omega}$
the velocity
${\it\bf\Omega}$
the velocity
![]() $\boldsymbol{v}$
is governed by the momentum equation,
$\boldsymbol{v}$
is governed by the momentum equation,
 $$\begin{eqnarray}\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+{\it\rho}^{-1}\boldsymbol{{\rm\nabla}}p=-{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}U_{e}+\mathit{E}\,{\rm\nabla}^{2}\boldsymbol{v}-\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}+\mathit{El}~{\it\rho}^{-1}\boldsymbol{F}_{L},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}+{\it\rho}^{-1}\boldsymbol{{\rm\nabla}}p=-{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}U_{e}+\mathit{E}\,{\rm\nabla}^{2}\boldsymbol{v}-\mathit{Po}\,\dot{{\it\bf\Omega}}\times \boldsymbol{r}+\mathit{El}~{\it\rho}^{-1}\boldsymbol{F}_{L},\end{eqnarray}$$
where
 $\dot{{\it\bf\Omega}}:=\text{d}{\it\bf\Omega}/\text{d}t$
,
$\dot{{\it\bf\Omega}}:=\text{d}{\it\bf\Omega}/\text{d}t$
,
![]() $\boldsymbol{r}$
is the radius vector and
$\boldsymbol{r}$
is the radius vector and
![]() $U_{e}$
is the effective gravitational potential modified by the centripetal acceleration
$U_{e}$
is the effective gravitational potential modified by the centripetal acceleration
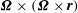 ${\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r})$
. If the fluid is electrically conducting there is also the Lorentz force
${\it\bf\Omega}\times ({\it\bf\Omega}\times \boldsymbol{r})$
. If the fluid is electrically conducting there is also the Lorentz force
![]() $\boldsymbol{F}_{L}$
. The pressure has been non-dimensionalised with a typical pressure
$\boldsymbol{F}_{L}$
. The pressure has been non-dimensionalised with a typical pressure
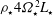 ${\it\rho}_{\star }4{\it\Omega}_{\star }^{2}L_{\star }$
. The dimensionless rotation rate
${\it\rho}_{\star }4{\it\Omega}_{\star }^{2}L_{\star }$
. The dimensionless rotation rate
![]() ${\it\bf\Omega}$
may be time-dependent with only
${\it\bf\Omega}$
may be time-dependent with only
![]() $|{\it\bf\Omega}|\approx 1$
; if
$|{\it\bf\Omega}|\approx 1$
; if
![]() ${\it\bf\Omega}$
is constant, then
${\it\bf\Omega}$
is constant, then
![]() ${\it\bf\Omega}$
is a unit vector, which will be denoted
${\it\bf\Omega}$
is a unit vector, which will be denoted
![]() $\widehat{{\it\bf\Omega}}$
. The dimensionless Rossby, Ekman, Poincaré and Elsasser numbers,
$\widehat{{\it\bf\Omega}}$
. The dimensionless Rossby, Ekman, Poincaré and Elsasser numbers,
![]() $\mathit{Ro}$
,
$\mathit{Ro}$
,
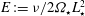 $\mathit{E}:={\it\nu}/2{\it\Omega}_{\star }L_{\star }^{2}$
,
$\mathit{E}:={\it\nu}/2{\it\Omega}_{\star }L_{\star }^{2}$
,
![]() $\mathit{Po}$
and
$\mathit{Po}$
and
![]() $\mathit{El}$
, are typical magnitude ratios of the advective, viscous, Poincaré and Lorentz forces to the Coriolis force. The factor
$\mathit{El}$
, are typical magnitude ratios of the advective, viscous, Poincaré and Lorentz forces to the Coriolis force. The factor
![]() $(1/2)$
in (1.3) is due to the definition of the Rossby number and arises from the time scale. We are interested in the rapid-rotation regime
$(1/2)$
in (1.3) is due to the definition of the Rossby number and arises from the time scale. We are interested in the rapid-rotation regime
![]() $\mathit{Ro}\ll 1$
and
$\mathit{Ro}\ll 1$
and
![]() $\mathit{E}\ll 1$
. The limit
$\mathit{E}\ll 1$
. The limit
![]() $\mathit{E}\rightarrow 0$
removes the viscous term in an inertial frame, since
$\mathit{E}\rightarrow 0$
removes the viscous term in an inertial frame, since
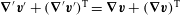 $\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }+(\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime })^{\text{T}}=\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}$
and
$\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime }+(\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{v}^{\prime })^{\text{T}}=\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}$
and
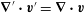 $\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{\cdot }\boldsymbol{v}^{\prime }=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}$
imply
$\boldsymbol{{\rm\nabla}}^{\prime }\boldsymbol{\cdot }\boldsymbol{v}^{\prime }=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}$
imply
 $\mathit{E}(\boldsymbol{{\rm\nabla}}^{\prime })^{2}\boldsymbol{v}^{\prime }=\mathit{E}\,\mathit{Ro}\,{\rm\nabla}^{2}\boldsymbol{v}$
. In the non-magnetic rapid-rotation limit
$\mathit{E}(\boldsymbol{{\rm\nabla}}^{\prime })^{2}\boldsymbol{v}^{\prime }=\mathit{E}\,\mathit{Ro}\,{\rm\nabla}^{2}\boldsymbol{v}$
. In the non-magnetic rapid-rotation limit
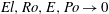 $\mathit{El},\mathit{Ro},\mathit{E},\mathit{Po}\rightarrow 0$
, with constant angular velocity and uniform density (
$\mathit{El},\mathit{Ro},\mathit{E},\mathit{Po}\rightarrow 0$
, with constant angular velocity and uniform density (
![]() ${\it\rho}=1$
), the momentum equation (1.3) and its solution
${\it\rho}=1$
), the momentum equation (1.3) and its solution
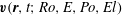 $\boldsymbol{v}(\boldsymbol{r},t;\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El})$
reduce on setting
$\boldsymbol{v}(\boldsymbol{r},t;\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El})$
reduce on setting
 $\mathit{El}=\mathit{Ro}=\mathit{E}=\mathit{Po}=0$
to
$\mathit{El}=\mathit{Ro}=\mathit{E}=\mathit{Po}=0$
to
 $$\begin{eqnarray}\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}P,\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{v}+{\it\bf\Omega}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}P,\end{eqnarray}$$
where the velocity is
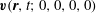 $\boldsymbol{v}(\boldsymbol{r},t;0,0,0,0)$
and
$\boldsymbol{v}(\boldsymbol{r},t;0,0,0,0)$
and
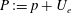 $P:=p+U_{e}$
. We do not consider in the present work if the velocity
$P:=p+U_{e}$
. We do not consider in the present work if the velocity
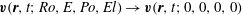 $\boldsymbol{v}(\boldsymbol{r},t;\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El})\rightarrow \boldsymbol{v}(\boldsymbol{r},t;0,0,0,0)$
as
$\boldsymbol{v}(\boldsymbol{r},t;\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El})\rightarrow \boldsymbol{v}(\boldsymbol{r},t;0,0,0,0)$
as
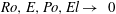 $\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El}\rightarrow ~0$
.
$\mathit{Ro},\mathit{E},\mathit{Po},\mathit{El}\rightarrow ~0$
.
We assume
![]() $\partial V$
is impenetrable, so
$\partial V$
is impenetrable, so
 $\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{v}-\boldsymbol{v}_{\partial V})=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{v}-\boldsymbol{v}_{\partial V})=0$
on
![]() $\partial V$
, where
$\partial V$
, where
![]() $\boldsymbol{n}$
is a (possibly non-unit) normal on
$\boldsymbol{n}$
is a (possibly non-unit) normal on
![]() $\partial V$
. We further assume that
$\partial V$
. We further assume that
![]() $\partial V$
rotates with a constant angular velocity, which is consistent with the almost rigid rotation flows. We do not consider free surfaces or impulsive motion of
$\partial V$
rotates with a constant angular velocity, which is consistent with the almost rigid rotation flows. We do not consider free surfaces or impulsive motion of
![]() $\partial V$
(e.g. see Bryan Reference Bryan1889 and Hough Reference Hough1895). Henceforth,
$\partial V$
(e.g. see Bryan Reference Bryan1889 and Hough Reference Hough1895). Henceforth,
![]() $O$
is the boundary frame,
$O$
is the boundary frame,
![]() $\boldsymbol{n}$
is steady and the boundary condition reduces to
$\boldsymbol{n}$
is steady and the boundary condition reduces to
 $$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{on }\partial V.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{on }\partial V.\end{eqnarray}$$
We assume the flow is incompressible,
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{in }V,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{in }V,\end{eqnarray}$$
except for a brief discussion in the final section § 9.
Mathematically the inertial wave problem consists of (1.4)–(1.6). Analytic solutions are usually derived from the formulation in terms of the pressure
![]() $P$
outlined in § 2. The velocity can be eliminated, yielding the free Poincaré equation,
$P$
outlined in § 2. The velocity can be eliminated, yielding the free Poincaré equation,
 $$\begin{eqnarray}\partial _{t}^{2}{\rm\nabla}^{2}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}P=0.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}^{2}{\rm\nabla}^{2}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}P=0.\end{eqnarray}$$
Thomson (Reference Thomson1880) determined the solutions for inertial waves in a cylinder and cylindrical shell rotating about the cylindrical axis. Poincaré (Reference Poincaré1885a
, pp. 355–365) (not to be confused with Poincaré (Reference Poincaré1885b
,Reference Poincaré
c
) of the same title), in a study of the stability of a fluid ellipsoid with a free surface, gave an incomplete derivation of the inertial modes for an ellipsoid rotating about a principal axis in terms of Lamé functions; see also Hough (Reference Hough1895, Appendix p. 479). Bryan (Reference Bryan1889) gave a full derivation of the inertial modes in terms of spheroidal harmonics for a spheroid rotating about its symmetry axis; see also Kudlick (Reference Kudlick1966). Taylor (Reference Taylor1922), Rao (Reference Rao1966) and Nurijanyan, Bokhove & Maas (Reference Nurijanyan, Bokhove and Maas2013) computed the inertial modes for a rectangular prism rotating about a centred axis perpendicular to a face. Rieutord (Reference Rieutord1991) and Rieutord & Valdettaro (Reference Rieutord and Valdettaro1997) computed the viscous inertial modes for a spherical shell with no-slip and stress-free boundary conditions. Solutions for the periodic plane layer and the periodic duct rotating about a centred axis perpendicular to impenetrable plane boundaries are well known. Pedlosky & Greenspan (Reference Pedlosky and Greenspan1967) derived approximate solutions for the sliced cylinder
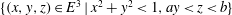 $\{(x,y,z)\in E^{3}\mid x^{2}+y^{2}<1,ay<z<b\}$
, where
$\{(x,y,z)\in E^{3}\mid x^{2}+y^{2}<1,ay<z<b\}$
, where
![]() $E^{3}$
is Euclidean space with a set of Cartesian coordinates
$E^{3}$
is Euclidean space with a set of Cartesian coordinates
![]() $(x,y,z)$
and
$(x,y,z)$
and
![]() $a$
,
$a$
,
![]() $b$
are constants. Inertial waves underlie many geophysical and astrophysical phenomena (see Zhang Reference Zhang1993; Cui, Zhang & Liao Reference Cui, Zhang and Liao2014).
$b$
are constants. Inertial waves underlie many geophysical and astrophysical phenomena (see Zhang Reference Zhang1993; Cui, Zhang & Liao Reference Cui, Zhang and Liao2014).
To study the spatial modes of inertial waves we consider the steady incompressible Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
defined by
$\boldsymbol{{\mathcal{C}}}$
defined by
 $$\begin{eqnarray}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}:=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}:=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p,\end{eqnarray}$$
subject to
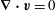 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V$
and
$V$
and
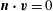 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V$
, i.e. (1.5) and (1.6). The operator
$\partial V$
, i.e. (1.5) and (1.6). The operator
![]() $\boldsymbol{{\mathcal{C}}}$
is a time-independent linear operator. This definition of
$\boldsymbol{{\mathcal{C}}}$
is a time-independent linear operator. This definition of
![]() $\boldsymbol{{\mathcal{C}}}$
is incomplete until the auxiliary function or pressure
$\boldsymbol{{\mathcal{C}}}$
is incomplete until the auxiliary function or pressure
![]() $p$
has been defined. We require that
$p$
has been defined. We require that
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
satisfies (1.6) and (1.5), i.e.
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
satisfies (1.6) and (1.5), i.e.
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=0\quad \text{on }\partial V,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=0\quad \text{on }\partial V,\end{eqnarray}$$
and hence
![]() $p$
must satisfy the elliptic Poisson–Neumann problem,
$p$
must satisfy the elliptic Poisson–Neumann problem,
 $$\begin{eqnarray}{\rm\nabla}^{2}p=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\quad \text{in }V;\quad \partial _{n}p=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\quad \text{on }\partial V,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}p=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\quad \text{in }V;\quad \partial _{n}p=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\quad \text{on }\partial V,\end{eqnarray}$$
where
![]() $\boldsymbol{v}$
is prescribed. This associates to each
$\boldsymbol{v}$
is prescribed. This associates to each
![]() $\boldsymbol{v}$
a
$\boldsymbol{v}$
a
![]() $p$
which is unique, if the condition
$p$
which is unique, if the condition
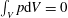 $\int _{V}p\text{d}V=0$
is imposed. We give an explicit expression for
$\int _{V}p\text{d}V=0$
is imposed. We give an explicit expression for
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
in terms of
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
in terms of
![]() $\boldsymbol{v}$
in § 3.
$\boldsymbol{v}$
in § 3.
It is useful to formulate the problem in terms of the space of functions
![]() $\boldsymbol{v}$
on which
$\boldsymbol{v}$
on which
![]() $\boldsymbol{{\mathcal{C}}}$
acts. Let
$\boldsymbol{{\mathcal{C}}}$
acts. Let
![]() $\boldsymbol{{\mathcal{V}}}^{k}(V)$
, where
$\boldsymbol{{\mathcal{V}}}^{k}(V)$
, where
![]() $k$
is a positive integer, be the space of
$k$
is a positive integer, be the space of
![]() $C^{k}$
(
$C^{k}$
(
![]() $k$
-times continuously differentiable) inviscid solenoidal velocities in
$k$
-times continuously differentiable) inviscid solenoidal velocities in
![]() $V$
, i.e. which satisfy (1.5) and (1.6). Thus
$V$
, i.e. which satisfy (1.5) and (1.6). Thus
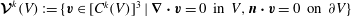 $\boldsymbol{{\mathcal{V}}}^{k}(V):=\{\boldsymbol{v}\in [C^{k}(V)]^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0~\text{in }V,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0~\text{on}~\partial V\}$
with the inner product
$\boldsymbol{{\mathcal{V}}}^{k}(V):=\{\boldsymbol{v}\in [C^{k}(V)]^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0~\text{in }V,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0~\text{on}~\partial V\}$
with the inner product
 $$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2}):=\int _{V}\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{v}_{2}^{\ast }\text{d}V,\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2}):=\int _{V}\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{v}_{2}^{\ast }\text{d}V,\end{eqnarray}$$
where the asterisk denotes complex conjugation and
![]() $C^{k}(V)$
is the space of complex-valued
$C^{k}(V)$
is the space of complex-valued
![]() $C^{k}$
scalar functions on
$C^{k}$
scalar functions on
![]() $V$
. The associated norm is
$V$
. The associated norm is
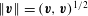 $\Vert \boldsymbol{v}\Vert =(\boldsymbol{v},\boldsymbol{v})^{1/2}$
,
$\Vert \boldsymbol{v}\Vert =(\boldsymbol{v},\boldsymbol{v})^{1/2}$
,
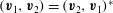 $(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{2},\boldsymbol{v}_{1})^{\ast }$
and the Cauchy–Schwartz inequality
$(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{2},\boldsymbol{v}_{1})^{\ast }$
and the Cauchy–Schwartz inequality
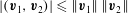 $|(\boldsymbol{v}_{1},\boldsymbol{v}_{2})|\leqslant \Vert \boldsymbol{v}_{1}\Vert \,\Vert \boldsymbol{v}_{2}\Vert$
holds. The flows have finite kinetic energy. Thus we require that the linear operator
$|(\boldsymbol{v}_{1},\boldsymbol{v}_{2})|\leqslant \Vert \boldsymbol{v}_{1}\Vert \,\Vert \boldsymbol{v}_{2}\Vert$
holds. The flows have finite kinetic energy. Thus we require that the linear operator
![]() $\boldsymbol{{\mathcal{C}}}$
maps flows in
$\boldsymbol{{\mathcal{C}}}$
maps flows in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
into
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
into
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The space
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The space
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
is not complete and therefore not a Hilbert space; but see the discussion in § 9. This does not limit the present results since we do not need to prove the general existence of solutions. Instead we consider restrictions of
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
is not complete and therefore not a Hilbert space; but see the discussion in § 9. This does not limit the present results since we do not need to prove the general existence of solutions. Instead we consider restrictions of
![]() $\boldsymbol{{\mathcal{C}}}$
to finite-dimensional spaces of polynomial flows and use the Weierstrass theorem on uniform polynomial approximation of continuous functions in a bounded region to approximate flows in
$\boldsymbol{{\mathcal{C}}}$
to finite-dimensional spaces of polynomial flows and use the Weierstrass theorem on uniform polynomial approximation of continuous functions in a bounded region to approximate flows in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. We also introduce the associated space of pressures on
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. We also introduce the associated space of pressures on
![]() $V$
,
$V$
,
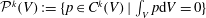 ${\mathcal{P}}^{k}(V):=\{p\in C^{k}(V)\mid \int _{V}p\text{d}V=0\}$
, with inner product
${\mathcal{P}}^{k}(V):=\{p\in C^{k}(V)\mid \int _{V}p\text{d}V=0\}$
, with inner product
 $$\begin{eqnarray}(p_{1},p_{2}):=\int _{V}\boldsymbol{{\rm\nabla}}p_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{2}^{\ast }\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}(p_{1},p_{2}):=\int _{V}\boldsymbol{{\rm\nabla}}p_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{2}^{\ast }\text{d}V.\end{eqnarray}$$
A second useful operator associated with the Navier–Stokes equation (1.3) is the Stokes operator,
 $$\begin{eqnarray}\boldsymbol{{\mathcal{S}}}\boldsymbol{v}:=-{\rm\nabla}^{2}\boldsymbol{v}+\boldsymbol{{\rm\nabla}}p\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\mathcal{S}}}\boldsymbol{v}:=-{\rm\nabla}^{2}\boldsymbol{v}+\boldsymbol{{\rm\nabla}}p\end{eqnarray}$$
with
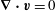 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V$
,
$V$
,
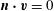 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V$
, additionally subject to either the no-slip condition
$\partial V$
, additionally subject to either the no-slip condition
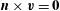 $\boldsymbol{n}\times \boldsymbol{v}=\mathbf{0}$
or the stress-free condition
$\boldsymbol{n}\times \boldsymbol{v}=\mathbf{0}$
or the stress-free condition
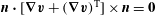 $\boldsymbol{n}\boldsymbol{\cdot }[\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}]\times \boldsymbol{n}=\mathbf{0}$
on
$\boldsymbol{n}\boldsymbol{\cdot }[\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}]\times \boldsymbol{n}=\mathbf{0}$
on
![]() $\partial V$
.
$\partial V$
.
![]() $\boldsymbol{{\mathcal{S}}}$
maps a flow
$\boldsymbol{{\mathcal{S}}}$
maps a flow
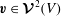 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{2}(V)$
into
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{2}(V)$
into
![]() $\boldsymbol{{\mathcal{V}}}^{2}(V)$
. Here
$\boldsymbol{{\mathcal{V}}}^{2}(V)$
. Here
![]() $p$
must satisfy the Poisson–Neumann problem,
$p$
must satisfy the Poisson–Neumann problem,
 $$\begin{eqnarray}{\rm\nabla}^{2}p=0\quad \text{in }V;\quad \partial _{n}p=\boldsymbol{n}\boldsymbol{\cdot }{\rm\nabla}^{2}\boldsymbol{v}\quad \text{on }\partial V.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}p=0\quad \text{in }V;\quad \partial _{n}p=\boldsymbol{n}\boldsymbol{\cdot }{\rm\nabla}^{2}\boldsymbol{v}\quad \text{on }\partial V.\end{eqnarray}$$
In terms of the operators
![]() $\boldsymbol{{\mathcal{C}}}$
and
$\boldsymbol{{\mathcal{C}}}$
and
![]() $\boldsymbol{{\mathcal{S}}}$
with associated pressures
$\boldsymbol{{\mathcal{S}}}$
with associated pressures
![]() $p_{C}$
and
$p_{C}$
and
![]() $p_{S}$
, the Navier–Stokes equation (1.3) with uniform density or in the Boussinesq approximation can be written as
$p_{S}$
, the Navier–Stokes equation (1.3) with uniform density or in the Boussinesq approximation can be written as
 $$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}(p-p_{C}-p_{S})+\mathit{Po}\,\boldsymbol{F}_{P}+{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{F}_{a}+\mathit{El}\,\boldsymbol{F}_{L}+\boldsymbol{F}_{g},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}(p-p_{C}-p_{S})+\mathit{Po}\,\boldsymbol{F}_{P}+{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{F}_{a}+\mathit{El}\,\boldsymbol{F}_{L}+\boldsymbol{F}_{g},\end{eqnarray}$$
where
![]() $\boldsymbol{F}_{P}$
,
$\boldsymbol{F}_{P}$
,
![]() $\boldsymbol{F}_{a}$
,
$\boldsymbol{F}_{a}$
,
![]() $\boldsymbol{F}_{L}$
,
$\boldsymbol{F}_{L}$
,
![]() $\boldsymbol{F}_{g}$
are the Poincaré, advective, Lorentz and gravitational or buoyancy force. The forces
$\boldsymbol{F}_{g}$
are the Poincaré, advective, Lorentz and gravitational or buoyancy force. The forces
![]() $\boldsymbol{F}_{P}$
,
$\boldsymbol{F}_{P}$
,
![]() $\boldsymbol{F}_{a}$
,
$\boldsymbol{F}_{a}$
,
![]() $\boldsymbol{F}_{L}$
,
$\boldsymbol{F}_{L}$
,
![]() $\boldsymbol{F}_{g}$
can be projected individually onto
$\boldsymbol{F}_{g}$
can be projected individually onto
![]() $\boldsymbol{{\mathcal{V}}}^{k}(V)$
by subtracting a pressure gradient:
$\boldsymbol{{\mathcal{V}}}^{k}(V)$
by subtracting a pressure gradient:
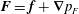 $\boldsymbol{F}=\boldsymbol{f}+\boldsymbol{{\rm\nabla}}p_{F}$
and
$\boldsymbol{F}=\boldsymbol{f}+\boldsymbol{{\rm\nabla}}p_{F}$
and
![]() $p_{F}$
is chosen so that
$p_{F}$
is chosen so that
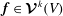 $\boldsymbol{f}\in \boldsymbol{{\mathcal{V}}}^{k}(V)$
, i.e.
$\boldsymbol{f}\in \boldsymbol{{\mathcal{V}}}^{k}(V)$
, i.e.
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{f}=0\quad \text{on }\partial V.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{f}=0\quad \text{on }\partial V.\end{eqnarray}$$
Thus the pressure
![]() $p_{F}$
is the solution of the Poisson–Neumann problem,
$p_{F}$
is the solution of the Poisson–Neumann problem,
 $$\begin{eqnarray}{\rm\nabla}^{2}p_{F}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{F}\quad \text{in }V;\quad \partial _{n}p_{F}=-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{F}\quad \text{on }\partial V;\quad \int _{V}p_{F}\text{d}V=0.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}p_{F}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{F}\quad \text{in }V;\quad \partial _{n}p_{F}=-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{F}\quad \text{on }\partial V;\quad \int _{V}p_{F}\text{d}V=0.\end{eqnarray}$$
Observe that this problem, and the specific cases (1.10) and (1.15), are self-consistent. Hence projecting
![]() $\boldsymbol{F}_{P}$
,
$\boldsymbol{F}_{P}$
,
![]() $\boldsymbol{F}_{a}$
,
$\boldsymbol{F}_{a}$
,
![]() $\boldsymbol{F}_{L}$
,
$\boldsymbol{F}_{L}$
,
![]() $\boldsymbol{F}_{g}$
yields
$\boldsymbol{F}_{g}$
yields
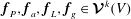 $\boldsymbol{f}_{P},\boldsymbol{f}_{a},\boldsymbol{f}_{L},\boldsymbol{f}_{g}\in \boldsymbol{{\mathcal{V}}}^{k}(V)$
with associated pressures
$\boldsymbol{f}_{P},\boldsymbol{f}_{a},\boldsymbol{f}_{L},\boldsymbol{f}_{g}\in \boldsymbol{{\mathcal{V}}}^{k}(V)$
with associated pressures
![]() $p_{P}$
,
$p_{P}$
,
![]() $p_{a}$
,
$p_{a}$
,
![]() $p_{L}$
,
$p_{L}$
,
![]() $p_{g}$
satisfying (1.17). The momentum equation reduces to
$p_{g}$
satisfying (1.17). The momentum equation reduces to
 $$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathit{Po}\,\boldsymbol{f}_{P}+{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{f}_{a}+\mathit{El}\,\boldsymbol{f}_{L}+\boldsymbol{f}_{g}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathit{Po}\,\boldsymbol{f}_{P}+{\textstyle \frac{1}{2}}\mathit{Ro}\,\boldsymbol{f}_{a}+\mathit{El}\,\boldsymbol{f}_{L}+\boldsymbol{f}_{g}.\end{eqnarray}$$
The divergence of (1.15) yields
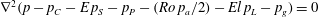 ${\rm\nabla}^{2}(p-p_{C}-\mathit{E}\,p_{S}-p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g})=0$
. Further, since
${\rm\nabla}^{2}(p-p_{C}-\mathit{E}\,p_{S}-p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g})=0$
. Further, since
![]() $\boldsymbol{n}$
is independent of time, taking the dot product of
$\boldsymbol{n}$
is independent of time, taking the dot product of
![]() $\boldsymbol{n}$
with (1.16) yields
$\boldsymbol{n}$
with (1.16) yields
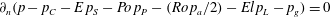 $\partial _{n}(p-p_{C}-\mathit{E}\,p_{S}-\mathit{Po}\,p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g})=0$
on the boundary
$\partial _{n}(p-p_{C}-\mathit{E}\,p_{S}-\mathit{Po}\,p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g})=0$
on the boundary
![]() $\partial V$
. Hence
$\partial V$
. Hence
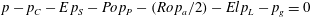 $p-p_{C}-\mathit{E}\,p_{S}-\mathit{Po}\,p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g}=0$
. Thus we consider the model forced-momentum equation in the rapid-rotation limit,
$p-p_{C}-\mathit{E}\,p_{S}-\mathit{Po}\,p_{P}-(\mathit{Ro}\,p_{a}/2)-\mathit{El}\,p_{L}-p_{g}=0$
. Thus we consider the model forced-momentum equation in the rapid-rotation limit,
 $$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f},\end{eqnarray}$$
where
![]() $\boldsymbol{f}$
satisfies conditions (1.16).
$\boldsymbol{f}$
satisfies conditions (1.16).
We consider properties of
![]() $\boldsymbol{{\mathcal{C}}}$
for general fluid volumes
$\boldsymbol{{\mathcal{C}}}$
for general fluid volumes
![]() $V$
in § 3, in particular we show that
$V$
in § 3, in particular we show that
![]() $\boldsymbol{{\mathcal{C}}}$
is a bounded operator on
$\boldsymbol{{\mathcal{C}}}$
is a bounded operator on
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
and
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
and
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric on
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric on
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Our primary interest is the discrete spectrum of
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Our primary interest is the discrete spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
, which consists of the eigenvalues
$\boldsymbol{{\mathcal{C}}}$
, which consists of the eigenvalues
![]() ${\it\lambda}$
of
${\it\lambda}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
, and the eigenfunctions
$\boldsymbol{{\mathcal{C}}}$
, and the eigenfunctions
![]() $\boldsymbol{v}~(\neq \mathbf{0})$
, which satisfy
$\boldsymbol{v}~(\neq \mathbf{0})$
, which satisfy
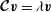 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
. Throughout we associate with an eigenvalue
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
. Throughout we associate with an eigenvalue
![]() ${\it\lambda}$
of
${\it\lambda}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
an angular frequency
$\boldsymbol{{\mathcal{C}}}$
an angular frequency
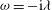 ${\it\omega}=-\text{i}{\it\lambda}$
, so that
${\it\omega}=-\text{i}{\it\lambda}$
, so that
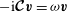 $-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
. We will refer to
$-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
. We will refer to
![]() $(\boldsymbol{v},{\it\lambda})$
as a (discrete) Coriolis mode. Physically, Coriolis modes are geostrophic modes or the spatial modes of inertial waves, or more generally Rossby waves, e.g. in a sliced cylinder (Pedlosky & Greenspan Reference Pedlosky and Greenspan1967). We will refer to Coriolis modes of zero and non-zero frequency as geostrophic and inertial modes respectively. In § 4 we enumerate by construction the Coriolis velocity modes
$(\boldsymbol{v},{\it\lambda})$
as a (discrete) Coriolis mode. Physically, Coriolis modes are geostrophic modes or the spatial modes of inertial waves, or more generally Rossby waves, e.g. in a sliced cylinder (Pedlosky & Greenspan Reference Pedlosky and Greenspan1967). We will refer to Coriolis modes of zero and non-zero frequency as geostrophic and inertial modes respectively. In § 4 we enumerate by construction the Coriolis velocity modes
![]() $\boldsymbol{v}_{n,j}^{m}$
in a sphere. The index
$\boldsymbol{v}_{n,j}^{m}$
in a sphere. The index
![]() $n$
is the polynomial degree of the velocity mode,
$n$
is the polynomial degree of the velocity mode,
![]() $m$
is the azimuthal wavenumber and
$m$
is the azimuthal wavenumber and
![]() $j$
labels the frequency. For the zero frequency, an infinite orthogonal set of geostrophic modes must be constructed, since it is infinitely degenerate.
$j$
labels the frequency. For the zero frequency, an infinite orthogonal set of geostrophic modes must be constructed, since it is infinitely degenerate.
In § 5 we determine the dimension of the space of polynomial flows in a sphere. This together with Theorem 6.4 provides an alternative method for enumerating the Coriolis modes which avoids explicit construction of the modes. In § 6 we show in Theorem 6.3 that the Coriolis operator is well defined on the space of polynomial flows in a sphere. Theorem 6.4 follows from this. This is based on the fundamental tool, Theorem 6.2, that the solution in a sphere of the polynomial Poisson–Neumann problem, i.e. Poisson’s equation with a Neumann boundary condition and polynomial data, is polynomial.
Consider the integral
 $$\begin{eqnarray}I_{n_{1},j_{1},n_{2},j_{2}}^{m_{1},m_{2}}:=({\rm\nabla}^{2}\boldsymbol{v}_{n_{1},j_{1}}^{m_{1}},\boldsymbol{v}_{n_{2},j_{2}}^{m_{2}}).\end{eqnarray}$$
$$\begin{eqnarray}I_{n_{1},j_{1},n_{2},j_{2}}^{m_{1},m_{2}}:=({\rm\nabla}^{2}\boldsymbol{v}_{n_{1},j_{1}}^{m_{1}},\boldsymbol{v}_{n_{2},j_{2}}^{m_{2}}).\end{eqnarray}$$
Zhang et al. (Reference Zhang, Earnshaw, Liao and Busse2001) derived a representation for
![]() $\boldsymbol{v}_{n,j}^{m}$
in terms of the monomial basis
$\boldsymbol{v}_{n,j}^{m}$
in terms of the monomial basis
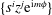 $\{s^{i}z^{j}\text{e}^{\text{i}m{\it\phi}}\}$
and showed that
$\{s^{i}z^{j}\text{e}^{\text{i}m{\it\phi}}\}$
and showed that
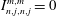 $I_{n,j,n,j}^{m,m}=0$
for a sphere. Zhang, Liao & Earnshaw (Reference Zhang, Liao and Earnshaw2004) extended this result to a spheroid rotating about its axis. Liao & Zhang (Reference Liao and Zhang2009) showed that
$I_{n,j,n,j}^{m,m}=0$
for a sphere. Zhang, Liao & Earnshaw (Reference Zhang, Liao and Earnshaw2004) extended this result to a spheroid rotating about its axis. Liao & Zhang (Reference Liao and Zhang2009) showed that
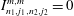 $I_{n_{1},j_{1},n_{2},j_{2}}^{m,m}=0$
for a sphere if
$I_{n_{1},j_{1},n_{2},j_{2}}^{m,m}=0$
for a sphere if
![]() $n_{1}\leqslant n_{2}$
. A proof of this directly from the governing equations remains elusive. Indeed, these remarkable results were our original motivation for studying the polynomial properties of inertial modes and the Coriolis operator. It is shown in § 7 that
$n_{1}\leqslant n_{2}$
. A proof of this directly from the governing equations remains elusive. Indeed, these remarkable results were our original motivation for studying the polynomial properties of inertial modes and the Coriolis operator. It is shown in § 7 that
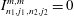 $I_{n_{1},j_{1},n_{2},j_{2}}^{m,m}=0$
for a sphere if
$I_{n_{1},j_{1},n_{2},j_{2}}^{m,m}=0$
for a sphere if
 $n_{1}\leqslant n_{2}+1$
, as a simple corollary of the results in § 6.
$n_{1}\leqslant n_{2}+1$
, as a simple corollary of the results in § 6.
In § 8 we again use Theorem 6.2 to establish the most important result of the paper, namely Theorem 8.1, that the Coriolis modes in a sphere
![]() $V$
are complete. Completeness of inertial modes has been established for a periodic duct (Cui et al.
Reference Cui, Zhang and Liao2014).
$V$
are complete. Completeness of inertial modes has been established for a periodic duct (Cui et al.
Reference Cui, Zhang and Liao2014).
In the concluding § 9 we outline an abstract existence theorem for Coriolis modes in a general bounded fluid volume. We also briefly discuss applications and the generalisations of the important time-dependent incompressible Coriolis operator and the anelastic Coriolis operator.
2. Poincaré’s equation
Since
![]() ${\it\bf\Omega}$
is constant in time, the velocity
${\it\bf\Omega}$
is constant in time, the velocity
![]() $\boldsymbol{v}$
can be eliminated from (1.19) and (1.6) as follows. The cross product of (1.19) with
$\boldsymbol{v}$
can be eliminated from (1.19) and (1.6) as follows. The cross product of (1.19) with
![]() $\widehat{{\it\bf\Omega}}$
, noting (1.8), gives
$\widehat{{\it\bf\Omega}}$
, noting (1.8), gives
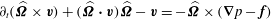 $\partial _{t}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}-\boldsymbol{v}=-\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})$
. Substituting
$\partial _{t}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}-\boldsymbol{v}=-\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})$
. Substituting
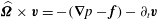 $\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=-(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})-\partial _{t}\boldsymbol{v}$
,
$\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=-(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})-\partial _{t}\boldsymbol{v}$
,
 $$\begin{eqnarray}\partial _{t}^{2}\boldsymbol{v}+\boldsymbol{v}=-\partial _{t}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}^{2}\boldsymbol{v}+\boldsymbol{v}=-\partial _{t}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
The dot product of (1.19) with
![]() $\widehat{{\it\bf\Omega}}$
gives
$\widehat{{\it\bf\Omega}}$
gives
 $$\begin{eqnarray}\partial _{t}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})=-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f}).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})=-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f}).\end{eqnarray}$$
Differentiating (2.1) with respect to
![]() $t$
and using the previous equation (2.2) to eliminate
$t$
and using the previous equation (2.2) to eliminate
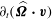 $\partial _{t}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})$
from the right-hand side,
$\partial _{t}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})$
from the right-hand side,
 $$\begin{eqnarray}\partial _{t}^{3}\boldsymbol{v}+\partial _{t}\boldsymbol{v}=-\partial _{t}^{2}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\times \partial _{t}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}^{3}\boldsymbol{v}+\partial _{t}\boldsymbol{v}=-\partial _{t}^{2}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\times \partial _{t}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
The divergence of (2.3) yields the forced Poincaré equation,
 $$\begin{eqnarray}\partial _{t}^{2}{\rm\nabla}^{2}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}p=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \partial _{t}\,\boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}^{2}{\rm\nabla}^{2}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}p=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \partial _{t}\,\boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}),\end{eqnarray}$$
noting
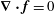 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=0$
. Since the boundary
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=0$
. Since the boundary
![]() $\partial V$
and
$\partial V$
and
![]() $\boldsymbol{n}$
are steady in the rotating frame
$\boldsymbol{n}$
are steady in the rotating frame
![]() $O$
, the dot product of (2.3) with
$O$
, the dot product of (2.3) with
![]() $\boldsymbol{n}$
yields the boundary condition,
$\boldsymbol{n}$
yields the boundary condition,
 $$\begin{eqnarray}\partial _{t}^{2}\partial _{n}p-\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\partial _{t}\boldsymbol{{\rm\nabla}}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \partial _{t}\boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}^{2}\partial _{n}p-\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\partial _{t}\boldsymbol{{\rm\nabla}}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \partial _{t}\boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}},\end{eqnarray}$$
noting
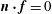 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{f}=0$
.
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{f}=0$
.
The initial value problems consisting of (1.19), subject to (1.6) and (1.5), or (2.4), subject to (2.5), with
![]() $\boldsymbol{v}$
or
$\boldsymbol{v}$
or
![]() $p$
prescribed at
$p$
prescribed at
![]() $t=0$
can be solved in principle using Laplace transforms in
$t=0$
can be solved in principle using Laplace transforms in
![]() $t$
. Alternatively, there is the modal approach adopted here of separating the time dependence. Thus, if
$t$
. Alternatively, there is the modal approach adopted here of separating the time dependence. Thus, if
 $\boldsymbol{f}(\boldsymbol{r},t)=\boldsymbol{f}(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
, then (1.19) has a forced solution of the form
$\boldsymbol{f}(\boldsymbol{r},t)=\boldsymbol{f}(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
, then (1.19) has a forced solution of the form
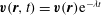 $\boldsymbol{v}(\boldsymbol{r},t)=\boldsymbol{v}(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
with
$\boldsymbol{v}(\boldsymbol{r},t)=\boldsymbol{v}(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
with
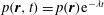 $p(\boldsymbol{r},t)=p(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
. The time dependence can also be expressed in terms of the angular frequency
$p(\boldsymbol{r},t)=p(\boldsymbol{r})\text{e}^{-{\it\lambda}t}$
. The time dependence can also be expressed in terms of the angular frequency
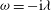 ${\it\omega}=-\text{i}{\it\lambda}$
introduced in the introduction. The momentum equation (2.1) and Poincaré’s equation (2.4) reduce to
${\it\omega}=-\text{i}{\it\lambda}$
introduced in the introduction. The momentum equation (2.1) and Poincaré’s equation (2.4) reduce to
 $$\begin{eqnarray}\displaystyle & -{\it\lambda}\boldsymbol{v}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}p+\boldsymbol{f} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & -{\it\lambda}\boldsymbol{v}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}p+\boldsymbol{f} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\it\lambda}^{2}{\rm\nabla}^{2}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}p=-{\it\lambda}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\lambda}^{2}{\rm\nabla}^{2}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})^{2}p=-{\it\lambda}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}). & \displaystyle\end{eqnarray}$$
 $a\boldsymbol{x}+\boldsymbol{b}\times \boldsymbol{x}=\boldsymbol{c}$
implies
$a\boldsymbol{x}+\boldsymbol{b}\times \boldsymbol{x}=\boldsymbol{c}$
implies
 $(a^{2}+b^{2})\boldsymbol{x}=a\boldsymbol{c}-\boldsymbol{b}\times \boldsymbol{c}+(\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{c}/a)\boldsymbol{b}$
in (2.7),
$(a^{2}+b^{2})\boldsymbol{x}=a\boldsymbol{c}-\boldsymbol{b}\times \boldsymbol{c}+(\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{c}/a)\boldsymbol{b}$
in (2.7),  $$\begin{eqnarray}{\it\lambda}(1+{\it\lambda}^{2})\boldsymbol{v}={\it\lambda}^{2}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+{\it\lambda}\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\lambda}(1+{\it\lambda}^{2})\boldsymbol{v}={\it\lambda}^{2}(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+{\it\lambda}\widehat{{\it\bf\Omega}}\times (\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }(\boldsymbol{{\rm\nabla}}p-\boldsymbol{f})\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
The boundary condition (2.4) becomes
 $$\begin{eqnarray}{\it\lambda}^{2}\partial _{n}p+{\it\lambda}\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}={\it\lambda}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\lambda}^{2}\partial _{n}p+{\it\lambda}\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}={\it\lambda}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{f}+\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{f}\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}.\end{eqnarray}$$
The forced Poincaré equation (2.7) in
![]() $V$
must be solved subject to this condition on
$V$
must be solved subject to this condition on
![]() $\partial V$
.
$\partial V$
.
For real frequencies
![]() ${\it\omega}$
, (2.7) is elliptic if
${\it\omega}$
, (2.7) is elliptic if
![]() $|{\it\omega}|\geqslant 1$
and hyperbolic if
$|{\it\omega}|\geqslant 1$
and hyperbolic if
![]() $|{\it\omega}|<1$
. The characteristics of (2.7) are the cones
$|{\it\omega}|<1$
. The characteristics of (2.7) are the cones
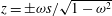 $z=\pm {\it\omega}s/\sqrt{1-{\it\omega}^{2}}$
, which are real in the hyperbolic case. The kinetic energy of the mode
$z=\pm {\it\omega}s/\sqrt{1-{\it\omega}^{2}}$
, which are real in the hyperbolic case. The kinetic energy of the mode
![]() $\{\boldsymbol{v},{\it\omega}\}$
is
$\{\boldsymbol{v},{\it\omega}\}$
is
![]() $(\boldsymbol{v},\boldsymbol{v})/2$
, which is constant since
$(\boldsymbol{v},\boldsymbol{v})/2$
, which is constant since
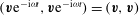 $(\boldsymbol{v}\text{e}^{-\text{i}{\it\omega}t},\boldsymbol{v}\text{e}^{-\text{i}{\it\omega}t})=(\boldsymbol{v},\boldsymbol{v})$
. If
$(\boldsymbol{v}\text{e}^{-\text{i}{\it\omega}t},\boldsymbol{v}\text{e}^{-\text{i}{\it\omega}t})=(\boldsymbol{v},\boldsymbol{v})$
. If
![]() $V$
is axisymmetric,
$V$
is axisymmetric,
![]() $\widehat{{\it\bf\Omega}}$
and the
$\widehat{{\it\bf\Omega}}$
and the
![]() $z$
-axis are co-axial with the symmetry axis, then the solutions decouple into azimuthal modes
$z$
-axis are co-axial with the symmetry axis, then the solutions decouple into azimuthal modes
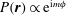 $P(\boldsymbol{r})\propto \text{e}^{\text{i}m{\it\phi}}$
,
$P(\boldsymbol{r})\propto \text{e}^{\text{i}m{\it\phi}}$
,
![]() $m\in \mathbb{Z}$
and
$m\in \mathbb{Z}$
and
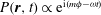 $P(\boldsymbol{r},t)\propto \text{e}^{\text{i}(m{\it\phi}-{\it\omega}t)}$
. Thus we adopt the convention that
$P(\boldsymbol{r},t)\propto \text{e}^{\text{i}(m{\it\phi}-{\it\omega}t)}$
. Thus we adopt the convention that
![]() ${\it\omega}>0$
corresponds to eastward (westward) propagation for positive (negative) azimuthal wavenumbers
${\it\omega}>0$
corresponds to eastward (westward) propagation for positive (negative) azimuthal wavenumbers
 $m>0~(m<0)$
.
$m>0~(m<0)$
.
3. The Coriolis operator
In this section we prove some general results for the Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
acting on the space
$\boldsymbol{{\mathcal{C}}}$
acting on the space
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
for a general bounded fluid region
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
for a general bounded fluid region
![]() $V$
, not just for a sphere. Given
$V$
, not just for a sphere. Given
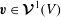 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
, then
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
, then
 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
if the pressure
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
if the pressure
![]() $p$
is determined from the Poisson–Neumann problem (1.10). This elliptic problem is well posed, unlike the ill-posed hyperbolic problem, equations (2.7) and (2.9) for real
$p$
is determined from the Poisson–Neumann problem (1.10). This elliptic problem is well posed, unlike the ill-posed hyperbolic problem, equations (2.7) and (2.9) for real
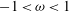 $-1<{\it\omega}<1$
, which determines the pressure. The infinite-dimensional operator
$-1<{\it\omega}<1$
, which determines the pressure. The infinite-dimensional operator
![]() $\boldsymbol{{\mathcal{C}}}$
is linear, non-local and can be expressed explicitly in terms of
$\boldsymbol{{\mathcal{C}}}$
is linear, non-local and can be expressed explicitly in terms of
![]() $\boldsymbol{v}$
,
$\boldsymbol{v}$
,
 $$\begin{eqnarray}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\int _{V}[\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}^{\prime }G(\boldsymbol{r}^{\prime },\boldsymbol{r})]\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v}^{\prime })\text{d}V^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\int _{V}[\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}^{\prime }G(\boldsymbol{r}^{\prime },\boldsymbol{r})]\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v}^{\prime })\text{d}V^{\prime },\end{eqnarray}$$
where
![]() $G$
is the Green’s function of the Poisson–Neumann problem,
$G$
is the Green’s function of the Poisson–Neumann problem,
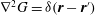 ${\rm\nabla}^{2}G={\it\delta}(\boldsymbol{r}-\boldsymbol{r}^{\prime })$
in
${\rm\nabla}^{2}G={\it\delta}(\boldsymbol{r}-\boldsymbol{r}^{\prime })$
in
![]() $V$
with
$V$
with
![]() $\partial _{n}G=0$
on
$\partial _{n}G=0$
on
![]() $\partial V$
. Equation (3.1) can be derived using Green’s representation formula,
$\partial V$
. Equation (3.1) can be derived using Green’s representation formula,
 $$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=-\int _{V}{\displaystyle \frac{{\rm\nabla}^{2}p}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\text{d}V-\int _{\partial V}\text{d}\boldsymbol{S}\boldsymbol{\cdot }\left\{p\boldsymbol{{\rm\nabla}}\left({\displaystyle \frac{1}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right)-{\displaystyle \frac{\boldsymbol{{\rm\nabla}}p}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right\},\quad \boldsymbol{r}^{\prime }\in V.\end{eqnarray}$$
$$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=-\int _{V}{\displaystyle \frac{{\rm\nabla}^{2}p}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\text{d}V-\int _{\partial V}\text{d}\boldsymbol{S}\boldsymbol{\cdot }\left\{p\boldsymbol{{\rm\nabla}}\left({\displaystyle \frac{1}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right)-{\displaystyle \frac{\boldsymbol{{\rm\nabla}}p}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right\},\quad \boldsymbol{r}^{\prime }\in V.\end{eqnarray}$$
Substituting from (1.10) yields
 $$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=\int _{V}{\displaystyle \frac{\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\text{d}V-\int _{\partial V}\text{d}\boldsymbol{S}\boldsymbol{\cdot }\left\{p\boldsymbol{{\rm\nabla}}\left({\displaystyle \frac{1}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right)+{\displaystyle \frac{\widehat{{\it\bf\Omega}}\times \boldsymbol{v}}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=\int _{V}{\displaystyle \frac{\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\text{d}V-\int _{\partial V}\text{d}\boldsymbol{S}\boldsymbol{\cdot }\left\{p\boldsymbol{{\rm\nabla}}\left({\displaystyle \frac{1}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right)+{\displaystyle \frac{\widehat{{\it\bf\Omega}}\times \boldsymbol{v}}{4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}}\right\}.\end{eqnarray}$$
To eliminate
![]() $p$
from the surface integral choose a harmonic function
$p$
from the surface integral choose a harmonic function
![]() $h(\boldsymbol{r},\boldsymbol{r}^{\prime })$
such that
$h(\boldsymbol{r},\boldsymbol{r}^{\prime })$
such that
 $$\begin{eqnarray}{\rm\nabla}^{2}h(\boldsymbol{r},\boldsymbol{r}^{\prime })=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h(\boldsymbol{r},\boldsymbol{r}^{\prime })=-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1}\quad \text{on }\partial V.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}h(\boldsymbol{r},\boldsymbol{r}^{\prime })=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h(\boldsymbol{r},\boldsymbol{r}^{\prime })=-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1}\quad \text{on }\partial V.\end{eqnarray}$$
Then, by Green’s first theorem in
![]() $p$
and
$p$
and
![]() $h$
,
$h$
,
 $$\begin{eqnarray}\int _{V}h(\boldsymbol{r},\boldsymbol{r}^{\prime })\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V-\int _{\partial V}[p\boldsymbol{{\rm\nabla}}h(\boldsymbol{r},\boldsymbol{r}^{\prime })+h(\boldsymbol{r},\boldsymbol{r}^{\prime })\widehat{{\it\bf\Omega}}\times \boldsymbol{v}]\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}h(\boldsymbol{r},\boldsymbol{r}^{\prime })\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V-\int _{\partial V}[p\boldsymbol{{\rm\nabla}}h(\boldsymbol{r},\boldsymbol{r}^{\prime })+h(\boldsymbol{r},\boldsymbol{r}^{\prime })\widehat{{\it\bf\Omega}}\times \boldsymbol{v}]\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0.\end{eqnarray}$$
Combining the last two integral equations,
 $$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=-\int _{V}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V+\int _{\partial V}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
$$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=-\int _{V}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V+\int _{\partial V}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
where
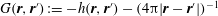 $G(\boldsymbol{r},\boldsymbol{r}^{\prime }):=-h(\boldsymbol{r},\boldsymbol{r}^{\prime })-(4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1}$
is the (interior) Neumann Green’s function for
$G(\boldsymbol{r},\boldsymbol{r}^{\prime }):=-h(\boldsymbol{r},\boldsymbol{r}^{\prime })-(4{\rm\pi}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1}$
is the (interior) Neumann Green’s function for
![]() $V$
. Integrating by parts gives
$V$
. Integrating by parts gives
 $$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=\int _{V}\boldsymbol{{\rm\nabla}}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V\end{eqnarray}$$
$$\begin{eqnarray}p(\boldsymbol{r}^{\prime })=\int _{V}\boldsymbol{{\rm\nabla}}G(\boldsymbol{r},\boldsymbol{r}^{\prime })\,\boldsymbol{\cdot }(\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V\end{eqnarray}$$
and interchanging
![]() $\boldsymbol{r}$
and
$\boldsymbol{r}$
and
![]() $\boldsymbol{r}^{\prime }$
yields (3.1). For the sphere
$\boldsymbol{r}^{\prime }$
yields (3.1). For the sphere
![]() $r<a$
,
$r<a$
,
 $$\begin{eqnarray}4{\rm\pi}G(\boldsymbol{r},\boldsymbol{r}^{\prime })=\frac{1}{a}\ln (a^{2}-\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}^{\prime }+|\boldsymbol{r}r^{\prime }-a^{2}\boldsymbol{r}^{\prime }/r^{\prime }|)-\frac{a}{|\boldsymbol{r}r^{\prime }-a^{2}\boldsymbol{r}^{\prime }/r^{\prime }|}-\frac{1}{|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}.\end{eqnarray}$$
$$\begin{eqnarray}4{\rm\pi}G(\boldsymbol{r},\boldsymbol{r}^{\prime })=\frac{1}{a}\ln (a^{2}-\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}^{\prime }+|\boldsymbol{r}r^{\prime }-a^{2}\boldsymbol{r}^{\prime }/r^{\prime }|)-\frac{a}{|\boldsymbol{r}r^{\prime }-a^{2}\boldsymbol{r}^{\prime }/r^{\prime }|}-\frac{1}{|\boldsymbol{r}-\boldsymbol{r}^{\prime }|}.\end{eqnarray}$$
The operator
![]() $\boldsymbol{{\mathcal{C}}}$
is bounded (Chossat Reference Chossat1979) on
$\boldsymbol{{\mathcal{C}}}$
is bounded (Chossat Reference Chossat1979) on
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
, since
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
, since
 $$\begin{eqnarray}\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert ^{2}=(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\widehat{{\it\bf\Omega}}\times \boldsymbol{v})+(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \,\Vert \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \,\Vert \boldsymbol{v}\Vert ,\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert ^{2}=(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\widehat{{\it\bf\Omega}}\times \boldsymbol{v})+(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \,\Vert \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \,\Vert \boldsymbol{v}\Vert ,\end{eqnarray}$$
using the Cauchy–Schwartz inequality and noting
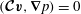 $(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=0$
by the divergence theorem,
$(\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=0$
by the divergence theorem,
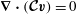 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=0$
in
![]() $V$
and
$V$
and
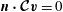 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=0$
on
![]() $\partial V$
. Hence
$\partial V$
. Hence
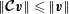 $\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert$
or, in terms of the operator norm
$\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert$
or, in terms of the operator norm
![]() $\Vert \boldsymbol{{\mathcal{C}}}\Vert$
of
$\Vert \boldsymbol{{\mathcal{C}}}\Vert$
of
![]() $\boldsymbol{{\mathcal{C}}}$
induced by the vector norm
$\boldsymbol{{\mathcal{C}}}$
induced by the vector norm
![]() $\Vert \boldsymbol{v}\Vert$
,
$\Vert \boldsymbol{v}\Vert$
,
 $$\begin{eqnarray}\Vert \boldsymbol{{\mathcal{C}}}\Vert :=\sup _{\boldsymbol{v}\neq \mathbf{0}}\frac{\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert }{\Vert \boldsymbol{v}\Vert }=\sup _{\Vert \boldsymbol{v}\Vert =1}\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{{\mathcal{C}}}\Vert :=\sup _{\boldsymbol{v}\neq \mathbf{0}}\frac{\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert }{\Vert \boldsymbol{v}\Vert }=\sup _{\Vert \boldsymbol{v}\Vert =1}\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant 1.\end{eqnarray}$$
A useful property of the operator norm used below is
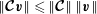 $\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}\Vert$
, which follows directly from its definition. Thus
$\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}\Vert$
, which follows directly from its definition. Thus
![]() $\boldsymbol{{\mathcal{C}}}$
is bounded and continuous, since, if
$\boldsymbol{{\mathcal{C}}}$
is bounded and continuous, since, if
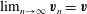 $\lim _{n\rightarrow \infty }\boldsymbol{v}_{n}=\boldsymbol{v}$
then
$\lim _{n\rightarrow \infty }\boldsymbol{v}_{n}=\boldsymbol{v}$
then
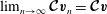 $\lim _{n\rightarrow \infty }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{n}=\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
in
$\lim _{n\rightarrow \infty }\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{n}=\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Since
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Since
![]() $\boldsymbol{{\mathcal{C}}}$
is bounded, it is the generator of a uniformly continuous semigroup (see Pazy Reference Pazy1983, § 1.1),
$\boldsymbol{{\mathcal{C}}}$
is bounded, it is the generator of a uniformly continuous semigroup (see Pazy Reference Pazy1983, § 1.1),
 $\boldsymbol{{\mathcal{T}}}(t)=\exp (-t\boldsymbol{{\mathcal{C}}})=\sum _{k=0}^{\infty }(-t\boldsymbol{{\mathcal{C}}})^{k}/k!$
. The solution of
$\boldsymbol{{\mathcal{T}}}(t)=\exp (-t\boldsymbol{{\mathcal{C}}})=\sum _{k=0}^{\infty }(-t\boldsymbol{{\mathcal{C}}})^{k}/k!$
. The solution of
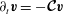 $\partial _{t}\boldsymbol{v}=-\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
with
$\partial _{t}\boldsymbol{v}=-\boldsymbol{{\mathcal{C}}}\boldsymbol{v}$
with
![]() $\boldsymbol{v}=\boldsymbol{v}_{0}$
at
$\boldsymbol{v}=\boldsymbol{v}_{0}$
at
![]() $t=0$
can be written in terms of the operator
$t=0$
can be written in terms of the operator
![]() $\boldsymbol{{\mathcal{T}}}$
as
$\boldsymbol{{\mathcal{T}}}$
as
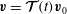 $\boldsymbol{v}=\boldsymbol{{\mathcal{T}}}(t)\boldsymbol{v}_{0}$
.
$\boldsymbol{v}=\boldsymbol{{\mathcal{T}}}(t)\boldsymbol{v}_{0}$
.
3.1. The spectrum of
 $\boldsymbol{{\mathcal{C}}}$
$\boldsymbol{{\mathcal{C}}}$
The spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
may be defined in terms of its resolvent operator
$\boldsymbol{{\mathcal{C}}}$
may be defined in terms of its resolvent operator
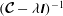 $(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
on
$(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
on
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The resolvent set
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The resolvent set
![]() ${\it\Gamma}$
of
${\it\Gamma}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
is the set of
$\boldsymbol{{\mathcal{C}}}$
is the set of
![]() ${\it\lambda}$
in the complex plane
${\it\lambda}$
in the complex plane
![]() $\mathbb{C}$
for which
$\mathbb{C}$
for which
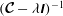 $(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
is a bounded operator. The forced solution of (2.6) is given in terms of the resolvent by
$(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
is a bounded operator. The forced solution of (2.6) is given in terms of the resolvent by
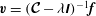 $\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
. The solution is well behaved, and in particular no resonance occurs, if
$\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
. The solution is well behaved, and in particular no resonance occurs, if
![]() ${\it\lambda}$
lies in the resolvent set. The resolvent has been useful in the analysis of stability problems with non-normal operators (see the review by Trefethen Reference Trefethen1997).
${\it\lambda}$
lies in the resolvent set. The resolvent has been useful in the analysis of stability problems with non-normal operators (see the review by Trefethen Reference Trefethen1997).
Theorem 3.1. The resolvent set
![]() ${\it\Gamma}$
of
${\it\Gamma}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
contains
$\boldsymbol{{\mathcal{C}}}$
contains
 $\mathbb{C}\setminus [-\text{i},\text{i}]$
.
$\mathbb{C}\setminus [-\text{i},\text{i}]$
.
Proof. The inner product of (2.6) with
![]() $\boldsymbol{v}$
gives
$\boldsymbol{v}$
gives
 $$\begin{eqnarray}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})-{\it\lambda}(\boldsymbol{v},\boldsymbol{v})=(\boldsymbol{f},\boldsymbol{v}),\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})-{\it\lambda}(\boldsymbol{v},\boldsymbol{v})=(\boldsymbol{f},\boldsymbol{v}),\end{eqnarray}$$
since
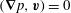 $(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v})=0$
by the divergence theorem,
$(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v})=0$
by the divergence theorem,
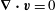 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V$
and
$V$
and
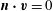 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V$
. The identity
$\partial V$
. The identity
 $$\begin{eqnarray}(\boldsymbol{v}\times \boldsymbol{v}^{\ast })^{\ast }=-\boldsymbol{v}\times \boldsymbol{v}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}\times \boldsymbol{v}^{\ast })^{\ast }=-\boldsymbol{v}\times \boldsymbol{v}^{\ast },\end{eqnarray}$$
implies
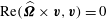 $\text{Re}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})=0$
and thus, if
$\text{Re}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})=0$
and thus, if
![]() ${\it\lambda}_{r}$
,
${\it\lambda}_{r}$
,
![]() ${\it\lambda}_{i}$
are the real and imaginary parts of
${\it\lambda}_{i}$
are the real and imaginary parts of
![]() ${\it\lambda}$
,
${\it\lambda}$
,
 $$\begin{eqnarray}{\it\lambda}_{r}\Vert \boldsymbol{v}\Vert ^{2}=-\text{Re}(\boldsymbol{f},\boldsymbol{v}),\quad {\it\lambda}_{i}\Vert \boldsymbol{v}\Vert ^{2}=-\text{i}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})-\text{Im}(\boldsymbol{f},\boldsymbol{v}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\lambda}_{r}\Vert \boldsymbol{v}\Vert ^{2}=-\text{Re}(\boldsymbol{f},\boldsymbol{v}),\quad {\it\lambda}_{i}\Vert \boldsymbol{v}\Vert ^{2}=-\text{i}(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})-\text{Im}(\boldsymbol{f},\boldsymbol{v}).\end{eqnarray}$$
By the Cauchy–Schwartz inequality
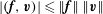 $|(\boldsymbol{f},\boldsymbol{v})|\leqslant \Vert \boldsymbol{f}\Vert \,\Vert \boldsymbol{v}\Vert$
and
$|(\boldsymbol{f},\boldsymbol{v})|\leqslant \Vert \boldsymbol{f}\Vert \,\Vert \boldsymbol{v}\Vert$
and
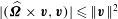 $|(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})|\leqslant \Vert \boldsymbol{v}\Vert ^{2}$
. Hence
$|(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\boldsymbol{v})|\leqslant \Vert \boldsymbol{v}\Vert ^{2}$
. Hence
 $$\begin{eqnarray}\Vert \boldsymbol{v}\Vert \leqslant |{\it\lambda}_{r}|^{-1}\,\Vert \boldsymbol{f}\Vert ;\quad \Vert \boldsymbol{v}\Vert \leqslant (|{\it\lambda}_{i}|-1)^{-1}\,\Vert \boldsymbol{f}\Vert ,\quad \text{if }|{\it\lambda}_{i}|>1.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{v}\Vert \leqslant |{\it\lambda}_{r}|^{-1}\,\Vert \boldsymbol{f}\Vert ;\quad \Vert \boldsymbol{v}\Vert \leqslant (|{\it\lambda}_{i}|-1)^{-1}\,\Vert \boldsymbol{f}\Vert ,\quad \text{if }|{\it\lambda}_{i}|>1.\end{eqnarray}$$
Since
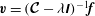 $\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
,
$\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
,
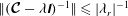 $\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\Vert \leqslant |{\it\lambda}_{r}|^{-1}$
and
$\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\Vert \leqslant |{\it\lambda}_{r}|^{-1}$
and
 $\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\Vert \leqslant (|{\it\lambda}_{i}|-1)^{-1}$
if
$\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\Vert \leqslant (|{\it\lambda}_{i}|-1)^{-1}$
if
![]() $|{\it\lambda}_{i}|>1$
. Hence the resolvent set contains all
$|{\it\lambda}_{i}|>1$
. Hence the resolvent set contains all
![]() ${\it\lambda}$
such that
${\it\lambda}$
such that
![]() ${\it\lambda}_{r}\neq 0$
or
${\it\lambda}_{r}\neq 0$
or
![]() $|{\it\lambda}_{i}|>1$
.
$|{\it\lambda}_{i}|>1$
.
The spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
is the complement
$\boldsymbol{{\mathcal{C}}}$
is the complement
![]() $\mathbb{C}\setminus {\it\Gamma}$
of the resolvent set
$\mathbb{C}\setminus {\it\Gamma}$
of the resolvent set
![]() ${\it\Gamma}$
in the complex plane
${\it\Gamma}$
in the complex plane
![]() $\mathbb{C}$
. Theorem 3.1 shows that the spectrum lies in
$\mathbb{C}$
. Theorem 3.1 shows that the spectrum lies in
![]() $[-\text{i},\text{i}]$
on the imaginary axis. In general, the spectrum is the disjoint union of the point (or discrete) spectrum
$[-\text{i},\text{i}]$
on the imaginary axis. In general, the spectrum is the disjoint union of the point (or discrete) spectrum
![]() ${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
, the continuous spectrum
${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
, the continuous spectrum
![]() ${\it\sigma}_{c}(\boldsymbol{{\mathcal{C}}})$
and the residual spectrum
${\it\sigma}_{c}(\boldsymbol{{\mathcal{C}}})$
and the residual spectrum
![]() ${\it\sigma}_{r}(\boldsymbol{{\mathcal{C}}})$
. The discrete spectrum
${\it\sigma}_{r}(\boldsymbol{{\mathcal{C}}})$
. The discrete spectrum
![]() ${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
consists of the eigenvalues of
${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
consists of the eigenvalues of
![]() $\boldsymbol{{\mathcal{C}}}$
, i.e. the values of
$\boldsymbol{{\mathcal{C}}}$
, i.e. the values of
![]() ${\it\lambda}\in \mathbb{C}$
for which
${\it\lambda}\in \mathbb{C}$
for which
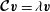 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
for some non-zero
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
for some non-zero
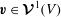 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
. These discrete modes, which we will refer to simply as Coriolis modes, are the free modes (
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
. These discrete modes, which we will refer to simply as Coriolis modes, are the free modes (
![]() $\boldsymbol{f}=\mathbf{0}$
) of
$\boldsymbol{f}=\mathbf{0}$
) of
![]() $\boldsymbol{{\mathcal{C}}}$
and can be physically interpreted as inertial modes or geostrophic modes, or Rossby modes, of frequency
$\boldsymbol{{\mathcal{C}}}$
and can be physically interpreted as inertial modes or geostrophic modes, or Rossby modes, of frequency
 ${\it\omega}=-\text{i}{\it\lambda}$
. As indicated in the introduction we regard the Coriolis modes of zero and non-zero frequency as the geostrophic modes and inertial spatial modes respectively. There is a further discussion of
${\it\omega}=-\text{i}{\it\lambda}$
. As indicated in the introduction we regard the Coriolis modes of zero and non-zero frequency as the geostrophic modes and inertial spatial modes respectively. There is a further discussion of
![]() ${\it\sigma}_{c}(\boldsymbol{{\mathcal{C}}})$
and
${\it\sigma}_{c}(\boldsymbol{{\mathcal{C}}})$
and
![]() ${\it\sigma}_{r}(\boldsymbol{{\mathcal{C}}})$
in § 9. The following theorem is important for the spectrum of
${\it\sigma}_{r}(\boldsymbol{{\mathcal{C}}})$
in § 9. The following theorem is important for the spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
, but particularly for
$\boldsymbol{{\mathcal{C}}}$
, but particularly for
![]() ${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
.
${\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
.
Theorem 3.2. The operator
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric, i.e.
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric, i.e.
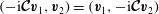 $(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
for all
$(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
for all
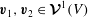 $\boldsymbol{v}_{1},\boldsymbol{v}_{2}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
.
$\boldsymbol{v}_{1},\boldsymbol{v}_{2}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
.
Proof. There exists a pressure
![]() $p_{1}\in {\mathcal{P}}$
such that
$p_{1}\in {\mathcal{P}}$
such that
 $(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(-\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{1},\boldsymbol{v}_{2})-\text{i}(\boldsymbol{{\rm\nabla}}p_{1},\boldsymbol{v}_{2})$
. But
$(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(-\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{1},\boldsymbol{v}_{2})-\text{i}(\boldsymbol{{\rm\nabla}}p_{1},\boldsymbol{v}_{2})$
. But
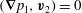 $(\boldsymbol{{\rm\nabla}}p_{1},\boldsymbol{v}_{2})=0$
, noting
$(\boldsymbol{{\rm\nabla}}p_{1},\boldsymbol{v}_{2})=0$
, noting
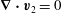 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{2}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{2}=0$
in
![]() $V$
, applying the divergence theorem and
$V$
, applying the divergence theorem and
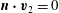 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}_{2}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}_{2}=0$
on
![]() $\partial V$
. Interchanging subscripts yields
$\partial V$
. Interchanging subscripts yields
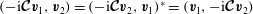 $(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2},\boldsymbol{v}_{1})^{\ast }=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
, since
$(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2},\boldsymbol{v}_{1})^{\ast }=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
, since
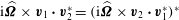 $\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{v}_{2}^{\ast }=(\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{2}\boldsymbol{\cdot }\boldsymbol{v}_{1}^{\ast })^{\ast }$
.
$\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{v}_{2}^{\ast }=(\text{i}\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{2}\boldsymbol{\cdot }\boldsymbol{v}_{1}^{\ast })^{\ast }$
.
The values
![]() ${\it\lambda}=\pm \text{i}$
are not eigenvalues of
${\it\lambda}=\pm \text{i}$
are not eigenvalues of
![]() $\boldsymbol{{\mathcal{C}}}$
, i.e.
$\boldsymbol{{\mathcal{C}}}$
, i.e.
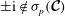 $\pm \text{i}\notin {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
. Physically, there are no Coriolis modes of frequency
$\pm \text{i}\notin {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
. Physically, there are no Coriolis modes of frequency
![]() ${\it\omega}=\pm 1$
, but if the fluid occupies all space
${\it\omega}=\pm 1$
, but if the fluid occupies all space
![]() $E^{3}$
, modes with frequency
$E^{3}$
, modes with frequency
![]() ${\it\omega}=\pm 1$
are possible. Equation (2.6) with
${\it\omega}=\pm 1$
are possible. Equation (2.6) with
![]() ${\it\lambda}=\text{i}$
and
${\it\lambda}=\text{i}$
and
![]() $\boldsymbol{f}=\mathbf{0}$
implies
$\boldsymbol{f}=\mathbf{0}$
implies
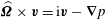 $\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p$
and hence
$\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p$
and hence
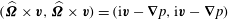 $(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\widehat{{\it\bf\Omega}}\times \boldsymbol{v})=(\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p,\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p)$
. Simplifying using
$(\widehat{{\it\bf\Omega}}\times \boldsymbol{v},\widehat{{\it\bf\Omega}}\times \boldsymbol{v})=(\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p,\text{i}\boldsymbol{v}-\boldsymbol{{\rm\nabla}}p)$
. Simplifying using
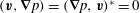 $(\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v})^{\ast }=0$
yields
$(\boldsymbol{v},\boldsymbol{{\rm\nabla}}p)=(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v})^{\ast }=0$
yields
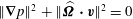 $\Vert \boldsymbol{{\rm\nabla}}p\Vert ^{2}+\Vert \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}\Vert ^{2}=0$
. Thus
$\Vert \boldsymbol{{\rm\nabla}}p\Vert ^{2}+\Vert \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}\Vert ^{2}=0$
. Thus
![]() $p$
is constant and
$p$
is constant and
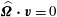 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=0$
. Equation (2.6) reduces to
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=0$
. Equation (2.6) reduces to
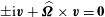 $\pm \text{i}\boldsymbol{v}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=\mathbf{0}$
. From
$\pm \text{i}\boldsymbol{v}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}=\mathbf{0}$
. From
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
, it follows that
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
, it follows that
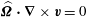 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}=0$
. Hence, there exists a potential
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}=0$
. Hence, there exists a potential
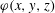 ${\it\varphi}(x,y,z)$
such that
${\it\varphi}(x,y,z)$
such that
 $\boldsymbol{v}=\boldsymbol{{\rm\nabla}}_{\bot }{\it\varphi}$
, where
$\boldsymbol{v}=\boldsymbol{{\rm\nabla}}_{\bot }{\it\varphi}$
, where
![]() $\boldsymbol{{\rm\nabla}}_{\bot }$
is the gradient perpendicular to
$\boldsymbol{{\rm\nabla}}_{\bot }$
is the gradient perpendicular to
![]() $\widehat{{\it\bf\Omega}}$
and
$\widehat{{\it\bf\Omega}}$
and
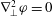 ${\rm\nabla}_{\bot }^{2}{\it\varphi}=0$
. Multiplying the last equation by
${\rm\nabla}_{\bot }^{2}{\it\varphi}=0$
. Multiplying the last equation by
![]() ${\it\varphi}^{\ast }$
and integrating by parts over a plane section of
${\it\varphi}^{\ast }$
and integrating by parts over a plane section of
![]() $V$
with
$V$
with
![]() $z$
constant yields
$z$
constant yields
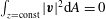 $\int _{z=\text{const}}|\boldsymbol{v}|^{2}\text{d}A=0$
, since
$\int _{z=\text{const}}|\boldsymbol{v}|^{2}\text{d}A=0$
, since
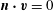 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on the boundary
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on the boundary
![]() $\partial V$
. It follows that
$\partial V$
. It follows that
![]() $\boldsymbol{v}=\mathbf{0}$
everywhere in
$\boldsymbol{v}=\mathbf{0}$
everywhere in
![]() $V$
. The case
$V$
. The case
![]() ${\it\lambda}=-\text{i}$
is similar.
${\it\lambda}=-\text{i}$
is similar.
3.2. Eigenvalues and orthogonality of Coriolis modes
Using the symmetry of
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
from Theorem 3.2, we now show the eigenvalues of
$-\text{i}\boldsymbol{{\mathcal{C}}}$
from Theorem 3.2, we now show the eigenvalues of
![]() $\boldsymbol{{\mathcal{C}}}$
are imaginary, i.e. the frequencies
$\boldsymbol{{\mathcal{C}}}$
are imaginary, i.e. the frequencies
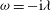 ${\it\omega}=-\text{i}{\it\lambda}$
are real, and that Coriolis modes with different eigenvalues are orthogonal. We also use the boundedness of
${\it\omega}=-\text{i}{\it\lambda}$
are real, and that Coriolis modes with different eigenvalues are orthogonal. We also use the boundedness of
![]() $\boldsymbol{{\mathcal{C}}}$
to show
$\boldsymbol{{\mathcal{C}}}$
to show
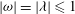 $|{\it\omega}|=|{\it\lambda}|\leqslant 1$
. These results are consistent with the restriction on the spectrum found in Theorem 3.1. We denote the pressure of the Coriolis modes by
$|{\it\omega}|=|{\it\lambda}|\leqslant 1$
. These results are consistent with the restriction on the spectrum found in Theorem 3.1. We denote the pressure of the Coriolis modes by
![]() $P$
.
$P$
.
Theorem 3.3. The Coriolis modes have the following properties: the eigenvalues
![]() ${\it\lambda}$
of
${\it\lambda}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
are imaginary and
$\boldsymbol{{\mathcal{C}}}$
are imaginary and
![]() $|{\it\lambda}|\leqslant 1$
: and modes
$|{\it\lambda}|\leqslant 1$
: and modes
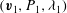 $(\boldsymbol{v}_{1},P_{1},{\it\lambda}_{1})$
and
$(\boldsymbol{v}_{1},P_{1},{\it\lambda}_{1})$
and
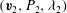 $(\boldsymbol{v}_{2},P_{2},{\it\lambda}_{2})$
with different eigenvalues (frequencies)
$(\boldsymbol{v}_{2},P_{2},{\it\lambda}_{2})$
with different eigenvalues (frequencies)
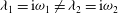 ${\it\lambda}_{1}=\text{i}{\it\omega}_{1}\neq {\it\lambda}_{2}=\text{i}{\it\omega}_{2}$
are orthogonal,
${\it\lambda}_{1}=\text{i}{\it\omega}_{1}\neq {\it\lambda}_{2}=\text{i}{\it\omega}_{2}$
are orthogonal,
 $(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=0$
.
$(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=0$
.
Proof. The proofs rely on the symmetry of
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
and the boundedness of
$-\text{i}\boldsymbol{{\mathcal{C}}}$
and the boundedness of
![]() $\boldsymbol{{\mathcal{C}}}$
. Alternative proofs are given in Greenspan (Reference Greenspan1968). From
$\boldsymbol{{\mathcal{C}}}$
. Alternative proofs are given in Greenspan (Reference Greenspan1968). From
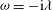 ${\it\omega}=-\text{i}{\it\lambda}$
,
${\it\omega}=-\text{i}{\it\lambda}$
,
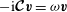 $-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
. Since
$-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
. Since
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric and
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric and
![]() $\boldsymbol{v}\neq \mathbf{0}$
,
$\boldsymbol{v}\neq \mathbf{0}$
,
 ${\it\omega}\Vert \boldsymbol{v}\Vert ^{2}=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{v})=(\boldsymbol{v},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v})={\it\omega}^{\ast }\Vert \boldsymbol{v}\Vert ^{2}$
, i.e.
${\it\omega}\Vert \boldsymbol{v}\Vert ^{2}=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v},\boldsymbol{v})=(\boldsymbol{v},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v})={\it\omega}^{\ast }\Vert \boldsymbol{v}\Vert ^{2}$
, i.e.
![]() ${\it\omega}$
is real. Since
${\it\omega}$
is real. Since
![]() $\Vert \boldsymbol{{\mathcal{C}}}\Vert \leqslant 1$
,
$\Vert \boldsymbol{{\mathcal{C}}}\Vert \leqslant 1$
,
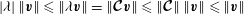 $|{\it\lambda}|\,\Vert \boldsymbol{v}\Vert \leqslant \Vert {\it\lambda}\boldsymbol{v}\Vert =\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert$
, i.e.
$|{\it\lambda}|\,\Vert \boldsymbol{v}\Vert \leqslant \Vert {\it\lambda}\boldsymbol{v}\Vert =\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert$
, i.e.
![]() $|{\it\lambda}|<1$
. Since
$|{\it\lambda}|<1$
. Since
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric,
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric,
 $0=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})-(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})=({\it\omega}_{1}-{\it\omega}_{2})(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
.
$0=(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})-(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})=({\it\omega}_{1}-{\it\omega}_{2})(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
.
The orthogonality property of Theorem 3.3 does not apply to modes of the same eigenvalue. Thus, for any eigenvalue with an eigenspace of dimension greater than one, as is true for the geostrophic modes in a sphere, an orthogonal basis must be constructed, for example using the Gram–Schmidt method. For this purpose it is useful to express the inner product of two inertial modes
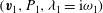 $(\boldsymbol{v}_{1},P_{1},{\it\lambda}_{1}=\text{i}{\it\omega}_{1})$
and
$(\boldsymbol{v}_{1},P_{1},{\it\lambda}_{1}=\text{i}{\it\omega}_{1})$
and
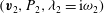 $(\boldsymbol{v}_{2},P_{2},{\it\lambda}_{2}=\text{i}{\it\omega}_{2})$
in terms of the pressures
$(\boldsymbol{v}_{2},P_{2},{\it\lambda}_{2}=\text{i}{\it\omega}_{2})$
in terms of the pressures
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
. Equation (2.2) with
$P_{2}$
. Equation (2.2) with
![]() $\boldsymbol{f}=\mathbf{0}$
or the dot product of (2.6) with
$\boldsymbol{f}=\mathbf{0}$
or the dot product of (2.6) with
![]() $\widehat{{\it\bf\Omega}}$
if
$\widehat{{\it\bf\Omega}}$
if
![]() ${\it\omega}^{2}\neq 1$
gives the useful result
${\it\omega}^{2}\neq 1$
gives the useful result
 $$\begin{eqnarray}\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P.\end{eqnarray}$$
$$\begin{eqnarray}\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P.\end{eqnarray}$$
Using (2.8) with
![]() $\boldsymbol{f}=\mathbf{0}$
, (3.15), integrating over
$\boldsymbol{f}=\mathbf{0}$
, (3.15), integrating over
![]() $V$
and using the boundary condition (1.6) yields, if
$V$
and using the boundary condition (1.6) yields, if
 ${\it\omega}_{1}{\it\omega}_{2}\neq 0$
,
${\it\omega}_{1}{\it\omega}_{2}\neq 0$
,
 $$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(1-{\it\omega}_{1}{\it\omega}_{2})^{-1}\int _{V}\left\{\boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast }+\frac{1}{{\it\omega}_{1}{\it\omega}_{2}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{1})(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast })\right\}\!\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(1-{\it\omega}_{1}{\it\omega}_{2})^{-1}\int _{V}\left\{\boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast }+\frac{1}{{\it\omega}_{1}{\it\omega}_{2}}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{1})(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast })\right\}\!\text{d}V.\end{eqnarray}$$
Formula (3.16) fails if one or both modes are geostrophic, since then
 ${\it\omega}_{1}{\it\omega}_{2}=0$
. The formula for the inner product of two geostrophic modes is derived in § 3.3 below.
${\it\omega}_{1}{\it\omega}_{2}=0$
. The formula for the inner product of two geostrophic modes is derived in § 3.3 below.
3.3. Inertial modes
In some simple geometries inertial modes can be constructed analytically using the pressure. With
![]() $\boldsymbol{f}=\mathbf{0}$
, (2.8) reduces to
$\boldsymbol{f}=\mathbf{0}$
, (2.8) reduces to
 $$\begin{eqnarray}\text{i}{\it\omega}(1-{\it\omega}^{2})\boldsymbol{v}=-{\it\omega}^{2}\boldsymbol{{\rm\nabla}}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P)\widehat{{\it\bf\Omega}}+\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P\quad \text{in }V\end{eqnarray}$$
$$\begin{eqnarray}\text{i}{\it\omega}(1-{\it\omega}^{2})\boldsymbol{v}=-{\it\omega}^{2}\boldsymbol{{\rm\nabla}}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P)\widehat{{\it\bf\Omega}}+\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P\quad \text{in }V\end{eqnarray}$$
and
 $$\begin{eqnarray}-{\it\omega}^{2}\partial _{n}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}+\text{i}{\it\omega}\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0\quad \text{in }\partial V.\end{eqnarray}$$
$$\begin{eqnarray}-{\it\omega}^{2}\partial _{n}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P)\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}+\text{i}{\it\omega}\boldsymbol{n}\times \widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0\quad \text{in }\partial V.\end{eqnarray}$$
Poincaré’s equation (1.7) must be solved for
![]() $P$
subject to the boundary condition (3.18) and the velocity then determined from (3.17). The construction for a sphere (Bryan Reference Bryan1889) is outlined in § 4 during the enumeration of the spherical inertial modes.
$P$
subject to the boundary condition (3.18) and the velocity then determined from (3.17). The construction for a sphere (Bryan Reference Bryan1889) is outlined in § 4 during the enumeration of the spherical inertial modes.
3.4. Geostrophic modes
The Coriolis modes of zero frequency, i.e. the geostrophic modes, require special treatment. Their properties can occasionally be found from those of inertial modes by taking the limit
![]() ${\it\omega}\rightarrow 0$
. Thus the limit as
${\it\omega}\rightarrow 0$
. Thus the limit as
![]() ${\it\omega}\rightarrow 0$
of (3.15) yields
${\it\omega}\rightarrow 0$
of (3.15) yields
 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
, i.e.
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
, i.e.
 $P=P(\boldsymbol{r}-\boldsymbol{r}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\widehat{{\it\bf\Omega}})$
, so these modes have no vertical structure.
$P=P(\boldsymbol{r}-\boldsymbol{r}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\widehat{{\it\bf\Omega}})$
, so these modes have no vertical structure.
The velocity
![]() $\boldsymbol{v}$
can be found by substituting (3.15) into (3.17), dividing by
$\boldsymbol{v}$
can be found by substituting (3.15) into (3.17), dividing by
![]() $\text{i}{\it\omega}$
and then taking the limit
$\text{i}{\it\omega}$
and then taking the limit
![]() ${\it\omega}\rightarrow 0$
to obtain
${\it\omega}\rightarrow 0$
to obtain
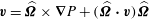 $\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}$
, or by taking the cross product of (2.6) with
$\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P+(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v})\widehat{{\it\bf\Omega}}$
, or by taking the cross product of (2.6) with
![]() $\widehat{{\it\bf\Omega}}$
. The axial component
$\widehat{{\it\bf\Omega}}$
. The axial component
![]() $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}$
of the flow is still undetermined. Letting
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}$
of the flow is still undetermined. Letting
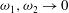 ${\it\omega}_{1},{\it\omega}_{2}\rightarrow 0$
in the inner product formula (3.16) using (3.15) leads to the undetermined axial components of
${\it\omega}_{1},{\it\omega}_{2}\rightarrow 0$
in the inner product formula (3.16) using (3.15) leads to the undetermined axial components of
![]() $\boldsymbol{v}_{1}$
,
$\boldsymbol{v}_{1}$
,
![]() $\boldsymbol{v}_{2}$
. We derive an expression for
$\boldsymbol{v}_{2}$
. We derive an expression for
![]() $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}$
in terms of the pressure and the geometry following Greenspan (Reference Greenspan1968). Let
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}$
in terms of the pressure and the geometry following Greenspan (Reference Greenspan1968). Let
![]() $(x,y,z)$
be Cartesian coordinates with the
$(x,y,z)$
be Cartesian coordinates with the
![]() $z$
-axis aligned along
$z$
-axis aligned along
![]() $\widehat{{\it\bf\Omega}}$
. We assume that any line parallel to
$\widehat{{\it\bf\Omega}}$
. We assume that any line parallel to
![]() $\widehat{{\it\bf\Omega}}$
intersects
$\widehat{{\it\bf\Omega}}$
intersects
![]() $\partial V$
in the top
$\partial V$
in the top
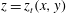 $z=z_{t}(x,y)$
and bottom
$z=z_{t}(x,y)$
and bottom
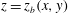 $z=z_{b}(x,y)$
boundaries, with outward normals
$z=z_{b}(x,y)$
boundaries, with outward normals
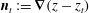 $\boldsymbol{n}_{t}:=\boldsymbol{{\rm\nabla}}(z-z_{t})$
and
$\boldsymbol{n}_{t}:=\boldsymbol{{\rm\nabla}}(z-z_{t})$
and
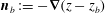 $\boldsymbol{n}_{b}:=-\boldsymbol{{\rm\nabla}}(z-z_{b})$
. Clearly
$\boldsymbol{n}_{b}:=-\boldsymbol{{\rm\nabla}}(z-z_{b})$
. Clearly
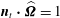 $\boldsymbol{n}_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=1$
and
$\boldsymbol{n}_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=1$
and
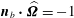 $\boldsymbol{n}_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=-1$
. Imposing
$\boldsymbol{n}_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}=-1$
. Imposing
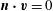 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V$
yields
$\partial V$
yields
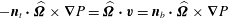 $-\boldsymbol{n}_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\boldsymbol{n}_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P$
or
$-\boldsymbol{n}_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\boldsymbol{n}_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P$
or
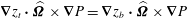 $\boldsymbol{{\rm\nabla}}z_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\boldsymbol{{\rm\nabla}}z_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P$
, i.e.
$\boldsymbol{{\rm\nabla}}z_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\boldsymbol{{\rm\nabla}}z_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P$
, i.e.
 $\boldsymbol{{\rm\nabla}}h\times \boldsymbol{{\rm\nabla}}z\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
, where
$\boldsymbol{{\rm\nabla}}h\times \boldsymbol{{\rm\nabla}}z\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
, where
 $h(x,y):=z_{t}-z_{b}$
is the height of the boundary. Hence,
$h(x,y):=z_{t}-z_{b}$
is the height of the boundary. Hence,
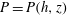 $P=P(h,z)$
, if
$P=P(h,z)$
, if
![]() $\boldsymbol{{\rm\nabla}}h\neq \mathbf{0}$
. But
$\boldsymbol{{\rm\nabla}}h\neq \mathbf{0}$
. But
 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
implies
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P=0$
implies
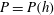 $P=P(h)$
and so
$P=P(h)$
and so
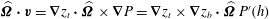 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\boldsymbol{{\rm\nabla}}z_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\boldsymbol{{\rm\nabla}}z_{t}\times \boldsymbol{{\rm\nabla}}z_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\,P^{\prime }(h)$
. So the horizontal structure of geostrophic flows is restricted to one degree of freedom. Finally, using
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{v}=\boldsymbol{{\rm\nabla}}z_{t}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P=\boldsymbol{{\rm\nabla}}z_{t}\times \boldsymbol{{\rm\nabla}}z_{b}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\,P^{\prime }(h)$
. So the horizontal structure of geostrophic flows is restricted to one degree of freedom. Finally, using
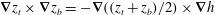 $\boldsymbol{{\rm\nabla}}z_{t}\times \boldsymbol{{\rm\nabla}}z_{b}=-\boldsymbol{{\rm\nabla}}((z_{t}+z_{b})/2)\times \boldsymbol{{\rm\nabla}}h$
,
$\boldsymbol{{\rm\nabla}}z_{t}\times \boldsymbol{{\rm\nabla}}z_{b}=-\boldsymbol{{\rm\nabla}}((z_{t}+z_{b})/2)\times \boldsymbol{{\rm\nabla}}h$
,
 $$\begin{eqnarray}\boldsymbol{v}=[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})]\times \boldsymbol{{\rm\nabla}}P=P^{\prime }(h)\,\boldsymbol{t},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})]\times \boldsymbol{{\rm\nabla}}P=P^{\prime }(h)\,\boldsymbol{t},\end{eqnarray}$$
where
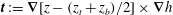 $\boldsymbol{t}:=\boldsymbol{{\rm\nabla}}[z-(z_{t}+z_{b})/2]\times \boldsymbol{{\rm\nabla}}h$
is tangent to the streamlines of
$\boldsymbol{t}:=\boldsymbol{{\rm\nabla}}[z-(z_{t}+z_{b})/2]\times \boldsymbol{{\rm\nabla}}h$
is tangent to the streamlines of
![]() $\boldsymbol{v}$
. The inner product of two geostrophic modes with pressures
$\boldsymbol{v}$
. The inner product of two geostrophic modes with pressures
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
is
$P_{2}$
is
 $$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=\int _{V}\left[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})\right]\times \boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\left[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})\right]\times \boldsymbol{{\rm\nabla}}P_{2}^{\ast }\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=\int _{V}\left[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})\right]\times \boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\left[\widehat{{\it\bf\Omega}}-\boldsymbol{{\rm\nabla}}{\textstyle \frac{1}{2}}(z_{t}+z_{b})\right]\times \boldsymbol{{\rm\nabla}}P_{2}^{\ast }\text{d}V.\end{eqnarray}$$
If
![]() $V$
is symmetrical about some
$V$
is symmetrical about some
![]() $z$
-plane, then
$z$
-plane, then
![]() $z_{t}+z_{b}$
is constant and the inner product reduces to
$z_{t}+z_{b}$
is constant and the inner product reduces to
 $$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=\int _{V}\boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast }\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})=\int _{V}\boldsymbol{{\rm\nabla}}P_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{2}^{\ast }\text{d}V.\end{eqnarray}$$
An orthogonal set of geostrophic modes can be constructed by applying Gram–Schmidt orthogonalisation to a linearly independent set of geostrophic pressure modes using the inner product (3.21).
The spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
depends only on the geometry of
$\boldsymbol{{\mathcal{C}}}$
depends only on the geometry of
![]() $V$
and
$V$
and
![]() $\widehat{{\it\bf\Omega}}$
, not on the rotation rate nor on any flow parameters. The simplest dependence is between closed curves and geostrophic modes. The intersection of the level surfaces of
$\widehat{{\it\bf\Omega}}$
, not on the rotation rate nor on any flow parameters. The simplest dependence is between closed curves and geostrophic modes. The intersection of the level surfaces of
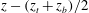 $z-(z_{t}+z_{b})/2$
and
$z-(z_{t}+z_{b})/2$
and
![]() $h$
, which depend only on
$h$
, which depend only on
![]() $V$
and
$V$
and
![]() $\widehat{{\it\bf\Omega}}$
, are called geostrophic curves, or contours if they lie on the boundary
$\widehat{{\it\bf\Omega}}$
, are called geostrophic curves, or contours if they lie on the boundary
![]() $z=z_{t}$
or
$z=z_{t}$
or
![]() $z=z_{b}$
. The streamlines of the geostrophic flow (3.19) are geostrophic curves. If
$z=z_{b}$
. The streamlines of the geostrophic flow (3.19) are geostrophic curves. If
![]() $G$
is a geostrophic curve,
$G$
is a geostrophic curve,
 $$\begin{eqnarray}\oint _{G}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{l}=P^{\prime }(h)\oint _{G}|\boldsymbol{t}|\text{d}l\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}\oint _{G}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{l}=P^{\prime }(h)\oint _{G}|\boldsymbol{t}|\text{d}l\neq 0.\end{eqnarray}$$
There is no non-zero geostrophic flow along a curve which terminates on the boundary with
 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{t}\neq 0$
. If all curves are of this form there is no geostrophic flow, e.g. as in a sliced cylinder rotating about its axis, and therefore no Coriolis mode of frequency zero. Of course, curves need not terminate on the boundary, as in the case of a sliced cone rotating about its axis.
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{t}\neq 0$
. If all curves are of this form there is no geostrophic flow, e.g. as in a sliced cylinder rotating about its axis, and therefore no Coriolis mode of frequency zero. Of course, curves need not terminate on the boundary, as in the case of a sliced cone rotating about its axis.
Geostrophic and inertial modes can be separated by frequency or orthogonality, but also geometrically by geostrophic cylinder average. The geostrophic contours that have the same boundary projections along
![]() $\widehat{{\it\bf\Omega}}$
generate a geostrophic cylinder of constant height, which need not be of circular cross-section. The geostrophic cylinder average of a vector field
$\widehat{{\it\bf\Omega}}$
generate a geostrophic cylinder of constant height, which need not be of circular cross-section. The geostrophic cylinder average of a vector field
![]() $\boldsymbol{F}$
over a geostrophic cylinder
$\boldsymbol{F}$
over a geostrophic cylinder
![]() $C$
is
$C$
is
 $$\begin{eqnarray}\langle \boldsymbol{F}\rangle _{C}:=\frac{1}{|C|}\int _{C}\boldsymbol{F}\boldsymbol{\cdot }\widehat{\boldsymbol{t}}\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{F}\rangle _{C}:=\frac{1}{|C|}\int _{C}\boldsymbol{F}\boldsymbol{\cdot }\widehat{\boldsymbol{t}}\text{d}S,\end{eqnarray}$$
where
![]() $|C|$
is the surface area of
$|C|$
is the surface area of
![]() $C$
and
$C$
and
![]() $\widehat{\boldsymbol{t}}$
is the unit tangent field along the geostrophic curves generating
$\widehat{\boldsymbol{t}}$
is the unit tangent field along the geostrophic curves generating
![]() $C$
. We show that, if
$C$
. We show that, if
![]() $C$
divides the fluid into two disjoint components
$C$
divides the fluid into two disjoint components
 $V=V_{1}\cup V_{2}$
, then
$V=V_{1}\cup V_{2}$
, then
 $$\begin{eqnarray}{\it\omega}\langle \boldsymbol{v}\rangle _{C}=0,\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}\langle \boldsymbol{v}\rangle _{C}=0,\end{eqnarray}$$
and hence for the inertial modes (
![]() ${\it\omega}\neq 0$
) the geostrophic cylinder average of
${\it\omega}\neq 0$
) the geostrophic cylinder average of
![]() $\boldsymbol{v}$
vanishes:
$\boldsymbol{v}$
vanishes:
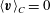 $\langle \boldsymbol{v}\rangle _{C}=0$
. The proof follows from the geostrophic cylinder average of (2.6),
$\langle \boldsymbol{v}\rangle _{C}=0$
. The proof follows from the geostrophic cylinder average of (2.6),
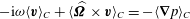 $-\text{i}{\it\omega}\langle \boldsymbol{v}\rangle _{C}+\langle \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\rangle _{C}=-\langle \boldsymbol{{\rm\nabla}}p\rangle _{C}$
and
$-\text{i}{\it\omega}\langle \boldsymbol{v}\rangle _{C}+\langle \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\rangle _{C}=-\langle \boldsymbol{{\rm\nabla}}p\rangle _{C}$
and
 $$\begin{eqnarray}0=\int _{V_{i}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}\text{d}V=\int _{C}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=\iint _{C}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\times \widehat{{\it\bf\Omega}}\text{d}z=|C|\langle \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\rangle _{C},\end{eqnarray}$$
$$\begin{eqnarray}0=\int _{V_{i}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}\text{d}V=\int _{C}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=\iint _{C}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\times \widehat{{\it\bf\Omega}}\text{d}z=|C|\langle \widehat{{\it\bf\Omega}}\times \boldsymbol{v}\rangle _{C},\end{eqnarray}$$
using
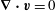 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V_{i}$
and
$V_{i}$
and
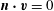 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on the boundary. Also
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0$
on the boundary. Also
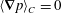 $\langle \boldsymbol{{\rm\nabla}}p\rangle _{C}=0$
, since
$\langle \boldsymbol{{\rm\nabla}}p\rangle _{C}=0$
, since
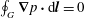 $\oint _{G}\boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\text{d}\boldsymbol{l}=0$
for any geostrophic contour
$\oint _{G}\boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\text{d}\boldsymbol{l}=0$
for any geostrophic contour
![]() $G$
on
$G$
on
![]() $C$
. So, unlike geostrophic modes, inertial modes have vertical structure
$C$
. So, unlike geostrophic modes, inertial modes have vertical structure
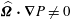 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P\neq 0$
and hence an axial flow along the rotation axis by (3.15). The result (3.24) is also known as the mean circulation theorem (Greenspan Reference Greenspan1968), that the circulation of a depth-averaged inertial (geostrophic) mode around a closed geostrophic contour is zero (non-zero).
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P\neq 0$
and hence an axial flow along the rotation axis by (3.15). The result (3.24) is also known as the mean circulation theorem (Greenspan Reference Greenspan1968), that the circulation of a depth-averaged inertial (geostrophic) mode around a closed geostrophic contour is zero (non-zero).
3.5. Angular momentum of Coriolis modes
Inertial and geostrophic modes also differ in angular momentum effects. Geostrophic modes transmit the component of the pressure torque along the rotation axis between the ends of a geostrophic cylinder or annulus. Inertial modes lose torque to the angular momentum of the fluid. This mechanism of torque transfer is significant if the region is periphractic, i.e. the outer fluid boundary encloses one or more inner fluid boundaries so not every closed surface in
![]() $V$
can be continuously shrunk to a point without leaving
$V$
can be continuously shrunk to a point without leaving
![]() $V$
(Maxwell Reference Maxwell1891, pp. 18, 24, 25). For then the geostrophic modes transmit the axial component of the pressure torque from the outer boundary to the inner boundary (Hide Reference Hide1995). The results follow from the identity
$V$
(Maxwell Reference Maxwell1891, pp. 18, 24, 25). For then the geostrophic modes transmit the axial component of the pressure torque from the outer boundary to the inner boundary (Hide Reference Hide1995). The results follow from the identity
 $$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\int _{\partial C}\boldsymbol{r}\times P\text{d}\boldsymbol{S}=\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{C}-\frac{\text{d}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}})}{\text{d}t},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\int _{\partial C}\boldsymbol{r}\times P\text{d}\boldsymbol{S}=\text{i}{\it\omega}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{C}-\frac{\text{d}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}})}{\text{d}t},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D644}_{C}$
and
$\unicode[STIX]{x1D644}_{C}$
and
![]() $\unicode[STIX]{x1D647}_{C}$
are the inertia tensor of
$\unicode[STIX]{x1D647}_{C}$
are the inertia tensor of
![]() $C$
and the angular momentum of
$C$
and the angular momentum of
![]() $C$
in the rotating frame, noting that
$C$
in the rotating frame, noting that
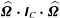 $\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}$
is constant if
$\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}$
is constant if
![]() $C$
is a geostrophic cylinder or annulus. In dimensional form,
$C$
is a geostrophic cylinder or annulus. In dimensional form,
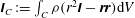 $\unicode[STIX]{x1D644}_{C}:=\int _{C}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V$
and
$\unicode[STIX]{x1D644}_{C}:=\int _{C}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V$
and
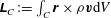 $\unicode[STIX]{x1D647}_{C}:=\int _{C}\boldsymbol{r}\times {\it\rho}\boldsymbol{v}\text{d}V$
. Since
$\unicode[STIX]{x1D647}_{C}:=\int _{C}\boldsymbol{r}\times {\it\rho}\boldsymbol{v}\text{d}V$
. Since
![]() $\widehat{{\it\bf\Omega}}$
is constant the last term in (3.26) vanishes, giving the result. For a sphere or spherical shell the result is trivial. Identity (3.26) is established by combining the dimensional identities
$\widehat{{\it\bf\Omega}}$
is constant the last term in (3.26) vanishes, giving the result. For a sphere or spherical shell the result is trivial. Identity (3.26) is established by combining the dimensional identities
 $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D644}_{C}}{\text{d}t}=\int _{C}{\it\rho}D_{t}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V+\int _{\partial C}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D644}_{C}}{\text{d}t}=\int _{C}{\it\rho}D_{t}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\text{d}V+\int _{\partial C}{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
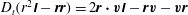 $D_{t}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})=2\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{v}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{v}-\boldsymbol{v}\boldsymbol{r}$
and
$D_{t}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})=2\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{v}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{v}-\boldsymbol{v}\boldsymbol{r}$
and
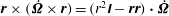 $\boldsymbol{r}\times (\dot{{\it\bf\Omega}}\times \boldsymbol{r})=(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\boldsymbol{\cdot }\dot{{\it\bf\Omega}}$
to yield the following identity for the moments of the Coriolis and Poincaré forces,
$\boldsymbol{r}\times (\dot{{\it\bf\Omega}}\times \boldsymbol{r})=(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})\boldsymbol{\cdot }\dot{{\it\bf\Omega}}$
to yield the following identity for the moments of the Coriolis and Poincaré forces,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{C}\boldsymbol{r}\times ({\it\rho}2{\it\bf\Omega}\times \boldsymbol{v})\text{d}V+\int _{C}\boldsymbol{r}\times ({\it\rho}\dot{{\it\bf\Omega}}\times \boldsymbol{r})\text{d}V\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\partial C}{\it\bf\Omega}\boldsymbol{\cdot }{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\text{d}\boldsymbol{S}=\frac{\text{d}({\it\bf\Omega}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C})}{\text{d}t}+{\it\bf\Omega}\times \unicode[STIX]{x1D647}_{C}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{C}\boldsymbol{r}\times ({\it\rho}2{\it\bf\Omega}\times \boldsymbol{v})\text{d}V+\int _{C}\boldsymbol{r}\times ({\it\rho}\dot{{\it\bf\Omega}}\times \boldsymbol{r})\text{d}V\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\partial C}{\it\bf\Omega}\boldsymbol{\cdot }{\it\rho}(r^{2}\unicode[STIX]{x1D644}-\boldsymbol{r}\boldsymbol{r})(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\text{d}\boldsymbol{S}=\frac{\text{d}({\it\bf\Omega}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C})}{\text{d}t}+{\it\bf\Omega}\times \unicode[STIX]{x1D647}_{C}.\end{eqnarray}$$
If
![]() $\dot{{\it\bf\Omega}}=\mathbf{0}$
and
$\dot{{\it\bf\Omega}}=\mathbf{0}$
and
![]() $C$
moves so that
$C$
moves so that
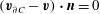 $(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\boldsymbol{n}=0$
, which implies the angular momentum flux across the boundary
$(\boldsymbol{v}_{\partial C}-\boldsymbol{v})\boldsymbol{\cdot }\boldsymbol{n}=0$
, which implies the angular momentum flux across the boundary
![]() $\partial C$
due to
$\partial C$
due to
![]() ${\it\bf\Omega}$
vanishes, the (dimensionless) identity reduces to
${\it\bf\Omega}$
vanishes, the (dimensionless) identity reduces to
 $$\begin{eqnarray}\frac{\text{d}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C})}{\text{d}t}+\widehat{{\it\bf\Omega}}\times \unicode[STIX]{x1D647}_{C}=\int _{C}\boldsymbol{r}\times (\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V=\text{i}{\it\omega}\int _{C}\boldsymbol{r}\times \boldsymbol{v}\text{d}V-\int _{\partial C}\boldsymbol{r}\times P\text{d}\boldsymbol{S}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}(\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\unicode[STIX]{x1D644}_{C})}{\text{d}t}+\widehat{{\it\bf\Omega}}\times \unicode[STIX]{x1D647}_{C}=\int _{C}\boldsymbol{r}\times (\widehat{{\it\bf\Omega}}\times \boldsymbol{v})\text{d}V=\text{i}{\it\omega}\int _{C}\boldsymbol{r}\times \boldsymbol{v}\text{d}V-\int _{\partial C}\boldsymbol{r}\times P\text{d}\boldsymbol{S}.\end{eqnarray}$$
The component along the rotation axis gives (3.26).
3.6. Inversion of
 $\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644}$
and resonance
$\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644}$
and resonance
Applications usually require, in principle, calculation of the resolvent
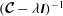 $(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
and forced solutions
$(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}$
and forced solutions
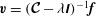 $\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
, where
$\boldsymbol{v}=(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}$
, where
![]() $\boldsymbol{f}$
satisfies (1.16). For this the velocity can be eliminated as in (2.7) and (2.9), which can be solved for
$\boldsymbol{f}$
satisfies (1.16). For this the velocity can be eliminated as in (2.7) and (2.9), which can be solved for
![]() $p$
. Equation (2.8) then gives
$p$
. Equation (2.8) then gives
![]() $\boldsymbol{v}$
. Alternatively, elimination of
$\boldsymbol{v}$
. Alternatively, elimination of
![]() $p$
from (1.19) yields the vorticity equation,
$p$
from (1.19) yields the vorticity equation,
 $$\begin{eqnarray}\partial _{t}\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{f},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{f},\end{eqnarray}$$
or from (2.6) the modal form,
 $$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}+{\it\lambda}\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}\times \boldsymbol{f}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}+{\it\lambda}\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}=-\boldsymbol{{\rm\nabla}}\times \boldsymbol{f}.\end{eqnarray}$$
Uncurling recovers (1.19) or (2.6). In principle, if
![]() ${\it\lambda}$
is in the resolvent set
${\it\lambda}$
is in the resolvent set
![]() ${\it\Gamma}$
of
${\it\Gamma}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
, this can be done for all
$\boldsymbol{{\mathcal{C}}}$
, this can be done for all
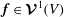 $\boldsymbol{f}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
. However, if
$\boldsymbol{f}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
. However, if
![]() ${\it\lambda}$
is in the spectrum
${\it\lambda}$
is in the spectrum
![]() $\mathbb{C}\setminus {\it\Gamma}$
,
$\mathbb{C}\setminus {\it\Gamma}$
,
![]() $\boldsymbol{f}$
may have to satisfy non-resonance conditions.
$\boldsymbol{f}$
may have to satisfy non-resonance conditions.
We consider only the point spectrum
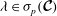 ${\it\lambda}\in {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
. If
${\it\lambda}\in {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
. If
![]() ${\it\lambda}=0$
, (1.19) reduces to the steady form
${\it\lambda}=0$
, (1.19) reduces to the steady form
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
and the resolvent is then the inverse of
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
and the resolvent is then the inverse of
![]() $\boldsymbol{{\mathcal{C}}}$
. If a geostrophic mode exists, then
$\boldsymbol{{\mathcal{C}}}$
. If a geostrophic mode exists, then
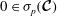 $0\in {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
and
$0\in {\it\sigma}_{p}(\boldsymbol{{\mathcal{C}}})$
and
![]() $\boldsymbol{{\mathcal{C}}}$
is not invertible. Taylor (Reference Taylor1963) considered this important case for the dynamo problem in the rapid-rotation limit
$\boldsymbol{{\mathcal{C}}}$
is not invertible. Taylor (Reference Taylor1963) considered this important case for the dynamo problem in the rapid-rotation limit
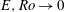 $\mathit{E},\mathit{Ro}\rightarrow 0$
. In this case the force
$\mathit{E},\mathit{Ro}\rightarrow 0$
. In this case the force
![]() $\boldsymbol{f}$
is the (projected) Lorentz force
$\boldsymbol{f}$
is the (projected) Lorentz force
![]() $\boldsymbol{f}_{L}$
and the force balance is magnetostrophic. We state a general existence theorem, Theorem 3.4, for solutions of
$\boldsymbol{f}_{L}$
and the force balance is magnetostrophic. We state a general existence theorem, Theorem 3.4, for solutions of
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
; a constructive proof is given in appendix A. We assume the region
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
; a constructive proof is given in appendix A. We assume the region
![]() $V$
is axisymmetric with
$V$
is axisymmetric with
![]() $\widehat{{\it\bf\Omega}}$
oriented along the symmetry
$\widehat{{\it\bf\Omega}}$
oriented along the symmetry
![]() $z$
-axis. We assume the top and bottom boundaries,
$z$
-axis. We assume the top and bottom boundaries,
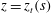 $z=z_{t}(s)$
and
$z=z_{t}(s)$
and
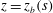 $z=z_{b}(s)$
, where the cylindrical radius
$z=z_{b}(s)$
, where the cylindrical radius
![]() $s$
satisfies
$s$
satisfies
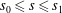 $s_{0}\leqslant s\leqslant s_{1}$
, are smooth. For a given
$s_{0}\leqslant s\leqslant s_{1}$
, are smooth. For a given
![]() $\widehat{{\it\bf\Omega}}$
,
$\widehat{{\it\bf\Omega}}$
,
![]() $V$
is geostrophically guided if there is exactly one geostrophic contour through each point on the boundary. We assume
$V$
is geostrophically guided if there is exactly one geostrophic contour through each point on the boundary. We assume
![]() $V$
is geostrophically guided:
$V$
is geostrophically guided:
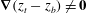 $\boldsymbol{{\rm\nabla}}(z_{t}-z_{b})\neq \mathbf{0}$
except at isolated values of
$\boldsymbol{{\rm\nabla}}(z_{t}-z_{b})\neq \mathbf{0}$
except at isolated values of
![]() $s$
.
$s$
.
Theorem 3.4. A necessary and sufficient condition for the existence of a single-valued solution
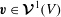 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
of
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
of
 $$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}\times \boldsymbol{f},\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=g\quad \text{on }\partial V,\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}\times \boldsymbol{f},\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\quad \text{in }V,\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=g\quad \text{on }\partial V,\end{eqnarray}$$
where
![]() $\boldsymbol{f}$
and
$\boldsymbol{f}$
and
![]() $g$
are prescribed subject to the consistency condition
$g$
are prescribed subject to the consistency condition
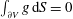 $\int _{\partial V}g\,\text{d}S=0$
, is
$\int _{\partial V}g\,\text{d}S=0$
, is
 $$\begin{eqnarray}|C(s)|\langle \boldsymbol{f}\rangle _{C(s)}+\int _{S(s)}g\text{d}S=0,\end{eqnarray}$$
$$\begin{eqnarray}|C(s)|\langle \boldsymbol{f}\rangle _{C(s)}+\int _{S(s)}g\text{d}S=0,\end{eqnarray}$$
for all geostrophic cylinders
![]() $C(s)$
, where
$C(s)$
, where
![]() $S(s)$
are the caps of
$S(s)$
are the caps of
![]() $C(s)$
. The solution is only determined up to an arbitrary additive function of
$C(s)$
. The solution is only determined up to an arbitrary additive function of
![]() $s$
to
$s$
to
![]() $v_{{\it\phi}}$
. If the further condition,
$v_{{\it\phi}}$
. If the further condition,
 $$\begin{eqnarray}\langle \boldsymbol{v}\rangle _{C(s)}=0\quad \text{for all }s_{0}\leqslant s\leqslant s_{1},\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{v}\rangle _{C(s)}=0\quad \text{for all }s_{0}\leqslant s\leqslant s_{1},\end{eqnarray}$$
is imposed, then the solution is unique.
The function
![]() $g$
allows for Ekman suction or a moving boundary. Imposing
$g$
allows for Ekman suction or a moving boundary. Imposing
![]() $g=0$
gives the result for the Coriolis operator.
$g=0$
gives the result for the Coriolis operator.
Corollary 3.1. A necessary and sufficient condition for the existence of a single-valued solution
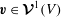 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
of
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
of
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
is that all geostrophic cylinder averages of
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
is that all geostrophic cylinder averages of
![]() $\boldsymbol{f}$
vanish,
$\boldsymbol{f}$
vanish,
 $$\begin{eqnarray}\langle \boldsymbol{f}\rangle _{C(s)}=0.\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{f}\rangle _{C(s)}=0.\end{eqnarray}$$
The non-resonance or solvability condition (3.35) is well known in dynamo theory as Taylor’s (Reference Taylor1963) condition for the magnetostrophic momentum equation. The theorem fails if
![]() $z_{t}(s)$
or
$z_{t}(s)$
or
![]() $z_{b}(s)$
are not smooth, e.g. in a spherical shell. The proof produces a smooth solution
$z_{b}(s)$
are not smooth, e.g. in a spherical shell. The proof produces a smooth solution
![]() $\boldsymbol{v}$
over each interval of
$\boldsymbol{v}$
over each interval of
![]() $s$
for which
$s$
for which
![]() $z_{t}(s)$
and
$z_{t}(s)$
and
![]() $z_{b}(s)$
are smooth but the smooth pieces of
$z_{b}(s)$
are smooth but the smooth pieces of
![]() $\boldsymbol{v}$
do not fit together smoothly. This remains an outstanding problem (Hollerbach & Proctor Reference Hollerbach, Proctor, Matthews, Proctor and Rucklidge1993; Hollerbach Reference Hollerbach1994a
,Reference Hollerbach
b
; Kleeorin et al.
Reference Kleeorin, Rogachevskii, Ruzmaikin, Soward and Starchenko1997; Dormy, Cardin & Jault Reference Dormy, Cardin and Jault1998; Soward & Hollerbach Reference Soward and Hollerbach2000; Livermore & Hollerbach Reference Livermore and Hollerbach2012).
$\boldsymbol{v}$
do not fit together smoothly. This remains an outstanding problem (Hollerbach & Proctor Reference Hollerbach, Proctor, Matthews, Proctor and Rucklidge1993; Hollerbach Reference Hollerbach1994a
,Reference Hollerbach
b
; Kleeorin et al.
Reference Kleeorin, Rogachevskii, Ruzmaikin, Soward and Starchenko1997; Dormy, Cardin & Jault Reference Dormy, Cardin and Jault1998; Soward & Hollerbach Reference Soward and Hollerbach2000; Livermore & Hollerbach Reference Livermore and Hollerbach2012).
The invertibility of
![]() $\boldsymbol{{\mathcal{C}}}$
can also be treated spectrally:
$\boldsymbol{{\mathcal{C}}}$
can also be treated spectrally:
Theorem 3.5. If
![]() $\boldsymbol{f}$
has an expansion in discrete Coriolis modes,
$\boldsymbol{f}$
has an expansion in discrete Coriolis modes,
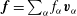 $\boldsymbol{f}=\sum _{{\it\alpha}}f_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
with
$\boldsymbol{f}=\sum _{{\it\alpha}}f_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
with
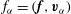 $f_{{\it\alpha}}=(\boldsymbol{f},\boldsymbol{v}_{{\it\alpha}})$
, then
$f_{{\it\alpha}}=(\boldsymbol{f},\boldsymbol{v}_{{\it\alpha}})$
, then
![]() $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
has the solution
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\boldsymbol{f}$
has the solution
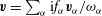 $\boldsymbol{v}=\sum _{{\it\alpha}}\text{i}f_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}/{\it\omega}_{{\it\alpha}}$
, if the non-resonance or solvability conditions,
$\boldsymbol{v}=\sum _{{\it\alpha}}\text{i}f_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}/{\it\omega}_{{\it\alpha}}$
, if the non-resonance or solvability conditions,
 $$\begin{eqnarray}(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=0,\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=0,\end{eqnarray}$$
hold for all
![]() ${\it\omega}_{{\it\beta}}=0$
, i.e. for all geostrophic modes, and
${\it\omega}_{{\it\beta}}=0$
, i.e. for all geostrophic modes, and
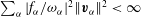 $\sum _{{\it\alpha}}|f_{{\it\alpha}}/{\it\omega}_{{\it\alpha}}|^{2}\Vert \boldsymbol{v}_{{\it\alpha}}\Vert ^{2}<\infty$
.
$\sum _{{\it\alpha}}|f_{{\it\alpha}}/{\it\omega}_{{\it\alpha}}|^{2}\Vert \boldsymbol{v}_{{\it\alpha}}\Vert ^{2}<\infty$
.
The proof is elementary. The solvability conditions in Theorem 3.5 are equivalent to condition (3.34) in Theorem 3.4, but may be more tractable. If the Coriolis modes are complete, so that any
![]() $\boldsymbol{f}$
can be expanded in discrete Coriolis modes, then the spectral inversion in Theorem 3.5 works for any
$\boldsymbol{f}$
can be expanded in discrete Coriolis modes, then the spectral inversion in Theorem 3.5 works for any
![]() $\boldsymbol{f}$
which satisfies the solvability conditions. This highlights the usefulness and importance of completeness for the Coriolis modes, which we prove in § 8 if
$\boldsymbol{f}$
which satisfies the solvability conditions. This highlights the usefulness and importance of completeness for the Coriolis modes, which we prove in § 8 if
![]() $V$
is a sphere. For the general forced problem,
$V$
is a sphere. For the general forced problem,
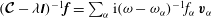 $(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}=\sum _{{\it\alpha}}\text{i}({\it\omega}-{\it\omega}_{{\it\alpha}})^{-1}f_{{\it\alpha}}\,\boldsymbol{v}_{{\it\alpha}}$
, where
$(\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})^{-1}\boldsymbol{f}=\sum _{{\it\alpha}}\text{i}({\it\omega}-{\it\omega}_{{\it\alpha}})^{-1}f_{{\it\alpha}}\,\boldsymbol{v}_{{\it\alpha}}$
, where
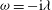 ${\it\omega}=-\text{i}{\it\lambda}$
, if
${\it\omega}=-\text{i}{\it\lambda}$
, if
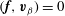 $(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=0$
for all
$(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=0$
for all
![]() ${\it\beta}$
for which
${\it\beta}$
for which
![]() ${\it\omega}={\it\omega}_{{\it\beta}}$
.
${\it\omega}={\it\omega}_{{\it\beta}}$
.
4. Coriolis modes in a sphere
In §§ 4–8 the fluid region
![]() $V$
is the (non-dimensionalised) sphere
$V$
is the (non-dimensionalised) sphere
![]() $|\boldsymbol{r}|<1$
. In the present section we enumerate the Coriolis modes in a sphere. The geostrophic modes require special treatment due to the zero frequency.
$|\boldsymbol{r}|<1$
. In the present section we enumerate the Coriolis modes in a sphere. The geostrophic modes require special treatment due to the zero frequency.
4.1. Inertial pressure modes
Poincaré’s equation (2.7) in cylindrical polar coordinates
![]() $(s,{\it\phi},z)$
with
$(s,{\it\phi},z)$
with
![]() $\boldsymbol{f}=\mathbf{0}$
is
$\boldsymbol{f}=\mathbf{0}$
is
 $$\begin{eqnarray}s^{-1}\partial _{s}(s\partial _{s}P)+s^{-2}\partial _{{\it\phi}}^{2}P-({\it\omega}^{-2}-1)\partial _{z}^{2}P=0,\quad s^{2}+z^{2}<1\end{eqnarray}$$
$$\begin{eqnarray}s^{-1}\partial _{s}(s\partial _{s}P)+s^{-2}\partial _{{\it\phi}}^{2}P-({\it\omega}^{-2}-1)\partial _{z}^{2}P=0,\quad s^{2}+z^{2}<1\end{eqnarray}$$
and the boundary condition (2.8) is
 $$\begin{eqnarray}{\it\omega}^{2}s\,\partial _{s}P+\text{i}{\it\omega}\partial _{{\it\phi}}P-(1-{\it\omega}^{2})z\,\partial _{z}P=0,\quad s^{2}+z^{2}=1,\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}^{2}s\,\partial _{s}P+\text{i}{\it\omega}\partial _{{\it\phi}}P-(1-{\it\omega}^{2})z\,\partial _{z}P=0,\quad s^{2}+z^{2}=1,\end{eqnarray}$$
since
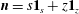 $\boldsymbol{n}=s\mathbf{1}_{s}+z\mathbf{1}_{z}$
. We transform the problem to the non-orthogonal frequency-dependent spheroidal coordinates
$\boldsymbol{n}=s\mathbf{1}_{s}+z\mathbf{1}_{z}$
. We transform the problem to the non-orthogonal frequency-dependent spheroidal coordinates
 $({\it\xi},{\it\zeta},{\it\phi})$
(Bryan Reference Bryan1889) given by
$({\it\xi},{\it\zeta},{\it\phi})$
(Bryan Reference Bryan1889) given by
 $$\begin{eqnarray}{\it\sigma}s=\sqrt{1-{\it\zeta}^{2}}\sqrt{1-{\it\xi}^{2}},\quad {\it\omega}z={\it\xi}{\it\zeta},\quad 0\leqslant {\it\zeta}\leqslant {\it\omega},~{\it\omega}\leqslant {\it\xi}\leqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}{\it\sigma}s=\sqrt{1-{\it\zeta}^{2}}\sqrt{1-{\it\xi}^{2}},\quad {\it\omega}z={\it\xi}{\it\zeta},\quad 0\leqslant {\it\zeta}\leqslant {\it\omega},~{\it\omega}\leqslant {\it\xi}\leqslant 1,\end{eqnarray}$$
where
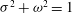 ${\it\sigma}^{2}+{\it\omega}^{2}=1$
. The relation between
${\it\sigma}^{2}+{\it\omega}^{2}=1$
. The relation between
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\it\omega}$
removes the mixed second derivative from Poincaré’s equation, allowing the variables to separate into Legendre’s equation in
${\it\omega}$
removes the mixed second derivative from Poincaré’s equation, allowing the variables to separate into Legendre’s equation in
![]() ${\it\zeta}$
and in
${\it\zeta}$
and in
![]() ${\it\xi}$
, and also ensures the spherical boundary
${\it\xi}$
, and also ensures the spherical boundary
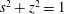 $s^{2}+z^{2}=1$
is a
$s^{2}+z^{2}=1$
is a
![]() ${\it\zeta}$
-surface,
${\it\zeta}$
-surface,
![]() ${\it\zeta}={\it\omega}$
. The transformation is degenerate if
${\it\zeta}={\it\omega}$
. The transformation is degenerate if
![]() ${\it\omega}=0$
. The
${\it\omega}=0$
. The
![]() ${\it\zeta}$
-surfaces (
${\it\zeta}$
-surfaces (
![]() ${\it\xi}$
-surfaces) are non-confocal oblate (prolate) spheroids with semi-axes
${\it\xi}$
-surfaces) are non-confocal oblate (prolate) spheroids with semi-axes
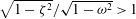 $\sqrt{1-{\it\zeta}^{2}}/\sqrt{1-{\it\omega}^{2}}>1$
and
$\sqrt{1-{\it\zeta}^{2}}/\sqrt{1-{\it\omega}^{2}}>1$
and
![]() ${\it\zeta}/{\it\omega}<1$
(respectively,
${\it\zeta}/{\it\omega}<1$
(respectively,
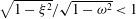 $\sqrt{1-{\it\xi}^{2}}/\sqrt{1-{\it\omega}^{2}}<1$
and
$\sqrt{1-{\it\xi}^{2}}/\sqrt{1-{\it\omega}^{2}}<1$
and
![]() ${\it\xi}/{\it\omega}>1$
), co-axial with the
${\it\xi}/{\it\omega}>1$
), co-axial with the
![]() $z$
-axis. Thus the spherical inertial modes are
$z$
-axis. Thus the spherical inertial modes are
 $$\begin{eqnarray}P=P_{n,{\it\omega}}^{m}:=P_{n}^{m}({\it\zeta}_{{\it\omega}})\,P_{n}^{m}({\it\xi}_{{\it\omega}})\text{e}^{\text{i}m{\it\phi}},\end{eqnarray}$$
$$\begin{eqnarray}P=P_{n,{\it\omega}}^{m}:=P_{n}^{m}({\it\zeta}_{{\it\omega}})\,P_{n}^{m}({\it\xi}_{{\it\omega}})\text{e}^{\text{i}m{\it\phi}},\end{eqnarray}$$
where
![]() $P_{n}^{m}$
is the associated Legendre function of degree
$P_{n}^{m}$
is the associated Legendre function of degree
![]() $n$
and order
$n$
and order
![]() $m$
,
$m$
,
![]() $m\in \mathbb{Z}$
,
$m\in \mathbb{Z}$
,
![]() $|m|\leqslant n$
,
$|m|\leqslant n$
,
![]() ${\it\omega}\neq 0$
and the
${\it\omega}\neq 0$
and the
![]() ${\it\omega}$
-dependence of
${\it\omega}$
-dependence of
![]() ${\it\zeta}$
and
${\it\zeta}$
and
![]() ${\it\xi}$
is indicated.
${\it\xi}$
is indicated.
The product
 $P_{n}^{m}({\it\xi})P_{n}^{m}({\it\zeta})$
is a polynomial in
$P_{n}^{m}({\it\xi})P_{n}^{m}({\it\zeta})$
is a polynomial in
![]() $s$
and
$s$
and
![]() $z$
of degree
$z$
of degree
![]() $n$
, and
$n$
, and
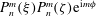 $P_{n}^{m}({\it\xi})P_{n}^{m}({\it\zeta})\text{e}^{\text{i}m{\it\phi}}$
is a polynomial in
$P_{n}^{m}({\it\xi})P_{n}^{m}({\it\zeta})\text{e}^{\text{i}m{\it\phi}}$
is a polynomial in
![]() $x,y,z$
of degree
$x,y,z$
of degree
![]() $n$
(Kudlick Reference Kudlick1966; Zhang et al.
Reference Zhang, Earnshaw, Liao and Busse2001), even if
$n$
(Kudlick Reference Kudlick1966; Zhang et al.
Reference Zhang, Earnshaw, Liao and Busse2001), even if
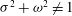 ${\it\sigma}^{2}+{\it\omega}^{2}\neq 1$
. In fact,
${\it\sigma}^{2}+{\it\omega}^{2}\neq 1$
. In fact,
 $$\begin{eqnarray}P_{n,{\it\omega}}^{m}=\left\{\begin{array}{@{}ll@{}}({\it\sigma}s\text{e}^{\text{i}{\it\phi}})^{m}({\it\omega}z)^{q}U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2}),\quad & \text{if }m\geqslant 0;\\ ({\it\sigma}s\text{e}^{-\text{i}{\it\phi}})^{|m|}({\it\omega}z)^{q}U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2}),\quad & \text{if }m<0;\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}P_{n,{\it\omega}}^{m}=\left\{\begin{array}{@{}ll@{}}({\it\sigma}s\text{e}^{\text{i}{\it\phi}})^{m}({\it\omega}z)^{q}U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2}),\quad & \text{if }m\geqslant 0;\\ ({\it\sigma}s\text{e}^{-\text{i}{\it\phi}})^{|m|}({\it\omega}z)^{q}U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2}),\quad & \text{if }m<0;\end{array}\right.\end{eqnarray}$$
where
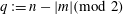 $q:=n-|m|(\text{mod}~2)$
is either 0 or 1, and
$q:=n-|m|(\text{mod}~2)$
is either 0 or 1, and
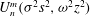 $U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2})$
is a polynomial in
$U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2})$
is a polynomial in
![]() ${\it\sigma}^{2}s^{2}$
and
${\it\sigma}^{2}s^{2}$
and
![]() ${\it\omega}^{2}z^{2}$
of degree
${\it\omega}^{2}z^{2}$
of degree
 $(n-|m|-q)/2$
. To establish this, note the associated Legendre function
$(n-|m|-q)/2$
. To establish this, note the associated Legendre function
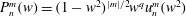 $P_{n}^{m}(w)=(1-w^{2})^{|m|/2}w^{q}u_{n}^{m}(w^{2})$
, where
$P_{n}^{m}(w)=(1-w^{2})^{|m|/2}w^{q}u_{n}^{m}(w^{2})$
, where
![]() $u_{n}^{m}(w^{2})$
is a polynomial in
$u_{n}^{m}(w^{2})$
is a polynomial in
![]() $w^{2}$
of degree
$w^{2}$
of degree
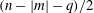 $(n-|m|-q)/2$
. Thus
$(n-|m|-q)/2$
. Thus
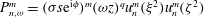 $P_{n,{\it\omega}}^{m}=({\it\sigma}s\text{e}^{\text{i}{\it\phi}})^{m}({\it\omega}z)^{q}u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
if
$P_{n,{\it\omega}}^{m}=({\it\sigma}s\text{e}^{\text{i}{\it\phi}})^{m}({\it\omega}z)^{q}u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
if
![]() $m\geqslant 0$
; and
$m\geqslant 0$
; and
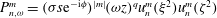 $P_{n,{\it\omega}}^{m}=({\it\sigma}s\text{e}^{-\text{i}{\it\phi}})^{|m|}({\it\omega}z)^{q}u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
if
$P_{n,{\it\omega}}^{m}=({\it\sigma}s\text{e}^{-\text{i}{\it\phi}})^{|m|}({\it\omega}z)^{q}u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
if
![]() $m<0$
. The result (4.5) follows, since the product
$m<0$
. The result (4.5) follows, since the product
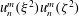 $u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
is a polynomial
$u_{n}^{m}({\it\xi}^{2})u_{n}^{m}({\it\zeta}^{2})$
is a polynomial
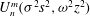 $U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2})$
in
$U_{n}^{m}({\it\sigma}^{2}s^{2},{\it\omega}^{2}z^{2})$
in
![]() $({\it\sigma}s)^{2}$
and
$({\it\sigma}s)^{2}$
and
![]() $({\it\omega}z)^{2}$
of degree
$({\it\omega}z)^{2}$
of degree
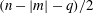 $(n-|m|-q)/2$
with coefficients independent of
$(n-|m|-q)/2$
with coefficients independent of
![]() ${\it\omega}$
and
${\it\omega}$
and
![]() ${\it\sigma}$
by the following lemma. Expressions (4.5) are polynomials in
${\it\sigma}$
by the following lemma. Expressions (4.5) are polynomials in
![]() $x,y,z$
since
$x,y,z$
since
 $s\text{e}^{\pm \text{i}{\it\phi}}=x\pm \text{i}y$
. The
$s\text{e}^{\pm \text{i}{\it\phi}}=x\pm \text{i}y$
. The
![]() $z$
-parity of
$z$
-parity of
![]() $P_{n,{\it\omega}}^{m}$
, which is not immediately apparent from
$P_{n,{\it\omega}}^{m}$
, which is not immediately apparent from
![]() ${\it\zeta}$
and
${\it\zeta}$
and
![]() ${\it\xi}$
, is determined by
${\it\xi}$
, is determined by
![]() $q$
.
$q$
.
Lemma 4.1. Let
 $s_{1}=\sqrt{1-{\it\zeta}^{2}}\sqrt{1-{\it\xi}^{2}}$
,
$s_{1}=\sqrt{1-{\it\zeta}^{2}}\sqrt{1-{\it\xi}^{2}}$
,
![]() $z_{1}={\it\xi}{\it\zeta}$
. If
$z_{1}={\it\xi}{\it\zeta}$
. If
![]() $p(w)$
is a polynomial of degree
$p(w)$
is a polynomial of degree
![]() $K$
, then
$K$
, then
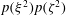 $p({\it\xi}^{2})p({\it\zeta}^{2})$
is a polynomial in
$p({\it\xi}^{2})p({\it\zeta}^{2})$
is a polynomial in
![]() $s_{1}^{2}$
and
$s_{1}^{2}$
and
![]() $z_{1}^{2}$
of degree
$z_{1}^{2}$
of degree
![]() $K$
.
$K$
.
Proof. Let
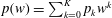 $p(w)=\sum _{k=0}^{K}p_{k}w^{k}$
, where the
$p(w)=\sum _{k=0}^{K}p_{k}w^{k}$
, where the
![]() $p_{k}$
are constants. Then
$p_{k}$
are constants. Then
 $$\begin{eqnarray}p({\it\xi}^{2})p({\it\zeta}^{2})=\mathop{\sum }_{k=0}^{K}\left\{p_{k}^{2}z_{1}^{2k}+\mathop{\sum }_{l=1}^{K-k}p_{k}p_{k+l}z_{1}^{2k}({\it\xi}^{2l}+{\it\zeta}^{2l})\right\}.\end{eqnarray}$$
$$\begin{eqnarray}p({\it\xi}^{2})p({\it\zeta}^{2})=\mathop{\sum }_{k=0}^{K}\left\{p_{k}^{2}z_{1}^{2k}+\mathop{\sum }_{l=1}^{K-k}p_{k}p_{k+l}z_{1}^{2k}({\it\xi}^{2l}+{\it\zeta}^{2l})\right\}.\end{eqnarray}$$
By rearranging the binomial expansion of
 $({\it\xi}^{2}+{\it\zeta}^{2})^{l}$
in the form,
$({\it\xi}^{2}+{\it\zeta}^{2})^{l}$
in the form,
 $$\begin{eqnarray}{\it\xi}^{2l}+{\it\zeta}^{2l}=({\it\xi}^{2}+{\it\zeta}^{2})^{l}-\mathop{\sum }_{j=1}^{\left\lfloor \frac{l-1}{2}\right\rfloor }~^{l}C_{j}({\it\xi}{\it\zeta})^{2j}({\it\xi}^{2(l-2j)}+{\it\zeta}^{2(l-2j)})\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}^{2l}+{\it\zeta}^{2l}=({\it\xi}^{2}+{\it\zeta}^{2})^{l}-\mathop{\sum }_{j=1}^{\left\lfloor \frac{l-1}{2}\right\rfloor }~^{l}C_{j}({\it\xi}{\it\zeta})^{2j}({\it\xi}^{2(l-2j)}+{\it\zeta}^{2(l-2j)})\end{eqnarray}$$
and using the identity
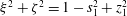 ${\it\xi}^{2}+{\it\zeta}^{2}=1-s_{1}^{2}+z_{1}^{2}$
, it follows by induction that
${\it\xi}^{2}+{\it\zeta}^{2}=1-s_{1}^{2}+z_{1}^{2}$
, it follows by induction that
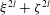 ${\it\xi}^{2l}+{\it\zeta}^{2l}$
is a polynomial in
${\it\xi}^{2l}+{\it\zeta}^{2l}$
is a polynomial in
![]() $s_{1}^{2}$
and
$s_{1}^{2}$
and
![]() $z_{1}^{2}$
of degree
$z_{1}^{2}$
of degree
![]() $l$
. Hence
$l$
. Hence
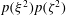 $p({\it\xi}^{2})p({\it\zeta}^{2})$
is a polynomial in
$p({\it\xi}^{2})p({\it\zeta}^{2})$
is a polynomial in
![]() $s_{1}^{2}$
and
$s_{1}^{2}$
and
![]() $z_{1}^{2}$
of degree
$z_{1}^{2}$
of degree
![]() $K$
.
$K$
.
The boundary
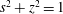 $s^{2}+z^{2}=1$
is given by
$s^{2}+z^{2}=1$
is given by
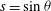 $s=\sin {\it\theta}$
and
$s=\sin {\it\theta}$
and
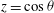 $z=\cos {\it\theta}$
, or in oblate spheroidal coordinates by
$z=\cos {\it\theta}$
, or in oblate spheroidal coordinates by
 ${\it\xi}=\cos {\it\theta}$
and
${\it\xi}=\cos {\it\theta}$
and
![]() ${\it\zeta}={\it\omega}$
. The boundary condition implies
${\it\zeta}={\it\omega}$
. The boundary condition implies
![]() ${\it\omega}$
is a root of
${\it\omega}$
is a root of
 $$\begin{eqnarray}(1-{\it\omega}^{2})\frac{\text{d}P_{n}^{m}({\it\omega})}{\text{d}{\it\omega}}+mP_{n}^{m}({\it\omega})=0.\end{eqnarray}$$
$$\begin{eqnarray}(1-{\it\omega}^{2})\frac{\text{d}P_{n}^{m}({\it\omega})}{\text{d}{\it\omega}}+mP_{n}^{m}({\it\omega})=0.\end{eqnarray}$$
Now
 $P_{n}^{m}({\it\omega})=(1-{\it\omega}^{2})^{|m|/2}p_{n}^{m}({\it\omega})$
, where
$P_{n}^{m}({\it\omega})=(1-{\it\omega}^{2})^{|m|/2}p_{n}^{m}({\it\omega})$
, where
![]() $p_{n}^{m}({\it\omega})$
is a polynomial in
$p_{n}^{m}({\it\omega})$
is a polynomial in
![]() ${\it\omega}$
of degree
${\it\omega}$
of degree
![]() $n-|m|$
. Moreover,
$n-|m|$
. Moreover,
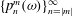 $\{p_{n}^{m}({\it\omega})\}_{n=|m|}^{\infty }$
form an orthogonal set of polynomials on
$\{p_{n}^{m}({\it\omega})\}_{n=|m|}^{\infty }$
form an orthogonal set of polynomials on
![]() $[-1,1]$
with weight function
$[-1,1]$
with weight function
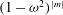 $(1-{\it\omega}^{2})^{|m|}$
even in
$(1-{\it\omega}^{2})^{|m|}$
even in
![]() ${\it\omega}$
, since
${\it\omega}$
, since
 $$\begin{eqnarray}\frac{1}{2}\int _{-1}^{1}P_{n}^{m}({\it\omega})P_{N}^{m}({\it\omega})\text{d}{\it\omega}={\it\delta}_{nN}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2}\int _{-1}^{1}P_{n}^{m}({\it\omega})P_{N}^{m}({\it\omega})\text{d}{\it\omega}={\it\delta}_{nN}.\end{eqnarray}$$
Thus
![]() $p_{n}^{m}({\it\omega})$
has
$p_{n}^{m}({\it\omega})$
has
![]() $n-|m|$
simple zeros
$n-|m|$
simple zeros
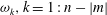 ${\it\omega}_{k},k=1:n-|m|$
, on
${\it\omega}_{k},k=1:n-|m|$
, on
![]() $(-1,1)$
symmetric about
$(-1,1)$
symmetric about
![]() ${\it\omega}=0$
and hence
${\it\omega}=0$
and hence
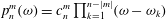 $p_{n}^{m}({\it\omega})=c_{n}^{m}\prod _{k=1}^{n-|m|}({\it\omega}-{\it\omega}_{k})$
, where
$p_{n}^{m}({\it\omega})=c_{n}^{m}\prod _{k=1}^{n-|m|}({\it\omega}-{\it\omega}_{k})$
, where
![]() $c_{n}^{m}$
is a constant. The frequency equation (3.4) can be written as
$c_{n}^{m}$
is a constant. The frequency equation (3.4) can be written as
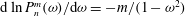 $\text{d}\ln P_{n}^{m}({\it\omega})/\text{d}{\it\omega}=-m/(1-{\it\omega}^{2})$
or
$\text{d}\ln P_{n}^{m}({\it\omega})/\text{d}{\it\omega}=-m/(1-{\it\omega}^{2})$
or
 $$\begin{eqnarray}\mathop{\sum }_{k=1}^{n-|m|}\frac{1}{{\it\omega}-{\it\omega}_{k}}=-\frac{{\textstyle \frac{1}{2}}(|m|+m)}{{\it\omega}+1}-\frac{{\textstyle \frac{1}{2}}(|m|-m)}{{\it\omega}-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=1}^{n-|m|}\frac{1}{{\it\omega}-{\it\omega}_{k}}=-\frac{{\textstyle \frac{1}{2}}(|m|+m)}{{\it\omega}+1}-\frac{{\textstyle \frac{1}{2}}(|m|-m)}{{\it\omega}-1}.\end{eqnarray}$$
For
![]() $m\neq 0$
this equation has
$m\neq 0$
this equation has
![]() $n-|m|$
zeros; for
$n-|m|$
zeros; for
![]() $m=0$
there are
$m=0$
there are
![]() $n-1$
zeros. Figure 1 shows the generic case for
$n-1$
zeros. Figure 1 shows the generic case for
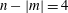 $n-|m|=4$
. The zeros are not symmetrically distributed about
$n-|m|=4$
. The zeros are not symmetrically distributed about
![]() ${\it\omega}=0$
. Geostrophic modes
${\it\omega}=0$
. Geostrophic modes
![]() ${\it\omega}=0$
occur if and only if
${\it\omega}=0$
occur if and only if
![]() $m=0$
and
$m=0$
and
![]() $n$
is even. There are no
$n$
is even. There are no
![]() $m=\pm n$
modes: in fact, the dispersion relation gives
$m=\pm n$
modes: in fact, the dispersion relation gives
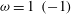 ${\it\omega}=1~(-1)$
for
${\it\omega}=1~(-1)$
for
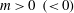 $m>0~({<}0)$
in these cases. Thus we label the non-zero frequencies for
$m>0~({<}0)$
in these cases. Thus we label the non-zero frequencies for
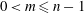 $0<m\leqslant n-1$
by
$0<m\leqslant n-1$
by
![]() ${\it\omega}_{n,j}^{m}$
, where
${\it\omega}_{n,j}^{m}$
, where
![]() $j\in \mathbb{Z}$
,
$j\in \mathbb{Z}$
,
![]() $j\neq 0$
and
$j\neq 0$
and
 $j=-(n-m+1)/2:(n-m-1)/2$
, if
$j=-(n-m+1)/2:(n-m-1)/2$
, if
![]() $n-m$
is odd, or
$n-m$
is odd, or
 $j=-(n-m)/2:(n-m)/2$
, if
$j=-(n-m)/2:(n-m)/2$
, if
![]() $n-m$
is even. The zero frequencies are
$n-m$
is even. The zero frequencies are
![]() ${\it\omega}_{n,0}^{0}$
, where
${\it\omega}_{n,0}^{0}$
, where
![]() $n$
is even,
$n$
is even,
![]() $m=0$
and
$m=0$
and
![]() $j=0$
. For
$j=0$
. For
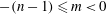 $-(n-1)\leqslant m<0$
,
$-(n-1)\leqslant m<0$
,
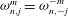 ${\it\omega}_{n,j}^{m}={\it\omega}_{n,-j}^{-m}$
. We define the associated inertial pressure mode for the non-zero frequency
${\it\omega}_{n,j}^{m}={\it\omega}_{n,-j}^{-m}$
. We define the associated inertial pressure mode for the non-zero frequency
![]() ${\it\omega}_{n,j}^{m}$
by
${\it\omega}_{n,j}^{m}$
by
 $$\begin{eqnarray}P_{n,j}^{m}:=P_{n,{\it\omega}_{n,j}^{m}}^{m}.\end{eqnarray}$$
$$\begin{eqnarray}P_{n,j}^{m}:=P_{n,{\it\omega}_{n,j}^{m}}^{m}.\end{eqnarray}$$
Note that
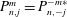 $P_{n,j}^{m}=P_{n,-j}^{-m\ast }$
. We construct the geostrophic modes in § 4.2.
$P_{n,j}^{m}=P_{n,-j}^{-m\ast }$
. We construct the geostrophic modes in § 4.2.

Figure 1. Schematic plot of the two sides of (5.6) for inertial frequencies
![]() ${\it\omega}$
with
${\it\omega}$
with
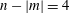 $n-|m|=4$
. The right-hand side curves are labelled by
$n-|m|=4$
. The right-hand side curves are labelled by
![]() $m>0$
and
$m>0$
and
![]() $m<0$
; the
$m<0$
; the
![]() $m=0$
curve is the
$m=0$
curve is the
![]() ${\it\omega}$
axis.
${\it\omega}$
axis.
The number of Coriolis pressure modes of degree
![]() $N+1$
or less, which equals the number of Coriolis velocity modes of degree
$N+1$
or less, which equals the number of Coriolis velocity modes of degree
![]() $N$
or less, is
$N$
or less, is
 $$\begin{eqnarray}C_{N}=\mathop{\sum }_{n=1}^{N+1}\mathop{\sum }_{m=-n}^{n}(n-|m|-{\it\delta}_{0}^{m})=\frac{1}{6}N(N+1)(2N+7).\end{eqnarray}$$
$$\begin{eqnarray}C_{N}=\mathop{\sum }_{n=1}^{N+1}\mathop{\sum }_{m=-n}^{n}(n-|m|-{\it\delta}_{0}^{m})=\frac{1}{6}N(N+1)(2N+7).\end{eqnarray}$$
For
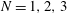 $N=1,2,3$
there are
$N=1,2,3$
there are
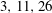 $3,11,26$
modes and for
$3,11,26$
modes and for
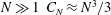 $N\gg 1~C_{N}\approx N^{3}/3$
. Greenspan (Reference Greenspan1968) counts
$N\gg 1~C_{N}\approx N^{3}/3$
. Greenspan (Reference Greenspan1968) counts
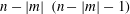 $n-|m|~(n-|m|-1)$
inertial modes if
$n-|m|~(n-|m|-1)$
inertial modes if
![]() $n-m$
is even (odd), in agreement with (4.12).
$n-m$
is even (odd), in agreement with (4.12).
4.2. Geostrophic pressure modes
We construct the geostrophic modes by taking the limit
![]() ${\it\omega}\rightarrow 0$
in the solutions (4.4). They are the natural choice, since they are hierarchical in polynomial degree. These geostrophic modes can also be constructed by applying Gram–Schmidt orthogonalisation with the inner product (1.11) to the polynomials
${\it\omega}\rightarrow 0$
in the solutions (4.4). They are the natural choice, since they are hierarchical in polynomial degree. These geostrophic modes can also be constructed by applying Gram–Schmidt orthogonalisation with the inner product (1.11) to the polynomials
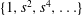 $\{1,s^{2},s^{4},\dots \}$
. See figure 2. Other geostrophic bases are possible.
$\{1,s^{2},s^{4},\dots \}$
. See figure 2. Other geostrophic bases are possible.
Lemma 4.2. For
![]() $m=0$
and
$m=0$
and
![]() ${\it\omega}\rightarrow 0$
the solutions (4.4) reduce to the geostrophic modes,
${\it\omega}\rightarrow 0$
the solutions (4.4) reduce to the geostrophic modes,
 $$\begin{eqnarray}P_{n,0}^{0}(s)=P_{n}(0)\,P_{n}(\sqrt{1-s^{2}})-[P_{n}(0)]^{2},\end{eqnarray}$$
$$\begin{eqnarray}P_{n,0}^{0}(s)=P_{n}(0)\,P_{n}(\sqrt{1-s^{2}})-[P_{n}(0)]^{2},\end{eqnarray}$$
where
![]() $n$
is even. Here,
$n$
is even. Here,
![]() $P_{n,0}^{0}(s)$
is a polynomial in
$P_{n,0}^{0}(s)$
is a polynomial in
![]() $s^{2}$
of even degree
$s^{2}$
of even degree
![]() $n$
in
$n$
in
![]() $s$
and
$s$
and
![]() $P_{n}$
is the Legendre polynomial of degree
$P_{n}$
is the Legendre polynomial of degree
![]() $n$
.
$n$
.
Proof. From (4.3)
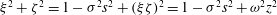 ${\it\xi}^{2}+{\it\zeta}^{2}=1-{\it\sigma}^{2}s^{2}+({\it\xi}{\it\zeta})^{2}=1-{\it\sigma}^{2}s^{2}+{\it\omega}^{2}z^{2}$
. Thus as
${\it\xi}^{2}+{\it\zeta}^{2}=1-{\it\sigma}^{2}s^{2}+({\it\xi}{\it\zeta})^{2}=1-{\it\sigma}^{2}s^{2}+{\it\omega}^{2}z^{2}$
. Thus as
![]() ${\it\omega}\rightarrow 0$
,
${\it\omega}\rightarrow 0$
,
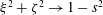 ${\it\xi}^{2}+{\it\zeta}^{2}\rightarrow 1-s^{2}$
and, by (4.7),
${\it\xi}^{2}+{\it\zeta}^{2}\rightarrow 1-s^{2}$
and, by (4.7),
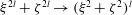 ${\it\xi}^{2l}+{\it\zeta}^{2l}\rightarrow ({\it\xi}^{2}+{\it\zeta}^{2})^{l}$
, since
${\it\xi}^{2l}+{\it\zeta}^{2l}\rightarrow ({\it\xi}^{2}+{\it\zeta}^{2})^{l}$
, since
![]() ${\it\sigma}\rightarrow 1$
and
${\it\sigma}\rightarrow 1$
and
 $({\it\xi}{\it\zeta})^{2}={\it\omega}^{2}z^{2}\rightarrow 0$
. If
$({\it\xi}{\it\zeta})^{2}={\it\omega}^{2}z^{2}\rightarrow 0$
. If
![]() $n$
is even,
$n$
is even,
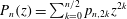 $P_{n}(z)=\sum _{k=0}^{n/2}p_{n,2k}z^{2k}$
, where the
$P_{n}(z)=\sum _{k=0}^{n/2}p_{n,2k}z^{2k}$
, where the
![]() $p_{n,2k}$
are constants, and
$p_{n,2k}$
are constants, and
 $$\begin{eqnarray}P_{n}({\it\xi})\,P_{n}({\it\zeta})=p_{n,0}\left[\mathop{\sum }_{k=0}^{n/2}p_{n,2k}({\it\xi}^{2k}+{\it\zeta}^{2k})-p_{n,0}\right]+\mathop{\sum }_{k=1}^{n/2}\mathop{\sum }_{l=1}^{n/2}p_{n,2k}p_{l,2k}{\it\xi}^{2k}{\it\zeta}^{2l}.\end{eqnarray}$$
$$\begin{eqnarray}P_{n}({\it\xi})\,P_{n}({\it\zeta})=p_{n,0}\left[\mathop{\sum }_{k=0}^{n/2}p_{n,2k}({\it\xi}^{2k}+{\it\zeta}^{2k})-p_{n,0}\right]+\mathop{\sum }_{k=1}^{n/2}\mathop{\sum }_{l=1}^{n/2}p_{n,2k}p_{l,2k}{\it\xi}^{2k}{\it\zeta}^{2l}.\end{eqnarray}$$
The double sum is
![]() $O({\it\xi}{\it\zeta})^{2}$
. Thus, for
$O({\it\xi}{\it\zeta})^{2}$
. Thus, for
![]() $n$
even,
$n$
even,
 $P_{n}({\it\xi})\,P_{n}({\it\zeta})\rightarrow P_{n,0}^{0}$
in (4.13) as
$P_{n}({\it\xi})\,P_{n}({\it\zeta})\rightarrow P_{n,0}^{0}$
in (4.13) as
![]() ${\it\omega}\rightarrow 0$
, since
${\it\omega}\rightarrow 0$
, since
 $p_{n,0}=P_{n}(0)$
. If
$p_{n,0}=P_{n}(0)$
. If
![]() $n$
is odd,
$n$
is odd,
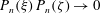 $P_{n}({\it\xi})\,P_{n}({\it\zeta})\rightarrow 0$
as
$P_{n}({\it\xi})\,P_{n}({\it\zeta})\rightarrow 0$
as
![]() ${\it\omega}\rightarrow 0$
.
${\it\omega}\rightarrow 0$
.
Linearly independent Coriolis modes of the same frequency may be non-orthogonal. The modes (4.13) are orthogonal: evaluating the inner product
![]() $(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
of two modes using (3.21), noting
$(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
of two modes using (3.21), noting
![]() $n_{1}$
and
$n_{1}$
and
![]() $n_{2}$
are even and substituting
$n_{2}$
are even and substituting
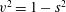 $v^{2}=1-s^{2}$
yields, apart from the factor
$v^{2}=1-s^{2}$
yields, apart from the factor
 $P_{n_{1}}(0)P_{n_{2}}(0)$
,
$P_{n_{1}}(0)P_{n_{2}}(0)$
,
 $$\begin{eqnarray}\int _{V}\boldsymbol{{\rm\nabla}}P_{n_{1}}(\sqrt{1-s^{2}})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{n_{2}}(\sqrt{1-s^{2}})\text{d}V=2{\rm\pi}\int _{-1}^{1}P_{n_{1}}^{\prime }(v)(1-v^{2})P_{n_{2}}^{\prime }(v)\text{d}v.\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}\boldsymbol{{\rm\nabla}}P_{n_{1}}(\sqrt{1-s^{2}})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{n_{2}}(\sqrt{1-s^{2}})\text{d}V=2{\rm\pi}\int _{-1}^{1}P_{n_{1}}^{\prime }(v)(1-v^{2})P_{n_{2}}^{\prime }(v)\text{d}v.\end{eqnarray}$$
An integration by parts and Legendre’s differential equation shows the last integral vanishes if
![]() $n_{1}\neq n_{2}$
.
$n_{1}\neq n_{2}$
.

Figure 2. The geostrophic modes
![]() $P_{n,0}^{0}$
as a function of cylindrical radius
$P_{n,0}^{0}$
as a function of cylindrical radius
![]() $s$
for
$s$
for
 $n=2,4,6,8,10$
.
$n=2,4,6,8,10$
.
4.3. Velocity modes
The velocity modes are constructed from the pressure modes using (3.17). Thus associated with the pressure mode
![]() $P_{n+1,j}^{m}$
is the velocity mode
$P_{n+1,j}^{m}$
is the velocity mode
![]() $\boldsymbol{v}_{n,j}^{m}$
. Define
$\boldsymbol{v}_{n,j}^{m}$
. Define
 $$\begin{eqnarray}\boldsymbol{v}_{n}^{m}({\it\omega}):=\left\{\begin{array}{@{}l@{}}\displaystyle \frac{\text{i}{\it\omega}}{1-{\it\omega}^{2}}(\boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m}-{\it\omega}^{-2}\widehat{{\it\bf\Omega}}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m})+\frac{1}{1-{\it\omega}^{2}}\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m},\quad {\it\omega}\neq 0;\quad \\ \widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P_{n+1,0}^{0},\quad {\it\omega}=0,m=0,n\text{ odd}.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{n}^{m}({\it\omega}):=\left\{\begin{array}{@{}l@{}}\displaystyle \frac{\text{i}{\it\omega}}{1-{\it\omega}^{2}}(\boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m}-{\it\omega}^{-2}\widehat{{\it\bf\Omega}}\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m})+\frac{1}{1-{\it\omega}^{2}}\widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P_{n+1,{\it\omega}}^{m},\quad {\it\omega}\neq 0;\quad \\ \widehat{{\it\bf\Omega}}\times \boldsymbol{{\rm\nabla}}P_{n+1,0}^{0},\quad {\it\omega}=0,m=0,n\text{ odd}.\quad \end{array}\right.\end{eqnarray}$$
The Coriolis velocity modes are thus
 $$\begin{eqnarray}\boldsymbol{v}_{n,j}^{m}:=N_{n,j}^{m}\boldsymbol{v}_{n}^{m}({\it\omega}_{n+1,j}^{m}),\quad |m|\leqslant n,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{n,j}^{m}:=N_{n,j}^{m}\boldsymbol{v}_{n}^{m}({\it\omega}_{n+1,j}^{m}),\quad |m|\leqslant n,\end{eqnarray}$$
where
 $j=-(n-m+1)/2:(n-m-1)/2$
if
$j=-(n-m+1)/2:(n-m-1)/2$
if
![]() $n-m$
is odd,
$n-m$
is odd,
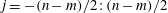 $j=-(n-m)/2:(n-m)/2$
if
$j=-(n-m)/2:(n-m)/2$
if
![]() $n-m$
is even, and
$n-m$
is even, and
![]() $j\neq 0$
unless
$j\neq 0$
unless
![]() $m=0$
and
$m=0$
and
![]() $n$
is odd. The normalisation constant
$n$
is odd. The normalisation constant
![]() $N_{n,j}^{m}>0$
is chosen so that the mode is normalised to
$N_{n,j}^{m}>0$
is chosen so that the mode is normalised to
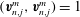 $(\boldsymbol{v}_{n,j}^{m},\boldsymbol{v}_{n,j}^{m})=1$
. The complex conjugate
$(\boldsymbol{v}_{n,j}^{m},\boldsymbol{v}_{n,j}^{m})=1$
. The complex conjugate
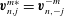 $\boldsymbol{v}_{n,j}^{m\ast }=\boldsymbol{v}_{n,-j}^{-m}$
. No modes
$\boldsymbol{v}_{n,j}^{m\ast }=\boldsymbol{v}_{n,-j}^{-m}$
. No modes
![]() $\boldsymbol{v}_{n,{\it\omega}}^{m}$
arise from
$\boldsymbol{v}_{n,{\it\omega}}^{m}$
arise from
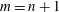 $m=n+1$
, i.e.
$m=n+1$
, i.e.
![]() $P_{n+1}^{\pm (n+1)}$
. For
$P_{n+1}^{\pm (n+1)}$
. For
![]() $m\neq 0$
the associated inertial waves propagate eastward (westward) if
$m\neq 0$
the associated inertial waves propagate eastward (westward) if
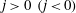 $j>0~(j<0)$
. Equatorial symmetries are determined by
$j>0~(j<0)$
. Equatorial symmetries are determined by
![]() $n-m$
: the velocity modes are quadrupole symmetric if
$n-m$
: the velocity modes are quadrupole symmetric if
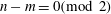 $n-m=0(\text{mod}~2)$
and dipole symmetric if
$n-m=0(\text{mod}~2)$
and dipole symmetric if
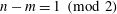 $n-m=1~(\text{mod}~2)$
; and rotational symmetries about
$n-m=1~(\text{mod}~2)$
; and rotational symmetries about
![]() $\widehat{{\it\bf\Omega}}$
are determined by
$\widehat{{\it\bf\Omega}}$
are determined by
![]() $m$
. The velocities of the geostrophic modes (4.13) agree with Liao & Zhang (Reference Liao and Zhang2010a
) up to normalisation and phase: in terms of Jacobi polynomials their
$m$
. The velocities of the geostrophic modes (4.13) agree with Liao & Zhang (Reference Liao and Zhang2010a
) up to normalisation and phase: in terms of Jacobi polynomials their
![]() ${\it\phi}$
-components can be written as
${\it\phi}$
-components can be written as
 $$\begin{eqnarray}v_{2n-1,0}^{0}=N_{2n-1,0}^{0}\frac{\text{d}P_{2n,0}^{0}(s)}{\text{d}s}=N_{2n-1,0}^{0}(-)^{n}(2n+1)P_{2n}(0)sP_{n}^{(1/2,1)}(2s^{2}-1).\end{eqnarray}$$
$$\begin{eqnarray}v_{2n-1,0}^{0}=N_{2n-1,0}^{0}\frac{\text{d}P_{2n,0}^{0}(s)}{\text{d}s}=N_{2n-1,0}^{0}(-)^{n}(2n+1)P_{2n}(0)sP_{n}^{(1/2,1)}(2s^{2}-1).\end{eqnarray}$$
Below we label the Coriolis modes using a 3-index Greek letter, e.g.
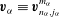 $\boldsymbol{v}_{{\it\alpha}}\equiv \boldsymbol{v}_{n_{{\it\alpha}},j_{{\it\alpha}}}^{m_{{\it\alpha}}}$
, and denote the degree of the polynomial flow
$\boldsymbol{v}_{{\it\alpha}}\equiv \boldsymbol{v}_{n_{{\it\alpha}},j_{{\it\alpha}}}^{m_{{\it\alpha}}}$
, and denote the degree of the polynomial flow
![]() $\boldsymbol{v}_{{\it\alpha}}$
by
$\boldsymbol{v}_{{\it\alpha}}$
by
![]() $\deg {\it\alpha}$
.
$\deg {\it\alpha}$
.
5. Polynomial flows in a sphere
Let
![]() ${\mathcal{P}}_{N}$
be the space of polynomials in
${\mathcal{P}}_{N}$
be the space of polynomials in
![]() $(x,y,z)$
of degree
$(x,y,z)$
of degree
![]() $N$
or less with complex coefficients. The space
$N$
or less with complex coefficients. The space
![]() ${\mathcal{P}}_{N}^{3}$
of polynomial vectors in
${\mathcal{P}}_{N}^{3}$
of polynomial vectors in
![]() $(x,y,z)$
of degree
$(x,y,z)$
of degree
![]() $N$
or less with complex coefficients has finite dimension
$N$
or less with complex coefficients has finite dimension
 $$\begin{eqnarray}\dim \,{\mathcal{P}}_{N}^{3}=3\mathop{\sum }_{0\leqslant i+j+k\leqslant N}1=\frac{1}{2}(N+1)(N+2)(N+3).\end{eqnarray}$$
$$\begin{eqnarray}\dim \,{\mathcal{P}}_{N}^{3}=3\mathop{\sum }_{0\leqslant i+j+k\leqslant N}1=\frac{1}{2}(N+1)(N+2)(N+3).\end{eqnarray}$$
We define the space of (inviscid) complex polynomial flows of degree
![]() $N$
on
$N$
on
![]() $V$
,
$V$
,
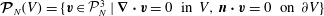 $\boldsymbol{{\mathcal{P}}}_{N}(V)=\{\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\,\text{ in}~V,\,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0\,\text{ on}~\partial V\}$
with inner product (1.11). It is not immediately obvious, due to the boundary condition (1.5), that
$\boldsymbol{{\mathcal{P}}}_{N}(V)=\{\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\,\text{ in}~V,\,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{v}=0\,\text{ on}~\partial V\}$
with inner product (1.11). It is not immediately obvious, due to the boundary condition (1.5), that
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
contains non-zero flows; for a sphere
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
contains non-zero flows; for a sphere
![]() $\boldsymbol{n}$
is a polynomial. We now show that, if
$\boldsymbol{n}$
is a polynomial. We now show that, if
![]() $V$
is a sphere, the dimension of
$V$
is a sphere, the dimension of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
is
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
is
![]() $C_{N}$
given by (4.12), the number of Coriolis modes of degree
$C_{N}$
given by (4.12), the number of Coriolis modes of degree
![]() $N$
or less. Since
$N$
or less. Since
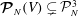 $\boldsymbol{{\mathcal{P}}}_{N}(V)\subsetneq {\mathcal{P}}_{N}^{3}$
,
$\boldsymbol{{\mathcal{P}}}_{N}(V)\subsetneq {\mathcal{P}}_{N}^{3}$
,
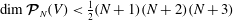 $\dim \boldsymbol{{\mathcal{P}}}_{N}(V)<{\textstyle \frac{1}{2}}(N+1)(N+2)(N+3)$
.
$\dim \boldsymbol{{\mathcal{P}}}_{N}(V)<{\textstyle \frac{1}{2}}(N+1)(N+2)(N+3)$
.
Constructing or even enumerating a basis of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
from linear combinations of the power basis
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
from linear combinations of the power basis
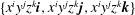 $\{x^{i}y^{j}z^{k}\boldsymbol{i},x^{i}y^{j}z^{k}\boldsymbol{j},x^{i}y^{j}z^{k}\boldsymbol{k}\}$
,
$\{x^{i}y^{j}z^{k}\boldsymbol{i},x^{i}y^{j}z^{k}\boldsymbol{j},x^{i}y^{j}z^{k}\boldsymbol{k}\}$
,
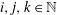 $i,j,k\in \mathbb{N}$
and
$i,j,k\in \mathbb{N}$
and
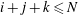 $i+j+k\leqslant N$
, of
$i+j+k\leqslant N$
, of
![]() ${\mathcal{P}}_{N}^{3}$
is difficult due to the solenoidal condition and particularly the boundary condition (1.5). It is much simpler to construct a basis for
${\mathcal{P}}_{N}^{3}$
is difficult due to the solenoidal condition and particularly the boundary condition (1.5). It is much simpler to construct a basis for
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
using spherical toroidal and poloidal fields: if
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
using spherical toroidal and poloidal fields: if
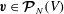 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
then
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
then
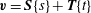 $\boldsymbol{v}=\boldsymbol{S}\{s\}+\boldsymbol{T}\{t\}$
, where
$\boldsymbol{v}=\boldsymbol{S}\{s\}+\boldsymbol{T}\{t\}$
, where
 $$\begin{eqnarray}\boldsymbol{T}\{t\}:=\boldsymbol{{\rm\nabla}}\times t\boldsymbol{r},\quad \boldsymbol{S}\{s\}:=\boldsymbol{{\rm\nabla}}\times \boldsymbol{T}\{s\},\quad \oint t\text{d}{\it\Omega}=0,\quad \oint s\text{d}{\it\Omega}=0,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}\{t\}:=\boldsymbol{{\rm\nabla}}\times t\boldsymbol{r},\quad \boldsymbol{S}\{s\}:=\boldsymbol{{\rm\nabla}}\times \boldsymbol{T}\{s\},\quad \oint t\text{d}{\it\Omega}=0,\quad \oint s\text{d}{\it\Omega}=0,\end{eqnarray}$$
with
![]() $t\in {\mathcal{P}}_{N}$
,
$t\in {\mathcal{P}}_{N}$
,
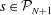 $s\in {\mathcal{P}}_{N+1}$
and
$s\in {\mathcal{P}}_{N+1}$
and
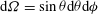 $\text{d}{\it\Omega}=\sin {\it\theta}\text{d}{\it\theta}\text{d}{\it\phi}$
the element of solid angle, and conversely if
$\text{d}{\it\Omega}=\sin {\it\theta}\text{d}{\it\theta}\text{d}{\it\phi}$
the element of solid angle, and conversely if
![]() $t\in {\mathcal{P}}_{N}$
,
$t\in {\mathcal{P}}_{N}$
,
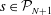 $s\in {\mathcal{P}}_{N+1}$
then
$s\in {\mathcal{P}}_{N+1}$
then
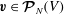 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Note that
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Note that
![]() $t$
and
$t$
and
![]() $s$
are not the time nor the cylindrical radius in this section. The boundary condition (1.5) is equivalent to
$s$
are not the time nor the cylindrical radius in this section. The boundary condition (1.5) is equivalent to
![]() $s=0$
on
$s=0$
on
![]() $r=1$
. Indeed, the Cartesian component of
$r=1$
. Indeed, the Cartesian component of
![]() $\boldsymbol{v}$
in the direction of a constant vector
$\boldsymbol{v}$
in the direction of a constant vector
![]() $\boldsymbol{c}$
is
$\boldsymbol{c}$
is
 $\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{v}=-(\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{r}){\rm\nabla}^{2}s+\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}s)-\boldsymbol{c}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}t$
. Thus, if
$\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{v}=-(\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{r}){\rm\nabla}^{2}s+\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}s)-\boldsymbol{c}\times \boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}t$
. Thus, if
![]() $t\in {\mathcal{P}}_{N}$
and
$t\in {\mathcal{P}}_{N}$
and
 $s\in {\mathcal{P}}_{N+1}$
, then
$s\in {\mathcal{P}}_{N+1}$
, then
![]() $\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}$
. Conversely, if
$\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}$
. Conversely, if
![]() $\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}$
, then
$\boldsymbol{v}\in {\mathcal{P}}_{N}^{3}$
, then
![]() $t\in {\mathcal{P}}_{N}$
and
$t\in {\mathcal{P}}_{N}$
and
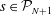 $s\in {\mathcal{P}}_{N+1}$
, since for any spherical harmonic
$s\in {\mathcal{P}}_{N+1}$
, since for any spherical harmonic
![]() $Y_{n}^{m}$
of degree
$Y_{n}^{m}$
of degree
![]() $n\geqslant 1$
and order
$n\geqslant 1$
and order
![]() $m$
,
$m$
,
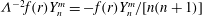 ${\it\Lambda}^{-2}f(r)Y_{n}^{m}=-f(r)Y_{n}^{m}/[n(n+1)]$
for any radial function
${\it\Lambda}^{-2}f(r)Y_{n}^{m}=-f(r)Y_{n}^{m}/[n(n+1)]$
for any radial function
![]() $f(r)$
, where
$f(r)$
, where
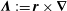 ${\it\bf\Lambda}:=\boldsymbol{r}\times \boldsymbol{{\rm\nabla}}$
.
${\it\bf\Lambda}:=\boldsymbol{r}\times \boldsymbol{{\rm\nabla}}$
.
To construct a polynomial toroidal–poloidal basis of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
and for the theorems in § 6, we need the spherical harmonic expansion of a polynomial
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
and for the theorems in § 6, we need the spherical harmonic expansion of a polynomial
![]() $f\in {\mathcal{P}}_{N}$
(see MacRobert Reference MacRobert1947, p. 140),
$f\in {\mathcal{P}}_{N}$
(see MacRobert Reference MacRobert1947, p. 140),
 $$\begin{eqnarray}f=\mathop{\sum }_{n=0}^{N}\!\vphantom{\sum }^{\prime }\mathop{\sum }_{p=n}^{N}\mathop{\sum }_{m=-n}^{n}f_{n,p}^{m}r^{p}Y_{n}^{m}({\it\theta},{\it\phi})\end{eqnarray}$$
$$\begin{eqnarray}f=\mathop{\sum }_{n=0}^{N}\!\vphantom{\sum }^{\prime }\mathop{\sum }_{p=n}^{N}\mathop{\sum }_{m=-n}^{n}f_{n,p}^{m}r^{p}Y_{n}^{m}({\it\theta},{\it\phi})\end{eqnarray}$$
where the
![]() $f_{n,p}^{m}$
are constant and the prime on the
$f_{n,p}^{m}$
are constant and the prime on the
![]() $p$
-sum indicates summation over
$p$
-sum indicates summation over
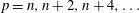 $p=n,n+2,n+4,\dots \,$
. The polynomial
$p=n,n+2,n+4,\dots \,$
. The polynomial
![]() $f$
is not necessarily harmonic. Thus, noting (5.2), the potentials
$f$
is not necessarily harmonic. Thus, noting (5.2), the potentials
![]() $t\in {\mathcal{P}}_{N}$
and
$t\in {\mathcal{P}}_{N}$
and
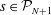 $s\in {\mathcal{P}}_{N+1}$
have spherical harmonic expansions of the form
$s\in {\mathcal{P}}_{N+1}$
have spherical harmonic expansions of the form
 $$\begin{eqnarray}\displaystyle & \displaystyle t=\mathop{\sum }_{n=1}^{N}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N-n)\right\rfloor }t_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle t=\mathop{\sum }_{n=1}^{N}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N-n)\right\rfloor }t_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle s=\mathop{\sum }_{n=1}^{N+1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor }\tilde{s}_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle s=\mathop{\sum }_{n=1}^{N+1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor }\tilde{s}_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}=\mathop{\sum }_{n=1}^{N}\mathop{\sum }_{m=-n}^{n}\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N-n)\right\rfloor }1=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{6}}N(N^{2}+6N+8),\quad & N\text{ even};\\ {\textstyle \frac{1}{6}}(N+1)(N^{2}+5N+3),\quad & N\text{ odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}=\mathop{\sum }_{n=1}^{N}\mathop{\sum }_{m=-n}^{n}\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N-n)\right\rfloor }1=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{6}}N(N^{2}+6N+8),\quad & N\text{ even};\\ {\textstyle \frac{1}{6}}(N+1)(N^{2}+5N+3),\quad & N\text{ odd}.\end{array}\right.\end{eqnarray}$$
The boundary condition (1.5) must still be imposed on the poloidal flows: on
![]() $r=1$
,
$r=1$
,
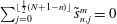 $\sum _{j=0}^{\lfloor \frac{1}{2}(N+1-n)\rfloor }\tilde{s}_{n,j}^{m}=0$
. Elimination of
$\sum _{j=0}^{\lfloor \frac{1}{2}(N+1-n)\rfloor }\tilde{s}_{n,j}^{m}=0$
. Elimination of
![]() $\tilde{s}_{n,0}^{m}$
gives
$\tilde{s}_{n,0}^{m}$
gives
 $$\begin{eqnarray}s=\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=1}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor }\tilde{s}_{n,j}^{m}(r^{2j}-1)\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}s=\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=1}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor }\tilde{s}_{n,j}^{m}(r^{2j}-1)\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
from which it is clear that
![]() $1-r^{2}$
is a factor of
$1-r^{2}$
is a factor of
![]() $s$
. Hence we can write
$s$
. Hence we can write
 $$\begin{eqnarray}s=(1-r^{2})\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor -1}s_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}s=(1-r^{2})\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\left(\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor -1}s_{n,j}^{m}r^{2j}\right)r^{n}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
where the new coefficients
![]() $s_{n,j}^{m}$
are independent. Thus the dimension of the poloidal subspace
$s_{n,j}^{m}$
are independent. Thus the dimension of the poloidal subspace
![]() $\boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}$
of
$\boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}$
of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
is
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
is
 $$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}=\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor -1}1=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{6}}N(N^{2}+3N-1),\quad & N\text{ even};\\ {\textstyle \frac{1}{6}}(N-1)(N+1)(N+3),\quad & N\text{ odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}=\mathop{\sum }_{n=1}^{N-1}\mathop{\sum }_{m=-n}^{n}\mathop{\sum }_{j=0}^{\left\lfloor \frac{1}{2}(N+1-n)\right\rfloor -1}1=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{6}}N(N^{2}+3N-1),\quad & N\text{ even};\\ {\textstyle \frac{1}{6}}(N-1)(N+1)(N+3),\quad & N\text{ odd}.\end{array}\right.\end{eqnarray}$$
Finally,
 $$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}(V)=\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}(V)+\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}(V)={\textstyle \frac{1}{6}}N(N+1)(2N+7)=C_{N},\end{eqnarray}$$
$$\begin{eqnarray}\dim \boldsymbol{{\mathcal{P}}}_{N}(V)=\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}(V)+\dim \boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}(V)={\textstyle \frac{1}{6}}N(N+1)(2N+7)=C_{N},\end{eqnarray}$$
i.e. the dimension of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
equals the number of Coriolis velocity modes of degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
equals the number of Coriolis velocity modes of degree
![]() $N$
or less as in (4.12). If
$N$
or less as in (4.12). If
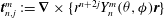 $\boldsymbol{t}_{n,j}^{m}:=\boldsymbol{{\rm\nabla}}\times \{r^{n+2j}Y_{n}^{m}({\it\theta},{\it\phi})\boldsymbol{r}\}$
, then
$\boldsymbol{t}_{n,j}^{m}:=\boldsymbol{{\rm\nabla}}\times \{r^{n+2j}Y_{n}^{m}({\it\theta},{\it\phi})\boldsymbol{r}\}$
, then
![]() $\{\boldsymbol{t}_{n,j}^{m}\}$
, where
$\{\boldsymbol{t}_{n,j}^{m}\}$
, where
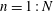 $n=1:N$
,
$n=1:N$
,
![]() $|m|\leqslant n$
,
$|m|\leqslant n$
,
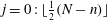 $j=0:\lfloor {\textstyle \frac{1}{2}}(N-n)\rfloor$
, is a basis of
$j=0:\lfloor {\textstyle \frac{1}{2}}(N-n)\rfloor$
, is a basis of
![]() $\boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}(V)$
. Similarly, if
$\boldsymbol{{\mathcal{P}}}_{N}^{\text{T}}(V)$
. Similarly, if
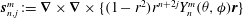 $\boldsymbol{s}_{n,j}^{m}:=\boldsymbol{{\rm\nabla}}\times \boldsymbol{{\rm\nabla}}\times \{(1-r^{2})r^{n+2j}Y_{n}^{m}({\it\theta},{\it\phi})\boldsymbol{r}\}$
, then
$\boldsymbol{s}_{n,j}^{m}:=\boldsymbol{{\rm\nabla}}\times \boldsymbol{{\rm\nabla}}\times \{(1-r^{2})r^{n+2j}Y_{n}^{m}({\it\theta},{\it\phi})\boldsymbol{r}\}$
, then
![]() $\{\boldsymbol{s}_{n,j}^{m}\}$
for
$\{\boldsymbol{s}_{n,j}^{m}\}$
for
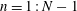 $n=1:N-1$
,
$n=1:N-1$
,
![]() $|m|\leqslant n$
,
$|m|\leqslant n$
,
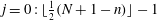 $j=0:\lfloor {\textstyle \frac{1}{2}}(N+1-n)\rfloor -1$
is a basis of
$j=0:\lfloor {\textstyle \frac{1}{2}}(N+1-n)\rfloor -1$
is a basis of
![]() $\boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}(V)$
.
$\boldsymbol{{\mathcal{P}}}_{N}^{\text{P}}(V)$
.
6. The Coriolis operator on polynomial flows in a sphere
If the Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
is restricted to act on polynomial flows
$\boldsymbol{{\mathcal{C}}}$
is restricted to act on polynomial flows
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
of degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
of degree
![]() $N$
or less, it is not true that
$N$
or less, it is not true that
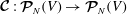 $\boldsymbol{{\mathcal{C}}}:\boldsymbol{{\mathcal{P}}}_{N}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
for any
$\boldsymbol{{\mathcal{C}}}:\boldsymbol{{\mathcal{P}}}_{N}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
for any
![]() $V$
, i.e. that it produces only polynomial flows of degree
$V$
, i.e. that it produces only polynomial flows of degree
![]() $N$
or less. However, if
$N$
or less. However, if
![]() $V$
is a sphere the restricted Coriolis operator
$V$
is a sphere the restricted Coriolis operator
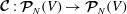 $\boldsymbol{{\mathcal{C}}}:\boldsymbol{{\mathcal{P}}}_{N}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
is well defined, i.e.
$\boldsymbol{{\mathcal{C}}}:\boldsymbol{{\mathcal{P}}}_{N}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
is well defined, i.e.
![]() $\boldsymbol{{\mathcal{C}}}$
maps polynomial flows to polynomial flows of the same degree. This is the essential result of the paper, Theorem 6.3, and follows from the fundamental tool, Theorem 6.2.
$\boldsymbol{{\mathcal{C}}}$
maps polynomial flows to polynomial flows of the same degree. This is the essential result of the paper, Theorem 6.3, and follows from the fundamental tool, Theorem 6.2.
Theorem 6.1 (Polynomial Laplace–Neumann Problem in a Sphere).
There exists a unique solution
![]() ${\it\varphi}$
of Laplace’s equation
${\it\varphi}$
of Laplace’s equation
 ${\rm\nabla}^{2}{\it\varphi}=0$
in the sphere
${\rm\nabla}^{2}{\it\varphi}=0$
in the sphere
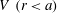 $V~(r<a)$
, subject to
$V~(r<a)$
, subject to
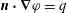 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
on
![]() $\partial V$
, where
$\partial V$
, where
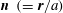 $\boldsymbol{n}~(=\,\boldsymbol{r}/a)$
is a linear polynomial and
$\boldsymbol{n}~(=\,\boldsymbol{r}/a)$
is a linear polynomial and
![]() $q\in {\mathcal{P}}_{N_{1}}$
, and to the respective uniqueness and consistency conditions,
$q\in {\mathcal{P}}_{N_{1}}$
, and to the respective uniqueness and consistency conditions,
 $$\begin{eqnarray}\int _{V}{\it\varphi}\text{d}V=0,\quad \int _{\partial V}q\text{d}S=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}{\it\varphi}\text{d}V=0,\quad \int _{\partial V}q\text{d}S=0,\end{eqnarray}$$
and
![]() ${\it\varphi}\in {\mathcal{P}}_{N_{1}}$
.
${\it\varphi}\in {\mathcal{P}}_{N_{1}}$
.
Proof. Since
![]() $\boldsymbol{n}=\boldsymbol{r}/a$
,
$\boldsymbol{n}=\boldsymbol{r}/a$
,
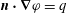 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
reduces to
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
reduces to
![]() $\partial _{r}{\it\varphi}=q$
on
$\partial _{r}{\it\varphi}=q$
on
![]() $r=a$
. On
$r=a$
. On
![]() $r=a$
,
$r=a$
,
 $\partial _{r}{\it\varphi}=\sum _{n=1}^{N_{1}}\sum _{m=-n}^{n}q_{n}^{m}Y_{n}^{m}({\it\theta},{\it\phi})$
, since
$\partial _{r}{\it\varphi}=\sum _{n=1}^{N_{1}}\sum _{m=-n}^{n}q_{n}^{m}Y_{n}^{m}({\it\theta},{\it\phi})$
, since
![]() $q\in {\mathcal{P}}_{N_{1}}$
. The general solution of
$q\in {\mathcal{P}}_{N_{1}}$
. The general solution of
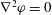 ${\rm\nabla}^{2}{\it\varphi}=0$
is
${\rm\nabla}^{2}{\it\varphi}=0$
is
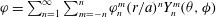 ${\it\varphi}=\sum _{n=1}^{\infty }\sum _{m=-n}^{n}{\it\varphi}_{n}^{m}(r/a)^{n}Y_{n}^{m}({\it\theta},{\it\phi})$
. Thus
${\it\varphi}=\sum _{n=1}^{\infty }\sum _{m=-n}^{n}{\it\varphi}_{n}^{m}(r/a)^{n}Y_{n}^{m}({\it\theta},{\it\phi})$
. Thus
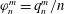 ${\it\varphi}_{n}^{m}=q_{n}^{m}/n$
for
${\it\varphi}_{n}^{m}=q_{n}^{m}/n$
for
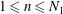 $1\leqslant n\leqslant N_{1}$
and
$1\leqslant n\leqslant N_{1}$
and
![]() ${\it\varphi}_{n}^{m}=0$
for
${\it\varphi}_{n}^{m}=0$
for
![]() $n>N_{1}$
, i.e.
$n>N_{1}$
, i.e.
![]() ${\it\varphi}\in {\mathcal{P}}_{N_{1}}$
.
${\it\varphi}\in {\mathcal{P}}_{N_{1}}$
.
Lemma 6.1 (Polynomial Integral of the Polynomial Poisson–Neumann Problem in
 $E^{3}$
).
$E^{3}$
).
If
![]() $f\in {\mathcal{P}}_{N_{2}}$
, then there exists a solution
$f\in {\mathcal{P}}_{N_{2}}$
, then there exists a solution
![]() ${\it\varphi}_{p}$
of Poisson’s equation
${\it\varphi}_{p}$
of Poisson’s equation
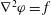 ${\rm\nabla}^{2}{\it\varphi}=f$
with
${\rm\nabla}^{2}{\it\varphi}=f$
with
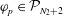 ${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
in
${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
in
![]() $E^{3}$
.
$E^{3}$
.
Proof. Since
![]() $f\in {\mathcal{P}}_{N_{2}}$
, it can be expanded in spherical harmonics as in (5.3). Define
$f\in {\mathcal{P}}_{N_{2}}$
, it can be expanded in spherical harmonics as in (5.3). Define
 $$\begin{eqnarray}{\it\varphi}_{p}:=\mathop{\sum }_{n=0}^{N_{2}}\!\vphantom{\sum }^{\prime }\mathop{\sum }_{p=n}^{N_{2}}\mathop{\sum }_{m=-n}^{n}{\it\varphi}_{n,p}^{m}r^{p+2}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{p}:=\mathop{\sum }_{n=0}^{N_{2}}\!\vphantom{\sum }^{\prime }\mathop{\sum }_{p=n}^{N_{2}}\mathop{\sum }_{m=-n}^{n}{\it\varphi}_{n,p}^{m}r^{p+2}Y_{n}^{m}({\it\theta},{\it\phi}),\end{eqnarray}$$
where
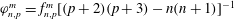 ${\it\varphi}_{n,p}^{m}=f_{n,p}^{m}[(p+2)(p+3)-n(n+1)]^{-1}$
and
${\it\varphi}_{n,p}^{m}=f_{n,p}^{m}[(p+2)(p+3)-n(n+1)]^{-1}$
and
![]() $p\geqslant n$
. Then
$p\geqslant n$
. Then
 ${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
and
${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
and
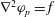 ${\rm\nabla}^{2}{\it\varphi}_{p}=f$
.
${\rm\nabla}^{2}{\it\varphi}_{p}=f$
.
The fundamental theorem of the paper is
Theorem 6.2 (Polynomial Poisson–Neumann Problem in a Sphere).
There exists a unique solution
![]() ${\it\varphi}$
of Poisson’s equation
${\it\varphi}$
of Poisson’s equation
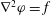 ${\rm\nabla}^{2}{\it\varphi}=f$
in the sphere
${\rm\nabla}^{2}{\it\varphi}=f$
in the sphere
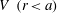 $V~(r<a)$
subject to
$V~(r<a)$
subject to
![]() $f\in {\mathcal{P}}_{N_{2}}$
,
$f\in {\mathcal{P}}_{N_{2}}$
,
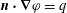 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}=q$
on
![]() $\partial V$
, where
$\partial V$
, where
![]() $\boldsymbol{n}=\boldsymbol{r}/a$
and
$\boldsymbol{n}=\boldsymbol{r}/a$
and
![]() $q\in {\mathcal{P}}_{N_{1}}$
, and to the respective uniqueness and consistency conditions
$q\in {\mathcal{P}}_{N_{1}}$
, and to the respective uniqueness and consistency conditions
 $$\begin{eqnarray}\int _{V}{\it\varphi}\text{d}V=0,\quad \int _{V}f\text{d}V=\int _{\partial V}q\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}{\it\varphi}\text{d}V=0,\quad \int _{V}f\text{d}V=\int _{\partial V}q\text{d}S,\end{eqnarray}$$
and
![]() ${\it\varphi}\in {\mathcal{P}}_{N_{3}}$
, where
${\it\varphi}\in {\mathcal{P}}_{N_{3}}$
, where
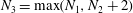 $N_{3}=\max (N_{1},N_{2}+2)$
.
$N_{3}=\max (N_{1},N_{2}+2)$
.
Proof. By Lemma 6.1 there exists a polynomial
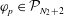 ${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
such that
${\it\varphi}_{p}\in {\mathcal{P}}_{N_{2}+2}$
such that
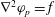 ${\rm\nabla}^{2}{\it\varphi}_{p}=f$
and
${\rm\nabla}^{2}{\it\varphi}_{p}=f$
and
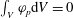 $\int _{V}{\it\varphi}_{p}\text{d}V=0$
. Thus
$\int _{V}{\it\varphi}_{p}\text{d}V=0$
. Thus
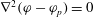 ${\rm\nabla}^{2}({\it\varphi}-{\it\varphi}_{p})=0$
in
${\rm\nabla}^{2}({\it\varphi}-{\it\varphi}_{p})=0$
in
![]() $V$
and
$V$
and
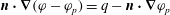 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}({\it\varphi}-{\it\varphi}_{p})=q-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}_{p}$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}({\it\varphi}-{\it\varphi}_{p})=q-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}_{p}$
on
![]() $\partial V$
. Since the uniqueness and consistency conditions of Theorem 6.1 hold, i.e.
$\partial V$
. Since the uniqueness and consistency conditions of Theorem 6.1 hold, i.e.
 $\int _{V}({\it\varphi}-{\it\varphi}_{p})\text{d}V=0$
and
$\int _{V}({\it\varphi}-{\it\varphi}_{p})\text{d}V=0$
and
 $$\begin{eqnarray}\int _{\partial V}(q-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}_{p})\text{d}S=\int _{\partial V}q\text{d}S-\int _{V}{\rm\nabla}^{2}{\it\varphi}_{p}\text{d}V=\int _{\partial V}q\text{d}S-\int _{V}f\text{d}V=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{\partial V}(q-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varphi}_{p})\text{d}S=\int _{\partial V}q\text{d}S-\int _{V}{\rm\nabla}^{2}{\it\varphi}_{p}\text{d}V=\int _{\partial V}q\text{d}S-\int _{V}f\text{d}V=0,\end{eqnarray}$$
Theorem 6.1 applies and implies
 ${\it\varphi}-{\it\varphi}_{p}\in {\mathcal{P}}_{N_{1}}$
. Hence
${\it\varphi}-{\it\varphi}_{p}\in {\mathcal{P}}_{N_{1}}$
. Hence
![]() ${\it\varphi}\in {\mathcal{P}}_{N_{3}}$
.
${\it\varphi}\in {\mathcal{P}}_{N_{3}}$
.
The essential theorem of the paper is that
![]() $\boldsymbol{{\mathcal{C}}}$
maps polynomial flows of degree
$\boldsymbol{{\mathcal{C}}}$
maps polynomial flows of degree
![]() $N$
or less in a sphere to polynomial flows of degree
$N$
or less in a sphere to polynomial flows of degree
![]() $N$
or less.
$N$
or less.
Theorem 6.3 (Invariance of Polynomial Flows in a Sphere).
The space
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
of polynomial flows of degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
of polynomial flows of degree
![]() $N$
or less on a sphere
$N$
or less on a sphere
![]() $V$
is invariant under
$V$
is invariant under
![]() $\boldsymbol{{\mathcal{C}}}$
, i.e.
$\boldsymbol{{\mathcal{C}}}$
, i.e.
 $\boldsymbol{{\mathcal{C}}}\boldsymbol{{\mathcal{P}}}_{N}(V)\subseteq \boldsymbol{{\mathcal{P}}}_{N}(V)$
.
$\boldsymbol{{\mathcal{C}}}\boldsymbol{{\mathcal{P}}}_{N}(V)\subseteq \boldsymbol{{\mathcal{P}}}_{N}(V)$
.
Proof. To show the Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
is well defined on
$\boldsymbol{{\mathcal{C}}}$
is well defined on
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
we must show for
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
we must show for
 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
that the pressure
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
that the pressure
![]() $p$
exists,
$p$
exists,
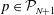 $p\in {\mathcal{P}}_{N+1}$
and
$p\in {\mathcal{P}}_{N+1}$
and
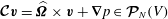 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Note that
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Note that
![]() $\boldsymbol{v}$
is a polynomial flow, but not necessarily an inertial mode, i.e. of the form (4.4). We can construct
$\boldsymbol{v}$
is a polynomial flow, but not necessarily an inertial mode, i.e. of the form (4.4). We can construct
![]() $p$
as in (1.10) so that
$p$
as in (1.10) so that
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}+{\rm\nabla}^{2}p=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}+{\rm\nabla}^{2}p=0$
in
![]() $V$
and
$V$
and
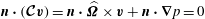 $\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{{\mathcal{C}}}\boldsymbol{v})=\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}+\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0$
on
![]() $\partial V$
, by Theorem 6.2 with
$\partial V$
, by Theorem 6.2 with
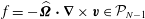 $f=-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}\in {\mathcal{P}}_{N-1}$
and
$f=-\widehat{{\it\bf\Omega}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}\in {\mathcal{P}}_{N-1}$
and
 $q=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\in {\mathcal{P}}_{N+1}$
. Thus
$q=-\boldsymbol{n}\boldsymbol{\cdot }\widehat{{\it\bf\Omega}}\times \boldsymbol{v}\in {\mathcal{P}}_{N+1}$
. Thus
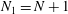 $N_{1}=N+1$
and
$N_{1}=N+1$
and
 $N_{2}=N-1$
in that theorem, i.e.
$N_{2}=N-1$
in that theorem, i.e.
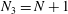 $N_{3}=N+1$
and hence
$N_{3}=N+1$
and hence
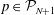 $p\in {\mathcal{P}}_{N+1}$
. Of course,
$p\in {\mathcal{P}}_{N+1}$
. Of course,
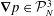 $\boldsymbol{{\rm\nabla}}p\in {\mathcal{P}}_{N}^{3}$
and thus
$\boldsymbol{{\rm\nabla}}p\in {\mathcal{P}}_{N}^{3}$
and thus
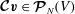 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
.
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
.
We now show the operator
![]() $\boldsymbol{{\mathcal{C}}}$
on
$\boldsymbol{{\mathcal{C}}}$
on
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
is non-defective, i.e. its eigenvectors span
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
is non-defective, i.e. its eigenvectors span
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
. In fact,
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
. In fact,
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
can be represented by a hermitian matrix. The proof is simple on the finite-dimensional space
$-\text{i}\boldsymbol{{\mathcal{C}}}$
can be represented by a hermitian matrix. The proof is simple on the finite-dimensional space
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
and does not require the explicit construction of the modes as a basis of
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
and does not require the explicit construction of the modes as a basis of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
. The result is used to prove the completeness of the Coriolis modes in the infinite-dimensional space
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
. The result is used to prove the completeness of the Coriolis modes in the infinite-dimensional space
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
in Theorem 8.1.
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
in Theorem 8.1.
Theorem 6.4 (Existence and Polynomial Nature of Coriolis Modes in a Sphere).
The finite-dimensional operator
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
on
$-\text{i}\boldsymbol{{\mathcal{C}}}$
on
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
is self-adjoint. The eigenvalues
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
is self-adjoint. The eigenvalues
![]() ${\it\lambda}=\text{i}{\it\omega}$
of
${\it\lambda}=\text{i}{\it\omega}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
are purely imaginary and satisfy
$\boldsymbol{{\mathcal{C}}}$
are purely imaginary and satisfy
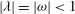 $|{\it\lambda}|=|{\it\omega}|<1$
and the eigenvectors of distinct eigenvalues of
$|{\it\lambda}|=|{\it\omega}|<1$
and the eigenvectors of distinct eigenvalues of
![]() $\boldsymbol{{\mathcal{C}}}$
are orthogonal. The eigenvectors of
$\boldsymbol{{\mathcal{C}}}$
are orthogonal. The eigenvectors of
![]() $\boldsymbol{{\mathcal{C}}}$
span the finite-dimensional space
$\boldsymbol{{\mathcal{C}}}$
span the finite-dimensional space
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
. The number of Coriolis modes of degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
. The number of Coriolis modes of degree
![]() $N$
or less is
$N$
or less is
![]() $C_{N}$
.
$C_{N}$
.
Proof. If
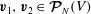 $\boldsymbol{v}_{1},\boldsymbol{v}_{2}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
, then
$\boldsymbol{v}_{1},\boldsymbol{v}_{2}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
, then
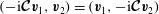 $(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
by Theorem 3.2 and
$(-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{1},\boldsymbol{v}_{2})=(\boldsymbol{v}_{1},-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}_{2})$
by Theorem 3.2 and
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is self-adjoint since
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is self-adjoint since
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
is finite-dimensional. Thus the eigenvectors of
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
is finite-dimensional. Thus the eigenvectors of
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
span
$-\text{i}\boldsymbol{{\mathcal{C}}}$
span
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
, the eigenvectors of distinct eigenvalues are orthogonal and its eigenvalues are real. If
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
, the eigenvectors of distinct eigenvalues are orthogonal and its eigenvalues are real. If
![]() $\boldsymbol{v}$
is an eigenvector of
$\boldsymbol{v}$
is an eigenvector of
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
corresponding to the eigenvalue
$-\text{i}\boldsymbol{{\mathcal{C}}}$
corresponding to the eigenvalue
![]() ${\it\omega}$
, then
${\it\omega}$
, then
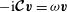 $-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
and hence
$-\text{i}\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\omega}\boldsymbol{v}$
and hence
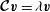 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
, i.e.
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}={\it\lambda}\boldsymbol{v}$
, i.e.
![]() $\boldsymbol{v}$
is an eigenvector of
$\boldsymbol{v}$
is an eigenvector of
![]() $\boldsymbol{{\mathcal{C}}}$
corresponding to the eigenvalue
$\boldsymbol{{\mathcal{C}}}$
corresponding to the eigenvalue
![]() ${\it\lambda}=\text{i}{\it\omega}$
. Thus the eigenvectors of
${\it\lambda}=\text{i}{\it\omega}$
. Thus the eigenvectors of
![]() $\boldsymbol{{\mathcal{C}}}$
are complete in the finite-dimensional space
$\boldsymbol{{\mathcal{C}}}$
are complete in the finite-dimensional space
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
and its eigenvalues are purely imaginary. The bound
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
and its eigenvalues are purely imaginary. The bound
![]() $|{\it\omega}|<1$
follows as in Theorem 3.3 and the result that
$|{\it\omega}|<1$
follows as in Theorem 3.3 and the result that
![]() ${\it\omega}\neq \pm 1$
.
${\it\omega}\neq \pm 1$
.
The spaces
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
are hierarchical in the sense that if
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
are hierarchical in the sense that if
![]() $N_{1}\leqslant N_{2}$
and
$N_{1}\leqslant N_{2}$
and
![]() $(\boldsymbol{v},{\it\omega})$
is an eigenmode of
$(\boldsymbol{v},{\it\omega})$
is an eigenmode of
![]() $\boldsymbol{{\mathcal{C}}}$
in
$\boldsymbol{{\mathcal{C}}}$
in
![]() $\boldsymbol{{\mathcal{P}}}_{N_{1}}(V)$
then
$\boldsymbol{{\mathcal{P}}}_{N_{1}}(V)$
then
![]() $(\boldsymbol{v},{\it\omega})$
is an eigenmode of
$(\boldsymbol{v},{\it\omega})$
is an eigenmode of
![]() $\boldsymbol{{\mathcal{C}}}$
in
$\boldsymbol{{\mathcal{C}}}$
in
![]() $\boldsymbol{{\mathcal{P}}}_{N_{2}}(V)$
. Moreover,
$\boldsymbol{{\mathcal{P}}}_{N_{2}}(V)$
. Moreover,
![]() $(\boldsymbol{v},{\it\omega})$
is an eigenmode of
$(\boldsymbol{v},{\it\omega})$
is an eigenmode of
![]() $\boldsymbol{{\mathcal{C}}}$
in
$\boldsymbol{{\mathcal{C}}}$
in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Moreover, for any polynomial flow
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. Moreover, for any polynomial flow
 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
,
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
,
 $(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})=0$
for all Coriolis modes
$(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})=0$
for all Coriolis modes
![]() $\boldsymbol{v}_{{\it\alpha}}$
with
$\boldsymbol{v}_{{\it\alpha}}$
with
 $\deg {\it\alpha}>N$
.
$\deg {\it\alpha}>N$
.
7. The Stokes and other operators in the Coriolis basis
The Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
restricted to polynomial flows in a sphere
$\boldsymbol{{\mathcal{C}}}$
restricted to polynomial flows in a sphere
![]() $V$
of degree
$V$
of degree
![]() $n$
or less
$n$
or less
![]() $\boldsymbol{{\mathcal{P}}}_{n}(V)$
is a diagonal
$\boldsymbol{{\mathcal{P}}}_{n}(V)$
is a diagonal
![]() $C_{n}\times C_{n}$
matrix in the Coriolis basis
$C_{n}\times C_{n}$
matrix in the Coriolis basis
![]() $\boldsymbol{v}_{{\it\alpha}}$
with
$\boldsymbol{v}_{{\it\alpha}}$
with
 $\deg {\it\alpha}\leqslant n$
. What forms do other operators restricted to
$\deg {\it\alpha}\leqslant n$
. What forms do other operators restricted to
![]() $\boldsymbol{{\mathcal{P}}}_{n}(V)$
take in the Coriolis basis? Consider the operator
$\boldsymbol{{\mathcal{P}}}_{n}(V)$
take in the Coriolis basis? Consider the operator
![]() ${\rm\nabla}^{2}$
: if
${\rm\nabla}^{2}$
: if
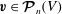 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
, it does not follow that
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
, it does not follow that
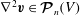 ${\rm\nabla}^{2}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
, due to the impenetrable boundary condition. Instead, we can adjust
${\rm\nabla}^{2}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
, due to the impenetrable boundary condition. Instead, we can adjust
![]() ${\rm\nabla}^{2}\boldsymbol{v}$
by subtracting the gradient of a harmonic function
${\rm\nabla}^{2}\boldsymbol{v}$
by subtracting the gradient of a harmonic function
![]() $p$
, where
$p$
, where
![]() $p$
is the solution of the Poisson–Neumann problem (1.14). This leads naturally to the Stokes operator
$p$
is the solution of the Poisson–Neumann problem (1.14). This leads naturally to the Stokes operator
 $\boldsymbol{{\mathcal{S}}}\boldsymbol{v}:=-{\rm\nabla}^{2}\boldsymbol{v}+\boldsymbol{{\rm\nabla}}p$
. Since
$\boldsymbol{{\mathcal{S}}}\boldsymbol{v}:=-{\rm\nabla}^{2}\boldsymbol{v}+\boldsymbol{{\rm\nabla}}p$
. Since
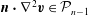 $\boldsymbol{n}\boldsymbol{\cdot }{\rm\nabla}^{2}\boldsymbol{v}\in {\mathcal{P}}_{n-1}$
, it follows from Theorem 6.2 that
$\boldsymbol{n}\boldsymbol{\cdot }{\rm\nabla}^{2}\boldsymbol{v}\in {\mathcal{P}}_{n-1}$
, it follows from Theorem 6.2 that
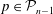 $p\in {\mathcal{P}}_{n-1}$
and
$p\in {\mathcal{P}}_{n-1}$
and
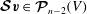 $\boldsymbol{{\mathcal{S}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n-2}(V)$
. Hence, for any
$\boldsymbol{{\mathcal{S}}}\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n-2}(V)$
. Hence, for any
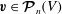 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
there exist coefficients
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{n}(V)$
there exist coefficients
![]() $u_{{\it\alpha}}$
such that
$u_{{\it\alpha}}$
such that
 $$\begin{eqnarray}\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant n-2}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant n-2}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}\end{eqnarray}$$
and for any
![]() $\boldsymbol{v}_{{\it\beta}}$
with
$\boldsymbol{v}_{{\it\beta}}$
with
 $\deg {\it\beta}\geqslant n-1$
,
$\deg {\it\beta}\geqslant n-1$
,
 $$\begin{eqnarray}({\rm\nabla}^{2}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=({\rm\nabla}^{2}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})-(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v}_{{\it\beta}})=-(\boldsymbol{{\mathcal{S}}}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant n-2}u_{{\it\alpha}}(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}_{{\it\beta}})=0,\end{eqnarray}$$
$$\begin{eqnarray}({\rm\nabla}^{2}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=({\rm\nabla}^{2}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})-(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v}_{{\it\beta}})=-(\boldsymbol{{\mathcal{S}}}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant n-2}u_{{\it\alpha}}(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}_{{\it\beta}})=0,\end{eqnarray}$$
since
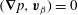 $(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v}_{{\it\beta}})=0$
. In particular,
$(\boldsymbol{{\rm\nabla}}p,\boldsymbol{v}_{{\it\beta}})=0$
. In particular,
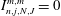 $I_{n,j,N,J}^{m,m}=0$
if
$I_{n,j,N,J}^{m,m}=0$
if
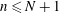 $n\leqslant N+1$
, which is consistent with Liao & Zhang (Reference Liao and Zhang2009). The Stokes matrix in the Coriolis basis decomposes further on subspaces of
$n\leqslant N+1$
, which is consistent with Liao & Zhang (Reference Liao and Zhang2009). The Stokes matrix in the Coriolis basis decomposes further on subspaces of
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
invariant under rotations about the rotation axis and subspaces invariant under reflection in the equator. Analogous results hold for the operators
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
invariant under rotations about the rotation axis and subspaces invariant under reflection in the equator. Analogous results hold for the operators
![]() $\partial _{x}^{2}$
,
$\partial _{x}^{2}$
,
![]() $\partial _{y}^{2}$
,
$\partial _{y}^{2}$
,
![]() $\partial _{z}^{2}$
,
$\partial _{z}^{2}$
,
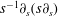 $s^{-1}\partial _{s}(s\partial _{s})$
or
$s^{-1}\partial _{s}(s\partial _{s})$
or
![]() $s^{-2}\partial _{{\it\phi}}^{2}$
.
$s^{-2}\partial _{{\it\phi}}^{2}$
.
The advection operator
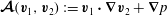 $\boldsymbol{{\mathcal{A}}}(\boldsymbol{v}_{1},\boldsymbol{v}_{2}):=\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{2}+\boldsymbol{{\rm\nabla}}p$
maps two polynomial flows
$\boldsymbol{{\mathcal{A}}}(\boldsymbol{v}_{1},\boldsymbol{v}_{2}):=\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{2}+\boldsymbol{{\rm\nabla}}p$
maps two polynomial flows
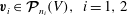 $\boldsymbol{v}_{i}\in \boldsymbol{{\mathcal{P}}}_{n_{i}}(V),~i=1,2$
, of degrees
$\boldsymbol{v}_{i}\in \boldsymbol{{\mathcal{P}}}_{n_{i}}(V),~i=1,2$
, of degrees
![]() $n_{1}$
and
$n_{1}$
and
![]() $n_{2}$
to a polynomial flow of degree
$n_{2}$
to a polynomial flow of degree
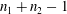 $n_{1}+n_{2}-1$
, if
$n_{1}+n_{2}-1$
, if
![]() $p$
satisfies (1.17) with
$p$
satisfies (1.17) with
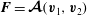 $\boldsymbol{F}=\boldsymbol{{\mathcal{A}}}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
. In particular, for any three Coriolis modes
$\boldsymbol{F}=\boldsymbol{{\mathcal{A}}}(\boldsymbol{v}_{1},\boldsymbol{v}_{2})$
. In particular, for any three Coriolis modes
![]() $\boldsymbol{v}_{{\it\alpha}}$
,
$\boldsymbol{v}_{{\it\alpha}}$
,
![]() $\boldsymbol{v}_{{\it\beta}}$
and
$\boldsymbol{v}_{{\it\beta}}$
and
![]() $\boldsymbol{v}_{{\it\gamma}}$
, if
$\boldsymbol{v}_{{\it\gamma}}$
, if
 $\deg {\it\alpha}+\deg {\it\beta}\leqslant \deg {\it\gamma}$
or
$\deg {\it\alpha}+\deg {\it\beta}\leqslant \deg {\it\gamma}$
or
 $m_{{\it\alpha}}+m_{{\it\beta}}\neq m_{{\it\gamma}}$
,
$m_{{\it\alpha}}+m_{{\it\beta}}\neq m_{{\it\gamma}}$
,
 $$\begin{eqnarray}(\boldsymbol{v}_{{\it\alpha}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{{\it\beta}},\boldsymbol{v}_{{\it\gamma}})=\int _{V}(\boldsymbol{v}_{{\it\alpha}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{{\it\beta}})\boldsymbol{\cdot }\boldsymbol{v}_{{\it\gamma}}^{\ast }\text{d}V=0.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v}_{{\it\alpha}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{{\it\beta}},\boldsymbol{v}_{{\it\gamma}})=\int _{V}(\boldsymbol{v}_{{\it\alpha}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{{\it\beta}})\boldsymbol{\cdot }\boldsymbol{v}_{{\it\gamma}}^{\ast }\text{d}V=0.\end{eqnarray}$$
Thus the operator
![]() $\boldsymbol{{\mathcal{A}}}$
maps
$\boldsymbol{{\mathcal{A}}}$
maps
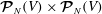 $\boldsymbol{{\mathcal{P}}}_{N}(V)\times \boldsymbol{{\mathcal{P}}}_{N}(V)$
to
$\boldsymbol{{\mathcal{P}}}_{N}(V)\times \boldsymbol{{\mathcal{P}}}_{N}(V)$
to
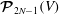 $\boldsymbol{{\mathcal{P}}}_{2N-1}(V)$
. In fact, if
$\boldsymbol{{\mathcal{P}}}_{2N-1}(V)$
. In fact, if
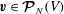 $\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
, there exist coefficients
$\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)$
, there exist coefficients
![]() $u_{{\it\alpha}}$
such that
$u_{{\it\alpha}}$
such that
 $$\begin{eqnarray}\boldsymbol{{\mathcal{A}}}(\boldsymbol{v},\boldsymbol{v})=\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant 2N-1}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\mathcal{A}}}(\boldsymbol{v},\boldsymbol{v})=\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant 2N-1}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}},\end{eqnarray}$$
and for any
![]() $\boldsymbol{v}_{{\it\beta}}$
with
$\boldsymbol{v}_{{\it\beta}}$
with
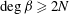 $\deg {\it\beta}\geqslant 2N$
,
$\deg {\it\beta}\geqslant 2N$
,
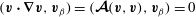 $(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=(\boldsymbol{{\mathcal{A}}}(\boldsymbol{v},\boldsymbol{v}),\boldsymbol{v}_{{\it\beta}})=0$
.
$(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v},\boldsymbol{v}_{{\it\beta}})=(\boldsymbol{{\mathcal{A}}}(\boldsymbol{v},\boldsymbol{v}),\boldsymbol{v}_{{\it\beta}})=0$
.
8. Completeness of the Coriolis modes in a sphere
In this section we establish in Theorem 8.1 the most important result in the paper, that the Coriolis modes in a sphere are complete in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The proof relies on the uniform polynomial approximation theorem of Weierstrass to approximate a flow in
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
. The proof relies on the uniform polynomial approximation theorem of Weierstrass to approximate a flow in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
by a polynomial vector field and the fundamental Theorem 6.2 to project this polynomial field onto
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
by a polynomial vector field and the fundamental Theorem 6.2 to project this polynomial field onto
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
for sufficiently high degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
for sufficiently high degree
![]() $N$
by subtracting a pressure gradient.
$N$
by subtracting a pressure gradient.
Theorem 8.1. The Coriolis modes in a sphere
![]() $V$
are complete in
$V$
are complete in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
.
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
.
Proof. Let
 $\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
and
$\boldsymbol{v}\in \boldsymbol{{\mathcal{V}}}^{1}(V)$
and
![]() ${\it\epsilon}>0$
. By application of the Weierstrass approximation theorem (see Davis Reference Davis1975, § 6.6) to each Cartesian component of
${\it\epsilon}>0$
. By application of the Weierstrass approximation theorem (see Davis Reference Davis1975, § 6.6) to each Cartesian component of
![]() $\boldsymbol{v}$
, there exists an integer
$\boldsymbol{v}$
, there exists an integer
![]() $N>0$
and a vector polynomial
$N>0$
and a vector polynomial
![]() $\boldsymbol{u}\in {\mathcal{P}}_{N}^{3}$
, such that
$\boldsymbol{u}\in {\mathcal{P}}_{N}^{3}$
, such that
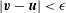 $|\boldsymbol{v}-\boldsymbol{u}|<{\it\epsilon}$
in
$|\boldsymbol{v}-\boldsymbol{u}|<{\it\epsilon}$
in
![]() $V$
. However,
$V$
. However,
![]() $\boldsymbol{u}\in \boldsymbol{{\mathcal{P}}}_{N}$
may be false, since the conditions
$\boldsymbol{u}\in \boldsymbol{{\mathcal{P}}}_{N}$
may be false, since the conditions
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0$
in
![]() $V$
and
$V$
and
 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}=0$
on
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}=0$
on
![]() $\partial V$
do not necessarily hold. By Theorem 6.2 there exists a polynomial
$\partial V$
do not necessarily hold. By Theorem 6.2 there exists a polynomial
 ${\it\pi}\in {\mathcal{P}}_{N+1}$
such that
${\it\pi}\in {\mathcal{P}}_{N+1}$
such that
 $\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi}\in \boldsymbol{{\mathcal{P}}}_{N}$
. Hence there are constants
$\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi}\in \boldsymbol{{\mathcal{P}}}_{N}$
. Hence there are constants
![]() $u_{{\it\alpha}}$
such that
$u_{{\it\alpha}}$
such that
 $$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{{\rm\nabla}}{\it\pi}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}=\boldsymbol{{\rm\nabla}}{\it\pi}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{{\rm\nabla}}{\it\pi}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}u_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}=\boldsymbol{{\rm\nabla}}{\it\pi}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}},\end{eqnarray}$$
where the
![]() $\boldsymbol{v}_{{\it\alpha}}$
are the orthonormal Coriolis modes in
$\boldsymbol{v}_{{\it\alpha}}$
are the orthonormal Coriolis modes in
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
. Now, using (8.1),
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
. Now, using (8.1),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\Vert \boldsymbol{v}-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}=\left\Vert (\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi})+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\Vert \boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi}\Vert ^{2}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})^{\ast }(\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}_{{\it\alpha}})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi})+\left\Vert \mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}-\boldsymbol{u})-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}|(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert \boldsymbol{v}-\boldsymbol{u}\Vert ^{2}+\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \,\Vert \boldsymbol{v}-\boldsymbol{u}\Vert ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\Vert \boldsymbol{v}-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}=\left\Vert (\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi})+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\Vert \boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi}\Vert ^{2}+\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})^{\ast }(\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}_{{\it\alpha}})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi})+\left\Vert \mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(\boldsymbol{v}-\boldsymbol{u}+\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}-\boldsymbol{u})-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}|(\boldsymbol{u}-\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert \boldsymbol{v}-\boldsymbol{u}\Vert ^{2}+\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \,\Vert \boldsymbol{v}-\boldsymbol{u}\Vert ,\end{eqnarray}$$
since
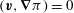 $(\boldsymbol{v},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
,
$(\boldsymbol{v},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
,
 $(\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
as
$(\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
as
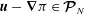 $\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi}\in \boldsymbol{{\mathcal{P}}}_{N}$
,
$\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi}\in \boldsymbol{{\mathcal{P}}}_{N}$
,
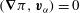 $(\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}_{{\it\alpha}})=0$
and
$(\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{v}_{{\it\alpha}})=0$
and
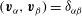 $(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}_{{\it\beta}})={\it\delta}_{{\it\alpha}{\it\beta}}$
. We bound
$(\boldsymbol{v}_{{\it\alpha}},\boldsymbol{v}_{{\it\beta}})={\it\delta}_{{\it\alpha}{\it\beta}}$
. We bound
![]() $\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert$
in terms of
$\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert$
in terms of
![]() $\Vert \boldsymbol{v}\Vert$
. Now
$\Vert \boldsymbol{v}\Vert$
. Now
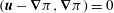 $(\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
implies
$(\boldsymbol{u}-\boldsymbol{{\rm\nabla}}{\it\pi},\boldsymbol{{\rm\nabla}}{\it\pi})=0$
implies
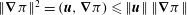 $\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert ^{2}=(\boldsymbol{u},\boldsymbol{{\rm\nabla}}{\it\pi})\leqslant \Vert \boldsymbol{u}\Vert \,\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert$
, i.e.
$\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert ^{2}=(\boldsymbol{u},\boldsymbol{{\rm\nabla}}{\it\pi})\leqslant \Vert \boldsymbol{u}\Vert \,\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert$
, i.e.
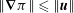 $\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{u}\Vert$
, and
$\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{u}\Vert$
, and
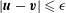 $|\boldsymbol{u}-\boldsymbol{v}|\leqslant {\it\epsilon}$
implies
$|\boldsymbol{u}-\boldsymbol{v}|\leqslant {\it\epsilon}$
implies
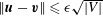 $\Vert \boldsymbol{u}-\boldsymbol{v}\Vert \leqslant {\it\epsilon}\sqrt{|V|}$
. Thus
$\Vert \boldsymbol{u}-\boldsymbol{v}\Vert \leqslant {\it\epsilon}\sqrt{|V|}$
. Thus
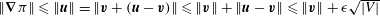 $\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{u}\Vert =\Vert \boldsymbol{v}+(\boldsymbol{u}-\boldsymbol{v})\Vert \leqslant \Vert \boldsymbol{v}\Vert +\Vert \boldsymbol{u}-\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert +{\it\epsilon}\sqrt{|V|}$
, where
$\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{u}\Vert =\Vert \boldsymbol{v}+(\boldsymbol{u}-\boldsymbol{v})\Vert \leqslant \Vert \boldsymbol{v}\Vert +\Vert \boldsymbol{u}-\boldsymbol{v}\Vert \leqslant \Vert \boldsymbol{v}\Vert +{\it\epsilon}\sqrt{|V|}$
, where
![]() $|V|$
is the volume of
$|V|$
is the volume of
![]() $V$
; i.e.
$V$
; i.e.
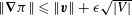 $\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{v}\Vert +{\it\epsilon}\sqrt{|V|}$
. Thus finally,
$\Vert \boldsymbol{{\rm\nabla}}{\it\pi}\Vert \leqslant \Vert \boldsymbol{v}\Vert +{\it\epsilon}\sqrt{|V|}$
. Thus finally,
 $$\begin{eqnarray}\left\Vert \boldsymbol{v}-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\leqslant \sqrt{|V|}(\Vert \boldsymbol{v}\Vert +2{\it\epsilon}\sqrt{|V|}){\it\epsilon}.\end{eqnarray}$$
$$\begin{eqnarray}\left\Vert \boldsymbol{v}-\mathop{\sum }_{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}\right\Vert ^{2}\leqslant \sqrt{|V|}(\Vert \boldsymbol{v}\Vert +2{\it\epsilon}\sqrt{|V|}){\it\epsilon}.\end{eqnarray}$$
Since the right-hand side is independent of
![]() $N$
,
$N$
,
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() ${\it\pi}$
, it follows that
${\it\pi}$
, it follows that
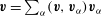 $\boldsymbol{v}=\sum _{{\it\alpha}}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}$
in
$\boldsymbol{v}=\sum _{{\it\alpha}}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}$
in
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
, where the sum is over Coriolis modes. The Coriolis modes are therefore complete in a sphere.
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
, where the sum is over Coriolis modes. The Coriolis modes are therefore complete in a sphere.
We showed that the Coriolis modes are polynomials by construction in § 4. We now show this also follows from Theorem 6.2 and that there are no missed eigenfunctions.
Theorem 8.2. The spherical Coriolis modes are polynomials.
Proof. Let
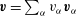 $\boldsymbol{v}=\sum _{{\it\alpha}}v_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
and
$\boldsymbol{v}=\sum _{{\it\alpha}}v_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
and
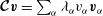 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\sum _{{\it\alpha}}{\it\lambda}_{{\it\alpha}}v_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
, then
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}=\sum _{{\it\alpha}}{\it\lambda}_{{\it\alpha}}v_{{\it\alpha}}\boldsymbol{v}_{{\it\alpha}}$
, then
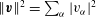 $\Vert \boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|v_{{\it\alpha}}|^{2}$
and
$\Vert \boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|v_{{\it\alpha}}|^{2}$
and
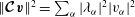 $\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|{\it\lambda}_{{\it\alpha}}|^{2}|v_{{\it\alpha}}|^{2}$
. If
$\Vert \boldsymbol{{\mathcal{C}}}\boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|{\it\lambda}_{{\it\alpha}}|^{2}|v_{{\it\alpha}}|^{2}$
. If
![]() $(\boldsymbol{v},{\it\lambda})$
is an eigenmode, then
$(\boldsymbol{v},{\it\lambda})$
is an eigenmode, then
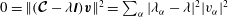 $0=\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})\boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|{\it\lambda}_{{\it\alpha}}-{\it\lambda}|^{2}|v_{{\it\alpha}}|^{2}$
. The series all converge since the kinetic energy is finite,
$0=\Vert (\boldsymbol{{\mathcal{C}}}-{\it\lambda}\unicode[STIX]{x1D644})\boldsymbol{v}\Vert ^{2}=\sum _{{\it\alpha}}|{\it\lambda}_{{\it\alpha}}-{\it\lambda}|^{2}|v_{{\it\alpha}}|^{2}$
. The series all converge since the kinetic energy is finite,
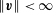 $\Vert \boldsymbol{v}\Vert <\infty$
, and
$\Vert \boldsymbol{v}\Vert <\infty$
, and
![]() $|{\it\lambda}_{{\it\alpha}}|<1$
for all
$|{\it\lambda}_{{\it\alpha}}|<1$
for all
![]() ${\it\alpha}$
. Thus
${\it\alpha}$
. Thus
![]() ${\it\lambda}={\it\lambda}_{{\it\beta}}$
for some index
${\it\lambda}={\it\lambda}_{{\it\beta}}$
for some index
![]() ${\it\beta}$
,
${\it\beta}$
,
![]() $v_{{\it\beta}}\neq 0$
and
$v_{{\it\beta}}\neq 0$
and
![]() $v_{{\it\alpha}}=0$
for
$v_{{\it\alpha}}=0$
for
![]() ${\it\alpha}\neq {\it\beta}$
.
${\it\alpha}\neq {\it\beta}$
.
The operator
![]() $\boldsymbol{{\mathcal{C}}}$
can be approximated elementwise by a finite-rank operator
$\boldsymbol{{\mathcal{C}}}$
can be approximated elementwise by a finite-rank operator
![]() $\boldsymbol{{\mathcal{C}}}_{N}$
, i.e. an operator with a finite-dimensional range. Let
$\boldsymbol{{\mathcal{C}}}_{N}$
, i.e. an operator with a finite-dimensional range. Let
![]() $\boldsymbol{P}_{N}$
be the projection onto
$\boldsymbol{P}_{N}$
be the projection onto
![]() $\boldsymbol{{\mathcal{P}}}_{N}$
,
$\boldsymbol{{\mathcal{P}}}_{N}$
,
 $\boldsymbol{v}_{N}=\boldsymbol{P}_{N}\boldsymbol{v}:=\sum _{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}$
and
$\boldsymbol{v}_{N}=\boldsymbol{P}_{N}\boldsymbol{v}:=\sum _{\text{deg}\,{\it\alpha}\leqslant N}(\boldsymbol{v},\boldsymbol{v}_{{\it\alpha}})\boldsymbol{v}_{{\it\alpha}}$
and
 $\boldsymbol{{\mathcal{C}}}_{N}:=\boldsymbol{{\mathcal{C}}}\circ \boldsymbol{P}_{N}:\boldsymbol{{\mathcal{V}}}^{1}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Then
$\boldsymbol{{\mathcal{C}}}_{N}:=\boldsymbol{{\mathcal{C}}}\circ \boldsymbol{P}_{N}:\boldsymbol{{\mathcal{V}}}^{1}(V)\rightarrow \boldsymbol{{\mathcal{P}}}_{N}(V)$
. Then
 $$\begin{eqnarray}\Vert (\boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N})\boldsymbol{v}\Vert =\Vert \boldsymbol{{\mathcal{C}}}(\boldsymbol{v}-\boldsymbol{v}_{N})\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}-\boldsymbol{v}_{N}\Vert \leqslant \sqrt{\sqrt{|V|}(1+2{\it\epsilon}\sqrt{|V|})}\,\sqrt{{\it\epsilon}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (\boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N})\boldsymbol{v}\Vert =\Vert \boldsymbol{{\mathcal{C}}}(\boldsymbol{v}-\boldsymbol{v}_{N})\Vert \leqslant \Vert \boldsymbol{{\mathcal{C}}}\Vert \,\Vert \boldsymbol{v}-\boldsymbol{v}_{N}\Vert \leqslant \sqrt{\sqrt{|V|}(1+2{\it\epsilon}\sqrt{|V|})}\,\sqrt{{\it\epsilon}}\end{eqnarray}$$
using (8.3). However, the approximation is non-uniform, since
![]() $N$
in (8.3) depends not only on
$N$
in (8.3) depends not only on
![]() ${\it\epsilon}$
but also
${\it\epsilon}$
but also
![]() $\boldsymbol{v}$
. Hence it does not follow from (8.4) that for all
$\boldsymbol{v}$
. Hence it does not follow from (8.4) that for all
![]() ${\it\epsilon}>0$
there exists
${\it\epsilon}>0$
there exists
![]() $N$
such that
$N$
such that
![]() $\boldsymbol{{\mathcal{C}}}_{N}$
approximates
$\boldsymbol{{\mathcal{C}}}_{N}$
approximates
![]() $\boldsymbol{{\mathcal{C}}}$
in the uniform operator norm, i.e.
$\boldsymbol{{\mathcal{C}}}$
in the uniform operator norm, i.e.
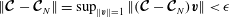 $\Vert \boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N}\Vert =\sup _{\Vert \boldsymbol{v}\Vert =1}\Vert (\boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N})\boldsymbol{v}\Vert <{\it\epsilon}$
, which would imply that
$\Vert \boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N}\Vert =\sup _{\Vert \boldsymbol{v}\Vert =1}\Vert (\boldsymbol{{\mathcal{C}}}-\boldsymbol{{\mathcal{C}}}_{N})\boldsymbol{v}\Vert <{\it\epsilon}$
, which would imply that
![]() $\boldsymbol{{\mathcal{C}}}$
is a compact operator. In fact, we show in the next theorem that
$\boldsymbol{{\mathcal{C}}}$
is a compact operator. In fact, we show in the next theorem that
![]() $\boldsymbol{{\mathcal{C}}}$
is not compact and hence cannot be uniformly approximated by the
$\boldsymbol{{\mathcal{C}}}$
is not compact and hence cannot be uniformly approximated by the
![]() $\boldsymbol{{\mathcal{C}}}_{N}$
or any finite-rank operator (Schechter Reference Schechter1971, § 4.3).
$\boldsymbol{{\mathcal{C}}}_{N}$
or any finite-rank operator (Schechter Reference Schechter1971, § 4.3).
Theorem 8.3. The Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
is not compact if
$\boldsymbol{{\mathcal{C}}}$
is not compact if
![]() $V$
is a sphere.
$V$
is a sphere.
Proof. We prove the theorem by contradiction. Assume
![]() $\boldsymbol{{\mathcal{C}}}$
is compact. Then the only point of accumulation of the frequencies
$\boldsymbol{{\mathcal{C}}}$
is compact. Then the only point of accumulation of the frequencies
![]() ${\it\omega}_{n,j}^{m}$
of
${\it\omega}_{n,j}^{m}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
is zero (Friedman Reference Friedman1982, Corollary 5.3.3), i.e. for all
$\boldsymbol{{\mathcal{C}}}$
is zero (Friedman Reference Friedman1982, Corollary 5.3.3), i.e. for all
![]() ${\it\delta}>0$
there are finitely many frequencies
${\it\delta}>0$
there are finitely many frequencies
![]() ${\it\omega}$
with
${\it\omega}$
with
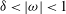 ${\it\delta}<|{\it\omega}|<1$
. However, from § 4 the
${\it\delta}<|{\it\omega}|<1$
. However, from § 4 the
![]() $m=0$
frequencies
$m=0$
frequencies
![]() ${\it\omega}_{n,j}^{0}$
are interlaced by the zeros
${\it\omega}_{n,j}^{0}$
are interlaced by the zeros
![]() ${\it\omega}_{j}$
of
${\it\omega}_{j}$
of
![]() $P_{n}$
which satisfy
$P_{n}$
which satisfy
 $\cos [2j{\rm\pi}/(2n+1)]\leqslant {\it\omega}_{j}\leqslant \cos [(2j-1){\rm\pi}/(2n+1)]$
, i.e. there exists a
$\cos [2j{\rm\pi}/(2n+1)]\leqslant {\it\omega}_{j}\leqslant \cos [(2j-1){\rm\pi}/(2n+1)]$
, i.e. there exists a
![]() ${\it\delta}>0$
such that
${\it\delta}>0$
such that
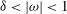 ${\it\delta}<|{\it\omega}|<1$
contains infinitely many
${\it\delta}<|{\it\omega}|<1$
contains infinitely many
![]() $m=0$
frequencies, a contradiction. Hence
$m=0$
frequencies, a contradiction. Hence
![]() $\boldsymbol{{\mathcal{C}}}$
is not compact.
$\boldsymbol{{\mathcal{C}}}$
is not compact.
Despite the lack of a uniform finite-dimensional approximation of
![]() $\boldsymbol{{\mathcal{C}}}$
, Theorem 8.3 importantly precludes an accumulation of near-resonance conditions, i.e.
$\boldsymbol{{\mathcal{C}}}$
, Theorem 8.3 importantly precludes an accumulation of near-resonance conditions, i.e.
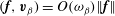 $(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=O({\it\omega}_{{\it\beta}})\Vert \boldsymbol{f}\Vert$
with
$(\boldsymbol{f},\boldsymbol{v}_{{\it\beta}})=O({\it\omega}_{{\it\beta}})\Vert \boldsymbol{f}\Vert$
with
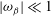 $|{\it\omega}_{{\it\beta}}|\ll 1$
compared to (3.36). Although Theorem 8.3 is only a partial result, the proof shows that
$|{\it\omega}_{{\it\beta}}|\ll 1$
compared to (3.36). Although Theorem 8.3 is only a partial result, the proof shows that
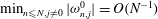 $\min _{n\leqslant N,j\neq 0}|{\it\omega}_{n,j}^{0}|=O(N^{-1})$
, which indicates that with axisymmetry frequencies near zero behave uniformly with
$\min _{n\leqslant N,j\neq 0}|{\it\omega}_{n,j}^{0}|=O(N^{-1})$
, which indicates that with axisymmetry frequencies near zero behave uniformly with
![]() $N$
and allow some regularity in inverting
$N$
and allow some regularity in inverting
![]() $\boldsymbol{{\mathcal{C}}}$
. The behaviour is also true for
$\boldsymbol{{\mathcal{C}}}$
. The behaviour is also true for
![]() $m\neq 0$
, since
$m\neq 0$
, since
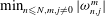 $\min _{n\leqslant N,m,j\neq 0}|{\it\omega}_{n,j}^{m}|$
is
$\min _{n\leqslant N,m,j\neq 0}|{\it\omega}_{n,j}^{m}|$
is
![]() $O(N^{-1})$
, using the estimate
$O(N^{-1})$
, using the estimate
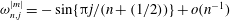 ${\it\omega}_{n,j}^{|m|}=-\sin \{{\rm\pi}j/(n+(1/2))\}+o(n^{-1})$
(see Ivanov & Papaloizou Reference Ivanov and Papaloizou2010), equation (B5) with
${\it\omega}_{n,j}^{|m|}=-\sin \{{\rm\pi}j/(n+(1/2))\}+o(n^{-1})$
(see Ivanov & Papaloizou Reference Ivanov and Papaloizou2010), equation (B5) with
![]() $j$
shifted so that
$j$
shifted so that
![]() ${\it\omega}_{n,0}^{|m|}=0$
. Thus the convergence condition on
${\it\omega}_{n,0}^{|m|}=0$
. Thus the convergence condition on
![]() $\boldsymbol{v}$
in Theorem 8.3 becomes
$\boldsymbol{v}$
in Theorem 8.3 becomes
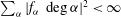 $\sum _{{\it\alpha}}|f_{{\it\alpha}}\,\deg {\it\alpha}|^{2}<\infty$
, where the sum is over the spherical inertial modes. Splitting the sum into
$\sum _{{\it\alpha}}|f_{{\it\alpha}}\,\deg {\it\alpha}|^{2}<\infty$
, where the sum is over the spherical inertial modes. Splitting the sum into
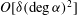 $O[{\it\delta}(\deg {\it\alpha})^{2}]$
frequencies in the range
$O[{\it\delta}(\deg {\it\alpha})^{2}]$
frequencies in the range
 $O(\deg {\it\alpha})^{-1}<|{\it\omega}_{{\it\alpha}}|\leqslant {\it\delta}<1$
near 0 and
$O(\deg {\it\alpha})^{-1}<|{\it\omega}_{{\it\alpha}}|\leqslant {\it\delta}<1$
near 0 and
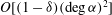 $O[(1-{\it\delta})(\deg {\it\alpha})^{2}]$
frequencies in
$O[(1-{\it\delta})(\deg {\it\alpha})^{2}]$
frequencies in
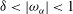 ${\it\delta}<|{\it\omega}_{{\it\alpha}}|<1$
gives an upper bound of order
${\it\delta}<|{\it\omega}_{{\it\alpha}}|<1$
gives an upper bound of order
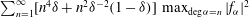 $\sum _{n=1}^{\infty }[n^{4}{\it\delta}+n^{2}{\it\delta}^{-2}(1-{\it\delta})]\,\max _{\text{deg}\,{\it\alpha}=n}|f_{{\it\alpha}}|^{2}$
. Minimising over
$\sum _{n=1}^{\infty }[n^{4}{\it\delta}+n^{2}{\it\delta}^{-2}(1-{\it\delta})]\,\max _{\text{deg}\,{\it\alpha}=n}|f_{{\it\alpha}}|^{2}$
. Minimising over
![]() ${\it\delta}$
yields
${\it\delta}$
yields
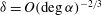 ${\it\delta}=O(\deg {\it\alpha})^{-2/3}$
and the convergence condition
${\it\delta}=O(\deg {\it\alpha})^{-2/3}$
and the convergence condition
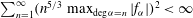 $\sum _{n=1}^{\infty }(n^{5/3}\,\max _{\text{deg}\,{\it\alpha}=n}|f_{{\it\alpha}}|)^{2}<\infty$
.
$\sum _{n=1}^{\infty }(n^{5/3}\,\max _{\text{deg}\,{\it\alpha}=n}|f_{{\it\alpha}}|)^{2}<\infty$
.
9. Discussion and conclusions
We defined the Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
, which maps the space of continuously differentiable incompressible flows
$\boldsymbol{{\mathcal{C}}}$
, which maps the space of continuously differentiable incompressible flows
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
in a bounded region
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
in a bounded region
![]() $V$
to itself. We showed that
$V$
to itself. We showed that
![]() $\boldsymbol{{\mathcal{C}}}$
is bounded with
$\boldsymbol{{\mathcal{C}}}$
is bounded with
![]() $\Vert \boldsymbol{{\mathcal{C}}}\Vert \leqslant 1$
and
$\Vert \boldsymbol{{\mathcal{C}}}\Vert \leqslant 1$
and
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric, thus establishing that the Coriolis modes are orthogonal with real frequencies
$-\text{i}\boldsymbol{{\mathcal{C}}}$
is symmetric, thus establishing that the Coriolis modes are orthogonal with real frequencies
![]() ${\it\omega}$
,
${\it\omega}$
,
![]() $|{\it\omega}|<1$
. We proved the polynomial Poisson–Neumann Theorem 6.2 for a sphere, thus showing that the space of incompressible polynomial flows
$|{\it\omega}|<1$
. We proved the polynomial Poisson–Neumann Theorem 6.2 for a sphere, thus showing that the space of incompressible polynomial flows
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
of degree
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
of degree
![]() ${\leqslant}N$
in a sphere is invariant under
${\leqslant}N$
in a sphere is invariant under
![]() $\boldsymbol{{\mathcal{C}}}$
. This and the self-adjointness of
$\boldsymbol{{\mathcal{C}}}$
. This and the self-adjointness of
![]() $-\text{i}\boldsymbol{{\mathcal{C}}}$
on
$-\text{i}\boldsymbol{{\mathcal{C}}}$
on
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
enabled us to simply enumerate the Coriolis modes in a sphere and to establish their completeness, by invoking the Weierstrass approximation theorem and using Theorem 6.2 again. We also enumerated the modes directly from the known analytic solutions, with careful consideration given to the geostrophic modes.
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
enabled us to simply enumerate the Coriolis modes in a sphere and to establish their completeness, by invoking the Weierstrass approximation theorem and using Theorem 6.2 again. We also enumerated the modes directly from the known analytic solutions, with careful consideration given to the geostrophic modes.
The first approach, based on the polynomial Poisson–Neumann Theorem 6.2, is especially useful, since it does not require analytic expressions for the Coriolis modes. It will be shown elsewhere that Theorem 6.2 can be extended to spheroids and tri-axial ellipsoids, even if the rotation axis is tilted from the principal axes, and hence that the Coriolis modes are polynomials and complete in these cases. In fact, it has been known since Poincaré (Reference Poincaré1885a
) (see also Hough Reference Hough1895) that the inertial modes in a tri-axial ellipsoid are polynomials in Cartesian coordinates. It will also be shown that the spaces of incompressible rotating periodic plane layer flows and rotating periodic duct flows can be decomposed using Fourier techniques into a sum of finite-dimensional spaces, which are invariant under the Coriolis operator
![]() $\boldsymbol{{\mathcal{C}}}$
. Consequently, the Coriolis modes are complete in periodic plane layer flows and a rotating periodic duct (Cui et al.
Reference Cui, Zhang and Liao2014). Decomposition of incompressible flows in a rotating rectangular prism into finite-dimensional spaces invariant under the Coriolis operator fails.
$\boldsymbol{{\mathcal{C}}}$
. Consequently, the Coriolis modes are complete in periodic plane layer flows and a rotating periodic duct (Cui et al.
Reference Cui, Zhang and Liao2014). Decomposition of incompressible flows in a rotating rectangular prism into finite-dimensional spaces invariant under the Coriolis operator fails.
Theorem 6.2 has no analogue in some simple geometries, which is consistent with these geometries having non-polynomial Coriolis modes. Thus the inertial pressure modes of a finite circular cylinder of radius
![]() $a$
rotating about its axis (Thomson Reference Thomson1880) are
$a$
rotating about its axis (Thomson Reference Thomson1880) are
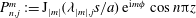 $P_{n,j}^{m}:=\text{J}_{|m|}({\it\lambda}_{|m|,j}s/a)\,\text{e}^{\text{i}m{\it\phi}}\,\cos n{\rm\pi}z$
, where
$P_{n,j}^{m}:=\text{J}_{|m|}({\it\lambda}_{|m|,j}s/a)\,\text{e}^{\text{i}m{\it\phi}}\,\cos n{\rm\pi}z$
, where
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
![]() $m\in \mathbb{Z}$
,
$m\in \mathbb{Z}$
,
![]() $\text{J}_{|m|}$
is a Bessel function of the first kind and
$\text{J}_{|m|}$
is a Bessel function of the first kind and
![]() ${\it\lambda}_{|m|,j}$
is the
${\it\lambda}_{|m|,j}$
is the
![]() $j$
th positive zero of
$j$
th positive zero of
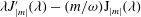 ${\it\lambda}J_{|m|}^{\prime }({\it\lambda})-(m/{\it\omega})\text{J}_{|m|}({\it\lambda})$
. The frequencies are given by
${\it\lambda}J_{|m|}^{\prime }({\it\lambda})-(m/{\it\omega})\text{J}_{|m|}({\it\lambda})$
. The frequencies are given by
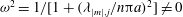 ${\it\omega}^{2}=1/[1+({\it\lambda}_{|m|,j}/n{\rm\pi}a)^{2}]\neq 0$
. If
${\it\omega}^{2}=1/[1+({\it\lambda}_{|m|,j}/n{\rm\pi}a)^{2}]\neq 0$
. If
![]() $m=0$
and
$m=0$
and
![]() ${\it\omega}\rightarrow 0$
this condition reduces to
${\it\omega}\rightarrow 0$
this condition reduces to
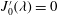 $J_{0}^{\prime }({\it\lambda})=0$
. Thus the geostrophic pressure modes are
$J_{0}^{\prime }({\it\lambda})=0$
. Thus the geostrophic pressure modes are
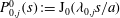 $P_{0,j}^{0}(s):=\text{J}_{0}({\it\lambda}_{0,j}s/a)$
, where
$P_{0,j}^{0}(s):=\text{J}_{0}({\it\lambda}_{0,j}s/a)$
, where
![]() ${\it\lambda}_{0,j}$
is the
${\it\lambda}_{0,j}$
is the
![]() $j$
th positive zero of
$j$
th positive zero of
 $J_{0}^{\prime }({\it\lambda})=0$
. The Coriolis modes are clearly not polynomials, specifically
$J_{0}^{\prime }({\it\lambda})=0$
. The Coriolis modes are clearly not polynomials, specifically
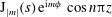 $\text{J}_{|m|}(s)\,\text{e}^{\text{i}m{\it\phi}}\,\cos n{\rm\pi}z$
is not polynomial. Thus it is not possible to construct the pressure
$\text{J}_{|m|}(s)\,\text{e}^{\text{i}m{\it\phi}}\,\cos n{\rm\pi}z$
is not polynomial. Thus it is not possible to construct the pressure
![]() $p$
in the Coriolis operator so that it maps
$p$
in the Coriolis operator so that it maps
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
to
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
to
![]() $\boldsymbol{{\mathcal{P}}}_{N}(V)$
, if
$\boldsymbol{{\mathcal{P}}}_{N}(V)$
, if
![]() $V$
is a cylinder, and Theorem 6.2 has no analogue in this case. Completeness of the discrete Coriolis modes for a cylinder is currently an open question; as the abstract completeness result outlined below indicates, it depends on the continuous spectrum.
$V$
is a cylinder, and Theorem 6.2 has no analogue in this case. Completeness of the discrete Coriolis modes for a cylinder is currently an open question; as the abstract completeness result outlined below indicates, it depends on the continuous spectrum.
A full analytical solution for the Coriolis modes in a spherical shell is not known. The difficulty with the separable solutions of the Poincaré’s equation in the coordinate system (4.3) is that only one
![]() ${\it\zeta}$
-surface is spherical,
${\it\zeta}$
-surface is spherical,
![]() ${\it\zeta}={\it\omega}$
corresponding to
${\it\zeta}={\it\omega}$
corresponding to
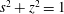 $s^{2}+z^{2}=1$
. Theorem 6.1 for polynomial solutions of the Laplace–Neumann problem fails in a shell. Hence the existence Theorem 6.3 and the polynomial form of such modes also fails. Ray theory arguments suggest that the continuous spectrum is non-empty for a spherical shell (Israeli Reference Israeli1972; see also Stewartson Reference Stewartson1972; Rieutord & Valdettaro Reference Rieutord and Valdettaro1997). In fact, the existence of inertial modes in a spherical shell has been questioned (Stewartson & Rickard Reference Stewartson and Rickard1969; Rieutord, Georgeot & Valdettaro Reference Rieutord, Georgeot and Valdettaro2001).
$s^{2}+z^{2}=1$
. Theorem 6.1 for polynomial solutions of the Laplace–Neumann problem fails in a shell. Hence the existence Theorem 6.3 and the polynomial form of such modes also fails. Ray theory arguments suggest that the continuous spectrum is non-empty for a spherical shell (Israeli Reference Israeli1972; see also Stewartson Reference Stewartson1972; Rieutord & Valdettaro Reference Rieutord and Valdettaro1997). In fact, the existence of inertial modes in a spherical shell has been questioned (Stewartson & Rickard Reference Stewartson and Rickard1969; Rieutord, Georgeot & Valdettaro Reference Rieutord, Georgeot and Valdettaro2001).
We outline a general abstract existence argument for the Coriolis modes in a bounded volume with smooth boundaries. By a standard theorem in functional analysis the inner-product space
![]() $\boldsymbol{{\mathcal{V}}}^{1}(V)$
can be completed to a Hilbert space
$\boldsymbol{{\mathcal{V}}}^{1}(V)$
can be completed to a Hilbert space
![]() $\overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
, although the elements of the space may be difficult to characterise. The operator
$\overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
, although the elements of the space may be difficult to characterise. The operator
![]() $\boldsymbol{{\mathcal{C}}}$
can be extended to a bounded linear operator
$\boldsymbol{{\mathcal{C}}}$
can be extended to a bounded linear operator
![]() $\overline{\boldsymbol{{\mathcal{C}}}}$
on
$\overline{\boldsymbol{{\mathcal{C}}}}$
on
![]() $\overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
, using continuity, and the operator
$\overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
, using continuity, and the operator
![]() $-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
is therefore a bounded self-adjoint operator. It follows (Friedman Reference Friedman1982) that the residual spectrum
$-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
is therefore a bounded self-adjoint operator. It follows (Friedman Reference Friedman1982) that the residual spectrum
![]() ${\it\sigma}_{r}$
of
${\it\sigma}_{r}$
of
![]() $\boldsymbol{{\mathcal{C}}}$
is empty and that the spectrum of
$\boldsymbol{{\mathcal{C}}}$
is empty and that the spectrum of
![]() $\boldsymbol{{\mathcal{C}}}$
, which is the union of the discrete and continuous spectrums, lies in
$\boldsymbol{{\mathcal{C}}}$
, which is the union of the discrete and continuous spectrums, lies in
![]() $[-\text{i},\text{i}]$
. The spectral theorem for bounded self-adjoint operators (Friedman Reference Friedman1982, § 6.7, Kreyszig Reference Kreyszig1978, § 9.9 or Taylor & Lay Reference Taylor and Lay1980, § 6.6) applies to
$[-\text{i},\text{i}]$
. The spectral theorem for bounded self-adjoint operators (Friedman Reference Friedman1982, § 6.7, Kreyszig Reference Kreyszig1978, § 9.9 or Taylor & Lay Reference Taylor and Lay1980, § 6.6) applies to
![]() $-i\overline{\boldsymbol{{\mathcal{C}}}}$
and implies that there exists a unique family of projection operators
$-i\overline{\boldsymbol{{\mathcal{C}}}}$
and implies that there exists a unique family of projection operators
![]() $\boldsymbol{{\mathcal{E}}}_{{\it\omega}}$
, which satisfy the conditions
$\boldsymbol{{\mathcal{E}}}_{{\it\omega}}$
, which satisfy the conditions
![]() $\boldsymbol{{\mathcal{E}}}_{{\it\omega}}=0$
if
$\boldsymbol{{\mathcal{E}}}_{{\it\omega}}=0$
if
![]() ${\it\omega}\leqslant -1$
and
${\it\omega}\leqslant -1$
and
![]() $\boldsymbol{{\mathcal{E}}}_{{\it\omega}}=\unicode[STIX]{x1D644}$
if
$\boldsymbol{{\mathcal{E}}}_{{\it\omega}}=\unicode[STIX]{x1D644}$
if
![]() ${\it\omega}>1$
, such that
${\it\omega}>1$
, such that
![]() $-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
has the following representation in terms of a Riemann–Stieltjes integral (with a right upper limit following Friedman Reference Friedman1982),
$-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
has the following representation in terms of a Riemann–Stieltjes integral (with a right upper limit following Friedman Reference Friedman1982),
 $$\begin{eqnarray}-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}=\int _{-1}^{1+}{\it\omega}\text{d}\boldsymbol{{\mathcal{E}}}_{{\it\omega}}.\end{eqnarray}$$
$$\begin{eqnarray}-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}=\int _{-1}^{1+}{\it\omega}\text{d}\boldsymbol{{\mathcal{E}}}_{{\it\omega}}.\end{eqnarray}$$
Moreover, any
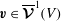 $\boldsymbol{v}\in \overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
has the spectral resolution
$\boldsymbol{v}\in \overline{\boldsymbol{{\mathcal{V}}}}^{1}(V)$
has the spectral resolution
 $$\begin{eqnarray}\boldsymbol{v}=\int _{-1}^{1+}\text{d}\boldsymbol{{\mathcal{E}}}_{{\it\omega}}\boldsymbol{v}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\int _{-1}^{1+}\text{d}\boldsymbol{{\mathcal{E}}}_{{\it\omega}}\boldsymbol{v}.\end{eqnarray}$$
This is the general completeness result for the discrete and continuous modes of
![]() $\overline{\boldsymbol{{\mathcal{C}}}}$
. If the spectrum is purely discrete the Riemann–Stieltjes integral reduces to a sum over the eigenvalues of
$\overline{\boldsymbol{{\mathcal{C}}}}$
. If the spectrum is purely discrete the Riemann–Stieltjes integral reduces to a sum over the eigenvalues of
![]() $-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
. The difficulty with the spectral theorem is that explicit construction of the spectral resolution is not possible except in special cases. Simple and practical characterisation of the spectral resolution is the subject of future work.
$-\text{i}\overline{\boldsymbol{{\mathcal{C}}}}$
. The difficulty with the spectral theorem is that explicit construction of the spectral resolution is not possible except in special cases. Simple and practical characterisation of the spectral resolution is the subject of future work.
Spherical Coriolis modes are useful in applications and potentially even in computations, due to their explicit polynomial form and completeness. Spherical harmonic expansions of the pressure modes, toroidal–poloidal potentials and vector spherical harmonic expansions of the velocity modes will be given elsewhere. One application is to viscous solutions of the momentum equation,
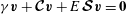 ${\it\gamma}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathbf{0}$
, or the viscous form of Poincaré’s equation, and how the modes for
${\it\gamma}\boldsymbol{v}+\boldsymbol{{\mathcal{C}}}\boldsymbol{v}+\mathit{E}\,\boldsymbol{{\mathcal{S}}}\boldsymbol{v}=\mathbf{0}$
, or the viscous form of Poincaré’s equation, and how the modes for
![]() $E=0$
approximate solutions in the limit
$E=0$
approximate solutions in the limit
![]() $E\rightarrow 0$
. Viscous asymptotic approximations have been given for spheres (Liao & Zhang Reference Liao and Zhang2010b
) and for a slender torus approximation to a spherical shell (Rieutord, Valdettaro & Georgeot Reference Rieutord, Valdettaro and Georgeot2002). A second application is magnetohydrodynamic dynamos, including the kinematic dynamo action of Coriolis modes. It is known that plane inertial modes have maximal helicity, a property exploited by Moffatt (Reference Moffatt1970) to produce a mean-field dynamo alpha effect. In the spherical case simple spatial inertial modes are not mean-field dynamos at leading order, due to the absence of any Stokes drift (Herreman & Lesaffre Reference Herreman and Lesaffre2011), but simple linear combinations of spatial Coriolis modes do act as dynamos, such as polynomial Dudley–James flows (Dudley & James Reference Dudley and James1989). The minimum magnetic Reynolds number
$E\rightarrow 0$
. Viscous asymptotic approximations have been given for spheres (Liao & Zhang Reference Liao and Zhang2010b
) and for a slender torus approximation to a spherical shell (Rieutord, Valdettaro & Georgeot Reference Rieutord, Valdettaro and Georgeot2002). A second application is magnetohydrodynamic dynamos, including the kinematic dynamo action of Coriolis modes. It is known that plane inertial modes have maximal helicity, a property exploited by Moffatt (Reference Moffatt1970) to produce a mean-field dynamo alpha effect. In the spherical case simple spatial inertial modes are not mean-field dynamos at leading order, due to the absence of any Stokes drift (Herreman & Lesaffre Reference Herreman and Lesaffre2011), but simple linear combinations of spatial Coriolis modes do act as dynamos, such as polynomial Dudley–James flows (Dudley & James Reference Dudley and James1989). The minimum magnetic Reynolds number
 $\min _{\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)}R_{m}$
for dynamo action over polynomial flows of degree
$\min _{\boldsymbol{v}\in \boldsymbol{{\mathcal{P}}}_{N}(V)}R_{m}$
for dynamo action over polynomial flows of degree
![]() $N$
or less would be interesting, as would some analogue for Coriolis modes. A third application is forcing with feedback, such as in magnetohydromagnetic torsional oscillations, where the forcing depends on the magnetic field, which depends on the velocity via the magnetic induction equation.
$N$
or less would be interesting, as would some analogue for Coriolis modes. A third application is forcing with feedback, such as in magnetohydromagnetic torsional oscillations, where the forcing depends on the magnetic field, which depends on the velocity via the magnetic induction equation.
Extensions of the Coriolis operator are possible. If the rotation is time-dependent, such as in precession, the incompressible Coriolis operator is time-dependent,
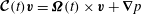 $\boldsymbol{{\mathcal{C}}}(t)\boldsymbol{v}={\it\bf\Omega}(t)\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p$
, where
$\boldsymbol{{\mathcal{C}}}(t)\boldsymbol{v}={\it\bf\Omega}(t)\times \boldsymbol{v}+\boldsymbol{{\rm\nabla}}p$
, where
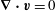 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
in
![]() $V(t)$
and
$V(t)$
and
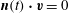 $\boldsymbol{n}(t)\boldsymbol{\cdot }\boldsymbol{v}=0$
on
$\boldsymbol{n}(t)\boldsymbol{\cdot }\boldsymbol{v}=0$
on
![]() $\partial V(t)$
. A useful extension to fully compressible flows appears unlikely due to the variable density. Morton & Shaughnessy (Reference Morton and Shaughnessy1972), Gans (Reference Gans1974) and Miles (Reference Miles1981) considered fully compressible inertial waves of an ideal gas in a cylinder rotating about its axis. Restricted compressible flows occur in various forms of the anelastic approximation, which all neglect the time dependence of the density in the equation for mass conservation (see Jones et al.
Reference Jones, Boronski, Brun, Glatzmaier, Gastine, Miesch and Wicht2011, § 2). If
$\partial V(t)$
. A useful extension to fully compressible flows appears unlikely due to the variable density. Morton & Shaughnessy (Reference Morton and Shaughnessy1972), Gans (Reference Gans1974) and Miles (Reference Miles1981) considered fully compressible inertial waves of an ideal gas in a cylinder rotating about its axis. Restricted compressible flows occur in various forms of the anelastic approximation, which all neglect the time dependence of the density in the equation for mass conservation (see Jones et al.
Reference Jones, Boronski, Brun, Glatzmaier, Gastine, Miesch and Wicht2011, § 2). If
![]() ${\it\rho}^{\prime }$
and
${\it\rho}^{\prime }$
and
![]() $p^{\prime }$
are the density and pressure perturbations of the basic state values
$p^{\prime }$
are the density and pressure perturbations of the basic state values
![]() $\bar{{\it\rho}}$
and
$\bar{{\it\rho}}$
and
![]() $\bar{p}$
of a stably stratified gas shell modelling gaseous planets and stars, a generalisation of the Coriolis operator to this case (see Jones et al.
Reference Jones, Boronski, Brun, Glatzmaier, Gastine, Miesch and Wicht2011, Eq. (15)) is
$\bar{p}$
of a stably stratified gas shell modelling gaseous planets and stars, a generalisation of the Coriolis operator to this case (see Jones et al.
Reference Jones, Boronski, Brun, Glatzmaier, Gastine, Miesch and Wicht2011, Eq. (15)) is
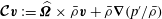 $\boldsymbol{{\mathcal{C}}}\boldsymbol{v}:=\widehat{{\it\bf\Omega}}\times \bar{{\it\rho}}\boldsymbol{v}+\bar{{\it\rho}}\boldsymbol{{\rm\nabla}}(p^{\prime }/\bar{{\it\rho}})$
with
$\boldsymbol{{\mathcal{C}}}\boldsymbol{v}:=\widehat{{\it\bf\Omega}}\times \bar{{\it\rho}}\boldsymbol{v}+\bar{{\it\rho}}\boldsymbol{{\rm\nabla}}(p^{\prime }/\bar{{\it\rho}})$
with
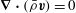 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\bar{{\it\rho}}\boldsymbol{v})=0$
. The properties of this
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\bar{{\it\rho}}\boldsymbol{v})=0$
. The properties of this
![]() $\boldsymbol{{\mathcal{C}}}$
, which clearly depend on
$\boldsymbol{{\mathcal{C}}}$
, which clearly depend on
![]() $\bar{{\it\rho}}$
, are not pursued any further here. Further work is also required on anelastic approximations with
$\bar{{\it\rho}}$
, are not pursued any further here. Further work is also required on anelastic approximations with
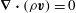 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0$
, for which the Coriolis operator may be generalised to
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0$
, for which the Coriolis operator may be generalised to
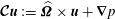 $\boldsymbol{{\mathcal{C}}}\boldsymbol{u}:=\widehat{{\it\bf\Omega}}\times \boldsymbol{u}+\boldsymbol{{\rm\nabla}}p$
, where
$\boldsymbol{{\mathcal{C}}}\boldsymbol{u}:=\widehat{{\it\bf\Omega}}\times \boldsymbol{u}+\boldsymbol{{\rm\nabla}}p$
, where
![]() $\boldsymbol{u}:={\it\rho}\boldsymbol{v}$
. This operator can be restricted to the space of polynomial momentum densities of degree
$\boldsymbol{u}:={\it\rho}\boldsymbol{v}$
. This operator can be restricted to the space of polynomial momentum densities of degree
![]() $N$
or less,
$N$
or less,
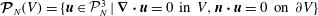 $\boldsymbol{{\mathcal{P}}}_{N}(V)=\{\boldsymbol{u}\in {\mathcal{P}}_{N}^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0~\text{in}~V,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}=0~\text{on}~\partial V\}$
and the results for the incompressible operator would follow in this compressible case. An extension to moving boundaries, when
$\boldsymbol{{\mathcal{P}}}_{N}(V)=\{\boldsymbol{u}\in {\mathcal{P}}_{N}^{3}\mid \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0~\text{in}~V,\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}=0~\text{on}~\partial V\}$
and the results for the incompressible operator would follow in this compressible case. An extension to moving boundaries, when
![]() $\boldsymbol{v}=\mathbf{0}$
is not a viscous solution in any rotating frame, is possible through linearisation. For example, consider a spherical shell with differentially rotating boundaries (Baruteau & Rieutord Reference Baruteau and Rieutord2013). The flow
$\boldsymbol{v}=\mathbf{0}$
is not a viscous solution in any rotating frame, is possible through linearisation. For example, consider a spherical shell with differentially rotating boundaries (Baruteau & Rieutord Reference Baruteau and Rieutord2013). The flow
![]() $\boldsymbol{v}=\mathbf{0}$
is a valid inviscid flow in any rotating reference frame concentric with the shell, but it is incompatible with a viscous solution. Let
$\boldsymbol{v}=\mathbf{0}$
is a valid inviscid flow in any rotating reference frame concentric with the shell, but it is incompatible with a viscous solution. Let
![]() $\boldsymbol{v}_{0}$
satisfy
$\boldsymbol{v}_{0}$
satisfy
 $$\begin{eqnarray}\boldsymbol{v}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{0}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{0}=-\boldsymbol{{\rm\nabla}}p_{0}+E{\rm\nabla}^{2}\boldsymbol{v}_{0}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{0}+\widehat{{\it\bf\Omega}}\times \boldsymbol{v}_{0}=-\boldsymbol{{\rm\nabla}}p_{0}+E{\rm\nabla}^{2}\boldsymbol{v}_{0}\end{eqnarray}$$
and
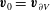 $\boldsymbol{v}_{0}=\boldsymbol{v}_{\partial V}$
, e.g. Taylor–Couette flow, and consider
$\boldsymbol{v}_{0}=\boldsymbol{v}_{\partial V}$
, e.g. Taylor–Couette flow, and consider
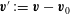 $\boldsymbol{v}^{\prime }:=\boldsymbol{v}-\boldsymbol{v}_{0}$
. The linearised inviscid problem for
$\boldsymbol{v}^{\prime }:=\boldsymbol{v}-\boldsymbol{v}_{0}$
. The linearised inviscid problem for
![]() $\boldsymbol{v}^{\prime }$
is
$\boldsymbol{v}^{\prime }$
is
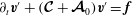 $\partial _{t}\boldsymbol{v}^{\prime }+(\boldsymbol{{\mathcal{C}}}+\boldsymbol{{\mathcal{A}}}_{0})\boldsymbol{v}^{\prime }=\boldsymbol{f}$
, where the linearised advective operator
$\partial _{t}\boldsymbol{v}^{\prime }+(\boldsymbol{{\mathcal{C}}}+\boldsymbol{{\mathcal{A}}}_{0})\boldsymbol{v}^{\prime }=\boldsymbol{f}$
, where the linearised advective operator
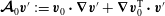 $\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}^{\prime }:=\boldsymbol{v}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}^{\prime }+\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{0}^{\text{T}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }$
. It is easily shown that
$\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}^{\prime }:=\boldsymbol{v}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}^{\prime }+\boldsymbol{{\rm\nabla}}\boldsymbol{v}_{0}^{\text{T}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }$
. It is easily shown that
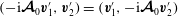 $(-\text{i}\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}_{1}^{\prime },\boldsymbol{v}_{2}^{\prime })=(\boldsymbol{v}_{1}^{\prime },-\text{i}\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}_{2}^{\prime })$
and hence
$(-\text{i}\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}_{1}^{\prime },\boldsymbol{v}_{2}^{\prime })=(\boldsymbol{v}_{1}^{\prime },-\text{i}\boldsymbol{{\mathcal{A}}}_{0}\boldsymbol{v}_{2}^{\prime })$
and hence
![]() $-i\boldsymbol{{\mathcal{A}}}_{0}$
is symmetric; but it is unbounded, unlike
$-i\boldsymbol{{\mathcal{A}}}_{0}$
is symmetric; but it is unbounded, unlike
![]() $\boldsymbol{{\mathcal{C}}}$
.
$\boldsymbol{{\mathcal{C}}}$
.
Acknowledgements
AJ is grateful for support through ERC Grant No. 247303 (MFECE). The authors are grateful to the anonymous referees for their constructive comments.
Appendix Proof of Theorem 3.4
We give an extension of Taylor’s Reference Taylor1963 proof to Theorem 3.4.
Proof. Condition (3.33) is necessary, since integration of the
![]() ${\it\phi}$
-component of (2.6) with
${\it\phi}$
-component of (2.6) with
![]() ${\it\lambda}=0$
over
${\it\lambda}=0$
over
![]() $C(s)$
gives
$C(s)$
gives
 $$\begin{eqnarray}\int _{C(s)}f_{{\it\phi}}\text{d}S=\int _{C(s)}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=-\int _{S(s)}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=-\int _{S(s)}g\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}\int _{C(s)}f_{{\it\phi}}\text{d}S=\int _{C(s)}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=-\int _{S(s)}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=-\int _{S(s)}g\text{d}S,\end{eqnarray}$$
noting that the total flux through the side
![]() $C(s)$
and ends
$C(s)$
and ends
![]() $S(s)$
of the cylinder
$S(s)$
of the cylinder
![]() $V(s)$
is zero by (3.32c
).
$V(s)$
is zero by (3.32c
).
Condition (3.33) is also sufficient. Let
![]() $\boldsymbol{n}_{t}~(\boldsymbol{n}_{b})$
be the outward unit normal on the top (bottom) boundary
$\boldsymbol{n}_{t}~(\boldsymbol{n}_{b})$
be the outward unit normal on the top (bottom) boundary
 $z=z_{t}~(z=z_{b})$
. Then
$z=z_{t}~(z=z_{b})$
. Then
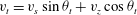 $v_{t}=v_{s}\sin {\it\theta}_{t}+v_{z}\cos {\it\theta}_{t}$
and
$v_{t}=v_{s}\sin {\it\theta}_{t}+v_{z}\cos {\it\theta}_{t}$
and
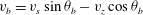 $v_{b}=v_{s}\sin {\it\theta}_{b}-v_{z}\cos {\it\theta}_{b}$
, where
$v_{b}=v_{s}\sin {\it\theta}_{b}-v_{z}\cos {\it\theta}_{b}$
, where
 $\cos {\it\theta}_{t}=\mathbf{1}_{z}\boldsymbol{\cdot }\boldsymbol{n}_{t}$
and
$\cos {\it\theta}_{t}=\mathbf{1}_{z}\boldsymbol{\cdot }\boldsymbol{n}_{t}$
and
 $\cos {\it\theta}_{b}=-\mathbf{1}_{z}\boldsymbol{\cdot }\boldsymbol{n}_{b}$
, and
$\cos {\it\theta}_{b}=-\mathbf{1}_{z}\boldsymbol{\cdot }\boldsymbol{n}_{b}$
, and
 $$\begin{eqnarray}v_{s}=\frac{v_{t}\cos {\it\theta}_{b}+v_{b}\cos {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\quad v_{z}=\frac{v_{t}\sin {\it\theta}_{b}-v_{b}\sin {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}.\end{eqnarray}$$
$$\begin{eqnarray}v_{s}=\frac{v_{t}\cos {\it\theta}_{b}+v_{b}\cos {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\quad v_{z}=\frac{v_{t}\sin {\it\theta}_{b}-v_{b}\sin {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}.\end{eqnarray}$$
Integration of the
![]() $\boldsymbol{n}_{t}$
and
$\boldsymbol{n}_{t}$
and
![]() $\boldsymbol{n}_{b}$
components of (3.32a
) yields
$\boldsymbol{n}_{b}$
components of (3.32a
) yields
 $$\begin{eqnarray}v_{t}=g_{t}-\int _{z_{t}}^{z}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{t}\text{d}z,\quad v_{b}=g_{b}-\int _{z_{b}}^{z}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{b}\text{d}z.\end{eqnarray}$$
$$\begin{eqnarray}v_{t}=g_{t}-\int _{z_{t}}^{z}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{t}\text{d}z,\quad v_{b}=g_{b}-\int _{z_{b}}^{z}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{b}\text{d}z.\end{eqnarray}$$
Transforming (A 2) to cylindrical polar coordinates yields
 $$\begin{eqnarray}v_{s}=v_{s}^{0}(\boldsymbol{f})+\frac{g_{t}\cos {\it\theta}_{b}+g_{b}\cos {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\quad v_{z}=v_{z}^{0}(\boldsymbol{F})+\frac{g_{t}\sin {\it\theta}_{b}-g_{b}\sin {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\end{eqnarray}$$
$$\begin{eqnarray}v_{s}=v_{s}^{0}(\boldsymbol{f})+\frac{g_{t}\cos {\it\theta}_{b}+g_{b}\cos {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\quad v_{z}=v_{z}^{0}(\boldsymbol{F})+\frac{g_{t}\sin {\it\theta}_{b}-g_{b}\sin {\it\theta}_{t}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle v_{s}^{0}(\boldsymbol{f}) & = & \displaystyle -\left(\frac{\sin {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{t}}^{z}+\frac{\cos {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z}\right)(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}z\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\cos {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z_{t}}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}z\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{s}^{0}(\boldsymbol{f}) & = & \displaystyle -\left(\frac{\sin {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{t}}^{z}+\frac{\cos {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z}\right)(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}z\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\cos {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z_{t}}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}z\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle v_{z}^{0}(\boldsymbol{f}) & = & \displaystyle -\left(\frac{\cos {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{t}}^{z}+\frac{\sin {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z}\right)(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}z\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\sin {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z_{t}}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}z.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{z}^{0}(\boldsymbol{f}) & = & \displaystyle -\left(\frac{\cos {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{t}}^{z}+\frac{\sin {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z}\right)(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}z\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\sin {\it\theta}_{t}\sin {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\int _{z_{b}}^{z_{t}}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}z.\end{eqnarray}$$
The component
![]() $v_{{\it\phi}}$
must be determined by integrating (3.32b
) and the
$v_{{\it\phi}}$
must be determined by integrating (3.32b
) and the
![]() ${\it\phi}$
-component of (3.32a
), namely
${\it\phi}$
-component of (3.32a
), namely
 $$\begin{eqnarray}\partial _{{\it\phi}}v_{{\it\phi}}=-\partial _{s}(sv_{s})-s\partial _{z}v_{z},\quad \partial _{z}v_{{\it\phi}}=\partial _{s}f_{z}-\partial _{z}f_{s},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{{\it\phi}}v_{{\it\phi}}=-\partial _{s}(sv_{s})-s\partial _{z}v_{z},\quad \partial _{z}v_{{\it\phi}}=\partial _{s}f_{z}-\partial _{z}f_{s},\end{eqnarray}$$
where
![]() $v_{s}$
and
$v_{s}$
and
![]() $v_{z}$
are given by (A 5) and (A 6). The equations (A 7) are integrable since the divergence of the right-hand side of (3.32a
) is identically zero. When the
$v_{z}$
are given by (A 5) and (A 6). The equations (A 7) are integrable since the divergence of the right-hand side of (3.32a
) is identically zero. When the
![]() ${\it\phi}$
-integration in (A 7) is performed, a single-valued solution is obtained if and only if
${\it\phi}$
-integration in (A 7) is performed, a single-valued solution is obtained if and only if
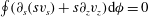 $\oint (\partial _{s}(sv_{s})+s\partial _{z}v_{z})\text{d}{\it\phi}=0$
. Substitution of the
$\oint (\partial _{s}(sv_{s})+s\partial _{z}v_{z})\text{d}{\it\phi}=0$
. Substitution of the
![]() $z$
-component of (3.32a
) and (A 7) yields
$z$
-component of (3.32a
) and (A 7) yields
 $$\begin{eqnarray}\oint (\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}{\it\phi}=-\partial _{z}\oint f_{{\it\phi}}\text{d}{\it\phi},\quad \oint (\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}{\it\phi}=\frac{1}{s}\partial _{s}s\oint f_{{\it\phi}}\text{d}{\it\phi},\end{eqnarray}$$
$$\begin{eqnarray}\oint (\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{s}\text{d}{\it\phi}=-\partial _{z}\oint f_{{\it\phi}}\text{d}{\it\phi},\quad \oint (\boldsymbol{{\rm\nabla}}\times \boldsymbol{f})_{z}\text{d}{\it\phi}=\frac{1}{s}\partial _{s}s\oint f_{{\it\phi}}\text{d}{\it\phi},\end{eqnarray}$$
 $$\begin{eqnarray}\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S=\int _{z_{b}}^{z_{t}}\partial _{s}s\oint f_{{\it\phi}}\text{d}{\it\phi}\text{d}z+\left[s\oint f_{{\it\phi}}\text{d}{\it\phi}\frac{\text{d}z}{\text{d}s}\right]_{z_{b}}^{z_{t}},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S=\int _{z_{b}}^{z_{t}}\partial _{s}s\oint f_{{\it\phi}}\text{d}{\it\phi}\text{d}z+\left[s\oint f_{{\it\phi}}\text{d}{\it\phi}\frac{\text{d}z}{\text{d}s}\right]_{z_{b}}^{z_{t}},\end{eqnarray}$$
 $\text{d}z_{t}/\text{d}s=-\text{tan}{\it\theta}_{t}$
and
$\text{d}z_{t}/\text{d}s=-\text{tan}{\it\theta}_{t}$
and
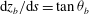 $\text{d}z_{b}/\text{d}s=\tan {\it\theta}_{b}$
gives
$\text{d}z_{b}/\text{d}s=\tan {\it\theta}_{b}$
gives
 $$\begin{eqnarray}\oint (\partial _{s}(sv_{s})+s\partial _{z}v_{z})\text{d}{\it\phi}=\partial _{s}\left(s\oint \frac{\cos {\it\theta}_{b}g_{t}+\cos {\it\theta}_{t}g_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\text{d}{\it\phi}+\frac{\cos {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S\right).\end{eqnarray}$$
$$\begin{eqnarray}\oint (\partial _{s}(sv_{s})+s\partial _{z}v_{z})\text{d}{\it\phi}=\partial _{s}\left(s\oint \frac{\cos {\it\theta}_{b}g_{t}+\cos {\it\theta}_{t}g_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\text{d}{\it\phi}+\frac{\cos {\it\theta}_{t}\cos {\it\theta}_{b}}{\sin ({\it\theta}_{t}+{\it\theta}_{b})}\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S\right).\end{eqnarray}$$
The last expression vanishes since
 $$\begin{eqnarray}s\oint (\sec {\it\theta}_{t}g_{t}+\sec {\it\theta}_{b}g_{b})\text{d}{\it\phi}+\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S=0,\end{eqnarray}$$
$$\begin{eqnarray}s\oint (\sec {\it\theta}_{t}g_{t}+\sec {\it\theta}_{b}g_{b})\text{d}{\it\phi}+\partial _{s}\int _{C(s)}f_{{\it\phi}}\text{d}S=0,\end{eqnarray}$$
which follows by differentiating (3.33) with respect to
![]() $s$
, noting that
$s$
, noting that
 $\text{d}S=\sec {\it\theta}_{t}s\text{d}s{\it\phi}$
(
$\text{d}S=\sec {\it\theta}_{t}s\text{d}s{\it\phi}$
(
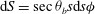 $\text{d}S=\sec {\it\theta}_{b}s\text{d}s{\it\phi}$
) on
$\text{d}S=\sec {\it\theta}_{b}s\text{d}s{\it\phi}$
) on
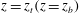 $z=z_{t}(z=z_{b})$
. Hence (3.33) is a necessary and sufficient condition for the single valuedness of
$z=z_{t}(z=z_{b})$
. Hence (3.33) is a necessary and sufficient condition for the single valuedness of
![]() $v_{{\it\phi}}$
. The non-uniqueness of
$v_{{\it\phi}}$
. The non-uniqueness of
![]() $v_{{\it\phi}}$
up to an arbitrary function of
$v_{{\it\phi}}$
up to an arbitrary function of
![]() $s$
is obvious, as is the uniqueness from imposing condition (3.34).
$s$
is obvious, as is the uniqueness from imposing condition (3.34).