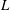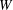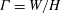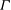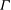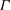1 Introduction
Thermal turbulence is ubiquitous in both nature and industrial applications. Turbulent Rayleigh–Bénard (RB) convection, a fluid layer heated from the bottom and cooled from the top has become a paradigm for the study of general convection phenomena. Over the years, there have been extensive studies addressing how the heat transport and flow dynamics of turbulent RB convection are determined by two control parameters, i.e. the Rayleigh number
![]() $Ra={\it\alpha}g{\rm\Delta}TH^{3}/{\it\nu}{\it\kappa}$
and the Prandtl number
$Ra={\it\alpha}g{\rm\Delta}TH^{3}/{\it\nu}{\it\kappa}$
and the Prandtl number
![]() $Pr={\it\nu}/{\it\kappa}$
, where
$Pr={\it\nu}/{\it\kappa}$
, where
![]() ${\rm\Delta}T$
is the temperature difference across the fluid layer of height
${\rm\Delta}T$
is the temperature difference across the fluid layer of height
![]() $H$
,
$H$
,
![]() $g$
is the acceleration due to gravity and
$g$
is the acceleration due to gravity and
![]() ${\it\alpha}$
,
${\it\alpha}$
,
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
are the thermal expansion coefficient, the kinematic viscosity and the thermal diffusivity of the working fluid, respectively (for reviews, see Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013). In laboratory experiments, the convective flows are always confined in containers with different geometries. It is generally believed that different geometric configurations will result in different flow structures and thus different associated flow properties. Therefore, the third control parameter that characterizes the effects of geometric confinement, aspect ratio
${\it\kappa}$
are the thermal expansion coefficient, the kinematic viscosity and the thermal diffusivity of the working fluid, respectively (for reviews, see Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013). In laboratory experiments, the convective flows are always confined in containers with different geometries. It is generally believed that different geometric configurations will result in different flow structures and thus different associated flow properties. Therefore, the third control parameter that characterizes the effects of geometric confinement, aspect ratio
![]() ${\it\Gamma}$
(lateral dimension of the fluid layer over its height), comes into the problem.
${\it\Gamma}$
(lateral dimension of the fluid layer over its height), comes into the problem.
Most of the existing studies on the confinement effects in turbulent RB convection were made in 3-D geometry (Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005; Nikolaenko et al.
Reference Nikolaenko, Brown, Funfschilling and Ahlers2005; Sun et al.
Reference Sun, Ren, Song and Xia2005a
; Niemela & Sreenivasan Reference Niemela and Sreenivasan2006; du Puits, Resagk & Thess Reference du Puits, Resagk and Thess2007; Xia, Sun & Cheung Reference Xia, Sun and Cheung2008; Bailon-Cuba, Emran & Schumacher Reference Bailon-Cuba, Emran and Schumacher2010; Roche et al.
Reference Roche, Gauthier, Kaiser and Salort2010; Wu & Libchaber Reference Wu and Libchaber2012; Zhou et al.
Reference Zhou, Liu, Li and Zhong2012) and the general findings were: (i) the single-roll structure changes to a multi-roll pattern with increasing
![]() ${\it\Gamma}$
; (ii) the heat transfer efficiency, characterized by the Nusselt number Nu, decreases slightly as
${\it\Gamma}$
; (ii) the heat transfer efficiency, characterized by the Nusselt number Nu, decreases slightly as
![]() ${\it\Gamma}$
increases and the asymptotic large-
${\it\Gamma}$
increases and the asymptotic large-
![]() ${\it\Gamma}$
behaviour may have been reached for
${\it\Gamma}$
behaviour may have been reached for
![]() ${\it\Gamma}\gtrsim 10$
. These findings have led one to conclude that the flow structures do not strongly influence the heat transport properties (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). Recently, there has been a growing interest in 2-D RB flow (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens and Lohse2013; van der Poel et al.
Reference van der Poel, Stevens, Sugiyama and Lohse2012; Chandra & Verma Reference Chandra and Verma2013; Huang & Zhou Reference Huang and Zhou2013; Podvin & Sergent Reference Podvin and Sergent2015). It was found that such a geometry will result in a stronger and more complicated
${\it\Gamma}\gtrsim 10$
. These findings have led one to conclude that the flow structures do not strongly influence the heat transport properties (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). Recently, there has been a growing interest in 2-D RB flow (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens and Lohse2013; van der Poel et al.
Reference van der Poel, Stevens, Sugiyama and Lohse2012; Chandra & Verma Reference Chandra and Verma2013; Huang & Zhou Reference Huang and Zhou2013; Podvin & Sergent Reference Podvin and Sergent2015). It was found that such a geometry will result in a stronger and more complicated
![]() ${\it\Gamma}$
-dependence of Nu, which was ascribed to the different flow structures in the 2-D system (van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012, Reference van der Poel, Stevens and Lohse2013). Although the flow dynamics in the 2-D system, which strictly can only be realized numerically, may share certain features with those in the quasi-2-D case (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), a true 2-D system is fundamentally different from a quasi-2-D one. Indeed, recent studies by Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) found that simple geometric confinement in the quasi-2-D system can significantly enhance convective heat transport, which is brought about by the change in the dynamics and morphology of the thermal plumes. Such a striking phenomenon has not been observed in previous studies in 3-D and true 2-D systems. In this paper, we further investigate the confinement effects in quasi-2-D turbulent RB convection by experimentally studying various flow properties, including flow dynamics, local temperature fluctuation and global heat transport. The results will complement the findings reported in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015). As will be shown in the paper, in the quasi-2-D geometry, the geometric confinement not only can strongly influence the local flow properties, but also has a significant effect on the global properties, which are very different from the previous findings in 3-D and true 2-D systems (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010; van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012, Reference van der Poel, Stevens and Lohse2013; Chandra & Verma Reference Chandra and Verma2013).
${\it\Gamma}$
-dependence of Nu, which was ascribed to the different flow structures in the 2-D system (van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012, Reference van der Poel, Stevens and Lohse2013). Although the flow dynamics in the 2-D system, which strictly can only be realized numerically, may share certain features with those in the quasi-2-D case (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), a true 2-D system is fundamentally different from a quasi-2-D one. Indeed, recent studies by Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) found that simple geometric confinement in the quasi-2-D system can significantly enhance convective heat transport, which is brought about by the change in the dynamics and morphology of the thermal plumes. Such a striking phenomenon has not been observed in previous studies in 3-D and true 2-D systems. In this paper, we further investigate the confinement effects in quasi-2-D turbulent RB convection by experimentally studying various flow properties, including flow dynamics, local temperature fluctuation and global heat transport. The results will complement the findings reported in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015). As will be shown in the paper, in the quasi-2-D geometry, the geometric confinement not only can strongly influence the local flow properties, but also has a significant effect on the global properties, which are very different from the previous findings in 3-D and true 2-D systems (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010; van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012, Reference van der Poel, Stevens and Lohse2013; Chandra & Verma Reference Chandra and Verma2013).
The rest of this paper is organized as follows. The experimental set-up and measurement techniques are described in § 2. The main results are presented in § 3, which is divided into three parts. We first show the results obtained from the flow field and reversal measurements in § 3.1. The influences of geometric confinement on the local temperature fluctuation and the global heat transport will be presented in §§ 3.2 and 3.3. A summary of our findings comes in § 4.
2 Experimental apparatus and methods
The experiments were conducted in the range
![]() $8.6\times 10^{7}\leqslant Ra\leqslant 2.50\times 10^{9}$
with the bulk temperature of the fluid (deionized and degassed water)
$8.6\times 10^{7}\leqslant Ra\leqslant 2.50\times 10^{9}$
with the bulk temperature of the fluid (deionized and degassed water)
![]() $T_{c}$
maintained at
$T_{c}$
maintained at
![]() $40.0\,^{\circ }\text{C}$
, corresponding to
$40.0\,^{\circ }\text{C}$
, corresponding to
![]() $Pr=4.3$
. The convection cells used in the experiments were similar to the one described in Xia, Sun & Zhou (Reference Xia, Sun and Zhou2003). Briefly, they were of rectangular shape and were built independently with their own Plexiglas side walls and conducting plates (but of identical design), where the bottom plates were heated with constant power and the top plates were kept at constant temperature. The height
$Pr=4.3$
. The convection cells used in the experiments were similar to the one described in Xia, Sun & Zhou (Reference Xia, Sun and Zhou2003). Briefly, they were of rectangular shape and were built independently with their own Plexiglas side walls and conducting plates (but of identical design), where the bottom plates were heated with constant power and the top plates were kept at constant temperature. The height
![]() $H$
and length
$H$
and length
![]() $L$
of the cells were the same and fixed at 12.6 cm, thus the aspect ratio
$L$
of the cells were the same and fixed at 12.6 cm, thus the aspect ratio
![]() ${\it\Gamma}_{\Vert }$
(
${\it\Gamma}_{\Vert }$
(
![]() $=L/H$
) in the plane parallel to the large-scale circulation (LSC) plane is one; whereas the width
$=L/H$
) in the plane parallel to the large-scale circulation (LSC) plane is one; whereas the width
![]() $W$
of the cells had values 7.56, 3.84, 2.56, 1.92 and 1.27 cm, giving rise to aspect ratios in the plane perpendicular to the LSC plane (
$W$
of the cells had values 7.56, 3.84, 2.56, 1.92 and 1.27 cm, giving rise to aspect ratios in the plane perpendicular to the LSC plane (
![]() ${\it\Gamma}_{\bot }=W/H$
, hereafter simply
${\it\Gamma}_{\bot }=W/H$
, hereafter simply
![]() ${\it\Gamma}$
) of 0.6, 0.3, 0.2, 0.15 and 0.1, respectively. With these geometric configurations, the confinement on the flow is expected to increase as
${\it\Gamma}$
) of 0.6, 0.3, 0.2, 0.15 and 0.1, respectively. With these geometric configurations, the confinement on the flow is expected to increase as
![]() ${\it\Gamma}$
decreases. Having exactly the same height is one important feature of the present study, as it allows measurements in different cells to be made over exactly the same range of Ra, so that results obtained from different cells can be compared directly.
${\it\Gamma}$
decreases. Having exactly the same height is one important feature of the present study, as it allows measurements in different cells to be made over exactly the same range of Ra, so that results obtained from different cells can be compared directly.
To obtain an overall picture of the confinement effects on the flow dynamics, we made 2-D velocity measurements in the vertical plane midway between the front and back walls of the convection cell at two selected aspect ratios, i.e.
![]() ${\it\Gamma}=0.3$
and 0.15, using a commercial particle image velocimetry (PIV) system that has been introduced elsewhere (Xia et al.
Reference Xia, Sun and Zhou2003). In the PIV measurements, the fluid was seeded with polyamide particles of
${\it\Gamma}=0.3$
and 0.15, using a commercial particle image velocimetry (PIV) system that has been introduced elsewhere (Xia et al.
Reference Xia, Sun and Zhou2003). In the PIV measurements, the fluid was seeded with polyamide particles of
![]() $50~{\rm\mu}\text{m}$
in diameter. Each flow field contained
$50~{\rm\mu}\text{m}$
in diameter. Each flow field contained
![]() $127\times 127$
velocity vectors and a total of 10 000 vector maps were acquired with a sampling rate
$127\times 127$
velocity vectors and a total of 10 000 vector maps were acquired with a sampling rate
![]() ${\sim}2~\text{Hz}$
. The statistical behaviour of flow reversal, a phenomenon that the LSC suddenly reverses its flow direction in an erratic manner (Sreenivasan, Bershadskii & Niemela Reference Sreenivasan, Bershadskii and Niemela2002; Brown & Ahlers Reference Brown and Ahlers2007; Xi & Xia Reference Xi and Xia2007), were studied with the so-called temperature contrast method (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni, Huang & Xia Reference Ni, Huang and Xia2015). For ease of presentation, the details of this technique will be described in § 3.1. The temperature fluctuations in the cell centre were measured with a small thermistor with a size of
${\sim}2~\text{Hz}$
. The statistical behaviour of flow reversal, a phenomenon that the LSC suddenly reverses its flow direction in an erratic manner (Sreenivasan, Bershadskii & Niemela Reference Sreenivasan, Bershadskii and Niemela2002; Brown & Ahlers Reference Brown and Ahlers2007; Xi & Xia Reference Xi and Xia2007), were studied with the so-called temperature contrast method (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni, Huang & Xia Reference Ni, Huang and Xia2015). For ease of presentation, the details of this technique will be described in § 3.1. The temperature fluctuations in the cell centre were measured with a small thermistor with a size of
![]() $200~{\rm\mu}\text{m}$
. Except in the PIV measurements, where a transparent window was required, several layers of thermal insulation were wrapped to the whole convection cell to prevent the heat leakage. To minimize influence from the surroundings, all the measurements were made in a thermostat with a stability of better than
$200~{\rm\mu}\text{m}$
. Except in the PIV measurements, where a transparent window was required, several layers of thermal insulation were wrapped to the whole convection cell to prevent the heat leakage. To minimize influence from the surroundings, all the measurements were made in a thermostat with a stability of better than
![]() $0.1\,^{\circ }\text{C}$
.
$0.1\,^{\circ }\text{C}$
.
3 Results and discussions
3.1 Flow dynamics
It is one’s intuition that the flow dynamics should strongly depend on geometry. To find out how the flow dynamics responds to geometric confinement, we show in figure 1(a–c) the PIV-measured mean velocity fields for
![]() ${\it\Gamma}=0.3$
(the unconfined case) and 0.15. The first thing we can see is that there exists a well-defined LSC with two counter-rotating corner rolls in the
${\it\Gamma}=0.3$
(the unconfined case) and 0.15. The first thing we can see is that there exists a well-defined LSC with two counter-rotating corner rolls in the
![]() ${\it\Gamma}=0.3$
cell, as found in previous studies with similar aspect ratios (Xia et al.
Reference Xia, Sun and Zhou2003; Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). For the
${\it\Gamma}=0.3$
cell, as found in previous studies with similar aspect ratios (Xia et al.
Reference Xia, Sun and Zhou2003; Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). For the
![]() ${\it\Gamma}=0.15$
cell, however, one finds a quite different flow pattern in the long time-averaged field: The single-roll structure has disappeared, instead, we have a four-roll structure. One way such a four-roll pattern in the mean field can arise is for the LSC to frequently reverse its flow direction, which had been experimentally demonstrated in an earlier study (Sun, Xia & Tong Reference Sun, Xia and Tong2005b
). Indeed, by taking short time averages of the instantaneous velocity fields, we can obtain LSCs with both clockwise and counter-clockwise flow directions in the
${\it\Gamma}=0.15$
cell, however, one finds a quite different flow pattern in the long time-averaged field: The single-roll structure has disappeared, instead, we have a four-roll structure. One way such a four-roll pattern in the mean field can arise is for the LSC to frequently reverse its flow direction, which had been experimentally demonstrated in an earlier study (Sun, Xia & Tong Reference Sun, Xia and Tong2005b
). Indeed, by taking short time averages of the instantaneous velocity fields, we can obtain LSCs with both clockwise and counter-clockwise flow directions in the
![]() ${\it\Gamma}=0.15$
cell (see figure 1
c for the counter-clockwise case), which was also illustrated in a recent numerical study with a similar
${\it\Gamma}=0.15$
cell (see figure 1
c for the counter-clockwise case), which was also illustrated in a recent numerical study with a similar
![]() ${\it\Gamma}$
(Kaczorowski, Chong & Xia Reference Kaczorowski, Chong and Xia2014). The second difference between these two
${\it\Gamma}$
(Kaczorowski, Chong & Xia Reference Kaczorowski, Chong and Xia2014). The second difference between these two
![]() ${\it\Gamma}$
cells is that the magnitude of the time-averaged LSC is smaller for
${\it\Gamma}$
cells is that the magnitude of the time-averaged LSC is smaller for
![]() ${\it\Gamma}=0.15$
, as indicated clearly by the scale bar. While the increased drag force from the walls can certainly slow down the flow, a more fluctuating flow can also result in a smaller mean velocity. Larger fluctuations in the flow field for small
${\it\Gamma}=0.15$
, as indicated clearly by the scale bar. While the increased drag force from the walls can certainly slow down the flow, a more fluctuating flow can also result in a smaller mean velocity. Larger fluctuations in the flow field for small
![]() ${\it\Gamma}$
are evident in the root-mean-square (r.m.s.) velocity field (see figure 1
d–f), which shows that the fluctuations in the bulk of the
${\it\Gamma}$
are evident in the root-mean-square (r.m.s.) velocity field (see figure 1
d–f), which shows that the fluctuations in the bulk of the
![]() ${\it\Gamma}=0.15$
cell become stronger and the region of strong fluctuations also becomes larger. It has been found in Xia et al. (Reference Xia, Sun and Zhou2003) that larger velocity fluctuations are associated with plume clusters, therefore the r.m.s. velocity fields measured here indicate that there are more thermal plumes going through the bulk region in the highly confined geometry, rather than rising and falling along the side walls as is the case for larger
${\it\Gamma}=0.15$
cell become stronger and the region of strong fluctuations also becomes larger. It has been found in Xia et al. (Reference Xia, Sun and Zhou2003) that larger velocity fluctuations are associated with plume clusters, therefore the r.m.s. velocity fields measured here indicate that there are more thermal plumes going through the bulk region in the highly confined geometry, rather than rising and falling along the side walls as is the case for larger
![]() ${\it\Gamma}$
. Note that the reversal of the LSC could also contribute to a larger velocity fluctuation in the bulk region. However, we found that the r.m.s. velocity field in the
${\it\Gamma}$
. Note that the reversal of the LSC could also contribute to a larger velocity fluctuation in the bulk region. However, we found that the r.m.s. velocity field in the
![]() ${\it\Gamma}=0.15$
cell for the situation when a LSC can still be identified by short time averaging is quite similar to the one with a four-roll pattern (see figure 1
e,f), suggesting that the major contributors for larger fluctuations in the bulk flow are the thermal plumes.
${\it\Gamma}=0.15$
cell for the situation when a LSC can still be identified by short time averaging is quite similar to the one with a four-roll pattern (see figure 1
e,f), suggesting that the major contributors for larger fluctuations in the bulk flow are the thermal plumes.

Figure 1. Coarse-grained vector maps of mean velocity field (a–c) and the corresponding contour maps of the r.m.s. velocity field (d–f) at
![]() $Ra=1.1\times 10^{9}$
. (a,d)
$Ra=1.1\times 10^{9}$
. (a,d)
![]() ${\it\Gamma}=0.3$
cell by long time averaging; (b,e)
${\it\Gamma}=0.3$
cell by long time averaging; (b,e)
![]() ${\it\Gamma}=0.15$
cell with a four-roll pattern by long time averaging; (c,f)
${\it\Gamma}=0.15$
cell with a four-roll pattern by long time averaging; (c,f)
![]() ${\it\Gamma}=0.15$
cell with a well-identified LSC by short time averaging. The velocity is coded in both colour scale and vector length in units of
${\it\Gamma}=0.15$
cell with a well-identified LSC by short time averaging. The velocity is coded in both colour scale and vector length in units of
![]() $\text{cm}~\text{s}^{-1}$
. The r.m.s. velocity is represented by the colour coding in units of
$\text{cm}~\text{s}^{-1}$
. The r.m.s. velocity is represented by the colour coding in units of
![]() $\text{cm}~\text{s}^{-1}$
.
$\text{cm}~\text{s}^{-1}$
.

Figure 2. A schematic sketch of the reversal process changing from (a) state I to (b) state II. (c) A typical time series of the temperature contrast
![]() ${\it\delta}$
between the two sensors embedded in the bottom plate for
${\it\delta}$
between the two sensors embedded in the bottom plate for
![]() $Ra=1.1\times 10^{9}$
. The red solid circles indicate detections of flow reversal events based on the criteria described in the text. The red dashed lines indicate the two flow states I and II shown in (a) and (b), respectively. (d) The corresponding PDF of the data shown in (c). The blue dashed lines are two independent Gaussian function fits to the data and the red solid line is the superposition of them. It is seen that the data can be excellently fitted with a double-Gaussian function. See text for the explanations of
$Ra=1.1\times 10^{9}$
. The red solid circles indicate detections of flow reversal events based on the criteria described in the text. The red dashed lines indicate the two flow states I and II shown in (a) and (b), respectively. (d) The corresponding PDF of the data shown in (c). The blue dashed lines are two independent Gaussian function fits to the data and the red solid line is the superposition of them. It is seen that the data can be excellently fitted with a double-Gaussian function. See text for the explanations of
![]() $d$
and
$d$
and
![]() ${\it\sigma}$
. Note that similar results were obtained from the top plate.
${\it\sigma}$
. Note that similar results were obtained from the top plate.
That flow reversals become more probable in quasi-2-D cells with smaller
![]() ${\it\Gamma}$
was also observed in some previous studies (Vasilev & Frick Reference Vasilev and Frick2011; Wagner & Shishkina Reference Wagner and Shishkina2013; Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but their statistical properties have not been examined. Here, we used the temperature contrast method (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni et al.
Reference Ni, Huang and Xia2015) to detect flow reversal events over long time periods. This method is based on the idea that a region where cold plumes impinge should have a lower temperature than that where hot plumes emit. As illustrated in figure 2, when the LSC circulates in the counter-clockwise direction (state I as sketched in figure 2
a), the temperature in the left side of the bottom plate is lower than that in the right side; when the flow reverses its circulation directing and changes to state II (figure 2
b), the temperature in the left side becomes higher. Therefore, the temperature contrast
${\it\Gamma}$
was also observed in some previous studies (Vasilev & Frick Reference Vasilev and Frick2011; Wagner & Shishkina Reference Wagner and Shishkina2013; Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but their statistical properties have not been examined. Here, we used the temperature contrast method (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni et al.
Reference Ni, Huang and Xia2015) to detect flow reversal events over long time periods. This method is based on the idea that a region where cold plumes impinge should have a lower temperature than that where hot plumes emit. As illustrated in figure 2, when the LSC circulates in the counter-clockwise direction (state I as sketched in figure 2
a), the temperature in the left side of the bottom plate is lower than that in the right side; when the flow reverses its circulation directing and changes to state II (figure 2
b), the temperature in the left side becomes higher. Therefore, the temperature contrast
![]() ${\it\delta}=T_{right}-T_{left}$
will change its sign during a reversal event and thus is a good indicator of reversals (see figure 2
c). Besides the sign change of
${\it\delta}=T_{right}-T_{left}$
will change its sign during a reversal event and thus is a good indicator of reversals (see figure 2
c). Besides the sign change of
![]() ${\it\delta}$
, we set three more criteria to count true reversal events. The first one is that the two circulation states can be clearly distinguished from each other. This is quantified with the PDF of
${\it\delta}$
, we set three more criteria to count true reversal events. The first one is that the two circulation states can be clearly distinguished from each other. This is quantified with the PDF of
![]() ${\it\delta}$
, as shown in figure 2(d). To be specific, the distance
${\it\delta}$
, as shown in figure 2(d). To be specific, the distance
![]() $d$
between the two most probable values in the PDF should be larger than the r.m.s. value
$d$
between the two most probable values in the PDF should be larger than the r.m.s. value
![]() ${\it\sigma}$
so that the two peaks can be clearly distinguished, where
${\it\sigma}$
so that the two peaks can be clearly distinguished, where
![]() $d$
and
$d$
and
![]() ${\it\sigma}$
were obtained by a double-Gaussian function fit as shown in figure 2(d). The second criterion is that when the flow changes from one state to the other,
${\it\sigma}$
were obtained by a double-Gaussian function fit as shown in figure 2(d). The second criterion is that when the flow changes from one state to the other,
![]() ${\it\delta}$
should first crossover the peak, i.e. the value of
${\it\delta}$
should first crossover the peak, i.e. the value of
![]() ${\it\delta}$
should be larger (smaller) than the peak value in the PDF corresponding to state I (II). The third one is that the flow should stay at the new state for more than one turnover time
${\it\delta}$
should be larger (smaller) than the peak value in the PDF corresponding to state I (II). The third one is that the flow should stay at the new state for more than one turnover time
![]() $t_{LSC}$
of the LSC, which was obtained from the correlation function of the temperature signals inside the plates (Brown, Funfschilling & Ahlers Reference Brown, Funfschilling and Ahlers2007). With these criteria, we are ready to examine the flow reversals quantitatively.
$t_{LSC}$
of the LSC, which was obtained from the correlation function of the temperature signals inside the plates (Brown, Funfschilling & Ahlers Reference Brown, Funfschilling and Ahlers2007). With these criteria, we are ready to examine the flow reversals quantitatively.

Figure 3. Examples of flow reversals at
![]() $Ra=1.1\times 10^{9}$
for (a)
$Ra=1.1\times 10^{9}$
for (a)
![]() ${\it\Gamma}=0.3$
, (b)
${\it\Gamma}=0.3$
, (b)
![]() ${\it\Gamma}=0.2$
and (c)
${\it\Gamma}=0.2$
and (c)
![]() ${\it\Gamma}=0.15$
. The red solid circles indicate detections of flow reversal events based on the criteria described in the text. (d) The normalized flow reversal frequency
${\it\Gamma}=0.15$
. The red solid circles indicate detections of flow reversal events based on the criteria described in the text. (d) The normalized flow reversal frequency
![]() $f_{rev}/f_{LSC}$
as a function of
$f_{rev}/f_{LSC}$
as a function of
![]() ${\it\Gamma}$
for different
${\it\Gamma}$
for different
![]() $Ra$
, where
$Ra$
, where
![]() $f_{rev}=1/\langle {\it\tau}\rangle$
,
$f_{rev}=1/\langle {\it\tau}\rangle$
,
![]() $f_{LSC}=1/t_{LSC}$
, and
$f_{LSC}=1/t_{LSC}$
, and
![]() $\langle {\it\tau}\rangle$
is the mean time interval between successive reversals.
$\langle {\it\tau}\rangle$
is the mean time interval between successive reversals.
We first show in figure 3(a–c) some examples of flow reversals at
![]() $Ra=1.1\times 10^{9}$
for
$Ra=1.1\times 10^{9}$
for
![]() ${\it\Gamma}=0.3$
, 0.2 and 0.15, respectively. It is seen clearly that the LSC reverses its circulating direction with a drastically increased frequency as
${\it\Gamma}=0.3$
, 0.2 and 0.15, respectively. It is seen clearly that the LSC reverses its circulating direction with a drastically increased frequency as
![]() ${\it\Gamma}$
decreases, which is quantified in figure 3(d). However, when
${\it\Gamma}$
decreases, which is quantified in figure 3(d). However, when
![]() ${\it\Gamma}$
is further reduced from 0.15 to 0.1, the reversal frequency does not show a significant increase anymore, so we do not show the examples for
${\it\Gamma}$
is further reduced from 0.15 to 0.1, the reversal frequency does not show a significant increase anymore, so we do not show the examples for
![]() ${\it\Gamma}=0.1$
here. It is further observed in figure 3(d) that the increase in the reversal frequency is
${\it\Gamma}=0.1$
here. It is further observed in figure 3(d) that the increase in the reversal frequency is
![]() $Ra$
-dependent: the higher Ra becomes, the larger the increase (by more than 1000-fold for the highest value of Rayleigh number reached in the experiment), suggesting that the impact of confinement on the LSC dynamics is stronger for higher
$Ra$
-dependent: the higher Ra becomes, the larger the increase (by more than 1000-fold for the highest value of Rayleigh number reached in the experiment), suggesting that the impact of confinement on the LSC dynamics is stronger for higher
![]() $Ra$
. Note that the measurements in smaller
$Ra$
. Note that the measurements in smaller
![]() ${\it\Gamma}$
cells did not go to lower Ra, because
${\it\Gamma}$
cells did not go to lower Ra, because
![]() ${\it\sigma}$
becomes comparable with
${\it\sigma}$
becomes comparable with
![]() $d$
in these cases, thus the first criterion is not satisfied anymore. This is a limitation of the measurement technique. We also remark that no flow reversal was observed in the
$d$
in these cases, thus the first criterion is not satisfied anymore. This is a limitation of the measurement technique. We also remark that no flow reversal was observed in the
![]() ${\it\Gamma}=0.6$
cell, even with a long time measurement of up to 15 000
${\it\Gamma}=0.6$
cell, even with a long time measurement of up to 15 000
![]() $t_{LSC}$
(more than two weeks) at
$t_{LSC}$
(more than two weeks) at
![]() $Ra=2.8\times 10^{8}$
, at which flow reversals are supposed to have a higher probability of occurrence than at higher Ra (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni et al.
Reference Ni, Huang and Xia2015).
$Ra=2.8\times 10^{8}$
, at which flow reversals are supposed to have a higher probability of occurrence than at higher Ra (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Ni et al.
Reference Ni, Huang and Xia2015).

Figure 4. A semi-log plot of the normalized mean time interval between successive reversals
![]() $\langle {\it\tau}\rangle /t_{LSC}$
as a function of
$\langle {\it\tau}\rangle /t_{LSC}$
as a function of
![]() $(d/2{\it\sigma})^{2}$
for different
$(d/2{\it\sigma})^{2}$
for different
![]() ${\it\Gamma}$
. The solid lines are fittings to individual data sets according to the formula
${\it\Gamma}$
. The solid lines are fittings to individual data sets according to the formula
![]() $\langle {\it\tau}\rangle /t_{LSC}=C_{p}({\it\Gamma})\exp [(d/2{\it\sigma})^{2}]$
obtained in a model developed by Ni et al. (Reference Ni, Huang and Xia2015) recently. Inset: The fitting coefficient
$\langle {\it\tau}\rangle /t_{LSC}=C_{p}({\it\Gamma})\exp [(d/2{\it\sigma})^{2}]$
obtained in a model developed by Ni et al. (Reference Ni, Huang and Xia2015) recently. Inset: The fitting coefficient
![]() $C_{p}$
versus
$C_{p}$
versus
![]() ${\it\Gamma}$
.
${\it\Gamma}$
.
In a recent study using quasi-2-D cells similar to the ones used in the present experiment, Ni et al. (Reference Ni, Huang and Xia2015) have shown that the mean time interval between successive reversals
![]() $\langle {\it\tau}\rangle$
follows a stochastic process, i.e.
$\langle {\it\tau}\rangle$
follows a stochastic process, i.e.
![]() $\langle {\it\tau}\rangle /t_{LSC}=C_{p}({\it\Gamma})\exp [(d/2{\it\sigma})^{2}]$
, where
$\langle {\it\tau}\rangle /t_{LSC}=C_{p}({\it\Gamma})\exp [(d/2{\it\sigma})^{2}]$
, where
![]() $d$
is taken as the relative strength of the LSC and
$d$
is taken as the relative strength of the LSC and
![]() ${\it\sigma}$
is its fluctuation. Figure 4 shows the data
${\it\sigma}$
is its fluctuation. Figure 4 shows the data
![]() $\langle {\it\tau}\rangle /t_{LSC}$
versus
$\langle {\it\tau}\rangle /t_{LSC}$
versus
![]() $(d/2{\it\sigma})^{2}$
for different
$(d/2{\it\sigma})^{2}$
for different
![]() ${\it\Gamma}$
cells in a semi-log plot. It is seen that the data can be nicely fitted with the formula above, with a strong
${\it\Gamma}$
cells in a semi-log plot. It is seen that the data can be nicely fitted with the formula above, with a strong
![]() ${\it\Gamma}$
-dependent prefactor
${\it\Gamma}$
-dependent prefactor
![]() $C_{p}$
, as shown in the inset, indicting that the model developed in Ni et al. (Reference Ni, Huang and Xia2015) can also well describe the reversal behaviours in a highly confined geometry. Since the value of
$C_{p}$
, as shown in the inset, indicting that the model developed in Ni et al. (Reference Ni, Huang and Xia2015) can also well describe the reversal behaviours in a highly confined geometry. Since the value of
![]() $d/{\it\sigma}$
can be used to characterize the stability of the LSC, we further examine their values separately to see how confinement affects the properties of the LSC. It is seen in figure 5 that as
$d/{\it\sigma}$
can be used to characterize the stability of the LSC, we further examine their values separately to see how confinement affects the properties of the LSC. It is seen in figure 5 that as
![]() ${\it\Gamma}$
decreases,
${\it\Gamma}$
decreases,
![]() $d$
decreases on one hand, and
$d$
decreases on one hand, and
![]() ${\it\sigma}$
increases on the other, which suggests that LSC becomes weaker and experiences stronger fluctuations in highly confined geometry, thus confirming the PIV-measured results. As
${\it\sigma}$
increases on the other, which suggests that LSC becomes weaker and experiences stronger fluctuations in highly confined geometry, thus confirming the PIV-measured results. As
![]() $d$
is essentially the temperature difference between the left and right sides of the conducting plates, smaller
$d$
is essentially the temperature difference between the left and right sides of the conducting plates, smaller
![]() $d$
also suggests that the temperature is more uniform in the plate for small
$d$
also suggests that the temperature is more uniform in the plate for small
![]() ${\it\Gamma}$
cells, consistent with the findings in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013).
${\it\Gamma}$
cells, consistent with the findings in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013).

Figure 5. (a) The strength of the LSC
![]() $d$
and (b) its fluctuation
$d$
and (b) its fluctuation
![]() ${\it\sigma}$
normalized by the global temperature difference
${\it\sigma}$
normalized by the global temperature difference
![]() ${\rm\Delta}T$
as a function of
${\rm\Delta}T$
as a function of
![]() ${\it\Gamma}$
for different
${\it\Gamma}$
for different
![]() $Ra$
. Note that
$Ra$
. Note that
![]() ${\rm\Delta}T$
for different
${\rm\Delta}T$
for different
![]() ${\it\Gamma}$
cells are the same for the same
${\it\Gamma}$
cells are the same for the same
![]() $Ra$
, as they have the same height.
$Ra$
, as they have the same height.

Figure 6. PDFs of the normalized time interval between successive flow reversals at
![]() $Ra=1.1\times 10^{9}$
for (a)
$Ra=1.1\times 10^{9}$
for (a)
![]() ${\it\Gamma}=0.2$
and (b)
${\it\Gamma}=0.2$
and (b)
![]() ${\it\Gamma}=0.15$
, respectively. The straight lines indicate exponential fittings.
${\it\Gamma}=0.15$
, respectively. The straight lines indicate exponential fittings.
In figure 6, we show the PDFs of time interval between successive reversals
![]() ${\it\tau}/t_{LSC}$
for
${\it\tau}/t_{LSC}$
for
![]() ${\it\Gamma}=0.2$
and 0.15 cells on a semi-log scale. It is seen that the data for both
${\it\Gamma}=0.2$
and 0.15 cells on a semi-log scale. It is seen that the data for both
![]() ${\it\Gamma}$
are in good agreement with the exponential function
${\it\Gamma}$
are in good agreement with the exponential function
![]() $p({\it\tau}/t_{LSC})\sim \exp (-{\it\tau}/t_{LSC})$
. (The levelling off of the PDFs at the large values of
$p({\it\tau}/t_{LSC})\sim \exp (-{\it\tau}/t_{LSC})$
. (The levelling off of the PDFs at the large values of
![]() ${\it\tau}/t_{LSC}$
is caused by the insufficient statistics.) These results indicate that flow reversals in the quasi-2-D geometry obey Poisson statistics as in the 3-D case (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Brown & Ahlers Reference Brown and Ahlers2007; Xi & Xia Reference Xi and Xia2007), which suggests that it may be possible to develop a geometry-independent model to explain the apparently different LSC dynamics in different geometries.
${\it\tau}/t_{LSC}$
is caused by the insufficient statistics.) These results indicate that flow reversals in the quasi-2-D geometry obey Poisson statistics as in the 3-D case (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Brown & Ahlers Reference Brown and Ahlers2007; Xi & Xia Reference Xi and Xia2007), which suggests that it may be possible to develop a geometry-independent model to explain the apparently different LSC dynamics in different geometries.

Figure 7. (a,b) Time series of temperatures measured at the cell centre for (a)
![]() $Ra=1.1\times 10^{9}$
and (b)
$Ra=1.1\times 10^{9}$
and (b)
![]() $Ra=8.6\times 10^{7}$
. From top to bottom,
$Ra=8.6\times 10^{7}$
. From top to bottom,
![]() ${\it\Gamma}=0.1$
, 0.15, 0.2, 0.3 and 0.6. (c,d) The corresponding PDFs of temperature fluctuations shown in (a,b): (c)
${\it\Gamma}=0.1$
, 0.15, 0.2, 0.3 and 0.6. (c,d) The corresponding PDFs of temperature fluctuations shown in (a,b): (c)
![]() $Ra=1.1\times 10^{9}$
and (d)
$Ra=1.1\times 10^{9}$
and (d)
![]() $Ra=8.6\times 10^{7}$
. Note that the data for different
$Ra=8.6\times 10^{7}$
. Note that the data for different
![]() ${\it\Gamma}$
have been upshifted for clarity. The green and orange lines represent exponential and Gaussian fits, respectively.
${\it\Gamma}$
have been upshifted for clarity. The green and orange lines represent exponential and Gaussian fits, respectively.
3.2 Local temperature fluctuations
In Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013), it was simply mentioned that with decreasing
![]() ${\it\Gamma}$
the local temperature fluctuation in the cell centre increases significantly and its PDF changes from exponential to Gaussian. Here, we present the details. Figure 7(a,b) shows the time series of temperatures measured at the cell centre for
${\it\Gamma}$
the local temperature fluctuation in the cell centre increases significantly and its PDF changes from exponential to Gaussian. Here, we present the details. Figure 7(a,b) shows the time series of temperatures measured at the cell centre for
![]() $Ra=1.1\times 10^{9}$
and
$Ra=1.1\times 10^{9}$
and
![]() $Ra=8.6\times 10^{7}$
, respectively. It is seen clearly that the fluctuations in small
$Ra=8.6\times 10^{7}$
, respectively. It is seen clearly that the fluctuations in small
![]() ${\it\Gamma}$
cells are stronger than those in large ones. Besides the change in fluctuation magnitude, the corresponding PDFs (shown in figure 7
c,d) also change their forms: as
${\it\Gamma}$
cells are stronger than those in large ones. Besides the change in fluctuation magnitude, the corresponding PDFs (shown in figure 7
c,d) also change their forms: as
![]() ${\it\Gamma}$
is reduced, there is a transition from (stretched) exponential to Gaussian-like. The strong geometric dependency of the temperature fluctuation PDF found in the quasi-2-D system is consistent with a recent numerical simulation using similar geometries (Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but quite different from previous studies conducted in 3-D systems, in which a universal form for different geometries was observed (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010). The functional form of the temperature fluctuation PDF is one important hallmark for different flow states (Heslot, Castaing & Libchaber Reference Heslot, Castaing and Libchaber1987; Castaing et al.
Reference Castaing, Gunaratne, Kadanoff, Libchaber and Heslot1989; Massaioli, Benzi & Succi Reference Massaioli, Benzi and Succi1993) and the plume distribution in the convection cell (Xia & Lui Reference Xia and Lui1997), thus these changes confirm that the flow state has been changed and/or there are more plumes passing though the cell centre as a result of confinement.
${\it\Gamma}$
is reduced, there is a transition from (stretched) exponential to Gaussian-like. The strong geometric dependency of the temperature fluctuation PDF found in the quasi-2-D system is consistent with a recent numerical simulation using similar geometries (Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but quite different from previous studies conducted in 3-D systems, in which a universal form for different geometries was observed (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010). The functional form of the temperature fluctuation PDF is one important hallmark for different flow states (Heslot, Castaing & Libchaber Reference Heslot, Castaing and Libchaber1987; Castaing et al.
Reference Castaing, Gunaratne, Kadanoff, Libchaber and Heslot1989; Massaioli, Benzi & Succi Reference Massaioli, Benzi and Succi1993) and the plume distribution in the convection cell (Xia & Lui Reference Xia and Lui1997), thus these changes confirm that the flow state has been changed and/or there are more plumes passing though the cell centre as a result of confinement.

Figure 8. (a) Normalized temperature fluctuation
![]() ${\it\sigma}_{c}/{\rm\Delta}T$
at the cell centre as a function of
${\it\sigma}_{c}/{\rm\Delta}T$
at the cell centre as a function of
![]() $Ra$
for different
$Ra$
for different
![]() ${\it\Gamma}$
. The solid lines represent power-law fits to the individual data sets. (b) The corresponding flatness versus
${\it\Gamma}$
. The solid lines represent power-law fits to the individual data sets. (b) The corresponding flatness versus
![]() $Ra$
.
$Ra$
.
To examine these changes quantitatively, we plot the Ra-dependence of the normalized r.m.s. temperature
![]() ${\it\sigma}_{c}/{\rm\Delta}T$
and their flatness values in figure 8. From figure 8(a), one can see that while the magnitude of
${\it\sigma}_{c}/{\rm\Delta}T$
and their flatness values in figure 8. From figure 8(a), one can see that while the magnitude of
![]() ${\it\sigma}_{c}/{\rm\Delta}T$
increases as
${\it\sigma}_{c}/{\rm\Delta}T$
increases as
![]() ${\it\Gamma}$
decreases, its
${\it\Gamma}$
decreases, its
![]() $Ra$
-scaling exponent in general decreases (see table 1 for detailed values). Large variations in the Ra dependency of temperature fluctuations due to geometric effects have also been found in earlier studies (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010). We note that the scalings for the
$Ra$
-scaling exponent in general decreases (see table 1 for detailed values). Large variations in the Ra dependency of temperature fluctuations due to geometric effects have also been found in earlier studies (Daya & Ecke Reference Daya and Ecke2001; Song & Tong Reference Song and Tong2010). We note that the scalings for the
![]() ${\it\Gamma}=0.6$
and 0.3 cells are the same as those found in a recent simulation of turbulent RB convection in a cubic geometry (Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but very different from the value
${\it\Gamma}=0.6$
and 0.3 cells are the same as those found in a recent simulation of turbulent RB convection in a cubic geometry (Kaczorowski et al.
Reference Kaczorowski, Chong and Xia2014), but very different from the value
![]() $-$
0.49 reported in Daya & Ecke (Reference Daya and Ecke2001) in a convection cell with square cross-section. The
$-$
0.49 reported in Daya & Ecke (Reference Daya and Ecke2001) in a convection cell with square cross-section. The
![]() ${\it\Gamma}=0.3$
cell also has similar flatness values with the
${\it\Gamma}=0.3$
cell also has similar flatness values with the
![]() ${\it\Gamma}=0.6$
cell (see figure 8
b), suggesting that the convective flow has not sensed the confinement effects from the walls for
${\it\Gamma}=0.6$
cell (see figure 8
b), suggesting that the convective flow has not sensed the confinement effects from the walls for
![]() ${\it\Gamma}=0.3$
. However, when
${\it\Gamma}=0.3$
. However, when
![]() ${\it\Gamma}$
is further reduced, there is a sudden drop in the flatness values; and these values gradually decrease to
${\it\Gamma}$
is further reduced, there is a sudden drop in the flatness values; and these values gradually decrease to
![]() ${\sim}$
3 (Gaussian case) for smaller
${\sim}$
3 (Gaussian case) for smaller
![]() ${\it\Gamma}$
and lower
${\it\Gamma}$
and lower
![]() $Ra$
, which is consistent with the change in the form of temperature fluctuation PDF shown in figure 7. Special attention is paid to the abnormal
$Ra$
, which is consistent with the change in the form of temperature fluctuation PDF shown in figure 7. Special attention is paid to the abnormal
![]() $Ra$
dependence of flatness in the
$Ra$
dependence of flatness in the
![]() ${\it\Gamma}=0.1$
cell, which is also reflected in its very different time series signals and the bimodal shaped PDF at
${\it\Gamma}=0.1$
cell, which is also reflected in its very different time series signals and the bimodal shaped PDF at
![]() $Ra=8.6\times 10^{7}$
. Based on the recent finding by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015), these strange behaviours for
$Ra=8.6\times 10^{7}$
. Based on the recent finding by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015), these strange behaviours for
![]() ${\it\Gamma}=0.1$
could be due to the fact that the LSC no longer exists in this case.
${\it\Gamma}=0.1$
could be due to the fact that the LSC no longer exists in this case.
Table 1. Fitting coefficients for the single power law
![]() $Nu=ARa^{{\it\alpha}}$
, the combined power law
$Nu=ARa^{{\it\alpha}}$
, the combined power law
![]() $Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
and the normalized temperature fluctuation
$Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
and the normalized temperature fluctuation
![]() ${\it\sigma}_{c}/{\rm\Delta}T=BRa^{{\it\beta}}$
measured in different
${\it\sigma}_{c}/{\rm\Delta}T=BRa^{{\it\beta}}$
measured in different
![]() ${\it\Gamma}$
cells. For an easier data referring, the uncertainties presented here are the maximum values of the fitting errors among all the cells.
${\it\Gamma}$
cells. For an easier data referring, the uncertainties presented here are the maximum values of the fitting errors among all the cells.

3.3 Heat transport
We now examine the influences of spatial confinement on the heat transport properties. Figure 9 shows a semi-log plot of the compensated Nu versus Ra for different
![]() ${\it\Gamma}$
cells. As the heat transfer in a cubic cell (i.e.
${\it\Gamma}$
cells. As the heat transfer in a cubic cell (i.e.
![]() ${\it\Gamma}=1$
) is identical to that in a cylinder (Qiu & Xia Reference Qiu and Xia1998b
), for clarity and easy comparison, we plot in figure 9 the results measured in a cylindrical cell of
${\it\Gamma}=1$
) is identical to that in a cylinder (Qiu & Xia Reference Qiu and Xia1998b
), for clarity and easy comparison, we plot in figure 9 the results measured in a cylindrical cell of
![]() ${\it\Gamma}=1$
(Wei, Ni & Xia Reference Wei, Ni and Xia2012), which is the most commonly used geometry in the study of turbulent RB convection. From figure 9, we find that: (i) the data for the
${\it\Gamma}=1$
(Wei, Ni & Xia Reference Wei, Ni and Xia2012), which is the most commonly used geometry in the study of turbulent RB convection. From figure 9, we find that: (i) the data for the
![]() ${\it\Gamma}=0.6$
cell collapse well with those measured in the
${\it\Gamma}=0.6$
cell collapse well with those measured in the
![]() ${\it\Gamma}=1$
cell; (ii) Nu first decreases a little when
${\it\Gamma}=1$
cell; (ii) Nu first decreases a little when
![]() ${\it\Gamma}$
is changed from 0.6 to 0.3 and then increases significantly afterwards, up to 17 % for the parameter range explored in the present study. Note that the Nu data have been reported in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013). We plot them here in a different form to understand the confinement effects in turbulent thermal convection from a different point of view.
${\it\Gamma}$
is changed from 0.6 to 0.3 and then increases significantly afterwards, up to 17 % for the parameter range explored in the present study. Note that the Nu data have been reported in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013). We plot them here in a different form to understand the confinement effects in turbulent thermal convection from a different point of view.

Figure 9. Compensated
![]() $Nu$
as a function of
$Nu$
as a function of
![]() $Ra$
from different
$Ra$
from different
![]() ${\it\Gamma}$
cells as indicated by different symbols. The solid lines are power-law fits to individual data sets. The solid hexagons are the results measured in a cylindrical cell of
${\it\Gamma}$
cells as indicated by different symbols. The solid lines are power-law fits to individual data sets. The solid hexagons are the results measured in a cylindrical cell of
![]() ${\it\Gamma}=1$
(Wei, Ni & Xia Reference Wei, Ni and Xia2012).
${\it\Gamma}=1$
(Wei, Ni & Xia Reference Wei, Ni and Xia2012).

Figure 10. Fitting coefficients for the combined power law
![]() $Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
as a function of
$Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
as a function of
![]() ${\it\Gamma}$
: (a)
${\it\Gamma}$
: (a)
![]() $C_{1}$
and (b)
$C_{1}$
and (b)
![]() $C_{2}$
. (c) The ratio between
$C_{2}$
. (c) The ratio between
![]() $C_{2}Ra^{1/4}$
and
$C_{2}Ra^{1/4}$
and
![]() $C_{1}Ra^{1/3}$
versus
$C_{1}Ra^{1/3}$
versus
![]() $Ra$
in different
$Ra$
in different
![]() ${\it\Gamma}$
cells.
${\it\Gamma}$
cells.
The solid lines in figure 9 represent power-law fits
![]() $Nu=ARa^{{\it\alpha}}$
to the measured data with the scaling exponent
$Nu=ARa^{{\it\alpha}}$
to the measured data with the scaling exponent
![]() ${\it\alpha}$
varying from 0.27 to 0.29 (see table 1 for detailed values). These values are in general agreement with those found in previous studies in the same parameter ranges of
${\it\alpha}$
varying from 0.27 to 0.29 (see table 1 for detailed values). These values are in general agreement with those found in previous studies in the same parameter ranges of
![]() $Ra$
and
$Ra$
and
![]() $Pr$
(Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). We recall that the Grossmann–Lohse (GL) model splits the globally averaged dissipation rate into bulk and boundary layer (BL) contributions and suggests that different linear combinations of power laws for different parameter ranges should be used for the
$Pr$
(Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). We recall that the Grossmann–Lohse (GL) model splits the globally averaged dissipation rate into bulk and boundary layer (BL) contributions and suggests that different linear combinations of power laws for different parameter ranges should be used for the
![]() $Nu$
–
$Nu$
–
![]() $Ra$
fitting (Grossmann & Lohse Reference Grossmann and Lohse2000). Based on this idea, we fit to each set of data with a combination of two power laws proposed in the GL model, i.e.
$Ra$
fitting (Grossmann & Lohse Reference Grossmann and Lohse2000). Based on this idea, we fit to each set of data with a combination of two power laws proposed in the GL model, i.e.
![]() $Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
, in which
$Nu=C_{1}Ra^{1/3}+C_{2}Ra^{1/4}$
, in which
![]() $C_{1}Ra^{1/3}$
and
$C_{1}Ra^{1/3}$
and
![]() $C_{2}Ra^{1/4}$
represent the contributions from the bulk and BLs, respectively. The obtained fitting coefficients
$C_{2}Ra^{1/4}$
represent the contributions from the bulk and BLs, respectively. The obtained fitting coefficients
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
for different
$C_{2}$
for different
![]() ${\it\Gamma}$
are plotted in figures 10(a) and 10(b), respectively (see table 1 for detailed values). It is seen that the
${\it\Gamma}$
are plotted in figures 10(a) and 10(b), respectively (see table 1 for detailed values). It is seen that the
![]() ${\it\Gamma}$
dependencies of
${\it\Gamma}$
dependencies of
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
have an opposite trend: the decrease (increase) in
$C_{2}$
have an opposite trend: the decrease (increase) in
![]() $C_{1}$
is accompanied by an increase (decrease) in
$C_{1}$
is accompanied by an increase (decrease) in
![]() $C_{2}$
. Interestingly, the behaviour of
$C_{2}$
. Interestingly, the behaviour of
![]() $C_{2}$
is similar to that of the global Nu: It first decreases when
$C_{2}$
is similar to that of the global Nu: It first decreases when
![]() ${\it\Gamma}$
is changed from 0.6 to 0.3 and then increases with decreasing
${\it\Gamma}$
is changed from 0.6 to 0.3 and then increases with decreasing
![]() ${\it\Gamma}$
afterwards (see figure 1 in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013)). This is because in the present parameter range, the heat transport, in terms of the energy dissipation rate, is dominated by the contributions from the boundary layers, which is supported by comparing the magnitudes between
${\it\Gamma}$
afterwards (see figure 1 in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013)). This is because in the present parameter range, the heat transport, in terms of the energy dissipation rate, is dominated by the contributions from the boundary layers, which is supported by comparing the magnitudes between
![]() $C_{1}Ra^{1/3}$
and
$C_{1}Ra^{1/3}$
and
![]() $C_{2}Ra^{1/4}$
as shown in figure 10(c). The change in the ratio of
$C_{2}Ra^{1/4}$
as shown in figure 10(c). The change in the ratio of
![]() $C_{2}Ra^{1/4}$
over
$C_{2}Ra^{1/4}$
over
![]() $C_{1}Ra^{1/3}$
as
$C_{1}Ra^{1/3}$
as
![]() ${\it\Gamma}$
is decreased suggests that the confinement increases the contribution from the BLs in the global heat transport and weakens that from the bulk. This result is consistent with the finding in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013), in which it was found that the confinement suppresses the large-scale turbulent flow in the bulk and enables thermal plumes (commonly viewed as detached thermal BLs) to pass through the entire cell, rather than being confined in its periphery.
${\it\Gamma}$
is decreased suggests that the confinement increases the contribution from the BLs in the global heat transport and weakens that from the bulk. This result is consistent with the finding in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013), in which it was found that the confinement suppresses the large-scale turbulent flow in the bulk and enables thermal plumes (commonly viewed as detached thermal BLs) to pass through the entire cell, rather than being confined in its periphery.
Why have such significant changes in Nu not been observed in previous studies in 3-D and true 2-D systems? Note that even for the smallest
![]() ${\it\Gamma}$
explored in the present study, the width of the cell (its smallest dimension) is still much larger than the thermal boundary layer thickness, therefore it is unlikely that the geometric effects will directly lead to any change in the BLs and hence Nu. Thus, the reasons must be connected to the flow structures. It has been shown by Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) that the confinement restricts the plume’s movement near the BLs into a 1-D motion, resulting in the formation of highly coherent plumes. These highly coherent plumes turn out to have a stronger interaction with the BLs, which is supported by the mean velocity fields as shown in figure 1. It is seen that in the
${\it\Gamma}$
explored in the present study, the width of the cell (its smallest dimension) is still much larger than the thermal boundary layer thickness, therefore it is unlikely that the geometric effects will directly lead to any change in the BLs and hence Nu. Thus, the reasons must be connected to the flow structures. It has been shown by Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) that the confinement restricts the plume’s movement near the BLs into a 1-D motion, resulting in the formation of highly coherent plumes. These highly coherent plumes turn out to have a stronger interaction with the BLs, which is supported by the mean velocity fields as shown in figure 1. It is seen that in the
![]() ${\it\Gamma}=0.3$
cell the mean flow near the boundary layers has a large horizontal component, whereas in the
${\it\Gamma}=0.3$
cell the mean flow near the boundary layers has a large horizontal component, whereas in the
![]() ${\it\Gamma}=0.15$
case, the mean flow is largely perpendicular and thus perturbs the BLs directly. Therefore, geometric confinement in the quasi-2-D geometry not only changes the morphology and dynamics of thermal plumes, but also strengthens the interaction between the flow structures in the bulk and the BLs, both of which have not been observed in previous studies in 3-D systems. This explains why these studies found a weak
${\it\Gamma}=0.15$
case, the mean flow is largely perpendicular and thus perturbs the BLs directly. Therefore, geometric confinement in the quasi-2-D geometry not only changes the morphology and dynamics of thermal plumes, but also strengthens the interaction between the flow structures in the bulk and the BLs, both of which have not been observed in previous studies in 3-D systems. This explains why these studies found a weak
![]() ${\it\Gamma}$
effect on heat transport. In the true 2-D case, there is no lateral confinement of the plumes when the aspect ratio is changed. As the coherent properties of plumes are not modified in this case but the flow structures are changed as a result of the aspect ratio variation,
${\it\Gamma}$
effect on heat transport. In the true 2-D case, there is no lateral confinement of the plumes when the aspect ratio is changed. As the coherent properties of plumes are not modified in this case but the flow structures are changed as a result of the aspect ratio variation,
![]() $Nu$
is found to be sensitive to the nature of the flow structures in the 2-D geometry (van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012).
$Nu$
is found to be sensitive to the nature of the flow structures in the 2-D geometry (van der Poel et al.
Reference van der Poel, Stevens and Lohse2011, Reference van der Poel, Stevens, Sugiyama and Lohse2012).
In a recent numerical simulation of 2-D turbulent convection (Chandra & Verma Reference Chandra and Verma2013), extremely large fluctuations and even negative values of global Nu were observed during the flow reversal processes, which was attributed to the strong geometric constraints to the flow. Since the confinement also leads to more frequent flow reversals, it would be interesting to examine the instantaneous Nu for different
![]() ${\it\Gamma}$
during reversals. As we can see in figure 11(a,b), neither negative values nor very large fluctuations are observed in the time series of instantaneous Nu for all the cases, which is also reflected by their PDFs, shown in figure 11(c,d). Although there is a trend that the fluctuations of instantaneous Nu increase as
${\it\Gamma}$
during reversals. As we can see in figure 11(a,b), neither negative values nor very large fluctuations are observed in the time series of instantaneous Nu for all the cases, which is also reflected by their PDFs, shown in figure 11(c,d). Although there is a trend that the fluctuations of instantaneous Nu increase as
![]() ${\it\Gamma}$
decreases, the fluctuation values for all the
${\it\Gamma}$
decreases, the fluctuation values for all the
![]() ${\it\Gamma}$
and the differences between them are so small that they are all within 1 % of the mean values. These results further suggest that the quasi-2-D geometry is different from the true 2-D case.
${\it\Gamma}$
and the differences between them are so small that they are all within 1 % of the mean values. These results further suggest that the quasi-2-D geometry is different from the true 2-D case.

Figure 11. (a,b) Time series of instantaneous Nu for (a)
![]() $Ra=1.1\times 10^{9}$
and (b)
$Ra=1.1\times 10^{9}$
and (b)
![]() $Ra=8.6\times 10^{7}$
. From top to bottom,
$Ra=8.6\times 10^{7}$
. From top to bottom,
![]() ${\it\Gamma}=0.1$
, 0.15, 0.2, 0.6 and 0.3. (c,d) The corresponding PDFs of the Nu fluctuations shown in (a,b): (c)
${\it\Gamma}=0.1$
, 0.15, 0.2, 0.6 and 0.3. (c,d) The corresponding PDFs of the Nu fluctuations shown in (a,b): (c)
![]() $Ra=1.1\times 10^{9}$
and (d)
$Ra=1.1\times 10^{9}$
and (d)
![]() $Ra=8.6\times 10^{7}$
.
$Ra=8.6\times 10^{7}$
.
4 Conclusion
In summary, our experiments reveal rich physics in quasi-2-D turbulent RB flow under geometric confinement.
-
(i) With the increasing degree of confinement, the large-scale flow slows down and there are more plumes traveling through the bulk region. Moreover, the LSC reverses its circulation direction more frequently in smaller
 ${\it\Gamma}$
cells, by more than 1000-fold for the highest value of Rayleigh number reached in the experiment. Despite the significant changes in the flow pattern and dynamics, it is found that the reversal process still follows Poissonian statistics, as in the 3-D system, and the reversal frequency could be well described by the stochastic model of Ni et al. (Reference Ni, Huang and Xia2015), which is closely related to the models used in other geometries (Brown & Ahlers Reference Brown and Ahlers2007; Song et al.
Reference Song, Brown, Hawkins and Tong2014). These common features are good circumstantial evidence for a potentially general model of LSC dynamics in different geometries.
${\it\Gamma}$
cells, by more than 1000-fold for the highest value of Rayleigh number reached in the experiment. Despite the significant changes in the flow pattern and dynamics, it is found that the reversal process still follows Poissonian statistics, as in the 3-D system, and the reversal frequency could be well described by the stochastic model of Ni et al. (Reference Ni, Huang and Xia2015), which is closely related to the models used in other geometries (Brown & Ahlers Reference Brown and Ahlers2007; Song et al.
Reference Song, Brown, Hawkins and Tong2014). These common features are good circumstantial evidence for a potentially general model of LSC dynamics in different geometries. -
(ii) The impact of geometric confinement on the flow dynamics is also reflected in the local temperature fluctuation. It is found that the bulk temperature fluctuations in different
 ${\it\Gamma}$
cells differ from each other not only in the magnitude and
${\it\Gamma}$
cells differ from each other not only in the magnitude and
 $Ra$
-dependent scaling, but also in the PDF shapes. These changes are the outcome of the changes in the flow state and/or plume distribution in the convection cell.
$Ra$
-dependent scaling, but also in the PDF shapes. These changes are the outcome of the changes in the flow state and/or plume distribution in the convection cell. -
(iii) Despite a slower flow, remarkable enhancement of heat transport is observed. By analysing the
 $Nu$
–
$Nu$
–
 $Ra$
behaviours according to the GL model, our results suggest that as
$Ra$
behaviours according to the GL model, our results suggest that as
 ${\it\Gamma}$
decreases, the relative weight of the boundary layer contribution to the global heat transport increases and at the same time that from the bulk decreases. In addition, we did not observe large variations nor negative values in global Nu during the reversal processes as found in true 2-D systems, which provides another evidence for the difference between the quasi-2-D and the true 2-D geometries.
${\it\Gamma}$
decreases, the relative weight of the boundary layer contribution to the global heat transport increases and at the same time that from the bulk decreases. In addition, we did not observe large variations nor negative values in global Nu during the reversal processes as found in true 2-D systems, which provides another evidence for the difference between the quasi-2-D and the true 2-D geometries.
These geometric confinement induced changes in quasi-2-D turbulent RB convection show that the interaction between the LSC, the thermal plumes and the BLs in thermal convection is more complicated than previous thought. These striking phenomena have not been observed in previous studies in 3-D and true 2-D systems, and could not be accounted for with the existing models for aspect ratio dependence (Grossmann & Lohse Reference Grossmann and Lohse2003; Ching & Tam Reference Ching and Tam2006). We end by stressing that our present understanding of the confinement effects in quasi-2-D turbulent convection are 2-fold: the first is the changes in the morphology and dynamics of thermal plumes and the modification of the flow structures in the bulk; the second is the strengthening of the interaction between the flow structures in the bulk and the BLs. Given this, the influence of geometric confinement in the small-
![]() ${\it\Gamma}$
limit would be an interesting topic for future studies.
${\it\Gamma}$
limit would be an interesting topic for future studies.
Acknowledgements
We thank S.-Q. Zhou and X.-D. Shang for kindly making their PIV apparatus available to us. We also thank F. Wang and L. Qu for their help with the experiments. This work was supported by the Hong Kong Research Grants Council under grant nos CUHK 403712 and 404513.