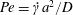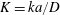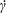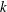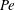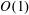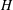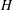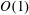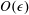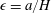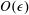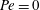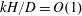1 Introduction
Mass transfer of a reactant by diffusion and convection in a fluid coupled with a chemical reaction at a surface occurs in numerous processes. For the surfaces that are uniformly reactive with known reaction kinetics, the analytical description for determining the total reaction rate and the reactant concentration distribution in the fluid is well established. In practice, however, the surfaces are often heterogeneous, and determining the concentration distribution accounting fully for the heterogeneity remains challenging. We examine here a simplified model in which the surface is smooth and consists of reactive surfaces that are all circular disks of radius
![]() $a$
uniformly distributed on an otherwise non-reactive surface. The kinetics at these disks are simple, characterized by a first-order surface-reaction rate constant
$a$
uniformly distributed on an otherwise non-reactive surface. The kinetics at these disks are simple, characterized by a first-order surface-reaction rate constant
![]() $k$
(units:
$k$
(units:
![]() $\text{m}~\text{s}^{-1}$
). If the scale of the heterogeneity (i.e.
$\text{m}~\text{s}^{-1}$
). If the scale of the heterogeneity (i.e.
![]() $a$
) is small compared to the macroscale
$a$
) is small compared to the macroscale
![]() $H$
(e.g. the width of a channel formed by two parallel heterogeneous walls), then it may be possible to solve an appropriate microscale problem – on the scale of the disk radius – and use the solution to prescribe the boundary conditions appropriate for the macroscale problem. This was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) who first determined the total reaction rate per disk as a function of the fraction
$H$
(e.g. the width of a channel formed by two parallel heterogeneous walls), then it may be possible to solve an appropriate microscale problem – on the scale of the disk radius – and use the solution to prescribe the boundary conditions appropriate for the macroscale problem. This was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) who first determined the total reaction rate per disk as a function of the fraction
![]() $\unicode[STIX]{x1D719}$
of the area occupied by the disks, the Péclet number
$\unicode[STIX]{x1D719}$
of the area occupied by the disks, the Péclet number
![]() $Pe=\dot{\unicode[STIX]{x1D6FE}}a^{2}/D$
, and the non-dimensional reaction rate
$Pe=\dot{\unicode[STIX]{x1D6FE}}a^{2}/D$
, and the non-dimensional reaction rate
![]() $K=ka/D$
, known as the Damköhler number. Here,
$K=ka/D$
, known as the Damköhler number. Here,
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate in the fluid near the wall and
$\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate in the fluid near the wall and
![]() $D$
is the diffusivity of the reactant in the fluid. These investigators next carried out a matched asymptotic analysis for small
$D$
is the diffusivity of the reactant in the fluid. These investigators next carried out a matched asymptotic analysis for small
![]() $\unicode[STIX]{x1D716}\equiv a/H$
to show that the boundary condition for the macroscale problem corresponds to treating the entire surface with a homogeneous effective surface-reaction rate constant
$\unicode[STIX]{x1D716}\equiv a/H$
to show that the boundary condition for the macroscale problem corresponds to treating the entire surface with a homogeneous effective surface-reaction rate constant
![]() $k_{eff}$
, which they determined for several values of
$k_{eff}$
, which they determined for several values of
![]() $Pe$
,
$Pe$
,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $K$
for both periodic as well as random arrays of the reactive disks. The microscale problem solved by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) assumed that the average concentration at the surface is constant. The macroscale concentration, however, varies, in general, along the surface, and the conditions under which the calculations based on the constant average concentration assumption may be used for the macroscale analysis were not discussed.
$K$
for both periodic as well as random arrays of the reactive disks. The microscale problem solved by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) assumed that the average concentration at the surface is constant. The macroscale concentration, however, varies, in general, along the surface, and the conditions under which the calculations based on the constant average concentration assumption may be used for the macroscale analysis were not discussed.
The limit
![]() $\unicode[STIX]{x1D716}=a/H\rightarrow 0$
for a given reactive system can be examined in at least two different manners. In the first one, the non-dimensional numbers based on the radius of the reactive disks (i.e.
$\unicode[STIX]{x1D716}=a/H\rightarrow 0$
for a given reactive system can be examined in at least two different manners. In the first one, the non-dimensional numbers based on the radius of the reactive disks (i.e.
![]() $ka/D$
and
$ka/D$
and
![]() $\dot{\unicode[STIX]{x1D6FE}}a^{2}/D$
) and
$\dot{\unicode[STIX]{x1D6FE}}a^{2}/D$
) and
![]() $\unicode[STIX]{x1D719}$
are treated as fixed, i.e.
$\unicode[STIX]{x1D719}$
are treated as fixed, i.e.
![]() $O(1)$
quantities, as
$O(1)$
quantities, as
![]() $H$
becomes increasingly large in the limit process. This is the limit investigated in detail by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). A consequence of fixing the non-dimensional numbers based on the microscale and then taking the limit
$H$
becomes increasingly large in the limit process. This is the limit investigated in detail by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). A consequence of fixing the non-dimensional numbers based on the microscale and then taking the limit
![]() $a/H\rightarrow 0$
is that the non-dimensional reaction rate and the Péclet number based on the macroscale become large, of
$a/H\rightarrow 0$
is that the non-dimensional reaction rate and the Péclet number based on the macroscale become large, of
![]() $O(\unicode[STIX]{x1D716}^{-1})$
and
$O(\unicode[STIX]{x1D716}^{-1})$
and
![]() $O(\unicode[STIX]{x1D716}^{-2})$
, respectively. The mass transfer process in this limit is therefore diffusion–convection limited on the macroscale and even the simple boundary condition of vanishing concentration of the reactant at the wall is sufficient for determining the concentration distribution in the fluid and the mass flux at the wall, making it somewhat unnecessary to specify the mixed reactive boundary condition at the walls in the macroscale description, unless determining the small, but finite, concentration near the wall is of interest. The other limit process, the one that we shall examine in the present study, treats the non-dimensional rate constant and the Péclet number based on the macroscale
$O(\unicode[STIX]{x1D716}^{-2})$
, respectively. The mass transfer process in this limit is therefore diffusion–convection limited on the macroscale and even the simple boundary condition of vanishing concentration of the reactant at the wall is sufficient for determining the concentration distribution in the fluid and the mass flux at the wall, making it somewhat unnecessary to specify the mixed reactive boundary condition at the walls in the macroscale description, unless determining the small, but finite, concentration near the wall is of interest. The other limit process, the one that we shall examine in the present study, treats the non-dimensional rate constant and the Péclet number based on the macroscale
![]() $H$
as
$H$
as
![]() $O(1)$
quantities. In this limit, the leading-order microscale description becomes reaction rate dominated since the non-dimensional reaction rate based on
$O(1)$
quantities. In this limit, the leading-order microscale description becomes reaction rate dominated since the non-dimensional reaction rate based on
![]() $a$
is vanishingly small, of
$a$
is vanishingly small, of
![]() $O(\unicode[STIX]{x1D716})$
. To obtain useful results for the case when both
$O(\unicode[STIX]{x1D716})$
. To obtain useful results for the case when both
![]() $ka/D$
and
$ka/D$
and
![]() $a/H$
are small but finite, it is necessary to evaluate several terms in the matched asymptotic expansions on the micro- and macroscales. The present analysis shows that the macroscale boundary condition can be expressed in terms of an effective rate constant only up to
$a/H$
are small but finite, it is necessary to evaluate several terms in the matched asymptotic expansions on the micro- and macroscales. The present analysis shows that the macroscale boundary condition can be expressed in terms of an effective rate constant only up to
![]() $O(\unicode[STIX]{x1D716})$
and that this effective rate constant can be determined by solving the microscale problem by taking the average concentration to be constant as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). At
$O(\unicode[STIX]{x1D716})$
and that this effective rate constant can be determined by solving the microscale problem by taking the average concentration to be constant as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). At
![]() $O(\unicode[STIX]{x1D716}^{2})$
, the surface-reaction rate depends, in general, on both the concentration and its macroscale gradient along the surface suggesting thereby that the concept of an effective rate constant which yields the macroscale reaction rate in terms of macroscale concentration is not always valid. In the limit process pursued in the present study, the effective reaction rate constant at
$O(\unicode[STIX]{x1D716}^{2})$
, the surface-reaction rate depends, in general, on both the concentration and its macroscale gradient along the surface suggesting thereby that the concept of an effective rate constant which yields the macroscale reaction rate in terms of macroscale concentration is not always valid. In the limit process pursued in the present study, the effective reaction rate constant at
![]() $O(1)$
is given by the trivial result
$O(1)$
is given by the trivial result
![]() $k_{eff}=\unicode[STIX]{x1D719}k$
while the next, the
$k_{eff}=\unicode[STIX]{x1D719}k$
while the next, the
![]() $O(\unicode[STIX]{x1D716})$
correction to the effective reaction rate, requires solving a simpler problem involving the Laplace equation on the microscale. We determine this correction analytically for both the spatially periodic and the random arrangement of the disks. While the analysis is strictly valid for small
$O(\unicode[STIX]{x1D716})$
correction to the effective reaction rate, requires solving a simpler problem involving the Laplace equation on the microscale. We determine this correction analytically for both the spatially periodic and the random arrangement of the disks. While the analysis is strictly valid for small
![]() $K$
, we find that its Padé approximant provides surprisingly accurate estimates even when
$K$
, we find that its Padé approximant provides surprisingly accurate estimates even when
![]() $K$
is not small. We also show that the results are also useful for estimating the effective reaction rate constant for a problem recently examined by Shah, Lin & Shaqfeh (Reference Shah, Lin and Shaqfeh2017) in which the disks are chemically inert but the surrounding surface is reactive.
$K$
is not small. We also show that the results are also useful for estimating the effective reaction rate constant for a problem recently examined by Shah, Lin & Shaqfeh (Reference Shah, Lin and Shaqfeh2017) in which the disks are chemically inert but the surrounding surface is reactive.
We also consider a related problem of determining the current density at a surface consisting of an array of microelectrodes that was examined in detail previously by Lucas, Sipcic & Stone (Reference Lucas, Sipcic and Stone1997) and show that the analytical results obtained for the effective reaction rate can be applied to this problem as well provided that the non-dimensional bulk reaction rate constant is small.
2 Formulation of the problem
The reactant concentration satisfies the following non-dimensional equation under steady state conditions:
Here, the distances are non-dimensionalized by diving by the macroscale length
![]() $H$
, the velocity is non-dimensionalized by the characteristic fluid velocity
$H$
, the velocity is non-dimensionalized by the characteristic fluid velocity
![]() $U$
, and
$U$
, and
![]() $Pe_{o}=UH/D$
is the macroscale Péclet number. The above equation is valid when the diffusion coefficient is constant and the mass flux generated by the diffusion is small compared to the mass flux due to the fluid flow, conditions that are often satisfied in practice. We are interested in determining the macroscale boundary condition at the reacting walls. The mass flux of the reactant at the wall due to diffusion must equal the rate of consumption by the reaction at the surface, i.e.
$Pe_{o}=UH/D$
is the macroscale Péclet number. The above equation is valid when the diffusion coefficient is constant and the mass flux generated by the diffusion is small compared to the mass flux due to the fluid flow, conditions that are often satisfied in practice. We are interested in determining the macroscale boundary condition at the reacting walls. The mass flux of the reactant at the wall due to diffusion must equal the rate of consumption by the reaction at the surface, i.e.
where
![]() $q_{w}$
is the rate of reaction per unit area of the wall and
$q_{w}$
is the rate of reaction per unit area of the wall and
![]() $n_{j}$
is the unit vector normal to the wall and pointing into the fluid. For the first-order reaction kinetics, the rate at a point
$n_{j}$
is the unit vector normal to the wall and pointing into the fluid. For the first-order reaction kinetics, the rate at a point
![]() $\boldsymbol{x}_{w}$
is given by
$\boldsymbol{x}_{w}$
is given by
where
![]() $p(\boldsymbol{x})$
is the probability density for finding a disk with its centre at
$p(\boldsymbol{x})$
is the probability density for finding a disk with its centre at
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $\langle c\rangle _{1}(\boldsymbol{x}_{w}|\boldsymbol{x})$
is the conditionally averaged concentration with the centre of a disk fixed at
$\langle c\rangle _{1}(\boldsymbol{x}_{w}|\boldsymbol{x})$
is the conditionally averaged concentration with the centre of a disk fixed at
![]() $\boldsymbol{x}$
. The integration is carried out over the centres of all the disks on the plane
$\boldsymbol{x}$
. The integration is carried out over the centres of all the disks on the plane
![]() $x_{3}=0$
that contain
$x_{3}=0$
that contain
![]() $\boldsymbol{x}_{w}$
. This integral can be related to the integral over a disk whose centre is at
$\boldsymbol{x}_{w}$
. This integral can be related to the integral over a disk whose centre is at
![]() $\boldsymbol{x}_{w}$
by treating the conditionally averaged concentration as a function of two variables, with the first representing the position vector relative to the centre of a disk and the second representing the centre of the disk:
$\boldsymbol{x}_{w}$
by treating the conditionally averaged concentration as a function of two variables, with the first representing the position vector relative to the centre of a disk and the second representing the centre of the disk:
Since the variations with respect to the second variable are expected to be small as they depend on the macroscale variations, we can use the Taylor series expansion to obtain
 $$\begin{eqnarray}\displaystyle q_{w}(\boldsymbol{x}_{w}) & = & \displaystyle k\int _{r\leqslant \unicode[STIX]{x1D716}}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A-k\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{iw}}\int _{r\leqslant \unicode[STIX]{x1D716}}r_{i}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k}{2!}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}x_{iw}\unicode[STIX]{x2202}x_{jw}}\int _{r\leqslant \unicode[STIX]{x1D716}}r_{i}r_{j}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle q_{w}(\boldsymbol{x}_{w}) & = & \displaystyle k\int _{r\leqslant \unicode[STIX]{x1D716}}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A-k\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{iw}}\int _{r\leqslant \unicode[STIX]{x1D716}}r_{i}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k}{2!}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}x_{iw}\unicode[STIX]{x2202}x_{jw}}\int _{r\leqslant \unicode[STIX]{x1D716}}r_{i}r_{j}\langle c\rangle _{1}(\boldsymbol{r},\boldsymbol{x}_{w})p(\boldsymbol{x}_{w})\,\text{d}A+\cdots \,.\end{eqnarray}$$
To determine the conditionally averaged field near a disk, let us rescale the distances by the radius of the disk according to
The region near the disk, with
![]() $\boldsymbol{X}=O(1)$
, will be referred to as the inner region and the concentration
$\boldsymbol{X}=O(1)$
, will be referred to as the inner region and the concentration
![]() $\langle c\rangle _{1}$
in this region will be denoted by
$\langle c\rangle _{1}$
in this region will be denoted by
![]() $C$
to distinguish it from the outer region concentration
$C$
to distinguish it from the outer region concentration
![]() $\langle c\rangle _{1}$
, which will be denoted simply by
$\langle c\rangle _{1}$
, which will be denoted simply by
![]() $c$
. For the sake of simplicity, we shall consider the case of uni-directional flow along the
$c$
. For the sake of simplicity, we shall consider the case of uni-directional flow along the
![]() $x_{1}$
-axis, as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). The mass conservation equation for this special case reduces in the inner region to
$x_{1}$
-axis, as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). The mass conservation equation for this special case reduces in the inner region to
where
![]() $\unicode[STIX]{x1D70F}_{w}=(\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{3})_{w}$
is the non-dimensional shear rate at the wall,
$\unicode[STIX]{x1D70F}_{w}=(\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{3})_{w}$
is the non-dimensional shear rate at the wall,
![]() $x_{3}$
-axis being along the normal vector
$x_{3}$
-axis being along the normal vector
![]() $n_{j}$
and
$n_{j}$
and
![]() $\unicode[STIX]{x1D6FB}_{X}^{2}$
is the Laplacian operator based on the inner region variable
$\unicode[STIX]{x1D6FB}_{X}^{2}$
is the Laplacian operator based on the inner region variable
![]() $\boldsymbol{X}$
. The boundary condition at the wall
$\boldsymbol{X}$
. The boundary condition at the wall
![]() $X_{3}=0$
is given by
$X_{3}=0$
is given by
where
![]() $K_{o}=kH/D$
is the non-dimensional rate constant based on the macroscale. The boundary conditions far from the centre of the disk are obtained from the matching requirement with the solution in the outer region. The latter must be obtained by solving the macroscale equations (2.1)–(2.2) together with a suitable closure relation for
$K_{o}=kH/D$
is the non-dimensional rate constant based on the macroscale. The boundary conditions far from the centre of the disk are obtained from the matching requirement with the solution in the outer region. The latter must be obtained by solving the macroscale equations (2.1)–(2.2) together with a suitable closure relation for
![]() $q_{w}$
.
$q_{w}$
.
Let the macroscale concentration expanded near
![]() $\boldsymbol{x}_{w}$
be given by
$\boldsymbol{x}_{w}$
be given by
Equation (2.9) then provides the matching condition for the inner region solution,
![]() $C$
, as
$C$
, as
![]() $|\boldsymbol{X}|\rightarrow \infty$
. Let us expand, subject to a posteriori verification, the concentration in the inner region in the powers of
$|\boldsymbol{X}|\rightarrow \infty$
. Let us expand, subject to a posteriori verification, the concentration in the inner region in the powers of
![]() $\unicode[STIX]{x1D716}$
:
$\unicode[STIX]{x1D716}$
:
The leading-order term
![]() $C^{0}$
is trivial to determine since it satisfiesthe Laplace equation with a vanishing flux at
$C^{0}$
is trivial to determine since it satisfiesthe Laplace equation with a vanishing flux at
![]() $X_{3}=0$
, and the matching with the outer region solution therefore yields
$X_{3}=0$
, and the matching with the outer region solution therefore yields
Substituting
![]() $\langle c\rangle _{1}=c_{w}$
in (2.5) yields the leading-order estimate for
$\langle c\rangle _{1}=c_{w}$
in (2.5) yields the leading-order estimate for
![]() $q_{w}$
:
$q_{w}$
:
where
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}^{2}p(\boldsymbol{x}_{w})$
is the area fraction of the disks. To this leading-order approximation, the wall flux is independent of the shape or the spatial distribution of the reactive patches on the surface. This, of course, is not the case for the higher-order corrections. The next term,
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}^{2}p(\boldsymbol{x}_{w})$
is the area fraction of the disks. To this leading-order approximation, the wall flux is independent of the shape or the spatial distribution of the reactive patches on the surface. This, of course, is not the case for the higher-order corrections. The next term,
![]() $C^{1}$
, in the inner region satisfies the Laplace equation with the boundary condition at the wall given by
$C^{1}$
, in the inner region satisfies the Laplace equation with the boundary condition at the wall given by
plus the matching requirement with the outer region (cf. (2.9))
The solvability condition for a quantity satisfying the Laplace equation requires that the total flux at
![]() $X_{3}=0$
must match that at the infinity:
$X_{3}=0$
must match that at the infinity:
Unlike
![]() $C^{0}$
, the spatial distribution of the disks must also be specified to determine
$C^{0}$
, the spatial distribution of the disks must also be specified to determine
![]() $C^{1}$
. Let us suppose that the disks are arranged in a periodic array with each unit cell consisting of
$C^{1}$
. Let us suppose that the disks are arranged in a periodic array with each unit cell consisting of
![]() $N$
disks. Let the centres of the disks in the basic unit cell be denoted by
$N$
disks. Let the centres of the disks in the basic unit cell be denoted by
![]() $\boldsymbol{X}^{\unicode[STIX]{x1D6FC}}$
,
$\boldsymbol{X}^{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D6FC}=1,2,\ldots ,N$
, with
$\unicode[STIX]{x1D6FC}=1,2,\ldots ,N$
, with
![]() $\boldsymbol{X}^{1}=\mathbf{0}$
being the test disk, fixed at
$\boldsymbol{X}^{1}=\mathbf{0}$
being the test disk, fixed at
![]() $\boldsymbol{x}=\boldsymbol{x}_{w}$
.
$\boldsymbol{x}=\boldsymbol{x}_{w}$
.
This completes the formulation of the problem for
![]() $C^{1}$
. In the next section, we present the results for the special cases corresponding to a simple periodic array with
$C^{1}$
. In the next section, we present the results for the special cases corresponding to a simple periodic array with
![]() $N=1$
and a random array with
$N=1$
and a random array with
![]() $N\gg 1$
.
$N\gg 1$
.
3 Results for
 $C^{1}$
$C^{1}$
The concentration
![]() $C^{1}$
is given by the sum of the terms that vary linearly in the plane parallel to the wall plus a term that depends linearly on the constant
$C^{1}$
is given by the sum of the terms that vary linearly in the plane parallel to the wall plus a term that depends linearly on the constant
![]() $c_{w}$
:
$c_{w}$
:
with
![]() $C^{\ast }$
satisfying the Laplace equation together with the conditions given by (2.13) at
$C^{\ast }$
satisfying the Laplace equation together with the conditions given by (2.13) at
![]() $X_{3}=0$
.
$X_{3}=0$
.
It can be shown that
where
![]() $G$
is the periodic Green’s function for the Laplace equation satisfying
$G$
is the periodic Green’s function for the Laplace equation satisfying
Here,
![]() $\unicode[STIX]{x1D6FF}_{D}$
is the Dirac’s delta function and
$\unicode[STIX]{x1D6FF}_{D}$
is the Dirac’s delta function and
![]() $\boldsymbol{X}_{L}$
are the lattice position vectors of the periodic array. The sum is over all the lattice vectors. This Green’s function has the limiting behaviour
$\boldsymbol{X}_{L}$
are the lattice position vectors of the periodic array. The sum is over all the lattice vectors. This Green’s function has the limiting behaviour
where
![]() $\unicode[STIX]{x1D70F}$
is the area of the unit cell. Physically, the Green’s function represents a solution of the heat conduction problem with heat sources at the lattice points of a doubly periodic array on the plane
$\unicode[STIX]{x1D70F}$
is the area of the unit cell. Physically, the Green’s function represents a solution of the heat conduction problem with heat sources at the lattice points of a doubly periodic array on the plane
![]() $X_{3}=0$
. Far from these sources, i.e. at distances large compared to the lattice dimension, the temperature decreases linearly with
$X_{3}=0$
. Far from these sources, i.e. at distances large compared to the lattice dimension, the temperature decreases linearly with
![]() $|X_{3}|$
. The last condition gives
$|X_{3}|$
. The last condition gives
![]() $C^{\ast }\rightarrow K_{o}N\unicode[STIX]{x03C0}X_{3}c_{w}/\unicode[STIX]{x1D70F}=K_{o}\unicode[STIX]{x1D719}c_{w}X_{3}$
, which upon using (2.15), can be shown to satisfy the matching condition for
$C^{\ast }\rightarrow K_{o}N\unicode[STIX]{x03C0}X_{3}c_{w}/\unicode[STIX]{x1D70F}=K_{o}\unicode[STIX]{x1D719}c_{w}X_{3}$
, which upon using (2.15), can be shown to satisfy the matching condition for
![]() $C^{1}$
.
$C^{1}$
.
Note that, since the boundary condition at
![]() $X_{3}=0$
is independent of the tangential components of the concentration gradient, the dependence of
$X_{3}=0$
is independent of the tangential components of the concentration gradient, the dependence of
![]() $C^{1}$
on the surface gradient of the concentration is trivial and this simplifies the analysis considerably.
$C^{1}$
on the surface gradient of the concentration is trivial and this simplifies the analysis considerably.
The Green’s function
![]() $G$
is related to the function
$G$
is related to the function
![]() $\unicode[STIX]{x1D713}_{1}$
in Sangani & Behl (Reference Sangani and Behl1989) by
$\unicode[STIX]{x1D713}_{1}$
in Sangani & Behl (Reference Sangani and Behl1989) by
Sangani & Behl (Reference Sangani and Behl1989) have described in detail the methods for evaluating
![]() $\unicode[STIX]{x1D713}_{1}$
. This function decays exponentially at large
$\unicode[STIX]{x1D713}_{1}$
. This function decays exponentially at large
![]() $|X_{3}|$
.
$|X_{3}|$
.
It should be noted that
![]() $C^{\ast }$
can be evaluated simply by carrying out integrations in (3.2). This is in contrast to the most multi-particle interaction problems in which an integral equation must be solved for determining the concentration or the velocity field. This simplification occurs in the present problem because of the Neumann boundary condition at the wall
$C^{\ast }$
can be evaluated simply by carrying out integrations in (3.2). This is in contrast to the most multi-particle interaction problems in which an integral equation must be solved for determining the concentration or the velocity field. This simplification occurs in the present problem because of the Neumann boundary condition at the wall
![]() $X_{3}=0$
which specifies the flux at the boundary.
$X_{3}=0$
which specifies the flux at the boundary.
The overall rate of reaction per unit area of the wall,
![]() $q_{w}$
, can be evaluated to
$q_{w}$
, can be evaluated to
![]() $O(\unicode[STIX]{x1D716})$
using the expression for
$O(\unicode[STIX]{x1D716})$
using the expression for
![]() $C^{1}$
as given by (3.1). The integral of the first two terms on the right-hand side of (3.1) over the test disk vanishes and therefore only
$C^{1}$
as given by (3.1). The integral of the first two terms on the right-hand side of (3.1) over the test disk vanishes and therefore only
![]() $C^{\ast }$
, which is proportional to
$C^{\ast }$
, which is proportional to
![]() $c_{w}$
, contributes to the integral. Thus, to
$c_{w}$
, contributes to the integral. Thus, to
![]() $O(\unicode[STIX]{x1D716})$
, the reaction rate can be expressed in terms of an effective surface-reaction rate constant
$O(\unicode[STIX]{x1D716})$
, the reaction rate can be expressed in terms of an effective surface-reaction rate constant
![]() $k_{eff}$
, i.e.
$k_{eff}$
, i.e.
![]() $q_{w}=k_{eff}c_{w}$
, with
$q_{w}=k_{eff}c_{w}$
, with
where
![]() $F$
is related to the average of
$F$
is related to the average of
![]() $C^{\ast }$
over the test disk:
$C^{\ast }$
over the test disk:
We shall evaluate
![]() $F$
for two special cases.
$F$
for two special cases.
3.1 Periodic array
Let us first consider the case of a periodic array with
![]() $N=1$
. To evaluate the integrals in (3.7), we decompose the Green’s function into singular and regular terms at the origin:
$N=1$
. To evaluate the integrals in (3.7), we decompose the Green’s function into singular and regular terms at the origin:
![]() $G=G^{s}+G^{r}$
with
$G=G^{s}+G^{r}$
with
![]() $G^{s}(\boldsymbol{X})=1/|\boldsymbol{X}|$
, and integrate the two separately. The singular part is integrated using the formulas
$G^{s}(\boldsymbol{X})=1/|\boldsymbol{X}|$
, and integrate the two separately. The singular part is integrated using the formulas
Equation (3.8) was derived using the Taylor series expansion of the integrand for small
![]() $\boldsymbol{Y}$
and integrating each term separately while (3.9) was obtained using the Taylor series expansion for
$\boldsymbol{Y}$
and integrating each term separately while (3.9) was obtained using the Taylor series expansion for
![]() $\boldsymbol{X}$
.
$\boldsymbol{X}$
.
Substituting (3.8) and (3.9) into (3.7) and carrying out integration over
![]() $\boldsymbol{X}$
we obtain the contribution to
$\boldsymbol{X}$
we obtain the contribution to
![]() $F$
resulting from the singular part of the Green’s function:
$F$
resulting from the singular part of the Green’s function:
The last equality in (3.10) was obtained by making use of the fact that the infinite series is related to a well-known integral identity for the Euler integral
![]() $K$
:
$K$
:
The result (3.10) was also obtained previously using the Hankel transform technique by Bender & Stone (Reference Bender and Stone1993) who examined the reaction–diffusion problem for an isolated disk.
Next, let us evaluate the contribution from the regular part
![]() $G^{r}$
of the Green’s function at the origin arising from the rest of the lattice points. Since this function is regular over the entire disk area, we use the Taylor series expansion:
$G^{r}$
of the Green’s function at the origin arising from the rest of the lattice points. Since this function is regular over the entire disk area, we use the Taylor series expansion:
where we have used the notation
with
![]() $\boldsymbol{S}=\boldsymbol{X}-\boldsymbol{Y}$
. We next use the binomial expansion
$\boldsymbol{S}=\boldsymbol{X}-\boldsymbol{Y}$
. We next use the binomial expansion
to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|\boldsymbol{X}|\leqslant 1}\int _{|\boldsymbol{Y}|\leqslant 1}G^{r}(\boldsymbol{X}-\boldsymbol{Y})\,\text{d}A_{\boldsymbol{X}}\,\text{d}A_{\boldsymbol{Y}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=0}^{\infty }\mathop{\sum }_{s=0}^{n}\frac{n!}{(n-s)!s!}\int _{|\boldsymbol{X}|\leqslant 1}\,\text{d}A_{\boldsymbol{X}}\,\boldsymbol{X}^{(s)}\int _{|\boldsymbol{Y}|\leqslant 1}\,\text{d}A_{\boldsymbol{Y}}\,\boldsymbol{Y}^{(n-s)}(\cdot )^{n}\unicode[STIX]{x1D735}^{(n)}G^{r}(0).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|\boldsymbol{X}|\leqslant 1}\int _{|\boldsymbol{Y}|\leqslant 1}G^{r}(\boldsymbol{X}-\boldsymbol{Y})\,\text{d}A_{\boldsymbol{X}}\,\text{d}A_{\boldsymbol{Y}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=0}^{\infty }\mathop{\sum }_{s=0}^{n}\frac{n!}{(n-s)!s!}\int _{|\boldsymbol{X}|\leqslant 1}\,\text{d}A_{\boldsymbol{X}}\,\boldsymbol{X}^{(s)}\int _{|\boldsymbol{Y}|\leqslant 1}\,\text{d}A_{\boldsymbol{Y}}\,\boldsymbol{Y}^{(n-s)}(\cdot )^{n}\unicode[STIX]{x1D735}^{(n)}G^{r}(0).\end{eqnarray}$$
We carry out the angular integration of
![]() $X^{(s)}$
over a circle of constant radius
$X^{(s)}$
over a circle of constant radius
![]() $|X|$
first. For even values of
$|X|$
first. For even values of
![]() $s$
, the integral can be expressed in terms of products of two-dimensional Kronecker delta functions in the
$s$
, the integral can be expressed in terms of products of two-dimensional Kronecker delta functions in the
![]() $x_{1}-x_{2}$
plane, i.e.
$x_{1}-x_{2}$
plane, i.e.
![]() $(\unicode[STIX]{x1D6FF}_{i1}+\unicode[STIX]{x1D6FF}_{i2})$
, which also equals
$(\unicode[STIX]{x1D6FF}_{i1}+\unicode[STIX]{x1D6FF}_{i2})$
, which also equals
![]() $\unicode[STIX]{x1D6FF}_{ij}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}$
, while the integral vanishes for the odd values of
$\unicode[STIX]{x1D6FF}_{ij}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}$
, while the integral vanishes for the odd values of
![]() $s$
. Since
$s$
. Since
![]() $G^{r}$
satisfies the Laplace equation, the terms resulting from the multiplication of
$G^{r}$
satisfies the Laplace equation, the terms resulting from the multiplication of
![]() $\unicode[STIX]{x1D6FF}_{ij}$
with the gradients of
$\unicode[STIX]{x1D6FF}_{ij}$
with the gradients of
![]() $G^{r}$
vanish. This gives
$G^{r}$
vanish. This gives
The integration over
![]() $\boldsymbol{Y}$
can be carried out in a similar manner and the final result for the double integration in (3.7) (with
$\boldsymbol{Y}$
can be carried out in a similar manner and the final result for the double integration in (3.7) (with
![]() $N=1$
) is
$N=1$
) is
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\frac{1}{2}G^{r}(0)-\frac{1}{8}\frac{\unicode[STIX]{x2202}^{2}G^{r}}{\unicode[STIX]{x2202}X_{3}^{2}}(0)+\frac{5}{128}\frac{\unicode[STIX]{x2202}^{4}G^{r}}{\unicode[STIX]{x2202}X_{3}^{4}}(0)+\cdots \nonumber\\ \displaystyle & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\mathop{\sum }_{n=0}^{\infty }c_{n}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{3}}\right)^{2n}G^{r}(0),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\frac{1}{2}G^{r}(0)-\frac{1}{8}\frac{\unicode[STIX]{x2202}^{2}G^{r}}{\unicode[STIX]{x2202}X_{3}^{2}}(0)+\frac{5}{128}\frac{\unicode[STIX]{x2202}^{4}G^{r}}{\unicode[STIX]{x2202}X_{3}^{4}}(0)+\cdots \nonumber\\ \displaystyle & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\mathop{\sum }_{n=0}^{\infty }c_{n}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{3}}\right)^{2n}G^{r}(0),\end{eqnarray}$$
with
![]() $c_{n}$
given by
$c_{n}$
given by
The derivatives of the Green’s function can be evaluated using the expressions given in Sangani & Behl (Reference Sangani and Behl1989). The details are given in the appendix where we take the opportunity to correct some of the expressions given in that study. Substituting for the numerical values of the derivatives of
![]() $G^{r}$
we obtain, for square arrays,
$G^{r}$
we obtain, for square arrays,
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\unicode[STIX]{x1D719}^{1/2} [-1.1002+0.2028\unicode[STIX]{x1D719}+0.1023\unicode[STIX]{x1D719}^{2}+0.0393\unicode[STIX]{x1D719}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,0.0481\unicode[STIX]{x1D719}^{4}+0.0288\unicode[STIX]{x1D719}^{5}+0.0400\unicode[STIX]{x1D719}^{6}+\cdots ],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\unicode[STIX]{x1D719}^{1/2} [-1.1002+0.2028\unicode[STIX]{x1D719}+0.1023\unicode[STIX]{x1D719}^{2}+0.0393\unicode[STIX]{x1D719}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,0.0481\unicode[STIX]{x1D719}^{4}+0.0288\unicode[STIX]{x1D719}^{5}+0.0400\unicode[STIX]{x1D719}^{6}+\cdots ],\end{eqnarray}$$
and for, hexagonal arrays,
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\unicode[STIX]{x1D719}^{1/2} [-1.1061+0.1996\unicode[STIX]{x1D719}+0.0316\unicode[STIX]{x1D719}^{2}+0.0116\unicode[STIX]{x1D719}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,0.0058\unicode[STIX]{x1D719}^{4}+0.0034\unicode[STIX]{x1D719}^{5}+0.0022\unicode[STIX]{x1D719}^{6}+\cdots ].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\unicode[STIX]{x1D719}^{1/2} [-1.1061+0.1996\unicode[STIX]{x1D719}+0.0316\unicode[STIX]{x1D719}^{2}+0.0116\unicode[STIX]{x1D719}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,0.0058\unicode[STIX]{x1D719}^{4}+0.0034\unicode[STIX]{x1D719}^{5}+0.0022\unicode[STIX]{x1D719}^{6}+\cdots ].\end{eqnarray}$$
Figure 1 shows the results for
![]() $F$
obtained by including up to the first 32 terms in the series for both square and hexagonal arrays. We see that, at least up to
$F$
obtained by including up to the first 32 terms in the series for both square and hexagonal arrays. We see that, at least up to
![]() $\unicode[STIX]{x1D719}=0.7$
,
$\unicode[STIX]{x1D719}=0.7$
,
![]() $F$
as a function of
$F$
as a function of
![]() $\unicode[STIX]{x1D719}$
is essentially the same for both arrays and lower than for the random arrays to be considered next. The expressions given by (3.19) and (3.20) are accurate to within about 5 % for
$\unicode[STIX]{x1D719}$
is essentially the same for both arrays and lower than for the random arrays to be considered next. The expressions given by (3.19) and (3.20) are accurate to within about 5 % for
![]() $\unicode[STIX]{x1D719}$
up to 0.35.
$\unicode[STIX]{x1D719}$
up to 0.35.

Figure 1.
![]() $F$
as a function of the area fraction
$F$
as a function of the area fraction
![]() $\unicode[STIX]{x1D719}$
of the disks for hexagonal (solid line), square (stars) and random arrays (dashed line).
$\unicode[STIX]{x1D719}$
of the disks for hexagonal (solid line), square (stars) and random arrays (dashed line).
3.2 Random arrays
Let us now consider the case in which the disks are arranged randomly, with the spatial distribution corresponding to a hard-disk molecular system. The results for this case will be obtained by first considering
![]() $N$
randomly placed disks within a unit cell of a periodic array and then taking the limit
$N$
randomly placed disks within a unit cell of a periodic array and then taking the limit
![]() $N\rightarrow \infty$
. Taking ensemble average of (3.7) over many hard-disk configurations, we obtain
$N\rightarrow \infty$
. Taking ensemble average of (3.7) over many hard-disk configurations, we obtain
where
![]() $P(\boldsymbol{R}|\mathbf{0})$
is the pair-probability density (in the inner region scaled variables) for finding a disk with its centre at
$P(\boldsymbol{R}|\mathbf{0})$
is the pair-probability density (in the inner region scaled variables) for finding a disk with its centre at
![]() $\boldsymbol{R}$
given that a disk exists at the origin of the unit cell and the integration over
$\boldsymbol{R}$
given that a disk exists at the origin of the unit cell and the integration over
![]() $\boldsymbol{R}$
is over the entire unit cell while that over
$\boldsymbol{R}$
is over the entire unit cell while that over
![]() $\boldsymbol{X}$
and
$\boldsymbol{X}$
and
![]() $\boldsymbol{Y}$
are over the area of the two disks at the origin and at
$\boldsymbol{Y}$
are over the area of the two disks at the origin and at
![]() $\boldsymbol{R}$
. The pair-probability density for the hard-disk configuration is given by
$\boldsymbol{R}$
. The pair-probability density for the hard-disk configuration is given by
where
![]() $g(R)$
is the radial distribution function and
$g(R)$
is the radial distribution function and
![]() $\unicode[STIX]{x1D6FF}_{2D}$
is Dirac’s delta function in the two-dimensional space. The integration over
$\unicode[STIX]{x1D6FF}_{2D}$
is Dirac’s delta function in the two-dimensional space. The integration over
![]() $\boldsymbol{R}$
is split into two parts with the singular, Dirac delta function part of the pair-probability density yielding the contribution to
$\boldsymbol{R}$
is split into two parts with the singular, Dirac delta function part of the pair-probability density yielding the contribution to
![]() $F$
corresponding to an isolated disk, i.e.
$F$
corresponding to an isolated disk, i.e.
![]() $8/3\unicode[STIX]{x03C0}$
. For
$8/3\unicode[STIX]{x03C0}$
. For
![]() $R>2$
, the integrations over
$R>2$
, the integrations over
![]() $\boldsymbol{X}$
and
$\boldsymbol{X}$
and
![]() $\boldsymbol{Y}$
can be carried out also as before using the Taylor series expansion. This yields
$\boldsymbol{Y}$
can be carried out also as before using the Taylor series expansion. This yields
with
![]() $c_{n}$
given by (3.18). In the limit
$c_{n}$
given by (3.18). In the limit
![]() $N\rightarrow \infty$
, the unit cell size is much larger than unity and
$N\rightarrow \infty$
, the unit cell size is much larger than unity and
![]() $G$
may be replaced by the infinite-space Green’s function:
$G$
may be replaced by the infinite-space Green’s function:
![]() $G=1/R+O(N^{-1/2})$
for
$G=1/R+O(N^{-1/2})$
for
![]() $R$
of
$R$
of
![]() $O(1)$
. This approximation for the Green’s function can be used for evaluating the terms with
$O(1)$
. This approximation for the Green’s function can be used for evaluating the terms with
![]() $n\geqslant 1$
in the above expression since they decay as
$n\geqslant 1$
in the above expression since they decay as
![]() $R^{-3}$
or faster. The
$R^{-3}$
or faster. The
![]() $n=0$
term needs to be treated separately. Accordingly, we write
$n=0$
term needs to be treated separately. Accordingly, we write
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\frac{\unicode[STIX]{x1D719}}{\unicode[STIX]{x03C0}}\left[c_{0}\int _{R\geqslant 2}G(\boldsymbol{R})\,\text{d}A_{\boldsymbol{R}}+c_{0}\int _{R\geqslant 2}G(\boldsymbol{R})[g(R)-1]\,\text{d}A_{\boldsymbol{R}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\int _{R\geqslant 2}\mathop{\sum }_{n=1}^{\infty }c_{n}\frac{\unicode[STIX]{x2202}^{2n}R^{-1}}{\unicode[STIX]{x2202}X_{3}^{2n}}g(R)\,\text{d}A_{\boldsymbol{R}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \frac{8}{3\unicode[STIX]{x03C0}}+\frac{\unicode[STIX]{x1D719}}{\unicode[STIX]{x03C0}}\left[c_{0}\int _{R\geqslant 2}G(\boldsymbol{R})\,\text{d}A_{\boldsymbol{R}}+c_{0}\int _{R\geqslant 2}G(\boldsymbol{R})[g(R)-1]\,\text{d}A_{\boldsymbol{R}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\int _{R\geqslant 2}\mathop{\sum }_{n=1}^{\infty }c_{n}\frac{\unicode[STIX]{x2202}^{2n}R^{-1}}{\unicode[STIX]{x2202}X_{3}^{2n}}g(R)\,\text{d}A_{\boldsymbol{R}}\right].\end{eqnarray}$$
The first integral on the right-hand side of the above expression is evaluated using the fact that the average of
![]() $G$
over the unit cell is zero. Therefore
$G$
over the unit cell is zero. Therefore
where we have used
![]() $G=1/R$
for
$G=1/R$
for
![]() $R<2$
. The remaining two integrals in (3.25) can be evaluated by substituting
$R<2$
. The remaining two integrals in (3.25) can be evaluated by substituting
![]() $G=1/R$
and carrying out integrals from
$G=1/R$
and carrying out integrals from
![]() $R=2$
to
$R=2$
to
![]() $\infty$
provided that
$\infty$
provided that
![]() $g(R)-1$
decays faster than
$g(R)-1$
decays faster than
![]() $1/R$
at infinity. The derivatives of
$1/R$
at infinity. The derivatives of
![]() $G$
are evaluated using
$G$
are evaluated using
For very dilute hard-disk arrays
![]() $g(R)=1+O(\unicode[STIX]{x1D719})$
. Substituting for
$g(R)=1+O(\unicode[STIX]{x1D719})$
. Substituting for
![]() $c_{n}$
from (3.18) into (3.24) and carrying out integrations yields
$c_{n}$
from (3.18) into (3.24) and carrying out integrations yields
The radial distribution function for the non-dilute hard-disk random arrays can be determined approximately by solving the Percus–Yevick equation. For the three-dimensional (3-D) case of hard-spheres, this equation permits an analytical solution but for the 2-D case of hard disks, this equation must be solved numerically (Chae, Ree & Ree Reference Chae, Ree and Ree1969; Adda-Bedia, Katzav & Vella Reference Adda-Bedia, Katzav and Vella2008). We used the method described by Adda-Bedia et al. (Reference Adda-Bedia, Katzav and Vella2008), according to which
![]() $g(R)$
is expanded in powers of
$g(R)$
is expanded in powers of
![]() $\unicode[STIX]{x1D719}$
:
$\unicode[STIX]{x1D719}$
:
and
![]() $g_{k}(R)$
subsequently determined by solving an integro-differential equation.
$g_{k}(R)$
subsequently determined by solving an integro-differential equation.
![]() $g_{k}$
has a compact support, being non-zero only for
$g_{k}$
has a compact support, being non-zero only for
![]() $2\leqslant R\leqslant 2k+2$
. Adda-Bedia et al. (Reference Adda-Bedia, Katzav and Vella2008) computed terms up to
$2\leqslant R\leqslant 2k+2$
. Adda-Bedia et al. (Reference Adda-Bedia, Katzav and Vella2008) computed terms up to
![]() $k=50$
and compared the radial distribution function thus determined with the results obtained using Monte Carlo simulations for
$k=50$
and compared the radial distribution function thus determined with the results obtained using Monte Carlo simulations for
![]() $\unicode[STIX]{x1D719}=0.62$
and found an excellent agreement. The integro-differential equation for each
$\unicode[STIX]{x1D719}=0.62$
and found an excellent agreement. The integro-differential equation for each
![]() $g_{k}$
is solved numerically by converting it into a system of linear algebraic equation by discretizing both the derivative and the integral terms. Calculations were done for four different discretizations, with the minimum being
$g_{k}$
is solved numerically by converting it into a system of linear algebraic equation by discretizing both the derivative and the integral terms. Calculations were done for four different discretizations, with the minimum being
![]() $\unicode[STIX]{x0394}R=0.02$
, and the results were used to extrapolate for
$\unicode[STIX]{x0394}R=0.02$
, and the results were used to extrapolate for
![]() $\unicode[STIX]{x0394}R=0$
. The coefficient of the
$\unicode[STIX]{x0394}R=0$
. The coefficient of the
![]() $O(\unicode[STIX]{x1D719}^{k})$
term
$O(\unicode[STIX]{x1D719}^{k})$
term
![]() $f_{k}$
in the expansion for
$f_{k}$
in the expansion for
![]() $F$
in powers of
$F$
in powers of
![]() $\unicode[STIX]{x1D719}$
is then evaluated using
$\unicode[STIX]{x1D719}$
is then evaluated using
Substituting (3.28) into (3.24), it is possible to determine
![]() $F$
in power series of
$F$
in power series of
![]() $\unicode[STIX]{x1D719}$
. The first few terms are given below
$\unicode[STIX]{x1D719}$
. The first few terms are given below
The coefficients of the last two terms are only approximate as their convergence with decreasing
![]() $\unicode[STIX]{x0394}R$
is somewhat slow. This, however, does not affect significantly the overall value of
$\unicode[STIX]{x0394}R$
is somewhat slow. This, however, does not affect significantly the overall value of
![]() $F$
shown in figure 1 where we see that
$F$
shown in figure 1 where we see that
![]() $F$
for random arrays is significantly greater than for square and hexagonal arrays.
$F$
for random arrays is significantly greater than for square and hexagonal arrays.
4 The
 $O(\unicode[STIX]{x1D716}^{2})$
problem
$O(\unicode[STIX]{x1D716}^{2})$
problem
Since the leading
![]() $O(1)$
term
$O(1)$
term
![]() $C^{0}$
in the inner region is a constant, the convective term in (2.7) does not contribute to the inner region governing equation even for the
$C^{0}$
in the inner region is a constant, the convective term in (2.7) does not contribute to the inner region governing equation even for the
![]() $O(\unicode[STIX]{x1D716}^{2})$
correction
$O(\unicode[STIX]{x1D716}^{2})$
correction
![]() $C^{2}$
. In other words,
$C^{2}$
. In other words,
![]() $C^{2}$
also satisfies the Laplace equation. The boundary condition on the surface of the reactive disks at the wall is given by
$C^{2}$
also satisfies the Laplace equation. The boundary condition on the surface of the reactive disks at the wall is given by
and the matching with the outer region requires that
Since
![]() $C^{\ast }$
is linear in
$C^{\ast }$
is linear in
![]() $c_{w}$
, we see that
$c_{w}$
, we see that
![]() $C^{2}$
is linear in both the concentration and its surface gradients. This is similar to
$C^{2}$
is linear in both the concentration and its surface gradients. This is similar to
![]() $C^{1}$
which also depended linearly on both the concentration and its gradients. But, whereas the part of
$C^{1}$
which also depended linearly on both the concentration and its gradients. But, whereas the part of
![]() $C^{1}$
that depended on the gradients did not contribute to the overall reaction rate, it can be shown that
$C^{1}$
that depended on the gradients did not contribute to the overall reaction rate, it can be shown that
![]() $O(\unicode[STIX]{x1D716}^{2})$
contribution to the rate will depend on both the concentration and its surface gradient. In other words, the concept of the effective rate constant does not hold in general at
$O(\unicode[STIX]{x1D716}^{2})$
contribution to the rate will depend on both the concentration and its surface gradient. In other words, the concept of the effective rate constant does not hold in general at
![]() $O(\unicode[STIX]{x1D716}^{2})$
. We should note that the last two integrals on the right-hand side of (2.5) do not contribute to the macroscopic flux up to
$O(\unicode[STIX]{x1D716}^{2})$
. We should note that the last two integrals on the right-hand side of (2.5) do not contribute to the macroscopic flux up to
![]() $O(\unicode[STIX]{x1D716})$
but may also contribute at
$O(\unicode[STIX]{x1D716})$
but may also contribute at
![]() $O(\unicode[STIX]{x1D716}^{2})$
. Finally, it can be shown, from the formal solution for
$O(\unicode[STIX]{x1D716}^{2})$
. Finally, it can be shown, from the formal solution for
![]() $C^{2}$
, that the part of the overall flux that depends linearly on the surface gradient involves a lattice sum that is not absolutely convergent suggesting thereby that its contribution to
$C^{2}$
, that the part of the overall flux that depends linearly on the surface gradient involves a lattice sum that is not absolutely convergent suggesting thereby that its contribution to
![]() $q_{w}$
will depend on the location of
$q_{w}$
will depend on the location of
![]() $\boldsymbol{x}_{w}$
relative to the macroscopic boundaries of the wall. Thus, estimating the
$\boldsymbol{x}_{w}$
relative to the macroscopic boundaries of the wall. Thus, estimating the
![]() $O(\unicode[STIX]{x1D716}^{2})$
correction to the flux will be far more cumbersome.
$O(\unicode[STIX]{x1D716}^{2})$
correction to the flux will be far more cumbersome.
5 Comparison with the Shah and Shaqfeh analysis
As mentioned in the introduction, Shah & Shaqfeh (Reference Shah and Shaqfeh2015) considered the case when the non-dimensional numbers based on the radius
![]() $a$
of the disks, i.e.
$a$
of the disks, i.e.
![]() $K\equiv ak/D=\unicode[STIX]{x1D716}K_{o}$
and
$K\equiv ak/D=\unicode[STIX]{x1D716}K_{o}$
and
![]() $Pe=a^{2}\dot{\unicode[STIX]{x1D6FE}}/$
$Pe=a^{2}\dot{\unicode[STIX]{x1D6FE}}/$
![]() $D=Pe_{o}\unicode[STIX]{x1D70F}_{w}\unicode[STIX]{x1D716}^{2}$
are
$D=Pe_{o}\unicode[STIX]{x1D70F}_{w}\unicode[STIX]{x1D716}^{2}$
are
![]() $O(1)$
constants. The analysis by Juhasz & Deen (Reference Juhasz and Deen1991) also considered the same case except that these investigators examined one-dimensional heterogeneous surfaces with the strips of reactive patches. In both studies, the outer region equations are given by, in lieu of (2.1) and (2.2),
$O(1)$
constants. The analysis by Juhasz & Deen (Reference Juhasz and Deen1991) also considered the same case except that these investigators examined one-dimensional heterogeneous surfaces with the strips of reactive patches. In both studies, the outer region equations are given by, in lieu of (2.1) and (2.2),
where
![]() $q_{w}^{\ast }=aq_{w}/D$
. We note that both
$q_{w}^{\ast }=aq_{w}/D$
. We note that both
![]() $\unicode[STIX]{x1D70F}_{w}$
and
$\unicode[STIX]{x1D70F}_{w}$
and
![]() $q_{w}^{\ast }/c_{w}$
are
$q_{w}^{\ast }/c_{w}$
are
![]() $O(1)$
when the macroscale Reynolds number and
$O(1)$
when the macroscale Reynolds number and
![]() $ka/D$
are
$ka/D$
are
![]() $O(1)$
. Both studies provided no justification for ignoring gradients in the average (macroscale) concentration parallel to the wall.
$O(1)$
. Both studies provided no justification for ignoring gradients in the average (macroscale) concentration parallel to the wall.
According to (5.1), the outer region is convection dominated so that, to leading order, the concentration does not change along the streamline, and hence at the wall
![]() $x_{3}\rightarrow 0$
(in the outer region). There exists a mass transfer boundary layer of thickness
$x_{3}\rightarrow 0$
(in the outer region). There exists a mass transfer boundary layer of thickness
![]() $O((\unicode[STIX]{x1D716}^{2}/Pe)^{1/3})$
which is small compared to the macroscale but large compared to the microscale. Under these conditions the flux of the solute normal to the wall will be much greater than that along the wall and therefore the surface gradient of the solute concentration is relatively unimportant. In the case of small or zero Péclet numbers, where one may expect the average concentration variation along the surface to become important, we can estimate the magnitude of the concentration gradient parallel to the surface as follows. Let us suppose that we have a diffusion in a long pore with heterogeneous wall and that the average concentration is depleting along its axis, which coincides with the
$O((\unicode[STIX]{x1D716}^{2}/Pe)^{1/3})$
which is small compared to the macroscale but large compared to the microscale. Under these conditions the flux of the solute normal to the wall will be much greater than that along the wall and therefore the surface gradient of the solute concentration is relatively unimportant. In the case of small or zero Péclet numbers, where one may expect the average concentration variation along the surface to become important, we can estimate the magnitude of the concentration gradient parallel to the surface as follows. Let us suppose that we have a diffusion in a long pore with heterogeneous wall and that the average concentration is depleting along its axis, which coincides with the
![]() $x_{1}$
-axis, due to the reaction at the pore wall. We must then have the diffusion term
$x_{1}$
-axis, due to the reaction at the pore wall. We must then have the diffusion term
![]() $\unicode[STIX]{x2202}^{2}c/\unicode[STIX]{x2202}x_{1}^{2}$
comparable to the rate of reaction, i.e.
$\unicode[STIX]{x2202}^{2}c/\unicode[STIX]{x2202}x_{1}^{2}$
comparable to the rate of reaction, i.e.
![]() $\unicode[STIX]{x1D716}^{-1}K_{eff}c$
, where
$\unicode[STIX]{x1D716}^{-1}K_{eff}c$
, where
![]() $K_{eff}=k_{eff}a/D$
is the effective Damköhler number based on the radius of the disks. This yields
$K_{eff}=k_{eff}a/D$
is the effective Damköhler number based on the radius of the disks. This yields
![]() $\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}x_{1}\sim \unicode[STIX]{x1D716}^{-1/2}c$
since
$\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}x_{1}\sim \unicode[STIX]{x1D716}^{-1/2}c$
since
![]() $K_{eff}$
is
$K_{eff}$
is
![]() $O(1)$
when
$O(1)$
when
![]() $ka/D=O(1)$
. Therefore, the boundary condition in terms of an effective rate constant remains valid to
$ka/D=O(1)$
. Therefore, the boundary condition in terms of an effective rate constant remains valid to
![]() $O(1)$
regardless of the Péclet number as long as
$O(1)$
regardless of the Péclet number as long as
![]() $ka/D$
is
$ka/D$
is
![]() $O(1)$
or
$O(1)$
or
![]() $K_{o}$
is
$K_{o}$
is
![]() $O(\unicode[STIX]{x1D716}^{-1})$
. The error due to the neglect of the variation in the macroscale concentration along the surface is
$O(\unicode[STIX]{x1D716}^{-1})$
. The error due to the neglect of the variation in the macroscale concentration along the surface is
![]() $O(\unicode[STIX]{x1D716}^{1/2})$
when
$O(\unicode[STIX]{x1D716}^{1/2})$
when
![]() $Pe=0$
and
$Pe=0$
and
![]() $O(\unicode[STIX]{x1D716})$
when
$O(\unicode[STIX]{x1D716})$
when
![]() $Pe$
is
$Pe$
is
![]() $O(1)$
.
$O(1)$
.
The terms containing the concentration gradient parallel to the wall in (4.1) can be neglected when
![]() $K_{o}$
is large and one may proceed with the calculation of
$K_{o}$
is large and one may proceed with the calculation of
![]() $C^{2}$
and the higher-order terms to produce an expression for
$C^{2}$
and the higher-order terms to produce an expression for
![]() $k_{eff}$
in a series of powers of
$k_{eff}$
in a series of powers of
![]() $K_{o}$
but solving numerically the integral equation for selected values of
$K_{o}$
but solving numerically the integral equation for selected values of
![]() $K_{o}$
or, equivalently,
$K_{o}$
or, equivalently,
![]() $K$
would be less cumbersome as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015).
$K$
would be less cumbersome as was done by Shah & Shaqfeh (Reference Shah and Shaqfeh2015).
It is interesting to compare the results obtained in the present study with those by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) even though they correspond to different limits. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) presented their results in terms of a Sherwood number, which is the same as the effective Damköhler number based on the radius of the disk divided by the area fraction of the reactive disks, i.e.
with
![]() $K=\unicode[STIX]{x1D716}K_{o}=ka/D$
. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) presented results for
$K=\unicode[STIX]{x1D716}K_{o}=ka/D$
. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) presented results for
![]() $K$
equal to 0.1, 1, 10 and 300 at various
$K$
equal to 0.1, 1, 10 and 300 at various
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $Pe$
for both square and random arrays. Since our analysis is accurate only for small
$Pe$
for both square and random arrays. Since our analysis is accurate only for small
![]() $K$
and
$K$
and
![]() $Pe$
, we choose the following equivalent Padé approximant for comparison purposes, which ensures that
$Pe$
, we choose the following equivalent Padé approximant for comparison purposes, which ensures that
![]() $Sh$
is finite even when
$Sh$
is finite even when
![]() $K=\infty$
:
$K=\infty$
:
Let us first consider the case of an isolated disk
![]() $(\unicode[STIX]{x1D719}\rightarrow 0)$
for which
$(\unicode[STIX]{x1D719}\rightarrow 0)$
for which
![]() $F=8/$
$F=8/$
![]() $(3\unicode[STIX]{x03C0})\simeq 0.85$
. The term on the extreme right-hand side of (5.4) expanded for small
$(3\unicode[STIX]{x03C0})\simeq 0.85$
. The term on the extreme right-hand side of (5.4) expanded for small
![]() $K$
gives
$K$
gives
![]() $Sh=K[1-0.85K+0.72K^{2}-0.61K^{3}+\cdots \,]$
which compares well with the exact result obtained by Bender & Stone (Reference Bender and Stone1993):
$Sh=K[1-0.85K+0.72K^{2}-0.61K^{3}+\cdots \,]$
which compares well with the exact result obtained by Bender & Stone (Reference Bender and Stone1993):
![]() $Sh=K[1-0.85K+0.73K^{2}-0.63K^{3}+O(K^{4})]$
. At the other extreme (i.e.
$Sh=K[1-0.85K+0.73K^{2}-0.63K^{3}+O(K^{4})]$
. At the other extreme (i.e.
![]() $K\rightarrow \infty$
),
$K\rightarrow \infty$
),
![]() $Sh\rightarrow 3\unicode[STIX]{x03C0}/8\simeq 1.18$
according to the above approximation. This is within approximately 7 % of the exact result
$Sh\rightarrow 3\unicode[STIX]{x03C0}/8\simeq 1.18$
according to the above approximation. This is within approximately 7 % of the exact result
![]() $Sh\rightarrow 4/\unicode[STIX]{x03C0}\simeq 1.27$
for
$Sh\rightarrow 4/\unicode[STIX]{x03C0}\simeq 1.27$
for
![]() $K=\infty$
. Thus, the Padé approximation (5.4) provides reasonably accurate estimates for the entire range of values of
$K=\infty$
. Thus, the Padé approximation (5.4) provides reasonably accurate estimates for the entire range of values of
![]() $K$
for the single disk. Since
$K$
for the single disk. Since
![]() $F$
decreases as
$F$
decreases as
![]() $\unicode[STIX]{x1D719}$
is increased, one may expect that the Padé approximant given by (5.4) will provide reasonably accurate estimates for the entire range of values of
$\unicode[STIX]{x1D719}$
is increased, one may expect that the Padé approximant given by (5.4) will provide reasonably accurate estimates for the entire range of values of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $K$
for
$K$
for
![]() $Pe=0$
.
$Pe=0$
.
Shah & Shaqfeh (Reference Shah and Shaqfeh2015) present somewhat limited results for small
![]() $Pe$
. For
$Pe$
. For
![]() $Pe=10^{-3}$
they present results for
$Pe=10^{-3}$
they present results for
![]() $\unicode[STIX]{x1D719}=0.00126$
and
$\unicode[STIX]{x1D719}=0.00126$
and
![]() $\unicode[STIX]{x1D719}=0.064$
in their figure 9. The results for the former are essentially the same as for an isolated disks and so we shall compare only the results for
$\unicode[STIX]{x1D719}=0.064$
in their figure 9. The results for the former are essentially the same as for an isolated disks and so we shall compare only the results for
![]() $\unicode[STIX]{x1D719}=0.064$
for which
$\unicode[STIX]{x1D719}=0.064$
for which
![]() $F=0.57$
(cf. figure 1). For
$F=0.57$
(cf. figure 1). For
![]() $K=1$
, the approximation (5.4) predicts
$K=1$
, the approximation (5.4) predicts
![]() $Sh=0.64$
which is essentially the same as one obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). For
$Sh=0.64$
which is essentially the same as one obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). For
![]() $K=10$
, the approximation gives
$K=10$
, the approximation gives
![]() $Sh=1.49$
compared to approximately 1.51 obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015), and for
$Sh=1.49$
compared to approximately 1.51 obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015), and for
![]() $K=300$
,
$K=300$
,
![]() $Sh=1.94$
predicted by (5.4) is approximately 8 % lower than that obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015).
$Sh=1.94$
predicted by (5.4) is approximately 8 % lower than that obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015).
Additional results for non-dilute arrays are presented in figure 12 of Shah & Shaqfeh (Reference Shah and Shaqfeh2015) in terms a variable
![]() $\unicode[STIX]{x1D702}\equiv K/Sh-1$
, which, in our approximation, simply equals
$\unicode[STIX]{x1D702}\equiv K/Sh-1$
, which, in our approximation, simply equals
![]() $KF$
. These calculations were limited to
$KF$
. These calculations were limited to
![]() $Pe=2$
. For
$Pe=2$
. For
![]() $\unicode[STIX]{x1D719}=0.4$
,
$\unicode[STIX]{x1D719}=0.4$
,
![]() $F=0.208$
and, therefore
$F=0.208$
and, therefore
![]() $\unicode[STIX]{x1D702}=0.208$
for
$\unicode[STIX]{x1D702}=0.208$
for
![]() $K=1$
, a result that is in perfect agreement with Shah & Shaqfeh (Reference Shah and Shaqfeh2015). Likewise, for
$K=1$
, a result that is in perfect agreement with Shah & Shaqfeh (Reference Shah and Shaqfeh2015). Likewise, for
![]() $\unicode[STIX]{x1D719}=0.6$
,
$\unicode[STIX]{x1D719}=0.6$
,
![]() $F$
equals 0.104 so that
$F$
equals 0.104 so that
![]() $\unicode[STIX]{x1D702}$
is also 0.104 for
$\unicode[STIX]{x1D702}$
is also 0.104 for
![]() $K=1$
which, once again, is essentially the same as the one obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). The same applies to
$K=1$
which, once again, is essentially the same as the one obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015). The same applies to
![]() $\unicode[STIX]{x1D719}=0.2$
for which
$\unicode[STIX]{x1D719}=0.2$
for which
![]() $F=0.376$
.
$F=0.376$
.
Shah & Shaqfeh (Reference Shah and Shaqfeh2015) also show the results for random arrays in their figure 12. Here, surprisingly, they find that the results for the random arrays are essentially the same as those for the periodic arrays in contrast to the results of the present study. For example, according to the results shown in figure 1,
![]() $F$
, and hence
$F$
, and hence
![]() $\unicode[STIX]{x1D702}/K$
, for random arrays is approximately 0.52 for
$\unicode[STIX]{x1D702}/K$
, for random arrays is approximately 0.52 for
![]() $\unicode[STIX]{x1D719}=0.2$
, which is approximately 40 % greater than 0.376 for square arrays. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) obtained
$\unicode[STIX]{x1D719}=0.2$
, which is approximately 40 % greater than 0.376 for square arrays. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) obtained
![]() $\unicode[STIX]{x1D702}/K$
equal to approximately 0.41 for the entire range of
$\unicode[STIX]{x1D702}/K$
equal to approximately 0.41 for the entire range of
![]() $K$
, a result that is significantly lower. Similar discrepancy is observed for other values of
$K$
, a result that is significantly lower. Similar discrepancy is observed for other values of
![]() $\unicode[STIX]{x1D719}$
. These investigators used random arrays with only ten disks per unit cell in obtaining their results and it is possible that this resulted in a gross underestimate of
$\unicode[STIX]{x1D719}$
. These investigators used random arrays with only ten disks per unit cell in obtaining their results and it is possible that this resulted in a gross underestimate of
![]() $\unicode[STIX]{x1D702}$
. The particle–particle interactions are long ranged and lead to substantial errors for small
$\unicode[STIX]{x1D702}$
. The particle–particle interactions are long ranged and lead to substantial errors for small
![]() $N$
, especially at small
$N$
, especially at small
![]() $K$
for which the conditionally averaged disturbance is not screened. This is similar to the well-studied problem of finite
$K$
for which the conditionally averaged disturbance is not screened. This is similar to the well-studied problem of finite
![]() $N$
errors in the Stokes flow sedimentation problem (see, e.g. Ladd (Reference Ladd1990); Mo & Sangani (Reference Mo and Sangani1994); Dodd et al. (Reference Dodd, Hammer, Sangani and Koch1995)). It can be shown that for small
$N$
errors in the Stokes flow sedimentation problem (see, e.g. Ladd (Reference Ladd1990); Mo & Sangani (Reference Mo and Sangani1994); Dodd et al. (Reference Dodd, Hammer, Sangani and Koch1995)). It can be shown that for small
![]() $K$
,
$K$
,
![]() $F(N)$
determined from the numerical simulations with
$F(N)$
determined from the numerical simulations with
![]() $N$
disks per unit cell of a square array is given by
$N$
disks per unit cell of a square array is given by
This correction arises due to the influence of the periodic images of the test disk and its immediate vicinity. Here,
![]() $S(0)$
is the zero-wavenumber structure factor for the array. Its value for random arrays with hard-disk configurations can be estimated using the expression given by Chae et al. (Reference Chae, Ree and Ree1969) (also given by equation (28) in Dodd et al. (Reference Dodd, Hammer, Sangani and Koch1995)). For
$S(0)$
is the zero-wavenumber structure factor for the array. Its value for random arrays with hard-disk configurations can be estimated using the expression given by Chae et al. (Reference Chae, Ree and Ree1969) (also given by equation (28) in Dodd et al. (Reference Dodd, Hammer, Sangani and Koch1995)). For
![]() $\unicode[STIX]{x1D719}=0.2$
,
$\unicode[STIX]{x1D719}=0.2$
,
![]() $S(0)=0.42$
and therefore the finite
$S(0)=0.42$
and therefore the finite
![]() $N$
error in
$N$
error in
![]() $F$
equals 0.07. If we add this correction to the result obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) we obtain
$F$
equals 0.07. If we add this correction to the result obtained by Shah & Shaqfeh (Reference Shah and Shaqfeh2015) we obtain
![]() $F=0.48$
, a value that is approximately 10 % lower than that indicated in figure 1. For
$F=0.48$
, a value that is approximately 10 % lower than that indicated in figure 1. For
![]() $\unicode[STIX]{x1D719}=0.4$
,
$\unicode[STIX]{x1D719}=0.4$
,
![]() $S(0)$
equals 0.15 and the finite
$S(0)$
equals 0.15 and the finite
![]() $N$
correction to
$N$
correction to
![]() $F$
is approximately 0.03. According to figure 1,
$F$
is approximately 0.03. According to figure 1,
![]() $F$
equals 0.2 and 0.3, respectively, for square and random arrays. The corresponding results as read from figure 12 of Shah & Shaqfeh (Reference Shah and Shaqfeh2015) are approximately 0.21 and 0.25. Once again if we add the finite
$F$
equals 0.2 and 0.3, respectively, for square and random arrays. The corresponding results as read from figure 12 of Shah & Shaqfeh (Reference Shah and Shaqfeh2015) are approximately 0.21 and 0.25. Once again if we add the finite
![]() $N$
correction to their random array result, then we obtain an estimate that is approximately 10 % different. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) obtained their results for
$N$
correction to their random array result, then we obtain an estimate that is approximately 10 % different. Shah & Shaqfeh (Reference Shah and Shaqfeh2015) obtained their results for
![]() $Pe=2$
and it is possible that the finite
$Pe=2$
and it is possible that the finite
![]() $Pe$
affects the random array results more than for the square arrays as the concentration wakes in the latter case would be expected to be shielded by the upstream disks.
$Pe$
affects the random array results more than for the square arrays as the concentration wakes in the latter case would be expected to be shielded by the upstream disks.
Apart from the above differences, which are most likely resulting from the finite
![]() $N$
simulations by Shah & Shaqfeh (Reference Shah and Shaqfeh2015), we conclude that (5.4) provides reasonably accurate estimates for
$N$
simulations by Shah & Shaqfeh (Reference Shah and Shaqfeh2015), we conclude that (5.4) provides reasonably accurate estimates for
![]() $Sh$
for most values of
$Sh$
for most values of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $K$
, at small Péclet numbers.
$K$
, at small Péclet numbers.
It may be noted that (5.4) may be expressed alternatively as
![]() $Sh^{-1}=K^{-1}+F$
according to which the overall resistance can be thought of as the sum of the resistances due to finite reaction and diffusion times.
$Sh^{-1}=K^{-1}+F$
according to which the overall resistance can be thought of as the sum of the resistances due to finite reaction and diffusion times.
5.1 Reactive surfaces blocked by inert disks
In a sequel, Shah et al. (Reference Shah, Lin and Shaqfeh2017) examined the inverse problem in which the surface
![]() $X_{3}=0$
consists of a periodic array of non-reactive disks embedded onto an otherwise reactive surface with a first-order kinetics characterized by the rate constant
$X_{3}=0$
consists of a periodic array of non-reactive disks embedded onto an otherwise reactive surface with a first-order kinetics characterized by the rate constant
![]() $k$
. If, once again, we consider the case when
$k$
. If, once again, we consider the case when
![]() $K_{o}$
and
$K_{o}$
and
![]() $\unicode[STIX]{x1D719}$
are
$\unicode[STIX]{x1D719}$
are
![]() $O(1)$
, then the concentration in the inner region is given by
$O(1)$
, then the concentration in the inner region is given by
with
![]() $C^{\ast }$
given by (3.2). The first term inside the square brackets on the right-hand side of the above equation ensures that the concentration gradient component normal to the wall equals
$C^{\ast }$
given by (3.2). The first term inside the square brackets on the right-hand side of the above equation ensures that the concentration gradient component normal to the wall equals
![]() $K_{o}c_{w}$
on the reactive surface. The last term inside the square brackets has an opposite sign compared to that in (3.1) and it ensures that the flux on the inert disk is zero. Since the integral of
$K_{o}c_{w}$
on the reactive surface. The last term inside the square brackets has an opposite sign compared to that in (3.1) and it ensures that the flux on the inert disk is zero. Since the integral of
![]() $C^{\ast }$
over the unit cell is zero, the integral over the reactive surface is just the opposite of the integral over the inert disks. We therefore obtain the following expression for the effective reaction rate:
$C^{\ast }$
over the unit cell is zero, the integral over the reactive surface is just the opposite of the integral over the inert disks. We therefore obtain the following expression for the effective reaction rate:
where
![]() $\unicode[STIX]{x1D719}$
is the area fraction of the inert disks. The above result is equivalent to its Padé approximant
$\unicode[STIX]{x1D719}$
is the area fraction of the inert disks. The above result is equivalent to its Padé approximant
Shah et al. (Reference Shah, Lin and Shaqfeh2017) present their results in terms of the effective Damköhler number normalized by the area fraction of the reactive surface,
![]() $S_{p}\equiv k_{eff}a/(D(1-\unicode[STIX]{x1D719}))$
. Substituting
$S_{p}\equiv k_{eff}a/(D(1-\unicode[STIX]{x1D719}))$
. Substituting
![]() $K=ka/D=\unicode[STIX]{x1D716}K_{o}$
in (5.8) we obtain
$K=ka/D=\unicode[STIX]{x1D716}K_{o}$
in (5.8) we obtain
The above results is exact for small
![]() $K$
up to
$K$
up to
![]() $O(K^{2})$
. Let us examine its behaviour for
$O(K^{2})$
. Let us examine its behaviour for
![]() $K\rightarrow \infty$
and
$K\rightarrow \infty$
and
![]() $\unicode[STIX]{x1D719}\rightarrow 0$
. It satisfies the obvious condition that
$\unicode[STIX]{x1D719}\rightarrow 0$
. It satisfies the obvious condition that
![]() $S_{p}=K$
if
$S_{p}=K$
if
![]() $\unicode[STIX]{x1D719}=0$
for all
$\unicode[STIX]{x1D719}=0$
for all
![]() $K$
. On the other hand,
$K$
. On the other hand,
![]() $S_{p}\rightarrow 1/(\unicode[STIX]{x1D719}F(0))=3\unicode[STIX]{x03C0}/(8\unicode[STIX]{x1D719})$
if
$S_{p}\rightarrow 1/(\unicode[STIX]{x1D719}F(0))=3\unicode[STIX]{x03C0}/(8\unicode[STIX]{x1D719})$
if
![]() $K=\infty$
and
$K=\infty$
and
![]() $\unicode[STIX]{x1D719}\rightarrow 0$
– half the correct asymptote
$\unicode[STIX]{x1D719}\rightarrow 0$
– half the correct asymptote
![]() $S_{p}\rightarrow 3\unicode[STIX]{x03C0}/(4\unicode[STIX]{x1D719})$
(Tio & Sadhal (Reference Tio and Sadhal1991); Shah et al. (Reference Shah, Lin and Shaqfeh2017)). Therefore we expect (5.9) to provide reasonably accurate estimates provided that
$S_{p}\rightarrow 3\unicode[STIX]{x03C0}/(4\unicode[STIX]{x1D719})$
(Tio & Sadhal (Reference Tio and Sadhal1991); Shah et al. (Reference Shah, Lin and Shaqfeh2017)). Therefore we expect (5.9) to provide reasonably accurate estimates provided that
![]() $K$
is not too large and
$K$
is not too large and
![]() $\unicode[STIX]{x1D719}$
is not too small.
$\unicode[STIX]{x1D719}$
is not too small.
Numerical results for
![]() $Pe=0$
are presented in figure 6 of Shah et al. (Reference Shah, Lin and Shaqfeh2017) for
$Pe=0$
are presented in figure 6 of Shah et al. (Reference Shah, Lin and Shaqfeh2017) for
![]() $K=1$
, 10 and 300 and for
$K=1$
, 10 and 300 and for
![]() $\unicode[STIX]{x1D719}=0.05$
, 0.1, 0.2 and 0.3. The results for
$\unicode[STIX]{x1D719}=0.05$
, 0.1, 0.2 and 0.3. The results for
![]() $K=1$
are essentially the same as given by the approximate relation (5.9). The variation in
$K=1$
are essentially the same as given by the approximate relation (5.9). The variation in
![]() $S_{p}$
is rather small for
$S_{p}$
is rather small for
![]() $K=1$
as it varies from 0.97 to 0.89 as
$K=1$
as it varies from 0.97 to 0.89 as
![]() $\unicode[STIX]{x1D719}$
is varied from 0.05 to 0.3. It is interesting to note that at
$\unicode[STIX]{x1D719}$
is varied from 0.05 to 0.3. It is interesting to note that at
![]() $\unicode[STIX]{x1D719}=0.5$
the result
$\unicode[STIX]{x1D719}=0.5$
the result
![]() $S_{p}=0.87$
for the inert disks is the same as for
$S_{p}=0.87$
for the inert disks is the same as for
![]() $Sh$
for the reactive disks so that at least for this case the same effective Damköhler number is obtained whether the disks are reactive or inert. For
$Sh$
for the reactive disks so that at least for this case the same effective Damköhler number is obtained whether the disks are reactive or inert. For
![]() $K=10$
, the approximate relation (5.9) predicts
$K=10$
, the approximate relation (5.9) predicts
![]() $S_{p}$
to vary from 7.6 to 4.5 as
$S_{p}$
to vary from 7.6 to 4.5 as
![]() $\unicode[STIX]{x1D719}$
is varied from 0.05 to 0.3 compared to the respective range from 8.5 to 5 obtained by Shah et al. (Reference Shah, Lin and Shaqfeh2017) indicating that (5.9) may be used to estimate
$\unicode[STIX]{x1D719}$
is varied from 0.05 to 0.3 compared to the respective range from 8.5 to 5 obtained by Shah et al. (Reference Shah, Lin and Shaqfeh2017) indicating that (5.9) may be used to estimate
![]() $S_{p}$
to within approximately 10 % for
$S_{p}$
to within approximately 10 % for
![]() $K\leqslant 10$
.
$K\leqslant 10$
.
Note that (5.9) may be expressed alternatively in terms of resistances due to finite reaction and diffusion times:
![]() $S_{p}^{-1}=K^{-1}+\unicode[STIX]{x1D719}F/(1-\unicode[STIX]{x1D719})$
. The diffusive resistance due to the inert disks is
$S_{p}^{-1}=K^{-1}+\unicode[STIX]{x1D719}F/(1-\unicode[STIX]{x1D719})$
. The diffusive resistance due to the inert disks is
![]() $\unicode[STIX]{x1D719}/(1-\unicode[STIX]{x1D719})$
times that due to the reactive disks.
$\unicode[STIX]{x1D719}/(1-\unicode[STIX]{x1D719})$
times that due to the reactive disks.
6 Steady state current in arrays of surface microelectrodes
A related problem of determining current through a heterogeneous electrode surface consisting of a square array of circular microelectrodes was examined by Lucas et al. (Reference Lucas, Sipcic and Stone1997). The problem formulation is described in detail by Bender & Stone (Reference Bender and Stone1993) in which a species is generated by a first-order reaction in the bulk electrolyte, diffuses through the electrolyte, and releases an electron via a reversible reaction at the electrodes. A suitably defined non-dimensional concentration
![]() $\unicode[STIX]{x1D6F7}$
satisfies
$\unicode[STIX]{x1D6F7}$
satisfies
with the boundary condition
![]() $\unicode[STIX]{x1D6F7}\rightarrow 0$
at infinity and
$\unicode[STIX]{x1D6F7}\rightarrow 0$
at infinity and
at the surface of the circular electrodes of radii unity on the plane
![]() $X_{3}=0$
. On the remaining passive surface at
$X_{3}=0$
. On the remaining passive surface at
![]() $X_{3}=0$
, the flux
$X_{3}=0$
, the flux
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}X_{3}$
equals zero. The quantity of interest is the current density, which can be related to the integral of the species flux over an electrode:
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x2202}X_{3}$
equals zero. The quantity of interest is the current density, which can be related to the integral of the species flux over an electrode:
The constant
![]() $\unicode[STIX]{x1D6FC}^{2}$
in (6.1) is the non-dimensional reaction rate constant for the reaction in the bulk while
$\unicode[STIX]{x1D6FC}^{2}$
in (6.1) is the non-dimensional reaction rate constant for the reaction in the bulk while
![]() $K$
is the constant based on the reactions at the microelectrode surface. Lucas et al. (Reference Lucas, Sipcic and Stone1997) have examined the same set of equations for a periodic array of microelectrodes. They presented results for
$K$
is the constant based on the reactions at the microelectrode surface. Lucas et al. (Reference Lucas, Sipcic and Stone1997) have examined the same set of equations for a periodic array of microelectrodes. They presented results for
![]() $Q$
as a function of
$Q$
as a function of
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $K$
, and the area fraction
$K$
, and the area fraction
![]() $\unicode[STIX]{x1D719}$
of the microelectrodes. In this section we show that their results for small
$\unicode[STIX]{x1D719}$
of the microelectrodes. In this section we show that their results for small
![]() $\unicode[STIX]{x1D6FC}$
can be related to the those obtained in the present study.
$\unicode[STIX]{x1D6FC}$
can be related to the those obtained in the present study.
We consider the case when both
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $K$
are small, with
$K$
are small, with
![]() $K=\unicode[STIX]{x1D6FC}K_{o}$
,
$K=\unicode[STIX]{x1D6FC}K_{o}$
,
![]() $K_{o}$
being
$K_{o}$
being
![]() $O(1)$
. In the outer region, at large distances from the electrodes,
$O(1)$
. In the outer region, at large distances from the electrodes,
![]() $\unicode[STIX]{x1D6F7}$
is given by
$\unicode[STIX]{x1D6F7}$
is given by
with the constant
![]() $\unicode[STIX]{x1D6F7}_{w}$
expanded in the power series:
$\unicode[STIX]{x1D6F7}_{w}$
expanded in the power series:
This outer region solution provides boundary conditions for the inner region expansion as
![]() $X_{3}\rightarrow \infty$
. In the inner region we write
$X_{3}\rightarrow \infty$
. In the inner region we write
where both
![]() $\unicode[STIX]{x1D6F7}^{0}$
and
$\unicode[STIX]{x1D6F7}^{0}$
and
![]() $\unicode[STIX]{x1D6F7}^{1}$
satisfy the Laplace equation, and
$\unicode[STIX]{x1D6F7}^{1}$
satisfy the Laplace equation, and
![]() $\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F7}^{2}=\unicode[STIX]{x1D6F7}^{0}$
. It is easy to show that
$\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F7}^{2}=\unicode[STIX]{x1D6F7}^{0}$
. It is easy to show that
![]() $\unicode[STIX]{x1D6F7}^{0}\equiv \unicode[STIX]{x1D6F7}_{w}^{0}$
and that
$\unicode[STIX]{x1D6F7}^{0}\equiv \unicode[STIX]{x1D6F7}_{w}^{0}$
and that
![]() $\unicode[STIX]{x1D6F7}^{1}$
is the same as that given by (3.2) for
$\unicode[STIX]{x1D6F7}^{1}$
is the same as that given by (3.2) for
![]() $C^{\ast }$
with
$C^{\ast }$
with
![]() $Kc_{w}$
in that equation replaced by
$Kc_{w}$
in that equation replaced by
![]() $K_{o}(\unicode[STIX]{x1D6F7}_{w}^{0}-1)$
. Therefore it can be shown that, as
$K_{o}(\unicode[STIX]{x1D6F7}_{w}^{0}-1)$
. Therefore it can be shown that, as
![]() $X_{3}\rightarrow \infty$
, the inner region solution behaves as
$X_{3}\rightarrow \infty$
, the inner region solution behaves as
which, on comparing with (6.5) for small
![]() $X_{3}$
, leads to
$X_{3}$
, leads to
The integrated flux over an electrode is therefore given by
On substituting
![]() $K=\unicode[STIX]{x1D6FC}K_{o}$
and rearranging the above expression requiring that
$K=\unicode[STIX]{x1D6FC}K_{o}$
and rearranging the above expression requiring that
![]() $Q$
must remain positive for all values of
$Q$
must remain positive for all values of
![]() $K$
yields
$K$
yields
The behaviour for large
![]() $X_{3}$
as given by (6.7) requires that
$X_{3}$
as given by (6.7) requires that
![]() $X_{3}$
be large compared to the unit cell size. The outer region solution given by (6.4) is therefore valid provided that
$X_{3}$
be large compared to the unit cell size. The outer region solution given by (6.4) is therefore valid provided that
![]() $\unicode[STIX]{x1D6FC}^{-1}\gg \unicode[STIX]{x1D719}^{-1/2}$
, or for
$\unicode[STIX]{x1D6FC}^{-1}\gg \unicode[STIX]{x1D719}^{-1/2}$
, or for
![]() $\unicode[STIX]{x1D719}>\unicode[STIX]{x1D6FC}^{2}\gg 1$
. Our analysis is of course valid strictly for
$\unicode[STIX]{x1D719}>\unicode[STIX]{x1D6FC}^{2}\gg 1$
. Our analysis is of course valid strictly for
![]() $\unicode[STIX]{x1D6FC}\ll 1$
but the use of the Padé approximant (6.10) may extend the range of applicability to even the case when
$\unicode[STIX]{x1D6FC}\ll 1$
but the use of the Padé approximant (6.10) may extend the range of applicability to even the case when
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $K$
are not small. Lucas et al. (Reference Lucas, Sipcic and Stone1997) present results for
$K$
are not small. Lucas et al. (Reference Lucas, Sipcic and Stone1997) present results for
![]() $Q$
for several values of
$Q$
for several values of
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $K$
, and
$K$
, and
![]() $\unicode[STIX]{x1D719}$
in their figures 7–9, 11 and 12. Their results are in very good agreement, within 5 %–10 %, with those given by (6.10) as long as
$\unicode[STIX]{x1D719}$
in their figures 7–9, 11 and 12. Their results are in very good agreement, within 5 %–10 %, with those given by (6.10) as long as
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D719}^{1/2}<1$
even for
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D719}^{1/2}<1$
even for
![]() $K=\infty$
. For example, for
$K=\infty$
. For example, for
![]() $\unicode[STIX]{x1D6FC}=0.5$
and
$\unicode[STIX]{x1D6FC}=0.5$
and
![]() $K=\infty$
, equation (6.10) predicts
$K=\infty$
, equation (6.10) predicts
![]() $Q$
equal to 2.73, 3.38 and 4.06 for, respectively,
$Q$
equal to 2.73, 3.38 and 4.06 for, respectively,
![]() $\unicode[STIX]{x1D719}$
equal to 0.5, 0.35 and 0.2. These agree reasonably well with, respectively, 2.8, 3.55 and 4.4 obtained by Lucas et al. (Reference Lucas, Sipcic and Stone1997) for the same conditions. Likewise, for
$\unicode[STIX]{x1D719}$
equal to 0.5, 0.35 and 0.2. These agree reasonably well with, respectively, 2.8, 3.55 and 4.4 obtained by Lucas et al. (Reference Lucas, Sipcic and Stone1997) for the same conditions. Likewise, for
![]() $\unicode[STIX]{x1D6FC}=1$
,
$\unicode[STIX]{x1D6FC}=1$
,
![]() $K=\infty$
and
$K=\infty$
and
![]() $\unicode[STIX]{x1D719}=0.71$
, equation (6.10) predicts
$\unicode[STIX]{x1D719}=0.71$
, equation (6.10) predicts
![]() $Q=4.05$
which compares well with 4.1 obtained by Lucas et al. (Reference Lucas, Sipcic and Stone1997). For
$Q=4.05$
which compares well with 4.1 obtained by Lucas et al. (Reference Lucas, Sipcic and Stone1997). For
![]() $\unicode[STIX]{x1D719}=0.5$
the corresponding values are, respectively, 4.83 and 5.2. Note that for this last case
$\unicode[STIX]{x1D719}=0.5$
the corresponding values are, respectively, 4.83 and 5.2. Note that for this last case
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D719}^{1/2}=1.4$
somewhat higher than the aforementioned restriction. This suggests that (6.10) may also be used for estimating
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D719}^{1/2}=1.4$
somewhat higher than the aforementioned restriction. This suggests that (6.10) may also be used for estimating
![]() $Q$
for random arrays provided that
$Q$
for random arrays provided that
![]() $\unicode[STIX]{x1D719}$
is not too small.
$\unicode[STIX]{x1D719}$
is not too small.
Finally, it should be noted that (6.10) may be expressed alternatively as
![]() $\unicode[STIX]{x03C0}/Q=K^{-1}+F+\unicode[STIX]{x1D719}/\unicode[STIX]{x1D6FC}$
according to which the overall resistance is the sum of resistances due to finite surface reaction, diffusion and bulk reaction times.
$\unicode[STIX]{x03C0}/Q=K^{-1}+F+\unicode[STIX]{x1D719}/\unicode[STIX]{x1D6FC}$
according to which the overall resistance is the sum of resistances due to finite surface reaction, diffusion and bulk reaction times.
7 Conclusion
We have examined three problems involving heterogeneous surfaces. The reaction problems are characterized by
![]() $a/H$
,
$a/H$
,
![]() $ka/D$
,
$ka/D$
,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $Pe$
. Depending on their values there are different possibilities of how the limit
$Pe$
. Depending on their values there are different possibilities of how the limit
![]() $a/H\rightarrow 0$
should be taken to model a given system. The present study is applicable to the reaction rate dominated systems that are relevant to heterogeneous catalysis as properly designed catalyst typically employ minimal amount of catalyst and the trend in catalysis is towards making nanoscale deposition of the catalytic material on passive substrates for which the Péclet number based on the microscale is typically small. We showed that for such systems, the first correction accounting for the finite diffusion time is relatively straightforward as it requires a simple double integration to be carried out over the reactive regions. At higher orders, the concept of a simple effective reaction rate is valid only if
$a/H\rightarrow 0$
should be taken to model a given system. The present study is applicable to the reaction rate dominated systems that are relevant to heterogeneous catalysis as properly designed catalyst typically employ minimal amount of catalyst and the trend in catalysis is towards making nanoscale deposition of the catalytic material on passive substrates for which the Péclet number based on the microscale is typically small. We showed that for such systems, the first correction accounting for the finite diffusion time is relatively straightforward as it requires a simple double integration to be carried out over the reactive regions. At higher orders, the concept of a simple effective reaction rate is valid only if
![]() $a/H$
is small compared to
$a/H$
is small compared to
![]() $ka/D$
. We also found that the Padé approximants based on this asymptotic analysis provides estimates that are accurate over surprisingly large range of values of
$ka/D$
. We also found that the Padé approximants based on this asymptotic analysis provides estimates that are accurate over surprisingly large range of values of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $ka/D$
. Although the analysis was carried out for the special case of a first-order reaction kinetics, its extension to more complex kinetics is relatively straightforward as only the linearized rate expression around
$ka/D$
. Although the analysis was carried out for the special case of a first-order reaction kinetics, its extension to more complex kinetics is relatively straightforward as only the linearized rate expression around
![]() $c_{w}$
is necessary for evaluating the leading effect of the finite diffusion time. Finally, we also derived an expression for the current density for an array of microelectrodes for the case when the bulk reaction rate constant
$c_{w}$
is necessary for evaluating the leading effect of the finite diffusion time. Finally, we also derived an expression for the current density for an array of microelectrodes for the case when the bulk reaction rate constant
![]() $\unicode[STIX]{x1D6FC}^{2}$
is small and showed that the Padé approximant of this also provides estimates that are accurate over wide ranges of values of the parameters.
$\unicode[STIX]{x1D6FC}^{2}$
is small and showed that the Padé approximant of this also provides estimates that are accurate over wide ranges of values of the parameters.
Appendix. Evaluation of the derivatives of the periodic Green’s function
The derivatives of the Green’s function were evaluated using the expressions given in Sangani & Behl (Reference Sangani and Behl1989). Note that
![]() $G=\unicode[STIX]{x1D713}_{1}-(2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D70F})|X_{3}|$
. Sangani & Behl (Reference Sangani and Behl1989) present three methods for evaluating the derivatives of
$G=\unicode[STIX]{x1D713}_{1}-(2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D70F})|X_{3}|$
. Sangani & Behl (Reference Sangani and Behl1989) present three methods for evaluating the derivatives of
![]() $\unicode[STIX]{x1D713}_{1}$
, of which the method 2 based on the Ewald’s technique is suitable for evaluating the lower-order, and the method 3 for the higher-order derivatives. The method 1, which is suitable for larger values of
$\unicode[STIX]{x1D713}_{1}$
, of which the method 2 based on the Ewald’s technique is suitable for evaluating the lower-order, and the method 3 for the higher-order derivatives. The method 1, which is suitable for larger values of
![]() $X_{3}$
, is not needed in the present study. The expressions given by Sangani & Behl (Reference Sangani and Behl1989) contained errors in their equations (20), (25) and (28). These are corrected here. The correct expression for
$X_{3}$
, is not needed in the present study. The expressions given by Sangani & Behl (Reference Sangani and Behl1989) contained errors in their equations (20), (25) and (28). These are corrected here. The correct expression for
![]() $\unicode[STIX]{x1D713}_{1}$
using the Ewald’s technique is
$\unicode[STIX]{x1D713}_{1}$
using the Ewald’s technique is
with
![]() $C_{I}$
–
$C_{I}$
–
![]() $C_{III}$
defined as in Sangani & Behl (Reference Sangani and Behl1989). Note that the sign in the front of
$C_{III}$
defined as in Sangani & Behl (Reference Sangani and Behl1989). Note that the sign in the front of
![]() $C_{III}$
was incorrect in Sangani & Behl (Reference Sangani and Behl1989). The derivatives at
$C_{III}$
was incorrect in Sangani & Behl (Reference Sangani and Behl1989). The derivatives at
![]() $\boldsymbol{X}=0$
are evaluated by the following expressions according to the method 2:
$\boldsymbol{X}=0$
are evaluated by the following expressions according to the method 2:
Here,
![]() $\boldsymbol{X}_{\boldsymbol{L}}$
and
$\boldsymbol{X}_{\boldsymbol{L}}$
and
![]() $\boldsymbol{q}_{\boldsymbol{L}}$
are, respectively, the vectors in the real and reciprocal space,
$\boldsymbol{q}_{\boldsymbol{L}}$
are, respectively, the vectors in the real and reciprocal space,
![]() $\unicode[STIX]{x1D70C}$
is an arbitrary constant whose value may be chosen such that the sums in both the real and reciprocal space converge rapidly (
$\unicode[STIX]{x1D70C}$
is an arbitrary constant whose value may be chosen such that the sums in both the real and reciprocal space converge rapidly (
![]() $\unicode[STIX]{x1D70C}=h^{2}$
was chosen in the present study), and
$\unicode[STIX]{x1D70C}=h^{2}$
was chosen in the present study), and
![]() $\unicode[STIX]{x1D6F7}$
is the incomplete Gamma function. Since we are interested in only the regular part of the derivatives of
$\unicode[STIX]{x1D6F7}$
is the incomplete Gamma function. Since we are interested in only the regular part of the derivatives of
![]() $G^{r}$
at origin, the incomplete Gamma function should be evaluated by its regular part at origin as given by
$G^{r}$
at origin, the incomplete Gamma function should be evaluated by its regular part at origin as given by
The above equations are specialized form of the more general expressions given in Sangani & Behl (Reference Sangani and Behl1989) and correct two additional errors in that study. (
![]() $\unicode[STIX]{x1D6F7}_{n-s-m-1/2}$
in their (25) should be
$\unicode[STIX]{x1D6F7}_{n-s-m-1/2}$
in their (25) should be
![]() $\unicode[STIX]{x1D6F7}_{n-s-m+1/2}$
and the factor
$\unicode[STIX]{x1D6F7}_{n-s-m+1/2}$
and the factor
![]() $p-2m-1/2$
in the denominator in their (28) should be replaced by
$p-2m-1/2$
in the denominator in their (28) should be replaced by
![]() $p-m+1/2$
. Note that all the computational results reported in Sangani & Behl (Reference Sangani and Behl1989) were free of these errors that resulted only during the preparation of the manuscript of that study.)
$p-m+1/2$
. Note that all the computational results reported in Sangani & Behl (Reference Sangani and Behl1989) were free of these errors that resulted only during the preparation of the manuscript of that study.)
For higher-order derivatives, the method 3 can be used, according to which
The above sum is convergent for
![]() $n\geqslant 2$
. We used the method 2 for
$n\geqslant 2$
. We used the method 2 for
![]() $n\leqslant 6$
and the method 3 for larger
$n\leqslant 6$
and the method 3 for larger
![]() $n$
although, for verification purposes, both methods were used for
$n$
although, for verification purposes, both methods were used for
![]() $n=4$
and
$n=4$
and
![]() $n=6$
to check that the derivatives evaluated by the two methods method agree with each other.
$n=6$
to check that the derivatives evaluated by the two methods method agree with each other.