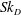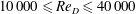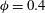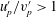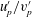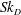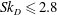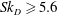1 Introduction
Particle-laden turbulent jets are an important class of flow that are utilised in a broad range of scientific and industrial applications, most notably in the combustion of solid fuels and, more recently, in concentrated solar thermal reactors (Steinfeld Reference Steinfeld2005). In these flows, the distributions of particle velocity and concentration (number density) are important as they can significantly affect the instantaneous flow field and chemistry, which in turn influence thermal performance and emissions (Nathan et al. Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006). A wide range of investigations have been performed to identify the important roles of key dimensionless parameters such as mass loading (Modarress, Tan & Elghobashi Reference Modarress, Tan and Elghobashi1984a ; Ferrand, Bazile & Borée Reference Ferrand, Bazile and Borée2001), particle-to-jet diameter (Tsuji et al. Reference Tsuji, Morikawa, Tanaka, Karimine and Nishida1988; Sheen, Jou & Lee Reference Sheen, Jou and Lee1994) and Stokes number (Hardalupas, Taylor & Whitelaw Reference Hardalupas, Taylor and Whitelaw1989; Prevost et al. Reference Prevost, Boree, Nuglisch and Charnay1996) in these flows. Nevertheless, the detailed understanding of these flows is limited by a lack of systematic and detailed measurements in well-characterised flows that report the inflow conditions together with both the particle velocity and concentration. This paper aims to meet this need through a detailed assessment of the influence of Stokes number on the velocity and concentration distributions in a well-characterised jet in a co-flow.
From previous studies of two-phase flows it is now well known that particle–fluid interactions are characterised by the dimensionless Stokes number, defined as the ratio of the particle-to-eddy response times (Eaton & Fessler Reference Eaton and Fessler1994; Balachandar & Eaton Reference Balachandar and Eaton2010; Monchaux, Bourgoin & Cartellier Reference Monchaux, Bourgoin and Cartellier2012). While a range of eddy response times exist within any turbulent flow, in particle-laden turbulent jets it is convenient to define the exit Stokes number using the large eddy time scale, that is,
where
![]() $\unicode[STIX]{x1D70C}_{p}$
is the particle density,
$\unicode[STIX]{x1D70C}_{p}$
is the particle density,
![]() $\overline{d}_{p}$
is the mean (or nominal) particle diameter,
$\overline{d}_{p}$
is the mean (or nominal) particle diameter,
![]() $U_{g,b}$
is the gas-phase bulk-mean velocity,
$U_{g,b}$
is the gas-phase bulk-mean velocity,
![]() $\unicode[STIX]{x1D707}$
is the fluid dynamic viscosity and
$\unicode[STIX]{x1D707}$
is the fluid dynamic viscosity and
![]() $D$
is the pipe diameter. Despite the importance of the Stokes number there is currently a paucity of systematic and reliable data of the influence of this parameter on the flow-field distribution in turbulent, particle-laden jets, especially in the two-way coupling regime (Elghobashi Reference Elghobashi2006) where the particle mass loading is sufficiently high such that the particle phase significantly affects the gas phase. This is attributable to the combination of the squared relationship between the Stokes number and particle size, which limits the range of Stokes number that can feasibly be investigated, and the significantly greater challenge of performing measurements in multiphase flows than their single-phase counterparts, particularly in the two-way coupling regime. To the authors’ knowledge, apart from our previously published data (Lau & Nathan Reference Lau and Nathan2014), there are only a handful of experimental measurements of turbulent jets that have utilised a mono-disperse distribution of particle sizes (Modarress et al.
Reference Modarress, Tan and Elghobashi1984a
; Modarress, Wuerer & Elghobashi Reference Modarress, Wuerer and Elghobashi1984b
; Mostafa et al.
Reference Mostafa, Mongia, McDonell and Samuelsen1989), and of these none of them investigated the effect of Stokes number on the flow (see table 1). In another study, Prevost et al. (Reference Prevost, Boree, Nuglisch and Charnay1996) attempted to investigate the effect of Stokes number indirectly by binning the measurements made in a poly-disperse particle-laden jet into different particle size ranges. While this has provided some useful insights, the method of binning is not truly quantitative, partly because the probe volume is typically larger than the particle size so that it is impossible to isolate the sizes of single particles in the measurement volume and partly because of the relatively large uncertainty in the measurement of particle sizes. Furthermore, the binning of data into particle size ranges does not isolate the effect of Stokes number on the flow because the poly-disperse particle phase will have an integrated effect on the gas phase which cannot be decoupled from the measurements by data processing.
$D$
is the pipe diameter. Despite the importance of the Stokes number there is currently a paucity of systematic and reliable data of the influence of this parameter on the flow-field distribution in turbulent, particle-laden jets, especially in the two-way coupling regime (Elghobashi Reference Elghobashi2006) where the particle mass loading is sufficiently high such that the particle phase significantly affects the gas phase. This is attributable to the combination of the squared relationship between the Stokes number and particle size, which limits the range of Stokes number that can feasibly be investigated, and the significantly greater challenge of performing measurements in multiphase flows than their single-phase counterparts, particularly in the two-way coupling regime. To the authors’ knowledge, apart from our previously published data (Lau & Nathan Reference Lau and Nathan2014), there are only a handful of experimental measurements of turbulent jets that have utilised a mono-disperse distribution of particle sizes (Modarress et al.
Reference Modarress, Tan and Elghobashi1984a
; Modarress, Wuerer & Elghobashi Reference Modarress, Wuerer and Elghobashi1984b
; Mostafa et al.
Reference Mostafa, Mongia, McDonell and Samuelsen1989), and of these none of them investigated the effect of Stokes number on the flow (see table 1). In another study, Prevost et al. (Reference Prevost, Boree, Nuglisch and Charnay1996) attempted to investigate the effect of Stokes number indirectly by binning the measurements made in a poly-disperse particle-laden jet into different particle size ranges. While this has provided some useful insights, the method of binning is not truly quantitative, partly because the probe volume is typically larger than the particle size so that it is impossible to isolate the sizes of single particles in the measurement volume and partly because of the relatively large uncertainty in the measurement of particle sizes. Furthermore, the binning of data into particle size ranges does not isolate the effect of Stokes number on the flow because the poly-disperse particle phase will have an integrated effect on the gas phase which cannot be decoupled from the measurements by data processing.
Table 1. Summary of previous experimental measurements of particle-laden turbulent jets issuing from a long pipe. Here
![]() $U$
is velocity,
$U$
is velocity,
![]() $\unicode[STIX]{x1D6E9}$
is particle concentration and
$\unicode[STIX]{x1D6E9}$
is particle concentration and
![]() $M$
is the mass flux. The subscripts
$M$
is the mass flux. The subscripts
![]() $0$
,
$0$
,
![]() $g$
and
$g$
and
![]() $p$
denote the single, gas and particle phases, respectively, while the subscript
$p$
denote the single, gas and particle phases, respectively, while the subscript
![]() $\infty$
denotes the co-flow. Values marked with an asterisk denote values that were calculated or inferred indirectly from the literature. In instances where the centreline velocity (
$\infty$
denotes the co-flow. Values marked with an asterisk denote values that were calculated or inferred indirectly from the literature. In instances where the centreline velocity (
![]() $U_{c}$
) was provided in lieu of the bulk velocity (
$U_{c}$
) was provided in lieu of the bulk velocity (
![]() $U_{b}$
), it was assumed that
$U_{b}$
), it was assumed that
![]() $U_{c}/U_{b}=1.2$
. Abbreviations: OF
$U_{c}/U_{b}=1.2$
. Abbreviations: OF
![]() $=$
Optical Fibre, LDA
$=$
Optical Fibre, LDA
![]() $=$
Laser Doppler Anemometry, PDPA
$=$
Laser Doppler Anemometry, PDPA
![]() $=$
Phase Doppler Particle Anemometry, IS
$=$
Phase Doppler Particle Anemometry, IS
![]() $=$
Isokinetic Sampling, PIV
$=$
Isokinetic Sampling, PIV
![]() $=$
Particle Image Velocimetry, PN
$=$
Particle Image Velocimetry, PN
![]() $=$
Planar Nephelometry and N/P
$=$
Planar Nephelometry and N/P
![]() $=$
not provided.
$=$
not provided.

An additional limitation of the available data is that all previous measurements, summarised in table 1, have been performed in flows for which
![]() $Sk_{D}\gtrsim O(10)$
. This is a significant limitation because no data are available in either the regime for which the Stokes number is less than, or of the order of, unity. Not only does the Stokes number in these regimes have a strong influence on the exit distribution of particles in a jet from a long pipe (Lau & Nathan Reference Lau and Nathan2014), but there is also growing evidence of its influence on particle clustering. The pioneering work of Eaton and co-workers (Fessler, Kulick & Eaton Reference Fessler, Kulick and Eaton1994; Rouson & Eaton Reference Rouson and Eaton2001), and more recently of Lau & Nathan (Reference Lau and Nathan0000), found that in free-shear flows particles preferentially cluster for Stokes numbers of the order of unity. Furthermore, these lower Stokes numbers jets more closely match the conditions found in industrial pulverised coal burners (Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006; Lau & Nathan Reference Lau and Nathan2014), which highlights the need for an investigation of particle-laden jets across a range of Stokes numbers which include
$Sk_{D}\gtrsim O(10)$
. This is a significant limitation because no data are available in either the regime for which the Stokes number is less than, or of the order of, unity. Not only does the Stokes number in these regimes have a strong influence on the exit distribution of particles in a jet from a long pipe (Lau & Nathan Reference Lau and Nathan2014), but there is also growing evidence of its influence on particle clustering. The pioneering work of Eaton and co-workers (Fessler, Kulick & Eaton Reference Fessler, Kulick and Eaton1994; Rouson & Eaton Reference Rouson and Eaton2001), and more recently of Lau & Nathan (Reference Lau and Nathan0000), found that in free-shear flows particles preferentially cluster for Stokes numbers of the order of unity. Furthermore, these lower Stokes numbers jets more closely match the conditions found in industrial pulverised coal burners (Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006; Lau & Nathan Reference Lau and Nathan2014), which highlights the need for an investigation of particle-laden jets across a range of Stokes numbers which include
![]() $Sk_{D}\approx O(1)$
.
$Sk_{D}\approx O(1)$
.
Previous numerical investigations of particle distributions in two-phase turbulent flows using direct numerical simulations (DNS) are also of limited value in providing quantitative data of the influence of Stokes number in turbulent jets, particularly in the two-way coupling regime (Fan et al. Reference Fan, Luo, Ha and Cen2004; Yan et al. Reference Yan, Luo, Fan, Tsuji and Cen2008; Picano et al. Reference Picano, Sardina, Gualtieri and Casciola2010). This is due to the high computational expense of resolving both high particle loadings and large computational domains, even before addressing the further challenge of fully resolving the flow around the particles, which, if adopted, would significantly increasing the computational requirement. Therefore, for the foreseeable future, simulations of particle-laden turbulent flows in the two-way coupling regime where particle–fluid interactions are significant will require the utilisation of two-phase models (Crowe, Troutt & Chung Reference Crowe, Troutt and Chung1996; Loth Reference Loth2000; Mashayek & Pandya Reference Mashayek and Pandya2003; Balachandar & Eaton Reference Balachandar and Eaton2010). Hence reliable, comprehensive and systematic datasets are needed for the development and validation of these two-phase models.
For the reasons described above, this study, of which the present paper is a substantial extension of work we have previous published (Lau & Nathan Reference Lau and Nathan2014), aims to systematically investigate the influence of the Stokes number on the distributions of particle velocity and concentration in a well-characterised turbulent, particle-laden jet under conditions suitable for model development and validation, spanning the three Stokes number regimes,
![]() $Sk_{D}<1$
,
$Sk_{D}<1$
,
![]() $Sk_{D}\approx 1$
and
$Sk_{D}\approx 1$
and
![]() $Sk_{D}>1$
. More specifically, the current study aims to characterise the influence of Stokes number on the distributions of particle velocity and number density within the first 30 diameters of a turbulent round jet issuing from a long, round pipe into a weak co-flow over the range
$Sk_{D}>1$
. More specifically, the current study aims to characterise the influence of Stokes number on the distributions of particle velocity and number density within the first 30 diameters of a turbulent round jet issuing from a long, round pipe into a weak co-flow over the range
![]() $0.3\leqslant Sk_{D}\leqslant 22.4$
utilising particles with a narrow distribution of diameters.
$0.3\leqslant Sk_{D}\leqslant 22.4$
utilising particles with a narrow distribution of diameters.

Figure 1. Schematic diagram of the experimental arrangement. All diameters refer to internal diameters.
2 Experimental arrangement
The experiment consisted of a particle-laden turbulent jet issuing from a long, round pipe into a low velocity co-flow, as shown in figure 1. The pipe was a Swagelok® stainless steel tube of inner diameter
![]() $D=12.7$
mm and a length of
$D=12.7$
mm and a length of
![]() $L_{pipe}=2080$
mm, resulting in a pipe length-to-diameter ratio of
$L_{pipe}=2080$
mm, resulting in a pipe length-to-diameter ratio of
![]() $L_{pipe}/D=163.8$
. This was found to be sufficiently high to result in conditions that approach a fully developed two-phase flow at the pipe exit (Lau & Nathan Reference Lau and Nathan2014). The outer diameter of the pipe was 15.88 mm. The pipe was mounted concentrically within an annulus of inner diameter
$L_{pipe}/D=163.8$
. This was found to be sufficiently high to result in conditions that approach a fully developed two-phase flow at the pipe exit (Lau & Nathan Reference Lau and Nathan2014). The outer diameter of the pipe was 15.88 mm. The pipe was mounted concentrically within an annulus of inner diameter
![]() $D_{ann}=69$
mm. Both the pipe and annulus were mounted vertically within an open-loop wind tunnel with a working cross-section of
$D_{ann}=69$
mm. Both the pipe and annulus were mounted vertically within an open-loop wind tunnel with a working cross-section of
![]() $650\times 650$
mm such that the pipe axis was equidistant from all four side walls of the tunnel. At the furthest downstream measurement location,
$650\times 650$
mm such that the pipe axis was equidistant from all four side walls of the tunnel. At the furthest downstream measurement location,
![]() $x/D=31.5$
, where
$x/D=31.5$
, where
![]() $x$
is the axial distance from the pipe exit, the width of the jet was approximately 30 mm (measured from the jet axis). Therefore, the edge of the jet within the measurement region was at least
$x$
is the axial distance from the pipe exit, the width of the jet was approximately 30 mm (measured from the jet axis). Therefore, the edge of the jet within the measurement region was at least
![]() $23D$
from the tunnel side walls, ensuring that boundary effects were negligible. A compressed air reservoir, operating at a constant pressure of 200 kPa (gauge) provided the unladen gas flow to the annulus and the central pipe. The gas flow was measured using two separate flowmeters and subsequently corrected to account for differences in air densities within the flowmeters and within the working section, the latter of which was at approximately atmospheric pressure. The velocity of the annular flow was matched to the wind tunnel velocity to within
$23D$
from the tunnel side walls, ensuring that boundary effects were negligible. A compressed air reservoir, operating at a constant pressure of 200 kPa (gauge) provided the unladen gas flow to the annulus and the central pipe. The gas flow was measured using two separate flowmeters and subsequently corrected to account for differences in air densities within the flowmeters and within the working section, the latter of which was at approximately atmospheric pressure. The velocity of the annular flow was matched to the wind tunnel velocity to within
![]() $\pm 5\,\%$
, resulting in a uniform co-flow. The annulus allowed the seeding of a limited region of the co-flow around the jet, thereby reducing the effects of light attenuation and signal trapping while also reducing the risk of wall contamination. Seeding of the co-flow was only performed for the single-phase measurements (§ 4). The jet-to-co-flow velocity was fixed at
$\pm 5\,\%$
, resulting in a uniform co-flow. The annulus allowed the seeding of a limited region of the co-flow around the jet, thereby reducing the effects of light attenuation and signal trapping while also reducing the risk of wall contamination. Seeding of the co-flow was only performed for the single-phase measurements (§ 4). The jet-to-co-flow velocity was fixed at
![]() $\unicode[STIX]{x1D706}=12$
. The influence of the co-flow on the jet at any particular axial location can be characterised using the momentum radius, here defined as
$\unicode[STIX]{x1D706}=12$
. The influence of the co-flow on the jet at any particular axial location can be characterised using the momentum radius, here defined as
where
is the excess momentum flux at the jet exit,
![]() $\unicode[STIX]{x1D70C}_{j}$
is the density of the two-phase jet,
$\unicode[STIX]{x1D70C}_{j}$
is the density of the two-phase jet,
![]() $\unicode[STIX]{x1D70C}_{g}$
is the fluid density,
$\unicode[STIX]{x1D70C}_{g}$
is the fluid density,
![]() $U_{g,e}$
is the fluid velocity at the pipe exit,
$U_{g,e}$
is the fluid velocity at the pipe exit,
![]() $U_{\infty }$
is the co-flow velocity and
$U_{\infty }$
is the co-flow velocity and
![]() $r$
is the radial distance from the jet axis. Here we take the opportunity to note that, throughout this paper, subscripts 0,
$r$
is the radial distance from the jet axis. Here we take the opportunity to note that, throughout this paper, subscripts 0,
![]() $g$
and
$g$
and
![]() $p$
refer to the single, gas and particle phases, respectively, as summarised in table 2 along with other commonly used subscripts in the current paper. For low values of
$p$
refer to the single, gas and particle phases, respectively, as summarised in table 2 along with other commonly used subscripts in the current paper. For low values of
![]() $x/\unicode[STIX]{x1D703}\lesssim x^{\ast }$
, where
$x/\unicode[STIX]{x1D703}\lesssim x^{\ast }$
, where
![]() $x^{\ast }$
is some threshold value, the co-flowing jet approaches that of an unconfined jet (Pitts Reference Pitts1991a
; Sautet & Stepowski Reference Sautet and Stepowski1995). From previous measurements made in co-flowing single-phase jets it can be inferred that
$x^{\ast }$
is some threshold value, the co-flowing jet approaches that of an unconfined jet (Pitts Reference Pitts1991a
; Sautet & Stepowski Reference Sautet and Stepowski1995). From previous measurements made in co-flowing single-phase jets it can be inferred that
![]() $x^{\ast }\approx 10$
(Nickels & Perry Reference Nickels and Perry1996; Davidson & Wang Reference Davidson and Wang2002), while Sautet & Stepowski (Reference Sautet and Stepowski1995) suggest
$x^{\ast }\approx 10$
(Nickels & Perry Reference Nickels and Perry1996; Davidson & Wang Reference Davidson and Wang2002), while Sautet & Stepowski (Reference Sautet and Stepowski1995) suggest
![]() $x^{\ast }\approx 3.95$
. Utilising the lower of these values, this suggests that the current jet approximates a free jet for
$x^{\ast }\approx 3.95$
. Utilising the lower of these values, this suggests that the current jet approximates a free jet for
![]() $x/D\lesssim x^{\ast }\unicode[STIX]{x1D703}/D\approx 49$
, i.e. the effect of the co-flow on the jet is expected to be negligible throughout the measurement region.
$x/D\lesssim x^{\ast }\unicode[STIX]{x1D703}/D\approx 49$
, i.e. the effect of the co-flow on the jet is expected to be negligible throughout the measurement region.
Table 2. Summary of subscripts used in the current study.


Figure 2. The probability density function (p.d.f.) of particle size distribution.
The pipe was seeded with spherical, polymer particles of density
![]() $\unicode[STIX]{x1D70C}_{p}=1200~\text{kg}~\text{m}^{-3}$
and diameter
$\unicode[STIX]{x1D70C}_{p}=1200~\text{kg}~\text{m}^{-3}$
and diameter
![]() $d_{p}=10\pm 1~\unicode[STIX]{x03BC}\text{m}$
,
$d_{p}=10\pm 1~\unicode[STIX]{x03BC}\text{m}$
,
![]() $20\pm 1~\unicode[STIX]{x03BC}\text{m}$
and
$20\pm 1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $40\pm 2~\unicode[STIX]{x03BC}\text{m}$
. The size distribution of the particles is shown in figure 2. The use of particles with a narrow size distribution resulted in a truly mono-disperse particle-laden flow. The exit Stokes number was varied within the range
$40\pm 2~\unicode[STIX]{x03BC}\text{m}$
. The size distribution of the particles is shown in figure 2. The use of particles with a narrow size distribution resulted in a truly mono-disperse particle-laden flow. The exit Stokes number was varied within the range
![]() $0.3\leqslant Sk_{D}\leqslant 22.4$
by changing the flow velocity and/or the particle diameter (summarised in table 3). It should be noted that the cases
$0.3\leqslant Sk_{D}\leqslant 22.4$
by changing the flow velocity and/or the particle diameter (summarised in table 3). It should be noted that the cases
![]() $Sk_{D}=0.3$
, 1.4 and 11.2, which we previously reported (Lau & Nathan Reference Lau and Nathan2014), were repeated in the current experiments, and therefore the current measurements are completely new.
$Sk_{D}=0.3$
, 1.4 and 11.2, which we previously reported (Lau & Nathan Reference Lau and Nathan2014), were repeated in the current experiments, and therefore the current measurements are completely new.
The resultant Reynolds number, defined as
was in the range
![]() $10\,000\leqslant Re_{D}\leqslant 40\,000$
. In this range, the effect of Reynolds number on the flow is expected to be small (Popper, Abuaf & Hetsroni Reference Popper, Abuaf and Hetsroni1974). The gas-phase bulk velocity,
$10\,000\leqslant Re_{D}\leqslant 40\,000$
. In this range, the effect of Reynolds number on the flow is expected to be small (Popper, Abuaf & Hetsroni Reference Popper, Abuaf and Hetsroni1974). The gas-phase bulk velocity,
![]() $U_{g,b}$
, was calculated using the pipe diameter and the gas flow rate (measured using flowmeters, as noted above). The air temperature at the inlet of the wind tunnel was measured as
$U_{g,b}$
, was calculated using the pipe diameter and the gas flow rate (measured using flowmeters, as noted above). The air temperature at the inlet of the wind tunnel was measured as
![]() $294\pm 1$
K.
$294\pm 1$
K.
The particle mass loading, defined as the ratio of the particle-to-gas mass flow rate was fixed at
![]() $\unicode[STIX]{x1D719}=0.4$
. This is sufficiently high to result in significant particle–fluid interactions, i.e. the flow was in the two-way coupling regime (Elghobashi Reference Elghobashi2006). The use of a constant mass loading and three different particle diameters resulted in three values of bulk particle number density,
$\unicode[STIX]{x1D719}=0.4$
. This is sufficiently high to result in significant particle–fluid interactions, i.e. the flow was in the two-way coupling regime (Elghobashi Reference Elghobashi2006). The use of a constant mass loading and three different particle diameters resulted in three values of bulk particle number density,
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }$
, as shown in table 3. The approach of varying
$\unicode[STIX]{x1D6E9}_{b}^{\ast }$
, as shown in table 3. The approach of varying
![]() $Sk_{D}$
at constant mass loading rather than constant
$Sk_{D}$
at constant mass loading rather than constant
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }$
was chosen because the available evidence suggests that, in the two-way coupling regime, a two-phase flow is more significantly influenced by momentum transfer between the two phases rather than inter-particle effects such as particle-to-particle collisions (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1989; Elghobashi Reference Elghobashi2006; Balachandar & Eaton Reference Balachandar and Eaton2010). In addition, the data reported in the appendix of Lau & Nathan (Reference Lau and Nathan2014) suggests that
$\unicode[STIX]{x1D6E9}_{b}^{\ast }$
was chosen because the available evidence suggests that, in the two-way coupling regime, a two-phase flow is more significantly influenced by momentum transfer between the two phases rather than inter-particle effects such as particle-to-particle collisions (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1989; Elghobashi Reference Elghobashi2006; Balachandar & Eaton Reference Balachandar and Eaton2010). In addition, the data reported in the appendix of Lau & Nathan (Reference Lau and Nathan2014) suggests that
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }$
has little influence on the exit distributions from a pipe. Furthermore, a constant value of
$\unicode[STIX]{x1D6E9}_{b}^{\ast }$
has little influence on the exit distributions from a pipe. Furthermore, a constant value of
![]() $\unicode[STIX]{x1D719}$
also maintains a fixed value of mean particle-to-particle spacing relative to the particle diameter.
$\unicode[STIX]{x1D719}$
also maintains a fixed value of mean particle-to-particle spacing relative to the particle diameter.
Table 3. Summary of experimental parameters. The pipe diameter was fixed at
![]() $D=12.7$
mm and the particle mass loading was fixed at
$D=12.7$
mm and the particle mass loading was fixed at
![]() $\unicode[STIX]{x1D719}=0.4$
.
$\unicode[STIX]{x1D719}=0.4$
.

Table 4. Details of the imaging configuration. Axial imaging extent measured from jet exit, while length components are radial
![]() $\times$
axial. The light sheet thickness was fixed at
$\times$
axial. The light sheet thickness was fixed at
![]() ${\approx}350~\unicode[STIX]{x03BC}\text{m}$
. The abbreviation IW stands for ‘interrogation window’.
${\approx}350~\unicode[STIX]{x03BC}\text{m}$
. The abbreviation IW stands for ‘interrogation window’.

The instantaneous particle velocity and concentration were simultaneously measured using digital particle image velocimetry (PIV) and planar nephelometry (PN), respectively. Planar nephelometry is a laser diagnostic technique that infers particle concentration (number density) from the intensity of the Mie scattering signal from the particles. This technique does not necessarily rely on the resolution of individual particles, and is therefore useful for the measurement of particle concentration in densely seeded flows. The source of illumination was a frequency-doubled, pulsed Nd:YAG laser, operating at a fixed frequency of 10 Hz and a wavelength of 532 nm. The maximum laser power was approximately 300 mJ per pulse, although the actual laser power used during the experiments was
![]() ${\approx}100$
mJ per pulse. The laser beam was shaped into a light sheet of thickness
${\approx}100$
mJ per pulse. The laser beam was shaped into a light sheet of thickness
![]() ${\approx}350\pm 50~\unicode[STIX]{x03BC}\text{m}$
which illuminated the entire measurement volume. Three Kodak Megaplus cameras were used to record images of three different regions of the jet, as summarised in table 4 (see also figure 1). A fourth Kodak Megaplus camera was used to record the instantaneous beam profile. For each experimental run, ‘background’ measurements were also made with the flow turned off. This allowed corrections for background and beam profile, as well as laser attenuation on a shot-by-shot basis using a previously developed method (Kalt & Nathan Reference Kalt and Nathan2007; Cheong, Birzer & Lau Reference Cheong, Birzer and Lau2015).
${\approx}350\pm 50~\unicode[STIX]{x03BC}\text{m}$
which illuminated the entire measurement volume. Three Kodak Megaplus cameras were used to record images of three different regions of the jet, as summarised in table 4 (see also figure 1). A fourth Kodak Megaplus camera was used to record the instantaneous beam profile. For each experimental run, ‘background’ measurements were also made with the flow turned off. This allowed corrections for background and beam profile, as well as laser attenuation on a shot-by-shot basis using a previously developed method (Kalt & Nathan Reference Kalt and Nathan2007; Cheong, Birzer & Lau Reference Cheong, Birzer and Lau2015).
2.1 PIV error analysis
The random errors associated with the PIV measurements were estimated by assuming that for any velocity component
![]() $U$
, the measured value
$U$
, the measured value
![]() $U_{m}$
is
$U_{m}$
is
where
![]() $\overline{U}$
and
$\overline{U}$
and
![]() $u$
are the actual mean and fluctuating components of
$u$
are the actual mean and fluctuating components of
![]() $U$
,
$U$
,
![]() $\unicode[STIX]{x1D716}$
is the measurement error and
$\unicode[STIX]{x1D716}$
is the measurement error and
![]() $u_{m}$
is the measured fluctuating component of
$u_{m}$
is the measured fluctuating component of
![]() $U$
. If the ensembles
$U$
. If the ensembles
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D716}$
are normally distributed, then utilising basic statistical analysis the random error in the mean measurement of
$\unicode[STIX]{x1D716}$
are normally distributed, then utilising basic statistical analysis the random error in the mean measurement of
![]() $U$
is
$U$
is
where
![]() $u^{\prime }=\langle u^{2}\rangle ^{0.5}$
,
$u^{\prime }=\langle u^{2}\rangle ^{0.5}$
,
![]() $\unicode[STIX]{x1D716}^{\prime }=\langle \unicode[STIX]{x1D716}^{2}\rangle ^{0.5}$
, the angled brackets
$\unicode[STIX]{x1D716}^{\prime }=\langle \unicode[STIX]{x1D716}^{2}\rangle ^{0.5}$
, the angled brackets
![]() $\langle ~\rangle$
denote an ensemble-averaging procedure and
$\langle ~\rangle$
denote an ensemble-averaging procedure and
![]() $N$
is the number of samples. Similarly, the error in the fluctuating (or root-mean-square, r.m.s.) component of velocity is
$N$
is the number of samples. Similarly, the error in the fluctuating (or root-mean-square, r.m.s.) component of velocity is
The random source of error was assumed to be that of the subpixel accuracy of the PIV processing algorithm, which is typically the dominant source of random error in PIV measurements (Raffel et al.
Reference Raffel, Willert, Wereley and Kompenhans2007). The subpixel accuracy was estimated by assessing the probability density functions (p.d.f.s) of
![]() $u_{m}$
(in both axial and radial directions) at different flow rates (not shown here). In most cases, the p.d.f.s of
$u_{m}$
(in both axial and radial directions) at different flow rates (not shown here). In most cases, the p.d.f.s of
![]() $u_{m}$
display two peaks, one corresponding to the actual velocity fluctuations due to turbulence, and the second corresponding to the errors in subpixel accuracy. For the same optical arrangement and with the same processing algorithm the former was found to vary with the flow rate, while the latter was approximately constant. From this it was estimated that
$u_{m}$
display two peaks, one corresponding to the actual velocity fluctuations due to turbulence, and the second corresponding to the errors in subpixel accuracy. For the same optical arrangement and with the same processing algorithm the former was found to vary with the flow rate, while the latter was approximately constant. From this it was estimated that
![]() $\unicode[STIX]{x1D716}^{\prime }\approx 0.071$
pixels, which is consistent with typical PIV measurements (Adrian & Westerweel Reference Adrian and Westerweel2011).
$\unicode[STIX]{x1D716}^{\prime }\approx 0.071$
pixels, which is consistent with typical PIV measurements (Adrian & Westerweel Reference Adrian and Westerweel2011).
The maximum error in the mean velocity was estimated based on the velocity at the most distant downstream location of the measurement region (i.e.
![]() $x/D=31.5$
), where the magnitude of the velocity is lowest. Using data from similar single-phase turbulent jets (Ball, Fellouah & Pollard Reference Ball, Fellouah and Pollard2012),
$x/D=31.5$
), where the magnitude of the velocity is lowest. Using data from similar single-phase turbulent jets (Ball, Fellouah & Pollard Reference Ball, Fellouah and Pollard2012),
![]() $\overline{U}\approx 0.2\overline{U}_{ec}$
and
$\overline{U}\approx 0.2\overline{U}_{ec}$
and
![]() $u^{\prime }/\overline{U}=0.25$
at
$u^{\prime }/\overline{U}=0.25$
at
![]() $x/D=31.5$
, where
$x/D=31.5$
, where
![]() $\overline{U}_{ec}$
is the mean centreline velocity at the jet exit and
$\overline{U}_{ec}$
is the mean centreline velocity at the jet exit and
![]() $u^{\prime }$
is the fluctuating component of the axial velocity. As the time separation between the recording of PIV image pairs was selected such that
$u^{\prime }$
is the fluctuating component of the axial velocity. As the time separation between the recording of PIV image pairs was selected such that
![]() $\overline{U}_{ec}$
, which is the highest expected velocity within the measurement region, corresponds to a maximum particle displacement of
$\overline{U}_{ec}$
, which is the highest expected velocity within the measurement region, corresponds to a maximum particle displacement of
![]() ${\approx}1/3\,(32)\approx 10.67$
pixels (i.e.
${\approx}1/3\,(32)\approx 10.67$
pixels (i.e.
![]() $1/3$
of the smallest interrogation window size), and considering that the lowest sample size in the current experiments was
$1/3$
of the smallest interrogation window size), and considering that the lowest sample size in the current experiments was
![]() $N=640$
, then using (2.5) the estimated maximum error in the mean velocity is
$N=640$
, then using (2.5) the estimated maximum error in the mean velocity is
![]() $\unicode[STIX]{x1D716}_{U}\approx 1\,\%$
. Also using single-phase data, the maximum uncertainty in the fluctuating component of velocity was estimated to be
$\unicode[STIX]{x1D716}_{U}\approx 1\,\%$
. Also using single-phase data, the maximum uncertainty in the fluctuating component of velocity was estimated to be
![]() $\unicode[STIX]{x1D716}_{u^{\prime }}\approx 23.5\,\%$
using (2.6), on the assumption that the minimum value of
$\unicode[STIX]{x1D716}_{u^{\prime }}\approx 23.5\,\%$
using (2.6), on the assumption that the minimum value of
![]() $u^{\prime }$
(which corresponds to the highest uncertainty in the r.m.s.) occurs close to the pipe exit where
$u^{\prime }$
(which corresponds to the highest uncertainty in the r.m.s.) occurs close to the pipe exit where
![]() $u^{\prime }/\overline{U}_{ec}\approx 0.01$
.
$u^{\prime }/\overline{U}_{ec}\approx 0.01$
.
3 Similarity equations
In the far field of axisymmetric turbulent jet flows, it is well established that the mean centreline velocity and scalar quantities (such as species concentration) decrease linearly with axial distance while the jet half-width increases linearly with it (Townsend Reference Townsend1976). For turbulent jets in a weak co-flow (
![]() $\unicode[STIX]{x1D706}\gg 1$
), the centreline decay of mean concentration and velocity can be written as (Sautet & Stepowski Reference Sautet and Stepowski1995)
$\unicode[STIX]{x1D706}\gg 1$
), the centreline decay of mean concentration and velocity can be written as (Sautet & Stepowski Reference Sautet and Stepowski1995)
while the jet expansion can be expressed as
where
![]() $\unicode[STIX]{x1D6FD}$
is the property of interest (e.g. mean velocity,
$\unicode[STIX]{x1D6FD}$
is the property of interest (e.g. mean velocity,
![]() $U$
or mean concentration,
$U$
or mean concentration,
![]() $\unicode[STIX]{x1D6E9}$
),
$\unicode[STIX]{x1D6E9}$
),
![]() $x_{o1,\unicode[STIX]{x1D6FD}}$
and
$x_{o1,\unicode[STIX]{x1D6FD}}$
and
![]() $x_{o2,\unicode[STIX]{x1D6FD}}$
are virtual origins based on the decay and expansion rates, respectively,
$x_{o2,\unicode[STIX]{x1D6FD}}$
are virtual origins based on the decay and expansion rates, respectively,
![]() $K_{1,\unicode[STIX]{x1D6FD}}$
is the decay coefficient,
$K_{1,\unicode[STIX]{x1D6FD}}$
is the decay coefficient,
![]() $K_{2,\unicode[STIX]{x1D6FD}}$
is the expansion coefficient and
$K_{2,\unicode[STIX]{x1D6FD}}$
is the expansion coefficient and
![]() $d_{\unicode[STIX]{x1D716}}$
is the equivalent diameter, the subscript
$d_{\unicode[STIX]{x1D716}}$
is the equivalent diameter, the subscript
![]() $c$
refers to the centreline value and the subscript
$c$
refers to the centreline value and the subscript
![]() $e$
refers to the value at the jet exit (see also table 2). The commonly accepted form of the equivalent diameter is (Papadopoulos & Pitts Reference Papadopoulos and Pitts1998; Mi, Nobes & Nathan Reference Mi, Nobes and Nathan2001)
$e$
refers to the value at the jet exit (see also table 2). The commonly accepted form of the equivalent diameter is (Papadopoulos & Pitts Reference Papadopoulos and Pitts1998; Mi, Nobes & Nathan Reference Mi, Nobes and Nathan2001)
where
and
is the mass and momentum flux of the jet at the exit, respectively. Here,
![]() $\unicode[STIX]{x1D70C}_{j}=$
is the density of the two-phase jet,
$\unicode[STIX]{x1D70C}_{j}=$
is the density of the two-phase jet,
![]() $\unicode[STIX]{x1D70C}_{\infty }$
is the density of the co-flow and
$\unicode[STIX]{x1D70C}_{\infty }$
is the density of the co-flow and
![]() $U_{e}$
is the gas-phase velocity profile at the jet exit. In the current experiments, the equivalent diameter was constant at
$U_{e}$
is the gas-phase velocity profile at the jet exit. In the current experiments, the equivalent diameter was constant at
![]() $d_{\unicode[STIX]{x1D716}}/D=1.17$
. The use of the equivalent diameter and the ‘correction’ term
$d_{\unicode[STIX]{x1D716}}/D=1.17$
. The use of the equivalent diameter and the ‘correction’ term
![]() $\sqrt{1-\unicode[STIX]{x1D706}^{-1}}$
in (3.1) and (3.2) takes into account the exit density, velocity profile and jet-to-co-flow velocity ratio, facilitating comparison between different configuration of jets on a more equitable basis (Pitts Reference Pitts1991a
; Sautet & Stepowski Reference Sautet and Stepowski1995; Mi et al.
Reference Mi, Nobes and Nathan2001).
$\sqrt{1-\unicode[STIX]{x1D706}^{-1}}$
in (3.1) and (3.2) takes into account the exit density, velocity profile and jet-to-co-flow velocity ratio, facilitating comparison between different configuration of jets on a more equitable basis (Pitts Reference Pitts1991a
; Sautet & Stepowski Reference Sautet and Stepowski1995; Mi et al.
Reference Mi, Nobes and Nathan2001).
4 Single-phase measurements
Single-phase measurements were also performed under identical conditions to the two-phase experiments described in § 2, except that both the jet and annular co-flow was seeded with alumina particles of diameter
![]() $0.5~\unicode[STIX]{x03BC}\text{m}$
and density
$0.5~\unicode[STIX]{x03BC}\text{m}$
and density
![]() $3950~\text{kg}~\text{m}^{-3}$
. The mass loading of the seeding particles within the jet and co-flow was maintained at
$3950~\text{kg}~\text{m}^{-3}$
. The mass loading of the seeding particles within the jet and co-flow was maintained at
![]() $\unicode[STIX]{x1D719}=0.4$
and
$\unicode[STIX]{x1D719}=0.4$
and
![]() $\unicode[STIX]{x1D719}\approx 0.04$
, respectively, such that the jet and co-flow densities match the two-phase experiments to within 4 %.
$\unicode[STIX]{x1D719}\approx 0.04$
, respectively, such that the jet and co-flow densities match the two-phase experiments to within 4 %.
For these single-phase measurements, the resultant exit Stokes number at the highest investigated Reynolds number of
![]() $Re_{D}=40\,000$
was
$Re_{D}=40\,000$
was
![]() $Sk_{D}\approx 0.01$
. As this value of Stokes number is two orders of magnitude smaller than unity, these particles are expected to faithfully follow the flow. The single-phase velocity measurements were also used to estimate the mean gas-phase velocity field, particularly at the exit plane of the jet, on the basis of previous measurements in particle-laden jets (Modarress et al.
Reference Modarress, Wuerer and Elghobashi1984b
; Sheen et al.
Reference Sheen, Jou and Lee1994; Gillandt et al.
Reference Gillandt, Fritsching and Bauckhage2001), which have demonstrated that, under similar or higher mass loadings (albeit only for
$Sk_{D}\approx 0.01$
. As this value of Stokes number is two orders of magnitude smaller than unity, these particles are expected to faithfully follow the flow. The single-phase velocity measurements were also used to estimate the mean gas-phase velocity field, particularly at the exit plane of the jet, on the basis of previous measurements in particle-laden jets (Modarress et al.
Reference Modarress, Wuerer and Elghobashi1984b
; Sheen et al.
Reference Sheen, Jou and Lee1994; Gillandt et al.
Reference Gillandt, Fritsching and Bauckhage2001), which have demonstrated that, under similar or higher mass loadings (albeit only for
![]() $Sk_{D}>10$
), single-phase measurements yield a reasonable approximation of the gas-phase flow field. (Note that further experiments are in progress to also measure the gas-phase velocity distributions in the two-phase cases, noting that the gas-phase velocity must differ from the single-phase case because the flow is in the two-way coupling regime.)
$Sk_{D}>10$
), single-phase measurements yield a reasonable approximation of the gas-phase flow field. (Note that further experiments are in progress to also measure the gas-phase velocity distributions in the two-phase cases, noting that the gas-phase velocity must differ from the single-phase case because the flow is in the two-way coupling regime.)

Figure 3. Mean velocity and turbulence intensity profiles of the single-phase flow at the jet exit. Also shown are the results from Mi et al. (Reference Mi, Nobes and Nathan2001) for a jet emerging from a fully developed pipe flow and at
![]() $Re_{D}=16\,000$
, together with the
$Re_{D}=16\,000$
, together with the
![]() $1/7$
th power law for mean velocity.
$1/7$
th power law for mean velocity.
Figure 3 presents the radial profiles of normalised mean axial velocity
![]() $U_{0}/U_{0,c}$
, axial turbulence intensity
$U_{0}/U_{0,c}$
, axial turbulence intensity
![]() $u_{0}^{\prime }/U_{0}$
and radial turbulence intensity,
$u_{0}^{\prime }/U_{0}$
and radial turbulence intensity,
![]() $v_{0}^{\prime }/U_{0}$
, at the exit (
$v_{0}^{\prime }/U_{0}$
, at the exit (
![]() $x/D\approx 0.2$
) of the single-phase jet, where we take this opportunity to remind the reader that the subscript
$x/D\approx 0.2$
) of the single-phase jet, where we take this opportunity to remind the reader that the subscript
![]() $0$
denotes the single-phase case. Here,
$0$
denotes the single-phase case. Here,
![]() $u_{0}^{\prime }=\langle u_{0}^{2}\rangle ^{0.5}$
and
$u_{0}^{\prime }=\langle u_{0}^{2}\rangle ^{0.5}$
and
![]() $v_{0}^{\prime }=\langle v_{0}^{2}\rangle ^{0.5}$
where
$v_{0}^{\prime }=\langle v_{0}^{2}\rangle ^{0.5}$
where
![]() $u_{0}$
and
$u_{0}$
and
![]() $v_{0}$
are the fluctuating components of the velocity in the axial and radial directions and
$v_{0}$
are the fluctuating components of the velocity in the axial and radial directions and
![]() $U_{0,c}$
is the mean centreline velocity. The mean velocity of the jet displays a profile that closely matches the
$U_{0,c}$
is the mean centreline velocity. The mean velocity of the jet displays a profile that closely matches the
![]() $1/7$
th power law, which is consistent with a fully developed pipe flow, while the co-flow velocity is uniform. It should be noted that the present comparisons of the single-phase jet with previous investigations has selected only those configurations employing a fully developed pipe for the initial flow, since previous work (Mi et al.
Reference Mi, Nobes and Nathan2001; Xu & Antonia Reference Xu and Antonia2002) has demonstrated that the rates of spread and decay for this pipe jet differ from the more commonly investigated single-phase jet from a smooth contraction nozzle.
$1/7$
th power law, which is consistent with a fully developed pipe flow, while the co-flow velocity is uniform. It should be noted that the present comparisons of the single-phase jet with previous investigations has selected only those configurations employing a fully developed pipe for the initial flow, since previous work (Mi et al.
Reference Mi, Nobes and Nathan2001; Xu & Antonia Reference Xu and Antonia2002) has demonstrated that the rates of spread and decay for this pipe jet differ from the more commonly investigated single-phase jet from a smooth contraction nozzle.
The results also show that the turbulence intensity profiles asymptote to the constant values of the co-flow. Within the jet (
![]() $r/D\leqslant 0.5$
), the radial profile of
$r/D\leqslant 0.5$
), the radial profile of
![]() $u_{0}^{\prime }/U_{0}$
is qualitatively similar to the profile of a free jet issuing from a long pipe as measured by Mi et al. (Reference Mi, Nobes and Nathan2001) at
$u_{0}^{\prime }/U_{0}$
is qualitatively similar to the profile of a free jet issuing from a long pipe as measured by Mi et al. (Reference Mi, Nobes and Nathan2001) at
![]() $Re_{D}=16\,000$
, although the current values of
$Re_{D}=16\,000$
, although the current values of
![]() $u_{0}^{\prime }/U_{0}$
are slightly higher. This may be due to differences in the surface roughness of both pipes or the presence of a co-flow in the present jet, which generates a boundary layer on the outside of the pipe. The strong peak in
$u_{0}^{\prime }/U_{0}$
are slightly higher. This may be due to differences in the surface roughness of both pipes or the presence of a co-flow in the present jet, which generates a boundary layer on the outside of the pipe. The strong peak in
![]() $u_{0}^{\prime }/U_{0}$
and
$u_{0}^{\prime }/U_{0}$
and
![]() $v_{0}^{\prime }/U_{0}$
at
$v_{0}^{\prime }/U_{0}$
at
![]() $r/D\approx 0.56$
is due to the wake from the
$r/D\approx 0.56$
is due to the wake from the
![]() ${\approx}1.59~\text{mm}$
thick of the pipe wall.
${\approx}1.59~\text{mm}$
thick of the pipe wall.

Figure 4. The axial evolution of the entrainment,
![]() $E_{0}$
(see also (4.1)), for the single-phase case (round markers). Also included is the entrainment coefficient,
$E_{0}$
(see also (4.1)), for the single-phase case (round markers). Also included is the entrainment coefficient,
![]() $C_{el,0}$
(blue line), calculated from a curve fit of
$C_{el,0}$
(blue line), calculated from a curve fit of
![]() $E_{0}$
(red line). Here,
$E_{0}$
(red line). Here,
![]() $c_{1}=0.1325$
,
$c_{1}=0.1325$
,
![]() $c_{2}=0.4149$
and
$c_{2}=0.4149$
and
![]() $x^{\ast \ast }/D=6$
. Note that the experimental measurements of
$x^{\ast \ast }/D=6$
. Note that the experimental measurements of
![]() $E$
only presents every fifth data point to improve clarity.
$E$
only presents every fifth data point to improve clarity.
Figure 4 presents the axial evolution of the co-flow entrainment into the single-phase jet. Here the entrainment is defined as
where
is the jet excess mass flow rate and
![]() $M_{0,ex,e}$
is the value of
$M_{0,ex,e}$
is the value of
![]() $M_{0,ex}$
at the exit plane. Measurements of entrainment are reported only for the single-phase case because the gas phase was not measured for the two-phase jet. It can be seen that the entrainment rate is only linear in the near field and decreases approximately exponentially with axial distance for
$M_{0,ex}$
at the exit plane. Measurements of entrainment are reported only for the single-phase case because the gas phase was not measured for the two-phase jet. It can be seen that the entrainment rate is only linear in the near field and decreases approximately exponentially with axial distance for
![]() $x/D\gtrsim 10$
. This is consistent with the influence of the co-flow causing the jet to depart from self-similarity (Nickels & Perry Reference Nickels and Perry1996; Han & Mungal Reference Han and Mungal2001). Defining the local rate of entrainment coefficient as
$x/D\gtrsim 10$
. This is consistent with the influence of the co-flow causing the jet to depart from self-similarity (Nickels & Perry Reference Nickels and Perry1996; Han & Mungal Reference Han and Mungal2001). Defining the local rate of entrainment coefficient as
the average rate of entrainment within the region
![]() $0\leqslant x/D\leqslant 2$
was calculated as
$0\leqslant x/D\leqslant 2$
was calculated as
![]() $\overline{C}_{el,0}=0.1165$
utilising a linear curve fit of the data. This is lower than the value of
$\overline{C}_{el,0}=0.1165$
utilising a linear curve fit of the data. This is lower than the value of
![]() $\overline{C}_{el,0}=0.136$
found by Crow & Champagne (Reference Crow and Champagne1971) within the same region for a smooth contraction jet, which is expected as pipe jets typically have lower rates of entrainment than smooth contraction jets (Mi et al.
Reference Mi, Nobes and Nathan2001; Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006). Nevertheless, this discrepancy can be partly attributed to the sensitivity of the gradient term in (4.3) to the noise in the measured data, particularly if only a small number of data points are used. To reduce these errors,
$\overline{C}_{el,0}=0.136$
found by Crow & Champagne (Reference Crow and Champagne1971) within the same region for a smooth contraction jet, which is expected as pipe jets typically have lower rates of entrainment than smooth contraction jets (Mi et al.
Reference Mi, Nobes and Nathan2001; Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006). Nevertheless, this discrepancy can be partly attributed to the sensitivity of the gradient term in (4.3) to the noise in the measured data, particularly if only a small number of data points are used. To reduce these errors,
![]() $C_{el,0}$
was calculated from a curve fit of
$C_{el,0}$
was calculated from a curve fit of
![]() $E_{0}(x)$
of the form
$E_{0}(x)$
of the form
 $$\begin{eqnarray}E_{0}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle c_{1}(x/D)+1\quad & \text{for }x\leqslant x^{\ast \ast }\\ \displaystyle c_{1}x^{\ast \ast }\left[(1+c_{2})\ln \left(\frac{x/x^{\ast \ast }+c_{2}}{1+c_{2}}\right)+1\right]+1\quad & \text{for }x\geqslant x^{\ast \ast },\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}E_{0}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle c_{1}(x/D)+1\quad & \text{for }x\leqslant x^{\ast \ast }\\ \displaystyle c_{1}x^{\ast \ast }\left[(1+c_{2})\ln \left(\frac{x/x^{\ast \ast }+c_{2}}{1+c_{2}}\right)+1\right]+1\quad & \text{for }x\geqslant x^{\ast \ast },\end{array}\right.\end{eqnarray}$$
where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are constants. This curve fit was obtained on the basis of assuming that the rate of entrainment is proportional to the excess velocity, i.e.
$c_{2}$
are constants. This curve fit was obtained on the basis of assuming that the rate of entrainment is proportional to the excess velocity, i.e.
![]() $\unicode[STIX]{x2202}E/\unicode[STIX]{x2202}x\propto (U-U_{\infty })$
, together with the assumption that the jet mean velocity
$\unicode[STIX]{x2202}E/\unicode[STIX]{x2202}x\propto (U-U_{\infty })$
, together with the assumption that the jet mean velocity
![]() $U$
is approximately constant for
$U$
is approximately constant for
![]() $x\leqslant x^{\ast \ast }$
, where
$x\leqslant x^{\ast \ast }$
, where
![]() $x^{\ast \ast }$
is some location downstream of the exit, and
$x^{\ast \ast }$
is some location downstream of the exit, and
![]() $U\propto 1/x$
for
$U\propto 1/x$
for
![]() $x\geqslant x^{\ast \ast }$
. The entrainment coefficient was obtained by analytically differentiating equation (4.4), that is,
$x\geqslant x^{\ast \ast }$
. The entrainment coefficient was obtained by analytically differentiating equation (4.4), that is,
 $$\begin{eqnarray}C_{el,0}=\left\{\begin{array}{@{}ll@{}}\displaystyle c_{1}(d_{\unicode[STIX]{x1D716}}/D)\quad & \text{for }x\leqslant x^{\ast \ast }\\ \displaystyle \frac{c_{1}(1+c_{2})}{(x/x^{\ast \ast }+c_{2})}\left(\frac{d_{\unicode[STIX]{x1D716}}}{D}\right)\quad & \text{for }x\geqslant x^{\ast \ast }.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}C_{el,0}=\left\{\begin{array}{@{}ll@{}}\displaystyle c_{1}(d_{\unicode[STIX]{x1D716}}/D)\quad & \text{for }x\leqslant x^{\ast \ast }\\ \displaystyle \frac{c_{1}(1+c_{2})}{(x/x^{\ast \ast }+c_{2})}\left(\frac{d_{\unicode[STIX]{x1D716}}}{D}\right)\quad & \text{for }x\geqslant x^{\ast \ast }.\end{array}\right.\end{eqnarray}$$
Utilizing a value of
![]() $x^{\ast \ast }/D=6$
(Sautet & Stepowski Reference Sautet and Stepowski1995), we obtain
$x^{\ast \ast }/D=6$
(Sautet & Stepowski Reference Sautet and Stepowski1995), we obtain
![]() $c_{1}=0.1325$
and
$c_{1}=0.1325$
and
![]() $c_{2}=0.4149$
. The curves described by (4.4) and (4.5) are also presented in figure 4. The results show that in the far field,
$c_{2}=0.4149$
. The curves described by (4.4) and (4.5) are also presented in figure 4. The results show that in the far field,
![]() $C_{el,0}$
decreases with increasing streamwise distance, as is expected for a co-flowing jet. In the near field,
$C_{el,0}$
decreases with increasing streamwise distance, as is expected for a co-flowing jet. In the near field,
![]() $0\leqslant x/D\leqslant 6$
,
$0\leqslant x/D\leqslant 6$
,
![]() $C_{el,0}=0.155$
, which is broadly consistent with the values of
$C_{el,0}=0.155$
, which is broadly consistent with the values of
![]() $0.11\lesssim C_{el,0}\lesssim 0.19$
in the region
$0.11\lesssim C_{el,0}\lesssim 0.19$
in the region
![]() $1\leqslant x/D\leqslant 2.88$
(Hill Reference Hill1972) and
$1\leqslant x/D\leqslant 2.88$
(Hill Reference Hill1972) and
![]() $0.1\lesssim C_{el,0}\lesssim 0.15$
in the region
$0.1\lesssim C_{el,0}\lesssim 0.15$
in the region
![]() $1\lesssim x/D\lesssim 4$
(Liepmann & Gharib Reference Liepmann and Gharib1992) found in other studies of turbulent free jets. However, an exact comparison is not possible because of the wide range of differing conditions and measurement techniques. For example, all previous measurements of entrainment were performed with free jets (rather than co-flowing jets) issuing from a smooth contraction nozzle (instead of a long pipe). A free jet has a higher spreading rate than a co-flowing jet, while a smooth contraction jet has a greater rate of entrainment than a pipe jet (Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006). However, the current study utilises measurements with a higher spatial resolution than the previous measurements, which is expected to result in greater values of axial gradients, including
$1\lesssim x/D\lesssim 4$
(Liepmann & Gharib Reference Liepmann and Gharib1992) found in other studies of turbulent free jets. However, an exact comparison is not possible because of the wide range of differing conditions and measurement techniques. For example, all previous measurements of entrainment were performed with free jets (rather than co-flowing jets) issuing from a smooth contraction nozzle (instead of a long pipe). A free jet has a higher spreading rate than a co-flowing jet, while a smooth contraction jet has a greater rate of entrainment than a pipe jet (Nathan et al.
Reference Nathan, Mi, Alwahabi, Newbold and Nobes2006). However, the current study utilises measurements with a higher spatial resolution than the previous measurements, which is expected to result in greater values of axial gradients, including
![]() $C_{el,0}$
. Hence the present agreement is sufficient to provide confidence in the current measurements and to provide a reference against which future measurements of entrainment in the two-phase case can be compared.
$C_{el,0}$
. Hence the present agreement is sufficient to provide confidence in the current measurements and to provide a reference against which future measurements of entrainment in the two-phase case can be compared.

Figure 5. The mean velocity profiles, normalised by the bulk velocity,
![]() $U/U_{g,b}$
, at the jet exit (
$U/U_{g,b}$
, at the jet exit (
![]() $x/D\approx 0.2$
) for the particle phase (markers) and the single phase (black dashed line). The solid colored lines represent a curve fit to the particle-phase data using (5.1). Note that only every second data point is plotted for clarity.
$x/D\approx 0.2$
) for the particle phase (markers) and the single phase (black dashed line). The solid colored lines represent a curve fit to the particle-phase data using (5.1). Note that only every second data point is plotted for clarity.
5 Results
5.1 Velocity measurements
Figure 5 presents the radial profiles of the mean velocity normalised by the bulk-mean gas velocity,
![]() $U/U_{g,b}$
, at the jet exit for both the particle phase (subscript
$U/U_{g,b}$
, at the jet exit for both the particle phase (subscript
![]() $p$
) and the single phase (subscript 0). It should be noted that while we have previously published similar data for
$p$
) and the single phase (subscript 0). It should be noted that while we have previously published similar data for
![]() $Sk_{D}=0.3$
, 1.4 and 11.2 (Lau & Nathan Reference Lau and Nathan2014), the current dataset is completely new as it not only includes new cases but also fully repeats these previous measurements. Additionally, the current measurements are virtually indistinguishable from the previous measurements (comparison not shown here for brevity). The current results show that the mean velocity profiles become ‘flatter’ and the velocity gradients near to the jet edge decreases as the Stokes number is increased. The particle velocity lags the single-phase velocity (presented as black dashed lines in figure 5) for all Stokes numbers within the central region of the jet (
$Sk_{D}=0.3$
, 1.4 and 11.2 (Lau & Nathan Reference Lau and Nathan2014), the current dataset is completely new as it not only includes new cases but also fully repeats these previous measurements. Additionally, the current measurements are virtually indistinguishable from the previous measurements (comparison not shown here for brevity). The current results show that the mean velocity profiles become ‘flatter’ and the velocity gradients near to the jet edge decreases as the Stokes number is increased. The particle velocity lags the single-phase velocity (presented as black dashed lines in figure 5) for all Stokes numbers within the central region of the jet (
![]() $-0.4\lesssim r/D\lesssim 0.4$
), however the magnitude of particle lag (or slip) decreases as the Stokes number is decreased, as expected. For all Stokes numbers, the shape of the profile is well described by the power law
$-0.4\lesssim r/D\lesssim 0.4$
), however the magnitude of particle lag (or slip) decreases as the Stokes number is decreased, as expected. For all Stokes numbers, the shape of the profile is well described by the power law
which is commonly employed for single-phase fully developed pipe jets (also shown in figure 5 as the coloured solid lines). In general, there is good agreement between the power law and the mean velocity profiles for all investigated Stokes numbers, with a lowest recorded regression coefficient of
![]() $R^{2}=0.9416$
occurring at the highest Stokes number of
$R^{2}=0.9416$
occurring at the highest Stokes number of
![]() $Sk_{D}=22.4$
.
$Sk_{D}=22.4$
.

Figure 6. The dependence of the exponent
![]() $n$
in the power law given by (5.1), and the bulk-to-centreline velocity ratio,
$n$
in the power law given by (5.1), and the bulk-to-centreline velocity ratio,
![]() $U_{b}/U_{c}$
, on the exit Stokes number,
$U_{b}/U_{c}$
, on the exit Stokes number,
![]() $Sk_{D}$
, for both the particle phase (open symbols) and single phase (closed symbols). The inset shows the relationship between
$Sk_{D}$
, for both the particle phase (open symbols) and single phase (closed symbols). The inset shows the relationship between
![]() $\log (Sk_{D})$
and
$\log (Sk_{D})$
and
![]() $\log (n_{p}-n_{0})$
, where
$\log (n_{p}-n_{0})$
, where
![]() $n_{0}=6.05$
is the value of
$n_{0}=6.05$
is the value of
![]() $n$
for the single-phase case. The value
$n$
for the single-phase case. The value
![]() $m$
in the inset is the gradient of the linear curve fit of the data.
$m$
in the inset is the gradient of the linear curve fit of the data.
The exponent
![]() $n$
in (5.1) and the bulk-to-centreline velocity ratio
$n$
in (5.1) and the bulk-to-centreline velocity ratio
![]() $U_{b}/U_{c}$
are presented in figure 6 as a function of exit Stokes number. Here, the particle-phase bulk-mean velocity
$U_{b}/U_{c}$
are presented in figure 6 as a function of exit Stokes number. Here, the particle-phase bulk-mean velocity
![]() $U_{p,b}$
was calculated using
$U_{p,b}$
was calculated using
It should be noted that
![]() $U_{p,b}$
will not necessarily equal to the gas-phase bulk velocity,
$U_{p,b}$
will not necessarily equal to the gas-phase bulk velocity,
![]() $U_{g,b}$
, due to slip between the particle and gas phases. Consistent with the observations above, the exponent
$U_{g,b}$
, due to slip between the particle and gas phases. Consistent with the observations above, the exponent
![]() $n$
can be found to increase, corresponding to the flattening of the profile, as the Stokes number is increased, as does the value of
$n$
can be found to increase, corresponding to the flattening of the profile, as the Stokes number is increased, as does the value of
![]() $U_{p,b}/U_{p,c}$
. These trends are consistent with the expectation that as
$U_{p,b}/U_{p,c}$
. These trends are consistent with the expectation that as
![]() $Sk_{D}\rightarrow \infty$
,
$Sk_{D}\rightarrow \infty$
,
![]() $n_{p}\rightarrow \infty$
so that
$n_{p}\rightarrow \infty$
so that
![]() $U_{p,b}/U_{p,c}\rightarrow 1$
. At these limits, equation (5.1) is expected to approach an exact match to the particle-phase velocity profile, which is consistent with the above observation that the lowest
$U_{p,b}/U_{p,c}\rightarrow 1$
. At these limits, equation (5.1) is expected to approach an exact match to the particle-phase velocity profile, which is consistent with the above observation that the lowest
![]() $R^{2}$
value was measured for the highest
$R^{2}$
value was measured for the highest
![]() $Sk_{D}$
case. The data for
$Sk_{D}$
case. The data for
![]() $(n_{p}-n_{0})$
, where
$(n_{p}-n_{0})$
, where
![]() $n_{0}=6.05$
is the single-phase value of
$n_{0}=6.05$
is the single-phase value of
![]() $n$
, is plotted against
$n$
, is plotted against
![]() $Sk_{D}$
in a log–log format in the inset of figure 6. The results show that there is a strong linear correlation between
$Sk_{D}$
in a log–log format in the inset of figure 6. The results show that there is a strong linear correlation between
![]() $\log (n_{p}-n_{0})$
and
$\log (n_{p}-n_{0})$
and
![]() $\log (Sk_{D})$
, with a linear curve fit to this data resulting in a coefficient of determination of
$\log (Sk_{D})$
, with a linear curve fit to this data resulting in a coefficient of determination of
![]() $R^{2}=0.9932$
. The gradient to this linear curve fit was calculated as
$R^{2}=0.9932$
. The gradient to this linear curve fit was calculated as
![]() $m=0.58$
, suggesting that
$m=0.58$
, suggesting that
![]() $(n_{p}-n_{0})\propto Sk_{D}^{0.58}$
, although it should be noted that this relationship was calculated from a small number of data points within a limited Stokes number range. Further work is required, particularly in the regimes
$(n_{p}-n_{0})\propto Sk_{D}^{0.58}$
, although it should be noted that this relationship was calculated from a small number of data points within a limited Stokes number range. Further work is required, particularly in the regimes
![]() $Sk_{D}<0.3$
and
$Sk_{D}<0.3$
and
![]() $Sk_{D}>22.4$
, to assess this relationship over a wider range of conditions.
$Sk_{D}>22.4$
, to assess this relationship over a wider range of conditions.
Additionally, the current measurements provide further evidence that the effect of particle number density,
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }$
, is second order to that of Stokes number. This is because, the use of six values of
$\unicode[STIX]{x1D6E9}_{b}^{\ast }$
, is second order to that of Stokes number. This is because, the use of six values of
![]() $Sk_{D}$
and three values of
$Sk_{D}$
and three values of
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }$
(namely
$\unicode[STIX]{x1D6E9}_{b}^{\ast }$
(namely
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }=749~\text{mm}^{-3}$
for
$\unicode[STIX]{x1D6E9}_{b}^{\ast }=749~\text{mm}^{-3}$
for
![]() $Sk_{D}=0.3$
,
$Sk_{D}=0.3$
,
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }=94~\text{mm}^{-3}$
for
$\unicode[STIX]{x1D6E9}_{b}^{\ast }=94~\text{mm}^{-3}$
for
![]() $Sk_{D}=1.4$
and 2.8, and
$Sk_{D}=1.4$
and 2.8, and
![]() $\unicode[STIX]{x1D6E9}_{b}^{\ast }=12~\text{mm}^{-3}$
for
$\unicode[STIX]{x1D6E9}_{b}^{\ast }=12~\text{mm}^{-3}$
for
![]() $Sk_{D}=5.6$
, 11.2 and 22.4, as shown in table 3), yield an approximately linear correlation between
$Sk_{D}=5.6$
, 11.2 and 22.4, as shown in table 3), yield an approximately linear correlation between
![]() $\log (n_{p}-n_{0})$
and
$\log (n_{p}-n_{0})$
and
![]() $\log (Sk_{D})$
, together with a monotonic increase in
$\log (Sk_{D})$
, together with a monotonic increase in
![]() $n$
with
$n$
with
![]() $Sk_{D}$
. That is, there is no evidence of a significant correlation between the measured particle mean velocity and the bulk particle number density. Nevertheless, an independent and systematic study is required to better assess the magnitude of this influence.
$Sk_{D}$
. That is, there is no evidence of a significant correlation between the measured particle mean velocity and the bulk particle number density. Nevertheless, an independent and systematic study is required to better assess the magnitude of this influence.

Figure 7. The pseudo-slip ratio,
![]() $U_{p,c}/U_{0,c}$
, and particle Reynolds number,
$U_{p,c}/U_{0,c}$
, and particle Reynolds number,
![]() $Re_{p}$
, at the jet exit centreline as a function of exit Stokes number.
$Re_{p}$
, at the jet exit centreline as a function of exit Stokes number.
Figure 7 presents the dependence of the pseudo-slip ratio,
![]() $U_{p,c}/U_{0,c}$
and particle Reynolds number,
$U_{p,c}/U_{0,c}$
and particle Reynolds number,
![]() $Re_{p}$
, measured on the centreline at the jet exit as a function of exit Stokes number,
$Re_{p}$
, measured on the centreline at the jet exit as a function of exit Stokes number,
![]() $Sk_{D}$
. Here, the particle Reynolds number is defined as
$Sk_{D}$
. Here, the particle Reynolds number is defined as
The results show that the pseudo-slip ratio approaches unity as the Stokes number is decreased, with
![]() $U_{p,c}/U_{0,c}\approx 0.95$
for the two lower Stokes numbers,
$U_{p,c}/U_{0,c}\approx 0.95$
for the two lower Stokes numbers,
![]() $Sk_{D}=0.3$
and 1.4, decreasing monotonically as
$Sk_{D}=0.3$
and 1.4, decreasing monotonically as
![]() $Sk_{D}$
is increased consistent with the expectation that the pseudo-slip ratio tends to zero as
$Sk_{D}$
is increased consistent with the expectation that the pseudo-slip ratio tends to zero as
![]() $Sk_{D}\rightarrow \infty$
. The largest recorded particle Reynolds number,
$Sk_{D}\rightarrow \infty$
. The largest recorded particle Reynolds number,
![]() $Re_{p}\approx 40$
, occurring at
$Re_{p}\approx 40$
, occurring at
![]() $Sk_{D}=22.4$
, is substantially lower than the particle Reynolds number threshold of
$Sk_{D}=22.4$
, is substantially lower than the particle Reynolds number threshold of
![]() $Re_{p}\approx 110$
where turbulence enhancement due to vortex shedding around particles is expected to occur (Hetsroni Reference Hetsroni1989). As the particle mass loading is sufficiently high to result in two-way coupling between the gas and particle phases, turbulence modulation of the gas phase by the particle phase is expected to occur for all Stokes numbers at the jet exit.
$Re_{p}\approx 110$
where turbulence enhancement due to vortex shedding around particles is expected to occur (Hetsroni Reference Hetsroni1989). As the particle mass loading is sufficiently high to result in two-way coupling between the gas and particle phases, turbulence modulation of the gas phase by the particle phase is expected to occur for all Stokes numbers at the jet exit.
Figure 8 presents the radial profiles of the turbulence intensity in the axial,
![]() $u^{\prime }/U$
, and radial,
$u^{\prime }/U$
, and radial,
![]() $v^{\prime }/U$
, directions, respectively, together with the non-dimensional Reynolds stress,
$v^{\prime }/U$
, directions, respectively, together with the non-dimensional Reynolds stress,
![]() $\langle uv\rangle /U^{2}$
and the ratio
$\langle uv\rangle /U^{2}$
and the ratio
![]() $u^{\prime }/v^{\prime }$
at the jet exit for both the particle phase and the single phase. In comparing the single-phase case with the measurements of particle velocity, it should be noted that the single-phase measurement includes the contribution of the entrained co-flow (which is seeded), while that of the particle phase does not.
$u^{\prime }/v^{\prime }$
at the jet exit for both the particle phase and the single phase. In comparing the single-phase case with the measurements of particle velocity, it should be noted that the single-phase measurement includes the contribution of the entrained co-flow (which is seeded), while that of the particle phase does not.

Figure 8. Radial profiles of normalised r.m.s. axial velocity,
![]() $u^{\prime }/U$
, r.m.s. radial velocity,
$u^{\prime }/U$
, r.m.s. radial velocity,
![]() $v^{\prime }/U$
, Reynolds stress,
$v^{\prime }/U$
, Reynolds stress,
![]() $\langle uv\rangle /U^{2}$
and the ratio
$\langle uv\rangle /U^{2}$
and the ratio
![]() $u^{\prime }/v^{\prime }$
at the jet exit (
$u^{\prime }/v^{\prime }$
at the jet exit (
![]() $x/D\approx 0.2$
) for both the particle phase (
$x/D\approx 0.2$
) for both the particle phase (
![]() $p$
) and the single phase (0). Note that all panels use identical legends and only every fourth data point is plotted for clarity.
$p$
) and the single phase (0). Note that all panels use identical legends and only every fourth data point is plotted for clarity.
Nevertheless, it can be seen that the magnitude of the turbulence intensity decreases with an increase in Stokes number, due to the reduction in particle response to turbulent eddies, as expected. Furthermore, the particle turbulence intensities in both directions are lower than the single-phase case for all Stokes numbers. Noting that the single-phase velocity profiles are expected to be approximately the same as the gas phase at the jet exit (Modarress et al.
Reference Modarress, Wuerer and Elghobashi1984b
; Sheen et al.
Reference Sheen, Jou and Lee1994; Gillandt et al.
Reference Gillandt, Fritsching and Bauckhage2001), the lower values of
![]() $u_{p}^{\prime }/U_{p}$
and
$u_{p}^{\prime }/U_{p}$
and
![]() $v_{p}^{\prime }/U_{p}$
for the particle phase is expected to correlate with lower rates of energy transfer between the gas and solid phases. It should also be noted that in the present experiments, the effect of ‘trajectory crossing’, whereby heavy particles drift from one region of the flow to another due to the presence of gravity leading to reduced particle residence times in turbulent eddies (Yudine Reference Yudine1959; Crowe et al.
Reference Crowe, Troutt and Chung1996), is expected to be small. This is because the maximum estimated drift velocity, defined as the difference between the particle velocity in the presence of, and in the absence of, gravity, is
$v_{p}^{\prime }/U_{p}$
for the particle phase is expected to correlate with lower rates of energy transfer between the gas and solid phases. It should also be noted that in the present experiments, the effect of ‘trajectory crossing’, whereby heavy particles drift from one region of the flow to another due to the presence of gravity leading to reduced particle residence times in turbulent eddies (Yudine Reference Yudine1959; Crowe et al.
Reference Crowe, Troutt and Chung1996), is expected to be small. This is because the maximum estimated drift velocity, defined as the difference between the particle velocity in the presence of, and in the absence of, gravity, is
![]() ${\approx}0.005U_{p}$
, which is sufficiently low that the effect of ‘trajectory crossing’ is negligible (Wells & Stock Reference Wells and Stock1983).
${\approx}0.005U_{p}$
, which is sufficiently low that the effect of ‘trajectory crossing’ is negligible (Wells & Stock Reference Wells and Stock1983).
The results also show that the turbulence intensities between the lowest Stokes number case (
![]() $Sk_{D}=0.3$
) and the single-phase case match quite closely except for near the jet edge, where the discrepancy between
$Sk_{D}=0.3$
) and the single-phase case match quite closely except for near the jet edge, where the discrepancy between
![]() $v_{p}^{\prime }/U_{p}$
and
$v_{p}^{\prime }/U_{p}$
and
![]() $v_{0}^{\prime }/U_{0}$
is particularly large. These discrepancies are consistent with the measurement of the entrained fluid from the co-flow, which is only seeded in the single-phase case (see also § 4). Nevertheless, given that within the central region of the jet exit the mean and r.m.s. particle velocities match the single-phase values closely for
$v_{0}^{\prime }/U_{0}$
is particularly large. These discrepancies are consistent with the measurement of the entrained fluid from the co-flow, which is only seeded in the single-phase case (see also § 4). Nevertheless, given that within the central region of the jet exit the mean and r.m.s. particle velocities match the single-phase values closely for
![]() $Sk_{D}=0.3\sim O(10^{-1})$
but depart for
$Sk_{D}=0.3\sim O(10^{-1})$
but depart for
![]() $Sk_{D}\gtrsim 1.4\sim O(1)$
, and assuming that particles respond to eddies of characteristic length
$Sk_{D}\gtrsim 1.4\sim O(1)$
, and assuming that particles respond to eddies of characteristic length
![]() $L$
for
$L$
for
![]() $Sk_{L}=\unicode[STIX]{x1D70C}_{p}d_{p}^{2}U/(18\unicode[STIX]{x1D707}L)\approx Sk_{D}(D/L)\lesssim O(1)$
, it can be deduced that the dominant turbulence length scales at the exit of the pipe are of the order of
$Sk_{L}=\unicode[STIX]{x1D70C}_{p}d_{p}^{2}U/(18\unicode[STIX]{x1D707}L)\approx Sk_{D}(D/L)\lesssim O(1)$
, it can be deduced that the dominant turbulence length scales at the exit of the pipe are of the order of
![]() $10^{-1}D$
or larger, consistent with the deductions of Hetsroni (Reference Hetsroni1989).
$10^{-1}D$
or larger, consistent with the deductions of Hetsroni (Reference Hetsroni1989).
Figure 8 also shows that the Reynolds stress increases approximately linearly with radial distance within the central region of the pipe (
![]() $-0.4\lesssim r/D\lesssim 0.4$
). This is expected, because the total stress in a fully developed pipe flow varies approximately linearly across the pipe radius and the viscous stresses within the core region of the pipe are small (Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994). Close to the edge of the jet,
$-0.4\lesssim r/D\lesssim 0.4$
). This is expected, because the total stress in a fully developed pipe flow varies approximately linearly across the pipe radius and the viscous stresses within the core region of the pipe are small (Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994). Close to the edge of the jet,
![]() $|r/D|\approx 0.5$
, the Reynolds stresses increase substantially due to the low values of
$|r/D|\approx 0.5$
, the Reynolds stresses increase substantially due to the low values of
![]() $U_{p}$
at this location even though there are some inconsistencies in the present measurements of Reynolds stress. In particular, the values of
$U_{p}$
at this location even though there are some inconsistencies in the present measurements of Reynolds stress. In particular, the values of
![]() $\langle u_{p}v_{p}\rangle /U_{p}^{2}\approx 0$
at
$\langle u_{p}v_{p}\rangle /U_{p}^{2}\approx 0$
at
![]() $r/D\approx -0.5$
for the
$r/D\approx -0.5$
for the
![]() $Sk_{D}=0.3$
case, which is not internally consistent with the remainder of the current measurements. Furthermore, the profile of
$Sk_{D}=0.3$
case, which is not internally consistent with the remainder of the current measurements. Furthermore, the profile of
![]() $\langle u_{0}v_{0}\rangle /U_{0}^{2}$
for the single-phase case shows multiple inflection points near the axis, which is not consistent with other single-phase measurements of pipes (Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994) and co-flowing jets (Nickels & Perry Reference Nickels and Perry1996). These discrepancies are attributed to PIV errors, which can be substantial in the measurements of higher-order turbulence statistics. Utilising similar arguments made in § 2.1, the error in the Reynolds stress was estimated at
$\langle u_{0}v_{0}\rangle /U_{0}^{2}$
for the single-phase case shows multiple inflection points near the axis, which is not consistent with other single-phase measurements of pipes (Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994) and co-flowing jets (Nickels & Perry Reference Nickels and Perry1996). These discrepancies are attributed to PIV errors, which can be substantial in the measurements of higher-order turbulence statistics. Utilising similar arguments made in § 2.1, the error in the Reynolds stress was estimated at
![]() $\langle u_{p}v_{p}\rangle /U_{p}^{2}\approx \pm 2\times 10^{4}$
. Nevertheless, the results show a general trend of decreasing radial gradients of
$\langle u_{p}v_{p}\rangle /U_{p}^{2}\approx \pm 2\times 10^{4}$
. Nevertheless, the results show a general trend of decreasing radial gradients of
![]() $\langle u_{p}v_{p}\rangle /U_{p}^{2}$
with an increase in
$\langle u_{p}v_{p}\rangle /U_{p}^{2}$
with an increase in
![]() $Sk_{D}$
, consistent with the reduction in particle response to turbulent motions in the flow.
$Sk_{D}$
, consistent with the reduction in particle response to turbulent motions in the flow.
The results also show that the magnitude of
![]() $u_{p}^{\prime }/U_{p}$
is higher than
$u_{p}^{\prime }/U_{p}$
is higher than
![]() $v_{p}^{\prime }/U_{p}$
for all cases, inferring a high degree of anisotropy in the current two-phase jet. The anisotropy, presented directly in figure 8(d), shows that the lowest value of
$v_{p}^{\prime }/U_{p}$
for all cases, inferring a high degree of anisotropy in the current two-phase jet. The anisotropy, presented directly in figure 8(d), shows that the lowest value of
![]() $u_{p}^{\prime }/v_{p}^{\prime }\approx 2$
at the centreline and increases towards the jet edge because the pipe boundary tends to reduce radial fluctuations more than the axial (Laufer Reference Laufer1954). For the single-phase case,
$u_{p}^{\prime }/v_{p}^{\prime }\approx 2$
at the centreline and increases towards the jet edge because the pipe boundary tends to reduce radial fluctuations more than the axial (Laufer Reference Laufer1954). For the single-phase case,
![]() $u_{0}^{\prime }/v_{0}^{\prime }=2.3$
at the centreline, which is slightly higher than the value of
$u_{0}^{\prime }/v_{0}^{\prime }=2.3$
at the centreline, which is slightly higher than the value of
![]() $u_{0}^{\prime }/v_{0}^{\prime }\approx 1.85$
found by Boguslawski & Popiel (Reference Boguslawski and Popiel1979) at the same location in a similar single-phase jet albeit at a higher Reynolds number of
$u_{0}^{\prime }/v_{0}^{\prime }\approx 1.85$
found by Boguslawski & Popiel (Reference Boguslawski and Popiel1979) at the same location in a similar single-phase jet albeit at a higher Reynolds number of
![]() $Re_{D}>50\,000$
. For the two-phase case, Hardalupas et al. (Reference Hardalupas, Taylor and Whitelaw1989) obtained a value of
$Re_{D}>50\,000$
. For the two-phase case, Hardalupas et al. (Reference Hardalupas, Taylor and Whitelaw1989) obtained a value of
![]() $u_{p}^{\prime }/v_{p}^{\prime }\approx 2.3$
on the axis at the pipe exit for
$u_{p}^{\prime }/v_{p}^{\prime }\approx 2.3$
on the axis at the pipe exit for
![]() $Sk_{D}=8.6$
, which is slightly lower than the value of
$Sk_{D}=8.6$
, which is slightly lower than the value of
![]() $u_{p}^{\prime }/v_{p}^{\prime }\approx 2.6$
measured here at the same Stokes number (obtained by interpolating data between the
$u_{p}^{\prime }/v_{p}^{\prime }\approx 2.6$
measured here at the same Stokes number (obtained by interpolating data between the
![]() $Sk_{D}=5.6$
and
$Sk_{D}=5.6$
and
![]() $Sk_{D}=11.2$
cases). The measurements of Hardalupas et al., however, were performed at a higher mass loading of
$Sk_{D}=11.2$
cases). The measurements of Hardalupas et al., however, were performed at a higher mass loading of
![]() $\unicode[STIX]{x1D719}=0.8$
than the present experiments (
$\unicode[STIX]{x1D719}=0.8$
than the present experiments (
![]() $\unicode[STIX]{x1D719}=0.4$
), which may indicate that the anisotropy in the jet is influenced by particle mass loading. Nevertheless, in general the measurements indicate that there is a high degree of anisotropy in both the single- and two-phase jets, which is a finding that is of particular relevance to the development of computational models, which often assume isotropic conditions within the flow (Launder, Reece & Rodi Reference Launder, Reece and Rodi1975; Loth Reference Loth2000; Mashayek & Pandya Reference Mashayek and Pandya2003; Fairweather & Hurn Reference Fairweather and Hurn2008).
$\unicode[STIX]{x1D719}=0.4$
), which may indicate that the anisotropy in the jet is influenced by particle mass loading. Nevertheless, in general the measurements indicate that there is a high degree of anisotropy in both the single- and two-phase jets, which is a finding that is of particular relevance to the development of computational models, which often assume isotropic conditions within the flow (Launder, Reece & Rodi Reference Launder, Reece and Rodi1975; Loth Reference Loth2000; Mashayek & Pandya Reference Mashayek and Pandya2003; Fairweather & Hurn Reference Fairweather and Hurn2008).

Figure 9. Axial evolution of inverse normalised mean velocity,
![]() $U_{ec}/U_{c}$
, velocity half-width,
$U_{ec}/U_{c}$
, velocity half-width,
![]() $r_{0.5,U}/D$
, axial turbulence intensity,
$r_{0.5,U}/D$
, axial turbulence intensity,
![]() $u_{c}^{\prime }/U_{c}$
, radial turbulence intensity,
$u_{c}^{\prime }/U_{c}$
, radial turbulence intensity,
![]() $v_{c}^{\prime }/U_{c}$
, ratio
$v_{c}^{\prime }/U_{c}$
, ratio
![]() $u_{c}^{\prime }/v_{c}^{\prime }$
along the jet centreline for both the particle phase (
$u_{c}^{\prime }/v_{c}^{\prime }$
along the jet centreline for both the particle phase (
![]() $p$
) and the single phase (0). Also included is the axial evolution of the centreline Stokes number,
$p$
) and the single phase (0). Also included is the axial evolution of the centreline Stokes number,
![]() $Sk_{c}$
. Note that all panels use identical legends.
$Sk_{c}$
. Note that all panels use identical legends.
Figure 9 presents the axial evolution of the inverse mean velocity,
![]() $U_{ec}/U_{c}$
, velocity half-width,
$U_{ec}/U_{c}$
, velocity half-width,
![]() $r_{0.5,U}/D$
, axial turbulence intensity,
$r_{0.5,U}/D$
, axial turbulence intensity,
![]() $u_{c}^{\prime }/U_{c}$
, radial turbulence intensity,
$u_{c}^{\prime }/U_{c}$
, radial turbulence intensity,
![]() $v_{c}^{\prime }/U_{c}$
, and the ratio
$v_{c}^{\prime }/U_{c}$
, and the ratio
![]() $u_{c}^{\prime }/v_{c}^{\prime }$
along the jet centreline for both the particle-phase and single-phase measurements. Also included is the axial profile of the local centreline Stokes number, defined as
$u_{c}^{\prime }/v_{c}^{\prime }$
along the jet centreline for both the particle-phase and single-phase measurements. Also included is the axial profile of the local centreline Stokes number, defined as
That is, the centreline mean velocity and velocity half-width of the single phase,
![]() $U_{0,c}$
and
$U_{0,c}$
and
![]() $r_{0.5,U0}$
, respectively, are used to characterise the local velocity and length scales of turbulence. The results show that the rates of decay of both the axial mean velocity and the velocity half-width decrease with an increase in Stokes number, which is consistent with previous trends (Yuu et al.
Reference Yuu, Yasukouchi, Hirosawa and Jotaki1978; Fleckhaus et al.
Reference Fleckhaus, Hishida and Maeda1987; Picano et al.
Reference Picano, Sardina, Gualtieri and Casciola2010). However, the velocity half-width for the
$r_{0.5,U0}$
, respectively, are used to characterise the local velocity and length scales of turbulence. The results show that the rates of decay of both the axial mean velocity and the velocity half-width decrease with an increase in Stokes number, which is consistent with previous trends (Yuu et al.
Reference Yuu, Yasukouchi, Hirosawa and Jotaki1978; Fleckhaus et al.
Reference Fleckhaus, Hishida and Maeda1987; Picano et al.
Reference Picano, Sardina, Gualtieri and Casciola2010). However, the velocity half-width for the
![]() $Sk_{D}=0.3$
and
$Sk_{D}=0.3$
and
![]() $Sk_{D}=1.4$
cases are almost equal to those of the single-phase case, with the axial evolution of
$Sk_{D}=1.4$
cases are almost equal to those of the single-phase case, with the axial evolution of
![]() $r_{0.5,Up}$
observed to change significantly with increasing Stokes number for
$r_{0.5,Up}$
observed to change significantly with increasing Stokes number for
![]() $Sk_{D}>1.4$
. This suggests that the particle-phase velocity approaches the gas-phase velocity for sufficiently low Stokes numbers. Furthermore, as the single-phase experiments includes simultaneous seeding of the jet and co-flow while the particle-phase measurements only include measurements within the jet, the close similarity in the values of
$Sk_{D}>1.4$
. This suggests that the particle-phase velocity approaches the gas-phase velocity for sufficiently low Stokes numbers. Furthermore, as the single-phase experiments includes simultaneous seeding of the jet and co-flow while the particle-phase measurements only include measurements within the jet, the close similarity in the values of
![]() $r_{0.5,U}$
between the single-phase and the
$r_{0.5,U}$
between the single-phase and the
![]() $Sk_{D}=0.3$
cases implies that the measurement of the entrained flow from the co-flow into the jet does not significantly bias the results. Close to the jet exit, the velocity half-widths are larger for higher Stokes numbers due to the velocity profile tending towards a uniform profile (see figure 5). The two lower Stokes number cases,
$Sk_{D}=0.3$
cases implies that the measurement of the entrained flow from the co-flow into the jet does not significantly bias the results. Close to the jet exit, the velocity half-widths are larger for higher Stokes numbers due to the velocity profile tending towards a uniform profile (see figure 5). The two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and
$Sk_{D}=0.3$
and
![]() $Sk_{D}=1.4$
, appear to approach the self-similar regime (see (3.1) and (3.2)) where
$Sk_{D}=1.4$
, appear to approach the self-similar regime (see (3.1) and (3.2)) where
![]() $U_{p,ec}/U_{p,c}\propto x$
and
$U_{p,ec}/U_{p,c}\propto x$
and
![]() $r_{0.5,Up}\propto x$
at
$r_{0.5,Up}\propto x$
at
![]() $x/D\approx 15$
. This transition to the self-similar regime occurs further downstream at higher exit Stokes numbers, with the transition occurring at
$x/D\approx 15$
. This transition to the self-similar regime occurs further downstream at higher exit Stokes numbers, with the transition occurring at
![]() $x/D\approx 25$
for the
$x/D\approx 25$
for the
![]() $Sk_{D}=11.2$
and
$Sk_{D}=11.2$
and
![]() $Sk_{D}=22.4$
cases.
$Sk_{D}=22.4$
cases.
The results presented in figure 9 also show that the centreline turbulence intensity of the particle phase is always lower than that of the corresponding single-phase jet except for the near field of the lower Stokes number case,
![]() $Sk_{D}=0.3$
. Importantly, in the near field corresponding to
$Sk_{D}=0.3$
. Importantly, in the near field corresponding to
![]() $0\lesssim x/D\lesssim 10$
, where the rates of co-flow entrainment are the greatest (see figure 4), the values of
$0\lesssim x/D\lesssim 10$
, where the rates of co-flow entrainment are the greatest (see figure 4), the values of
![]() $v_{c}^{\prime }/U_{c}$
for the single-phase case and the
$v_{c}^{\prime }/U_{c}$
for the single-phase case and the
![]() $Sk_{D}=0.3$
case are almost identical. This is further evidence that the measurement of the entrained co-flow, which was performed exclusively for the single-phase case, does not have a significant impact on the results. The results show that the difference between the particle-phase and single-phase turbulence intensities increase with
$Sk_{D}=0.3$
case are almost identical. This is further evidence that the measurement of the entrained co-flow, which was performed exclusively for the single-phase case, does not have a significant impact on the results. The results show that the difference between the particle-phase and single-phase turbulence intensities increase with
![]() $Sk_{D}$
. These findings can be explained, at least in part, by the partial response of the particles to turbulent fluctuations. Nevertheless, the local centreline Stokes number within the region
$Sk_{D}$
. These findings can be explained, at least in part, by the partial response of the particles to turbulent fluctuations. Nevertheless, the local centreline Stokes number within the region
![]() $x/D\gtrsim 20$
for the
$x/D\gtrsim 20$
for the
![]() $Sk_{D}=0.3$
case is
$Sk_{D}=0.3$
case is
![]() $Sk_{c}\sim O(10^{-2})$
(see figure 9
f), which is sufficiently low to suggest that under these conditions the particles respond strongly to the flow. The minimum local centreline particle volume fraction within the measured region of the jet is
$Sk_{c}\sim O(10^{-2})$
(see figure 9
f), which is sufficiently low to suggest that under these conditions the particles respond strongly to the flow. The minimum local centreline particle volume fraction within the measured region of the jet is
![]() ${\approx}7\times 10^{-5}$
based on a conservative concentration decay coefficient of
${\approx}7\times 10^{-5}$
based on a conservative concentration decay coefficient of
![]() $K_{1,\unicode[STIX]{x1D6E9}}=4.9$
found in a similar single-phase turbulent co-flowing jet with
$K_{1,\unicode[STIX]{x1D6E9}}=4.9$
found in a similar single-phase turbulent co-flowing jet with
![]() $Re_{D}=12\,000$
and
$Re_{D}=12\,000$
and
![]() $\unicode[STIX]{x1D706}=20$
(Pitts Reference Pitts1991b
). This is an order of magnitude higher than the estimated minimum volume loading required for two-way coupling, which is
$\unicode[STIX]{x1D706}=20$
(Pitts Reference Pitts1991b
). This is an order of magnitude higher than the estimated minimum volume loading required for two-way coupling, which is
![]() ${\approx}1\times 10^{-6}$
(Elghobashi Reference Elghobashi2006), implying that the particles influence the gas phase throughout the jet. In addition, the particle Reynolds numbers found in this study (see figure 7) are below the threshold where the gas-phase turbulence is enhanced (Hetsroni Reference Hetsroni1989). Hence turbulence modulation of the gas phase can be concluded to contribute to the reduction in turbulence intensity of the particle phase relative to that of the single phase. Furthermore, the difference between the
${\approx}1\times 10^{-6}$
(Elghobashi Reference Elghobashi2006), implying that the particles influence the gas phase throughout the jet. In addition, the particle Reynolds numbers found in this study (see figure 7) are below the threshold where the gas-phase turbulence is enhanced (Hetsroni Reference Hetsroni1989). Hence turbulence modulation of the gas phase can be concluded to contribute to the reduction in turbulence intensity of the particle phase relative to that of the single phase. Furthermore, the difference between the
![]() $Sk_{D}=0.3$
and the single-phase case is typically greater for
$Sk_{D}=0.3$
and the single-phase case is typically greater for
![]() $u_{p,c}^{\prime }$
than it is for
$u_{p,c}^{\prime }$
than it is for
![]() $v_{p,c}^{\prime }$
. From this, it can be deduced that the gas-phase axial velocity fluctuations are damped more significantly than the radial velocity fluctuations.
$v_{p,c}^{\prime }$
. From this, it can be deduced that the gas-phase axial velocity fluctuations are damped more significantly than the radial velocity fluctuations.
Figure 9 also shows that
![]() $u_{0,c}^{\prime }/U_{0,c}$
increases sharply in the region
$u_{0,c}^{\prime }/U_{0,c}$
increases sharply in the region
![]() $4\lesssim x/D\lesssim 9$
for the single-phase case. This sharp increase, which has also been implicitly shown in previous measurements (Boguslawski & Popiel Reference Boguslawski and Popiel1979; Fellouah, Ball & Pollard Reference Fellouah, Ball and Pollard2009), coincides with the region where the mixing layer converges onto the jet axis. The same trend can be observed for the particle phase, although the magnitude of the increase is not as great due to the partial response of the particles to the flow and turbulence modulation of the gas phase. The location of this increase also moves further downstream as the Stokes number is increased, probably due to the greater particle inertia. The single-phase axial profile of
$4\lesssim x/D\lesssim 9$
for the single-phase case. This sharp increase, which has also been implicitly shown in previous measurements (Boguslawski & Popiel Reference Boguslawski and Popiel1979; Fellouah, Ball & Pollard Reference Fellouah, Ball and Pollard2009), coincides with the region where the mixing layer converges onto the jet axis. The same trend can be observed for the particle phase, although the magnitude of the increase is not as great due to the partial response of the particles to the flow and turbulence modulation of the gas phase. The location of this increase also moves further downstream as the Stokes number is increased, probably due to the greater particle inertia. The single-phase axial profile of
![]() $v_{0,c}^{\prime }/U_{0,c}$
also exhibits a similar sharp increase in the region
$v_{0,c}^{\prime }/U_{0,c}$
also exhibits a similar sharp increase in the region
![]() $4\lesssim x/D\lesssim 9$
. However, the particle phase displays a similar increase in
$4\lesssim x/D\lesssim 9$
. However, the particle phase displays a similar increase in
![]() $v_{p,c}^{\prime }/U_{p,c}$
only for the two lower Stokes number cases,
$v_{p,c}^{\prime }/U_{p,c}$
only for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4. This indicates that particles with
$Sk_{D}=0.3$
and 1.4. This indicates that particles with
![]() $Sk_{D}>1.4$
have a significantly weak response to radial velocity fluctuations in the gas phase. Furthermore, the axial profiles of
$Sk_{D}>1.4$
have a significantly weak response to radial velocity fluctuations in the gas phase. Furthermore, the axial profiles of
![]() $v_{p,c}^{\prime }/U_{p,c}$
exhibit the strongest dependence on Stokes number over the range
$v_{p,c}^{\prime }/U_{p,c}$
exhibit the strongest dependence on Stokes number over the range
![]() $1.4\lesssim Sk_{D}\lesssim 11.2$
. In contrast with the mean velocity and velocity half-width, the axial profiles of
$1.4\lesssim Sk_{D}\lesssim 11.2$
. In contrast with the mean velocity and velocity half-width, the axial profiles of
![]() $u_{p,c}^{\prime }/U_{p,c}$
and
$u_{p,c}^{\prime }/U_{p,c}$
and
![]() $v_{p,c}^{\prime }/U_{p,c}$
have not approached the asymptotic pseudo-similar regime, with the turbulence intensities gradually increasing with axial distance throughout the measurement region (
$v_{p,c}^{\prime }/U_{p,c}$
have not approached the asymptotic pseudo-similar regime, with the turbulence intensities gradually increasing with axial distance throughout the measurement region (
![]() $0\leqslant x/D\leqslant 31.5$
). This is consistent with previous single-phase measurements, which reveal that the turbulence intensity only approaches an asymptotic value at
$0\leqslant x/D\leqslant 31.5$
). This is consistent with previous single-phase measurements, which reveal that the turbulence intensity only approaches an asymptotic value at
![]() $x/D\gtrsim 70$
(Panchapakesan & Lumley Reference Panchapakesan and Lumley1993). Extrapolation of the present trends in
$x/D\gtrsim 70$
(Panchapakesan & Lumley Reference Panchapakesan and Lumley1993). Extrapolation of the present trends in
![]() $u_{p,c}^{\prime }/U_{p,c}$
and
$u_{p,c}^{\prime }/U_{p,c}$
and
![]() $v_{p,c}^{\prime }/U_{p,c}$
suggest that these quantities will approach a constant value with increasing axial distance as the Stokes number is increased, at least within the region upstream of the influence of the co-flow. At
$v_{p,c}^{\prime }/U_{p,c}$
suggest that these quantities will approach a constant value with increasing axial distance as the Stokes number is increased, at least within the region upstream of the influence of the co-flow. At
![]() $x/D=30$
,
$x/D=30$
,
![]() $u_{0,c}^{\prime }/U_{0,c}\approx 0.25$
for the single-phase case, which is similar to the value
$u_{0,c}^{\prime }/U_{0,c}\approx 0.25$
for the single-phase case, which is similar to the value
![]() $u_{0,c}^{\prime }/U_{0,c}\approx 0.24$
reported for other single-phase jets at same axial distance (Ball et al.
Reference Ball, Fellouah and Pollard2012).
$u_{0,c}^{\prime }/U_{0,c}\approx 0.24$
reported for other single-phase jets at same axial distance (Ball et al.
Reference Ball, Fellouah and Pollard2012).
The axial profiles of
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
shows that the anisotropy of the turbulent fluctuations exhibited by the particles is significantly larger than unity throughout the entire measurement region for all investigated Stokes numbers. This further highlights the high degree of anisotropy in the jet, with
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
shows that the anisotropy of the turbulent fluctuations exhibited by the particles is significantly larger than unity throughout the entire measurement region for all investigated Stokes numbers. This further highlights the high degree of anisotropy in the jet, with
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
even reaching values of
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
even reaching values of
![]() ${\approx}4{-}5$
for the highest Stokes number case. These high levels of anisotropy have also been observed in a similar particle-laden jet by Hardalupas et al. (Reference Hardalupas, Taylor and Whitelaw1989), who measured
${\approx}4{-}5$
for the highest Stokes number case. These high levels of anisotropy have also been observed in a similar particle-laden jet by Hardalupas et al. (Reference Hardalupas, Taylor and Whitelaw1989), who measured
![]() $2.3\lesssim u_{p,c}^{\prime }/v_{p,c}^{\prime }\lesssim 5.8$
along the centreline at
$2.3\lesssim u_{p,c}^{\prime }/v_{p,c}^{\prime }\lesssim 5.8$
along the centreline at
![]() $Sk_{D}=8.6$
and
$Sk_{D}=8.6$
and
![]() $\unicode[STIX]{x1D719}=0.8$
. The axial profiles of
$\unicode[STIX]{x1D719}=0.8$
. The axial profiles of
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
are similar for the two lower Stokes number cases,
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
are similar for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4, as well as the two highest Stokes number cases,
$Sk_{D}=0.3$
and 1.4, as well as the two highest Stokes number cases,
![]() $Sk_{D}=11.2$
and 22.4. This suggests that the largest change in anisotropy occurs between
$Sk_{D}=11.2$
and 22.4. This suggests that the largest change in anisotropy occurs between
![]() $1.4\lesssim Sk_{D}\lesssim 11.2$
, consistent with the trends in
$1.4\lesssim Sk_{D}\lesssim 11.2$
, consistent with the trends in
![]() $v_{p,c}^{\prime }/U_{p,c}$
, as discussed previously. At large distances from the exit plane,
$v_{p,c}^{\prime }/U_{p,c}$
, as discussed previously. At large distances from the exit plane,
![]() $x/D\gtrsim 11$
,
$x/D\gtrsim 11$
,
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
decreases steadily for all Stokes numbers. This suggests that, for a self-similar jet,
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
decreases steadily for all Stokes numbers. This suggests that, for a self-similar jet,
![]() $u_{c}^{\prime }/v_{c}^{\prime }\rightarrow 1$
as
$u_{c}^{\prime }/v_{c}^{\prime }\rightarrow 1$
as
![]() $x/D\rightarrow \infty$
.
$x/D\rightarrow \infty$
.
The results also show that, for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4, the values of
$Sk_{D}=0.3$
and 1.4, the values of
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
are typically lower than the corresponding values for the single-phase case. As previously discussed, this is attributed to the preferential damping of the axial gas-phase velocity fluctuations over their radial counterparts by the presence of the particles (see also figure 9
c,d), although further measurements of the two phases simultaneously is required to confirm this. Throughout the axial extent of the measurement region, the anisotropy in the centreline velocity fluctuations increases as
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
are typically lower than the corresponding values for the single-phase case. As previously discussed, this is attributed to the preferential damping of the axial gas-phase velocity fluctuations over their radial counterparts by the presence of the particles (see also figure 9
c,d), although further measurements of the two phases simultaneously is required to confirm this. Throughout the axial extent of the measurement region, the anisotropy in the centreline velocity fluctuations increases as
![]() $Sk_{D}$
is increased, consistent with the measured anisotropy at the jet exit (figure 10). Interestingly, the axial profile of
$Sk_{D}$
is increased, consistent with the measured anisotropy at the jet exit (figure 10). Interestingly, the axial profile of
![]() $u_{p,c}^{\prime }/v_{p,c}^{\prime }$
for the
$u_{p,c}^{\prime }/v_{p,c}^{\prime }$
for the
![]() $Sk_{D}=2.8$
case approximately matches that of the single phase throughout the axial extent of the measurement region.
$Sk_{D}=2.8$
case approximately matches that of the single phase throughout the axial extent of the measurement region.

Figure 10. The influence of Stokes number,
![]() $Sk_{D}$
, on the axial,
$Sk_{D}$
, on the axial,
![]() $\overline{u_{c}^{\prime }/U_{c}}$
, and radial,
$\overline{u_{c}^{\prime }/U_{c}}$
, and radial,
![]() $\overline{v_{c}^{\prime }/U_{c}}$
, turbulence intensities, together with the ratio
$\overline{v_{c}^{\prime }/U_{c}}$
, turbulence intensities, together with the ratio
![]() $\overline{u_{c}^{\prime }}/\overline{v_{c}^{\prime }}$
on the centreline averaged over the region
$\overline{u_{c}^{\prime }}/\overline{v_{c}^{\prime }}$
on the centreline averaged over the region
![]() $20\leqslant x/D\leqslant 30$
for both the particle phase (open symbols) and the single phase (closed symbols).
$20\leqslant x/D\leqslant 30$
for both the particle phase (open symbols) and the single phase (closed symbols).
Figure 10 presents the axial and radial turbulence intensity averaged over the region
![]() $20\leqslant x/D\leqslant 30$
on centreline,
$20\leqslant x/D\leqslant 30$
on centreline,
![]() $\overline{u_{c}^{\prime }/U_{c}}$
and
$\overline{u_{c}^{\prime }/U_{c}}$
and
![]() $\overline{v_{c}^{\prime }/U_{c}}$
, respectively, as well as the ratio
$\overline{v_{c}^{\prime }/U_{c}}$
, respectively, as well as the ratio
![]() $\overline{u_{c}^{\prime }}/\overline{v_{c}^{\prime }}$
, as a function of exit Stokes number,
$\overline{u_{c}^{\prime }}/\overline{v_{c}^{\prime }}$
, as a function of exit Stokes number,
![]() $Sk_{D}$
. This figure more clearly illustrates our previous observation that an increase in
$Sk_{D}$
. This figure more clearly illustrates our previous observation that an increase in
![]() $Sk_{D}$
causes a decrease in the turbulence intensity and an increase in the anisotropy of the velocity fluctuations. Furthermore, the influence of
$Sk_{D}$
causes a decrease in the turbulence intensity and an increase in the anisotropy of the velocity fluctuations. Furthermore, the influence of
![]() $Sk_{D}$
on
$Sk_{D}$
on
![]() $\overline{u_{p,c}^{\prime }/U_{p,c}}$
and
$\overline{u_{p,c}^{\prime }/U_{p,c}}$
and
![]() $\overline{v_{p,c}^{\prime }/U_{p,c}}$
is greatest over the range
$\overline{v_{p,c}^{\prime }/U_{p,c}}$
is greatest over the range
![]() $0.3\leqslant Sk_{D}\leqslant 2.8$
. Importantly, the difference between
$0.3\leqslant Sk_{D}\leqslant 2.8$
. Importantly, the difference between
![]() $\overline{u_{p,c}^{\prime }/U_{p,c}}$
and
$\overline{u_{p,c}^{\prime }/U_{p,c}}$
and
![]() $\overline{u_{o,c}^{\prime }/U_{o,c}}$
is large relative to the corresponding difference between
$\overline{u_{o,c}^{\prime }/U_{o,c}}$
is large relative to the corresponding difference between
![]() $\overline{v_{p,c}^{\prime }/U_{p,c}}$
and
$\overline{v_{p,c}^{\prime }/U_{p,c}}$
and
![]() $\overline{v_{o,c}^{\prime }/U_{o,c}}$
(the latter shown as the closed square red symbol in figure 10) for all Stokes numbers, including the lowest Stokes number case of
$\overline{v_{o,c}^{\prime }/U_{o,c}}$
(the latter shown as the closed square red symbol in figure 10) for all Stokes numbers, including the lowest Stokes number case of
![]() $Sk_{D}=0.3$
. Since the particles for the
$Sk_{D}=0.3$
. Since the particles for the
![]() $Sk_{D}=0.3$
case are expected to exhibit good response to the velocity fluctuations in the flow due to the low local Stokes numbers (see figure 9
f), these differences are further evidence that the presence of particles causes modulation of the gas-phase velocity fluctuations that is more significant in the axial direction than the radial direction. This results in values of
$Sk_{D}=0.3$
case are expected to exhibit good response to the velocity fluctuations in the flow due to the low local Stokes numbers (see figure 9
f), these differences are further evidence that the presence of particles causes modulation of the gas-phase velocity fluctuations that is more significant in the axial direction than the radial direction. This results in values of
![]() $\overline{u_{p,c}^{\prime }}/\overline{v_{p,c}^{\prime }}$
for the two lower Stokes number cases,
$\overline{u_{p,c}^{\prime }}/\overline{v_{p,c}^{\prime }}$
for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4, which are lower than the corresponding value of the single-phase case. The value of
$Sk_{D}=0.3$
and 1.4, which are lower than the corresponding value of the single-phase case. The value of
![]() $\overline{u_{p,c}^{\prime }}/\overline{v_{p,c}^{\prime }}$
is above unity for all cases, highlighting that even at
$\overline{u_{p,c}^{\prime }}/\overline{v_{p,c}^{\prime }}$
is above unity for all cases, highlighting that even at
![]() $20\leqslant x/D\leqslant 30$
there remains significant anisotropy in the velocity fluctuations in both phases along the centreline of the jet.
$20\leqslant x/D\leqslant 30$
there remains significant anisotropy in the velocity fluctuations in both phases along the centreline of the jet.
It has previously been proposed that the large values of
![]() $u_{p}^{\prime }/v_{p}^{\prime }>1$
within a jet is due to a mechanism dubbed ‘fan spreading’. It has been hypothesised that, for a flow with significant velocity gradients in the radial direction, the radial velocity fluctuations in the particle phase cause an increase in
$u_{p}^{\prime }/v_{p}^{\prime }>1$
within a jet is due to a mechanism dubbed ‘fan spreading’. It has been hypothesised that, for a flow with significant velocity gradients in the radial direction, the radial velocity fluctuations in the particle phase cause an increase in
![]() $u_{p}^{\prime }$
that are in addition to the particle-phase axial velocity fluctuations caused by turbulence (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1989). However, this explanation predicts an increase in
$u_{p}^{\prime }$
that are in addition to the particle-phase axial velocity fluctuations caused by turbulence (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1989). However, this explanation predicts an increase in
![]() $u_{p}^{\prime }$
with
$u_{p}^{\prime }$
with
![]() $Sk_{D}$
, which is inconsistent with the current measurements (figure 9
c). Hence, there is a need for a different explanation.
$Sk_{D}$
, which is inconsistent with the current measurements (figure 9
c). Hence, there is a need for a different explanation.
As an alternative to the previously hypothesised ‘fan spreading’, we propose that the current measurements can be explained by assuming that the dominant turbulent fluid time and/or length scales in the axial direction are different from, and typically larger than, those in the radial direction. This difference in these scales can be explained by an anisotropic structure of the large-scale eddies, for which a helical mode seems to be most plausible. The helical mode has been shown to exist right from the exit plane of a turbulent pipe jet (Mullyadzhanov, Abdurakipov & Hanjalić Reference Mullyadzhanov, Abdurakipov and Hanjalić2016) and shown to be the dominant structure in the far field of round turbulent jets (Yoda, Hesselink & Mungal Reference Yoda, Hesselink and Mungal1992). In addition, it has been shown to increase radial fluid motion (and speed) while generating length scales that are smaller in the radial direction than the axial (Tso & Hussain Reference Tso and Hussain1989). The greater length scale in the axial direction relative to the radial direction is significant because it implies that the Stokes number in the two directions are also different. This, together with the earlier assessment that the effect of trajectory crossing due to gravity is negligible, implies that the Stokes number of a particle in the axial direction is lower than that in the radial direction, causing it to respond preferentially to the axial fluctuations regardless of the orientation of the jet.
However, the nonlinear relationship between the Stokes number and the particle response to turbulent motions, particularly in the regime where
![]() $Sk_{D}\approx 1$
, causes the anisotropy to increase with
$Sk_{D}\approx 1$
, causes the anisotropy to increase with
![]() $Sk_{D}$
in this regime. That is, the particle response to gas-phase velocity fluctuations in the radial direction will decrease at a greater rate than in the axial direction, resulting in an increase in
$Sk_{D}$
in this regime. That is, the particle response to gas-phase velocity fluctuations in the radial direction will decrease at a greater rate than in the axial direction, resulting in an increase in
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
, as
$u_{p}^{\prime }/v_{p}^{\prime }$
, as
![]() $Sk_{D}$
is increased in the regime where
$Sk_{D}$
is increased in the regime where
![]() $Sk_{D}\approx 1$
, consistent with the current measurements (see figures 9
c,d and 10). However, it can be anticipated that the values of
$Sk_{D}\approx 1$
, consistent with the current measurements (see figures 9
c,d and 10). However, it can be anticipated that the values of
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
will converge to a constant value where
$u_{p}^{\prime }/v_{p}^{\prime }$
will converge to a constant value where
![]() $Sk_{D}\gg 1$
. These results provide strong evidence that the response of a particle to the flow can only be adequately described by the use of two Stokes numbers, one for the axial and another for the radial direction, instead of the single Stokes number that has typically been used in the past.
$Sk_{D}\gg 1$
. These results provide strong evidence that the response of a particle to the flow can only be adequately described by the use of two Stokes numbers, one for the axial and another for the radial direction, instead of the single Stokes number that has typically been used in the past.
The above finding also implies that the modulation of the gas-phase turbulence by particles will also be different in the axial and radial directions. That is, the preferential response of particles to axial fluctuations at large
![]() $Sk_{D}$
implies that these particles will exhibit a greater ‘slip’ between the two phases in the radial direction than in the axial direction. This, in turn, implies that particles with larger
$Sk_{D}$
implies that these particles will exhibit a greater ‘slip’ between the two phases in the radial direction than in the axial direction. This, in turn, implies that particles with larger
![]() $Sk_{D}$
will preferentially dampen turbulent motions in the radial direction over those in the axial direction, which will further amplify anisotropy in the gas phase. Since this anisotropic modulation of the gas-phase turbulence by the particles is coupled with the anisotropic response of the particles to turbulent motions in the gas phase, these two processes cannot be modelled independently from each other. Furthermore, the decrease in local Stokes number with axial distance in a jet flow (figure 9
f) implies that the extent of this coupling will also change with axial distance, which further complicates these processes.
$Sk_{D}$
will preferentially dampen turbulent motions in the radial direction over those in the axial direction, which will further amplify anisotropy in the gas phase. Since this anisotropic modulation of the gas-phase turbulence by the particles is coupled with the anisotropic response of the particles to turbulent motions in the gas phase, these two processes cannot be modelled independently from each other. Furthermore, the decrease in local Stokes number with axial distance in a jet flow (figure 9
f) implies that the extent of this coupling will also change with axial distance, which further complicates these processes.

Figure 11. The influence of exit Stokes number,
![]() $Sk_{D}$
, on the inverse velocity decay coefficient,
$Sk_{D}$
, on the inverse velocity decay coefficient,
![]() $K_{1,U}^{-1}$
, and velocity half-width expansion coefficient,
$K_{1,U}^{-1}$
, and velocity half-width expansion coefficient,
![]() $K_{2,U}$
, for both the particle-phase (open symbols) and single-phase (closed symbols) cases.
$K_{2,U}$
, for both the particle-phase (open symbols) and single-phase (closed symbols) cases.
Figure 11 presents the dependence of the inverse velocity decay coefficient,
![]() $K_{1,U}^{-1}$
(see (3.1)) and jet expansion coefficient,
$K_{1,U}^{-1}$
(see (3.1)) and jet expansion coefficient,
![]() $K_{2,U}$
(see (3.2)), on
$K_{2,U}$
(see (3.2)), on
![]() $Sk_{D}$
. It can be seen that both
$Sk_{D}$
. It can be seen that both
![]() $K_{1,Up}^{-1}$
and
$K_{1,Up}^{-1}$
and
![]() $K_{2,Up}$
decrease with increasing
$K_{2,Up}$
decrease with increasing
![]() $Sk_{D}$
, consistent with previous measurements (Prevost et al.
Reference Prevost, Boree, Nuglisch and Charnay1996). In both cases, the most significant change occurs over the range
$Sk_{D}$
, consistent with previous measurements (Prevost et al.
Reference Prevost, Boree, Nuglisch and Charnay1996). In both cases, the most significant change occurs over the range
![]() $1.4\lesssim Sk_{D}\lesssim 11.2$
. The present measurements of
$1.4\lesssim Sk_{D}\lesssim 11.2$
. The present measurements of
![]() $K_{1,U0}=6.1$
and
$K_{1,U0}=6.1$
and
![]() $K_{2,U0}=0.081$
for the single phase are consistent with previously measured values of
$K_{2,U0}=0.081$
for the single phase are consistent with previously measured values of
![]() $5.9\leqslant K_{1,U0}\leqslant 6.5$
(Boguslawski & Popiel Reference Boguslawski and Popiel1979; Xu & Antonia Reference Xu and Antonia2002) and
$5.9\leqslant K_{1,U0}\leqslant 6.5$
(Boguslawski & Popiel Reference Boguslawski and Popiel1979; Xu & Antonia Reference Xu and Antonia2002) and
![]() $0.07\leqslant K_{2,U0}\leqslant 0.086$
(Boguslawski & Popiel Reference Boguslawski and Popiel1979; Sautet & Stepowski Reference Sautet and Stepowski1995; Xu & Antonia Reference Xu and Antonia2002) performed in unconfined, single-phase pipe jets. The jet expansion coefficient for the two lower Stokes number cases,
$0.07\leqslant K_{2,U0}\leqslant 0.086$
(Boguslawski & Popiel Reference Boguslawski and Popiel1979; Sautet & Stepowski Reference Sautet and Stepowski1995; Xu & Antonia Reference Xu and Antonia2002) performed in unconfined, single-phase pipe jets. The jet expansion coefficient for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4, closely matches the single-phase case. However, the jet decay coefficient for the two-phase jet is significantly lower than the single-phase jet, suggesting that the presence of particles affects the jet decay rate more significantly than the spreading rate.
$Sk_{D}=0.3$
and 1.4, closely matches the single-phase case. However, the jet decay coefficient for the two-phase jet is significantly lower than the single-phase jet, suggesting that the presence of particles affects the jet decay rate more significantly than the spreading rate.

Figure 12. The normalised mean velocity,
![]() $U/U_{c}$
, as a function of normalised radial distance,
$U/U_{c}$
, as a function of normalised radial distance,
![]() $r/r_{0.5,U}$
, for both the particle phase (
$r/r_{0.5,U}$
, for both the particle phase (
![]() $p$
) and the single phase (0) at the axial location
$p$
) and the single phase (0) at the axial location
![]() $x/D=10$
.
$x/D=10$
.
Figure 12 presents the normalised radial distribution of mean axial velocity at the axial location
![]() $x/D=10$
. The results show that
$x/D=10$
. The results show that
![]() $U_{p}/U_{p,c}$
collapse onto a similar profile, suggesting that the mean particle velocity approaches self-similarity by
$U_{p}/U_{p,c}$
collapse onto a similar profile, suggesting that the mean particle velocity approaches self-similarity by
![]() $x/D\approx 10$
for all
$x/D\approx 10$
for all
![]() $Sk_{D}$
. The radial profiles closely match a Gaussian profile of the form
$Sk_{D}$
. The radial profiles closely match a Gaussian profile of the form
![]() $U/U_{c}=\exp [\unicode[STIX]{x1D6FC}(r/r_{0.5,U})^{2}]$
for all Stokes numbers, including the single phase, where
$U/U_{c}=\exp [\unicode[STIX]{x1D6FC}(r/r_{0.5,U})^{2}]$
for all Stokes numbers, including the single phase, where
![]() $\unicode[STIX]{x1D6FC}=\ln 0.5=-0.693$
following the definition of
$\unicode[STIX]{x1D6FC}=\ln 0.5=-0.693$
following the definition of
![]() $r_{0.5,U}$
. This value of
$r_{0.5,U}$
. This value of
![]() $\unicode[STIX]{x1D6FC}$
matches closely the value of
$\unicode[STIX]{x1D6FC}$
matches closely the value of
![]() $\unicode[STIX]{x1D6FC}=-0.691$
found for a similar but unconfined single-phase turbulent pipe jet (Boguslawski & Popiel Reference Boguslawski and Popiel1979).
$\unicode[STIX]{x1D6FC}=-0.691$
found for a similar but unconfined single-phase turbulent pipe jet (Boguslawski & Popiel Reference Boguslawski and Popiel1979).

Figure 13. The axial and radial turbulence intensities,
![]() $u^{\prime }/U$
and
$u^{\prime }/U$
and
![]() $v^{\prime }/U$
, respectively, as well as the ratio
$v^{\prime }/U$
, respectively, as well as the ratio
![]() $u^{\prime }/v^{\prime }$
, as a function of normalised radial distance,
$u^{\prime }/v^{\prime }$
, as a function of normalised radial distance,
![]() $r/r_{0.5,U}$
, for both the particle phase (
$r/r_{0.5,U}$
, for both the particle phase (
![]() $p$
) and the single phase (0) at
$p$
) and the single phase (0) at
![]() $x/D=10$
(a,c,e) and
$x/D=10$
(a,c,e) and
![]() $x/D=30$
(b,d,f). Note that all panels use identical legends.
$x/D=30$
(b,d,f). Note that all panels use identical legends.
Figure 13 presents the radial profiles of axial and radial turbulence intensities,
![]() $u^{\prime }/U$
and
$u^{\prime }/U$
and
![]() $v^{\prime }/U$
, respectively, as well as the ratio
$v^{\prime }/U$
, respectively, as well as the ratio
![]() $u^{\prime }/v^{\prime }$
, at
$u^{\prime }/v^{\prime }$
, at
![]() $x/D=10$
and
$x/D=10$
and
![]() $x/D=30$
for both the particle-phase and single-phase cases. In general, the turbulence intensities of the particle phase are lower than the single phase, due to the partial response of the particles to turbulent motions in the gas phase, together with a possible role of turbulence modulation of the gas phase. Interestingly, at
$x/D=30$
for both the particle-phase and single-phase cases. In general, the turbulence intensities of the particle phase are lower than the single phase, due to the partial response of the particles to turbulent motions in the gas phase, together with a possible role of turbulence modulation of the gas phase. Interestingly, at
![]() $x/D=10$
for the
$x/D=10$
for the
![]() $Sk_{D}=0.3$
case, the radial profile of
$Sk_{D}=0.3$
case, the radial profile of
![]() $v_{p}^{\prime }/U_{p}$
matches the single-phase case while the radial profile of
$v_{p}^{\prime }/U_{p}$
matches the single-phase case while the radial profile of
![]() $u_{p}^{\prime }/U_{p}$
departs the single-phase case. Furthermore, at
$u_{p}^{\prime }/U_{p}$
departs the single-phase case. Furthermore, at
![]() $x/D=30$
where the local Stokes number is sufficiently small (
$x/D=30$
where the local Stokes number is sufficiently small (
![]() $Sk_{c}\approx 0.02$
, see figure 9
f) for the
$Sk_{c}\approx 0.02$
, see figure 9
f) for the
![]() $Sk_{D}=0.3$
case such that the particles are expected to respond strongly to turbulent fluctuations in the flow, the difference between the particle phase and the single phase is more significant in the radial profiles of
$Sk_{D}=0.3$
case such that the particles are expected to respond strongly to turbulent fluctuations in the flow, the difference between the particle phase and the single phase is more significant in the radial profiles of
![]() $u_{p}^{\prime }/U_{p}$
than it is in the radial profiles of
$u_{p}^{\prime }/U_{p}$
than it is in the radial profiles of
![]() $v_{p}^{\prime }/U_{p}$
. These findings are consistent with the preferred modulation of the gas-phase axial velocity fluctuations over the radial velocity fluctuations by the presence of the particles, as previously discussed. The preferential damping of axial velocity fluctuations over radial velocity fluctuations results in values of
$v_{p}^{\prime }/U_{p}$
. These findings are consistent with the preferred modulation of the gas-phase axial velocity fluctuations over the radial velocity fluctuations by the presence of the particles, as previously discussed. The preferential damping of axial velocity fluctuations over radial velocity fluctuations results in values of
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
that are lower than the single-phase case across the span of the jet, at least for the two lower Stokes number cases,
$u_{p}^{\prime }/v_{p}^{\prime }$
that are lower than the single-phase case across the span of the jet, at least for the two lower Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4.
$Sk_{D}=0.3$
and 1.4.
The results also show that, at
![]() $x/D=10$
, the turbulence intensities for the single-phase case increase with radial distance
$x/D=10$
, the turbulence intensities for the single-phase case increase with radial distance
![]() $r/r_{0.5,U}$
. While these trends are also observed in the particle-phase radial profiles of
$r/r_{0.5,U}$
. While these trends are also observed in the particle-phase radial profiles of
![]() $u_{p}^{\prime }/U_{p}$
for all
$u_{p}^{\prime }/U_{p}$
for all
![]() $Sk_{D},$
they are only observed in the radial profiles of
$Sk_{D},$
they are only observed in the radial profiles of
![]() $v_{p}^{\prime }/U_{p}$
for the two lowest Stokes number cases,
$v_{p}^{\prime }/U_{p}$
for the two lowest Stokes number cases,
![]() $Sk_{D}=0.3$
and 1.4. Furthermore, at both
$Sk_{D}=0.3$
and 1.4. Furthermore, at both
![]() $x/D=10$
and 30, the values of
$x/D=10$
and 30, the values of
![]() $v_{p}^{\prime }/U_{p}$
decrease with an increase in
$v_{p}^{\prime }/U_{p}$
decrease with an increase in
![]() $Sk_{D}$
at a greater rate than do the values of
$Sk_{D}$
at a greater rate than do the values of
![]() $u_{p}^{\prime }/U_{p}$
. These findings are further evidence that the particles respond to axial velocity fluctuations in the gas phase differently than to the radial velocity fluctuations, so that a single Stokes number cannot adequately characterise the response of particles to a turbulent flow. As previously discussed, the different response of the particles to axial and radial velocity fluctuations leads to an increase in
$u_{p}^{\prime }/U_{p}$
. These findings are further evidence that the particles respond to axial velocity fluctuations in the gas phase differently than to the radial velocity fluctuations, so that a single Stokes number cannot adequately characterise the response of particles to a turbulent flow. As previously discussed, the different response of the particles to axial and radial velocity fluctuations leads to an increase in
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
with
$u_{p}^{\prime }/v_{p}^{\prime }$
with
![]() $Sk_{D}$
, consistent with the radial measurements at both axial locations
$Sk_{D}$
, consistent with the radial measurements at both axial locations
![]() $x/D=10$
and
$x/D=10$
and
![]() $x/D=30$
(figure 13). From figure 13 it can also be seen that the peak values of the ratio
$x/D=30$
(figure 13). From figure 13 it can also be seen that the peak values of the ratio
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
occur for the higher Stokes number cases, most notably at
$u_{p}^{\prime }/v_{p}^{\prime }$
occur for the higher Stokes number cases, most notably at
![]() $r/r_{0.5,Up}\approx 0.5$
, 0.55 and 0.7 for
$r/r_{0.5,Up}\approx 0.5$
, 0.55 and 0.7 for
![]() $Sk_{D}=5.6$
, 11.2 and 22.4, respectively at the axial location
$Sk_{D}=5.6$
, 11.2 and 22.4, respectively at the axial location
![]() $x/D=10$
. However, the extent of the anisotropy varies only weakly with radial distance. This is consistent with the motions being dominated by large-scale coherent structures that have different turbulence scales in the axial and radial directions.
$x/D=10$
. However, the extent of the anisotropy varies only weakly with radial distance. This is consistent with the motions being dominated by large-scale coherent structures that have different turbulence scales in the axial and radial directions.

Figure 14. The mean distributions of particle concentration normalised by the bulk-mean concentration,
![]() $\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, for all investigated Stokes numbers,
$\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, for all investigated Stokes numbers,
![]() $Sk_{D}$
.
$Sk_{D}$
.
5.2 Concentration measurements
Figure 14 presents the mean (time-averaged) distributions of particle concentration
![]() $\unicode[STIX]{x1D6E9}$
, normalised by the bulk concentration,
$\unicode[STIX]{x1D6E9}$
, normalised by the bulk concentration,
![]() $\unicode[STIX]{x1D6E9}_{b}$
, within the turbulent jet for all investigated Stokes numbers. Here, the bulk concentration is defined as
$\unicode[STIX]{x1D6E9}_{b}$
, within the turbulent jet for all investigated Stokes numbers. Here, the bulk concentration is defined as
Here we reiterate that although we have published similar results for
![]() $Sk_{D}=0.3$
, 1.4 and 11.2 (Lau & Nathan Reference Lau and Nathan2014), the current dataset, in its entirety, is completely new. The results show that the concentration distributions are different for each Stokes number case, with the distributions of the three lower Stokes numbers,
$Sk_{D}=0.3$
, 1.4 and 11.2 (Lau & Nathan Reference Lau and Nathan2014), the current dataset, in its entirety, is completely new. The results show that the concentration distributions are different for each Stokes number case, with the distributions of the three lower Stokes numbers,
![]() $Sk_{D}=0.3$
, 1.4 and 2.8 differing quite significantly from the three higher Stokes,
$Sk_{D}=0.3$
, 1.4 and 2.8 differing quite significantly from the three higher Stokes,
![]() $Sk_{D}=5.6$
, 11.2 and 22.4. For the three lower Stokes numbers, the concentration distributions at the exit appear relatively uniform except for the regions close to the edges of the pipe (
$Sk_{D}=5.6$
, 11.2 and 22.4. For the three lower Stokes numbers, the concentration distributions at the exit appear relatively uniform except for the regions close to the edges of the pipe (
![]() $r/D=\pm 0.5$
) for
$r/D=\pm 0.5$
) for
![]() $Sk_{D}=0.3$
and 1.4. By contrast, for the three higher Stokes numbers the particles are preferentially concentrated along the pipe axis at the jet exit.
$Sk_{D}=0.3$
and 1.4. By contrast, for the three higher Stokes numbers the particles are preferentially concentrated along the pipe axis at the jet exit.

Figure 15. The radial profile of particle concentration normalised by the bulk-mean value,
![]() $\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, at the jet exit (
$\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, at the jet exit (
![]() $x/D\approx 0.2$
) for all investigated Stokes numbers,
$x/D\approx 0.2$
) for all investigated Stokes numbers,
![]() $Sk_{D}$
.
$Sk_{D}$
.
Figure 15 presents the radial profiles of the particle concentration normalised by the bulk-mean value,
![]() $\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, at the pipe exit for all investigated Stokes numbers. The results show that the particle concentration profile is significantly influenced by the Stokes number, with the particles preferentially concentrated at the jet edge resulting in a ‘
$\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{b}$
, at the pipe exit for all investigated Stokes numbers. The results show that the particle concentration profile is significantly influenced by the Stokes number, with the particles preferentially concentrated at the jet edge resulting in a ‘
![]() $\cup$
-shaped’ profile for
$\cup$
-shaped’ profile for
![]() $Sk_{D}=0.3$
and 1.4, and preferentially concentrated at the pipe axis with an approximately linear increase in concentration from the edge to the axis resulting in a ‘
$Sk_{D}=0.3$
and 1.4, and preferentially concentrated at the pipe axis with an approximately linear increase in concentration from the edge to the axis resulting in a ‘
![]() $\wedge$
- shaped’ profile for
$\wedge$
- shaped’ profile for
![]() $Sk_{D}=5.6$
, 11.2 and 22.4. Of the latter three Stokes number cases, the concentration profile appears the most narrow for
$Sk_{D}=5.6$
, 11.2 and 22.4. Of the latter three Stokes number cases, the concentration profile appears the most narrow for
![]() $Sk_{D}=5.6$
, becoming less narrow as the Stokes number is increased. This is attributed to the thinning of the boundary layer with increasing Reynolds number, as the
$Sk_{D}=5.6$
, becoming less narrow as the Stokes number is increased. This is attributed to the thinning of the boundary layer with increasing Reynolds number, as the
![]() $Sk_{D}=5.6$
, 11.2 and 22.4 cases were measured at
$Sk_{D}=5.6$
, 11.2 and 22.4 cases were measured at
![]() $Re_{D}=10\,000$
,
$Re_{D}=10\,000$
,
![]() $20\,000$
and
$20\,000$
and
![]() $40\,000$
, respectively. For the
$40\,000$
, respectively. For the
![]() $Sk_{D}=2.8$
case, the concentration profile is approximately uniform, which is a result of the transition between the two aforementioned concentration profiles. The significant difference in the concentration profile between the
$Sk_{D}=2.8$
case, the concentration profile is approximately uniform, which is a result of the transition between the two aforementioned concentration profiles. The significant difference in the concentration profile between the
![]() $Sk_{D}=1.4$
and
$Sk_{D}=1.4$
and
![]() $Sk_{D}=2.8$
cases, which were performed at the same particle number density (see table 3), is further evidence that the effect of number density is secondary to the influence of Stokes number, consistent with our previous measurements (Lau & Nathan Reference Lau and Nathan2014). An explanation for the overall trends in the exit concentration profile has also been proposed in our previous publication (Lau & Nathan Reference Lau and Nathan2014). It is hypothesised that these results can be predominantly attributed to the combined effects of turbophoresis and Saffman lift. Turbophoresis, which causes particles to migrate towards regions of low turbulence intensity in the gas phase (Reeks Reference Reeks1983; Young & Leeming Reference Young and Leeming1997), is deduced to be dominant for low Stokes number particles, resulting in particles migrating towards the viscous sublayer within the pipe (i.e. close to the pipe wall). Saffman lift, which causes particles to migrate towards regions of high axial gas-phase velocity in flows where these particles lag the gas phase (Saffman Reference Saffman1965), is deduced to be dominant for higher Stokes number particles, resulting in an increase in the concentration of these particles at the pipe axis.
$Sk_{D}=2.8$
cases, which were performed at the same particle number density (see table 3), is further evidence that the effect of number density is secondary to the influence of Stokes number, consistent with our previous measurements (Lau & Nathan Reference Lau and Nathan2014). An explanation for the overall trends in the exit concentration profile has also been proposed in our previous publication (Lau & Nathan Reference Lau and Nathan2014). It is hypothesised that these results can be predominantly attributed to the combined effects of turbophoresis and Saffman lift. Turbophoresis, which causes particles to migrate towards regions of low turbulence intensity in the gas phase (Reeks Reference Reeks1983; Young & Leeming Reference Young and Leeming1997), is deduced to be dominant for low Stokes number particles, resulting in particles migrating towards the viscous sublayer within the pipe (i.e. close to the pipe wall). Saffman lift, which causes particles to migrate towards regions of high axial gas-phase velocity in flows where these particles lag the gas phase (Saffman Reference Saffman1965), is deduced to be dominant for higher Stokes number particles, resulting in an increase in the concentration of these particles at the pipe axis.
The axial evolution of the normalised centreline concentration,
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
is presented in figure 16. Consistent with previous understanding, the centreline concentration profile is significantly affected by the Stokes number, partly due to the differences in the exit concentration profiles (as shown in figure 15) (Lau & Nathan Reference Lau and Nathan2014). While
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
is presented in figure 16. Consistent with previous understanding, the centreline concentration profile is significantly affected by the Stokes number, partly due to the differences in the exit concentration profiles (as shown in figure 15) (Lau & Nathan Reference Lau and Nathan2014). While
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
is approximately constant for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
is approximately constant for
![]() $x/D\lesssim 2$
for all
$x/D\lesssim 2$
for all
![]() $Sk_{D}$
, further downstream it increases beyond the exit value for the three lower Stokes numbers,
$Sk_{D}$
, further downstream it increases beyond the exit value for the three lower Stokes numbers,
![]() $Sk_{D}=0.3$
, 1.4 and 2.8, with the highest increase found for the
$Sk_{D}=0.3$
, 1.4 and 2.8, with the highest increase found for the
![]() $Sk_{D}=1.4$
case. In contrast, for
$Sk_{D}=1.4$
case. In contrast, for
![]() $x/D\gtrsim 2$
, the centreline concentration decays approximately linearly with axial distance for the three higher Stokes number cases. Interestingly, there are also subtle local ‘humps’ in the axial concentration profile for these higher Stokes number cases, at
$x/D\gtrsim 2$
, the centreline concentration decays approximately linearly with axial distance for the three higher Stokes number cases. Interestingly, there are also subtle local ‘humps’ in the axial concentration profile for these higher Stokes number cases, at
![]() $x/D\approx 9$
, 11 and 12 for
$x/D\approx 9$
, 11 and 12 for
![]() $Sk_{D}=5.6$
, 11.2 and 22.4, respectively. Further downstream from these local humps,
$Sk_{D}=5.6$
, 11.2 and 22.4, respectively. Further downstream from these local humps,
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
decays at a different rate than upstream from them, suggesting that these humps mark a transition between two regimes of centreline concentration decay. There is also a clear trend that the axial location of the local peaks and humps increases with
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
decays at a different rate than upstream from them, suggesting that these humps mark a transition between two regimes of centreline concentration decay. There is also a clear trend that the axial location of the local peaks and humps increases with
![]() $Sk_{D}$
.
$Sk_{D}$
.

Figure 16. The axial evolution of the normalised centreline concentration,
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
. Also included are the results obtained from a direct numerical simulation of a free particle-laden jet by Picano et al. (Reference Picano, Sardina, Gualtieri and Casciola2010).
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
. Also included are the results obtained from a direct numerical simulation of a free particle-laden jet by Picano et al. (Reference Picano, Sardina, Gualtieri and Casciola2010).
The current observation of peaks and humps in the axial concentration profile are consistent with trends from direct numerical (Picano et al.
Reference Picano, Sardina, Gualtieri and Casciola2010) and large eddy (Wang, Law & Adams Reference Wang, Law and Adams2013) simulations of turbulent particle-laden free jets. The DNS data of Picano et al. taken at
![]() $Sk_{D}=1.0$
and
$Sk_{D}=1.0$
and
![]() $2.0$
are similar to the current measurements at
$2.0$
are similar to the current measurements at
![]() $Sk_{D}=1.4$
and 2.8 (see figure 16), with the magnitude and axial location of the peak
$Sk_{D}=1.4$
and 2.8 (see figure 16), with the magnitude and axial location of the peak
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
approximately equal. However, the current measurements differ significantly from the DNS calculations for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
approximately equal. However, the current measurements differ significantly from the DNS calculations for
![]() $Sk_{D}>2$
. Furthermore, the present measurements also contrast their finding that the humps in
$Sk_{D}>2$
. Furthermore, the present measurements also contrast their finding that the humps in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
coincide with the axial location where the local centreline Stokes number,
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{ec}$
coincide with the axial location where the local centreline Stokes number,
![]() $Sk_{c}\approx 0.5$
, which is not found here (see figure 9
f). A likely explanation for this apparent contradiction can be found in their assumption that the flow is in the one-way coupling regime, that is, their DNS assumes that the particle phase has no influence on the gas phase. This assumption is not valid in the current experiment due to the high particle loading. Additionally, the DNS also utilises exit conditions that differ to the conditions measured in the current experiment. Most notably, the DNS assumes that the particle concentration at exit plane is uniform, while the current experimental measurements show that the exit particle concentration profile is significantly influenced by
$Sk_{c}\approx 0.5$
, which is not found here (see figure 9
f). A likely explanation for this apparent contradiction can be found in their assumption that the flow is in the one-way coupling regime, that is, their DNS assumes that the particle phase has no influence on the gas phase. This assumption is not valid in the current experiment due to the high particle loading. Additionally, the DNS also utilises exit conditions that differ to the conditions measured in the current experiment. Most notably, the DNS assumes that the particle concentration at exit plane is uniform, while the current experimental measurements show that the exit particle concentration profile is significantly influenced by
![]() $Sk_{D}$
(figure 15). These differences are expected to cause further discrepancies in the centreline concentration profiles between the DNS of Picano et al. and the current measurements.
$Sk_{D}$
(figure 15). These differences are expected to cause further discrepancies in the centreline concentration profiles between the DNS of Picano et al. and the current measurements.

Figure 17. The axial evolution of the inverse centreline concentration,
![]() $\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and normalised concentration half-width,
$\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and normalised concentration half-width,
![]() $r_{0.5,\unicode[STIX]{x1D6E9}}/D$
.
$r_{0.5,\unicode[STIX]{x1D6E9}}/D$
.

Figure 18. The influence of exit Stokes number,
![]() $Sk_{D}$
, on the inverse concentration decay coefficient,
$Sk_{D}$
, on the inverse concentration decay coefficient,
![]() $K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
, and concentration half-width expansion coefficient,
$K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
, and concentration half-width expansion coefficient,
![]() $K_{2,\unicode[STIX]{x1D6E9}}$
. Also included are data from passive scalar measurements made in a single-phase turbulent pipe jet (Mi et al.
Reference Mi, Nobes and Nathan2001).
$K_{2,\unicode[STIX]{x1D6E9}}$
. Also included are data from passive scalar measurements made in a single-phase turbulent pipe jet (Mi et al.
Reference Mi, Nobes and Nathan2001).
Figure 17 presents the axial evolution of the normalised inverse centreline concentration,
![]() $\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and concentration half-width,
$\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and concentration half-width,
![]() $r_{0.5,\unicode[STIX]{x1D6E9}}/D$
. The axial distance where the centreline concentration and concentration half-width approaches the regime where
$r_{0.5,\unicode[STIX]{x1D6E9}}/D$
. The axial distance where the centreline concentration and concentration half-width approaches the regime where
![]() $\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}\propto x$
and
$\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}\propto x$
and
![]() $r_{0.5,\unicode[STIX]{x1D6E9}}/D\propto x$
(see (3.1) and (3.2)) is shown to increase with increasing Stokes number, due to the lower response of the particles to the flow (Lau & Nathan Reference Lau and Nathan2014). For the two lower Stokes numbers,
$r_{0.5,\unicode[STIX]{x1D6E9}}/D\propto x$
(see (3.1) and (3.2)) is shown to increase with increasing Stokes number, due to the lower response of the particles to the flow (Lau & Nathan Reference Lau and Nathan2014). For the two lower Stokes numbers,
![]() $Sk_{D}=0.3$
and 1.4, this linear concentration decay and expansion regime occurs at
$Sk_{D}=0.3$
and 1.4, this linear concentration decay and expansion regime occurs at
![]() $x/D\approx 16$
, increasing to
$x/D\approx 16$
, increasing to
![]() $x/D\approx 22$
and
$x/D\approx 22$
and
![]() $x/D\approx 25$
for
$x/D\approx 25$
for
![]() $Sk_{D}=2.8$
and 5.6, respectively. For the two highest Stokes number cases,
$Sk_{D}=2.8$
and 5.6, respectively. For the two highest Stokes number cases,
![]() $Sk_{D}=11.2$
and 22.4,
$Sk_{D}=11.2$
and 22.4,
![]() $\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and
$\unicode[STIX]{x1D6E9}_{ec}/\unicode[STIX]{x1D6E9}_{c}$
and
![]() $r_{0.5,\unicode[STIX]{x1D6E9}}/D$
do not reach the regime of self-similar mean flow within the axial extent of the measurement region.
$r_{0.5,\unicode[STIX]{x1D6E9}}/D$
do not reach the regime of self-similar mean flow within the axial extent of the measurement region.
Interestingly, the centreline concentration decay rate downstream of the near field,
![]() $x/D\gtrsim 25$
, appears to be higher for the
$x/D\gtrsim 25$
, appears to be higher for the
![]() $Sk_{D}=2.8$
and
$Sk_{D}=2.8$
and
![]() $Sk_{D}=5.6$
cases than for the
$Sk_{D}=5.6$
cases than for the
![]() $Sk_{D}=0.3$
and
$Sk_{D}=0.3$
and
![]() $Sk_{D}=1.4$
cases. This is more clearly illustrated in figure 18, which presents the influence of exit Stokes number on the inverse concentration decay coefficient,
$Sk_{D}=1.4$
cases. This is more clearly illustrated in figure 18, which presents the influence of exit Stokes number on the inverse concentration decay coefficient,
![]() $K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
, and concentration expansion coefficient,
$K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
, and concentration expansion coefficient,
![]() $K_{2,\unicode[STIX]{x1D6E9}}$
(see also (3.1) and (3.2)). The inverse concentration decay coefficient
$K_{2,\unicode[STIX]{x1D6E9}}$
(see also (3.1) and (3.2)). The inverse concentration decay coefficient
![]() $K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
increases with
$K_{1,\unicode[STIX]{x1D6E9}}^{-1}$
increases with
![]() $Sk_{D}$
to reach a peak at
$Sk_{D}$
to reach a peak at
![]() $Sk_{D}=5.6$
, beyond which it decreases with further increases in
$Sk_{D}=5.6$
, beyond which it decreases with further increases in
![]() $Sk_{D}$
. For the
$Sk_{D}$
. For the
![]() $Sk_{D}=2.4$
and 5.6 cases,
$Sk_{D}=2.4$
and 5.6 cases,
![]() $K_{1,\unicode[STIX]{x1D6E9}}^{-1}=0.211$
and 0.212, respectively, which are even higher than the value of
$K_{1,\unicode[STIX]{x1D6E9}}^{-1}=0.211$
and 0.212, respectively, which are even higher than the value of
![]() $K_{1,\unicode[STIX]{x1D6E9}}^{-1}=0.216$
previously measured in a single-phase turbulent pipe jet (Mi et al.
Reference Mi, Nobes and Nathan2001). This is because the preferential concentration of the particles on the jet centreline at the pipe exit increases with Stokes number over the range
$K_{1,\unicode[STIX]{x1D6E9}}^{-1}=0.216$
previously measured in a single-phase turbulent pipe jet (Mi et al.
Reference Mi, Nobes and Nathan2001). This is because the preferential concentration of the particles on the jet centreline at the pipe exit increases with Stokes number over the range
![]() $0.3\leqslant Sk_{D}\leqslant 5.6$
(see figure 15), which increases the absolute particle concentration along the centreline downstream of the exit plane. This consequently leads to greater rates of particle diffusion away from the centreline, which in turn increases the centreline concentration decay rate. For
$0.3\leqslant Sk_{D}\leqslant 5.6$
(see figure 15), which increases the absolute particle concentration along the centreline downstream of the exit plane. This consequently leads to greater rates of particle diffusion away from the centreline, which in turn increases the centreline concentration decay rate. For
![]() $Sk_{D}\geqslant 5.6$
, where the particle exit concentration profiles are similar, the centreline concentration decay rate reduces as the Stokes number is increased due to the lower particle response to the flow, as is expected.
$Sk_{D}\geqslant 5.6$
, where the particle exit concentration profiles are similar, the centreline concentration decay rate reduces as the Stokes number is increased due to the lower particle response to the flow, as is expected.
The axial evolution of the concentration half-width presented in figure 17 also exhibits subtle local troughs in the concentration half-widths for all exit Stokes numbers, for example, at
![]() $x/D=5.5$
for
$x/D=5.5$
for
![]() $Sk_{D}=1.4$
and
$Sk_{D}=1.4$
and
![]() $x/D=7$
for
$x/D=7$
for
![]() $Sk_{D}=2.8$
. The location of these troughs move further downstream with increased exit Stokes number and approximately corresponds to the location of the humps in the centreline concentration (figure 16). This is expected because a high peak centreline concentration typically implies that most of the particles are concentrated along the axis, causing the concentration half-width to be small.
$Sk_{D}=2.8$
. The location of these troughs move further downstream with increased exit Stokes number and approximately corresponds to the location of the humps in the centreline concentration (figure 16). This is expected because a high peak centreline concentration typically implies that most of the particles are concentrated along the axis, causing the concentration half-width to be small.

Figure 19. The normalised mean particle concentration,
![]() $\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{c}$
, as a function of normalised radial distance,
$\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D6E9}_{c}$
, as a function of normalised radial distance,
![]() $r/r_{0.5,\unicode[STIX]{x1D6E9}}$
, at the axial location
$r/r_{0.5,\unicode[STIX]{x1D6E9}}$
, at the axial location
![]() $x/D=10$
. Note that symbols are only plotted at every fifth data point for clarity.
$x/D=10$
. Note that symbols are only plotted at every fifth data point for clarity.
Figure 19 presents the mean particle concentration,
![]() $\unicode[STIX]{x1D6E9}$
, normalised by the mean centreline value,
$\unicode[STIX]{x1D6E9}$
, normalised by the mean centreline value,
![]() $\unicode[STIX]{x1D6E9}_{c}$
as a function of normalised radial distance
$\unicode[STIX]{x1D6E9}_{c}$
as a function of normalised radial distance
![]() $r/r_{0.5,\unicode[STIX]{x1D6E9}}$
at the axial location
$r/r_{0.5,\unicode[STIX]{x1D6E9}}$
at the axial location
![]() $x/D=10$
. Similar to the particle velocity profile at the same axial location (figure 12), the radial concentration profiles closely match a Gaussian profile, consistent with single-phase scalar measurements in a turbulent free jet (Mi et al.
Reference Mi, Nobes and Nathan2001), although there are some departures from a pure Gaussian distribution particularly at
$x/D=10$
. Similar to the particle velocity profile at the same axial location (figure 12), the radial concentration profiles closely match a Gaussian profile, consistent with single-phase scalar measurements in a turbulent free jet (Mi et al.
Reference Mi, Nobes and Nathan2001), although there are some departures from a pure Gaussian distribution particularly at
![]() $r/r_{0.5,\unicode[STIX]{x1D6E9}}\gtrsim 1.2$
. This shows that by
$r/r_{0.5,\unicode[STIX]{x1D6E9}}\gtrsim 1.2$
. This shows that by
![]() $x/D=10$
, the radial concentration profiles have approached a Gaussian-like profile for all exit Stokes numbers, even for the low
$x/D=10$
, the radial concentration profiles have approached a Gaussian-like profile for all exit Stokes numbers, even for the low
![]() $Sk_{D}$
cases where the exit profiles differ significantly from a Gaussian profiles (see figure 15). Not surprisingly, the radial concentration profile of the
$Sk_{D}$
cases where the exit profiles differ significantly from a Gaussian profiles (see figure 15). Not surprisingly, the radial concentration profile of the
![]() $Sk_{D}=0.3$
case most closely approximates a Gaussian distribution, because the particle phase at this low Stokes number most closely approaches a passive scalar field. However, for
$Sk_{D}=0.3$
case most closely approximates a Gaussian distribution, because the particle phase at this low Stokes number most closely approaches a passive scalar field. However, for
![]() $Sk_{D}\geqslant 1.4$
, the radial concentration profile increasingly departs from a Gaussian distribution as the Stokes number decreases. This is attributed to the exit concentration profiles, which increasingly depart from a Gaussian distribution as the exit Stokes number decreases. This also implies that, for the relatively low exit Stokes number of
$Sk_{D}\geqslant 1.4$
, the radial concentration profile increasingly departs from a Gaussian distribution as the Stokes number decreases. This is attributed to the exit concentration profiles, which increasingly depart from a Gaussian distribution as the exit Stokes number decreases. This also implies that, for the relatively low exit Stokes number of
![]() $Sk_{D}=1.4$
, the particle concentration field departs significantly from that of a passive tracer, at least for
$Sk_{D}=1.4$
, the particle concentration field departs significantly from that of a passive tracer, at least for
![]() $x/D\lesssim 10$
.
$x/D\lesssim 10$
.
To provide more insight into the cause for the observed humps in the centreline concentration (figure 16), a mass balance is performed on the (compressible) particle phase resulting in
where
and
![]() $\tilde{r}=r/D$
. The last term in (5.6) is zero on the axis because
$\tilde{r}=r/D$
. The last term in (5.6) is zero on the axis because
![]() $V_{p}=0$
there (the mean flow is axisymmetric). On this basis, the increase in the particle concentration on the axis,
$V_{p}=0$
there (the mean flow is axisymmetric). On this basis, the increase in the particle concentration on the axis,
![]() $\unicode[STIX]{x1D6E9}_{c}$
, can be attributed to two independent mechanisms, the axial deceleration of particles along the centreline,
$\unicode[STIX]{x1D6E9}_{c}$
, can be attributed to two independent mechanisms, the axial deceleration of particles along the centreline,
![]() $\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}$
, and the radial particle migration towards the centreline
$\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}$
, and the radial particle migration towards the centreline
![]() $\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, corresponding to the second and third terms in (5.6), respectively. Furthermore, these trends can be expected to apply beyond the axis within the near field because the value of
$\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, corresponding to the second and third terms in (5.6), respectively. Furthermore, these trends can be expected to apply beyond the axis within the near field because the value of
![]() $V_{p}/U_{p}$
is small within this region.
$V_{p}/U_{p}$
is small within this region.

Figure 20. The normalised axial gradients of particle concentration,
![]() $\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6E9}}_{c}/\unicode[STIX]{x2202}\tilde{x}$
, particle axial velocity,
$\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6E9}}_{c}/\unicode[STIX]{x2202}\tilde{x}$
, particle axial velocity,
![]() $\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}$
and normalised radial gradient of particle radial velocity,
$\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}$
and normalised radial gradient of particle radial velocity,
![]() $\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, along the centreline for
$\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, along the centreline for
![]() $Sk_{D}=1.4$
(a) and
$Sk_{D}=1.4$
(a) and
![]() $Sk_{D}=11.2$
(b). Note that both panels use the same legend.
$Sk_{D}=11.2$
(b). Note that both panels use the same legend.
The axial evolution of the first three gradient terms on the left-hand side of (5.6) along the jet centreline are presented in figure 20 for
![]() $Sk_{D}=1.4$
and
$Sk_{D}=1.4$
and
![]() $Sk_{D}=11.2$
, which correspond to the cases where the exit concentration is preferentially distributed on the jet edge and axis, respectively (Lau & Nathan Reference Lau and Nathan2014). The results show that, while axial deceleration along the centreline is negligible within the first few pipe diameters of the exit plane for both exit Stokes numbers cases, the axial deceleration in particle velocity becomes significant at
$Sk_{D}=11.2$
, which correspond to the cases where the exit concentration is preferentially distributed on the jet edge and axis, respectively (Lau & Nathan Reference Lau and Nathan2014). The results show that, while axial deceleration along the centreline is negligible within the first few pipe diameters of the exit plane for both exit Stokes numbers cases, the axial deceleration in particle velocity becomes significant at
![]() $x/D\gtrsim 4$
for
$x/D\gtrsim 4$
for
![]() $Sk_{D}=1.4$
and
$Sk_{D}=1.4$
and
![]() $x/D\gtrsim 6$
for
$x/D\gtrsim 6$
for
![]() $Sk_{D}=11.2,$
consistent with the centreline velocity data presented in figure 9. Furthermore, the radial gradients in particle velocity,
$Sk_{D}=11.2,$
consistent with the centreline velocity data presented in figure 9. Furthermore, the radial gradients in particle velocity,
![]() $\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, reveal that, for
$\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
, reveal that, for
![]() $Sk_{D}=1.4$
the particles migrate toward the axis in the region
$Sk_{D}=1.4$
the particles migrate toward the axis in the region
![]() $0\lesssim x/D\lesssim 5.5$
. In contrast, for the
$0\lesssim x/D\lesssim 5.5$
. In contrast, for the
![]() $Sk_{D}=11.2$
case, particles migrate away from the axis in the region
$Sk_{D}=11.2$
case, particles migrate away from the axis in the region
![]() $0\lesssim x/D\lesssim 8$
. For both cases, the magnitude of particle migration firstly increases with axial distance, and then subsequently decreases approaching zero towards the end of this region. Beyond this initial region, particles migrate away from the jet axis throughout the axial extent of the measurement region, due to the expansion of the jet. As
$0\lesssim x/D\lesssim 8$
. For both cases, the magnitude of particle migration firstly increases with axial distance, and then subsequently decreases approaching zero towards the end of this region. Beyond this initial region, particles migrate away from the jet axis throughout the axial extent of the measurement region, due to the expansion of the jet. As
![]() $x/D\rightarrow \infty$
, it is expected that all three gradient terms approach zero as the jet approaches the co-flow.
$x/D\rightarrow \infty$
, it is expected that all three gradient terms approach zero as the jet approaches the co-flow.
From these results, it can be deduced that within the initial ‘core’ region the particle phase undergoes a process of reorganisation whereby the concentration profile transitions from the exit profile (figure 15) towards a Gaussian-like profile (figure 19). This, in turn, causes the concentration half-width,
![]() $r_{0.5,\unicode[STIX]{x1D6E9}}/D$
, to decrease (figure 17
b). The reorganisation involves particle migration towards the axis, resulting in an increase in
$r_{0.5,\unicode[STIX]{x1D6E9}}/D$
, to decrease (figure 17
b). The reorganisation involves particle migration towards the axis, resulting in an increase in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
with axial distance, for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
with axial distance, for
![]() $Sk_{D}\leqslant 2.4$
and particle migration away from the axis, leading to a decrease in
$Sk_{D}\leqslant 2.4$
and particle migration away from the axis, leading to a decrease in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
with axial distance, for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
with axial distance, for
![]() $Sk_{D}\geqslant 5.6$
(figure 16). At the end of the core region, the reorganisation process approaches completion and radial particle migration reduces to zero. The combination of particle radial migration and particle axial deceleration causes a strong hump in
$Sk_{D}\geqslant 5.6$
(figure 16). At the end of the core region, the reorganisation process approaches completion and radial particle migration reduces to zero. The combination of particle radial migration and particle axial deceleration causes a strong hump in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
![]() $Sk_{D}\leqslant 2.4$
, and a weaker localised hump in
$Sk_{D}\leqslant 2.4$
, and a weaker localised hump in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
![]() $Sk_{D}\geqslant 5.6$
. The location of the humps corresponds to the location at which the rate of increase in centreline particle concentration due to particle deceleration exactly matches the rate of particle migration away from the centreline (due to jet expansion), i.e.
$Sk_{D}\geqslant 5.6$
. The location of the humps corresponds to the location at which the rate of increase in centreline particle concentration due to particle deceleration exactly matches the rate of particle migration away from the centreline (due to jet expansion), i.e.
![]() $\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}=-\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
. This is always downstream from the end of the core because particle deceleration occurs upstream from the end of the core. It then follows that the particle concentration profile at the exit not only influences the rate of decay of centreline concentration, as previously shown (Lau & Nathan Reference Lau and Nathan2014), but also impacts the particle distributions throughout the entire jet.
$\unicode[STIX]{x2202}\tilde{U} _{p,c}/\unicode[STIX]{x2202}\tilde{x}=-\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}$
. This is always downstream from the end of the core because particle deceleration occurs upstream from the end of the core. It then follows that the particle concentration profile at the exit not only influences the rate of decay of centreline concentration, as previously shown (Lau & Nathan Reference Lau and Nathan2014), but also impacts the particle distributions throughout the entire jet.

Figure 21. The departure of the radial concentration profile from a true Gaussian distribution,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
, as a function of axial distance normalised by the core length,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
, as a function of axial distance normalised by the core length,
![]() $x/x_{core}$
.
$x/x_{core}$
.
Figure 21 presents the departure of the radial concentration profile from a true Gaussian distribution,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
, as a function of axial distance normalised by the core length,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
, as a function of axial distance normalised by the core length,
![]() $x/x_{core}$
, where the departure parameter is defined as
$x/x_{core}$
, where the departure parameter is defined as
the
![]() $\langle ~\rangle$
brackets denote an averaging procedure and the core length
$\langle ~\rangle$
brackets denote an averaging procedure and the core length
![]() $x_{core}$
is defined as the first axial location downstream from the exit plane where
$x_{core}$
is defined as the first axial location downstream from the exit plane where
![]() $\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}=0$
(see also figure 20). The results show that the radial concentration profiles depart from a Gaussian profile most significantly at the exit plane and that this departure
$\unicode[STIX]{x2202}\tilde{V}_{p,c}/\unicode[STIX]{x2202}\tilde{r}=0$
(see also figure 20). The results show that the radial concentration profiles depart from a Gaussian profile most significantly at the exit plane and that this departure
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
is most significant at lower Stokes numbers,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
is most significant at lower Stokes numbers,
![]() $Sk_{D}\leqslant 2.4$
, as expected. The departure decreases with axial distance to reach a minima at
$Sk_{D}\leqslant 2.4$
, as expected. The departure decreases with axial distance to reach a minima at
![]() $x/x_{core}\approx 1$
for all Stokes numbers. This is further evidence that the particle phase undergoes a reorganisation towards a Gaussian-like profile within the core region of the jet and that the current definition of core length, i.e. the location where the particle migration reduces to zero, coincides with the end of this reorganisation region. Further downstream from the core,
$x/x_{core}\approx 1$
for all Stokes numbers. This is further evidence that the particle phase undergoes a reorganisation towards a Gaussian-like profile within the core region of the jet and that the current definition of core length, i.e. the location where the particle migration reduces to zero, coincides with the end of this reorganisation region. Further downstream from the core,
![]() $x/x_{core}>1$
, the departure increases due to the effect of the co-flow. For
$x/x_{core}>1$
, the departure increases due to the effect of the co-flow. For
![]() $x/x_{core}\gtrsim 2$
,
$x/x_{core}\gtrsim 2$
,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
approaches a constant non-zero value, indicating that the concentration profiles approach a self-similar non-Gaussian profile in the far field of the jet.
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E9}}$
approaches a constant non-zero value, indicating that the concentration profiles approach a self-similar non-Gaussian profile in the far field of the jet.

Figure 22. The influence of exit Stokes number,
![]() $Sk_{D}$
, on the normalised core length,
$Sk_{D}$
, on the normalised core length,
![]() $x_{core}/D$
, location of the hump in centreline concentration,
$x_{core}/D$
, location of the hump in centreline concentration,
![]() $x_{\unicode[STIX]{x1D6E9},hump}/D$
, normalised particle velocity at the end of the core,
$x_{\unicode[STIX]{x1D6E9},hump}/D$
, normalised particle velocity at the end of the core,
![]() $U_{p,c}/U_{p,ce}|_{x=x_{core}}$
and normalised particle velocity at the location of the concentration hump,
$U_{p,c}/U_{p,ce}|_{x=x_{core}}$
and normalised particle velocity at the location of the concentration hump,
![]() $U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}$
.
$U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}$
.
Figure 22 presents the influence of exit Stokes number on the normalised core length,
![]() $x_{core}/D$
, together with the normalised location of the hump in centreline concentration,
$x_{core}/D$
, together with the normalised location of the hump in centreline concentration,
![]() $x_{\unicode[STIX]{x1D6E9},hump}/D$
. Also included in the figure are the normalised particle velocities at these axial locations,
$x_{\unicode[STIX]{x1D6E9},hump}/D$
. Also included in the figure are the normalised particle velocities at these axial locations,
![]() $U_{p,c}/U_{p,ce}|_{x=x_{core}}$
and
$U_{p,c}/U_{p,ce}|_{x=x_{core}}$
and
![]() $U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}$
, respectively. These results show that both
$U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}$
, respectively. These results show that both
![]() $x_{core}$
and
$x_{core}$
and
![]() $x_{\unicode[STIX]{x1D6E9},hump}$
increase with Stokes number, consistent with the measurements of Prevost et al. (Reference Prevost, Boree, Nuglisch and Charnay1996) and Picano et al. (Reference Picano, Sardina, Gualtieri and Casciola2010), although it should be noted that in all three measurements a different definition of core length is used. The values of
$x_{\unicode[STIX]{x1D6E9},hump}$
increase with Stokes number, consistent with the measurements of Prevost et al. (Reference Prevost, Boree, Nuglisch and Charnay1996) and Picano et al. (Reference Picano, Sardina, Gualtieri and Casciola2010), although it should be noted that in all three measurements a different definition of core length is used. The values of
![]() $x_{\unicode[STIX]{x1D6E9},hump}/D$
are larger than
$x_{\unicode[STIX]{x1D6E9},hump}/D$
are larger than
![]() $x_{core}/D$
for all Stokes numbers, as previously discussed. The core length is found to increase with Stokes number at a different rate for
$x_{core}/D$
for all Stokes numbers, as previously discussed. The core length is found to increase with Stokes number at a different rate for
![]() $Sk_{D}\leqslant 2.8$
compared with
$Sk_{D}\leqslant 2.8$
compared with
![]() $Sk_{D}\geqslant 5.6$
. This is because for
$Sk_{D}\geqslant 5.6$
. This is because for
![]() $Sk_{D}\geqslant 5.6$
, the initial concentration profiles (see figure 15) are not significantly different from the Gaussian-like profile expected at the end of the core and therefore the increase in core length as the Stokes number increases is solely due to the lower response of the particles to axial changes in the flow. However, for
$Sk_{D}\geqslant 5.6$
, the initial concentration profiles (see figure 15) are not significantly different from the Gaussian-like profile expected at the end of the core and therefore the increase in core length as the Stokes number increases is solely due to the lower response of the particles to axial changes in the flow. However, for
![]() $Sk_{D}\leqslant 2.8$
, the increase in Stokes number has the additional impact of lowering the particle response to radial motions, which increases the development length required to transition from the significantly non-Gaussian exit profile to the Gaussian-like profile observed at the end of the core.
$Sk_{D}\leqslant 2.8$
, the increase in Stokes number has the additional impact of lowering the particle response to radial motions, which increases the development length required to transition from the significantly non-Gaussian exit profile to the Gaussian-like profile observed at the end of the core.
The normalised particle centreline velocity at the location of the hump is typically within the range
![]() $0.9\lesssim U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}\lesssim 0.94$
for all investigated exit Stokes numbers, although this particle velocity decreases with increasing Stokes number. The normalised particle velocity at the end of the core is approximately constant at
$0.9\lesssim U_{p,c}/U_{p,ce}|_{x=x_{\unicode[STIX]{x1D6E9},hump}}\lesssim 0.94$
for all investigated exit Stokes numbers, although this particle velocity decreases with increasing Stokes number. The normalised particle velocity at the end of the core is approximately constant at
![]() $U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.985$
for
$U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.985$
for
![]() $Sk_{D}\geqslant 5.6$
. This value is close to unity, which shows that, for these high Stokes number cases, the axial location where the centreline velocity starts to decay coincides closely with the end of the jet core. For
$Sk_{D}\geqslant 5.6$
. This value is close to unity, which shows that, for these high Stokes number cases, the axial location where the centreline velocity starts to decay coincides closely with the end of the jet core. For
![]() $Sk_{D}=1.4$
and 2.8,
$Sk_{D}=1.4$
and 2.8,
![]() $U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.95$
, which is lower than is found for the higher Stokes number cases. This is attributed to the exit concentration profiles of the
$U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.95$
, which is lower than is found for the higher Stokes number cases. This is attributed to the exit concentration profiles of the
![]() $Sk_{D}=1.4$
and 2.8 cases, which have a stronger departure from a Gaussian profile compared to the higher exit Stokes number cases. Therefore, the
$Sk_{D}=1.4$
and 2.8 cases, which have a stronger departure from a Gaussian profile compared to the higher exit Stokes number cases. Therefore, the
![]() $Sk_{D}=1.4$
and 2.8 cases require a greater development length to transition towards the Gaussian-like profile expected at the end of the core. For the
$Sk_{D}=1.4$
and 2.8 cases require a greater development length to transition towards the Gaussian-like profile expected at the end of the core. For the
![]() $Sk_{D}=0.3$
case,
$Sk_{D}=0.3$
case,
![]() $U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.98$
, which is higher than the
$U_{p,c}/U_{p,ce}|_{x=x_{core}}\approx 0.98$
, which is higher than the
![]() $Sk_{D}=1.4$
and 2.8 cases, despite having an initial concentration profile that departs most significantly from a Gaussian profile (see figure 21). This is because the particles at
$Sk_{D}=1.4$
and 2.8 cases, despite having an initial concentration profile that departs most significantly from a Gaussian profile (see figure 21). This is because the particles at
![]() $Sk_{D}=0.3$
are sufficiently responsive to the flow so that its initial concentration profile does not extend its core length significantly. This further implies that an exit Stokes number of
$Sk_{D}=0.3$
are sufficiently responsive to the flow so that its initial concentration profile does not extend its core length significantly. This further implies that an exit Stokes number of
![]() $Sk_{D}=1.4$
is not sufficiently low to result in a particle phase that can be treated as a passive flow tracer.
$Sk_{D}=1.4$
is not sufficiently low to result in a particle phase that can be treated as a passive flow tracer.
6 Conclusions
New details of the relationships between particle concentration and velocity distributions in the evolution of a turbulent, particle-laden jet have been revealed by a systematic and comprehensive dataset. Importantly, the data reveal that it is impossible to adequately characterise the evolution with a single Stokes number. Instead, the evolution is better described by using different Stokes numbers for the axial and radial flow components. For the present flow it is deduced that the effective Stokes number in the axial direction is less than the corresponding value in the radial direction. This is attributed to the greater length scale in the axial than the radial motions, which is possibly explained by a helical flow mode. This interpretation also provides an explanation for the observed preferential response of the particles to gas-phase axial velocity fluctuations over radial velocity fluctuations. It is also consistent with the large magnitude of the measured values of
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
which are above unity and may reach values as high as
$u_{p}^{\prime }/v_{p}^{\prime }$
which are above unity and may reach values as high as
![]() ${\approx}5$
. The different effective Stokes numbers in the axial and radial directions also provides an explanation for the observed greater rate at which
${\approx}5$
. The different effective Stokes numbers in the axial and radial directions also provides an explanation for the observed greater rate at which
![]() $v_{p}^{\prime }/U_{p}$
reduces than
$v_{p}^{\prime }/U_{p}$
reduces than
![]() $u_{p}^{\prime }/U_{p}$
as
$u_{p}^{\prime }/U_{p}$
as
![]() $Sk_{D}$
is increased, as evidenced by measurements of turbulence intensities along the centreline as well as radially across the jet at
$Sk_{D}$
is increased, as evidenced by measurements of turbulence intensities along the centreline as well as radially across the jet at
![]() $x/D=10$
and 30. It also explains the increase in anisotropy in in the velocity fluctuations,
$x/D=10$
and 30. It also explains the increase in anisotropy in in the velocity fluctuations,
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
, as
$u_{p}^{\prime }/v_{p}^{\prime }$
, as
![]() $Sk_{D}$
is increased.
$Sk_{D}$
is increased.
The deduction that the Stokes number in the axial direction is lower than that in the radial direction also implies that there is a further mechanism by which the two phases are coupled. The larger effective Stokes numbers in the radial direction relative to the axial direction implies that the ‘slip’ between the two phases is greater in the radial than the axial directions, which in turn leads to preferential damping of radial velocity fluctuations over axial velocity fluctuations in the gas phase. This amplifies the difference between the axial and radial fluctuations, contributing to a further increase in the values of
![]() $u_{p}^{\prime }/v_{p}^{\prime }$
as
$u_{p}^{\prime }/v_{p}^{\prime }$
as
![]() $Sk_{D}$
is increased.
$Sk_{D}$
is increased.
New details are also revealed of the dependence of the particle concentration and velocity profile on the Stokes number within a fully developed pipe flow (which is the exit profile to the present jet). In addition to providing more comprehensive information about the transition between a
![]() $\cup$
-shaped concentration profile for
$\cup$
-shaped concentration profile for
![]() $Sk_{D}\leqslant 1.4$
, and a
$Sk_{D}\leqslant 1.4$
, and a
![]() $\wedge$
-shaped concentration profile for
$\wedge$
-shaped concentration profile for
![]() $Sk_{D}\geqslant 5.6$
, they reveal that the transition between these two regimes occurs at
$Sk_{D}\geqslant 5.6$
, they reveal that the transition between these two regimes occurs at
![]() $Sk_{D}\approx 2.8$
, where the exit concentration profile is approximately uniform. This progressive change in exit concentration profile as
$Sk_{D}\approx 2.8$
, where the exit concentration profile is approximately uniform. This progressive change in exit concentration profile as
![]() $Sk_{D}$
is increased from
$Sk_{D}$
is increased from
![]() $Sk_{D}=0.3$
to
$Sk_{D}=0.3$
to
![]() $Sk_{D}=5.6$
leads to an increase in absolute particle concentration along the centreline, which in turn increases particle diffusion away from the centreline. This causes the centreline concentration axial decay to increase at a significantly greater rate than the single-phase counterpart as the exit Stokes number is increased from
$Sk_{D}=5.6$
leads to an increase in absolute particle concentration along the centreline, which in turn increases particle diffusion away from the centreline. This causes the centreline concentration axial decay to increase at a significantly greater rate than the single-phase counterpart as the exit Stokes number is increased from
![]() $Sk_{D}=0.3$
to
$Sk_{D}=0.3$
to
![]() $Sk_{D}=5.6$
. By contrast, the present results reveal that
$Sk_{D}=5.6$
. By contrast, the present results reveal that
![]() $Sk_{D}$
has the strongest influence on the particle-phase exit velocity profiles over the range
$Sk_{D}$
has the strongest influence on the particle-phase exit velocity profiles over the range
![]() $1.4\leqslant Sk_{D}\leqslant 11.2$
.
$1.4\leqslant Sk_{D}\leqslant 11.2$
.
Analysis of the measurements has demonstrated that the region within the first few diameters of the exit plane, referred to as the ‘core’ region, is characterised by the reorganisation of particle distributions from those at the exit plane of the pipe to their Gaussian-like far-field profiles. For low Stokes number cases,
![]() $Sk_{D}\leqslant 2.8$
, this reorganisation process involves significant particle migration from the jet edge towards the axis, which causes an increase in the centreline particle concentration. For
$Sk_{D}\leqslant 2.8$
, this reorganisation process involves significant particle migration from the jet edge towards the axis, which causes an increase in the centreline particle concentration. For
![]() $Sk_{D}\geqslant 5.6$
, the reorganisation process involves a modest migration of particles away from the jet axis, which decreases the centreline concentration. In both cases, the concentration half-width decreases through the near field as a result of this particle migration. At the end of the core region, the reorganisation process concludes, and radial particle migration on the axis reduces to zero. Downstream from the core end, particles migrate away from the axis as the jet expands.
$Sk_{D}\geqslant 5.6$
, the reorganisation process involves a modest migration of particles away from the jet axis, which decreases the centreline concentration. In both cases, the concentration half-width decreases through the near field as a result of this particle migration. At the end of the core region, the reorganisation process concludes, and radial particle migration on the axis reduces to zero. Downstream from the core end, particles migrate away from the axis as the jet expands.
Within the first few diameters of the exit plane, the particle velocity along the axis remains constant. However, beyond this and upstream from the end of the core region, the particles begin to decelerate, i.e.
![]() $\unicode[STIX]{x2202}U_{p,c}/\unicode[STIX]{x2202}x<0$
. Due to continuity along the axis, this increases the axial gradients of particle concentration,
$\unicode[STIX]{x2202}U_{p,c}/\unicode[STIX]{x2202}x<0$
. Due to continuity along the axis, this increases the axial gradients of particle concentration,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x2202}x$
, which in turn augments the increase in centreline concentration due to particle migration for
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x2202}x$
, which in turn augments the increase in centreline concentration due to particle migration for
![]() $Sk_{D}\leqslant 2.8$
. This provides an explanation for the strong near-field peaks in
$Sk_{D}\leqslant 2.8$
. This provides an explanation for the strong near-field peaks in
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
for
![]() $Sk_{D}\leqslant 2.8$
. For the larger Stokes number cases,
$Sk_{D}\leqslant 2.8$
. For the larger Stokes number cases,
![]() $Sk_{D}\geqslant 5.6$
, the deceleration of particles along the axis results in subtle humps in the axial profile of
$Sk_{D}\geqslant 5.6$
, the deceleration of particles along the axis results in subtle humps in the axial profile of
![]() $\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
near the core end where particle migration away from the axis is negligible. In all cases, the location of these humps was found to be downstream of the core end.
$\unicode[STIX]{x1D6E9}_{c}/\unicode[STIX]{x1D6E9}_{e}$
near the core end where particle migration away from the axis is negligible. In all cases, the location of these humps was found to be downstream of the core end.
The axial length of the core region was found to increase with increasing exit Stokes number, but at greater rates for the
![]() $Sk_{D}\leqslant 2.8$
than the
$Sk_{D}\leqslant 2.8$
than the
![]() $Sk_{D}\geqslant 5.6$
cases. This is attributed to the reduction in the particle’s response to the flow, which impacts the
$Sk_{D}\geqslant 5.6$
cases. This is attributed to the reduction in the particle’s response to the flow, which impacts the
![]() $Sk_{D}\leqslant 2.8$
cases more than the
$Sk_{D}\leqslant 2.8$
cases more than the
![]() $Sk_{D}\geqslant 5.6$
cases because more significant radial particle migration occurs in the core region in the lower Stokes number cases.
$Sk_{D}\geqslant 5.6$
cases because more significant radial particle migration occurs in the core region in the lower Stokes number cases.
Acknowledgement
The authors are pleased to acknowledge the financial contributions of the Australian government through the Australian Research Council (grant no. DP120102961) and the Australian Renewable Energy Agency (grant no. USO034). The authors would also like to thank Mr I. Saridakis for his useful contributions in the laboratory.