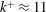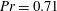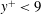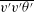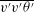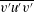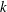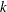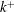1. Introduction
Understanding the physics of spatially developing thermal turbulent boundary layers over smooth and rough surfaces is an essential step in the design and optimization of heat control tools for industrial applications, and also in turbulence modelling development for Reynolds averaged Navier–Stokes (RANS) and large eddy simulations (LES). Many studies have been performed on the subject of heat transfer in turbulent boundary layers over smooth surfaces, but as of today, direct numerical simulation (DNS) of realistic surface roughness and heat transfer in a spatially developing turbulent boundary layer has not been reported. Problems such as flow over pitted gas turbine blades, fouled heat exchangers or the atmospheric flows over urban areas are related to thermal fields over rough surfaces. Experimental and numerical studies have been conducted for several decades to investigate thermal field statistics and fundamental mechanisms of momentum and heat transport in smooth-wall and rough-wall thermal turbulent boundary layers (Pimenta, Moffat & Kays Reference Pimenta, Moffat and Kays1975; Miyake, Tsujimoto & Nakaji Reference Miyake, Tsujimoto and Nakaji2001; Belnap, van Rij & Ligrani Reference Belnap, van Rij and Ligrani2002). However, resolving the viscous region, even on smooth surfaces, has been a challenge for computations and experiments. We use the statistics from our DNS database to test two long-standing concepts in wall-bounded turbulent flows: the Reynolds analogy and the Townsend’s Reynolds number similarity hypothesis.
The Reynolds analogy asserts that transports of momentum and heat are similar, with the consequence that the turbulent Prandtl number,
$Pr_{t}$
, is constant and close to one.
$Pr_{t}$
is defined as the ratio of the eddy viscosity,
${\it\nu}_{t}=-\overline{u^{\prime }v^{\prime }}/(\text{d}\overline{U}/\text{d}y)$
, to the eddy diffusivity,
${\it\kappa}_{t}=\overline{v^{\prime }{\it\theta}^{\prime }}/(\text{d}\overline{{\it\Theta}}/\text{d}y)$
. Here,
$u^{\prime }$
and
$v^{\prime }$
are the streamwise and wall-normal components of velocity fluctuations,
${\it\theta}^{\prime }$
is the temperature fluctuation,
$\overline{U}$
is the mean streamwise velocity,
$\overline{{\it\Theta}}$
is the mean temperature, and the overbar represents time averaging. This is a useful reference concept, and its value provides a useful relationship for calculating the turbulent heat transfer by knowing the velocity field in smooth and rough walls.
Although there have been many experimental studies in determining
$Pr_{t}$
, as reported by Kays (Reference Kays1994), the accurate and simultaneous measurements of the four quantities (turbulent shear stress, turbulent heat flux, gradient of temperature and gradient of velocity) needed to calculate
$Pr_{t}$
at a single point are extremely difficult to obtain. This difficulty has led to large scatter in experimental results. In a review paper, Kays (Reference Kays1994) presented available experimental data for the turbulent boundary layer in proximity of a smooth wall which showed that
$Pr_{t}$
ranged from 0.8 to 1, agreeing fairly well with the Reynolds analogy. However, this approach is not always valid, especially for complex flows. Pimenta et al. (Reference Pimenta, Moffat and Kays1975) experimentally studied a zero-pressure-gradient turbulent boundary layer with
$20<Re_{k}<150$
, where
$Re_{k}=k^{+}=u_{{\it\tau}}k/{\it\nu}$
,
$k$
is the roughness height,
${\it\nu}$
is the kinematic molecular viscosity, and
$u_{{\it\tau}}$
(
$=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, where
${\it\tau}_{w}$
is the wall shear stress and
${\it\rho}$
is the fluid density) is the friction velocity. They found that a transitionally rough surface flow retained some characteristics of smooth-wall flow. For instance,
$Pr_{t}$
was constant with a value close to unity for the rough case for the closest distance from the wall at
$y^{+}\approx 250$
(where
$y^{+}$
was the distance from the wall normalized in inner units), as was speculated earlier by Owen & Thomson (Reference Owen and Thomson1963).
Belnap et al. (Reference Belnap, van Rij and Ligrani2002) conducted experiments of a transitionally rough channel flow at
$10\,000<Re_{D_{h}}<25\,000$
, where
$Re_{D_{h}}=VD_{h}/{\it\nu}$
,
$V$
is the mean streamwise velocity of pipe flow, and
$D_{h}$
is the hydraulic diameter of pipe. They indicated that surface roughness only modified the ratio
$St/(C_{f}/2)$
slightly, which was another representation of the Reynolds analogy, where
$St$
is the Stanton number and
$C_{f}$
is the skin friction coefficient.
Miyake et al. (Reference Miyake, Tsujimoto and Nakaji2001) performed a numerical study in a fully developed turbulent channel flow with sand-grain roughness modelled as straight cones on one side of channel and
$Re_{{\it\tau}}=150$
, where
$Re_{{\it\tau}}=hu_{{\it\tau}}/{\it\nu}$
, with
$h$
the half-height of the channel. They reported that
$Pr_{t}$
remained unchanged and close to unity in the rough case, but the question regarding the validity of Reynolds analogy in higher Reynolds numbers over a rough surface in spatially developing flows has remained unanswered.
Townsend (Reference Townsend1976) proposed the Reynolds number similarity hypothesis, which states that at sufficiently high Reynolds numbers and outside the roughness sublayer, the characteristics of turbulent flow are independent of the Reynolds number and surface roughness. Raupach, Antonia & Rajagopalan (Reference Raupach, Antonia and Rajagopalan1991) also concluded that at high Reynolds numbers, above the roughness sublayer, turbulence structures were similar. Experiments by Flack, Schultz & Shapiro (Reference Flack, Schultz and Shapiro2005) supported the Townsend’s Reynolds number similarity hypothesis for turbulent boundary layer flow over a uniform, three-dimensional, fully rough wall at
$Re_{{\it\theta}}=14\,000$
, where
$Re_{{\it\theta}}={\it\theta}U_{\infty }/{\it\nu}$
is the Reynolds number based on momentum thickness, and
${\it\theta}$
is the momentum thickness. They found that the rough-wall modifications to the flow were confined to the roughness sublayer, provided that the roughness elements were sufficiently small compared to the boundary thickness. Jiménez (Reference Jiménez2004) proposed a criterion for satisfying the latter condition which requires that
$k/{\it\delta}<0.02$
. However, the validity of Townsend’s hypothesis is still in question for the thermal and velocity field at moderate Reynolds numbers.
DNS of the velocity field over a spatially developing ZPG-boundary layer (zero pressure gradient) subjected to transitional, 24-grit sandpaper surface roughness was carried out by Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). The Reynolds stresses were decreased by roughness when scaled by inner units, but were increased by roughness when scaled by outer units; thus showing a scaling dependency. Two-point correlations distinctly showed an effect due to roughness at
$y^{+}=5$
; however, velocity fluctuations were slightly less correlated in the outer region for the rough case. The POD analysis demonstrated that low-order modes of the streamwise velocity fluctuations possessed characteristic wavelengths of the order of
$3{\it\delta}$
for the smooth case, while the same modes for the rough case exhibited characteristic wavelengths of the order of
${\it\delta}$
, where
${\it\delta}$
was the boundary layer thickness.
The performed literature review has revealed that publications on the effects of roughness on turbulent thermal boundary layers are rather scarce. With many unanswered questions about rough surface thermal turbulent boundary layers, it is obvious that more accurate and extensive methods, such as DNS, are needed to shed some light on the thermal turbulent boundary layer over rough surfaces and to develop turbulence models for lower-level numerical approaches, such as RANS and LES. Therefore, the present study’s objective is to gain better knowledge of the thermal field behaviour in spatially developing turbulent boundary layers under the effect of small surface roughness at moderate Reynolds numbers by adding a passive scalar into the DNS performed in Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). The most important questions we seek to answer are how structural modifications caused by roughness in the velocity field are translated to the thermal field, particularly in the heat-flux terms. Further, we seek to understand the interaction of heat fluxes between the inner and outer layers of the boundary layer. These investigations allow us to further evaluate the validity of the Reynolds analogy in the vicinity of the rough wall by accurately computing the turbulent Prandtl number and to examine the validity of Townsend’s Reynolds number similarity hypothesis for the velocity and thermal field in flow over transitionally rough surfaces. The paper is organized as follows: § 2 deals with basis of the dynamic multiscale approach employed in the simulations, § 3 describes the roughness modelling and flow solver description, § 4 discusses the velocity and thermal field results and § 5 presents the concluding remarks.
Figure 1. Schematic of the rough thermal boundary layer with different regions and planes: inlet, test and recycle stations.
2. The dynamic multiscale approach (DMA) for spatially evolving thermal flows
In order to prescribe realistic thermal turbulent inlet flow conditions we have adapted the dynamic multiscale approach (DMA) developed by Araya et al. (Reference Araya, Castillo, Meneveau and Jansen2011) to thermal rough walls in the present study. The DMA is based on the rescaling–recycling methodology of Lund, Wu & Squires (Reference Lund, Wu and Squires1998), which prescribes time-dependent turbulence information at the inlet plane by using a flow scaled from the downstream solution at the recycle plane, as shown in figure 1. The major differences between the DMA and the original rescaling–recycling method (henceforth ORRM) by Lund et al. (Reference Lund, Wu and Squires1998) are threefold: (i) the precursor auxiliary domain is removed (single domain); (ii) different scaling functions in the inner and outer regions of the boundary layer (i.e. multiscale) are imposed; and (iii) the friction velocity
$u_{{\it\tau}}$
and flow parameters at the inlet of the computational domain are deduced dynamically by using a ‘test plane’ located between the inlet and recycle planes (Araya et al.
Reference Araya, Castillo, Meneveau and Jansen2011), as shown in figure 1. The previously mentioned improvements have made the DMA a more versatile, robust and computational-resource-saving method, without the need for empirical correlations in the rescaling process, especially at the inlet plane that generates a short developing section. The DMA has also been applied to thermal boundary layers over smooth surfaces with and without streamwise pressure gradients (Araya & Castillo Reference Araya and Castillo2012, Reference Araya and Castillo2013). In this method, the instantaneous temperature,
${\it\Theta}$
, is represented as a mean value,
$\overline{{\it\Theta}}$
plus a fluctuating component,
${\it\theta}^{\prime }$
, given as
$$\begin{eqnarray}{\it\Theta}(x,y,z,t)=\overline{{\it\Theta}}(x,y)+{\it\theta}^{\prime }(x,y,z,t).\end{eqnarray}$$
In the inner region, the mean temperature follows a thermal law of the wall, as expressed by
$$\begin{eqnarray}{\it\Theta}_{w}-\overline{{\it\Theta}}^{inner}=T_{si}(x)g_{si}(y_{T}^{+},Pr),\end{eqnarray}$$
where
${\it\Theta}_{w}$
stands for wall temperature, the superscript
$^{inner}$
stands for inner layer,
$T_{si}$
is the temperature scale for the inner region, and
$g_{si}$
is the inner similarity function, which depends on the inner thermal length scale,
$y_{T}^{+}=(yU_{\infty }/{\it\nu})\sqrt{St}$
, and the molecular Prandtl number (
$Pr$
), where
$St=q_{w}/({\it\rho}C_{p}U_{\infty }({\it\Theta}_{w}-{\it\Theta}_{\infty }))$
,
$q_{w}$
is the wall heat flux and
$C_{p}$
is the specific heat. In the outer region, a defect law is used as follows,
$$\begin{eqnarray}\overline{{\it\Theta}}^{outer}-{\it\Theta}_{\infty }=T_{so}(x)g_{so}(\overline{y}_{T},Pr),\end{eqnarray}$$
where the superscript
$^{outer}$
indicates outer layer,
${\it\Theta}_{\infty }$
is the free-stream temperature,
$T_{so}$
is the temperature scale for the outer region, and
$g_{so}$
is the outer similarity function. The wall-normal similarity coordinate in the outer region is expressed as
$\overline{y}_{T}=y/{\it\delta}_{T}$
, where
${\it\delta}_{T}$
is the thermal boundary layer thickness where the temperature is 99 % of the free-stream temperature. A similar procedure is carried out for thermal fluctuations,
$$\begin{eqnarray}\displaystyle {\it\theta}^{\prime inner} & = & \displaystyle T_{si}^{\prime }(x)g_{si}^{\prime }(y_{T}^{+},z,t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\theta}^{\prime outer} & = & \displaystyle T_{so}^{\prime }(x)g_{so}^{\prime }(\overline{y}_{T},z,t).\end{eqnarray}$$
$T_{si}(x),T_{so}(x),T_{si}^{\prime }(x)$
and
$T_{so}^{\prime }(x)$
) employed in the present study were developed by performing an equilibrium similarity analysis of the governing equations of the inner and outer flow (Wang & Castillo Reference Wang and Castillo2003) shown in table 1, where
${\it\delta}_{T}^{\ast }$
is computed as
$\int _{0}^{\infty }[1-{\it\Theta}/{\it\Theta}_{\infty }]\,\text{d}y$
, and
$C_{f}={\it\tau}_{w}/({\it\rho}U_{\infty }^{2}/2)$
is the skin friction. By relating (2.2)–(2.5) in the inlet plane and the recycle plane, respectively, the mean and fluctuating components of the temperature can be obtained at the inlet from the flow solution at the recycle station. Finally, a composite thermal profile can be written for the entire boundary layer at the inlet plane at every time step, by defining a weighted average of the inner and outer profiles, as follows, 
$$\begin{eqnarray}{\it\Theta}_{inl}=[\overline{{\it\Theta}}_{inl}^{inner}+{\it\theta}_{inl}^{\prime inner}][1-W(\overline{y}_{T,inl})]+[\overline{{\it\Theta}}_{inl}^{outer}+{\it\theta}_{inl}^{\prime outer}]W(\overline{y}_{T,inl}),\end{eqnarray}$$
Table 1. Thermal scaling functions.
where
$W(\overline{y}_{T,inl})$
is a weighting function going smoothly from zero near the wall to 1 in the outer region. For
$W(\overline{y}_{T,inl})$
, the tanh profile of Lund et al. (Reference Lund, Wu and Squires1998), Kong, Choi & Lee (Reference Kong, Choi and Lee2000) was used, given as
$$\begin{eqnarray}W({\it\eta}_{T})=0.5\left.\left[1+\tanh \left[\frac{{\it\alpha}({\it\eta}_{T}-b)}{(1-2b){\it\eta}_{T}+b}\right]\right/\tanh ({\it\alpha})\right],\end{eqnarray}$$
where
${\it\eta}_{T}=\overline{y}_{T,inl}$
,
${\it\alpha}=4$
and
$b=0.2$
.
The rescaling method requires computation of thermal scaling functions at the inlet and recycle stations (the similarity functions
$g$
are universal, hence, they cancel each other). Furthermore, all variables involved in the thermal scaling functions can be computed from the mean flow solution, except the Stanton number at the inlet plane. This is because, at the inlet, the thermal boundary layer thickness is prescribed; therefore, prescribing the inlet
$St$
as well would be redundant. In order to connect the corresponding Stanton number at the inlet to the computed value from the flow solution at the recycle plane, a dynamic method for computation of
$St_{inl}$
based on the downstream solution is also employed in the present study. Since the calculation of
$St$
number based on the wall thermal gradient will be very difficult in boundary layers with surface roughness, we have utilized the energy integral equation, given as
$$\begin{eqnarray}St=\frac{\text{d}{\it\Delta}_{2}}{\text{d}x},\end{eqnarray}$$
where
${\it\Delta}_{2}$
is the enthalpy thickness and
$x$
is the streamwise coordinate. In order to compute (2.8), we have assumed a power-law variation for the enthalpy thickness as a function of the streamwise Reynolds number,
$Re_{x}$
, in the form
${\it\Delta}_{2}/x\sim Re_{x}^{{\it\gamma}_{{\it\Delta}}}$
, where
$Re_{x}=U_{\infty }x/{\it\nu}$
. The streamwise coordinate is defined as
$x=x^{\prime }+x_{inl}$
, where
$x=0$
indicates the virtual origin of the boundary layer,
$x^{\prime }=0$
means the computational box origin and
$x_{inl}$
is the distance between the virtual origin and the inlet plane. This methodology of calculating the ratio of Stanton numbers (i.e.
$St_{\mathit{inl}}/St_{\mathit{rec}}$
) has been found to be more accurate and stable (particularly, during the transient stage) than computing (2.8) via finite difference. Furthermore, a similar procedure to compute dynamically the ratio of friction velocities (i.e.
$u_{{\it\tau}\,inl}/u_{{\it\tau}\,rec}$
) for rough walls based on the momentum integral equation has been successfully implemented in Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). The unknown power
${\it\gamma}_{{\it\Delta}}$
can be obtained by relating the downstream flow solutions, as follows:
$$\begin{eqnarray}{\it\gamma}_{{\it\Delta}}=\frac{\ln [({\it\Delta}_{2}/x)_{test}/({\it\Delta}_{2}/x)_{rec}]}{\ln [(Re_{x})_{test}/(Re_{x})_{rec}]},\end{eqnarray}$$
where subscripts
$_{test}$
and
$_{rec}$
stand for test and recycle planes, respectively. The enthalpy thicknesses are computed at each streamwise station by means of the trapezoidal rule. And the Stanton number ratio between inlet and recycle stations is calculated as
$St_{inl}/St_{rec}=(Re_{x\,\,inl}/Re_{x\,\,rec})^{{\it\gamma}_{{\it\Delta}}}$
. Figure 2 shows the temporal trend of the
${\it\gamma}_{{\it\Delta}}$
parameter. It can be seen that after an initial transient,
${\it\gamma}_{{\it\Delta}}$
tends approximately to a value of
$-$
0.23, which is consistent with the empirical value proposed by Kong et al. (Reference Kong, Choi and Lee2000) (i.e.
${\it\gamma}_{{\it\Delta}}=-0.2$
) for smooth boundary layers at moderate
$Re$
numbers and isothermal wall conditions. Simulations were run for approximately
$45\,000u_{{\it\tau}}^{2}/{\it\nu}$
dimensionless time and statistics were computed in the last 1200 time steps, which represents a dimensionless time of approximately
$6000u_{{\it\tau}}^{2}/{\it\nu}$
in wall units.
Figure 2. Time series of the dynamically computed power-law exponent,
${\it\gamma}_{{\it\Delta}}$
, for the smooth case.
3. Surface roughness modelling, flow solver and boundary conditions
To include surface roughness in the computational domain, a modification to the original dynamic multiscale approach was incorporated, as explained in Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). Direct simulations of the Navier–Stokes and heat transfer equations are performed by using the PHASTA code (parallel hierarchic adaptive stabilized transient analysis), which is based on the finite element method with a streamline upwind Petrov–Galerkin (SUPG) stabilization (Jansen Reference Jansen1999; Whiting & Jansen Reference Whiting and Jansen2001). The PHASTA code was also employed in the study by Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013) and the velocity field results were validated by the experimental data of Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008). Furthermore, the fully coupled momentum and continuity equations are solved with multiple nonlinear iterations (two nonlinear iterations are performed on each step). An additional discrete pressure Poisson equation is solved between each iteration, to maintain a tight tolerance on the continuity equation (Whiting & Jansen Reference Whiting and Jansen2001; Sun Reference Sun2008). Linear elements were used which yielded global second-order accuracy in space. Moreover, satisfactory results have been achieved with this set-up (Araya, Jansen & Castillo Reference Araya, Jansen and Castillo2009; Araya et al. Reference Araya, Castillo, Meneveau and Jansen2011; Cardillo et al. Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). In order to characterize the surface roughness, a new subroutine has been added to the PHASTA code. The subroutine employs a ‘displaced-boundary’ method. It works by taking the no-slip condition, which is originally assigned to the bottom wall of the computational domain, and displacing it to the height of the roughness element at the corresponding node. The roughness distribution has been prescribed based on the topographical data by Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008), which consists of laser measurements of the surface of 24-grit sandpaper.
For the velocity field, the no-slip condition is imposed at the wall and displaced to the height of the roughness element at the corresponding node for the rough case; meanwhile at the free-stream location, the streamwise velocity is given by
$U_{\infty }$
and zero derivatives of the normal and spanwise velocities are prescribed. Temperature is assumed to be a passive scalar with wall isothermal conditions, whereas a free-stream temperature value is considered at the top surface. At the inlet station, the time-dependent inflow conditions for the velocity and temperature fields are generated based on the dynamic multiscale approach by Araya et al. (Reference Araya, Castillo, Meneveau and Jansen2011). Periodic boundary conditions are prescribed in the spanwise direction for the instantaneous velocity and temperature.
At the outflow, pressure is weakly prescribed. Outflow boundary conditions play an important role in the numerical simulation of spatially developing turbulent flows, particularly for the velocity–pressure field. The finite element formulation of the PHASTA code together with initial and boundary condition discussion is well documented in several papers, such as Whiting & Jansen (Reference Whiting and Jansen2001), Whiting, Jansen & Dey (Reference Whiting, Jansen and Dey2003), particularly in journals whose scopes are more related to the description of computational methods in science and engineering. For convenience, a summary of the PHASTA formulation (mathematical expressions) is discussed below. We will start from the outflow pressure boundary condition. The strong form of the continuity and momentum balance equations for incompressible flows, written in advective and index forms (Whiting & Jansen Reference Whiting and Jansen2001), are as follows:
$$\begin{eqnarray}\displaystyle u_{i,i} & = & \displaystyle 0\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dot{u_{i}}+u_{j}u_{i,i} & = & \displaystyle -p_{,i}+{\it\tau}_{ij,i},\end{eqnarray}$$
$u_{i}$
is the
$i$
th component of velocity,
$p$
is the pressure divided by the density
${\it\rho}$
(assumed constant), and
${\it\tau}_{ij}$
is the viscous stress tensor given by
${\it\tau}_{ij}={\it\nu}(u_{i,j}+u_{j,i})$
where
${\it\nu}$
is the fluid kinematic viscosity and the summation convention is used throughout (sum on repeated indices). To proceed with the finite element discretization of the weak form of the Navier–Stokes equations (3.1) and (3.2), they are written in continuous function space. The next step is to discretize the weight and solution function spaces using polynomial functions. Recall that
$\overline{{\it\Omega}}\subset \mathbb{R}^{N}$
(with
$N=3$
) represents the closure of the physical spatial domain,
${\it\Omega}\cup {\it\Gamma}$
, where
${\it\Omega}$
indicates the fluid domain and
${\it\Gamma}$
represents its boundary. To obtain the weak formulation, the strategy is to multiply the continuity equation (3.1) by
$q$
and the momentum equation (3.2) by
$w_{i}$
, the weight functions for the pressure and velocity fields, respectively. The diffusive term, pressure term and continuity equation are all integrated by parts in the domain and by making use of the gradient theorem; 
$$\begin{eqnarray}\int _{{\it\Omega}}[-q_{,i}u_{i}+w_{i}(\dot{u_{i}}+u_{j}u_{i,j})-w_{i,j}(p{\it\delta}_{ij}-{\it\tau}_{ij})]\,\text{d}{\it\Omega}+\int _{{\it\Gamma}}[qu_{i}n_{i}+w_{i}(pn_{i}-{\it\tau}_{ij}n_{j})]\,\text{d}{\it\Gamma}=0,\end{eqnarray}$$
where
$n_{i}$
indicates the unitary normal vector to the surface boundaries. The boundary integral term in
${\it\Gamma}$
arises from the integration by parts and is only carried out over the portion of the domain without essential velocity boundary conditions (Dirichlet).
To be more precise, over the inflow and no-slip surfaces, velocity boundary conditions are applied, and this makes the corresponding weight functions (
$w_{i}$
) zero, but on the outflow boundary, these weights take on arbitrary values. Thus, this boundary integral remains active. In this way, the finite element method allows for a weak application of the outflow pressure instead of a strong (Dirichlet) application of pressure. This has the effect of forcing the solution to match the integral of pressure over the surface, which allows the continuity equation to still remain in the system. Such a boundary condition allows for pressure perturbations to pass through the boundary with minimal reflection, which results in better numerical stability for the method. In incompressible flows, unless the buoyancy forces are taken into consideration for natural convection, the momentum and energy equations are uncoupled. In this case, temperature acts as a passive scalar and only continuity and momentum equations must be solved simultaneously, which is the case of the present study. The strong form of the energy equation reads
$$\begin{eqnarray}\dot{{\it\Theta}}+u_{i}{\it\Theta}_{,i}={\it\alpha}{\it\Theta}_{,ii},\end{eqnarray}$$
where
${\it\alpha}$
is the fluid thermal diffusivity. The weak form is obtained by multiplying equation (3.4) by the temperature weight function
$w_{t}$
. After integration by parts in the whole domain
${\it\Omega}\cup {\it\Gamma}$
and by using the gradient theorem result;
$$\begin{eqnarray}\int _{{\it\Omega}}[w_{t}(\dot{{\it\Theta}}+u_{i}{\it\Theta}_{,i})+w_{t,i}{\it\alpha}{\it\Theta}_{,i}]\,\text{d}{\it\Omega}-\int _{{\it\Gamma}}[w_{t}{\it\alpha}{\it\Theta}_{,i}n_{i}]\,\text{d}{\it\Gamma}=0.\end{eqnarray}$$
Again,
$n_{i}$
indicates the unitary normal vector to the surface boundaries. Therefore, at the outflow the normal thermal derivative,
${\it\Theta}_{,i}n_{i}$
, is prescribed a zero value (no streamwise heat transfer by conduction at the outflow). As with the pressure boundary condition described above, this boundary condition is applied in an integral or weak sense and thus not applied pointwise, which results in better stability for the method.
In order to have good performance for turbulent simulations, structured meshes with hexahedral elements were employed. In the wall-normal direction, non-uniform mesh sizes are used with the mesh properties indicated in table 2. From this table, it is observed that the smooth and rough cases are very similar in terms of the Reynolds number range and inlet boundary layer thicknesses. The differences between the two simulations are mainly the spatio-temporal resolution (i.e.
${\rm\Delta}x^{+},{\rm\Delta}y^{+},{\rm\Delta}z^{+}$
and
${\rm\Delta}t^{+}$
), the sample time and
${\it\delta}_{inl}^{+}$
. A grid independence test and computation of the Obukhoff–Corrsin lengths and Kolmogorov time scales can be found in appendices A and B, respectively. Furthermore, suitability of the streamwise domain length is addressed in appendix C. Both cases were run on 128 processors (
$N_{procs}$
).
Table 2. Table showing proposed DNS cases and domain parameters for smooth and rough ZPG simulations.
4. Numerical results
4.1. Displacement height
In order to ensure that the rough and smooth surface statistics are comparable, a displacement of the origin in the wall-normal direction for the profiles was employed. This origin displacement appears in the profile diagrams as a reference height for vertical coordinates, and data is shifted by the displacement height. Due to the lack of any models for flow characteristics around roughness elements, this height cannot be determined analytically. Consequently, based on the total average roughness height (
$k^{+}=11$
) the reference height was chosen, given by
${\it\varepsilon}^{+}=11$
, at a streamwise station where the local momentum thickness Reynolds number is 2465. For the smooth case, averaging is done in time and in the full spanwise direction. On the other hand, for the rough case the mean flow is, in principle, only averaged in time (to locally compute the fluctuation as instantaneous minus mean flow). Additionally, we have selected 16 spanwise locations with similar roughness heights around the total average value of
$k^{+}$
(i.e.
$k_{local}^{+}\approx 11$
). Once the statistics were computed, the corresponding homogeneous spanwise values have been averaged.
In figure 3, a schematic streamwise profile of the roughness elements with a line denoting the reference height,
${\it\varepsilon}^{+}$
, and the corresponding boundary layer regions can be seen. Given the moderate Reynolds number of the simulations (i.e. as compared to typical high Reynolds numbers of experiments), an inertial sublayer is not present, only a mesolayer region exists. As shown in figure 3, the roughness elements in the current study occupy most of the linear sublayer, significantly altering the viscous sublayer, and extending it into the lower part of the buffer layer (
$y^{+}\approx 11$
).
Figure 3. Schematic of the boundary layer with roughness elements for high Reynolds numbers.
Figure 4. Mean temperature profile comparison for rough and smooth DNS cases with experimental smooth ZPG data for validation.
4.2. Thermal field
Figure 4 compares the mean temperature profiles of the current DNS database, with smooth ZPG experimental results by Blackwell (Reference Blackwell1972), Hoffmann & Perry (Reference Hoffmann and Perry1979), Nagano, Tsuji & Houra (Reference Nagano, Tsuji and Houra1998) in classical coordinates (i.e.
$y^{+}=u_{{\it\tau}}y/{\it\nu};{\it\Theta}^{+}={\it\Theta}/{\it\theta}_{{\it\tau}}$
, where
${\it\theta}_{{\it\tau}}=q_{w}/({\it\rho}C_{p}u_{{\it\tau}})$
is the friction temperature). Excellent agreement is observed with the experimental data for the smooth case. As shown, the smooth-case profiles from the simulations and the experiments follow the linear profile (
$\overline{{\it\Theta}}^{+}=Pry^{+}$
) and the log-law profile (
$\overline{{\it\Theta}}^{+}=0.48^{-1}\ln y^{+}+3.8$
); however, surface roughness provokes the typical downward shift of the mean temperature profile in the log region.
Figure 5. (a) Streamwise variation of Stanton number. (b) Streamwise variation of
$St/(C_{f}/2)$
.
Figure 5(a) depicts the streamwise variation of the Stanton number values for the smooth and rough cases. During postprocessing, the rough case Stanton number was computed using the constant heat-flux equation (Teitel & Antonia Reference Teitel and Antonia1993), given as
$$\begin{eqnarray}\frac{1}{Pr}\frac{\partial \overline{{\it\Theta}}^{+}}{\partial y^{+}}-\overline{v^{\prime }{\it\theta}^{\prime }}^{+}=-1.\end{eqnarray}$$
Furthermore, the main contributions to the wall heat flux,
$q_{w}$
, in the inner region (i.e. the wall-normal gradient of the mean temperature and wall-normal turbulent heat fluxes) have been averaged at five points around the
$\overline{v^{\prime }{\it\theta}^{\prime }}_{max}$
location (i.e. the constant heat-flux layer) to estimate
$St$
; whereas the wall thermal gradient is employed for the smooth
$St$
number calculation. We have also checked the
$St$
number computation in the smooth case by means of the constant heat-flux equation (4.1) and obtained differences within 2 % with respect to the wall thermal gradient methodology.
The constant heat-flux equation is more accurate than the energy integral equation (2.8) for the computation of
$St$
. However, (2.8) is simpler to implement (with a faster rate of convergence, particularly in the transient stage) since it only requires the knowledge of the mean thermal flow. Moreover, the dynamic multiscale approach only demands the ratio of the Stanton number values at the inlet and recycle planes, not the actual values of
$St$
, which produces an error compensation. For instance, the computed value of
$St_{inl}/St_{rec}$
at the end of the collected sample by means of the energy integral equation was just 1 % lower than that obtained by the constant heat-flux equation. A similar methodology was implemented in Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013) to compute the
$C_{f}$
in the rough case by means of the constant stress layer equation.
As observed in figure 5(a), there is a good agreement of the present smooth
$St$
with the experimental and theoretical data of Blackwell (Reference Blackwell1972), Kays & Crawford (Reference Kays and Crawford1993), Wang, Castillo & Araya (Reference Wang, Castillo and Araya2008). From this figure it is evident that the transitionally rough surface with
$k^{+}\approx 11$
increased the heat transfer rate by as much as 12 % compared to the smooth case at
$Re_{{\it\theta}}\approx 2100$
. Since the Stanton number can be expressed as
$St=Nu/(Re_{{\it\theta}}Pr)$
, where
$Nu$
is the Nusselt number, it is proportional to the Nusselt number (ratio of the convective to conductive heat transfer). This, it is clear that the Nusselt number for the rough case is increased as well. This increase in
$Nu$
is attributed to the enhancement of the turbulent convective heat transfer.
In figure 5(b), the streamwise variation of
$St/(C_{f}/2)$
is shown. Evidently this ratio is around
$1$
in both smooth and rough cases; it shows a high correlation between surface friction and the heat transfer coefficient. In an expression suggested by Kays & Crawford (Reference Kays and Crawford1993), for smooth turbulent ZPG and isothermal conditions,
$$\begin{eqnarray}St/(C_{f}/2)=Pr^{-0.4},\end{eqnarray}$$
for
$Pr=0.71$
,
$St/(C_{f}/2)$
adopts the value of
$1.147$
, which is consistent with the results presented for the smooth case here.
We also observe that the
$St/(C_{f}/2)$
ratio is closer to one for the rough case. For higher Reynolds numbers, this unitary value does not change much (a change of the order of 1 % in this range), and the relating expression for local Stanton number and local surface skin friction factor can be applied to a transitionally rough surface of
$k^{+}\approx 11$
. This expression is useful for estimating heat transfer rates in situations in which the skin friction is known.
The increase in the
$C_{f}$
value is larger than the increase in
$St$
over the transitionally rough surface case. This increase is consistent with the experiments by Dipprey & Sabersky (Reference Dipprey and Sabersky1963). With the presence of surface roughness, the
$C_{f}$
and
$St$
both increased by approximately 17 % and 12%, respectively, which is the primary reason of the observed decrease of the
$St/(C_{f}/2)$
ratio.
Figure 6. Mean temperature profiles in Wang–Castillo scaling for the smooth and rough cases with (a) inner and (b) outer scaling.
Figure 7. (a)
${\it\theta}_{rms}^{\prime }$
fluctuations profiles of the smooth and rough cases with outer Wang–Castillo (main) and inner (inset) classical scaling. (b) Wall-normal turbulent heat fluxes using Wang–Castillo scaling for the smooth and rough cases with outer (main) and inner units (inset).
Figure 6(a) is in inner Wang–Castillo scaling, it can be observed that the mean temperature is influenced by the rough surface, and the normalized temperature profile of the rough surface flow lies below that of the smooth surface flow. The smooth and rough Reynolds numbers are slightly different. However, the authors verified that the DNS data’s Reynolds number dependence was negligible. The downward shifted thermal profile may indicate that surface roughness enhances mixing (i.e. lower temperature difference with the wall). Also note that the Stanton number is larger for the rough case. A very good collapse is observed in the inner region, indicating absorption of roughness effects by the Wang–Castillo scaling in the inner region. For the outer scaling, as shown in figure 6(b), a perfect collapse in the outer region of boundary layer is observed as well. This collapse indicates that the selected scaling absorbs the effects induced by the surface roughness in the outer region.
Figure 7(a), shows the r.m.s. of temperature fluctuations in inner classical and outer Wang–Castillo scaling.
${\it\theta}_{rms}^{\prime +}$
is altered minimally in the inner and outer regions of the boundary layer. In figure 7(a), the peak value of
${\it\theta}_{rms}^{\prime +}$
in the rough case is slightly reduced compared to the smooth case in the inner layer. However, a fair collapse between the
${\it\theta}_{rms}^{\prime +}$
profiles is noticed in the outer region, with a slight increase in the rough case, particularly at the ‘shoulder’ location (i.e. for
$0.1<(y+{\it\varepsilon})/{\it\delta}_{T}<0.5$
). The wall-normal turbulent heat fluxes across the boundary layer are examined in figure 7(b) for inner and outer Wang–Castillo scaling. In the main figure, in the outer region, vertical turbulent heat flux is lower for the rough case, but from
$(y+{\it\varepsilon})/{\it\delta}_{T}=0.4$
a nice collapse can be seen. For the inner layer, in the inset of figure 7(b), it is observed that
$\overline{v^{\prime }{\it\theta}^{\prime }}^{+}$
is lower for the rough case compared to smooth case all across the inner layer. The peak value of wall-normal heat flux is slightly moved away from the wall.
It is evident that roughness plays a significant role in the inner region up to
$(y+{\it\varepsilon})/{\it\delta}_{T}<0.4$
for the wall-normal turbulent heat fluxes, which corresponds to
$(y+{\it\varepsilon})^{+}<100$
, since the profiles are self-similar beyond this wall-normal location. This is consistent with Jiménez (Reference Jiménez2004), who showed that in flows with
${\it\delta}/k\leqslant 50$
the effect of roughness extends across the boundary layer. However, we have
${\it\delta}/k\approx 71$
, and therefore the effects of surface roughness on wall-normal heat fluxes are approximately restricted to
$(y+{\it\varepsilon})/{\it\delta}_{T}<0.4$
.
Figure 8. Smooth and rough turbulent Prandtl numbers, (a) up to
$(y+{\it\varepsilon})^{+}=600$
, and (b) in the near-wall region.
The Reynolds analogy is a relationship between turbulent momentum and heat transfer, and one outcome of this analogy is to relate the molecular wall heat transfer to the local wall viscous stress. In the Reynolds analogy for turbulent flows, according to Tennekes & Lumley (Reference Tennekes and Lumley1972), the turbulent Prandtl number,
$Pr_{t}$
, is assumed to be constant and close to one. Figure 8(a) shows the variation of
$Pr_{t}$
across the boundary layer. These results are consistent for the smooth case with the review by Kays (Reference Kays1994), in which he concluded that in the log region of boundary layer
$Pr_{t}$
has a value from 0.8 to 1. Our results in figure 8(b) for the smooth case show a value of 1.1 at the wall and start to decrease away from the wall. Up to
$y^{+}=7$
we have
$Pr_{t}>1$
, and then reach a value of 0.9 around
$y^{+}=60$
, 0.8 around
$y^{+}=140$
, and far away from the wall a value of approximately 0.7 is obtained, which is consistent with the DNS values of
$Pr_{t}$
for the smooth case of Li et al. (Reference Li, Schlatter, Brandt and Henningson2009) at
$Re_{{\it\theta}}=820$
for
$Pr=0.71$
. However, in the DNS study by Wu & Moin (Reference Wu and Moin2010) a wall value of
$Pr_{t}=1.9$
was reported for the turbulent boundary layer at
$Re_{{\it\theta}}=1840$
and
$Pr=1.0$
. In the present DNS simulation, the data indicated no secondary peak, similar to Wu & Moin (Reference Wu and Moin2010), but contrary to other studies which reported a secondary peak for the
$Pr_{t}$
number close to the smooth wall around
$y^{+}\approx 35$
, e.g. Kong et al. (Reference Kong, Choi and Lee2000), Li et al. (Reference Li, Schlatter, Brandt and Henningson2009), which can be attributed to the low Reynolds numbers considered in the latter studies. We can assert that the Reynolds analogy is strictly valid for the smooth case from the wall up to
$y^{+}\approx 60$
, where the
$Pr_{t}$
attains the value of 0.9 and for
$y^{+}>60$
it varies from 0.9 to 0.6 at the boundary layer edge; thus the Reynolds analogy is approximately valid. For the rough surface, the
$Pr_{t}$
starts from a value of
$1.3$
at the wall and exhibits negative values in the region
$5<(y+{\it\varepsilon})^{+}<8$
. Later,
$Pr_{t}$
increases to the smooth-case value at
$(y+{\it\varepsilon})^{+}=9$
, and above that the rough- and smooth-case values are very similar. The ratio of the mean thermal gradient
$\text{d}\overline{{\it\Theta}}/\text{d}y$
to the mean streamwise velocity gradient
$\text{d}\overline{U}/\text{d}y$
in the rough case remains similar to the smooth case given by
$\text{d}\overline{{\it\Theta}}/\text{d}\overline{U}$
in figure 9(a). The ratios of Reynolds shear stresses to wall-normal turbulent heat fluxes in figure 9(b) approximately exhibit the same trend in both cases, except for the region
$5<(y+{\it\varepsilon})^{+}<8$
, where the rough profile significantly deviates from the smooth one. This is the principal reason for the strong dissimilarity of the smooth and rough
$Pr_{t}$
values in that zone. The rough profiles of
$\overline{u^{\prime }v^{\prime }}^{+}$
and
$\overline{v^{\prime }{\it\theta}^{\prime }}^{+}$
exhibit positive values for
$(y+{\it\varepsilon})^{+}<6$
. Thus, it is inferred that roughness mainly promotes outward (
$Q1$
) and inward (
$Q3$
) interactions instead of the typical
$Q2$
(ejections) and
$Q4$
(sweeps) events that principally contribute to
$\overline{u^{\prime }v^{\prime }}^{+}$
and
$\overline{v^{\prime }{\it\theta}^{\prime }}^{+}$
in smooth boundary layers. Evidence of the
$Q1$
and
$Q3$
enhancement due to the presence of roughness is shown later by a quadrant analysis. From figure 9(b) it is observed that the turbulent momentum transport is more pronounced than the turbulent transport of heat in the rough case for
$(y+{\it\varepsilon})^{+}<4$
(i.e. ratio of
$\overline{u^{\prime }v^{\prime }}/\overline{v^{\prime }{\it\theta}^{\prime }}\approx 1.5$
). In the region
$4<(y+{\it\varepsilon})^{+}<9$
the opposite occurs, with values of the ratio
$\overline{u^{\prime }v^{\prime }}/\overline{v^{\prime }{\it\theta}^{\prime }}$
much lower than 1, meaning that the Reynolds analogy is not satisfied in the region
$(y+{\it\varepsilon})^{+}<9$
. Above
$y^{+}\approx 9$
, up to
$(y+{\it\varepsilon})^{+}\approx 60$
, the rough surface
$Pr_{t}$
varies from 1 to 0.9, so the Reynolds analogy is valid. Above this region, similar to the smooth case,
$Pr_{t}$
varies from 0.9 to 0.6, indicating approximate validity of the Reynolds analogy.
Figure 9. Turbulent Prandtl number decomposition, (a)
$\text{d}\overline{{\it\Theta}}/\text{d}\overline{U}$
, (b)
$\overline{u^{\prime }v^{\prime }}/\overline{v^{\prime }{\it\theta}^{\prime }}$
.
Figure 10(a) shows the net force exerted by the Reynolds shear stress, which vanishes at the location of the maximum value. This zero net Reynolds force occurs at
$(y+{\it\varepsilon})^{+}\approx 45$
for the smooth and rough cases at the same wall-normal location. For the zero net turbulent heat flux, as shown in figure 10(b), the maximum value of
$\overline{v^{\prime }{\it\theta}^{\prime }}$
occurs at
$(y+{\it\varepsilon})^{+}\approx 58$
for the smooth case, and at
$(y+{\it\varepsilon})^{+}\approx 73$
for the rough case, a difference of approximately 15 wall units. Thus surface roughness induces more significant changes in the thermal transport than in the turbulent transport. Furthermore, the peak values in each figure 10(a,b) representing maximum thermal and turbulent transport, are increased and also moved away from the wall by approximately two wall units for the rough surface compared to the smooth surface. According to Adrian (Reference Adrian2007) this increase in the maximum value of
$\text{d}(\overline{u^{\prime }v^{\prime }}^{+}/\text{d}y^{+})$
causes an increase in the mean transport of turbulent momentum. Furthermore, the similarity between the turbulent momentum and thermal transports is remarkable, even for the rough case. Notice that the net force and net turbulent heat flux are positive for
$(y+{\it\varepsilon})^{+}<4$
in the rough case, which indicates local positive curvatures of the mean streamwise velocity and mean temperature. Furthermore, in the near-wall region (i.e.
$(y+{\it\varepsilon})^{+}<7$
) the net force and net turbulent heat flux are lower for the rough case compared to the smooth case, leading to less acceleration of the flow near the wall. This retardation of the flow will lead to deterioration of the heat and mass transfer, as mentioned by Yaglom & Kader (Reference Yaglom and Kader1974) close to the rough surface. Accordingly, we can conclude that the reduced zero net turbulent heat flux close to the wall leads to the decrease of the mean turbulent thermal transport near the wall.
Figure 10. Comparison of location of (a) zero net Reynolds force, (b) zero net turbulent heat, for the smooth and rough cases, in the wall-normal direction.
Figure 11. Comparison of production of (a) temperature fluctuations and (b) TKE, for smooth and rough cases.
4.3. Thermal/turbulence production, transport and higher-order moments
Figure 11(a) shows production of temperature fluctuations computed by the following equation,
$$\begin{eqnarray}-\overline{u_{i}^{\prime }{\it\theta}^{\prime }}^{+}\frac{\partial \overline{{\it\Theta}}^{+}}{\partial x_{i}^{+}}.\end{eqnarray}$$
It can be seen that the peak of thermal production is reduced by approximately 5 % for the rough surface compared to the smooth surface. In the inner region the thermal production is much lower in the rough case, which can be attributed to the increased thermal dissipation. Up to
$(y+{\it\varepsilon})^{+}\approx 5$
we observe a negative region of thermal production which is due to the negative value of streamwise and vertical production components. In this region both
$\overline{u^{\prime }{\it\theta}^{\prime }}^{+}$
and
$\partial \overline{{\it\Theta}}^{+}/\partial x^{+}$
are positive, and also
$\overline{v^{\prime }{\it\theta}^{\prime }}^{+}$
is positive in a small region, while
$\partial \overline{{\it\Theta}}^{+}/\partial y^{+}$
is positive, leading to a negative production of temperature fluctuations. Furthermore, it can be inferred that the imposed rough surface does not affect production of thermal fluctuations beyond
$(y+{\it\varepsilon})^{+}>30$
. Similarly, in figure 11(b), production of turbulence kinetic energy (TKE) is shown and computed as follows,
$$\begin{eqnarray}-\overline{u_{i}^{\prime }u_{j}^{\prime }}^{+}\frac{\partial \overline{U_{i}}^{+}}{\partial x_{j}^{+}}.\end{eqnarray}$$
It is observed that the peak in production of TKE is reduced by as much as 17 % for the rough case compared to the smooth case, which is consistent with observations of turbulent heat flux and zero net Reynolds force. Additionally, in the inner layer, for
$(y+{\it\varepsilon})^{+}<20$
, turbulence production is much lower in the rough case, mainly due to an increase of TKE dissipation and pressure diffusion due to roughness (not shown). Moreover, for
$(y+{\it\varepsilon})^{+}>30$
, a good collapse between smooth and rough surface flow is observed in the turbulent kinetic energy production. Notice that the shape of profiles for production of thermal fluctuations and TKE are indeed similar.
Figure 12. Turbulent transports of (a) Reynolds shear stresses and (b) turbulent heat flux.
Figure 12(a,b) show the vertical transport of the Reynolds shear stresses and wall-normal heat fluxes by the wall-normal fluctuations, normalized in wall coordinates. The presence of surface roughness enhances the wall-normal transport of the Reynolds stresses and turbulent heat fluxes towards the wall in the near-wall region. On the other hand, it reduces the transport away from the wall in the regions further away from the wall. It may be due to the fact that roughness curtails the larger structures in the outer flow, as shown in Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). This phenomena inhibits the flow to convect energy in the turbulent boundary layer.
Figure 13. (a) Skewness factor
$S_{{\it\theta}}$
and (b) flatness factor
$F_{{\it\theta}}$
for
${\it\theta}^{\prime }$
.
Figure 14. Skewness factor for (a)
$u^{\prime }$
,
$S_{u}$
, and (b)
$v^{\prime }$
,
$S_{v}$
.
The skewness factor distributions for
${\it\theta}^{\prime }$
are shown in figure 13(a), where the horizontal line indicate the Gaussian level. For
$(y+{\it\varepsilon})^{+}>4$
an excellent agreement for the smooth and rough profiles is observed. However, close to the wall the skewness is higher for the rough case compared to the smooth case. In figure 13(b) the flatness factor,
$F_{{\it\theta}}$
, for
${\it\theta}^{\prime }$
is shown and a good collapse is observed for
$(y+{\it\varepsilon})^{+}>5$
, particularly in the outer layer. For
$(y+{\it\varepsilon})^{+}<5$
,
$F_{{\it\theta}}$
is observed to be much higher for the rough case compared to the smooth case. Since flatness is a measure of the intermittency, it is inferred that roughness significantly enhances intermittency of thermal fluctuations. In figure 14 the skewness factor profiles,
$S_{u}$
and
$S_{v}$
, for
$u^{\prime }$
and
$v^{\prime }$
, respectively, are depicted. Good agreement is observed for
$S_{u}$
at
$(y+{\it\varepsilon})^{+}>5$
, and closer to the wall, the skewness factor is higher for the rough case compared to the smooth case. The skewness factor value of
$S_{v}$
is drastically higher for the rough case compared to the smooth case near the wall, and there is a fair collapse at
$(y+{\it\varepsilon})^{+}>17$
. It is also noticeable that the skewness factors
$S_{u}$
and
$S_{{\it\theta}}$
are very similar in shape, and they both look quite different compared to the skewness factor of
$S_{v}$
. Figure 15 shows the flatness factor distributions,
$F_{u}$
and
$F_{v}$
, for
$u^{\prime }$
and
$v^{\prime }$
. A very good collapse is observed for
$F_{u}$
at
$(y+{\it\varepsilon})^{+}>6$
and for
$F_{v}$
at
$(y+{\it\varepsilon})^{+}>30$
. For
$F_{u}$
it can be observed that the flatness factor is higher for the rough case close to the wall, whereas
$F_{v}$
is lower for the rough case close to the wall. It is evident that both flatness factors
$F_{u}$
and
$F_{v}$
reach the Gaussian level for
$(y+{\it\varepsilon})^{+}>40$
, whereas
$F_{{\it\theta}}$
reaches a value lower than the Gaussian level. In general, since the level of smoothness in the higher-order statistics profiles (i.e. skewness and flatness) of fluctuations is very good, it is inferred that the collected sample size is quite appropriate.
Figure 15. Flatness factor for (a)
$u^{\prime }$
,
$F_{u}$
, and (b)
$v^{\prime }$
,
$F_{v}$
.
In figure 16(a) the fractional contribution of quadrant events to the wall-normal turbulent heat flux is shown. It is observed that the presence of surface roughness significantly promotes all quadrant motions, especially the
$Q1$
,
$Q3$
and
$Q4$
or sweep events. A perfect collapse between smooth and rough data is observed for
$(y+{\it\varepsilon})^{+}>20$
. Figure 16(b) shows the contribution of quadrant motions to Reynolds shear stress. Rough surfaces enhance all quadrant motions, similar to the wall-normal turbulent heat-flux motions. In both cases it can be concluded that surface roughness promotes the sweep motions and inward interactions (
$Q3$
) towards the wall in the near-wall region (as observed in the turbulent transport of Reynolds stresses and turbulent heat fluxes), which is consistent with increased transport towards the wall, and also the increased skewness observed earlier for the rough surface. This can be due to the less rigid wall-normal boundary conditions for the rough surface.
Figure 16. Fractional contributions from quadrant motions to (a) vertical turbulent heat flux and (b) Reynolds shear stress. Solid lines: smooth,
${\it\varepsilon}^{+}=0$
; dash-dot lines: rough,
$k^{+}=11$
,
${\it\varepsilon}^{+}=11$
.
The transport equation for
$\overline{v^{\prime +}{\it\theta}^{\prime +}}$
is given as
$$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{-\overline{U}_{i}^{+}\frac{\partial (\overline{v^{\prime +}{\it\theta}^{\prime +}})}{\partial x_{i}^{+}}}_{\text{Convection}}\underbrace{-\overline{u_{i}^{\prime +}v^{\prime +}}\frac{\partial \overline{{\it\Theta}}^{+}}{\partial x_{i}^{+}}-\overline{u_{i}^{\prime +}{\it\theta}^{\prime +}}\frac{\partial \overline{V}^{+}}{\partial x_{i}^{+}}}_{\text{Production}}\underbrace{-\frac{\partial (\overline{{\it\theta}^{\prime +}v^{\prime +}u_{i}^{\prime +}})}{\partial x_{i}^{+}}}_{\text{Turbulent diffusion}}\underbrace{-\left(1+\frac{1}{Pr}\right)\overline{\frac{\partial {\it\theta}^{\prime +}}{\partial x_{i}^{+}}\frac{\partial v^{\prime +}}{\partial x_{i}^{+}}}}_{\text{Dissipation}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad \underbrace{+\overline{p^{\prime +}\frac{\partial {\it\theta}^{\prime +}}{\partial y^{+}}}}_{\text{Press-temp. grad. correl.}}\underbrace{+\frac{\partial }{\partial x_{i}^{+}}\left(\overline{{\it\theta}^{\prime +}\frac{\partial v^{\prime +}}{\partial x_{i}^{+}}}+\frac{1}{Pr}\overline{v^{\prime +}\frac{\partial {\it\theta}^{\prime +}}{\partial x_{i}^{+}}}\right)}_{\text{Molecular diffusion}}\underbrace{-\frac{\partial }{\partial y^{+}}\left(\overline{p^{\prime +}{\it\theta}^{\prime +}}\right)}_{\text{Pressure diffusion}}=0. & \displaystyle\end{eqnarray}$$
Figure 17(a,b) shows energy budget terms for the turbulent vertical heat flux
$\overline{v^{\prime }{\it\theta}^{\prime }}$
. Near the wall, the convection term is negligible in the smooth case, but for the rough case this term is significantly enhanced close to the wall, due to the less rigid wall-normal velocity condition at the wall for the rough surface flow. Although the convective term is enhanced, it is still negligible compared to the other terms.
The dissipation term is slightly increased in the rough case compared to the smooth case and the molecular diffusion for the rough case is very similar to the smooth case. The contribution from the production term is slightly decreased for the rough case compared to the smooth case, whereas the contribution from turbulent diffusion is slightly enhanced in the rough case. Further, in figure 17(a), pressure diffusion (PD) and pressure–temperature gradient correlation (PTG) terms can be seen. The pressure terms are observed to be slightly modified close to the wall, with a slight displacement away from the wall for the rough case compared to the smooth case. It is also observed that the pressure diffusion term is slightly enhanced for the rough case.
Figure 17. Energy budgets of wall-normal turbulent heat flux
$\overline{v^{\prime }{\it\theta}^{\prime }}$
. Solid lines: smooth,
${\it\varepsilon}^{+}=0$
; dash-dot lines: rough,
$k^{+}=11$
,
${\it\varepsilon}^{+}=11$
. (a) Strong contributions and (b) weak contributions.
According to Tennekes & Lumley (Reference Tennekes and Lumley1972), the energy budget of Reynolds stresses is expressed as follows,
$$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{-\overline{U_{j}^{+}}\frac{\partial \overline{R_{ij}^{\prime +}}}{\partial x_{j}^{+}}}_{\text{Convection}}\underbrace{-\frac{\partial \overline{u_{i}^{\prime +}u_{j}^{\prime +}u_{k}^{\prime +}}}{\partial x_{k}^{+}}}_{\text{Turbulent diffusion}}\underbrace{+\overline{\left(p^{\prime +}\frac{\partial u_{i}^{\prime +}}{\partial x_{j}}+p^{\prime +}\frac{\partial u_{j}^{\prime +}}{\partial x_{i}}\right)}}_{\text{Pressure strain correlation}}\underbrace{-\frac{\partial }{\partial x_{k}^{+}}(\overline{p^{\prime +}u_{j}^{\prime +}}{\it\delta}_{ik}+\overline{p^{\prime +}u_{i}^{\prime +}}{\it\delta}_{jk})}_{\text{Pressure diffusion}} & \displaystyle \nonumber\\ \displaystyle & \underbrace{+\frac{\partial ^{2}\overline{R_{ij}^{\prime +}}}{\partial x_{k}^{+2}}}_{\text{Molecular diffusion}}\underbrace{-\overline{u_{i}^{\prime +}u_{k}^{\prime +}}\frac{\partial \overline{U_{j}^{+}}}{\partial x_{k}^{+}}-\overline{u_{j}^{\prime +}u_{k}^{\prime +}}\frac{\partial \overline{U_{i}^{+}}}{\partial x_{k}^{+}}}_{\text{Production}}\underbrace{-2\overline{\frac{\partial u_{i}^{\prime +}}{\partial x_{k}^{+}}\frac{\partial u_{j}^{\prime +}}{\partial x_{k}^{+}}}}_{\text{Dissipation}}=0, & \displaystyle\end{eqnarray}$$
where
$R_{11}$
,
$R_{22}$
,
$R_{33}$
and
$R_{12}$
represent Reynolds normal stresses and Reynolds shear stresses, respectively, and
${\it\delta}_{ij}$
corresponds to the Kronecker delta. The energy budget terms of Reynolds shear stress
$\overline{u^{\prime }v^{\prime }}$
are shown in near-wall region in figure 18(a,b). The contribution of the convection term is negligible near the smooth wall, as expected; however, in the rough case it is slightly enhanced and visible around
$(y+{\it\varepsilon})^{+}\approx 7$
and
$(y+{\it\varepsilon})^{+}\approx 13$
. This is mainly due to the increase in the mean wall-normal velocity, although its contribution is still negligible compared to other terms. Similar to the vertical turbulent heat flux, the dissipation term is enhanced close to the wall in the rough case compared to the smooth case. The molecular diffusion term is negligible for both smooth and rough cases for
$(y+{\it\varepsilon})^{+}>30$
, and close to the wall both positive and negative peaks are enhanced in the rough case. Regarding the turbulent diffusion term, an increase in the peak value is observed for the rough case compared to the smooth case around
$(y+{\it\varepsilon})^{+}\approx 9$
. However, the production term is slightly suppressed in the rough case up to
$(y+{\it\varepsilon})^{+}\approx 15$
. The examination of the energy redistribution (pressure diffusion and pressure-strain correlation (PS)) terms in figure 18(a) reveals that surface roughness modifies these terms close to the wall. The peaks close to the wall are intensified and also moved away from the wall for the rough case. In figure 19, the temperature–pressure gradient correlation (
$\text{TPG}=\text{PD}-\text{PTG}$
) and velocity–pressure gradient correlation (
$\text{VPG}=\text{PD}-\text{PS}$
) are depicted. It is concluded that the significant discrepancies of the smooth and rough cases disappear when considering the total contribution of pressure terms, i.e. TPG and VPG. In general, similar trends are observed for the Reynolds shear stress and vertical turbulent heat-flux budgets, which means that the similarity between
$\overline{u^{\prime }v^{\prime }}$
and
$\overline{v^{\prime }{\it\theta}^{\prime }}$
somehow still holds for the type of roughness utilized in the present study. In addition, the role of pressure fluctuations due to roughness play a significant role in the energy exchange for
$\overline{v^{\prime }{\it\theta}^{\prime }}$
and
$\overline{u^{\prime }v^{\prime }}$
in the near-wall region for
$(y+{\it\varepsilon})^{+}<20$
.
Figure 18. Energy budgets of Reynolds shear stress
$\overline{u^{\prime }v^{\prime }}$
. Solid lines: smooth,
${\it\varepsilon}^{+}=0$
; dash-dot lines: rough,
$k^{+}=11$
,
${\it\varepsilon}^{+}=11$
. (a) Strong contributions and (b) weak contributions.
Figure 19. Sum of the pressure-related terms in budgets. (a) Pressure–temperature gradient correlation
$+$
pressure diffusion for
$\overline{v^{\prime }{\it\theta}^{\prime }}$
. (b) Pressure–strain correlation
$+$
pressure diffusion for
$\overline{u^{\prime }v^{\prime }}$
.
4.4. Vorticity
Figure 20(a,b) compares the r.m.s. of the vorticity fluctuation components for smooth and rough cases, normalized by
${\it\nu}/u_{{\it\tau}}^{2}$
. All three components are nearly identical for smooth and rough cases away from the wall for
$(y+{\it\varepsilon})^{+}>50$
. For the
$x$
component, a peak is observed at
$(y+{\it\varepsilon})^{+}\approx 3$
for the rough case. In the smooth case, a local minimum is observed at
$y^{+}\approx 5.5$
before it attains a local maximum at
$y^{+}\approx 10.5$
. Kim, Moin & Moser (Reference Kim, Moin and Moser1987) attributed this behaviour to near-wall streamwise vortices. They explained that the location of the local maximum is the average location of the axis centre of the streamwise vortices and the first peak at the wall is due to the streamwise vortices with opposite sign formed close to the wall due to the no-slip condition. The local minimum is the average location at which two counter-rotating streamwise vortices encounter each other. In the rough case, no such local minimum of maximum is observed, which may indicate that the rough wall is disrupting the formation of opposite sign streamwise vortices near the wall. For
${\it\omega}_{y}^{\prime +}$
, the changes are not significant and a slight increase in the peak is observed around
$(y+{\it\varepsilon})^{+}\approx 12$
.
${\it\omega}_{y}^{\prime +}$
is primarily generated on streak flanks (Schoppa & Hussain Reference Schoppa and Hussain2002), so it can be inferred that the height of streak is unchanged by roughness. Moreover, up to
$(y+{\it\varepsilon})^{+}\approx 40$
,
${\it\omega}_{x}^{\prime +}$
for the rough surface is larger than the
${\it\omega}_{x}^{\prime +}$
for the smooth surface and it can be inferred that hairpin legs have shallower inclination in the buffer region. In the
$z$
direction, the vorticity magnitude of
${\it\omega}_{z}^{\prime +}$
has increased significantly up to
$y^{+}\approx 20$
. A peak is observed at
$y^{+}\approx 3$
, which coincides with the drop in
${\it\omega}_{x}^{\prime +}$
.
Figure 20. R.m.s. of vorticity fluctuation components, (a) for the
$x$
and
$y$
directions, (b) for the
$z$
direction.
4.5. Townsend’s hypothesis
As used in the study of turbulent flow over rough surfaces, Townsend’s Reynolds number similarity hypothesis states that the mean relative motion and the motion of the energy-containing eddies do not depend on viscosity or the surface roughness in the region above the roughness layer, provided the Reynolds number is high enough, and the roughness layer is small enough. While viscous stresses and the size and shape of the roughness elements are dominant factors within the roughness layer, they only manifest their effects in the outer layer through the mean velocity and mean turbulent stress created at the top of the roughness layer. These values define boundary conditions for the outer region. An important and obvious implication of the hypothesis is that neither the viscous length scale, nor the scale of the roughness height are appropriate in the similarity region, leaving the outer length scale as the proper property for non-dimensionalization. Measurements of moments as high as fourth order support Townsend’s hypothesis for the velocity field (Schultz & Flack Reference Schultz and Flack2007; Nickels Reference Nickels2010).
We have tested the validity of Townsend’s hypothesis for the velocity and temperature fields by comparing the statistical moments of the smooth-wall and rough-wall cases. Since the hypothesis implies no effect of the roughness in the outer layer, any statistically significant differences in the outer layer would invalidate it. Comparisons of the profiles of many different statistical moments are contained in the results already presented. For example, in figure 20 the r.m.s. values of each component of vorticity converge above
$(y+{\it\varepsilon})^{+}\approx 30{-}50$
, beyond which they are the same with and without roughness. Thus, Townsend’s hypothesis is supported by the behaviour of the r.m.s. vorticity in the outer layer. The single-point statistics profiles shown in this paper in terms of wall units can be viewed as plots in outer units, because
$y^{+}=(y/{\it\delta}){\it\delta}^{+}$
, and
${\it\delta}^{+}$
is nearly the same constant for the smooth and the rough data. Regarding other moments, with our statistics of turbulent flow over smooth and rough surfaces, we can examine the validity of Townsend’s hypothesis. Presented results indicate that mean temperature defect profiles collapse above the roughness sublayer with the outer scaling for the smooth and rough cases in figure 6(b). Thus, the higher-order statistics of the turbulence fields for smooth and rough surfaces reveal that they also support Townsend’s hypothesis.
The net force of the Reynolds shear stress and the net flux of the wall-normal turbulent heat flux (figure 10), the production of temperature variance and turbulent kinetic energy (figure 11), and the skewness and flatness of temperature and velocity (figures 13–15), all support Townsend’s hypothesis in the outer region above a few roughness heights, i.e.
$(3{-}5)k$
. Remarkably, the terms of the budgets of turbulent heat flux (figure 17) and turbulent kinetic energy (figure 18) each indicate absence of a roughness effect in the outer layer, as do fractional contributions of quadrant motions to the total Reynolds shear stress and the vertical turbulent heat flux (figure 16). However, it is observed from flow statistics,
${\it\theta}_{rms}^{\prime }$
(figure 7
a),
$\overline{v^{\prime }{\it\theta}^{\prime }}$
(figure 7
b),
$\overline{v^{\prime }u^{\prime }v^{\prime }}$
(figure 12
a) and
$\overline{v^{\prime }v^{\prime }{\it\theta}^{\prime }}$
(figure 12
b) that the effects of roughness can extend beyond
$3k{-}5k$
. Furthermore, a fair collapse (with deviations within 15 %) of the previously mentioned smooth and rough profiles was obtained beyond
$y^{+}\approx 80{-}90$
, which corresponds to a roughness layer of approximately
$7k{-}8k$
. We therefore conclude that Townsend’s hypothesis applies both to the temperature and velocity fields.
5. Conclusions
Thermal statistics from direct numerical simulations of a zero pressure gradient turbulent boundary layer, over a transitionally rough surface at
$Re_{{\it\theta}}\approx 2400$
, and molecular Prandtl number of 0.71, are presented for the first time. The roughness elements can be considered to be small compared to the boundary layer thickness. The data from the smooth surface simulations were validated with existing experimental data for the velocity field by Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). Like the statistics of the velocity field, the statistics of the temperature field are affected by the surface roughness in the inner layer up to
$(y+{\it\varepsilon})^{+}\approx 100$
at most.
Based on the values of the turbulent Prandtl number, the Reynolds analogy does not hold in the rough case for
$(y+{\it\varepsilon})^{+}<9$
. The rough surface decreased the ratio of Reynolds stress to turbulent heat flux in the near-wall region, leading to a decreased turbulent Prandtl number, while remaining unchanged above
$y^{+}\approx 9$
. This is attributed to the fact that the ratio of thermal to turbulent mixing is enhanced more than the ratio of molecular heat transfer to viscous stress in the rough case in that zone. This dissimilarity between the velocity and thermal field (no Reynolds analogy) might be associated with the modification of pressure-related terms.
In addition, it was found that roughness enhances wall-normal heat-flux transport in the inner layer, and reduces it in the outer region of the boundary layer. Surface roughness suppresses the production of TKE and turbulent temperature fluctuations, and moves the zero turbulent heat location away from the wall. Examining the energy budget terms of Reynolds stress and turbulent heat flux, revealed the significant role of pressure fluctuations due to surface roughness in the energy exchange for Reynolds stresses and turbulent heat fluxes, below the buffer region. This supports the idea of pressure fluctuations as the principal mean of energy transport over rough surfaces. In addition, they play a key role in the presence of convective terms near the wall region for the rough surface.
Our results indicate that Townsend’s Reynolds number similarity hypothesis applies to the thermal field, as well as the velocity field. Various statistics of the temperature field coincide for smooth and rough walls in the outer region, where it is known that the velocity statistics are independent of Reynolds number and roughness. Thus, even though our simulation pertains to a single Reynolds number, it can be concluded that the similarity in the outer region is independent of Reynolds number for smooth and rough surfaces. Furthermore, the observed similarity of velocity and thermal fields in the outer region does not imply that the structures will not be modified in the outer region for the rough surface flow.
Table 3. Characteristics of the employed meshes in smooth ZPG simulations.
Acknowledgement
Computational resources were supplied by XSEDE (Project Number: TG-CTS120046) and SCOREC (Scientific Computation Research Center) from Rensselaer Polytechnic Institute. G.A. acknowledges HYDAC Corporation for grant no. 23C475, and NSF-CBET no. 0829020. Dr Y. Chen is greatly acknowledged for his important insight and comments to this work.
Appendix A. Grid independence test
Two different meshes composed of linear hexahedral elements are tested in the smooth ZPG case. Both meshes are structured with equidistant points along the streamwise (
$x$
) and spanwise (
$z$
) directions. The mesh is stretched in the wall-normal direction (
$y$
). More grid points are clustered near the wall. The main features of the coarse and refined meshes are depicted in table 3, such as number of points along the directions, number of hexahedral elements and mesh resolution.
Figure 21 depicts the mean temperature, temperature fluctuations and vertical turbulent heat flux in wall units obtained in the coarse and refined meshes at
$Re_{{\it\theta}}=2239$
. The mean temperature profiles normalized in wall units exhibit a very analogous behaviour for both meshes, as shown in figure 21(a). However, in the outer region it shows some differences, which can be attributed to some discrepancies in the computed friction temperature for the coarse and refined meshes. Furthermore, the friction temperature is proportional to the Stanton number, which has shown good agreement with available smooth experimental and theoretical data in figure 5(a) for the refined mesh. Moreover, the obtained temperature profile by means of the refined mesh is validated with existing experimental studies in figure 4.
Nevertheless, the temperature fluctuations and vertical heat-flux profiles show some differences in both meshes. Particularly, in the turbulent heat fluxes as seen in figure 21(b), for the coarse mesh the value is higher than
$1$
, which is not realistic and may be attributed to a poor resolution in the constant heat-flux layer. In contrast, for the refined mesh the value becomes lower than
$1$
. Furthermore, the strategy has been to initiate the numerical simulations with a somehow coarse grid and to later interpolate the flow solution onto the refined grid, which saved considerable computational resources. Finally, all results shown in this paper were computed by means of the refined mesh.
Figure 21. Grid independence test: (a) mean temperature profile, (b) temperature fluctuations and vertical turbulent heat flux at
$Re_{{\it\theta}}=2239$
.
Appendix B. Obukhoff–Corrsin length and Kolmogorov time scales
In this section, suitability of the mesh resolution and time step are demonstrated by means of the Obukhoff–Corrsin length and Kolmogorov time scale calculation. According to Batchelor (Reference Batchelor1959), the smallest resolved length scale in DNS should be of the order of the Obukhoff–Corrsin length scale,
$l_{C}$
for
$Pr<1$
, or Batchelor scale,
${\it\lambda}_{B}$
for
$Pr\geqslant 1$
. The Kolmogorov length scale is defined as
${\it\eta}_{k}=({\it\nu}^{3}/{\it\epsilon})^{1/4}$
, where
${\it\epsilon}$
is the average rate of energy dissipation per unit mass, and
${\it\nu}$
is the kinematic viscosity of the fluid. For the studied case (
$Pr=0.71$
), the Obukhoff–Corrsin length scale is defined as
$l_{C}={\it\eta}_{k}Pr^{-3/4}$
, which is bigger than the Kolmogorov length scale, so by resolving the Kolmogorov length scales, the Obukhoff–Corrsin length scales should also be captured. Table 4 shows the Obukhoff–Corrsin length scales at five different wall distances for the smooth and rough DNS cases. Vertical locations have been selected in such a way as to explore the Obukhoff–Corrsin length scales at critical points; very close to the wall, peak locations of fluctuations and outer region. The first wall distance being the distance where the smallest length scale or maximum dissipation
${\it\epsilon}^{+}$
is observed in the computational domain (e.g.
$(y+{\it\varepsilon})^{+}=0.5$
and 13 for the smooth and rough cases, respectively). One can observe that the presence of the roughness causes the maximum dissipation of turbulent kinetic energy to be offset further from the wall. Consequently, the minimum Obukhoff–Corrsin length scale was observed at
$(y+{\it\varepsilon})^{+}\approx 13$
(computation not shown). Furthermore, it can be inferred that the mesh resolutions are of the order of
$l_{C}$
(i.e.
${\rm\Delta}y<10l_{C}$
). Therefore, the grid points for the current mesh are sufficient to resolve even the smallest scales in the flow. However, the mesh for the rough DNS case may be marginally adequate to fully resolve all the details of the sand grit surface topography, particularly in the streamwise direction.
Table 4. Obukhoff–Corrsin length scales.
Similarly, table 5 exhibits the Kolmogorov time scales also at five different wall distances for the smooth and rough cases. The Kolmogorov time scale is defined as
${\it\tau}_{{\it\eta}}=({\it\nu}/{\it\epsilon})^{1/2}$
. In the present study, the time steps are chosen by considering the Courant–Friedrichs–Levy (CFL) parameters approximately equal to 0.5, which results in accurate prediction of turbulence statistics. According to Choi & Moin (Reference Choi and Moin1994), ‘turbulence fluctuations can only be sustained if the computational time step is appreciably less than the Kolmogorov time scale’. Clearly, it can be appreciated from table 5 that the selected time steps in wall units (i.e.
${\rm\Delta}t^{+}$
) are much lower than the corresponding dimensionless Kolmogorov time scales,
${\it\tau}_{{\it\eta}}^{+}$
, at all vertical coordinates considered for the smooth and rough cases.
Table 5. Kolmogorov time scales.
Appendix C. Inlet recovery of turbulent scales and suitability of the streamwise domain length
C.1. Inlet recovery length or developing section
One of the main challenges in direct numerical simulations (DNS) of spatially evolving turbulent boundary layers is the prescription of time-dependent turbulent inflow information. In the last few decades, several numerical ‘tripping’ methodologies have been introduced with different degrees of success ‘and the Reynolds numbers of the resulting simulations have steadily increased although often using relatively short domains and coarse resolutions’, (Jiménez et al.
Reference Jiménez, Hoyas, Simens and Mizuno2010). Perhaps the most employed inflow generation technique (and its variants) has been the rescaling–recycling method by Lund et al. (Reference Lund, Wu and Squires1998). Jiménez’s group has performed a detailed assessment of the rescaling–recycling method over extremely long domains. Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009) used the original rescaling–recycling method (henceforth ORRM) by Lund et al. (Reference Lund, Wu and Squires1998) in direct simulation of incompressible boundary layers over a flat plate. They found that boundary layer simulations recovered from synthetic inflow conditions after an initial length of approximately
$0.25L_{x}$
(where
$L_{x}$
is the streamwise domain length) by analysing local maxima of fluctuations and the decay of the space–time velocity correlations. Therefore, this developing section had to be discarded from the statistics computation. According to Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009), this is not a flaw of the ORRM by Lund but a property of the boundary layer. The turnover time of the largest scales is of the order of
${\it\delta}/u_{{\it\tau}}$
, and the large eddies are advected over a distance
$U_{\infty }{\it\delta}/u_{{\it\tau}}$
by assuming a convection velocity of
$U_{\infty }$
. Moreover, they found that ‘at least one eddy turnover is required for most flow scales to decorrelate from the inlet’ (Sillero, Jiménez & Moser Reference Sillero, Jiménez and Moser2013), which roughly corresponds to
$20{\it\delta}$
. Furthermore, Sillero et al. (Reference Sillero, Jiménez and Moser2013) showed that ‘the recovery length of the largest scales is considerable longer than the decorrelation length mentioned above’. We will demonstrate in this section that the recovery length of the large scales in our direct simulations represents just a small fraction of the whole domain by analysing the evolution of the same flow parameters utilized in Sillero et al. (Reference Sillero, Jiménez and Moser2013). This discrepancy might be attributed to the different turbulent inflow generator utilized. We strongly believe that high-quality inflow conditions ensure a fast recovery of the flow structures. The dynamic multiscale approach (DMA) by Araya et al. (Reference Araya, Castillo, Meneveau and Jansen2011) employed in this study for turbulent inflow generation is an improvement of the ORRM. As stated at the beginning of § 2, the major differences between the DMA and the ORRM are: (i) different scaling functions in the inner and outer regions of the boundary layer (i.e. multiscale) are imposed; and (ii) the friction velocity and friction temperature at the inlet of the computational domain are deduced dynamically by using a ‘test plane’ located between the inlet and recycle planes. These improvements have made the DMA a more versatile, robust and computational-resource-saving method, without the need for empirical correlations in the rescaling process which enable us to better absorb external effects such as different Reynolds numbers or streamwise pressure gradients. In addition, another important feature of the DMA is that the inlet developing section (a zone where flow structures behave in a non-physical sense) is very short, attributed to the high-quality turbulent inlet conditions. The skin friction coefficient,
$C_{f}$
(a near-wall property, according to Sillero et al. (Reference Sillero, Jiménez and Moser2013)) for the smooth and rough cases shows a nearly negligible developing section in figure 6 of Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013). Furthermore, the outer flow parameters such as the shape factor (
$H$
), momentum thickness (
${\it\theta}$
) and boundary layer thickness (
${\it\delta}$
) can be linked to larger turbulent scales (Sillero et al.
Reference Sillero, Jiménez and Moser2013). From figures 7(b,c) of (Cardillo et al.
Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013), the outer parameters
${\it\theta}$
and
${\it\delta}$
decrease at the beginning of the computational domain, and later exhibit an increasing trend. Therefore, it can be inferred that larger scales relax slowly; however, they only demanded approximately 10 % of the streamwise domain length for full recovery in our smooth and rough cases. Also, it can be observed from figures 6 and 7 of Cardillo et al. (Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013) that the present direct simulations (and the computational box) have appropriately reproduced the streamwise development of the boundary layer parameters in the near-wall region (
$C_{f}$
) and in the outer region (
$H$
,
${\it\theta}$
and
${\it\delta}$
), as compared with rough experimental data by Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008). Notice that, in the present DNS, the same roughness topology as in Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008) has been modelled at similar Reynolds numbers. Moreover, in Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008) the LDA measurements were carried out far away from the trip wire (1.05–2.05 m), which corresponds to roughly 35–69 boundary layer thicknesses, and once the flow has relaxed from its initial tripping perturbations. This feature plus the high Reynolds number range considered (
$Re_{{\it\theta}}\approx 2600{-}3900$
) in experiments ensure a well-established boundary layer Erm & Joubert (Reference Erm and Joubert1991), Schlatter & Örlü (Reference Schlatter and Örlü2012).
Figure 22. Downstream evolution of local maxima of (a) the Reynolds shear stresses, (b) the wall-normal turbulent heat fluxes.
We have also plotted local maxima of the Reynolds shear stresses for the DNS rough case in figure 22(a). Following Sillero et al. (Reference Sillero, Jiménez and Moser2013), these maxima of
$\overline{u^{\prime }v^{\prime }}^{+}$
are near-wall quantities at
$y^{+}\approx O({\it\delta}^{+1/2})$
, and thus might be related to the small scales in the near-wall region. After a short initial developing section (of the order of
$1{\it\delta}_{inlet}$
), as represented by the vertical dashed lines, the absolute values of
$(\overline{u^{\prime }v^{\prime }}^{+})_{max}$
exactly follow the downstream evolution of experimental data by Brzek et al. (Reference Brzek, Cal, Johansson and Castillo2008). There is a small ‘downtick’ at the end of the domain, caused by the prescribed pressure outflow boundary condition. However, the recycle plane is selected sufficiently far away from the outflow in such a way that the flow solution is not affected at this recycling station. Similarly, figure 22(b) depicts the downstream evolution of the local maxima of the wall-normal turbulent heat fluxes in the DNS rough case. The near-wall thermal structures require approximately
$1{\it\delta}_{inlet}$
for full relaxation. The ‘downtick’ on the
$(\overline{v^{\prime }{\it\theta}^{\prime }}^{+})_{max}$
at the domain end is more obvious than in
$(\overline{u^{\prime }v^{\prime }}^{+})_{max}$
; however, it is still negligible. The numerically contaminated inflow and outflow zones represent approximately 12 % of the total computational domain and have been discarded for final statistics computation.
Figure 23. Two-point streamwise correlations for thermal fluctuations at
$y^{+}=500$
, for smooth and rough cases, (a)
$R_{uu}$
, (b)
$R_{{\it\theta}{\it\theta}}$
.
C.2. Suitability of the streamwise domain length
The suitability of the streamwise domain size has been demonstrated by computing: (i) two-point correlation functions of velocity and thermal fluctuations from a reference downstream location where larger outer scales are fully relaxed from inlet synthetic conditions (
$x_{relax}\approx 0.1L_{x}$
, where
$L_{x}$
is the streamwise domain length), and (ii) superstructure dimensions based on the model proposed by Hutchins & Marusic (Reference Hutchins and Marusic2007). Furthermore, the two-point correlation analysis quantitatively documents the correlation levels involved in the domain size chosen after the initial relaxation zone of the larger scales. This is the standard way to justify whether or not a computational domain is appropriate, as used by Kim et al. (Reference Kim, Moin and Moser1987) to justify their streamwise domain length. With respect to the streamwise domain size, decorrelation of the velocity and thermal fluctuations (i.e.
$R_{uu}$
and
$R_{{\it\theta}{\it\theta}}$
) is achieved by
$x^{+}\approx 2000$
, as seen in figure 23(a,b) in the outer region at
$y^{+}=500$
where large turbulent scales are usually found, indicating that the computational domain (
$L_{x}^{+}\approx 8660{-}9410$
) and recycle lengths (
$x_{rec}^{+}\approx 7770{-}8440$
) are large enough in the streamwise direction for the smooth and rough cases. Notice that the reference planes, i.e.
$x_{relax}^{+}$
, are located at 897 and 959 in wall units for the smooth and rough case, respectively. The presence of a peak is also observed at the recycle plane, which is expected since it is highly correlated with the inlet. A similar finding about the two-point correlations of velocity fluctuations at the recycle station was reported in Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009), Stolz & Adams (Reference Stolz and Adams2003) in DNS of ZPG flows by employing the rescaling–recycling approach of Lund et al. (Reference Lund, Wu and Squires1998). More details about two-point correlation analysis can also be found in Araya et al. (Reference Araya, Castillo, Meneveau and Jansen2011), Araya & Castillo (Reference Araya and Castillo2013).
Regarding superstructures in the boundary layer, Hutchins & Marusic (Reference Hutchins and Marusic2007) have stated that superstructures populate the log region of turbulent boundary layers. They have also concluded that superstructures become increasingly large in comparison to the near-wall structures as the Reynolds number increases (Hutchins & Marusic (Reference Hutchins and Marusic2007) carried out experiments up to
$Re_{{\it\tau}}\approx 20\,000$
). They approximated the superstructure length with respect to the near-wall structure length by a factor of at least
$6Re_{{\it\tau}}/1000$
, where
$Re_{{\it\tau}}$
is the Reynolds number based on boundary layer thickness,
${\it\delta}$
, and the friction velocity,
$u_{{\it\tau}}$
. Consequently, we have estimated the superstructure lengths in our simulations according to the factor
$6Re_{{\it\tau}}/1000$
given by Hutchins & Marusic (Reference Hutchins and Marusic2007) by considering an average streamwise length of near-wall streaky structures of approximately 1000 in wall units. Table 6 shows the corresponding superstructure and useful region lengths for the smooth and rough case in wall units. It is inferred that our computational domains are able to capture superstructures of the order of 5538–5694 in wall units since the corresponding useful regions are, at least, 46 % longer (8096–8659 wall units), which is more than enough to capture large-scale motions.
Table 6. Superstructure lengths in present simulations.
