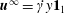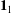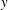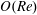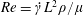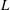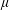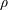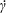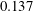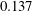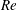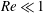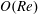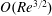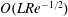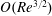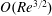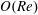1 Introduction
In the Stokes limit, it is well known that, in simple shear flow, a spheroid rotates in any of a one-parameter family of orbits (Jeffery Reference Jeffery1922), eponymously called the Jeffery orbits. The generic Jeffery orbit is a spherical ellipse corresponding to a time-dependent three-dimensional precessional motion of the orientation vector about the vorticity axis. The limiting members of the aforementioned family are the tumbling orbit, a great circle in the flow–gradient plane, and the spinning orbit, where the angular velocity vector is time-independent and aligned with the ambient vorticity (see figure 1
a,b,d). In the Stokes limit, a spheroid will continue to rotate in a Jeffery orbit determined by its initial orientation for all time. It was shown recently that weak inertia in the suspending fluid and that of the particle, at
![]() $O(Re)$
and
$O(Re)$
and
![]() $O(St)$
respectively, stabilize either the spinning or the tumbling orbit (Einarsson et al.
Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015; Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2016; Marath, Dwivedi & Subramanian Reference Marath, Dwivedi and Subramanian2017). Here,
$O(St)$
respectively, stabilize either the spinning or the tumbling orbit (Einarsson et al.
Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015; Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2016; Marath, Dwivedi & Subramanian Reference Marath, Dwivedi and Subramanian2017). Here,
![]() $Re$
and
$Re$
and
![]() $St$
are the Reynolds and Stokes numbers, with
$St$
are the Reynolds and Stokes numbers, with
![]() $Re=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$
and
$Re=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$
and
![]() $St=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D707}$
, where
$St=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D707}$
, where
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate corresponding to the ambient flow given by
$\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate corresponding to the ambient flow given by
![]() $\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}y\mathbf{1}_{1}$
(see figure 1
a),
$\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}y\mathbf{1}_{1}$
(see figure 1
a),
![]() $L$
is the length of the semimajor axis of the spheroid,
$L$
is the length of the semimajor axis of the spheroid,
![]() $\unicode[STIX]{x1D707}$
is the viscosity of the fluid, and
$\unicode[STIX]{x1D707}$
is the viscosity of the fluid, and
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D70C}_{p}$
are the densities of the fluid and particle respectively. Marath et al. (Reference Marath, Dwivedi and Subramanian2017), in particular, showed that the orientation dynamics in the presence of both inertia and rotary Brownian motion allows for an elegant thermodynamic interpretation which has similarities to the coil–stretch transition described in the polymer physics literature (De Gennes Reference De Gennes1974; Hinch Reference Hinch1974). In Dabade et al. (Reference Dabade, Marath and Subramanian2016), it was pointed out that weak inertial effects at
$\unicode[STIX]{x1D70C}_{p}$
are the densities of the fluid and particle respectively. Marath et al. (Reference Marath, Dwivedi and Subramanian2017), in particular, showed that the orientation dynamics in the presence of both inertia and rotary Brownian motion allows for an elegant thermodynamic interpretation which has similarities to the coil–stretch transition described in the polymer physics literature (De Gennes Reference De Gennes1974; Hinch Reference Hinch1974). In Dabade et al. (Reference Dabade, Marath and Subramanian2016), it was pointed out that weak inertial effects at
![]() $O(Re)$
and
$O(Re)$
and
![]() $O(St)$
do not alter the time period of rotation from its leading-order Stokesian value given by
$O(St)$
do not alter the time period of rotation from its leading-order Stokesian value given by
![]() $T_{jeff}=2\unicode[STIX]{x03C0}\dot{\unicode[STIX]{x1D6FE}}^{-1}(\unicode[STIX]{x1D705}+1/\unicode[STIX]{x1D705})$
and
$T_{jeff}=2\unicode[STIX]{x03C0}\dot{\unicode[STIX]{x1D6FE}}^{-1}(\unicode[STIX]{x1D705}+1/\unicode[STIX]{x1D705})$
and
![]() $T_{jeff}=4\unicode[STIX]{x03C0}$
respectively for the tumbling and spinning orbits. Here,
$T_{jeff}=4\unicode[STIX]{x03C0}$
respectively for the tumbling and spinning orbits. Here,
![]() $\unicode[STIX]{x1D705}=L/b(b/L)$
is the aspect ratio of the prolate (oblate) spheroid, where
$\unicode[STIX]{x1D705}=L/b(b/L)$
is the aspect ratio of the prolate (oblate) spheroid, where
![]() $b$
is the semiminor axis of the spheroid. As shown later, for a spheroid rotating in the tumbling orbit, the aforementioned vanishing of the
$b$
is the semiminor axis of the spheroid. As shown later, for a spheroid rotating in the tumbling orbit, the aforementioned vanishing of the
![]() $O(Re)$
correction is true only for spheroids with aspect ratios of order unity.
$O(Re)$
correction is true only for spheroids with aspect ratios of order unity.
Dabade et al. (Reference Dabade, Marath and Subramanian2016) also calculated the
![]() $O(St^{2})$
correction to the tumbling period, a simpler calculation due to its regular nature, and showed that the time period decreases from the aforementioned Jeffery value at the said order. This decrease is on account of the inertial persistence of the angular velocity maximum in the vicinity of the gradient–vorticity plane for a prolate spheroid (the flow–vorticity plane for an oblate one). On account of being a singular perturbation problem, the correction due to fluid inertia, which comes at
$O(St^{2})$
correction to the tumbling period, a simpler calculation due to its regular nature, and showed that the time period decreases from the aforementioned Jeffery value at the said order. This decrease is on account of the inertial persistence of the angular velocity maximum in the vicinity of the gradient–vorticity plane for a prolate spheroid (the flow–vorticity plane for an oblate one). On account of being a singular perturbation problem, the correction due to fluid inertia, which comes at
![]() $O(Re^{3/2})$
for spheroids with order-unity aspect ratios, needs a more elaborate analysis and was not investigated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). A recent simulation effort (Mao & Alexeev Reference Mao and Alexeev2014) has shown that, in contrast to particle inertia, fluid inertia increases the time period of rotation in the stable orbits from its leading-order Jeffery value, although the simulations largely explored
$O(Re^{3/2})$
for spheroids with order-unity aspect ratios, needs a more elaborate analysis and was not investigated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). A recent simulation effort (Mao & Alexeev Reference Mao and Alexeev2014) has shown that, in contrast to particle inertia, fluid inertia increases the time period of rotation in the stable orbits from its leading-order Jeffery value, although the simulations largely explored
![]() $Re$
values of order unity and only aspect ratios of
$Re$
values of order unity and only aspect ratios of
![]() $0.5,0.8,1.2$
and
$0.5,0.8,1.2$
and
![]() $2$
; the small-
$2$
; the small-
![]() $Re$
regime, characterizing the first effects of inertia, has not been systematically investigated. In this paper, we calculate the first effects of fluid inertia at
$Re$
regime, characterizing the first effects of inertia, has not been systematically investigated. In this paper, we calculate the first effects of fluid inertia at
![]() $O(Re^{3/2})$
on the time period of rotation as a function of the aspect ratio for both prolate and oblate spheroids, and for triaxial ellipsoids over a restricted range of two-axis ratios which includes the value examined in a recent numerical investigation (Rosen Reference Rosen2016). Towards the end of the paper, the
$O(Re^{3/2})$
on the time period of rotation as a function of the aspect ratio for both prolate and oblate spheroids, and for triaxial ellipsoids over a restricted range of two-axis ratios which includes the value examined in a recent numerical investigation (Rosen Reference Rosen2016). Towards the end of the paper, the
![]() $O(Re^{3/2})$
analysis is combined with the
$O(Re^{3/2})$
analysis is combined with the
![]() $O(Re)$
analysis given in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The latter continues to predict the critical Reynolds number for the arrest of rotation of extreme-aspect-ratio spheroids (both slender fibres and flat disks). The critical Reynolds number is
$O(Re)$
analysis given in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The latter continues to predict the critical Reynolds number for the arrest of rotation of extreme-aspect-ratio spheroids (both slender fibres and flat disks). The critical Reynolds number is
![]() $O(\unicode[STIX]{x1D705})$
for flat disks and
$O(\unicode[STIX]{x1D705})$
for flat disks and
![]() $O(\ln \unicode[STIX]{x1D705}/\unicode[STIX]{x1D705})$
for slender fibres, the latter being the same as that originally predicted by Subramanian & Koch (Reference Subramanian and Koch2005) based on slender-body theory.
$O(\ln \unicode[STIX]{x1D705}/\unicode[STIX]{x1D705})$
for slender fibres, the latter being the same as that originally predicted by Subramanian & Koch (Reference Subramanian and Koch2005) based on slender-body theory.

Figure 1. (a) The orientation vector (red) defined by the angles
![]() $\unicode[STIX]{x1D703}_{j}$
and
$\unicode[STIX]{x1D703}_{j}$
and
![]() $\unicode[STIX]{x1D719}_{j}$
in the space-fixed coordinate system
$\unicode[STIX]{x1D719}_{j}$
in the space-fixed coordinate system
![]() $XYZ$
. The
$XYZ$
. The
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
axes correspond to the flow, the gradient and the vorticity directions of the simple shear flow. (b) Jeffery orbits (blue) for an oblate spheroid of aspect ratio 0.05 for different initial conditions. The limiting orbits, that is the tumbling and spinning modes, are indicated. (c) The repeller (red) for an oblate spheroid of aspect ratio 0.05, which divides the unit hemisphere into two distinct basins of attractions. The trajectories of the spheroid due to fluid inertial drift at
$Z$
axes correspond to the flow, the gradient and the vorticity directions of the simple shear flow. (b) Jeffery orbits (blue) for an oblate spheroid of aspect ratio 0.05 for different initial conditions. The limiting orbits, that is the tumbling and spinning modes, are indicated. (c) The repeller (red) for an oblate spheroid of aspect ratio 0.05, which divides the unit hemisphere into two distinct basins of attractions. The trajectories of the spheroid due to fluid inertial drift at
![]() $O(Re)$
, starting from either side of the repeller and ending at the attractors of the corresponding basins, are shown as purple and green curves. (d) Jeffery orbits (blue) for a prolate spheroid of aspect ratio 2. (e) The
$O(Re)$
, starting from either side of the repeller and ending at the attractors of the corresponding basins, are shown as purple and green curves. (d) Jeffery orbits (blue) for a prolate spheroid of aspect ratio 2. (e) The
![]() $O(Re)$
inertial trajectory (purple), which ends in the tumbling orbit, for the same prolate spheroid.
$O(Re)$
inertial trajectory (purple), which ends in the tumbling orbit, for the same prolate spheroid.
In a simple shear flow, the
![]() $O(Re^{3/2})$
correction arises due to fluid inertia becoming important in a region of the order of and beyond the inertial screening length, defined as
$O(Re^{3/2})$
correction arises due to fluid inertia becoming important in a region of the order of and beyond the inertial screening length, defined as
![]() $LRe^{-1/2}$
(
$LRe^{-1/2}$
(
![]() $Re\ll 1$
). In this so-called outer region, the Stokes approximation breaks down and inertial forces balance viscous forces at leading order. The aforementioned inertial screening length can be obtained from this balance as follows: the Stokes disturbance field due to a freely rotating spheroid in simple shear flow decays as
$Re\ll 1$
). In this so-called outer region, the Stokes approximation breaks down and inertial forces balance viscous forces at leading order. The aforementioned inertial screening length can be obtained from this balance as follows: the Stokes disturbance field due to a freely rotating spheroid in simple shear flow decays as
![]() $O(1/r^{2})$
. Here,
$O(1/r^{2})$
. Here,
![]() $r$
is the distance (scaled with
$r$
is the distance (scaled with
![]() $L$
) from the centre of the spheroid. The inertial terms, for instance
$L$
) from the centre of the spheroid. The inertial terms, for instance
![]() $\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{r}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}$
, would scale as
$\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{r}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}$
, would scale as
![]() $Re/r^{2}$
and the viscous term would scale as
$Re/r^{2}$
and the viscous term would scale as
![]() $1/r^{4}$
; a balance gives
$1/r^{4}$
; a balance gives
![]() $r\sim Re^{-1/2}$
(
$r\sim Re^{-1/2}$
(
![]() $\unicode[STIX]{x1D71E}$
is the non-dimensional velocity gradient tensor for simple shear, and
$\unicode[STIX]{x1D71E}$
is the non-dimensional velocity gradient tensor for simple shear, and
![]() $\boldsymbol{u}$
is the spheroid disturbance velocity field). Calculation of the effects of fluid inertia based on an analysis of the outer region is non-trivial. Saffman was one of the first to use an analysis based on the outer region to calculate the lift force on a translating sphere ‘slipping’ past an ambient simple shear flow (Saffman Reference Saffman1965). The Fourier-space analysis in Saffman (Reference Saffman1965) was earlier employed by Childress (Reference Childress1964) in the context of estimating the correction to the well-known Stokes drag formula for the slow translation of a sphere along the axis of rotation of a rotating ambient flow. In the rheological context, Lin, Peery & Schowalter (Reference Lin, Peery and Schowalter1970) (see also Stone, Brady & Lovalenti Reference Stone, Brady and Lovalenti2000) analysed the effects of fluid inertia to
$\boldsymbol{u}$
is the spheroid disturbance velocity field). Calculation of the effects of fluid inertia based on an analysis of the outer region is non-trivial. Saffman was one of the first to use an analysis based on the outer region to calculate the lift force on a translating sphere ‘slipping’ past an ambient simple shear flow (Saffman Reference Saffman1965). The Fourier-space analysis in Saffman (Reference Saffman1965) was earlier employed by Childress (Reference Childress1964) in the context of estimating the correction to the well-known Stokes drag formula for the slow translation of a sphere along the axis of rotation of a rotating ambient flow. In the rheological context, Lin, Peery & Schowalter (Reference Lin, Peery and Schowalter1970) (see also Stone, Brady & Lovalenti Reference Stone, Brady and Lovalenti2000) analysed the effects of fluid inertia to
![]() $O(Re^{3/2})$
in order to characterize the
$O(Re^{3/2})$
in order to characterize the
![]() $O(\unicode[STIX]{x1D719})$
rheology of a dilute suspension of rigid neutrally buoyant spheres; here,
$O(\unicode[STIX]{x1D719})$
rheology of a dilute suspension of rigid neutrally buoyant spheres; here,
![]() $\unicode[STIX]{x1D719}$
is the volume fraction of the suspended spheres. Specifically, in Lin et al. (Reference Lin, Peery and Schowalter1970), a matched asymptotic expansion approach was used to determine both the normal stress differences at
$\unicode[STIX]{x1D719}$
is the volume fraction of the suspended spheres. Specifically, in Lin et al. (Reference Lin, Peery and Schowalter1970), a matched asymptotic expansion approach was used to determine both the normal stress differences at
![]() $O(\unicode[STIX]{x1D719}Re)$
and
$O(\unicode[STIX]{x1D719}Re)$
and
![]() $O(\unicode[STIX]{x1D719}Re^{3/2})$
, and the correction to the suspension shear viscosity that appears at the latter order; the inertial correction to the viscosity contributes to a shear thickening rheology. Stone et al. (Reference Stone, Brady and Lovalenti2000) performed the
$O(\unicode[STIX]{x1D719}Re^{3/2})$
, and the correction to the suspension shear viscosity that appears at the latter order; the inertial correction to the viscosity contributes to a shear thickening rheology. Stone et al. (Reference Stone, Brady and Lovalenti2000) performed the
![]() $O(\unicode[STIX]{x1D719}Re^{3/2})$
calculation again using a concise Fourier-space formulation based on a reciprocal theorem formulation by treating the sphere as a force-dipole singularity. The concise formulation was used by Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011) to characterize the complete non-Newtonian rheology of an emulsion to
$O(\unicode[STIX]{x1D719}Re^{3/2})$
calculation again using a concise Fourier-space formulation based on a reciprocal theorem formulation by treating the sphere as a force-dipole singularity. The concise formulation was used by Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011) to characterize the complete non-Newtonian rheology of an emulsion to
![]() $O(\unicode[STIX]{x1D719}Re^{3/2})$
for arbitrary ratios of the disperse (drop) to continuous phase viscosities, including the
$O(\unicode[STIX]{x1D719}Re^{3/2})$
for arbitrary ratios of the disperse (drop) to continuous phase viscosities, including the
![]() $O(\unicode[STIX]{x1D719}Re^{3/2})$
Reynolds stress contributions neglected by earlier authors.
$O(\unicode[STIX]{x1D719}Re^{3/2})$
Reynolds stress contributions neglected by earlier authors.
In all of the cases mentioned above, the disturbance velocity field due to the particle is steady on account of its spherical shape. This steady velocity field may also be used to determine the inertial correction to the angular velocity of a freely rotating sphere. The absence of a regular correction at
![]() $O(Re)$
, in simple shear flow, is easily seen. Such a correction would have to be quadratic in the shear rate, and, being a pseudovector, would have to be proportional to
$O(Re)$
, in simple shear flow, is easily seen. Such a correction would have to be quadratic in the shear rate, and, being a pseudovector, would have to be proportional to
![]() $\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D640}$
, where
$\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D640}$
, where
![]() $\unicode[STIX]{x1D640}$
and
$\unicode[STIX]{x1D640}$
and
![]() $\unicode[STIX]{x1D74E}$
are the rate-of-strain tensor and the vorticity vector in the ambient simple shear respectively. Since
$\unicode[STIX]{x1D74E}$
are the rate-of-strain tensor and the vorticity vector in the ambient simple shear respectively. Since
![]() $\unicode[STIX]{x1D74E}$
is perpendicular to the plane of the flow,
$\unicode[STIX]{x1D74E}$
is perpendicular to the plane of the flow,
![]() $\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D640}=0$
. This remains true in the absence of ambient vortex stretching, and, therefore, for the one-parameter family of planar linear flows (Subramanian & Koch Reference Subramanian and Koch2006b
). It should be noted that, for linear flows other than simple shear, the sphere will deviate from the fluid streamlines at finite
$\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D640}=0$
. This remains true in the absence of ambient vortex stretching, and, therefore, for the one-parameter family of planar linear flows (Subramanian & Koch Reference Subramanian and Koch2006b
). It should be noted that, for linear flows other than simple shear, the sphere will deviate from the fluid streamlines at finite
![]() $Re$
due to an inertial lag, but the angular velocity correction is unchanged at leading order since the velocity gradient tensor is a constant. The first effects of inertia therefore appear at
$Re$
due to an inertial lag, but the angular velocity correction is unchanged at leading order since the velocity gradient tensor is a constant. The first effects of inertia therefore appear at
![]() $O(Re^{3/2})$
,
$O(Re^{3/2})$
,
![]() $Re$
being defined based on the sphere radius, and the inertial correction has been found to be
$Re$
being defined based on the sphere radius, and the inertial correction has been found to be
![]() $-0.054Re^{3/2}$
(Stone et al.
Reference Stone, Brady and Lovalenti2000; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). Thus, for small but finite
$-0.054Re^{3/2}$
(Stone et al.
Reference Stone, Brady and Lovalenti2000; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). Thus, for small but finite
![]() $Re$
, the time period of rotation of a sphere increases by
$Re$
, the time period of rotation of a sphere increases by
![]() $1.355Re^{3/2}$
.
$1.355Re^{3/2}$
.
The disturbance velocity field for a spheroid in a spinning orbit is steady, and therefore the scaling of the inertial correction to the angular velocity would be similar to that of a sphere. Indeed, as shown in a later section, the detailed calculation is easily carried out based on the
![]() $O(Re^{3/2})$
Fourier-space formulation, and predicts slowing down of the spinning spheroid due to inertial effects. The inertial correction to the spin is, in fact, proportional to the correction for a sphere, the multiplicative constant being given by a function of the aspect ratio. The
$O(Re^{3/2})$
Fourier-space formulation, and predicts slowing down of the spinning spheroid due to inertial effects. The inertial correction to the spin is, in fact, proportional to the correction for a sphere, the multiplicative constant being given by a function of the aspect ratio. The
![]() $O(Re^{3/2})$
correction in the spinning orbit has recently been determined using the traditional matched asymptotic expansion approach (Meibohm et al.
Reference Meibohm, Candelier, Rosén, Einarsson, Lundell and Mehlig2016), and we validate our calculation with this result. In the tumbling orbit, however, the disturbance velocity field due to the spheroid is unsteady, and the torque-free spheroid acts as a time-dependent force-dipole singularity in the outer region. This dependence, when represented in frequency space, is an infinite Fourier series, and this makes evaluation of the
$O(Re^{3/2})$
correction in the spinning orbit has recently been determined using the traditional matched asymptotic expansion approach (Meibohm et al.
Reference Meibohm, Candelier, Rosén, Einarsson, Lundell and Mehlig2016), and we validate our calculation with this result. In the tumbling orbit, however, the disturbance velocity field due to the spheroid is unsteady, and the torque-free spheroid acts as a time-dependent force-dipole singularity in the outer region. This dependence, when represented in frequency space, is an infinite Fourier series, and this makes evaluation of the
![]() $O(Re^{3/2})$
correction to the angular velocity, as a function of the instantaneous spheroid orientation, a difficult proposition. However, as is shown later, if one only has to evaluate the time period correction at
$O(Re^{3/2})$
correction to the angular velocity, as a function of the instantaneous spheroid orientation, a difficult proposition. However, as is shown later, if one only has to evaluate the time period correction at
![]() $O(Re^{3/2})$
, one only needs the Jeffery-averaged angular velocity correction. The relevant infinite series then reduces to three terms, allowing one to determine the correction without the need for truncation.
$O(Re^{3/2})$
, one only needs the Jeffery-averaged angular velocity correction. The relevant infinite series then reduces to three terms, allowing one to determine the correction without the need for truncation.
The correctness of the angular velocity correction, predicted at
![]() $O(Re^{3/2})$
for a sphere, and the associated increase in time period have been confirmed in a numerical investigation by Mikulencak & Morris (Reference Mikulencak and Morris2004). These authors extended the results for the inertial correction to
$O(Re^{3/2})$
for a sphere, and the associated increase in time period have been confirmed in a numerical investigation by Mikulencak & Morris (Reference Mikulencak and Morris2004). These authors extended the results for the inertial correction to
![]() $Re$
values of order unity, with inertia continuing to slow down the rotation. As mentioned earlier, Mao & Alexeev (Reference Mao and Alexeev2014) have recently investigated the effect of inertia on the time period of rotation of spheroids with different aspect ratios using the lattice Boltzmann method. This work concluded that the time period of rotation increases with the Reynolds number, but the authors found the scaling for the inertial correction to be
$Re$
values of order unity, with inertia continuing to slow down the rotation. As mentioned earlier, Mao & Alexeev (Reference Mao and Alexeev2014) have recently investigated the effect of inertia on the time period of rotation of spheroids with different aspect ratios using the lattice Boltzmann method. This work concluded that the time period of rotation increases with the Reynolds number, but the authors found the scaling for the inertial correction to be
![]() $O(Re)$
for small Reynolds numbers. However, based on the
$O(Re)$
for small Reynolds numbers. However, based on the
![]() $O(Re)$
correction of the angular velocity derived in Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016), it can be easily seen that the correction to the time period at this order is zero for spheroids with order-unity aspect ratios. This apparent contradiction might arise due to the bounded domain used in the simulations. An accurate estimation of the
$O(Re)$
correction of the angular velocity derived in Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016), it can be easily seen that the correction to the time period at this order is zero for spheroids with order-unity aspect ratios. This apparent contradiction might arise due to the bounded domain used in the simulations. An accurate estimation of the
![]() $O(Re^{3/2})$
inertial correction, in a numerical effort, is not easy since the correction originates in the outer region and requires that the outer boundary for the computational domain be much farther away than the (large) inertial screening length.
$O(Re^{3/2})$
inertial correction, in a numerical effort, is not easy since the correction originates in the outer region and requires that the outer boundary for the computational domain be much farther away than the (large) inertial screening length.
It is of interest to note that the arguments leading to the
![]() $O(Re^{3/2})$
scaling for the angular velocity correction remain valid even for a general triaxial ellipsoid provided that one of its principal axes remains aligned with the ambient vorticity. It is known that for
$O(Re^{3/2})$
scaling for the angular velocity correction remain valid even for a general triaxial ellipsoid provided that one of its principal axes remains aligned with the ambient vorticity. It is known that for
![]() $Re=0$
, and for sufficiently long times, the orientation dynamics of a triaxial ellipsoid differs significantly from that of a spheroid even for small departures from axisymmetry. For a general triaxial ellipsoid, quasiperiodic and chaotic trajectories coexist in orientation space, and an ellipsoid may exhibit dynamics of either type depending on its initial orientation. Nearly axisymmetric ellipsoids, and those with moderate aspect ratios, exhibit a quasiperiodic orientation dynamics for the most part, as shown originally by Hinch & Leal (Reference Hinch and Leal1979); on the other hand, the orientation dynamics is largely chaotic for slender ellipsoids (Yarin, Gottlieb & Roisman Reference Yarin, Gottlieb and Roisman1997). It has been shown very recently, using Lattice Boltzmann simulations (Rosen Reference Rosen2016), that the first effects of inertia render the rotation about the intermediate axis stable for certain values of the axis ratios (
$Re=0$
, and for sufficiently long times, the orientation dynamics of a triaxial ellipsoid differs significantly from that of a spheroid even for small departures from axisymmetry. For a general triaxial ellipsoid, quasiperiodic and chaotic trajectories coexist in orientation space, and an ellipsoid may exhibit dynamics of either type depending on its initial orientation. Nearly axisymmetric ellipsoids, and those with moderate aspect ratios, exhibit a quasiperiodic orientation dynamics for the most part, as shown originally by Hinch & Leal (Reference Hinch and Leal1979); on the other hand, the orientation dynamics is largely chaotic for slender ellipsoids (Yarin, Gottlieb & Roisman Reference Yarin, Gottlieb and Roisman1997). It has been shown very recently, using Lattice Boltzmann simulations (Rosen Reference Rosen2016), that the first effects of inertia render the rotation about the intermediate axis stable for certain values of the axis ratios (
![]() $\unicode[STIX]{x1D705}_{1}=b/a=1/3$
and
$\unicode[STIX]{x1D705}_{1}=b/a=1/3$
and
![]() $\unicode[STIX]{x1D705}_{2}=c/a=1/4$
), where
$\unicode[STIX]{x1D705}_{2}=c/a=1/4$
), where
![]() $2a$
,
$2a$
,
![]() $2b$
and
$2b$
and
![]() $2c$
are the lengths of the three axes of the triaxial ellipsoid, with
$2c$
are the lengths of the three axes of the triaxial ellipsoid, with
![]() $a>b>c$
(the analogous rotation in the Stokesian limit is neutrally stable). The natural question to ask is with regard to the time period of rotation in this inertially stabilized configuration. We show that the correction to the time period for a triaxial ellipsoid in this configuration again arises at
$a>b>c$
(the analogous rotation in the Stokesian limit is neutrally stable). The natural question to ask is with regard to the time period of rotation in this inertially stabilized configuration. We show that the correction to the time period for a triaxial ellipsoid in this configuration again arises at
![]() $O(Re^{3/2})$
, and evaluate the correction. Assuming stability of the intermediate-axis-aligned rotation, we also examine a sequence of triaxial ellipsoids approaching a tumbling ellipse, and characterize the divergence of the time period in this limit.
$O(Re^{3/2})$
, and evaluate the correction. Assuming stability of the intermediate-axis-aligned rotation, we also examine a sequence of triaxial ellipsoids approaching a tumbling ellipse, and characterize the divergence of the time period in this limit.
The inertial correction above remains
![]() $O(Re^{3/2})$
provided that the inertial screening length of
$O(Re^{3/2})$
provided that the inertial screening length of
![]() $O(Re^{-1/2})$
is much larger than any of the principal axes. At the other extreme, when the largest axis is much larger than the inertial screening length (which is still much larger than the other two axes), and is in addition parallel to the ambient vorticity, the determination of the inertial correction reduces to a two-dimensional scenario involving a freely rotating elliptic cylinder in simple shear flow. The inertial correction is now larger, being
$O(Re^{-1/2})$
is much larger than any of the principal axes. At the other extreme, when the largest axis is much larger than the inertial screening length (which is still much larger than the other two axes), and is in addition parallel to the ambient vorticity, the determination of the inertial correction reduces to a two-dimensional scenario involving a freely rotating elliptic cylinder in simple shear flow. The inertial correction is now larger, being
![]() $O(Re)$
, due to the more gradual
$O(Re)$
, due to the more gradual
![]() $O(1/r)$
decay of the force-dipole velocity field in two dimensions. An analytical determination of the
$O(1/r)$
decay of the force-dipole velocity field in two dimensions. An analytical determination of the
![]() $O(Re)$
angular velocity correction has been carried out for a circular cylinder by Robertson & Acrivos (Reference Robertson and Acrivos1970); the analogous scaling for an elliptic cylinder has been verified in computations by Mikulencak & Morris (Reference Mikulencak and Morris2004).
$O(Re)$
angular velocity correction has been carried out for a circular cylinder by Robertson & Acrivos (Reference Robertson and Acrivos1970); the analogous scaling for an elliptic cylinder has been verified in computations by Mikulencak & Morris (Reference Mikulencak and Morris2004).
This paper is organized as follows. In § 2, we derive the expression for the inertial correction to the angular velocity of a spheroid using a reciprocal theorem formulation. We express the reciprocal theorem in terms of Fourier-space integrals similarly to Stone et al. (Reference Stone, Brady and Lovalenti2000) and Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). In § 3, we summarize the Stokesian scenario and the results of the
![]() $O(Re)$
calculation made in Dabade et al. (Reference Dabade, Marath and Subramanian2016). Aside from determining the
$O(Re)$
calculation made in Dabade et al. (Reference Dabade, Marath and Subramanian2016). Aside from determining the
![]() $O(Re)$
drift across orbits, this latter calculation shows that the time period correction vanishes at
$O(Re)$
drift across orbits, this latter calculation shows that the time period correction vanishes at
![]() $O(Re)$
in the stabilized (spinning or tumbling) orbits. We then consider the simpler case of the spinning spheroid in § 4, and show that the Fourier-space integral for the
$O(Re)$
in the stabilized (spinning or tumbling) orbits. We then consider the simpler case of the spinning spheroid in § 4, and show that the Fourier-space integral for the
![]() $O(Re^{3/2})$
angular velocity correction reduces to that of the sphere, as given in Stone et al. (Reference Stone, Brady and Lovalenti2000). A numerical evaluation of this integral yields the spinning correction over the relevant range of aspect ratios. As mentioned above, this is expected since a torque-free spinning spheroid acts as a time-independent force-dipole singularity. In § 5, we evaluate the reciprocal theorem integral for the more involved case of the tumbling orbit, the difficulty arising from the time-dependent nature of the force-dipole singularity. The inertial correction to the tumbling time period reduces to a sum of a three- and a four-dimensional integral. These integrals are evaluated numerically and the results are presented in § 6. In § 7, we calculate the time period correction for a triaxial ellipsoid rotating about its intermediate principal axis for a restricted set of axis-ratio pairs. In § 8, we first summarize our results. Then, we combine the findings of the
$O(Re^{3/2})$
angular velocity correction reduces to that of the sphere, as given in Stone et al. (Reference Stone, Brady and Lovalenti2000). A numerical evaluation of this integral yields the spinning correction over the relevant range of aspect ratios. As mentioned above, this is expected since a torque-free spinning spheroid acts as a time-independent force-dipole singularity. In § 5, we evaluate the reciprocal theorem integral for the more involved case of the tumbling orbit, the difficulty arising from the time-dependent nature of the force-dipole singularity. The inertial correction to the tumbling time period reduces to a sum of a three- and a four-dimensional integral. These integrals are evaluated numerically and the results are presented in § 6. In § 7, we calculate the time period correction for a triaxial ellipsoid rotating about its intermediate principal axis for a restricted set of axis-ratio pairs. In § 8, we first summarize our results. Then, we combine the findings of the
![]() $O(Re)$
analysis in Dabade et al. (Reference Dabade, Marath and Subramanian2016) and the current one, to present a description of the effects of weak inertia valid for all aspect ratios. In particular, we show that the
$O(Re)$
analysis in Dabade et al. (Reference Dabade, Marath and Subramanian2016) and the current one, to present a description of the effects of weak inertia valid for all aspect ratios. In particular, we show that the
![]() $O(Re^{3/2})$
inertial terms do not affect the leading-order estimate of the critical Reynolds number (based on the
$O(Re^{3/2})$
inertial terms do not affect the leading-order estimate of the critical Reynolds number (based on the
![]() $O(Re)$
inertial correction) required for arrest of the rotation of extreme-aspect-ratio spheroids.
$O(Re)$
inertial correction) required for arrest of the rotation of extreme-aspect-ratio spheroids.
2 Formulation for the time period: the reciprocal theorem
In this section, we derive the formal expression for the correction to the time period of rotation of a spheroid, in a simple shear flow, for small
![]() $Re$
. The time period is related to the angular velocity of the spheroid, and the latter can be evaluated using a generalized reciprocal theorem. The reciprocal theorem relates the velocity and stress fields of two problems, the first being the problem of interest and the second being a simpler test problem with a known solution. The flow physics in the two problems can be different; however, the configuration, size and shape of the particle, a spheroid in an unbounded fluid domain, are the same (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006a
; Dabade et al.
Reference Dabade, Marath and Subramanian2016). The problem of interest here is a torque-free spheroid rotating in a simple shear flow, accounting for the inertial acceleration of the fluid in an unbounded domain. The objective is to relate its angular velocity,
$Re$
. The time period is related to the angular velocity of the spheroid, and the latter can be evaluated using a generalized reciprocal theorem. The reciprocal theorem relates the velocity and stress fields of two problems, the first being the problem of interest and the second being a simpler test problem with a known solution. The flow physics in the two problems can be different; however, the configuration, size and shape of the particle, a spheroid in an unbounded fluid domain, are the same (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006a
; Dabade et al.
Reference Dabade, Marath and Subramanian2016). The problem of interest here is a torque-free spheroid rotating in a simple shear flow, accounting for the inertial acceleration of the fluid in an unbounded domain. The objective is to relate its angular velocity,
![]() $\unicode[STIX]{x1D734}_{1}$
, to the time period of rotation, for small
$\unicode[STIX]{x1D734}_{1}$
, to the time period of rotation, for small
![]() $Re$
, and thereby determine the latter to
$Re$
, and thereby determine the latter to
![]() $O(Re^{3/2})$
. The test problem corresponds to the Stokesian rotation of a spheroid in a quiescent ambient with an angular velocity
$O(Re^{3/2})$
. The test problem corresponds to the Stokesian rotation of a spheroid in a quiescent ambient with an angular velocity
![]() $\unicode[STIX]{x1D734}_{2}$
, and with the same instantaneous orientation as that of the spheroid in the problem of interest. The velocity and stress fields in the problem of interest are denoted by
$\unicode[STIX]{x1D734}_{2}$
, and with the same instantaneous orientation as that of the spheroid in the problem of interest. The velocity and stress fields in the problem of interest are denoted by
![]() $\boldsymbol{u}^{(1)}$
and
$\boldsymbol{u}^{(1)}$
and
![]() $\unicode[STIX]{x1D748}^{(1)}$
, and those in the test problem are
$\unicode[STIX]{x1D748}^{(1)}$
, and those in the test problem are
![]() $\boldsymbol{u}^{(2)}$
and
$\boldsymbol{u}^{(2)}$
and
![]() $\unicode[STIX]{x1D748}^{(2)}$
. The reciprocal theorem is formulated in terms of the scaled disturbance fields (both stress and velocity) in the problem of interest, which are given by
$\unicode[STIX]{x1D748}^{(2)}$
. The reciprocal theorem is formulated in terms of the scaled disturbance fields (both stress and velocity) in the problem of interest, which are given by
![]() $\unicode[STIX]{x1D748}^{\prime (1)}=\unicode[STIX]{x1D748}^{(1)}-2\unicode[STIX]{x1D640}$
and
$\unicode[STIX]{x1D748}^{\prime (1)}=\unicode[STIX]{x1D748}^{(1)}-2\unicode[STIX]{x1D640}$
and
![]() $\boldsymbol{u}^{\prime (1)}=\boldsymbol{u}^{(1)}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
, where
$\boldsymbol{u}^{\prime (1)}=\boldsymbol{u}^{(1)}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
, where
![]() $\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
is the ambient simple shear defined in a coordinate system whose origin is at the centre of the spheroid. The space-fixed coordinate system has its
$\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
is the ambient simple shear defined in a coordinate system whose origin is at the centre of the spheroid. The space-fixed coordinate system has its
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
axes along the flow, gradient and vorticity directions respectively of the ambient simple shear (see figure 1), with the unit vectors in the
$Z$
axes along the flow, gradient and vorticity directions respectively of the ambient simple shear (see figure 1), with the unit vectors in the
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
directions being
$Z$
directions being
![]() $\mathbf{1}_{1}$
,
$\mathbf{1}_{1}$
,
![]() $\mathbf{1}_{2}$
and
$\mathbf{1}_{2}$
and
![]() $\mathbf{1}_{3}$
respectively. The disturbance velocity and stress fields are scaled with
$\mathbf{1}_{3}$
respectively. The disturbance velocity and stress fields are scaled with
![]() $\dot{\unicode[STIX]{x1D6FE}}L$
and
$\dot{\unicode[STIX]{x1D6FE}}L$
and
![]() $\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}L$
. Thus,
$\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}L$
. Thus,
![]() $\unicode[STIX]{x1D71E}=\mathbf{1}_{1}\mathbf{1}_{2}$
and
$\unicode[STIX]{x1D71E}=\mathbf{1}_{1}\mathbf{1}_{2}$
and
![]() $\unicode[STIX]{x1D640}=(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})/2$
are the transpose of the non-dimensional velocity gradient and the rate-of-strain tensors respectively. The expression for the inertial angular velocity has already been derived in Dabade et al. (Reference Dabade, Marath and Subramanian2016) (equation (2.19)), using a reciprocal theorem formulation, and takes the following form in non-dimensional terms:
$\unicode[STIX]{x1D640}=(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})/2$
are the transpose of the non-dimensional velocity gradient and the rate-of-strain tensors respectively. The expression for the inertial angular velocity has already been derived in Dabade et al. (Reference Dabade, Marath and Subramanian2016) (equation (2.19)), using a reciprocal theorem formulation, and takes the following form in non-dimensional terms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{\prime (1)}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (1)}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{\prime (1)}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (1)}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D734}_{1}$
and
$\unicode[STIX]{x1D734}_{1}$
and
![]() $\boldsymbol{{\mathcal{L}}}_{2}$
are respectively the angular velocity of the spheroid in the problem of interest and the torque acting on the spheroid in the test problem. The latter is given by
$\boldsymbol{{\mathcal{L}}}_{2}$
are respectively the angular velocity of the spheroid in the problem of interest and the torque acting on the spheroid in the test problem. The latter is given by
![]() $\boldsymbol{{\mathcal{L}}}_{2}=-8\unicode[STIX]{x03C0}(X_{C}\boldsymbol{p}\boldsymbol{p}+Y_{C}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
,
$\boldsymbol{{\mathcal{L}}}_{2}=-8\unicode[STIX]{x03C0}(X_{C}\boldsymbol{p}\boldsymbol{p}+Y_{C}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
,
![]() $\boldsymbol{p}$
here being the orientation vector of the spheroid, and the torque coefficients being given by
$\boldsymbol{p}$
here being the orientation vector of the spheroid, and the torque coefficients being given by
![]() $X_{C}=4(\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(2\unicode[STIX]{x1D709}_{0}-2(\unicode[STIX]{x1D709}_{0}^{2}-1)\coth ^{-1}\unicode[STIX]{x1D709}_{0}))$
and
$X_{C}=4(\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(2\unicode[STIX]{x1D709}_{0}-2(\unicode[STIX]{x1D709}_{0}^{2}-1)\coth ^{-1}\unicode[STIX]{x1D709}_{0}))$
and
![]() $Y_{C}=4(2\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(2(\unicode[STIX]{x1D709}_{0}^{2}+1)\coth ^{-1}\unicode[STIX]{x1D709}_{0}-2\unicode[STIX]{x1D709}_{0}))$
for a prolate spheroid (Kim & Karrila Reference Kim and Karrila1991), where
$Y_{C}=4(2\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(2(\unicode[STIX]{x1D709}_{0}^{2}+1)\coth ^{-1}\unicode[STIX]{x1D709}_{0}-2\unicode[STIX]{x1D709}_{0}))$
for a prolate spheroid (Kim & Karrila Reference Kim and Karrila1991), where
![]() $\unicode[STIX]{x1D709}_{0}$
is the inverse of the eccentricity of the spheroid (
$\unicode[STIX]{x1D709}_{0}$
is the inverse of the eccentricity of the spheroid (
![]() $\unicode[STIX]{x1D709}_{0}=1/\sqrt{1-1/\unicode[STIX]{x1D705}^{2}}$
for a prolate spheroid). The expressions for
$\unicode[STIX]{x1D709}_{0}=1/\sqrt{1-1/\unicode[STIX]{x1D705}^{2}}$
for a prolate spheroid). The expressions for
![]() $X_{C}$
and
$X_{C}$
and
![]() $Y_{C}$
, for an oblate spheroid, can be obtained by using the transformation
$Y_{C}$
, for an oblate spheroid, can be obtained by using the transformation
![]() $\unicode[STIX]{x1D709}_{0}=\text{i}\sqrt{\unicode[STIX]{x1D709}_{0}^{2}-1}$
and
$\unicode[STIX]{x1D709}_{0}=\text{i}\sqrt{\unicode[STIX]{x1D709}_{0}^{2}-1}$
and
![]() $d=-\text{i}d$
(
$d=-\text{i}d$
(
![]() $d$
is the interfocal distance) in the dimensional forms of the prolate torque coefficients (
$d$
is the interfocal distance) in the dimensional forms of the prolate torque coefficients (
![]() $\unicode[STIX]{x1D709}_{0}=1/\sqrt{1-\unicode[STIX]{x1D705}^{2}}$
for an oblate spheroid). The term proportional to
$\unicode[STIX]{x1D709}_{0}=1/\sqrt{1-\unicode[STIX]{x1D705}^{2}}$
for an oblate spheroid). The term proportional to
![]() $St$
in (2.1), where
$St$
in (2.1), where
![]() $St$
is the Stokes number defined as
$St$
is the Stokes number defined as
![]() $\unicode[STIX]{x1D70C}_{p}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D70C}_{p}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$
and
![]() $\boldsymbol{I}_{p}$
is the moment of inertia of the spheroid, gives the contribution to the angular velocity due to particle inertia. For a neutrally buoyant spheroid, the case considered here,
$\boldsymbol{I}_{p}$
is the moment of inertia of the spheroid, gives the contribution to the angular velocity due to particle inertia. For a neutrally buoyant spheroid, the case considered here,
![]() $St=Re$
. The volume integral on the right-hand side of (2.1) gives the contribution to the angular velocity due to fluid inertia, the domain of integration being the unbounded fluid volume outside the spheroid. The leading-order contribution due to fluid inertia, at
$St=Re$
. The volume integral on the right-hand side of (2.1) gives the contribution to the angular velocity due to fluid inertia, the domain of integration being the unbounded fluid volume outside the spheroid. The leading-order contribution due to fluid inertia, at
![]() $O(Re)$
, can be obtained by replacing
$O(Re)$
, can be obtained by replacing
![]() $\boldsymbol{u}^{\prime (1)}$
with the disturbance velocity field in the Stokes limit (
$\boldsymbol{u}^{\prime (1)}$
with the disturbance velocity field in the Stokes limit (
![]() $\boldsymbol{u}^{\prime (s)}$
) in the integral. The resulting integral is convergent, implying the regular nature of the
$\boldsymbol{u}^{\prime (s)}$
) in the integral. The resulting integral is convergent, implying the regular nature of the
![]() $O(Re)$
correction. This correction has been evaluated in Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016), and it stabilizes certain Stokesian orbits of the spheroid. Specifically, while, at
$O(Re)$
correction. This correction has been evaluated in Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016), and it stabilizes certain Stokesian orbits of the spheroid. Specifically, while, at
![]() $Re=0$
, the spheroid may rotate in any of a one-parameter family of precessional orbits known as Jeffery orbits (Jeffery Reference Jeffery1922), for finite
$Re=0$
, the spheroid may rotate in any of a one-parameter family of precessional orbits known as Jeffery orbits (Jeffery Reference Jeffery1922), for finite
![]() $Re$
, only the limiting members of this family (the tumbling and the spinning modes; see figure 1
b) are rendered stable by the drift induced by inertia at
$Re$
, only the limiting members of this family (the tumbling and the spinning modes; see figure 1
b) are rendered stable by the drift induced by inertia at
![]() $O(Re)$
. As shown in § 3, the
$O(Re)$
. As shown in § 3, the
![]() $O(Re)$
correction to the angular velocity of a spheroid rotating in either of the asymptotic states above does not change the time period of rotation from its leading-order value given in non-dimensional terms by
$O(Re)$
correction to the angular velocity of a spheroid rotating in either of the asymptotic states above does not change the time period of rotation from its leading-order value given in non-dimensional terms by
![]() $T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
. However, as mentioned in § 1, numerical simulations have shown a change in the time period in the presence of fluid inertia (Mao & Alexeev Reference Mao and Alexeev2014), although the scaling for this change has not been rigorously characterized in the limit
$T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
. However, as mentioned in § 1, numerical simulations have shown a change in the time period in the presence of fluid inertia (Mao & Alexeev Reference Mao and Alexeev2014), although the scaling for this change has not been rigorously characterized in the limit
![]() $Re\ll 1$
. Thus, there is a need to characterize the first correction to the time period. As shown later in this section, this comes at
$Re\ll 1$
. Thus, there is a need to characterize the first correction to the time period. As shown later in this section, this comes at
![]() $O(Re^{3/2})$
.
$O(Re^{3/2})$
.
To calculate the
![]() $O(Re^{3/2})$
correction, we first examine the assumptions made when replacing
$O(Re^{3/2})$
correction, we first examine the assumptions made when replacing
![]() $\boldsymbol{u}^{\prime (1)}$
with
$\boldsymbol{u}^{\prime (1)}$
with
![]() $\boldsymbol{u}^{\prime (s)}$
to obtain the
$\boldsymbol{u}^{\prime (s)}$
to obtain the
![]() $O(Re)$
correction. The equation governing
$O(Re)$
correction. The equation governing
![]() $\boldsymbol{u}^{\prime (1)}$
is given by
$\boldsymbol{u}^{\prime (1)}$
is given by
This equation is obtained by taking the difference of the governing equations for the full velocity field
![]() $\boldsymbol{u}^{(1)}$
and the ambient
$\boldsymbol{u}^{(1)}$
and the ambient
![]() $\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
. By neglecting the inertial terms proportional to
$\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x}$
. By neglecting the inertial terms proportional to
![]() $Re$
in (2.2), one gets the Stokes equations whose solution is
$Re$
in (2.2), one gets the Stokes equations whose solution is
![]() $\boldsymbol{u}^{\prime (s)}$
. It is well known that
$\boldsymbol{u}^{\prime (s)}$
. It is well known that
![]() $\boldsymbol{u}^{\prime (s)}$
is not a uniformly valid approximation for the velocity field throughout the unbounded domain outside the spheroid. The inertial terms on the right-hand side decay as
$\boldsymbol{u}^{\prime (s)}$
is not a uniformly valid approximation for the velocity field throughout the unbounded domain outside the spheroid. The inertial terms on the right-hand side decay as
![]() $1/r^{2}$
, and cannot be neglected when
$1/r^{2}$
, and cannot be neglected when
![]() $r\approx Re^{-1/2}$
, the inertial screening length, and the Stokes solution ceases to be a good approximation to the disturbance velocity field at distances of the order of and beyond this length. The region around the sphere can therefore be divided into two, depending on whether the inertial terms can be neglected compared with the viscous terms: the inner region (
$r\approx Re^{-1/2}$
, the inertial screening length, and the Stokes solution ceases to be a good approximation to the disturbance velocity field at distances of the order of and beyond this length. The region around the sphere can therefore be divided into two, depending on whether the inertial terms can be neglected compared with the viscous terms: the inner region (
![]() $r\sim 1$
) and the outer region (
$r\sim 1$
) and the outer region (
![]() $r\sim O(Re^{-1/2})$
). The Stokes velocity field is a good approximation to the actual disturbance velocity field only in the inner region. The leading-order velocity field in the outer region should be obtained by solving the linearized version of (2.2). The velocity fields in the inner (
$r\sim O(Re^{-1/2})$
). The Stokes velocity field is a good approximation to the actual disturbance velocity field only in the inner region. The leading-order velocity field in the outer region should be obtained by solving the linearized version of (2.2). The velocity fields in the inner (
![]() $\boldsymbol{u}^{inner}$
) and outer (
$\boldsymbol{u}^{inner}$
) and outer (
![]() $\boldsymbol{u}^{outer}$
) regions, however, reduce to the same functional form (
$\boldsymbol{u}^{outer}$
) regions, however, reduce to the same functional form (
![]() $\boldsymbol{u}^{match}$
) in a matching region (
$\boldsymbol{u}^{match}$
) in a matching region (
![]() $1\ll r\ll Re^{-1/2}$
). To calculate the
$1\ll r\ll Re^{-1/2}$
). To calculate the
![]() $O(Re^{3/2})$
correction to the angular velocity,
$O(Re^{3/2})$
correction to the angular velocity,
![]() $\boldsymbol{u}^{\prime (1)}$
is written, formally, as the following uniformly valid expansion (Hinch Reference Hinch1991):
$\boldsymbol{u}^{\prime (1)}$
is written, formally, as the following uniformly valid expansion (Hinch Reference Hinch1991):
Next, defining
![]() $\boldsymbol{u}^{f}=\boldsymbol{u}^{outer}-\boldsymbol{u}^{match}$
, the reciprocal theorem in (2.1) becomes
$\boldsymbol{u}^{f}=\boldsymbol{u}^{outer}-\boldsymbol{u}^{match}$
, the reciprocal theorem in (2.1) becomes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f}+\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f}+\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\end{eqnarray}$$
In the inner region,
![]() $\boldsymbol{u}^{f}$
comes at a higher order, and in the outer region, the nonlinear cross terms,
$\boldsymbol{u}^{f}$
comes at a higher order, and in the outer region, the nonlinear cross terms,
![]() $\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}$
and
$\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}$
and
![]() $\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}$
, decay faster than the linear terms, and therefore the integrals involving the cross terms in (2.4) contribute at a higher order. The third term on the right-hand side in (2.4) gives the
$\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}$
, decay faster than the linear terms, and therefore the integrals involving the cross terms in (2.4) contribute at a higher order. The third term on the right-hand side in (2.4) gives the
![]() $O(Re)$
correction to the angular velocity (
$O(Re)$
correction to the angular velocity (
![]() $\unicode[STIX]{x1D734}_{1}$
), arising from the inner region with
$\unicode[STIX]{x1D734}_{1}$
), arising from the inner region with
![]() $\boldsymbol{u}^{inner}=\boldsymbol{u}^{\prime (s)}$
, and is evaluated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The fourth term on the right-hand side is the contribution to the angular velocity from the outer region. To explicitly see the scaling with respect to
$\boldsymbol{u}^{inner}=\boldsymbol{u}^{\prime (s)}$
, and is evaluated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The fourth term on the right-hand side is the contribution to the angular velocity from the outer region. To explicitly see the scaling with respect to
![]() $Re$
for this contribution, the velocity fields in the fourth term are written in terms of a rescaled coordinate defined as
$Re$
for this contribution, the velocity fields in the fourth term are written in terms of a rescaled coordinate defined as
![]() $\unicode[STIX]{x1D70C}=Re^{1/2}r$
. The rescaled coordinate is
$\unicode[STIX]{x1D70C}=Re^{1/2}r$
. The rescaled coordinate is
![]() $O(1)$
when
$O(1)$
when
![]() $r$
is of the order of the inertial screening length, and is therefore appropriate for the outer region. The radial vector and the differential volume can be expressed in the outer coordinate as
$r$
is of the order of the inertial screening length, and is therefore appropriate for the outer region. The radial vector and the differential volume can be expressed in the outer coordinate as
![]() $\unicode[STIX]{x1D746}=Re^{1/2}\boldsymbol{x}$
,
$\unicode[STIX]{x1D746}=Re^{1/2}\boldsymbol{x}$
,
![]() $\text{d}V_{\unicode[STIX]{x1D70C}}=Re^{3/2}\,\text{d}V$
. Since the neutrally buoyant spheroid acts as a force-dipole singularity for
$\text{d}V_{\unicode[STIX]{x1D70C}}=Re^{3/2}\,\text{d}V$
. Since the neutrally buoyant spheroid acts as a force-dipole singularity for
![]() $r\gg 1$
, the disturbance velocity fields in the problem of interest as well as the test problem decay as
$r\gg 1$
, the disturbance velocity fields in the problem of interest as well as the test problem decay as
![]() $1/r^{2}$
when
$1/r^{2}$
when
![]() $1\ll r\ll Re^{-1/2}$
, and can be written as
$1\ll r\ll Re^{-1/2}$
, and can be written as
![]() $\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}=Re^{-1}\boldsymbol{u}^{f}$
and
$\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}=Re^{-1}\boldsymbol{u}^{f}$
and
![]() $\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}=Re^{-1}\boldsymbol{u}^{(2)}$
. It should be noted that, as defined,
$\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}=Re^{-1}\boldsymbol{u}^{(2)}$
. It should be noted that, as defined,
![]() $\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}=(\boldsymbol{u}^{outer\unicode[STIX]{x1D70C}}-\boldsymbol{u}^{match\unicode[STIX]{x1D70C}})$
, the superscript
$\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}=(\boldsymbol{u}^{outer\unicode[STIX]{x1D70C}}-\boldsymbol{u}^{match\unicode[STIX]{x1D70C}})$
, the superscript
![]() $\unicode[STIX]{x1D70C}$
indicating that these velocity fields are now expressed in the outer coordinate
$\unicode[STIX]{x1D70C}$
indicating that these velocity fields are now expressed in the outer coordinate
![]() $\unicode[STIX]{x1D70C}$
. The reciprocal theorem statement in (2.4), with the fourth term on the right-hand side expressed in terms of the rescaled outer coordinate, is given by
$\unicode[STIX]{x1D70C}$
. The reciprocal theorem statement in (2.4), with the fourth term on the right-hand side expressed in terms of the rescaled outer coordinate, is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\frac{\text{d}}{\text{d}t}(\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\nonumber\\ \displaystyle & & \displaystyle +\,Re^{3/2}\int _{V_{\unicode[STIX]{x1D70C}}}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\unicode[STIX]{x1D746})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}\,\text{d}V_{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\frac{\text{d}}{\text{d}t}(\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\nonumber\\ \displaystyle & & \displaystyle +\,Re^{3/2}\int _{V_{\unicode[STIX]{x1D70C}}}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\unicode[STIX]{x1D746})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}\,\text{d}V_{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
It should be noted that the nonlinear term
![]() $\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}$
in the fourth term in (2.4), when expressed in terms of the outer coordinate, contributes at a higher order, and is neglected in the fourth term on the right-hand side of (2.5). It is evident from (2.5) that the correction from the outer region comes at
$\boldsymbol{u}^{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f}$
in the fourth term in (2.4), when expressed in terms of the outer coordinate, contributes at a higher order, and is neglected in the fourth term on the right-hand side of (2.5). It is evident from (2.5) that the correction from the outer region comes at
![]() $O(Re^{3/2})$
. The volume of the spheroid expressed in outer variables is
$O(Re^{3/2})$
. The volume of the spheroid expressed in outer variables is
![]() $O(Re^{3/2})$
, and its omission only leads to an error of
$O(Re^{3/2})$
, and its omission only leads to an error of
![]() $O(Re^{3})$
. The omission is equivalent to treating the spheroid as an equivalent point-force-dipole singularity. Thus, the outer integral in (2.5) may be extended right until the origin, and the resulting calculation is then more conveniently performed in Fourier space. The convolution theorem (Arfken, Weber & Harris Reference Arfken, Weber and Harris2011) is applied to the
$O(Re^{3})$
. The omission is equivalent to treating the spheroid as an equivalent point-force-dipole singularity. Thus, the outer integral in (2.5) may be extended right until the origin, and the resulting calculation is then more conveniently performed in Fourier space. The convolution theorem (Arfken, Weber & Harris Reference Arfken, Weber and Harris2011) is applied to the
![]() $O(Re^{3/2})$
integral in (2.5) to obtain
$O(Re^{3/2})$
integral in (2.5) to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{V_{\unicode[STIX]{x1D70C}}}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\unicode[STIX]{x1D746})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}\,\text{d}V_{\unicode[STIX]{x1D70C}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int \left[\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\right]\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{V_{\unicode[STIX]{x1D70C}}}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\unicode[STIX]{x1D746})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}\,\text{d}V_{\unicode[STIX]{x1D70C}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int \left[\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\right]\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})\,\text{d}\boldsymbol{k},\end{eqnarray}$$
where the hatted variables denote the Fourier transformed fields, the transform being defined as
![]() $\hat{f}(\boldsymbol{k})=\int f(\boldsymbol{r})\text{e}^{-\text{i}2\unicode[STIX]{x03C0}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}\,\text{d}\boldsymbol{r}$
. In (2.6),
$\hat{f}(\boldsymbol{k})=\int f(\boldsymbol{r})\text{e}^{-\text{i}2\unicode[STIX]{x03C0}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}\,\text{d}\boldsymbol{r}$
. In (2.6),
![]() $\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})$
and
$\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})$
and
![]() $\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
are the Fourier transforms of the test velocity field
$\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
are the Fourier transforms of the test velocity field
![]() $\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}$
and the velocity field in the problem of interest
$\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}$
and the velocity field in the problem of interest
![]() $\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}$
. The ambient simple shear flow takes the form
$\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}$
. The ambient simple shear flow takes the form
![]() $\hat{\boldsymbol{u}}^{\infty }=-k_{1}\mathbf{1}_{2}$
(
$\hat{\boldsymbol{u}}^{\infty }=-k_{1}\mathbf{1}_{2}$
(
![]() $\unicode[STIX]{x1D71E}^{\dagger }=\mathbf{1}_{2}\mathbf{1}_{1}$
) in Fourier space. Here,
$\unicode[STIX]{x1D71E}^{\dagger }=\mathbf{1}_{2}\mathbf{1}_{1}$
) in Fourier space. Here,
![]() $k_{1}$
is the component of the wavevector
$k_{1}$
is the component of the wavevector
![]() $\boldsymbol{k}$
in the
$\boldsymbol{k}$
in the
![]() $X$
direction.
$X$
direction.
To evaluate (2.6), we need to find
![]() $\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
and
$\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
and
![]() $\hat{\boldsymbol{u}}^{(2)}(\boldsymbol{k})$
. The governing equation for
$\hat{\boldsymbol{u}}^{(2)}(\boldsymbol{k})$
. The governing equation for
![]() $\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}$
is
$\boldsymbol{u}^{(2_{\unicode[STIX]{x1D70C}})}$
is
where
![]() $\unicode[STIX]{x1D64E}^{(2)}$
is the time-dependent force-dipole singularity corresponding to a spheroid rotating in a quiescent fluid. The term
$\unicode[STIX]{x1D64E}^{(2)}$
is the time-dependent force-dipole singularity corresponding to a spheroid rotating in a quiescent fluid. The term
![]() $\unicode[STIX]{x1D64E}^{(2)}$
is given by
$\unicode[STIX]{x1D64E}^{(2)}$
is given by
where
![]() $\boldsymbol{p}$
is the spheroid orientation vector and the constants
$\boldsymbol{p}$
is the spheroid orientation vector and the constants
![]() $B_{1}$
,
$B_{1}$
,
![]() $B_{2}$
and
$B_{2}$
and
![]() $B_{3}$
for a prolate spheroid are given by
$B_{3}$
for a prolate spheroid are given by
The terms proportional to
![]() $B_{2}$
and
$B_{2}$
and
![]() $B_{3}$
correspond to the rotlet singularities and the one multiplying
$B_{3}$
correspond to the rotlet singularities and the one multiplying
![]() $B_{1}$
corresponds to the stresslet induced by the rotating spheroid. In the limit
$B_{1}$
corresponds to the stresslet induced by the rotating spheroid. In the limit
![]() $\unicode[STIX]{x1D709}_{0}\rightarrow \infty$
, that is for a sphere,
$\unicode[STIX]{x1D709}_{0}\rightarrow \infty$
, that is for a sphere,
![]() $B_{3}=-4\unicode[STIX]{x03C0}$
, and
$B_{3}=-4\unicode[STIX]{x03C0}$
, and
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are
$B_{2}$
are
![]() $O(1/\unicode[STIX]{x1D709}_{0}^{2})$
, consistent with a rotating sphere acting as a pure rotlet singularity. As before, the constants for an oblate spheroid can be obtained using the transformation
$O(1/\unicode[STIX]{x1D709}_{0}^{2})$
, consistent with a rotating sphere acting as a pure rotlet singularity. As before, the constants for an oblate spheroid can be obtained using the transformation
![]() $\unicode[STIX]{x1D709}_{0}=\text{i}\sqrt{\unicode[STIX]{x1D709}_{0}^{2}-1}$
and
$\unicode[STIX]{x1D709}_{0}=\text{i}\sqrt{\unicode[STIX]{x1D709}_{0}^{2}-1}$
and
![]() $d=-\text{i}d$
, mentioned below (2.1) (alternatively, see Kim & Karrila (Reference Kim and Karrila1991)). The Fourier transform of (2.7) gives
$d=-\text{i}d$
, mentioned below (2.1) (alternatively, see Kim & Karrila (Reference Kim and Karrila1991)). The Fourier transform of (2.7) gives
To evaluate
![]() $\hat{\boldsymbol{u}}^{f}$
, we need the equation governing
$\hat{\boldsymbol{u}}^{f}$
, we need the equation governing
![]() $\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}$
, which can be derived from the equations governing
$\boldsymbol{u}^{f_{\unicode[STIX]{x1D70C}}}$
, which can be derived from the equations governing
![]() $\boldsymbol{u}^{outer\unicode[STIX]{x1D70C}}$
and
$\boldsymbol{u}^{outer\unicode[STIX]{x1D70C}}$
and
![]() $\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}$
, given by
$\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}$
, given by
and
respectively. Equation (2.13) is the far-field approximation of (2.2), where the boundary conditions on the surface of the freely rotating spheroid are replaced by a singular forcing at the origin. Here, to the order of approximation desired,
![]() $\unicode[STIX]{x1D64E}$
is the time-dependent force-dipole singularity corresponding to a torque-free spheroid in a simple shear flow at
$\unicode[STIX]{x1D64E}$
is the time-dependent force-dipole singularity corresponding to a torque-free spheroid in a simple shear flow at
![]() $Re=0$
, given by
$Re=0$
, given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E} & = & \displaystyle A_{1}\frac{3}{2}(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\,\left(\boldsymbol{p}\boldsymbol{p}-\frac{\unicode[STIX]{x1D644}}{3}\right)+A_{2}((\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p}\boldsymbol{p}+\boldsymbol{p}\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))\nonumber\\ \displaystyle & & \displaystyle +\,A_{3}\left((\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})+(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\frac{(\unicode[STIX]{x1D640}\mathbf{:}\boldsymbol{p}\boldsymbol{p})}{2}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E} & = & \displaystyle A_{1}\frac{3}{2}(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\,\left(\boldsymbol{p}\boldsymbol{p}-\frac{\unicode[STIX]{x1D644}}{3}\right)+A_{2}((\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p}\boldsymbol{p}+\boldsymbol{p}\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))\nonumber\\ \displaystyle & & \displaystyle +\,A_{3}\left((\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})+(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\frac{(\unicode[STIX]{x1D640}\mathbf{:}\boldsymbol{p}\boldsymbol{p})}{2}\right).\end{eqnarray}$$
To understand
![]() $\unicode[STIX]{x1D64E}$
in more detail, we note that the Stokesian disturbance field induced in an ambient linear flow can be split into five component flows corresponding to the five degrees of freedom of the rate-of-strain tensor. These may conveniently be regarded as an axisymmetric extensional flow and pairs of planar extensional flows in the longitudinal (containing
$\unicode[STIX]{x1D64E}$
in more detail, we note that the Stokesian disturbance field induced in an ambient linear flow can be split into five component flows corresponding to the five degrees of freedom of the rate-of-strain tensor. These may conveniently be regarded as an axisymmetric extensional flow and pairs of planar extensional flows in the longitudinal (containing
![]() $\boldsymbol{p}$
) and transverse (orthogonal to
$\boldsymbol{p}$
) and transverse (orthogonal to
![]() $\boldsymbol{p}$
) planes (Dabade et al.
Reference Dabade, Marath and Subramanian2016), with the component amplitude dependent on the spheroid orientation. Due to its axisymmetry, a spheroid responds identically to the two extensions in the longitudinal and transverse planes. Therefore, the stresslet singularity in (2.15) can be written as a sum of only three terms, with the terms proportional to
$\boldsymbol{p}$
) planes (Dabade et al.
Reference Dabade, Marath and Subramanian2016), with the component amplitude dependent on the spheroid orientation. Due to its axisymmetry, a spheroid responds identically to the two extensions in the longitudinal and transverse planes. Therefore, the stresslet singularity in (2.15) can be written as a sum of only three terms, with the terms proportional to
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
and
$A_{2}$
and
![]() $A_{3}$
being the stresslets induced by the axisymmetric extension and the longitudinal and transverse planar extensional flows respectively. The constants for a prolate spheroid (Kim & Karrila Reference Kim and Karrila1991) are
$A_{3}$
being the stresslets induced by the axisymmetric extension and the longitudinal and transverse planar extensional flows respectively. The constants for a prolate spheroid (Kim & Karrila Reference Kim and Karrila1991) are
For a sphere, all three constants equal
![]() $-20\unicode[STIX]{x03C0}/3$
, so that
$-20\unicode[STIX]{x03C0}/3$
, so that
![]() $\lim _{\unicode[STIX]{x1D709}_{0}\rightarrow \infty }\unicode[STIX]{x1D64E}=-(20\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D640}$
, corresponding to the well-known stresslet singularity of a freely rotating sphere (
$\lim _{\unicode[STIX]{x1D709}_{0}\rightarrow \infty }\unicode[STIX]{x1D64E}=-(20\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D640}$
, corresponding to the well-known stresslet singularity of a freely rotating sphere (
![]() $n\lim _{\unicode[STIX]{x1D709}_{0}\rightarrow \infty }\unicode[STIX]{x1D64E}$
yields the well-known Einstein correction). The equation governing
$n\lim _{\unicode[STIX]{x1D709}_{0}\rightarrow \infty }\unicode[STIX]{x1D64E}$
yields the well-known Einstein correction). The equation governing
![]() $\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}$
is derived using (2.13) and (2.14), and is given by
$\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}$
is derived using (2.13) and (2.14), and is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D735}p^{f\unicode[STIX]{x1D70C}} & = & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D735}p^{f\unicode[STIX]{x1D70C}} & = & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{f\unicode[STIX]{x1D70C}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{match\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
The bracketed term on the right-hand side of (2.6) is obtained by taking the Fourier transform of (2.19), and is given by
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f} & = & \displaystyle -4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-\text{i}2\unicode[STIX]{x03C0}\boldsymbol{k}\hat{p}^{f}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f} & = & \displaystyle -4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-\text{i}2\unicode[STIX]{x03C0}\boldsymbol{k}\hat{p}^{f}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The Fourier transformed matching velocity field (
![]() $\hat{\boldsymbol{u}}^{match}$
) in (2.20) is obtained by taking the Fourier transform of (2.14), and is given by
$\hat{\boldsymbol{u}}^{match}$
) in (2.20) is obtained by taking the Fourier transform of (2.14), and is given by
with
![]() $\unicode[STIX]{x1D64E}$
given by (2.15). By substituting (2.12) and (2.20) into (2.6), the reciprocal theorem relation in (2.5) becomes
$\unicode[STIX]{x1D64E}$
given by (2.15). By substituting (2.12) and (2.20) into (2.6), the reciprocal theorem relation in (2.5) becomes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+\,Re\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle -\,Re^{3/2}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left(\frac{\text{i}\unicode[STIX]{x1D64E}^{(2)}\boldsymbol{\cdot }\boldsymbol{k}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right)\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\mathbf{L}_{2} & = & \displaystyle \unicode[STIX]{x1D71E}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}(\unicode[STIX]{x1D748}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+\,Re\frac{\text{d}}{\text{d}t}({\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}}_{1})\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{inner}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{inner}+\boldsymbol{u}^{inner}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{inner}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle -\,Re^{3/2}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left(\frac{\text{i}\unicode[STIX]{x1D64E}^{(2)}\boldsymbol{\cdot }\boldsymbol{k}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right)\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
It should be noted that the term containing the Fourier transformed pressure field in (2.20), which is proportional to
![]() $\boldsymbol{k}$
, vanishes when contracted with
$\boldsymbol{k}$
, vanishes when contracted with
![]() $\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})$
, and, therefore, does not appear in (2.22). For the test problem, we define two second-order tensors
$\hat{\boldsymbol{u}}^{(2)}(-\boldsymbol{k})$
, and, therefore, does not appear in (2.22). For the test problem, we define two second-order tensors
![]() $\unicode[STIX]{x1D647}_{2}$
and
$\unicode[STIX]{x1D647}_{2}$
and
![]() $\unicode[STIX]{x1D650}_{2}$
, and two third-order tensors
$\unicode[STIX]{x1D650}_{2}$
, and two third-order tensors
![]() $\unicode[STIX]{x1D72E}^{(2)}$
and
$\unicode[STIX]{x1D72E}^{(2)}$
and
![]() $\unicode[STIX]{x1D64E}^{2t}$
, such that
$\unicode[STIX]{x1D64E}^{2t}$
, such that
![]() $\boldsymbol{{\mathcal{L}}}_{2}=\unicode[STIX]{x1D647}_{2}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(
$\boldsymbol{{\mathcal{L}}}_{2}=\unicode[STIX]{x1D647}_{2}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(
![]() $\boldsymbol{{\mathcal{L}}}_{2}$
is defined below (2.1)),
$\boldsymbol{{\mathcal{L}}}_{2}$
is defined below (2.1)),
![]() $\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}_{2}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
,
$\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}_{2}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
,
![]() $\unicode[STIX]{x1D748}^{(2)}=\unicode[STIX]{x1D72E}^{(2)}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(see Dabade et al.
Reference Dabade, Marath and Subramanian2016) and
$\unicode[STIX]{x1D748}^{(2)}=\unicode[STIX]{x1D72E}^{(2)}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(see Dabade et al.
Reference Dabade, Marath and Subramanian2016) and
![]() $\unicode[STIX]{x1D64E}^{(2)}=\unicode[STIX]{x1D64E}^{2t}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(
$\unicode[STIX]{x1D64E}^{(2)}=\unicode[STIX]{x1D64E}^{2t}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{2}$
(
![]() $\unicode[STIX]{x1D64E}^{(2)}$
is defined in (2.8)). In terms of these newly defined tensors, the relation (2.22) becomes independent of the angular velocity of the test spheroid (
$\unicode[STIX]{x1D64E}^{(2)}$
is defined in (2.8)). In terms of these newly defined tensors, the relation (2.22) becomes independent of the angular velocity of the test spheroid (
![]() $\unicode[STIX]{x1D734}_{2}$
).
$\unicode[STIX]{x1D734}_{2}$
).
Next, the angular velocity in the problem of interest (
![]() $\unicode[STIX]{x1D734}_{1}$
) is expanded as
$\unicode[STIX]{x1D734}_{1}$
) is expanded as
![]() $\unicode[STIX]{x1D734}_{jeff}+Re\,\unicode[STIX]{x1D734}_{c1}+Re^{3/2}\unicode[STIX]{x1D734}_{c2}$
, and substitution of the expansion as well as the newly defined tensors in (2.22) leads to
$\unicode[STIX]{x1D734}_{jeff}+Re\,\unicode[STIX]{x1D734}_{c1}+Re^{3/2}\unicode[STIX]{x1D734}_{c2}$
, and substitution of the expansion as well as the newly defined tensors in (2.22) leads to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{c1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{2} & = & \displaystyle \int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{\prime (s)}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (s)}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (s)}+\boldsymbol{u}^{\prime (s)}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (s)}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}_{2}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\text{d}}{\text{d}t}(\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{c1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{2} & = & \displaystyle \int _{V}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{\prime (s)}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (s)}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (s)}+\boldsymbol{u}^{\prime (s)}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime (s)}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}_{2}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\text{d}}{\text{d}t}(\boldsymbol{I}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1}),\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{c2}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{2} & = & \displaystyle -\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left(\frac{\text{i}\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right)\,\text{d}\boldsymbol{k}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D734}_{c2}\boldsymbol{\cdot }\unicode[STIX]{x1D647}_{2} & = & \displaystyle -\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left(\frac{\text{i}\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right)\,\text{d}\boldsymbol{k}\end{eqnarray}$$
at successive orders. The detailed expression for
![]() $\boldsymbol{u}^{\prime (s)}$
, obtained using a spheroidal harmonics formalism, has already been used to evaluate
$\boldsymbol{u}^{\prime (s)}$
, obtained using a spheroidal harmonics formalism, has already been used to evaluate
![]() $\unicode[STIX]{x1D734}_{c1}$
in Dabade et al. (Reference Dabade, Marath and Subramanian2016). To evaluate the
$\unicode[STIX]{x1D734}_{c1}$
in Dabade et al. (Reference Dabade, Marath and Subramanian2016). To evaluate the
![]() $O(Re^{3/2})$
correction,
$O(Re^{3/2})$
correction,
![]() $\unicode[STIX]{x1D734}_{c2}$
, using (2.25), one needs
$\unicode[STIX]{x1D734}_{c2}$
, using (2.25), one needs
![]() $\hat{\boldsymbol{u}}^{f}$
, which can be obtained by solving (2.20). This is a rather elaborate calculation, and is presented later in §§ 4 and 5.
$\hat{\boldsymbol{u}}^{f}$
, which can be obtained by solving (2.20). This is a rather elaborate calculation, and is presented later in §§ 4 and 5.
3 Summary: time period at leading order and at
 $O(Re)$
$O(Re)$
The leading-order angular velocity
![]() $\unicode[STIX]{x1D734}_{jeff}$
in (2.23) may be expressed in terms of the rates of change of the polar and azimuthal angles
$\unicode[STIX]{x1D734}_{jeff}$
in (2.23) may be expressed in terms of the rates of change of the polar and azimuthal angles
![]() $\unicode[STIX]{x1D703}_{j}$
and
$\unicode[STIX]{x1D703}_{j}$
and
![]() $\unicode[STIX]{x1D719}_{j}$
(Jeffery Reference Jeffery1922), defined in figure 1(a), and these are given by
$\unicode[STIX]{x1D719}_{j}$
(Jeffery Reference Jeffery1922), defined in figure 1(a), and these are given by
There is an additional spin component given by
![]() $\dot{\unicode[STIX]{x1D713}}=-\text{cos}\,\unicode[STIX]{x1D703}_{j}/2-\dot{\unicode[STIX]{x1D719}}_{jeff}\cos \unicode[STIX]{x1D703}_{j}$
. As is well known, the solution of (3.1) and (3.2) shows that the spheroid rotates in any of a one-parameter family of closed orbits (figure 1
b), the particular orbit being determined by its initial orientation. The parameter is the orbit constant
$\dot{\unicode[STIX]{x1D713}}=-\text{cos}\,\unicode[STIX]{x1D703}_{j}/2-\dot{\unicode[STIX]{x1D719}}_{jeff}\cos \unicode[STIX]{x1D703}_{j}$
. As is well known, the solution of (3.1) and (3.2) shows that the spheroid rotates in any of a one-parameter family of closed orbits (figure 1
b), the particular orbit being determined by its initial orientation. The parameter is the orbit constant
![]() $C$
, which takes values from 0 to
$C$
, which takes values from 0 to
![]() $\infty$
. The orbital or so-called natural coordinates (
$\infty$
. The orbital or so-called natural coordinates (
![]() $C,\unicode[STIX]{x1D70F}$
) were originally introduced by Leal & Hinch (Reference Leal and Hinch1971), with the constant-
$C,\unicode[STIX]{x1D70F}$
) were originally introduced by Leal & Hinch (Reference Leal and Hinch1971), with the constant-
![]() $C$
lines being Jeffery orbits and the constant-
$C$
lines being Jeffery orbits and the constant-
![]() $\unicode[STIX]{x1D70F}$
lines (
$\unicode[STIX]{x1D70F}$
lines (
![]() $\unicode[STIX]{x1D70F}$
being the phase along the Jeffery orbit) being the constant-
$\unicode[STIX]{x1D70F}$
being the phase along the Jeffery orbit) being the constant-
![]() $\unicode[STIX]{x1D719}$
lines on the unit sphere. In these coordinates, the aforementioned rates of change take on a much simpler form, namely
$\unicode[STIX]{x1D719}$
lines on the unit sphere. In these coordinates, the aforementioned rates of change take on a much simpler form, namely
![]() $\text{d}C/\text{d}t=0$
and
$\text{d}C/\text{d}t=0$
and
![]() $\text{d}\unicode[STIX]{x1D70F}/\text{d}t=\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D705}^{2}+1)$
.
$\text{d}\unicode[STIX]{x1D70F}/\text{d}t=\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D705}^{2}+1)$
.
If a spheroid is initially aligned with the ambient vorticity axis, it will continue to spin in that orientation. This particular orbit with
![]() $C=0(\unicode[STIX]{x1D703}_{j}=0)$
is called a log-rolling (spinning) orbit for a prolate (oblate) spheroid. At leading order, the angular velocity of the spinning spheroid is a constant, and is therefore independent of the aspect ratio and equal to
$C=0(\unicode[STIX]{x1D703}_{j}=0)$
is called a log-rolling (spinning) orbit for a prolate (oblate) spheroid. At leading order, the angular velocity of the spinning spheroid is a constant, and is therefore independent of the aspect ratio and equal to
![]() $-(1/2)\mathbf{1}_{3}$
. The disturbance velocity field is steady in this orbit, just like a sphere, and the time period of rotation is
$-(1/2)\mathbf{1}_{3}$
. The disturbance velocity field is steady in this orbit, just like a sphere, and the time period of rotation is
![]() $4\unicode[STIX]{x03C0}$
. If the initial orientation of the spheroid is in the flow–gradient plane, the orbit is a unit circle in this plane and is called a tumbling orbit (
$4\unicode[STIX]{x03C0}$
. If the initial orientation of the spheroid is in the flow–gradient plane, the orbit is a unit circle in this plane and is called a tumbling orbit (
![]() $\unicode[STIX]{x1D703}_{j}=\unicode[STIX]{x03C0}/2,C=\infty$
). The rotation in a Jeffery orbit is not uniform for any orbits other than the log-rolling (spinning) orbit. The disturbance velocity field due to a spheroid in these orbits, including the tumbling one in particular, is unsteady. The Stokesian disturbance field due to a spheroid rotating in any of these orbits exhibits a periodic dependence on time. The time period of rotation may be obtained based on
$\unicode[STIX]{x1D703}_{j}=\unicode[STIX]{x03C0}/2,C=\infty$
). The rotation in a Jeffery orbit is not uniform for any orbits other than the log-rolling (spinning) orbit. The disturbance velocity field due to a spheroid in these orbits, including the tumbling one in particular, is unsteady. The Stokesian disturbance field due to a spheroid rotating in any of these orbits exhibits a periodic dependence on time. The time period of rotation may be obtained based on
![]() $\dot{\unicode[STIX]{x1D719}}_{jeff}$
, and is given by
$\dot{\unicode[STIX]{x1D719}}_{jeff}$
, and is given by
![]() $T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
. It should be noted that the period is the same for all orbits because
$T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
. It should be noted that the period is the same for all orbits because
![]() $\dot{\unicode[STIX]{x1D719}}_{jeff}$
is independent of
$\dot{\unicode[STIX]{x1D719}}_{jeff}$
is independent of
![]() $\unicode[STIX]{x1D703}_{j}$
. Further, the disturbance velocity field in the tumbling orbit has a period of
$\unicode[STIX]{x1D703}_{j}$
. Further, the disturbance velocity field in the tumbling orbit has a period of
![]() $T_{jeff}/2$
, due to the
$T_{jeff}/2$
, due to the
![]() $\boldsymbol{p}\leftrightarrow -\boldsymbol{p}$
symmetry.
$\boldsymbol{p}\leftrightarrow -\boldsymbol{p}$
symmetry.
As mentioned in § 2, the correction to the angular velocity at
![]() $O(Re)$
,
$O(Re)$
,
![]() $\unicode[STIX]{x1D734}_{c1}$
, given in (2.24), is evaluated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The angular velocity components expressed in terms of the angles defined above are of the form
$\unicode[STIX]{x1D734}_{c1}$
, given in (2.24), is evaluated in Dabade et al. (Reference Dabade, Marath and Subramanian2016). The angular velocity components expressed in terms of the angles defined above are of the form
For a neutrally buoyant spheroid, the functions
![]() $F_{i}^{n}$
and
$F_{i}^{n}$
and
![]() $G_{i}^{n}$
are defined as
$G_{i}^{n}$
are defined as
![]() $F_{i}^{n}=F_{i}^{p}+F_{i}^{f}$
and
$F_{i}^{n}=F_{i}^{p}+F_{i}^{f}$
and
![]() $G_{i}^{n}=G_{i}^{p}+G_{i}^{f}$
, with
$G_{i}^{n}=G_{i}^{p}+G_{i}^{f}$
, with
![]() $F_{i}^{p}$
,
$F_{i}^{p}$
,
![]() $F_{i}^{f}$
,
$F_{i}^{f}$
,
![]() $G_{i}^{p}$
and
$G_{i}^{p}$
and
![]() $G_{i}^{f}$
defined for a prolate spheroid in Dabade et al. (Reference Dabade, Marath and Subramanian2016); the corresponding functions for an oblate spheroid are obtained using the transformation defined in § 2. The superscripts ‘
$G_{i}^{f}$
defined for a prolate spheroid in Dabade et al. (Reference Dabade, Marath and Subramanian2016); the corresponding functions for an oblate spheroid are obtained using the transformation defined in § 2. The superscripts ‘
![]() $f$
’ and ‘
$f$
’ and ‘
![]() $p$
’ correspond to fluid and particle inertia contributions respectively. The rates of change defined in (3.3) and (3.4) lead to an inertial drift across Jeffery orbits. The orbital drift, defined as the average change in
$p$
’ correspond to fluid and particle inertia contributions respectively. The rates of change defined in (3.3) and (3.4) lead to an inertial drift across Jeffery orbits. The orbital drift, defined as the average change in
![]() $C$
over one complete rotation of the spheroid, can be obtained from a multiple time scale analysis and has been used to analyse the effect of inertia at
$C$
over one complete rotation of the spheroid, can be obtained from a multiple time scale analysis and has been used to analyse the effect of inertia at
![]() $O(Re)$
in planar linear flows (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006a
; Dabade et al.
Reference Dabade, Marath and Subramanian2016; Marath & Subramanian Reference Marath and Subramanian2017; Marath et al.
Reference Marath, Dwivedi and Subramanian2017). For simple shear flow, in particular, it has been found that on time scales of
$O(Re)$
in planar linear flows (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006a
; Dabade et al.
Reference Dabade, Marath and Subramanian2016; Marath & Subramanian Reference Marath and Subramanian2017; Marath et al.
Reference Marath, Dwivedi and Subramanian2017). For simple shear flow, in particular, it has been found that on time scales of
![]() $O(Re^{-1})$
, a neutrally buoyant prolate spheroid of any aspect ratio settles into the tumbling orbit, and a neutrally buoyant oblate spheroid with aspect ratio
$O(Re^{-1})$
, a neutrally buoyant prolate spheroid of any aspect ratio settles into the tumbling orbit, and a neutrally buoyant oblate spheroid with aspect ratio
![]() $\unicode[STIX]{x1D705}$
in the range
$\unicode[STIX]{x1D705}$
in the range
![]() $0.137<\unicode[STIX]{x1D705}<1$
asymptotes to the spinning orbit. For neutrally buoyant oblate spheroids with
$0.137<\unicode[STIX]{x1D705}<1$
asymptotes to the spinning orbit. For neutrally buoyant oblate spheroids with
![]() $\unicode[STIX]{x1D705}<0.137$
, a repeller exists on the unit sphere (see the red curve in figure 1
c), dividing the orientation hemisphere into two basins of attraction, with the attractors being the spinning and tumbling orbits, and, in the absence of stochastic fluctuations, the spheroid can settle into either of these depending on its initial orientation. In the analysis below, we focus on the effect of inertia on the time periods of rotation of both prolate and oblate spheroids, in the orbits into which they settle for times longer than
$\unicode[STIX]{x1D705}<0.137$
, a repeller exists on the unit sphere (see the red curve in figure 1
c), dividing the orientation hemisphere into two basins of attraction, with the attractors being the spinning and tumbling orbits, and, in the absence of stochastic fluctuations, the spheroid can settle into either of these depending on its initial orientation. In the analysis below, we focus on the effect of inertia on the time periods of rotation of both prolate and oblate spheroids, in the orbits into which they settle for times longer than
![]() $O(Re^{-1})$
, due to the aforementioned
$O(Re^{-1})$
, due to the aforementioned
![]() $O(Re)$
drift.
$O(Re)$
drift.
The correction to the spinning period is zero at
![]() $O(Re)$
. The argument leading to an analogous conclusion for a sphere has already been given in the introduction. The argument remains unchanged for a spheroid since
$O(Re)$
. The argument leading to an analogous conclusion for a sphere has already been given in the introduction. The argument remains unchanged for a spheroid since
![]() $\unicode[STIX]{x1D74E}$
and
$\unicode[STIX]{x1D74E}$
and
![]() $\boldsymbol{p}$
are coincident in the spinning mode. In the tumbling orbit,
$\boldsymbol{p}$
are coincident in the spinning mode. In the tumbling orbit,
![]() $\dot{\unicode[STIX]{x1D719}}_{j}$
is not a constant, and depends on
$\dot{\unicode[STIX]{x1D719}}_{j}$
is not a constant, and depends on
![]() $\boldsymbol{p}$
, which is orthogonal to
$\boldsymbol{p}$
, which is orthogonal to
![]() $\unicode[STIX]{x1D74E}$
. The tumbling time period is given by
$\unicode[STIX]{x1D74E}$
. The tumbling time period is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\text{d}\unicode[STIX]{x1D719}_{j}}{\dot{\unicode[STIX]{x1D719}}_{jeff}+Re\,\dot{\unicode[STIX]{x1D719}}_{c1}+Re^{3/2}\,\dot{\unicode[STIX]{x1D719}}_{c2}}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{1}{\dot{\unicode[STIX]{x1D719}}_{jeff}}\,\text{d}\unicode[STIX]{x1D719}_{j}-Re\int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\dot{\unicode[STIX]{x1D719}}_{c1}}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\unicode[STIX]{x1D719}_{j}+O(Re^{3/2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\text{d}\unicode[STIX]{x1D719}_{j}}{\dot{\unicode[STIX]{x1D719}}_{jeff}+Re\,\dot{\unicode[STIX]{x1D719}}_{c1}+Re^{3/2}\,\dot{\unicode[STIX]{x1D719}}_{c2}}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{1}{\dot{\unicode[STIX]{x1D719}}_{jeff}}\,\text{d}\unicode[STIX]{x1D719}_{j}-Re\int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\dot{\unicode[STIX]{x1D719}}_{c1}}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\unicode[STIX]{x1D719}_{j}+O(Re^{3/2}),\end{eqnarray}$$
where the expansion is valid for
![]() $\unicode[STIX]{x1D705}\sim O(1)$
, when
$\unicode[STIX]{x1D705}\sim O(1)$
, when
![]() $\dot{\unicode[STIX]{x1D719}}_{c1}Re\ll \dot{\unicode[STIX]{x1D719}}_{jeff}$
. The leading-order integral on the right-hand side evaluates to
$\dot{\unicode[STIX]{x1D719}}_{c1}Re\ll \dot{\unicode[STIX]{x1D719}}_{jeff}$
. The leading-order integral on the right-hand side evaluates to
![]() $2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
, which is, of course, the Jeffery period. The
$2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}$
, which is, of course, the Jeffery period. The
![]() $O(Re)$
integral in the above equation evaluates to zero after substituting for
$O(Re)$
integral in the above equation evaluates to zero after substituting for
![]() $\dot{\unicode[STIX]{x1D719}}_{jeff}$
and
$\dot{\unicode[STIX]{x1D719}}_{jeff}$
and
![]() $\dot{\unicode[STIX]{x1D719}}_{c1}$
from (3.1) and (3.4) respectively. The vanishing of this integral can also be seen by noting that the
$\dot{\unicode[STIX]{x1D719}}_{c1}$
from (3.1) and (3.4) respectively. The vanishing of this integral can also be seen by noting that the
![]() $O(Re)$
correction to the angular velocity given in (3.4) is antisymmetric about the gradient axis (
$O(Re)$
correction to the angular velocity given in (3.4) is antisymmetric about the gradient axis (
![]() $\unicode[STIX]{x1D719}_{j}=\unicode[STIX]{x03C0}/2$
). Therefore, the contribution to the integral from the first quadrant (
$\unicode[STIX]{x1D719}_{j}=\unicode[STIX]{x03C0}/2$
). Therefore, the contribution to the integral from the first quadrant (
![]() $\unicode[STIX]{x1D719}_{j}$
varies from 0 to
$\unicode[STIX]{x1D719}_{j}$
varies from 0 to
![]() $\unicode[STIX]{x03C0}/2$
) cancels the contribution from the second quadrant (
$\unicode[STIX]{x03C0}/2$
) cancels the contribution from the second quadrant (
![]() $\unicode[STIX]{x1D719}_{j}$
varies from
$\unicode[STIX]{x1D719}_{j}$
varies from
![]() $\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}/2$
to
![]() $\unicode[STIX]{x03C0}$
) (this symmetry follows from the Stokesian velocity field due to the regular nature of the correction).
$\unicode[STIX]{x03C0}$
) (this symmetry follows from the Stokesian velocity field due to the regular nature of the correction).
The correction to the time period due to fluid inertia arises at
![]() $O(Re^{3/2})$
for both the tumbling and the spinning orbits. As mentioned in the introduction, the
$O(Re^{3/2})$
for both the tumbling and the spinning orbits. As mentioned in the introduction, the
![]() $O(Re^{3/2})$
correction for a rigid sphere is evaluated in Stone et al. (Reference Stone, Brady and Lovalenti2000) and Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). The evaluation of the correction for a spheroid in the spinning orbit is simpler in that it follows that for a sphere, and is presented in § 4. The correction for a tumbling spheroid is more involved, in having to account for the unsteadiness of the disturbance velocity field, and is presented in § 5.
$O(Re^{3/2})$
correction for a rigid sphere is evaluated in Stone et al. (Reference Stone, Brady and Lovalenti2000) and Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). The evaluation of the correction for a spheroid in the spinning orbit is simpler in that it follows that for a sphere, and is presented in § 4. The correction for a tumbling spheroid is more involved, in having to account for the unsteadiness of the disturbance velocity field, and is presented in § 5.
4 Evaluation: time period – spinning orbit
In this section, we focus on the effect of fluid inertia on spinning spheroids. The spinning mode is the only steady-state orbit for oblate spheroids with aspect ratios larger than
![]() $0.137$
, and one of two for oblate spheroids with aspect ratio less than
$0.137$
, and one of two for oblate spheroids with aspect ratio less than
![]() $0.137$
. The leading-order spin is
$0.137$
. The leading-order spin is
![]() $-(1/2)\mathbf{1}_{3}$
. Defining the correction to the spin, at
$-(1/2)\mathbf{1}_{3}$
. Defining the correction to the spin, at
![]() $O(Re^{3/2})$
, as
$O(Re^{3/2})$
, as
![]() $\dot{\unicode[STIX]{x1D713}}_{c2}\mathbf{1}_{3}$
,
$\dot{\unicode[STIX]{x1D713}}_{c2}\mathbf{1}_{3}$
,
![]() $\dot{\unicode[STIX]{x1D713}}_{c2}$
being independent of the spin angle
$\dot{\unicode[STIX]{x1D713}}_{c2}$
being independent of the spin angle
![]() $\unicode[STIX]{x1D713}$
due to symmetry, one obtains
$\unicode[STIX]{x1D713}$
due to symmetry, one obtains
Here,
![]() $\dot{\unicode[STIX]{x1D713}}_{c2}$
can be obtained by contracting (2.25) with
$\dot{\unicode[STIX]{x1D713}}_{c2}$
can be obtained by contracting (2.25) with
![]() $\mathbf{1}_{3}$
, and is given by
$\mathbf{1}_{3}$
, and is given by
 $$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D713}}_{c2} & = & \displaystyle \frac{1}{8\unicode[STIX]{x03C0}X_{C}}\displaystyle \int [4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D713}}_{c2} & = & \displaystyle \frac{1}{8\unicode[STIX]{x03C0}X_{C}}\displaystyle \int [4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k},\end{eqnarray}$$
where all of the terms in the integrand are evaluated at
![]() $\unicode[STIX]{x1D703}_{j}=0$
, corresponding to the spinning orbit, and
$\unicode[STIX]{x1D703}_{j}=0$
, corresponding to the spinning orbit, and
![]() $X_{C}$
is the torque coefficient corresponding to spinning motion, defined in § 2. The Fourier transformed velocity fields
$X_{C}$
is the torque coefficient corresponding to spinning motion, defined in § 2. The Fourier transformed velocity fields
![]() $\hat{\boldsymbol{u}}^{match}$
and
$\hat{\boldsymbol{u}}^{match}$
and
![]() $\hat{\boldsymbol{u}}^{f}$
are now independent of time. The integral for the time period in (4.1) then becomes
$\hat{\boldsymbol{u}}^{f}$
are now independent of time. The integral for the time period in (4.1) then becomes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{spin} & = & \displaystyle -\frac{Re^{3/2}}{X_{C}}\int [-4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{match}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{spin} & = & \displaystyle -\frac{Re^{3/2}}{X_{C}}\int [-4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{match}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
The term within braces above is again independent of time, and simplifies to
using (2.8), and, to within a constant of proportionality, is just the Fourier transformed rotlet field. For a sphere,
![]() $B_{2}+B_{3}$
above reduces to
$B_{2}+B_{3}$
above reduces to
![]() $-4\unicode[STIX]{x03C0}$
, which equals half of the torque exerted by a unit sphere rotating with a unit non-dimensional angular velocity.
$-4\unicode[STIX]{x03C0}$
, which equals half of the torque exerted by a unit sphere rotating with a unit non-dimensional angular velocity.
The singularity
![]() $\unicode[STIX]{x1D64E}$
in the actual problem takes the form
$\unicode[STIX]{x1D64E}$
in the actual problem takes the form
![]() $\unicode[STIX]{x1D64E}=A_{3}\unicode[STIX]{x1D640}$
, and, therefore,
$\unicode[STIX]{x1D64E}=A_{3}\unicode[STIX]{x1D640}$
, and, therefore,
![]() $\hat{\boldsymbol{u}}^{match}(\boldsymbol{k})$
is
$\hat{\boldsymbol{u}}^{match}(\boldsymbol{k})$
is
![]() $-\text{i}A_{3}\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{k}/(2\unicode[STIX]{x03C0}k^{2})\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{k}\boldsymbol{k}/k^{2})$
from (2.21), which is the Fourier transformed stresslet velocity field, but with a
$-\text{i}A_{3}\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{k}/(2\unicode[STIX]{x03C0}k^{2})\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-\boldsymbol{k}\boldsymbol{k}/k^{2})$
from (2.21), which is the Fourier transformed stresslet velocity field, but with a
![]() $\unicode[STIX]{x1D709}_{0}$
-dependent coefficient (
$\unicode[STIX]{x1D709}_{0}$
-dependent coefficient (
![]() $A_{3}=-20\unicode[STIX]{x03C0}/3$
for a sphere). The inertial terms in (4.3) involving
$A_{3}=-20\unicode[STIX]{x03C0}/3$
for a sphere). The inertial terms in (4.3) involving
![]() $\hat{\boldsymbol{u}}^{match}$
take the form
$\hat{\boldsymbol{u}}^{match}$
take the form
where
![]() $\boldsymbol{R}_{1}^{spin}$
is given by
$\boldsymbol{R}_{1}^{spin}$
is given by
The Fourier transformed velocity field
![]() $\hat{\boldsymbol{u}}^{f}$
in (4.3) is governed by (2.20). After eliminating the pressure term, (2.20) reduces, for the spinning case, to
$\hat{\boldsymbol{u}}^{f}$
in (4.3) is governed by (2.20). After eliminating the pressure term, (2.20) reduces, for the spinning case, to
 $$\begin{eqnarray}\displaystyle & & \displaystyle -(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}=\boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)=\boldsymbol{Q}^{spin}\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{A_{3}}{k^{6}\unicode[STIX]{x03C0}}\left(-\text{i}k_{1}^{3}k_{2}^{2}\mathbf{1}_{1}+\text{i}k_{1}^{2}k_{2}\left(k_{1}^{2}+k_{3}^{2}\right)\mathbf{1}_{2}-\text{i}k_{1}^{2}k_{2}^{2}k_{3}\mathbf{1}_{3}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}=\boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)=\boldsymbol{Q}^{spin}\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{A_{3}}{k^{6}\unicode[STIX]{x03C0}}\left(-\text{i}k_{1}^{3}k_{2}^{2}\mathbf{1}_{1}+\text{i}k_{1}^{2}k_{2}\left(k_{1}^{2}+k_{3}^{2}\right)\mathbf{1}_{2}-\text{i}k_{1}^{2}k_{2}^{2}k_{3}\mathbf{1}_{3}\right).\end{eqnarray}$$
The components of (4.7) in a space-fixed coordinate system are given as
where the subscripts
![]() $1$
,
$1$
,
![]() $2$
and
$2$
and
![]() $3$
denote the components along the
$3$
denote the components along the
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
axes. While the components along the flow (
$Z$
axes. While the components along the flow (
![]() $\hat{u} _{1}^{f}$
) and the vorticity (
$\hat{u} _{1}^{f}$
) and the vorticity (
![]() $\hat{u} _{3}^{f}$
) axes are coupled to the one along the gradient axis (
$\hat{u} _{3}^{f}$
) axes are coupled to the one along the gradient axis (
![]() $\hat{u} _{2}^{f}$
), the equation governing the latter is independent of the other two, and is therefore solved first. In (4.8)–(4.10), one can identify a simple shear flow in Fourier space, given by
$\hat{u} _{2}^{f}$
), the equation governing the latter is independent of the other two, and is therefore solved first. In (4.8)–(4.10), one can identify a simple shear flow in Fourier space, given by
![]() $\hat{\boldsymbol{u}}^{\ast \infty }(\boldsymbol{k})=-k_{1}\mathbf{1}_{2}$
, orthogonal to the one in physical space, (
$\hat{\boldsymbol{u}}^{\ast \infty }(\boldsymbol{k})=-k_{1}\mathbf{1}_{2}$
, orthogonal to the one in physical space, (
![]() $\boldsymbol{u}^{\infty }(\boldsymbol{x})=x_{2}\mathbf{1}_{1}$
), convecting the Fourier transformed velocity field. The orthogonality arises because the wavevector is oriented normal to the wavefronts, the latter being turned by the simple shear flow in physical space (see figure 2). The components of the Fourier transformed velocity field are convected by the Fourier-space simple shear flow. This convection has the effect that
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=x_{2}\mathbf{1}_{1}$
), convecting the Fourier transformed velocity field. The orthogonality arises because the wavevector is oriented normal to the wavefronts, the latter being turned by the simple shear flow in physical space (see figure 2). The components of the Fourier transformed velocity field are convected by the Fourier-space simple shear flow. This convection has the effect that
![]() $\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
, for a given
$\hat{\boldsymbol{u}}^{f}(\boldsymbol{k})$
, for a given
![]() $\boldsymbol{k}$
, has contributions from all wavevectors turned onto
$\boldsymbol{k}$
, has contributions from all wavevectors turned onto
![]() $\boldsymbol{k}$
from orientations further upstream. The viscous term, proportional to
$\boldsymbol{k}$
from orientations further upstream. The viscous term, proportional to
![]() $4\unicode[STIX]{x03C0}^{2}k^{2}$
in (4.8)–(4.10), causes an exponential decay in amplitude with an argument that involves an integral over the square of the changing wavevector over this ‘turning’ period. Defining the streamlines of the Fourier-space simple shear flow as
$4\unicode[STIX]{x03C0}^{2}k^{2}$
in (4.8)–(4.10), causes an exponential decay in amplitude with an argument that involves an integral over the square of the changing wavevector over this ‘turning’ period. Defining the streamlines of the Fourier-space simple shear flow as
![]() $k_{2}^{\prime }=k_{2}+k_{1}s$
,
$k_{2}^{\prime }=k_{2}+k_{1}s$
,
![]() $s$
being a time-like variable, the solutions for the individual components
$s$
being a time-like variable, the solutions for the individual components
![]() $\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
,
$\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
,
![]() $\hat{u} _{1}^{f}$
and
$\hat{u} _{1}^{f}$
and
![]() $\hat{u} _{3}^{f}$
may be written as follows:
$\hat{u} _{3}^{f}$
may be written as follows:
 $$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{1}{k^{2}}\right)\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{\prime 4}\unicode[STIX]{x03C0}}\,\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{1}{k^{2}}\right)\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{\prime 4}\unicode[STIX]{x03C0}}\,\text{d}s,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{u} _{1}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(-\frac{\text{i}k_{1}^{3}(k_{2}+k_{1}s)^{2}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}-\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })\right)\text{d}s\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{1}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(-\frac{\text{i}k_{1}^{3}(k_{2}+k_{1}s)^{2}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}-\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })\right)\text{d}s\end{eqnarray}$$

Figure 2. The red lines denote the wavefronts. Here,
![]() $\boldsymbol{k}$
is the wavevector which gets turned due to a simple shear flow of the form
$\boldsymbol{k}$
is the wavevector which gets turned due to a simple shear flow of the form
![]() $\boldsymbol{u}^{\infty }(\boldsymbol{x})=x_{2}\mathbf{1}_{1}$
. This is equivalent to a convection by a simple shear flow of the form
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=x_{2}\mathbf{1}_{1}$
. This is equivalent to a convection by a simple shear flow of the form
![]() $\hat{\boldsymbol{u}}^{\ast \infty }(\boldsymbol{k})=-k_{1}\mathbf{1}_{2}$
in the Fourier space.
$\hat{\boldsymbol{u}}^{\ast \infty }(\boldsymbol{k})=-k_{1}\mathbf{1}_{2}$
in the Fourier space.
and
 $$\begin{eqnarray}\displaystyle \hat{u} _{3}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(-\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)^{2}k_{3}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}+\frac{2k_{1}k_{3}}{k^{\prime 2}}\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })\right)\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{3}^{f}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(-\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)^{2}k_{3}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}+\frac{2k_{1}k_{3}}{k^{\prime 2}}\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })\right)\text{d}s,\end{eqnarray}$$
where the components in the flow and vorticity directions are coupled to the component in the gradient direction through the term
![]() $\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
. Here,
$\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
. Here,
![]() $\boldsymbol{k}^{\prime }=(k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}s)\mathbf{1}_{2}+k_{3}\mathbf{1}_{3})$
and
$\boldsymbol{k}^{\prime }=(k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}s)\mathbf{1}_{2}+k_{3}\mathbf{1}_{3})$
and
![]() $k^{\prime }=|\boldsymbol{k}^{\prime }|$
, and
$k^{\prime }=|\boldsymbol{k}^{\prime }|$
, and
![]() $\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
in (4.12) and (4.13) is given by
$\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
in (4.12) and (4.13) is given by
 $$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f}(\boldsymbol{k}^{\prime }) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}(k_{2}+k_{1}s)s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{1}{k^{\prime 2}}\right)\frac{\text{i}k_{1}^{2}k_{2}^{\prime \prime }\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{\prime \prime 4}\unicode[STIX]{x03C0}}\,\text{d}s^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f}(\boldsymbol{k}^{\prime }) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}(k_{2}+k_{1}s)s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{1}{k^{\prime 2}}\right)\frac{\text{i}k_{1}^{2}k_{2}^{\prime \prime }\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{\prime \prime 4}\unicode[STIX]{x03C0}}\,\text{d}s^{\prime },\end{eqnarray}$$
where
![]() $\boldsymbol{k}^{\prime \prime }=(k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}(s+s^{\prime }))\mathbf{1}_{2}+k_{3}\mathbf{1}_{3})$
,
$\boldsymbol{k}^{\prime \prime }=(k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}(s+s^{\prime }))\mathbf{1}_{2}+k_{3}\mathbf{1}_{3})$
,
![]() $k^{\prime \prime }=|\boldsymbol{k}^{\prime \prime }|$
and
$k^{\prime \prime }=|\boldsymbol{k}^{\prime \prime }|$
and
![]() $k_{2}^{\prime \prime }=(k_{2}+k_{1}(s+s^{\prime }))$
. Thus,
$k_{2}^{\prime \prime }=(k_{2}+k_{1}(s+s^{\prime }))$
. Thus,
![]() $\hat{u} _{1}^{f}(\boldsymbol{k}^{\prime })$
and
$\hat{u} _{1}^{f}(\boldsymbol{k}^{\prime })$
and
![]() $\hat{u} _{3}^{f}(\boldsymbol{k}^{\prime })$
given in (4.11) and (4.13) include a one-dimensional and a two-dimensional integral, whereas
$\hat{u} _{3}^{f}(\boldsymbol{k}^{\prime })$
given in (4.11) and (4.13) include a one-dimensional and a two-dimensional integral, whereas
![]() $\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
given in (4.12) consists of only a one-dimensional integral.
$\hat{u} _{2}^{f}(\boldsymbol{k}^{\prime })$
given in (4.12) consists of only a one-dimensional integral.
The Fourier transformed test velocity field given in (4.4), the inertial terms involving
![]() $\hat{u} ^{match}$
given by (4.5)–(4.6) and
$\hat{u} ^{match}$
given by (4.5)–(4.6) and
![]() $\hat{u} ^{f}$
given by (4.11)–(4.13) are now substituted in (4.3) to obtain
$\hat{u} ^{f}$
given by (4.11)–(4.13) are now substituted in (4.3) to obtain
The different terms in the integral above can be expressed in a spherical coordinate system with
![]() $k_{1}=k\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
,
$k_{1}=k\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
,
![]() $k_{2}=k\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}$
,
$k_{2}=k\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}$
,
![]() $k_{3}=k\cos \unicode[STIX]{x1D703}$
and
$k_{3}=k\cos \unicode[STIX]{x1D703}$
and
![]() $\text{d}\boldsymbol{k}=k^{2}\sin \unicode[STIX]{x1D703}\,\text{d}k\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}$
as
$\text{d}\boldsymbol{k}=k^{2}\sin \unicode[STIX]{x1D703}\,\text{d}k\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}$
as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin})\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\frac{\text{i}k_{1}^{3}k_{2}^{\prime 2}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}\left[\frac{\text{i}(B_{2}+B_{3})k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[\frac{\text{i}(B_{2}+B_{3})k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right]\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\frac{\text{i}k_{1}^{2}k_{2}^{\prime \prime }(k_{1}^{2}+k_{3}^{2})A_{3}}{k^{\prime \prime 4}k^{\prime 2}\unicode[STIX]{x03C0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin})\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\frac{\text{i}k_{1}^{3}k_{2}^{\prime 2}A_{3}}{k^{\prime 6}\unicode[STIX]{x03C0}}\left[\frac{\text{i}(B_{2}+B_{3})k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[\frac{\text{i}(B_{2}+B_{3})k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right]\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\frac{\text{i}k_{1}^{2}k_{2}^{\prime \prime }(k_{1}^{2}+k_{3}^{2})A_{3}}{k^{\prime \prime 4}k^{\prime 2}\unicode[STIX]{x03C0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int 4\unicode[STIX]{x03C0}^{2}\left\{\left[\frac{-\text{i}(B_{2}+B_{3})k_{1}}{2\unicode[STIX]{x03C0}}\right]\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{2}k^{\prime 4}\unicode[STIX]{x03C0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int 4\unicode[STIX]{x03C0}^{2}\left\{\left[\frac{-\text{i}(B_{2}+B_{3})k_{1}}{2\unicode[STIX]{x03C0}}\right]\frac{\text{i}k_{1}^{2}(k_{2}+k_{1}s)\left(k_{1}^{2}+k_{3}^{2}\right)A_{3}}{k^{2}k^{\prime 4}\unicode[STIX]{x03C0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k} & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{-\frac{A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k} & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{-\frac{A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
where we have retained the Cartesian notation for the wavevector components for brevity, and the terms grouped within the braces are such that they are independent of
![]() $k$
. The test velocity field does not have a vorticity component, and therefore the contribution to (4.15) due to the term proportional to
$k$
. The test velocity field does not have a vorticity component, and therefore the contribution to (4.15) due to the term proportional to
![]() $\hat{u} _{3}^{f}$
is zero.
$\hat{u} _{3}^{f}$
is zero.
The right-hand side of (4.16) is sum of a four-dimensional and a five-dimensional integral, whereas that of (4.17) is a single four-dimensional integral. In the four-dimensional integrals, the integration over
![]() $k$
gives a term proportional to
$k$
gives a term proportional to
![]() $1/s^{3/2}$
, which is divergent in the integration over
$1/s^{3/2}$
, which is divergent in the integration over
![]() $s$
as
$s$
as
![]() $s\rightarrow 0$
, as follows:
$s\rightarrow 0$
, as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}/3)^{3/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}/3)^{3/2}}.\end{eqnarray}$$
The three-dimensional integral on the right-hand side of (4.19) diverges in the limit
![]() $k\rightarrow \infty$
. Although, individually, the abovementioned integrals are divergent, the sum is nevertheless convergent. This divergence arises because, while deriving the expression for the angular velocity in (2.22), we had rewritten the three terms proportional to
$k\rightarrow \infty$
. Although, individually, the abovementioned integrals are divergent, the sum is nevertheless convergent. This divergence arises because, while deriving the expression for the angular velocity in (2.22), we had rewritten the three terms proportional to
![]() $\hat{u} ^{f}$
in (2.6) as a sum of a term proportional to
$\hat{u} ^{f}$
in (2.6) as a sum of a term proportional to
![]() $k^{2}\hat{u} ^{f}$
and three terms proportional to
$k^{2}\hat{u} ^{f}$
and three terms proportional to
![]() $\hat{u} ^{match}$
, and each of these four terms is divergent in the limit of
$\hat{u} ^{match}$
, and each of these four terms is divergent in the limit of
![]() $k\rightarrow \infty$
(the original terms were convergent with
$k\rightarrow \infty$
(the original terms were convergent with
![]() $\hat{u} ^{f}$
decaying as
$\hat{u} ^{f}$
decaying as
![]() $1/k^{3}$
, the scaling obtained from the large-
$1/k^{3}$
, the scaling obtained from the large-
![]() $k$
limit of (4.11)–(4.13)). To eliminate the divergence, an additional integral over a dummy variable
$k$
limit of (4.11)–(4.13)). To eliminate the divergence, an additional integral over a dummy variable
![]() $s$
is introduced in (4.19) as follows:
$s$
is introduced in (4.19) as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\frac{-A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\text{e}^{-4\unicode[STIX]{x03C0}^{2}k^{2}s}\,\text{d}s\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\frac{-A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\text{e}^{-4\unicode[STIX]{x03C0}^{2}k^{2}s}\,\text{d}s\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
It should be noted that
![]() $\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\exp (-4\unicode[STIX]{x03C0}^{2}k^{2}s)\,\text{d}s=1$
. The additional integral, when integrated over
$\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\exp (-4\unicode[STIX]{x03C0}^{2}k^{2}s)\,\text{d}s=1$
. The additional integral, when integrated over
![]() $k$
, gives a term proportional to
$k$
, gives a term proportional to
![]() $1/s^{3/2}$
, and (4.21) takes the form
$1/s^{3/2}$
, and (4.21) takes the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\frac{-A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\frac{1}{8\sqrt{\unicode[STIX]{x03C0}}s^{3/2}}\,\text{d}s\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \boldsymbol{R}_{1}^{spin}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{spin}\,\text{d}\boldsymbol{k}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\frac{-A_{3}k_{1}^{3}(k^{2}-4k_{2}^{2})}{\unicode[STIX]{x03C0}k^{6}}\frac{(B_{2}+B_{3})k_{2}}{4\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,\frac{A_{3}k_{1}^{2}k_{2}(3k^{2}-4k_{2}^{2})}{k^{6}\unicode[STIX]{x03C0}}\frac{(B_{2}+B_{3})k_{1}}{4\unicode[STIX]{x03C0}}\right\}\frac{1}{8\sqrt{\unicode[STIX]{x03C0}}s^{3/2}}\,\text{d}s\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
The integration over
![]() $k$
in the five-dimensional integral in (4.16) gives
$k$
in the five-dimensional integral in (4.16) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\frac{s^{\prime }}{12}\left(3\left(4+s^{2}-s^{2}\cos 2\unicode[STIX]{x1D703}+2s\sin ^{2}\unicode[STIX]{x1D703}(s\cos 2\unicode[STIX]{x1D719}+2\sin 2\unicode[STIX]{x1D719})\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,4\cos \unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D703}s^{\prime }\left(3\sin \unicode[STIX]{x1D719}+\cos \unicode[STIX]{x1D719}\left(3s+s^{\prime }\right)\right)\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(f^{exp}(s,s^{\prime },\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}))^{3/2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\frac{s^{\prime }}{12}\left(3\left(4+s^{2}-s^{2}\cos 2\unicode[STIX]{x1D703}+2s\sin ^{2}\unicode[STIX]{x1D703}(s\cos 2\unicode[STIX]{x1D719}+2\sin 2\unicode[STIX]{x1D719})\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,4\cos \unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D703}s^{\prime }\left(3\sin \unicode[STIX]{x1D719}+\cos \unicode[STIX]{x1D719}\left(3s+s^{\prime }\right)\right)\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(f^{exp}(s,s^{\prime },\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}))^{3/2}},\end{eqnarray}$$
where
![]() $f^{exp}$
is the function that multiplies
$f^{exp}$
is the function that multiplies
![]() $-4\unicode[STIX]{x03C0}^{2}k^{2}$
in the exponent of the integrand. It should be noted that there is no divergence for the five-dimensional integral in the limit of
$-4\unicode[STIX]{x03C0}^{2}k^{2}$
in the exponent of the integrand. It should be noted that there is no divergence for the five-dimensional integral in the limit of
![]() $s\rightarrow 0$
or
$s\rightarrow 0$
or
![]() $s^{\prime }\rightarrow 0$
. The integration over
$s^{\prime }\rightarrow 0$
. The integration over
![]() $k$
for the four-dimensional integrals given in (4.16) and (4.17) is substituted from (4.20), and the sum of the resulting three-dimensional integral together with the matching term contribution given in (4.22) is convergent in the limit of
$k$
for the four-dimensional integrals given in (4.16) and (4.17) is substituted from (4.20), and the sum of the resulting three-dimensional integral together with the matching term contribution given in (4.22) is convergent in the limit of
![]() $s\rightarrow 0$
. This sum, which is a three-dimensional integral (over
$s\rightarrow 0$
. This sum, which is a three-dimensional integral (over
![]() $s$
,
$s$
,
![]() $\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D703}$
,
![]() $\unicode[STIX]{x1D719}$
) and a four-dimensional integral (over
$\unicode[STIX]{x1D719}$
) and a four-dimensional integral (over
![]() $s$
,
$s$
,
![]() $s^{\prime }$
,
$s^{\prime }$
,
![]() $\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D703}$
,
![]() $\unicode[STIX]{x1D719}$
) obtained from the five-dimensional ones in (4.16) and (4.17), after substituting from (4.23), is evaluated numerically using Gaussian quadrature to give the time period correction as
$\unicode[STIX]{x1D719}$
) obtained from the five-dimensional ones in (4.16) and (4.17), after substituting from (4.23), is evaluated numerically using Gaussian quadrature to give the time period correction as
The angular velocity correction at
![]() $O(Re^{3/2})$
can be obtained by using (4.1) and is given by
$O(Re^{3/2})$
can be obtained by using (4.1) and is given by
![]() $\unicode[STIX]{x0394}T^{spin}/(8\unicode[STIX]{x03C0})$
, which leads to
$\unicode[STIX]{x0394}T^{spin}/(8\unicode[STIX]{x03C0})$
, which leads to
For an oblate spheroid,
![]() $A_{3}(B_{2}+B_{3})/X_{c}=128\unicode[STIX]{x03C0}^{2}/(9\,\text{cosec}^{-1}\unicode[STIX]{x1D709}_{0}\unicode[STIX]{x1D709}_{0}^{5}-6\unicode[STIX]{x1D709}_{0}\sqrt{-1+\unicode[STIX]{x1D709}_{0}^{2}}-9\unicode[STIX]{x1D709}_{0}^{3}\sqrt{-1+\unicode[STIX]{x1D709}_{0}^{2}})$
. For a sphere,
$A_{3}(B_{2}+B_{3})/X_{c}=128\unicode[STIX]{x03C0}^{2}/(9\,\text{cosec}^{-1}\unicode[STIX]{x1D709}_{0}\unicode[STIX]{x1D709}_{0}^{5}-6\unicode[STIX]{x1D709}_{0}\sqrt{-1+\unicode[STIX]{x1D709}_{0}^{2}}-9\unicode[STIX]{x1D709}_{0}^{3}\sqrt{-1+\unicode[STIX]{x1D709}_{0}^{2}})$
. For a sphere,
![]() $A_{3}(B_{2}+B_{3})/X_{c}=80\unicode[STIX]{x03C0}^{2}/3$
and the angular velocity reduces to that obtained by Stone et al. (Reference Stone, Brady and Lovalenti2000) and Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). The reason for the absence of the
$A_{3}(B_{2}+B_{3})/X_{c}=80\unicode[STIX]{x03C0}^{2}/3$
and the angular velocity reduces to that obtained by Stone et al. (Reference Stone, Brady and Lovalenti2000) and Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). The reason for the absence of the
![]() $O(Re)$
correction in (4.25) has already been pointed out in §§ 1 and 3. The correction given in (4.25) matches with that derived using a matched asymptotic expansion approach in Meibohm et al. (Reference Meibohm, Candelier, Rosén, Einarsson, Lundell and Mehlig2016). The plot of the correction to the time period in (4.24) against eccentricity is given in § 6.
$O(Re)$
correction in (4.25) has already been pointed out in §§ 1 and 3. The correction given in (4.25) matches with that derived using a matched asymptotic expansion approach in Meibohm et al. (Reference Meibohm, Candelier, Rosén, Einarsson, Lundell and Mehlig2016). The plot of the correction to the time period in (4.24) against eccentricity is given in § 6.
The correction derived in (4.24) is also valid for a spinning prolate spheroid, with
![]() $A_{3}(B_{2}+B_{3})/X_{c}=128\unicode[STIX]{x03C0}^{2}(\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(-3\unicode[STIX]{x1D709}_{0}^{3}+3(\unicode[STIX]{x1D709}_{0}^{2}-1)^{2}\coth ^{-1}\unicode[STIX]{x1D709}_{0}+5\unicode[STIX]{x1D709}_{0}))$
. Although not relevant to inertial correction in three dimensions, consideration of this mode allows one to connect to the effect of inertia in the two-dimensional scenario. As mentioned in the introduction, the inertial correction for a circular cylinder arises at
$A_{3}(B_{2}+B_{3})/X_{c}=128\unicode[STIX]{x03C0}^{2}(\unicode[STIX]{x1D709}_{0}^{2}-1)/(3\unicode[STIX]{x1D709}_{0}^{3}(-3\unicode[STIX]{x1D709}_{0}^{3}+3(\unicode[STIX]{x1D709}_{0}^{2}-1)^{2}\coth ^{-1}\unicode[STIX]{x1D709}_{0}+5\unicode[STIX]{x1D709}_{0}))$
. Although not relevant to inertial correction in three dimensions, consideration of this mode allows one to connect to the effect of inertia in the two-dimensional scenario. As mentioned in the introduction, the inertial correction for a circular cylinder arises at
![]() $O(Re)$
, as shown by Robertson & Acrivos (Reference Robertson and Acrivos1970). This scaling emerges from the
$O(Re)$
, as shown by Robertson & Acrivos (Reference Robertson and Acrivos1970). This scaling emerges from the
![]() $O(Re^{3/2})$
correction for a spinning prolate spheroid in the limit of
$O(Re^{3/2})$
correction for a spinning prolate spheroid in the limit of
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
. To see this, one first writes (4.24) in terms of the Reynolds number based on the spheroid minor axis (
$\unicode[STIX]{x1D705}\rightarrow \infty$
. To see this, one first writes (4.24) in terms of the Reynolds number based on the spheroid minor axis (
![]() $\tilde{Re}$
), yielding
$\tilde{Re}$
), yielding
![]() $\unicode[STIX]{x0394}T^{spin}=\tilde{Re}^{3/2}\unicode[STIX]{x1D705}^{3}A_{3}(B_{2}+B_{3})/X_{c}$
, which in the large-aspect-ratio limit is proportional to
$\unicode[STIX]{x0394}T^{spin}=\tilde{Re}^{3/2}\unicode[STIX]{x1D705}^{3}A_{3}(B_{2}+B_{3})/X_{c}$
, which in the large-aspect-ratio limit is proportional to
![]() $\tilde{Re}^{3/2}\unicode[STIX]{x1D705}$
. As expected, the transition from
$\tilde{Re}^{3/2}\unicode[STIX]{x1D705}$
. As expected, the transition from
![]() $O(Re^{3/2})$
to the two-dimensional
$O(Re^{3/2})$
to the two-dimensional
![]() $O(Re)$
scaling occurs when
$O(Re)$
scaling occurs when
![]() $\unicode[STIX]{x1D705}$
is
$\unicode[STIX]{x1D705}$
is
![]() $O(\tilde{Re}^{-1/2})$
.
$O(\tilde{Re}^{-1/2})$
.
5 Evaluation: time period – tumbling orbit
In this section, we focus on the tumbling orbit, which is the long-time orbit for prolate spheroids of any aspect ratio and one of two for oblate spheroids with aspect ratios less than 0.137. The inertial correction to the tumbling time period may be obtained by considering the explicit form of the
![]() $O(Re^{3/2})$
term in (3.5), and is given by
$O(Re^{3/2})$
term in (3.5), and is given by
In (5.1), we have changed the variable of integration back to time based on
![]() $\text{d}\unicode[STIX]{x1D719}_{j}/\text{d}t=\dot{\unicode[STIX]{x1D719}}_{jeff}$
, since the error affects the time period only at
$\text{d}\unicode[STIX]{x1D719}_{j}/\text{d}t=\dot{\unicode[STIX]{x1D719}}_{jeff}$
, since the error affects the time period only at
![]() $O(Re^{5/2})$
. The angular velocity of the tumbling spheroid, at
$O(Re^{5/2})$
. The angular velocity of the tumbling spheroid, at
![]() $O(Re^{3/2})$
,
$O(Re^{3/2})$
,
![]() $\dot{\unicode[STIX]{x1D719}}_{c2}$
, may be obtained by contracting (2.25) with
$\dot{\unicode[STIX]{x1D719}}_{c2}$
, may be obtained by contracting (2.25) with
![]() $\mathbf{1}_{3}$
, which gives
$\mathbf{1}_{3}$
, which gives
 $$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D719}}_{c2} & = & \displaystyle \frac{1}{8\unicode[STIX]{x03C0}Y_{C}}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dot{\unicode[STIX]{x1D719}}_{c2} & = & \displaystyle \frac{1}{8\unicode[STIX]{x03C0}Y_{C}}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}\boldsymbol{k},\end{eqnarray}$$
where all of the terms in the integrand are evaluated at
![]() $\unicode[STIX]{x1D703}_{j}=\unicode[STIX]{x03C0}/2$
(tumbling orbit), and
$\unicode[STIX]{x1D703}_{j}=\unicode[STIX]{x03C0}/2$
(tumbling orbit), and
![]() $Y_{c}$
, the torque coefficient corresponding to transverse rotation, is defined in § 2. Substitution of (5.2) into (5.1) leads to the
$Y_{c}$
, the torque coefficient corresponding to transverse rotation, is defined in § 2. Substitution of (5.2) into (5.1) leads to the
![]() $O(Re^{3/2})$
correction to the time period, given by
$O(Re^{3/2})$
correction to the time period, given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{c}}\displaystyle \int \int _{0}^{T_{jeff}}\left[-4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}\,\dot{\unicode[STIX]{x1D719}}_{jeff}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}t\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{c}}\displaystyle \int \int _{0}^{T_{jeff}}\left[-4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}-\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}-\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}\,\dot{\unicode[STIX]{x1D719}}_{jeff}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\text{d}t\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
The integral above is evaluated in the space-fixed coordinate system (
![]() $XYZ$
in figure 1
a) and the details are presented in §§ 5.1–5.4 below. The reciprocal theorem restricts the orientation of the spheroid in the test problem to be the same as that of the spheroid in the problem of interest. Therefore, in the tumbling orbit, the velocity field is unsteady in the test problem too. The singularities corresponding to both problems are time-dependent point-force-dipole singularities (a stresslet in the actual problem and both a stresslet and a rotlet in the test problem), the time dependence arising from the motion of
$XYZ$
in figure 1
a) and the details are presented in §§ 5.1–5.4 below. The reciprocal theorem restricts the orientation of the spheroid in the test problem to be the same as that of the spheroid in the problem of interest. Therefore, in the tumbling orbit, the velocity field is unsteady in the test problem too. The singularities corresponding to both problems are time-dependent point-force-dipole singularities (a stresslet in the actual problem and both a stresslet and a rotlet in the test problem), the time dependence arising from the motion of
![]() $\boldsymbol{p}$
along the tumbling orbit. The time-dependent
$\boldsymbol{p}$
along the tumbling orbit. The time-dependent
![]() $\boldsymbol{p}$
determines
$\boldsymbol{p}$
determines
![]() $\unicode[STIX]{x1D64E}^{(2t)}$
,
$\unicode[STIX]{x1D64E}^{(2t)}$
,
![]() $\unicode[STIX]{x1D64E}$
and thence
$\unicode[STIX]{x1D64E}$
and thence
![]() $\hat{\boldsymbol{u}}^{match}$
and
$\hat{\boldsymbol{u}}^{match}$
and
![]() $\hat{\boldsymbol{u}}^{f}$
via (2.21) and (2.20). Thus, the term involving the test velocity field, given within braces in (5.3), and the inertial terms in the problem of interest, given in square brackets, are functions of time.
$\hat{\boldsymbol{u}}^{f}$
via (2.21) and (2.20). Thus, the term involving the test velocity field, given within braces in (5.3), and the inertial terms in the problem of interest, given in square brackets, are functions of time.
To evaluate the integral in (5.3), in § 5.1, the term within braces is expressed in the aforementioned coordinate system as a Fourier time series which involves a combination of three Fourier modes, namely the mode independent of time that is already present for a sphere, and modes proportional to
![]() $\cos (4\unicode[STIX]{x03C0}t/T_{jeff})$
and
$\cos (4\unicode[STIX]{x03C0}t/T_{jeff})$
and
![]() $\sin (4\unicode[STIX]{x03C0}t/T_{jeff})$
,
$\sin (4\unicode[STIX]{x03C0}t/T_{jeff})$
,
![]() $T_{jeff}$
being the Jeffery period. The combination
$T_{jeff}$
being the Jeffery period. The combination
![]() $\unicode[STIX]{x1D64E}^{(2t)}/\dot{\unicode[STIX]{x1D719}}_{jeff}$
leads to a finite Fourier series, a fact crucial to the evaluation of the time period correction; the time dependence of
$\unicode[STIX]{x1D64E}^{(2t)}/\dot{\unicode[STIX]{x1D719}}_{jeff}$
leads to a finite Fourier series, a fact crucial to the evaluation of the time period correction; the time dependence of
![]() $\unicode[STIX]{x1D64E}^{(2t)}$
alone, for instance, would have led to an infinite Fourier time series. The two time-dependent modes have a frequency that is twice the Jeffery frequency (
$\unicode[STIX]{x1D64E}^{(2t)}$
alone, for instance, would have led to an infinite Fourier time series. The two time-dependent modes have a frequency that is twice the Jeffery frequency (
![]() $\unicode[STIX]{x1D714}_{g}=2\unicode[STIX]{x03C0}/T_{jeff}$
), this being due to the fore–aft symmetry of the spheroid, which leads to the same disturbance field for orientations
$\unicode[STIX]{x1D714}_{g}=2\unicode[STIX]{x03C0}/T_{jeff}$
), this being due to the fore–aft symmetry of the spheroid, which leads to the same disturbance field for orientations
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $-\boldsymbol{p}$
. In (5.3), since one is only interested in the integration over a time period, only the terms corresponding to these three Fourier modes in the Fourier expansion of the inertial acceleration terms will lead to non-zero contributions. The expansions for the inertial terms involving
$-\boldsymbol{p}$
. In (5.3), since one is only interested in the integration over a time period, only the terms corresponding to these three Fourier modes in the Fourier expansion of the inertial acceleration terms will lead to non-zero contributions. The expansions for the inertial terms involving
![]() $\hat{\boldsymbol{u}}^{match}$
are made in § 5.2, and that for the inertial term proportional to
$\hat{\boldsymbol{u}}^{match}$
are made in § 5.2, and that for the inertial term proportional to
![]() $\hat{\boldsymbol{u}}^{f}$
is made in § 5.3. The details of the evaluation of the integral are presented in § 5.4.
$\hat{\boldsymbol{u}}^{f}$
is made in § 5.3. The details of the evaluation of the integral are presented in § 5.4.
5.1 The term proportional to the singularity in the test problem
In the tumbling orbit,
![]() $\boldsymbol{p}$
has the form
$\boldsymbol{p}$
has the form
![]() $\cos \unicode[STIX]{x1D719}_{j}\mathbf{1}_{1}+\sin \unicode[STIX]{x1D719}_{j}\mathbf{1}_{2}$
, with
$\cos \unicode[STIX]{x1D719}_{j}\mathbf{1}_{1}+\sin \unicode[STIX]{x1D719}_{j}\mathbf{1}_{2}$
, with
![]() $\tan \unicode[STIX]{x1D719}_{j}=1/(\unicode[STIX]{x1D705}\tan (\unicode[STIX]{x1D714}_{g}t))$
, which is the solution of the Jeffery equations (3.1)–(3.2). This relation is used for both the orientation in the test problem and that in the problem of interest. The term corresponding to the test velocity field in braces, in (5.3), simplifies to
$\tan \unicode[STIX]{x1D719}_{j}=1/(\unicode[STIX]{x1D705}\tan (\unicode[STIX]{x1D714}_{g}t))$
, which is the solution of the Jeffery equations (3.1)–(3.2). This relation is used for both the orientation in the test problem and that in the problem of interest. The term corresponding to the test velocity field in braces, in (5.3), simplifies to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}\dot{\unicode[STIX]{x1D719}}_{jeff}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)=\boldsymbol{T}_{1}^{tumb}+\boldsymbol{T}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{T}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\boldsymbol{T}_{1}\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}+\boldsymbol{T}_{2}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}+\left(\boldsymbol{T}_{1}\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}+\boldsymbol{T}_{2}\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\cos (2\unicode[STIX]{x1D714}_{g}t)-\boldsymbol{T}_{3}\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\sin (2\unicode[STIX]{x1D714}_{g}t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}\dot{\unicode[STIX]{x1D719}}_{jeff}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)=\boldsymbol{T}_{1}^{tumb}+\boldsymbol{T}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{T}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\boldsymbol{T}_{1}\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}+\boldsymbol{T}_{2}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}+\left(\boldsymbol{T}_{1}\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}+\boldsymbol{T}_{2}\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\cos (2\unicode[STIX]{x1D714}_{g}t)-\boldsymbol{T}_{3}\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\sin (2\unicode[STIX]{x1D714}_{g}t),\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D714}_{g}=2\unicode[STIX]{x03C0}/T_{jeff}$
. The vectors
$\unicode[STIX]{x1D714}_{g}=2\unicode[STIX]{x03C0}/T_{jeff}$
. The vectors
![]() $\boldsymbol{T}_{1}$
,
$\boldsymbol{T}_{1}$
,
![]() $\boldsymbol{T}_{2}$
and
$\boldsymbol{T}_{2}$
and
![]() $\boldsymbol{T}_{3}$
above are given by
$\boldsymbol{T}_{3}$
above are given by
The constants
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{3}$
above are defined in (2.9) and (2.11) for a prolate spheroid. In the tumbling mode, one need not consider the axial spin singularity corresponding to
$B_{3}$
above are defined in (2.9) and (2.11) for a prolate spheroid. In the tumbling mode, one need not consider the axial spin singularity corresponding to
![]() $B_{2}$
, since the orientation vector is perpendicular to the angular velocity and, thus, equation (5.4) is independent of
$B_{2}$
, since the orientation vector is perpendicular to the angular velocity and, thus, equation (5.4) is independent of
![]() $B_{2}$
. As is evident in (5.4), there are only three Fourier modes for an arbitrary-aspect-ratio spheroid. In the limiting case of a sphere (
$B_{2}$
. As is evident in (5.4), there are only three Fourier modes for an arbitrary-aspect-ratio spheroid. In the limiting case of a sphere (
![]() $\unicode[STIX]{x1D705}\rightarrow 1$
),
$\unicode[STIX]{x1D705}\rightarrow 1$
),
![]() $B_{1}\rightarrow 0$
, and therefore
$B_{1}\rightarrow 0$
, and therefore
![]() $\boldsymbol{T}_{2}^{tumb},\boldsymbol{T}_{3}^{tumb}\rightarrow 0$
, and only the time-independent mode survives. In the limit of a flat disk (
$\boldsymbol{T}_{2}^{tumb},\boldsymbol{T}_{3}^{tumb}\rightarrow 0$
, and only the time-independent mode survives. In the limit of a flat disk (
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
),
$\unicode[STIX]{x1D705}\rightarrow 0$
),
![]() $B_{1}=B_{3}=-16/3$
, and
$B_{1}=B_{3}=-16/3$
, and
![]() $\boldsymbol{T}_{3}^{tumb}$
is
$\boldsymbol{T}_{3}^{tumb}$
is
![]() $O(\unicode[STIX]{x1D705})$
smaller than both
$O(\unicode[STIX]{x1D705})$
smaller than both
![]() $\boldsymbol{T}_{1}^{tumb}$
and
$\boldsymbol{T}_{1}^{tumb}$
and
![]() $\boldsymbol{T}_{2}^{tumb}$
, and can therefore be neglected. Therefore, for a flat disk, (5.4) scales as
$\boldsymbol{T}_{2}^{tumb}$
, and can therefore be neglected. Therefore, for a flat disk, (5.4) scales as
![]() $O(1/\unicode[STIX]{x1D705}^{2})$
. In the limit of a slender fibre (
$O(1/\unicode[STIX]{x1D705}^{2})$
. In the limit of a slender fibre (
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
),
$\unicode[STIX]{x1D705}\rightarrow \infty$
),
![]() $B_{1}=-B_{3}=4\unicode[STIX]{x03C0}/(3\log \unicode[STIX]{x1D705})$
, consistent with viscous slender-body theory, and
$B_{1}=-B_{3}=4\unicode[STIX]{x03C0}/(3\log \unicode[STIX]{x1D705})$
, consistent with viscous slender-body theory, and
![]() $\boldsymbol{T}_{3}^{tumb}$
is
$\boldsymbol{T}_{3}^{tumb}$
is
![]() $O(1/\unicode[STIX]{x1D705})$
smaller than both
$O(1/\unicode[STIX]{x1D705})$
smaller than both
![]() $\boldsymbol{T}_{1}^{tumb}$
and
$\boldsymbol{T}_{1}^{tumb}$
and
![]() $\boldsymbol{T}_{2}^{tumb}$
, and can again be neglected. Therefore, for a slender fibre, (5.4) scales as
$\boldsymbol{T}_{2}^{tumb}$
, and can again be neglected. Therefore, for a slender fibre, (5.4) scales as
![]() $O(\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705})$
. The scalings for
$O(\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705})$
. The scalings for
![]() $\unicode[STIX]{x0394}T^{tumb}$
, for these extreme-aspect-ratio particles, are further analysed in § 5.5.
$\unicode[STIX]{x0394}T^{tumb}$
, for these extreme-aspect-ratio particles, are further analysed in § 5.5.
5.2 The inertial terms with
 $\hat{\boldsymbol{u}}^{match}$
$\hat{\boldsymbol{u}}^{match}$
In this section, we expand the three terms involving
![]() $\hat{\boldsymbol{u}}^{match}$
, in the integrand in (5.3), as a Fourier series. The general Fourier expansion has an infinite number of terms, but one only needs to retain terms corresponding to the three modes in (5.4). As for the test velocity field, the expression for
$\hat{\boldsymbol{u}}^{match}$
, in the integrand in (5.3), as a Fourier series. The general Fourier expansion has an infinite number of terms, but one only needs to retain terms corresponding to the three modes in (5.4). As for the test velocity field, the expression for
![]() $\hat{\boldsymbol{u}}^{match}$
given in (2.21) now depends on time through the stresslet singularity coefficient
$\hat{\boldsymbol{u}}^{match}$
given in (2.21) now depends on time through the stresslet singularity coefficient
![]() $\unicode[STIX]{x1D64E}$
. Hence, we expand
$\unicode[STIX]{x1D64E}$
. Hence, we expand
![]() $\unicode[STIX]{x1D64E}$
as a Fourier series in time and retain only the aforementioned terms. This truncated expansion takes the form
$\unicode[STIX]{x1D64E}$
as a Fourier series in time and retain only the aforementioned terms. This truncated expansion takes the form
where
where the
![]() $A_{i}$
terms are defined in (2.16)–(2.18). In deriving (5.8), we have again used the Jeffery solution for
$A_{i}$
terms are defined in (2.16)–(2.18). In deriving (5.8), we have again used the Jeffery solution for
![]() $\unicode[STIX]{x1D719}_{j}$
(see § 5.1). For a sphere,
$\unicode[STIX]{x1D719}_{j}$
(see § 5.1). For a sphere,
![]() $A_{1}=A_{2}=A_{3}=-20\unicode[STIX]{x03C0}/3$
, and therefore
$A_{1}=A_{2}=A_{3}=-20\unicode[STIX]{x03C0}/3$
, and therefore
![]() $\unicode[STIX]{x1D64E}$
in (5.8) reduces to
$\unicode[STIX]{x1D64E}$
in (5.8) reduces to
![]() $-10\unicode[STIX]{x03C0}/3(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})=-(20\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D640}$
. For a flat disk,
$-10\unicode[STIX]{x03C0}/3(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})=-(20\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D640}$
. For a flat disk,
![]() $2A_{1}=A_{3}=-64/9$
and
$2A_{1}=A_{3}=-64/9$
and
![]() $A_{2}$
is
$A_{2}$
is
![]() $-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}/3$
, therefore (5.8) is
$-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}/3$
, therefore (5.8) is
![]() $O(\unicode[STIX]{x1D705})$
. For a slender fibre,
$O(\unicode[STIX]{x1D705})$
. For a slender fibre,
![]() $A_{1}=-8\unicode[STIX]{x03C0}/(9\log \unicode[STIX]{x1D705})$
,
$A_{1}=-8\unicode[STIX]{x03C0}/(9\log \unicode[STIX]{x1D705})$
,
![]() $A_{2}$
and
$A_{2}$
and
![]() $A_{3}$
are
$A_{3}$
are
![]() $O(1/\unicode[STIX]{x1D705}^{2})$
, and (5.8) is therefore
$O(1/\unicode[STIX]{x1D705}^{2})$
, and (5.8) is therefore
![]() $O(1/(\unicode[STIX]{x1D705}\log \unicode[STIX]{x1D705}))$
.
$O(1/(\unicode[STIX]{x1D705}\log \unicode[STIX]{x1D705}))$
.
Using (2.21) and (5.8), the truncated Fourier expansion of the terms involving
![]() $\hat{\boldsymbol{u}}^{match}$
, to be used in (5.3), is obtained as
$\hat{\boldsymbol{u}}^{match}$
, to be used in (5.3), is obtained as
where
![]() $\boldsymbol{R}_{1}^{tumb}$
,
$\boldsymbol{R}_{1}^{tumb}$
,
![]() $\boldsymbol{R}_{2}^{tumb}$
and
$\boldsymbol{R}_{2}^{tumb}$
and
![]() $\boldsymbol{R}_{3}^{tumb}$
are functions of
$\boldsymbol{R}_{3}^{tumb}$
are functions of
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
,
$k_{2}$
,
![]() $k_{3}$
,
$k_{3}$
,
![]() $\unicode[STIX]{x1D714}_{g}$
and the
$\unicode[STIX]{x1D714}_{g}$
and the
![]() $A_{ijk}$
terms defined in (5.9)–(5.13), and are given by
$A_{ijk}$
terms defined in (5.9)–(5.13), and are given by
 $$\begin{eqnarray}\displaystyle \boldsymbol{R}_{2}^{tumb} & = & \displaystyle \frac{2\text{i}k_{1}\left(A_{122}k_{1}^{2}\left(k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}\left(-k^{2}+k_{1}^{2}\right)+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\text{i}k_{2}\left(A_{122}k_{1}^{2}\left(3k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}k_{1}^{2}+A_{222}\left(-k^{2}+k_{2}^{2}\right)+A_{332}k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\,\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\text{i}k_{3}\left(A_{122}k_{1}^{2}\left(k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\,\mathbf{1}_{3},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{R}_{2}^{tumb} & = & \displaystyle \frac{2\text{i}k_{1}\left(A_{122}k_{1}^{2}\left(k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}\left(-k^{2}+k_{1}^{2}\right)+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\text{i}k_{2}\left(A_{122}k_{1}^{2}\left(3k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}k_{1}^{2}+A_{222}\left(-k^{2}+k_{2}^{2}\right)+A_{332}k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\,\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\text{i}k_{3}\left(A_{122}k_{1}^{2}\left(k^{2}-4k_{2}^{2}\right)+\unicode[STIX]{x1D714}_{g}k^{2}\left(A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\,\mathbf{1}_{3},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{R}_{3}^{tumb} & = & \displaystyle \left(-\frac{2\text{i}\unicode[STIX]{x1D714}_{g}A_{122}\left(k^{2}-2k_{1}^{2}\right)k_{2}}{k^{4}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{112}k_{1}^{2}\left(-k^{2}+4k_{1}^{2}\right)k_{2}}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\text{i}A_{222}k_{2}\left(-k^{2}\left(k^{2}+2k_{1}^{2}\right)+\left(k^{2}+4k_{1}^{2}\right)k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{332}\left(k^{2}+4k_{1}^{2}\right)k_{2}k_{3}^{2}}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\left(-\frac{2\text{i}\unicode[STIX]{x1D714}_{g}A_{122}k_{1}\left(k^{2}-2k_{2}^{2}\right)}{k^{4}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{112}k_{1}^{3}\left(-k^{2}+4k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{\text{i}A_{222}k_{1}\left(k-k_{2}\right)\left(k+k_{2}\right)\left(-k^{2}+4k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}-\frac{\text{i}A_{332}k_{1}\left(k^{2}-4k_{2}^{2}\right)k_{3}^{2}}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\left(\frac{4\text{i}\unicode[STIX]{x1D714}_{g}A_{122}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}+\frac{4\text{i}A_{112}k_{1}^{3}k_{2}k_{3}}{k^{6}\unicode[STIX]{x03C0}}+\frac{2\text{i}A_{222}k_{1}k_{2}\left(-k^{2}+2k_{2}^{2}\right)k_{3}}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{2\text{i}A_{332}k_{1}k_{2}k_{3}\left(-k^{2}+2k_{3}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{R}_{3}^{tumb} & = & \displaystyle \left(-\frac{2\text{i}\unicode[STIX]{x1D714}_{g}A_{122}\left(k^{2}-2k_{1}^{2}\right)k_{2}}{k^{4}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{112}k_{1}^{2}\left(-k^{2}+4k_{1}^{2}\right)k_{2}}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\text{i}A_{222}k_{2}\left(-k^{2}\left(k^{2}+2k_{1}^{2}\right)+\left(k^{2}+4k_{1}^{2}\right)k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{332}\left(k^{2}+4k_{1}^{2}\right)k_{2}k_{3}^{2}}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\left(-\frac{2\text{i}\unicode[STIX]{x1D714}_{g}A_{122}k_{1}\left(k^{2}-2k_{2}^{2}\right)}{k^{4}\unicode[STIX]{x03C0}}+\frac{\text{i}A_{112}k_{1}^{3}\left(-k^{2}+4k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{\text{i}A_{222}k_{1}\left(k-k_{2}\right)\left(k+k_{2}\right)\left(-k^{2}+4k_{2}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}-\frac{\text{i}A_{332}k_{1}\left(k^{2}-4k_{2}^{2}\right)k_{3}^{2}}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\left(\frac{4\text{i}\unicode[STIX]{x1D714}_{g}A_{122}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}+\frac{4\text{i}A_{112}k_{1}^{3}k_{2}k_{3}}{k^{6}\unicode[STIX]{x03C0}}+\frac{2\text{i}A_{222}k_{1}k_{2}\left(-k^{2}+2k_{2}^{2}\right)k_{3}}{k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{2\text{i}A_{332}k_{1}k_{2}k_{3}\left(-k^{2}+2k_{3}^{2}\right)}{k^{6}\unicode[STIX]{x03C0}}\right)\,\mathbf{1}_{3}.\end{eqnarray}$$
Again, for a sphere, only the time-independent mode survives in (5.14). In the limit of extreme aspect ratios, that is, for a fibre or a flat disk, one needs to consider only the constant term and the one proportional to
![]() $\cos (2\unicode[STIX]{x1D714}_{g}t)$
in (5.14), since the test singularity has only those two modes, as seen later in § 5.5.
$\cos (2\unicode[STIX]{x1D714}_{g}t)$
in (5.14), since the test singularity has only those two modes, as seen later in § 5.5.
5.3 The inertial term proportional to
 $\hat{\boldsymbol{u}}^{f}$
$\hat{\boldsymbol{u}}^{f}$
In this section, we expand the lone term proportional to
![]() $\hat{\boldsymbol{u}}^{f}$
in the integrand in (5.3) as a Fourier series. As in the previous section, we only need to find the coefficients of the three modes present in (5.4). To begin with, (2.20) is contracted with
$\hat{\boldsymbol{u}}^{f}$
in the integrand in (5.3) as a Fourier series. As in the previous section, we only need to find the coefficients of the three modes present in (5.4). To begin with, (2.20) is contracted with
![]() $(\unicode[STIX]{x1D644}-\boldsymbol{k}\boldsymbol{k}/k^{2})$
to eliminate the pressure, leading to the following governing equation for
$(\unicode[STIX]{x1D644}-\boldsymbol{k}\boldsymbol{k}/k^{2})$
to eliminate the pressure, leading to the following governing equation for
![]() $\hat{\boldsymbol{u}}^{f}$
:
$\hat{\boldsymbol{u}}^{f}$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\left(\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right)\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\left(\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right)\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right).\end{eqnarray}$$
The expression on the right-hand side above is evaluated using (5.14) to give
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}\nonumber\\ \displaystyle & & \displaystyle \qquad =(\boldsymbol{R}_{1}^{tumb}+\boldsymbol{R}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{R}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t))\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \{0,2,-2\}}\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}\text{e}^{\text{i}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D714}_{g}t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{f}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{f}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{f}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-2\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)+4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}\nonumber\\ \displaystyle & & \displaystyle \qquad =(\boldsymbol{R}_{1}^{tumb}+\boldsymbol{R}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{R}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t))\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \{0,2,-2\}}\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}\text{e}^{\text{i}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D714}_{g}t},\end{eqnarray}$$
where
![]() $\boldsymbol{Q}^{0}=\boldsymbol{R}_{1}^{tumb}-(\boldsymbol{R}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{k}/k^{2}$
,
$\boldsymbol{Q}^{0}=\boldsymbol{R}_{1}^{tumb}-(\boldsymbol{R}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{k}/k^{2}$
,
![]() $\boldsymbol{Q}^{2}=((\boldsymbol{R}_{2}^{tumb}-\text{i}\boldsymbol{R}_{3}^{tumb})/2)\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-(\boldsymbol{k}\boldsymbol{k}/k^{2}))$
and
$\boldsymbol{Q}^{2}=((\boldsymbol{R}_{2}^{tumb}-\text{i}\boldsymbol{R}_{3}^{tumb})/2)\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-(\boldsymbol{k}\boldsymbol{k}/k^{2}))$
and
![]() $\boldsymbol{Q}^{-2}=((\boldsymbol{R}_{2}^{tumb}+\text{i}\boldsymbol{R}_{3}^{tumb})/2)\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-(\boldsymbol{k}\boldsymbol{k}/k^{2}))$
. The
$\boldsymbol{Q}^{-2}=((\boldsymbol{R}_{2}^{tumb}+\text{i}\boldsymbol{R}_{3}^{tumb})/2)\boldsymbol{\cdot }(\unicode[STIX]{x1D644}-(\boldsymbol{k}\boldsymbol{k}/k^{2}))$
. The
![]() $\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}$
terms for
$\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}$
terms for
![]() $\unicode[STIX]{x1D6FD}=0,2$
and
$\unicode[STIX]{x1D6FD}=0,2$
and
![]() $-2$
are given as follows:
$-2$
are given as follows:
 $$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{2Re} & = & \displaystyle \left(\frac{k_{2}\left(-k^{4}A_{222}-2\unicode[STIX]{x1D714}_{g}k^{2}A_{122}\left(k^{2}-2k_{1}^{2}\right)+A_{112}k_{1}^{2}\left(-k^{2}+2k_{1}^{2}\right)\right)}{2k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{k_{2}\left(A_{222}\left(k^{2}+2k_{1}^{2}\right)k_{2}^{2}+A_{332}\left(k^{2}+2k_{1}^{2}\right)k_{3}^{2}\right)}{2k^{6}\unicode[STIX]{x03C0}}\right)\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\left(-\frac{k_{1}\left(k^{2}-2k_{2}^{2}\right)A_{112}k_{1}^{2}}{2k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{k_{1}\left(k^{2}-2k_{2}^{2}\right)\left(+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}+k^{2}\left(-A_{222}+2A_{122}\unicode[STIX]{x1D714}_{g}\right)\right)}{2k^{6}\unicode[STIX]{x03C0}}\right)\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{1}k_{2}k_{3}\left(2\unicode[STIX]{x1D714}_{g}k^{2}A_{122}+A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{3},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{2Re} & = & \displaystyle \left(\frac{k_{2}\left(-k^{4}A_{222}-2\unicode[STIX]{x1D714}_{g}k^{2}A_{122}\left(k^{2}-2k_{1}^{2}\right)+A_{112}k_{1}^{2}\left(-k^{2}+2k_{1}^{2}\right)\right)}{2k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{k_{2}\left(A_{222}\left(k^{2}+2k_{1}^{2}\right)k_{2}^{2}+A_{332}\left(k^{2}+2k_{1}^{2}\right)k_{3}^{2}\right)}{2k^{6}\unicode[STIX]{x03C0}}\right)\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\left(-\frac{k_{1}\left(k^{2}-2k_{2}^{2}\right)A_{112}k_{1}^{2}}{2k^{6}\unicode[STIX]{x03C0}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{k_{1}\left(k^{2}-2k_{2}^{2}\right)\left(+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}+k^{2}\left(-A_{222}+2A_{122}\unicode[STIX]{x1D714}_{g}\right)\right)}{2k^{6}\unicode[STIX]{x03C0}}\right)\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{1}k_{2}k_{3}\left(2\unicode[STIX]{x1D714}_{g}k^{2}A_{122}+A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{3},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{2i} & = & \displaystyle \frac{k_{1}\left(-2A_{122}k_{1}^{2}k_{2}^{2}+k^{2}\left(A_{112}\left(-k^{2}+k_{1}^{2}\right)+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{2}\left(2A_{122}k_{1}^{2}\left(k^{2}-k_{2}^{2}\right)+k^{2}\left(A_{112}k_{1}^{2}+A_{222}\left(-k^{2}+k_{2}^{2}\right)+A_{332}k_{3}^{2}\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{3}\left(-2A_{122}k_{1}^{2}k_{2}^{2}+k^{2}\left(A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{2i} & = & \displaystyle \frac{k_{1}\left(-2A_{122}k_{1}^{2}k_{2}^{2}+k^{2}\left(A_{112}\left(-k^{2}+k_{1}^{2}\right)+A_{222}k_{2}^{2}+A_{332}k_{3}^{2}\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{2}\left(2A_{122}k_{1}^{2}\left(k^{2}-k_{2}^{2}\right)+k^{2}\left(A_{112}k_{1}^{2}+A_{222}\left(-k^{2}+k_{2}^{2}\right)+A_{332}k_{3}^{2}\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{k_{3}\left(-2A_{122}k_{1}^{2}k_{2}^{2}+k^{2}\left(A_{112}k_{1}^{2}+A_{222}k_{2}^{2}+A_{332}\left(-k^{2}+k_{3}^{2}\right)\right)\unicode[STIX]{x1D714}_{g}\right)}{k^{6}\unicode[STIX]{x03C0}}\mathbf{1}_{3}.\end{eqnarray}$$
We have written the Fourier modes in complex exponential form in (5.19) to simplify the analysis that follows. To reiterate, the general solution for
![]() $\hat{\boldsymbol{u}}^{f}$
would contain a forcing on the right-hand side of (5.19) that involves an infinite Fourier series. However, only the three terms corresponding to the values of
$\hat{\boldsymbol{u}}^{f}$
would contain a forcing on the right-hand side of (5.19) that involves an infinite Fourier series. However, only the three terms corresponding to the values of
![]() $\unicode[STIX]{x1D6FD}$
above (
$\unicode[STIX]{x1D6FD}$
above (
![]() $0,2,-2$
) contribute to the change in the time period of rotation.
$0,2,-2$
) contribute to the change in the time period of rotation.
To obtain the solution of (5.19),
![]() $\hat{\boldsymbol{u}}^{f}$
is expanded as a complex exponential Fourier series, given by
$\hat{\boldsymbol{u}}^{f}$
is expanded as a complex exponential Fourier series, given by
By substituting the expansion above into (5.19), the governing equations for each of the components of the Fourier transformed velocity field may be written as
The equations above are similar to the ones seen for the spinning case in (4.8)–(4.10) except for an additional frequency-dependent term (involving
![]() $\unicode[STIX]{x1D714}_{g}$
) on the left-hand side and a frequency-dependent forcing amplitude on the right-hand side. Obtainment of the solution to (5.26)–(5.28) therefore proceeds in a manner similar to that of the spinning case, and the gradient component, being independent of the others, is solved first. The solution of (5.26)–(5.28) arising from the substitution of (5.25) corresponds to the neglect of an exponentially decaying transient, which governs the relaxation from a general initial condition, and a restriction to the long-time dynamics corresponding to the frequencies present in the applied forcing. The steady linear flow ensures that there is a one-to-one correspondence between the Fourier amplitudes of the forcing and the velocity field, with inertia determining the frequency-dependent phase lag between the two via the terms proportional to
$\unicode[STIX]{x1D714}_{g}$
) on the left-hand side and a frequency-dependent forcing amplitude on the right-hand side. Obtainment of the solution to (5.26)–(5.28) therefore proceeds in a manner similar to that of the spinning case, and the gradient component, being independent of the others, is solved first. The solution of (5.26)–(5.28) arising from the substitution of (5.25) corresponds to the neglect of an exponentially decaying transient, which governs the relaxation from a general initial condition, and a restriction to the long-time dynamics corresponding to the frequencies present in the applied forcing. The steady linear flow ensures that there is a one-to-one correspondence between the Fourier amplitudes of the forcing and the velocity field, with inertia determining the frequency-dependent phase lag between the two via the terms proportional to
![]() $\text{i}\unicode[STIX]{x1D714}_{g}$
in (5.26)–(5.28). It should be noted again that
$\text{i}\unicode[STIX]{x1D714}_{g}$
in (5.26)–(5.28). It should be noted again that
![]() $\sum _{\unicode[STIX]{x1D6FD}\in \{0,2,-2\}}\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}\text{e}^{\text{i}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D714}_{g}t}$
does not determine the complete outer velocity field, but the part that is relevant for the determination of
$\sum _{\unicode[STIX]{x1D6FD}\in \{0,2,-2\}}\boldsymbol{Q}^{\unicode[STIX]{x1D6FD}}\text{e}^{\text{i}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D714}_{g}t}$
does not determine the complete outer velocity field, but the part that is relevant for the determination of
![]() $\unicode[STIX]{x0394}T^{tumb}$
.
$\unicode[STIX]{x0394}T^{tumb}$
.
Again, defining
![]() $k_{2}^{\prime }=k_{2}+k_{1}s$
, where
$k_{2}^{\prime }=k_{2}+k_{1}s$
, where
![]() $s$
is a time-like variable, the solutions for the individual components
$s$
is a time-like variable, the solutions for the individual components
![]() $\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
,
$\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
,
![]() $\hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}$
and
$\hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}$
and
![]() $\hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}$
are written in terms of
$\hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}$
are written in terms of
![]() $s$
as follows:
$s$
as follows:
 $$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{2}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{2}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{1}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,\int _{0}^{\infty }\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{2k_{1}^{2}}{\left(k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s\right)}\right)\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{1}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,\int _{0}^{\infty }\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{2k_{1}^{2}}{\left(k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s\right)}\right)\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{3}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{\infty }\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{2k_{1}k_{3}}{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}\right)\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}Q_{3}^{\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{\infty }\text{e}^{-\text{i}\unicode[STIX]{x1D714}_{g}\unicode[STIX]{x1D6FD}s}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{2k_{1}k_{3}}{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}\right)\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}(k_{1},k_{2}+k_{1}s,k_{3})\,\text{d}s.\end{eqnarray}$$
The solutions for
![]() $\hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}$
and
$\hat{u} _{1}^{f\unicode[STIX]{x1D6FD}}$
and
![]() $\hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}$
are coupled with
$\hat{u} _{3}^{f\unicode[STIX]{x1D6FD}}$
are coupled with
![]() $\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
, as expected, and are given as a sum of a one-dimensional and a two-dimensional integral, with the latter integral arising from the coupling with
$\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
, as expected, and are given as a sum of a one-dimensional and a two-dimensional integral, with the latter integral arising from the coupling with
![]() $\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
. The contributions in (5.29)–(5.31), for the different
$\hat{u} _{2}^{f\unicode[STIX]{x1D6FD}}$
. The contributions in (5.29)–(5.31), for the different
![]() $\unicode[STIX]{x1D6FD}$
terms, are substituted in (5.25) to obtain the components of
$\unicode[STIX]{x1D6FD}$
terms, are substituted in (5.25) to obtain the components of
![]() $\hat{\boldsymbol{u}}^{f}$
in the space-fixed coordinate system, and are given by
$\hat{\boldsymbol{u}}^{f}$
in the space-fixed coordinate system, and are given by
where we have written the components as a sum of a time-independent term (superscript ‘
![]() $f0$
’) and time-dependent term (superscript ‘
$f0$
’) and time-dependent term (superscript ‘
![]() $ft$
’). Denoting the convected wavevector,
$ft$
’). Denoting the convected wavevector,
![]() $k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}s)\mathbf{1}_{2}+k_{3}\mathbf{1}_{3}$
, as
$k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}s)\mathbf{1}_{2}+k_{3}\mathbf{1}_{3}$
, as
![]() $\boldsymbol{k}^{\prime }$
and
$\boldsymbol{k}^{\prime }$
and
![]() $k^{\prime }=|\boldsymbol{k}^{\prime }|$
, the time-dependent and time-independent contributions in (5.32)–(5.34) may be conveniently expressed in the form
$k^{\prime }=|\boldsymbol{k}^{\prime }|$
, the time-dependent and time-independent contributions in (5.32)–(5.34) may be conveniently expressed in the form
 $$\begin{eqnarray}\displaystyle \hat{u} _{2}^{ft}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{2}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{2}^{ft}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{2}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{u} _{1}^{ft}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{1}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{1}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{1}^{ft}(\boldsymbol{k}) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{1}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{1}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{u} _{3}^{ft}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{3}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{3}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{3}^{ft}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{3}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{3}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the terms
![]() $Q_{j}^{2Re}$
,
$Q_{j}^{2Re}$
,
![]() $Q_{j}^{2i}$
are given in (5.23)–(5.24), with ‘
$Q_{j}^{2i}$
are given in (5.23)–(5.24), with ‘
![]() $j$
’ denoting the component along the 1, 2 and 3 directions. The coefficients of
$j$
’ denoting the component along the 1, 2 and 3 directions. The coefficients of
![]() $\cos (2\unicode[STIX]{x1D714}_{g}t)$
and
$\cos (2\unicode[STIX]{x1D714}_{g}t)$
and
![]() $\sin (2\unicode[STIX]{x1D714}_{g}t)$
in (5.36) and (5.42) are denoted by
$\sin (2\unicode[STIX]{x1D714}_{g}t)$
in (5.36) and (5.42) are denoted by
![]() $\hat{u} ^{ftcos}$
and
$\hat{u} ^{ftcos}$
and
![]() $\hat{u} ^{ftsin}$
. The flow and vorticity components are coupled to the gradient component through
$\hat{u} ^{ftsin}$
. The flow and vorticity components are coupled to the gradient component through
![]() $\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)$
and
$\hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t)$
and
![]() $\hat{u} _{2}^{f0}(\boldsymbol{k}^{\prime })$
, which are given by
$\hat{u} _{2}^{f0}(\boldsymbol{k}^{\prime })$
, which are given by
 $$\begin{eqnarray}\displaystyle \hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s^{\prime }\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{u} _{2}^{ft}(\boldsymbol{k}^{\prime },t) & = & \displaystyle \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\cos (2\unicode[STIX]{x1D714}_{g}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}s^{\prime }\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and
respectively. As defined in § 4, the primed variables in (5.44) and (5.45) are given as
![]() $\boldsymbol{k}^{\prime \prime }=k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}(s+s^{\prime }))\mathbf{1}_{2}+k_{3}\mathbf{1}_{3}$
,
$\boldsymbol{k}^{\prime \prime }=k_{1}\mathbf{1}_{1}+(k_{2}+k_{1}(s+s^{\prime }))\mathbf{1}_{2}+k_{3}\mathbf{1}_{3}$
,
![]() $k_{2}^{\prime }=k_{2}+k_{1}s$
and
$k_{2}^{\prime }=k_{2}+k_{1}s$
and
![]() $k^{\prime \prime }=|\boldsymbol{k}^{\prime \prime }|$
. The coefficients of
$k^{\prime \prime }=|\boldsymbol{k}^{\prime \prime }|$
. The coefficients of
![]() $\cos (2\unicode[STIX]{x1D714}_{g}t)$
and
$\cos (2\unicode[STIX]{x1D714}_{g}t)$
and
![]() $\sin (2\unicode[STIX]{x1D714}_{g}t)$
in the time-dependent terms are defined as
$\sin (2\unicode[STIX]{x1D714}_{g}t)$
in the time-dependent terms are defined as
![]() $\hat{u} _{i}^{ftcos}(\boldsymbol{k},t)$
and
$\hat{u} _{i}^{ftcos}(\boldsymbol{k},t)$
and
![]() $\hat{u} _{i}^{ftsin}(\boldsymbol{k},t)$
respectively. The components along the flow and vorticity directions given in (5.38)–(5.43) are therefore sums of a one-dimensional integral and a two-dimensional integral. The two-dimensional integrals in (5.38)–(5.43) are coupled with the velocity in the gradient direction and are given by (5.44) and (5.45).
$\hat{u} _{i}^{ftsin}(\boldsymbol{k},t)$
respectively. The components along the flow and vorticity directions given in (5.38)–(5.43) are therefore sums of a one-dimensional integral and a two-dimensional integral. The two-dimensional integrals in (5.38)–(5.43) are coupled with the velocity in the gradient direction and are given by (5.44) and (5.45).
5.4 Evaluation of integrals
The integral for the tumbling time period given in (5.3) is evaluated in this section. The inertial terms given in (5.14) along with the term involving the singularity in the test problem in (5.4) are substituted in (5.3) to obtain the final form of the integral as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{c}}\nonumber\\ \displaystyle & & \displaystyle \times \int \int _{0}^{T_{jeff}}[-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{f}\mathbf{1}_{1}+\hat{u} _{2}^{f}\mathbf{1}_{2}+\hat{u} _{3}^{f}\mathbf{1}_{3})+\boldsymbol{R}_{1}+\boldsymbol{R}_{2}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{R}_{3}\sin (2\unicode[STIX]{x1D714}_{g}t)]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left(\boldsymbol{T}_{1}^{tumb}+\boldsymbol{T}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{T}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}t\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{c}}\nonumber\\ \displaystyle & & \displaystyle \times \int \int _{0}^{T_{jeff}}[-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{f}\mathbf{1}_{1}+\hat{u} _{2}^{f}\mathbf{1}_{2}+\hat{u} _{3}^{f}\mathbf{1}_{3})+\boldsymbol{R}_{1}+\boldsymbol{R}_{2}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{R}_{3}\sin (2\unicode[STIX]{x1D714}_{g}t)]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\,\left(\boldsymbol{T}_{1}^{tumb}+\boldsymbol{T}_{2}^{tumb}\cos (2\unicode[STIX]{x1D714}_{g}t)+\boldsymbol{T}_{3}^{tumb}\sin (2\unicode[STIX]{x1D714}_{g}t)\right)\,\text{d}t\,\text{d}\boldsymbol{k},\end{eqnarray}$$
where the components of
![]() $\hat{\boldsymbol{u}}^{f}$
are given in (5.32)–(5.34). The integration over time in (5.46) is straightforward, and leads to
$\hat{\boldsymbol{u}}^{f}$
are given in (5.32)–(5.34). The integration over time in (5.46) is straightforward, and leads to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{C}}\int \left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{1}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{f0}\mathbf{1}_{1}+\hat{u} _{2}^{f0}\mathbf{1}_{2}+\hat{u} _{3}^{f0}\mathbf{1}_{3}))\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{2}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{ftcos}\mathbf{1}_{1}+\hat{u} _{2}^{ftcos}\mathbf{1}_{2}+\hat{u} _{3}^{ftcos}\mathbf{1}_{3}))\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{3}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{ftsin}\mathbf{1}_{1}+\hat{u} _{2}^{ftsin}\mathbf{1}_{2}+\hat{u} _{3}^{ftsin}\mathbf{1}_{3}))\right]\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \frac{Re^{3/2}}{8\unicode[STIX]{x03C0}Y_{C}}\int \left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{1}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{f0}\mathbf{1}_{1}+\hat{u} _{2}^{f0}\mathbf{1}_{2}+\hat{u} _{3}^{f0}\mathbf{1}_{3}))\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{2}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{ftcos}\mathbf{1}_{1}+\hat{u} _{2}^{ftcos}\mathbf{1}_{2}+\hat{u} _{3}^{ftcos}\mathbf{1}_{3}))\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }(\boldsymbol{R}_{3}-4\unicode[STIX]{x03C0}^{2}k^{2}(\hat{u} _{1}^{ftsin}\mathbf{1}_{1}+\hat{u} _{2}^{ftsin}\mathbf{1}_{2}+\hat{u} _{3}^{ftsin}\mathbf{1}_{3}))\right]\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
The expressions for
![]() $\hat{u} ^{fi}$
(
$\hat{u} ^{fi}$
(
![]() $i$
$i$
![]() $=$
‘0’,‘cos’,‘sin’) are given in (5.35)–(5.43). Each of the terms proportional to
$=$
‘0’,‘cos’,‘sin’) are given in (5.35)–(5.43). Each of the terms proportional to
![]() $\hat{u} _{1}^{fi}$
and
$\hat{u} _{1}^{fi}$
and
![]() $\hat{u} _{3}^{fi}$
(
$\hat{u} _{3}^{fi}$
(
![]() $i$
$i$
![]() $=$
‘0’,‘cos’,‘sin’) in (5.47) is a sum of four-dimensional and five-dimensional integrals. The terms proportional to
$=$
‘0’,‘cos’,‘sin’) in (5.47) is a sum of four-dimensional and five-dimensional integrals. The terms proportional to
![]() $\hat{u} _{2}^{fi}$
are four-dimensional integrals and the terms proportional to
$\hat{u} _{2}^{fi}$
are four-dimensional integrals and the terms proportional to
![]() $\boldsymbol{R}_{1}$
,
$\boldsymbol{R}_{1}$
,
![]() $\boldsymbol{R}_{2}$
and
$\boldsymbol{R}_{2}$
and
![]() $\boldsymbol{R}_{3}$
involve three-dimensional integrals. The numerical evaluation of the integrals proceeds in a manner similar to that of the spinning case in § 4. In a spherical coordinate system, the three-dimensional and four-dimensional integrals involved in (5.47) are again seen to be divergent (after a
$\boldsymbol{R}_{3}$
involve three-dimensional integrals. The numerical evaluation of the integrals proceeds in a manner similar to that of the spinning case in § 4. In a spherical coordinate system, the three-dimensional and four-dimensional integrals involved in (5.47) are again seen to be divergent (after a
![]() $k$
integration), with the combination of the integrals nevertheless being convergent, as explained in § 4. These integrals are evaluated numerically to obtain the time period.
$k$
integration), with the combination of the integrals nevertheless being convergent, as explained in § 4. These integrals are evaluated numerically to obtain the time period.
To illustrate the aforementioned simplification of (5.47) to an equation involving convergent integrals alone, we focus on the evaluation of the integrals proportional to
![]() $\hat{u} _{1}^{f0}$
,
$\hat{u} _{1}^{f0}$
,
![]() $\boldsymbol{R}_{1}$
,
$\boldsymbol{R}_{1}$
,
![]() $\boldsymbol{R}_{2}$
and
$\boldsymbol{R}_{2}$
and
![]() $\boldsymbol{R}_{3}$
. The simplification of the other terms in the integral follows the same method as presented below. We present the final simplified form of the integrals for the other terms in appendix A. We write the four-dimensional and five-dimensional integrals for the term proportional to
$\boldsymbol{R}_{3}$
. The simplification of the other terms in the integral follows the same method as presented below. We present the final simplified form of the integrals for the other terms in appendix A. We write the four-dimensional and five-dimensional integrals for the term proportional to
![]() $\hat{u} _{1}^{f0}$
as follows:
$\hat{u} _{1}^{f0}$
as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f0}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int 4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)Q_{1}^{0}(\boldsymbol{k}^{\prime })\,\text{d}s\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int 4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\,\text{d}s^{\prime }\,\text{d}s\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f0}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int 4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)Q_{1}^{0}(\boldsymbol{k}^{\prime })\,\text{d}s\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int 4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\,\text{d}s^{\prime }\,\text{d}s\,\text{d}\boldsymbol{k}.\end{eqnarray}$$
The first and second integrals on the right-hand side are respectively four-dimensional and five-dimensional integrals. The five-dimensional integral arises due to the coupling with the velocity component in the gradient direction. When writing the five-dimensional integral, we have used the definition of
![]() $\hat{u} _{2}^{f0}$
in (5.45) and substituted in (5.38). The term in the square brackets in (5.47) corresponds to the
$\hat{u} _{2}^{f0}$
in (5.45) and substituted in (5.38). The term in the square brackets in (5.47) corresponds to the
![]() $\mathbf{1}_{1}$
component of
$\mathbf{1}_{1}$
component of
![]() $\boldsymbol{T}_{1}^{tumb}$
and is obtained from (5.4). The integrals in (5.47) can be expressed in a spherical coordinate system with
$\boldsymbol{T}_{1}^{tumb}$
and is obtained from (5.4). The integrals in (5.47) can be expressed in a spherical coordinate system with
![]() $k_{1}=k\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
,
$k_{1}=k\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
,
![]() $k_{2}=k\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}$
,
$k_{2}=k\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}$
,
![]() $k_{3}=k\cos \unicode[STIX]{x1D703}$
and
$k_{3}=k\cos \unicode[STIX]{x1D703}$
and
![]() $\text{d}\boldsymbol{k}=k^{2}\sin \unicode[STIX]{x1D703}\,\text{d}k\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}$
. Rewriting (5.48) to isolate the
$\text{d}\boldsymbol{k}=k^{2}\sin \unicode[STIX]{x1D703}\,\text{d}k\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}$
. Rewriting (5.48) to isolate the
![]() $k$
integral in the spherical coordinate system (again, for brevity, we have retained the notation
$k$
integral in the spherical coordinate system (again, for brevity, we have retained the notation
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
and
$k_{2}$
and
![]() $k_{3}$
), one obtains
$k_{3}$
), one obtains
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f0}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}Q_{1}^{0}(\boldsymbol{k}^{\prime })\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \quad \times \,\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{f0}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}Q_{1}^{0}(\boldsymbol{k}^{\prime })\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{(\unicode[STIX]{x1D705}^{2}+1)^{2}}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \quad \times \,\left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
where the term in the braces is independent of
![]() $k$
because
$k$
because
![]() $Q_{1}^{0}$
(the ‘1’ component of
$Q_{1}^{0}$
(the ‘1’ component of
![]() $\boldsymbol{Q}^{0}$
, see (5.20)) and the term in the square brackets above are proportional to
$\boldsymbol{Q}^{0}$
, see (5.20)) and the term in the square brackets above are proportional to
![]() $1/k$
. The
$1/k$
. The
![]() $k$
integrals above are evaluated for the four-dimensional case, given by
$k$
integrals above are evaluated for the four-dimensional case, given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}/3)^{3/2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}/3)^{3/2}},\end{eqnarray}$$
and the five-dimensional case, given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4k^{2}\unicode[STIX]{x03C0}^{2}\frac{sp}{3}\left(3(4+s^{2}-s^{2}\cos 2\unicode[STIX]{x1D703}+2s\sin ^{2}\unicode[STIX]{x1D703}(s\cos 2\unicode[STIX]{x1D719}+2\sin 2\unicode[STIX]{x1D719}))\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,4\cos \unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D703}s^{\prime }(3\sin \unicode[STIX]{x1D719}+\cos \unicode[STIX]{x1D719}(3s+s^{\prime }))\right)\!\!\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(f^{exp}(s,s^{\prime },\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}))^{3/2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\int k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}k^{2}\left(s+\sin ^{2}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\sin \unicode[STIX]{x1D719}s^{2}+\frac{\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\exp \left(-4k^{2}\unicode[STIX]{x03C0}^{2}\frac{sp}{3}\left(3(4+s^{2}-s^{2}\cos 2\unicode[STIX]{x1D703}+2s\sin ^{2}\unicode[STIX]{x1D703}(s\cos 2\unicode[STIX]{x1D719}+2\sin 2\unicode[STIX]{x1D719}))\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.+\,4\cos \unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D703}s^{\prime }(3\sin \unicode[STIX]{x1D719}+\cos \unicode[STIX]{x1D719}(3s+s^{\prime }))\right)\!\!\right)\,\text{d}k\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{32\unicode[STIX]{x03C0}^{5/2}(f^{exp}(s,s^{\prime },\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}))^{3/2}},\end{eqnarray}$$
where
![]() $f^{exp}$
is the function that multiplies
$f^{exp}$
is the function that multiplies
![]() $-4\unicode[STIX]{x03C0}^{2}k^{2}$
in the exponent of the integrand. The result of the
$-4\unicode[STIX]{x03C0}^{2}k^{2}$
in the exponent of the integrand. The result of the
![]() $k$
integration for the four-dimensional integral is proportional to
$k$
integration for the four-dimensional integral is proportional to
![]() $1/s^{3/2}$
and therefore diverges in the limit of
$1/s^{3/2}$
and therefore diverges in the limit of
![]() $s\rightarrow 0$
. The sum of all of the four-dimensional divergent integrals in the expressions of terms proportional to
$s\rightarrow 0$
. The sum of all of the four-dimensional divergent integrals in the expressions of terms proportional to
![]() $\hat{u} _{2}^{f0}$
,
$\hat{u} _{2}^{f0}$
,
![]() $\hat{u} _{2}^{f0}$
,
$\hat{u} _{2}^{f0}$
,
![]() $\hat{u} _{j}^{fi}$
(
$\hat{u} _{j}^{fi}$
(
![]() $j=1,2$
and 3 and
$j=1,2$
and 3 and
![]() $\text{i}$
$\text{i}$
![]() $=$
‘
$=$
‘
![]() $t\cos$
’,‘
$t\cos$
’,‘
![]() $t\sin$
’), given in appendix (A 1)–(A 9), as well as the one in (5.49) for
$t\sin$
’), given in appendix (A 1)–(A 9), as well as the one in (5.49) for
![]() $\hat{u} _{1}^{f0}$
, and the three-dimensional integral presented below in (5.52), is however convergent. The reason for the divergence has already been explained in § 4. It should be noted that the
$\hat{u} _{1}^{f0}$
, and the three-dimensional integral presented below in (5.52), is however convergent. The reason for the divergence has already been explained in § 4. It should be noted that the
![]() $k$
integrals in (A 1)–(A 9) are identical to that of (5.49).
$k$
integrals in (A 1)–(A 9) are identical to that of (5.49).
The three-dimensional integral proportional to
![]() $\boldsymbol{R}_{1}$
,
$\boldsymbol{R}_{1}$
,
![]() $\boldsymbol{R}_{2}$
and
$\boldsymbol{R}_{2}$
and
![]() $\boldsymbol{R}_{3}$
in (5.48) is
$\boldsymbol{R}_{3}$
in (5.48) is
The terms
![]() $\boldsymbol{R}_{1}$
,
$\boldsymbol{R}_{1}$
,
![]() $\boldsymbol{R}_{2}$
,
$\boldsymbol{R}_{2}$
,
![]() $\boldsymbol{R}_{3}$
,
$\boldsymbol{R}_{3}$
,
![]() $\boldsymbol{T}_{1}^{tumb}$
,
$\boldsymbol{T}_{1}^{tumb}$
,
![]() $\boldsymbol{T}_{2}^{tumb}$
and
$\boldsymbol{T}_{2}^{tumb}$
and
![]() $\boldsymbol{T}_{3}^{tumb}$
(see (5.15)–(5.17) and (5.4)–(5.7)) are proportional to
$\boldsymbol{T}_{3}^{tumb}$
(see (5.15)–(5.17) and (5.4)–(5.7)) are proportional to
![]() $(1/k)$
, and
$(1/k)$
, and
![]() $\text{d}\boldsymbol{k}$
is proportional to
$\text{d}\boldsymbol{k}$
is proportional to
![]() $k^{2}\,\text{d}k$
in (5.52), making the
$k^{2}\,\text{d}k$
in (5.52), making the
![]() $k$
integral divergent as
$k$
integral divergent as
![]() $k\rightarrow \infty$
. The divergence here can again be isolated by introducing an integral over a dummy variable
$k\rightarrow \infty$
. The divergence here can again be isolated by introducing an integral over a dummy variable
![]() $s$
. Noting that
$s$
. Noting that
![]() $\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\exp (-4\unicode[STIX]{x03C0}^{2}k^{2}s)=1$
, the integrals proportional to
$\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\exp (-4\unicode[STIX]{x03C0}^{2}k^{2}s)=1$
, the integrals proportional to
![]() $\boldsymbol{R}_{1}$
,
$\boldsymbol{R}_{1}$
,
![]() $\boldsymbol{R}_{2}$
and
$\boldsymbol{R}_{2}$
and
![]() $\boldsymbol{R}_{3}$
are written as
$\boldsymbol{R}_{3}$
are written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x03C0}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{1}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{2}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{3}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,k^{2}\text{e}^{-4\unicode[STIX]{x03C0}^{2}k^{2}s}\,\text{d}sk^{2}\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x03C0}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{1}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{2}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{3}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,k^{2}\text{e}^{-4\unicode[STIX]{x03C0}^{2}k^{2}s}\,\text{d}sk^{2}\,\text{d}k\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
where we have added an additional integral over
![]() $s$
. The
$s$
. The
![]() $k$
integral can be readily evaluated, and (5.53) becomes
$k$
integral can be readily evaluated, and (5.53) becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x03C0}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{1}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{2}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{3}\right]k^{2}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\frac{1}{32\unicode[STIX]{x03C0}^{5/2}s^{3/2}}\,\text{d}s\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x03C0}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\left\{\left[\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{1}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{1}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{2}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{2}+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D714}_{g}}\boldsymbol{T}_{3}^{tumb}\boldsymbol{\cdot }\boldsymbol{R}_{3}\right]k^{2}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\frac{1}{32\unicode[STIX]{x03C0}^{5/2}s^{3/2}}\,\text{d}s\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
where the term in the braces above is independent of
![]() $k$
.
$k$
.
In (5.49) and (A 1)–(A 9), the results of the
![]() $k$
integration from (5.50) and (5.51) are substituted, and they are combined with (5.54), to obtain the final integral for the time period. The final integral is evaluated numerically using Gaussian quadrature. The numerical integration has to be carried out for each of the aspect ratios. This is unlike the spinning case, where the aspect-ratio-dependent term factored out from the integral (see (4.24)). However, in the limit of extreme aspect ratios (
$k$
integration from (5.50) and (5.51) are substituted, and they are combined with (5.54), to obtain the final integral for the time period. The final integral is evaluated numerically using Gaussian quadrature. The numerical integration has to be carried out for each of the aspect ratios. This is unlike the spinning case, where the aspect-ratio-dependent term factored out from the integral (see (4.24)). However, in the limit of extreme aspect ratios (
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
for an oblate spheroid and
$\unicode[STIX]{x1D705}\rightarrow 0$
for an oblate spheroid and
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
for a prolate spheroid), one can again pull out the aspect-ratio dependence and obtain the appropriate limiting forms. This is discussed in § 5.5. The correction to the tumbling period obtained from the numerical integration is presented in § 6.
$\unicode[STIX]{x1D705}\rightarrow \infty$
for a prolate spheroid), one can again pull out the aspect-ratio dependence and obtain the appropriate limiting forms. This is discussed in § 5.5. The correction to the tumbling period obtained from the numerical integration is presented in § 6.
5.5 Extreme-aspect-ratio analysis
In this section, we evaluate the scaling of the
![]() $O(Re^{3/2})$
inertial correction to the time period for spheroids with extreme aspect ratios (
$O(Re^{3/2})$
inertial correction to the time period for spheroids with extreme aspect ratios (
![]() $\unicode[STIX]{x1D705}\ll 1$
or
$\unicode[STIX]{x1D705}\ll 1$
or
![]() $\unicode[STIX]{x1D705}\gg 1$
) rotating in the tumbling orbit. At
$\unicode[STIX]{x1D705}\gg 1$
) rotating in the tumbling orbit. At
![]() $Re=0$
, an oblate (prolate) spends a time of
$Re=0$
, an oblate (prolate) spends a time of
![]() $O(1/\unicode[STIX]{x1D705})$
(
$O(1/\unicode[STIX]{x1D705})$
(
![]() $O(\unicode[STIX]{x1D705})$
) in the nearly aligned phase, and a time of
$O(\unicode[STIX]{x1D705})$
) in the nearly aligned phase, and a time of
![]() $O(1)$
in the non-aligned phase (flipping between nearly aligned orientations). The nearly aligned phase for a thin prolate spheroid (slender fibre) corresponds to
$O(1)$
in the non-aligned phase (flipping between nearly aligned orientations). The nearly aligned phase for a thin prolate spheroid (slender fibre) corresponds to
![]() $\boldsymbol{p}$
being close to the flow axis (
$\boldsymbol{p}$
being close to the flow axis (
![]() $\unicode[STIX]{x1D719}_{j}\sim O(1/\unicode[STIX]{x1D705})$
,
$\unicode[STIX]{x1D719}_{j}\sim O(1/\unicode[STIX]{x1D705})$
,
![]() $\unicode[STIX]{x03C0}+O(1/\unicode[STIX]{x1D705})$
), while that for a thin oblate spheroid (flat disk) corresponds to
$\unicode[STIX]{x03C0}+O(1/\unicode[STIX]{x1D705})$
), while that for a thin oblate spheroid (flat disk) corresponds to
![]() $\boldsymbol{p}$
being close to the gradient axis (
$\boldsymbol{p}$
being close to the gradient axis (
![]() $\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x1D719}_{j}+\unicode[STIX]{x03C0}/2\sim O(\unicode[STIX]{x1D705})$
). In both cases, the Jeffery angular velocity is asymptotically small, of
$\unicode[STIX]{x1D719}_{j}+\unicode[STIX]{x03C0}/2\sim O(\unicode[STIX]{x1D705})$
). In both cases, the Jeffery angular velocity is asymptotically small, of
![]() $O(\unicode[STIX]{x1D705}^{2})$
(
$O(\unicode[STIX]{x1D705}^{2})$
(
![]() $O(1/\unicode[STIX]{x1D705}^{2})$
) for the oblate (prolate) case. Thus, one would expect inertia to primarily alter the time period during the nearly aligned phase. As mentioned in the introduction, for extreme aspect ratios, the
$O(1/\unicode[STIX]{x1D705}^{2})$
) for the oblate (prolate) case. Thus, one would expect inertia to primarily alter the time period during the nearly aligned phase. As mentioned in the introduction, for extreme aspect ratios, the
![]() $O(Re)$
correction can balance the slow Stokesian rotation in the aligned phase, leading to a threshold
$O(Re)$
correction can balance the slow Stokesian rotation in the aligned phase, leading to a threshold
![]() $Re$
beyond which the spheroid is stationary. For a fixed
$Re$
beyond which the spheroid is stationary. For a fixed
![]() $Re$
, this places a natural restriction on the
$Re$
, this places a natural restriction on the
![]() $O(Re^{3/2})$
analysis for extreme aspect ratios. The relevant aspect-ratio bounds arising from the scalings obtained here are given in § 8.
$O(Re^{3/2})$
analysis for extreme aspect ratios. The relevant aspect-ratio bounds arising from the scalings obtained here are given in § 8.
The integral in (5.3), when expressed in terms of
![]() $\unicode[STIX]{x1D719}_{j}$
, takes the form
$\unicode[STIX]{x1D719}_{j}$
, takes the form
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle -Re^{3/2}\int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\dot{\unicode[STIX]{x1D719}}_{c2}}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{1}{8\unicode[STIX]{x03C0}Y_{c}}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\frac{1}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D719}_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle -Re^{3/2}\int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{\dot{\unicode[STIX]{x1D719}}_{c2}}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x03C0}}^{-\unicode[STIX]{x03C0}}\frac{1}{8\unicode[STIX]{x03C0}Y_{c}}\int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\frac{1}{\dot{\unicode[STIX]{x1D719}}_{jeff}^{2}}\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D719}_{j}.\end{eqnarray}$$
The dominant contribution arising from the aligned phase may be seen by considering a flat disk with
![]() $\unicode[STIX]{x1D705}=0$
(a slender fibre with
$\unicode[STIX]{x1D705}=0$
(a slender fibre with
![]() $\unicode[STIX]{x1D705}=\infty$
); it is sufficient to focus on one of the aligned phases, since the contribution of the other phase is identical from symmetry considerations. The angular velocity of a nearly aligned disk (slender fibre) is
$\unicode[STIX]{x1D705}=\infty$
); it is sufficient to focus on one of the aligned phases, since the contribution of the other phase is identical from symmetry considerations. The angular velocity of a nearly aligned disk (slender fibre) is
![]() $O((\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D719}_{j})^{2})$
(
$O((\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D719}_{j})^{2})$
(
![]() $O(\unicode[STIX]{x1D719}_{j}^{2})$
). The term in braces in (5.55) is proportional to
$O(\unicode[STIX]{x1D719}_{j}^{2})$
). The term in braces in (5.55) is proportional to
![]() $\boldsymbol{T}_{1}+\boldsymbol{T}_{2}\cos (2\unicode[STIX]{x1D719}_{j})+\boldsymbol{T}_{3}\sin (2\unicode[STIX]{x1D719}_{j})$
, with the
$\boldsymbol{T}_{1}+\boldsymbol{T}_{2}\cos (2\unicode[STIX]{x1D719}_{j})+\boldsymbol{T}_{3}\sin (2\unicode[STIX]{x1D719}_{j})$
, with the
![]() $\boldsymbol{T}_{i}$
terms given in (5.5)–(5.7), and therefore reduces to
$\boldsymbol{T}_{i}$
terms given in (5.5)–(5.7), and therefore reduces to
![]() $\boldsymbol{T}_{1}+\boldsymbol{T}_{2}$
and
$\boldsymbol{T}_{1}+\boldsymbol{T}_{2}$
and
![]() $\boldsymbol{T}_{1}-\boldsymbol{T}_{2}$
respectively, for a slender fibre and a flat disk. In the slender-fibre limit,
$\boldsymbol{T}_{1}-\boldsymbol{T}_{2}$
respectively, for a slender fibre and a flat disk. In the slender-fibre limit,
![]() $\boldsymbol{T}_{1}$
and
$\boldsymbol{T}_{1}$
and
![]() $\boldsymbol{T}_{2}$
scale as
$\boldsymbol{T}_{2}$
scale as
![]() $1/\text{log}\,\unicode[STIX]{x1D705}$
, and in the flat-disk limit, they are constants of order unity. Noting that the velocity field
$1/\text{log}\,\unicode[STIX]{x1D705}$
, and in the flat-disk limit, they are constants of order unity. Noting that the velocity field
![]() $\hat{\boldsymbol{u}}^{f}$
is driven by
$\hat{\boldsymbol{u}}^{f}$
is driven by
![]() $\hat{\boldsymbol{u}}^{match}$
, it can be seen that the term in square brackets in (5.55) is proportional to
$\hat{\boldsymbol{u}}^{match}$
, it can be seen that the term in square brackets in (5.55) is proportional to
![]() $\hat{\boldsymbol{u}}^{match}$
, which in the flat-disk limit is proportional to
$\hat{\boldsymbol{u}}^{match}$
, which in the flat-disk limit is proportional to
![]() $A_{2}/2(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})+(A_{1}+A_{3})(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)/2\,\mathbf{1}_{1}\mathbf{1}_{1}-A_{1}(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)\mathbf{1}_{2}\mathbf{1}_{2}+(A_{1}-A_{3})(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)/2\,\mathbf{1}_{3}\mathbf{1}_{3}$
. In the slender-fibre limit, the term is proportional to
$A_{2}/2(\mathbf{1}_{1}\mathbf{1}_{2}+\mathbf{1}_{2}\mathbf{1}_{1})+(A_{1}+A_{3})(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)/2\,\mathbf{1}_{1}\mathbf{1}_{1}-A_{1}(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)\mathbf{1}_{2}\mathbf{1}_{2}+(A_{1}-A_{3})(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)/2\,\mathbf{1}_{3}\mathbf{1}_{3}$
. In the slender-fibre limit, the term is proportional to
![]() $A_{1}\unicode[STIX]{x1D719}_{j}\,\mathbf{1}_{1}\mathbf{1}_{1}-A_{1}\unicode[STIX]{x1D719}_{j}/(2)\,(\mathbf{1}_{2}\mathbf{1}_{2}+\mathbf{1}_{3}\mathbf{1}_{3})$
; see (2.16)–(2.18) for the definition of the constants
$A_{1}\unicode[STIX]{x1D719}_{j}\,\mathbf{1}_{1}\mathbf{1}_{1}-A_{1}\unicode[STIX]{x1D719}_{j}/(2)\,(\mathbf{1}_{2}\mathbf{1}_{2}+\mathbf{1}_{3}\mathbf{1}_{3})$
; see (2.16)–(2.18) for the definition of the constants
![]() $A_{i}$
. It should be recalled that for a slender fibre,
$A_{i}$
. It should be recalled that for a slender fibre,
![]() $A_{1}$
scales as
$A_{1}$
scales as
![]() $1/\text{log}\,\unicode[STIX]{x1D705}$
, and both
$1/\text{log}\,\unicode[STIX]{x1D705}$
, and both
![]() $A_{2}$
and
$A_{2}$
and
![]() $A_{3}$
scale as
$A_{3}$
scale as
![]() $1/\unicode[STIX]{x1D705}^{2}$
. For a flat disk,
$1/\unicode[STIX]{x1D705}^{2}$
. For a flat disk,
![]() $A_{2}$
scales as
$A_{2}$
scales as
![]() $\unicode[STIX]{x1D705}$
, whereas
$\unicode[STIX]{x1D705}$
, whereas
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{3}$
are constants. The integral in (5.55) therefore diverges as
$A_{3}$
are constants. The integral in (5.55) therefore diverges as
![]() $O(\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)^{3})$
for a flat disk and as
$O(\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D719}_{j}-\unicode[STIX]{x03C0}/2)^{3})$
for a flat disk and as
![]() $O(1/(\unicode[STIX]{x1D719}_{j}^{2}\log \unicode[STIX]{x1D705}))$
for a slender fibre. This clearly implies that the contribution comes from the nearly aligned phases in the two cases. The divergence is cut off for
$O(1/(\unicode[STIX]{x1D719}_{j}^{2}\log \unicode[STIX]{x1D705}))$
for a slender fibre. This clearly implies that the contribution comes from the nearly aligned phases in the two cases. The divergence is cut off for
![]() $\unicode[STIX]{x1D719}_{j}$
of
$\unicode[STIX]{x1D719}_{j}$
of
![]() $O(\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D705})$
for a flat disk and
$O(\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D705})$
for a flat disk and
![]() $\unicode[STIX]{x1D719}_{j}$
of
$\unicode[STIX]{x1D719}_{j}$
of
![]() $O(1/\unicode[STIX]{x1D705})$
for a slender fibre, leading to inertial time period estimates of
$O(1/\unicode[STIX]{x1D705})$
for a slender fibre, leading to inertial time period estimates of
![]() $O(1/\unicode[STIX]{x1D705}^{2})$
and
$O(1/\unicode[STIX]{x1D705}^{2})$
and
![]() $O(\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705})$
in the two cases.
$O(\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705})$
in the two cases.
Having estimated the scalings of the time period, we proceed to calculate the numerical prefactor, which requires evaluation of the integral using a rescaled angular coordinate that remains
![]() $O(1)$
in the nearly aligned phase. For the flat disk, this boundary layer variable is given by
$O(1)$
in the nearly aligned phase. For the flat disk, this boundary layer variable is given by
![]() $\hat{\unicode[STIX]{x1D719}}=(-\unicode[STIX]{x03C0}/2+\unicode[STIX]{x1D719}_{j})/\unicode[STIX]{x1D705}$
. In terms of
$\hat{\unicode[STIX]{x1D719}}=(-\unicode[STIX]{x03C0}/2+\unicode[STIX]{x1D719}_{j})/\unicode[STIX]{x1D705}$
. In terms of
![]() $\hat{\unicode[STIX]{x1D719}}$
, one may rewrite (5.55) in the boundary layer variable as
$\hat{\unicode[STIX]{x1D719}}$
, one may rewrite (5.55) in the boundary layer variable as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \int _{\infty }^{-\infty }\frac{1}{8\unicode[STIX]{x03C0}Y_{c}}\displaystyle \int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\frac{1}{\unicode[STIX]{x1D705}^{3}(\hat{\unicode[STIX]{x1D719}}^{2}+1)^{2}}\,\text{d}\boldsymbol{k}\,\text{d}\hat{\unicode[STIX]{x1D719}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T^{tumb} & = & \displaystyle \int _{\infty }^{-\infty }\frac{1}{8\unicode[STIX]{x03C0}Y_{c}}\displaystyle \int \left[4\unicode[STIX]{x03C0}^{2}k^{2}\hat{\boldsymbol{u}}^{f}+\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{match}}{\unicode[STIX]{x2202}t}-(\unicode[STIX]{x1D71E}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}^{match}+\unicode[STIX]{x1D71E}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{match}\right]\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{\cdot }\left\{\frac{\text{i}(\unicode[STIX]{x1D64E}^{(2t)}\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\mathbf{1}_{3}}{2\unicode[STIX]{x03C0}k^{2}}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{k}\boldsymbol{k}}{k^{2}}\right)\right\}\,\frac{1}{\unicode[STIX]{x1D705}^{3}(\hat{\unicode[STIX]{x1D719}}^{2}+1)^{2}}\,\text{d}\boldsymbol{k}\,\text{d}\hat{\unicode[STIX]{x1D719}}.\end{eqnarray}$$
At the leading order in
![]() $\unicode[STIX]{x1D705}$
, the term within braces in (5.56) becomes
$\unicode[STIX]{x1D705}$
, the term within braces in (5.56) becomes
where
![]() $\boldsymbol{T}_{1}$
and
$\boldsymbol{T}_{1}$
and
![]() $\boldsymbol{T}_{2}$
are defined in (5.5)–(5.6), with
$\boldsymbol{T}_{2}$
are defined in (5.5)–(5.6), with
![]() $B_{1}=B_{3}=-16/3$
in the flat-disk limit. The term proportional to the singularity in the test problem is therefore independent of
$B_{1}=B_{3}=-16/3$
in the flat-disk limit. The term proportional to the singularity in the test problem is therefore independent of
![]() $\unicode[STIX]{x1D705}$
. The leading-order term in
$\unicode[STIX]{x1D705}$
. The leading-order term in
![]() $\hat{\boldsymbol{u}}^{match}$
takes the form
$\hat{\boldsymbol{u}}^{match}$
takes the form
It should be recalled that
![]() $A_{2}$
is the coefficient of the longitudinal extension and is equal to
$A_{2}$
is the coefficient of the longitudinal extension and is equal to
![]() $-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}/3$
in the flat-disk limit (see below (5.13)). The inertial term in the square brackets in (5.56) is therefore proportional to
$-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}/3$
in the flat-disk limit (see below (5.13)). The inertial term in the square brackets in (5.56) is therefore proportional to
![]() $\unicode[STIX]{x1D705}$
. Although the contribution from the inertial terms involving the singularities in the axisymmetric extension and transverse extensions, proportional to
$\unicode[STIX]{x1D705}$
. Although the contribution from the inertial terms involving the singularities in the axisymmetric extension and transverse extensions, proportional to
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{3}$
, comes at
$A_{3}$
, comes at
![]() $O(\unicode[STIX]{x1D705})$
, this contribution is also proportional to the boundary layer variable
$O(\unicode[STIX]{x1D705})$
, this contribution is also proportional to the boundary layer variable
![]() $\hat{\unicode[STIX]{x1D719}}$
, and the integration over
$\hat{\unicode[STIX]{x1D719}}$
, and the integration over
![]() $\hat{\unicode[STIX]{x1D719}}$
in (5.56) is zero for this contribution. The evaluation of the integral in (5.56) leads to
$\hat{\unicode[STIX]{x1D719}}$
in (5.56) is zero for this contribution. The evaluation of the integral in (5.56) leads to
for a flat disk.
The estimation of the correction for the slender-fibre case is slightly non-trivial. If one proceeds in a manner similar to that for the flat disk given above, one can see that the scaling of the leading-order term in (5.55), when expressed in the boundary layer variable (
![]() $\hat{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D719}/\unicode[STIX]{x1D705}$
), is
$\hat{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D719}/\unicode[STIX]{x1D705}$
), is
![]() $\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705}$
. It should be noted that the scaling of
$\unicode[STIX]{x1D705}^{2}/\text{log}\,\unicode[STIX]{x1D705}$
. It should be noted that the scaling of
![]() $1/\text{log}\,\unicode[STIX]{x1D705}$
arises because the axisymmetric extensional flow with
$1/\text{log}\,\unicode[STIX]{x1D705}$
arises because the axisymmetric extensional flow with
![]() $A_{1}\propto 1/\text{log}\,\unicode[STIX]{x1D705}$
is dominant in the slender-fibre limit (Subramanian & Koch Reference Subramanian and Koch2005). It turns out, however, that the leading-order term is an odd function of the boundary layer variable (
$A_{1}\propto 1/\text{log}\,\unicode[STIX]{x1D705}$
is dominant in the slender-fibre limit (Subramanian & Koch Reference Subramanian and Koch2005). It turns out, however, that the leading-order term is an odd function of the boundary layer variable (
![]() $\hat{\unicode[STIX]{x1D719}}$
), and therefore the integral over
$\hat{\unicode[STIX]{x1D719}}$
), and therefore the integral over
![]() $\hat{\unicode[STIX]{x1D719}}$
is zero. The correction should therefore come in at a smaller order (
$\hat{\unicode[STIX]{x1D719}}$
is zero. The correction should therefore come in at a smaller order (
![]() $\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705}$
).
$\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705}$
).
6 Results:
 $O(Re^{3/2})$
correction for spheroids
$O(Re^{3/2})$
correction for spheroids
In this section, we summarize the numerical results obtained using the analytical expressions derived in the previous two sections. The scaled correction to the tumbling time period is plotted against the eccentricity (
![]() $e$
) for a prolate spheroid in figure 3(a). For a sphere (
$e$
) for a prolate spheroid in figure 3(a). For a sphere (
![]() $e=0$
), the correction is
$e=0$
), the correction is
![]() $1.355$
, and it first decreases with increasing eccentricity (increasing aspect ratio) until an
$1.355$
, and it first decreases with increasing eccentricity (increasing aspect ratio) until an
![]() $e$
of approximately
$e$
of approximately
![]() $0.75$
, as shown in the inset plot, before eventually diverging in the slender-fibre limit. The correction normalized with the Jeffery period, which diverges as
$0.75$
, as shown in the inset plot, before eventually diverging in the slender-fibre limit. The correction normalized with the Jeffery period, which diverges as
![]() $O(\unicode[STIX]{x1D705})$
as
$O(\unicode[STIX]{x1D705})$
as
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
, is plotted against the eccentricity in figure 3(b). As is clear from the dip in the plot for large
$\unicode[STIX]{x1D705}\rightarrow \infty$
, is plotted against the eccentricity in figure 3(b). As is clear from the dip in the plot for large
![]() $\unicode[STIX]{x1D705}$
, the divergence of the inertial correction is slower than
$\unicode[STIX]{x1D705}$
, the divergence of the inertial correction is slower than
![]() $O(\unicode[STIX]{x1D705})$
for
$O(\unicode[STIX]{x1D705})$
for
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
. To obtain the scaling for this divergence, we have plotted
$\unicode[STIX]{x1D705}\rightarrow \infty$
. To obtain the scaling for this divergence, we have plotted
![]() $\unicode[STIX]{x0394}T^{tumb}\log \unicode[STIX]{x1D705}$
on a log–log scale in figure 3(c) together with a line of slope 1 (red) for purposes of comparison. The plot suggests a scaling of
$\unicode[STIX]{x0394}T^{tumb}\log \unicode[STIX]{x1D705}$
on a log–log scale in figure 3(c) together with a line of slope 1 (red) for purposes of comparison. The plot suggests a scaling of
![]() $O(\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705})$
, consistent with the arguments at the end of § 5.5.
$O(\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705})$
, consistent with the arguments at the end of § 5.5.

Figure 3. (a) The
![]() $O(Re^{3/2})$
inertial correction plotted against the eccentricity (
$O(Re^{3/2})$
inertial correction plotted against the eccentricity (
![]() $e$
) for a prolate spheroid in the tumbling orbit. The inset plot shows a zoomed view of
$e$
) for a prolate spheroid in the tumbling orbit. The inset plot shows a zoomed view of
![]() $e<0.8$
. (b) The
$e<0.8$
. (b) The
![]() $O(Re^{3/2})$
inertial correction scaled with the Jeffery period plotted as a function of the prolate spheroid eccentricity. (c) The inertial correction times
$O(Re^{3/2})$
inertial correction scaled with the Jeffery period plotted as a function of the prolate spheroid eccentricity. (c) The inertial correction times
![]() $\log \unicode[STIX]{x1D705}$
is plotted on a log–log scale for large aspect ratios; the red line shown in the plot has a slope of unity.
$\log \unicode[STIX]{x1D705}$
is plotted on a log–log scale for large aspect ratios; the red line shown in the plot has a slope of unity.
The correction to the time period is plotted against the eccentricity, for an oblate spheroid in the tumbling orbit, in figure 4(a). The correction starts again from that for the sphere (
![]() $e=0$
) and, to begin with, decreases slightly with increasing eccentricity (decreasing aspect ratio), as shown in the inset plot, before eventually diverging in the limit of a flat disk. The blue circles in figure 4(a) correspond to the aspect ratios for which the tumbling orbit is always unstable. The correction scaled with the Jeffery period (which diverges as
$e=0$
) and, to begin with, decreases slightly with increasing eccentricity (decreasing aspect ratio), as shown in the inset plot, before eventually diverging in the limit of a flat disk. The blue circles in figure 4(a) correspond to the aspect ratios for which the tumbling orbit is always unstable. The correction scaled with the Jeffery period (which diverges as
![]() $1/\unicode[STIX]{x1D705}$
as
$1/\unicode[STIX]{x1D705}$
as
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
) is plotted in figure 4(b), and, in contrast to the prolate case, continues to diverge in the limit
$\unicode[STIX]{x1D705}\rightarrow 0$
) is plotted in figure 4(b), and, in contrast to the prolate case, continues to diverge in the limit
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
. We have plotted the flat-disk asymptote (red) given by (5.59) as well as the numerical results on a log–log scale in figure 4(c); the asymptote compares well with the numerical results, and validates the predicted
$\unicode[STIX]{x1D705}\rightarrow 0$
. We have plotted the flat-disk asymptote (red) given by (5.59) as well as the numerical results on a log–log scale in figure 4(c); the asymptote compares well with the numerical results, and validates the predicted
![]() $O(\unicode[STIX]{x1D705}^{-2})$
divergence. In figure 5, we have plotted the correction against the eccentricity for an oblate spheroid in its spinning orbit. Starting from the sphere value of 1.355, the scaled correction decreases with increasing eccentricity, approaching a finite value of 0.47 for the flat disk. This is unlike the case of a prolate spheroid in spinning mode, in which case the correction increases with increasing aspect ratio, eventually leading to a change in the scaling from
$O(\unicode[STIX]{x1D705}^{-2})$
divergence. In figure 5, we have plotted the correction against the eccentricity for an oblate spheroid in its spinning orbit. Starting from the sphere value of 1.355, the scaled correction decreases with increasing eccentricity, approaching a finite value of 0.47 for the flat disk. This is unlike the case of a prolate spheroid in spinning mode, in which case the correction increases with increasing aspect ratio, eventually leading to a change in the scaling from
![]() $O(Re^{3/2})$
to
$O(Re^{3/2})$
to
![]() $O(\tilde{Re})$
, as is appropriate for a cylinder, where
$O(\tilde{Re})$
, as is appropriate for a cylinder, where
![]() $\tilde{Re}$
is the Reynolds number based on the smallest axis of the spheroid (see § 4).
$\tilde{Re}$
is the Reynolds number based on the smallest axis of the spheroid (see § 4).

Figure 4. (a) The
![]() $O(Re^{3/2})$
inertial correction plotted against the eccentricity for an oblate spheroid in the tumbling orbit. The blue points indicate the aspect ratios for which the tumbling orbit is unstable; the black points correspond to conditional stability (initial-orientation-dependent). The inset plot shows the zoomed view for
$O(Re^{3/2})$
inertial correction plotted against the eccentricity for an oblate spheroid in the tumbling orbit. The blue points indicate the aspect ratios for which the tumbling orbit is unstable; the black points correspond to conditional stability (initial-orientation-dependent). The inset plot shows the zoomed view for
![]() $e<0.8$
. (b) The
$e<0.8$
. (b) The
![]() $O(Re^{3/2})$
inertial correction scaled with the Jeffery period plotted as a function of the oblate spheroid eccentricity. (c) The inertial correction is plotted on a log–log scale for small aspect ratios. The red line is the asymptote given in (5.59).
$O(Re^{3/2})$
inertial correction scaled with the Jeffery period plotted as a function of the oblate spheroid eccentricity. (c) The inertial correction is plotted on a log–log scale for small aspect ratios. The red line is the asymptote given in (5.59).
The
![]() $O(Re^{3/2})$
time period corrections for both the prolate and oblate spheroids have been found to be positive, implying an increase in the time period of rotation due to inertia in all relevant cases.
$O(Re^{3/2})$
time period corrections for both the prolate and oblate spheroids have been found to be positive, implying an increase in the time period of rotation due to inertia in all relevant cases.

Figure 5. The
![]() $O(Re^{3/2})$
inertial correction is plotted against the eccentricity for an oblate spheroid in the spinning orbit.
$O(Re^{3/2})$
inertial correction is plotted against the eccentricity for an oblate spheroid in the spinning orbit.
7 Evaluation of the
 $O(Re^{3/2})$
time period correction for triaxial ellipsoids
$O(Re^{3/2})$
time period correction for triaxial ellipsoids
In this section, we calculate the inertial correction to the time period of rotation for a triaxial ellipsoid that is rotating in an orbit stabilized by weak inertia. In the Stokes limit, it is known that the orientation dynamics of a triaxial ellipsoid may range from quasiperiodic to chaotic, depending on the axis ratios and the initial orientation (Yarin et al.
Reference Yarin, Gottlieb and Roisman1997). For
![]() $Re=0$
, the angular velocity of a triaxial ellipsoid rotating in a simple shear flow can be written as (Kim & Karrila Reference Kim and Karrila1991)
$Re=0$
, the angular velocity of a triaxial ellipsoid rotating in a simple shear flow can be written as (Kim & Karrila Reference Kim and Karrila1991)
In (7.1),
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $\boldsymbol{q}$
and
$\boldsymbol{q}$
and
![]() $\boldsymbol{r}$
are respectively the unit vectors along the longest (of length
$\boldsymbol{r}$
are respectively the unit vectors along the longest (of length
![]() $2a$
), intermediate (of length
$2a$
), intermediate (of length
![]() $2b$
) and shortest (of length
$2b$
) and shortest (of length
![]() $2c$
) principal axes of the triaxial ellipsoid. Here,
$2c$
) principal axes of the triaxial ellipsoid. Here,
![]() $\unicode[STIX]{x1D705}_{1}$
and
$\unicode[STIX]{x1D705}_{1}$
and
![]() $\unicode[STIX]{x1D705}_{2}$
are the axis ratios of the triaxial ellipsoid, defined as
$\unicode[STIX]{x1D705}_{2}$
are the axis ratios of the triaxial ellipsoid, defined as
![]() $\unicode[STIX]{x1D705}_{1}=b/a$
and
$\unicode[STIX]{x1D705}_{1}=b/a$
and
![]() $\unicode[STIX]{x1D705}_{2}=c/a$
. For
$\unicode[STIX]{x1D705}_{2}=c/a$
. For
![]() $\unicode[STIX]{x1D705}_{1}=1$
, the ellipsoid becomes an oblate spheroid with aspect ratio
$\unicode[STIX]{x1D705}_{1}=1$
, the ellipsoid becomes an oblate spheroid with aspect ratio
![]() $\unicode[STIX]{x1D705}_{2}$
, and for
$\unicode[STIX]{x1D705}_{2}$
, and for
![]() $\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
, the ellipsoid becomes a prolate spheroid with aspect ratio
$\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
, the ellipsoid becomes a prolate spheroid with aspect ratio
![]() $1/\unicode[STIX]{x1D705}_{1}$
.
$1/\unicode[STIX]{x1D705}_{1}$
.
Recently, Rosen (Reference Rosen2016) simulated the inertial orientation dynamics of a triaxial ellipsoid in simple shear flow as a function of
![]() $Re$
(based on the length of the longest principal axis), using lattice Boltzmann simulations. Rosen (Reference Rosen2016) examined the stability of principal-axis-aligned rotations for a triaxial ellipsoid with
$Re$
(based on the length of the longest principal axis), using lattice Boltzmann simulations. Rosen (Reference Rosen2016) examined the stability of principal-axis-aligned rotations for a triaxial ellipsoid with
![]() $\unicode[STIX]{x1D705}_{1}=1/3$
and
$\unicode[STIX]{x1D705}_{1}=1/3$
and
![]() $\unicode[STIX]{x1D705}_{2}=1/4$
for
$\unicode[STIX]{x1D705}_{2}=1/4$
for
![]() $Re$
ranging from 0 to 100. A particular result was the ability of inertia to stabilize the intermediate-axis-aligned rotation even for small but finite
$Re$
ranging from 0 to 100. A particular result was the ability of inertia to stabilize the intermediate-axis-aligned rotation even for small but finite
![]() $Re$
, an aspect that comes under the purview of the current small-
$Re$
, an aspect that comes under the purview of the current small-
![]() $Re$
analysis. The triangular region in figure 6 covers all axis ratios of interest for a triaxial ellipsoid, with one of its sides (
$Re$
analysis. The triangular region in figure 6 covers all axis ratios of interest for a triaxial ellipsoid, with one of its sides (
![]() $\unicode[STIX]{x1D705}_{1}=1$
) corresponding to an oblate spheroid, the other (
$\unicode[STIX]{x1D705}_{1}=1$
) corresponding to an oblate spheroid, the other (
![]() $\unicode[STIX]{x1D705}_{2}=0$
) corresponding to an elliptical flat disk, and the hypotenuse (
$\unicode[STIX]{x1D705}_{2}=0$
) corresponding to an elliptical flat disk, and the hypotenuse (
![]() $\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
) corresponding to a prolate spheroid. The analysis below can predict the time period correction for an ellipsoid with axis ratios of order unity, provided that the ellipsoid rotates about one of its principal axes. The particular pair of axis ratios examined by Rosen (Reference Rosen2016) is shown as a filled (black) circle in figure 6. We also use the analysis to predict the time period corrections for a sequence of axis-ratio pairs approaching an elliptical flat disk (marked using crosses in figure 6). It is known from Dabade et al. (Reference Dabade, Marath and Subramanian2016) that a circular flat disk (an infinitely thin oblate spheroid) tumbles starting from almost any initial orientation. Therefore, it is reasonable to assume that rotation about the intermediate axis remains stable for ellipsoids with axis ratios approaching that of an elliptical flat disk. The stability of such a rotation needs to nevertheless be validated using a numerical approach as given in Rosen (Reference Rosen2016) or an
$\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
) corresponding to a prolate spheroid. The analysis below can predict the time period correction for an ellipsoid with axis ratios of order unity, provided that the ellipsoid rotates about one of its principal axes. The particular pair of axis ratios examined by Rosen (Reference Rosen2016) is shown as a filled (black) circle in figure 6. We also use the analysis to predict the time period corrections for a sequence of axis-ratio pairs approaching an elliptical flat disk (marked using crosses in figure 6). It is known from Dabade et al. (Reference Dabade, Marath and Subramanian2016) that a circular flat disk (an infinitely thin oblate spheroid) tumbles starting from almost any initial orientation. Therefore, it is reasonable to assume that rotation about the intermediate axis remains stable for ellipsoids with axis ratios approaching that of an elliptical flat disk. The stability of such a rotation needs to nevertheless be validated using a numerical approach as given in Rosen (Reference Rosen2016) or an
![]() $O(Re)$
analytical calculation. It should be noted that the assumption of stable intermediate-axis-aligned rotation cannot be true for triaxial ellipsoids with axis ratios lying close to the blue segment in figure 6 (corresponding to triaxial ellipsoids with axis-ratio pairs close to that of an oblate spheroid with
$O(Re)$
analytical calculation. It should be noted that the assumption of stable intermediate-axis-aligned rotation cannot be true for triaxial ellipsoids with axis ratios lying close to the blue segment in figure 6 (corresponding to triaxial ellipsoids with axis-ratio pairs close to that of an oblate spheroid with
![]() $\unicode[STIX]{x1D705}_{2}>0.137$
). This is because as
$\unicode[STIX]{x1D705}_{2}>0.137$
). This is because as
![]() $\unicode[STIX]{x1D705}_{1}\rightarrow 1$
, a triaxial ellipsoid approaches the limiting oblate spheroid via the intermediate axis lengthening to equal the longest one. Stable intermediate-axis-aligned rotation would therefore correspond to a tumbling rather than a spinning oblate spheroid.
$\unicode[STIX]{x1D705}_{1}\rightarrow 1$
, a triaxial ellipsoid approaches the limiting oblate spheroid via the intermediate axis lengthening to equal the longest one. Stable intermediate-axis-aligned rotation would therefore correspond to a tumbling rather than a spinning oblate spheroid.

Figure 6. The orbits stabilized by inertia from earlier analysis for general triaxial ellipsoids are indicated in the figure. The filled black circle corresponds to the ellipsoid for which the numerical simulation by Rosen (Reference Rosen2016) has shown that the rotation about the intermediate axis is stable. The orbits stabilized for prolate and oblate spheroids are indicated (Dabade et al. Reference Dabade, Marath and Subramanian2016). For the ellipsoids indicated by crosses, we assume that the inertia stabilizes the rotation about the intermediate axis.
To calculate the correction, we again use the reciprocal theorem formulation of § 2, with the problem of interest being a neutrally buoyant triaxial ellipsoid rotating in a simple shear flow with its intermediate axis aligned with the ambient vorticity. In the test problem, we consider the same triaxial ellipsoid rotating in a quiescent fluid. The expression for the angular velocity of a triaxial ellipsoid obtained from the reciprocal theorem is the same as that of a spheroid given in (2.24)–(2.25), with the velocity fields and torque constants replaced with those of the ellipsoid. As for the spheroid, the
![]() $O(Re)$
correction to the time period for any triaxial ellipsoid rotating in a principal-axis-aligned orientation is zero. At
$O(Re)$
correction to the time period for any triaxial ellipsoid rotating in a principal-axis-aligned orientation is zero. At
![]() $O(Re)$
, the angular velocity of the triaxial ellipsoid must be quadratic in the flow parameters (
$O(Re)$
, the angular velocity of the triaxial ellipsoid must be quadratic in the flow parameters (
![]() $\unicode[STIX]{x1D640}$
and
$\unicode[STIX]{x1D640}$
and
![]() $\unicode[STIX]{x1D74E}$
) and be invariant under any of the transformations
$\unicode[STIX]{x1D74E}$
) and be invariant under any of the transformations
![]() $\boldsymbol{p}\leftrightarrow -\boldsymbol{p}$
,
$\boldsymbol{p}\leftrightarrow -\boldsymbol{p}$
,
![]() $\boldsymbol{q}\leftrightarrow -\boldsymbol{q}$
and
$\boldsymbol{q}\leftrightarrow -\boldsymbol{q}$
and
![]() $\boldsymbol{r}\leftrightarrow -\boldsymbol{r}$
. The invariance implies that for a rotation with any of the principal axes aligned with the ambient vorticity, the angular dependence of the time period integral at
$\boldsymbol{r}\leftrightarrow -\boldsymbol{r}$
. The invariance implies that for a rotation with any of the principal axes aligned with the ambient vorticity, the angular dependence of the time period integral at
![]() $O(Re)$
, given in (3.5), is such that it evaluates to zero when integrated over
$O(Re)$
, given in (3.5), is such that it evaluates to zero when integrated over
![]() $\unicode[STIX]{x1D719}_{j}$
. For rotation about the intermediate axis
$\unicode[STIX]{x1D719}_{j}$
. For rotation about the intermediate axis
![]() $\boldsymbol{q}$
,
$\boldsymbol{q}$
,
![]() $\unicode[STIX]{x1D719}_{j}$
would correspond to the angle made by the vector
$\unicode[STIX]{x1D719}_{j}$
would correspond to the angle made by the vector
![]() $\boldsymbol{p}$
with the flow axis (the vectors
$\boldsymbol{p}$
with the flow axis (the vectors
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{r}$
lie in the flow–gradient plane). Thus, the correction to the time period of rotation about the intermediate axis arises at
$\boldsymbol{r}$
lie in the flow–gradient plane). Thus, the correction to the time period of rotation about the intermediate axis arises at
![]() $O(Re^{3/2})$
. The calculation of this correction follows the same steps as that for a tumbling spheroid seen in § 5. We therefore define the singularity coefficients that completely characterize the far-field disturbance forms in the problem of interest and the test problem, and directly state the correction to the time period at
$O(Re^{3/2})$
. The calculation of this correction follows the same steps as that for a tumbling spheroid seen in § 5. We therefore define the singularity coefficients that completely characterize the far-field disturbance forms in the problem of interest and the test problem, and directly state the correction to the time period at
![]() $O(Re^{3/2})$
for the ellipsoids shown in figure 6 without going into the details of the calculation.
$O(Re^{3/2})$
for the ellipsoids shown in figure 6 without going into the details of the calculation.
To calculate the
![]() $O(Re^{3/2})$
correction to the time period, one has to evaluate the integral given in (5.3). The singularity coefficient for a triaxial ellipsoid rotating with angular velocity
$O(Re^{3/2})$
correction to the time period, one has to evaluate the integral given in (5.3). The singularity coefficient for a triaxial ellipsoid rotating with angular velocity
![]() $\unicode[STIX]{x1D734}^{(2)}$
in a quiescent ambient is given by
$\unicode[STIX]{x1D734}^{(2)}$
in a quiescent ambient is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(2)} & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D716}_{ijk}(H_{1}(\unicode[STIX]{x1D705}_{1}^{2}+\unicode[STIX]{x1D705}_{2}^{2})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{p})p_{j}+H_{2}(1+\unicode[STIX]{x1D705}_{2}^{2})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{q})q_{j}+H_{3}(\unicode[STIX]{x1D705}_{1}^{2}+1)(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{r})r_{j})\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{H_{3}}{2}(1-\unicode[STIX]{x1D705}_{1}^{2})(p_{i}q_{k}+p_{k}q_{i})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }(\boldsymbol{p}\times \boldsymbol{q}))\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{H_{1}}{2}(\unicode[STIX]{x1D705}_{1}^{2}-\unicode[STIX]{x1D705}_{2}^{2})(r_{i}q_{k}+r_{k}q_{i})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }(\boldsymbol{q}\times \boldsymbol{r}))\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(2)} & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D716}_{ijk}(H_{1}(\unicode[STIX]{x1D705}_{1}^{2}+\unicode[STIX]{x1D705}_{2}^{2})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{p})p_{j}+H_{2}(1+\unicode[STIX]{x1D705}_{2}^{2})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{q})q_{j}+H_{3}(\unicode[STIX]{x1D705}_{1}^{2}+1)(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }\boldsymbol{r})r_{j})\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{H_{3}}{2}(1-\unicode[STIX]{x1D705}_{1}^{2})(p_{i}q_{k}+p_{k}q_{i})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }(\boldsymbol{p}\times \boldsymbol{q}))\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{H_{1}}{2}(\unicode[STIX]{x1D705}_{1}^{2}-\unicode[STIX]{x1D705}_{2}^{2})(r_{i}q_{k}+r_{k}q_{i})(\unicode[STIX]{x1D734}^{(2)}\boldsymbol{\cdot }(\boldsymbol{q}\times \boldsymbol{r}))\end{eqnarray}$$
with constants
![]() $H_{i}$
defined as (Kim & Karrila Reference Kim and Karrila1991)
$H_{i}$
defined as (Kim & Karrila Reference Kim and Karrila1991)
and
In the limit of a spheroid, the singularity in (7.3) reduces to that given in (2.8), with the first three terms reducing to the rotlet proportional to
![]() $B_{2}$
and
$B_{2}$
and
![]() $B_{3}$
, and the last three terms reducing to the stresslet proportional to
$B_{3}$
, and the last three terms reducing to the stresslet proportional to
![]() $B_{1}$
. For the particular case of rotation about the intermediate axis, this singularity reduces to
$B_{1}$
. For the particular case of rotation about the intermediate axis, this singularity reduces to
The stresslet singularity coefficient corresponding to a triaxial ellipsoid rotating in simple shear flow is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(1)} & = & \displaystyle J_{1}\unicode[STIX]{x1D6FC}_{0}^{\prime \prime }(3p_{i}p_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})+J_{1}\unicode[STIX]{x1D6FD}_{0}^{\prime \prime }(3q_{i}q_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{q}\boldsymbol{q})+J_{1}\unicode[STIX]{x1D6FE}_{0}^{\prime \prime }(3r_{i}r_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{r})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{3}}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}+\unicode[STIX]{x1D6FD}_{0}}{\unicode[STIX]{x1D6FE}_{0}^{\prime }}-\frac{(1-\unicode[STIX]{x1D705}_{1}^{2})^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{q})(p_{i}q_{k}+q_{i}p_{k})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{1}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FD}_{0}}{\unicode[STIX]{x1D6FC}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-\unicode[STIX]{x1D705}_{1}^{2})^{2}}{(\unicode[STIX]{x1D705}_{2}^{2}+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{q})(r_{i}q_{k}+q_{i}r_{k})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{2}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FC}_{0}}{\unicode[STIX]{x1D6FD}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-1)^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{p})(r_{i}p_{k}+p_{i}r_{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(1)} & = & \displaystyle J_{1}\unicode[STIX]{x1D6FC}_{0}^{\prime \prime }(3p_{i}p_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})+J_{1}\unicode[STIX]{x1D6FD}_{0}^{\prime \prime }(3q_{i}q_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{q}\boldsymbol{q})+J_{1}\unicode[STIX]{x1D6FE}_{0}^{\prime \prime }(3r_{i}r_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{r})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{3}}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}+\unicode[STIX]{x1D6FD}_{0}}{\unicode[STIX]{x1D6FE}_{0}^{\prime }}-\frac{(1-\unicode[STIX]{x1D705}_{1}^{2})^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{q})(p_{i}q_{k}+q_{i}p_{k})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{1}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FD}_{0}}{\unicode[STIX]{x1D6FC}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-\unicode[STIX]{x1D705}_{1}^{2})^{2}}{(\unicode[STIX]{x1D705}_{2}^{2}+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{q})(r_{i}q_{k}+q_{i}r_{k})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{2}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FC}_{0}}{\unicode[STIX]{x1D6FD}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-1)^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{p})(r_{i}p_{k}+p_{i}r_{k}),\end{eqnarray}$$
with the constants above defined as (Kim & Karrila Reference Kim and Karrila1991)
It should be noted that, unlike the singularity for a spheroid given in (2.15), there are six constants in (7.9), with three constants corresponding to axisymmetric extensional flows, aligned with each of the ellipsoidal axes (first three terms in (7.9)), and the last three corresponding to planar extensional flows in the planes formed by the three axes (taken two at a time). The first term within the brackets of the latter three constants in (7.9) is obtained by imposing the torque-free condition on the ellipsoid. For the particular case of the rotation about the intermediate axis, (7.9) reduces to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(1)} & = & \displaystyle J_{1}\unicode[STIX]{x1D6FC}_{0}^{\prime \prime }(3p_{i}p_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})+J_{1}\unicode[STIX]{x1D6FE}_{0}^{\prime \prime }(3r_{i}r_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{r})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{2}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FC}_{0}}{\unicode[STIX]{x1D6FD}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-1)^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{p})(r_{i}p_{k}+p_{i}r_{k}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E}_{ik}^{(1)} & = & \displaystyle J_{1}\unicode[STIX]{x1D6FC}_{0}^{\prime \prime }(3p_{i}p_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})+J_{1}\unicode[STIX]{x1D6FE}_{0}^{\prime \prime }(3r_{i}r_{k}-\unicode[STIX]{x1D6FF}_{ik})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{r})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{H_{2}}{2}\left(\frac{\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FC}_{0}}{\unicode[STIX]{x1D6FD}_{0}^{\prime }}-\frac{(\unicode[STIX]{x1D705}_{2}^{2}-1)^{2}}{(1+\unicode[STIX]{x1D705}_{1}^{2})}\right)(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{r}\boldsymbol{p})(r_{i}p_{k}+p_{i}r_{k}).\end{eqnarray}$$
The correction to the time period takes the same form as in (5.3), with the constants
![]() $Y_{c}$
(the torque coefficient for the rotation about the intermediate principal axis) and
$Y_{c}$
(the torque coefficient for the rotation about the intermediate principal axis) and
![]() $\dot{\unicode[STIX]{x1D719}}_{jeff}$
(the magnitude of the leading-order angular velocity of the triaxial ellipsoid) given by
$\dot{\unicode[STIX]{x1D719}}_{jeff}$
(the magnitude of the leading-order angular velocity of the triaxial ellipsoid) given by
The detailed calculation, for the triaxial ellipsoids indicated in figure 6, leads to the time period corrections given in table 1. We have also listed the ratio of the correction(
![]() $\unicode[STIX]{x0394}T_{corrE}$
) to the leading-order time period (
$\unicode[STIX]{x0394}T_{corrE}$
) to the leading-order time period (
![]() $T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}_{2}+\unicode[STIX]{x1D705}_{2}^{-1})$
) in the table. As shown in figure 7, this ratio scales as
$T_{jeff}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D705}_{2}+\unicode[STIX]{x1D705}_{2}^{-1})$
) in the table. As shown in figure 7, this ratio scales as
![]() $1/\unicode[STIX]{x1D705}_{2}^{0.87}$
for
$1/\unicode[STIX]{x1D705}_{2}^{0.87}$
for
![]() $\unicode[STIX]{x1D705}_{2}\rightarrow 0$
. Unlike the case of the prolate spheroid in figure 3, where the ratio decreases with increasing aspect ratio (slender fibres), here it increases with decreasing
$\unicode[STIX]{x1D705}_{2}\rightarrow 0$
. Unlike the case of the prolate spheroid in figure 3, where the ratio decreases with increasing aspect ratio (slender fibres), here it increases with decreasing
![]() $\unicode[STIX]{x1D705}_{2}$
(thin ellipses). This increase is similar to that seen for a tumbling oblate spheroid with decreasing aspect ratio (see figure 4).
$\unicode[STIX]{x1D705}_{2}$
(thin ellipses). This increase is similar to that seen for a tumbling oblate spheroid with decreasing aspect ratio (see figure 4).

Figure 7. The ratio
![]() $\unicode[STIX]{x0394}T_{corrE}/T_{jeff}$
plotted against
$\unicode[STIX]{x0394}T_{corrE}/T_{jeff}$
plotted against
![]() $1/\unicode[STIX]{x1D705}_{2}$
in a log–log scale. The red line has a slope of 0.87.
$1/\unicode[STIX]{x1D705}_{2}$
in a log–log scale. The red line has a slope of 0.87.
Table 1. Inertial time periods for torque-free triaxial ellipsoids in simple shear flow.

In principle, the analogue of the
![]() $O(Re)$
integral given in (2.24), for a triaxial ellipsoid, would allow one to analytically determine the stability of the principal-axis-aligned rotations for axis ratios other than the one examined in simulations (Rosen Reference Rosen2016). However, the analysis involved is likely to be exceedingly complicated, since the
$O(Re)$
integral given in (2.24), for a triaxial ellipsoid, would allow one to analytically determine the stability of the principal-axis-aligned rotations for axis ratios other than the one examined in simulations (Rosen Reference Rosen2016). However, the analysis involved is likely to be exceedingly complicated, since the
![]() $O(Re)$
correction arises from a region around the ellipsoid of the order of its own size, and thus the Stokes velocity field required for the
$O(Re)$
correction arises from a region around the ellipsoid of the order of its own size, and thus the Stokes velocity field required for the
![]() $O(Re)$
computation would involve nonlinear combinations of the ellipsoidal harmonics used by Jeffery (Reference Jeffery1922). In contrast, the
$O(Re)$
computation would involve nonlinear combinations of the ellipsoidal harmonics used by Jeffery (Reference Jeffery1922). In contrast, the
![]() $O(Re^{3/2})$
correction is insensitive to these details, and, as seen above, one only needs the force-dipole singularity that the ellipsoids in the actual and test problems correspond to. A calculation of the time period correction over the entire parameter space indicated in figure 6 will, however, have to wait until a more comprehensive investigation of inertia-induced stability of the principal-axis-aligned rotations.
$O(Re^{3/2})$
correction is insensitive to these details, and, as seen above, one only needs the force-dipole singularity that the ellipsoids in the actual and test problems correspond to. A calculation of the time period correction over the entire parameter space indicated in figure 6 will, however, have to wait until a more comprehensive investigation of inertia-induced stability of the principal-axis-aligned rotations.
8 Conclusions and future work
In this paper, we have evaluated the leading-order fluid inertial correction, at
![]() $O(Re^{3/2})$
, to the time period of rotation a spheroid, in simple shear flow, rotating in the tumbling and spinning orbits. The first effects of inertia occur at
$O(Re^{3/2})$
, to the time period of rotation a spheroid, in simple shear flow, rotating in the tumbling and spinning orbits. The first effects of inertia occur at
![]() $O(Re)$
, but at this order, inertia only acts to stabilize either one of two Jeffery orbits, depending on the spheroid aspect ratio and its initial orientation, leaving the time period of rotation unchanged. Specifically, it has been shown by Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016) that the stable orbit for a prolate spheroid of any aspect ratio is the tumbling one, and is the spinning one for an oblate spheroid with
$O(Re)$
, but at this order, inertia only acts to stabilize either one of two Jeffery orbits, depending on the spheroid aspect ratio and its initial orientation, leaving the time period of rotation unchanged. Specifically, it has been shown by Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015) and Dabade et al. (Reference Dabade, Marath and Subramanian2016) that the stable orbit for a prolate spheroid of any aspect ratio is the tumbling one, and is the spinning one for an oblate spheroid with
![]() $\unicode[STIX]{x1D705}>0.137$
. The stable orbit for an oblate spheroid with
$\unicode[STIX]{x1D705}>0.137$
. The stable orbit for an oblate spheroid with
![]() $\unicode[STIX]{x1D705}<0.137$
is either spinning or tumbling, depending on the initial orientation.
$\unicode[STIX]{x1D705}<0.137$
is either spinning or tumbling, depending on the initial orientation.
The correction to the angular velocity at
![]() $O(Re^{3/2})$
is formulated as an integral in Fourier space, based on a reciprocal theorem formulation, the details of which are given in § 2. The disturbance velocity field around a spinning spheroid is steady, and, therefore, the correction to the angular velocity at
$O(Re^{3/2})$
is formulated as an integral in Fourier space, based on a reciprocal theorem formulation, the details of which are given in § 2. The disturbance velocity field around a spinning spheroid is steady, and, therefore, the correction to the angular velocity at
![]() $O(Re^{3/2})$
is trivially related to the correction to the time period through (4.1). The calculation proceeds in a manner similar to earlier calculations for a sphere (Stone et al.
Reference Stone, Brady and Lovalenti2000; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011), and the result is given in (4.24). The disturbance velocity field around a spheroid is unsteady in the tumbling orbit, and the evaluation of the time period correction is therefore not trivial. However, we show in § 5 that by expanding the integrand in the reciprocal theorem as a Fourier series in time, one can evaluate the correction without the need for truncation. The numerical results for the tumbling and spinning orbits are summarized in § 6. It is shown that the time period of rotation increases with the fluid inertia, at
$O(Re^{3/2})$
is trivially related to the correction to the time period through (4.1). The calculation proceeds in a manner similar to earlier calculations for a sphere (Stone et al.
Reference Stone, Brady and Lovalenti2000; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011), and the result is given in (4.24). The disturbance velocity field around a spheroid is unsteady in the tumbling orbit, and the evaluation of the time period correction is therefore not trivial. However, we show in § 5 that by expanding the integrand in the reciprocal theorem as a Fourier series in time, one can evaluate the correction without the need for truncation. The numerical results for the tumbling and spinning orbits are summarized in § 6. It is shown that the time period of rotation increases with the fluid inertia, at
![]() $O(Re^{3/2})$
in both tumbling and spinning orbits, consistent with earlier simulations. It was shown in Dabade et al. (Reference Dabade, Marath and Subramanian2016) that the particle inertia decreases the tumbling time period at
$O(Re^{3/2})$
in both tumbling and spinning orbits, consistent with earlier simulations. It was shown in Dabade et al. (Reference Dabade, Marath and Subramanian2016) that the particle inertia decreases the tumbling time period at
![]() $O(St^{2})$
. For the tumbling neutrally buoyant spheroids considered here,
$O(St^{2})$
. For the tumbling neutrally buoyant spheroids considered here,
![]() $St=Re$
, and the increase due to fluid inertia is therefore dominant. Particle inertia plays no role for spinning spheroids.
$St=Re$
, and the increase due to fluid inertia is therefore dominant. Particle inertia plays no role for spinning spheroids.
Although not considered here, for a general spheroid orientation, the
![]() $O(Re^{3/2})$
correction should also contribute to an orbital drift. This correction is of little consequence for the rheology of a dilute suspension of neutrally buoyant prolate spheroids, on account of the stability, at
$O(Re^{3/2})$
correction should also contribute to an orbital drift. This correction is of little consequence for the rheology of a dilute suspension of neutrally buoyant prolate spheroids, on account of the stability, at
![]() $O(Re)$
, of the tumbling mode for all aspect ratios. However, the
$O(Re)$
, of the tumbling mode for all aspect ratios. However, the
![]() $O(Re^{3/2})$
correction will affect the rheology of a suspension of oblate spheroids by altering the location of the repeller identified in Dabade et al. (Reference Dabade, Marath and Subramanian2016), and that separates the basins of attraction (on the unit hemisphere) corresponding to the tumbling and spinning modes. The altered repeller location, for aspect ratios lower than
$O(Re^{3/2})$
correction will affect the rheology of a suspension of oblate spheroids by altering the location of the repeller identified in Dabade et al. (Reference Dabade, Marath and Subramanian2016), and that separates the basins of attraction (on the unit hemisphere) corresponding to the tumbling and spinning modes. The altered repeller location, for aspect ratios lower than
![]() $0.137$
(this threshold is itself subject to an
$0.137$
(this threshold is itself subject to an
![]() $O(Re^{1/2})$
correction), will contribute to an
$O(Re^{1/2})$
correction), will contribute to an
![]() $O(Re^{1/2})$
correction to the shear viscosity. This is in contrast to the
$O(Re^{1/2})$
correction to the shear viscosity. This is in contrast to the
![]() $O(Re^{3/2})$
modification expected from the direct effects of inertia (via corrections to the stresslet integral, and the acceleration and Reynolds stresses); see Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). An analogous effect is expected in the presence of weak Brownian motion, with the critical aspect ratio, corresponding to the tumbling–spinning transition in simple shear flow, being altered by
$O(Re^{3/2})$
modification expected from the direct effects of inertia (via corrections to the stresslet integral, and the acceleration and Reynolds stresses); see Subramanian et al. (Reference Subramanian, Koch, Zhang and Yang2011). An analogous effect is expected in the presence of weak Brownian motion, with the critical aspect ratio, corresponding to the tumbling–spinning transition in simple shear flow, being altered by
![]() $O(Re^{1/2})$
(see Marath et al.
Reference Marath, Dwivedi and Subramanian2017).
$O(Re^{1/2})$
(see Marath et al.
Reference Marath, Dwivedi and Subramanian2017).
In § 7, we have evaluated the time period correction for the triaxial ellipsoids indicated in figure 6. The calculation proceeds in a manner similar to that of a tumbling spheroid, and the results are presented in § 7. In performing this calculation, we have assumed that fluid inertia, at
![]() $O(Re)$
, stabilizes the rotation about the intermediate principal axis for ellipsoids other than the one already analysed in Rosen (Reference Rosen2016). Examination of a sequence of triaxial ellipsoids asymptoting to an elliptical disk of eccentricity
$O(Re)$
, stabilizes the rotation about the intermediate principal axis for ellipsoids other than the one already analysed in Rosen (Reference Rosen2016). Examination of a sequence of triaxial ellipsoids asymptoting to an elliptical disk of eccentricity
![]() $(8/9)^{1/2}$
, rotating in the assumed manner, leads to the inertial correction to the time period diverging in a manner similar to the oblate spheroid. The assumption of intermediate-axis-aligned rotation is, however, not likely for axis ratios close to the blue segment in figure 6. Inertial stabilization, at
$(8/9)^{1/2}$
, rotating in the assumed manner, leads to the inertial correction to the time period diverging in a manner similar to the oblate spheroid. The assumption of intermediate-axis-aligned rotation is, however, not likely for axis ratios close to the blue segment in figure 6. Inertial stabilization, at
![]() $O(Re)$
, of principal-axis-aligned rotations requires a more comprehensive simulation programme than the one given in Rosen (Reference Rosen2016), or a small-
$O(Re)$
, of principal-axis-aligned rotations requires a more comprehensive simulation programme than the one given in Rosen (Reference Rosen2016), or a small-
![]() $Re$
analytical approach. The latter appears to be particularly forbidding, keeping in mind the ellipsoidal harmonics used for constructing the Stokes velocity field around an arbitrarily oriented triaxial ellipsoid (Jeffery Reference Jeffery1922).
$Re$
analytical approach. The latter appears to be particularly forbidding, keeping in mind the ellipsoidal harmonics used for constructing the Stokes velocity field around an arbitrarily oriented triaxial ellipsoid (Jeffery Reference Jeffery1922).
The analysis of the period of rotation of a tumbling inertial spheroid has thus far assumed an aspect ratio of order unity, and we make this estimate more precise in the arguments that follow. An order-unity aspect ratio leads to the inertial contributions to the angular velocity being asymptotically small in comparison with the Stokesian one, and, as seen in (3.5), the time period may then be expanded in a perturbative manner for small
![]() $Re$
. This is no longer possible for extreme-aspect-ratio spheroids. As described in § 5.5, at
$Re$
. This is no longer possible for extreme-aspect-ratio spheroids. As described in § 5.5, at
![]() $Re=0$
, such spheroids rotate very slowly during the aligned phase. Thus, even in the limit
$Re=0$
, such spheroids rotate very slowly during the aligned phase. Thus, even in the limit
![]() $Re\ll 1$
, the
$Re\ll 1$
, the
![]() $O(Re)$
inertial correction becomes comparable to the leading-order Stokesian rotation, and, as first shown by Subramanian & Koch (Reference Subramanian and Koch2005), this leads to an arrest of rotation beyond a modest threshold
$O(Re)$
inertial correction becomes comparable to the leading-order Stokesian rotation, and, as first shown by Subramanian & Koch (Reference Subramanian and Koch2005), this leads to an arrest of rotation beyond a modest threshold
![]() $Re$
. To analyse this arrest for both slender fibres (
$Re$
. To analyse this arrest for both slender fibres (
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
) and flat disks (
$\unicode[STIX]{x1D705}\rightarrow \infty$
) and flat disks (
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
), we consider the asymptotic forms of the equation for
$\unicode[STIX]{x1D705}\rightarrow 0$
), we consider the asymptotic forms of the equation for
![]() $\dot{\unicode[STIX]{x1D719}}_{j}$
, given by
$\dot{\unicode[STIX]{x1D719}}_{j}$
, given by
and
for slender fibres and flat disks respectively. Here,
![]() $G_{i}^{\infty }=\lim _{\unicode[STIX]{x1D705}\rightarrow \infty }G_{i}^{n}(\unicode[STIX]{x1D709}_{0})$
,
$G_{i}^{\infty }=\lim _{\unicode[STIX]{x1D705}\rightarrow \infty }G_{i}^{n}(\unicode[STIX]{x1D709}_{0})$
,
![]() $G_{i}^{0}=\lim _{\unicode[STIX]{x1D705}\rightarrow 0}G_{i}^{n}(\unicode[STIX]{x1D709}_{0})$
, and these terms are given in Dabade et al. (Reference Dabade, Marath and Subramanian2016). We consider a slender fibre to begin with; the arguments for a flat disk follow in an analogous manner. For
$G_{i}^{0}=\lim _{\unicode[STIX]{x1D705}\rightarrow 0}G_{i}^{n}(\unicode[STIX]{x1D709}_{0})$
, and these terms are given in Dabade et al. (Reference Dabade, Marath and Subramanian2016). We consider a slender fibre to begin with; the arguments for a flat disk follow in an analogous manner. For
![]() $\log \unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}\ll Re\ll 1$
, the arrest of rotation for a fibre occurs when the
$\log \unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}\ll Re\ll 1$
, the arrest of rotation for a fibre occurs when the
![]() $O(Re)$
term in (8.2) equals the slender-body contribution of
$O(Re)$
term in (8.2) equals the slender-body contribution of
![]() $(\unicode[STIX]{x1D719}_{j}^{2})$
, so the orientation of the nearly aligned stationary fibre is
$(\unicode[STIX]{x1D719}_{j}^{2})$
, so the orientation of the nearly aligned stationary fibre is
![]() $O(Re/\text{log}\,\unicode[STIX]{x1D705})$
. At the onset of arrest, the non-slender-body term proportional to
$O(Re/\text{log}\,\unicode[STIX]{x1D705})$
. At the onset of arrest, the non-slender-body term proportional to
![]() $\unicode[STIX]{x1D705}^{-2}$
in (8.2) must also be of the same order, and this leads to a threshold given by
$\unicode[STIX]{x1D705}^{-2}$
in (8.2) must also be of the same order, and this leads to a threshold given by
![]() $Re_{c}=((30\log \unicode[STIX]{x1D705})/\unicode[STIX]{x1D705})$
, the resulting stationary orientation being
$Re_{c}=((30\log \unicode[STIX]{x1D705})/\unicode[STIX]{x1D705})$
, the resulting stationary orientation being
![]() $O(1/\unicode[STIX]{x1D705})$
(see Subramanian & Koch Reference Subramanian and Koch2005). We now examine the
$O(1/\unicode[STIX]{x1D705})$
(see Subramanian & Koch Reference Subramanian and Koch2005). We now examine the
![]() $O(Re^{3/2})$
correction in order to show that the estimate for
$O(Re^{3/2})$
correction in order to show that the estimate for
![]() $Re_{c}$
above, obtained by considering only the
$Re_{c}$
above, obtained by considering only the
![]() $O(Re)$
contribution, is not altered at leading order. One first needs an estimate for
$O(Re)$
contribution, is not altered at leading order. One first needs an estimate for
![]() $\dot{\unicode[STIX]{x1D719}}_{c2}$
, which may be obtained from the definition
$\dot{\unicode[STIX]{x1D719}}_{c2}$
, which may be obtained from the definition
![]() $\unicode[STIX]{x0394}T_{tumb}=Re^{3/2}\textstyle \int _{0}^{T_{jeff}}\text{d}t(\dot{\unicode[STIX]{x1D719}}_{c2}/\dot{\unicode[STIX]{x1D719}}_{jeff})$
and the fact that
$\unicode[STIX]{x0394}T_{tumb}=Re^{3/2}\textstyle \int _{0}^{T_{jeff}}\text{d}t(\dot{\unicode[STIX]{x1D719}}_{c2}/\dot{\unicode[STIX]{x1D719}}_{jeff})$
and the fact that
![]() $\unicode[STIX]{x0394}T_{tumb}\sim O(Re^{3/2}\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705})$
, as shown in § 5.5. For the aligned phase,
$\unicode[STIX]{x0394}T_{tumb}\sim O(Re^{3/2}\unicode[STIX]{x1D705}/\text{log}\,\unicode[STIX]{x1D705})$
, as shown in § 5.5. For the aligned phase,
![]() $\text{d}t\sim O(\unicode[STIX]{x1D705})$
and
$\text{d}t\sim O(\unicode[STIX]{x1D705})$
and
![]() $\dot{\unicode[STIX]{x1D719}}_{jeff}\sim O(1/\unicode[STIX]{x1D705}^{2})$
, and this leads to
$\dot{\unicode[STIX]{x1D719}}_{jeff}\sim O(1/\unicode[STIX]{x1D705}^{2})$
, and this leads to
![]() $\dot{\unicode[STIX]{x1D719}}_{c2}\sim 1/(\unicode[STIX]{x1D705}^{2}\log \unicode[STIX]{x1D705})$
. Using this, the higher-order inertial correction in (8.2) is
$\dot{\unicode[STIX]{x1D719}}_{c2}\sim 1/(\unicode[STIX]{x1D705}^{2}\log \unicode[STIX]{x1D705})$
. Using this, the higher-order inertial correction in (8.2) is
![]() $O(Re^{3/2}/\unicode[STIX]{x1D705}^{2}\log \unicode[STIX]{x1D705})$
. It should be noted that the singular origin of this contribution implies that the angular velocity at this order remains finite even for an aligned spheroid; this is unlike the regular
$O(Re^{3/2}/\unicode[STIX]{x1D705}^{2}\log \unicode[STIX]{x1D705})$
. It should be noted that the singular origin of this contribution implies that the angular velocity at this order remains finite even for an aligned spheroid; this is unlike the regular
![]() $O(Re)$
contribution, which goes to zero as
$O(Re)$
contribution, which goes to zero as
![]() $O(\unicode[STIX]{x1D719}_{j})$
, being proportional to the instantaneous angular acceleration of the fluid elements (approximated based on the Stokesian field). Using the aforementioned estimate of
$O(\unicode[STIX]{x1D719}_{j})$
, being proportional to the instantaneous angular acceleration of the fluid elements (approximated based on the Stokesian field). Using the aforementioned estimate of
![]() $Re_{c}$
, one finds that the
$Re_{c}$
, one finds that the
![]() $O(Re^{3/2})$
correction is
$O(Re^{3/2})$
correction is
![]() $O[(\text{log}\,\unicode[STIX]{x1D705})^{1/2}/\unicode[STIX]{x1D705}^{7/2}]$
at arrest, while the Stokesian and
$O[(\text{log}\,\unicode[STIX]{x1D705})^{1/2}/\unicode[STIX]{x1D705}^{7/2}]$
at arrest, while the Stokesian and
![]() $O(Re)$
inertial contributions are
$O(Re)$
inertial contributions are
![]() $O(1/\unicode[STIX]{x1D705}^{2})$
, and, therefore, asymptotically larger. Thus, the inclusion of the
$O(1/\unicode[STIX]{x1D705}^{2})$
, and, therefore, asymptotically larger. Thus, the inclusion of the
![]() $O(Re^{3/2})$
contribution only decreases
$O(Re^{3/2})$
contribution only decreases
![]() $Re_{c}$
, relative to its leading-order estimate, by
$Re_{c}$
, relative to its leading-order estimate, by
![]() $O[(\text{log}\,\unicode[STIX]{x1D705})^{1/2}/\unicode[STIX]{x1D705}^{3/2}]$
. In summary, for a given
$O[(\text{log}\,\unicode[STIX]{x1D705})^{1/2}/\unicode[STIX]{x1D705}^{3/2}]$
. In summary, for a given
![]() $Re$
, the analysis in this paper predicts an
$Re$
, the analysis in this paper predicts an
![]() $O(Re^{3/2})$
inertia-induced increase in the time period of a prolate spheroid for
$O(Re^{3/2})$
inertia-induced increase in the time period of a prolate spheroid for
![]() $1\ll \unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{c}$
, with
$1\ll \unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{c}$
, with
![]() $\log \unicode[STIX]{x1D705}_{c}/\unicode[STIX]{x1D705}_{c}\sim Re$
(or
$\log \unicode[STIX]{x1D705}_{c}/\unicode[STIX]{x1D705}_{c}\sim Re$
(or
![]() $\unicode[STIX]{x1D705}_{c}\sim Re\log Re$
at leading logarithmic order). However, the arrest of rotation for large
$\unicode[STIX]{x1D705}_{c}\sim Re\log Re$
at leading logarithmic order). However, the arrest of rotation for large
![]() $\unicode[STIX]{x1D705}$
values of
$\unicode[STIX]{x1D705}$
values of
![]() $O(\unicode[STIX]{x1D705}_{c})$
is still controlled by the
$O(\unicode[STIX]{x1D705}_{c})$
is still controlled by the
![]() $O(Re)$
inertial correction first obtained by Subramanian & Koch (Reference Subramanian and Koch2005). For a flat disk, similar arguments show that the threshold for arrest corresponds to
$O(Re)$
inertial correction first obtained by Subramanian & Koch (Reference Subramanian and Koch2005). For a flat disk, similar arguments show that the threshold for arrest corresponds to
![]() $Re_{c}=15\unicode[STIX]{x1D705}$
, based on the
$Re_{c}=15\unicode[STIX]{x1D705}$
, based on the
![]() $O(Re)$
correction, and inclusion of the
$O(Re)$
correction, and inclusion of the
![]() $O(Re^{3/2})$
contribution obtained here only decreases
$O(Re^{3/2})$
contribution obtained here only decreases
![]() $Re_{c}$
by
$Re_{c}$
by
![]() $O(\unicode[STIX]{x1D705}^{1/2})$
relative to this estimate. This in turn implies that the
$O(\unicode[STIX]{x1D705}^{1/2})$
relative to this estimate. This in turn implies that the
![]() $O(Re^{3/2})$
analysis given here for oblate spheroids is only valid provided that
$O(Re^{3/2})$
analysis given here for oblate spheroids is only valid provided that
![]() $\unicode[STIX]{x1D705}\gg O(Re)$
. Thus, the
$\unicode[STIX]{x1D705}\gg O(Re)$
. Thus, the
![]() $O(Re^{3/2})$
analysis for a spheroid is valid only for
$O(Re^{3/2})$
analysis for a spheroid is valid only for
![]() $Re\ll \unicode[STIX]{x1D705}\ll Re\log Re$
. This
$Re\ll \unicode[STIX]{x1D705}\ll Re\log Re$
. This
![]() $Re$
-dependent aspect-ratio interval makes the limitation of order-unity aspect ratios mentioned earlier precise. Importantly, combination of the
$Re$
-dependent aspect-ratio interval makes the limitation of order-unity aspect ratios mentioned earlier precise. Importantly, combination of the
![]() $O(Re^{3/2})$
contribution with the
$O(Re^{3/2})$
contribution with the
![]() $O(Re)$
contribution given in Dabade et al. (Reference Dabade, Marath and Subramanian2016) allows one to predict the first effects of inertia for all aspect ratios, including the arrest of rotation of extreme-aspect-ratio spheroids.
$O(Re)$
contribution given in Dabade et al. (Reference Dabade, Marath and Subramanian2016) allows one to predict the first effects of inertia for all aspect ratios, including the arrest of rotation of extreme-aspect-ratio spheroids.
Appendix A. The integrals in (5.47)
The four-dimensional and five-dimensional integrals for the terms proportional to
![]() $\hat{u} _{1}^{fi}$
(
$\hat{u} _{1}^{fi}$
(
![]() $i$
$i$
![]() $=$
‘0’,‘
$=$
‘0’,‘
![]() $t\cos$
’,‘
$t\cos$
’,‘
![]() $t\sin$
’),
$t\sin$
’),
![]() $\hat{u} _{3}^{fi}$
(
$\hat{u} _{3}^{fi}$
(
![]() $i$
$i$
![]() $=$
‘0’,‘
$=$
‘0’,‘
![]() $t\cos$
’,‘
$t\cos$
’,‘
![]() $t\sin$
’) and the four-dimensional integral for
$t\sin$
’) and the four-dimensional integral for
![]() $\hat{u} _{2}^{fi}$
(‘
$\hat{u} _{2}^{fi}$
(‘
![]() $t\cos$
’,‘
$t\cos$
’,‘
![]() $t\sin$
’) in (5.47) are given below in the spherical coordinate system.
$t\sin$
’) in (5.47) are given below in the spherical coordinate system.
The integral proportional to
![]() $\hat{u} _{2}^{f0}$
is written using (5.35) and (5.4),
$\hat{u} _{2}^{f0}$
is written using (5.35) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f0}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{3}k_{1}}{2k^{2}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\left.\frac{\text{i}B_{1}k_{1}(k^{2}-2k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}Q_{2}^{0}(\boldsymbol{k}^{\prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f0}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{3}k_{1}}{2k^{2}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\left.\frac{\text{i}B_{1}k_{1}(k^{2}-2k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}Q_{2}^{0}(\boldsymbol{k}^{\prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{3}^{f0}$
is written using (5.41) and (5.4),
$\hat{u} _{3}^{f0}$
is written using (5.41) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{f0}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]Q_{3}^{0}(\boldsymbol{k}^{\prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\frac{2k_{1}k_{3}}{k^{\prime 2}}\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\text{d}s^{\prime }\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{f0}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{1}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]Q_{3}^{0}(\boldsymbol{k}^{\prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1-\unicode[STIX]{x1D705}^{4})}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\frac{2k_{1}k_{3}}{k^{\prime 2}}\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)Q_{2}^{0}(\boldsymbol{k}^{\prime \prime })\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\text{d}s^{\prime }\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{1}^{ftcos}$
is written using (5.39) and (5.4),
$\hat{u} _{1}^{ftcos}$
is written using (5.39) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{ftcos}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}=-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\left.\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\left(Q_{1}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\left\{\left[\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\times \left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{ftcos}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}=-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\left.\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\left(Q_{1}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2k^{2}\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}k^{2}\left\{\left[\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}\frac{\text{i}B_{3}k_{2}}{2k^{2}\unicode[STIX]{x03C0}}+\frac{\text{i}B_{1}(k^{2}-2k_{1}^{2})k_{2}}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\times \left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{2}^{ftcos}$
is written using (5.36) and (5.4),
$\hat{u} _{2}^{ftcos}$
is written using (5.36) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{ftcos}(\boldsymbol{k})\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{-\text{i}B_{3}k_{1}}{2k^{2}\unicode[STIX]{x03C0}}\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}+\frac{\text{i}B_{1}k_{1}(k^{2}-2k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{ftcos}(\boldsymbol{k})\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{-\text{i}B_{3}k_{1}}{2k^{2}\unicode[STIX]{x03C0}}\frac{(\unicode[STIX]{x1D705}^{4}-1)}{2\unicode[STIX]{x1D705}^{2}}+\frac{\text{i}B_{1}k_{1}(k^{2}-2k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\left(Q_{2}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{3}^{ftcos}$
is written using (5.42) and (5.6),
$\hat{u} _{3}^{ftcos}$
is written using (5.42) and (5.6),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{ftcos}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}=-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{3}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\!\right\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{ftcos}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{2}^{tumb})\,\text{d}\boldsymbol{k}=-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{3}^{2i}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)-Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\left\{4\unicode[STIX]{x03C0}^{2}k^{2}\left[-\frac{\text{i}B_{1}k_{1}k_{2}k_{3}}{k^{4}\unicode[STIX]{x03C0}}\frac{(1+\unicode[STIX]{x1D705}^{2})^{2}}{2\unicode[STIX]{x1D705}^{2}}\right]\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))-Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\!\right\}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{1}^{ftsin}$
is written using (5.39) and (5.4),
$\hat{u} _{1}^{ftsin}$
is written using (5.39) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{ftsin}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{1}(k^{2}-k_{1}^{2}+k_{2}^{2})k_{1}}{2k^{4}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.\times \left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\right]\left(Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{1}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{1}(k^{2}-k_{1}^{2}+k_{2}^{2})k_{1}}{2k^{4}\unicode[STIX]{x03C0}}\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{1}^{ftsin}(\boldsymbol{k})\,\mathbf{1}_{1}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{1}(k^{2}-k_{1}^{2}+k_{2}^{2})k_{1}}{2k^{4}\unicode[STIX]{x03C0}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\left.\times \left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\right]\left(Q_{1}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{1}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[\frac{\text{i}B_{1}(k^{2}-k_{1}^{2}+k_{2}^{2})k_{1}}{2k^{4}\unicode[STIX]{x03C0}}\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left(1-\frac{2k_{1}^{2}}{k^{\prime 2}}\right)\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{2}^{ftsin}$
is written using (5.36) and (5.4),
$\hat{u} _{2}^{ftsin}$
is written using (5.36) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f0}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}k_{2}(k^{2}+k_{1}^{2}-k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\times \left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{2}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{2}^{f0}(\boldsymbol{k})\,\mathbf{1}_{2}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}k_{2}(k^{2}+k_{1}^{2}-k_{2}^{2})}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.\times \left(\frac{k^{2}+k_{1}^{2}s^{2}+2k_{1}k_{2}s}{k^{2}}\right)\left(Q_{2}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{2}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s)\right)\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
The integral proportional to
![]() $\hat{u} _{3}^{ftsin}$
is written using (5.42) and (5.4),
$\hat{u} _{3}^{ftsin}$
is written using (5.42) and (5.4),
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{ftsin}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}(k_{1}^{2}-k_{2}^{2})k_{3}}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{3}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}(k_{1}^{2}-k_{2}^{2})k_{3}}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int (-4\unicode[STIX]{x03C0}^{2}k^{2}\,\hat{u} _{3}^{ftsin}(\boldsymbol{k})\,\mathbf{1}_{3}\boldsymbol{\cdot }\boldsymbol{T}_{3}^{tumb})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}(k_{1}^{2}-k_{2}^{2})k_{3}}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.(Q_{3}^{2Re}(\boldsymbol{k}^{\prime })\cos (2\unicode[STIX]{x1D714}_{g}s)+Q_{3}^{2i}(\boldsymbol{k}^{\prime })\sin (2\unicode[STIX]{x1D714}_{g}s))\!\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }4\unicode[STIX]{x03C0}^{2}\left\{k^{2}\left[-\left(\frac{\unicode[STIX]{x1D705}^{2}+1}{\unicode[STIX]{x1D705}}\right)\frac{\text{i}B_{1}(k_{1}^{2}-k_{2}^{2})k_{3}}{2k^{4}\unicode[STIX]{x03C0}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{2k_{1}k_{3}}{k^{\prime 2}}\right)(Q_{2}^{2Re}(\boldsymbol{k}^{\prime \prime })\cos (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime }))+Q_{2}^{2i}(\boldsymbol{k}^{\prime \prime })\sin (2\unicode[STIX]{x1D714}_{g}(s+s^{\prime })))\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \left.\left(\frac{k^{\prime 2}+k_{1}^{2}s^{\prime 2}+2k_{1}k_{2}^{\prime }s^{\prime }}{k^{\prime 2}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \int _{0}^{\infty }\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{2}s+k_{1}k_{2}s^{2}+\frac{k_{1}^{2}s^{3}}{3}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\text{i}2\exp \left(-4\unicode[STIX]{x03C0}^{2}\left(k^{\prime 2}s^{\prime }+k_{1}k_{2}^{\prime }s^{\prime 2}+\frac{k_{1}^{2}s^{\prime 3}}{3}\right)\right)k^{2}\,\text{d}k\,\text{d}s^{\prime }\,\text{d}s\,\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D719}.\qquad\end{eqnarray}$$