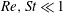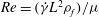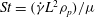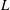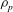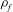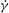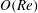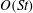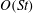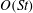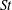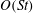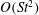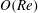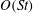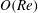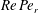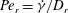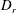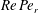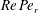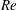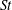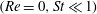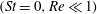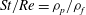1 Introduction
The present paper is concerned with the theoretical determination of the viscosity of a dilute non-interacting suspension of non-Brownian anisotropic particles as a function of the particle volume fraction, a classical problem in microhydrodynamics (Batchelor Reference Batchelor1977). The relevant volume fraction here is the hydrodynamic one,
![]() $nL^{3}$
, where
$nL^{3}$
, where
![]() $n$
is the particle number density and
$n$
is the particle number density and
![]() $L$
is the largest characteristic dimension of an individual particle;
$L$
is the largest characteristic dimension of an individual particle;
![]() $nL^{3}\ll 1$
implies hydrodynamic diluteness. We consider the simplest geometry for a non-spherical particle, that of a spheroid, wherein the deviation from sphericity is characterized by a single parameter, the particle aspect ratio, and in which case
$nL^{3}\ll 1$
implies hydrodynamic diluteness. We consider the simplest geometry for a non-spherical particle, that of a spheroid, wherein the deviation from sphericity is characterized by a single parameter, the particle aspect ratio, and in which case
![]() $L$
would be the semimajor axis. The analogous problem for spheres was first analysed by Einstein in 1906 (Leal Reference Leal1992) who showed that a suspension of rigid spheres, in the dilute non-interacting limit, behaves as a Newtonian fluid with an effective viscosity that is enhanced relative to that of the suspending fluid by a factor
$L$
would be the semimajor axis. The analogous problem for spheres was first analysed by Einstein in 1906 (Leal Reference Leal1992) who showed that a suspension of rigid spheres, in the dilute non-interacting limit, behaves as a Newtonian fluid with an effective viscosity that is enhanced relative to that of the suspending fluid by a factor
![]() $(5/2){\it\phi}$
,
$(5/2){\it\phi}$
,
![]() ${\it\phi}$
(
${\it\phi}$
(
![]() $\ll 1$
) being the volume fraction, and the factor
$\ll 1$
) being the volume fraction, and the factor
![]() $5/2$
often referred to as the Einstein coefficient. The determination of the analogue of the Einstein coefficient for a suspension of spheroids, a dimensionless function of the spheroid aspect ratio that multiplies
$5/2$
often referred to as the Einstein coefficient. The determination of the analogue of the Einstein coefficient for a suspension of spheroids, a dimensionless function of the spheroid aspect ratio that multiplies
![]() $nL^{3}$
, turns out to be considerably more involved. Stokesian hydrodynamics alone does not, in fact, provide for a unique answer in this regard.
$nL^{3}$
, turns out to be considerably more involved. Stokesian hydrodynamics alone does not, in fact, provide for a unique answer in this regard.
In order to better understand the above difficulty, one may again examine a suspension of spheres, where a similar difficulty occurs in determining the
![]() $O({\it\phi}^{2})$
correction to the effective viscosity. This calculation, which includes the first effects of hydrodynamic interactions, was accomplished much later (than Einstein) by Batchelor and Green in 1972 (Batchelor & Green Reference Batchelor and Green1972a
,Reference Batchelor and Green
b
). The difficulty in the pair problem arises because a naive summation of the long-ranged pair interactions in the suspension viscosity problem, and in other related problems that include the determination of the hindered settling velocity (Batchelor Reference Batchelor1972) and the permeability of a dilute fixed bed (Hinch Reference Hinch1977), leads to either divergent or conditionally convergent integrals, and only in the 1970s was it shown that appropriate renormalizations were needed to sensibly characterize the effects of hydrodynamic interactions on the bulk characteristics of Stokesian suspensions. For the suspension viscosity problem in particular, even after the renormalization, the notion of the particulate phase modifying the shear viscosity to
$O({\it\phi}^{2})$
correction to the effective viscosity. This calculation, which includes the first effects of hydrodynamic interactions, was accomplished much later (than Einstein) by Batchelor and Green in 1972 (Batchelor & Green Reference Batchelor and Green1972a
,Reference Batchelor and Green
b
). The difficulty in the pair problem arises because a naive summation of the long-ranged pair interactions in the suspension viscosity problem, and in other related problems that include the determination of the hindered settling velocity (Batchelor Reference Batchelor1972) and the permeability of a dilute fixed bed (Hinch Reference Hinch1977), leads to either divergent or conditionally convergent integrals, and only in the 1970s was it shown that appropriate renormalizations were needed to sensibly characterize the effects of hydrodynamic interactions on the bulk characteristics of Stokesian suspensions. For the suspension viscosity problem in particular, even after the renormalization, the notion of the particulate phase modifying the shear viscosity to
![]() $O({\it\phi}^{2})$
, and, thence, of a Newtonian rheology for a Stokesian suspension at this order, was found to be crucially dependent on the topology of the pair-sphere trajectories. This is due to the occurrence of closed pair pathlines, and the resulting indeterminacy of the pair-distribution function on such trajectories in the purely hydrodynamic limit (Batchelor & Green Reference Batchelor and Green1972a
). The occurrence of closed particle (Kao, Cox & Mason Reference Kao, Cox and Mason1977) or fluid trajectories (Subramanian & Koch Reference Subramanian and Koch2006a
,Reference Subramanian and Koch
c
, Reference Subramanian and Koch2007) in Stokes flows is not uncommon, the underlying reason being the principle of reversibility associated with the quasisteady Stokes equations. The above indeterminacy associated with the pair probability on closed pair-particle pathlines prevents a straightforward determination of the stress tensor, at
$O({\it\phi}^{2})$
, and, thence, of a Newtonian rheology for a Stokesian suspension at this order, was found to be crucially dependent on the topology of the pair-sphere trajectories. This is due to the occurrence of closed pair pathlines, and the resulting indeterminacy of the pair-distribution function on such trajectories in the purely hydrodynamic limit (Batchelor & Green Reference Batchelor and Green1972a
). The occurrence of closed particle (Kao, Cox & Mason Reference Kao, Cox and Mason1977) or fluid trajectories (Subramanian & Koch Reference Subramanian and Koch2006a
,Reference Subramanian and Koch
c
, Reference Subramanian and Koch2007) in Stokes flows is not uncommon, the underlying reason being the principle of reversibility associated with the quasisteady Stokes equations. The above indeterminacy associated with the pair probability on closed pair-particle pathlines prevents a straightforward determination of the stress tensor, at
![]() $O({\it\phi}^{2})$
, for a range of linear flows that includes the rheologically important case of simple shear flow (Kao et al.
Reference Kao, Cox and Mason1977). Any calculation of the
$O({\it\phi}^{2})$
, for a range of linear flows that includes the rheologically important case of simple shear flow (Kao et al.
Reference Kao, Cox and Mason1977). Any calculation of the
![]() $O({\it\phi}^{2})$
contribution in such flows must therefore appeal to physics outside of Stokesian hydrodynamics in the dilute regime, such as three-particle interactions, weak particle (Subramanian & Brady Reference Subramanian and Brady2006) or fluid inertia (Morris, Yan & Koplik Reference Morris, Yan and Koplik2007) or weak Brownian motion (Morris & Brady Reference Morris and Brady1997).
$O({\it\phi}^{2})$
contribution in such flows must therefore appeal to physics outside of Stokesian hydrodynamics in the dilute regime, such as three-particle interactions, weak particle (Subramanian & Brady Reference Subramanian and Brady2006) or fluid inertia (Morris, Yan & Koplik Reference Morris, Yan and Koplik2007) or weak Brownian motion (Morris & Brady Reference Morris and Brady1997).
For a suspension of spheroids, the aforementioned rheological indeterminacy is already present at
![]() $O(nL^{3})$
, that is, even in the absence of hydrodynamic interactions. The aspect-ratio-dependent analogue of the Einstein coefficient depends only on the single-particle orientation distribution (owing to the absence of positional correlations at this order), and the latter is indeterminate. It was shown originally by Jeffery (Reference Jeffery1922) that an isolated spheroid in simple shear flow rotates along any of a one-parameter family of closed orbits now known as Jeffery orbits. The Jeffery orbits are spherical ellipses, with those for a prolate spheroid having their major axes aligned with the flow direction; the ones for an oblate spheroid are obtained via a 90° rotation. The existence of such closed orbits on the unit sphere of orientations leads to the indeterminacy above. In the convective limit (that is, for large values of the rotary Péclet number defined as
$O(nL^{3})$
, that is, even in the absence of hydrodynamic interactions. The aspect-ratio-dependent analogue of the Einstein coefficient depends only on the single-particle orientation distribution (owing to the absence of positional correlations at this order), and the latter is indeterminate. It was shown originally by Jeffery (Reference Jeffery1922) that an isolated spheroid in simple shear flow rotates along any of a one-parameter family of closed orbits now known as Jeffery orbits. The Jeffery orbits are spherical ellipses, with those for a prolate spheroid having their major axes aligned with the flow direction; the ones for an oblate spheroid are obtained via a 90° rotation. The existence of such closed orbits on the unit sphere of orientations leads to the indeterminacy above. In the convective limit (that is, for large values of the rotary Péclet number defined as
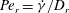 $Pe_{r}=\dot{{\it\gamma}}/D_{r}$
,
$Pe_{r}=\dot{{\it\gamma}}/D_{r}$
,
![]() $D_{r}$
being the Brownian rotary diffusivity, and
$D_{r}$
being the Brownian rotary diffusivity, and
![]() $\dot{{\it\gamma}}$
being the shear rate), the orientation probability density may be conveniently written in the form
$\dot{{\it\gamma}}$
being the shear rate), the orientation probability density may be conveniently written in the form
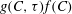 $g(C,{\it\tau})f(C)$
(Leal & Hinch Reference Leal and Hinch1971). The coordinates (
$g(C,{\it\tau})f(C)$
(Leal & Hinch Reference Leal and Hinch1971). The coordinates (
![]() $C,{\it\tau}$
) form a non-orthogonal system on the unit sphere that characterizes the particle motion along Jeffery orbits, with
$C,{\it\tau}$
) form a non-orthogonal system on the unit sphere that characterizes the particle motion along Jeffery orbits, with
![]() $C$
being an orbit constant that ranges from 0 to
$C$
being an orbit constant that ranges from 0 to
![]() $\infty$
and
$\infty$
and
![]() ${\it\tau}$
being the phase that changes at a constant aspect-ratio-dependent rate along a given orbit. The first factor in the orientation probability density,
${\it\tau}$
being the phase that changes at a constant aspect-ratio-dependent rate along a given orbit. The first factor in the orientation probability density,
![]() $g(C,{\it\tau})$
, determines the distribution of orientations along a Jeffery orbit, while the second factor,
$g(C,{\it\tau})$
, determines the distribution of orientations along a Jeffery orbit, while the second factor,
![]() $f(C)$
, determines the distribution of orientations across the various Jeffery orbits. Strictly speaking, neither of these two components is uniquely determined in the convective limit in the absence of interparticle interactions. A tiny polydispersity in the particle aspect ratio, however, is sufficient for the orientation distribution along a single Jeffery orbit to converge to a unique steady distribution given by the inverse rate of change of the azimuthal angle as found by Jeffery, and is a function of the particle aspect ratio (Okagawa, Cox & Mason Reference Okagawa, Cox and Mason1973a
,Reference Okagawa, Cox and Mason
b
). On the other hand, the function
$f(C)$
, determines the distribution of orientations across the various Jeffery orbits. Strictly speaking, neither of these two components is uniquely determined in the convective limit in the absence of interparticle interactions. A tiny polydispersity in the particle aspect ratio, however, is sufficient for the orientation distribution along a single Jeffery orbit to converge to a unique steady distribution given by the inverse rate of change of the azimuthal angle as found by Jeffery, and is a function of the particle aspect ratio (Okagawa, Cox & Mason Reference Okagawa, Cox and Mason1973a
,Reference Okagawa, Cox and Mason
b
). On the other hand, the function
![]() $f(C)$
is, by definition, unchanged by particle motion along Jeffery orbits, and therefore preserves its functional form in the absence of interactions. As a result, one predicts a sensitive dependence of the rheology of a dilute non-interacting suspension of non-Brownian spheroids on the initial orientation distribution! As for spherical particle suspensions, earlier authors have appealed to mechanisms such as Brownian motion (Leal & Hinch Reference Leal and Hinch1971; Hinch & Leal Reference Hinch and Leal1972), viscoelasticity (Leal Reference Leal1975), fluid and particle inertia (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
), and pair-hydrodynamic interactions in the limit of large aspect ratios (Okagawa et al.
Reference Okagawa, Cox and Mason1973a
; Rahnama, Koch & Shaqfeh Reference Rahnama, Koch and Shaqfeh1995), to obtain a drift across Jeffery orbits in an effort to endow the suspension with a finite memory and, thereby, arrive at a unique steady-state distribution across Jeffery orbits.
$f(C)$
is, by definition, unchanged by particle motion along Jeffery orbits, and therefore preserves its functional form in the absence of interactions. As a result, one predicts a sensitive dependence of the rheology of a dilute non-interacting suspension of non-Brownian spheroids on the initial orientation distribution! As for spherical particle suspensions, earlier authors have appealed to mechanisms such as Brownian motion (Leal & Hinch Reference Leal and Hinch1971; Hinch & Leal Reference Hinch and Leal1972), viscoelasticity (Leal Reference Leal1975), fluid and particle inertia (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
), and pair-hydrodynamic interactions in the limit of large aspect ratios (Okagawa et al.
Reference Okagawa, Cox and Mason1973a
; Rahnama, Koch & Shaqfeh Reference Rahnama, Koch and Shaqfeh1995), to obtain a drift across Jeffery orbits in an effort to endow the suspension with a finite memory and, thereby, arrive at a unique steady-state distribution across Jeffery orbits.
In this paper, we appeal specifically to weak inertial effects as a mechanism leading to a unique distribution of orientations across Jeffery orbits independent of initial conditions, a unique value for the Einstein coefficient analogue, and, thereby, a unique steady-state rheology in simple shear flow. We consider inertia of both the particle and that of the suspending fluid, and determine the inertial drift, at leading order, for both prolate and oblate spheroids of an arbitrary aspect ratio using a reciprocal theorem formulation together with a novel spheroidal harmonics formalism. The relevant non-dimensional measures of fluid and particle inertia are the Reynolds and Stokes numbers defined as
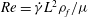 $Re=\dot{{\it\gamma}}L^{2}{\it\rho}_{f}/{\it\mu}$
and
$Re=\dot{{\it\gamma}}L^{2}{\it\rho}_{f}/{\it\mu}$
and
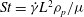 $St=\dot{{\it\gamma}}L^{2}{\it\rho}_{p}/{\it\mu}$
, and the leading-order drifts occur at
$St=\dot{{\it\gamma}}L^{2}{\it\rho}_{p}/{\it\mu}$
, and the leading-order drifts occur at
![]() $O(Re)$
and
$O(Re)$
and
![]() $O(St)$
, respectively; here,
$O(St)$
, respectively; here,
![]() ${\it\rho}_{p}$
and
${\it\rho}_{p}$
and
![]() ${\it\rho}_{f}$
are the particle and fluid densities,
${\it\rho}_{f}$
are the particle and fluid densities,
![]() $L$
the semimajor axis, and
$L$
the semimajor axis, and
![]() ${\it\mu}$
the suspending fluid viscosity. The time period of rotation remains equal to the Jeffery period to this order. For particle inertia alone, the analysis, being simpler, is extended to
${\it\mu}$
the suspending fluid viscosity. The time period of rotation remains equal to the Jeffery period to this order. For particle inertia alone, the analysis, being simpler, is extended to
![]() $O(St^{2})$
, and it is thereby shown that particle inertia acts to decrease the time period of rotation of a prolate spheroid, consistent with recent simulation results (see discussion below). The effect of fluid inertia on the time period of rotation occurs at
$O(St^{2})$
, and it is thereby shown that particle inertia acts to decrease the time period of rotation of a prolate spheroid, consistent with recent simulation results (see discussion below). The effect of fluid inertia on the time period of rotation occurs at
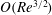 $O(Re^{3/2})$
for spheroids with aspect ratios of order unity, and an analysis of the same will be reported separately.
$O(Re^{3/2})$
for spheroids with aspect ratios of order unity, and an analysis of the same will be reported separately.
Jeffery (Reference Jeffery1922) himself had hypothesized that weak inertial effects would eventually move the particle to an orbit of minimum dissipation. These correspond to the log-rolling and tumbling orbits for prolate and oblate spheroids, respectively. Initial experimental investigations (Taylor Reference Taylor1923; Trevelyan & Mason Reference Trevelyan and Mason1951) were inconclusive. The earliest analytical investigation to study the effect of weak fluid inertia on a nearly spherical particle in simple shear flow was that of Saffman (Reference Saffman1956), and appeared to confirm Jeffery’s hypothesis, although no details were given. In the same paper, the author concluded that particle inertia does not lead to any drift. In contrast, Karnis, Goldsmith & Mason (Reference Karnis, Goldsmith and Mason1966), in experiments with disks and rods in Couette flow, observed the particles to migrate towards orbits of maximum energy dissipation. Later, Harper & Chang (Reference Harper and Chang1968) analysed the motion of a dumbbell-shaped particle, in simple shear flow, in the limit when the intersphere separation is much greater than the inertial screening length (of
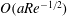 $O(aRe^{-1/2})$
,
$O(aRe^{-1/2})$
,
![]() $a$
being the sphere radius). The torque leading to the drift was regarded as arising from inertial lift forces (Saffman Reference Saffman1965) acting independently on each sphere and, as a result, the dumbbell was found to move towards a tumbling mode. However, as argued in Subramanian & Koch (Reference Subramanian and Koch2005), use of the Saffman lift force is inconsistent with the limit considered by the authors. There have been more recent investigations for the inertial drift, based on a reciprocal theorem formulation, that are either limited to particles with large aspect ratios (Subramanian & Koch Reference Subramanian and Koch2005), with the attendant simplifications arising from viscous slender body theory (Batchelor Reference Batchelor1970a
), or to particles with aspect ratios near unity which allow for a regular perturbation expansion about a sphere (Subramanian & Koch Reference Subramanian and Koch2006b
). For nearly spherical axisymmetric particles, Subramanian & Koch (Reference Subramanian and Koch2006b
) conclude that the effect of fluid inertia is in accordance with Jeffery’s hypothesis (as we show later, in appendix D, this is incorrect). Particle inertia was found to cause prolate and oblate near-spheres to drift towards tumbling and spinning modes, respectively. For slender fibres, Subramanian & Koch (Reference Subramanian and Koch2005) found a fluid inertial drift towards the tumbling mode, a decrease in the speed of rotation with increasing
$a$
being the sphere radius). The torque leading to the drift was regarded as arising from inertial lift forces (Saffman Reference Saffman1965) acting independently on each sphere and, as a result, the dumbbell was found to move towards a tumbling mode. However, as argued in Subramanian & Koch (Reference Subramanian and Koch2005), use of the Saffman lift force is inconsistent with the limit considered by the authors. There have been more recent investigations for the inertial drift, based on a reciprocal theorem formulation, that are either limited to particles with large aspect ratios (Subramanian & Koch Reference Subramanian and Koch2005), with the attendant simplifications arising from viscous slender body theory (Batchelor Reference Batchelor1970a
), or to particles with aspect ratios near unity which allow for a regular perturbation expansion about a sphere (Subramanian & Koch Reference Subramanian and Koch2006b
). For nearly spherical axisymmetric particles, Subramanian & Koch (Reference Subramanian and Koch2006b
) conclude that the effect of fluid inertia is in accordance with Jeffery’s hypothesis (as we show later, in appendix D, this is incorrect). Particle inertia was found to cause prolate and oblate near-spheres to drift towards tumbling and spinning modes, respectively. For slender fibres, Subramanian & Koch (Reference Subramanian and Koch2005) found a fluid inertial drift towards the tumbling mode, a decrease in the speed of rotation with increasing
![]() $Re$
, and a relatively modest critical
$Re$
, and a relatively modest critical
![]() $Re$
above which the particle ceases to rotate. It was also argued herein that the effects of particle inertia would be asymptotically small for large aspect ratios. Recently, the effect of particle inertia on the orientation of axisymmetric particles of arbitrary aspect ratios, to
$Re$
above which the particle ceases to rotate. It was also argued herein that the effects of particle inertia would be asymptotically small for large aspect ratios. Recently, the effect of particle inertia on the orientation of axisymmetric particles of arbitrary aspect ratios, to
![]() $O(St)$
, has been examined by Einarsson, Angilella & Mehlig (Reference Einarsson, Angilella and Mehlig2014). The authors obtain the correction to the leading-order Jeffery angular velocity, and conclude that prolate and oblate spheroids drift towards the tumbling and spinning modes, respectively, consistent with the near-sphere analysis of Subramanian & Koch (Reference Subramanian and Koch2006b
). Even more recently, Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015a
,Reference Einarsson, Candelier, Lundell, Angilella and Mehlig
b
) have looked at the effect of both particle and fluid inertia on spheroids of an arbitrary aspect ratio, and we comment on this effort in § 8.
$O(St)$
, has been examined by Einarsson, Angilella & Mehlig (Reference Einarsson, Angilella and Mehlig2014). The authors obtain the correction to the leading-order Jeffery angular velocity, and conclude that prolate and oblate spheroids drift towards the tumbling and spinning modes, respectively, consistent with the near-sphere analysis of Subramanian & Koch (Reference Subramanian and Koch2006b
). Even more recently, Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015a
,Reference Einarsson, Candelier, Lundell, Angilella and Mehlig
b
) have looked at the effect of both particle and fluid inertia on spheroids of an arbitrary aspect ratio, and we comment on this effort in § 8.
There have been several recent numerical investigations that examine the orientation dynamics of anisotropic particles in simple shear flow. These may be conveniently divided into those that analyse the orientational motion of neutrally buoyant spheroids
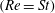 $(Re=St)$
, over a wide range of
$(Re=St)$
, over a wide range of
![]() $Re$
, via (mainly) Lattice Boltzmann simulations (Aidun, Lu & Ding Reference Aidun, Lu and Ding1998; Ding & Aidun Reference Ding and Aidun2000; Qi & Luo Reference Qi and Luo2003; Huang et al.
Reference Huang, Yang, Krafczyk and Lu2012; Mao & Alexeev Reference Mao and Alexeev2014) and via the distributed Lagrangian multiplier based fictitious domain method (Yu, Phan-Thien & Tanner Reference Yu, Phan-Thien and Tanner2007), and those that examine the orientation dynamics of massive spheroids and triaxial ellipsoids in shear flow in the absence of fluid inertia, but over a wide range of
$Re$
, via (mainly) Lattice Boltzmann simulations (Aidun, Lu & Ding Reference Aidun, Lu and Ding1998; Ding & Aidun Reference Ding and Aidun2000; Qi & Luo Reference Qi and Luo2003; Huang et al.
Reference Huang, Yang, Krafczyk and Lu2012; Mao & Alexeev Reference Mao and Alexeev2014) and via the distributed Lagrangian multiplier based fictitious domain method (Yu, Phan-Thien & Tanner Reference Yu, Phan-Thien and Tanner2007), and those that examine the orientation dynamics of massive spheroids and triaxial ellipsoids in shear flow in the absence of fluid inertia, but over a wide range of
![]() $St$
, via a numerical integration of the governing ODE’s (Lundell & Carlsson Reference Lundell and Carlsson2010, Reference Lundell and Carlsson2011; Challabotla, Nilsen & Andersson Reference Challabotla, Nilsen and Andersson2015). One of the main conclusions of the second group of investigations is a rather sharp transition, across a narrow range in
$St$
, via a numerical integration of the governing ODE’s (Lundell & Carlsson Reference Lundell and Carlsson2010, Reference Lundell and Carlsson2011; Challabotla, Nilsen & Andersson Reference Challabotla, Nilsen and Andersson2015). One of the main conclusions of the second group of investigations is a rather sharp transition, across a narrow range in
![]() $St$
, from a small-
$St$
, from a small-
![]() $St$
to a large-
$St$
to a large-
![]() $St$
dynamics. In the former regime, as would be expected, the inertial drift leads to a spiralling trajectory for the orientation vector, with each turn of the spiral closely resembling a Jeffery orbit. In the latter regime, the drift is again asymptotically slow but has a very different character, akin to the classical Euler top (Goldstein Reference Goldstein1962) with a superposed secular drift, that is outside the scope of the current investigation. The first group of investigations above, culminating in the recent effort of Huang et al. (Reference Huang, Yang, Krafczyk and Lu2012), has identified a series of transitions in the rotation mode as a function of
$St$
dynamics. In the former regime, as would be expected, the inertial drift leads to a spiralling trajectory for the orientation vector, with each turn of the spiral closely resembling a Jeffery orbit. In the latter regime, the drift is again asymptotically slow but has a very different character, akin to the classical Euler top (Goldstein Reference Goldstein1962) with a superposed secular drift, that is outside the scope of the current investigation. The first group of investigations above, culminating in the recent effort of Huang et al. (Reference Huang, Yang, Krafczyk and Lu2012), has identified a series of transitions in the rotation mode as a function of
![]() $Re$
for both prolate and oblate spheroids. With increasing
$Re$
for both prolate and oblate spheroids. With increasing
![]() $Re$
, the sequence of rotation modes are tumbling, log-rolling, inclined rolling, precession and nutation around an inclined axis and, finally, a stationary state at the highest
$Re$
, the sequence of rotation modes are tumbling, log-rolling, inclined rolling, precession and nutation around an inclined axis and, finally, a stationary state at the highest
![]() $Re$
values (Huang et al.
Reference Huang, Yang, Krafczyk and Lu2012), for a prolate spheroid. For an oblate spheroid, this sequence is simpler, consisting of a low-
$Re$
values (Huang et al.
Reference Huang, Yang, Krafczyk and Lu2012), for a prolate spheroid. For an oblate spheroid, this sequence is simpler, consisting of a low-
![]() $Re$
, spinning mode followed by an inclined spinning mode, and a stationary state at the highest
$Re$
, spinning mode followed by an inclined spinning mode, and a stationary state at the highest
![]() $Re$
values. The general focus of these simulation efforts has been more on the transition in rotations, and less on the dependence of the period of rotation on
$Re$
values. The general focus of these simulation efforts has been more on the transition in rotations, and less on the dependence of the period of rotation on
![]() $Re$
; although it is clear that, over the lower range of
$Re$
; although it is clear that, over the lower range of
![]() $Re$
values, the period increases monotonically due to the onset of fluid inertial effects. The work by Mao & Alexeev (Reference Mao and Alexeev2014) is an exception in this regard, and the authors find that the effects of particle and fluid inertia are, respectively, to decrease and increase the time period of rotation from the inertialess Jeffery value. Note that, in two dimensions, increasing
$Re$
values, the period increases monotonically due to the onset of fluid inertial effects. The work by Mao & Alexeev (Reference Mao and Alexeev2014) is an exception in this regard, and the authors find that the effects of particle and fluid inertia are, respectively, to decrease and increase the time period of rotation from the inertialess Jeffery value. Note that, in two dimensions, increasing
![]() $Re$
had already been shown to eventually arrest rotation of an elliptic cylinder (Ding & Aidun Reference Ding and Aidun2000). In three dimensions, for sufficiently slender bodies, such an arrest has been predicted to occur at a fairly modest
$Re$
had already been shown to eventually arrest rotation of an elliptic cylinder (Ding & Aidun Reference Ding and Aidun2000). In three dimensions, for sufficiently slender bodies, such an arrest has been predicted to occur at a fairly modest
![]() $Re$
of
$Re$
of
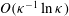 $O({\it\kappa}^{-1}\ln {\it\kappa})$
,
$O({\it\kappa}^{-1}\ln {\it\kappa})$
,
![]() ${\it\kappa}$
being the large aspect ratio (Subramanian & Koch Reference Subramanian and Koch2005). As is the case for numerical investigations, the above efforts for neutrally buoyant spheroids (and, to a lesser extent, those for massive spheroids) are limited in the number of aspect ratios examined and in terms of analysing the detailed dependence of the nature of the final steady or time-periodic state on the particular initial orientation. For instance, excepting Mao & Alexeev (Reference Mao and Alexeev2014), all other efforts only look at prolate and oblate spheroids with aspect ratios of 2 and 0.5, respectively. Further, the numerical simulations of neutrally buoyant spheroids are necessarily limited to wall-bounded domains with periodic boundary conditions in the flow and vorticity directions. The effect of the wall confinement on the aforementioned transitions is not small, and the effects of periodicity are uncertain. There is also some disagreement, between different efforts, with regard to the detailed sequence of transitions, and the precise estimates of the associated critical
${\it\kappa}$
being the large aspect ratio (Subramanian & Koch Reference Subramanian and Koch2005). As is the case for numerical investigations, the above efforts for neutrally buoyant spheroids (and, to a lesser extent, those for massive spheroids) are limited in the number of aspect ratios examined and in terms of analysing the detailed dependence of the nature of the final steady or time-periodic state on the particular initial orientation. For instance, excepting Mao & Alexeev (Reference Mao and Alexeev2014), all other efforts only look at prolate and oblate spheroids with aspect ratios of 2 and 0.5, respectively. Further, the numerical simulations of neutrally buoyant spheroids are necessarily limited to wall-bounded domains with periodic boundary conditions in the flow and vorticity directions. The effect of the wall confinement on the aforementioned transitions is not small, and the effects of periodicity are uncertain. There is also some disagreement, between different efforts, with regard to the detailed sequence of transitions, and the precise estimates of the associated critical
![]() $Re$
values. This appears partly due to the differing nature of the numerical methods, and partly due to the different initial orientations examined in different investigations. The analysis given here will serve as a very useful point of validation for any numerical effort. Although restricted to
$Re$
values. This appears partly due to the differing nature of the numerical methods, and partly due to the different initial orientations examined in different investigations. The analysis given here will serve as a very useful point of validation for any numerical effort. Although restricted to
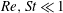 $Re,St\ll 1$
, the qualitative nature of the orientation dynamics is expected to conform to predictions even when
$Re,St\ll 1$
, the qualitative nature of the orientation dynamics is expected to conform to predictions even when
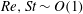 $Re,St\sim O(1)$
. In sharp contrast to the above numerical investigations and the earlier theoretical efforts, we cover the entire range of aspect ratios for both prolate and oblate spheroids, and show that, for sufficiently thin oblate spheroids (aspect ratios smaller than approximately 0.14, which have not been examined in any of the above simulations), the long-time orientation dynamics is a function of the initial orientation, with the unit sphere being divided into distinct basins of attraction corresponding to the tumbling and spinning modes. For the dilute regime of relevance here, the dependence on initial conditions for the said aspect ratios is expected to be eliminated, over much longer times, on account of weak thermal or hydrodynamically induced orientation fluctuations. The case of weak Brownian motion is analysed here in some detail.
$Re,St\sim O(1)$
. In sharp contrast to the above numerical investigations and the earlier theoretical efforts, we cover the entire range of aspect ratios for both prolate and oblate spheroids, and show that, for sufficiently thin oblate spheroids (aspect ratios smaller than approximately 0.14, which have not been examined in any of the above simulations), the long-time orientation dynamics is a function of the initial orientation, with the unit sphere being divided into distinct basins of attraction corresponding to the tumbling and spinning modes. For the dilute regime of relevance here, the dependence on initial conditions for the said aspect ratios is expected to be eliminated, over much longer times, on account of weak thermal or hydrodynamically induced orientation fluctuations. The case of weak Brownian motion is analysed here in some detail.
Very recently, there have been a pair of numerical investigations of both neutrally and non-neutrally buoyant prolate spheroids, again using variants of the Lattice Boltzmann method. Rosen, Lundell & Aidun (Reference Rosen, Lundell and Aidun2014) examined a neutrally buoyant prolate spheroid with aspect ratio 4 (in contrast to the aspect ratio of 2 considered in virtually all of the aforementioned numerical efforts) in simple shear flow with increasing
![]() $Re$
. A sequence of rotational states, similar to that found earlier by Huang et al. (Reference Huang, Yang, Krafczyk and Lu2012) for a prolate spheroid of aspect ratio 2, was found, although the transition Reynolds numbers differed in magnitude (lower for the higher aspect ratio). Importantly, the authors interpreted the transitions from one rotational state to the other in terms of the analogous bifurcations of the fixed points of a model two-dimensional two-parameter vector field. This dynamical systems perspective is crucial to understand the underlying system symmetries. For instance, the analogy with the model dynamical system naturally explains the presence of two possible inclined log-rolling and precessing modes, symmetrically disposed about the ambient vorticity axis; as to which one is actually observed in a simulation depends on the initial orientation. The authors also observed the tumbling mode of the spheroid to coexist with other rotational states at higher
$Re$
. A sequence of rotational states, similar to that found earlier by Huang et al. (Reference Huang, Yang, Krafczyk and Lu2012) for a prolate spheroid of aspect ratio 2, was found, although the transition Reynolds numbers differed in magnitude (lower for the higher aspect ratio). Importantly, the authors interpreted the transitions from one rotational state to the other in terms of the analogous bifurcations of the fixed points of a model two-dimensional two-parameter vector field. This dynamical systems perspective is crucial to understand the underlying system symmetries. For instance, the analogy with the model dynamical system naturally explains the presence of two possible inclined log-rolling and precessing modes, symmetrically disposed about the ambient vorticity axis; as to which one is actually observed in a simulation depends on the initial orientation. The authors also observed the tumbling mode of the spheroid to coexist with other rotational states at higher
![]() $Re$
, until the tumbling period diverged at a critical Reynolds number, via a saddle-node bifurcation, in a manner similar to that found earlier by one of the authors for two-dimensional elliptic cylinders (Ding & Aidun Reference Ding and Aidun2000). Rosen et al. (Reference Rosen, Do-Quang, Aidun and Lundell2015) have extended the study of Rosen et al. (Reference Rosen, Lundell and Aidun2014) to non-neutrally buoyant spheroids, and examine in detail the effects of varying particle inertia and aspect ratio (prolate spheroids with aspect ratios ranging from 2 to 6) on the different transition Reynolds numbers (tumbling
$Re$
, until the tumbling period diverged at a critical Reynolds number, via a saddle-node bifurcation, in a manner similar to that found earlier by one of the authors for two-dimensional elliptic cylinders (Ding & Aidun Reference Ding and Aidun2000). Rosen et al. (Reference Rosen, Do-Quang, Aidun and Lundell2015) have extended the study of Rosen et al. (Reference Rosen, Lundell and Aidun2014) to non-neutrally buoyant spheroids, and examine in detail the effects of varying particle inertia and aspect ratio (prolate spheroids with aspect ratios ranging from 2 to 6) on the different transition Reynolds numbers (tumbling
![]() $\rightarrow$
tumbling/log-rolling, tumbling/log-rolling
$\rightarrow$
tumbling/log-rolling, tumbling/log-rolling
![]() $\rightarrow$
tumbling/inclined log-rolling, etc).
$\rightarrow$
tumbling/inclined log-rolling, etc).
The rheology of anisotropic particle suspensions is relevant to a wide range of problems and applications. Blood rheology is sensitively dependent on the orientation distribution of the dominant suspended constituent – red blood cells (Caro et al. Reference Caro, Pedley, Schroter and Seed2012). Magma is a three-phase mixture of inorganic silicate melt, gas bubbles and anisotropic mineral crystals. While the role of bubbles on magma rheology (which determines the nature of the volcanic eruption) has been investigated in some detail earlier (Manga et al. Reference Manga, Castro, Cashman and Loewenberg1998; Llewellin, Mader & Wilson Reference Llewellin, Mader and Wilson2002), the importance of suspended crystals on magma rheology has only been recognized recently (Mueller, Llewellin & Mader Reference Mueller, Llewellin and Mader2011). It has, in fact, been shown that the shear viscosity increases significantly with increasing anisotropy (tending either towards a fibre or a disk morphology) of the suspended particles (Mueller, Llewellin & Mader Reference Mueller, Llewellin and Mader2010). Apart from the rheological significance, analysing the dynamics of anisotropic particles in shearing flows is also important in other contexts. For instance, reflective flakes, with sizes of the order of micrometres and often having extreme aspect ratios, are routinely used for flow visualization purposes (Thoroddsen & Bauer Reference Thoroddsen and Bauer1999; Goto, Kida & Fujiwara Reference Goto, Kida and Fujiwara2011). Interpretation of the scattered intensity patterns that arise from the suspended flakes depend crucially on knowledge of their orientation dynamics in the local shearing flow, and there have been investigations in this regard (Savas Reference Savas1985; Gauthier, Gondret & Rabaud Reference Gauthier, Gondret and Rabaud1998). Although not directly relevant to the present investigation, the emerging field of inertial microfluidics (Carlo Reference Carlo2009; Amini, Lee & Carlo Reference Amini, Lee and Carlo2014) involves high-throughput particle separation protocols in microfluidic channels that rely on the unique (transverse) equilibrium positions adopted by spherical particles under the action of inertial lift forces. Recently, it has been found that unique equilibrium positions, that arise from aspect-ratio-dependent lift forces, can also lead to shape sorting of particulate matter (Masaeli et al. Reference Masaeli, Sollier, Amini, Mao, Camacho, Doshi, Mitragotri, Alexeev and Carlo2012). The shape-selective nature of inertial lift forces relies crucially on the coupled positional and orientation dynamics of anisotropic particles in the bounded channel geometry. Other applications of interest, pertaining to atmospheric and geophysical scenarios, have been mentioned in Dabade, Marath & Subramanian (Reference Dabade, Marath and Subramanian2015).
The paper is organized as follows. In § 2, a reciprocal theorem formulation (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
) is used to obtain the governing equation for the angular velocity of a spheroid in simple shear flow, accounting for both fluid and particle inertia. The analysis of particle inertia is a fairly straightforward exercise, involving a regular expansion of the angular velocity for small
![]() $St$
, with the leading-order term being the Jeffery angular velocity. The analysis of even weak fluid inertia is a difficult exercise in general, but it is shown that the
$St$
, with the leading-order term being the Jeffery angular velocity. The analysis of even weak fluid inertia is a difficult exercise in general, but it is shown that the
![]() $O(Re)$
correction has a regular character, with its calculation requiring only a knowledge of the Stokes velocity fields. Thus, in § 3, we derive an analytical expression for the disturbance velocity field due to a freely rotating spheroid in simple shear flow, at
$O(Re)$
correction has a regular character, with its calculation requiring only a knowledge of the Stokes velocity fields. Thus, in § 3, we derive an analytical expression for the disturbance velocity field due to a freely rotating spheroid in simple shear flow, at
![]() $Re=0$
, based on a vector spheroidal harmonics formalism developed originally by Kushch and co-workers in the context of elastic composites (Kushch Reference Kushch1997, Reference Kushch1998; Kushch & Sangani Reference Kushch and Sangani2003). The general velocity field is expressed in spheroidal coordinates as a sum of five contributions, each corresponding to a simpler canonical linear flow, the relative amplitudes of these component flows being determined by the instantaneous orientation of the spheroid. As a validation exercise, this velocity field is first used to obtain the Jeffery equations for the spheroidal angular velocity in § 4. We then analyse the effects of particle and fluid inertia in §§ 5 and 6, respectively. Section 5.1 analyses the
$Re=0$
, based on a vector spheroidal harmonics formalism developed originally by Kushch and co-workers in the context of elastic composites (Kushch Reference Kushch1997, Reference Kushch1998; Kushch & Sangani Reference Kushch and Sangani2003). The general velocity field is expressed in spheroidal coordinates as a sum of five contributions, each corresponding to a simpler canonical linear flow, the relative amplitudes of these component flows being determined by the instantaneous orientation of the spheroid. As a validation exercise, this velocity field is first used to obtain the Jeffery equations for the spheroidal angular velocity in § 4. We then analyse the effects of particle and fluid inertia in §§ 5 and 6, respectively. Section 5.1 analyses the
![]() $O(St)$
drift for both prolate and oblate spheroids, while § 5.2 examines the
$O(St)$
drift for both prolate and oblate spheroids, while § 5.2 examines the
![]() $O(St^{2})$
alteration in the period of rotation of a tumbling prolate spheroid. Sections 6.1 and 6.2 analyse the
$O(St^{2})$
alteration in the period of rotation of a tumbling prolate spheroid. Sections 6.1 and 6.2 analyse the
![]() $O(Re)$
inertial drift for prolate and oblate spheroids, respectively, with a detailed characterization of the bifurcation in the orientation dynamics that occurs in the latter case for aspect ratios smaller than 0.142. Section 6.3 examines the drift, arising from both particle and fluid inertia, for non-neutrally buoyant prolate and oblate spheroids, as a function of the density ratio (
$O(Re)$
inertial drift for prolate and oblate spheroids, respectively, with a detailed characterization of the bifurcation in the orientation dynamics that occurs in the latter case for aspect ratios smaller than 0.142. Section 6.3 examines the drift, arising from both particle and fluid inertia, for non-neutrally buoyant prolate and oblate spheroids, as a function of the density ratio (
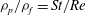 ${\it\rho}_{p}/{\it\rho}_{f}=St/Re$
); for neutrally buoyant oblate spheroids, in particular, the aspect ratio for the aforementioned bifurcation decreases slightly to 0.137. In § 7, we present the calculation of the steady-state shear viscosity, to
${\it\rho}_{p}/{\it\rho}_{f}=St/Re$
); for neutrally buoyant oblate spheroids, in particular, the aspect ratio for the aforementioned bifurcation decreases slightly to 0.137. In § 7, we present the calculation of the steady-state shear viscosity, to
![]() $O(nL^{3})$
, of a dilute suspension of neutrally buoyant spheroids. In § 7.1, the shear viscosity is calculated for a suspension of non-Brownian spheroids, and the aforementioned bifurcation in the orientation dynamics implies a kink in the shear-viscosity curve for oblate spheroids at the critical aspect ratio of 0.137, and a dependence of the viscosity on the initial orientation distribution, for smaller aspect ratios, via the relative proportions of particles in the tumbling and spinning modes at the initial instant. Next, in § 7.2, we show that even asymptotically weak Brownian motion, acting over sufficiently long times, eliminates this dependence. The resulting unique steady shear viscosity now exhibits a jump across a considerably smaller aspect ratio of approximately 0.0126 (for oblate spheroids) owing to a discontinuous transition in the peak of the orientation distribution from the vicinity of the spinning mode (aspect ratios greater than 0.0126) to the vicinity of the tumbling mode (aspect ratios less than 0.0126) in the convective limit (
$O(nL^{3})$
, of a dilute suspension of neutrally buoyant spheroids. In § 7.1, the shear viscosity is calculated for a suspension of non-Brownian spheroids, and the aforementioned bifurcation in the orientation dynamics implies a kink in the shear-viscosity curve for oblate spheroids at the critical aspect ratio of 0.137, and a dependence of the viscosity on the initial orientation distribution, for smaller aspect ratios, via the relative proportions of particles in the tumbling and spinning modes at the initial instant. Next, in § 7.2, we show that even asymptotically weak Brownian motion, acting over sufficiently long times, eliminates this dependence. The resulting unique steady shear viscosity now exhibits a jump across a considerably smaller aspect ratio of approximately 0.0126 (for oblate spheroids) owing to a discontinuous transition in the peak of the orientation distribution from the vicinity of the spinning mode (aspect ratios greater than 0.0126) to the vicinity of the tumbling mode (aspect ratios less than 0.0126) in the convective limit (
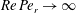 $Re\,Pe_{r}\rightarrow \infty$
). In § 8, we begin with a summary of the main results, and then examine the steady shear viscosity for finite
$Re\,Pe_{r}\rightarrow \infty$
). In § 8, we begin with a summary of the main results, and then examine the steady shear viscosity for finite
![]() $Re\,Pe_{r}$
, showing, in particular, that a dilute inertial suspension of thin oblate spheroids exhibits a pronounced shear-thickening rheology for aspect ratios greater than 0.0126.
$Re\,Pe_{r}$
, showing, in particular, that a dilute inertial suspension of thin oblate spheroids exhibits a pronounced shear-thickening rheology for aspect ratios greater than 0.0126.
2 Formulation for the inertial drift: the generalized reciprocal theorem
The generalized reciprocal theorem relates the velocity and stress fields of the problem of interest and those of a simpler test problem for which the solution is known. Both sets of fields are solutions for the flow past a given body (a spheroid with a given orientation in the present case), but with different boundary conditions and possibly governed by different dynamical equations (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
). Since the quantity of interest here is the inertial correction to the angular velocity of a spheroid in simple shear flow, the first problem,
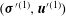 $({\bf\sigma}^{\prime (1)},\boldsymbol{u}^{\prime (1)})$
, is taken to correspond to a spheroid suspended in a Newtonian fluid undergoing simple shear flow with the inertial acceleration, both of the particle and that of the fluid, being taken into account. Here,
$({\bf\sigma}^{\prime (1)},\boldsymbol{u}^{\prime (1)})$
, is taken to correspond to a spheroid suspended in a Newtonian fluid undergoing simple shear flow with the inertial acceleration, both of the particle and that of the fluid, being taken into account. Here,
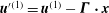 $\boldsymbol{u}^{\prime (1)}=\boldsymbol{u}^{(1)}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
is the disturbance velocity field,
$\boldsymbol{u}^{\prime (1)}=\boldsymbol{u}^{(1)}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
is the disturbance velocity field,
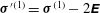 ${\bf\sigma}^{\prime (1)}={\bf\sigma}^{(1)}-2\unicode[STIX]{x1D640}$
is the corresponding stress field, and
${\bf\sigma}^{\prime (1)}={\bf\sigma}^{(1)}-2\unicode[STIX]{x1D640}$
is the corresponding stress field, and
![]() ${\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
is the ambient simple shear defined with the origin at the centre of the spheroid, all in non-dimensional form.
${\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
is the ambient simple shear defined with the origin at the centre of the spheroid, all in non-dimensional form.
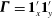 ${\it\bf\Gamma}=\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }$
and
${\it\bf\Gamma}=\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }$
and
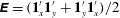 $\unicode[STIX]{x1D640}=(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })/2$
are the transpose of the non-dimensional velocity gradient and rate-of-strain tensors, respectively, in a space-fixed coordinate system;
$\unicode[STIX]{x1D640}=(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })/2$
are the transpose of the non-dimensional velocity gradient and rate-of-strain tensors, respectively, in a space-fixed coordinate system;
![]() $X^{\prime }$
,
$X^{\prime }$
,
![]() $Y^{\prime }$
and
$Y^{\prime }$
and
![]() $Z^{\prime }$
being the flow, gradient and vorticity directions, respectively, of the ambient simple shear. The test problem,
$Z^{\prime }$
being the flow, gradient and vorticity directions, respectively, of the ambient simple shear. The test problem,
 $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, corresponds to the Stokesian rotation of a spheroid, with the same instantaneous orientation, in an otherwise quiescent ambient. The reciprocal theorem then yields the following identity:
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, corresponds to the Stokesian rotation of a spheroid, with the same instantaneous orientation, in an otherwise quiescent ambient. The reciprocal theorem then yields the following identity:
 $$\begin{eqnarray}\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S-\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\boldsymbol{\cdot }{\bf\sigma}^{(1)}\,\text{d}S=Re\int _{V}\frac{\text{D}\boldsymbol{u}^{(1)}}{\text{D}t}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\end{eqnarray}$$
$$\begin{eqnarray}\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S-\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\boldsymbol{\cdot }{\bf\sigma}^{(1)}\,\text{d}S=Re\int _{V}\frac{\text{D}\boldsymbol{u}^{(1)}}{\text{D}t}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V,\end{eqnarray}$$
where
![]() $\boldsymbol{n}$
is the unit normal into the fluid domain
$\boldsymbol{n}$
is the unit normal into the fluid domain
![]() $V$
and
$V$
and
![]() $S$
includes all bounding surfaces. Here,
$S$
includes all bounding surfaces. Here,
![]() $Re$
is a non-dimensional measure of fluid inertia in relation to viscous forces, and is defined as
$Re$
is a non-dimensional measure of fluid inertia in relation to viscous forces, and is defined as
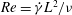 $Re=\dot{{\it\gamma}}L^{2}/{\it\nu}$
, where
$Re=\dot{{\it\gamma}}L^{2}/{\it\nu}$
, where
![]() $\dot{{\it\gamma}}$
is the ambient shear rate,
$\dot{{\it\gamma}}$
is the ambient shear rate,
![]() $L$
is taken to be the spheroid semimajor axis,
$L$
is taken to be the spheroid semimajor axis,
 ${\it\nu}={\it\mu}/{\it\rho}_{f}$
is the kinematic viscosity of the suspending fluid, with
${\it\nu}={\it\mu}/{\it\rho}_{f}$
is the kinematic viscosity of the suspending fluid, with
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() ${\it\rho}_{f}$
being its viscosity and density, respectively. The velocity fields
${\it\rho}_{f}$
being its viscosity and density, respectively. The velocity fields
![]() $\boldsymbol{u}^{\prime (1)}$
and
$\boldsymbol{u}^{\prime (1)}$
and
![]() $\boldsymbol{u}^{(2)}$
decay sufficiently rapidly for the surface integrals at infinity to be neglected, and the bounding surface
$\boldsymbol{u}^{(2)}$
decay sufficiently rapidly for the surface integrals at infinity to be neglected, and the bounding surface
![]() $S$
in (2.1) reduces to that of the spheroid (
$S$
in (2.1) reduces to that of the spheroid (
![]() $S_{p}$
). The inertial acceleration
$S_{p}$
). The inertial acceleration
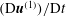 $(\text{D}\boldsymbol{u}^{(1)})/\text{D}t$
in (2.1) is written in terms of
$(\text{D}\boldsymbol{u}^{(1)})/\text{D}t$
in (2.1) is written in terms of
![]() ${\it\bf\Gamma}$
and
${\it\bf\Gamma}$
and
![]() $\boldsymbol{u}^{\prime (1)}$
below (see (2.11)). The no-slip boundary conditions in the two problems imply that, on
$\boldsymbol{u}^{\prime (1)}$
below (see (2.11)). The no-slip boundary conditions in the two problems imply that, on
![]() $S_{P}$
,
$S_{P}$
,
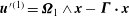 $\boldsymbol{u}^{\prime (1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
and
$\boldsymbol{u}^{\prime (1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}$
and
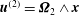 $\boldsymbol{u}^{(2)}={\it\bf\Omega}_{2}\wedge \boldsymbol{x}$
, where
$\boldsymbol{u}^{(2)}={\it\bf\Omega}_{2}\wedge \boldsymbol{x}$
, where
![]() ${\it\bf\Omega}_{1}$
and
${\it\bf\Omega}_{1}$
and
![]() ${\it\bf\Omega}_{2}$
are the angular velocities of the spheroid in the actual problem and test problem, respectively. In this paper, we determine
${\it\bf\Omega}_{2}$
are the angular velocities of the spheroid in the actual problem and test problem, respectively. In this paper, we determine
![]() ${\it\bf\Omega}_{1}$
to
${\it\bf\Omega}_{1}$
to
![]() $O(Re)$
, and to
$O(Re)$
, and to
![]() $O(St^{2})$
, where
$O(St^{2})$
, where
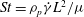 $St={\it\rho}_{p}\dot{{\it\gamma}}L^{2}/{\it\mu}$
is a dimensionless measure of particle inertia,
$St={\it\rho}_{p}\dot{{\it\gamma}}L^{2}/{\it\mu}$
is a dimensionless measure of particle inertia,
![]() ${\it\rho}_{p}$
being the particle density. The relative importance of particle and fluid inertia is determined by the ratio
${\it\rho}_{p}$
being the particle density. The relative importance of particle and fluid inertia is determined by the ratio
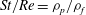 $St/Re={\it\rho}_{p}/{\it\rho}_{f}$
. Thus, for a gas–solid system we have
$St/Re={\it\rho}_{p}/{\it\rho}_{f}$
. Thus, for a gas–solid system we have
![]() $St\gg Re$
, but for solid–liquid systems
$St\gg Re$
, but for solid–liquid systems
![]() $St\approx Re$
; for neutrally buoyant particles in particular,
$St\approx Re$
; for neutrally buoyant particles in particular,
![]() $St=Re$
.
$St=Re$
.
Accounting for the boundary conditions above, the surface integrals in (2.1) may now be expressed as:
 $$\begin{eqnarray}\displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\boldsymbol{\cdot }{\bf\sigma}^{(1)}\,\text{d}S & = & \displaystyle {\it\bf\Omega}_{2}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\boldsymbol{\cdot }{\bf\sigma}^{(1)}\,\text{d}S & = & \displaystyle {\it\bf\Omega}_{2}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{1},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle St\,{\it\bf\Omega}_{2}\boldsymbol{\cdot }\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle St\,{\it\bf\Omega}_{2}\boldsymbol{\cdot }\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S & = & \displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }({\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S & = & \displaystyle \int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }({\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }{\bf\sigma}^{(2)}\,\text{d}S,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2}-{\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2}-{\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S,\end{eqnarray}$$
where we have assumed the absence of any external torque in the problem of interest. As a result, the hydrodynamic torque
![]() $(\boldsymbol{{\mathcal{L}}}_{1})$
must equal the angular acceleration, and
$(\boldsymbol{{\mathcal{L}}}_{1})$
must equal the angular acceleration, and
![]() $\unicode[STIX]{x1D644}_{p}$
above is the moment of inertia tensor of the spheroid. For an inertialess particle, the torque-free condition would mean
$\unicode[STIX]{x1D644}_{p}$
above is the moment of inertia tensor of the spheroid. For an inertialess particle, the torque-free condition would mean
![]() $\boldsymbol{{\mathcal{L}}}_{1}=0$
. The identity (2.1) now takes the form:
$\boldsymbol{{\mathcal{L}}}_{1}=0$
. The identity (2.1) now takes the form:
 $$\begin{eqnarray}{\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\right]\boldsymbol{\cdot }{\it\bf\Omega}_{2}+Re\int _{V}\frac{\text{D}\boldsymbol{u}^{(1)}}{\text{D}t}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}{\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\right]\boldsymbol{\cdot }{\it\bf\Omega}_{2}+Re\int _{V}\frac{\text{D}\boldsymbol{u}^{(1)}}{\text{D}t}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\end{eqnarray}$$
The non-dimensional equations of motion and the continuity equation for the problem of interest,
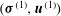 $({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, are given by:
$({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle Re\left[\frac{\partial \boldsymbol{u}^{(1)}}{\partial t}+\boldsymbol{u}^{(1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}\right]=-\boldsymbol{{\rm\nabla}}p^{(1)}+{\rm\nabla}^{2}\boldsymbol{u}^{(1)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Re\left[\frac{\partial \boldsymbol{u}^{(1)}}{\partial t}+\boldsymbol{u}^{(1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}\right]=-\boldsymbol{{\rm\nabla}}p^{(1)}+{\rm\nabla}^{2}\boldsymbol{u}^{(1)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{(1)}=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{(1)}=0. & \displaystyle\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(1)}\rightarrow {\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(1)}\rightarrow {\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
In terms of the disturbance field used in the reciprocal theorem formulation above, we have:
 $$\begin{eqnarray}\displaystyle & \displaystyle Re\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]=-\boldsymbol{{\rm\nabla}}p^{\prime (1)}+{\rm\nabla}^{2}\boldsymbol{u}^{\prime (1)},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Re\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]=-\boldsymbol{{\rm\nabla}}p^{\prime (1)}+{\rm\nabla}^{2}\boldsymbol{u}^{\prime (1)},\quad & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}=0, & \displaystyle\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{\prime (1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{\prime (1)}={\it\bf\Omega}_{1}\wedge \boldsymbol{x}-{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{\prime (1)}\rightarrow 0\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{\prime (1)}\rightarrow 0\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
The test problem,
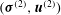 $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, in (2.1), is defined by
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, in (2.1), is defined by
 $$\begin{eqnarray}\displaystyle & \displaystyle -\boldsymbol{{\rm\nabla}}p^{(2)}+{\rm\nabla}^{2}\boldsymbol{u}^{(2)}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\boldsymbol{{\rm\nabla}}p^{(2)}+{\rm\nabla}^{2}\boldsymbol{u}^{(2)}=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}=0, & \displaystyle\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(2)}={\it\bf\Omega}_{2}\wedge \boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(2)}={\it\bf\Omega}_{2}\wedge \boldsymbol{x}\quad \text{for}~\boldsymbol{x}\,\in \,S_{p}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(2)}\rightarrow 0\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{(2)}\rightarrow 0\quad \text{for}~\boldsymbol{x}\rightarrow \infty . & \displaystyle\end{eqnarray}$$
For
![]() $St=0$
,
$St=0$
,
![]() ${\it\bf\Omega}_{2}$
may be chosen orthogonal to the spheroidal symmetry axis since the axial rotation of the spheroid does not couple to a change in its orientation. An inertialess spheroid, as it rotates along a Jeffery orbit, spins at a rate commensurate with the ambient vorticity vector projected along its axis. However, with particle inertia, the presence of gyroscopic forces implies that orientation and spin dynamics are coupled, and the test problem must therefore include both the axial and transverse rotation problems (Subramanian & Koch Reference Subramanian and Koch2006b
).
${\it\bf\Omega}_{2}$
may be chosen orthogonal to the spheroidal symmetry axis since the axial rotation of the spheroid does not couple to a change in its orientation. An inertialess spheroid, as it rotates along a Jeffery orbit, spins at a rate commensurate with the ambient vorticity vector projected along its axis. However, with particle inertia, the presence of gyroscopic forces implies that orientation and spin dynamics are coupled, and the test problem must therefore include both the axial and transverse rotation problems (Subramanian & Koch Reference Subramanian and Koch2006b
).

Figure 1. The body-fixed and space-fixed coordinate systems for a spheroid in simple shear flow.
Using the form of the inertial acceleration in (2.11), (2.6) may be rewritten as:
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2} & = & \displaystyle {\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\right]\boldsymbol{\cdot }{\it\bf\Omega}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\boldsymbol{{\mathcal{L}}}_{2} & = & \displaystyle {\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\bf\sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\right]\boldsymbol{\cdot }{\it\bf\Omega}_{2}\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V.\qquad \quad\end{eqnarray}$$
Further, noting that the velocity field in the test problem is linear in
![]() ${\it\bf\Omega}_{2}$
, one may write
${\it\bf\Omega}_{2}$
, one may write
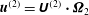 $\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
,
$\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
,
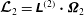 $\boldsymbol{{\mathcal{L}}}_{2}=\unicode[STIX]{x1D647}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
and
$\boldsymbol{{\mathcal{L}}}_{2}=\unicode[STIX]{x1D647}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
and
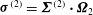 ${\bf\sigma}^{(2)}={\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
, where
${\bf\sigma}^{(2)}={\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}_{2}$
, where
![]() $\unicode[STIX]{x1D650}^{(2)}$
and
$\unicode[STIX]{x1D650}^{(2)}$
and
![]() $\unicode[STIX]{x1D647}^{(2)}$
are second-order tensors, and
$\unicode[STIX]{x1D647}^{(2)}$
are second-order tensors, and
![]() ${\it\bf\Sigma}^{(2)}$
is a third-order tensor, dependent only on the geometry of the spheroidal particle, and are known in closed form as a function of the aspect ratio (see § 3; also see Dabade et al. (Reference Dabade, Marath and Subramanian2015)). Accounting for
${\it\bf\Sigma}^{(2)}$
is a third-order tensor, dependent only on the geometry of the spheroidal particle, and are known in closed form as a function of the aspect ratio (see § 3; also see Dabade et al. (Reference Dabade, Marath and Subramanian2015)). Accounting for
![]() ${\it\bf\Omega}_{2}$
being arbitrary, (2.19) takes the form:
${\it\bf\Omega}_{2}$
being arbitrary, (2.19) takes the form:
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad +\,Re\int _{V}\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad +\,Re\int _{V}\left[\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\qquad \quad\end{eqnarray}$$
valid for arbitrary
![]() $Re$
and
$Re$
and
![]() $St$
. In § 3, we obtain expressions for the disturbance fields that appear in (2.20), using a spheroidal harmonics formalism, in a body-fixed coordinate system aligned with the spheroid symmetry axis. As a result, it becomes convenient to evaluate the unsteady acceleration involved in the last integral on the right-hand side of (2.20) in a coordinate system that rotates with the spheroid (
$St$
. In § 3, we obtain expressions for the disturbance fields that appear in (2.20), using a spheroidal harmonics formalism, in a body-fixed coordinate system aligned with the spheroid symmetry axis. As a result, it becomes convenient to evaluate the unsteady acceleration involved in the last integral on the right-hand side of (2.20) in a coordinate system that rotates with the spheroid (
![]() $XYZ$
in figure 1), but with the
$XYZ$
in figure 1), but with the
![]() $Y$
-axis constrained to lie in the flow–gradient plane. The constraint implies that while the axes of this coordinate system section rotate with the spheroid, the resulting spin about the spheroid axis (
$Y$
-axis constrained to lie in the flow–gradient plane. The constraint implies that while the axes of this coordinate system section rotate with the spheroid, the resulting spin about the spheroid axis (
![]() $Z$
) differs from the actual rate of spin. Using the relation between the time derivatives in the two coordinate systems, we have:
$Z$
) differs from the actual rate of spin. Using the relation between the time derivatives in the two coordinate systems, we have:
 $$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)} & = & \displaystyle \frac{\text{d}\boldsymbol{u}^{\prime (1)}}{\text{d}t}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)} & = & \displaystyle \frac{\text{d}\boldsymbol{u}^{\prime (1)}}{\text{d}t}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\text{d}\boldsymbol{u}^{\prime (1)}}{\text{d}t}\right)_{r}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\text{d}\boldsymbol{u}^{\prime (1)}}{\text{d}t}\right)_{r}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+\boldsymbol{u}_{r}^{(1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+\boldsymbol{u}_{r}^{(1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)},\end{eqnarray}$$
where
![]() ${\it\bf\Omega}_{b}$
is the angular velocity of the body-fixed coordinate system, and we have used that the total time derivative in the rotating coordinate system involves calculating the rate of change for an element that moves with the velocity in the rotating coordinate system, which is given in terms of the original disturbance field as
${\it\bf\Omega}_{b}$
is the angular velocity of the body-fixed coordinate system, and we have used that the total time derivative in the rotating coordinate system involves calculating the rate of change for an element that moves with the velocity in the rotating coordinate system, which is given in terms of the original disturbance field as
 $\boldsymbol{u}_{r}^{(1)}=\boldsymbol{u}^{\prime (1)}-{\it\bf\Omega}_{b}\wedge \boldsymbol{x}$
. Using this relation, (2.23) takes the form:
$\boldsymbol{u}_{r}^{(1)}=\boldsymbol{u}^{\prime (1)}-{\it\bf\Omega}_{b}\wedge \boldsymbol{x}$
. Using this relation, (2.23) takes the form:
 $$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)} & = & \displaystyle \left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)}-({\it\bf\Omega}_{b}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)} & = & \displaystyle \left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)}-({\it\bf\Omega}_{b}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the third term arises from the usual rate of change of the rotating unit vector triad relative to a space-fixed coordinate system, while the fourth term denotes the rate of change due to the spatially inhomogeneous disturbance velocity field being swept past a space-fixed point with velocity
![]() ${\it\bf\Omega}_{b}\wedge \boldsymbol{x}$
. Using (2.24) in (2.20), we have the following form for the reciprocal theorem identity:
${\it\bf\Omega}_{b}\wedge \boldsymbol{x}$
. Using (2.24) in (2.20), we have the following form for the reciprocal theorem identity:
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)} & = & \displaystyle {\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)}-({\it\bf\Omega}_{b}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\vphantom{\left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)} & = & \displaystyle {\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,Re\int _{V}\left[\left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}^{\prime (1)}+\boldsymbol{u}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\it\bf\Omega}_{b}\wedge \boldsymbol{u}^{\prime (1)}-({\it\bf\Omega}_{b}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime (1)}\vphantom{\left(\frac{\partial \boldsymbol{u}^{\prime (1)}}{\partial t}\right)_{r}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\end{eqnarray}$$
which will be used in conjunction with the expressions for the disturbance velocity fields derived in § 3.
In order to estimate the
![]() $O(Re)$
correction to
$O(Re)$
correction to
![]() ${\it\bf\Omega}_{1}$
, it is sufficient to use the leading-order Jeffery approximation for
${\it\bf\Omega}_{1}$
, it is sufficient to use the leading-order Jeffery approximation for
![]() ${\it\bf\Omega}_{b}$
in the volume integral in (2.25), since the neglected terms of
${\it\bf\Omega}_{b}$
in the volume integral in (2.25), since the neglected terms of
![]() $O(ReSt)$
and
$O(ReSt)$
and
![]() $O(Re^{2})$
are asymptotically smaller than those retained. This leading-order angular velocity, obtained from neglecting the inertial contributions in (2.25), is given by:
$O(Re^{2})$
are asymptotically smaller than those retained. This leading-order angular velocity, obtained from neglecting the inertial contributions in (2.25), is given by:
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S. & & \displaystyle\end{eqnarray}$$
The components of
![]() ${\it\bf\Omega}_{jeff}$
orthogonal to
${\it\bf\Omega}_{jeff}$
orthogonal to
![]() $\boldsymbol{p}$
, obtained from (2.26), lead to the well-known Jeffery orbit equations for a spheroid (see § 4) which, in non-dimensional form, are given by Leal & Hinch (Reference Leal and Hinch1971), Kim & Karrila (Reference Kim and Karrila1991):
$\boldsymbol{p}$
, obtained from (2.26), lead to the well-known Jeffery orbit equations for a spheroid (see § 4) which, in non-dimensional form, are given by Leal & Hinch (Reference Leal and Hinch1971), Kim & Karrila (Reference Kim and Karrila1991):
 $$\begin{eqnarray}\dot{\boldsymbol{p}}_{jeff}={\bf\omega}\wedge \boldsymbol{p}+\frac{{\it\kappa}^{2}-1}{{\it\kappa}^{2}+1}[\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p}-\boldsymbol{p}(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})],\end{eqnarray}$$
$$\begin{eqnarray}\dot{\boldsymbol{p}}_{jeff}={\bf\omega}\wedge \boldsymbol{p}+\frac{{\it\kappa}^{2}-1}{{\it\kappa}^{2}+1}[\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p}-\boldsymbol{p}(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})],\end{eqnarray}$$
where
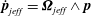 $\dot{\boldsymbol{p}}_{jeff}={\it\bf\Omega}_{jeff}\wedge \boldsymbol{p}$
,
$\dot{\boldsymbol{p}}_{jeff}={\it\bf\Omega}_{jeff}\wedge \boldsymbol{p}$
,
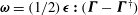 ${\bf\omega}=(1/2)\,{\bf\epsilon}\boldsymbol{ : }({\it\bf\Gamma}-{\it\bf\Gamma}^{\dagger })$
, with
${\bf\omega}=(1/2)\,{\bf\epsilon}\boldsymbol{ : }({\it\bf\Gamma}-{\it\bf\Gamma}^{\dagger })$
, with
![]() ${\it\bf\Gamma}$
as defined before, is the ambient vorticity vector and
${\it\bf\Gamma}$
as defined before, is the ambient vorticity vector and
![]() ${\it\kappa}$
is the spheroid aspect ratio; if
${\it\kappa}$
is the spheroid aspect ratio; if
![]() $b$
be the semiminor axis,
$b$
be the semiminor axis,
![]() ${\it\kappa}=L/b$
and
${\it\kappa}=L/b$
and
![]() $b/L$
for prolate and oblate spheroids, respectively. Since the spheroid spins at a rate commensurate with the projected ambient vorticity, we have
$b/L$
for prolate and oblate spheroids, respectively. Since the spheroid spins at a rate commensurate with the projected ambient vorticity, we have
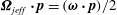 ${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}=({\bf\omega}\boldsymbol{\cdot }\boldsymbol{p})/2$
. The solution of (2.27) may be written in terms of spherical coordinates (with the ambient vorticity direction as the polar axis) as:
${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}=({\bf\omega}\boldsymbol{\cdot }\boldsymbol{p})/2$
. The solution of (2.27) may be written in terms of spherical coordinates (with the ambient vorticity direction as the polar axis) as:
 $$\begin{eqnarray}\displaystyle & \displaystyle \tan {\it\phi}_{j}=\frac{1}{{\it\kappa}\tan \left[\displaystyle \frac{{\it\kappa}t}{({\it\kappa}^{2}+1)}\right]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tan {\it\phi}_{j}=\frac{1}{{\it\kappa}\tan \left[\displaystyle \frac{{\it\kappa}t}{({\it\kappa}^{2}+1)}\right]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \tan {\it\theta}_{j}=\frac{C{\it\kappa}}{({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})^{1/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tan {\it\theta}_{j}=\frac{C{\it\kappa}}{({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})^{1/2}}, & \displaystyle\end{eqnarray}$$
where
![]() ${\it\theta}_{j}$
is the angle between the symmetry axis of the spheroid and the direction (
${\it\theta}_{j}$
is the angle between the symmetry axis of the spheroid and the direction (
![]() $Z^{\prime }$
) of ambient vorticity and
$Z^{\prime }$
) of ambient vorticity and
![]() ${\it\phi}_{j}$
is the dihedral angle between the flow–vorticity plane (
${\it\phi}_{j}$
is the dihedral angle between the flow–vorticity plane (
![]() $X^{\prime }Z^{\prime }$
) and the orientation–vorticity plane (
$X^{\prime }Z^{\prime }$
) and the orientation–vorticity plane (
![]() $ZZ^{\prime }$
) – see figure 1. Here,
$ZZ^{\prime }$
) – see figure 1. Here,
![]() $C$
is the orbit constant, ranging from zero (log-rolling motion for a prolate spheroid, and spinning for an oblate spheroid, about the ambient vorticity) to infinity (tumbling motion in the flow–gradient plane), and
$C$
is the orbit constant, ranging from zero (log-rolling motion for a prolate spheroid, and spinning for an oblate spheroid, about the ambient vorticity) to infinity (tumbling motion in the flow–gradient plane), and
 ${\it\tau}={\it\kappa}t/({\it\kappa}^{2}+1)$
is the phase along an orbit (Leal & Hinch Reference Leal and Hinch1971; Kim & Karrila Reference Kim and Karrila1991). The period of rotation is independent of the orbit constant, being given by
${\it\tau}={\it\kappa}t/({\it\kappa}^{2}+1)$
is the phase along an orbit (Leal & Hinch Reference Leal and Hinch1971; Kim & Karrila Reference Kim and Karrila1991). The period of rotation is independent of the orbit constant, being given by
 $T_{jeff}=2{\rm\pi}({\it\kappa}+1/{\it\kappa})$
for all
$T_{jeff}=2{\rm\pi}({\it\kappa}+1/{\it\kappa})$
for all
![]() $C$
. Thus,
$C$
. Thus,
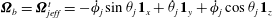 ${\it\bf\Omega}_{b}={\it\bf\Omega}_{jeff}^{t}=-\dot{{\it\phi}}_{j}\sin {\it\theta}_{j}\,\mathbf{1}_{x}+\dot{{\it\theta}}_{j}\,\mathbf{1}_{y}+\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}\,\mathbf{1}_{z}$
, with
${\it\bf\Omega}_{b}={\it\bf\Omega}_{jeff}^{t}=-\dot{{\it\phi}}_{j}\sin {\it\theta}_{j}\,\mathbf{1}_{x}+\dot{{\it\theta}}_{j}\,\mathbf{1}_{y}+\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}\,\mathbf{1}_{z}$
, with
![]() ${\it\phi}_{j}$
and
${\it\phi}_{j}$
and
![]() ${\it\theta}_{j}$
satisfying the Jeffery equations above; the superscript
${\it\theta}_{j}$
satisfying the Jeffery equations above; the superscript
![]() $^{\prime }t^{\prime }$
emphasizes the difference in the spin component of
$^{\prime }t^{\prime }$
emphasizes the difference in the spin component of
![]() ${\it\bf\Omega}_{b}$
compared to
${\it\bf\Omega}_{b}$
compared to
![]() ${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}$
.
${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}$
.
To determine
![]() ${\it\bf\Omega}_{1}$
to
${\it\bf\Omega}_{1}$
to
![]() $O(Re)$
, one may also use the Stokes approximation (
$O(Re)$
, one may also use the Stokes approximation (
![]() $\boldsymbol{u}_{s}^{\prime (1)}$
) for the velocity field
$\boldsymbol{u}_{s}^{\prime (1)}$
) for the velocity field
![]() $\boldsymbol{u}^{\prime (1)}$
in (2.25). That this approximation leads to a convergent integral may be seen by noting that, for a linear flow at
$\boldsymbol{u}^{\prime (1)}$
in (2.25). That this approximation leads to a convergent integral may be seen by noting that, for a linear flow at
![]() $Re=0$
, we have
$Re=0$
, we have
 $\boldsymbol{u}_{s}^{\prime (1)}\sim O(1/r^{2})$
for
$\boldsymbol{u}_{s}^{\prime (1)}\sim O(1/r^{2})$
for
![]() $r\gg L$
, and from (2.11), it is then seen that
$r\gg L$
, and from (2.11), it is then seen that
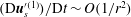 $(\text{D}\boldsymbol{u}_{s}^{\prime (1)})/\text{D}t\sim O(1/r^{2})$
for large
$(\text{D}\boldsymbol{u}_{s}^{\prime (1)})/\text{D}t\sim O(1/r^{2})$
for large
![]() $r$
. Since
$r$
. Since
 $\boldsymbol{u}^{(2)}\sim O(1/r^{2})$
for
$\boldsymbol{u}^{(2)}\sim O(1/r^{2})$
for
![]() $r\gg L$
, the
$r\gg L$
, the
![]() $O(Re)$
integrand based on the Stokes approximation is
$O(Re)$
integrand based on the Stokes approximation is
![]() $O(1/r^{4})$
for
$O(1/r^{4})$
for
![]() $r\gg L$
, implying convergence. As for the case of sedimentation in a quiescent fluid (Dabade et al.
Reference Dabade, Marath and Subramanian2015), this points to the regular nature of the
$r\gg L$
, implying convergence. As for the case of sedimentation in a quiescent fluid (Dabade et al.
Reference Dabade, Marath and Subramanian2015), this points to the regular nature of the
![]() $O(Re)$
correction, with the dominant contribution to the
$O(Re)$
correction, with the dominant contribution to the
![]() $O(Re)$
torque arising due to fluid inertial forces acting within a volume of order the size of the particle itself. It may be shown that the next correction to the angular velocity is
$O(Re)$
torque arising due to fluid inertial forces acting within a volume of order the size of the particle itself. It may be shown that the next correction to the angular velocity is
 $O(Re^{3/2})$
, and is singular in character, arising from the effects of inertia acting on length scales of
$O(Re^{3/2})$
, and is singular in character, arising from the effects of inertia acting on length scales of
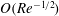 $O(Re^{-1/2})$
. The non-uniformity of the Stokes approximation must be accounted for at this order (Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). As will be seen later, while the
$O(Re^{-1/2})$
. The non-uniformity of the Stokes approximation must be accounted for at this order (Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). As will be seen later, while the
![]() $O(Re)$
correction evaluated here is sufficient to account for an inertial drift across Jeffery orbits, the effects of inertia on the Jeffery period, observed in recent simulations (Mao & Alexeev Reference Mao and Alexeev2014), where the spheroid rotation in either the tumbling or spinning mode is observed to slow down with increasing
$O(Re)$
correction evaluated here is sufficient to account for an inertial drift across Jeffery orbits, the effects of inertia on the Jeffery period, observed in recent simulations (Mao & Alexeev Reference Mao and Alexeev2014), where the spheroid rotation in either the tumbling or spinning mode is observed to slow down with increasing
![]() $Re$
, requires an analysis of the next correction at
$Re$
, requires an analysis of the next correction at
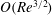 $O(Re^{3/2})$
, and this will be reported separately.
$O(Re^{3/2})$
, and this will be reported separately.
To
![]() $O(Re)$
, (2.25) may now be written as:
$O(Re)$
, (2.25) may now be written as:
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}-St\,\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\int _{V}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\boldsymbol{u}_{s}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\vphantom{\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}-St\,\frac{\text{d}}{\text{d}t}({\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+Re\int _{V}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\boldsymbol{u}_{s}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\vphantom{\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V,\end{eqnarray}$$
which is the final form on which subsequent calculations are based. Note that
![]() $St$
in (2.30) is still arbitrary. The operator on the left-hand side, when considered alone, governs the rotations of an axisymmetric free body arising from a balance of centrifugal and gyroscopic forces. These are known from classical mechanics (the Euler top), and correspond to the limit
$St$
in (2.30) is still arbitrary. The operator on the left-hand side, when considered alone, governs the rotations of an axisymmetric free body arising from a balance of centrifugal and gyroscopic forces. These are known from classical mechanics (the Euler top), and correspond to the limit
![]() $St\rightarrow \infty$
(Goldstein Reference Goldstein1962). Herein, we assume
$St\rightarrow \infty$
(Goldstein Reference Goldstein1962). Herein, we assume
![]() $St$
to be small, and only consider the effects of weak particle inertia to
$St$
to be small, and only consider the effects of weak particle inertia to
![]() $O(St^{2})$
. The surface integral on the right-hand side must lead to the well-known Jeffery orbits (Jeffery Reference Jeffery1922) in the inertialess limit, while the second term, the volume integral, captures fluid inertial effects to
$O(St^{2})$
. The surface integral on the right-hand side must lead to the well-known Jeffery orbits (Jeffery Reference Jeffery1922) in the inertialess limit, while the second term, the volume integral, captures fluid inertial effects to
![]() $O(Re)$
. The analysis of the leading-order effects of fluid inertia therefore requires the Stokes disturbance velocity field (
$O(Re)$
. The analysis of the leading-order effects of fluid inertia therefore requires the Stokes disturbance velocity field (
![]() $\boldsymbol{u}_{s}^{\prime (1)}$
) due to a torque-free spheroid, of an arbitrary orientation, in an ambient simple shear flow.
$\boldsymbol{u}_{s}^{\prime (1)}$
) due to a torque-free spheroid, of an arbitrary orientation, in an ambient simple shear flow.
3 The solutions of the Stokes equations in spheroidal coordinates
The reciprocal theorem formulation in its final form, (2.30), requires the Stokes velocity disturbance field due to a torque-free spheroidal particle in a simple shear flow. Following Subramanian & Koch (Reference Subramanian and Koch2006b
), the velocity disturbance field for an arbitrarily oriented spheroid may be obtained by resolving the ambient shear flow into five canonical component linear flows. Since the ambient vorticity tensor does not induce a disturbance field in the Stokes regime, such a resolution reflects the decomposition of the ambient rate-of-strain tensor into five canonical components in a body-fixed coordinate system with its
![]() $z$
-axis aligned with the spheroid axis of symmetry. In terms of the angles
$z$
-axis aligned with the spheroid axis of symmetry. In terms of the angles
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
defined earlier in § 2, the ambient rate-of-strain tensor, given by
${\it\phi}_{j}$
defined earlier in § 2, the ambient rate-of-strain tensor, given by
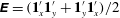 $\unicode[STIX]{x1D640}=(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })/2$
in the original space-fixed coordinate system, may now be written as:
$\unicode[STIX]{x1D640}=(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })/2$
in the original space-fixed coordinate system, may now be written as:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D640} & = & \displaystyle \cos ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}\mathbf{1}_{x}+{\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})(\mathbf{1}_{x}\mathbf{1}_{y}+\mathbf{1}_{y}\mathbf{1}_{x})\nonumber\\ \displaystyle & & \displaystyle +\,\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}(\mathbf{1}_{x}\mathbf{1}_{z}+\mathbf{1}_{z}\mathbf{1}_{x})-\cos {\it\phi}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}\mathbf{1}_{y}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})(\mathbf{1}_{y}\mathbf{1}_{z}+\mathbf{1}_{z}\mathbf{1}_{y})+\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\mathbf{1}_{z}\mathbf{1}_{z}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D640} & = & \displaystyle \cos ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}\mathbf{1}_{x}+{\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})(\mathbf{1}_{x}\mathbf{1}_{y}+\mathbf{1}_{y}\mathbf{1}_{x})\nonumber\\ \displaystyle & & \displaystyle +\,\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}(\mathbf{1}_{x}\mathbf{1}_{z}+\mathbf{1}_{z}\mathbf{1}_{x})-\cos {\it\phi}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}\mathbf{1}_{y}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})(\mathbf{1}_{y}\mathbf{1}_{z}+\mathbf{1}_{z}\mathbf{1}_{y})+\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\mathbf{1}_{z}\mathbf{1}_{z}\end{eqnarray}$$
in terms of the body-fixed unit vector triplet
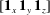 $[\mathbf{1}_{x}\,\mathbf{1}_{y}\,\mathbf{1}_{z}]$
. Note that the
$[\mathbf{1}_{x}\,\mathbf{1}_{y}\,\mathbf{1}_{z}]$
. Note that the
![]() $Y$
-axis of the body-fixed coordinate system is constrained to lie in the flow–gradient (
$Y$
-axis of the body-fixed coordinate system is constrained to lie in the flow–gradient (
![]() $X^{\prime }Y^{\prime }$
) plane at all times (reflected in the equality of the
$X^{\prime }Y^{\prime }$
) plane at all times (reflected in the equality of the
![]() $xz$
and
$xz$
and
![]() $zx$
component of the rate-of-strain tensor in (3.1)), and the relations between the unit vectors in the two coordinate systems are given by
$zx$
component of the rate-of-strain tensor in (3.1)), and the relations between the unit vectors in the two coordinate systems are given by
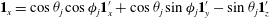 $\mathbf{1}_{x}=\cos {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }-\sin {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
,
$\mathbf{1}_{x}=\cos {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }-\sin {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
,
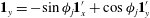 $\mathbf{1}_{y}=-\text{sin}\,{\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\phi}_{j}\mathbf{1}_{y}^{\prime }$
and
$\mathbf{1}_{y}=-\text{sin}\,{\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\phi}_{j}\mathbf{1}_{y}^{\prime }$
and
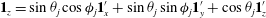 $\mathbf{1}_{z}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }+\cos {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
. The aforementioned decomposition of
$\mathbf{1}_{z}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }+\cos {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
. The aforementioned decomposition of
![]() $\unicode[STIX]{x1D640}$
may now be written in the following form in terms of the respective matrix representations:
$\unicode[STIX]{x1D640}$
may now be written in the following form in terms of the respective matrix representations:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\begin{array}{@{}ccc@{}}\cos ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\\ {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & -\text{cos}\,{\it\phi}_{j}\sin {\it\phi}_{j} & {\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\\ \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & {\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & \sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\begin{array}{@{}ccc@{}}-{\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\\ 0 & -{\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0\\ 0 & 0 & \sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}{\textstyle \frac{1}{2}}(\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\\ 0 & -{\textstyle \frac{1}{2}}(\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0\\ 0 & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0\\ {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0 & 0\\ 0 & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & 0 & \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\\ 0 & 0 & 0\\ \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ 0 & 0 & {\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\\ 0 & {\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\begin{array}{@{}ccc@{}}\cos ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\\ {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & -\text{cos}\,{\it\phi}_{j}\sin {\it\phi}_{j} & {\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\\ \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & {\textstyle \frac{1}{2}}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & \sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\begin{array}{@{}ccc@{}}-{\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\\ 0 & -{\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0\\ 0 & 0 & \sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}{\textstyle \frac{1}{2}}(\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\\ 0 & -{\textstyle \frac{1}{2}}(\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0\\ 0 & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0\\ {\textstyle \frac{1}{2}}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0 & 0\\ 0 & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & 0 & \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}\\ 0 & 0 & 0\\ \sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j} & 0 & 0\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ 0 & 0 & {\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\\ 0 & {\textstyle \frac{1}{2}}\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}) & 0\end{array}\right].\end{eqnarray}$$
The five component matrices above correspond, respectively, to an axisymmetric extensional flow (uniaxial or biaxial depending on the sign of
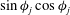 $\sin {\it\phi}_{j}\cos {\it\phi}_{j}$
) along the spheroidal axis (
$\sin {\it\phi}_{j}\cos {\it\phi}_{j}$
) along the spheroidal axis (
![]() $z$
) of symmetry with an amplitude proportional to
$z$
) of symmetry with an amplitude proportional to
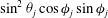 $\sin ^{2}{\it\theta}_{j}\cos {\it\phi}_{j}\sin {\it\phi}_{j}$
; a pair of extensional flows in the plane (
$\sin ^{2}{\it\theta}_{j}\cos {\it\phi}_{j}\sin {\it\phi}_{j}$
; a pair of extensional flows in the plane (
![]() $xy$
) transverse to the axis of symmetry, one of them being obtained from the other via a 45° rotation about the symmetry axis, and with amplitudes proportional to
$xy$
) transverse to the axis of symmetry, one of them being obtained from the other via a 45° rotation about the symmetry axis, and with amplitudes proportional to
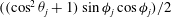 $((\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j})/2$
and
$((\cos ^{2}{\it\theta}_{j}+1)\sin {\it\phi}_{j}\cos {\it\phi}_{j})/2$
and
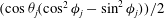 $(\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}))/2$
; and a pair of longitudinal extensional flows in planes containing the axis of symmetry (the
$(\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}))/2$
; and a pair of longitudinal extensional flows in planes containing the axis of symmetry (the
![]() $xz$
and
$xz$
and
![]() $yz$
planes) and with amplitudes proportional to
$yz$
planes) and with amplitudes proportional to
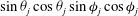 $\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}$
and
$\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}$
and
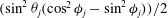 $(\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}))/2$
.
$(\sin ^{2}{\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j}))/2$
.
Denoting the disturbance fields corresponding to the five component linear flows as
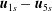 $\boldsymbol{u}_{1s}-\boldsymbol{u}_{5s}$
, we have
$\boldsymbol{u}_{1s}-\boldsymbol{u}_{5s}$
, we have
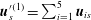 $\boldsymbol{u}_{s}^{\prime (1)}=\sum _{i=1}^{5}\boldsymbol{u}_{is}$
, with
$\boldsymbol{u}_{s}^{\prime (1)}=\sum _{i=1}^{5}\boldsymbol{u}_{is}$
, with
![]() $\boldsymbol{u}_{1s}$
corresponding to the axisymmetric extension,
$\boldsymbol{u}_{1s}$
corresponding to the axisymmetric extension,
![]() $\boldsymbol{u}_{2s},\boldsymbol{u}_{3s}$
corresponding to the two planar extensions, and
$\boldsymbol{u}_{2s},\boldsymbol{u}_{3s}$
corresponding to the two planar extensions, and
![]() $\boldsymbol{u}_{4s},\boldsymbol{u}_{5s}$
corresponding to the pair of longitudinal extensions above. While the expressions for these component Stokesian velocity fields may be obtained using earlier results based on the method of singularities (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975), herein we use the vector spheroidal harmonics formalism developed by Kushch and co-workers (Kushch Reference Kushch1997, Reference Kushch1998). The reasons for this choice have been outlined in Dabade et al. (Reference Dabade, Marath and Subramanian2015), where the formalism was used for a single sedimenting particle in an otherwise quiescent fluid. Since the structure of the formalism, and a comparison with a similar expansion of the velocity field in terms of spherical harmonics, originally given by Lamb (for instance, see Kim & Karrila (Reference Kim and Karrila1991, chap. 4)), has already been explained in some detail in Dabade et al. (Reference Dabade, Marath and Subramanian2015), we will be brief here. The formalism is based on expressing the general solution of the Stokes equations, around an arbitrary number of spheroidal particles, as a superposition of growing and decaying vector harmonics in local spheroidal coordinates defined with respect to a Cartesian system centred at each particle, and aligned with the particle axis of symmetry. For a prolate spheroid, the spheroidal coordinates (
$\boldsymbol{u}_{4s},\boldsymbol{u}_{5s}$
corresponding to the pair of longitudinal extensions above. While the expressions for these component Stokesian velocity fields may be obtained using earlier results based on the method of singularities (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975), herein we use the vector spheroidal harmonics formalism developed by Kushch and co-workers (Kushch Reference Kushch1997, Reference Kushch1998). The reasons for this choice have been outlined in Dabade et al. (Reference Dabade, Marath and Subramanian2015), where the formalism was used for a single sedimenting particle in an otherwise quiescent fluid. Since the structure of the formalism, and a comparison with a similar expansion of the velocity field in terms of spherical harmonics, originally given by Lamb (for instance, see Kim & Karrila (Reference Kim and Karrila1991, chap. 4)), has already been explained in some detail in Dabade et al. (Reference Dabade, Marath and Subramanian2015), we will be brief here. The formalism is based on expressing the general solution of the Stokes equations, around an arbitrary number of spheroidal particles, as a superposition of growing and decaying vector harmonics in local spheroidal coordinates defined with respect to a Cartesian system centred at each particle, and aligned with the particle axis of symmetry. For a prolate spheroid, the spheroidal coordinates (
![]() ${\it\xi},{\it\eta},{\it\phi}$
) are related to Cartesian coordinates
${\it\xi},{\it\eta},{\it\phi}$
) are related to Cartesian coordinates
![]() $(x,y,z)$
as
$(x,y,z)$
as
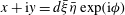 $x+\text{i}y=d\bar{{\it\xi}}\bar{{\it\eta}}\exp (\text{i}{\it\phi})$
and
$x+\text{i}y=d\bar{{\it\xi}}\bar{{\it\eta}}\exp (\text{i}{\it\phi})$
and
![]() $z=d{\it\xi}{\it\eta}$
, with
$z=d{\it\xi}{\it\eta}$
, with
 $\bar{{\it\xi}}=\sqrt{({\it\xi}^{2}-1)}$
and
$\bar{{\it\xi}}=\sqrt{({\it\xi}^{2}-1)}$
and
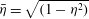 $\bar{{\it\eta}}=\sqrt{(1-{\it\eta}^{2})}$
, where
$\bar{{\it\eta}}=\sqrt{(1-{\it\eta}^{2})}$
, where
![]() $d$
is the interfocal distance. Here, the constant-
$d$
is the interfocal distance. Here, the constant-
![]() ${\it\xi}$
-surfaces denote a family of confocal prolate spheroids with the interfoci distance being equal to
${\it\xi}$
-surfaces denote a family of confocal prolate spheroids with the interfoci distance being equal to
![]() $2d$
;
$2d$
;
![]() ${\it\xi}_{0}$
denotes the surface of the particle. The constant-
${\it\xi}_{0}$
denotes the surface of the particle. The constant-
![]() ${\it\eta}$
-surfaces represent a family of confocal two-sheeted hyperboloids, while the constant-
${\it\eta}$
-surfaces represent a family of confocal two-sheeted hyperboloids, while the constant-
![]() ${\it\phi}$
-surfaces are planes passing through the axis of symmetry. The disturbance field due to a single particle in an infinite viscous ambient must involve only decaying spheroidal harmonics, and may therefore be written in the form:
${\it\phi}$
-surfaces are planes passing through the axis of symmetry. The disturbance field due to a single particle in an infinite viscous ambient must involve only decaying spheroidal harmonics, and may therefore be written in the form:
 $$\begin{eqnarray}\boldsymbol{u}(\boldsymbol{x})=\mathop{\sum }_{i=1}^{3}\mathop{\sum }_{t=0}^{\infty }\mathop{\sum }_{s=-t}^{t}A_{ts}^{(i)}\boldsymbol{S}_{ts}^{(i)}(\boldsymbol{r},d),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}(\boldsymbol{x})=\mathop{\sum }_{i=1}^{3}\mathop{\sum }_{t=0}^{\infty }\mathop{\sum }_{s=-t}^{t}A_{ts}^{(i)}\boldsymbol{S}_{ts}^{(i)}(\boldsymbol{r},d),\end{eqnarray}$$
where the decaying (singular) partial vectorial solutions are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{S}_{ts}^{(1)}=\boldsymbol{e}_{1}F_{t+1}^{s-1}-\boldsymbol{e}_{2}F_{t+1}^{s+1}+\mathbf{1}_{z}F_{t+1}^{s}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{S}_{ts}^{(1)}=\boldsymbol{e}_{1}F_{t+1}^{s-1}-\boldsymbol{e}_{2}F_{t+1}^{s+1}+\mathbf{1}_{z}F_{t+1}^{s}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{S}_{ts}^{(2)}=\frac{1}{t}[\boldsymbol{e}_{1}(t+s)F_{t}^{s-1}+\boldsymbol{e}_{2}(t-s)F_{t}^{s+1}+\mathbf{1}_{z}sF_{t}^{s}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{S}_{ts}^{(2)}=\frac{1}{t}[\boldsymbol{e}_{1}(t+s)F_{t}^{s-1}+\boldsymbol{e}_{2}(t-s)F_{t}^{s+1}+\mathbf{1}_{z}sF_{t}^{s}], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}F_{t-1}^{s-1}-({\it\xi}_{0}^{2}-1)d\text{D}_{1}F_{t}^{s}+(t+s-1)(t+s){\it\beta}_{-(t+1)}F_{t-1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}F_{t-1}^{s+1}-({\it\xi}_{0}^{2}-1)d\text{D}_{2}F_{t}^{s}-(t-s-1)(t-s){\it\beta}_{-(t+1)}F_{t-1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{t-1}^{s}-{\it\xi}_{0}^{2}d\text{D}_{3}F_{t}^{s}-C_{-(t+1),s}F_{t-1}^{s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}F_{t-1}^{s-1}-({\it\xi}_{0}^{2}-1)d\text{D}_{1}F_{t}^{s}+(t+s-1)(t+s){\it\beta}_{-(t+1)}F_{t-1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}F_{t-1}^{s+1}-({\it\xi}_{0}^{2}-1)d\text{D}_{2}F_{t}^{s}-(t-s-1)(t-s){\it\beta}_{-(t+1)}F_{t-1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{t-1}^{s}-{\it\xi}_{0}^{2}d\text{D}_{3}F_{t}^{s}-C_{-(t+1),s}F_{t-1}^{s}],\end{eqnarray}$$
with
![]() $\boldsymbol{S}_{ts}^{(i)}\rightarrow \mathbf{0}$
for
$\boldsymbol{S}_{ts}^{(i)}\rightarrow \mathbf{0}$
for
![]() $\boldsymbol{r}\rightarrow \infty$
. Here,
$\boldsymbol{r}\rightarrow \infty$
. Here,
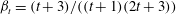 ${\it\beta}_{t}=(t+3)/((t+1)(2t+3))$
,
${\it\beta}_{t}=(t+3)/((t+1)(2t+3))$
,
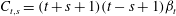 $C_{t,s}=(t+s+1)(t-s+1){\it\beta}_{t}$
, with
$C_{t,s}=(t+s+1)(t-s+1){\it\beta}_{t}$
, with
 $t=0,1,\ldots ;|s|\leqslant t$
; further,
$t=0,1,\ldots ;|s|\leqslant t$
; further,
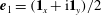 $\boldsymbol{e}_{1}=(\mathbf{1}_{x}+\text{i}\mathbf{1}_{y})/2$
,
$\boldsymbol{e}_{1}=(\mathbf{1}_{x}+\text{i}\mathbf{1}_{y})/2$
,
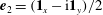 $\boldsymbol{e}_{2}=(\mathbf{1}_{x}-\text{i}\mathbf{1}_{y})/2$
, with
$\boldsymbol{e}_{2}=(\mathbf{1}_{x}-\text{i}\mathbf{1}_{y})/2$
, with
![]() $\mathbf{1}_{z}$
, as before, being directed along the axis of symmetry of the spheroidal coordinate system. The
$\mathbf{1}_{z}$
, as before, being directed along the axis of symmetry of the spheroidal coordinate system. The
![]() $\text{D}_{i}$
denote differential operators with
$\text{D}_{i}$
denote differential operators with
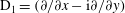 $\text{D}_{1}=(\partial /\partial x-\text{i}\partial /\partial y)$
,
$\text{D}_{1}=(\partial /\partial x-\text{i}\partial /\partial y)$
,
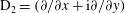 $\text{D}_{2}=(\partial /\partial x+\text{i}\partial /\partial y)$
, and
$\text{D}_{2}=(\partial /\partial x+\text{i}\partial /\partial y)$
, and
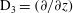 $\text{D}_{3}=(\partial /\partial z)$
. In (3.4)–(3.6), the functions
$\text{D}_{3}=(\partial /\partial z)$
. In (3.4)–(3.6), the functions
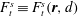 $F_{t}^{s}\equiv F_{t}^{s}(\boldsymbol{r},d)$
are the singular solid spheroidal harmonics of the form
$F_{t}^{s}\equiv F_{t}^{s}(\boldsymbol{r},d)$
are the singular solid spheroidal harmonics of the form
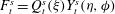 $F_{t}^{s}=Q_{t}^{s}({\it\xi})Y_{t}^{s}({\it\eta},{\it\phi})$
, with
$F_{t}^{s}=Q_{t}^{s}({\it\xi})Y_{t}^{s}({\it\eta},{\it\phi})$
, with
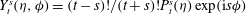 $Y_{t}^{s}({\it\eta},{\it\phi})=(t-s)!/(t+s)!P_{t}^{s}({\it\eta})\exp (\text{i}s{\it\phi})$
being the familiar scalar surface harmonics, and
$Y_{t}^{s}({\it\eta},{\it\phi})=(t-s)!/(t+s)!P_{t}^{s}({\it\eta})\exp (\text{i}s{\it\phi})$
being the familiar scalar surface harmonics, and
![]() $P_{t}^{s}$
and
$P_{t}^{s}$
and
![]() $Q_{t}^{s}$
being the associated Legendre functions of the first and second kind, respectively (Morse & Feshbach Reference Morse and Feshbach1953). The analogues of all of the above expressions, for an oblate spheroid, can be derived from using the transformation
$Q_{t}^{s}$
being the associated Legendre functions of the first and second kind, respectively (Morse & Feshbach Reference Morse and Feshbach1953). The analogues of all of the above expressions, for an oblate spheroid, can be derived from using the transformation
![]() ${\it\xi}\leftrightarrow \text{i}\bar{{\it\xi}}$
and
${\it\xi}\leftrightarrow \text{i}\bar{{\it\xi}}$
and
 $d\leftrightarrow -\text{i}d$
(Dabade et al.
Reference Dabade, Marath and Subramanian2015).
$d\leftrightarrow -\text{i}d$
(Dabade et al.
Reference Dabade, Marath and Subramanian2015).
Now, the
![]() $\boldsymbol{S}_{ts}^{(1)}$
and
$\boldsymbol{S}_{ts}^{(1)}$
and
![]() $\boldsymbol{S}_{ts}^{(2)}$
are harmonic functions, while the
$\boldsymbol{S}_{ts}^{(2)}$
are harmonic functions, while the
![]() $\boldsymbol{S}_{ts}^{(3)}$
satisfy the biharmonic equation, and are therefore the only vectorial solutions associated with a non-trivial pressure field. The index
$\boldsymbol{S}_{ts}^{(3)}$
satisfy the biharmonic equation, and are therefore the only vectorial solutions associated with a non-trivial pressure field. The index
![]() $t$
in
$t$
in
![]() $\boldsymbol{S}_{ts}^{(i)}$
is a measure of the rapidity of decay of the velocity disturbance field for large
$\boldsymbol{S}_{ts}^{(i)}$
is a measure of the rapidity of decay of the velocity disturbance field for large
![]() $r$
, with
$r$
, with
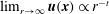 $\lim _{r\rightarrow \infty }\boldsymbol{u}(\boldsymbol{x})\propto r^{-t}$
, this arising from the large-
$\lim _{r\rightarrow \infty }\boldsymbol{u}(\boldsymbol{x})\propto r^{-t}$
, this arising from the large-
![]() ${\it\xi}$
behaviour of the
${\it\xi}$
behaviour of the
![]() $Q_{t}^{s}$
. Since the
$Q_{t}^{s}$
. Since the
![]() $\boldsymbol{S}_{ts}^{(3)}$
alone include the fundamental singularities of the Stokes equations, in light of the large-
$\boldsymbol{S}_{ts}^{(3)}$
alone include the fundamental singularities of the Stokes equations, in light of the large-
![]() $r$
behaviour indicated above, one expects the
$r$
behaviour indicated above, one expects the
![]() $\boldsymbol{S}_{1s}^{(3)}$
to be relevant to the translation problem where
$\boldsymbol{S}_{1s}^{(3)}$
to be relevant to the translation problem where
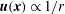 $\boldsymbol{u}(\boldsymbol{x})\propto 1/r$
; and the
$\boldsymbol{u}(\boldsymbol{x})\propto 1/r$
; and the
![]() $\boldsymbol{S}_{2s}^{(3)}$
to come into play for both transverse rotations and the disturbance fields in an ambient linear flow, for all of which
$\boldsymbol{S}_{2s}^{(3)}$
to come into play for both transverse rotations and the disturbance fields in an ambient linear flow, for all of which
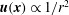 $\boldsymbol{u}(\boldsymbol{x})\propto 1/r^{2}$
– see (3.7)–(3.15) and (3.27)–(3.29) below. Note that axial rotation is an exception in that it does not generate a pressure field and the velocity disturbance in this case is harmonic, being proportional to
$\boldsymbol{u}(\boldsymbol{x})\propto 1/r^{2}$
– see (3.7)–(3.15) and (3.27)–(3.29) below. Note that axial rotation is an exception in that it does not generate a pressure field and the velocity disturbance in this case is harmonic, being proportional to
![]() $\boldsymbol{S}_{20}^{(2)}$
(see (3.36)). The second index
$\boldsymbol{S}_{20}^{(2)}$
(see (3.36)). The second index
![]() $s$
in all these cases denotes the variation of the velocity field as a function of the azimuthal angle in the plane transverse to the symmetry axis, with
$s$
in all these cases denotes the variation of the velocity field as a function of the azimuthal angle in the plane transverse to the symmetry axis, with
![]() $s=0$
corresponding to an axisymmetric exterior field; for instance, the disturbance velocity field in an ambient axisymmetric extensional flow must involve
$s=0$
corresponding to an axisymmetric exterior field; for instance, the disturbance velocity field in an ambient axisymmetric extensional flow must involve
![]() $\boldsymbol{S}_{20}^{(3)}$
.
$\boldsymbol{S}_{20}^{(3)}$
.
For a prolate spheroid, use of the surface boundary condition at
![]() ${\it\xi}={\it\xi}_{0}$
leads to the following expressions, in terms of the
${\it\xi}={\it\xi}_{0}$
leads to the following expressions, in terms of the
![]() $\boldsymbol{S}_{ts}^{(3)}$
, for the disturbance velocity and pressure fields corresponding to the five canonical linear flows above:
$\boldsymbol{S}_{ts}^{(3)}$
, for the disturbance velocity and pressure fields corresponding to the five canonical linear flows above:
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{1s}=\frac{-d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\boldsymbol{S}_{20}^{(3)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{1s}=\frac{-d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\boldsymbol{S}_{20}^{(3)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{1s}=\frac{-2d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\text{D}_{3}F_{1}^{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{1s}=\frac{-2d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\text{D}_{3}F_{1}^{0}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{2s}=-\frac{d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\sin {\it\phi}_{j}\cos {\it\phi}_{j}(1+\cos ^{2}{\it\theta}_{j})](\boldsymbol{S}_{22}^{(3)}+\boldsymbol{S}_{2,-2}^{(3)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{2s}=-\frac{d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\sin {\it\phi}_{j}\cos {\it\phi}_{j}(1+\cos ^{2}{\it\theta}_{j})](\boldsymbol{S}_{22}^{(3)}+\boldsymbol{S}_{2,-2}^{(3)}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{2s}=-\frac{2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\sin {\it\phi}_{j}\cos {\it\phi}_{j}(1+\cos ^{2}{\it\theta}_{j})](\text{D}_{3}F_{1}^{2}+\text{D}_{3}F_{1}^{-2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{2s}=-\frac{2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\sin {\it\phi}_{j}\cos {\it\phi}_{j}(1+\cos ^{2}{\it\theta}_{j})](\text{D}_{3}F_{1}^{2}+\text{D}_{3}F_{1}^{-2}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{3s}=\frac{\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\cos {\it\theta}_{j}\cos 2{\it\phi}_{j}](\boldsymbol{S}_{22}^{(3)}-\boldsymbol{S}_{2,-2}^{(3)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{3s}=\frac{\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\cos {\it\theta}_{j}\cos 2{\it\phi}_{j}](\boldsymbol{S}_{22}^{(3)}-\boldsymbol{S}_{2,-2}^{(3)}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{3s}=\frac{2\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\cos {\it\theta}_{j}\cos 2{\it\phi}_{j}](\text{D}_{3}F_{1}^{2}-\text{D}_{3}F_{1}^{-2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{3s}=\frac{2\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}[\cos {\it\theta}_{j}\cos 2{\it\phi}_{j}](\text{D}_{3}F_{1}^{2}-\text{D}_{3}F_{1}^{-2}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{4s}=\frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})(\boldsymbol{S}_{21}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{4s}=\frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})(\boldsymbol{S}_{21}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{4s}=\frac{4d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})(\text{D}_{3}F_{1}^{1}-\text{D}_{3}F_{1}^{-1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{4s}=\frac{4d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})(\text{D}_{3}F_{1}^{1}-\text{D}_{3}F_{1}^{-1}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{5s}=-\frac{\text{i}d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}[\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})](\boldsymbol{S}_{21}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{5s}=-\frac{\text{i}d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}[\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})](\boldsymbol{S}_{21}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{5s}=-\frac{2\text{i}d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}[\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})](\text{D}_{3}F_{1}^{1}+\text{D}_{3}F_{1}^{-1}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{5s}=-\frac{2\text{i}d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}[\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})](\text{D}_{3}F_{1}^{1}+\text{D}_{3}F_{1}^{-1}). & \displaystyle\end{eqnarray}$$
On substitution of the expressions for the
![]() $\boldsymbol{S}_{ts}^{(3)}$
and
$\boldsymbol{S}_{ts}^{(3)}$
and
![]() $F_{t}^{s}$
, given in (3.6), the disturbance velocity fields take the following forms:
$F_{t}^{s}$
, given in (3.6), the disturbance velocity fields take the following forms:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1s} & = & \displaystyle -\frac{d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{0}Q_{1}^{0})-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{2}^{0}Q_{2}^{0})-d\bar{{\it\xi}}_{0}^{2}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{0}Q_{2}^{0})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1s} & = & \displaystyle -\frac{d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{0}Q_{1}^{0})-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{2}^{0}Q_{2}^{0})-d\bar{{\it\xi}}_{0}^{2}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{0}Q_{2}^{0})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{1s} & = & \displaystyle -\frac{2d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{0}Q_{1}^{0}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{1s} & = & \displaystyle -\frac{2d\bar{{\it\xi}}_{0}}{(Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\sin ^{2}{\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{0}Q_{1}^{0}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{2s} & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{({\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})-3Q_{1}^{1}({\it\xi}_{0}))}(1+\cos ^{2}{\it\theta}_{j})\sin {\it\phi}_{j}\cos {\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\left\{\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right\}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}Q_{2}^{2}\cos 2{\it\phi})-\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}Q_{2}^{2}\cos 2{\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{2s} & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{({\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})-3Q_{1}^{1}({\it\xi}_{0}))}(1+\cos ^{2}{\it\theta}_{j})\sin {\it\phi}_{j}\cos {\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\left\{\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right\}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}Q_{2}^{2}\cos 2{\it\phi})-\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}Q_{2}^{2}\cos 2{\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{2s} & = & \displaystyle \frac{2d\bar{{\it\xi}}_{0}}{({\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})-3Q_{1}^{1}({\it\xi}_{0}))}(1+\cos ^{2}{\it\theta}_{j})\sin {\it\phi}_{j}\cos {\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{2s} & = & \displaystyle \frac{2d\bar{{\it\xi}}_{0}}{({\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})-3Q_{1}^{1}({\it\xi}_{0}))}(1+\cos ^{2}{\it\theta}_{j})\sin {\it\phi}_{j}\cos {\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{3s} & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\left\{\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right\}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}Q_{2}^{2}\sin 2{\it\phi})+\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}Q_{2}^{2}\sin 2{\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{3s} & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\left\{\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right\}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}Q_{2}^{2}\sin 2{\it\phi})+\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}Q_{2}^{2}\sin 2{\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{3s} & = & \displaystyle \frac{2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{3s} & = & \displaystyle \frac{2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}\cos {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{4s} & = & \displaystyle \frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})-\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{4s} & = & \displaystyle \frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})-\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{4s} & = & \displaystyle \frac{4d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{4s} & = & \displaystyle \frac{4d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}(\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{5s} & = & \displaystyle \frac{d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})-\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{5s} & = & \displaystyle \frac{d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})-\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{5s} & = & \displaystyle \frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{5s} & = & \displaystyle \frac{2d{\it\xi}_{0}\bar{{\it\xi}}_{0}}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}^{2}-1)}\sin {\it\theta}_{j}(\cos ^{2}{\it\phi}_{j}-\sin ^{2}{\it\phi}_{j})\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi}).\end{eqnarray}$$
As shown by Dabade et al. (Reference Dabade, Marath and Subramanian2015), the test velocity fields in (2.30), corresponding to transverse rotations about the
![]() $x$
and
$x$
and
![]() $y$
axes, are given by:
$y$
axes, are given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sx}^{(2)} & = & \displaystyle \frac{\text{i}d(2{\it\xi}_{0}^{2}-1)}{2Q_{1}^{0}({\it\xi}_{0}){\it\xi}_{0}-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{1,1}^{(2)}-\boldsymbol{S}_{1,-1}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\text{i}d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2Q_{1}^{0}({\it\xi}_{0}){\it\xi}_{0}-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{2,1}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sx}^{(2)} & = & \displaystyle \frac{\text{i}d(2{\it\xi}_{0}^{2}-1)}{2Q_{1}^{0}({\it\xi}_{0}){\it\xi}_{0}-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{1,1}^{(2)}-\boldsymbol{S}_{1,-1}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\text{i}d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2Q_{1}^{0}({\it\xi}_{0}){\it\xi}_{0}-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{2,1}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -\frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{y}+P_{1}^{1}Q_{1}^{1}\sin {\it\phi}\mathbf{1}_{z})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{d}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{y}+P_{1}^{1}Q_{1}^{1}\sin {\it\phi}\mathbf{1}_{z})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{d}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sy}^{(2)} & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{1,1}^{(2)}+\boldsymbol{S}_{1,-1}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sy}^{(2)} & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{1,1}^{(2)}+\boldsymbol{S}_{1,-1}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{x}+P_{1}^{1}Q_{1}^{1}\cos {\it\phi}\mathbf{1}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{x}+P_{1}^{1}Q_{1}^{1}\cos {\it\phi}\mathbf{1}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\left[\boldsymbol{r}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d\bar{{\it\xi}}_{0}^{2}}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right],\end{eqnarray}$$
respectively, with the corresponding pressure fields being given by:
 $$\begin{eqnarray}\displaystyle p_{sx}^{(2)} & = & \displaystyle \frac{2\text{i}d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(D_{2}^{1}+D_{2}^{-1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{sx}^{(2)} & = & \displaystyle \frac{2\text{i}d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(D_{2}^{1}+D_{2}^{-1}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -\frac{2d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\frac{2d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle p_{sy}^{(2)} & = & \displaystyle \frac{2({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(D_{2}^{1}-D_{2}^{-1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{sy}^{(2)} & = & \displaystyle \frac{2({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}(D_{2}^{1}-D_{2}^{-1}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{2d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{2d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\bar{{\it\xi}}_{0}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\bar{{\it\xi}}_{0}Q_{1}^{1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\end{eqnarray}$$
where
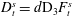 $D_{t}^{s}=d\text{D}_{3}F_{t}^{s}$
. The test velocity field corresponding to rotation about the
$D_{t}^{s}=d\text{D}_{3}F_{t}^{s}$
. The test velocity field corresponding to rotation about the
![]() $z$
-axis is given by:
$z$
-axis is given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sz}^{(2)} & = & \displaystyle \frac{2\text{i}d\bar{{\it\xi}}_{0}}{Q_{1}^{1}({\it\xi}_{0})}\boldsymbol{S}_{10}^{(2)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{sz}^{(2)} & = & \displaystyle \frac{2\text{i}d\bar{{\it\xi}}_{0}}{Q_{1}^{1}({\it\xi}_{0})}\boldsymbol{S}_{10}^{(2)},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{Q_{1}^{1}({\it\xi}_{0})}(-\text{sin}\,{\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y})(P_{1}^{1}Q_{1}^{1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d\bar{{\it\xi}}_{0}}{Q_{1}^{1}({\it\xi}_{0})}(-\text{sin}\,{\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y})(P_{1}^{1}Q_{1}^{1}),\end{eqnarray}$$
with
![]() $p_{sz}^{(2)}=0$
, there being no associated pressure field with axial rotation. The magnitudes of the torque for axial and transverse rotations are given by
$p_{sz}^{(2)}=0$
, there being no associated pressure field with axial rotation. The magnitudes of the torque for axial and transverse rotations are given by
![]() $8{\rm\pi}X_{C}$
and
$8{\rm\pi}X_{C}$
and
![]() $8{\rm\pi}Y_{C}$
respectively, with
$8{\rm\pi}Y_{C}$
respectively, with
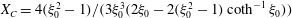 $X_{C}=4({\it\xi}_{0}^{2}-1)/(3{\it\xi}_{0}^{3}(2{\it\xi}_{0}-2({\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}))$
and
$X_{C}=4({\it\xi}_{0}^{2}-1)/(3{\it\xi}_{0}^{3}(2{\it\xi}_{0}-2({\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}))$
and
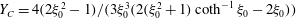 $Y_{C}=4(2{\it\xi}_{0}^{2}-1)/(3{\it\xi}_{0}^{3}(2({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}-2{\it\xi}_{0}))$
. The second-order tensors characterizing the test problem that appear in (2.30) are therefore given by
$Y_{C}=4(2{\it\xi}_{0}^{2}-1)/(3{\it\xi}_{0}^{3}(2({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}-2{\it\xi}_{0}))$
. The second-order tensors characterizing the test problem that appear in (2.30) are therefore given by
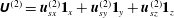 $\unicode[STIX]{x1D650}^{(2)}=\boldsymbol{u}_{sx}^{(2)}\mathbf{1}_{x}+\boldsymbol{u}_{sy}^{(2)}\mathbf{1}_{y}+\boldsymbol{u}_{sz}^{(2)}\mathbf{1}_{z}$
and
$\unicode[STIX]{x1D650}^{(2)}=\boldsymbol{u}_{sx}^{(2)}\mathbf{1}_{x}+\boldsymbol{u}_{sy}^{(2)}\mathbf{1}_{y}+\boldsymbol{u}_{sz}^{(2)}\mathbf{1}_{z}$
and
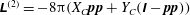 $\unicode[STIX]{x1D647}^{(2)}=-8{\rm\pi}(X_{C}\boldsymbol{p}\boldsymbol{p}+Y_{C}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))$
, with
$\unicode[STIX]{x1D647}^{(2)}=-8{\rm\pi}(X_{C}\boldsymbol{p}\boldsymbol{p}+Y_{C}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p}))$
, with
![]() $\boldsymbol{p}=\mathbf{1}_{z}$
.
$\boldsymbol{p}=\mathbf{1}_{z}$
.
4 Jeffery orbits using spheroidal harmonics
To begin with, we validate the spheroidal harmonics formalism by considering (2.30) in the limit
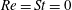 $Re=St=0$
, in which case
$Re=St=0$
, in which case
![]() ${\it\bf\Omega}_{1}$
, at each instant, is directly given in terms of the surface integral (rather than being governed by a differential equation):
${\it\bf\Omega}_{1}$
, at each instant, is directly given in terms of the surface integral (rather than being governed by a differential equation):
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S. & & \displaystyle\end{eqnarray}$$
In the inertialess limit, the transverse and axial rotation problems are decoupled. The spheroid spins at a rate commensurate with the ambient vorticity, that is,
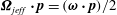 ${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}=({\bf\omega}\boldsymbol{\cdot }\boldsymbol{p})/2$
. Thus, in (4.1) one may consider only the components of
${\it\bf\Omega}_{jeff}\boldsymbol{\cdot }\boldsymbol{p}=({\bf\omega}\boldsymbol{\cdot }\boldsymbol{p})/2$
. Thus, in (4.1) one may consider only the components of
![]() $\unicode[STIX]{x1D647}^{(2)}$
corresponding to transverse rotation. With
$\unicode[STIX]{x1D647}^{(2)}$
corresponding to transverse rotation. With
![]() $\boldsymbol{n}=\mathbf{1}_{{\it\xi}}$
, we have the following expression for the stress vector:
$\boldsymbol{n}=\mathbf{1}_{{\it\xi}}$
, we have the following expression for the stress vector:
 $$\begin{eqnarray}{\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\mathbf{1}_{{\it\xi}}=-\boldsymbol{P}^{(2)}\mathbf{1}_{{\it\xi}}+2\left[\frac{\bar{{\it\xi}}}{d({\it\xi}^{2}-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\xi}}\unicode[STIX]{x1D650}^{(2)}+\frac{1}{2}\mathbf{1}_{{\it\xi}}\wedge (\boldsymbol{{\rm\nabla}}\wedge \unicode[STIX]{x1D650}^{(2)})\right],\end{eqnarray}$$
$$\begin{eqnarray}{\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\mathbf{1}_{{\it\xi}}=-\boldsymbol{P}^{(2)}\mathbf{1}_{{\it\xi}}+2\left[\frac{\bar{{\it\xi}}}{d({\it\xi}^{2}-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\xi}}\unicode[STIX]{x1D650}^{(2)}+\frac{1}{2}\mathbf{1}_{{\it\xi}}\wedge (\boldsymbol{{\rm\nabla}}\wedge \unicode[STIX]{x1D650}^{(2)})\right],\end{eqnarray}$$
all quantities being evaluated at
![]() ${\it\xi}={\it\xi}_{0}$
. Here,
${\it\xi}={\it\xi}_{0}$
. Here,
![]() $\boldsymbol{P}^{(2)}$
is a pressure vector corresponding to the transverse rotations. Based on (4.2), it is convenient to identify three contributions to each angular velocity component – one pressure (
$\boldsymbol{P}^{(2)}$
is a pressure vector corresponding to the transverse rotations. Based on (4.2), it is convenient to identify three contributions to each angular velocity component – one pressure (
![]() $p$
) and two viscous (
$p$
) and two viscous (
![]() $v1$
and
$v1$
and
![]() $v2$
) ones. The detailed calculation, following the substitution of (4.2) in (4.1), yields the following expressions for these contributions:
$v2$
) ones. The detailed calculation, following the substitution of (4.2) in (4.1), yields the following expressions for these contributions:
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{p}^{x} & = & \displaystyle \frac{3}{4(2{\it\xi}_{0}^{2}-1)}\left[-2{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\left(2{\it\xi}_{0}^{2}-\frac{4}{3}\right)\right]\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}-\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{p}^{x} & = & \displaystyle \frac{3}{4(2{\it\xi}_{0}^{2}-1)}\left[-2{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\left(2{\it\xi}_{0}^{2}-\frac{4}{3}\right)\right]\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}-\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{v1}^{x} & = & \displaystyle \frac{\sin {\it\theta}_{j}}{2{\it\xi}_{0}^{2}-1}\left[\left(\frac{\bar{{\it\xi}}_{0}^{2}(1-5{\it\xi}_{0}^{2})}{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+\frac{{\it\xi}_{0}^{2}}{2}(5{\it\xi}_{0}^{2}-7)\right)\sin ^{2}{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{\bar{{\it\xi}}_{0}^{2}}{2}\left({\it\xi}_{0}(5-7{\it\xi}_{0}^{2})\coth ^{-1}{\it\xi}_{0}+7{\it\xi}_{0}^{2}\right)\cos ^{2}{\it\phi}_{j}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{v1}^{x} & = & \displaystyle \frac{\sin {\it\theta}_{j}}{2{\it\xi}_{0}^{2}-1}\left[\left(\frac{\bar{{\it\xi}}_{0}^{2}(1-5{\it\xi}_{0}^{2})}{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+\frac{{\it\xi}_{0}^{2}}{2}(5{\it\xi}_{0}^{2}-7)\right)\sin ^{2}{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{\bar{{\it\xi}}_{0}^{2}}{2}\left({\it\xi}_{0}(5-7{\it\xi}_{0}^{2})\coth ^{-1}{\it\xi}_{0}+7{\it\xi}_{0}^{2}\right)\cos ^{2}{\it\phi}_{j}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{v2}^{x} & = & \displaystyle \frac{\sin {\it\theta}_{j}}{2{\it\xi}_{0}^{2}-1}\left[\left(\frac{{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}(2{\it\xi}_{0}^{2}-1)}{2}\coth ^{-1}{\it\xi}_{0}+\frac{3{\it\xi}_{0}^{2}}{2}\left(1-\frac{2{\it\xi}_{0}^{2}}{3}\right)\right)\sin ^{2}{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\bar{{\it\xi}}_{0}^{2}\left(2{\it\xi}_{0}^{2}+{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})\coth ^{-1}{\it\xi}_{0}\right)\cos ^{2}{\it\phi}_{j}\vphantom{\left(\frac{\bar{{\it\xi}}_{0}^{2}(1-5{\it\xi}_{0}^{2})}{2}\right)}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{v2}^{x} & = & \displaystyle \frac{\sin {\it\theta}_{j}}{2{\it\xi}_{0}^{2}-1}\left[\left(\frac{{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}(2{\it\xi}_{0}^{2}-1)}{2}\coth ^{-1}{\it\xi}_{0}+\frac{3{\it\xi}_{0}^{2}}{2}\left(1-\frac{2{\it\xi}_{0}^{2}}{3}\right)\right)\sin ^{2}{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\bar{{\it\xi}}_{0}^{2}\left(2{\it\xi}_{0}^{2}+{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})\coth ^{-1}{\it\xi}_{0}\right)\cos ^{2}{\it\phi}_{j}\vphantom{\left(\frac{\bar{{\it\xi}}_{0}^{2}(1-5{\it\xi}_{0}^{2})}{2}\right)}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{p}^{y} & = & \displaystyle -{\textstyle \frac{1}{8}}(3{\it\xi}_{0}^{2}-3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}-2)\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{p}^{y} & = & \displaystyle -{\textstyle \frac{1}{8}}(3{\it\xi}_{0}^{2}-3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}-2)\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{v1}^{y} & = & \displaystyle \frac{{\it\xi}_{0}(-6{\it\xi}_{0}^{3}+7{\it\xi}_{0}+(6{\it\xi}_{0}^{4}-9{\it\xi}_{0}^{2}+3)\coth ^{-1}{\it\xi}_{0})}{4(2{\it\xi}_{0}^{2}-1)}\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{v1}^{y} & = & \displaystyle \frac{{\it\xi}_{0}(-6{\it\xi}_{0}^{3}+7{\it\xi}_{0}+(6{\it\xi}_{0}^{4}-9{\it\xi}_{0}^{2}+3)\coth ^{-1}{\it\xi}_{0})}{4(2{\it\xi}_{0}^{2}-1)}\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Omega}_{v2}^{y} & = & \displaystyle \frac{{\it\xi}_{0}({\it\xi}_{0}(6{\it\xi}_{0}^{2}-7)+(-6{\it\xi}_{0}^{4}+9{\it\xi}_{0}^{2}-3)\coth ^{-1}{\it\xi}_{0})}{8(2{\it\xi}_{0}^{2}-1)}\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}_{v2}^{y} & = & \displaystyle \frac{{\it\xi}_{0}({\it\xi}_{0}(6{\it\xi}_{0}^{2}-7)+(-6{\it\xi}_{0}^{4}+9{\it\xi}_{0}^{2}-3)\coth ^{-1}{\it\xi}_{0})}{8(2{\it\xi}_{0}^{2}-1)}\sin 2{\it\theta}_{j}\sin 2{\it\phi}_{j},\end{eqnarray}$$
with
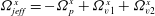 ${\it\Omega}_{jeff}^{x}=-{\it\Omega}_{p}^{x}+{\it\Omega}_{v1}^{x}+{\it\Omega}_{v2}^{x}$
and
${\it\Omega}_{jeff}^{x}=-{\it\Omega}_{p}^{x}+{\it\Omega}_{v1}^{x}+{\it\Omega}_{v2}^{x}$
and
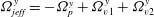 ${\it\Omega}_{jeff}^{y}=-{\it\Omega}_{p}^{y}+{\it\Omega}_{v1}^{y}+{\it\Omega}_{v2}^{y}$
. The rates of change of
${\it\Omega}_{jeff}^{y}=-{\it\Omega}_{p}^{y}+{\it\Omega}_{v1}^{y}+{\it\Omega}_{v2}^{y}$
. The rates of change of
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
are now related to the transverse angular velocity vector,
${\it\phi}_{j}$
are now related to the transverse angular velocity vector,
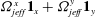 ${\it\Omega}_{jeff}^{x}\mathbf{1}_{x}+{\it\Omega}_{jeff}^{y}\mathbf{1}_{y}$
, as
${\it\Omega}_{jeff}^{x}\mathbf{1}_{x}+{\it\Omega}_{jeff}^{y}\mathbf{1}_{y}$
, as
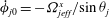 $\dot{{\it\phi}}_{j0}=-{\it\Omega}_{jeff}^{x}/\text{sin}\,{\it\theta}_{j}$
and
$\dot{{\it\phi}}_{j0}=-{\it\Omega}_{jeff}^{x}/\text{sin}\,{\it\theta}_{j}$
and
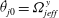 $\dot{{\it\theta}}_{j0}={\it\Omega}_{jeff}^{y}$
, leading to the following equations for a prolate spheroid:
$\dot{{\it\theta}}_{j0}={\it\Omega}_{jeff}^{y}$
, leading to the following equations for a prolate spheroid:
 $$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{0}=\frac{1}{(2{\it\xi}_{0}^{2}-1)}\,\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{0}=\frac{1}{(2{\it\xi}_{0}^{2}-1)}\,\sin {\it\theta}_{j}\cos {\it\theta}_{j}\sin {\it\phi}_{j}\cos {\it\phi}_{j}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{0}=-\frac{1}{(2{\it\xi}_{0}^{2}-1)}[{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{0}=-\frac{1}{(2{\it\xi}_{0}^{2}-1)}[{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}], & \displaystyle\end{eqnarray}$$
where the subscript ‘0’ denotes the Stokesian limit. The equivalent relations for an oblate spheroid, obtained using
![]() ${\it\xi}_{0}\leftrightarrow \text{i}\bar{{\it\xi}}_{0}$
in (4.10). These reduce to the invariant form given in (2.27) on noting that
${\it\xi}_{0}\leftrightarrow \text{i}\bar{{\it\xi}}_{0}$
in (4.10). These reduce to the invariant form given in (2.27) on noting that
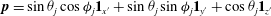 $\boldsymbol{p}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x^{\prime }}+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y^{\prime }}+\cos {\it\theta}_{j}\mathbf{1}_{z^{\prime }}$
, and with the spheroid aspect ratio being given by
$\boldsymbol{p}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x^{\prime }}+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y^{\prime }}+\cos {\it\theta}_{j}\mathbf{1}_{z^{\prime }}$
, and with the spheroid aspect ratio being given by
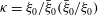 ${\it\kappa}={\it\xi}_{0}/\bar{{\it\xi}}_{0}(\bar{{\it\xi}}_{0}/{\it\xi}_{0})$
for prolate (oblate) spheroids.
${\it\kappa}={\it\xi}_{0}/\bar{{\it\xi}}_{0}(\bar{{\it\xi}}_{0}/{\it\xi}_{0})$
for prolate (oblate) spheroids.
Taken together, (4.9) and (4.10) describe Jeffery orbits on the unit sphere. As is well known, the orbits for a general aspect ratio are the non-planar curves of intersection of a cone, with an elliptical cross-section, with the unit sphere (Trevelyan & Mason Reference Trevelyan and Mason1951). For spheres (
![]() ${\it\xi}_{0}\rightarrow \infty$
), these orbits reduce to circles oriented perpendicularly to the ambient vorticity. In the limiting cases of a slender fibre and a flat disk (accounting for the prolate–oblate transformation, both limits correspond to
${\it\xi}_{0}\rightarrow \infty$
), these orbits reduce to circles oriented perpendicularly to the ambient vorticity. In the limiting cases of a slender fibre and a flat disk (accounting for the prolate–oblate transformation, both limits correspond to
![]() ${\it\xi}_{0}\rightarrow 1$
), the orbits become meridional in character, with the polar axis corresponding to the flow and gradient axes, respectively. In the absence of additional physical mechanisms such as inertia (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
), viscoelasticity, Brownian motion (Leal & Hinch Reference Leal and Hinch1971) or hydrodynamic interactions (Okagawa et al.
Reference Okagawa, Cox and Mason1973a
,Reference Okagawa, Cox and Mason
b
), a given spheroidal particle is confined to its initial Jeffery orbit for all times. This is readily seen in the
${\it\xi}_{0}\rightarrow 1$
), the orbits become meridional in character, with the polar axis corresponding to the flow and gradient axes, respectively. In the absence of additional physical mechanisms such as inertia (Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
), viscoelasticity, Brownian motion (Leal & Hinch Reference Leal and Hinch1971) or hydrodynamic interactions (Okagawa et al.
Reference Okagawa, Cox and Mason1973a
,Reference Okagawa, Cox and Mason
b
), a given spheroidal particle is confined to its initial Jeffery orbit for all times. This is readily seen in the
![]() $(C,{\it\tau})$
coordinates introduced by Leal & Hinch (Reference Leal and Hinch1971), and defined by:
$(C,{\it\tau})$
coordinates introduced by Leal & Hinch (Reference Leal and Hinch1971), and defined by:
 $$\begin{eqnarray}\displaystyle & \displaystyle C=\tan {\it\theta}_{j}\frac{[{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}]^{1/2}}{{\it\xi}_{0}};\quad {\it\tau}=\tan ^{-1}\left[\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}\tan {\it\phi}_{j}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C=\tan {\it\theta}_{j}\frac{[{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}]^{1/2}}{{\it\xi}_{0}};\quad {\it\tau}=\tan ^{-1}\left[\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}\tan {\it\phi}_{j}}\right], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle C=\tan {\it\theta}_{j}\frac{[\bar{{\it\xi}}_{0}^{2}\sin ^{2}{\it\phi}_{j}+{\it\xi}_{0}^{2}\cos ^{2}{\it\phi}_{j}]^{1/2}}{\overline{{\it\xi}}_{0}};\quad {\it\tau}=\tan ^{-1}\left[\displaystyle \frac{{\it\xi}_{0}}{\overline{{\it\xi}}_{0}\tan {\it\phi}_{j}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C=\tan {\it\theta}_{j}\frac{[\bar{{\it\xi}}_{0}^{2}\sin ^{2}{\it\phi}_{j}+{\it\xi}_{0}^{2}\cos ^{2}{\it\phi}_{j}]^{1/2}}{\overline{{\it\xi}}_{0}};\quad {\it\tau}=\tan ^{-1}\left[\displaystyle \frac{{\it\xi}_{0}}{\overline{{\it\xi}}_{0}\tan {\it\phi}_{j}}\right], & \displaystyle\end{eqnarray}$$
for prolate and oblate spheroids, respectively. Using (4.9) and (4.10), the Stokesian orientation dynamics in terms of
![]() $C$
and
$C$
and
![]() ${\it\tau}$
, reduces to:
${\it\tau}$
, reduces to:
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\tau}}{\text{d}t}=\frac{{\it\xi}_{0}\bar{{\it\xi}}_{0}}{2{\it\xi}_{0}^{2}-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\tau}}{\text{d}t}=\frac{{\it\xi}_{0}\bar{{\it\xi}}_{0}}{2{\it\xi}_{0}^{2}-1}, & \displaystyle\end{eqnarray}$$
for both prolate and oblate spheroids. Thus, the Jeffery orbits are conveniently parametrized by the orbit constant
![]() $C$
, and the limiting members of this one-parameter family correspond to a tumbling motion of the spheroid in the flow–gradient plane (
$C$
, and the limiting members of this one-parameter family correspond to a tumbling motion of the spheroid in the flow–gradient plane (
![]() $C=\infty$
) and a log-rolling or spinning (
$C=\infty$
) and a log-rolling or spinning (
![]() $C=0$
) motion about the vorticity axis. Unlike the azimuthal angle, the phase
$C=0$
) motion about the vorticity axis. Unlike the azimuthal angle, the phase
![]() ${\it\tau}$
changes at a constant albeit aspect-ratio-dependent rate. The Jeffery period is the time required for
${\it\tau}$
changes at a constant albeit aspect-ratio-dependent rate. The Jeffery period is the time required for
![]() ${\it\tau}$
to complete a
${\it\tau}$
to complete a
![]() $2{\rm\pi}$
-cycle, and is given by
$2{\rm\pi}$
-cycle, and is given by
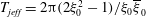 $T_{jeff}=2{\rm\pi}(2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}\overline{{\it\xi}}_{0}$
; the Jeffery period diverges as
$T_{jeff}=2{\rm\pi}(2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}\overline{{\it\xi}}_{0}$
; the Jeffery period diverges as
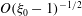 $O({\it\xi}_{0}-1)^{-1/2}$
in the limit of a slender fibre or a flat disk, with the particle spending most of this time in the flow-aligned or gradient-aligned orientation, respectively. The particle flips between aligned orientations, moving along the aforementioned nearly meridional trajectories, in a small
$O({\it\xi}_{0}-1)^{-1/2}$
in the limit of a slender fibre or a flat disk, with the particle spending most of this time in the flow-aligned or gradient-aligned orientation, respectively. The particle flips between aligned orientations, moving along the aforementioned nearly meridional trajectories, in a small
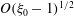 $O({\it\xi}_{0}-1)^{1/2}$
fraction of the rotation period. For later purposes, we note that, in the limit of a slender fibre, (4.11a,b
) reduces to
$O({\it\xi}_{0}-1)^{1/2}$
fraction of the rotation period. For later purposes, we note that, in the limit of a slender fibre, (4.11a,b
) reduces to
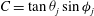 $C=\tan {\it\theta}_{j}\sin {\it\phi}_{j}$
. For a flat disk, on the other hand, one finds
$C=\tan {\it\theta}_{j}\sin {\it\phi}_{j}$
. For a flat disk, on the other hand, one finds
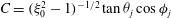 $C=({\it\xi}_{0}^{2}-1)^{-1/2}\tan {\it\theta}_{j}\cos {\it\phi}_{j}$
from (4.12a,b
) with
$C=({\it\xi}_{0}^{2}-1)^{-1/2}\tan {\it\theta}_{j}\cos {\it\phi}_{j}$
from (4.12a,b
) with
![]() ${\it\xi}_{0}\rightarrow 1$
, implying that
${\it\xi}_{0}\rightarrow 1$
, implying that
![]() $\bar{{\it\xi}}_{0}C$
, rather than
$\bar{{\it\xi}}_{0}C$
, rather than
![]() $C$
, is a more appropriate choice for the orbit constant, since
$C$
, is a more appropriate choice for the orbit constant, since
![]() $O(1)$
values of
$O(1)$
values of
![]() $C$
in the flat-disk limit correspond to a vanishingly small neighbourhood of the gradient–vorticity plane.
$C$
in the flat-disk limit correspond to a vanishingly small neighbourhood of the gradient–vorticity plane.
5 The effect of particle inertia: massive spheroids
 $(Re=0,St\ll 1)$
$(Re=0,St\ll 1)$
In this section, we present results for the
![]() $O(St)$
and
$O(St)$
and
![]() $O(St^{2})$
corrections to the Jeffery angular velocity. Section 5.1 details the
$O(St^{2})$
corrections to the Jeffery angular velocity. Section 5.1 details the
![]() $O(St)$
analysis and examines the resulting drift across Jeffery orbits. It is shown, consistent with earlier results (Subramanian & Koch Reference Subramanian and Koch2006b
; Einarsson et al.
Reference Einarsson, Angilella and Mehlig2014), that a prolate spheroid asymptotes to a tumbling mode while an oblate spheroid approaches a spinning mode. The absence of an angular acceleration implies that particle inertia can have no effect after an oblate spheroid has drifted across Jeffery orbits to a steadily spinning configuration. This is not true for a prolate spheroid, and the analysis in § 5.2 shows that particle inertia modifies the tumbling period at
$O(St)$
analysis and examines the resulting drift across Jeffery orbits. It is shown, consistent with earlier results (Subramanian & Koch Reference Subramanian and Koch2006b
; Einarsson et al.
Reference Einarsson, Angilella and Mehlig2014), that a prolate spheroid asymptotes to a tumbling mode while an oblate spheroid approaches a spinning mode. The absence of an angular acceleration implies that particle inertia can have no effect after an oblate spheroid has drifted across Jeffery orbits to a steadily spinning configuration. This is not true for a prolate spheroid, and the analysis in § 5.2 shows that particle inertia modifies the tumbling period at
![]() $O(St^{2})$
.
$O(St^{2})$
.
Considering (2.30) with
![]() $Re=0$
, one obtains:
$Re=0$
, one obtains:
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\,\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1}), & & \displaystyle\end{eqnarray}$$
where the second term on the right-hand side denotes the
![]() $O(St)$
rate of change of the angular momentum in the inertial reference frame. It is convenient to evaluate this in the body-fixed coordinate system, rotating with
$O(St)$
rate of change of the angular momentum in the inertial reference frame. It is convenient to evaluate this in the body-fixed coordinate system, rotating with
![]() ${\it\bf\Omega}_{b}$
, chosen to evaluate the fluid inertia terms in (2.30), and given by
${\it\bf\Omega}_{b}$
, chosen to evaluate the fluid inertia terms in (2.30), and given by
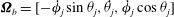 ${\it\bf\Omega}_{b}=[-\dot{{\it\phi}}_{j}\sin {\it\theta}_{j},\dot{{\it\theta}}_{j},\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}]$
; recall that the spin (
${\it\bf\Omega}_{b}=[-\dot{{\it\phi}}_{j}\sin {\it\theta}_{j},\dot{{\it\theta}}_{j},\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}]$
; recall that the spin (
![]() $Z$
) component,
$Z$
) component,
![]() $\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}$
, is that needed to constrain the
$\dot{{\it\phi}}_{j}\cos {\it\theta}_{j}$
, is that needed to constrain the
![]() $Y$
-axis to the flow–gradient plane. The space-fixed rate of change is related to the body-fixed rate of change as
$Y$
-axis to the flow–gradient plane. The space-fixed rate of change is related to the body-fixed rate of change as
 $(\text{d}/\text{d}t)(\cdot )=((\text{d}/\text{d}t)(\cdot ))_{b}+{\it\bf\Omega}_{b}\wedge (\cdot )$
, and (5.2) takes the form:
$(\text{d}/\text{d}t)(\cdot )=((\text{d}/\text{d}t)(\cdot ))_{b}+{\it\bf\Omega}_{b}\wedge (\cdot )$
, and (5.2) takes the form:
 $$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\left(\frac{\text{d}{\it\bf\Omega}_{1}}{\text{d}t}\right)_{b}+{\it\bf\Omega}_{b}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1})\right], & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Omega}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}={\it\bf\Gamma}\boldsymbol{ : }\int _{S_{p}}\boldsymbol{x}({\it\bf\Sigma}^{(2)}\boldsymbol{\cdot }\boldsymbol{n})\,\text{d}S+St\left[\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\left(\frac{\text{d}{\it\bf\Omega}_{1}}{\text{d}t}\right)_{b}+{\it\bf\Omega}_{b}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1})\right], & & \displaystyle\end{eqnarray}$$
the moment of inertia tensor being a constant in the body-fixed coordinate system. The formal expressions for the inertial corrections to the Jeffery angular velocity are readily obtained. Using a regular expansion of the form
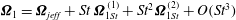 ${\it\bf\Omega}_{1}={\it\bf\Omega}_{jeff}+St\,{\it\bf\Omega}_{1St}^{(1)}+St^{2}{\it\bf\Omega}_{1St}^{(2)}+O(St^{3})$
for the particle angular velocity,
${\it\bf\Omega}_{1}={\it\bf\Omega}_{jeff}+St\,{\it\bf\Omega}_{1St}^{(1)}+St^{2}{\it\bf\Omega}_{1St}^{(2)}+O(St^{3})$
for the particle angular velocity,
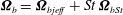 ${\it\bf\Omega}_{b}={\it\bf\Omega}_{bjeff}+St\,{\it\bf\Omega}_{bSt}$
for the angular velocity of the body-fixed coordinate system, and the expansion
${\it\bf\Omega}_{b}={\it\bf\Omega}_{bjeff}+St\,{\it\bf\Omega}_{bSt}$
for the angular velocity of the body-fixed coordinate system, and the expansion
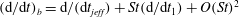 $(\text{d}/\text{d}t)_{b}=\text{d}/(\text{d}t_{jeff})+St(\text{d}/\text{d}t_{1})+O(St)^{2}$
for the time rate of change, in (5.2), one obtains:
$(\text{d}/\text{d}t)_{b}=\text{d}/(\text{d}t_{jeff})+St(\text{d}/\text{d}t_{1})+O(St)^{2}$
for the time rate of change, in (5.2), one obtains:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\bf\Omega}_{1St}^{(1)}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}=\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\frac{\text{d}{\it\bf\Omega}_{jeff}}{\text{d}t_{jeff}}+{\it\bf\Omega}_{bjeff}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{jeff}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\bf\Omega}_{1St}^{(1)}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}=\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\frac{\text{d}{\it\bf\Omega}_{jeff}}{\text{d}t_{jeff}}+{\it\bf\Omega}_{bjeff}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{jeff}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\bf\Omega}_{1St}^{(2)}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}=\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\left(\frac{\text{d}{\it\bf\Omega}_{jeff}}{\text{d}t_{1}}+\frac{\text{d}{\it\bf\Omega}_{1St}^{(1)}}{\text{d}t_{jeff}}\right)+{\it\bf\Omega}_{bjeff}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1St}^{(1)})+{\it\bf\Omega}_{bSt}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{jeff}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\bf\Omega}_{1St}^{(2)}\boldsymbol{\cdot }\unicode[STIX]{x1D647}^{(2)}=\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }\left(\frac{\text{d}{\it\bf\Omega}_{jeff}}{\text{d}t_{1}}+\frac{\text{d}{\it\bf\Omega}_{1St}^{(1)}}{\text{d}t_{jeff}}\right)+{\it\bf\Omega}_{bjeff}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{1St}^{(1)})+{\it\bf\Omega}_{bSt}\wedge (\unicode[STIX]{x1D644}_{p}\boldsymbol{\cdot }{\it\bf\Omega}_{jeff}), & \displaystyle\end{eqnarray}$$
at
![]() $O(St)$
and
$O(St)$
and
![]() $O(St^{2})$
, respectively. Here,
$O(St^{2})$
, respectively. Here,
 $\text{d}/(\text{d}t_{jeff})$
denotes the rate of change along a Jeffery orbit, and is given by (4.9) and (4.10) in terms of
$\text{d}/(\text{d}t_{jeff})$
denotes the rate of change along a Jeffery orbit, and is given by (4.9) and (4.10) in terms of
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
. The derivative
${\it\phi}_{j}$
. The derivative
![]() $\text{d}/\text{d}t_{1}$
denotes the correction to this rate of change due to the
$\text{d}/\text{d}t_{1}$
denotes the correction to this rate of change due to the
![]() $O(St)$
deviation from a Jeffery orbit. Knowing
$O(St)$
deviation from a Jeffery orbit. Knowing
![]() ${\it\bf\Omega}_{1St}^{(1)}$
,
${\it\bf\Omega}_{1St}^{(1)}$
,
![]() $\text{d}/\text{d}t_{1}$
may be expressed in terms of corrections to the Jeffery rates of change of
$\text{d}/\text{d}t_{1}$
may be expressed in terms of corrections to the Jeffery rates of change of
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
. The test-torque tensor,
${\it\phi}_{j}$
. The test-torque tensor,
![]() $\unicode[STIX]{x1D647}^{(2)}$
, in (5.3) and (5.4) has already been defined at the end of § 3. The non-dimensional moment of inertia tensor,
$\unicode[STIX]{x1D647}^{(2)}$
, in (5.3) and (5.4) has already been defined at the end of § 3. The non-dimensional moment of inertia tensor,
![]() $\unicode[STIX]{x1D644}_{p}$
, is given by
$\unicode[STIX]{x1D644}_{p}$
, is given by
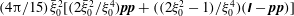 $(4{\rm\pi}/15)\bar{{\it\xi}}_{0}^{2}[(2\bar{{\it\xi}}_{0}^{2}/{\it\xi}_{0}^{4})\boldsymbol{p}\boldsymbol{p}+((2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}^{4})(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})]$
and
$(4{\rm\pi}/15)\bar{{\it\xi}}_{0}^{2}[(2\bar{{\it\xi}}_{0}^{2}/{\it\xi}_{0}^{4})\boldsymbol{p}\boldsymbol{p}+((2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}^{4})(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})]$
and
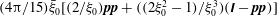 $(4{\rm\pi}/15)\bar{{\it\xi}}_{0}[(2/{\it\xi}_{0})\boldsymbol{p}\boldsymbol{p}+((2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}^{3})(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})]$
for prolate and oblate spheroids, respectively.
$(4{\rm\pi}/15)\bar{{\it\xi}}_{0}[(2/{\it\xi}_{0})\boldsymbol{p}\boldsymbol{p}+((2{\it\xi}_{0}^{2}-1)/{\it\xi}_{0}^{3})(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})]$
for prolate and oblate spheroids, respectively.
5.1 The
 $O(St)$
analysis: drift due to particle inertia
$O(St)$
analysis: drift due to particle inertia
The
![]() $O(St)$
correction to
$O(St)$
correction to
![]() ${\it\bf\Omega}_{jeff}$
may be evaluated from (5.3) in a straightforward manner. We only note that
${\it\bf\Omega}_{jeff}$
may be evaluated from (5.3) in a straightforward manner. We only note that
![]() ${\it\bf\Omega}_{jeff}$
in (5.3) includes the spin component, and the transverse components of
${\it\bf\Omega}_{jeff}$
in (5.3) includes the spin component, and the transverse components of
![]() ${\it\bf\Omega}_{1St}^{(1)}$
, that drive the
${\it\bf\Omega}_{1St}^{(1)}$
, that drive the
![]() $O(St)$
drift, therefore couple to the axial spin at leading order. For nearly spherical particles, Subramanian & Koch (Reference Subramanian and Koch2006b
) argued that the inertial drift may be interpreted as arising from an imbalance between the centrifugal and gyroscopic torques, both of which depend on the axial spin. Defining
$O(St)$
drift, therefore couple to the axial spin at leading order. For nearly spherical particles, Subramanian & Koch (Reference Subramanian and Koch2006b
) argued that the inertial drift may be interpreted as arising from an imbalance between the centrifugal and gyroscopic torques, both of which depend on the axial spin. Defining
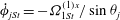 $\dot{{\it\phi}}_{jSt}=-{\it\Omega}_{1St}^{(1)x}/\sin {\it\theta}_{j}$
and
$\dot{{\it\phi}}_{jSt}=-{\it\Omega}_{1St}^{(1)x}/\sin {\it\theta}_{j}$
and
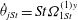 $\dot{{\it\theta}}_{jSt}=St{\it\Omega}_{1St}^{(1)y}$
, the equations for the rates of change, at
$\dot{{\it\theta}}_{jSt}=St{\it\Omega}_{1St}^{(1)y}$
, the equations for the rates of change, at
![]() $O(St)$
, have the following general form:
$O(St)$
, have the following general form:
 $$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St} & = & \displaystyle \sin {\it\theta}_{j}\cos {\it\theta}_{j} [F_{1}^{p}({\it\xi}_{0})+F_{2}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+F_{3}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+F_{4}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle +\,F_{5}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}-4{\it\phi}_{j})+F_{6}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}+4{\it\phi}_{j})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St} & = & \displaystyle \sin {\it\theta}_{j}\cos {\it\theta}_{j} [F_{1}^{p}({\it\xi}_{0})+F_{2}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+F_{3}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+F_{4}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle +\,F_{5}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}-4{\it\phi}_{j})+F_{6}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}+4{\it\phi}_{j})],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St} & = & \displaystyle \sin {\it\phi}_{j}\cos {\it\phi}_{j} [G_{1}^{p}({\it\xi}_{0})+G_{2}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+G_{3}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle +\,G_{4}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j})\cos (2{\it\phi}_{j})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St} & = & \displaystyle \sin {\it\phi}_{j}\cos {\it\phi}_{j} [G_{1}^{p}({\it\xi}_{0})+G_{2}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+G_{3}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}\nonumber\\ \displaystyle & & \displaystyle +\,G_{4}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j})\cos (2{\it\phi}_{j})],\end{eqnarray}$$
for both prolate and oblate spheroids. The aspect-ratio-dependent functions are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{p}({\it\xi}_{0})=\frac{(4{\it\xi}_{0}^{4}-7{\it\xi}_{0}^{2}+3)({\it\xi}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{160{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{p}({\it\xi}_{0})=\frac{(4{\it\xi}_{0}^{4}-7{\it\xi}_{0}^{2}+3)({\it\xi}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{160{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{2}^{p}({\it\xi}_{0})=\frac{\bar{{\it\xi}}_{0}^{4}(\coth ^{-1}{\it\xi}_{0}+{\it\xi}_{0}({\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}-1))}{40{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{2}^{p}({\it\xi}_{0})=\frac{\bar{{\it\xi}}_{0}^{4}(\coth ^{-1}{\it\xi}_{0}+{\it\xi}_{0}({\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}-1))}{40{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{3}^{p}({\it\xi}_{0})=F_{4}^{p}({\it\xi}_{0})=-\frac{\bar{{\it\xi}}_{0}^{2}({\it\xi}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{160{\it\xi}_{0}(2{\it\xi}_{0}^{2}-1)^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{3}^{p}({\it\xi}_{0})=F_{4}^{p}({\it\xi}_{0})=-\frac{\bar{{\it\xi}}_{0}^{2}({\it\xi}_{0}^{2}\coth ^{-1}{\it\xi}_{0}+\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{160{\it\xi}_{0}(2{\it\xi}_{0}^{2}-1)^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{5}^{p}({\it\xi}_{0})=F_{6}^{p}({\it\xi}_{0})=-\frac{F_{3}^{p}({\it\xi}_{0})}{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{5}^{p}({\it\xi}_{0})=F_{6}^{p}({\it\xi}_{0})=-\frac{F_{3}^{p}({\it\xi}_{0})}{2}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle G_{1}^{p}({\it\xi}_{0})=-\frac{(3{\it\xi}_{0}^{4}-5{\it\xi}_{0}^{2}+2)(({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{40{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G_{1}^{p}({\it\xi}_{0})=-\frac{(3{\it\xi}_{0}^{4}-5{\it\xi}_{0}^{2}+2)(({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})}{40{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle G_{2}^{p}({\it\xi}_{0})={\it\xi}_{0}^{2}G_{3}^{p}({\it\xi}_{0})=-{\it\xi}_{0}^{2}G_{4}^{p}({\it\xi}_{0})=\frac{{\it\xi}_{0}(-{\it\xi}_{0}^{3}+{\it\xi}_{0}+({\it\xi}_{0}^{4}-1)\coth ^{-1}{\it\xi}_{0})}{40(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G_{2}^{p}({\it\xi}_{0})={\it\xi}_{0}^{2}G_{3}^{p}({\it\xi}_{0})=-{\it\xi}_{0}^{2}G_{4}^{p}({\it\xi}_{0})=\frac{{\it\xi}_{0}(-{\it\xi}_{0}^{3}+{\it\xi}_{0}+({\it\xi}_{0}^{4}-1)\coth ^{-1}{\it\xi}_{0})}{40(1-2{\it\xi}_{0}^{2})^{2}}, & \displaystyle\end{eqnarray}$$
for a prolate spheroid, and for an oblate spheroid the functions can be obtained using the prolate–oblate transformation (note that the transformation
![]() ${\it\xi}_{0}\leftrightarrow \text{i}\bar{{\it\xi}}_{0}$
and
${\it\xi}_{0}\leftrightarrow \text{i}\bar{{\it\xi}}_{0}$
and
 $d\leftrightarrow -\text{i}d$
, has to be applied on the relevant dimensional angular velocity, having accounted for the aspect-ratio dependence that occurs in the relevant non-dimensional parameter –
$d\leftrightarrow -\text{i}d$
, has to be applied on the relevant dimensional angular velocity, having accounted for the aspect-ratio dependence that occurs in the relevant non-dimensional parameter –
![]() $St$
here and
$St$
here and
![]() $Re$
in § 6.2). Although not needed for the calculations here, we note that the correction to the axial spin at
$Re$
in § 6.2). Although not needed for the calculations here, we note that the correction to the axial spin at
![]() $O(St)$
,
$O(St)$
,
![]() ${\it\Omega}_{1St}^{(1)z}$
, is given by
${\it\Omega}_{1St}^{(1)z}$
, is given by
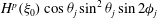 $H^{p}({\it\xi}_{0})\cos {\it\theta}_{j}\sin ^{2}{\it\theta}_{j}\sin 2{\it\phi}_{j}$
, with
$H^{p}({\it\xi}_{0})\cos {\it\theta}_{j}\sin ^{2}{\it\theta}_{j}\sin 2{\it\phi}_{j}$
, with
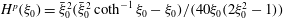 $H^{p}({\it\xi}_{0})=\bar{{\it\xi}}_{0}^{2}(\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})/(40{\it\xi}_{0}(2{\it\xi}_{0}^{2}-1))$
, for a prolate spheroid. Thus, including particle inertia leads to an increased spin in the extensional quadrants of the simple shear flow and a reduction in the compressional quadrants, since the persistence of spin, at
$H^{p}({\it\xi}_{0})=\bar{{\it\xi}}_{0}^{2}(\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0}-{\it\xi}_{0})/(40{\it\xi}_{0}(2{\it\xi}_{0}^{2}-1))$
, for a prolate spheroid. Thus, including particle inertia leads to an increased spin in the extensional quadrants of the simple shear flow and a reduction in the compressional quadrants, since the persistence of spin, at
![]() $O(St)$
, is proportional to the instantaneous rate of change of spin along a Jeffery orbit. The spin remains the same, to
$O(St)$
, is proportional to the instantaneous rate of change of spin along a Jeffery orbit. The spin remains the same, to
![]() $O(St)$
, for orientations in the flow–vorticity (
$O(St)$
, for orientations in the flow–vorticity (
 ${\it\phi}_{j}=0,{\rm\pi}$
) and gradient–vorticity planes (
${\it\phi}_{j}=0,{\rm\pi}$
) and gradient–vorticity planes (
 ${\it\phi}_{j}={\rm\pi}/2,3{\rm\pi}/2$
), since the rate of change of spin, at leading order, is zero for these orientations.
${\it\phi}_{j}={\rm\pi}/2,3{\rm\pi}/2$
), since the rate of change of spin, at leading order, is zero for these orientations.
From the definition of
![]() $C$
for a prolate spheroid, the irreversible orbital drift, at
$C$
for a prolate spheroid, the irreversible orbital drift, at
![]() $O(St)$
, may now be obtained as:
$O(St)$
, may now be obtained as:
 $$\begin{eqnarray}\displaystyle \frac{\text{d}C}{\text{d}t} & = & \displaystyle \frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\frac{\text{d}{\it\theta}_{j}}{\text{d}t}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\frac{\text{d}{\it\phi}_{j}}{\text{d}t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}C}{\text{d}t} & = & \displaystyle \frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\frac{\text{d}{\it\theta}_{j}}{\text{d}t}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\frac{\text{d}{\it\phi}_{j}}{\text{d}t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle St\left[\frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle St\left[\frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}\right],\end{eqnarray}$$
where
 $(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
and
$(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
and
 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
are given by (5.5) and (5.6). For
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
are given by (5.5) and (5.6). For
![]() $St\ll 1$
, the weak inertial drift leads to a tightly spiralling trajectory of the spheroidal axis, with each turn of this spiral closely approximating a Jeffery orbit. It is convenient to characterize the drift in terms of the pitch of this spiral measured in units of
$St\ll 1$
, the weak inertial drift leads to a tightly spiralling trajectory of the spheroidal axis, with each turn of this spiral closely approximating a Jeffery orbit. It is convenient to characterize the drift in terms of the pitch of this spiral measured in units of
![]() $C$
. The pitch equals the change in
$C$
. The pitch equals the change in
![]() $C$
in a single Jeffery period,
$C$
in a single Jeffery period,
![]() ${\rm\Delta}C$
, and
${\rm\Delta}C$
, and
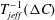 $T_{jeff}^{-1}({\rm\Delta}C)$
may be regarded as the
$T_{jeff}^{-1}({\rm\Delta}C)$
may be regarded as the
![]() $C$
-component of an averaged inertial drift velocity. One obtains:
$C$
-component of an averaged inertial drift velocity. One obtains:
 $$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle \int _{0}^{T_{jeff}}\frac{\text{d}C}{\text{d}t}\,\text{d}t,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle \int _{0}^{T_{jeff}}\frac{\text{d}C}{\text{d}t}\,\text{d}t,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\text{d}{\it\tau}}{\text{d}t}\right)^{-1}\int _{0}^{2{\rm\pi}}\frac{\text{d}C}{\text{d}t}\,\text{d}{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{\text{d}{\it\tau}}{\text{d}t}\right)^{-1}\int _{0}^{2{\rm\pi}}\frac{\text{d}C}{\text{d}t}\,\text{d}{\it\tau},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle St\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\int _{0}^{2{\rm\pi}}\left[\frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}\right]\text{d}{\it\tau},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle St\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\int _{0}^{2{\rm\pi}}\left[\frac{C}{\sin {\it\theta}_{j}\cos {\it\theta}_{j}}\left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{St}+\frac{C\cos {\it\phi}_{j}\sin {\it\phi}_{j}}{{\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}\right]\text{d}{\it\tau},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the subscript ‘
![]() $p$
’ denotes particle inertia, and the
$p$
’ denotes particle inertia, and the
![]() ${\it\tau}$
-integrals are to be evaluated for
${\it\tau}$
-integrals are to be evaluated for
![]() $C$
fixed. Using (5.5) and (5.6):
$C$
fixed. Using (5.5) and (5.6):
 $$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle St\,C\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\left\{\int _{0}^{2{\rm\pi}} [F_{1}^{p}({\it\xi}_{0})+F_{2}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+F_{3}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+F_{4}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle +\,F_{5}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}-4{\it\phi}_{j})+F_{6}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}+4{\it\phi}_{j})]\,\text{d}{\it\tau}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{2{\rm\pi}}\frac{\sin ^{2}{\it\phi}_{j}\cos ^{2}{\it\phi}_{j}}{({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j})} [G_{1}^{p}({\it\xi}_{0})+G_{2}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}\nonumber\\ \displaystyle & & \displaystyle +\left.G_{3}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+G_{4}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}\cos 2{\it\phi}_{j} ]\,\text{d}{\it\tau}\vphantom{\displaystyle \int _{0}^{2{\rm\pi}}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle St\,C\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\left\{\int _{0}^{2{\rm\pi}} [F_{1}^{p}({\it\xi}_{0})+F_{2}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+F_{3}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}+F_{4}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}\right.\nonumber\\ \displaystyle & & \displaystyle +\,F_{5}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}-4{\it\phi}_{j})+F_{6}^{p}({\it\xi}_{0})\cos (2{\it\theta}_{j}+4{\it\phi}_{j})]\,\text{d}{\it\tau}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{2{\rm\pi}}\frac{\sin ^{2}{\it\phi}_{j}\cos ^{2}{\it\phi}_{j}}{({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j})} [G_{1}^{p}({\it\xi}_{0})+G_{2}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}\nonumber\\ \displaystyle & & \displaystyle +\left.G_{3}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+G_{4}^{p}({\it\xi}_{0})\cos 2{\it\theta}_{j}\cos 2{\it\phi}_{j} ]\,\text{d}{\it\tau}\vphantom{\displaystyle \int _{0}^{2{\rm\pi}}}\right\}.\end{eqnarray}$$
This may in turn be written as:
 $$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle St\,C\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\{[I_{1}F_{1}^{p}({\it\xi}_{0})+I_{2}F_{2}^{p}({\it\xi}_{0})+I_{3}F_{3}^{p}({\it\xi}_{0})+I_{4}F_{4}^{p}({\it\xi}_{0})+I_{5}F_{5}^{p}({\it\xi}_{0})+I_{6}F_{6}^{p}({\it\xi}_{0})]\nonumber\\ \displaystyle & & \displaystyle +\,[J_{1}G_{1}^{p}({\it\xi}_{0})+J_{2}G_{2}^{p}({\it\xi}_{0})+J_{3}G_{3}^{p}({\it\xi}_{0})+J_{4}G_{4}^{p}({\it\xi}_{0})]\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Delta}C_{p} & = & \displaystyle St\,C\frac{(2{\it\xi}_{0}^{2}-1)}{{\it\xi}_{0}\bar{{\it\xi}}_{0}}\{[I_{1}F_{1}^{p}({\it\xi}_{0})+I_{2}F_{2}^{p}({\it\xi}_{0})+I_{3}F_{3}^{p}({\it\xi}_{0})+I_{4}F_{4}^{p}({\it\xi}_{0})+I_{5}F_{5}^{p}({\it\xi}_{0})+I_{6}F_{6}^{p}({\it\xi}_{0})]\nonumber\\ \displaystyle & & \displaystyle +\,[J_{1}G_{1}^{p}({\it\xi}_{0})+J_{2}G_{2}^{p}({\it\xi}_{0})+J_{3}G_{3}^{p}({\it\xi}_{0})+J_{4}G_{4}^{p}({\it\xi}_{0})]\},\end{eqnarray}$$
where the values of
![]() $I_{i}$
and
$I_{i}$
and
![]() $J_{i}$
result from integrating the corresponding trigonometric functions in (5.18) over
$J_{i}$
result from integrating the corresponding trigonometric functions in (5.18) over
![]() ${\it\tau}$
. To evaluate the drift to
${\it\tau}$
. To evaluate the drift to
![]() $O(St)$
, the trigonometric functions involved may be related to
$O(St)$
, the trigonometric functions involved may be related to
![]() $C$
and
$C$
and
![]() ${\it\tau}$
using (4.11a,b
), the error in this approximation being
${\it\tau}$
using (4.11a,b
), the error in this approximation being
![]() $O(St^{2})$
. The expressions for
$O(St^{2})$
. The expressions for
![]() $I_{1}$
to
$I_{1}$
to
![]() $I_{6}$
and
$I_{6}$
and
![]() $J_{1}$
to
$J_{1}$
to
![]() $J_{4}$
as functions of
$J_{4}$
as functions of
![]() $C$
and
$C$
and
![]() ${\it\xi}_{0}$
are given in appendix C.
${\it\xi}_{0}$
are given in appendix C.

Figure 2. The drift due to the particle inertia, as characterized by the normalized change in the orbit constant in a single Jeffery period,
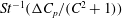 $St^{-1}({\rm\Delta}C_{p}/(C^{2}+1))$
, plotted as a function of
$St^{-1}({\rm\Delta}C_{p}/(C^{2}+1))$
, plotted as a function of
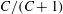 $C/(C+1)$
, for a prolate spheroid;
$C/(C+1)$
, for a prolate spheroid;
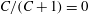 $C/(C+1)=0$
and
$C/(C+1)=0$
and
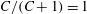 $C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
$C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
![]() ${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
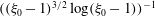 $(({\it\xi}_{0}-1)^{3/2}\log ({\it\xi}_{0}-1))^{-1}$
, to make the drift finite in the slender-fibre limit (
$(({\it\xi}_{0}-1)^{3/2}\log ({\it\xi}_{0}-1))^{-1}$
, to make the drift finite in the slender-fibre limit (
![]() ${\it\xi}_{0}\rightarrow 1$
).
${\it\xi}_{0}\rightarrow 1$
).
The drift for a prolate spheroid that results from using (5.19) and (C 1)–(C 9) is plotted as a function of the normalized orbit constant,
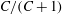 $C/(C+1)$
in figure 2 for various aspect ratios. The drift is evidently zero for
$C/(C+1)$
in figure 2 for various aspect ratios. The drift is evidently zero for
![]() $C=0$
and
$C=0$
and
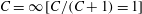 $C=\infty \,[C/(C+1)=1]$
on account of symmetry, but is positive for all other values of
$C=\infty \,[C/(C+1)=1]$
on account of symmetry, but is positive for all other values of
![]() $C$
and for all aspect ratios. Thus, a massive prolate spheroid always drifts towards the tumbling mode. In the near-sphere limit (
$C$
and for all aspect ratios. Thus, a massive prolate spheroid always drifts towards the tumbling mode. In the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
),
${\it\xi}_{0}\rightarrow \infty$
),
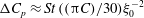 ${\rm\Delta}C_{p}\approx St\,(({\rm\pi}C)/30){\it\xi}_{0}^{-2}$
, as is expected on account of the drift being proportional to the square of the eccentricity (
${\rm\Delta}C_{p}\approx St\,(({\rm\pi}C)/30){\it\xi}_{0}^{-2}$
, as is expected on account of the drift being proportional to the square of the eccentricity (
![]() $e=1/{\it\xi}_{0}$
). In the limit of a slender fibre (
$e=1/{\it\xi}_{0}$
). In the limit of a slender fibre (
![]() ${\it\xi}_{0}\rightarrow 1$
), one finds
${\it\xi}_{0}\rightarrow 1$
), one finds
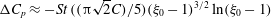 ${\rm\Delta}C_{p}\approx -St\,(({\rm\pi}\sqrt{2}C)/5)({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)$
. A leading-order estimate from the non-aligned phase of a rotating fibre comes out to be larger than
${\rm\Delta}C_{p}\approx -St\,(({\rm\pi}\sqrt{2}C)/5)({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)$
. A leading-order estimate from the non-aligned phase of a rotating fibre comes out to be larger than
 $O[({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)]$
. This estimate arises from transverse moments of inertia of
$O[({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)]$
. This estimate arises from transverse moments of inertia of
 $O({\it\xi}_{0}-1)$
driving a drift against a resistive torque of
$O({\it\xi}_{0}-1)$
driving a drift against a resistive torque of
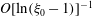 $O[\ln ({\it\xi}_{0}-1)]^{-1}$
predicted by slender body theory; the next correction in the non-aligned phase is
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
predicted by slender body theory; the next correction in the non-aligned phase is
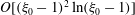 $O[({\it\xi}_{0}-1)^{2}\ln ({\it\xi}_{0}-1)]$
. The actual estimate of
$O[({\it\xi}_{0}-1)^{2}\ln ({\it\xi}_{0}-1)]$
. The actual estimate of
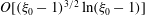 $O[({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)]$
above must therefore involve the dominant flow-aligned phase of the fibre. These near-sphere and slender-fibre scalings, together with a normalizing factor of
$O[({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)]$
above must therefore involve the dominant flow-aligned phase of the fibre. These near-sphere and slender-fibre scalings, together with a normalizing factor of
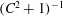 $(C^{2}+1)^{-1}$
, are accounted for in figure 2 in order to render the
$(C^{2}+1)^{-1}$
, are accounted for in figure 2 in order to render the
![]() ${\rm\Delta}C_{p}$
curve, in the relevant asymptotic limit, a finite one for all
${\rm\Delta}C_{p}$
curve, in the relevant asymptotic limit, a finite one for all
![]() $C$
.
$C$
.
The drift due to particle inertia for an oblate spheroid may be obtained in a similar manner with expressions for the analogues of the
![]() $I_{i}$
and
$I_{i}$
and
![]() $J_{i}$
now being obtained using (4.12a,b
). The normalized
$J_{i}$
now being obtained using (4.12a,b
). The normalized
![]() ${\rm\Delta}C_{p}$
for a massive oblate spheroid is plotted as a function of
${\rm\Delta}C_{p}$
for a massive oblate spheroid is plotted as a function of
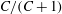 $C/(C+1)$
in figure 3, and is negative for all values of
$C/(C+1)$
in figure 3, and is negative for all values of
![]() $C$
and aspect ratios, implying that the spheroid would asymptote to a steady spinning mode starting from any initial orientation. In the near-sphere limit,
$C$
and aspect ratios, implying that the spheroid would asymptote to a steady spinning mode starting from any initial orientation. In the near-sphere limit,
![]() ${\rm\Delta}C_{p}$
is just the negative of that for a prolate spheroid. In contrast to a prolate spheroid, however, a normalization based on this near-sphere scaling of
${\rm\Delta}C_{p}$
is just the negative of that for a prolate spheroid. In contrast to a prolate spheroid, however, a normalization based on this near-sphere scaling of
![]() $O({\it\xi}_{0}^{-2})$
alone suffices for plotting
$O({\it\xi}_{0}^{-2})$
alone suffices for plotting
![]() ${\rm\Delta}C_{p}$
, since the inertial drift remains finite in the flat-disk limit –
${\rm\Delta}C_{p}$
, since the inertial drift remains finite in the flat-disk limit –
 $\lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{p}\approx -{\rm\pi}^{2}(((C^{2}+1)^{1/2}-1)/(20C))$
. The moments of inertia of a thin oblate spheroid are only
$\lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{p}\approx -{\rm\pi}^{2}(((C^{2}+1)^{1/2}-1)/(20C))$
. The moments of inertia of a thin oblate spheroid are only
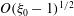 $O({\it\xi}_{0}-1)^{1/2}$
, but their smallness appears to be compensated by the long,
$O({\it\xi}_{0}-1)^{1/2}$
, but their smallness appears to be compensated by the long,
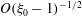 $O({\it\xi}_{0}-1)^{-1/2}$
, period available for inertia to act, leading to
$O({\it\xi}_{0}-1)^{-1/2}$
, period available for inertia to act, leading to
![]() ${\rm\Delta}C_{p}$
being
${\rm\Delta}C_{p}$
being
![]() $O(1)$
for
$O(1)$
for
![]() ${\it\xi}_{0}\rightarrow 1$
. Note that the
${\it\xi}_{0}\rightarrow 1$
. Note that the
![]() ${\rm\Delta}C_{p}$
curve for any oblate spheroid crosses that of a near-sphere, with this cross-over point moving in from
${\rm\Delta}C_{p}$
curve for any oblate spheroid crosses that of a near-sphere, with this cross-over point moving in from
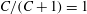 $C/(C+1)=1$
to a limiting value of approximately 0.75 for a flat disk. thus, for sufficiently thin spheroids, the inertial drift increases in magnitude below this cross-over
$C/(C+1)=1$
to a limiting value of approximately 0.75 for a flat disk. thus, for sufficiently thin spheroids, the inertial drift increases in magnitude below this cross-over
![]() $C$
, while decreasing for greater
$C$
, while decreasing for greater
![]() $C$
values.
$C$
values.

Figure 3. The drift due to the particle inertia, as characterized by the normalized change in the orbit constant in a single Jeffery period,
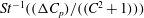 $St^{-1}(({\rm\Delta}C_{p})/((C^{2}+1)))$
, plotted as a function of
$St^{-1}(({\rm\Delta}C_{p})/((C^{2}+1)))$
, plotted as a function of
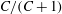 $C/(C+1)$
, for an oblate spheroid;
$C/(C+1)$
, for an oblate spheroid;
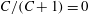 $C/(C+1)=0$
and
$C/(C+1)=0$
and
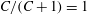 $C/(C+1)=1$
correspond to the spinning and the tumbling modes, respectively.
$C/(C+1)=1$
correspond to the spinning and the tumbling modes, respectively.
The expressions for
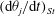 $(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
and
$(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
and
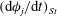 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
do not match those given in Subramanian & Koch (Reference Subramanian and Koch2006b
) for a near-sphere in the limit
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
do not match those given in Subramanian & Koch (Reference Subramanian and Koch2006b
) for a near-sphere in the limit
![]() ${\it\xi}_{0}\rightarrow \infty$
. The expression for
${\it\xi}_{0}\rightarrow \infty$
. The expression for
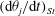 $(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
given in Subramanian & Koch (Reference Subramanian and Koch2006b
, (3.15) therein) missed a
$(\text{d}{\it\theta}_{j}/\text{d}t)_{St}$
given in Subramanian & Koch (Reference Subramanian and Koch2006b
, (3.15) therein) missed a
![]() $1/2$
in the term that multiplies
$1/2$
in the term that multiplies
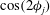 $\cos (2{\it\phi}_{j})$
and the expression (3.16) for
$\cos (2{\it\phi}_{j})$
and the expression (3.16) for
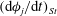 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
missed a factor of
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
missed a factor of
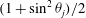 $(1+\sin ^{2}{\it\theta}_{j})/2$
. The expressions for the transverse components of the
$(1+\sin ^{2}{\it\theta}_{j})/2$
. The expressions for the transverse components of the
![]() $O(St)$
angular velocity have been recently obtained by Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014), for an arbitrary-aspect-ratio spheroid, directly from the equations of motion. On account of the spheroidal coordinates used here, and in order to facilitate a smooth transition to the
$O(St)$
angular velocity have been recently obtained by Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014), for an arbitrary-aspect-ratio spheroid, directly from the equations of motion. On account of the spheroidal coordinates used here, and in order to facilitate a smooth transition to the
![]() $O(St^{2})$
results presented in the next subsection, we have rederived the equations governing the
$O(St^{2})$
results presented in the next subsection, we have rederived the equations governing the
![]() $O(St)$
drift. The
$O(St)$
drift. The
![]() $O(St)$
rates of change
$O(St)$
rates of change
![]() $\dot{{\it\phi}_{j}}$
and
$\dot{{\it\phi}_{j}}$
and
![]() $\dot{{\it\theta}_{j}}$
in (5.5) and (5.6) match with those given in Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014), although the results therein are not interpreted in terms of an orbital drift. The latter offers a convenient interpretation, and also a physically significant one. The influence of additional physical mechanisms on the orientation distribution, either the weak Brownian motion considered in § 7.2, or orientation fluctuations of a hydrodynamic origin that might arise at higher volume fractions from pair interactions, are best interpreted, in
$\dot{{\it\theta}_{j}}$
in (5.5) and (5.6) match with those given in Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014), although the results therein are not interpreted in terms of an orbital drift. The latter offers a convenient interpretation, and also a physically significant one. The influence of additional physical mechanisms on the orientation distribution, either the weak Brownian motion considered in § 7.2, or orientation fluctuations of a hydrodynamic origin that might arise at higher volume fractions from pair interactions, are best interpreted, in
![]() $(C,{\it\tau})$
coordinates, in terms of the distribution of Jeffery orbits arising from a balance of a deterministic inertial drift and diffusion along the
$(C,{\it\tau})$
coordinates, in terms of the distribution of Jeffery orbits arising from a balance of a deterministic inertial drift and diffusion along the
![]() $C$
coordinate.
$C$
coordinate.
Finally, it will be seen in §§ 6.1 and 6.2, where we determine the orbital drift
![]() ${\rm\Delta}C_{f}$
driven by fluid inertia, that, for extreme aspect ratios, fluid inertia always dominates particle inertia. This is because the moment of inertia of a slender fibre (
${\rm\Delta}C_{f}$
driven by fluid inertia, that, for extreme aspect ratios, fluid inertia always dominates particle inertia. This is because the moment of inertia of a slender fibre (
 $O({\it\rho}L^{3}b^{2})$
) or a flat disk (
$O({\it\rho}L^{3}b^{2})$
) or a flat disk (
 $O({\it\rho}L^{4}b)$
) is asymptotically smaller than the moment of inertia of the disturbed fluid sphere (
$O({\it\rho}L^{4}b)$
) is asymptotically smaller than the moment of inertia of the disturbed fluid sphere (
![]() $O({\it\rho}L^{5})$
) around the rotating particle that contributes to the fluid inertial forces and governs the
$O({\it\rho}L^{5})$
) around the rotating particle that contributes to the fluid inertial forces and governs the
![]() $O(Re)$
drift (Subramanian & Koch Reference Subramanian and Koch2005).
$O(Re)$
drift (Subramanian & Koch Reference Subramanian and Koch2005).
5.2 The
 $O(St^{2})$
analysis: effect of particle inertia on the time period of rotation
$O(St^{2})$
analysis: effect of particle inertia on the time period of rotation
There is no correction to the period of rotation at
![]() $O(St)$
for a Jeffery orbit with any
$O(St)$
for a Jeffery orbit with any
![]() $C$
. This may be seen by writing the period
$C$
. This may be seen by writing the period
![]() $T$
as
$T$
as
 $T=\int _{{\rm\pi}}^{-{\rm\pi}}\,\text{d}{\it\phi}_{j}/\dot{{\it\phi}}_{j}$
, and using
$T=\int _{{\rm\pi}}^{-{\rm\pi}}\,\text{d}{\it\phi}_{j}/\dot{{\it\phi}}_{j}$
, and using
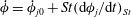 $\dot{{\it\phi}}=\dot{{\it\phi}}_{j0}+St(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
, with
$\dot{{\it\phi}}=\dot{{\it\phi}}_{j0}+St(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
, with
![]() $\dot{{\it\phi}}_{j0}$
and
$\dot{{\it\phi}}_{j0}$
and
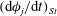 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
being given by (4.10) and (5.6), respectively. The
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
being given by (4.10) and (5.6), respectively. The
![]() $O(St)$
correction to the Jeffery period then takes the form
$O(St)$
correction to the Jeffery period then takes the form
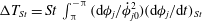 ${\rm\Delta}T_{St}=St\,\int _{{\rm\pi}}^{-{\rm\pi}}(\text{d}{\it\phi}_{j}/\dot{{\it\phi}}_{j0}^{2})(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
, which integrates to 0 for any fixed
${\rm\Delta}T_{St}=St\,\int _{{\rm\pi}}^{-{\rm\pi}}(\text{d}{\it\phi}_{j}/\dot{{\it\phi}}_{j0}^{2})(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
, which integrates to 0 for any fixed
![]() $C$
. The correction to the time period for an inertial spheroid, comes at
$C$
. The correction to the time period for an inertial spheroid, comes at
![]() $O(St^{2})$
for all orbits except for the spinning mode (
$O(St^{2})$
for all orbits except for the spinning mode (
![]() $C=0$
). As will be seen later in § 6, the rate of change of
$C=0$
). As will be seen later in § 6, the rate of change of
![]() ${\it\phi}_{j}$
due to the fluid inertia at
${\it\phi}_{j}$
due to the fluid inertia at
![]() $O(Re)$
takes the same form as (5.6), and therefore there is no correction to the time period of rotation at
$O(Re)$
takes the same form as (5.6), and therefore there is no correction to the time period of rotation at
![]() $O(Re)$
either. For fluid inertia, as mentioned in earlier sections, the modification of the period arises at
$O(Re)$
either. For fluid inertia, as mentioned in earlier sections, the modification of the period arises at
 $O(Re^{3/2})$
and not at
$O(Re^{3/2})$
and not at
![]() $O(Re^{2})$
, and the singular origin implies that such a modification would be present for both the tumbling and (steadily) spinning modes; the slowing down of a freely rotating sphere in simple shear has already been analysed (Lin, Peery & Schowalter Reference Lin, Peery and Schowalter1970; Stone, John & Lovalenti Reference Stone, John and Lovalenti2000).
$O(Re^{2})$
, and the singular origin implies that such a modification would be present for both the tumbling and (steadily) spinning modes; the slowing down of a freely rotating sphere in simple shear has already been analysed (Lin, Peery & Schowalter Reference Lin, Peery and Schowalter1970; Stone, John & Lovalenti Reference Stone, John and Lovalenti2000).
In what follows, we determine the correction to the Jeffery period for a tumbling prolate spheroid. Using
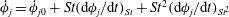 $\dot{{\it\phi}}_{j}=\dot{{\it\phi}}_{j0}+St(\text{d}{\it\phi}_{j}/\text{d}t)_{St}+St^{2}(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
, the
$\dot{{\it\phi}}_{j}=\dot{{\it\phi}}_{j0}+St(\text{d}{\it\phi}_{j}/\text{d}t)_{St}+St^{2}(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
, the
![]() $O(St^{2})$
correction to the period of rotation comes out to be:
$O(St^{2})$
correction to the period of rotation comes out to be:
 $$\begin{eqnarray}{\rm\Delta}T_{St^{2}}=St^{2}\int _{{\rm\pi}}^{-{\rm\pi}}\left[\frac{1}{\dot{{\it\phi}}_{j0}^{3}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}^{2}-\frac{1}{\dot{{\it\phi}}_{j0}^{2}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St^{2}}\right],\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}T_{St^{2}}=St^{2}\int _{{\rm\pi}}^{-{\rm\pi}}\left[\frac{1}{\dot{{\it\phi}}_{j0}^{3}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St}^{2}-\frac{1}{\dot{{\it\phi}}_{j0}^{2}}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St^{2}}\right],\end{eqnarray}$$
where
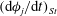 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
is given by (5.6). Starting from (5.4), the final expression for
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St}$
is given by (5.6). Starting from (5.4), the final expression for
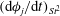 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
valid for arbitrary
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
valid for arbitrary
![]() $C$
is very lengthy. Owing to the sign of the
$C$
is very lengthy. Owing to the sign of the
![]() $O(St)$
drift, for long times, one only needs the limiting form relevant for a tumbling mode (
$O(St)$
drift, for long times, one only needs the limiting form relevant for a tumbling mode (
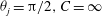 ${\it\theta}_{j}={\rm\pi}/2,C=\infty$
). This is significantly simpler and given by:
${\it\theta}_{j}={\rm\pi}/2,C=\infty$
). This is significantly simpler and given by:
 $$\begin{eqnarray}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St^{2}}=H_{1}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+H_{2}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}+H_{3}^{p}({\it\xi}_{0})\cos 6{\it\phi}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{\text{d}{\it\phi}_{j}}{\text{d}t}\right)_{St^{2}}=H_{1}^{p}({\it\xi}_{0})\cos 2{\it\phi}_{j}+H_{2}^{p}({\it\xi}_{0})\cos 4{\it\phi}_{j}+H_{3}^{p}({\it\xi}_{0})\cos 6{\it\phi}_{j},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle H_{1}^{p}({\it\xi}_{0})=-\frac{(16{\it\xi}_{0}^{4}-16{\it\xi}_{0}^{2}+5)(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{3200{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{1}^{p}({\it\xi}_{0})=-\frac{(16{\it\xi}_{0}^{4}-16{\it\xi}_{0}^{2}+5)(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{3200{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle H_{2}^{p}({\it\xi}_{0})=\frac{(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{400({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{2}^{p}({\it\xi}_{0})=\frac{(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{400({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle H_{3}^{p}({\it\xi}_{0})=-\frac{3(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{3200{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{3}^{p}({\it\xi}_{0})=-\frac{3(\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}+(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0})^{2}}{3200{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}. & \displaystyle\end{eqnarray}$$
Using (5.21)–(5.24) in (5.20), the change induced by particle inertia in the period of rotation of a tumbling prolate spheroid is given by:
 $$\begin{eqnarray}{\rm\Delta}T_{St^{2}}=St^{2}\frac{{\rm\pi}[2{\it\xi}_{0}(\bar{{\it\xi}}_{0}-{\it\xi}_{0})+1][(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0}+{\it\xi}_{0}^{3}-{\it\xi}_{0}]^{2}}{100{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)}.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}T_{St^{2}}=St^{2}\frac{{\rm\pi}[2{\it\xi}_{0}(\bar{{\it\xi}}_{0}-{\it\xi}_{0})+1][(1-{\it\xi}_{0}^{4})\coth ^{-1}{\it\xi}_{0}+{\it\xi}_{0}^{3}-{\it\xi}_{0}]^{2}}{100{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)}.\end{eqnarray}$$
The analysis in the earlier section also shows that, at
![]() $O(St)$
, inertial persistence leads to a shift in the locations of the angular velocity extrema relative to those for the original Jeffery orbit. The angular displacements are of
$O(St)$
, inertial persistence leads to a shift in the locations of the angular velocity extrema relative to those for the original Jeffery orbit. The angular displacements are of
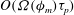 $O({\it\Omega}({\it\phi}_{m}){\it\tau}_{p})$
,
$O({\it\Omega}({\it\phi}_{m}){\it\tau}_{p})$
,
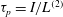 ${\it\tau}_{p}=I/L^{(2)}$
being the inertial relaxation time that governs the persistence of the angular velocity. Here,
${\it\tau}_{p}=I/L^{(2)}$
being the inertial relaxation time that governs the persistence of the angular velocity. Here,
![]() ${\it\Omega}({\it\phi}_{m})$
is the angular speed at the extremum,
${\it\Omega}({\it\phi}_{m})$
is the angular speed at the extremum,
![]() $I$
is the (non-dimensional) equatorial moment of inertia relevant to the tumbling mode, while
$I$
is the (non-dimensional) equatorial moment of inertia relevant to the tumbling mode, while
![]() $L^{(2)}$
is the aspect-ratio scale for the test-torque coefficient. In the near-sphere limit, the angular displacements are
$L^{(2)}$
is the aspect-ratio scale for the test-torque coefficient. In the near-sphere limit, the angular displacements are
![]() $O(St)$
for both the maxima and minima, while for the slender-fibre limit, the test-torque coefficient is
$O(St)$
for both the maxima and minima, while for the slender-fibre limit, the test-torque coefficient is
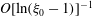 $O[\ln ({\it\xi}_{0}-1)]^{-1}$
, and these displacements are
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
, and these displacements are
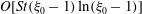 $O[St({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)]$
and
$O[St({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)]$
and
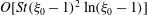 $O[St({\it\xi}_{0}-1)^{2}\ln ({\it\xi}_{0}-1)]$
for the maxima (
$O[St({\it\xi}_{0}-1)^{2}\ln ({\it\xi}_{0}-1)]$
for the maxima (
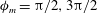 ${\it\phi}_{m}={\rm\pi}/2,3{\rm\pi}/2$
) and minima (
${\it\phi}_{m}={\rm\pi}/2,3{\rm\pi}/2$
) and minima (
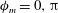 ${\it\phi}_{m}=0,{\rm\pi}$
), respectively. This
${\it\phi}_{m}=0,{\rm\pi}$
), respectively. This
![]() $O(St)$
alteration in the angular velocity profile does not, however, change the period due to the antisymmetry of the angular acceleration profiles in the compressional and extensional quadrants of the Jeffery orbit. At
$O(St)$
alteration in the angular velocity profile does not, however, change the period due to the antisymmetry of the angular acceleration profiles in the compressional and extensional quadrants of the Jeffery orbit. At
![]() $O(St^{2})$
, this antisymmetry is broken, with the result that the decrease in the traversal time of the extensional quadrants is greater than the corresponding increase in the compressional quadrants, leading to a net decrease in the period of rotation. For a near-sphere, this reduction in period is smaller than expected owing to a cancellation at
$O(St^{2})$
, this antisymmetry is broken, with the result that the decrease in the traversal time of the extensional quadrants is greater than the corresponding increase in the compressional quadrants, leading to a net decrease in the period of rotation. For a near-sphere, this reduction in period is smaller than expected owing to a cancellation at
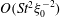 $O(St^{2}{\it\xi}_{0}^{-2})$
; (5.25) gives
$O(St^{2}{\it\xi}_{0}^{-2})$
; (5.25) gives
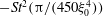 $-St^{2}({\rm\pi}/(450{\it\xi}_{0}^{4}))$
. For a slender fibre, the changes in angular velocity over the meridional portion of the trajectory (the non-aligned phase) govern the reduction in period. The
$-St^{2}({\rm\pi}/(450{\it\xi}_{0}^{4}))$
. For a slender fibre, the changes in angular velocity over the meridional portion of the trajectory (the non-aligned phase) govern the reduction in period. The
![]() $O(St)$
angular acceleration of a non-aligned slender fibre combines with a moment of inertia of
$O(St)$
angular acceleration of a non-aligned slender fibre combines with a moment of inertia of
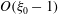 $O({\it\xi}_{0}-1)$
, leading to a change in angular velocity of
$O({\it\xi}_{0}-1)$
, leading to a change in angular velocity of
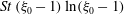 $St\,({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)$
. An analogous argument implies that the change in angular velocity at
$St\,({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1)$
. An analogous argument implies that the change in angular velocity at
![]() $O(St^{2})$
is
$O(St^{2})$
is
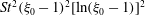 $St^{2}({\it\xi}_{0}-1)^{2}[\ln ({\it\xi}_{0}-1)]^{2}$
, which then gives the aspect-ratio scaling for the reduction in the period; the limiting form of (5.25) gives
$St^{2}({\it\xi}_{0}-1)^{2}[\ln ({\it\xi}_{0}-1)]^{2}$
, which then gives the aspect-ratio scaling for the reduction in the period; the limiting form of (5.25) gives
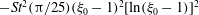 $-St^{2}({\rm\pi}/25)({\it\xi}_{0}-1)^{2}[\ln ({\it\xi}_{0}-1)]^{2}$
.
$-St^{2}({\rm\pi}/25)({\it\xi}_{0}-1)^{2}[\ln ({\it\xi}_{0}-1)]^{2}$
.

Figure 4. The
![]() $O(St^{2})$
corrections to the time period and the angular velocity extrema, as a function of
$O(St^{2})$
corrections to the time period and the angular velocity extrema, as a function of
![]() ${\it\xi}_{0}$
, for a prolate spheroid in the tumbling mode.
${\it\xi}_{0}$
, for a prolate spheroid in the tumbling mode.
It turns out that the minimum and maximum angular velocities in the tumbling mode are unaltered at
![]() $O(St)$
. Starting from (5.21), one obtains the following expressions, to
$O(St)$
. Starting from (5.21), one obtains the following expressions, to
![]() $O(St^{2})$
, for the angular velocity extrema:
$O(St^{2})$
, for the angular velocity extrema:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\Omega}_{max}=-\frac{{\it\xi}_{0}^{2}}{2{\it\xi}_{0}^{2}-1}+St^{2}\frac{{\it\xi}_{0}^{2}[-{\it\xi}_{0}^{3}+{\it\xi}_{0}+({\it\xi}_{0}^{4}-1)\coth ^{-1}{\it\xi}_{0}]^{2}}{400(2{\it\xi}_{0}^{2}-1)^{3}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\Omega}_{max}=-\frac{{\it\xi}_{0}^{2}}{2{\it\xi}_{0}^{2}-1}+St^{2}\frac{{\it\xi}_{0}^{2}[-{\it\xi}_{0}^{3}+{\it\xi}_{0}+({\it\xi}_{0}^{4}-1)\coth ^{-1}{\it\xi}_{0}]^{2}}{400(2{\it\xi}_{0}^{2}-1)^{3}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\Omega}_{min}=-\frac{\bar{{\it\xi}}_{0}^{2}}{2{\it\xi}_{0}^{2}-1}-St^{2}\frac{\bar{{\it\xi}}_{0}^{8}[{\it\xi}_{0}-({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}]^{2}}{400{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\Omega}_{min}=-\frac{\bar{{\it\xi}}_{0}^{2}}{2{\it\xi}_{0}^{2}-1}-St^{2}\frac{\bar{{\it\xi}}_{0}^{8}[{\it\xi}_{0}-({\it\xi}_{0}^{2}+1)\coth ^{-1}{\it\xi}_{0}]^{2}}{400{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}}. & \displaystyle\end{eqnarray}$$
The corrections to the time period, maximum and minimum angular velocities are plotted as a function of the prolate spheroid eccentricity (
![]() $e=1/{\it\xi}_{0}$
) in figure 4. The effect of particle inertia is to make the angular velocity extrema approach each other, consistent with the general notion of an inertial resistance to angular acceleration (for large
$e=1/{\it\xi}_{0}$
) in figure 4. The effect of particle inertia is to make the angular velocity extrema approach each other, consistent with the general notion of an inertial resistance to angular acceleration (for large
![]() $St$
, the particle begins to rotate with a constant angular velocity of
$St$
, the particle begins to rotate with a constant angular velocity of
![]() $4{\rm\pi}$
in the flow–gradient plane (Lundell Reference Lundell2011)). Although the changes in the maxima and minima are of opposite signs, the correction to time period is negative for all
$4{\rm\pi}$
in the flow–gradient plane (Lundell Reference Lundell2011)). Although the changes in the maxima and minima are of opposite signs, the correction to time period is negative for all
![]() ${\it\xi}_{0}$
, implying that the time period decreases at
${\it\xi}_{0}$
, implying that the time period decreases at
![]() $O(St^{2})$
. This decrease is consistent with recent simulations (Mao & Alexeev Reference Mao and Alexeev2014), although a quantitative comparison is not possible due to the simulations being carried out for much larger
$O(St^{2})$
. This decrease is consistent with recent simulations (Mao & Alexeev Reference Mao and Alexeev2014), although a quantitative comparison is not possible due to the simulations being carried out for much larger
![]() $St$
. A couple of points are in order before moving on to an analysis of fluid inertial effects. The expression for
$St$
. A couple of points are in order before moving on to an analysis of fluid inertial effects. The expression for
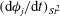 $(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
, valid for arbitrary
$(\text{d}{\it\phi}_{j}/\text{d}t)_{St^{2}}$
, valid for arbitrary
![]() $C$
, in (5.20), shows that particle inertia acts to decrease the period of rotation for arbitrary
$C$
, in (5.20), shows that particle inertia acts to decrease the period of rotation for arbitrary
![]() $C$
. Further, since the analysis does not explicitly depend on the disturbance velocity field, it can easily be generalized to an arbitrary axisymmetric particle, provided one uses the appropriate moment of inertia tensor, and the geometric aspect ratio is replaced by the effective aspect ratio (as obtained from the Jeffery rotation period; see Bretherton (Reference Bretherton1962)).
$C$
. Further, since the analysis does not explicitly depend on the disturbance velocity field, it can easily be generalized to an arbitrary axisymmetric particle, provided one uses the appropriate moment of inertia tensor, and the geometric aspect ratio is replaced by the effective aspect ratio (as obtained from the Jeffery rotation period; see Bretherton (Reference Bretherton1962)).
6 The orbital drift due to fluid inertia: hollow spheroids
 $(St=0,Re\ll 1)$
$(St=0,Re\ll 1)$
At
![]() $O(Re)$
, the general form for the rates of change of
$O(Re)$
, the general form for the rates of change of
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
are identical to those at
${\it\phi}_{j}$
are identical to those at
![]() $O(St)$
, that is, (5.5) and (5.6) in § 5.1, with
$O(St)$
, that is, (5.5) and (5.6) in § 5.1, with
![]() $Re$
now replacing
$Re$
now replacing
![]() $St$
, and with differing expressions for the aspect-ratio-dependent functions now denoted by the superscript ‘
$St$
, and with differing expressions for the aspect-ratio-dependent functions now denoted by the superscript ‘
![]() $f$
’. The forms of these functions, for arbitrary
$f$
’. The forms of these functions, for arbitrary
![]() ${\it\xi}_{0}$
, are given in the subsections that follow. Knowing these, the resulting change in orbit constant in a single Jeffery period may be determined as before using (5.19), with the expressions for the
${\it\xi}_{0}$
, are given in the subsections that follow. Knowing these, the resulting change in orbit constant in a single Jeffery period may be determined as before using (5.19), with the expressions for the
![]() $I_{i}$
and
$I_{i}$
and
![]() $J_{i}$
being the same as those in § 5.1.
$J_{i}$
being the same as those in § 5.1.
6.1 The
 $O(Re)$
orbital drift for prolate spheroids
$O(Re)$
orbital drift for prolate spheroids
The aspect-ratio-dependent functions appearing in the fluid inertial analogues of (5.5) and (5.6) are given by:
 $$\begin{eqnarray}\displaystyle F_{1}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(-648{\it\xi}_{0}^{12}+1350{\it\xi}_{0}^{10}-5571{\it\xi}_{0}^{8}+11\,841{\it\xi}_{0}^{6}-9269{\it\xi}_{0}^{4}+2263{\it\xi}_{0}^{2}+6)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(24{\it\xi}_{0}^{8}-14{\it\xi}_{0}^{6}-19{\it\xi}_{0}^{4}+16{\it\xi}_{0}^{2}-3)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}\nonumber\\ \displaystyle & & \displaystyle +\,9{\it\xi}_{0}(288{\it\xi}_{0}^{12}-564{\it\xi}_{0}^{10}-20{\it\xi}_{0}^{8}+799{\it\xi}_{0}^{6}-743{\it\xi}_{0}^{4}+261{\it\xi}_{0}^{2}-29)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\xi}_{0} (2592{\it\xi}_{0}^{14}-7020{\it\xi}_{0}^{12}+13\,932{\it\xi}_{0}^{10}-21\,123{\it\xi}_{0}^{8}+14\,255{\it\xi}_{0}^{6}-577{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle -\,2711{\it\xi}_{0}^{2}+652)\coth ^{-1}{\it\xi}_{0}-3(1296{\it\xi}_{0}^{16}-4320{\it\xi}_{0}^{14}+5346{\it\xi}_{0}^{12}-1477{\it\xi}_{0}^{10}\nonumber\\ \displaystyle & & \displaystyle -\,4260{\it\xi}_{0}^{8}+6116{\it\xi}_{0}^{6}-3492{\it\xi}_{0}^{4}+849{\it\xi}_{0}^{2}-58)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (480{\it\xi}_{0}^{2}(-1+2{\it\xi}_{0}^{2})^{3}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{1}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(-648{\it\xi}_{0}^{12}+1350{\it\xi}_{0}^{10}-5571{\it\xi}_{0}^{8}+11\,841{\it\xi}_{0}^{6}-9269{\it\xi}_{0}^{4}+2263{\it\xi}_{0}^{2}+6)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(24{\it\xi}_{0}^{8}-14{\it\xi}_{0}^{6}-19{\it\xi}_{0}^{4}+16{\it\xi}_{0}^{2}-3)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}\nonumber\\ \displaystyle & & \displaystyle +\,9{\it\xi}_{0}(288{\it\xi}_{0}^{12}-564{\it\xi}_{0}^{10}-20{\it\xi}_{0}^{8}+799{\it\xi}_{0}^{6}-743{\it\xi}_{0}^{4}+261{\it\xi}_{0}^{2}-29)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\xi}_{0} (2592{\it\xi}_{0}^{14}-7020{\it\xi}_{0}^{12}+13\,932{\it\xi}_{0}^{10}-21\,123{\it\xi}_{0}^{8}+14\,255{\it\xi}_{0}^{6}-577{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle -\,2711{\it\xi}_{0}^{2}+652)\coth ^{-1}{\it\xi}_{0}-3(1296{\it\xi}_{0}^{16}-4320{\it\xi}_{0}^{14}+5346{\it\xi}_{0}^{12}-1477{\it\xi}_{0}^{10}\nonumber\\ \displaystyle & & \displaystyle -\,4260{\it\xi}_{0}^{8}+6116{\it\xi}_{0}^{6}-3492{\it\xi}_{0}^{4}+849{\it\xi}_{0}^{2}-58)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (480{\it\xi}_{0}^{2}(-1+2{\it\xi}_{0}^{2})^{3}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{2}^{f}({\it\xi}_{0}) & = & \displaystyle -(\bar{{\it\xi}}_{0}^{2} (-9{\it\xi}_{0}^{9}+30{\it\xi}_{0}^{7}-115{\it\xi}_{0}^{5}+90{\it\xi}_{0}^{3}-12{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,9\bar{{\it\xi}}_{0}^{8}({\it\xi}_{0}^{2}+1){\it\xi}_{0}^{2}\coth ^{-1}({\it\xi}_{0})^{3}-3\bar{{\it\xi}}_{0}^{4} (9{\it\xi}_{0}^{6}-10{\it\xi}_{0}^{4}-17{\it\xi}_{0}^{2}+14){\it\xi}_{0}\coth ^{-1}({\it\xi}_{0})^{2}\nonumber\\ \displaystyle & & \displaystyle +\,(27{\it\xi}_{0}^{10}-87{\it\xi}_{0}^{8}+133{\it\xi}_{0}^{6}-33{\it\xi}_{0}^{4}-52{\it\xi}_{0}^{2}+12)\coth ^{-1}{\it\xi}_{0} ))\nonumber\\ \displaystyle & & \displaystyle \times (40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{2}^{f}({\it\xi}_{0}) & = & \displaystyle -(\bar{{\it\xi}}_{0}^{2} (-9{\it\xi}_{0}^{9}+30{\it\xi}_{0}^{7}-115{\it\xi}_{0}^{5}+90{\it\xi}_{0}^{3}-12{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,9\bar{{\it\xi}}_{0}^{8}({\it\xi}_{0}^{2}+1){\it\xi}_{0}^{2}\coth ^{-1}({\it\xi}_{0})^{3}-3\bar{{\it\xi}}_{0}^{4} (9{\it\xi}_{0}^{6}-10{\it\xi}_{0}^{4}-17{\it\xi}_{0}^{2}+14){\it\xi}_{0}\coth ^{-1}({\it\xi}_{0})^{2}\nonumber\\ \displaystyle & & \displaystyle +\,(27{\it\xi}_{0}^{10}-87{\it\xi}_{0}^{8}+133{\it\xi}_{0}^{6}-33{\it\xi}_{0}^{4}-52{\it\xi}_{0}^{2}+12)\coth ^{-1}{\it\xi}_{0} ))\nonumber\\ \displaystyle & & \displaystyle \times (40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{3}^{f}({\it\xi}_{0}) & = & \displaystyle -({\it\xi}_{0}^{2}(378{\it\xi}_{0}^{10}+801{\it\xi}_{0}^{8}-4731{\it\xi}_{0}^{6}+5551{\it\xi}_{0}^{4}-2369{\it\xi}_{0}^{2}+342)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(6{\it\xi}_{0}^{6}+{\it\xi}_{0}^{4}-4{\it\xi}_{0}^{2}+1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+9{\it\xi}_{0} (12{\it\xi}_{0}^{10}+28{\it\xi}_{0}^{8}-201{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,273{\it\xi}_{0}^{4}-147{\it\xi}_{0}^{2}+27)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-972{\it\xi}_{0}^{13}-324{\it\xi}_{0}^{11}+7365{\it\xi}_{0}^{9}\nonumber\\ \displaystyle & & \displaystyle -\,10\,409{\it\xi}_{0}^{7}+5143{\it\xi}_{0}^{5}-847{\it\xi}_{0}^{3}+44{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}+3(216{\it\xi}_{0}^{14}-378{\it\xi}_{0}^{12}\nonumber\\ \displaystyle & & \displaystyle +\,109{\it\xi}_{0}^{10}-412{\it\xi}_{0}^{8}+1204{\it\xi}_{0}^{6}-1028{\it\xi}_{0}^{4}+311{\it\xi}_{0}^{2}-22)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (480{\it\xi}_{0}^{2}(-1+2{\it\xi}_{0}^{2})^{3}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0} )((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{3}^{f}({\it\xi}_{0}) & = & \displaystyle -({\it\xi}_{0}^{2}(378{\it\xi}_{0}^{10}+801{\it\xi}_{0}^{8}-4731{\it\xi}_{0}^{6}+5551{\it\xi}_{0}^{4}-2369{\it\xi}_{0}^{2}+342)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(6{\it\xi}_{0}^{6}+{\it\xi}_{0}^{4}-4{\it\xi}_{0}^{2}+1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+9{\it\xi}_{0} (12{\it\xi}_{0}^{10}+28{\it\xi}_{0}^{8}-201{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,273{\it\xi}_{0}^{4}-147{\it\xi}_{0}^{2}+27)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-972{\it\xi}_{0}^{13}-324{\it\xi}_{0}^{11}+7365{\it\xi}_{0}^{9}\nonumber\\ \displaystyle & & \displaystyle -\,10\,409{\it\xi}_{0}^{7}+5143{\it\xi}_{0}^{5}-847{\it\xi}_{0}^{3}+44{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}+3(216{\it\xi}_{0}^{14}-378{\it\xi}_{0}^{12}\nonumber\\ \displaystyle & & \displaystyle +\,109{\it\xi}_{0}^{10}-412{\it\xi}_{0}^{8}+1204{\it\xi}_{0}^{6}-1028{\it\xi}_{0}^{4}+311{\it\xi}_{0}^{2}-22)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (480{\it\xi}_{0}^{2}(-1+2{\it\xi}_{0}^{2})^{3}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0} )((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{4}^{f}({\it\xi}_{0}) & = & \displaystyle -2F_{5}^{f}({\it\xi}_{0})=-2F_{6}^{f}({\it\xi}_{0})=F_{3}^{f}({\it\xi}_{0})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{4}^{f}({\it\xi}_{0}) & = & \displaystyle -2F_{5}^{f}({\it\xi}_{0})=-2F_{6}^{f}({\it\xi}_{0})=F_{3}^{f}({\it\xi}_{0})\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle G_{1}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(81{\it\xi}_{0}^{10}-414{\it\xi}_{0}^{8}+1074{\it\xi}_{0}^{6}-1162{\it\xi}_{0}^{4}+479{\it\xi}_{0}^{2}-54)\nonumber\\ \displaystyle & & \displaystyle +\,9{\it\xi}_{0}^{2}(9{\it\xi}_{0}^{6}-7{\it\xi}_{0}^{2}+2)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}-3{\it\xi}_{0} (108{\it\xi}_{0}^{10}-246{\it\xi}_{0}^{8}+69{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,167{\it\xi}_{0}^{4}-129{\it\xi}_{0}^{2}+23)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-324{\it\xi}_{0}^{13}+1566{\it\xi}_{0}^{11}\nonumber\\ \displaystyle & & \displaystyle -\,3309{\it\xi}_{0}^{9}+3133{\it\xi}_{0}^{7}-1023{\it\xi}_{0}^{5}-79{\it\xi}_{0}^{3}+36{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,(486{\it\xi}_{0}^{14}-2214{\it\xi}_{0}^{12}+3819{\it\xi}_{0}^{10}-2568{\it\xi}_{0}^{8}-222{\it\xi}_{0}^{6}+1036{\it\xi}_{0}^{4}-355{\it\xi}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,18)\coth ^{-1}({\it\xi}_{0})^{2} )(40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{1}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(81{\it\xi}_{0}^{10}-414{\it\xi}_{0}^{8}+1074{\it\xi}_{0}^{6}-1162{\it\xi}_{0}^{4}+479{\it\xi}_{0}^{2}-54)\nonumber\\ \displaystyle & & \displaystyle +\,9{\it\xi}_{0}^{2}(9{\it\xi}_{0}^{6}-7{\it\xi}_{0}^{2}+2)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}-3{\it\xi}_{0} (108{\it\xi}_{0}^{10}-246{\it\xi}_{0}^{8}+69{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,167{\it\xi}_{0}^{4}-129{\it\xi}_{0}^{2}+23)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-324{\it\xi}_{0}^{13}+1566{\it\xi}_{0}^{11}\nonumber\\ \displaystyle & & \displaystyle -\,3309{\it\xi}_{0}^{9}+3133{\it\xi}_{0}^{7}-1023{\it\xi}_{0}^{5}-79{\it\xi}_{0}^{3}+36{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,(486{\it\xi}_{0}^{14}-2214{\it\xi}_{0}^{12}+3819{\it\xi}_{0}^{10}-2568{\it\xi}_{0}^{8}-222{\it\xi}_{0}^{6}+1036{\it\xi}_{0}^{4}-355{\it\xi}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,18)\coth ^{-1}({\it\xi}_{0})^{2} )(40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle G_{2}^{f}({\it\xi}_{0}) & = & \displaystyle (-{\it\xi}_{0}^{2}(27{\it\xi}_{0}^{10}-180{\it\xi}_{0}^{8}+204{\it\xi}_{0}^{6}+68{\it\xi}_{0}^{4}-133{\it\xi}_{0}^{2}+18)\nonumber\\ \displaystyle & & \displaystyle -\,9{\it\xi}_{0}^{4}(3{\it\xi}_{0}^{4}+2{\it\xi}_{0}^{2}-1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+3{\it\xi}_{0} (36{\it\xi}_{0}^{10}-78{\it\xi}_{0}^{8}+73{\it\xi}_{0}^{6}-69{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle +\,35{\it\xi}_{0}^{2}-5)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+{\it\xi}_{0} (108{\it\xi}_{0}^{12}-630{\it\xi}_{0}^{10}+1041{\it\xi}_{0}^{8}-617{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,115{\it\xi}_{0}^{4}-29{\it\xi}_{0}^{2}+12)\coth ^{-1}{\it\xi}_{0}+ (-162{\it\xi}_{0}^{14}+810{\it\xi}_{0}^{12}-1551{\it\xi}_{0}^{10}\nonumber\\ \displaystyle & & \displaystyle +\,1600{\it\xi}_{0}^{8}-1054{\it\xi}_{0}^{6}+448{\it\xi}_{0}^{4}-97{\it\xi}_{0}^{2}+6)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0} )((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{2}^{f}({\it\xi}_{0}) & = & \displaystyle (-{\it\xi}_{0}^{2}(27{\it\xi}_{0}^{10}-180{\it\xi}_{0}^{8}+204{\it\xi}_{0}^{6}+68{\it\xi}_{0}^{4}-133{\it\xi}_{0}^{2}+18)\nonumber\\ \displaystyle & & \displaystyle -\,9{\it\xi}_{0}^{4}(3{\it\xi}_{0}^{4}+2{\it\xi}_{0}^{2}-1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+3{\it\xi}_{0} (36{\it\xi}_{0}^{10}-78{\it\xi}_{0}^{8}+73{\it\xi}_{0}^{6}-69{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle +\,35{\it\xi}_{0}^{2}-5)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+{\it\xi}_{0} (108{\it\xi}_{0}^{12}-630{\it\xi}_{0}^{10}+1041{\it\xi}_{0}^{8}-617{\it\xi}_{0}^{6}\nonumber\\ \displaystyle & & \displaystyle +\,115{\it\xi}_{0}^{4}-29{\it\xi}_{0}^{2}+12)\coth ^{-1}{\it\xi}_{0}+ (-162{\it\xi}_{0}^{14}+810{\it\xi}_{0}^{12}-1551{\it\xi}_{0}^{10}\nonumber\\ \displaystyle & & \displaystyle +\,1600{\it\xi}_{0}^{8}-1054{\it\xi}_{0}^{6}+448{\it\xi}_{0}^{4}-97{\it\xi}_{0}^{2}+6)\coth ^{-1}({\it\xi}_{0})^{2} )\nonumber\\ \displaystyle & & \displaystyle \times (40({\it\xi}_{0}-2{\it\xi}_{0}^{3})^{2}(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0} )((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle G_{3}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(378{\it\xi}_{0}^{10}+801{\it\xi}_{0}^{8}-4731{\it\xi}_{0}^{6}+5551{\it\xi}_{0}^{4}-2369{\it\xi}_{0}^{2}+342)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(6{\it\xi}_{0}^{6}+{\it\xi}_{0}^{4}-4{\it\xi}_{0}^{2}+1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+9{\it\xi}_{0} (12{\it\xi}_{0}^{10}+28{\it\xi}_{0}^{8}\nonumber\\ \displaystyle & & \displaystyle -\,201{\it\xi}_{0}^{6}+273{\it\xi}_{0}^{4}-147{\it\xi}_{0}^{2}+27)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-972{\it\xi}_{0}^{13}\nonumber\\ \displaystyle & & \displaystyle -\,324{\it\xi}_{0}^{11}+7365{\it\xi}_{0}^{9}-10\,409{\it\xi}_{0}^{7}+5143{\it\xi}_{0}^{5}-847{\it\xi}_{0}^{3}+44{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,3(216{\it\xi}_{0}^{14}-378{\it\xi}_{0}^{12}+109{\it\xi}_{0}^{10}-412{\it\xi}_{0}^{8}+1204{\it\xi}_{0}^{6}-1028{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle +\,311{\it\xi}_{0}^{2}-22){\coth ^{-1}({\it\xi}_{0})}^{2} )(120{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})\nonumber\\ \displaystyle & & \displaystyle \times \,((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{3}^{f}({\it\xi}_{0}) & = & \displaystyle ({\it\xi}_{0}^{2}(378{\it\xi}_{0}^{10}+801{\it\xi}_{0}^{8}-4731{\it\xi}_{0}^{6}+5551{\it\xi}_{0}^{4}-2369{\it\xi}_{0}^{2}+342)\nonumber\\ \displaystyle & & \displaystyle -\,27{\it\xi}_{0}^{2}(6{\it\xi}_{0}^{6}+{\it\xi}_{0}^{4}-4{\it\xi}_{0}^{2}+1)\bar{{\it\xi}}_{0}^{8}\coth ^{-1}({\it\xi}_{0})^{4}+9{\it\xi}_{0} (12{\it\xi}_{0}^{10}+28{\it\xi}_{0}^{8}\nonumber\\ \displaystyle & & \displaystyle -\,201{\it\xi}_{0}^{6}+273{\it\xi}_{0}^{4}-147{\it\xi}_{0}^{2}+27)\bar{{\it\xi}}_{0}^{4}\coth ^{-1}({\it\xi}_{0})^{3}+ (-972{\it\xi}_{0}^{13}\nonumber\\ \displaystyle & & \displaystyle -\,324{\it\xi}_{0}^{11}+7365{\it\xi}_{0}^{9}-10\,409{\it\xi}_{0}^{7}+5143{\it\xi}_{0}^{5}-847{\it\xi}_{0}^{3}+44{\it\xi}_{0} )\coth ^{-1}{\it\xi}_{0}\nonumber\\ \displaystyle & & \displaystyle +\,3(216{\it\xi}_{0}^{14}-378{\it\xi}_{0}^{12}+109{\it\xi}_{0}^{10}-412{\it\xi}_{0}^{8}+1204{\it\xi}_{0}^{6}-1028{\it\xi}_{0}^{4}\nonumber\\ \displaystyle & & \displaystyle +\,311{\it\xi}_{0}^{2}-22){\coth ^{-1}({\it\xi}_{0})}^{2} )(120{\it\xi}_{0}^{2}(2{\it\xi}_{0}^{2}-1)^{3}\nonumber\\ \displaystyle & & \displaystyle \times \,(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}}_{0}^{2}{\it\xi}_{0}\coth ^{-1}{\it\xi}_{0}+2)(-3{\it\xi}_{0}^{3}+5{\it\xi}_{0}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})\nonumber\\ \displaystyle & & \displaystyle \times \,((3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}))^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle G_{4}^{f}({\it\xi}_{0}) & = & \displaystyle -G_{3}^{f}({\it\xi}_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{4}^{f}({\it\xi}_{0}) & = & \displaystyle -G_{3}^{f}({\it\xi}_{0}).\end{eqnarray}$$
The near-sphere limits of the above functions (
![]() ${\it\xi}_{0}\rightarrow \infty$
) are given by:
${\it\xi}_{0}\rightarrow \infty$
) are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})\approx \frac{11}{280{\it\xi}_{0}^{2}},\quad F_{2}^{f}({\it\xi}_{0})\approx -\frac{37}{840{\it\xi}_{0}^{2}},\quad F_{3}^{f}({\it\xi}_{0})\approx -\frac{163}{31\,360{\it\xi}_{0}^{4}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})\approx \frac{11}{280{\it\xi}_{0}^{2}},\quad F_{2}^{f}({\it\xi}_{0})\approx -\frac{37}{840{\it\xi}_{0}^{2}},\quad F_{3}^{f}({\it\xi}_{0})\approx -\frac{163}{31\,360{\it\xi}_{0}^{4}} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{71}G_{1}^{f}({\it\xi}_{0})=\frac{1}{3}G_{2}^{f}({\it\xi}_{0})\approx \frac{1}{840{\it\xi}_{0}^{2}},\quad G_{3}^{f}({\it\xi}_{0})\approx \frac{163}{7840{\it\xi}_{0}^{4}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{71}G_{1}^{f}({\it\xi}_{0})=\frac{1}{3}G_{2}^{f}({\it\xi}_{0})\approx \frac{1}{840{\it\xi}_{0}^{2}},\quad G_{3}^{f}({\it\xi}_{0})\approx \frac{163}{7840{\it\xi}_{0}^{4}}, & \displaystyle\end{eqnarray}$$
and the slender-fibre limits (
![]() ${\it\xi}_{0}\rightarrow 1$
) are given by:
${\it\xi}_{0}\rightarrow 1$
) are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})=-F_{3}^{f}({\it\xi}_{0})\approx -\frac{7}{240[\log ({\it\xi}_{0}-1)-\log 2+3]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})=-F_{3}^{f}({\it\xi}_{0})\approx -\frac{7}{240[\log ({\it\xi}_{0}-1)-\log 2+3]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{2}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{2}{5}}({\it\xi}_{0}-1), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{2}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{2}{5}}({\it\xi}_{0}-1), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle G_{1}^{f}({\it\xi}_{0})=-G_{2}^{f}({\it\xi}_{0})=-\frac{3}{7}G_{3}^{f}({\it\xi}_{0})\approx \frac{1}{20[\log ({\it\xi}_{0}-1)-\log 2+3]}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G_{1}^{f}({\it\xi}_{0})=-G_{2}^{f}({\it\xi}_{0})=-\frac{3}{7}G_{3}^{f}({\it\xi}_{0})\approx \frac{1}{20[\log ({\it\xi}_{0}-1)-\log 2+3]}. & \displaystyle\end{eqnarray}$$
The inertial drift evaluated using the above near-sphere and slender-fibre asymptotes above are compared with the earlier analytical results of Subramanian & Koch (Reference Subramanian and Koch2005) and Subramanian & Koch (Reference Subramanian and Koch2006b ) in appendix D.
The normalized change in the drift constant (
![]() ${\rm\Delta}C_{f}$
) is plotted as a function of
${\rm\Delta}C_{f}$
) is plotted as a function of
![]() $C$
in figure 5 for various aspect ratios.
$C$
in figure 5 for various aspect ratios.
![]() ${\rm\Delta}C_{f}$
is positive for all aspect ratios and for all values of
${\rm\Delta}C_{f}$
is positive for all aspect ratios and for all values of
![]() $C$
. Fluid inertia therefore causes a prolate spheroid to drift towards the tumbling mode starting from an arbitrary initial orientation. For a near-sphere,
$C$
. Fluid inertia therefore causes a prolate spheroid to drift towards the tumbling mode starting from an arbitrary initial orientation. For a near-sphere,
![]() ${\rm\Delta}C_{f}$
reduces to:
${\rm\Delta}C_{f}$
reduces to:
 $$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow \infty }{\rm\Delta}C_{f}=\frac{11{\rm\pi}C}{70{\it\xi}_{0}^{2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow \infty }{\rm\Delta}C_{f}=\frac{11{\rm\pi}C}{70{\it\xi}_{0}^{2}}, & & \displaystyle\end{eqnarray}$$
at leading order and, for a slender fibre, one obtains:
 $$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{f}=-\frac{\sqrt{2}{\rm\pi}C}{15({\it\xi}_{0}-1)^{1/2}\ln ({\it\xi}_{0}-1)}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{f}=-\frac{\sqrt{2}{\rm\pi}C}{15({\it\xi}_{0}-1)^{1/2}\ln ({\it\xi}_{0}-1)}. & & \displaystyle\end{eqnarray}$$
These expressions motivate the normalizations used in figure 5. The factor
![]() ${\it\xi}_{0}^{2}$
in the near-sphere limit is identical to that for particle inertia, as would be expected since an inertial drift in either case would scale with the square of the eccentricity. In the limit of a slender fibre, the inertial terms may be linearized at leading order, being proportional to the leading-order Stokes disturbance field of
${\it\xi}_{0}^{2}$
in the near-sphere limit is identical to that for particle inertia, as would be expected since an inertial drift in either case would scale with the square of the eccentricity. In the limit of a slender fibre, the inertial terms may be linearized at leading order, being proportional to the leading-order Stokes disturbance field of
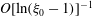 $O[\ln ({\it\xi}_{0}-1)]^{-1}$
associated with the axisymmetric extensional component of the simple shear (given by (3.7) in § 3). The resulting inertial angular velocity is
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
associated with the axisymmetric extensional component of the simple shear (given by (3.7) in § 3). The resulting inertial angular velocity is
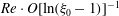 $Re\cdot O[\ln ({\it\xi}_{0}-1)]^{-1}$
. Over the
$Re\cdot O[\ln ({\it\xi}_{0}-1)]^{-1}$
. Over the
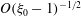 $O({\it\xi}_{0}-1)^{-1/2}$
Jeffery period, this leads to an angular displacement and a
$O({\it\xi}_{0}-1)^{-1/2}$
Jeffery period, this leads to an angular displacement and a
![]() ${\rm\Delta}C_{f}$
of
${\rm\Delta}C_{f}$
of
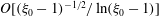 $O[({\it\xi}_{0}-1)^{-1/2}/\ln ({\it\xi}_{0}-1)]$
, as in (6.15). Recall from § 5.1 that
$O[({\it\xi}_{0}-1)^{-1/2}/\ln ({\it\xi}_{0}-1)]$
, as in (6.15). Recall from § 5.1 that
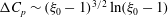 ${\rm\Delta}C_{p}\sim ({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)$
, so
${\rm\Delta}C_{p}\sim ({\it\xi}_{0}-1)^{3/2}\ln ({\it\xi}_{0}-1)$
, so
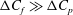 ${\rm\Delta}C_{f}\gg {\rm\Delta}C_{p}$
, and fluid inertia is dominant for
${\rm\Delta}C_{f}\gg {\rm\Delta}C_{p}$
, and fluid inertia is dominant for
![]() ${\it\xi}_{0}\rightarrow 1$
. In other words, one requires an asymptotically large density ratio of
${\it\xi}_{0}\rightarrow 1$
. In other words, one requires an asymptotically large density ratio of
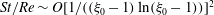 $St/Re\sim O[1/(({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1))]^{2}$
for particle inertia to influence the inertial drift of a slender fibre.
$St/Re\sim O[1/(({\it\xi}_{0}-1)\ln ({\it\xi}_{0}-1))]^{2}$
for particle inertia to influence the inertial drift of a slender fibre.

Figure 5. The drift due to fluid inertia, as characterized by the normalized change in the orbit constant in a single Jeffery period,
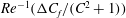 $Re^{-1}({\rm\Delta}C_{f}/(C^{2}+1))$
, plotted as a function of
$Re^{-1}({\rm\Delta}C_{f}/(C^{2}+1))$
, plotted as a function of
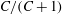 $C/(C+1)$
, for a prolate spheroid;
$C/(C+1)$
, for a prolate spheroid;
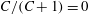 $C/(C+1)=0$
and
$C/(C+1)=0$
and
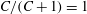 $C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
$C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
![]() ${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
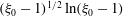 $({\it\xi}_{0}-1)^{1/2}\ln ({\it\xi}_{0}-1)$
, to render the drift finite in the slender-fibre limit (
$({\it\xi}_{0}-1)^{1/2}\ln ({\it\xi}_{0}-1)$
, to render the drift finite in the slender-fibre limit (
![]() ${\it\xi}_{0}\rightarrow 1$
).
${\it\xi}_{0}\rightarrow 1$
).

Figure 6. The drift due to fluid inertia, as characterized by the normalized change in the orbit constant in a single Jeffery period,
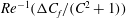 $Re^{-1}({\rm\Delta}C_{f}/(C^{2}+1))$
, plotted as a function of
$Re^{-1}({\rm\Delta}C_{f}/(C^{2}+1))$
, plotted as a function of
 $C/(C+1)$
, for an oblate spheroid;
$C/(C+1)$
, for an oblate spheroid;
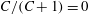 $C/(C+1)=0$
and
$C/(C+1)=0$
and
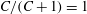 $C/(C+1)=1$
correspond to the spinning and the tumbling modes, respectively. (a) Uses the additional normalization factor of
$C/(C+1)=1$
correspond to the spinning and the tumbling modes, respectively. (a) Uses the additional normalization factor of
![]() ${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
 $({\it\xi}_{0}-1)^{1/2}$
, to render the drift finite in the flat-disk limit (
$({\it\xi}_{0}-1)^{1/2}$
, to render the drift finite in the flat-disk limit (
![]() ${\it\xi}_{0}\rightarrow 1$
). (c) Magnified view highlighting the shift in the repeller location with changing
${\it\xi}_{0}\rightarrow 1$
). (c) Magnified view highlighting the shift in the repeller location with changing
![]() ${\it\xi}_{0}$
.
${\it\xi}_{0}$
.
6.2 The
 $O(Re)$
orbital drift for oblate spheroids
$O(Re)$
orbital drift for oblate spheroids
The functions,
![]() $F_{i}^{f}({\it\xi}_{0})$
and
$F_{i}^{f}({\it\xi}_{0})$
and
![]() $G_{i}^{f}({\it\xi}_{0})$
, for an oblate spheroid are obtained from those for a prolate spheroid in the usual manner. The flat-disk limits of the resulting functions are given by
$G_{i}^{f}({\it\xi}_{0})$
, for an oblate spheroid are obtained from those for a prolate spheroid in the usual manner. The flat-disk limits of the resulting functions are given by
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{29}{480}},\quad F_{2}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{1}{20}},\quad F_{3}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{11}{480}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{29}{480}},\quad F_{2}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{1}{20}},\quad F_{3}^{f}({\it\xi}_{0})\approx -{\textstyle \frac{11}{480}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle G_{1}^{f}({\it\xi}_{0})\approx {\textstyle \frac{3}{40}},\quad G_{2}^{f}({\it\xi}_{0})\approx {\textstyle \frac{1}{40}},\quad G_{3}^{f}({\it\xi}_{0})\approx {\textstyle \frac{11}{120}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{1}^{f}({\it\xi}_{0})\approx {\textstyle \frac{3}{40}},\quad G_{2}^{f}({\it\xi}_{0})\approx {\textstyle \frac{1}{40}},\quad G_{3}^{f}({\it\xi}_{0})\approx {\textstyle \frac{11}{120}}. & & \displaystyle\end{eqnarray}$$
To calculate
![]() ${\rm\Delta}C_{f}$
, aside from the aspect-ratio-dependent functions given above, one also needs to replace the integrals
${\rm\Delta}C_{f}$
, aside from the aspect-ratio-dependent functions given above, one also needs to replace the integrals
![]() $I_{i}$
and
$I_{i}$
and
![]() $J_{i}$
by their oblate analogues. The
$J_{i}$
by their oblate analogues. The
![]() ${\rm\Delta}C_{f}$
for an oblate spheroid is plotted against
${\rm\Delta}C_{f}$
for an oblate spheroid is plotted against
![]() $C$
in figure 6. In contrast to the particle inertia case (see figure 3), the near-sphere normalization alone is not sufficient for an oblate spheroid. The inertial angular velocity approaches a finite
$C$
in figure 6. In contrast to the particle inertia case (see figure 3), the near-sphere normalization alone is not sufficient for an oblate spheroid. The inertial angular velocity approaches a finite
![]() $O(Re)$
value independent of aspect ratio in the flat-disk limit, and this leads to
$O(Re)$
value independent of aspect ratio in the flat-disk limit, and this leads to
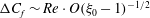 ${\rm\Delta}C_{f}\sim Re\cdot O({\it\xi}_{0}-1)^{-1/2}$
for
${\rm\Delta}C_{f}\sim Re\cdot O({\it\xi}_{0}-1)^{-1/2}$
for
![]() ${\it\xi}_{0}\rightarrow 1$
owing to the diverging Jeffery period. The differing scalings for particle and fluid inertia imply that the density ratio
${\it\xi}_{0}\rightarrow 1$
owing to the diverging Jeffery period. The differing scalings for particle and fluid inertia imply that the density ratio
![]() $St/Re$
must become asymptotically large, of
$St/Re$
must become asymptotically large, of
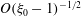 $O({\it\xi}_{0}-1)^{-1/2}$
(although still far smaller than the corresponding prolate estimate), before particle inertia can begin to exert an influence on the orientation distribution of flat disks. Figure 6 includes separate plots of
$O({\it\xi}_{0}-1)^{-1/2}$
(although still far smaller than the corresponding prolate estimate), before particle inertia can begin to exert an influence on the orientation distribution of flat disks. Figure 6 includes separate plots of
![]() ${\rm\Delta}C_{f}$
with the near-sphere and the flat-disk normalizations.
${\rm\Delta}C_{f}$
with the near-sphere and the flat-disk normalizations.
From the plots in figure 6, we note that, unlike a prolate spheroid,
![]() ${\rm\Delta}C_{f}$
is no longer single-signed. Now,
${\rm\Delta}C_{f}$
is no longer single-signed. Now,
![]() ${\rm\Delta}C_{f}$
must certainly be negative, for all values of
${\rm\Delta}C_{f}$
must certainly be negative, for all values of
![]() $C$
, for a near-sphere, as is implied by the prolate–oblate transformation and a
$C$
, for a near-sphere, as is implied by the prolate–oblate transformation and a
![]() ${\rm\Delta}C_{f}$
of
${\rm\Delta}C_{f}$
of
![]() $O({\it\xi}_{0}^{-2})$
. This remains true for aspect ratios greater than approximately
$O({\it\xi}_{0}^{-2})$
. This remains true for aspect ratios greater than approximately
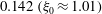 $0.142\,({\it\xi}_{0}\approx 1.01)$
, and such oblate spheroids drift towards a steady spinning mode starting from any initial orientation. For aspect ratios smaller than this critical value, the
$0.142\,({\it\xi}_{0}\approx 1.01)$
, and such oblate spheroids drift towards a steady spinning mode starting from any initial orientation. For aspect ratios smaller than this critical value, the
![]() ${\rm\Delta}C_{f}$
curves cross the
${\rm\Delta}C_{f}$
curves cross the
![]() $C$
-axis, so the drift becomes positive beyond a critical value of
$C$
-axis, so the drift becomes positive beyond a critical value of
![]() $C$
(say,
$C$
(say,
![]() $C^{\ast }$
).
$C^{\ast }$
).
![]() $C^{\ast }$
is a function of
$C^{\ast }$
is a function of
![]() ${\it\xi}_{0}$
, and equals
${\it\xi}_{0}$
, and equals
![]() $\infty$
for an oblate spheroid with the critical aspect ratio (0.142), decreasing to
$\infty$
for an oblate spheroid with the critical aspect ratio (0.142), decreasing to
![]() $\sqrt{35}$
in the limit
$\sqrt{35}$
in the limit
![]() ${\it\xi}_{0}\rightarrow 1$
. For a flat disk,
${\it\xi}_{0}\rightarrow 1$
. For a flat disk,
![]() ${\rm\Delta}C_{f}$
is given by:
${\rm\Delta}C_{f}$
is given by:
 $$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{f}=\frac{{\rm\pi}(7+C^{2}-7(1+C^{2})^{1/2})}{15\sqrt{2}C({\it\xi}_{0}-1)^{1/2}}=\frac{{\rm\pi}(\sqrt{1+C^{2}}-1)(\sqrt{1+C^{2}}-\sqrt{1+{C^{\ast }}^{2}})}{15\sqrt{2}C({\it\xi}_{0}-1)^{1/2}}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{{\it\xi}_{0}\rightarrow 1}{\rm\Delta}C_{f}=\frac{{\rm\pi}(7+C^{2}-7(1+C^{2})^{1/2})}{15\sqrt{2}C({\it\xi}_{0}-1)^{1/2}}=\frac{{\rm\pi}(\sqrt{1+C^{2}}-1)(\sqrt{1+C^{2}}-\sqrt{1+{C^{\ast }}^{2}})}{15\sqrt{2}C({\it\xi}_{0}-1)^{1/2}}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The movement of
![]() $C^{\ast }$
towards its limiting value in the range
$C^{\ast }$
towards its limiting value in the range
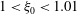 $1<{\it\xi}_{0}<1.01$
is highlighted by the magnified view in figure 6. As the aspect ratio decreases below 0.142, a pair of repellers (which are Jeffery orbits at this order of approximation) bifurcate from the tumbling orbit, separating the unit sphere into distinct basins of attraction. The region on the unit sphere between the repelling orbits, extending across the plane of symmetry of the ambient shear, corresponds now to orientations that asymptote towards a tumbling mode, while the region around the vorticity axis enclosed by each of the repellers corresponds to orientations that asymptote towards a steady spinning mode. With decreasing aspect ratio, the two repelling orbits flatten out into increasingly thin ellipses centred about the gradient–vorticity plane. Eventually, in the flat-disk limit, the repellers reduce to a pair of arcs (with an angular extent of approximately 161°) on the great circle in which the gradient–vorticity plane intersects the unit sphere. As a result, a flat disk, like a prolate spheroid, approaches a tumbling mode from almost any initial orientation (except for a set of measure zero corresponding to the repellers). This happens despite the movement of
$1<{\it\xi}_{0}<1.01$
is highlighted by the magnified view in figure 6. As the aspect ratio decreases below 0.142, a pair of repellers (which are Jeffery orbits at this order of approximation) bifurcate from the tumbling orbit, separating the unit sphere into distinct basins of attraction. The region on the unit sphere between the repelling orbits, extending across the plane of symmetry of the ambient shear, corresponds now to orientations that asymptote towards a tumbling mode, while the region around the vorticity axis enclosed by each of the repellers corresponds to orientations that asymptote towards a steady spinning mode. With decreasing aspect ratio, the two repelling orbits flatten out into increasingly thin ellipses centred about the gradient–vorticity plane. Eventually, in the flat-disk limit, the repellers reduce to a pair of arcs (with an angular extent of approximately 161°) on the great circle in which the gradient–vorticity plane intersects the unit sphere. As a result, a flat disk, like a prolate spheroid, approaches a tumbling mode from almost any initial orientation (except for a set of measure zero corresponding to the repellers). This happens despite the movement of
![]() $C^{\ast }$
towards a finite limiting value (from
$C^{\ast }$
towards a finite limiting value (from
![]() $\infty$
to
$\infty$
to
![]() $\sqrt{35}$
) for
$\sqrt{35}$
) for
![]() ${\it\xi}_{0}\rightarrow 1$
. This is because, as noted earlier in § 4, for sufficiently thin oblate spheroids, the orbit constant is appropriately defined as
${\it\xi}_{0}\rightarrow 1$
. This is because, as noted earlier in § 4, for sufficiently thin oblate spheroids, the orbit constant is appropriately defined as
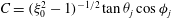 $C=({\it\xi}_{0}^{2}-1)^{-1/2}\tan {\it\theta}_{j}\cos {\it\phi}_{j}$
, so that for a given Jeffery orbit to remain bounded away from the gradient–vorticity plane as
$C=({\it\xi}_{0}^{2}-1)^{-1/2}\tan {\it\theta}_{j}\cos {\it\phi}_{j}$
, so that for a given Jeffery orbit to remain bounded away from the gradient–vorticity plane as
![]() ${\it\xi}_{0}\rightarrow 1$
,
${\it\xi}_{0}\rightarrow 1$
,
![]() $C$
must diverge as
$C$
must diverge as
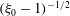 $({\it\xi}_{0}-1)^{-1/2}$
; in other words, Jeffery orbits corresponding to any finite
$({\it\xi}_{0}-1)^{-1/2}$
; in other words, Jeffery orbits corresponding to any finite
![]() $C$
in the flat-disk limit (including the
$C$
in the flat-disk limit (including the
 $C^{\ast }=\sqrt{35}$
, the zero crossing of the
$C^{\ast }=\sqrt{35}$
, the zero crossing of the
![]() ${\rm\Delta}C_{f}$
curve for a flat disk) must collapse onto the gradient–vorticity plane (the angular extent of the resulting arc is
${\rm\Delta}C_{f}$
curve for a flat disk) must collapse onto the gradient–vorticity plane (the angular extent of the resulting arc is
 $C/\sqrt{1+C^{2}}$
, and with
$C/\sqrt{1+C^{2}}$
, and with
![]() $C=C^{\ast }$
, this gives 161° as mentioned above). To illustrate the approach of the
$C=C^{\ast }$
, this gives 161° as mentioned above). To illustrate the approach of the
![]() ${\rm\Delta}C_{f}$
zero crossing towards
${\rm\Delta}C_{f}$
zero crossing towards
![]() $C=0$
for a flat disk, the fluid inertial drift is plotted against the rescaled orbital coordinate
$C=0$
for a flat disk, the fluid inertial drift is plotted against the rescaled orbital coordinate
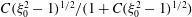 $C({\it\xi}_{0}^{2}-1)^{1/2}/(1+C({\it\xi}_{0}^{2}-1)^{1/2})$
in figure 7. Figure 8 illustrates the repelling (Jeffery) orbits starting from the equator of the unit sphere (
$C({\it\xi}_{0}^{2}-1)^{1/2}/(1+C({\it\xi}_{0}^{2}-1)^{1/2})$
in figure 7. Figure 8 illustrates the repelling (Jeffery) orbits starting from the equator of the unit sphere (
![]() $C=\infty$
), and moving towards smaller
$C=\infty$
), and moving towards smaller
![]() $C$
values with decreasing aspect ratio. Figure 9 shows the nature of the finite-
$C$
values with decreasing aspect ratio. Figure 9 shows the nature of the finite-
![]() $Re$
spiralling trajectories of the orientation vector on either side of these repellers. The emergence of the repellers may also be interpreted as a subcritical pitchfork bifurcation (figure 10), with
$Re$
spiralling trajectories of the orientation vector on either side of these repellers. The emergence of the repellers may also be interpreted as a subcritical pitchfork bifurcation (figure 10), with
![]() $1/C$
being the relevant coordinate, and the spheroid aspect ratio being the relevant parameter. For aspect ratios less than 0.142, the tumbling orbit is a local attractor bounded by a pair of unstable solutions (repeller). The coalescence of the three (two unstable and one stable) solutions, at the critical aspect ratio, renders the tumbling orbit unstable, and the system migrates to a distant equilibrium (the spinning mode). In the vicinity of the critical aspect ratio, the repeller locations are given by
$1/C$
being the relevant coordinate, and the spheroid aspect ratio being the relevant parameter. For aspect ratios less than 0.142, the tumbling orbit is a local attractor bounded by a pair of unstable solutions (repeller). The coalescence of the three (two unstable and one stable) solutions, at the critical aspect ratio, renders the tumbling orbit unstable, and the system migrates to a distant equilibrium (the spinning mode). In the vicinity of the critical aspect ratio, the repeller locations are given by
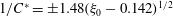 $1/C^{\ast }=\pm 1.48({\it\xi}_{0}-0.142)^{1/2}$
.
$1/C^{\ast }=\pm 1.48({\it\xi}_{0}-0.142)^{1/2}$
.

Figure 7. (a) Magnified view of the drift for the oblate spheroid plotted against a rescaled orbital coordinate shown in (b). The cross-over point shifts towards zero with decreasing aspect ratio.

Figure 8. The repeller orbit location for various aspect ratios. As the aspect ratios decreases below 0.142 (
 ${\it\xi}_{0}=1.01$
) a repeller orbit (denoted by thick black lines) emerges from
${\it\xi}_{0}=1.01$
) a repeller orbit (denoted by thick black lines) emerges from
 $C/(C+1)=1$
(the tumbling orbit). With further decrease in the aspect ratio, the repeller progressively shrinks, collapsing into the vicinity of the gradient–vorticity plane in the flat-disk limit.
$C/(C+1)=1$
(the tumbling orbit). With further decrease in the aspect ratio, the repeller progressively shrinks, collapsing into the vicinity of the gradient–vorticity plane in the flat-disk limit.

Figure 9. The nature of the spiralling trajectories on either side of the repeller is shown for a pair of aspect ratios. For the purpose of illustration, a large Stokes number (
![]() $St=0.8$
) is chosen.
$St=0.8$
) is chosen.

Figure 10. The oblate spheroid orientation dynamics from a dynamical systems perspective: a subcritical pitchfork bifurcation at an aspect ratio of
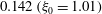 $0.142\,({\it\xi}_{0}=1.01)$
.
$0.142\,({\it\xi}_{0}=1.01)$
.
6.3 Drift due to fluid and particle inertia: role of the particle-to-fluid density ratio (
 $St/Re={\it\rho}_{p}/{\it\rho}_{f}$
)
$St/Re={\it\rho}_{p}/{\it\rho}_{f}$
)
For a neutrally buoyant spheroid, the inertial drift is given by (5.19), but with the aspect-ratio-dependent functions now being the sums of the
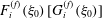 $F_{i}^{(f)}({\it\xi}_{0})\,[G_{i}^{(f)}({\it\xi}_{0})]$
and the
$F_{i}^{(f)}({\it\xi}_{0})\,[G_{i}^{(f)}({\it\xi}_{0})]$
and the
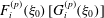 $F_{i}^{(p)}({\it\xi}_{0})\,[G_{i}^{(p)}({\it\xi}_{0})]$
. The drifts for neutrally buoyant prolate and oblate spheroids are plotted against the normalized orbit constant in figures 11 and 12, respectively. These curves closely resemble those in figures 5 and 6, showing that fluid inertia dominates the inertia of the particle for most aspect ratios. Accordingly, the critical aspect ratio at which
$F_{i}^{(p)}({\it\xi}_{0})\,[G_{i}^{(p)}({\it\xi}_{0})]$
. The drifts for neutrally buoyant prolate and oblate spheroids are plotted against the normalized orbit constant in figures 11 and 12, respectively. These curves closely resemble those in figures 5 and 6, showing that fluid inertia dominates the inertia of the particle for most aspect ratios. Accordingly, the critical aspect ratio at which
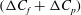 $({\rm\Delta}C_{f}+{\rm\Delta}C_{p})$
first changes sign (for
$({\rm\Delta}C_{f}+{\rm\Delta}C_{p})$
first changes sign (for
![]() $C\rightarrow \infty$
) is only slightly altered from the original value, 0.142, for hollow oblate spheroids (fluid inertia acting alone), to 0.137 for a neutrally buoyant oblate spheroid.
$C\rightarrow \infty$
) is only slightly altered from the original value, 0.142, for hollow oblate spheroids (fluid inertia acting alone), to 0.137 for a neutrally buoyant oblate spheroid.
The effect of density ratio (
![]() $St/Re$
) is best illustrated for small aspect-ratio oblate spheroids, since the particle inertial (single signed) and fluid inertial (zero crossing for aspect ratios below a critical value) drift curves are distinct in character in this case. As
$St/Re$
) is best illustrated for small aspect-ratio oblate spheroids, since the particle inertial (single signed) and fluid inertial (zero crossing for aspect ratios below a critical value) drift curves are distinct in character in this case. As
![]() $St/Re$
increases from 0, for a fixed aspect ratio below 0.142, one expects the location of the repeller to move towards the tumbling orbit, and
$St/Re$
increases from 0, for a fixed aspect ratio below 0.142, one expects the location of the repeller to move towards the tumbling orbit, and
![]() ${\rm\Delta}C$
to eventually become single-signed. This is shown in figure 13 for an oblate spheroid with an aspect ratio of
${\rm\Delta}C$
to eventually become single-signed. This is shown in figure 13 for an oblate spheroid with an aspect ratio of
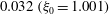 $0.032\,({\it\xi}_{0}=1.001)$
; the
$0.032\,({\it\xi}_{0}=1.001)$
; the
![]() $St$
and
$St$
and
![]() $Re$
here vary from 0 to 0.15 (
$Re$
here vary from 0 to 0.15 (
![]() $St^{\ast }$
) and 0.0033 (
$St^{\ast }$
) and 0.0033 (
![]() $Re^{\ast }$
), respectively, the maximum values being chosen so as to make the particle and the fluid inertial drifts of the same order. The actual drift is proportional to
$Re^{\ast }$
), respectively, the maximum values being chosen so as to make the particle and the fluid inertial drifts of the same order. The actual drift is proportional to
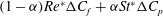 $(1-{\it\alpha})Re^{\ast }{\rm\Delta}C_{f}+{\it\alpha}St^{\ast }{\rm\Delta}C_{p}$
, with the value of
$(1-{\it\alpha})Re^{\ast }{\rm\Delta}C_{f}+{\it\alpha}St^{\ast }{\rm\Delta}C_{p}$
, with the value of
![]() ${\it\alpha}$
fixing the ratio
${\it\alpha}$
fixing the ratio
![]() $St/Re$
. It is worth noting that, even for the chosen small aspect ratio, the drift becomes single-signed only at
$St/Re$
. It is worth noting that, even for the chosen small aspect ratio, the drift becomes single-signed only at
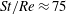 $St/Re\approx 75$
. Since both particle and fluid inertia induce a drift in the same direction for a prolate spheroid, one expects no qualitative changes in the drift curve with varying
$St/Re\approx 75$
. Since both particle and fluid inertia induce a drift in the same direction for a prolate spheroid, one expects no qualitative changes in the drift curve with varying
![]() $St/Re$
. Hence, in figure 14, we have plotted separately the normalized fluid and particle inertial drifts for a prolate spheroid of aspect ratio 4 to again reinforce the dominance of fluid inertia. The peak drift values are 0.238 and 0.0058 for the particle and fluid inertia cases (attained at
$St/Re$
. Hence, in figure 14, we have plotted separately the normalized fluid and particle inertial drifts for a prolate spheroid of aspect ratio 4 to again reinforce the dominance of fluid inertia. The peak drift values are 0.238 and 0.0058 for the particle and fluid inertia cases (attained at
![]() $C$
values of 1.20 and 1.10 respectively), implying that particle inertia begins to control the inertial drift of the prolate spheroid of aspect ratio 4 only when the density ratio exceeds approximately 41. Thus, for a prolate spheroid of any reasonable aspect ratio and a density ratio of order unity, the drift is controlled by fluid inertial forces, and it is only for gas–solid systems that particle inertia becomes significant.
$C$
values of 1.20 and 1.10 respectively), implying that particle inertia begins to control the inertial drift of the prolate spheroid of aspect ratio 4 only when the density ratio exceeds approximately 41. Thus, for a prolate spheroid of any reasonable aspect ratio and a density ratio of order unity, the drift is controlled by fluid inertial forces, and it is only for gas–solid systems that particle inertia becomes significant.
The above fact needs particular emphasis in light of the recent comments of Aidun and co-workers (Rosen et al.
Reference Rosen, Lundell and Aidun2014), which might in turn might be due to the incorrect fluid inertial analysis of Subramanian & Koch (Reference Subramanian and Koch2006b
) that predicted a nearly spherical prolate particle to drift towards the vorticity axis (see appendix D). For instance, it has been emphasized on more than one occasion by Rosen et al. (Reference Rosen, Lundell and Aidun2014) that the initial tumbling phase (for small
![]() $Re$
) arises due to centrifuging effects associated with particle inertia, and fluid inertial effects act in opposition to this tendency, leading to subsequent bifurcations at higher
$Re$
) arises due to centrifuging effects associated with particle inertia, and fluid inertial effects act in opposition to this tendency, leading to subsequent bifurcations at higher
![]() $Re$
to log-rolling and kayaking modes. The authors also attempt to rationalize the results of some early experiments by Mason and co-workers (Karnis, Goldsmith & Mason Reference Karnis, Goldsmith and Mason1963), who found cylindrical particles to apparently conform to the minimum dissipation hypothesis for
$Re$
to log-rolling and kayaking modes. The authors also attempt to rationalize the results of some early experiments by Mason and co-workers (Karnis, Goldsmith & Mason Reference Karnis, Goldsmith and Mason1963), who found cylindrical particles to apparently conform to the minimum dissipation hypothesis for
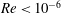 $Re<10^{-6}$
. The present analysis, reinforced by figure 14, shows that this is clearly not true, and it is almost entirely due to fluid inertia alone that a prolate spheroid of any reasonable aspect ratio, suspended in a liquid, approaches the tumbling mode for small
$Re<10^{-6}$
. The present analysis, reinforced by figure 14, shows that this is clearly not true, and it is almost entirely due to fluid inertia alone that a prolate spheroid of any reasonable aspect ratio, suspended in a liquid, approaches the tumbling mode for small
![]() $Re$
.
$Re$
.
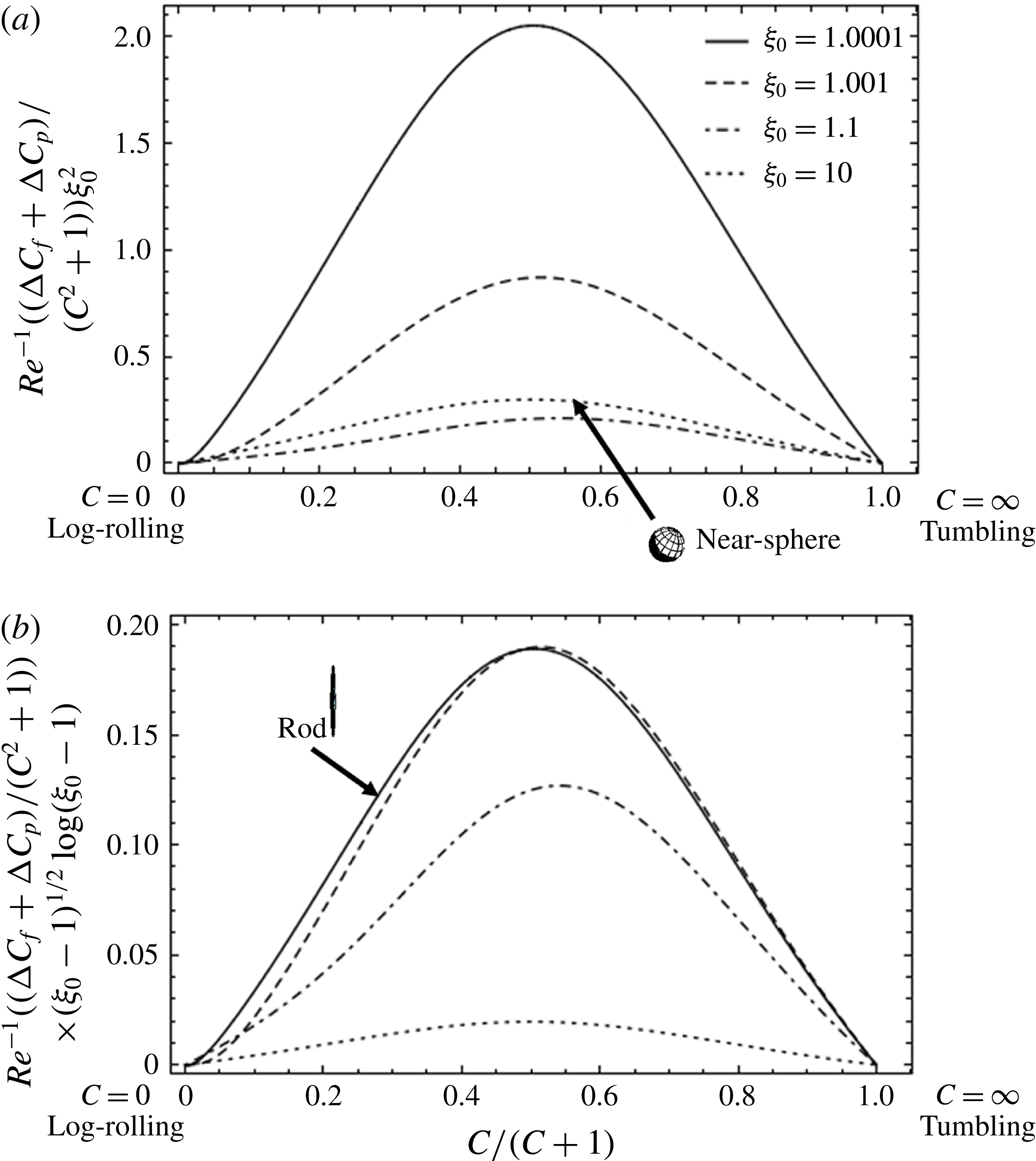
Figure 11. The drift due to fluid and particle inertia for a prolate (neutrally buoyant) spheroid, as characterized by the normalized change in the orbit constant in a single Jeffery period,
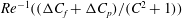 $Re^{-1}(({\rm\Delta}C_{f}+{\rm\Delta}C_{p})/(C^{2}+1))$
, plotted as a function of
$Re^{-1}(({\rm\Delta}C_{f}+{\rm\Delta}C_{p})/(C^{2}+1))$
, plotted as a function of
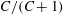 $C/(C+1)$
;
$C/(C+1)$
;
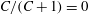 $C/(C+1)=0$
and
$C/(C+1)=0$
and
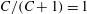 $C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
$C/(C+1)=1$
correspond to the log-rolling and tumbling modes, respectively. (a) Uses the additional normalization factor of
![]() ${\it\xi}_{0}^{2}$
, so that the drift remains finite in the near-sphere limit (
${\it\xi}_{0}^{2}$
, so that the drift remains finite in the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
${\it\xi}_{0}\rightarrow \infty$
). (b) Uses the normalization factor
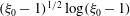 $({\it\xi}_{0}-1)^{1/2}\log ({\it\xi}_{0}-1)$
such that the drift remains finite in the slender rod limit (
$({\it\xi}_{0}-1)^{1/2}\log ({\it\xi}_{0}-1)$
such that the drift remains finite in the slender rod limit (
![]() ${\it\xi}_{0}\rightarrow 1$
). The contribution due to fluid inertia dominates particle inertia for all aspect ratios.
${\it\xi}_{0}\rightarrow 1$
). The contribution due to fluid inertia dominates particle inertia for all aspect ratios.

Figure 12. The drift due to fluid and particle inertia for an oblate (neutrally buoyant) spheroid, as characterized by the normalized change in the orbit constant in a single Jeffery period,
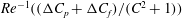 $Re^{-1}(({\rm\Delta}C_{p}+{\rm\Delta}C_{f})/(C^{2}+1))$
, plotted as a function of
$Re^{-1}(({\rm\Delta}C_{p}+{\rm\Delta}C_{f})/(C^{2}+1))$
, plotted as a function of
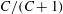 $C/(C+1)$
;
$C/(C+1)$
;
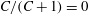 $C/(C+1)=0$
and
$C/(C+1)=0$
and
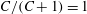 $C/(C+1)=1$
correspond to the spinning and tumbling modes, respectively. The plot uses the additional normalization factor of
$C/(C+1)=1$
correspond to the spinning and tumbling modes, respectively. The plot uses the additional normalization factor of
![]() ${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
${\it\xi}_{0}^{2}$
, so the drift remains finite in the near-sphere limit (
![]() ${\it\xi}_{0}\rightarrow \infty$
).
${\it\xi}_{0}\rightarrow \infty$
).

Figure 13. (it a) Magnified view close to the tumbling orbit of the combined drift due to particle and fluid inertia plotted for various values of the ratio
![]() $St/Re$
with
$St/Re$
with
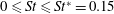 $0\leqslant St\leqslant St^{\ast }=0.15$
and
$0\leqslant St\leqslant St^{\ast }=0.15$
and
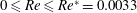 $0\leqslant Re\leqslant Re^{\ast }=0.0033$
for
$0\leqslant Re\leqslant Re^{\ast }=0.0033$
for
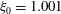 ${\it\xi}_{0}=1.001$
shown in (b).
${\it\xi}_{0}=1.001$
shown in (b).

Figure 14. The drifts due to fluid and particle inertia are plotted for a prolate spheroid of aspect ratio 4.
7 The rheology of a dilute suspension of neutrally buoyant spheroids
In this section, we determine the shear viscosity of a dilute suspension of non-Brownian neutrally buoyant spheroidal particles as a function of the particle aspect ratio. The contribution of the particulate phase to the averaged suspension stress may be written as
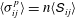 $\langle {\it\sigma}_{ij}^{p}\rangle =n\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
, where, in the infinitely dilute limit, the stresslet,
$\langle {\it\sigma}_{ij}^{p}\rangle =n\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
, where, in the infinitely dilute limit, the stresslet,
![]() $\unicode[STIX]{x1D61A}_{ij}$
, is that associated with an isolated torque-free spheroid immersed in an ambient linear flow. This stresslet is a function of the instantaneous spheroid orientation
$\unicode[STIX]{x1D61A}_{ij}$
, is that associated with an isolated torque-free spheroid immersed in an ambient linear flow. This stresslet is a function of the instantaneous spheroid orientation
![]() $\boldsymbol{p}$
, and the angled brackets therefore denote an average over the relevant orientation probability density. Thus,
$\boldsymbol{p}$
, and the angled brackets therefore denote an average over the relevant orientation probability density. Thus,
![]() $\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
is given by:
$\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
is given by:
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D61A}_{ij}\rangle =\int {\it\Omega}(\boldsymbol{p})\,\text{d}\boldsymbol{p}\int _{S_{p}}\frac{1}{2}\left[{\it\sigma}_{ik}x_{j}n_{k}+{\it\sigma}_{jk}x_{i}n_{k}-\frac{2}{3}\,{\it\delta}_{ij}({\it\sigma}_{lk}x_{l}n_{k})\right]\text{d}A,\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D61A}_{ij}\rangle =\int {\it\Omega}(\boldsymbol{p})\,\text{d}\boldsymbol{p}\int _{S_{p}}\frac{1}{2}\left[{\it\sigma}_{ik}x_{j}n_{k}+{\it\sigma}_{jk}x_{i}n_{k}-\frac{2}{3}\,{\it\delta}_{ij}({\it\sigma}_{lk}x_{l}n_{k})\right]\text{d}A,\end{eqnarray}$$
where
![]() $S_{p}$
denotes the surface of the spheroid. For finite
$S_{p}$
denotes the surface of the spheroid. For finite
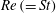 $Re\,(=\,St)$
, as originally shown by Batchelor (Reference Batchelor1970b
), the suspension stress contains additional terms involving both the particle phase acceleration and the fluid phase velocity fluctuations, and these have been shown to lead to a non-Newtonian rheology even for suspensions of spherical inclusions (Lin et al.
Reference Lin, Peery and Schowalter1970; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). However, these effects scale with
$Re\,(=\,St)$
, as originally shown by Batchelor (Reference Batchelor1970b
), the suspension stress contains additional terms involving both the particle phase acceleration and the fluid phase velocity fluctuations, and these have been shown to lead to a non-Newtonian rheology even for suspensions of spherical inclusions (Lin et al.
Reference Lin, Peery and Schowalter1970; Subramanian et al.
Reference Subramanian, Koch, Zhang and Yang2011). However, these effects scale with
![]() $Re$
, and become vanishingly small for
$Re$
, and become vanishingly small for
![]() $Re\rightarrow 0$
. Thus, for small but finite
$Re\rightarrow 0$
. Thus, for small but finite
![]() $Re$
, the dominant effect of inertia is an indirect one in terms of determining the steady-state orientation probability density (and thereby, the shear viscosity). As shown in §§ 7.1 and 7.2, this steady-state probability density is independent of
$Re$
, the dominant effect of inertia is an indirect one in terms of determining the steady-state orientation probability density (and thereby, the shear viscosity). As shown in §§ 7.1 and 7.2, this steady-state probability density is independent of
![]() $Re$
, and this indirect effect of inertia on the rheology is therefore of order unity. Note that the steady-state orientation distribution is set up by the weak inertial drift determined in previous sections, with or without Brownian diffusion, on an asymptotically long time scale. In the absence of Brownian motion, this time scale is
$Re$
, and this indirect effect of inertia on the rheology is therefore of order unity. Note that the steady-state orientation distribution is set up by the weak inertial drift determined in previous sections, with or without Brownian diffusion, on an asymptotically long time scale. In the absence of Brownian motion, this time scale is
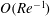 $O(Re^{-1})$
; in the presence of Brownian motion, this time scale continues to be the relevant one for prolate spheroids and oblate spheroids greater than the critical aspect ratio (0.137). For thinner oblate spheroids, the orientation distribution set up by the bidirectional inertial drift is sensitive to the initial orientation distribution, and the eventual initial-condition-independent steady state is set up by weak Brownian motion on an exponentially long time scale (
$O(Re^{-1})$
; in the presence of Brownian motion, this time scale continues to be the relevant one for prolate spheroids and oblate spheroids greater than the critical aspect ratio (0.137). For thinner oblate spheroids, the orientation distribution set up by the bidirectional inertial drift is sensitive to the initial orientation distribution, and the eventual initial-condition-independent steady state is set up by weak Brownian motion on an exponentially long time scale (
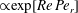 $\propto \text{exp}[Re\,Pe_{r}]$
).
$\propto \text{exp}[Re\,Pe_{r}]$
).
The instantaneous stresslet as a function of
![]() $\boldsymbol{p}$
may be written down from symmetry arguments as:
$\boldsymbol{p}$
may be written down from symmetry arguments as:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61A}_{ij}(\boldsymbol{p}) & = & \displaystyle {\textstyle \frac{3}{2}}D_{1}^{(p/o)}({\it\xi}_{0})(\unicode[STIX]{x1D60C}_{kl}p_{k}p_{l})(p_{i}p_{j}-{\textstyle \frac{1}{3}}\,{\it\delta}_{ij})+D_{2}^{(p/o)}({\it\xi}_{0})[\hspace{2.39996pt}({\it\delta}_{ik}-p_{i}p_{k})\unicode[STIX]{x1D60C}_{kl}p_{l}p_{j}\nonumber\\ \displaystyle & & \displaystyle +\,({\it\delta}_{jk}-p_{j}p_{k})\unicode[STIX]{x1D60C}_{kl}p_{l}p_{i} ]+\,D_{3}^{(p/o)}({\it\xi}_{0})[\hspace{2.39996pt}({\it\delta}_{ik}-p_{i}p_{k})\unicode[STIX]{x1D60C}_{kl}({\it\delta}_{jl}-p_{l}p_{j})\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}(\unicode[STIX]{x1D60C}_{kl}p_{k}p_{l})({\it\delta}_{ij}-p_{i}p_{j})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61A}_{ij}(\boldsymbol{p}) & = & \displaystyle {\textstyle \frac{3}{2}}D_{1}^{(p/o)}({\it\xi}_{0})(\unicode[STIX]{x1D60C}_{kl}p_{k}p_{l})(p_{i}p_{j}-{\textstyle \frac{1}{3}}\,{\it\delta}_{ij})+D_{2}^{(p/o)}({\it\xi}_{0})[\hspace{2.39996pt}({\it\delta}_{ik}-p_{i}p_{k})\unicode[STIX]{x1D60C}_{kl}p_{l}p_{j}\nonumber\\ \displaystyle & & \displaystyle +\,({\it\delta}_{jk}-p_{j}p_{k})\unicode[STIX]{x1D60C}_{kl}p_{l}p_{i} ]+\,D_{3}^{(p/o)}({\it\xi}_{0})[\hspace{2.39996pt}({\it\delta}_{ik}-p_{i}p_{k})\unicode[STIX]{x1D60C}_{kl}({\it\delta}_{jl}-p_{l}p_{j})\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}(\unicode[STIX]{x1D60C}_{kl}p_{k}p_{l})({\it\delta}_{ij}-p_{i}p_{j})],\end{eqnarray}$$
where the coefficients
![]() $D_{1}^{(p/o)}$
,
$D_{1}^{(p/o)}$
,
![]() $D_{2}^{(p/o)}$
and
$D_{2}^{(p/o)}$
and
![]() $D_{3}^{(p/o)}$
, respectively, denote the aspect-ratio-dependent strength of the stresslet singularities corresponding to the component flows (axisymmetric, longitudinal and transverse extensions) that make up the ambient simple shear in the body-fixed reference frame for prolate (
$D_{3}^{(p/o)}$
, respectively, denote the aspect-ratio-dependent strength of the stresslet singularities corresponding to the component flows (axisymmetric, longitudinal and transverse extensions) that make up the ambient simple shear in the body-fixed reference frame for prolate (
![]() $p$
) and oblate (
$p$
) and oblate (
![]() $o$
) spheroids. The number of coefficients (three) is fewer than the number of component flows (five), since the axisymmetry of the spheroid implies identical responses to the two longitudinal (
$o$
) spheroids. The number of coefficients (three) is fewer than the number of component flows (five), since the axisymmetry of the spheroid implies identical responses to the two longitudinal (
![]() $\boldsymbol{u}_{4s}$
and
$\boldsymbol{u}_{4s}$
and
![]() $\boldsymbol{u}_{5s}$
) and transverse extensional flows (
$\boldsymbol{u}_{5s}$
) and transverse extensional flows (
![]() $\boldsymbol{u}_{2s}$
and
$\boldsymbol{u}_{2s}$
and
![]() $\boldsymbol{u}_{3s}$
), which combine to give the terms proportional to
$\boldsymbol{u}_{3s}$
), which combine to give the terms proportional to
![]() $D_{2}$
and
$D_{2}$
and
![]() $D_{3}$
, respectively, in (7.2). For the limiting case of a sphere,
$D_{3}$
, respectively, in (7.2). For the limiting case of a sphere,
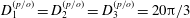 $D_{1}^{(p/o)}=D_{2}^{(p/o)}=D_{3}^{(p/o)}=20{\rm\pi}/3$
, and (7.2) takes the familiar form
$D_{1}^{(p/o)}=D_{2}^{(p/o)}=D_{3}^{(p/o)}=20{\rm\pi}/3$
, and (7.2) takes the familiar form
 $\unicode[STIX]{x1D61A}_{ij}=(20{\rm\pi}/3)\unicode[STIX]{x1D60C}_{ij}$
which yields the Einstein coefficient. From Kim & Karrila (Reference Kim and Karrila1991), the expressions for the coefficients, translated to our notation, are given by:
$\unicode[STIX]{x1D61A}_{ij}=(20{\rm\pi}/3)\unicode[STIX]{x1D60C}_{ij}$
which yields the Einstein coefficient. From Kim & Karrila (Reference Kim and Karrila1991), the expressions for the coefficients, translated to our notation, are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{1}^{(p)}({\it\xi}_{0})=\frac{16{\rm\pi}}{9{\it\xi}_{0}^{3}[(3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{1}^{(p)}({\it\xi}_{0})=\frac{16{\rm\pi}}{9{\it\xi}_{0}^{3}[(3{\it\xi}_{0}^{2}-1)\coth ^{-1}{\it\xi}_{0}-3{\it\xi}_{0}]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{2}^{(p)}({\it\xi}_{0})=\frac{16{\rm\pi}\bar{{\it\xi}}_{0}^{2}}{[3{\it\xi}_{0}^{2}(1-2{\it\xi}_{0}^{2})(2-3{\it\xi}_{0}^{2}+3{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0})]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{2}^{(p)}({\it\xi}_{0})=\frac{16{\rm\pi}\bar{{\it\xi}}_{0}^{2}}{[3{\it\xi}_{0}^{2}(1-2{\it\xi}_{0}^{2})(2-3{\it\xi}_{0}^{2}+3{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}\coth ^{-1}{\it\xi}_{0})]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{3}^{(p)}({\it\xi}_{0})=\frac{32{\rm\pi}\bar{{\it\xi}}_{0}^{2}}{3{\it\xi}_{0}^{3}(5{\it\xi}_{0}-3{\it\xi}_{0}^{3}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{3}^{(p)}({\it\xi}_{0})=\frac{32{\rm\pi}\bar{{\it\xi}}_{0}^{2}}{3{\it\xi}_{0}^{3}(5{\it\xi}_{0}-3{\it\xi}_{0}^{3}+3\bar{{\it\xi}}_{0}^{4}\coth ^{-1}{\it\xi}_{0})}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{1}^{(o)}({\it\xi}_{0})=\frac{16{\rm\pi}}{9{\it\xi}_{0}^{3}[(3{\it\xi}_{0}^{2}-2)\cot ^{-1}\bar{{\it\xi}}_{0}-3\bar{{\it\xi}}_{0}]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{1}^{(o)}({\it\xi}_{0})=\frac{16{\rm\pi}}{9{\it\xi}_{0}^{3}[(3{\it\xi}_{0}^{2}-2)\cot ^{-1}\bar{{\it\xi}}_{0}-3\bar{{\it\xi}}_{0}]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{2}^{(o)}({\it\xi}_{0})=\frac{16{\rm\pi}\bar{{\it\xi}}_{0}}{[3{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})(1-3{\it\xi}_{0}^{2}+3{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}\cot ^{-1}\bar{{\it\xi}}_{0})]}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{2}^{(o)}({\it\xi}_{0})=\frac{16{\rm\pi}\bar{{\it\xi}}_{0}}{[3{\it\xi}_{0}(1-2{\it\xi}_{0}^{2})(1-3{\it\xi}_{0}^{2}+3{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}\cot ^{-1}\bar{{\it\xi}}_{0})]}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{3}^{(o)}({\it\xi}_{0})=\frac{32{\rm\pi}}{3{\it\xi}_{0}(-(2+3{\it\xi}_{0}^{2})\bar{{\it\xi}}_{0}+3{\it\xi}_{0}^{4}\cot ^{-1}\bar{{\it\xi}}_{0})}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{3}^{(o)}({\it\xi}_{0})=\frac{32{\rm\pi}}{3{\it\xi}_{0}(-(2+3{\it\xi}_{0}^{2})\bar{{\it\xi}}_{0}+3{\it\xi}_{0}^{4}\cot ^{-1}\bar{{\it\xi}}_{0})}. & \displaystyle\end{eqnarray}$$
The above expressions may also be obtained from the far-field limit (for
![]() ${\it\xi}\rightarrow \infty$
) of each of the component velocity fields (
${\it\xi}\rightarrow \infty$
) of each of the component velocity fields (
 $\boldsymbol{u}_{1s}-\boldsymbol{u}_{5s}$
), of the form
$\boldsymbol{u}_{1s}-\boldsymbol{u}_{5s}$
), of the form
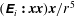 $(\unicode[STIX]{x1D640}_{i}\boldsymbol{ : }\boldsymbol{x}\boldsymbol{x})\boldsymbol{x}/r^{5}$
,
$(\unicode[STIX]{x1D640}_{i}\boldsymbol{ : }\boldsymbol{x}\boldsymbol{x})\boldsymbol{x}/r^{5}$
,
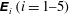 $\unicode[STIX]{x1D640}_{i}\,(i=1{-}5)$
being the component rate-of-strain tensor (see (3.2)), with the constant of proportionality, a function of
$\unicode[STIX]{x1D640}_{i}\,(i=1{-}5)$
being the component rate-of-strain tensor (see (3.2)), with the constant of proportionality, a function of
![]() ${\it\xi}_{0}$
, giving the
${\it\xi}_{0}$
, giving the
![]() ${\it\xi}_{0}$
-dependent stresslet coefficient.
${\it\xi}_{0}$
-dependent stresslet coefficient.
The excess stress in a dilute suspension is therefore given by:
 $$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\unicode[STIX]{x1D60C}_{kl}\int \left\{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}p_{k}p_{l}\left(p_{i}p_{j}-\frac{1}{3}\,{\it\delta}_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,D_{2}^{(p/o)}({\it\xi}_{0})[({\it\delta}_{ik}-p_{i}p_{k})p_{l}p_{j}+({\it\delta}_{jk}-p_{j}p_{k})p_{l}p_{i}]\nonumber\\ \displaystyle & & \displaystyle +\left.D_{3}^{(p/o)}({\it\xi}_{0})\left[({\it\delta}_{ik}-p_{i}p_{k})({\it\delta}_{jl}-p_{l}p_{j})+\frac{1}{2}p_{k}p_{l}({\it\delta}_{ij}-p_{i}p_{j})\right]\vphantom{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}}\!\right\}{\it\Omega}(\boldsymbol{p})\,\text{d}\boldsymbol{p},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\unicode[STIX]{x1D60C}_{kl}\int \left\{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}p_{k}p_{l}\left(p_{i}p_{j}-\frac{1}{3}\,{\it\delta}_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,D_{2}^{(p/o)}({\it\xi}_{0})[({\it\delta}_{ik}-p_{i}p_{k})p_{l}p_{j}+({\it\delta}_{jk}-p_{j}p_{k})p_{l}p_{i}]\nonumber\\ \displaystyle & & \displaystyle +\left.D_{3}^{(p/o)}({\it\xi}_{0})\left[({\it\delta}_{ik}-p_{i}p_{k})({\it\delta}_{jl}-p_{l}p_{j})+\frac{1}{2}p_{k}p_{l}({\it\delta}_{ij}-p_{i}p_{j})\right]\vphantom{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}}\!\right\}{\it\Omega}(\boldsymbol{p})\,\text{d}\boldsymbol{p},\end{eqnarray}$$
where the functional form of
![]() ${\it\Omega}(\boldsymbol{p})$
depends on
${\it\Omega}(\boldsymbol{p})$
depends on
![]() ${\it\xi}_{0}$
and
${\it\xi}_{0}$
and
![]() $Re\,Pe_{r}$
. As mentioned in § 1, the distribution of orientations along a Jeffery orbit is determined in the athermal limit, even in the absence of interparticle hydrodynamic interactions, being given by the inverse of the azimuthal component of the Jeffery angular velocity. In terms of
$Re\,Pe_{r}$
. As mentioned in § 1, the distribution of orientations along a Jeffery orbit is determined in the athermal limit, even in the absence of interparticle hydrodynamic interactions, being given by the inverse of the azimuthal component of the Jeffery angular velocity. In terms of
![]() ${\it\phi}_{j}$
, the probability density along a Jeffery orbit is proportional to
${\it\phi}_{j}$
, the probability density along a Jeffery orbit is proportional to
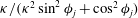 ${\it\kappa}/({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})$
for a spheroid. In
${\it\kappa}/({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})$
for a spheroid. In
![]() $(C,{\it\tau})$
coordinates,
$(C,{\it\tau})$
coordinates,
![]() ${\it\Omega}(\boldsymbol{p})$
may be written in the form
${\it\Omega}(\boldsymbol{p})$
may be written in the form
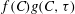 $f(C)g(C,{\it\tau})$
, where the function
$f(C)g(C,{\it\tau})$
, where the function
![]() $g(C,{\it\tau})$
corresponds to the aforementioned distribution of azimuthal angles, and is given by:
$g(C,{\it\tau})$
corresponds to the aforementioned distribution of azimuthal angles, and is given by:
 $$\begin{eqnarray}\displaystyle g(C,{\it\tau})=\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(C,{\it\tau})=\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}, & & \displaystyle\end{eqnarray}$$
and
![]() $f(C)$
corresponds to the distribution of orientation across orbits. In (7.10),
$f(C)$
corresponds to the distribution of orientation across orbits. In (7.10),
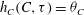 $h_{C}(C,{\it\tau})={\it\theta}_{C}$
and
$h_{C}(C,{\it\tau})={\it\theta}_{C}$
and
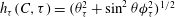 $h_{{\it\tau}}(C,{\it\tau})=({\it\theta}_{{\it\tau}}^{2}+\sin ^{2}{\it\theta}{\it\phi}_{{\it\tau}}^{2})^{1/2}$
are the diagonal elements of the metric tensor, with the angle between the coordinate lines being given by
$h_{{\it\tau}}(C,{\it\tau})=({\it\theta}_{{\it\tau}}^{2}+\sin ^{2}{\it\theta}{\it\phi}_{{\it\tau}}^{2})^{1/2}$
are the diagonal elements of the metric tensor, with the angle between the coordinate lines being given by
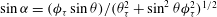 $\sin {\it\alpha}=({\it\phi}_{{\it\tau}}\sin {\it\theta})/({\it\theta}_{{\it\tau}}^{2}+\sin ^{2}{\it\theta}{\it\phi}_{{\it\tau}}^{2})^{1/2}$
. Thus, the sides of the elemental parallelogram in the
$\sin {\it\alpha}=({\it\phi}_{{\it\tau}}\sin {\it\theta})/({\it\theta}_{{\it\tau}}^{2}+\sin ^{2}{\it\theta}{\it\phi}_{{\it\tau}}^{2})^{1/2}$
. Thus, the sides of the elemental parallelogram in the
![]() $(C,{\it\tau})$
system are
$(C,{\it\tau})$
system are
![]() $h_{C}\,\text{d}C$
and
$h_{C}\,\text{d}C$
and
![]() $h_{{\it\tau}}\,\text{d}{\it\tau}$
, the area of the parallelogram being
$h_{{\it\tau}}\,\text{d}{\it\tau}$
, the area of the parallelogram being
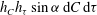 $h_{C}h_{{\it\tau}}\sin {\it\alpha}\,\text{d}C\,\text{d}{\it\tau}$
. The suffixes here denote derivatives with respect to the relevant variables, which may be obtained using the expressions given in § 4; see appendix B. Using (7.10), the excess stress due to the suspended particles may be written as:
$h_{C}h_{{\it\tau}}\sin {\it\alpha}\,\text{d}C\,\text{d}{\it\tau}$
. The suffixes here denote derivatives with respect to the relevant variables, which may be obtained using the expressions given in § 4; see appendix B. Using (7.10), the excess stress due to the suspended particles may be written as:
 $$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\unicode[STIX]{x1D60C}_{kl}\int \left\{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}p_{k}p_{l}\left(p_{i}p_{j}-\frac{1}{3}\,{\it\delta}_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,D_{2}^{(p/o)}({\it\xi}_{0})[({\it\delta}_{ik}-p_{i}p_{k})p_{l}p_{j}+({\it\delta}_{jk}-p_{j}p_{k})p_{l}p_{i}]\nonumber\\ \displaystyle & & \displaystyle +\left.D_{3}^{(p/o)}({\it\xi}_{0})\left[({\it\delta}_{ik}-p_{i}p_{k})({\it\delta}_{jl}-p_{l}p_{j})+\frac{1}{2}p_{k}p_{l}({\it\delta}_{ij}-p_{i}p_{j})\right]\vphantom{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}}\!\right\}\frac{f(C)}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\,\text{d}\boldsymbol{p},\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\unicode[STIX]{x1D60C}_{kl}\int \left\{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}p_{k}p_{l}\left(p_{i}p_{j}-\frac{1}{3}\,{\it\delta}_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,D_{2}^{(p/o)}({\it\xi}_{0})[({\it\delta}_{ik}-p_{i}p_{k})p_{l}p_{j}+({\it\delta}_{jk}-p_{j}p_{k})p_{l}p_{i}]\nonumber\\ \displaystyle & & \displaystyle +\left.D_{3}^{(p/o)}({\it\xi}_{0})\left[({\it\delta}_{ik}-p_{i}p_{k})({\it\delta}_{jl}-p_{l}p_{j})+\frac{1}{2}p_{k}p_{l}({\it\delta}_{ij}-p_{i}p_{j})\right]\vphantom{\frac{3D_{1}^{(p/o)}({\it\xi}_{0})}{2}}\!\right\}\frac{f(C)}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\,\text{d}\boldsymbol{p},\qquad \quad\end{eqnarray}$$
for the case of the spheroids, with
![]() $f(C)$
being the only unknown. The orientation-space integration element in (7.11) is left as
$f(C)$
being the only unknown. The orientation-space integration element in (7.11) is left as
![]() $\text{d}\boldsymbol{p}$
, since it turns out that the integration is easiest in the usual spherical coordinates in the non-Brownian case (§ 7.1), while the
$\text{d}\boldsymbol{p}$
, since it turns out that the integration is easiest in the usual spherical coordinates in the non-Brownian case (§ 7.1), while the
![]() $C{-}{\it\tau}$
coordinate system is more convenient with the inclusion of weak Brownian motion (§ 7.2), as is necessary for neutrally buoyant oblate spheroids with aspect ratios less than 0.137 on account of the bifurcation in the orientation dynamics induced by fluid inertia. The space-fixed form of the rate-of-strain tensor,
$C{-}{\it\tau}$
coordinate system is more convenient with the inclusion of weak Brownian motion (§ 7.2), as is necessary for neutrally buoyant oblate spheroids with aspect ratios less than 0.137 on account of the bifurcation in the orientation dynamics induced by fluid inertia. The space-fixed form of the rate-of-strain tensor,
![]() $\unicode[STIX]{x1D640}$
, is most convenient for the rheology calculations based on (7.11).
$\unicode[STIX]{x1D640}$
, is most convenient for the rheology calculations based on (7.11).
7.1 The shear viscosity of a suspension of non-Brownian spheroids
While the distribution across Jeffery orbits is indeterminate in the Stokes limit, accounting for the drift due to either particle or fluid inertia, and in the absence of stochastic de-correlation mechanisms (of either a thermal or hydrodynamic origin), must lead to a singular steady-state orientation distribution. For sufficiently long times, the spheroids are confined to the tumbling and/or spinning modes, and
![]() ${\it\Omega}(\boldsymbol{p})$
must therefore involve delta functions at either or both of
${\it\Omega}(\boldsymbol{p})$
must therefore involve delta functions at either or both of
![]() ${\it\theta}_{j}=0$
and
${\it\theta}_{j}=0$
and
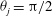 ${\it\theta}_{j}={\rm\pi}/2$
. Evidently, only one of these delta functions is present when the drift is single-signed over the entire unit sphere of orientations. As already seen, fluid inertia alone led to a change in sign of the drift for oblate spheroids with aspect ratios smaller than 0.142. For neutrally buoyant spheroids with
${\it\theta}_{j}={\rm\pi}/2$
. Evidently, only one of these delta functions is present when the drift is single-signed over the entire unit sphere of orientations. As already seen, fluid inertia alone led to a change in sign of the drift for oblate spheroids with aspect ratios smaller than 0.142. For neutrally buoyant spheroids with
![]() $Re=St$
, as seen in § 6.3, the drift arises from the combined effects of particle and fluid inertia, and the single-signed drift regime for oblate spheroids is then found to extend down to a slightly smaller aspect ratio of 0.137 owing to the
$Re=St$
, as seen in § 6.3, the drift arises from the combined effects of particle and fluid inertia, and the single-signed drift regime for oblate spheroids is then found to extend down to a slightly smaller aspect ratio of 0.137 owing to the
![]() $O(St)$
component of the drift stabilizing the spinning mode. Note that the drift is virtually unaltered close to the flat-disk limit, where the fluid inertial contribution is greater than that due to particle inertia by a factor of
$O(St)$
component of the drift stabilizing the spinning mode. Note that the drift is virtually unaltered close to the flat-disk limit, where the fluid inertial contribution is greater than that due to particle inertia by a factor of
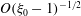 $O({\it\xi}_{0}-1)^{-1/2}$
; in particular, the change in sign of the drift continues to occur at
$O({\it\xi}_{0}-1)^{-1/2}$
; in particular, the change in sign of the drift continues to occur at
 $C^{\ast }\approx \sqrt{35}$
for
$C^{\ast }\approx \sqrt{35}$
for
![]() ${\it\xi}_{0}\rightarrow 1$
.
${\it\xi}_{0}\rightarrow 1$
.
As a result, for prolate spheroids of any aspect ratio:
 $$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{\bar{{\it\xi}}_{0}{\it\xi}_{0}{\it\delta}\left({\it\theta}_{j}-\displaystyle \frac{{\rm\pi}}{2}\right)}{2{\rm\pi}\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j})}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{\bar{{\it\xi}}_{0}{\it\xi}_{0}{\it\delta}\left({\it\theta}_{j}-\displaystyle \frac{{\rm\pi}}{2}\right)}{2{\rm\pi}\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\sin ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\cos ^{2}{\it\phi}_{j})}, & & \displaystyle\end{eqnarray}$$
and for neutrally buoyant oblate spheroids with aspect ratios greater than 0.137:
 $$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{{\it\delta}({\it\theta}_{j})}{2{\rm\pi}\sin {\it\theta}_{j}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{{\it\delta}({\it\theta}_{j})}{2{\rm\pi}\sin {\it\theta}_{j}}. & & \displaystyle\end{eqnarray}$$
For neutrally buoyant oblate spheroids with aspect ratios less than 0.137:
 $$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{{\mathcal{A}}_{1}(C^{\ast }){\it\delta}({\it\theta}_{j})}{2{\rm\pi}\sin {\it\theta}_{j}}+\frac{\bar{{\it\xi}}_{0}{\it\xi}_{0}\left[{\mathcal{A}}_{2}(C^{\ast }){\it\delta}\left({\it\theta}_{j}-\displaystyle \frac{{\rm\pi}}{2}\right)\right]}{2{\rm\pi}\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\cos ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\sin ^{2}{\it\phi}_{j})}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}(\boldsymbol{p})=\frac{{\mathcal{A}}_{1}(C^{\ast }){\it\delta}({\it\theta}_{j})}{2{\rm\pi}\sin {\it\theta}_{j}}+\frac{\bar{{\it\xi}}_{0}{\it\xi}_{0}\left[{\mathcal{A}}_{2}(C^{\ast }){\it\delta}\left({\it\theta}_{j}-\displaystyle \frac{{\rm\pi}}{2}\right)\right]}{2{\rm\pi}\sin {\it\theta}_{j}({\it\xi}_{0}^{2}\cos ^{2}{\it\phi}_{j}+\bar{{\it\xi}}_{0}^{2}\sin ^{2}{\it\phi}_{j})}, & & \displaystyle\end{eqnarray}$$
where the constants
![]() ${\mathcal{A}}_{1}$
and
${\mathcal{A}}_{1}$
and
![]() ${\mathcal{A}}_{2}$
, in addition to depending on
${\mathcal{A}}_{2}$
, in addition to depending on
![]() $C^{\ast }$
(and thereby on the aspect ratio), are functions of the initial orientation distribution. This dependence arises because the relative proportions of oblate spheroids asymptoting to the tumbling and spinning modes depend on the number of particles located on either side of the repeller (the Jeffery orbit with
$C^{\ast }$
(and thereby on the aspect ratio), are functions of the initial orientation distribution. This dependence arises because the relative proportions of oblate spheroids asymptoting to the tumbling and spinning modes depend on the number of particles located on either side of the repeller (the Jeffery orbit with
 $C=C^{\ast }({\it\xi}_{0})$
) on the unit sphere at the initial instant. For an initial isotropic distribution, for instance,
$C=C^{\ast }({\it\xi}_{0})$
) on the unit sphere at the initial instant. For an initial isotropic distribution, for instance,
![]() ${\mathcal{A}}_{1}$
and
${\mathcal{A}}_{1}$
and
![]() ${\mathcal{A}}_{2}$
are, respectively, proportional to the areas enclosed within and in between the pair of Jeffery-orbit repellers. Thus, for non-Brownian neutrally buoyant oblate spheroids in the range of aspect ratios
${\mathcal{A}}_{2}$
are, respectively, proportional to the areas enclosed within and in between the pair of Jeffery-orbit repellers. Thus, for non-Brownian neutrally buoyant oblate spheroids in the range of aspect ratios
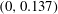 $(0,0.137)$
, the inertial suspension rheology, at leading order, still depends on the initial state of the dilute suspension. While inclusion of weak inertial effects does make the functional form of the steady-state orientation distribution determinate, in that
$(0,0.137)$
, the inertial suspension rheology, at leading order, still depends on the initial state of the dilute suspension. While inclusion of weak inertial effects does make the functional form of the steady-state orientation distribution determinate, in that
![]() ${\it\Omega}(\boldsymbol{p})$
always consists of a pair of delta functions, the relative amplitudes of these delta functions continues to depend on the initial distribution of orientations. In what follows, for oblate spheroids in the above range of aspect ratios, we evaluate the shear viscosity in the dilute regime assuming an initially isotropic orientation distribution.
${\it\Omega}(\boldsymbol{p})$
always consists of a pair of delta functions, the relative amplitudes of these delta functions continues to depend on the initial distribution of orientations. In what follows, for oblate spheroids in the above range of aspect ratios, we evaluate the shear viscosity in the dilute regime assuming an initially isotropic orientation distribution.

Figure 15. The intrinsic viscosity coefficient as a function of eccentricity for a dilute suspension of neutrally buoyant prolate spheroids: scaled with
![]() $nd^{3}{\it\xi}_{0}^{3}$
(a); scaled with
$nd^{3}{\it\xi}_{0}^{3}$
(a); scaled with
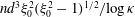 $nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}/\text{log}\,{\it\kappa}$
(b).
$nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}/\text{log}\,{\it\kappa}$
(b).
For the prolate case, using (7.12) in (7.11) with
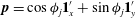 $\boldsymbol{p}=\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }$
, one obtains:
$\boldsymbol{p}=\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }$
, one obtains:
 $$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle =n\left[D_{2}^{(p)}({\it\xi}_{0})+\left(\frac{3}{2}D_{1}^{(p)}({\it\xi}_{0})-2D_{2}^{(p)}({\it\xi}_{0})+\frac{D_{3}^{(p)}({\it\xi}_{0})}{2}\right)\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}+\right]\unicode[STIX]{x1D60C}_{ij}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle =n\left[D_{2}^{(p)}({\it\xi}_{0})+\left(\frac{3}{2}D_{1}^{(p)}({\it\xi}_{0})-2D_{2}^{(p)}({\it\xi}_{0})+\frac{D_{3}^{(p)}({\it\xi}_{0})}{2}\right)\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}+\right]\unicode[STIX]{x1D60C}_{ij}. & & \displaystyle\end{eqnarray}$$
The rheology is evidently Newtonian. In terms of an effective viscosity
![]() ${\it\mu}_{eff}$
, we have from (7.15) that
${\it\mu}_{eff}$
, we have from (7.15) that
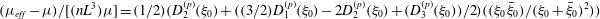 $({\it\mu}_{eff}-{\it\mu})/[(nL^{3}){\it\mu}]=(1/2)(D_{2}^{(p)}({\it\xi}_{0})+((3/2)D_{1}^{(p)}({\it\xi}_{0})-2D_{2}^{(p)}({\it\xi}_{0})+(D_{3}^{(p)}({\it\xi}_{0}))/2)(({\it\xi}_{0}\,\bar{{\it\xi}}_{0})/({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}))$
for a suspension of prolate spheroids at small but finite
$({\it\mu}_{eff}-{\it\mu})/[(nL^{3}){\it\mu}]=(1/2)(D_{2}^{(p)}({\it\xi}_{0})+((3/2)D_{1}^{(p)}({\it\xi}_{0})-2D_{2}^{(p)}({\it\xi}_{0})+(D_{3}^{(p)}({\it\xi}_{0}))/2)(({\it\xi}_{0}\,\bar{{\it\xi}}_{0})/({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}))$
for a suspension of prolate spheroids at small but finite
![]() $Re$
. Figure 15(a) shows this intrinsic viscosity coefficient as a function of the spheroid eccentricity. It is seen to vary from a value corresponding to the Einstein coefficient (the value near 10 comes from the factor
$Re$
. Figure 15(a) shows this intrinsic viscosity coefficient as a function of the spheroid eccentricity. It is seen to vary from a value corresponding to the Einstein coefficient (the value near 10 comes from the factor
![]() $4{\rm\pi}/3$
involved in the spherical volume fraction) for a near-sphere to a vanishingly small contribution for a slender spheroid. This happens due to a change in the scaling of
$4{\rm\pi}/3$
involved in the spherical volume fraction) for a near-sphere to a vanishingly small contribution for a slender spheroid. This happens due to a change in the scaling of
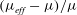 $({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
from
$({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
from
![]() $O(nL^{3})$
in the near-sphere limit to
$O(nL^{3})$
in the near-sphere limit to
 $O(nL^{2}b)/\ln {\it\kappa}$
in the slender-fibre limit; from (7.15),
$O(nL^{2}b)/\ln {\it\kappa}$
in the slender-fibre limit; from (7.15),
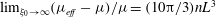 $\lim _{{\it\xi}_{0}\rightarrow \infty }({\it\mu}_{eff}-{\it\mu})/{\it\mu}=(10{\rm\pi}/3)nL^{3}$
and
$\lim _{{\it\xi}_{0}\rightarrow \infty }({\it\mu}_{eff}-{\it\mu})/{\it\mu}=(10{\rm\pi}/3)nL^{3}$
and
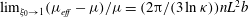 $\lim _{{\it\xi}_{0}\rightarrow 1}({\it\mu}_{eff}-{\it\mu})/{\it\mu}=(2{\rm\pi}/(3\ln {\it\kappa}))nL^{2}b$
. For large aspect ratios (
$\lim _{{\it\xi}_{0}\rightarrow 1}({\it\mu}_{eff}-{\it\mu})/{\it\mu}=(2{\rm\pi}/(3\ln {\it\kappa}))nL^{2}b$
. For large aspect ratios (
![]() ${\it\kappa}\rightarrow \infty$
), the dominant contribution to the averaged stresslet is from non-aligned fibres, with the probability of such orientations only being
${\it\kappa}\rightarrow \infty$
), the dominant contribution to the averaged stresslet is from non-aligned fibres, with the probability of such orientations only being
![]() $O({\it\kappa}^{-1})$
. From viscous slender body theory, the stresslet for a non-aligned fibre arises from a linear force density of
$O({\it\kappa}^{-1})$
. From viscous slender body theory, the stresslet for a non-aligned fibre arises from a linear force density of
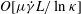 $O[{\it\mu}\dot{{\it\gamma}}L/\ln {\it\kappa}]$
acting with a moment arm of
$O[{\it\mu}\dot{{\it\gamma}}L/\ln {\it\kappa}]$
acting with a moment arm of
![]() $O(L)$
over the length of the spheroid, and is
$O(L)$
over the length of the spheroid, and is
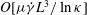 $O[{\it\mu}\dot{{\it\gamma}}L^{3}/\ln {\it\kappa}]$
. The resulting (dimensional) stress is
$O[{\it\mu}\dot{{\it\gamma}}L^{3}/\ln {\it\kappa}]$
. The resulting (dimensional) stress is
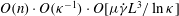 $O(n)\cdot O({\it\kappa}^{-1})\cdot O[{\it\mu}\dot{{\it\gamma}}L^{3}/\ln {\it\kappa}]$
, leading to an effective viscosity
$O(n)\cdot O({\it\kappa}^{-1})\cdot O[{\it\mu}\dot{{\it\gamma}}L^{3}/\ln {\it\kappa}]$
, leading to an effective viscosity
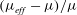 $({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
of
$({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
of
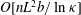 $O[nL^{2}b/\ln {\it\kappa}]$
. The stresslet for flow-aligned fibres is smaller than the non-aligned contribution by
$O[nL^{2}b/\ln {\it\kappa}]$
. The stresslet for flow-aligned fibres is smaller than the non-aligned contribution by
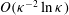 $O({\it\kappa}^{-2}\ln {\it\kappa})$
, and only contributes to a small correction of
$O({\it\kappa}^{-2}\ln {\it\kappa})$
, and only contributes to a small correction of
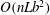 $O(nLb^{2})$
to the above estimate. Figure 15(b) uses the slender-fibre scaling above to obtain a finite viscosity coefficient in the slender-fibre limit; note that the near-sphere asymptote is zero in these units owing to the additional logarithmic factor involved. The scaling of the intrinsic viscosity with aspect ratio, in the slender-fibre limit, is controlled by the anisotropy of orientations within a given Jeffery orbit, and thus, Leal and Hinch’s (Leal & Hinch Reference Leal and Hinch1971) original calculation, involving the effect of weak Brownian diffusion in setting up a steady smooth distribution across Jeffery orbits, also leads to a viscosity coefficient of
$O(nLb^{2})$
to the above estimate. Figure 15(b) uses the slender-fibre scaling above to obtain a finite viscosity coefficient in the slender-fibre limit; note that the near-sphere asymptote is zero in these units owing to the additional logarithmic factor involved. The scaling of the intrinsic viscosity with aspect ratio, in the slender-fibre limit, is controlled by the anisotropy of orientations within a given Jeffery orbit, and thus, Leal and Hinch’s (Leal & Hinch Reference Leal and Hinch1971) original calculation, involving the effect of weak Brownian diffusion in setting up a steady smooth distribution across Jeffery orbits, also leads to a viscosity coefficient of
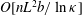 $O[nL^{2}b/\ln {\it\kappa}]$
for large aspect ratios, albeit with a different
$O[nL^{2}b/\ln {\it\kappa}]$
for large aspect ratios, albeit with a different
![]() $O(1)$
coefficient.
$O(1)$
coefficient.
For oblate spheroids with aspect ratios greater than 0.137,
![]() $\boldsymbol{p}=\mathbf{1}_{z}^{\prime }$
, and only the two transverse planar extensions in (3.2) contribute to the rheology. Using (7.13), (7.11) reduces to:
$\boldsymbol{p}=\mathbf{1}_{z}^{\prime }$
, and only the two transverse planar extensions in (3.2) contribute to the rheology. Using (7.13), (7.11) reduces to:
 $$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle =nD_{3}^{(o)}({\it\xi}_{0})\unicode[STIX]{x1D60C}_{ij}\quad 1.01<{\it\xi}_{0}<\infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle =nD_{3}^{(o)}({\it\xi}_{0})\unicode[STIX]{x1D60C}_{ij}\quad 1.01<{\it\xi}_{0}<\infty . & & \displaystyle\end{eqnarray}$$
For oblate spheroids with aspect ratios smaller than 0.137, (7.14) is used in (7.11) to obtain:
 $$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\left[D_{3}^{(o)}({\it\xi}_{0})\,{\mathcal{A}}_{1}+\left(D_{2}^{(o)}({\it\xi}_{0})+\left(\frac{3}{2}D_{1}^{(o)}({\it\xi}_{0})-2D_{2}^{(o)}({\it\xi}_{0})+\frac{D_{3}^{(o)}({\it\xi}_{0})}{2}\right)\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.(1-{\mathcal{A}}_{1})\vphantom{\left(\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}\right)}\right]\unicode[STIX]{x1D60C}_{ij}\quad 1<{\it\xi}_{0}<1.01.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\it\sigma}_{ij}^{p}\rangle & = & \displaystyle n\left[D_{3}^{(o)}({\it\xi}_{0})\,{\mathcal{A}}_{1}+\left(D_{2}^{(o)}({\it\xi}_{0})+\left(\frac{3}{2}D_{1}^{(o)}({\it\xi}_{0})-2D_{2}^{(o)}({\it\xi}_{0})+\frac{D_{3}^{(o)}({\it\xi}_{0})}{2}\right)\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.(1-{\mathcal{A}}_{1})\vphantom{\left(\frac{{\it\xi}_{0}\,\bar{{\it\xi}}_{0}}{({\it\xi}_{0}+\bar{{\it\xi}}_{0})^{2}}\right)}\right]\unicode[STIX]{x1D60C}_{ij}\quad 1<{\it\xi}_{0}<1.01.\end{eqnarray}$$
The area within a Jeffery orbit, with an orbit constant
![]() $C$
, is given by
$C$
, is given by
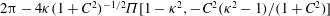 $2{\rm\pi}-4{\it\kappa}(1+C^{2})^{-1/2}{\it\Pi}[1-{\it\kappa}^{2},-C^{2}({\it\kappa}^{2}-1)/(1+C^{2})]$
, and normalizing by the area of the unit hemisphere, one obtains
$2{\rm\pi}-4{\it\kappa}(1+C^{2})^{-1/2}{\it\Pi}[1-{\it\kappa}^{2},-C^{2}({\it\kappa}^{2}-1)/(1+C^{2})]$
, and normalizing by the area of the unit hemisphere, one obtains
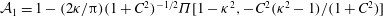 ${\mathcal{A}}_{1}=1-(2{\it\kappa}/{\rm\pi})(1+C^{2})^{-1/2}{\it\Pi}[1-{\it\kappa}^{2},-C^{2}({\it\kappa}^{2}-1)/(1+C^{2})]$
and
${\mathcal{A}}_{1}=1-(2{\it\kappa}/{\rm\pi})(1+C^{2})^{-1/2}{\it\Pi}[1-{\it\kappa}^{2},-C^{2}({\it\kappa}^{2}-1)/(1+C^{2})]$
and
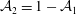 ${\mathcal{A}}_{2}=1-{\mathcal{A}}_{1}$
for an initially isotropic orientation distribution,
${\mathcal{A}}_{2}=1-{\mathcal{A}}_{1}$
for an initially isotropic orientation distribution,
![]() ${\it\Pi}(x,y)$
being the complete elliptic function of the third kind (Gradshteyn & Ryzhik Reference Gradshteyn and Ryzhik2007). The intrinsic viscosity coefficient,
${\it\Pi}(x,y)$
being the complete elliptic function of the third kind (Gradshteyn & Ryzhik Reference Gradshteyn and Ryzhik2007). The intrinsic viscosity coefficient,
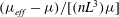 $({\it\mu}_{eff}-{\it\mu})/[(nL^{3}){\it\mu}]$
for a suspension of oblate spheroids, over the entire range of eccentricities is plotted in figure 16(a). There is a kink (a discontinuity in slope) in the curve at
$({\it\mu}_{eff}-{\it\mu})/[(nL^{3}){\it\mu}]$
for a suspension of oblate spheroids, over the entire range of eccentricities is plotted in figure 16(a). There is a kink (a discontinuity in slope) in the curve at
![]() $e\approx 0.99$
due to the oblate spheroids transitioning from a pure spinning mode to a weighted combination of spinning and tumbling modes. The part of the viscosity curve for
$e\approx 0.99$
due to the oblate spheroids transitioning from a pure spinning mode to a weighted combination of spinning and tumbling modes. The part of the viscosity curve for
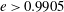 $e>0.9905$
(aspect ratios smaller than 0.137) is plotted as a discrete sequence of points because the relative proportions of spinning and tumbling spheroids in this range of aspect ratios is a function of the repeller location
$e>0.9905$
(aspect ratios smaller than 0.137) is plotted as a discrete sequence of points because the relative proportions of spinning and tumbling spheroids in this range of aspect ratios is a function of the repeller location
![]() $C^{\ast }$
, and this is found numerically from the zero crossing in a plot of
$C^{\ast }$
, and this is found numerically from the zero crossing in a plot of
![]() ${\rm\Delta}C$
against
${\rm\Delta}C$
against
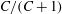 $C/(C+1)$
for a particular aspect ratio (similar to figure 6). Figure 16(b) shows a magnified view of the aforementioned kink. Here, the curve corresponding to the pure spinning mode is continued until
$C/(C+1)$
for a particular aspect ratio (similar to figure 6). Figure 16(b) shows a magnified view of the aforementioned kink. Here, the curve corresponding to the pure spinning mode is continued until
![]() $e=1$
to emphasize the transition from spinning oblate spheroids, of aspect ratio 0.137, at
$e=1$
to emphasize the transition from spinning oblate spheroids, of aspect ratio 0.137, at
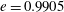 $e=0.9905$
, to tumbling flat disks at
$e=0.9905$
, to tumbling flat disks at
![]() $e=1$
. Note that the spinning-mode curve would terminate in a finite coefficient at
$e=1$
. Note that the spinning-mode curve would terminate in a finite coefficient at
![]() $e=1$
, since the viscosity coefficient for spinning disks is
$e=1$
, since the viscosity coefficient for spinning disks is
![]() $O(nL^{3})$
as for spheres. The bifurcation at
$O(nL^{3})$
as for spheres. The bifurcation at
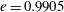 $e=0.9905$
, however, implies that the viscosity coefficient at
$e=0.9905$
, however, implies that the viscosity coefficient at
![]() $e=1$
, arises almost entirely from tumbling flat disks, and is asymptotically smaller than
$e=1$
, arises almost entirely from tumbling flat disks, and is asymptotically smaller than
![]() $O(nL^{3})$
. The appropriate scale in the flat-disk limit may be obtained by noting that the averaged stresslet arises from the combination of an
$O(nL^{3})$
. The appropriate scale in the flat-disk limit may be obtained by noting that the averaged stresslet arises from the combination of an
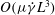 $O({\it\mu}\dot{{\it\gamma}}L^{3})$
stresslet associated with an
$O({\it\mu}\dot{{\it\gamma}}L^{3})$
stresslet associated with an
![]() $O({\it\kappa})$
fraction of spinning disks, and a comparable
$O({\it\kappa})$
fraction of spinning disks, and a comparable
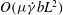 $O({\it\mu}\dot{{\it\gamma}}bL^{2})$
stresslet associated with disks that tumble in the flow–gradient plane (unlike the prolate case, both aligned and non-aligned flat disks end up contributing, at the same order, to the tumbling stress component). This leads to an effective viscosity
$O({\it\mu}\dot{{\it\gamma}}bL^{2})$
stresslet associated with disks that tumble in the flow–gradient plane (unlike the prolate case, both aligned and non-aligned flat disks end up contributing, at the same order, to the tumbling stress component). This leads to an effective viscosity
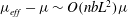 ${\it\mu}_{eff}-{\it\mu}\sim O(nbL^{2}){\it\mu}$
in the flat-disk limit. Figure 17 plots
${\it\mu}_{eff}-{\it\mu}\sim O(nbL^{2}){\it\mu}$
in the flat-disk limit. Figure 17 plots
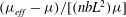 $({\it\mu}_{eff}-{\it\mu})/[(nbL^{2}){\it\mu}]$
as a function of the spheroid eccentricity, which leads to a finite value in the flat-disk limit; the spinning-mode coefficient diverges as
$({\it\mu}_{eff}-{\it\mu})/[(nbL^{2}){\it\mu}]$
as a function of the spheroid eccentricity, which leads to a finite value in the flat-disk limit; the spinning-mode coefficient diverges as
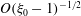 $O({\it\xi}_{0}-1)^{-1/2}$
with this normalization. The viscosity coefficient for sufficiently thin oblate spheroids is again controlled by the anisotropy of orientations within a given Jeffery orbit, and the effects of weak Brownian motion, although resulting in a different distribution across Jeffery orbits, lead to a similar scale in the flat-disk limit (Leal & Hinch Reference Leal and Hinch1971).
$O({\it\xi}_{0}-1)^{-1/2}$
with this normalization. The viscosity coefficient for sufficiently thin oblate spheroids is again controlled by the anisotropy of orientations within a given Jeffery orbit, and the effects of weak Brownian motion, although resulting in a different distribution across Jeffery orbits, lead to a similar scale in the flat-disk limit (Leal & Hinch Reference Leal and Hinch1971).

Figure 16. (a) Intrinsic viscosity coefficient as a function of eccentricity for a dilute suspension of neutrally buoyant oblate spheroids (scaled with
![]() $nd^{3}{\it\xi}_{0}^{3}$
). An initial isotropic orientation distribution is assumed while calculating the viscosity for aspect ratios less than the critical aspect ratio (0.137). The dotted line denotes the viscosity coefficient for these viscosity ratios. (b) Magnified view of the viscosity coefficient transitioning from the spinning to the tumbling asymptote close to the flat-disk limit.
$nd^{3}{\it\xi}_{0}^{3}$
). An initial isotropic orientation distribution is assumed while calculating the viscosity for aspect ratios less than the critical aspect ratio (0.137). The dotted line denotes the viscosity coefficient for these viscosity ratios. (b) Magnified view of the viscosity coefficient transitioning from the spinning to the tumbling asymptote close to the flat-disk limit.

Figure 17. (a) Intrinsic viscosity coefficient as a function of eccentricity for a dilute suspension of neutrally buoyant oblate spheroids presented in figure 16, is now appropriately rescaled in the flat-disk limit (scaled with
 $nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}$
). (b) Magnified view of (a).
$nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}$
). (b) Magnified view of (a).
Apart from the kink at
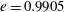 $e=0.9905$
discussed above, there are two points worth noting in figure 17. The first is that the intrinsic viscosity curve corresponds to a steady-state orientation distribution. Within the framework of an orbital drift, the time required to attain such a steady state diverges in the flat-disk limit owing to the diverging Jeffery period; recall that the Jeffery period is
$e=0.9905$
discussed above, there are two points worth noting in figure 17. The first is that the intrinsic viscosity curve corresponds to a steady-state orientation distribution. Within the framework of an orbital drift, the time required to attain such a steady state diverges in the flat-disk limit owing to the diverging Jeffery period; recall that the Jeffery period is
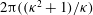 $2{\rm\pi}(({\it\kappa}^{2}+1)/{\it\kappa})$
and is
$2{\rm\pi}(({\it\kappa}^{2}+1)/{\it\kappa})$
and is
![]() $O({\it\kappa}^{-1})$
for
$O({\it\kappa}^{-1})$
for
![]() ${\it\kappa}\rightarrow 0$
. Note, however, that the orbital drift interpretation, that assumes the inertial trajectory to be a tightly wound spiral, becomes increasingly restrictive for both large and small aspect ratios (see § 8). Notwithstanding this restriction, the viscosity coefficient, plotted for any finite time, will deviate from the steady-state plot for sufficiently thin oblate spheroids, asymptoting to a (frozen-in-time) isotropic orientation distribution at
${\it\kappa}\rightarrow 0$
. Note, however, that the orbital drift interpretation, that assumes the inertial trajectory to be a tightly wound spiral, becomes increasingly restrictive for both large and small aspect ratios (see § 8). Notwithstanding this restriction, the viscosity coefficient, plotted for any finite time, will deviate from the steady-state plot for sufficiently thin oblate spheroids, asymptoting to a (frozen-in-time) isotropic orientation distribution at
![]() $e=1$
. For longer times, this deviation from the steady-state curve will occur at progressively smaller aspect ratios. The second feature is the difference between the value of the intrinsic viscosity coefficient at
$e=1$
. For longer times, this deviation from the steady-state curve will occur at progressively smaller aspect ratios. The second feature is the difference between the value of the intrinsic viscosity coefficient at
![]() $e=1$
, and that corresponding to a suspension consisting only of tumbling flat disks (indicated by the horizontal dashed line in figure 17(b)). This jump comes from the implicit assumption of an infinite suspension for which a statistical description, in terms of an orientation probability density, is appropriate. For any finite-sized system, there will be a small enough aspect ratio when the area within the Jeffery repeller, corresponding to
$e=1$
, and that corresponding to a suspension consisting only of tumbling flat disks (indicated by the horizontal dashed line in figure 17(b)). This jump comes from the implicit assumption of an infinite suspension for which a statistical description, in terms of an orientation probability density, is appropriate. For any finite-sized system, there will be a small enough aspect ratio when the area within the Jeffery repeller, corresponding to
 $C^{\ast }=\sqrt{35}$
, is small enough that the number of spheroid orientations in this tiny region of the unit sphere is of order unity, and a probabilistic description is no longer valid. Below such an aspect ratio, the viscosity coefficient will approach the lower value corresponding to the pure tumbling mode (again of
$C^{\ast }=\sqrt{35}$
, is small enough that the number of spheroid orientations in this tiny region of the unit sphere is of order unity, and a probabilistic description is no longer valid. Below such an aspect ratio, the viscosity coefficient will approach the lower value corresponding to the pure tumbling mode (again of
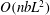 $O(nbL^{2})$
). Said differently, the jump in the viscosity coefficient at
$O(nbL^{2})$
). Said differently, the jump in the viscosity coefficient at
![]() $e=1$
is an artefact of the thermodynamic limit.
$e=1$
is an artefact of the thermodynamic limit.
7.2 The rheology of a suspension of oblate spheroids with aspect ratio less than 0.137: the role of weak Brownian motion
In this section, in an effort to resolve the indeterminacy in the steady-state rheology that arose in § 7.1 for oblate spheroids with aspect ratios less than 0.137, we include the effects of weak Brownian motion (large but finite rotary Péclet number
![]() $Pe_{r}$
). As will be seen below, Brownian motion together with the inertial drift does lead to a steady state independent of initial conditions. To examine this steady state, we write down the governing drift–diffusion equation for the orientation probability density:
$Pe_{r}$
). As will be seen below, Brownian motion together with the inertial drift does lead to a steady state independent of initial conditions. To examine this steady state, we write down the governing drift–diffusion equation for the orientation probability density:
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\boldsymbol{\cdot }(\dot{\boldsymbol{p}}{\it\Omega})=\frac{1}{Pe_{r}}{\rm\nabla}_{\boldsymbol{p}}^{2}{\it\Omega}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\boldsymbol{\cdot }(\dot{\boldsymbol{p}}{\it\Omega})=\frac{1}{Pe_{r}}{\rm\nabla}_{\boldsymbol{p}}^{2}{\it\Omega}.\end{eqnarray}$$
The left-hand side denotes the convection of
![]() ${\it\Omega}$
with
${\it\Omega}$
with
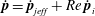 $\dot{\boldsymbol{p}}=\dot{\boldsymbol{p}}_{jeff}+Re\,\dot{\boldsymbol{p}}_{i}$
, where
$\dot{\boldsymbol{p}}=\dot{\boldsymbol{p}}_{jeff}+Re\,\dot{\boldsymbol{p}}_{i}$
, where
![]() $\dot{\boldsymbol{p}}_{jeff}$
is the Stokesian rate of change of orientation along a Jeffery orbit, and
$\dot{\boldsymbol{p}}_{jeff}$
is the Stokesian rate of change of orientation along a Jeffery orbit, and
![]() $\dot{\boldsymbol{p}}_{i}$
denotes the inertial drift with components both along and perpendicular to the Jeffery orbits. The orientational Laplacian on the right-hand side denotes the Brownian motion of
$\dot{\boldsymbol{p}}_{i}$
denotes the inertial drift with components both along and perpendicular to the Jeffery orbits. The orientational Laplacian on the right-hand side denotes the Brownian motion of
![]() $\boldsymbol{p}$
on the unit sphere. The
$\boldsymbol{p}$
on the unit sphere. The
![]() $(C,{\it\tau})$
coordinate system is most convenient for solving (7.18), since in this coordinate system,
$(C,{\it\tau})$
coordinate system is most convenient for solving (7.18), since in this coordinate system,
![]() $\dot{\boldsymbol{p}}_{jeff}$
has only a
$\dot{\boldsymbol{p}}_{jeff}$
has only a
![]() ${\it\tau}$
component, and determines only the orientation distribution along any Jeffery orbit (
${\it\tau}$
component, and determines only the orientation distribution along any Jeffery orbit (
![]() $g(C,{\it\tau})$
as given by (7.10)), while the distribution across orbits (
$g(C,{\it\tau})$
as given by (7.10)), while the distribution across orbits (
![]() $f(C)$
in (7.11)) emerges from a one-dimensional drift–diffusion balance, in the
$f(C)$
in (7.11)) emerges from a one-dimensional drift–diffusion balance, in the
![]() $C$
coordinate, between inertial convection and Brownian diffusion. The nature of this reduced distribution,
$C$
coordinate, between inertial convection and Brownian diffusion. The nature of this reduced distribution,
![]() $f(C)$
, is controlled by the parameter
$f(C)$
, is controlled by the parameter
![]() $Re\,Pe_{r}$
, which determines the relative magnitudes of inertial drift and thermal diffusion. While § 7.1 dealt with the case
$Re\,Pe_{r}$
, which determines the relative magnitudes of inertial drift and thermal diffusion. While § 7.1 dealt with the case
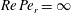 $Re\,Pe_{r}=\infty$
, the focus here is on the (singular) nearly athermal limit
$Re\,Pe_{r}=\infty$
, the focus here is on the (singular) nearly athermal limit
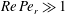 $Re\,Pe_{r}\gg 1$
. The additional contribution to the suspension stress (the so-called Brownian or diffusion stress) is asymptotically small in this limit, and the suspension stress is still given by
$Re\,Pe_{r}\gg 1$
. The additional contribution to the suspension stress (the so-called Brownian or diffusion stress) is asymptotically small in this limit, and the suspension stress is still given by
![]() $n\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
, as in § 7.1.
$n\langle \unicode[STIX]{x1D61A}_{ij}\rangle$
, as in § 7.1.
To obtain the governing equation for
![]() $f(C)$
, we again follow Leal & Hinch (Reference Leal and Hinch1971), and integrate (7.18) over the area enclosed by a single Jeffery orbit (
$f(C)$
, we again follow Leal & Hinch (Reference Leal and Hinch1971), and integrate (7.18) over the area enclosed by a single Jeffery orbit (
![]() $2{\rm\pi}{\mathcal{A}}_{1}$
, as defined in § 7.1):
$2{\rm\pi}{\mathcal{A}}_{1}$
, as defined in § 7.1):
 $$\begin{eqnarray}\int _{{\mathcal{A}}_{1}}Re\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\boldsymbol{\cdot }(\dot{\boldsymbol{p}}{\it\Omega})\,\text{d}S=\frac{1}{Pe_{r}}\int _{{\mathcal{A}}_{1}}{\rm\nabla}_{\boldsymbol{p}}^{2}{\it\Omega}\,\text{d}S.\end{eqnarray}$$
$$\begin{eqnarray}\int _{{\mathcal{A}}_{1}}Re\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\boldsymbol{\cdot }(\dot{\boldsymbol{p}}{\it\Omega})\,\text{d}S=\frac{1}{Pe_{r}}\int _{{\mathcal{A}}_{1}}{\rm\nabla}_{\boldsymbol{p}}^{2}{\it\Omega}\,\text{d}S.\end{eqnarray}$$
Application of the divergence theorem leads to:
 $$\begin{eqnarray}\int _{C_{1}}Re(\dot{\boldsymbol{p}}_{i}\boldsymbol{\cdot }\boldsymbol{n}_{j}){\it\Omega}\,\text{d}l=\frac{1}{Pe_{r}}\int _{C_{1}}\boldsymbol{n}_{j}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}{\it\Omega}\,\text{d}l,\end{eqnarray}$$
$$\begin{eqnarray}\int _{C_{1}}Re(\dot{\boldsymbol{p}}_{i}\boldsymbol{\cdot }\boldsymbol{n}_{j}){\it\Omega}\,\text{d}l=\frac{1}{Pe_{r}}\int _{C_{1}}\boldsymbol{n}_{j}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}{\it\Omega}\,\text{d}l,\end{eqnarray}$$
where the term involving the Jeffery convection integrates to zero. Here,
![]() $C_{1}$
is the Jeffery orbit with orbit constant
$C_{1}$
is the Jeffery orbit with orbit constant
![]() $C$
,
$C$
,
 $\text{d}l=h_{{\it\tau}}\,\text{d}{\it\tau}$
being the arclength element along this orbit, and
$\text{d}l=h_{{\it\tau}}\,\text{d}{\it\tau}$
being the arclength element along this orbit, and
![]() $\boldsymbol{n}_{j}$
is the unit vector, in the tangent plane of the unit sphere, and normal to this Jeffery orbit. We now write the inertial drift in
$\boldsymbol{n}_{j}$
is the unit vector, in the tangent plane of the unit sphere, and normal to this Jeffery orbit. We now write the inertial drift in
![]() $(C,{\it\tau})$
coordinates as
$(C,{\it\tau})$
coordinates as
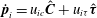 $\dot{\boldsymbol{p}}_{i}=u_{ic}\hat{\boldsymbol{C}}+u_{i{\it\tau}}\hat{{\bf\tau}}$
, with
$\dot{\boldsymbol{p}}_{i}=u_{ic}\hat{\boldsymbol{C}}+u_{i{\it\tau}}\hat{{\bf\tau}}$
, with
![]() $\hat{\boldsymbol{C}}=\mathbf{1}_{{\it\theta}}$
and
$\hat{\boldsymbol{C}}=\mathbf{1}_{{\it\theta}}$
and
![]() $\hat{{\bf\tau}}$
tangent to the Jeffery orbit. Using
$\hat{{\bf\tau}}$
tangent to the Jeffery orbit. Using
 $\hat{{\bf\tau}}\boldsymbol{\cdot }\boldsymbol{n}_{j}=0$
and
$\hat{{\bf\tau}}\boldsymbol{\cdot }\boldsymbol{n}_{j}=0$
and
 $\hat{\boldsymbol{C}}\boldsymbol{\cdot }\boldsymbol{n}_{j}=\sin {\it\alpha}$
, and the definition of the gradient operator (see appendix B 6), (7.20) becomes
$\hat{\boldsymbol{C}}\boldsymbol{\cdot }\boldsymbol{n}_{j}=\sin {\it\alpha}$
, and the definition of the gradient operator (see appendix B 6), (7.20) becomes
 $$\begin{eqnarray}Re\,Pe_{r}\int _{0}^{2{\rm\pi}}u_{ic}\sin {\it\alpha}\,{\it\Omega}\,h_{{\it\tau}}\,\text{d}{\it\tau}=\int _{0}^{2{\rm\pi}}\left(\frac{h_{{\it\tau}}}{h_{C}\sin {\it\alpha}}\frac{\partial {\it\Omega}}{\partial C}-\cot {\it\alpha}\frac{\partial {\it\Omega}}{\partial {\it\tau}}\right)\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}Re\,Pe_{r}\int _{0}^{2{\rm\pi}}u_{ic}\sin {\it\alpha}\,{\it\Omega}\,h_{{\it\tau}}\,\text{d}{\it\tau}=\int _{0}^{2{\rm\pi}}\left(\frac{h_{{\it\tau}}}{h_{C}\sin {\it\alpha}}\frac{\partial {\it\Omega}}{\partial C}-\cot {\it\alpha}\frac{\partial {\it\Omega}}{\partial {\it\tau}}\right)\text{d}{\it\tau}.\end{eqnarray}$$
Using
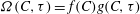 ${\it\Omega}(C,{\it\tau})=f(C)g(C,{\it\tau})$
, with
${\it\Omega}(C,{\it\tau})=f(C)g(C,{\it\tau})$
, with
![]() $g(C,{\it\tau})$
given by (7.10), (7.21) becomes:
$g(C,{\it\tau})$
given by (7.10), (7.21) becomes:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[Re\,Pe_{r}\int _{0}^{2{\rm\pi}}\frac{u_{ic}}{h_{C}}\,\text{d}{\it\tau}-\int _{0}^{2{\rm\pi}}\left(\frac{h_{{\it\tau}}}{h_{C}\sin {\it\alpha}}\frac{\partial g}{\partial C}-\cot {\it\alpha}\frac{\partial g}{\partial {\it\tau}}\right)\text{d}{\it\tau}\right]f(C)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\int _{0}^{2{\rm\pi}}\frac{1}{h_{C}^{2}\sin ^{2}{\it\alpha}}\,\text{d}{\it\tau}\right)\frac{\text{d}f}{\text{d}C}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[Re\,Pe_{r}\int _{0}^{2{\rm\pi}}\frac{u_{ic}}{h_{C}}\,\text{d}{\it\tau}-\int _{0}^{2{\rm\pi}}\left(\frac{h_{{\it\tau}}}{h_{C}\sin {\it\alpha}}\frac{\partial g}{\partial C}-\cot {\it\alpha}\frac{\partial g}{\partial {\it\tau}}\right)\text{d}{\it\tau}\right]f(C)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\int _{0}^{2{\rm\pi}}\frac{1}{h_{C}^{2}\sin ^{2}{\it\alpha}}\,\text{d}{\it\tau}\right)\frac{\text{d}f}{\text{d}C}.\end{eqnarray}$$
Expectedly, (7.22) is a
![]() ${\it\tau}$
-averaged drift–diffusion equation where the drift includes both the inertial contribution and a Brownian contribution that arises due to the curvature and non-orthogonality of the
${\it\tau}$
-averaged drift–diffusion equation where the drift includes both the inertial contribution and a Brownian contribution that arises due to the curvature and non-orthogonality of the
![]() $(C,{\it\tau})$
coordinates. Now,
$(C,{\it\tau})$
coordinates. Now,
 $u_{ic}/h_{C}=\text{d}C/\text{d}t$
, and the inertial drift term in (7.22) may be written as
$u_{ic}/h_{C}=\text{d}C/\text{d}t$
, and the inertial drift term in (7.22) may be written as
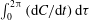 $\int _{0}^{2{\rm\pi}}(\text{d}C/\text{d}t)\,\text{d}{\it\tau}$
, which, from (5.17), equals
$\int _{0}^{2{\rm\pi}}(\text{d}C/\text{d}t)\,\text{d}{\it\tau}$
, which, from (5.17), equals
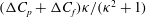 $({\rm\Delta}C_{p}+{\rm\Delta}C_{f}){\it\kappa}/({\it\kappa}^{2}+1)$
for neutrally buoyant spheroids. This is just the dimensionless Jeffery-orbit-averaged drift velocity, of a neutrally buoyant oblate spheroid, with the distance (across Jeffery orbits) measured in units of
$({\rm\Delta}C_{p}+{\rm\Delta}C_{f}){\it\kappa}/({\it\kappa}^{2}+1)$
for neutrally buoyant spheroids. This is just the dimensionless Jeffery-orbit-averaged drift velocity, of a neutrally buoyant oblate spheroid, with the distance (across Jeffery orbits) measured in units of
![]() $C$
and time measured in units of the inverse shear rate. The expressions for
$C$
and time measured in units of the inverse shear rate. The expressions for
![]() ${\rm\Delta}C_{p}$
and
${\rm\Delta}C_{p}$
and
![]() ${\rm\Delta}C_{f}$
, as functions of the aspect ratio (or
${\rm\Delta}C_{f}$
, as functions of the aspect ratio (or
![]() ${\it\xi}_{0}$
), have already been given in §§ 5.1 and 6.2, respectively. Defining
${\it\xi}_{0}$
), have already been given in §§ 5.1 and 6.2, respectively. Defining
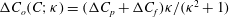 ${\rm\Delta}C_{o}(C;{\it\kappa})=({\rm\Delta}C_{p}+{\rm\Delta}C_{f}){\it\kappa}/({\it\kappa}^{2}+1)$
, (7.22) takes the form:
${\rm\Delta}C_{o}(C;{\it\kappa})=({\rm\Delta}C_{p}+{\rm\Delta}C_{f}){\it\kappa}/({\it\kappa}^{2}+1)$
, (7.22) takes the form:
 $$\begin{eqnarray}{\it\chi}_{1}\frac{\text{d}f}{\text{d}C}=\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}}{{\rm\pi}}-\frac{{\it\chi}_{2}}{C}\right)f,\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}_{1}\frac{\text{d}f}{\text{d}C}=\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}}{{\rm\pi}}-\frac{{\it\chi}_{2}}{C}\right)f,\end{eqnarray}$$
where
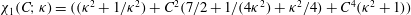 ${\it\chi}_{1}(C;{\it\kappa})=(({\it\kappa}^{2}+1/{\it\kappa}^{2})+C^{2}(7/2+1/(4{\it\kappa}^{2})+{\it\kappa}^{2}/4)+C^{4}({\it\kappa}^{2}+1))$
and
${\it\chi}_{1}(C;{\it\kappa})=(({\it\kappa}^{2}+1/{\it\kappa}^{2})+C^{2}(7/2+1/(4{\it\kappa}^{2})+{\it\kappa}^{2}/4)+C^{4}({\it\kappa}^{2}+1))$
and
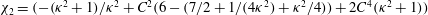 ${\it\chi}_{2}=(-({\it\kappa}^{2}+1)/{\it\kappa}^{2}+C^{2}(6-(7/2+1/(4{\it\kappa}^{2})+{\it\kappa}^{2}/4))+2C^{4}({\it\kappa}^{2}+1))$
are obtained by evaluating the
${\it\chi}_{2}=(-({\it\kappa}^{2}+1)/{\it\kappa}^{2}+C^{2}(6-(7/2+1/(4{\it\kappa}^{2})+{\it\kappa}^{2}/4))+2C^{4}({\it\kappa}^{2}+1))$
are obtained by evaluating the
![]() ${\it\tau}$
-integrals in (7.22). Equation (7.23) can readily be integrated formally to obtain:
${\it\tau}$
-integrals in (7.22). Equation (7.23) can readily be integrated formally to obtain:
 $$\begin{eqnarray}f(C)=N\exp \left[\int ^{C}\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}(C^{\prime };{\it\kappa})}{{\rm\pi}}-\frac{{\it\chi}_{2}(C^{\prime };{\it\kappa})}{C^{\prime }}\right)\frac{1}{{\it\chi}_{1}(C^{\prime };{\it\kappa})}\,\text{d}C^{\prime }\right],\end{eqnarray}$$
$$\begin{eqnarray}f(C)=N\exp \left[\int ^{C}\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}(C^{\prime };{\it\kappa})}{{\rm\pi}}-\frac{{\it\chi}_{2}(C^{\prime };{\it\kappa})}{C^{\prime }}\right)\frac{1}{{\it\chi}_{1}(C^{\prime };{\it\kappa})}\,\text{d}C^{\prime }\right],\end{eqnarray}$$
where
![]() $N$
is a normalization constant determined from the constraint
$N$
is a normalization constant determined from the constraint
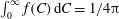 $\int _{0}^{\infty }f(C)\,\text{d}C=1/4{\rm\pi}$
. Since (7.24) is the solution of a drift–diffusion balance in one dimension, it is an equilibrium distribution with the flux being zero at every point along the
$\int _{0}^{\infty }f(C)\,\text{d}C=1/4{\rm\pi}$
. Since (7.24) is the solution of a drift–diffusion balance in one dimension, it is an equilibrium distribution with the flux being zero at every point along the
![]() $C$
-axis, the no-flux conditions at the boundary conditions (one of them at infinity) being automatically satisfied. In this sense, the solution is analogous to the much simpler Gaussian equilibrium for a Brownian particle in a bounded harmonic potential (Wax Reference Wax2013). Interpreting (7.24) within the framework of the harmonic potential problem, the equivalent
$C$
-axis, the no-flux conditions at the boundary conditions (one of them at infinity) being automatically satisfied. In this sense, the solution is analogous to the much simpler Gaussian equilibrium for a Brownian particle in a bounded harmonic potential (Wax Reference Wax2013). Interpreting (7.24) within the framework of the harmonic potential problem, the equivalent
![]() $C$
-dependent potential for the present case is given by
$C$
-dependent potential for the present case is given by
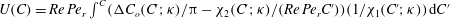 $U(C)=Re\,Pe_{r}\int ^{C}({\rm\Delta}C_{o}(C^{\prime };{\it\kappa})/{\rm\pi}-{\it\chi}_{2}(C^{\prime };{\it\kappa})/(Re\,Pe_{r}C^{\prime }))(1/{\it\chi}_{1}(C^{\prime };{\it\kappa}))\,\text{d}C^{\prime }$
where, unlike the harmonic oscillator case,
$U(C)=Re\,Pe_{r}\int ^{C}({\rm\Delta}C_{o}(C^{\prime };{\it\kappa})/{\rm\pi}-{\it\chi}_{2}(C^{\prime };{\it\kappa})/(Re\,Pe_{r}C^{\prime }))(1/{\it\chi}_{1}(C^{\prime };{\it\kappa}))\,\text{d}C^{\prime }$
where, unlike the harmonic oscillator case,
![]() $U(C)$
also incorporates the
$U(C)$
also incorporates the
![]() $C$
-dependence of the diffusivity in (7.23);
$C$
-dependence of the diffusivity in (7.23);
 $(Re\,Pe_{r})^{-1}$
is the dimensionless temperature. Figure 18 shows a plot of
$(Re\,Pe_{r})^{-1}$
is the dimensionless temperature. Figure 18 shows a plot of
![]() $U(C)$
against
$U(C)$
against
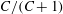 $C/(C+1)$
, for different
$C/(C+1)$
, for different
![]() $Re\,Pe_{r}$
, for an oblate spheroid of aspect ratio 0.0135. In the limit
$Re\,Pe_{r}$
, for an oblate spheroid of aspect ratio 0.0135. In the limit
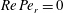 $Re\,Pe_{r}=0$
, the potential has only one minimum, corresponding to Brownian motion alone, and this is located close to the tumbling mode. But, as the value of
$Re\,Pe_{r}=0$
, the potential has only one minimum, corresponding to Brownian motion alone, and this is located close to the tumbling mode. But, as the value of
![]() $Re\,Pe_{r}$
increases, the inertial drift towards the spinning mode (for
$Re\,Pe_{r}$
increases, the inertial drift towards the spinning mode (for
![]() $C<C^{\ast }$
with
$C<C^{\ast }$
with
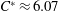 $C^{\ast }\approx 6.07$
for an aspect ratio of 0.0135) causes the potential to become a bistable one with a second shallow minimum developing in the vicinity of the spinning mode. Note that the minima of the bistable potential, for any finite
$C^{\ast }\approx 6.07$
for an aspect ratio of 0.0135) causes the potential to become a bistable one with a second shallow minimum developing in the vicinity of the spinning mode. Note that the minima of the bistable potential, for any finite
![]() $Re\,Pe_{r}$
, are not exactly at
$Re\,Pe_{r}$
, are not exactly at
![]() $C=0$
and
$C=0$
and
![]() $C=\infty$
due to the presence of an additional Brownian drift component; such a coincidence occurs only at
$C=\infty$
due to the presence of an additional Brownian drift component; such a coincidence occurs only at
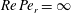 $Re\,Pe_{r}=\infty$
. The bistable nature of
$Re\,Pe_{r}=\infty$
. The bistable nature of
![]() $U(C)$
implies that
$U(C)$
implies that
![]() $f(C)$
will have a pair of peaks corresponding to the two minima, and this is borne out in the plots that follow. It is worth noting that, although the
$f(C)$
will have a pair of peaks corresponding to the two minima, and this is borne out in the plots that follow. It is worth noting that, although the
![]() $U(C)$
minimum and the
$U(C)$
minimum and the
![]() $f(C)$
maximum (see below), in the vicinity of
$f(C)$
maximum (see below), in the vicinity of
![]() $C=0$
, appear quite shallow, they would be much sharper in terms of the actual angular coordinates since, as already mentioned, close to the flat-disk limit, all the finite-
$C=0$
, appear quite shallow, they would be much sharper in terms of the actual angular coordinates since, as already mentioned, close to the flat-disk limit, all the finite-
![]() $C$
Jeffery orbits are squished to within an asymptotically small interval in the vicinity of the gradient–vorticity plane (figure 8).
$C$
Jeffery orbits are squished to within an asymptotically small interval in the vicinity of the gradient–vorticity plane (figure 8).

Figure 18. The
![]() $C$
-dependent potential for an oblate spheroid of aspect ratio 0.0135 is plotted against
$C$
-dependent potential for an oblate spheroid of aspect ratio 0.0135 is plotted against
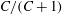 $C/(C+1)$
for various values of
$C/(C+1)$
for various values of
![]() $Re\,Pe_{r}$
.
$Re\,Pe_{r}$
.
For
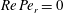 $Re\,Pe_{r}=0$
, (7.23) reduces to the equation solved by Leal & Hinch (Reference Leal and Hinch1971), who analysed the effect of Brownian motion alone in determining
$Re\,Pe_{r}=0$
, (7.23) reduces to the equation solved by Leal & Hinch (Reference Leal and Hinch1971), who analysed the effect of Brownian motion alone in determining
![]() $f(C)$
. The deviation in
$f(C)$
. The deviation in
![]() $f(C)$
from the ‘Leal–Hinch distribution’ due to the emergence of an inertial drift, for moderate
$f(C)$
from the ‘Leal–Hinch distribution’ due to the emergence of an inertial drift, for moderate
![]() $Re\,Pe_{r}$
, is shown in figure 19, again for an oblate spheroid with aspect ratio 0.0135. Figure 20 shows the normalized
$Re\,Pe_{r}$
, is shown in figure 19, again for an oblate spheroid with aspect ratio 0.0135. Figure 20 shows the normalized
![]() $f(C)$
for much larger values of
$f(C)$
for much larger values of
![]() $Re\,Pe_{r}$
for four different aspect ratios in the range 0.011–0.0135 (the purely Brownian Leal–Hinch curve is also shown for comparison in each figure). One expects to obtain bimodal distributions over some range of large
$Re\,Pe_{r}$
for four different aspect ratios in the range 0.011–0.0135 (the purely Brownian Leal–Hinch curve is also shown for comparison in each figure). One expects to obtain bimodal distributions over some range of large
![]() $Re\,Pe_{r}$
values owing to the bidirectional inertial drift for aspect ratios less than 0.137; the original delta functions used in § 7.1, for the rheology calculation, will now be smoothed by Brownian motion into finite peaks with a small spread that varies in some inverse proportion with
$Re\,Pe_{r}$
values owing to the bidirectional inertial drift for aspect ratios less than 0.137; the original delta functions used in § 7.1, for the rheology calculation, will now be smoothed by Brownian motion into finite peaks with a small spread that varies in some inverse proportion with
![]() $Re\,Pe_{r}$
. The precise scaling of the spinning and tumbling peak widths may be found from the asymptotic forms of the drift and diffusivity coefficients for small and large
$Re\,Pe_{r}$
. The precise scaling of the spinning and tumbling peak widths may be found from the asymptotic forms of the drift and diffusivity coefficients for small and large
![]() $C$
. For
$C$
. For
![]() $C\rightarrow 0$
,
$C\rightarrow 0$
,
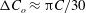 ${\rm\Delta}C_{o}\approx {\rm\pi}C/30$
and (7.23) takes the form
${\rm\Delta}C_{o}\approx {\rm\pi}C/30$
and (7.23) takes the form
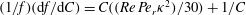 $(1/f)(\text{d}f/\text{d}C)=C((Re\,Pe_{r}{\it\kappa}^{2})/30)+1/C$
, implying a spinning peak width of
$(1/f)(\text{d}f/\text{d}C)=C((Re\,Pe_{r}{\it\kappa}^{2})/30)+1/C$
, implying a spinning peak width of
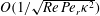 $O(1/\sqrt{Re\,Pe_{r}{\it\kappa}^{2}})$
; for
$O(1/\sqrt{Re\,Pe_{r}{\it\kappa}^{2}})$
; for
![]() $C\rightarrow \infty$
,
$C\rightarrow \infty$
,
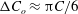 ${\rm\Delta}C_{o}\approx {\rm\pi}C/6$
and (7.23) takes the form
${\rm\Delta}C_{o}\approx {\rm\pi}C/6$
and (7.23) takes the form
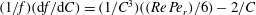 $(1/f)(\text{d}f/\text{d}C)=(1/C^{3})((Re\,Pe_{r})/6)-2/C$
, implying a tumbling peak width of
$(1/f)(\text{d}f/\text{d}C)=(1/C^{3})((Re\,Pe_{r})/6)-2/C$
, implying a tumbling peak width of
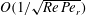 $O(1/\sqrt{Re\,Pe_{r}})$
. The smoothing effect of Brownian motion is, of course, expected, and is of a relatively minor significance in the rheological context, since the regularization of the delta functions only leads to a vanishingly small correction to the steady-state shear viscosity for
$O(1/\sqrt{Re\,Pe_{r}})$
. The smoothing effect of Brownian motion is, of course, expected, and is of a relatively minor significance in the rheological context, since the regularization of the delta functions only leads to a vanishingly small correction to the steady-state shear viscosity for
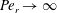 $Pe_{r}\rightarrow \infty$
. This has, for instance, been done in the context of particle inertia by Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014) with
$Pe_{r}\rightarrow \infty$
. This has, for instance, been done in the context of particle inertia by Einarsson et al. (Reference Einarsson, Angilella and Mehlig2014) with
![]() $St\,Pe_{r}$
being the relevant parameter.
$St\,Pe_{r}$
being the relevant parameter.

Figure 19. The
![]() $f(C)$
for an oblate spheroid of aspect ratio 0.0135 is plotted against
$f(C)$
for an oblate spheroid of aspect ratio 0.0135 is plotted against
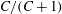 $C/(C+1)$
for moderate values of
$C/(C+1)$
for moderate values of
![]() $Re\,Pe_{r}$
. The Leal–Hinch distribution corresponds to
$Re\,Pe_{r}$
. The Leal–Hinch distribution corresponds to
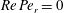 $Re\,Pe_{r}=0$
.
$Re\,Pe_{r}=0$
.
The non-trivial effect of Brownian motion is in determining the ratio of the tumbling-to-spinning peak amplitude, which, in sharp contrast to § 7.1, is now independent of initial conditions. This independence is evident from (7.24), where the ratio of tumbling-to-spinning peak amplitudes is proportional to the exponential of the difference in the corresponding potentials (
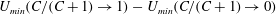 $U_{min}(C/(C+1)\rightarrow 1)-U_{min}(C/(C+1)\rightarrow 0)$
). Figure 20 shows that this ratio crosses unity, as the aspect ratio decreases from 0.137 and approaches zero, implying a transition from a dominance of spinning oblate spheroids to tumbling oblate spheroids. For really large values of
$U_{min}(C/(C+1)\rightarrow 1)-U_{min}(C/(C+1)\rightarrow 0)$
). Figure 20 shows that this ratio crosses unity, as the aspect ratio decreases from 0.137 and approaches zero, implying a transition from a dominance of spinning oblate spheroids to tumbling oblate spheroids. For really large values of
![]() $Re\,Pe_{r}$
, this transition occurs at approximately an aspect ratio of 0.0126 (notice the shift in dominant peak from the spinning to the tumbling one at
$Re\,Pe_{r}$
, this transition occurs at approximately an aspect ratio of 0.0126 (notice the shift in dominant peak from the spinning to the tumbling one at
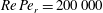 $Re\,Pe_{r}=200\,000$
, as one changes the aspect ratio from 0.0127 to 0.0124); this may also be seen from the relative depths of the two minima of
$Re\,Pe_{r}=200\,000$
, as one changes the aspect ratio from 0.0127 to 0.0124); this may also be seen from the relative depths of the two minima of
![]() $U(C)$
for
$U(C)$
for
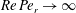 $Re\,Pe_{r}\rightarrow \infty$
. In the athermal limit of interest here, the difference between potential minima is enormously magnified by the factor
$Re\,Pe_{r}\rightarrow \infty$
. In the athermal limit of interest here, the difference between potential minima is enormously magnified by the factor
![]() $Re\,Pe_{r}$
, and a change in sign of
$Re\,Pe_{r}$
, and a change in sign of
 $U(\infty )-U(0)$
implies, for long enough times, a transition from a suspension of spinning spheroids to one of tumbling spheroids. The interval of aspect ratios over which such a transition (spinning
$U(\infty )-U(0)$
implies, for long enough times, a transition from a suspension of spinning spheroids to one of tumbling spheroids. The interval of aspect ratios over which such a transition (spinning
![]() $\rightarrow$
tumbling) occurs (with decreasing aspect ratio) must scale inversely with
$\rightarrow$
tumbling) occurs (with decreasing aspect ratio) must scale inversely with
![]() $Re\,Pe_{r}$
, implying that the intrinsic viscosity coefficient, in the limit
$Re\,Pe_{r}$
, implying that the intrinsic viscosity coefficient, in the limit
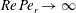 $Re\,Pe_{r}\rightarrow \infty$
, must undergo a jump at the critical aspect ratio of 0.0126 from a large
$Re\,Pe_{r}\rightarrow \infty$
, must undergo a jump at the critical aspect ratio of 0.0126 from a large
![]() $O(nL^{3})$
value to a much smaller
$O(nL^{3})$
value to a much smaller
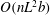 $O(nL^{2}b)$
value. Figure 21 evaluates the viscosity coefficient with an
$O(nL^{2}b)$
value. Figure 21 evaluates the viscosity coefficient with an
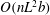 $O(nL^{2}b)$
normalization using an orientation distribution given by (7.13) above this critical aspect ratio, and the oblate analogue of (7.12) below it. Note that the aforementioned critical aspect ratio differs from the critical value of 0.137 found in the absence of Brownian motion (
$O(nL^{2}b)$
normalization using an orientation distribution given by (7.13) above this critical aspect ratio, and the oblate analogue of (7.12) below it. Note that the aforementioned critical aspect ratio differs from the critical value of 0.137 found in the absence of Brownian motion (
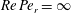 $Re\,Pe_{r}=\infty$
), implying the singular role of Brownian motion; the viscosity coefficient now varies smoothly across the earlier critical value. This singular effect of thermal forces is contingent on taking the limit
$Re\,Pe_{r}=\infty$
), implying the singular role of Brownian motion; the viscosity coefficient now varies smoothly across the earlier critical value. This singular effect of thermal forces is contingent on taking the limit
![]() $t\rightarrow \infty$
before
$t\rightarrow \infty$
before
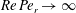 $Re\,Pe_{r}\rightarrow \infty$
, thereby allowing even weak Brownian motion to act over an asymptotically large period of time (this ordering of limits is in the same sense as that in the original Leal–Hinch analysis (Leal & Hinch Reference Leal and Hinch1971), except that
$Re\,Pe_{r}\rightarrow \infty$
, thereby allowing even weak Brownian motion to act over an asymptotically large period of time (this ordering of limits is in the same sense as that in the original Leal–Hinch analysis (Leal & Hinch Reference Leal and Hinch1971), except that
![]() $Pe_{r}$
is now replaced by
$Pe_{r}$
is now replaced by
![]() $Re\,Pe_{r}$
).
$Re\,Pe_{r}$
).

Figure 20. The
![]() $f(C)$
for different aspect ratios (a) 0.0124; (b) 0.0127; (c) 0.011 and (d) 0.0135 is plotted against the orbital coordinate for various values of
$f(C)$
for different aspect ratios (a) 0.0124; (b) 0.0127; (c) 0.011 and (d) 0.0135 is plotted against the orbital coordinate for various values of
![]() $Re\,Pe_{r}$
(0–2000 000). As
$Re\,Pe_{r}$
(0–2000 000). As
![]() $ReP_{r}$
increases, for aspect ratios less than 0.0126, the probability leaks towards the tumbling mode, and for aspect ratios greater than 0.0126, the leak is towards the spinning mode.
$ReP_{r}$
increases, for aspect ratios less than 0.0126, the probability leaks towards the tumbling mode, and for aspect ratios greater than 0.0126, the leak is towards the spinning mode.
The aforementioned critical aspect ratio can also be calculated from the asymptotic forms that the distribution,
![]() $f(C)$
, takes as
$f(C)$
, takes as
![]() $C\rightarrow \infty$
and
$C\rightarrow \infty$
and
![]() $C\rightarrow 0$
. In the latter case,
$C\rightarrow 0$
. In the latter case,
![]() $f(C)$
takes the form
$f(C)$
takes the form
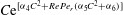 $C\text{e}^{[{\it\alpha}_{4}C^{2}+Re\,Pe_{r}({\it\alpha}_{5}C^{2}+{\it\alpha}_{6})]}$
, and for
$C\text{e}^{[{\it\alpha}_{4}C^{2}+Re\,Pe_{r}({\it\alpha}_{5}C^{2}+{\it\alpha}_{6})]}$
, and for
![]() $C\rightarrow \infty$
,
$C\rightarrow \infty$
,
![]() $f(C)$
takes the form
$f(C)$
takes the form
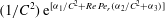 $(1/C^{2})\,\text{e}^{[{\it\alpha}_{1}/C^{2}+Re\,Pe_{r}({\it\alpha}_{2}/C^{2}+{\it\alpha}_{3})]}$
, where the
$(1/C^{2})\,\text{e}^{[{\it\alpha}_{1}/C^{2}+Re\,Pe_{r}({\it\alpha}_{2}/C^{2}+{\it\alpha}_{3})]}$
, where the
![]() ${\it\alpha}_{i}$
are functions of the spheroid aspect ratio. The ratio of the maxima of these two asymptotes must be equated to unity to obtain the critical aspect ratio corresponding to the spinning–tumbling transition. This gives
${\it\alpha}_{i}$
are functions of the spheroid aspect ratio. The ratio of the maxima of these two asymptotes must be equated to unity to obtain the critical aspect ratio corresponding to the spinning–tumbling transition. This gives
![]() ${\it\alpha}_{3}={\it\alpha}_{6}$
at the leading order with corrections of
${\it\alpha}_{3}={\it\alpha}_{6}$
at the leading order with corrections of
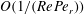 $O(1/(Re\,Pe_{r}))$
. The aspect-ratio functions,
$O(1/(Re\,Pe_{r}))$
. The aspect-ratio functions,
![]() ${\it\alpha}_{3}$
and
${\it\alpha}_{3}$
and
![]() ${\it\alpha}_{6}$
, are plotted in figure 22 for aspect ratios ranging from 0 to 0.136, and the curves cross at the aspect ratio of 0.0126.
${\it\alpha}_{6}$
, are plotted in figure 22 for aspect ratios ranging from 0 to 0.136, and the curves cross at the aspect ratio of 0.0126.

Figure 21. (a) Intrinsic viscosity for a suspension of Brownian oblate spheroids is plotted as a function of the aspect ratio (scaled with
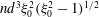 $nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}$
). (b) Shows the jump from the spinning to the tumbling value at the critical aspect ratio of 0.0126.
$nd^{3}{\it\xi}_{0}^{2}({\it\xi}_{0}^{2}-1)^{1/2}$
). (b) Shows the jump from the spinning to the tumbling value at the critical aspect ratio of 0.0126.

Figure 22. (a) The functions
![]() ${\it\alpha}_{3}$
and
${\it\alpha}_{3}$
and
![]() ${\it\alpha}_{6}$
, in the large
${\it\alpha}_{6}$
, in the large
![]() $C$
and the small
$C$
and the small
![]() $C$
asymptotic forms of distribution are plotted against the aspect ratio in (a). The cross-over of the two functions gives the critical aspect ratio. (b) Zoomed view of (a) which shows the crossing of the functions at 0.0126.
$C$
asymptotic forms of distribution are plotted against the aspect ratio in (a). The cross-over of the two functions gives the critical aspect ratio. (b) Zoomed view of (a) which shows the crossing of the functions at 0.0126.
Starting from an arbitrary initial condition, the orientation probability density evolves in a non-trivial fashion for
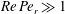 $Re\,Pe_{r}\gg 1$
. The inertial drift must, on a shorter time scale of
$Re\,Pe_{r}\gg 1$
. The inertial drift must, on a shorter time scale of
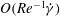 $O(Re^{-1}\dot{{\it\gamma}})$
(the time required for a spheroid orientation to drift across the unit sphere), lead to the establishment of the tumbling and spinning peaks whose amplitudes depend on the initial orientation distribution as found in § 7.1. The establishment of these peaks must then be followed by a process of ‘equilibration’ that involves the slow transfer of probability (of spheroid orientations) from the tumbling to the spinning peak, or vice versa, depending on whether one is above or below the aforementioned critical aspect ratio, leading to the peak ratio eventually approaching an initial-condition-independent value. This second (slower) process may be interpreted as an activated (barrier-hopping) process that requires an activation energy of
$O(Re^{-1}\dot{{\it\gamma}})$
(the time required for a spheroid orientation to drift across the unit sphere), lead to the establishment of the tumbling and spinning peaks whose amplitudes depend on the initial orientation distribution as found in § 7.1. The establishment of these peaks must then be followed by a process of ‘equilibration’ that involves the slow transfer of probability (of spheroid orientations) from the tumbling to the spinning peak, or vice versa, depending on whether one is above or below the aforementioned critical aspect ratio, leading to the peak ratio eventually approaching an initial-condition-independent value. This second (slower) process may be interpreted as an activated (barrier-hopping) process that requires an activation energy of
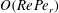 $O(Re\,Pe_{r})$
corresponding to the potential maximum in figure 18, and the classical analysis of Kramer in the context of reaction-rate theory implies that the time scale for equilibration between the peak amplitudes would scale as
$O(Re\,Pe_{r})$
corresponding to the potential maximum in figure 18, and the classical analysis of Kramer in the context of reaction-rate theory implies that the time scale for equilibration between the peak amplitudes would scale as
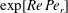 $\exp [Re\,Pe_{r}]$
(Wax Reference Wax2013). This is, of course, much longer than the
$\exp [Re\,Pe_{r}]$
(Wax Reference Wax2013). This is, of course, much longer than the
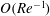 $O(Re^{-1})$
scale associated with the inertial drift setting up the initial-condition-dependent peaks for large
$O(Re^{-1})$
scale associated with the inertial drift setting up the initial-condition-dependent peaks for large
![]() $Re\,Pe_{r}$
. An analogy may also be drawn between the tumbling–spinning transition analysed here and the coil-stretch transition in the polymer physics context, with the strain rate replacing the aspect ratio as the relevant parameter (De Gennes Reference De Gennes1974; Hinch Reference Hinch1974), and the tumbling and spinning modes corresponding, respectively, to the coiled and stretched configurations, respectively. In the thermodynamic limit, and for sufficiently long times, there must be a complete transition of all polymer molecules from the coiled to the stretched configuration when a dilute polymer solution is subjected to a supercritical extension rate (greater than a Deborah number of
$Re\,Pe_{r}$
. An analogy may also be drawn between the tumbling–spinning transition analysed here and the coil-stretch transition in the polymer physics context, with the strain rate replacing the aspect ratio as the relevant parameter (De Gennes Reference De Gennes1974; Hinch Reference Hinch1974), and the tumbling and spinning modes corresponding, respectively, to the coiled and stretched configurations, respectively. In the thermodynamic limit, and for sufficiently long times, there must be a complete transition of all polymer molecules from the coiled to the stretched configuration when a dilute polymer solution is subjected to a supercritical extension rate (greater than a Deborah number of
![]() $1/2$
; Hsieh & Larson Reference Hsieh and Larson2005). It is also, however, true that the importance of the so-called coil-stretch hysteresis is precisely due to the long-lived metastable states (either the coiled or the stretched configurations, depending on whether the extension rate is above or below the critical value). For instance, as pointed out by Hinch (Reference Hinch1974), a weak subcritical flow can indeed maintain a stretched polymer molecule, although the stretching would have originally required the imposition of a supercritical extension. Based on this analogy with the coil-stretch transition, one expects a similar hysteresis with regard to the tumbling and spinning modes in the present context. In other words, for time scales much shorter than the peak-equilibration time above, both tumbling and spinning modes are allowed configurations for oblate spheroids with aspect ratios less than 0.137. The simpler spheroidal geometry also allows us to identify the basins of attraction corresponding to the tumbling and spinning modes on the unit sphere; the corresponding basins of attraction for the coiled and stretched states of a polymer molecule in the absence of Brownian motion, although unphysical, would necessitate examination of a much more complicated configuration space.
$1/2$
; Hsieh & Larson Reference Hsieh and Larson2005). It is also, however, true that the importance of the so-called coil-stretch hysteresis is precisely due to the long-lived metastable states (either the coiled or the stretched configurations, depending on whether the extension rate is above or below the critical value). For instance, as pointed out by Hinch (Reference Hinch1974), a weak subcritical flow can indeed maintain a stretched polymer molecule, although the stretching would have originally required the imposition of a supercritical extension. Based on this analogy with the coil-stretch transition, one expects a similar hysteresis with regard to the tumbling and spinning modes in the present context. In other words, for time scales much shorter than the peak-equilibration time above, both tumbling and spinning modes are allowed configurations for oblate spheroids with aspect ratios less than 0.137. The simpler spheroidal geometry also allows us to identify the basins of attraction corresponding to the tumbling and spinning modes on the unit sphere; the corresponding basins of attraction for the coiled and stretched states of a polymer molecule in the absence of Brownian motion, although unphysical, would necessitate examination of a much more complicated configuration space.
It again needs emphasis that, for any finite
![]() $Re\,Pe_{r}$
, there will be a non-trivial distribution of spheroid orientations spread across the entire unit sphere. In the athermal limit, however, the preponderance of spheroid orientations would be in the vicinity of either the tumbling or spinning modes, whichever is stable in the sense of corresponding to a lower potential. Thus, the primary effect of Brownian motion, at leading order, is only in determining the relative stability of these modes; the smoothing of the peaks, and the resulting finite spread of orientations, are second-order effects that become vanishingly small for
$Re\,Pe_{r}$
, there will be a non-trivial distribution of spheroid orientations spread across the entire unit sphere. In the athermal limit, however, the preponderance of spheroid orientations would be in the vicinity of either the tumbling or spinning modes, whichever is stable in the sense of corresponding to a lower potential. Thus, the primary effect of Brownian motion, at leading order, is only in determining the relative stability of these modes; the smoothing of the peaks, and the resulting finite spread of orientations, are second-order effects that become vanishingly small for
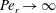 $Pe_{r}\rightarrow \infty$
. It is especially worth noting that, although the specific case of Brownian motion has been analysed above in some detail, an alternate (weak) stochastic mechanism, in the presence of a bidirectional inertial drift, should also lead to a unique steady-state orientation distribution in a similar manner, although the existence of, and the actual value of a critical aspect ratio, depends on the details of the mechanism. For instance, outside the infinitely dilute limit, pair-hydrodynamic interactions would have the same qualitative effect. For oblate spheroids, successive uncorrelated pair interactions would lead to a relaxation process in orientation space similar to Brownian motion, although the process is non-local owing to each pair interaction leading to, in general, a large jump in orientation (these jumps become small, of
$Pe_{r}\rightarrow \infty$
. It is especially worth noting that, although the specific case of Brownian motion has been analysed above in some detail, an alternate (weak) stochastic mechanism, in the presence of a bidirectional inertial drift, should also lead to a unique steady-state orientation distribution in a similar manner, although the existence of, and the actual value of a critical aspect ratio, depends on the details of the mechanism. For instance, outside the infinitely dilute limit, pair-hydrodynamic interactions would have the same qualitative effect. For oblate spheroids, successive uncorrelated pair interactions would lead to a relaxation process in orientation space similar to Brownian motion, although the process is non-local owing to each pair interaction leading to, in general, a large jump in orientation (these jumps become small, of
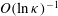 $O(\ln {\it\kappa})^{-1}$
, and the associated pair interactions are describable in terms of a hydrodynamic rotary diffusivity, only for slender prolate spheroids (Rahnama et al.
Reference Rahnama, Koch and Shaqfeh1995). Thus, if hydrodynamically induced orientation de-correlations were responsible for setting up a steady-state orientation distribution,
$O(\ln {\it\kappa})^{-1}$
, and the associated pair interactions are describable in terms of a hydrodynamic rotary diffusivity, only for slender prolate spheroids (Rahnama et al.
Reference Rahnama, Koch and Shaqfeh1995). Thus, if hydrodynamically induced orientation de-correlations were responsible for setting up a steady-state orientation distribution,
![]() $f(C)$
would be governed by a Boltzmann-like integro-differential equation in the
$f(C)$
would be governed by a Boltzmann-like integro-differential equation in the
![]() $C$
-coordinate of the form:
$C$
-coordinate of the form:
 $$\begin{eqnarray}\frac{\partial f}{\partial t}+\frac{\partial }{\partial C}\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}}{{\rm\pi}}f\right)+\frac{f}{{\it\tau}[f(C)]}-\int \text{d}C_{1}^{\prime }{\mathcal{K}}(C,C^{\prime }\mid C_{1},C_{1}^{\prime })[f(C_{1})f(C_{1}^{\prime })]=0\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f}{\partial t}+\frac{\partial }{\partial C}\left(\frac{Re\,Pe_{r}{\rm\Delta}C_{o}}{{\rm\pi}}f\right)+\frac{f}{{\it\tau}[f(C)]}-\int \text{d}C_{1}^{\prime }{\mathcal{K}}(C,C^{\prime }\mid C_{1},C_{1}^{\prime })[f(C_{1})f(C_{1}^{\prime })]=0\end{eqnarray}$$
where both the relaxation time (which depends on
![]() $f(C)$
, and is
$f(C)$
, and is
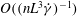 $O((nL^{3}\dot{{\it\gamma}})^{-1})$
in the dilute limit of interest) and the kernel
$O((nL^{3}\dot{{\it\gamma}})^{-1})$
in the dilute limit of interest) and the kernel
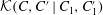 ${\mathcal{K}}(C,C^{\prime }\mid C_{1},C_{1}^{\prime })$
depends on the details of the pair-hydrodynamic interactions between spheroids (an unsolved problem). In summary, although we have analysed specifically the role of weak Brownian motion in eliminating the rheological indeterminacy associated with a dilute suspension of oblate spheroids, with aspect ratios less than 0.137, one expects the proposed scenario to remain qualitatively valid even outside the restricted regime considered. A similar situation would prevail even at finite
${\mathcal{K}}(C,C^{\prime }\mid C_{1},C_{1}^{\prime })$
depends on the details of the pair-hydrodynamic interactions between spheroids (an unsolved problem). In summary, although we have analysed specifically the role of weak Brownian motion in eliminating the rheological indeterminacy associated with a dilute suspension of oblate spheroids, with aspect ratios less than 0.137, one expects the proposed scenario to remain qualitatively valid even outside the restricted regime considered. A similar situation would prevail even at finite
![]() $Re$
, and at higher volume fractions until the inertial trajectory topology begins to differ qualitatively from that implied by the
$Re$
, and at higher volume fractions until the inertial trajectory topology begins to differ qualitatively from that implied by the
![]() $O(Re)$
analysis here (due to, for instance, the inertial drift no longer being bidirectional or from hydrodynamic fluctuations affecting the distribution of orientation within a Jeffery orbit). The role of Brownian motion above will now be replaced by hydrodynamic orientation fluctuations (at either zero or finite
$O(Re)$
analysis here (due to, for instance, the inertial drift no longer being bidirectional or from hydrodynamic fluctuations affecting the distribution of orientation within a Jeffery orbit). The role of Brownian motion above will now be replaced by hydrodynamic orientation fluctuations (at either zero or finite
![]() $Re$
) with the single dimensionless parameter governing the orientation distribution (and the rheology) now being
$Re$
) with the single dimensionless parameter governing the orientation distribution (and the rheology) now being
![]() $Re/nL^{3}$
(
$Re/nL^{3}$
(
![]() $1/nL^{3}$
playing the role of
$1/nL^{3}$
playing the role of
![]() $Pe_{r}$
, since the Brownian diffusion time of
$Pe_{r}$
, since the Brownian diffusion time of
![]() $O(D_{r}^{-1})$
is now replaced by the time between successive pair interactions of
$O(D_{r}^{-1})$
is now replaced by the time between successive pair interactions of
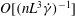 $O[(nL^{3}\dot{{\it\gamma}})^{-1}]$
).
$O[(nL^{3}\dot{{\it\gamma}})^{-1}]$
).
8 Conclusions and future work
There have been a fair number of analytical and numerical investigations which have examined the effects of both particle and fluid inertia on axisymmetric particles in a simple shear flow. The analytical investigations have thus far mainly focused on the first effects of inertia for slender fibres and nearly spherical particles; an exception is the recent work of Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015b
) which is discussed below. In the present effort, using a novel spheroidal harmonics formalism (see § 3), we have calculated the
![]() $O(Re)$
and the
$O(Re)$
and the
![]() $O(St)$
corrections to the Jeffery angular velocity for prolate and oblate spheroids of an arbitrary aspect ratio. The resulting inertial angular velocity components are given by (5.5) and (5.6). The aspect-ratio-dependent functions that appear in these equations are given by (5.7)–(5.12) for the case of particle inertia, while the same functions for the fluid inertial case are given by (6.1)–(6.8). The inertial drift is interpreted in terms of the change in orbit constant over a single Jeffery period,
$O(St)$
corrections to the Jeffery angular velocity for prolate and oblate spheroids of an arbitrary aspect ratio. The resulting inertial angular velocity components are given by (5.5) and (5.6). The aspect-ratio-dependent functions that appear in these equations are given by (5.7)–(5.12) for the case of particle inertia, while the same functions for the fluid inertial case are given by (6.1)–(6.8). The inertial drift is interpreted in terms of the change in orbit constant over a single Jeffery period,
![]() ${\rm\Delta}C$
, and the plots for
${\rm\Delta}C$
, and the plots for
![]() ${\rm\Delta}C$
for all relevant cases are given in §§ 5.1 (particle inertia: prolate and oblate) and 6 (fluid inertia: prolate and oblate).
${\rm\Delta}C$
for all relevant cases are given in §§ 5.1 (particle inertia: prolate and oblate) and 6 (fluid inertia: prolate and oblate).
![]() ${\rm\Delta}C$
is positive for a prolate spheroid, at both
${\rm\Delta}C$
is positive for a prolate spheroid, at both
![]() $O(Re)$
and
$O(Re)$
and
![]() $O(St)$
, and a prolate spheroid always drifts towards a tumbling mode. For an oblate spheroid,
$O(St)$
, and a prolate spheroid always drifts towards a tumbling mode. For an oblate spheroid,
![]() ${\rm\Delta}C$
is negative at
${\rm\Delta}C$
is negative at
![]() $O(St)$
for all aspect ratios, and at
$O(St)$
for all aspect ratios, and at
![]() $O(Re)$
, for aspect ratios greater than (approximately) 0.142. In all these cases, the oblate spheroid drifts towards a spinning mode. For oblate spheroids with aspect ratios less than 0.142, the
$O(Re)$
, for aspect ratios greater than (approximately) 0.142. In all these cases, the oblate spheroid drifts towards a spinning mode. For oblate spheroids with aspect ratios less than 0.142, the
![]() ${\rm\Delta}C$
curve, at
${\rm\Delta}C$
curve, at
![]() $O(Re)$
, exhibits a single zero crossing at
$O(Re)$
, exhibits a single zero crossing at
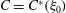 $C=C^{\ast }({\it\xi}_{0})$
. The change in sign implies that the unit sphere is now divided into distinct basins of attraction corresponding to the spinning and tumbling modes. With decreasing aspect ratio (below 0.142), the basin of attraction corresponding to the tumbling mode expands, eventually filling up the entire unit sphere in the flat-disk limit. Finally, in § 5.2, we extend the analysis for particle inertia to
$C=C^{\ast }({\it\xi}_{0})$
. The change in sign implies that the unit sphere is now divided into distinct basins of attraction corresponding to the spinning and tumbling modes. With decreasing aspect ratio (below 0.142), the basin of attraction corresponding to the tumbling mode expands, eventually filling up the entire unit sphere in the flat-disk limit. Finally, in § 5.2, we extend the analysis for particle inertia to
![]() $O(St^{2})$
, showing that there is a decrease in the period of rotation at this order.
$O(St^{2})$
, showing that there is a decrease in the period of rotation at this order.
Although the predictions above are expected to be quantitatively accurate only in the limit
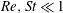 $Re,St\ll 1$
, it would be interesting if future simulations, carried out at lower values of
$Re,St\ll 1$
, it would be interesting if future simulations, carried out at lower values of
![]() $Re$
and
$Re$
and
![]() $St$
, help delineate the precise regimes of validity for the theoretical expressions obtained here. To account for non-trivial aspect-ratio-related factors entering the particle inertia regime of validity, one may define an effective Stokes number (
$St$
, help delineate the precise regimes of validity for the theoretical expressions obtained here. To account for non-trivial aspect-ratio-related factors entering the particle inertia regime of validity, one may define an effective Stokes number (
![]() $\bar{St}$
) that is the ratio of the moment of inertia to the viscous torque coefficient, given by
$\bar{St}$
) that is the ratio of the moment of inertia to the viscous torque coefficient, given by
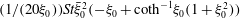 $(1/(20{\it\xi}_{0}))St\bar{{\it\xi}}_{0}^{2}(-{\it\xi}_{0}+\text{coth}^{-1}{\it\xi}_{0}(1+{\it\xi}_{0}^{2}))$
and
$(1/(20{\it\xi}_{0}))St\bar{{\it\xi}}_{0}^{2}(-{\it\xi}_{0}+\text{coth}^{-1}{\it\xi}_{0}(1+{\it\xi}_{0}^{2}))$
and
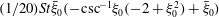 $(1/20)St\bar{{\it\xi}}_{0}(-\text{csc}^{-1}{\it\xi}_{0}(-2+{\it\xi}_{0}^{2})+\bar{{\it\xi}}_{0})$
for prolate and oblate spheroids, respectively.
$(1/20)St\bar{{\it\xi}}_{0}(-\text{csc}^{-1}{\it\xi}_{0}(-2+{\it\xi}_{0}^{2})+\bar{{\it\xi}}_{0})$
for prolate and oblate spheroids, respectively.
![]() $\bar{St}$
thus defined above is the true measure of particle inertia, especially for extreme aspect ratios for which
$\bar{St}$
thus defined above is the true measure of particle inertia, especially for extreme aspect ratios for which
![]() $St$
based on the length (
$St$
based on the length (
![]() $d{\it\xi}_{0}$
) overestimates the inertia. The present analysis is then valid when
$d{\it\xi}_{0}$
) overestimates the inertia. The present analysis is then valid when
![]() $\bar{St}\ll 1$
regardless of aspect ratio. With regard to fluid inertia, of particular interest would be a simulation effort that continues the small-
$\bar{St}\ll 1$
regardless of aspect ratio. With regard to fluid inertia, of particular interest would be a simulation effort that continues the small-
![]() $Re$
bifurcation found here, for oblate spheroids, to
$Re$
bifurcation found here, for oblate spheroids, to
![]() $Re$
values of order unity, and thereby establishes the
$Re$
values of order unity, and thereby establishes the
![]() $Re$
-interval over which the bifurcation persists as well as the
$Re$
-interval over which the bifurcation persists as well as the
![]() $Re$
-dependence of the critical aspect ratio starting from its limiting value of 0.142 (for
$Re$
-dependence of the critical aspect ratio starting from its limiting value of 0.142 (for
![]() $Re\rightarrow 0$
); this would require simulating oblate spheroids having aspect ratios much smaller than those considered earlier. The presence of multiple attractors at finite
$Re\rightarrow 0$
); this would require simulating oblate spheroids having aspect ratios much smaller than those considered earlier. The presence of multiple attractors at finite
![]() $Re$
, with disjoint basins of attraction, would again imply that stochastic orientation fluctuations, acting over long times, dictate the steady-state rheology.
$Re$
, with disjoint basins of attraction, would again imply that stochastic orientation fluctuations, acting over long times, dictate the steady-state rheology.
It is also worth mentioning that the interpretation in terms of an orbital drift at
![]() $O(Re)$
in § 6 is not a uniformly valid one. For any
$O(Re)$
in § 6 is not a uniformly valid one. For any
![]() $Re$
, however small, the change in orbit constant due to the inertial drift, acting over a whole (or half) of a Jeffery period, will eventually get to be large when the aspect ratio becomes sufficiently small or large. From the limiting expressions obtained for
$Re$
, however small, the change in orbit constant due to the inertial drift, acting over a whole (or half) of a Jeffery period, will eventually get to be large when the aspect ratio becomes sufficiently small or large. From the limiting expressions obtained for
![]() ${\rm\Delta}C$
, it is seen that
${\rm\Delta}C$
, it is seen that
![]() ${\rm\Delta}C$
becomes
${\rm\Delta}C$
becomes
![]() $O(1)$
when
$O(1)$
when
![]() ${\it\kappa}$
is
${\it\kappa}$
is
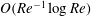 $O(Re^{-1}\log Re)$
for prolate spheroids, and when
$O(Re^{-1}\log Re)$
for prolate spheroids, and when
![]() ${\it\kappa}$
is
${\it\kappa}$
is
![]() $O(Re)$
for oblate spheroids. This happens because the Jeffery rotation becomes arbitrarily slow for large or small
$O(Re)$
for oblate spheroids. This happens because the Jeffery rotation becomes arbitrarily slow for large or small
![]() ${\it\kappa}$
(being
${\it\kappa}$
(being
![]() $O({\it\kappa}^{-2})$
and
$O({\it\kappa}^{-2})$
and
![]() $O({\it\kappa}^{2})$
, respectively, for a slender fibre and a flat disk nearly aligned with the flow–vorticity and gradient–vorticity planes, respectively), allowing inertia to act over a large time, and secondly because the nearly meridional Jeffery orbits are closely bunched together in these regions. Under these circumstances, the inertial trajectory of the spheroid is no longer a tightly wound spiral with individual turns resembling Jeffery orbits. Rather, the trajectory would consist of Jeffery orbits having a meridional character (corresponding to the non-aligned phases) connected by phases dominated by inertia where the drift is predominantly parallel to the flow–vorticity (slender fibre) or gradient–vorticity plane (flat disk). While this may be done in principle, it would require a separate analysis. The drift equation (5.19) is obtained from approximating the unsteady acceleration term in (2.30) based on a rotational motion along Jeffery orbits, and this is no longer valid for aligned particles that rotate across Jeffery orbits at leading order. This in turn would mean that the orbital drift for such particles cannot be obtained by integrating over
$O({\it\kappa}^{2})$
, respectively, for a slender fibre and a flat disk nearly aligned with the flow–vorticity and gradient–vorticity planes, respectively), allowing inertia to act over a large time, and secondly because the nearly meridional Jeffery orbits are closely bunched together in these regions. Under these circumstances, the inertial trajectory of the spheroid is no longer a tightly wound spiral with individual turns resembling Jeffery orbits. Rather, the trajectory would consist of Jeffery orbits having a meridional character (corresponding to the non-aligned phases) connected by phases dominated by inertia where the drift is predominantly parallel to the flow–vorticity (slender fibre) or gradient–vorticity plane (flat disk). While this may be done in principle, it would require a separate analysis. The drift equation (5.19) is obtained from approximating the unsteady acceleration term in (2.30) based on a rotational motion along Jeffery orbits, and this is no longer valid for aligned particles that rotate across Jeffery orbits at leading order. This in turn would mean that the orbital drift for such particles cannot be obtained by integrating over
![]() ${\it\tau}$
at a constant
${\it\tau}$
at a constant
![]() $C$
(as given by (5.17)), but has to be determined by solving the governing equation for
$C$
(as given by (5.17)), but has to be determined by solving the governing equation for
![]() $\text{d}C/\text{d}{\it\tau}$
, with
$\text{d}C/\text{d}{\it\tau}$
, with
![]() ${\it\tau}$
corresponding to the aligned phase of the spheroid orbit. Note that, for such particles with extreme aspect ratios, a modest
${\it\tau}$
corresponding to the aligned phase of the spheroid orbit. Note that, for such particles with extreme aspect ratios, a modest
![]() $Re$
is also sufficient to arrest particle rotation (as seen in the flow–gradient plane), as first shown by Subramanian & Koch (Reference Subramanian and Koch2005).
$Re$
is also sufficient to arrest particle rotation (as seen in the flow–gradient plane), as first shown by Subramanian & Koch (Reference Subramanian and Koch2005).
We have used the phrase ‘the flat-disk limit’ several times in this paper to refer to oblate spheroids of a vanishing aspect ratio. It is important here to reiterate that this limit is specific to the spheroidal geometry considered here. Disk-shaped particles, with edge profiles differing from that of a spheroid, exhibit a different rotational behaviour in simple shear flow. It has been shown by Singh et al. (Reference Singh, Koch, Subramanian and Stroock2014) that the period of rotation of a disk-shaped particle, with a sufficiently blunt edge, is asymptotically small in comparison to a spheroidal particle of the same aspect ratio; for disk-shaped particles (
![]() ${\it\kappa}\rightarrow 0$
), with edge profiles of the form
${\it\kappa}\rightarrow 0$
), with edge profiles of the form
 $(1-r^{2})^{{\it\alpha}}$
, the time period is
$(1-r^{2})^{{\it\alpha}}$
, the time period is
![]() $O({\it\kappa}^{-1})$
for
$O({\it\kappa}^{-1})$
for
![]() ${\it\alpha}>1/4$
(the spheroid corresponds to
${\it\alpha}>1/4$
(the spheroid corresponds to
![]() ${\it\alpha}=1/2$
); but only diverges as
${\it\alpha}=1/2$
); but only diverges as
 $O({\it\kappa}^{-3/4(1-{\it\alpha})})$
for
$O({\it\kappa}^{-3/4(1-{\it\alpha})})$
for
![]() ${\it\kappa}\rightarrow 0$
and
${\it\kappa}\rightarrow 0$
and
![]() ${\it\alpha}<1/4$
. The inertial drift for such particles would evidently exhibit a different scaling with aspect ratio even in the limit that the aspect ratio becomes vanishingly small.
${\it\alpha}<1/4$
. The inertial drift for such particles would evidently exhibit a different scaling with aspect ratio even in the limit that the aspect ratio becomes vanishingly small.
Inertia eliminates the rheological degeneracy, associated with the existence of Jeffery orbits in the Stokes limit, although the manner of elimination depends on the aspect ratio for oblate spheroids. For neutrally buoyant prolate spheroids, and for neutrally buoyant oblate spheroids with aspect ratios greater than 0.137, the inertial drift leads to a singular orientation distribution localized at either the tumbling or the spinning mode, depending on whether
![]() ${\rm\Delta}C$
is positive (prolate) or negative (oblate). In § 7.1, we calculate the associated intrinsic viscosity coefficients, in the absence of Brownian motion, as a function of the particle aspect ratio (see (7.15) and (7.16) for prolate and oblate spheroids, respectively) arising from the aforementioned singular distribution. Weak Brownian motion only leads to asymptotically small corrections to this estimate. In contrast, for oblate spheroids with aspect ratios smaller than 0.137, the inertial drift acting alone leads to an initial-condition-dependent rheology, and it is only with the inclusion of weak Brownian motion that a unique steady-state rheology results. In § 7.1, we calculate the initial-condition-dependent intrinsic viscosity for the non-Brownian case for an initial isotropic orientation distribution (see (7.17)). In § 7.2, we analyse in some detail the steady-state distribution across Jeffery orbits in the presence of weak Brownian motion, the inclusion of which implies a dependence of the steady-state rheology on the parameter
${\rm\Delta}C$
is positive (prolate) or negative (oblate). In § 7.1, we calculate the associated intrinsic viscosity coefficients, in the absence of Brownian motion, as a function of the particle aspect ratio (see (7.15) and (7.16) for prolate and oblate spheroids, respectively) arising from the aforementioned singular distribution. Weak Brownian motion only leads to asymptotically small corrections to this estimate. In contrast, for oblate spheroids with aspect ratios smaller than 0.137, the inertial drift acting alone leads to an initial-condition-dependent rheology, and it is only with the inclusion of weak Brownian motion that a unique steady-state rheology results. In § 7.1, we calculate the initial-condition-dependent intrinsic viscosity for the non-Brownian case for an initial isotropic orientation distribution (see (7.17)). In § 7.2, we analyse in some detail the steady-state distribution across Jeffery orbits in the presence of weak Brownian motion, the inclusion of which implies a dependence of the steady-state rheology on the parameter
![]() $Re\,Pe_{r}$
. Interestingly, the steady-state Jeffery-orbit distribution may be interpreted in terms of a one-dimensional drift–diffusion equilibrium along the orbit constant coordinate, with
$Re\,Pe_{r}$
. Interestingly, the steady-state Jeffery-orbit distribution may be interpreted in terms of a one-dimensional drift–diffusion equilibrium along the orbit constant coordinate, with
![]() $Re\,Pe_{r}$
governing the relative magnitudes of the convective and diffusive fluxes in orientation space. This distribution has a bimodal character, with peaks corresponding to the tumbling and spinning modes, for sufficiently large
$Re\,Pe_{r}$
governing the relative magnitudes of the convective and diffusive fluxes in orientation space. This distribution has a bimodal character, with peaks corresponding to the tumbling and spinning modes, for sufficiently large
![]() $Re\,Pe_{r}$
. For any finite
$Re\,Pe_{r}$
. For any finite
![]() $Re\,Pe_{r}$
, the shear viscosity varies smoothly with changing aspect ratio of the oblate spheroid, but in the limit
$Re\,Pe_{r}$
, the shear viscosity varies smoothly with changing aspect ratio of the oblate spheroid, but in the limit
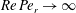 $Re\,Pe_{r}\rightarrow \infty$
, the shear viscosity must exhibit a jump across a much smaller (in relation to the non-Brownian value of 0.142) critical aspect ratio of 0.0126 owing to a transition in the (limiting) orientation distribution from a delta function localized at
$Re\,Pe_{r}\rightarrow \infty$
, the shear viscosity must exhibit a jump across a much smaller (in relation to the non-Brownian value of 0.142) critical aspect ratio of 0.0126 owing to a transition in the (limiting) orientation distribution from a delta function localized at
![]() $C=0$
(the spinning mode) to one localized at the tumbling mode (
$C=0$
(the spinning mode) to one localized at the tumbling mode (
![]() $C=\infty$
). As mentioned in § 7, we calculate here only the leading-order (indirect) effect of inertia on the suspension rheology. For prolate spheroids, and oblate spheroids with aspect ratios greater than 0.137, the direct effects of inertia enter at
$C=\infty$
). As mentioned in § 7, we calculate here only the leading-order (indirect) effect of inertia on the suspension rheology. For prolate spheroids, and oblate spheroids with aspect ratios greater than 0.137, the direct effects of inertia enter at
![]() $O(Re)$
. Interestingly for oblate spheroids with aspect ratios less than 0.137, the next correction to the drift occurs at
$O(Re)$
. Interestingly for oblate spheroids with aspect ratios less than 0.137, the next correction to the drift occurs at
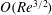 $O(Re^{3/2})$
, and this implies a larger
$O(Re^{3/2})$
, and this implies a larger
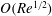 $O(Re^{1/2})$
correction to the leading-order rheology.
$O(Re^{1/2})$
correction to the leading-order rheology.
In § 7.2, although we discussed the Jeffery-orbit distribution,
![]() $f(C)$
, as a function of
$f(C)$
, as a function of
![]() $Re\,Pe_{r}$
, the resulting variation of the shear viscosity with aspect ratio was only analysed in the limit
$Re\,Pe_{r}$
, the resulting variation of the shear viscosity with aspect ratio was only analysed in the limit
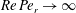 $Re\,Pe_{r}\rightarrow \infty$
, corresponding to a singular orientation distribution. It is, however, evident from figure 20 that this limit might only be achieved at very large values of
$Re\,Pe_{r}\rightarrow \infty$
, corresponding to a singular orientation distribution. It is, however, evident from figure 20 that this limit might only be achieved at very large values of
![]() $Re\,Pe_{r}$
, especially for aspect ratios close to the critical value (0.0126), and even for
$Re\,Pe_{r}$
, especially for aspect ratios close to the critical value (0.0126), and even for
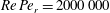 $Re\,Pe_{r}=2000\,000$
,
$Re\,Pe_{r}=2000\,000$
,
![]() $f(C)$
is far from being singular especially for small values of
$f(C)$
is far from being singular especially for small values of
![]() $C$
. To get an idea of how large
$C$
. To get an idea of how large
![]() $Re\,Pe_{r}$
might become (even while
$Re\,Pe_{r}$
might become (even while
![]() $Re$
remains small), consider a thin oblate disk with an equatorial radius of
$Re$
remains small), consider a thin oblate disk with an equatorial radius of
 $100~{\rm\mu}\text{m}$
in an aqueous solution, subjected to a shear flow of strength of
$100~{\rm\mu}\text{m}$
in an aqueous solution, subjected to a shear flow of strength of
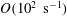 $O(10^{2}~\text{s}^{-1})$
, the
$O(10^{2}~\text{s}^{-1})$
, the
![]() $Re$
would be of
$Re$
would be of
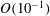 $O(10^{-1})$
and the
$O(10^{-1})$
and the
![]() $Pe_{r}$
of
$Pe_{r}$
of
![]() $O(10^{8})$
, which makes
$O(10^{8})$
, which makes
![]() $Re\,Pe_{r}$
of
$Re\,Pe_{r}$
of
![]() $O(10^{7})$
, which is an order of magnitude greater than the
$O(10^{7})$
, which is an order of magnitude greater than the
![]() $Re\,Pe_{r}$
in figure 20. So, a relevant question is, given the results for the intrinsic viscosity coefficient obtained here, what is the implication for the variation of the steady shear viscosity of a dilute suspension of spheroids, as a function of a suitable non-dimensional shear rate, for different aspect ratios. The detailed review by Brenner (Reference Brenner1974) describes the variation of the intrinsic viscosity coefficient for a non-interacting suspension of Brownian spheroids, as a function of
$Re\,Pe_{r}$
in figure 20. So, a relevant question is, given the results for the intrinsic viscosity coefficient obtained here, what is the implication for the variation of the steady shear viscosity of a dilute suspension of spheroids, as a function of a suitable non-dimensional shear rate, for different aspect ratios. The detailed review by Brenner (Reference Brenner1974) describes the variation of the intrinsic viscosity coefficient for a non-interacting suspension of Brownian spheroids, as a function of
![]() $Pe_{r}$
, in the inertialess limit (see figures 7 and 10 therein). As expected, for a general complex fluid with an isotropic microstructure at equilibrium, the imposition of shear and the resulting flow alignment of the spheroidal particles leads to a shear-thinning rheology. More specifically, for a spheroid of a given aspect ratio, either prolate or oblate,
$Pe_{r}$
, in the inertialess limit (see figures 7 and 10 therein). As expected, for a general complex fluid with an isotropic microstructure at equilibrium, the imposition of shear and the resulting flow alignment of the spheroidal particles leads to a shear-thinning rheology. More specifically, for a spheroid of a given aspect ratio, either prolate or oblate,
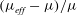 $({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
decreases from a zero-shear-rate plateau of
$({\it\mu}_{eff}-{\it\mu})/{\it\mu}$
decreases from a zero-shear-rate plateau of
![]() $O(nL^{3})$
, arising from a combination of the hydrodynamic and Brownian stress contributions for a nearly isotropic orientation distribution, to a smaller
$O(nL^{3})$
, arising from a combination of the hydrodynamic and Brownian stress contributions for a nearly isotropic orientation distribution, to a smaller
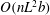 $O(nL^{2}b)$
high-shear plateau, arising solely from the hydrodynamic stress contribution associated with a flow-aligned orientation distribution. The high-shear plateau values were first calculated by Leal & Hinch (Reference Leal and Hinch1971), numerically for arbitrary aspect-ratio spheroids (see Kim & Karrila Reference Kim and Karrila1991), and analytically in the slender-fibre and flat-disk limits. These plateaus correspond to the limit
$O(nL^{2}b)$
high-shear plateau, arising solely from the hydrodynamic stress contribution associated with a flow-aligned orientation distribution. The high-shear plateau values were first calculated by Leal & Hinch (Reference Leal and Hinch1971), numerically for arbitrary aspect-ratio spheroids (see Kim & Karrila Reference Kim and Karrila1991), and analytically in the slender-fibre and flat-disk limits. These plateaus correspond to the limit
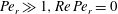 $Pe_{r}\gg 1,Re\,Pe_{r}=0$
for spheroids with aspect ratios of order unity. For extreme aspect ratios, a more stringent requirement arises from the neglect of Brownian motion even close to the flow–vorticity (gradient–vorticity) plane for slender fibres (flat disks) given by
$Pe_{r}\gg 1,Re\,Pe_{r}=0$
for spheroids with aspect ratios of order unity. For extreme aspect ratios, a more stringent requirement arises from the neglect of Brownian motion even close to the flow–vorticity (gradient–vorticity) plane for slender fibres (flat disks) given by
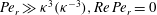 $Pe_{r}\gg {\it\kappa}^{3}({\it\kappa}^{-3}),Re\,Pe_{r}=0$
(Hinch & Leal Reference Hinch and Leal1972); this, so the orientation distribution along a Jeffery orbit is determined solely by the Jeffery angular velocity with
$Pe_{r}\gg {\it\kappa}^{3}({\it\kappa}^{-3}),Re\,Pe_{r}=0$
(Hinch & Leal Reference Hinch and Leal1972); this, so the orientation distribution along a Jeffery orbit is determined solely by the Jeffery angular velocity with
![]() $g(C,{\it\tau})$
given by (7.10). The analysis here helps extend the behaviour of the intrinsic viscosity coefficient beyond the ‘Leal–Hinch plateaus’, as a function of
$g(C,{\it\tau})$
given by (7.10). The analysis here helps extend the behaviour of the intrinsic viscosity coefficient beyond the ‘Leal–Hinch plateaus’, as a function of
![]() $Re\,Pe_{r}$
, up until the point where
$Re\,Pe_{r}$
, up until the point where
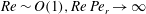 $Re\sim O(1),Re\,Pe_{r}\rightarrow \infty$
. Said differently, the shear-thinning rheology of a dilute inertialess suspension of spheroids is known up until a
$Re\sim O(1),Re\,Pe_{r}\rightarrow \infty$
. Said differently, the shear-thinning rheology of a dilute inertialess suspension of spheroids is known up until a
![]() $Pe_{r}$
where a limiting Newtonian plateau results from Brownian motion only determining the distribution of orientations across Jeffery orbits. The viscosity versus shear rate curves given below, both the schematic and the actual numerical calculations, start from this point and determine the non-Newtonian rheology at higher
$Pe_{r}$
where a limiting Newtonian plateau results from Brownian motion only determining the distribution of orientations across Jeffery orbits. The viscosity versus shear rate curves given below, both the schematic and the actual numerical calculations, start from this point and determine the non-Newtonian rheology at higher
![]() $Pe_{r}$
due to the Jeffery-orbit distribution, as shown in § 7.2, being determined by the competing effects of inertial and thermal forces.
$Pe_{r}$
due to the Jeffery-orbit distribution, as shown in § 7.2, being determined by the competing effects of inertial and thermal forces.
As shown in figure 23, accounting for a non-zero
![]() $Re\,Pe_{r}$
will always lead to a shear-thickening rheology (relative to the Leal–Hinch plateau) for prolate spheroids owing to the drift towards the maximum dissipation (tumbling) orbit. The inertial plateau for
$Re\,Pe_{r}$
will always lead to a shear-thickening rheology (relative to the Leal–Hinch plateau) for prolate spheroids owing to the drift towards the maximum dissipation (tumbling) orbit. The inertial plateau for
 $Re\,Pe_{r}\rightarrow \infty$
exceeds even the zero-shear plateau (
$Re\,Pe_{r}\rightarrow \infty$
exceeds even the zero-shear plateau (
![]() $Pe_{r}\rightarrow 0$
) provided the spheroid aspect ratio is less than 1.7. The behaviour for oblate spheroids depends on the whether the aspect ratio is above or below 0.0126. In the former case, an overall shear-thickening rheology (relative to both the zero-shear and Leal–Hinch plateaus) results for sufficiently large
$Pe_{r}\rightarrow 0$
) provided the spheroid aspect ratio is less than 1.7. The behaviour for oblate spheroids depends on the whether the aspect ratio is above or below 0.0126. In the former case, an overall shear-thickening rheology (relative to both the zero-shear and Leal–Hinch plateaus) results for sufficiently large
![]() $Re\,Pe_{r}$
, while for the latter case, the suspension continues to shear thin even with the onset of inertia. Accordingly, figure 24 shows the viscosity versus shear curves, corresponding to the two aspect-ratio groups, separating out in the limit
$Re\,Pe_{r}$
, while for the latter case, the suspension continues to shear thin even with the onset of inertia. Accordingly, figure 24 shows the viscosity versus shear curves, corresponding to the two aspect-ratio groups, separating out in the limit
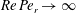 $Re\,Pe_{r}\rightarrow \infty$
, this being consistent with a jump in the shear viscosity in this limit (see § 7.2). The actual plots of the intrinsic viscosity coefficient plotted against
$Re\,Pe_{r}\rightarrow \infty$
, this being consistent with a jump in the shear viscosity in this limit (see § 7.2). The actual plots of the intrinsic viscosity coefficient plotted against
![]() $Re\,Pe_{r}$
are shown attached to the schematics in figures 23 and 24. These reveal the scenario for oblate spheroids, with aspect ratios greater than 0.0126, to be a little more complicated than that shown in the schematic, owing to the suspension first shear thinning substantially with increasing
$Re\,Pe_{r}$
are shown attached to the schematics in figures 23 and 24. These reveal the scenario for oblate spheroids, with aspect ratios greater than 0.0126, to be a little more complicated than that shown in the schematic, owing to the suspension first shear thinning substantially with increasing
![]() $Re\,Pe_{r}$
, for aspect ratios just above the critical value, before eventually shear thickening for sufficiently large
$Re\,Pe_{r}$
, for aspect ratios just above the critical value, before eventually shear thickening for sufficiently large
![]() $Re\,Pe_{r}$
. This non-monotonicity arises because of an initial Brownian peak close to tumbling, and the transition from this to a spinning peak with increasing
$Re\,Pe_{r}$
. This non-monotonicity arises because of an initial Brownian peak close to tumbling, and the transition from this to a spinning peak with increasing
![]() $Re\,Pe_{r}$
; the transition involves a sharpening of the tumbling peak (leading to shear thinning) prior to the development of a spinning peak. A similar calculation for oblate spheroids with smaller aspect ratios shows a monotonic shear thinning; the viscosity coefficient here is plotted against
$Re\,Pe_{r}$
; the transition involves a sharpening of the tumbling peak (leading to shear thinning) prior to the development of a spinning peak. A similar calculation for oblate spheroids with smaller aspect ratios shows a monotonic shear thinning; the viscosity coefficient here is plotted against
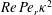 $Re\,Pe_{r}{\it\kappa}^{2}$
, this being the actual ratio of drift to diffusion for
$Re\,Pe_{r}{\it\kappa}^{2}$
, this being the actual ratio of drift to diffusion for
![]() ${\it\kappa}\ll 1$
. For the prolate case, the viscosity coefficient again rises monotonically to the inertial high-shear plateau for all aspect ratios examined. For higher shear rates,
${\it\kappa}\ll 1$
. For the prolate case, the viscosity coefficient again rises monotonically to the inertial high-shear plateau for all aspect ratios examined. For higher shear rates,
![]() $Re$
would be of order unity or larger, and the rheology will begin to be influenced by the finite-
$Re$
would be of order unity or larger, and the rheology will begin to be influenced by the finite-
![]() $Re$
bifurcations that have been identified in numerical simulations. Depending on
$Re$
bifurcations that have been identified in numerical simulations. Depending on
![]() $Re$
as well as the aspect ratio, the suspension can exhibit shear thickening as well as shear-thinning behaviour (Rosen et al.
Reference Rosen, Do-Quang, Aidun and Lundell2015). It is important to note that the presence of multiple attractors at finite
$Re$
as well as the aspect ratio, the suspension can exhibit shear thickening as well as shear-thinning behaviour (Rosen et al.
Reference Rosen, Do-Quang, Aidun and Lundell2015). It is important to note that the presence of multiple attractors at finite
![]() $Re$
would again point to the role of stochastic orientation fluctuations in establishing a steady-state rheology.
$Re$
would again point to the role of stochastic orientation fluctuations in establishing a steady-state rheology.

Figure 23. (a) Schematic of the expected variation of intrinsic viscosity for a suspension of Brownian prolate spheroids. (b) Variation of the viscosity, scaled with
![]() $nd^{3}{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}$
, with
$nd^{3}{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}$
, with
![]() $Re\,Pe_{r}$
. The dotted lines in (b) are the
$Re\,Pe_{r}$
. The dotted lines in (b) are the
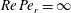 $Re\,Pe_{r}=\infty$
asymptotes.
$Re\,Pe_{r}=\infty$
asymptotes.

Figure 24. (a) Schematic of the expected variation of intrinsic viscosity for a suspension of Brownian oblate spheroids. (b),(c) Magnified view and full view, respectively, of the variation of the viscosity, scaled with
![]() $nd^{3}{\it\xi}_{0}^{3}$
, with
$nd^{3}{\it\xi}_{0}^{3}$
, with
![]() $Re\,Pe_{r}$
for aspect ratios greater than the critical aspect ratio of 0.0126. (d) Variation of the viscosity, scaled with
$Re\,Pe_{r}$
for aspect ratios greater than the critical aspect ratio of 0.0126. (d) Variation of the viscosity, scaled with
![]() $nd^{3}{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}$
, with
$nd^{3}{\it\xi}_{0}^{2}\bar{{\it\xi}}_{0}$
, with
![]() $Re\,Pe_{r}$
for aspect ratios smaller than the critical aspect ratio of 0.0126. An aspect ratio greater than the critical aspect ratio is also included in the lower plot. The dotted lines in (b)–(d) are the
$Re\,Pe_{r}$
for aspect ratios smaller than the critical aspect ratio of 0.0126. An aspect ratio greater than the critical aspect ratio is also included in the lower plot. The dotted lines in (b)–(d) are the
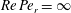 $Re\,Pe_{r}=\infty$
asymptotes.
$Re\,Pe_{r}=\infty$
asymptotes.
Finally, we note that a very recent work (Einarsson et al.
Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015a
,Reference Einarsson, Candelier, Lundell, Angilella and Mehlig
b
) has also investigated the effect of weak fluid inertia on spheroidal particles of arbitrary aspect ratio. The reciprocal theorem volume integral for the rate of change of the orientation vector of the spheroid is written in a general tensorial form, and is evaluated after applying symmetry arguments to reduce it to a set of four scalar integrals. The authors investigate the stability of the spinning and tumbling modes for both prolate and oblate spheroids and arrive at the same conclusions as the present work with respect to the stability of the tumbling and log-rolling/spinning modes. As explained above, the results of the present effort are based on a novel spheroidal harmonics formalism which is significantly broader in scope. As mentioned in Dabade et al. (Reference Dabade, Marath and Subramanian2015), this formalism, with the aid of addition theorems, may be extended to multiple interacting spheroids. We provide closed-form expressions for the aspect-ratio-dependent functions present in the expressions for the inertial angular velocities. Aside from detailed scaling arguments in all relevant asymptotic limits, the effect of inertia is interpreted here in terms of a physically significant orbital drift. Importantly, the consequences for a unique steady-state rheology are also explored. For oblate spheroids, the interpretation in terms of an orbital drift competing with thermal fluctuations may, in fact, be given a more profound interpretation. The small-
![]() $C$
and large-
$C$
and large-
![]() $C$
orbits may be interpreted as orientationally ordered phases that determine the two-phase envelope region (ending in a critical point) in a non-equilibrium phase diagram. Here, the spheroid aspect ratio plays the role of a pressure, the normalized orbit constant replaces the specific volume, and
$C$
orbits may be interpreted as orientationally ordered phases that determine the two-phase envelope region (ending in a critical point) in a non-equilibrium phase diagram. Here, the spheroid aspect ratio plays the role of a pressure, the normalized orbit constant replaces the specific volume, and
![]() $Re\,Pe_{r}$
plays the role of an inverse non-equilibrium temperature.
$Re\,Pe_{r}$
plays the role of an inverse non-equilibrium temperature.
Appendix A. The Kushch and Chwang & Wu velocity fields
Herein, we show that the expressions for the disturbance velocity fields given in § 3, in terms of the spheroidal vector harmonic functions, are identical to those derived earlier by Chwang & Wu (Reference Chwang and Wu1974, Reference Chwang and Wu1975) and Chwang (Reference Chwang1975), using the method of singularities, for a prolate spheroid of an arbitrary aspect ratio. We consider the different canonical motions of the spheroid involved in the reciprocal theorem formulation (axisymmetric, longitudinal and transverse extensional flows in the actual problem and rotations in the test problem) in sequence.
A.1 Axisymmetric extensional flow
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid with its major axis along the
![]() $z$
-axis in an axisymmetric extensional flow given by
$z$
-axis in an axisymmetric extensional flow given by
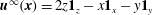 $\boldsymbol{u}^{\infty }(\boldsymbol{x})=2z\mathbf{1}_{z}-x\mathbf{1}_{x}-y\mathbf{1}_{y}$
:
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=2z\mathbf{1}_{z}-x\mathbf{1}_{x}-y\mathbf{1}_{y}$
:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \mathbf{1}_{z}2\left[2({\it\alpha}_{5}+6{\it\beta}_{5})zB_{1,0}-({\it\alpha}_{5}+4{\it\beta}_{5})(R_{1}-R_{2})\left(3+\frac{a^{2}e^{2}}{R_{1}R_{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\it\alpha}_{5}aez\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right]-(x\mathbf{1}_{x}+y\mathbf{1}_{y}){\it\rho}\left[2({\it\alpha}_{5}+6{\it\beta}_{5})\!\left(B_{1,0}-ae\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4{\it\beta}_{5}\left(3z\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)+(a^{2}e^{2}-3z^{2})B_{3,0}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \mathbf{1}_{z}2\left[2({\it\alpha}_{5}+6{\it\beta}_{5})zB_{1,0}-({\it\alpha}_{5}+4{\it\beta}_{5})(R_{1}-R_{2})\left(3+\frac{a^{2}e^{2}}{R_{1}R_{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\it\alpha}_{5}aez\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right]-(x\mathbf{1}_{x}+y\mathbf{1}_{y}){\it\rho}\left[2({\it\alpha}_{5}+6{\it\beta}_{5})\!\left(B_{1,0}-ae\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4{\it\beta}_{5}\left(3z\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)+(a^{2}e^{2}-3z^{2})B_{3,0}\right)\right],\end{eqnarray}$$
where
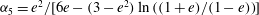 ${\it\alpha}_{5}=e^{2}/[6e-(3-e^{2})\ln ((1+e)/(1-e))]$
and
${\it\alpha}_{5}=e^{2}/[6e-(3-e^{2})\ln ((1+e)/(1-e))]$
and
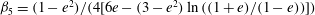 ${\it\beta}_{5}=(1-e^{2})/(4[6e-(3-e^{2})\ln ((1+e)/(1-e))])$
and
${\it\beta}_{5}=(1-e^{2})/(4[6e-(3-e^{2})\ln ((1+e)/(1-e))])$
and
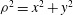 ${\it\rho}^{2}=x^{2}+y^{2}$
. Further,
${\it\rho}^{2}=x^{2}+y^{2}$
. Further,
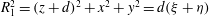 $R_{1}^{2}=(z+d)^{2}+x^{2}+y^{2}=d({\it\xi}+{\it\eta})$
,
$R_{1}^{2}=(z+d)^{2}+x^{2}+y^{2}=d({\it\xi}+{\it\eta})$
,
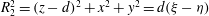 $R_{2}^{2}=(z-d)^{2}+x^{2}+y^{2}=d({\it\xi}-{\it\eta})$
and
$R_{2}^{2}=(z-d)^{2}+x^{2}+y^{2}=d({\it\xi}-{\it\eta})$
and
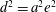 $d^{2}=a^{2}e^{2}$
. The functions
$d^{2}=a^{2}e^{2}$
. The functions
![]() $B_{m,n}$
are defined via the recurrence relation
$B_{m,n}$
are defined via the recurrence relation
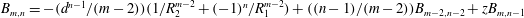 $B_{m,n}=-(d^{n-1}/(m-2))(1/R_{2}^{m-2}+(-1)^{n}/R_{1}^{m-2})+((n-1)/(m-2))B_{m-2,n-2}+zB_{m,n-1}$
. Using this relation, and the expressions for
$B_{m,n}=-(d^{n-1}/(m-2))(1/R_{2}^{m-2}+(-1)^{n}/R_{1}^{m-2})+((n-1)/(m-2))B_{m-2,n-2}+zB_{m,n-1}$
. Using this relation, and the expressions for
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
above, in terms of the spheroidal coordinates, one finds
$R_{2}$
above, in terms of the spheroidal coordinates, one finds
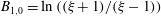 $B_{1,0}=\ln (({\it\xi}+1)/({\it\xi}-1))$
and
$B_{1,0}=\ln (({\it\xi}+1)/({\it\xi}-1))$
and
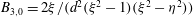 $B_{3,0}=2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2}))$
. The axial component of the disturbance field in (A 1) is given by:
$B_{3,0}=2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2}))$
. The axial component of the disturbance field in (A 1) is given by:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=2\left[2({\it\alpha}_{5}+6{\it\beta}_{5})zB_{1,0}-({\it\alpha}_{5}+4{\it\beta}_{5})(R_{1}-R_{2})\left(3+\frac{a^{2}e^{2}}{R_{1}R_{2}}\right)+{\it\alpha}_{5}aez\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right].\hspace{-6.0pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=2\left[2({\it\alpha}_{5}+6{\it\beta}_{5})zB_{1,0}-({\it\alpha}_{5}+4{\it\beta}_{5})(R_{1}-R_{2})\left(3+\frac{a^{2}e^{2}}{R_{1}R_{2}}\right)+{\it\alpha}_{5}aez\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right].\hspace{-6.0pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Using
![]() $e=1/{\it\xi}_{0}$
, and expressing
$e=1/{\it\xi}_{0}$
, and expressing
![]() ${\it\alpha}_{1}$
and
${\it\alpha}_{1}$
and
![]() ${\it\beta}_{1}$
in terms of
${\it\beta}_{1}$
in terms of
![]() ${\it\xi}_{0}$
, and by expressing
${\it\xi}_{0}$
, and by expressing
![]() $R_{1},R_{2}$
and
$R_{1},R_{2}$
and
![]() $B_{1,0}$
in terms of
$B_{1,0}$
in terms of
![]() ${\it\xi}$
, after some simplification one finds:
${\it\xi}$
, after some simplification one finds:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[\frac{-{\it\eta}}{2}\left(\frac{2{\it\xi}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}-{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{{\it\eta}{\it\xi}_{0}^{2}}{2}\left(3{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}-2\left(3+\frac{1}{{\it\xi}^{2}-{\it\eta}^{2}}\right)\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[\frac{-{\it\eta}}{2}\left(\frac{2{\it\xi}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}-{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{{\it\eta}{\it\xi}_{0}^{2}}{2}\left(3{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}-2\left(3+\frac{1}{{\it\xi}^{2}-{\it\eta}^{2}}\right)\right)\right].\end{eqnarray}$$
Next, using the expressions for the
![]() $P_{t}^{s}$
and
$P_{t}^{s}$
and
![]() $Q_{t}^{s}$
, the terms in the above parentheses may be written as:
$Q_{t}^{s}$
, the terms in the above parentheses may be written as:
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \frac{-{\it\eta}}{2}\left(\frac{2{\it\xi}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}-{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\\ \quad \displaystyle =d{\it\xi}{\it\eta}\left(\frac{{\it\eta}({\it\xi}^{2}-1)}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{1}^{0}({\it\eta})Q_{1}^{0}({\it\xi}),\\ \displaystyle \frac{-{\it\eta}{\it\xi}_{0}^{2}}{2}\left(3{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}-2\left(3+\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right)\\ \quad \displaystyle =-d{\it\xi}_{0}^{2}\left(\frac{{\it\eta}({\it\xi}^{2}-1)}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \frac{-{\it\eta}}{2}\left(\frac{2{\it\xi}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}-{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\\ \quad \displaystyle =d{\it\xi}{\it\eta}\left(\frac{{\it\eta}({\it\xi}^{2}-1)}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{1}^{0}({\it\eta})Q_{1}^{0}({\it\xi}),\\ \displaystyle \frac{-{\it\eta}{\it\xi}_{0}^{2}}{2}\left(3{\it\xi}\ln \frac{{\it\xi}+1}{{\it\xi}-1}-2\left(3+\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right)\\ \quad \displaystyle =-d{\it\xi}_{0}^{2}\left(\frac{{\it\eta}({\it\xi}^{2}-1)}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi}).\end{array}\right\}\end{eqnarray}$$
Reverting back to Cartesian derivatives and using the fact that
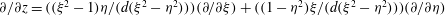 $\partial /\partial z=(({\it\xi}^{2}-1){\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\xi})+((1-{\it\eta}^{2}){\it\xi}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\eta})$
and substituting
$\partial /\partial z=(({\it\xi}^{2}-1){\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\xi})+((1-{\it\eta}^{2}){\it\xi}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\eta})$
and substituting
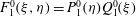 $F_{1}^{0}({\it\xi},{\it\eta})=P_{1}^{0}({\it\eta})Q_{1}^{0}({\it\xi})$
, one may write (A 3) as:
$F_{1}^{0}({\it\xi},{\it\eta})=P_{1}^{0}({\it\eta})Q_{1}^{0}({\it\xi})$
, one may write (A 3) as:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\,[z\text{D}_{3}(F_{1}^{0})-d{\it\xi}_{0}^{2}\text{D}_{3}(F_{2}^{0})]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\,[z\text{D}_{3}(F_{1}^{0})-d{\it\xi}_{0}^{2}\text{D}_{3}(F_{2}^{0})]. & & \displaystyle\end{eqnarray}$$
Now consider the radial component of (A 1), which is given by:
 $$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle -{\it\rho}\left[2({\it\alpha}_{5}+6{\it\beta}_{5})\left(B_{1,0}-ae\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4{\it\beta}_{5}\left(3z\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)+(a^{2}e^{2}-3z^{2})B_{3,0}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle -{\it\rho}\left[2({\it\alpha}_{5}+6{\it\beta}_{5})\left(B_{1,0}-ae\left(\frac{1}{R_{2}}+\frac{1}{R_{1}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4{\it\beta}_{5}\left(3z\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)+(a^{2}e^{2}-3z^{2})B_{3,0}\right)\right].\end{eqnarray}$$
Using the expressions for the
![]() $R_{i}$
and
$R_{i}$
and
![]() $B_{m,n}$
in terms of the spheroidal coordinates, and rewriting
$B_{m,n}$
in terms of the spheroidal coordinates, and rewriting
![]() ${\it\alpha}_{5}$
and
${\it\alpha}_{5}$
and
![]() ${\it\beta}_{5}$
in terms of
${\it\beta}_{5}$
in terms of
![]() ${\it\xi}_{0}$
, after some simplification one finds
${\it\xi}_{0}$
, after some simplification one finds
 $$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[\bar{{\it\xi}}_{0}^{2}\left(3\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}(3({\it\xi}^{2}-{\it\eta}^{2})-2)}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[\bar{{\it\xi}}_{0}^{2}\left(3\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}(3({\it\xi}^{2}-{\it\eta}^{2})-2)}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right].\end{eqnarray}$$
Using the fact that
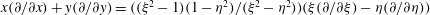 $x(\partial /\partial x)+y(\partial /\partial y)=(({\it\xi}^{2}-1)(1-{\it\eta}^{2})/({\it\xi}^{2}-{\it\eta}^{2}))({\it\xi}(\partial /\partial {\it\xi})-{\it\eta}(\partial /\partial {\it\eta}))$
and
$x(\partial /\partial x)+y(\partial /\partial y)=(({\it\xi}^{2}-1)(1-{\it\eta}^{2})/({\it\xi}^{2}-{\it\eta}^{2}))({\it\xi}(\partial /\partial {\it\xi})-{\it\eta}(\partial /\partial {\it\eta}))$
and
 ${\it\rho}=d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}$
, one can simplify the coefficient of
${\it\rho}=d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}$
, one can simplify the coefficient of
![]() $({\it\xi}_{0}^{2}-1)$
in the above expression as follows:
$({\it\xi}_{0}^{2}-1)$
in the above expression as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\left[({\it\xi}_{0}^{2}-1)\left(3\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}(3({\it\xi}^{2}-{\it\eta}^{2})-2)}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-({\it\xi}_{0}^{2}-1)\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}{{\it\xi}^{2}-{\it\eta}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left({\it\xi}\frac{\partial }{\partial {\it\xi}}-{\it\eta}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi}),\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-({\it\xi}_{0}^{2}-1)}{\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}\right)\left(x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-d({\it\xi}_{0}^{2}-1)}{{\it\rho}}\right)(x\mathbf{1}_{x}+y\mathbf{1}_{y})\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\left[({\it\xi}_{0}^{2}-1)\left(3\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}(3({\it\xi}^{2}-{\it\eta}^{2})-2)}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-({\it\xi}_{0}^{2}-1)\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}{{\it\xi}^{2}-{\it\eta}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left({\it\xi}\frac{\partial }{\partial {\it\xi}}-{\it\eta}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi}),\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-({\it\xi}_{0}^{2}-1)}{\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}}\right)\left(x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}\right)P_{2}^{0}({\it\eta})Q_{2}^{0}({\it\xi})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left(\frac{-d({\it\xi}_{0}^{2}-1)}{{\it\rho}}\right)(x\mathbf{1}_{x}+y\mathbf{1}_{y})\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
One can modify the coefficient multiplying 2 within the parentheses of expression (A 7) using a substitution similar to what was as done in (A 4), and write the following:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[2\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}[{\it\rho}\text{D}_{3}(F_{1}^{0})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[2\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}[{\it\rho}\text{D}_{3}(F_{1}^{0})].\end{eqnarray}$$
Combining (A 8) and (A 9) the total radial velocity is given by:
 $$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[{\it\rho}\text{D}_{3}(F_{1}^{0})-\frac{d({\it\xi}_{0}^{2}-1)}{{\it\rho}}(x\mathbf{1}_{x}+y\mathbf{1}_{y})\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{{\it\rho}}^{\prime CW} & = & \displaystyle \frac{-d\sqrt{{\it\xi}^{2}-1}\sqrt{{\it\eta}^{2}-1}}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[{\it\rho}\text{D}_{3}(F_{1}^{0})-\frac{d({\it\xi}_{0}^{2}-1)}{{\it\rho}}(x\mathbf{1}_{x}+y\mathbf{1}_{y})\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}\right].\end{eqnarray}$$
Summing the expressions in (A 5) and (A 10), gives us the following total disturbance velocity field:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\text{D}_{3}F_{1}^{0}-d\left({\it\xi}_{0}^{2}\text{D}_{3}F_{2}^{0}\mathbf{1}_{z}+({\it\xi}_{0}^{2}-1)\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{-4d}{\left[6{\it\xi}_{0}-(3{\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[\boldsymbol{x}\text{D}_{3}F_{1}^{0}-d\left({\it\xi}_{0}^{2}\text{D}_{3}F_{2}^{0}\mathbf{1}_{z}+({\it\xi}_{0}^{2}-1)\left(\frac{\partial }{\partial x}\mathbf{1}_{x}+\frac{\partial }{\partial y}\mathbf{1}_{y}\right)F_{2}^{0}\right)\right],\end{eqnarray}$$
where
 $\text{D}_{3}=\partial /\partial z$
.
$\text{D}_{3}=\partial /\partial z$
.
From the spheroidal harmonics formalism, the disturbance velocity field is given by (see (3.7)):
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-2d}{[Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})]}\boldsymbol{S}_{2,0}^{(3)}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-2d}{[Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0})]}\boldsymbol{S}_{2,0}^{(3)}, & & \displaystyle\end{eqnarray}$$
where
![]() $\boldsymbol{S}_{2,0}^{(3)}$
, from (3.6) with
$\boldsymbol{S}_{2,0}^{(3)}$
, from (3.6) with
 $t=2,s=0$
, is given by:
$t=2,s=0$
, is given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{S}_{2,0}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}[-(x-\text{i}y)\text{D}_{2}F_{1}^{-1}-d({\it\xi}_{0}^{2}-1)\text{D}_{1}F_{2}^{0}]+\boldsymbol{e}_{2}[(x+\text{i}y)D_{1}F_{1}^{1}-d({\it\xi}_{0}^{2}-1)\text{D}_{2}F_{2}^{0}]\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{1}^{0}-d{\it\xi}_{0}^{2}D_{3}F_{2}^{0}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{S}_{2,0}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}[-(x-\text{i}y)\text{D}_{2}F_{1}^{-1}-d({\it\xi}_{0}^{2}-1)\text{D}_{1}F_{2}^{0}]+\boldsymbol{e}_{2}[(x+\text{i}y)D_{1}F_{1}^{1}-d({\it\xi}_{0}^{2}-1)\text{D}_{2}F_{2}^{0}]\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{1}^{0}-d{\it\xi}_{0}^{2}D_{3}F_{2}^{0}].\end{eqnarray}$$
Using the relations
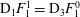 $\text{D}_{1}F_{1}^{1}=\text{D}_{3}F_{1}^{0}$
,
$\text{D}_{1}F_{1}^{1}=\text{D}_{3}F_{1}^{0}$
,
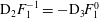 $\text{D}_{2}F_{1}^{-1}=-\text{D}_{3}F_{1}^{0}$
, and the expressions for
$\text{D}_{2}F_{1}^{-1}=-\text{D}_{3}F_{1}^{0}$
, and the expressions for
![]() $\boldsymbol{e}_{1}$
,
$\boldsymbol{e}_{1}$
,
![]() $\boldsymbol{e}_{2}$
,
$\boldsymbol{e}_{2}$
,
![]() $\text{D}_{1}$
and
$\text{D}_{1}$
and
![]() $\text{D}_{2}$
in terms of
$\text{D}_{2}$
in terms of
![]() $\mathbf{1}_{x}$
,
$\mathbf{1}_{x}$
,
![]() $\mathbf{1}_{y}$
,
$\mathbf{1}_{y}$
,
![]() $\partial /\partial x$
and
$\partial /\partial x$
and
![]() $\partial /\partial y$
, the above expression, when substituted in (A 12), reduces to (A 11).
$\partial /\partial y$
, the above expression, when substituted in (A 12), reduces to (A 11).
A.2 Longitudinal extensional flow
The method of singularities yields the following expression for the disturbance velocity field due to a torque-free prolate spheroid placed with its major axis along the
![]() $z$
-axis in a longitudinal extensional flow given by
$z$
-axis in a longitudinal extensional flow given by
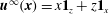 $\boldsymbol{u}^{\infty }(\boldsymbol{x})=x\mathbf{1}_{z}+z\mathbf{1}_{x}$
:
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=x\mathbf{1}_{z}+z\mathbf{1}_{x}$
:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \left({\it\alpha}_{3}-{\it\alpha}_{3}^{\prime }+\frac{e^{2}}{2-e^{2}}({\it\alpha}_{3}+{\it\alpha}_{3}^{\prime })\right)[(2A_{1}+A_{3})\mathbf{1}_{z}+2{\it\rho}\boldsymbol{e}_{{\it\rho}}B_{3,1}]x\nonumber\\ \displaystyle & & \displaystyle +\,4\left({\it\beta}_{3}-{\it\beta}_{3}^{\prime }+\frac{e^{2}}{2-e^{2}}({\it\beta}_{3}+{\it\beta}_{3}^{\prime })\right)\boldsymbol{{\rm\nabla}}[x(d^{2}B_{3,1}-B_{3,3})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \left({\it\alpha}_{3}-{\it\alpha}_{3}^{\prime }+\frac{e^{2}}{2-e^{2}}({\it\alpha}_{3}+{\it\alpha}_{3}^{\prime })\right)[(2A_{1}+A_{3})\mathbf{1}_{z}+2{\it\rho}\boldsymbol{e}_{{\it\rho}}B_{3,1}]x\nonumber\\ \displaystyle & & \displaystyle +\,4\left({\it\beta}_{3}-{\it\beta}_{3}^{\prime }+\frac{e^{2}}{2-e^{2}}({\it\beta}_{3}+{\it\beta}_{3}^{\prime })\right)\boldsymbol{{\rm\nabla}}[x(d^{2}B_{3,1}-B_{3,3})],\end{eqnarray}$$
where
 ${\it\alpha}_{3}=2e^{2}(1-e^{2})[-2e+\ln ((1+e)/(1-e))]/([-2e+(1+e^{2})\ln ((1+e)/(1-e))][2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))])$
,
${\it\alpha}_{3}=2e^{2}(1-e^{2})[-2e+\ln ((1+e)/(1-e))]/([-2e+(1+e^{2})\ln ((1+e)/(1-e))][2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))])$
,
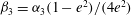 ${\it\beta}_{3}={\it\alpha}_{3}(1-e^{2})/(4e^{2})$
,
${\it\beta}_{3}={\it\alpha}_{3}(1-e^{2})/(4e^{2})$
,
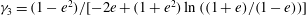 ${\it\gamma}_{3}=(1-e^{2})/[-2e+(1+e^{2})\ln ((1+e)/(1-e))]$
,
${\it\gamma}_{3}=(1-e^{2})/[-2e+(1+e^{2})\ln ((1+e)/(1-e))]$
,
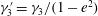 ${\it\gamma}_{3}^{\prime }={\it\gamma}_{3}/(1-e^{2})$
,
${\it\gamma}_{3}^{\prime }={\it\gamma}_{3}/(1-e^{2})$
,
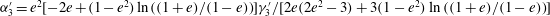 ${\it\alpha}_{3}^{\prime }=e^{2}[-2e+(1-e^{2})\ln ((1+e)/(1-e))]{\it\gamma}_{3}^{\prime }/[2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))]$
and
${\it\alpha}_{3}^{\prime }=e^{2}[-2e+(1-e^{2})\ln ((1+e)/(1-e))]{\it\gamma}_{3}^{\prime }/[2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))]$
and
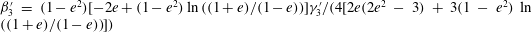 ${\it\beta}_{3}^{\prime }=(1-e^{2})[-2e+(1-e^{2})\ln ((1+e)/(1-e))]{\it\gamma}_{3}^{\prime }/(4[2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))])$
. Writing the
${\it\beta}_{3}^{\prime }=(1-e^{2})[-2e+(1-e^{2})\ln ((1+e)/(1-e))]{\it\gamma}_{3}^{\prime }/(4[2e(2e^{2}-3)+3(1-e^{2})\ln ((1+e)/(1-e))])$
. Writing the
![]() ${\it\alpha}_{i}$
and
${\it\alpha}_{i}$
and
![]() ${\it\beta}_{i}$
in terms of
${\it\beta}_{i}$
in terms of
![]() ${\it\xi}_{0}$
, using
${\it\xi}_{0}$
, using
 $A_{1}=2{\it\xi}/({\it\xi}^{2}-{\it\eta}^{2})$
,
$A_{1}=2{\it\xi}/({\it\xi}^{2}-{\it\eta}^{2})$
,
 $A_{3}=(2{\it\xi}/({\it\xi}^{2}-1))\ln (({\it\xi}+1)/({\it\xi}-1))$
and expanding the
$A_{3}=(2{\it\xi}/({\it\xi}^{2}-1))\ln (({\it\xi}+1)/({\it\xi}-1))$
and expanding the
![]() $B_{m,n}$
in terms of
$B_{m,n}$
in terms of
![]() ${\it\xi}$
the disturbance velocity in (A 15) simplifies to:
${\it\xi}$
the disturbance velocity in (A 15) simplifies to:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{2{\it\xi}_{0}({\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}^{2}-1)\left[2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \,[x[(2A_{1}+A_{3})\mathbf{1}_{z}+2{\it\rho}\boldsymbol{e}_{{\it\rho}}B_{3,1}]+({\it\xi}_{0}^{2}-1)\boldsymbol{{\rm\nabla}}(x(d^{2}B_{3,1}-B_{3,3}))].\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{2{\it\xi}_{0}({\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}^{2}-1)\left[2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln \displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \,[x[(2A_{1}+A_{3})\mathbf{1}_{z}+2{\it\rho}\boldsymbol{e}_{{\it\rho}}B_{3,1}]+({\it\xi}_{0}^{2}-1)\boldsymbol{{\rm\nabla}}(x(d^{2}B_{3,1}-B_{3,3}))].\quad\end{eqnarray}$$
The
![]() $z$
-component of the disturbance velocity in (A 15) is given by:
$z$
-component of the disturbance velocity in (A 15) is given by:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{2{\it\xi}_{0}({\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}^{2}-1)\left[2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[x\left(2A_{1}+A_{3}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}(d^{2}B_{3,1}-B_{3,3})\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{2{\it\xi}_{0}({\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}^{2}-1)\left[2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln {\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \left[x\left(2A_{1}+A_{3}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}(d^{2}B_{3,1}-B_{3,3})\right)\right].\end{eqnarray}$$
One can verify that the term in the parentheses of (A 16) can be written as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle x\left(2A_{1}+A_{3}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}(d^{2}B_{3,1}-B_{3,3})\right)\nonumber\\ \displaystyle & & \displaystyle \quad =2d{\it\xi}{\it\eta}\left(\frac{{\it\eta}(1-{\it\xi}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{2d{\it\xi}_{0}^{2}}{3}\left(\frac{({\it\xi}^{2}-1){\it\eta}}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{(1-{\it\eta}^{2}){\it\xi}}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{1}({\it\eta})Q_{2}^{1}({\it\xi})\cos {\it\phi}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle x\left(2A_{1}+A_{3}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}(d^{2}B_{3,1}-B_{3,3})\right)\nonumber\\ \displaystyle & & \displaystyle \quad =2d{\it\xi}{\it\eta}\left(\frac{{\it\eta}(1-{\it\xi}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{2d{\it\xi}_{0}^{2}}{3}\left(\frac{({\it\xi}^{2}-1){\it\eta}}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}+\frac{(1-{\it\eta}^{2}){\it\xi}}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\right)P_{2}^{1}({\it\eta})Q_{2}^{1}({\it\xi})\cos {\it\phi}.\end{eqnarray}$$
Reverting back to Cartesian derivatives and using the fact that
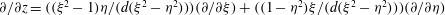 $\partial /\partial z=(({\it\xi}^{2}-1){\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\xi})+((1-{\it\eta}^{2}){\it\xi}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\eta})$
, also noting that
$\partial /\partial z=(({\it\xi}^{2}-1){\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\xi})+((1-{\it\eta}^{2}){\it\xi}/(d({\it\xi}^{2}-{\it\eta}^{2})))(\partial /\partial {\it\eta})$
, also noting that
![]() $z=d{\it\xi}{\it\eta}$
and
$z=d{\it\xi}{\it\eta}$
and
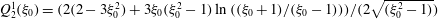 $Q_{2}^{1}({\it\xi}_{0})=(2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln (({\it\xi}_{0}+1)/({\it\xi}_{0}-1)))/(2\sqrt{({\it\xi}_{0}^{2}-1)})$
, the
$Q_{2}^{1}({\it\xi}_{0})=(2(2-3{\it\xi}_{0}^{2})+3{\it\xi}_{0}({\it\xi}_{0}^{2}-1)\ln (({\it\xi}_{0}+1)/({\it\xi}_{0}-1)))/(2\sqrt{({\it\xi}_{0}^{2}-1)})$
, the
![]() $z$
-component can be written as:
$z$
-component can be written as:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=\frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(Q_{2}^{1}({\it\xi}_{0})2{\it\xi}_{0}^{2}-1)}\left[z\frac{\partial }{\partial z}P_{1}^{1}Q_{1}^{1}\cos {\it\phi}-\frac{d{\it\xi}_{0}^{2}}{3}\frac{\partial }{\partial z}P_{2}^{1}Q_{2}^{1}\cos {\it\phi}\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW}=\frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(Q_{2}^{1}({\it\xi}_{0})2{\it\xi}_{0}^{2}-1)}\left[z\frac{\partial }{\partial z}P_{1}^{1}Q_{1}^{1}\cos {\it\phi}-\frac{d{\it\xi}_{0}^{2}}{3}\frac{\partial }{\partial z}P_{2}^{1}Q_{2}^{1}\cos {\it\phi}\right]. & & \displaystyle\end{eqnarray}$$
We now match the reminder of the disturbance velocity
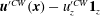 $\boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z}$
, which can be written as follows:
$\boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z}$
, which can be written as follows:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z} & = & \displaystyle \frac{2{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\vphantom{\left(\frac{\partial }{\partial y}\right)}2x^{2}B_{3,1}\mathbf{1}_{x}+2xyB_{3,1}\mathbf{1}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.({\it\xi}_{0}^{2}-1)\left(\frac{\partial }{\partial x}(xd^{2}B_{3,1}-xB_{3,3})\mathbf{1}_{x}+\frac{\partial }{\partial y}(xd^{2}B_{3,1}-xB_{3,3})\mathbf{1}_{y}\right)\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z} & = & \displaystyle \frac{2{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\vphantom{\left(\frac{\partial }{\partial y}\right)}2x^{2}B_{3,1}\mathbf{1}_{x}+2xyB_{3,1}\mathbf{1}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.({\it\xi}_{0}^{2}-1)\left(\frac{\partial }{\partial x}(xd^{2}B_{3,1}-xB_{3,3})\mathbf{1}_{x}+\frac{\partial }{\partial y}(xd^{2}B_{3,1}-xB_{3,3})\mathbf{1}_{y}\right)\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We use the following formulae to simplify (A 19):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x^{2}B_{3,1}=\frac{2d{\it\eta}({\it\eta}^{2}-1)\cos ^{2}{\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}=xd\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\\ \displaystyle xyB_{3,1}=\frac{2d{\it\eta}({\it\eta}^{2}-1)\cos {\it\phi}\sin {\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}=yd\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\\ \displaystyle x(d^{2}B_{3,1}-B_{3,3})=-{\textstyle \frac{2}{3}}d^{2}P_{2}^{1}Q_{2}^{1}\cos {\it\phi}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x^{2}B_{3,1}=\frac{2d{\it\eta}({\it\eta}^{2}-1)\cos ^{2}{\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}=xd\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\\ \displaystyle xyB_{3,1}=\frac{2d{\it\eta}({\it\eta}^{2}-1)\cos {\it\phi}\sin {\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}=yd\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi}),\\ \displaystyle x(d^{2}B_{3,1}-B_{3,3})=-{\textstyle \frac{2}{3}}d^{2}P_{2}^{1}Q_{2}^{1}\cos {\it\phi}.\end{array}\right\}\end{eqnarray}$$
With these substitutions
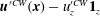 $\boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z}$
simplifies to:
$\boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z}$
simplifies to:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z} & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[x\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\mathbf{1}_{x}+y\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\mathbf{1}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\frac{\partial }{\partial x}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\mathbf{1}_{x}+\frac{\partial }{\partial y}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\mathbf{1}_{y}\right)\right].\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})-u_{z}^{\prime CW}\mathbf{1}_{z} & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[x\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\mathbf{1}_{x}+y\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\mathbf{1}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\frac{\partial }{\partial x}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\mathbf{1}_{x}+\frac{\partial }{\partial y}(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\mathbf{1}_{y}\right)\right].\qquad\end{eqnarray}$$
Summing up (A 18) and (A 21) we get the total disturbance velocity as:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
From the spheroidal harmonics formalism, the disturbance velocity field is given by (see (3.13)):
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}). & & \displaystyle\end{eqnarray}$$
Again, using the expressions for
![]() $\boldsymbol{S}_{2,1}^{(3)}$
and
$\boldsymbol{S}_{2,1}^{(3)}$
and
![]() $\boldsymbol{S}_{2,-1}^{(3)}$
from (3.6), (A 23) can be written as:
$\boldsymbol{S}_{2,-1}^{(3)}$
from (3.6), (A 23) can be written as:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\mathbf{1}_{x}-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\mathbf{1}_{x}-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
Hence, the expressions in (A 24) and (A 22) are identical.
Similarly, one can show disturbance velocity field, due to a torque-free prolate spheroid placed in a longitudinal extensional flow given by
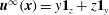 $\boldsymbol{u}^{\infty }(\boldsymbol{x})=y\mathbf{1}_{z}+z\mathbf{1}_{y}$
, is given in terms of the following combination of vector spheroidal harmonics:
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=y\mathbf{1}_{z}+z\mathbf{1}_{y}$
, is given in terms of the following combination of vector spheroidal harmonics:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-\text{i}2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{2,1}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-\text{i}2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}(\boldsymbol{S}_{2,1}^{(3)}+\boldsymbol{S}_{2,-1}^{(3)}). & & \displaystyle\end{eqnarray}$$
Using the expressions for
![]() $\boldsymbol{S}_{2,1}^{(3)}$
and
$\boldsymbol{S}_{2,1}^{(3)}$
and
![]() $\boldsymbol{S}_{2,-1}^{(3)}$
from (3.6), (A 25) simplifies to:
$\boldsymbol{S}_{2,-1}^{(3)}$
from (3.6), (A 25) simplifies to:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\mathbf{1}_{x}-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2d{\it\xi}_{0}\sqrt{{\it\xi}_{0}^{2}-1}}{(2{\it\xi}_{0}^{2}-1)Q_{2}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin {\it\phi})\mathbf{1}_{x}-\frac{d{\it\xi}_{0}^{2}}{3}\left(\mathbf{1}_{z}\frac{\partial }{\partial z}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\sin {\it\phi})\right].\end{eqnarray}$$
A.3 Transverse extensional flow
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid with its major axis along the
![]() $z$
-axis in a transverse extensional flow given by
$z$
-axis in a transverse extensional flow given by
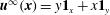 $\boldsymbol{u}^{\infty }(\boldsymbol{x})=y\mathbf{1}_{x}+x\mathbf{1}_{y}$
:
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=y\mathbf{1}_{x}+x\mathbf{1}_{y}$
:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle 2{\it\alpha}_{4}[2xy\,B_{3,1}\mathbf{1}_{z}+3xy{\it\rho}(d^{2}B_{5,0}-B_{5,2})\boldsymbol{e}_{{\it\rho}}]\nonumber\\ \displaystyle & & \displaystyle +\,2\,{\it\beta}_{4}\boldsymbol{{\rm\nabla}}[3x\,y(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle 2{\it\alpha}_{4}[2xy\,B_{3,1}\mathbf{1}_{z}+3xy{\it\rho}(d^{2}B_{5,0}-B_{5,2})\boldsymbol{e}_{{\it\rho}}]\nonumber\\ \displaystyle & & \displaystyle +\,2\,{\it\beta}_{4}\boldsymbol{{\rm\nabla}}[3x\,y(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})],\end{eqnarray}$$
where
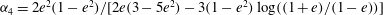 ${\it\alpha}_{4}=2e^{2}(1-e^{2})/[2e(3-5e^{2})-3(1-e^{2})\log ((1+e)/(1-e))]$
,
${\it\alpha}_{4}=2e^{2}(1-e^{2})/[2e(3-5e^{2})-3(1-e^{2})\log ((1+e)/(1-e))]$
,
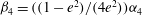 ${\it\beta}_{4}=((1-e^{2})/(4e^{2})){\it\alpha}_{4}$
,
${\it\beta}_{4}=((1-e^{2})/(4e^{2})){\it\alpha}_{4}$
,
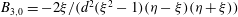 $B_{3,0}=-2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
$B_{3,0}=-2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
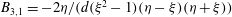 $B_{3,1}=-2{\it\eta}/(d({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
$B_{3,1}=-2{\it\eta}/(d({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
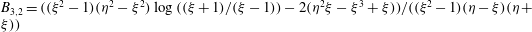 $B_{3,2}=(({\it\xi}^{2}-1)({\it\eta}^{2}-{\it\xi}^{2})\log (({\it\xi}+1)/({\it\xi}-1))-2({\it\eta}^{2}{\it\xi}-{\it\xi}^{3}+{\it\xi}))/(({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
$B_{3,2}=(({\it\xi}^{2}-1)({\it\eta}^{2}-{\it\xi}^{2})\log (({\it\xi}+1)/({\it\xi}-1))-2({\it\eta}^{2}{\it\xi}-{\it\xi}^{3}+{\it\xi}))/(({\it\xi}^{2}-1)({\it\eta}-{\it\xi})({\it\eta}+{\it\xi}))$
,
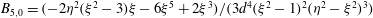 $B_{5,0}=(-2{\it\eta}^{2}({\it\xi}^{2}-3){\it\xi}-6{\it\xi}^{5}+2{\it\xi}^{3})/(3d^{4}({\it\xi}^{2}-1)^{2}({\it\eta}^{2}-{\it\xi}^{2})^{3})$
,
$B_{5,0}=(-2{\it\eta}^{2}({\it\xi}^{2}-3){\it\xi}-6{\it\xi}^{5}+2{\it\xi}^{3})/(3d^{4}({\it\xi}^{2}-1)^{2}({\it\eta}^{2}-{\it\xi}^{2})^{3})$
,
 $B_{5,4}=(1/3)((2{\it\xi}({\it\eta}^{6}(5-3{\it\xi}^{2})+{\it\eta}^{4}(9{\it\xi}^{4}-15{\it\xi}^{2}+4)+{\it\eta}^{2}(-9{\it\xi}^{6}+15{\it\xi}^{4}-9{\it\xi}^{2}+3)+3{\it\xi}^{8}-5{\it\xi}^{6}+{\it\xi}^{4}+{\it\xi}^{2}))/(({\it\xi}^{2}-1)^{2}({\it\eta}-{\it\xi})^{3}({\it\eta}+{\it\xi})^{3})+3\log (({\it\xi}+1)/({\it\xi}-1)))$
and
$B_{5,4}=(1/3)((2{\it\xi}({\it\eta}^{6}(5-3{\it\xi}^{2})+{\it\eta}^{4}(9{\it\xi}^{4}-15{\it\xi}^{2}+4)+{\it\eta}^{2}(-9{\it\xi}^{6}+15{\it\xi}^{4}-9{\it\xi}^{2}+3)+3{\it\xi}^{8}-5{\it\xi}^{6}+{\it\xi}^{4}+{\it\xi}^{2}))/(({\it\xi}^{2}-1)^{2}({\it\eta}-{\it\xi})^{3}({\it\eta}+{\it\xi})^{3})+3\log (({\it\xi}+1)/({\it\xi}-1)))$
and
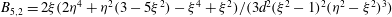 $B_{5,2}=2{\it\xi}(2{\it\eta}^{4}+{\it\eta}^{2}(3-5{\it\xi}^{2})-{\it\xi}^{4}+{\it\xi}^{2})/(3d^{2}({\it\xi}^{2}-1)^{2}({\it\eta}^{2}-{\it\xi}^{2})^{3})$
. Writing
$B_{5,2}=2{\it\xi}(2{\it\eta}^{4}+{\it\eta}^{2}(3-5{\it\xi}^{2})-{\it\xi}^{4}+{\it\xi}^{2})/(3d^{2}({\it\xi}^{2}-1)^{2}({\it\eta}^{2}-{\it\xi}^{2})^{3})$
. Writing
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
in terms of
${\it\beta}$
in terms of
![]() ${\it\xi}_{0}$
the disturbance velocity field takes the form:
${\it\xi}_{0}$
the disturbance velocity field takes the form:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle -\frac{({{\it\xi}_{0}}^{2}-1)^{3}[2xy\,B_{3,1}\mathbf{1}_{z}+3xy{\it\rho}(d^{2}B_{5,0}-B_{5,2})\boldsymbol{e}_{{\it\rho}}]}{2\left(4{\it\xi}_{0}(5-3{{\it\xi}_{0}}^{2})+6({{\it\xi}_{0}}^{2}-1)^{2}\log \left(\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right)\right)}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{({{\it\xi}_{0}}^{2}-1)^{2}}{-3{{\it\xi}_{0}}^{3}+3({{\it\xi}_{0}}^{2}-1)^{2}\coth ^{-1}({\it\xi}_{0})+5{\it\xi}_{0}}\boldsymbol{{\rm\nabla}}[3x\,y\,(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle -\frac{({{\it\xi}_{0}}^{2}-1)^{3}[2xy\,B_{3,1}\mathbf{1}_{z}+3xy{\it\rho}(d^{2}B_{5,0}-B_{5,2})\boldsymbol{e}_{{\it\rho}}]}{2\left(4{\it\xi}_{0}(5-3{{\it\xi}_{0}}^{2})+6({{\it\xi}_{0}}^{2}-1)^{2}\log \left(\displaystyle \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right)\right)}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{({{\it\xi}_{0}}^{2}-1)^{2}}{-3{{\it\xi}_{0}}^{3}+3({{\it\xi}_{0}}^{2}-1)^{2}\coth ^{-1}({\it\xi}_{0})+5{\it\xi}_{0}}\boldsymbol{{\rm\nabla}}[3x\,y\,(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We observe that the terms in the square brackets of (A 28) can be written as follows:
 $$\begin{eqnarray}\displaystyle 2B_{3,1}xy & = & \displaystyle \text{d}z\left(\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d^{2}}{12}\frac{\partial }{\partial z}(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2B_{3,1}xy & = & \displaystyle \text{d}z\left(\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d^{2}}{12}\frac{\partial }{\partial z}(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle 3xy(d^{2}B_{5,0}-B_{5,2})=d\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+d\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi}) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 3xy(d^{2}B_{5,0}-B_{5,2})=d\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+d\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi}) & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle 3xy(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})=\frac{d^{2}}{3}P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 3xy(d^{4}B_{5,0}+B_{5,4}-2d^{2}B_{5,2})=\frac{d^{2}}{3}P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi}. & \displaystyle\end{eqnarray}$$
Rearranging the expression on the right-hand side of (A 28) by using expressions in (A 30), (A 31) and (A 29) and defining
![]() $K_{3}$
as
$K_{3}$
as
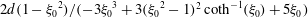 $2d(1-{\it\xi}_{0}^{2})/(-3{{\it\xi}_{0}}^{3}+3({{\it\xi}_{0}}^{2}-1)^{2}\coth ^{-1}({\it\xi}_{0})+5{\it\xi}_{0})$
, the disturbance velocity field can be written as:
$2d(1-{\it\xi}_{0}^{2})/(-3{{\it\xi}_{0}}^{3}+3({{\it\xi}_{0}}^{2}-1)^{2}\coth ^{-1}({\it\xi}_{0})+5{\it\xi}_{0})$
, the disturbance velocity field can be written as:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle K_{3}\left((x\mathbf{1}_{x}+y\mathbf{1}_{y}+z\mathbf{1}_{z})\left(\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d({\it\xi}_{0}^{2}-1)}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi})\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi})\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle K_{3}\left((x\mathbf{1}_{x}+y\mathbf{1}_{y}+z\mathbf{1}_{z})\left(\frac{\partial }{\partial x}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\sin {\it\phi})+\frac{\partial }{\partial y}(P_{1}^{1}({\it\eta})Q_{1}^{1}({\it\xi})\cos {\it\phi})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d({\it\xi}_{0}^{2}-1)}{12}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi})\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{d{\it\xi}_{0}^{2}}{12}\mathbf{1}_{z}\frac{\partial }{\partial z}(P_{2}^{2}({\it\eta})Q_{2}^{2}({\it\xi})\sin 2{\it\phi})\right).\end{eqnarray}$$
Using the expressions for
![]() $\boldsymbol{S}_{2,2}^{(3)}$
and
$\boldsymbol{S}_{2,2}^{(3)}$
and
![]() $\boldsymbol{S}_{2,-2}^{(3)}$
from (3.6) and with some simplification of
$\boldsymbol{S}_{2,-2}^{(3)}$
from (3.6) and with some simplification of
![]() $K_{3}$
, we see that:
$K_{3}$
, we see that:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{2\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{22}^{(3)}-\boldsymbol{S}_{2,-2}^{(3)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{2\text{i}d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{22}^{(3)}-\boldsymbol{S}_{2,-2}^{(3)}). & & \displaystyle\end{eqnarray}$$
We see that the above expression (A 33) is the same as the disturbance velocity field due to transverse extensional flow as given in (3.11), with prefactor
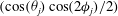 $(\cos ({\it\theta}_{j})\cos (2{\it\phi}_{j})/2)$
due to the flow set to 1.
$(\cos ({\it\theta}_{j})\cos (2{\it\phi}_{j})/2)$
due to the flow set to 1.
Similarly, one can show disturbance velocity field, due to a torque-free prolate spheroid placed in a transverse extensional flow given by
 $\boldsymbol{u}^{\infty }(\boldsymbol{x})=-x\mathbf{1}_{x}+y\mathbf{1}_{y}$
, is given in terms of the following combination of vector spheroidal harmonics:
$\boldsymbol{u}^{\infty }(\boldsymbol{x})=-x\mathbf{1}_{x}+y\mathbf{1}_{y}$
, is given in terms of the following combination of vector spheroidal harmonics:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{22}^{(3)}+\boldsymbol{S}_{2,-2}^{(3)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\frac{-2d\bar{{\it\xi}}_{0}}{(3Q_{1}^{1}({\it\xi}_{0})-{\it\xi}_{0}Q_{2}^{1}({\it\xi}_{0}))}(\boldsymbol{S}_{22}^{(3)}+\boldsymbol{S}_{2,-2}^{(3)}). & & \displaystyle\end{eqnarray}$$
A.4 Axisymmetric rotation about the symmetry axis of the spheroid
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid with its major axis along the
![]() $z$
-axis and rotating about its axis of symmetry:
$z$
-axis and rotating about its axis of symmetry:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})={\it\beta}_{0}\frac{1}{{\it\rho}}\left((d-z)R_{1}+(d+z)R_{2}+{\it\rho}^{2}\log \left(\frac{R_{1}-z-d}{R_{2}-z+d}\right)\right)(-\sin {\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y}),\hspace{-12.0pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})={\it\beta}_{0}\frac{1}{{\it\rho}}\left((d-z)R_{1}+(d+z)R_{2}+{\it\rho}^{2}\log \left(\frac{R_{1}-z-d}{R_{2}-z+d}\right)\right)(-\sin {\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y}),\hspace{-12.0pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
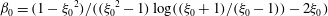 ${\it\beta}_{0}=(1-{{\it\xi}_{0}}^{2})/(({{\it\xi}_{0}}^{2}-1)\log (({\it\xi}_{0}+1)/({\it\xi}_{0}-1))-2{\it\xi}_{0})$
. The right-hand side of (A 35) can be simplified by noting that
${\it\beta}_{0}=(1-{{\it\xi}_{0}}^{2})/(({{\it\xi}_{0}}^{2}-1)\log (({\it\xi}_{0}+1)/({\it\xi}_{0}-1))-2{\it\xi}_{0})$
. The right-hand side of (A 35) can be simplified by noting that
 $R_{1}=d({\it\xi}+{\it\eta})$
and
$R_{1}=d({\it\xi}+{\it\eta})$
and
 $R_{2}=d({\it\xi}-{\it\eta})$
, and this substitution gives us:
$R_{2}=d({\it\xi}-{\it\eta})$
, and this substitution gives us:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})=\frac{d({{\it\xi}_{0}}^{2}-1)\sqrt{\displaystyle \frac{1-{\it\eta}^{2}}{{\it\xi}^{2}-1}}(({\it\xi}^{2}-1)\coth ^{-1}({\it\xi})-{\it\xi})}{({{\it\xi}_{0}}^{2}-1)\coth ^{-1}({\it\xi}_{0})-{\it\xi}_{0}}(-\sin {\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y}),\qquad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x})=\frac{d({{\it\xi}_{0}}^{2}-1)\sqrt{\displaystyle \frac{1-{\it\eta}^{2}}{{\it\xi}^{2}-1}}(({\it\xi}^{2}-1)\coth ^{-1}({\it\xi})-{\it\xi})}{({{\it\xi}_{0}}^{2}-1)\coth ^{-1}({\it\xi}_{0})-{\it\xi}_{0}}(-\sin {\it\phi}\mathbf{1}_{x}+\cos {\it\phi}\mathbf{1}_{y}),\qquad & & \displaystyle\end{eqnarray}$$
which is same as the velocity field obtained by simplifying the expression in equation (3.36), derived using the spheroidal harmonics formalism.
The velocity fields for the two transverse rotations of a spheroid have already been shown to be equivalent to those derived by Chwang and Wu in Dabade et al. (Reference Dabade, Marath and Subramanian2015).
Appendix B. The
 $C{-}{\it\tau}$
coordinate system
$C{-}{\it\tau}$
coordinate system
The details of the
![]() $(C,{\it\tau})$
coordinate system are given below. The orbital coordinates (
$(C,{\it\tau})$
coordinate system are given below. The orbital coordinates (
![]() $C,{\it\tau}$
) are related to spherical coordinate angles,
$C,{\it\tau}$
) are related to spherical coordinate angles,
![]() ${\it\theta}_{j}$
and
${\it\theta}_{j}$
and
![]() ${\it\phi}_{j}$
, as
${\it\phi}_{j}$
, as
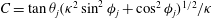 $C=\tan {\it\theta}_{j}({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})^{1/2}/{\it\kappa}$
and
$C=\tan {\it\theta}_{j}({\it\kappa}^{2}\sin ^{2}{\it\phi}_{j}+\cos ^{2}{\it\phi}_{j})^{1/2}/{\it\kappa}$
and
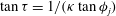 $\tan {\it\tau}=1/({\it\kappa}\tan {\it\phi}_{j})$
. The Jeffery angular velocity components in the
$\tan {\it\tau}=1/({\it\kappa}\tan {\it\phi}_{j})$
. The Jeffery angular velocity components in the
![]() $(C,{\it\tau})$
coordinate system are given by
$(C,{\it\tau})$
coordinate system are given by
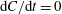 $\text{d}C/\text{d}t=0$
and
$\text{d}C/\text{d}t=0$
and
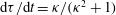 $\text{d}{\it\tau}/\text{d}t={\it\kappa}/({\it\kappa}^{2}+1)$
. The unit vectors
$\text{d}{\it\tau}/\text{d}t={\it\kappa}/({\it\kappa}^{2}+1)$
. The unit vectors
![]() $\hat{\boldsymbol{C}}$
and
$\hat{\boldsymbol{C}}$
and
![]() $\hat{{\bf\tau}}$
are given by
$\hat{{\bf\tau}}$
are given by
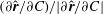 $(\partial \hat{\boldsymbol{r}}/\partial C)/|\partial \hat{\boldsymbol{r}}/\partial C|$
and
$(\partial \hat{\boldsymbol{r}}/\partial C)/|\partial \hat{\boldsymbol{r}}/\partial C|$
and
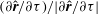 $(\partial \hat{\boldsymbol{r}}/\partial {\it\tau})/|\partial \hat{\boldsymbol{r}}/\partial {\it\tau}|$
respectively, where
$(\partial \hat{\boldsymbol{r}}/\partial {\it\tau})/|\partial \hat{\boldsymbol{r}}/\partial {\it\tau}|$
respectively, where
![]() $\hat{\boldsymbol{r}}$
is the unit radial vector in spherical coordinates (
$\hat{\boldsymbol{r}}$
is the unit radial vector in spherical coordinates (
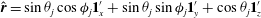 $\hat{\boldsymbol{r}}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }+\cos {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
). The metric factors
$\hat{\boldsymbol{r}}=\sin {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\sin {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }+\cos {\it\theta}_{j}\mathbf{1}_{z}^{\prime }$
). The metric factors
![]() $h_{C}$
and
$h_{C}$
and
![]() $h_{{\it\tau}}$
are given by
$h_{{\it\tau}}$
are given by
![]() $|\partial \hat{\boldsymbol{r}}/\partial C|$
and
$|\partial \hat{\boldsymbol{r}}/\partial C|$
and
![]() $|\partial \hat{\boldsymbol{r}}/\partial {\it\tau}|$
respectively. Simplifying, one gets:
$|\partial \hat{\boldsymbol{r}}/\partial {\it\tau}|$
respectively. Simplifying, one gets:
 $$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{C}}=\cos {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }-\sin {\it\theta}_{j}\mathbf{1}_{z}^{\prime }=\hat{{\bf\theta}_{\boldsymbol{j}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{C}}=\cos {\it\theta}_{j}\cos {\it\phi}_{j}\mathbf{1}_{x}^{\prime }+\cos {\it\theta}_{j}\sin {\it\phi}_{j}\mathbf{1}_{y}^{\prime }-\sin {\it\theta}_{j}\mathbf{1}_{z}^{\prime }=\hat{{\bf\theta}_{\boldsymbol{j}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \hat{{\bf\tau}}=\frac{\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}{\sqrt{\left(\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}\hat{{\bf\theta}_{\boldsymbol{j}}}+\frac{\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\sin {\it\theta}_{j}}{\sqrt{\left(\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}\hat{{\bf\phi}_{\boldsymbol{j}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{{\bf\tau}}=\frac{\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}{\sqrt{\left(\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}\hat{{\bf\theta}_{\boldsymbol{j}}}+\frac{\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\sin {\it\theta}_{j}}{\sqrt{\left(\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}\hat{{\bf\phi}_{\boldsymbol{j}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle h_{C}=\frac{\partial {\it\theta}_{j}}{\partial C}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle h_{C}=\frac{\partial {\it\theta}_{j}}{\partial C}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle h_{{\it\tau}}=\sqrt{\left(\frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle h_{{\it\tau}}=\sqrt{\left(\frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}\right)^{2}+\left(\frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}\right)^{2}\sin ^{2}{\it\theta}_{j}}, & \displaystyle\end{eqnarray}$$
where
![]() $\hat{{\bf\theta}_{\boldsymbol{j}}}$
and
$\hat{{\bf\theta}_{\boldsymbol{j}}}$
and
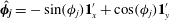 $\hat{{\bf\phi}_{\boldsymbol{j}}}=-\sin ({\it\phi}_{j})\mathbf{1}_{x}^{\prime }+\cos ({\it\phi}_{j})\mathbf{1}_{y}^{\prime }$
are the polar and azimuthal unit vectors in spherical coordinate system, and
$\hat{{\bf\phi}_{\boldsymbol{j}}}=-\sin ({\it\phi}_{j})\mathbf{1}_{x}^{\prime }+\cos ({\it\phi}_{j})\mathbf{1}_{y}^{\prime }$
are the polar and azimuthal unit vectors in spherical coordinate system, and
![]() $\hat{{\bf\tau}}$
is tangent to a Jeffery orbit. The
$\hat{{\bf\tau}}$
is tangent to a Jeffery orbit. The
![]() $(C,{\it\tau})$
is a non-orthogonal coordinate system and the angle(
$(C,{\it\tau})$
is a non-orthogonal coordinate system and the angle(
![]() ${\it\alpha}$
) between the unit vectors
${\it\alpha}$
) between the unit vectors
![]() $\hat{\boldsymbol{C}}$
and
$\hat{\boldsymbol{C}}$
and
![]() $\hat{{\bf\tau}}$
is given by:
$\hat{{\bf\tau}}$
is given by:
 $$\begin{eqnarray}\cos {\it\alpha}=\frac{{\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}}{\sqrt{\left({\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}\right)^{2}+\left({\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}.\end{eqnarray}$$
$$\begin{eqnarray}\cos {\it\alpha}=\frac{{\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}}{\sqrt{\left({\displaystyle \frac{\partial {\it\theta}_{j}}{\partial {\it\tau}}}\right)^{2}+\left({\displaystyle \frac{\partial {\it\phi}_{j}}{\partial {\it\tau}}}\right)^{2}\sin ^{2}{\it\theta}_{j}}}.\end{eqnarray}$$
The
![]() $\hat{{\bf\tau}}$
can then be written as
$\hat{{\bf\tau}}$
can then be written as
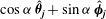 $\cos {\it\alpha}\,\hat{{\bf\theta}_{\boldsymbol{j}}}+\sin {\it\alpha}\,\hat{{\bf\phi}_{\boldsymbol{j}}}$
. The gradient operator in the
$\cos {\it\alpha}\,\hat{{\bf\theta}_{\boldsymbol{j}}}+\sin {\it\alpha}\,\hat{{\bf\phi}_{\boldsymbol{j}}}$
. The gradient operator in the
![]() $(C,{\it\tau})$
coordinate system is given by:
$(C,{\it\tau})$
coordinate system is given by:
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}f=\left(\frac{1}{h_{C}\sin ^{2}{\it\alpha}}\frac{\partial f}{\partial C}-\frac{\cot {\it\alpha}}{h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial f}{\partial {\it\tau}}\right)\hat{\boldsymbol{C}}+\left(\frac{1}{h_{{\it\tau}}\sin ^{2}{\it\alpha}}\frac{\partial f}{\partial {\it\tau}}-\frac{\cot {\it\alpha}}{h_{C}\sin {\it\alpha}}\frac{\partial f}{\partial C}\right)\hat{{\bf\tau}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}f=\left(\frac{1}{h_{C}\sin ^{2}{\it\alpha}}\frac{\partial f}{\partial C}-\frac{\cot {\it\alpha}}{h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial f}{\partial {\it\tau}}\right)\hat{\boldsymbol{C}}+\left(\frac{1}{h_{{\it\tau}}\sin ^{2}{\it\alpha}}\frac{\partial f}{\partial {\it\tau}}-\frac{\cot {\it\alpha}}{h_{C}\sin {\it\alpha}}\frac{\partial f}{\partial C}\right)\hat{{\bf\tau}}.\end{eqnarray}$$
The divergence operator in the
![]() $(C,{\it\tau})$
coordinate system is given by:
$(C,{\it\tau})$
coordinate system is given by:
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial }{\partial C}\left(h_{{\it\tau}}\sin {\it\alpha}\boldsymbol{f}\boldsymbol{\cdot }\hat{\boldsymbol{C}}\right)+\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial }{\partial {\it\tau}}\left(h_{C}\sin {\it\alpha}\boldsymbol{f}\boldsymbol{\cdot }\hat{{\bf\tau}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial }{\partial C}\left(h_{{\it\tau}}\sin {\it\alpha}\boldsymbol{f}\boldsymbol{\cdot }\hat{\boldsymbol{C}}\right)+\frac{1}{h_{C}h_{{\it\tau}}\sin {\it\alpha}}\frac{\partial }{\partial {\it\tau}}\left(h_{C}\sin {\it\alpha}\boldsymbol{f}\boldsymbol{\cdot }\hat{{\bf\tau}}\right).\end{eqnarray}$$
The unit normal vector to a Jeffery orbit (
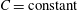 $C=\text{constant}$
) is
$C=\text{constant}$
) is
 $$\begin{eqnarray}\hat{\boldsymbol{n}}=\sin {\it\alpha}\,\hat{{\bf\theta}_{\boldsymbol{j}}}-\cos {\it\alpha}\,\hat{{\bf\phi}_{\boldsymbol{j}}},\end{eqnarray}$$
$$\begin{eqnarray}\hat{\boldsymbol{n}}=\sin {\it\alpha}\,\hat{{\bf\theta}_{\boldsymbol{j}}}-\cos {\it\alpha}\,\hat{{\bf\phi}_{\boldsymbol{j}}},\end{eqnarray}$$
which gives
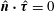 $\hat{\boldsymbol{n}}\boldsymbol{\cdot }\hat{{\bf\tau}}=0$
and
$\hat{\boldsymbol{n}}\boldsymbol{\cdot }\hat{{\bf\tau}}=0$
and
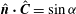 $\hat{\boldsymbol{n}}\boldsymbol{\cdot }\hat{\boldsymbol{C}}=\sin {\it\alpha}$
. Recall that
$\hat{\boldsymbol{n}}\boldsymbol{\cdot }\hat{\boldsymbol{C}}=\sin {\it\alpha}$
. Recall that
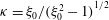 ${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}$
for a prolate spheroid and
${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}$
for a prolate spheroid and
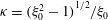 ${\it\kappa}=({\it\xi}_{0}^{2}-1)^{1/2}/{\it\xi}_{0}$
for an oblate spheroid.
${\it\kappa}=({\it\xi}_{0}^{2}-1)^{1/2}/{\it\xi}_{0}$
for an oblate spheroid.
Appendix C. The expressions for the functions
 $I_{i}$
and
$I_{i}$
and
 $J_{i}$
in (5.19)
$J_{i}$
in (5.19)
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{2}=2{\rm\pi}({\it\kappa}-1)({\it\kappa}+1)^{-1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{2}=2{\rm\pi}({\it\kappa}-1)({\it\kappa}+1)^{-1} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{3}=2{\rm\pi}(2((C^{2}+1)(C^{2}{\it\kappa}^{2}+1))^{-1/2}-1) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{3}=2{\rm\pi}(2((C^{2}+1)(C^{2}{\it\kappa}^{2}+1))^{-1/2}-1) & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{4}=2{\rm\pi}({\it\kappa}-1)^{2}({\it\kappa}+1)^{-2} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{4}=2{\rm\pi}({\it\kappa}-1)^{2}({\it\kappa}+1)^{-2} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle I_{5}+I_{6} & = & \displaystyle -\left(4{\rm\pi}\left(2{\it\kappa}^{2}\left(3\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-8C^{2}-6\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,4{\it\kappa}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}+\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\nonumber\\ \displaystyle & & \displaystyle +\,4(4C^{2}+1){\it\kappa}^{3}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\nonumber\\ \displaystyle & & \displaystyle \left.+\left.{\it\kappa}^{4}\left(\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-16(C^{4}+C^{2})-2\right)-2\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(({\it\kappa}^{2}-1)^{2}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\right)^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{5}+I_{6} & = & \displaystyle -\left(4{\rm\pi}\left(2{\it\kappa}^{2}\left(3\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-8C^{2}-6\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,4{\it\kappa}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}+\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\nonumber\\ \displaystyle & & \displaystyle +\,4(4C^{2}+1){\it\kappa}^{3}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\nonumber\\ \displaystyle & & \displaystyle \left.+\left.{\it\kappa}^{4}\left(\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-16(C^{4}+C^{2})-2\right)-2\right)\right)\nonumber\\ \displaystyle & & \displaystyle \times \left(({\it\kappa}^{2}-1)^{2}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\right)^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{1}={\rm\pi}({\it\kappa}-1)({\it\kappa}+1)^{-1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{1}={\rm\pi}({\it\kappa}-1)({\it\kappa}+1)^{-1} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{2}=-{\rm\pi}\left(-4\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}+C^{2}({\it\kappa}+1)^{2}+4\right)C^{-2}({\it\kappa}^{2}-1)^{-1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{2}=-{\rm\pi}\left(-4\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}+C^{2}({\it\kappa}+1)^{2}+4\right)C^{-2}({\it\kappa}^{2}-1)^{-1} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{3}={\rm\pi}({\it\kappa}-1)^{2}({\it\kappa}+1)^{-2} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{3}={\rm\pi}({\it\kappa}-1)^{2}({\it\kappa}+1)^{-2} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle J_{4} & = & \displaystyle -2{\rm\pi}\left(8C^{4}{\it\kappa}^{3}+C^{2}\left(({\it\kappa}+1)^{4}-8{\it\kappa}^{2}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4({\it\kappa}^{2}+1)\left(\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-1\right)\right)C^{-2}({\it\kappa}^{2}-1)^{-2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{4} & = & \displaystyle -2{\rm\pi}\left(8C^{4}{\it\kappa}^{3}+C^{2}\left(({\it\kappa}+1)^{4}-8{\it\kappa}^{2}\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.4({\it\kappa}^{2}+1)\left(\sqrt{(C^{2}+1)(C^{2}{\it\kappa}^{2}+1)}-1\right)\right)C^{-2}({\it\kappa}^{2}-1)^{-2}.\end{eqnarray}$$
Note that only
![]() $I_{5}+I_{6}$
matters since
$I_{5}+I_{6}$
matters since
 $F_{5}^{p}({\it\xi}_{0})=F_{6}^{p}({\it\xi}_{0})$
(see (5.10)) and
$F_{5}^{p}({\it\xi}_{0})=F_{6}^{p}({\it\xi}_{0})$
(see (5.10)) and
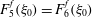 $F_{5}^{f}({\it\xi}_{0})=F_{6}^{f}({\it\xi}_{0})$
(see (6.4)). Recall that
$F_{5}^{f}({\it\xi}_{0})=F_{6}^{f}({\it\xi}_{0})$
(see (6.4)). Recall that
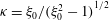 ${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}$
for a prolate spheroid and
${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}$
for a prolate spheroid and
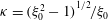 ${\it\kappa}=({\it\xi}_{0}^{2}-1)^{1/2}/{\it\xi}_{0}$
for an oblate spheroid.
${\it\kappa}=({\it\xi}_{0}^{2}-1)^{1/2}/{\it\xi}_{0}$
for an oblate spheroid.
Appendix D. Comparison with previous analytical theories: the near-sphere and flat-disk limits
In the following two subsections, we compare the limiting forms of (5.5) and (5.6) with the aspect-ratio functions defined in §§ 5.1 and 6.1, in the limits
![]() ${\it\xi}_{0}\rightarrow 1$
and
${\it\xi}_{0}\rightarrow 1$
and
![]() ${\it\xi}_{0}\rightarrow \infty$
, to the recent analytical results of Subramanian & Koch (Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
).
${\it\xi}_{0}\rightarrow \infty$
, to the recent analytical results of Subramanian & Koch (Reference Subramanian and Koch2005, Reference Subramanian and Koch2006b
).
D.1 The slender-fibre theory of Subramanian & Koch (Reference Subramanian and Koch2005)
Subramanian & Koch (Reference Subramanian and Koch2005) obtained the
![]() $O(Re)$
drift of a neutrally buoyant slender fibre in simple shear flow, at leading logarithmic order in the aspect ratio, using viscous slender body theory. This was accomplished using a reciprocal theorem formulation with the inertial drift, as in (2.19), being expressible in terms of a volume integral of the inertial acceleration. Since the Stokes disturbance velocity field is only
$O(Re)$
drift of a neutrally buoyant slender fibre in simple shear flow, at leading logarithmic order in the aspect ratio, using viscous slender body theory. This was accomplished using a reciprocal theorem formulation with the inertial drift, as in (2.19), being expressible in terms of a volume integral of the inertial acceleration. Since the Stokes disturbance velocity field is only
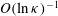 $O(\ln {\it\kappa})^{-1}$
for large aspect ratios, the inertial terms were linearized to leading logarithmic order [
$O(\ln {\it\kappa})^{-1}$
for large aspect ratios, the inertial terms were linearized to leading logarithmic order [
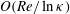 $O(Re/\ln {\it\kappa})$
]. A convolution theorem was then used to write this linearized inertial integral in terms of the corresponding Fourier transformed velocity fields, which are much simpler in form. Further, the unsteady term (
$O(Re/\ln {\it\kappa})$
]. A convolution theorem was then used to write this linearized inertial integral in terms of the corresponding Fourier transformed velocity fields, which are much simpler in form. Further, the unsteady term (
![]() $\partial \boldsymbol{u}^{\prime }/\partial t$
) in Subramanian & Koch (Reference Subramanian and Koch2005) was evaluated in invariant terms, in space-fixed coordinates, using the known expression for
$\partial \boldsymbol{u}^{\prime }/\partial t$
) in Subramanian & Koch (Reference Subramanian and Koch2005) was evaluated in invariant terms, in space-fixed coordinates, using the known expression for
![]() $\dot{\boldsymbol{p}}$
which, at leading logarithmic order in the aspect ratio and in the absence of inertia, describes the meridional trajectories of an infinitely thin fibre [
$\dot{\boldsymbol{p}}$
which, at leading logarithmic order in the aspect ratio and in the absence of inertia, describes the meridional trajectories of an infinitely thin fibre [
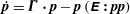 $\dot{\boldsymbol{p}}={\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{p}-\boldsymbol{p}\,(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})$
]. In what follows, we examine briefly the manner in which the slender-fibre drift of Subramanian & Koch (Reference Subramanian and Koch2005) emerges as a special case of (2.30). With the Fourier transform in space-fixed coordinates (
$\dot{\boldsymbol{p}}={\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{p}-\boldsymbol{p}\,(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})$
]. In what follows, we examine briefly the manner in which the slender-fibre drift of Subramanian & Koch (Reference Subramanian and Koch2005) emerges as a special case of (2.30). With the Fourier transform in space-fixed coordinates (
![]() $\boldsymbol{x}_{sp}$
) defined as
$\boldsymbol{x}_{sp}$
) defined as
 $\hat{f}(\boldsymbol{k},t)=\int \text{d}\boldsymbol{x}_{sp}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}_{sp}}f(\boldsymbol{x}_{sp},t)$
, application of the convolution theorem to the volume integral in (2.25) gives:
$\hat{f}(\boldsymbol{k},t)=\int \text{d}\boldsymbol{x}_{sp}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}_{sp}}f(\boldsymbol{x}_{sp},t)$
, application of the convolution theorem to the volume integral in (2.25) gives:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\boldsymbol{u}_{s}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\vphantom{\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle \quad =\int \text{d}\boldsymbol{k}\left[\mathscr{F}\left(\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s}^{\prime (1)}\vphantom{\left(\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}\right)}\right]\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D650}}^{(2)}(-\boldsymbol{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\boldsymbol{u}_{s}^{\prime (1)}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\vphantom{\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D650}^{(2)}\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle \quad =\int \text{d}\boldsymbol{k}\left[\mathscr{F}\left(\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s}^{\prime (1)}\vphantom{\left(\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}\right)}\right]\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D650}}^{(2)}(-\boldsymbol{k}),\end{eqnarray}$$
where recall that
![]() $\boldsymbol{u}_{s}^{\prime (1)}$
is defined in a body-fixed coordinate system rotating with
$\boldsymbol{u}_{s}^{\prime (1)}$
is defined in a body-fixed coordinate system rotating with
![]() ${\it\bf\Omega}_{b}$
and
${\it\bf\Omega}_{b}$
and
![]() $\mathscr{F}$
denotes the Fourier transform of the bracketed expression. In (D 1), we have neglected the
$\mathscr{F}$
denotes the Fourier transform of the bracketed expression. In (D 1), we have neglected the
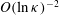 $O(\ln {\it\kappa})^{-2}$
nonlinear inertial term. Unlike the other terms, the Fourier transform of the bracketed expression in (D 1) depends on the choice of space-fixed (
$O(\ln {\it\kappa})^{-2}$
nonlinear inertial term. Unlike the other terms, the Fourier transform of the bracketed expression in (D 1) depends on the choice of space-fixed (
![]() $\boldsymbol{x}_{sp}$
) vis-a-vis body-fixed (
$\boldsymbol{x}_{sp}$
) vis-a-vis body-fixed (
![]() $\boldsymbol{x}$
) coordinates. The relation between the disturbance velocity fields in the two coordinate systems given by
$\boldsymbol{x}$
) coordinates. The relation between the disturbance velocity fields in the two coordinate systems given by
 $\boldsymbol{u}_{s(sp)}^{\prime (1)}(\boldsymbol{x}_{sp},t)=\unicode[STIX]{x1D64D}(t)\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}(\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{x}_{sp},t)$
, with
$\boldsymbol{u}_{s(sp)}^{\prime (1)}(\boldsymbol{x}_{sp},t)=\unicode[STIX]{x1D64D}(t)\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime (1)}(\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{x}_{sp},t)$
, with
 $\boldsymbol{x}=\unicode[STIX]{x1D64D}^{\dagger }\boldsymbol{\cdot }\boldsymbol{x}_{sp}$
defining the space-fixed–body-fixed relation, and
$\boldsymbol{x}=\unicode[STIX]{x1D64D}^{\dagger }\boldsymbol{\cdot }\boldsymbol{x}_{sp}$
defining the space-fixed–body-fixed relation, and
 $\text{d}\unicode[STIX]{x1D64D}/\text{d}t={\it\bf\Omega}_{jeff}^{t}\wedge \unicode[STIX]{x1D64D}$
defining the rotation matrix that relates the space-fixed and body-fixed configurations at time
$\text{d}\unicode[STIX]{x1D64D}/\text{d}t={\it\bf\Omega}_{jeff}^{t}\wedge \unicode[STIX]{x1D64D}$
defining the rotation matrix that relates the space-fixed and body-fixed configurations at time
![]() $t$
. The space-fixed Fourier transform of the aforementioned combination of terms may be written as:
$t$
. The space-fixed Fourier transform of the aforementioned combination of terms may be written as:
 $$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}_{sp}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}_{sp}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}_{sp}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}_{sp}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right]. & & \displaystyle\end{eqnarray}$$
In body-fixed coordinates, one obtains:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \quad =\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \hat{\boldsymbol{u}}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad =\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \hat{\boldsymbol{u}}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)},\end{eqnarray}$$
with
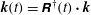 $\boldsymbol{k}(t)=\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{k}$
. We have used
$\boldsymbol{k}(t)=\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{k}$
. We have used
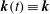 $\boldsymbol{k}(t)\equiv \boldsymbol{k}$
in the second and third terms since the time dependence of the wavevector affects only the first term in (D 4). The first term may now be written in the form:
$\boldsymbol{k}(t)\equiv \boldsymbol{k}$
in the second and third terms since the time dependence of the wavevector affects only the first term in (D 4). The first term may now be written in the form:
 $$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t} & = & \displaystyle \frac{\text{d}}{\text{d}t}\left[\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)}\right]+\boldsymbol{k}^{\prime }(t)\boldsymbol{\cdot }\int \text{d}\boldsymbol{x}(2{\rm\pi}\text{i}\boldsymbol{x})\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)},\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D64D}^{\dagger }}{\text{d}t}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s(sp)}^{\prime (1)}+\unicode[STIX]{x1D64D}^{\dagger }\boldsymbol{\cdot }\frac{\partial \hat{\boldsymbol{u}}_{s(sp)}^{\prime (1)}}{\partial t}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\frac{\partial }{\partial \boldsymbol{k}(t)}\left[\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t} & = & \displaystyle \frac{\text{d}}{\text{d}t}\left[\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)}\right]+\boldsymbol{k}^{\prime }(t)\boldsymbol{\cdot }\int \text{d}\boldsymbol{x}(2{\rm\pi}\text{i}\boldsymbol{x})\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)},\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D64D}^{\dagger }}{\text{d}t}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s(sp)}^{\prime (1)}+\unicode[STIX]{x1D64D}^{\dagger }\boldsymbol{\cdot }\frac{\partial \hat{\boldsymbol{u}}_{s(sp)}^{\prime (1)}}{\partial t}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D64D}^{\dagger }(t)\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\frac{\partial }{\partial \boldsymbol{k}(t)}\left[\int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\boldsymbol{u}_{s}^{\prime (1)}\right].\end{eqnarray}$$
Using
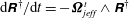 $\text{d}\unicode[STIX]{x1D64D}^{\dagger }/\text{d}t=-{\it\bf\Omega}_{jeff}^{t}\wedge \unicode[STIX]{x1D64D}^{\dagger }$
, and the coincidence of the space-fixed and body-fixed coordinate systems at time
$\text{d}\unicode[STIX]{x1D64D}^{\dagger }/\text{d}t=-{\it\bf\Omega}_{jeff}^{t}\wedge \unicode[STIX]{x1D64D}^{\dagger }$
, and the coincidence of the space-fixed and body-fixed coordinate systems at time
![]() $t$
(so that
$t$
(so that
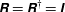 $\unicode[STIX]{x1D64D}=\unicode[STIX]{x1D64D}^{\dagger }=\unicode[STIX]{x1D644}$
), one may drop the additional subscript
$\unicode[STIX]{x1D64D}=\unicode[STIX]{x1D64D}^{\dagger }=\unicode[STIX]{x1D644}$
), one may drop the additional subscript
![]() $^{\prime }sp^{\prime }$
, and (D 5) becomes:
$^{\prime }sp^{\prime }$
, and (D 5) becomes:
 $$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}=\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}-{\it\bf\Omega}_{jeff}^{t}\wedge \hat{\boldsymbol{u}}_{s}^{\prime (1)}+({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}=\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}-{\it\bf\Omega}_{jeff}^{t}\wedge \hat{\boldsymbol{u}}_{s}^{\prime (1)}+({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}, & & \displaystyle\end{eqnarray}$$
so that
 $$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right]=\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{x}\,\text{e}^{-2{\rm\pi}\text{i}\boldsymbol{k}(t)\boldsymbol{\cdot }\boldsymbol{x}}\left[\frac{\partial \boldsymbol{u}_{s}^{\prime (1)}}{\partial t}+{\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{u}_{s}^{\prime (1)}-({\it\bf\Omega}_{jeff}^{t}\wedge \boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{s}^{\prime (1)}\right]=\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}, & & \displaystyle\end{eqnarray}$$
and the Fourier-space integral in (D 1) takes the form:
 $$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{k}\left[\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}-({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s}^{\prime (1)}\right]\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D650}}^{(2)}(-\boldsymbol{k}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \text{d}\boldsymbol{k}\left[\frac{\partial \hat{\boldsymbol{u}}_{s}^{\prime (1)}}{\partial t}-({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ k}}\hat{\boldsymbol{u}}_{s}^{\prime (1)}+{\it\bf\Gamma}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{s}^{\prime (1)}\right]\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D650}}^{(2)}(-\boldsymbol{k}), & & \displaystyle\end{eqnarray}$$
which is precisely the integral that yields the
![]() $O(Re)$
drift for a neutrally buoyant fibre in a simple shear flow. Substitution of the well-known expressions for the transformed fields finally leads to the following orbit equations:
$O(Re)$
drift for a neutrally buoyant fibre in a simple shear flow. Substitution of the well-known expressions for the transformed fields finally leads to the following orbit equations:
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\theta}_{j}}{\text{d}t}=-\frac{7\cos {\it\theta}_{j}\sin ^{2}{\it\phi}_{j}\cos ^{2}{\it\phi}_{j}\sin ^{3}{\it\theta}_{j}}{15\log ({\it\xi}_{0}-1)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\theta}_{j}}{\text{d}t}=-\frac{7\cos {\it\theta}_{j}\sin ^{2}{\it\phi}_{j}\cos ^{2}{\it\phi}_{j}\sin ^{3}{\it\theta}_{j}}{15\log ({\it\xi}_{0}-1)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\phi}_{j}}{\text{d}t}=\frac{(3-7\cos 2{\it\phi}_{j})\cos {\it\phi}_{j}\sin {\it\phi}_{j}\sin ^{2}{\it\theta}_{j}}{30\log ({\it\xi}_{0}-1)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\phi}_{j}}{\text{d}t}=\frac{(3-7\cos 2{\it\phi}_{j})\cos {\it\phi}_{j}\sin {\it\phi}_{j}\sin ^{2}{\it\theta}_{j}}{30\log ({\it\xi}_{0}-1)}, & \displaystyle\end{eqnarray}$$
at leading logarithmic order. It is worth noting that, at
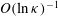 $O(\ln {\it\kappa})^{-1}$
, the disturbance velocity field contributing to the inertial drift only arises on account of the fibre inextensibility, and therefore involves a response to the axisymmetric extensional component of the ambient shear alone. The responses to the longitudinal extensional components are smaller by
$O(\ln {\it\kappa})^{-1}$
, the disturbance velocity field contributing to the inertial drift only arises on account of the fibre inextensibility, and therefore involves a response to the axisymmetric extensional component of the ambient shear alone. The responses to the longitudinal extensional components are smaller by
 $O({\it\xi}_{0}-1)^{1/2}$
, and those to the transverse extensional components are smaller by
$O({\it\xi}_{0}-1)^{1/2}$
, and those to the transverse extensional components are smaller by
 $O({\it\xi}_{0}-1)$
. Thus, only one of the five canonical velocity field components (
$O({\it\xi}_{0}-1)$
. Thus, only one of the five canonical velocity field components (
![]() $\boldsymbol{u}_{1s}$
) detailed in § 3 contributes to the inertial drift. This must remain true to all logarithmic orders, although Subramanian & Koch (Reference Subramanian and Koch2005) only calculated the leading logarithmic order contribution. For slender spheroidal fibres, the drift, to within algebraic errors in the aspect ratio, may be obtained by replacing
$\boldsymbol{u}_{1s}$
) detailed in § 3 contributes to the inertial drift. This must remain true to all logarithmic orders, although Subramanian & Koch (Reference Subramanian and Koch2005) only calculated the leading logarithmic order contribution. For slender spheroidal fibres, the drift, to within algebraic errors in the aspect ratio, may be obtained by replacing
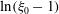 $\ln ({\it\xi}_{0}-1)$
by
$\ln ({\it\xi}_{0}-1)$
by
 $[3-\log (2)+\log ({\it\xi}_{0}-1)]$
in (D 9) and (D 10) above. The results (D 9) and (D 10) match those of Subramanian & Koch (Reference Subramanian and Koch2005) except for a factor of
$[3-\log (2)+\log ({\it\xi}_{0}-1)]$
in (D 9) and (D 10) above. The results (D 9) and (D 10) match those of Subramanian & Koch (Reference Subramanian and Koch2005) except for a factor of
![]() $1/8{\rm\pi}$
, which has been pointed out in Shin, Subramanian & Koch (Reference Shin, Subramanian and Koch2009).
$1/8{\rm\pi}$
, which has been pointed out in Shin, Subramanian & Koch (Reference Shin, Subramanian and Koch2009).
D.2 The near-sphere theory of Subramanian & Koch (Reference Subramanian and Koch2006b )
Subramanian & Koch (Reference Subramanian and Koch2006b
) analysed the leading-order effects of both particle and fluid inertia on the orientation of nearly spherical particles in simple shear flow. Their result for the
![]() $O(St)$
drift induced by particle inertia misses a factor of
$O(St)$
drift induced by particle inertia misses a factor of
![]() $1/2$
in the term multiplying
$1/2$
in the term multiplying
![]() $\cos (2{\it\phi})$
((3.18) in Subramanian & Koch (Reference Subramanian and Koch2006b
)). As seen from the limiting cases considered above, notwithstanding the drift-reversal that occurs close to the flat-disk limit, the direction of the drift of a near-sphere remains the same as that for arbitrary aspect ratios. The authors found fluid inertia to cause a prolate near-sphere to drift towards the vorticity axis at
$\cos (2{\it\phi})$
((3.18) in Subramanian & Koch (Reference Subramanian and Koch2006b
)). As seen from the limiting cases considered above, notwithstanding the drift-reversal that occurs close to the flat-disk limit, the direction of the drift of a near-sphere remains the same as that for arbitrary aspect ratios. The authors found fluid inertia to cause a prolate near-sphere to drift towards the vorticity axis at
![]() $O(Re)$
, with an oblate near-sphere doing the opposite, both occurring on a time scale of
$O(Re)$
, with an oblate near-sphere doing the opposite, both occurring on a time scale of
 $O({\it\epsilon}Re\dot{{\it\gamma}})^{-1}$
; the parameter
$O({\it\epsilon}Re\dot{{\it\gamma}})^{-1}$
; the parameter
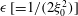 ${\it\epsilon}\,[=1/(2{\it\xi}_{0}^{2})]$
is the deviation from sphericity with the near-sphere described by
${\it\epsilon}\,[=1/(2{\it\xi}_{0}^{2})]$
is the deviation from sphericity with the near-sphere described by
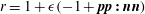 $r=1+{\it\epsilon}(-1+\boldsymbol{p}\boldsymbol{p}\boldsymbol{ : }\boldsymbol{n}\boldsymbol{n})$
. These contradict the results of the analysis given here, and are incorrect. As we show below, the method proposed to calculate the
$r=1+{\it\epsilon}(-1+\boldsymbol{p}\boldsymbol{p}\boldsymbol{ : }\boldsymbol{n}\boldsymbol{n})$
. These contradict the results of the analysis given here, and are incorrect. As we show below, the method proposed to calculate the
![]() $O(Re)$
near-sphere drift is, however, correct, and the error arose in the detailed calculation of the integrals.
$O(Re)$
near-sphere drift is, however, correct, and the error arose in the detailed calculation of the integrals.
The calculation of Subramanian & Koch (Reference Subramanian and Koch2006b
) was again based on a generalized reciprocal theorem formulation. While the actual problem was the free rotation of a near-sphere in a simple shear flow, the test problem was not that of the same near-sphere rotating in a quiescent fluid. To minimize the algebraic complexity, and exploit the known results for the
![]() $O(Re)$
velocity field around a sphere (Lin et al.
Reference Lin, Peery and Schowalter1970; Subramanian & Koch Reference Subramanian and Koch2006a
), the test velocity field was chosen as a composite field, consisting of a rigid-body rotation within a fluid sphere circumscribing the near-sphere, and a rotlet velocity field outside. Such a velocity field can only be maintained by a distribution of forces localized on the surface of the fluid sphere, and the stress field of the test problem is therefore no longer divergence-free (as would be the case for the usual choice of the Stokesian rotation of a near-sphere). The inertial correction to the Jeffery angular velocity involves two integrals, a surface integral arising from the singular force field in the test problem (a delta function) and a volume integral of the inertial forces similar to that in (2.30), and satisfies the relation:
$O(Re)$
velocity field around a sphere (Lin et al.
Reference Lin, Peery and Schowalter1970; Subramanian & Koch Reference Subramanian and Koch2006a
), the test velocity field was chosen as a composite field, consisting of a rigid-body rotation within a fluid sphere circumscribing the near-sphere, and a rotlet velocity field outside. Such a velocity field can only be maintained by a distribution of forces localized on the surface of the fluid sphere, and the stress field of the test problem is therefore no longer divergence-free (as would be the case for the usual choice of the Stokesian rotation of a near-sphere). The inertial correction to the Jeffery angular velocity involves two integrals, a surface integral arising from the singular force field in the test problem (a delta function) and a volume integral of the inertial forces similar to that in (2.30), and satisfies the relation:
 $$\begin{eqnarray}\displaystyle -3\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \{\boldsymbol{u}^{\prime (0)}(\boldsymbol{n})+{\it\epsilon}\boldsymbol{u}^{\prime (1)}(\boldsymbol{n})\}-Re\int \frac{\boldsymbol{r}\wedge \boldsymbol{f}}{r^{3}}\,\text{d}V=0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -3\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \{\boldsymbol{u}^{\prime (0)}(\boldsymbol{n})+{\it\epsilon}\boldsymbol{u}^{\prime (1)}(\boldsymbol{n})\}-Re\int \frac{\boldsymbol{r}\wedge \boldsymbol{f}}{r^{3}}\,\text{d}V=0. & & \displaystyle\end{eqnarray}$$
Here,
![]() $\boldsymbol{f}$
denotes the inertial terms in the equations of motion, and the integral in (D 11) is to be evaluated over the volume outside the near-sphere. The unknown angular velocity enters via the disturbance velocity field (
$\boldsymbol{f}$
denotes the inertial terms in the equations of motion, and the integral in (D 11) is to be evaluated over the volume outside the near-sphere. The unknown angular velocity enters via the disturbance velocity field (
![]() $\boldsymbol{u}^{\prime }$
) in the surface integral – for a sphere in Stokes flow,
$\boldsymbol{u}^{\prime }$
) in the surface integral – for a sphere in Stokes flow,
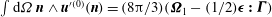 $\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \boldsymbol{u}^{\prime (0)}(\boldsymbol{n})=(8{\rm\pi}/3)({\it\bf\Omega}_{1}-(1/2){\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma})$
, leading to the well-known result of a sphere rotating at a rate commensurate with the ambient vorticity. Since there is no
$\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \boldsymbol{u}^{\prime (0)}(\boldsymbol{n})=(8{\rm\pi}/3)({\it\bf\Omega}_{1}-(1/2){\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma})$
, leading to the well-known result of a sphere rotating at a rate commensurate with the ambient vorticity. Since there is no
![]() $O(Re)$
correction associated with a sphere in simple shear, the inertial angular velocity correction must be
$O(Re)$
correction associated with a sphere in simple shear, the inertial angular velocity correction must be
![]() $O({\it\epsilon}Re)$
; further, from (5.14), it may be shown that, for
$O({\it\epsilon}Re)$
; further, from (5.14), it may be shown that, for
![]() ${\it\xi}_{0}\rightarrow \infty$
, the inertial drift is determined, at
${\it\xi}_{0}\rightarrow \infty$
, the inertial drift is determined, at
![]() $O({\it\xi}_{0}^{-2})$
, by
$O({\it\xi}_{0}^{-2})$
, by
![]() $\text{d}{\it\theta}_{j}/\text{d}t$
with the
$\text{d}{\it\theta}_{j}/\text{d}t$
with the
![]() $O(Re)$
correction to
$O(Re)$
correction to
![]() $\text{d}{\it\phi}_{j}/\text{d}t$
coming in only at
$\text{d}{\it\phi}_{j}/\text{d}t$
coming in only at
![]() $({\it\xi}_{0}^{-4})$
. There are three different contributions at
$({\it\xi}_{0}^{-4})$
. There are three different contributions at
![]() $O({\it\epsilon}Re)$
. Two of these arise from the volume integral in (2.30); the first one arises from integrating the exact inertial terms for a sphere over the
$O({\it\epsilon}Re)$
. Two of these arise from the volume integral in (2.30); the first one arises from integrating the exact inertial terms for a sphere over the
![]() $O({\it\epsilon})$
annular volume between the near-sphere and the aforementioned circumscribing fluid sphere, and its contribution to
$O({\it\epsilon})$
annular volume between the near-sphere and the aforementioned circumscribing fluid sphere, and its contribution to
![]() $\text{d}{\it\theta}_{j}/\text{d}t$
equals
$\text{d}{\it\theta}_{j}/\text{d}t$
equals
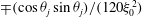 $\mp (\cos {\it\theta}_{j}\sin {\it\theta}_{j})/(120{\it\xi}_{0}^{2})$
; the second arises from integrating the
$\mp (\cos {\it\theta}_{j}\sin {\it\theta}_{j})/(120{\it\xi}_{0}^{2})$
; the second arises from integrating the
![]() $O({\it\epsilon})$
terms in the inertial acceleration over the volume exterior to the unit sphere, and this contribution equals
$O({\it\epsilon})$
terms in the inertial acceleration over the volume exterior to the unit sphere, and this contribution equals
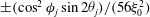 $\pm (\cos ^{2}{\it\phi}_{j}\sin 2{\it\theta}_{j})/(56{\it\xi}_{0}^{2})$
. Both these contributions are also present with the usual choice of test problem (a rotating near-sphere) and, for reasons mentioned in § 2, may be evaluated from knowledge of the Stokesian fields. The third contribution that, with this usual choice, would arise from integrating the
$\pm (\cos ^{2}{\it\phi}_{j}\sin 2{\it\theta}_{j})/(56{\it\xi}_{0}^{2})$
. Both these contributions are also present with the usual choice of test problem (a rotating near-sphere) and, for reasons mentioned in § 2, may be evaluated from knowledge of the Stokesian fields. The third contribution that, with this usual choice, would arise from integrating the
![]() $O({\it\epsilon})$
terms in the test velocity field with the inertial acceleration for a sphere, is now contained in the surface integral in (D 11). The evaluation of this surface integral requires knowledge of the
$O({\it\epsilon})$
terms in the test velocity field with the inertial acceleration for a sphere, is now contained in the surface integral in (D 11). The evaluation of this surface integral requires knowledge of the
![]() $O(Re)$
velocity field. But, following Subramanian & Koch (Reference Subramanian and Koch2006b
), it may be calculated knowing both
$O(Re)$
velocity field. But, following Subramanian & Koch (Reference Subramanian and Koch2006b
), it may be calculated knowing both
![]() $\boldsymbol{u}^{\prime }$
and
$\boldsymbol{u}^{\prime }$
and
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }$
for a sphere, to
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }$
for a sphere, to
![]() $O(Re)$
(Subramanian & Koch Reference Subramanian and Koch2006a
), and the relation (D 11) takes the form:
$O(Re)$
(Subramanian & Koch Reference Subramanian and Koch2006a
), and the relation (D 11) takes the form:
 $$\begin{eqnarray}\displaystyle & & \displaystyle -3\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \{\boldsymbol{u}^{\prime (0)}(\boldsymbol{n})+{\it\epsilon}\boldsymbol{u}^{\prime (1)}(\boldsymbol{n})\}\nonumber\\ \displaystyle & & \displaystyle \quad =-8{\rm\pi}{\it\bf\Omega}_{1}^{(1)}+{\it\epsilon}\frac{{\rm\pi}}{480}\left[-\frac{104}{7}\{2\boldsymbol{p}\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})+2(\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{p})+({\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{616}{7}\{2\boldsymbol{p}\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})+2(\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{p})+({\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma}^{\dagger })(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.792\boldsymbol{p}\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }{\it\bf\Gamma})\boldsymbol{\cdot }\boldsymbol{p}-232\boldsymbol{p}\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }{\it\bf\Gamma}^{\dagger })\boldsymbol{\cdot }\boldsymbol{p}\vphantom{\frac{104}{7}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -3\int \text{d}{\it\Omega}\,\boldsymbol{n}\wedge \{\boldsymbol{u}^{\prime (0)}(\boldsymbol{n})+{\it\epsilon}\boldsymbol{u}^{\prime (1)}(\boldsymbol{n})\}\nonumber\\ \displaystyle & & \displaystyle \quad =-8{\rm\pi}{\it\bf\Omega}_{1}^{(1)}+{\it\epsilon}\frac{{\rm\pi}}{480}\left[-\frac{104}{7}\{2\boldsymbol{p}\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})+2(\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }\boldsymbol{p})+({\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma})(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{616}{7}\{2\boldsymbol{p}\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})+2(\unicode[STIX]{x1D640}\boldsymbol{\cdot }\boldsymbol{p})\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }\boldsymbol{p})+({\bf\epsilon}\boldsymbol{ : }{\it\bf\Gamma}^{\dagger })(\unicode[STIX]{x1D640}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.792\boldsymbol{p}\wedge ({\it\bf\Gamma}^{\dagger }\boldsymbol{\cdot }{\it\bf\Gamma})\boldsymbol{\cdot }\boldsymbol{p}-232\boldsymbol{p}\wedge ({\it\bf\Gamma}\boldsymbol{\cdot }{\it\bf\Gamma}^{\dagger })\boldsymbol{\cdot }\boldsymbol{p}\vphantom{\frac{104}{7}}\right],\end{eqnarray}$$
in terms of the
![]() $O(Re)$
inertial correction
$O(Re)$
inertial correction
![]() ${\it\bf\Omega}_{1}^{(1)}$
. Adding the three contributions, one obtains:
${\it\bf\Omega}_{1}^{(1)}$
. Adding the three contributions, one obtains:
 $$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{Re}=\pm \frac{(33-37\cos 2{\it\phi}_{j})\sin 2{\it\theta}_{j}}{1680{\it\xi}_{0}^{2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\text{d}{\it\theta}_{j}}{\text{d}t}\right)_{Re}=\pm \frac{(33-37\cos 2{\it\phi}_{j})\sin 2{\it\theta}_{j}}{1680{\it\xi}_{0}^{2}}, & & \displaystyle\end{eqnarray}$$
with the plus sign corresponding to a prolate spheroid. This matches up exactly with (5.5) on using the limiting forms of the fluid inertial aspect-ratio functions,
![]() $F_{i}^{f}({\it\xi}_{0})$
, for
$F_{i}^{f}({\it\xi}_{0})$
, for
![]() ${\it\xi}_{0}\rightarrow \infty$
.
${\it\xi}_{0}\rightarrow \infty$
.