Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-21T04:33:52.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection

Published online by Cambridge University Press:  01 February 2013

Yi-Chao Xie ,
Ping Wei  and
Ke-Qing Xia
Yi-Chao Xie
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ping Wei
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: kxia@phy.cuhk.edu.hk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We report experimental investigations of the dynamics of the large-scale circulation (LSC) in turbulent Rayleigh–Bénard convection at high Prandtl number 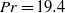$\mathit{Pr}= 19. 4$ (and also 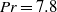$\mathit{Pr}= 7. 8$) and Rayleigh number 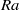$\mathit{Ra}$ varying from 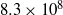$8. 3\times 1{0}^{8} $ to 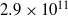$2. 9\times 1{0}^{11} $ in a cylindrical convection cell with aspect ratio unity. The dynamics of the LSC is measured using the multithermal probe technique. Both the sinusoidal-fitting (SF) and the temperature-extrema-extraction (TEE) methods are used to analyse the properties of the LSC. It is found that the LSC in high-$\mathit{Pr}$ regime remains a single-roll structure. The azimuthal motion of the LSC is a diffusive process, which is the same as those for $\mathit{Pr}$ around 1. However, the azimuthal diffusion of the LSC, characterized by the angular speed 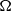$\Omega $ is almost two orders of magnitude smaller when compared with that in water. The non-dimensional time-averaged amplitude of the angular speed 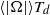$\langle \vert \Omega \vert \rangle {T}_{d} $ (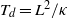${T}_{d} = {L}^{2} / \kappa $ is the thermal diffusion time) of the LSC at the mid-height of the convection cell increases with 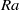$\mathit{Ra}$ as a power law, which is 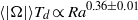$\langle \vert \Omega \vert \rangle {T}_{d} \propto {\mathit{Ra}}^{0. 36\pm 0. 01} $. The 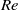$\mathit{Re}$ number based on the oscillation frequency of the LSC is found to scale with 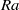$\mathit{Ra}$ as 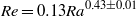$\mathit{Re}= 0. 13{\mathit{Ra}}^{0. 43\pm 0. 01} $. It is also found that the normalized flow strength 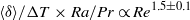$\langle \delta \rangle / \mrm{\Delta} T\times \mathit{Ra}/ \mathit{Pr}\propto {\mathit{Re}}^{1. 5\pm 0. 1} $, with the exponent in good agreement with that predicted by Brown & Ahlers (Phys. Fluids, vol. 20, 2008, p. 075101). A wealth of dynamical features of the LSC, such as the cessations, flow reversals, flow mode transitions, torsional and sloshing oscillations are observed in the high-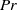$\mathit{Pr}$ regime as well.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 322 - 346
Copyright
©2013 Cambridge University Press

References

Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 641, 157–167.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Ashkenazi, S. & Steinberg, V. 1999 High Rayleigh number turbulent convection in a gas near the gas–liquid critical point. Phys. Rev. Lett. 83, 3641–3644.Google Scholar
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95, 024502.Google Scholar
Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on the large-scale circulation of turbulent Rayleigh–Bénard convection. Phys. Fluids 18 (12), 125108.Google Scholar
Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20 (7), 075101.Google Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 10005.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.Google Scholar
Kaczorowski, M., Shishkina, O., Shishkin, A., Wagner, C. & Xia, K.-Q. 2011 Analysis of the large-scale circulation and the boundary layers in turbulent Rayleigh–Bénard convection. In Direct and Large-Eddy Simulation VIII (ed. Kuerten, H., Geurts, B., Armenio, V. & Frhlich, J.), vol. 15, pp. 383–388. Springer.Google Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.Google Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.Google Scholar
Sano, M., Wu, X.-Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.Google Scholar
Shang, X.-D. & Xia, K.-Q. 2001 Scaling of the velocity power spectra in turbulent thermal convection. Phys. Rev. E 64, 065301.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005a Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.Google Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google Scholar
Sun, C. & Xia, K.-Q. 2007 Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection. J. Fluid Mech. 570, 479–489.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
Takeshita, T., Segawa, T., Glazier, J. A. & Sano, M. 1996 Thermal turbulence in mercury. Phys. Rev. Lett. 76, 1465–1468.Google Scholar
Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio $\Gamma = 0. 50$ and Prandtl number . J. Fluid Mech. 676, 5–40.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transitions in turbulent thermal convection. Phys. Fluids 20 (5), 055104.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q. 2011 How heat transfer efficiencies in turbulent thermal convection depend on internal flow modes. J. Fluid Mech. 676, 1–4.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.Google Scholar