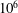1 Introduction
Being ubiquitous in nature, thermal convection presents itself in many natural flows. Warm air rising above solar-heated land or water generates convective cells that contribute to all weather systems. Large-scale oceanic circulation is also generated by thermal convection, as cold surface water at high latitudes sinks deep and flows towards the equator and warm equator water floats towards higher latitudes, resulting in an overturning circulation. These natural convection events occur in fluid. Given enough time, thermal convection can even occur in Earth’s solid mantle by means of solid-state creep (Turcotte & Schubert Reference Turcotte and Schubert2002). In fact, the realization that the mantle can exhibit viscous behaviour on a geologic time scale is crucial in conjuring up mantle convection as the driving force for continental drift, which leads to the birth of the revolutionary theory of plate tectonics (Schubert, Turcotte & Olson Reference Schubert, Turcotte and Olson2001).
Compared to the oceanic lithosphere, the average heat loss through continents is much lower (Pollack, Hurter & Johnson Reference Pollack, Hurter and Johnson1993; Lenardic et al. Reference Lenardic, Moresi, Jellinek and Manga2005). The presence of continents limits local surface heat flux and warms up the underlying mantle, thus modifying the underlying flow structure, which in turn affects continent motion. Therefore, continents and the mantle form a strongly coupled dynamic system. This is analogous to a simplified model of an insulating plate drifting over a thermally convecting fluid, which has been adopted in laboratory experiments (Elder Reference Elder1967; Zhang & Libchaber Reference Zhang and Libchaber2000; Zhong & Zhang Reference Zhong and Zhang2005; Whitehead, Shea & Behn Reference Whitehead, Shea and Behn2011). The process was also modelled experimentally by a freely moving heat source over a thermally convecting fluid (Howard, Malkus & Whitehead Reference Howard, Malkus and Whitehead1970; Whitehead Reference Whitehead1972). Simplified though they are, these models capture the essential factors and the basic mechanisms, in particular, (1) a thermally convecting fluid subject to basal heating; (2) a plate drifting on top of the fluid; (3) the dynamic feedback between the plate and the convecting fluid.
In the present study, the emphasis is placed on the dynamic feedback between a freely drifting plate and the thermally convecting fluid underneath it. How does a freely drifting plate affect underlying convection and what dynamic states can it trigger? Replacing the freely drifting plate with a rigid wall sealing the top of the fluid results in the classic problem of Rayleigh–Bénard convection, for which one of the key issues is the overall efficiency of heat transport through the fluid (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). For the present coupled system, we will investigate how a freely drifting plate affects the overall heat transport efficiency of the fluid as compared to the case with a fixed plate.
Rather than being a passive drifter, a floating plate moves without requiring a pre-existing stream in the fluid, as discovered very early through laboratory experiments (Elder Reference Elder1967). More recently, laboratory experiments show that a floating plate over a convecting fluid oscillates periodically between the two end walls of the fluid domain (Zhang & Libchaber Reference Zhang and Libchaber2000; Zhong & Zhang Reference Zhong and Zhang2005). This suggests that low-dimensional behaviour can be restored in turbulent Bénard convection by introducing a freely moving boundary. As the plate covers an increasing portion of the top surface, a trapped state starts to appear in which the floating plate stays in the middle of the flow domain and makes only small excursions in response to the competition between the two underlying convection cells (Zhong & Zhang Reference Zhong and Zhang2007a ,Reference Zhong and Zhang b ). Nevertheless, the fluid in these experiments is water, the Prandtl number of which is far from that of the mantle. Furthermore, the aspect ratios of the fluid domain in these experiments are much smaller than that of the Earth. These differences bring uncertainty when applying the experimental results to the Earth itself.
Meanwhile, numerical methods utilizing dynamically determined boundary conditions have captured processes of continent aggregation and dispersion and the simultaneous development of underlying mantle flow (Gurnis Reference Gurnis1988; Lowman & Jarvis Reference Lowman and Jarvis1993, Reference Lowman and Jarvis1995; Lowman & Gable Reference Lowman and Gable1999; Honda et al. Reference Honda, Yoshida, Ootorii and Iwase2000; Heron & Lowman Reference Heron and Lowman2011). Moreover, important light has been shed on the long-term dynamic feedback between the plate and the underlying flow (Gurnis Reference Gurnis1988; Zhong & Gurnis Reference Zhong and Gurnis1993; Phillips & Bunge Reference Phillips and Bunge2005; Whitehead & Behn Reference Whitehead and Behn2015). An interesting feature is that time series of plate velocity had suggested that a plate’s motion varies with its size: very large plates always have an appreciable velocity, whereas the velocity of small plate is episodic, with low velocities interrupted by bursts of high velocities (Gurnis Reference Gurnis1988; Phillips & Bunge Reference Phillips and Bunge2005). But the details of this variation and the mechanism underlying this variation are unclear. More recently, a ‘continental drift convection cell’ has been observed in the numerical study of Whitehead & Behn (Reference Whitehead and Behn2015), in which a single convection cell is always identified underlying the drifting plate, moving with the plate and absorbing ambient cells on its way. However, the presence of the single cell and the periodic motion of the plate are only steady for relatively large plates. What happens when plates are small? It is expected that small plates are less capable of modulating the underlying mantle flow and should behave more passively. Therefore, plate motion and the evolution of underlying flow are expected to vary with plate size. But how exactly plate motion and the associated underlying flow depend on plate size is still unclear.
To answer this question, we numerically simulate the coupled dynamic system with a mobile plate of a wide range of sizes over a thermally convecting fluid with infinite Prandtl number. Our results shed light on the above question and reveal three different coupling modes: namely, the stagnant mode I (SM I), stagnant mode II (SM II) and the unidirectionally moving mode (UMM) as plate size increases. These different modes might illustrate, to a certain extent, the variation of continent–mantle coupling over the convective mantle, as discussed in § 5.
The remainder of the paper is organized as follows: First, the numerical model and techniques are given in § 2. The evolutions of three distinct coupling modes are then demonstrated in detail for the two-dimensional (2-D) cases in § 3 and briefly for the three-dimensional (3-D) cases later in § 4.6. Section 4 presents detailed analysis on the simulation results. In this section, the variation of plate speed with plate size is analysed, and a comparison of Nusselt number is made between cases with a freely moving plate and those with a fixed plate. The variation of plate motion with Rayleigh number, the effect of internal heating on plate motion, and the evolution of different modes in three dimensions are also investigated in this section. Finally, a brief summary and the relation of the identified coupling modes to real geophysical phenomena are given in § 5.
2 Numerical simulations
Most of the simulations in the present study are performed for the 2-D models, but some 3-D simulation results are presented in § 4.6. Our numerical model incorporates several simplifications, as in previous studies (for example, Gurnis Reference Gurnis1988; Whitehead & Behn Reference Whitehead and Behn2015): a 2-D or a 3-D rectangular geometry, the Boussinesq approximation, a uniform viscosity for the convecting fluid, and the dropping of the inertia and advection terms in the momentum equation owing to the large Prandtl number of the mantle. Here, we focus on revealing the different coupling modes caused by the ‘thermal blanket effect’, which may be obscured when complex Earth-like factors are considered. Therefore, the ‘thermal blanket effect’ of continents is studied in isolation and the simulation is conducted in a much reduced system with only the essential factors. A Cartesian coordinate system is considered, with coordinate components
![]() $x_{i}$
(
$x_{i}$
(
![]() $i=1,2$
for the 2-D system;
$i=1,2$
for the 2-D system;
![]() $i=1$
, 2, 3 for the 3-D system), where
$i=1$
, 2, 3 for the 3-D system), where
![]() $x_{2}$
represents the vertical coordinate. The velocity components are denoted as
$x_{2}$
represents the vertical coordinate. The velocity components are denoted as
![]() $u_{i}$
, and the symbols
$u_{i}$
, and the symbols
![]() $t$
,
$t$
,
![]() $P$
,
$P$
,
![]() $T$
, and
$T$
, and
![]() $h$
represent time, pressure, temperature and internal heating rate, respectively. With the above assumptions, the dimensionless governing equations become:
$h$
represent time, pressure, temperature and internal heating rate, respectively. With the above assumptions, the dimensionless governing equations become:
where the symbol
![]() $\unicode[STIX]{x1D6FF}_{ij}$
denotes the Kronecker delta (
$\unicode[STIX]{x1D6FF}_{ij}$
denotes the Kronecker delta (
![]() $\unicode[STIX]{x1D6FF}_{ij}=1$
if
$\unicode[STIX]{x1D6FF}_{ij}=1$
if
![]() $i=j$
,
$i=j$
,
![]() $\unicode[STIX]{x1D6FF}_{ij}=0$
if
$\unicode[STIX]{x1D6FF}_{ij}=0$
if
![]() $i\neq j$
). The Rayleigh number
$i\neq j$
). The Rayleigh number
![]() $Ra$
is defined as
$Ra$
is defined as
![]() $Ra=g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}TD^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
$Ra=g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}TD^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
![]() $g$
,
$g$
,
![]() $\unicode[STIX]{x0394}T$
,
$\unicode[STIX]{x0394}T$
,
![]() $D$
,
$D$
,
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D705}$
are the acceleration due to gravity, temperature difference between the bottom and the top of the fluid, the depth of the fluid domain, thermal expansion coefficient, kinematic viscosity, and thermal diffusivity of the fluid, respectively. The flow can be turbulent even for infinite Prandtl number, owing to the nonlinearity in the energy equation (2.3). The average Nusselt number
$\unicode[STIX]{x1D705}$
are the acceleration due to gravity, temperature difference between the bottom and the top of the fluid, the depth of the fluid domain, thermal expansion coefficient, kinematic viscosity, and thermal diffusivity of the fluid, respectively. The flow can be turbulent even for infinite Prandtl number, owing to the nonlinearity in the energy equation (2.3). The average Nusselt number
![]() $Nu$
over the bottom surface is defined as
$Nu$
over the bottom surface is defined as
where
![]() $k$
is the thermal conductivity and
$k$
is the thermal conductivity and
![]() $q$
is the average heat flux at the bottom of the flow domain. Equations (2.1)–(2.3) are made dimensionless with the following scales: the coordinate
$q$
is the average heat flux at the bottom of the flow domain. Equations (2.1)–(2.3) are made dimensionless with the following scales: the coordinate
![]() $x_{i}$
scale
$x_{i}$
scale
![]() $D$
, the time
$D$
, the time
![]() $t$
scale
$t$
scale
![]() $D^{2}/\unicode[STIX]{x1D705}$
, the temperature
$D^{2}/\unicode[STIX]{x1D705}$
, the temperature
![]() $T$
(relative to the top surface temperature) scale
$T$
(relative to the top surface temperature) scale
![]() $\unicode[STIX]{x0394}T$
, the velocity
$\unicode[STIX]{x0394}T$
, the velocity
![]() $u_{i}$
scale
$u_{i}$
scale
![]() $\unicode[STIX]{x1D705}/D$
, the pressure gradient
$\unicode[STIX]{x1D705}/D$
, the pressure gradient
![]() $\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}x_{i}$
scale
$\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}x_{i}$
scale
![]() $\unicode[STIX]{x1D70C}_{0}g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T$
(
$\unicode[STIX]{x1D70C}_{0}g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T$
(
![]() $\unicode[STIX]{x1D70C}_{0}$
is the fluid density), the internal heating rate
$\unicode[STIX]{x1D70C}_{0}$
is the fluid density), the internal heating rate
![]() $h$
scale
$h$
scale
![]() $\unicode[STIX]{x1D70C}_{0}c_{p}\unicode[STIX]{x1D705}\unicode[STIX]{x0394}T/D^{2}$
(
$\unicode[STIX]{x1D70C}_{0}c_{p}\unicode[STIX]{x1D705}\unicode[STIX]{x0394}T/D^{2}$
(
![]() $c_{p}$
is the specific heat). For simplicity, the indicial notation is substituted hereinafter by the basic Cartesian notation, where
$c_{p}$
is the specific heat). For simplicity, the indicial notation is substituted hereinafter by the basic Cartesian notation, where
![]() $x=x_{1}$
,
$x=x_{1}$
,
![]() $y=x_{2}$
,
$y=x_{2}$
,
![]() $z=x_{3}$
. Correspondingly, the velocity components
$z=x_{3}$
. Correspondingly, the velocity components
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{2}$
,
$u_{2}$
,
![]() $u_{3}$
are denoted as
$u_{3}$
are denoted as
![]() $u$
,
$u$
,
![]() $v$
,
$v$
,
![]() $w$
, respectively. The vertical normal stress
$w$
, respectively. The vertical normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
, discussed later, is normalized by
$\unicode[STIX]{x1D70E}_{yy}$
, discussed later, is normalized by
![]() $\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}/D^{2}$
.
$\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}/D^{2}$
.

Figure 1. Sketch of the model and specification of boundary conditions for the 2-D cases.
The fluid is initially stationary and isothermal (
![]() $T=1$
). The vertical end walls are set to be adiabatic. The bottom of the chamber is set to be isothermal (
$T=1$
). The vertical end walls are set to be adiabatic. The bottom of the chamber is set to be isothermal (
![]() $T=1$
). Cooling (
$T=1$
). Cooling (
![]() $T=0$
) is imposed on top of the fluid. The limited heat flux through the continent is simplified by setting it to zero at the plate–fluid interface, i.e. the plate bottom, as also adopted by Whitehead & Behn (Reference Whitehead and Behn2015). All the boundaries of the fluid are set to be stress-free except the plate–fluid interface, which is set to be non-slip, i.e. flow at the interface has the same velocity as the plate. A schematic figure of the 2-D model is shown in figure 1 with the boundary conditions denoted, where variables with a subscript denote the partial derivatives with respect to the subscript (for example,
$T=0$
) is imposed on top of the fluid. The limited heat flux through the continent is simplified by setting it to zero at the plate–fluid interface, i.e. the plate bottom, as also adopted by Whitehead & Behn (Reference Whitehead and Behn2015). All the boundaries of the fluid are set to be stress-free except the plate–fluid interface, which is set to be non-slip, i.e. flow at the interface has the same velocity as the plate. A schematic figure of the 2-D model is shown in figure 1 with the boundary conditions denoted, where variables with a subscript denote the partial derivatives with respect to the subscript (for example,
![]() $u_{y}=\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$
). For the 2-D models, a 2-D convection domain with an aspect ratio of 8 (
$u_{y}=\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$
). For the 2-D models, a 2-D convection domain with an aspect ratio of 8 (
![]() $W/D=8$
, where
$W/D=8$
, where
![]() $W$
and
$W$
and
![]() $D$
are the horizontal span and the depth of the fluid domain, respectively) is considered (figure 1). The plate length
$D$
are the horizontal span and the depth of the fluid domain, respectively) is considered (figure 1). The plate length
![]() $L$
, normalized by
$L$
, normalized by
![]() $D$
, varies from 0.25 to 5.
$D$
, varies from 0.25 to 5.
For fluid with infinite Prandtl number, body forces are balanced by viscous forces, and thus there is no acceleration or net force on any mass element (Gable, O’Connell & Travis Reference Gable, O’Connell and Travis1991). The plate has no inertia. Therefore, the plate velocity is determined by setting the net horizontal shear force exerted by the flow on the plate–fluid interface (plate bottom) to zero. Plate velocity determined this way was first used by Gable et al. (Reference Gable, O’Connell and Travis1991). It ensures energy conservation, neither adding nor subtracting energy from the convecting system (Lowman & Jarvis Reference Lowman and Jarvis1999). Therefore, plate velocity is specified by the integral of flow velocity at the first grid cell below the interface. Both the flow velocity and the plate position are updated at each time step. When the plate encounters the end walls, its speed is set to be zero until the net underlying flow reverses. The governing equations along with the specified boundary and initial conditions are solved numerically using the finite-volume method. The code has been used and validated when solving natural convection problems (for example, Mao, Lei & Patterson Reference Mao, Lei and Patterson2009, Reference Mao, Lei and Patterson2010). The SIMPLE scheme (Patankar Reference Patankar1980) is adopted for pressure–velocity coupling and the QUICK scheme (Leonard Reference Leonard1979) is applied for spatial derivatives. A second-order implicit scheme is applied for time discretization.
For each run of the 2-D cases, the plate is first fixed in the middle at the top of the fluid (
![]() $y=0$
) until a quasi-steady-state is reached, and then the plate is set free. A mesh and time-step dependency test has been conducted for three different meshes,
$y=0$
) until a quasi-steady-state is reached, and then the plate is set free. A mesh and time-step dependency test has been conducted for three different meshes,
![]() $400\times 50$
,
$400\times 50$
,
![]() $800\times 100$
,
$800\times 100$
,
![]() $1200\times 150$
, for the fixed plate case in the 2-D system with a plate length of
$1200\times 150$
, for the fixed plate case in the 2-D system with a plate length of
![]() $L=0.25$
and
$L=0.25$
and
![]() $Ra=10^{6}$
(Appendix). All the meshes were equidistant and the time step is adjusted so that the Courant–Friedrichs–Lewy (CFL) number remains the same for different meshes. The averaged Nusselt number
$Ra=10^{6}$
(Appendix). All the meshes were equidistant and the time step is adjusted so that the Courant–Friedrichs–Lewy (CFL) number remains the same for different meshes. The averaged Nusselt number
![]() $Nu$
at quasi-steady-state (averaged from
$Nu$
at quasi-steady-state (averaged from
![]() $t=0.3$
to 0.5) for the three different meshes (from the coarsest to the finest) is 13.88, 16.66, 17.25. The difference of
$t=0.3$
to 0.5) for the three different meshes (from the coarsest to the finest) is 13.88, 16.66, 17.25. The difference of
![]() $Nu$
decreases from 20.0 % between the former two meshes to 3.5 % between the latter two. In order to ensure the accuracy of the solutions while keeping the calculation time manageable, the
$Nu$
decreases from 20.0 % between the former two meshes to 3.5 % between the latter two. In order to ensure the accuracy of the solutions while keeping the calculation time manageable, the
![]() $800\times 100$
mesh is used in all the following 2-D simulations with a time step of
$800\times 100$
mesh is used in all the following 2-D simulations with a time step of
![]() $5\times 10^{-7}$
.
$5\times 10^{-7}$
.
For the 3-D coordinate system, the axes of
![]() $x$
and
$x$
and
![]() $z$
lie within the horizontal domain, and the
$z$
lie within the horizontal domain, and the
![]() $y$
axis is also in the direction of the depth as in the 2-D system. A mesh of
$y$
axis is also in the direction of the depth as in the 2-D system. A mesh of
![]() $400\times 400\times 50$
was adopted for a
$400\times 400\times 50$
was adopted for a
![]() $8\times 8\times 1$
fluid domain (
$8\times 8\times 1$
fluid domain (
![]() $8\times 8$
is the horizontal dimension and 1 is the depth). Similar to the 2-D cases, there is no net force on the plate exerted by the fluid to ensure energy conservation of the convecting system. As a result, the translational movement of the plate in the
$8\times 8$
is the horizontal dimension and 1 is the depth). Similar to the 2-D cases, there is no net force on the plate exerted by the fluid to ensure energy conservation of the convecting system. As a result, the translational movement of the plate in the
![]() $x$
–
$x$
–
![]() $z$
plane ensures that there is no net force in the directions of the two horizontal axes,
$z$
plane ensures that there is no net force in the directions of the two horizontal axes,
![]() $x$
and
$x$
and
![]() $z$
. Therefore, both the integral of shear stress
$z$
. Therefore, both the integral of shear stress
![]() $\unicode[STIX]{x1D70F}_{xy}$
(proportional to
$\unicode[STIX]{x1D70F}_{xy}$
(proportional to
![]() $\unicode[STIX]{x2202}(u-u_{c})/\unicode[STIX]{x2202}y$
, where
$\unicode[STIX]{x2202}(u-u_{c})/\unicode[STIX]{x2202}y$
, where
![]() $u$
is the
$u$
is the
![]() $x$
-component of fluid speed adjacent the interface and
$x$
-component of fluid speed adjacent the interface and
![]() $u_{c}$
is the
$u_{c}$
is the
![]() $x$
-component of the net plate speed) and the integral of
$x$
-component of the net plate speed) and the integral of
![]() $\unicode[STIX]{x1D70F}_{zy}$
(proportional to
$\unicode[STIX]{x1D70F}_{zy}$
(proportional to
![]() $\unicode[STIX]{x2202}(w-w_{c})/\unicode[STIX]{x2202}y$
, where
$\unicode[STIX]{x2202}(w-w_{c})/\unicode[STIX]{x2202}y$
, where
![]() $w$
is the
$w$
is the
![]() $z$
-component of fluid speed adjacent the interface and
$z$
-component of fluid speed adjacent the interface and
![]() $w_{c}$
is the
$w_{c}$
is the
![]() $z$
-component of the net plate speed) on the interface (plate bottom) are zero. The rotational movement of the plate in the horizontal plane ensures no net shear force
$z$
-component of the net plate speed) on the interface (plate bottom) are zero. The rotational movement of the plate in the horizontal plane ensures no net shear force
![]() $\unicode[STIX]{x1D70F}_{xz}$
(proportional to
$\unicode[STIX]{x1D70F}_{xz}$
(proportional to
![]() $2^{-1}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}x)-\unicode[STIX]{x1D714}_{c}$
, where
$2^{-1}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}x)-\unicode[STIX]{x1D714}_{c}$
, where
![]() $\unicode[STIX]{x1D714}_{c}$
is the angular speed of the plate, the rotational axis is parallel to the
$\unicode[STIX]{x1D714}_{c}$
is the angular speed of the plate, the rotational axis is parallel to the
![]() $y$
axis at plate centre) is exerted by the flow on plate bottom. These conditions uniquely determine the movement of the plate. Three plate sizes, with horizontal dimensions of
$y$
axis at plate centre) is exerted by the flow on plate bottom. These conditions uniquely determine the movement of the plate. Three plate sizes, with horizontal dimensions of
![]() $0.5\times 0.5$
,
$0.5\times 0.5$
,
![]() $1.5\times 1.5$
and
$1.5\times 1.5$
and
![]() $2.5\times 2.5$
are adopted to demonstrate the presence of three different modes in three dimensions. The plate is initially placed at the centre of the top surface of the fluid domain. Different from the 2-D case, the plate is set free to move from the beginning when the entire flow is isothermal and stationary. Since 3-D simulation is much more time-consuming than 2-D simulation, a much shorter time series is obtained for the 3-D cases than the 2-D cases.
$2.5\times 2.5$
are adopted to demonstrate the presence of three different modes in three dimensions. The plate is initially placed at the centre of the top surface of the fluid domain. Different from the 2-D case, the plate is set free to move from the beginning when the entire flow is isothermal and stationary. Since 3-D simulation is much more time-consuming than 2-D simulation, a much shorter time series is obtained for the 3-D cases than the 2-D cases.
3 Coupling modes
A plate moves along with the underlying flow when it rides on a single convection cell; however, the scenario differs remarkably when the leading edge of the plate encounters impeding flow structures. Three coupling modes are identified and elucidated below.
3.1 Stagnant mode I
A small plate is easily trapped when it encounters a downwelling and a counter-rotating convection cell, as the opposing flows of the two cells converge beneath the plate (figure 2
a,b). The opposing forces exerted by these opposing flows on the bottom of the plate tend to balance each other by adjusting the plate position. This is a stable mode, since the plate will be pulled back if it is moved slightly away from the balanced position. As a result, the plate is trapped for a long time, which we term stagnant mode I (SM I). For a small plate of
![]() $L=0.25$
, it never shows significant displacement after being arrested by the downwelling (figure 2
c) and the underlying flow structure remains approximately the same. Nevertheless, the system shows an alternation of quiescence (figure 2
a) and activity (figure 2
b). The former is characterized by a more regular flow structure (figure 2
a) and smaller fluctuations of plate velocity and flow properties with time (figure 2
c). Furthermore, during the quiescent duration, the thermal plumes are striking almost vertically towards the opposing boundaries (figure 2
a). In contrast, they show significant bifurcation and variation during the active duration (figure 2
b).
$L=0.25$
, it never shows significant displacement after being arrested by the downwelling (figure 2
c) and the underlying flow structure remains approximately the same. Nevertheless, the system shows an alternation of quiescence (figure 2
a) and activity (figure 2
b). The former is characterized by a more regular flow structure (figure 2
a) and smaller fluctuations of plate velocity and flow properties with time (figure 2
c). Furthermore, during the quiescent duration, the thermal plumes are striking almost vertically towards the opposing boundaries (figure 2
a). In contrast, they show significant bifurcation and variation during the active duration (figure 2
b).

Figure 2. Stagnant mode I (SM I) for
![]() $L=0.25$
at
$L=0.25$
at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
. (a,b) Snapshots of streamlines and temperature for the quiescent duration and the active duration, respectively, with a sketch of the flow structure of SM I on the right-hand side. The corresponding times are marked in (c) with red circles and cyan lines. The solid and dashed streamlines represent anticlockwise and clockwise flows, respectively. (c) Time series of plate centre location
$h=0$
. (a,b) Snapshots of streamlines and temperature for the quiescent duration and the active duration, respectively, with a sketch of the flow structure of SM I on the right-hand side. The corresponding times are marked in (c) with red circles and cyan lines. The solid and dashed streamlines represent anticlockwise and clockwise flows, respectively. (c) Time series of plate centre location
![]() $x$
, plate velocity
$x$
, plate velocity
![]() $u$
, the average temperature
$u$
, the average temperature
![]() $T$
and average normal stress
$T$
and average normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.
$\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.

Figure 3. Alternation of stagnant mode I (SM I) and velocity bursts for
![]() $L=0.5$
at
$L=0.5$
at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
. (a–g) Snapshots of streamlines and temperature with sketches on the right-hand side. (h) Time series of plate centre location
$h=0$
. (a–g) Snapshots of streamlines and temperature with sketches on the right-hand side. (h) Time series of plate centre location
![]() $x$
, plate velocity
$x$
, plate velocity
![]() $u$
, average temperature
$u$
, average temperature
![]() $T$
and average normal stress
$T$
and average normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.
$\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.
For a small plate of
![]() $L=0.25$
, the two convection cells underlying the plate do not show significant variation in size over time. As the plate becomes larger, its capability to modify the flow increases. As a result, as
$L=0.25$
, the two convection cells underlying the plate do not show significant variation in size over time. As the plate becomes larger, its capability to modify the flow increases. As a result, as
![]() $L$
increases to 0.5, the two convection cells underneath shrink gradually as the two associated hot plumes approach the plate, which is evident by comparing figure 3(a) with 3(b), and figure 3(d) with 3(e) (supplementary movie 1 available at https://doi.org/10.1017/jfm.2019.189). Such an evolution of flow pattern is due to the thermal blanket effect as the plate reduces the local heat loss and weakens the downwelling. As the two cells shrink, one of them eventually vanishes and the remaining one merges with the neighbouring cell of the same sign (this evolution is evident by comparing figure 3
b with 3
c, and figure 3
f with 3
g), thus the plate rides on a single convection cell and exhibits a burst in velocity (supplementary movie 1). This process of cell vanishing and merging is accomplished when one of the two associated hot plumes reaches the plate. As a result, the bursts in plate velocity are accompanied by evident bursts in temperature
$L$
increases to 0.5, the two convection cells underneath shrink gradually as the two associated hot plumes approach the plate, which is evident by comparing figure 3(a) with 3(b), and figure 3(d) with 3(e) (supplementary movie 1 available at https://doi.org/10.1017/jfm.2019.189). Such an evolution of flow pattern is due to the thermal blanket effect as the plate reduces the local heat loss and weakens the downwelling. As the two cells shrink, one of them eventually vanishes and the remaining one merges with the neighbouring cell of the same sign (this evolution is evident by comparing figure 3
b with 3
c, and figure 3
f with 3
g), thus the plate rides on a single convection cell and exhibits a burst in velocity (supplementary movie 1). This process of cell vanishing and merging is accomplished when one of the two associated hot plumes reaches the plate. As a result, the bursts in plate velocity are accompanied by evident bursts in temperature
![]() $T$
at plate bottom and alleviations of the extensional (positive) normal stress
$T$
at plate bottom and alleviations of the extensional (positive) normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
there (figure 3
h).
$\unicode[STIX]{x1D70E}_{yy}$
there (figure 3
h).
3.2 Stagnant mode II
Another stagnant mode, i.e. stagnant mode II (SM II) (supplementary movie 2), starts to appear at
![]() $L\sim 0.75$
and gradually becomes dominant at
$L\sim 0.75$
and gradually becomes dominant at
![]() $L\sim 1.5$
. For
$L\sim 1.5$
. For
![]() $L=1.5$
, the plate rides on a single convection cell most of the time (for example, figure 4
a,e,h). However, plate motion can be severely hindered when the leading edge of the plate encounters a counter-rotating cell and the associated downwelling. As the plate slows down and becomes stagnant, a new downwelling starts to form at the other end of the plate and a hot plume develops underneath, initiating two counter-rotating convection cells underneath and a divergent flow at plate bottom (figure 4
b,f, supplementary movie 2). The two cells underlying the plate together with the neighbouring cells on each side of the plate form a flow structure that traps the plate, which we term stagnant mode II (SM II). This is a stable structure, since a minor shift of the plate position will be inhibited by the opposing flow of the neighbouring cell.
$L=1.5$
, the plate rides on a single convection cell most of the time (for example, figure 4
a,e,h). However, plate motion can be severely hindered when the leading edge of the plate encounters a counter-rotating cell and the associated downwelling. As the plate slows down and becomes stagnant, a new downwelling starts to form at the other end of the plate and a hot plume develops underneath, initiating two counter-rotating convection cells underneath and a divergent flow at plate bottom (figure 4
b,f, supplementary movie 2). The two cells underlying the plate together with the neighbouring cells on each side of the plate form a flow structure that traps the plate, which we term stagnant mode II (SM II). This is a stable structure, since a minor shift of the plate position will be inhibited by the opposing flow of the neighbouring cell.

Figure 4. The evolution of stagnant mode II (SM II) for
![]() $L=1.5$
at
$L=1.5$
at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
. (a–h) Snapshots of streamlines and temperature with sketches of flow structure on the right-hand side. (i) Time series of plate centre location
$h=0$
. (a–h) Snapshots of streamlines and temperature with sketches of flow structure on the right-hand side. (i) Time series of plate centre location
![]() $x$
, plate velocity
$x$
, plate velocity
![]() $u$
, average temperature
$u$
, average temperature
![]() $T$
and average normal stress
$T$
and average normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.
$\unicode[STIX]{x1D70E}_{yy}$
at plate bottom.
Under the insulating plate, the hot plume grows and the two convection cells expand. Meanwhile, the neighbouring hot plume on each side of the plate moves towards the plate. As a result, the two underlying convection cells merge respectively with the nearest cell of the same sign on each side of the plate at the cost of a counter-rotating cell, which is evident by comparing figure 4(c) with 4(d), and figure 4(f) with 4(g) (supplementary movie 2). This is contrary to the shrinkage of the underlying cells in SM I. Nevertheless, SM II becomes unstable when the two underlying cells merge with the neighbouring cells and become large (figure 4
d,g), since a small shift of the plate position will be amplified rather than inhibited as in SM I. One of the two cells soon becomes dominant in moving the plate and thus the plate rides on a single cell again (figure 4
e,h), ending its stagnant state. Since the downwelling which initially slows down the plate tends to drag the plate downwards, the decrease in plate speed
![]() $u$
owing to the encounter of downwelling is accompanied by an increase in the extensional stress
$u$
owing to the encounter of downwelling is accompanied by an increase in the extensional stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at the plate bottom, and a decrease in the average temperature
$\unicode[STIX]{x1D70E}_{yy}$
at the plate bottom, and a decrease in the average temperature
![]() $T$
there (figure 4
i). Conversely, during the stagnant duration, the growth of hot plumes underneath the plate leads to a gradual increase of
$T$
there (figure 4
i). Conversely, during the stagnant duration, the growth of hot plumes underneath the plate leads to a gradual increase of
![]() $T$
and a decrease of
$T$
and a decrease of
![]() $\unicode[STIX]{x1D70E}_{yy}$
(figure 4
i). As the insulating effect of the plate increases with its size, a larger plate needs a shorter time to warm up the underlying flow and modify the underlying flow structure. Therefore, SM II is much shorter-lived than SM I.
$\unicode[STIX]{x1D70E}_{yy}$
(figure 4
i). As the insulating effect of the plate increases with its size, a larger plate needs a shorter time to warm up the underlying flow and modify the underlying flow structure. Therefore, SM II is much shorter-lived than SM I.
3.3 Unidirectional moving mode

Figure 5. The unidirectional moving mode (UMM) for
![]() $L=2.5$
at
$L=2.5$
at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
. (a–g) Snapshots of streamlines and temperature with sketches of flow structure on the right-hand side. (h) Time series of plate centre location
$h=0$
. (a–g) Snapshots of streamlines and temperature with sketches of flow structure on the right-hand side. (h) Time series of plate centre location
![]() $x$
, plate velocity
$x$
, plate velocity
![]() $u$
, average temperature
$u$
, average temperature
![]() $T$
and average normal stress
$T$
and average normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at plate bottom. Except moments of forced stop in (d), a single large convection cell is always identified underlying the plate.
$\unicode[STIX]{x1D70E}_{yy}$
at plate bottom. Except moments of forced stop in (d), a single large convection cell is always identified underlying the plate.
As the plate size increases to
![]() $L=2.5$
, the aforementioned two stagnant modes disappear and the unidirectional moving mode (UMM) emerges (supplementary movie 3). In this mode, the plate rides most of the time on a single large convection cell and moves unidirectionally until it encounters the end walls (figure 5), where it is forced to stop until hot plumes rise up underneath and the net underlying horizontal flow reverses (figure 5
d), similar to that observed by Whitehead & Behn (Reference Whitehead and Behn2015). the leading edge of the plate encounters a cold downwelling, instead of being stopped as in the stagnant modes, the plate slows down transiently but continues moving forwards, taking the cold plume along with it (supplementary movie 3). Meanwhile, the underlying convection cell merges with the frontal cell of the same sign, at the cost of a counter-rotating cell, which is evident by comparing figure 5(a) with 5(b), and figure 5(e) with 5(f). On the other hand, when the underlying convection cell becomes large through merging, it disintegrates by forming new hot upwelling near the trailing edge of the plate, which is evident by comparing figure 5(b) with 5(c), and figure 5(f) with 5(g). Such a process of cell merging near the leading edge and disintegration near the trailing edge continues, resulting in the propagation of a large convection cell with the moving plate (supplementary movie 3).
$L=2.5$
, the aforementioned two stagnant modes disappear and the unidirectional moving mode (UMM) emerges (supplementary movie 3). In this mode, the plate rides most of the time on a single large convection cell and moves unidirectionally until it encounters the end walls (figure 5), where it is forced to stop until hot plumes rise up underneath and the net underlying horizontal flow reverses (figure 5
d), similar to that observed by Whitehead & Behn (Reference Whitehead and Behn2015). the leading edge of the plate encounters a cold downwelling, instead of being stopped as in the stagnant modes, the plate slows down transiently but continues moving forwards, taking the cold plume along with it (supplementary movie 3). Meanwhile, the underlying convection cell merges with the frontal cell of the same sign, at the cost of a counter-rotating cell, which is evident by comparing figure 5(a) with 5(b), and figure 5(e) with 5(f). On the other hand, when the underlying convection cell becomes large through merging, it disintegrates by forming new hot upwelling near the trailing edge of the plate, which is evident by comparing figure 5(b) with 5(c), and figure 5(f) with 5(g). Such a process of cell merging near the leading edge and disintegration near the trailing edge continues, resulting in the propagation of a large convection cell with the moving plate (supplementary movie 3).
A comparison of the average normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
at the plate bottom among different cases suggests that as plate size increases, the value of
$\unicode[STIX]{x1D70E}_{yy}$
at the plate bottom among different cases suggests that as plate size increases, the value of
![]() $\unicode[STIX]{x1D70E}_{yy}$
changes from generally positive to generally negative (figures 2–5), suggesting that the plate transfers from being dragged down by cold downwelling to being uplifted by hot upwelling. This is consistent with the generally larger number of hot plumes identified underneath the larger plate (figures 2–5), which embodies the increase of the thermal blanket effect with plate size.
$\unicode[STIX]{x1D70E}_{yy}$
changes from generally positive to generally negative (figures 2–5), suggesting that the plate transfers from being dragged down by cold downwelling to being uplifted by hot upwelling. This is consistent with the generally larger number of hot plumes identified underneath the larger plate (figures 2–5), which embodies the increase of the thermal blanket effect with plate size.
4 Analysis on the simulation results
4.1 Variation of plate speed with plate size
It is clear now that plate motion varies significantly with its size. Very small plates (
![]() $L\leqslant \sim 0.25$
) are permanently trapped in SM I with no significant displacement once being trapped (figure 6,
$L\leqslant \sim 0.25$
) are permanently trapped in SM I with no significant displacement once being trapped (figure 6,
![]() $L=0.25$
). As plate size increases to
$L=0.25$
). As plate size increases to
![]() $L=0.5$
, the plate shows long durations of stagnancy punctuated by short episodes of velocity burst (figure 6). Excluding the forced stop at the end walls, the duration of stagnancy decreases with increasing plate size (figure 6). For
$L=0.5$
, the plate shows long durations of stagnancy punctuated by short episodes of velocity burst (figure 6). Excluding the forced stop at the end walls, the duration of stagnancy decreases with increasing plate size (figure 6). For
![]() $L\geqslant 2.5$
, the plate shows unidirectional movement until it encounters the end walls (figure 6
a,
$L\geqslant 2.5$
, the plate shows unidirectional movement until it encounters the end walls (figure 6
a,
![]() $L=2.5,4.0$
).
$L=2.5,4.0$
).

Figure 6. (a) Plate centre position
![]() $x$
and (b) plate velocity
$x$
and (b) plate velocity
![]() $u$
for
$u$
for
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
. Time starts from when the plate is freed. The red horizontal lines denote the maximum range of plate centre position
$h=0$
. Time starts from when the plate is freed. The red horizontal lines denote the maximum range of plate centre position
![]() $x$
.
$x$
.
An analysis on the time series of plate speed
![]() $|u|$
reveals that as a plate becomes larger, it is less likely to be stagnant and its speed becomes increasingly concentrated on high values (figure 7
a), suggesting its increasing capability to overcome impeding flow structures and maintain a steady motion. As
$|u|$
reveals that as a plate becomes larger, it is less likely to be stagnant and its speed becomes increasingly concentrated on high values (figure 7
a), suggesting its increasing capability to overcome impeding flow structures and maintain a steady motion. As
![]() $L$
increases to 2.5, the probability of a plate to be stagnant (low speed, for example,
$L$
increases to 2.5, the probability of a plate to be stagnant (low speed, for example,
![]() $|u|<100$
) approaches zero (figure 7
a,b), corresponding to the UMM of large plates. The enhanced moving capability of larger plates is also manifested in the increase of the average plate speed
$|u|<100$
) approaches zero (figure 7
a,b), corresponding to the UMM of large plates. The enhanced moving capability of larger plates is also manifested in the increase of the average plate speed
![]() $|u|_{mean}$
with plate size (figure 7
c). The standard deviation of plate speed reaches a maximum at a plate size of
$|u|_{mean}$
with plate size (figure 7
c). The standard deviation of plate speed reaches a maximum at a plate size of
![]() $L=1.5$
–2 (figure 7
c). This is because towards the lower end of plate size, the plate shows an increasing tendency to be stagnant, and thus the standard deviation decreases. Towards the upper end, the increasing steadiness of the unidirectional plate motion also results in a decrease of the standard deviation.
$L=1.5$
–2 (figure 7
c). This is because towards the lower end of plate size, the plate shows an increasing tendency to be stagnant, and thus the standard deviation decreases. Towards the upper end, the increasing steadiness of the unidirectional plate motion also results in a decrease of the standard deviation.

Figure 7. Analysis of plate speed
![]() $|u|$
for different plate size
$|u|$
for different plate size
![]() $L$
at
$L$
at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
(a) Probability density of plate speed
$h=0$
(a) Probability density of plate speed
![]() $|u|$
. (b) Percentage of low plate speed
$|u|$
. (b) Percentage of low plate speed
![]() $|u|$
in the time series of
$|u|$
in the time series of
![]() $|u|$
. (c) Mean plate speed
$|u|$
. (c) Mean plate speed
![]() $|u|_{mean}$
with the standard deviation denoted by the upper and lower bars, and the maximum plate speed
$|u|_{mean}$
with the standard deviation denoted by the upper and lower bars, and the maximum plate speed
![]() $|u|_{max}$
. Dashed vertical lines indicate the rough boundaries between different modes (
$|u|_{max}$
. Dashed vertical lines indicate the rough boundaries between different modes (
![]() $\text{SM I}+\text{II}$
denotes a transition from SM I to SM II, where both modes exist). (d) Streamlines and temperature for
$\text{SM I}+\text{II}$
denotes a transition from SM I to SM II, where both modes exist). (d) Streamlines and temperature for
![]() $L=3$
(upper panel) and 4 (lower panel) when the plate starts to ride on a single convection cell again after the forced stop at the end wall. The two red lines at the top denote the range of the end-wall cell. Plate speeds affected by this cell are excluded from the analysis.
$L=3$
(upper panel) and 4 (lower panel) when the plate starts to ride on a single convection cell again after the forced stop at the end wall. The two red lines at the top denote the range of the end-wall cell. Plate speeds affected by this cell are excluded from the analysis.
The maximum plate speed is reached at a plate size of
![]() $L\sim 0.75$
(figure 7
c). Since plate speed reflects the average flow speed at the plate–fluid interface, an increase in plate size has the effect of smoothing out local fluctuations and results in more steady plate movement. Therefore, as plate size increases, it is less susceptible to local velocity pulses caused by local flows and thus its maximum speed decreases. On the other hand, a very small plate (e.g.
$L\sim 0.75$
(figure 7
c). Since plate speed reflects the average flow speed at the plate–fluid interface, an increase in plate size has the effect of smoothing out local fluctuations and results in more steady plate movement. Therefore, as plate size increases, it is less susceptible to local velocity pulses caused by local flows and thus its maximum speed decreases. On the other hand, a very small plate (e.g.
![]() $L=0.25$
) is always trapped in SM I, and therefore its maximum speed is also small. It is worth noting that data at the very initial stage when the plate is just freed are excluded from the above analysis in order to exclude the start-up effect. Furthermore, plate speed affected by the artificially forced stop at the end walls is also excluded, starting from when the plate is forced to stop until it returns back and rides on a single convection cell again (figure 7
d). A comparison of the single convection cell underlying different plates suggests that it becomes larger as plate size increases (figure 7
d). For a large plate of
$L=0.25$
) is always trapped in SM I, and therefore its maximum speed is also small. It is worth noting that data at the very initial stage when the plate is just freed are excluded from the above analysis in order to exclude the start-up effect. Furthermore, plate speed affected by the artificially forced stop at the end walls is also excluded, starting from when the plate is forced to stop until it returns back and rides on a single convection cell again (figure 7
d). A comparison of the single convection cell underlying different plates suggests that it becomes larger as plate size increases (figure 7
d). For a large plate of
![]() $L=4$
, there is not much room left for the development of impeding flow structures for the plate (figure 7
d). Therefore, for
$L=4$
, there is not much room left for the development of impeding flow structures for the plate (figure 7
d). Therefore, for
![]() $L=4$
, the distribution of plate velocity is much more concentrated on relatively high values (figure 7
a), showing a rather steady plate movement.
$L=4$
, the distribution of plate velocity is much more concentrated on relatively high values (figure 7
a), showing a rather steady plate movement.
4.2 Comparison of
 $Nu$
with fixed-plate cases
$Nu$
with fixed-plate cases

Figure 8. (a) Time series of
![]() $Nu$
at the bottom of the flow domain for
$Nu$
at the bottom of the flow domain for
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $h=0$
with fixed and freely moving plates. (b) Time-averaged
$h=0$
with fixed and freely moving plates. (b) Time-averaged
![]() $Nu$
during the quasi-steady-state at
$Nu$
during the quasi-steady-state at
![]() $Ra=10^{6}$
for cases with fixed and free plates and their difference (
$Ra=10^{6}$
for cases with fixed and free plates and their difference (
![]() $\unicode[STIX]{x0394}Nu$
). (c) Temperature and streamlines at the quasi-steady-state for cases with a fixed plate. (d) Time-averaged
$\unicode[STIX]{x0394}Nu$
). (c) Temperature and streamlines at the quasi-steady-state for cases with a fixed plate. (d) Time-averaged
![]() $Nu$
during the quasi-steady-state for
$Nu$
during the quasi-steady-state for
![]() $L=2.5$
at different
$L=2.5$
at different
![]() $Ra$
.
$Ra$
.
Compared to cases with a fixed plate, the Nusselt number
![]() $Nu$
, increases when the plate is free to move (figure 8
a,b). The value of this increase,
$Nu$
, increases when the plate is free to move (figure 8
a,b). The value of this increase,
![]() $\unicode[STIX]{x0394}Nu$
, depends on plate size
$\unicode[STIX]{x0394}Nu$
, depends on plate size
![]() $L$
, increasing dramatically with
$L$
, increasing dramatically with
![]() $L$
up to
$L$
up to
![]() $L=0.75$
, staying approximately constant for
$L=0.75$
, staying approximately constant for
![]() $L$
ranging from 0.75 to 2.5, and decreasing gradually with
$L$
ranging from 0.75 to 2.5, and decreasing gradually with
![]() $L$
for
$L$
for
![]() $L>2.5$
(figure 8
b). Compared to heat transfer by conduction, the thermal plumes that bring fluid from one horizontal boundary straightforwardly towards the opposing boundary present a more efficient means of heat transfer. These thermal plumes are henceforth termed striking thermals since they strike the opposing boundary, in contrast to those short thermals that move fast horizontally with the convective flow until uniting with the striking thermals. Therefore, the presence of a larger number of striking thermals should be associated with a higher efficiency of heat transfer, and hence larger
$L>2.5$
(figure 8
b). Compared to heat transfer by conduction, the thermal plumes that bring fluid from one horizontal boundary straightforwardly towards the opposing boundary present a more efficient means of heat transfer. These thermal plumes are henceforth termed striking thermals since they strike the opposing boundary, in contrast to those short thermals that move fast horizontally with the convective flow until uniting with the striking thermals. Therefore, the presence of a larger number of striking thermals should be associated with a higher efficiency of heat transfer, and hence larger
![]() $Nu$
.
$Nu$
.
For cases with a fixed plate,
![]() $Nu$
decreases dramatically with
$Nu$
decreases dramatically with
![]() $L$
up to
$L$
up to
![]() $L=0.75$
and less abruptly as
$L=0.75$
and less abruptly as
![]() $L$
continues to increase (figure 8
b, blue line). The dramatic decrease of
$L$
continues to increase (figure 8
b, blue line). The dramatic decrease of
![]() $Nu$
corresponds to the dramatic decrease of convection cells from five to two, or the associated striking thermals from six to three as
$Nu$
corresponds to the dramatic decrease of convection cells from five to two, or the associated striking thermals from six to three as
![]() $L$
increases from 0.25 to 0.75 (figure 8
c). As
$L$
increases from 0.25 to 0.75 (figure 8
c). As
![]() $L$
continues to increase, the number of convection cells (or striking thermals) becomes constant (figure 8
c) and therefore the decrease of
$L$
continues to increase, the number of convection cells (or striking thermals) becomes constant (figure 8
c) and therefore the decrease of
![]() $Nu$
with
$Nu$
with
![]() $L$
becomes less abrupt. For
$L$
becomes less abrupt. For
![]() $0.75\leqslant L\leqslant 2.5$
, only two convection cells, or three associated striking thermals are present for cases with a fixed plate (figure 8
c). However, the corresponding cases with a freely moving plate have evidently more convection cells (or striking thermals) (figures 3–5), which lead to a higher efficiency of heat transfer and therefore higher
$0.75\leqslant L\leqslant 2.5$
, only two convection cells, or three associated striking thermals are present for cases with a fixed plate (figure 8
c). However, the corresponding cases with a freely moving plate have evidently more convection cells (or striking thermals) (figures 3–5), which lead to a higher efficiency of heat transfer and therefore higher
![]() $Nu$
. For large plates of
$Nu$
. For large plates of
![]() $L>2.5$
, the convection cell underneath the moving plate occupies a large portion of the flow domain (for example, figure 7
d). In this case, the space left for the development of other convection cells (or the associated striking thermals) becomes quite limited and it decreases with increasing
$L>2.5$
, the convection cell underneath the moving plate occupies a large portion of the flow domain (for example, figure 7
d). In this case, the space left for the development of other convection cells (or the associated striking thermals) becomes quite limited and it decreases with increasing
![]() $L$
(figure 7
d). Therefore, as
$L$
(figure 7
d). Therefore, as
![]() $L$
increases, the number of striking thermals for fixed-plate cases and that for free-plate cases gradually becomes close, and thus
$L$
increases, the number of striking thermals for fixed-plate cases and that for free-plate cases gradually becomes close, and thus
![]() $\unicode[STIX]{x0394}Nu$
, the difference of
$\unicode[STIX]{x0394}Nu$
, the difference of
![]() $Nu$
between cases with free and fixed plates, decreases with
$Nu$
between cases with free and fixed plates, decreases with
![]() $L$
for
$L$
for
![]() $L>2.5$
. It is expected that
$L>2.5$
. It is expected that
![]() $\unicode[STIX]{x0394}Nu$
approaches zero as
$\unicode[STIX]{x0394}Nu$
approaches zero as
![]() $L$
approaches the length of the fluid domain.
$L$
approaches the length of the fluid domain.
For a unit square box, the boundary layer theory has predicted a power-law relation of
![]() $Nu$
being linearly proportional to
$Nu$
being linearly proportional to
![]() $Ra^{1/3}$
(Turcotte & Schubert Reference Turcotte and Schubert2002). Nevertheless, the present configuration is significantly different from a unit square box, not only in the horizontal size of the flow domain but also in the top boundary condition. Therefore, to obtain the
$Ra^{1/3}$
(Turcotte & Schubert Reference Turcotte and Schubert2002). Nevertheless, the present configuration is significantly different from a unit square box, not only in the horizontal size of the flow domain but also in the top boundary condition. Therefore, to obtain the
![]() $Nu$
–
$Nu$
–
![]() $Ra$
power-law relation (
$Ra$
power-law relation (
![]() $Nu=\unicode[STIX]{x1D6FC}\,Ra^{\unicode[STIX]{x1D6FD}}$
) for the case of
$Nu=\unicode[STIX]{x1D6FC}\,Ra^{\unicode[STIX]{x1D6FD}}$
) for the case of
![]() $L=2.5$
, both the exponent
$L=2.5$
, both the exponent
![]() $\unicode[STIX]{x1D6FD}$
and the coefficient
$\unicode[STIX]{x1D6FD}$
and the coefficient
![]() $\unicode[STIX]{x1D6FC}$
are set as the fitting parameters. Our results suggest that the average
$\unicode[STIX]{x1D6FC}$
are set as the fitting parameters. Our results suggest that the average
![]() $Nu$
over the quasi-steady-state scales with
$Nu$
over the quasi-steady-state scales with
![]() $Ra^{0.2831}$
for the fixed-plate cases, and
$Ra^{0.2831}$
for the fixed-plate cases, and
![]() $Ra^{0.2565}$
for the free-plate cases, and therefore the exponents are much smaller than the theoretical value of
$Ra^{0.2565}$
for the free-plate cases, and therefore the exponents are much smaller than the theoretical value of
![]() $1/3$
predicted for a unit square box.
$1/3$
predicted for a unit square box.
4.3 Variation of plate motion with Ra
For
![]() $L=2.5$
, the plate moves unidirectionally under different Rayleigh numbers until it encounters the end wall (figure 9
a). Nevertheless, for
$L=2.5$
, the plate moves unidirectionally under different Rayleigh numbers until it encounters the end wall (figure 9
a). Nevertheless, for
![]() $Ra=2\times 10^{5}$
, the plate motion can still be severely hindered when the plate encounters impeding flow structures (figure 9
b). As
$Ra=2\times 10^{5}$
, the plate motion can still be severely hindered when the plate encounters impeding flow structures (figure 9
b). As
![]() $Ra$
increases, the probability of low plate speed (for example,
$Ra$
increases, the probability of low plate speed (for example,
![]() $|u|<100$
) decreases significantly, approaching zero for
$|u|<100$
) decreases significantly, approaching zero for
![]() $Ra\geqslant 10^{6}$
(figure 9
c). Therefore, apart from plate size, the increase of
$Ra\geqslant 10^{6}$
(figure 9
c). Therefore, apart from plate size, the increase of
![]() $Ra$
also increases plate capacity to overcome impeding flow structures. Excluding data affected by the end-wall effect, the mean plate speed scales relatively well with
$Ra$
also increases plate capacity to overcome impeding flow structures. Excluding data affected by the end-wall effect, the mean plate speed scales relatively well with
![]() $Ra^{2/3}$
, which is consistent with the scaling prediction for the mantle flow (Turcotte & Schubert Reference Turcotte and Schubert2002; Grigné, Labrosse & Tackley Reference Grigné, Labrosse and Tackley2005). However, for
$Ra^{2/3}$
, which is consistent with the scaling prediction for the mantle flow (Turcotte & Schubert Reference Turcotte and Schubert2002; Grigné, Labrosse & Tackley Reference Grigné, Labrosse and Tackley2005). However, for
![]() $Ra=2\times 10^{5}$
, the mean plate speed is evidently lower than the scaling prediction (figure 9
d). This is because for this lower
$Ra=2\times 10^{5}$
, the mean plate speed is evidently lower than the scaling prediction (figure 9
d). This is because for this lower
![]() $Ra$
, plate movement is often significantly hindered by impeding flow, which counteracts the main flow that drives the plate (figure 9
b), and therefore the plate speed is lower than the speed of the underlying flow predicted by the scaling.
$Ra$
, plate movement is often significantly hindered by impeding flow, which counteracts the main flow that drives the plate (figure 9
b), and therefore the plate speed is lower than the speed of the underlying flow predicted by the scaling.

Figure 9. Variation of plate motion with
![]() $Ra$
for
$Ra$
for
![]() $L=2.5$
and
$L=2.5$
and
![]() $h=0$
. (a) Time series of plate centre location
$h=0$
. (a) Time series of plate centre location
![]() $x$
for
$x$
for
![]() $Ra=2\times 10^{5}$
,
$Ra=2\times 10^{5}$
,
![]() $5\times 10^{5}$
,
$5\times 10^{5}$
,
![]() $10^{6}$
,
$10^{6}$
,
![]() $2\times 10^{6}$
,
$2\times 10^{6}$
,
![]() $5\times 10^{6}$
from top to bottom. (b) Time series of the corresponding plate velocity
$5\times 10^{6}$
from top to bottom. (b) Time series of the corresponding plate velocity
![]() $u$
. (c) Probability density of plate speed
$u$
. (c) Probability density of plate speed
![]() $|u|$
. (d) Time-averaged plate speed
$|u|$
. (d) Time-averaged plate speed
![]() $|u|_{mean}$
during the quasi-steady-state, the straight line is a fit to the value at
$|u|_{mean}$
during the quasi-steady-state, the straight line is a fit to the value at
![]() $Ra=5\times 10^{6}$
and is given by
$Ra=5\times 10^{6}$
and is given by
![]() $|u|_{mean}=0.0627\,Ra^{2/3}$
.
$|u|_{mean}=0.0627\,Ra^{2/3}$
.
4.4 The correlation between plate movement and thermal signals of the flow
The presence of the plate affects the underlying thermal structure, as shown by the isotherms and streamlines in § 3. Further, plate movement or stagnancy can affect the thermal signals of the flow. Some of the thermal signals, including the spatial root mean square temperature
![]() $T_{rms}$
, the average temperature
$T_{rms}$
, the average temperature
![]() $\overline{T}$
over the flow domain, the average temperature
$\overline{T}$
over the flow domain, the average temperature
![]() $\overline{T}_{i}$
at the plate–fluid interface and the Nusselt number
$\overline{T}_{i}$
at the plate–fluid interface and the Nusselt number
![]() $Nu$
are shown in figure 10.
$Nu$
are shown in figure 10.
For a very small plate of
![]() $L=0.25$
, the quiescent duration (highlighted by the cyan bands in figure 10
a) is characterized by lower plate velocity
$L=0.25$
, the quiescent duration (highlighted by the cyan bands in figure 10
a) is characterized by lower plate velocity
![]() $u$
, lower
$u$
, lower
![]() $T_{rms}$
and higher
$T_{rms}$
and higher
![]() $Nu$
than the active duration (figure 10
a). The lower
$Nu$
than the active duration (figure 10
a). The lower
![]() $T_{rms}$
corresponds to the more regular flow structure during the quiescent duration (figure 2
a). The higher
$T_{rms}$
corresponds to the more regular flow structure during the quiescent duration (figure 2
a). The higher
![]() $Nu$
during the quiescent duration corresponds to the more straightforward movement of the thermals towards the opposing boundaries. The vertically moving thermals during the quiescent duration bring colder/warmer material to the lower/upper boundary than the bifurcating and inclining thermals during the active duration (figure 2
a,b), resulting in a higher efficiency of heat transfer, and therefore higher
$Nu$
during the quiescent duration corresponds to the more straightforward movement of the thermals towards the opposing boundaries. The vertically moving thermals during the quiescent duration bring colder/warmer material to the lower/upper boundary than the bifurcating and inclining thermals during the active duration (figure 2
a,b), resulting in a higher efficiency of heat transfer, and therefore higher
![]() $Nu$
. Over the quiescent duration, the time series of the average temperature
$Nu$
. Over the quiescent duration, the time series of the average temperature
![]() $\overline{T}$
over the flow domain shows a general trend of slow increase and is much smoother than over the active duration (figure 10
a). On the other hand, the average temperature
$\overline{T}$
over the flow domain shows a general trend of slow increase and is much smoother than over the active duration (figure 10
a). On the other hand, the average temperature
![]() $\overline{T}_{i}$
at the plate–fluid interface exhibits higher values (suggesting weaker downwellings underneath the plate) during the active durations, consistent with the snapshots of temperature (figure 2
a,b).
$\overline{T}_{i}$
at the plate–fluid interface exhibits higher values (suggesting weaker downwellings underneath the plate) during the active durations, consistent with the snapshots of temperature (figure 2
a,b).

Figure 10. The response of thermal signals to plate movement for different plate sizes at
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
: time series of plate centre location
$h=0$
: time series of plate centre location
![]() $x$
, plate velocity
$x$
, plate velocity
![]() $u$
, the spatial root mean square temperature
$u$
, the spatial root mean square temperature
![]() $T_{rms}$
, the average temperature of the flow domain
$T_{rms}$
, the average temperature of the flow domain
![]() $\overline{T}$
, the average temperature
$\overline{T}$
, the average temperature
![]() $\overline{T}_{i}$
over the plate–fluid interface, and the average Nusselt number
$\overline{T}_{i}$
over the plate–fluid interface, and the average Nusselt number
![]() $Nu$
at the bottom boundary. (a)
$Nu$
at the bottom boundary. (a)
![]() $L=0.25$
, the cyan bands highlight the quiescent durations, the red line in the time series of
$L=0.25$
, the cyan bands highlight the quiescent durations, the red line in the time series of
![]() $Nu$
shows the result of
$Nu$
shows the result of
![]() $Nu$
after the plate is removed at
$Nu$
after the plate is removed at
![]() $t=0.47$
. (b)
$t=0.47$
. (b)
![]() $L=0.5$
, the magenta bands highlight the velocity bursts. (c)
$L=0.5$
, the magenta bands highlight the velocity bursts. (c)
![]() $L=1.5$
, the cyan bands highlight the durations when the plate slows down and becomes stagnant. (d)
$L=1.5$
, the cyan bands highlight the durations when the plate slows down and becomes stagnant. (d)
![]() $L=2.5$
, the cyan bands highlight the durations when the plate slows down at first but retains or even increases its speed afterwards.
$L=2.5$
, the cyan bands highlight the durations when the plate slows down at first but retains or even increases its speed afterwards.
To investigate the effect of a very small mobile plate (
![]() $L=0.25$
) on the flow pattern underneath, we remove the plate (at time
$L=0.25$
) on the flow pattern underneath, we remove the plate (at time
![]() $t=0.47$
) after the coupled system reaches a quasi-steady-state. It is found that the quasi-steady-state flow pattern for the no-plate case is similar to the flow pattern for the case with a small plate of
$t=0.47$
) after the coupled system reaches a quasi-steady-state. It is found that the quasi-steady-state flow pattern for the no-plate case is similar to the flow pattern for the case with a small plate of
![]() $L=0.25$
, shown in figure 2(a), in which the flow domain is occupied by five convection rolls of similar size. Nevertheless, for the no-plate case, the differentiation between the active and the quiescent duration is less noticeable and the fluctuation of flow properties with time is much smaller, as illustrated by the time series of
$L=0.25$
, shown in figure 2(a), in which the flow domain is occupied by five convection rolls of similar size. Nevertheless, for the no-plate case, the differentiation between the active and the quiescent duration is less noticeable and the fluctuation of flow properties with time is much smaller, as illustrated by the time series of
![]() $Nu$
(red line in figure 10
a). Therefore, rather than being a completely passive tracer, the small plate magnifies the fluctuation of flow properties during the active duration and lowers the average
$Nu$
(red line in figure 10
a). Therefore, rather than being a completely passive tracer, the small plate magnifies the fluctuation of flow properties during the active duration and lowers the average
![]() $Nu$
.
$Nu$
.
As plate size increases to
![]() $L=0.5$
, the plate experiences long durations of stagnancy on top of cold downwelling until hot upwelling arrives underneath and brings it a velocity burst. As the plate alternates between stagnancy and velocity burst, the thermal signals, including
$L=0.5$
, the plate experiences long durations of stagnancy on top of cold downwelling until hot upwelling arrives underneath and brings it a velocity burst. As the plate alternates between stagnancy and velocity burst, the thermal signals, including
![]() $T_{rms}$
,
$T_{rms}$
,
![]() $\overline{T}$
,
$\overline{T}$
,
![]() $\overline{T}_{i}$
and
$\overline{T}_{i}$
and
![]() $Nu$
, exhibit consistent trend of variation over time (figure 10
b). Plate velocity burst is associated with a general increase of
$Nu$
, exhibit consistent trend of variation over time (figure 10
b). Plate velocity burst is associated with a general increase of
![]() $T_{rms}$
, a maximum of
$T_{rms}$
, a maximum of
![]() $\overline{T}$
, a burst of
$\overline{T}$
, a burst of
![]() $\overline{T}_{i}$
, and a decrease of
$\overline{T}_{i}$
, and a decrease of
![]() $Nu$
(highlighted by the magenta bands in figure 10
b). Since plate velocity bursts happen when hot upwelling arrives underneath, bursts of plate velocity correspond to bursts of temperature
$Nu$
(highlighted by the magenta bands in figure 10
b). Since plate velocity bursts happen when hot upwelling arrives underneath, bursts of plate velocity correspond to bursts of temperature
![]() $\overline{T_{i}}$
at the interface. When the plate experiences a velocity burst, the position of the plate changes abruptly. Corresponding to this abrupt change, the underlying convection cells undergo a process of reorganization. During this process, the plume pattern becomes less regular and the number of convection cells decreases (figure 3
b,c). As a result of flow reorganization, bursts of plate velocity correspond to general increases of
$\overline{T_{i}}$
at the interface. When the plate experiences a velocity burst, the position of the plate changes abruptly. Corresponding to this abrupt change, the underlying convection cells undergo a process of reorganization. During this process, the plume pattern becomes less regular and the number of convection cells decreases (figure 3
b,c). As a result of flow reorganization, bursts of plate velocity correspond to general increases of
![]() $T_{rms}$
and general decreases of
$T_{rms}$
and general decreases of
![]() $Nu$
, as highlighted by the magenta bands in figure 10(b). Shortly after the velocity burst, the plate arrives at another downwelling and becomes stagnant again. The thermal plumes and the convection cells reorganize to adjust to the changed plate position. As the process of reorganization goes on, the spatial pattern of convection cells and the associated plumes becomes more regular and the number of convection cells increases (figure 3
d,e), resulting in a decrease/increase of
$Nu$
, as highlighted by the magenta bands in figure 10(b). Shortly after the velocity burst, the plate arrives at another downwelling and becomes stagnant again. The thermal plumes and the convection cells reorganize to adjust to the changed plate position. As the process of reorganization goes on, the spatial pattern of convection cells and the associated plumes becomes more regular and the number of convection cells increases (figure 3
d,e), resulting in a decrease/increase of
![]() $T_{rms}/Nu$
. This process of variation in
$T_{rms}/Nu$
. This process of variation in
![]() $T_{rms}$
and
$T_{rms}$
and
![]() $Nu$
persists as the plate alternates between stagnancy and velocity burst. Since a stagnant plate accumulates heat underneath more efficiently than a fast moving plate, the burst in plate velocity is associated with the start of a sharp decrease in the average temperature
$Nu$
persists as the plate alternates between stagnancy and velocity burst. Since a stagnant plate accumulates heat underneath more efficiently than a fast moving plate, the burst in plate velocity is associated with the start of a sharp decrease in the average temperature
![]() $\overline{T}$
(figure 10
b). This decrease persists for a while after the plate reaches a new downwelling. After the plate sits on top of the downwelling for a sufficiently long time, its thermal blanket effect becomes evident and the value of
$\overline{T}$
(figure 10
b). This decrease persists for a while after the plate reaches a new downwelling. After the plate sits on top of the downwelling for a sufficiently long time, its thermal blanket effect becomes evident and the value of
![]() $\overline{T}$
begins to increase with time. As a result, the average temperature
$\overline{T}$
begins to increase with time. As a result, the average temperature
![]() $\overline{T}$
reaches a maximum around the time when the plate shows a velocity burst, as highlighted by the magenta bands in figure 10(b).
$\overline{T}$
reaches a maximum around the time when the plate shows a velocity burst, as highlighted by the magenta bands in figure 10(b).
As plate size increases to
![]() $L\geqslant 1.5$
, the overall shape of thermal plumes becomes more irregular and their movement towards the opposing boundary becomes less straightforward (figures 4 and 5). The alternation between stagnancy (SM II) and movement becomes less distinct and less differentiable. Further, the duration of stagnancy (SM II) is much shorter than that of SM I for smaller plates, leaving a very limited time for the fluid to reorganize and respond to the newly settled plate position. As a result, the variation of the thermal signals of the fluid with plate movement becomes less obvious (figure 10
c). Nevertheless, a decrease in plate velocity
$L\geqslant 1.5$
, the overall shape of thermal plumes becomes more irregular and their movement towards the opposing boundary becomes less straightforward (figures 4 and 5). The alternation between stagnancy (SM II) and movement becomes less distinct and less differentiable. Further, the duration of stagnancy (SM II) is much shorter than that of SM I for smaller plates, leaving a very limited time for the fluid to reorganize and respond to the newly settled plate position. As a result, the variation of the thermal signals of the fluid with plate movement becomes less obvious (figure 10
c). Nevertheless, a decrease in plate velocity
![]() $u$
and its subsequent stagnation are associated with an evident decrease and then a subsequent increase in the average temperature
$u$
and its subsequent stagnation are associated with an evident decrease and then a subsequent increase in the average temperature
![]() $\overline{T}_{i}$
at the interface (highlighted by the cyan bands in figure 10
c). This corresponding variation in plate velocity
$\overline{T}_{i}$
at the interface (highlighted by the cyan bands in figure 10
c). This corresponding variation in plate velocity
![]() $u$
and
$u$
and
![]() $\overline{T}_{i}$
is consistent with the temporal evolution of the stagnant mode II. The encounter of cold downwelling at the leading edge of the plate initiates a slowdown of plate velocity and a decrease in
$\overline{T}_{i}$
is consistent with the temporal evolution of the stagnant mode II. The encounter of cold downwelling at the leading edge of the plate initiates a slowdown of plate velocity and a decrease in
![]() $\overline{T}_{i}$
, which is evident by comparing figure 4(a) with 4(b), and figure 4(e) with 4(f). As the plate slows down, it gradually enters into the stagnant mode II and nurtures the growth of hot upwelling underneath the plate (figure 4
b,c), resulting in an increase of
$\overline{T}_{i}$
, which is evident by comparing figure 4(a) with 4(b), and figure 4(e) with 4(f). As the plate slows down, it gradually enters into the stagnant mode II and nurtures the growth of hot upwelling underneath the plate (figure 4
b,c), resulting in an increase of
![]() $\overline{T}_{i}$
at the interface. This variation of
$\overline{T}_{i}$
at the interface. This variation of
![]() $\overline{T}_{i}$
after the slowdown of plate velocity is also observed for the even larger plate case of
$\overline{T}_{i}$
after the slowdown of plate velocity is also observed for the even larger plate case of
![]() $L=2.5$
. As the thermal blanket effect is enhanced with increasing plate size, the decrease and the subsequent increase in
$L=2.5$
. As the thermal blanket effect is enhanced with increasing plate size, the decrease and the subsequent increase in
![]() $\overline{T}_{i}$
(highlighted by the cyan bands in figure 10
d) is completed in shorter durations for the case of
$\overline{T}_{i}$
(highlighted by the cyan bands in figure 10
d) is completed in shorter durations for the case of
![]() $L=2.5$
than for the case of
$L=2.5$
than for the case of
![]() $L=1.5$
(figure 10
c,d). Further, the large plate of
$L=1.5$
(figure 10
c,d). Further, the large plate of
![]() $L=2.5$
slows down when it encounters a cold downwelling, but the plate soon warms up the downwelling, resulting in the decrease of the spatial root mean square temperature
$L=2.5$
slows down when it encounters a cold downwelling, but the plate soon warms up the downwelling, resulting in the decrease of the spatial root mean square temperature
![]() $T_{rms}$
with decreasing
$T_{rms}$
with decreasing
![]() $u$
. Conversely, an increase of plate velocity from zero, after the forced stop at the end wall, is associated with the generation of hot thermal plumes underneath the plate (figure 5
d), which is reflected in the increase of
$u$
. Conversely, an increase of plate velocity from zero, after the forced stop at the end wall, is associated with the generation of hot thermal plumes underneath the plate (figure 5
d), which is reflected in the increase of
![]() $T_{rms}$
as
$T_{rms}$
as
![]() $u$
increases from zero (figure 10
d).
$u$
increases from zero (figure 10
d).
4.5 The effect of internal heating on plate movement
Apart from bottom heating at the core–mantle boundary, radioactive decay provides an essential heating source for the interior of the Earth (Turcotte & Schubert Reference Turcotte and Schubert2002). To investigate the effect of internal heating on plate movement, simulations were conducted by applying different intensities of internal heating for the case of
![]() $L=2.5$
(figure 11). Time series of the plate centre position
$L=2.5$
(figure 11). Time series of the plate centre position
![]() $x$
and plate velocity
$x$
and plate velocity
![]() $u$
show increasing steadiness of plate movement as the intensity of internal heating
$u$
show increasing steadiness of plate movement as the intensity of internal heating
![]() $h$
increases (figure 11
a,b). As
$h$
increases (figure 11
a,b). As
![]() $h$
increases, the distribution of plate speed
$h$
increases, the distribution of plate speed
![]() $|u|$
becomes increasingly concentrated on high values (figure 11
c), suggesting an increasing steadiness of plate movement and an increasing overall plate speed. Meanwhile, as
$|u|$
becomes increasingly concentrated on high values (figure 11
c), suggesting an increasing steadiness of plate movement and an increasing overall plate speed. Meanwhile, as
![]() $h$
increases, the probability and the percentage of low plate speed decrease (figure 11
c,d), suggesting a decreasing likelihood of plate movement being severely hindered by impeding flow structures. The average plate speed
$h$
increases, the probability and the percentage of low plate speed decrease (figure 11
c,d), suggesting a decreasing likelihood of plate movement being severely hindered by impeding flow structures. The average plate speed
![]() $|u|$
increases with increasing
$|u|$
increases with increasing
![]() $h$
(figure 11
e). Therefore, plate mobility or its capability to overcome impeding flow structures increases with increasing internal heating intensity
$h$
(figure 11
e). Therefore, plate mobility or its capability to overcome impeding flow structures increases with increasing internal heating intensity
![]() $h$
.
$h$
.

Figure 11. The effect of internal heating on plate movement illustrated with a parameter setting of
![]() $L=2.5$
,
$L=2.5$
,
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0$
, 2, 4, 8. (a) Plate centre position
$h=0$
, 2, 4, 8. (a) Plate centre position
![]() $x$
and (b) plate velocity
$x$
and (b) plate velocity
![]() $u$
for
$u$
for
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $L=2.5$
with different internal heating rates,
$L=2.5$
with different internal heating rates,
![]() $h=0$
, 2, 4, 8. Time starts from when the plate is freed. The red horizontal lines denote the maximum range of plate centre position
$h=0$
, 2, 4, 8. Time starts from when the plate is freed. The red horizontal lines denote the maximum range of plate centre position
![]() $x$
. (c) Probability density of plate speed
$x$
. (c) Probability density of plate speed
![]() $|u|$
. (d) Percentage of low plate speed
$|u|$
. (d) Percentage of low plate speed
![]() $|u|$
in the time series of
$|u|$
in the time series of
![]() $|u|$
. (e) Time-averaged plate speed
$|u|$
. (e) Time-averaged plate speed
![]() $|u|$
during the quasi-steady-state. Data shown in (d,e) exclude those when plate movement is affected by the artificially forced stop at the end wall.
$|u|$
during the quasi-steady-state. Data shown in (d,e) exclude those when plate movement is affected by the artificially forced stop at the end wall.
A comparison was also made between one case with
![]() $h=0$
(no internal heating) and another one with
$h=0$
(no internal heating) and another one with
![]() $h=8$
for a small plate size of
$h=8$
for a small plate size of
![]() $L=0.5$
. Time series of plate centre position
$L=0.5$
. Time series of plate centre position
![]() $x$
and plate velocity
$x$
and plate velocity
![]() $u$
show that plate mobility increases significantly as internal heating is switched on (figure 12
a). For
$u$
show that plate mobility increases significantly as internal heating is switched on (figure 12
a). For
![]() $h=8$
, as a result of the enhanced plate mobility, the distinction between stagnation and velocity burst becomes less differentiable in the times series of plate velocity
$h=8$
, as a result of the enhanced plate mobility, the distinction between stagnation and velocity burst becomes less differentiable in the times series of plate velocity
![]() $u$
, and the plate is able to reach the end walls (figure 12
a). Consequently, the probability of plate stagnation (low plate speed
$u$
, and the plate is able to reach the end walls (figure 12
a). Consequently, the probability of plate stagnation (low plate speed
![]() $|u|$
) decreases significantly as
$|u|$
) decreases significantly as
![]() $h$
increases from 0 to 8 (figure 12
b).
$h$
increases from 0 to 8 (figure 12
b).

Figure 12. The effect of internal heating on plate movement illustrated with a parameter setting of
![]() $L=0.5$
,
$L=0.5$
,
![]() $Ra=10^{6}$
,
$Ra=10^{6}$
,
![]() $h=0,8$
. (a) Plate centre position
$h=0,8$
. (a) Plate centre position
![]() $x$
and plate velocity
$x$
and plate velocity
![]() $u$
for
$u$
for
![]() $Ra=10^{6}$
with
$Ra=10^{6}$
with
![]() $h=0$
(black line) and
$h=0$
(black line) and
![]() $h=8$
(red dashed line). Time starts from when the plate is freed. (b) Probability density of plate speed
$h=8$
(red dashed line). Time starts from when the plate is freed. (b) Probability density of plate speed
![]() $|u|$
.
$|u|$
.
4.6 The presence of different modes in three dimensions
To illustrate the presence of different modes in three dimensions, 3-D simulations were conducted in a
![]() $8\times 8\times 1$
(
$8\times 8\times 1$
(
![]() $8\times 8$
is the horizontal dimensional size and 1 is the depth) convective domain with a square plate of different sizes floating on top of it. Although the plate is set free to move from the beginning when the entire flow is isothermal and stationary, it is observed that all of the plates remain stagnant at the initial stage and only begin to move at a more developed stage.
$8\times 8$
is the horizontal dimensional size and 1 is the depth) convective domain with a square plate of different sizes floating on top of it. Although the plate is set free to move from the beginning when the entire flow is isothermal and stationary, it is observed that all of the plates remain stagnant at the initial stage and only begin to move at a more developed stage.
The addition of a new dimension in space introduces much richer dynamics in the fluid domain and more possibilities in plate movement. Nevertheless, the three different coupling modes (SM I, SM II and UMM) revealed in two dimensions are all identified in three dimensions, and the basic characteristics of the different modes are consistent with those observed in two dimensions.
For a small plate with a horizontal size of
![]() $0.5\times 0.5$
, the plate shows a short episode of velocity burst when its underlying flow is coherently flowing in one direction, from a site of hot upwelling towards a site of cold downwelling (figure 13
a,d). When the plate arrives at the site of downwelling, the underlying flow converges underneath the plate and flows downwards towards the bottom of the fluid domain. The convergence of flow underneath the plate involves flows in two opposing directions for the 2-D cases (figures 2
a, 3
a,e), but involves flows in all horizontal directions for the 3-D case (figure 13
b,c). The coupled system achieves a balance by adjusting the plate position so that the forces exerted by the underlying flow on the plate are balanced. This is a stable mode since the plate will be pulled back to the balanced position if it is moved slightly away from it. Figure 13(b) shows the snapshot of two isothermal surfaces and streamlines of SM I at an early stage of flow development, while the presence of SM I at a more developed stage is illustrated in figure 13(c). The convergence of flow underneath the plate is shown by the streamlines there, and the presence of cold downwelling at the plate position is demonstrated by the translucent blue isothermal surface.
$0.5\times 0.5$
, the plate shows a short episode of velocity burst when its underlying flow is coherently flowing in one direction, from a site of hot upwelling towards a site of cold downwelling (figure 13
a,d). When the plate arrives at the site of downwelling, the underlying flow converges underneath the plate and flows downwards towards the bottom of the fluid domain. The convergence of flow underneath the plate involves flows in two opposing directions for the 2-D cases (figures 2
a, 3
a,e), but involves flows in all horizontal directions for the 3-D case (figure 13
b,c). The coupled system achieves a balance by adjusting the plate position so that the forces exerted by the underlying flow on the plate are balanced. This is a stable mode since the plate will be pulled back to the balanced position if it is moved slightly away from it. Figure 13(b) shows the snapshot of two isothermal surfaces and streamlines of SM I at an early stage of flow development, while the presence of SM I at a more developed stage is illustrated in figure 13(c). The convergence of flow underneath the plate is shown by the streamlines there, and the presence of cold downwelling at the plate position is demonstrated by the translucent blue isothermal surface.

Figure 13. The evolution of stagnant mode I in three dimensions with a plate size of
![]() $0.5\times 0.5$
,
$0.5\times 0.5$
,
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–c) are snapshots of isothermal surface and streamlines. (a) Corresponds to a time when plate shows velocity burst. (b,c) Correspond to the time when the plate shows SM I at an early and a more developed stage respectively. (d) Time series of plate velocity components,
$h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–c) are snapshots of isothermal surface and streamlines. (a) Corresponds to a time when plate shows velocity burst. (b,c) Correspond to the time when the plate shows SM I at an early and a more developed stage respectively. (d) Time series of plate velocity components,
![]() $u$
,
$u$
,
![]() $w$
and its horizontal speed
$w$
and its horizontal speed
![]() $(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–c) are marked with cyan dots and lines in (d).
$(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–c) are marked with cyan dots and lines in (d).

Figure 14. The evolution of stagnant mode II in three dimensions with a plate size of
![]() $1.5\times 1.5$
,
$1.5\times 1.5$
,
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–d) Snapshots of isothermal surface and streamlines. (a) Corresponds to the time when the plate shows velocity burst. (b) Corresponds to the time when plate begins to show SM II. (c) Corresponds to the time when the SM II is about to end. (d) Corresponds to the time when the plate shows velocity burst again. (e) Time series of plate velocity components,
$h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–d) Snapshots of isothermal surface and streamlines. (a) Corresponds to the time when the plate shows velocity burst. (b) Corresponds to the time when plate begins to show SM II. (c) Corresponds to the time when the SM II is about to end. (d) Corresponds to the time when the plate shows velocity burst again. (e) Time series of plate velocity components,
![]() $u$
,
$u$
,
![]() $w$
and its horizontal speed
$w$
and its horizontal speed
![]() $(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–d) are marked with cyan dots and lines in (e). The grey bands mark the duration when plate velocity is affected by the end wall, i.e. the plate is not allowed to penetrate the end wall.
$(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–d) are marked with cyan dots and lines in (e). The grey bands mark the duration when plate velocity is affected by the end wall, i.e. the plate is not allowed to penetrate the end wall.
For a larger plate with a horizontal size of
![]() $1.5\times 1.5$
, the presence of SM II is illustrated in figure 14. Figure 14(a) shows the snapshot of isothermal surfaces and streamlines when the fluid underneath the plate flows almost coherently in one direction, nearly parallel to the
$1.5\times 1.5$
, the presence of SM II is illustrated in figure 14. Figure 14(a) shows the snapshot of isothermal surfaces and streamlines when the fluid underneath the plate flows almost coherently in one direction, nearly parallel to the
![]() $z$
axis. It is about to encounter flows in different directions at its leading edge. As the plate moves ahead, the coherent flow structure underneath the plate disappears and the plate slows down. This slowing down of plate enhances the thermal blanket effect of the plate to the underlying flow and nurtures the growth of hot thermal plumes underneath the plate. Consequently, a hot plume starts to rise up underneath the plate (figure 14
b), similar to the 2-D case (figure 4
b,f). The presence of the hot plume underneath the plate gives a divergent flow structure there, as shown by the streamlines (figure 14
b), analogous to the 2-D case (figure 4
b,f). As the plume grows and the underlying flow evolves with time, the flow in the direction parallel to the positive
$z$
axis. It is about to encounter flows in different directions at its leading edge. As the plate moves ahead, the coherent flow structure underneath the plate disappears and the plate slows down. This slowing down of plate enhances the thermal blanket effect of the plate to the underlying flow and nurtures the growth of hot thermal plumes underneath the plate. Consequently, a hot plume starts to rise up underneath the plate (figure 14
b), similar to the 2-D case (figure 4
b,f). The presence of the hot plume underneath the plate gives a divergent flow structure there, as shown by the streamlines (figure 14
b), analogous to the 2-D case (figure 4
b,f). As the plume grows and the underlying flow evolves with time, the flow in the direction parallel to the positive
![]() $x$
axis starts to become dominant (figure 14
c), and the plate is about to move in the same direction as the dominant flow. Figure 14(d) shows the termination of SM II, in which the plate rides on a coherent flow again, almost parallel to the positive
$x$
axis starts to become dominant (figure 14
c), and the plate is about to move in the same direction as the dominant flow. Figure 14(d) shows the termination of SM II, in which the plate rides on a coherent flow again, almost parallel to the positive
![]() $x$
axis. During this evolution of SM II, the plate changes its direction from originally moving parallel to the
$x$
axis. During this evolution of SM II, the plate changes its direction from originally moving parallel to the
![]() $z$
axis before the stagnation mode to moving parallel to the
$z$
axis before the stagnation mode to moving parallel to the
![]() $x$
axis after the stagnation mode, as illustrated by the direction of streamlines in figure 14(a,d). This change of direction is also evident in the time series of velocity components, in which the
$x$
axis after the stagnation mode, as illustrated by the direction of streamlines in figure 14(a,d). This change of direction is also evident in the time series of velocity components, in which the
![]() $w$
component decreases and the
$w$
component decreases and the
![]() $u$
component increases during the evolution of SM II (figure 14
e).
$u$
component increases during the evolution of SM II (figure 14
e).
For an even larger plate with a horizontal size of
![]() $2.5\times 2.5$
, the presence of the unidirectional moving mode is illustrated in figure 15. The plate is observed to move almost straightforwardly until it encounters the end wall. Figure 15(a) shows the snapshot when the plate rides on a coherent flow structure and is about to encounter impeding flow structure at its leading edge. Hot thermals are observed to rise up at its trailing edge while cold downwellings occur close to its leading edge, similar to the pattern of a single underlying convection cell in the 2-D case. When the plate encounters the downwelling and the associated impeding flow structure at its leading edge, it slows down but continues its movement forwards, taking the cold downwelling along with it (figure 15
b). As a result, the cold downwelling is observed to dip at an angle beneath the moving plate, similar to the 2-D case (figure 5
b). This slowing down of plate enhances the thermal blanket effect of plate to the underlying flow and the underlying flow quickly readjusts by forming new uprising hot plumes which are observed at a later stage (figure 15
c). The underlying flow quickly reorganizes by merging with the frontal flow of the same direction and disintegrating at the trailing edge of the plate. As a result of this reorganization, the plate rides on top of a strong coherent flow again and resumes its fast motion (figure 15
c). This process of flow merging at the leading edge and disintegrating near the trailing edge is consistent with that observed in the 2-D case (figure 5).
$2.5\times 2.5$
, the presence of the unidirectional moving mode is illustrated in figure 15. The plate is observed to move almost straightforwardly until it encounters the end wall. Figure 15(a) shows the snapshot when the plate rides on a coherent flow structure and is about to encounter impeding flow structure at its leading edge. Hot thermals are observed to rise up at its trailing edge while cold downwellings occur close to its leading edge, similar to the pattern of a single underlying convection cell in the 2-D case. When the plate encounters the downwelling and the associated impeding flow structure at its leading edge, it slows down but continues its movement forwards, taking the cold downwelling along with it (figure 15
b). As a result, the cold downwelling is observed to dip at an angle beneath the moving plate, similar to the 2-D case (figure 5
b). This slowing down of plate enhances the thermal blanket effect of plate to the underlying flow and the underlying flow quickly readjusts by forming new uprising hot plumes which are observed at a later stage (figure 15
c). The underlying flow quickly reorganizes by merging with the frontal flow of the same direction and disintegrating at the trailing edge of the plate. As a result of this reorganization, the plate rides on top of a strong coherent flow again and resumes its fast motion (figure 15
c). This process of flow merging at the leading edge and disintegrating near the trailing edge is consistent with that observed in the 2-D case (figure 5).

Figure 15. The unidirectional moving mode (UMM) in three dimensions with a plate size of
![]() $2.5\times 2.5$
,
$2.5\times 2.5$
,
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–c) Snapshots of isothermal surface and streamlines. (a) Corresponds to the time when the plate is about to encounter impeding flow. (b) Corresponds to the time when plate slows down after it encounters downwelling. (c) Corresponds to the time when the underlying convective flow reorganizes and the plate resumes its velocity. (d) Time series of plate velocity components,
$h=0$
. The translucent blue and red iso-surfaces represent isothermal surfaces of 0.25 and 0.8, respectively. The grey lines represent streamlines around the plate. (a–c) Snapshots of isothermal surface and streamlines. (a) Corresponds to the time when the plate is about to encounter impeding flow. (b) Corresponds to the time when plate slows down after it encounters downwelling. (c) Corresponds to the time when the underlying convective flow reorganizes and the plate resumes its velocity. (d) Time series of plate velocity components,
![]() $u$
,
$u$
,
![]() $w$
and its horizontal speed
$w$
and its horizontal speed
![]() $(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–c) are marked with cyan dots and lines in (d). The grey bands mark the duration when plate velocity is affected by the end wall, i.e. the plate is not allowed to penetrate the end wall.
$(u^{2}+w^{2})^{1/2}$
. The corresponding times of (a–c) are marked with cyan dots and lines in (d). The grey bands mark the duration when plate velocity is affected by the end wall, i.e. the plate is not allowed to penetrate the end wall.
The time series of plate centre position is shown in figure 16. While a small plate (
![]() $0.5\times 0.5$
) remains almost in the same position after a velocity burst, larger plates (
$0.5\times 0.5$
) remains almost in the same position after a velocity burst, larger plates (
![]() $1.5\times 1.5$
,
$1.5\times 1.5$
,
![]() $2.5\times 2.5$
) show increased mobility. As the flow develops to a relatively mature stage, the largest plate (
$2.5\times 2.5$
) show increased mobility. As the flow develops to a relatively mature stage, the largest plate (
![]() $2.5\times 2.5$
) shows almost a unidirectional movement until it encounters the end wall. Whereas the medium plate (
$2.5\times 2.5$
) shows almost a unidirectional movement until it encounters the end wall. Whereas the medium plate (
![]() $1.5\times 1.5$
) detours during its movement, since it is easily affected by the flow structure it encounters and changes its direction afterwards (figure 14). These characteristics of plate movement agree with the time series of velocity components (figures 13
d, 14
e, 15
d) and are consistent with the characteristics of plate motion in the corresponding 2-D cases.
$1.5\times 1.5$
) detours during its movement, since it is easily affected by the flow structure it encounters and changes its direction afterwards (figure 14). These characteristics of plate movement agree with the time series of velocity components (figures 13
d, 14
e, 15
d) and are consistent with the characteristics of plate motion in the corresponding 2-D cases.

Figure 16. Time series of plate centre position
![]() $x$
,
$x$
,
![]() $z$
with three plate sizes of
$z$
with three plate sizes of
![]() $0.5\times 0.5$
,
$0.5\times 0.5$
,
![]() $1.5\times 1.5$
,
$1.5\times 1.5$
,
![]() $2.5\times 2.5$
,
$2.5\times 2.5$
,
![]() $Ra=10^{6}$
and
$Ra=10^{6}$
and
![]() $h=0$
.
$h=0$
.
5 Discussions and conclusions
Plate size is revealed to have a strong influence on its motion over a thermally convecting fluid. A small plate, with a weak capability to modulate the underlying flow, easily falls into stagnancy when encountering impeding flow structures, whereas a large plate (
![]() $L\geqslant 2.5$
) quickly modifies the impeding flow and moves unidirectionally along with a single convection cell underneath it. As a plate becomes larger, it becomes less likely to be stagnant. Two stagnant modes are identified, i.e., SM I and SM II, characterized by the presence of cold downwelling and hot upwelling underneath the plate, respectively, corresponding to convergent and divergent underlying flow, respectively. For
$L\geqslant 2.5$
) quickly modifies the impeding flow and moves unidirectionally along with a single convection cell underneath it. As a plate becomes larger, it becomes less likely to be stagnant. Two stagnant modes are identified, i.e., SM I and SM II, characterized by the presence of cold downwelling and hot upwelling underneath the plate, respectively, corresponding to convergent and divergent underlying flow, respectively. For
![]() $Ra=10^{6}$
, the plate is permanently trapped in SM I for
$Ra=10^{6}$
, the plate is permanently trapped in SM I for
![]() $L\leqslant 0.25$
. As
$L\leqslant 0.25$
. As
![]() $L$
increases to 0.5, the plate experiences an alternation of SM I and velocity bursts. A small plate gradually escapes from SM I as the two underlying convection cells shrink and the neighbouring hot plumes move towards it. As
$L$
increases to 0.5, the plate experiences an alternation of SM I and velocity bursts. A small plate gradually escapes from SM I as the two underlying convection cells shrink and the neighbouring hot plumes move towards it. As
![]() $L$
increases to 0.75, SM II starts to appear and this mode becomes dominant in trapping the plate at
$L$
increases to 0.75, SM II starts to appear and this mode becomes dominant in trapping the plate at
![]() $L=1.5$
. The plate escapes from SM II as the underlying hot plume grows and the neighbouring hot plumes move towards it. This results in the merging of underlying convection cells with the neighbouring cells and thus the enlargement of the two underlying cells, which is contrary to their shrinkage in SM I. For
$L=1.5$
. The plate escapes from SM II as the underlying hot plume grows and the neighbouring hot plumes move towards it. This results in the merging of underlying convection cells with the neighbouring cells and thus the enlargement of the two underlying cells, which is contrary to their shrinkage in SM I. For
![]() $L\geqslant 2.5$
, the plate moves unidirectionally by quickly modifying impeding flow structures on its way. As a result, a single convection cell is maintained underneath the plate, merging with frontal cells of the same direction and disintegrating at the back as the plate moves ahead. Although the possibilities of plate movement and flow dynamics in three dimensions are much richer than in two dimensions, the coupling modes between the plate and the underlying fluid are essentially the same. The three coupling modes revealed in two dimensions, namely SM I, SM II and UMM, are all identified in three dimensions.
$L\geqslant 2.5$
, the plate moves unidirectionally by quickly modifying impeding flow structures on its way. As a result, a single convection cell is maintained underneath the plate, merging with frontal cells of the same direction and disintegrating at the back as the plate moves ahead. Although the possibilities of plate movement and flow dynamics in three dimensions are much richer than in two dimensions, the coupling modes between the plate and the underlying fluid are essentially the same. The three coupling modes revealed in two dimensions, namely SM I, SM II and UMM, are all identified in three dimensions.
Although the present simplified model is far from representing Earth itself, the identified coupling modes are reminiscent of some real Earth cases. While most continents have been moving from geoid highs to geoid lows along with the underlying mantle flow since the breakup of Pangaea approximately 170 Myr ago (Turcotte & Schubert Reference Turcotte and Schubert2002), some have been rather stagnant. One of them is the African continent, which has been staying roughly stationary in a deep mantle plume reference frame since the breakup of Pangaea (Burke & Torsvik Reference Burke and Torsvik2004; Torsvik et al.
Reference Torsvik, Steinberger, Cocks and Burke2008, Reference Torsvik, Burke, Steinberger, Webb and Ashwal2010). It is being uplifted by a huge mantle plume (hot upwelling) in the eastern and southern part (Ebinger & Sleep Reference Ebinger and Sleep1998; Ritsema, van Heijst & Woodhouse Reference Ritsema, van Heijst and Woodhouse1999), and high velocity anomalies, which correspond to cold downwelling, were identified near the edge of the continent (Ritsema et al.
Reference Ritsema, van Heijst and Woodhouse1999). This thermal structure conforms to SM II. The average width of the African continent is
![]() ${\sim}1.2D$
(
${\sim}1.2D$
(
![]() $D$
is the mantle depth, which is approximately 2900 km) from the middle towards its southern part and
$D$
is the mantle depth, which is approximately 2900 km) from the middle towards its southern part and
![]() ${\sim}1.8D$
in the northern part, both of which fall into the size range for the occurrence of SM II (figure 6
c). Another stagnant continent, Zealandia, i.e. the largely submerged continent of New Zealand, has been straddling the oceanic subduction site at the Pacific–Australia plate boundary since its arrival there 25 Ma ago (Sutherland Reference Sutherland1999; Cande & Stock Reference Cande and Stock2004). As a subduction site corresponds to cold downwelling, the thermal structure of the mantle flow underneath Zealandia is reminiscent of SM I. The average width of Zealandia is approximately 0.4 D, which falls into the size range for the occurrence of SM I, as suggested by the above simulation results (figure 6
c). Interestingly, these two stagnant continents are associated with extreme elevation anomalies. Over 90 % of Zealandia is below water (Suggate, Stevens & Te Punga Reference Suggate, Stevens and Te Punga1978), whereas the southern and eastern African plateau stands more than 1 km above sea level (Lithgow-Bertelloni & Silver Reference Lithgow-Bertelloni and Silver1998). These elevation anomalies suggest that Zealandia is being dragged down by cold downwelling, whereas the African continent is being uplifted by hot upwelling, correlating well with the positive (extensional) and the negative (compressional) vertical normal stress
${\sim}1.8D$
in the northern part, both of which fall into the size range for the occurrence of SM II (figure 6
c). Another stagnant continent, Zealandia, i.e. the largely submerged continent of New Zealand, has been straddling the oceanic subduction site at the Pacific–Australia plate boundary since its arrival there 25 Ma ago (Sutherland Reference Sutherland1999; Cande & Stock Reference Cande and Stock2004). As a subduction site corresponds to cold downwelling, the thermal structure of the mantle flow underneath Zealandia is reminiscent of SM I. The average width of Zealandia is approximately 0.4 D, which falls into the size range for the occurrence of SM I, as suggested by the above simulation results (figure 6
c). Interestingly, these two stagnant continents are associated with extreme elevation anomalies. Over 90 % of Zealandia is below water (Suggate, Stevens & Te Punga Reference Suggate, Stevens and Te Punga1978), whereas the southern and eastern African plateau stands more than 1 km above sea level (Lithgow-Bertelloni & Silver Reference Lithgow-Bertelloni and Silver1998). These elevation anomalies suggest that Zealandia is being dragged down by cold downwelling, whereas the African continent is being uplifted by hot upwelling, correlating well with the positive (extensional) and the negative (compressional) vertical normal stress
![]() $\unicode[STIX]{x1D70E}_{yy}$
identified at the plate bottom for SM I (figure 2
g) and SM II (figure 3
i), respectively.
$\unicode[STIX]{x1D70E}_{yy}$
identified at the plate bottom for SM I (figure 2
g) and SM II (figure 3
i), respectively.
The Earth system is much more complex than the present oversimplified model. Several other factors should be taken into account when applying the present results to the Earth itself. First, the present study is conducted at a Rayleigh number of
![]() $Ra=10^{6}$
, which is still on the lower end of Rayleigh number for mantle convection. For an estimation of the Rayleigh number for the mantle, the following parameters are taken from Turcotte & Schubert (Reference Turcotte and Schubert2002), a thermal diffusivity of
$Ra=10^{6}$
, which is still on the lower end of Rayleigh number for mantle convection. For an estimation of the Rayleigh number for the mantle, the following parameters are taken from Turcotte & Schubert (Reference Turcotte and Schubert2002), a thermal diffusivity of
![]() $\unicode[STIX]{x1D705}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, a dynamic viscosity of
$\unicode[STIX]{x1D705}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, a dynamic viscosity of
![]() $\unicode[STIX]{x1D707}=10^{21}$
Pa s, a thermal expansion coefficient of
$\unicode[STIX]{x1D707}=10^{21}$
Pa s, a thermal expansion coefficient of
![]() $\unicode[STIX]{x1D6FD}=3\times 10^{-5}~\text{K}^{-1}$
, an average density of
$\unicode[STIX]{x1D6FD}=3\times 10^{-5}~\text{K}^{-1}$
, an average density of
![]() $\unicode[STIX]{x1D70C}=4000~\text{kg}~\text{m}^{-3}$
, a temperature difference of
$\unicode[STIX]{x1D70C}=4000~\text{kg}~\text{m}^{-3}$
, a temperature difference of
![]() $\unicode[STIX]{x0394}T=2900$
K and a mantle depth of
$\unicode[STIX]{x0394}T=2900$
K and a mantle depth of
![]() $D=2880$
km, resulting in a Rayleigh number of approximately
$D=2880$
km, resulting in a Rayleigh number of approximately
![]() $8\times 10^{7}$
. Nevertheless, this value is associated with uncertainties, largely because of the uncertainties in the value of viscosity, which is temperature- and pressure-dependent and varies significantly with depth (Turcotte & Schubert Reference Turcotte and Schubert2002). While the viscosity of the upper mantle is of the order of
$8\times 10^{7}$
. Nevertheless, this value is associated with uncertainties, largely because of the uncertainties in the value of viscosity, which is temperature- and pressure-dependent and varies significantly with depth (Turcotte & Schubert Reference Turcotte and Schubert2002). While the viscosity of the upper mantle is of the order of
![]() $10^{21}$
Pa s (Mitrovica Reference Mitrovica1996), several geoid studies, which are reviewed in King (Reference King1995), have suggested a viscosity jump by a factor of approximately 30 for the lower mantle. Using the high viscosity value of the lower mantle in the calculation of
$10^{21}$
Pa s (Mitrovica Reference Mitrovica1996), several geoid studies, which are reviewed in King (Reference King1995), have suggested a viscosity jump by a factor of approximately 30 for the lower mantle. Using the high viscosity value of the lower mantle in the calculation of
![]() $Ra$
would decrease the above
$Ra$
would decrease the above
![]() $Ra$
value by a factor of 30. If the detailed radial profile of viscosity was known, an effective Rayleigh number could be calculated using the volume average of viscosity. Moreover, for the layered mantle convection model, a much lower
$Ra$
value by a factor of 30. If the detailed radial profile of viscosity was known, an effective Rayleigh number could be calculated using the volume average of viscosity. Moreover, for the layered mantle convection model, a much lower
![]() $Ra$
is expected for the upper mantle convection, as the values of both
$Ra$
is expected for the upper mantle convection, as the values of both
![]() $\unicode[STIX]{x0394}T$
and the depth of the fluid layer
$\unicode[STIX]{x0394}T$
and the depth of the fluid layer
![]() $D$
are much smaller than those for the whole-mantle convection model. For instance, a value of
$D$
are much smaller than those for the whole-mantle convection model. For instance, a value of
![]() $2.55\times 10^{5}$
has been estimated by Jarvis & Peltier (Reference Jarvis, Peltier and Peltier1989) as the Rayleigh number for the upper mantle convection. In fact, a wide range of values, from
$2.55\times 10^{5}$
has been estimated by Jarvis & Peltier (Reference Jarvis, Peltier and Peltier1989) as the Rayleigh number for the upper mantle convection. In fact, a wide range of values, from
![]() ${\sim}10^{5}$
to
${\sim}10^{5}$
to
![]() ${\sim}10^{9}$
, with most falling into the range
${\sim}10^{9}$
, with most falling into the range
![]() $10^{5}$
–
$10^{5}$
–
![]() $10^{8}$
, have been adopted as the Rayleigh number in numerical simulations of mantle convection induced by bottom heating. The selection of a relatively low
$10^{8}$
, have been adopted as the Rayleigh number in numerical simulations of mantle convection induced by bottom heating. The selection of a relatively low
![]() $Ra$
value is sometimes dictated by computational considerations, since cases with lower
$Ra$
value is sometimes dictated by computational considerations, since cases with lower
![]() $Ra$
are usually less time-consuming. The above discussion of
$Ra$
are usually less time-consuming. The above discussion of
![]() $Ra$
values is concerned with mantle convection subject to pure bottom heating. On the other hand, the Rayleigh number defined for mantle convection subject to pure internal heating ranges from
$Ra$
values is concerned with mantle convection subject to pure bottom heating. On the other hand, the Rayleigh number defined for mantle convection subject to pure internal heating ranges from
![]() ${\sim}10^{6}$
for the upper mantle convection and
${\sim}10^{6}$
for the upper mantle convection and
![]() ${\sim}10^{9}$
for the whole mantle convection (Turcotte & Schubert Reference Turcotte and Schubert2002). Since the mantle of the Earth is subject to both bottom heating and internal heating, further studies on the coupling modes are worth pursing using a model that adopts both thermal forcings, with a proportion that is close to the Earth.
${\sim}10^{9}$
for the whole mantle convection (Turcotte & Schubert Reference Turcotte and Schubert2002). Since the mantle of the Earth is subject to both bottom heating and internal heating, further studies on the coupling modes are worth pursing using a model that adopts both thermal forcings, with a proportion that is close to the Earth.
Our simulation results for
![]() $L=2.5$
under various
$L=2.5$
under various
![]() $Ra$
indicate that plates are less likely to be stagnant as
$Ra$
indicate that plates are less likely to be stagnant as
![]() $Ra$
increases. It would be interesting to conduct simulations at higher
$Ra$
increases. It would be interesting to conduct simulations at higher
![]() $Ra$
and investigate the effect of
$Ra$
and investigate the effect of
![]() $Ra$
on the transition of different modes and the distribution of plate speed. It has been revealed that the horizontal length of the convection cell increases with
$Ra$
on the transition of different modes and the distribution of plate speed. It has been revealed that the horizontal length of the convection cell increases with
![]() $Ra$
(Grigne, Labrosse & Tackley Reference Grigné, Labrosse and Tackley2007). Therefore, for cases with larger
$Ra$
(Grigne, Labrosse & Tackley Reference Grigné, Labrosse and Tackley2007). Therefore, for cases with larger
![]() $Ra$
, it is expected that a plate will travel longer distances before being impeded and there will be fewer impeding flow structures within the flow domain.
$Ra$
, it is expected that a plate will travel longer distances before being impeded and there will be fewer impeding flow structures within the flow domain.
Second, the present study focuses on the influence of a single continent. In reality, continents of different sizes are simultaneously modulating the mantle flow and thus affecting the velocity of each other, and they sometimes break or collide with each other. Therefore, one must be cautious when applying the present evolution of different modes to real continents. Nevertheless, SM I provides a possible mechanism for continent accretion. As it takes a long time for a small continent to escape from stagnancy by itself, other continents may collide and amalgamate with it before it generates a velocity burst by itself. Conversely, SM II promotes continent breakup. In SM II, the evolution of a divergent mantle flow underneath the continent is analogous to that after continent collision, in which hot plumes develop underneath the supercontinent and stay underneath it until continent breaks up and disperses away with the divergent convection flow (Lowman & Jarvis Reference Lowman and Jarvis1993, Reference Lowman and Jarvis1995). Furthermore, the specified forced stop of a plate at the end of the flow domain is analogous to the cessation of movement when continents collide. The flow development afterwards is also characterized by hot plumes rising up underneath the continent and the generation of a divergent flow (figure 4 d). For future investigations, modelling with a periodic boundary condition at the vertical boundaries is worth pursuing, in which the fluid and the part of the plate passing through one side of the flow domain automatically reappear on the opposite side with the same velocity.
In the present study, oceanic regions are differentiated from the continental regions by a prescribed isothermal free-slip boundary condition. Although this approach is adopted in many mantle convection studies, since oceanic plate can subduct into the mantle and is often regarded as an integral part of mantle convection, it neglects the influence of the rigidity of oceanic plates on mantle convection. In fact, many studies have shown that the presence of large plates significantly influences the thermal structure of the mantle (Bunge & Richards Reference Bunge and Richards1996; Zhong et al. Reference Zhong, Zuber, Moresi and Gurnis2000; Lowman, King & Gable Reference Lowman, King and Gable2001; Monnereau & Quéré Reference Monnereau and Quéré2001). Rigid plates are revealed to control the scale or the dominant wavelength of thermal structures (Davies Reference Davies1988; Zhong et al. Reference Zhong, Zuber, Moresi and Gurnis2000). The structure of rigid oceanic plates lying over the soft asthenosphere is expected to induce larger convection cells than in the present model. Moreover, owing to the rigidity of the oceanic plate, continents will encounter higher resistance during their movement, which needs to be taken into account for a more realistic representation. Nevertheless, the existence of the different coupling modes revealed in the present study is unlikely to be affected by the rigidity of oceanic plate.
Results show that an increase in the intensity of internal heating results in an increased mobility of plate. Therefore, plates will be less stagnant and more mobile in the early days of Earth’s history when the intensity of internal heating by radioactive decay was much higher than today (Turcotte & Schubert Reference Turcotte and Schubert2002). The presently revealed variation of coupling modes with plate size, shown in figure 7(c), is under the assumption of pure bottom heating and no internal heating. An increase in internal heating increases plate mobility and therefore will probably lead to a decrease of the critical plate size of different modes. For example, the UMM appears only when the plate size is larger than approximately 2.5 for
![]() $Ra=10^{6}$
with pure bottom heating. However, this value will probably decrease with the switching on of internal heating, and the appearance of the stagnant modes of SM I and SM II will probably be limited to smaller plates. Further simulations with internal heating switched on are worth pursuing to verify this.
$Ra=10^{6}$
with pure bottom heating. However, this value will probably decrease with the switching on of internal heating, and the appearance of the stagnant modes of SM I and SM II will probably be limited to smaller plates. Further simulations with internal heating switched on are worth pursuing to verify this.
Another simplification of the present study is the assumption of a uniform viscosity. In reality, the viscosity of the mantle is dependent on temperature, pressure and composition, which leads to a layering of viscosity with lower values in the upper mantle. The lowest viscosity value is present in the asthenosphere. This layering of mantle viscosity leads to long-wavelength flow, i.e. large convection cells with large horizontal extent (Bunge, Richards & Baumgardner Reference Bunge, Richards and Baumgardner1996, Reference Bunge, Richards and Baumgardner1997; Bunge & Richards Reference Bunge and Richards1996; Tackley Reference Tackley1996; Zhong et al. Reference Zhong, Zuber, Moresi and Gurnis2000; Lenardic, Richards & Busse Reference Lenardic, Richards and Busse2006; Höink & Lenardic Reference Höink and Lenardic2008). Consequently, the plate will move longer distances with the convective flow until it encounters impeding flow structures associated with downwellings, resulting in a decreased chance of being impeded. Further study of the coupling modes with a model that gives a closer representation of the Earth is worth pursuing in the future.
Acknowledgements
We thank A. van den Berg for helpful discussions. This work was supported by the National Natural Science Foundation of China (grant nos. 11472250 and 41630317 (Y.M.), 11472106 (J.Z.), 11572230 (J.-Q.Z.)).
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.189.
Appendix. The mesh and time-step dependency test
Table 1. Effect of mesh size and time step on the Nusselt number at the bottom of the flow domain for
![]() $Ra=10^{6}$
.
$Ra=10^{6}$
.

The parameters of the mesh and time-step dependency test are listed in table 1. The time series of Nusselt number (
![]() $Nu$
) at the bottom of the flow domain is shown in figure 17 for the three different meshes (
$Nu$
) at the bottom of the flow domain is shown in figure 17 for the three different meshes (
![]() $400\times 50$
,
$400\times 50$
,
![]() $800\times 100$
,
$800\times 100$
,
![]() $1200\times 150$
) for the fixed-plate case with
$1200\times 150$
) for the fixed-plate case with
![]() $L=0.25$
and
$L=0.25$
and
![]() $Ra=10^{6}$
. The difference of
$Ra=10^{6}$
. The difference of
![]() $Nu$
decreases from 20.0 % between the former two meshes to 3.5 % between the latter two. Based on this test, a mesh of
$Nu$
decreases from 20.0 % between the former two meshes to 3.5 % between the latter two. Based on this test, a mesh of
![]() $800\times 100$
is adopted in the present simulations with a time step of
$800\times 100$
is adopted in the present simulations with a time step of
![]() $5\times 10^{-7}$
.
$5\times 10^{-7}$
.

Figure 17. Time series of Nusselt number at the bottom of the flow domain for the fixed-plate case with
![]() $L=0.25$
and
$L=0.25$
and
![]() $Ra=10^{6}$
.
$Ra=10^{6}$
.