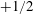1 Introduction
Active matter represents a class of far-away-from-equilibrium systems comprising self-driven particles (Ramaswamy Reference Ramaswamy2010; Marchetti et al. Reference Marchetti, Joanny, Ramaswamy, Liverpool, Prost, Rao and Simha2013; Shelley Reference Shelley2016). When immersed in a fluid, motile microstructures exert forces upon the ambient liquid, which itself acts as a coupling medium for generation of multiscale dynamics; this presents challenges in design, analysis and control of novel active materials. To take advantage of the anomalous properties (e.g. large-scale induced motion, enhanced diffusion and energy conversion), it is essential to guide active matter to perform useful mechanical work. One way of doing this is to tune the suspension concentration and the amount of chemical fuels (Sokolov et al. Reference Sokolov, Aranson, Kessler and Goldstein2007; Sanchez et al. Reference Sanchez, Chen, Decamp, Heymann and Dogic2012; Henkin et al. Reference Henkin, Decamp, Chen, Sanchez and Dogic2014). Alternatively, it is possible to make use of the particle interactions, either individually or collectively, with obstacles and geometric boundaries for more direct manipulation. By trapping active suspensions (such as pusher swimmers and Quincke rollers) within straight and curved boundaries, experimental and numerical studies have revealed stable coherent structures and flow types (Woodhouse & Goldstein Reference Woodhouse and Goldstein2012; Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013; Ravnik & Yeomans Reference Ravnik and Yeomans2013; Wioland et al. Reference Wioland, Woodhouse, Dunkel, Kessler and Goldstein2013; Ezhilan & Saintillan Reference Ezhilan and Saintillan2015; Tsang & Kanso Reference Tsang and Kanso2016; Guillamat, Ignés-Mullol & Sagués Reference Guillamat, Ignés-Mullol and Sagués2016a ; Guillamat et al. Reference Guillamat, Ignés-Mullol, Shankar, Marchetti and Sagués2016b ; Theillard, Alonso-Matilla & Saintillan Reference Theillard, Alonso-Matilla and Saintillan2017; Wu et al. Reference Wu, Hishamunda, Chen, Decamp, Chang, Fernández-Nieves, Fraden and Dogic2017).
In this paper, we study the complex dynamics of a two-dimensional (2D) apolar active suspension confined in an annulus. The rod-like microparticles are non-motile but mobile, and are only advected by fluid flow. In the meantime, they elongate through nearly symmetric stretching or growth to exert extensile dipolar stresses on the solvent, and interact with one another through hydrodynamic coupling and steric alignment torques, which we have previously referred to as ‘extensor’ particles (Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017). Examples include bacterial cell division (Adams & Errington Reference Adams and Errington2009), microtubule (MT) bundles undergoing polarity sorting driven by molecular motors (Sanchez et al.
Reference Sanchez, Chen, Decamp, Heymann and Dogic2012) and tripartite Au–Pt–Au nanomotors generating surface flows due to catalytic reactions (Jewell, Wang & Malloukl Reference Jewell, Wang and Malloukl2016; Wykes et al.
Reference Wykes, Palacci, Adachi, Ristroph, Zhong, Ward, Zhang and Shelley2016). In the previous works by Gao et al. (Reference Gao, Betterton, Jhang and Shelley2017) and Gao & Li (Reference Gao and Li2017), a macroscale liquid-crystal model, i.e. ‘
![]() $BQ$
’-tensor theory, was derived from a kinetic theory that describes the ensemble dynamics of extensors. Compared with macro models for motile suspensions (Saintillan & Shelley Reference Saintillan and Shelley2013), where the coupled evolution equations for the suspension concentration, polarity and tensorial order parameter need to be solved together, we have shown that the apolar
$BQ$
’-tensor theory, was derived from a kinetic theory that describes the ensemble dynamics of extensors. Compared with macro models for motile suspensions (Saintillan & Shelley Reference Saintillan and Shelley2013), where the coupled evolution equations for the suspension concentration, polarity and tensorial order parameter need to be solved together, we have shown that the apolar
![]() $BQ$
-tensor model naturally conserves the local concentration and the global particle numbers, and can be characterized by the evolution equation of the second-moment tensor only. Through theoretical analyses and numerical simulations for extensor suspensions both in unbounded domains and confined in circular chambers, we have demonstrated that this active fluid model, while being apolar, inherits all of the basic transitions and instabilities associated with motile suspensions, and exhibits a rich set of collective dynamics.
$BQ$
-tensor model naturally conserves the local concentration and the global particle numbers, and can be characterized by the evolution equation of the second-moment tensor only. Through theoretical analyses and numerical simulations for extensor suspensions both in unbounded domains and confined in circular chambers, we have demonstrated that this active fluid model, while being apolar, inherits all of the basic transitions and instabilities associated with motile suspensions, and exhibits a rich set of collective dynamics.
We examine both dilute and concentrated extensor suspensions confined in an annulus geometry. For the dilute cases, we identify emergent coherent structures that resemble those observed in ‘polar’ active suspensions of pusher particles (Wioland, Lushi & Goldstein Reference Wioland, Lushi and Goldstein2016; Theillard et al.
Reference Theillard, Alonso-Matilla and Saintillan2017) by varying the particle activity and annulus gap width. Linear stability analyses are performed to reveal the underlying physical mechanisms of a series of hydrodynamic instabilities starting from a near-isotropic state. At a finite concentration, we show that the internal collective dynamics can be effectively inhibited when confined in thin gaps; the particles rise when the gap width is large enough so that a bending instability can develop in the radial direction to generate active nematic flows. In particular, we capture an intriguing quasi-steady-state at a finite gap width featuring oscillating
![]() $+1/2$
-order defects and travelling-wave flows that switch circulation directions periodically.
$+1/2$
-order defects and travelling-wave flows that switch circulation directions periodically.
2 Mathematical model
We consider a collection of extensor particles suspended in a Newtonian fluid. These active particles are non-motile but can elongate or stretch near-symmetrically to produce extensional flows that effectively exert dipolar stresses upon the liquid. As shown by Gao et al. (Reference Gao, Betterton, Jhang and Shelley2017) and Gao & Li (Reference Gao and Li2017), the ensemble dynamics of extensor particles whose centre-of-mass position is located at
![]() $\boldsymbol{x}$
with an orientation
$\boldsymbol{x}$
with an orientation
![]() $\boldsymbol{p}$
(
$\boldsymbol{p}$
(
![]() $|\boldsymbol{p}|=1$
) can be described by a probability distribution function
$|\boldsymbol{p}|=1$
) can be described by a probability distribution function
![]() $\unicode[STIX]{x1D6F9}(\boldsymbol{x},\boldsymbol{p},t)$
through a Smoluchowski equation. The particles exert stresses
$\unicode[STIX]{x1D6F9}(\boldsymbol{x},\boldsymbol{p},t)$
through a Smoluchowski equation. The particles exert stresses
![]() $\unicode[STIX]{x1D72E}$
on the liquid to drive fluid motion, which is governed by the (dimensionless) incompressible Stokes equation,
$\unicode[STIX]{x1D72E}$
on the liquid to drive fluid motion, which is governed by the (dimensionless) incompressible Stokes equation,
where
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
are the fluid velocity and pressure respectively. The extra stress tensor
$p$
are the fluid velocity and pressure respectively. The extra stress tensor
![]() $\unicode[STIX]{x1D72E}$
can be written as (Saintillan & Shelley Reference Saintillan and Shelley2008; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
)
$\unicode[STIX]{x1D72E}$
can be written as (Saintillan & Shelley Reference Saintillan and Shelley2008; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
)
where
![]() $\unicode[STIX]{x1D640}=1/2(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the rate-of-strain tensor;
$\unicode[STIX]{x1D640}=1/2(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the rate-of-strain tensor;
![]() $\unicode[STIX]{x1D63F}=\int _{p}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
and
$\unicode[STIX]{x1D63F}=\int _{p}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
and
![]() $\unicode[STIX]{x1D64E}=\int _{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
are the second- and fourth-moment tensors respectively, and are calculated by taking the average of
$\unicode[STIX]{x1D64E}=\int _{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
are the second- and fourth-moment tensors respectively, and are calculated by taking the average of
![]() $\boldsymbol{p}$
on the surface of a unit sphere. In (2.3), the first term represents a dipolar extensile stress that arises from the local extensional flows, with the dimensionless coefficient
$\boldsymbol{p}$
on the surface of a unit sphere. In (2.3), the first term represents a dipolar extensile stress that arises from the local extensional flows, with the dimensionless coefficient
![]() $\unicode[STIX]{x1D6FC}<0$
quantifying particle activity (Saintillan & Shelley Reference Saintillan and Shelley2008; Hohenegger & Shelley Reference Hohenegger and Shelley2011). The second term is a constraining stress due to particle rigidity (Doi & Edwards Reference Doi and Edwards1988; Ezhilan, Shelley & Saintillan Reference Ezhilan, Shelley and Saintillan2013), with an effective shape factor
$\unicode[STIX]{x1D6FC}<0$
quantifying particle activity (Saintillan & Shelley Reference Saintillan and Shelley2008; Hohenegger & Shelley Reference Hohenegger and Shelley2011). The second term is a constraining stress due to particle rigidity (Doi & Edwards Reference Doi and Edwards1988; Ezhilan, Shelley & Saintillan Reference Ezhilan, Shelley and Saintillan2013), with an effective shape factor
![]() $\unicode[STIX]{x1D6FD}>0$
characterizing the particle aspect ratio. The third term is due to steric interactions through a Maier–Saupe potential with a strength coefficient
$\unicode[STIX]{x1D6FD}>0$
characterizing the particle aspect ratio. The third term is due to steric interactions through a Maier–Saupe potential with a strength coefficient
![]() $\unicode[STIX]{x1D701}$
(Maier & Saupe Reference Maier and Saupe1958; Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
). It should be noted that both the constraining and the steric interaction stresses are proportional to the effective volume fraction of the suspension, and hence cannot be neglected for concentrated suspensions (Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
).
$\unicode[STIX]{x1D701}$
(Maier & Saupe Reference Maier and Saupe1958; Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
). It should be noted that both the constraining and the steric interaction stresses are proportional to the effective volume fraction of the suspension, and hence cannot be neglected for concentrated suspensions (Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
).
The flow equation is coupled with the evolution equation of the
![]() $\unicode[STIX]{x1D63F}$
tensor, which is derived from the kinetic model by taking a standard moment average (Doi & Edwards Reference Doi and Edwards1988; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017),
$\unicode[STIX]{x1D63F}$
tensor, which is derived from the kinetic model by taking a standard moment average (Doi & Edwards Reference Doi and Edwards1988; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017),
where
![]() $\unicode[STIX]{x1D63F}^{\unicode[STIX]{x1D735}}=\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D63F}-(\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}+\unicode[STIX]{x1D63F}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is an upper-convected derivative, and
$\unicode[STIX]{x1D63F}^{\unicode[STIX]{x1D735}}=\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D63F}-(\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}+\unicode[STIX]{x1D63F}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is an upper-convected derivative, and
![]() $d_{R}$
and
$d_{R}$
and
![]() $d_{T}$
are the rotational and translational diffusion coefficients respectively. It is worthwhile to mention that in the classical Landau–de Gennes approach for liquid-crystalline fluids (de Gennes Reference de Gennes1974),
$d_{T}$
are the rotational and translational diffusion coefficients respectively. It is worthwhile to mention that in the classical Landau–de Gennes approach for liquid-crystalline fluids (de Gennes Reference de Gennes1974),
![]() $d_{R}$
and
$d_{R}$
and
![]() $d_{T}$
are essentially the linear terms in a Landau potential and the Frank elastic constant for a nematic liquid crystal respectively. In non-dimensionalization, we assume that there are
$d_{T}$
are essentially the linear terms in a Landau potential and the Frank elastic constant for a nematic liquid crystal respectively. In non-dimensionalization, we assume that there are
![]() $N$
extensor particles of length
$N$
extensor particles of length
![]() $l$
and width
$l$
and width
![]() $b$
(
$b$
(
![]() $b/l\ll 1$
) distributed in a volume
$b/l\ll 1$
) distributed in a volume
![]() $V$
, and introduce an effective volume fraction
$V$
, and introduce an effective volume fraction
![]() $\unicode[STIX]{x1D708}=nbl^{2}$
, where
$\unicode[STIX]{x1D708}=nbl^{2}$
, where
![]() $n=N/V$
is the mean number density (Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017). Then, we choose the length scale
$n=N/V$
is the mean number density (Ezhilan et al.
Reference Ezhilan, Shelley and Saintillan2013; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017). Then, we choose the length scale
![]() $l_{c}=b/\unicode[STIX]{x1D708}$
, the velocity scale
$l_{c}=b/\unicode[STIX]{x1D708}$
, the velocity scale
![]() $|u_{0}|$
, which represents the surface velocity due to elongation or stretching motion, and the stress scale
$|u_{0}|$
, which represents the surface velocity due to elongation or stretching motion, and the stress scale
![]() $\unicode[STIX]{x1D707}|u_{0}|/l_{c}$
. Equation (2.4) can be closed by expressing the fourth-moment tensor
$\unicode[STIX]{x1D707}|u_{0}|/l_{c}$
. Equation (2.4) can be closed by expressing the fourth-moment tensor
![]() $\unicode[STIX]{x1D64E}$
in terms of
$\unicode[STIX]{x1D64E}$
in terms of
![]() $\unicode[STIX]{x1D63F}$
through the so-called Bingham closure (Bingham Reference Bingham1974; Chaubal & Leal Reference Chaubal and Leal1998; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017), which reconstructs a distribution function
$\unicode[STIX]{x1D63F}$
through the so-called Bingham closure (Bingham Reference Bingham1974; Chaubal & Leal Reference Chaubal and Leal1998; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017), which reconstructs a distribution function
![]() $\unicode[STIX]{x1D6F9}_{B}(\boldsymbol{x},\boldsymbol{p},t)$
in terms of a traceless symmetric tensor
$\unicode[STIX]{x1D6F9}_{B}(\boldsymbol{x},\boldsymbol{p},t)$
in terms of a traceless symmetric tensor
![]() $\unicode[STIX]{x1D64F}(\boldsymbol{x},t)$
, to yield
$\unicode[STIX]{x1D64F}(\boldsymbol{x},t)$
, to yield
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]=\frac{\exp (\unicode[STIX]{x1D64F}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})}{\displaystyle \int _{p}\exp (\unicode[STIX]{x1D64F}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\,\text{d}\boldsymbol{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]=\frac{\exp (\unicode[STIX]{x1D64F}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})}{\displaystyle \int _{p}\exp (\unicode[STIX]{x1D64F}\boldsymbol{ : }\boldsymbol{p}\boldsymbol{p})\,\text{d}\boldsymbol{p}}.\end{eqnarray}$$
We determine the tensor
![]() $\unicode[STIX]{x1D64F}$
numerically by solving the relation
$\unicode[STIX]{x1D64F}$
numerically by solving the relation
![]() $\unicode[STIX]{x1D63F}=\int _{p}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]\boldsymbol{p}\boldsymbol{p}\,\text{d}\boldsymbol{p}$
. Given
$\unicode[STIX]{x1D63F}=\int _{p}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]\boldsymbol{p}\boldsymbol{p}\,\text{d}\boldsymbol{p}$
. Given
![]() $\unicode[STIX]{x1D64F}$
, the fourth-moment tensor
$\unicode[STIX]{x1D64F}$
, the fourth-moment tensor
![]() $\unicode[STIX]{x1D64E}$
is then approximated by
$\unicode[STIX]{x1D64E}$
is then approximated by
![]() $\unicode[STIX]{x1D64E}_{B}=\int _{p}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\,\text{d}\boldsymbol{p}$
as
$\unicode[STIX]{x1D64E}_{B}=\int _{p}\unicode[STIX]{x1D6F9}_{B}[\unicode[STIX]{x1D64F}]\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\boldsymbol{p}\,\text{d}\boldsymbol{p}$
as
![]() $\unicode[STIX]{x1D6F9}_{B}$
is determined by assuming that
$\unicode[STIX]{x1D6F9}_{B}$
is determined by assuming that
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() $\unicode[STIX]{x1D63F}$
are co-aligned in the principal coordinates of
$\unicode[STIX]{x1D63F}$
are co-aligned in the principal coordinates of
![]() $\unicode[STIX]{x1D63F}$
. We refer to the above model as the ‘
$\unicode[STIX]{x1D63F}$
. We refer to the above model as the ‘
![]() $BQ$
-tensor’ model (Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017). In the following, we define the 2D tensor order parameter
$BQ$
-tensor’ model (Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017). In the following, we define the 2D tensor order parameter
![]() $\unicode[STIX]{x1D64C}(\boldsymbol{x},t)=\unicode[STIX]{x1D63F}/\unicode[STIX]{x1D719}(\boldsymbol{x},t)-\unicode[STIX]{x1D644}/2$
(here
$\unicode[STIX]{x1D64C}(\boldsymbol{x},t)=\unicode[STIX]{x1D63F}/\unicode[STIX]{x1D719}(\boldsymbol{x},t)-\unicode[STIX]{x1D644}/2$
(here
![]() $\unicode[STIX]{x1D719}(\boldsymbol{x},t)=\int _{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
is the concentration) whose maximal non-negative eigenvalue
$\unicode[STIX]{x1D719}(\boldsymbol{x},t)=\int _{p}\unicode[STIX]{x1D6F9}\,\text{d}\boldsymbol{p}$
is the concentration) whose maximal non-negative eigenvalue
![]() $\unicode[STIX]{x1D706}_{max}$
of
$\unicode[STIX]{x1D706}_{max}$
of
![]() $\unicode[STIX]{x1D64C}$
satisfies
$\unicode[STIX]{x1D64C}$
satisfies
![]() $0\leqslant \unicode[STIX]{x1D706}_{max}\leqslant 1/2$
. We call its associated unit eigenvector the nematic director
$0\leqslant \unicode[STIX]{x1D706}_{max}\leqslant 1/2$
. We call its associated unit eigenvector the nematic director
![]() $\boldsymbol{m}$
, and
$\boldsymbol{m}$
, and
![]() $0\leqslant s=2\unicode[STIX]{x1D706}_{max}\leqslant 1$
the scalar order parameter.
$0\leqslant s=2\unicode[STIX]{x1D706}_{max}\leqslant 1$
the scalar order parameter.
3 Results and discussion
When simulating the confined active fluid motion, we solve the
![]() $\unicode[STIX]{x1D63F}$
dynamics equation (2.4) together with the incompressible Navier–Stokes equation at small Reynolds numbers (
$\unicode[STIX]{x1D63F}$
dynamics equation (2.4) together with the incompressible Navier–Stokes equation at small Reynolds numbers (
![]() $Re=10^{-3}$
) using a mixed finite element method (Hu, Zhu & Patankar Reference Hu, Zhu and Patankar2001; Gao & Hu Reference Gao and Hu2009; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). At the inner (
$Re=10^{-3}$
) using a mixed finite element method (Hu, Zhu & Patankar Reference Hu, Zhu and Patankar2001; Gao & Hu Reference Gao and Hu2009; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). At the inner (
![]() $r=R_{1}$
) and outer (
$r=R_{1}$
) and outer (
![]() $r=R_{2}$
) boundaries, a no-slip condition
$r=R_{2}$
) boundaries, a no-slip condition
![]() $\boldsymbol{u}=\mathbf{0}$
is imposed for the velocity field, and a no-flux condition
$\boldsymbol{u}=\mathbf{0}$
is imposed for the velocity field, and a no-flux condition
![]() $(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D63F}=\mathbf{0}$
is used for the second-moment tensor
$(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D63F}=\mathbf{0}$
is used for the second-moment tensor
![]() $\unicode[STIX]{x1D63F}$
. It should be noted that, in this way, we do not enforce any particular alignment direction at the boundary but guarantee global particle number conservation. For all of the simulation results below, we vary
$\unicode[STIX]{x1D63F}$
. It should be noted that, in this way, we do not enforce any particular alignment direction at the boundary but guarantee global particle number conservation. For all of the simulation results below, we vary
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $R_{1,2}$
, and fix
$R_{1,2}$
, and fix
![]() $d_{T}=d_{R}=0.025$
(for both dilute and concentrated suspensions), as well as
$d_{T}=d_{R}=0.025$
(for both dilute and concentrated suspensions), as well as
![]() $\unicode[STIX]{x1D701}=0.5,\unicode[STIX]{x1D6FD}=0.874$
(for concentrated suspensions).
$\unicode[STIX]{x1D701}=0.5,\unicode[STIX]{x1D6FD}=0.874$
(for concentrated suspensions).
3.1 Dilute suspension
We first examine the case of a confined dilute suspension by neglecting both the steric interaction stress (
![]() $\unicode[STIX]{x1D701}=0$
) and the constraining stress (
$\unicode[STIX]{x1D701}=0$
) and the constraining stress (
![]() $\unicode[STIX]{x1D6FD}=0$
), and start simulations from an initially near-isotropic state. As shown in figure 1(a–f), where
$\unicode[STIX]{x1D6FD}=0$
), and start simulations from an initially near-isotropic state. As shown in figure 1(a–f), where
![]() $R_{1}=1.0$
and
$R_{1}=1.0$
and
![]() $R_{2}=2.0$
are fixed, characteristic nematic structures and flow patterns are highlighted at different regimes of
$R_{2}=2.0$
are fixed, characteristic nematic structures and flow patterns are highlighted at different regimes of
![]() $|\unicode[STIX]{x1D6FC}|$
. As shown in (a), a unidirectional circulating flow first appears when
$|\unicode[STIX]{x1D6FC}|$
. As shown in (a), a unidirectional circulating flow first appears when
![]() $|\unicode[STIX]{x1D6FC}|$
goes beyond a certain critical value
$|\unicode[STIX]{x1D6FC}|$
goes beyond a certain critical value
![]() $\unicode[STIX]{x1D6FC}_{cr}$
(in this case,
$\unicode[STIX]{x1D6FC}_{cr}$
(in this case,
![]() $\unicode[STIX]{x1D6FC}_{cr}=-1.23$
). While the nematic order is still low, as shown in (d), it clearly shows that particles become aligned in the azimuthal direction due to fluid shear (Saintillan & Shelley Reference Saintillan and Shelley2008; Thampi et al.
Reference Thampi, Doostmohammadi, Golestanian and Yeomans2015), with a stronger alignment near rigid walls. As
$\unicode[STIX]{x1D6FC}_{cr}=-1.23$
). While the nematic order is still low, as shown in (d), it clearly shows that particles become aligned in the azimuthal direction due to fluid shear (Saintillan & Shelley Reference Saintillan and Shelley2008; Thampi et al.
Reference Thampi, Doostmohammadi, Golestanian and Yeomans2015), with a stronger alignment near rigid walls. As
![]() $|\unicode[STIX]{x1D6FC}|$
further increases up to 10.0 in (b), a circulating flow pattern still dominates but the streamlines exhibit periodic bending deformations in the radial direction to form travelling waves, leading to counterclockwise (CCW) and clockwise (CW) vortices near the inner and outer boundaries respectively. Such oscillatory patterns have also been seen in other active liquid crystal systems due to bending (or splay) deformations (Voituriez, Joanny & Prost Reference Voituriez, Joanny and Prost2005; Giomi et al.
Reference Giomi, Mahadevan, Chakraborty and Hagan2011, Reference Giomi, Mahadevan, Chakraborty and Hagan2012). In (e), the flow-induced alignment is further enhanced to form low-order structures (blue colour). At even higher values of
$|\unicode[STIX]{x1D6FC}|$
further increases up to 10.0 in (b), a circulating flow pattern still dominates but the streamlines exhibit periodic bending deformations in the radial direction to form travelling waves, leading to counterclockwise (CCW) and clockwise (CW) vortices near the inner and outer boundaries respectively. Such oscillatory patterns have also been seen in other active liquid crystal systems due to bending (or splay) deformations (Voituriez, Joanny & Prost Reference Voituriez, Joanny and Prost2005; Giomi et al.
Reference Giomi, Mahadevan, Chakraborty and Hagan2011, Reference Giomi, Mahadevan, Chakraborty and Hagan2012). In (e), the flow-induced alignment is further enhanced to form low-order structures (blue colour). At even higher values of
![]() $|\unicode[STIX]{x1D6FC}|$
, the flow pattern in (c) becomes seemingly chaotic. The resultant nematic field exhibits a typical active liquid-crystalline phase (Sanchez et al.
Reference Sanchez, Chen, Decamp, Heymann and Dogic2012; Giomi et al.
Reference Giomi, Bowick, Ma and Marchetti2013; Thampi, Golestanian & Yeomans Reference Thampi, Golestanian and Yeomans2014; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
; Shelley Reference Shelley2016), in which
$|\unicode[STIX]{x1D6FC}|$
, the flow pattern in (c) becomes seemingly chaotic. The resultant nematic field exhibits a typical active liquid-crystalline phase (Sanchez et al.
Reference Sanchez, Chen, Decamp, Heymann and Dogic2012; Giomi et al.
Reference Giomi, Bowick, Ma and Marchetti2013; Thampi, Golestanian & Yeomans Reference Thampi, Golestanian and Yeomans2014; Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
; Shelley Reference Shelley2016), in which
![]() $\pm 1/2$
disclination defects stream around, and are constantly generated/annihilated during interactions (see f).
$\pm 1/2$
disclination defects stream around, and are constantly generated/annihilated during interactions (see f).
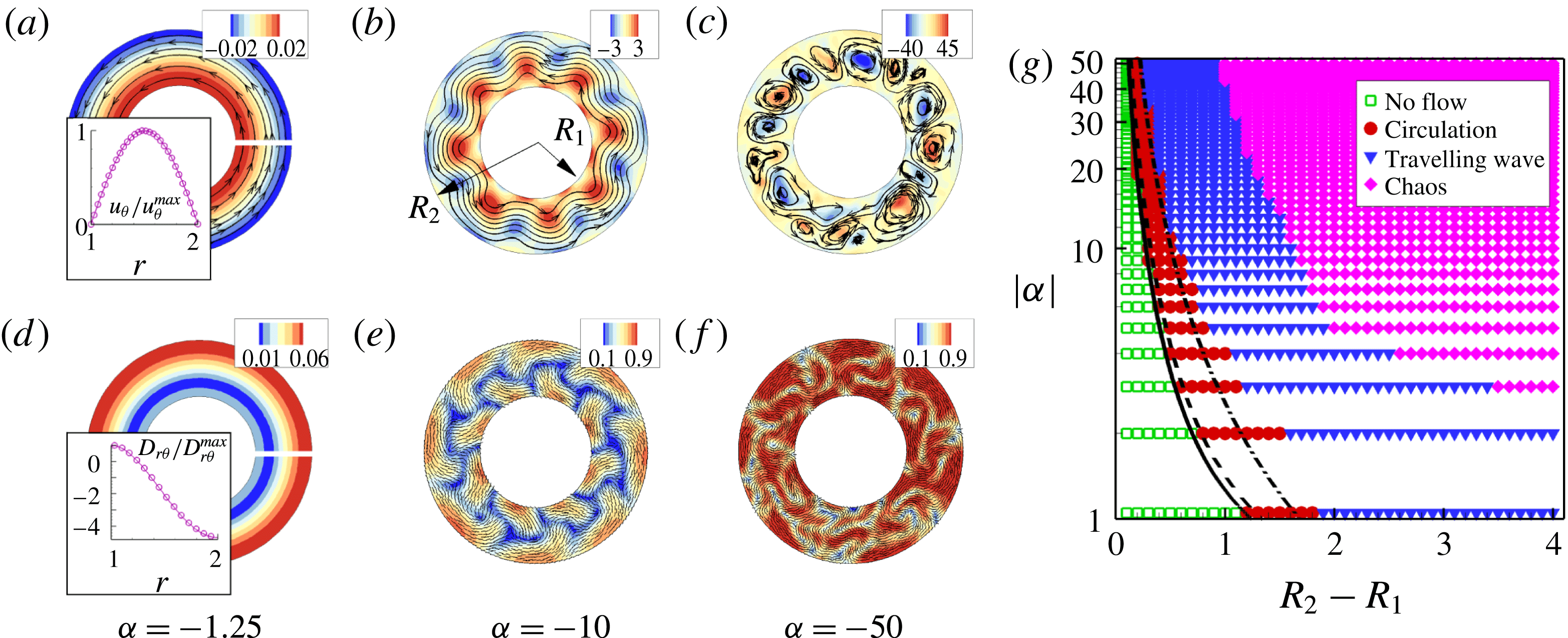
Figure 1. (a–c) Characteristic flow patterns (streamline overlaid on the colourmap of vorticity
![]() $\unicode[STIX]{x1D6FA}$
) and (d–f) nematic structures (nematic director
$\unicode[STIX]{x1D6FA}$
) and (d–f) nematic structures (nematic director
![]() $\boldsymbol{m}$
field overlaid on the colourmap of scalar order parameter
$\boldsymbol{m}$
field overlaid on the colourmap of scalar order parameter
![]() $s$
) when choosing
$s$
) when choosing
![]() $R_{1}=1.0$
and
$R_{1}=1.0$
and
![]() $R_{2}=2.0$
. The insets in (a) and (d) are comparisons between the analytical (solid lines) and numerical (open circles) results for normalized
$R_{2}=2.0$
. The insets in (a) and (d) are comparisons between the analytical (solid lines) and numerical (open circles) results for normalized
![]() $u_{\unicode[STIX]{x1D703}}$
and
$u_{\unicode[STIX]{x1D703}}$
and
![]() $D_{r\unicode[STIX]{x1D703}}$
components taken along the white lines when
$D_{r\unicode[STIX]{x1D703}}$
components taken along the white lines when
![]() $|\unicode[STIX]{x1D6FC}|$
slightly goes beyond the critical value
$|\unicode[STIX]{x1D6FC}|$
slightly goes beyond the critical value
![]() $|\unicode[STIX]{x1D6FC}|_{cr}=1.23$
for the isotropy–circulation instability. (g) Phase diagram of (
$|\unicode[STIX]{x1D6FC}|_{cr}=1.23$
for the isotropy–circulation instability. (g) Phase diagram of (
![]() $|\unicode[STIX]{x1D6FC}|,R_{2}-R_{1}$
) when fixing
$|\unicode[STIX]{x1D6FC}|,R_{2}-R_{1}$
) when fixing
![]() $R_{1}=1.0$
. The solid and dashed lines characterize the isotropy–circulation instability in an annulus and a straight channel respectively. The dash–dotted line characterizes the circulation–travelling-wave instability in a straight channel for sharply aligned rods by neglecting the rotational diffusion.
$R_{1}=1.0$
. The solid and dashed lines characterize the isotropy–circulation instability in an annulus and a straight channel respectively. The dash–dotted line characterizes the circulation–travelling-wave instability in a straight channel for sharply aligned rods by neglecting the rotational diffusion.
It should be noted that while our model is apolar, the observed phenomena are very similar to those reported for polar active suspensions where effects of self-swimming motions of microparticles (e.g. bacteria) are taken into account (Lushi, Wioland & Goldstein Reference Lushi, Wioland and Goldstein2014; Wioland et al.
Reference Wioland, Lushi and Goldstein2016; Theillard et al.
Reference Theillard, Alonso-Matilla and Saintillan2017). It is essential to recognize that the nonlinear dynamics is governed by a concatenation of hydrodynamic instabilities as
![]() $\unicode[STIX]{x1D6FC}$
increases, and can be characterized by a series of instabilities including isotropy to circulation, circulation to travelling wave and travelling wave to chaos. An overview of the instabilities is presented in a phase diagram plotted in the (
$\unicode[STIX]{x1D6FC}$
increases, and can be characterized by a series of instabilities including isotropy to circulation, circulation to travelling wave and travelling wave to chaos. An overview of the instabilities is presented in a phase diagram plotted in the (
![]() $|\unicode[STIX]{x1D6FC}|,R_{2}-R_{1}$
) plane in (g), where
$|\unicode[STIX]{x1D6FC}|,R_{2}-R_{1}$
) plane in (g), where
![]() $R_{1}$
is fixed to be 1.0. Furthermore, the marginal stability curve that delineates the isotropy–circulation instability can be calculated analytically in the polar coordinates. To do this, we perturb the near-isotropic solutions as
$R_{1}$
is fixed to be 1.0. Furthermore, the marginal stability curve that delineates the isotropy–circulation instability can be calculated analytically in the polar coordinates. To do this, we perturb the near-isotropic solutions as
![]() $\unicode[STIX]{x1D63F}=\unicode[STIX]{x1D644}/2+\unicode[STIX]{x1D716}\unicode[STIX]{x1D63F}^{\prime }(r)$
and
$\unicode[STIX]{x1D63F}=\unicode[STIX]{x1D644}/2+\unicode[STIX]{x1D716}\unicode[STIX]{x1D63F}^{\prime }(r)$
and
![]() $\boldsymbol{u}=\unicode[STIX]{x1D716}\boldsymbol{u}^{\prime }(r)$
(
$\boldsymbol{u}=\unicode[STIX]{x1D716}\boldsymbol{u}^{\prime }(r)$
(
![]() $\unicode[STIX]{x1D716}\ll 1$
) by assuming azimuthal symmetry. Following the procedure of Woodhouse & Goldstein (Reference Woodhouse and Goldstein2012), we examine an initially exponential growth
$\unicode[STIX]{x1D716}\ll 1$
) by assuming azimuthal symmetry. Following the procedure of Woodhouse & Goldstein (Reference Woodhouse and Goldstein2012), we examine an initially exponential growth
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}^{\prime }/\unicode[STIX]{x2202}t=\unicode[STIX]{x1D705}\unicode[STIX]{x1D63F}^{\prime }$
with the growth factor
$\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}^{\prime }/\unicode[STIX]{x2202}t=\unicode[STIX]{x1D705}\unicode[STIX]{x1D63F}^{\prime }$
with the growth factor
![]() $\unicode[STIX]{x1D705}\geqslant 0$
. After some algebra, we find
$\unicode[STIX]{x1D705}\geqslant 0$
. After some algebra, we find
![]() $D_{rr}^{\prime }=D_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}^{\prime }=0$
, and the hydrodynamic instability arises from the following coupled linearized equations for
$D_{rr}^{\prime }=D_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}^{\prime }=0$
, and the hydrodynamic instability arises from the following coupled linearized equations for
![]() $u_{\unicode[STIX]{x1D703}}^{\prime }$
and
$u_{\unicode[STIX]{x1D703}}^{\prime }$
and
![]() $D_{r\unicode[STIX]{x1D703}}^{\prime }$
:
$D_{r\unicode[STIX]{x1D703}}^{\prime }$
:
where
![]() $\unicode[STIX]{x1D6FE}=-((16d_{R}+4\unicode[STIX]{x1D705}+\unicode[STIX]{x1D6FC})/4d_{T})$
. We are able to seek the solutions
$\unicode[STIX]{x1D6FE}=-((16d_{R}+4\unicode[STIX]{x1D705}+\unicode[STIX]{x1D6FC})/4d_{T})$
. We are able to seek the solutions
![]() $D_{r\unicode[STIX]{x1D703}}^{\prime }=-(A_{0}/4\unicode[STIX]{x1D6FE}d_{T}r^{2})+A_{1}(\unicode[STIX]{x2202}\text{J}_{2}(\sqrt{\unicode[STIX]{x1D6FE}}r)/\unicode[STIX]{x2202}r)+A_{2}(\unicode[STIX]{x2202}\text{N}_{2}(\sqrt{\unicode[STIX]{x1D6FE}}r)/\unicode[STIX]{x2202}r)$
and
$D_{r\unicode[STIX]{x1D703}}^{\prime }=-(A_{0}/4\unicode[STIX]{x1D6FE}d_{T}r^{2})+A_{1}(\unicode[STIX]{x2202}\text{J}_{2}(\sqrt{\unicode[STIX]{x1D6FE}}r)/\unicode[STIX]{x2202}r)+A_{2}(\unicode[STIX]{x2202}\text{N}_{2}(\sqrt{\unicode[STIX]{x1D6FE}}r)/\unicode[STIX]{x2202}r)$
and
![]() $u_{\unicode[STIX]{x1D703}}^{\prime }=-(A_{0}/2r)(1+\unicode[STIX]{x1D6FC}/4\unicode[STIX]{x1D6FE}d_{T})+(2A_{1}/\sqrt{\unicode[STIX]{x1D6FE}})\text{J}_{1}(\sqrt{\unicode[STIX]{x1D6FE}}r)+(2A_{2}/\sqrt{\unicode[STIX]{x1D6FE}})\text{N}_{1}(\sqrt{\unicode[STIX]{x1D6FE}}r)+A_{3}r$
, where
$u_{\unicode[STIX]{x1D703}}^{\prime }=-(A_{0}/2r)(1+\unicode[STIX]{x1D6FC}/4\unicode[STIX]{x1D6FE}d_{T})+(2A_{1}/\sqrt{\unicode[STIX]{x1D6FE}})\text{J}_{1}(\sqrt{\unicode[STIX]{x1D6FE}}r)+(2A_{2}/\sqrt{\unicode[STIX]{x1D6FE}})\text{N}_{1}(\sqrt{\unicode[STIX]{x1D6FE}}r)+A_{3}r$
, where
![]() $\text{J}_{j}$
and
$\text{J}_{j}$
and
![]() $\text{N}_{j}$
are respectively Bessel functions of the first and second kinds, with coefficients
$\text{N}_{j}$
are respectively Bessel functions of the first and second kinds, with coefficients
![]() $A_{j}$
to be determined. By applying boundary conditions
$A_{j}$
to be determined. By applying boundary conditions
![]() $\unicode[STIX]{x2202}D_{r\unicode[STIX]{x1D703}}^{\prime }/\unicode[STIX]{x2202}r=0$
and
$\unicode[STIX]{x2202}D_{r\unicode[STIX]{x1D703}}^{\prime }/\unicode[STIX]{x2202}r=0$
and
![]() $u_{\unicode[STIX]{x1D703}}^{\prime }=0$
on the two walls, we then solve the eigenvalues of
$u_{\unicode[STIX]{x1D703}}^{\prime }=0$
on the two walls, we then solve the eigenvalues of
![]() $\unicode[STIX]{x1D6FE}$
numerically at
$\unicode[STIX]{x1D6FE}$
numerically at
![]() $\unicode[STIX]{x1D705}=0$
(solid line in g), as well as the velocity and
$\unicode[STIX]{x1D705}=0$
(solid line in g), as well as the velocity and
![]() $\unicode[STIX]{x1D63F}$
field (insets in a,d), which, again, confirm our simulation results.
$\unicode[STIX]{x1D63F}$
field (insets in a,d), which, again, confirm our simulation results.
Next, we reveal the nature of the hydrodynamic instabilities and gain physical insight into the formation of the observed coherent structures in figure 1. As shown below, while analytical approaches are feasible for the isotropy–circulation and circulation–travelling-wave transitions, the travelling-wave–chaos instability is highly nonlinear and hence can only be explored numerically. Here, we avoid tedious mathematical manipulations in the polar coordinates to simplify our analysis by considering confinement in a straight periodic channel (i.e. in the limit
![]() $R_{1,2}\rightarrow \infty$
), where very similar collective dynamics and hydrodynamic instabilities are observed (Theillard et al.
Reference Theillard, Alonso-Matilla and Saintillan2017). For the two cases considered, we employ a homogeneous base-state solution of
$R_{1,2}\rightarrow \infty$
), where very similar collective dynamics and hydrodynamic instabilities are observed (Theillard et al.
Reference Theillard, Alonso-Matilla and Saintillan2017). For the two cases considered, we employ a homogeneous base-state solution of
![]() $\unicode[STIX]{x1D63F}_{0}$
without background flow (i.e.
$\unicode[STIX]{x1D63F}_{0}$
without background flow (i.e.
![]() $\boldsymbol{u}_{0}=\mathbf{0}$
,
$\boldsymbol{u}_{0}=\mathbf{0}$
,
![]() $p_{0}=0$
), and introduce perturbations (
$p_{0}=0$
), and introduce perturbations (
![]() $\unicode[STIX]{x1D63F}^{\prime },\boldsymbol{u}^{\prime },p^{\prime }$
) to yield the following linearized equations:
$\unicode[STIX]{x1D63F}^{\prime },\boldsymbol{u}^{\prime },p^{\prime }$
) to yield the following linearized equations:
with boundary conditions
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}^{\prime }/\unicode[STIX]{x2202}y=0$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D63F}^{\prime }/\unicode[STIX]{x2202}y=0$
and
![]() $\boldsymbol{u}^{\prime }=0$
on the upper (
$\boldsymbol{u}^{\prime }=0$
on the upper (
![]() $y=h$
) and bottom (
$y=h$
) and bottom (
![]() $y=-h$
) walls. (It should be noted here that
$y=-h$
) walls. (It should be noted here that
![]() $D_{11}^{\prime }+D_{22}^{\prime }=0$
.) We then take a Fourier transform in the
$D_{11}^{\prime }+D_{22}^{\prime }=0$
.) We then take a Fourier transform in the
![]() $x$
direction of all perturbed quantities
$x$
direction of all perturbed quantities
![]() $\boldsymbol{f}^{\prime }$
such that
$\boldsymbol{f}^{\prime }$
such that
![]() $\boldsymbol{f}^{\prime }(x,y)=\tilde{\boldsymbol{f}}(k,y)\exp (\text{i}kx+\unicode[STIX]{x1D70E}t)$
, where
$\boldsymbol{f}^{\prime }(x,y)=\tilde{\boldsymbol{f}}(k,y)\exp (\text{i}kx+\unicode[STIX]{x1D70E}t)$
, where
![]() $\tilde{\boldsymbol{f}}$
is the amplitude function,
$\tilde{\boldsymbol{f}}$
is the amplitude function,
![]() $k$
is the wavenumber and
$k$
is the wavenumber and
![]() $\unicode[STIX]{x1D70E}$
is the complex-valued growth rate.
$\unicode[STIX]{x1D70E}$
is the complex-valued growth rate.
Case 1: isotropy–circulation instability. In this case, the instability grows from an initially isotropic state, i.e.
![]() $\unicode[STIX]{x1D63F}_{0}=\unicode[STIX]{x1D644}/2$
. The linearized equations in (3.3) and (3.5) become
$\unicode[STIX]{x1D63F}_{0}=\unicode[STIX]{x1D644}/2$
. The linearized equations in (3.3) and (3.5) become
where
![]() $\unicode[STIX]{x1D6FF}^{(n)}=\text{d}^{n}/\text{d}y^{n}$
represents the
$\unicode[STIX]{x1D6FF}^{(n)}=\text{d}^{n}/\text{d}y^{n}$
represents the
![]() $n$
th derivative of
$n$
th derivative of
![]() $y$
, and
$y$
, and
![]() $\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D70E}+4d_{R})/d_{T}+k^{2}$
. We find that the general solution of the above equations has the vector form
$\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D70E}+4d_{R})/d_{T}+k^{2}$
. We find that the general solution of the above equations has the vector form
where
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FC}/4d_{T}$
, and
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FC}/4d_{T}$
, and
![]() $\boldsymbol{F}_{j}$
can be written as
$\boldsymbol{F}_{j}$
can be written as
By implementing the eight boundary conditions
![]() $\unicode[STIX]{x1D6FF}\tilde{D}_{11}=\unicode[STIX]{x1D6FF}\tilde{D}_{12}=\unicode[STIX]{x1D6FF}\tilde{v}=\tilde{v}=0$
at
$\unicode[STIX]{x1D6FF}\tilde{D}_{11}=\unicode[STIX]{x1D6FF}\tilde{D}_{12}=\unicode[STIX]{x1D6FF}\tilde{v}=\tilde{v}=0$
at
![]() $y=\pm h$
, we obtain a linear system for
$y=\pm h$
, we obtain a linear system for
![]() $B_{j}$
. The existence of non-trivial solutions gives
$B_{j}$
. The existence of non-trivial solutions gives
![]() $\unicode[STIX]{x1D714}$
and hence
$\unicode[STIX]{x1D714}$
and hence
![]() $\unicode[STIX]{x1D70E}$
. On the other hand, we find that the long-wave solution has to be solved separately due to a singularity at
$\unicode[STIX]{x1D70E}$
. On the other hand, we find that the long-wave solution has to be solved separately due to a singularity at
![]() $k=0$
. By making use of the fact that the solution is unidirectional, we are able to obtain the equilibrium solution,
$k=0$
. By making use of the fact that the solution is unidirectional, we are able to obtain the equilibrium solution,
![]() $(\tilde{D}_{11},\tilde{D}_{12},\tilde{v})=(0,\sin (\sqrt{(\unicode[STIX]{x1D6FC}+4\unicode[STIX]{x1D70E}+16d_{R})/4d_{T}}y),\cos (\sqrt{(\unicode[STIX]{x1D6FC}+4\unicode[STIX]{x1D70E}+16d_{R})/4d_{T}}y))$
, which yields the growth rate
$(\tilde{D}_{11},\tilde{D}_{12},\tilde{v})=(0,\sin (\sqrt{(\unicode[STIX]{x1D6FC}+4\unicode[STIX]{x1D70E}+16d_{R})/4d_{T}}y),\cos (\sqrt{(\unicode[STIX]{x1D6FC}+4\unicode[STIX]{x1D70E}+16d_{R})/4d_{T}}y))$
, which yields the growth rate
As shown by the comparisons in figure 2(a), we find that the real parts of the growth rates of the long-wave modes (diamond symbols) are always larger than those of the corresponding finite-wavelength ones (solid lines), and hence dominate the instability. Moreover, (3.14) suggests a marginal stability condition,
![]() $|\unicode[STIX]{x1D6FC}|>4(\unicode[STIX]{x03C0}/2h)^{2}d_{T}+16d_{R}$
, which recovers the theoretical predictions for unbounded suspensions in the limit
$|\unicode[STIX]{x1D6FC}|>4(\unicode[STIX]{x03C0}/2h)^{2}d_{T}+16d_{R}$
, which recovers the theoretical predictions for unbounded suspensions in the limit
![]() $h\rightarrow \infty$
(Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
). When making connections to the annulus geometry by replacing the gap width
$h\rightarrow \infty$
(Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
). When making connections to the annulus geometry by replacing the gap width
![]() $2h$
by
$2h$
by
![]() $R_{2}-R_{1}$
, we find that the marginal instability curve in figure 1(g) can be accurately fitted as a function of the form
$R_{2}-R_{1}$
, we find that the marginal instability curve in figure 1(g) can be accurately fitted as a function of the form
![]() $K(R_{2}-R_{1})^{-2}d_{T}+16d_{R}$
but with a different constant
$K(R_{2}-R_{1})^{-2}d_{T}+16d_{R}$
but with a different constant
![]() $K$
due to curved geometries (in this case,
$K$
due to curved geometries (in this case,
![]() $K\approx 28.7$
). It is apparent that the prediction in the straight periodic channel (dashed line in figure 1
g) agrees well with that of the curved annulus, suggesting that (3.14) in fact provides a reasonable estimate of the time scale of the isotropy–circulation instability under a general parallel confinement.
$K\approx 28.7$
). It is apparent that the prediction in the straight periodic channel (dashed line in figure 1
g) agrees well with that of the curved annulus, suggesting that (3.14) in fact provides a reasonable estimate of the time scale of the isotropy–circulation instability under a general parallel confinement.
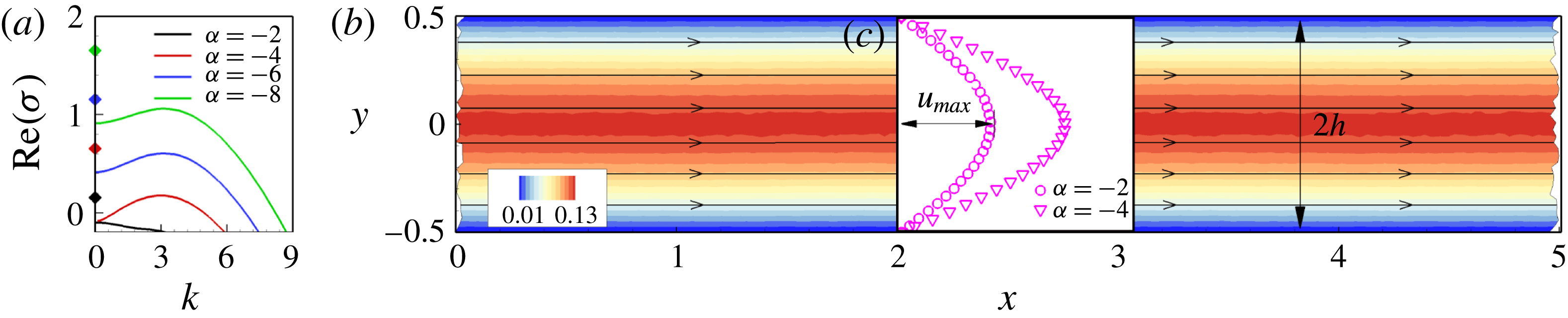
Figure 2. (a) The growth rate
![]() $\text{Re}(\unicode[STIX]{x1D70E})$
for the long-wave (diamonds) and finite-wavelength (lines) instabilities as a function of the wavenumber
$\text{Re}(\unicode[STIX]{x1D70E})$
for the long-wave (diamonds) and finite-wavelength (lines) instabilities as a function of the wavenumber
![]() $k$
for isotropy–circulation instabilities in a periodic straight channel when choosing
$k$
for isotropy–circulation instabilities in a periodic straight channel when choosing
![]() $h=0.5$
,
$h=0.5$
,
![]() $d_{T}=d_{R}=0.025$
. (b) Streamlines overlaid on the colourmap of the
$d_{T}=d_{R}=0.025$
. (b) Streamlines overlaid on the colourmap of the
![]() $u$
velocity component at
$u$
velocity component at
![]() $\unicode[STIX]{x1D6FC}=-4.0$
. (c) Velocity profiles at
$\unicode[STIX]{x1D6FC}=-4.0$
. (c) Velocity profiles at
![]() $\unicode[STIX]{x1D6FC}=-2.0$
(
$\unicode[STIX]{x1D6FC}=-2.0$
(
![]() $u_{max}=0.07$
) and
$u_{max}=0.07$
) and
![]() $\unicode[STIX]{x1D6FC}=-4.0$
(
$\unicode[STIX]{x1D6FC}=-4.0$
(
![]() $u_{max}=0.13$
) respectively.
$u_{max}=0.13$
) respectively.

Figure 3. (a) The growth rate
![]() $\text{Re}(\unicode[STIX]{x1D70E})$
as a function of the wavenumber
$\text{Re}(\unicode[STIX]{x1D70E})$
as a function of the wavenumber
![]() $k$
for bending instabilities of the sharply aligned extensors when confined in a periodic straight channel when choosing
$k$
for bending instabilities of the sharply aligned extensors when confined in a periodic straight channel when choosing
![]() $h=0.5$
,
$h=0.5$
,
![]() $d_{R}=0$
and
$d_{R}=0$
and
![]() $d_{T}=0.025$
. The maximum growth rates at the critical wavenumbers
$d_{T}=0.025$
. The maximum growth rates at the critical wavenumbers
![]() $k_{cr}$
are marked by solid circles. (b,c) The vorticity field
$k_{cr}$
are marked by solid circles. (b,c) The vorticity field
![]() $\unicode[STIX]{x1D6FA}$
as the bending instability starts to grow at
$\unicode[STIX]{x1D6FA}$
as the bending instability starts to grow at
![]() $\unicode[STIX]{x1D6FC}=-4.0$
and
$\unicode[STIX]{x1D6FC}=-4.0$
and
![]() $\unicode[STIX]{x1D6FC}=-8.0$
respectively. The solid black scales represent the length scales
$\unicode[STIX]{x1D6FC}=-8.0$
respectively. The solid black scales represent the length scales
![]() $\unicode[STIX]{x03C0}/k_{cr}$
that match the separation distance between the neighbouring vortices.
$\unicode[STIX]{x03C0}/k_{cr}$
that match the separation distance between the neighbouring vortices.
Case 2: circulation–travelling-wave instability. It needs to kept in mind that the circulation–travelling-wave instability is in fact a secondary instability developed from a shear-induced aligned state whose analytical form, however, is lacking. Nevertheless, we consider a reduced model where all of the extensor particles are initially aligned in the
![]() $x$
direction, and neglect the rotational diffusion by choosing
$x$
direction, and neglect the rotational diffusion by choosing
![]() $d_{R}=0$
(Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). For such a ‘sharply aligned’ configuration, the homogeneous base-state solution is simply
$d_{R}=0$
(Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). For such a ‘sharply aligned’ configuration, the homogeneous base-state solution is simply
![]() $\unicode[STIX]{x1D63F}_{0}=\operatorname{diag}\{1,0\}$
. After some algebra, we are able to eliminate several unknown variables, and show that the hydrodynamic instability is determined by the following sixth-order ordinary differential equation for the off-diagonal component
$\unicode[STIX]{x1D63F}_{0}=\operatorname{diag}\{1,0\}$
. After some algebra, we are able to eliminate several unknown variables, and show that the hydrodynamic instability is determined by the following sixth-order ordinary differential equation for the off-diagonal component
![]() $\tilde{D}_{12}$
:
$\tilde{D}_{12}$
:
which admits the general solution
![]() $\tilde{D}_{12}=\sum _{j=1}^{6}C_{j}\exp (\unicode[STIX]{x1D706}_{j}y)$
. The eigenvalues
$\tilde{D}_{12}=\sum _{j=1}^{6}C_{j}\exp (\unicode[STIX]{x1D706}_{j}y)$
. The eigenvalues
![]() $\unicode[STIX]{x1D706}_{j}$
and hence the growth rate
$\unicode[STIX]{x1D706}_{j}$
and hence the growth rate
![]() $\unicode[STIX]{x1D70E}$
are then solved numerically by applying the converted boundary conditions
$\unicode[STIX]{x1D70E}$
are then solved numerically by applying the converted boundary conditions
![]() $(\unicode[STIX]{x1D70E}+d_{T}k^{2})\tilde{D}_{12}-d_{T}\unicode[STIX]{x1D6FF}^{(2)}\tilde{D}_{12}=0$
and
$(\unicode[STIX]{x1D70E}+d_{T}k^{2})\tilde{D}_{12}-d_{T}\unicode[STIX]{x1D6FF}^{(2)}\tilde{D}_{12}=0$
and
![]() $\unicode[STIX]{x1D6FF}\tilde{D}_{12}=\unicode[STIX]{x1D6FF}^{(3)}\tilde{D}_{12}=0$
at
$\unicode[STIX]{x1D6FF}\tilde{D}_{12}=\unicode[STIX]{x1D6FF}^{(3)}\tilde{D}_{12}=0$
at
![]() $y=\pm h$
, and seeking non-trivial solutions. The real parts of the growth rates as a function of
$y=\pm h$
, and seeking non-trivial solutions. The real parts of the growth rates as a function of
![]() $k$
are plotted in figure 3(a) at different values of
$k$
are plotted in figure 3(a) at different values of
![]() $\unicode[STIX]{x1D6FC}$
, showing that the maximum growth rates occur at finite critical wavenumbers
$\unicode[STIX]{x1D6FC}$
, showing that the maximum growth rates occur at finite critical wavenumbers
![]() $k_{cr}>0$
. In (b,c), we set up the corresponding numerical simulations with the same initial conditions, and highlight the snapshots of the vorticity field
$k_{cr}>0$
. In (b,c), we set up the corresponding numerical simulations with the same initial conditions, and highlight the snapshots of the vorticity field
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y-\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}x$
. The simulation results show the generation of fluid jets that are perpendicular to the particle alignment direction due to the nematic bending instability, which leads to uniformly spaced vortices of alternating signs. The separation distance between neighbouring vortex pairs can be accurately measured by the characteristic length scale
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y-\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}x$
. The simulation results show the generation of fluid jets that are perpendicular to the particle alignment direction due to the nematic bending instability, which leads to uniformly spaced vortices of alternating signs. The separation distance between neighbouring vortex pairs can be accurately measured by the characteristic length scale
![]() $\unicode[STIX]{x03C0}/k_{cr}$
.
$\unicode[STIX]{x03C0}/k_{cr}$
.
While the above analysis is for a reduced model by assuming particle alignment in the
![]() $x$
direction without background flow, it reveals the finite-wavelength nature of the bending instability, and provides quantitative measurements for the intrinsic time and length scales selected by the parallel confinement. Similarly to case 1, the predicted circulation–travelling-wave borderline (dash–dotted line in (g)) in the straight channel indeed agrees with the simulation results for the annulus geometry, especially in the regime of high
$x$
direction without background flow, it reveals the finite-wavelength nature of the bending instability, and provides quantitative measurements for the intrinsic time and length scales selected by the parallel confinement. Similarly to case 1, the predicted circulation–travelling-wave borderline (dash–dotted line in (g)) in the straight channel indeed agrees with the simulation results for the annulus geometry, especially in the regime of high
![]() $|\unicode[STIX]{x1D6FC}|$
and small
$|\unicode[STIX]{x1D6FC}|$
and small
![]() $R_{2}-R_{1}$
, where particles are strongly aligned and hence close to the sharp-alignment approximation. Beyond the travelling-wave regime, the transition towards chaotic flows is highly nonlinear, and can only be determined by numerical simulations.
$R_{2}-R_{1}$
, where particles are strongly aligned and hence close to the sharp-alignment approximation. Beyond the travelling-wave regime, the transition towards chaotic flows is highly nonlinear, and can only be determined by numerical simulations.
3.2 Concentrated suspension
In this section, we examine the nonlinear dynamics of concentrated suspensions where both
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D701}$
are non-zero. A mean-field torque is introduced to govern the rotational dynamics of extensor particles in the kinetic model through a Maier–Saupe steric potential (Maier & Saupe Reference Maier and Saupe1958). As shown by Gao et al. (Reference Gao, Blackwell, Glaser, Betterton and Shelley2015a
,Reference Gao, Blackwell, Glaser, Betterton and Shelley
b
, Reference Gao, Betterton, Jhang and Shelley2017), for rod-like particles, the resultant enhanced steric interactions spontaneously drive the system away from an initially isotropic state to form a nematically aligned state when
$\unicode[STIX]{x1D701}$
are non-zero. A mean-field torque is introduced to govern the rotational dynamics of extensor particles in the kinetic model through a Maier–Saupe steric potential (Maier & Saupe Reference Maier and Saupe1958). As shown by Gao et al. (Reference Gao, Blackwell, Glaser, Betterton and Shelley2015a
,Reference Gao, Blackwell, Glaser, Betterton and Shelley
b
, Reference Gao, Betterton, Jhang and Shelley2017), for rod-like particles, the resultant enhanced steric interactions spontaneously drive the system away from an initially isotropic state to form a nematically aligned state when
![]() $\unicode[STIX]{x1D701}>4d_{R}$
.
$\unicode[STIX]{x1D701}>4d_{R}$
.
Compared with the dilute cases where isotropy is the only admissible equilibrium state, we have obtained the steady-state solutions of
![]() $\unicode[STIX]{x1D63F}$
without flows at relatively small values of
$\unicode[STIX]{x1D63F}$
without flows at relatively small values of
![]() $|\unicode[STIX]{x1D6FC}|$
, which exhibit much more complicated nematic configurations, as shown in figure 4. For passive particles, when choosing
$|\unicode[STIX]{x1D6FC}|$
, which exhibit much more complicated nematic configurations, as shown in figure 4. For passive particles, when choosing
![]() $\unicode[STIX]{x1D6FC}=0$
, figure 4(a) reveals that the system quickly relaxes to a homogeneous nematic state where the equilibrium solution satisfies a 2D distribution of Bingham form (Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
, Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017),
$\unicode[STIX]{x1D6FC}=0$
, figure 4(a) reveals that the system quickly relaxes to a homogeneous nematic state where the equilibrium solution satisfies a 2D distribution of Bingham form (Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
, Reference Gao, Betterton, Jhang and Shelley2017; Gao & Li Reference Gao and Li2017),
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{B}(\unicode[STIX]{x1D719})=\frac{\exp [\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\cos (2\unicode[STIX]{x1D719})]}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D719}^{\prime }\exp [\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\cos (2\unicode[STIX]{x1D719}^{\prime })]},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{B}(\unicode[STIX]{x1D719})=\frac{\exp [\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\cos (2\unicode[STIX]{x1D719})]}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D719}^{\prime }\exp [\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\cos (2\unicode[STIX]{x1D719}^{\prime })]},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}$
is the rod orientation angle and
$\unicode[STIX]{x1D719}$
is the rod orientation angle and
![]() $\unicode[STIX]{x1D6FF}$
is a function of the coefficient
$\unicode[STIX]{x1D6FF}$
is a function of the coefficient
![]() $\unicode[STIX]{x1D709}=2\unicode[STIX]{x1D701}/d_{R}$
. Therefore, the degree of alignment is in fact determined by the ratio between
$\unicode[STIX]{x1D709}=2\unicode[STIX]{x1D701}/d_{R}$
. Therefore, the degree of alignment is in fact determined by the ratio between
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $d_{R}$
. As
$d_{R}$
. As
![]() $\unicode[STIX]{x1D6FC}$
increases, it is seen that the nematic field lines in figure 4(b) become distorted to spiral outwards to the annulus boundaries, reminiscent of the defect structures of active nematics when confined in a circular disk (Woodhouse & Goldstein Reference Woodhouse and Goldstein2012; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). As
$\unicode[STIX]{x1D6FC}$
increases, it is seen that the nematic field lines in figure 4(b) become distorted to spiral outwards to the annulus boundaries, reminiscent of the defect structures of active nematics when confined in a circular disk (Woodhouse & Goldstein Reference Woodhouse and Goldstein2012; Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). As
![]() $|\unicode[STIX]{x1D6FC}|$
approximately goes beyond 0.5, the nematic structures in figure 4(c,d) switch to become azimuthal-symmetric and independent of the values of
$|\unicode[STIX]{x1D6FC}|$
approximately goes beyond 0.5, the nematic structures in figure 4(c,d) switch to become azimuthal-symmetric and independent of the values of
![]() $\unicode[STIX]{x1D6FC}$
, which can be solved analytically by setting the right-hand side of (2.5) to be zero and then seeking the steady-state solution of
$\unicode[STIX]{x1D6FC}$
, which can be solved analytically by setting the right-hand side of (2.5) to be zero and then seeking the steady-state solution of
![]() $\unicode[STIX]{x1D63F}$
as a function of
$\unicode[STIX]{x1D63F}$
as a function of
![]() $r$
only. The observed variations in the equilibrium nematic states can be illustrated by examining the system transient dynamics that evolves from near-isotropy. One interesting example is shown in figure 5 when choosing
$r$
only. The observed variations in the equilibrium nematic states can be illustrated by examining the system transient dynamics that evolves from near-isotropy. One interesting example is shown in figure 5 when choosing
![]() $\unicode[STIX]{x1D6FC}=-2.0$
. An isotropy–circulation instability first occurs in figure 5(a) to reorient particles, due to the combined effect of the circulating flow and the Maier–Saupe steric interactions. However, in this case, the confinement effect in the thin gap is so strong that it suppresses the bending deformation occurring in the radial direction. As a result, the induced circulating flow gradually diminishes and the system eventually relaxes to an axisymmetric equilibrium state where all particles are approximately aligned in the azimuthal direction; see the insets in figure 5(b–d).
$\unicode[STIX]{x1D6FC}=-2.0$
. An isotropy–circulation instability first occurs in figure 5(a) to reorient particles, due to the combined effect of the circulating flow and the Maier–Saupe steric interactions. However, in this case, the confinement effect in the thin gap is so strong that it suppresses the bending deformation occurring in the radial direction. As a result, the induced circulating flow gradually diminishes and the system eventually relaxes to an axisymmetric equilibrium state where all particles are approximately aligned in the azimuthal direction; see the insets in figure 5(b–d).

Figure 4. Equilibrium solutions of nematically aligned states at different values of
![]() $\unicode[STIX]{x1D6FC}$
when choosing
$\unicode[STIX]{x1D6FC}$
when choosing
![]() $R_{1}=1.0$
and
$R_{1}=1.0$
and
![]() $R_{2}=2.0$
; the nematic director field is overlaid on the colourmap of
$R_{2}=2.0$
; the nematic director field is overlaid on the colourmap of
![]() $s$
. Inset in (d): comparisons between the analytical (solid line) and numerical (open symbols) results at
$s$
. Inset in (d): comparisons between the analytical (solid line) and numerical (open symbols) results at
![]() $\unicode[STIX]{x1D6FC}=-0.5,-2.0$
for the
$\unicode[STIX]{x1D6FC}=-0.5,-2.0$
for the
![]() $D_{rr}$
component. The numerical data are taken along the white line marked in (c).
$D_{rr}$
component. The numerical data are taken along the white line marked in (c).
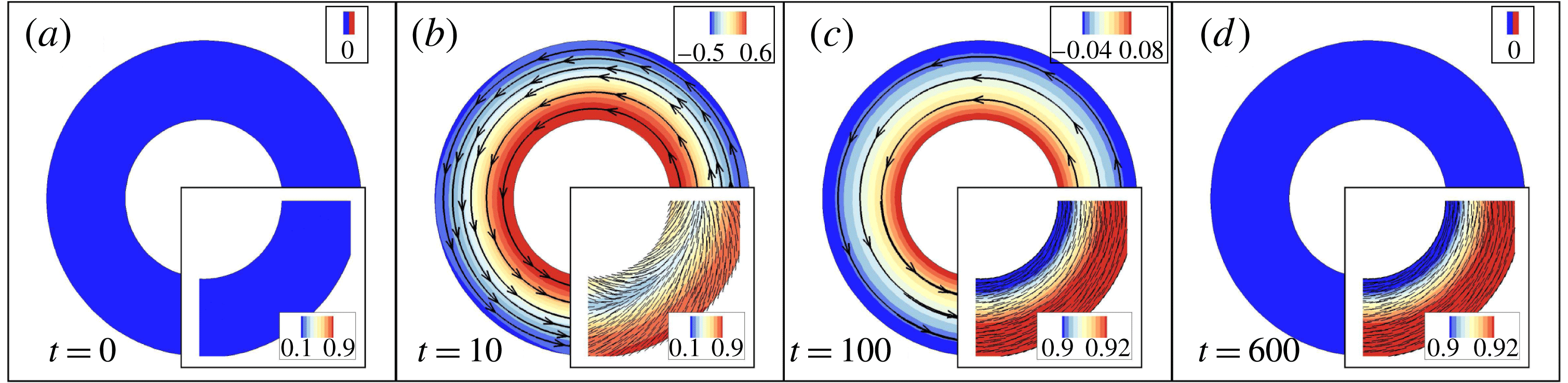
Figure 5. Evolution of the flow patterns for a concentrated extensor suspension when choosing
![]() $\unicode[STIX]{x1D6FC}=-2.0$
,
$\unicode[STIX]{x1D6FC}=-2.0$
,
![]() $R_{1}=1.0$
and
$R_{1}=1.0$
and
![]() $R_{2}=2.0$
. Insets: the nematic director field overlaid on the colourmap of
$R_{2}=2.0$
. Insets: the nematic director field overlaid on the colourmap of
![]() $s$
.
$s$
.

Figure 6. (a–d) Flow patterns (streamline overlaid on the colourmap of
![]() $\unicode[STIX]{x1D6FA}$
) and (e–h) nematic structures (nematic director field overlaid on the colourmap of
$\unicode[STIX]{x1D6FA}$
) and (e–h) nematic structures (nematic director field overlaid on the colourmap of
![]() $s$
) that characterize the long-time dynamics of a confined extensor suspension when choosing
$s$
) that characterize the long-time dynamics of a confined extensor suspension when choosing
![]() $\unicode[STIX]{x1D6FC}=-2.0$
,
$\unicode[STIX]{x1D6FC}=-2.0$
,
![]() $R_{1}=0.75$
and
$R_{1}=0.75$
and
![]() $R_{2}=2.0$
.
$R_{2}=2.0$
.

Figure 7. (a–d) Short-time evolution of the flow (velocity vector overlaid on the colourmap of
![]() $\unicode[STIX]{x1D6FA}$
) and (e–h) nematic fields (nematic director overlaid on the colourmap of
$\unicode[STIX]{x1D6FA}$
) and (e–h) nematic fields (nematic director overlaid on the colourmap of
![]() $s$
) for the case shown in figure 6. In (e–h), the black arrows show the direction of the crack formation and
$s$
) for the case shown in figure 6. In (e–h), the black arrows show the direction of the crack formation and
![]() $+1/2$
defect movement.
$+1/2$
defect movement.
Increase of the gap width relaxes the confinement effect to facilitate the active flow generation through the bending instability, which can be similarly explained by the analysis in the dilute cases above. As shown in figure 6, the system long-time dynamics clearly exhibits an isotropy–circulation (b,f) and then a circulation–travelling-wave (c,g) instability. Compared with the stable structures observed in the dilute cases, the structure formation and evolution in concentrated suspensions are much more complicated. In (c), it is shown that the active flows bend the streamlines to form travelling waves, leading to six evenly spaced ‘incipient cracks’ growing from the inner wall into the bulk regime shown in (g). Disclination defects of charge
![]() $\pm 1/2$
are seen to be born along these cracks, move around and undergo nucleation/annihilation when interacting with each other as well as with rigid boundaries. Interestingly, the system gradually approaches a quasi-steady-state where four
$\pm 1/2$
are seen to be born along these cracks, move around and undergo nucleation/annihilation when interacting with each other as well as with rigid boundaries. Interestingly, the system gradually approaches a quasi-steady-state where four
![]() $+1/2$
defects oscillate around their equilibrium positions; see (h). The flow field remains travelling-wave-like but also periodically switches directions; see (d). The entire history of the complex dynamics is shown in the supplementary movie S1 (available at https://doi.org/10.1017/jfm.2017.759).
$+1/2$
defects oscillate around their equilibrium positions; see (h). The flow field remains travelling-wave-like but also periodically switches directions; see (d). The entire history of the complex dynamics is shown in the supplementary movie S1 (available at https://doi.org/10.1017/jfm.2017.759).
As shown in figure 7, a close look at the short-time dynamics of oscillating
![]() $+1/2$
defects and the accompanying swirling flow reveals the subtle interplay among the nematic structure variation, the active flow generation and their interactions with the curved walls. The swirling flow drives the upward movement of the
$+1/2$
defects and the accompanying swirling flow reveals the subtle interplay among the nematic structure variation, the active flow generation and their interactions with the curved walls. The swirling flow drives the upward movement of the
![]() $+1/2$
disclination defect and, in the mean time, induces an opposite bending deformation nearby to form an incipient crack. As shown in (f,g), the crack ‘head’ keeps moving downward to become a
$+1/2$
disclination defect and, in the mean time, induces an opposite bending deformation nearby to form an incipient crack. As shown in (f,g), the crack ‘head’ keeps moving downward to become a
![]() $+1/2$
defect (see (h)), while its ‘tail’ gradually merges with the up-moving
$+1/2$
defect (see (h)), while its ‘tail’ gradually merges with the up-moving
![]() $+1/2$
defect before it hits the wall. Corresponding to the nematic structure change, the resultant CCW (CW) vorticity is seen to be strengthened (weakened) when the crack and defect interact, and then weakened (strengthened) during their annihilation. We find that such an oscillating state is very robust when choosing
$+1/2$
defect before it hits the wall. Corresponding to the nematic structure change, the resultant CCW (CW) vorticity is seen to be strengthened (weakened) when the crack and defect interact, and then weakened (strengthened) during their annihilation. We find that such an oscillating state is very robust when choosing
![]() $R_{1}$
less than 1.5, and the gap width
$R_{1}$
less than 1.5, and the gap width
![]() $R_{2}-R_{1}$
between 1.0 and 1.5 (see also movie S2 for the similar dynamics observed in a smaller annulus). As shown in movie S3, more complex defect dynamics and seemingly chaotic flows dominate when
$R_{2}-R_{1}$
between 1.0 and 1.5 (see also movie S2 for the similar dynamics observed in a smaller annulus). As shown in movie S3, more complex defect dynamics and seemingly chaotic flows dominate when
![]() $R_{2}-R_{1}>2.0$
, resembling the active nematic flows observed in an unbounded domain (Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
, Reference Gao, Betterton, Jhang and Shelley2017).
$R_{2}-R_{1}>2.0$
, resembling the active nematic flows observed in an unbounded domain (Gao et al.
Reference Gao, Blackwell, Glaser, Betterton and Shelley2015b
, Reference Gao, Betterton, Jhang and Shelley2017).
4 Conclusion
In this work, we have studied the nonlinear dynamics and flow patterns of apolar extensor suspensions confined in an annulus geometry through modelling and simulation. The
![]() $BQ$
-tensor model with the Bingham closure, which was coarse-grained from a mesoscale kinetic model, was used to describe the evolution of the second-moment
$BQ$
-tensor model with the Bingham closure, which was coarse-grained from a mesoscale kinetic model, was used to describe the evolution of the second-moment
![]() $\unicode[STIX]{x1D63F}$
tensor (Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). The
$\unicode[STIX]{x1D63F}$
tensor (Gao et al.
Reference Gao, Betterton, Jhang and Shelley2017). The
![]() $\unicode[STIX]{x1D63F}$
dynamics equation was coupled with the incompressible Navier–Stokes equations, which were solved by using a Galerkin mixed element method at low Reynolds numbers. We have observed active flow generation and spontaneous coherent structures in both dilute and concentrated suspensions. We have gained physical insights into the analytical structure, hydrodynamic instabilities, and characteristic time and length scales under parallel confinement by performing stability analyses for dilute suspensions in a periodic straight channel. In particular, we have shown analytically the long-wave and finite-wavelength nature of the isotropy–circulation and circulation–travelling-wave instabilities respectively. By using similar models and analyses, we will be able to explore more challenging situations when active fluids are confined in complex geometries at high dimensions.
$\unicode[STIX]{x1D63F}$
dynamics equation was coupled with the incompressible Navier–Stokes equations, which were solved by using a Galerkin mixed element method at low Reynolds numbers. We have observed active flow generation and spontaneous coherent structures in both dilute and concentrated suspensions. We have gained physical insights into the analytical structure, hydrodynamic instabilities, and characteristic time and length scales under parallel confinement by performing stability analyses for dilute suspensions in a periodic straight channel. In particular, we have shown analytically the long-wave and finite-wavelength nature of the isotropy–circulation and circulation–travelling-wave instabilities respectively. By using similar models and analyses, we will be able to explore more challenging situations when active fluids are confined in complex geometries at high dimensions.
Acknowledgements
T.G. acknowledges useful discussions with M. Shelley and D. Saintillan. This work is partially supported by NSF grant DMS-1619960.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.759.