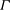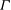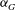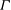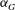1. Introduction
Axisymmetric turbulent forced plumes produced by horizontal, circular sources of constant buoyancy, momentum and volume fluxes have been the subject of considerable research over the last 70 years or so. Zel’dovich (Reference Zel’dovich1937), Priestley & Ball (Reference Priestley and Ball1955) and Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956) developed the classic plume model assuming a conceptual point source of buoyancy flux alone, complete dynamical self-similarity, fully developed turbulence, small density differences and negligible diffusion and radiation. The backbone of this theory has remained virtually unchanged since. The validation of this theory has been comprehensive and has essentially fallen into two categories: the first through widespread application where the bulk flow of plumes occurring over a range of different scales, in the natural and built environments, and in industry, are of interest; and the second through predominantly experimental campaigns focusing on the details of the internal flow. Although relatively few in number, the latter have provided a quantification of some of the key dynamical quantities, such as the entrainment coefficient, the mean to turbulent ratio of the vertical fluxes and of the radial spread of the buoyancy and velocity profiles. These quantities are however characterised by a non-negligible scatter, with differences that can exceed 20–25 % (Linden Reference Linden, Batchelor, Moffatt and Worster2000). Despite this scatter, the classic plume solutions provide a robust and reliable model for buoyant plumes in geophysical and industrial contexts and have been extended to account for stratified environments (Batchelor Reference Batchelor1954; Caulfield & Woods Reference Caulfield and Woods1998; Kaye & Scase Reference Kaye and Scase2011), non-constant source strengths (Scase et al. Reference Scase, Caulfield, Dalziel and Hunt2006), negative buoyancy (Baines, Turner & Campbell Reference Baines, Turner and Campbell1990; Carazzo, Kaminski & Tait Reference Carazzo, Kaminski and Tait2008; Burridge & Hunt Reference Burridge and Hunt2012; Mehaddi, Vauquelin & Candelier Reference Mehaddi, Vauquelin and Candelier2012), chemical reactions (Zhou Reference Zhou2002; Campbell & Cardoso Reference Campbell and Cardoso2010; Ülpre, Eames & Greig Reference Ülpre, Eames and Greig2013) and their non-Boussinesq counterparts (Rooney & Linden Reference Rooney and Linden1996; Carlotti & Hunt Reference Carlotti and Hunt2005). For further reading on the development of plume theory, review papers by List (Reference List1982), Kaye (Reference Kaye2008), Woods (Reference Woods2010) and Hunt & van den Bremer (Reference Hunt and van den Bremer2011) are recommended as is the text of Linden (Reference Linden, Batchelor, Moffatt and Worster2000).
More generally, we can assert that the dynamical properties of buoyant jets in their asymptotic states of ‘pure jet’ and ‘pure plume’ are nowadays widely identified in the literature. Much less is known about the variability characterising the dynamics of buoyant releases in what may be regarded as the ‘transition’ states between these asymptotic states, for example as the buoyancy flux of a highly forced plume is systematically increased. Assuming a fully turbulent Boussinesq plume, with negligible influence of diffusive phenomena, developing in an unstratified quiescent ambient fluid, the flow dynamics can be shown to depend on a single non-dimensional parameter: the plume Richardson number
${\it\Gamma}$
. This may be evaluated at any height
$z$
above the source (at
$z=0$
) based on the local volume, momentum and buoyancy fluxes (Hunt & Kaye Reference Hunt and Kaye2001) as
$$\begin{eqnarray}{\it\Gamma}(z)=\frac{5}{2^{7/2}{\rm\pi}^{1/2}{\it\alpha}_{ref}}\frac{Q(z)^{2}B(z)}{M(z)^{5/2}}\end{eqnarray}$$
where
${\it\alpha}_{ref}$
denotes the reference value of the entrainment coefficient for Gaussian profiles and the mean fluxes of volume
$Q$
, specific momentum
$M$
and specific buoyancy
$B$
are defined as
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle Q(z)=2{\rm\pi}\int _{0}^{\infty }w(r,z)r\text{d}r\\ \displaystyle M(z)=2{\rm\pi}\int _{0}^{\infty }w^{2}(r,z)r\text{d}r\\ \displaystyle B(z)=2{\rm\pi}\int _{0}^{\infty }w(r,z)g^{\prime }(r,z)r\text{d}r,\end{array}\right\}\end{eqnarray}$$
where
$w$
is the Reynolds-averaged vertical velocity,
$r$
denotes the radial coordinate of the axisymmetric plume (figure 1) and
$g^{\prime }=g(({\it\rho}_{e}-{\it\rho})/{\it\rho}_{e})$
denotes the Reynolds-averaged buoyancy (
$g$
is the gravitational acceleration) of the plume fluid, of density
${\it\rho}(r,z)$
, relative to a fixed representative density
${\it\rho}_{e}$
of the ambient.
Figure 1. Schematic of the experimental set-up for PIV on thermal air plumes with the coordinate system
$(r,z)$
employed herein.
It is worth mentioning that when the plume density is significantly lower than that of the ambient, such that the conditions are non-Boussinesq (Rooney & Linden Reference Rooney and Linden1996; Carlotti & Hunt Reference Carlotti and Hunt2005; van den Bremer & Hunt Reference van den Bremer and Hunt2010), the ratio
${\it\rho}/{\it\rho}_{e}$
has to be considered as a second non-dimensional parameter on which the flow dynamics depend.
The dependence of the plume dynamics on
${\it\Gamma}$
and on
${\it\rho}/{\it\rho}_{e}$
has rarely been investigated experimentally and represents nowadays a major research axis in this field. In order to focus on this variability, and primarily on the role of
${\it\Gamma}$
, benefitting from advancement in visualisation and data acquisition techniques, we have performed experiments on steady, thermal air plumes injected into a nominally quiescent, unstratified laboratory enclosure at differing source Richardson number. The remainder of this paper is structured as follows. We begin by reviewing the major findings of previous experimental works on buoyant plumes in order to motivate a further experimental investigation. The experimental set-up and plume source conditions investigated are outlined in § 2. Radial profiles of time-averaged velocities derived from particle image velocimetry (PIV) velocity and thermocouple temperature measurements are examined in § 3. From the high spatial resolution of the PIV measurements, we investigate the turbulent intensities, the turbulent momentum transfer and the spatial structure of the turbulent flow (§ 4). Finally, in § 5 we present different estimates of the entrainment coefficient that allow us to conclude on the influence of
${\it\Gamma}$
on the entrainment process.
1.1. Previous experimental results
In early experimental work, Ricou & Spalding (Reference Ricou and Spalding1961) injected air radially inwards towards buoyant jets enclosed by a porous cylinder until they measured a zero pressure drop across the cylinder. This satisfied what they called the ‘entrainment appetite’ of the flow and, as a result, they determined the entrainment coefficient for buoyant gas jets of varying densities. Although the releases were buoyant, the forcing at source was such that the flows were relatively jet-like over the region of interest. The major contribution of their work was to establish a dependence of the entrainment coefficient on the ratio
${\it\rho}_{0}/{\it\rho}_{e}$
of the injected fluid density (
${\it\rho}_{0}={\it\rho}(z=0)$
) to the ambient fluid density; the subscript ‘0’ is used throughout to denote the value of quantities at the source.
George, Alpert & Tamanini (Reference George, Alpert and Tamanini1977) investigated the buoyant plume and made concurrent temperature and velocity measurements using two-wire probes. The plumes were neither Boussinesq nor fully turbulent at the source. They found that the velocity profiles were Gaussian and approximately 10 % wider than their buoyancy counterparts. Their measurements of the fluctuating flow components show that these were still developing at heights exceeding 20 source radii, yet also tend towards Gaussian profiles. The entrainment coefficient in the far field was estimated as
${\it\alpha}_{G}=0.108$
(throughout the paper we always refer to Gaussian entrainment coefficients, a factor
$\sqrt{2}$
lower than the top-hat equivalent in classic plume theory). Finally, George et al. (Reference George, Alpert and Tamanini1977) estimated that the turbulent fluxes of momentum, i.e. related to the standard deviation of the vertical velocity
${\it\sigma}_{w}^{2}$
, and of buoyancy, i.e. related to the correlation of vertical velocity and temperature
$\overline{\tilde{w}\tilde{T}}$
, are responsible for 8 and 15 % of the overall fluxes, respectively. The same experimental apparatus was used by Shabbir & George (Reference Shabbir and George1994), who conducted simultaneous velocity and temperature measurements by means of a set of hot-wire and cold-wire probes. In this case, the experimental facility was completed by a rack of thermocouples to monitor the ambient air stratification and by concentric screens placed around the source to prevent horizontal plume drift: the latter may have inadvertently influenced plume entrainment. Source Reynolds numbers were slightly higher than those attained by George et al. (Reference George, Alpert and Tamanini1977), but not high enough to produce fully turbulent plumes at the source. The study extended the George et al. (Reference George, Alpert and Tamanini1977) analysis to third-order moments of the velocity components, of the temperature and of their correlations. A relatively poor fit of the mean vertical velocity data to a Gaussian curve is presented. Given this poor fit of the key first statistical moment of the data, the validity of the computation of second and third moments is questionable. Nevertheless, good agreement is achieved between the measurements of the vertical fluxes and the power-law relationships predicted by the classic plume model. Both George et al. (Reference George, Alpert and Tamanini1977) and Shabbir & George (Reference Shabbir and George1994) focus on the region where the flow reaches the truly plume-like asymptotic condition, i.e.
${\it\Gamma}=1$
, and do not provide any information on the transition region, as the flow adjusts from either jet-like (
${\it\Gamma}\ll 1$
) or highly lazy (
${\it\Gamma}\gg 1$
) states at its source.
A first systematic investigation of buoyant jets examining the role of the plume Richardson number at the source was performed by Papanicolaou & List (Reference Papanicolaou and List1988). They used laser-Doppler anemometry (LDA) combined with laser-induced fluorescence (LIF) to simultaneously measure velocities and concentrations in saline plumes at frequencies of up to 50 Hz over a vertical extent of 80 cm (
${\approx}40{-}100b_{0}$
, where
$b_{0}$
is the source radius) from an orifice measuring 0.75–2.0 cm in diameter. The spatial resolution of their measurements was an order of magnitude lower than that reported herein and their velocity data was acquired at points rather than over a plane. However, the simultaneous measurement of salinity and velocity signals enabled correlation of the two, and thereby one of the few published estimates of the turbulent buoyancy flux in plumes: of approximately 16 % of the mean buoyancy flux. The source Richardson number varied from jet-like to plume-like buoyant releases. Papanicolaou & List (Reference Papanicolaou and List1988) found that the forced plume examined behaved in a jet-like manner for
$z/L_{M}<1$
, a plume-like manner for
$z/L_{M}>5$
and a smooth vertical transition between the two regimes occurred over
$1<z/L_{M}<5$
,
$L_{M}=\mathscr{C}\cdot M_{0}^{3/4}/B_{0}^{1/2}$
denoting a characteristic length known as the ‘jet length’ (with
$\mathscr{C}=(5/9{\it\alpha}_{ref})^{1/2}(2/{\rm\pi})^{1/4}$
). The vertical extent of these regions agrees well with the theoretical prediction of Morton (Reference Morton1959). Their measurements showed that the radial profiles of the statistics of density and velocity within jet-like and plume-like releases do not differ significantly from each other. Furthermore, these profiles do not show any significant discrepancy with the LDA measurements on isothermal jets performed by Hussein, Capp & George (Reference Hussein, Capp and George1994). The noteworthy differences observed were related to the transport of buoyancy produced turbulence, with almost twice the flux in pure plumes as in jet-like releases. Other major differences concerned the ratio of length scales
$$\begin{eqnarray}{\it\varphi}=b_{g^{\prime }}/b_{w}\end{eqnarray}$$
between the spread of buoyancy
$b_{g^{\prime }}$
and velocity
$b_{w}$
profiles that took an average value of
${\it\varphi}=1.19$
in plume-like releases and
${\it\varphi}=1.33$
in jet-like releases, thereby contradicting the findings of George, Alpert & Tamanini (Reference George, Alpert and Tamanini1977). Finally, the entrainment coefficient
${\it\alpha}_{G}$
was found to be equal to
${\it\alpha}_{j}=0.0545$
in pure jets and
${\it\alpha}_{p}=0.0875$
in pure plumes. The investigation of the dependence of
${\it\varphi}$
and
${\it\alpha}_{G}$
with the plume Richardson number, however, was beyond the scope of their study.
Only relatively recently have plume dynamics been investigated with PIV thereby allowing for higher spatial resolution of the velocity measurements than earlier techniques. Wang & Law (Reference Wang and Law2002) performed simultaneous velocity and density measurements with PIV and planar laser-induced fluorescence (PLIF). They performed experiments over a large number of saline plumes that were all highly forced at the source, i.e.
${\it\Gamma}_{0}\ll 1$
. As far as we are aware, this is the first experimental study reporting the variability of
${\it\varphi}$
and
${\it\alpha}_{G}$
with the local Richardson number. Wang & Law (Reference Wang and Law2002) found a general trend of a decreasing
${\it\varphi}$
with increasing Richardson number, whereas
${\it\alpha}_{G}$
was shown to increase with the Richardson number. Both features will be widely discussed throughout the present paper. More recently Pham, Plourde & Kim (Reference Pham, Plourde and Kim2005) focused on the dynamics of a thermal plume generated by a heated plate maintained at a constant temperature
$T_{0}=400\,^{\circ }\text{C}$
. Pham et al. (Reference Pham, Plourde and Kim2005) provided a detailed description of the three-dimensional structure of the velocity field by means of stereoscopic PIV, but did not report any temperature or density measurement. From their PIV measurements they directly measured the entrainment coefficient and compared it with estimates provided by classic indirect methods. However, the lack of temperature data prevented them from linking the values of the entrainment coefficient to the variation of
${\it\Gamma}$
.
This overview of previous studies highlights the general lack of knowledge on the behaviour of a buoyant plume in the transition state characterised by a local variation of the plume Richardson number. This lack of knowledge motivates our work, which aims to shed light on the dynamical variability of buoyant plumes. To this end we performed experiments on plumes with highly contrasting conditions at the source, characterised by values of
${\it\Gamma}_{0}$
varying over three orders of magnitude.
2. Experimental set-up and parameters
We measured velocities and temperatures using PIV and thermocouples, respectively, in thermal air plumes in a windowless, thermally insulated enclosure.
The experimental set-up is shown in figure 1. Air was fed from a compressor to a mass flow-rate meter, where the mass flux was monitored and controlled by an electronic feedback system. A small fraction of the air (
${\approx}5\,\%$
by volume) passed via a chamber where it was seeded with incense particles. The seeded air rejoined the unseeded air immediately upstream of the heating element. The heated air then passed through a diverging–converging section, over a turbulence grid and finally through a diaphragm opening. Air temperature was monitored continuously at the diaphragm to ensure steady source conditions. The ambient air was seeded using a stage smoke generator, which filled the whole enclosure with approximately spherical
$1~{\rm\mu}\text{m}$
polyethylene glycol particles. Over a 10 min period, the release of smoke spread to fill the enclosure uniformly. When the ambient air motion induced by the initial jet of smoke dissipated, acquisition of data could begin. Approximately one smoke injection per hour seeded the ambient sufficiently. Seeding both plume and ambient air was necessary in order to obtain proper velocity statistics, statistics which would otherwise be biased when solely seeding the plume.
Temperature measurements were made with a horizontal rake of thermocouples spaced at 10 mm intervals. The uncertainty associated with these measurements was estimated as
$\pm 0.5~\text{K}$
. The rake was sequentially displaced vertically at increments of 10 mm, from
$z=12$
to
$z=512~\text{mm}$
. Temperatures were measured for 3 min at 10 Hz.
We acquired and processed PIV data using LaVision’s DaVis 7.2 software. Circular interrogation areas with a 50 % overlap were employed, resulting in a spatial resolution of 0.7 mm. To achieve this resolution, the measurement plane was split into various fields of view with 3000 image pairs acquired sequentially for each field. In order to record sufficiently large particle images to allow for PIV processing at
$16\times 16~\text{pixels}$
and to minimise peak-locking, we split the acquisition into 8 adjacent fields of view measuring approximately 150 mm (horizontal)
$\times$
100 mm (vertical) with a 15 mm vertical overlap between successive fields to ensure continuity of data. The camera could not be moved further than 1.5 m from the laser plane to prevent peak-locking from becoming significant. Subpixel accuracy of the processing algorithm was thus maintained. Measurements on plumes at a spatial resolution of less than 1 mm have seldom been undertaken and those presented herein represent a resource for numerical practitioners, experimentalists and theoreticians alike. Velocity measurements were made at a frequency of 4 Hz, and the duration of each acquisition was 12.5 min. Dynamic statistics were obtained from the 3000 instantaneous measurements.
In order to compare the spatial and temporal resolutions of our measurements with characteristic (turbulent) time and length scales of the flows, estimates of a typical length scale
$\ell$
and velocity scale
${\it\upsilon}$
, the former approximately equal to the plume radius and the latter to the standard deviation of the vertical velocities, were computed. In the flows analysed here,
$\ell$
varied from a minimum of approximately 10 mm in the near field of release J to a maximum of 75 mm in the far field of release P (see table 1), whereas
${\it\upsilon}$
is of the order
$1~\text{m}~\text{s}^{-1}$
in release J and
$0.1~\text{m}~\text{s}^{-1}$
in release P. From these we obtained typical time scales
${\it\tau}\sim \ell /{\it\upsilon}$
of the order
$10^{-2}~\text{s}$
for release J and
$10^{-1}~\text{s}$
for release P. The temporal resolution of the PIV and thermocouple measurements are therefore slightly larger than
${\it\tau}$
and insufficient to allow the computation of turbulent velocity and temperature spectra. The spatial resolution of the PIV measurements is at least one order of magnitude lower than
$\ell$
allowing for a detailed description of the velocity field structure. Conversely, for thermocouple measurements the spatial resolution is coarser and approaches
$\ell$
in the near field of release J.
Table 1. The three source conditions of the releases investigated giving the plume Richardson number
${\it\Gamma}_{0}=\{0.001,0.034,0.96\}$
; note that the value
${\it\alpha}_{ref}=0.1$
has been assumed when calculating
${\it\Gamma}_{0}$
from (1.1). The source buoyancy is
$g_{0}^{\prime }=g({\rm\Delta}T_{0}/T_{0})$
. Here J refers to jet-like, F to forced plume and P to pure plume. We use
$z_{B}$
to denote the non-Boussinesq length scale (2.1),
$L_{M}=\mathscr{C}\cdot M_{0}^{3/4}/B_{0}^{1/2}$
to denote the jet-length, with
$\mathscr{C}=(5/9{\it\alpha}_{ref})^{1/2}(2/{\rm\pi})^{1/4}$
. The final two columns report, respectively, the limiting measurement heights,
$z_{max}$
, scaled on the source radius,
$b_{0}$
, and on the jet length,
$L_{M}$
.
The injected air velocity was kept as high as practicable in order to maximise the Reynolds number and reduce the influence of background disturbances. A nozzle was selected with a maximum radius of 2.5 cm. With the 2 kW coiled heating element, a maximum temperature difference of
${\rm\Delta}T_{0}=T_{0}-T_{e}\approx 90{-}100~\text{K}$
(
$T_{e}$
is the ambient air temperature) was possible and this enabled us to achieve a relatively high source buoyancy flux at the lower velocities we considered. Table 1 summarises the three different releases studied, where the letters J, F and P refer to jet-like, forced and pure plume releases, respectively. Measurements were made over a vertical extent ranging from 1 to 70 cm above the source. The corresponding non-dimensional heights are listed in the final two columns of table 1.
For our set-up, the Reynolds number at the source (
$\mathit{Re}_{0}=(w_{0}b_{0})/{\it\nu}$
,
$w_{0}$
denoting the velocity at the source and
${\it\nu}$
the air kinematic viscosity) decreases with increasing
${\it\Gamma}_{0}$
. The higher source Richardson number (table 1) of the pure plume required relatively low flow velocities so that
$\mathit{Re}_{0}\approx 1000$
, implying that the near-source flow field is not fully turbulent (we return to this in § 3). The temperature at the source reached 393 K, producing flow conditions that are nominally beyond the limits of the Boussinesq approximation. Woods (Reference Woods1997) suggested a length scale over which non-Boussinesq effects are significant as
$$\begin{eqnarray}z_{B}=\frac{5}{3}\left(\frac{B_{0}^{2}}{20{\it\alpha}_{ref}^{4}g^{3}}\right)^{1/5}.\end{eqnarray}$$
An estimate of this length scale for our experiments leads to
$z_{B}\sim 15~\text{cm}$
. A non-negligible part of the domain could therefore be affected by non-Boussinesq effects on the flow dynamics.
The experimental apparatus was conceived to produce buoyant turbulent plumes within an unstratified quiescent environment. We however observed two main features inducing non-negligible departures from these ideal conditions. The first concerned the diffusion of heat along the horizontal rigid wooden base plate within which the nozzle was mounted (figure 1). Heat transferred from this plate (at
$z=0$
) resulted in a region, of approximately 5 % of the vertical extent of the domain, where the ambient air temperatures could not be considered to be uniform. Figure 2 shows the mean temperatures in the ambient measured over the course of the three experiments using a rack of thermocouples. From these we estimate the temperature gradient to be
$1~\text{K}~\text{cm}^{-1}$
over a layer approximately 3 cm thick immediately above the plate. The second concerned the ambient air which was not perfectly still. Background air motion was unavoidable for a number of reasons: the release induces a flow within the confines of the test room as it was necessary to seed the environment with smoke. Mean air velocities in the background, as estimated by PIV measurements, never exceeded 10 % (for releases J and F this percentage was far lower) of the mean centreline plume velocity
$w_{m}$
and the standard deviation of this fluctuation about this mean was always less than
$0.1w_{m}$
: equivalent to an actual velocity of
$7~\text{cm}~\text{s}^{-1}$
. These intensities of background motion are directly comparable with those in previous plume studies.
Figure 2. Vertical profiles of ambient temperature
$T$
(degrees centigrade) registered in experiments for releases (a) J, (b) F and (c) P.
3. Mean flow and temperature field
First, we focus on the evolution of mean velocity and buoyancy (temperature). We examine the radial evolution of the vertical component of the mean velocity and of the mean temperature. Whilst over 800 velocity profiles were gathered for each release, plotting all of the data collected was unhelpful in explaining the trends; for this reason each plot shows 13 radial profiles equally spaced in height and spanning the entire vertical extent of each experiment. See table 2 for heights and symbols used in these plots. Mean temperature profiles are given at these same distances from the source. We discuss the reliability of the assumption of Gaussian profiles (§§ 3.1 and 3.2), profiles which allow us to readily identify characteristic scales for the plume width, velocity and buoyancy with height. The analysis of the variation with height of these local scales (§§ 3.3.1 and 3.3.2) provides first evidence of the dynamical behaviour of the three releases. To discuss this further, we compute the vertical evolution of the plume Richardson number
${\it\Gamma}(z)$
by integrating the radial profiles of mean vertical velocity and temperature (§ 3.3.3). Finally, we discuss the implication of self-similarity of radial profiles in light of the concept of ‘local self-similarity’ proposed by George et al. (Reference George, Alpert and Tamanini1977).
3.1. Radial profiles of mean vertical velocity
From each profile of the measured averaged vertical velocity,
$w(r,z)$
, a Gaussian profile centred on
$r=0$
was fitted to the data. The form of each profile
$$\begin{eqnarray}\frac{w(r,z)}{w_{m}(z)}=\exp \left\{\frac{-r^{2}}{b_{w}^{2}(z)}\right\},\end{eqnarray}$$
is determined by
$b_{w}$
, which we define to be the plume width and by
$w_{m}$
, the mean vertical centreline velocity, which, in a quiescent environment, corresponds to the maximum mean velocity. Due to background air motion and camera positioning uncertainties (estimated to be
$\pm 2~\text{mm}$
horizontally) the maximum mean velocity did not always perfectly coincide with the axis (
$r=0$
) of the experiment. When this was the case, the maximum value of
$w(r)$
was recorded and the radial coordinate system locally translated so that
$w_{m}(z)=w(0,z)$
, so as not to introduce errors in the determination of the plume radius and the bulk quantities. These adjustments were never more than
$\pm 3~\text{mm}$
.
Figure 3 shows non-dimensionalised radial profiles of mean vertical velocity. Figure 3(a,b) shows that the mean vertical velocity for plumes J and F exhibit a clear self-similarity and collapse tightly on to a Gaussian curve. Examination of figure 3(c) reveals a slightly increased scatter for plume P, compared to cases J and F. The reasons are twofold. Given the intermediate source Reynolds number,
$\mathit{Re}_{0}\approx 10^{3}$
, in plume P (table 1), self-similarity of even the mean flow field is not to be expected in the near-source region. Moreover, the profiles for release P were at lower non-dimensional distances above the source (see table 1), where the flow was still influenced by the source profile. However, we verified that the Gaussian function provided a very good fit to the data, with
$R^{2}\geqslant 0.95$
, for
$z/b_{0}>5$
.
Figure 3. Non-dimensionalised radial profiles of time-averaged vertical velocity in releases (a) J (profiles plotted in the range
$9<z/b_{0}<94$
); (b) F (profiles plotted in the range
$3<z/b_{0}<32$
); and (c) P (profiles plotted in the range
$2<z/b_{0}<19$
).
3.2. Buoyancy profiles
The radial profiles of buoyancy are now examined. Figure 4 shows that, albeit with non-negligible scatter, the buoyancy profiles exhibit approximate self-similarity at all heights and in all experiments, even close to the source. The near-source behaviour noted in the velocity profiles is not observed, probably due to the cooling from the injector walls which resulted in a more pronounced parabolic shape of the outlet profiles. An identical curve-fitting procedure was used as that described in the previous section, with a fit of the form
$$\begin{eqnarray}\frac{g^{\prime }(r,z)}{g_{m}^{\prime }(z)}=\exp \left\{\!\frac{-r^{2}}{b_{g^{\prime }}^{2}(z)}\!\right\}.\end{eqnarray}$$
Figure 4. Non-dimensionalised profiles of buoyancy
$g^{\prime }/g_{m}^{\prime }$
for releases (a) J, (b) F and (c) P plotted over the same vertical extent as in figure 3.
The characteristic length scale is now the standard deviation of the Gaussian buoyancy profiles, denoted
$b_{g^{\prime }}$
, and the characteristic buoyancy scale is the maximum centreline buoyancy,
$g_{m}^{\prime }$
. The goodness of the fit with a Gaussian function is lower than for the velocity profiles, with
$R^{2}\geqslant 0.95$
for releases J and F, and
$R^{2}\geqslant 0.9$
for release P.
3.3. Vertical evolution of plume dynamics
In order to unravel the dynamical evolution with height of the releases considered, we plot the vertical evolution of the centreline velocity and buoyancy, the plume radii and the local Richardson number
${\it\Gamma}(z)$
.
To allow for direct comparisons between the different releases and the experimental data of others, the dynamic quantities are scaled on their source values and all lengths on the source radius,
$b_{0}$
.
3.3.1. Radial growth from velocity and temperature profiles
Figure 5 shows how the normalised plume radius
$b_{w}/b_{0}$
evolves with height. From this we observe that all three releases tend to spread linearly with height in the far field, but at different rates.
Figure 5. Comparison of normalised widths of velocity profiles
$b_{w}/b_{0}$
and buoyancy profiles
$b_{g^{\prime }}/b_{0}$
with height
$z/b_{0}$
for releases (a) J, (b) F and (c) P. Filled circles denote
$b_{w}/b_{0}$
, hollow circles denote
$b_{g^{\prime }}/b_{0}$
.
While in both forced releases, J and F, the radius grows monotonically from very close to the source, albeit in a less-than-linear fashion, release P exhibits a different behaviour. The pure plume P appears to be straight-sided over a vertical distance of approximately
$5b_{0}$
, indicating that entrainment is substantially reduced in this section.
In the same figure we show the vertical evolution of the radius
$b_{g^{\prime }}$
as estimated from the temperature profiles;
$b_{g^{\prime }}$
equals or exceeds
$b_{w}$
for all releases and at all heights. This suggests that the radial turbulent transfer of heat is more effective than that of momentum. A further discussion on the physical implications of this feature is provided in § 4.3.
It is worth noting that the estimates of
$b_{g^{\prime }}$
, as shown in figure 5, are characterised by a non-negligible scatter: scatter that becomes increasingly visible from release J to release P, as we ‘zoom in’ the spatial resolution (note the difference in the vertical axis scale in figure 5
a–c). We attribute this scatter to the experimental uncertainties in temperature measurement which lead to a variability in the estimates of
$b_{g^{\prime }}$
of approximately
$\pm 5\,\%$
. The uncertainty related to
$b_{w}$
was approximately
$\pm 2.5\,\%$
.
3.3.2. Centreline vertical velocity and buoyancy
We plot in figures 6 and 7 the vertical variations of centreline vertical velocity and centreline buoyancy, showing as a reference their theoretical pure-plume and pure-jet dependencies, that is
$w_{j}/w_{0}\sim (z/b_{0})^{-1}$
and
$g_{j}^{\prime }/g_{m0}^{\prime }\sim (z/b_{0})^{-1}$
in pure jets (Fischer et al.
Reference Fischer, List, Koh, Imberger and Brooks1979) and
$w_{p}/w_{0}\sim (z/b_{0})^{-1/3}$
and
$g_{p}^{\prime }/g_{m0}^{\prime }\sim (z/b_{0})^{-5/3}$
in pure plumes (Morton et al.
Reference Morton, Taylor and Turner1956).
Figure 6. Vertical dependency of normalised centreline velocity
$w_{m}/w_{0}$
for the three releases J, F, P with the pure jet,
${\sim}(z/b_{0})^{-1}$
, and pure plume,
${\sim}(z/b_{0})^{-1/3}$
, power laws.
Figure 7. Vertical dependency of normalised centreline buoyancy
$g_{m}^{\prime }/g_{m0}^{\prime }$
for the three releases J, F, P, with the pure plume,
${\sim}(z^{-5/3})$
, and pure jet,
${\sim}(z^{-1})$
, dependencies.
Figures 6 and 7 highlight a substantial variation in the nature of the velocity decay with height for the three releases (in figure 6, data for plume P has been shifted to the left for ease of comparison). Release J, the most jet-like, closely follows the
${\sim}(z/b_{0})^{-1}$
trend (dashed line) for both
$w_{m}/w_{0}$
and
$g_{m}^{\prime }/g_{m0}^{\prime }$
: the latter for sufficiently large
$z/b_{0}$
. This data indicates that heat is little more than a passive scalar quantity in this flow and the source momentum flux completely dominates that induced by the action of the buoyancy force. This is unsurprising as
$z_{max}\approx L_{M}/3$
, so the entire experiment is well within one jet-length of the source.
In release F, fluid decelerates and dilutes at a rate intermediate to the pure jet and pure plume. Even at a non-dimensional height of
$z/b_{0}\approx 40$
, the behaviour shows no appreciable tendency to approach the
$w_{m}/w_{0}\sim (z/b_{0})^{-1/3}$
and
$g_{m}^{\prime }/g_{m0}^{\prime }\sim (z/b_{0})^{-5/3}$
behaviour (dot–dashed line). Experiment F reaches a height of
$z_{max}\approx 2L_{M}$
and is therefore entirely within the five jet lengths over which the flow is expected to exhibit a smooth transition between the near-field jet-like and the far-field plume-like asymptotic states (Morton Reference Morton1959; Papanicolaou & List Reference Papanicolaou and List1988).
As expected, release P exhibits a vertical behaviour that is fully consistent with the scaling laws of a purely buoyancy-driven plume, with a deceleration of the form
$w_{m}/w_{0}\sim (z/b_{0})^{-1/3}$
and a dilution of buoyancy
$g_{p}^{\prime }/g_{m0}^{\prime }\sim (z/b_{0})^{-5/3}$
.
It is worth noting that figures 6 and 7 show that close to the source, i.e. for
$z/b_{0}\leqslant 5$
, all releases dilute and decelerate slowly, suggesting the presence of a non-turbulent core that, in turn, may be related to a reduced entrainment rate of ambient air. This tendency is particularly evident in release P. As figure 6 shows, the centreline velocity increases in release P by up to 20 % over the interval
$0\lesssim z/b_{0}\lesssim 5$
; this is a similar height range to that required for the velocity profiles to exhibit approximate self-similarity. The near-source acceleration is likely to be due to the relatively low Reynolds number in the near-source zone which implies a suppression of entrainment into the plume. In this condition, the unmixed fluid released accelerates due to its buoyancy. This acceleration persists until the flow becomes sufficiently turbulent to entrain at a rate consistent with a fully developed turbulent plume, with a radial momentum transfer that acts to reduce the centreline velocity.
This simple analysis of the vertical variation of
$w_{m}$
and
$g_{m}^{\prime }$
clearly shows that the dilution rate with increasing distance from the source varies significantly between the three cases considered. Therefore, behind an apparent similarity of the radial profiles of mean velocity and mean buoyancy, the flows develop with different dynamical behaviours which results in the entrainment of ambient air at different rates.
3.3.3. Plume Richardson number
An estimate of the plume Richardson number,
${\it\Gamma}(z)$
from (1.1), is essential in order to physically interpret the different behaviour of the three releases.
The plume Richardson number could be estimated at all heights by means of the mean vertical fluxes of volume, momentum and buoyancy. These fluxes were explicitly computed by means of the integrals (1.2), fitting the experimental data with the Gaussian profiles presented in §§ 3.1 and 3.2 and assuming rotational symmetry. Figure 8 shows this estimate for
${\it\Gamma}$
. Error bars of amplitude 15 %, are associated primarily with uncertainty in the estimates of
$b_{g^{\prime }}$
and
$b_{w}$
(§ 3.3.1).
Figure 8. Vertical dependency of plume Richardson number
${\it\Gamma}$
.
Encouragingly, the values of
${\it\Gamma}$
near to the source closely match those in table 1, indicating that the source Richardson numbers achieved were very similar to those intended.
As has been customary, in this section we begin with an assessment of releases J and F; both low Richardson number, high Reynolds number flows at source. As expected, for both,
${\it\Gamma}$
tends towards unity, release F at an increased rate compared to J as the theoretical models predict (Hunt & Kaye Reference Hunt and Kaye2001).
The behaviour of
${\it\Gamma}(z)$
in plume P for small
$z/b_{0}$
may appear surprising, since the Richardson number slightly ‘overshoots’ unity for
$z/b_{0}\leqslant 5$
– i.e.
${\it\Gamma}$
first increases above unity and then decreases to unity with height. A similar behaviour can be observed in the numerical simulation performed by Devenish, Rooney & Thomson (Reference Devenish, Rooney and Thomson2010). However, in our case, the ‘overshoot’ has to be attributed to a numerical artefact associated with the significant errors in the interpolation of the near-source velocity profiles with a Gaussian curve, and has therefore no physical significance.
Figure 8 clearly captures the variability of the dynamical state of the three releases examined. It is worth noting that, although there is considerable dynamical variability, the mean radial profiles previously examined showed a self-similar profile over the majority of the rise height. This then provides a clear example of what George (Reference George, Arndt and George1989) defines as a ‘local self-preserving flow’, i.e. a flow that appears to scale with local quantities even though the equations of motion do not admit self-similar solutions, since any solution should account for the variability of
${\it\Gamma}$
. However, as is evident in the analysis of the vertical variation of the centreline velocity and centreline buoyancy, behind this local self-similarity the plumes develop different dynamical behaviour with height that results, notably, in a different mixing rate with the ambient.
4. Turbulence
The aim here is to use turbulent statistics of the velocity data to illuminate the discussion that follows in § 5, particularly with regards to the (non-constant) entrainment coefficient.
4.1. Turbulence intensities
Figure 9 contains plots showing non-dimensionalised radial profiles of second-order moments of the velocity statistics, namely the vertical and radial turbulence intensities,
$I_{w}={\it\sigma}_{w}/w_{m}$
and
$I_{u}={\it\sigma}_{u}/w_{m}$
(where
${\it\sigma}_{w}$
and
${\it\sigma}_{u}$
are the root mean squares (r.m.s.) of the vertical and radial velocity), respectively. Heights of the radial profiles and symbols used in these plots are the same as those used for the mean velocities, as specified in table 2.
Figure 9. Non-dimensionalised radial profiles of the normalised r.m.s. vertical
$I_{w}$
and radial
$I_{u}$
velocities: (a,b) release J (profiles plotted in the range
$9<z/b_{0}<94$
); (c,d) release F (profiles plotted in the range
$3<z/b_{0}<32$
); (e, f) release P (profiles plotted in the range
$2<z/b_{0}<19$
).
For release J, the turbulence intensity (figure 9
a,b) exhibits a very good collapse on to a single curve with the exception of the four lowermost profiles. Neither these near-source profiles, nor those further from the source, are approximately Gaussian in contrast to the suggestion of Papanicolaou & List (Reference Papanicolaou and List1988). Rather, the maximum turbulence intensities are approximately constant within the range
$|r/b_{w}|<1$
(at
$I_{u}=0.2$
and
$I_{w}=0.25$
). As the other experimental results demonstrate in due course, these turbulence intensity profiles are consistent for the three release conditions in the developed flow field and, what is more, they are consistent with previous data (Hussein et al.
Reference Hussein, Capp and George1994; Shabbir & George Reference Shabbir and George1994; Wang & Law Reference Wang and Law2002).
Figure 9(c,d) reveal that the lowermost turbulence intensity profiles for release F differ significantly from the developed profiles. A core of reduced turbulent intensities centred on the plume axis is clearly identifiable, becoming less pronounced with height. This appears to correspond to the zone of flow establishment, where the shear layer which develops on the plume perimeter has not fully penetrated into the plume interior. The fully developed turbulence intensity profiles approximately match those in release J. For F and J, the peak values of
$I_{w}$
and
$I_{u}$
show good agreement with the experimental results for non-buoyant jets of Hussein et al. (Reference Hussein, Capp and George1994), namely
$I_{w}\simeq 0.27$
and
$I_{u}\simeq 0.22$
, Shabbir & George (Reference Shabbir and George1994), namely
$I_{w}\simeq 0.32$
and
$I_{u}\simeq 0.19$
, and Wang & Law (Reference Wang and Law2002), namely
$I_{w}\simeq 0.3$
and
$I_{u}\simeq 0.2$
. This confirms one major finding of the previous results; even though the increased buoyancy within the plume enhances local turbulence production, the excess of turbulent kinetic energy (t.k.e.)
$\propto I^{2}$
appears to be fully scalable with the local variables
$w_{m}$
and
$b_{w}$
. In other words, the intensity of the t.k.e. and its spatial distribution within the plume appear to be independent of the processes that are responsible for its generation, i.e. related to inertial instabilities or thermal stratification. The concept of local self similarity can therefore also be extended to the t.k.e. levels within the release.
For release P, plots 9(e, f) show that for small
$z/b_{0}$
the turbulent intensities are as low as 5 % inside the plume, indicating a quasi-laminar flow. The core of reduced turbulent intensity persists over approximately 5 source diameters and is noticeable in plots of both
$I_{w}$
and
$I_{u}$
. The maximum turbulence intensity is slightly increased in magnitude compared with the previous, more forced cases. However, this could be reasonably attributed to the higher scatter in the data and to the role of ambient turbulence (due to an ambient that is not perfectly quiescent) which increases as the velocities in the plume are reduced. Similar features can be observed in the measurements, obtained with the same measurement technique, of Wang & Law (Reference Wang and Law2002). Their radial profiles of both
$I_{w}$
and
$I_{u}$
exhibit a similar scatter, and a similar tendency to approach a value of approximately 0.1 (i.e. non-zero) beyond the plume borders.
A final remark concerns the fetch needed by the second-order velocity statistics to become (locally) self-similar. The analysis of the radial profiles of
$I_{u}$
and
$I_{w}$
suggest that self-similarity is attained between
$30<z/b_{0}<35$
for release J,
$10<z/b_{0}<15$
for F and
$5<z/b_{0}<10$
for P. This observation is in agreement with the idea that the higher the value of
${\it\Gamma}$
at the source, the more rapid is the transition toward an asymptotic state of plume equilibrium. However, given the non-identical nozzle geometry for the three releases and their different source Reynolds numbers, these relationships between
${\it\Gamma}_{0}$
and the fetch required to attain self-similarity cannot be considered to be general values.
4.2. Radial turbulent transfer of momentum and buoyancy
4.2.1. Reynolds stress and turbulent viscosity
Figure 10(a) shows radial profiles of the Reynolds stress
$\overline{\tilde{u} \tilde{w}}$
(
$\tilde{u}$
is the fluctuation of the radial velocity) for the jet-like, high-source-Reynolds-number release J. Evidently, the Reynolds stress profiles tend towards a single profile at sufficiently high elevation. The form of the Reynolds stress profile is qualitatively very similar to that published in the numerical work of Zhou (Reference Zhou2001) and with the measurements of Hussein et al. (Reference Hussein, Capp and George1994) in isothermal jets, with a maximum stress value of approximately
$|\overline{\tilde{u} \tilde{w}}/w_{m}^{2}|\simeq 0.025$
. Examination of figure 10(c) for release F leads to the same broad observations as those above. As in release J, the Reynolds stresses for release F tend toward a single profile and show profiles very similar to those in figure 10(a). These observations are in very good agreement with the findings of Wang & Law (Reference Wang and Law2002).
Figure 10. Radial profiles of non-dimensional Reynolds stress (a,c,e) and non-dimensional turbulent viscosity
$\widehat{{\it\nu}_{T}}={\it\nu}_{T}/(w_{m}b_{w})$
(b,d,f) for (a,b) release J (profiles plotted in the range
$9<z/b_{0}<94$
), (c,d) release F (profiles plotted for
$3<z/b_{0}<32$
) and (e, f) release P (profiles plotted for
$2<z/b_{0}<19$
). The continuous (red online) line represents the fit of the experimental data of Hussein et al. (Reference Hussein, Capp and George1994) in a non-buoyant jet.
For the nominally pure plume release P, near to the source the Reynolds stresses (figure 10 e) are negligible and approximately constant across the plume. However, with increasing distance from the source, the profiles begin to converge towards a self-similar profile which is similar in form to release F.
The high spatial resolution of the velocity statistics gathered allows us to achieve an experimental estimate of the turbulent viscosity, usually defined as
$$\begin{eqnarray}{\it\nu}_{T}(r,z)=-\overline{\tilde{u} \tilde{w}}(r,z)/\biggl(\frac{\partial w(r,z)}{\partial r}\biggr).\end{eqnarray}$$
This quantity provides potentially important information concerning both the turbulence dynamics and the momentum transfer within the plume. The curves for the corresponding non-dimensional turbulent viscosity
$\widehat{{\it\nu}_{T}}={\it\nu}_{T}/(w_{m}b_{w})$
are shown in figure 10. Near the plume axis, the small Reynolds stress is divided by a small velocity gradient which explains why the turbulent viscosity peaks here. In the two releases characterised by high Reynolds number, namely J and F, the radial profiles of
$\widehat{{\it\nu}_{T}}$
(figure 10
b,d), although scattered, tend towards a single profile at sufficiently high elevations that is similar to that identified by Hussein et al. (Reference Hussein, Capp and George1994) for non-buoyant jets. This confirms that the momentum transfer within the releases is almost unaffected by buoyancy, as are the t.k.e. levels (see § 4.1), in the sense that any variation can be fully rescaled on local quantities leading to the same local self-similar curves.
It is questionable whether the values of
$\widehat{{\it\nu}_{T}}$
in release P (figure 10
f) genuinely exceed those of the other plumes. Non-dimensional profiles are far from collapsing on to a single curve (and the data is affected by significant scatter) which indicates the varying dynamical nature of the plume with height. Despite this, several profiles show a qualitative tendency that is very similar to that observed for releases J and F.
We can therefore conclude that evidently there is no one-to-one dependence of
$\widehat{{\it\nu}_{T}}$
on
${\it\Gamma}$
, i.e. that the increased role played by buoyancy in the dynamics as
${\it\Gamma}$
increases does not necessarily result in a more effective turbulent radial transfer of momentum as is consistent with an increase in
$\widehat{{\it\nu}_{T}}$
. Just as for the other turbulent quantities examined, variations in the turbulent viscosity can be completely rescaled by local quantities confirming the ‘local’ self-similar behaviour.
To unravel the influence of
${\it\Gamma}$
on the radial turbulent transfer of momentum it is instructive to examine the vertical evolution of a non-dimensional bulk turbulent viscosity
$\langle \widehat{{\it\nu}_{T}}\rangle$
, representing a spatial average of
$\widehat{{\it\nu}_{T}}$
over the plume section. Values of
$\langle \widehat{{\it\nu}_{T}}\rangle$
were estimated as those giving the best agreement on fitting the
$\overline{\tilde{u} \tilde{w}}$
profiles with a function of the form
$$\begin{eqnarray}\mathscr{F}(r,z)=2\langle \widehat{{\it\nu}_{T}}\rangle \frac{r^{2}}{b_{w}^{2}}\exp \frac{r^{2}}{b_{w}^{2}}\end{eqnarray}$$
i.e. assuming the Gaussian form of the velocity profile (3.1). The vertical evolution of
$\langle \widehat{{\it\nu}_{T}}\rangle$
plotted in figure 11 sheds light on the influence of a varying
${\it\Gamma}$
on the plume dynamics. Despite a non-negligible uncertainty in the estimate of
$\langle \widehat{{\it\nu}_{T}}\rangle$
, which is reflected in error bars of
$10{-}25\,\%$
, figure 11 depicts a clear tendency in its vertical evolution for the three releases considered. The quantity
$\langle \widehat{{\it\nu}_{T}}\rangle$
evolves with height up to a far-field value of approximately 0.035 in all three cases, as could also be inferred by examining figure 10(b,d,f). It is however evident that the enhanced role of buoyancy in the plume dynamics accelerates significantly this evolution. As a result, for release J,
$\langle \widehat{{\it\nu}_{T}}\rangle$
requires a distance of almost 100 radii to attain its far-field value. By contrast, for release P the evolution to the far-field value occurs over a fetch of approximately 10
$b_{0}$
. As discussed in § 5, this feature plays a major role in the way the different releases entrain ambient air.
Figure 11. Vertical evolution of the non-dimensional bulk turbulent viscosity
$\langle \widehat{{\it\nu}_{T}}\rangle$
for releases J, F and P.
4.3. Turbulent Prandtl number
An experimental estimate of the radial turbulent transfer of heat (or mass) requires simultaneous measurement of velocity and temperature (or solute concentration
$c$
) in order to assess the radial variability of the correlation between fluctuations of temperature
$\tilde{T}$
(or concentration
$\tilde{c}$
) and radial velocity. Just as for the momentum transfer, the adoption of a gradient closure model of the form (4.1), leads to an estimate of a turbulent diffusivity of heat (or mass)
$D_{T}$
, and therefore to the turbulent Prandtl (or Schmidt) number
$\mathit{Pr}_{T}={\it\nu}_{T}/D_{T}$
, that characterises the relative effectiveness of the two transport phenomena.
This kind of simultaneous measurement has seldom been undertaken and represents a major challenge in the experimental investigation of buoyant plumes. Shabbir & George (Reference Shabbir and George1994) performed these measurements in air plumes with hot-wire anemometry. Despite the remarkable experimental effort however, the radial profiles of
$\overline{\tilde{u} \tilde{T}}$
presented in their study were affected by a considerable scatter, showing the limitations of wire anemometry in evaluating the variation of
$\overline{\tilde{u} \tilde{T}}$
for varying dynamical plume conditions. Far smoother profiles were obtained by means of optical techniques in saline plumes by Papanicolaou & List (Reference Papanicolaou and List1988) and Wang & Law (Reference Wang and Law2002). Both papers report profiles of
$\overline{\tilde{u} \tilde{w}}$
and
$\overline{\tilde{u} \tilde{c}}$
in jets and plumes with similar results. Far-field profiles of
$\overline{\tilde{u} \tilde{w}}/w_{m}^{2}$
were insensitive to enhanced buoyancy, whereas
$\overline{\tilde{u} \tilde{c}}/w_{m}c_{m}$
showed a clear tendency to be higher in plumes compared with jets. Papanicolaou & List (Reference Papanicolaou and List1988) found that
$\overline{\tilde{u} \tilde{c}}/w_{m}c_{m}\simeq 0.12$
in jets and
$\simeq 0.25$
in plumes, whereas Wang & Law (Reference Wang and Law2002) found
$\overline{\tilde{u} \tilde{c}}/w_{m}c_{m}\simeq 0.15{-}0.2$
in jets and
$\simeq 0.25{-}0.3$
in plumes. Both studies indicate a general tendency of
$\mathit{Pr}_{T}$
to decrease as
${\it\Gamma}$
increases.
Given the difficulty associated with the direct estimation of
$\mathit{Pr}_{T}$
, several authors could only infer its spatial average (over the plume section) by estimating the ratio
${\it\varphi}=b_{g^{\prime }}/b_{w}$
between the local spread of the buoyancy and velocity profiles. Assuming Gaussian profiles, the (spatially averaged) turbulent Prandtl number can be estimated as
$$\begin{eqnarray}\langle \mathit{Pr}_{T}\rangle ={\it\varphi}^{-2},\quad {\it\varphi}=\frac{b_{g^{\prime }}}{b_{w}}.\end{eqnarray}$$
It is worth noting that the values for
${\it\varphi}$
in the open literature show a high variability. For example, Papanicolaou & List (Reference Papanicolaou and List1988) find
${\it\varphi}=1.19$
in nominally pure plumes. Their estimates are consistent with their direct measurements of the radial turbulent fluxes of momentum and mass, and indicate that the spread of buoyancy exceeds that of the velocity owing to turbulence radially transferring buoyancy more effectively than momentum. However, experiments of other researchers on buoyancy-dominated plumes, including George et al. (Reference George, Alpert and Tamanini1977) and Nakagome & Hirata (Reference Nakagome and Hirata1977), led to the contradictory conclusion that
${\it\varphi}<1$
. This unexplained contradiction in the experimental results is particularly evident in the study of Wang & Law (Reference Wang and Law2002). Their measurements indicate that
${\it\varphi}$
decreases with increasing
${\it\Gamma}$
, from a value of approximately 1.25 for a pure jet close to the source, toward unity for a pure plume in the far field. We stress here that this decrease is in contrast to the results of Papanicolaou & List (Reference Papanicolaou and List1988) and with Wang & Law’s own experimental results, results that showed a tendency for
$\overline{\tilde{u} \tilde{c}}/w_{m}c_{m}$
to increase with
${\it\Gamma}$
.
The ratio
${\it\varphi}$
, as a function of the normalised distance from the source, obtained from the estimates of
$b_{g^{\prime }}~(\pm 5\,\%)$
and
$b_{w}~(\pm 2.5\,\%)$
(see § 3.3.1 for details) is plotted in figure 12. A cursory examination clearly shows that the width of the error bars on
${\it\varphi}$
are of the same order as its variation over the plume’s vertical extent. This feature highlights a striking difference between the vertical evolution of
${\it\varphi}$
(and
$\mathit{Pr}_{T}$
) and that of
$\langle \widehat{{\it\nu}_{T}}\rangle$
(see figure 11) and
${\it\Gamma}$
(see figure 8); while the trends in
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\Gamma}$
are clear, the precise trend in
${\it\varphi}$
is less clear.
Figure 12. Vertical evolution of
${\it\varphi}=b_{g^{\prime }}/b_{w}$
for releases J, F and P.
Beyond this general uncertainty one could argue that there is a tendency in releases J and F for
${\it\varphi}$
to increase with height. For release P the values of
${\it\varphi}$
are higher although it is difficult to discern a clear trend. In all three cases,
${\it\varphi}$
tends to a far-field value slightly higher than 1.2, which corresponds to
$\langle \mathit{Pr}_{T}\rangle =1/1.2^{2}\simeq 0.7$
: a result that supports the findings of Papanicolaou & List (Reference Papanicolaou and List1988) and Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993) who found
${\it\varphi}\approx 1.2$
for pure plumes.
Kaminski, Tait & Carazzo (Reference Kaminski, Tait and Carazzo2005) suggested that the considerable discrepancy reported in the literature in the values of
${\it\varphi}$
could be explained by the distance from the source at which profiles were measured. They noticed that researchers who obtained
${\it\varphi}<1$
acquired data close to the source (
$z/b_{0}\sim 10$
), whereas measurements further away (
$z/b_{0}\sim 100$
) resulted in
${\it\varphi}>1$
. Kaminski et al. (Reference Kaminski, Tait and Carazzo2005) plotted the parameter
$A=(2/3)({\it\varphi}^{2}+1)$
against
$z/b_{0}$
, which varied from approximately
$A=1.1$
for
$z/b_{0}\leqslant 10$
to approximately
$A=1.9$
for
$z/b_{0}\simeq 100$
. This led them to conclude that
${\it\varphi}$
increases slowly with height, with typical values of
${\it\varphi}<1$
in the near field and
${\it\varphi}\simeq 1.36~(\langle \mathit{Pr}_{T}\rangle \simeq 0.56)$
in the far field. They referred to this evolution in the value of
${\it\varphi}$
as ‘similarity drift’.
Our data plotted in figure 12 partially supports their assertion. For releases J and F,
${\it\varphi}$
shows a tendency to increase with
$z/b_{0}$
to attain slightly higher values compared with those reviewed by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005). In contrast, the data for release P suggests a tendency of
${\it\varphi}$
to decrease with height, a tendency that is not consistent with ‘similarity drift’. As already mentioned, a similar anomalous (with respect to the ‘similarity drift’ model) decrease of
${\it\varphi}$
can be observed in the data of Wang & Law (Reference Wang and Law2002). In the present case however, it is worth noting that this tendency is captured only over a limited vertical range from the source, since
$z_{max}/b_{0}=19$
for plume P, and is inconclusive given the significant amplitude of the error bars. We therefore conclude that our data agrees partially with the concept of ‘similarity drift’ and that the non-negligible uncertainty in the estimates of
${\it\varphi}$
does not bring to an end this controversy.
However, our experimental results highlight two important features that concern the nature of this ‘drift’. These warrant discussion as they could help in explaining the wide spread of the literature data. First, whilst at the outset it may have been tempting to examine the variation of
${\it\varphi}$
with
${\it\Gamma}$
, we cannot identify any clear one-to-one relationship between them, and therefore between
$\mathit{Pr}_{T}$
and
${\it\Gamma}$
(or indeed between
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\Gamma}$
). Second, for two of the releases we observed a tendency of
${\it\varphi}$
to increase. These aspects suggest that the evolution of
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\varphi}$
is similar. From the nozzle the flow develops seeking its equilibrium state, with a near-field evolution whose rapidity is influenced by
${\it\Gamma}$
. Therefore, at a given distance from the source, a forced plume can exhibit varying
${\it\varphi}$
depending on its
${\it\Gamma}_{0}$
( just as it can exhibit different
$\langle \widehat{{\it\nu}_{T}}\rangle$
), which explains the variety of values presented in the literature.
There is another reason that can potentially explain this variability. In their analysis, Kaminski et al. (Reference Kaminski, Tait and Carazzo2005) refer to data from 9 different experimental data sets; 5 of these refer to measurements taken between 10 and 30 radii from the source. It is well known from the literature data, and as discussed in §§ 4 and 4.2.1, that in this region intermediate to near field and to far field, the flow has not necessarily reached conditions for self-similarity. The region of the ‘drift’ is therefore, at least partially, a region within which the flow retains some memory of its source state. We cannot then exclude that the observed variability of
${\it\varphi}$
is due to the influence of the source conditions (conditions that cannot be perfectly controlled by the experimentalist) on the subsequent evolution of the flow dynamics. It is customary to refer to the source condition as given by steady and self-similar radial profiles of velocity and temperature (or concentration), so that we can fully characterise the release by the governing parameters:
${\it\Gamma}_{0}$
,
$\mathit{Re}_{0}$
and
$T_{0}/T_{e}$
. The actual source flow conditions reproduced in an experiment (or in a numerical simulation) may, however, exhibit non-negligible departures from these idealised reference conditions. This can be due, for example, to a different form of the velocity and temperature profiles, to non-null intensities of the turbulent fluctuations or of the Reynolds stress. Thus, for identical values of
${\it\Gamma}_{0}$
,
$\mathit{Re}_{0}$
and
$T_{0}/T_{e}$
(defined by means of spatially averaged quantities), we can then have a variety of source conditions; these can exert their influence over a distance of several source diameters (see figure 8), along which the release evolves toward a condition of dynamical equilibrium and may exhibit a high variability of the local
${\it\Gamma}$
. We stress that, if the uncertainties associated with the conditions imposed at the source do indeed have a significant influence on the near-field plume behaviour, it would be unclear how to dissociate them from the dependence of flow variables, such as
${\it\varphi}$
(or
${\it\alpha}_{G}$
), on the local variation of
${\it\Gamma}$
(or
$\mathit{Re}$
).
4.4. Turbulence structure
To provide further information on the turbulence dynamics we investigated its spatial structure by computing two-point velocity correlations throughout the domain. We focus here on the two-point correlation functions
$R_{uu}$
and
$R_{ww}$
of the vertical and radial velocity components, defined as
$$\begin{eqnarray}\displaystyle & \displaystyle R_{uu}(\boldsymbol{x}_{0},\boldsymbol{s})=\frac{\overline{\tilde{u} (\boldsymbol{x}_{0})\tilde{u} (\boldsymbol{x}_{0}+\boldsymbol{s})}}{{\it\sigma}_{u}^{2}(\boldsymbol{x}_{0})} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle R_{ww}(\boldsymbol{x}_{0},\boldsymbol{s})=\frac{\overline{\tilde{w}(\boldsymbol{x}_{0})\tilde{w}(\boldsymbol{x}_{0}+\boldsymbol{s})}}{{\it\sigma}_{w}^{2}(\boldsymbol{x}_{0})} & \displaystyle\end{eqnarray}$$
$\boldsymbol{x}_{0}$
is any point in the domain,
$\boldsymbol{s}$
is a displacement relative to
$\boldsymbol{x}_{0}$
and the ensemble averaging is performed over the 3000 instantaneous velocity field measurements.
The integral over
$\boldsymbol{s}$
of the functions (4.4) and (4.5) gives a length scale, referred to as an Eulerian integral length scale, which is representative of the maximal distance over which the velocities are correlated and, thus, provides an indication of the scale of an eddy. As an example we have plotted, in figures 13 and 14, isolines of
$R_{uu}$
and
$R_{ww}$
for releases F and P, computed on the centreline at the same non-dimensional distance from the source (
$z/b_{0}=15$
). Two main features are shown. First, a clear anisotropy of the turbulent field is evident with vertical velocity correlations that are considerably larger than their horizontal counterparts and with higher correlations. Second, the correlations for release P are higher than for release F. The influence of buoyancy in marginally widening (figure 13) and in elongating (figure 14) the eddy structure is immediately evident.
Figure 13. Correlation coefficient
$R_{uu}=(\overline{\tilde{u} (x_{0})\tilde{u} (x_{0}+\boldsymbol{r})})/{\it\sigma}_{u}^{2}$
computed on the centreline at
$z/b_{0}=15$
for release: (a) F and (b) P. Isolines vary from 0.8 for the inner contour to 0.3 for the outer.
Figure 14. Correlation coefficient
$R_{ww}=(\overline{\tilde{w}(x_{0})\tilde{w}(x_{0}+\boldsymbol{r})})/{\it\sigma}_{w}^{2}$
computed on the centreline at
$z/b_{0}=15$
for release: (a) F and (b) P. Isolines vary from 0.8 for the inner contour to 0.3 for the outer.
In order to quantify these differences and investigate the spatial variation of the Eulerian integral length scales we have attempted to estimate typical correlation distances over the whole domain. To that end, we have assumed that the two-point correlation functions can be modelled as an exponential function. Accordingly, we fitted the vertical and horizontal sections of
$R_{uu}$
and
$R_{ww}$
with functions of the form
$$\begin{eqnarray}\displaystyle & f(r)=\exp \{-r/\mathscr{L}_{uu}\} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f(z)=\exp \{-z/\mathscr{L}_{ww}\}. & \displaystyle\end{eqnarray}$$
Values of the parameters
$\mathscr{L}_{uu}$
and
$\mathscr{L}_{ww}$
, fitting this exponential curve to the data, provide a measure of a radial and a vertical integral length scale, respectively. The resulting non-dimensional integral length scale profiles are shown in figure 15 and are compared with the results of Wygnanski & Fiedler (Reference Wygnanski and Fiedler1969) for non-buoyant releases.
Figure 15. Radial profiles of the integral length scales, horizontal scale
$\mathscr{L}_{uu}$
and vertical scale
$\mathscr{L}_{ww}$
, non-dimensionalised on plume width,
$b_{w}$
, for (a,b) release J (profiles plotted in range
$9<z/b_{0}<94$
), (c,d) release F (profiles plotted in range
$3<z/b_{0}<32$
) and (e, f) release P (profiles plotted in range
$2<z/b_{0}<19$
). The continuous line indicates the experimental estimates by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1969) for a non-buoyant jet.
This data highlights the anisotropy of the large-scale turbulent motion, as the vertical length scale,
$\mathscr{L}_{ww}$
, is 1–3 times larger than the radial scale
$\mathscr{L}_{uu}$
. Results bolster the findings of § 3 showing that approximate self-similarity of the profiles is achieved for each of the three release conditions. The local self-similar behaviour, however, differs slightly from release J to release F, and markedly from release P. Data for J and F agrees well with Wygnanski & Fiedler’s (Reference Wygnanski and Fiedler1969) measurements of non-buoyant plumes showing, once again, that the effect of an excess of buoyancy on the plume dynamics can be fully re-scaled by local quantities, thereby indicating a local self-similarity of the flow, characterising even the local turbulence structure. The only difference that can be observed between releases J and F is the slightly higher values of non-dimensional
$\mathscr{L}_{ww}$
towards the perimeter of release F. Conversely, a clear departure from this self-similar behaviour can be observed for plume P, which is also characterised by higher values of both
$\mathscr{L}_{uu}$
and
$\mathscr{L}_{ww}$
compared with the others. This departure from self-similarity can be reasonably attributed to two features. First, to the vorticity production by the baroclinic torque, whose effect is enhanced for higher
${\it\Gamma}$
. This produces a coalescence of vortices that extends, both laterally and vertically, the larger eddies within the plume. Second, the higher values of
$\mathscr{L}_{uu}$
observed for higher
${\it\Gamma}$
can be also attributed to the meandering that characterises the morphology of release P: meandering that was hardly detectable in releases J and F.
5. Entrainment coefficient
Finally, we focus on the rate of entrainment. Our aim is twofold. First, we aim to quantify the apparent differential entrainment coefficient evidenced by the vertical profiles of centreline buoyancy examined in § 3.3.2. Second, in light of the analysis of the flow structure performed so far, we aim to shed light on the dynamical causes of this variation.
The entrainment coefficient
${\it\alpha}_{G}=u_{e}/w_{m}$
is defined as the ratio of two velocities, the entrainment velocity
$u_{e}$
and the mean centreline vertical velocity, and represents the simplest way to close the volume flux conservation equation:
$$\begin{eqnarray}\frac{\text{d}Q}{\text{d}z}=2{\rm\pi}b_{w}u_{e}=2{\rm\pi}b_{w}{\it\alpha}_{G}w_{m}.\end{eqnarray}$$
Although widely and successfully applied to many problems of practical interest (Turner Reference Turner1986), this form of turbulence closure that attempts to capture the turbulent process, by which ambient fluid is entrained across the shear layers forming the plume boundary and into the plume, is nonetheless a rather crude model of a complex physical phenomenon. Many researchers have attempted to infer the entrainment coefficient from experimental observations (Turner Reference Turner1986) as it is central to plume theory. A major problem in the experimental estimates of
${\it\alpha}_{G}$
reported in the literature, for both jets and plumes, is the consistent scatter in the data. A comprehensive review of the estimates of the entrainment coefficient provided by previous authors is presented by Linden (Reference Linden, Batchelor, Moffatt and Worster2000) and by Carazzo, Kaminski & Tait (Reference Carazzo, Kaminski and Tait2006). For Gaussian profiles, the entrainment coefficient is in the range
$0.045<{\it\alpha}_{j}<0.056$
in pure momentum-dominated jets and
$0.07<{\it\alpha}_{p}<0.11$
in pure buoyancy-dominated plumes (Carazzo et al.
Reference Carazzo, Kaminski and Tait2006). Whilst this variability remains only partially explained it can, in part, be attributed to different conditions at the source, the nozzle geometry, or to the different experimental techniques deployed. In addition to this uncertainty, however, we can expect that buoyant plumes produce different entrainment rates according to their local dynamical condition. Assuming fully-turbulent plumes with relatively low density differences, we may therefore expect the dynamics of the entrainment process to depend on the plume Richardson number
${\it\Gamma}$
. Previous authors have tried to define the functional dependence of
${\it\alpha}_{G}$
on
${\it\Gamma}$
, or to equivalent non-dimensional parameters (the Froude number). Among these, we cite the semi-empirical model derived from the theoretical analysis of Priestley & Ball (Reference Priestley and Ball1955)
$$\begin{eqnarray}{\it\alpha}_{G}({\it\Gamma})={\it\alpha}_{j}+({\it\alpha}_{p}-{\it\alpha}_{j}){\it\Gamma},\end{eqnarray}$$
which assumes a linear variation between two asymptotic values (determined experimentally) for a pure jet
${\it\alpha}_{j}$
and a pure plume
${\it\alpha}_{p}$
. Then 50 years later Kaminski et al. (Reference Kaminski, Tait and Carazzo2005), following Priestley & Ball (Reference Priestley and Ball1955), proposed a formulation of the entrainment coefficient based on a mean kinetic energy budget, and that includes explicitly the direct contribution of the variation of
${\it\Gamma}$
on
${\it\alpha}_{G}$
.
The entrainment coefficient is computed herein from the PIV velocity estimates of the mean vertical volume flux
$Q(z)$
. To avoid scatter in the data due to spatial discretisation, prior to determining its derivative, the volume flux variation with height was fitted by means of a sixth-order polynomial, and thereafter
${\it\alpha}_{G}$
estimated from (5.1). Results are shown in figure 16, where we plot the entrainment coefficient for the three releases as a function of
${\it\Gamma}$
. We have excluded only the data of release P for
$z/b_{0}\leqslant 5$
, data that was highly affected by the non-fully turbulent condition of the flow, as widely discussed in §§ 3.3.1, 3.3.3 and 4.
Figure 16. Entrainment coefficient
${\it\alpha}_{G}$
plotted against local plume Richardson number
${\it\Gamma}$
. Experimental data of the present study refers to release J (○), F (
$+$
) and P (
$\Box$
). The grey shaded area represents estimates based on the Priestley & Ball model (5.2) assuming an upper and lower bound provided by maximal and minimal entrainment values for jets and plumes from the literature data (see the text). Experimental data from Wang & Law (Reference Wang and Law2002) is referred to as W&L.
Results are compared with the model of Priestley & Ball (Reference Priestley and Ball1955) discussed above and with experimental results reported by Wang & Law (Reference Wang and Law2002). To the best of the authors’ knowledge, Wang & Law (Reference Wang and Law2002) provide the only experimental estimate of the entrainment coefficient as a function of the local Richardson number in the literature. The data of Wang & Law (Reference Wang and Law2002) was originally plotted against a non-dimensional parameter, denoted here as
$\mathit{Fr}$
, which is related to the plume Richardson number via
${\it\Gamma}=\mathit{Fr}^{2}(5/(2^{7/2}\sqrt{{\rm\pi}}{\it\alpha}_{ref}))$
. Wang & Law (Reference Wang and Law2002) estimated
$\mathit{Fr}$
, taking also into account the turbulent fluxes of buoyancy and momentum, which are neglected in (1.1). Since the turbulent fluxes constitute approximately 20 % of the total buoyancy flux and 10 % of the total momentum flux, neglecting these leads to overestimates of
${\it\Gamma}$
of approximately 5 %. The outcome of the Priestley & Ball (Reference Priestley and Ball1955) model is plotted assuming the two limits for both asymptotic values of
${\it\alpha}_{G}$
identified by Carazzo et al. (Reference Carazzo, Kaminski and Tait2006), i.e.
${\it\alpha}_{j}=0.045$
and
${\it\alpha}_{j}=0.056$
for
${\it\Gamma}\rightarrow 0$
, and
${\it\alpha}_{p}=0.07$
and
${\it\alpha}_{p}=0.11$
for
${\it\Gamma}\rightarrow 1$
.
As a general remark we note that our estimates show a clear tendency for
${\it\alpha}_{G}$
to increase with
${\it\Gamma}$
. For the condition of a ‘highly forced plume’,
${\it\Gamma}\rightarrow 0$
, our
${\it\alpha}_{G}$
tends to be slightly lower than that in the literature for jets. For increasing
${\it\Gamma}$
, our results show generally good agreement with the lower bound defined by the semi-empirical model of Priestley & Ball (Reference Priestley and Ball1955). Across the whole range of forced plume conditions
$0<{\it\Gamma}<1$
, our estimates are systematically lower than those provided by Wang & Law (Reference Wang and Law2002). This discrepancy is significantly reduced for pure plume conditions. In addition, our estimates show good agreement with the other literature on pure plumes, in particular the PIV estimates by Pham et al. (Reference Pham, Plourde and Kim2005) within a thermal plume rising above a heated plate.
To help explain the differences between our estimates of
${\it\alpha}_{G}$
and the estimates of Wang & Law (Reference Wang and Law2002), as well as the differences in
${\it\alpha}_{G}$
in our own data at a given value of
${\it\Gamma}$
(i.e. for releases J and F for
$0.06<{\it\Gamma}<0.2$
) we turn to the expression developed by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005) for the entrainment coefficient. Following recent developments proposed by Craske & van Reeuwijk (Reference Craske and van Reeuwijk2014) for the analysis of unsteady jets, we adopt a formulation that makes no assumption about the slenderness of the flow. In particular, this allows us to quantify the behaviour of the entrainment in the very near field, where the usual assumption of ‘thin plume’ (negligible vertical gradients of second-order statistics compared with radial gradients) does not necessarily hold. Assuming that the radial profiles of velocity and buoyancy are well approximated by a Gaussian, even close to the source (as we verified in §§ 3.1 and 3.2), and adopting a simple gradient-law closure to model the Reynolds stress, the entrainment coefficient can be expressed as
$$\begin{eqnarray}{\it\alpha}_{G}=(2{\it\varphi}^{2}-1)\frac{2{\it\alpha}_{ref}}{5}{\it\Gamma}+\frac{3}{2}\langle \widehat{{\it\nu}_{T}}\rangle +{\it\alpha}_{nf}-{\it\alpha}_{m}\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}_{nf}=3b_{w}I_{7}-2b_{w}\frac{\text{d}I_{6}}{\text{d}z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}_{m}=2b_{w}I_{6}\frac{\text{d}}{\text{d}z}\ln \left(b_{w}^{2}w_{m}^{2}\right), & \displaystyle\end{eqnarray}$$
$I_{6}$
and
$I_{7}$
are related to integrals of radial profiles of second-order velocity statistics. Details on the derivation of (5.3) are provided in the appendix A.
The formulation of the entrainment coefficient (5.3) helps to clarify the role of the different terms in the entrainment process and their physical meaning. The first term
$(2{\it\varphi}^{2}-1)(2{\it\alpha}_{ref}/5){\it\Gamma}$
reflects the effect of the radial gradient of hydrostatic pressure, induced by the presence of a column of warm air, in drawing ambient air into the plume. This term is therefore related to the mean radial velocity field. The second term
$(3/2)\langle \widehat{{\it\nu}_{T}}\rangle$
is directly linked to the local production of t.k.e. by inertial instabilities (Kaminski et al.
Reference Kaminski, Tait and Carazzo2005), i.e. to the product of Reynolds stress and mean vertical velocity radial gradient. It is therefore related to the fluctuating component of the velocity field. The remaining two terms, originally neglected by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005), are both related to the t.k.e. production and to the vertical mean kinetic energy transfer (and thereby related to the vertical gradient of the first- and second-order velocity statistics). The term
${\it\alpha}_{nf}$
tends to zero in the far field, as the second-order velocity statistics attain self-similarity and therefore plays a role only in the very near field. The term
${\it\alpha}_{m}$
tends to zero in the far field only in pure jets,
${\it\Gamma}=0$
, as the mean momentum flux maintains a constant value. Its contribution however is non-null for buoyant releases. It is instructive to evaluate the magnitude of
${\it\alpha}_{m}$
in the case of a nominal pure plume, i.e.
${\it\Gamma}\approx 1$
. Considering simple scaling relations for a pure plume, i.e.
$b_{w}^{2}w_{m}^{2}\propto z^{4/3}$
and
$b_{w}\propto (6/5){\it\alpha}_{ref}z$
, and estimating the integral
$I_{6}\simeq 0.05$
from our experimental data, we can estimate
${\it\alpha}_{m}\simeq 1.6\times 10^{-2}$
, which represents a contribution of approximately 10 % to the total entrainment.
As pointed out in appendix A, it is worth noting that, under the assumption of Gaussian radial profiles of mean vertical velocity and temperature, the contribution to
${\it\alpha}_{G}$
given by the ‘drift term’ and pointed out by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005) vanishes, even in the case of a varying
${\it\varphi}$
.
A systematic comparison of estimates of the entrainment coefficient obtained from (5.1) with those from (5.3) offers a means to explain the variability of
${\it\alpha}_{G}={\it\alpha}_{G}({\it\Gamma})$
shown in figure 16.
First, we analyse the Wang & Law (Reference Wang and Law2002) data. Their estimates of
${\it\alpha}_{G}$
are obtained for releases with
$0.01<{\it\Gamma}_{0}<0.1$
and in the range
$60<z/b_{0}<110$
. In contrast to us, Wang & Law (Reference Wang and Law2002) focus on the far-field region, i.e. where
$\langle \widehat{{\it\nu}_{T}}\rangle$
is expected to have reached its asymptotic value, and where the second-order statistics have clearly already attained a condition of self-similarity, so that the contribution of the term
${\it\alpha}_{nf}$
is null. An examination of their Reynolds stress and mean velocity vertical profiles suggests
$\langle \widehat{{\it\nu}_{T}}\rangle \simeq 0.35$
, which leads to values of the parameter
$C=(3/2)\langle \widehat{{\it\nu}_{T}}\rangle ({\it\varphi}^{2}+1)$
(see appendix A) in the range
$0.12<C<0.14$
(Kaminski et al.
Reference Kaminski, Tait and Carazzo2005). This value of
$\langle \widehat{{\it\nu}_{T}}\rangle$
corresponds approximately to the same value as observed in the far field of all three releases examined here (see figure 11). Over a similar range of distances from the source Wang & Law (Reference Wang and Law2002) data exhibits a decrease of
${\it\varphi}$
, from a near-field value of 1.25 down to 1.05 in the far field. As a first approximation, we neglect the contribution of
${\it\alpha}_{m}$
in (5.3), and estimate the entrainment coefficient as
$$\begin{eqnarray}{\it\alpha}_{G}\simeq (2{\it\varphi}^{2}-1)\frac{2{\it\alpha}_{ref}}{5}{\it\Gamma}+\frac{3}{2}\langle \widehat{{\it\nu}_{T}}\rangle .\end{eqnarray}$$
On imposing
$\langle \widehat{{\it\nu}_{T}}\rangle =0.35$
we plot
${\it\alpha}_{G}$
from (5.6) for
${\it\varphi}=$
1.05, 1.15 and 1.25. As is clear from figure 17, the tendency of
${\it\alpha}_{G}={\it\alpha}_{G}({\it\Gamma})$
from Wang & Law (Reference Wang and Law2002) can be fully reproduced by (5.6) with
${\it\varphi}=1.05$
. For
${\it\Gamma}\geqslant 10^{-1}$
we note that entrainment responds sensitively to
${\it\varphi}$
, with variation of
${\it\varphi}$
less than 10 % inducing considerable variation in
${\it\alpha}_{G}$
. As a consequence of this sensitivity, the actual variation of
${\it\varphi}$
with height in the Wang & Law (Reference Wang and Law2002) experiments, that we have here neglected, is likely to alter the close agreement seen. However, a detailed estimate of all terms in (5.3) for the Wang & Law releases is clearly beyond the scope of the present study and requires further information on the velocity statistics, specifically those related to the term
${\it\alpha}_{m}$
. Our aim here is only to demonstrate that the estimates of
${\it\alpha}_{G}$
provided by Wang & Law (Reference Wang and Law2002) are consistent with the plume dynamics in the far field, where both
${\it\varphi}$
and
$\langle \widehat{{\it\nu}_{T}}\rangle$
have reached their asymptotic values: values that closely match their experimental estimates.
Figure 17. Entrainment coefficient
${\it\alpha}_{G}$
plotted against local plume Richardson number
${\it\Gamma}$
. Experimental data from Wang & Law (Reference Wang and Law2002) and estimates of the formulation of Kaminski et al. (Reference Kaminski, Tait and Carazzo2005) given by (5.6) for a fixed
$\langle \widehat{{\it\nu}_{T}}\rangle =0.035$
and three different values of
${\it\varphi}$
(see text).
Second, we focus on our three releases J, F and P. The measurements gathered during our experimental campaign allow for a direct estimate of all terms comprising
${\it\alpha}_{G}$
in (5.3). However, an estimate of the terms in
${\it\alpha}_{nf}$
, involving vertical derivatives of second-order velocity statistics, is characterised by a large uncertainty due to an insufficient number of sampled velocity fields. Accurate estimates of these terms would require a number of samples of at least an order of magnitude larger. For these reasons, in estimating
${\it\alpha}_{G}$
by means of (5.3), we consider as a first approximation,
${\it\alpha}_{nf}=0$
which we expect to lead to underestimations of
${\it\alpha}_{G}$
in the near field.
Since release P exhibits almost no variation of
${\it\Gamma}$
, the evolution of the estimates of
${\it\alpha}_{G}$
provided by (5.1) and (5.3) shown in figure 18 is plotted against
$z/b_{0}$
, rather than against
${\it\Gamma}$
. Estimates from (5.3) are shown for all three releases with 20 % error bars, evaluated taking into account the uncertainties related to
${\it\Gamma}$
(figure 8),
$\langle \widehat{{\it\nu}_{T}}\rangle$
(figure 11) and
${\it\varphi}$
(figure 12).
For releases J and F, estimates from (5.3) tend to systematically underestimate those from (5.1) in the near field. This can be explained by the neglected contribution of
${\it\alpha}_{nf}$
. Even in the case of plume P, the two estimates of
${\it\alpha}_{G}$
differ significantly in the near field. This difference can primarily be attributed to the non-fully turbulent condition of the plume for
$z/b_{0}<5$
, conditions that invalidate the formulation of (5.3). Discrepancies in the near-field region can also be attributed to the two features discussed in § 2, i.e. eventual non-Boussinesq effects and the thermal stratification of the ambient very close to the source (in a region that extends up to
$z/b_{0}\sim 6$
for release J,
$z/b_{0}\sim 2$
for F and
$z/b_{0}\sim 2$
for P). Both features are not accounted for in the formulation of (5.3). However, despite the non-negligible extent of the error bars, we observe a relatively good agreement between the two estimates for releases J, F and P. This allows us to interpret the physical variation of
${\it\alpha}_{G}$
with
$z/b_{0}$
as given by the variations with
$z/b_{0}$
of the terms on the right-hand side (r.h.s.) of (5.3) and to shed light on the role of
${\it\Gamma}$
in the intensity of the entrainment of ambient air. Focusing on the first two terms on the r.h.s. of (5.3), terms that represent the highest contribution to the total entrainment, we may assert that the role of
${\it\Gamma}$
is twofold: directly through term
$(2{\it\varphi}^{2}-1)(2{\it\alpha}_{ref}/5){\it\Gamma}$
and indirectly through the vertical evolution of
$\langle \widehat{{\it\nu}_{T}}\rangle$
.
The relatively low values of
${\it\alpha}_{G}$
in the near field of releases J and F can then be fully explained by the corresponding low values of
$\langle \widehat{{\it\nu}_{T}}\rangle$
(figure 11). Moving away from the source,
${\it\Gamma}\rightarrow 1$
and the contribution of
$\langle \widehat{{\it\nu}_{T}}\rangle$
to
${\it\alpha}_{G}$
increases (at a rate that depends on
${\it\Gamma}$
) as does the direct contribution of the term including
${\it\Gamma}$
. As widely discussed in § 4, a buoyant release can exhibit different
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\varphi}$
for a given
${\it\Gamma}$
, depending on the release conditions and distance from the source. This explains why, in general, a plume can exhibit a different value of
${\it\alpha}_{G}$
for the same local
${\it\Gamma}$
and provides, in this particular case, a robust justification for the differences observed between our estimates of
${\it\alpha}_{G}$
and those reported by Wang & Law (Reference Wang and Law2002). This feature is also likely to explain the high variability of values of the entrainment coefficient reported in the literature.
6. Summary of findings
We have presented a highly resolved set of velocity and temperature measurements carried out on three turbulent plumes of source Richardson number (1.1) in the range
$10^{-2}<{\it\Gamma}_{0}<1$
. These measurements have been used to assess local dynamical self-similarity, to confirm the evolution of key dynamic quantities, to investigate the large scale structure of the flow and the variability of the rate of entrainment with height from the source.
Despite a variable local dynamical condition, characterised by a varying plume Richardson number
${\it\Gamma}$
, the radial profiles of the mean and of the r.m.s. of the velocity components can be rescaled on local quantities, namely the mean centerline velocity
$w_{m}$
and the mean plume radius
$b_{w}$
, to yield self-similar profiles for the flow variables for a wide range of distances from the source. This local self-similarity applies also to the mean temperature (buoyancy) profiles and to the turbulent viscosity
$\widehat{{\it\nu}_{T}}$
, showing that even the increased radial turbulent momentum transfer induced by an excess of buoyancy can be fully rescaled by local quantities. Even the Eulerian length scales
$\mathscr{L}_{uu}$
and
$\mathscr{L}_{ww}$
appear to rescale locally when normalised with the plume radius. In contrast to the other flow variables however, the local self-similar function describing the spatial evolution of the Eulerian length scales differs significantly depending on
${\it\Gamma}$
.
The influence of
${\it\Gamma}$
on the turbulence dynamics within each release was studied by focusing on the evolution of radial profiles of second-order velocity statistics and estimating bulk quantities, including the spatially averaged turbulent viscosity
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\varphi}=b_{g^{\prime }}/b_{w}$
which is directly linked to the spatially averaged turbulent Prandtl number. Summarising, our results show that:
-
(a) the higher the value of
${\it\Gamma}$
, the lower is the fetch required for second-order statistics to attain local self-similarity; -
(b) the higher the value of
${\it\Gamma}$
, the more rapid the rate of increase of
$\langle \widehat{{\it\nu}_{T}}\rangle$
toward its asymptotic value; -
(c) the influence of
${\it\Gamma}$
on
${\it\varphi}$
is likely to be similar to the influence of
${\it\Gamma}$
on
$\langle \widehat{{\it\nu}_{T}}\rangle$
, but this effect is difficult to unequivocally confirm, given the vertical variation of
${\it\varphi}$
exhibited by a buoyant release is comparable with the uncertainty associated with its experimental estimate; -
(d) neither
$\langle \widehat{{\it\nu}_{T}}\rangle$
nor
${\it\varphi}$
do not show a one-to-one dependence with
${\it\Gamma}$
, since their magnitude depends, at least in a region of flow transition, also on the distance from the source.
The study culminated with an analysis of the influence of
${\it\Gamma}$
on the rate of entrainment of ambient air as quantified by the entrainment coefficient
${\it\alpha}_{G}$
. Two distinct experimental estimates of
${\it\alpha}_{G}$
were obtained. The first by estimating the vertical variation of the volume flux. The second adopting a formulation of
${\it\alpha}_{G}$
similar to that originally proposed by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005), and that makes explicit the role of the main non-dimensional parameters governing the dynamics of the plume, i.e.
${\it\Gamma}$
,
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\varphi}$
. In this way we could fully explain the observed variations of
${\it\alpha}_{G}$
in the three releases studied as well as in the existing literature data, depending on
${\it\Gamma}$
and on the distance from the source.
Our analysis shows that it is not possible to identify a one-to-one dependence of
${\it\alpha}_{G}$
on
${\it\Gamma}$
, since its variations are due also to changes in
$\langle \widehat{{\it\nu}_{T}}\rangle$
and
${\it\varphi}$
, whose magnitude, for a given
${\it\Gamma}$
depends on the distances from the source and the value of
${\it\Gamma}$
at the source.
Acknowledgements
We would like to express our gratitude to C. Nicot and N. Grosjean who contributed their laboratory expertise. Also our thanks go to the EPSRC for their financial support through the doctoral training scheme at Imperial College London and Bourse Ministérielle at LMFA for financing the work in Lyon. G.R.H. would like to thank the CNRS for funding his visiting position at the Ecole Centrale de Lyon. P.S. would like to thank M. Marro for invaluable help in data processing and C. Cancelli, M. van Reeuwijk, M. Creyssels and S. Vaux for fruitful discussions.
Appendix A
Following the analysis undertaken by Craske & van Reeuwijk (Reference Craske and van Reeuwijk2014) on unsteady jets, we present an extension of the model of Kaminski et al. (Reference Kaminski, Tait and Carazzo2005). For clarity, the notation will be kept as similar as possible to that adopted by Kaminski et al. (Reference Kaminski, Tait and Carazzo2005). We begin by writing the steady balance equations for mass, momentum and buoyancy in cylindrical coordinates under the Boussinesq approximation and assuming negligible viscous effects:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial rw}{\partial r}+\frac{\partial ru}{\partial r}=0,\\ \displaystyle \frac{\partial }{\partial z}(rw^{2})+\frac{\partial }{\partial r}(ruw)=rg^{\prime }-\frac{\partial }{\partial r}(r\overline{\tilde{u} \tilde{w}})-\frac{1}{{\it\rho}_{e}}\frac{\partial }{\partial z}(\,pr)-\frac{\partial }{\partial z}({\it\sigma}_{w}^{2}r),\\ \displaystyle \frac{\partial }{\partial z}(rwg^{\prime }+r\overline{\tilde{w}\tilde{g^{\prime }}})+\frac{\partial }{\partial r}(rug^{\prime }+r\overline{\tilde{u} \tilde{g^{\prime }}})=0,\end{array}\right\}\end{eqnarray}$$
where
$p$
represents the difference from hydrostatic pressure
$p_{e}={\it\rho}_{e}gz$
. In contrast to Kaminski et al. (Reference Kaminski, Tait and Carazzo2005), equation (A 1) includes the vertical derivatives of
${\it\sigma}_{w}^{2}$
and pressure. Since the pressure distribution is difficult to measure, its vertical gradient is usually modelled as (Hussein et al.
Reference Hussein, Capp and George1994; Shabbir & George Reference Shabbir and George1994; Wang & Law Reference Wang and Law2002)
$$\begin{eqnarray}-\frac{\partial p}{{\it\rho}_{e}\partial z}\approx \frac{\partial ({\it\sigma}_{u}^{2}+{\it\sigma}_{v}^{2})}{2\partial z}\approx \frac{\partial {\it\sigma}_{u}^{2}}{\partial z},\end{eqnarray}$$
where
${\it\sigma}_{v}$
denotes the standard deviation of the azimuthal velocity component.
By combining mass and momentum balances, we can write the mean kinetic energy balance as
$$\begin{eqnarray}\frac{\partial }{\partial z}\left(\frac{1}{2}rw^{3}\right)+\frac{\partial }{\partial r}\left(\frac{1}{2}ruw^{2}\right)=rwg^{\prime }-w\frac{\partial }{\partial r}\left(r\overline{\tilde{u} \tilde{w}}\right)-w\frac{\partial }{\partial z}\left({\it\sigma}_{w}^{2}-{\it\sigma}_{u}^{2}\right)r.\end{eqnarray}$$
The balance equations (A 1) can be integrated over
$r$
, from 0 to
$\infty$
, assuming as boundary conditions that
$\lim _{r\rightarrow \infty }ruw=\lim _{r\rightarrow \infty }r\overline{\tilde{u} \tilde{w}}=\lim _{r\rightarrow \infty }rug^{\prime }=\lim _{r\rightarrow \infty }r\overline{\tilde{u} \tilde{g^{\prime }}}=0$
, so that
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}}{\text{d}z}\int _{0}^{\infty }rw\text{d}r=-\left[ru\right]_{0}^{\infty },\\ \displaystyle \frac{\text{d}}{\text{d}z}\int _{0}^{\infty }rw^{2}\text{d}r=\int _{0}^{\infty }rg^{\prime }\text{d}r-\frac{\text{d}}{\text{d}z}\int _{0}^{\infty }\left({\it\sigma}_{w}^{2}-{\it\sigma}_{u}^{2}\right)r\text{d}r,\\ \displaystyle \frac{\text{d}}{\text{d}z}\int _{0}^{\infty }(rwg^{\prime }+r\overline{\tilde{w}\tilde{g^{\prime }}})\text{d}r=0,\\ \displaystyle \frac{\text{d}}{\text{d}z}\int _{0}^{\infty }\frac{1}{2}rw^{3}\text{d}r=\int _{0}^{\infty }rwg^{\prime }\text{d}r+\int _{0}^{\infty }r\overline{\tilde{u} \tilde{w}}\frac{\partial w}{\partial r}\text{d}r-\int _{0}^{\infty }rw\frac{\partial }{\partial z}\left({\it\sigma}_{w}^{2}-{\it\sigma}_{u}^{2}\right)\text{d}r.\end{array}\right\}\end{eqnarray}$$
As in Kaminski et al. (Reference Kaminski, Tait and Carazzo2005), the mean and variance of the vertical velocity, the mean buoyancy and the Reynolds stress are expressed by shape functions:
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}w(r,z)=w_{m}(z)f(r,z),\\ g^{\prime }(r,z)=g_{m}^{\prime }(z)h(r,z),\\ \overline{\tilde{u} \tilde{w}}=-{\textstyle \frac{1}{2}}w_{m}(z)^{2}j(r,z),\\ {\it\sigma}_{w}^{2}-{\it\sigma}_{u}^{2}={\textstyle \frac{1}{2}}w_{m}^{2}l(r,z).\end{array}\right\}\end{eqnarray}$$
With reference to (4.2) in § 4.2.1 we note that, for Gaussian profiles,
$j(r,z)=2\mathscr{F}(r,z)$
. These shape functions allow the computation of the integrals in (A 4) without making any assumption regarding the similarity of the profiles,
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle I_{0}=\int _{0}^{\infty }r^{\ast }f(r^{\ast },z)\text{d}r^{\ast },\\ \displaystyle I_{1}=\int _{0}^{\infty }r^{\ast }f(r^{\ast },z)h(r^{\ast },z)\text{d}r^{\ast },\\ \displaystyle I_{2}=\int _{0}^{\infty }r^{\ast }h(r^{\ast },z)\text{d}r^{\ast },\\ \displaystyle I_{3}=\int _{0}^{\infty }r^{\ast }f(r^{\ast },z)^{2}\text{d}r^{\ast },\\ \displaystyle I_{4}=\int _{0}^{\infty }r^{\ast }f(r^{\ast },z)^{3}\text{d}r^{\ast },\\ \displaystyle I_{5}=\int _{0}^{\infty }r^{\ast }j(r^{\ast },z)\frac{\partial f}{\partial r^{\ast }}\text{d}r^{\ast },\\ \displaystyle I_{6}=\int _{0}^{\infty }r^{\ast }l(r^{\ast },z)\text{d}r^{\ast },\\ \displaystyle I_{7}=\int _{0}^{\infty }\left(2l\frac{\text{d}}{\text{d}z}\ln w_{m}+\frac{\partial l}{\partial z}\right)f(r^{\ast },z)r^{\ast }\text{d}r^{\ast },\end{array}\right\}\end{eqnarray}$$
where
$r^{\ast }=r/b_{m}$
, with
$b_{m}$
denoting a generic radius scale.
Top-hat variables are defined according to the following relations
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle R^{2}W^{2}=\int _{0}^{\infty }rw^{2}\text{d}r,\\ \displaystyle R^{2}G^{\prime }=\int _{0}^{\infty }rg^{\prime }\text{d}r,\\ \displaystyle R^{2}WG^{\prime }=\int _{0}^{\infty }rwg^{\prime }\text{d}r,\\ \displaystyle R^{2}{\it\Sigma}_{q}^{2}=\int _{0}^{\infty }({\it\sigma}_{w}^{2}-{\it\sigma}_{u}^{2})r\text{d}r.\end{array}\right\}\end{eqnarray}$$
With the integrals (A 7), introducing the usual entrainment assumption in the volume balance equation (A 4)
$$\begin{eqnarray}-[ru]_{0}^{\infty }={\it\alpha}_{G}b_{m}w_{m},\end{eqnarray}$$
and neglecting the vertical turbulent transfer of buoyancy (i.e.
$\overline{\tilde{w}\tilde{g^{\prime }}}$
), the system (A 4) can be rewritten in top-hat equation form as
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}}{\text{d}z}R^{2}W=2RW{\it\alpha}_{t},\\ \displaystyle \frac{\text{d}}{\text{d}z}R^{2}W^{2}=R^{2}G^{\prime }-\frac{\text{d}}{\text{d}z}R^{2}{\it\Sigma}_{q}^{2},\\ \displaystyle \frac{\text{d}}{\text{d}z}R^{2}WG^{\prime }=0,\\ \displaystyle \frac{\text{d}}{\text{d}z}R^{2}W^{3}=\frac{2}{A}R^{2}WG^{\prime }-R^{2}W^{3}\frac{\text{d}\ln A}{\text{d}z}-W^{3}R(C+RD),\end{array}\right\}\end{eqnarray}$$
where the relations between ‘top-hat’ variables and the real variables are
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle R=\frac{I_{3}^{1/2}I_{2}}{I_{1}}b_{m},\\ \displaystyle W=\frac{I_{1}}{I_{2}}w_{m},\\ \displaystyle G^{\prime }=\frac{I_{1}^{2}}{I_{2}I_{3}}g_{m}^{\prime },\\ \displaystyle {\it\Sigma}_{q}^{2}=\frac{1}{2}\frac{I_{1}^{2}I_{6}}{I_{2}^{2}I_{3}}w_{m}^{2},\end{array}\right\}\end{eqnarray}$$
where
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A=\frac{I_{2}I_{4}}{I_{1}I_{3}},\\ \displaystyle C=\frac{I_{2}I_{3}^{1/2}I_{5}}{I_{1}I_{4}},\\ \displaystyle D=\frac{I_{7}}{I_{4}},\end{array}\right\}\end{eqnarray}$$
and where the top-hat entrainment coefficient
${\it\alpha}_{t}$
in (A 9) is related to the Gaussian coefficient
${\it\alpha}_{G}$
in (A 8) by
$$\begin{eqnarray}{\it\alpha}_{t}=\left[\frac{{\it\alpha}_{G}}{2}\frac{I_{3}^{1/2}I_{2}}{I_{1}I_{0}}-\frac{R}{2}\frac{\text{d}}{\text{d}z}\ln \frac{I_{1}I_{0}}{I_{3}I_{2}}\right].\end{eqnarray}$$
It is worth noting that the relation between the ‘top-hat’ entrainment coefficient
${\it\alpha}_{t}$
and
${\it\alpha}_{G}$
is not simply given by a proportionality coefficient, i.e.
$\sqrt{2}$
, as in the classic top-hat formulations of the plume equations (Morton et al.
Reference Morton, Taylor and Turner1956). This is due to the fact that the definitions of the top-hat variables in (A 7) differ from those of Morton et al. (Reference Morton, Taylor and Turner1956).
With some algebra, the top-hat momentum and mean kinetic energy balance can be manipulated in order to conveniently express the continuity equation as
$$\begin{eqnarray}\frac{\text{d}}{\text{d}z}R^{2}W=2RW\left[\mathit{Ri}\underbrace{\left(1-\frac{1}{A}\right)+\frac{1}{2}R\frac{\text{d}\ln A}{\text{d}z}+\frac{1}{2}C+\frac{1}{2}RD-\frac{1}{RW^{2}}\frac{\text{d}}{\text{d}z}\left({\it\Sigma}_{q}^{2}R^{2}\right)}_{{\it\alpha}_{t}}\right],\end{eqnarray}$$
where the term within the square brackets is equal to the entrainment coefficient
${\it\alpha}_{t}$
in (A 9) and
$\mathit{Ri}\equiv (RG^{\prime })/W^{2}$
represents a bulk Richardson number. The volume flux balance (A 13) provides a formulation for
${\it\alpha}_{t}$
that allows for its direct estimate from first- and second-order velocity statistics.
We now assume local self-similarity of the first-order velocity statistics (but not of second-order statistics) and adopt Gaussian profiles of velocity and buoyancy of the form
$f=\text{e}^{-r\ast ^{2}}$
and
$h=\text{e}^{-(r\ast ^{2}/{\it\varphi}^{2})}$
, with
$r\ast =r/b_{w}$
. Furthermore, we model the Reynolds stress by a gradient law of the form
$j=\langle \widehat{{\it\nu}_{T}}\rangle (\partial f/\partial r^{\ast })$
. The integrals in (A 6) then reduce to
$I_{0}=1/2$
,
$I_{1}={\it\varphi}^{2}/(2({\it\varphi}^{2}+1))$
,
$I_{2}={\it\varphi}^{2}/2$
,
$I_{3}=1/4$
,
$I_{4}=1/6$
,
$I_{5}=\langle \widehat{{\it\nu}_{T}}\rangle /2$
, so that the relations in (A 10), (A 11) can be written
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}R={\textstyle \frac{1}{2}}({\it\varphi}^{2}+1)b_{w},\\ \displaystyle W=\frac{w_{m}}{{\it\varphi}^{2}+1},\\ \displaystyle G^{\prime }=\frac{2{\it\varphi}^{2}}{({\it\varphi}^{2}+1)^{2}}g_{m}^{\prime },\\ \displaystyle {\it\Sigma}_{q}^{2}=\frac{2}{({\it\varphi}^{2}+1)^{2}}I_{6}w_{m}^{2},\\ A={\textstyle \frac{2}{3}}({\it\varphi}^{2}+1),\\ C={\textstyle \frac{3}{2}}\langle \widehat{{\it\nu}_{T}}\rangle ({\it\varphi}^{2}+1),\\ D=6I_{7}\end{array}\right\}\end{eqnarray}$$
and the Richardson number
$\mathit{Ri}$
in (A 13) can be expressed as
$$\begin{eqnarray}\mathit{Ri}\equiv \frac{b_{w}g_{m}^{\prime }}{w_{m}^{2}}{\it\varphi}^{2}({\it\varphi}^{2}+1)=\frac{2{\it\alpha}_{ref}}{5}({\it\varphi}^{2}+1)^{2}{\it\Gamma}.\end{eqnarray}$$
From (A 12), the relation linking the entrainment coefficients
${\it\alpha}_{G}$
and
${\it\alpha}_{t}$
then reduces to
$$\begin{eqnarray}{\it\alpha}_{G}=\frac{2}{{\it\varphi}^{2}+1}{\it\alpha}_{t}-\frac{b_{w}}{2}\frac{\text{d}}{\text{d}z}\ln ({\it\varphi}^{2}+1).\end{eqnarray}$$
By combining (A 13)–(A 16) we finally obtain an expression for the Gaussian entrainment coefficient as a function of the first- and second-order velocity statistics
$$\begin{eqnarray}{\it\alpha}_{G}=(2{\it\varphi}^{2}-1)\frac{2{\it\alpha}_{ref}}{5}{\it\Gamma}+\frac{3}{2}\langle \widehat{{\it\nu}_{T}}\rangle +3b_{w}I_{7}-\frac{2}{b_{w}w_{m}^{2}}\frac{\text{d}}{\text{d}z}\left(I_{6}b_{w}^{2}w_{m}^{2}\right).\end{eqnarray}$$
Note that, assuming Gaussian radial profiles of mean vertical velocity and buoyancy, even with a variable
${\it\varphi}$
, the ‘drift’ term
$(R(\text{d}\ln A/\text{d}z))/2$
in (A 13) vanishes when converting
${\it\alpha}_{t}$
in
${\it\alpha}_{G}$
. The last term can be expressed as
$$\begin{eqnarray}\frac{2b_{w}}{b_{w}^{2}w_{m}^{2}}\frac{\text{d}}{\text{d}z}\left(I_{6}b_{w}^{2}w_{m}^{2}\right)=2b_{w}\frac{\text{d}I_{6}}{\text{d}z}+2b_{w}I_{6}\frac{\text{d}}{\text{d}z}\ln \left(b_{w}^{2}w_{m}^{2}\right),\end{eqnarray}$$
so that (A 17) can be finally written as
$$\begin{eqnarray}{\it\alpha}_{G}=(2{\it\varphi}^{2}-1)\frac{2{\it\alpha}_{ref}}{5}{\it\Gamma}+\frac{3}{2}\langle \widehat{{\it\nu}_{T}}\rangle +{\it\alpha}_{nf}-{\it\alpha}_{m},\end{eqnarray}$$
with
$$\begin{eqnarray}{\it\alpha}_{nf}=3b_{w}I_{7}-2b_{w}\frac{\text{d}I_{6}}{\text{d}z},\end{eqnarray}$$
and
$$\begin{eqnarray}{\it\alpha}_{m}=2b_{w}I_{6}\frac{\text{d}}{\text{d}z}\ln \left(b_{w}^{2}w_{m}^{2}\right).\end{eqnarray}$$
