1 Introduction
Dynamic wetting refers to the displacement of one immiscible fluid by another on a solid substrate. This phenomenon is ubiquitous in applications such as oil recovery (Gerritsen & Durlofsky Reference Gerritsen and Durlofsky2005), microfluidics (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004) and coating processes (Weinstein & Ruschak Reference Weinstein and Ruschak2004). In coating processes, steady dynamic wetting occurs when a liquid is deposited on a solid substrate that moves at a speed 
$U$. However, at a critical substrate speed 
$U^{crit}$, the liquid is no longer uniformly deposited on the substrate and the flow transitions from steady to unsteady and from two-dimensional (2-D) to three-dimensional (3-D). This critical substrate speed corresponds to a critical capillary number 
$Ca^{crit}=\unicode[STIX]{x1D707}U_{crit}/\unicode[STIX]{x1D70E}$, where 
$\unicode[STIX]{x1D707}$ and 
$\unicode[STIX]{x1D70E}$ are the viscosity and surface tension of the liquid, respectively. When the displaced fluid is air, dynamic wetting failure leads to air entrainment: a sawtooth-shaped meniscus appears at the contact line that serves as a visual marker of 
$Ca^{crit}$ (Wilkinson Reference Wilkinson1975; Burley & Kennedy Reference Burley and Kennedy1976; Blake & Ruschak Reference Blake and Ruschak1979; Vandre, Carvalho & Kumar Reference Vandre, Carvalho and Kumar2014; Liu, Carvalho & Kumar Reference Liu, Carvalho and Kumar2017; He & Nagel Reference He and Nagel2019). Air bubbles break off the tip of the sawteeth and are entrained in the liquid. Since this phenomenon is detrimental to the final quality of the coating, understanding the underlying mechanisms is of considerable industrial importance.
Vandre, Carvalho & Kumar (Reference Vandre, Carvalho and Kumar2013) proposed a mechanism for the onset of air entrainment by considering the displacement of air by a Newtonian liquid between two parallel plates, one of which is stationary while the other moves horizontally at a constant speed. Their two-dimensional finite-element calculations showed that as long as the capillary-stress gradients are larger than the air-pressure gradients in the vicinity of the contact line, steady dynamic wetting can be sustained. In this case, the capillary-stress gradients act to pump air away from the contact-line region, thereby allowing the liquid to displace the air. However, when the capillary number (dimensionless plate speed) reaches a critical value, the air-pressure gradients become equal to the capillary-stress gradients, and the air cannot be pumped away fast enough to sustain a steady state at speeds above this critical value. This provides a way to determine 
$Ca^{crit}$ from the calculations, and the model predictions for physically reasonable slip lengths agree well with values of 
$Ca^{crit}$ obtained from flow visualization experiments (Vandre, Carvalho & Kumar Reference Vandre, Carvalho and Kumar2012; Vandre et al. Reference Vandre, Carvalho and Kumar2013, Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b, Reference Liu, Carvalho and Kumar2017).
Although the fundamental understanding of dynamic wetting failure in Newtonian liquids has been significantly advanced by these studies, dynamic wetting failure in non-Newtonian liquids remains poorly understood. Wetting failure is a common problem in the liquid-applied coatings industry, where non-Newtonian liquids are widely used. In practice, coating liquids can exhibit multiple types of non-Newtonian rheological behaviour including shear thinning, shear thickening and viscoelasticity.
Experimental studies suggest shear thinning can increase the maximum speed at which a coating process can operate before defects occur. Ning, Tsai & Liu (Reference Ning, Tsai and Liu1996) and Yang, Wong & Liu (Reference Yang, Wong and Liu2004) conducted slot-coating experiments using a Newtonian base of glycerol–water solutions and added either polyacrylamide powder or carboxymethylcellulose powder to create shear-thinning solutions. They showed that there exists an optimal concentration for each polymer additive at which the maximum coating speed is increased when compared to that of the Newtonian base solution. Bhamidipati et al. (Reference Bhamidipati, Didari, Bedell and Harris2011) also conducted slot-coating experiments but used blackstrap molasses as a shear-thinning liquid. In addition, they performed volume-of-fluid simulations using a power-law model to describe the liquid rheology. Their simulations revealed that the maximum coating speed was increased for liquids with a lower power-law index, which corresponds to more pronounced shear thinning. In the experiments, only one liquid was used, and the maximum speed observed agreed well with the simulation prediction. A later study using the same liquid and simulation method also reported good agreement (Didari et al. Reference Didari, Ahmad, Veldhorst and Harris2014). Apart from published papers, the patent literature suggests that shear thinning helps postpone air entrainment to higher speeds (Blake et al. Reference Blake, Dobson, Batts and Harrison1995).
In contrast, other experiments suggest that shear thickening can decrease the maximum speed at which a coating process can operate before defects occur. Khandavalli & Rothstein (Reference Khandavalli and Rothstein2016) investigated the effect of shear thickening on the stability of slot coating. They controlled the extent of shear thickening by changing the concentration of fumed silica nanoparticles in polypropylene glycol. Their results show that, for liquids with more pronounced shear thickening, the maximum coating speed is decreased. The influence of viscoelasticity on air entrainment has also been investigated, via experiments in which a substrate is plunged into a liquid (Cohu & Benkreira Reference Cohu and Benkreira1998; Wei et al. Reference Wei, Rame, Walker and Garoff2009b). The results of these experiments suggest that viscoelasticity itself may have little influence on the critical speed needed for air entrainment, whereas changes in the liquid viscosity may play a much more important role.
Notably, liquid-plunging experiments with shear-thinning liquids at speeds low enough to avoid air entrainment indicate that shear thinning reduces the viscous bending of the liquid–air interface near the contact line (Seevaratnam et al. Reference Seevaratnam, Suo, Ramé, Walker and Garoff2007; Wei, Garoff & Walker Reference Wei, Garoff and Walker2009a). This leads to a lower dynamic contact angle at a given substrate speed, suggesting that air entrainment (which occurs as the dynamic contact angle approaches 
$180^{\circ }$) would be delayed in shear-thinning liquids.
It should be noted that in the slot-coating experiments described above (Ning et al. Reference Ning, Tsai and Liu1996; Yang et al. Reference Yang, Wong and Liu2004; Bhamidipati et al. Reference Bhamidipati, Didari, Bedell and Harris2011; Khandavalli & Rothstein Reference Khandavalli and Rothstein2016), no vacuum was applied at the upstream meniscus. As a consequence, the upstream meniscus can get dragged toward the feed slot as the coating speed increases. This causes the coating bead to become three-dimensional, leading to defects that can appear as entrained air (Romero et al. Reference Romero, Suszynski, Scriven and Carvalho2004). In this work, we make a distinction between such defects and actual wetting failure, which is associated with the inability to remove air quickly enough from the contact-line region in the absence of any other instability of the coating bead.
While the above experiments (Ning et al. Reference Ning, Tsai and Liu1996; Yang et al. Reference Yang, Wong and Liu2004; Bhamidipati et al. Reference Bhamidipati, Didari, Bedell and Harris2011; Khandavalli & Rothstein Reference Khandavalli and Rothstein2016) suggest that shear thinning may be beneficial for reducing coating defects, several outstanding issues need to be resolved to establish whether shear thinning can delay the onset of dynamic wetting failure and the resulting air entrainment. First, as already noted, the above experiments were conducted in complicated coating geometries where other types of defects such as ribbing and bead breakup can occur. Thus, it is not apparent whether the observed increase in the maximum coating speed corresponds to a suppression of these defects by shear thinning or to a true delay of wetting failure itself. Such a delay would correspond to an enhancement in the ability of the liquid to displace air from the contact line (Vandre et al. Reference Vandre, Carvalho and Kumar2012, Reference Vandre, Carvalho and Kumar2013, Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016a,Reference Liu, Vandre, Carvalho and Kumarb, Reference Liu, Carvalho and Kumar2017; Liu, Carvalho & Kumar Reference Liu, Carvalho and Kumar2019). Second, it is not clear whether the increase in the maximum coating speed is due to shear thinning itself or to changes in the zero-shear viscosity. Finally, there has not been a systematic theoretical investigation of the role of shear thinning and the underlying physical mechanisms, especially for a simpler geometry in which complicated features present in real coating flows (e.g. feed flows, film formation) are absent.
The principal objective of this work is to carry out a theoretical investigation using the parallel-plate geometry employed in our prior work (Vandre et al. Reference Vandre, Carvalho and Kumar2012, Reference Vandre, Carvalho and Kumar2013, Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b, Reference Liu, Carvalho and Kumar2017). In addition to examining the effect of shear thinning, we will also explore the role of shear thickening. To further clarify the influence shear thinning can have on dynamic wetting failure and air entrainment, some brief motivating experiments are presented in § 2. The mathematical model and solution method are discussed in § 3, followed by a presentation of results in § 4 and a discussion of physical mechanisms in § 5. In § 6, we comment on the possible implications of our results for developing models of low-speed dynamic wetting in non-Newtonian liquids, which is important for understanding phenomena such as droplet spreading. Finally, concluding remarks are given in § 7.
2 Motivating experiments
As noted in § 1, it is not clear from previous studies whether any delay in dynamic wetting failure observed in shear-thinning liquids is due to shear thinning itself or to changes in the zero-shear viscosity. One simple way to address this issue is to perform experiments with a shear-thinning liquid and with a Newtonian liquid having a similar zero-shear viscosity and surface tension.
We present here the results of such experiments using a curtain-coating geometry. Although curtain coating is complex geometrically and dynamically due the presence of a feed flow and two liquid–air interfaces, wetting failure and air entrainment can more readily be identified compared to slot coating, where bead breakup can occur at high enough coating speeds (Romero et al. Reference Romero, Suszynski, Scriven and Carvalho2004). It should be noted that we also tried experiments similar to those in our prior work with Newtonian liquids where a rotating cylindrical roll or a tape-like substrate is plunged into a liquid bath (Vandre et al. Reference Vandre, Carvalho and Kumar2012, Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Carvalho and Kumar2017). However, we found that the shear-thinning liquid we used quickly became turbid, making it difficult to conduct flow visualization experiments. Thus, we focus on curtain coating in these brief motivating experiments. We emphasize that these experiments are intended simply to provide a qualitative illustration rather than a comprehensive quantitative study.
2.1 Experimental set-up
The experimental apparatus is shown in figure 1. The system consists of a hollow, custom-made rotating glass roll exposed to air, measuring 15 cm in diameter and 17 cm in length. A custom-made coating die is positioned above the glass roll at a height of 10 cm. Liquid is pumped out of a reservoir with the use of a gear pump (Zenith) and flows through a Coriolis-type mass flow meter (KROHNE), which measures the mass flow rate 
$Q$. The flow rate is controlled by the pump motor speed controller. The liquid flows through the coating die and falls vertically to form a liquid curtain, guided by two stainless steel edge guides, until it impinges on the rotating glass roll and forms a liquid film. A squeegee is installed to remove liquid from the glass roll, and the removed liquid is recycled back to the reservoir. A mirror is placed inside the hollow roll at such an angle as to reflect the contact-line image. A camera is focused at the mirror to allow for flow visualization of the reflected contact line. The camera is connected to a computer and display where real-time video is projected and recorded.
Figure 1. Schematic of the experimental apparatus.
Figure 2. Viscosity 
$\unicode[STIX]{x1D707}$ as a function of the shear rate 
$\dot{\unicode[STIX]{x1D6FE}}$.
A Newtonian solution of aqueous glycerol (Brenntag) and a shear-thinning solution of aqueous glycerol mixed with xanthan gum (Nature’s Oil) were used in the experiments. The properties of the two solutions are shown in table 1. The surface tension 
$\unicode[STIX]{x1D70E}$ was measured with a Krüss digital tensiometer (K10ST). The viscosity 
$\unicode[STIX]{x1D707}$ of the two liquids was measured as a function of the shear rate 
$\dot{\unicode[STIX]{x1D6FE}}$ using a concentric-cylinder rheometer (TA Instruments), and is shown in figure 2. Note that the two liquids have similar viscosities 
$\unicode[STIX]{x1D707}_{0}$ for low 
$\dot{\unicode[STIX]{x1D6FE}}$, but as 
$\dot{\unicode[STIX]{x1D6FE}}$ increases, the viscosity of the shear-thinning liquid decreases.
Table 1. Physical properties of the liquids used in the experiments.
The experimental procedure involves several steps. First, the flow rate 
$Q$ is set to a certain value through the flow controller. Second, the roller speed is gradually increased and the system is allowed to reach steady state. Third, air entrainment is observed on the display and the critical speed 
$U_{crit}$ at which it occurs is recorded. Finally, the flow rate is changed to another value and the procedure is repeated. These steps were followed for both liquids, and the second and third steps were repeated to obtain at least three sets of data for every flow rate 
$Q$.
2.2 Experimental results
In figure 3, the flow rate 
$Q$ is plotted against the corresponding critical speed of the roll 
$U^{crit}$ at which the onset of air entrainment occurs. The blue line represents pairs of 
$(U^{crit},Q)$ obtained for the Newtonian liquid. Error bars on the 
$x$-axis represent uncertainty of the flow-rate measurements. On the 
$y$-axis, error bars are the standard error of at least three measurements.
As the flow rate increases, so does the critical speed (figure 3); it is assumed that air entrainment is still present for 
$U>U^{crit}$. This behaviour reflects the phenomenon of ‘hydrodynamic assist’ (Blake, Clarke & Ruschak Reference Blake, Clarke and Ruschak1994), where the hydrodynamic pressure generated by the inertia of the impinging curtain creates larger gradients in interface curvature near the dynamic contact line (Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016a, Reference Liu, Carvalho and Kumar2019). This effect is most prominent when the curtain flow rate is such that the contact line is directly under the the liquid curtain. These larger interface curvature gradients produce stronger capillary-stress gradients that are more effective at pumping air away from the contact-line region, resulting in larger values of 
$U^{crit}$.
Although experiments were conducted with the shear-thinning liquid as well, air entrainment could not be observed for the same flow-rate range even at the maximum speed of the roll. As a result, pairs of 
$(U^{crit},Q)$ could not be obtained.
Figure 3. Onset of air entrainment for the Newtonian liquid. The blue line corresponds to the critical operating conditions after which air entrainment occurs (shaded area). Air entrainment was not observed for the shear-thinning liquid.
Flow visualization images of the contact line for both liquids are shown in figure 4. For a given flow rate 
$Q$, the formation of a sawtooth-shaped meniscus leading to air entrainment is clearly observed for the Newtonian liquid (figure 4a). However, the contact line for the shear-thinning liquid remains straight even when the roll speed is set to its maximum value (figure 4b). Note that although multiple sawtooth shapes are observed along the contact line for the Newtonian liquid, we have shown only one in this image. For both liquids, the dynamic contact line is directly underneath the liquid curtain and no heel-formation or bead-pulling phenomena (Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016a, Reference Liu, Carvalho and Kumar2019) were observed. This indicates that the effects of hydrodynamic assist are similar for both liquids and that the observed difference in maximum speeds is principally due to shear thinning. For Newtonian liquids, decreasing the liquid viscosity generally produces higher critical speeds (Blake, Bracke & Shikhmurzaev Reference Blake, Bracke and Shikhmurzaev1999; Vandre et al. Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Carvalho and Kumar2017). Our results thus suggest that shear thinning may lead to a lower effective viscosity, an idea we explore later in this paper.
Figure 4. Flow visualization of the contact line for the (a) Newtonian liquid and (b) shear-thinning liquid. The contact line for both liquids is shown with a white dashed line. The flow rate is 
$Q=28.2\pm 0.2~\text{g}~\text{s}^{-1}$ in both cases but the speed is (a) 
$U=1.79\pm 0.03~\text{m}~\text{s}^{-1}$ and (b) 
$U=1.91\pm 0.01~\text{m}~\text{s}^{-1}$ (maximum roll speed). The scale bar is 4.25 mm.
Although a comprehensive experimental study is beyond the scope of the present work, the above results support the idea that shear thinning is beneficial for postponing dynamic wetting failure and air entrainment. They thus serve to motivate development of a mathematical model in a parallel-plate geometry, where we can isolate the role of shear thinning from the complex geometric and dynamic features present in curtain coating.
3 Mathematical model
3.1 Governing equations and boundary conditions
We develop a hydrodynamic model describing the displacement of a receding fluid by an advancing fluid within two parallel boundaries separated by a distance 
$H$, as shown in figure 5(a). The top boundary remains stationary while the bottom boundary moves at a speed 
$U$. Symbols 
$x$ and 
$y$ represent the Cartesian coordinates and we take 
$s$ to be the arclength along the fluid interface, measured from the contact line at the top boundary to the point where 
$y=h$. The projection of the interface in the 
$x$-direction is denoted by 
$L$. The viscosities of the advancing and receding fluids are denoted by 
$\unicode[STIX]{x1D707}_{rec}$ and 
$\unicode[STIX]{x1D707}_{adv}$, respectively. Because our principal focus is on air entrainment, we take the receding phase to be air and the advancing phase to be a liquid.
Figure 5. (a) Schematic of the model geometry. (b) Enlarged view of the contact-line region near the bottom substrate. The inflection point occurs where 
$\unicode[STIX]{x1D703}_{M}$ is maximum along the interface and is characterized by height 
$h_{f}$ and radial distance 
$r_{f}$ from the contact line. Figure adapted from Liu et al. (Reference Liu, Vandre, Carvalho and Kumar2016b).
Two types of contact angle are used to describe the interface shape and are displayed in figure 5(b). The microscopic contact angle 
$\unicode[STIX]{x1D703}_{mic}$ arises where the interface contacts the substrate, whereas the macroscopic or apparent contact angle 
$\unicode[STIX]{x1D703}_{M}$ is a result of the deformation of the interface and is measured at some distance away from the dynamic contact line. The microscopic contact angle for the top substrate is 
$\unicode[STIX]{x1D703}_{mic,T}$ and that for the bottom substrate is 
$\unicode[STIX]{x1D703}_{mic,B}$. In this work, we take 
$\unicode[STIX]{x1D703}_{M}$ to be the maximum surface angle along the interface, so the position it occurs at corresponds to the interface inflection point (IP). The inflection point is characterized by a height 
$h_{f}$ and a radial distance 
$r_{f}$ from the bottom contact line.
The dimensionless momentum and mass conservation equations for the advancing phase are
$$\begin{eqnarray}\displaystyle & \displaystyle Re\left(\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\right)=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\pmb{\unicode[STIX]{x1D70F}}+St\boldsymbol{g}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0. & \displaystyle\end{eqnarray}$$ Here, lengths, velocities, stresses and time have been scaled by 
$H$, 
$U$, 
$\unicode[STIX]{x1D707}_{0}U/H$ and 
$H/U$, respectively, where 
$\unicode[STIX]{x1D707}_{0}$ is the zero-shear viscosity of the advancing phase. The two dimensionless parameters that appear in (3.1) are the Reynolds number, 
$Re=\unicode[STIX]{x1D70C}UH/\unicode[STIX]{x1D707}_{0}$, which measures the relative importance of inertial to viscous forces, and the Stokes number, 
$St=\unicode[STIX]{x1D70C}gH^{2}/\unicode[STIX]{x1D707}_{0}U$, which measures the relative importance of gravitational to viscous forces. Both 
$Re$ and 
$St$ contain the density 
$\unicode[STIX]{x1D70C}$ and the zero-shear viscosity 
$\unicode[STIX]{x1D707}_{0}$ of the advancing phase. The velocity vector is denoted by 
$\boldsymbol{u}$, the pressure by 
$p$, the viscous-stress tensor by 
$\pmb{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}_{adv}(\dot{\unicode[STIX]{x1D6FE}})[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]$ and the gravitational acceleration vector by 
$\boldsymbol{g}$. The viscosity is assumed to depend on a scalar measure of the deformation rate, 
$\dot{\unicode[STIX]{x1D6FE}}$.
To isolate the influence of non-Newtonian rheology, we neglect inertial and gravitational effects by setting 
$Re=St=0$. Thus, equation (3.1) simplifies to
$$\begin{eqnarray}\unicode[STIX]{x1D735}p=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\pmb{\unicode[STIX]{x1D70F}}.\end{eqnarray}$$The dimensionless boundary conditions applied to the fluid interface are
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}|_{rec}=\boldsymbol{u}|_{adv}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{t}|_{adv}=\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{t}|_{rec}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}=Ca[\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{n}|_{adv}-\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{n}|_{rec}]. & \displaystyle\end{eqnarray}$$ Here, 
$Ca=\unicode[STIX]{x1D707}_{0}U/\unicode[STIX]{x1D70E}$ is the capillary number, which is a ratio of viscous to surface-tension forces, where 
$\unicode[STIX]{x1D70E}$ is the surface tension between the advancing and receding phases. Equations (3.4) and (3.5) are the no-slip and no-penetration boundary conditions and equations (3.6) and (3.7) are the tangential and normal stress balances at the interface. Subscripts rec and adv correspond to the receding and advancing phases. With 
$\boldsymbol{n}$ and 
$\boldsymbol{t}$ we denote the unit vectors that are normal (pointing toward the receding phase) and tangent to the interface. The curvature of the interface at each point is denoted by 
$\unicode[STIX]{x1D705}$, and 
$\unicode[STIX]{x1D64F}$ is the total-stress tensor. For the advancing phase, 
$\unicode[STIX]{x1D64F}=-p\unicode[STIX]{x1D644}+\pmb{\unicode[STIX]{x1D70F}}$. For the receding phase, we take 
$\unicode[STIX]{x1D64F}=-p_{rec}\unicode[STIX]{x1D644}+\unicode[STIX]{x1D707}_{rec}[\unicode[STIX]{x1D735}\boldsymbol{u}_{rec}+(\unicode[STIX]{x1D735}\boldsymbol{u}_{rec})^{\text{T}}]$, where 
$\unicode[STIX]{x1D707}_{rec}$ is taken to be constant, and 
$p_{rec}$ and 
$\boldsymbol{u}_{rec}$ are the pressure and velocity vector in the receding phase.
A Navier-slip boundary condition is applied at the bottom boundary to remove the stress singularity caused by applying the no-slip boundary condition at the dynamic (bottom) contact line (Huh & Scriven Reference Huh and Scriven1971; Dussan V. Reference Dussan V.1976; Chan et al. Reference Chan, Srivastava, Marchand, Andreotti, Biferale, Toschi and Snoeijer2013; Sibley, Nold & Kalliadasis Reference Sibley, Nold and Kalliadasis2015),
$$\begin{eqnarray}\boldsymbol{t}_{s}\boldsymbol{\cdot }(\boldsymbol{u}-\boldsymbol{U})=\unicode[STIX]{x1D706}[\boldsymbol{n}_{s}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{t}_{s}].\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D706}=l_{slip}/H$ is the dimensionless slip length with 
$l_{slip}$ being the dimensional slip length. In our previous work (Vandre et al. Reference Vandre, Carvalho and Kumar2012, Reference Vandre, Carvalho and Kumar2013, Reference Vandre, Carvalho and Kumar2014; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b, Reference Liu, Carvalho and Kumar2017), model predictions were found to agree well with experimental data for 
$\unicode[STIX]{x1D706}\leqslant 10^{-4}$. Thus, 
$\unicode[STIX]{x1D706}=10^{-4}$ is chosen here unless otherwise noted. For Newtonian liquids, increasing the value of 
$\unicode[STIX]{x1D706}$ increases the values of 
$Ca^{crit}$ but does not change the qualitative features of the results (Vandre et al. Reference Vandre, Carvalho and Kumar2012). Additional calculations we have performed confirm that this is also the case for the non-Newtonian liquids considered here, which is why we choose a fixed value of 
$\unicode[STIX]{x1D706}$. The vectors 
$\boldsymbol{t}_{s}$ and 
$\boldsymbol{n}_{s}$ are the unit vectors tangential and normal (pointing upward) to the bottom substrate, and 
$\boldsymbol{U}$ is the velocity vector of the bottom substrate. Equation (3.8) recovers the no-slip boundary condition for distances greater than 
$l_{slip}$ from the dynamic contact line (Vandre et al. Reference Vandre, Carvalho and Kumar2012). Additionally, the no-penetration boundary condition (3.5) is applied to both boundaries, whereas the no-slip boundary condition is applied only to the top substrate.
The microscopic contact angles serve as boundary conditions at the two ends of the fluid interface. Although these angles may be speed dependent in general (Blake Reference Blake2006; Wilson et al. Reference Wilson, Summers, Shikhmurzaev, Clarke and Blake2006; Shikhmurzaev Reference Shikhmurzaev2007; Snoeijer & Andreotti Reference Snoeijer and Andreotti2013), here, we assume that 
$\unicode[STIX]{x1D703}_{mic}$ is constant and equal to the static contact angle to isolate the influence of non-Newtonian rheology. To eliminate the influence of surface wettability, the microscopic contact angles are set to 
$90^{\circ }$ for both boundaries. For Newtonian liquids, decreasing the value of 
$\unicode[STIX]{x1D703}_{mic,B}$ increases the values of 
$Ca^{crit}$ (Vandre et al. Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b). We have performed additional calculations and find that this also holds true for the non-Newtonian liquids considered here. For this reason, we consider a single value of 
$\unicode[STIX]{x1D703}_{mic,B}$ when presenting results.
As noted earlier, we take the receding phase to be air to focus on the case of air entrainment. In this case, the receding phase becomes long and thin, so lubrication theory and the quasi-parallel (QP) approximation can be used to describe the flow in that phase. In the QP approximation, it is assumed that the curvature gradients along the 
$x$-coordinate are equal to those along the arclength 
$s$, i.e. 
$\text{d}\unicode[STIX]{x1D705}/\text{d}x\approx \text{d}\unicode[STIX]{x1D705}/\text{d}s$ (Jacqmin Reference Jacqmin2004; Sbragaglia, Sugiyama & Biferale Reference Sbragaglia, Sugiyama and Biferale2008; Qin & Gao Reference Qin and Gao2018). With these assumptions, mass and momentum conservation in the receding phase are simplified to a set of 1-D equations
$$\begin{eqnarray}\displaystyle & \displaystyle Ah+{\displaystyle \frac{1}{2}}Bh^{2}+{\displaystyle \frac{1}{6}}{\displaystyle \frac{\text{d}p_{rec}}{\text{d}s}}h^{3}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left.{\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}}\right|_{s}=B+{\displaystyle \frac{\text{d}p_{rec}}{\text{d}s}}h,\quad \text{where }A={\displaystyle \frac{\unicode[STIX]{x1D712}h+\unicode[STIX]{x1D712}\unicode[STIX]{x1D706}u_{s}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\text{d}p_{rec}}{\text{d}s}}h^{2}\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D706}+h}},B={\displaystyle \frac{-\unicode[STIX]{x1D712}+A}{\unicode[STIX]{x1D706}}}.\quad & \displaystyle\end{eqnarray}$$ Here, 
$h$ is the interface height (see figure 5a), 
$p_{rec}$ is the air pressure, 
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y|_{s}$ is the velocity gradient at the interface and 
$u_{s}$ is the horizontal velocity evaluated at the interface. The dimensionless slip length 
$\unicode[STIX]{x1D706}$ is defined in (3.8), and 
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D707}_{rec}/\unicode[STIX]{x1D707}_{0}$ is the viscosity ratio between the receding and advancing phases. Since we focus on the displacement of air by a liquid, we set 
$\unicode[STIX]{x1D712}=10^{-3}$ in this work. For Newtonian liquids, decreasing the value of 
$\unicode[STIX]{x1D712}$ increases the values of 
$Ca^{crit}$ (Vandre et al. Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b). We have found that this is also the case for the non-Newtonian liquids considered here. For simplicity, we ignore any effects due to Knudsen diffusion (Sprittles Reference Sprittles2015, Reference Sprittles2017).
We note that this hybrid approach of a 1-D description of the receding phase and a 2-D description of the advancing phase has been implemented in our previous work (Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016a,Reference Liu, Vandre, Carvalho and Kumarb, Reference Liu, Carvalho and Kumar2017, Reference Liu, Carvalho and Kumar2019). Predictions of this model for the onset of dynamic wetting failure match the predictions of a full 2-D description of both the receding and advancing phases over a wide range of microscopic contact angles, including 
$90^{\circ }$ (Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b).
3.2 Constitutive model
We employ a Carreau-type constitutive model (Bird Reference Bird1976; Carreau, Kee & Daroux Reference Carreau, Kee and Daroux1979) since it provides one of the simplest descriptions of shear thinning and it can also be easily modified to describe shear thickening. For this model,
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\dot{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D707}_{\infty }+(\unicode[STIX]{x1D707}_{0}-\unicode[STIX]{x1D707}_{\infty })[1+(\unicode[STIX]{x1D706}_{s}\dot{\unicode[STIX]{x1D6FE}})^{2}]^{(n-1)/2},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D707}_{\infty }$ is the infinite-shear viscosity, 
$\unicode[STIX]{x1D707}_{0}$ is the zero-shear viscosity, 
$n$ is a power-law exponent and 
$\unicode[STIX]{x1D706}_{s}$ is a time constant (relaxation time) that determines the onset of shear thinning or shear thickening.
As a scalar measure of the deformation rate, we take 
$\dot{\unicode[STIX]{x1D6FE}}=\sqrt{2II_{D}}$, where 
$II_{D}$ is the second invariant of the rate-of-deformation tensor (Morrison Reference Morrison2001), 
$\unicode[STIX]{x1D63F}=[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]/2$. In Cartesian coordinates,
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}}=\left[\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}\right)^{2}+2\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}\right)^{2}+2\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}\right)^{2}\right]^{1/2},\end{eqnarray}$$ where 
$u$ and 
$v$ are the 
$x$- and 
$y$-components of the velocity vector 
$\boldsymbol{u}$, respectively.
The dimensionless form of (3.11) is
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\dot{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D6FD}+(1-\unicode[STIX]{x1D6FD})[1+(De\dot{\unicode[STIX]{x1D6FE}})^{2}]^{(n-1)/2},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D707}_{\infty }/\unicode[STIX]{x1D707}_{0}$ is the ratio of the infinite-shear to the zero-shear viscosity. Note that 
$\unicode[STIX]{x1D6FD}$ is less than unity for shear-thinning liquids (
$\unicode[STIX]{x1D6FD}<1$), greater than unity for shear-thickening liquids (
$\unicode[STIX]{x1D6FD}>1$) and equal to unity for Newtonian liquids (
$\unicode[STIX]{x1D6FD}=1$). Values of 
$\unicode[STIX]{x1D6FD}$ can range from 0.01 to 0.5 for shear-thinning liquids (Carreau et al. Reference Carreau, Kee and Daroux1979; Tamjid & Guenther Reference Tamjid and Guenther2010) and from 3 to 15 for shear-thickening liquids (Galindo-Rosales, Rubio-Hernández & Velázquez-Navarro Reference Galindo-Rosales, Rubio-Hernández and Velázquez-Navarro2009; Galindo-Rosales, Rubio-Hernández & Sevilla Reference Galindo-Rosales, Rubio-Hernández and Sevilla2011). The Deborah number 
$De=\unicode[STIX]{x1D706}_{s}/(H/U)$ is the ratio of the relaxation time to the characteristic flow time. As 
$De$ increases, shear-thinning or shear-thickening effects become apparent at lower deformation rates 
$\dot{\unicode[STIX]{x1D6FE}}$. Also, as the power-law index 
$n$ is reduced, shear-thinning or shear-thickening effects become more pronounced, as shown in figure 6. Typical values of 
$n$ range from 0.2 to 1 (Carreau et al. Reference Carreau, Kee and Daroux1979). For 
$n=1$, the constitutive model for a Newtonian liquid is recovered.
Figure 6. Effect of 
$n$ on the viscosity of a (a) shear-thinning liquid with 
$\unicode[STIX]{x1D6FD}=0.1$ and (b) shear-thickening liquid with 
$\unicode[STIX]{x1D6FD}=3.5$ described by a Carreau-type model (3.13).
3.3 Solution method
Equations (3.2)–(3.10) are solved using a Galerkin finite-element method with elliptic mesh generation; for more details we refer readers to our previous work (Vandre et al. Reference Vandre, Carvalho and Kumar2012, Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b). For a given set of dimensionless parameters, we look for a family of steady-state solutions by increasing the capillary number 
$Ca$. The key dimensionless parameters in our model are summarized in table 2. The steady-state solutions include the fluid interface shape, pressure in the air phase and pressure and velocity in the liquid phase. By post-processing the interface-shape data, we calculate the surface angle at each point of the interface and take the maximum angle as the macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$. We then track the macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$ as a function of the capillary number 
$Ca$ until a critical capillary number 
$Ca^{crit}$ beyond which we are unable to find 2-D steady-state solutions. We assume that the onset of wetting failure happens when 
$Ca=Ca^{crit}$.
Table 2. Model parameters and corresponding definitions and physical meanings.
4 Effect of shear thinning and shear thickening on 
$Ca^{crit}$
In this section we characterize the influence of shear thinning and shear thickening on the critical capillary number 
$Ca^{crit}$ at which dynamic wetting failure is assumed to occur. Before doing so, we briefly discuss the flow kinematics.
4.1 Kinematics
In figure 7, we plot the magnitude of the rate-of-deformation tensor 
$\Vert \unicode[STIX]{x1D63F}\Vert$, and the magnitude of the vorticity tensor 
$\Vert \unicode[STIX]{x1D734}\Vert$, for a Newtonian liquid. The magnitudes of these tensors are defined as
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D63F}\Vert =\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D63F}\boldsymbol{ : }\unicode[STIX]{x1D63F}^{\text{T}}}{2}}},\quad \Vert \unicode[STIX]{x1D734}\Vert =\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D734}\boldsymbol{ : }\unicode[STIX]{x1D734}^{\text{T}}}{2}}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D63F}=[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]/2$ and 
$\unicode[STIX]{x1D734}=[\unicode[STIX]{x1D735}\boldsymbol{u}-(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]/2$. The rate-of-deformation tensor 
$\unicode[STIX]{x1D63F}$ measures the deformation of fluid line elements whereas 
$\unicode[STIX]{x1D734}$ quantifies the rotation speed of fluid line elements. Contour plots of the magnitudes of the two tensors are almost identical, meaning that, locally, the flow behaves like a simple shear flow everywhere. This suggests that for the problem considered here, shear rheology is likely to be more important than extensional rheology in affecting dynamic wetting failure.
Figure 7. Magnitude of the (a) rate-of-deformation tensor (b) vorticity tensor for a Newtonian liquid. Other parameters are 
$Ca=0.40,\unicode[STIX]{x1D712}=10^{-3},\unicode[STIX]{x1D706}=10^{-4}$ and 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$.
4.2 Steady-state solution families
We now compare steady-state solution families of the macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$ as a function of the capillary number 
$Ca$ for shear-thinning, shear-thickening and Newtonian liquids. To highlight the effect of rheology on 
$Ca^{crit}$, we use the same zero-shear viscosity 
$\unicode[STIX]{x1D707}_{0}$ and surface tension 
$\unicode[STIX]{x1D70E}$ for the Newtonian and non-Newtonian liquids and vary only the power-law index 
$n$.
For a given non-Newtonian liquid, 
$De$ will increase as 
$Ca$ does. However, to isolate the influence of individual parameters, it is easiest to fix 
$De$ when constructing solution families. Thus, for most of the calculations in this paper, we fix 
$De=0.1$. We will discuss below the influence of varying 
$De$ and show examples of solution families where we allow 
$De$ to increase as 
$Ca$ does.
Figure 8. (a) Steady-state solution families of shear-thinning liquids (
$\unicode[STIX]{x1D6FD}=0.1$) with
$n=0.5$, 0.8 and 
$n=1$ (Newtonian liquid). (b) Steady-state solution families of shear-thickening liquids (
$\unicode[STIX]{x1D6FD}=3.5$) with 
$n=0.5,0.8$ and 
$n=1$ (Newtonian liquid). (a) (Inset) Solution families of (a) plotted with 
$Ca_{eff}$. (b) (Inset) Solution families of (b) plotted with 
$Ca_{eff}$. Other parameters are 
$\unicode[STIX]{x1D712}=10^{-3},\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
Figure 8(a) shows the macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$ as a function of the capillary number 
$Ca$ for a Newtonian liquid (
$n=1$) and two shear-thinning liquids at 
$De=0.1$ with viscosity ratio 
$\unicode[STIX]{x1D6FD}=0.1$ and power-law indices 
$n=0.5$ and 
$n=0.8$. For all liquids, 
$\unicode[STIX]{x1D703}_{M}$ increases with increasing 
$Ca$. However, the rate at which 
$\unicode[STIX]{x1D703}_{M}$ increases is lower for 
$n=0.5$ and 
$n=0.8$, revealing a weaker dependence of 
$\unicode[STIX]{x1D703}_{M}$ on 
$Ca$ for shear-thinning liquids, consistent with experimental observations (Seevaratnam et al. Reference Seevaratnam, Suo, Ramé, Walker and Garoff2007; Wei et al. Reference Wei, Garoff and Walker2009a). (For Newtonian liquids, the increase in 
$\unicode[STIX]{x1D703}_{M}$ with 
$Ca$ is consistent with reported experiments (Burley & Kennedy Reference Burley and Kennedy1976)).
The macroscopic contact angle increases until a certain 
$Ca$ beyond which we are unable to find 2-D steady-state solutions. This 
$Ca$ is the critical capillary number, 
$Ca^{crit}$, and is represented by the circles on the steady-state solution families. As discussed in prior work, the turning point in a family of steady-state solutions is a bifurcation that separates the steady (lower) branch from the unsteady (upper) branch of steady-state solutions (Jacqmin Reference Jacqmin2004; Sbragaglia et al. Reference Sbragaglia, Sugiyama and Biferale2008; Vandre et al. Reference Vandre, Carvalho and Kumar2013). In this work, we simply identify 
$Ca^{crit}$ from the solution families and do not perform a detailed stability analysis.
As 
$n$ decreases, the onset of dynamic wetting failure occurs at a larger value of 
$Ca^{crit}$. Since 
$Ca^{crit}=\unicode[STIX]{x1D707}_{0}U^{crit}/\unicode[STIX]{x1D70E}$, and 
$\unicode[STIX]{x1D707}_{0}$ and 
$\unicode[STIX]{x1D70E}$ are the same for the three liquids, we can conclude that the critical substrate speed 
$U^{crit}$ increases as the power-law index 
$n$ decreases.
Since the solution families in figure 8(a) all have a similar shape, it is natural to ask whether the capillary number can be re-defined for the shear-thinning cases such that all the solution families collapse onto a single curve. We do this simply by defining an effective capillary number 
$Ca_{eff}=\unicode[STIX]{x1D707}_{eff}U/\unicode[STIX]{x1D70E}$, where 
$\unicode[STIX]{x1D707}_{eff}$ is a constant effective viscosity chosen so that the solution families collapse. Note that in general, the value of 
$\unicode[STIX]{x1D707}_{eff}$ will change as 
$n$ does. The results of this procedure are shown in the inset to figure 8(a), and the values of 
$\unicode[STIX]{x1D707}_{eff}$ are shown in table 3.
It is seen from table 3 that the value of 
$\unicode[STIX]{x1D707}_{eff}$ decreases as shear thinning becomes more significant (smaller 
$n$). The critical substrate speed can be expressed as 
$U^{crit}=Ca_{eff}^{crit}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{eff}$. Since the values of 
$\unicode[STIX]{x1D70E}$ and 
$Ca_{eff}^{crit}$ are the same for all three cases shown in figure 8(a), stronger shear thinning leads to larger values of 
$U^{crit}$, suggesting that shear-thinning postpones wetting failure. Note that the values of 
$\unicode[STIX]{x1D707}_{eff}/\unicode[STIX]{x1D707}_{0}$ are larger than 
$\unicode[STIX]{x1D6FD}$, the dimensionless infinite-shear viscosity.
To gain additional insight into the values of 
$\unicode[STIX]{x1D707}_{eff}$, we can compare them to values of 
$\unicode[STIX]{x1D707}_{ave}$, a viscosity calculated from (3.13) for an average shear rate 
$\dot{\unicode[STIX]{x1D6FE}}_{ave}=1/l_{c}$, where the numerator of unity represents a characteristic dimensionless velocity change and the denominator 
$l_{c}$ represents a characteristic length scale over which there are significant viscosity changes. Because we expect the most significant viscosity changes to occur near the contact line (where the shear rates are largest), a reasonable order-of-magnitude estimate of 
$l_{c}$ might be the air-film thickness 
$h_{f}$ (figure 5b). We thus set 
$l_{c}=h_{f}^{crit}$, the air-film thickness at the critical conditions.
As seen in table 3, the values of 
$\unicode[STIX]{x1D707}_{ave}$ are fairly close to the values of 
$\unicode[STIX]{x1D707}_{eff}$, confirming the above conjecture. We note that an alternative choice of 
$l_{c}$ would be the radial distance to the interface inflection point from the contact line, 
$r_{f}$ (figure 5b), at the critical conditions. It turns out that these values are about four to eight times as large as the 
$h_{f}^{crit}$ values for the cases in table 3. As a consequence, the corresponding values of 
$\unicode[STIX]{x1D707}_{eff}$ are up to twice as large for the shear-thinning liquids and approximately 60 %–70 % of the values for the shear thickening liquids. Because the values of 
$\unicode[STIX]{x1D707}_{eff}$ do not change by orders of magnitude, the radial distance to the inflection point also provides a reasonable order-of-magnitude estimate of the length scale over which there are significant viscosity changes. Overall, the collapse the solution families onto a single curve (inset of figure 8a) suggests that the underlying mechanism of dynamic wetting failure is likely to be similar for Newtonian and shear-thinning liquids, a point we will return to in § 5.
Table 3. Viscosity comparison.
In contrast to the shear-thinning case, figure 8(b) shows that 
$Ca^{crit}$ decreases as the liquid becomes more shear thickening (decreasing 
$n$), indicating that the critical substrate speed 
$U^{crit}$ decreases as the power-law index 
$n$ decreases. We also note that 
$\unicode[STIX]{x1D703}_{M}$ increases at a larger rate for smaller 
$n$, revealing a stronger dependence of 
$\unicode[STIX]{x1D703}_{M}$ on 
$Ca$ for shear-thickening liquids.
Rescaling 
$Ca$ as 
$Ca_{eff}=\unicode[STIX]{x1D707}_{eff}U/\unicode[STIX]{x1D70E}$ results in the collapse of all the solution families onto a single curve, as shown in the inset to figure 8(b). This suggests that the mechanism of wetting failure is likely to be similar for Newtonian and shear-thickening liquids. Note that the values of 
$\unicode[STIX]{x1D707}_{eff}/\unicode[STIX]{x1D707}_{0}$ (table 3) are smaller than 
$\unicode[STIX]{x1D6FD}$, the dimensionless infinite-shear viscosity.
We compare 
$\unicode[STIX]{x1D707}_{eff}$ to 
$\unicode[STIX]{x1D707}_{ave}$ for the shear-thickening liquids in table 3. As in the shear-thinning case, the two viscosities agree fairly well, but here the value of 
$\unicode[STIX]{x1D707}_{eff}$ increases as shear thickening becomes more significant (smaller 
$n$). Since 
$U^{crit}=Ca_{eff}^{crit}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{eff}$, and the values of 
$\unicode[STIX]{x1D70E}$ and 
$Ca_{eff}^{crit}$ are the same for the three liquids, we can conclude that the critical substrate speed 
$U^{crit}$ decreases as the power-law index 
$n$ decreases, suggesting that shear-thickening promotes wetting failure.
It should be noted that that the solution families shown in figure 8 also collapse onto a single curve when 
$Ca$ is scaled by 
$Ca^{crit}$ (see supplementary material available online at https://doi.org/10.1017/jfm.2020.154). This collapse, along with those shown in the insets of figure 8 suggest that similar physical mechanisms govern dynamic wetting failure in Newtonian, shear-thinning and shear-thickening liquids. Before examining physical mechanisms in § 5, we perform a more detailed characterization of interface shapes and discuss the influence of 
$De$.
4.3 Characterization of interface shapes and influence of $De$
To characterize interface shapes near 
$Ca^{crit}$, the solution families for 
$n=0.5$ and 
$n=1$ from figure 8(a) are shown again in figure 9(a), with several points identified by circles (marked 1, 2 and 3) that denote three different wetting states. A given pair of points has approximately the same macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$ but a different capillary number 
$Ca$. The interfacial shapes corresponding to these point pairs are shown in figure 9(b). It can be seen that for the points labelled 2 and 3, the interface is less elongated for the shear-thinning liquid. The differences are more readily apparent when plotted with a semilog scale, as shown in figure 9(c). The smaller elongation for the shear-thinning liquid corresponds to an air film that has not penetrated as far into the liquid for a given 
$\unicode[STIX]{x1D703}_{M}$. This suggests that shear thinning postpones wetting failure by inhibiting the formation of a thin air film near the contact line.
Figure 9. (a) Solution families of a shear-thinning liquid with 
$\unicode[STIX]{x1D6FD}=0.1$ (
$n=0.5$, red solid line) and a Newtonian liquid (
$n=1$, black solid line). (b) Interface shapes of the two liquids at points 1, 2 and 3 (red dashed line for 
$n=0.5$ and black solid line for 
$n=1$). (c) Semilog plot of the interface profiles shown in (b). Other parameters are
$\unicode[STIX]{x1D712}=10^{-3},\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
The same characterization is made for the shear-thickening case. Figure 10(a) illustrates the solution families for 
$n=0.5$ and 
$n=1$ as they appear in figure 8(b). In this case, the interfacial elongation is larger for the shear-thickening liquid as shown in figures 10(b) and 10(c). This implies that shear thickening helps the receding air phase penetrate into the advancing liquid, thereby promoting wetting failure.
Figure 10. (a) Solution families of a shear-thickening liquid with 
$\unicode[STIX]{x1D6FD}=3.5$ (
$n=0.5$, red solid line) and a Newtonian liquid (
$n=1$, black solid line). (b) Interface shapes of the two liquids at points 1, 2 and 3 (red dashed line for 
$n=0.5$ and black solid line for 
$n=1$). (c) Semilog plot of the interface profiles shown in (b). Other parameters are 
$\unicode[STIX]{x1D712}=10^{-3},\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
We now discuss the influence of varying 
$De$. Figure 11 shows solution families for 
$n=0.5$ with 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D6FD}=3.5$ at different values of 
$De$. For shear-thinning liquids, increasing the value of 
$De$ causes 
$Ca^{crit}$ to increase (figure 11a), whereas the opposite is observed for shear-thickening liquids (figure 11b). Note that for 
$De\ll 1$, the solution family approaches that for a Newtonian liquid at the zero-shear viscosity, whereas for 
$De\gg 1$, the solution family approaches that for a Newtonian liquid at the infinite-shear viscosity.
For a given non-Newtonian liquid, 
$De$ will increase as 
$Ca$ does. Solution families can also be obtained at constant elasticity number 
$E$, defined as 
$E=De/Ca=(\unicode[STIX]{x1D706}_{s}\unicode[STIX]{x1D70E})/(\unicode[STIX]{x1D707}H)$. This parameter is only a function of liquid properties and the flow geometry, and is independent of the substrate speed, so solution families at constant 
$E$ correspond to solution families for a given liquid.
The dashed lines in figure 11 are solution families at fixed values of 
$E$. These values of 
$E$ correspond to conditions where 
$De=0.1$ when 
$Ca=Ca^{crit}$ (turning point in solution family). It is seen that these solution families have a similar shape to those obtained at constant 
$De$. The results of figures 8 and 11 thus demonstrate that for a given non-Newtonian liquid, shear thinning will postpone wetting failure whereas shear thickening will promote wetting failure, relative to a Newtonian liquid of the same zero-shear viscosity.
Figure 11. Steady-state solution families of (a) shear-thinning liquids (
$\unicode[STIX]{x1D6FD}=0.1$ and 
$n=0.5$), and (b) shear-thickening liquids (
$\unicode[STIX]{x1D6FD}=3.5$ and 
$n=0.5$) with 
$De=0.01$, 0.1, and 1. The dashed lines are examples of what solution families would look like for a given non-Newtonian liquid, where 
$De$ increases as 
$Ca$ does (
$E=0.095$ in (a) and 
$E=0.58$ in (b), where 
$E=Ca/De$). Other parameters are 
$\unicode[STIX]{x1D712}=10^{-3},\unicode[STIX]{x1D706}=10^{-4}$ and 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$.
5 Physical mechanisms
In Newtonian liquids, dynamic wetting failure occurs when the capillary-stress gradients can no longer provide the pressure gradients needed to pump the receding fluid away from the contact line (Vandre et al. Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016a,Reference Liu, Vandre, Carvalho and Kumarb, Reference Liu, Carvalho and Kumar2019). In this section, we show that a similar physical mechanism holds for shear-thinning and shear-thickening liquids.
By applying lubrication theory to the receding phase, it can be shown that the receding-phase pressure gradients scale as (Vandre et al. Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b)
$$\begin{eqnarray}\left|{\displaystyle \frac{\text{d}p}{\text{d}x}}\right|\sim {\displaystyle \frac{\unicode[STIX]{x1D712}}{h_{f}^{2}}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D712}$ is the viscosity ratio and 
$h_{f}$ is the height of the inflection point (see figure 5b). When the Navier-slip boundary condition (3.8) is applied on the bottom substrate, the interface curvature 
$\unicode[STIX]{x1D705}$ diverges as a function of 
$r$ (
$\unicode[STIX]{x1D705}\sim \ln r$) (Snoeijer & Andreotti Reference Snoeijer and Andreotti2013), where 
$r$ is the radial distance of a point on the interface from the contact line on the bottom substrate. Thus, the capillary-stress gradients in the advancing phase scale as
$$\begin{eqnarray}{\displaystyle \frac{1}{Ca}}\left|{\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}x}}\right|\sim {\displaystyle \frac{1}{Ca}}{\displaystyle \frac{1}{r_{f}}},\end{eqnarray}$$ where 
$r_{f}$ is the distance of the inflection point from the contact line (see figure 5b).
Figure 12. Magnitude of stress gradients at the inflection point for (a) Newtonian liquid (
$\unicode[STIX]{x1D6FD}=1$, black diamonds), shear-thinning liquid (
$\unicode[STIX]{x1D6FD}=0.1$, red circles) and (b) Newtonian liquid (
$\unicode[STIX]{x1D6FD}=1$, black diamonds), shear-thickening liquid (
$\unicode[STIX]{x1D6FD}=3.5$, blue circles). Capillary-stress gradients (filled symbols) meet the receding-phase pressure gradients (open symbols) at 
$Ca^{crit}$ (vertical dashed line) for all cases. Black (
$\unicode[STIX]{x1D6FD}=1$), red (
$\unicode[STIX]{x1D6FD}=0.1$) and blue (
$\unicode[STIX]{x1D6FD}=3.5$) dashed lines correspond to (5.1) and black (
$\unicode[STIX]{x1D6FD}=1$), red (
$\unicode[STIX]{x1D6FD}=0.1$) and blue (
$\unicode[STIX]{x1D6FD}=3.5$) solid lines correspond to (5.2). Magnitude of stress gradients of (a,b) are replotted using 
$Ca_{eff}$ (§ 4.2) in (c,d). Other parameter values are 
$\unicode[STIX]{x1D712}=10^{-3},n=0.5,\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
The capillary-stress gradients and the receding-phase pressure gradients of a Newtonian liquid (
$\unicode[STIX]{x1D6FD}=1$) are plotted as a function of 
$Ca$ and compared to those of a shear-thinning liquid with 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$n=0.5$ (figure 12a) and a shear-thickening liquid with 
$\unicode[STIX]{x1D6FD}=3.5$ and 
$n=0.5$ (figure 12b) at 
$De=0.1$. For both 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D6FD}=3.5$, these quantities become equal at 
$Ca^{crit}$. This confirms that the wetting-failure mechanism in shear-thinning and shear-thickening liquids is similar to that for Newtonian liquids. Moreover, the scaling relationships (5.1) and (5.2) match the numerical results well in both cases. The receding-phase pressure gradients grow (with respect to 
$Ca$) at a lower rate for 
$\unicode[STIX]{x1D6FD}=0.1$ and at a higher rate for 
$\unicode[STIX]{x1D6FD}=3.5$ when compared to those of the Newtonian liquid. This results in a higher 
$Ca^{crit}$ for the shear-thinning liquid and a lower 
$Ca^{crit}$ for the shear-thickening liquid. Notably, the non-Newtonian rheology does not have as significant an effect on the values of the capillary-stress gradients.
As noted earlier, 
$De$ will increase as 
$Ca$ does for a given non-Newtonian liquid. Suppose we consider the case where 
$De=De^{\ast }$ at the point of wetting failure and perform calculations in which we allow 
$De$ to increase as 
$Ca$ does, keeping 
$E=De/Ca$ constant. Then, the receding-phase pressure gradients for a shear-thinning liquid will grow more rapidly with 
$Ca$ relative to the case where 
$De$ is held fixed at 
$De^{\ast }$. However, they will still grow more slowly relative to those for a Newtonian liquid at the same zero-shear viscosity, leading to a larger value of 
$Ca^{crit}$. Similarly, the receding-phase pressure gradients for a shear-thickening liquid will grow more slowly with 
$Ca$ relative to the case where 
$De$ is held fixed at 
$De^{\ast }$, but they will still grow more rapidly relative to those for a Newtonian liquid at the same zero-shear viscosity, leading to a smaller value of 
$Ca^{crit}$.
The magnitudes of the stress gradients shown in figures 12(a) and 12(b) are replotted using 
$Ca_{eff}$ (§ 4.2) in figures 12(c) and 12(d), respectively. In figure 12(c), the magnitudes of the capillary-stress gradients of the Newtonian and shear-thinning liquids collapse on a single curve and so do the magnitudes of the receding-phase pressure gradients. For the shear-thickening liquid, the magnitudes of the stress gradients behave similarly, as shown in figure 12(d). This data collapse suggests that the underlying mechanism of dynamic wetting failure is similar for Newtonian, shear-thinning and shear-thickening liquids. Note that in figures 12(c) and 12(d), the dashed lines appearing in figures 12(a) and 12(b) have been omitted for clarity. Additionally, the data of figures 12(a) and 12(b) also collapse when rescaled by their respective critical values and plotted using 
$Ca/Ca^{crit}$ (see supplementary material).
Figure 13. Tangential stresses at the inflection point for (a) Newtonian liquid (
$\unicode[STIX]{x1D6FD}=1$, black diamonds), shear-thinning liquid (
$\unicode[STIX]{x1D6FD}=0.1$, red circles) and (b) Newtonian liquid (
$\unicode[STIX]{x1D6FD}=1$, black diamonds), shear-thickening liquid (
$\unicode[STIX]{x1D6FD}=3.5$, blue circles). Dashed lines correspond to (5.3). The insets show the tangential stresses versus 
$Ca_{eff}$. Other parameter values are 
$\unicode[STIX]{x1D712}=10^{-3},n=0.5,\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
To understand why shear thinning postpones and shear thickening promotes the onset of dynamic wetting failure, the tangential stresses at the interface inflection point for 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D6FD}=3.5$ are plotted as a function of 
$Ca$ and compared to those of a Newtonian liquid in figures 13(a) and 13(b), respectively. According to the tangential stress balance (3.6), the tangential stresses in the advancing phase are equal to those in the receding phase. Figure 13(a) shows that shear thinning decreases the tangential stresses at the inflection point. Since the receding-phase tangential stresses are approximated as 
$\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{t}|_{rec}\approx \unicode[STIX]{x1D712}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)|_{rec}$ (Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b), the velocity gradients in the receding phase, 
$(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)|_{rec}$, decrease. It will be shown later that this reduction is achieved by a thickened air film (figure 15a). In contrast, shear thickening increases the tangential stresses (figure 13b) leading to a thinner air film (figure 15b).
The insets of figures 13(a) and 13(b) show the tangential stresses versus 
$Ca_{eff}$ (§ 4.2). When replotted in this way, the data collapse well. In addition, by normalizing the tangential stresses with their respective critical value and replotting with 
$Ca/Ca^{crit}$, the data shown in figures 13(a) and 13(b) each nearly collapse onto a single curve. For brevity, the rescaled data are not shown here but can be found in the supplementary material.
Application of lubrication theory to the receding phase shows that the receding-phase tangential stresses scale as (Vandre et al. Reference Vandre, Carvalho and Kumar2013; Liu et al. Reference Liu, Vandre, Carvalho and Kumar2016b)
$$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{t}|_{rec}\sim {\displaystyle \frac{\unicode[STIX]{x1D712}}{h_{f}}},\end{eqnarray}$$ where 
$h_{f}$ is the height of the interface inflection point (figure 5b) and 
$\unicode[STIX]{x1D712}$ is the viscosity ratio. Equation (5.3) is included in figures 13(a) and 13(b) and it shows good agreement with the numerical data for all liquids.
Figures 14(a) and 14(b) show contour plots of the dimensionless viscosity for 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D6FD}=3.5$ at their respective values of 
$Ca^{crit}$. In the liquid bulk, the viscosity remains almost constant and approximately equal to the zero-shear viscosity. But in the vicinity of the contact line where the shear rates are higher, the viscosity is reduced for 
$\unicode[STIX]{x1D6FD}=0.1$ and increased for 
$\unicode[STIX]{x1D6FD}=3.5$. This is of course due to the shear-thinning and shear-thickening natures of the liquids as described by (3.13). The length scale over which the viscosity varies significantly is consistent with the values of 
$h_{f}$ and 
$r_{f}$ (figure 5b), as discussed in § 4.2.
The change in viscosity near the contact line explains the reduced tangential stresses for 
$\unicode[STIX]{x1D6FD}=0.1$ and increased tangential stresses for 
$\unicode[STIX]{x1D6FD}=3.5$, as shown in figures 13(a) and 13(b), respectively. The viscosity changes also suggest that relative to a Newtonian liquid of the same zero-shear viscosity, there will be less viscous bending of the interface for a shear-thinning liquid, and thus smaller values of 
$\unicode[STIX]{x1D703}_{M}$ (figure 8a). Similarly, for a shear-thickening liquid there will be more viscous bending and larger values of 
$\unicode[STIX]{x1D703}_{M}$ (figure 8b).
Figure 14. (a) Viscosity contours for 
$\unicode[STIX]{x1D6FD}=0.1$ at 
$Ca=Ca^{crit}=1.05$. (b) Viscosity contours for 
$\unicode[STIX]{x1D6FD}=3.5$ at 
$Ca=Ca^{crit}=1.71\times 10^{-1}$. Other parameters are 
$\unicode[STIX]{x1D712}=10^{-3},n=0.5,\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
To further characterize how shear thinning and shear thickening influence the interface shape, the characteristic length scales 
$h_{f}$ and 
$r_{f}$ (figure 5b) are plotted as a function of the capillary number 
$Ca$ for 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D6FD}=1$ in figure 15(a) and 
$\unicode[STIX]{x1D6FD}=1$ and 
$\unicode[STIX]{x1D6FD}=3.5$ in figure 15(b). The characteristic length scales of all three liquids decrease with increasing 
$Ca$, which means that the inflection point approaches the contact line, and the air film is thinned and stretched.
Figure 15. Characterization of interface shape. Black symbols are used for Newtonian (
$\unicode[STIX]{x1D6FD}=1$), red for shear-thinning (
$\unicode[STIX]{x1D6FD}=0.1$) and blue for shear-thickening (
$\unicode[STIX]{x1D6FD}=3.5$) liquids. (a,b) Interfacial length scales 
$h_{f}$ (open symbols) and 
$r_{f}$ (closed symbols) as a function of 
$Ca$. (c) Interface length 
$L$ as a function of 
$Ca$. (d) Height of inflection point 
$h_{f}$ as a function of interface length 
$L$. Other parameters are 
$\unicode[STIX]{x1D712}=10^{-3},n=0.5,\unicode[STIX]{x1D706}=10^{-4}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$ and 
$De=0.1$.
For 
$\unicode[STIX]{x1D6FD}=0.1$, both 
$h_{f}$ and 
$r_{f}$ are larger compared to those for 
$\unicode[STIX]{x1D6FD}=1$, which corresponds to a thicker air film for the shear-thinning liquid (figure 15a). The thicker air film reduces the tangential stresses in the receding phase, allowing it to balance the reduced tangential stresses in the advancing phase (figures 13a and 14a). The thicker air film also leads to smaller receding-phase pressure gradients for 
$\unicode[STIX]{x1D6FD}=0.1$ (figure 12a), which results in a postponement of wetting failure.
In contrast, 
$r_{f}$ and 
$h_{f}$ for 
$\unicode[STIX]{x1D6FD}=3.5$ are smaller than those for 
$\unicode[STIX]{x1D6FD}=1$ (figure 15b), corresponding to a thinner air film for the shear-thickening liquid. The thinner air film increases the tangential stresses in the receding phase, allowing it to balance the increased tangential stresses in the advancing phase (figures 13b and 14b). The thinner air film also leads to larger receding-phase pressure gradients for 
$\unicode[STIX]{x1D6FD}=3.5$ (figure 12b), meaning that wetting failure is promoted. These effects become more pronounced as 
$\unicode[STIX]{x1D6FD}$ increases from unity, and the strong deformation of the interface that results from the increased viscous forces makes convergence of the calculations difficult when 
$\unicode[STIX]{x1D6FD}$ becomes too large. Note that for 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$Ca\sim$
$10^{-3}$, the inflection point is located at higher 
$y$ than that for 
$\unicode[STIX]{x1D6FD}=1$, as opposed to 
$\unicode[STIX]{x1D6FD}=3.5$ where it is located at a lower 
$y$ compared to 
$\unicode[STIX]{x1D6FD}=1$. By normalizing 
$h_{f}$ and 
$r_{f}$ with their respective critical values and the 
$x$-axis by 
$Ca^{crit}$ or 
$Ca_{eff}$, the 
$h_{f}$ and 
$r_{f}$ curves of all three liquids have a similar shape (see supplementary material).
In figure 15(c), the interface length 
$L$ (see figure 5a) is plotted as a function of 
$Ca$. The interface elongates with increasing 
$Ca$ for all 
$\unicode[STIX]{x1D6FD}$, but for 
$\unicode[STIX]{x1D6FD}=0.1$ a smaller elongation is obtained at larger 
$Ca$. This reduced elongation is a result of shear thinning, and means that penetration of the receding phase has been inhibited. In contrast, the elongation for 
$\unicode[STIX]{x1D6FD}=3.5$ is much larger, which leads to a smaller 
$Ca^{crit}$. Note that when both axes are normalized with their respective critical values (or 
$Ca_{eff}$ is used for the horizontal axis), the data for all three liquids nearly collapse onto a single curve (see supplementary material).
To see how elongation affects the air-film thickness, 
$h_{f}$ is plotted with 
$L$ in figure 15(d). For all liquids, the air-film thickness gets reduced with increasing interfacial elongation. After a certain 
$L$ the three curves collapse onto each other, suggesting that the mechanism of interfacial elongation in shear-thinning and shear-thickening liquids is similar to that in Newtonian liquids. When the axes are normalized with their respective critical values, the curves for all three liquids still retain a similar shape (see supplementary material).
6 Low-speed dynamic wetting
Although the focus of this paper is on high-speed dynamic wetting near the limit of air entrainment, the results reported here may also be useful for developing models of low-speed dynamic wetting in non-Newtonian liquids. Such models are useful for understanding phenomena such as droplet spreading (de Gennes Reference de Gennes1985; Bonn et al. Reference Bonn, Eggers, Indekeu and Meunier2009).
The standard theory for low-speed dynamic wetting in Newtonian liquids was developed by Cox, who applied asymptotic analysis to describe the behaviour of the apparent contact angle 
$\unicode[STIX]{x1D703}_{ap}$ as a function of the capillary number 
$Ca$, during two-phase displacement (Cox Reference Cox1986),
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle g(\unicode[STIX]{x1D703}_{mic};\unicode[STIX]{x1D712})-g(\unicode[STIX]{x1D703}_{ap};\unicode[STIX]{x1D712})=Ca\ln (\unicode[STIX]{x1D706}_{Cox}),\\ \displaystyle \!g(\unicode[STIX]{x1D703};\unicode[STIX]{x1D712})=\displaystyle \int _{0}^{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D712}(x^{2}-\sin ^{2}x)[(\unicode[STIX]{x03C0}-x)+\sin x\cos x]+[(\unicode[STIX]{x03C0}-x)^{2}-\sin ^{2}x](x-\sin x\cos x)}{2\sin x[\unicode[STIX]{x1D712}^{2}(x^{2}-\sin ^{2}x)+2\unicode[STIX]{x1D712}[x(\unicode[STIX]{x03C0}-x)+\sin ^{2}x]+[(\unicode[STIX]{x03C0}-x)^{2}-\sin ^{2}x]]}}\,\text{d}x.\end{array}\right\}\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D703}_{mic}$ is the microscopic contact angle, 
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D707}_{rec}/\unicode[STIX]{x1D707}_{0}$ is the viscosity ratio and 
$\unicode[STIX]{x1D706}_{Cox}=l_{mic}/l_{M}$ is the ratio between a characteristic microscopic length scale 
$l_{mic}$ and a characteristic macroscopic length scale 
$l_{M}$. The scale 
$l_{mic}$ is of the order of molecular dimensions (
${\sim}1~\text{nm}$) (Petrov & Petrov Reference Petrov and Petrov1992; Blake Reference Blake2006) whereas the scale 
$l_{M}$ (
${\sim}10~\unicode[STIX]{x03BC}\text{m}-1~\text{mm}$) may be set by the system geometry or gravity. Cox’s theory neglects inertial effects and is limited to low-speed steady wetting (
$Ca\ll 1$) with slowly varying interface angles (
$Ca|\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}x|\ll 1$). For the case of vanishing 
$\unicode[STIX]{x1D712}$, 
$g(\unicode[STIX]{x1D703})\approx \unicode[STIX]{x1D703}^{3}/9$.
Note that 
$l_{mic}$ is not necessarily equal to the slip length, and 
$\unicode[STIX]{x1D703}_{ap}$ is not necessarily equal to the macroscopic contact angle 
$\unicode[STIX]{x1D703}_{M}$. Nevertheless, by identifying 
$\unicode[STIX]{x1D703}_{ap}$ with 
$\unicode[STIX]{x1D703}_{M}$ or a measured apparent contact angle, and treating 
$\unicode[STIX]{x1D706}_{Cox}$ as a fitting parameter, equation (6.1) can be fit to data from experiments or simulations to see how well it works.
In our previous work (Vandre et al. Reference Vandre, Carvalho and Kumar2013), equation (6.1) was found to describe well data for small 
$Ca$ obtained from simulations for Newtonian liquids like those conducted here. It was generally found that 
$\unicode[STIX]{x1D706}_{Cox}$ was an order of magnitude larger than the dimensionless slip length 
$\unicode[STIX]{x1D706}$. Given the similarities in dynamic wetting failure between Newtonian, shear-thinning and shear-thickening liquids reported in the present paper, it is natural to ask how well (6.1) can describe the simulation data for the non-Newtonian liquids. Because we are interested in how 
$\unicode[STIX]{x1D703}_{M}$ varies with 
$Ca$ at low 
$Ca$ for a given liquid, for the calculations in this section we present results at fixed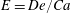 
$E=De/Ca$.
Figure 16 shows a comparison between the finite-element calculations and the predictions of (6.1), where 
$\unicode[STIX]{x1D706}_{Cox}$ is treated as a fitting parameter and 
$\unicode[STIX]{x1D703}_{M}$ is used in place of 
$\unicode[STIX]{x1D703}_{ap}$. Our simulation results are compared with results obtained from (6.1) for a Newtonian (
$\unicode[STIX]{x1D6FD}=1$), a shear-thinning (
$\unicode[STIX]{x1D6FD}=0.1$) and a shear-thickening liquid (
$\unicode[STIX]{x1D6FD}=3.5$) for 
$\unicode[STIX]{x1D712}=0$ (figure 16a) and 
$\unicode[STIX]{x1D712}=10^{-3}$ (figure 16b). Simulation results are shown with open symbols and results from (6.1) are given by dashed lines. For simplicity, the same values of 
$\unicode[STIX]{x1D706}_{Cox}$ are used for both values of 
$\unicode[STIX]{x1D712}$, and these are obtained from fitting (6.1) to the 
$\unicode[STIX]{x1D712}=0$ simulation results.
Figure 16. Comparison of solution families for (a) 
$\unicode[STIX]{x1D712}=0$ and (b) 
$\unicode[STIX]{x1D712}=10^{-3}$ with results obtained from (6.1). Black diamonds correspond to 
$\unicode[STIX]{x1D6FD}=1$, red circles to 
$\unicode[STIX]{x1D6FD}=0.1$ and blue squares to 
$\unicode[STIX]{x1D6FD}=3.5$. Results from the asymptotic theory (6.1) are shown with dashed lines (black for 
$\unicode[STIX]{x1D6FD}=1$, red for 
$\unicode[STIX]{x1D6FD}=0.1$ and blue for 
$\unicode[STIX]{x1D6FD}=3.5$). 
$\unicode[STIX]{x1D706}_{Cox,newt}=0.06$ (for 
$\unicode[STIX]{x1D6FD}=1$), 
$\unicode[STIX]{x1D706}_{Cox,thin}=0.55$ (for 
$\unicode[STIX]{x1D6FD}=0.1$) and 
$\unicode[STIX]{x1D706}_{Cox,thick}=3.8\times 10^{-4}$ (for 
$\unicode[STIX]{x1D6FD}=3.5$). (c,d) Data in (a) and (b) replotted with 
$Ca_{eff}$, respectively. Other parameters are 
$n=0.5$, 
$\unicode[STIX]{x1D706}=10^{-2}$, 
$\unicode[STIX]{x1D703}_{mic,T}=\unicode[STIX]{x1D703}_{mic,B}=90^{\circ }$. In all cases, 
$E=De/Ca=10$.
At low 
$Ca$, equation (6.1) agrees well with our simulation data for all 
$\unicode[STIX]{x1D6FD}$ and both 
$\unicode[STIX]{x1D712}$. As 
$Ca$ increases, a disagreement is observed. However, such a disagreement might be expected (Kamal et al. Reference Kamal, Sprittles, Snoeijer and Eggers2019) since Cox’s theory is derived for Newtonian liquids with small 
$Ca$ and does not take into account any effects that a shear-rate-dependent viscosity may have on contact-line dynamics. Note that for all cases, 
$\unicode[STIX]{x1D706}_{Cox}$ is within approximately an order-of-magnitude of 
$\unicode[STIX]{x1D706}$, similar to what was found in our previous work. This is consistent with the idea that the mechanics of dynamic wetting in Newtonian, shear-thinning and shear-thickening liquids have strong similarities.
Shear-thinning liquids appear to have a larger value of 
$\unicode[STIX]{x1D706}_{Cox}$ compared to Newtonian liquids, whereas shear-thickening liquids appear to have a smaller value. This may reflect the idea that slip plays a stronger role in shear-thinning liquids due to the reduced viscosities near the dynamic contact line, whereas it plays a weaker role in shear-thickening liquids. The influence of viscosity is also seen in the values of 
$\unicode[STIX]{x1D703}_{M}$: smaller viscosities near the contact line lead to less viscous bending and smaller values of 
$\unicode[STIX]{x1D703}_{M}$ compared to the Newtonian case, whereas larger viscosities lead to more viscous bending and larger values of 
$\unicode[STIX]{x1D703}_{M}$ (Seevaratnam et al. Reference Seevaratnam, Suo, Ramé, Walker and Garoff2007; Wei et al. Reference Wei, Garoff and Walker2009a). The weaker dependence of 
$\unicode[STIX]{x1D703}_{M}$ on 
$Ca$ for shear-thinning liquids is consistent with experimental observations (Seevaratnam et al. Reference Seevaratnam, Suo, Ramé, Walker and Garoff2007; Wei et al. Reference Wei, Garoff and Walker2009a).
Figures 16(c) and 16(d) show the collapse of the simulation data (open symbols) of figures 16(a) and 16(b), respectively, when plotted using 
$Ca_{eff}=\unicode[STIX]{x1D707}_{eff}U/\unicode[STIX]{x1D70E}$ (§ 4.2). For both values of 
$\unicode[STIX]{x1D712}$, we use the same values of 
$\unicode[STIX]{x1D707}_{eff}$, 
$\unicode[STIX]{x1D707}_{eff}=0.18\unicode[STIX]{x1D707}_{0}$ for 
$\unicode[STIX]{x1D6FD}=0.1$ and 
$\unicode[STIX]{x1D707}_{eff}=3\unicode[STIX]{x1D707}_{0}$ for 
$\unicode[STIX]{x1D6FD}=3.5$. The good collapse of the data, especially at low 
$Ca_{eff}$, suggests that the mechanics of low-speed dynamic wetting in Newtonian, shear-thinning and shear-thickening liquids are similar. As in § 4.2, the values of 
$\unicode[STIX]{x1D707}_{eff}$ imply that the effective viscosity for a non-Newtonian liquid is likely an averaged value in the vicinity of the contact line.
Although development of an asymptotic theory like Cox’s for non-Newtonian liquids is beyond the scope of the present work, the results presented here may provide guidance in developing such a theory. In particular, one might imagine an inner region that behaves like a Newtonian liquid at the infinite-shear viscosity, an outer region that behaves like a Newtonian liquid at a higher viscosity (shear-thinning liquid) or lower viscosity (shear-thickening liquid), and an intermediate region that connects the two. Regardless of whether this conjecture is borne out, development of a rigorous theory for non-Newtonian liquids along the lines of Cox’s work would likely shed light on the limitations of various approximate theories of low-speed dynamic wetting in non-Newtonian liquids that have been developed specifically in the context of droplet spreading (Carré & Eustache Reference Carré and Eustache2000; Betelú & Fontelos Reference Betelú and Fontelos2003; Starov et al. Reference Starov, Tyatyushkin, Velarde and Zhdanov2003; Betelú & Fontelos Reference Betelú and Fontelos2004; Wang et al. Reference Wang, Lee, Peng and Lai2007a,Reference Wang, Zhang, Lee and Pengb; Liang et al. Reference Liang, Wang, Duan and Min2012; Lu, Wang & Duan Reference Lu, Wang and Duan2016; Wang et al. Reference Wang, Min, Zhang and Duan2018).
7 Conclusions
The results of our work indicate that shear thinning postpones the onset of dynamic wetting failure whereas shear thickening promotes it. Strong viscosity gradients arise near the dynamic contact line, influencing the tangential stress balance there. In shear-thinning liquids, a lower tangential stress arises in the liquid phase (compared to a Newtonian liquid of the same zero-shear viscosity), so a lower tangential stress is required in the air phase to balance this. This lower tangential stress is achieved through a thickening of the air film, which in turn lowers the pressure gradients in the air phase near the contact line. As a result, the capillary-stress gradients are more effective at pumping air away from the contact line, increasing the maximum speed at which steady wetting can be maintained. The opposite scenario arises in shear-thickening liquids. Our results can be interpreted in terms of an effective viscosity, and demonstrate that similar physical mechanisms govern dynamic wetting failure in Newtonian, shear-thinning and shear-thickening liquids. Shear thinning leads to a lower effective viscosity, whereas shear thickening leads to a higher effective viscosity.
For low-speed dynamic wetting, our results indicate that shear thinning leads to less viscous bending of the interface and thus smaller values of the dynamic contact angle relative to a Newtonian liquid of the same zero-shear viscosity, consistent with experimental observations (Seevaratnam et al. Reference Seevaratnam, Suo, Ramé, Walker and Garoff2007; Wei et al. Reference Wei, Garoff and Walker2009a). In contrast, shear thickening leads to more viscous bending and larger values of the dynamic contact angle. The dependence of the dynamic contact angle on the capillary number appears to be well described by the asymptotic theory of Cox (Reference Cox1986).
The results of this work appear to be qualitatively consistent with the motivating experiments described in § 2 as well as other experiments described in § 1. While outside the scope of the present work, a systematic experimental study using a plunge-tank geometry will be essential for making a more quantitative comparison between model predictions and experiments. Similarly, extension of the model to account for the more complex geometries encountered in actual coating processes (e.g. curtain coating) would be extremely valuable. The results of such studies will provide further insight into the mechanisms underlying dynamic wetting failure in non-Newtonian liquids, and insight into how liquid rheology can be controlled to postpone air entrainment as much as possible.
Acknowledgements
This work is supported by the National Science Foundation under grant no. CBET-1434016. V.C. was also supported by the Onassis Foundation – Scholarship ID: F ZP 059-1/2019-2020.
Declaration of interests
The authors report no conflict of interest.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2020.154.
