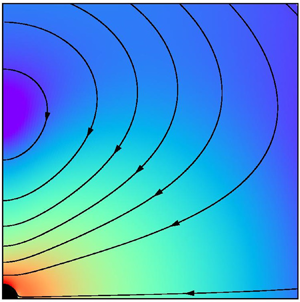
1. Introduction
Problems regarding viscous drag and thermophoresis on spherical particles immersed in a rarefied gas are classical in the field of rarefied gas dynamics and have been investigated by many authors over the years; see, e.g. Yamamoto & Ishihara (Reference Yamamoto and Ishihara1988), Takata, Aoki & Sone (Reference Takata, Aoki, Sone, Shizgal and Weaver1992), Loyalka (Reference Loyalka1992), Beresnev & Chernyak (Reference Beresnev and Chernyak1995), Takata & Sone (Reference Takata and Sone1995) and Chernyak & Sograbi (Reference Chernyak and Sograbi2019). The study of this topic is motivated by its fundamental importance for the understanding of the physics underlying some phenomena, such as the transport of aerosols in the atmosphere, and for practical applications such as the development of technologies in the fields of microfluidics, semiconductor industry, security of nuclear plants, etc. The well-known equations of continuum mechanics, namely the Navier–Stokes–Fourier equations (see, e.g. Landau & Lifshitz Reference Landau and Lifshitz1989), can be used to calculate the drag and the thermophoretic forces acting on a sphere, as well as the macroscopic characteristics of the gas flow around it, only in situations where the molecular mean free path is significantly smaller than a characteristic length of the gas flow domain so that the continuum hypothesis is still valid. The Knudsen number (
$Kn$), defined as the ratio of the molecular mean free path to a characteristic length of the gas flow, is the parameter often used to classify the gas flow regimes. The equations of continuum mechanics are valid when 
$Kn \ll 1$. For instance, in air at standard conditions, the molecular mean free path is approximately 0.065 
$\mathrm {\mu }$m. Then, for small particles originated from several sources moving through the air, the Knudsen number varies from about 0 to 65 when the size of particles ranges from 100 to 10
$^{-3}$
$\mathrm {\mu }$m. Therefore, the modelling of the gas flow around aerosols in the atmosphere, as well as the movement of these particles itself, cannot be accurately described by the classical equations of continuum mechanics. Moreover, even in the continuum regime, the Navier–Stokes–Fourier equations cannot predict the negative thermophoresis, which means the movement of aerosol particles from cold to hot regions. This phenomenon was first predicted theoretically, and satisfactorily explained as a result of the thermal stress slip flow, by Sone (Reference Sone1972) in case of aerosol particles with high thermal conductivity related to that of the carrier gas. However, experimental data regarding this phenomenon are still scarce in the literature because the detection is very difficult. Actually, the more recent experimental data concerning negative thermophoresis are provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016), in which the thermophoretic force on a copper sphere in argon gas was measured in a wide range of the gas rarefaction.
Historically, the viscous drag force on a sphere was first investigated by Stokes (Reference Stokes1845) via hydrodynamic analysis based on the Navier–Stokes–Fourier equations, with the derivation of his famous formula for the drag force on a sphere in a slow flow; see, e.g. Landau & Lifshitz (Reference Landau and Lifshitz1989). Regarding the thermophoresis, the first attempt to calculate the thermal force on a sphere in a gas with a temperature gradient was done by Epstein (Reference Epstein1967). Since the theories of both Stokes and Epstein were valid in the continuum regime, many attempts to modify the equations of continuum mechanics as well as the boundary conditions were proposed over the years to increase their range of applicability in the Knudsen number. For instance, the correction factor proposed by Cunningham (Reference Cunningham1910) to consider the non-continuum effects of gas slippage on the boundary was incorporated in the Stokes formula so that its applicability was extended to the so-called slip flow regime. Concerning the thermophoresis, a continuum analysis based on the Navier–Stokes–Fourier equations with slip corrections in the boundary condition was first carried out by Brock (Reference Brock1962) in an attempt to improve the previous theory proposed by Epstein. Methods based on the use of higher-order kinetic theory approximations, as that first proposed by Grad (Reference Grad1949), were also employed to solve the problems of drag and thermophoresis on a sphere. For instance, Sone (Reference Sone1972) obtained an expression for the thermophoretic force acting on a sphere with uniform temperature corrected up to the second order in the Knudsen number using an asymptotic theory for small Knudsen numbers, and predicted the negative thermophoresis as a result of the thermal stress slip flow. In a more recent paper, Torrilhon (Reference Torrilhon2010) investigated a slow flow past a sphere on the basis of the regularized 13-moment equations as proposed by Struchtrup & Torrilhon (Reference Struchtrup and Torrilhon2003), a method which relies on the combination of the moment approximation and asymptotic expansion in kinetic theory of gases. Similarly, Padrino, Sprittles & Lockerby (Reference Padrino, Sprittles and Lockerby2019) investigated the thermophoresis on a sphere by employing the same method and predicted the negative thermophoresis. According to Torrilhon (Reference Torrilhon2010) and Padrino et al. (Reference Padrino, Sprittles and Lockerby2019), the regularized 13-moment method can be used to describe the drag and the thermophoresis on a sphere when 
$Kn < 1$. In fact, although many efforts have been done over the years to expand the validity of the continuum models in the description of gas flows, it is well known that all the theories and methods currently available fail in describing gas flows properly when 
$Kn \sim 1$ or 
$Kn \gg 1$. In these kinds of situations, corresponding to transition and free molecular regimes, the problem must be solved at the microscopic level via the methods of rarefied gas dynamics, which are based on either the solution of the Boltzmann equation, e.g. Cercignani (Reference Cercignani1988) and Sharipov (Reference Sharipov2016), and its related kinetic models, e.g. Bhatnagar, Gross & Krook (Reference Bhatnagar, Gross and Krook1954) and Shakhov (Reference Shakhov1968), or the direct simulation Monte Carlo method as pioneered by Bird (Reference Bird1994).
Although an extensive literature concerning the topic under investigation in the whole range of the Knudsen number based on kinetic theory is available, most of the papers rely on the assumption of diffuse reflection or complete accommodation of gas molecules on the surface; see, e.g. the reviews on thermophoresis by Zheng (Reference Zheng2002) and Young (Reference Young2011). However, in practice, the assumption of complete accommodation of gas molecules on the surface is not always valid and its use can lead to large deviations of theoretical predictions from experimental data. As pointed out by Zheng (Reference Zheng2002), actually the gas–surface interaction law is most probably something between the widely used diffuse and specular reflection models. Thus, the so-called accommodation coefficients on the surface should be conveniently introduced to accurately describe the gas–surface interaction. To the best of our knowledge, Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Beresnev, Chernyak & Fomyagin (Reference Beresnev, Chernyak and Fomyagin1990) were the first authors to study the influence of the gas–surface interaction law on the drag and thermophoretic forces acting on a sphere with basis on a kinetic model to the Boltzmann equation in the whole range of the Knudsen number. These authors solved numerically the linearized kinetic equation proposed by Shakhov (Reference Shakhov1968) by using the integral-moment method with the boundary condition written in terms of accommodation coefficients of momentum and energy as proposed by Shen (Reference Shen1967). According to this condition, the distribution function of molecules reflected from the surface is expanded in Hermite polynomials and unknown accommodation coefficients are determined from the conservation laws of momentum and energy on the surface. The qualitative results presented by the authors show a strong dependence of the drag and thermophoretic forces on the accommodation coefficients. Moreover, their results predict the negative thermophoresis in the case of a highly heat conducting sphere in the continuum regime as dependent on the tangential momentum accommodation coefficient. However, Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990) applied the variational method which implies the use of trial functions. In other words, the macroscopic quantities are assumed a priori to be parametric functions of the radial coordinate. Then, the functions parameters are calculated using some variational principle. Such an assumption introduces a numerical error which cannot be estimated without a direct numerical solution of the kinetic equation. Recently, Chernyak & Sograbi (Reference Chernyak and Sograbi2019) calculated the drag and thermophoretic forces for several models on a non-diffuse gas–surface interaction, but their results are restricted to the free molecular regime. Thus, till now, no numerical solution of the kinetic equation subject to a non-diffuse scattering is available in the literature for rarefied gas flows past a sphere. In contrast to the variational solution by Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990), direct numerical calculations based on the kinetic equation requires more detailed information about the gas–surface interaction, namely, the scattering kernel. Maxwell (Reference Maxwell1879) proposed the diffuse-specular model assuming that only a portion of the incident particles is reflected diffusely, while the remaining portion is reflected specularly. As pointed out by Sharipov (Reference Sharipov2003b), this widely used model contradicts some experimental data. For instance, several experimental works (see, e.g. Podgursky & Davis Reference Podgursky and Davis1961 and Edmonds & Hobson Reference Edmonds and Hobson1965) showed that the exponent in the thermomolecular pressure difference (TPD) at low pressures varies from 0.4 to 0.5, but the model by Maxwell always provides the TPD index equal to 0.5 in the free molecular regime. To improve the Maxwell model, Epstein (Reference Epstein1967) assumed that the probability of the diffuse reflection depends on the velocity of the incident particles. This model contains some parameters which a priori do not have any physical meaning. The model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) has two parameters having the physical meaning, namely, the tangential momentum accommodation coefficient (TMAC) and normal energy accommodation coefficient (NEAC). Later, Cercignani (Reference Cercignani1972) derived this kernel from a physical model of a surface based on the Fokker–Planck equation. Some authors (see, e.g. Liang, Li & Ye Reference Liang, Li and Ye2013 and Spijker et al. Reference Spijker, Markvoort, Nedea and Hilbers2010) analysed several gas–surface interaction models to microflows and nanoflows, specifically the models proposed by Maxwell (Reference Maxwell1879), Cercignani & Lampis (Reference Cercignani and Lampis1971) and Yamamoto, Takeuchi & Hyakutake (Reference Yamamoto, Takeuchi and Hyakutake2007), and concluded that the Cercignani–Lampis model shows a better comparison with molecular dynamics simulation. Kosuge et al. (Reference Kosuge, Aoki, Takata, Hattori and Sakai2011) analysed the influence of the gas–surface interaction model on the gas flow induced by thermal effects in the vicinity of a boundary, e.g. the thermal creep flow, the thermal stress slip flow and the thermal edge flow which are peculiar to rarefied gases. This type of flow induced solely by thermal effects vanishes in the free molecular regime when the Maxwell model of gas–surface interaction is used in the boundary condition. Kosuge et al. (Reference Kosuge, Aoki, Takata, Hattori and Sakai2011) carried out a deterministic computation based on the integral equation as well as on the direct simulation Monte Carlo (DSMC) method and concluded that the Cercignani–Lampis boundary condition accurately predicts the steady flow induced by thermal effects even in the free molecular limit. Sazhin et al. (Reference Sazhin, Kulev, Borisov and Gimelshein2007), Yakunchikov, Kovalev & Utyuzhnikov (Reference Yakunchikov, Kovalev and Utyuzhnikov2012) and Chernyak & Sograbi (Reference Chernyak and Sograbi2019) analysed both Epstein and Cercignani–Lampis (CL) models, but they were not able to point out which of these models was better. Yakunchikov et al. (Reference Yakunchikov, Kovalev and Utyuzhnikov2012), based on numerical results from molecular dynamics, and Wu & Struchtrup (Reference Wu and Struchtrup2017), based on the comparison between experimental data and numerical results obtained from the Boltzmann equation, proposed a combination of the Epstein and CL models which significantly increased the number of adjusting parameters. Thus, the Cercignani–Lampis scattering kernel can be actually considered the most reliable model of the gas–surface interaction because it provides a correct physical description of many transport phenomena in gases which are not described correctly by other models available in the literature.
As mentioned above, the CL model contains two independent accommodation coefficients, namely TMAC ranging from 0 to 2 and NEAC varying from 0 to 1. In practice, the values of these accommodation coefficients extracted from experiments can be found in the literature; see, e.g. Semyonov, Borisov & Suetin (Reference Semyonov, Borisov and Suetin1984), Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011), Sazhin, Borisov & Sharipov (Reference Sazhin, Borisov and Sharipov2001) and Sharipov & Moldover (Reference Sharipov and Moldover2016) for several gases and surfaces. For instance, according to Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011) and Sharipov & Moldover (Reference Sharipov and Moldover2016), the NEAC ranges from 0 to 0.1 for helium and from 0.5 to 0.95 for argon at ambient temperature and several different smooth metallic surfaces such as aluminum, platinum and stainless steel. Moreover, the TMAC of helium and argon ranges from 0.5 to 1 at the same conditions. According to the results presented by Chernyak & Sograbi (Reference Chernyak and Sograbi2019), in the free molecular regime the thermophoretic force is sensitive to both TMAC and NEAC.
As is known, the thermophoretic force is the so-called cross-effect from the viewpoint of non-equilibrium thermodynamics (see, e.g. De Groot & Mazur Reference De Groot and Mazur1984), i.e. it is coupled with another cross-effect by the reciprocity relation. Basing on the general properties of the Boltzmann equation and its boundary condition, Sharipov (Reference Sharipov2010) showed that the thermophoretic force of a particle is related to a heat flux around the same particle in the drag force problem. However, this relation has not been verified numerically because of its complexity.
In the present work, the influence of the gas–surface interaction law on the drag and thermophoretic forces acting on a sphere of high thermal conductivity immersed in a monatomic rarefied gas is investigated by employing the CL scattering kernel. The linearized kinetic equation proposed by Shakhov (Reference Shakhov1968) is solved numerically by the discrete velocity method taking into account the discontinuity of the distribution function of molecular velocities around a convex body; see, e.g. Sone (Reference Sone1966) and Sone & Takata (Reference Sone and Takata1992). It is worth mentioning that the linearized approach is legitimate in the majority of problems concerning aerosols because the Mach number of the induced flow, as well as the temperature and density deviations, are very small.
The linearized Shakhov model is the most suitable to deal with the problem in question because it maintains the original properties of the Boltzmann equation and provides the correct Prandtl number, i.e. the correct values of both gas viscosity and heat conductivity. The advantage of using this model is that its solution requires a modest computational effort in comparison to that required to solve the Boltzmann equation itself. At the same time it provides a good accuracy. For instance, Graur & Polikarpov (Reference Graur and Polikarpov2009) calculated the heat flux between parallel plates from the Shakhov kinetic equation and showed that the deviation of their results from those obtained by Ohwada (Reference Ohwada1996) from the Boltzmann equation and hard-spheres potential is less than 3 %. In the case of planar Couette flow, a comparison presented by Sharipov (Reference Sharipov2016) between the results obtained from the solution of the Shakhov model via the discrete velocity method and those obtained by Siewert (Reference Siewert2003) from the linearized Boltzmann equation based on hard-spheres potential and the DSMC method based on the ab initio potential for argon gas given by Sharipov & Strapasson (Reference Sharipov and Strapasson2013) shows that the discrepancy among results obtained from quite different methods does not exceed 1 %. Concerning the problems of drag and thermophoresis on a sphere, the comparison is still scarce in the literature. Nonetheless, Beresnev & Chernyak (Reference Beresnev and Chernyak1995) showed that the discrepancy between their results for the thermophoretic force on a sphere obtained from the Shakhov model is not greater than 5 %–7 % from those obtained by Takata et al. (Reference Takata, Aoki, Sone, Shizgal and Weaver1992) from the linearized Boltzmann equation for hard-spheres potential. Thus, the reliability of the Shakhov model is supported by literature.
The viscous drag and the thermophoretic forces on the sphere, as well as the macroscopic characteristics of the gas flow around it, are calculated in a range of the gas rarefaction which allows us to verify the influence of the accommodation coefficients on these forces in the free molecular, transition and hydrodynamic regimes. The values of the TMAC and NEAC are chosen with basis on experimental data as given by Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011) and Sharipov & Moldover (Reference Sharipov and Moldover2016).
The reciprocity relation between the cross phenomena is verified and used as an accuracy criterion of the numerical calculations. The results obtained for both the drag and thermophoretic forces on the sphere in the whole range of the gas rarefaction are compared to those results provided by Beresnev & Chernyak (Reference Beresnev and Chernyak1995), Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990), Takata et al. (Reference Takata, Aoki, Sone, Shizgal and Weaver1992) and Takata, Sone & Aoki (Reference Takata, Sone and Aoki1993) in case of diffuse scattering on the surface. Moreover, the results obtained for the forces in the free molecular regime are compared to those presented by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) in a wide range of TMAC and NEAC.
Regarding the comparison with experimental data, it is worth mentioning that although many data are available in the literature, such a comparison is still a difficult task because in most of the experiments the carrier gas is air or a polyatomic gas, and the results are limited to a certain range of the Knudsen number which usually covers the continuum and near-continuum regimes. Moreover, the experiments involve particles of different materials and some physical properties of matter, such as the thermal conductivity, which may play an important role in the description of phoretic phenomena. A list of measurements concerning thermophoresis on spherical particles can be found in the review by Young (Reference Young2011), while a critical review on the drag force on a sphere in the transition regime which includes experimental data is given by Bailey et al. (Reference Bailey, Barber, Emerson, Lockerby and Reese2004). In the present work a comparison with the more recent data on thermophoresis provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) in the case of a copper sphere in argon gas is presented.
2. Formulation of the problem
We consider a sphere of radius 
$R_0$ at rest placed in a monatomic rarefied gas. Far from the sphere, the gas flows with a constant bulk velocity 
$U_{\infty }$ and has a temperature gradient 
$\nabla T_{\infty }=\partial T/\partial z'$ in the 
$z'$-direction as shown in figure 1. Due to the problem geometry, it is convenient to introduce spherical coordinates 
$(r',\theta ,\phi )$ in the physical space. Then according to figure 1, the components of the position vector 
${\boldsymbol r}'$ of gas molecules are given as
\begin{gather} x'=r'\sin{\theta}\cos{\phi}, \end{gather}
\begin{gather}y'=r'\sin{\theta}\sin{\phi}, \end{gather}
\begin{gather}z'=r'\cos{\theta}. \end{gather}
Moreover, the components of the molecular velocity vector 
${\boldsymbol v}$ read as
\begin{gather} v_x=(v_r\sin{\theta}+v_{\theta}\cos{\theta})\cos{\phi}-v_{\phi}\sin{\phi}, \end{gather}
\begin{gather}v_y=(v_r\sin{\theta}+v_{\theta}\cos{\theta})\sin{\phi}+v_{\phi}\cos{\phi}, \end{gather}
\begin{gather}v_z=v_r\cos{\theta}-v_{\theta}\sin{\theta}, \end{gather}
where 
$v_r$, 
$v_{\theta }$ and 
$v_{\phi }$ are the radial, polar and azimuthal components of the molecular velocity vector, respectively, which are written in spherical coordinates 
$(v,\theta ',\phi ')$ in the velocity space as
\begin{gather} v_r=v\cos{\theta'}, \end{gather}
\begin{gather}v_{\theta}=v_t\cos{\phi'}, \end{gather}
\begin{gather}v_{\phi}=v_t\sin{\phi'}, \end{gather}with the tangential component given as
\begin{equation} v_t=\sqrt{v_{\theta}^{2}+v_{\phi}^{2}}=v\sin{\theta'}. \end{equation}
Figure 1. Formulation of the problem.
It is assumed that the thermal conductivity of the spherical particle is significantly higher than that corresponding to the carrier gas. As a consequence, the temperature of the sphere is uniform and equal to the gas temperature in equilibrium. Let us denote by 
$n_0$, 
$T_0$ and 
$p_0$ the number density, temperature and pressure of the gas in thermodynamic equilibrium, respectively. Two dimensionless thermodynamic forces are introduced here as follows:
\begin{equation} X_u=\frac{U_{\infty}}{v_0},\quad X_T=\frac{\ell_0}{T_0} \frac{\partial T} {\partial z'}.\end{equation}
Here 
$\ell _0$ and 
$v_0$ denote the equivalent free path and the most probable molecular velocity, defined as
\begin{equation} \ell_0=\frac{\mu_0v_0}{p_0}, \quad v_0=\sqrt{\frac{2kT_0}{m}}, \end{equation}
where 
$\mu _0$ denotes the viscosity of the gas at temperature 
$T_0$, while 
$m$ and 
$k$ are the molecular mass and the Boltzmann constant, respectively. It is assumed that the thermodynamic forces defined in (2.5a,b) are very small, i.e.
\begin{equation} |X_u| \ll 1, \quad |X_T| \ll 1. \end{equation}These assumptions of weak disturbance from equilibrium allow us to split the problem into two independent parts corresponding to viscous drag and thermophoresis on the sphere. Hereafter, the dimensionless sphere radius as well as the molecular position and velocity vectors are introduced as follows:
\begin{equation} r_0=\frac{R_0}{\ell_0},\quad {\boldsymbol r}=\frac{{\boldsymbol r}'}{\ell_0},\quad {\boldsymbol c}=\frac{{\boldsymbol v}}{v_0}. \end{equation}
The pressure of the gas is constant and it is given by the state equation of an ideal gas as 
$p_0=n_0kT_0$. As a consequence, the asymptotic behaviour of the number density 
$n({\boldsymbol r})$ and temperature 
$T({\boldsymbol r})$ of the gas far from the sphere are given as
\begin{gather} n_{\infty}=\lim_{r\rightarrow \infty} n({\boldsymbol r})=n_0(1-zX_T), \end{gather}
\begin{gather}T_{\infty}=\lim_{r\rightarrow \infty}T({\boldsymbol r})=T_0(1+zX_T). \end{gather}
The main parameter of the problem is the rarefaction parameter, 
$\delta$, which is inversely proportional to the Knudsen number, but defined as the ratio of the sphere radius to the equivalent molecular free path, i.e.
\begin{equation} \delta=\frac{R_0}{\ell_0}=r_0. \end{equation}
When 
$\delta \ll 1$ the gas is in the free molecular regime, while the opposite limit, 
$\delta \gg 1$, corresponds to the continuum or hydrodynamic regime. In other situations, the gas is in the so-called transition regime.
The model of gas–surface interaction law proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) is employed in the boundary condition. According to this model, the type of gas–surface interaction is chosen by setting appropriate values of NEAC and TMAC. Henceforth, these accommodation coefficients will be denoted by 
$\alpha _n$ and 
$\alpha _t$, respectively. The diffuse scattering or complete accommodation on the surface corresponds to 
$\alpha _n =1$ and 
$\alpha _t=1$.
The viscous drag and thermophoretic forces acting on the sphere are calculated in a range of the gas rarefaction parameter, 
$\delta$, which covers all the regimes of the gas flow, i.e. the free molecular, transitional and hydrodynamic regimes. Moreover, various values of accommodation coefficients are considered in the calculations in order to analyse the influence of the gas–surface interaction law on the solution of the problem. The flow fields, i.e. the density and temperature deviations from equilibrium, bulk velocity and heat flux around the sphere are also calculated. Some numerical results are compared to those found in the literature. The reciprocity relation between cross phenomena is obtained at an arbitrary distance from the sphere and then verified numerically.
3. Kinetic equation
For the problem in question, the Boltzmann equation in the absence of external forces reads as
\begin{equation} {\boldsymbol v}\boldsymbol{\cdot} \frac{\partial f}{\partial {\boldsymbol r}'}=Q(\,ff_*),\end{equation}
where 
$f=f({\boldsymbol r}',{\boldsymbol v})$ is the distribution function of molecular velocities and 
$Q(\,ff_*)$ is the collision integral whose expression can be found in the literature; see, e.g. Ferziger & Kaper (Reference Ferziger and Kaper1972), Cercignani (Reference Cercignani1975) and Sharipov (Reference Sharipov2016). Here, the model proposed by Shakhov (Reference Shakhov1968) for the collision integral is employed due to its reliability to deal with problems regarding both mass and heat transfer. Then, the collision integral reads as
\begin{equation} Q(\,ff_*)=Q_S=\nu_S\left\{f^{M}\left[1+\frac{4}{15}\left(\frac{V^{2}}{v_0^{2}}-\frac 52\right) \frac{{\boldsymbol Q}\boldsymbol{\cdot} {\boldsymbol V}}{p_0v_0^{2}}\right]-f({\boldsymbol r}',{\boldsymbol v}) \right\}, \end{equation}where
\begin{equation} f^{M}({\boldsymbol r}',{\boldsymbol v})=\left[\frac{m}{2{\rm \pi} kT({\boldsymbol r}')}\right]^{3/2}\exp{\left[-\frac{m{\boldsymbol V}^{2}}{2kT({\boldsymbol r}')}\right]} \end{equation}
is the local Maxwellian function. The quantity 
$\nu _S$ has the order of the intermolecular interaction frequency and 
${\boldsymbol V}={\boldsymbol v}-{\boldsymbol U}$ is the peculiar velocity so that 
$V=|{\boldsymbol V}|$ denotes its magnitude. We denote by 
${\boldsymbol U}({\boldsymbol r}')$ and 
${\boldsymbol Q}({\boldsymbol r}')$ the bulk velocity and heat flux vectors, respectively.
The assumptions of smallness of the thermodynamic forces, given in (2.7a,b), allow us to linearize the kinetic equation by representing the distribution function as
\begin{equation} f({\boldsymbol r},{\boldsymbol c})=f_R^{M}[1+h^{(T)}({\boldsymbol r},{\boldsymbol v})X_T + h^{(u)}({\boldsymbol r},{\boldsymbol v})X_u], \end{equation}
where 
$h^{(T)}$ and 
$h^{(u)}$ are the perturbation functions due to the thermodynamic forces 
$X_T$ and 
$X_u$. The reference Maxwellian function is given by
\begin{equation} f_R^{M}=f^{M}=f_0\left[1+z\left(c^{2}-\tfrac 52\right)X_T+2c_zX_u\right], \end{equation}
where 
$f_0$ is the global Maxwellian function and 
$c=|{\boldsymbol c}|$ is the magnitude of the dimensionless molecular velocity defined in (2.8a–c).
Then, after introducing the representation (3.4) into (3.1), and also introducing the dimensionless quantities given by (2.8a–c), the linearized kinetic equation corresponding to each thermodynamic force is written as
\begin{equation} \hat{D}h^{(n)}=\hat{L}_Sh^{(n)} + g^{(n)}({\boldsymbol r},{\boldsymbol c}),\quad n=T, u, \end{equation}where the operator
\begin{equation} \hat{D}={\boldsymbol c}\boldsymbol{\cdot}\frac{\partial}{\partial {\boldsymbol r}} \end{equation}and the linearized collision integral reads as
\begin{equation} \hat{L}_Sh^{(n)}=\nu^{(n)}+\left(c^{2}-\tfrac 32\right) \tau^{(n)}+2{\boldsymbol c}\boldsymbol{\cdot}{\boldsymbol u}^{(n)}+\tfrac{4}{15}\left(c^{2}-\tfrac 52\right){\boldsymbol c}\boldsymbol{\cdot} {\boldsymbol q}^{(n)}-h^{(n)}. \end{equation}The free terms are given by
\begin{equation} g^{(T)}=-c_z\left(c^{2}-\tfrac 52\right),\quad g^{(u)}=0. \end{equation} The dimensionless quantities on the right-hand side of (3.8) correspond to the density and temperature deviations from equilibrium, bulk velocity and heat flux vectors, respectively, due to the corresponding thermodynamic force. These quantities are calculated in terms of the distribution function of molecular velocities, and details regarding these calculations are given by Ferziger & Kaper (Reference Ferziger and Kaper1972). In our notation, these quantities are written in terms of the perturbation function 
$h^{(n)}$ corresponding to each thermodynamic force as
\begin{gather} \nu^{(n)}({\boldsymbol r})=\frac{1}{{\rm \pi}^{3/2}}\int h^{(n)}({\boldsymbol r},{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}, \end{gather}
\begin{gather}\tau^{(n)}({\boldsymbol r})=\frac{2}{3{\rm \pi}^{3/2}}\int\left(c^{2}-\frac 32\right)h^{(n)}({\boldsymbol r},{\boldsymbol c})\,\text{e}^{-c^{2}}\, \text{d}{\boldsymbol c}, \end{gather}
\begin{gather}{\boldsymbol u}^{(n)}({\boldsymbol r})=\frac{1}{{\rm \pi}^{3/2}}\int {\boldsymbol c}h^{(n)}({\boldsymbol r},{\boldsymbol c})\,\text{e}^{-c^{2}}\, \text{d}{\boldsymbol c}, \end{gather}
\begin{gather}{\boldsymbol q}^{(n)}({\boldsymbol r})=\frac{1}{{\rm \pi}^{3/2}}\int{\boldsymbol c}\left(c^{2}-\frac 52\right)h^{(n)}({\boldsymbol r},{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}. \end{gather} Far from the sphere (
${\boldsymbol r}\rightarrow \infty$), the asymptotic behaviour of the perturbation functions are obtained from the Chapmann–Enskog solution for the linearized kinetic equation as
\begin{gather} h_{\infty}^{(T)}=\lim_{{\boldsymbol r}\rightarrow \infty}h^{(T)}({\boldsymbol r},{\boldsymbol c})=-\frac 32 c_z\left(c^{2}-\frac 52\right), \end{gather}
\begin{gather}h_{\infty}^{(u)}=\lim_{{\boldsymbol r}\rightarrow \infty}h^{(u)}({\boldsymbol r},{\boldsymbol c})=0. \end{gather} Due to the spherical geometry of the problem, it is convenient to write the kinetic equation (3.6) in spherical coordinates in both physical and molecular velocity spaces. Details regarding this transformation are given by Shakhov (Reference Shakhov1967). Moreover, the problem has symmetry on the azimuthal angle 
$\phi$. Therefore, after some algebraic manipulation, the left-hand side of the kinetic equation (3.6) is written as
\begin{equation} \hat{D}h^{(n)}=c_r\frac{\partial h^{(n)}}{\partial r}- \frac{c_t}{r} \frac{\partial h^{(n)}}{\partial \theta'}+\frac{c_t}{r}\cos{\phi'} \frac{\partial h^{(n)}}{\partial \theta}- \frac{c_t}{r}\sin{\phi'}\cot{\theta}\frac{\partial h^{(n)}}{\partial \phi'}, \end{equation}
where 
$h^{(n)}=h^{(n)}(r,\theta ,{\boldsymbol c})$ and 
${\boldsymbol c}=(c, \theta ',\phi ')$. The symmetry of the solution on the azimuthal angle also allows us to eliminate the dependence of the moments of the perturbation function on the angle 
$\phi$. Thus, the density and temperature deviations given in (3.10) and (3.11) are written as
\begin{gather} \nu^{(n)}(r,\theta)=\frac{1}{{\rm \pi}^{3/2}}\int h^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}, \end{gather}
\begin{gather}\tau^{(n)}(r,\theta)=\frac{2}{3{\rm \pi}^{3/2}}\int \left(c^{2}-\frac 32\right)h^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}, \end{gather}
where 
$\text {d}{\boldsymbol c}=c^{2}\sin {\theta '}\,\text {d}c\,\text {d}\theta '\,\text {d}\phi '$. Moreover, the non-zero components of the bulk velocity and heat flux vectors given in (3.12) and (3.13) are written as
\begin{gather} u_r^{(n)}(r,\theta)=\frac{1}{{\rm \pi}^{3/2}}\int c_rh^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\, \text{d}{\boldsymbol c}, \end{gather}
\begin{gather}u_{\theta}^{(n)}(r,\theta)=\frac{1}{{\rm \pi}^{3/2}}\int c_{\theta}h^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}, \end{gather}
\begin{gather}q_r^{(n)}(r,\theta)=\frac{1}{{\rm \pi}^{3/2}}\int c_r\left(c^{2}-\frac 52\right)h^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\,\text{d}{\boldsymbol c}, \end{gather}
\begin{gather}q_{\theta}^{(n)}(r,\theta)=\frac{1}{{\rm \pi}^{3/2}}\int c_{\theta}\left(c^{2}-\frac 52\right)h^{(n)}(r,\theta,{\boldsymbol c})\,\text{e}^{-c^{2}}\, \text{d}{\boldsymbol c}. \end{gather} Similarly to the moments appearing in the kinetic equation, the force on the sphere in the 
$z'$-direction is calculated in terms of the distribution function of molecular velocities on the boundary as
\begin{equation} F_z'=-\int_{\Sigma'_w}\text{d}\Sigma'_w\int mv_rv_z \,f({\boldsymbol r}_0,{\boldsymbol v})\, \text{d}{\boldsymbol v}, \end{equation}
where 
$\text {d}\Sigma '_w=R_0^{2}\sin {\theta }\,\text {d}\theta \,\text {d}\phi$ is an area element taken in the surface of the sphere. For convenience, the dimensionless force is introduced here as
\begin{equation} F_z=\frac{F_z'}{4{\rm \pi} R_0^{2} p_0}. \end{equation}Then, after the introduction of the representation (3.4) into (3.23) and some algebraic manipulation, the dimensionless force acting on the sphere reads as
\begin{equation} F_z=F_TX_T + F_uX_u, \end{equation}where the dimensionless thermophoretic and drag forces are given as
\begin{gather} F_T=-\frac{1}{2{\rm \pi}^{5/2}}\int_{\Sigma_w}\text{d}\Sigma_w \int c_rc_z\,\text{e}^{-c^{2}}\left[h^{(T)}(r_0,\theta, {\boldsymbol c})+z_0 \left(c^{2}-\frac 52\right)\right]\text{d}{\boldsymbol c}, \end{gather}
\begin{gather}F_u=-\frac{1}{2{\rm \pi}^{5/2}}\int_{\Sigma_w}\text{d}\Sigma_w \int c_rc_z\,\text{e}^{-c^{2}}[h^{(u)}(r_0,\theta,{\boldsymbol c})+2c_z]\,\text{d}{\boldsymbol c}, \end{gather}
with 
$\text {d}\Sigma _w=\text {d}\Sigma '_w/R_0^{2}$.
4. Boundary condition
The boundary conditions for both the drag and thermophoresis on the spherical surface are obtained from the relation between the distribution functions of incident particles on the wall and reflected particles from the wall. According to Cercignani (Reference Cercignani1975) and Sharipov (Reference Sharipov2016), the general form of the linearized boundary condition at the surface reads as
\begin{equation} h^{+(n)}=\hat{A}h^{-(n)}+h_w^{(n)}-\hat{A}h_w^{(n)}, \end{equation}
where the signal ‘
$+$’ denotes the reflected particles from the surface, while the signal ‘
$-$’ denotes the incident particles on the surface. The source terms, obtained from (3.5), are given as
\begin{equation} h_w^{(T)}=-z_0\left(c^{2}-\tfrac 52\right),\quad h_w^{(u)}=-2c_z, \end{equation}
where 
$z_0=r_0\cos {\theta }$ and 
$c_z=c_r\cos {\theta }-c_{\theta }\sin {\theta }$.
In the spherical coordinates the scattering operator 
$\hat {A}$ can be decomposed as
\begin{equation} \hat{A}h^{(n)}=\hat{A}_r\hat{A}_{\theta}\hat{A}_{\phi}h^{(n)}, \end{equation}where
\begin{gather} \hat{A}_r\xi=-\frac{1}{c_r}\int_{c_r'<0}c_r'\exp{(c_r^{2}-c_r'^{2})}R_r(c_r\rightarrow c_r')\xi\,\text{d}c_r', \end{gather}
\begin{gather}\hat{A}_i\xi=\int_{-\infty}^{\infty}\exp{(c_i^{2}-c_i'^{2})}R_i(c_i\rightarrow c_i')\xi \,\text{d}c_i',\quad i=\theta, \phi, \end{gather}
for an arbitrary 
$\xi$ as a function of the molecular velocity. The functions 
$R_r$, 
$R_{\theta }$ and 
$R_{\phi }$ are components of the scattering kernel proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971), i.e.
\begin{equation} R({\boldsymbol c}\rightarrow {\boldsymbol c}')=R_r(c_r\rightarrow c_r')R_{\theta}(c_{\theta} \rightarrow c_{\theta}')R_{\phi}(c_{\phi}\rightarrow c_{\phi}'), \end{equation}where
\begin{gather} R_r(c_r\rightarrow c_r')=\frac{2c_r}{\alpha_n}\exp{\left[-\frac{c_r^{2}+(1-\alpha_n)c_r'^{2}}{\alpha_n}\right]} I_0\left(\frac{2\sqrt{1-\alpha_n}}{\alpha_n}c_rc_r'\right), \end{gather}
\begin{gather}R_i(c_i\rightarrow c_i')=\frac{1}{\sqrt{{\rm \pi} \alpha_t(2-\alpha_t)}}\exp{\left\{-\frac{[c_i-(1-\alpha_t) c_i']^{2}}{\alpha_t(2-\alpha_t)}\right\}},\quad i=\theta, \phi. \end{gather}
Here 
$I_0$ denotes the modified Bessel function of first kind and zeroth order. According to this model, the accommodation coefficients can vary in the ranges 
$0 \le \alpha _t \le 2$ and 
$0\le \alpha _n \le 1$. The case 
$\alpha _t=1$ and 
$\alpha _n=1$ corresponds to diffuse scattering or complete accommodation on the spherical surface, while the case 
$\alpha _t=0$ and 
$\alpha _n=0$ corresponds to specular reflection at the surface. It is worth noting that, for intermediate values of 
$\alpha _t$ and 
$\alpha _n$, the scattering kernel proposed by Cercignani–Lampis differs significantly from the diffuse specular which have just one accommodation coefficient.
It can be shown that the following relations are satisfied:
\begin{gather} \hat{A}_ic_i=(1-\alpha_t)c_i,\quad i=\theta, \phi, \end{gather}
\begin{gather}\hat{A}_ic_i^{2}=(1-\alpha_t)^{2}c_i^{2}+\tfrac 12 \alpha_t(2-\alpha_t), \end{gather}
\begin{gather}\hat{A}_ic_i^{3}=(1-\alpha_t)^{3}c_i^{3}+\tfrac 32 \alpha_t(2-\alpha_t)(1-\alpha_t)c_i, \end{gather}
\begin{gather}\hat{A}_rc_r=-\sqrt{\alpha_n}H_1(\eta), \end{gather}
\begin{gather}\hat{A}_rc_r^{2}=\alpha_n + (1-\alpha_n)c_r^{2}, \end{gather}
\begin{gather}\hat{A}_rc_r^{3}=-\alpha_n^{3/2}H_3(\eta). \end{gather}Here
\begin{equation} H_j(\eta)=2\,\text{e}^{-\eta^{2}}\int_{0}^{\infty}\xi^{j+1}\,\text{e}^{-\xi^{2}}I_0(2\eta \xi)\,\text{d}\xi,\quad \xi=\frac{c_r'}{\sqrt{\alpha_n}},\quad j=1, 3, \end{equation}and
\begin{equation} \eta=c_r\sqrt{\frac{1}{\alpha_n}-1}. \end{equation} Therefore, with the help of the relations (4.9)–(4.14), the boundary conditions at 
$r=r_0$ and 
$c_r > 0$, for each thermodynamic force are obtained from (4.1) as
\begin{gather} h^{+(T)}=\hat{A}h^{-(T)}+z_0[\alpha_n(1-c_r^{2})+\alpha_t(2-\alpha_t)(1-c_t^{2})], \end{gather}
\begin{gather}h^{+(u)}=\hat{A}h^{-(u)}-2\frac{z_0}{\delta}[(1-\alpha_t) c_r+\sqrt{\alpha_n}H_1(\eta)]-2\alpha_tc_z. \end{gather}5. Reciprocity relation
As it is known from the non-equilibrium thermodynamics (see, e.g. De Groot & Mazur Reference De Groot and Mazur1984) the reciprocity relations between cross phenomena represent an important criterion to verify the numerical precision in calculations regarding small deviations from thermodynamic equilibrium. According to Sharipov (Reference Sharipov2006, Reference Sharipov2010) and Sharipov & Kalempa (Reference Sharipov and Kalempa2006), the reciprocity relation for the problem in question can be written as
\begin{equation} \Lambda_{uT}^{t}=\Lambda_{Tu}^{t}, \end{equation}where the time reversal kinetic coefficients are defined as
\begin{equation} \Lambda_{kn}^{t}=((\hat{T}g'^{(k)},h^{(n)}))+\int_{\Sigma_w}(\hat{T}v_rh_w^{(k)},h^{(n)})\,\text{d}\Sigma +\frac 12 \int_{\Sigma_g}(\hat{T}v_rh^{(k)},h^{(n)})\,\text{d}\Sigma. \end{equation}
The dimension free terms 
$g'^{(n)}=v_0g^{(n)}/\ell _0$ (
$n=u, T$), where 
$g^{(n)}$ are given in (3.9a,b). The source terms 
$h_w^{(n)}$ are given in (4.2a,b). Here, the time reversal operator 
$\hat {T}$ just changes the sign of the molecular velocity, i.e. 
$\hat {T}h({\boldsymbol v})=h(-{\boldsymbol v})$. The scalar products are defined as
\begin{equation} (\xi_1,\xi_2)=\int f_0\xi_1({\boldsymbol r}',{\boldsymbol v})\xi_2({\boldsymbol r}',{\boldsymbol v})\,\text{d}{\boldsymbol v}, \end{equation}and
\begin{equation} ((g,h))=\int_{\Omega}(g,h)\,\text{d}{\boldsymbol r}'. \end{equation}
Here 
$\Omega$ means the gas flow domain, while 
$\Sigma _w$ and 
$\Sigma _g$ mean the solid spherical surface and the imaginary spherical surface at 
$r'>R_0$ which enclose the gas domain.
Then, after some algebraic manipulation, the time reversed kinetic coefficients are written as
\begin{gather} \Lambda_{uT}^{t}=-4{\rm \pi} R_0^{2} n_0v_0F_T - \frac 12 \int_{\Sigma_g}(\hat{T}v_rh^{(T)},h^{(u)})\,\text{d}\Sigma, \end{gather}
\begin{gather}\Lambda_{Tu}^{t}=v_0n_0\int_{\Sigma_g}zq_r^{(u)}(r,\theta)\, \text{d}\Sigma + \frac 12 \int_{\Sigma_g}(\hat{T}v_rh^{(T)},h^{(u)})\, \text{d}\Sigma. \end{gather}Therefore, after substituting (5.5) and (5.6) into (5.1), the thermophoretic force on the sphere is related to the solution of the drag force problem as
\begin{align} F_T &= -\frac{r^{2}}{2\delta^{2}}\left[r\int_{0}^{\rm \pi}q_r^{(u)}(r,\theta)\cos{\theta}\sin{\theta}\,\text{d}\theta \right.\nonumber\\ &\quad \left.+\frac{1}{{\rm \pi}^{3/2}}\int_{0}^{\rm \pi}\int c_rh^{(T)}(r,\theta,-{\boldsymbol c})h^{(u)}(r, \theta,{\boldsymbol c})\,\text{e}^{-c^{2}} \sin{\theta}\,\text{d}{\boldsymbol c}\,\text{d}\theta\right], \end{align}
where 
$r$ is the radius of the imaginary spherical surface 
$\Sigma _g$, which can be arbitrary. The right-hand side of the relation (5.7) was calculated numerically for 
$r=1$, 5, 10 and 40 and the fulfillment of such a relation was verified numerically within the numerical error of 0.1 %.
6. Method of solution
6.1. Free molecular regime
In the free molecular regime, i.e. 
$\delta \ll 1$, the collision integral which appears in the Boltzmann equation (3.1) can be neglected. As a consequence, in this regime of the gas flow, the problem is solved analytically via solution of a differential equation for each thermodynamic force. Thus, the linearized equation is obtained from (3.6) as
\begin{equation} \hat{D} h^{(n)}=g^{(n)}, \end{equation}
whose solution must satisfy the boundary condition given in (4.1) for the corresponding thermodynamic force. Moreover, in this regime of the gas flow, the distribution function of incident gas particles on the surface is not perturbed, which means that 
$h^{-(n)}=h_{\infty }^{(n)}$ as given by (3.14) and (3.15). The method of the characteristics allows us to solve the previous equations for each thermodynamic force and obtain analytic expressions for the thermophoretic and drag forces acting on the sphere. Details regarding the solution are presented in appendix A. Then, after substituting the solutions given in (A 1) into (3.26) and (3.27), the forces of interest are obtained as
\begin{gather} F_T=-\frac{1}{2\sqrt{\rm \pi}}\left[\frac{1+\alpha_t}{2}+ 2\alpha_n^{1/2}\int_{0}^{\infty}c_r^{2}\,\text{e}^{-c_r^{2}} \left(\alpha_nH_3(\eta)-\frac 32 H_1(\eta)\right)\text{d}c_r \right], \end{gather}
\begin{gather}F_u=\frac{2}{3\sqrt{\rm \pi}}\left(1+\alpha_t+2\alpha_n^{1/2}\int_0^{\infty} c_r^{2}\,\text{e}^{-c_r^{2}} H_1(\eta)\,\text{d}c_r\right), \end{gather}
with 
$H_1(\eta )$, 
$H_3(\eta )$, 
$\eta$ and 
$\xi$ defined in (4.15a,b) and (4.16). In case of diffuse scattering, i.e. 
$\alpha _t=1$ and 
$\alpha _n=1$, the thermophoretic and drag forces given in (6.2) and (6.3) correspond to those found in the literature; see, e.g. Takata et al. (Reference Takata, Sone and Aoki1993), Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Sone (Reference Sone2007).
The macrocroscopic characteristics of the gas flow around the sphere due to each thermodynamic force can be obtained just by substituting the corresponding solution given in (A 1) into the expressions (3.17)–(3.22).
6.2. Arbitrary gas rarefaction
In order to consider arbitrary values of the gas rarefaction, the problem is solved numerically by employing the linearized kinetic equations given in (3.16) for each thermodynamic force subject to the corresponding boundary condition. Here, these equations are solved by the discrete velocity method, whose details can be found in the literature; see, e.g. Sharipov & Subbotin (Reference Sharipov and Subbotin1993) and Sharipov (Reference Sharipov2016). Moreover, the split method proposed by Naris & Valougeorgis (Reference Naris and Valougeorgis2005) to deal with the problem of the discontinuity of the distribution function of molecular velocities on the boundary is employed. In rarefied gas dynamics, the problem of the discontinuity of the distribution function is a peculiarity inherent to gas flows around convex bodies (see, e.g. Sone & Takata Reference Sone and Takata1992) and must be treated carefully when a finite-difference scheme is used. The idea of the split method is the decomposition of the perturbation function into two parts as
\begin{equation} h^{(n)}({\boldsymbol r},{\boldsymbol c})=h_0^{(n)}({\boldsymbol r},{\boldsymbol c})+ \tilde{h}^{(n)}({\boldsymbol r},{\boldsymbol c}), \end{equation}
where the function 
$h_0^{(n)}$ is obtained from the solution of the differential equation
\begin{equation} \hat{D} h_0^{(n)}+h_0^{(n)}=0, \end{equation}with boundary condition
\begin{equation} h_0^{+(n)}=h_w^{(n)}-\hat{A}h_w^{(n)}, \end{equation}
where 
$h_w^{(n)}$ is given in (4.2a,b) for the corresponding thermodynamic force.
The function 
$\tilde {h}^{(n)}$ satisfy the kinetic equation (3.6) just replacing 
$h^{(n)}$ by 
$\tilde {h}^{(n)}$, but with the boundary condition
\begin{equation} \tilde{h}^{+(n)}=\hat{A}\tilde{h}^{-(n)}. \end{equation}
Moreover, the asymptotic behaviour of the perturbation functions 
$h_0^{(n)}$ and 
$\tilde {h}^{(n)}$, obtained from (3.14) and (3.15), reads as
\begin{equation} h_{0_{\infty}}^{(n)}=\lim_{r\rightarrow \infty} h_0^{(n)}=0,\quad \tilde{h}_{\infty}^{(n)}=\lim_{r\rightarrow \infty} \tilde{h}^{(n)}=h_{\infty}^{(n)}, \end{equation}
where 
$h_{\infty }^{(T)}$ and 
$h_{\infty }^{(u)}$ are given in (3.14) and (3.15), respectively.
The advantage of the split method is that the discontinuous function 
$h_0^{(n)}$ can be obtained analytically by employing the method of characteristics to solve a partial differential equation, while the function 
$\tilde {h}^{(n)}$ is sufficiently smooth so that a finite-difference scheme leads to a smaller numerical error. For convenience, the analytic solutions 
$h_0^{(n)}$ for both thermodynamic forces are presented in appendix B as well as their moments. To reduce the number of variables of the perturbation function 
$\tilde {h}^{(n)}$, its dependence on the variables 
$\theta$ and 
$\phi '$ is eliminated by employing the similarity solution proposed by Sone & Aoki (Reference Sone and Aoki1983). Then, in our notation, the perturbation function 
$\tilde {h}^{(n)}$ is represented as
\begin{equation} \tilde{h}^{(n)}(r,\theta,{\boldsymbol c})=\tilde{h}_c^{(n)}(r,c,\theta')\cos{\theta}+ \tilde{h}_s^{(n)}(r,c,\theta')c_{\theta}\sin{\theta}. \end{equation}
The substitution of the representation (6.9) into the kinetic equation (3.6) leads to a system of kinetic equations for the new perturbation functions 
$\tilde {h}_c^{(n)}$ and 
$\tilde {h}_s^{(n)}$, which are solved numerically with the boundary conditions (6.7) and asymptotic behaviours obtained from (6.8a,b).
Regarding the boundary conditions, the representation (6.9) is compatible with the CL boundary condition taking the form
\begin{equation} \hat{A}\tilde{h}^{-(n)}=\cos{\theta}\hat{A}_r\hat{A}_t^{(0)}\tilde{h}_c^{-(n)}+ \sin{\theta}\cos{\phi'}\hat{A}_r\hat{A}_t^{(1)}\tilde{h}_s^{-(n)}, \end{equation}where
\begin{align} \hat{A}_r\xi &= \frac{2}{\alpha_n}\int_{0}^{\infty}c_r'\exp{\left[-\frac{(1-\alpha_n)c_r^{2}+c_r'^{2}}{\alpha_n}\right]} \nonumber\\ &\quad \times I_0\left(\frac{2\sqrt{1-\alpha_n}c_rc_r'}{\alpha_n}\right)\xi(-c_r',c_t')\,\text{d}c_r', \end{align}
\begin{align} \hat{A}_t^{(i)}\xi &= \frac{2}{\alpha_t(2-\alpha_t)}\int_{0}^{\infty}c_t'^{(i+1)} \exp{\left[-\frac{(1-\alpha_t)^{2}c_t^{2}+c_t'^{2}} {\alpha_t(2-\alpha_t)}\right]} \nonumber\\ &\quad \times I_i\left[\frac{2(1-\alpha_t)c_tc_t'}{\alpha_t(2-\alpha_t)}\right] \xi(c_r',c_t')\, \text{d}c_t', \end{align}
where 
$I_i$ (
$i=0, 1$) is the modified Bessel function of the first kind and 
$i$th order.
Therefore, the boundary conditions for the perturbation functions 
$\tilde {h}_c^{(n)}$ and 
$\tilde {h}_s^{(n)}$ are obtained from (6.7) as follows:
\begin{equation} \tilde{h}_c^{+(n)}=\hat{A}_r\hat{A}_t^{(0)}\tilde{h}_c^{-(n)},\quad \tilde{h}_s^{+(n)}=\frac{1}{c_t}\hat{A}_r\hat{A}_t^{(1)}\tilde{h}_s^{-(n)}. \end{equation} Moreover, from (6.8a,b), the asymptotic behaviours for the perturbation functions 
$\tilde {h}_c^{(n)}$ and 
$\tilde {h}_s^{(n)}$ are given as
\begin{gather} \tilde{h}_{c_{\infty}}^{(T)}=\lim_{r\rightarrow \infty} \tilde{h}_c^{(T)}=-\frac 32 c_r\left(c^{2}-\frac 52\right),\quad \tilde{h}_{s_{\infty}}^{(T)}=\lim_{r\rightarrow \infty}\tilde{h}_s^{(T)}=\frac 32 \left(c^{2}-\frac 52\right), \end{gather}
\begin{gather}\tilde{h}_{c_{\infty}}^{(u)}=\lim_{r\rightarrow \infty} \tilde{h}_c^{(u)}=0,\quad \tilde{h}_{s_{\infty}}^{(u)}=\lim_{r\rightarrow \infty}\tilde{h}_s^{(u)}=0. \end{gather}Further details regarding the complete set of equations solved numerically are presented in appendix B.
It is worth noting that the moments defined in (3.17)–(3.22), and the dimensionless forces defined in (3.26) and (3.27), are also decomposed into two parts due to the representation (6.4). Then after some algebraic manipulation, the moments corresponding to the density and temperature deviations from equilibrium, and the radial and polar components of the bulk velocity and heat flux vectors can be written as
\begin{equation} \left.\begin{array}{c@{}} \nu^{(n)}(r,\theta)=\nu^{*(n)}(r) \cos{\theta},\\ \tau^{(n)}(r,\theta)=\tau^{*(n)}(r)\cos{\theta},\\ u_r^{(n)}(r,\theta)=u_r^{*(n)}(r)\cos{\theta},\\ u_{\theta}^{(n)}(r,\theta)=u_{\theta}^{*(n)}(r)\sin{\theta},\\ q_r^{(n)}(r,\theta)=q_r^{*(n)}(r)\cos{\theta},\\ q_{\theta}^{(n)}(r,\theta)=q_{\theta}^{*(n)}(r)\sin{\theta}, \end{array}\right\}\end{equation}
where the quantities dependent only on the radial coordinate 
$r$ on right-hand side are given in (B 6)–(B 11). The final expressions to calculate the thermophoretic and drag forces on the sphere are also given in appendix B, specifically in (B 18).
Then, the system of kinetic equations for the functions 
$\tilde {h}_c^{(n)}$ and 
$\tilde {h}_s^{(n)}$ subject to the corresponding boundary condition and asymptotic behaviour for each thermodynamic force was solved numerically via the discrete velocity method with an accuracy of 0.1 % for the moments of the perturbation functions at the boundary. Details regarding the discrete velocity method can be found in the literature; see, e.g. Sharipov (Reference Sharipov2016). The Gaussian quadrature was used to discretize the molecular velocity and calculate the moments of the perturbation function. The numerical values of the nodes and weights as well as the technique to calculate them are described in Krylov (Reference Krylov2005). Moreover, a central finite-difference scheme was used to approximate the derivatives which appear in the kinetic equation. The accuracy was estimated by varying the grid parameters 
$N_r$, 
$N_{c}$ and 
$N_{\theta }$ corresponding to the number of nodes in the radial coordinate 
$r$, molecular speed 
$c$ and angle 
$\theta '$, as well as the maximum value of the radial coordinate, denoted here as 
$r_{max}$, which defines the gas flow domain. The values of these parameters providing such an accuracy were 
$N_c$ and 
$N_{\theta }$ fixed at 12 and 200, respectively, while 
$N_r$ varied according to the distance 
$r_{max}$ so that the increment 
${\rm \Delta} r \sim 10^{-3}$. The maximum distance 
$r_{max}$ varied from 10 to 100 when the rarefaction parameter varied from 0.01 to 10. For instance, for 
$\delta =1$, 
$r_{\textit{max}}=40 $ and 
$N_r =10\,000 $, while for 
$\delta=10 $, 
$r_{\textit{max}}=100 $ and 
$N_r =40\,000 $ were used. Moreover, the reciprocal relation (5.7) was verified and confirmed within the numerical error.
7. Results and discussion
7.1. Free molecular regime
Firstly, the results obtained from the analytic solutions (6.2) and (6.3) were compared to those given by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) in the free molecular regime. The analytic expressions given by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) to calculate the thermophoretic and drag forces were obtained in the limit 
$(1-\alpha _t)\ll 1$ and 
$(1-\alpha _n)\ll 1$, which means almost complete accommodation of gas particles on the sphere. However, the figures presented by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) show the profiles of the dimensionless thermophoretic and drag forces on the sphere as functions of the TMAC, 
$\alpha _t$, and fixed values of NEAC corresponding to 
$\alpha _n= 0.1, 0.5$ and 0.9. Moreover, the forces as functions of the NEAC and fixed values of TMAC corresponding to 
$\alpha _t=0, 0.4, 0.8$ and 1 are also presented by the authors. The comparison shows a good agreement between the results obtained in the present work and those given by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) for the drag force in the whole range of accommodation coefficients. There is a small difference between the results only for small values of NEAC. On the contrary, there is a large disagreement between the present results and those given by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) for the thermophoretic force in the whole range of the accommodation coefficients. In fact, the expression derived by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) for the thermophoretic force on the sphere is not correct even in the limit of diffuse scattering. As one can see, under the assumption of diffuse scattering, (6.2) and (6.3) lead to the following expressions for the thermophoretic and drag forces on the sphere:
\begin{gather} F_{T}=-\frac{1}{2\sqrt{\rm \pi}}, \end{gather}
\begin{gather}F_u=\frac{4}{3\sqrt{\rm \pi}}\left(1+\frac{\rm \pi}{8}\right). \end{gather}These expressions are well known from the literature, e.g. Takata et al. (Reference Takata, Sone and Aoki1993), Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Sone (Reference Sone2007). The figures showing the comparison with the results presented by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) are provided as online supplementary material available at https://doi.org/10.1017/jfm.2020.523.
It is also worth mentioning that the reciprocity relation between cross phenomena was not verified by Chernyak & Sograbi (Reference Chernyak and Sograbi2019), while in the present work the reciprocity relation given by (5.7) was fulfilled within the numerical error for arbitrary values of accommodation coefficients. Table 1 presents the comparison between the values of the thermophoretic force on the sphere calculated by (5.7) and (6.2). Moreover, numerical results for both forces in the free molecular regime are given in tables 2 and 3. According to these tables, the numerical results obtained via the kinetic equation for small values of the rarefaction parameter tend to those given by (6.2) and (6.3).
Table 1. Thermophoretic force on the sphere: verification of the reciprocity relation.
$^{a}$Analytical solution in the free molecular regime.
$^{b}$Numerical solution due to 
$X_T$ (
$n=T$).
Table 2. Dimensionless thermophoretic force on the sphere.
$^{a}$Equation (6.2), free molecular regime.
Table 3. Dimensionless viscous drag force on the sphere.
$^{{\textit{a}}}$Equation (6.3), free molecular regime.
7.2. Transitional regime
Under the assumption of complete accommodation of gas particles on the surface, the results obtained for the thermophoretic and viscous drag forces were compared to those presented by Beresnev & Chernyak (Reference Beresnev and Chernyak1995), Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990), Takata et al. (Reference Takata, Aoki, Sone, Shizgal and Weaver1992) and Takata et al. (Reference Takata, Sone and Aoki1993). The comparison is shown in figures 2 and 3, in which 
$F_{T}^{*}$ and 
$F_u^{*}$ denote the ratio of the thermophoretic and drag forces to the corresponding values in the free molecular regime given in (7.1) and (7.2). Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990) used the integral-moment method to solve the same linearized kinetic equation of the present work and also the variational method to calculate the macroscopic quantities. On the other hand, Takata et al. (Reference Takata, Aoki, Sone, Shizgal and Weaver1992) and Takata et al. (Reference Takata, Sone and Aoki1993) solved the full linearized Boltzmann equation via a finite-difference scheme method and the similarity solution proposed by Sone (Reference Sone1966). It is worth noting that the integral-moment method consists of obtaining a set of integral equations for the moments of the distribution function and its advantage is that only the physical space must be discretized. However, this method requires much more computational memory and CPU time than that required when the discrete velocity method is employed. Regarding the solution of the full Boltzmann equation, in spite of the great computational infrastructure currently available, finding this solution is still a difficult task which requires considerable computational effort and so the use of kinetic model equations still plays an important role in solving problems of practical interest in the field of rarefied gas dynamics. According to figures 2 and 3, there is a good agreement between our results and those provided by the other authors when diffuse scattering is assumed. Moreover, in case of thermophoresis, the results obtained in the present work are in better agreement with the data reported by Takata et al. (Reference Takata, Sone and Aoki1993) than those obtained by Beresnev & Chernyak (Reference Beresnev and Chernyak1995) in the considered range of the gas rarefaction. Since our results and those by Beresnev & Chernyak (Reference Beresnev and Chernyak1995) are based on the solution of the same kinetic equation, one can conclude that the better agreement with the results obtained from the Boltzmann equation is due to the numerical technique used in our work, i.e. the discrete velocity method. The reciprocity relation (5.7) is fulfilled within the numerical error. Table 1 shows the fulfillment of the reciprocity relation (5.7) when 
$\delta =0.1$ and 1 for some sets of accommodation coefficients.
Figure 2. Ratio of the thermophoretic force on the sphere to its value in the free molecular regime: comparison to the results presented by Beresnev & Chernyak (Reference Beresnev and Chernyak1995) and Takata et al. (Reference Takata, Aoki, Sone, Shizgal and Weaver1992) for diffuse scattering.
Figure 3. Ratio of the drag force on the sphere to its value in the free molecular regime: comparison to the results presented by Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990) and Takata et al. (Reference Takata, Sone and Aoki1993) for diffuse scattering.
For other kinds of gas–surface interaction law, some numerical results obtained in the present work are presented in tables 2 and 3 for a range of rarefaction parameters 
$\delta$ which covers the free molecular, transitional and hydrodynamic regimes. The values of the accommodation coefficients considered in the calculations were chosen because, in practice, the coefficients vary in the ranges 
$0.6 \le \alpha _t \le 1$ and 
$0.1 \le \alpha _n \le 1$ for some gases; see, e.g. Sharipov (Reference Sharipov1999) and Sharipov & Moldover (Reference Sharipov and Moldover2016). According to table 2, the thermophoretic force can be either in the direction of the temperature gradient or in the opposite direction to it. Usually, the thermophoretic force is in the opposite direction to the temperature gradient, i.e. the force tends to move the particle from a hot to cold region in the gas. However, in some situations the movement of the particle from a cold to hot region can occur and such a phenomenon is known as negative thermophoresis, which corresponds to a force in the same direction of the temperature gradient. The negative thermophoresis of particles with high thermal conductivity is expected to appear at large values of rarefaction parameter, i.e. in the continuum and near-continuum regimes. The thermal creep flow, or thermal slip flow, which is induced in the vicinity of a boundary subject to a temperature gradient along it, is the main mechanism of thermophoresis. The thermal creep flow is strongly sensitive to both the TMAC and NEAC (see, e.g. Sharipov Reference Sharipov2011) and it appears in an approximation of first order in the Knudsen number so that the equations of continuum mechanics with the usual slip boundary conditions lead to it. In the case of particles with low and moderate thermal conductivity related to that of the gas, the thermal creep flow is dominant. However, in the case of particles with high thermal conductivity, the more accepted explanation for the reversal of the thermophoretic force is still that given by Sone (Reference Sone1966, Reference Sone1972, Reference Sone2007) with the introduction of the so-called thermal stress slip flow, which is an effect of second order in the Knudsen number caused by the non-uniformity of the temperature field in the gas and also dependent on the gas–surface interaction law. Minute details regarding the thermal stress slip flow are given by Sone (Reference Sone1966, Reference Sone1972, Reference Sone2007). Nevertheless, it is important to point out that the dependence of the thermal stress slip flow on the TMAC and NEAC as introduced by Cercignani & Lampis (Reference Cercignani and Lampis1971) is not known yet. Table 2 shows the appearance of the negative thermophoresis when 
$\delta =10$ for some sets of accommodation coefficients. For instance, when 
$\alpha _n=0.1$ and 
$\alpha _t$ varies from 1 to 0.5, the force is reversed, i.e. the force is positive in the direction of the temperature gradient. These results show that the occurrence of the negative thermophoresis depends not only on the rarefaction degree of the gas flow and thermal conductivity of aerosol particles, but also on the accommodation coefficients on the surface. Therefore, the appropriate modelling of the gas–surface interaction plays a fundamental role for the correct description of the thermophoresis phenomenon.
According to tables 2 and 3, the thermophoretic and drag forces depend on both accommodation coefficients in the whole range of the gas rarefaction. As one can see in table 2, for fixed values of 
$\alpha _n$, when the thermophoretic force is in the opposite direction to the temperature gradient, its magnitude decreases as 
$\alpha _t$ varies from 1 to 0.5. Moreover, for fixed values of 
$\alpha _t$, the magnitude of the thermophoretic force increases when 
$\alpha _n$ varies from 1 to 0.1. The same qualitative behaviour is observed in table 3 for the drag force on the sphere. In fact, this kind of behaviour is due to the fact that an increase of 
$\alpha _t$ means an increase of tangential stress acting on the sphere, while an increase of 
$\alpha _n$ means an increase of normal stress on the sphere. However, when the force is reversed, the bevavior of the thermal force on the accommodation coefficients is opposite, i.e. the larger the NEAC the larger the magnitude of the thermophoretic force, and the larger the TMAC the smaller the magnitude of the thermophoretic force on the sphere. The results given in these tables also show us that, in spite of the smallness of the thermophoretic force in comparison to the drag force on the sphere, the dependence of the thermophoretic force on the accommodation coefficients is stronger than that observed for the drag force. For instance, the maximum deviation of the thermophoretic force from the corresponding value for complete accommodation is around 50 % when 
$\delta =0.1$, 94 % when 
$\delta =1$ and larger than 100 % when 
$\delta =10$. On the other hand, the maximum deviation of the drag force from that value in the case of diffuse scattering is around 7 % when 
$\delta =0.1$, 5 % when 
$\delta =1$ and 0.5 % when 
$\delta =10$. It can also be seen that the dependence of the thermophoretic force on the accommodation coefficients is larger in the hydrodynamic regime, while for the drag force such a dependence is larger in the free molecular regime.
7.3. Slip flow regime
In situations where 
$\delta \gg 1$, the drag force acting on the sphere can be obtained from the solution of the Navier–Stokes equations with slip boundary condition. Thus, according to Sharipov (Reference Sharipov2011), the dimensionless drag force is written as
\begin{equation} F_u=\frac {3}{2\delta}\left(1-\frac{\sigma_{P}}{\delta}\right),\end{equation}
where 
$\sigma _{P}$ is the viscous slip coefficient, which strongly depends on the TMAC. Siewert & Sharipov (Reference Siewert and Sharipov2002) and Sharipov (Reference Sharipov2003a) provide some values of 
$\sigma _{P}$ for a single gas obtained numerically via the solution of the Shakhov kinetic equation and the CL model of gas–surface interaction. For practical applications, a formula which perfectly interpolates the results provided by Siewert & Sharipov (Reference Siewert and Sharipov2002) and Sharipov (Reference Sharipov2003a) is presented by Sharipov (Reference Sharipov2011) as
\begin{equation} \sigma_{P}=\frac{1.772}{\alpha_t}-0.754. \end{equation}
The results obtained from (7.3) are in good agreement with the experimental data found in the literature. For instance, in the case of 
$\alpha _t=1$ and 
$\delta > 10$, the results obtained from (7.3) agree very well with the experimental data provided by Allen & Raabe (Reference Allen and Raabe1985) and Hutchinson, Harper & Felder (Reference Hutchinson, Harper and Felder1995) for the drag force on spherical particles of polystyrene latex in air at ambient conditions.
Similarly, for situations where 
$\delta > 10$, an expression for the thermophoretic force on the sphere can be obtained from the solution of the Navier–Stokes–Fourier equations with slip velocity and temperature jump boundary conditions, e.g. Brock (Reference Brock1962). However, the thermophoretic force predicted from these equations have a large deviation from experimental data for high thermal conductivity particles, e.g. Jacobsen & Brock (Reference Jacobsen and Brock1965). This failure is attributed to the fact that the first-order slip solution cannot account for the phenomena arising in the vicinity of the particle, which is a region with large departure from local thermodynamic equilibrium. On the contrary, theories based on higher-order approximation in the Knudsen number, as that proposed by Sone (Reference Sone1966), are able to predict the thermophoretic force on high thermal conductivity particles in the continuum and near continuum or slip flow regimes. However, it is worth mentioning that the solutions obtained from higher-order approximations in the Knudsen number rely on the accurate determination of the slip velocity and temperature jump coefficients, and these quantities can be strongly dependent on the accommodation coefficients and intermolecular interaction potential. As pointed out in the review by Sharipov (Reference Sharipov2011), to obtain more reliable theoretical values of the slip and jump coefficients, numerical methods to solve the Boltzmann equation with a realistic potential of intermolecular interaction and new models of the gas–surface interaction should be developed as well as carrying out more experiments.
7.4. Flow fields
The macroscopic characteristics of the gas flow around the sphere are dependent on the accommodation coefficients. Figures 4–7 show the profiles of the radial and polar components of the bulk velocity, density and temperature deviations from equilibrium, respectively, due to the thermodynamic force 
$X_T$, as functions of the distance 
$r/\delta$, when 
$\delta =0.1$, 1 and 10. Similarly, figures 8 and 9 show the profiles of the radial and polar components of the bulk velocity, the density and temperature deviations from equilibrium, but due to the thermodynamic force 
$X_u$. Since it was verified that there is no influence of the NEAC on the gas bulk velocity due to 
$X_u$, and the influence of the TMAC on the density and temperature deviations from equilibrium due to the same thermodynamic force is negligible, the profiles of these quantities as functions of the distance 
$r/\delta$ are provided as online supplementary material. Note that, according to the definitions given in (2.8a–c) and (2.10), the dimensionless distance 
$r/\delta$ corresponds to the ratio of the dimension radial distance 
$r'$ from the sphere to the radius 
$R_0$ of the sphere. The dependence on the TMAC is shown in figures 4, 5 and 8, with the NEAC fixed at 
$\alpha _n=0.1$. The dependence on the NEAC is shown in figures 6, 7 and 9, with the TMAC fixed at 
$\alpha _t=1$. The fixed values of 
$\alpha _n$ and 
$\alpha _t$ were chosen because, as noted in tables 2 and 3, the larger deviations of the thermophoretic and drag forces from those values in the case of diffuse scattering occurs when 
$\alpha _n=0.1$ and 
$\alpha _t=1$.
Figure 4. Components of the bulk velocity as functions of the radial distance from the sphere due to the thermodynamic force 
$X_T$ for fixed 
$\alpha _n=0.1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
Figure 5. Density and temperature deviations as functions of the radial distance from the sphere due to the thermodynamic force 
$X_T$ for fixed 
$\alpha _n=0.1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
Figure 6. Components of the bulk velocity as functions of the radial distance from the sphere due to the thermodynamic force 
$X_T$ for fixed 
$\alpha _t=1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
Figure 7. Density and temperature deviations as functions of the radial distance from the sphere due to the thermodynamic force 
$X_T$ for fixed 
$\alpha _t=1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
Figure 8. Components of the bulk velocity as functions of the radial distance from the sphere due to the thermodynamic force 
$X_u$ for fixed 
$\alpha _n=0.1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
Figure 9. Density and temperature deviations as functions of the radial distance from the sphere due to the thermodynamic force 
$X_u$ for fixed 
$\alpha _t=1$. (a) Rarefaction parameter 
$\delta =0.1$; (b) rarefaction parameter 
$\delta =1$; (c) rarefaction parameter 
$\delta =10$.
From figures 4–7, regarding the macroscopic quantities due to the thermodynamic force 
$X_T$, one can conclude the following. (i) According to figures 4 and 6, the radial and polar components of the bulk velocity depend on both accommodation coefficients. However, the dependence on the TMAC tends to be larger as the gas flow tends to the free molecular regime, while the dependence on the NEAC tends to be larger as the gas flow tends to the hydrodynamic regime. Quantitatively, the dependence on the NEAC is larger than that on the TMAC. Figure 6 shows us that when 
$\delta =10$, 
$\alpha _n=\alpha _t=1$, the bulk velocity of the gas in the vicinity of the sphere starts to change direction, which means the starting of the negative thermophoresis on the sphere. In order to see the dependence of the bulk velocity of the gas flow due to the temperature gradient on the NEAC and the appearance of the negative thermophoresis, the speed contour and the velocity streamlines are given in figure 10 for 
$\delta =10$, the TMAC is fixed at 
$\alpha _t=0.5$ and the NEAC at 
$\alpha _n=0.1$ and 1. According to this figure, the bulk velocity of the gas flow strongly depends on the NEAC and it is even reversed when 
$\alpha _n=1$, which means a gas flow in the opposite direction to the temperature gradient and, thus, the movement of the particle in the same direction of the temperature gradient, i.e. the negative thermophoresis on the sphere. From figure 10, it is worth noting that the NEAC also influences the flow field far from the sphere, which can be noted by the vortex position in the figure. (ii) The temperature of the gas flow tends to increase in the vicinity of the sphere in free molecular and transition regimes. However, in the hydrodynamic regime the temperature of the gas decreases near the sphere. The qualitative behaviour is the same for arbitrary values of accommodation coefficients, but the influence of the NEAC is larger than that on the TMAC.
Figure 10. Speed contour and velocity streamlines for fixed 
$\alpha _t=0.5$ and 
$\delta =10$. (a) 
$\alpha _n=0.1$ and (b) 
$\alpha _n=1$.
From figures 8 and 9, regarding the macroscopic quantities due to the thermodynamic force 
$X_u$, one can conclude the following. (i) According to figure 8, near the sphere the radial component of the bulk velocity tends to decrease while the polar component tends to increase. This situation corresponds to a decrease in the bulk velocity of the gas flow due to the presence of the sphere. This qualitative behaviour is already known from the literature. As previously mentioned, it was verified that there was no influence of the NEAC on the bulk velocity of the gas flow due to 
$X_u$. However, as one can see from figure 8, there is a small dependence on the TMAC. (ii) Regarding the number density and temperature of the gas flow around the sphere, according to figure 9, these quantities always decrease in the vicinity of the sphere. However, while the dependence of the density and temperature deviations on the TMAC is negligible, there is a significant dependence on the NEAC. As one can see in figure 9, when 
$\alpha _n$ varies from 1 to 0.1, the temperature deviation near the sphere strongly deviates from the corresponding plot for diffuse scattering in the three situations of gas rarefaction considered, i.e. 
$\delta =0.1$, 1 and 10. The dependence of the density deviation on the NEAC is negligible in the free molecular regime, but it tends to be significant as the gas flow tends to the hydrodynamic regime.
7.5. Comparison with experiment
Figure 11 shows the comparison between the results obtained in the present work for the dimension thermophoretic force, in 
$\mathrm {\mu }$N, and those provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) for a copper sphere in argon gas in a wide range of the gas rarefaction. The experimental apparatus employed by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) consisted of measuring the thermophoretic force acting on a sphere, with a radius of about 0.025 m, and fixed in the middle of two 
$61~\textrm {cm}\times 61~\textrm {cm}\times 0.9~\textrm {cm}$ copper plates placed within a vacuum chamber filled with argon gas at ambient temperature and pressure ranging from 13.3 to 0.013 Pa. The distance between the plates was fixed at 40 cm and their temperatures were set up to establish a temperature gradient of 35 K m
$^{-1}$ between them. However, in rarefied conditions, the profile of the gas temperature between the plates is not linear and there is a temperature jump at the plates. Moreover, the temperature gradient through the gas tends to decrease as the pressure decreases. Therefore, to compare our numerical results with the experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016), these effects must be taken into account. For pressures lower than 1 Pa, the temperature gradient can be estimated with basis on the temperature profiles presented by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) in figure 5, which were obtained numerically via the DSMC method. The temperature jump coefficient necessary to estimate the gas temperature at the walls can be obtained from the interpolating formula given by Sharipov & Moldover (Reference Sharipov and Moldover2016). Here, it is worth noting that the experimental configuration provides the maximum radial coordinate 
$r'=8\delta \ell _0$, where the equivalent mean free path 
$\ell _0$ is defined in (2.6a,b). Nonetheless, the convergence of the numerical calculations within the numerical error was achieved by considering the maximum radial coordinate varying from 10
$\ell _0$ to 100
$\ell _0$ as the rarefaction parameter 
$\delta$ varied from 0.01 to 10. Therefore, in the present work, as the rarefaction parameter decreases, the comparison between our numerical results and the experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) is valid only at approximately 
$\delta =1$. For 
$\delta < 1$, the comparison is no longer valid because the experimental configuration, i.e. the distance between the plates and sphere radius, does not provide our problem assumption of local equilibrium far from the sphere. According to the literature (see, e.g. Sazhin et al. Reference Sazhin, Borisov and Sharipov2001 and Sharipov & Moldover Reference Sharipov and Moldover2016) in the case of argon gas and a metallic surface, the more reliable values of accommodation coefficients supported by experimental data are 
$\alpha _t=1$ and 
$\alpha _n=0.9$ on an atomically clean surface whereas on a contaminated surface the gas–surface interaction is closer to diffuse scattering. Then, the results obtained in the present work for diffuse scattering, i.e. 
$\alpha _t=1$ and 
$\alpha _n=1$, and also 
$\alpha _t=1$ and 
$\alpha _n=0.9$, are given in figure 11. The viscosity of the gas was obtained from Vogel et al. (Reference Vogel, Jaeger, Hellmann and Bich2010). According to figure 11, there is a good agreement between the results obtained in the present work and the experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) in the range 
$1 \le \delta \le 10$. However, although the negative thermophoresis was detected in the experiment carried out by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016), in the present work it was not predicted numerically for the chosen set of accommodation coefficients. Nonetheless, according to the results presented in table 2, the negative thermophoresis is predicted numerically for 
$\delta =10$ only for some sets of accommodation coefficients. From figure 11 one can also see that, in the range 
$1\le \delta \le 10$, the results corresponding to 
$\alpha _t=1$ and 
$\alpha _n=0.9$ are closer to the experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) than those corresponding to diffuse scattering.
Figure 11. Dimensional thermophoretic force: comparison with experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016) for a copper sphere in argon gas.
8. Concluding remarks
In the present work, the classical problems of thermophoresis and viscous drag on a sphere with high thermal conductivity were investigated on the basis of the linearized kinetic equation proposed by Shakhov and the Cercignani–Lampis model to the gas–surface interaction law. In the free molecular regime the solutions for both problems were obtained analytically, while in the transitional and hydrodynamic regimes the problems were solved numerically via the discrete velocity method with a proper method to take into account the discontinuity of the distribution function around a convex body. The reciprocity relation between the cross phenomena was obtained and verified numerically within the numerical error. The thermophoretic and drag forces acting on the sphere, as well as the macroscopic characteristics of the gas flow around it, were calculated for some sets of TMAC and NEAC which were chosen according to the data available in the literature concerning experiments for monatomic gases at various surfaces. The results show a strong dependence of the thermophoretic force on both accommodation coefficients, including the appearance of the negative thermophoresis in the hydrodynamic regime as TMAC and the NEAC vary. Moreover, the results show a dependence of the viscous drag force on the accommodation coefficients, but such a dependence is smaller than that observed for the thermophoretic force. Similarly, the flow fields around the sphere also depend on the accommodation coefficients, but the dependence of the quantities due to the thermodynamic force 
$X_u$ is smaller than that observed for the quantities due to the thermodynamic force 
$X_T$. As the gas tends to the hydrodynamic regime, the drag force tends to be independent of the NEAC as predicted by the expression obtained from the Navier–Stokes equations with slip boundary conditions at the spherical surface. Regarding the comparison with experimental data provided by Bosworth et al. (Reference Bosworth, Ventura, Ketsdever and Gimelshein2016), a good agreement was verified for the case of a copper sphere in argon gas when 
$\alpha _t=1$ and 
$\alpha _n=0.9$ in the range of the rarefaction parameter 
$1\le \delta \le 10$. For smaller values of 
$\delta$, the comparison is no longer valid because the assumption of local equilibrium far from the sphere is not valid. Moreover, in the comparison with experiment our results did not predict the negative thermophoresis for 
$\delta =10$ and the chosen sets of accommodation coefficients. However, in the present work, the negative thermophoresis is predicted for other sets of accommodation coefficients. Thus, according to the results of the present work, a better understanding of the transport phenomena of spherical aerosols relies on the correct description of the gas–surface interaction law so that further investigations on this research topic must be encouraged, experimentally and numerically. Moreover, since the data on this topic are still scarce in the literature, the results provided in the present work represent a significant contribution towards a better understanding of the phoretic phenomena.
Acknowledgements
The present calculations were carried out at the Laboratório Central de Processamento de Alto Desempenho (LCPAD) of Universidade Federal do Paraná (UFPR, Brazil). The authors acknowledge the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant 304831/2018-2, and the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), grant 2015/20650-5, for support of the research.
Declaration of interests
The authors report no conflict of interest.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2020.523.
Figures 1–4 show the comparison between our results and those provided by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) for the drag and thermophoretic forces in the free molecular regime as the NEAC and TMAC vary.
Figure 5 shows the profiles of the radial and polar components of the bulk velocity due to 
$X_u$ as functions of the distance 
$r/\delta$ when 
$\delta =0.1$, 1 and 10. The TMAC is fixed at 
$\alpha _t=1$, while the NEAC assumes the values 
$\alpha _n=0.1$, 0.5, 0.8 and 1.
Figure 6 shows the profiles of the density and temperature deviations due to 
$X_u$ as functions of the distance 
$r/\delta$ when 
$\delta =0.1$, 1 and 10. The NEAC is fixed at 
$\alpha _n=0.1$, while the TMAC assumes the values 
$\alpha _t=0.5$, 0.8 and 1.
Appendix A. Analytic solution in the free molecular regime
The method of the characteristics allows us to obtain the solution of the collisionless kinetic equation (6.1) for each thermodynamic force (
$n=T$, 
$u$) as
\begin{equation} h^{(n)}(r,\theta,{\boldsymbol c})=\begin{cases} h_c^{(n)}\cos{\theta}+h_s^{(n)}c_{\theta}\sin{\theta}+g^{(n)}\dfrac Sc, & 0\le \theta' \le \theta_0,\\ h_{\infty}^{(n)}, & \theta_0 \le \theta'\le {\rm \pi}, \end{cases} \end{equation}where
\begin{gather} h_c^{(n)}(r,c,\theta')=C_1^{(n)}\left(r-\frac Sc c_r\right) - C_2^{(n)}c_r, \end{gather}
\begin{gather}h_s^{(n)}(r,c,\theta')=C_1^{(n)}\frac Sc + C_2^{(n)}. \end{gather}
The free terms 
$g^{(n)}$ are given in (3.9a,b). The functions 
$h_{\infty }^{(n)}$ are given in (3.14) and (3.15) and, for convenience, they can be written as
\begin{equation} h_{\infty}^{(n)}=h_{c_{\infty}}^{(n)}\cos{\theta} + h_{s_{\infty}}^{(n)}c_{\theta}\sin{\theta}, \end{equation}where
\begin{equation} h_{c_{\infty}}^{(T)}=-\tfrac 32 c_r\left(c^{2} -\tfrac 52 \right),\quad h_{s_{\infty}}^{(T)}=\tfrac 32 \left(c^{2}-\tfrac 52 \right), \end{equation}and
\begin{equation} h_{c_{\infty}}^{(u)}=0,\quad h_{s_{\infty}}^{(u)}=0. \end{equation} We denote by 
$S$ the distance between a point in the gas flow domain with Cartesian coordinates 
$(x,y,z)$ and a point on the spherical surface with Cartesian coordinates 
$(x_0,y_0,z_0)$ which is written as
\begin{equation} S=r\cos{\theta'}-\sqrt{r_0^{2}-r^{2}\sin^{2}{\theta'}}. \end{equation}
It is worth noting that the vector 
${\boldsymbol S}$ is directed towards -
${\boldsymbol c}$ and, consequently, the following relation is valid:
\begin{equation} z_0=z-\frac Sc c_z. \end{equation}
The angle 
$\theta _0$ is given by
\begin{equation} \theta_0=\arcsin{\left(\frac{r_0}{r}\right)}. \end{equation} The quantities 
$C_1^{(T)}$ and 
$C_2^{(T)}$ are obtained from the boundary condition (4.17) as follows:
\begin{align} C_1^{(T)}&=\frac{3}{2r_0}\left\{\alpha_n^{3/2}H_3(\eta)+\alpha_n^{1/2}H_1(\eta) \left[\alpha_t(2-\alpha_t)+(1-\alpha_t)^{2}c_t^{2}-\frac 52 \right] \right\} \nonumber\\ &\quad +\alpha_n(1-c_r^{2})+\alpha_t(2-\alpha_t)-\alpha_t(2-\alpha_t)c_t^{2} +C_2^{(T)}\frac{c_r}{r_0}, \end{align}
\begin{align} C_2^{(T)}&=\frac 32 (1-\alpha_t)\left[\alpha_n+(1-\alpha_n)c_r^{2}+(1-\alpha_t)^{2}c_t^{2}+2\alpha_t(2-\alpha_t)- \frac 52\right]. \end{align} Similarly, the quantities 
$C_1^{(u)}$ and 
$C_2^{(u)}$ are obtained from the boundary condition (4.18) as
\begin{gather} C_1^{(u)}=-\frac{2[(1-\alpha_t)c_r+\sqrt{\alpha_n}H_1(\eta)]}{r_0}, \end{gather}
\begin{gather}C_2^{(u)}=2\alpha_t. \end{gather}The integrals 
$H_1(\eta )$ and 
$H_3(\eta )$ are defined in (4.15a,b).
Appendix B. Split method to solve the kinetic equation
The differential equation (6.5) subject to the boundary condition (6.6) is solved analytically via the method of characteristics and its solution is written as
\begin{equation} h_0^{(n)}(r,\theta,{\boldsymbol c}=\begin{cases} [h_c^{(n)}\cos{\theta}+h_s^{(n)}\sin{\theta}]\,\text{e}^{-S/c}, & 0 \le \theta' \le \theta_0,\\ 0, & \theta_0 < \theta' \le {\rm \pi}, \end{cases} \end{equation}
where the distance 
$S$ along the characteristic line and the angle 
$\theta _0$ are given in (A 7) and (A 9). The functions 
$h_c^{(n)}$ and 
$h_s^{(n)}$ are given in (A 2) and (A 3), but here
\begin{equation} C_1^{(T)}=\alpha_n(1-c_r^{2})+\alpha_t(2-\alpha_t)(1-c_t^{2}),\quad C_2^{(T)}=0, \end{equation}
while 
$C_1^{(u)}$ and 
$C_2^{(u)}$ are given in (A 12) and (A 13).
The system of kinetic equations obtained from the substitution of the representation (6.9) into the kinetic equation for the function 
$\tilde {h}^{(n)}$ reads as
\begin{align} & c_r\frac{\partial \tilde{h}_c^{(n)}}{\partial r}-\frac{c_t}{r} \frac{\partial \tilde{h}_c^{(n)}}{\partial \theta'}+\frac{c_t^{2}}{r}\tilde{h}_s^{(n)}=\nu^{*(n)}+ \left(c^{2}-\frac 32\right)\tau^{*(n)}+2c_ru_r^{*(n)} \nonumber\\ &\quad +\frac{4}{15}c_r\left(c^{2}-\frac 52 \right)q_r^{*(n)}-\tilde{h}_c^{(n)}+g_1^{*(n)}, \end{align}
\begin{align} & c_r\frac{\partial \tilde{h}_s^{(n)}}{\partial r}-\frac{c_t}{r}\frac{\partial \tilde{h}_s^{(n)}}{\partial \theta'}- \frac{c_r}{r}\tilde{h}_s^{(n)}-\frac 1r\tilde{h}_c^{(n)}=2u_{\theta}^{*(n)} \nonumber\\ &\quad +\frac{4}{15}\left(c^{2}-\frac 52\right)q_{\theta}^{*(n)}-\tilde{h}_s^{(n)}+g_2^{*(n)}, \end{align}where the free terms for each thermodynamic force are given as
\begin{equation} g_1^{*(T)}=-c_r\left(c^{2}-\tfrac 52\right),\quad g_2^{*(T)}=c^{2}-\tfrac 52,\quad g_1^{*(u)}=g_2^{*(u)}=0. \end{equation}Then, from (3.17)–(3.22) and (6.16), the dimensionless moments which appear on the right-hand side of (B 3) and (B 4) are written as
\begin{gather} \nu^{*(n)}(r)=\nu_0^{(n)}(r)+\frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi}c_t\tilde{h}_c^{(n)}\,\text{e}^{-c^{2}} c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}\tau^{*(n)}(r)=\tau_0^{(n)}(r)+\frac{4}{3\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi} \left(c^{2}-\frac 32\right)c_t\tilde{h}_c^{(n)}\,\text{e}^{-c^{2}}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}u_r^{*(n)}(r)=u_{r0}^{(n)}(r)+\frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi}c_rc_t \tilde{h}_c^{(n)}\,\text{e}^{-c^{2}}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}u_{\theta}^{*(n)}(r)=u_{\theta 0}^{(n)}(r) + \frac{1}{\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi} c_t^{3}\tilde{h}_s^{(n)}\,\text{e}^{-c^{2}}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}q_r^{*(n)}(r)=q_{r0}^{(n)}(r) + \frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi}c_rc_t\left(c^{2}-\frac 52\right)\tilde{h}_c^{(n)}\,\text{e}^{-c^{2}} c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}q_{\theta}^{*(n)}(r)=q_{\theta 0}^{(n)}(r) + \frac{1}{\sqrt{\rm \pi}}\int_{0}^{\infty}\int_{0}^{\rm \pi}c_t^{3}\left(c^{2}-\frac 52\right)\tilde{h}_s^{(n)}\,\text{e}^{-c^{2}}c\,\text{d}c\,\text{d}\theta', \end{gather}
where the quantities with subscript zero are calculated using the known functions 
$h_0^{(n)}$, given in (B 1), and read as
\begin{gather} \nu_0^{(n)}(r)=\frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0} c_t h_c^{(n)}\,\text{e}^{-c^{2}-S/c}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}\tau_0^{(n)}(r)=\frac{4}{3\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0}\left(c^{2}-\frac 32\right) c_t h_c^{(n)}\,\text{e}^{-c^{2}-S/c}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}u_{r0}^{(n)}(r)=\frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0} c_rc_t h_c^{(n)}\,\text{e}^{-c^{2}-S/c}c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}u_{\theta 0}^{(n)}(r)=\frac{1}{\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0} c_t^{3} h_s^{(n)}\,\text{e}^{-c^{2}-S/c} c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}q_{r0}^{(n)}(r)=\frac{2}{\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0} c_rc_t \left(c^{2}-\frac 52\right) h_c^{(n)}\,\text{e}^{-c^{2}-S/c} c\,\text{d}c\,\text{d}\theta', \end{gather}
\begin{gather}q_{\theta 0}^{(n)}(r)=\frac{1}{\sqrt{\rm \pi}}\int_{0}^{\infty} \int_{0}^{\theta_0} c_rc_t \left(c^{2}-\frac 52\right) h_s^{(n)}\,\text{e}^{-c^{2}-S/c}c\,\text{d}c\,\text{d}\theta'. \end{gather}The dimensionless drag and thermophoretic forces on the sphere, which are defined in (3.26) and (3.27), are written as
\begin{align} F_n &= F_{n0}-\frac{4}{3\sqrt{\rm \pi}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} c_r^{2}c_t\tilde{h}_c^{(n)}(r_0,c_r,c_t)\,\text{e}^{-c^{2}}\,\text{d}c_r\,\text{d}c_{t} \nonumber\\ &\quad + \frac{4}{3\sqrt{\rm \pi}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} c_rc_t^{3}\tilde{h}_s^{(n)}(r_0,c_r,c_t)\,\text{e}^{-c^{2}}\,\text{d}c_r\,\text{d}c_{t}, \end{align}
where 
$F_{n0}$ is obtained by substituting the solution (B 1) into (3.26) and (3.27) when 
$r=r_0$.
