2. Problem formulation and computational details

2.1. Governing equations

In our prior studies we have successfully used a fully spectral, three-dimensional parallel algorithm to predict high-order nonlinear viscoelastic TC flow transitions (Thomas et al. Reference Thomas, Al-Mubaiyedh, Sureshkumar and Khomami2006a,Reference Thomas, Khomami and Sureshkumarb, Reference Thomas, Khomami and Sureshkumar2009) and study viscoelastic TC turbulence (Liu & Khomami Reference Liu and Khomami2013a,Reference Liu and Khomamib; Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). In this study, we have used a modified version of this code to avoid use of artificial diffusion (AD) to stabilize numerical integration of the conformation tensor evolution equation (see below for details). Similar to our prior studies, the FENE-P constitutive equation is used to model the polymer contribution to the total stress. The physical connection of the FENE-P model to real elastic liquids, i.e. dilute solutions of high molecular weight, finitely extensible flexible polymers in a theta solvent, makes it a model of choice for this class of simulations. This model captures the essential rheological response of this class of fluids both in shear and extension. The maximum chain extensibility is defined as $L$, and remains constant in the simulations. Thus, flow-induced polymer chain scission is not captured in our simulations. Overall, chain scission in stochastic flows has not been extensively studied; even if a model existed that could accurately capture flow-induced chain scission in this class of flows, its implementation in DNS of viscoelastic flows would require computational power well beyond today's most advanced supercomputers. We have chosen $d=R_o-R_i$, $d/\varOmega R_i$, $\varOmega R_i$, $\rho (\varOmega R_i)^{2}$ and $\eta _p \varOmega R_i / d$ as scales for length, time, velocity $\boldsymbol {u}$, pressure $p$ and polymer stress $\boldsymbol {\tau }$, respectively. Here, $\rho$ represents the solution density, and the total zero-shear solution viscosity $\eta _t$ is the sum of the solvent ($\eta _s$) and polymeric ($\eta _p$) contributions. Further, we scale the conformation tensor $\boldsymbol{\mathsf{C}}$, which represents the ensemble average of the second moment of the end-to-end vector of the polymer chain, with respect to $BT/H$, where $B$, $T$ and $H$ denote the Boltzmann constant, absolute temperature and the Hookean spring constant of the elastic dumbbell model, respectively. The resulting dimensionless equations governing the motion of an incompressible FENE-P fluid are as follows:

(2.1)$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u} = 0, \end{gather}$$

(2.2)$$\begin{gather}\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u} ={-}\boldsymbol{\nabla} P+\frac{\beta}{Re}\nabla^{2}\boldsymbol{u}+\frac{1-\beta}{Re}\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{\tau}, \end{gather}$$

and

(2.3)\begin{equation} \frac{\partial \boldsymbol{\mathsf{C}}}{\partial t} + \boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{\mathsf{C}}=\boldsymbol{\mathsf{C}}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u} +(\boldsymbol{\nabla}\boldsymbol{u})^\textrm{T}\boldsymbol{\cdot}\boldsymbol{\mathsf{C}}-\boldsymbol{\tau}, \end{equation}

where polymer molecules are modelled as dumbbells composed of two beads and a nonlinear spring, and the polymer stress $\boldsymbol {\tau }$ can be related to the stress conformation tensor $\boldsymbol{\mathsf{C}}$ via the relationship

(2.4)\begin{equation} \boldsymbol{\tau}=\frac{f(\boldsymbol{\mathsf{C}})\boldsymbol{\mathsf{C}}-\boldsymbol{\mathsf{I}}}{Wi}. \end{equation}

The function $f(\boldsymbol{\mathsf{C}})$, known as the Peterlin function, is defined as

(2.5)\begin{equation} f(\boldsymbol{\mathsf{C}})=\frac{L^{2}-3}{L^{2}-\textrm{trace}(\boldsymbol{\mathsf{C}})}. \end{equation}

In the above equations, $\beta =\eta _s / \eta _t$ is the solvent to total viscosity ratio; the Reynolds number is defined as $Re=\rho \varOmega R_i d /\eta _t$, and the Weissenberg number as $Wi=\lambda R_i \varOmega /d$. The velocity vector $\boldsymbol {u}$ is composed of three components $u_r$, $u_\theta$ and $u_z$ in the $r$, $\theta$ and $z$ directions, respectively, in a cylindrical coordinate system, where the $z$-axis coincides with the cylinder axis. The length of the computational domain along the cylinder axis is set as $L_z={\rm \pi} d$, so the effects of large-scale TV in the gap and turbulent fluctuations can be obtained reliably (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015). The governing equations are also supplemented by no-slip boundary conditions at the walls, as well as periodic boundary conditions in the $z$ direction.

2.3. Code assessment

In order to demonstrate the accuracy of our HM code, a multi-step hierarchical validation strategy has been adopted: (i) comparison with analytical solution of laminar flow, (ii) faithfully capturing a unique flow pattern in viscoelastic TC flow, namely, ribbon or RSW flow (Groisman & Steinberg Reference Groisman and Steinberg1996, Reference Groisman and Steinberg1998a; Thomas et al. Reference Thomas, Khomami and Sureshkumar2009) and (iii) the inertio-elastic turbulent flow. In the present study, $\langle \,\rangle =\langle \langle \langle \, \rangle _\theta \rangle _z\rangle _t$, denotes hereafter averaging in the $\theta$-direction ($\langle \, \rangle _\theta$), the $z$-direction ($\langle \, \rangle _z$) and time ($\langle \, \rangle _t$), and the fluctuating part of variable $v$ is obtained as $v'=v-\langle v\rangle$. In addition, $\tilde {r}=(r-R_i)/d$ is the dimensionless distance to the inner cylinder wall.

A comparison of the HM numerical results with the analytical solutions of laminar viscoelastic TC flow is depicted in figure 1. The simulation parameters correspond to a laminar Couette flow with parameters extracted from linear stability analysis results (Thomas Reference Thomas2006). Specifically, the simulation is performed at $Re=40, Wi=1$ with $L=100, \beta =0.8$ with a unit tensor as the initial condition for the conformation tensor; the mean tangential ($\langle C_{r\theta }\rangle$) and normal ($\langle C_{\theta \theta }\rangle$) components of the conformation tensor obtained by HM are in excellent agreement with the analytical solution.

Figure 1. Profiles of (a) mean conformation component $\langle C_{r\theta }\rangle$ and (b) $\langle C_{\theta \theta }\rangle$ obtained by analytical solution and HM simulation at $Re=40, Wi=1, L=100, \beta =0.8$.

A ribbon flow state simulated by HM and SM without use of AD has also been examined. The ribbon patterns obtained by the two methods shown in figure 2(a) are indistinguishable; their checkerboard-like features signifying the expected alternative regions of radial inflow (blue) and outflow (red) are accurately captured (Groisman & Steinberg Reference Groisman and Steinberg1996, Reference Groisman and Steinberg1998a; Thomas et al. Reference Thomas, Khomami and Sureshkumar2009). The time periods associated with the fluctuating radial velocity in the ribbons are approximately $14.45\lambda$ and $14.62\lambda$ for SM and HM, respectively. Moreover, in figure 2(b), the time series of total drag force ($F_{t}$) and its components of Newtonian viscous shear stress ($F_s$) and elastic shear stress ($F_p$) obtained by these two methods show good agreements with relative error less than $0.06\,\%$.

Figure 2. (a) Space–time plots of radial velocity $u_r$ along the axial line positioned at $r=(R_i+R_o)/2$ and $\theta ={\rm \pi}$ showing flow states calculated by SM and HM methods at $Re=86.6, Wi=4.33, L=100, \beta =0.8$. (b) Time series of drag forces at the inner cylinder wall. Here, total drag forces $F_t$ is the sum of solvent $F_s$ and polymer $F_p$ contributions, $F_s=2\beta \int _0^{L_z}\mathrm {d}z\int _0^{2{\rm \pi} }S_{r \theta }r\,\mathrm {d}\theta /Re/L_z$, $F_p=(1-\beta )\int _0^{L_z}\mathrm {d}z\int _0^{2{\rm \pi} }\tau _{r \theta }r\,\mathrm {d}\theta /Re/L_z$, where $S_{r\theta }$ is the ($r,\theta$) component of the velocity gradient tensor $\boldsymbol{\mathsf{S}}=(\boldsymbol {\nabla }\boldsymbol {u}+(\boldsymbol {\nabla }\boldsymbol {u})^\textrm {T})/2$.

Finally, a comparison between the results of the high-$Re$ viscoelastic TC turbulence simulated by previously developed SM and the new HM is made. Due to the aforementioned numerical stability problem, a global AD term is added to the SM for simulation of dilute polymer solution at $\beta =0.9$ and large extensibility $L=100$ at $Re=3000$, $Wi=30$. Thus, the validation in this part can also be viewed as a critical examination of the effects of AD on the flow structure and the turbulence statistics in the elasto-inertial turbulent TC flow. The profiles of mean velocity $\langle u_\theta \rangle$ and polymer shear stress $\langle \tau _{r\theta }\rangle$ are shown in figure 3(a,b). Excellent agreements between the computed velocity and shear stress profiles are observed, particularly at high $Sc$. Furthermore, the profiles of fluctuations in velocity and elastic shear stress depicted in figure 3(c,d) shows minor differences between the two schemes at high $Sc$. The modifications of flow structures can be further quantified by the differences in the one-dimensional spanwise spectra of the turbulent kinetic energy (TKE) and polymer stretch for different $Sc$ (see figure 4). The energy in the high-wavenumber regime is lower for the SM results of finite $S_c$ than that obtained by the HM technique. However, in the low-wavenumber regime, the profiles collapse indicating the large-scale flow structures remain nearly unchanged for the range of $S_c$ considered. To this end, these comparisons taken together have revealed that the HM code can faithfully reproduce high-$Re$ viscoelastic TC turbulence flow features and statistics (Liu & Khomami Reference Liu and Khomami2013b; Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). At the same time, the $Sc$ sensitivity analysis suggests that $Sc\sim {O}(1)$ can capture the essential features of the velocity and polymer stress fields in high-$Re$ viscoelastic TC simulations. However, it should be noted that the addition of the AD term mainly modifies/reduces the large polymer stress gradients in the flow field that give rise to small-scale structures as evinced by the small-scale elastic GV formed near the inner cylinder walls where large stress gradients exist (Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). To this end, addition of AD mainly affects/dissipates small-scale elastic flow structures (see figure 4). This is consistent with the previous findings regarding the influence of AD on simulations of inertia-driven and elasto-inertial viscoelastic turbulence (Sid et al. Reference Sid, Terrapon and Dubief2018; Gupta & Vincenzi Reference Gupta and Vincenzi2019; Zhu & Xi Reference Zhu and Xi2020). Based on our earlier studies of the curvature dependence of viscoelastic TC turbulence (Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019), decreasing the gap (larger $\eta$) is expected to lead to weakening and elimination of the small-scale elastic GV, due to the fact that elastic effects are more significant at smaller $\eta$. That is, a decrease in $\eta$ leads to an increase in curvature and commensurately higher hoop stresses (Larson et al. Reference Larson, Shaqfeh and Muller1990; Groisman & Steinberg Reference Groisman and Steinberg1998b). Thus the AD effect is more prominent near the walls where significant polymer stretch is realized due to the mean-flow shear. This in turn, leads to larger polymer stress gradients and formation of an elastic boundary layer. Evidently, the AD effect is more pronounced in small gap systems.

Figure 3. Profiles of (a) mean azimuthal velocity $\langle u_\theta \rangle$ and (b) mean polymer shear stress component $\langle \tau _{r\theta }\rangle$, (c) root-mean-square (r.m.s.) values of three velocity components and (d) polymer stress component $\tau _{r\theta }$ at $Re=3000, Wi=30, L=100$ with various $Sc$.

Figure 4. One-dimensional spectra of the turbulent kinetic energy ($\langle \boldsymbol {u}^{\prime }\boldsymbol {\cdot }\boldsymbol {u}^{\prime }\rangle /2$) (a) and polymer stretching ($\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle$) (b) sampled at the middle of the gap for viscoelastic flows of $Re=3000, Wi=30, L=100$ with various $Sc$.

It should be noted that figure 3(c,d) depicts that the most accurate results correspond to those of the full pseudo-spectral calculation with the highest $Sc=3.33$. Evidently, the predictions of the HM technique fall between the spectral results obtained with two different global AD values. This underscores the fact that introduction of a low-order upwind finite-difference approximation for the convection term introduces numerical diffusion mainly in the radial direction. However, the scheme does produce results that are very similar to fully spectral techniques with small global AD of $Sc\sim {O}(1)$. In addition, it ensures positive definiteness of the conformation tensor and the hyperbolic-like nature of the constitutive equation. Hence, if SM with sufficiently high-order approximating function and $Sc\sim {O}(1)$ is coupled with available schemes that ensure positive definiteness of the conformation tensor (Housiadas, Wang & Beris Reference Housiadas, Wang and Beris2010), reliable results can be obtained. To this end, the HM technique used in this study can be viewed as an equivalent technique to traditional SM with a sufficiently high $Sc$ value.

2.4. Simulation parameters

The viscoelastic TC flow of a dilute long chain polymer solution with $\beta =0.9$ and $L=100$, at $Wi=30$ is investigated in the Reynolds number range of $500$ to $8000$ to scrutinize the influence of fluid inertia on the inertio-elastic turbulent flow structures and statistics. This corresponds to $El$ in the range of $0.00375\sim 0.06$. All the simulations are started from a fully developed inertio-elastic turbulent flow at $Re=3000$, $Wi=30$ with radius ratio $\eta =R_i/R_o=0.5$. Based on this flow field, we decrease the Reynolds number to $1000, 500$ to obtain results for the low-$Re$ regime and increase it to $5000, 8000$ for the high-$Re$ regime. Simulation parameters and the grid resolutions are summarized in table 1. As Gauss–Lobatto–Chebyshev polynomials are applied in the wall normal ($r$-) direction and Fourier series in the periodic ($\theta$- and $z$-) directions, mesh grids are clustered near the inner and outer walls in the $r$-direction, and uniform in the $\theta$- and $z$-directions. The time scale is made dimensionless by the convective time unit, $T=d/(\varOmega R_1)$. Sufficiently long simulations (at least $300T=10\lambda$) have been performed to ensure that statistically steady flow states are realized. To evaluate the turbulence statistics, ensemble averaging is performed for time periods of approximately $120T$.

Table 1. Numerical parameters and grid resolutions. The superscript ‘$+$’ is used to denote the quantities non-dimensionalized by the viscous length scale $\delta _\tau =\eta _t/\rho /u_\tau$; the friction velocity is defined as $u_\tau =\sqrt {\tau _w/\rho }$, where $\tau _w$ is the total wall stress; the friction Reynolds number is defined as $Re_\tau =\rho u_\tau d/\eta _t$.

3. Small-scale elastic GV

In this section, the flow structures in turbulent TC flow with particular emphasis on small-scale GV near the inner cylinder wall are discussed in detail. Similar to our previous findings in the viscoelastic turbulent TC flow at this radius ratio (Liu & Khomami Reference Liu and Khomami2013b; Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019), the well-organized large-scale TV identified in the Newtonian flow are no longer observed in the time and $\theta$-direction averaged flow fields at all $Re$ considered (see figure 5a). Instead, a large number of vortices span across the entire gap. Also, the GV are smaller in size and higher in number near the inner wall. The instantaneous flow fields depicted in figure 5(b), show that increasing $Re$ leads to a monotonic increase in number of the vortices. Specifically, at $Re\leqslant 3000$, the gap is occupied by a few larger-scale vortices in the bulk region along with some GV near the inner wall. As the Reynolds numbers is increased to $Re\geqslant 5000$, larger-scale vortices observed at smaller $Re$ become severely distorted and break down into smaller vortices, in turn, the GV become closer to the wall. This finding is consistent with experimental observation of Baumert and Muller (Baumert & Muller Reference Baumert and Muller1995, Reference Baumert and Muller1997, Reference Baumert and Muller1999). In a wider gap (smaller radius ratio $\eta$) TC cell, in addition to large counter-rotating vortices spanning across the gap, Baumert and Muller also observed additional small and irregular vortices formed near the inner cylinder wall (Baumert & Muller Reference Baumert and Muller1999). The more prominent appearance of small-scale vortices near the inner wall with increasing curvature of the TC cell has also been confirmed by our DNS study of curvature-dependent viscoelastic turbulent TC flows (Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). Moreover, as pointed out in our previous study, these small-scale vortices are mainly generated through an elastic mechanism, as a result they have been dubbed ‘elastic Görtler vortices’.

Figure 5. (a) Time and $\theta$-direction averaged vectors of radial ($\langle u_r\rangle _{\theta , t}$) and axial ($\langle u_z\rangle _{\theta , t}$) velocities and contour plots of streamwise vorticity $\langle \omega _\theta \rangle _{\theta , t}$ in ($r, z$) plane; (b) instantaneous vectors of radial ($u_r$) and axial ($u_z$) velocities and contour plots of streamwise vorticity $\omega _\theta$ in ($r, z$) plane with $\theta ={\rm \pi} /2$ for various $Re$ with $Wi=30$.

The existence of near-wall elastic GV and the effect of fluid inertia on their scales can be quantified via examination of the streamwise vorticity fluctuations $\omega _{\theta \,rms}^{\prime }$ as depicted in figure 6. Specifically, all $\omega _{\theta \, rms}^{\prime }$ profiles exhibit a local maximum and minimum in the inner-wall region. The near-wall quasi-streamwise vortices (QSV) model proposed by Kim, Moin & Moser (Reference Kim, Moin and Moser1987), ascribes the difference between the local minimum and maximum of $\omega _{\theta \,rms}^{\prime }$ to the average intensity of the QSV that are generated as a consequence of a turbulent shear instability (Stone, Waleffe & Graham Reference Stone, Waleffe and Graham2002; Li et al. Reference Li, Sureshkumar and Khomami2006); the radial positions of the local minimum and maximum correspond to the average locations of the edge and centre of the QSV, respectively. Thus their distance is roughly proportional to the average size of the QSV. Near the inner wall, increasing $Re$ makes the local maximum and minimum of $\omega _{\theta \,rms}^{\prime }$ more pronounced (see figure 6a), consequently smaller size vortices appear as $Re$ is increased (also see figure 7). Evidently, the small-scale GV become stronger in intensity and smaller in size with increasing $Re$, which indicates a gradual enhancement of the intensity of the turbulent shear instability in the inner-wall region. In contrast, vorticity fluctuations exhibit the opposite trend in polymer-induced drag reduction channel flows where near-wall QSV obtain an increase in size and a reduction in number and become highly elongated in the streamwise direction (Li et al. Reference Li, Sureshkumar and Khomami2006; Kim et al. Reference Kim, Li, Sureshkumar, Balachandar and Adrian2007; Xi & Graham Reference Xi and Graham2012; Li et al. Reference Li, Sureshkumar and Khomami2015; Teng et al. Reference Teng, Liu, Lu and Khomami2018). However, as shown in figures 5 and 6(b), small-scale GV are not observed in the outer-wall region for all $Re$ considered here. This is in contrast to our earlier findings where slightly larger inertio-elastic GV formed near the outer cylinder wall (Liu & Khomami Reference Liu and Khomami2013b; Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). This points to the fact that the elastic effects needed to generate these inertio-elastic GV are not sufficient near the outer wall due to the smaller $Wi$ and larger solvent to total viscosity ratio ($\beta =0.9$) used in the present study.

Figure 6. The r.m.s. values of azimuthal (streamwise) vorticity component for various $Re$ with $Wi=30$: (a) near the inner wall and (b) near the outer wall.

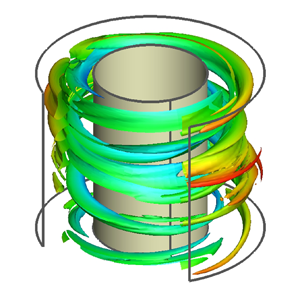
Figure 7. Instantaneous vortical structures visualized by $Q$-criterion with $Q=0.001$ and coloured by the distance to the inner wall for the three main regimes of viscoelastic TC flow at (a) $Re=500$, (b) $Re=3000$, (c) $Re=8000$, with $Wi=30$. The flow structures in the region $\theta \in [3/2{\rm \pi} ,2{\rm \pi} ]$ and $\tilde {r}\in [1/2,1]$ are not shown to clearly display the small-scale vortical structures near the inner wall.

Although the small and irregular elastic GV formed near the inner cylinder wall have been observed in a series of prior experiments (Lee et al. Reference Lee, Sengupta and Wei1995; Baumert & Muller Reference Baumert and Muller1995, Reference Baumert and Muller1997, Reference Baumert and Muller1999), the generation mechanism of these structures remains poorly understood due to the lack of polymer stress/body force measurements. To this end, a comparison of the production terms of the mean streamwise enstrophy budget equations (Dimitropoulos et al. Reference Dimitropoulos, Sureshkumar, Beris and Handler2001; Kim et al. Reference Kim, Li, Sureshkumar, Balachandar and Adrian2007) near the inner wall is performed to shed light on the generation mechanism of the elastic GV. A detailed description of the budget equations for mean enstrophy is given in Appendix A. Here, we take the $\theta$-component of the mean vorticity ($W_\theta$) in (A3) and obtain the transport equation for mean streamwise enstrophy ($E_{\omega \theta }=W_\theta ^{2}/2$). As seen in figure 8(a), the total streamwise enstrophy is balanced near the inner wall for $Re=500$, demonstrating that a statistical steady state has been achieved. At $Re=500$, $E_{\omega \theta }$ is mainly produced by the elastic effect $T_\omega$ that is almost balanced by viscous dissipation ($\varepsilon _\omega$) since other typical shear production terms, i.e. production by mean ($PM_\omega$) and fluctuating ($PF_\omega$) strain of the mean vorticity as well as fluctuating enstrophy ($FE_\omega$) are negligible. In addition, local balance (redistribution to opposite direction with equal magnitude) is achieved by two diffusive transports of the mean enstrophy, namely, by the solvent ($DS_\omega$) and polymer ($DT_\omega$) viscosity. The distributions of the main production terms with various $Re$ are depicted in 8(b). Specifically, it is shown that the elastic production $T_\omega$ acts as the dominant source term for the ${E_\omega }_\theta$ budgets as opposed to the typical shear term $S_\omega$ that is the sole generating mechanism for streamwise vortical structures in Newtonian TC flow. So, it is rational to label these near-inner-wall small-scale vortices as elastic GV (Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). However, increasing $Re$ leads to a monotonic decrease of the dominant radial region of $T_\omega$ and a commensurate change in its position, i.e. it gets closer to the inner wall. This confirms that the decrease in size of these elastic GV discussed above indeed occurs by the redistribution of the streamwise vorticity fluctuations (see figure 6a). To this end, it is rational to expect that the entire gap will be filled with inertia-dominated vortical structures when $Re$ gets much higher resulting in a gradual elimination of the elastic vortical structures.

Figure 8. (a) Balance of mean streamwise enstrophy $E_{\omega \theta }$ of $Re=500$, $Wi=30$ near the inner cylinder wall. (b) Production terms of $E_{\omega \theta }$ for the viscoelastic TC flows for various $Re$ with $Wi=30$. Here, $S_\omega$ denotes the typical shear production including the mean and fluctuating strain as well as the fluctuating enstrophy, and $T_\omega$ represents the elastic production.

It has been confirmed that the GV near the cylinder walls will cause near-wall streaky structures to form herringbone-like patterns in the Newtonian turbulent TC flows (Wei et al. Reference Wei, Kline, Lee and Woodruff1992; Dong Reference Dong2007). Similarly, as depicted in figure 9, herringbone-like patterns can also be observed from the spatial-temporal characteristics of the radial velocity near the inner wall in the inertio-elastic turbulent TC flows, especially at high $Re$. Evidently, it is the radial inflows and outflows at the boundaries of the counter-rotating elastic GV pairs that cause the streaky structures. Specifically, at $Re=500$, only a few large and long herringbone streaks are distributed in disjoint bands around the outflow boundaries of the elastic GV and streaks from neighbouring bands barely intersect. As $Re$ is increased, a considerable increase in the population of streaks is observed, and the spacing between neighbouring streaks is substantially decreased. Finally, at $Re=8000$, the herringbone streaks become significantly finer and more closely packed, and their population is dramatically increased. However, the streaks become less coherent as evinced by their broken appearances, shorter lengths and scattered nature. The herringbone steaks in elastically dominated turbulent TC flows have sufficiently longer time life than their Newtonian counterparts due to their elastic origin. This is attributed to the fact that the fluid relaxation time ($\lambda$) governs this dynamical process in the elasticity-dominated regime. Consequently, increasing fluid inertia leads to a monotonic decrease in the lifetime of the herringbone steaks as a result of a significant reduction of elastic effects.

Figure 9. Space–time plots of radial velocity $u_r$ along the axial line positioned at $\tilde {r}=0.01$ and $\theta ={\rm \pi}$ showing radial inflows (blue) and outflows (red) at (a) $Re=500$, (b) $Re=1000$, (c) $Re=3000$, (d) $Re=5000$, (e) $Re=8000$, with $Wi=30$.

4. Polymer-induced turbulence dynamics

The flow structures discussed above (shown in figures 5, 7, 9) clearly demonstrate that the turbulent flow states are achieved for all $Re$ considered. It should be noted that the Newtonian counterparts of $Re=500$ and $Re=1000$ are laminar flow states at radius ratio $\eta =0.5$ (Dong Reference Dong2007); thus the turbulence at $Re=500$ and $Re=1000$ is elasticity induced. As expected, in figure 10(a) the mean azimuthal velocity profiles obtain large radial gradients near both walls and an almost flat plateau in the bulk. The velocity gradient becomes larger and the flat region gets wider as the Reynolds number increases, suggesting an enhanced mean momentum transport in the wall regions and efficient mixing in the bulk due to the intense vortical circulations. Generally, the angular momentum $ru_\theta$ is the preferred variable to quantify the transport dynamics in a TC flow system, where the current of $ru_\theta$ is a conserved quantity that is transported from the inner to the outer cylinder (or vice versa) (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). Instead of an essentially constant mean angular momentum of $0.5\varOmega R_i^{2}$ observed in the bulk of Newtonian turbulent TC flow (Dong Reference Dong2007), the mean angular momentum for the viscoelastic TC flow depicted in figure 10(b) is less than $0.5\varOmega R_i^{2}$ and exhibits obvious positive gradients at the same $Re$; this indicates an efficient transport but an inefficient mixing of the mean angular momentum in the inertio-elastic turbulent TC flows.

Figure 10. Profiles of (a) mean azimuthal velocity $\langle u_\theta \rangle$ and (b) mean angular momentum $\langle ru_\theta \rangle$ for various $Re$ with $Wi=30$.

For the viscoelastic turbulent TC flow, the same procedure used by Eckhardt et al. (Reference Eckhardt, Grossmann and Lohse2007) is applied to derive the angular momentum current $J^{\omega }$ as

(4.1)\begin{equation} J^{\omega}=r^{3}[\langle u_r\omega \rangle-\nu_s \partial_r \langle\omega\rangle - \nu_p \langle\tau_{r\theta}\rangle/r], \end{equation}

where $\nu _s$ and $\nu _p$ are dimensionless kinematic viscosities for solvent and polymers respectively, and $\nu _s=\beta /Re$, $\nu _p=(1-\beta )/Re$. The right-hand terms of (4.1) represent in sequence the convective flux ($J^{\omega }_c$), the diffusive flux ($J^{\omega }_d$) and the elastic source/sink term ($J^{\omega }_p$) to angular momentum (Song et al. Reference Song, Teng, Liu, Ding, Lu and Khomami2019). For a statistically stationary turbulent TC flow, the angular momentum current should be conserved (Eckhardt et al. Reference Eckhardt, Grossmann and Lohse2007; Dong Reference Dong2008), corresponding to a fact that the total torque exerted on the cylindrical fluid layers at a given radial position should be a $r$-independent constant (Van Gils et al. Reference Van Gils, Huisman, Bruggert, Sun and Lohse2011). As expected, in figure 11, different yet constant values of the total angular momentum current are realized for all the viscoelastic TC flows. For all $Re$ considered, the diffusive flux ($J^{\omega }_d$) has the dominant contribution to $J^{\omega }$ in the wall regions, while $J^{\omega }_p$ has the most significant contribution away from the walls (which is positive and thus a source term). However, with increasing $Re$, the convective flux ($J^{\omega }_c$) gradually plays a more significant role in transport of the angular momentum in the bulk region. It should be noted that the diffusive flux ($J^{\omega }_d$) makes a larger contribution than the convective flux ($J^{\omega }_c$) in the entire gap at $Re=500$, clearly demonstrating the negligible effect of convective flux in the flow (see figure 11a). The overall angular momentum current balance clearly underscores the fact that increasing the $Re$ leads to a monotonic increase of the inertial contribution but a decrease of the elastic contribution to the $J^{\omega }$-transport in the inertio-elastic TC flow.

Figure 11. Balance of angular momentum current across the gap for viscoelastic TC flows of (a) $Re=500$, (b) $Re=1000$, (c) $Re=3000$ and (d) $Re=8000$, with $Wi=30$.

As a consequence, near the inner wall the corresponding elastic shear stress (figure 12a) and inertial shear stress (figure 12b) both exhibit a monotonic increase with $Re$. Specifically, at all $Re$ the mean elastic shear stress $\langle \tau _{r\theta }\rangle$ increases monotonically between its minimum in the inner-wall region and the local minimum of markedly higher value in the outer-wall region (see figure 12a). Elastic GV as expected (see figure 5a) enhance transverse momentum exchange and turbulent mixing of $\tau _{r\theta }$ via their vortical circulations. It should be noted that the minimum value of $\langle \tau _{r\theta }\rangle$ occurs close to the inner wall while the magnitude of this minimum decreases remarkably with increasing $Re$. Further, for each $Re$, a sharp decrease of $\langle \tau _{r\theta }\rangle$ in the inner-wall region indicates that the elastic GV have developed a $\langle \tau _{r\theta }\rangle$ boundary layer in the turbulent flow. Moreover, the radial position of the minimum of $\langle \tau _{r\theta }\rangle$ shifts slightly toward the inner wall for higher $Re$, leading to a further reduction of the polymer shear stress boundary layer thickness $\delta _{\tau _{r\theta }}$. In a turbulent TC flow, shear stress $\langle u'_r u'_\theta \rangle$ is mainly caused by the shear instability induced by the coupling of radial and azimuthal fluctuating motions that are generated by the vortical circulations (Bilson & Bremhorst Reference Bilson and Bremhorst2007; Dong Reference Dong2007). Specifically, the large-scale vortices in the bulk mainly generate the energetic radial fluctuating motions at the inflow/outflow vortex cell boundaries, while the small-scale vortices in the near-wall region are responsible for the intense azimuthal fluctuating motions. Hence, the distributions of inertial shear stress as shown in figure 12(b) clearly demonstrate a change from a regime dominated by large-scale centre-region vortices at low $Re\leqslant 1000$ to a small-scale near-wall vortices regime at high $Re\geqslant 5000$ (see figure 7). At the same time, the strong shear instability that results from these elastic GV causes a local maximum of $\langle u'_r u'_\theta \rangle$ for large $Re$. Moreover, for higher $Re$ flows, a much higher inner-wall peak value of $\langle u'_r u'_\theta \rangle$ indicates a higher intensity of turbulent shear instability over the inner wall as compared with that over the outer wall.

Figure 12. Mean polymer shear stress component $(1-\beta )\langle \tau _{r\theta }\rangle /Re$ (a) and Reynolds shear stress component $\langle u'_r u'_\theta \rangle$ (b) for various $Re$ with $Wi=30$. Here, $\delta _{\tau _{r\theta }}$ represents the thickness of boundary layer of $\langle \tau _{r\theta }\rangle$ for the inertio-elastic turbulent TC flows, defined as the distance from the inner wall to the radial position where the minimum of $\langle \tau _{r\theta }\rangle$ occurs.

The influence of $Re$ on the inertio-elastic TC flows can also be quantitatively measured by comparing the power spectral density at various Re. The one-dimensional spectra of the TKE depicted in figure 13 capture approximately eight orders of magnitude of decay, indicating that the grid resolution is sufficient to cover the relevant spatial scales. For both the streamwise and the spanwise spectra, the small-scale values monotonically increase with $Re$ and in the small-wavenumber (k) range the scaling of approximately $k^{-5/3}$ gradually appears. In EIT of channel flows, scaling law of $k^{-5/3}$ in the low-wavenumber range is also observed (Dubief et al. Reference Dubief, Terrapon and Soria2013). Generally, the Kolmogorov spectrum law of $-5/3$ is the hallmark of classical inertial turbulence. Thus, the progressive disappearance of the $-5/3$ scaling at large scales as $Re$ is decreased, unequivocally demonstrates the gradual weakening of inertial effects on the flow. In fact, the scaling of velocity power spectra over a broad range of wavenumbers can be fitted by the power-law decay with the exponent of nearly $k^{-14/3}$, even at large $Re$. To this end, as $Re$ is progressively decreased, the wavenumber range of the dissipation range progressively increases; correspondingly the wavenumber range where the power-law decay with the exponent of approximately $k^{-14/3}$ increases (see figure 13). Intriguingly, in the dissipation range the scaling with the exponent of nearly $k^{-14/3}$ is consistent with EIT in channel and decaying isotropic turbulent flows, where energy spectra often displays a scaling law of $k^{-\gamma }$ in the high-wavenumber range and $\gamma$ is between $3.8$ and $4.7$ (Dubief et al. Reference Dubief, Terrapon and Soria2013; Watanabea & Gotoh Reference Watanabea and Gotoh2013, Reference Watanabea and Gotoh2014; Sid et al. Reference Sid, Terrapon and Dubief2018).

Figure 13. One-dimensional streamwise (a) and spanwise (b) spectra of the TKE ($\langle \boldsymbol {u}^{\prime }\boldsymbol {\cdot }\boldsymbol {u}^{\prime }\rangle /2$) normalized by streamwise TKE ($\langle u'_\theta u'_\theta \rangle /2$ ) sampled at the middle of the gap for various $Re$ with $Wi=30$.

The polymer-induced changes in turbulence fluctuations can be ascertained via examination of energy exchange across the gap with a particular emphasis on the wall regions. To this end, the budgets of mean kinetic energy and TKE are analysed as they are good analytical tools to advance mechanistic understanding of complicated flow dynamics in wall-bounded turbulence (Dimitropoulos et al. Reference Dimitropoulos, Sureshkumar, Beris and Handler2001; Dallas & Vassilicos Reference Dallas and Vassilicos2010; Thais, Gatski & Mompean Reference Thais, Gatski and Mompean2012, Reference Thais, Gatski and Mompean2013; Teng et al. Reference Teng, Liu, Lu and Khomami2018). The budget equations to quantify the energy cascade of viscoelastic turbulent TC flow are given below; the budget equation for the mean kinetic energy $E=\boldsymbol {U}^{2}/2$ is given by

(4.2)\begin{align} \frac{\partial E}{\partial t}+\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla} E & = \boldsymbol{\nabla}\boldsymbol{\cdot}( \underbrace{-P\boldsymbol{U}}_{D_{mp}} \underbrace{+2\nu_s\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\mathsf{S}}}_{D_{ms}} \underbrace{+\nu_p\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{T}}_{D_{me}} \underbrace{-\langle\boldsymbol{uu}\rangle \boldsymbol{\cdot}\boldsymbol{U}}_{D_{mt}}) \nonumber\\ &\quad\underbrace{-2\nu_s(\boldsymbol{\nabla}\boldsymbol{U}):\boldsymbol{\mathsf{S}}}_{\varepsilon_m} \underbrace{-\nu_p(\boldsymbol{\nabla}\boldsymbol{U}): \boldsymbol{T}}_{P_{me}} \underbrace{+\langle\boldsymbol{u}^{\prime}\boldsymbol{u}^{\prime}\rangle:(\boldsymbol{\nabla}\boldsymbol{U})}_{P_{t}}, \end{align}

and for the TKE $e=\langle \boldsymbol {u}^{\prime } \boldsymbol {\cdot } \boldsymbol {u}^{\prime }\rangle /2$

(4.3)\begin{align} \frac{\partial e}{\partial t}+\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla} e & = \boldsymbol{\nabla}\boldsymbol{\cdot}( \underbrace{-\langle P^{\prime} \boldsymbol{u}^{\prime}\rangle}_{D_{p}}+\underbrace{2\nu_s\langle\boldsymbol{u}^{\prime} \boldsymbol{\cdot}\boldsymbol{\mathsf{s}}^{\prime}\rangle}_{D_{s}}+\underbrace{\nu_p\langle\boldsymbol{u}^{\prime} \boldsymbol{\cdot}\boldsymbol{\tau}^{\prime}\rangle}_{D_{e}}-\underbrace{\langle\boldsymbol{u}^{\prime} \boldsymbol{u}^{\prime}\boldsymbol{\cdot}\boldsymbol{u}^{\prime}\rangle/2}_{D_{t}} ) \nonumber\\ &\quad \underbrace{-2\nu_s\langle(\boldsymbol{\nabla}\boldsymbol{u}^{\prime}):\boldsymbol{\mathsf{s}}^{\prime}\rangle}_{\varepsilon} \underbrace{-\nu_p\langle(\boldsymbol{\nabla}\boldsymbol{u}^{\prime}):\boldsymbol{\tau}^{\prime}\rangle}_{P_{e}} \underbrace{-\langle\boldsymbol{u}^{\prime}\boldsymbol{u}^{\prime}\rangle:(\boldsymbol{\nabla}\boldsymbol{U})}_{P_{t}}. \end{align}

The mean strain rate and the fluctuating strain rate tensors are given by $\boldsymbol{\mathsf{S}}=(\boldsymbol {\nabla }\boldsymbol {U}+(\boldsymbol {\nabla }\boldsymbol {U})^\textrm {T})/2$ and $\boldsymbol{\mathsf{s}}^{\prime }=(\boldsymbol {\nabla }\boldsymbol {u}^{\prime } + (\boldsymbol {\nabla }\boldsymbol {u}^{\prime })^\textrm {T})/2$, respectively. Specifically, in (4.2) and (4.3), the left side is merely the total time derivative of $E$ or $e$ following a mean-flow fluid particle, while the right side represents the various mechanisms that bring about changes in $E$ or $e$. The first four divergence terms on right side are energy transport and redistribution caused by pressure ($D_{mp}, D_p$), viscous diffusion ($D_{ms}, D_s$), polymeric elastic stress ($D_{me}, D_e$) and turbulent stress ($D_{mt}, D_t$), respectively. When integrated over the entire gap, these terms will not contribute to the total budget. The fifth term represents the direct viscous dissipation of kinetic energy ($\varepsilon _m, \varepsilon$) via its conversion into heat. It is important to emphasize that the sixth term represents the energy production associated with polymer stretch, which has been used to quantify energy exchange between kinetic and elastic energy, denoted as $P_{me}$ and $P_{e}$, respectively. And the last term is turbulence shear production term $P_t$ that arises due to interaction of the mean streamwise velocity gradient and Reynolds shear stress; $P_t$ quantifies the loss of mean kinetic energy in (4.2), but the gain of TKE in (4.3).

The TKE budgets for Newtonian TC turbulence have been examined in detail by Bilson & Bremhorst (Reference Bilson and Bremhorst2007). Specifically, it is clearly shown how velocity fluctuations are produced, dissipated and transported across the gap. In what follows, the budget terms of key importance to the energy exchange processes are discussed. Of particular interest is the energy budget of EDT at $Re=500$. Interestingly, the energy budgets terms at higher Reynolds numbers have a similar radial variation; however, the magnitude of each term has a large $Re$ dependence.

As shown in figures 14(a) and 15(a), a total balance is obtained for the budget equations of the mean kinetic energy ($E$-budget) and TKE ($e$-budget) when a stationary steady turbulent state is realized. For the $E$-budget depicted in figure 14(a), the pressure and Reynolds stress transport terms, i.e. $D_{mp}$ and $D_{mt}$ are relatively small as compared with the viscous diffusion term $D_{ms}$ and the polymeric diffusion term $D_{me}$. Here, $D_{ms}$ acts to bring high-velocity fluids close to the walls, where $D_{me}$ plays an important role in moving them away from the inner-wall vicinity. Dissipation term $\varepsilon _m$ approaches its maximum value (acting as a loss) as the inner wall is approached, and in the inner-wall region it is balanced approximately by the viscous diffusion term $D_{ms}$. Additionally, the turbulent shear ($P_{t}$) and mean elastic potential energy ($P_{me}$) production terms are both negative across the entire gap, indicating the transformation of kinetic energy of mean flow to turbulent fluctuations and elastic potential energy associated with polymer stretch. Specifically, for all $Re$ considered (see figure 14b), polymer chains extract energy across the entire gap from the mean flow via chain stretch. Moreover, $P_{me}$ obtains a local minimum that corresponds to the radial position of the elastic GV at each $Re$; this minimum displays a monotonic increase with $Re$. Thus, increasing fluid inertia hinders the energy extraction process by which the mean elastic potential energy is generated. This also leads to a reduction of the magnitude of the mean polymer shear stress (see figure 12a).

Figure 14. (a) Mean kinetic energy $E$-budget for viscoelastic TC flow of $Re=500$, $Wi=30$, (b) the elastic production $P_{me}$ of $E$ for various $Re$ with $Wi=30$.

Figure 15. (a) TKE $e$-budget for viscoelastic TC flow of $Re=500$, $Wi=30$, (b) the elastic production $P_e$ of $e$ for various $Re$ with $Wi=30$.

The $e$-budget is illustrated in figure 15(a); the pressure term $D_p$ and turbulent transport term $D_t$ approximately mirror each other. Specifically, they alternate as gain and loss terms of relatively small magnitudes. The viscous and polymer diffusion terms, i.e. $D_s$ and $D_e$ transport the high-fluctuating velocity fluids close to the wall to the bulk region, and in turn the TKE is dissipated by the viscous dissipation term $\varepsilon$, particularly near the walls, and in turn it is extracted by the macromolecules via chain stretch term $P_{e}$ in the bulk region. For the gain of $e$, the mean shear production term $P_{t}$ has a maximum near the inner wall and a descending value away from the inner wall. However, the additional elastic production term $P_{e}$ attains two local positive maximum values near the two walls that are much larger than the classical turbulent shear production term $P_{t}$. Thus, the turbulence generating mechanism in EDT is dominated by elastic effects.

The value of $P_{e}$ is commonly used to quantify energy exchange between $e$ and elastic potential energy $\epsilon =\nu _p (L^{2}-3)\langle \ln (f(\boldsymbol{\mathsf{C}}))\rangle /2Wi$ (Dallas & Vassilicos Reference Dallas and Vassilicos2010). Specifically, negative $P_{e}$ means that the kinetic energy carried by fluctuating motions is absorbed and stored as elastic potential energy in stretched polymer chains; positive $P_{e}$ means that elastic potential energy is released from the stretched polymer chains back to the turbulent flow. In fact, three energy exchange regions based on the sign of $P_{e}$, namely, the wall vicinity region with $P_{e}< 0$, the near-wall region with $P_{e}> 0$, and the core region with $P_{e}< 0$, have been identified in drag reduced or drag enhanced viscoelastic turbulent flows (Tsukahara et al. Reference Tsukahara, Ishigamia, Yub and Kawaguchia2011; Teng et al. Reference Teng, Liu, Lu and Khomami2018; Zhu et al. Reference Zhu, Song, Liu, Lu and Khomami2020). As shown in figure 15(b), these three typical energy exchange regions are also observed in the present study. In fact, the second (positive $P_{e}$) region becomes smaller as $Re$ is enhanced. The gradual disappearance of this second region implies that the turbulence derived from the elastic energy is inhibited by enhanced inertia. As a consequence, at high Reynolds number, $Re\geqslant 5000$, $e$ is mainly produced by mean-flow shear production $P_t$ (not show here), indicating an inertia-dominated global turbulence dynamics.

As a salient feature of EIT in pipe and channel flows, the markedly lower Reynolds shear stress than their Newtonian counterparts has been observed and interpreted as a qualitative result of the suppression of self-sustaining process of wall turbulence (Samanta et al. Reference Samanta, Dubief, Holzner, Schafer, Morozov, Wagner and Hof2013; Choueiri et al. Reference Choueiri, Lopez and Hof2018; Lopez et al. Reference Lopez, Choueiri and Hof2019). However, the mechanism underlying the modification of $\langle u'_r u'_\theta \rangle$ by the elastic effect is still not well understood. To this end, budgets of the Reynolds shear stress $\langle u'_r u'_\theta \rangle$ are examined here with the aim of explaining how $\langle u'_r u'_\theta \rangle$ is produced, dissipated and transported across the gap. The equation describing the budget for $\langle u'_r u'_\theta \rangle$ is given as

(4.4)\begin{equation} \frac{\partial \langle u'_r u'_\theta\rangle}{\partial t}= P_{r\theta}+C_{r\theta}+TD_{r\theta}+PD_{r\theta}+ PS_{r\theta}+D_{r\theta}+\varepsilon_{r\theta}+ED_{r\theta}+E_{r\theta}, \end{equation}

(4.5) \begin{equation} \left. \begin{gathered} \displaystyle P_{r\theta}={-}\left(\langle u'_r u'_r\rangle \frac{\partial U_\theta}{\partial r}-\frac{U_\theta}{r}\langle u'_\theta u'_\theta\rangle\right), \quad C_{r\theta}={-}\frac{U_\theta}{r}(\langle u'_r u'_r\rangle-\langle u'_\theta u'_\theta\rangle), \\ \displaystyle TD_{r\theta}={-}\frac{1}{r}\left[\frac{\partial (r\langle u'_r u'_r u'_\theta\rangle)}{\partial r}+\langle u'_r u'_r u'_\theta\rangle-\langle u'_\theta u'_\theta u'_\theta\rangle\right], \\ PD_{r\theta}={-}\left[\frac{1}{r}\frac{\partial (r\langle u'_\theta p' \rangle)}{\partial r}-\frac{2}{r}\langle u'_\theta p' \rangle\right], \quad PS_{r\theta}=\left\langle p'\left[\frac{1}{r}\left(\frac{\partial u'_r}{\partial \theta}-u'_\theta\right)+ \frac{\partial u'_\theta}{\partial r}\right]\right\rangle, \\ D_{r\theta}=\nu_s\left[\frac{1}{r}\frac{\partial (r\partial\langle u'_r u'_\theta\rangle/\partial r)}{\partial r}-\frac{4}{r^{2}}\langle u'_r u'_\theta\rangle\right],\\ \varepsilon_{r\theta}={-}2\nu_s\left[\left\langle\frac{\partial u'_r}{\partial r}\frac{\partial u'_\theta}{\partial r}\right\rangle +\frac{1}{r^{2}}\left\langle\left(\frac{\partial u'_r}{\partial \theta}-u'_\theta\right) \left(\frac{\partial u'_\theta}{\partial \theta}+u'_r\right)\right\rangle+\left\langle\frac{\partial u'_r}{\partial z}\frac{\partial u'_\theta}{\partial z}\right\rangle\right],\\ ED_{r\theta}=\nu_p\left[\frac{\partial \langle \tau'_{rr} u'_\theta + \tau'_{r\theta} u'_r \rangle}{\partial r}+\frac{1}{r}(\langle \tau'_{rr} u'_\theta \rangle-2\langle \tau'_{\theta\theta} u'_\theta \rangle+3\langle \tau'_{r\theta} u'_r \rangle)\right],\\ E_{r\theta}={-}\nu_p\left\{\left\langle \tau'_{rr} \frac{\partial u'_\theta}{\partial r}\right\rangle+\left\langle \tau'_{r\theta} \frac{\partial u'_r}{\partial r}\right\rangle+\frac{1}{r}\left[\left\langle \tau'_{r\theta} \left(\frac{\partial u'_\theta}{\partial \theta}+u'_r\right)\right\rangle+\left\langle \tau'_{\theta\theta} \left(\frac{\partial u'_r}{\partial \theta}-u'_\theta\right) \right\rangle\right] \right.\\ \hspace{-15pc}\left.+\left\langle \tau'_{rz} \frac{\partial u'_\theta}{\partial z}\right\rangle +\left\langle \tau'_{\theta z} \frac{\partial u'_r}{\partial z}\right\rangle\right\}, \end{gathered}\right\} \end{equation}

where the terms on the right-hand side of (4.4) are the shear production ($P_{r\theta }$), the convection production ($C_{r\theta }$), the turbulence stress transport ($TD_{r\theta }$), the pressure diffusion ($PD_{r\theta }$), the pressure strain ($PS_{r\theta }$), the molecular diffusion ($D_{r\theta }$) and the dissipation ($\varepsilon _{r\theta }$). The last two terms are the polymer diffusion ($ED_{r\theta }$) and elastic production ($E_{r\theta }$) that are only present in viscoelastic flow. The budget terms in (4.5) are interpreted in the same manner as previously documented for Newtonian turbulent TC flow (Bilson & Bremhorst Reference Bilson and Bremhorst2007).

As depicted in figure 16(a), the budget of the Reynolds stress $\langle u'_r u'_\theta \rangle$ is dominated by the production term $P_{r\theta }$, bulk gradient production term $C_{r\theta }$ and pressure terms ($PS_{r\theta }$, $PD_{r\theta }$) for inertio-elastic TC flow. In the entire gap, $\langle u'_r u'_\theta \rangle$ is mainly produced by $P_{r\theta }$ and $C_{r\theta }$. Other terms like the dissipation term $\varepsilon _{r\theta }$, viscous diffusion term $D_{r\theta }$ and turbulent transport term $TD_{r\theta }$ are non-zero, but substantially smaller in magnitude as also seen in Newtonian TC turbulence (Bilson & Bremhorst Reference Bilson and Bremhorst2007). However, the polymer diffusion term $ED_{r\theta }$ plays an important role in moving the high-fluctuating stress to the inner-wall region, which in turn is absorbed by the elastic stress work ($E_{r\theta }$). As a consequence, in viscoelastic TC flows $\langle u'_r u'_\theta \rangle$ decreases mainly at the inner-wall region, while in the bulk region, $E_{r\theta }$ makes a positive contribution to the production of $\langle u'_r u'_\theta \rangle$. The $Re$-effects on the elastic work ($E_{r\theta }$) are illustrated in figure 16(b). Intriguingly, in the bulk and outer-wall vicinity, $E_{r\theta }$ has positive values. This indicates that the elastic work facilitates the production of turbulent shear stress especially at low Reynolds numbers, $Re\leqslant 1000$. In contrast, near the inner wall and slightly away from the outer wall, $E_{r\theta }$ has negative values; hence, elastic work acts to suppress the production of turbulent shear stress. Both the facilitation and suppression scenarios in modification of the Reynolds shear stress become less significant as $Re$ is enhanced. This is consistent with the variation of $\langle u'_r u'_\theta \rangle$ shown in figure 12(b).

Figure 16. (a) Reynolds shear stress $\langle u'_r u'_\theta \rangle$-budget for viscoelastic TC flow of $Re=500$, $Wi=30$, (b) the elastic production $E_{r\theta }$ of $\langle u'_r u'_\theta \rangle$ for various $Re$ with $Wi=30$.

5. Flow–microstructure coupling

As discussed above, the most critical flow changes occur as a result of flow-induced polymer chain stretch in the wall regions. To address the details of polymer-induced flow–microstructure coupling, this section is devoted to examination of the polymer stretch/relaxation and the resulting polymeric elastic stress and body force that lead to flow modifications.

The extent of average polymer stretch can be quantified by the chain fractional extension ($\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$) defined as the ratio of the trace of the conformation tensor to the maximum polymer chain extensibility. As depicted in figure 17(a), for all $Re$ considered, two local maxima of $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ are observed, one near the inner wall with the polymer chains almost fully stretched ($\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}\geqslant 80\,\%$) and another near the outer wall with relatively lower fractional extension. As $Re$ is enhanced $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ increases almost in the entire gap, which is merely due to enhanced intensity of shear flow that results from the vortical circulations. However, the decrease in $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ as a function of radial position indicates that highly stretched polymer chains gradually relax as they are moved away from the inner-wall region. This observation is consistent with the fact that in drag reduced channel flows higher chain extension is realized in the near-wall region (Sureshkumar et al. Reference Sureshkumar, Beris and Avgousti1997; Li et al. Reference Li, Sureshkumar and Khomami2006; Kim et al. Reference Kim, Li, Sureshkumar, Balachandar and Adrian2007; Samanta et al. Reference Samanta, Dubief, Holzner, Schafer, Morozov, Wagner and Hof2013). As a consequence, the aforementioned polymer stretch leads to significant hoop stresses $\langle \tau _{\theta \theta } \rangle$ across the gap, see figure 17(b). Specifically, a higher $\langle \tau _{\theta \theta } \rangle$ is realized in the inner-wall region where a higher extension is realized. It is important to emphasize that an unstable stratification of the hoop stress is the prerequisite for the occurrence of solitary coherent structures like oscillatory strips and diwhirls in the elastically driven TC flows (Groisman & Steinberg Reference Groisman and Steinberg1997; Baumert & Muller Reference Baumert and Muller1999; Kumar & Graham Reference Kumar and Graham2000; Thomas et al. Reference Thomas, Khomami and Sureshkumar2006b). As a consequence, the strong hoop stresses near the inner wall in inertio-elastic turbulent TC flow facilitate the generation of elastic GV structures (see figures 5, 7). Therefore, increasing fluid inertia hinders the hoop-stress generation, leading to a suppression for the elastic GV. Specifically, a sharp increase in $\langle \tau _{\theta \theta } \rangle$ is also observed in the inner wall region, indicating the existence of a inner-wall hoop-stress boundary layer $\delta _{\tau _{\theta \theta }}$ in the flow (see figure 17b). The progressive thinning of the boundary layer $\delta _{\tau _{\theta \theta }}$ with $Re$ confirms the suppressed role of the local elastic instability acting for the flow dynamics.

Figure 17. (a) Ensemble averaged chain fractional extension $\langle tr(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ and (b) mean hoop stress $(1-\beta )\langle \tau _{\theta \theta } \rangle /Re$ for various $Re$ with $Wi=30$. Here, $\delta _{\tau _{\theta \theta }}$ represents the thickness of boundary layer of $\langle \tau _{\theta \theta }\rangle$ for the inertio-elastic turbulent TC flows, defined as the distance from the inner wall to the radial position where the maximum of $\langle \tau _{\theta \theta }\rangle$ occurs.

Generally, the role of hoop stress $\tau _{\theta \theta }$ in the viscoelastic TC flows can also be quantified by ascertaining its contribution to the radial polymer body force $f_{pr}$ (Kumar & Graham Reference Kumar and Graham2000; Thomas et al. Reference Thomas, Khomami and Sureshkumar2009; Liu & Khomami Reference Liu and Khomami2013a,Reference Liu and Khomamib). Specifically, the radial polymer body force mainly results from the radial body force $N_1/r$ and the radial stress gradient $\nu _p \langle \partial \tau _{rr} /\partial r\rangle$, where $N_1=\nu _p \langle \tau _{rr}-\tau _{\theta \theta }\rangle$ is the first normal stress difference. As seen in figure 18(a), $N_1/r$ is negative in the entire gap as $\langle \tau _{\theta \theta } \rangle$ is much greater than $\langle \tau _{rr}\rangle$ and $N_1/r$ obtains a local minimum near the inner wall. Evidently, increasing $Re$ leads to a monotonic decrease of the magnitude of $N_1/r$ across the gap due to the weakening of hoop stresses (see figure 17b). As seen in figure 18(b), although the radial stress gradient obtains a positive value near the inner wall, $f_{pr}$ is negative in the entire gap, even at the highest $Re$. Consequently, for all $Re$ considered, this observation points to the fact that hoop stresses $\langle \tau _{\theta \theta } \rangle$ (via $N_1/r$ ) are the major contributor to the radial elastic body force and the main driving force for the elastic Görtler instability that occurs near the inner wall. In fact, in the inertio-elastic flow regime, the high fluctuations in polymer extension are closely associated with the small-scale elastic GV near the inner wall. Specifically, concentrated regions of high and low $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ appear alternately along the inner and outer walls, and they are located at the centres of the inflow and outflow boundaries of adjacent counter-rotating vortex pairs (see figure 19a). At the inner wall, the regions of high $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ are concentrated near the stagnation points of the radial outflow between two adjacent counter-rotating large-scale vortex cells (see figure 19b), where the outflow accelerates away from the inner wall and attains its maximum radial velocity (i.e. $\partial u_r/\partial r <0$); hence, the incompressible fluid flow becomes transversely extensional. As a consequence, the substantially stretched polymer chains develop significant hoop stresses that trigger the elastic Görtler instability in this region leading to generation of a pair of elastic GV. It is well known that elastically driven solitary vortical structures such as oscillatory strips and diwhirls appear due to highly localized polymer extension in the radial inflow regions near the outer wall (Baumert & Muller Reference Baumert and Muller1997, Reference Baumert and Muller1999; Groisman & Steinberg Reference Groisman and Steinberg1997, Reference Groisman and Steinberg1998a; Kumar & Graham Reference Kumar and Graham2000; Thomas et al. Reference Thomas, Al-Mubaiyedh, Sureshkumar and Khomami2006a, Reference Thomas, Khomami and Sureshkumar2009). Conversely, the localized elastic GV structures in inertio-elastic turbulent TC flow result from the radial hoop stresses present near the inner cylinder.

Figure 18. (a) Ensemble averaged radial body force $N_1/r$ and (b) polymer radial stress gradient $(1-\beta )\langle \partial \tau _{rr} /\partial r\rangle /Re$ for various $Re$ with $Wi=30$. Where the first normal stress difference $N_1= (1-\beta ) \langle \tau _{rr} -\tau _{\theta \theta }\rangle /Re$.

Figure 19. (a) Time and $\theta$-direction averaged chain fractional extension $\langle \textrm {tr}(\boldsymbol{\mathsf{C}})\rangle /L^{2}$ in ($r, z$) plane for various $Re$ with $Wi=30$. (b) Magnified image of (a) for $Re=3000$ near the inner wall. The ($r, z$) plane streamlines in (b) are plotted using the ($u_r, u_z$) velocities. Here, the purple circles are used to mark the localized regions with high polymer extension (the red regions of $\langle\textrm {tr}(\boldsymbol{\mathsf{C}})\rangle/L^{2}$ at the inner wall), the red dashed rectangle to mark the radial outflow ($u_r > 0$) region and blue dashed rectangle the radial inflow ($u_r < 0$) region.