1 Introduction
Insight into turbulent buoyancy-driven geophysical processes often rely on energy-based arguments. The nature and evolution of spatio-temporal processes that transfer energy between different reservoirs, and of the sources and sinks of energy can provide considerable insights on the processes that link geophysical motions over a range of scales. (In this paper, we take a ‘Boussinesq’ point of view, which relegates the internal energy as a purely passive form of energy. Thus, for us, energy means the sum of kinetic and potential energy, which is not conserved under diabatic effects.)
For homogeneous (constant density), incompressible fluids contained in a rigid vessel, gravity can be eliminated from the equations by a redefinition of the pressure, leaving the kinetic energy density
$\unicode[STIX]{x1D70C}_{0}\boldsymbol{u}^{2}/2$
, where
$\unicode[STIX]{x1D70C}_{0}$
is the uniform density and
$\boldsymbol{u}$
the velocity field as the lone contributor to the total energy. Writing its evolution along Lagrangian trajectories highlights the role of
$\unicode[STIX]{x1D716}\equiv 2\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ji}$
(where
$\unicode[STIX]{x1D61A}_{ij}$
is the symmetric component of the velocity gradient tensor), which quantifies the rate at which frictional forces convert kinetic energy into heat. The energetics framework becomes less obvious for variable-density fluids where gravitational effects become a source of vorticity, and thus cannot be ‘hidden’ into a redefined pressure. Indeed, the evolution of the potential energy density
$\unicode[STIX]{x1D70C}gZ$
, where
$\unicode[STIX]{x1D70C}$
is the spatially variable density of the fluid,
$g$
the local acceleration of gravity and
$Z$
the geopotential height, along Lagrangian trajectories does not illuminate how mixing, i.e. the irreversible loss of the variance of the active tracer, affects the energetics. Yet, we know that to homogenize an active tracer whose concentration varies along the vertical direction in such a way that density decreases with height requires a larger input of energy than it would be required if the tracer was purely passive. (For simplicity here we consider a single stratifying agent.) From this point of view, the problem consists in finding ‘recipes’ to relate the rate of dissipation of variance of the stratifying agent to its impact on the energetics (Ivey, Winters & Koseff Reference Ivey, Winters and Koseff2008). Often, one way to measure such impact is to look at how irreversible mixing raises the centre of mass of the system. However, it is easy to conceive cases where mixing does not raise the centre of mass of the system, yet it still affects the energetics of the system, e.g. by diminishing the amount of useful work that can be extracted from the system. For example, consider a simple fluid set-up such that at a given time the isopycnals are vertical: vigorous diapycnal mixing across the vertical isopycnals does not change the elevation of the centre of mass, yet it reduces, and in the limit of infinitely fast mixing, all but eliminates any energy that can be extracted from the system by, e.g. deploying a turbine in the fluid. Indeed, this example highlights the guiding principle of this paper, namely to define a framework that can be used to answer, inter alia, the following question: How do diabatic processes (irreversible mixing and viscous dissipation) impact the amount of work that can be extracted from a system under certain limiting conditions? Conversely, how much external work is needed to bring a system to a given (mixed) state? How much energy needs to be supplied to a system to be kept in a statistically stationary state if the latter does not coincide with a state of minimum energy compatible with the appropriate constraints?
The inadequacy of the standard energetic framework based on
$\unicode[STIX]{x1D70C}gZ$
as a definition of potential energy in answering these questions was recognized long time ago, and a solution was proposed by Margules (Reference Margules1903) at the beginning of the last century. In a nutshell, Margules’ idea was to (i) calculate a minimum-energy state (or ground state) compatible with certain constraints and (ii) use the energy of such state to ‘gauge’ the amount of energy effectively available to the system. This pioneering framework amounts to the first definition of the available energy for a given system. While Margules was thinking about isolated atmospheric storms, his theory required a closed system. Half a century later, Lorenz (Reference Lorenz1955) applied Margules’ idea to the entire atmosphere, assuming that the flow is a perturbation of a minimum-energy state that depends only on the mass distribution. That the reference state may depend on factors other than the mass distribution was not lost on Lorenz. In the introduction to his 1955 seminal paper, he wrote: ‘There is no assurance in any individual case that all the available potential energy will be converted into kinetic energy. For example, if the flow is purely zonal, and the mass and momentum distributions are in dynamically stable equilibrium, no kinetic energy at all can be realized. It might seem desirable to redefine available potential energy, so that, in particular, it will be zero in the above example. But the available potential energy so defined would depend upon both the mass and momentum distributions (Lorenz Reference Lorenz1955)’.
While attempts to introduce more general reference states have been proposed in the atmospheric literature (see, e.g. Codoban & Shepherd Reference Codoban and Shepherd2003), following the work of Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995), Lorenz’s bias in favour of a reference state at rest still dominates the literature (Tailleux Reference Tailleux2018), especially the one concerned with mixing in the ocean (see, e.g. von Storch et al. Reference von Storch, Eden, Fast, Haak, Hernàndez-Deckers, Maier-Reimer, Marotzke and Stammer2012; Zemskova, White & Scotti Reference Zemskova, White and Scotti2015; MacCready & Giddings Reference MacCready and Giddings2016). Since in this case the ground state is characterized by flat isopycnals, and it is at rest, the available energy is de facto measured by the available potential energy (APE), i.e. the potential energy gauged to the potential energy of the reference state.
By focusing on the APE, as opposed to the traditional potential energy definition, Winters and coworkers showed that it was possible to construct a positive definite quantity, the dissipation rate of APE, analogous to the dissipation rate of kinetic energy,
$\unicode[STIX]{x1D716}$
. The use of the dissipation rate of APE makes it possible to separate the reversible exchange between kinetic energy (KE) and APE due to internal waves from the irreversible exchange due to irreversible turbulent fluctuations. It also shows that APE is lost whenever there is diabatic flux across isopycnals, regardless of the orientation of the latter (Winters & D’Asaro Reference Winters and D’Asaro1996), thus it can be naturally applied to the vertical isopycnals example discussed earlier.
Winters et al.’s approach considers the global effects of mixing (i.e. diabatic effects) on a closed system. For this, it relies on a definition of APE for the system as a whole. There are however situations that call for a definition that applies to localized regions of the domain, e.g. when measuring the energy carried by nonlinear internal waves (Scotti, Beardsley & Butman Reference Scotti, Beardsley and Butman2006; Lamb Reference Lamb2008), when partitioning energy between mean and fluctuating components in a cyclone (Kucharski & Thorpe Reference Kucharski and Thorpe2000), in determining the efficiency of different mixing systems (Scotti & White Reference Scotti and White2014) and in studying mixing and turbulence in spatially inhomogeneous systems (Passaggia, Scotti & White Reference Passaggia, Scotti and White2017). Recently, Venaille, Gostiaux & Sommeria (Reference Venaille, Gostiaux and Sommeria2017) applied mathematical tools traditionally used in the context of statistical mechanics to the APE framework. This alternative approach allowed them to derive bounds on mixing efficiency for decaying flows but the main advantage is their coarse-grained computational technique, used to compute the partition between the mean flow and the fluctuations, which could be robust enough to be extended to large Reynolds or Péclet numbers where the available data might be under-resolved. In all these studies, the starting point is the local definitions of APE developed in the early 1980s by Holliday & McIntyre (Reference Holliday and McIntyre1981) for incompressible flows and by Andrews (Reference Andrews1981) for compressible flows, based on a reference state that depends only on the mass distribution. Interestingly, the fact that the global APE introduced by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) coincides with the volume integrated local APE based on Holliday & McIntyre (Reference Holliday and McIntyre1981) was not realized until much later (Winters & Barkan Reference Winters and Barkan2012), although in hindsight it should have been clear that they must be equal (or at least related by a gauge symmetry), since the volume averaged transport equation for the Holliday & McIntyre local APE (see, e.g. Scotti et al. (Reference Scotti, Beardsley and Butman2006), for a derivation) coincides, up to boundary terms, with the equation derived by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) for the global APE. While Winters & Barkan’s proof of equivalence is rather convoluted and specific to the Holliday and McIntyre APE, within the framework that we develop in this paper the proof is almost trivial.
Our framework is built in two steps: first we generalize Margules’ intuitive notion of available energy of a system as the energy that can be realized given a set of constraints; we then introduce a local quantity
${\mathcal{E}}$
, the local diagnostic energy, whose evolution along Lagrangian trajectories quantifies how diabatic processes modify the available energy of the system. It is important to note that in our framework
${\mathcal{E}}$
, while having the dimension of an energy, cannot be in general interpreted as a local available energy. For us, available energy remains a property of the system as whole, even though there are special cases when
${\mathcal{E}}$
can be modified to become a local available energy. Essentially this occurs for those systems where our formalism recovers Winters et al. theory, which is included as a special case.
Our point of departure is Shepherd’s observation that, because of the non-canonical nature of the Hamiltonian mechanics that describes the evolution of these flows in the inviscid limit (Littlejohn Reference Littlejohn1982; Salmon Reference Salmon1988; Shepherd Reference Shepherd1993), the Hamiltonian possesses a local (in phase space) gauge symmetry, related to the existence of so-called Casimir functions (In modern algebraic terms, non-canonicity means that the Poisson algebra that underpins the Hamiltonian structure has a non-trivial centre.). From this point of view, the problem of defining a suitable diagnostic framework reduces to the problem of selecting a specific gauge condition that accounts for the appropriate constraints on the system. Following Shepherd (Reference Shepherd1993), we first lay down in § 2 the general theoretical framework that applies to generic systems that in the adiabatic limit have a non-canonical Hamiltonian description. From there, we introduce the specific gauge-fixing condition that, when applied to the equivalence class of Hamiltonians, identifies the one whose density is the local diagnostic energy that we seek. In practice, the gauge-fixing condition identifies which Casimir needs to be the added to the original Hamiltonian (i.e. the sum of kinetic and potential energy) to obtain
${\mathcal{E}}$
. At the same time, we also obtain the equations that specify the appropriate reference state. In practice
${\mathcal{E}}$
is the sum of the traditional energy functional, the sum of kinetic and potential, and the gauge-fixed Casimir. Changes in available energy due to diabatic effects are due to changes in the energy of the flow and changes in the energy of the ground state, since the latter evolves in time responding to changes in the constraints due to diabatic processes (e.g. mixing). The gauge-fixed Casimir measures changes of the latter. In particular, it is possible to envision scenarios where at times, diabatic effects may lessen the constraints acting on the system and thus may increase the amount of available energy.
What differentiates our approach from these past studies is that we do not specify a priori the form of the ground state. Rather, our approach seeks (numerically, if necessary) the ground state which is compatible with the constraints imposed on the system, the latter being related to quantities that are conserved along Lagrangian trajectories by the adiabatic dynamics (Lagrangian invariants). Our approach bears similarities to the work of Renaud, Venaille & Bouchet (Reference Renaud, Venaille and Bouchet2016) and Venaille et al. (Reference Venaille, Gostiaux and Sommeria2017). In these works, the authors approached the problem of generating extremal states of fluid systems from a statistical mechanics point of view, subject to additional constraints: the distribution of potential vorticity moments in a shallow water system in the former, conservation of volume (buoyancy) in a stratified Boussinesq flow in the latter. The statistical nature of these approaches can only be applied to studying the properties of the final states of a nominally adiabatic dynamics (i.e. a dynamics in the limit of infinite Reynolds number and finite Prandtl number). These works show that under the conditions specified above, the systems are attracted to a state in which energy is split between a coarse grained profile and fine-grained fluctuations. For a stratified Boussinesq flow, Venaille et al. show that the attractor consists of a stable buoyancy profile with a lower overall potential energy relative to the initial state (the statistical mechanics nature of the analysis allows irreversible mixing in the absence of an explicitly irreversible microscopic dynamics), and that fine-grained fluctuations carry kinetic energy. A similar split exists in the shallow water case: in particular, absent rotation or bottom topography, the coarse-grained state is quiescent, and the fine-grained field carries energy as inertia–gravity waves. Here, we consider the possibility that multiple constraints may exists, and we take a deterministic approach, so that we can study diabatic effects at finite values of the relevant-order parameters, even though we do not need to specify a priori a particular dissipative mechanism. Since the approach is deterministic, we can in principle apply the framework to study the impact of specific mixing processes acting at any given time on the system. Here, we apply our method to Boussinesq flows in inertial and non-inertial channels.
The rest of the paper is organized as follows: the framework is developed in § 2 in rather general terms. In § 3 we specialize it to consider Euler equations in the Boussinesq approximation for a continuously stratified flow. Both inertial and non-inertial (i.e. rotating) frames are considered. We give general properties for both the gauge-fixed Casimir and the reference state. In simple geometric configurations, we calculate analytically the solution or a suitable approximation, and we show under what conditions our framework recovers the traditional Winters et al. approach. An interesting result that applies to the rotating Boussinesq equations is that the local diagnostic energy associated with low Rossby number reference states has a universal character. This has potential application to study the turbulent energetics of submesoscale fronts, a topic that has generated a considerable amount of attention recently (DAsaro et al. Reference DAsaro, Lee, Rainville, Harcourt and Thomas2011; Arobone & Sarkar Reference Arobone and Sarkar2015; Haney et al. Reference Haney, Fox-Kemper, Julien and Webb2015; Marino, Pouquet & Rosenberg Reference Marino, Pouquet and Rosenberg2015). In § 4 we provide an example of how the gauge-fixed Casimir can be calculated analytically, followed by our conclusions. We provide mathematical details in the appendix A.
2 Theoretical background: non-canonical Hamiltonian systems, local gauge symmetries and Casimirs
We begin this section with a brief review of the basic elements that enter the Hamiltonian formulation of mechanical systems. For an in depth review of the Hamiltonian formulation of fluid systems the reader is referred to Salmon (Reference Salmon1988). The three basic ingredients are: (i) a phase space whose points
$\mathfrak{q}$
describe the state of the system; (ii) a vector space of functionals on the phase space (i.e. real-valued functions on the phase space) with a suitable algebraic structure, the Poisson bracket; and finally (iii) a specific functional, the Hamiltonian. For example, consider a point unit mass constrained to move along a straight line: the phase space consists of the pairs
$\mathfrak{q}=(p,x)$
where
$p$
is the momentum and
$x$
the position on the line. The Poisson bracket
$\{F[\mathfrak{q}],G[\mathfrak{q}]\}=\unicode[STIX]{x2202}(F,G)/\unicode[STIX]{x2202}(p,x)$
is the standard Jacobian determinant. Different motions are described by different Hamiltonians:
$H_{f}[p,x]=p^{2}/2$
describes a free particle, while
$H_{s}[p,x]=(p^{2}+x^{2})/2$
describes a point mass attached to a linear spring. However, even in this simple example, the choice of Hamiltonian is not unique. Indeed,
$H^{\prime }[p,x]=H[p,x]+f(t)$
, where
$f(t)$
is an arbitrary function of time, is dynamically indistinguishable from
$H[p,x]$
, regardless of how the latter depends on its arguments. This is an example of a global symmetry, since Hamiltonians belonging to the same equivalence class differ by a quantity which is constant over the entire phase space. Note that the existence (and character) of the symmetry is determined by the Poisson bracket. In the particular example considered here, solutions of
$$\begin{eqnarray}\{f[\mathfrak{q}],G[\mathfrak{q}]\}=0,\quad \forall G[\mathfrak{q}]\end{eqnarray}$$
are those functionals
$f$
that are constant on the phase space (though may depend on time). In this case, we say that the algebra is non-degenerate. In general, solutions to (2.1) are called Casimirs.
If, however, the Poisson algebra is degenerate (this can happen both in finite- and infinite-dimensional phase spaces, see Littlejohn (Reference Littlejohn1982)), i.e. there are non-constant solutions to (2.1), then the equivalence class for Hamiltonians can be much wider. If that is the case, the global symmetry, manifested by the invariance of the dynamics under the addition of a (time varying) constant to the Hamiltonian at every point in phase space, widens to a local (in phase space) symmetry, i.e. the Hamiltonian can be altered by the addition of a Casimir that can depend on the location in phase space, and still yield the same dynamical equations. From a field-theoretical point of view, the Hamiltonian in this case possesses a local gauge symmetry.
It is important to remark that the existence of non-trivial Casimirs depends on the degeneracy of the Poisson algebra, rather than on the particular choice of the Hamiltonian. If the algebra is degenerate, equilibrium solutions need not be (and in general, are not) extrema of the Hamiltonian.
For notational purposes, here and thereafter we will denote with
$H[\mathfrak{q}]$
the ‘naive’ Hamiltonian, which for the systems considered here can be considered to be the sum of kinetic and potential energy, while
${\mathcal{H}}[\mathfrak{q}]$
will denote a member of the class of equivalent Hamiltonians, which can be written as
${\mathcal{H}}[\mathfrak{q}]=H[\mathfrak{q}]+C[\mathfrak{q}]$
, the sum of the naive Hamiltonian and a Casimir. Since we are interested in systems where the phase space is infinitely dimensional, it is also convenient to introduce the following notation: to any functional
$F[\mathfrak{q}]$
we associate the corresponding density
$F(\mathfrak{q})$
, i.e.
$$\begin{eqnarray}F[\mathfrak{q}]=\int _{\mathbb{D}}F(\mathfrak{q})dV,\end{eqnarray}$$
where
$\mathbb{D}$
is the manifold that contains the flow. To summarize, square brackets
$[\cdot ]$
denote a manifold integrated quantity, with the corresponding local density indicated by the use of
$(\cdot )$
.
For fluid systems, Casimirs can be constructed as follows (see Shepherd (Reference Shepherd1990), Abarbanel et al. (Reference Abarbanel, Holm, Marsden and Ratiu1986), for an exhaustive compilation of Hamiltonians and Casimirs associated with flows of geophysical relevance): let
$s_{1}(\boldsymbol{x}),\ldots ,s_{p}(\boldsymbol{x})$
be
$p$
Lagrangian invariants, by which we mean they are intensive quantities constant along Lagrangian trajectories, i.e.
$$\begin{eqnarray}\frac{\text{D}s_{i}}{\text{D}t}=0,\quad i=1,\ldots ,p,\end{eqnarray}$$
with
$\text{D}/\text{D}t$
being the material derivative. We also need a conserved density
$\mathfrak{D}$
, that is an extensive quantity which is also materially conserved, that is
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\mathfrak{D}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{v}\mathfrak{D})=0.\end{eqnarray}$$
Then
$$\begin{eqnarray}C[\mathfrak{q}]=\int _{\mathbb{D}}C(s_{1}(\boldsymbol{x}),\ldots ,s_{p}(\boldsymbol{x}))\mathfrak{D}dV,\end{eqnarray}$$
where
$C(s_{1},\ldots ,s_{p})$
is any real-valued function which depends on its arguments algebraically (i.e. we are not allowing
$C$
to depend on derivatives of the
$s_{i}$
). It is trivial to verify that
$\text{d}C/\text{d}t\cong 0$
(here and thereafter
$\cong$
means equality up to boundary terms). Note that there may be more general classes of Casimirs (e.g. which may depend on derivatives of the conserved quantities). However we limit this paper to Casimirs that can be written as (2.5).
2.1 Holonomic brakes and available energy
It is straightforward to reformulate Margules’ intuitive idea of available energy within the framework of a non-canonical Hamiltonian system.
Consider a system described at time
$t=0$
by a point
$\mathfrak{q}_{0}$
in phase space. Under adiabatic conditions, the system is described by a trajectory
$\mathfrak{q}(t)$
in phase space such that along the trajectory
${\mathcal{H}}[\mathfrak{q}(t)]={\mathcal{H}}[\mathfrak{q}_{0}]$
, where
${\mathcal{H}}[\mathfrak{q}]$
is any member of the class of equivalent Hamiltonian functionals.
Gay-Balmaz & Holm (Reference Gay-Balmaz and Holm2013) modified the underlying Hamiltonian geometry so that Casimirs are not conserved. Here, we consider the complementary approach, i.e. we modify the dynamics so that it is the naive energy that is dissipated, while still conserving the Casimirs. We do this following an idea first introduced by Vallis, Carnevale & Young (Reference Vallis, Carnevale and Young1989), later expanded by Shepherd (Reference Shepherd1990), which involves modifying the system by adding what here we call a holonomic brake.
The idea behind this strategy is to reduce the total energy of the system as quantified by
$H[\mathfrak{q}(t)]$
(hence a brake) while ensuring that the
$s_{i}$
remain Lagrangian invariants (hence the brake is holonomic), and
$\mathfrak{D}$
remains materially conserved, i.e. (2.3) and (2.4) are still satisfied. Thus, the holonomic brake leaves the Casimirs invariant. We will show later how holonomic brakes can be realized in actual systems. Of course, realistic diabatic processes modify both the naive energy as well as the Casimirs. The holonomic brake is an expedient that allows one to separate the action of diabatic processes on the naive energy from their effect on the dynamical constraint, since both determine the evolution of the available energy of the system.
With the brake turned on, it follows that
$\text{d}{\mathcal{H}}[\mathfrak{q}(t)]/\text{d}t\leqslant 0$
and, since the brake is holonomic, any decrease in
${\mathcal{H}}[\mathfrak{q}(t)]$
is entirely due to a decrease in the ‘naive’ Hamiltonian
$H[\mathfrak{q}(t)]$
. We assume that, in the limit
$t\rightarrow \infty$
, the application of the brake causes the system to relax to a stationary ‘ground’ state
$\mathfrak{q}_{\ast }$
. If such a ground state exists, the energy extracted by the holonomic brake from the system which is initially at
$\mathfrak{q}_{0}$
, is the difference
$E_{AE}[\mathfrak{q}_{0}]\equiv H[\mathfrak{q}_{0}]-H[\mathfrak{q}_{\ast }]$
. We identify
$E_{AE}$
with the available energy envisioned by Margules. In other words, this is the maximum amount of energy that can be extracted from the system under the constraint that Lagrangian invariants are conserved. We therefore have the following definition: the available energy is the energy of the system referenced to the energy of the ground state, the latter being the state that the system settles to when subjected to a holonomic brake.
We shall see presently that, in the process of determining
$\mathfrak{q}_{\ast }$
, a gauge-fixing condition will naturally arise which selects an element
${\mathcal{H}}_{\ast }$
of the equivalence class of Hamiltonians. The rate of change in time of
${\mathcal{H}}_{\ast }[\mathfrak{q}(t)]$
measures the loss or gain of available energy when
$\mathfrak{q}(t)$
evolves under full diabatic conditions. It is worth noticing that the rest state obtained with the resorting method proposed by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) can be obtained solving the viscous equations in the limit of infinite Prandtl number, the viscous term
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
acting as a brake. With the diffusivity turned off, buoyancy is still conserved along trajectories. However, this specific brake does not conserve the other Lagrangian invariant of the system, the potential vorticity. We will go back to this point in § 3.
2.2 A special family of Casimirs: the mass distribution function
The main postulate of our approach is that the ground state
$q_{\ast }$
to which the system relaxes after the holonomic brake is turned on is the point that minimizes the naive Hamiltonian subject to a set of constraints required by the conservation of the
$s_{i}$
along trajectories, which are not affected by the brake. Thus, the extremal point of
$H[\mathfrak{q}]$
must be sought among the points that satisfy an extra set of conditions, the definition of which is the subject of this section.
Consider a Lagrangian set of coordinates
$\unicode[STIX]{x1D736}=(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{n})$
. A Lagrangian particle characterized by a
$p$
-tuple
$\boldsymbol{s}=(s_{1},\ldots ,s_{p})$
of Lagrangian invariants retains its identity. The mass of all Lagrangian particles whose
$p$
-tuple falls between
$\boldsymbol{s}$
and
$\boldsymbol{s}\,+\,\text{d}\boldsymbol{s}$
is given by
$$\begin{eqnarray}\unicode[STIX]{x0394}M(\boldsymbol{s})=\left(\int _{\mathbb{D}}\left[\mathop{\prod }_{i=1}^{p}\unicode[STIX]{x1D6FF}(s_{i}(\unicode[STIX]{x1D736})-s_{i})\right]\mathfrak{D}(\unicode[STIX]{x1D736})dV_{\unicode[STIX]{x1D736}}\right)\,\text{d}\boldsymbol{s},\end{eqnarray}$$
where
$\mathfrak{D}(\unicode[STIX]{x1D736})$
is the density expressed in Lagrangian coordinates,
$dV_{\unicode[STIX]{x1D736}}$
is the volume element in Lagrangian coordinates and
$\unicode[STIX]{x1D6FF}$
is Dirac’s delta (not to be confused with the
$\unicode[STIX]{x1D6FF}$
used to denote variations). Integrating
$\unicode[STIX]{x0394}M$
over the
$p$
-tuples, from
$s_{i}$
to its maximum value
$S_{i}\equiv \max \{s_{i}(\unicode[STIX]{x1D736}),\unicode[STIX]{x1D736}\in \mathbb{D}\}$
for each
$i$
, we obtain the mass distribution function
$$\begin{eqnarray}\displaystyle M(\boldsymbol{s})=\int _{s_{1}}^{S_{1}}\cdots \int _{s_{p}}^{S_{p}}\unicode[STIX]{x0394}M(\boldsymbol{s}^{\prime })=\int _{\mathbb{ D}}\left[\mathop{\prod }_{i=1}^{p}\unicode[STIX]{x1D703}(s_{i}(\unicode[STIX]{x1D736})-s_{i})\right]\mathfrak{D}(\unicode[STIX]{x1D736})dV_{\unicode[STIX]{x1D736}}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D703}(s)=\int _{\infty }^{s}\unicode[STIX]{x1D6FF}(t)\,\text{d}t,\end{eqnarray}$$
is the Heaviside function and
$dV_{\unicode[STIX]{x1D736}}$
is the volume element in Lagrangian coordinates. It represents the mass of all Lagrangian particles with values of the
$p$
-tuple greater than
$(s_{1},\ldots ,s_{n})$
. (Methven & Berrisford (Reference Methven and Berrisford2015) used a similar approach to construct a background state in an atmospheric context.) If we wish to express the theory in Eulerian coordinates, we just need to replace Eulerian coordinates
$x^{i}=x^{i}(\unicode[STIX]{x1D736},t)$
in (2.7) and integrate over the corresponding Eulerian density
$$\begin{eqnarray}\mathfrak{D}(\boldsymbol{x})=\left(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D736})\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{n})}{\unicode[STIX]{x2202}(x^{1},\ldots ,x^{n})}(t)\right).\end{eqnarray}$$
By construction, the mass distribution function is a
$p$
-parameter family of Casimirs, one for each
$p$
-tuple. Mass distribution functions introduce a phase space ‘foliation’: with the holonomic brake turned off,
$\mathfrak{q}(t)$
moves on a leaf of the foliation along isolines
$H[\mathfrak{q}]$
; when the brake is turned on,
$\mathfrak{q}(t)$
still moves on the same leaf, but crosses the isolines of
$H[\mathfrak{q}]$
on its way to
$\mathfrak{q}_{\ast }$
, which, by our hypothesis, is where the naive Hamiltonian attains its minimum on the leaf (see figure 1).
Figure 1. Sketch of phase space with two leaves. The dashed line shows a trajectory under the action of a holonomic brake.
Two remarks are in order: while it may be possible to use (2.6) to quantify the constraints, the integral version (2.7) has the advantage of including bulk constraints, such as conservation of total mass; also, for incompressible flows in the Boussinesq approximation, we can replace the density
$\mathfrak{D}$
with a function constant and equal to 1, since Boussinesq flows conserve volume, in which case we should properly speak of a volume distribution function. For simplicity, we will still refer to
$M(\boldsymbol{s})$
as the mass distribution function.
To solve the minimization problem, we introduce a suitable Lagrange multiplier
$\unicode[STIX]{x1D713}(\boldsymbol{s})$
, defined on the support of the mass distribution function
$M^{0}(\boldsymbol{s})$
that specifies the leaf. That is, we seek to render the Lagrangian functional
$$\begin{eqnarray}L[\mathfrak{q},\unicode[STIX]{x1D713}]\equiv H[\mathfrak{q}]+\int \unicode[STIX]{x1D713}(\boldsymbol{s})\left[\int _{\mathbb{D}}\mathop{\prod }_{i=1}^{p}\unicode[STIX]{x1D703}(s_{i}(\boldsymbol{x})-s_{i})\mathfrak{D}(\boldsymbol{x})dV_{\boldsymbol{x}}-M^{0}(\boldsymbol{s})\right]d\boldsymbol{s}\end{eqnarray}$$
stationary, by varying both
$\mathfrak{q}$
and
$\unicode[STIX]{x1D713}$
(recall that
$s_{i}(\boldsymbol{x})$
is the value of the
$i$
th Lagrangian invariant at
$\boldsymbol{x}$
calculated from the fields in
$\mathfrak{q}$
), that is we seek the solution
$\mathfrak{q}_{\ast },\unicode[STIX]{x1D713}_{\ast }$
of
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}L}{\unicode[STIX]{x1D6FF}\mathfrak{q}}\cong 0,\quad \frac{\unicode[STIX]{x1D6FF}L}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}=0.\end{eqnarray}$$
(Although we should admit the possibility that more than one extremal (minimal) solution exists, for simplicity we assume that the minimal solution is unique.) If all the
$s_{i}$
depend algebraically on the field in
$\mathfrak{q}$
, then the
$\cong 0$
can be replaced by equality stricto sensu. From now on,
$\mathfrak{q}_{\ast }$
will be referred to as the ‘ground state’.
2.3 The gauge-fixing condition
Let
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}[\mathfrak{q}]\equiv \int _{\mathbb{D}}\left[\int \unicode[STIX]{x1D713}(\boldsymbol{s})\left(\mathop{\prod }_{i=1}^{p}\unicode[STIX]{x1D703}(s_{i}(\boldsymbol{x})-s_{i})\right)d\boldsymbol{s}\right]\mathfrak{D}(\boldsymbol{x})dV_{\boldsymbol{x}},\end{eqnarray}$$
be the Casimir associated with the Lagrange multiplier and let
$$\begin{eqnarray}{\mathcal{H}}[\mathfrak{q}]=H[\mathfrak{q}]+\unicode[STIX]{x1D6F9}[\mathfrak{q}].\end{eqnarray}$$
By switching the integral over the
$p$
-tuples
$\boldsymbol{s}$
with the integral over the manifold
$\mathbb{D}$
, the Lagrange functional can be rewritten as
$$\begin{eqnarray}L[\mathfrak{q},\unicode[STIX]{x1D713}]={\mathcal{H}}[\mathfrak{q}]-\int \unicode[STIX]{x1D713}(\boldsymbol{s})M^{0}(\boldsymbol{s})d\boldsymbol{s}.\end{eqnarray}$$
Since the last term in (2.14) does not depend on
$\mathfrak{q}$
, the Lagrangian multiplier
$\unicode[STIX]{x1D713}_{\ast }$
associated with the ground state
$\mathfrak{q}_{\ast }$
can be used to define the following gauge-fixing condition to the equivalence class of Hamiltonians
$$\begin{eqnarray}\left.\frac{\unicode[STIX]{x1D6FF}{\mathcal{H}}}{\unicode[STIX]{x1D6FF}\mathfrak{q}}\right|_{\mathfrak{q}_{\ast }}\cong 0,\end{eqnarray}$$
which is satisfied when
${\mathcal{E}}[\mathfrak{q}]=H[\mathfrak{q}]+\unicode[STIX]{x1D6F9}_{\ast }[\mathfrak{q}]$
, where the Casimir
$\unicode[STIX]{x1D6F9}_{\ast }[\mathfrak{q}]$
is related to the Lagrange multiplier
$\unicode[STIX]{x1D713}_{\ast }$
by (2.12). We leave to the reader to verify that for any two states
$\mathfrak{q}_{1}$
and
$\mathfrak{q}_{2}$
belonging to the same leaf (i.e. having the same mass distribution function)
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\ast }[\mathfrak{q}_{1}]=\unicode[STIX]{x1D6F9}_{\ast }[\mathfrak{q}_{2}].\end{eqnarray}$$
We are now in a position to define the local diagnostic energy as follows: the local diagnostic energy
${\mathcal{E}}$
is the scalar density of the Hamiltonian which satisfies the gauge-fixing condition (2.15), with the ground state
$\mathfrak{q}_{\ast }$
obtained from (2.11), i.e.
$$\begin{eqnarray}{\mathcal{E}}(\mathfrak{q})=H(\mathfrak{q})+\unicode[STIX]{x1D6F9}_{\ast }(\mathfrak{q}).\end{eqnarray}$$
In terms of the local diagnostic energy, the available energy is
$$\begin{eqnarray}E_{AE}[\mathfrak{q}]\equiv {\mathcal{E}}[\mathfrak{q}]-{\mathcal{E}}[\mathfrak{q}_{\ast }]=H[\mathfrak{q}]-H[\mathfrak{q}_{\ast }],\end{eqnarray}$$
where the last equality follows from (2.16), since
$\mathfrak{q}$
and
$\mathfrak{q}_{\ast }$
belong to the same leaf. Later we will show that the local APE of Holliday & McIntyre (Reference Holliday and McIntyre1981) is a particular solution of the gauge-fixing condition when the mass distribution function satisfies certain symmetries. Then, the equivalence between the global APE of Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) and the volume integrated local APE of Holliday & McIntyre, the latter being
${\mathcal{E}}(\mathfrak{q})-{\mathcal{E}}(\mathfrak{q}_{\ast })$
, follows trivially from (2.18), itself a consequence of (2.16) which is true when the two states belong to the same leaf.
Thus, the gauge-fixing condition selects, out of the class of dynamically equivalent Hamiltonians, the one that returns the same available energy as the naive Hamiltonian, when referenced to the ground state. Of course, the naive Hamiltonian is physically interpreted as being the energy of the system. What makes the local diagnostic energy interesting is how the evolution of the available energy under full diabatic conditions is related to the local diagnostic energy.
2.4 Evolution of the available energy under diabatic conditions
The Hamiltonian selected by the gauge-fixing condition (2.15) acquires a special role when we apply non-holonomic forces which break the invariance of the
$s_{i}$
values along Lagrangian trajectories. Without brakes, the motion occurs on a leaf along trajectories of constant energy. With a holonomic brake, the motion still occurs within the leaf, crossing the isolines of the naive Hamiltonian. Finally with the full non-holonomic brake on, the mass distribution function becomes time dependent and
$\mathfrak{q}(t)$
drifts across leaves. At each time, we can still calculate a ground state solving (2.10)–(2.11) with
$M^{0}(\boldsymbol{s})$
replaced by its instantaneous value
$M^{t}(\boldsymbol{s})$
calculated from
$\mathfrak{q}(t)$
. Thus, starting from a time series of
$\mathfrak{q}(t)$
states, we obtain a sequence of ground states
$\mathfrak{q}_{\ast }(t)$
with the corresponding Lagrange multipliers
$\unicode[STIX]{x1D713}_{\ast }(\boldsymbol{s},t)$
. Note that (2.16) still holds on the pairs
$(\mathfrak{q}(t),\mathfrak{q}_{\ast }(t))$
.
Based on our definition of local diagnostic energy,
$$\begin{eqnarray}{\mathcal{E}}(\mathfrak{q}_{\ast }(t))=H(\mathfrak{q}_{\ast }(t))+\unicode[STIX]{x1D6F9}_{\ast }(\mathfrak{q}_{\ast }(t),t),\end{eqnarray}$$
where the second argument in
$\unicode[STIX]{x1D6F9}_{\ast }(\cdot ,t)$
is a reminder that the time dependence of the Casimir is due both to the time dependence of the ground state as well as to the intrinsic time dependence of
$\unicode[STIX]{x1D713}_{\ast }$
. The rate of change of the integrated local diagnostic energy of the ground state is
$$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{E}}[\mathfrak{q}_{\ast }(t)]}{\text{d}t} & = & \displaystyle \left.\left(\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\mathfrak{q}}+\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F9}_{\ast }}{\unicode[STIX]{x1D6FF}\mathfrak{q}}\right)\right|_{(\mathfrak{q}_{\ast }(t),t)}\left[\frac{\text{d}\mathfrak{q}_{\ast }}{\text{d}t}\right]+\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}_{\ast }}{\unicode[STIX]{x2202}t}\right|_{(\mathfrak{q}_{\ast }(t),t)}\nonumber\\ \displaystyle & \cong & \displaystyle \left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}_{\ast }}{\unicode[STIX]{x2202}t}\right|_{(\mathfrak{q}_{\ast }(t),t)},\end{eqnarray}$$
where the last equality is made possible by the gauge-fixing condition. Note that the last partial derivative only applies to the explicit dependence on time in the gauge-fixed Casimir. (In the following, when we speak of the Casimir, we will intend the gauge-fixed Casimir, as opposed to a generic Casimir. The context will usually suffice to make the distinction clear.) Since
$\mathfrak{q}(t)$
and
$\mathfrak{q}_{\ast }(t)$
are on the same leaf, we have
$$\begin{eqnarray}\frac{\text{d}{\mathcal{E}}[\mathfrak{q}_{\ast }(t)]}{\text{d}t}\cong \left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}_{\ast }}{\unicode[STIX]{x2202}t}\right|_{(\mathfrak{q}(t),t)},\end{eqnarray}$$
where now the Casimir is evaluated on
$\mathfrak{q}(t)$
, rather than on the ground state
$\mathfrak{q}_{\ast }(t)$
. Therefore, the rate of change of the available energy
$$\begin{eqnarray}\displaystyle \frac{\text{d}E_{AE}[\mathfrak{q}(t)]}{\text{d}t} & \cong & \displaystyle \left.\frac{\unicode[STIX]{x1D6FF}{\mathcal{E}}}{\unicode[STIX]{x1D6FF}\mathfrak{q}}\right|_{(\mathfrak{q}(t),t)}\left[\frac{\text{d}\mathfrak{q}}{\text{d}t}\right]\nonumber\\ \displaystyle & \cong & \displaystyle \left.\left(\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\mathfrak{q}}+\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F9}_{\ast }}{\unicode[STIX]{x1D6FF}\mathfrak{q}}\right)\right|_{(\mathfrak{q}(t),t)}\left[\frac{\text{d}\mathfrak{q}}{\text{d}t}\right],\end{eqnarray}$$
can be expressed solely in terms of the rate of change of the local diagnostic energy evaluated on
$\mathfrak{q}$
.
The rate of change of the naive Hamiltonian reflects the action of the holonomic and non-holonomic components of the diabatic processes, while the change in the Casimir is due solely to the non-holonomic component. From a local point of view, how
$H$
evolves along Lagrangian trajectories is usually well known. For example, for a Boussinesq fluid, the loss of energy due to diabatic effects is quantified by
$\unicode[STIX]{x1D716}$
, the rate of loss of kinetic energy. Usually, the latter is mediated by turbulent cascade, but our framework will work regardless of the precise nature of the diabatic effects.
The local evolution of the Casimir
$\unicode[STIX]{x1D6F9}_{\ast }$
along trajectories quantifies how (non-holonomic) diabatic effects modify the available energy. Interestingly, such effects may actually increase the available energy, at least temporarily. We will return to this point in the discussion. What is important to remember is that the (potentially, time-varying) gauge-fixed Casimir is the quantity that needs to be analysed in order to understand how diabatic processes modify the available energy. To study such processes we do not need to know what the ground state is. Knowledge of the latter is required only if we actually want to calculate the total available energy. For systems that are maintained by external factors away from a state of minimum energy, the information we are often after is the energetic cost of keeping the system away from equilibrium, that is the rate of change of available energy. In this case, the gauge-fixed Casimir is the quantity of interest. It is for this reason that in the following section we will mostly focus on the gauge-fixed Casimir.
3 A specific flow model: Boussinesq fluids
The theory developed in the preceding sections is quite general, and applies to any type of system that can be described in the adiabatic limit with a non-canonical Hamiltonian structure. In this section, we apply the theory to continuously stratified flows in the Boussinesq approximation. The two Lagrangian invariants are the relative concentration of the stratifying agent and the Potential Vorticity. Within the confines of the Boussinesq approximation, we can replace the former with the buoyancy.
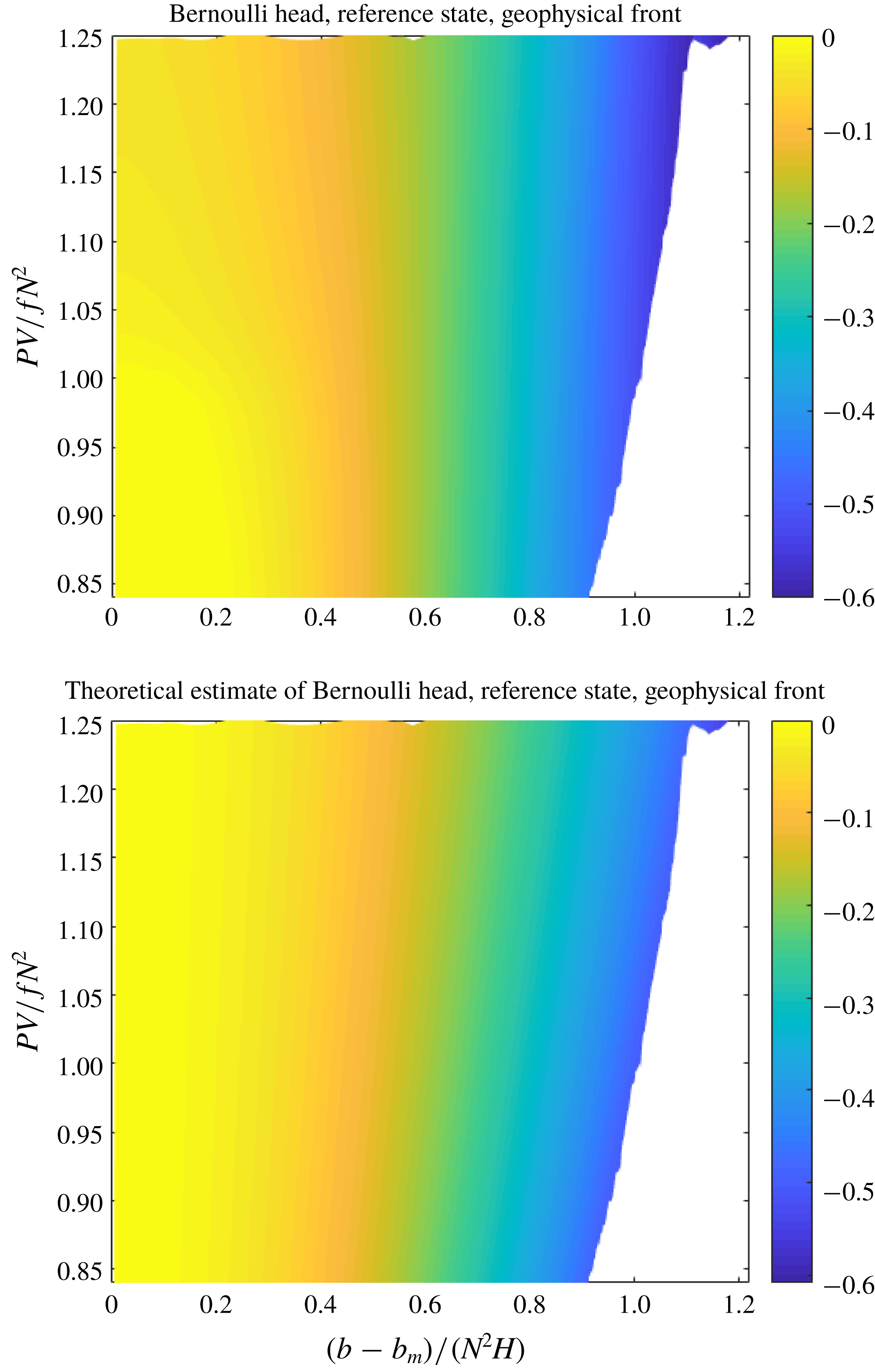
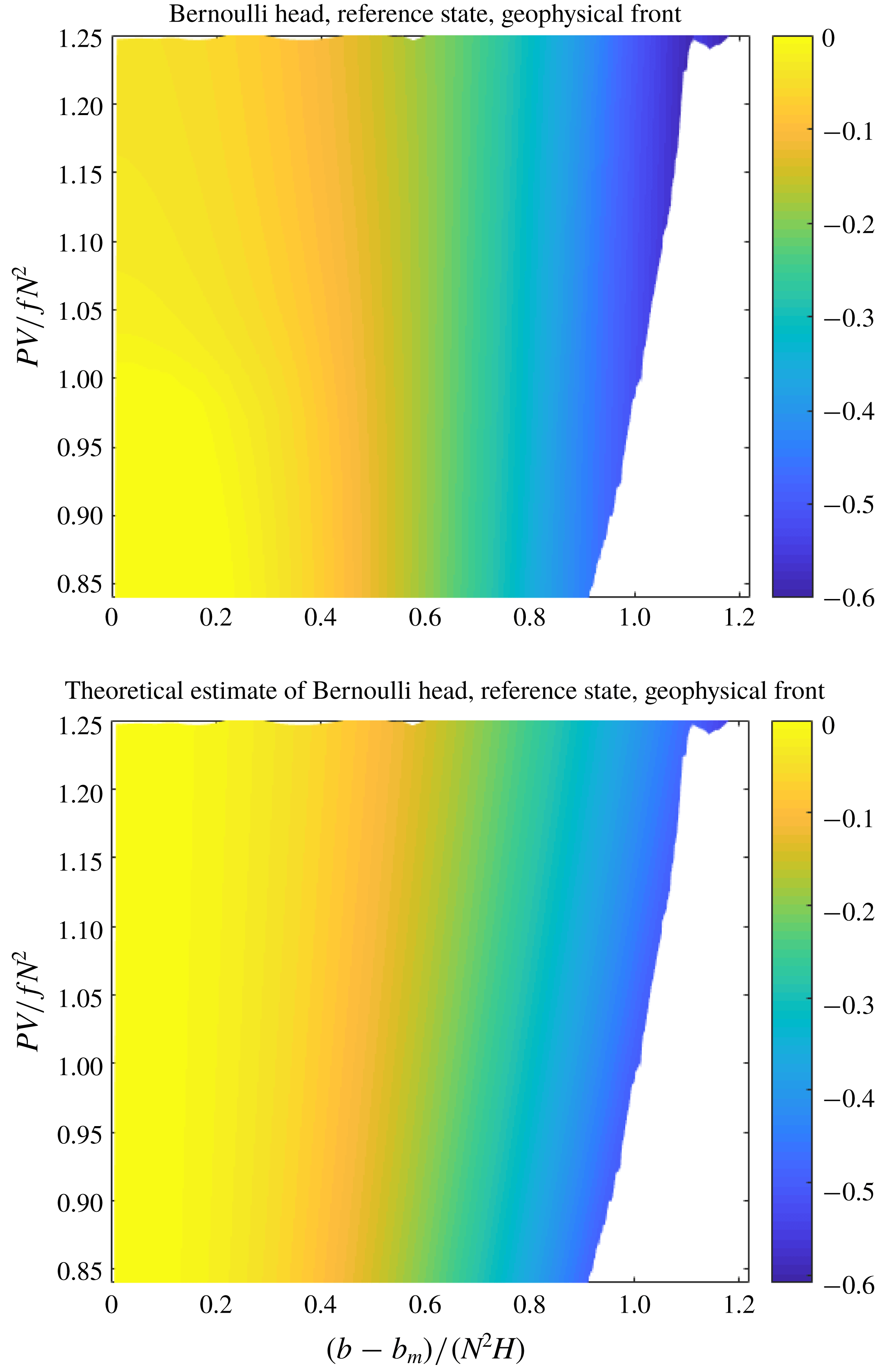
The main result of this section, that in strongly rotating systems, to leading order, the Casimir is independent on the details of the mass distribution function, relies on the fact that the Casimir is related via a simple transformation to the Bernoulli head of the ground state.
3.1 Stratified Boussinesq flows
A continuously stratified flow in the Boussinesq approximation is described by the pair
$\mathfrak{q}\equiv (b,\boldsymbol{v})$
, where
$b\equiv g(\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x1D70C})/\unicode[STIX]{x1D70C}_{0}$
is the buoyancy,
$\boldsymbol{v}$
is the velocity field. Together, they satisfy
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}=-\boldsymbol{v}\times \unicode[STIX]{x1D74E}-\unicode[STIX]{x1D735}(P+Ek)+b\unicode[STIX]{x1D735}Z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}b}{\unicode[STIX]{x2202}t}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}b=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$
$P$
is the pressure,
$Z$
the geopotential height and
$Ek=\boldsymbol{v}^{2}/2$
the kinetic energy per unit mass. The total vorticity
$\unicode[STIX]{x1D74E}\equiv \unicode[STIX]{x1D735}\times \boldsymbol{v}+\boldsymbol{f}$
is the sum of the relative vorticity
$\unicode[STIX]{x1D735}\times \boldsymbol{v}$
and the frame vorticity
$\boldsymbol{f}$
. Let
$(x^{1},x^{2},x^{3})$
be a set of geometric coordinates and
$g=g_{ij}dx^{i}\otimes dx^{j}=g^{ij}\boldsymbol{\unicode[STIX]{x2202}}_{i}\otimes \boldsymbol{\unicode[STIX]{x2202}}_{j}$
be the metric tensor. Einstein convention (summation over repeated indexes) is implied, and we follow modern notation by denoting with
$\boldsymbol{\unicode[STIX]{x2202}}_{i}=\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{x}^{i}$
,
$i=1,\ldots ,3$
the elements of a basis fitted to the coordinates in a local patch.
There are two independent Lagrangian invariants: the buoyancy
$b$
itself and the potential vorticity
$q\equiv \unicode[STIX]{x1D735}b\boldsymbol{\cdot }\unicode[STIX]{x1D74E}$
. (if
$f(b)$
is any (smooth) function of
$b$
, then
$f(b)$
is also a Lagrangian invariant, and so is
$(\unicode[STIX]{x1D735}f(b)\boldsymbol{\cdot }\unicode[STIX]{x1D74E})$
. This will be reflected in certain degrees of freedom available in the definition of the gauge-fixed Casimir.)
The naive Hamiltonian is
$$\begin{eqnarray}H[\mathfrak{q}]=\int _{\mathbb{D}}(Ek-bZ)dV,\end{eqnarray}$$
while Casimirs have the general form
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}[\mathfrak{q}]=\int _{\mathbb{D}}\unicode[STIX]{x1D6F9}(b,q)dV.\end{eqnarray}$$
In terms of the Lagrange multiplier, the density of the gauge-fixed Casimir is
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(b,q)=\int _{b_{min}}^{b}\int _{q_{min}}^{q}\unicode[STIX]{x1D713}(q^{\prime },b^{\prime })dq^{\prime }db^{\prime }.\end{eqnarray}$$
3.1.1 The gauge-fixing condition
The Frèchet derivatives of the naive energy with respect to
$\boldsymbol{v}$
and
$b$
are trivial. We concentrate here on the variations of the Casimir written as in (3.3). The variation with respect to
$b$
is given by
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x1D6FF}b}\unicode[STIX]{x1D6FF}b & = & \displaystyle (\unicode[STIX]{x1D6F9}_{,b}\unicode[STIX]{x1D6FF}b+\unicode[STIX]{x1D6F9}_{,q}\unicode[STIX]{x1D6FF}q)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6F9}_{,b}\unicode[STIX]{x1D6FF}b+\unicode[STIX]{x1D6F9}_{,q}(\unicode[STIX]{x1D735}(\unicode[STIX]{x1D6FF}b)\boldsymbol{\cdot }\unicode[STIX]{x1D74E}))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6F9}_{,b}\unicode[STIX]{x1D6FF}b-\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D6F9}_{,q}\unicode[STIX]{x1D714})\unicode[STIX]{x1D6FF}b\nonumber\\ \displaystyle & = & \displaystyle [(\unicode[STIX]{x1D6F9}-q\unicode[STIX]{x1D6F9}_{,q})_{,b}-\unicode[STIX]{x1D6F9}_{,qq}(\unicode[STIX]{x1D735}q\boldsymbol{\cdot }\unicode[STIX]{x1D74E})]\unicode[STIX]{x1D6FF}b,\end{eqnarray}$$
while the variation with respect to
$\boldsymbol{v}$
is given by
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x1D6FF}\boldsymbol{v}}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{v}=\unicode[STIX]{x1D6F9}_{,q}\frac{\unicode[STIX]{x1D6FF}q}{\unicode[STIX]{x1D6FF}\boldsymbol{v}}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{v}=\unicode[STIX]{x1D6F9}_{,qq}(\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}b)\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{v}.\end{eqnarray}$$
Note that to avoid notational clutter we use the comma derivative notation, i.e.
$$\begin{eqnarray}f_{,a}\equiv \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}a},\quad f_{,ab}\equiv \frac{\unicode[STIX]{x2202}^{2}f}{\unicode[STIX]{x2202}a\unicode[STIX]{x2202}b},\ldots\end{eqnarray}$$
Given the mass distribution function
$V(q,b)$
, the ground state and the gauge-fixed Casimir are found solving
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}{\mathcal{H}}}{\unicode[STIX]{x1D6FF}b} & \cong & \displaystyle [-Z+(\unicode[STIX]{x1D6F9}-q\unicode[STIX]{x1D6F9}_{,q})_{,b}]-\unicode[STIX]{x1D6F9}_{,qq}(\unicode[STIX]{x1D735}q\boldsymbol{\cdot }\unicode[STIX]{x1D74E})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}{\mathcal{H}}}{\unicode[STIX]{x1D6FF}\boldsymbol{v}} & \cong & \displaystyle \boldsymbol{v}+\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D6F9}_{,q}\unicode[STIX]{x1D735}b)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}{\mathcal{H}}}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}} & = & \displaystyle \int _{\mathbb{D}}[\unicode[STIX]{x1D703}(q(\boldsymbol{x})-q)\unicode[STIX]{x1D703}(b(\boldsymbol{x})-b)]dV=V(q,b).\end{eqnarray}$$
3.1.2 Non-quiescent ground states and natural coordinates
While our theory recovers Winters et al.’s quiescent ground state (i.e. having zero KE) as a special case, we are mainly interested in characterizing ground states with non-zero kinetic energy, and in which streamlines do not end in stagnation points, which requires
$\unicode[STIX]{x1D6F9}_{\ast ,qq}\neq 0$
and
$\unicode[STIX]{x1D735}q_{\ast }\times \unicode[STIX]{x1D735}b_{\ast }\neq 0$
or else from (3.8b
)
$\boldsymbol{v}_{\ast }=0$
. Also, we assume that the mass distribution function is a continuous and differentiable function, i.e. buoyancy and potential vorticity are continuously distributed. More complicated cases consisting of layers where buoyancy and/or potential vorticity are interleaved with layers where one or the other are constant will not be considered here.
The form of the equations, and the fact that buoyancy and potential vorticity are an obvious choice for Lagrangian coordinates, suggest that the ground state is more conveniently expressed with a ‘natural’ set of coordinates which is given by buoyancy, potential vorticity and a third coordinate
$t$
. The latter is defined so that the relationship between ‘geometric’
$(x^{1},x^{2},x^{3})$
and natural coordinates
$(q,b,t)$
is such that the volume element becomes
$$\begin{eqnarray}\sqrt{|g|}dx^{1}dx^{2}dx^{3}=\unicode[STIX]{x1D6F9}_{\ast ,qq}dbdqdt.\end{eqnarray}$$
This can be achieved if locally the relationship between geometric and natural coordinates is obtained by integrating the Pfaffian system
$$\begin{eqnarray}dx^{i}=v_{\ast }^{i}dt,\quad i=1,\ldots ,3\end{eqnarray}$$
where
$\boldsymbol{v}_{\ast }=-\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D6F9}_{\ast ,q}\unicode[STIX]{x1D735}b_{\ast })$
is the velocity field of the ground state, i.e. the solution of (3.8b
) and the subscript
$_{\ast }$
reminds us that these are ground state fields (see § A.2 for a derivation of (3.9) from (3.10)). In the following sections, we explore some of the general properties of the ground states that are solutions of (3.8a
)–(3.8c
). The analysis relies on the following general property: if
$\boldsymbol{v}_{\ast },b_{\ast }$
are solutions of (3.8a
)–(3.8c
), the Casimir
$\unicode[STIX]{x1D6F9}_{\ast }$
of the ground state, is related to the Bernoulli head
$$\begin{eqnarray}B_{\ast }(q,b)=\boldsymbol{v}_{\ast }(q,b)^{2}/2-bZ_{\ast }(q,b)+P_{\ast }(q,b)\end{eqnarray}$$
of the ground state expressed in natural coordinates, via
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F9}}_{\ast }\equiv q\unicode[STIX]{x1D6F9}_{\ast ,q}-\unicode[STIX]{x1D6F9}_{\ast }=B_{\ast }(q,b),\end{eqnarray}$$
whose general solution is
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\ast }=q\int _{q_{min}}^{q}\frac{B_{\ast }(q^{\prime },b)}{{q^{\prime }}^{2}}dq^{\prime }\end{eqnarray}$$
(see § A.1).
3.1.3 Apedic ground states and their properties
As a first application of our framework, we wish to characterize under what conditions we recover Winters et al. APE definition.
Let us start with a general definition: an apedic (from the Greek 
meaning level, flat) ground state is a ground state such that
$b_{\ast }=b_{\ast }(Z)$
. By extension, the leaf in phase space to which an apedic ground state belongs is called an apedic leaf.
If we express the absolute vorticity of a ground state as
$$\begin{eqnarray}\unicode[STIX]{x1D74E}_{\ast }=\unicode[STIX]{x1D714}^{t}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q+\unicode[STIX]{x1D714}^{b}\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}t+\unicode[STIX]{x1D714}^{q}\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b,\end{eqnarray}$$
then the ground state is apedic if and only if
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{,t}^{q} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{,t}^{t} & = & \displaystyle 0,\end{eqnarray}$$
$t$
must be independent on
$t$
for a ground state to be apedic. This follows from taking the curl of (3.1a
) (assuming stationarity) and since
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}=0$
, we obtain after some simple algebra 
$$\begin{eqnarray}\unicode[STIX]{x1D735}Z\times \unicode[STIX]{x1D735}b+\unicode[STIX]{x1D714}_{,t}^{t}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q+\unicode[STIX]{x1D714}_{,t}^{q}\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b=0,\end{eqnarray}$$
which the ground state must satisfy. This equation is satisfied if and only if (3.15a
)–(3.15b
) hold, since
$\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q$
and
$\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b$
are independent vectors, and on an apedic manifold
$\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}Z=0$
by definition.
Let us now explore some more properties of apedic ground states. Let
$\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }$
be the acceleration along streamlines, where
$\unicode[STIX]{x1D735}$
is the Levi-Civita connection on the manifold, i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }=\left[x_{,tt}^{j}+\unicode[STIX]{x1D6E4}_{mp}^{j}x_{,t}^{m}x_{,t}^{p}\right]\boldsymbol{\unicode[STIX]{x2202}}_{j},\end{eqnarray}$$
where the
$x^{j}(t)$
are the coordinates along streamlines parameterized with
$t$
, i.e. the solution to
$dx^{i}=v_{\ast }^{i}dt$
and
$\unicode[STIX]{x1D6E4}_{mp}^{i}$
are the Christoffel symbols of the Levi-Civita connection. Then it is a matter of straightforward algebra (see § A.3) to show that for a ground state to be apedic the conditions (3.15a
)–(3.15b
) require
$$\begin{eqnarray}\displaystyle \left(\frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }\right)_{,q} & = & \displaystyle \left(\frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{q}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }\right)_{,b},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }\right)_{,t} & = & \displaystyle Ek_{\ast ,tb}.\end{eqnarray}$$
Thus, a sufficient condition for a ground state to be apedic is that streamlines are geodesics in an inertial frame and the kinetic energy depends only on either
$q$
and
$t$
or
$q$
and
$b$
.
Also, it is worth remarking that the notion of apedicity, depends on the local direction of the plumb line, and thus it is not frame independent. Thus, a flow in solid body rotation will appear apedic to an observer in solid body rotation with the flow, but not to an inertial observer.
3.1.4 The Casimir of inertial apedic ground states
Under the assumption that the ground state is apedic in an inertial system, we can make further analytic inroads. Let
$Ek_{\ast }=g_{ij}x_{,t}^{i}x_{,t}^{j}/2=g_{tt}/2$
be the kinetic energy of the ground state. Assuming that apedicity is due to the trajectories being inertial, we have (see § A.3)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{\ast }^{b} & = & \displaystyle Ek_{\ast ,q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{\ast }^{q} & = & \displaystyle -Ek_{\ast ,b},\end{eqnarray}$$
that is
$$\begin{eqnarray}\unicode[STIX]{x1D74E}_{\ast }=\unicode[STIX]{x1D735}\times (Ek_{\ast }\unicode[STIX]{x1D735}t)+\unicode[STIX]{x1D714}_{\ast }^{t}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q,\end{eqnarray}$$
which, substituted in (3.1a
) (recall that
$\boldsymbol{v}_{\ast }$
is parallel to
$\unicode[STIX]{x1D735}t$
)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}(P_{\ast })=b_{\ast }\unicode[STIX]{x1D735}Z=\unicode[STIX]{x1D735}\left(\int ^{Z}b_{\ast }\,\text{d}Z\right), & & \displaystyle\end{eqnarray}$$
indicates that the pressure distribution in apedic ground states is hydrostatic.
The definitions of local available potential energy proposed in the past that rely on a Casimir (e.g. Holliday & McIntyre Reference Holliday and McIntyre1981), usually, (but not always, see, e.g. Codoban & Shepherd (Reference Codoban and Shepherd2003)) include only the potential and pressure term, combined in
$\int ^{b}Zdb$
. This is not surprising, since the traditional available energy approach is to define the background potential energy as the energy of the restratified flow. In our formalism, it can be recovered by enforcing only conservation of buoyancy when we seek the ground state. Indeed, in this case,
$\unicode[STIX]{x1D6F9}_{\ast }$
depends only on buoyancy, and (3.8a
)–(3.8b
) show that
$Z_{\ast }=Z_{\ast }(b)$
and
$\boldsymbol{v}_{\ast }=0$
. Of course, this is a solution of the full problem if the state
$\mathfrak{q}$
has zero potential vorticity throughout. If we want to enforce both buoyancy and potential vorticity conservation, the corresponding ground state in general must have kinetic energy, and thus the system will have a lower available energy. Superficially, it would seem that enforcing potential vorticity conservation on the ground state would necessarily lead to ground states with kinetic energy, thus lowering the amount of available energy, unless
$\mathfrak{q}$
has zero potential vorticity. In fact, the set of states whose ground state is described by the Winters et al. ground state is wider, and they will be discussed in the next section, where we apply the theory to simple channel geometries, both inertial and rotating.
3.1.5 Boussinesq channel flows
For arbitrary mass distribution functions and geometries, (3.8a
)–(3.8c
) constitute a formidable nonlinear optimization problem for the ground state. It is therefore of advantage to solve this optimization problem by other means, for instance, integrating numerically the Euler equations with a holonomic brake to find the ground state. Once the pair
$b_{\ast },\boldsymbol{v}_{\ast }$
is known, the Casimir can be calculated from its Bernoulli head.
Nevertheless, analytic progress can be made if we are willing to sacrifice geometric complexity. We consider simple ‘open’ channel geometries, which can be geometrically described by Cartesian coordinates. For definiteness, let
$0\leqslant Z\leqslant L_{z}$
be the vertical direction,
$0\leqslant y\leqslant L_{y}$
the spanwise direction and
$0\leqslant x\leqslant L_{x}$
the streamwise direction. The bottom, top and side walls are free-slip boundaries, while the flow is periodic in the streamwise direction. For simplicity, we limit the search of ground states to states that are
$2.5$
-dimensional: these are states defined by
$Z=Z(b,q)$
and
$y=y(b,q)$
, and such that the velocity, which depends on two dimensions
$(b,q)$
is normal to the
$Z,y$
plane (the
$1/2$
dimension).
3.1.6 Apedic ground states in inertial channels
In this section, we prove that 2.5-dimensional ground states (as defined above) in inertial channels are apedic. Further if, for any value of
$b$
, the mass distribution function
$V$
is such that
$V_{,qb}$
is an even function of
$q$
, the kinetic energy of the ground state is zero.
The method to construct an apedic ground state for simple flow geometries is a natural extension of the technique introduced by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) and consists of three steps:
(i) Determine the resorted height
$Z_{\ast }(b)$
solving (3.8c
) in the limit
$q\rightarrow q_{min}$
. This coincides with the restratification of the fluid.(ii) Compute the resorted distribution of potential vorticity along the spanwise direction
$y_{\ast }(q)$
.(iii) Finally, determine the kinetic energy
$Ek_{\ast }$
of the ground state.
Later, we will modify this recipe to calculate the ground state and associated Casimir of rotating flows characterized by a low Rossby number ground state, with the Rossby number being defined as
$Ro=O(|(\unicode[STIX]{x1D735}\times \boldsymbol{v})\boldsymbol{\cdot }\unicode[STIX]{x1D735}b|/\boldsymbol{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}b)$
, in other words, flows in which the leading-order contribution to potential vorticity is provided by the frame vorticity.
It is straightforward to verify that 2.5-dimensional ground states in inertial channels are apedic. In geometric coordinates, the components of the velocity vector are
$[0,0,v_{\ast }(b(Z,y),q(Z,y))]$
, thus
$dx=v(b,q)dt$
and
$dy=dZ=0$
, which implies that the velocity is uniform along geodesics. Rather than working in ‘natural’ coordinates, we work with ‘hybrid’ coordinates
$(b,q,x)$
. Being apedic
$Z_{\ast }=Z_{\ast }(b)$
, (here, as we have done before, quantities used as coordinates will not carry the
$_{\ast }$
subscript) which can be calculated from the limit
$q\rightarrow q_{min}$
of (3.8c
)
$$\begin{eqnarray}\displaystyle \int \unicode[STIX]{x1D703}(b_{\ast }(Z)-s)dZdydx & = & \displaystyle -L_{y}L_{x}\int _{b_{min}}^{b_{Max}}\unicode[STIX]{x1D703}(b-s)\frac{dZ_{\ast }}{db}db\nonumber\\ \displaystyle & = & \displaystyle V(q_{min},s),\end{eqnarray}$$
whose solution is
$$\begin{eqnarray}Z_{\ast }(b)=L_{z}\left(1-\frac{V(q_{min},b)}{V(q_{min},b_{min})}\right).\end{eqnarray}$$
Its functional inverse
$b_{\ast }(Z)$
is the buoyancy distribution of the ground state. From this, we can calculate the hydrostatic pressure of the ground state. Also, for later convenience, we define
$N_{\ast }^{-2}\equiv Z_{\ast ,b}(b)$
.
Next, consider the volume element
$$\begin{eqnarray}\mathfrak{V}=dZdydx=\left|\frac{\unicode[STIX]{x2202}(Z,y)}{\unicode[STIX]{x2202}(b,q)}\right|dbdqdx.\end{eqnarray}$$
Using again (3.8c )
$$\begin{eqnarray}\left|\frac{\unicode[STIX]{x2202}(Z,y)}{\unicode[STIX]{x2202}(b,q)}\right|=\frac{V_{,qb}}{L_{x}},\end{eqnarray}$$
we obtain
$y=y(q,b)$
solving
$$\begin{eqnarray}\frac{V_{,qb}}{L_{x}}=\left|\frac{\unicode[STIX]{x2202}(Z,y)}{\unicode[STIX]{x2202}(b,q)}\right|=\left|\frac{V_{,b}(q_{min},b)}{L_{x}L_{y}}\frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}q}\right|.\end{eqnarray}$$
The solution that spans the domain is
$$\begin{eqnarray}y_{\ast }=L_{y}\frac{V_{,b}(q_{min},b)-V_{,b}(q,b)}{V_{,b}(q_{min},b)}.\end{eqnarray}$$
Note that in this apedic ground state, isopycnals are flat, whereas surfaces of constant potential vorticity are not and the relationship between natural and geometric coordinates is invariant under the dilation
$V\rightarrow e^{s}V$
.
At this point, all we have left is to calculate the kinetic energy of the ground state. By construction, we must have
$\boldsymbol{v}=F\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}x$
and
$\unicode[STIX]{x1D735}\times \boldsymbol{v}=F_{,b}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}x+F_{,q}\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}x$
. Using the definition of potential vorticity (A 6) and (3.26) we may try as a first ansatz a solution to
$$\begin{eqnarray}F_{,q}=\frac{qV_{,qb}}{L_{x}},\end{eqnarray}$$
with the constant of integration set along planes of constant buoyancy so that the total momentum along the
$x$
direction is conserved. In the special case
$$\begin{eqnarray}V_{,qb}=\unicode[STIX]{x1D6FF}(q)\tilde{V}_{,b},\end{eqnarray}$$
which corresponds to a leaf characterized by a uniformly zero distribution of potential vorticity,
$F$
and the kinetic energy of the ground state are zero. The Casimir then reduces (up to a factor
$qf(b)$
which does not concern us) to
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\ast }=\int _{b_{min}}^{b}Z(s)ds,\end{eqnarray}$$
and the ground state to a quiescent fluid restratified according to (3.24). Two-dimensional flows contained in a vertical plane have zero potential vorticity, and thus satisfy (3.30). In this case, as mentioned earlier, we recover the same definition of available energy used by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995).
Consider a three-dimensional flow at time
$t$
which evolved from an initially two-dimensional flow contained in the vertical plane seeded with random infinitesimal perturbations along the third dimension. At
$t=0$
the mass distribution function is very well approximated by
$V_{,q}=\widetilde{V}_{,b}\unicode[STIX]{x1D6FF}(q)$
. As the flow develops instabilities, the delta-like distribution in the mass distribution function develops tails. Let us assume that in the absence of any mechanism that breaks the symmetry, the potential vorticity that the diabatic processes generate ex nihilo is equally distributed around the origin. In other words, we assume that whatever mechanism generates potential vorticity, it is not biased against either positive or negative potential vorticity. While this hypothesis seems reasonable, and it is supported by analysis of numerical experiments of different flow configurations, where a stretched exponential appears to give a good fit (figure 2), we cannot prove it. Thus, it must be considered as a conjecture. Here, we explore its consequences. Without loss of generality, we can assume that at time
$t$
$$\begin{eqnarray}V_{,qb}\simeq \frac{L_{y}L_{x}N_{\ast }^{-2}(b)}{\unicode[STIX]{x1D70E}(b)}w\left(\frac{q}{\unicode[STIX]{x1D70E}(b)}\right),\end{eqnarray}$$
where
$w(x)$
is a suitable even function. As long as it decays sufficiently rapidly, we can replace
$p_{min}$
with
$-\infty$
and
$p_{Max}$
with
$+\infty$
.
$\unicode[STIX]{x1D70E}(b)$
measures the spread (i.e. the variance if the distribution was Gaussian) in potential vorticity near a given buoyancy level. Let
$W(x)=\int _{-\infty }^{x}tw(t)dt$
and
$\overline{W}_{n}=\int _{-\infty }^{\infty }W^{n}(t)dt$
. Integration of (3.29) yields for the velocity the following expression (setting the integration constant to zero for the moment)
$$\begin{eqnarray}F(q,b)=\int _{-\infty }^{q}q\frac{V_{,qb}}{L_{x}}\,\text{d}q=L_{y}W\left(\frac{q}{\unicode[STIX]{x1D70E}(b)}\right)N_{\ast }^{-2}(b)\unicode[STIX]{x1D70E}(b),\end{eqnarray}$$
from which the kinetic energy per unit volume of the ground state can be easily calculated
$$\begin{eqnarray}\displaystyle Ek_{\ast } & = & \displaystyle \int _{-\infty }^{+\infty }\left(\int _{b_{min}}^{b_{Max}}\frac{F^{2}}{2}V_{,bq}\,\text{d}b\right)\text{d}q\left/\int _{-\infty }^{+\infty }\left(\int _{b_{min}}^{b_{Max}}V_{,bq}\,\text{d}b\right)\,\text{d}q\right.\nonumber\\ \displaystyle & = & \displaystyle \frac{L_{y}^{2}}{2}\left(\frac{\overline{W}_{2}}{L_{z}}\int _{0}^{L_{z}}N_{\ast }^{-2}(b_{\ast }(Z)\unicode[STIX]{x1D70E}(b_{\ast }(Z)))^{2}dZ\right),\end{eqnarray}$$
the inescapable consequence of which is that the kinetic energy per unit volume of this point on the leaf grows with the width
$L_{y}$
of the channel squared. While we have derived this result assuming that the mass distribution function has the particular form given by (3.32), it fundamentally rests on the fact that under the dilation
$V\rightarrow e^{s}V$
we have
$F\rightarrow e^{s}F$
and
$Ek\rightarrow e^{2s}Ek$
. Therefore, what we have derived cannot be the ground state that we are seeking. To understand what went wrong, and to find a cure for it, in figure 3 we plot
$F$
calculated using (3.29) where the mass distribution function was obtained from a direct numerical simulation of stratified Couette flow (Scotti Reference Scotti2015) (indicated with the label (1)).
Figure 2. Value of
$\log _{10}(V_{,qb})$
in stratified shear flows. (a) A stratified Couette flow: the inset shows
$V_{,qb}(q,0.5)$
(blue line) superimposed to a stretched exponential
$\exp -|q/0.3|^{0.6}$
(orange line). (b) A time-evolving shear layer, after the initial break-up of the Kelvin–Helmholtz instabilities. In this case too, a stretched exponential with a similar exponent fits the profile (
$\exp -|q/4.5|^{0.6}$
). Note how, in both cases, profiles of
$V_{qp}$
along lines of constant buoyancy are symmetric around the origin.
Figure 3. (a) Value of
$F(b_{0},q)$
versus
$q$
where
$F$
is obtained solving (3.29) in a time-evolving stratified shear layer, where
$b_{0}=(b_{min}+b_{Max})/2$
is the midplane buoyancy. (b) Value of
$F(b_{0},q)$
versus
$y(b_{0},q)$
obtained using one (1), two (2) or four (4) charts to cover the domain.
In this set-up, the Lagrangian parcels with high negative potential vorticity are shunted on one side of the domain, most of the domain is filled by the (many) particles with little potential vorticity, while the parcels with large positive vorticity are pushed to the other side of the physical domain. We can see immediately two problems with this approach: first, having separated the large negative from the large positive potential vorticity particles, we have created a large, sustained shear that forces the velocity to reach a large value in the centre of the domain. Second, while this set-up does not violate a free-slip boundary condition at the side walls, it cannot accommodate periodic boundary conditions.
Indeed, no matter what the details of the mass distribution function are, a single
$(b,q,x)\overset{\unicode[STIX]{x1D709}}{\rightarrow }(z,y,x)$
chart cannot cover the manifold if the latter is periodic in the
$y$
direction. Let us explore then what happens if we allow two charts to cover the manifold. The first chart maps the
$(b,q,x)$
space to the half of the channel such that
$0\leqslant y\leqslant L_{y}/2$
, while the second covers the other half. Further, since the mass distribution function is an extensive quantity by definition, we require that each half of the physical domain contributes exactly one half to the total mass distribution function. In each half, we proceed exactly as we did before, and since
$F(q,b)\overset{q\rightarrow \pm \infty }{\longrightarrow }0$
it is possible to stitch together the velocity at the edge of every subdomain to obtain the profile shown on figure 3(b) labelled (2). Because in each half the mass distribution function is half of the original one, the energy per unit volume in each half (an intensive quantity) is now 25 % of the energy per unit volume obtained using only one chart. As a bonus, the velocity field is now periodic. Again, what makes this possible is the fact that
$V_{,qb}$
is an even function of
$q$
.
Of course, there is no reason to stop at two charts. The procedure can be repeated with
$4,8,\ldots$
, charts, each covering
$1/4,1/8,\ldots$
of the channel, and each time obtaining a field with a kinetic energy per unit volume
$1/16,1/64,\ldots$
of the previous (figure 3 shows the profiles obtained using one, two and four charts). Thus, we generate a sequence of velocity fields in which potential vorticity is interleaved at finer and finer scales, while at the same time reducing the overall kinetic energy by a factor
$4$
with each iteration. Barring the existence of a cutoff scale, this shows how to construct a sequence of states which in the limit approaches a ground state with zero kinetic energy. These ground states are also obviously global minima on their leaf, since the only way to further lower the total energy would break the conservation of volume constraint.
Naturally, it is possible to consider initial conditions in which the symmetry in
$q$
is broken ab initio, even in the absence of rotation. For example, consider filling a channel, which, as before, has dimensions
$(L_{z},L_{y},L_{x})$
with a fluid whose buoyancy has a uniform gradient along the spanwise direction
$\unicode[STIX]{x1D735}b=N_{0}^{2}\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{y}$
, and flowing (in a way consistent with Boussinesq dynamics) such that
$\boldsymbol{v}=\unicode[STIX]{x0394}v_{0}(Z/L_{z})\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{x}$
, so that
$\unicode[STIX]{x1D6FA}=-\unicode[STIX]{x0394}v_{0}/L_{z}\unicode[STIX]{x1D735}x\times \unicode[STIX]{x1D735}Z$
. Thus, the potential vorticity is uniform and equal to
$-N_{0}^{2}\unicode[STIX]{x0394}v_{0}/L_{z}$
. We can handle this singular limit by ‘smearing’ the potential vorticity distribution around its constant value by an amount
$O(\unicode[STIX]{x1D716})$
, carry out the calculation and finally taking the
$\unicode[STIX]{x1D716}\rightarrow 0$
limit. In this case, the buoyancy of the ground state is such that
$\unicode[STIX]{x1D735}b_{\ast }=N_{0}^{2}(L_{y}/L_{z})\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{Z}$
and
$\boldsymbol{v}_{\ast }=\unicode[STIX]{x0394}v_{0}(y/L_{y})\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{x}$
. Interestingly, the ground state contains as much kinetic energy as the initial state, and thus the available energy per unit volume is simply the difference between the potential energy of the initial and ground state
$(\unicode[STIX]{x0394}bL_{z}/12)$
. (It is important to realize that this ground state, like any other ground state as defined in our theory, is stable relative to perturbations that belong to the same leaf of the ground state. The ground state considered in the last example belongs to a class of flows whose stability has been studied by Deloncle, Chomaz & Billant (Reference Deloncle, Chomaz and Billant2007). The potential vorticity of the unstable modes is such that the unstable modes can be excited in the rest state only via the action of non-holonomic forces (forces that alter the potential vorticity distribution). This example confirms that non-holonomic forces can increase the available energy, which is used by the unstable modes to grow. In other words, the introduction of unstable modes moves the state to a different leaf, on which the ground state has a lower energy.) We must however emphasize that when the mass distribution function symmetry in
$q$
is broken, the global apedic minimum on the leaf could be three-dimensional.
3.1.7 Rotating channels in the low Rossby number limit: geostrophic ground states
Another class of ground states that is amenable to analytic treatment are the ground states of flows contained in rotating channels where the frame vorticity is much larger than the relative vorticity. In other words, we look for ground states characterized by a small value of the Rossby number (as defined earlier). We also assume that the Burger number
$Bu=(N_{\ast }H/fL)^{2}$
is kept finite, and as such we drop it from the asymptotics. We call low-
$Ro$
ground states geostrophic ground states. We work with natural
$(b,q,t)$
coordinates assuming that the ground state is 2.5-dimensional.
Under these assumptions, the main source of non-inertiality along trajectories in the ground state is due to the frame vorticity
$\unicode[STIX]{x1D6EF}=f\unicode[STIX]{x1D735}y\times \unicode[STIX]{x1D735}x$
, which we write as
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}^{t}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q+\unicode[STIX]{x1D6EF}^{b}\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}t+\unicode[STIX]{x1D6EF}^{q}\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b,\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}^{t} & = & \displaystyle f(y_{,b}x_{,q}-y_{,q}x_{,b}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}^{b} & = & \displaystyle fy_{,q}x_{,t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}^{p} & = & \displaystyle -fy_{,b}x_{,t},\end{eqnarray}$$
$f$
is the Coriolis parameter (recall that
$y_{,t}=0$
). Under the 2.5-dimensional assumption and in the limit of vanishing Rossby numbers,
$x_{,t}=\sqrt{2Ek}$
, and the steady state version of (3.1a
) becomes (Pedlosky Reference Pedlosky1986, p. 45)
$$\begin{eqnarray}\unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D6F9}}=f\sqrt{2Ek}\,\unicode[STIX]{x1D735}y-Z\unicode[STIX]{x1D735}b+O(Ro),\end{eqnarray}$$
where we made use of (3.36b
)–(3.36c
). Thus, to
$O(Ro)$
the integrability condition
$$\begin{eqnarray}f\sqrt{2Ek}_{,Z}\unicode[STIX]{x1D735}Z\times \unicode[STIX]{x1D735}y=b_{,y}\unicode[STIX]{x1D735}Z\times \unicode[STIX]{x1D735}y,\end{eqnarray}$$
shows that the ground state is in the so-called thermal wind balance. As we did for flows in inertial channels, we endeavour to construct the ground state explicitly by seeking first the coordinate maps
$Z_{\ast }=Z(b,q)$
and
$y_{\ast }=y(b,q)$
. The solution can be expressed as (for details see § A.4)
$$\begin{eqnarray}\displaystyle Z_{\ast } & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }Z_{n}(q)(b-b_{min})^{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{\ast } & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }y_{n}(q)(b-b_{min})^{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{2Ek_{\ast }} & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }v_{l}(q)(b-b_{min})^{n}.\end{eqnarray}$$
$V_{,bq}$
as a power series in
$b-b_{min}$
$$\begin{eqnarray}V_{,qb}=L_{x}\mathop{\sum }_{n=0}^{\infty }F_{n}(q)(b-b_{min})^{n},\end{eqnarray}$$
the coefficients of (3.39a )–(3.39c ) are given by
$$\begin{eqnarray}y_{n}=f^{-1}\int _{q_{min}}^{q}sF_{n}(s)ds,\end{eqnarray}$$
$$\begin{eqnarray}Z_{1}=\frac{f}{q},\quad Z_{l+1}=\frac{\displaystyle lZ_{1,q}y_{l}-\mathop{\sum }_{n=2}^{l}(nZ_{n}y_{l+1-n,q}-(l+1-n)Z_{n,q}y_{l+1-n})}{(l+1)y_{0,q}},\end{eqnarray}$$
$$\begin{eqnarray}v_{0}=v_{1}=0,\quad v_{l+1}=\frac{\displaystyle -Z_{l,q}+f\mathop{\sum }_{n=1}^{l}(nv_{l+1-n,q}y_{n}-(l+1-n)v_{l+1-n}y_{n,q})}{f(l+1)y_{0,q}}.\end{eqnarray}$$
With the complete solution in hand, it is now time to revisit the small-
$Ro$
assumption made at the beginning. The goal is to characterize the mass distribution functions that lead to small-
$Ro$
ground states. It is straightforward to calculate the relative vorticity of the ground state (It follows from the fact that the infinitesimal contribution to the circulation is
$\boldsymbol{v}\boldsymbol{\cdot }d\boldsymbol{l}=\sqrt{2Ek}dx^{3}=2Ekdt$
, from which we can calculate the curl.)
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\ast }=-(2Ek)_{,b}\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b+(2Ek)_{,q}\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}t.\end{eqnarray}$$
Let us start from the special case that leads to (A 34). The most stringent condition is
$$\begin{eqnarray}Ro=O\left(\frac{(\sqrt{2Ek_{\ast }})_{,Z}}{f}\right)=\frac{L_{z}}{f^{2}qF_{0}(q)}\ll 1.\end{eqnarray}$$
We can estimate
$$\begin{eqnarray}O(qF_{0})=\overline{q}\frac{L_{y}L_{z}}{\unicode[STIX]{x0394}q\unicode[STIX]{x0394}b}=\overline{q}\frac{L_{y}}{\unicode[STIX]{x0394}pN^{2}},\end{eqnarray}$$
where
$N^{2}=\unicode[STIX]{x0394}b/L_{z}$
. Here
$\unicode[STIX]{x0394}q$
is a measure of the spread of potential vorticity, e.g. the root-mean-square (r.m.s.) of the fluctuations,
$\unicode[STIX]{x0394}b$
is a measure of the spread of buoyancy and
$\overline{q}$
the mean potential vorticity (which, when needed, can be estimated as
$fN^{2}$
). Thus, the ground state satisfies the low-
$Ro$
condition if the following condition on the spread of potential vorticity
$$\begin{eqnarray}\frac{\unicode[STIX]{x0394}q}{\overline{q}}\ll \frac{L_{y}L_{z}}{L_{R}^{2}},\end{eqnarray}$$
where
$L_{R}\equiv L_{z}N/f$
is the internal Rossby radius of deformation, is satisfied.
Let us now consider the more general case of a mass distribution function which is not linear in the buoyancy, but which still satisfies (3.45). We have
$$\begin{eqnarray}O(qF_{n})=Ro^{-1}\frac{L_{R}^{2}}{\unicode[STIX]{x0394}b}(\unicode[STIX]{x0394}b)^{-n},\end{eqnarray}$$
whence
$$\begin{eqnarray}\displaystyle O(fy_{n}) & = & \displaystyle O(\unicode[STIX]{x0394}q\,qF_{n})=fL_{y}(\unicode[STIX]{x0394}b)^{-n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle O(fy_{n,q}) & = & \displaystyle O(qF_{n})=Ro^{-1}\frac{L_{R}^{2}}{\unicode[STIX]{x0394}b}(\unicode[STIX]{x0394}b)^{-n}.\end{eqnarray}$$
$$\begin{eqnarray}O(Z_{2}(b-b_{min})^{2})=Ro\frac{L_{y}L_{z}}{L_{R}^{2}}L_{z}.\end{eqnarray}$$
Given the nature of the recurrence relation (A 29), it follows that all the other terms in the series for
$Z$
are
$O(Ro)$
, and thus
$$\begin{eqnarray}Z_{\ast }=\frac{f}{q}(b-b_{min})+O(Ro).\end{eqnarray}$$
Along essentially the same lines we have that
$\sqrt{2Ek_{\ast }}=O(Ro)$
, and thus to
$O(Ro)$
the pressure in the ground state is hydrostatic. Hence
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F9}}=-\frac{f}{2}\frac{(b-b_{min})^{2}}{q}+O(Ro),\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\ast }=\frac{f}{4}\frac{(b-b_{min})^{2}}{q}+O(Ro),\end{eqnarray}$$
which shows that the Casimir of geostrophic leaves, defined as leaves characterized by a geostrophic ground state (i.e. a low-
$Ro$
state) does not depend, to leading order, on the details of the mass distribution function that defines the leaf to which the ground state belongs. A field on a geostrophic leaf does not need to be in geostrophic equilibrium, but the ageostrophic component must be such that the overall spread in potential vorticity is small when looked over the entire field. As long as the diabatic dynamics does not cause a significant spread in potential vorticity, the flow remains on a geostrophic leaf and the diagnostic energy
${\mathcal{E}}$
is to leading order independent of the mass distribution function. Thus, the local diagnostic energy has, to
$O(Ro)$
a universal character.
3.2 The non-holonomic dynamics of Casimirs in Boussinesq flows
Once the gauge-fixed Casimir is known, non-holonomic effects on the available energy can be analysed by considering how the Casimir evolves along Lagrangian trajectories. In apedic manifolds characterized by an even distribution of potential vorticity, our theory recovers the standard local APE formulation based on Holliday & McIntyre (Reference Holliday and McIntyre1981) (here, we reinstate the qualified potential, since the ground state has no kinetic energy). In particular, under the Boussinesq approximation, the sink of APE is quantified by
$-\unicode[STIX]{x1D705}\overline{\unicode[STIX]{x1D713}}_{,bb}|\unicode[STIX]{x1D735}b|^{2}$
, where
$\unicode[STIX]{x1D705}$
is the diffusivity of the stratifying agent. Archetypal flows for small-scale mixing (e.g. shear layers, Couette flows,…) fall into this category. On geostrophic manifolds, the evolution of the Casimir depends on the details of the non-holonomic brake. Assuming a standard diffusion term in the buoyancy equation, the sink term due to mixing of the stratifying agent
$-\unicode[STIX]{x1D705}\overline{\unicode[STIX]{x1D713}}_{,bb}|\unicode[STIX]{x1D735}b|^{2}$
is equal to
$\unicode[STIX]{x1D705}f/q|\unicode[STIX]{x1D735}b|^{2}+O(Ro)$
. However, diabatic momentum fluxes will change the potential vorticity along trajectories and thus can either increase or decrease the available energy. In light of the discussion regarding the Casimir associated with states with a symmetric distribution of potential vorticity around the origin, it becomes clear how diabatic processes that tend to drive the potential vorticity of a flow which originally had a skewed potential vorticity distribution toward a distribution symmetrical around the origin, such as winds blowing down front along oceanic fronts (Thomas Reference Thomas2005; Taylor & Ferrari Reference Taylor and Ferrari2010) have the effect of increasing the available energy of the flow. The existence of a skewed potential vorticity distribution requires the background state to have KE, and thus lowers the available energy of the system.
4 An example
As an application of the framework discussed in the preceding sections, we calculate the available energy and the gauge-fixed Casimir of an oceanic-type front. The dynamics of submesoscale fronts has received widespread attention recently since it provides routes for energy dissipation in the world’s oceans (Nikurashin, Vallis & Adcroft Reference Nikurashin, Vallis and Adcroft2013; Callies et al. Reference Callies, Ferrari, Klymak and Gula2015; McWilliams Reference McWilliams2016; Thomas Reference Thomas2017). Mesoscale fronts also provide a mechanism for driving vertical mixing through submesoscale and small-scale turbulent processes and power the biological pump by exchanging nutrients, marine geochemical species and biology (Lévy et al. Reference Lévy, Ferrari, Franks, Martin and Rivière2012; Mahadevan Reference Mahadevan2016).
Here, we consider a simple set-up, consisting of a channel periodic in the
$y$
direction, bounded by vertical walls located at
$x=\pm L_{x}/2$
, and extending from
$z=-H$
, where the isopycnals are flat, to the surface
$z=0$
. The initial stratification consists of a linear profile with a
$x$
-dependent vertical length scale
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle b(z)\equiv g(\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x1D70C})/\unicode[STIX]{x1D70C}_{0}=HN^{2}\frac{(z+H)}{\ell (x)},\\ \displaystyle \ell (x)=H(1+\unicode[STIX]{x1D716}\tanh (x/\unicode[STIX]{x1D6E5})),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
resulting in isopycnals outcropping at the surface. The characteristics of the frontal region (
$\unicode[STIX]{x1D6E5}=30H$
and
$\unicode[STIX]{x1D716}=0.2$
), and the ratio of stratification to Coriolis force
$N/f=60$
are illustrative of mid-latitude oceanic fronts (Simpson & Lynn Reference Simpson and Lynn1990; Zhang, Wang & Qiu Reference Zhang, Wang and Qiu2014). The width of the channel
$L_{y}=12\unicode[STIX]{x1D6E5}$
is large enough to avoid end-channel effects. To calculate the available energy and the Casimir, we solve numerically the Navier–Stokes equations in the Boussinesq approximation with a holonomic brake added as a body force to the right-hand side
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t} & = & \displaystyle -\boldsymbol{u}\times (\unicode[STIX]{x1D74E}+f\boldsymbol{k})-\unicode[STIX]{x1D735}p+b\boldsymbol{k}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}-\frac{\unicode[STIX]{x1D6FC}}{fN^{2}}(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}b)\unicode[STIX]{x1D735}b,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{D}b}{\text{D}t} & = & \displaystyle \unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}b,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u} & = & \displaystyle 0.\end{eqnarray}$$
$-\unicode[STIX]{x1D70F}(|\boldsymbol{u}|,b)(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{j})\boldsymbol{j}$
, with
$\boldsymbol{j}=\unicode[STIX]{x1D735}b/|\unicode[STIX]{x1D735}b|$
and
$\unicode[STIX]{x1D70F}>0$
a time scale function, so that its effect on the evolution of vorticity is limited to the components normal to
$\unicode[STIX]{x1D735}b$
. Here we choose
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FC}|\unicode[STIX]{x1D735}b|^{2}/fN^{2}$
. Physically, it siphons energy whenever there is a component of the flow normal to the isopycnals. Note that there are other possible classes of holonomic brakes that can be applied, e.g. the ones investigated by Vallis et al. (Reference Vallis, Carnevale and Young1989). We use this form since it does not change the nature of the advecting field, and it is thus easier to implement in an existing numerical model. The viscosity
$\unicode[STIX]{x1D708}$
and diffusivity
$\unicode[STIX]{x1D705}$
are taken equal, and chosen so that the Reynolds number
$NH^{2}/\unicode[STIX]{x1D708}=1.5\times 10^{5}$
is large enough to ensure numerical stability without significantly affecting the mass distribution function and overall energy of the system over the time required to bring the system to rest. Since we seek a 2.5-dimensional ground state, the equations are solved in the
$(x,z)$
plane on a uniform grid
$512\times 64$
, starting from a quiescent initial condition with buoyancy distribution given by (4.1). We keep the solution 2.5-dimensional for two reasons: consistent with the approach taken so far, we assume that on a given leaf the extremal point is unique and for these simple systems 2.5-dimensional, although, in principle, the extremal point may be a saddle, rather than a (local) minimum; also, since the numerical discretization is not guaranteed to conserve the Lagrangian invariants, we want to minimize the possibility that instabilities not belonging to the leaf (i.e. with a different mass distribution function) be introduced by numerical noise. We experimented with different values for the non-dimensional strength of the holonomic brake
$\unicode[STIX]{x1D6FC}$
. Ideally,
$\unicode[STIX]{x1D6FC}$
should be set to achieve critical damping. Here we show results with
$\unicode[STIX]{x1D6FC}=16.7$
, which is still below the critical value. For more complex situations, a feedback method based on the optimization of the low pass filter should be implemented to achieve optimal damping (Åkervik et al.
Reference Åkervik, Brandt, Henningson, Hœpffner, Marxen and Schlatter2006; Cunha, Passaggia & Lazareff Reference Cunha, Passaggia and Lazareff2015), but we leave this to a future publication. Under the action of the holonomic brake, the system converges in about 4 inertial periods to the ground state (figure 4), which, as expected, is characterized by a zonal jet in thermal-wind balance with the front (figure 5). The kinetic energy of the front in the ground state is approximately 37 % of the difference
$\unicode[STIX]{x0394}PE$
between the potential energy associated with the initial profile and the potential energy of the ground state, the rest being dissipated by the holonomic brake. Thus, in this case, the available energy of the initial state is 63 % of
$\unicode[STIX]{x0394}PE$
, much less than what one would infer by using as ground state the restratified fluid, (see for instance the example computed in Simpson & Lynn (Reference Simpson and Lynn1990)). Furthermore, it seems reasonable to assume that the ground state calculated by evolving the initial condition with the holonomic brake on does not depend on the meridional (i.e. along the
$x$
direction) extent of the channel, whereas the restratified ground state would. In other words, it is reasonable to assume that the available energy and the Casimir converge to a finite value as
$L_{x}\rightarrow \infty$
.
Figure 4. Evolution of the kinetic energy of an initially unbalanced front under the action of a holonomic brake.
Finally, the actual Casimir (as given by the Bernoulli Head) compares well with the approximated Casimir derived in the preceding section under geostrophic conditions (figure 6).
Figure 5. The ground state for an initial out of balance front, calculated evolving the initial front with a holonomic brake. The curtain plot shows the intensity of the zonal jet. The solid lines show the position of representative isopycnals of the ground state, while the dashed lines show the isopycnals of the initial front. Here,
$L=30H$
is the horizontal scale of the front. The zonal velocity is shown as a local Rossby number.
5 Conclusions
In this paper, we have developed a framework to diagnose diabatic effects on flows that can be described by a non-canonical Hamiltonian formalism in the adiabatic limit.
Margules’ available energy concept in our framework becomes the energy that can be extracted from the system by any mechanism that does not violate the conservation of the Lagrangian invariants. It is a property of the system as a whole.
We show that a specific gauge-fixing condition can be imposed to select a specific Hamiltonian that can be used to define a local diagnostic energy with the following property: the temporal rate of change of the available energy under diabatic conditions is given by the diabatic evolution of the local diagnostic energy.
When the framework is applied to fluid described by the Boussinesq approximation, it recovers Winters et al.’s global APE and Holliday & McIntyre’s local APE as special cases which apply to non-rotating flows, provided the distribution of potential vorticity in the flow is even around the origin. Most archetypal flows used to study small-scale mixing start as two-dimensional flows contained in a vertical plane. For such flows, under the assumption that the diabatic dynamics does not favour negative over positive potential vorticity, approaches based on the Holliday & McIntyre APE definition (e.g. Winters et al. Reference Winters, Lombard, Riley and D’Asaro1995; Scotti & White Reference Scotti and White2014) remain correct.
Our definition of local diagnostic energy extends naturally to rotating Boussinesq flows. Under the effect of rotation, the conservation of potential vorticity imposes a strong constraint, which is not accounted for by approaches based on Holliday & McIntyre’s APE. In particular, when the flow is obtained from a general-form perturbation which preserves both the potential vorticity and the buoyancy distribution of a low Rossby number state in near-geostrophic equilibrium, to lowest order in the Rossby number, we show that the expression for the local diagnostic energy has a universal character.
Once the functional form of the local diagnostic energy is known (i.e. when the right Casimir is found via the gauge-fixing condition), it can be used to study the effect of diabatic processes. The effect of these processes, which in general break the conservation of the Lagrangian invariants, on the change of the available energy can be studied following the evolution of the local diagnostic energy along Lagrangian trajectories. Such processes can locally increase the available energy. This is not too surprising, since diabatic processes erode the potential vorticity constraint, which is what in general keeps energy locked up in the ground state field.
Our framework provides a unified procedure to calculate the available energy for a given state. Also, we show how for such a defined available energy, it is possible to introduce a local diagnostic quantity to study how local diabatic effects modify the available energy. The analysis shows that the evolution of the gauge-fixed Casimir under non-holonomic forces is essential in describing how the latter modify the available energy via the erosion of the constraints.
It is also important to emphasize some of the limitations of the current analysis. The results were derived under the assumption that the ground state is unique. Of course, we can envision situations where there exists multiple minima of the energy for a given set of constraints. In this case, it cannot be ruled out that the application of different holonomic brakes may lead to different ground states, especially if the system is close to the separatrix between the basins of attraction. On the other hand, if the system is not too far from a minimum, then it is not unreasonable to assume that most holonomic brakes will lead to the same extremal point, even though there may exist other ground states with overall less energy. Related to this issue, we have considered here only very simple geometries. Since the theory relies on a number of equalities that contain boundary terms that were neglected, it is possible that topographic boundaries may introduce an extra level of complexity. As an example, consider a basin which is divided in two sub-basins by a submerged ridge. Even restricting ourselves to apedic cases, one can imagine multiple local minima obtained filling the two sub-basins with a different combinations of less buoyant fluid.
While in simple inertial channels we showed that the global minimum is indeed 2.5-dimensional if the mass distribution function enjoys certain properties, it is possible that in more general situations the global minimum may be three-dimensional. Indeed, Renaud et al. (Reference Renaud, Venaille and Bouchet2016) showed in that in the shallow water case bottom topography modifies the circulation of the ground state and we therefore expect a similar behaviour in the Boussinesq case. In order to answer these questions, we need to develop a robust algorithm to calculate extremal points, which is the subject of ongoing investigation.
In conclusion, the formalism presented in this paper extends Margules’ original idea to include the role that multiple constraints play in the available energetics framework. Since the mass distribution function, or, for incompressible flows, the volume distribution function plays a central role in defining the gauge-fixing condition, our approach applies to flows contained on a finite volume. However, the possibility that other ways to enforce the constraints, not dependent on the system having a finite volume, exist should not be discarded. Since the applicability of any local diagnostic tool is constrained by the data available for the analysis, it can rarely be considered independent from the flow data themselves.
Acknowledgements
The authors would like to thank K. Lamb and two anonymous reviewers for their constructive criticism. This work was supported in part by NSF grants OCE-115558, OCE-1736989 and OCE-1459506.
Appendix A
We provide in the next sections results that were used in the paper. In the first two sections we use exterior calculus. While these statements can be considered with standard vector calculus (see, e.g. Holm (Reference Holm2008), for a proof of (6.3)), exterior calculus provides much shorter and elegant proofs. We hope that the reader may be motivated to explore further the potential of modern geometric tools, which have recently found application in fluid mechanics problems (Besse & Frisch Reference Besse and Frisch2017; Gilbert & Vanneste Reference Gilbert and Vanneste2018). To fix the notation,
$d$
denotes the exterior derivative,
$\wedge$
the exterior product,
$i_{\boldsymbol{v}}\unicode[STIX]{x1D6FC}$
the interior product of the vector field
$\boldsymbol{v}$
with the form
$\unicode[STIX]{x1D6FC}$
and
$\star$
the Hodge star (i.e. the isomorphism between
$n$
-forms and
$(D-n)$
-forms, where
$D$
is the dimension of the manifold and
$n=0,\ldots ,D$
). (We do not intend to provide an exhaustive introduction to the calculus of exterior differential forms. The reader is referred to the appendix in Besse & Frisch (Reference Besse and Frisch2017) and Gilbert & Vanneste (Reference Gilbert and Vanneste2018, §2) for a more comprehensive treatment. The topics is also covered in a number of excellent textbooks, such as Frankel (Reference Frankel2011) and Sternberg (Reference Sternberg2012).) The volume
$3$
-form of the manifold in arbitrary coordinates
$(x^{1},x^{2},x^{3})$
is
$$\begin{eqnarray}\mathfrak{V}=\sqrt{g}dx^{1}\wedge dx^{2}\wedge dx^{3},\end{eqnarray}$$
where
$\sqrt{g}$
is the square root of the determinant of the metric tensor. In the following, the property of the Hodge star that we need is
$$\begin{eqnarray}\star \mathfrak{V}=1.\end{eqnarray}$$
Since the Hodge star, like any other operator in exterior calculus, is coordinate independent, equation (A 2) holds in any coordinate system.
A.1 The gauge-fixed Casimir dependence on the Bernoulli head of the ground state
We intend to prove the following: up to an inconsequential constant, the gauge-fixed Casimir for the ground state of a flow described in the inviscid limit by the Boussinesq equations (3.1a )–(3.1c ) is given by
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\ast }=q\int _{q_{min}}^{q}\frac{B_{\ast }(s,b)}{s^{2}}ds,\end{eqnarray}$$
where
$B_{\ast }=Ek_{\ast }(q,b)-bZ_{\ast }(q,b)+P_{\ast }(q,b)$
is the Bernoulli head of the ground state expressed in natural coordinates.
First of all, it is trivial to see that for a quiescent ground state (A 3) is satisfied. Thus, we proceed assuming that the ground state is not quiescent, and thus
$\unicode[STIX]{x1D6F9}_{\ast ,qq}\neq 0$
.
Assuming that the ground state is not quiescent, we introduce the natural set of coordinates, which include the buoyancy, the potential vorticity and the time-like coordinate, in terms of which the volume 3-form is
$\mathfrak{V}=\unicode[STIX]{x1D6F9}_{,qq}db\wedge dq\wedge dt$
(see § A.2 below). The total vorticity
$2$
-form
$\unicode[STIX]{x1D6FA}=d(\boldsymbol{v}^{\flat })+\unicode[STIX]{x1D6EF}$
, where
$\boldsymbol{v}^{\flat }=v_{i}dx^{i}$
is the
$1$
-form associated via the musical isomorphism with the velocity field
$\boldsymbol{v}=v^{i}\boldsymbol{\unicode[STIX]{x2202}}_{i}$
(here understood as a differential operator) is the sum of the relative vorticity and
$\unicode[STIX]{x1D6EF}$
, the frame vorticity. The isomorphism
$\flat$
is completely defined by its action on the basis vectors, that is
$\boldsymbol{\unicode[STIX]{x2202}}_{i}^{\flat }=g_{ij}dx^{j}$
. The vorticity in natural coordinates reads
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}^{b}dq\wedge dt+\unicode[STIX]{x1D6FA}^{q}dt\wedge db+\unicode[STIX]{x1D6FA}^{t}db\wedge dq.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D6FA}$
is closed by definition
$$\begin{eqnarray}(\unicode[STIX]{x1D6FA}^{b})_{,b}+(\unicode[STIX]{x1D6FA}^{q})_{,q}+(\unicode[STIX]{x1D6FA}^{t})_{,t}=0.\end{eqnarray}$$
From the definition of potential vorticity,
$$\begin{eqnarray}q=\star (db\wedge \unicode[STIX]{x1D6FA})=\unicode[STIX]{x1D6FA}^{b}\star (db\wedge dq\wedge dt)=\unicode[STIX]{x1D6FA}^{b}(\unicode[STIX]{x1D6F9}_{,qq})^{-1}.\end{eqnarray}$$
We introduce
$\overline{\unicode[STIX]{x1D6F9}}_{\ast }=q\unicode[STIX]{x1D6F9}_{\ast ,q}-\unicode[STIX]{x1D6F9}_{\ast }$
. Taking the Hodge star of
$$\begin{eqnarray}[-Z+(\unicode[STIX]{x1D6F9}_{\ast }-q\unicode[STIX]{x1D6F9}_{\ast ,q})_{,b}]\mathfrak{V}-\unicode[STIX]{x1D6F9}_{\ast ,qq}dq\wedge \unicode[STIX]{x1D6FA}=0,\end{eqnarray}$$
(which is (3.8a ) rewritten in exterior calculus), and using (A 2) we get
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F9}}_{\ast ,b} & = & \displaystyle -(Z_{\ast }+\unicode[STIX]{x1D6FA}^{q}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F9}}_{\ast ,q} & = & \displaystyle \unicode[STIX]{x1D6FA}^{b},\end{eqnarray}$$
$\overline{\unicode[STIX]{x1D6F9}}_{\ast ,q}=q\unicode[STIX]{x1D6F9}_{\ast ,qq}$
and (A 6). These two equations can be combined into a single equation 
$$\begin{eqnarray}d(\overline{\unicode[STIX]{x1D6F9}}_{\ast }+Z_{\ast }b)=bdZ-\unicode[STIX]{x1D6FA}^{q}db+\unicode[STIX]{x1D6FA}^{b}dq=bdZ_{\ast }-i_{\boldsymbol{v}_{\ast }}\unicode[STIX]{x1D6FA}_{\ast }.\end{eqnarray}$$
We have derived the above expression in natural coordinates, where
$\boldsymbol{v}_{\ast }$
has the simple expression
$\boldsymbol{v}_{\ast }=\boldsymbol{\unicode[STIX]{x2202}}/\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{t}$
, but (A 9) is coordinate free. Thus, comparing (A 9) with (3.1a
), which in exterior calculus reads
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{v}^{\flat }}{\unicode[STIX]{x2202}t}=-i_{\boldsymbol{v}}\unicode[STIX]{x1D6FA}-d(Ek+P)+bdZ,\end{eqnarray}$$
we see immediately that
$\overline{\unicode[STIX]{x1D6F9}}_{\ast }$
is, up to a constant, the Bernoulli head of the ground state, and thus we have proven the theorem. (For a proof using standard vector calculus see (Holm Reference Holm2008).)
A.2 The volume element in natural coordinates
Consider the three
$1$
-forms
$\unicode[STIX]{x1D719}^{i}=dx^{i}-v_{\ast }^{i}dt,\,i=1,\ldots ,3$
defined on 4-dimensional space
$\mathbb{D}\times \mathbb{R}$
. The
$3$
-form
$$\begin{eqnarray}\displaystyle \mathfrak{O} & = & \displaystyle \sqrt{g}\,\unicode[STIX]{x1D719}^{1}\wedge \unicode[STIX]{x1D719}^{2}\wedge \unicode[STIX]{x1D719}^{3}\nonumber\\ \displaystyle & = & \displaystyle \sqrt{g}(dx^{1}\wedge dx^{2}\wedge dx^{3}-v_{\ast }^{1}dx^{2}\wedge dx^{3}\wedge dt-v_{\ast }^{2}dx^{3}\wedge dx^{1}\wedge dt-v_{\ast }^{3}dx^{1}\wedge dx^{2}\wedge dt)\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{V}-(i_{\boldsymbol{v}_{\ast }}\mathfrak{V})dt=\mathfrak{V}-\unicode[STIX]{x1D6F7}_{\ast }\wedge dt=\mathfrak{V}-\unicode[STIX]{x1D6F9}_{\ast ,qq}db\wedge dq\wedge dt.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D6F7}_{\ast }$
is the flux
$2$
-form, which associates with a two-dimensional surface in
$\mathbb{D}$
the flux across it, and the last equality follows from (3.8b
), which in exterior calculus reads
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\ast }=\unicode[STIX]{x1D6F9}_{\ast ,qq}db\wedge dq.\end{eqnarray}$$
Let
$(b,q,t)\xrightarrow[{}]{\unicode[STIX]{x1D701}}(x^{1},x^{2},x^{3})$
the (local) map from natural to geometric coordinates, and
$(b,q,t)\xrightarrow[{}]{\hat{\unicode[STIX]{x1D701}}}(\unicode[STIX]{x1D701}(b,q,t),t)$
the map that embeds
$\mathbb{D}$
into
$\mathbb{D}\times \mathbb{R}$
. Then, since
$\unicode[STIX]{x1D701}$
is the local solution to the Pfaffian system
$\unicode[STIX]{x1D719}^{i}=0,\,i=1,\ldots ,3$
, under the pullback
$\hat{\unicode[STIX]{x1D701}}^{\ast }\mathfrak{O}=0$
, thus
$$\begin{eqnarray}\mathfrak{V}=\unicode[STIX]{x1D6F9}_{\ast ,qq}db\wedge dq\wedge dt,\end{eqnarray}$$
which shows that indeed
$\unicode[STIX]{x1D6F9}_{\ast ,qq}db\wedge dq\wedge dt$
is the volume form in natural coordinates. Note that the Pfaffian system is integrable since it satisfies the integrability conditions (Flanders Reference Flanders1989)
$$\begin{eqnarray}d\unicode[STIX]{x1D719}^{i}\wedge \mathfrak{O}=0,\quad i=1,\ldots ,3.\end{eqnarray}$$
A.3 The vorticity of the ground state expressed in terms of the acceleration along streamlines
From (3.8b ) we know that in an inertial system, the vorticity of the ground state
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74E}_{\ast } & = & \displaystyle \unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D6F9}_{\ast ,qq}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D735}\times (g_{bt}\unicode[STIX]{x1D735}b+g_{qt}\unicode[STIX]{x1D735}q+g_{tt}\unicode[STIX]{x1D735}t)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}^{t}\unicode[STIX]{x1D735}b\times \unicode[STIX]{x1D735}q+\unicode[STIX]{x1D714}^{q}\unicode[STIX]{x1D735}t\times \unicode[STIX]{x1D735}b+\unicode[STIX]{x1D714}^{b}\unicode[STIX]{x1D735}q\times \unicode[STIX]{x1D735}t,\end{eqnarray}$$
where
$g_{XY}=x_{,X}^{i}x_{,Y}^{j}g_{ij}$
is the
$XY$
component of the metric expressed in natural coordinates, and here
$X$
and
$Y$
are placeholders for
$b$
,
$q$
or
$t$
. Hence,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{t} & = & \displaystyle g_{qt,b}-g_{bt,q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{q} & = & \displaystyle g_{bt,t}-g_{tt,b},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{b} & = & \displaystyle g_{tt,q}-g_{qt,t}.\end{eqnarray}$$
$g_{ij,X}=g_{ij,k}x_{,X}^{k}$
, and
$g_{ij}x_{,t}^{i}x_{,t}^{j}=2Ek_{\ast }$
, we have the following 
$$\begin{eqnarray}\displaystyle g_{tt,X} & = & \displaystyle 2Ek_{\ast ,X},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{Xt,t} & = & \displaystyle g_{ij,t}x_{,X}^{i}x_{,t}^{j}+g_{ij}x_{,Xt}^{i}x_{,t}^{j}+g_{ij}x_{,X}^{i}x_{,tt}^{j}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}(x_{,t}^{i}x_{,t}^{j}g_{ij})_{,q}-\frac{1}{2}x_{,t}^{i}x_{,t}^{j}g_{ij,X}+g_{ij,t}x_{,X}^{i}x_{,t}^{j}+g_{ij}x_{,q}^{i}x_{,tt}^{j}\nonumber\\ \displaystyle & = & \displaystyle Ek_{\ast ,X}+g_{ij}x_{,q}^{i}x_{,tt}^{j}+\frac{1}{2}(g_{ij,k}x_{,t}^{k}+g_{ji,k}x_{,t}^{k})x_{,X}^{i}x_{,t}^{j}-\frac{1}{2}g_{ij,k}x_{,X}^{k}x_{,t}^{i}x_{,t}^{j}\nonumber\\ \displaystyle & = & \displaystyle Ek_{\ast ,X}+x_{,X}^{i}g_{ij}(x_{,tt}^{j}+\unicode[STIX]{x1D6E4}_{mp}^{j}x_{,t}^{m}x_{,t}^{p})=Ek_{\ast ,X}+\frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{q} & = & \displaystyle \frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }-Ek_{\ast ,b},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{b} & = & \displaystyle Ek_{\ast ,q}-\frac{\boldsymbol{\unicode[STIX]{x2202}}}{\boldsymbol{\unicode[STIX]{x2202}}\boldsymbol{q}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}_{\ast }}\boldsymbol{v}_{\ast }.\end{eqnarray}$$
A.4 The ground state of geostrophic rotating channels: mathematical details
Along a streamline extending from one end of the domain to the other,
$\int dt=L_{x}/\sqrt{2Ek}$
. From the definition of mass distribution function
$$\begin{eqnarray}\frac{L_{x}}{\sqrt{2Ek}}\unicode[STIX]{x1D6F9}_{,qq}=V_{,qb},\end{eqnarray}$$
which, combined with (A 8b ) gives
$$\begin{eqnarray}fy_{\ast ,q}=\frac{pV_{,qb}}{L_{x}}.\end{eqnarray}$$
A second equation involving the coordinates is (3.26),
$$\begin{eqnarray}\left|\frac{\unicode[STIX]{x2202}(Z_{\ast },y_{\ast })}{\unicode[STIX]{x2202}(b,q)}\right|=Z_{\ast ,b}y_{\ast ,q}-Z_{\ast ,q}y_{\ast ,b}=\frac{V_{,qb}}{L_{x}}.\end{eqnarray}$$
In choosing the sign, we assume that
$f>0$
. We seek solutions of (A 20)–(A 21) in power series of
$(b-b_{min})$
as follows
$$\begin{eqnarray}\displaystyle Z_{\ast } & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }Z_{n}(q)(b-b_{min})^{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{\ast } & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }y_{n}(q)(b-b_{min})^{n},\end{eqnarray}$$
$b=b_{min}$
. We also write 
$$\begin{eqnarray}\frac{V_{,qb}}{L_{x}}=\mathop{\sum }_{n=0}^{\infty }F_{n}(q)(b-b_{min})^{n}\end{eqnarray}$$
as a power series. (From a computational point of view, it may be more advantageous to use orthogonal polynomials. Here, we use a simple power series for convenience.) Inserting (A 22b
) into (A 20) we obtain the coefficients of the power series for
$y$
as
$$\begin{eqnarray}y_{n}=f^{-1}\int _{q_{min}}^{q}sF_{n}(s)ds,\end{eqnarray}$$
while combining (A 20) and (A 21)
$$\begin{eqnarray}\mathop{\sum }_{l=0}^{\infty }\mathop{\sum }_{n=1}^{l+1}(nZ_{n}y_{l+1-n,q}-(l+1-n)Z_{n,q}y_{l+1-n})(b-b_{min})^{l}=\mathop{\sum }_{l=0}^{\infty }F_{l}(b-b_{min})^{l},\end{eqnarray}$$
which yields the following upper triangular set of algebraic equations for the coefficients
$Z_{n}$
of the series for
$Z$
$$\begin{eqnarray}\mathop{\sum }_{n=1}^{l+1}(nZ_{n}y_{l+1-n,q}-(l+1-n)Z_{n,q}y_{l+1-n})=F_{l}.\end{eqnarray}$$
The equation for the first term
$$\begin{eqnarray}Z_{1}y_{0,q}=F_{0}\end{eqnarray}$$
can be readily solved using (A 24)
$$\begin{eqnarray}Z_{1}=\frac{f}{q},\end{eqnarray}$$
while the other terms satisfy the following recurrence relation
$$\begin{eqnarray}Z_{l+1}=[(l+1)y_{0,q}]^{-1}\left[lZ_{1,q}y_{l}-\mathop{\sum }_{n=2}^{l}(nZ_{n}y_{l+1-n,q}-(l+1-n)Z_{n,q}y_{l+1-n})\right],\quad l\geqslant 1.\end{eqnarray}$$
Note how
$Z_{l+1}$
depends on the
$y_{n}$
with
$n\geqslant 1$
.
Having determined the map from natural to physical coordinates, we now calculate the kinetic energy of the ground state, by solving the thermal wind equation (3.38), which expressed in
$(b,q)$
coordinates reads
$$\begin{eqnarray}(\sqrt{2Ek})_{,q}y_{,b}-(\sqrt{2Ek})_{,b}y_{,q}=f^{-1}Z_{,q}.\end{eqnarray}$$
Once again, we look for a power series solution
$$\begin{eqnarray}\sqrt{2Ek}=\mathop{\sum }_{l=0}^{\infty }v_{l}(q)(b-b_{min})^{l},\end{eqnarray}$$
and, since we have assumed that
$b=b_{min}$
is the level of no motion,
$v_{0}=0$
. Substituting into (A 30) and rearranging we again obtain a triangular algebraic set of equations for the
$v_{l}$
values (no surprise here, as we are dealing with the same nonlinear operator)
$$\begin{eqnarray}\displaystyle v_{1} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{l+1} & = & \displaystyle \frac{\displaystyle -Z_{l,q}+f\mathop{\sum }_{n=1}^{l}(nv_{l+1-n,q}y_{n}-(l+1-n)v_{l+1-n}y_{n,q})}{f(l+1)y_{0,q}},\quad l\geqslant 1.\end{eqnarray}$$
$v_{l}$
with
$l\geqslant 3$
depend on the
$y_{n}$
with
$n\geqslant 1$
. In particular, 
$$\begin{eqnarray}fy_{0,q}v_{2}=\frac{f}{2q^{2}}.\end{eqnarray}$$
A special case is when
$F_{n}=0,\,n>0$
, i.e. the mass distribution function is linear in the buoyancy. In this case, the solution has the very simple form
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle y_{\ast }=f^{-1}\int _{q_{min}}^{q}sF_{0}(s)ds,\quad Z_{\ast }=f\frac{b-b_{min}}{q},\\ \displaystyle \sqrt{2Ek_{\ast }}=\frac{f(b-b_{min})^{2}}{2q^{2}}[qF_{0}(q)]^{-1}.\end{array}\right\}\end{eqnarray}$$
