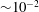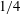1. Introduction
Kelvin–Helmholtz (KH) instability of a stratified shear layer is an important mechanism in all natural (and many fabricated) fluid systems because it can trigger turbulence (e.g. Smyth & Moum Reference Smyth and Moum2012). The standard theory assumes that the initial state is laminar and inviscid (Rayleigh Reference Rayleigh1880), whereas naturally occurring shear layers invariably coexist with some level of ambient turbulence (e.g. remnants of previous instability events). Thorpe, Smyth & Li (Reference Thorpe, Smyth and Li2013, hereafter referred to as T13) investigated the stability of a stratified shear layer in which ambient turbulence was represented as vertically variable eddy viscosity and diffusivity. That study found, counterintuitively, that in some circumstances variable viscosity acts to amplify instability. This amplification could speed the onset of a new turbulent episode or allow its development in flows that would otherwise be stable.
We are motivated by these results to (i) explain the physics underlying the destabilization phenomenon and (ii) assess its relevance over a broader range of initial conditions. This line of research is part of an ongoing effort to understand the relationship between instability and turbulence in the ocean. The resulting theory has found useful application in studies of mixing in tidally driven stratified shear flows in the Clyde Sea (west of Scotland; Liu, Thorpe & Smyth Reference Liu, Thorpe and Smyth2012) and has led to a potential explanation for diurnally varying, near-surface turbulence in the equatorial Pacific (Smyth, Moum & Li Reference Smyth, Moum and Li2013, hereafter referred to as S13).
T13 worked with a perturbation theory that assumed (i) the wavenumber was close to a stability boundary and (ii) that viscosity and diffusivity were small. In this paper, we extend the method numerically to allow arbitrarily large viscosity and diffusivity and mean flows that are far from any stability boundary, e.g. the fastest-growing instability for a given initial state. We explore these effects over a broad range of initial states and propose a mechanistic explanation for the amplification of instability. In geophysical flows, observed mean profiles of velocity, density and turbulence magnitude vary greatly (e.g. S13). Here, we seek conceptual understanding by focusing on a few idealized profile shapes that are expected to have general relevance. Our model for a stratified shear layer is the Holmboe flow, in which mean velocity and buoyancy are both proportional to
$\tanh (z)$
, where
$z$
is the height. Eddy viscosity and diffusivity are assumed to act on vertical gradients only, and have one of three simple vertical profiles (uniform, minimum within shear layer and maximum within shear layer).
We begin by reviewing the mechanism of shear instability and considering the potential effects of stable stratification and uniform viscosity and mass diffusivity. Imagine two fluid layers moving opposite to one another, separated by a transition layer (or shear layer) in which the vorticity is concentrated. Now suppose that the transition layer suffers a sinusoidal vertical displacement (figure 1 a). This creates constrictions in the upper and lower layers where the horizontal flow must accelerate. The accelerated flow preferentially advects vorticity toward a convergence point (located at the centre of 1 a). The resulting accumulation of vorticity (figure 1 b) induces enhanced clockwise motion that acts to amplify the original sinusoidal displacement. The result is a positive feedback loop that leads to exponential growth.
Figure 1. Schematic representation of the positive feedback that regulates shear instability: (a) vorticity accumulation due to horizontal advection; (b) amplification of the initial wave by induced vertical motions. Buoyancy perturbations (indicated as
${\it\delta}b<0$
,
${\it\delta}b>0$
) generate a baroclinic torque that retards growth.
If the fluid is stably stratified, the vertical displacement induces buoyancy perturbations
${\it\delta}b$
of opposite sign in the crests and troughs (figure 1
b). This creates a counterclockwise baroclinic torque that acts to impede growth. Only when the former effect (vorticity accumulation) dominates the latter (baroclinic torque) can the perturbation grow.
The effect of uniform viscosity is to disperse the vorticity accumulation and hence to weaken the instability. In contrast, uniform diffusivity reduces the buoyancy contrast and its attendant baroclinic torque, allowing the perturbation to grow more rapidly. These effects operate the same whether the eddy viscosity and diffusivity act on vertical gradients, horizontal gradients or both. As we will see, though, spatial non-uniformities in the viscosity and diffusivity can lead to very different effects.
The destabilizing influence of uniform mass diffusivity has been documented recently by T13. The stabilizing effect of viscosity has been demonstrated explicitly in many studies. Betchov & Szewczyk (Reference Betchov and Szewczyk1963) studied the stability of a uniformly viscous, homogeneous, hyperbolic tangent shear layer. Viscosity was found to damp the growth rate for a perturbation of any wavenumber. Maslowe & Thompson (Reference Maslowe and Thompson1971) extended this work to include stable stratification, with the Prandtl number (the ratio of viscosity to diffusivity)
$\mathit{Pr}=0.72$
, as is typical of air. They found that instability is damped as viscosity and diffusivity are increased.
Defina, Lanzoni & Susin (Reference Defina, Lanzoni and Susin1999) explored the effect of uniform viscosity on the instability of a stratified shear flow in a tilted tube both theoretically and experimentally. This study assumed
$\mathit{Pr}\gg 1$
(i.e. the diffusion is small compared with viscosity). The damping action of viscosity was found to reduce the critical Richardson number with respect to the inviscid limit
$\mathit{Ri}=0.25$
. The critical Richardson number decreases as viscosity increases.
These studies find that both viscosity and diffusivity have a stabilizing effect on KH instability. In each case, however, the viscosity and diffusivity were assumed to be uniform, and the range of Prandtl numbers tested was limited. Here, we allow viscosity and diffusivity to vary in space, and test values of
$\mathit{Pr}$
covering two orders of magnitude. This gives a more comprehensive, and in some respects very different, view of viscous and diffusive effects.
Section 2 describes the background profiles of the shear flow and methods used in the analysis. Section 3 reviews the results near the neutral stability boundary (T13). Section 4 gives the numerical results away from the stability boundary, retaining the assumption of small viscosity and diffusivity. Section 5 extends viscosity and diffusivity to larger values. In § 6 an analysis of the enstrophy budget is applied to identify the mechanism of destabilization, and an explanation is proposed for the anomalous effects of viscosity variations. In § 7, we describe the dependence on the Prandtl number. Conclusions are summarized in § 8.
2. Methods
Our calculation is carried on a vertical plane measured by Cartesian coordinates
$x$
(streamwise) and
$z$
(vertical). The fluid is assumed to be incompressible. Because small-scale turbulent fluxes in geophysical flows are primarily vertical, we assume here that eddy viscosity and diffusion act on vertical gradients only. The Boussinesq equations for this case are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}=-\frac{\boldsymbol{{\rm\nabla}}p}{{\it\rho}_{0}}+b\hat{z}+\frac{\partial }{\partial z}\left(A\frac{\partial \boldsymbol{u}}{\partial z}\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}b}{\text{d}t}=\frac{\partial }{\partial z}\left(K\frac{\partial b}{\partial z}\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0. & \displaystyle\end{eqnarray}$$
$b=-g({\it\rho}-{\it\rho}_{0})/{\it\rho}_{0}$
where
${\it\rho}_{0}$
is a reference density,
$\hat{\boldsymbol{z}}$
is the vertical unit vector and
$p$
is the pressure. Here
$A(z)$
and
$K(z)$
denote the vertical eddy viscosity and mass diffusivity, respectively. Eddy viscosity and diffusivity components that act on horizontal gradients (e.g. Liu et al.
Reference Liu, Thorpe and Smyth2012) are not included in the present study.
Following Liu et al. (Reference Liu, Thorpe and Smyth2012), we assume a steady mean flow with stable stratification, and use the method of normal modes to study the evolution of small perturbations. Velocity, buoyancy and pressure are expressed in terms of a mean profile and a small perturbation:
$\boldsymbol{u}=[U(z)+u^{\prime }(x,z,t),w^{\prime }(x,z,t)]$
where
$U(z)$
is the horizontal mean flow and
$u^{\prime }(x,z,t)$
and
$w^{\prime }(x,z,t)$
are velocity perturbations. Buoyancy
$b=B(z)+b^{\prime }(x,z,t)$
and pressure
$p=P(z)+p^{\prime }(x,z,t)$
. The normal mode form is assumed for the perturbation
${\it\phi}^{\prime }=\hat{{\it\phi}}(z)\exp (\text{i}kx+{\it\sigma}t)$
where
${\it\phi}$
represents
$u,w,b$
or
$p$
. Here
${\it\sigma}={\it\sigma}_{r}+\text{i}{\it\sigma}_{i}$
where
${\it\sigma}_{r}$
is the growth rate and
${\it\sigma}_{i}$
is the frequency. The wavenumber
$k$
of the perturbation is real. The complex vertical structure function
$\hat{{\it\phi}}$
depends only on
$z$
.
Linearizing the equations of motion for small perturbations leads to
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\sigma}\left(\frac{\partial ^{2}}{\partial z^{2}}-k^{2}\right){\hat{w}}=\left[-\text{i}kU\left(\frac{\partial ^{2}}{\partial z^{2}}-k^{2}\right)+\text{i}k\frac{\partial ^{2}U}{\partial z^{2}}+F_{w}\right]{\hat{w}}-k^{2}\hat{b} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\sigma}\hat{b}=-N^{2}{\hat{w}}+[-\text{i}kU+F_{b}]\hat{b} & \displaystyle\end{eqnarray}$$
where
$N^{2}=\text{d}B/\text{d}z$
. In (2.2)
${\hat{w}}$
and
$\hat{b}$
are structure functions of vertical velocity and buoyancy perturbation. The effects of eddy viscosity and diffusivity are expressed by
$$\begin{eqnarray}\displaystyle & \displaystyle F_{w}=\frac{\text{d}^{2}}{\text{d}z^{2}}\left(A\frac{\text{d}^{2}}{\text{d}z^{2}}\right)-k^{2}\frac{\text{d}}{\text{d}z}\left(A\frac{\text{d}}{\text{d}z}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{b}=\frac{\text{d}}{\text{d}z}\left(K\frac{\text{d}}{\text{d}z}\right). & \displaystyle\end{eqnarray}$$
This can be written in a matrix form and treated as a generalized eigenvalue problem:
$$\begin{eqnarray}{\it\sigma}\left[\begin{array}{@{}cc@{}}{\rm\nabla}^{2} & 0\\ 0 & \unicode[STIX]{x1D644}\end{array}\right]\left[\begin{array}{@{}c@{}}{\hat{w}}\\ \hat{b}\end{array}\right]=\left[\begin{array}{@{}cc@{}}-\text{i}kU{\rm\nabla}^{2}+\text{i}kU_{zz}+F_{w} & -k^{2}\\ -N^{2} & -\text{i}kU+F_{b}\end{array}\right]\left[\begin{array}{@{}c@{}}{\hat{w}}\\ \hat{b}\end{array}\right],\end{eqnarray}$$
where
$\unicode[STIX]{x1D644}$
is the identity matrix. The submatrix
${\rm\nabla}^{2}=\text{d}^{2}/\text{d}z^{2}-k^{2}$
and the second derivative
$\text{d}^{2}/\text{d}z^{2}$
is replaced by a second-order finite difference. Given a certain background velocity
$U(z)$
, buoyancy frequency profile
$N(z)$
and eddy coefficients
$A(z)$
and
$K(z)$
, eigenvalues of
${\it\sigma}$
and corresponding eigenfunctions
${\hat{w}}$
and
$\hat{b}$
can be calculated using standard numerical methods.
A hyperbolic tangent profile is assumed for both the background velocity and buoyancy:
$$\begin{eqnarray}\frac{U(z)}{{\rm\Delta}U}=\frac{B(z)}{{\rm\Delta}B}=\tanh \!\frac{z}{h}\end{eqnarray}$$
where
$h$
is the half-thickness of the shear layer and
${\rm\Delta}U$
and
${\rm\Delta}B$
are the half-changes of velocity and buoyancy, respectively (figure 2
a). Three choices are made for eddy coefficients of viscosity and diffusivity:
$$\begin{eqnarray}\frac{A}{A_{0}}=\frac{K}{K_{0}}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{profile 1}\\ \tanh \!^{2}\displaystyle \frac{z}{h}\quad & \text{profile 2}\\ \text{sech}^{2}\displaystyle \frac{z}{h}\quad & \text{profile 3.}\end{array}\right.\end{eqnarray}$$
In each profile
$A_{0}$
and
$K_{0}$
characterize the maximum values of the vertical eddy coefficients of viscosity and diffusivity. Note that
$\mathit{Pr}=A/K$
is independent of
$z$
in these profiles.
Figure 2. (a) Background profiles of scaled velocity and buoyancy; (b) scaled vertical eddy viscosity and diffusivity. Only the centre part of the shear layer is shown in this figure. The boundaries for the calculation are at
$z=\pm 10h$
.
For profile 1 the viscosity/diffusivity is uniform through the whole depth, as in previous studies (Betchov & Szewczyk Reference Betchov and Szewczyk1963; Maslowe & Thompson Reference Maslowe and Thompson1971; Defina et al. Reference Defina, Lanzoni and Susin1999). Profile 2 represents a viscosity/diffusivity distribution that is smaller within the shear layer and larger away from it. Profile 2 may be thought of as a layer of locally weak ambient turbulence where instability is about to begin, e.g. a thermohaline staircase (Gregg & Sanford Reference Gregg and Sanford1987), or a stable layer of the sort formed when eddy diffusivity varies inversely with stratification (e.g. Phillips Reference Phillips1972; Posmentier Reference Posmentier1977), exposed to shear due to internal waves (e.g. Kimura, Smyth & Kunze Reference Kimura, Smyth and Kunze2011). In profile 3 the viscosity/diffusivity is greatest in the shear layer and decays away from it. Profile 3 may represent a region where instability has occurred recently and has left behind a layer of turbulence.
After scaling with
$h$
and
${\rm\Delta}U$
, the solution depends on four non-dimensional parameters. The Richardson number
$\mathit{Ri}=h{\rm\Delta}B/{\rm\Delta}U^{2}$
. The non-dimensional maximum viscosity
$A_{0}/h{\rm\Delta}U$
, and diffusivity
$K_{0}/h{\rm\Delta}U$
are the inverses of the Reynolds and Péclet numbers, respectively. The Prandtl number is
$\mathit{Pr}=A/K=A_{0}/K_{0}$
. In what follows all quantities are non-dimensionalized by
$h$
and
${\rm\Delta}U$
.
Ideally, we would assume an infinite vertical domain, as in T13. Due to finite computer capacity, we must assume a finite domain. We choose the domain half-depth
$H=10$
and the increment of the vertical coordinate
$\text{d}z=0.01$
. We run the calculation with different values of
$H$
and
$\text{d}z$
and confirm that the results are well converged. Boundary conditions
${\hat{w}}=0$
and
$\hat{b}=0$
are imposed at upper and lower boundaries
$z=\pm H$
.
3. Effects of weak ambient turbulence near the stability boundary
We now review pertinent results from the perturbation theory of T13. Near the stability boundary in the inviscid, non-diffusive limit, the change of the growth rate due to a small viscosity and diffusivity is
$$\begin{eqnarray}{\it\delta}{\it\sigma}_{r}=A_{0}kf_{A}(k)+K_{0}kf_{K}(k)\end{eqnarray}$$
where the coefficients
$kf_{A}(k)$
and
$kf_{K}(k)$
quantify the sensitivity of
${\it\sigma}_{r}$
to small increments of viscosity and diffusivity. Equation (3.1) shows that the effects of the two eddy coefficients are additive, so it is convenient to study them separately.
The circle at the top of figure 3 represents the case where instability first appears as shear is increased or stratification is decreased. The solid curve is the stability boundary for
$A_{0}=K_{0}=0$
(Holmboe’s inviscid and non-diffusive solution); everywhere below this curve
${\it\sigma}_{r}>0$
(unstable), while above it
${\it\sigma}_{r}=0$
(neutral). For a given
$\mathit{Ri}$
, the fastest growing inviscid and non-diffusive mode is shown by the dashed curve. With the introduction of small viscosity or diffusivity, modes on the inviscid stability boundary shown in figure 3 generally acquire non-zero growth rates
${\it\delta}{\it\sigma}_{r}$
, with
${\it\delta}{\it\sigma}_{r}<0\;({>}0)$
indicating that viscosity/diffusivity has a stabilizing (destabilizing) effect.
Figure 3. The solid curve,
$\mathit{Ri}=k(1-k)$
, is the neutral stability boundary on which the growth rates are zero (J. Holmboe 1960, personal communication). The dashed line shows where the fastest growing modes lie, obtained with numerical method. The arrow represents the departure from T13.
Changes to the growth rate by vertically variable viscosity and diffusivity profiles near the neutral stability boundary curve are discussed in detail by T13. Values of
$kf_{A}$
and
$kf_{K}$
computed for the profiles used here are in table 1. For profile 2,
$kf_{A}>0$
. This tells us that, near the neutral stability boundary, the effect of eddy viscosity profile 2 is to destabilize the flow. This presents a striking contrast with the finding of all previous studies that viscosity stabilizes a shear layer (Betchov & Szewczyk Reference Betchov and Szewczyk1963; Maslowe & Thompson Reference Maslowe and Thompson1971; Defina et al.
Reference Defina, Lanzoni and Susin1999). Also interesting is that adding a small eddy diffusivity
$K$
with profile 2 stabilizes the shear flow. This effect is opposite to that of the other two profiles of
$K$
.
Table 1. Effects on stability for three vertical eddy viscosity and diffusivity profiles. Results pertain to the limiting case of small viscosity and diffusivity and close proximity to the inviscid stability boundary (T13).
4. Effects of weak ambient turbulence away from the stability boundary
Here we explore the effects of moving
$\mathit{Ri}$
away from the small neighbourhood of 0.25 considered by T13 (dashed curve and arrow on figure 3), with
$A_{0}$
and
$K_{0}$
kept small. The results of increasing
$A_{0}$
and
$K_{0}$
will be examined separately.
In the inviscid limit, the fastest growth rate for a given
$\mathit{Ri}$
decreases from 0.1897 at
$\mathit{Ri}=0$
(where
$k=0.445$
) to 0 at
$\mathit{Ri}=0.25$
(
$k=0.5$
) as shown in figure 4(a). Here we will describe the change of this growth rate due to variable eddy viscosity or diffusivity (figure 4
b,c):
$$\begin{eqnarray}{\rm\Delta}{\it\sigma}_{r}={\it\sigma}_{r}(\mathit{Ri},A_{0},K_{0},k,n)-{\it\sigma}_{r}(\mathit{Ri},0,0,k_{0},n),\end{eqnarray}$$
where the wavenumbers
$k$
and
$k_{0}$
correspond to the fastest-growing modes of the viscous case and in the inviscid limit, respectively, and
$n=1,2,3$
specifies profiles 1–3 given by (2.5). The change of growth rate due to viscosity or diffusivity of profile 2 is small relative to the other two profiles and is therefore plotted in a separate panel.
4.1. Effects of non-zero eddy viscosity
$A$
The three solid curves in figure 4(b,c) show the change of the fastest growth rate when a small eddy viscosity with vertical dependence (2.5) is added to the inviscid flow. In this calculation
$A_{0}=10^{-5}$
and
$K_{0}=0$
. For profiles 1 and 3 the change of the growth rate is negative for all
$0<\mathit{Ri}<0.25$
so these two viscosity profiles are stabilizing. The stabilizing effect is stronger at higher
$\mathit{Ri}$
. In the limit
$\mathit{Ri}\rightarrow 0.25$
,
${\rm\Delta}{\it\sigma}_{r}$
approaches the value predicted using the T13 perturbation theory as expected (figure 4
b, asterisks). When
$\mathit{Ri}>0.13$
, viscosity with profile 3 (the
$\text{sech}^{2}z$
case) has a stabilizing effect greater than that of uniform viscosity.
In the case of profile 2 (the
$\tanh \!^{2}z$
viscosity profile), at higher Richardson numbers, the change of the fastest growth rates is positive, i.e. the addition of viscosity with this profile is destabilizing as predicted by T13 for the limiting case
$\mathit{Ri}\rightarrow 0.25$
(asterisk on 4
c). Farther from the stability boundary (i.e. for
$\mathit{Ri}<0.25$
), this change is reduced. When
$\mathit{Ri}<0.13$
the destabilizing effect is reversed. We conclude that the anomalous destabilizing effect of the
$\tanh \!^{2}z$
viscosity profile is not restricted to the immediate vicinity of the stability boundary (as explored by T13) but instead operates over a range of
$\mathit{Ri}$
extending down to
$\mathit{Ri}=0.13$
.
Because (3.1) is linear in
$A_{0}$
, the changes due to the different viscosity profiles described above are related to each other through the identity
$\tanh \!^{2}z+\text{sech}^{2}z=1$
. The change of the fastest growth rates due to profile 1 is equal to the summed effects of profiles 2 and 3. For example, in the parameter range
$\mathit{Ri}>0.13$
where profile 2 is destabilizing, profile 3 is more stabilizing than profile 1. While for
$\mathit{Ri}<0.13$
, profile 3 is less stabilizing than profile 1, and correspondingly profile 2 becomes stabilizing.
Figure 4. Numerical results for three profiles,
$A_{0}=10^{-5}$
,
$K_{0}=10^{-5}$
. (a) Fastest growth rate of the inviscid flow. (b) The change of the fastest growth rate due to a small viscosity or diffusivity disturbance from the inviscid flow for profiles 1 and 3. (c) The change of the fastest growth rate due to a small viscosity or diffusivity disturbance from the inviscid flow for profile 2. The asterisks at the right are values at
$k=0.5$
;
$\mathit{Ri}=0.25$
from table 1 of T13.
4.2. Effects of non-zero eddy diffusivity
$K$
In this calculation
$K_{0}=10^{-5}$
and
$A_{0}=0$
. The three dashed curves in figure 4(b,c) show
${\rm\Delta}{\it\sigma}_{r}$
for the three profiles of
$K$
described in (2.5). For profiles 1 and 3,
$K$
is destabilizing as we expect, and increases with
$\mathit{Ri}$
to match the asymptotic results of T13. In the case of profile 2, diffusivity is destabilizing for most
$\mathit{Ri}$
, but the effect is reversed when
$\mathit{Ri}>0.22$
. In contrast to viscosity, the effects of diffusivity approach zero in the limit
$\mathit{Ri}\rightarrow 0$
, because there are no buoyancy perturbations on which the diffusivity can act.
5. Effects of strong ambient turbulence
So far, the calculations are performed at small values of eddy viscosity and diffusivity where
${\rm\Delta}{\it\sigma}_{r}$
is small and varies linearly with
$A_{0}$
and
$K_{0}$
as described by (3.1). At larger values, the variation of
${\rm\Delta}{\it\sigma}_{r}$
becomes more complicated. A representative example, with
$\mathit{Ri}=0.2$
, is shown in figure 5. In this log–log representation, the slopes are very close to unity for small
$A_{0}$
and
$K_{0}$
, indicating that the linear relationship (3.1) remains approximately correct. The linear relationship breaks down when
$A_{0}$
(or
$K_{0}$
) exceeds
${\sim}10^{-2}$
. At that extreme,
${\rm\Delta}{\it\sigma}_{r}$
is comparable with the inviscid growth rate. In the common case
$\mathit{Pr}=1$
, this criterion is equivalent to
$\mathit{Re}<100$
. This is consistent with existing indications of the magnitude of
$\mathit{Re}$
at which viscous effects are no longer ‘small’. For example, when
$\mathit{Ri}=0.2$
, instability is damped completely when
$\mathit{Re}<25$
(Maslowe & Thompson Reference Maslowe and Thompson1971). At the other extreme, viscous effects on KH instability are generally negligible when
$\mathit{Re}$
is greater than a few hundred (e.g. Smyth, Klaassen & Peltier Reference Smyth, Klaassen and Peltier1988).
Figure 5. Growth rate increase versus eddy viscosity (diffusivity) for profile 2. The results are obtained for
$\mathit{Ri}=0.2$
and on the maximum growth rate curve of figure 3. The dashed line has unit slope.
6. Destabilization mechanism of the eddy viscosity for the
$\tanh \!^{2}z$
profile
The destabilization by eddy viscosity
$\propto \!\tanh \!^{2}z$
(profile 2) bears further discussion. Here, we offer a physical explanation based on the perturbation enstrophy budget. Perturbation enstrophy is defined as
$$\begin{eqnarray}Z={\textstyle \frac{1}{2}}|{\it\omega}|^{2}\end{eqnarray}$$
where
${\it\omega}={\hat{w}}_{x}-\hat{u} _{z}$
is the vorticity. The subscripts
$x$
and
$z$
denote partial derivatives. Based on (2.1c
), the eigenfunction of horizontal velocity is
$\hat{u} =\text{i}{\hat{w}}_{z}/k$
.
The equation of motion (2.1a ) implies the normal mode enstrophy balance,
$$\begin{eqnarray}\frac{\partial Z}{\partial t}=\overbrace{\mathbb{R}({\hat{w}}{\it\omega}^{\ast })U_{zz}}^{\mathscr{E}_{1}}+\underbrace{\mathbb{R}(\hat{b}_{x}{\it\omega}^{\ast })}_{\mathscr{E}_{2}}\overbrace{-A|{\it\omega}_{z}|^{2}}^{\mathscr{E}_{3}}\underbrace{-A_{z}Z_{z}}_{\mathscr{E}_{4}}\overbrace{-\mathbb{R}[(A_{z}{\hat{w}}_{x})_{z}{\it\omega}^{\ast }]}^{\mathscr{E}_{5}}+\underbrace{\frac{\partial }{\partial z}(AZ_{z}+2A_{z}Z)}_{\mathscr{E}_{6}}.\end{eqnarray}$$
-
(i) Here
$\mathscr{E}_{1}$
is analogous to the shear production term in the kinetic energy budget (e.g. Smyth & Peltier Reference Smyth and Peltier1989). The asterisk denotes the complex conjugate and
$\mathbb{R}$
indicates the real part. Here
$\mathscr{E}_{1}$
is a correlation between the perturbation vorticity and its rate of change due to vertical advection of the mean gradient
$U_{zz}$
. If vertical advection reinforces the existing vorticity distribution, as is the case with KH billows, the term supports growth. -
(ii) We use
$\mathscr{E}_{2}$
to represent changes in enstrophy due to buoyancy. In contrast with the corresponding term in the kinetic energy budget, this buoyancy production term is positive definite for all growing modes. In the case of KH instability, the baroclinic torque opposes the vorticity concentration that drives the growth of the large vortex (figure 1), but it also generates intense shear in the thin braids separating the billows of the wave train (Corcos & Sherman Reference Corcos and Sherman1976; Staquet Reference Staquet1995; Smyth Reference Smyth2003) and thereby contributes positively to the net enstrophy. -
(iii) Here
$\mathscr{E}_{3}$
is dissipation due to viscosity. It is negative definite. -
(iv) The term
$\mathscr{E}_{4}$
is non-zero only for variable viscosity profiles. We will see later that this is the main factor in the destabilization mechanism. -
(v) Like
$\mathscr{E}_{4}$
,
$\mathscr{E}_{5}$
is only non-zero for variable viscosity. Its magnitude is negligible in the present case. -
(vi) The final term,
$\mathscr{E}_{6}$
, is a flux divergence which vanishes when (6.2) is integrated over the whole range of
$z$
.
We now integrate (6.2) over
$-H\leqslant z\leqslant H$
and divide each side by
$\langle 2Z\rangle =2\int \!Z\,\text{d}z$
, isolating
${\it\sigma}_{r}$
on the left-hand side. The growth rate can now be decomposed into several partial growth rates, each corresponding to a term on the right-hand side of (6.2):
$$\begin{eqnarray}{\it\sigma}_{r}={\it\sigma}_{SP}+{\it\sigma}_{BP}+{\it\sigma}_{{\it\epsilon}}+{\it\sigma}_{A1}+{\it\sigma}_{A2}.\end{eqnarray}$$
The partial growth rate terms on the right-hand side are defined as
$$\begin{eqnarray}\displaystyle & {\it\sigma}_{SP}=\mathscr{E}_{1}/\langle 2Z\rangle & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\sigma}_{BP}=\mathscr{E}_{2}/\langle 2Z\rangle & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\sigma}_{{\it\epsilon}}=\mathscr{E}_{3}/\langle 2Z\rangle & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\sigma}_{A1}=\mathscr{E}_{4}/\langle 2Z\rangle & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\sigma}_{A2}=\mathscr{E}_{5}/\langle 2Z\rangle . & \displaystyle\end{eqnarray}$$
The change of the fastest growth rates
${\rm\Delta}{\it\sigma}_{r}$
from the inviscid limit is determined by the balance among the changes of these partial growth rates of (6.3). For profile 2, the effect of viscosity is to increase
${\it\sigma}_{SP}$
and decrease
${\it\sigma}_{BP}$
(figure 6), the only two non-zero partial growth rate terms in the inviscid limit. The change of the growth rate due to the shear production,
${\rm\Delta}{\it\sigma}_{SP}$
, is always positive, but decreases to a value very close to zero as
$\mathit{Ri}$
approaches 0.25. Hence, it cannot be the main contribution to the destabilization effect of this viscosity profile. The change of the growth rate due to the buoyancy production term
${\rm\Delta}{\it\sigma}_{BP}$
is always negative. Due to dissipation
${\rm\Delta}{\it\sigma}_{{\it\epsilon}}$
is always negative and does not vary much with the increase of
$\mathit{Ri}$
. Here
${\rm\Delta}{\it\sigma}_{A2}$
is negative, and its magnitude is small. As
$\mathit{Ri}$
approaches 0.25,
${\rm\Delta}{\it\sigma}_{A1}$
is the dominant source of destabilization (thick solid line in figure 6).
Figure 6. The change of partial growth rate from inviscid case due to eddy viscosity profile 2 with
$A_{0}=10^{-5}$
. It is the term
${\rm\Delta}{\it\sigma}_{A1}$
that makes the change of growth rate positive. Note that
${\rm\Delta}{\it\sigma}_{{\it\epsilon}}={\it\sigma}_{{\it\epsilon}}$
,
${\rm\Delta}{\it\sigma}_{A1}={\it\sigma}_{A1}$
and
${\rm\Delta}{\it\sigma}_{A2}={\it\sigma}_{A2}$
since none of the three processes exist in the inviscid limit.
To understand how
${\it\sigma}_{A1}$
makes the growth rate increase, we interpret
$-A_{z}Z_{z}$
((6.2), (6.4d
)) as an advection process, with equivalent vertical velocity
$w_{e}=-A_{z}$
. For profile 2,
$w_{e}$
is negative for
$z>0$
and positive for
$z<0$
(figure 7
a); hence, the effective vertical velocity converges. The enstrophy maximum (figure 7
b) is thereby reinforced, and the growth rate increases. At lower
$\mathit{Ri}$
(e.g. figure 7
c), this mechanism is less effective due to the double-peaked structure of
$Z$
.
Figure 7. (a) Equivalent vertical velocity
$w_{e}=-A_{z}$
for profile 2. Enstrophy profiles for high-
$\mathit{Ri}$
(b) and low-
$\mathit{Ri}$
(c) cases.
If
$w_{e}$
diverges, as in profile 3 where
$A$
is a maximum at
$z=0$
, the effect is opposite: the enstrophy maximum at the centre of the flow is diffused and viscosity tends to damp the instability. This explains why, when
$0.13<\mathit{Ri}<0.25$
, viscosity with profile 3 has a damping effect greater than that of uniform viscosity as noted in § 4.1.
The change in the enstrophy profile with
$\mathit{Ri}$
, which governs the behaviour of the destabilizing term
${\it\sigma}_{A1}$
, can be understood in terms of the wave resonance mechanism of shear instability. At low
$\mathit{Ri}$
, the instability is primarily a resonance between waves supported by the vorticity gradients on the upper and lower flanks of the shear layer, so enstrophy is concentrated there (Baines & Mitsudera Reference Baines and Mitsudera1994; Carpenter et al.
Reference Carpenter, Tedford, Heifitz and Lawrence2013). When stratification is stronger (i.e. as
$\mathit{Ri}$
approaches 0.25), the resonance includes a gravity wave centred at the stratification maximum,
$z=0$
, and that wave dominates the enstrophy profile.
7. Dependence on the Prandtl number for small viscosity and diffusivity
When viscosity and diffusivity are small, the effect of varying
$\mathit{Pr}$
is easily predicted because (3.1) holds (see figure 5 and the accompanying discussion). Figure 4(b) shows that for profiles 1 and 3, if the same amounts of viscosity and diffusivity are added to the inviscid flow (i.e. if
$\mathit{Pr}=1$
), the stabilizing effect of viscosity is greater than the destabilizing effect of diffusivity. Only if diffusivity is much greater than viscosity (
$\mathit{Pr}\ll 1$
) does the destabilizing effect dominate, and this is not generally true for geophysical turbulence. This is why diffusive destabilization was not evident in the studies of Maslowe & Thompson (Reference Maslowe and Thompson1971) and Defina et al. (Reference Defina, Lanzoni and Susin1999) who used
$\mathit{Pr}\sim 1$
and
$\mathit{Pr}\gg 1$
, respectively.
Now we explore the dependence of
${\rm\Delta}{\it\sigma}_{r}$
on
$\mathit{Ri}$
and
$\mathit{Pr}$
for profile 2. Profile 2 is more complicated than cases 1 and 3. Diffusion is destabilizing (figure 4
c) except for a very small range of
$0.22<\mathit{Ri}\leqslant 0.25$
. Viscosity, in contrast, is destabilizing for
$\mathit{Ri}>0.13$
but stabilizing for
$\mathit{Ri}<0.13$
. For
$\mathit{Ri}<0.13$
, if
$\mathit{Pr}$
is sufficiently large, the stabilizing effect of viscosity dominates the destabilizing effect of diffusion and the net effect is stabilization. The Prandtl number needed for viscous stabilization to dominate becomes smaller as
$\mathit{Ri}$
decreases (and vice versa). At
$\mathit{Pr}=1$
, a typical value for geophysical turbulence, stabilization occurs for
$0<\mathit{Ri}<0.08$
, and destabilization occurs for
$0.08<\mathit{Ri}<0.22$
. For
$0.22<\mathit{Ri}<0.25$
, diffusion is weakly stabilizing, but the destabilizing effect of viscosity dominates unless
$\mathit{Pr}<0.23$
(calculated with the values of
$kf_{A}$
and
$kf_{K}$
at
$k=0.5$
in table 1).
Figure 8. The Prandtl number dependence for profile 2, i.e.
$A,K\propto \tanh \!^{2}z$
. On the two curves the change of growth rate
${\rm\Delta}{\it\sigma}_{r}=0$
. In the shaded area
${\rm\Delta}{\it\sigma}_{r}>0$
which means the net effect from viscosity and diffusivity is destabilizing in this area. Outside this area
${\rm\Delta}{\it\sigma}_{r}<0$
and the viscosity and diffusivity are stabilizing.
8. Conclusions
We have examined the effects of vertically varying turbulent viscosity and mass diffusion on the KH instability of a stratified shear layer. In the double limit of weak turbulence and
$\mathit{Ri}$
approaching 0.25, these effects are accurately predicted by the perturbation analyses of T13. When non-dimensional eddy viscosity and diffusivity (or the inverse Reynolds and Péclet numbers, respectively) exceed
$O(10^{-2})$
, the results change quantitatively, though not qualitatively. When
$\mathit{Ri}$
departs from the neighbourhood of 0.25, dramatically different results may be found depending on the vertical structure of the turbulence.
When turbulent eddy coefficients are localized within the shear layer (profile 3), as might happen if the latter is colocated with a previous turbulent event, the effects of turbulence are similar to those of uniform viscosity and diffusivity: viscosity tends to stabilize the flow; diffusion tends to destabilize it.
The results are very different when an unstable shear layer develops in a region of weak ambient turbulence (profile 2), as is often observed (S13). In that case, eddy viscosity tends to diffuse vorticity inward from the flanks of the shear layer to the centre. When
$\mathit{Ri}>0.13$
, the enstrophy profile is sharply peaked at
$z=0$
, and is therefore reinforced by this turbulent vorticity diffusion, resulting in accelerated growth. When
$\mathit{Ri}<0.13$
, enstrophy is concentrated away from the shear layer, and vorticity diffusion has the opposite effect, impeding growth. This difference in the shape of the perturbation enstrophy profile, which determines its response to turbulent vorticity diffusion, can be understood in terms of the wave resonance mechanism of instability growth (e.g. Baines & Mitsudera Reference Baines and Mitsudera1994; Carpenter et al.
Reference Carpenter, Tedford, Heifitz and Lawrence2013).
For
$\mathit{Ri}<0.13$
and profile 2, the effects of eddy viscosity and mass diffusion act oppositely, and the net effect can be stabilizing or destabilizing depending on the turbulent Prandtl number. For any
$\mathit{Pr}$
, there is a value of
$\mathit{Ri}$
below which the stabilizing effect of eddy viscosity dominates, while at larger
$\mathit{Ri}$
, the destabilizing effect of mass diffusion dominates. At
$\mathit{Pr}=1$
, for example, the flow is destabilized if
$\mathit{Ri}>0.08$
. When
$\mathit{Ri}>0.13$
, the flow is destabilized regardless of
$\mathit{Pr}$
since eddy viscosity and diffusion act in the same sense.
This stability theory has already proven useful in the analysis of oceanographic observations by Liu et al. (Reference Liu, Thorpe and Smyth2012) and S13. The analyses of S13 revealed that the damping of unstable modes by pre-existing turbulence is an important facet of the diurnal cycle of near-surface turbulence. Observed profiles are complicated, however, and conceptual understanding of the instability characteristics is aided considerably by the study of simple, canonical profiles such as those examined here. Future work will include a broader range of velocity, buoyancy, viscosity and diffusivity profiles.
This theory may also lend insight into marginal instability, the property of sheared, stratified turbulence wherein the Richardson number fluctuates about the critical value
$1/4$
due to the interaction of external forcing, instabilities and ambient turbulence (Thorpe & Liu Reference Thorpe and Liu2009; Smyth & Moum Reference Smyth and Moum2013).
The effects of ambient turbulence on instability evolution will ultimately be investigated via direct numerical simulations that include small-scale turbulence as part of the initial conditions (e.g. Brucker & Sarkar Reference Brucker and Sarkar2007). This will bypass two important idealizations made in the present model: the neglect of nonlinear terms and the representation of turbulence via eddy coefficients.
Acknowledgements
The authors are most grateful to the three reviewers for the very helpful suggestions. This work was funded by the US National Science Foundation under grant OCE-1030772.
