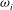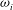1. Introduction
Linear stability theory predicts the evolution of small disturbances superposed on a laminar base flow. For many flow scenarios, the underlying linear growth mechanism determines the initial path in the complex transition process from laminar to turbulent flow and has therefore been the subject of interest over a long period (Schmid & Henningson Reference Schmid and Henningson2001; Criminale, Jackson & Joslin Reference Criminale, Jackson and Joslin2003). Even though the linear approach ceases to be applicable in the later nonlinear stages of the transition process, for many flows the initial linear mechanism orchestrates the subsequent cascade that creates harmonics and subharmonics of some fundamental disturbance and eventually leads to a fully turbulent state. Traditionally, the linearised disturbance equations, derived from the governing Navier–Stokes equations, are transformed by introducing a normal mode ansatz, i.e. assuming wave-like disturbances of the form
$\text{exp}[\text{i}({\it\alpha}x-{\it\omega}t)]$
, which reduces the initial-value problem to an eigenvalue problem. For incompressible viscous flow and the assumption of a stationary parallel base flow, this eigenvalue problem is governed by the famous Orr–Sommerfeld equation (see e.g. Schmid & Henningson Reference Schmid and Henningson2001; Drazin & Reid Reference Drazin and Reid2004). The analogue of the Orr–Sommerfeld equation for compressible flow is given by Malik (Reference Malik1990) and Criminale et al. (Reference Criminale, Jackson and Joslin2003) as a coupled set of ordinary differential equations. Together with proper boundary conditions, one can pose the temporal stability problem, where a real wavenumber
${\it\alpha}_{r}$
is given and one solves for the complex angular frequency
${\it\omega}={\it\omega}_{r}+\text{i}{\it\omega}_{i}$
. Here,
${\it\omega}_{r}$
denotes the real angular frequency which is related to the phase speed by
$c={\it\omega}_{r}/{\it\alpha}_{r}$
, and
${\it\omega}_{i}$
is the temporal disturbance growth rate that determines disturbance growth (
${\it\omega}_{i}>0$
) or decay (
${\it\omega}_{i}<0$
).
Solving the linear eigenvalue problem directly yields the eigenvalues
${\it\omega}$
, however without revealing additional information on the underlying principles that lead to a specific solution. In particular, for the temporal growth rate
${\it\omega}_{i}$
an understanding of the mechanisms that induce temporal growth or decay is of great interest because it would clarify which factors determine the linear stability of a given flow. For incompressible viscous flow the individual components that, when summed up, yield the temporal growth rate can be derived from the well-known Reynolds–Orr equation by introducing the normal mode ansatz and solving for
${\it\omega}_{i}$
(Schmid & Henningson Reference Schmid and Henningson2001).
More recently, Malik, Alam & Dey (Reference Malik, Alam and Dey2006), Malik, Dey & Alam (Reference Malik, Dey and Alam2008) presented a study of the transient energy growth in the context of linear stability theory for plane compressible Couette flow. They decomposed the time evolution of the perturbation energy into four contributions, namely the energy transfer rate from the base flow, the viscous dissipation rate, the thermal diffusion rate and the shear-work rate. However, their formulation is only applicable to confined flows without energy flux across a domain boundary. We have removed this restriction by including the flux terms at the domain boundaries. Additionally, Malik et al. (Reference Malik, Alam and Dey2006, Reference Malik, Dey and Alam2008) do not provide a direct relation between
${\it\omega}_{i}$
and the components that determine the temporal energy evolution. Tritarelli (Reference Tritarelli2011) has derived a detailed formulation for the energy evolution in a spatial linear stability framework and applied it to hypersonic boundary layers.
The temporal growth or decay characteristics of a disturbance contained in an arbitrary volume are obviously dependent on the details of the balance between production, dissipation and the flux of disturbance energy across the boundaries of the considered volume. In this paper, we present a novel decomposition of the temporal growth rate for bounded as well as unbounded compressible viscous flow. Our analysis is based on the disturbance energy balance by Chu (Reference Chu1965), the analogue of the Reynolds–Orr equation for compressible flow, and offers a decomposition of
${\it\omega}_{i}$
into production, dissipation, and flux terms (§ 2). This allows us to identify the major contributing terms and to uncover their corresponding growth mechanisms. A detailed classification of the individual contributions helps to analyse the change of instability properties for varying flow conditions, as we will show in § 3 for two well-studied base flows, namely plane Couette flow and plane jet flow. The example of supersonic jet flow highlights the importance of including the flux terms in the growth-rate decomposition.
2. Method
2.1. Governing equations
Two-dimensional compressible gas flow is governed by the Navier–Stokes equations, i.e. the conservation equations of mass, momentum, and energy
$$\begin{eqnarray}\displaystyle \mathscr{D}_{t}{\it\varrho}+{\it\varrho}(\partial _{x}u+\partial _{y}v) & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\varrho}\,\mathscr{D}_{t}u+\partial _{x}p-\partial _{x}{\it\tau}_{xx}-\partial _{y}{\it\tau}_{xy} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\varrho}\,\mathscr{D}_{t}v+\partial _{y}p-\partial _{x}{\it\tau}_{xy}-\partial _{y}{\it\tau}_{yy} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\varrho}c_{v}\,\mathscr{D}_{t}T+p(\partial _{x}u+\partial _{y}v)+\partial _{x}q_{x}+\partial _{y}q_{y}-{\it\Phi} & = & \displaystyle 0,\end{eqnarray}$$
$\mathscr{D}_{t}\equiv \partial _{t}+u\,\partial _{x}+v\,\partial _{y}$
. We use non-dimensional variables where the spatial coordinates
$(x,y)$
are normalised by some characteristic reference length
$L^{\circ }$
, the velocity components
$(u,v)$
by some reference velocity
$\bar{u}_{0}^{\circ }$
, the time
$t$
by the characteristic time
$L^{\circ }/\bar{u}_{0}^{\circ }$
and the thermodynamic pressure
$p$
by the dynamic pressure
$\bar{{\it\varrho}}_{0}^{\circ }\bar{u}_{0}^{\circ 2}$
. Here,
$(\cdot )^{\circ }$
denotes a dimensional quantity and
$(\bar{\cdot })_{0}^{\circ }$
the dimensional base-flow value at a reference point
$(x_{0}^{\circ },y_{0}^{\circ })$
. Mass density
${\it\varrho}$
and absolute temperature
$T$
are normalised by their base-flow value
$(\bar{\cdot })_{0}^{\circ }$
. All dimensional reference quantities are combined into the dimensionless groups 
$$\begin{eqnarray}Re=\bar{{\it\varrho}}_{0}^{\circ }\bar{u}_{0}^{\circ }L^{\circ }/\bar{{\it\mu}}_{0}^{\circ },\quad \mathit{Ma}=\bar{u}_{0}^{\circ }/\bar{a}_{0}^{\circ },\quad Pr=\bar{{\it\mu}}_{0}^{\circ }c_{p}^{\circ }/\bar{k}_{0}^{\circ },\end{eqnarray}$$
known as the Reynolds number, Mach number, and Prandtl number, respectively. In the definition of the Mach number, the speed of sound at the reference point is given as
$\bar{a}_{0}^{\circ }=\sqrt{{\it\gamma}\text{R}^{\circ }\bar{T}_{0}^{\circ }}$
with
$\text{R}^{\circ }$
being the specific gas constant.
We consider a calorically perfect gas with constant specific heats for constant pressure
$c_{p}=[({\it\gamma}-1)\mathit{Ma}^{2}]^{-1}$
and constant volume
$c_{v}=[{\it\gamma}({\it\gamma}-1)\mathit{Ma}^{2}]^{-1}$
, respectively, that obeys the equation of state
$$\begin{eqnarray}p={\it\varrho}T/({\it\gamma}\mathit{Ma}^{2}).\end{eqnarray}$$
The ratio of specific heats is defined as
${\it\gamma}=c_{p}^{\circ }/c_{v}^{\circ }$
. We assume a Newtonian fluid, i.e. a linear deformation law for the shear stress components
$$\begin{eqnarray}\displaystyle & {\it\tau}_{xx}=(2{\it\mu}+{\it\lambda})/Re\,\partial _{x}u+{\it\lambda}/Re\,\partial _{y}v, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\tau}_{xy}={\it\mu}/Re\,(\partial _{y}u+\partial _{x}v), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\tau}_{yy}=(2{\it\mu}+{\it\lambda})/Re\,\partial _{y}v+{\it\lambda}/Re\,\partial _{x}u. & \displaystyle\end{eqnarray}$$
${\it\mu}(T)$
and
${\it\lambda}(T)$
are assumed to be functions of temperature only. Further, we consider Fourier’s law for heat transfer by conduction so that the heat-flux components are given by 
$$\begin{eqnarray}q_{x}=-k/[({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}]\,\partial _{x}T,\quad q_{y}=-k/[({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}]\,\partial _{y}T,\end{eqnarray}$$
where
$k(T)$
indicates the temperature-dependent coefficient of thermal conductivity. Finally, the dissipation function in the equation of energy is defined as
$$\begin{eqnarray}{\it\Phi}={\it\tau}_{xx}\,\partial _{x}u+{\it\tau}_{xy}(\partial _{y}u+\partial _{x}v)+{\it\tau}_{yy}\,\partial _{y}v.\end{eqnarray}$$
Together with appropriate boundary conditions, (2.1)–(2.6) describe the motion of fluid flow under the stated assumptions. If (2.3) is substituted into (2.1), the pressure variable
$p$
can be eliminated so that the unknowns are reduced to the primitive variables
$\boldsymbol{q}=\boldsymbol{q}(x,y,t)=({\it\varrho},u,v,T)^{\text{T}}$
and the Navier–Stokes equations (2.1) can be abbreviated in symbolic form as
$$\begin{eqnarray}{\mathcal{N}}{\mathcal{S}}\{\boldsymbol{q}\}=0.\end{eqnarray}$$
Here,
${\mathcal{N}}{\mathcal{S}}\{\cdot \}$
is the nonlinear Navier–Stokes operator that operates on the primitive-variable vector
$\boldsymbol{q}$
. This notation is used in the following derivations to avoid writing out the lengthy full equations.
2.2. Linear disturbance equations
We assume a stationary parallel base flow, indicated by
$(\bar{\cdot })$
, that depends on the
$y$
-coordinate only, i.e.
$\bar{\boldsymbol{q}}=\bar{\boldsymbol{q}}(y)$
with
$\bar{u}=\bar{u}(y)$
and
$\bar{v}=0$
, satisfying
${\mathcal{N}}{\mathcal{S}}\{\bar{\boldsymbol{q}}\}=0$
. The perturbed base flow is expanded as
$\boldsymbol{q}(x,y,t)=\bar{\boldsymbol{q}}(y)+{\it\varepsilon}\tilde{\boldsymbol{q}}(x,y,t)+O({\it\varepsilon}^{2})$
with
$(\tilde{\cdot })$
denoting first-order disturbance variables. We focus on small disturbances and therefore linearise the governing equations (2.7) around the base-flow solution
$\bar{\boldsymbol{q}}(y)$
by
$\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})\,\tilde{\boldsymbol{q}}=[\partial _{{\it\varepsilon}}{\mathcal{N}}{\mathcal{S}}\{\bar{\boldsymbol{q}}+{\it\varepsilon}\tilde{\boldsymbol{q}}+O({\it\varepsilon}^{2})\}]_{{\it\varepsilon}=0}$
. Here,
$\widetilde{{\mathcal{N}}{\mathcal{S}}}(\cdot )$
is the linear disturbance operator that depends on the base flow
$\bar{\boldsymbol{q}}$
and operates on first-order disturbances
$\tilde{\boldsymbol{q}}$
. The evolution equations for small disturbances
$\tilde{\boldsymbol{q}}$
are then given as
$$\begin{eqnarray}\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})\tilde{\boldsymbol{q}}=0,\end{eqnarray}$$
with the elements of the disturbance operator
$\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})$
provided in the Appendix.
2.3. Disturbance energy balance
In order to derive a balance equation for the disturbance energy we follow Chu (Reference Chu1965) and multiply the continuity equation (2.8)1 by
$\bar{a}^{2}\tilde{{\it\varrho}}/({\it\gamma}\bar{{\it\varrho}})$
with
$\bar{a}^{2}=\bar{T}/\mathit{Ma}^{2}$
, the momentum equation in the
$x$
-direction (2.8)2 by
$\tilde{u}$
, the momentum equation in the
$y$
-direction (2.8)3 by
$\tilde{v}$
, and the energy equation (2.8)4 by
$\tilde{T}/\bar{T}$
and integrate their sum over an arbitrary, but time-independent, domain
${\it\Omega}\subset \mathbb{R}\times \mathbb{R}$
. The resulting scalar equation can symbolically be written as
$$\begin{eqnarray}\int _{{\it\Omega}}\left[\tilde{\boldsymbol{p}}^{\text{T}}\,\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})\,\tilde{\boldsymbol{q}}\right]\text{d}V=0,\end{eqnarray}$$
where the multiplication factors are collected in the vector
$\tilde{\boldsymbol{p}}=(\bar{a}^{2}\tilde{{\it\varrho}}/({\it\gamma}\bar{{\it\varrho}}),\tilde{u} ,\tilde{v},\tilde{T}/\bar{T})^{\text{T}}$
and
$\text{d}V=\text{d}x\,\text{d}y$
denotes an infinitesimal area element. According to Chu (Reference Chu1965) all terms in (2.9) with time derivatives are collected and the disturbance energy is consequently defined as
$$\begin{eqnarray}\tilde{E}=\int _{{\it\Omega}}\left[\frac{1}{2}\bar{{\it\varrho}}\left(\tilde{u} ^{2}+\tilde{v}^{2}\right)+\frac{1}{2}\frac{\bar{a}^{2}\tilde{{\it\varrho}}^{2}}{{\it\gamma}\bar{{\it\varrho}}}+\frac{1}{2}\frac{\bar{{\it\varrho}}c_{v}\tilde{T}^{2}}{\bar{T}}\right]\text{d}V.\end{eqnarray}$$
By considering (2.10) and with the aid of Gauss’ divergence theorem (integration by parts in space) we can rearrange (2.9) into the balance equation for the disturbance energy
$$\begin{eqnarray}\frac{\text{d}\tilde{E}}{\text{d}t}=-\int _{{\it\Omega}}\bar{{\it\varrho}}\tilde{u} \tilde{v}\,\frac{\text{d}\bar{u}}{\text{d}y}\,\text{d}V-\int _{{\it\Omega}}\bar{{\it\varrho}}\tilde{v}\tilde{s}\,\frac{\text{d}\bar{T}}{\text{d}y}\,\text{d}V+\int _{{\it\Omega}}\frac{\tilde{T}}{\bar{T}}\tilde{Q}\,\text{d}V\end{eqnarray}$$
$$\begin{eqnarray}-\int _{{\it\Omega}}\left[\tilde{{\it\tau}}_{xx}\,\partial _{x}\tilde{u} +\tilde{{\it\tau}}_{xy}(\partial _{y}\tilde{u} +\partial _{x}\tilde{v})+\tilde{{\it\tau}}_{yy}\,\partial _{y}\tilde{v}\right]\,\text{d}V+\int _{{\it\Omega}}[\tilde{q}_{x}\,\partial _{x}+\tilde{q}_{y}\,\partial _{y}]\frac{\tilde{T}}{\bar{T}}\,\text{d}V\end{eqnarray}$$
$$\begin{eqnarray}-\int _{\partial {\it\Omega}}\tilde{p}[\tilde{u} n_{x}+\tilde{v}n_{y}]\,\text{d}S+\int _{\partial {\it\Omega}}\left[\tilde{{\it\tau}}_{xx}\tilde{u} n_{x}+\tilde{{\it\tau}}_{xy}(\tilde{u} n_{y}+\tilde{v}n_{x})+\tilde{{\it\tau}}_{yy}\tilde{v}n_{y}\right]\,\text{d}S\end{eqnarray}$$
$$\begin{eqnarray}-\int _{\partial {\it\Omega}}\frac{\tilde{T}}{\bar{T}}[\tilde{q}_{x}n_{x}+\tilde{q}_{y}n_{y}]\,\text{d}S\end{eqnarray}$$
$$\begin{eqnarray}+\frac{1}{Re}\int _{{\it\Omega}}\partial _{y}\left[\tilde{u} \tilde{T}\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}\right]\text{d}V+\frac{1}{Re}\int _{{\it\Omega}}\partial _{x}\left[\tilde{v}\tilde{T}\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}\right]\text{d}V\end{eqnarray}$$
$$\begin{eqnarray}-\int _{{\it\Omega}}\partial _{x}\left[\frac{1}{2}\bar{u}\bar{p}\frac{\tilde{{\it\varrho}}^{2}}{\bar{{\it\varrho}}^{2}}+\frac{1}{2}\frac{\bar{u}\bar{p}}{{\it\gamma}-1}\frac{\tilde{T}^{2}}{\bar{T}^{2}}+\frac{1}{2}\bar{u}\bar{{\it\varrho}}(\tilde{u} ^{2}+\tilde{v}^{2})\right]\text{d}V.\end{eqnarray}$$
Unlike Chu (Reference Chu1965) we take non-vanishing disturbances at the domain boundary
$\partial {\it\Omega}$
into account which yields the additional terms (2.11f–h
). The outward unit vector to
$\partial {\it\Omega}$
is denoted as
$(n_{x},n_{y})^{\text{T}}$
and the infinitesimal line element on
$\partial {\it\Omega}$
as
$\text{d}S$
. The disturbance shear stress components are defined as
$$\begin{eqnarray}\displaystyle \tilde{{\it\tau}}_{xx}=\frac{2\bar{{\it\mu}}+\bar{{\it\lambda}}}{Re}\partial _{x}\tilde{u} +\frac{\bar{{\it\lambda}}}{Re}\partial _{y}\tilde{v},\quad \tilde{{\it\tau}}_{xy}=\frac{\bar{{\it\mu}}}{Re}(\partial _{y}\tilde{u} +\partial _{x}\tilde{v}),\quad \tilde{{\it\tau}}_{yy}=\frac{2\bar{{\it\mu}}+\bar{{\it\lambda}}}{Re}\partial _{y}\tilde{v}+\frac{\bar{{\it\lambda}}}{Re}\partial _{x}\tilde{u} , & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
the disturbance heat-flux components as
$$\begin{eqnarray}\tilde{q}_{x}=-\frac{\bar{k}}{({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}}\partial _{x}\tilde{T},\quad \tilde{q}_{y}=-\frac{\bar{k}}{({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}}\partial _{y}\tilde{T}\end{eqnarray}$$
and the specific disturbance heat source as
$$\begin{eqnarray}\displaystyle \tilde{Q} & = & \displaystyle \frac{1}{Re}\left(2\bar{{\it\mu}}-\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\bar{T}\right)\frac{\text{d}\bar{u}}{\text{d}y}\left(\frac{\partial \tilde{u} }{\partial y}+\frac{\partial \tilde{v}}{\partial x}\right)+\frac{1}{({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}}\frac{\bar{k}}{\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\frac{\partial \tilde{T}}{\partial y}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{Re}\tilde{T}\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\left(\frac{\text{d}\bar{u}}{\text{d}y}\right)^{2}+\frac{1}{({\it\gamma}-1)Re\,Pr\,\mathit{Ma}^{2}}\frac{\partial }{\partial y}\left(\tilde{T}\frac{\text{d}\bar{k}}{\text{d}\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\right).\end{eqnarray}$$
The specific disturbance entropy introduced in (2.11b
) is given as
$\tilde{s}=[({\it\gamma}-1)^{-1}\tilde{T}/\bar{T}-\tilde{{\it\varrho}}/\bar{{\it\varrho}}]/({\it\gamma}\mathit{Ma}^{2})$
, where the relation
$s-s_{0}=c_{v}\ln (T/T_{0})+\text{R}\ln ({\it\varrho}_{0}/{\it\varrho})$
for a calorically perfect gas with the specific gas constant
$\text{R}=1/({\it\gamma}\mathit{Ma}^{2})$
was used (Moran & Shapiro Reference Moran and Shapiro2000).
2.4. Decomposition of temporal growth rate
${\it\omega}_{i}$
We are interested in the temporal evolution of the disturbance energy for normal modes, i.e. disturbances with wave-like shape. Thus, we introduce the normal mode ansatz
$$\begin{eqnarray}\tilde{q}(x,y,t)=\text{Re}\left[\hat{q}({\it\alpha}_{r},y,{\it\omega})\,\text{e}^{\text{i}({\it\alpha}_{r}x-{\it\omega}t)}\right],\quad q\in \{{\it\varrho},u,v,T,s\},\end{eqnarray}$$
where
$\hat{q}({\it\alpha}_{r},y,{\it\omega})$
denotes the complex first-order disturbance amplitude,
${\it\alpha}_{r}\in \mathbb{R}$
the streamwise wavenumber and
${\it\omega}=({\it\omega}_{r}+\text{i}{\it\omega}_{i})\in \mathbb{C}$
the complex angular frequency. The wave-like disturbances are spatially periodic in the
$x$
-direction and restricted to a finite domain in the
$y$
-direction,
$y^{-}\leqslant y\leqslant y^{+}$
. Hence it is sufficient to consider the fluid domain
${\it\Omega}^{\text{t}}=[0,2{\rm\pi}/{\it\alpha}_{r})\times [y^{-},y^{+}]$
, where
$2{\rm\pi}/{\it\alpha}_{r}$
denotes the disturbance wavelength.
We evaluate the integrals in (2.10) and (2.11) over the domain
${\it\Omega}^{\text{t}}$
for normal modes and use the relation
$$\begin{eqnarray}\int _{0}^{2{\rm\pi}/{\it\alpha}_{r}}\tilde{f}\tilde{g}\,\text{d}x=\frac{{\rm\pi}}{{\it\alpha}_{r}}\text{e}^{2{\it\omega}_{i}t}\langle \hat{f},{\hat{g}}\rangle\end{eqnarray}$$
for products of disturbance quantities, e.g.
$\tilde{f}\tilde{g}\in \mathbb{R}$
with
$\tilde{f},\tilde{g}\in \{\tilde{{\it\varrho}},\tilde{u} ,\tilde{v},\tilde{T},\tilde{s}\}$
. The inner product is given by
$\langle \hat{f},{\hat{g}}\rangle \equiv (\hat{f}^{\ast }{\hat{g}}+\hat{f}{\hat{g}}^{\ast })/2$
where
$(\cdot )^{\ast }$
stands for the complex conjugate. Terms (2.11j,k
) as well as the boundary integrals
$\int _{\partial {\it\Omega}^{\text{t}}}(\cdot )\,n_{x}\,\text{d}S$
in (2.11f–h
) vanish because of disturbance periodicity in the
$x$
-direction, and from (2.16) it follows that
$\text{d}\tilde{E}/\text{d}t=2{\it\omega}_{i}\tilde{E}$
. We can therefore rewrite equation (2.11) for normal modes in the domain
${\it\Omega}^{\text{t}}$
as the decomposition
$$\begin{eqnarray}{\it\omega}_{i}=\mathop{\sum }_{i=1}^{3}\frac{\hat{P}_{i}}{2\hat{E}}+\mathop{\sum }_{j=1}^{2}\frac{\hat{D}_{j}}{2\hat{E}}+\mathop{\sum }_{k=1}^{4}\frac{\hat{F}_{k}}{2\hat{E}},\end{eqnarray}$$
where
$$\begin{eqnarray}\hat{E}=\frac{1}{2}\int _{y^{-}}^{y^{+}}\left[\bar{{\it\varrho}}(\langle \hat{u} ,\hat{u} \rangle +\langle \hat{v},\hat{v}\rangle )+\frac{\bar{a}^{2}\langle \hat{{\it\varrho}},\hat{{\it\varrho}}\rangle }{{\it\gamma}\bar{{\it\varrho}}}+\frac{\bar{{\it\varrho}}c_{v}\langle \hat{T},\hat{T}\rangle }{\bar{T}}\right]\text{d}y\end{eqnarray}$$
denotes the disturbance energy amplitude and
$$\begin{eqnarray}\displaystyle \hat{P}_{1}=\int _{y^{-}}^{y^{+}}-\bar{{\it\varrho}}\langle \hat{u} ,\hat{v}\rangle \,\frac{\text{d}\bar{u}}{\text{d}y}\,\text{d}y,\quad \hat{P}_{2}=\int _{y^{-}}^{y^{+}}-\bar{{\it\varrho}}\langle \hat{v},{\hat{s}}\rangle \,\frac{\text{d}\bar{T}}{\text{d}y}\,\text{d}y,\quad \hat{P}_{3}=\int _{y^{-}}^{y^{+}}\frac{\langle \hat{T},\hat{Q}\rangle }{\bar{T}}\,\text{d}y, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\hat{D}_{1}=\int _{y^{-}}^{y^{+}}-\!\left[\langle \hat{{\it\tau}}_{xx},\text{i}{\it\alpha}_{r}\hat{u} \rangle +\langle \hat{{\it\tau}}_{xy},\mathscr{D}_{y}\hat{u} \rangle +\langle \hat{{\it\tau}}_{xy},\text{i}{\it\alpha}_{r}\hat{v}\rangle +\langle \hat{{\it\tau}}_{yy},\mathscr{D}_{y}\hat{v}\rangle \right]\text{d}y,\end{eqnarray}$$
$$\begin{eqnarray}\hat{D}_{2}=\int _{y^{-}}^{y^{+}}\frac{\langle \hat{q}_{x},\text{i}{\it\alpha}_{r}\hat{T}\rangle +\langle \hat{q}_{y},\mathscr{D}_{y}\hat{T}\rangle }{\bar{T}}\,\text{d}y,\end{eqnarray}$$
$$\begin{eqnarray}\hat{F}_{1}=-\langle \hat{p},\hat{v}\rangle \big|_{y^{-}}^{y^{+}},\quad \hat{F}_{2}=\langle \hat{{\it\tau}}_{xy},\hat{u} \rangle \big|_{y^{-}}^{y^{+}}+\langle \hat{{\it\tau}}_{yy},\hat{v}\rangle \big|_{y^{-}}^{y^{+}},\end{eqnarray}$$
$$\begin{eqnarray}\hat{F}_{3}=\left.-\frac{\langle \hat{T},\hat{q}_{y}\rangle }{\bar{T}}\right|_{y^{-}}^{y^{+}},\quad \hat{F}_{4}=\frac{1}{Re}\left[\langle \hat{u} ,\hat{T}\rangle \frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}\right]_{y^{-}}^{y^{+}}\end{eqnarray}$$
define amplitudes of production
$\hat{P}_{i}$
, of dissipation
$\hat{D}_{j}$
, and of flux
$\hat{F}_{k}$
, respectively, with
$\mathscr{D}_{y}\equiv \text{d}/\text{d}y$
.
The production term
$\hat{P}_{1}$
describes the interaction of Reynolds stress
$-\bar{{\it\varrho}}\langle \hat{u} ,\hat{v}\rangle$
with the base-flow velocity gradient
$\text{d}\bar{u}/\text{d}y$
and is the key component for inviscid flow. Interaction between entropy flux density
$-\bar{{\it\varrho}}\langle \hat{v},{\hat{s}}\rangle$
and base-flow temperature gradient
$\text{d}\bar{T}/\text{d}y$
characterises the production term
$\hat{P}_{2}$
. The third term
$\hat{P}_{3}$
includes production of disturbance energy due to change of transport properties
${\it\mu}$
and
$k$
with temperature. Production terms
$\hat{P}_{i}$
can be positive and negative and therefore enhance disturbance growth or decay. Pure dissipative effects are incorporated in the dissipation terms
$\hat{D}_{1}$
and
$\hat{D}_{2}$
, which describe viscous and thermal dissipation, respectively. Disturbance energy convected across the domain boundary
$\partial {\it\Omega}$
is represented by the flux terms
$\hat{F}_{k}$
. Terms
$\hat{F}_{1}$
and
$\hat{F}_{2}$
describe the net flux of mechanical energy and
$\hat{F}_{3}$
the net flux of thermal disturbance energy across the domain boundary. The last flux term
$\hat{F}_{4}$
arises due to the temperature-dependence of the viscosity.
Figure 1. Disturbance amplitudes of mode-II instability for plane compressible Couette flow at
$Re=2.5\times 10^{5}$
,
$\mathit{Ma}=5$
,
${\it\alpha}_{r}=2.4$
. (a,d)
$x$
-component of disturbance velocity
$\hat{u}$
, (b,e)
$y$
-component of disturbance velocity
$\hat{v}$
, (c, f) temperature disturbance
$\hat{T}$
. (a–c) Magnified sections of (d–f) near the top boundary layer at
$y^{+}=1$
. Magnitude (solid lines), real part (dashed lines), imaginary part (dash-dotted lines).
3. Results
In the following, we briefly present the application of the theory using two examples, namely compressible Couette flow and plane jet flow. We would like to stress that the goal of this section is not a comprehensive study of the linear stability of these flows, since this has been carried out before (see e.g. Duck, Erlebacher & Hussaini Reference Duck, Erlebacher and Hussaini1994; Hu & Zhong Reference Hu and Zhong1998 and Parras & Le Dizès Reference Parras and Le Dizès2010), but rather to exemplify the more profound physical understanding of instability mechanisms that can be gained from the proposed decomposition of the temporal growth rate
${\it\omega}_{i}$
.
The spectra of both examples are obtained from a linear stability solver, where the disturbance equations for the temporal problem were discretised using the Chebyshev collocation method (Malik Reference Malik1990; Peyret Reference Peyret2002) and the resulting generalised eigenvalue problem was solved by the QZ algorithm. The integrals in (2.18) and (2.19) are evaluated numerically by applying the Chebyshev–Gauss quadrature of the second kind on the computed discrete eigenfunctions (Abramowitz & Stegun Reference Abramowitz and Stegun1972).
3.1. Plane Couette flow
Compressible plane Couette flow is the solution of (2.1) subject to the boundary conditions
$u(y^{-})=0$
,
$u(y^{+})=1$
,
$T(y^{-})=T_{w}$
,
$T(y^{+})=1$
with the fluid domain
$[y^{-},y^{+}]=[0,1]$
and the recovery temperature
$T_{w}=1+({\it\gamma}-1)Pr\mathit{Ma}^{2}/2$
. The linear stability of this flow was extensively studied by Duck et al. (Reference Duck, Erlebacher and Hussaini1994) and Hu & Zhong (Reference Hu and Zhong1998). Here, we provide further insight into the growth mechanisms of compressible Couette flow by exemplarily applying the decomposition proposed in § 2 to the so-called mode-II instability (Hu & Zhong Reference Hu and Zhong1998). Disturbance amplitudes for mode II at
$Re=2.5\times 10^{5}$
,
$\mathit{Ma}=5$
,
${\it\alpha}_{r}=2.4$
are plotted in figure 1. The
$x$
-component of the disturbance velocity and the temperature disturbance show large gradients near the top boundary which obeys the Dirichlet boundary condition.
Figure 2. Decomposition of temporal growth rate
${\it\omega}_{i}$
according to (2.17) of mode-II instability (Hu & Zhong Reference Hu and Zhong1998) for plane compressible Couette flow as a function of
$Re$
;
$\mathit{Ma}=5$
,
${\it\alpha}_{r}=2.4$
.
The temporal growth rate
${\it\omega}_{i}$
and its decomposition into production and dissipation terms for
$\mathit{Ma}=5$
,
${\it\alpha}_{r}=2.4$
as a function of
$Re$
are shown in figure 2. The flux terms are all zero because of the vanishing velocity, temperature and heat-flux fluctuations at the boundary. The production terms
$\hat{P}_{2}/2\hat{E}$
and
$\hat{P}_{3}/2\hat{E}$
and the dissipation term
$\hat{D}_{1}/2\hat{E}$
are small and roughly cancel each other. Therefore, the production term
$\hat{P}_{1}/2\hat{E}$
and the dissipation term
$\hat{D}_{2}/2\hat{E}$
are the major components of
${\it\omega}_{i}$
. In the low-
$Re$
regime (
$Re<10^{5}$
), the growth rate is dominated by the strongly negative dissipation term
$\hat{D}_{2}/2\hat{E}$
, which is related to thermal dissipation, whereas viscous dissipation plays a minor role. With rising
$Re$
, the influence of the thermal dissipation is reduced while the production term
$\hat{P}_{1}/2\hat{E}$
rises to its maximum resulting in a positive temporal growth rate
${\it\omega}_{i}$
. For even higher
$Re$
, the production term
$\hat{P}_{1}/2\hat{E}$
, which quantifies the interaction between Reynolds stress and base-flow velocity gradient, decreases and hence the growth rate also becomes smaller.
Figure 3. Integrands of (a,c) production term
$\hat{P}_{1}$
and (b,d) dissipation term
$\hat{D}_{2}$
for mode-II instability of plane compressible Couette flow at
$Re=2.5\times 10^{5}$
,
$\mathit{Ma}=5$
,
${\it\alpha}_{r}=2.4$
. (a,b) Magnified sections of (c,d) near the top boundary layer at
$y^{+}=1$
.
For a deeper level of understanding we further analyse the major terms of the decomposition for the given flow, namely production
$\hat{P}_{1}$
(2.19a
) and dissipation
$\hat{D}_{2}$
(2.19e
). Both terms are defined as integrals over the domain
$[y^{-},y^{+}]$
. The respective integrands are plotted in figure 3 for the same flow parameters as in figure 1. The integrand of production
$\hat{P}_{1}$
, which measures the interaction of Reynolds stress with base-flow velocity gradient, is nearly constant except for the spike at the top boundary
$y^{+}$
and the gradual decrease at the bottom boundary
$y^{-}$
. On the other hand, the integrand of the thermal dissipation
$\hat{D}_{2}$
is zero except in the very thin boundary layer near
$y^{+}=1$
, where the integrand sharply drops to a negative value due to large fluctuations in the heat-flux component
$\hat{q}_{y}$
. This analysis of the integrands reveals that the disturbance production is nearly homogeneously distributed over the domain
$[y^{-},y^{+}]$
, whereas the major thermal dissipation is limited to a small region near the top boundary.
3.2. Plane jet flow
The local temporal linear stability of supersonic round jet flow has been studied recently by Parras & Le Dizès (Reference Parras and Le Dizès2010). In the following, we consider a plane supersonic jet. We will show that under certain conditions the flux terms can be used to quantify a stabilising mechanism due to radiation which is observed for certain supersonic jet instability modes.
As base-flow velocity we choose the profile proposed by Michalke (Reference Michalke1984)
$$\begin{eqnarray}\bar{u}(y)=\frac{1}{2}\left[1+\text{tanh}\left(\frac{1}{4{\it\theta}}\left(\frac{1}{|y|}-|y|\right)\right)\right],\end{eqnarray}$$
where we set the momentum thickness
${\it\theta}=0.1$
. According to this definition, the velocity shear layers are located at
$y=\pm 1$
. The temperature profile
$\bar{T}(y)$
is computed according to the Crocco–Busemann relation (Busemann Reference Busemann1935), which for a temperature ratio
$\bar{T}(\infty )/\bar{T}(0)=1$
and a vanishing ambient velocity
$\bar{u}(\infty )=0$
simplifies to
$$\begin{eqnarray}\bar{T}(y)=1+\mathit{Ma}^{2}({\it\gamma}-1)\left(\bar{u}(y)-\bar{u}^{2}(y)\right).\end{eqnarray}$$
We set the physical domain to
$[y^{-},y^{+}]=[-20,+20]$
and apply the coordinate mapping proposed by Bayliss & Turkel (Reference Bayliss and Turkel1992) to accumulate the collocation points near the shear layers. At the domain boundaries
$y^{\pm }$
, we use the far-field boundary condition given by Thompson (Reference Thompson1987).
Figure 5. (a,b) Decomposition of temporal growth rate
${\it\omega}_{i}$
according to (2.17) of (a) mode-I and (b) mode-II instability for plane jet flow at various
${\it\alpha}$
. (c,d) Streamwise velocity component
$\hat{u}$
of (c) mode I and (d) mode II for
${\it\alpha}=0.5$
. Magnitude
$|\hat{u} |$
(solid lines), real part
$\text{Re}\,\hat{u}$
(dashed lines), imaginary part
$\text{Im}\,\hat{u}$
(dash-dotted lines).
Figure 4 shows different types of temporally unstable modes for the given base flow at
$\mathit{Ma}=2.5$
and
$Re=10^{6}$
. Here, these modes are called modes I to III and they exhibit partially overlapping ranges of unstable streamwise wavenumbers. Mode II reaches maximum temporal growth for
${\it\alpha}\approx 0.55$
. In the following, we demonstrate the importance of flux terms by comparing results of mode I and mode II. The decomposition of the temporal growth rates and representative eigenfunctions
$\hat{u} (z)$
of both modes are shown in figure 5. Mode II is of classical Kelvin–Helmholtz type, which is characterised by large disturbance amplitudes in the base-flow shear layer and small amplitudes elsewhere (figure 5
d). Its decomposition (figure 5
b) reveals only contributions of
$\hat{P}_{1}/2\hat{E}$
(interaction of Reynolds stress with base-flow velocity gradient) and
$\hat{P}_{2}/2\hat{E}$
(interaction of entropy flux density with base-flow temperature gradient). The remaining components of (2.17) are negligibly small due to the large Reynolds number and the vanishing disturbance amplitudes in the far field. Compared to mode II, we recognise the additional negative flux term
$\hat{F}_{1}/2\hat{E}$
in the decomposition of mode I (figure 5
a). This flux term quantifies the net flux of mechanical disturbance energy across the domain boundary and is caused by the radiating Mach-wave character of mode I (Tam & Hu Reference Tam and Hu1989). This mode features non-vanishing eigenfunctions in the far field (figure 5
c) and therefore exhibits an additional stabilising mechanism due to sound radiation.
4. Discussion
In this paper, a detailed formulation for the decomposition of the temporal growth rate of linear instability modes has been derived for two-dimensional parallel compressible viscous gas flow. The contributing terms can be classified as production, dissipation and flux terms. The analysis identifies the relevant underlying mechanisms that determine the linear stability of a given flow and quantifies the relative influence of different base-flow properties such as velocity shear, temperature gradients, compressibility or viscous effects, to name but a few.
The usefulness of this formulation in gaining a deeper understanding of linear instability in compressible flows and the capability to quantify the sensitivity of eigenmodes with respect to changes in the parameter space have been demonstrated for plane Couette flow (figure 2) and plane jet flow (figure 5) at supersonic Mach numbers. These examples highlight the distinct physical mechanisms that are responsible for disturbance growth under certain flow conditions. Furthermore, inclusion of flux terms allows the quantification of damping effects which can be present in unconfined flows, e.g. due to Mach-wave radiation in supersonic open shear flows.
Appendix A. Linear disturbance equations
The linear disturbance equations for plane compressible flow were derived in § 2.2 under the assumption of a calorically perfect gas and a stationary parallel base flow (
$\bar{\boldsymbol{q}}=\bar{\boldsymbol{q}}(y)$
,
$\bar{v}=0$
). Here we provide the full disturbance equations by listing the non-zero elements of the linear disturbance operator
$\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})$
, i.e.
$$\begin{eqnarray}\widetilde{{\mathcal{N}}{\mathcal{S}}}(\bar{\boldsymbol{q}})\,\tilde{\boldsymbol{q}}=\left[\begin{array}{@{}cccc@{}}\widetilde{{\mathcal{N}}{\mathcal{S}}}_{11} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{12} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{13} & 0\\ \widetilde{{\mathcal{N}}{\mathcal{S}}}_{21} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{22} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{23} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{24}\\ \widetilde{{\mathcal{N}}{\mathcal{S}}}_{31} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{32} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{33} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{34}\\ 0 & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{42} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{43} & \widetilde{{\mathcal{N}}{\mathcal{S}}}_{44}\end{array}\right]\left[\begin{array}{@{}c@{}}\tilde{{\it\varrho}}\\ \tilde{u} \\ \tilde{v}\\ \tilde{T}\end{array}\right]=0,\end{eqnarray}$$
with the coefficients for the equation of continuity
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{11}=\partial _{t}+\bar{u}\,\partial _{x}\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{12}=\bar{{\it\varrho}}\,\partial _{x}\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{13}=\frac{\text{d}\bar{{\it\varrho}}}{\text{d}y}+\bar{{\it\varrho}}\,\partial _{y},\end{array}\right\}\end{eqnarray}$$
the coefficients for the equation of momentum in the
$x$
-direction
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{21}=\frac{\bar{T}}{\mathit{Ma}^{2}{\it\gamma}}\partial _{x}\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{22}=\bar{{\it\varrho}}\,\partial _{t}+\bar{u}\bar{{\it\varrho}}\,\partial _{x}-\frac{1}{Re}\bigg((\bar{{\it\lambda}}+2\bar{{\it\mu}})\,\partial _{x}^{2}+\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\,\partial _{y}+\bar{{\it\mu}}\,\partial _{y}^{2}\bigg)\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{23}=\bar{{\it\varrho}}\frac{\text{d}\bar{u}}{\text{d}y}-\frac{1}{Re}\bigg(\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\,\partial _{x}+(\bar{{\it\lambda}}+\bar{{\it\mu}})\,\partial _{x}\partial _{y}\bigg)\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{24}=\frac{\bar{{\it\varrho}}}{\mathit{Ma}^{2}{\it\gamma}}\partial _{x}-\frac{1}{Re}\bigg(\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}^{2}\bar{u}}{\text{d}y^{2}}+\frac{\text{d}^{2}\bar{{\it\mu}}}{\text{d}\bar{T}^{2}}\frac{\text{d}\bar{u}}{\text{d}y}\frac{\text{d}\bar{T}}{\text{d}y}+\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}\partial _{y}\bigg),\end{array}\right\}\end{eqnarray}$$
the coefficients for the equation of momentum in the
$y$
-direction
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{31}=\frac{1}{\mathit{Ma}^{2}{\it\gamma}}\bigg(\frac{\text{d}\bar{T}}{\text{d}y}+\bar{T}\,\partial _{y}\bigg)\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{32}=-\frac{1}{Re}\bigg(\frac{\text{d}\bar{{\it\lambda}}}{\text{d}\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\,\partial _{x}+(\bar{{\it\lambda}}+\bar{{\it\mu}})\,\partial _{x}\partial _{y}\bigg)\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{33}=\bar{{\it\varrho}}\,\partial _{t}+\bar{u}\bar{{\it\varrho}}\,\partial _{x}-\frac{1}{Re}\bigg[\bar{{\it\mu}}\,\partial _{x}^{2}+\bigg(\frac{\text{d}\bar{{\it\lambda}}}{\text{d}\bar{T}}+2\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\bigg)\frac{\text{d}\bar{T}}{\text{d}y}\,\partial _{y}+(\bar{{\it\lambda}}+2\bar{{\it\mu}})\,\partial _{y}^{2}\bigg]\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{34}=\frac{1}{\mathit{Ma}^{2}{\it\gamma}}\bigg(\frac{\text{d}\bar{{\it\varrho}}}{\text{d}y}+\bar{{\it\varrho}}\,\partial _{y}\bigg)-\frac{1}{Re}\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}\,\partial _{x},\end{array}\right\}\end{eqnarray}$$
and the coefficients for the equation of energy
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{42}=\frac{\bar{{\it\varrho}}\bar{T}}{\mathit{Ma}^{2}{\it\gamma}}\,\partial _{x}-\frac{2\bar{{\it\mu}}}{Re}\frac{\text{d}\bar{u}}{\text{d}y}\partial _{y}\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{43}=\frac{\bar{{\it\varrho}}}{\mathit{Ma}^{2}{\it\gamma}}\bigg(\frac{1}{{\it\gamma}-1}\frac{\text{d}\bar{T}}{\text{d}y}+\bar{T}\,\partial _{y}\bigg)-\frac{2\bar{{\it\mu}}}{Re}\frac{\text{d}\bar{u}}{\text{d}y}\,\partial _{x}\\ \displaystyle \widetilde{{\mathcal{N}}{\mathcal{S}}}_{44}=\frac{1}{\mathit{Ma}^{2}({\it\gamma}-1)}\bigg\{\frac{\bar{{\it\varrho}}}{{\it\gamma}}(\partial _{t}+\bar{u}\partial _{x})-\frac{1}{RePr}\bigg[\frac{\text{d}\bar{k}}{\text{d}\bar{T}}\frac{\text{d}^{2}\bar{T}}{\text{d}y^{2}}+\frac{\text{d}^{2}\bar{k}}{\text{d}\bar{T}^{2}}\bigg(\frac{\text{d}\bar{T}}{\text{d}y}\bigg)^{2}\\ \displaystyle \phantom{\widetilde{{\mathcal{N}}{\mathcal{S}}}_{44}=}+2\frac{\text{d}\bar{k}}{\text{d}\bar{T}}\frac{\text{d}\bar{T}}{\text{d}y}\,\partial _{y}+\bar{k}(\partial _{x}^{2}+\partial _{y}^{2})\bigg]\!\bigg\}-\frac{1}{Re}\frac{\text{d}\bar{{\it\mu}}}{\text{d}\bar{T}}\frac{\text{d}\bar{u}}{\text{d}y}^{2}.\end{array}\right\}\end{eqnarray}$$
