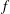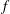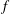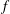1. Introduction
Atmospheric gravity waves (inertia–gravity waves) whose restoring force is buoyancy and
![]() $f$
(Coriolis parameter) are small-scale waves compared to vortical flows, which directly influence the daily weather system. Nevertheless, it is now widely known that gravity waves play an essential role in the atmosphere, especially in the middle atmosphere, where gravity waves drive the general circulation (cf. Holton et al.
Reference Holton, Haynes, McIntyre, Douglass, Road and Pfister1995; Fritts & Alexander Reference Fritts and Alexander2003). Since gravity waves propagate far from their source region, usually the lower atmosphere with high density, they carry a significant amount of energy and momentum to the upper atmosphere with low density. This role of gravity waves is quite important for climate modelling and simulation, since the general circulation and material transport in the middle atmosphere significantly affect the climate. It is therefore important to understand precisely the dynamical processes of gravity waves, i.e. radiation, propagation and dissipation, in order to obtain reliable projections of future climate change. In the present study, we focus on an important radiation process of gravity waves, called ‘spontaneous (gravity wave) radiation’ (see Ford, McIntyre & Norton Reference Ford, McIntyre and Norton2000), since gravity waves are spontaneously radiated from unsteady nearly balanced vortical flows.
$f$
(Coriolis parameter) are small-scale waves compared to vortical flows, which directly influence the daily weather system. Nevertheless, it is now widely known that gravity waves play an essential role in the atmosphere, especially in the middle atmosphere, where gravity waves drive the general circulation (cf. Holton et al.
Reference Holton, Haynes, McIntyre, Douglass, Road and Pfister1995; Fritts & Alexander Reference Fritts and Alexander2003). Since gravity waves propagate far from their source region, usually the lower atmosphere with high density, they carry a significant amount of energy and momentum to the upper atmosphere with low density. This role of gravity waves is quite important for climate modelling and simulation, since the general circulation and material transport in the middle atmosphere significantly affect the climate. It is therefore important to understand precisely the dynamical processes of gravity waves, i.e. radiation, propagation and dissipation, in order to obtain reliable projections of future climate change. In the present study, we focus on an important radiation process of gravity waves, called ‘spontaneous (gravity wave) radiation’ (see Ford, McIntyre & Norton Reference Ford, McIntyre and Norton2000), since gravity waves are spontaneously radiated from unsteady nearly balanced vortical flows.
Recently, many observational studies have reported that gravity waves are radiated not only from orographic sources and convection but also from unsteady flows, such as polar night jets (Yoshiki & Sato Reference Yoshiki and Sato2000; Sato & Yoshiki Reference Sato and Yoshiki2008), subtropical jets (Uccelini & Koch Reference Uccelini and Koch1987; Kitamura & Hirota Reference Kitamura and Hirota1989; Sato Reference Sato1994; Plougonven, Teitelbaum & Zeitlin Reference Plougonven, Teitelbaum and Zeitlin2003) and tropical cyclones (Pfister et al.
Reference Pfister, Chan, Bui, Bowen, Legg, Gary, Kelly, Proffitt and Starr1993; May Reference May1996; Wu & Eckermann Reference Wu and Eckermann2008). The radiation process in the atmosphere was initially investigated by a numerical simulation of the baroclinic life cycle (O’Sullivan & Dunkerton Reference O’Sullivan and Dunkerton1995) and is now widely recognized as spontaneous gravity wave radiation. Many numerical (e.g. Schecter & Montgomery Reference Schecter and Montgomery2004; Zhang Reference Zhang2004; Dritschel & Vanneste Reference Dritschel and Vanneste2006; Plougonven & Snyder Reference Plougonven and Snyder2007; Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007; Wang, Zhang & Snyder Reference Wang, Zhang and Snyder2009), theoretical (Vanneste Reference Vanneste2008; Yasuda, Sato & Sugimoto Reference Yasuda, Sato and Sugimoto2015a
,Reference Yasuda, Sato and Sugimoto
b
) and experimental (Williams, Read & Haine Reference Williams, Read and Haine2003; Williams, Haine & Read Reference Williams, Haine and Read2005; Afanasyev, Rhines & Lindahl Reference Afanasyev, Rhines and Lindahl2008; Williams, Haine & Read Reference Williams, Haine and Read2008) studies have been made on this topic, from both practical and theoretical perspectives, since the process is directly related to the accuracy of ‘balanced models’ (for example, the quasi-geostrophic system). In a balanced model, slow balanced vortical motions are free from fast inertia–gravity waves, and the time evolution of the flow field is completely determined by vortical motions. The accuracy of a balanced model is determined by the time-scale separation of these modes for a small Rossby number (
![]() $\mathit{Ro}$
), which corresponds to strong rotation of the Earth. However, the separation is not complete, and the time evolution of vortical motions inevitably radiates gravity waves spontaneously (Ford et al.
Reference Ford, McIntyre and Norton2000; Vanneste Reference Vanneste2008). Recent comprehensive reviews of this topic can be found in Vanneste (Reference Vanneste2013) and Plougonven & Zhang (Reference Plougonven and Zhang2014).
$\mathit{Ro}$
), which corresponds to strong rotation of the Earth. However, the separation is not complete, and the time evolution of vortical motions inevitably radiates gravity waves spontaneously (Ford et al.
Reference Ford, McIntyre and Norton2000; Vanneste Reference Vanneste2008). Recent comprehensive reviews of this topic can be found in Vanneste (Reference Vanneste2013) and Plougonven & Zhang (Reference Plougonven and Zhang2014).
A shallow water system is the simplest system in which both vortical flows and gravity waves exist. If the effect of the Earth’s rotation is negligibly small, this system is equivalent to a two-dimensional adiabatic gas system with a specific heat ratio of
![]() ${\it\gamma}_{s}=2$
. Then, gravity waves in a shallow water system are analogous to sound waves in compressible gas systems. In a shallow water system, Ford (Reference Ford1994) investigated spontaneous gravity wave radiation from a vortex train for the first time. His study was extended to an unsteady jet (Sugimoto, Ishioka & Yoden Reference Sugimoto, Ishioka and Yoden2007b
; Sugimoto, Ishioka & Ishii Reference Sugimoto, Ishioka and Ishii2008) and a spherical domain (Sugimoto & Ishii Reference Sugimoto and Ishii2012). Since previous studies reported gravity wave radiation from complicated unsteady vortical flows, in the present study we use a co-rotating vortex pair, which is one of the simplest basic states. In the field of fluid dynamics, aeroacoustic sound wave radiation from a co-rotating vortex pair has been investigated theoretically (e.g. Powell Reference Powell1964) and numerically (Mitchell, Lele & Moin Reference Mitchell, Lele and Moin1995). We extend those works to an
${\it\gamma}_{s}=2$
. Then, gravity waves in a shallow water system are analogous to sound waves in compressible gas systems. In a shallow water system, Ford (Reference Ford1994) investigated spontaneous gravity wave radiation from a vortex train for the first time. His study was extended to an unsteady jet (Sugimoto, Ishioka & Yoden Reference Sugimoto, Ishioka and Yoden2007b
; Sugimoto, Ishioka & Ishii Reference Sugimoto, Ishioka and Ishii2008) and a spherical domain (Sugimoto & Ishii Reference Sugimoto and Ishii2012). Since previous studies reported gravity wave radiation from complicated unsteady vortical flows, in the present study we use a co-rotating vortex pair, which is one of the simplest basic states. In the field of fluid dynamics, aeroacoustic sound wave radiation from a co-rotating vortex pair has been investigated theoretically (e.g. Powell Reference Powell1964) and numerically (Mitchell, Lele & Moin Reference Mitchell, Lele and Moin1995). We extend those works to an
![]() $f$
-plane shallow water system. In this experimental setting, it is possible to derive an analytical form of the far field of gravity waves in the presence of the Earth’s rotation, assuming that point vortices exist and keep their structure. It should be mentioned that, for the non-rotating cases, Gryanik (Reference Gryanik1983) derived an analytical estimate of sound wave emission from linear vortex filaments. His study was extended by Zeitlin (Reference Zeitlin1991) to Kirchhoff elliptic vortex focusing on the back-reaction of acoustic radiation. Further, Plougonven & Zeitlin (Reference Plougonven and Zeitlin2002) used a three-dimensional Kirchhoff vortex to investigate gravity wave radiation in strongly stratified flows.
$f$
-plane shallow water system. In this experimental setting, it is possible to derive an analytical form of the far field of gravity waves in the presence of the Earth’s rotation, assuming that point vortices exist and keep their structure. It should be mentioned that, for the non-rotating cases, Gryanik (Reference Gryanik1983) derived an analytical estimate of sound wave emission from linear vortex filaments. His study was extended by Zeitlin (Reference Zeitlin1991) to Kirchhoff elliptic vortex focusing on the back-reaction of acoustic radiation. Further, Plougonven & Zeitlin (Reference Plougonven and Zeitlin2002) used a three-dimensional Kirchhoff vortex to investigate gravity wave radiation in strongly stratified flows.
In a shallow water system, Zeitlin (Reference Zeitlin2007) described gravity wave radiation from a co-rotating vortex pair for the non-rotating case and sketched the generalization to the rotating case. He discussed the effect of the Earth’s rotation on gravity wave propagation and showed that the propagating gravity waves exist only for large
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${>}1$
) under the influence of inertial cutoff frequency. It is also important that a shallow water system has an asymmetry between cyclones and anticyclones under the effect of the Earth’s rotation (e.g. Stegner & Dritschel Reference Stegner and Dritschel2000). In previous numerical studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012), it has also been reported that gravity waves are radiated from the source term originating in the Coriolis force at relatively smaller
${>}1$
) under the influence of inertial cutoff frequency. It is also important that a shallow water system has an asymmetry between cyclones and anticyclones under the effect of the Earth’s rotation (e.g. Stegner & Dritschel Reference Stegner and Dritschel2000). In previous numerical studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012), it has also been reported that gravity waves are radiated from the source term originating in the Coriolis force at relatively smaller
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\leqslant}10$
) in addition to the usual source term produced by vortical flows. Moreover, Sugimoto et al. (Reference Sugimoto, Ishioka and Ishii2008) found that the amplitude of gravity waves has its local maximum at an intermediate
${\leqslant}10$
) in addition to the usual source term produced by vortical flows. Moreover, Sugimoto et al. (Reference Sugimoto, Ishioka and Ishii2008) found that the amplitude of gravity waves has its local maximum at an intermediate
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\sim}10$
). In the present study, we focus on the asymmetry between cyclone pairs and anticyclone pairs through the process of spontaneous gravity wave radiation. Note that cyclone–anticyclone asymmetry in gravity waves is also found in continuously stratified systems (cf. Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007; Wang et al.
Reference Wang, Zhang and Snyder2009; Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015b
). Although it has been pointed out that spontaneous radiation in a shallow water system, which is called ‘Lighthill radiation’, is different from that in a continuously stratified system (see McIntyre Reference McIntyre2009), investigating fundamental mechanisms of cyclone–anticyclone asymmetry in gravity waves in a simplified configuration of an
${\sim}10$
). In the present study, we focus on the asymmetry between cyclone pairs and anticyclone pairs through the process of spontaneous gravity wave radiation. Note that cyclone–anticyclone asymmetry in gravity waves is also found in continuously stratified systems (cf. Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007; Wang et al.
Reference Wang, Zhang and Snyder2009; Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015b
). Although it has been pointed out that spontaneous radiation in a shallow water system, which is called ‘Lighthill radiation’, is different from that in a continuously stratified system (see McIntyre Reference McIntyre2009), investigating fundamental mechanisms of cyclone–anticyclone asymmetry in gravity waves in a simplified configuration of an
![]() $f$
-plane shallow water system is a necessary step towards the general understanding of spontaneous gravity wave radiation from more complex vortical flows in the real atmosphere.
$f$
-plane shallow water system is a necessary step towards the general understanding of spontaneous gravity wave radiation from more complex vortical flows in the real atmosphere.
In order to verify the derived analytical form of the far field of gravity waves, direct numerical simulation is a useful tool. However, there are several difficulties to simulate spontaneous gravity wave radiation numerically. It is well known that the energy of gravity waves radiated from vortical motions is very small in a shallow water system owing to the strong density difference at the free surface. Therefore, we have to use a numerical model with high resolution and accuracy. Recently, with the aid of conformal mapping from the closed domain to an unbounded domain, spectral methods in unbounded domains for the one- and two-dimensional cases were proposed by Ishioka (Reference Ishioka2008). It is then possible to position many grid points in the near field of a vortical region and a few points in the far field of waves. This method also includes pseudo-hyperviscosity, which acts like usual hyperviscosity in the near field, while it acts like a sponge layer in the far field to effectively damp waves. The method enables us to simulate vortical motion accompanied by wave radiation with high accuracy. The method for a one-dimensional domain has already been applied to simulate spontaneous gravity wave radiation from an unsteady jet (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008). In the present study, we apply the method for a two-dimensional domain to an
![]() $f$
-plane shallow water system expressed in cylindrical coordinates in order to compare the amplitude of gravity waves between the analytical study and numerical simulation.
$f$
-plane shallow water system expressed in cylindrical coordinates in order to compare the amplitude of gravity waves between the analytical study and numerical simulation.
The present study has several goals. First, we derive an analytical form of the far field of gravity waves from a co-rotating vortex pair and reveal cyclone–anticyclone asymmetry. It will also be shown that the amplitude of gravity waves has its local maximum at an intermediate
![]() $f$
only for the case of anticyclone pairs. Second, we verify the analytical solution by using the results of a newly developed numerical model. The comparison of the analytical results with the numerical ones is aimed at checking not only the analytical derivation but also the numerical model itself. One of the important goals is to demonstrate the feasibility of the numerical model and show a possible path for future studies of gravity wave radiation from more complex flows.
$f$
only for the case of anticyclone pairs. Second, we verify the analytical solution by using the results of a newly developed numerical model. The comparison of the analytical results with the numerical ones is aimed at checking not only the analytical derivation but also the numerical model itself. One of the important goals is to demonstrate the feasibility of the numerical model and show a possible path for future studies of gravity wave radiation from more complex flows.
This paper is organized as follows. In § 2 we describe the basic equations. In § 3 the analytical form of the far field is derived using the Lighthill–Ford equation in an
![]() $f$
-plane shallow water system. In § 4 we report the results of nonlinear numerical experiments, including the model description and experimental setting. A summary and discussion are presented in § 5.
$f$
-plane shallow water system. In § 4 we report the results of nonlinear numerical experiments, including the model description and experimental setting. A summary and discussion are presented in § 5.
2. Basic equation
We consider gravity wave radiation from vortical motions in an
![]() $f$
-plane shallow water system. The basic equations are expressed as
$f$
-plane shallow water system. The basic equations are expressed as
Equations (2.1)–(2.3) are the same as for vortex sound if the effect of the Earth’s rotation is negligibly small. From the flux forms of (2.1)–(2.3), the divergence and vorticity equations are derived. Combining them with the conservation-of-mass equation, we obtain the Lighthill–Ford equation (Lighthill Reference Lighthill1952; Ford Reference Ford1994) in this system:
Here
![]() $x_{1}=x$
,
$x_{1}=x$
,
![]() $x_{2}=y$
, and we use the Einstein summation convention; and
$x_{2}=y$
, and we use the Einstein summation convention; and
![]() $c_{0}=\sqrt{gh_{0}}$
and
$c_{0}=\sqrt{gh_{0}}$
and
![]() ${\rm\nabla}^{2}$
denote the phase speed of the fastest gravity wave and the horizontal Laplacian, respectively. The left-hand side of (2.4) is the wave operator of a linear gravity wave, and the right-hand side can be regarded as the source of gravity waves. Here,
${\rm\nabla}^{2}$
denote the phase speed of the fastest gravity wave and the horizontal Laplacian, respectively. The left-hand side of (2.4) is the wave operator of a linear gravity wave, and the right-hand side can be regarded as the source of gravity waves. Here,
![]() $T_{ij}$
is written as
$T_{ij}$
is written as
where
![]() ${\it\epsilon}_{12}=-{\it\epsilon}_{21}=1$
,
${\it\epsilon}_{12}=-{\it\epsilon}_{21}=1$
,
![]() ${\it\epsilon}_{11}={\it\epsilon}_{22}=0$
,
${\it\epsilon}_{11}={\it\epsilon}_{22}=0$
,
![]() $u_{1}=u_{c}$
,
$u_{1}=u_{c}$
,
![]() $u_{2}=v_{c}$
and
$u_{2}=v_{c}$
and
![]() ${\it\delta}_{ij}$
is the Kronecker delta.
${\it\delta}_{ij}$
is the Kronecker delta.
The key point in the Lighthill–Ford theory is that we assume the source term
![]() $T_{ij}$
is non-zero only over a small enough region that the right-hand side of (2.4) may be approximated by a quadrupole point source. A further assumption is that the source flow
$T_{ij}$
is non-zero only over a small enough region that the right-hand side of (2.4) may be approximated by a quadrupole point source. A further assumption is that the source flow
![]() $T_{ij}$
may be regarded as being known only in terms of vortex dynamics. Then, we can compute the source term without knowledge of the wavefield (Ford Reference Ford1994). In the limit of small
$T_{ij}$
may be regarded as being known only in terms of vortex dynamics. Then, we can compute the source term without knowledge of the wavefield (Ford Reference Ford1994). In the limit of small
![]() $\mathit{Fr}$
(Froude number; the ratio of the flow velocity to the phase speed of the gravity waves), both assumptions are valid. Then the vortical flow is governed by the equations for a two-dimensional incompressible fluid, and the wavelength of gravity waves is
$\mathit{Fr}$
(Froude number; the ratio of the flow velocity to the phase speed of the gravity waves), both assumptions are valid. Then the vortical flow is governed by the equations for a two-dimensional incompressible fluid, and the wavelength of gravity waves is
![]() $O(\mathit{Fr}^{-1})$
larger than the scale of vortical flows (Ford et al.
Reference Ford, McIntyre and Norton2000). Note that
$O(\mathit{Fr}^{-1})$
larger than the scale of vortical flows (Ford et al.
Reference Ford, McIntyre and Norton2000). Note that
![]() $\mathit{Fr}$
corresponds to the Mach number (the ratio of the flow velocity to the phase speed of sound waves) in the field of aeroacoustic sound wave radiation. It has also been confirmed in previous studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012) that for large
$\mathit{Fr}$
corresponds to the Mach number (the ratio of the flow velocity to the phase speed of sound waves) in the field of aeroacoustic sound wave radiation. It has also been confirmed in previous studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012) that for large
![]() $\mathit{Ro}$
(small
$\mathit{Ro}$
(small
![]() $f$
) the primary source of gravity waves is the first term on the right-hand side of (2.5), which is the usual source term produced by vortical flows, while the second term, which originates in the Coriolis force, is sometimes comparable to the first term for relatively smaller
$f$
) the primary source of gravity waves is the first term on the right-hand side of (2.5), which is the usual source term produced by vortical flows, while the second term, which originates in the Coriolis force, is sometimes comparable to the first term for relatively smaller
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\leqslant}10$
; large
${\leqslant}10$
; large
![]() $f$
). Since the third term is always small, we neglect this term.
$f$
). Since the third term is always small, we neglect this term.
3. Far field
In this section, we analytically derive the far field of gravity waves spontaneously radiated from a co-rotating point vortex pair in an
![]() $f$
-plane shallow water system. Here, we assume point vortices exist and keep their structure, although it is impossible to realize a point vortex as a balanced state in an
$f$
-plane shallow water system. Here, we assume point vortices exist and keep their structure, although it is impossible to realize a point vortex as a balanced state in an
![]() $f$
-plane shallow water system. The depth of the fluid inevitably vanishes at the position of a point vortex, because the surface elevation, which needs to be in balance with the velocity field induced by a point vortex, becomes infinite. We use a co-rotating point vortex pair to estimate the major sources of gravity waves, which are the first and second terms on the right-hand side of (2.5). As shown later, the second term leads to cyclone–anticyclone asymmetry in gravity waves.
$f$
-plane shallow water system. The depth of the fluid inevitably vanishes at the position of a point vortex, because the surface elevation, which needs to be in balance with the velocity field induced by a point vortex, becomes infinite. We use a co-rotating point vortex pair to estimate the major sources of gravity waves, which are the first and second terms on the right-hand side of (2.5). As shown later, the second term leads to cyclone–anticyclone asymmetry in gravity waves.
A vortex pair with the same sign and strength co-rotates due to the flow field produced by each point vortex. A schematic of this configuration is shown in figure 1. For aeroacoustic vortex sound wave radiation, several theoretical studies (e.g. Powell Reference Powell1964; Howe Reference Howe2003) and numerical simulations (Mitchell et al.
Reference Mitchell, Lele and Moin1995) of this configuration have been reported. Zeitlin (Reference Zeitlin2007) also derived an analytical solution for non-rotating shallow water and sketched the generalization to the rotating case. Here, we extend the previous theory to an
![]() $f$
-plane shallow water system and derive an analytical form of the far field of gravity waves by taking into account the Coriolis effect in the source of gravity waves.
$f$
-plane shallow water system and derive an analytical form of the far field of gravity waves by taking into account the Coriolis effect in the source of gravity waves.

Figure 1. Schematic of experimental configuration.
We assume that a vortex pair, each vortex having a circulation
![]() ${\it\Gamma}$
and positioning at distance
${\it\Gamma}$
and positioning at distance
![]() $2l$
, co-rotates at an angular velocity of
$2l$
, co-rotates at an angular velocity of
![]() ${\it\Omega}={\it\Gamma}/4{\rm\pi}l^{2}$
(cyclone,
${\it\Omega}={\it\Gamma}/4{\rm\pi}l^{2}$
(cyclone,
![]() ${\it\Omega}>0$
). The positions of each point vortex at
${\it\Omega}>0$
). The positions of each point vortex at
![]() $t$
are expressed as
$t$
are expressed as
Then, the vorticity distribution
![]() ${\bf\omega}$
and velocity
${\bf\omega}$
and velocity
![]() $\boldsymbol{v}$
associated with the vortices are expressed as
$\boldsymbol{v}$
associated with the vortices are expressed as
where
![]() $\boldsymbol{k}$
is a unit vector in the
$\boldsymbol{k}$
is a unit vector in the
![]() $z$
direction, parallel to the vortices, and
$z$
direction, parallel to the vortices, and
![]() ${\it\delta}$
is a delta function. The vortex convection velocities
${\it\delta}$
is a delta function. The vortex convection velocities
![]() $\boldsymbol{v}=(u_{1},u_{2})$
are
$\boldsymbol{v}=(u_{1},u_{2})$
are
We assume the characteristic velocity scale
![]() $U={\it\Omega}l\ll c_{0}$
. Then since
$U={\it\Omega}l\ll c_{0}$
. Then since
![]() $\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{s})=-\boldsymbol{s}$
, we have
$\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{s})=-\boldsymbol{s}$
, we have
On the right-hand side of (2.4), the primary source of gravity waves is the first term on the right-hand side of (2.5). For
![]() $\mathit{Fr}\equiv U/c_{0}\ll 1$
and under the assumption of a compact source, we can safely assume non-divergent flows, namely,
$\mathit{Fr}\equiv U/c_{0}\ll 1$
and under the assumption of a compact source, we can safely assume non-divergent flows, namely,
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
and
![]() $h\approx h_{0}$
. Then we obtain
$h\approx h_{0}$
. Then we obtain
Here we neglect the second term on the right-hand side of (3.5) on the assumption that
![]() $\mathit{Fr}\ll 1$
, since the far field of gravity waves from the second term is
$\mathit{Fr}\ll 1$
, since the far field of gravity waves from the second term is
![]() $O(\mathit{Fr}^{2})$
smaller than that from the first term in the theory of aeroacoustic vortex sound wave radiation (Howe Reference Howe2003). Then the source of gravity waves produced by the unsteady motions of a co-rotating vortex pair is approximated as follows. If we expand (3.5) in powers of the radius
$O(\mathit{Fr}^{2})$
smaller than that from the first term in the theory of aeroacoustic vortex sound wave radiation (Howe Reference Howe2003). Then the source of gravity waves produced by the unsteady motions of a co-rotating vortex pair is approximated as follows. If we expand (3.5) in powers of the radius
![]() $l$
of the circular orbit for small
$l$
of the circular orbit for small
![]() $\mathit{Fr}\ll 1$
, the
$\mathit{Fr}\ll 1$
, the
![]() $i$
th component of the first non-zero term is
$i$
th component of the first non-zero term is
Then, the time variation of
is regarded as the quadrupole source of gravity waves, which corresponds to the first term on the right-hand side of (2.5).
As mentioned in the previous section, since the second term on the right-hand side of (2.5) is comparable to the first term for relatively smaller
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\leqslant}10$
; large
${\leqslant}10$
; large
![]() $f$
) (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012), we derive the source originating in the Coriolis force in a similar way. Taking into account the symmetry, we consider the next term,
$f$
) (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012), we derive the source originating in the Coriolis force in a similar way. Taking into account the symmetry, we consider the next term,
where we again assume non-divergent flows,
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
and
![]() $h\approx h_{0}$
, for
$h\approx h_{0}$
, for
![]() $\mathit{Fr}\ll 1$
and under the assumption of a compact source. Because
$\mathit{Fr}\ll 1$
and under the assumption of a compact source. Because
![]() $\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{s})=-\boldsymbol{s}$
, we have
$\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{s})=-\boldsymbol{s}$
, we have
Then we have
For small
![]() $\mathit{Fr}\ll 1$
,
$\mathit{Fr}\ll 1$
,
Now the source originating in the Coriolis force is expressed as follows:
We regard (3.7) and (3.12) as the sources of gravity waves. As mentioned before, we neglect the third term on the right-hand side of (2.5), because it is always small.
Next, we derive the far field of gravity waves radiated from (3.7) and (3.12) using a Green’s function. First, the Green’s function of (2.4) in the two-dimensional domain incorporating time variation is defined from the following Klein–Gordon equation:
where
![]() ${\it\mu}=f/c_{0}$
. The form of the Green’s function is given by
${\it\mu}=f/c_{0}$
. The form of the Green’s function is given by
 $$\begin{eqnarray}G_{2}(\boldsymbol{x},t,\boldsymbol{x}^{\prime },t^{\prime })=\frac{c_{0}}{2{\rm\pi}}\frac{\cos \left({\it\mu}\sqrt{c_{0}^{2}(t-t^{\prime })^{2}-|\boldsymbol{x}-\boldsymbol{ x}^{\prime }|^{2}}\,\right)}{\sqrt{c_{0}^{2}(t-t^{\prime })^{2}-|\boldsymbol{x}-\boldsymbol{ x}^{\prime }|^{2}}}\,{\it\theta}_{s}(c_{0}(t-t^{\prime })-|\boldsymbol{x}-\boldsymbol{x}^{\prime }|),\end{eqnarray}$$
$$\begin{eqnarray}G_{2}(\boldsymbol{x},t,\boldsymbol{x}^{\prime },t^{\prime })=\frac{c_{0}}{2{\rm\pi}}\frac{\cos \left({\it\mu}\sqrt{c_{0}^{2}(t-t^{\prime })^{2}-|\boldsymbol{x}-\boldsymbol{ x}^{\prime }|^{2}}\,\right)}{\sqrt{c_{0}^{2}(t-t^{\prime })^{2}-|\boldsymbol{x}-\boldsymbol{ x}^{\prime }|^{2}}}\,{\it\theta}_{s}(c_{0}(t-t^{\prime })-|\boldsymbol{x}-\boldsymbol{x}^{\prime }|),\end{eqnarray}$$
where
![]() ${\it\theta}_{s}$
is the Heaviside function. Using this form of the Green’s function, the far field of gravity waves radiated from the source (3.7) is estimated analytically by analogy with the derivation by Howe (Reference Howe2003) as
${\it\theta}_{s}$
is the Heaviside function. Using this form of the Green’s function, the far field of gravity waves radiated from the source (3.7) is estimated analytically by analogy with the derivation by Howe (Reference Howe2003) as
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial h(\boldsymbol{x},t)}{\partial t}\right)_{V} & = & \displaystyle \frac{1}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial (h\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\bf\omega}\times \boldsymbol{v}))}{\partial t^{\prime }}\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime }\nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{h_{0}}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial }{\partial t^{\prime }}\left[\frac{\partial ^{2}}{\partial {x_{i}}^{\prime }{x_{j}}^{\prime }}(2{\it\Gamma}{\it\Omega}s_{i}(t^{\prime })s_{j}(t^{\prime }){\it\delta}(\boldsymbol{x}^{\prime }))\right]\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime },\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial h(\boldsymbol{x},t)}{\partial t}\right)_{V} & = & \displaystyle \frac{1}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial (h\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\bf\omega}\times \boldsymbol{v}))}{\partial t^{\prime }}\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime }\nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{h_{0}}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial }{\partial t^{\prime }}\left[\frac{\partial ^{2}}{\partial {x_{i}}^{\prime }{x_{j}}^{\prime }}(2{\it\Gamma}{\it\Omega}s_{i}(t^{\prime })s_{j}(t^{\prime }){\it\delta}(\boldsymbol{x}^{\prime }))\right]\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime },\qquad\end{eqnarray}$$
where subscript
![]() $V$
indicates the far field of gravity waves radiated from the source (3.7), which is related to unsteady motions of the vortex. Then we can integrate the delta function, which yields
$V$
indicates the far field of gravity waves radiated from the source (3.7), which is related to unsteady motions of the vortex. Then we can integrate the delta function, which yields
To proceed further, since
where
![]() $r=\sqrt{x_{1}^{2}+x_{2}^{2}}$
is the distance from the origin, we use the following approximation in the far field (
$r=\sqrt{x_{1}^{2}+x_{2}^{2}}$
is the distance from the origin, we use the following approximation in the far field (
![]() $r\gg 1$
):
$r\gg 1$
):
where terms in the parentheses vanish for large
![]() $r$
. Since
$r$
. Since
![]() $(x_{i}x_{j})/r^{2}$
is independent of
$(x_{i}x_{j})/r^{2}$
is independent of
![]() $\partial ^{2}/\partial r^{2}$
, it follows from (3.16) that
$\partial ^{2}/\partial r^{2}$
, it follows from (3.16) that
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial h}{\partial t}\right)_{V} & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}h_{0}}{c_{0}^{2}}\frac{\partial ^{2}}{\partial r^{2}}\int _{-\infty }^{\infty }G_{2}\frac{x_{i}x_{j}}{r^{2}}\frac{\partial (s_{i}(t^{\prime })s_{j}(t^{\prime }))}{\partial t^{\prime }}\,\text{d}t^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}^{2}l^{2}h_{0}}{c_{0}^{2}}\frac{\partial ^{2}}{\partial r^{2}}\int _{-\infty }^{\infty }G_{2}\sin (2{\it\theta}-2{\it\Omega}t^{\prime })\,\text{d}t^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial h}{\partial t}\right)_{V} & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}h_{0}}{c_{0}^{2}}\frac{\partial ^{2}}{\partial r^{2}}\int _{-\infty }^{\infty }G_{2}\frac{x_{i}x_{j}}{r^{2}}\frac{\partial (s_{i}(t^{\prime })s_{j}(t^{\prime }))}{\partial t^{\prime }}\,\text{d}t^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}^{2}l^{2}h_{0}}{c_{0}^{2}}\frac{\partial ^{2}}{\partial r^{2}}\int _{-\infty }^{\infty }G_{2}\sin (2{\it\theta}-2{\it\Omega}t^{\prime })\,\text{d}t^{\prime },\end{eqnarray}$$
where
![]() ${\it\theta}$
is the angle in cylindrical coordinates, with
${\it\theta}$
is the angle in cylindrical coordinates, with
![]() $\boldsymbol{x}=r(\cos {\it\theta},\sin {\it\theta})$
.
$\boldsymbol{x}=r(\cos {\it\theta},\sin {\it\theta})$
.
In a similar way, using the same form of Green’s function (3.14), we derive the far field of gravity waves radiated from the source (3.12) as
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial h(\boldsymbol{x},t)}{\partial t}\right)_{F} & = & \displaystyle -\frac{1}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\,fh_{0}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\boldsymbol{k}\times ({\bf\omega}\times \boldsymbol{v})]\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime }\nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{fh_{0}}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial ^{2}}{\partial {x_{i}}^{\prime }{x_{j}}^{\prime }}(2{\it\Gamma}{\it\Omega}{\it\epsilon}_{ik}s_{k}(t^{\prime })s_{j}(t^{\prime }){\it\delta}(\boldsymbol{x}^{\prime }))\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial h(\boldsymbol{x},t)}{\partial t}\right)_{F} & = & \displaystyle -\frac{1}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\,fh_{0}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\boldsymbol{k}\times ({\bf\omega}\times \boldsymbol{v})]\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime }\nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{fh_{0}}{c_{0}^{2}}\iiint _{-\infty }^{\infty }G_{2}\frac{\partial ^{2}}{\partial {x_{i}}^{\prime }{x_{j}}^{\prime }}(2{\it\Gamma}{\it\Omega}{\it\epsilon}_{ik}s_{k}(t^{\prime })s_{j}(t^{\prime }){\it\delta}(\boldsymbol{x}^{\prime }))\,\text{d}^{2}\boldsymbol{x}^{\prime }\,\text{d}t^{\prime },\end{eqnarray}$$
where subscript
![]() $F$
indicates the far field of gravity waves radiated from the source (3.12), which originates in the Coriolis force. With the aid of (3.18), we obtain a similar form to that in (3.19):
$F$
indicates the far field of gravity waves radiated from the source (3.12), which originates in the Coriolis force. With the aid of (3.18), we obtain a similar form to that in (3.19):
By combining (3.19) and (3.21) with (3.14), we obtain
 $$\begin{eqnarray}\frac{\partial h}{\partial t}=\left(1-\frac{\,f}{2{\it\Omega}}\right)\frac{{\it\Gamma}{\it\Omega}^{2}l^{2}h_{0}}{{\rm\pi}c_{0}}\frac{\partial ^{2}}{\partial r^{2}}\underbrace{\int _{-\infty }^{t}\frac{\sin (2{\it\theta}-2{\it\Omega}t^{\prime })\cos ({\it\mu}\sqrt{{\it\tau}})}{\sqrt{{\it\tau}}}\,{\it\theta}_{s}(c_{0}(t-t^{\prime })-r)\,\text{d}t^{\prime }}_{B},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial h}{\partial t}=\left(1-\frac{\,f}{2{\it\Omega}}\right)\frac{{\it\Gamma}{\it\Omega}^{2}l^{2}h_{0}}{{\rm\pi}c_{0}}\frac{\partial ^{2}}{\partial r^{2}}\underbrace{\int _{-\infty }^{t}\frac{\sin (2{\it\theta}-2{\it\Omega}t^{\prime })\cos ({\it\mu}\sqrt{{\it\tau}})}{\sqrt{{\it\tau}}}\,{\it\theta}_{s}(c_{0}(t-t^{\prime })-r)\,\text{d}t^{\prime }}_{B},\end{eqnarray}$$
where
![]() ${\it\tau}=c_{0}^{2}(t-t^{\prime })^{2}-r^{2}$
.
${\it\tau}=c_{0}^{2}(t-t^{\prime })^{2}-r^{2}$
.
Next, we change variables to calculate the integral in (3.22), which is labelled as
![]() $B$
: i.e.
$B$
: i.e.
![]() $t-t^{\prime }=(r/c_{0})\cosh {\it\varphi}$
and
$t-t^{\prime }=(r/c_{0})\cosh {\it\varphi}$
and
![]() $\sqrt{{\it\tau}}=r\sinh {\it\varphi}$
. Then, we obtain
$\sqrt{{\it\tau}}=r\sinh {\it\varphi}$
. Then, we obtain
 $$\begin{eqnarray}\displaystyle B & = & \displaystyle \frac{1}{c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}\right)\cos ({\it\mu}r\sinh {\it\varphi})\,\text{d}{\it\varphi}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}+{\it\mu}r\sinh {\it\varphi}\right)\,\text{d}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}-{\it\mu}r\sinh {\it\varphi}\right)\,\text{d}{\it\varphi}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B & = & \displaystyle \frac{1}{c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}\right)\cos ({\it\mu}r\sinh {\it\varphi})\,\text{d}{\it\varphi}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}+{\it\mu}r\sinh {\it\varphi}\right)\,\text{d}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2c_{0}}\int _{0}^{\infty }\sin \!\left(2{\it\theta}-2{\it\Omega}t+\frac{2{\it\Omega}r}{c_{0}}\cosh {\it\varphi}-{\it\mu}r\sinh {\it\varphi}\right)\,\text{d}{\it\varphi}.\end{eqnarray}$$
In order to complete the derivation, we use an addition theorem of trigonometric functions and composition of hyperbolic functions. Finally, with the aid of the integral form of Hankel’s function (
![]() $\text{H}_{0}(x)$
; see appendix A for special functions), we obtain for a cyclone pair (
$\text{H}_{0}(x)$
; see appendix A for special functions), we obtain for a cyclone pair (
![]() ${\it\Omega}>0$
, (A 1a
)) and an anticyclone pair (
${\it\Omega}>0$
, (A 1a
)) and an anticyclone pair (
![]() ${\it\Omega}<0$
, (A 1c
)):
${\it\Omega}<0$
, (A 1c
)):
 $$\begin{eqnarray}\displaystyle B & = & \displaystyle \frac{1}{2c_{0}}\text{Re}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(r\sqrt{\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}-{\it\mu}^{2}}\right)\right]\sin (2{\it\theta}-2{\it\Omega}t)\nonumber\\ \displaystyle & & \displaystyle -\,\text{sgn}(\,f)\text{sgn}({\it\Omega})\frac{1}{2c_{0}}\text{Im}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(r\sqrt{\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}-{\it\mu}^{2}}\right)\right]\cos (2{\it\theta}-2{\it\Omega}t),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B & = & \displaystyle \frac{1}{2c_{0}}\text{Re}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(r\sqrt{\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}-{\it\mu}^{2}}\right)\right]\sin (2{\it\theta}-2{\it\Omega}t)\nonumber\\ \displaystyle & & \displaystyle -\,\text{sgn}(\,f)\text{sgn}({\it\Omega})\frac{1}{2c_{0}}\text{Im}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(r\sqrt{\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}-{\it\mu}^{2}}\right)\right]\cos (2{\it\theta}-2{\it\Omega}t),\qquad\end{eqnarray}$$
where we use (A 2) for
![]() $(r/c_{0})\sqrt{4{\it\Omega}^{2}-f^{2}}\gg 1$
and the sign function
$(r/c_{0})\sqrt{4{\it\Omega}^{2}-f^{2}}\gg 1$
and the sign function
![]() $\text{sgn}(x)$
, where we define
$\text{sgn}(x)$
, where we define
![]() $\text{sgn}(0)=1$
. By use of (A 3), we obtain
$\text{sgn}(0)=1$
. By use of (A 3), we obtain
Finally, with the aid of (A 4), the far field of gravity waves is estimated by
 $$\begin{eqnarray}\displaystyle \frac{\partial h(\boldsymbol{x},t)}{\partial t} & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}^{4}l^{2}h_{0}}{c_{0}^{4}}\left(1-\frac{\,f}{2{\it\Omega}}\right)\!\left[1-\!\left(\frac{\,f}{2{\it\Omega}}\right)^{2}\right]\!\left[\text{Y}_{0}\!\left(\frac{r}{c_{0}}\sqrt{4{\it\Omega}^{2}-f^{2}}\right)\sin (2{\it\theta}-2{\it\Omega}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\text{sgn}(\,f)\text{sgn}({\it\Omega})\text{J}_{0}\!\left(\frac{r}{c_{0}}\sqrt{4{\it\Omega}^{2}-f^{2}}\right)\cos (2{\it\theta}-2{\it\Omega}t)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial h(\boldsymbol{x},t)}{\partial t} & = & \displaystyle \frac{2{\it\Gamma}{\it\Omega}^{4}l^{2}h_{0}}{c_{0}^{4}}\left(1-\frac{\,f}{2{\it\Omega}}\right)\!\left[1-\!\left(\frac{\,f}{2{\it\Omega}}\right)^{2}\right]\!\left[\text{Y}_{0}\!\left(\frac{r}{c_{0}}\sqrt{4{\it\Omega}^{2}-f^{2}}\right)\sin (2{\it\theta}-2{\it\Omega}t)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\text{sgn}(\,f)\text{sgn}({\it\Omega})\text{J}_{0}\!\left(\frac{r}{c_{0}}\sqrt{4{\it\Omega}^{2}-f^{2}}\right)\cos (2{\it\theta}-2{\it\Omega}t)\right],\end{eqnarray}$$
where
![]() $\text{J}_{0}$
and
$\text{J}_{0}$
and
![]() $\text{Y}_{0}$
are the zeroth-order Bessel functions of the first and second kind, respectively. Equation (3.26) is applicable for both cyclone pairs and anticyclone pairs regardless of the signs of
$\text{Y}_{0}$
are the zeroth-order Bessel functions of the first and second kind, respectively. Equation (3.26) is applicable for both cyclone pairs and anticyclone pairs regardless of the signs of
![]() $f$
.
$f$
.
In the case of evanescent gravity waves for
![]() $4{\it\Omega}^{2}\leqslant f^{2}$
, the analytical estimate is also derived in a similar way. Since we have to use (A 1b
) for
$4{\it\Omega}^{2}\leqslant f^{2}$
, the analytical estimate is also derived in a similar way. Since we have to use (A 1b
) for
![]() $4{\it\Omega}^{2}\leqslant f^{2}$
in (3.23),
$4{\it\Omega}^{2}\leqslant f^{2}$
in (3.23),
![]() $B$
expressed in (3.24) is replaced by
$B$
expressed in (3.24) is replaced by
 $$\begin{eqnarray}\displaystyle B^{\prime } & = & \displaystyle \frac{1}{2c_{0}}\text{Re}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(\text{i}r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\right]\sin (2{\it\theta}-2{\it\Omega}t)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2c_{0}}\text{Im}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(\text{i}r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\right]\cos (2{\it\theta}-2{\it\Omega}t).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B^{\prime } & = & \displaystyle \frac{1}{2c_{0}}\text{Re}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(\text{i}r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\right]\sin (2{\it\theta}-2{\it\Omega}t)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2c_{0}}\text{Im}\left[\text{i}{\rm\pi}\text{H}_{0}^{(1)}\!\left(\text{i}r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\right]\cos (2{\it\theta}-2{\it\Omega}t).\end{eqnarray}$$
By using (A 7),
![]() $B^{\prime }$
is expressed as
$B^{\prime }$
is expressed as
 $$\begin{eqnarray}B^{\prime }=\frac{1}{c_{0}}\text{K}_{0}\!\left(r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\sin (2{\it\theta}-2{\it\Omega}t),\end{eqnarray}$$
$$\begin{eqnarray}B^{\prime }=\frac{1}{c_{0}}\text{K}_{0}\!\left(r\sqrt{{\it\mu}^{2}-\left(\frac{2{\it\Omega}}{c_{0}}\right)^{2}}\right)\sin (2{\it\theta}-2{\it\Omega}t),\end{eqnarray}$$
where
![]() $\text{K}_{0}(x)$
is the zeroth-order modified Bessel function of the second kind. Finally, with the aid of (A 8), the far field of evanescent gravity waves is estimated by
$\text{K}_{0}(x)$
is the zeroth-order modified Bessel function of the second kind. Finally, with the aid of (A 8), the far field of evanescent gravity waves is estimated by
Equation (3.26) includes the effect of the Earth’s rotation as the second term in the first and second parentheses and a square root term. In the two-dimensional domain, we have to perform a long-time integration to estimate the far field of waves, since the influence of the source persists. In the absence of the Earth’s rotation (in the limit of
![]() $f\rightarrow 0$
), (3.26) corresponds to the analytical form of the vortex sound from a co-rotating point vortex pair (Mitchell et al.
Reference Mitchell, Lele and Moin1995). It is easy to see that large
$f\rightarrow 0$
), (3.26) corresponds to the analytical form of the vortex sound from a co-rotating point vortex pair (Mitchell et al.
Reference Mitchell, Lele and Moin1995). It is easy to see that large
![]() $f$
inhibits gravity wave radiation because of a negative value in the square root term. In addition, the second term in the first parentheses indicates that gravity waves are radiated from the source originating in the Coriolis force. For cyclone pairs
$f$
inhibits gravity wave radiation because of a negative value in the square root term. In addition, the second term in the first parentheses indicates that gravity waves are radiated from the source originating in the Coriolis force. For cyclone pairs
![]() $({\it\Omega}>0)$
the effect of the Earth’s rotation suppresses gravity wave radiation because of the same positive signs of
$({\it\Omega}>0)$
the effect of the Earth’s rotation suppresses gravity wave radiation because of the same positive signs of
![]() ${\it\Omega}$
and
${\it\Omega}$
and
![]() $f$
(
$f$
(
![]() ${\geqslant}0$
). On the other hand, for anticyclone pairs
${\geqslant}0$
). On the other hand, for anticyclone pairs
![]() $({\it\Omega}<0)$
the source originating in the Coriolis force enhances gravity wave radiation because of the opposite signs of
$({\it\Omega}<0)$
the source originating in the Coriolis force enhances gravity wave radiation because of the opposite signs of
![]() ${\it\Omega}$
and
${\it\Omega}$
and
![]() $f$
. Therefore, the second term in the first parentheses can be regarded as an indicator of the asymmetry of gravity wave radiation from cyclone pairs and anticyclone pairs. Since
$f$
. Therefore, the second term in the first parentheses can be regarded as an indicator of the asymmetry of gravity wave radiation from cyclone pairs and anticyclone pairs. Since
![]() $f$
also leads to the suppression of gravity wave radiation in the second parentheses, the amplitude of gravity waves for anticyclone pairs also goes to zero asymptotically for
$f$
also leads to the suppression of gravity wave radiation in the second parentheses, the amplitude of gravity waves for anticyclone pairs also goes to zero asymptotically for
![]() $f\rightarrow |2{\it\Omega}|$
. Note that, in the case of reverse Earth’s rotation for
$f\rightarrow |2{\it\Omega}|$
. Note that, in the case of reverse Earth’s rotation for
![]() $f\leqslant 0$
, the amplitude of gravity waves is larger from a vortex pair of
$f\leqslant 0$
, the amplitude of gravity waves is larger from a vortex pair of
![]() ${\it\Omega}>0$
than that from a vortex pair of
${\it\Omega}>0$
than that from a vortex pair of
![]() ${\it\Omega}<0$
. It should be mentioned that, while the analytical results obtained here are basically a combination of the approach of Ford (Reference Ford1994) with the non-rotating calculation of Mitchell et al. (Reference Mitchell, Lele and Moin1995), the novelty is to include the source (3.12), which leads to cyclone–anticyclone asymmetry. In addition, it is worth noting that a new approach of (3.18) regarding the space derivatives is required to derive (3.26) precisely in the presence of
${\it\Omega}<0$
. It should be mentioned that, while the analytical results obtained here are basically a combination of the approach of Ford (Reference Ford1994) with the non-rotating calculation of Mitchell et al. (Reference Mitchell, Lele and Moin1995), the novelty is to include the source (3.12), which leads to cyclone–anticyclone asymmetry. In addition, it is worth noting that a new approach of (3.18) regarding the space derivatives is required to derive (3.26) precisely in the presence of
![]() $f$
, since space derivatives cannot be replaced by time derivatives easily as in the case of the acoustic far field. This is because of the quadratic relation between
$f$
, since space derivatives cannot be replaced by time derivatives easily as in the case of the acoustic far field. This is because of the quadratic relation between
![]() $x$
and
$x$
and
![]() $t$
in the argument of the Green’s function in (3.14).
$t$
in the argument of the Green’s function in (3.14).
Snapshots of several parameter values of
![]() $\mathit{Ro}\equiv U_{l}/f\,l$
(Rossby number; the ratio of the advective term to the Coriolis term) and
$\mathit{Ro}\equiv U_{l}/f\,l$
(Rossby number; the ratio of the advective term to the Coriolis term) and
![]() $\mathit{Fr}\equiv U_{l}/\sqrt{gh_{0}}$
are shown in figure 2 for a cyclone pair. Here,
$\mathit{Fr}\equiv U_{l}/\sqrt{gh_{0}}$
are shown in figure 2 for a cyclone pair. Here,
![]() $U_{l}$
is the typical value of the velocity, and we fix
$U_{l}$
is the typical value of the velocity, and we fix
![]() ${\it\Omega}=0.1$
,
${\it\Omega}=0.1$
,
![]() $U_{l}=0.5$
and
$U_{l}=0.5$
and
![]() $l=0.5$
. These values are chosen to be consistent with those of the numerical simulation, as will be shown in § 4. The double spiral pattern clearly illustrates the rotating quadrupole nature of the radiated waves. For
$l=0.5$
. These values are chosen to be consistent with those of the numerical simulation, as will be shown in § 4. The double spiral pattern clearly illustrates the rotating quadrupole nature of the radiated waves. For
![]() $\mathit{Ro}=\infty$
, namely
$\mathit{Ro}=\infty$
, namely
![]() $f=0$
, (3.26) corresponds to the analytical form of the vortex sound from a co-rotating point vortex pair (Mitchell et al.
Reference Mitchell, Lele and Moin1995). Note also that gravity waves are cylindrical in the far field for
$f=0$
, (3.26) corresponds to the analytical form of the vortex sound from a co-rotating point vortex pair (Mitchell et al.
Reference Mitchell, Lele and Moin1995). Note also that gravity waves are cylindrical in the far field for
![]() $\mathit{Fr}=0.6~(gh_{0}=25/36)$
in figure 2(a). For small
$\mathit{Fr}=0.6~(gh_{0}=25/36)$
in figure 2(a). For small
![]() $\mathit{Fr}=0.3~(gh_{0}=25/9)$
, gravity waves with long wavelength are radiated due to the fast phase speed of gravity waves in figure 2(b). For relatively small
$\mathit{Fr}=0.3~(gh_{0}=25/9)$
, gravity waves with long wavelength are radiated due to the fast phase speed of gravity waves in figure 2(b). For relatively small
![]() $\mathit{Ro}=6.0~(\,f=1/6)$
, the radiation and propagation of small-scale gravity waves is suppressed by the effect of the Earth’s rotation, and the horizontal scale of the waves becomes large in figure 2(c). This tendency was also verified by the dispersion relation of gravity waves (Sugimoto et al.
Reference Sugimoto, Ishioka and Yoden2007b
). When
$\mathit{Ro}=6.0~(\,f=1/6)$
, the radiation and propagation of small-scale gravity waves is suppressed by the effect of the Earth’s rotation, and the horizontal scale of the waves becomes large in figure 2(c). This tendency was also verified by the dispersion relation of gravity waves (Sugimoto et al.
Reference Sugimoto, Ishioka and Yoden2007b
). When
![]() $f$
exceeds the critical value
$f$
exceeds the critical value
![]() $f\geqslant 0.2$
, which corresponds to
$f\geqslant 0.2$
, which corresponds to
![]() $\mathit{Ro}\leqslant 5$
, there is no gravity wave radiation. This is due to inertial cutoff of gravity wave radiation and propagation, since the square root term in (3.26) is negative (cf. Zeitlin Reference Zeitlin2007).
$\mathit{Ro}\leqslant 5$
, there is no gravity wave radiation. This is due to inertial cutoff of gravity wave radiation and propagation, since the square root term in (3.26) is negative (cf. Zeitlin Reference Zeitlin2007).

Figure 2. Snapshots of the far field (
![]() $r\leqslant 100$
) of gravity waves (
$r\leqslant 100$
) of gravity waves (
![]() $\text{d}{\it\Phi}/\text{d}t$
, where
$\text{d}{\it\Phi}/\text{d}t$
, where
![]() ${\it\Phi}\equiv gh$
) radiated from a co-rotating vortex pair with various parameter values: (a)
${\it\Phi}\equiv gh$
) radiated from a co-rotating vortex pair with various parameter values: (a)
![]() $\mathit{Ro}=\infty ~(\,f=0)$
,
$\mathit{Ro}=\infty ~(\,f=0)$
,
![]() $\mathit{Fr}=0.6~(gh_{0}=25/36)$
, contour interval
$\mathit{Fr}=0.6~(gh_{0}=25/36)$
, contour interval
![]() $=1.5\times 10^{-5}$
; (b)
$=1.5\times 10^{-5}$
; (b)
![]() $\mathit{Ro}=\infty$
,
$\mathit{Ro}=\infty$
,
![]() $\mathit{Fr}=0.3~(gh_{0}=25/9)$
, contour interval
$\mathit{Fr}=0.3~(gh_{0}=25/9)$
, contour interval
![]() $=4\times 10^{-6}$
; and (c)
$=4\times 10^{-6}$
; and (c)
![]() $\mathit{Ro}=6~(\,f=1/6)$
,
$\mathit{Ro}=6~(\,f=1/6)$
,
![]() $\mathit{Fr}=0.6$
, contour interval
$\mathit{Fr}=0.6$
, contour interval
![]() $=8\times 10^{-6}$
. The circles behind the contours denote
$=8\times 10^{-6}$
. The circles behind the contours denote
![]() $r=5$
, 10, 20, 30, 40 and 50, respectively.
$r=5$
, 10, 20, 30, 40 and 50, respectively.
The dependence on
![]() $f/2{\it\Omega}$
of the intensity of gravity waves for both cyclone pairs and anticyclone pairs is shown in figure 3. Here, by defining geopotential
$f/2{\it\Omega}$
of the intensity of gravity waves for both cyclone pairs and anticyclone pairs is shown in figure 3. Here, by defining geopotential
![]() ${\it\Phi}\equiv gh$
, we calculate
${\it\Phi}\equiv gh$
, we calculate
as the intensity of gravity waves, since this value is the same at any
![]() $r$
in the far field due to (A 6a,b
) as follows:
$r$
in the far field due to (A 6a,b
) as follows:
Note that
![]() $I$
depends on
$I$
depends on
![]() $f$
not only from the term
$f$
not only from the term
![]() $f/2{\it\Omega}$
in the coefficients in (3.26) but also from the arguments of
$f/2{\it\Omega}$
in the coefficients in (3.26) but also from the arguments of
![]() $\text{Y}_{0}$
and
$\text{Y}_{0}$
and
![]() $\text{J}_{0}$
.
$\text{J}_{0}$
.

Figure 3. Analytical estimate of the dependence on
![]() $f/2{\it\Omega}$
of the intensity of gravity waves (
$f/2{\it\Omega}$
of the intensity of gravity waves (
![]() $I$
) calculated from (3.30), for cyclone pairs (
$I$
) calculated from (3.30), for cyclone pairs (
![]() ${\it\Omega}\geqslant 0$
) and anticyclone pairs (
${\it\Omega}\geqslant 0$
) and anticyclone pairs (
![]() ${\it\Omega}\leqslant 0$
).
${\it\Omega}\leqslant 0$
).
For anticyclone pairs, a local maximum,
![]() $I_{max}$
, appears at
$I_{max}$
, appears at
![]() $f/2{\it\Omega}=-0.4$
, which corresponds to medium
$f/2{\it\Omega}=-0.4$
, which corresponds to medium
![]() $\mathit{Ro}=12.5$
(
$\mathit{Ro}=12.5$
(
![]() $\,f=2/25$
). From (3.31),
$\,f=2/25$
). From (3.31),
![]() $I_{max}$
is about 1.51 times larger than that for the case of
$I_{max}$
is about 1.51 times larger than that for the case of
![]() $\mathit{Ro}=\infty$
(
$\mathit{Ro}=\infty$
(
![]() $\,f=0$
). On the other hand, the amplitude of gravity waves for cyclone pairs decreases monotonically as
$\,f=0$
). On the other hand, the amplitude of gravity waves for cyclone pairs decreases monotonically as
![]() $f$
increases (
$f$
increases (
![]() $\mathit{Ro}$
decreases). Cyclone–anticyclone asymmetry appears due to the signs of
$\mathit{Ro}$
decreases). Cyclone–anticyclone asymmetry appears due to the signs of
![]() ${\it\Omega}$
; the direction of rotation of vortex pairs. The
${\it\Omega}$
; the direction of rotation of vortex pairs. The
![]() $\mathit{Ro}$
dependence for anticyclone pairs corresponds to previous numerical results of gravity wave radiation from unsteady jet flows (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008), in which the gravity wave flux has a local maximum at intermediate
$\mathit{Ro}$
dependence for anticyclone pairs corresponds to previous numerical results of gravity wave radiation from unsteady jet flows (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008), in which the gravity wave flux has a local maximum at intermediate
![]() $\mathit{Ro}\sim 10$
. Further, previous numerical studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012) have reported that gravity waves are radiated from the source originating in the Coriolis force for relatively smaller
$\mathit{Ro}\sim 10$
. Further, previous numerical studies (Sugimoto et al.
Reference Sugimoto, Ishioka and Ishii2008; Sugimoto & Ishii Reference Sugimoto and Ishii2012) have reported that gravity waves are radiated from the source originating in the Coriolis force for relatively smaller
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\leqslant}10$
), which is also consistent with the analytical estimate obtained here.
${\leqslant}10$
), which is also consistent with the analytical estimate obtained here.
4. Numerical simulation
4.1. Experimental setting
In this section, we perform numerical simulations in order to verify the analytical solution derived in § 3. First, in this subsection we explain the experimental setting.
There are several difficulties in investigating gravity wave radiation from vortical motions in a numerical simulation. These difficulties include the large extent of the far field of gravity waves compared to the near field of vortical motions, the small energy of the wavefield, the possibility that numerical discretization may serve as a significant source of waves, and the errors arising from inaccurate boundary conditions. Gravity waves are so much faster than vortical flows that they soon propagate to the boundary, and wave reflection from the boundary often influences the results. Since gravity waves in an
![]() $f$
-plane shallow water system exhibit dispersion, there is no accurate non-reflective boundary condition. Applying a sponge layer is not an efficient way of introducing a boundary condition, because we have to prepare a very wide region, and trial and error is required to determine the damping coefficient and the width of the sponge layer. Furthermore, for parameter sweep experiments, different coefficients and widths of the sponge layer will be needed because of variations of the phase speed of gravity waves.
$f$
-plane shallow water system exhibit dispersion, there is no accurate non-reflective boundary condition. Applying a sponge layer is not an efficient way of introducing a boundary condition, because we have to prepare a very wide region, and trial and error is required to determine the damping coefficient and the width of the sponge layer. Furthermore, for parameter sweep experiments, different coefficients and widths of the sponge layer will be needed because of variations of the phase speed of gravity waves.
In order to avoid the above difficulties, it is advantageous to use a spectral method in an unbounded domain on a non-uniform grid system without reflection of waves. An effective method has been proposed recently by Ishioka (Reference Ishioka2008), as an extension of earlier work (Matsushima & Marcus Reference Matsushima and Marcus1997). In the present study, we apply this method to an
![]() $f$
-plane shallow water system. While a test simulation for a collapsing vortex has already been performed in preliminary work (Murakami Reference Murakami2008), we will further check the numerical model by comparing the results with the analytical estimates in a wide range of
$f$
-plane shallow water system. While a test simulation for a collapsing vortex has already been performed in preliminary work (Murakami Reference Murakami2008), we will further check the numerical model by comparing the results with the analytical estimates in a wide range of
![]() $\mathit{Ro}$
. We also perform simulations with different resolutions and several values of hyperviscosity to confirm the applicability of the numerical model. Note that the basic idea in Ishioka (Reference Ishioka2008) is applicable to several equations and is not limited to a shallow water system.
$\mathit{Ro}$
. We also perform simulations with different resolutions and several values of hyperviscosity to confirm the applicability of the numerical model. Note that the basic idea in Ishioka (Reference Ishioka2008) is applicable to several equations and is not limited to a shallow water system.
In order to implement the method, we start with a shallow water system on an
![]() $f$
-plane in cylindrical coordinates for the basic equations, which are derived by the coordinate transformation from (2.1) to (2.3):
$f$
-plane in cylindrical coordinates for the basic equations, which are derived by the coordinate transformation from (2.1) to (2.3):
The basic equations (4.1)–(4.3) are transformed to the equations of relative vorticity
![]() ${\it\zeta}$
, divergence
${\it\zeta}$
, divergence
![]() ${\it\gamma}$
and geopotential
${\it\gamma}$
and geopotential
![]() ${\it\Phi}\equiv gh$
for the convenience of numerical calculation. Then, (4.1)–(4.3) are reduced to
${\it\Phi}\equiv gh$
for the convenience of numerical calculation. Then, (4.1)–(4.3) are reduced to
To solve (4.4)–(4.6), we use a mapping method (Ishioka Reference Ishioka2008). In this method, we use a conformal mapping from a sphere with radius
![]() $R$
in spherical coordinates
$R$
in spherical coordinates
![]() $({\it\lambda},{\it\phi})$
to a plane in cylindrical coordinates
$({\it\lambda},{\it\phi})$
to a plane in cylindrical coordinates
![]() $(r,{\it\theta})$
with the aid of the following relation:
$(r,{\it\theta})$
with the aid of the following relation:
A schematic of this mapping is shown in figure 4. Then, the transformation of the coordinates is expressed as
By this mapping, we can calculate the phenomena on a two-dimensional unbounded plane from the phenomena on a sphere with an ordinary spectral method, such as spherical harmonics. In addition, we set the grid points non-uniformly so that many grid points are positioned in the near field of vortical flows, while few are in the far field of gravity waves. This model enables us to simulate gravity wave radiation from vortical flows localized in the centre region with high accuracy.

Figure 4. Schematic of the mapping method from
![]() $P_{i}({\it\lambda},{\it\phi})$
on a sphere to
$P_{i}({\it\lambda},{\it\phi})$
on a sphere to
![]() $Q_{i}(r,{\it\theta})$
on a plane.
$Q_{i}(r,{\it\theta})$
on a plane.
In addition, the Laplacian on the plane is easily related to that on the sphere by the following equation:
Here
![]() ${\rm\Delta}_{s}$
is the Laplacian on the sphere expressed as
${\rm\Delta}_{s}$
is the Laplacian on the sphere expressed as
Since
![]() ${\it\zeta}$
and
${\it\zeta}$
and
![]() ${\it\gamma}$
are obtained by the Laplacian of
${\it\gamma}$
are obtained by the Laplacian of
![]() ${\it\psi}$
and
${\it\psi}$
and
![]() ${\it\chi}$
, respectively, (4.4)–(4.6) are easily calculated on a sphere by the usual properties of spherical harmonics, as follows:
${\it\chi}$
, respectively, (4.4)–(4.6) are easily calculated on a sphere by the usual properties of spherical harmonics, as follows:
A notable feature of this method is pseudo-hyperviscosity. In the numerical simulation, we include the following type of hyperviscosity:
where
![]() ${\it\nu}$
,
${\it\nu}$
,
![]() $p$
and
$p$
and
![]() $P=({\it\zeta},{\it\gamma},{\it\Phi})$
are the viscosity coefficient, order of viscosity and physical variables, respectively. This form of hyperviscosity has two advantages. One is that the hyperviscosity (4.17) acts as a sponge layer far from the vortical region, since (4.17) is transformed from (4.14) to
$P=({\it\zeta},{\it\gamma},{\it\Phi})$
are the viscosity coefficient, order of viscosity and physical variables, respectively. This form of hyperviscosity has two advantages. One is that the hyperviscosity (4.17) acts as a sponge layer far from the vortical region, since (4.17) is transformed from (4.14) to
It can be easily seen that, while this term acts as usual hyperviscosity for small
![]() ${\it\phi}$
, the viscosity becomes very large far from the vortex region for large
${\it\phi}$
, the viscosity becomes very large far from the vortex region for large
![]() ${\it\phi}$
. Since this role is directly linked to a sponge layer, we call this type of hyperviscosity ‘pseudo-hyperviscosity’.
${\it\phi}$
. Since this role is directly linked to a sponge layer, we call this type of hyperviscosity ‘pseudo-hyperviscosity’.
The second advantage is that the Laplacian operator on a sphere is easily calculated by spherical harmonics (4.16). Thus, the pseudo-hyperviscosity (4.17) is easy to code in the numerical simulation as follows:
While it has been reported that results using hyperviscosity do not always simulate inviscid dynamics nor molecular-diffusive dynamics (e.g. Jiménez Reference Jiménez1994; Mariotti, Legras & Dritschel Reference Mariotti, Legras and Dritschel1994; Yao, Zabusky & Dritschel Reference Yao, Zabusky and Dritschel1995), we include hyperviscosity to prevent numerical instability and set a value of the viscosity coefficient
![]() ${\it\nu}$
as small as possible to keep the intensity of vortex and to damp radiated gravity waves effectively in the far field. We will discuss the influence of hyperviscosity later.
${\it\nu}$
as small as possible to keep the intensity of vortex and to damp radiated gravity waves effectively in the far field. We will discuss the influence of hyperviscosity later.
As an initial state, we use a co-rotating Gaussian vortex pair, which is expressed as
where
![]() $A$
and
$A$
and
![]() ${\it\sigma}$
determine the amplitude and radius of the vortices, respectively. The signs in (4.20) are positive for a cyclone pair and negative for an anticyclone pair. The depth of the fluid
${\it\sigma}$
determine the amplitude and radius of the vortices, respectively. The signs in (4.20) are positive for a cyclone pair and negative for an anticyclone pair. The depth of the fluid
![]() ${\it\Phi}$
is set to be in gradient wind balance with the Gaussian vortex. Although the vortices are assumed to be point vortices in § 3, it is not possible to produce a balanced state of the vortices in a shallow water system in the presence of surface elevation. Note that, since the Coriolis force acts in opposite directions for cyclones and anticyclones, the vortices in an
${\it\Phi}$
is set to be in gradient wind balance with the Gaussian vortex. Although the vortices are assumed to be point vortices in § 3, it is not possible to produce a balanced state of the vortices in a shallow water system in the presence of surface elevation. Note that, since the Coriolis force acts in opposite directions for cyclones and anticyclones, the vortices in an
![]() $f$
-plane shallow water system have cyclone–anticyclone asymmetry for the depth of the fluid, especially for large
$f$
-plane shallow water system have cyclone–anticyclone asymmetry for the depth of the fluid, especially for large
![]() $f$
.
$f$
.
The non-dimensional parameters in the numerical simulation are defined by the initial state of the Gaussian vortex:
We fix
![]() $A=20$
and
$A=20$
and
![]() ${\it\sigma}=0.05$
in (4.20). This leads to the maximum velocity
${\it\sigma}=0.05$
in (4.20). This leads to the maximum velocity
![]() $U_{i}\sim 0.5$
in the
$U_{i}\sim 0.5$
in the
![]() ${\it\theta}$
direction for the initial vortices. The initial positions of the vortices are also fixed to
${\it\theta}$
direction for the initial vortices. The initial positions of the vortices are also fixed to
![]() $l=0.5$
and
$l=0.5$
and
![]() ${\it\theta}_{1}={\rm\pi}/4$
. Then
${\it\theta}_{1}={\rm\pi}/4$
. Then
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{Fr}$
are the non-dimensional reciprocals of
$\mathit{Fr}$
are the non-dimensional reciprocals of
![]() $f$
and
$f$
and
![]() ${\it\Phi}_{0}=gh_{0}$
, respectively. Note that the definitions of (4.21) correspond to those of the analytical study in § 3.
${\it\Phi}_{0}=gh_{0}$
, respectively. Note that the definitions of (4.21) correspond to those of the analytical study in § 3.
An example of an initial Gaussian vortex (cyclone) with
![]() $\mathit{Ro}=20~(\,f=1/20)$
and
$\mathit{Ro}=20~(\,f=1/20)$
and
![]() $\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
is shown in figure 5. The vorticity
$\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
is shown in figure 5. The vorticity
![]() ${\it\zeta}$
, velocity
${\it\zeta}$
, velocity
![]() $u$
in the
$u$
in the
![]() ${\it\theta}$
direction and geopotential height
${\it\theta}$
direction and geopotential height
![]() ${\it\Phi}$
along the section of the centre of the vortices are shown. Since we use strong vortices at the initial state, both cyclones and anticyclones have a shallower depth at the centre of the vortices, where the term ‘anticyclone’ indicates an anticyclonic rotation, not a high-pressure system.
${\it\Phi}$
along the section of the centre of the vortices are shown. Since we use strong vortices at the initial state, both cyclones and anticyclones have a shallower depth at the centre of the vortices, where the term ‘anticyclone’ indicates an anticyclonic rotation, not a high-pressure system.

Figure 5. Basic state of an initial Gaussian vortex (cyclone) for the run with
![]() $\mathit{Ro}=20~(\,f=1/20)$
and
$\mathit{Ro}=20~(\,f=1/20)$
and
![]() $\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
: (a) vorticity
$\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
: (a) vorticity
![]() ${\it\zeta}$
, (b) velocity
${\it\zeta}$
, (b) velocity
![]() $u$
in the
$u$
in the
![]() ${\it\theta}$
direction, and (c) geopotential height
${\it\theta}$
direction, and (c) geopotential height
![]() ${\it\Phi}$
. One vortex is shown.
${\it\Phi}$
. One vortex is shown.
In the numerical simulation, we set
![]() $R=8$
and
$R=8$
and
![]() $T=682$
, where
$T=682$
, where
![]() $T$
is the truncation wavenumber of the spherical harmonics for the spectral method, in order to match the numerical results with the analytical estimates sufficiently. Then there are 2048 and 1024 grid points in the
$T$
is the truncation wavenumber of the spherical harmonics for the spectral method, in order to match the numerical results with the analytical estimates sufficiently. Then there are 2048 and 1024 grid points in the
![]() ${\it\theta}$
and
${\it\theta}$
and
![]() $r$
directions, respectively. Using this resolution, the grid intervals in the
$r$
directions, respectively. Using this resolution, the grid intervals in the
![]() $r$
direction
$r$
direction
![]() $({\rm\Delta}r)$
in the near field (
$({\rm\Delta}r)$
in the near field (
![]() $r\leqslant 2$
) are
$r\leqslant 2$
) are
![]() ${\rm\Delta}r\leqslant 0.0249$
, and the farthest grid points are positioned at
${\rm\Delta}r\leqslant 0.0249$
, and the farthest grid points are positioned at
![]() $r\sim 13\,632$
. We set
$r\sim 13\,632$
. We set
![]() ${\it\nu}=10^{-11}$
and
${\it\nu}=10^{-11}$
and
![]() $p=3$
to prevent any artificial disturbance. A time integration is performed by the fourth-order Runge–Kutta method with an increment time of 0.025. The numerical calculation is continued to the end of time 200, which corresponds to 8000 total time steps.
$p=3$
to prevent any artificial disturbance. A time integration is performed by the fourth-order Runge–Kutta method with an increment time of 0.025. The numerical calculation is continued to the end of time 200, which corresponds to 8000 total time steps.
The computational cost per time step is
![]() $O(NT)$
for this spectral method, where
$O(NT)$
for this spectral method, where
![]() $N$
is the number of grid points and
$N$
is the number of grid points and
![]() $T$
is the truncation wavenumber. Although this cost is higher than that for the finite difference method (
$T$
is the truncation wavenumber. Although this cost is higher than that for the finite difference method (
![]() $O(N)$
), we adopt the spectral method for the following three advantages. First, the present spectral method has higher accuracy than the finite difference method with the same resolution. Second, a longer time step can be used for the present method than for the finite difference method because the present method can relax the severe Courant–Friedrichs–Lewy (CFL) condition arising from the concentration of the grid points near the origin. Third, the present method can suppress the spurious reflection of waves from the boundary of the computational domain thanks to the pseudo-hyperviscosity as explained above.
$O(N)$
), we adopt the spectral method for the following three advantages. First, the present spectral method has higher accuracy than the finite difference method with the same resolution. Second, a longer time step can be used for the present method than for the finite difference method because the present method can relax the severe Courant–Friedrichs–Lewy (CFL) condition arising from the concentration of the grid points near the origin. Third, the present method can suppress the spurious reflection of waves from the boundary of the computational domain thanks to the pseudo-hyperviscosity as explained above.
4.2. Cyclone pair (
 $\mathit{Ro}=20$
and
$\mathit{Ro}=20$
and
 $\mathit{Fr}=0.6$
)
$\mathit{Fr}=0.6$
)
Here we compare the results of the numerical simulation with those of the analytical study for a co-rotating cyclone pair. The non-dimensional parameters are set to be
![]() $\mathit{Ro}=20~(\,f=1/20)$
and
$\mathit{Ro}=20~(\,f=1/20)$
and
![]() $\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
. Although these values are not realistic for slow vortical phenomena in the atmosphere on the Earth, the results are typical and easy to understand for cyclone–anticyclone asymmetry in spontaneous gravity wave radiation.
$\mathit{Fr}=0.6~({\it\Phi}_{0}=25/36)$
. Although these values are not realistic for slow vortical phenomena in the atmosphere on the Earth, the results are typical and easy to understand for cyclone–anticyclone asymmetry in spontaneous gravity wave radiation.
Snapshots of the time evolution for a run of a cyclone pair are shown in figure 6. Three prognostic physical variables,
![]() ${\it\zeta}$
,
${\it\zeta}$
,
![]() ${\it\gamma}$
and
${\it\gamma}$
and
![]() ${\it\Phi}$
, are shown here, because we use them to integrate (4.4)–(4.6) numerically. The near field (
${\it\Phi}$
, are shown here, because we use them to integrate (4.4)–(4.6) numerically. The near field (
![]() $r\leqslant 2$
) of vortices is enlarged in the left and right columns, while the far field (
$r\leqslant 2$
) of vortices is enlarged in the left and right columns, while the far field (
![]() $r\leqslant 100$
) of gravity waves is shown in the centre column. As a vortex pair co-rotates, gravity waves with double spiral structure are radiated in the divergent field (centre). While gravity waves with small scales and amplitudes are radiated from the initial geostrophic adjustment process (centre panels in figure 6
b,c), they are dissipated subsequently by pseudo-hyperviscosity as they propagate to the far field (centre panels in figure 6
d,e). As the initial vortices radiate gravity waves, they are weakened slightly due to energy dissipation by gravity wave radiation and hyperviscosity. Nevertheless, they keep enough strength to co-rotate, and it is clearly seen that gravity waves are radiated continuously in the divergent field. Initially, one turnover time is 64 as a rough estimate, and it takes longer for another turnover. Then, a wave of about four wavelengths is radiated at
$r\leqslant 100$
) of gravity waves is shown in the centre column. As a vortex pair co-rotates, gravity waves with double spiral structure are radiated in the divergent field (centre). While gravity waves with small scales and amplitudes are radiated from the initial geostrophic adjustment process (centre panels in figure 6
b,c), they are dissipated subsequently by pseudo-hyperviscosity as they propagate to the far field (centre panels in figure 6
d,e). As the initial vortices radiate gravity waves, they are weakened slightly due to energy dissipation by gravity wave radiation and hyperviscosity. Nevertheless, they keep enough strength to co-rotate, and it is clearly seen that gravity waves are radiated continuously in the divergent field. Initially, one turnover time is 64 as a rough estimate, and it takes longer for another turnover. Then, a wave of about four wavelengths is radiated at
![]() $t=120$
(figure 6
e). Note that the divergent field is depicted in the area which gravity waves reach from the initial time (
$t=120$
(figure 6
e). Note that the divergent field is depicted in the area which gravity waves reach from the initial time (
![]() $t=0$
). In the vorticity field, there is also a weak vorticity spreading all around the streamlines connecting the hyperbolic points because of hyperviscosity. However, it is confirmed that these vorticity filaments do not radiate significant gravity waves in the present study.
$t=0$
). In the vorticity field, there is also a weak vorticity spreading all around the streamlines connecting the hyperbolic points because of hyperviscosity. However, it is confirmed that these vorticity filaments do not radiate significant gravity waves in the present study.

Figure 6. Snapshots of the time evolution of a run of a cyclone pair with
![]() $\mathit{Ro}=20$
and
$\mathit{Ro}=20$
and
![]() $\mathit{Fr}=0.6$
: (left) vorticity
$\mathit{Fr}=0.6$
: (left) vorticity
![]() ${\it\zeta}$
, (centre) divergence
${\it\zeta}$
, (centre) divergence
![]() ${\it\gamma}$
and (right) geopotential height
${\it\gamma}$
and (right) geopotential height
![]() ${\it\Phi}$
, with
${\it\Phi}$
, with
![]() ${\it\zeta}$
and
${\it\zeta}$
and
![]() ${\it\Phi}$
shown in the near field (
${\it\Phi}$
shown in the near field (
![]() $r\leqslant 2$
) and
$r\leqslant 2$
) and
![]() ${\it\gamma}$
shown in the far field (
${\it\gamma}$
shown in the far field (
![]() $r\leqslant 100$
). The time steps are (a)
$r\leqslant 100$
). The time steps are (a)
![]() $t=0$
, (b)
$t=0$
, (b)
![]() $t=30$
, (c)
$t=30$
, (c)
![]() $t=60$
, (d)
$t=60$
, (d)
![]() $t=90$
and (e)
$t=90$
and (e)
![]() $t=120$
. The circles behind the contours in the centre panels denote
$t=120$
. The circles behind the contours in the centre panels denote
![]() $r=5$
, 10, 20, 30, 40 and 50, respectively.
$r=5$
, 10, 20, 30, 40 and 50, respectively.
Figure 7 shows snapshots of the far field (
![]() $r\leqslant 100$
) of gravity waves,
$r\leqslant 100$
) of gravity waves,
![]() $\text{d}{\it\Phi}/\text{d}t$
, for a run of a cyclone pair at
$\text{d}{\it\Phi}/\text{d}t$
, for a run of a cyclone pair at
![]() $t=150$
in comparison with the analytical estimate (3.26) with the same parameter values:
$t=150$
in comparison with the analytical estimate (3.26) with the same parameter values:
![]() $\text{d}{\it\Phi}/\text{d}t$
is estimated from (4.6) except for the effect of the hyperviscosity. Since the initial Gaussian vortices in the numerical simulation are not point vortices as assumed in the analytical study, we estimate the intensity of the vortices
$\text{d}{\it\Phi}/\text{d}t$
is estimated from (4.6) except for the effect of the hyperviscosity. Since the initial Gaussian vortices in the numerical simulation are not point vortices as assumed in the analytical study, we estimate the intensity of the vortices
![]() ${\it\Gamma}\sim 0.98\times (2{\rm\pi}{\it\sigma}^{2}A)$
(thus
${\it\Gamma}\sim 0.98\times (2{\rm\pi}{\it\sigma}^{2}A)$
(thus
![]() ${\it\Omega}={\it\Gamma}/4{\rm\pi}l^{2}\sim 0.098$
) in the analytical calculation of (3.26) in order to ensure that the rotation rate, namely, angular velocity
${\it\Omega}={\it\Gamma}/4{\rm\pi}l^{2}\sim 0.098$
) in the analytical calculation of (3.26) in order to ensure that the rotation rate, namely, angular velocity
![]() ${\it\Omega}$
, has the same value as that in the numerical simulation. This intensity is nearly consistent with that of the analytical estimate for a Gaussian vortex,
${\it\Omega}$
, has the same value as that in the numerical simulation. This intensity is nearly consistent with that of the analytical estimate for a Gaussian vortex,
where
![]() $\boldsymbol{S}$
indicates a plane perpendicular to the direction of
$\boldsymbol{S}$
indicates a plane perpendicular to the direction of
![]() ${\bf\omega}$
. The reason that
${\bf\omega}$
. The reason that
![]() ${\it\Gamma}$
in the numerical simulation is slightly smaller than that in the analytical estimate (4.22) might be due to the effect of hyperviscosity, which weakens vortices in the time evolution gradually. We also choose an appropriate time for the analytical estimate to coincide with the numerical results. The double spiral structures are quite similar between the two cases. Since two gravity waves are radiated in one turnover time of
${\it\Gamma}$
in the numerical simulation is slightly smaller than that in the analytical estimate (4.22) might be due to the effect of hyperviscosity, which weakens vortices in the time evolution gradually. We also choose an appropriate time for the analytical estimate to coincide with the numerical results. The double spiral structures are quite similar between the two cases. Since two gravity waves are radiated in one turnover time of
![]() $2{\rm\pi}/{\it\Omega}\sim 64.1$
, the wavelength is estimated to be
$2{\rm\pi}/{\it\Omega}\sim 64.1$
, the wavelength is estimated to be
![]() $32.06\times c_{0}({\sim}0.8333)\sim 26.7$
. Figure 7 indicates that the process of spontaneous gravity wave radiation, propagation, phase speed and wavelength are sufficiently well simulated in the numerical model. Note that the rotation rate is modified by the finite wave speed and may be derived analytically. It is, however, almost the same as that for the non-rotating (or barotropic) case for large
$32.06\times c_{0}({\sim}0.8333)\sim 26.7$
. Figure 7 indicates that the process of spontaneous gravity wave radiation, propagation, phase speed and wavelength are sufficiently well simulated in the numerical model. Note that the rotation rate is modified by the finite wave speed and may be derived analytically. It is, however, almost the same as that for the non-rotating (or barotropic) case for large
![]() $\mathit{Ro}$
, because the separation distance between vortices is sufficiently smaller than the deformation radius,
$\mathit{Ro}$
, because the separation distance between vortices is sufficiently smaller than the deformation radius,
![]() $2l\ll \sqrt{{\it\Phi}_{0}}/f$
.
$2l\ll \sqrt{{\it\Phi}_{0}}/f$
.

Figure 7. Snapshots of the far field (
![]() $r\leqslant 100$
) of gravity waves (
$r\leqslant 100$
) of gravity waves (
![]() $\text{d}{\it\Phi}/\text{d}t$
) for a cyclone pair with
$\text{d}{\it\Phi}/\text{d}t$
) for a cyclone pair with
![]() $\mathit{Ro}=20$
and
$\mathit{Ro}=20$
and
![]() $\mathit{Fr}=0.6$
: (a) the analytical estimate (3.26), contour interval
$\mathit{Fr}=0.6$
: (a) the analytical estimate (3.26), contour interval
![]() $=1.5\times 10^{-5}$
; and (b) the numerical simulation (at
$=1.5\times 10^{-5}$
; and (b) the numerical simulation (at
![]() $t=150$
), contour interval
$t=150$
), contour interval
![]() $1.5\times 10^{-2}$
. The circles behind the contours denote
$1.5\times 10^{-2}$
. The circles behind the contours denote
![]() $r=5$
, 10, 20, 30, 40 and 50, respectively.
$r=5$
, 10, 20, 30, 40 and 50, respectively.
Moreover, the amplitudes of gravity waves in the far field between the two results are almost the same. Figure 8 shows line plots of radiated gravity waves from a cyclone pair,
![]() $\text{d}{\it\Phi}/\text{d}t$
, against
$\text{d}{\it\Phi}/\text{d}t$
, against
![]() $r$
for both the analytical estimate (solid line) and numerical simulation (broken line). The line plot in the
$r$
for both the analytical estimate (solid line) and numerical simulation (broken line). The line plot in the
![]() ${\it\theta}={\rm\pi}/4$
section at
${\it\theta}={\rm\pi}/4$
section at
![]() $t=200$
is shown for the numerical simulation, while we again choose an appropriate time for the analytical estimate to coincide with the numerical results. The results of the numerical simulation are in excellent agreement with those of the analytical estimate, especially at
$t=200$
is shown for the numerical simulation, while we again choose an appropriate time for the analytical estimate to coincide with the numerical results. The results of the numerical simulation are in excellent agreement with those of the analytical estimate, especially at
![]() $65\leqslant r\leqslant 105$
. It should be emphasized that our configuration of the numerical experiments is not the same as that of the analytical study, since we assume point vortices in (3.26) excluding a surface elevation. Nevertheless, radiated gravity waves are quite similar, in both spatial scale and amplitude. A slight difference of the phase in the numerical simulation appears in the inner part (
$65\leqslant r\leqslant 105$
. It should be emphasized that our configuration of the numerical experiments is not the same as that of the analytical study, since we assume point vortices in (3.26) excluding a surface elevation. Nevertheless, radiated gravity waves are quite similar, in both spatial scale and amplitude. A slight difference of the phase in the numerical simulation appears in the inner part (
![]() $r<65$
). This might be due to the effect of hyperviscosity, which weakens vortices in the time evolution gradually but shortens the separation distance. It is possible to set smaller
$r<65$
). This might be due to the effect of hyperviscosity, which weakens vortices in the time evolution gradually but shortens the separation distance. It is possible to set smaller
![]() ${\it\Omega}$
(
${\it\Omega}$
(
![]() ${<}0.098$
) for the analytical estimate to coincide with the results of the numerical simulation for
${<}0.098$
) for the analytical estimate to coincide with the results of the numerical simulation for
![]() $r<65$
(for later time). In that case, the far field of gravity waves (
$r<65$
(for later time). In that case, the far field of gravity waves (
![]() $65\leqslant r$
) does not coincide with the analytical estimate as a trade-off. Note that deviations at the inner region (
$65\leqslant r$
) does not coincide with the analytical estimate as a trade-off. Note that deviations at the inner region (
![]() $r\leqslant 10$
) in the numerical simulation are not gravity waves that propagate to the far field but a balanced component associated with vortical motions.
$r\leqslant 10$
) in the numerical simulation are not gravity waves that propagate to the far field but a balanced component associated with vortical motions.

Figure 8. The far field (
![]() $r\leqslant 150$
) of gravity waves (
$r\leqslant 150$
) of gravity waves (
![]() $\text{d}{\it\Phi}/\text{d}t$
) for a cyclone pair with
$\text{d}{\it\Phi}/\text{d}t$
) for a cyclone pair with
![]() $\mathit{Ro}=20$
and
$\mathit{Ro}=20$
and
![]() $\mathit{Fr}=0.6$
for the analytical estimate (3.26) (solid line) and numerical simulation in the
$\mathit{Fr}=0.6$
for the analytical estimate (3.26) (solid line) and numerical simulation in the
![]() ${\it\theta}={\rm\pi}/4$
section at
${\it\theta}={\rm\pi}/4$
section at
![]() $t=200$
(broken line).
$t=200$
(broken line).
4.3. Cyclone–anticyclone asymmetry in gravity wave radiation
We perform the numerical simulation with several
![]() $\mathit{Ro}~(=4,6,8,10,12,15,20,\infty )$
for fixed
$\mathit{Ro}~(=4,6,8,10,12,15,20,\infty )$
for fixed
![]() $\mathit{Fr}=0.6$
for both cases of cyclone pairs and anticyclone pairs to investigate cyclone–anticyclone asymmetry in gravity wave radiation. The other experimental setting is the same as a cyclone pair of
$\mathit{Fr}=0.6$
for both cases of cyclone pairs and anticyclone pairs to investigate cyclone–anticyclone asymmetry in gravity wave radiation. The other experimental setting is the same as a cyclone pair of
![]() $\mathit{Ro}=20$
and
$\mathit{Ro}=20$
and
![]() $\mathit{Fr}=0.6$
as shown in § 4.2. As an anticyclone pair co-rotates in the opposite direction to a cyclone pair, gravity waves are spontaneously radiated from vortical flows in the same way as a cyclone pair (not shown). The structure in the far field of gravity waves is also a double spiral, while the direction of rotation is opposite to that from a cyclone pair. Although the spontaneous gravity wave radiation from an anticyclone pair is qualitatively similar to that from a cyclone pair, the amplitude of gravity waves is different at finite values of
$\mathit{Fr}=0.6$
as shown in § 4.2. As an anticyclone pair co-rotates in the opposite direction to a cyclone pair, gravity waves are spontaneously radiated from vortical flows in the same way as a cyclone pair (not shown). The structure in the far field of gravity waves is also a double spiral, while the direction of rotation is opposite to that from a cyclone pair. Although the spontaneous gravity wave radiation from an anticyclone pair is qualitatively similar to that from a cyclone pair, the amplitude of gravity waves is different at finite values of
![]() $f$
.
$f$
.
In order to elucidate cyclone–anticyclone asymmetry, line plots of radiated gravity waves from cyclone pairs (a,c,e) and anticyclone pairs (b,d, f) are shown in figure 9 for
![]() $\mathit{Ro}=\infty$
, 12 and 8, respectively. Both the analytical estimate (solid line) and numerical simulation (broken line) of
$\mathit{Ro}=\infty$
, 12 and 8, respectively. Both the analytical estimate (solid line) and numerical simulation (broken line) of
![]() $\text{d}{\it\Phi}/\text{d}t$
are shown. The line plots in the
$\text{d}{\it\Phi}/\text{d}t$
are shown. The line plots in the
![]() ${\it\theta}={\rm\pi}/4$
section at
${\it\theta}={\rm\pi}/4$
section at
![]() $t=200$
are shown for the numerical simulation, while we again choose an appropriate time for the analytical estimate to coincide with the numerical results. The results of the numerical simulation are in excellent agreement with those of the analytical estimate. The important result is that gravity waves radiated from anticyclone pairs have larger amplitude than those from cyclone pairs for a finite value of
$t=200$
are shown for the numerical simulation, while we again choose an appropriate time for the analytical estimate to coincide with the numerical results. The results of the numerical simulation are in excellent agreement with those of the analytical estimate. The important result is that gravity waves radiated from anticyclone pairs have larger amplitude than those from cyclone pairs for a finite value of
![]() $f$
. For an anticyclone pair with
$f$
. For an anticyclone pair with
![]() $\mathit{Ro}=12$
, the amplitude of gravity waves is larger than that with
$\mathit{Ro}=12$
, the amplitude of gravity waves is larger than that with
![]() $\mathit{Ro}=\infty$
and 8, which clearly indicates a local maximum at around
$\mathit{Ro}=\infty$
and 8, which clearly indicates a local maximum at around
![]() $\mathit{Ro}=12$
. On the other hand, the amplitudes of gravity waves for cyclone pairs monotonically decrease as
$\mathit{Ro}=12$
. On the other hand, the amplitudes of gravity waves for cyclone pairs monotonically decrease as
![]() $\mathit{Ro}$
decreases. Note that for
$\mathit{Ro}$
decreases. Note that for
![]() $\mathit{Ro}=8$
a slight deviation appears in the far field (
$\mathit{Ro}=8$
a slight deviation appears in the far field (
![]() $120\leqslant r$
), which is larger for an anticyclone pair. One reason might be due to gravity wave radiation from an initial geostrophic adjustment process. It is supposed that gravity waves are damped by the effect of hyperviscosity, since pseudo-hyperviscosity acts as a sponge layer in the far field. At relatively smaller
$120\leqslant r$
), which is larger for an anticyclone pair. One reason might be due to gravity wave radiation from an initial geostrophic adjustment process. It is supposed that gravity waves are damped by the effect of hyperviscosity, since pseudo-hyperviscosity acts as a sponge layer in the far field. At relatively smaller
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\leqslant}10$
), the phase differences between analytical estimates and numerical results may also be caused by the modification of the rotation rate due to the finite deformation radius.
${\leqslant}10$
), the phase differences between analytical estimates and numerical results may also be caused by the modification of the rotation rate due to the finite deformation radius.

Figure 9. The far field (
![]() $r\leqslant 150$
) of gravity waves (
$r\leqslant 150$
) of gravity waves (
![]() $\text{d}{\it\Phi}/\text{d}t$
) for (a,c,e) cyclone pairs and (b,d, f) anticyclone pairs for the analytical estimate (3.26) (solid line) and the numerical simulation in the
$\text{d}{\it\Phi}/\text{d}t$
) for (a,c,e) cyclone pairs and (b,d, f) anticyclone pairs for the analytical estimate (3.26) (solid line) and the numerical simulation in the
![]() ${\it\theta}={\rm\pi}/4$
section at
${\it\theta}={\rm\pi}/4$
section at
![]() $t=200$
(broken line) with
$t=200$
(broken line) with
![]() $\mathit{Fr}=0.6$
: (a,b)
$\mathit{Fr}=0.6$
: (a,b)
![]() $\mathit{Ro}=\infty$
, (c,d)
$\mathit{Ro}=\infty$
, (c,d)
![]() $\mathit{Ro}=12$
and (e, f)
$\mathit{Ro}=12$
and (e, f)
![]() $\mathit{Ro}=8$
.
$\mathit{Ro}=8$
.
Furthermore, the intensity of gravity waves (
![]() $I$
) is calculated from (3.30) for the numerical simulation. Figure 10 shows the dependence on
$I$
) is calculated from (3.30) for the numerical simulation. Figure 10 shows the dependence on
![]() $f/2{\it\Omega}$
of
$f/2{\it\Omega}$
of
![]() $I$
normalized by that of
$I$
normalized by that of
![]() $f=0~(I/I_{f=0})$
for the analytical estimate (solid line) and numerical simulation (symbols). Again, numerical results agree very well with analytical ones for both cyclone pairs (crosses) and anticyclone pairs (circles). In figure 10, the analytical estimate excluding the source (3.12) is also shown (dotted line). It is clear that cyclone–anticyclone asymmetry comes from the source (3.12), which originates in the Coriolis force.
$f=0~(I/I_{f=0})$
for the analytical estimate (solid line) and numerical simulation (symbols). Again, numerical results agree very well with analytical ones for both cyclone pairs (crosses) and anticyclone pairs (circles). In figure 10, the analytical estimate excluding the source (3.12) is also shown (dotted line). It is clear that cyclone–anticyclone asymmetry comes from the source (3.12), which originates in the Coriolis force.

Figure 10. The dependence on
![]() $f/2{\it\Omega}$
of the intensity of gravity waves normalized by that of
$f/2{\it\Omega}$
of the intensity of gravity waves normalized by that of
![]() $f=0~(I/I_{f=0})$
for the analytical estimate (solid line) and the numerical simulation (symbols). Circles and crosses are for anticyclone pairs and cyclone pairs with
$f=0~(I/I_{f=0})$
for the analytical estimate (solid line) and the numerical simulation (symbols). Circles and crosses are for anticyclone pairs and cyclone pairs with
![]() $\mathit{Ro}=8$
, 12, 20 and
$\mathit{Ro}=8$
, 12, 20 and
![]() $\infty$
. The dotted line shows the analytical estimate excluding the source (3.12).
$\infty$
. The dotted line shows the analytical estimate excluding the source (3.12).
The overall results indicate that the analytical solution derived in § 3 is verified successfully by the newly developed numerical model. Note that we additionally perform numerical simulations with different
![]() $\mathit{Fr}$
. The results in the numerical simulations coincide sufficiently with those of the analytical study (not shown). We have checked the results with different values of the hyperviscosity and different resolutions (with different radius
$\mathit{Fr}$
. The results in the numerical simulations coincide sufficiently with those of the analytical study (not shown). We have checked the results with different values of the hyperviscosity and different resolutions (with different radius
![]() $R$
). With a smaller hyperviscosity (
$R$
). With a smaller hyperviscosity (
![]() ${\it\nu}\leqslant 10^{-12}$
), while the gravity waves radiated from a co-rotating vortex pair are qualitatively the same, gravity waves are not damped in the far field (
${\it\nu}\leqslant 10^{-12}$
), while the gravity waves radiated from a co-rotating vortex pair are qualitatively the same, gravity waves are not damped in the far field (
![]() $r>150$
), thus eventually the numerical simulation collapses. In contrast, with a large hyperviscosity (
$r>150$
), thus eventually the numerical simulation collapses. In contrast, with a large hyperviscosity (
![]() ${\it\nu}\geqslant 10^{-10}$
), the amplitude of vortices gradually weakens and broadens. Then the numerical results do not coincide with the analytical estimate. Gravity waves with small scales and amplitudes are also radiated from the weakened vortex pair through the mechanism of geostrophic adjustment by the dissipation. This is also true for a simulation with a medium resolution of
${\it\nu}\geqslant 10^{-10}$
), the amplitude of vortices gradually weakens and broadens. Then the numerical results do not coincide with the analytical estimate. Gravity waves with small scales and amplitudes are also radiated from the weakened vortex pair through the mechanism of geostrophic adjustment by the dissipation. This is also true for a simulation with a medium resolution of
![]() $T=341$
with a larger value of hyperviscosity. Excellent agreements with the analytical estimate are obtained only for the
$T=341$
with a larger value of hyperviscosity. Excellent agreements with the analytical estimate are obtained only for the
![]() $T=682$
simulation with
$T=682$
simulation with
![]() ${\it\nu}=10^{-11}$
. The main difficulty is that we have to keep the Gaussian vortex similar to the point vortex in the numerical simulation because we assume point vortices in the analytical study. Thus a high-resolution numerical model with sufficiently small hyperviscosity is required to mimic a pair of point vortices. It is also necessary to damp gravity waves propagating to the far field by the effect of pseudo-hyperviscosity.
${\it\nu}=10^{-11}$
. The main difficulty is that we have to keep the Gaussian vortex similar to the point vortex in the numerical simulation because we assume point vortices in the analytical study. Thus a high-resolution numerical model with sufficiently small hyperviscosity is required to mimic a pair of point vortices. It is also necessary to damp gravity waves propagating to the far field by the effect of pseudo-hyperviscosity.
While the results for
![]() $T=341$
deviate slightly from those of the analytical estimate owing to the weakened and broadened vortices, the overall features of the radiated gravity waves are reproduced sufficiently well. It should be emphasized that the discrepancy between the analytical results and numerical ones does not mean that the numerical model is insufficient, but merely indicates that it is impossible to keep the Gaussian vortex similar to the point vortex in the numerical model with given resolution and hyperviscosity. It is supposed that our numerical model will have sufficient accuracy to investigate spontaneous gravity wave radiation from more complex vortical flows from which we cannot derive the far field of gravity waves analytically. In future work, it would be possible to use a medium resolution for parameter sweep experiments of gravity wave radiation from several configurations of vortical flows. Note that we set a very small hyperviscosity in high-resolution simulations to keep the intensity and shape of vortices so that vortices in the numerical simulations will mimic point vortices in the analytical study. For different types of vortical motions, such as coalescence of vortices, collapsing vortex and turbulent flows, it is safe to set a larger hyperviscosity to avoid accumulation of enstrophy at small scales. It should also be mentioned that, when focusing on the small-scale phenomena such as turbulent flows or vortex filaments, careful treatment of hyperviscosity is required, since it is possible to maintain ‘spurious’ small scales by the effect of hyperviscosity as revealed in several studies (e.g. Jiménez Reference Jiménez1994; Mariotti et al.
Reference Mariotti, Legras and Dritschel1994; Yao et al.
Reference Yao, Zabusky and Dritschel1995).
$T=341$
deviate slightly from those of the analytical estimate owing to the weakened and broadened vortices, the overall features of the radiated gravity waves are reproduced sufficiently well. It should be emphasized that the discrepancy between the analytical results and numerical ones does not mean that the numerical model is insufficient, but merely indicates that it is impossible to keep the Gaussian vortex similar to the point vortex in the numerical model with given resolution and hyperviscosity. It is supposed that our numerical model will have sufficient accuracy to investigate spontaneous gravity wave radiation from more complex vortical flows from which we cannot derive the far field of gravity waves analytically. In future work, it would be possible to use a medium resolution for parameter sweep experiments of gravity wave radiation from several configurations of vortical flows. Note that we set a very small hyperviscosity in high-resolution simulations to keep the intensity and shape of vortices so that vortices in the numerical simulations will mimic point vortices in the analytical study. For different types of vortical motions, such as coalescence of vortices, collapsing vortex and turbulent flows, it is safe to set a larger hyperviscosity to avoid accumulation of enstrophy at small scales. It should also be mentioned that, when focusing on the small-scale phenomena such as turbulent flows or vortex filaments, careful treatment of hyperviscosity is required, since it is possible to maintain ‘spurious’ small scales by the effect of hyperviscosity as revealed in several studies (e.g. Jiménez Reference Jiménez1994; Mariotti et al.
Reference Mariotti, Legras and Dritschel1994; Yao et al.
Reference Yao, Zabusky and Dritschel1995).
5. Summary and discussion
Cyclone–anticyclone asymmetry in spontaneous gravity wave radiation from a co-rotating vortex pair is investigated in an
![]() $f$
-plane shallow water system both analytically and numerically. We derived analytically the far field of gravity waves by analogy with the theory of aeroacoustic sound wave radiation (Lighthill theory) in the presence of the Earth’s rotation. The newly derived form is a natural extension of the theory of sound wave radiation from a co-rotating vortex pair, but the Earth’s rotation affects not only the propagation of gravity waves but also their source. In the limit of
$f$
-plane shallow water system both analytically and numerically. We derived analytically the far field of gravity waves by analogy with the theory of aeroacoustic sound wave radiation (Lighthill theory) in the presence of the Earth’s rotation. The newly derived form is a natural extension of the theory of sound wave radiation from a co-rotating vortex pair, but the Earth’s rotation affects not only the propagation of gravity waves but also their source. In the limit of
![]() $f\rightarrow 0$
the results correspond to the previous theory of vortex sound. For finite values of
$f\rightarrow 0$
the results correspond to the previous theory of vortex sound. For finite values of
![]() $f$
, however, there is an asymmetry of gravity wave radiation between cyclone pairs and anticyclone pairs due to the effect of the Earth’s rotation. It was shown that an anticyclone pair radiates gravity waves more intensely than a cyclone pair under the same parameter values. Furthermore, the local maximum of intensity of gravity waves appears at an intermediate value of
$f$
, however, there is an asymmetry of gravity wave radiation between cyclone pairs and anticyclone pairs due to the effect of the Earth’s rotation. It was shown that an anticyclone pair radiates gravity waves more intensely than a cyclone pair under the same parameter values. Furthermore, the local maximum of intensity of gravity waves appears at an intermediate value of
![]() $f$
only for anticyclone pairs. To verify the analytical solution, series of numerical simulations with experimental configuration similar to analytical study are also performed.
$f$
only for anticyclone pairs. To verify the analytical solution, series of numerical simulations with experimental configuration similar to analytical study are also performed.
In the numerical simulation, we use a spectral method for an unbounded domain with the aid of a conformal mapping from a sphere to a plane. It is then possible to position many grid points in the near field of vortices and few points in the far field of waves. In addition, the model includes pseudo-hyperviscosity, which acts as usual hyperviscosity in the near field and as a sponge layer in the far field to damp waves. Thus, we are able to simulate vortical motion accompanied by wave radiation with high accuracy. The results of the numerical simulation were compared with those of the analytical study, and the results were found to be in excellent agreement with each other. Again, cyclone–anticyclone asymmetry in spontaneous gravity wave radiation appeared at finite values of
![]() $f$
in the numerical simulation. It was also confirmed that the amplitude of the gravity waves from an anticyclone pair was always larger than that from a cyclone pair under the same parameter values. Therefore, analytical derivation is verified successfully by the numerical simulations. Moreover, it is confirmed that the developed numerical model has sufficient accuracy to estimate amplitudes of gravity waves far from vortical flows.
$f$
in the numerical simulation. It was also confirmed that the amplitude of the gravity waves from an anticyclone pair was always larger than that from a cyclone pair under the same parameter values. Therefore, analytical derivation is verified successfully by the numerical simulations. Moreover, it is confirmed that the developed numerical model has sufficient accuracy to estimate amplitudes of gravity waves far from vortical flows.
A key finding in the present study is the cyclone–anticyclone asymmetry in spontaneous gravity wave radiation. This asymmetry comes from the Coriolis effect in the source of gravity waves. In Sugimoto et al. (Reference Sugimoto, Ishioka and Ishii2008), it was reported that a local maximum of the gravity wave flux due to an unsteady jet appears, because the source originating in the Coriolis force is larger than that produced by unsteady motions of the vortex at a medium value of
![]() $f$
. It is strongly suggested that the local maximum appears because of gravity wave radiation from anticyclones as shown in the present study. Cyclone–anticyclone asymmetry has also been reported in a linear stability analysis (Sugimoto, Ishioka & Yoden Reference Sugimoto, Ishioka and Yoden2007a
). While in rotating shallow water linear stability analysis (Stegner & Dritschel Reference Stegner and Dritschel2000) and nonlinear simulations for one layer (Polvani et al.
Reference Polvani, McWilliams, Spall and Ford1994) and two layers (Lahaye & Zeitlin Reference Lahaye and Zeitlin2012a
) show that anticyclones tend to be more stable than cyclones due to the effect of the finite deformation radius, gravity wave radiation is enhanced for anticyclones in the present study. The physical mechanism for cyclone–anticyclone asymmetry in gravity wave radiation has not yet been clarified. The enhancement of gravity wave radiation is caused by the opposite signs of
$f$
. It is strongly suggested that the local maximum appears because of gravity wave radiation from anticyclones as shown in the present study. Cyclone–anticyclone asymmetry has also been reported in a linear stability analysis (Sugimoto, Ishioka & Yoden Reference Sugimoto, Ishioka and Yoden2007a
). While in rotating shallow water linear stability analysis (Stegner & Dritschel Reference Stegner and Dritschel2000) and nonlinear simulations for one layer (Polvani et al.
Reference Polvani, McWilliams, Spall and Ford1994) and two layers (Lahaye & Zeitlin Reference Lahaye and Zeitlin2012a
) show that anticyclones tend to be more stable than cyclones due to the effect of the finite deformation radius, gravity wave radiation is enhanced for anticyclones in the present study. The physical mechanism for cyclone–anticyclone asymmetry in gravity wave radiation has not yet been clarified. The enhancement of gravity wave radiation is caused by the opposite signs of
![]() ${\it\Omega}$
and
${\it\Omega}$
and
![]() $f$
. While the Coriolis and centrifugal forces act in the same directions for cyclones, they act oppositely for anticyclones. One possible mechanism might be that anticyclones tend to fluctuate when the Coriolis and centrifugal forces are comparable at an intermediate
$f$
. While the Coriolis and centrifugal forces act in the same directions for cyclones, they act oppositely for anticyclones. One possible mechanism might be that anticyclones tend to fluctuate when the Coriolis and centrifugal forces are comparable at an intermediate
![]() $\mathit{Ro}$
. Another possible mechanism may be that background rotation
$\mathit{Ro}$
. Another possible mechanism may be that background rotation
![]() $f$
intensifies the apparent
$f$
intensifies the apparent
![]() ${\it\Omega}_{a}$
in a rotating reference frame for the case of anticyclones, while it weakens
${\it\Omega}_{a}$
in a rotating reference frame for the case of anticyclones, while it weakens
![]() ${\it\Omega}_{a}$
for cyclones. A promising next step is to investigate cyclone–anticyclone asymmetry in gravity wave radiation in a wide parameter space of
${\it\Omega}_{a}$
for cyclones. A promising next step is to investigate cyclone–anticyclone asymmetry in gravity wave radiation in a wide parameter space of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{Fr}$
, focusing on the frequency of the source originating in the Coriolis force. It would also be interesting to investigate gravity wave radiation from several configurations of vortical flows, such as the merger of a cyclone pair and an anticyclone pair, in a collapsing vortex and for turbulent flows as in the case of sound wave emission (e.g. Knio, Collorec & Juvé Reference Knio, Collorec and Juvé1995)
$\mathit{Fr}$
, focusing on the frequency of the source originating in the Coriolis force. It would also be interesting to investigate gravity wave radiation from several configurations of vortical flows, such as the merger of a cyclone pair and an anticyclone pair, in a collapsing vortex and for turbulent flows as in the case of sound wave emission (e.g. Knio, Collorec & Juvé Reference Knio, Collorec and Juvé1995)
Since an
![]() $f$
-plane shallow water system is introduced on the assumption of strong stratification, this system has external gravity waves that propagate only in the horizontal direction. This leads to a large spectral gap between balanced and unbalanced motions and large
$f$
-plane shallow water system is introduced on the assumption of strong stratification, this system has external gravity waves that propagate only in the horizontal direction. This leads to a large spectral gap between balanced and unbalanced motions and large
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${>}1$
) is required to radiate gravity waves (cf. Zeitlin Reference Zeitlin2007). As a consequence, very weak gravity waves are spontaneously radiated from prescribed sources of vortical flows. This is the feature of ‘Lighthill radiation’ (Ford et al.
Reference Ford, McIntyre and Norton2000). Further, there is no wave capture mechanism (Bühler & McIntyre Reference Bühler and McIntyre2005) in this system. In contrast, in a continuously stratified system where scale separation between inertial gravity waves and vortical flows is no longer large, gravity waves are spontaneously radiated for smaller
${>}1$
) is required to radiate gravity waves (cf. Zeitlin Reference Zeitlin2007). As a consequence, very weak gravity waves are spontaneously radiated from prescribed sources of vortical flows. This is the feature of ‘Lighthill radiation’ (Ford et al.
Reference Ford, McIntyre and Norton2000). Further, there is no wave capture mechanism (Bühler & McIntyre Reference Bühler and McIntyre2005) in this system. In contrast, in a continuously stratified system where scale separation between inertial gravity waves and vortical flows is no longer large, gravity waves are spontaneously radiated for smaller
![]() $\mathit{Ro}$
and the spatial scale of gravity waves radiated from a jet is much smaller than that of the local jet itself (e.g. O’Sullivan & Dunkerton Reference O’Sullivan and Dunkerton1995; Zhang Reference Zhang2004; Plougonven & Snyder Reference Plougonven and Snyder2007). Here, advection by vortical flows plays crucial roles. Radiated gravity waves are captured in the vortical flows (Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007) and significant back-reaction of gravity waves occurs (Wang et al.
Reference Wang, Zhang and Snyder2009). Taking into account the Doppler shift by vortical flows is also necessary for time-scale matching, which is called ‘quasi-resonance’, in order to explain spontaneous gravity wave radiation theoretically (Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015a
). Therefore, it is difficult to apply results obtained in the present study and those of ‘Lighthill radiation’ directly to phenomena in the real atmosphere. While cyclone–anticyclone asymmetry in spontaneous gravity waves from dipoles has also been reported in several numerical simulations of the continuously stratified system (e.g. Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007; Wang et al.
Reference Wang, Zhang and Snyder2009; Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015b
) in which gravity waves are more strongly wrapped in the anticyclone, the mechanism has not yet been revealed. Our results would give a first step towards a fundamental understanding of cyclone–anticyclone asymmetry in spontaneous gravity wave radiation in the real atmosphere, though
$\mathit{Ro}$
and the spatial scale of gravity waves radiated from a jet is much smaller than that of the local jet itself (e.g. O’Sullivan & Dunkerton Reference O’Sullivan and Dunkerton1995; Zhang Reference Zhang2004; Plougonven & Snyder Reference Plougonven and Snyder2007). Here, advection by vortical flows plays crucial roles. Radiated gravity waves are captured in the vortical flows (Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007) and significant back-reaction of gravity waves occurs (Wang et al.
Reference Wang, Zhang and Snyder2009). Taking into account the Doppler shift by vortical flows is also necessary for time-scale matching, which is called ‘quasi-resonance’, in order to explain spontaneous gravity wave radiation theoretically (Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015a
). Therefore, it is difficult to apply results obtained in the present study and those of ‘Lighthill radiation’ directly to phenomena in the real atmosphere. While cyclone–anticyclone asymmetry in spontaneous gravity waves from dipoles has also been reported in several numerical simulations of the continuously stratified system (e.g. Snyder et al.
Reference Snyder, Muraki, Plougonven and Zhang2007; Viúdez Reference Viúdez2007; Wang et al.
Reference Wang, Zhang and Snyder2009; Yasuda et al.
Reference Yasuda, Sato and Sugimoto2015b
) in which gravity waves are more strongly wrapped in the anticyclone, the mechanism has not yet been revealed. Our results would give a first step towards a fundamental understanding of cyclone–anticyclone asymmetry in spontaneous gravity wave radiation in the real atmosphere, though
![]() $\mathit{Ro}$
used in the present study is larger than that of typical synoptic-scale flows on the Earth. In the context of the present study at intermediate
$\mathit{Ro}$
used in the present study is larger than that of typical synoptic-scale flows on the Earth. In the context of the present study at intermediate
![]() $\mathit{Ro}$
(
$\mathit{Ro}$
(
![]() ${\sim}10$
), there is a possibility of cyclone–anticyclone asymmetry in gravity waves from the Florida Current, which is a very strong flow close to shore. Further, on slowly rotating planets, such as Venus,
${\sim}10$
), there is a possibility of cyclone–anticyclone asymmetry in gravity waves from the Florida Current, which is a very strong flow close to shore. Further, on slowly rotating planets, such as Venus,
![]() $\mathit{Ro}$
is supposed to be large for barotropic or baroclinic vortices in super-rotating flow (e.g. Sugimoto, Takagi & Matsuda Reference Sugimoto, Takagi and Matsuda2014). It is inferred that intense gravity waves may be radiated from anticyclones and have a significant impact on the atmosphere of Venus. It would also be interesting to verify cyclone–anticyclone asymmetry in gravity waves in laboratory experiments as an extension of previous work (e.g. Williams et al.
Reference Williams, Read and Haine2003). Since structures similar to wave capture have been observed recently in a two-layer rotating shallow water system (Lahaye & Zeitlin Reference Lahaye and Zeitlin2012b
), it might be important to extend the present study to the two-layer system.
$\mathit{Ro}$
is supposed to be large for barotropic or baroclinic vortices in super-rotating flow (e.g. Sugimoto, Takagi & Matsuda Reference Sugimoto, Takagi and Matsuda2014). It is inferred that intense gravity waves may be radiated from anticyclones and have a significant impact on the atmosphere of Venus. It would also be interesting to verify cyclone–anticyclone asymmetry in gravity waves in laboratory experiments as an extension of previous work (e.g. Williams et al.
Reference Williams, Read and Haine2003). Since structures similar to wave capture have been observed recently in a two-layer rotating shallow water system (Lahaye & Zeitlin Reference Lahaye and Zeitlin2012b
), it might be important to extend the present study to the two-layer system.
Another point worth noting is the applicability of the numerical model used in the present study. We have applied the method proposed by Ishioka (Reference Ishioka2008) to an
![]() $f$
-plane shallow water system. The method can be extended to several equations in principle. For a one-dimensional domain, the method has already been applied to a two-layer shallow water system (Harada & Ishioka Reference Harada and Ishioka2011). It is possible to apply two- or three-dimensional Navier–Stokes equations and more realistic three-dimensional primitive equations. The method will be powerful for investigating wave radiation from vortex motions localized in the centre region. For future work, it is of interest to simulate gravity wave radiation from three-dimensional vortical flows as an extension of the proposed method. Sound wave radiation from vortex motion is also an important subject for both theoretical and engineering purposes, especially in the field of noise reduction. It is expected that various applications could be realized using this method.
$f$
-plane shallow water system. The method can be extended to several equations in principle. For a one-dimensional domain, the method has already been applied to a two-layer shallow water system (Harada & Ishioka Reference Harada and Ishioka2011). It is possible to apply two- or three-dimensional Navier–Stokes equations and more realistic three-dimensional primitive equations. The method will be powerful for investigating wave radiation from vortex motions localized in the centre region. For future work, it is of interest to simulate gravity wave radiation from three-dimensional vortical flows as an extension of the proposed method. Sound wave radiation from vortex motion is also an important subject for both theoretical and engineering purposes, especially in the field of noise reduction. It is expected that various applications could be realized using this method.
It is well known that a strict slow manifold (purely balanced model), which is free from gravity wave radiation, for atmospheric motion does not exist (e.g. Ford et al.
Reference Ford, McIntyre and Norton2000). However, the parameter dependence of the amplitude of gravity waves is not yet understood clearly (cf. Saujani & Shepherd Reference Saujani and Shepherd2002; Vanneste Reference Vanneste2008, Reference Vanneste2013). The numerical model used in the present study offers the possibility of revealing the dependence of the amplitude of gravity waves on small
![]() $\mathit{Ro}$
by numerical simulation with ultra-high resolution. Further studies will be needed to comprehensively describe spontaneous gravity wave radiation.
$\mathit{Ro}$
by numerical simulation with ultra-high resolution. Further studies will be needed to comprehensively describe spontaneous gravity wave radiation.
Acknowledgements
The work by N.S. is supported by the JSPS Grant-in-Aid for Young Scientists (B) (no. 25800265). The GFD-DENNOU Library was used for drawing the figures. ISPACK (Ishioka Reference Ishioka2011) was used for numerical simulation and analysis. We thank H. Niino, K. Sato, K. Iga, T. Horinouchi, S. Shima, P. D. Williams, R. Plougonven, M. E. McIntyre and three anonymous referees for their constructive comments.
Appendix A. Special functions
In this appendix, we show the special functions used in the present study. First, the integral form of Hankel’s function is written
 $$\begin{eqnarray}\int _{-\infty }^{\infty }\text{d}{\it\xi}\,\text{e}^{\text{i}{\it\alpha}(a\cosh {\it\xi}+b\sinh {\it\xi})}=\left\{\begin{array}{@{}ll@{}}\text{i}{\rm\pi}\text{H}_{0}^{(1)}({\it\alpha}\sqrt{b^{2}-a^{2}})\quad & \quad (b>|a|),\\ \text{i}{\rm\pi}\text{H}_{0}^{(1)}(\text{i}{\it\alpha}\sqrt{a^{2}-b^{2}})\quad & \quad (|a|>|b|),\\ -\text{i}{\rm\pi}\text{H}_{0}^{(2)}({\it\alpha}\sqrt{b^{2}-a^{2}})\quad & \quad (-b>|a|).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\int _{-\infty }^{\infty }\text{d}{\it\xi}\,\text{e}^{\text{i}{\it\alpha}(a\cosh {\it\xi}+b\sinh {\it\xi})}=\left\{\begin{array}{@{}ll@{}}\text{i}{\rm\pi}\text{H}_{0}^{(1)}({\it\alpha}\sqrt{b^{2}-a^{2}})\quad & \quad (b>|a|),\\ \text{i}{\rm\pi}\text{H}_{0}^{(1)}(\text{i}{\it\alpha}\sqrt{a^{2}-b^{2}})\quad & \quad (|a|>|b|),\\ -\text{i}{\rm\pi}\text{H}_{0}^{(2)}({\it\alpha}\sqrt{b^{2}-a^{2}})\quad & \quad (-b>|a|).\end{array}\right.\end{eqnarray}$$
For
![]() $ax\gg 1$
,
$ax\gg 1$
,
where
![]() $x$
and
$x$
and
![]() $a$
are a real variable and a constant, respectively. Then we obtain
$a$
are a real variable and a constant, respectively. Then we obtain
We also note that
In addition, for
![]() $\text{H}_{0}^{(1)}(\text{i}ax)$
,
$\text{H}_{0}^{(1)}(\text{i}ax)$
,
is real, where
![]() $\text{K}_{0}(x)$
is the zeroth-order modified Bessel function of the second kind. Then we obtain the following approximation for
$\text{K}_{0}(x)$
is the zeroth-order modified Bessel function of the second kind. Then we obtain the following approximation for
![]() $ax\gg 1$
,
$ax\gg 1$
,