1. Introduction
This paper is concerned with the control of stationary convective instabilities in the rotating disk boundary layer via a time-periodic modulation of the disk rotation rate. The steady flow on a rotating disk (without periodic modulation) develops when a disk of infinite extent rotates beneath an otherwise stationary body of fluid. The disk motion creates a thin boundary layer, whereby fluid near the disk centre spirals radially outwards, that is in turn replaced by an axial flow directed towards the disk surface. The resulting flow admits a similarity solution to the Navier–Stokes equations in cylindrical coordinates that was first derived by von Kármán (Reference von Kármán1921). Thus, the flow over a rotating disk is often referred to as the von Kármán flow and provides a canonical example of a three-dimensional boundary layer.
The von Kármán flow displays qualitatively similar stability mechanisms to those found in the boundary layer over a swept wing, as both flow configurations are susceptible to an inviscid cross-flow instability (Gregory, Stuart & Walker Reference Gregory, Stuart and Walker1955). Thus, strategies for controlling disturbance development in the rotating disk boundary layer may be used to identify control technologies that maintain laminar flow past a swept wing. Since the von Kármán flow has certain practical advantages over the swept wing configuration, including its experimental amenability, it is common practice to conduct laminar flow control studies on the rotating disk before extending the applications to complex swept wing geometries. However, it is important to emphasise that there are several differences between the two flow configurations. The rotating disk boundary layer is affected by Coriolis forces that are not present in the flow over a swept wing. Additionally, the former system permits an azimuthal periodicity that is not found in the latter flow configuration.
As stated in the review by Lingwood & Alfredsson (Reference Lingwood and Alfredsson2015), the rotating disk and family of related flows have many applications beyond the scope of swept wing boundary layers. Rotating flows encompass a range of complex three-dimensional configurations, including atmospheric and oceanic flows, rotating-cavity flows and computer storage devices. In electrochemistry, the rotating disk electrode is utilised to perform hydrodynamic voltammetry (Ahn et al. Reference Ahn, Frith, Fisher, Bond and Marken2014, Reference Ahn, Somasundaram, Nguyen, Birgersson, Lee, Gao, Fisher, Frith and Marken2016). In part, it is the simplicity of the model that has made the von Kármán flow an attractive candidate for studies of some of these more general three-dimensional boundary layers.
Using a china clay visualisation technique, Gregory et al. (Reference Gregory, Stuart and Walker1955) observed the cross-flow instability or type I mode as 28–32 stationary spiral vortex structures relative to the rotating disk surface. The number of cross-flow vortices is directly related to the integer-valued azimuthal mode number ![]() $n$ that represents the periodicity of the disturbance in the azimuthal direction. Experimental studies by Kobayashi, Kohama & Takamadate (Reference Kobayashi, Kohama and Takamadate1980) and Jarre, Le Gal & Chauve (Reference Jarre, Le Gal and Chauve1996) drew similar conclusions to Gregory et al. (Reference Gregory, Stuart and Walker1955), noting that stationary cross-flow modes
$n$ that represents the periodicity of the disturbance in the azimuthal direction. Experimental studies by Kobayashi, Kohama & Takamadate (Reference Kobayashi, Kohama and Takamadate1980) and Jarre, Le Gal & Chauve (Reference Jarre, Le Gal and Chauve1996) drew similar conclusions to Gregory et al. (Reference Gregory, Stuart and Walker1955), noting that stationary cross-flow modes ![]() $n\in [30,32]$ dominated the early stages of the laminar–turbulent transition process. Mack (Reference Mack1975) and Malik (Reference Malik1986) investigated the stability of the von Kármán flow using linear analysis and determined neutral conditions for the onset of the stationary cross-flow instability. It was determined by Malik (Reference Malik1986) and subsequently confirmed by many others (Dhanak, Kumar & Streett Reference Dhanak, Kumar and Streett1992; Cooper & Carpenter Reference Cooper and Carpenter1997; Lingwood Reference Lingwood1997; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) that this form of instability first appears for a Reynolds number
$n\in [30,32]$ dominated the early stages of the laminar–turbulent transition process. Mack (Reference Mack1975) and Malik (Reference Malik1986) investigated the stability of the von Kármán flow using linear analysis and determined neutral conditions for the onset of the stationary cross-flow instability. It was determined by Malik (Reference Malik1986) and subsequently confirmed by many others (Dhanak, Kumar & Streett Reference Dhanak, Kumar and Streett1992; Cooper & Carpenter Reference Cooper and Carpenter1997; Lingwood Reference Lingwood1997; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) that this form of instability first appears for a Reynolds number ![]() ${Re} \approx 286$. (A formal definition for the Reynolds number
${Re} \approx 286$. (A formal definition for the Reynolds number ![]() ${Re}$ is given below in (2.7).)
${Re}$ is given below in (2.7).)
In addition to the cross-flow instability, the rotating disk boundary layer is susceptible to several other types of instability. As a consequence of the curvature and Coriolis effects, a type II instability develops that is viscous in nature (Faller & Kaylor Reference Faller and Kaylor1966; Malik Reference Malik1986). A third type III mode was discovered by Mack (Reference Mack1975) that propagates radially inwards and is spatially damped. Modes I and II are both classified as convective instabilities, as the disturbance is convected radially downstream away from the location where it first appears. The primary goal of this investigation is to control these convectively unstable disturbances and in particular stationary cross-flow waves, via a time-periodic modulation applied to the disk rotation rate.
A region of absolute instability was identified by Lingwood (Reference Lingwood1995, Reference Lingwood1997) for a Reynolds number ![]() ${Re}\approx 507.3$, whereby the disturbance grows in time about all radial positions. Utilising a homogeneous flow approximation that neglects the radial dependence of the basic state, it was shown that this form of instability forms due to the coalescence of the type I and III modes. The effect of radial inhomogeneity and the impulse response of linear disturbances was subsequently investigated by Davies & Carpenter (Reference Davies and Carpenter2003) and Thomas & Davies (Reference Thomas and Davies2018) via direct numerical simulations. It was determined that disturbances only become globally linearly unstable for parameter settings significantly greater than that associated with the onset of absolute instability. Moreover, these global linearly unstable disturbances were characterised by a faster than exponential growth.
${Re}\approx 507.3$, whereby the disturbance grows in time about all radial positions. Utilising a homogeneous flow approximation that neglects the radial dependence of the basic state, it was shown that this form of instability forms due to the coalescence of the type I and III modes. The effect of radial inhomogeneity and the impulse response of linear disturbances was subsequently investigated by Davies & Carpenter (Reference Davies and Carpenter2003) and Thomas & Davies (Reference Thomas and Davies2018) via direct numerical simulations. It was determined that disturbances only become globally linearly unstable for parameter settings significantly greater than that associated with the onset of absolute instability. Moreover, these global linearly unstable disturbances were characterised by a faster than exponential growth.
Numerous investigations on the rotating disk have implemented control strategies, with the aim to suppress the growth of boundary layer instabilities and delay the onset of transition to turbulence. For instance, Dhanak et al. (Reference Dhanak, Kumar and Streett1992) and Lingwood (Reference Lingwood1997) applied uniform suction at the disk surface to control the convective and absolute instabilities, respectively. Cooper & Carpenter (Reference Cooper and Carpenter1997) modelled a disk with a compliant surface and found this to have a significant stabilising effect on the type I cross-flow instability. However, the effects on the type II Coriolis instability were more complex, with wall compliance promoting unstable behaviour in many instances. More recently, Cooper et al. (Reference Cooper, Harris, Garrett, Özkan and Thomas2015) and Garrett et al. (Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) used surface roughness to delay the onset of the type I instability, whereby roughness modelling was achieved via a spatial averaging of the undisturbed flow. Though similar to the observations on wall compliance, the type II instability was again destabilised. More recently, Miller et al. (Reference Miller, Griffiths, Hussain and Garrett2020) found that a stabilising effect can be established by a heated disk with a temperature-dependent viscous fluid.
The motivation for the current investigation, whereby the disk rotation rate undergoes a small time-periodic modulation, originates from the earlier study by Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2011) who found that a small level of oscillation in an otherwise steady flow can bring about a stabilising effect. Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2011) illustrated this stabilising effect for the flow in an oscillating channel by coupling the Stokes layer to the plane Poiseuille flow. For very large channel half-widths (or very high frequencies of oscillation), modulation promoted instability, which is consistent with the behaviour observed by Hall (Reference Hall1975) and Von Kerczek (Reference Von Kerczek1982). However, for sufficiently small channel half-widths (or frequencies), time-periodic modulation of the plane Poiseuille flow was found to increase the Reynolds number for the onset of linear instability. Thus, these time-modulated unidirectional flows were stabilised. These particular results complement the earlier investigations of Kelly & Cheers (Reference Kelly and Cheers1970) and Von Kerczek (Reference Von Kerczek1976), who found a similar stabilising effect in modulated plane Couette flow. Furthermore, Rosenblat (Reference Rosenblat1959) undertook a study on a torsionally oscillating disk, while Wise & Ricco (Reference Wise and Ricco2014) found that turbulent drag in a channel flow can be reduced via the application of oscillating disks.
The Stokes layer is the archetypal model for investigating unsteady flow behaviour and develops when a planar surface oscillates back and forth. An early review on time-periodic flows was given by Davis (Reference Davis1976), while Von Kerczek & Davis (Reference Von Kerczek and Davis1974) and Hall (Reference Hall1978) applied linear stability analyses to the respective finite and semi-infinite Stokes layers. In the latter investigation, linear stability calculations based on Floquet theory assume perturbations to the time-periodic base flow of the form ![]() $\exp (\mu t)f$, for a time-periodic function
$\exp (\mu t)f$, for a time-periodic function ![]() $f$ and a Floquet exponent
$f$ and a Floquet exponent ![]() $\mu$ that encompasses the net growth (or decay) of the disturbance. Hall (Reference Hall1978) was unable to locate any linearly unstable disturbances for the range of Reynolds numbers that the computational resources permitted at the time. However, following the advancement of computer technology, Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) were able to locate the critical conditions for the onset of linear instability. These calculations were later confirmed separately by Luo & Wu (Reference Luo and Wu2010) and Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2010), while Thomas et al. (Reference Thomas, Davies, Bassom and Blennerhassett2014) investigated the impulse response and spatiotemporal development of linear disturbances via direct numerical simulations. Cowley (Reference Cowley1987) and Hall (Reference Hall2003) used quasi-steady (Q-S) instability theory to study the large Reynolds number behaviour in the Stokes layer. Quasi-steady theory is an approximation of linear analyses, whereby the time-periodic flow is frozen and the phase of the time within the oscillation cycle is treated as a parameter. The attraction of this approach is that it allows the prediction of an instantaneous growth rate at each instant during the time-periodic motion. Indeed, the frozen profiles are found to become highly unstable at Reynolds numbers below that found by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) using Floquet theory. Moreover, Luo & Wu (Reference Luo and Wu2010) found that eigenfunctions computed using Floquet theory could be approximated by the corresponding Q-S eigenfunctions.
$\mu$ that encompasses the net growth (or decay) of the disturbance. Hall (Reference Hall1978) was unable to locate any linearly unstable disturbances for the range of Reynolds numbers that the computational resources permitted at the time. However, following the advancement of computer technology, Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) were able to locate the critical conditions for the onset of linear instability. These calculations were later confirmed separately by Luo & Wu (Reference Luo and Wu2010) and Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2010), while Thomas et al. (Reference Thomas, Davies, Bassom and Blennerhassett2014) investigated the impulse response and spatiotemporal development of linear disturbances via direct numerical simulations. Cowley (Reference Cowley1987) and Hall (Reference Hall2003) used quasi-steady (Q-S) instability theory to study the large Reynolds number behaviour in the Stokes layer. Quasi-steady theory is an approximation of linear analyses, whereby the time-periodic flow is frozen and the phase of the time within the oscillation cycle is treated as a parameter. The attraction of this approach is that it allows the prediction of an instantaneous growth rate at each instant during the time-periodic motion. Indeed, the frozen profiles are found to become highly unstable at Reynolds numbers below that found by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) using Floquet theory. Moreover, Luo & Wu (Reference Luo and Wu2010) found that eigenfunctions computed using Floquet theory could be approximated by the corresponding Q-S eigenfunctions.
The primary aim for the following investigation is to ascertain the viability of controlling stationary convective instabilities (type I cross-flow and type II Coriolis) in the rotating disk boundary layer via a time-periodic modulation of the disk rotation rate. Perturbations to the temporally periodic flow are decomposed into the Floquet mode form, with disturbance development modelled using the numerical formulation and methods developed by Davies & Carpenter (Reference Davies and Carpenter2001) and Morgan & Davies (Reference Morgan and Davies2020).
The remainder of this investigation is outlined as follows. The von Kármán flow subject to time-periodic modulation is modelled in the subsequent section. In § 3, the behaviour of the flow is investigated in the high-frequency limit with a small modulation amplitude. A linear stability study based on Floquet theory is undertaken in § 4, while an energy analysis of the disturbance structure that utilises the Q-S flow approximation is carried out in § 5. Finally, conclusions are given in § 6.
2. Unsteady base flow
2.1. Non-dimensionalisation
The similarity solution for the steady laminar flow over an infinite rotating disk with a constant rotation rate ![]() $\varOmega _0^{*}$, was first formulated by von Kármán (Reference von Kármán1921). In the following, we describe the necessary modifications to the base flow that arise with the inclusion of a time-periodic modulation. Cylindrical polar coordinates are used, where
$\varOmega _0^{*}$, was first formulated by von Kármán (Reference von Kármán1921). In the following, we describe the necessary modifications to the base flow that arise with the inclusion of a time-periodic modulation. Cylindrical polar coordinates are used, where ![]() $r^{*}$,
$r^{*}$, ![]() $\theta$ and
$\theta$ and ![]() $z^{*}$ denote the radial, azimuthal and wall-normal directions. (An asterisks denotes dimensional quantities.) The dimensional velocity field is defined by
$z^{*}$ denote the radial, azimuthal and wall-normal directions. (An asterisks denotes dimensional quantities.) The dimensional velocity field is defined by ![]() $\boldsymbol {U}^{*}=(U^{*}, V^{*},W^{*})$, while
$\boldsymbol {U}^{*}=(U^{*}, V^{*},W^{*})$, while ![]() $\nu ^{*}$ and
$\nu ^{*}$ and ![]() $\varOmega ^{*}(t^{*})$ denote the kinematic viscosity of the fluid and the unsteady angular velocity of the disk, respectively. Due to the inherent azimuthal periodicity of the problem, the dependence on the azimuthal
$\varOmega ^{*}(t^{*})$ denote the kinematic viscosity of the fluid and the unsteady angular velocity of the disk, respectively. Due to the inherent azimuthal periodicity of the problem, the dependence on the azimuthal ![]() $\theta$-direction is removed from the velocity field
$\theta$-direction is removed from the velocity field ![]() $\boldsymbol {U}^{*}$.
$\boldsymbol {U}^{*}$.
The unsteady base flow is computed in a non-rotating frame of reference. This strategy is implemented to facilitate the numerical solution that is based on Chebyshev methods (outlined in § 2.2). Boundary conditions on the disk surface are defined as
while in the far field they are
A small time-periodic modulation is applied to the constant disk rotation rate ![]() $\varOmega _0^{*}$ to give the total unsteady disk rotation rate
$\varOmega _0^{*}$ to give the total unsteady disk rotation rate
where ![]() $\lambda$ and
$\lambda$ and ![]() $\phi ^{*}$ denote the angular displacement and frequency of the modulation, respectively. The unsteady component of (2.2) has been shifted by a phase
$\phi ^{*}$ denote the angular displacement and frequency of the modulation, respectively. The unsteady component of (2.2) has been shifted by a phase ![]() ${\rm \pi} /2$, so that time
${\rm \pi} /2$, so that time ![]() $t^{*}=0$ is matched to the steady state. Moreover, in the instance
$t^{*}=0$ is matched to the steady state. Moreover, in the instance ![]() $\lambda = 0$, the steady von Kármán flow (without time-periodic modulation) is recovered.
$\lambda = 0$, the steady von Kármán flow (without time-periodic modulation) is recovered.
There are two length scales associated with the system that are based on the constant rotation rate ![]() $\varOmega _0^{*}$ and the modulation frequency
$\varOmega _0^{*}$ and the modulation frequency ![]() $\phi ^{*}$. These are, respectively, referred to as the von Kármán and the Stokes length scales,
$\phi ^{*}$. These are, respectively, referred to as the von Kármán and the Stokes length scales,
 \begin{equation} \delta^{*}_k = \sqrt{\frac{\nu^{*}}{\varOmega_0^{*}}} \quad \textrm{and} \quad \delta^{*}_s = \sqrt{\frac{2\nu^{*}}{\phi^{*}}}. \end{equation}
\begin{equation} \delta^{*}_k = \sqrt{\frac{\nu^{*}}{\varOmega_0^{*}}} \quad \textrm{and} \quad \delta^{*}_s = \sqrt{\frac{2\nu^{*}}{\phi^{*}}}. \end{equation}
(The subscript notation ![]() $k$ and
$k$ and ![]() $s$ references scales based on the von Kármán layer and the Stokes layer, respectively.) Additionally there are three temporal scales to consider. A local time scale is defined as the ratio of the circumferential speed of the rotating disk
$s$ references scales based on the von Kármán layer and the Stokes layer, respectively.) Additionally there are three temporal scales to consider. A local time scale is defined as the ratio of the circumferential speed of the rotating disk ![]() $r^{*}_L\varOmega ^{*}_0$ and the von Kármán length scale
$r^{*}_L\varOmega ^{*}_0$ and the von Kármán length scale ![]() $\delta ^{*}_k$,
$\delta ^{*}_k$,
for a reference radius ![]() $r_L^{*}$, while a global time scale is characterised by the constant disk angular velocity
$r_L^{*}$, while a global time scale is characterised by the constant disk angular velocity
A third time scale is based on the modulation frequency as follows:
In the subsequent analysis, the amplitude of the time-periodic modulation is assumed to be small. Thus, units of length are scaled on the von Kármán length scale (2.3a), while non-dimensional time is specified by (2.4a).
The dimensional unsteady base flow is defined as
where ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ represent the non-dimensional unsteady velocity profiles along the three coordinate directions. (Note that the subscript
$H$ represent the non-dimensional unsteady velocity profiles along the three coordinate directions. (Note that the subscript ![]() $k$ and superscript
$k$ and superscript ![]() $l$ notation in the non-dimensional time term
$l$ notation in the non-dimensional time term ![]() $\tau$ have been dropped for simplicity.) Scaling the velocity field
$\tau$ have been dropped for simplicity.) Scaling the velocity field ![]() $\boldsymbol {U}^{*}$ on the circumferential speed of the disk
$\boldsymbol {U}^{*}$ on the circumferential speed of the disk ![]() $r_L^{*}\varOmega _0^{*}$ gives the following definition for the non-dimensional unsteady velocity field
$r_L^{*}\varOmega _0^{*}$ gives the following definition for the non-dimensional unsteady velocity field ![]() $\boldsymbol {U}=(U,V,W)$ as
$\boldsymbol {U}=(U,V,W)$ as
where the Reynolds number ![]() ${Re}$, associated with the constant disk rotation rate
${Re}$, associated with the constant disk rotation rate ![]() $\varOmega ^{*}_0$, is given as
$\varOmega ^{*}_0$, is given as
A second, so-called Stokes Reynolds number ![]() ${Re}_s$, related to the time-periodic modulation of the disk, is defined as
${Re}_s$, related to the time-periodic modulation of the disk, is defined as
 \begin{equation} {Re}_s = \frac{\lambda r_L^{*}\phi^{*}\delta^{*}_s}{2\nu^{*}} = \lambda r_L\sqrt{\frac{\phi^{*}}{2\varOmega^{*}_0}} = \frac{\epsilon{Re}}{\sqrt{2\varphi}}, \end{equation}
\begin{equation} {Re}_s = \frac{\lambda r_L^{*}\phi^{*}\delta^{*}_s}{2\nu^{*}} = \lambda r_L\sqrt{\frac{\phi^{*}}{2\varOmega^{*}_0}} = \frac{\epsilon{Re}}{\sqrt{2\varphi}}, \end{equation}
where the non-dimensional frequency ![]() $\varphi = \phi ^{*}/\varOmega ^{*}_0$ corresponds to the number of cycles of time-periodic modulation during one full rotation of the disk. The dimensionless parameter
$\varphi = \phi ^{*}/\varOmega ^{*}_0$ corresponds to the number of cycles of time-periodic modulation during one full rotation of the disk. The dimensionless parameter
represents the modulation amplitude.
On substituting (2.5) into the Navier–Stokes equations in cylindrical coordinates, the following system of differential equations for ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ is derived:
$H$ is derived:
which is solved subject to the boundary conditions
and
Thus, velocity profiles are fully specified by the Reynolds number ![]() ${Re}$, the non-dimensional modulation frequency
${Re}$, the non-dimensional modulation frequency ![]() $\varphi$ and amplitude
$\varphi$ and amplitude ![]() $\epsilon$. (The steady von Kármán flow is recovered by setting
$\epsilon$. (The steady von Kármán flow is recovered by setting ![]() $\epsilon = 0$.)
$\epsilon = 0$.)
As our primary goal is to control stationary convective instabilities in the rotating disk boundary layer via the application of a small time-periodic modulation to the disk rotation rate, we restrict ![]() $\epsilon \leq 0.2$ for the remainder of this investigation. This ensures that the modulation is small relative to the constant disk rotation rate. Furthermore, the corresponding Stokes Reynolds number
$\epsilon \leq 0.2$ for the remainder of this investigation. This ensures that the modulation is small relative to the constant disk rotation rate. Furthermore, the corresponding Stokes Reynolds number ![]() ${Re}_s$ is small relative to that found by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) for the onset of linear instability in the semi-infinite Stokes layer,
${Re}_s$ is small relative to that found by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) for the onset of linear instability in the semi-infinite Stokes layer, ![]() ${Re}_{s}\approx 707$. Thus, the time-periodic modulation implemented here is unlikely to introduce any new forms of instability (other than those disturbances already present in the steady von Kármán flow). Validation for this particular argument is given in Morgan (Reference Morgan2018).
${Re}_{s}\approx 707$. Thus, the time-periodic modulation implemented here is unlikely to introduce any new forms of instability (other than those disturbances already present in the steady von Kármán flow). Validation for this particular argument is given in Morgan (Reference Morgan2018).
2.2. Numerical solution
Numerical solutions to the system of (2.10) and (2.11) are obtained using the following procedure. The three velocity components ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ are defined on the semi-infinite physical domain
$H$ are defined on the semi-infinite physical domain ![]() $z\in [0,\infty )$ and mapped onto the computational domain
$z\in [0,\infty )$ and mapped onto the computational domain ![]() $\eta \in (0,1]$ via the coordinate transformation
$\eta \in (0,1]$ via the coordinate transformation
where ![]() $l$ is a stretching factor. For this investigation
$l$ is a stretching factor. For this investigation ![]() $l=4$, and several checks were performed to ensure that this particular choice for
$l=4$, and several checks were performed to ensure that this particular choice for ![]() $l$ did not influence the stability calculations.
$l$ did not influence the stability calculations.
As a consequence of the decision to model the unsteady base flow in a non-rotating frame and the boundary conditions (2.11), velocity fields ![]() $F$ and
$F$ and ![]() $G$ are expanded using an odd Chebyshev series
$G$ are expanded using an odd Chebyshev series
 \begin{equation} q(z,\tau)=\sum_{k=1}^{M}q_k(\tau)T_{2k-1}(\eta), \end{equation}
\begin{equation} q(z,\tau)=\sum_{k=1}^{M}q_k(\tau)T_{2k-1}(\eta), \end{equation}
where ![]() $T_k$ is the
$T_k$ is the ![]() $k$th Chebyshev polynomial. On the other hand, the wall-normal velocity component
$k$th Chebyshev polynomial. On the other hand, the wall-normal velocity component ![]() $H$ is expanded as an even Chebyshev series
$H$ is expanded as an even Chebyshev series
 \begin{equation} q(z,\tau)=\frac{1}{2}q_0+\sum_{k=1}^{M}q_k(\tau)T_{2k}(\eta). \end{equation}
\begin{equation} q(z,\tau)=\frac{1}{2}q_0+\sum_{k=1}^{M}q_k(\tau)T_{2k}(\eta). \end{equation}
Furthermore, the coordinate transformation (2.12) allows derivatives with respect to the wall-normal ![]() $z$-direction to be reformulated as
$z$-direction to be reformulated as
Thus, after setting ![]() $\tilde {H} = \eta ^{2} H$, the system of (2.10) is recast as
$\tilde {H} = \eta ^{2} H$, the system of (2.10) is recast as
 \begin{gather} \frac{\partial F}{\partial \tau} - \frac{1}{{Re}}D^{2}F = \frac{1}{{Re}}\left(G^{2} - F^{2} +\frac{\tilde{H}}{l}\frac{\partial F}{\partial\eta} \right), \end{gather}
\begin{gather} \frac{\partial F}{\partial \tau} - \frac{1}{{Re}}D^{2}F = \frac{1}{{Re}}\left(G^{2} - F^{2} +\frac{\tilde{H}}{l}\frac{\partial F}{\partial\eta} \right), \end{gather} \begin{gather}\frac{\partial G}{\partial \tau} - \frac{1}{{Re}}D^{2}G = \frac{1}{{Re}}\left({-}2FG +\frac{\tilde{H}}{l}\frac{\partial G}{\partial\eta}\right), \end{gather}
\begin{gather}\frac{\partial G}{\partial \tau} - \frac{1}{{Re}}D^{2}G = \frac{1}{{Re}}\left({-}2FG +\frac{\tilde{H}}{l}\frac{\partial G}{\partial\eta}\right), \end{gather}Equation (2.15c) can be solved using an integrating factor to give
while the remaining two (2.15a) and (2.15b) require the implementation of a time-marching procedure. The temporal integration is performed via a three-point backward difference scheme of the form
and a time-step ![]() ${\rm \Delta} \tau$. Additionally, all terms on the right-hand side of (2.14a,b) are treated explicitly via a predictor–corrector method.
${\rm \Delta} \tau$. Additionally, all terms on the right-hand side of (2.14a,b) are treated explicitly via a predictor–corrector method.
Finally, second-order derivatives ![]() $D^{2}$ are treated implicitly to enhance the numerical stability of the scheme.
$D^{2}$ are treated implicitly to enhance the numerical stability of the scheme.
Equations (2.15a) and (2.15b) are integrated twice with respect to the mapped variable ![]() $\eta$ to give
$\eta$ to give
 \begin{gather} \int_0^{\eta}\int_0^{\eta'}\left(\frac{3}{2{\rm \Delta} \tau}-D^{2}\right)F^{l+1}\,\textrm{d} \eta''\,\textrm{d}\eta' = \int_0^{\eta}\int_0^{\eta'} \left(\frac{2}{{\rm \Delta} \tau} F^{l} - \frac{1}{2{\rm \Delta} \tau} F^{l-1} + \mathcal{R}_F^{l}\right) \,\textrm{d} \eta''\,\textrm{d}\eta', \end{gather}
\begin{gather} \int_0^{\eta}\int_0^{\eta'}\left(\frac{3}{2{\rm \Delta} \tau}-D^{2}\right)F^{l+1}\,\textrm{d} \eta''\,\textrm{d}\eta' = \int_0^{\eta}\int_0^{\eta'} \left(\frac{2}{{\rm \Delta} \tau} F^{l} - \frac{1}{2{\rm \Delta} \tau} F^{l-1} + \mathcal{R}_F^{l}\right) \,\textrm{d} \eta''\,\textrm{d}\eta', \end{gather} \begin{gather}\int_0^{\eta}\int_0^{\eta'}\left(\frac{3}{2{\rm \Delta} \tau}-D^{2}\right)G^{l+1}\,\textrm{d} \eta''\,\textrm{d}\eta' = \int_0^{\eta}\int_0^{\eta'} \left(\frac{2}{{\rm \Delta} \tau} G^{l} - \frac{1}{2{\rm \Delta} \tau} G^{l-1} + \mathcal{R}_G^{l}\right) \,\textrm{d} \eta''\,\textrm{d}\eta', \end{gather}
\begin{gather}\int_0^{\eta}\int_0^{\eta'}\left(\frac{3}{2{\rm \Delta} \tau}-D^{2}\right)G^{l+1}\,\textrm{d} \eta''\,\textrm{d}\eta' = \int_0^{\eta}\int_0^{\eta'} \left(\frac{2}{{\rm \Delta} \tau} G^{l} - \frac{1}{2{\rm \Delta} \tau} G^{l-1} + \mathcal{R}_G^{l}\right) \,\textrm{d} \eta''\,\textrm{d}\eta', \end{gather}
where ![]() $\mathcal {R}_F$ and
$\mathcal {R}_F$ and ![]() $\mathcal {R}_G$ encompass all terms on the right-hand side of (2.15a) and (2.15b), respectively. Moreover, the velocity field
$\mathcal {R}_G$ encompass all terms on the right-hand side of (2.15a) and (2.15b), respectively. Moreover, the velocity field ![]() $H$ is defined explicitly in terms of
$H$ is defined explicitly in terms of ![]() $F$ via (2.16).
$F$ via (2.16).
The Chebyshev polynomial representation allows the integral expressions (2.18) to be recast as matrix operators, while the time-marching procedure is achieved using matrix inversion and multiplication operations. A pseudo-spectral fast Fourier transform (FFT) is then utilised to transform quantities between the physical and Chebyshev space. In all subsequent numerical calculations, ![]() $M=64$ Chebyshev points were used to accurately compute the velocity profiles
$M=64$ Chebyshev points were used to accurately compute the velocity profiles ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$. Several tests were performed for larger values of
$H$. Several tests were performed for larger values of ![]() $M$ to ensure numerical convergence was achieved. Further details of the numerical procedure are described in Morgan (Reference Morgan2018).
$M$ to ensure numerical convergence was achieved. Further details of the numerical procedure are described in Morgan (Reference Morgan2018).
Figure 1 displays the three velocity fields ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ as a function of the wall-normal
$H$ as a function of the wall-normal ![]() $z$-direction, about four points in time during the modulation cycle, for the Reynolds number
$z$-direction, about four points in time during the modulation cycle, for the Reynolds number ![]() ${Re}=500$, modulation amplitude
${Re}=500$, modulation amplitude ![]() $\epsilon = 0.2$ and frequency
$\epsilon = 0.2$ and frequency ![]() $\varphi = 10$. Here
$\varphi = 10$. Here ![]() $T=2{\rm \pi} \varphi /{Re}$ denotes one full cycle of the time-periodic modulation. The illustration demonstrates that modulation of the disk rotation rate brings about a considerable change to the azimuthal velocity field
$T=2{\rm \pi} \varphi /{Re}$ denotes one full cycle of the time-periodic modulation. The illustration demonstrates that modulation of the disk rotation rate brings about a considerable change to the azimuthal velocity field ![]() $G$, while the radial
$G$, while the radial ![]() $F$ and wall-normal
$F$ and wall-normal ![]() $H$ components are less affected. The corresponding temporal evolution of the azimuthal velocity field
$H$ components are less affected. The corresponding temporal evolution of the azimuthal velocity field ![]() $G$ is plotted in figure 2 about three wall-normal
$G$ is plotted in figure 2 about three wall-normal ![]() $z$-locations, which further demonstrates the significant variation in this particular velocity component during the modulation cycle. Table 1 lists numerical values of the base flow fields
$z$-locations, which further demonstrates the significant variation in this particular velocity component during the modulation cycle. Table 1 lists numerical values of the base flow fields ![]() $\partial F/\partial z$ and
$\partial F/\partial z$ and ![]() $\partial G/\partial z$, at the disk wall and four points in time, for the above parameter settings and several other modulation amplitudes
$\partial G/\partial z$, at the disk wall and four points in time, for the above parameter settings and several other modulation amplitudes ![]() $\epsilon$.
$\epsilon$.

Figure 1. Velocity profiles ![]() $F,G$ and
$F,G$ and ![]() $H$ as a function of the wall-normal
$H$ as a function of the wall-normal ![]() $z$-direction, for the Reynolds number
$z$-direction, for the Reynolds number ![]() ${Re} = 500$, modulation amplitude
${Re} = 500$, modulation amplitude ![]() $\epsilon = 0.2$ and frequency
$\epsilon = 0.2$ and frequency ![]() $\varphi = 10$ for (a)
$\varphi = 10$ for (a) ![]() $\tau /T=0$, (b)
$\tau /T=0$, (b) ![]() $\tau /T={\rm \pi} /2$, (c)
$\tau /T={\rm \pi} /2$, (c) ![]() $\tau /T={\rm \pi}$ and (d)
$\tau /T={\rm \pi}$ and (d) ![]() $\tau /T=3{\rm \pi} /2$.
$\tau /T=3{\rm \pi} /2$.

Figure 2. Temporal evolution of the azimuthal component ![]() $G$ of the base flow, for
$G$ of the base flow, for ![]() $z=0$ (solid line),
$z=0$ (solid line), ![]() $z=0.1$ (dashed) and
$z=0.1$ (dashed) and ![]() $z=0.25$ (chain), over one period of time-periodic modulation. The Reynolds number
$z=0.25$ (chain), over one period of time-periodic modulation. The Reynolds number ![]() ${Re} = 500$, modulation amplitude
${Re} = 500$, modulation amplitude ![]() $\epsilon = 0.2$ and frequency
$\epsilon = 0.2$ and frequency ![]() $\varphi = 10$.
$\varphi = 10$.
Table 1. Numerical values of the base flow fields ![]() $\partial F/\partial z$ and
$\partial F/\partial z$ and ![]() $\partial G/\partial z$, at the disk wall
$\partial G/\partial z$, at the disk wall ![]() $z=0$ and four points in time
$z=0$ and four points in time ![]() $\tau /T$, for the Reynolds number
$\tau /T$, for the Reynolds number ![]() ${Re} = 500$, modulation frequency
${Re} = 500$, modulation frequency ![]() $\varphi = 10$ and variable modulation amplitudes
$\varphi = 10$ and variable modulation amplitudes ![]() $\epsilon$.
$\epsilon$.

3. High-frequency limit for small modulation amplitudes
Before undertaking a linear stability study on the effects of time-periodic modulation, we consider the behaviour of the base flow in the high-frequency ![]() $\varphi$-limit with small modulation amplitudes
$\varphi$-limit with small modulation amplitudes ![]() $\epsilon$. Hence, we assume the non-dimensional modulation frequency
$\epsilon$. Hence, we assume the non-dimensional modulation frequency ![]() $\varphi \gg 1$, while the modulation amplitude
$\varphi \gg 1$, while the modulation amplitude ![]() $\epsilon \ll 1$. The three velocity fields
$\epsilon \ll 1$. The three velocity fields ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ are then expanded in ascending powers of
$H$ are then expanded in ascending powers of ![]() $\epsilon$ as
$\epsilon$ as
On substituting (3.1) into the system of (2.10) and equating coefficients of order ![]() $\epsilon$, we obtain the following set of equations:
$\epsilon$, we obtain the following set of equations:
subject to the boundary conditions
and
The zeroth-order terms ![]() $F_0$,
$F_0$, ![]() $G_0$ and
$G_0$ and ![]() $H_0$ are obtained by equating coefficients of order
$H_0$ are obtained by equating coefficients of order ![]() $\epsilon ^{0}$. The subsequent system of equations is identical to (2.10), with the exception of the removal of the time
$\epsilon ^{0}$. The subsequent system of equations is identical to (2.10), with the exception of the removal of the time ![]() $\tau$-dependence. Hence, solutions for
$\tau$-dependence. Hence, solutions for ![]() $F_0$,
$F_0$, ![]() $G_0$ and
$G_0$ and ![]() $H_0$ correspond to the steady von Kármán flow.
$H_0$ correspond to the steady von Kármán flow.
In the high-frequency ![]() $\varphi$-limit, the flow evolves on a scale proportional to the Stokes layer thickness
$\varphi$-limit, the flow evolves on a scale proportional to the Stokes layer thickness ![]() $\delta _s^{*}$. Thus, using (2.3) and (2.4c) we set
$\delta _s^{*}$. Thus, using (2.3) and (2.4c) we set
for ![]() $\delta = \sqrt {2/\varphi }\ll 1$. Hence, (3.2) is rewritten as
$\delta = \sqrt {2/\varphi }\ll 1$. Hence, (3.2) is rewritten as
while the boundary conditions (3.3) are given as
and
Expanding the first-order velocity fields ![]() $F_1$,
$F_1$, ![]() $G_1$ and
$G_1$ and ![]() $H_1$ in ascending powers of
$H_1$ in ascending powers of ![]() $\delta$ as
$\delta$ as
transforms the system of (3.5) into the form
 \begin{gather} \frac{\partial F_1^{k}}{\partial \tilde{\tau}} = \frac{1}{2}\left(\frac{\partial^{2} F_1^{k}}{\partial \tilde{z}^{2}} + 2(G_0G_1^{k-2}-F_0F_1^{k-2} ) - H_1^{k-1}\frac{\partial F_0}{\partial \tilde{z}} - H_0\frac{\partial F_1^{k-1}}{\partial \tilde{z}} \right), \end{gather}
\begin{gather} \frac{\partial F_1^{k}}{\partial \tilde{\tau}} = \frac{1}{2}\left(\frac{\partial^{2} F_1^{k}}{\partial \tilde{z}^{2}} + 2(G_0G_1^{k-2}-F_0F_1^{k-2} ) - H_1^{k-1}\frac{\partial F_0}{\partial \tilde{z}} - H_0\frac{\partial F_1^{k-1}}{\partial \tilde{z}} \right), \end{gather} \begin{gather}\frac{\partial G_1^{k}}{\partial \tilde{\tau}} =\frac{1}{2}\left(\frac{\partial^{2} G_1^{k}}{\partial \tilde{z}^{2}} - 2(F_0G_1^{k-2}+G_0F_1^{k-2}) - H_1^{k-1}\frac{\partial G_0}{\partial \tilde{z}} - H_0\frac{\partial G_1^{k-1}}{\partial \tilde{z}}\right), \end{gather}
\begin{gather}\frac{\partial G_1^{k}}{\partial \tilde{\tau}} =\frac{1}{2}\left(\frac{\partial^{2} G_1^{k}}{\partial \tilde{z}^{2}} - 2(F_0G_1^{k-2}+G_0F_1^{k-2}) - H_1^{k-1}\frac{\partial G_0}{\partial \tilde{z}} - H_0\frac{\partial G_1^{k-1}}{\partial \tilde{z}}\right), \end{gather}
where the ![]() $k$th superscript denotes the order of the terms in the
$k$th superscript denotes the order of the terms in the ![]() $\delta$ expansion.
$\delta$ expansion.
Setting ![]() $k = 0$ in (3.8) gives the zeroth-order terms in
$k = 0$ in (3.8) gives the zeroth-order terms in ![]() $\delta$ as
$\delta$ as
which subject to the boundary conditions (3.6) gives
and
Thus, in the high-frequency, low-amplitude limit, the azimuthal velocity component ![]() $G_1$ is approximated by the Stokes solution for the flow established by a planar oscillating plate. Furthermore, the first-order azimuthal component
$G_1$ is approximated by the Stokes solution for the flow established by a planar oscillating plate. Furthermore, the first-order azimuthal component ![]() $G_1$ is at least an order of magnitude in
$G_1$ is at least an order of magnitude in ![]() $\delta$ greater than the corresponding radial
$\delta$ greater than the corresponding radial ![]() $F_1$ and wall-normal
$F_1$ and wall-normal ![]() $H_1$ velocity components.
$H_1$ velocity components.
Hence, for small amplitude ![]() $\epsilon$, high-frequency
$\epsilon$, high-frequency ![]() $\varphi$ modulations, the flow behaviour on a time-periodically modulated rotating disk is characterised by the addition of a Stokes layer to the azimuthal component of the steady rotating disk boundary layer,
$\varphi$ modulations, the flow behaviour on a time-periodically modulated rotating disk is characterised by the addition of a Stokes layer to the azimuthal component of the steady rotating disk boundary layer,
This is similar to that implemented by Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2011) for the flow in a two-dimensional oscillating channel. Furthermore, this particular observation is in excellent agreement with the numerical solutions depicted in figure 1, where variations brought about by the time-periodic modulation are considerably greater in the azimuthal ![]() $G$ velocity field than the other two components.
$G$ velocity field than the other two components.
In order to verify the above analysis, the system of (2.10) was solved numerically for modulation amplitudes ![]() $\epsilon = 0.1$ and
$\epsilon = 0.1$ and ![]() $\epsilon =0.2$, and frequencies
$\epsilon =0.2$, and frequencies ![]() $0< \varphi \leq 100$ at step intervals
$0< \varphi \leq 100$ at step intervals ![]() ${\rm \Delta} \varphi =0.25$. The numerical solution for the azimuthal velocity field
${\rm \Delta} \varphi =0.25$. The numerical solution for the azimuthal velocity field ![]() $G$ was then separated into its steady
$G$ was then separated into its steady ![]() $G_0$ and unsteady components
$G_0$ and unsteady components ![]() $G_{\textrm {u}}$:
$G_{\textrm {u}}$: ![]() $G=G_0+G_{\textrm {u}}$. (The steady solution
$G=G_0+G_{\textrm {u}}$. (The steady solution ![]() $G_0$ was obtained by solving for the von Kármán flow with the time dependence removed from (2.10).) Figure 3 displays the maximum absolute error
$G_0$ was obtained by solving for the von Kármán flow with the time dependence removed from (2.10).) Figure 3 displays the maximum absolute error ![]() $E$ between the exact unsteady velocity component
$E$ between the exact unsteady velocity component ![]() $G_{{u}}$ and the analytic Stokes layer solution
$G_{{u}}$ and the analytic Stokes layer solution ![]() $G_1^{0}$
$G_1^{0}$
across the boundary layer and over one modulation period ![]() $T$. As expected, the error
$T$. As expected, the error ![]() $E$ is greatest for low frequencies of modulation. Nevertheless, the error is still relatively small compared with the modulation amplitude
$E$ is greatest for low frequencies of modulation. Nevertheless, the error is still relatively small compared with the modulation amplitude ![]() $\epsilon$. As the modulation frequency
$\epsilon$. As the modulation frequency ![]() $\varphi$ increases, the error
$\varphi$ increases, the error ![]() $E$ decreases rapidly. Furthermore, the error appears to increase linearly with
$E$ decreases rapidly. Furthermore, the error appears to increase linearly with ![]() $\epsilon$. Thus, for suitable modulation amplitudes
$\epsilon$. Thus, for suitable modulation amplitudes ![]() $\epsilon$ and frequencies
$\epsilon$ and frequencies ![]() $\varphi$, the unsteady flow on a modulated rotating disk can be approximated by (3.12). Nevertheless, throughout the subsequent linear stability analyses, this approximation is not necessary, and the base flow is computed numerically by directly solving (2.10).
$\varphi$, the unsteady flow on a modulated rotating disk can be approximated by (3.12). Nevertheless, throughout the subsequent linear stability analyses, this approximation is not necessary, and the base flow is computed numerically by directly solving (2.10).

Figure 3. Maximum absolute error ![]() $E= \max _{\tilde {\tau },\tilde {z}}|G_{{u}} - G_1^{0}|$ as a function of the non-dimensional modulation frequency
$E= \max _{\tilde {\tau },\tilde {z}}|G_{{u}} - G_1^{0}|$ as a function of the non-dimensional modulation frequency ![]() $\varphi$, between the unsteady part
$\varphi$, between the unsteady part ![]() $G_{{u}}$ of the azimuthal velocity field and the analytic Stokes layer solution
$G_{{u}}$ of the azimuthal velocity field and the analytic Stokes layer solution ![]() $G_1^{0}$, for modulation amplitudes
$G_1^{0}$, for modulation amplitudes ![]() $\epsilon = 0.1$ (solid line) and
$\epsilon = 0.1$ (solid line) and ![]() $\epsilon = 0.2$ (dashed).
$\epsilon = 0.2$ (dashed).
4. Linear stability analysis
The linear stability of disturbances in the rotating disk boundary layer is modelled in a rotating frame of reference using the numerical formulation developed by Davies & Carpenter (Reference Davies and Carpenter2001). (Recall that the base flow velocity profiles were computed in the non-rotating frame to facilitate the implementation of the numerical method based on Chebyshev series expansions.) As a consequence of the change in reference frame, the base flow (2.6) must first undergo a transformation. This comprises a change in the boundary conditions (2.1c,e) for the azimuthal velocity component ![]() $G$ as
$G$ as
and by setting
Subscripts ![]() $r$ and
$r$ and ![]() $nr$ denote the rotating and non-rotating reference frames, respectively. Additionally, Coriolis and curvature effects are included in the governing perturbation equations.
$nr$ denote the rotating and non-rotating reference frames, respectively. Additionally, Coriolis and curvature effects are included in the governing perturbation equations.
In the subsequent local linear stability analysis, the homogeneous flow approximation is implemented, whereby the radial dependence of the base flow (2.6) is ignored. This amounts to the replacement of the radial coordinate ![]() $r$ with the Reynolds number
$r$ with the Reynolds number ![]() ${Re}$. Hence, the base flow (2.6) is given as
${Re}$. Hence, the base flow (2.6) is given as
4.1. Velocity–vorticity formulation
Linear stability analysis is performed using the vorticity-based formulation developed by Davies & Carpenter (Reference Davies and Carpenter2001) that requires the Chebyshev-tau method used by Bridges & Morris (Reference Bridges and Morris1984) and Cooper & Carpenter (Reference Cooper and Carpenter1997). Velocity and vorticity perturbations to the homogeneous base flow (4.3) are denoted by
Following Davies & Carpenter (Reference Davies and Carpenter2001), perturbation fields are separated into primary ![]() $(\xi _r,\xi _{\theta }, u_z)$ and secondary variables
$(\xi _r,\xi _{\theta }, u_z)$ and secondary variables ![]() $(u_r,u_{\theta },\xi _z)$. The three primary variables are then given as solutions of the following equations that are fully equivalent to the linearised Navier–Stokes equations:
$(u_r,u_{\theta },\xi _z)$. The three primary variables are then given as solutions of the following equations that are fully equivalent to the linearised Navier–Stokes equations:
where
and
Secondary variables ![]() $(u_r,u_{\theta }, \xi _z)$ are expressed in terms of the primary variables by rearranging the definition for vorticity and the solenoidal condition as follows:
$(u_r,u_{\theta }, \xi _z)$ are expressed in terms of the primary variables by rearranging the definition for vorticity and the solenoidal condition as follows:
Moreover, since the rotating disk is rigid, the no-slip conditions on the disk surface
can be reformulated using the definitions for ![]() $u_r$ and
$u_r$ and ![]() $u_{\theta }$ as the following integral constraints on the primary variables
$u_{\theta }$ as the following integral constraints on the primary variables ![]() $\xi _r$ and
$\xi _r$ and ![]() $\xi _{\theta }$:
$\xi _{\theta }$:
Furthermore, as per Davies & Carpenter (Reference Davies and Carpenter2001), all velocity and vorticity perturbation fields are assumed to vanish in the far-field limit, ![]() $z \to \infty$.
$z \to \infty$.
4.2. Floquet theory
Since the base flow (4.3) is time-dependent, perturbations ![]() $\boldsymbol {q}= (\boldsymbol {u},\boldsymbol {\xi })$ are decomposed into the form
$\boldsymbol {q}= (\boldsymbol {u},\boldsymbol {\xi })$ are decomposed into the form
where ![]() $\hat {\boldsymbol {q}}$ is time-periodic with the same period
$\hat {\boldsymbol {q}}$ is time-periodic with the same period ![]() $T$ as the disk modulation and
$T$ as the disk modulation and ![]() $\textrm {c.c.}$ denotes the complex conjugate. Due to the circumferential periodicity of the disk, the azimuthal mode number
$\textrm {c.c.}$ denotes the complex conjugate. Due to the circumferential periodicity of the disk, the azimuthal mode number ![]() $n=\beta {Re}$ is an integer. However, for practical purposes it is treated as a continuous parameter, similar to the azimuthal wavenumber
$n=\beta {Re}$ is an integer. However, for practical purposes it is treated as a continuous parameter, similar to the azimuthal wavenumber ![]() $\beta$ that is more commonly used in linear stability studies (Lingwood Reference Lingwood1995; Cooper & Carpenter Reference Cooper and Carpenter1997; Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015). The parameters
$\beta$ that is more commonly used in linear stability studies (Lingwood Reference Lingwood1995; Cooper & Carpenter Reference Cooper and Carpenter1997; Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015). The parameters ![]() $\alpha$ and
$\alpha$ and ![]() $\mu$ denote the radial wavenumber and Floquet exponent of the disturbance, respectively. Spatial growth is encompassed in the imaginary part of
$\mu$ denote the radial wavenumber and Floquet exponent of the disturbance, respectively. Spatial growth is encompassed in the imaginary part of ![]() $\alpha$, while the real part of
$\alpha$, while the real part of ![]() $\mu$ specifies the temporal growth of the perturbation. Additionally, all terms of
$\mu$ specifies the temporal growth of the perturbation. Additionally, all terms of ![]() $O(1/{Re}^{2})$ and higher are neglected, to ensure compatibility with earlier local linear stability studies.
$O(1/{Re}^{2})$ and higher are neglected, to ensure compatibility with earlier local linear stability studies.
The time-periodic function ![]() $\hat {\boldsymbol {q}}$ is decomposed into Fourier harmonics as
$\hat {\boldsymbol {q}}$ is decomposed into Fourier harmonics as
 \begin{equation} \hat{\boldsymbol{q}}(z,\tau) = \sum_{m={-}\infty}^{\infty}\boldsymbol{q}_m(z)\exp(\textrm{i}m\varphi\tau/{Re}), \end{equation}
\begin{equation} \hat{\boldsymbol{q}}(z,\tau) = \sum_{m={-}\infty}^{\infty}\boldsymbol{q}_m(z)\exp(\textrm{i}m\varphi\tau/{Re}), \end{equation}
where the factor ![]() $\varphi /{Re}$ ensures the harmonics have the same period as
$\varphi /{Re}$ ensures the harmonics have the same period as ![]() $\hat {\boldsymbol {q}}$. Similarly, the unsteady base flow (4.3) is decomposed into Fourier harmonics as
$\hat {\boldsymbol {q}}$. Similarly, the unsteady base flow (4.3) is decomposed into Fourier harmonics as
 \begin{equation} \boldsymbol{U}(z,\tau) = \boldsymbol{U}_0(z) + \sum_{k={-}\infty}^{\infty}\boldsymbol{U}_k(z)\exp(\textrm{i}k\varphi\tau/{Re}), \end{equation}
\begin{equation} \boldsymbol{U}(z,\tau) = \boldsymbol{U}_0(z) + \sum_{k={-}\infty}^{\infty}\boldsymbol{U}_k(z)\exp(\textrm{i}k\varphi\tau/{Re}), \end{equation}
where ![]() $\boldsymbol {U}_0$ represents the steady von Kármán flow.
$\boldsymbol {U}_0$ represents the steady von Kármán flow.
Numerical solutions are then obtained by truncating the number of harmonics in the two infinite series expressions (4.12) and (4.13) to finite values ![]() $N_F$ and
$N_F$ and ![]() $N_B$, respectively. Substituting (4.11) with the truncated series expressions (4.12) and (4.13), into the governing perturbation (4.5), establishes a coupled system of ordinary differential equations given by the dispersion relationship
$N_B$, respectively. Substituting (4.11) with the truncated series expressions (4.12) and (4.13), into the governing perturbation (4.5), establishes a coupled system of ordinary differential equations given by the dispersion relationship
The system of (4.14) is solved numerically using the methods outlined in Morgan & Davies (Reference Morgan and Davies2020), whereby perturbations are represented using the Chebyshev series expansion (2.13). The dispersion relationship (4.14) is then integrated twice with respect to the mapped variable ![]() $\eta$ (recall (2.12)), resulting in a numerical eigenvalue problem that is solved using the eigensolver routines in MATLAB.
$\eta$ (recall (2.12)), resulting in a numerical eigenvalue problem that is solved using the eigensolver routines in MATLAB.
There are two distinct types of analysis that may be undertaken. A temporal approach consists of specifying the radial wavenumber ![]() $\alpha \in \mathbb {R}$ and calculating the complex valued Floquet exponent
$\alpha \in \mathbb {R}$ and calculating the complex valued Floquet exponent ![]() $\mu$. On the other hand, a spatial analysis is achieved by setting
$\mu$. On the other hand, a spatial analysis is achieved by setting ![]() $\mu \in \mathbb {R}$ and computing the complex valued wavenumber
$\mu \in \mathbb {R}$ and computing the complex valued wavenumber ![]() $\alpha$. Since our primary aim is to suppress the growth of convectively unstable disturbances, and in particular stationary cross-flow vortices, a spatial analysis is undertaken.
$\alpha$. Since our primary aim is to suppress the growth of convectively unstable disturbances, and in particular stationary cross-flow vortices, a spatial analysis is undertaken.
4.3. Numerical validation
In the earlier Floquet stability study by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002) on the semi-infinite Stokes layer, numerical convergence was achieved for Fourier harmonics ![]() $N_F=0.8\alpha {Re}_s$, which was typically greater than
$N_F=0.8\alpha {Re}_s$, which was typically greater than ![]() $200$. Hence, significant computational resources were required to accurately determine conditions for linear instability. However, for the current study we do not anticipate any
$200$. Hence, significant computational resources were required to accurately determine conditions for linear instability. However, for the current study we do not anticipate any ![]() $O({Re})$ separation between the time scales of the base flow and the disturbance, at least for those small modulation amplitudes
$O({Re})$ separation between the time scales of the base flow and the disturbance, at least for those small modulation amplitudes ![]() $\epsilon$ modelled herein. Following careful calculations it was determined that a six (or greater) decimal place accuracy was realised, by setting the number of harmonics in the perturbation field (4.12) and base flow (4.13) as
$\epsilon$ modelled herein. Following careful calculations it was determined that a six (or greater) decimal place accuracy was realised, by setting the number of harmonics in the perturbation field (4.12) and base flow (4.13) as ![]() $N_F=6$ and
$N_F=6$ and ![]() $N_B=4$, respectively (see table 2 for a list of radial wavenumbers
$N_B=4$, respectively (see table 2 for a list of radial wavenumbers ![]() $\alpha$ computed for variable
$\alpha$ computed for variable ![]() $N_F$ and
$N_F$ and ![]() $N_B$). Thus, the computational requirements are significantly reduced. Additionally, setting the number of wall-normal Chebyshev polynomials,
$N_B$). Thus, the computational requirements are significantly reduced. Additionally, setting the number of wall-normal Chebyshev polynomials, ![]() $M=64$, was sufficient to ensure numerical convergence. Further details of the validation checks are presented in Morgan (Reference Morgan2018).
$M=64$, was sufficient to ensure numerical convergence. Further details of the validation checks are presented in Morgan (Reference Morgan2018).
4.4. Stationary convective disturbances
In addition to the Reynolds number ![]() ${Re}$, modulation amplitude
${Re}$, modulation amplitude ![]() $\epsilon$ and frequency
$\epsilon$ and frequency ![]() $\varphi$ (that fully specify the base flow (4.3)), a spatial analysis of the dispersion relationship (4.14) is based on the azimuthal mode number
$\varphi$ (that fully specify the base flow (4.3)), a spatial analysis of the dispersion relationship (4.14) is based on the azimuthal mode number ![]() $n$ and Floquet exponent
$n$ and Floquet exponent ![]() $\mu$. Since stationary cross-flow vortices play a significant role in the early stages of laminar–turbulent transition on a rotating disk (Gregory et al. Reference Gregory, Stuart and Walker1955), the following analysis is limited to stationary disturbances by setting the Floquet exponent
$\mu$. Since stationary cross-flow vortices play a significant role in the early stages of laminar–turbulent transition on a rotating disk (Gregory et al. Reference Gregory, Stuart and Walker1955), the following analysis is limited to stationary disturbances by setting the Floquet exponent ![]() $\mu =0$. The dispersion relationship (4.14) is then used to determine the complex valued radial wavenumber
$\mu =0$. The dispersion relationship (4.14) is then used to determine the complex valued radial wavenumber ![]() $\alpha$, where a negative imaginary part corresponds to unstable behaviour.
$\alpha$, where a negative imaginary part corresponds to unstable behaviour.
Stationary disturbances will be stabilised by the application of time-periodic modulation to the disk rotation rate, if
where ![]() $\alpha _i^{s}$ and
$\alpha _i^{s}$ and ![]() $\alpha _i^{m}$ denote the radial growth rates without and with modulation, respectively. (Note that the inequality is as given in (4.15), as a consequence of radial growth occurring when
$\alpha _i^{m}$ denote the radial growth rates without and with modulation, respectively. (Note that the inequality is as given in (4.15), as a consequence of radial growth occurring when ![]() $\alpha _i$ is negative.)
$\alpha _i$ is negative.)
Differences in the radial growth rates
are plotted in figure 4 as a function of the modulation frequency ![]() $\varphi$, for two modulation amplitudes
$\varphi$, for two modulation amplitudes ![]() $\epsilon$. Results correspond to the Reynolds number
$\epsilon$. Results correspond to the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$, while a positive (negative) valued
$n=32$, while a positive (negative) valued ![]() ${\rm \Delta} \alpha _i$ indicates a reduction (increase) in the radial growth rate and a stabilising (destabilising) effect. This particular azimuthal mode number was chosen to illustrate disturbance behaviour, since earlier investigations found this mode to be the most significant in the laminar–turbulent transition process. With the exception of very small modulation frequencies,
${\rm \Delta} \alpha _i$ indicates a reduction (increase) in the radial growth rate and a stabilising (destabilising) effect. This particular azimuthal mode number was chosen to illustrate disturbance behaviour, since earlier investigations found this mode to be the most significant in the laminar–turbulent transition process. With the exception of very small modulation frequencies, ![]() ${\rm \Delta} \alpha _i$ is always positive. Hence, time-periodic modulation of the disk rotation rate is stabilising and reduces the growth of the stationary cross-flow vortex. A peak level of stabilisation is observed for frequencies
${\rm \Delta} \alpha _i$ is always positive. Hence, time-periodic modulation of the disk rotation rate is stabilising and reduces the growth of the stationary cross-flow vortex. A peak level of stabilisation is observed for frequencies ![]() $\varphi \sim 8$, while modulation is found to have a negligible effect for very high frequencies. Thus, there is an optimal range of frequencies
$\varphi \sim 8$, while modulation is found to have a negligible effect for very high frequencies. Thus, there is an optimal range of frequencies ![]() $\varphi$ for which a considerable level of flow control is realised.
$\varphi$ for which a considerable level of flow control is realised.

Figure 4. Variation in the radial growth rate, ![]() ${\rm \Delta} \alpha _i$, as a function of the modulation frequency
${\rm \Delta} \alpha _i$, as a function of the modulation frequency ![]() $\varphi$, for the stationary type I cross-flow instability with the Reynolds number
$\varphi$, for the stationary type I cross-flow instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$. The modulation amplitude
$n=32$. The modulation amplitude ![]() $\epsilon = 0.1$ (solid) and
$\epsilon = 0.1$ (solid) and ![]() $\epsilon = 0.2$ (dashed), while
$\epsilon = 0.2$ (dashed), while ![]() ${\rm \Delta} \alpha _i > 0$ indicates a reduction in the radial growth rate and a stabilising effect.
${\rm \Delta} \alpha _i > 0$ indicates a reduction in the radial growth rate and a stabilising effect.
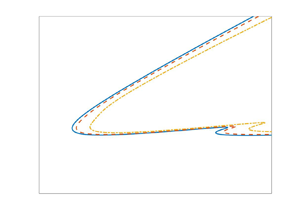
Figure 5 displays neutral stability curves for stationary disturbances in both the ![]() $({Re},\alpha _r)$- and
$({Re},\alpha _r)$- and ![]() $({Re},n)$-planes, with the modulation frequency
$({Re},n)$-planes, with the modulation frequency ![]() $\varphi = 6$ in 5(a,b) and
$\varphi = 6$ in 5(a,b) and ![]() $\varphi = 10$ in 5(c,d). Results are plotted for modulation amplitudes
$\varphi = 10$ in 5(c,d). Results are plotted for modulation amplitudes ![]() $\epsilon =0.1$ (dashed) and
$\epsilon =0.1$ (dashed) and ![]() $\epsilon =0.2$ (chain), while solid lines depict the solutions corresponding to the steady von Kármán flow without time-periodic modulation. (As the base flow (2.6) is dependent on the Reynolds number
$\epsilon =0.2$ (chain), while solid lines depict the solutions corresponding to the steady von Kármán flow without time-periodic modulation. (As the base flow (2.6) is dependent on the Reynolds number ![]() ${Re}$, it was necessary to compute the velocity profiles
${Re}$, it was necessary to compute the velocity profiles ![]() $F,G,H$ at every
$F,G,H$ at every ![]() ${Re}$ step in the neutral stability calculations.) Solutions demonstrate that the stabilising effect observed in figure 4 for the type I cross-flow instability is not an isolated occurrence, but is found for a range of modulation parameter settings
${Re}$ step in the neutral stability calculations.) Solutions demonstrate that the stabilising effect observed in figure 4 for the type I cross-flow instability is not an isolated occurrence, but is found for a range of modulation parameter settings ![]() $(\epsilon ,\varphi )$, Reynolds numbers
$(\epsilon ,\varphi )$, Reynolds numbers ![]() ${Re}$ and azimuthal mode numbers
${Re}$ and azimuthal mode numbers ![]() $n$. Furthermore, the neutral stability curves indicate that the type II Coriolis instability is marginally stabilised when modulating the disk with a frequency
$n$. Furthermore, the neutral stability curves indicate that the type II Coriolis instability is marginally stabilised when modulating the disk with a frequency ![]() $\varphi =6$, but undergoes a significant stabilisation in the instance
$\varphi =6$, but undergoes a significant stabilisation in the instance ![]() $\varphi =10$. (The type II instability is evidenced by those secondary protrusions near
$\varphi =10$. (The type II instability is evidenced by those secondary protrusions near ![]() ${Re}=450$ and
${Re}=450$ and ![]() $n=20$.) Thus, contrary to other flow control methods, such as surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) and wall compliance (Cooper & Carpenter Reference Cooper and Carpenter1997) that could only be used to control the type I mode, time-periodic modulation stabilises both the stationary cross-flow and Coriolis instabilities.
$n=20$.) Thus, contrary to other flow control methods, such as surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) and wall compliance (Cooper & Carpenter Reference Cooper and Carpenter1997) that could only be used to control the type I mode, time-periodic modulation stabilises both the stationary cross-flow and Coriolis instabilities.

Figure 5. Neutral stability curves for the onset of stationary disturbances in the ![]() $({Re},\alpha _r)$- and
$({Re},\alpha _r)$- and ![]() $({Re},n)$-planes. (a,b) The modulation frequency
$({Re},n)$-planes. (a,b) The modulation frequency ![]() $\varphi =6$; (c,d)
$\varphi =6$; (c,d) ![]() $\varphi =10$. The modulation amplitude
$\varphi =10$. The modulation amplitude ![]() $\epsilon =0$ (solid),
$\epsilon =0$ (solid), ![]() $\epsilon = 0.1$ (dashed) and
$\epsilon = 0.1$ (dashed) and ![]() $\epsilon = 0.2$ (chain).
$\epsilon = 0.2$ (chain).
Neutral stability curves are replotted in figure 6 over a reduced ![]() $({Re},\alpha _r)$ range for both
$({Re},\alpha _r)$ range for both ![]() $\varphi =6$ and
$\varphi =6$ and ![]() $\varphi =10$. The behaviour near the onset of the type I cross-flow instability and the type II Coriolis instability are shown in figure 6(a,c) and figure 6(b,d), respectively. The illustration further demonstrates the strong stabilising effect of time-periodic modulation on the cross-flow instability. However, the effect on the Coriolis instability is only noticeably different in the instance
$\varphi =10$. The behaviour near the onset of the type I cross-flow instability and the type II Coriolis instability are shown in figure 6(a,c) and figure 6(b,d), respectively. The illustration further demonstrates the strong stabilising effect of time-periodic modulation on the cross-flow instability. However, the effect on the Coriolis instability is only noticeably different in the instance ![]() $\varphi =10$. Moreover, results suggest that the stabilising effect found for the cross-flow instability increases as the modulation amplitude
$\varphi =10$. Moreover, results suggest that the stabilising effect found for the cross-flow instability increases as the modulation amplitude ![]() $\epsilon$ increases.
$\epsilon$ increases.

Figure 6. Same as figure 5 but over a reduced ![]() $({Re},\alpha _r)$ range, highlighting the behaviour near (a,c) the type I cross-flow instability and (b,d) the type II Coriolis instability. (a,b) The modulation frequency
$({Re},\alpha _r)$ range, highlighting the behaviour near (a,c) the type I cross-flow instability and (b,d) the type II Coriolis instability. (a,b) The modulation frequency ![]() $\varphi =6$; (c,d)
$\varphi =6$; (c,d) ![]() $\varphi =10$. The modulation amplitude
$\varphi =10$. The modulation amplitude ![]() $\epsilon =0$ (solid),
$\epsilon =0$ (solid), ![]() $\epsilon = 0.1$ (dashed) and
$\epsilon = 0.1$ (dashed) and ![]() $\epsilon = 0.2$ (chain).
$\epsilon = 0.2$ (chain).
The above analysis was extended to encompass a range of modulation frequencies ![]() $\varphi$ and two modulation amplitudes:
$\varphi$ and two modulation amplitudes: ![]() $\epsilon =0.1$ and
$\epsilon =0.1$ and ![]() $\epsilon =0.2$. Critical conditions for the onset of the stationary convective instability were then determined, with the critical Reynolds number
$\epsilon =0.2$. Critical conditions for the onset of the stationary convective instability were then determined, with the critical Reynolds number ![]() ${Re}_c$ and azimuthal mode number
${Re}_c$ and azimuthal mode number ![]() $n_c$ plotted in figure 7. The horizontal chain lines depict the critical conditions obtained for the rotating disk without modulation, where
$n_c$ plotted in figure 7. The horizontal chain lines depict the critical conditions obtained for the rotating disk without modulation, where ![]() ${Re}_c\approx 285.6$ and
${Re}_c\approx 285.6$ and ![]() $n_c\approx 22$. The calculations for
$n_c\approx 22$. The calculations for ![]() $\epsilon =0$ are consistent with those found in the earlier linear stability studies by Malik (Reference Malik1986) and Lingwood (Reference Lingwood1997), amongst many others. Table 3 presents numerical values for
$\epsilon =0$ are consistent with those found in the earlier linear stability studies by Malik (Reference Malik1986) and Lingwood (Reference Lingwood1997), amongst many others. Table 3 presents numerical values for ![]() ${Re}_c$ and
${Re}_c$ and ![]() $n_c$, alongside the critical radial wavenumber
$n_c$, alongside the critical radial wavenumber ![]() $\alpha _c$, for several modulation
$\alpha _c$, for several modulation ![]() $(\epsilon ,\varphi )$ settings. In all instances modelled, the most unstable disturbance corresponds to the cross-flow instability (given in bold); the type II Coriolis instability (given in brackets) emerges at significantly larger Reynolds numbers. Thus, the cross-flow instability is the most unstable form of disturbance and will ultimately be responsible for bringing about the early stages of laminar–turbulent transition on the modulated rotating disk. Furthermore, time-periodic modulation increases the Reynolds number for the onset of unstable behaviour, with a peak stabilising effect achieved for frequencies
$(\epsilon ,\varphi )$ settings. In all instances modelled, the most unstable disturbance corresponds to the cross-flow instability (given in bold); the type II Coriolis instability (given in brackets) emerges at significantly larger Reynolds numbers. Thus, the cross-flow instability is the most unstable form of disturbance and will ultimately be responsible for bringing about the early stages of laminar–turbulent transition on the modulated rotating disk. Furthermore, time-periodic modulation increases the Reynolds number for the onset of unstable behaviour, with a peak stabilising effect achieved for frequencies ![]() $\varphi \sim 8$. However, for modulation frequencies
$\varphi \sim 8$. However, for modulation frequencies ![]() $\varphi >25$, the stabilising effect is negligible. Finally, the critical azimuthal mode number
$\varphi >25$, the stabilising effect is negligible. Finally, the critical azimuthal mode number ![]() $n_c$ for linear instability is only marginally affected by modulating the disk rotation rate.
$n_c$ for linear instability is only marginally affected by modulating the disk rotation rate.

Figure 7. (a) Critical Reynolds number ![]() ${Re}_c$ and (b) azimuthal mode number
${Re}_c$ and (b) azimuthal mode number ![]() $n_c$ for the stationary type I cross-flow instability, as a function of the modulation frequency
$n_c$ for the stationary type I cross-flow instability, as a function of the modulation frequency ![]() $\varphi$. The modulation amplitude
$\varphi$. The modulation amplitude ![]() $\epsilon = 0.1$ (solid line) and
$\epsilon = 0.1$ (solid line) and ![]() $\epsilon = 0.2$ (dashed). Solutions corresponding to the steady von Kármán flow are indicated by the horizontal chain lines.
$\epsilon = 0.2$ (dashed). Solutions corresponding to the steady von Kármán flow are indicated by the horizontal chain lines.
Table 3. Critical conditions for the onset of the stationary type I cross-flow instability (bold) and type II Coriolis instability (brackets). The cross-flow mode is the most dangerous in all instances modelled.

Optimum modulation frequencies ![]() $\varphi$ are presented in table 4 that establish the greatest level of stabilisation for both the type I cross-flow instability (bold) and type II Coriolis instability (italics). Numerical calculations indicate that different modulation frequencies are required to achieve the maximum stabilisation effect for the two forms of instability. While we might expect optimum
$\varphi$ are presented in table 4 that establish the greatest level of stabilisation for both the type I cross-flow instability (bold) and type II Coriolis instability (italics). Numerical calculations indicate that different modulation frequencies are required to achieve the maximum stabilisation effect for the two forms of instability. While we might expect optimum ![]() $\varphi$ to be the same for both forms of instability, the differences reported in table 4 can be explained by noting that the two instabilities are brought about by very different mechanisms and so can be expected to react differently to the imposed modulation frequency. The cross-flow instability is inviscid in nature and is associated with an inflection point in the mean velocity profiles. On the other hand, the Coriolis instability is essentially viscous and is destabilised by the Coriolis forces present within the rotating disk boundary layer.
$\varphi$ to be the same for both forms of instability, the differences reported in table 4 can be explained by noting that the two instabilities are brought about by very different mechanisms and so can be expected to react differently to the imposed modulation frequency. The cross-flow instability is inviscid in nature and is associated with an inflection point in the mean velocity profiles. On the other hand, the Coriolis instability is essentially viscous and is destabilised by the Coriolis forces present within the rotating disk boundary layer.
Table 4. Optimum modulation frequencies ![]() $\varphi$ that establish the greatest level of stabilisation for the type I cross-flow instability (bold) and type II Coriolis instability (italics).
$\varphi$ that establish the greatest level of stabilisation for the type I cross-flow instability (bold) and type II Coriolis instability (italics).

5. Energy analysis
Following the approach of Cooper & Carpenter (Reference Cooper and Carpenter1997) on wall compliance and Cooper et al. (Reference Cooper, Harris, Garrett, Özkan and Thomas2015) and Garrett et al. (Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) on surface roughness, an integral energy equation for linear disturbances to the base flow ![]() $\boldsymbol {U}=(U,V,W)$ is derived. This allows us to assess the physical mechanisms behind the stabilising effect brought about by the application of time-periodic modulation to the disk rotation rate.
$\boldsymbol {U}=(U,V,W)$ is derived. This allows us to assess the physical mechanisms behind the stabilising effect brought about by the application of time-periodic modulation to the disk rotation rate.
5.1. Formulation
In order to compute the energy balance across a full period of modulation, a Q-S formulation is adopted, whereby the homogeneous base flow (4.3) is frozen at each time-step. Thus, time ![]() $\tau$ is treated as a parameter, and the Floquet mode structure (4.11) is replaced by the simpler normal mode form
$\tau$ is treated as a parameter, and the Floquet mode structure (4.11) is replaced by the simpler normal mode form
which is more commonly utilised in local stability studies on the steady rotating disk. The radial wavenumber and azimuthal mode number are again denoted by ![]() $\alpha$ and
$\alpha$ and ![]() $n$, while the frequency
$n$, while the frequency ![]() $\omega =0$ for stationary disturbances. On substituting (5.1) into the governing perturbation (4.5), a single system of ordinary differential equations is established, given by the dispersion relationship
$\omega =0$ for stationary disturbances. On substituting (5.1) into the governing perturbation (4.5), a single system of ordinary differential equations is established, given by the dispersion relationship
which is solved using the numerical methods outlined in § 4. By imposing the Q-S flow approximation, the stability problem is cast as a series of locally defined systems for a succession of different basic states at each phase during the modulation cycle.
The energy equation is formulated by multiplying the three linearised momentum equations by the respective velocity perturbation fields ![]() $\boldsymbol {u}=(u_r,u_{\theta },u_z)$, and summing together to give the following equation for the kinetic energy:
$\boldsymbol {u}=(u_r,u_{\theta },u_z)$, and summing together to give the following equation for the kinetic energy:
 \begin{align} &\left(\frac{\partial K}{\partial t} + U\frac{\partial K}{\partial r} + \frac{V}{r}\frac{\partial K}{\partial \theta} + W\frac{\partial K}{\partial z} \right) ={-}u_ru_z\frac{\partial U}{\partial z} - u_{\theta}u_z \frac{\partial V}{\partial z} - u_z^{2}\frac{\partial W}{\partial z} - u_r^{2}\frac{\partial U}{\partial r} - \frac{u_{\theta}^{2}U}{r} \nonumber\\ &\quad - \left(\frac{\partial}{\partial r}(u_rp) + \frac{1}{r}\frac{\partial }{\partial r}(u_{\theta}p) + \frac{\partial }{\partial z}(u_zp) + \frac{u_rp}{r}\right) + \left(\frac{\partial}{\partial x_i}(u_j\sigma_{ij}) - \sigma{ij}\frac{\partial u_j}{\partial x_i}\right), \end{align}
\begin{align} &\left(\frac{\partial K}{\partial t} + U\frac{\partial K}{\partial r} + \frac{V}{r}\frac{\partial K}{\partial \theta} + W\frac{\partial K}{\partial z} \right) ={-}u_ru_z\frac{\partial U}{\partial z} - u_{\theta}u_z \frac{\partial V}{\partial z} - u_z^{2}\frac{\partial W}{\partial z} - u_r^{2}\frac{\partial U}{\partial r} - \frac{u_{\theta}^{2}U}{r} \nonumber\\ &\quad - \left(\frac{\partial}{\partial r}(u_rp) + \frac{1}{r}\frac{\partial }{\partial r}(u_{\theta}p) + \frac{\partial }{\partial z}(u_zp) + \frac{u_rp}{r}\right) + \left(\frac{\partial}{\partial x_i}(u_j\sigma_{ij}) - \sigma{ij}\frac{\partial u_j}{\partial x_i}\right), \end{align}
where ![]() $p$ represents the pressure perturbation field,
$p$ represents the pressure perturbation field, ![]() $K = (u_r^{2} + u_{\theta }^{2} + w^{2})/2$, repeated suffices indicate summation and
$K = (u_r^{2} + u_{\theta }^{2} + w^{2})/2$, repeated suffices indicate summation and ![]() $\sigma _{ij}$ denotes the viscous stress terms
$\sigma _{ij}$ denotes the viscous stress terms
The ![]() $O(1/{Re}^{2})$ terms have been neglected for consistency with the Floquet analysis presented in § 4.
$O(1/{Re}^{2})$ terms have been neglected for consistency with the Floquet analysis presented in § 4.
By averaging over a single azimuthal mode number ![]() $n$ and integrating across the boundary layer, azimuthal
$n$ and integrating across the boundary layer, azimuthal ![]() $\theta$-derivatives are removed from (5.3) to give
$\theta$-derivatives are removed from (5.3) to give
 \begin{align} &\int_{0}^{\infty}\left(\frac{\partial \bar{K}}{\partial t} + \underbrace{U\frac{\partial \bar{K}}{\partial r}}_{{(A)}} + \underbrace{\frac{\partial\left(\bar{u_rp}\right)}{\partial r}}_{{(B)}} - \underbrace{\frac{\partial}{\partial r}\left(\bar{u_{r}\sigma_{11}} +\bar{u_{\theta}\sigma_{12}} + \bar{u_z\sigma_{13}}\right)}_{{(C)}}\right) \,\textrm{d} z \nonumber\\ &\quad = \underbrace{\int_{0}^{\infty}\left(-\bar{u_ru_z}\frac{\partial U}{\partial z} - \bar{u_{\theta}u_z}\frac{\partial V}{\partial z} - \bar{u_z^{2}}\frac{\partial W}{\partial z} \right)\,\textrm{d} z}_{{(I)}} - \underbrace{\int_{0}^{\infty}\left(\bar{\sigma_{ij}\frac{\partial u_{j}}{\partial i}}\right) \,\textrm{d} z}_{{(II)}} \nonumber\\ &\qquad - \underbrace{\int_{0}^{\infty}\left(\frac{\bar{u_rp}}{r}\right) \,\textrm{d} z \!+\! (u_zp)_w}_{{(III)}} \!-\! \underbrace{(u_r\sigma_{31} \!+\! u_{\theta}\sigma_{32})_w}_{{(IV)}} - \underbrace{\int_{0}^{\infty}\left(W\frac{\partial \bar{K}}{\partial z}+\bar{u_r^{2}}\frac{\partial U}{\partial r}+\frac{\overline{u_{\theta}^{2}}U}{r}\right) \,\textrm{d} z}_{{(V)}}. \end{align}
\begin{align} &\int_{0}^{\infty}\left(\frac{\partial \bar{K}}{\partial t} + \underbrace{U\frac{\partial \bar{K}}{\partial r}}_{{(A)}} + \underbrace{\frac{\partial\left(\bar{u_rp}\right)}{\partial r}}_{{(B)}} - \underbrace{\frac{\partial}{\partial r}\left(\bar{u_{r}\sigma_{11}} +\bar{u_{\theta}\sigma_{12}} + \bar{u_z\sigma_{13}}\right)}_{{(C)}}\right) \,\textrm{d} z \nonumber\\ &\quad = \underbrace{\int_{0}^{\infty}\left(-\bar{u_ru_z}\frac{\partial U}{\partial z} - \bar{u_{\theta}u_z}\frac{\partial V}{\partial z} - \bar{u_z^{2}}\frac{\partial W}{\partial z} \right)\,\textrm{d} z}_{{(I)}} - \underbrace{\int_{0}^{\infty}\left(\bar{\sigma_{ij}\frac{\partial u_{j}}{\partial i}}\right) \,\textrm{d} z}_{{(II)}} \nonumber\\ &\qquad - \underbrace{\int_{0}^{\infty}\left(\frac{\bar{u_rp}}{r}\right) \,\textrm{d} z \!+\! (u_zp)_w}_{{(III)}} \!-\! \underbrace{(u_r\sigma_{31} \!+\! u_{\theta}\sigma_{32})_w}_{{(IV)}} - \underbrace{\int_{0}^{\infty}\left(W\frac{\partial \bar{K}}{\partial z}+\bar{u_r^{2}}\frac{\partial U}{\partial r}+\frac{\overline{u_{\theta}^{2}}U}{r}\right) \,\textrm{d} z}_{{(V)}}. \end{align}
The ![]() $w$ subscript in
$w$ subscript in ![]() $(III)$ and
$(III)$ and ![]() $(IV)$ denotes a quantity evaluated at the disk wall, while overbars denote a period-averaged quantity. Velocity perturbation fields
$(IV)$ denotes a quantity evaluated at the disk wall, while overbars denote a period-averaged quantity. Velocity perturbation fields ![]() $\boldsymbol {u}$ are given as solutions of the dispersion relationship (5.2), while the pressure
$\boldsymbol {u}$ are given as solutions of the dispersion relationship (5.2), while the pressure ![]() $p$ perturbation field is obtained by integrating the linearised
$p$ perturbation field is obtained by integrating the linearised ![]() $z$-momentum component of the Navier–Stokes equations to give the formula
$z$-momentum component of the Navier–Stokes equations to give the formula
As described by Cooper and coauthors (Cooper & Carpenter Reference Cooper and Carpenter1997; Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016), each term in (5.5) has a physical interpretation in terms of its contribution to the system energy. On the left-hand side, ![]() $(A)$ represents the average kinetic energy convected by the radial component of the base flow,
$(A)$ represents the average kinetic energy convected by the radial component of the base flow, ![]() $(B)$ the work done by the pressure perturbation field and
$(B)$ the work done by the pressure perturbation field and ![]() $(C)$ the work done by the viscous stresses across some internal boundary in the fluid. For the subsequent analysis, the latter term
$(C)$ the work done by the viscous stresses across some internal boundary in the fluid. For the subsequent analysis, the latter term ![]() $(C)$ is negligible. On the right-hand side,
$(C)$ is negligible. On the right-hand side, ![]() $(I)$ represents the Reynolds stress energy production,
$(I)$ represents the Reynolds stress energy production, ![]() $(II)$ the viscous dissipation energy removal,
$(II)$ the viscous dissipation energy removal, ![]() $(III)$ the pressure work,
$(III)$ the pressure work, ![]() $(IV)$ the contributions from work done on the wall by viscous stresses and
$(IV)$ the contributions from work done on the wall by viscous stresses and ![]() $(V)$ the streamline curvature effects and the three-dimensionality of the mean flow.
$(V)$ the streamline curvature effects and the three-dimensionality of the mean flow.
Equation (5.5) is normalised by the integrated mechanical energy flux to give
 \begin{align} -2\alpha_i &={-}\frac{\partial K}{\partial t} + \underbrace{(P_1 + P_2 + P_3)}_{{(I)}} + \underbrace{D}_{{(II)}} + \underbrace{(PW_1 + PW_2)}_{{(III)}} \nonumber\\ &\quad + \underbrace{(S_1 + S_2 + S_3)}_{{(IV)}} + \underbrace{(G_1 + G_2 + G_3)}_{{(V)}}, \end{align}
\begin{align} -2\alpha_i &={-}\frac{\partial K}{\partial t} + \underbrace{(P_1 + P_2 + P_3)}_{{(I)}} + \underbrace{D}_{{(II)}} + \underbrace{(PW_1 + PW_2)}_{{(III)}} \nonumber\\ &\quad + \underbrace{(S_1 + S_2 + S_3)}_{{(IV)}} + \underbrace{(G_1 + G_2 + G_3)}_{{(V)}}, \end{align}
where all terms, including the mechanical energy flux, are time-dependent. In particular, terms are time-periodic with a period ![]() $T$. Positive terms correspond to an energy production, while negative terms are matched to the removal of energy from the system. A disturbance is then amplified when the energy production exceeds the energy dissipation from the system, which corresponds to a negative radial growth rate
$T$. Positive terms correspond to an energy production, while negative terms are matched to the removal of energy from the system. A disturbance is then amplified when the energy production exceeds the energy dissipation from the system, which corresponds to a negative radial growth rate ![]() $(\alpha _i < 0)$. All components of the energy balance equation (5.7) are then determined to identify those terms that are most affected by the time-periodic modulation.
$(\alpha _i < 0)$. All components of the energy balance equation (5.7) are then determined to identify those terms that are most affected by the time-periodic modulation.
It was shown by the Cooper group (Cooper & Carpenter Reference Cooper and Carpenter1997; Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) that the energy production due to the Reynolds stress ![]() $(P_2)$ and the viscous energy removal
$(P_2)$ and the viscous energy removal ![]() $(D)$ dominate (5.7) for the steady von Kármán flow, while
$(D)$ dominate (5.7) for the steady von Kármán flow, while ![]() $S_1, S_2, S_3$ and
$S_1, S_2, S_3$ and ![]() $PW_2$ are zero as a consequence of the boundary conditions. Furthermore, the remaining terms are negligible, with the exception of the geometric terms
$PW_2$ are zero as a consequence of the boundary conditions. Furthermore, the remaining terms are negligible, with the exception of the geometric terms ![]() $G_1$ and
$G_1$ and ![]() $G_3$ for the type II Coriolis instability.
$G_3$ for the type II Coriolis instability.
For the periodically modulated rotating disk flow (4.3), Q-S perturbations (5.1) and by extension the energy terms in (5.7), are computed over a full cycle ![]() $T$ of the time-periodic modulation. It is expected that quantities will vary across the period of modulation. Thus, to help draw comparisons with the solutions of the steady von Kármán flow, terms are averaged over one modulation period
$T$ of the time-periodic modulation. It is expected that quantities will vary across the period of modulation. Thus, to help draw comparisons with the solutions of the steady von Kármán flow, terms are averaged over one modulation period ![]() $T$, by computing the quantity
$T$, by computing the quantity
For instance, ![]() $\bar {\alpha }_i$ denotes the time-averaged (T-A) radial growth rate over one modulation period.
$\bar {\alpha }_i$ denotes the time-averaged (T-A) radial growth rate over one modulation period.
In the following analysis, we compute the energy terms in (5.7) for two specific flow conditions that are matched to the type I cross-flow instability and the type II Coriolis instability. In the former instance the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$, while in the latter case
$n=32$, while in the latter case ![]() ${Re}$ is unchanged but
${Re}$ is unchanged but ![]() $n=20$. The decision to focus on these modes, and in particular the
$n=20$. The decision to focus on these modes, and in particular the ![]() $n=32$ cross-flow mode, was made as a consequence of earlier experimental observations that found the early stages of laminar–turbulent transition were dominated by azimuthal modes
$n=32$ cross-flow mode, was made as a consequence of earlier experimental observations that found the early stages of laminar–turbulent transition were dominated by azimuthal modes ![]() $n\in [28,32]$ (Gregory et al. Reference Gregory, Stuart and Walker1955; Kobayashi et al. Reference Kobayashi, Kohama and Takamadate1980; Jarre et al. Reference Jarre, Le Gal and Chauve1996). The effects of time-periodic modulation are then determined for modulation amplitudes
$n\in [28,32]$ (Gregory et al. Reference Gregory, Stuart and Walker1955; Kobayashi et al. Reference Kobayashi, Kohama and Takamadate1980; Jarre et al. Reference Jarre, Le Gal and Chauve1996). The effects of time-periodic modulation are then determined for modulation amplitudes ![]() $\epsilon =0.1$ and
$\epsilon =0.1$ and ![]() $0.2$, and frequencies
$0.2$, and frequencies ![]() $\varphi =6$ and
$\varphi =6$ and ![]() $10$, and solutions compared against those results obtained for the steady von Kármán flow. These particular parameters were chosen as they correspond to a near optimal stabilisation of the cross-flow and Coriolis instabilities (recall figures 4–7). Although this only illustrates the effect of modulation on disturbance characteristics in a few specific instances, comparable behaviour was observed for other modulation settings and flow conditions.
$10$, and solutions compared against those results obtained for the steady von Kármán flow. These particular parameters were chosen as they correspond to a near optimal stabilisation of the cross-flow and Coriolis instabilities (recall figures 4–7). Although this only illustrates the effect of modulation on disturbance characteristics in a few specific instances, comparable behaviour was observed for other modulation settings and flow conditions.
5.2. Stationary type I cross-flow instability
The disturbance evolution matching the conditions given above for the stationary cross-flow instability are considered first. Figure 8(a) displays the variation of the radial wavenumber ![]() $\alpha$ in the complex
$\alpha$ in the complex ![]() $(\alpha _r,\alpha _i)$-plane, while figure 8(b) depicts the temporal evolution of the radial growth rate
$(\alpha _r,\alpha _i)$-plane, while figure 8(b) depicts the temporal evolution of the radial growth rate ![]() $\alpha _i$ as a function of time
$\alpha _i$ as a function of time ![]() $\tau$. Solutions are plotted over one full period of time-periodic modulation, for the modulation amplitude
$\tau$. Solutions are plotted over one full period of time-periodic modulation, for the modulation amplitude ![]() $\epsilon =0.2$ and frequency
$\epsilon =0.2$ and frequency ![]() $\varphi =10$. The radial growth rate
$\varphi =10$. The radial growth rate ![]() $\alpha$ obtained for the steady von Kármán flow is indicated by the blue circular marker and solid blue line in the respective illustrations. Cross and square markers in figure 8(a) display the Q-S and T-A solutions of the modulated system, while the equivalent results in figure 8(b) are indicated by dashed and chain lines. The Q-S radial growth rate
$\alpha$ obtained for the steady von Kármán flow is indicated by the blue circular marker and solid blue line in the respective illustrations. Cross and square markers in figure 8(a) display the Q-S and T-A solutions of the modulated system, while the equivalent results in figure 8(b) are indicated by dashed and chain lines. The Q-S radial growth rate ![]() $\alpha _i$ fluctuates over the time interval shown. A minimum and maximum growth rate are realised about the respective
$\alpha _i$ fluctuates over the time interval shown. A minimum and maximum growth rate are realised about the respective ![]() $\tau /T=1/4$ and
$\tau /T=1/4$ and ![]() $\tau /T=3/4$ stages of the modulation cycle, which coincides with the unsteady part of the disk rotation rate (2.2) achieving a maximum and minimum, respectively (recall figure 2). The corresponding T-A radial growth rate
$\tau /T=3/4$ stages of the modulation cycle, which coincides with the unsteady part of the disk rotation rate (2.2) achieving a maximum and minimum, respectively (recall figure 2). The corresponding T-A radial growth rate ![]() $\bar {\alpha }_i$ indicates that a reduction in growth is achieved over a modulation period compared with the steady von Kármán flow. Hence, time-periodic modulation of the disk rotation rate is stabilising, which is to be expected given the earlier Floquet analysis.
$\bar {\alpha }_i$ indicates that a reduction in growth is achieved over a modulation period compared with the steady von Kármán flow. Hence, time-periodic modulation of the disk rotation rate is stabilising, which is to be expected given the earlier Floquet analysis.

Figure 8. Evolution of the radial wavenumber ![]() $\alpha$, over one modulation period
$\alpha$, over one modulation period ![]() $T$, for the stationary type I cross-flow instability with the Reynolds number
$T$, for the stationary type I cross-flow instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$. The modulation amplitude
$n=32$. The modulation amplitude ![]() $\epsilon = 0.2$ and frequency
$\epsilon = 0.2$ and frequency ![]() $\varphi = 10$. (a) The
$\varphi = 10$. (a) The ![]() $(\alpha _r,\alpha _i)$-plane, (b)
$(\alpha _r,\alpha _i)$-plane, (b) ![]() $\alpha _i$ as a function of time
$\alpha _i$ as a function of time ![]() $\tau /T$.
$\tau /T$.
The corresponding radial wavenumber ![]() $\alpha$ obtained via Floquet linear stability theory is indicated by a star in figure 8(a), and coincides with the T-A wavenumber
$\alpha$ obtained via Floquet linear stability theory is indicated by a star in figure 8(a), and coincides with the T-A wavenumber ![]() $\bar {\alpha }$ (square marker). Indeed, as shown in table 5, agreement between the Floquet and T-A wavenumbers is realised to at least two decimal places for the above parameter settings and in many other instances.
$\bar {\alpha }$ (square marker). Indeed, as shown in table 5, agreement between the Floquet and T-A wavenumbers is realised to at least two decimal places for the above parameter settings and in many other instances.
Table 5. Radial growth rates obtained using Floquet theory and via a time-averaging of the Q-S solutions, for the stationary type I cross-flow instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$.
$n=32$.

The evolution of the Reynolds stress energy production ![]() $(P_2)$ and viscous dissipation
$(P_2)$ and viscous dissipation ![]() $(D)$ are plotted in figure 9, for modulation amplitudes
$(D)$ are plotted in figure 9, for modulation amplitudes ![]() $\epsilon =0.1$ and
$\epsilon =0.1$ and ![]() $0.2$, and the modulation frequency
$0.2$, and the modulation frequency ![]() $\varphi =10$. Line types for the steady and modulated systems are the same as that given in figure 8. Quasi-steady solutions again fluctuate over the modulation cycle. The energy production
$\varphi =10$. Line types for the steady and modulated systems are the same as that given in figure 8. Quasi-steady solutions again fluctuate over the modulation cycle. The energy production ![]() $(P_2)$ displays behaviour qualitatively similar to the above description of the radial growth rate
$(P_2)$ displays behaviour qualitatively similar to the above description of the radial growth rate ![]() $\alpha _i$. A minima and maxima are observed about the quarter and three-quarter stages of the modulation cycle, which coincides with the time-periodic modulation attaining, respectively, a maximum and minimum (recall (2.2) and figure 2). The behaviour is reversed for the viscous dissipation, with maximum and minimum absolute values realised about
$\alpha _i$. A minima and maxima are observed about the quarter and three-quarter stages of the modulation cycle, which coincides with the time-periodic modulation attaining, respectively, a maximum and minimum (recall (2.2) and figure 2). The behaviour is reversed for the viscous dissipation, with maximum and minimum absolute values realised about ![]() $\tau /T=1/4$ and
$\tau /T=1/4$ and ![]() $\tau /T=3/4$, respectively. This particular feature of the energy balance is to be expected, as a reduction (increase) in the radial growth rate will establish a comparable drop (rise) and rise (drop) in the respective energy terms
$\tau /T=3/4$, respectively. This particular feature of the energy balance is to be expected, as a reduction (increase) in the radial growth rate will establish a comparable drop (rise) and rise (drop) in the respective energy terms ![]() $P_2$ and
$P_2$ and ![]() $|D|$. Furthermore, as the modulation amplitude
$|D|$. Furthermore, as the modulation amplitude ![]() $\epsilon$ increases, there is a marginal increase in the maximum value of the energy production, while there is a significant decrease in the corresponding minimum value. On the other hand, the minimum absolute value of the viscous dissipation is relatively unchanged by increasing
$\epsilon$ increases, there is a marginal increase in the maximum value of the energy production, while there is a significant decrease in the corresponding minimum value. On the other hand, the minimum absolute value of the viscous dissipation is relatively unchanged by increasing ![]() $\epsilon$, while there is a noticeable increase in the maximum absolute value. Since the energy terms
$\epsilon$, while there is a noticeable increase in the maximum absolute value. Since the energy terms ![]() $P_2$ and
$P_2$ and ![]() $D$ are, respectively, positive and negative, and are matched to an energy production and reduction, this behaviour would suggest that the stabilising effect induced by modulating the disk rotation rate will become more pronounced as the modulation amplitude
$D$ are, respectively, positive and negative, and are matched to an energy production and reduction, this behaviour would suggest that the stabilising effect induced by modulating the disk rotation rate will become more pronounced as the modulation amplitude ![]() $\epsilon$ increases. Finally, as
$\epsilon$ increases. Finally, as ![]() $\epsilon$ increases, the T-A energy production
$\epsilon$ increases, the T-A energy production ![]() $(\bar {P}_2)$ decreases and the T-A viscous dissipation
$(\bar {P}_2)$ decreases and the T-A viscous dissipation ![]() $(\bar {D})$ attains a larger absolute value. Hence, the T-A calculations provide a further illustration of the stabilising effect brought about by the time-periodic modulation.
$(\bar {D})$ attains a larger absolute value. Hence, the T-A calculations provide a further illustration of the stabilising effect brought about by the time-periodic modulation.

Figure 9. Evolution of (a,b) the Reynolds stress energy production (![]() $P_2$) and (c,d) the viscous dissipation
$P_2$) and (c,d) the viscous dissipation ![]() $(D)$ across one full period
$(D)$ across one full period ![]() $T$ of disk modulation. Modulation amplitudes
$T$ of disk modulation. Modulation amplitudes ![]() $\epsilon$ are as given in the caption for the modulation frequency
$\epsilon$ are as given in the caption for the modulation frequency ![]() $\varphi =10$, for the stationary type I cross-flow instability with the Reynolds number
$\varphi =10$, for the stationary type I cross-flow instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$.
$n=32$.
Figure 10 depicts the full energy balance of those terms given in (5.7), for the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$. Results are plotted for the steady von Kármán flow and four time-periodically modulated systems that are based on the T-A calculations. Similar to the steady von Kármán flow, the Reynolds stress energy production and viscous dissipation energy removal are the most significant in all instances modelled. All remaining terms are again negligibly small. Furthermore, figure 10 displays behaviour comparable with the trends observed by Cooper & Carpenter (Reference Cooper and Carpenter1997) on wall compliance, and Garrett et al. (Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) on surface roughness. Similar to these other flow control strategies, the stabilising effect brought about by time-periodic modulation corresponds to a reduction in
$n=32$. Results are plotted for the steady von Kármán flow and four time-periodically modulated systems that are based on the T-A calculations. Similar to the steady von Kármán flow, the Reynolds stress energy production and viscous dissipation energy removal are the most significant in all instances modelled. All remaining terms are again negligibly small. Furthermore, figure 10 displays behaviour comparable with the trends observed by Cooper & Carpenter (Reference Cooper and Carpenter1997) on wall compliance, and Garrett et al. (Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) on surface roughness. Similar to these other flow control strategies, the stabilising effect brought about by time-periodic modulation corresponds to a reduction in ![]() $\bar {P}_2$ and an increase in
$\bar {P}_2$ and an increase in ![]() $\bar {D}$. The illustration infers that the stabilising effect, induced by modulating the disk rotation rate, is enhanced for larger modulation amplitudes
$\bar {D}$. The illustration infers that the stabilising effect, induced by modulating the disk rotation rate, is enhanced for larger modulation amplitudes ![]() $\epsilon$ and frequencies
$\epsilon$ and frequencies ![]() $\varphi \sim 6$, which is consistent with the earlier Floquet analysis.
$\varphi \sim 6$, which is consistent with the earlier Floquet analysis.

Figure 10. Energy balance terms in (5.7) for the stationary type I cross-flow instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=32$. The solutions to the steady system (blue) are compared against four time-periodically modulated systems based on the T-A computations.
$n=32$. The solutions to the steady system (blue) are compared against four time-periodically modulated systems based on the T-A computations.
The T-A Reynolds stress energy production and viscous dissipation are plotted in figure 11 as a function of the azimuthal mode number ![]() $n$. Solutions correspond to the stationary type I cross-flow instability, with the Reynolds number
$n$. Solutions correspond to the stationary type I cross-flow instability, with the Reynolds number ![]() ${Re}=500$ and modulation frequency
${Re}=500$ and modulation frequency ![]() $\varphi =10$. Results are plotted for three modulation amplitudes
$\varphi =10$. Results are plotted for three modulation amplitudes ![]() $\epsilon$, over the interval
$\epsilon$, over the interval ![]() $30\leq n\leq 40$ that are the most unstable mode numbers for the given parameter settings. There is a marked reduction and growth in the respective energy terms
$30\leq n\leq 40$ that are the most unstable mode numbers for the given parameter settings. There is a marked reduction and growth in the respective energy terms ![]() $\bar {P}_2$ and
$\bar {P}_2$ and ![]() $|\bar {D}|$, for all azimuthal mode numbers
$|\bar {D}|$, for all azimuthal mode numbers ![]() $n$ considered, which further emphasises the stabilising effect brought about by modulating the disk rotation rate.
$n$ considered, which further emphasises the stabilising effect brought about by modulating the disk rotation rate.

Figure 11. Variation in the T-A (a) Reynolds stress energy production (![]() $\bar {P}_2$) and (b) the viscous dissipation
$\bar {P}_2$) and (b) the viscous dissipation ![]() $(\bar {D})$ with the azimuthal mode number
$(\bar {D})$ with the azimuthal mode number ![]() $n$. Modulation amplitudes
$n$. Modulation amplitudes ![]() $\epsilon$ are as given in the caption for the modulation frequency
$\epsilon$ are as given in the caption for the modulation frequency ![]() $\varphi =10$ and the Reynolds number
$\varphi =10$ and the Reynolds number ![]() ${Re}=500$. Solutions correspond to the stationary type I cross-flow instability (
${Re}=500$. Solutions correspond to the stationary type I cross-flow instability (![]() $\bar {P}_2$ attains a maximum about
$\bar {P}_2$ attains a maximum about ![]() $n=34.55$,
$n=34.55$, ![]() $35.13$ and
$35.13$ and ![]() $36.33$, for
$36.33$, for ![]() $\epsilon =0$,
$\epsilon =0$, ![]() $0.1$ and
$0.1$ and ![]() $0.2$, respectively).
$0.2$, respectively).
5.3. Stationary type II Coriolis instability
The above analysis was extended to the type II Coriolis instability, where the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=20$. Figure 12 depicts the corresponding full energy balance terms in (5.7), with the modulation parameter settings and colourbars the same as those given in figure 10. The T-A Reynolds stress energy production and viscous dissipation energy removal again dominate the energy (5.7), while the geometric terms
$n=20$. Figure 12 depicts the corresponding full energy balance terms in (5.7), with the modulation parameter settings and colourbars the same as those given in figure 10. The T-A Reynolds stress energy production and viscous dissipation energy removal again dominate the energy (5.7), while the geometric terms ![]() $\bar {G}_1$ and
$\bar {G}_1$ and ![]() $\bar {G}_3$ are also significant. Unlike the earlier studies on surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) that observed an increase in the energy production and a destabilisation of the Coriolis instability, time-periodic modulation establishes a small reduction in the magnitude of
$\bar {G}_3$ are also significant. Unlike the earlier studies on surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016) that observed an increase in the energy production and a destabilisation of the Coriolis instability, time-periodic modulation establishes a small reduction in the magnitude of ![]() $\bar {P}_2$ and an increase in the absolute value of
$\bar {P}_2$ and an increase in the absolute value of ![]() $\bar {D}$. This behaviour is identical to the effect of modulation on the stationary cross-flow instability, although the effect is less pronounced. Hence, modulating the disk rotation rate acts to stabilise both the stationary type I and II instabilities.
$\bar {D}$. This behaviour is identical to the effect of modulation on the stationary cross-flow instability, although the effect is less pronounced. Hence, modulating the disk rotation rate acts to stabilise both the stationary type I and II instabilities.

Figure 12. Energy balance terms in (5.7) for the stationary type II Coriolis instability with the Reynolds number ![]() ${Re}=500$ and azimuthal mode number
${Re}=500$ and azimuthal mode number ![]() $n=20$. The solutions to the steady system (blue) are compared against four time-periodically modulated systems based on the T-A computations.
$n=20$. The solutions to the steady system (blue) are compared against four time-periodically modulated systems based on the T-A computations.
6. Conclusions
The effects of time-periodic modulation on the development of linear stationary disturbances in the rotating disk boundary layer have been investigated. Modulation was achieved via the addition of a sinusoidal motion to the otherwise constant disk rotation rate, while the modulation amplitude was sufficiently small to prevent the development of unsteady instability mechanisms (Blennerhassett & Bassom Reference Blennerhassett and Bassom2002). Base flow profiles were computed numerically for an extensive range of modulation frequencies and it was determined that the azimuthal velocity field changes significantly as a consequence of the time-periodic modulation. The radial and wall-normal components were less affected. Furthermore, in the high-frequency, low-amplitude limit, the analysis indicates that the basic state can be approximated by the addition of a Stokes layer to the azimuthal component of the steady von Kármán flow.
Linear stability calculations based on Floquet theory (Morgan & Davies Reference Morgan and Davies2020) that utilise the homogeneous flow approximation, suggest that time-periodic modulation can establish a stabilising effect, and suppress the growth and onset of the stationary convective instabilities. Indeed, it was shown that the critical Reynolds number ![]() ${Re}_c$ for the onset of the type I cross-flow instability was raised to significantly larger values than that found for the steady disk without modulation. An optimal level of flow control was realised for modulation frequencies
${Re}_c$ for the onset of the type I cross-flow instability was raised to significantly larger values than that found for the steady disk without modulation. An optimal level of flow control was realised for modulation frequencies ![]() $\varphi \sim 8$, while the effect of modulation was negligible for
$\varphi \sim 8$, while the effect of modulation was negligible for ![]() $\varphi \gg 25$. Furthermore, the type II Coriolis instability was also stabilised by modulating the disk rotation rate, with the greatest stabilisation achieved for
$\varphi \gg 25$. Furthermore, the type II Coriolis instability was also stabilised by modulating the disk rotation rate, with the greatest stabilisation achieved for ![]() $\varphi \sim 10$.
$\varphi \sim 10$.
An energy analysis was undertaken to ascertain the physical mechanisms responsible for stabilising the stationary cross-flow and Coriolis instabilities. A Q-S approach was implemented and T-A flow characteristics were determined to aid comparisons with solutions of the steady von Kármán flow. Similar to the earlier studies on wall compliance (Cooper & Carpenter Reference Cooper and Carpenter1997) and surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016), it was determined that time-periodic modulation induces a reduction in the Reynolds stress energy production and an increase in the viscous dissipation. However, while wall compliance and surface roughness were only found to control the type I cross-flow instability (and destabilise the Coriolis instability), time-periodic modulation was found to stabilise both stationary forms of convective instability. Hence, modulation of the disk rotation rate may prove to be more beneficial as a control mechanism than these other flow control technologies.
The unsteady base flow established by modulating the disk rotation rate can be described exactly without the need for any modelling or averaging, as is the case for models based on surface roughness (Cooper et al. Reference Cooper, Harris, Garrett, Özkan and Thomas2015; Garrett et al. Reference Garrett, Cooper, Harris, Özkan, Segalini and Thomas2016). Though there is an analogy between the roughness and modulated configurations, the roughness models implemented by Cooper and coworkers required a spatial averaging of the basic state that only accounts for second-order effects, since any change in the average basic state must be traced to nonlinearity. The first-order effects, in which the roughness induces an oscillatory spatial variation of the base flow, are removed by the averaging. Whereas, similar to the studies on plane Poiseuille flow (Thomas et al. Reference Thomas, Bassom, Blennerhassett and Davies2011), the oscillatory variation – in time rather than space – is fully retained in our study of the modulated rotating disk boundary layer. Thus, the favourable stability results presented herein are better established than those that have previously been published for disks with rough surfaces.
Although the stabilising effect brought about by the time-periodic modulation is relatively weak (compared with other flow control strategies, i.e. mass suction (Lingwood Reference Lingwood1997)), the modulation amplitudes considered in this study are comparatively small. Given the favourable stabilising trends observed above, we might expect greater control benefits to be realised for larger modulation amplitudes.
This study has focussed on the control of stationary convective instabilities, and in particular the cross-flow vortex (Gregory et al. Reference Gregory, Stuart and Walker1955) that is considered to be fundamental in the early stages of laminar–turbulent transition on a rotating disk. The control of travelling waves and absolute instability (Lingwood Reference Lingwood1995) that may play a role in the latter stages of transition have not been considered. Furthermore, the homogeneous flow approximation was utilised here to simplify the modelling. Thus, the effect of time-periodic modulation on the radially inhomogeneous flow and the corresponding global stability characteristics are yet to be determined (Davies & Carpenter Reference Davies and Carpenter2003; Appelquist et al. Reference Appelquist, Schlatter, Alfredsson and Lingwood2015, Reference Appelquist, Schlatter, Alfredsson and Lingwood2016, Reference Appelquist, Schlatter, Alfredsson and Lingwood2018; Thomas & Davies Reference Thomas and Davies2018).
Acknowledgements
We thank the referees for their helpful comments on this paper.
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council.
Declaration of interests
The authors report no conflict of interest.