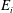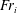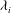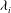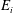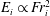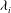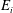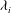1. Introduction
We theoretically examine ‘confined’ interfacial entrainment, that is, the turbulent downward transport of buoyant fluid across a gravitationally stable horizontal density interface separating two uniform fluid masses within the confines of a box. The last five decades have witnessed an extensive series of experimental investigations in which turbulent entrainment across density interfaces is examined, by necessity, within the confines of a transparent box or visual tank. The rate of interfacial entrainment has historically been parameterised solely in terms of quantities local to the interface. However, in the pursuit of a universal entrainment law (for example relating the entrainment flux to an interfacial Froude number), the effects of confinement, i.e. the role of the box, on the dynamics of interfacial entrainment have not, to our knowledge, been examined explicitly until now. By unravelling the role of confinement, we herein challenge the notion of a universal entrainment law. Indeed, we deduce that the role of the box may be sufficient to explain a spread in measured entrainment rates from quadratic to cubic power laws.

Figure 1. Schematics showing turbulent entrainment across an interface separating two uniform layers of densities
![]() ${\it\rho}_{1}$
(lower) and
${\it\rho}_{1}$
(lower) and
![]() ${\it\rho}_{2}<{\it\rho}_{1}$
(upper). A volume flux
${\it\rho}_{2}<{\it\rho}_{1}$
(upper). A volume flux
![]() $Q_{e}$
is entrained from the upper layer into the lower layer. (a) Layers confined in a box, as considered in this paper. A positively buoyant plume maintains the upper layer, a negatively buoyant impinging fountain drives interfacial entrainment, and a steady flow through a top opening into an external ambient is established. (b) The unconfined case, shown here with a neutrally buoyant impinging jet driving interfacial entrainment (cf. Shrinivas & Hunt Reference Shrinivas and Hunt2014).
$Q_{e}$
is entrained from the upper layer into the lower layer. (a) Layers confined in a box, as considered in this paper. A positively buoyant plume maintains the upper layer, a negatively buoyant impinging fountain drives interfacial entrainment, and a steady flow through a top opening into an external ambient is established. (b) The unconfined case, shown here with a neutrally buoyant impinging jet driving interfacial entrainment (cf. Shrinivas & Hunt Reference Shrinivas and Hunt2014).
From both experimental and theoretical viewpoints, it is appealing to investigate the classic transport phenomenon of interfacial entrainment (Fernando Reference Fernando1991) in a state of (quasi-) steady equilibrium. To this end, we consider the steady two-layer stratification established by a turbulent plume and a turbulent fountain in a box that connects to an external unbounded quiescent environment via an opening at the top. Figure 1(a) depicts the configuration we consider. The localised sources which give rise to the plume and the fountain are located at the base of the box and are sufficiently well separated so that the resulting plume and fountain are considered to be non-interacting. In the context of our study, the plume is essentially an artefact for enabling a buoyant upper layer of constant depth to be maintained. The impingement of the fountain with the interface, which separates the resulting upper layer from the fluid below (the lower layer), creates and sustains a localised turbulent region of eddying motions that drive entrainment of fluid across the interface. In other words, the plume establishes the two-layer stratification and the fountain provides the source of turbulence at the interface. As the flow, pre-impingement, is negatively buoyant relative to the lower layer, we refer to it as an impinging fountain. The appeal of this quasi-steady configuration is due to the steadiness eliminating the inherent complex time-dependent coupling between the entrainment flux across the interface and the evolution of a stratified intermediate layer. The main question we address is how does the confinement imposed by the physical boundaries of the box influence the rate of interfacial entrainment?
Our motivation to consider the role of confinement has been fuelled by the significant scatter in measurements of the entrainment rate. Coffey & Hunt (Reference Coffey and Hunt2010) comment that the underlying physical reason for this scatter is unknown and, as nominally identical configurations (e.g. plume/fountain impingement) and techniques have been used to induce and measure the entrainment rate, the scatter cannot be explained by experimental variabilities or systematic errors alone. Moreover, conflicting entrainment laws that stem from existing data currently shroud the understanding of the problem, thereby casting doubt on the most appropriate empirical entrainment model for application in engineering flows, the atmospheric sciences or oceanography, where interfacial entrainment is ubiquitous. Many of these applications are discussed in the review on mixing in stratified fluids by Fernando (Reference Fernando1991).
With the aim of quantifying the volume flux
![]() $Q_{e}$
entrained across a density interface, Shrinivas & Hunt (Reference Shrinivas and Hunt2014) analysed the large-time quasi-steady flow in an unconfined environment that is induced, and maintained, by the impingement of a turbulent axisymmetric jet on an interface separating two layers of uniform densities
$Q_{e}$
entrained across a density interface, Shrinivas & Hunt (Reference Shrinivas and Hunt2014) analysed the large-time quasi-steady flow in an unconfined environment that is induced, and maintained, by the impingement of a turbulent axisymmetric jet on an interface separating two layers of uniform densities
![]() ${\it\rho}_{1}$
and
${\it\rho}_{1}$
and
![]() ${\it\rho}_{2}<{\it\rho}_{1}$
(figure 1
b). Drawing on the wealth of previous observations, Shrinivas & Hunt (Reference Shrinivas and Hunt2014) modelled impingements with a small interfacial Froude number
${\it\rho}_{2}<{\it\rho}_{1}$
(figure 1
b). Drawing on the wealth of previous observations, Shrinivas & Hunt (Reference Shrinivas and Hunt2014) modelled impingements with a small interfacial Froude number
![]() $(\mathit{Fr}_{i})$
as a semi-ellipsoidal dome and characterised large-
$(\mathit{Fr}_{i})$
as a semi-ellipsoidal dome and characterised large-
![]() $\mathit{Fr}_{i}$
impingements as a fully penetrating turbulent fountain. For the high-Reynolds-number and high-Péclet-number flows of interest, the dimensionless entrainment flux
$\mathit{Fr}_{i}$
impingements as a fully penetrating turbulent fountain. For the high-Reynolds-number and high-Péclet-number flows of interest, the dimensionless entrainment flux
is governed solely by the interfacial Froude number
![]() $\mathit{Fr}_{i}=w_{i}/\sqrt{b_{i}{\rm\Delta}g^{\prime }}$
, a quantity which characterises the relative strengths of the inertial forcing associated with the energy-containing eddies that drive interfacial entrainment and the buoyancy force that acts to stabilise the interface. Here,
$\mathit{Fr}_{i}=w_{i}/\sqrt{b_{i}{\rm\Delta}g^{\prime }}$
, a quantity which characterises the relative strengths of the inertial forcing associated with the energy-containing eddies that drive interfacial entrainment and the buoyancy force that acts to stabilise the interface. Here,
![]() $b_{i}$
and
$b_{i}$
and
![]() $w_{i}$
denote the characteristic length scale and velocity scale at the interface (the radius and vertical velocity of the jet at the interface, respectively) and
$w_{i}$
denote the characteristic length scale and velocity scale at the interface (the radius and vertical velocity of the jet at the interface, respectively) and
![]() ${\rm\Delta}g^{\prime }=g({\it\rho}_{1}-{\it\rho}_{2})/{\it\rho}_{1}$
the buoyancy step in the environment across the interface. Shrinivas & Hunt (Reference Shrinivas and Hunt2014) showed that
${\rm\Delta}g^{\prime }=g({\it\rho}_{1}-{\it\rho}_{2})/{\it\rho}_{1}$
the buoyancy step in the environment across the interface. Shrinivas & Hunt (Reference Shrinivas and Hunt2014) showed that
![]() $E_{i}\propto \mathit{Fr}_{i}^{2}$
for small
$E_{i}\propto \mathit{Fr}_{i}^{2}$
for small
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() $E_{i}\propto \mathit{Fr}_{i}$
for large
$E_{i}\propto \mathit{Fr}_{i}$
for large
![]() $\mathit{Fr}_{i}$
. Figure 2 plots the solution for this unconfined entrainment model together with the experimental data from Baines (Reference Baines1975), Kumagai (Reference Kumagai1984), Baines, Corriveau & Reedman (Reference Baines, Corriveau and Reedman1993) and Lin & Linden (Reference Lin and Linden2005). These experimental studies measured interfacial entrainment driven by the localised impingement of a turbulent axisymmetric plume (Baines Reference Baines1975; Kumagai Reference Kumagai1984) or a turbulent axisymmetric fountain (Baines et al.
Reference Baines, Corriveau and Reedman1993; Lin & Linden Reference Lin and Linden2005). A comprehensive review of these and other previous studies is given in Shrinivas & Hunt (Reference Shrinivas and Hunt2014). Whilst the general trends are well captured by Shrinivas & Hunt’s (Reference Shrinivas and Hunt2014) model (figure 2), it is evident that there is a significant spread in both the individual and collective data sets, with experimental values of
$\mathit{Fr}_{i}$
. Figure 2 plots the solution for this unconfined entrainment model together with the experimental data from Baines (Reference Baines1975), Kumagai (Reference Kumagai1984), Baines, Corriveau & Reedman (Reference Baines, Corriveau and Reedman1993) and Lin & Linden (Reference Lin and Linden2005). These experimental studies measured interfacial entrainment driven by the localised impingement of a turbulent axisymmetric plume (Baines Reference Baines1975; Kumagai Reference Kumagai1984) or a turbulent axisymmetric fountain (Baines et al.
Reference Baines, Corriveau and Reedman1993; Lin & Linden Reference Lin and Linden2005). A comprehensive review of these and other previous studies is given in Shrinivas & Hunt (Reference Shrinivas and Hunt2014). Whilst the general trends are well captured by Shrinivas & Hunt’s (Reference Shrinivas and Hunt2014) model (figure 2), it is evident that there is a significant spread in both the individual and collective data sets, with experimental values of
![]() $E_{i}$
differing by an order of magnitude for a given
$E_{i}$
differing by an order of magnitude for a given
![]() $\mathit{Fr}_{i}$
. These disparities compound the inherent challenges and uncertainties experimentalists face when pursuing an entrainment law of the form
$\mathit{Fr}_{i}$
. These disparities compound the inherent challenges and uncertainties experimentalists face when pursuing an entrainment law of the form
![]() $E_{i}\propto \mathit{Fr}_{i}^{n}$
. Owing to the complexities associated with an experimental approach, there is wide variation in the reported values of the exponent
$E_{i}\propto \mathit{Fr}_{i}^{n}$
. Owing to the complexities associated with an experimental approach, there is wide variation in the reported values of the exponent
![]() $n$
, which include
$n$
, which include
![]() $n=0$
(Lin & Linden Reference Lin and Linden2005),
$n=0$
(Lin & Linden Reference Lin and Linden2005),
![]() $n=1$
(Baines et al.
Reference Baines, Corriveau and Reedman1993),
$n=1$
(Baines et al.
Reference Baines, Corriveau and Reedman1993),
![]() $n=2$
(Cardoso & Woods Reference Cardoso and Woods1993; Ching, Fernando & Noh Reference Ching, Fernando and Noh1993) and
$n=2$
(Cardoso & Woods Reference Cardoso and Woods1993; Ching, Fernando & Noh Reference Ching, Fernando and Noh1993) and
![]() $n=3$
(Baines Reference Baines1975; Coffey & Hunt Reference Coffey and Hunt2010). Although the model developed by Shrinivas & Hunt (Reference Shrinivas and Hunt2014) elucidates the dominant physics at the heart of the quadratic and linear power laws, it does not explain the cubic power law.
$n=3$
(Baines Reference Baines1975; Coffey & Hunt Reference Coffey and Hunt2010). Although the model developed by Shrinivas & Hunt (Reference Shrinivas and Hunt2014) elucidates the dominant physics at the heart of the quadratic and linear power laws, it does not explain the cubic power law.

Figure 2. Dimensionless entrainment flux
![]() $E_{i}$
against the interfacial Froude number
$E_{i}$
against the interfacial Froude number
![]() $\mathit{Fr}_{i}$
: comparison of the theoretical prediction of Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (solid line) with previous experimental measurements. The theoretical prediction approximates to
$\mathit{Fr}_{i}$
: comparison of the theoretical prediction of Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (solid line) with previous experimental measurements. The theoretical prediction approximates to
![]() $E_{i}=0.24\mathit{Fr}_{i}^{2}$
for
$E_{i}=0.24\mathit{Fr}_{i}^{2}$
for
![]() $\mathit{Fr}_{i}<1.4$
and
$\mathit{Fr}_{i}<1.4$
and
![]() $E_{i}=0.42\mathit{Fr}_{i}$
for
$E_{i}=0.42\mathit{Fr}_{i}$
for
![]() $\mathit{Fr}_{i}>3.8$
.
$\mathit{Fr}_{i}>3.8$
.
Box confinement is an intrinsic feature of all the aforementioned experiments and the disparities between the reported entrainment laws are irrefutable. This raises the question of whether interfacial entrainment and confinement are inextricably intertwined – confinement leading to secondary flows in the environment and secondary flows influencing measurements of the entrainment flux. Jirka & Harleman (Reference Jirka and Harleman1979) demonstrated that turbulent jets and plumes in a confined uniform fluid of finite depth induce a clearly defined flow pattern: a momentum jet forming circulation cells, and a buoyant plume forming a gravity current and a horizontal return flow. Ching et al. (Reference Ching, Fernando and Noh1993) studied the interaction of a turbulent line plume with the density interface of a two-layer fluid within the confines of a box whose width
![]() $W$
far exceeded its height
$W$
far exceeded its height
![]() $H$
(figure 3
a). Subsequent to its impingement with the interface, the plume formed an interfacial gravity current. Akin to the experiments of Jirka & Harleman (Reference Jirka and Harleman1979), they identified that horizontal secondary flows prevailed in the confined environment. Jirka & Harleman (Reference Jirka and Harleman1979) reported that entrainment into a jet/plume is influenced by secondary flows, and thus it is entirely conceivable that secondary flows in a confined two-layer system influence or modify interfacial entrainment.
$H$
(figure 3
a). Subsequent to its impingement with the interface, the plume formed an interfacial gravity current. Akin to the experiments of Jirka & Harleman (Reference Jirka and Harleman1979), they identified that horizontal secondary flows prevailed in the confined environment. Jirka & Harleman (Reference Jirka and Harleman1979) reported that entrainment into a jet/plume is influenced by secondary flows, and thus it is entirely conceivable that secondary flows in a confined two-layer system influence or modify interfacial entrainment.

Figure 3. (a) Schematic showing the set-up considered by Ching et al. (Reference Ching, Fernando and Noh1993), in which a turbulent line plume impinges on a density interface within the confines of a box. (b) Vertical profile of the dimensionless horizontal velocity
![]() $u/w_{i}$
in the environment measured by Ching et al. (Reference Ching, Fernando and Noh1993).
$u/w_{i}$
in the environment measured by Ching et al. (Reference Ching, Fernando and Noh1993).
Figure 3(b) shows a vertical profile of the horizontal velocity
![]() $u$
in the environment measured by Ching et al. (Reference Ching, Fernando and Noh1993). A flow in the upper layer, towards the interfacial dome, occurs by virtue of two independent mechanisms, which we now discuss in turn. First, plume impingement gives rise to a perpetual cycle of vertical excursions of the density interface (Ching et al.
Reference Ching, Fernando and Noh1993), and the surplus potential energy that becomes available, as a result of the interfacial deflections, is converted into kinetic energy that drives a bulk flow in the environment. This available potential energy is stored in the horizontal density gradients that manifest when the interface deflects. Entrainment into the dome (figure 3
a) and the requirement for volume conservation is the second mechanism by which a flow is induced in the upper layer. If we ignore the flow produced by interfacial deflections and consider just the mean velocity
$u$
in the environment measured by Ching et al. (Reference Ching, Fernando and Noh1993). A flow in the upper layer, towards the interfacial dome, occurs by virtue of two independent mechanisms, which we now discuss in turn. First, plume impingement gives rise to a perpetual cycle of vertical excursions of the density interface (Ching et al.
Reference Ching, Fernando and Noh1993), and the surplus potential energy that becomes available, as a result of the interfacial deflections, is converted into kinetic energy that drives a bulk flow in the environment. This available potential energy is stored in the horizontal density gradients that manifest when the interface deflects. Entrainment into the dome (figure 3
a) and the requirement for volume conservation is the second mechanism by which a flow is induced in the upper layer. If we ignore the flow produced by interfacial deflections and consider just the mean velocity
![]() $u_{in}$
of the flow induced by entrainment, continuity across a vertical section of the upper layer of depth
$u_{in}$
of the flow induced by entrainment, continuity across a vertical section of the upper layer of depth
![]() $D$
requires
$D$
requires
![]() $Q_{e}=u_{in}\mathit{WD}$
, that is,
$Q_{e}=u_{in}\mathit{WD}$
, that is,
![]() $u_{in}/w_{i}=E_{i}a_{i}/(\mathit{WD})$
. The area
$u_{in}/w_{i}=E_{i}a_{i}/(\mathit{WD})$
. The area
![]() $a_{i}$
of the localised impingement region is typically a small fraction of the box cross-sectional area (we note that
$a_{i}$
of the localised impingement region is typically a small fraction of the box cross-sectional area (we note that
![]() $a_{i}<0.1\mathit{WD}$
for the experiments of Ching et al. (Reference Ching, Fernando and Noh1993)) and
$a_{i}<0.1\mathit{WD}$
for the experiments of Ching et al. (Reference Ching, Fernando and Noh1993)) and
![]() $E_{i}\ll 1$
for small-
$E_{i}\ll 1$
for small-
![]() $\mathit{Fr}_{i}$
entrainment (figure 2). Thus, the flow induced by interfacial entrainment is weak, i.e.
$\mathit{Fr}_{i}$
entrainment (figure 2). Thus, the flow induced by interfacial entrainment is weak, i.e.
![]() $u_{in}/w_{i}\ll 1$
. However, figure 3 indicates that the velocity in the upper layer can be up to 30 % of
$u_{in}/w_{i}\ll 1$
. However, figure 3 indicates that the velocity in the upper layer can be up to 30 % of
![]() $w_{i}$
. We therefore expect that these relatively large velocities are primarily attributed to the flow produced by interfacial deflections. Hereinafter, we refer to the flow induced solely by the interfacial deflections as the ‘secondary flow’.
$w_{i}$
. We therefore expect that these relatively large velocities are primarily attributed to the flow produced by interfacial deflections. Hereinafter, we refer to the flow induced solely by the interfacial deflections as the ‘secondary flow’.
Herein, by considering the steady two-layer stratification established by a plume and a fountain in a box, we determine the influence of confinement on interfacial entrainment and establish what the term ‘confinement’ signifies dynamically. In § 2, we develop a model of turbulent interfacial entrainment in the presence of a secondary flow induced by vertical excursions of the interface. We reveal that, besides
![]() $\mathit{Fr}_{i}$
,
$\mathit{Fr}_{i}$
,
![]() $E_{i}$
is dependent on a second dimensionless quantity, namely a ‘confinement’ parameter
$E_{i}$
is dependent on a second dimensionless quantity, namely a ‘confinement’ parameter
![]() ${\it\lambda}_{i}$
, which characterises the length scale of interfacial turbulence relative to the vertical extent of the confinement, so that in general
${\it\lambda}_{i}$
, which characterises the length scale of interfacial turbulence relative to the vertical extent of the confinement, so that in general
![]() $E_{i}=E_{i}(\mathit{Fr}_{i},{\it\lambda}_{i})$
. Analysing the model predictions in § 3, we establish that for small
$E_{i}=E_{i}(\mathit{Fr}_{i},{\it\lambda}_{i})$
. Analysing the model predictions in § 3, we establish that for small
![]() ${\it\lambda}_{i}$
, the secondary flow is weak and has little influence on
${\it\lambda}_{i}$
, the secondary flow is weak and has little influence on
![]() $E_{i}$
. Hence we regard interfacial entrainment in this regime as weakly confined. By contrast,
$E_{i}$
. Hence we regard interfacial entrainment in this regime as weakly confined. By contrast,
![]() $E_{i}$
is significantly influenced by a strong secondary flow when
$E_{i}$
is significantly influenced by a strong secondary flow when
![]() ${\it\lambda}_{i}$
is sufficiently large, and hence we regard interfacial entrainment in this regime as strongly confined. In these limits of small
${\it\lambda}_{i}$
is sufficiently large, and hence we regard interfacial entrainment in this regime as strongly confined. In these limits of small
![]() ${\it\lambda}_{i}$
and large
${\it\lambda}_{i}$
and large
![]() ${\it\lambda}_{i}$
, the scaling of
${\it\lambda}_{i}$
, the scaling of
![]() $E_{i}$
on
$E_{i}$
on
![]() $\mathit{Fr}_{i}$
is distinct, giving
$\mathit{Fr}_{i}$
is distinct, giving
Our theory thereby offers a reason as to why some data sets support a cubic power law whilst others follow a quadratic power law. Deducing where possible the values of
![]() ${\it\lambda}_{i}$
for previous experiments, we highlight physical reasons for the scatter in the existing data (figure 2). Drawing on our predictions, in § 4 we offer guidance on an appropriate box geometry and configuration for experimentally and numerically examining interfacial entrainment.
${\it\lambda}_{i}$
for previous experiments, we highlight physical reasons for the scatter in the existing data (figure 2). Drawing on our predictions, in § 4 we offer guidance on an appropriate box geometry and configuration for experimentally and numerically examining interfacial entrainment.
2. A model for confined interfacial entrainment
Based on the experimental observations of Jirka & Harleman (Reference Jirka and Harleman1979) and Ching et al. (Reference Ching, Fernando and Noh1993), we hypothesise that secondary flows induced by the deflections of the interface within the confines of a box may influence or modify the dynamics of turbulent entrainment across a density interface. To investigate this hypothesis, we relax the condition of an unconfined environment and extend the model of Shrinivas & Hunt (Reference Shrinivas and Hunt2014) to describe interfacial entrainment within a box of height
![]() $H$
and plan area
$H$
and plan area
![]() $S$
. The box interior connects to an unbounded quiescent ambient of uniform density
$S$
. The box interior connects to an unbounded quiescent ambient of uniform density
![]() ${\it\rho}$
via an opening of area
${\it\rho}$
via an opening of area
![]() $a_{t}$
at the top (figure 4). At the base of the box
$a_{t}$
at the top (figure 4). At the base of the box
![]() $(z=0)$
, a continuous point source of constant buoyancy flux
$(z=0)$
, a continuous point source of constant buoyancy flux
![]() $B_{P}$
gives rise to a turbulent axisymmetric pure plume, and the continuous vertically forced upward injection of relatively dense fluid from a circular area source (radius
$B_{P}$
gives rise to a turbulent axisymmetric pure plume, and the continuous vertically forced upward injection of relatively dense fluid from a circular area source (radius
![]() $b_{f_{0}}$
), with constant fluxes of volume
$b_{f_{0}}$
), with constant fluxes of volume
![]() $Q_{f_{0}}$
, momentum
$Q_{f_{0}}$
, momentum
![]() $M_{f_{0}}$
and buoyancy
$M_{f_{0}}$
and buoyancy
![]() $B_{f_{0}}<0$
, produces a turbulent axisymmetric fountain. The two sources are sufficiently well separated that the resulting plume and fountain are regarded as non-interacting. As confirmed in the experiments of Lin & Linden (Reference Lin and Linden2005), these sources establish two buoyant layers, separated by a steady interface at height
$B_{f_{0}}<0$
, produces a turbulent axisymmetric fountain. The two sources are sufficiently well separated that the resulting plume and fountain are regarded as non-interacting. As confirmed in the experiments of Lin & Linden (Reference Lin and Linden2005), these sources establish two buoyant layers, separated by a steady interface at height
![]() $z=h$
, as depicted in figure 4. The boundaries of the box are purely a physical constraint and there are no buoyancy exchanges between them and the fluid. Our system is a direct analogue of the experiments of Lin & Linden (Reference Lin and Linden2005) and of numerous others (§ 1) that have examined entrainment across interfaces by using saline releases in water to create density contrasts.
$z=h$
, as depicted in figure 4. The boundaries of the box are purely a physical constraint and there are no buoyancy exchanges between them and the fluid. Our system is a direct analogue of the experiments of Lin & Linden (Reference Lin and Linden2005) and of numerous others (§ 1) that have examined entrainment across interfaces by using saline releases in water to create density contrasts.
The minimum separation distance between the sources corresponds to the distance at which the plume and fountain first interact at the top of the box
![]() $(z=H)$
. Kaye & Linden (Reference Kaye and Linden2004) showed that two plumes of similar strength coalesce at a height of approximately four times the separation of their sources. Thus, for a first approximation we may take the minimum separation distance between the sources as
$(z=H)$
. Kaye & Linden (Reference Kaye and Linden2004) showed that two plumes of similar strength coalesce at a height of approximately four times the separation of their sources. Thus, for a first approximation we may take the minimum separation distance between the sources as
![]() $H/4$
. This is consistent with Lin & Linden’s (2005) experiments.
$H/4$
. This is consistent with Lin & Linden’s (2005) experiments.
At steady state, the fluxes of volume and buoyancy supplied via the sources are exactly matched by the corresponding fluxes driven, by the buoyant layers, out through the top opening. We assume that the flow through the opening remains unidirectional. Hunt & Coffey (Reference Hunt and Coffey2010) showed that a Froude number
![]() $\mathit{Fr}_{t}$
associated with the flow through the top opening characterises the direction of flow and to achieve a unidirectional outflow requires
$\mathit{Fr}_{t}$
associated with the flow through the top opening characterises the direction of flow and to achieve a unidirectional outflow requires
![]() $\mathit{Fr}_{t}>0.33$
. This requirement restricts the range of possible dimensionless opening areas
$\mathit{Fr}_{t}>0.33$
. This requirement restricts the range of possible dimensionless opening areas
![]() $a_{t}/H^{2}$
, as discussed in Hunt & Coffey (Reference Hunt and Coffey2010).
$a_{t}/H^{2}$
, as discussed in Hunt & Coffey (Reference Hunt and Coffey2010).

Figure 4. Schematic showing the steady two-layer flow established by a turbulent fountain (left) and a turbulent pure plume (right) with sources at the base
![]() $(z=0)$
of a box of height
$(z=0)$
of a box of height
![]() $H$
. The steady density interface is at height
$H$
. The steady density interface is at height
![]() $z=h$
.
$z=h$
.
Our model is underpinned by the three key facets of interfacial entrainment noted by Turner (Reference Turner1986), namely, the dynamics of the energy source driving the entrainment, the entrainment mechanism and the influence of the energy source on the environment. We now consider each of these in turn. First, energy for interfacial entrainment is channelled to the interface via the fountain, the dynamics of which are well described by existing models (see, for example, the review by Hunt & Burridge Reference Hunt and Burridge2015). Second, the entrainment mechanism is attributed to the engulfment of fluid by baroclinic vortices around the periphery of the impingement dome. Shrinivas & Hunt (Reference Shrinivas and Hunt2014) developed a mechanistic description of this process and showed that, much as for plume entrainment, the entrainment velocity is proportional to a local vertical velocity. The third facet of the problem, namely that which pertains to the fountain–interface interaction and its influence on the two-layer stratification, has received little attention. We will see (§§ 2.2, 3) that fountain–interface interaction plays an instrumental role in the dynamics of confined interfacial entrainment.
Our system is similar to the experimental arrangement of Lin & Linden (Reference Lin and Linden2005). For a laboratory experiment our system would be inverted, with saline solution injected downwards, from a localised source, into a box of fresh water to generate a dense plume and by supplying fresh water downwards at the fountain source to produce a fountain in the steady state. For the Boussinesq flows of concern here, this reversal of direction of the buoyancy force is unimportant to the dynamics, apart from reversing the sense of motion. Following Lin & Linden (Reference Lin and Linden2005), we assume that the layers are of uniform density. Accordingly, the mean buoyancies
are assigned to the lower layer of density
![]() ${\it\rho}_{1}$
and the upper layer of density
${\it\rho}_{1}$
and the upper layer of density
![]() ${\it\rho}_{2}$
, respectively. The measurements of Lin & Linden (Reference Lin and Linden2005) showed that this is a very good assumption for the upper layer. Turbulent fluctuations associated with the downward entrainment flux across the interface give rise to weak density gradients adjacent to the interface. However, these gradients are confined in a relatively thin transitional region
${\it\rho}_{2}$
, respectively. The measurements of Lin & Linden (Reference Lin and Linden2005) showed that this is a very good assumption for the upper layer. Turbulent fluctuations associated with the downward entrainment flux across the interface give rise to weak density gradients adjacent to the interface. However, these gradients are confined in a relatively thin transitional region
![]() $({\sim}0.1H)$
, and so to a first approximation we assume two uniform layers.
$({\sim}0.1H)$
, and so to a first approximation we assume two uniform layers.
Entrainment of fluid from the upper layer into the lower layer is driven by energetic eddying motions contained within a localised region of turbulent flow above the interface (shown as a dome in figure 4) resulting from the impingement of the fountain. The morphology and dynamics of this turbulent flow above the interface are governed primarily by the interfacial Froude number
where
![]() $w_{i}$
and
$w_{i}$
and
![]() $b_{i}$
are the mean vertical velocity and mean radius of the fountain at the interface. When
$b_{i}$
are the mean vertical velocity and mean radius of the fountain at the interface. When
![]() $\mathit{Fr}_{i}$
is small
$\mathit{Fr}_{i}$
is small
![]() $(\mathit{Fr}_{i}\lesssim 1)$
, the interfacial impingement is weakly energetic (Shrinivas & Hunt Reference Shrinivas and Hunt2014), and strong buoyancy forces local to the interface arrest the penetration of dense fluid, resulting in the formation of a shallow dome-like upwelling (figure 4). This behaviour and morphology of flow is confirmed by several experimental studies (Kumagai Reference Kumagai1984; Shy Reference Shy1995; Hunt & Coffey Reference Hunt and Coffey2010). The shadowgraph images from Hunt & Coffey’s (Reference Hunt and Coffey2010) experiments clearly indicate the presence of impingement domes (figure 5). A volume flux
$(\mathit{Fr}_{i}\lesssim 1)$
, the interfacial impingement is weakly energetic (Shrinivas & Hunt Reference Shrinivas and Hunt2014), and strong buoyancy forces local to the interface arrest the penetration of dense fluid, resulting in the formation of a shallow dome-like upwelling (figure 4). This behaviour and morphology of flow is confirmed by several experimental studies (Kumagai Reference Kumagai1984; Shy Reference Shy1995; Hunt & Coffey Reference Hunt and Coffey2010). The shadowgraph images from Hunt & Coffey’s (Reference Hunt and Coffey2010) experiments clearly indicate the presence of impingement domes (figure 5). A volume flux
![]() $Q_{e}$
of buoyant fluid is entrained from the upper layer into the dome by baroclinic vortices around the periphery of the dome. The entrained fluid is transported downwards across the interface through an annular region. Our attention is centred around these small-
$Q_{e}$
of buoyant fluid is entrained from the upper layer into the dome by baroclinic vortices around the periphery of the dome. The entrained fluid is transported downwards across the interface through an annular region. Our attention is centred around these small-
![]() $\mathit{Fr}_{i}$
flows, and we shall restrict our model to
$\mathit{Fr}_{i}$
flows, and we shall restrict our model to
![]() $\mathit{Fr}_{i}<1.4$
(Shrinivas & Hunt Reference Shrinivas and Hunt2014). In § 2.1, we relate
$\mathit{Fr}_{i}<1.4$
(Shrinivas & Hunt Reference Shrinivas and Hunt2014). In § 2.1, we relate
![]() $Q_{e}$
to the interface position
$Q_{e}$
to the interface position
![]() $(z=h)$
and the layer buoyancies
$(z=h)$
and the layer buoyancies
![]() $(g_{1}^{\prime },g_{2}^{\prime })$
by considering conservation arguments for the buoyant layers. In §§ 2.2 and 2.3, we seek a solution for
$(g_{1}^{\prime },g_{2}^{\prime })$
by considering conservation arguments for the buoyant layers. In §§ 2.2 and 2.3, we seek a solution for
![]() $Q_{e}$
by analysing the local fountain–interface interaction.
$Q_{e}$
by analysing the local fountain–interface interaction.

Figure 5. Shadowgraph images from Hunt & Coffey’s (Reference Hunt and Coffey2010) experiments: (a) the local upward deflection of a density interface resulting from the impingement of a turbulent fountain; (b) the flow 15 s later when the interface has been temporarily restored back to horizontal.
2.1. Global conservation equations
For an incompressible flow, the volume flux
![]() $Q_{P_{i}}$
supplied to the upper layer by the plume at the interface is exactly balanced by the volume flux leaving this layer, i.e. via the sum of that entrained
$Q_{P_{i}}$
supplied to the upper layer by the plume at the interface is exactly balanced by the volume flux leaving this layer, i.e. via the sum of that entrained
![]() $Q_{e}$
and driven through the top opening
$Q_{e}$
and driven through the top opening
![]() $Q_{t}=Q_{f_{0}}$
. The buoyancy flux supplied to the upper layer comprises
$Q_{t}=Q_{f_{0}}$
. The buoyancy flux supplied to the upper layer comprises
![]() $B_{P}$
and the flux of buoyancy
$B_{P}$
and the flux of buoyancy
![]() $g_{1}^{\prime }Q_{P_{i}}$
entrained by the plume from the lower layer. The impinging fountain entrains a flux of buoyancy
$g_{1}^{\prime }Q_{P_{i}}$
entrained by the plume from the lower layer. The impinging fountain entrains a flux of buoyancy
![]() $g_{2}^{\prime }Q_{e}$
from the upper layer and the outflow from the box expels buoyant fluid at a rate
$g_{2}^{\prime }Q_{e}$
from the upper layer and the outflow from the box expels buoyant fluid at a rate
![]() $g_{2}^{\prime }Q_{t}$
. Thus, for the upper layer, conservation of volume and buoyancy require, respectively,
$g_{2}^{\prime }Q_{t}$
. Thus, for the upper layer, conservation of volume and buoyancy require, respectively,
Inspired by the long history of simplified models on turbulent plumes and fountains, top-hat profiles are adopted for the time-averaged horizontal variation of the vertical velocity and buoyancy of the plume and fountain. Following the classic plume theory of Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956),
where
![]() ${\it\alpha}_{P}$
is the top-hat entrainment coefficient for the plume. Following Turner (Reference Turner1986) we take
${\it\alpha}_{P}$
is the top-hat entrainment coefficient for the plume. Following Turner (Reference Turner1986) we take
![]() ${\it\alpha}_{P}=0.117$
. As the plume is merely an artefact in the problem, in (2.4) we have neglected the effects of the secondary flow on plume entrainment. Although the secondary flow may modify the entrainment coefficient
${\it\alpha}_{P}=0.117$
. As the plume is merely an artefact in the problem, in (2.4) we have neglected the effects of the secondary flow on plume entrainment. Although the secondary flow may modify the entrainment coefficient
![]() ${\it\alpha}_{P}$
, the choice of
${\it\alpha}_{P}$
, the choice of
![]() ${\it\alpha}_{P}$
does not influence the scaling of
${\it\alpha}_{P}$
does not influence the scaling of
![]() $Q_{e}$
, which is the quantity of primary interest to us.
$Q_{e}$
, which is the quantity of primary interest to us.
The source buoyancy flux of the fountain
![]() $B_{f_{0}}$
and the buoyancy flux turbulently entrained via the impingement dome from the upper layer
$B_{f_{0}}$
and the buoyancy flux turbulently entrained via the impingement dome from the upper layer
![]() $g_{2}^{\prime }Q_{e}$
are supplied to the lower layer. Due to entrainment into the plume, a flux of buoyancy
$g_{2}^{\prime }Q_{e}$
are supplied to the lower layer. Due to entrainment into the plume, a flux of buoyancy
![]() $g_{1}^{\prime }Q_{P_{i}}$
is removed from the lower layer. Thus, conservation of buoyancy for the lower layer requires
$g_{1}^{\prime }Q_{P_{i}}$
is removed from the lower layer. Thus, conservation of buoyancy for the lower layer requires
Denoting
![]() $b_{f_{0}}$
and
$b_{f_{0}}$
and
![]() $w_{f_{0}}$
as the radius and vertical velocity, respectively, of the fountain at its source,
$w_{f_{0}}$
as the radius and vertical velocity, respectively, of the fountain at its source,
The conservation equations, (2.3) and (2.5), are reduced to their simplest form by scaling the layer buoyancies on the source buoyancy
![]() $g_{f_{0}}^{\prime }=|B_{f_{0}}|/Q_{f_{0}}$
of the fountain and scaling the interface height on the box height
$g_{f_{0}}^{\prime }=|B_{f_{0}}|/Q_{f_{0}}$
of the fountain and scaling the interface height on the box height
![]() $H$
. Accordingly, we introduce the dimensionless variables
$H$
. Accordingly, we introduce the dimensionless variables
To proceed, we substitute (2.4) into (2.3a
) and rearrange for
![]() $h$
. We then substitute for
$h$
. We then substitute for
![]() $g_{1}^{\prime }$
from (2.5) into (2.3b
). Non-dimensionalising the resulting equations yields closed-form solutions for the dimensionless interface height and the dimensionless layer buoyancies:
$g_{1}^{\prime }$
from (2.5) into (2.3b
). Non-dimensionalising the resulting equations yields closed-form solutions for the dimensionless interface height and the dimensionless layer buoyancies:
The three resulting non-dimensional parameters (2.9) of our system are the buoyancy flux ratio
![]() ${\it\psi}$
, the fountain source Froude number
${\it\psi}$
, the fountain source Froude number
![]() $\mathit{Fr}_{0}$
and the dimensionless radius
$\mathit{Fr}_{0}$
and the dimensionless radius
![]() $\mathscr{L}$
of the fountain source:
$\mathscr{L}$
of the fountain source:
At this stage,
![]() $E=Q_{e}/Q_{f_{0}}$
is the single unknown dimensionless quantity. In order to determine
$E=Q_{e}/Q_{f_{0}}$
is the single unknown dimensionless quantity. In order to determine
![]() $Q_{e}$
and hence close the problem, we now model the fountain–interface interaction.
$Q_{e}$
and hence close the problem, we now model the fountain–interface interaction.
2.2. Secondary flow in the environment
The impingement of the fountain produces a ‘local’ upward deflection of the interface. To produce a local deflection, we require the radius of the impinging fountain
![]() $b_{i}\ll \sqrt{S}$
. Although the two-layer fluid remains close to hydrostatic equilibrium, the ‘tilting’ of the interface indicates that the surfaces of constant pressure and constant density are no longer parallel. The action of the resulting baroclinic torque reduces the horizontal density gradients eventuating from the interfacial deflection and restores the interface back to the horizontal. The sustained forcing of the interface by the fountain gives rise to a near-continuous cycle of vertical deflections from the horizontal. This perpetual process is confirmed by several experimental studies (Kumagai Reference Kumagai1984; Shy Reference Shy1995; Hunt & Coffey Reference Hunt and Coffey2010). Figure 5 shows shadowgraph images from Hunt & Coffey’s (Reference Hunt and Coffey2010) experiments; in figure 5(a), the interface between two saline layers of different density is deflected upwards due to the localised impingement of a fountain from below. A short time later, the interface has been temporarily restored to its stable horizontal orientation (figure 5
b).
$b_{i}\ll \sqrt{S}$
. Although the two-layer fluid remains close to hydrostatic equilibrium, the ‘tilting’ of the interface indicates that the surfaces of constant pressure and constant density are no longer parallel. The action of the resulting baroclinic torque reduces the horizontal density gradients eventuating from the interfacial deflection and restores the interface back to the horizontal. The sustained forcing of the interface by the fountain gives rise to a near-continuous cycle of vertical deflections from the horizontal. This perpetual process is confirmed by several experimental studies (Kumagai Reference Kumagai1984; Shy Reference Shy1995; Hunt & Coffey Reference Hunt and Coffey2010). Figure 5 shows shadowgraph images from Hunt & Coffey’s (Reference Hunt and Coffey2010) experiments; in figure 5(a), the interface between two saline layers of different density is deflected upwards due to the localised impingement of a fountain from below. A short time later, the interface has been temporarily restored to its stable horizontal orientation (figure 5
b).
When the interface tilts, (heavy) fluid of density
![]() ${\it\rho}_{1}$
within the lower layer is displaced upwards and (light) fluid of density
${\it\rho}_{1}$
within the lower layer is displaced upwards and (light) fluid of density
![]() ${\it\rho}_{2}$
within the upper layer is displaced downwards. Thence, as the baroclinic torque acts to restore the interface, the potential energy of the displaced fluids is released and a fraction of this energy is converted into kinetic energy that drives fluid motions. As a direct consequence of the near-continuous release of potential energy from the perpetual cycle of interfacial deflections, a quasi-steady secondary flow is established and maintained in the upper and lower layers (see appendix A for arguments on why the secondary flow is quasi-steady). Crucially, therefore, fluid with non-zero velocity is entrained into the impingement dome. Ching et al. (Reference Ching, Fernando and Noh1993) observed secondary flows in the environment with velocities in the upper layer of up to 30 % of the plume’s vertical velocity at the interface (figure 3). Accordingly, to account for the non-zero flux of momentum entrained into the dome, we consider a time-averaged picture and seek an expression for the mean velocity
${\it\rho}_{2}$
within the upper layer is displaced downwards. Thence, as the baroclinic torque acts to restore the interface, the potential energy of the displaced fluids is released and a fraction of this energy is converted into kinetic energy that drives fluid motions. As a direct consequence of the near-continuous release of potential energy from the perpetual cycle of interfacial deflections, a quasi-steady secondary flow is established and maintained in the upper and lower layers (see appendix A for arguments on why the secondary flow is quasi-steady). Crucially, therefore, fluid with non-zero velocity is entrained into the impingement dome. Ching et al. (Reference Ching, Fernando and Noh1993) observed secondary flows in the environment with velocities in the upper layer of up to 30 % of the plume’s vertical velocity at the interface (figure 3). Accordingly, to account for the non-zero flux of momentum entrained into the dome, we consider a time-averaged picture and seek an expression for the mean velocity
![]() $u_{2}$
of the secondary flow in the upper layer.
$u_{2}$
of the secondary flow in the upper layer.

Figure 6. Schematic showing the modelled maximum deflection of the interface resulting from the impingement of the fountain. The position of the undisturbed interface is
![]() $\acute{z} =0$
. Due to the deflection, fluid is displaced in shaded regions
$\acute{z} =0$
. Due to the deflection, fluid is displaced in shaded regions
![]() $\text{A}$
and
$\text{A}$
and
![]() $\text{B}$
. Solid arrows in the upper and lower layers indicate the secondary flow induced by interfacial tilting.
$\text{B}$
. Solid arrows in the upper and lower layers indicate the secondary flow induced by interfacial tilting.
In a given cycle of interfacial deflection, the interface attains a maximum vertical displacement of
![]() $\acute{z} ={\it\eta}$
from its equilibrium position at
$\acute{z} ={\it\eta}$
from its equilibrium position at
![]() $\acute{z} =0$
, as depicted in figure 6. Dense lower-layer fluid is displaced upwards above
$\acute{z} =0$
, as depicted in figure 6. Dense lower-layer fluid is displaced upwards above
![]() $\acute{z} =0$
in region A and an equal volume of light upper-layer fluid is displaced downwards below
$\acute{z} =0$
in region A and an equal volume of light upper-layer fluid is displaced downwards below
![]() $\acute{z} =0$
in region B (of horizontal extent
$\acute{z} =0$
in region B (of horizontal extent
![]() $l_{B}$
). Guided by observations (cf. figure 5), we assume that the horizontal extent,
$l_{B}$
). Guided by observations (cf. figure 5), we assume that the horizontal extent,
![]() $l_{A}$
, of the upward deflection is equal to the horizontal length scale,
$l_{A}$
, of the upward deflection is equal to the horizontal length scale,
![]() $b_{i}$
, of the forcing that produces the deflection. The deflection of the interface is thereby assumed to occur within a circular region of radius
$b_{i}$
, of the forcing that produces the deflection. The deflection of the interface is thereby assumed to occur within a circular region of radius
![]() $r_{id}=b_{i}+l_{A}+l_{B}=2b_{i}+l_{B}$
, which we refer to as the ‘zone of interfacial deflection’ (the subscript ‘
$r_{id}=b_{i}+l_{A}+l_{B}=2b_{i}+l_{B}$
, which we refer to as the ‘zone of interfacial deflection’ (the subscript ‘
![]() $id$
’ meaning ‘interfacial deflection’). Whilst the deflected interface typically exhibits a relatively smoothly varying profile (figure 5
a), the gradient of our assumed profile is discontinuous at
$id$
’ meaning ‘interfacial deflection’). Whilst the deflected interface typically exhibits a relatively smoothly varying profile (figure 5
a), the gradient of our assumed profile is discontinuous at
![]() $r=r_{id}$
. Nevertheless, we will see that our model provides a simple yet effective starting point for quantifying the velocity
$r=r_{id}$
. Nevertheless, we will see that our model provides a simple yet effective starting point for quantifying the velocity
![]() $u_{2}$
resulting from the deflections. For the impingement of an axisymmetric fountain, the deflected regions are characterised by an annular prism whose outer radius and inner radius are
$u_{2}$
resulting from the deflections. For the impingement of an axisymmetric fountain, the deflected regions are characterised by an annular prism whose outer radius and inner radius are
![]() $\{2b_{i},b_{i}\}$
for region A and
$\{2b_{i},b_{i}\}$
for region A and
![]() $\{2b_{i}+l_{B},2b_{i}\}$
for region B. Accordingly, in the displaced state
$\{2b_{i}+l_{B},2b_{i}\}$
for region B. Accordingly, in the displaced state
Rearranging (2.10) gives a quadratic in
![]() $l_{B}/b_{i}$
, which has a single positive root:
$l_{B}/b_{i}$
, which has a single positive root:
When the interface attains its maximum displacement (
![]() $\acute{z} ={\it\eta}$
), fluid in regions A and B momentarily comes to rest. Subsequently, as the interface is restored, the displaced fluids are set in motion. Thus, at the instant when maximum tilting occurs there is no flux of momentum into, or out of, region A. Hence, conservation of vertical momentum for this fluid volume requires
$\acute{z} ={\it\eta}$
), fluid in regions A and B momentarily comes to rest. Subsequently, as the interface is restored, the displaced fluids are set in motion. Thus, at the instant when maximum tilting occurs there is no flux of momentum into, or out of, region A. Hence, conservation of vertical momentum for this fluid volume requires
i.e. the interface is brought momentarily to rest when the upward excitation force (left-hand side) causing the interfacial deflection is balanced by the downward restoring buoyancy force (right-hand side) acting on the displaced fluid of volume
![]() $3{\rm\pi}b_{i}^{2}{\it\eta}/2$
(2.10). Here,
$3{\rm\pi}b_{i}^{2}{\it\eta}/2$
(2.10). Here,
![]() ${\it\rho}_{i}$
denotes the density of the fountain at the level of the undisturbed interface. Under the Boussinesq approximation, the maximum vertical displacement of the interface is, from (2.12),
${\it\rho}_{i}$
denotes the density of the fountain at the level of the undisturbed interface. Under the Boussinesq approximation, the maximum vertical displacement of the interface is, from (2.12),
As we shall see in § 2.3, the penetration depth of the impingement dome is
![]() $z_{d}/b_{i}=0.94\mathit{Fr}_{i}^{2}$
. Evidently, the scalings of
$z_{d}/b_{i}=0.94\mathit{Fr}_{i}^{2}$
. Evidently, the scalings of
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $z_{d}$
on
$z_{d}$
on
![]() $\mathit{Fr}_{i}$
are identical, which is not surprising given that both the origin of the interfacial deflection and the shallow-penetration dome is the vertical forcing by the fountain. We note that
$\mathit{Fr}_{i}$
are identical, which is not surprising given that both the origin of the interfacial deflection and the shallow-penetration dome is the vertical forcing by the fountain. We note that
![]() ${\it\eta}/z_{d}<1$
, a result one would expect on physical grounds. Moreover, our prediction that
${\it\eta}/z_{d}<1$
, a result one would expect on physical grounds. Moreover, our prediction that
![]() ${\it\eta}/z_{d}\approx 0.7$
is consistent with observations (cf. figure 5
a).
${\it\eta}/z_{d}\approx 0.7$
is consistent with observations (cf. figure 5
a).
Upon calculating the potential energy of the two-layer fluid in the displaced state
![]() $\text{PE}_{dis}$
and the potential energy of the equilibrium state
$\text{PE}_{dis}$
and the potential energy of the equilibrium state
![]() $\text{PE}_{eq}$
(see appendix B), we find that the surplus potential energy available for conversion into kinetic energy is
$\text{PE}_{eq}$
(see appendix B), we find that the surplus potential energy available for conversion into kinetic energy is
As the action of the baroclinic torque temporarily restores the tilted interface from the point of maximum deflection
![]() $(\acute{z} ={\it\eta})$
to the equilibrium position
$(\acute{z} ={\it\eta})$
to the equilibrium position
![]() $(\acute{z} =0)$
, the available potential energy (2.14) is converted into kinetic energy for driving fluid motion in the upper and lower layers primarily over the radial extent
$(\acute{z} =0)$
, the available potential energy (2.14) is converted into kinetic energy for driving fluid motion in the upper and lower layers primarily over the radial extent
![]() $r_{id}$
. A flow towards the impingement dome is established within the upper layer, whereby light fluid of density
$r_{id}$
. A flow towards the impingement dome is established within the upper layer, whereby light fluid of density
![]() ${\it\rho}_{2}$
replaces heavy fluid of density
${\it\rho}_{2}$
replaces heavy fluid of density
![]() ${\it\rho}_{1}$
in region A (figure 6). We note that the hydrostatic pressure variations established by the tilting, and indeed the entrainment into the dome, induce a flow towards the dome. Similarly, a flow towards the side walls of the box is established within the lower layer, whereby fluid of density
${\it\rho}_{1}$
in region A (figure 6). We note that the hydrostatic pressure variations established by the tilting, and indeed the entrainment into the dome, induce a flow towards the dome. Similarly, a flow towards the side walls of the box is established within the lower layer, whereby fluid of density
![]() ${\it\rho}_{1}$
replaces fluid of density
${\it\rho}_{1}$
replaces fluid of density
![]() ${\it\rho}_{2}$
in region B. In our time-averaged conceptualisation, the mean kinetic energy of the secondary flow prevailing in the upper layer is
${\it\rho}_{2}$
in region B. In our time-averaged conceptualisation, the mean kinetic energy of the secondary flow prevailing in the upper layer is
Given that we seek a local velocity for the bulk-flow-induced adjacent to the dome, in (2.15) we have calculated the kinetic energy of the flow within the region of interfacial deflection (i.e. for
![]() $r\leqslant r_{id}$
). Continuous vertical oscillations of the interface typically contribute to the generation of interfacial gravity waves that extract a fraction of the potential energy released from the interfacial deflections. Some of the available potential energy may also be dissipated due to viscous effects. Thus, a fraction
$r\leqslant r_{id}$
). Continuous vertical oscillations of the interface typically contribute to the generation of interfacial gravity waves that extract a fraction of the potential energy released from the interfacial deflections. Some of the available potential energy may also be dissipated due to viscous effects. Thus, a fraction
![]() $c$
of the available potential energy remains after dissipation. For simplicity, and indeed in the absence of data to support or justify a more complex energy balance, we apportion the available potential energy (after dissipation) equally between the kinetic energies of the flows in the upper and lower layers, i.e.
$c$
of the available potential energy remains after dissipation. For simplicity, and indeed in the absence of data to support or justify a more complex energy balance, we apportion the available potential energy (after dissipation) equally between the kinetic energies of the flows in the upper and lower layers, i.e.
![]() $\text{KE}_{2}=c(\text{APE}/2)$
. Seeking an upper-bound solution for
$\text{KE}_{2}=c(\text{APE}/2)$
. Seeking an upper-bound solution for
![]() $u_{2}$
, we neglect local energy losses so that
$u_{2}$
, we neglect local energy losses so that
![]() $c=1$
. Under the Boussinesq approximation, the dimensionless mean velocity
$c=1$
. Under the Boussinesq approximation, the dimensionless mean velocity
![]() $\tilde{u} _{2}$
of the secondary flow in the upper layer is then
$\tilde{u} _{2}$
of the secondary flow in the upper layer is then
where the ‘confinement’ parameter
Evidently,
![]() ${\it\lambda}_{i}$
characterises the length scale of interfacial turbulence relative to the vertical extent
${\it\lambda}_{i}$
characterises the length scale of interfacial turbulence relative to the vertical extent
![]() $(H-h)$
of the confinement. Accordingly, hereafter ‘confinement’ refers to ‘vertical confinement’. For a given
$(H-h)$
of the confinement. Accordingly, hereafter ‘confinement’ refers to ‘vertical confinement’. For a given
![]() $b_{i}$
and
$b_{i}$
and
![]() $\mathit{Fr}_{i}$
, a relatively weak secondary flow (
$\mathit{Fr}_{i}$
, a relatively weak secondary flow (
![]() $\tilde{u} _{2}\ll 1$
) is established in the upper layer when the impingement occurs at low elevations (
$\tilde{u} _{2}\ll 1$
) is established in the upper layer when the impingement occurs at low elevations (
![]() $h\ll H$
) in a tall box such that
$h\ll H$
) in a tall box such that
![]() ${\it\lambda}_{i}$
is relatively small. In this limit, we expect our prediction of
${\it\lambda}_{i}$
is relatively small. In this limit, we expect our prediction of
![]() $u_{2}$
to be less reliable as the local interfacial deflections are unlikely to induce fluid motions over the depth of a relatively deep upper layer. However, we note that in the absence of confinement
$u_{2}$
to be less reliable as the local interfacial deflections are unlikely to induce fluid motions over the depth of a relatively deep upper layer. However, we note that in the absence of confinement
![]() ${\it\lambda}_{i}\rightarrow 0$
and
${\it\lambda}_{i}\rightarrow 0$
and
![]() $\tilde{u} _{2}\rightarrow 0$
(2.16), which is entirely consistent with the unconfined case where interfacial entrainment occurs in the absence of a secondary flow (Shrinivas & Hunt Reference Shrinivas and Hunt2014).
$\tilde{u} _{2}\rightarrow 0$
(2.16), which is entirely consistent with the unconfined case where interfacial entrainment occurs in the absence of a secondary flow (Shrinivas & Hunt Reference Shrinivas and Hunt2014).
In contrast, the secondary flow is relatively strong when the impingement occurs at high elevations in a short box such that
![]() ${\it\lambda}_{i}$
is relatively large. In this limit, we expect our model to capture well the dynamics of the secondary flow as the interfacial deflections are likely to excite fluid motions over the full depth of a relatively shallow upper layer, as indicated in figure 3(b). Indeed, it is this limit that is of primary interest to us. Moreover, we will see that for previous experimental studies
${\it\lambda}_{i}$
is relatively large. In this limit, we expect our model to capture well the dynamics of the secondary flow as the interfacial deflections are likely to excite fluid motions over the full depth of a relatively shallow upper layer, as indicated in figure 3(b). Indeed, it is this limit that is of primary interest to us. Moreover, we will see that for previous experimental studies
![]() ${\it\lambda}_{i}$
varies in the range
${\it\lambda}_{i}$
varies in the range
![]() $0.1<{\it\lambda}_{i}<1$
, with the majority of the values of
$0.1<{\it\lambda}_{i}<1$
, with the majority of the values of
![]() ${\it\lambda}_{i}$
exceeding
${\it\lambda}_{i}$
exceeding
![]() ${\it\lambda}_{i}=0.3$
, i.e.
${\it\lambda}_{i}=0.3$
, i.e.
![]() ${\it\lambda}_{i}$
was relatively large for previous experiments. Given that we focus on
${\it\lambda}_{i}$
was relatively large for previous experiments. Given that we focus on
![]() $\mathit{Fr}_{i}\lesssim 1$
,
$\mathit{Fr}_{i}\lesssim 1$
,
![]() $\tilde{u} _{2}\sim O(1)$
(2.16). Thus, the velocity
$\tilde{u} _{2}\sim O(1)$
(2.16). Thus, the velocity
![]() $\tilde{u} _{2}$
of the secondary flow cannot be reasonably ignored. In § 3.1, we establish the range of
$\tilde{u} _{2}$
of the secondary flow cannot be reasonably ignored. In § 3.1, we establish the range of
![]() ${\it\lambda}_{i}$
that may be regarded as ‘small’ and ‘large’.
${\it\lambda}_{i}$
that may be regarded as ‘small’ and ‘large’.
2.3. Impingement dome
Having determined
![]() $u_{2}$
, our attention turns to the volume flux
$u_{2}$
, our attention turns to the volume flux
![]() $Q_{e}$
of buoyant fluid, with velocity
$Q_{e}$
of buoyant fluid, with velocity
![]() $u_{2}$
, turbulently entrained from the upper layer into the axisymmetric semi-ellipsoidal impingement dome atop the incident fountain (figure 7). To model the entrainment into the dome, we employ the theoretical framework developed in Shrinivas & Hunt (Reference Shrinivas and Hunt2014). The entrained fluid is transported across the interface through an annulus of width
$u_{2}$
, turbulently entrained from the upper layer into the axisymmetric semi-ellipsoidal impingement dome atop the incident fountain (figure 7). To model the entrainment into the dome, we employ the theoretical framework developed in Shrinivas & Hunt (Reference Shrinivas and Hunt2014). The entrained fluid is transported across the interface through an annulus of width
![]() $(b_{d}-b_{i})$
. Adopting top-hat profiles for the variation of the vertical downward velocity
$(b_{d}-b_{i})$
. Adopting top-hat profiles for the variation of the vertical downward velocity
![]() $\grave{w} _{d}<0$
and density
$\grave{w} _{d}<0$
and density
![]() ${\it\rho}_{d}$
across this annular region, conservation of volume for the impingement dome requires
${\it\rho}_{d}$
across this annular region, conservation of volume for the impingement dome requires
where
![]() $w_{d}=|\grave{w} _{d}|$
. The dome receives a flux of momentum
$w_{d}=|\grave{w} _{d}|$
. The dome receives a flux of momentum
![]() ${\rm\pi}{\it\rho}_{i}b_{i}^{2}w_{i}^{2}$
from the fountain and a flux of momentum
${\rm\pi}{\it\rho}_{i}b_{i}^{2}w_{i}^{2}$
from the fountain and a flux of momentum
![]() ${\rm\pi}{\it\rho}_{d}(b_{d}^{2}-b_{i}^{2})w_{d}^{2}$
is transported out of the dome through the annulus. Guided by the measurements of Ching et al. (Reference Ching, Fernando and Noh1993) (figure 3), we assume that the secondary flow in the vicinity of the dome boundary is horizontal. Accordingly, the flux of vertical momentum entrained into the dome is zero. Therefore, conservation of vertical momentum for the dome requires
${\rm\pi}{\it\rho}_{d}(b_{d}^{2}-b_{i}^{2})w_{d}^{2}$
is transported out of the dome through the annulus. Guided by the measurements of Ching et al. (Reference Ching, Fernando and Noh1993) (figure 3), we assume that the secondary flow in the vicinity of the dome boundary is horizontal. Accordingly, the flux of vertical momentum entrained into the dome is zero. Therefore, conservation of vertical momentum for the dome requires
where
![]() $g_{i}^{\prime }$
is the mean buoyancy experienced by dense fluid within the dome of volume
$g_{i}^{\prime }$
is the mean buoyancy experienced by dense fluid within the dome of volume
![]() $2{\rm\pi}b_{d}^{2}z_{d}/3$
. Substituting for
$2{\rm\pi}b_{d}^{2}z_{d}/3$
. Substituting for
![]() $w_{d}$
from (2.18) into (2.19) gives
$w_{d}$
from (2.18) into (2.19) gives
for Boussinesq flows, where
are the dimensionless penetration depth, the aspect ratio of the dome and the dimensionless buoyancy of the fountain at the interface, respectively. We will see (§§ 3.2, 3.3) that solutions of (2.8) are realised for fountains with source Froude numbers
![]() $\mathit{Fr}_{0}\gg 1$
and source buoyancy flux ratios
$\mathit{Fr}_{0}\gg 1$
and source buoyancy flux ratios
![]() ${\it\psi}\gg 1$
, i.e. the impinging fountain is highly forced at its source. For these source conditions, the fountain behaviour is jet-like over a significant fraction of the rise height, and hence its density
${\it\psi}\gg 1$
, i.e. the impinging fountain is highly forced at its source. For these source conditions, the fountain behaviour is jet-like over a significant fraction of the rise height, and hence its density
![]() ${\it\rho}_{i}$
at the interface is comparable with
${\it\rho}_{i}$
at the interface is comparable with
![]() ${\it\rho}_{1}$
for Boussinesq flows. Accordingly, we invoke the approximation that
${\it\rho}_{1}$
for Boussinesq flows. Accordingly, we invoke the approximation that
![]() ${\check{g}}_{i}^{\prime }\approx 1$
, which considerably simplifies the analysis whilst having little effect on the solution. By considering conservation of buoyancy for the dome, we find that our approximation
${\check{g}}_{i}^{\prime }\approx 1$
, which considerably simplifies the analysis whilst having little effect on the solution. By considering conservation of buoyancy for the dome, we find that our approximation
![]() ${\check{g}}_{i}=1$
leads to a marginal overprediction (by no more than 4 %) of
${\check{g}}_{i}=1$
leads to a marginal overprediction (by no more than 4 %) of
![]() $Q_{e}$
(see appendix C).
$Q_{e}$
(see appendix C).

Figure 7. Schematic showing (a) the small-
![]() $\mathit{Fr}_{i}$
axisymmetric semi-ellipsoidal impingement dome atop the impinging fountain and (b) the modelled vortex layer (shaded area) of the dome. In (b), the dashed box is the control volume considered for the inflow into the dome due to turbulent entrainment.
$\mathit{Fr}_{i}$
axisymmetric semi-ellipsoidal impingement dome atop the impinging fountain and (b) the modelled vortex layer (shaded area) of the dome. In (b), the dashed box is the control volume considered for the inflow into the dome due to turbulent entrainment.
To close the problem, it is necessary to describe the mechanism by which external fluid is entrained into the dome. The representation of turbulence, necessary to close the problem mathematically, forms the cornerstone of the mechanistic entrainment model developed by Shrinivas & Hunt (Reference Shrinivas and Hunt2014). Shy (Reference Shy1995) and Cotel et al. (Reference Cotel, Gjestvang, Ramkhelawan and Breidenthal1997) identified that the interaction between the incident vorticity within the impinging flow and the baroclinic vorticity generated at the interface, due to its tilting, results in the formation of strong persistent vortices within a relatively thin layer around the perimeter of the dome. These rotational motions are predominantly responsible for the entrainment into the dome. By modelling this peripheral region of strong vorticity as a finite-thickness vortex layer (the shaded region of the schematic of figure 7
b), Shrinivas & Hunt (Reference Shrinivas and Hunt2014) related the generation of baroclinic vorticity to the resulting mean entrainment velocity
![]() $u_{e}$
and showed that
$u_{e}$
and showed that
i.e. the entrainment velocity is proportional to a local buoyancy velocity. Here,
![]() ${\it\alpha}_{d}$
is an entrainment coefficient, an appropriate value for which is
${\it\alpha}_{d}$
is an entrainment coefficient, an appropriate value for which is
![]() ${\it\alpha}_{d}=0.1$
(Turner Reference Turner1986).
${\it\alpha}_{d}=0.1$
(Turner Reference Turner1986).
To account for the horizontal momentum
![]() $(\propto u_{2})$
of the fluid entrained from the upper layer, we consider a control volume of height
$(\propto u_{2})$
of the fluid entrained from the upper layer, we consider a control volume of height
![]() $\text{d}\acute{z}$
around the dome perimeter (figure 7
b). Owing to the secondary flow, a volume flux
$\text{d}\acute{z}$
around the dome perimeter (figure 7
b). Owing to the secondary flow, a volume flux
![]() $q_{2}$
per unit height with fluid of velocity
$q_{2}$
per unit height with fluid of velocity
![]() $u_{2}$
enters the control volume. A volume flux
$u_{2}$
enters the control volume. A volume flux
![]() $q^{\ast }$
per unit height leaves the control volume and enters the dome at velocity
$q^{\ast }$
per unit height leaves the control volume and enters the dome at velocity
![]() $u^{\ast }$
. Thus, conservation of horizontal momentum for the flow near the dome boundary requires
$u^{\ast }$
. Thus, conservation of horizontal momentum for the flow near the dome boundary requires
where
![]() $F_{e}$
denotes the inertial force of the peripheral energy-containing vortices that drive entrainment into the dome and
$F_{e}$
denotes the inertial force of the peripheral energy-containing vortices that drive entrainment into the dome and
![]() ${\it\rho}^{\ast }$
denotes the density of the fluid entering the vortex layer. Over a vertical extent
${\it\rho}^{\ast }$
denotes the density of the fluid entering the vortex layer. Over a vertical extent
![]() $\text{d}\acute{z}$
of the vortex layer, a volume
$\text{d}\acute{z}$
of the vortex layer, a volume
![]() $\text{d}V_{e}$
of external fluid is engulfed at velocity
$\text{d}V_{e}$
of external fluid is engulfed at velocity
![]() $u_{e}$
in a time
$u_{e}$
in a time
![]() $\text{d}t$
. Therefore, the inertial force associated with the energy-containing vortices that gives rise to and maintains the steady inflow into the dome is
$\text{d}t$
. Therefore, the inertial force associated with the energy-containing vortices that gives rise to and maintains the steady inflow into the dome is
Under the Boussinesq approximation, substituting for
![]() $F_{e}$
(2.24) into (2.23) and given that conservation of volume for the steady flow requires
$F_{e}$
(2.24) into (2.23) and given that conservation of volume for the steady flow requires
![]() $q_{2}\,\text{d}\acute{z} =q_{e}\,\text{d}\acute{z} =\text{d}V_{e}/\text{d}t$
, we obtain
$q_{2}\,\text{d}\acute{z} =q_{e}\,\text{d}\acute{z} =\text{d}V_{e}/\text{d}t$
, we obtain
i.e. the mean horizontal inflow velocity
![]() $u^{\ast }$
across the boundary between the turbulent flow and the external environment is given by the sum of the entrainment velocity of the peripheral vortices and the velocity of the secondary flow in the upper layer. To further support this entrainment formulation, we may draw a direct analogy between plumes rising in a weak crossflow and our dome in the midst of a predominantly horizontal secondary flow. The net entrainment into a plume rising in a crossflow is the sum of two parts, namely, the entrainment driven by the vertical shear and the entrainment of the crossflow (Hoult & Weil Reference Hoult and Weil1972; Lee & Chu Reference Lee and Chu1979; Devenish et al.
Reference Devenish, Rooney, Webster and Thomson2010). Similarly, the net entrainment into the dome in the presence of a secondary flow comprises two components, namely, the entrainment driven by baroclinic vortices and the entrainment of the secondary flow. Thus, (2.25) is consistent with well-established entrainment models for plumes in a crossflow.
$u^{\ast }$
across the boundary between the turbulent flow and the external environment is given by the sum of the entrainment velocity of the peripheral vortices and the velocity of the secondary flow in the upper layer. To further support this entrainment formulation, we may draw a direct analogy between plumes rising in a weak crossflow and our dome in the midst of a predominantly horizontal secondary flow. The net entrainment into a plume rising in a crossflow is the sum of two parts, namely, the entrainment driven by the vertical shear and the entrainment of the crossflow (Hoult & Weil Reference Hoult and Weil1972; Lee & Chu Reference Lee and Chu1979; Devenish et al.
Reference Devenish, Rooney, Webster and Thomson2010). Similarly, the net entrainment into the dome in the presence of a secondary flow comprises two components, namely, the entrainment driven by baroclinic vortices and the entrainment of the secondary flow. Thus, (2.25) is consistent with well-established entrainment models for plumes in a crossflow.
The total volume flux entrained into the dome over the height
![]() $0\leqslant \acute{z} \leqslant z_{d}$
is
$0\leqslant \acute{z} \leqslant z_{d}$
is
where
![]() $b_{p}$
is the radius of the dome at height
$b_{p}$
is the radius of the dome at height
![]() $\acute{z}$
. The dome perimeter is the semi-ellipse:
$\acute{z}$
. The dome perimeter is the semi-ellipse:
Substituting for
![]() $u_{2}$
(2.16),
$u_{2}$
(2.16),
![]() $u_{e}$
(2.22) and
$u_{e}$
(2.22) and
![]() $b_{p}$
(2.27) into (2.26) gives
$b_{p}$
(2.27) into (2.26) gives
To complete our solution we require the penetration depth
![]() $z_{d}$
of the dome. For the unconfined case, wherein interfacial entrainment occurs in the absence of a secondary flow (i.e.
$z_{d}$
of the dome. For the unconfined case, wherein interfacial entrainment occurs in the absence of a secondary flow (i.e.
![]() $\tilde{u} _{2}\rightarrow 0$
as
$\tilde{u} _{2}\rightarrow 0$
as
![]() ${\it\lambda}_{i}\rightarrow 0$
), Shrinivas & Hunt (Reference Shrinivas and Hunt2014) considered conservation of energy for the dome and showed that
${\it\lambda}_{i}\rightarrow 0$
), Shrinivas & Hunt (Reference Shrinivas and Hunt2014) considered conservation of energy for the dome and showed that
For the confined problem of interest here, entrainment of fluid into the dome results in an inflow of kinetic energy
![]() $\propto u_{2}^{2}$
and potential energy
$\propto u_{2}^{2}$
and potential energy
![]() $\propto {\rm\Delta}g^{\prime }z_{d}$
. Whilst both can be accounted for in the energy budget, an elegant approximation becomes evident on examining the relative magnitudes of the kinetic and potential energies entrained. Given that
$\propto {\rm\Delta}g^{\prime }z_{d}$
. Whilst both can be accounted for in the energy budget, an elegant approximation becomes evident on examining the relative magnitudes of the kinetic and potential energies entrained. Given that
![]() $z_{d}/b_{i}\propto \mathit{Fr}_{i}^{2}$
, the ratio of the entrained energies is
$z_{d}/b_{i}\propto \mathit{Fr}_{i}^{2}$
, the ratio of the entrained energies is
![]() $u_{2}^{2}/({\rm\Delta}g^{\prime }z_{d})\propto u_{2}^{2}/w_{i}^{2}$
. Noting that
$u_{2}^{2}/({\rm\Delta}g^{\prime }z_{d})\propto u_{2}^{2}/w_{i}^{2}$
. Noting that
![]() $u_{2}^{2}/w_{i}^{2}\ll 1$
(2.16) for the range of
$u_{2}^{2}/w_{i}^{2}\ll 1$
(2.16) for the range of
![]() $\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
considered, the kinetic energy entrained into the dome is relatively small and thus may reasonably be neglected. Hence, the secondary flow has a relatively minor influence on the energy budget for the dome. Thus, to a good approximation, the penetration depth of the confined dome is given by (2.29).
$\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
considered, the kinetic energy entrained into the dome is relatively small and thus may reasonably be neglected. Hence, the secondary flow has a relatively minor influence on the energy budget for the dome. Thus, to a good approximation, the penetration depth of the confined dome is given by (2.29).
With the problem fully closed, we substitute for
![]() $u_{2}$
(2.16) and
$u_{2}$
(2.16) and
![]() $z_{d}$
(2.29) into (2.28). The resulting expression is rearranged for the aspect ratio
$z_{d}$
(2.29) into (2.28). The resulting expression is rearranged for the aspect ratio
![]() $k$
and substituted into (2.20). This yields a cubic in
$k$
and substituted into (2.20). This yields a cubic in
![]() $E_{i}$
as a function of the interfacial Froude number and the confinement parameter:
$E_{i}$
as a function of the interfacial Froude number and the confinement parameter:
where
This cubic has a single positive root, namely
For
![]() $\mathit{Fr}_{i}<1$
and
$\mathit{Fr}_{i}<1$
and
![]() ${\it\lambda}_{i}<1$
, a two-step procedure (see appendix D) reduces (2.32) to the simple analytic solution
${\it\lambda}_{i}<1$
, a two-step procedure (see appendix D) reduces (2.32) to the simple analytic solution
which closely approximates the full solution. In (2.33),
The first term of (2.33) is the contribution to the total volume flux into the dome due to entrainment driven by peripheral vortices and the second term is the volume flux into the dome due to entrainment of the secondary flow.
When interfacial entrainment occurs in an unconfined environment,
![]() ${\it\lambda}_{i}\rightarrow 0$
and
${\it\lambda}_{i}\rightarrow 0$
and
![]() $\tilde{u} _{2}\rightarrow 0$
(2.16). In this limit
$\tilde{u} _{2}\rightarrow 0$
(2.16). In this limit
![]() $E_{i}=E_{i}(\mathit{Fr}_{i})$
and we recover our solution
$E_{i}=E_{i}(\mathit{Fr}_{i})$
and we recover our solution
![]() $E_{i}=A\mathit{Fr}_{i}^{2}$
for unconfined entrainment (Shrinivas & Hunt Reference Shrinivas and Hunt2014). When interfacial entrainment occurs within the confines of a box so that
$E_{i}=A\mathit{Fr}_{i}^{2}$
for unconfined entrainment (Shrinivas & Hunt Reference Shrinivas and Hunt2014). When interfacial entrainment occurs within the confines of a box so that
![]() ${\it\lambda}_{i}>0$
, a secondary flow persists (
${\it\lambda}_{i}>0$
, a secondary flow persists (
![]() $\tilde{u} _{2}>0$
) and
$\tilde{u} _{2}>0$
) and
![]() $E_{i}=E_{i}(\mathit{Fr}_{i},{\it\lambda}_{i})$
. Thus, the second term of (2.33) solely accounts for the role of confinement. To quantify the influence of confinement on
$E_{i}=E_{i}(\mathit{Fr}_{i},{\it\lambda}_{i})$
. Thus, the second term of (2.33) solely accounts for the role of confinement. To quantify the influence of confinement on
![]() $E_{i}$
, we consider the total entrainment flux
$E_{i}$
, we consider the total entrainment flux
![]() $E_{i}$
relative to the entrainment flux in the absence of confinement (i.e. the unconfined component in (2.33)). Accordingly, we introduce the ratio
$E_{i}$
relative to the entrainment flux in the absence of confinement (i.e. the unconfined component in (2.33)). Accordingly, we introduce the ratio
is the rate of entrainment of the secondary flow (the subscript ‘
![]() $c$
’ meaning ‘confined’). When
$c$
’ meaning ‘confined’). When
![]() ${\it\phi}\sim 1$
, the contribution of
${\it\phi}\sim 1$
, the contribution of
![]() $E_{i,c}$
to
$E_{i,c}$
to
![]() $E_{i}$
is small and box confinement does not significantly influence the rate of interfacial entrainment. When
$E_{i}$
is small and box confinement does not significantly influence the rate of interfacial entrainment. When
![]() ${\it\phi}\gg 1$
,
${\it\phi}\gg 1$
,
![]() $E_{i,c}$
provides a significant contribution to
$E_{i,c}$
provides a significant contribution to
![]() $E_{i}$
, and hence confinement plays an instrumental role in increasing the total entrainment flux
$E_{i}$
, and hence confinement plays an instrumental role in increasing the total entrainment flux
![]() $E_{i}$
.
$E_{i}$
.
2.4. Impinging fountain
To predict
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
, it is necessary to model the fountain. Assuming that the downflow of the fountain is fully incorporated into the lower layer, conservation of volume flux
${\it\lambda}_{i}$
, it is necessary to model the fountain. Assuming that the downflow of the fountain is fully incorporated into the lower layer, conservation of volume flux
![]() $({\rm\pi}b_{f}^{2}w_{f})$
, momentum flux
$({\rm\pi}b_{f}^{2}w_{f})$
, momentum flux
![]() $({\rm\pi}b_{f}^{2}w_{f}^{2})$
and buoyancy flux
$({\rm\pi}b_{f}^{2}w_{f}^{2})$
and buoyancy flux
![]() $(-{\rm\pi}b_{f}^{2}w_{f}g_{f}^{\prime })$
for the fountain upflow requires (Morton et al.
Reference Morton, Taylor and Turner1956)
$(-{\rm\pi}b_{f}^{2}w_{f}g_{f}^{\prime })$
for the fountain upflow requires (Morton et al.
Reference Morton, Taylor and Turner1956)
where
![]() ${\it\alpha}_{f}$
is the top-hat entrainment coefficient for the fountain. Following Kaye & Hunt (Reference Kaye and Hunt2006), we take
${\it\alpha}_{f}$
is the top-hat entrainment coefficient for the fountain. Following Kaye & Hunt (Reference Kaye and Hunt2006), we take
![]() ${\it\alpha}_{f}=0.085$
. Given that the fountain behaviour is jet-like for the majority of its rise height, the vertical velocity
${\it\alpha}_{f}=0.085$
. Given that the fountain behaviour is jet-like for the majority of its rise height, the vertical velocity
![]() $w_{f}$
of the fountain is large compared with the velocity of the secondary flow in the lower layer. Therefore, it is reasonable to assume that entrainment into the fountain is not significantly influenced by the secondary flow in the lower layer. Whilst the secondary flow may modify the entrainment coefficient
$w_{f}$
of the fountain is large compared with the velocity of the secondary flow in the lower layer. Therefore, it is reasonable to assume that entrainment into the fountain is not significantly influenced by the secondary flow in the lower layer. Whilst the secondary flow may modify the entrainment coefficient
![]() ${\it\alpha}_{f}$
, it is reassuring that the choice of
${\it\alpha}_{f}$
, it is reassuring that the choice of
![]() ${\it\alpha}_{f}$
does not influence the scaling of
${\it\alpha}_{f}$
does not influence the scaling of
![]() $E_{i}$
, the quantity of primary interest to us.
$E_{i}$
, the quantity of primary interest to us.
Scaling quantities of interest on their values at the fountain source, we seek the vertical variation of the dimensionless radius
![]() ${\it\beta}_{f}=b_{f}/b_{f_{0}}$
, vertical velocity
${\it\beta}_{f}=b_{f}/b_{f_{0}}$
, vertical velocity
![]() ${\it\omega}_{f}=w_{f}/w_{f_{0}}$
and local Froude number
${\it\omega}_{f}=w_{f}/w_{f_{0}}$
and local Froude number
![]() $\mathit{Fr}_{f}=w_{f}/\sqrt{b_{f}g_{f}^{\prime }}$
of the fountain. The non-dimensional governing equations for the fountain are
$\mathit{Fr}_{f}=w_{f}/\sqrt{b_{f}g_{f}^{\prime }}$
of the fountain. The non-dimensional governing equations for the fountain are
where
![]() $\mathscr{Z}=(6{\it\alpha}_{f}/5)z/b_{f_{0}}$
. The source conditions of the fountain are
$\mathscr{Z}=(6{\it\alpha}_{f}/5)z/b_{f_{0}}$
. The source conditions of the fountain are
![]() ${\it\beta}_{f}(\mathscr{Z}=0)=1$
,
${\it\beta}_{f}(\mathscr{Z}=0)=1$
,
![]() ${\it\omega}_{f}(\mathscr{Z}=0)=1$
and
${\it\omega}_{f}(\mathscr{Z}=0)=1$
and
![]() $\mathit{Fr}_{f}(\mathscr{Z}=0)=\mathit{Fr}_{0}$
.
$\mathit{Fr}_{f}(\mathscr{Z}=0)=\mathit{Fr}_{0}$
.
The non-dimensional parameters of our system (2.9) are the source Froude number
![]() $\mathit{Fr}_{0}$
of the fountain, the buoyancy flux ratio
$\mathit{Fr}_{0}$
of the fountain, the buoyancy flux ratio
![]() ${\it\psi}$
and the fountain source radius
${\it\psi}$
and the fountain source radius
![]() $\mathscr{L}$
. For a given
$\mathscr{L}$
. For a given
![]() $\{\mathit{Fr}_{0},{\it\psi},\mathscr{L}\}$
, solutions were obtained using an iterative procedure. First, by making an initial estimate of
$\{\mathit{Fr}_{0},{\it\psi},\mathscr{L}\}$
, solutions were obtained using an iterative procedure. First, by making an initial estimate of
![]() $E=Q_{e}/Q_{f_{0}}$
, the interface position
$E=Q_{e}/Q_{f_{0}}$
, the interface position
![]() $({\it\xi})$
and mean layer buoyancies
$({\it\xi})$
and mean layer buoyancies
![]() $({\it\delta}_{1},{\it\delta}_{2})$
were calculated from (2.8a−c
). Subsequently, the fountain equations (2.37) were solved to obtain the dimensionless vertical velocity
$({\it\delta}_{1},{\it\delta}_{2})$
were calculated from (2.8a−c
). Subsequently, the fountain equations (2.37) were solved to obtain the dimensionless vertical velocity
![]() ${\it\omega}_{i}$
and dimensionless radius
${\it\omega}_{i}$
and dimensionless radius
![]() ${\it\beta}_{i}$
of the fountain at the interface. The interfacial Froude number and the confinement parameter were determined from
${\it\beta}_{i}$
of the fountain at the interface. The interfacial Froude number and the confinement parameter were determined from
We then calculated the dimensionless entrainment flux
![]() $E_{i}$
(2.33) and re-estimated
$E_{i}$
(2.33) and re-estimated
![]() $E=E_{i}{\it\beta}_{i}^{2}{\it\omega}_{i}$
, the interface position and the layer buoyancies. This procedure was repeated until
$E=E_{i}{\it\beta}_{i}^{2}{\it\omega}_{i}$
, the interface position and the layer buoyancies. This procedure was repeated until
![]() $E_{i}$
,
$E_{i}$
,
![]() ${\it\xi}$
,
${\it\xi}$
,
![]() ${\it\delta}_{1}$
and
${\it\delta}_{1}$
and
![]() ${\it\delta}_{2}$
converged to fixed values.
${\it\delta}_{2}$
converged to fixed values.
3. Model predictions and analysis of results
3.1. Power laws for unconfined and confined entrainment
As an illustrative example of the role of confinement, figure 8(a) plots
![]() $E_{i}$
as a function of
$E_{i}$
as a function of
![]() ${\it\lambda}_{i}$
for
${\it\lambda}_{i}$
for
![]() $\mathit{Fr}_{i}=0.7$
. Also plotted is the power law
$\mathit{Fr}_{i}=0.7$
. Also plotted is the power law
![]() $E_{i}=A\mathit{Fr}_{i}^{2}$
for unconfined interfacial entrainment. As
$E_{i}=A\mathit{Fr}_{i}^{2}$
for unconfined interfacial entrainment. As
![]() ${\it\lambda}_{i}$
increases, and thus the confinement is enhanced, the velocity
${\it\lambda}_{i}$
increases, and thus the confinement is enhanced, the velocity
![]() $\tilde{u} _{2}(\propto \sqrt{{\it\lambda}_{i}})$
of the secondary flow increases (see § 3.3 for a further discussion on the role of
$\tilde{u} _{2}(\propto \sqrt{{\it\lambda}_{i}})$
of the secondary flow increases (see § 3.3 for a further discussion on the role of
![]() ${\it\lambda}_{i}$
). Therefore, the rate of entrainment
${\it\lambda}_{i}$
). Therefore, the rate of entrainment
![]() $E_{i,c}(\propto \tilde{u} _{2})$
of the secondary flow and hence
$E_{i,c}(\propto \tilde{u} _{2})$
of the secondary flow and hence
![]() $E_{i}$
increase with
$E_{i}$
increase with
![]() ${\it\lambda}_{i}$
(figure 8
a). Notably, when the radius of the impinging fountain equals the depth of the upper layer (i.e.
${\it\lambda}_{i}$
(figure 8
a). Notably, when the radius of the impinging fountain equals the depth of the upper layer (i.e.
![]() ${\it\lambda}_{i}=1$
),
${\it\lambda}_{i}=1$
),
![]() $E_{i}$
exceeds the rate of interfacial entrainment in an unconfined environment by a factor of three.
$E_{i}$
exceeds the rate of interfacial entrainment in an unconfined environment by a factor of three.

Figure 8. Dimensionless entrainment flux
![]() $E_{i}$
across the interface: (a) as a function of the confinement parameter
$E_{i}$
across the interface: (a) as a function of the confinement parameter
![]() ${\it\lambda}_{i}$
for
${\it\lambda}_{i}$
for
![]() $\mathit{Fr}_{i}=0.7$
and (b) as a function of the interfacial Froude number
$\mathit{Fr}_{i}=0.7$
and (b) as a function of the interfacial Froude number
![]() $\mathit{Fr}_{i}$
for
$\mathit{Fr}_{i}$
for
![]() ${\it\lambda}_{i}=\{0,0.5\}$
.
${\it\lambda}_{i}=\{0,0.5\}$
.
Figure 8(b) plots
![]() $E_{i}$
as a function of
$E_{i}$
as a function of
![]() $\mathit{Fr}_{i}$
for
$\mathit{Fr}_{i}$
for
![]() ${\it\lambda}_{i}=\{0,0.5\}$
and further emphasises the disparities between entrainment in unconfined and confined environments. As
${\it\lambda}_{i}=\{0,0.5\}$
and further emphasises the disparities between entrainment in unconfined and confined environments. As
![]() $\mathit{Fr}_{i}$
increases, and thus the vertical forcing of the interface is strengthened, larger deflections
$\mathit{Fr}_{i}$
increases, and thus the vertical forcing of the interface is strengthened, larger deflections
![]() ${\it\eta}$
${\it\eta}$
![]() $(\propto \mathit{Fr}_{i}^{2})$
are produced. Hence, for
$(\propto \mathit{Fr}_{i}^{2})$
are produced. Hence, for
![]() ${\it\lambda}_{i}>0$
a greater amount of potential energy is released and converted into kinetic energy of the secondary flow. Therefore,
${\it\lambda}_{i}>0$
a greater amount of potential energy is released and converted into kinetic energy of the secondary flow. Therefore,
![]() $\tilde{u} _{2}$
and
$\tilde{u} _{2}$
and
![]() $E_{i}$
increase with
$E_{i}$
increase with
![]() $\mathit{Fr}_{i}$
(figure 8
b). Significantly, when the diameter
$\mathit{Fr}_{i}$
(figure 8
b). Significantly, when the diameter
![]() $(2b_{i})$
of the impinging fountain equals the upper-layer depth (i.e.
$(2b_{i})$
of the impinging fountain equals the upper-layer depth (i.e.
![]() ${\it\lambda}_{i}=0.5$
), doubling
${\it\lambda}_{i}=0.5$
), doubling
![]() $\mathit{Fr}_{i}$
from
$\mathit{Fr}_{i}$
from
![]() $\mathit{Fr}_{i}=0.5$
to
$\mathit{Fr}_{i}=0.5$
to
![]() $\mathit{Fr}_{i}=1$
gives rise to a sevenfold increase in
$\mathit{Fr}_{i}=1$
gives rise to a sevenfold increase in
![]() $E_{i}$
; this compares with a fourfold increase in the unconfined case.
$E_{i}$
; this compares with a fourfold increase in the unconfined case.
Crucially, the scaling of
![]() $E_{i}$
on
$E_{i}$
on
![]() $\mathit{Fr}_{i}$
is determined by
$\mathit{Fr}_{i}$
is determined by
![]() ${\it\lambda}_{i}$
. From (2.33), our entrainment law follows
${\it\lambda}_{i}$
. From (2.33), our entrainment law follows
In other words, when
![]() ${\it\lambda}_{i}\ll {\it\lambda}_{i,c}$
, the secondary flow is sufficiently weak such that the contribution of
${\it\lambda}_{i}\ll {\it\lambda}_{i,c}$
, the secondary flow is sufficiently weak such that the contribution of
![]() $E_{i,c}$
to
$E_{i,c}$
to
![]() $E_{i}$
is small, and thus
$E_{i}$
is small, and thus
![]() $E_{i}$
is quadratic in
$E_{i}$
is quadratic in
![]() $\mathit{Fr}_{i}$
as per ‘unconfined’ entrainment (Shrinivas & Hunt Reference Shrinivas and Hunt2014). When
$\mathit{Fr}_{i}$
as per ‘unconfined’ entrainment (Shrinivas & Hunt Reference Shrinivas and Hunt2014). When
![]() ${\it\lambda}_{i}\gg {\it\lambda}_{i,c}$
, the secondary flow is sufficiently strong such that
${\it\lambda}_{i}\gg {\it\lambda}_{i,c}$
, the secondary flow is sufficiently strong such that
![]() $E_{i,c}$
provides the dominant contribution to
$E_{i,c}$
provides the dominant contribution to
![]() $E_{i}$
and thus,
$E_{i}$
and thus,
![]() $E_{i}$
is cubic in
$E_{i}$
is cubic in
![]() $\mathit{Fr}_{i}$
(2.33). We refer to interfacial entrainment in these small-
$\mathit{Fr}_{i}$
(2.33). We refer to interfacial entrainment in these small-
![]() ${\it\lambda}_{i}$
and large-
${\it\lambda}_{i}$
and large-
![]() ${\it\lambda}_{i}$
limits as weakly confined and strongly confined, respectively.
${\it\lambda}_{i}$
limits as weakly confined and strongly confined, respectively.

Figure 9. (a) Interface height
![]() ${\it\xi}$
against the source Froude number
${\it\xi}$
against the source Froude number
![]() $\mathit{Fr}_{0}$
of the fountain and (b) velocity
$\mathit{Fr}_{0}$
of the fountain and (b) velocity
![]() $\tilde{u} _{2}$
of secondary flow against the confinement parameter
$\tilde{u} _{2}$
of secondary flow against the confinement parameter
![]() ${\it\lambda}_{i}$
for buoyancy flux ratio
${\it\lambda}_{i}$
for buoyancy flux ratio
![]() ${\it\psi}=25$
and fountain source radius
${\it\psi}=25$
and fountain source radius
![]() $\mathscr{L}=0.1$
.
$\mathscr{L}=0.1$
.
This result provides a plausible physical explanation for why some experimental studies support a
![]() $E_{i}\propto \mathit{Fr}_{i}^{2}$
power law, whereas others report
$E_{i}\propto \mathit{Fr}_{i}^{2}$
power law, whereas others report
![]() $E_{i}\propto \mathit{Fr}_{i}^{3}$
. Our model (3.1) indicates that measurements of
$E_{i}\propto \mathit{Fr}_{i}^{3}$
. Our model (3.1) indicates that measurements of
![]() $E_{i}$
following a cubic power law (Baines Reference Baines1975; Coffey & Hunt Reference Coffey and Hunt2010) may have been influenced by a secondary flow owing to relatively large values of
$E_{i}$
following a cubic power law (Baines Reference Baines1975; Coffey & Hunt Reference Coffey and Hunt2010) may have been influenced by a secondary flow owing to relatively large values of
![]() ${\it\lambda}_{i}$
. Inferring values of
${\it\lambda}_{i}$
. Inferring values of
![]() ${\it\lambda}_{i}$
from previous works, we find that for the experiments of Coffey & Hunt (Reference Coffey and Hunt2010),
${\it\lambda}_{i}$
from previous works, we find that for the experiments of Coffey & Hunt (Reference Coffey and Hunt2010),
![]() ${\it\lambda}_{i}$
was as large as unity, as discussed in § 3.3. Conversely, measurements of
${\it\lambda}_{i}$
was as large as unity, as discussed in § 3.3. Conversely, measurements of
![]() $E_{i}$
supporting a quadratic power law (Cardoso & Woods Reference Cardoso and Woods1993; Ching et al.
Reference Ching, Fernando and Noh1993) were not significantly influenced by a secondary flow as
$E_{i}$
supporting a quadratic power law (Cardoso & Woods Reference Cardoso and Woods1993; Ching et al.
Reference Ching, Fernando and Noh1993) were not significantly influenced by a secondary flow as
![]() ${\it\lambda}_{i}$
was sufficiently small. Indeed, for the experiments of Ching et al. (Reference Ching, Fernando and Noh1993), a value of
${\it\lambda}_{i}$
was sufficiently small. Indeed, for the experiments of Ching et al. (Reference Ching, Fernando and Noh1993), a value of
![]() ${\it\lambda}_{i}=0.2$
was never exceeded. We will see (§ 3.3) that for previous studies,
${\it\lambda}_{i}=0.2$
was never exceeded. We will see (§ 3.3) that for previous studies,
![]() ${\it\lambda}_{i}$
exhibits wide variation, spanning the range
${\it\lambda}_{i}$
exhibits wide variation, spanning the range
![]() $0.1<{\it\lambda}_{i}<1$
. Hence, these studies capture
$0.1<{\it\lambda}_{i}<1$
. Hence, these studies capture
![]() $E_{i}$
not only within the weakly confined and strongly confined regimes, but also in the transitional regime where comparable contributions from the quadratic and cubic components are expected.
$E_{i}$
not only within the weakly confined and strongly confined regimes, but also in the transitional regime where comparable contributions from the quadratic and cubic components are expected.
3.2. Entrainment for varying
 $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
 ${\it\lambda}_{i}$
${\it\lambda}_{i}$
Thus far, we have focused on entrainment for constant
![]() $\mathit{Fr}_{i}$
or constant
$\mathit{Fr}_{i}$
or constant
![]() ${\it\lambda}_{i}$
(figure 8). The difficulty in achieving this in practice is exemplified by the significant variation of
${\it\lambda}_{i}$
(figure 8). The difficulty in achieving this in practice is exemplified by the significant variation of
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
in previous experiments (see § 3.3). To examine
${\it\lambda}_{i}$
in previous experiments (see § 3.3). To examine
![]() $E_{i}$
when both
$E_{i}$
when both
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
vary, we increase the source Froude number
${\it\lambda}_{i}$
vary, we increase the source Froude number
![]() $\mathit{Fr}_{0}$
of the fountain, whilst holding the source radius
$\mathit{Fr}_{0}$
of the fountain, whilst holding the source radius
![]() $\mathscr{L}$
and buoyancy flux ratio
$\mathscr{L}$
and buoyancy flux ratio
![]() ${\it\psi}$
constant. As this produces more energetic interfacial impingements, the rate of entrainment
${\it\psi}$
constant. As this produces more energetic interfacial impingements, the rate of entrainment
![]() $(E_{i})$
of fluid from the upper layer increases and hence the interface height
$(E_{i})$
of fluid from the upper layer increases and hence the interface height
![]() ${\it\xi}$
increases (figure 9
a). Consequently, the radius
${\it\xi}$
increases (figure 9
a). Consequently, the radius
![]() ${\it\beta}_{i}$
of the fountain at the interface increases. Therefore, increasing
${\it\beta}_{i}$
of the fountain at the interface increases. Therefore, increasing
![]() $\mathit{Fr}_{0}$
results in larger values of
$\mathit{Fr}_{0}$
results in larger values of
![]() ${\it\lambda}_{i}\propto {\it\beta}_{i}/(1-{\it\xi})$
. Enhancing the confinement in this way gives rise to stronger secondary flows, i.e.
${\it\lambda}_{i}\propto {\it\beta}_{i}/(1-{\it\xi})$
. Enhancing the confinement in this way gives rise to stronger secondary flows, i.e.
![]() $\tilde{u} _{2}$
increases with
$\tilde{u} _{2}$
increases with
![]() ${\it\lambda}_{i}$
, as shown in figure 9(b). Notably,
${\it\lambda}_{i}$
, as shown in figure 9(b). Notably,
![]() $u_{2}$
is approximately 25 % of the fountain’s vertical velocity
$u_{2}$
is approximately 25 % of the fountain’s vertical velocity
![]() $w_{i}$
at the interface when
$w_{i}$
at the interface when
![]() ${\it\lambda}_{i}\sim 1$
.
${\it\lambda}_{i}\sim 1$
.

Figure 10. Entrainment flux ratio
![]() ${\it\phi}$
(2.35): (a) against the interfacial Froude number
${\it\phi}$
(2.35): (a) against the interfacial Froude number
![]() $\mathit{Fr}_{i}$
and (b) against the confinement parameter
$\mathit{Fr}_{i}$
and (b) against the confinement parameter
![]() ${\it\lambda}_{i}$
for source buoyancy flux ratio
${\it\lambda}_{i}$
for source buoyancy flux ratio
![]() ${\it\psi}=25$
and fountain source radius
${\it\psi}=25$
and fountain source radius
![]() $\mathscr{L}=0.1$
.
$\mathscr{L}=0.1$
.
Figures 10(a) and 10(b) plot the entrainment flux ratio
![]() ${\it\phi}$
(2.35) against
${\it\phi}$
(2.35) against
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
, respectively. Two limiting cases can be identified: one in which
${\it\lambda}_{i}$
, respectively. Two limiting cases can be identified: one in which
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
are small and a second in which
${\it\lambda}_{i}$
are small and a second in which
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
are large. For
${\it\lambda}_{i}$
are large. For
![]() $\mathit{Fr}_{i}\ll 1$
a weak forcing of the interface by the fountain produces relatively small deflections as
$\mathit{Fr}_{i}\ll 1$
a weak forcing of the interface by the fountain produces relatively small deflections as
![]() ${\it\eta}\propto \mathit{Fr}_{i}^{2}$
, and for
${\it\eta}\propto \mathit{Fr}_{i}^{2}$
, and for
![]() ${\it\lambda}_{i}\ll 1$
the zone of interfacial deflection
${\it\lambda}_{i}\ll 1$
the zone of interfacial deflection
![]() $(r_{id}\propto b_{i})$
is small compared with the depth of the upper layer,
$(r_{id}\propto b_{i})$
is small compared with the depth of the upper layer,
![]() $r_{id}\ll D$
. Thus, a relatively small amount of potential energy
$r_{id}\ll D$
. Thus, a relatively small amount of potential energy
![]() $({\sim}b_{i}^{2}{\it\eta}^{2})$
is released from the deflections and converted into kinetic energy of a relatively large mass of upper-layer fluid. As a result, the secondary flow is weak (
$({\sim}b_{i}^{2}{\it\eta}^{2})$
is released from the deflections and converted into kinetic energy of a relatively large mass of upper-layer fluid. As a result, the secondary flow is weak (
![]() $\tilde{u} _{2}\ll 1$
), and hence the rate of entrainment
$\tilde{u} _{2}\ll 1$
), and hence the rate of entrainment
![]() $E_{i,c}$
of the secondary flow provides only a small contribution to
$E_{i,c}$
of the secondary flow provides only a small contribution to
![]() $E_{i}$
. For example,
$E_{i}$
. For example,
![]() ${\it\phi}\sim 1$
when
${\it\phi}\sim 1$
when
![]() $\{\mathit{Fr}_{i},{\it\lambda}_{i}\}\ll 1$
(figure 10). When
$\{\mathit{Fr}_{i},{\it\lambda}_{i}\}\ll 1$
(figure 10). When
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
are both large, the vertical excursions of the interface are relatively large (
${\it\lambda}_{i}$
are both large, the vertical excursions of the interface are relatively large (
![]() ${\it\eta}$
is comparable with
${\it\eta}$
is comparable with
![]() $b_{i}$
) and the zone of deflection is comparable with the upper-layer depth. Thus, a significant amount of potential energy is released and converted into kinetic energy of a relatively shallow mass of upper-layer fluid. As a result, the secondary flow is strong and hence,
$b_{i}$
) and the zone of deflection is comparable with the upper-layer depth. Thus, a significant amount of potential energy is released and converted into kinetic energy of a relatively shallow mass of upper-layer fluid. As a result, the secondary flow is strong and hence,
![]() $E_{i,c}$
provides a significant contribution to the total entrainment flux
$E_{i,c}$
provides a significant contribution to the total entrainment flux
![]() $E_{i}$
. For example,
$E_{i}$
. For example,
![]() ${\it\phi}\approx 4$
when
${\it\phi}\approx 4$
when
![]() $\{\mathit{Fr}_{i},{\it\lambda}_{i}\}\sim 1$
, i.e. with identical forcing, the entrainment flux in the confined environment exceeds that in an unconfined environment by a factor of almost four (figure 10).
$\{\mathit{Fr}_{i},{\it\lambda}_{i}\}\sim 1$
, i.e. with identical forcing, the entrainment flux in the confined environment exceeds that in an unconfined environment by a factor of almost four (figure 10).
3.3. Confinement in previous experimental studies
Figure 11 plots contours of constant
![]() $E_{i}$
in
$E_{i}$
in
![]() $\{{\it\lambda}_{i},\mathit{Fr}_{i}\}$
space, thereby encompassing the dynamics of interfacial entrainment in a confined environment. For a given
$\{{\it\lambda}_{i},\mathit{Fr}_{i}\}$
space, thereby encompassing the dynamics of interfacial entrainment in a confined environment. For a given
![]() $\mathit{Fr}_{i}$
,
$\mathit{Fr}_{i}$
,
![]() $E_{i}$
can vary by up to 80 % depending on
$E_{i}$
can vary by up to 80 % depending on
![]() ${\it\lambda}_{i}$
. For example with
${\it\lambda}_{i}$
. For example with
![]() $\mathit{Fr}_{i}=0.7$
,
$\mathit{Fr}_{i}=0.7$
,
![]() $E_{i}=0.18$
when
$E_{i}=0.18$
when
![]() ${\it\lambda}_{i}=0.1$
, whereas
${\it\lambda}_{i}=0.1$
, whereas
![]() $E_{i}=0.32$
when
$E_{i}=0.32$
when
![]() ${\it\lambda}_{i}=0.8$
. Given that
${\it\lambda}_{i}=0.8$
. Given that
![]() ${\it\lambda}_{i}$
plays an instrumental role in the entrainment dynamics, it is informative to examine the confinement in previous experimental studies.
${\it\lambda}_{i}$
plays an instrumental role in the entrainment dynamics, it is informative to examine the confinement in previous experimental studies.
A wide range of box geometries have been used in experiments to measure
![]() $E_{i}$
, with the box height
$E_{i}$
, with the box height
![]() $H$
differing by more than a factor of two: see table 1. Accordingly, it is instructive to examine the effect of the vertical extent
$H$
differing by more than a factor of two: see table 1. Accordingly, it is instructive to examine the effect of the vertical extent
![]() $H$
of the confinement on
$H$
of the confinement on
![]() $E_{i}$
. To this end, we vary the box height
$E_{i}$
. To this end, we vary the box height
![]() $H$
for constant
$H$
for constant
![]() $\{b_{f_{0}},\mathit{Fr}_{0},{\it\psi}\}$
, equivalent to varying
$\{b_{f_{0}},\mathit{Fr}_{0},{\it\psi}\}$
, equivalent to varying
![]() $\mathscr{L}\propto b_{f_{0}}/H$
, and calculate
$\mathscr{L}\propto b_{f_{0}}/H$
, and calculate
![]() $E_{i}$
. Figure 12 plots the entrainment flux ratio
$E_{i}$
. Figure 12 plots the entrainment flux ratio
![]() ${\it\phi}$
against
${\it\phi}$
against
![]() $\mathscr{L}$
. The values of
$\mathscr{L}$
. The values of
![]() $\mathscr{L}$
we consider span those of the experimental studies (table 1). Reducing
$\mathscr{L}$
we consider span those of the experimental studies (table 1). Reducing
![]() $H$
(i.e. increasing
$H$
(i.e. increasing
![]() $\mathscr{L}$
) strengthens the confinement and hence results in stronger secondary flows. Consequently, the rate of entrainment
$\mathscr{L}$
) strengthens the confinement and hence results in stronger secondary flows. Consequently, the rate of entrainment
![]() $E_{i,c}$
of the secondary flow increases, and thus
$E_{i,c}$
of the secondary flow increases, and thus
![]() ${\it\phi}$
increases with
${\it\phi}$
increases with
![]() $\mathscr{L}$
. For a typical source radius of
$\mathscr{L}$
. For a typical source radius of
![]() $b_{f_{0}}=0.6$
cm, the dashed lines in figure 12 indicate the values of
$b_{f_{0}}=0.6$
cm, the dashed lines in figure 12 indicate the values of
![]() ${\it\phi}$
corresponding to the minimum and maximum box heights used in experiment (table 1). Evidently, the enhancement of
${\it\phi}$
corresponding to the minimum and maximum box heights used in experiment (table 1). Evidently, the enhancement of
![]() $E_{i}$
due to the confinement increases by more than 50 % when the box height is decreased from
$E_{i}$
due to the confinement increases by more than 50 % when the box height is decreased from
![]() $H=50$
cm to
$H=50$
cm to
![]() $H=23$
cm.
$H=23$
cm.

Figure 11. Contours of constant entrainment flux
![]() $E_{i}$
in
$E_{i}$
in
![]() $\{{\it\lambda}_{i},\mathit{Fr}_{i}\}$
space.
$\{{\it\lambda}_{i},\mathit{Fr}_{i}\}$
space.
Table 1. Examples of the box height
![]() $H$
, source radius
$H$
, source radius
![]() $b_{f_{0}}$
and dimensionless source radius
$b_{f_{0}}$
and dimensionless source radius
![]() $\mathscr{L}$
used in previous experimental studies.
$\mathscr{L}$
used in previous experimental studies.


Figure 12. Entrainment flux ratio
![]() ${\it\phi}$
against dimensionless source radius
${\it\phi}$
against dimensionless source radius
![]() $\mathscr{L}$
for source Froude number
$\mathscr{L}$
for source Froude number
![]() $\mathit{Fr}_{0}=20$
and buoyancy flux ratio
$\mathit{Fr}_{0}=20$
and buoyancy flux ratio
![]() ${\it\psi}=10$
. The dashed lines indicate
${\it\psi}=10$
. The dashed lines indicate
![]() ${\it\phi}=\{2.75,1.8\}$
for box height
${\it\phi}=\{2.75,1.8\}$
for box height
![]() $H=\{23,50\}~\text{cm}$
and source radius
$H=\{23,50\}~\text{cm}$
and source radius
![]() $b_{f_{0}}=0.6$
cm.
$b_{f_{0}}=0.6$
cm.
These results highlight that confinement has a significant effect on the strength of the secondary flow and thus on the entrainment flux. Of course, this variation is entirely unwanted from a practical perspective as experiments have sought to determine a universal entrainment law.
To establish whether the role of confinement can shed new light on the significant spread in the existing measurements of
![]() $E_{i}$
(figure 2), figure 13 plots
$E_{i}$
(figure 2), figure 13 plots
![]() ${\it\lambda}_{i}$
for the experiments of Kumagai (Reference Kumagai1984), Lin & Linden (Reference Lin and Linden2005) and Coffey & Hunt (Reference Coffey and Hunt2010) in
${\it\lambda}_{i}$
for the experiments of Kumagai (Reference Kumagai1984), Lin & Linden (Reference Lin and Linden2005) and Coffey & Hunt (Reference Coffey and Hunt2010) in
![]() $\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
space. We note that Baines (Reference Baines1975) does not provide sufficient information to calculate
$\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
space. We note that Baines (Reference Baines1975) does not provide sufficient information to calculate
![]() ${\it\lambda}_{i}$
for his experiments. Evidently, the experimental values of
${\it\lambda}_{i}$
for his experiments. Evidently, the experimental values of
![]() ${\it\lambda}_{i}$
vary by up to an order of magnitude for a given
${\it\lambda}_{i}$
vary by up to an order of magnitude for a given
![]() $\mathit{Fr}_{i}$
. Notably, the range of experimental values of
$\mathit{Fr}_{i}$
. Notably, the range of experimental values of
![]() ${\it\lambda}_{i}$
${\it\lambda}_{i}$
![]() $(0.1<{\it\lambda}_{i}<1)$
corresponds to the range of values of
$(0.1<{\it\lambda}_{i}<1)$
corresponds to the range of values of
![]() ${\it\lambda}_{i}$
predicted by our model (figure 10
b). Moreover, there is no systematic variation of
${\it\lambda}_{i}$
predicted by our model (figure 10
b). Moreover, there is no systematic variation of
![]() ${\it\lambda}_{i}$
with
${\it\lambda}_{i}$
with
![]() $\mathit{Fr}_{i}$
, thus affirming that
$\mathit{Fr}_{i}$
, thus affirming that
![]() ${\it\lambda}_{i}$
is an independent parameter. Based on this evidence and given that the influence of
${\it\lambda}_{i}$
is an independent parameter. Based on this evidence and given that the influence of
![]() ${\it\lambda}_{i}$
on
${\it\lambda}_{i}$
on
![]() $E_{i}$
has not been previously considered, it is plausible and indeed we assert that the spread in the existing data of
$E_{i}$
has not been previously considered, it is plausible and indeed we assert that the spread in the existing data of
![]() $E_{i}$
is attributed, at least in part, to the dependence of
$E_{i}$
is attributed, at least in part, to the dependence of
![]() $E_{i}$
on
$E_{i}$
on
![]() ${\it\lambda}_{i}$
. To reinforce this assertion, also shown in figure 13 are our theoretical curves of constant
${\it\lambda}_{i}$
. To reinforce this assertion, also shown in figure 13 are our theoretical curves of constant
![]() ${\it\phi}=\{1.2,4\}$
. Clearly, almost all the data points lie within the shaded region bounded by these curves. In other words, we predict that for the majority of existing measurements, at least 20 % of
${\it\phi}=\{1.2,4\}$
. Clearly, almost all the data points lie within the shaded region bounded by these curves. In other words, we predict that for the majority of existing measurements, at least 20 % of
![]() $E_{i}$
may be attributed to the rate of entrainment
$E_{i}$
may be attributed to the rate of entrainment
![]() $E_{i,c}$
of the secondary flow, and that for strongly confined flows, the entrainment flux inferred from measurements is increased by a factor of four over that which may be expected for truly unconfined interfacial entrainment. This is compelling evidence that previous measurements have been influenced by a secondary flow and that the disparities in
$E_{i,c}$
of the secondary flow, and that for strongly confined flows, the entrainment flux inferred from measurements is increased by a factor of four over that which may be expected for truly unconfined interfacial entrainment. This is compelling evidence that previous measurements have been influenced by a secondary flow and that the disparities in
![]() $E_{i}$
are likely to be associated with variations in
$E_{i}$
are likely to be associated with variations in
![]() ${\it\lambda}_{i}$
.
${\it\lambda}_{i}$
.

Figure 13. Confinement parameter
![]() ${\it\lambda}_{i}$
against the interfacial Froude number
${\it\lambda}_{i}$
against the interfacial Froude number
![]() $\mathit{Fr}_{i}$
for the experiments of Kumagai (Reference Kumagai1984) (▫), Lin & Linden (Reference Lin and Linden2005)
$\mathit{Fr}_{i}$
for the experiments of Kumagai (Reference Kumagai1984) (▫), Lin & Linden (Reference Lin and Linden2005)
![]() $(+)$
and Coffey & Hunt (Reference Coffey and Hunt2010) (▵). Solid lines are our theoretical curves of constant entrainment flux ratio
$(+)$
and Coffey & Hunt (Reference Coffey and Hunt2010) (▵). Solid lines are our theoretical curves of constant entrainment flux ratio
![]() ${\it\phi}=\{1.2,4\}$
.
${\it\phi}=\{1.2,4\}$
.
Baines (Reference Baines1975), Kumagai (Reference Kumagai1984) and Coffey & Hunt (Reference Coffey and Hunt2010) inferred
![]() $E_{i}$
by tracking the position of a moving interface and, as a consequence,
$E_{i}$
by tracking the position of a moving interface and, as a consequence,
![]() ${\it\lambda}_{i}$
was time-dependent in their experiments. By using a wide tank, Ching et al. (Reference Ching, Fernando and Noh1993) measured the entrainment rate before the interfacial gravity current reached the side boundaries. Thus, the interface position and
${\it\lambda}_{i}$
was time-dependent in their experiments. By using a wide tank, Ching et al. (Reference Ching, Fernando and Noh1993) measured the entrainment rate before the interfacial gravity current reached the side boundaries. Thus, the interface position and
![]() ${\it\lambda}_{i}$
were invariant for the duration of interest. It is therefore unsurprising that their measurements of the entrainment rate exhibit considerably less scatter than the data sets of Baines (Reference Baines1975) and Kumagai (Reference Kumagai1984), for which
${\it\lambda}_{i}$
were invariant for the duration of interest. It is therefore unsurprising that their measurements of the entrainment rate exhibit considerably less scatter than the data sets of Baines (Reference Baines1975) and Kumagai (Reference Kumagai1984), for which
![]() ${\it\lambda}_{i}$
differs by almost an order of magnitude (figure 13).
${\it\lambda}_{i}$
differs by almost an order of magnitude (figure 13).
3.4. Implications for the design of an experiment
It is not immediately clear for a given experiment (or indeed from the wealth of previous measurements) how the individual components of
![]() $E_{i}$
(2.33) may be accurately determined. What is clear is that in search of a universal law it is the entrainment flux in the absence of confinement that has been, and arguably remains, the true goal. Our analysis raises the question of what is an appropriate box height
$E_{i}$
(2.33) may be accurately determined. What is clear is that in search of a universal law it is the entrainment flux in the absence of confinement that has been, and arguably remains, the true goal. Our analysis raises the question of what is an appropriate box height
![]() $H$
for measuring the entrainment flux. As a secondary flow persists for
$H$
for measuring the entrainment flux. As a secondary flow persists for
![]() $H>0$
, the influence of confinement on
$H>0$
, the influence of confinement on
![]() $E_{i}$
is inexorable. However, through careful selection of the box height, it is possible to tailor the contribution of
$E_{i}$
is inexorable. However, through careful selection of the box height, it is possible to tailor the contribution of
![]() $E_{i,c}$
to
$E_{i,c}$
to
![]() $E_{i}$
in an experiment so that
$E_{i}$
in an experiment so that
![]() ${\it\phi}=(A\mathit{Fr}_{i}^{2}+E_{i,c})/A\mathit{Fr}_{i}^{2}$
does not exceed an acceptable threshold,
${\it\phi}=(A\mathit{Fr}_{i}^{2}+E_{i,c})/A\mathit{Fr}_{i}^{2}$
does not exceed an acceptable threshold,
![]() ${\it\phi}_{T}$
. Based on the accuracy to which
${\it\phi}_{T}$
. Based on the accuracy to which
![]() $E_{i}$
is measured, experimentalists can specify
$E_{i}$
is measured, experimentalists can specify
![]() ${\it\phi}_{T}$
. By ensuring that
${\it\phi}_{T}$
. By ensuring that
![]() ${\it\phi}<{\it\phi}_{T}$
, the effect of confinement on
${\it\phi}<{\it\phi}_{T}$
, the effect of confinement on
![]() $E_{i}$
can, in principle, be restricted solely to the realms of experimental uncertainty.
$E_{i}$
can, in principle, be restricted solely to the realms of experimental uncertainty.
With a view to guiding future experiments, we seek the box height required to achieve a given
![]() ${\it\phi}={\it\phi}_{T}$
. While the plan area
${\it\phi}={\it\phi}_{T}$
. While the plan area
![]() $S$
of the box is needed to fully define the geometry, its precise value is not of concern, and implicit in the following discussion is that
$S$
of the box is needed to fully define the geometry, its precise value is not of concern, and implicit in the following discussion is that
![]() $S$
is sufficiently large that both the plume and fountain are free to entrain and their sources sufficiently well separated that they may be considered to be non-interacting. Moreover, the sources are sufficiently small in area that they approximate to localised sources (e.g.
$S$
is sufficiently large that both the plume and fountain are free to entrain and their sources sufficiently well separated that they may be considered to be non-interacting. Moreover, the sources are sufficiently small in area that they approximate to localised sources (e.g.
![]() $b_{f_{0}}\ll h$
). As the fountain exhibits jet-like behaviour below the interface (see § 2.3), its radius scales approximately linearly with height (Kaye & Hunt Reference Kaye and Hunt2006), and hence we take
$b_{f_{0}}\ll h$
). As the fountain exhibits jet-like behaviour below the interface (see § 2.3), its radius scales approximately linearly with height (Kaye & Hunt Reference Kaye and Hunt2006), and hence we take
![]() $b_{i}=c_{1}h$
, where
$b_{i}=c_{1}h$
, where
![]() $c_{1}$
is a constant. Recalling that
$c_{1}$
is a constant. Recalling that
![]() ${\it\lambda}_{i}=b_{i}/(H-h)$
, we substitute for
${\it\lambda}_{i}=b_{i}/(H-h)$
, we substitute for
![]() $b_{i}$
into (2.35) and rearrange for
$b_{i}$
into (2.35) and rearrange for
![]() $h/H$
to give
$h/H$
to give
Taking
![]() $c_{1}=0.17$
(Mizushina et al.
Reference Mizushina, Ogino, Takeuchi and Ikawa1982), figure 14 plots
$c_{1}=0.17$
(Mizushina et al.
Reference Mizushina, Ogino, Takeuchi and Ikawa1982), figure 14 plots
![]() $(h/H)_{design}$
(3.2) as a function of
$(h/H)_{design}$
(3.2) as a function of
![]() $\mathit{Fr}_{i}$
for
$\mathit{Fr}_{i}$
for
![]() ${\it\phi}_{T}=\{1.2,1.5,2.0,2.5\}$
. The region beneath a given curve of constant
${\it\phi}_{T}=\{1.2,1.5,2.0,2.5\}$
. The region beneath a given curve of constant
![]() ${\it\phi}_{T}$
encompasses the values of
${\it\phi}_{T}$
encompasses the values of
![]() $(h/H)_{design}$
for which
$(h/H)_{design}$
for which
![]() ${\it\phi}<{\it\phi}_{T}$
. Hence, for a given interface position
${\it\phi}<{\it\phi}_{T}$
. Hence, for a given interface position
![]() $h$
, figure 14 indicates the box height
$h$
, figure 14 indicates the box height
![]() $H$
required to limit the influence of the confinement on
$H$
required to limit the influence of the confinement on
![]() $E_{i}$
to
$E_{i}$
to
![]() ${\it\phi}={\it\phi}_{T}$
. For example, if the interface is established 12 cm above the base of the box and
${\it\phi}={\it\phi}_{T}$
. For example, if the interface is established 12 cm above the base of the box and
![]() $\mathit{Fr}_{i}=0.3$
, we would require
$\mathit{Fr}_{i}=0.3$
, we would require
![]() $H>47$
cm to restrict the rate of entrainment
$H>47$
cm to restrict the rate of entrainment
![]() $E_{i,c}$
of the secondary flow to no more than 20 % of
$E_{i,c}$
of the secondary flow to no more than 20 % of
![]() $E_{i}$
. Lower box heights could be used, but with the penalty of higher thresholds
$E_{i}$
. Lower box heights could be used, but with the penalty of higher thresholds
![]() ${\it\phi}_{T}$
.
${\it\phi}_{T}$
.

Figure 14. Interface height
![]() $h$
scaled on box height
$h$
scaled on box height
![]() $H$
as a function of
$H$
as a function of
![]() $\mathit{Fr}_{i}$
for a constant entrainment flux ratio
$\mathit{Fr}_{i}$
for a constant entrainment flux ratio
![]() ${\it\phi}_{T}=\{1.2,1.5,2.0,2.5\}$
.
${\it\phi}_{T}=\{1.2,1.5,2.0,2.5\}$
.
3.5. Summary of key modelling assumptions
Guided by previous experimental results and observations, a number of key modelling assumptions and simplifications have been made and these are as follows.
-
(i) The interfacial deflections occur within a circular region of finite radius.
-
(ii) The fountain, the dome and the plume occupy only a small fraction of the total volume of the box, so we may ignore the potential energies contained in these regions.
-
(iii) Interfacial deflections induce a flow predominantly within the zone of interfacial deflection.
-
(iv) Energy losses associated with the generation of interfacial waves and the energy dissipated due to viscous effects may be neglected in our analysis of the secondary flow.
-
(v) Persistent baroclinic vortices around the periphery of the dome are primarily responsible for entrainment into the dome.
-
(vi) The entrainment coefficients for the plume and the fountain are not significantly influenced by the secondary flow in the lower layer.
-
(vii) The available potential energy is apportioned equally between the kinetic energies of the secondary flows in the upper and lower layers.
Whilst the interfacial Froude number and the confinement parameter are instrumental in determining the entrainment flux across the interface, their values here are not specified a priori but span the range
![]() $0.1\lesssim {\it\lambda}_{i}\lesssim 1$
,
$0.1\lesssim {\it\lambda}_{i}\lesssim 1$
,
![]() $0.1\lesssim \mathit{Fr}_{i}\lesssim 1.4$
as a consequence of the system we consider (see figures 10 and 13).
$0.1\lesssim \mathit{Fr}_{i}\lesssim 1.4$
as a consequence of the system we consider (see figures 10 and 13).
4. Conclusions
Over the last five decades, a host of experimental studies have sought to determine the dimensionless volume flux
![]() $E_{i}$
turbulently entrained across a stable density interface. A wider understanding of this problem has been shrouded by the significant spread in the measurements of
$E_{i}$
turbulently entrained across a stable density interface. A wider understanding of this problem has been shrouded by the significant spread in the measurements of
![]() $E_{i}$
and by the conflicting power laws describing its dependence on the interfacial Froude number
$E_{i}$
and by the conflicting power laws describing its dependence on the interfacial Froude number
![]() $\mathit{Fr}_{i}$
. Whilst all experiments have been conducted, by necessity, within the confines of a (transparent) box or visual tank, the effects of confinement on interfacial entrainment have not been previously examined. Seeking to establish the role of confinement, we theoretically examined turbulent entrainment across an interface separating two uniform fluid masses within a box. Complexities associated with the time-dependent coupling between
$\mathit{Fr}_{i}$
. Whilst all experiments have been conducted, by necessity, within the confines of a (transparent) box or visual tank, the effects of confinement on interfacial entrainment have not been previously examined. Seeking to establish the role of confinement, we theoretically examined turbulent entrainment across an interface separating two uniform fluid masses within a box. Complexities associated with the time-dependent coupling between
![]() $E_{i}$
and the growth of a stratified intermediate layer were overcome by considering the steady two-layer stratification established by a turbulent plume and a turbulent fountain rising from the base of the box. The plume maintains the buoyant upper layer and the localised impingement of the fountain with the interface drives entrainment of fluid from the upper layer into the lower layer via an interfacial dome.
$E_{i}$
and the growth of a stratified intermediate layer were overcome by considering the steady two-layer stratification established by a turbulent plume and a turbulent fountain rising from the base of the box. The plume maintains the buoyant upper layer and the localised impingement of the fountain with the interface drives entrainment of fluid from the upper layer into the lower layer via an interfacial dome.
Guided by previous experimental studies, we developed a model describing the dynamics of fountain–interface interaction and the steady secondary flow in the environment that is induced and maintained by the perpetual cycle of interfacial deflections. We deduced that besides
![]() $\mathit{Fr}_{i}$
,
$\mathit{Fr}_{i}$
,
![]() $E_{i}$
is dependent on a confinement parameter
$E_{i}$
is dependent on a confinement parameter
![]() ${\it\lambda}_{i}$
which characterises the length scale of interfacial turbulence relative to the depth of the upper layer. For small
${\it\lambda}_{i}$
which characterises the length scale of interfacial turbulence relative to the depth of the upper layer. For small
![]() ${\it\lambda}_{i}$
, a weak secondary flow has little influence on
${\it\lambda}_{i}$
, a weak secondary flow has little influence on
![]() $E_{i}$
which is governed by a quadratic power law
$E_{i}$
which is governed by a quadratic power law
![]() $E_{i}\propto \mathit{Fr}_{i}^{2}$
. For large
$E_{i}\propto \mathit{Fr}_{i}^{2}$
. For large
![]() ${\it\lambda}_{i}$
, however,
${\it\lambda}_{i}$
, however,
![]() $E_{i}$
is significantly influenced by a strong secondary flow and is governed by a cubic power law
$E_{i}$
is significantly influenced by a strong secondary flow and is governed by a cubic power law
![]() $E_{i}\propto \mathit{Fr}_{i}^{3}$
. By establishing the range of
$E_{i}\propto \mathit{Fr}_{i}^{3}$
. By establishing the range of
![]() ${\it\lambda}_{i}$
that may be regarded as small and large, we classified the dynamics of confined interfacial entrainment into the weakly confined and strongly confined regimes.
${\it\lambda}_{i}$
that may be regarded as small and large, we classified the dynamics of confined interfacial entrainment into the weakly confined and strongly confined regimes.
Crucially, we established that a secondary flow persists for all box heights. Therefore, the effect of box confinement on
![]() $E_{i}$
is an inescapable feature of laboratory experiments. We showed that for previous experiments,
$E_{i}$
is an inescapable feature of laboratory experiments. We showed that for previous experiments,
![]() ${\it\lambda}_{i}$
varies in the range
${\it\lambda}_{i}$
varies in the range
![]() $0.1<{\it\lambda}_{i}<1$
. A key result from our model is that depending on
$0.1<{\it\lambda}_{i}<1$
. A key result from our model is that depending on
![]() ${\it\lambda}_{i}$
,
${\it\lambda}_{i}$
,
![]() $E_{i}$
can vary by up to an order of magnitude for a given
$E_{i}$
can vary by up to an order of magnitude for a given
![]() $\mathit{Fr}_{i}$
. Thus, the modification of
$\mathit{Fr}_{i}$
. Thus, the modification of
![]() $E_{i}$
due to the confinement provides a plausible physical explanation for the wide disparities evident in the existing data. Based on our model, we suggest that the effects of confinement on
$E_{i}$
due to the confinement provides a plausible physical explanation for the wide disparities evident in the existing data. Based on our model, we suggest that the effects of confinement on
![]() $E_{i}$
can be minimised by designing experimental configurations that satisfy
$E_{i}$
can be minimised by designing experimental configurations that satisfy
![]() ${\it\lambda}_{i}\ll 0.16\mathit{Fr}_{i}^{-2}$
.
${\it\lambda}_{i}\ll 0.16\mathit{Fr}_{i}^{-2}$
.
For unsteady experiments (e.g. Kumagai Reference Kumagai1984) wherein
![]() $E_{i}$
is inferred by tracking the position of a moving interface,
$E_{i}$
is inferred by tracking the position of a moving interface,
![]() ${\it\lambda}_{i}$
varies significantly with time, thereby compounding the inherent challenges associated with the pursuit of a universal relationship between
${\it\lambda}_{i}$
varies significantly with time, thereby compounding the inherent challenges associated with the pursuit of a universal relationship between
![]() $E_{i}$
and
$E_{i}$
and
![]() $\mathit{Fr}_{i}$
. To overcome this complexity, one could examine interfacial entrainment in a box whose width far exceeds its height. Measurements of
$\mathit{Fr}_{i}$
. To overcome this complexity, one could examine interfacial entrainment in a box whose width far exceeds its height. Measurements of
![]() $E_{i}$
can then be made prior to the interfacial gravity current reaching the side walls so that the interface position and
$E_{i}$
can then be made prior to the interfacial gravity current reaching the side walls so that the interface position and
![]() ${\it\lambda}_{i}$
remain constant. A second option is to consider a steady system. To this end, the steady two-layer stratification established by a plume and a fountain, as considered in this paper, provides a convenient means of measuring
${\it\lambda}_{i}$
remain constant. A second option is to consider a steady system. To this end, the steady two-layer stratification established by a plume and a fountain, as considered in this paper, provides a convenient means of measuring
![]() $E_{i}$
for a given
$E_{i}$
for a given
![]() ${\it\lambda}_{i}$
. With a view to guiding future experiments, we established (figure 14) box geometries which enable the contribution of confinement to the total entrainment flux to be bounded.
${\it\lambda}_{i}$
. With a view to guiding future experiments, we established (figure 14) box geometries which enable the contribution of confinement to the total entrainment flux to be bounded.
Our complementary studies of unconfined (Shrinivas & Hunt Reference Shrinivas and Hunt2014) and confined (herein)interfacial entrainmentelucidate the key physicsthat underpinsthe entrainment law
![]() $E_{i}\propto \mathit{Fr}_{i}^{n}$
. We have shown that
$E_{i}\propto \mathit{Fr}_{i}^{n}$
. We have shown that
![]() $n=1$
for large
$n=1$
for large
![]() $\mathit{Fr}_{i}$
,
$\mathit{Fr}_{i}$
,
![]() $n=2$
for small
$n=2$
for small
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() $n=3$
for large
$n=3$
for large
![]() ${\it\lambda}_{i}$
. The results and recommendations stemming from our investigation of confined entrainment may enable future studies to account for, or minimise, the effects of confinement in their experiments or numerical work. Nevertheless, the dependence of
${\it\lambda}_{i}$
. The results and recommendations stemming from our investigation of confined entrainment may enable future studies to account for, or minimise, the effects of confinement in their experiments or numerical work. Nevertheless, the dependence of
![]() $E_{i}$
on the confinement throws into question and challenges the notion of a universal entrainment law.
$E_{i}$
on the confinement throws into question and challenges the notion of a universal entrainment law.
Acknowledgements
The authors are grateful for the comments of anonymous referees.
Appendix A. Steadiness of the secondary flow
Linden (Reference Linden1974) and Shy (Reference Shy1995) showed that the time scale associated with the displacement of the interface is
![]() $T_{dis}\propto \sqrt{b_{i}/{\rm\Delta}g^{\prime }}$
. Prior to reaching the dome boundary, the secondary flow in the upper layer develops over the length scale
$T_{dis}\propto \sqrt{b_{i}/{\rm\Delta}g^{\prime }}$
. Prior to reaching the dome boundary, the secondary flow in the upper layer develops over the length scale
![]() $l_{A}+l_{\text{B}}$
(figure 6). Given that this flow is buoyancy-driven and is established within the zone of interfacial deflection of radial extent
$l_{A}+l_{\text{B}}$
(figure 6). Given that this flow is buoyancy-driven and is established within the zone of interfacial deflection of radial extent
![]() $r_{id}$
, its characteristic velocity scale is the buoyancy velocity
$r_{id}$
, its characteristic velocity scale is the buoyancy velocity
![]() $\sqrt{r_{id}{\rm\Delta}g^{\prime }}$
. Noting that
$\sqrt{r_{id}{\rm\Delta}g^{\prime }}$
. Noting that
![]() $l_{\text{A}}+l_{B}\approx 1.65b_{i}$
and
$l_{\text{A}}+l_{B}\approx 1.65b_{i}$
and
![]() $r_{id}=2.65b_{i}$
, the time scale for the secondary flow is
$r_{id}=2.65b_{i}$
, the time scale for the secondary flow is
Therefore,
i.e. the time scale associated with the interfacial deflections is approximately the same as the time scale for the secondary flow. Therefore, one would anticipate the secondary flow to be quasi-steady.
Appendix B. Potential energy of two-layer fluid in the displaced state and equilibrium state
For
![]() $r>r_{id}$
, the depths of the upper and lower layers are unaffected by interfacial tilting. Hence, the potential energy outside the zone of interfacial deflection
$r>r_{id}$
, the depths of the upper and lower layers are unaffected by interfacial tilting. Hence, the potential energy outside the zone of interfacial deflection
![]() $\text{PE}_{out}$
remains unchanged from the equilibrium state. The potential energy of the two-layer fluid in the displaced state is then
$\text{PE}_{out}$
remains unchanged from the equilibrium state. The potential energy of the two-layer fluid in the displaced state is then
where
![]() $V$
denotes volume and
$V$
denotes volume and
![]() $D=H-h$
is the upper-layer depth of the equilibrium state. In (B 1) we have implicitly assumed that the fountain, the dome and the plume occupy only a small fraction of the total volume of the box so we may ignore the potential energies contained in these regions. By definition, the non-zero potential energy of the equilibrium state
$D=H-h$
is the upper-layer depth of the equilibrium state. In (B 1) we have implicitly assumed that the fountain, the dome and the plume occupy only a small fraction of the total volume of the box so we may ignore the potential energies contained in these regions. By definition, the non-zero potential energy of the equilibrium state
![]() $\text{PE}_{eq}$
cannot be reduced by any adiabatic rearrangement of fluid parcels and hence this energy is unavailable for conversion into kinetic energy of fluid motion. Given that
$\text{PE}_{eq}$
cannot be reduced by any adiabatic rearrangement of fluid parcels and hence this energy is unavailable for conversion into kinetic energy of fluid motion. Given that
and
![]() $\text{PE}_{dis}>\text{PE}_{eq}$
, subtracting (B 2) from (B 1) gives the available potential energy APE (2.14).
$\text{PE}_{dis}>\text{PE}_{eq}$
, subtracting (B 2) from (B 1) gives the available potential energy APE (2.14).
Appendix C. Buoyancy of the impinging fountain
We seek the buoyancy
![]() $g_{i}^{\prime }$
(2.19) of the fluid supplied by the impinging fountain to the interfacial dome (figure 7). Conservation of buoyancy for the dome requires
$g_{i}^{\prime }$
(2.19) of the fluid supplied by the impinging fountain to the interfacial dome (figure 7). Conservation of buoyancy for the dome requires
where
![]() $Q_{i}$
and
$Q_{i}$
and
![]() $Q_{d}$
are the fluxes of volume into and out of the dome, respectively. The outflow from the dome via the annular region is turbulently mixed with the fluid in the lower layer. This is consistent with our argument (§ 2.4) that the fountain’s downflow (which is fed by the outflow from the dome) is fully incorporated into the lower layer. Our model assumes that the upper and lower layers are of uniform density. Thus, the density
$Q_{d}$
are the fluxes of volume into and out of the dome, respectively. The outflow from the dome via the annular region is turbulently mixed with the fluid in the lower layer. This is consistent with our argument (§ 2.4) that the fountain’s downflow (which is fed by the outflow from the dome) is fully incorporated into the lower layer. Our model assumes that the upper and lower layers are of uniform density. Thus, the density
![]() ${\it\rho}_{d}$
of the fluid entering the lower layer equals the density of the lower layer. As
${\it\rho}_{d}$
of the fluid entering the lower layer equals the density of the lower layer. As
![]() $Q_{d}=Q_{i}+Q_{e}$
, substituting
$Q_{d}=Q_{i}+Q_{e}$
, substituting
![]() ${\it\rho}_{d}={\it\rho}_{1}$
in (C 1) gives
${\it\rho}_{d}={\it\rho}_{1}$
in (C 1) gives
Owing to the dependence of
![]() ${\check{g}}_{i}^{\prime }$
on
${\check{g}}_{i}^{\prime }$
on
![]() $E_{i}$
, it is no longer possible to analytically solve (2.20) for
$E_{i}$
, it is no longer possible to analytically solve (2.20) for
![]() $E_{i}$
. To proceed, we non-dimensionalise equation (2.28) describing the entrainment mechanism for the dome. We recall that the equations describing the conservation of volume and momentum for the dome were combined to form a single expression (2.20). Thus, the non-dimensional equations governing
$E_{i}$
. To proceed, we non-dimensionalise equation (2.28) describing the entrainment mechanism for the dome. We recall that the equations describing the conservation of volume and momentum for the dome were combined to form a single expression (2.20). Thus, the non-dimensional equations governing
![]() $E_{i}$
are, from (2.20) and (2.28), respectively,
$E_{i}$
are, from (2.20) and (2.28), respectively,
Noting that the quantities
![]() $\hat{z}_{d}$
,
$\hat{z}_{d}$
,
![]() $\tilde{u} _{2}$
and
$\tilde{u} _{2}$
and
![]() ${\check{g}}_{i}^{\prime }$
are given by (2.29), (2.16) and (C 2), respectively, (C 3) can be solved to obtain
${\check{g}}_{i}^{\prime }$
are given by (2.29), (2.16) and (C 2), respectively, (C 3) can be solved to obtain
![]() $E_{i}$
for a given
$E_{i}$
for a given
![]() $\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
. To calculate
$\{\mathit{Fr}_{i},{\it\lambda}_{i}\}$
. To calculate
![]() $\mathit{Fr}_{i}$
and
$\mathit{Fr}_{i}$
and
![]() ${\it\lambda}_{i}$
, we follow the solution procedure outlined in § 2.4. Figure 15 plots
${\it\lambda}_{i}$
, we follow the solution procedure outlined in § 2.4. Figure 15 plots
![]() $E_{i}$
against
$E_{i}$
against
![]() $\mathit{Fr}_{i}$
for
$\mathit{Fr}_{i}$
for
![]() ${\check{g}}_{i}^{\prime }=1$
and when
${\check{g}}_{i}^{\prime }=1$
and when
![]() ${\check{g}}_{i}^{\prime }$
is given by (C 2). Evidently, the two solutions are graphically indistinguishable for
${\check{g}}_{i}^{\prime }$
is given by (C 2). Evidently, the two solutions are graphically indistinguishable for
![]() $\mathit{Fr}_{i}\lesssim 0.6$
and the difference between the solutions is less than 4 % at
$\mathit{Fr}_{i}\lesssim 0.6$
and the difference between the solutions is less than 4 % at
![]() $\mathit{Fr}_{i}=0.8$
. Hence, our simplifying assumption that
$\mathit{Fr}_{i}=0.8$
. Hence, our simplifying assumption that
![]() ${\check{g}}_{i}^{\prime }\approx 1$
has only a minor effect on the final solution. This simplification enables us to obtain an analytic solution (2.33) for
${\check{g}}_{i}^{\prime }\approx 1$
has only a minor effect on the final solution. This simplification enables us to obtain an analytic solution (2.33) for
![]() $E_{i}$
and deduce the scaling of
$E_{i}$
and deduce the scaling of
![]() $E_{i}$
on
$E_{i}$
on
![]() $\mathit{Fr}_{i}$
in the small-
$\mathit{Fr}_{i}$
in the small-
![]() ${\it\lambda}_{i}$
and large-
${\it\lambda}_{i}$
and large-
![]() ${\it\lambda}_{i}$
limits.
${\it\lambda}_{i}$
limits.

Figure 15. Entrainment flux
![]() $E_{i}$
against interfacial Froude number
$E_{i}$
against interfacial Froude number
![]() $\mathit{Fr}_{i}$
for
$\mathit{Fr}_{i}$
for
![]() ${\check{g}}_{i}^{\prime }=1$
(dashed line) and when
${\check{g}}_{i}^{\prime }=1$
(dashed line) and when
![]() ${\check{g}}_{i}^{\prime }$
is given by (C 2) (solid line). Solutions obtained for
${\check{g}}_{i}^{\prime }$
is given by (C 2) (solid line). Solutions obtained for
![]() ${\it\psi}=25$
and
${\it\psi}=25$
and
![]() $\mathscr{L}=0.1$
.
$\mathscr{L}=0.1$
.
Appendix D. Simplified solution for the entrainment flux
 $E_{i}$
$E_{i}$
For
![]() $\mathit{Fr}_{i}<1$
and
$\mathit{Fr}_{i}<1$
and
![]() ${\it\lambda}_{i}<1$
, a two-step procedure reduces (2.32) to a simple analytic solution that closely approximates the full solution. First, as
${\it\lambda}_{i}<1$
, a two-step procedure reduces (2.32) to a simple analytic solution that closely approximates the full solution. First, as
![]() $B\approx 0.94$
(2.29), the third term within the parenthesis of (2.31a
) is sufficiently small compared with
$B\approx 0.94$
(2.29), the third term within the parenthesis of (2.31a
) is sufficiently small compared with
![]() $2B/3$
that it may be neglected when
$2B/3$
that it may be neglected when
![]() $a_{3}^{2}\ll 2B/3\approx 0.6$
. Second, with
$a_{3}^{2}\ll 2B/3\approx 0.6$
. Second, with
![]() $C\approx 0.16$
(2.28), upon examining the relative magnitudes of the two terms
$C\approx 0.16$
(2.28), upon examining the relative magnitudes of the two terms
![]() $((a_{2}/2)^{2},(a_{1}/3)^{3})$
within the square-root in (2.32), we find that
$((a_{2}/2)^{2},(a_{1}/3)^{3})$
within the square-root in (2.32), we find that
Noting that our approximation holds for
![]() ${\it\lambda}_{i}\ll 0.9$
when
${\it\lambda}_{i}\ll 0.9$
when
![]() $\mathit{Fr}_{i}=1$
, and given that
$\mathit{Fr}_{i}=1$
, and given that
![]() ${\it\lambda}_{i}$
is inversely proportional to
${\it\lambda}_{i}$
is inversely proportional to
![]() $\mathit{Fr}_{i}$
, this constraint (D 1) on
$\mathit{Fr}_{i}$
, this constraint (D 1) on
![]() ${\it\lambda}_{i}$
is satisfied for the range of
${\it\lambda}_{i}$
is satisfied for the range of
![]() $\mathit{Fr}_{i}$
considered. Restricting our attention to these values of
$\mathit{Fr}_{i}$
considered. Restricting our attention to these values of
![]() ${\it\lambda}_{i}$
, we may simplify the full solution (2.32) to
${\it\lambda}_{i}$
, we may simplify the full solution (2.32) to
where
![]() $\text{i}=\sqrt{-1}$
. The only solutions for
$\text{i}=\sqrt{-1}$
. The only solutions for
![]() $\text{i}^{1/3}$
and
$\text{i}^{1/3}$
and
![]() $(-\text{i})^{1/3}$
that yield real, positive values of
$(-\text{i})^{1/3}$
that yield real, positive values of
![]() $E_{i}$
are
$E_{i}$
are
![]() $\text{i}^{1/3}=(\sqrt{3}+\text{i})/2$
and
$\text{i}^{1/3}=(\sqrt{3}+\text{i})/2$
and
![]() $(-\text{i})^{1/3}=(\sqrt{3}-\text{i})/2$
. Substituting
$(-\text{i})^{1/3}=(\sqrt{3}-\text{i})/2$
. Substituting
![]() $\text{i}^{1/3}=(\sqrt{3}+\text{i})/2$
and
$\text{i}^{1/3}=(\sqrt{3}+\text{i})/2$
and
![]() $(-\text{i})^{1/3}=(\sqrt{3}-\text{i})/2$
in (D 2) gives the analytic solution (2.33).
$(-\text{i})^{1/3}=(\sqrt{3}-\text{i})/2$
in (D 2) gives the analytic solution (2.33).