1 Introduction
Various microfluidic applications exploit multiphase flow of different types (Gunther & Jensen Reference Gunther and Jensen2006; Zhao Reference Zhao2013). One of them, called slug or segmented flow (Cahill Reference Cahill, Köhler and Cahill2014), is often generated at T or Y bifurcations of microfluidic channels (Dessimoz et al. Reference Dessimoz, Cavin, Renken and Kiwi-Minsker2008) or in flow-focusing devices (Li et al. Reference Li, Yamane, Li, Biswas, Reddy, Goettert, Nandakumar and Kumar2013). Two-phase flows of two immiscible liquids or gas–liquid flows are usually formed; however, more complex three-phase systems such as gas–(liquid–liquid) flows have been reported (Cech, Pribyl & Snita Reference Cech, Pribyl and Snita2013; Ladosz, Rigger & von Rohr Reference Ladosz, Rigger and von Rohr2016). Slug flow is characterized by continuous formation of small droplets or bubbles of one phase regularly dispersed in another immiscible phase. Droplets then move along a microfluidic channel or microcapillary. Regular separation of phases provides constant residence time of all slugs in a microfluidic device (Arndt, Thoming & Baumer Reference Arndt, Thoming and Baumer2013). Moreover, both phases are intensively stirred due to internal circulation, which has been predicted theoretically (Kashid et al. Reference Kashid, Gerlach, Goetz, Franzke, Acker, Platte, Agar and Turek2005) and confirmed experimentally (Meyer, Hoffmann & Schluter Reference Meyer, Hoffmann and Schluter2014). Slug flow also enhances mass transport in microreactors or microseparators due to the large interfacial area (Kashid & Agar Reference Kashid and Agar2007; Ghaini, Kashid & Agar Reference Ghaini, Kashid and Agar2010). There are many possibilities in terms of how to arrange a chemical reaction in a slug flow. One phase can serve as the reaction phase and the other phase as a simple separator, reservoir of reactants, catalyst or product container (Jovanovic et al. Reference Jovanovic, Rebrov, Nijhuis, Hessel and Schouten2010). The chemical or biological reaction can be confined to the interface itself (Cech et al. Reference Cech, Schrott, Slouka, Pribyl, Broz, Kuncova and Snita2012). Microchips for cellular and toxicology studies (Cao & Köhler Reference Cao and Köhler2015) and particle generators (Testino et al. Reference Testino, Pilger, Lucchini, Quinsaat, Staehli and Bowen2015) are among other applications of slug flow microdevices.
It is necessary to reliably control droplet transport in slug flow devices. Systems of precise dosing pumps sometimes coupled with different types of valves represent classical solutions of flow control (Iverson & Garimella Reference Iverson and Garimella2008). Flow in microfluidic devices is typically coupled with the use of expensive pumps that are able to overcome high pressure drops (Jovanovic et al. Reference Jovanovic, Zhou, Rebrov, Nijhuis, Hessel and Schouten2011). Electrokinetic phenomena represent alternatives to pressure-driven pumping (Wang et al. Reference Wang, Cheng, Wang and Liu2009). Aqueous electrolytes can be transported in a microfluidic structure by electroosmotic convection arising from the interaction of an imposed electric field and free electric charge formed at polarized microchannel walls; see e.g. Hrdlicka et al. (Reference Hrdlicka, Cervenka, Pribyl and Snita2010) and Hrdlicka et al. (Reference Hrdlicka, Cervenka, Jindra, Pribyl and Snita2013). Here we focus on a two-phase system with an aqueous droplet placed in a dielectric medium. Link et al. (Reference Link, Grasland-Mongrain, Duri, Sarrazin, Cheng, Cristobal, Marquez and Weitz2006) showed that an aqueous droplet can be efficiently addressed (transported to a specific place of a microfluidic chip) by a direct current (DC) electric field of proper strength and orientation in a complex microfluidic structure. An aqueous droplet is electrically charged at an electrode by electrochemical reaction in the first step. A DC electric field is then applied between two or more electrodes properly placed in a microfluidic chip. The Coulomb force attracts the droplet to the oppositely charged electrode and thus provides the addressing (i.e. controlled droplet motion to a particular place on a microfluidic chip). The same type of droplet addressing was used, for example, in Ahn et al. (Reference Ahn, Lee, Louge and Oh2009) and Ahn et al. (Reference Ahn, Lee, Panchapakesan and Oh2011). Recently, the Coulombic and dielectrophoretic contributions to the total electric force in different microelectrode arrangements were evaluated, which can aid in the efficient design of addressing microdevices (Ahn et al. Reference Ahn, Im, Yoo and Kang2015). Other phenomena such as electrocoalescence and droplet breakup (Bartlett, Genero & Bird Reference Bartlett, Genero and Bird2015) can also contribute to efficient droplet addressing.
Several research groups have reported oscillatory or rhythmic motion under a DC electric field in the system formed by an aqueous droplet, dielectric fluid and a pair of electrodes (Hase, Watanabe & Yoshikawa Reference Hase, Watanabe and Yoshikawa2006; Jung, Oh & Kang Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Mhatre & Thaokar Reference Mhatre and Thaokar2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). The oscillatory behaviour is caused by periodical injections of electric charge at one and the other electrode. Initially a charged droplet is attracted to the oppositely charged electrode. When the droplet touches the electrode, the electric charge polarity in the droplet is reversed due to a fast electrochemical reaction and the droplet is repelled back to the other electrode (Im et al. Reference Im, Ahn, Yoo, Moon, Lee and Kang2012). This process is periodic and depends on the electric field strength, composition of both phases and geometry of the system. Rhythmic motion has been observed in systems of two horizontal rod electrodes (Hase et al. Reference Hase, Watanabe and Yoshikawa2006), vertical parallel plate electrodes (Jung et al. Reference Jung, Oh and Kang2008; Jalaal, Khorshidi & Esmaeilzadeh Reference Jalaal, Khorshidi and Esmaeilzadeh2010; Im et al. Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012) and tip electrodes (Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013). The first investigation of droplet rhythmic motion in microfludic chips was reported in Beranek et al. (Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). It was found that the frequency of the droplet oscillations depends on the electric field strength, the ionic strength inside aqueous droplets and the electrode arrangement. The effects of the dielectrophoretic force on rhythmic motion in experimental systems with a non-homogeneous electric field have also been shown (Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Mhatre & Thaokar Reference Mhatre and Thaokar2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). Recently, it was shown that the presence of white noise enhances the regularity of droplet oscillation due to the coherent resonance phenomenon (Kurimura & Ichikawa Reference Kurimura and Ichikawa2016). Oscillatory behaviour in a DC electric field is not limited to aqueous droplets; for example, silver-coated glass particles were placed in a dielectric fluid and exhibited rhythmic motion, thereby providing intensive fluid mixing (Cartier, Drews & Bishop Reference Cartier, Drews and Bishop2014).
Mathematical models of droplet motion are usually based on simple force analysis (Hase et al. Reference Hase, Watanabe and Yoshikawa2006; Jung et al. Reference Jung, Oh and Kang2008; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Mhatre & Thaokar Reference Mhatre and Thaokar2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014) or force analysis derived from a detailed knowledge of the electric field around droplets (Ahn et al. Reference Ahn, Im, Yoo and Kang2015). They can be used to estimate the amount of electric charge stored in a droplet or the effective electrophoretic mobility. However, these models are not able to reveal the flow field in both phases, the pressure distribution or the character of droplet deformation during charge reversal. The growing power of computers and powerful numerical schemes allow for simulation of complex electrokinetics and electrohydrodynamics problems such as two-phase flow under an imposed electric field, electrowetting or Taylor cone phenomena (Saville Reference Saville1997; Zeng & Korsmeyer Reference Zeng and Korsmeyer2004; Bazant Reference Bazant2015; Schnitzer & Yariv Reference Schnitzer and Yariv2015). Lin, Skjetne & Carlson (Reference Lin, Skjetne and Carlson2012) formulated a phase field mathematical model based on the Cahn–Hilliard equation to study droplet deformation and electrocoalescence. Their two-phase model considered constant dielectric constants and conductivities in the bulk of each phase. Collins et al. (Reference Collins, Sambath, Harris and Basaran2013) developed a two-phase model for simulation of the Taylor cone formation and jetting of charged microdroplets from cone tips. They discovered scaling rules for the microdroplet formation. The presence of free electric charge was considered only on the interface. A spatially three-dimensional (3-D) mathematical model of slug flow under an imposed electric field was reported in Wehking & Kumar (Reference Wehking and Kumar2015). The model predicted induced deformations of flowing droplets previously observed in experiments. Wallau, Schlawitschek & Arellano-Garcia (Reference Wallau, Schlawitschek and Arellano-Garcia2016) developed a two-phase flow model to study merging of aqueous droplets under an imposed electric field. The model equation considers dielectrophoretic attraction of the droplets, but the effect of free electric charge is neglected. Recently, Pillai et al. (Reference Pillai, Berry, Harvie and Davidson2016) used Berry’s model (Berry, Davidson & Harvie Reference Berry, Davidson and Harvie2013) of two-phase flow to investigate deformation and jetting in the system formed by a droplet with ion charge carriers and an outer dielectric fluid. This model allows for the evaluation of free electric charge distribution in an electric double layer (EDL) localized at the interface. This sophisticated approach is applicable to systems with the ratio of the droplet diameter to the Debye layer thickness not much exceeding a value of one.
Here, we formulate a mathematical model of an axisymmetric cylindrical cell with an oscillating and deformable droplet. The momentum balances, together with the continuity equation and the Poisson equation, are numerically solved. To track the liquid–liquid interface, the level-set method is employed. The electrochemical charge injection occurring at the droplet–electrode interface is also included in the model. Although several simplifications are made, the model is able to qualitatively and meaningfully predict droplet behaviour. The paper is organized as follows. A detailed description of the model domain and governing equations and the validation of the numerical method are provided in the next section. The results and discussion section introduces the dynamics of droplet behaviour and displays snapshots of selected flow patterns. Furthermore, results of several studies focused on the effects of selected model parameters on the frequency of oscillations and other characteristics are discussed.
2 Governing equations and numerical methods
2.1 Model domain
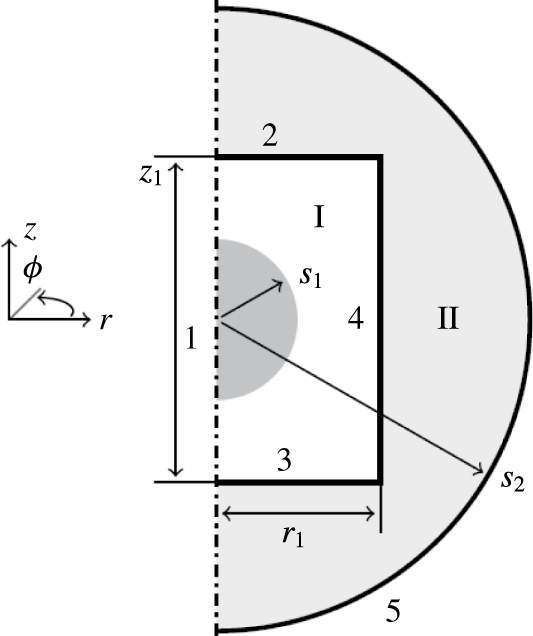
To avoid 3-D dynamical simulation of the model equations, an axisymmetric geometry is considered, as shown in figure 1. The cylindrical domain I contains an aqueous droplet immersed in a dielectric fluid. The domain is surrounded by circular electrodes (boundaries 2 and 3), a solid wall (boundary 4) and the axis of symmetry (boundary 1). The droplet moves between the electrodes, where it undergoes charge reversal due to electrochemical reactions. We assumed that the entire domain I is placed in a dielectric medium (domain II) surrounded by a ground electrode.
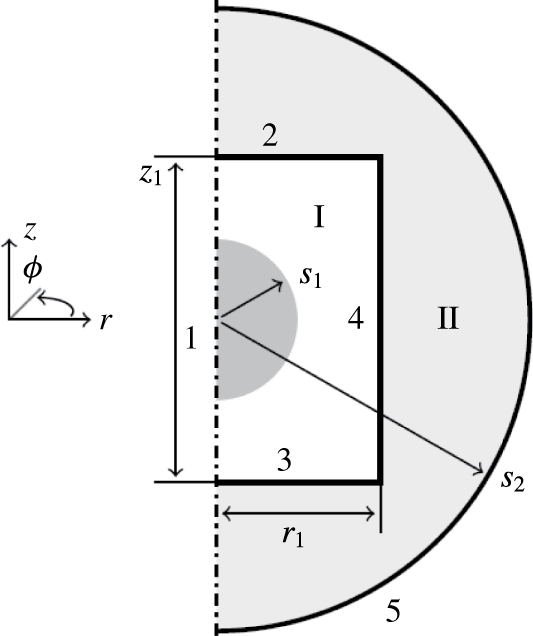
Figure 1. Domain geometry. Arabic and roman numerals denote boundary and domain indexes, respectively. The grey area represents the initial position of the droplet. The symbols
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
,
$s_{2}$
,
![]() $r_{1}$
and
$r_{1}$
and
![]() $z_{1}$
denote the initial droplet radius, radius of the grounded electrode, radius of the circular electrodes and spacing between the circular electrodes.
$z_{1}$
denote the initial droplet radius, radius of the grounded electrode, radius of the circular electrodes and spacing between the circular electrodes.
2.2 Governing equation and the main assumptions
Because both liquids in domain I are incompressible and Newtonian, the velocity and pressure fields are described by the Navier–Stokes and continuity equations
where the symbols
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D707}$
,
![]() $t$
,
$t$
,
![]() $p$
and
$p$
and
![]() $\boldsymbol{v}$
denote the liquid density, liquid dynamical viscosity, time, pressure and velocity vector, respectively. The symbols
$\boldsymbol{v}$
denote the liquid density, liquid dynamical viscosity, time, pressure and velocity vector, respectively. The symbols
![]() $\boldsymbol{f}_{e}$
,
$\boldsymbol{f}_{e}$
,
![]() $\boldsymbol{f}_{s}$
and
$\boldsymbol{f}_{s}$
and
![]() $\boldsymbol{f}_{g}$
represent volume forces in the system.
$\boldsymbol{f}_{g}$
represent volume forces in the system.
The inertial term in the Navier–Stokes equations is considered because the values of the Reynolds number (
![]() $Re$
) in experiments reported in Beranek et al. (Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014) were typically higher than 10. In such cases, the inertial forces in the fluid bulk dominate the viscous forces. As will be shown in § 3.1, our simulations predict
$Re$
) in experiments reported in Beranek et al. (Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014) were typically higher than 10. In such cases, the inertial forces in the fluid bulk dominate the viscous forces. As will be shown in § 3.1, our simulations predict
![]() $Re>100$
in some regimes.
$Re>100$
in some regimes.
The electric volume force
![]() $\boldsymbol{f}_{e}$
can be expressed as either the divergence of the Maxwell stress tensor (Saville Reference Saville1997) or the Korteweg–Helmholtz force density (Grodzinsky Reference Grodzinsky2011), which reads
$\boldsymbol{f}_{e}$
can be expressed as either the divergence of the Maxwell stress tensor (Saville Reference Saville1997) or the Korteweg–Helmholtz force density (Grodzinsky Reference Grodzinsky2011), which reads
where
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $\unicode[STIX]{x1D714}$
are the fluid permittivity and volume density of free electric charge. The first term on the right-hand side of (2.3) is called the electrostriction force density and is typically lumped with the pressure gradient in (2.1), which leads to a modified definition of pressure (Saville Reference Saville1997). Hence this term was not included in our study. The second and third terms come from the interactions between electric field and dipoles and between electric field and free charges, respectively. The dipole term is important in many electrohydrodynamics problems such as dielectrophoresis or droplet breakup. However, the mechanism of rhythmic droplet motion between two parallel electrodes is mainly driven by the interaction of injected free charge and imposed electric field (Jung et al.
Reference Jung, Oh and Kang2008; Jalaal et al.
Reference Jalaal, Khorshidi and Esmaeilzadeh2010; Im et al.
Reference Im, Noh, Moon and Kang2011). If the droplet will not be in the proximity of an electrode, the net dielectric force will be close to zero and will not significantly contribute to the droplet forcing. For that reason, only the term containing free electric charge is considered in our simulations.
$\unicode[STIX]{x1D714}$
are the fluid permittivity and volume density of free electric charge. The first term on the right-hand side of (2.3) is called the electrostriction force density and is typically lumped with the pressure gradient in (2.1), which leads to a modified definition of pressure (Saville Reference Saville1997). Hence this term was not included in our study. The second and third terms come from the interactions between electric field and dipoles and between electric field and free charges, respectively. The dipole term is important in many electrohydrodynamics problems such as dielectrophoresis or droplet breakup. However, the mechanism of rhythmic droplet motion between two parallel electrodes is mainly driven by the interaction of injected free charge and imposed electric field (Jung et al.
Reference Jung, Oh and Kang2008; Jalaal et al.
Reference Jalaal, Khorshidi and Esmaeilzadeh2010; Im et al.
Reference Im, Noh, Moon and Kang2011). If the droplet will not be in the proximity of an electrode, the net dielectric force will be close to zero and will not significantly contribute to the droplet forcing. For that reason, only the term containing free electric charge is considered in our simulations.
The formulation of the surface tension force in the form of divergence of the capillary pressure tensor
![]() $\boldsymbol{f}_{s}$
was adopted from Lafaurie et al. (Reference Lafaurie, Nardone, Scardovelli, Zaleski and Zanetti1994):
$\boldsymbol{f}_{s}$
was adopted from Lafaurie et al. (Reference Lafaurie, Nardone, Scardovelli, Zaleski and Zanetti1994):
where
![]() $\boldsymbol{I}$
,
$\boldsymbol{I}$
,
![]() $\boldsymbol{n}$
,
$\boldsymbol{n}$
,
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
are the unit tensor, normal vector to the liquid–liquid interface, interfacial tension and Dirac delta function (further defined in § 2.4), respectively.
$\unicode[STIX]{x1D6FF}$
are the unit tensor, normal vector to the liquid–liquid interface, interfacial tension and Dirac delta function (further defined in § 2.4), respectively.
The gravity volume force
![]() $\boldsymbol{f}_{g}$
is not involved in the Navier–Stokes equation due to the typically horizontal orientation of the microfluidic devices. In physical experiments with parallel plate electrodes, e.g. Im et al. (Reference Im, Noh, Moon and Kang2011), a highly viscous organic phase is used as well as large electrodes and an organic phase with density similar to that of water. All these measures suppress the effect of the gravity force.
$\boldsymbol{f}_{g}$
is not involved in the Navier–Stokes equation due to the typically horizontal orientation of the microfluidic devices. In physical experiments with parallel plate electrodes, e.g. Im et al. (Reference Im, Noh, Moon and Kang2011), a highly viscous organic phase is used as well as large electrodes and an organic phase with density similar to that of water. All these measures suppress the effect of the gravity force.
The liquid–liquid interface is tracked by means of the level-set method (Olsson & Kreiss Reference Olsson and Kreiss2005). Local values of the level-set function
![]() $\unicode[STIX]{x1D713}$
are calculated from
$\unicode[STIX]{x1D713}$
are calculated from
The symbol
![]() $R_{ls}$
represents a stabilizing term of the level-set method that is further discussed in § 2.4. The level-set function
$R_{ls}$
represents a stabilizing term of the level-set method that is further discussed in § 2.4. The level-set function
![]() $\unicode[STIX]{x1D713}\rightarrow 0$
in the dielectric liquid and
$\unicode[STIX]{x1D713}\rightarrow 0$
in the dielectric liquid and
![]() $\unicode[STIX]{x1D713}\rightarrow 1$
in the aqueous droplet. Physical properties of the liquids in domain I are then calculated using the level-set function
$\unicode[STIX]{x1D713}\rightarrow 1$
in the aqueous droplet. Physical properties of the liquids in domain I are then calculated using the level-set function
In electroquasistatic systems (Grodzinsky Reference Grodzinsky2011), the electric field
![]() $\boldsymbol{E}$
can be evaluated from
$\boldsymbol{E}$
can be evaluated from
where
![]() $\unicode[STIX]{x1D719}$
is the electric potential. The distribution of the electric potential is given by the Gauss law in the form of Poisson’s equation,
$\unicode[STIX]{x1D719}$
is the electric potential. The distribution of the electric potential is given by the Gauss law in the form of Poisson’s equation,
Due to the relatively high electrolytic conductivity of the aqueous phase, free electric charge will be collected in a thin EDL at the interface. The characteristic thickness of the EDL is called the Debye length and for a uni-univalent electrolyte (Hrdlicka et al. Reference Hrdlicka, Cervenka, Jindra, Pribyl and Snita2013) it is given by
where
![]() $R$
,
$R$
,
![]() $T$
,
$T$
,
![]() $c$
and
$c$
and
![]() $F$
are the molar gas constant, temperature, electrolyte concentration and Faradaic constant, respectively. Depending on the concentration, the Debye length in aqueous system ranges from
$F$
are the molar gas constant, temperature, electrolyte concentration and Faradaic constant, respectively. Depending on the concentration, the Debye length in aqueous system ranges from
![]() $1\times 10^{-10}$
to
$1\times 10^{-10}$
to
![]() $1\times 10^{-7}$
m. It is difficult to numerically solve dynamical problems where geometrical dimensions are several orders of magnitude larger than the Debye thickness. Pillai et al. (Reference Pillai, Berry, Harvie and Davidson2016) were able to simulate two-phase systems with the ratio of the droplet diameter to the Debye layer thickness equal to 25. The characteristic geometric dimensions of our system are
$1\times 10^{-7}$
m. It is difficult to numerically solve dynamical problems where geometrical dimensions are several orders of magnitude larger than the Debye thickness. Pillai et al. (Reference Pillai, Berry, Harvie and Davidson2016) were able to simulate two-phase systems with the ratio of the droplet diameter to the Debye layer thickness equal to 25. The characteristic geometric dimensions of our system are
![]() ${\sim}1\times 10^{-3}$
m. Thus the ratio ranges from
${\sim}1\times 10^{-3}$
m. Thus the ratio ranges from
![]() $1\times 10^{4}$
to
$1\times 10^{4}$
to
![]() $1\times 10^{7}$
. Solution of such problems is nearly impossible even if boundaries are non-moving (Hrdlicka et al.
Reference Hrdlicka, Cervenka, Pribyl and Snita2010). Instead we consider that an aqueous droplet is homogeneously charged. The volume concentration of electric charge within the droplet is
$1\times 10^{7}$
. Solution of such problems is nearly impossible even if boundaries are non-moving (Hrdlicka et al.
Reference Hrdlicka, Cervenka, Pribyl and Snita2010). Instead we consider that an aqueous droplet is homogeneously charged. The volume concentration of electric charge within the droplet is
![]() $\unicode[STIX]{x1D714}_{w}$
. This assumption makes it impossible to simulate jetting or Taylor cone formation. Moreover, the estimation of the dielectric force at the interface (not used in our study because the second right-hand term of (2.3) is neglected) would be imprecise due to a different distribution of the electric field within the droplet. However, it is still efficient to investigate the motion of electrically charged objects in an electric field and to study electrochemical charge injection at the electrodes. The volume density of free electric charge in domain I reads
$\unicode[STIX]{x1D714}_{w}$
. This assumption makes it impossible to simulate jetting or Taylor cone formation. Moreover, the estimation of the dielectric force at the interface (not used in our study because the second right-hand term of (2.3) is neglected) would be imprecise due to a different distribution of the electric field within the droplet. However, it is still efficient to investigate the motion of electrically charged objects in an electric field and to study electrochemical charge injection at the electrodes. The volume density of free electric charge in domain I reads
Other approaches for the treatment of the electric charge distribution in the droplet can be taken into account. For example, the problem can be divided into electric and fluid parts. In the electric part, the electric potential inside the droplet can be set in an iterative manner in order to conserve the surface electric charge of a droplet not attached to an electrode. The obtained field of electric potential can be used in the next integration step to obtain the velocity, pressure and level-set variable distribution. This procedure is extremely time consuming. Moreover, artificial redistribution of the electric charge on the droplet surface will locally violate the velocity field (2.1) and thus also the position of the interface and shape of the droplet. Other problems of this approach originate from the properties of the level-set method. The level-set function is smooth in the spatial domain and the sharpness of the interface is given by the density of finite elements which is, of course, limited. Physical fields (electric potential, velocity, pressure) are represented by the same variables in both phases. The level-set function smoothly switches physical properties such as electric permittivity. So it is difficult and maybe impossible to define the electric potential at an exact coordinate of the interface in each integration step.
As domains I and II are not hydrodynamically coupled, only the distribution of the electric potential is necessary to determine in domain II by the Laplace equation
In principle, it is not necessary to include domain II in the system geometry. However, it significantly helps with stability of the numerical simulations. One can imagine domain II as a cavity filled with air or other dielectric material and surrounded by a grounded Faradaic cage.
We have to consider electric charge balances to describe the electron transfer between the droplet and an electrode. Electrochemical reactions are typically limited by the electrochemical process itself or by mass transport under low or high overpotential (Bard & Faulkner Reference Bard and Faulkner2001; Cervenka et al.
Reference Cervenka, Hrdlicka, Pribyl and Snita2012). Because the electric field in experiments with oscillating droplets is typically
![]() ${\sim}10^{5}~\text{V}~\text{m}^{-1}$
, a regime limited by mass transport is more probable. We note that under low-intensity electric fields, one has to use Butler–Volmer kinetics or its modification to describe the process (Bard & Faulkner Reference Bard and Faulkner2001). The following charge balance at the electrode–electrolyte interface can then be written
${\sim}10^{5}~\text{V}~\text{m}^{-1}$
, a regime limited by mass transport is more probable. We note that under low-intensity electric fields, one has to use Butler–Volmer kinetics or its modification to describe the process (Bard & Faulkner Reference Bard and Faulkner2001). The following charge balance at the electrode–electrolyte interface can then be written
where
![]() $V_{d}$
is the droplet volume,
$V_{d}$
is the droplet volume,
![]() $\unicode[STIX]{x1D705}$
is the electrolytic conductivity of the aqueous droplet (alternatively it can be understood as a mass transfer coefficient) and
$\unicode[STIX]{x1D705}$
is the electrolytic conductivity of the aqueous droplet (alternatively it can be understood as a mass transfer coefficient) and
![]() $A$
is the droplet–electrode interfacial area. The electric field strength and electrolytic conductivity are spatially distributed in real aqueous droplets due to possible ionic depletion at the electrode surface under higher overpotential. Because EDL processes are not considered in this study, it is not meaningful to evaluate the distribution of electric conductivity within the droplet. Then a constant
$A$
is the droplet–electrode interfacial area. The electric field strength and electrolytic conductivity are spatially distributed in real aqueous droplets due to possible ionic depletion at the electrode surface under higher overpotential. Because EDL processes are not considered in this study, it is not meaningful to evaluate the distribution of electric conductivity within the droplet. Then a constant
![]() $\unicode[STIX]{x1D705}$
is assumed. Another simplification used here is that we replace the local value of
$\unicode[STIX]{x1D705}$
is assumed. Another simplification used here is that we replace the local value of
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{E}$
by the average electric field strength between the electrodes
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{E}$
by the average electric field strength between the electrodes
![]() $\bar{E}$
in (2.12). The average strength is calculated as the difference of electric potential between the electrodes divided by the electrode–electrode distance. Equation (2.12) finally simplifies to the form
$\bar{E}$
in (2.12). The average strength is calculated as the difference of electric potential between the electrodes divided by the electrode–electrode distance. Equation (2.12) finally simplifies to the form
The integral of the level-set function over the entire electrode surface represents the electrode–electrolyte interfacial area
![]() $A$
. Equation (2.13) uses classical chemical engineering philosophy regarding how to describe a rate
$A$
. Equation (2.13) uses classical chemical engineering philosophy regarding how to describe a rate
![]() $r$
of a complex mass transfer process. Typically
$r$
of a complex mass transfer process. Typically
![]() $r=k\unicode[STIX]{x0394}XA$
, where
$r=k\unicode[STIX]{x0394}XA$
, where
![]() $k$
is the mass transfer coefficient,
$k$
is the mass transfer coefficient,
![]() $\unicode[STIX]{x0394}X$
is the driving force and
$\unicode[STIX]{x0394}X$
is the driving force and
![]() $A$
is the contact area. The driving force, i.e. the gradient of electric potential, is approximated as
$A$
is the contact area. The driving force, i.e. the gradient of electric potential, is approximated as
![]() $\bar{E}$
and can be coupled with the constant
$\bar{E}$
and can be coupled with the constant
![]() $k$
to yield the charging constant (effective mass transfer coefficient)
$k$
to yield the charging constant (effective mass transfer coefficient)
![]() $K$
. The mass transfer coefficient
$K$
. The mass transfer coefficient
![]() $k$
depends on geometrical parameters (droplet volume) and the effective electrolyte conductivity at the interface. The conductivity at the interface can significantly differ from a bulk value, because the appearance of an ion-depleted zone is highly probable under an intensive electric field (Slouka et al.
Reference Slouka, Pribyl, Snita and Postler2007).
$k$
depends on geometrical parameters (droplet volume) and the effective electrolyte conductivity at the interface. The conductivity at the interface can significantly differ from a bulk value, because the appearance of an ion-depleted zone is highly probable under an intensive electric field (Slouka et al.
Reference Slouka, Pribyl, Snita and Postler2007).
2.3 Boundary conditions and initial conditions
Axisymmetric boundary conditions were considered for all quantities at boundary 1; see figure 1. Reference zero electric potential is set at the boundary 5. Wetted wall boundary conditions (Comsol 2013b
) with adjustable contact angle
![]() $\unicode[STIX]{x1D703}$
were applied to the boundaries 2, 3 and 4. Reference zero pressure is defined at a single point in domain I. Continuity of electric potential is considered at the boundaries 2, 3 and 4. The other condition at these boundaries results from the application of Gauss’s law (Grodzinsky Reference Grodzinsky2011) and reads
$\unicode[STIX]{x1D703}$
were applied to the boundaries 2, 3 and 4. Reference zero pressure is defined at a single point in domain I. Continuity of electric potential is considered at the boundaries 2, 3 and 4. The other condition at these boundaries results from the application of Gauss’s law (Grodzinsky Reference Grodzinsky2011) and reads
where
![]() $\unicode[STIX]{x1D70E}_{s}$
denotes the surface concentration of electric charge and the suffixes are the domain indexes. The dielectric constant in domain II was set to one, i.e.
$\unicode[STIX]{x1D70E}_{s}$
denotes the surface concentration of electric charge and the suffixes are the domain indexes. The dielectric constant in domain II was set to one, i.e.
![]() $\unicode[STIX]{x1D716}_{II}=\unicode[STIX]{x1D716}_{0}$
, where
$\unicode[STIX]{x1D716}_{II}=\unicode[STIX]{x1D716}_{0}$
, where
![]() $\unicode[STIX]{x1D716}_{0}$
is the vacuum permittivity. Zero surface charge is chosen at boundary 4. The boundaries 2 and 3 are considered to contain the same amount of electric charge
$\unicode[STIX]{x1D716}_{0}$
is the vacuum permittivity. Zero surface charge is chosen at boundary 4. The boundaries 2 and 3 are considered to contain the same amount of electric charge
![]() $\unicode[STIX]{x1D70E}$
with opposite polarity,
$\unicode[STIX]{x1D70E}$
with opposite polarity,
Zero reference pressure and zero velocity were set as the initial conditions in domain I. The phase field function was set to 1 at the position of the aqueous droplet and to 0 elsewhere. The droplet initially did not touch any electrode and the volume charge density was set to an initial value
![]() $\unicode[STIX]{x1D714}_{w}=\unicode[STIX]{x1D714}_{0}$
.
$\unicode[STIX]{x1D714}_{w}=\unicode[STIX]{x1D714}_{0}$
.
2.4 Numerical methods
Comsol Multiphysics 4.4 software (Comsol 2013a ) and the Microfludics module extension (Comsol 2013b ) based on the finite element method were used to solve the axisymmetric problem defined above. The solution was obtained in three steps. The solver internally initialized the level-set function in the first step, equation (2.5). The initial distribution of electric potential was then obtained by solving equations (2.8) and (2.11). Dynamical simulation of the full problem (equations (2.1), (2.2), (2.5), (2.8), (2.11), (2.13)) together with boundary conditions was carried out in the last step.
The Dirac function in (2.4) is approximated by (Comsol 2013b )
The stabilization term
![]() $R_{ls}$
in (2.5) reads (Comsol 2013b
)
$R_{ls}$
in (2.5) reads (Comsol 2013b
)
where
![]() $a_{1}=1$
m s
$a_{1}=1$
m s
![]() $^{-1}$
is the reinitialization parameter and
$^{-1}$
is the reinitialization parameter and
![]() $a_{2}$
is the parameter controlling the liquid–liquid interface thickness. The parameter
$a_{2}$
is the parameter controlling the liquid–liquid interface thickness. The parameter
![]() $a_{2}$
was set to one-half of the maximum finite element size.
$a_{2}$
was set to one-half of the maximum finite element size.
The multifrontal massively parallel sparse direct solver (Amestoy et al.
Reference Amestoy, Duff, Koster and L’Excellent2001) was used for the elimination of large sparse matrixes. The relative tolerance was set to
![]() $1\times 10^{-3}$
. A solver based on backward differential formulae of first and second order with automatically adjusted time stepping was used for the time integration of the model equations (Hindmarsh et al.
Reference Hindmarsh, Brown, Grant, Lee, Serban, Shumaker and Woodward2005). The relative tolerance of integration steps was set to
$1\times 10^{-3}$
. A solver based on backward differential formulae of first and second order with automatically adjusted time stepping was used for the time integration of the model equations (Hindmarsh et al.
Reference Hindmarsh, Brown, Grant, Lee, Serban, Shumaker and Woodward2005). The relative tolerance of integration steps was set to
![]() $1\times 10^{-2}$
.
$1\times 10^{-2}$
.
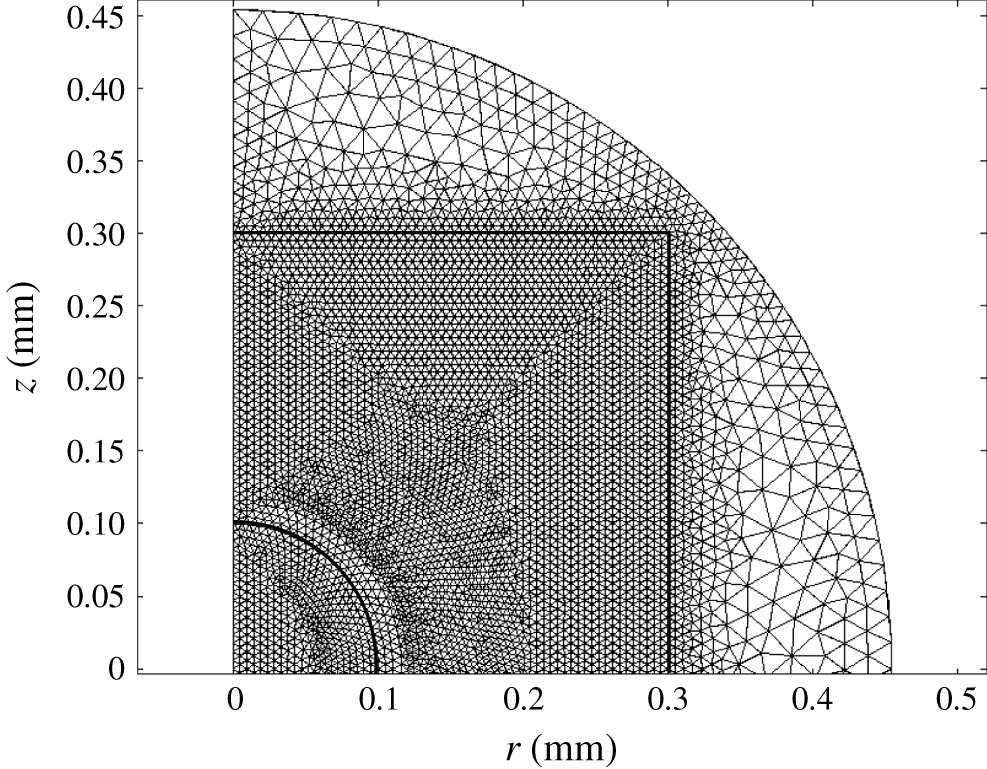
Spatial domains were discretized with triangular finite elements (figure 2). The mesh consists of approximately
![]() $1.7\times 10^{4}$
elements. Most of them are localized in domain I (more than
$1.7\times 10^{4}$
elements. Most of them are localized in domain I (more than
![]() $1.4\times 10^{4}$
). The distribution of boundary elements is the following: the axis of symmetry (boundary 1, 130 elements), electrodes (boundaries 2 and 3, 51 and 51 elements), solid wall (boundary 4, 102 elements), grounding electrode (boundary 5, 104 elements).
$1.4\times 10^{4}$
). The distribution of boundary elements is the following: the axis of symmetry (boundary 1, 130 elements), electrodes (boundaries 2 and 3, 51 and 51 elements), solid wall (boundary 4, 102 elements), grounding electrode (boundary 5, 104 elements).
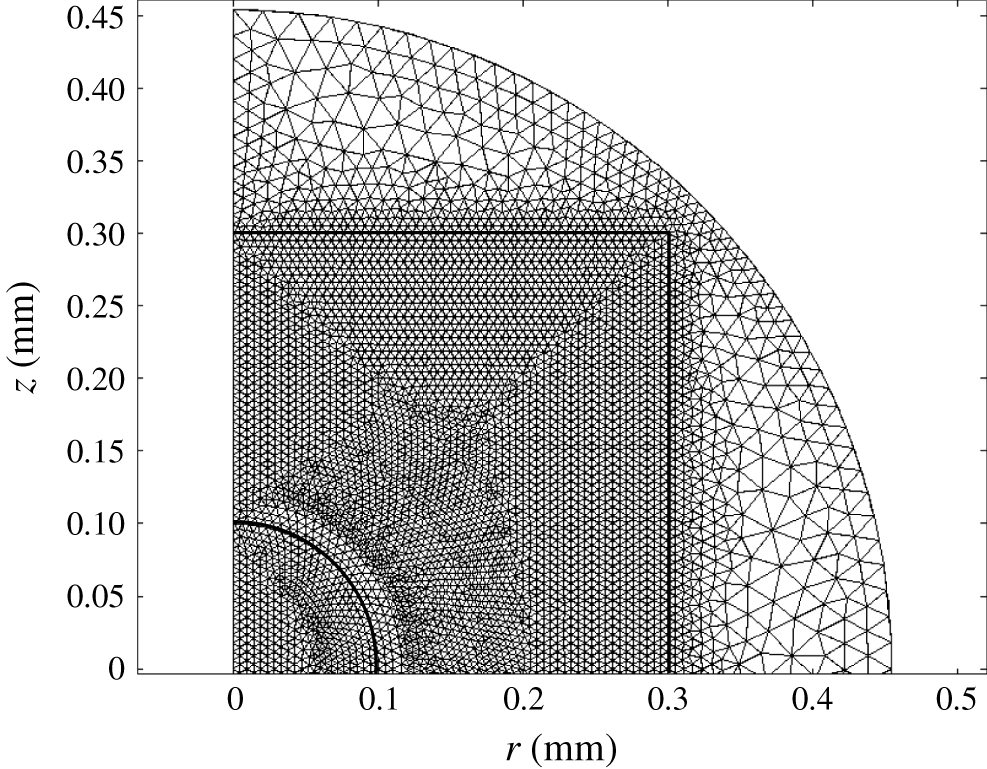
Figure 2. Distribution of triangular elements in one-half of the geometrical domain.
The basic set of values of the dimensional model parameters is summarized in table 1. Values of selected parameters were systematically varied in parametric studies.
Table 1. The basic set of values of the model parameters.

2.5 Mesh validation
To characterize the rhythmic motion of the droplet over a longer time period, several normalized characteristics of the system were defined. The normalized volume charge density, droplet–electrode contact area and droplet position read
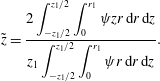 $$\begin{eqnarray}\displaystyle & \displaystyle \tilde{z}=\frac{2\displaystyle \int _{-z_{1}/2}^{z_{1}/2}\int _{0}^{r_{1}}\unicode[STIX]{x1D713}zr\,\text{d}r\,\text{d}z}{z_{1}\displaystyle \int _{-z_{1}/2}^{z_{1}/2}\int _{0}^{r_{1}}\unicode[STIX]{x1D713}r\,\text{d}r\,\text{d}z}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{z}=\frac{2\displaystyle \int _{-z_{1}/2}^{z_{1}/2}\int _{0}^{r_{1}}\unicode[STIX]{x1D713}zr\,\text{d}r\,\text{d}z}{z_{1}\displaystyle \int _{-z_{1}/2}^{z_{1}/2}\int _{0}^{r_{1}}\unicode[STIX]{x1D713}r\,\text{d}r\,\text{d}z}. & \displaystyle\end{eqnarray}$$
The volume charge density
![]() $\tilde{\unicode[STIX]{x1D714}}\in \left[-1,1\right]$
is normalized by the maximal absolute value of volume charge density in the regular periodic regime. The contact area is normalized by the enclosed area of a circle with a radius of
$\tilde{\unicode[STIX]{x1D714}}\in \left[-1,1\right]$
is normalized by the maximal absolute value of volume charge density in the regular periodic regime. The contact area is normalized by the enclosed area of a circle with a radius of
![]() $s_{1}$
. The droplet position is calculated as the mean integral value of the droplet position in domain I normalized by one-half of the electrode distance.
$s_{1}$
. The droplet position is calculated as the mean integral value of the droplet position in domain I normalized by one-half of the electrode distance.
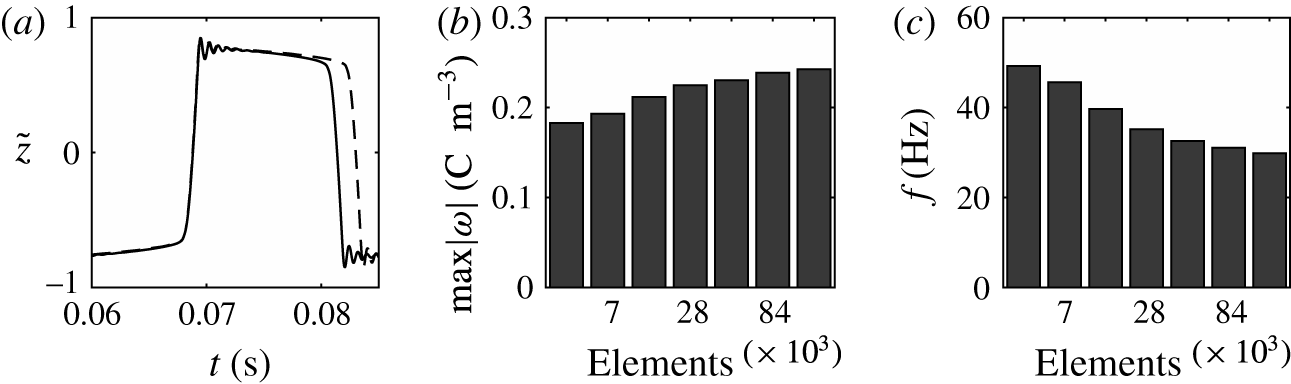
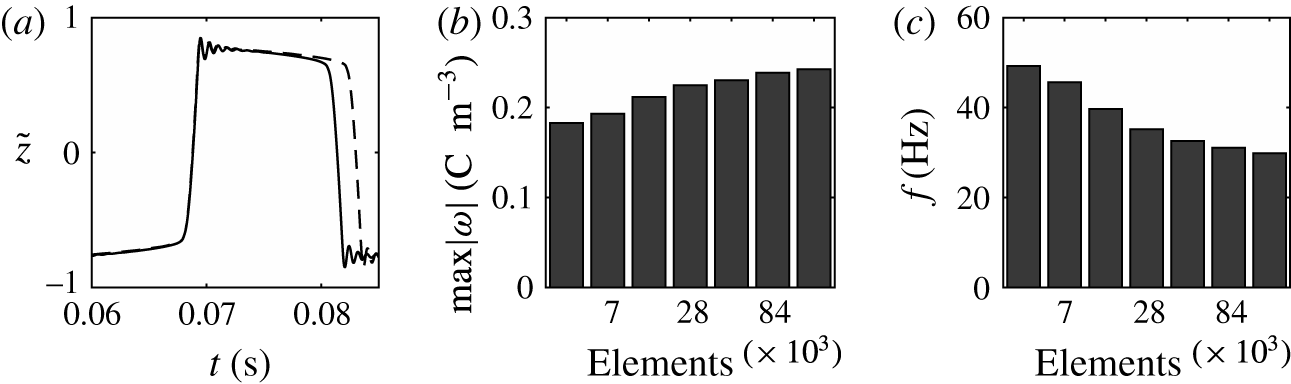
Figure 3. (a) Dependence of the normalized droplet position on time calculated with meshes consisting of 14 106 (solid line) and 28 212 (dashed line) elements in domain I. Effect of the number of mesh elements on the charge acquired by droplet (b) and on the frequency of droplet oscillations (c).
Numerical simulations of the model equations were carried out with several meshes of different quality. The corresponding normalized characteristics are plotted in figure 3. The dependences of the mean droplet position on time for the meshes with
![]() $1.4\times 10^{4}$
and
$1.4\times 10^{4}$
and
![]() $2.8\times 10^{4}$
elements are shown in figure 3(a). The dynamics of droplet transition from one electrode to the other is almost identical. The wavy parts of these time courses are also identical and correspond to damped droplet deformations that appear after touching the electrode. However, the durations of the droplet–electrode contact, i.e. the durations of electrochemical charging, differ by approximately 10 %. This results in slightly higher concentrations of free charge in the droplet (figure 3
b) and a decreased frequency (figure 3
c) in simulations with finer meshes. The time of droplet–electrode contact is affected by the sharpness of the liquid–liquid interface, which is always greater for a finer mesh. The droplet–electrode contact area and charge transfer are then also influenced. Because the mesh test revealed that the qualitative behaviour of the system does not depend on the mesh density and the quantitative characteristics do not differ by more than 15 % for the meshes with
$2.8\times 10^{4}$
elements are shown in figure 3(a). The dynamics of droplet transition from one electrode to the other is almost identical. The wavy parts of these time courses are also identical and correspond to damped droplet deformations that appear after touching the electrode. However, the durations of the droplet–electrode contact, i.e. the durations of electrochemical charging, differ by approximately 10 %. This results in slightly higher concentrations of free charge in the droplet (figure 3
b) and a decreased frequency (figure 3
c) in simulations with finer meshes. The time of droplet–electrode contact is affected by the sharpness of the liquid–liquid interface, which is always greater for a finer mesh. The droplet–electrode contact area and charge transfer are then also influenced. Because the mesh test revealed that the qualitative behaviour of the system does not depend on the mesh density and the quantitative characteristics do not differ by more than 15 % for the meshes with
![]() $1.4\times 10^{4}$
and
$1.4\times 10^{4}$
and
![]() $5.6\times 10^{4}$
elements, we decided to use the sparser mesh in our parametric studies. One simulation of 0.25 s time period with the mesh consisting of
$5.6\times 10^{4}$
elements, we decided to use the sparser mesh in our parametric studies. One simulation of 0.25 s time period with the mesh consisting of
![]() $1.4\times 10^{4}$
elements typically took only 14 h on 4-core Intel i7-4790 3.6 GHz processors. We further repeated the simulation plotted in figure 3 for
$1.4\times 10^{4}$
elements typically took only 14 h on 4-core Intel i7-4790 3.6 GHz processors. We further repeated the simulation plotted in figure 3 for
![]() $8.4\times 10^{4}$
and
$8.4\times 10^{4}$
and
![]() $1.12\times 10^{5}$
finite elements. The simulation with
$1.12\times 10^{5}$
finite elements. The simulation with
![]() $1.12\times 10^{5}$
elements takes more than 10 days of computational time. The numerical solver uses second-order elements to approximate the velocity field and electric potential and first-order elements to approximate the pressure field (Comsol 2013b
). The global error of numerical approximation is then directly proportional to the element size
$1.12\times 10^{5}$
elements takes more than 10 days of computational time. The numerical solver uses second-order elements to approximate the velocity field and electric potential and first-order elements to approximate the pressure field (Comsol 2013b
). The global error of numerical approximation is then directly proportional to the element size
![]() $({\sim}h^{1})$
and convergence is rather gradual. However, the memory demands of the solver grow with
$({\sim}h^{1})$
and convergence is rather gradual. However, the memory demands of the solver grow with
![]() ${\sim}h^{-2}$
. The mesh consisting of
${\sim}h^{-2}$
. The mesh consisting of
![]() $1.4\times 10^{4}$
elements thus represents a good compromise between the precision of the numerical approximation and the time demands of the simulations.
$1.4\times 10^{4}$
elements thus represents a good compromise between the precision of the numerical approximation and the time demands of the simulations.
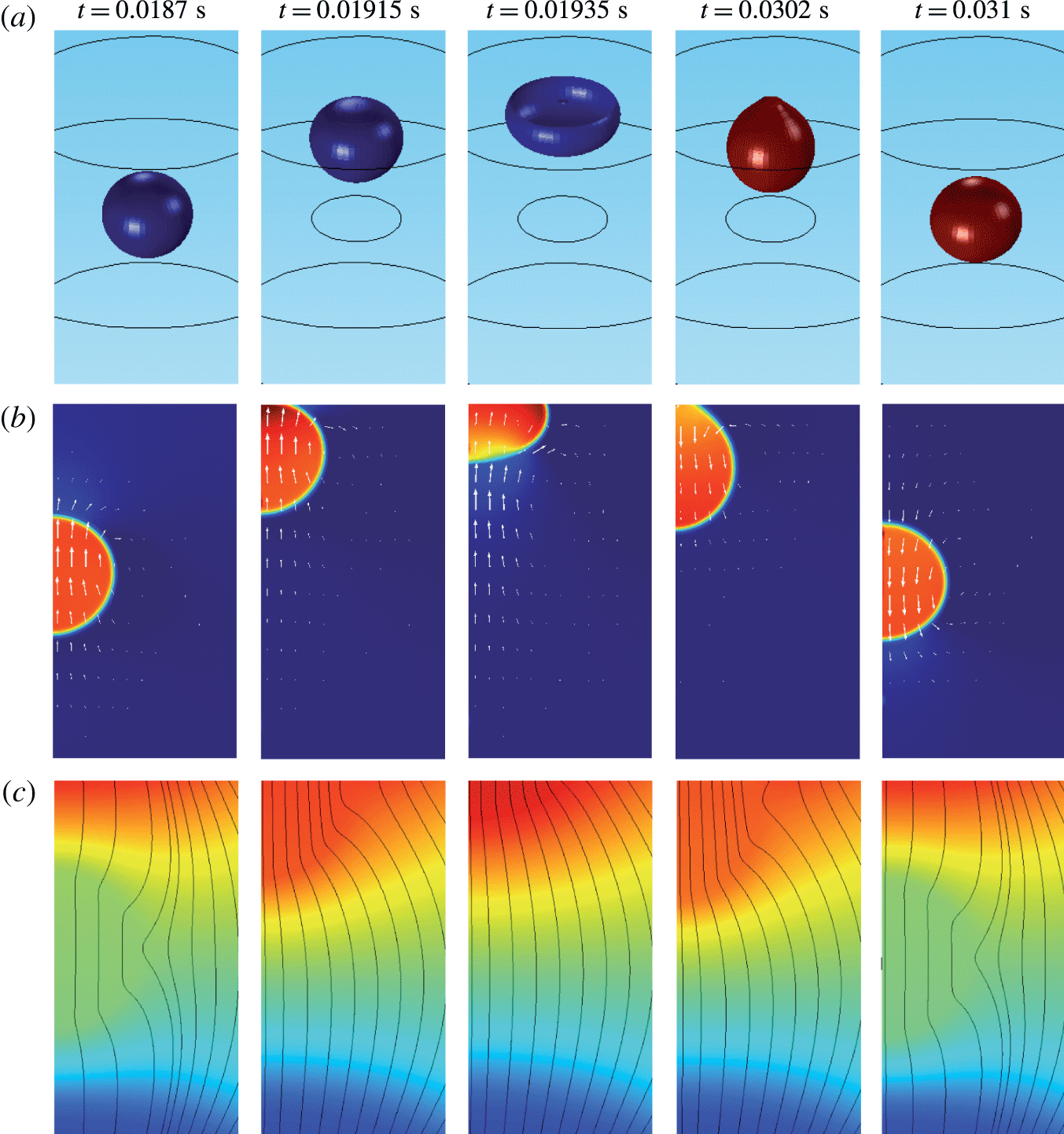
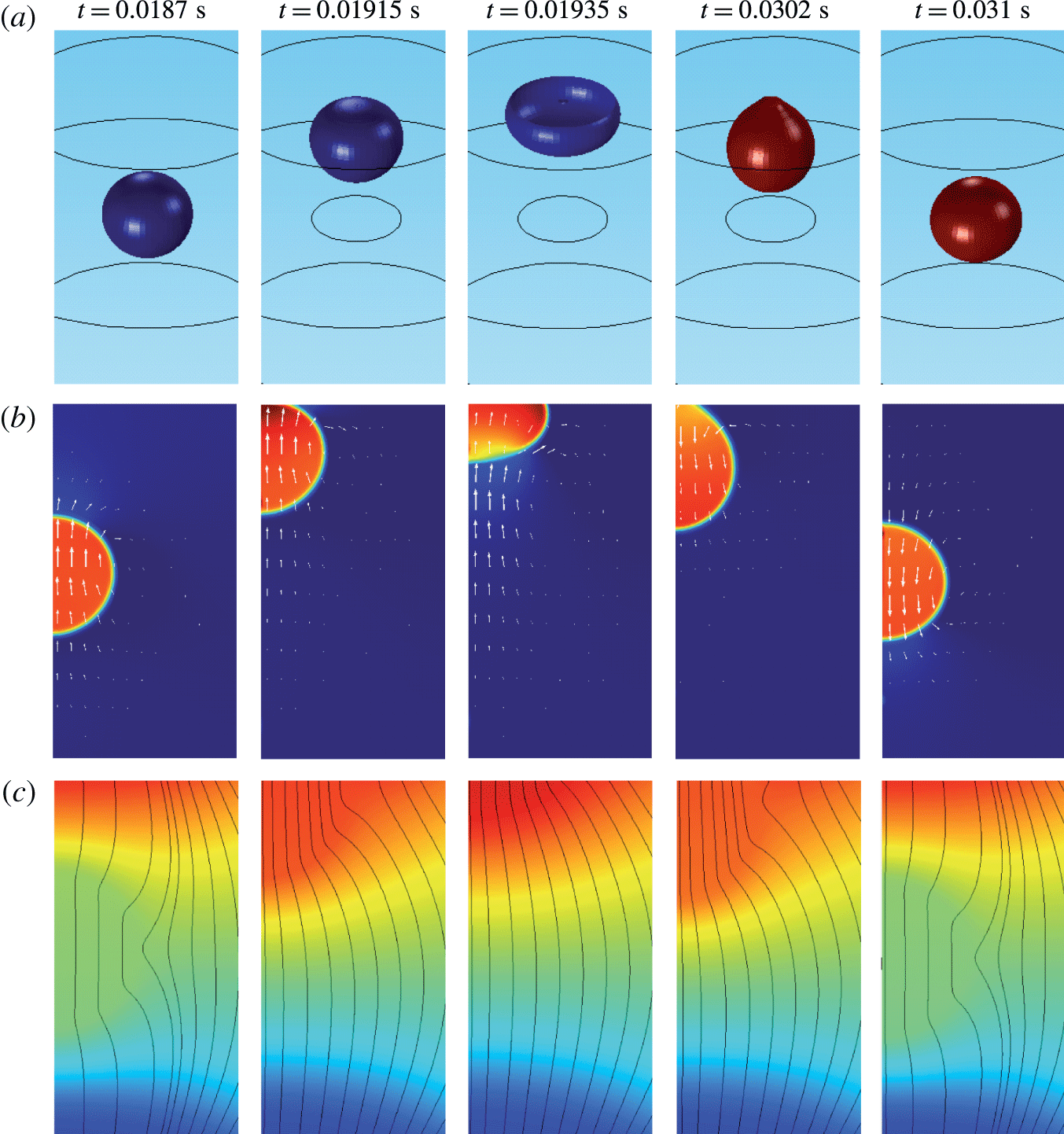
Figure 4. Snapshots of a oscillating droplet. (a) Droplet positions expressed as isosurface plots for
![]() $\unicode[STIX]{x1D713}=0.5$
. Droplet colour ranges from
$\unicode[STIX]{x1D713}=0.5$
. Droplet colour ranges from
![]() $\unicode[STIX]{x1D714}=-0.2~\text{C}~\text{m}^{-3}$
(blue) to
$\unicode[STIX]{x1D714}=-0.2~\text{C}~\text{m}^{-3}$
(blue) to
![]() $\unicode[STIX]{x1D714}=0.2~\text{C}~\text{m}^{-3}$
(red). (b) Relative pressure distribution and velocity field. Colour palette ranges from
$\unicode[STIX]{x1D714}=0.2~\text{C}~\text{m}^{-3}$
(red). (b) Relative pressure distribution and velocity field. Colour palette ranges from
![]() $p=-10$
Pa (blue) to
$p=-10$
Pa (blue) to
![]() $p=1.2$
kPa (red). White arrows indicate the vector field of velocity. (c) Electric field and electric potential distributions. Colour palette ranges from
$p=1.2$
kPa (red). White arrows indicate the vector field of velocity. (c) Electric field and electric potential distributions. Colour palette ranges from
![]() $\unicode[STIX]{x1D719}=-12$
kV (blue) to
$\unicode[STIX]{x1D719}=-12$
kV (blue) to
![]() $\unicode[STIX]{x1D719}=12$
kV (red). Black lines indicate the streamlines of the electric field.
$\unicode[STIX]{x1D719}=12$
kV (red). Black lines indicate the streamlines of the electric field.
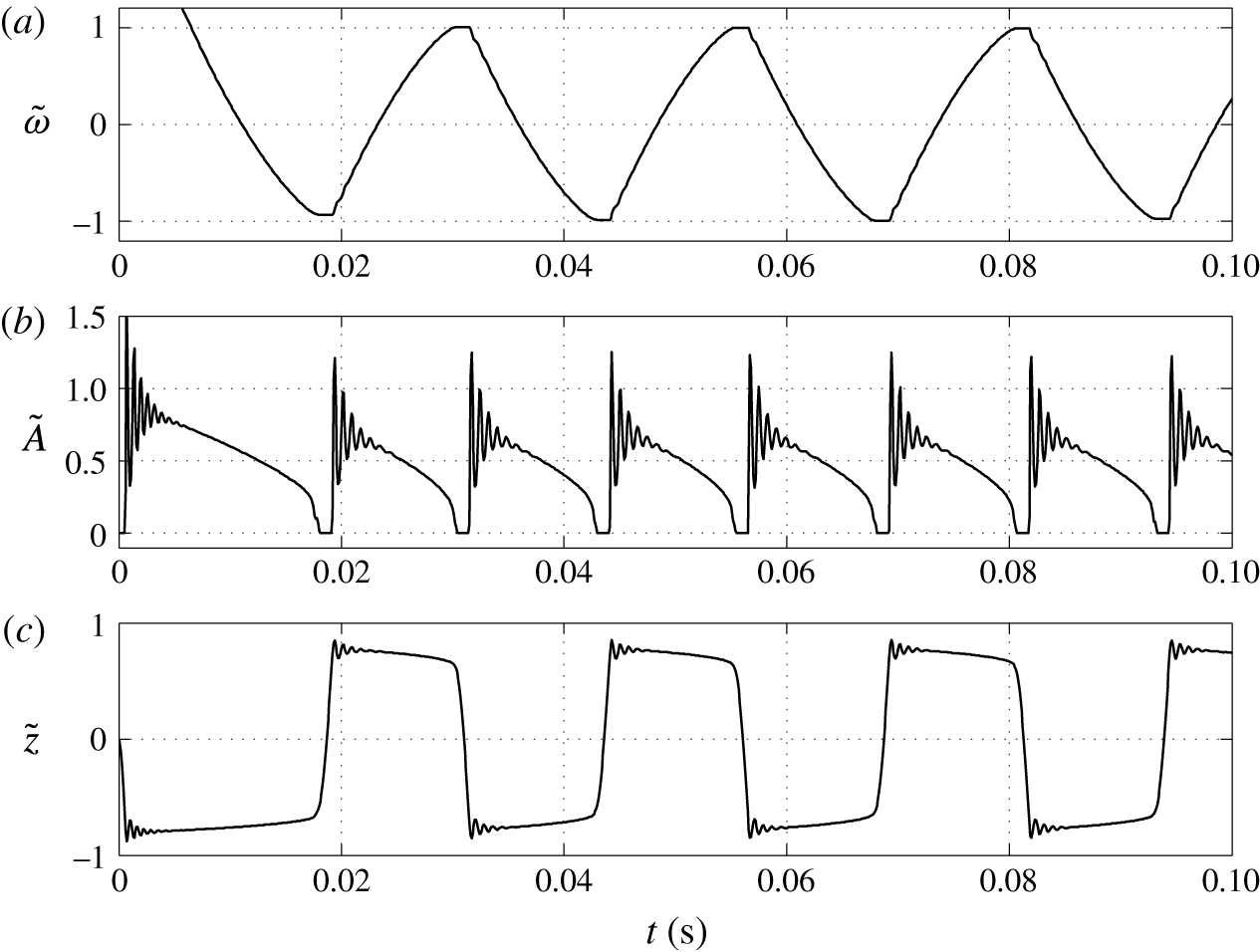
Figure 5. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position.
3 Results and discussion
3.1 Droplet dynamics and flow pattern
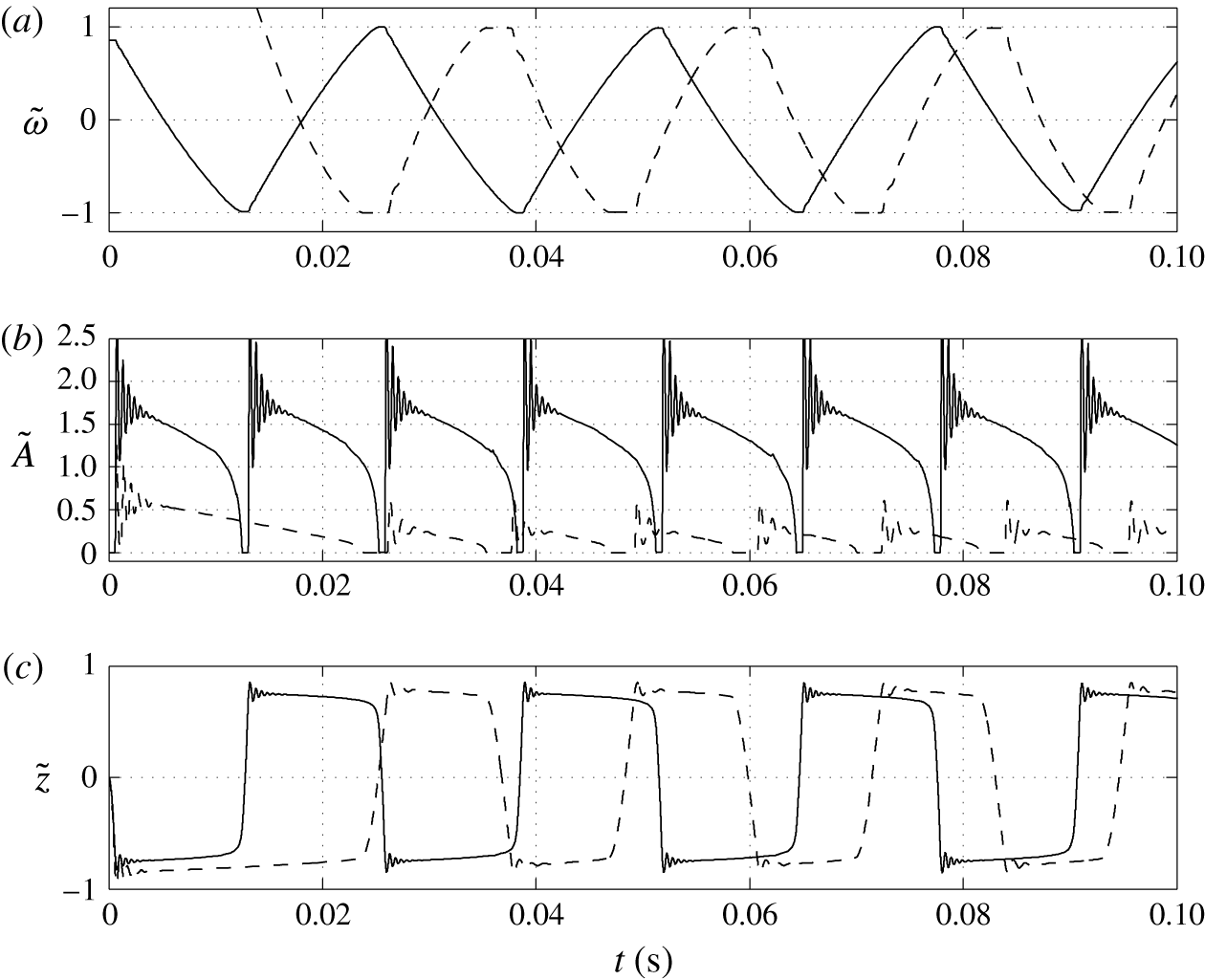
The dynamical behaviour of a charged droplet within a dielectric fluid for the basic set of model parameters is shown in figures 4 and 5 and supplementary movie 1 available at https://doi.org/10.1017/jfm.2017.230. The movie shows the detailed dynamics of droplet deformation and interaction with solid electrodes. One can see that the charged droplet is attracted to the oppositely charged electrode. Once attached, the droplet–electrode interface provides a reaction area for the electrochemical reaction.
The periodic motion of droplets between electrodes consists of a charging phase, where the droplet stays at an electrode, and a non-charging phase, where the droplet moves from one electrode to the other. The charging phase can be accompanied by damped shape oscillations (movie 1) and oscillations of the droplet–electrode contact area and droplet position (figure 5). This behaviour represents a kind of damped harmonic oscillation. Damped oscillators are characterized by a linear or nonlinear damping (friction) term, which is directly proportional to the droplet or object velocity. The van der Pol oscillator represents an oscillator with a nonlinear damping term (van der Pol Reference van der Pol1926). If forced, it can exhibit complex periodic or chaotic behaviour (Parlitz & Lauterborn Reference Parlitz and Lauterborn1987). The damped oscillations of droplet shape appear as a result of energy dissipation due to viscous friction in both liquids at their interface. The radial component of the velocity field is then described by spherical harmonics with a damping function
![]() $\exp (-\unicode[STIX]{x1D6FD}t)$
, where
$\exp (-\unicode[STIX]{x1D6FD}t)$
, where
![]() $\unicode[STIX]{x1D6FD}$
is the decay factor that can be estimated for different physical situations (Miller & Scriven Reference Miller and Scriven1968).
$\unicode[STIX]{x1D6FD}$
is the decay factor that can be estimated for different physical situations (Miller & Scriven Reference Miller and Scriven1968).
In relevant experiments (Hase et al.
Reference Hase, Watanabe and Yoshikawa2006; Jung et al.
Reference Jung, Oh and Kang2008; Im et al.
Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012), only tiny droplet tips mediated the charge transfer across the electrode–droplet interface, which is not in full agreement with the results of our numerical simulations. However, Jalaal et al. (Reference Jalaal, Khorshidi and Esmaeilzadeh2010) observed remarkable droplet deformations in the form of damped oscillations with large contact area at the droplet–electrode interface. The droplet–electrode contact area can be reduced in our simulations, e.g. by setting higher values of the charging constant
![]() $K$
or contact angle
$K$
or contact angle
![]() $\unicode[STIX]{x1D703}$
. Despite higher
$\unicode[STIX]{x1D703}$
. Despite higher
![]() $K$
or
$K$
or
![]() $\unicode[STIX]{x1D703}$
, the model predictions cannot be in full agreement with experimental observations, because spatially uniform droplet charging is assumed and the dielectrophoretic force neglected; see (2.12).
$\unicode[STIX]{x1D703}$
, the model predictions cannot be in full agreement with experimental observations, because spatially uniform droplet charging is assumed and the dielectrophoretic force neglected; see (2.12).
When the oscillations are completely damped, the interfacial area shrinks because the droplet becomes charged by electric charge of the same polarity as the electrode. At a certain moment, the electric volume force exceeds the force of interfacial tension, and the droplet is released into the dielectric fluid and moves to the other electrode. The elongation of the droplet and tip formation before the release have been observed experimentally (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012).
Damped oscillations of the droplet shape are observed after the release. Inertial forces are mostly responsible for these oscillations because the Reynolds number in this particular regime is approximately 120, which is quite far from the Stokes regime (
![]() $Re\ll 1$
). Here
$Re\ll 1$
). Here
![]() $Re$
is evaluated as
$Re$
is evaluated as
![]() $Re=2\bar{v}_{z}s_{1}\unicode[STIX]{x1D70C}_{w}/\unicode[STIX]{x1D702}_{w}$
, where the average axial velocity,
$Re=2\bar{v}_{z}s_{1}\unicode[STIX]{x1D70C}_{w}/\unicode[STIX]{x1D702}_{w}$
, where the average axial velocity,
![]() $\bar{v}_{z}\approx 0.6~\text{m}~\text{s}^{-1}$
, is estimated as the electrode spacing
$\bar{v}_{z}\approx 0.6~\text{m}~\text{s}^{-1}$
, is estimated as the electrode spacing
![]() $z_{1}$
divided by the duration of droplet shift between the electrodes. Similar shape deformations were observed experimentally (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014).
$z_{1}$
divided by the duration of droplet shift between the electrodes. Similar shape deformations were observed experimentally (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014).
We note that a Reynolds number significantly higher than 1 is not a very common situation in microfluidics. Typical applications of droplet microfluidics such as slug flow separators or microreactors are accompanied by Stokes flow (
![]() $Re<1$
). However, in our own experiments (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014)
$Re<1$
). However, in our own experiments (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014)
![]() $Re$
ranged from 10 to 60, which is a result of the high frequency of oscillations;
$Re$
ranged from 10 to 60, which is a result of the high frequency of oscillations;
![]() $Re=4$
was reported in Jalaal et al. (Reference Jalaal, Khorshidi and Esmaeilzadeh2010) for a more viscous organic phase. When the inertial forces dominate over the viscous forces, the linear Stokes equation cannot be used for the description of the velocity field. However, turbulent instabilities and intermittency typically appear for
$Re=4$
was reported in Jalaal et al. (Reference Jalaal, Khorshidi and Esmaeilzadeh2010) for a more viscous organic phase. When the inertial forces dominate over the viscous forces, the linear Stokes equation cannot be used for the description of the velocity field. However, turbulent instabilities and intermittency typically appear for
![]() $Re\sim 10^{3}$
. Thus the description based on the nonlinear Navier–Stokes equation should be satisfactory and the solution should remain axisymmetric.
$Re\sim 10^{3}$
. Thus the description based on the nonlinear Navier–Stokes equation should be satisfactory and the solution should remain axisymmetric.
Several snapshots of domain I preceding and following the contact of a negatively charged droplet with a positively charged electrode are shown in figure 4. A nearly spherical droplet approaches the electrode. The internal pressure within the droplet is higher than that in the dielectric fluid due to the interfacial tension. The velocity field clearly indicates motion of the droplet and the surrounding dielectric liquid. The electric field is significantly deformed and the streamlines preferentially enter the droplet because of high droplet permittivity. Once the droplet touches the electrode, pressure increases due to the force reaction of the fixed electrode. The middle snapshots show the droplet in the phase of maximal deformation that is accompanied by liquid suction behind the droplet and liquid pushing next to the droplet. When the electric charge within the droplet is reversed, the droplet elongates, touching the electrode with a tiny tip. After release, the nearly spherical droplet moves back to the negatively charged electrode.
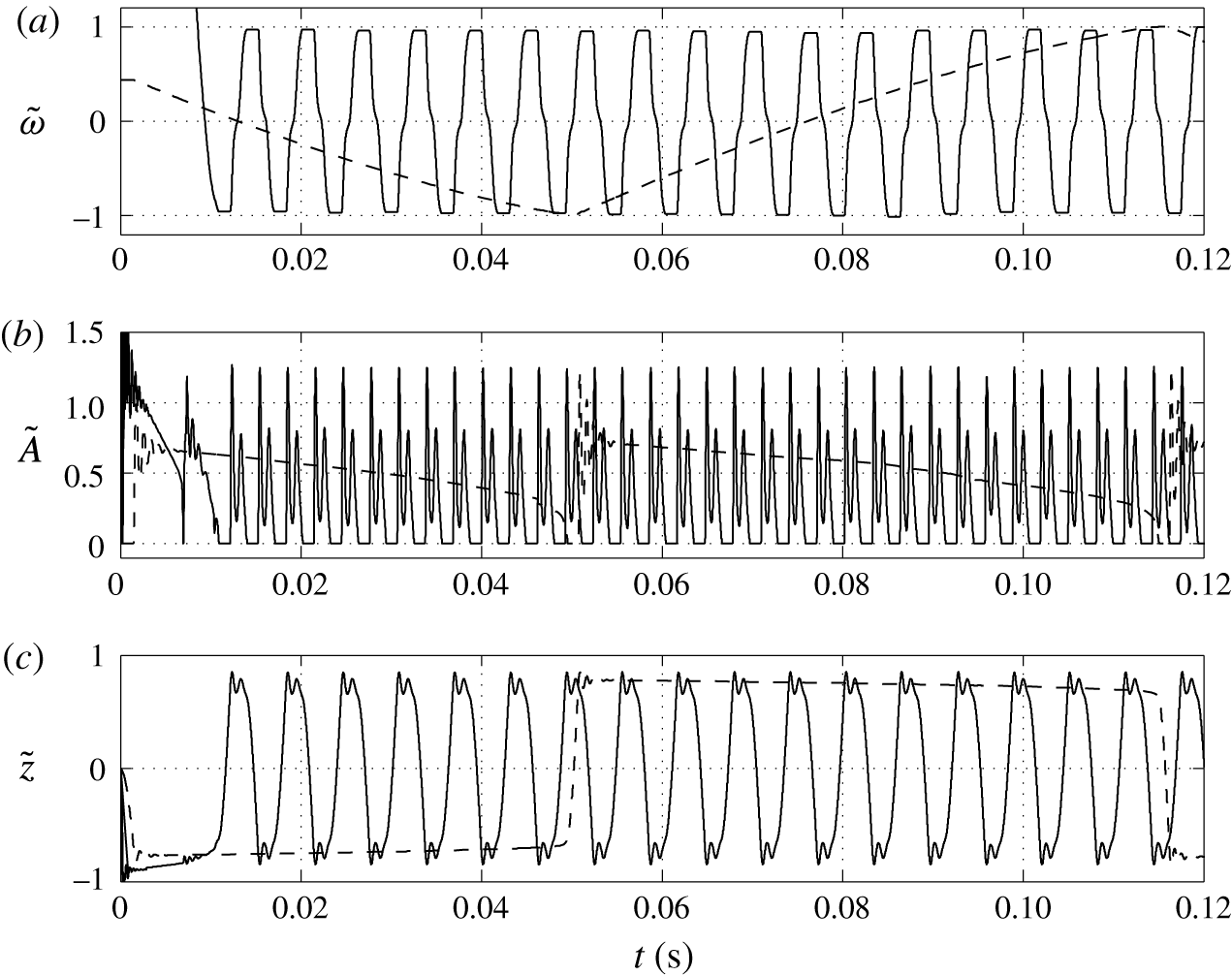
One can see that an almost regular periodic regime is attained after one charge reversal of the droplet (figure 5). The charging process is symmetric (figure 5
a) due to the same charging constant at both electrodes. In general, the charging dynamics can be asymmetric due to different kinetics of oxidation and reduction reactions (Bard & Faulkner Reference Bard and Faulkner2001) or asymmetric transport of ions with different electrophoretic mobilities (Grodzinsky Reference Grodzinsky2011). Im et al. (Reference Im, Noh, Moon and Kang2011) found that charging at the negative and positive electrodes differs at most by 5 %. The time dependence of the normalized contact area (figure 5
b) is characterized by damped oscillations that emerge immediately after droplet–electrode contact as a consequence of the shape deformation. As shown in figure 5(a), the oscillations do not significantly affect the charging dynamics. Figure 5(b) further reveals that the contact area can be temporarily larger than the largest cross-sectional area of an ideally spherical droplet of the same volume. The normalized droplet position (figure 5
c) indicates that the droplet remains in contact with the electrodes for
![]() ${\sim}10$
ms, the duration of droplet shift between the electrodes is
${\sim}10$
ms, the duration of droplet shift between the electrodes is
![]() ${\sim}1$
ms, and the oscillation frequency is approximately 40 Hz. The frequency of oscillations in experiments typically does not exceed 10 Hz (Hase et al.
Reference Hase, Watanabe and Yoshikawa2006; Im et al.
Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). The difference is caused by the very high electric field strength in this particular simulation (
${\sim}1$
ms, and the oscillation frequency is approximately 40 Hz. The frequency of oscillations in experiments typically does not exceed 10 Hz (Hase et al.
Reference Hase, Watanabe and Yoshikawa2006; Im et al.
Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). The difference is caused by the very high electric field strength in this particular simulation (
![]() ${\sim}40~\text{kV}~\text{mm}^{-1}$
). In experiments, the electric field strength is usually below 1
${\sim}40~\text{kV}~\text{mm}^{-1}$
). In experiments, the electric field strength is usually below 1
![]() $\text{kV}~\text{mm}^{-1}$
. We will show in our parametric studies that the oscillation frequency decreases with decreasing electric field strength and is sensitive to other model parameters.
$\text{kV}~\text{mm}^{-1}$
. We will show in our parametric studies that the oscillation frequency decreases with decreasing electric field strength and is sensitive to other model parameters.
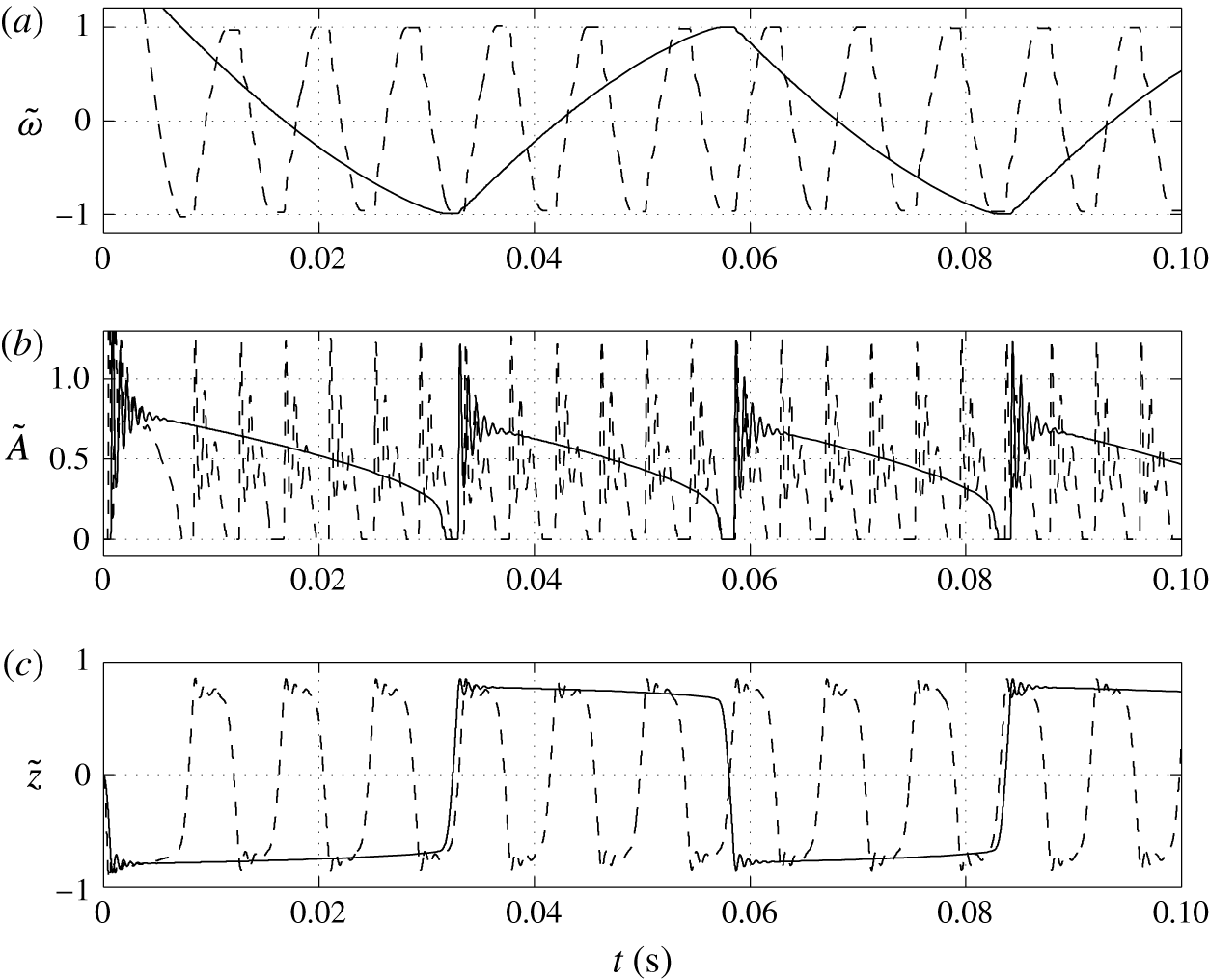
3.2 Effect of surface charge density
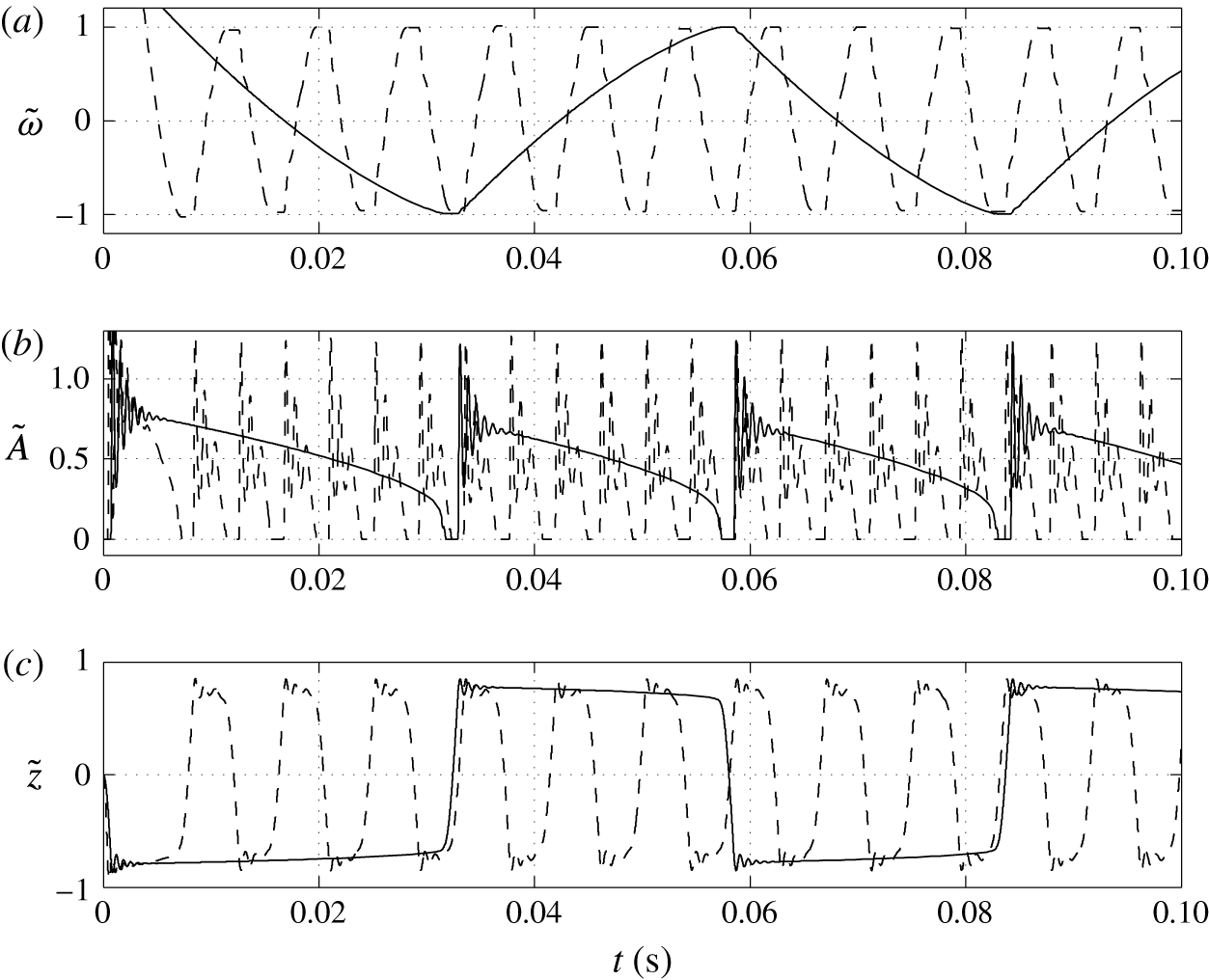
Figure 6. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position. Solid line,
![]() $\unicode[STIX]{x1D70E}=2~\text{mC}~\text{m}^{-2}$
; dashed line,
$\unicode[STIX]{x1D70E}=2~\text{mC}~\text{m}^{-2}$
; dashed line,
![]() $\unicode[STIX]{x1D70E}=6~\text{mC}~\text{m}^{-2}$
.
$\unicode[STIX]{x1D70E}=6~\text{mC}~\text{m}^{-2}$
.
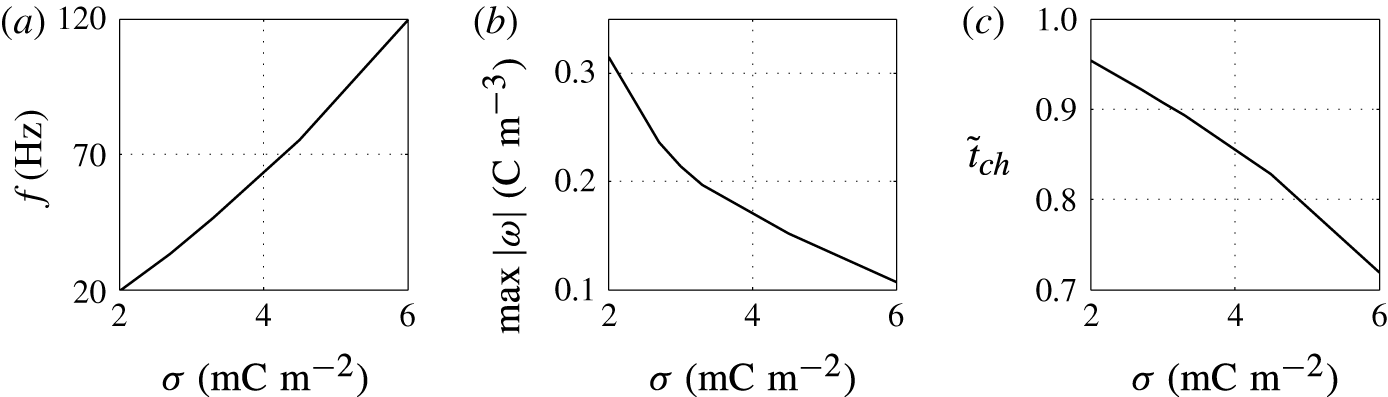
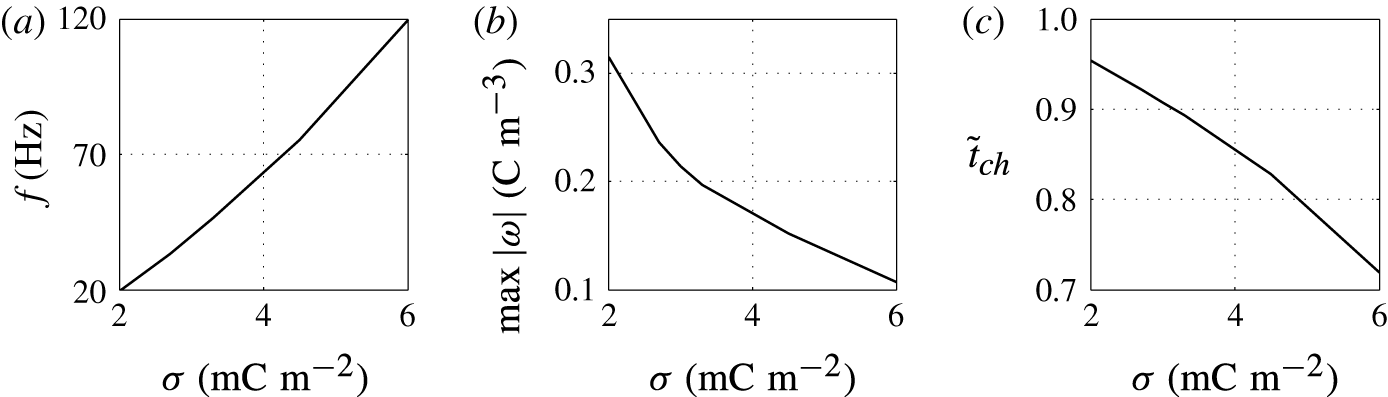
Figure 7. Effects of the surface charge density on (a) frequency of oscillations, (b) charge acquired by droplet and (c) relative time of charging.
The higher the surface charge density on the electrodes, the higher the electric field strength forces the droplet. Monotonic increase of the oscillation frequency with the charge density is observed (figures 6 and 7). This finding is in agreement with available experimental results (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). The dielectric effects, which are neglected in this study, are important only at the electrode surface, where instead of tiny tip formation, the droplet wets the electrode surface. This finally leads to the underestimation of the oscillation frequency because more energy is required for the droplet separation. The electric field strength affects not only the electric volume force acting on the free charge (2.1) but also the kinetics of the electrochemical reactions (2.12). This means that the droplet has to spend less time at a charging electrode to collect enough charge for detachment under a higher electric field strength; see figure 6(c).
In addition to frequency, two other characteristics are plotted in the parametric studies (figure 7). The charge acquired by the droplet,
![]() $\max |\unicode[STIX]{x1D714}|$
, is the absolute value of electric charge density acquired within one period of the stable periodic regime, and the relative time of charging,
$\max |\unicode[STIX]{x1D714}|$
, is the absolute value of electric charge density acquired within one period of the stable periodic regime, and the relative time of charging,
![]() $\tilde{t}_{ch}$
, is the duration of the charging process divided by the period of the stable periodic regime.
$\tilde{t}_{ch}$
, is the duration of the charging process divided by the period of the stable periodic regime.
The acquired charge decreases with growing surface charge density (figure 7
b). The electric force is the product of the electric field strength and the free charge density. Hence, a lower concentration of free electric charge is necessary to detach the droplet under a higher electric field strength. This finding is meaningful for droplets with relatively large droplet–electrode contact area. In such a case, the electric force required for droplet detachment is given by the droplet–electrode adhesion energy (expressed in the form of the contact angle
![]() $\unicode[STIX]{x1D70E}$
), which is kept constant in this parametric study. However, experiments with rhythmically moving droplets forming only tiny tips during the charging showed that the acquired charge monotonically increases with the electric field strength:
$\unicode[STIX]{x1D70E}$
), which is kept constant in this parametric study. However, experiments with rhythmically moving droplets forming only tiny tips during the charging showed that the acquired charge monotonically increases with the electric field strength:
![]() $\unicode[STIX]{x1D714}\propto \boldsymbol{E}^{1.33}$
(Jung et al.
Reference Jung, Oh and Kang2008) or
$\unicode[STIX]{x1D714}\propto \boldsymbol{E}^{1.33}$
(Jung et al.
Reference Jung, Oh and Kang2008) or
![]() $\unicode[STIX]{x1D714}\propto \boldsymbol{E}^{1.0}$
(Im et al.
Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012). Because of negligible adhesion energy in the tip-like interaction, the electric charge concentration in a droplet grows with increasing electric field strength as the kinetics of electrochemical charging becomes faster.
$\unicode[STIX]{x1D714}\propto \boldsymbol{E}^{1.0}$
(Im et al.
Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012). Because of negligible adhesion energy in the tip-like interaction, the electric charge concentration in a droplet grows with increasing electric field strength as the kinetics of electrochemical charging becomes faster.
The charging process is fast for high surface charge density on the electrode, which leads to a short time of charging and high frequency of droplet oscillations (figure 7 c).
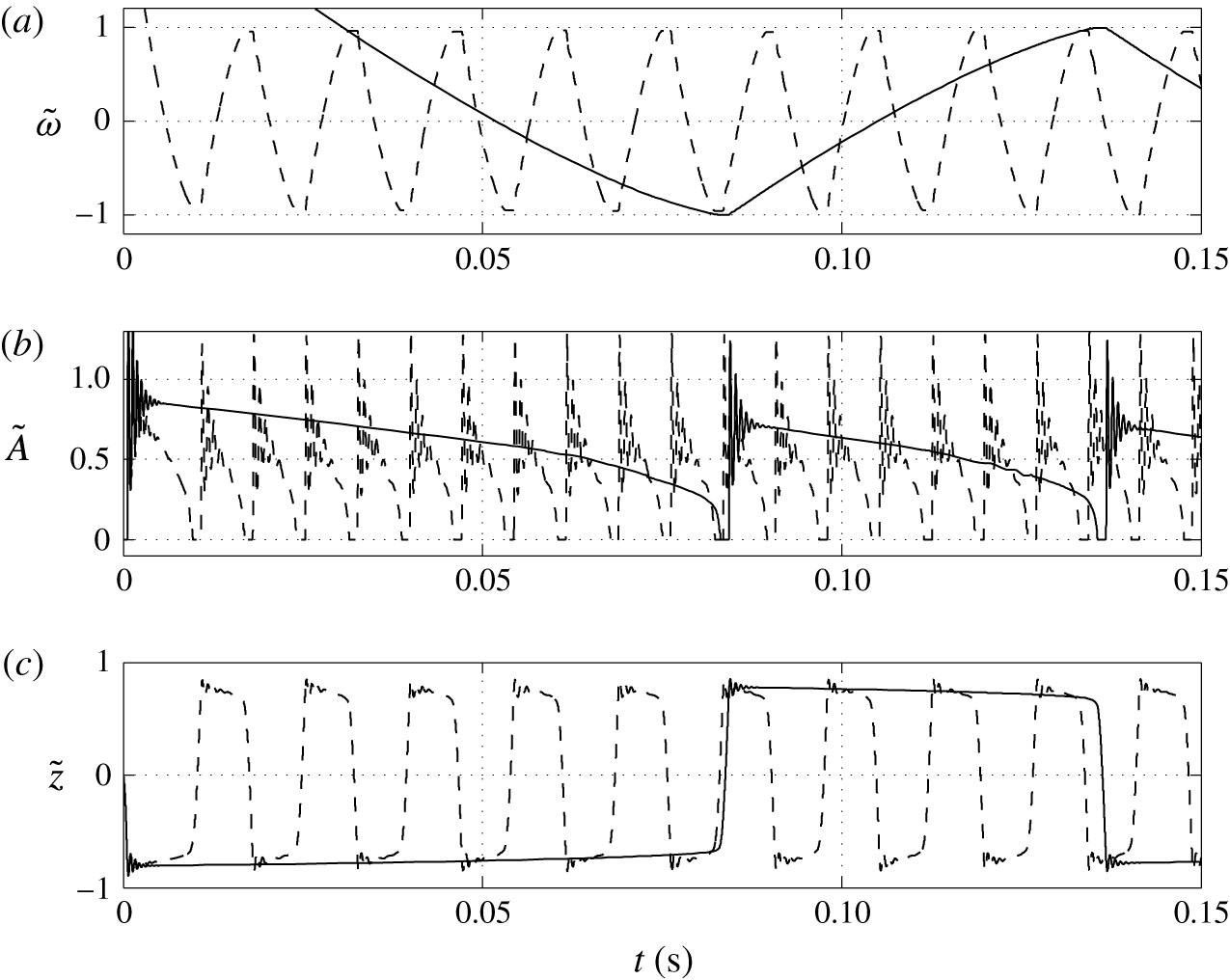
3.3 Effect of charging parameter
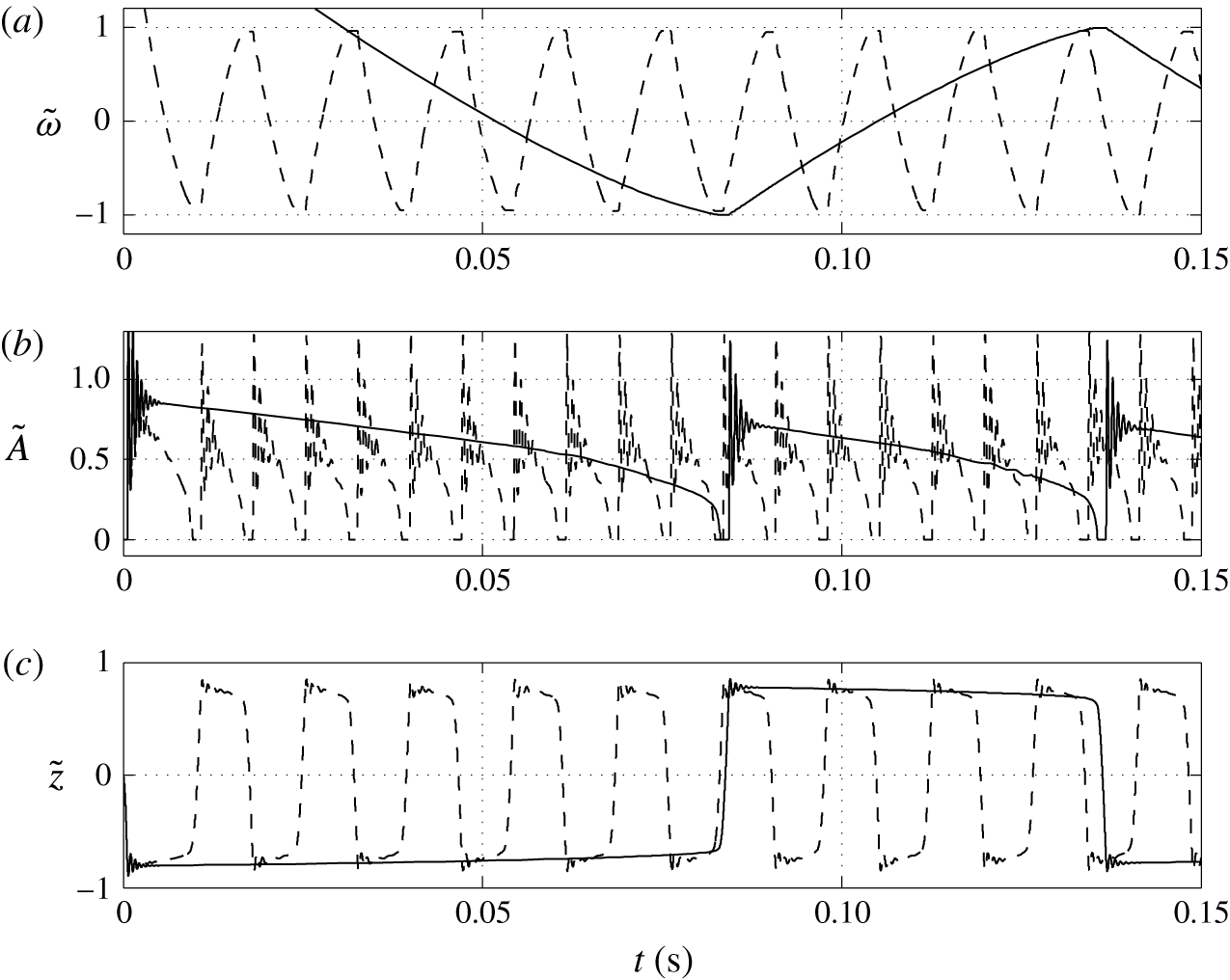
Figure 8. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position. Solid line,
![]() $K=0.002~\text{A}~\text{m}^{5}$
; dashed line,
$K=0.002~\text{A}~\text{m}^{5}$
; dashed line,
![]() $K=0.02~\text{A}~\text{m}^{5}$
.
$K=0.02~\text{A}~\text{m}^{5}$
.
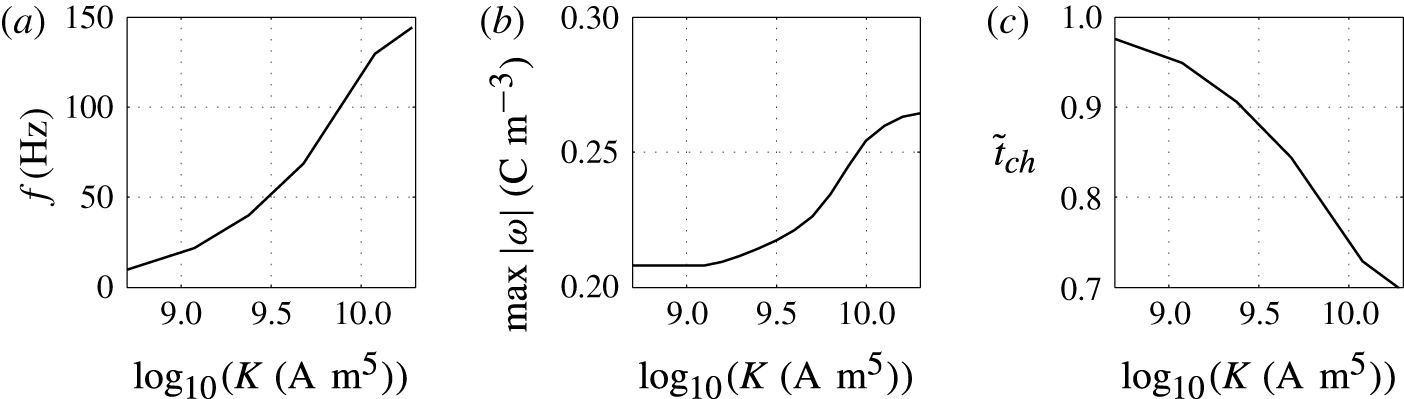
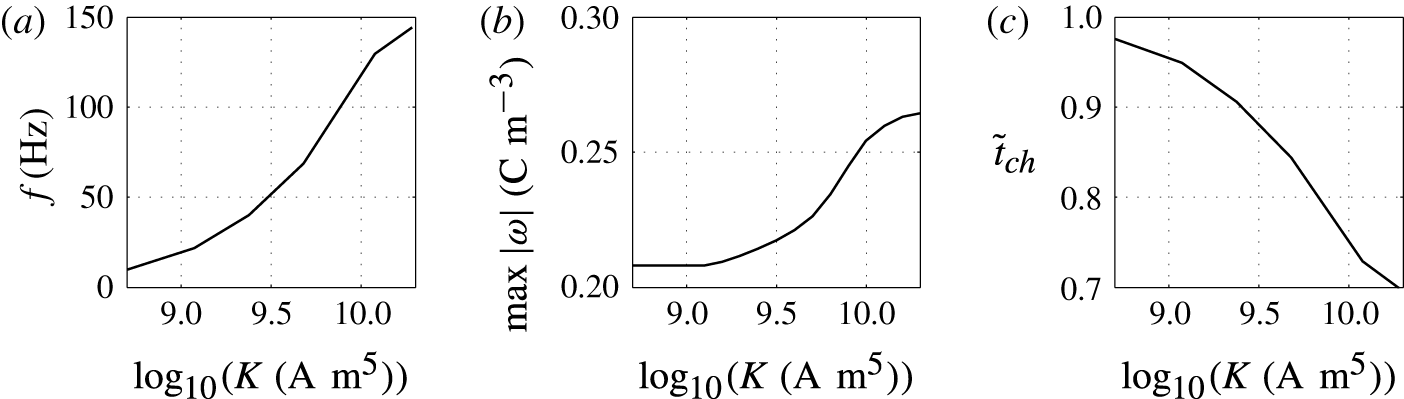
Figure 9. Effects of the charging parameter on (a) frequency of oscillations, (b) charge acquired by droplet and (c) relative time of charging.
The imposed electric field affects both the electrochemical kinetics (the charging process) and the electric volume force within the charged fluid. To decouple these two phenomena, it is useful to study the influence of the charging parameter
![]() $K$
on rhythmic motion of the droplet. The charging parameter can then be understood as an effective mass transfer coefficient multiplied by the fixed driving force (
$K$
on rhythmic motion of the droplet. The charging parameter can then be understood as an effective mass transfer coefficient multiplied by the fixed driving force (
![]() $\bar{E}$
).
$\bar{E}$
).
Figures 8 and 9 show that the larger the value of
![]() $K$
, the higher the oscillation frequency observed. High values of the charging parameter allow for fast droplet charging, significantly reducing the time that the droplet spends at the electrode surface (figure 9
c). Smaller values of
$K$
, the higher the oscillation frequency observed. High values of the charging parameter allow for fast droplet charging, significantly reducing the time that the droplet spends at the electrode surface (figure 9
c). Smaller values of
![]() $K$
provide an oscillation frequency comparable to that observed in microfluidic experiments (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014).
$K$
provide an oscillation frequency comparable to that observed in microfluidic experiments (Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014).
In contrast with the results plotted in figure 7(b), the dependence of the acquired charge on the charging parameter is an increasing function (figure 9
b). In this parametric study, the driving force
![]() $\bar{E}$
is fixed. A high value of
$\bar{E}$
is fixed. A high value of
![]() $K$
provides fast charge/mass transfer between the electrodes and droplet. Intensification of charge transfer is also responsible for the same trend observed in Jung et al. (Reference Jung, Oh and Kang2008) and Im et al. (Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012).
$K$
provides fast charge/mass transfer between the electrodes and droplet. Intensification of charge transfer is also responsible for the same trend observed in Jung et al. (Reference Jung, Oh and Kang2008) and Im et al. (Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012).
3.4 Effect of contact angle

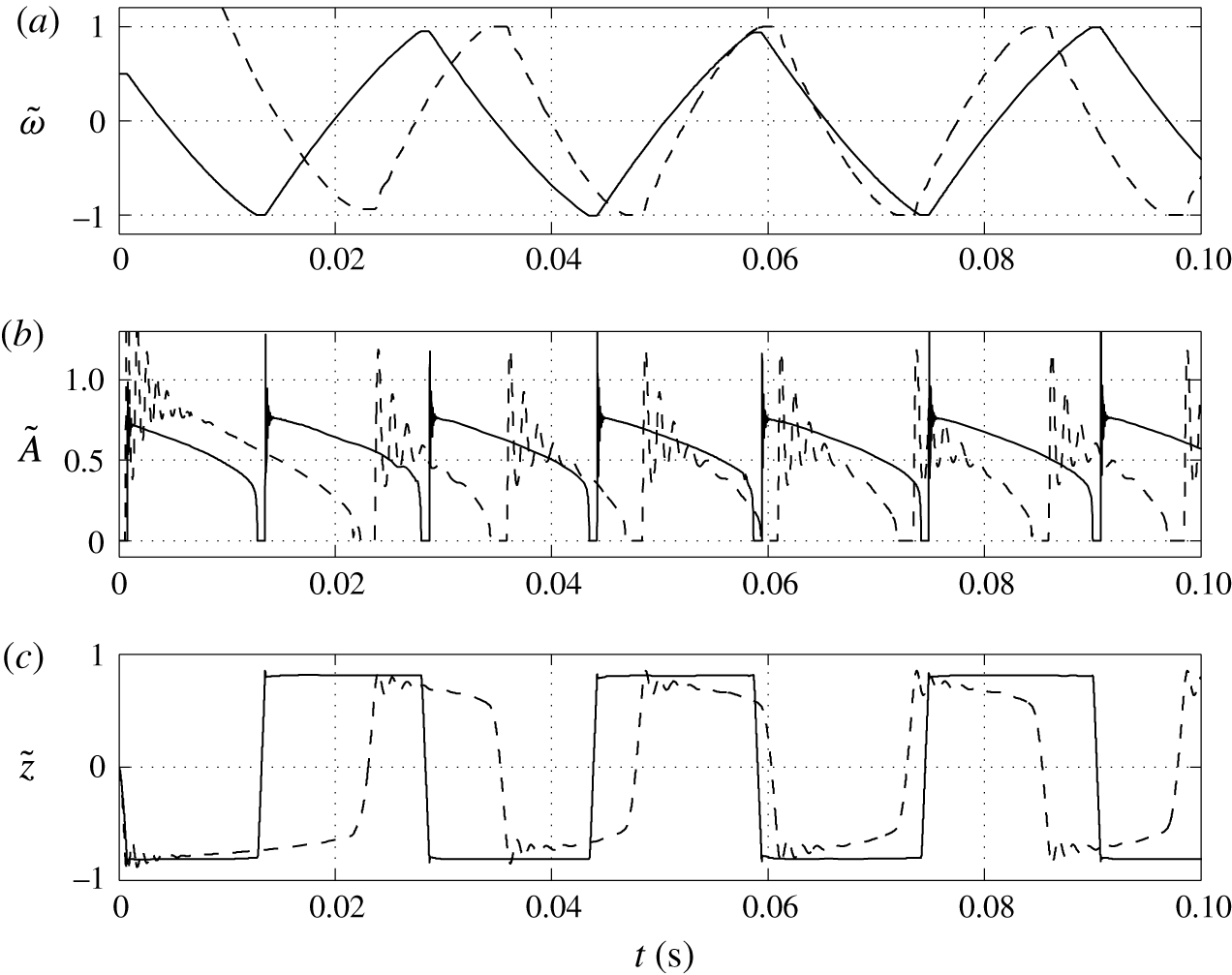
Figure 10. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position. Solid line,
![]() $\unicode[STIX]{x1D703}=90^{\circ }$
; dashed line,
$\unicode[STIX]{x1D703}=90^{\circ }$
; dashed line,
![]() $\unicode[STIX]{x1D703}=150^{\circ }$
.
$\unicode[STIX]{x1D703}=150^{\circ }$
.
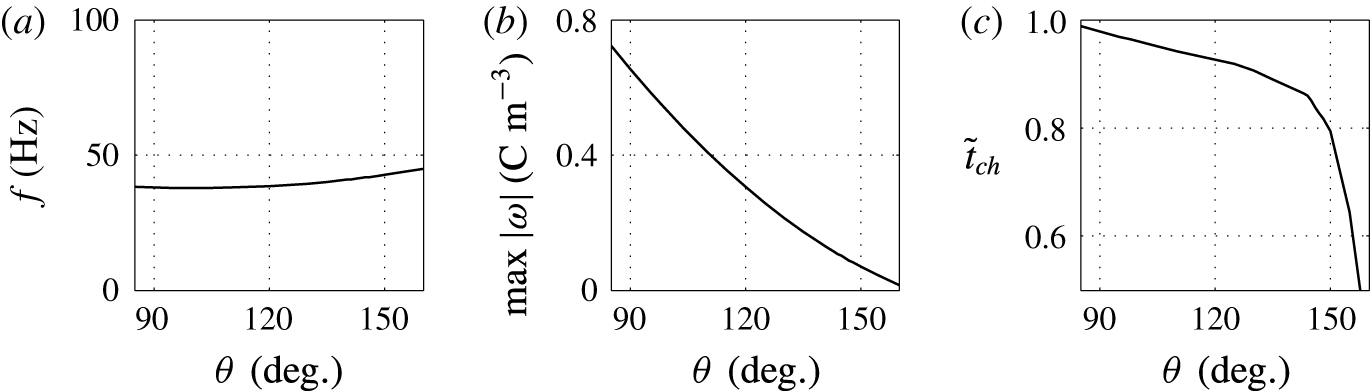
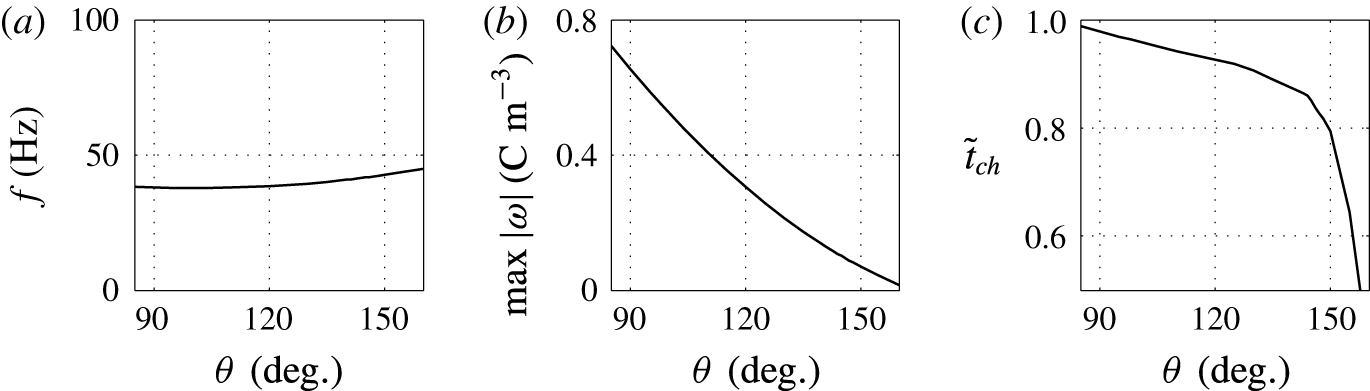
Figure 11. Effects of the contact angle on (a) frequency of oscillations, (b) charge acquired by droplet and (c) relative time of charging.
A lower value of the contact angle corresponds to a better wettability of an electrode by the droplet. While the oscillation frequency does not significantly depend on the contact angle, the electrode–droplet contact area remarkably decreases with growing contact angle; see figures 10 and 11. With larger contact area, the adhesion energy barrier increases. This has to be overcome by the electric volume force to detach the droplet. Under constant electric field strength, the force can be provided only by a larger electric charge injected into the droplet. That is the reason why the charging time is slightly longer for
![]() $\unicode[STIX]{x1D703}=90^{\circ }$
than for
$\unicode[STIX]{x1D703}=90^{\circ }$
than for
![]() $\unicode[STIX]{x1D703}=150^{\circ }$
(figures 10
c and 11
c). The fact that the acquired electric charge monotonically decreases with the contact angle is demonstrated in figure 11(b).
$\unicode[STIX]{x1D703}=150^{\circ }$
(figures 10
c and 11
c). The fact that the acquired electric charge monotonically decreases with the contact angle is demonstrated in figure 11(b).
The results plotted in figures 10 and 11 are physically meaningful, however, experimental studies focused on the contact angle effects in similar experimental system have not been reported.
3.5 Effect of droplet size
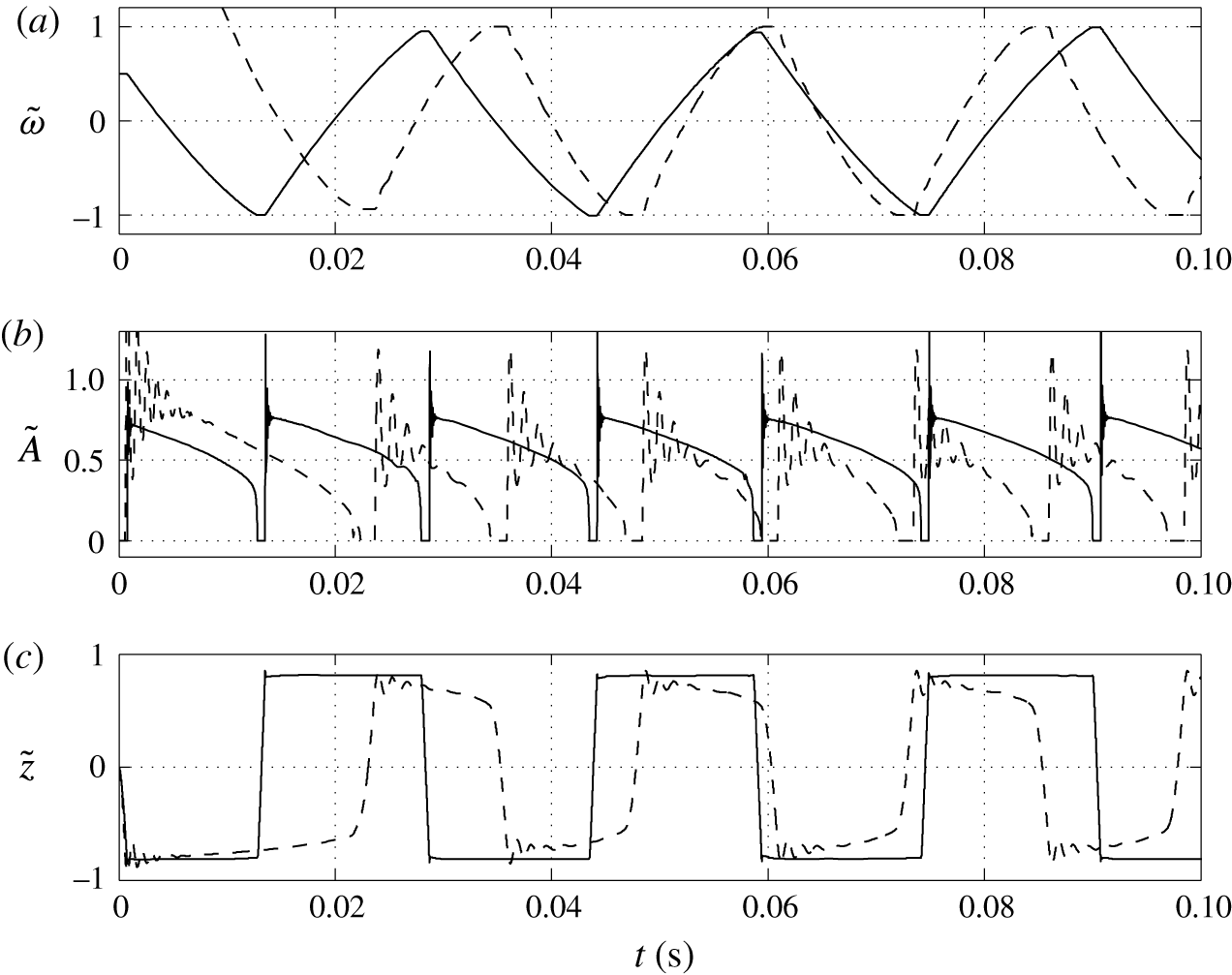
Figure 12. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position. Solid line,
![]() $s_{1}=0.03$
mm; dashed line,
$s_{1}=0.03$
mm; dashed line,
![]() $s_{1}=0.14$
mm.
$s_{1}=0.14$
mm.
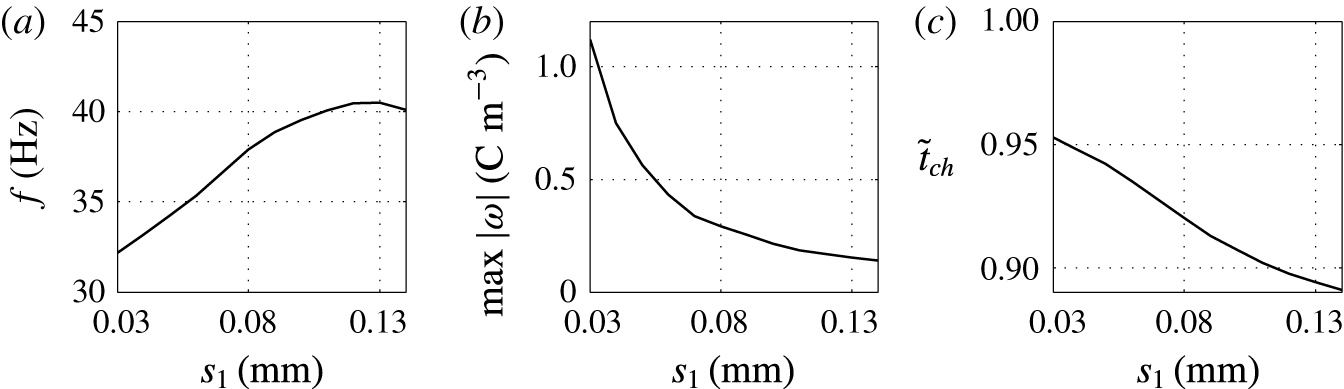
Figure 13. Effects of the droplet radius on (a) frequency of oscillations, (b) charge acquired by droplet and (c) relative time of charging.
Dependences of the velocity of oscillating droplets on the droplet radius were reported in several experimental papers (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Mhatre & Thaokar Reference Mhatre and Thaokar2013). Experiments with a pair of coplanar electrodes (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011), i.e. with geometry most relevant to our theoretical study, reveal that droplet velocity and thus oscillation frequency increases with the droplet radius. Despite the fact that bigger droplets exhibit higher hydrodynamic resistances, they are able to acquire more electric charge, which increases the electric volume force. These observations are in agreement with the results of numerical studies presented here; see figures 12 and 13.
Under a constant electric field, the total amount of acquired electric charge is proportional to the droplet–electrode contact area, equation (2.12), i.e. approximately
![]() $\propto s_{1}^{2}$
. Droplet volume
$\propto s_{1}^{2}$
. Droplet volume
![]() $V_{d}\propto s_{1}^{3}$
, hence the electric charge density
$V_{d}\propto s_{1}^{3}$
, hence the electric charge density
![]() $\unicode[STIX]{x1D714}\propto s_{1}^{-1}$
. This consideration is in agreement with the hyperbolic-like dependence plotted in figure 13(b).
$\unicode[STIX]{x1D714}\propto s_{1}^{-1}$
. This consideration is in agreement with the hyperbolic-like dependence plotted in figure 13(b).
As the droplet velocity is directly proportional to the total amount of acquired electric charge, the dependence of oscillation frequency on the droplet size should be approximately parabolic,
![]() $V_{d}\unicode[STIX]{x1D714}\propto s_{1}^{2}$
. Our simulation revealed the parabolic dependence only for droplets of size less than 0.08 mm (figure 13
a). If the droplet becomes bigger, the frequency increase is slower, then attains a maximum and finally decreases. This nonlinearity appears because friction forces between the droplet and the wall enveloping the two-phase system become important as
$V_{d}\unicode[STIX]{x1D714}\propto s_{1}^{2}$
. Our simulation revealed the parabolic dependence only for droplets of size less than 0.08 mm (figure 13
a). If the droplet becomes bigger, the frequency increase is slower, then attains a maximum and finally decreases. This nonlinearity appears because friction forces between the droplet and the wall enveloping the two-phase system become important as
![]() $s_{1}\rightarrow r_{1}$
.
$s_{1}\rightarrow r_{1}$
.
One feature of smaller droplets when touching an electrode is that there are only a few oscillations of shape. In contrast, large droplets exhibit damped oscillations during the entire period of droplet–electrode interaction (figure 12 b), which is caused by the relatively large inertial forces.
3.6 Effect of permittivity
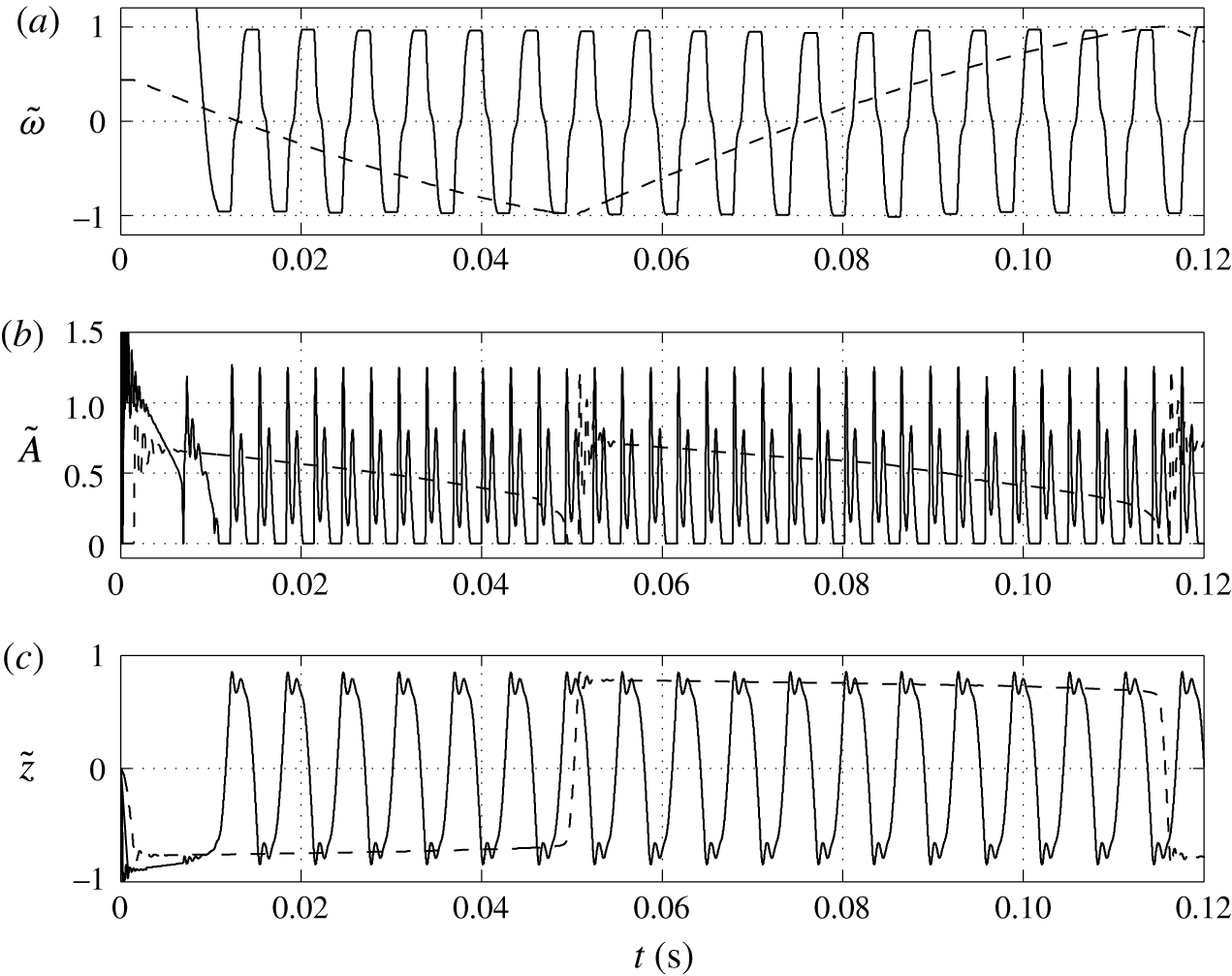
Figure 14. Time dependences of normalized (a) volume charge density, (b) droplet–electrode contact area and (c) droplet position. Solid line,
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}=2$
; dashed line,
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}=2$
; dashed line,
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}=210$
.
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}=210$
.
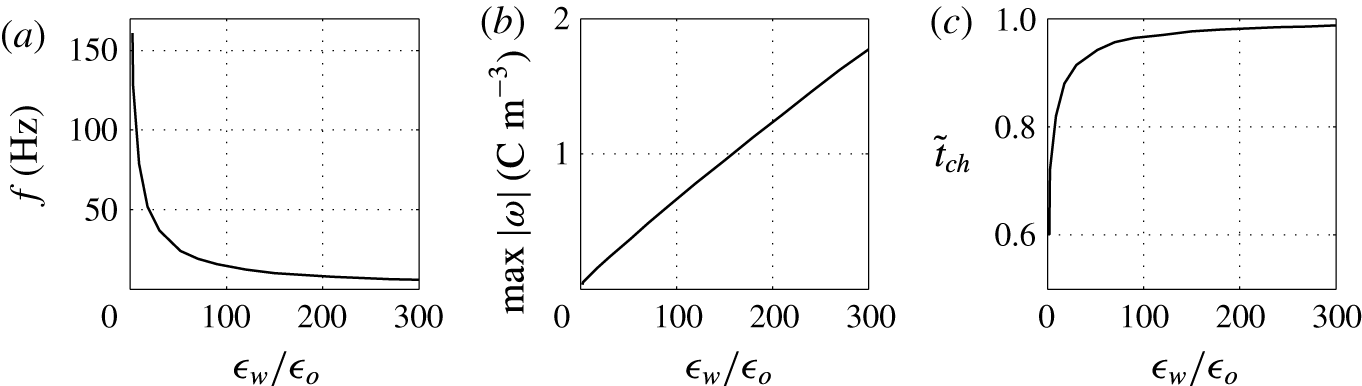
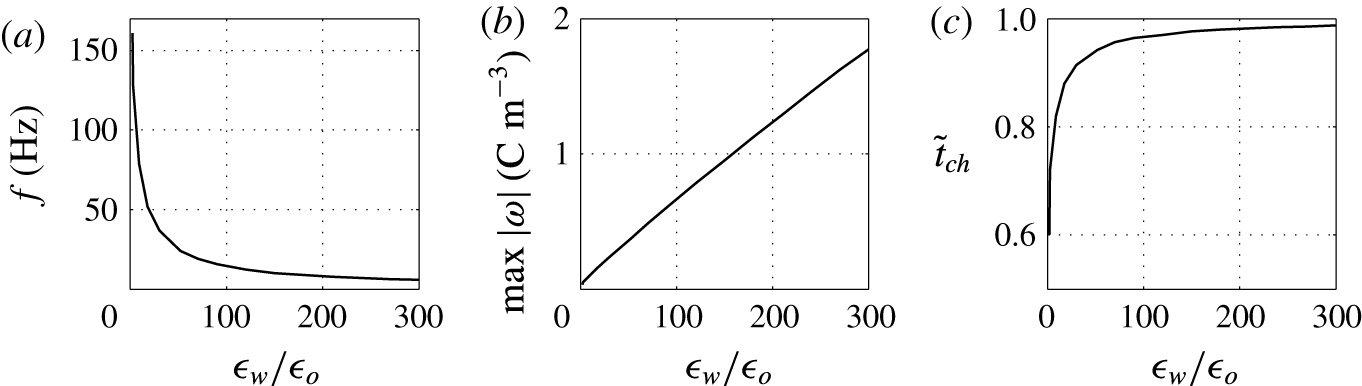
Figure 15. Effects of the permittivity ratio on (a) frequency of oscillations, (b) charge acquired by droplet and (c) relative time of charging.
Finally, the effects of the ratio of droplet to dielectric fluid permittivities
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
on the character of oscillations is examined; see figures 14 and 15. The bigger the ratio, the weaker the electric field present in the charged droplet and the stronger the electric field present in the dielectric fluid. In typical experiments with water droplets dispersed in kerosene,
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
on the character of oscillations is examined; see figures 14 and 15. The bigger the ratio, the weaker the electric field present in the charged droplet and the stronger the electric field present in the dielectric fluid. In typical experiments with water droplets dispersed in kerosene,
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}\approx 27$
. This indicates that the electric field in the droplet is much weaker than in the dielectric fluid. This is valid not only for a homogeneously charged droplet. As a thin EDL is formed in the water phase, the electric field in the droplet bulk will be even weaker.
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}\approx 27$
. This indicates that the electric field in the droplet is much weaker than in the dielectric fluid. This is valid not only for a homogeneously charged droplet. As a thin EDL is formed in the water phase, the electric field in the droplet bulk will be even weaker.
Figure 14 shows that high
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
can lead to an oscillation frequency below 10 Hz, which is typical for many reported experiments (Hase et al.
Reference Hase, Watanabe and Yoshikawa2006; Im et al.
Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). A weaker field in the droplet results in a significant decrease of the oscillation frequency (figure 15
a). A weaker electric field also requires more electric charge to detach the droplet from an electrode (figure 15
b). Hence, the relative time of charging monotonically increases with
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
can lead to an oscillation frequency below 10 Hz, which is typical for many reported experiments (Hase et al.
Reference Hase, Watanabe and Yoshikawa2006; Im et al.
Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Beranek et al.
Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). A weaker field in the droplet results in a significant decrease of the oscillation frequency (figure 15
a). A weaker electric field also requires more electric charge to detach the droplet from an electrode (figure 15
b). Hence, the relative time of charging monotonically increases with
![]() $\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
(figure 15
c).
$\unicode[STIX]{x1D716}_{w}/\unicode[STIX]{x1D716}_{o}$
(figure 15
c).
4 Summary and conclusion
According to our best knowledge we present a first attempt to numerically simulate a multiphysical model of a charged droplet oscillating under a DC electric field by means of computational fluid dynamics. Previously reported models relied mostly on force analysis for a rigid droplet (Hase et al. Reference Hase, Watanabe and Yoshikawa2006; Jung et al. Reference Jung, Oh and Kang2008; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Mhatre & Thaokar Reference Mhatre and Thaokar2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). Here we show that the level-set method can be used to study the dynamics of a deformable droplet that undergoes electric charge injection at a pair of electrodes.
Despite the model simplifications, most of the obtained results are in qualitative agreement with available experimental data: (i) the charging process is symmetric on the negative and positive electrodes as observed in Im et al. (Reference Im, Noh, Moon and Kang2011); (ii) only stable periodic regimes with period one were observed in parametric space, which is in agreement with experimental observations (Hase et al. Reference Hase, Watanabe and Yoshikawa2006; Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Kurimura et al. Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014); (iii) the model predicts a monotonic increase of the oscillation frequency for growing voltage/electric field strength/surface charge density on the electrodes as reported in Jung et al. (Reference Jung, Oh and Kang2008), Im et al. (Reference Im, Noh, Moon and Kang2011), Kurimura et al. (Reference Kurimura, Ichikawa, Takinoue and Yoshikawa2013) and Beranek et al. (Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014); (iv) predicted frequencies of oscillations are similar to those observed in experiments (Hase et al. Reference Hase, Watanabe and Yoshikawa2006; Im et al. Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014), especially for small values of the charging parameter, small densities of the electric charge on the electrodes and high ratios of permittivities of the dispersed and continuous phases; (v) the frequency of oscillations and droplet velocity increase with the droplet radius in agreement with experimental data available for coplanar electrodes (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011).
The main difference between experimental data and our theoretical predictions is found in the character of droplet–electrode interaction. The formation of only a tiny tip on the droplet surface was observed during charge injection in most of the experiments (Jung et al. Reference Jung, Oh and Kang2008; Im et al. Reference Im, Noh, Moon and Kang2011, Reference Im, Ahn, Yoo, Moon, Lee and Kang2012; Mhatre & Thaokar Reference Mhatre and Thaokar2013; Beranek et al. Reference Beranek, Flittner, Hrobar, Ethgen and Pribyl2014). However, experiments reported in Jalaal et al. (Reference Jalaal, Khorshidi and Esmaeilzadeh2010) exhibit a large droplet–electrode interface during the charging process. Our simulations show significant wetting of electrodes by the droplet. This difference stems from two simplifying assumptions we exploited: (i) homogeneous distribution of electric charge within the droplet; (ii) the neglect of the dielectrophoretic term in (2.3). Unfortunately, to treat EDL dynamics within an aqueous droplet represents quite a difficult task due to extreme differences between the characteristic dimensions of the model domain or droplet radius on the one hand and EDL thickness or thickness of the interface on the other.
Stable periodic regimes with period one were observed in all the parametric studies reported in this paper. However, there is a possibility of the emergence of more complex regimes in parametric space. The system is similar to dripping faucet oscillators, which frequently exhibit chaotic and higher-period regimes due to the interplay of surface tension and gravity, drag and inertial forces (Martien et al. Reference Martien, Pope, Scott and Shaw1985). Instead of the gravity force and continuous mass injection into a droplet, electric volume force and electrochemical charge injection are considered in our study.
It can be concluded that the mathematical model studied here confirms the idea that rhythmic droplet motion under a DC electric field emerges as a result of the electrochemical charging process and the interaction of free electric charge with the imposed electric field. The model is able to predict the existence of periodic oscillations in a wide region of parametric space.
Acknowledgements
The authors would like to thank the Czech Science Foundation (grant no. 14-01781S) and the Ministry of Education, Youth, and Sports of the Czech Republic (specific university research MSMT no. 20-SVV/2016) for financial support of this work.
Supplementary movie
A supplementary movie is available at https://doi.org/10.1017/jfm.2017.230.