1. Introduction
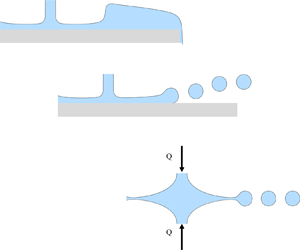
Stationary axisymmetric liquid structures formed by jet impacts have motivated an enormous amount of literature. Three examples that will be important here are sketched in figure 1. The first is the well-known circular hydraulic jump (Rayleigh Reference Rayleigh1914; Tani Reference Tani1949; Watson Reference Watson1964; Craik et al. Reference Craik, Latham, Fawkes and Gribbon1981; Bohr, Dimon & Putkaradze Reference Bohr, Dimon and Putkaradze1993; Bush & Aristoff Reference Bush and Aristoff2003; Duchesne, Lebon & Limat Reference Duchesne, Lebon and Limat2014; Mohajer & Li Reference Mohajer and Li2015; Bhagat et al. Reference Bhagat, Jha, Linden and Wilson2018; Salah et al. Reference Salah, Duchesne, De Cock, Massinon, Sassi, Abrougui, Lebeau and Dorbolo2018; Wang & Khayat Reference Wang and Khayat2019, Reference Wang and Khayat2021), shown in figure 1(a), with a well-developed liquid film extending all around. The second, in figure 1(b), is its equivalent on a ‘dry’ surface (atomization rim), obtained by superhydrophobic treatment (Maynes, Johnson & Webb Reference Maynes, Johnson and Webb2011; Sen et al. Reference Sen, Chatterjee, Crockett, Ganguly, Yu and Megaridis2019). A related, but different, configuration can be reached by simply impinging a vertical jet from below on a horizontal ceiling (Button et al. Reference Button, Davidson, Jameson and Sader2010; Jameson et al. Reference Jameson, Jenkins, Button and Sader2010). The final example is the well-known radial liquid sheet (Savart Reference Savart1833; Huang Reference Huang1970; Clanet & Villermaux Reference Clanet and Villermaux2002; Villermaux, Pistre & Lhuissier Reference Villermaux, Pistre and Lhuissier2013), formed either by impinging two opposite symmetrical liquid jets having the same central axis, or by impinging a liquid jet on a solid surface with a diameter similar to the jet diameter; this is depicted in figure 1(c).

Figure 1. Three axisymmetric film flows are discussed in the present article: (a) the classical circular hydraulic jump formed by a jet impacting a solid disk at its centre; (b) atomization ring formed by a jet impacting a dry surface, possibly superhydrophobic; (c) liquid sheet formed by impact of two liquid jets of opposite direction.
These three geometries are of course linked by the same general equation for the energy balance. In this article, we will therefore show that apparent paradoxes raised by the modelling of the surface tension on the circular hydraulic jump by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018) may be solved or at least clarified by considering the geometry depicted in figure 1(c).
The selection of jump radius ![]() $R_J$ in the circular hydraulic jump case (figure 1a) has motivated many studies. The two best-known approaches are that of Watson and Bush (Watson Reference Watson1964; Bush & Aristoff Reference Bush and Aristoff2003), in which the height of the outer film remains a control parameter, and that of Bohr et al. (Reference Bohr, Dimon and Putkaradze1993), devised instead for a liquid film extending all around at a large distance, and inspired by boundary-layer theories. As is well known, this second approach leads to a scaling law dependence of
$R_J$ in the circular hydraulic jump case (figure 1a) has motivated many studies. The two best-known approaches are that of Watson and Bush (Watson Reference Watson1964; Bush & Aristoff Reference Bush and Aristoff2003), in which the height of the outer film remains a control parameter, and that of Bohr et al. (Reference Bohr, Dimon and Putkaradze1993), devised instead for a liquid film extending all around at a large distance, and inspired by boundary-layer theories. As is well known, this second approach leads to a scaling law dependence of ![]() $R_J$ upon the flow rate
$R_J$ upon the flow rate ![]() $Q$ and the physical parameters (the kinematic viscosity of the fluid
$Q$ and the physical parameters (the kinematic viscosity of the fluid ![]() $\nu$, the gravity
$\nu$, the gravity ![]() $g$), which reads as follows:
$g$), which reads as follows:
Later, Duchesne et al. (Reference Duchesne, Lebon and Limat2014) emphasized the importance of logarithmic corrections to scaling, due to viscous dissipation in the outer film, yet observed numerically by Bohr. They also showed that the prefactor was experimentally linked to the value of the Froude number at the jump location (precisely at the immediate exit of the jump, in the outer part of the flow), which seemed to be locked to a critical value. This phenomenon was recovered by Mohajer & Li (Reference Mohajer and Li2015) and by Argentina et al. (Reference Argentina, Cerda, Duchesne and Limat2017) with a nonlinear modelling of film flow equations including the first finite slope terms.
Very recently, an attempt to revise this picture has been published by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), who performed new experiments and reported the observation of a different scaling, where surface tension ![]() $\gamma$ was involved, but not gravity:
$\gamma$ was involved, but not gravity:
where ![]() $\rho$ is the liquid density. To rationalize this finding, these authors claimed that most available approaches to the influence of surface tension lead to only small corrections (Bush & Aristoff Reference Bush and Aristoff2003) and that the description of the circular hydraulic jump had thus to be completely reconsidered. They introduced an energy balance, between two radii
$\rho$ is the liquid density. To rationalize this finding, these authors claimed that most available approaches to the influence of surface tension lead to only small corrections (Bush & Aristoff Reference Bush and Aristoff2003) and that the description of the circular hydraulic jump had thus to be completely reconsidered. They introduced an energy balance, between two radii ![]() $r$ and
$r$ and ![]() $r+\delta r$, which reads
$r+\delta r$, which reads
 \begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh \right]^{r+\delta r}_r= \left[\gamma r\bar u \right]^{r+\delta r}_r-\left[p \bar u h \right]^{r+\delta r}_r- \left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r, \end{equation}
\begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh \right]^{r+\delta r}_r= \left[\gamma r\bar u \right]^{r+\delta r}_r-\left[p \bar u h \right]^{r+\delta r}_r- \left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r, \end{equation}
with the notation ![]() $[A ]_r^{r+\delta r}= A(r+\delta r)-A(r)$, and where
$[A ]_r^{r+\delta r}= A(r+\delta r)-A(r)$, and where ![]() $\bar u$ designates the flux-average radial velocity,
$\bar u$ designates the flux-average radial velocity, ![]() $r$ the distance to the axis,
$r$ the distance to the axis, ![]() $h(r)$ the thickness of the liquid layer,
$h(r)$ the thickness of the liquid layer, ![]() $p(r)$ the pressure at
$p(r)$ the pressure at ![]() $z=0$ and
$z=0$ and ![]() $\tau _W$ the wall shear stress. The last term on the right designates the viscous dissipation by friction on the substrate, while the first one is an additional term compared to previous approaches, which is presumed to be ‘at the origin’ of the new scaling (1.2). This conjecture has been contested (Duchesne, Andersen & Bohr Reference Duchesne, Andersen and Bohr2019; Bohr & Scheichl Reference Bohr and Scheichl2021) (see also the answer in Bhagat & Linden (Reference Bhagat and Linden2020)), and it is also known that a scaling like (1.2) can also appear without such an assumption, as shown for instance by Button et al. (Reference Button, Davidson, Jameson and Sader2010) for liquid bells formed below a ceiling.
$\tau _W$ the wall shear stress. The last term on the right designates the viscous dissipation by friction on the substrate, while the first one is an additional term compared to previous approaches, which is presumed to be ‘at the origin’ of the new scaling (1.2). This conjecture has been contested (Duchesne, Andersen & Bohr Reference Duchesne, Andersen and Bohr2019; Bohr & Scheichl Reference Bohr and Scheichl2021) (see also the answer in Bhagat & Linden (Reference Bhagat and Linden2020)), and it is also known that a scaling like (1.2) can also appear without such an assumption, as shown for instance by Button et al. (Reference Button, Davidson, Jameson and Sader2010) for liquid bells formed below a ceiling.
Here it is useful to have a look at what would happen in the simplified geometry of figure 1(c), when applying this principle. As we shall show in § 2, this modelling leads to a velocity distribution in complete contradiction to the present knowledge of liquid sheets (and with Bernoulli's principle), which suggests that the argument of Bhagat et al. is flawed. In fact the flow field obtained is not new; it was previously proposed by Bouasse (Reference Bouasse1923), who attributed the calculation to Hagen (Reference Hagen1849) (it is worth noticing that this error has recently been pointed out by Bohr & Scheichl Reference Bohr and Scheichl2021). It will be instructive here to recall the argument followed by Hagen and Bouasse in a Lagrangian frame, analysing an expanding circular piece of film; we describe this argument in § 3. We will then show, in the same section, how one can correct the argument to get the more classical and now admitted result deduced from Bernoulli's principle of a uniform radial velocity around the impact point, and how, if some terms in the balance are missed, one can get the flawed result of Bouasse and Hagen. Finally, coming back to an Eulerian description, we will explain how these considerations affect the principle proposed in (1.3). We will show that an extra term exactly equal and opposite to the capillary contribution should cancel this one, in a way consistent with classical thermodynamics (i.e. surface tension can only produce a non-zero amount of global work when the surface area of the associated interface changes), leading to the expression usually written from the balance of momentum.
This does not mean, however, that the scaling discovery of Bhagat et al. is of no interest. In §§ 4 and 5, we will try to specify to which capillary structures – different from the stationary hydraulic jump observed by Bohr – it could apply, and a possible way to justify its occurrence.
2. A look at a simple situation: the axisymmetric liquid sheet
Let us try to apply the principle suggested in (1.3) to the case suggested in figure 1(c), i.e. to an axisymmetric sheet formed by the coaxial impact of two jets in a situation of negligible gravity. The viscous shear on the substrate having disappeared, (1.3) reduces to a very simple balance that reads as follows:
 \begin{equation} \left[ \rho rh \frac{ u^3}2 \right]^{r+\delta r}_r=\left[ \gamma r u \right]^{r+\delta r}_r, \end{equation}
\begin{equation} \left[ \rho rh \frac{ u^3}2 \right]^{r+\delta r}_r=\left[ \gamma r u \right]^{r+\delta r}_r, \end{equation}
where the horizontal velocity ![]() $u$ has no dependence upon the transverse direction, and coincides with any of its average values. This implies that the following quantity is constant all over the sheet:
$u$ has no dependence upon the transverse direction, and coincides with any of its average values. This implies that the following quantity is constant all over the sheet:
Combined with the mass balance ![]() $Q=2{\rm \pi} rhu$, this leads to the following expression for
$Q=2{\rm \pi} rhu$, this leads to the following expression for ![]() $u$:
$u$:
 \begin{equation} u=2 {\rm \pi}\frac\gamma{\rho Q}r+\sqrt{u_0^2-4 {\rm \pi}\frac\gamma{\rho Q}r_0 u_0+ 4 {\rm \pi}^2 \frac{\gamma^2}{\rho^2 Q^2}r^2}, \end{equation}
\begin{equation} u=2 {\rm \pi}\frac\gamma{\rho Q}r+\sqrt{u_0^2-4 {\rm \pi}\frac\gamma{\rho Q}r_0 u_0+ 4 {\rm \pi}^2 \frac{\gamma^2}{\rho^2 Q^2}r^2}, \end{equation}
where ![]() $r_0$ designates the jet radius at impact and
$r_0$ designates the jet radius at impact and ![]() $u_0$ the asymptotic value for
$u_0$ the asymptotic value for ![]() $u$, reached when
$u$, reached when ![]() $r=r_0$, which satisfies the equality
$r=r_0$, which satisfies the equality ![]() $Q={\rm \pi} r_0^2 u_0$ in a quasi-elastic shock approximation (Villermaux et al. Reference Villermaux, Pistre and Lhuissier2013). In the limit of large jet velocity, i.e.
$Q={\rm \pi} r_0^2 u_0$ in a quasi-elastic shock approximation (Villermaux et al. Reference Villermaux, Pistre and Lhuissier2013). In the limit of large jet velocity, i.e. ![]() $u_0^2 \gg 2\gamma /(\rho r_0 )$, this expression reduces to the following approximation, which is slowly varying upon
$u_0^2 \gg 2\gamma /(\rho r_0 )$, this expression reduces to the following approximation, which is slowly varying upon ![]() $r$:
$r$:
This is known to be false, as it has been checked experimentally that the velocity is constant all over the sheet, recovering Bernoulli's principle (see in particular figure 3 in Villermaux et al. Reference Villermaux, Pistre and Lhuissier2013). It is surprising, however, that a similar expression was proposed by Bouasse (Reference Bouasse1923), who attributed this result to Hagen (Reference Hagen1849), but with a slight sign change that is in fact due to a mistake of his own:
Though obtained erroneously, this expression is very seductive, and Bouasse used it to calculate the radius of the liquid sheet ![]() $R_{LS}$ assuming that the sheet border should stay at the place where
$R_{LS}$ assuming that the sheet border should stay at the place where ![]() $u$ vanishes, which leads to
$u$ vanishes, which leads to ![]() $R_{LS}=(\rho Q u_0)/(2{\rm \pi} \gamma ) =(\rho r_0^2 u_0^2)/(2\gamma )$. Surprisingly, this result coincides with the correct one, which is in fact obtained, now, by assuming a constant velocity, dictated by Bernoulli's principle, and the balance of momentum at the sheet perimeter, i.e.
$R_{LS}=(\rho Q u_0)/(2{\rm \pi} \gamma ) =(\rho r_0^2 u_0^2)/(2\gamma )$. Surprisingly, this result coincides with the correct one, which is in fact obtained, now, by assuming a constant velocity, dictated by Bernoulli's principle, and the balance of momentum at the sheet perimeter, i.e. ![]() $\rho hu^2=\gamma$ (Villermaux et al. Reference Villermaux, Pistre and Lhuissier2013). But on the other hand, we would like to stress that the radial velocity is uniform in the sheet of figure 1(c), which means that the principle proposed in (1.3), and therefore the basis of the theory developed by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), is flawed.
$\rho hu^2=\gamma$ (Villermaux et al. Reference Villermaux, Pistre and Lhuissier2013). But on the other hand, we would like to stress that the radial velocity is uniform in the sheet of figure 1(c), which means that the principle proposed in (1.3), and therefore the basis of the theory developed by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), is flawed.
3. Reconsidering Hagen's argument, and its implications for hydraulic jump
We now try to understand the fault underlying the principle of Bouasse and Hagen. Their line of thought is easier to explain if we consider a Lagrangian frame, and more precisely the balance of energy on an annular piece of fluid convected by the radial flow; this is in fact the method proposed by Bouasse himself in his treatise on fluid mechanics (Bouasse Reference Bouasse1923).
Let us consider an annular piece of film as in figure 2(a), convected and distorted by the flow. Mass conservation implies that, at any time ![]() $hr\delta r=Cte$, while the balance of energy for the whole annulus reads, in the limit of
$hr\delta r=Cte$, while the balance of energy for the whole annulus reads, in the limit of ![]() $\delta r$ small enough to satisfies the condition
$\delta r$ small enough to satisfies the condition ![]() $\delta r ({\partial u}/{\partial r}) \ll u$ of a slowly varying velocity field:
$\delta r ({\partial u}/{\partial r}) \ll u$ of a slowly varying velocity field:

Figure 2. Lagrangian (a) and Eulerian (b) frames used in the text for discussing energy balance in an annular portion of a liquid film.
The first term in the left-hand side of this equation stands for kinetic energy, and the second for the surface energy enclosed between ![]() $r$ and
$r$ and ![]() $r+\delta r$. The right-hand term comes from the work of surface forces, and does not vanish. Indeed, the same surface tension force is pulling on a different arc length, as the external boundary has a larger perimeter than the other (note that this is the intuitive argument underlying the analysis of Bhagat et al.). Still in the limit of a slowly varying velocity field at the scale
$r+\delta r$. The right-hand term comes from the work of surface forces, and does not vanish. Indeed, the same surface tension force is pulling on a different arc length, as the external boundary has a larger perimeter than the other (note that this is the intuitive argument underlying the analysis of Bhagat et al.). Still in the limit of a slowly varying velocity field at the scale ![]() $\delta r$, after noting that
$\delta r$, after noting that ![]() ${\partial }/{\partial t}=u {\partial }/{\partial r}$, (3.1) reads
${\partial }/{\partial t}=u {\partial }/{\partial r}$, (3.1) reads
In fact, the two surface tension terms are cancelling each other, which means that the work provided to the annulus by the surface tension of the outer interfaces is completely transformed into the surface energy stored at the free surface of the annulus, in agreement with simple thermodynamic considerations. As a result, the fluid velocity is unaffected by surface tension balance and remains constant, as one would deduce from a more classical argument in terms of Bernoulli's principle; i.e. ![]() $u(r)$ is in fact independent of
$u(r)$ is in fact independent of ![]() $r$:
$r$:
Note here that skipping from (3.1) to (3.2) is not completely trivial, as there is an extra ![]() $\gamma$ term remaining, but this vanishes for the constant and uniform
$\gamma$ term remaining, but this vanishes for the constant and uniform ![]() $u_0$ solution.
$u_0$ solution.
To reconnect with Bouasse, if instead one forgets the internal surface energy contribution in the left-hand member of (3.2), one obtains the following equation for ![]() $u$:
$u$:
After simplifying ![]() $\delta r$, and using the fact that
$\delta r$, and using the fact that ![]() $Q= 2{\rm \pi} r u h$, this equation leads to
$Q= 2{\rm \pi} r u h$, this equation leads to
which leads finally to (2.4). Alternatively, (2.5) is obtained when one forgets the work provided to the annulus by the outer parts of the liquid sheet, i.e. when one neglects the right-hand member of (3.2), following the intuitive but erroneous idea of Hagen (Reference Hagen1849) that surface tension could slow down the flow. Historically, Bouasse followed the first argument but made a sign error, obtaining (2.5), which was presumably physically more natural, in view of what Hagen said long ago.
To summarize, a correct treatment of the expansion of liquid annuli in the flow leads to the classical result of a uniform velocity, while the approximations defended by Hagen and Bouasse would follow from neglecting one or the other of the capillary terms. We believe that a similar problem is involved in (1.3). If we now consider an Eulerian description of the flow, as suggested in figure 2(b), the balance of energy will instead read
 \begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh +\gamma r\bar u \right]^{r+\delta r}_r= \left[\gamma r\bar u \right]^{r+\delta r}_r-\left[p \bar u h \right]^{r+\delta r}_r- \left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r, \end{equation}
\begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh +\gamma r\bar u \right]^{r+\delta r}_r= \left[\gamma r\bar u \right]^{r+\delta r}_r-\left[p \bar u h \right]^{r+\delta r}_r- \left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r, \end{equation}where, in the left-hand side, we have added the surface energy convected by the film. It is true that one can consider a capillary force, as in Bhagat et al., in the right-hand member, but in this case, one should not miss the surface flux crossing the two circles displayed in figure 2(b) in the left-hand side of the equation. And just as in a Lagrangian frame, the physics being the same in both frames, the capillary effects should exactly compensate for each other in this equation, which should then reduce to the more conventional form
 \begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh \right]^{r+\delta r}_r={-} \left[p \bar u h \right]^{r+\delta r}_r-\left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r. \end{equation}
\begin{equation} \left[\rho \frac{\bar u^2}2 \bar u rh \right]^{r+\delta r}_r={-} \left[p \bar u h \right]^{r+\delta r}_r-\left[\rho g \frac{h^2}2 r \bar u \right]^{r+\delta r}_r-r \tau_W\bar u \delta r. \end{equation}This, apart from some coefficients that will depend on the detailed structure of the flow profile, is consistent with what people are used to writing starting instead from the balance of momentum (Bohr et al. Reference Bohr, Dimon and Putkaradze1993). Therefore, in the interpretation of (1.2), we do not consider that one should add a new capillary force distributed throughout space as proposed by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018). In our opinion, this would merely reproduce the initial mistake of Hagen and Bouasse. However, in the same way that Bouasse's approach leads to the correct radius for the liquid sheet but with a biased approach, we may be able to show that the scaling of Bhagat et al. can be recovered by properly taking into account the boundary conditions. We now develop this idea further.
4. Alternative explanation of unusual scaling: the boundary condition at the ‘jump’ radius; comparison with atomization rings
To interpret the occurrence of the scaling of Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), we propose an alternative approach. We simply treat the two ideal situations of figures 1(a) and 1(b) with the same method, and see what happens. We will then see that the situation obtained in figure 1(b) may be compared to the one suggested by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018).
To simplify the analysis, the ‘internal’ flow for ![]() $r_0< r< R_J$ is assimilated to the one discussed long ago by Watson (Reference Watson1964), in which fluid inertia is progressively dissipated by viscous friction; i.e. for
$r_0< r< R_J$ is assimilated to the one discussed long ago by Watson (Reference Watson1964), in which fluid inertia is progressively dissipated by viscous friction; i.e. for ![]() $r< R_J$,
$r< R_J$,
where ![]() $c\approx 1.402$,
$c\approx 1.402$, ![]() $l=0.567r_0R$ (with
$l=0.567r_0R$ (with ![]() $R$ the Reynolds number of the jet) and
$R$ the Reynolds number of the jet) and ![]() $f$ is the function
$f$ is the function ![]() $f(\eta )=\sqrt {3}+1-{2\sqrt {3}}/{(1+cn(3^{1/4}c(1-\eta )))}$. Mass conservation implies that the flux of momentum is given by
$f(\eta )=\sqrt {3}+1-{2\sqrt {3}}/{(1+cn(3^{1/4}c(1-\eta )))}$. Mass conservation implies that the flux of momentum is given by
where ![]() $\langle u^2\rangle =\int_0^h u^2 \,\mathrm{d}z$. In the case of figure 1a, this flow must be matched for
$\langle u^2\rangle =\int_0^h u^2 \,\mathrm{d}z$. In the case of figure 1a, this flow must be matched for ![]() $r>R_J$ to a film flow under the action of gravity that, according to lubrication (Duchesne et al. Reference Duchesne, Lebon and Limat2014), has a thickness distribution
$r>R_J$ to a film flow under the action of gravity that, according to lubrication (Duchesne et al. Reference Duchesne, Lebon and Limat2014), has a thickness distribution ![]() $H(r)$ given by
$H(r)$ given by
where ![]() $R_\infty$ designates the outer radius of the substrate and the thickness H reaches a value called
$R_\infty$ designates the outer radius of the substrate and the thickness H reaches a value called ![]() $H_\infty$ that will depend on the specific geometrical conditions of the flow there (see figure 1a for the graphical definition). At
$H_\infty$ that will depend on the specific geometrical conditions of the flow there (see figure 1a for the graphical definition). At ![]() $r=R_J$, one must write some matching condition that is consistent with the approximations made on each side of
$r=R_J$, one must write some matching condition that is consistent with the approximations made on each side of ![]() $r=R_J$, and stands for a shock (Bélanger Reference Bélanger1841; Rayleigh Reference Rayleigh1914). If we assume
$r=R_J$, and stands for a shock (Bélanger Reference Bélanger1841; Rayleigh Reference Rayleigh1914). If we assume ![]() $h\ll H$ and neglect the surface tension at the shock (i.e. for sufficiently large circular hydraulic jumps , such as those considered by Bhagat et al. Reference Bhagat, Jha, Linden and Wilson2018), this shock condition reads
$h\ll H$ and neglect the surface tension at the shock (i.e. for sufficiently large circular hydraulic jumps , such as those considered by Bhagat et al. Reference Bhagat, Jha, Linden and Wilson2018), this shock condition reads
In the limit of negligible values for ![]() $H_\infty$ and
$H_\infty$ and ![]() $r_0$, compared to the other scales, it is easy to check that these equations lead to the following scaling law for
$r_0$, compared to the other scales, it is easy to check that these equations lead to the following scaling law for ![]() $R_J$:
$R_J$:
 \begin{equation} R_J ln \left(\frac {R_\infty} {R_J}\right)^{1/8}= \frac{(3c)^{3/4}}{2^{9/8} {\rm \pi}^{11/8}} \frac{Q^{5/8}}{\nu^{3/8}g^{1/8}}. \end{equation}
\begin{equation} R_J ln \left(\frac {R_\infty} {R_J}\right)^{1/8}= \frac{(3c)^{3/4}}{2^{9/8} {\rm \pi}^{11/8}} \frac{Q^{5/8}}{\nu^{3/8}g^{1/8}}. \end{equation}This is the scaling obtained by Bohr et al. (Reference Bohr, Dimon and Putkaradze1993), modified by logarithmic corrections.
We now consider the regime described in figure 1(b), which may be obtained in a stationary regime with a particular superhydrophobic treatment (Maynes et al. Reference Maynes, Johnson and Webb2011; Sen et al. Reference Sen, Chatterjee, Crockett, Ganguly, Yu and Megaridis2019). In this regime the force opposed to fluid inertia at the boundaries is dictated only by surface tension and not by gravity; there is no developed shock, no liquid ‘wall’. In other words, the flux of momentum is balanced only by surface tension, which means that (4.3) and (4.4) are now simply replaced by
with ![]() $\theta$ the static contact angle. This equation also applies to water bells obtained from the impact of a vertical jet below a ceiling, as detailed in Button et al. (Reference Button, Davidson, Jameson and Sader2010). In that case, the local contact angle has no influence and the flux of momentum is simply balanced by
$\theta$ the static contact angle. This equation also applies to water bells obtained from the impact of a vertical jet below a ceiling, as detailed in Button et al. (Reference Button, Davidson, Jameson and Sader2010). In that case, the local contact angle has no influence and the flux of momentum is simply balanced by ![]() $\gamma$. This means that (4.6) is still valid in this configuration if we assume
$\gamma$. This means that (4.6) is still valid in this configuration if we assume ![]() $\theta ={\rm \pi} /2$.
$\theta ={\rm \pi} /2$.
Using (4.2) in the limit ![]() $r=R_J\gg r_0$, this condition yields a new scaling that reads as follows:
$r=R_J\gg r_0$, this condition yields a new scaling that reads as follows:
 \begin{equation} R_J=\left(\frac{27\sqrt{3}c^3}{16{\rm \pi}^6}\right)^{1/4} (1-\cos \theta)^{1/4}Q^{3/4} \nu^{-(1/4)}\rho^{1/4}\gamma^{-(1/4)}. \end{equation}
\begin{equation} R_J=\left(\frac{27\sqrt{3}c^3}{16{\rm \pi}^6}\right)^{1/4} (1-\cos \theta)^{1/4}Q^{3/4} \nu^{-(1/4)}\rho^{1/4}\gamma^{-(1/4)}. \end{equation} This scaling is very close to the one suggested by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018) and previously by Button et al. (Reference Button, Davidson, Jameson and Sader2010). The only difference is an additional factor linked to the contact angle (![]() $=1$ for water bells as previously explained). This explains why the scaling obtained by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018) applies to the experimental data of Jameson et al. (Reference Jameson, Jenkins, Button and Sader2010) even if the theory leading to this scaling is not the right one.
$=1$ for water bells as previously explained). This explains why the scaling obtained by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018) applies to the experimental data of Jameson et al. (Reference Jameson, Jenkins, Button and Sader2010) even if the theory leading to this scaling is not the right one.
We thus do not believe that there is a ‘universal’ scaling that should hold for any circular ‘print’ formed around an impacting jet. Sometimes one may find Bohr's scaling and sometimes that of Bhagat et al. and Button et al.; what matters is the analysis of the conditions surrounding the impact.
5. Another possible occurrence of the scaling of Bhagat et al. and Button et al.
We now show that the scaling of Bhagat et al. may also be observed in classical circular hydraulic jumps. In Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), the authors consider an intermediate regime where the liquid has not yet reached the edge of the plate (see figure 3). In their experimental evidence the authors consider partial wetting conditions (they use Perspex, glass and Teflon) and aqueous solutions. Given that the front propagation speed is rather small, we can suppose that the liquid front height is approximately given by
 \begin{equation} h_{cap}\approx \sqrt 2\left(\frac \gamma {\rho g}\right)^{1/2} (1-\cos \theta)^{1/2}, \end{equation}
\begin{equation} h_{cap}\approx \sqrt 2\left(\frac \gamma {\rho g}\right)^{1/2} (1-\cos \theta)^{1/2}, \end{equation}as explained, for instance, in de Gennes, Brochard-Wyart & Quéré (Reference de Gennes, Brochard-Wyart and Quéré2004).

Figure 3. Sketch of the intermediate regime for a low-viscosity liquid in partial wetting.
According to Duchesne et al. (Reference Duchesne, Lebon and Limat2014) (and as also used in Mohajer & Li (Reference Mohajer and Li2015) and Ipatova, Smirnov & Mogilevskiy (Reference Ipatova, Smirnov and Mogilevskiy2021)), at low viscosity and moderate flow rate, ![]() $H(r)$ is nearly constant and approximately reduces to
$H(r)$ is nearly constant and approximately reduces to
Therefore the (simplified) shock condition (4.4) previously obtained leads to
Surprisingly, this argument leads again to the ‘surface-tension-dominated’ scaling with only a factor of ![]() $2^{1/4}$ in between:
$2^{1/4}$ in between:
 \begin{equation}R_J=\left(\frac{27\sqrt{3}c^3}{16{\rm \pi}^6}\right)^{1/4}2^{1/4} (1-\cos \theta)^{1/4}Q^{3/4}\nu^{-(1/4)}\rho^{1/4}\gamma^{-(1/4)}. \end{equation}
\begin{equation}R_J=\left(\frac{27\sqrt{3}c^3}{16{\rm \pi}^6}\right)^{1/4}2^{1/4} (1-\cos \theta)^{1/4}Q^{3/4}\nu^{-(1/4)}\rho^{1/4}\gamma^{-(1/4)}. \end{equation}Now, recovering a result from Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018), one can also deduce that the Weber number satisfies
i.e. a constant Weber number replaces the constant Froude number encountered in a fully established hydraulic jump with a complete, flowing outer film.
Taking ![]() $\theta={\rm \pi}/2$, we obtain
$\theta={\rm \pi}/2$, we obtain
which is the result for the Weber number obtained by Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018).
6. Conclusion
In summary, we have reconsidered the problem of scaling law selection of the ‘radius of influence’ in the problem of vertical jet impact on a horizontal solid surface. In our opinion, the ideal law (1.1) proposed by Bohr and colleagues (to which one should not forget to add logarithmic corrections as in Duchesne et al. Reference Duchesne, Lebon and Limat2014) corresponds to the ideal situation of a stationary hydraulic jump formed inside a liquid film extending across the whole solid surface. On the other hand, the scaling (1.2) suggested in Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018) holds in different situations, such as the following:
(i) stationary impact of a jet on a dry surface, possibly superhydrophobic (fully or partially as in Sen et al. Reference Sen, Chatterjee, Crockett, Ganguly, Yu and Megaridis2019), without formation of the outer film (atomization ring);
(ii) stationary impact of a jet on a dry surface in inverse gravity (impact of a jet on a ceiling);
(iii) transient regime of circular hydraulic jump formation for low-viscosity liquids in partial wetting.
It would be interesting to explore in more detail these three situations, and to identify possible other ones. In our opinion, there is no need to imagine some universal extra capillary term imposing the scaling (1.2) as imagined in Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018). Though this extra term really exists, it is in practice compensated for by another one (in a way consistent with classical thermodynamics) when the control volume contains the free surface of the film instead of excluding it. As usual in free surface flows, there is no increase or decrease of velocity that could be due solely to the action of surface tension, except when Marangoni effects are involved (Marmottant, Villermaux & Clanet Reference Marmottant, Villermaux and Clanet2000). To continue in this direction would be simply to reproduce, for thin film flows on a solid, the initial mistake of Hagen and Bouasse.
Returning to the matter of Bohr scaling, we have set aside somewhat the questions of the logarithmic corrections and the possible existence of a critical Froude number at the jump exit, as suggested in Duchesne et al. (Reference Duchesne, Lebon and Limat2014). The possible existence of this critical Froude number leads to a different exponent for the logarithmic corrections (![]() $3/8$ instead of
$3/8$ instead of ![]() $1/8$), and this question is still not resolved. As stated in the introduction, recent nonlinear analytical treatment of the film flow suggests that such a critical Froude number could exist, but this remains to be established and convincingly explained.
$1/8$), and this question is still not resolved. As stated in the introduction, recent nonlinear analytical treatment of the film flow suggests that such a critical Froude number could exist, but this remains to be established and convincingly explained.
A specific problem of great interest where these considerations should matter is the question of jet impacts on inclined plates. It is not obvious in this kind of problem whether or not a perfect hydraulic jump can exist, and the two scalings should compete against each other in a way that merits investigation. The influence of an external field, here the tangent component of gravity, on a circular shock is a fundamental question of great interest. Specific efforts should be made in this direction (Wilson et al. Reference Wilson, Le, Dao, Lai, Morison and Davidson2012; Duchesne, Lebon & Limat Reference Duchesne, Lebon and Limat2013).
Declaration of interests
The authors report no conflict of interest.