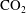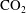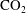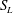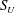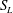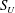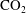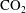1 Introduction
Geological storage of carbon dioxide (
![]() $\text{CO}_{2}$
) is considered to be a pragmatic solution for the mitigation of global warming by reducing
$\text{CO}_{2}$
) is considered to be a pragmatic solution for the mitigation of global warming by reducing
![]() $\text{CO}_{2}$
emissions from large and concentrated sources. The sequestration of
$\text{CO}_{2}$
emissions from large and concentrated sources. The sequestration of
![]() $\text{CO}_{2}$
is expected to be guaranteed during an extremely long time period by four basic trapping mechanisms: structural or stratigraphic, residual, solubility and mineral trapping (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005; Celia et al.
Reference Celia, Bachu, Nordbotten and Bandilla2015). In a deep saline heterogeneous aquifer the structural and residual trappings should be the dominant mechanisms during the injection and the short- to medium-term post-injection periods. Injected at the bottom of this reservoir, and far from the injection well, the supercritical
$\text{CO}_{2}$
is expected to be guaranteed during an extremely long time period by four basic trapping mechanisms: structural or stratigraphic, residual, solubility and mineral trapping (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005; Celia et al.
Reference Celia, Bachu, Nordbotten and Bandilla2015). In a deep saline heterogeneous aquifer the structural and residual trappings should be the dominant mechanisms during the injection and the short- to medium-term post-injection periods. Injected at the bottom of this reservoir, and far from the injection well, the supercritical
![]() $\text{CO}_{2}$
rises buoyantly due to its difference in density with the reservoir brine. When the plume reaches a low-permeability layer, it spreads beneath as a gravity current and continues its buoyant rise at the layer ends until it reaches another layer or the cap-rock at the top of the reservoir (Huppert & Neufeld Reference Huppert and Neufeld2014). Consequently, the layers act as flow barriers and disperse the
$\text{CO}_{2}$
rises buoyantly due to its difference in density with the reservoir brine. When the plume reaches a low-permeability layer, it spreads beneath as a gravity current and continues its buoyant rise at the layer ends until it reaches another layer or the cap-rock at the top of the reservoir (Huppert & Neufeld Reference Huppert and Neufeld2014). Consequently, the layers act as flow barriers and disperse the
![]() $\text{CO}_{2}$
plume, which increases the plume volume and the
$\text{CO}_{2}$
plume, which increases the plume volume and the
![]() $\text{CO}_{2}$
residual trapping. This stratification process is currently observed at the pilot site in Sleipner where
$\text{CO}_{2}$
residual trapping. This stratification process is currently observed at the pilot site in Sleipner where
![]() $\text{CO}_{2}$
has been injected into the Utsira aquifer since 1996 (Bickle et al.
Reference Bickle, Chadwick, Huppert, Hallworth and Lyle2007).
$\text{CO}_{2}$
has been injected into the Utsira aquifer since 1996 (Bickle et al.
Reference Bickle, Chadwick, Huppert, Hallworth and Lyle2007).
The gravity current model used by several authors to describe the
![]() $\text{CO}_{2}$
currents relies on two assumptions (Huppert & Woods Reference Huppert and Woods1995): (i) the
$\text{CO}_{2}$
currents relies on two assumptions (Huppert & Woods Reference Huppert and Woods1995): (i) the
![]() $\text{CO}_{2}$
and the brine are completely segregated and separated by a sharp interface; and (ii) the pressure in the
$\text{CO}_{2}$
and the brine are completely segregated and separated by a sharp interface; and (ii) the pressure in the
![]() $\text{CO}_{2}$
current is hydrostatic and its flow is principally parallel to the layer horizontal boundary and driven by the gradient of the current thickness. These assumptions are valid as long as the capillarity is neglected and the current thickness is considerably smaller than its lateral extent. This vertical equilibrium approximation, similar to the Dupuit–Forchheimer assumption in hydrology (Bear Reference Bear1988), has proven to be fruitful to model different sequestration situations and scenarios. This result is partly due to the self-similar properties of the equation governing the gravity current thickness, which allows for analytical solutions to be determined when boundary conditions are appropriate (Huppert & Woods Reference Huppert and Woods1995). Gravity current models have been applied to
$\text{CO}_{2}$
current is hydrostatic and its flow is principally parallel to the layer horizontal boundary and driven by the gradient of the current thickness. These assumptions are valid as long as the capillarity is neglected and the current thickness is considerably smaller than its lateral extent. This vertical equilibrium approximation, similar to the Dupuit–Forchheimer assumption in hydrology (Bear Reference Bear1988), has proven to be fruitful to model different sequestration situations and scenarios. This result is partly due to the self-similar properties of the equation governing the gravity current thickness, which allows for analytical solutions to be determined when boundary conditions are appropriate (Huppert & Woods Reference Huppert and Woods1995). Gravity current models have been applied to
![]() $\text{CO}_{2}$
injection in homogeneous horizontal confined aquifers, in two dimensions (Huppert & Woods Reference Huppert and Woods1995; Nordbotten & Celia Reference Nordbotten and Celia2006; Hesse et al.
Reference Hesse, Tchelepi, Cantwel and Orr2007), in 3-D axisymmetric geometries (Lyle et al.
Reference Lyle, Huppert, Hallworth, Bickle and Chadwick2005) and in 2-D sloping confined aquifers (Vella & Huppert Reference Vella and Huppert2006). They have also been used, for instance, to assess the
$\text{CO}_{2}$
injection in homogeneous horizontal confined aquifers, in two dimensions (Huppert & Woods Reference Huppert and Woods1995; Nordbotten & Celia Reference Nordbotten and Celia2006; Hesse et al.
Reference Hesse, Tchelepi, Cantwel and Orr2007), in 3-D axisymmetric geometries (Lyle et al.
Reference Lyle, Huppert, Hallworth, Bickle and Chadwick2005) and in 2-D sloping confined aquifers (Vella & Huppert Reference Vella and Huppert2006). They have also been used, for instance, to assess the
![]() $\text{CO}_{2}$
footprint in an aquifer by considering the residual trapping mechanism (Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Juanes, MacMinn & Szulczewski Reference Juanes, Macminn and Szulczewski2010), the dispersion of a
$\text{CO}_{2}$
footprint in an aquifer by considering the residual trapping mechanism (Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Juanes, MacMinn & Szulczewski Reference Juanes, Macminn and Szulczewski2010), the dispersion of a
![]() $\text{CO}_{2}$
plume in a 2-D periodic array of low-permeability layers (Hesse & Woods Reference Hesse and Woods2010) or the
$\text{CO}_{2}$
plume in a 2-D periodic array of low-permeability layers (Hesse & Woods Reference Hesse and Woods2010) or the
![]() $\text{CO}_{2}$
stratification beneath shale layers at the Sleipner site (Bickle et al.
Reference Bickle, Chadwick, Huppert, Hallworth and Lyle2007). For more applications, one can refer to the reviews of Huppert & Neufeld (Reference Huppert and Neufeld2014) and Celia et al. (Reference Celia, Bachu, Nordbotten and Bandilla2015). When the capillarity is considered, the classical gravity current assumptions are not valid. Because of capillary diffusion, there is no longer a sharp interface, however a transition zone exists between the two fluids. Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) extended the vertical equilibrium approach to the capillary case and proposed a two-phase gravity current model. These authors performed a sensitivity analysis of the current characteristics with respect to the Bond number, which provides a measure of the importance of capillarity compared to buoyancy. Later, the model was extended to the axisymmetric geometry (Golding, Huppert & Neufeld Reference Golding, Huppert and Neufeld2013). Different authors applied the single-phase current approach to the case in which the low-permeability layers, or the cap-rock, allowed the
$\text{CO}_{2}$
stratification beneath shale layers at the Sleipner site (Bickle et al.
Reference Bickle, Chadwick, Huppert, Hallworth and Lyle2007). For more applications, one can refer to the reviews of Huppert & Neufeld (Reference Huppert and Neufeld2014) and Celia et al. (Reference Celia, Bachu, Nordbotten and Bandilla2015). When the capillarity is considered, the classical gravity current assumptions are not valid. Because of capillary diffusion, there is no longer a sharp interface, however a transition zone exists between the two fluids. Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) extended the vertical equilibrium approach to the capillary case and proposed a two-phase gravity current model. These authors performed a sensitivity analysis of the current characteristics with respect to the Bond number, which provides a measure of the importance of capillarity compared to buoyancy. Later, the model was extended to the axisymmetric geometry (Golding, Huppert & Neufeld Reference Golding, Huppert and Neufeld2013). Different authors applied the single-phase current approach to the case in which the low-permeability layers, or the cap-rock, allowed the
![]() $\text{CO}_{2}$
to leak (Pritchard, Woods & Hogg Reference Pritchard, Woods and Hogg2001; Neufeld & Huppert Reference Neufeld and Huppert2009; Woods & Farcas Reference Woods and Farcas2009). Thus, they used the drainage approximation, in which the current remains in single phase and is governed by vertical equilibrium. In its simplest form, this leads to a gravity current equation with a source term proportional to the current height. Here, there is a strong analogy with certain hydrological problems, such as modelling an unconfined leaky aquifer (Bear Reference Bear1988).
$\text{CO}_{2}$
to leak (Pritchard, Woods & Hogg Reference Pritchard, Woods and Hogg2001; Neufeld & Huppert Reference Neufeld and Huppert2009; Woods & Farcas Reference Woods and Farcas2009). Thus, they used the drainage approximation, in which the current remains in single phase and is governed by vertical equilibrium. In its simplest form, this leads to a gravity current equation with a source term proportional to the current height. Here, there is a strong analogy with certain hydrological problems, such as modelling an unconfined leaky aquifer (Bear Reference Bear1988).
The single-phase approximation is no longer justified for a two-phase flow problem in a domain with a permeable matrix and a semi-permeable layer. This type of layer generally has a permeability of approximately one-tenth of the matrix permeability whereas a low-permeability layer has a permeability of approximately one hundredth or less. In a deep heterogeneous saline aquifer, the type of heterogeneity depends on the geological formation, studied facies and scale of investigation. In an aquifer such as Utsira at the Sleipner site, the kilometric mudstone layers are low-permeability units (Bickle et al.
Reference Bickle, Chadwick, Huppert, Hallworth and Lyle2007) whereas in other potential aquifers, the permeability contrast between the matrix and the heterogeneities may be less pronounced. This issue, which is site specific and scale dependent, is beyond the scope of this study and discussions may be found in Ambrose et al. (Reference Ambrose, Lakshminarasimhan, Holtz, Nunez-Lopez, Hovorka and Duncan2008) or Lengler, De Lucia & Kühn (Reference Lengler, De Lucia and Kühn2010). When the permeability of the layer becomes non-zero, the phase segregation is incomplete, the
![]() $\text{CO}_{2}$
and the brine can pass through the layer and the
$\text{CO}_{2}$
and the brine can pass through the layer and the
![]() $\text{CO}_{2}$
saturation in the current decreases while the permeability of the layer increases. The presence of the brine in the current and the two-phase flow at the interface between the matrix and the layer must be considered in the model. This is particularly true when the flow is counter-current: the
$\text{CO}_{2}$
saturation in the current decreases while the permeability of the layer increases. The presence of the brine in the current and the two-phase flow at the interface between the matrix and the layer must be considered in the model. This is particularly true when the flow is counter-current: the
![]() $\text{CO}_{2}$
ascending flow rate across a horizontal section of the domain is balanced by the descending brine flow rate. The counter-current flow corresponds to the inject-low-and-let-rise strategy, which aims to increase the residual trapping (Bryant, Lakshminarasimhan & Pope Reference Bryant, Lakshminarasimhan and Pope2008).
$\text{CO}_{2}$
ascending flow rate across a horizontal section of the domain is balanced by the descending brine flow rate. The counter-current flow corresponds to the inject-low-and-let-rise strategy, which aims to increase the residual trapping (Bryant, Lakshminarasimhan & Pope Reference Bryant, Lakshminarasimhan and Pope2008).
When the layers of a reservoir have a low permeability, such as at the Sleipner site, the
![]() $\text{CO}_{2}$
can sweep only a very limited volume of the reservoir: the gravity currents domain beneath the layers and the cap-rock, and the
$\text{CO}_{2}$
can sweep only a very limited volume of the reservoir: the gravity currents domain beneath the layers and the cap-rock, and the
![]() $\text{CO}_{2}$
chimneys at the layer extremities. When the layers are semi-permeable the
$\text{CO}_{2}$
chimneys at the layer extremities. When the layers are semi-permeable the
![]() $\text{CO}_{2}$
can sweep a much larger region as the
$\text{CO}_{2}$
can sweep a much larger region as the
![]() $\text{CO}_{2}$
can pass through the layers. This may have an important impact on the sequestration properties of the reservoir, and principally on its trapping efficiency. Two short-term or mid-term trapping mechanisms are distinguished in the literature: capillary trapping and
$\text{CO}_{2}$
can pass through the layers. This may have an important impact on the sequestration properties of the reservoir, and principally on its trapping efficiency. Two short-term or mid-term trapping mechanisms are distinguished in the literature: capillary trapping and
![]() $\text{CO}_{2}$
dissolution in the brine (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005). Capillary trapping is a post injection mechanism and takes place principally at the trailing edge of the plume where blobs of
$\text{CO}_{2}$
dissolution in the brine (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005). Capillary trapping is a post injection mechanism and takes place principally at the trailing edge of the plume where blobs of
![]() $\text{CO}_{2}$
are trapped in the reservoir pores (Doughty Reference Doughty2007; Hesse et al.
Reference Hesse, Orr and Tchelepi2008). The amount of trapped
$\text{CO}_{2}$
are trapped in the reservoir pores (Doughty Reference Doughty2007; Hesse et al.
Reference Hesse, Orr and Tchelepi2008). The amount of trapped
![]() $\text{CO}_{2}$
increases with the saturation in the plume. Therefore, this amount should be locally high in the high saturation regions described previously and low in the rest of the reservoir, as the saturation of
$\text{CO}_{2}$
increases with the saturation in the plume. Therefore, this amount should be locally high in the high saturation regions described previously and low in the rest of the reservoir, as the saturation of
![]() $\text{CO}_{2}$
flowing out the layers is expected to be low. Nevertheless, at the scale of the reservoir the global amount of trapped
$\text{CO}_{2}$
flowing out the layers is expected to be low. Nevertheless, at the scale of the reservoir the global amount of trapped
![]() $\text{CO}_{2}$
should be much more important than if layers were impermeable. The second trapping mechanism,
$\text{CO}_{2}$
should be much more important than if layers were impermeable. The second trapping mechanism,
![]() $\text{CO}_{2}$
dissolution, should be also enhanced as it depends on the contact volume between
$\text{CO}_{2}$
dissolution, should be also enhanced as it depends on the contact volume between
![]() $\text{CO}_{2}$
and brine (Huppert & Neufeld Reference Huppert and Neufeld2014). Dissolution is expected to give rise to mineral trapping which is considered as a long-term trapping mechanism (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005).
$\text{CO}_{2}$
and brine (Huppert & Neufeld Reference Huppert and Neufeld2014). Dissolution is expected to give rise to mineral trapping which is considered as a long-term trapping mechanism (Benson et al.
Reference Benson, Cook, Anderson, Bachu, Nimir, Basu, Bradshaw, Deguchi, Gale and von Goerne2005).
In this paper, we study this problem by considering the 2-D flow around and through a single semi-permeable layer of finite extent embedded in a permeable matrix. We consider three forces: buoyancy, capillarity and viscosity. There is no injection and the flow is counter-current at the scale of the reservoir, i.e. not at the local scale. The flow dynamics is essentially ruled by the interface conditions: capillary pressure continuity and total flux continuity at the layer matrix interface. In § 2, we recall the equations of the incompressible immiscible two-phase flow model, and we investigate this interface problem for a 1-D geometry (§ 3): a vertical column consisting of a piecewise homogeneous porous medium. Based on the studies performed by Cancès (Reference Cancès2010a
,Reference Cancès
b
) and Andreianov & Cancès (Reference Andreianov and Cancès2013), we demonstrate how to graphically determine the saturation discontinuity at the interface and the steady state saturation distributions in each domain of the column from the capillary and buoyant flux curves. In § 4, the 2-D problem is considered. Hence, we heuristically extend the model proposed by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) to the case of a semi-permeable layer. We separately consider the capillary-free and the gravity-dominant cases. The proposed model is compared to fine grid numerical simulations performed using DuMu
![]() $^{x}$
, which is an open-source simulator for flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). The comparison indicates that the model adequately describes the flow dynamics; however, in the capillary-free case, it also demonstrates that the total velocity fluctuations, which, on spatial averaging are zero, should be considered in the total flux function at the interface to improve the accuracy of the gravity current prediction.
$^{x}$
, which is an open-source simulator for flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). The comparison indicates that the model adequately describes the flow dynamics; however, in the capillary-free case, it also demonstrates that the total velocity fluctuations, which, on spatial averaging are zero, should be considered in the total flux function at the interface to improve the accuracy of the gravity current prediction.
2 Two-phase incompressible, immiscible flow model
The governing equations of two-phase incompressible, immiscible flow in a porous medium are given by Darcy’s law and the mass conservation equation (Helmig Reference Helmig1997)
with
![]() $S_{\unicode[STIX]{x1D6FC}_{r}}$
is the residual saturation of phase
$S_{\unicode[STIX]{x1D6FC}_{r}}$
is the residual saturation of phase
![]() $\unicode[STIX]{x1D6FC}$
. The normalized saturations of the wetting and non-wetting phases sum up to one:
$\unicode[STIX]{x1D6FC}$
. The normalized saturations of the wetting and non-wetting phases sum up to one:
![]() $S_{w_{e}}+S_{nw_{e}}=1$
. In what follows, the normalized saturation of the non-wetting phase
$S_{w_{e}}+S_{nw_{e}}=1$
. In what follows, the normalized saturation of the non-wetting phase
![]() $S_{nw_{e}}$
is written as
$S_{nw_{e}}$
is written as
![]() $S$
for simplicity. Thus, (2.3) and (2.4) become
$S$
for simplicity. Thus, (2.3) and (2.4) become
The capillary pressure is typically viewed as a function of the wetting saturation and can be given by either a Van Genuchten (Van Genuchten Reference Van Genuchten1980) or a Brooks and Corey (BC) (Brooks & Corey Reference Brooks and Corey1964) function. In this paper, only a BC capillary pressure expression is considered
where
![]() $J(S)=(1-S)^{-1/\unicode[STIX]{x1D706}}$
is the Leverett’s function, which is based on the saturation of the non-wetting phase and the pore size distribution parameter
$J(S)=(1-S)^{-1/\unicode[STIX]{x1D706}}$
is the Leverett’s function, which is based on the saturation of the non-wetting phase and the pore size distribution parameter
![]() $\unicode[STIX]{x1D706}$
; and
$\unicode[STIX]{x1D706}$
; and
![]() $\unicode[STIX]{x1D70E}~(\text{M}/(\text{LT}^{2}))$
is the interfacial tension between the phases. Here, we assume
$\unicode[STIX]{x1D70E}~(\text{M}/(\text{LT}^{2}))$
is the interfacial tension between the phases. Here, we assume
![]() $\unicode[STIX]{x1D706}=2$
, which is a standard choice in porous media studies. The entry pressure corresponds to the capillary pressure value when
$\unicode[STIX]{x1D706}=2$
, which is a standard choice in porous media studies. The entry pressure corresponds to the capillary pressure value when
![]() $S=0$
$S=0$
The hysteresis in the capillary pressures and the relative permeabilities curves are neglected, and the same capillary pressure function is used for both the imbibition and drainage processes.
By combining (2.1) and (2.8), the Darcian velocity of the non-wetting phase can be written as
where
![]() $\boldsymbol{q}_{t}$
is the total velocity, which can be expressed as
$\boldsymbol{q}_{t}$
is the total velocity, which can be expressed as
with
![]() $M=\unicode[STIX]{x1D707}_{nw}/\unicode[STIX]{x1D707}_{w}$
, i.e. the viscosity ratio, and
$M=\unicode[STIX]{x1D707}_{nw}/\unicode[STIX]{x1D707}_{w}$
, i.e. the viscosity ratio, and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{w}-\unicode[STIX]{x1D70C}_{nw}$
. The fractional flux function
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{w}-\unicode[STIX]{x1D70C}_{nw}$
. The fractional flux function
![]() $f(S)$
(2.13) is a monotonic increasing
$f(S)$
(2.13) is a monotonic increasing
![]() $S$
-shaped function (Helmig Reference Helmig1997) whereas the gravitational flux function
$S$
-shaped function (Helmig Reference Helmig1997) whereas the gravitational flux function
![]() $\unicode[STIX]{x1D6EC}(S)$
(2.14) has a bell-shaped form (Hayek, Mouche & Mügler Reference Hayek, Mouche and Mügler2009). By substituting (2.11) into (2.2), we obtain the non-wetting phase saturation transport equation
$\unicode[STIX]{x1D6EC}(S)$
(2.14) has a bell-shaped form (Hayek, Mouche & Mügler Reference Hayek, Mouche and Mügler2009). By substituting (2.11) into (2.2), we obtain the non-wetting phase saturation transport equation
where the total flux of the non-wetting phase
![]() $\unicode[STIX]{x1D731}$
is
$\unicode[STIX]{x1D731}$
is
The first term of the total flux is a convective flux, called viscous flux when produced by injection or pumping. The second term is the gravitational flux, which is also known as the buoyant flux and induced by the difference in the phase densities. The last term is the capillary flux, which is provoked by the difference in pressure across the phases interface at the pore scale. In the sequel, we denote
![]() $\boldsymbol{G}$
the gravitational flux
$\boldsymbol{G}$
the gravitational flux
We intentionally simplified the model to keep the discussion general and simple. The relative permeability functions could be more complex than Brooks and Corey’s laws with an exponent equal to two. However, Brooks–Corey model is often used in petroleum engineering and the exponent depends generally on the geology of the reservoir (Honarpour, Koederitz & Herbert Reference Honarpour, Koederitz and Herbert1986). Adopting such quadratic relative permeabilities as (2.6) and (2.7) with a viscosity ratio
![]() $M=1$
results in a symmetric buoyant flux function
$M=1$
results in a symmetric buoyant flux function
![]() $\unicode[STIX]{x1D6EC}(S)$
with respect to the saturation
$\unicode[STIX]{x1D6EC}(S)$
with respect to the saturation
![]() $S$
. Using a given viscosity ratio
$S$
. Using a given viscosity ratio
![]() $M\neq 1$
or another relative permeability law would lead to an asymmetry of
$M\neq 1$
or another relative permeability law would lead to an asymmetry of
![]() $\unicode[STIX]{x1D6EC}(S)$
and change the value of the different key saturations subsequently introduced in the paper, but not the dynamics. The important property conserved whatever the relative permeabilities is the bell shape of the buoyant flux function
$\unicode[STIX]{x1D6EC}(S)$
and change the value of the different key saturations subsequently introduced in the paper, but not the dynamics. The important property conserved whatever the relative permeabilities is the bell shape of the buoyant flux function
![]() $G(S)$
and its scale dependency with the permeability. Furthermore, it is worth noting that hysteresis is an important process in carbon sequestration studies but its inclusion into a model makes both the physics and numerics more complex (Doughty Reference Doughty2007). We discuss in the conclusion (§ 6) the effect of this process on the trapping efficiency of a reservoir.
$G(S)$
and its scale dependency with the permeability. Furthermore, it is worth noting that hysteresis is an important process in carbon sequestration studies but its inclusion into a model makes both the physics and numerics more complex (Doughty Reference Doughty2007). We discuss in the conclusion (§ 6) the effect of this process on the trapping efficiency of a reservoir.
3
 $\text{CO}_{2}$
buoyant migration in a vertical column filled with a piecewise homogeneous porous medium
$\text{CO}_{2}$
buoyant migration in a vertical column filled with a piecewise homogeneous porous medium
To study the flow of
![]() $\text{CO}_{2}$
through the interface between two porous media, we first consider a 1-D vertical
$\text{CO}_{2}$
through the interface between two porous media, we first consider a 1-D vertical
![]() $H$
(m) height column filled with a piecewise homogeneous porous medium consisting of two materials, permeable and semi-permeable. The interface
$H$
(m) height column filled with a piecewise homogeneous porous medium consisting of two materials, permeable and semi-permeable. The interface
![]() $\unicode[STIX]{x1D6E4}$
is located at
$\unicode[STIX]{x1D6E4}$
is located at
![]() $z=0~\text{m}$
(figure 1). For simplicity, only the absolute permeability is heterogeneous:
$z=0~\text{m}$
(figure 1). For simplicity, only the absolute permeability is heterogeneous:
![]() $k^{+}$
for the permeable material and
$k^{+}$
for the permeable material and
![]() $k^{-}$
for semi-permeable material, with a permeability ratio
$k^{-}$
for semi-permeable material, with a permeability ratio
![]() $k^{-}/k^{+}=1/2$
. The other material parameters are constant in the column. Moreover, we henceforth assume that the
$k^{-}/k^{+}=1/2$
. The other material parameters are constant in the column. Moreover, we henceforth assume that the
![]() $\text{CO}_{2}$
and brine viscosities are identical. This assumption is introduced to make the discussion simple but does not alter the results or the following discussions. The impact of the viscosity ratio on the flow dynamics is discussed further in § 3.4. We consider a counter-current flow,
$\text{CO}_{2}$
and brine viscosities are identical. This assumption is introduced to make the discussion simple but does not alter the results or the following discussions. The impact of the viscosity ratio on the flow dynamics is discussed further in § 3.4. We consider a counter-current flow,
![]() $\boldsymbol{q}_{t}=0$
, which indicates that there is no phase injection or pumping in the column. The non-wetting phase rises buoyantly upwards whereas the wetting phase flows downwards, and the volume in the first phase is replaced by the same volume of the second phase. The entire column is initially saturated with brine, and a constant non-wetting phase saturation is imposed at the bottom of the column which corresponds to an imposed buoyant flux value. A zero non-wetting saturation is imposed at the top to allow the
$\boldsymbol{q}_{t}=0$
, which indicates that there is no phase injection or pumping in the column. The non-wetting phase rises buoyantly upwards whereas the wetting phase flows downwards, and the volume in the first phase is replaced by the same volume of the second phase. The entire column is initially saturated with brine, and a constant non-wetting phase saturation is imposed at the bottom of the column which corresponds to an imposed buoyant flux value. A zero non-wetting saturation is imposed at the top to allow the
![]() $\text{CO}_{2}$
phase to migrate freely upwards (figure 1). We denote
$\text{CO}_{2}$
phase to migrate freely upwards (figure 1). We denote
![]() $k_{i}$
,
$k_{i}$
,
![]() $G_{i}$
and
$G_{i}$
and
![]() $\unicode[STIX]{x1D731}_{\boldsymbol{i}}$
as the absolute permeability, gravitational flux and total flux function in the material
$\unicode[STIX]{x1D731}_{\boldsymbol{i}}$
as the absolute permeability, gravitational flux and total flux function in the material
![]() $i$
, (
$i$
, (
![]() $i\in [l,u]$
), respectively, where the subscripts
$i\in [l,u]$
), respectively, where the subscripts
![]() $l$
and
$l$
and
![]() $u$
denote the lower and upper materials, respectively.
$u$
denote the lower and upper materials, respectively.

Figure 1. Sketch of the piecewise homogeneous porous medium column.
The 1-D hydrodynamics of a two-phase mixture at the interface of such a discontinuous medium under the simultaneous effects of the capillary and gravity forces has rarely been studied in the literature. A few authors considered either buoyancy (Langtangen, Tveito & Winther Reference Langtangen, Tveito and Winther1992; Kaasschieter Reference Kaasschieter1999; Adimurthi, Jaffré & Veerappa Gowda Reference Jaffré and Veerappa Gowda2004) or capillarity alone (Van Duijn & De Neef Reference Van Duijn and De Neef1998). Others studied the effects of capillarity in the viscous case but disregarded buoyancy, i.e. when one phase is injected at the inlet of a horizontal column (Van Duijn, Molenaar & De Neef Reference Van Duijn, Molenaar and De Neef1995; Mikelic, van Duijn & Pop Reference Mikelic, van Duijn and Pop2002; Buzzi, Lenzinger & Schweizer Reference Buzzi, Lenzinger and Schweizer2009). Cancès (Reference Cancès2010a ,Reference Cancès b ) considered both capillarity and buoyancy. He proved the existence of a weak solution that satisfies the total flux continuity and the capillary pressure matching condition at the interface between the two media. However, this author did not study the effects of the materials permeabilities and the inflow rate of the buoyant phase on the saturation distribution in the column.
3.1 One-dimensional vertical migration model and continuity conditions at the interface
Using (2.15) and (2.16), the
![]() $\text{CO}_{2}$
saturation transport equation in the vertical column is written as
$\text{CO}_{2}$
saturation transport equation in the vertical column is written as
To express this equation in a dimensionless form, we set the column height
![]() $H$
as the characteristic length scale and the time
$H$
as the characteristic length scale and the time
![]() $T=(\unicode[STIX]{x1D719}H\unicode[STIX]{x1D707}_{w})/(k_{0}g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C})$
for the
$T=(\unicode[STIX]{x1D719}H\unicode[STIX]{x1D707}_{w})/(k_{0}g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C})$
for the
![]() $\text{CO}_{2}$
to migrate buoyantly in a column filled only with the permeable material as the characteristic time. The intrinsic permeability
$\text{CO}_{2}$
to migrate buoyantly in a column filled only with the permeable material as the characteristic time. The intrinsic permeability
![]() $k^{+}$
is set as the permeability scale
$k^{+}$
is set as the permeability scale
![]() $k_{0}$
of the medium.
$k_{0}$
of the medium.
These scalings lead to the capillary number
![]() $N_{c}$
$N_{c}$
Then, the dimensionless transport equation can be written as
where
![]() $J_{s}^{\prime }=\text{d}J/\text{d}s$
. When the capillarity is neglected (
$J_{s}^{\prime }=\text{d}J/\text{d}s$
. When the capillarity is neglected (
![]() $N_{c}=0$
), the flux contains only the gravitational part and the (3.4) reduces to the well-known Buckley–Leverett equation with gravity (Kaasschieter Reference Kaasschieter1999)
$N_{c}=0$
), the flux contains only the gravitational part and the (3.4) reduces to the well-known Buckley–Leverett equation with gravity (Kaasschieter Reference Kaasschieter1999)
where
is the scaled gravitational flux.
The dynamics of the two-phase flow depends on the value of
![]() $N_{c}$
. The dynamics may be classified into four different flow regimes: capillarity dominant (
$N_{c}$
. The dynamics may be classified into four different flow regimes: capillarity dominant (
![]() $N_{c}\gg 1$
), balance case (
$N_{c}\gg 1$
), balance case (
![]() $N_{c}\approx 1$
), gravity dominant (
$N_{c}\approx 1$
), gravity dominant (
![]() $N_{c}\ll 1$
) and capillarity free (
$N_{c}\ll 1$
) and capillarity free (
![]() $N_{c}=0$
). When
$N_{c}=0$
). When
![]() $N_{c}\geqslant 1$
, the capillarity leads to pseudo-linear
$N_{c}\geqslant 1$
, the capillarity leads to pseudo-linear
![]() $\text{CO}_{2}$
saturation distributions in each material of the column. This case is not considered here and will be discussed in a forthcoming paper. The capillary-free case has been studied by Hayek et al. (Reference Hayek, Mouche and Mügler2009) in the framework of the theory of shocks and rarefaction waves. The authors demonstrated that the continuity of the buoyant flux
$\text{CO}_{2}$
saturation distributions in each material of the column. This case is not considered here and will be discussed in a forthcoming paper. The capillary-free case has been studied by Hayek et al. (Reference Hayek, Mouche and Mügler2009) in the framework of the theory of shocks and rarefaction waves. The authors demonstrated that the continuity of the buoyant flux
![]() $G(S)$
at the interface leads to a saturation discontinuity and, in certain conditions, a
$G(S)$
at the interface leads to a saturation discontinuity and, in certain conditions, a
![]() $\text{CO}_{2}$
stratification beneath the interface. This stratification can be qualified as a 1-D gravity current, and the phase segregation resulting in 2-D or 3-D gravity currents may be interpreted as a shock travelling in the direction of the gravity balanced by a lateral spreading of the saturation. Furthermore, the purely capillary case (no buoyancy) results in a saturation discontinuity (Van Duijn & De Neef Reference Van Duijn and De Neef1998). Here, the case of interest is the gravity-dominant flow with a low positive capillary number
$\text{CO}_{2}$
stratification beneath the interface. This stratification can be qualified as a 1-D gravity current, and the phase segregation resulting in 2-D or 3-D gravity currents may be interpreted as a shock travelling in the direction of the gravity balanced by a lateral spreading of the saturation. Furthermore, the purely capillary case (no buoyancy) results in a saturation discontinuity (Van Duijn & De Neef Reference Van Duijn and De Neef1998). Here, the case of interest is the gravity-dominant flow with a low positive capillary number
![]() $N_{c}\ll 1$
. As presented in the next section, based on the arrangement of the materials in the column (
$N_{c}\ll 1$
. As presented in the next section, based on the arrangement of the materials in the column (
![]() $k_{l}$
,
$k_{l}$
,
![]() $k_{u}$
)
$k_{u}$
)
![]() $\equiv$
(
$\equiv$
(
![]() $k^{-}$
,
$k^{-}$
,
![]() $k^{+}$
) or (
$k^{+}$
) or (
![]() $k_{l}$
,
$k_{l}$
,
![]() $k_{u}$
)
$k_{u}$
)
![]() $\equiv$
(
$\equiv$
(
![]() $k^{+}$
,
$k^{+}$
,
![]() $k^{-}$
), the buoyancy and capillarity may generate a
$k^{-}$
), the buoyancy and capillarity may generate a
![]() $\text{CO}_{2}$
stratification beneath the interface. Regardless of this arrangement, the difference in the entry capillary pressures between the two materials results in a
$\text{CO}_{2}$
stratification beneath the interface. Regardless of this arrangement, the difference in the entry capillary pressures between the two materials results in a
![]() $\text{CO}_{2}$
saturation discontinuity at the interface. The one-sided traces of saturation at the interface, known as
$\text{CO}_{2}$
saturation discontinuity at the interface. The one-sided traces of saturation at the interface, known as
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{U}$
with subscripts
$S_{U}$
with subscripts
![]() $L$
and
$L$
and
![]() $U$
denoting the lower and upper sub-domains, respectively, must fulfil two conditions: the continuity of the capillary pressure and the continuity of the total flux, which latter are expressed as follows
$U$
denoting the lower and upper sub-domains, respectively, must fulfil two conditions: the continuity of the capillary pressure and the continuity of the total flux, which latter are expressed as follows
When the capillarity disappears, the condition of the total flux continuity is reduced to only that of the gravitational flux
This limit, known as the vanishing capillarity limit, has been studied from a mathematical point of view by Andreianov & Cancès (Reference Andreianov and Cancès2013). For
![]() $(k_{l},k_{u})\equiv (k^{+},k^{-})$
, the matching condition of capillary pressure results in the threshold saturation
$(k_{l},k_{u})\equiv (k^{+},k^{-})$
, the matching condition of capillary pressure results in the threshold saturation
![]() $S^{\ast }$
$S^{\ast }$
A natural way to connect the capillary pressures at the interface between layers is to define the multi-valued capillary pressure function. This definition has been introduced by Cancès, Gallouët & Porretta (Reference Cancès, Gallouët and Porretta2009) and Buzzi et al. (Reference Buzzi, Lenzinger and Schweizer2009) to study of discontinuous-flux problems. Using the notations defined by these authors, the extended capillary pressure function can be written as
 $$\begin{eqnarray}\displaystyle \overline{p}_{c}(S):=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70E}\sqrt{\frac{\unicode[STIX]{x1D719}}{k(z)}}J(S) & \text{if }0<S<1,\\ \displaystyle (-\infty ,p_{c,min}] & \text{if }S=0,\\ \displaystyle [p_{c,max},+\infty ) & \text{if }S=1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{p}_{c}(S):=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70E}\sqrt{\frac{\unicode[STIX]{x1D719}}{k(z)}}J(S) & \text{if }0<S<1,\\ \displaystyle (-\infty ,p_{c,min}] & \text{if }S=0,\\ \displaystyle [p_{c,max},+\infty ) & \text{if }S=1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
![]() $p_{c,min}=\lim _{S{\searrow}0}p_{c}$
and
$p_{c,min}=\lim _{S{\searrow}0}p_{c}$
and
![]() $p_{c,max}=\lim _{S{\nearrow}1}p_{c}$
. Thus, the continuity of capillary pressure is expressed as
$p_{c,max}=\lim _{S{\nearrow}1}p_{c}$
. Thus, the continuity of capillary pressure is expressed as

Figure 2. Capillary pressure curves of the materials
![]() $k^{+}$
,
$k^{+}$
,
![]() $p_{c}^{+}$
and
$p_{c}^{+}$
and
![]() $k^{-}$
,
$k^{-}$
,
![]() $p_{c}^{-}$
, and paths of
$p_{c}^{-}$
, and paths of
![]() $(S_{L},S_{U})$
for the cases
$(S_{L},S_{U})$
for the cases
![]() $k^{-}\rightarrow k^{+}$
(a,b) and
$k^{-}\rightarrow k^{+}$
(a,b) and
![]() $k^{+}\rightarrow k^{-}$
(c,d). The thick curves represent the connected parts of the capillary pressure curves.
$k^{+}\rightarrow k^{-}$
(c,d). The thick curves represent the connected parts of the capillary pressure curves.
Figure 2 illustrates the path of
![]() $(S_{L},S_{U})$
on the capillary curves for the cases (
$(S_{L},S_{U})$
on the capillary curves for the cases (
![]() $k_{l}$
,
$k_{l}$
,
![]() $k_{u}$
)
$k_{u}$
)
![]() $\equiv$
(
$\equiv$
(
![]() $k^{-}$
,
$k^{-}$
,
![]() $k^{+}$
) and (
$k^{+}$
) and (
![]() $k_{l}$
,
$k_{l}$
,
![]() $k_{u}$
)
$k_{u}$
)
![]() $\equiv$
(
$\equiv$
(
![]() $k^{+}$
,
$k^{+}$
,
![]() $k^{-}$
), which is henceforth denoted by
$k^{-}$
), which is henceforth denoted by
![]() $k^{-}\rightarrow k^{+}$
and
$k^{-}\rightarrow k^{+}$
and
![]() $k^{+}\rightarrow k^{-}$
, respectively. In the first case,
$k^{+}\rightarrow k^{-}$
, respectively. In the first case,
![]() $k^{-}\rightarrow k^{+}$
, when
$k^{-}\rightarrow k^{+}$
, when
![]() $S_{L}=0$
,
$S_{L}=0$
,
![]() $S_{U}<S^{\ast }$
(figure 2
a), and when
$S_{U}<S^{\ast }$
(figure 2
a), and when
![]() $S_{U}>S^{\ast }$
,
$S_{U}>S^{\ast }$
,
![]() $S_{L}$
increases (figure 2
b). In the second case,
$S_{L}$
increases (figure 2
b). In the second case,
![]() $k^{+}\rightarrow k^{-}$
, the paths of
$k^{+}\rightarrow k^{-}$
, the paths of
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{U}$
are interchanged: when
$S_{U}$
are interchanged: when
![]() $S_{L}<S^{\ast }$
,
$S_{L}<S^{\ast }$
,
![]() $S_{U}=0$
(figure 2
c), and when
$S_{U}=0$
(figure 2
c), and when
![]() $S_{L}>S^{\ast }$
,
$S_{L}>S^{\ast }$
,
![]() $S_{U}$
increases (figure 2
d). Furthermore, these paths are constrained by the total flux continuity condition. To graphically observe the effects of this constraint on the couple
$S_{U}$
increases (figure 2
d). Furthermore, these paths are constrained by the total flux continuity condition. To graphically observe the effects of this constraint on the couple
![]() $(S_{L},S_{U})$
, the couple is represented on the gravitational flux curves for different values of
$(S_{L},S_{U})$
, the couple is represented on the gravitational flux curves for different values of
![]() $(S_{L},S_{U})$
(figure 3). For simplicity, we assume that in figure 3, and henceforth, the
$(S_{L},S_{U})$
(figure 3). For simplicity, we assume that in figure 3, and henceforth, the
![]() $\text{CO}_{2}$
and brine viscosities are identical. This assumption is introduced to make the discussion simple but does not alter the results or the following discussions. The impact of the viscosity ratio on the flow dynamics is discussed further in § 3.4. Figure 3 shows that, for a given couple
$\text{CO}_{2}$
and brine viscosities are identical. This assumption is introduced to make the discussion simple but does not alter the results or the following discussions. The impact of the viscosity ratio on the flow dynamics is discussed further in § 3.4. Figure 3 shows that, for a given couple
![]() $(S_{L},S_{U})$
, there is generally no continuity of the gravity flux. The difference is balanced by the capillary flux beneath the interface. The overall equilibrium at the interface depends on the value of the initial gravity flux. We examine now in detail the two cases
$(S_{L},S_{U})$
, there is generally no continuity of the gravity flux. The difference is balanced by the capillary flux beneath the interface. The overall equilibrium at the interface depends on the value of the initial gravity flux. We examine now in detail the two cases
![]() $k^{-}\rightarrow k^{+}$
and
$k^{-}\rightarrow k^{+}$
and
![]() $k^{+}\rightarrow k^{-}$
for a permeability ratio of
$k^{+}\rightarrow k^{-}$
for a permeability ratio of
![]() $k^{-}/k^{+}=1/2$
, which results in a threshold saturation of
$k^{-}/k^{+}=1/2$
, which results in a threshold saturation of
![]() $S^{\ast }=1/2$
. We simulate the transport of a
$S^{\ast }=1/2$
. We simulate the transport of a
![]() $\text{CO}_{2}$
plume generated by an imposed saturation
$\text{CO}_{2}$
plume generated by an imposed saturation
![]() $S_{i}$
at the bottom of the column (figure 1). These simulations are performed with a home-made code based on the algorithm of Cancès (Reference Cancès2008) using the Godunov discretisation scheme.
$S_{i}$
at the bottom of the column (figure 1). These simulations are performed with a home-made code based on the algorithm of Cancès (Reference Cancès2008) using the Godunov discretisation scheme.

Figure 3. Gravitational fluxes
![]() $G^{-}$
in the material
$G^{-}$
in the material
![]() $k^{-}$
(dashed line) and
$k^{-}$
(dashed line) and
![]() $G^{+}$
in the material
$G^{+}$
in the material
![]() $k^{+}$
(continuous line). Each pair of markers plotted on these curves represents a couple
$k^{+}$
(continuous line). Each pair of markers plotted on these curves represents a couple
![]() $(S_{L},S_{U})$
satisfying the capillary pressure continuity condition at the interface.
$(S_{L},S_{U})$
satisfying the capillary pressure continuity condition at the interface.
![]() $G_{M}^{-}$
and
$G_{M}^{-}$
and
![]() $G_{M}^{+}$
are the maximal gravitational fluxes in the layer and in the matrix respectively.
$G_{M}^{+}$
are the maximal gravitational fluxes in the layer and in the matrix respectively.
![]() $S_{M}$
is the saturation in the layer such that
$S_{M}$
is the saturation in the layer such that
![]() $G^{-}(S_{M})=G_{M}^{-}$
;
$G^{-}(S_{M})=G_{M}^{-}$
;
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
are the saturations in the matrix such that
$S_{2}$
are the saturations in the matrix such that
![]() $G^{+}(S_{1})=G^{+}(S_{2})=G_{M}^{-}$
.
$G^{+}(S_{1})=G^{+}(S_{2})=G_{M}^{-}$
.
3.2 Case
 $k^{-}\rightarrow k^{+}$
$k^{-}\rightarrow k^{+}$
Because the entry capillary pressure ratio is
![]() $p_{e}^{-}/p_{e}^{+}=\sqrt{2}$
, there is no capillary barrier. Therefore, when the
$p_{e}^{-}/p_{e}^{+}=\sqrt{2}$
, there is no capillary barrier. Therefore, when the
![]() $\text{CO}_{2}$
plume reaches the interface between the two media, the plume immediately crosses the interface. The saturation traces
$\text{CO}_{2}$
plume reaches the interface between the two media, the plume immediately crosses the interface. The saturation traces
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{U}$
are determined from the total flux continuity condition and the value of the imposed saturation
$S_{U}$
are determined from the total flux continuity condition and the value of the imposed saturation
![]() $S_{i}$
at the bottom of the column. The total flux continuity,
$S_{i}$
at the bottom of the column. The total flux continuity,
![]() $G^{-}(S_{i})=\unicode[STIX]{x1D6F7}^{+}(S_{U})=G^{+}(S_{U})$
, determines
$G^{-}(S_{i})=\unicode[STIX]{x1D6F7}^{+}(S_{U})=G^{+}(S_{U})$
, determines
![]() $S_{U}$
. In the case of
$S_{U}$
. In the case of
![]() $S_{U}\leqslant S^{\ast }$
,
$S_{U}\leqslant S^{\ast }$
,
![]() $S_{L}$
remains unchanged at zero, and the buoyant flux on the lower side of the interface is also equal to zero. Therefore, the total flux on this side is reduced to its capillary diffusion component. Figure 4(b) depicts the temporal evolution of the
$S_{L}$
remains unchanged at zero, and the buoyant flux on the lower side of the interface is also equal to zero. Therefore, the total flux on this side is reduced to its capillary diffusion component. Figure 4(b) depicts the temporal evolution of the
![]() $\text{CO}_{2}$
saturation distribution for
$\text{CO}_{2}$
saturation distribution for
![]() $S_{i}=0.3$
. The buoyant flux curves displayed in figure 4(a) indicate that the upper saturation trace is
$S_{i}=0.3$
. The buoyant flux curves displayed in figure 4(a) indicate that the upper saturation trace is
![]() $S_{U}\approx 0.2$
. The apparent non-zero
$S_{U}\approx 0.2$
. The apparent non-zero
![]() $S_{L}$
value at
$S_{L}$
value at
![]() $t=6.8$
is due to the finite difference discretisation scheme, where variables are assigned at the cell centres instead of the cell edges. The case
$t=6.8$
is due to the finite difference discretisation scheme, where variables are assigned at the cell centres instead of the cell edges. The case
![]() $S_{U}>S^{\ast }$
does not exist with our selection of parameters and relative permeability laws for which
$S_{U}>S^{\ast }$
does not exist with our selection of parameters and relative permeability laws for which
![]() $S^{\ast }=1/2$
. This case is improbable if not impossible because (i) in most of the reservoirs,
$S^{\ast }=1/2$
. This case is improbable if not impossible because (i) in most of the reservoirs,
![]() $S^{\ast }$
is greater than the saturation
$S^{\ast }$
is greater than the saturation
![]() $S_{M}$
for which the buoyant flux is maximum, here
$S_{M}$
for which the buoyant flux is maximum, here
![]() $S_{M}=0.5$
, and (ii) the capillary pressure continuity implies that
$S_{M}=0.5$
, and (ii) the capillary pressure continuity implies that
![]() $S_{U}>S_{L}$
, which indicates that
$S_{U}>S_{L}$
, which indicates that
![]() $S_{U}$
is greater than
$S_{U}$
is greater than
![]() $S_{M}$
and therefore describes a shock travelling downwards (Hayek et al.
Reference Hayek, Mouche and Mügler2009).
$S_{M}$
and therefore describes a shock travelling downwards (Hayek et al.
Reference Hayek, Mouche and Mügler2009).

Figure 4.
![]() $\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
$\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
![]() $G^{-}$
in the material
$G^{-}$
in the material
![]() $k^{-}$
(dashed line) and
$k^{-}$
(dashed line) and
![]() $G^{+}$
in the material
$G^{+}$
in the material
![]() $k^{+}$
(continuous line). The couple
$k^{+}$
(continuous line). The couple
![]() $(S_{i},S_{U})$
satisfies the gravitational flux continuity, where
$(S_{i},S_{U})$
satisfies the gravitational flux continuity, where
![]() $S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at four times. At
$S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at four times. At
![]() $t=6.8$
, the saturation is at steady state.
$t=6.8$
, the saturation is at steady state.
3.3 Case
 $k^{+}\rightarrow k^{-}$
$k^{+}\rightarrow k^{-}$
The continuity of the capillary pressure is no longer automatically satisfied as in the previous case,
![]() $k^{-}\rightarrow k^{+}$
. Therefore, the
$k^{-}\rightarrow k^{+}$
. Therefore, the
![]() $\text{CO}_{2}$
accumulation occurs beneath the interface until
$\text{CO}_{2}$
accumulation occurs beneath the interface until
![]() $S_{L}$
is equal to
$S_{L}$
is equal to
![]() $S^{\ast }$
. Beyond this value,
$S^{\ast }$
. Beyond this value,
![]() $\text{CO}_{2}$
can flow through the interface, and the couple of saturation
$\text{CO}_{2}$
can flow through the interface, and the couple of saturation
![]() $(S_{L},S_{U})$
satisfies the capillary pressure continuity (3.11) (figure 2
c). Andreianov & Cancès (Reference Andreianov and Cancès2013) indicated how to graphically determine this couple in the
$(S_{L},S_{U})$
satisfies the capillary pressure continuity (3.11) (figure 2
c). Andreianov & Cancès (Reference Andreianov and Cancès2013) indicated how to graphically determine this couple in the
![]() $(S_{L},S_{U})$
plane using the solution curves
$(S_{L},S_{U})$
plane using the solution curves
![]() $S_{U}(S_{L})$
of the capillary pressure continuity condition and the buoyant flux continuity relationship. Let us define
$S_{U}(S_{L})$
of the capillary pressure continuity condition and the buoyant flux continuity relationship. Let us define
![]() ${\mathcal{P}}$
as the curve
${\mathcal{P}}$
as the curve
![]() $S_{U}(S_{L})$
solution of the capillary pressure continuity condition
$S_{U}(S_{L})$
solution of the capillary pressure continuity condition
Furthermore,
![]() ${\mathcal{G}}$
is defined as the solution curve
${\mathcal{G}}$
is defined as the solution curve
![]() $S_{U}(S_{L})$
of the buoyant flux continuity relationship
$S_{U}(S_{L})$
of the buoyant flux continuity relationship
Curves
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{G}}$
are plotted in figure 5. Due to the bell shape of the buoyant flux, curve
${\mathcal{G}}$
are plotted in figure 5. Due to the bell shape of the buoyant flux, curve
![]() ${\mathcal{G}}$
consists of three branches:
${\mathcal{G}}$
consists of three branches:
![]() ${\mathcal{G}}_{1}$
and
${\mathcal{G}}_{1}$
and
![]() ${\mathcal{G}}_{2}$
, which correspond to
${\mathcal{G}}_{2}$
, which correspond to
![]() $(S_{L}<S_{1},S_{U}<S_{M})$
and
$(S_{L}<S_{1},S_{U}<S_{M})$
and
![]() $(S_{L}>S_{2},S_{U}<S_{M})$
, respectively, and
$(S_{L}>S_{2},S_{U}<S_{M})$
, respectively, and
![]() ${\mathcal{G}}_{3}$
, which corresponds to
${\mathcal{G}}_{3}$
, which corresponds to
![]() $(S_{1}<S_{L}<S_{2},S_{U}=S_{M})$
, where
$(S_{1}<S_{L}<S_{2},S_{U}=S_{M})$
, where
![]() $S_{M}=0.5$
is the saturation for which the gravitational flux is maximum, and
$S_{M}=0.5$
is the saturation for which the gravitational flux is maximum, and
![]() $S_{1}=0.265$
and
$S_{1}=0.265$
and
![]() $S_{2}=0.735$
are the saturations such that
$S_{2}=0.735$
are the saturations such that
![]() $G^{+}(S_{1})=G^{+}(S_{2})=G^{-}(S_{M})$
with
$G^{+}(S_{1})=G^{+}(S_{2})=G^{-}(S_{M})$
with
![]() $S_{1}<S_{2}$
(figure 3). The couple
$S_{1}<S_{2}$
(figure 3). The couple
![]() $\overline{S}_{LU}=(\overline{S}_{2},\overline{S}_{U})$
represented in figure 5 is the intersection point between the curves
$\overline{S}_{LU}=(\overline{S}_{2},\overline{S}_{U})$
represented in figure 5 is the intersection point between the curves
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{G}}$
in the (
${\mathcal{G}}$
in the (
![]() $S_{L},S_{U}$
) plane. This couple defines the maximum
$S_{L},S_{U}$
) plane. This couple defines the maximum
![]() $\text{CO}_{2}$
flux that can cross the interface and respects the continuity conditions at the interface. The two saturations
$\text{CO}_{2}$
flux that can cross the interface and respects the continuity conditions at the interface. The two saturations
![]() $\overline{S}_{1}$
,
$\overline{S}_{1}$
,
![]() $\overline{S}_{2}$
in figure 5 are fortuitously close to
$\overline{S}_{2}$
in figure 5 are fortuitously close to
![]() $S_{1}$
,
$S_{1}$
,
![]() $S_{2}$
. This should not be the case with a different set of relative permeabilities and capillary pressure laws.
$S_{2}$
. This should not be the case with a different set of relative permeabilities and capillary pressure laws.

Figure 5. Curves
![]() $S_{U}(S_{L})$
, solutions of the capillary pressure continuity condition, curve
$S_{U}(S_{L})$
, solutions of the capillary pressure continuity condition, curve
![]() ${\mathcal{P}}$
(continuous line), and the gravitational flux continuity relationship, curve
${\mathcal{P}}$
(continuous line), and the gravitational flux continuity relationship, curve
![]() ${\mathcal{G}}$
(dashed line). Curve
${\mathcal{G}}$
(dashed line). Curve
![]() ${\mathcal{P}}$
is composed of two segments:
${\mathcal{P}}$
is composed of two segments:
![]() ${\mathcal{P}}_{1}$
for
${\mathcal{P}}_{1}$
for
![]() $S_{L}\leqslant S^{\ast }$
and
$S_{L}\leqslant S^{\ast }$
and
![]() ${\mathcal{P}}_{2}$
for
${\mathcal{P}}_{2}$
for
![]() $S_{L}>S^{\ast }$
. Curve
$S_{L}>S^{\ast }$
. Curve
![]() ${\mathcal{G}}$
has three branches:
${\mathcal{G}}$
has three branches:
![]() ${\mathcal{G}}_{1}$
and
${\mathcal{G}}_{1}$
and
![]() ${\mathcal{G}}_{2}$
correspond to
${\mathcal{G}}_{2}$
correspond to
![]() $(S_{L}<S_{1},S_{U}<S_{M})$
and
$(S_{L}<S_{1},S_{U}<S_{M})$
and
![]() $(S_{L}>S_{2},S_{U}<S_{M})$
, respectively, and
$(S_{L}>S_{2},S_{U}<S_{M})$
, respectively, and
![]() ${\mathcal{G}}_{3}$
to
${\mathcal{G}}_{3}$
to
![]() $(S_{1}<S_{L}<S_{2},S_{U}=S_{M})$
. The intersection point
$(S_{1}<S_{L}<S_{2},S_{U}=S_{M})$
. The intersection point
![]() $\overline{S}_{LU}=(\overline{S}_{2},\overline{S}_{U})$
of
$\overline{S}_{LU}=(\overline{S}_{2},\overline{S}_{U})$
of
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{G}}$
is the steady state solution of the interface problem for
${\mathcal{G}}$
is the steady state solution of the interface problem for
![]() $S_{i}>\overline{S}_{1}$
, where
$S_{i}>\overline{S}_{1}$
, where
![]() $G^{+}(\overline{S}_{1})=G^{+}(\overline{S}_{2})=G^{-}(\overline{S}_{U})$
and
$G^{+}(\overline{S}_{1})=G^{+}(\overline{S}_{2})=G^{-}(\overline{S}_{U})$
and
![]() $\overline{S}_{1}<\overline{S}_{2}$
.
$\overline{S}_{1}<\overline{S}_{2}$
.
The saturation discontinuity and distribution in the column depends strongly on the imposed saturation
![]() $S_{i}$
at the bottom of the column. Two cases must be distinguished:
$S_{i}$
at the bottom of the column. Two cases must be distinguished:
![]() $S_{i}\leqslant \overline{S}_{1}$
, i.e. the buoyant inflow flux is lower than the maximum flux, which can flow into the material
$S_{i}\leqslant \overline{S}_{1}$
, i.e. the buoyant inflow flux is lower than the maximum flux, which can flow into the material
![]() $k^{-}$
, and the inverse case.
$k^{-}$
, and the inverse case.
To illustrate the first case,
![]() $S_{i}\leqslant \overline{S}_{1}$
, we consider
$S_{i}\leqslant \overline{S}_{1}$
, we consider
![]() $S_{i}$
= 0.15 (
$S_{i}$
= 0.15 (
![]() $\overline{S}_{1}$
= 0.26). The pathway showing the evolution of
$\overline{S}_{1}$
= 0.26). The pathway showing the evolution of
![]() $(S_{L},S_{U})$
towards their steady state values is depicted in figure 6(a), and the temporal evolution of the
$(S_{L},S_{U})$
towards their steady state values is depicted in figure 6(a), and the temporal evolution of the
![]() $\text{CO}_{2}$
saturation distribution in the column is depicted in figure 7(b). When the
$\text{CO}_{2}$
saturation distribution in the column is depicted in figure 7(b). When the
![]() $\text{CO}_{2}$
plume reaches the interface, the capillary barrier results in an accumulation beneath the interface. The trace of saturation
$\text{CO}_{2}$
plume reaches the interface, the capillary barrier results in an accumulation beneath the interface. The trace of saturation
![]() $S_{U}$
is derived from the flux continuity condition. For any imposed saturation
$S_{U}$
is derived from the flux continuity condition. For any imposed saturation
![]() $S_{i}\leqslant \overline{S}_{1}$
, there always exist a saturation
$S_{i}\leqslant \overline{S}_{1}$
, there always exist a saturation
![]() $S_{U}$
that satisfies the buoyant flux continuity relationship
$S_{U}$
that satisfies the buoyant flux continuity relationship
![]() $G^{+}(S_{U})=G^{-}(S_{i})$
(figure 6
a). The imposed saturation value
$G^{+}(S_{U})=G^{-}(S_{i})$
(figure 6
a). The imposed saturation value
![]() $S_{i}=0.15$
results in
$S_{i}=0.15$
results in
![]() $S_{U}=0.22$
(figures 6
a and 7
a). The trace of saturation
$S_{U}=0.22$
(figures 6
a and 7
a). The trace of saturation
![]() $S_{L}$
is determined from the continuity of the capillary pressure at the interface:
$S_{L}$
is determined from the continuity of the capillary pressure at the interface:
![]() $S_{L}=0.61$
. The difference between the buoyant fluxes
$S_{L}=0.61$
. The difference between the buoyant fluxes
![]() $G^{-}(S_{U})$
and
$G^{-}(S_{U})$
and
![]() $G^{+}(S_{L})$
is balanced by a capillary diffusion flux (figure 7
b). It is important to note that the saturation traces (
$G^{+}(S_{L})$
is balanced by a capillary diffusion flux (figure 7
b). It is important to note that the saturation traces (
![]() $S_{L},S_{U}$
), and the gravitational flux difference
$S_{L},S_{U}$
), and the gravitational flux difference
![]() $G^{+}(S_{L})$
-
$G^{+}(S_{L})$
-
![]() $G^{-}(S_{U})$
is thus not affected by a variation of the capillary number
$G^{-}(S_{U})$
is thus not affected by a variation of the capillary number
![]() $N_{c}$
(3.3). For the limit
$N_{c}$
(3.3). For the limit
![]() $N_{c}\rightarrow 0$
, the saturation gradient beneath the interface increases, and the
$N_{c}\rightarrow 0$
, the saturation gradient beneath the interface increases, and the
![]() $\text{CO}_{2}$
peak shrinks and disappears when the capillary pressure tends to zero; hence, the capillary-free case is recovered.
$\text{CO}_{2}$
peak shrinks and disappears when the capillary pressure tends to zero; hence, the capillary-free case is recovered.

Figure 6. Curves
![]() $S_{U}(S_{L})$
, solutions of the capillary pressure continuity condition, curve
$S_{U}(S_{L})$
, solutions of the capillary pressure continuity condition, curve
![]() ${\mathcal{P}}$
(continuous line), and the gravitational flux continuity relationship, curve
${\mathcal{P}}$
(continuous line), and the gravitational flux continuity relationship, curve
![]() ${\mathcal{G}}$
(dashed line) (see figure 5). The pathway to determine the steady state solution of the interface problem for
${\mathcal{G}}$
(dashed line) (see figure 5). The pathway to determine the steady state solution of the interface problem for
![]() $S_{i}<\overline{S}_{1}$
(a) and for
$S_{i}<\overline{S}_{1}$
(a) and for
![]() $S_{i}\geqslant \overline{S}_{1}$
(b). The arrows indicate the direction of increasing
$S_{i}\geqslant \overline{S}_{1}$
(b). The arrows indicate the direction of increasing
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{U}$
.
$S_{U}$
.

Figure 7.
![]() $\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
$\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
![]() $G^{-}$
in the material
$G^{-}$
in the material
![]() $k^{-}$
(dashed line) and
$k^{-}$
(dashed line) and
![]() $G^{+}$
in the material
$G^{+}$
in the material
![]() $k^{+}$
(continuous line). The couple
$k^{+}$
(continuous line). The couple
![]() $(S_{i},S_{U})$
satisfies the capillary pressure continuity, where
$(S_{i},S_{U})$
satisfies the capillary pressure continuity, where
![]() $S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at four times. At
$S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at four times. At
![]() $t=13.7$
, the saturation is at steady state.
$t=13.7$
, the saturation is at steady state.

Figure 8.
![]() $\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
$\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. (a) Gravitational fluxes
![]() $G^{-}$
in the material
$G^{-}$
in the material
![]() $k^{-}$
(dashed line) and
$k^{-}$
(dashed line) and
![]() $G^{+}$
in the material
$G^{+}$
in the material
![]() $k^{+}$
(continuous line). The couple
$k^{+}$
(continuous line). The couple
![]() $\overline{S}_{LU}=(\overline{S}_{L},\overline{S}_{U})$
satisfies the capillary pressure and the gravitational continuity conditions and
$\overline{S}_{LU}=(\overline{S}_{L},\overline{S}_{U})$
satisfies the capillary pressure and the gravitational continuity conditions and
![]() $S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at five times. At
$S_{i}$
is the imposed saturation at the bottom of the column. (b) Saturation distributions along the vertical axis of the column at five times. At
![]() $t=13.7$
, the saturation is at steady state.
$t=13.7$
, the saturation is at steady state.
In the second case,
![]() $S_{i}>\overline{S}_{1}$
,
$S_{i}>\overline{S}_{1}$
,
![]() $S_{L}$
increases until
$S_{L}$
increases until
![]() $\overline{S}_{2}=0.74$
for which
$\overline{S}_{2}=0.74$
for which
![]() $S_{U}=\overline{S}_{U}=0.46$
(figure 6
b). The difference between the initial buoyant flux
$S_{U}=\overline{S}_{U}=0.46$
(figure 6
b). The difference between the initial buoyant flux
![]() $G^{+}(S_{i})$
and this maximum flux corresponds to a backward shock travelling at a velocity
$G^{+}(S_{i})$
and this maximum flux corresponds to a backward shock travelling at a velocity
![]() $[G(S_{i})-G(S_{L})]/(S_{i}-S_{L})$
(Hayek et al.
Reference Hayek, Mouche and Mügler2009), as illustrated in figure 8(b).
$[G(S_{i})-G(S_{L})]/(S_{i}-S_{L})$
(Hayek et al.
Reference Hayek, Mouche and Mügler2009), as illustrated in figure 8(b).

Figure 9.
![]() $\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. Gravitational fluxes
$\text{CO}_{2}$
migration in a vertical column filled with a piecewise homogeneous porous medium. Gravitational fluxes
![]() $G^{-}$
in the material
$G^{-}$
in the material
![]() $k^{-}$
(dashed line) and
$k^{-}$
(dashed line) and
![]() $G^{+}$
in the material
$G^{+}$
in the material
![]() $k^{+}$
(continuous line) for two values of the viscosity ratio
$k^{+}$
(continuous line) for two values of the viscosity ratio
![]() $M$
: (a)
$M$
: (a)
![]() $M=0.1$
, (b)
$M=0.1$
, (b)
![]() $M=0.2$
. The couple
$M=0.2$
. The couple
![]() $\overline{S}_{LU}=(\overline{S}_{L},\overline{S}_{U})$
satisfies the capillary pressure and the gravitational continuity conditions and
$\overline{S}_{LU}=(\overline{S}_{L},\overline{S}_{U})$
satisfies the capillary pressure and the gravitational continuity conditions and
![]() $S_{i}$
is the imposed saturation at the bottom of the column.
$S_{i}$
is the imposed saturation at the bottom of the column.

Figure 10. Flow regime diagram showing the three regimes of
![]() $\text{CO}_{2}$
accumulation beneath the interface as a function of the permeability ratio
$\text{CO}_{2}$
accumulation beneath the interface as a function of the permeability ratio
![]() $k_{l}/k_{u}$
and the imposed saturation
$k_{l}/k_{u}$
and the imposed saturation
![]() $S_{i}$
at the bottom of the column.
$S_{i}$
at the bottom of the column.
3.4 Impact of the model parameters on the flow regime
For simplicity we assume in this work a viscosity ratio equal to one. For a viscosity ratio lying between
![]() $10^{-1}$
and
$10^{-1}$
and
![]() $10^{-2}$
, which is the usual range for carbon sequestration studies (Huppert & Neufeld Reference Huppert and Neufeld2014), the position of the maximum flux is shifted towards
$10^{-2}$
, which is the usual range for carbon sequestration studies (Huppert & Neufeld Reference Huppert and Neufeld2014), the position of the maximum flux is shifted towards
![]() $S=0$
. Using the notations of § 3.3 we have
$S=0$
. Using the notations of § 3.3 we have
![]() $S_{M}=0.25$
and
$S_{M}=0.25$
and
![]() $G_{M}=0.28$
for
$G_{M}=0.28$
for
![]() $M=0.1$
, whereas
$M=0.1$
, whereas
![]() $S_{M}=0.5$
and
$S_{M}=0.5$
and
![]() $G_{M}=0.13$
for
$G_{M}=0.13$
for
![]() $M=1$
. Figures 9(a) and 9(b) display the buoyant flux curves with different values of the couple (
$M=1$
. Figures 9(a) and 9(b) display the buoyant flux curves with different values of the couple (
![]() $S_{L},S_{U}$
) for
$S_{L},S_{U}$
) for
![]() $M=0.1$
and
$M=0.1$
and
![]() $M=0.2$
respectively. In the case
$M=0.2$
respectively. In the case
![]() $k^{+}\rightarrow k^{-}$
and for
$k^{+}\rightarrow k^{-}$
and for
![]() $S_{i}=0.15$
we see that
$S_{i}=0.15$
we see that
![]() $S_{i}>\overline{S}_{1}$
for
$S_{i}>\overline{S}_{1}$
for
![]() $M=0.1$
(
$M=0.1$
(
![]() $\overline{S}_{1}=0.13$
) and
$\overline{S}_{1}=0.13$
) and
![]() $S_{i}<\overline{S}_{1}$
for
$S_{i}<\overline{S}_{1}$
for
![]() $M=0.2$
(
$M=0.2$
(
![]() $\overline{S}_{1}=0.16$
). According to the previous discussion (§ 3.3) the
$\overline{S}_{1}=0.16$
). According to the previous discussion (§ 3.3) the
![]() $\text{CO}_{2}$
accumulation beneath the interface tends to a steady state for
$\text{CO}_{2}$
accumulation beneath the interface tends to a steady state for
![]() $M=0.2$
and becomes unsteady for
$M=0.2$
and becomes unsteady for
![]() $M=0.1$
. We report on figures 9(a) and 9(b) the couples (
$M=0.1$
. We report on figures 9(a) and 9(b) the couples (
![]() $S_{L},S_{U}$
) for these two cases where (
$S_{L},S_{U}$
) for these two cases where (
![]() $S_{L}=\overline{S}_{2},S_{U}=\overline{S}_{U}$
) for
$S_{L}=\overline{S}_{2},S_{U}=\overline{S}_{U}$
) for
![]() $M=0.1$
. Figure 10 summarizes the three different flow regimes in the space described by the axis
$M=0.1$
. Figure 10 summarizes the three different flow regimes in the space described by the axis
![]() $k_{l}/k_{u}$
and
$k_{l}/k_{u}$
and
![]() $S_{i}$
for a given viscosity ratio. The saturation range is limited to (
$S_{i}$
for a given viscosity ratio. The saturation range is limited to (
![]() $0,S_{M}$
) because any saturation greater than
$0,S_{M}$
) because any saturation greater than
![]() $S_{M}$
cannot migrate upwards. The key parameter is
$S_{M}$
cannot migrate upwards. The key parameter is
![]() $\overline{S}_{1}$
, and it is easy to show that it depends on the ratio
$\overline{S}_{1}$
, and it is easy to show that it depends on the ratio
![]() $k^{-}/k^{+}$
and
$k^{-}/k^{+}$
and
![]() $M$
.
$M$
.
4 Gravity current model for a semi-permeable layer of finite extent
We now consider a 2-D reservoir consisting of a single horizontal semi-permeable layer of finite length
![]() $2L$
embedded in a permeable matrix. The permeabilities of the matrix and the inclusion are
$2L$
embedded in a permeable matrix. The permeabilities of the matrix and the inclusion are
![]() $k^{+}$
and
$k^{+}$
and
![]() $k^{-}$
, respectively, with
$k^{-}$
, respectively, with
![]() $k^{-}/k^{+}\ll 1$
. The reservoir, initially filled with brine, is fed by a uniform
$k^{-}/k^{+}\ll 1$
. The reservoir, initially filled with brine, is fed by a uniform
![]() $\text{CO}_{2}$
buoyant flux generated by an imposed
$\text{CO}_{2}$
buoyant flux generated by an imposed
![]() $\text{CO}_{2}$
saturation at the bottom of the reservoir. The bottom is supposed to be far from the layer. Similar to the 1-D vertical column case studied previously in § 3, the flow is counter-current: the
$\text{CO}_{2}$
saturation at the bottom of the reservoir. The bottom is supposed to be far from the layer. Similar to the 1-D vertical column case studied previously in § 3, the flow is counter-current: the
![]() $\text{CO}_{2}$
ascending flow rate across a horizontal section of the reservoir is balanced by the descending brine flow rate. As there is no
$\text{CO}_{2}$
ascending flow rate across a horizontal section of the reservoir is balanced by the descending brine flow rate. As there is no
![]() $\text{CO}_{2}$
injection the flow rate of the total velocity
$\text{CO}_{2}$
injection the flow rate of the total velocity
![]() $\boldsymbol{q}_{t}$
across the section (2.12) is zero but the velocity may be locally non-zero. This system could schematically represent the post-injection migration of a
$\boldsymbol{q}_{t}$
across the section (2.12) is zero but the velocity may be locally non-zero. This system could schematically represent the post-injection migration of a
![]() $\text{CO}_{2}$
plume in a single layer reservoir.
$\text{CO}_{2}$
plume in a single layer reservoir.

Figure 11. Simulation of the gravity currents (
![]() $p_{c}=0$
) underlying an impervious (a) or a semi-permeable layer (b,c). The black lines delineate the interface between the matrix and the layer. Simulations are performed using the DuMu
$p_{c}=0$
) underlying an impervious (a) or a semi-permeable layer (b,c). The black lines delineate the interface between the matrix and the layer. Simulations are performed using the DuMu
![]() $^{x}$
code (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011).
$^{x}$
code (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011).
We study the buoyancy-dominant flow of
![]() $\text{CO}_{2}$
beneath and through the semi-permeable layer. The numerical simulations neglecting the capillary pressure indicate that this predominantly horizontal flow can be assimilated to a so-called gravity current driven by the density contrast between the
$\text{CO}_{2}$
beneath and through the semi-permeable layer. The numerical simulations neglecting the capillary pressure indicate that this predominantly horizontal flow can be assimilated to a so-called gravity current driven by the density contrast between the
![]() $\text{CO}_{2}$
and the surrounding brine (figure 11). For permeability ratios
$\text{CO}_{2}$
and the surrounding brine (figure 11). For permeability ratios
![]() $k^{-}/k^{+}\geqslant 0.1$
, figure 11 clearly indicates that there is a phase segregation and a neat interface between the gravity current and the remaining fluid. Furthermore, we can observe that when
$k^{-}/k^{+}\geqslant 0.1$
, figure 11 clearly indicates that there is a phase segregation and a neat interface between the gravity current and the remaining fluid. Furthermore, we can observe that when
![]() $k^{-}/k^{+}$
increases, the
$k^{-}/k^{+}$
increases, the
![]() $\text{CO}_{2}$
saturation in the gravity current
$\text{CO}_{2}$
saturation in the gravity current
![]() $S_{gc}$
decreases:
$S_{gc}$
decreases:
![]() $S_{gc}\approx 0.9$
for
$S_{gc}\approx 0.9$
for
![]() $k^{-}/k^{+}=0.1$
and
$k^{-}/k^{+}=0.1$
and
![]() $S_{gc}\approx 0.8$
for
$S_{gc}\approx 0.8$
for
![]() $k^{-}/k^{+}=0.25$
. The imposed saturation at the bottom of the reservoir is
$k^{-}/k^{+}=0.25$
. The imposed saturation at the bottom of the reservoir is
![]() $S_{i}=0.25$
.
$S_{i}=0.25$
.
The extension of gravity current models to semi-permeable layers is a complex theoretical issue which is beyond the scope of the paper. Indeed, this extension must be able to describe the flows of brine and
![]() $\text{CO}_{2}$
in the gravity current, in the layer and in the layer’s surrounding, while respecting the phase segregation condition. The objective of our modelling approach is to simplify the problem by decoupling the flows of the two phases and to describe the flow of
$\text{CO}_{2}$
in the gravity current, in the layer and in the layer’s surrounding, while respecting the phase segregation condition. The objective of our modelling approach is to simplify the problem by decoupling the flows of the two phases and to describe the flow of
![]() $\text{CO}_{2}$
by means of a single transport saturation equation with flux continuity conditions at the interfaces. For this purpose one must be able to circumvent the pressure equation, and therefore disregard the total velocity. Although this is not feasible in our 2-D problem one may hope that when flow is counter-current at the scale of the domain it is approximatively counter-current at the interfaces with the layer. Under this approximation the
$\text{CO}_{2}$
by means of a single transport saturation equation with flux continuity conditions at the interfaces. For this purpose one must be able to circumvent the pressure equation, and therefore disregard the total velocity. Although this is not feasible in our 2-D problem one may hope that when flow is counter-current at the scale of the domain it is approximatively counter-current at the interfaces with the layer. Under this approximation the
![]() $\text{CO}_{2}$
vertical flow is one-dimensional and counter-current and the horizontal flow in the gravity current is governed by the horizontal gradient of the gravity current height. Adopting these assumptions we here propose to extend the gravity current models developed for impermeable layers to semi-permeable layers. These assumptions are discussed and heuristically justified in the appendix A.
$\text{CO}_{2}$
vertical flow is one-dimensional and counter-current and the horizontal flow in the gravity current is governed by the horizontal gradient of the gravity current height. Adopting these assumptions we here propose to extend the gravity current models developed for impermeable layers to semi-permeable layers. These assumptions are discussed and heuristically justified in the appendix A.
Most of the studies on gravity currents in porous media use a sharp-interface approximation assuming that the regions within and without the current are fully saturated, and a macroscopic sharp interface exists between the two fluids (Huppert & Neufeld Reference Huppert and Neufeld2014). These single-phase gravity current models can only be applied when the capillary pressure is negligible compared to gravity and viscous forces. When capillarity is considered, the simulation indicates that both phases are present, and due to capillary diffusion, the vertical extent of the gravity current and its non-wetting phase saturation are greater and smaller, respectively, than that in the capillary-free case. Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) developed a model that considers the capillary effect on the saturation distribution within the current. The authors proposed a vertically integrated model for a two-phase gravity current along a horizontal impermeable barrier, in which the local capillary effect is encapsulated directly into the total flux function. Thereafter, we extend their model to study the two-phase gravity current along a semi-permeable barrier of finite extent (appendix A).
The two-phase gravity current model beneath an impermeable boundary is based on the assumption of a vertical gravity–capillary equilibrium which expresses the balance between the gravitational and the capillary force within the current (Golding et al. Reference Golding, Neufeld, Hesse and Huppert2011). We assume that this assumption is still valid when the boundary is semi-permeable (appendix A)
where the vertical axis
![]() $z$
is oriented downwards, and its origin is located at the centre of the low matrix inclusion interface. The relationship between the capillary pressure and the current height is determined by integrating equation (4.1) from
$z$
is oriented downwards, and its origin is located at the centre of the low matrix inclusion interface. The relationship between the capillary pressure and the current height is determined by integrating equation (4.1) from
![]() $z$
to the gravity current height
$z$
to the gravity current height
![]() $h$
as follows
$h$
as follows
where
![]() $S_{h}$
denotes the non-wetting phase saturation at
$S_{h}$
denotes the non-wetting phase saturation at
![]() $z=h$
, which is commonly equal to zero, except in our case where the gravity current is fed by a source distributed uniformly at the bottom of the reservoir, and
$z=h$
, which is commonly equal to zero, except in our case where the gravity current is fed by a source distributed uniformly at the bottom of the reservoir, and
![]() $p_{e}^{+}$
is the entry pressure of the permeable matrix. The expression of
$p_{e}^{+}$
is the entry pressure of the permeable matrix. The expression of
![]() $\text{CO}_{2}$
saturation within the current as a function of the current height
$\text{CO}_{2}$
saturation within the current as a function of the current height
![]() $h$
and
$h$
and
![]() $z$
is written as follows
$z$
is written as follows
where
![]() $h_{e}^{+}=p_{e}^{+}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g$
. The non-wetting phase saturation
$h_{e}^{+}=p_{e}^{+}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g$
. The non-wetting phase saturation
![]() $S_{0}^{+}$
at
$S_{0}^{+}$
at
![]() $z=0$
on the matrix side of the interface is
$z=0$
on the matrix side of the interface is
A vertical integration of the mass conservation equation (2.2) for the non-wetting phase over the gravity current yields
where
![]() $\unicode[STIX]{x1D6F7}_{in}$
,
$\unicode[STIX]{x1D6F7}_{in}$
,
![]() $\unicode[STIX]{x1D6F7}_{out}$
are the vertical feeding flux at
$\unicode[STIX]{x1D6F7}_{out}$
are the vertical feeding flux at
![]() $z=h$
and the vertical leakage term at the interface, respectively, with the semi-permeable layer at
$z=h$
and the vertical leakage term at the interface, respectively, with the semi-permeable layer at
![]() $z=0$
. The capillary effect on the gravity current is considered via the flux function
$z=0$
. The capillary effect on the gravity current is considered via the flux function
![]() ${\mathcal{F}}(h/h_{e}^{+})$
${\mathcal{F}}(h/h_{e}^{+})$
The current height at the layer ends is set to zero:
![]() $h(x=\pm L)=0$
. An analytical expression of
$h(x=\pm L)=0$
. An analytical expression of
![]() ${\mathcal{F}}$
is given by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) for
${\mathcal{F}}$
is given by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) for
![]() $S_{h}=0$
. Based on this expression, we derive
$S_{h}=0$
. Based on this expression, we derive
where
The flux
![]() $\unicode[STIX]{x1D6F7}_{in}$
is assumed to be equal to the buoyant flux
$\unicode[STIX]{x1D6F7}_{in}$
is assumed to be equal to the buoyant flux
![]() $G^{+}(S_{h})$
. At steady state, we have
$G^{+}(S_{h})$
. At steady state, we have
![]() $S_{h}=S_{i}$
, where
$S_{h}=S_{i}$
, where
![]() $S_{i}$
is the imposed saturation at the bottom of the reservoir. The saturation
$S_{i}$
is the imposed saturation at the bottom of the reservoir. The saturation
![]() $S_{0}^{+}$
on the matrix side of the interface between the low-permeability layer and the matrix and the flux
$S_{0}^{+}$
on the matrix side of the interface between the low-permeability layer and the matrix and the flux
![]() $\unicode[STIX]{x1D6F7}_{out}$
are given by the buoyant flux and the capillary pressure continuity conditions at the interface. Based on the previous analysis of the
$\unicode[STIX]{x1D6F7}_{out}$
are given by the buoyant flux and the capillary pressure continuity conditions at the interface. Based on the previous analysis of the
![]() $\text{CO}_{2}$
plume dynamics at the interface of a piecewise homogeneous porous medium (§ 3) the
$\text{CO}_{2}$
plume dynamics at the interface of a piecewise homogeneous porous medium (§ 3) the
![]() $\text{CO}_{2}$
can penetrate locally, i.e. for a given
$\text{CO}_{2}$
can penetrate locally, i.e. for a given
![]() $x$
, into the semi-permeable layer when the local capillary pressure in the gravity current at
$x$
, into the semi-permeable layer when the local capillary pressure in the gravity current at
![]() $z=0$
exceeds the entry capillary pressure of the layer
$z=0$
exceeds the entry capillary pressure of the layer
![]() $p_{e}^{-}$
. In terms of saturation, the vertical flow occurs locally if the local saturation
$p_{e}^{-}$
. In terms of saturation, the vertical flow occurs locally if the local saturation
![]() $S_{0}^{+}$
exceeds the threshold saturation
$S_{0}^{+}$
exceeds the threshold saturation
![]() $S_{0}^{\ast }$
defined by (3.9). The relationship between
$S_{0}^{\ast }$
defined by (3.9). The relationship between
![]() $S_{0}^{+}$
and the current height
$S_{0}^{+}$
and the current height
![]() $h$
expressed in (4.4) results in the notion of the threshold height
$h$
expressed in (4.4) results in the notion of the threshold height
![]() $h^{\ast }$
$h^{\ast }$
where
![]() $S_{0}^{\ast }$
is a function of the permeability contrast
$S_{0}^{\ast }$
is a function of the permeability contrast
![]() $k^{-}/k^{+}$
.
$k^{-}/k^{+}$
.
Woods & Farcas (Reference Woods and Farcas2009) investigated the influence of the entry capillary pressure on the leakage of single-phase gravity currents through a low-permeability layer. However, in their study, the threshold height of the single-phase gravity current
![]() $h^{\ast }$
is equal to
$h^{\ast }$
is equal to
![]() $h_{e}$
, and the impact of the permeability contrast between the matrix and the layer is not studied. At steady state, Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) introduced the dimensionless variables
$h_{e}$
, and the impact of the permeability contrast between the matrix and the layer is not studied. At steady state, Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) introduced the dimensionless variables
![]() $x=x/L$
and
$x=x/L$
and
![]() $h=h/h_{gc}$
, where
$h=h/h_{gc}$
, where
![]() $h_{gc}$
is the gravity current height scale corresponding to a steady state gravity current of the horizontal extent
$h_{gc}$
is the gravity current height scale corresponding to a steady state gravity current of the horizontal extent
![]() $2L$
, which was originally introduced by Huppert & Woods (Reference Huppert and Woods1995). In our system, this height scale is given as
$2L$
, which was originally introduced by Huppert & Woods (Reference Huppert and Woods1995). In our system, this height scale is given as
Hence, the governing equation of the current height reads
and
where
![]() $B$
is the Bond number
$B$
is the Bond number
The solution of (4.11) and (4.12) depends strongly on the Bond number
![]() $B$
and the capillary number
$B$
and the capillary number
![]() $N_{c}$
. Lastly, the dynamics of the system is essentially controlled by four variables or parameters: layer length
$N_{c}$
. Lastly, the dynamics of the system is essentially controlled by four variables or parameters: layer length
![]() $2L$
, entry pressure in the matrix
$2L$
, entry pressure in the matrix
![]() $h_{e}^{+}$
, imposed saturation at the bottom of the reservoir
$h_{e}^{+}$
, imposed saturation at the bottom of the reservoir
![]() $S_{i}$
and ratio of the permeabilities
$S_{i}$
and ratio of the permeabilities
![]() $k^{-}/k^{+}$
.
$k^{-}/k^{+}$
.
The outflux
![]() $\unicode[STIX]{x1D6F7}_{out}$
in (4.11) can be approximated by the buoyant flux on the inclusion side of the interface as follows
$\unicode[STIX]{x1D6F7}_{out}$
in (4.11) can be approximated by the buoyant flux on the inclusion side of the interface as follows
where the saturation
![]() $S_{0}^{-}$
is the saturation on the inclusion side of the interface, which is determined via the matching condition of capillary pressure at this interface
$S_{0}^{-}$
is the saturation on the inclusion side of the interface, which is determined via the matching condition of capillary pressure at this interface
where
![]() $S_{0}^{+}$
is related to the height of the gravity current
$S_{0}^{+}$
is related to the height of the gravity current
![]() $h$
via (4.4). In other words, the outflux
$h$
via (4.4). In other words, the outflux
![]() $\unicode[STIX]{x1D6F7}_{out}$
is also a function of
$\unicode[STIX]{x1D6F7}_{out}$
is also a function of
![]() $h$
. To determine
$h$
. To determine
![]() $h$
, equations (4.11) and (4.12) can be solved numerically using a predictor–corrector algorithm (Ames Reference Ames2014).
$h$
, equations (4.11) and (4.12) can be solved numerically using a predictor–corrector algorithm (Ames Reference Ames2014).
When the capillarity is neglected,
![]() $N_{c}=0$
, unlike the single-phase gravity current beneath impermeable boundaries, the zone occupied by the current is not saturated with
$N_{c}=0$
, unlike the single-phase gravity current beneath impermeable boundaries, the zone occupied by the current is not saturated with
![]() $\text{CO}_{2}$
because of the leakage term
$\text{CO}_{2}$
because of the leakage term
![]() $\unicode[STIX]{x1D6F7}_{out}$
through the layer. We can assume that at steady state, the saturation
$\unicode[STIX]{x1D6F7}_{out}$
through the layer. We can assume that at steady state, the saturation
![]() $S_{gc}$
within the current is constant and determined from the continuity condition of the buoyant flux at the interface. We emphasize that in most of the works the flux
$S_{gc}$
within the current is constant and determined from the continuity condition of the buoyant flux at the interface. We emphasize that in most of the works the flux
![]() $\unicode[STIX]{x1D6F7}_{out}$
is considered as a drainage term evaluated from the hydrostatic pressure assumption (Acton, Huppert & Worster Reference Acton, Huppert and Worster2001; Spannuth et al.
Reference Spannuth, Neufeld, Wettlaufer and Worster2009; Neufeld & Huppert Reference Neufeld and Huppert2009). This drainage assumption is not justified for a counter-current flow in a semi-permeable layer where the two-phase flow nature of the problem must be respected. Finally, we recover the equation describing the propagation of current given by Huppert & Woods (Reference Huppert and Woods1995) but with slight differences (appendix A)
$\unicode[STIX]{x1D6F7}_{out}$
is considered as a drainage term evaluated from the hydrostatic pressure assumption (Acton, Huppert & Worster Reference Acton, Huppert and Worster2001; Spannuth et al.
Reference Spannuth, Neufeld, Wettlaufer and Worster2009; Neufeld & Huppert Reference Neufeld and Huppert2009). This drainage assumption is not justified for a counter-current flow in a semi-permeable layer where the two-phase flow nature of the problem must be respected. Finally, we recover the equation describing the propagation of current given by Huppert & Woods (Reference Huppert and Woods1995) but with slight differences (appendix A)
For the capillary case, we introduce the dimensionless variables
![]() $x=x/L\text{ and }h=h/h_{gc}$
, where the gravity current height scale
$x=x/L\text{ and }h=h/h_{gc}$
, where the gravity current height scale
![]() $h_{gc}$
is given by (4.10), in which
$h_{gc}$
is given by (4.10), in which
![]() $k^{+}$
is replaced by
$k^{+}$
is replaced by
![]() $k^{+}k_{r_{nw}}(S_{gc})$
and
$k^{+}k_{r_{nw}}(S_{gc})$
and
![]() $\unicode[STIX]{x1D6F7}_{in}$
is replaced by
$\unicode[STIX]{x1D6F7}_{in}$
is replaced by
![]() $\unicode[STIX]{x1D6F7}_{in}-\unicode[STIX]{x1D6F7}_{out}$
. The profile of the single-phase gravity current at steady state is given by
$\unicode[STIX]{x1D6F7}_{in}-\unicode[STIX]{x1D6F7}_{out}$
. The profile of the single-phase gravity current at steady state is given by
where
![]() $\unicode[STIX]{x1D6F7}_{in}=G^{+}(S_{i})$
and
$\unicode[STIX]{x1D6F7}_{in}=G^{+}(S_{i})$
and
![]() $\unicode[STIX]{x1D6F7}_{out}=G^{+}(S_{gc})=G^{-}(S_{la})$
, with
$\unicode[STIX]{x1D6F7}_{out}=G^{+}(S_{gc})=G^{-}(S_{la})$
, with
![]() $S_{la}$
denoting the saturation in the layer. Because the layer is thin, this saturation is assumed to be homogeneous. The solution of (4.17) is
$S_{la}$
denoting the saturation in the layer. Because the layer is thin, this saturation is assumed to be homogeneous. The solution of (4.17) is
5 Numerical validation and discussion of the model
The reservoir introduced in the previous section is modelled as a rectangular domain with a width of
![]() $2L_{0}=80~\text{m}$
and a height of
$2L_{0}=80~\text{m}$
and a height of
![]() $H=100~\text{m}$
with a length layer of
$H=100~\text{m}$
with a length layer of
![]() $2L=72~\text{m}$
localized at the centre and leaving two gaps of
$2L=72~\text{m}$
localized at the centre and leaving two gaps of
![]() $l=L_{0}-L=4~\text{m}$
width on each side (figure 12). A
$l=L_{0}-L=4~\text{m}$
width on each side (figure 12). A
![]() $\text{CO}_{2}$
saturation
$\text{CO}_{2}$
saturation
![]() $S_{i}$
is imposed throughout the lower boundary of the domain which is initially saturated with brine. All of the other boundaries are impermeable and the brine is allowed to flow downwards through the lower boundary. The flow is counter-current: the brine initially located in the reservoir can flow downwards through the layer and the two gaps. This domain may be observed as the unit cell of a larger reservoir, which consists of a periodic array of identical horizontal layers with a length
$S_{i}$
is imposed throughout the lower boundary of the domain which is initially saturated with brine. All of the other boundaries are impermeable and the brine is allowed to flow downwards through the lower boundary. The flow is counter-current: the brine initially located in the reservoir can flow downwards through the layer and the two gaps. This domain may be observed as the unit cell of a larger reservoir, which consists of a periodic array of identical horizontal layers with a length
![]() $2L$
and a periodicity
$2L$
and a periodicity
![]() $2L_{0}$
. The petrophysical parameters of the reservoir for the two studied cases, i.e. capillary free and gravity dominant, and the parameters of the fluids are summarized in table 1. For reasons explained in § 3.1, the brine and the
$2L_{0}$
. The petrophysical parameters of the reservoir for the two studied cases, i.e. capillary free and gravity dominant, and the parameters of the fluids are summarized in table 1. For reasons explained in § 3.1, the brine and the
![]() $\text{CO}_{2}$
viscosities are assumed to be equal. The numerical validation of the model developed in the previous section is performed using DuMu
$\text{CO}_{2}$
viscosities are assumed to be equal. The numerical validation of the model developed in the previous section is performed using DuMu
![]() $^{x}$
, which is an open-source simulator for the flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). We successively discuss the cases without and with the capillarity. In this last case, we consider only the gravity-dominant flow,
$^{x}$
, which is an open-source simulator for the flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). We successively discuss the cases without and with the capillarity. In this last case, we consider only the gravity-dominant flow,
![]() $N_{c}\ll 1$
.
$N_{c}\ll 1$
.

Figure 12. Reservoir with a single embedded layer of permeability
![]() $k^{-}$
in a permeable matrix of permeability
$k^{-}$
in a permeable matrix of permeability
![]() $k^{+}$
.
$k^{+}$
.
Table 1. Parameters for the simulations of the capillary-free and gravity-dominant cases.


Figure 13. Gravitational flux curves of the layer and the matrix for
![]() $k^{-}/k^{+}=1/10$
.
$k^{-}/k^{+}=1/10$
.
5.1 Capillary-free case
We consider a permeability ratio
![]() $k^{-}/k^{+}=1/10$
for the capillary-free case. The buoyant flux functions are depicted in figure 13. First, we emphasize that in the finite width domain considered here the buoyant flux imposed at the bottom is limited by a critical value beyond which a steady state gravity current cannot be obtained. This critical flux can be defined by the equality
$k^{-}/k^{+}=1/10$
for the capillary-free case. The buoyant flux functions are depicted in figure 13. First, we emphasize that in the finite width domain considered here the buoyant flux imposed at the bottom is limited by a critical value beyond which a steady state gravity current cannot be obtained. This critical flux can be defined by the equality
where
![]() $G_{M}^{+}$
and
$G_{M}^{+}$
and
![]() $G_{M}^{-}$
are the maxima of the buoyant flux in the matrix and the layer respectively (figure 13). This equality defines a critical saturation
$G_{M}^{-}$
are the maxima of the buoyant flux in the matrix and the layer respectively (figure 13). This equality defines a critical saturation
![]() $S_{c}$
given by the relationship
$S_{c}$
given by the relationship
It is easy to find that the saturation
![]() $S_{1}$
defined by
$S_{1}$
defined by
![]() $G^{+}(S_{1})=G_{M}^{-}$
and shown in figure 13 is always lower than the critical saturation
$G^{+}(S_{1})=G_{M}^{-}$
and shown in figure 13 is always lower than the critical saturation
![]() $S_{c}$
. The saturation
$S_{c}$
. The saturation
![]() $S_{1}$
is the maximum saturation below which there is no gravity current, i.e. all of the imposed buoyant flux can pass through the layer. When
$S_{1}$
is the maximum saturation below which there is no gravity current, i.e. all of the imposed buoyant flux can pass through the layer. When
![]() $k^{-}\rightarrow k^{+}$
we have
$k^{-}\rightarrow k^{+}$
we have
![]() $S_{1}\rightarrow S_{c}\rightarrow S_{M}$
. For
$S_{1}\rightarrow S_{c}\rightarrow S_{M}$
. For
![]() $k^{-}/k^{+}=1/10$
we have
$k^{-}/k^{+}=1/10$
we have
![]() $S_{c}=0.156$
and
$S_{c}=0.156$
and
![]() $S_{1}=0.112$
, and for
$S_{1}=0.112$
, and for
![]() $k^{-}/k^{+}=1/4$
,
$k^{-}/k^{+}=1/4$
,
![]() $S_{c}=0.205$
and
$S_{c}=0.205$
and
![]() $S_{1}=0.180$
. Therefore, based on the continuity condition of the buoyant flux, three cases
$S_{1}=0.180$
. Therefore, based on the continuity condition of the buoyant flux, three cases
![]() $\boldsymbol{C}$
(1,2,3) must be identified:
$\boldsymbol{C}$
(1,2,3) must be identified:
-
(i)
 $\boldsymbol{C}.1:$
$\boldsymbol{C}.1:$
 $S_{i}\leqslant S_{1}$
. There is no gravity current and
$S_{i}\leqslant S_{1}$
. There is no gravity current and
 $\unicode[STIX]{x1D6F7}_{out}=\unicode[STIX]{x1D6F7}_{in}=G(S_{i})$
. The saturation in the layer is given by the buoyant flux continuity and equal to
$\unicode[STIX]{x1D6F7}_{out}=\unicode[STIX]{x1D6F7}_{in}=G(S_{i})$
. The saturation in the layer is given by the buoyant flux continuity and equal to
 $S_{i}$
on the matrix side of the upper interface of the layer.
$S_{i}$
on the matrix side of the upper interface of the layer. -
(ii)
 $\boldsymbol{C}.2:$
$\boldsymbol{C}.2:$
 $S_{1}\leqslant S_{i}\leqslant S_{c}$
. There is a gravity current and
$S_{1}\leqslant S_{i}\leqslant S_{c}$
. There is a gravity current and
 $\unicode[STIX]{x1D6F7}_{out}=G_{M}^{-}$
. After a relaxation period, which depends on
$\unicode[STIX]{x1D6F7}_{out}=G_{M}^{-}$
. After a relaxation period, which depends on
 $k^{-}$
the gravity current reaches a steady state. The saturation is
$k^{-}$
the gravity current reaches a steady state. The saturation is
 $S_{M}=0.5$
in the layer and
$S_{M}=0.5$
in the layer and
 $S_{1}$
on the matrix side of the upper interface of the layer.
$S_{1}$
on the matrix side of the upper interface of the layer. -
(iii)
 $\boldsymbol{C}.3:$
$\boldsymbol{C}.3:$
 $S_{c}\leqslant S_{i}$
. There is a gravity current but
$S_{c}\leqslant S_{i}$
. There is a gravity current but
 $\text{CO}_{2}$
flows back downwards beneath the layer and there is no steady state.
$\text{CO}_{2}$
flows back downwards beneath the layer and there is no steady state.
It must be remarked that the range of saturations inside which a steady state gravity current can take place,
![]() $[S_{1},S_{c}]$
, becomes narrow when
$[S_{1},S_{c}]$
, becomes narrow when
![]() $k^{-}\rightarrow k^{+}$
.
$k^{-}\rightarrow k^{+}$
.
Figure 14 illustrates these three cases at three different times: case
![]() $\boldsymbol{C}.1$
with
$\boldsymbol{C}.1$
with
![]() $S_{i}=0.10$
(figures 14
a–14
c), case
$S_{i}=0.10$
(figures 14
a–14
c), case
![]() $\boldsymbol{C}.2$
with
$\boldsymbol{C}.2$
with
![]() $S_{i}=0.15$
(figures 14
d–14
f) and case
$S_{i}=0.15$
(figures 14
d–14
f) and case
![]() $\boldsymbol{C}.3$
with
$\boldsymbol{C}.3$
with
![]() $S_{i}=0.20$
(figures 14
g–14
i).
$S_{i}=0.20$
(figures 14
g–14
i).

Figure 14. Capillary-free case.
![]() $\text{CO}_{2}$
distributions after an early time
$\text{CO}_{2}$
distributions after an early time
![]() $t_{1}$
(a,d,g) when the
$t_{1}$
(a,d,g) when the
![]() $\text{CO}_{2}$
plume has just reached the semi-permeable layer, at an intermediate time
$\text{CO}_{2}$
plume has just reached the semi-permeable layer, at an intermediate time
![]() $t_{2}$
(b,e,h) and a relatively long time
$t_{2}$
(b,e,h) and a relatively long time
![]() $t_{3}$
after the
$t_{3}$
after the
![]() $\text{CO}_{2}$
plume has reached the no-flow top of the reservoir (c,f,i).
$\text{CO}_{2}$
plume has reached the no-flow top of the reservoir (c,f,i).

Figure 15. Capillary-free case:
![]() $\text{CO}_{2}$
distributions from
$\text{CO}_{2}$
distributions from
![]() $Z=0~(\text{m})$
to the observation surface
$Z=0~(\text{m})$
to the observation surface
![]() $Z=60~(\text{m})$
modelled with the gravity current model (a) and simulated with DuMu
$Z=60~(\text{m})$
modelled with the gravity current model (a) and simulated with DuMu
![]() $^{x}$
(b). A moderate influx (
$^{x}$
(b). A moderate influx (
![]() $S_{i}=0.15$
) is imposed at the bottom of the reservoir.
$S_{i}=0.15$
) is imposed at the bottom of the reservoir.

Figure 16. Capillary-free case: (a)
![]() $\text{CO}_{2}$
saturation profile along the central vertical axis of the layer. Comparison between the numerical simulation results obtained using DuMu
$\text{CO}_{2}$
saturation profile along the central vertical axis of the layer. Comparison between the numerical simulation results obtained using DuMu
![]() $^{x}$
and the analytical gravity current models, with (
$^{x}$
and the analytical gravity current models, with (
![]() $\boldsymbol{q}_{t}\neq 0$
) and without (
$\boldsymbol{q}_{t}\neq 0$
) and without (
![]() $\boldsymbol{q}_{t}=0$
) the total velocity correction, for the case
$\boldsymbol{q}_{t}=0$
) the total velocity correction, for the case
![]() $S_{i}=0.15$
. (b) Vertical total flux function
$S_{i}=0.15$
. (b) Vertical total flux function
![]() $\unicode[STIX]{x1D6F7}(S)$
(solid line) and gravitational flux function
$\unicode[STIX]{x1D6F7}(S)$
(solid line) and gravitational flux function
![]() $G(S)$
(dotted line) at the interface between the matrix and the layer.
$G(S)$
(dotted line) at the interface between the matrix and the layer.
The 2-D steady state
![]() $\text{CO}_{2}$
saturation distributions given by the model and computed using DuMu
$\text{CO}_{2}$
saturation distributions given by the model and computed using DuMu
![]() $^{x}$
for
$^{x}$
for
![]() $S_{i}=0.15$
are depicted in figure 15, and the 1-D distributions along the vertical axis passing through the middle of the layer (
$S_{i}=0.15$
are depicted in figure 15, and the 1-D distributions along the vertical axis passing through the middle of the layer (
![]() $x=0$
) are plotted in figure 16(a). Only the lower part of the domain is illustrated in these figures. The model and numerical results match fairly well. Particularly, we can see that the model overestimates the current height. When the layer is impermeable, the current heights are nearly identical; therefore, the observed discrepancy for the semi-permeable case is not due to the Boussinesq approximation in the gravity current model. We attribute this discrepancy to the role of the total velocity
$x=0$
) are plotted in figure 16(a). Only the lower part of the domain is illustrated in these figures. The model and numerical results match fairly well. Particularly, we can see that the model overestimates the current height. When the layer is impermeable, the current heights are nearly identical; therefore, the observed discrepancy for the semi-permeable case is not due to the Boussinesq approximation in the gravity current model. We attribute this discrepancy to the role of the total velocity
![]() $\boldsymbol{q}_{t}$
(2.12), which is disregarded in our model. Because the flow is counter-current, the flow rate of the total velocity across a horizontal section is zero but the velocity is locally non-zero. The velocity increases the flux at the interface and therefore lowers the current height (figure 16
b). The flux continuity at the centre (
$\boldsymbol{q}_{t}$
(2.12), which is disregarded in our model. Because the flow is counter-current, the flow rate of the total velocity across a horizontal section is zero but the velocity is locally non-zero. The velocity increases the flux at the interface and therefore lowers the current height (figure 16
b). The flux continuity at the centre (
![]() $x=0$
) of the lower matrix–layer interface indicates
$x=0$
) of the lower matrix–layer interface indicates
where the saturations
![]() $S_{2}^{\prime }$
,
$S_{2}^{\prime }$
,
![]() $S_{m}^{\prime }$
are depicted in figure 16(b) and
$S_{m}^{\prime }$
are depicted in figure 16(b) and
![]() $q_{tn}$
is the component normal to the interface of
$q_{tn}$
is the component normal to the interface of
![]() $\boldsymbol{q}_{t}$
. When
$\boldsymbol{q}_{t}$
. When
![]() $\boldsymbol{q}_{t}=0$
, we have
$\boldsymbol{q}_{t}=0$
, we have
![]() $S_{2}^{\prime }=S_{2}$
and
$S_{2}^{\prime }=S_{2}$
and
![]() $S_{M}^{\prime }=S_{M}$
. The effects of the velocity
$S_{M}^{\prime }=S_{M}$
. The effects of the velocity
![]() $\boldsymbol{q}_{t}$
on the total flux continuity and the saturation discontinuity at an interface between two different porous media have been discussed by Hayek et al. (Reference Hayek, Mouche and Mügler2009). We can graphically see that an increase in
$\boldsymbol{q}_{t}$
on the total flux continuity and the saturation discontinuity at an interface between two different porous media have been discussed by Hayek et al. (Reference Hayek, Mouche and Mügler2009). We can graphically see that an increase in
![]() $q_{tn}$
increases the saturations on each side of the interface. Here, we estimate
$q_{tn}$
increases the saturations on each side of the interface. Here, we estimate
![]() $q_{tn}$
from the pressure gradient
$q_{tn}$
from the pressure gradient
![]() $\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}z$
across the layer obtained numerically using DuMu
$\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}z$
across the layer obtained numerically using DuMu
![]() $^{x}$
$^{x}$
Furthermore, one obtains
![]() $S_{M}^{\prime }$
by solving the following nonlinear system
$S_{M}^{\prime }$
by solving the following nonlinear system
where
![]() $\unicode[STIX]{x1D6F7}=q_{tn}f(S)+G^{+}(S)$
. Once
$\unicode[STIX]{x1D6F7}=q_{tn}f(S)+G^{+}(S)$
. Once
![]() $S_{M}^{\prime }$
is known,
$S_{M}^{\prime }$
is known,
![]() $S_{2}^{\prime }$
can be deduced from the flux continuity relationship (5.3). Here, we assume that
$S_{2}^{\prime }$
can be deduced from the flux continuity relationship (5.3). Here, we assume that
![]() $\unicode[STIX]{x1D6F7}(S_{M}^{\prime })<G^{+}(S_{i})$
so that the flux in the layer is at its maximum value. Additionally, we assume also that the total velocity in the layer is essentially vertical, and the saturation on the matrix side of the upper layer matrix interface is
$\unicode[STIX]{x1D6F7}(S_{M}^{\prime })<G^{+}(S_{i})$
so that the flux in the layer is at its maximum value. Additionally, we assume also that the total velocity in the layer is essentially vertical, and the saturation on the matrix side of the upper layer matrix interface is
![]() $S_{1}^{\prime }$
(figure 16
b).
$S_{1}^{\prime }$
(figure 16
b).
Both the saturation profiles computed with and without the total velocity correction are plotted in figure 16(a). We can see that this correction significantly improves the agreement with the simulation results. This is true regardless of the imposed saturation
![]() $S_{i}$
at the bottom of the domain. Figure 17 illustrates the time evolutions of the maximum current height at
$S_{i}$
at the bottom of the domain. Figure 17 illustrates the time evolutions of the maximum current height at
![]() $x=0$
, with (figure 17
a) and without (figure 17
b) the total velocity correction and for three values of
$x=0$
, with (figure 17
a) and without (figure 17
b) the total velocity correction and for three values of
![]() $S_{i}$
,
$S_{i}$
,
![]() $S_{i}=0.13,0.14$
and
$S_{i}=0.13,0.14$
and
![]() $0.15$
. We can see that ignoring the velocity results in a difference of the order of magnitude of the current height, i.e. a metre, but taking this velocity into account divides by ten the differences. These differences, showing a systematic underestimation of the model, should be improved with a refined spatial resolution.
$0.15$
. We can see that ignoring the velocity results in a difference of the order of magnitude of the current height, i.e. a metre, but taking this velocity into account divides by ten the differences. These differences, showing a systematic underestimation of the model, should be improved with a refined spatial resolution.
Considering the total velocity field should improve the model; however, it is not theoretically possible. Here, the proposed correction is only applicable in the central area of the layer, where the velocity is expected to be vertical. It should be noted that we could also use an approximation of the pressure gradient, as given by flow models around thin plates. Nevertheless, at the layer extremities, the velocity in the layer is not vertical, and its impact on the total flux continuity becomes more complex to model and analyse. Thus, we disregard the velocity in the model with the capillarity discussed below.

Figure 17. Capillary-free case: maximal gravity current height at the origin
![]() $x=0$
. Comparison between the numerical simulation results obtained using DuMu
$x=0$
. Comparison between the numerical simulation results obtained using DuMu
![]() $^{x}$
(continuous lines) and the analytical gravity current models, without (a) and with (b) the total velocity.
$^{x}$
(continuous lines) and the analytical gravity current models, without (a) and with (b) the total velocity.
5.2 Gravity-dominant case
We consider the gravity-dominant case characterized by a capillary number considerably lower than one,
![]() $N_{c}\ll 1$
. The permeability ratio is set to
$N_{c}\ll 1$
. The permeability ratio is set to
![]() $k^{-}/k^{+}=0.10$
. This ratio results in a threshold saturation
$k^{-}/k^{+}=0.10$
. This ratio results in a threshold saturation
![]() $S_{0}^{\ast }=0.90$
if the interfacial tensions of the matrix and the layer are identical. The imposed saturation at the bottom of the domain is
$S_{0}^{\ast }=0.90$
if the interfacial tensions of the matrix and the layer are identical. The imposed saturation at the bottom of the domain is
![]() $S_{i}=0.10$
, and only the capillarity can provoke a
$S_{i}=0.10$
, and only the capillarity can provoke a
![]() $\text{CO}_{2}$
gravity current beneath the layer. Three increasing values of the capillary number are considered:
$\text{CO}_{2}$
gravity current beneath the layer. Three increasing values of the capillary number are considered:
![]() $N_{c}=0$
,
$N_{c}=0$
,
![]() $N_{c}=0.01$
and
$N_{c}=0.01$
and
![]() $N_{c}=0.1$
. They correspond to increasing values of the entry pressure caused by the increase of the interfacial tension in the layer (table 1). The corresponding threshold heights of the gravity current as given by (4.9) are
$N_{c}=0.1$
. They correspond to increasing values of the entry pressure caused by the increase of the interfacial tension in the layer (table 1). The corresponding threshold heights of the gravity current as given by (4.9) are
![]() $h^{\ast }=0~\text{m}$
(
$h^{\ast }=0~\text{m}$
(
![]() $N_{c}=0$
),
$N_{c}=0$
),
![]() $h^{\ast }=1.054~\text{m}$
(
$h^{\ast }=1.054~\text{m}$
(
![]() $N_{c}=0.01$
) and
$N_{c}=0.01$
) and
![]() $h^{\ast }=10.54~\text{m}$
(
$h^{\ast }=10.54~\text{m}$
(
![]() $N_{c}=0.1$
). Figure 18 depicts the
$N_{c}=0.1$
). Figure 18 depicts the
![]() $\text{CO}_{2}$
distributions obtained using DuMu
$\text{CO}_{2}$
distributions obtained using DuMu
![]() $^{x}$
after a long time. In the capillary-free case,
$^{x}$
after a long time. In the capillary-free case,
![]() $h^{\ast }=0$
, there is no
$h^{\ast }=0$
, there is no
![]() $\text{CO}_{2}$
accumulation beneath the barrier. The saturation within the inclusion is obtained from the continuity condition of the gravitational flux (figure 18
a). When the capillary number is extremely small, i.e.
$\text{CO}_{2}$
accumulation beneath the barrier. The saturation within the inclusion is obtained from the continuity condition of the gravitational flux (figure 18
a). When the capillary number is extremely small, i.e.
![]() $N_{c}=0.01$
, the
$N_{c}=0.01$
, the
![]() $\text{CO}_{2}$
accumulation occurs because of the capillary barrier. The
$\text{CO}_{2}$
accumulation occurs because of the capillary barrier. The
![]() $\text{CO}_{2}$
can pass into the layer only in the zone of the interface where the gravity current height exceeds the threshold height
$\text{CO}_{2}$
can pass into the layer only in the zone of the interface where the gravity current height exceeds the threshold height
![]() $h^{\ast }$
: over the zone
$h^{\ast }$
: over the zone
![]() $-x^{\ast }\leqslant x\leqslant x^{\ast }$
with
$-x^{\ast }\leqslant x\leqslant x^{\ast }$
with
![]() $x^{\ast }$
being the point at which
$x^{\ast }$
being the point at which
![]() $h=h^{\ast }$
(figure 18
b). For a fairly high capillary number,
$h=h^{\ast }$
(figure 18
b). For a fairly high capillary number,
![]() $N_{c}=0.1$
, the threshold height
$N_{c}=0.1$
, the threshold height
![]() $h^{\ast }$
is also fairly high,
$h^{\ast }$
is also fairly high,
![]() $h^{\ast }=10.54$
m. Even at steady state the maximal height of the gravity current is not sufficient enough to overcome the capillary barrier (figure 18
c). Therefore, the layer is impermeable to
$h^{\ast }=10.54$
m. Even at steady state the maximal height of the gravity current is not sufficient enough to overcome the capillary barrier (figure 18
c). Therefore, the layer is impermeable to
![]() $\text{CO}_{2}$
.
$\text{CO}_{2}$
.

Figure 18. Gravity-dominant case with
![]() $k^{-}/k^{+}=0.10$
and
$k^{-}/k^{+}=0.10$
and
![]() $S_{i}=0.10$
. The
$S_{i}=0.10$
. The
![]() $\text{CO}_{2}$
saturation distributions after a long time when
$\text{CO}_{2}$
saturation distributions after a long time when
![]() $\text{CO}_{2}$
has reached the top of the domain. The simulation results are obtained for different values of the capillary number:
$\text{CO}_{2}$
has reached the top of the domain. The simulation results are obtained for different values of the capillary number:
![]() $N_{c}=0$
(a),
$N_{c}=0$
(a),
![]() $N_{c}=0.01$
(b), and
$N_{c}=0.01$
(b), and
![]() $N_{c}=0.1$
(c) for which the corresponding threshold heights of the gravity current are
$N_{c}=0.1$
(c) for which the corresponding threshold heights of the gravity current are
![]() $h^{\ast }=0,1.054$
and 10.54, respectively.
$h^{\ast }=0,1.054$
and 10.54, respectively.

Figure 19. Gravity-dominant case with
![]() $k^{-}/k^{+}=0.25$
,
$k^{-}/k^{+}=0.25$
,
![]() $N_{c}=0.1$
and
$N_{c}=0.1$
and
![]() $S_{i}=0.10$
. The
$S_{i}=0.10$
. The
![]() $\text{CO}_{2}$
distributions reconstructed from the semi-analytical solution (a) and simulated using DuMu
$\text{CO}_{2}$
distributions reconstructed from the semi-analytical solution (a) and simulated using DuMu
![]() $^{x}$
(b).
$^{x}$
(b).
Figure 19 depicts a comparison between the 2-D saturations in the domain computed using DuMu
![]() $^{x}$
and reconstructed from our semi-analytical solution for
$^{x}$
and reconstructed from our semi-analytical solution for
![]() $k^{+}/k^{-}=0.25$
,
$k^{+}/k^{-}=0.25$
,
![]() $S_{i}=0.10$
and
$S_{i}=0.10$
and
![]() $N_{c}=0.1$
(
$N_{c}=0.1$
(
![]() $h^{\ast }=4.73~\text{m}$
) (table 1). The two distributions agree qualitatively, and we can observe that the model accounts for the penetration of the
$h^{\ast }=4.73~\text{m}$
) (table 1). The two distributions agree qualitatively, and we can observe that the model accounts for the penetration of the
![]() $\text{CO}_{2}$
plume in a limited extent of the layer, i.e. where
$\text{CO}_{2}$
plume in a limited extent of the layer, i.e. where
![]() $h<h^{\ast }$
.
$h<h^{\ast }$
.
Figure 20 illustrates the 1-D saturation distributions along the vertical axis passing through the middle of the layer and along the interface
![]() $\unicode[STIX]{x1D6E4}$
between the matrix and the layer for two values of the imposed saturation,
$\unicode[STIX]{x1D6E4}$
between the matrix and the layer for two values of the imposed saturation,
![]() $S_{i}=0.10$
and
$S_{i}=0.10$
and
![]() $S_{i}=0.15$
. The two distributions, numerical and semi-analytical, are in good agreement for both
$S_{i}=0.15$
. The two distributions, numerical and semi-analytical, are in good agreement for both
![]() $S_{i}$
values. Nevertheless, a better agreement is obtained for the lowest
$S_{i}$
values. Nevertheless, a better agreement is obtained for the lowest
![]() $S_{i}$
value (see the appendix A for a discussion on the impact of
$S_{i}$
value (see the appendix A for a discussion on the impact of
![]() $S_{i}$
). The extension of the area where the
$S_{i}$
). The extension of the area where the
![]() $\text{CO}_{2}$
can penetrate is also well described by the model (limited by the vertical dotted lines in figure 20
a,c).
$\text{CO}_{2}$
can penetrate is also well described by the model (limited by the vertical dotted lines in figure 20
a,c).

Figure 20. Gravity-dominant case with
![]() $k^{-}/k^{+}=0.25$
and
$k^{-}/k^{+}=0.25$
and
![]() $N_{c}=0.1$
. The
$N_{c}=0.1$
. The
![]() $\text{CO}_{2}$
saturations reconstructed from the semi-analytical solution (solid line) and simulated with DuMu
$\text{CO}_{2}$
saturations reconstructed from the semi-analytical solution (solid line) and simulated with DuMu
![]() $^{x}$
(dotted line) along the horizontal interface
$^{x}$
(dotted line) along the horizontal interface
![]() $\unicode[STIX]{x1D6E4}$
(
$\unicode[STIX]{x1D6E4}$
(
![]() $\unicode[STIX]{x1D6E4}^{-}$
for the matrix side and
$\unicode[STIX]{x1D6E4}^{-}$
for the matrix side and
![]() $\unicode[STIX]{x1D6E4}^{+}$
for the inclusion side) (a,c), and along the vertical central axis
$\unicode[STIX]{x1D6E4}^{+}$
for the inclusion side) (a,c), and along the vertical central axis
![]() $x=0$
(b,d) for the cases
$x=0$
(b,d) for the cases
![]() $S_{i}=0.10$
(a,b) and
$S_{i}=0.10$
(a,b) and
![]() $S_{i}=0.15$
(c,d).
$S_{i}=0.15$
(c,d).
6 Summary and conclusions
We have studied by means of theoretical developments and numerical simulations the buoyancy- and capillary-driven counter-current flow of
![]() $\text{CO}_{2}$
and brine through and around a semi-permeable layer of finite extent embedded in a permeable matrix. This system schematically describes the local flow of
$\text{CO}_{2}$
and brine through and around a semi-permeable layer of finite extent embedded in a permeable matrix. This system schematically describes the local flow of
![]() $\text{CO}_{2}$
in a deep saline heterogeneous aquifer after injection has stopped or is far from the injection well. The three forces of a two-phase immiscible flow are considered: buoyancy, capillarity and viscosity.
$\text{CO}_{2}$
in a deep saline heterogeneous aquifer after injection has stopped or is far from the injection well. The three forces of a two-phase immiscible flow are considered: buoyancy, capillarity and viscosity.
Initially, we considered a 1-D vertical column filled with a piecewise homogeneous porous medium consisting of two materials: permeable and semi-permeable. We investigated the effects of the buoyant
![]() $\text{CO}_{2}$
inflow rate on the saturation distribution in the column and for the two arrangements of the materials, that is, permeable material at the top and semi-permeable at the bottom, and the reverse. For each configuration, we demonstrated how to graphically determine the saturation discontinuity at the interface and how the buoyant and capillary diffusion fluxes are balanced to respect the capillary pressure and total flux continuity conditions.
$\text{CO}_{2}$
inflow rate on the saturation distribution in the column and for the two arrangements of the materials, that is, permeable material at the top and semi-permeable at the bottom, and the reverse. For each configuration, we demonstrated how to graphically determine the saturation discontinuity at the interface and how the buoyant and capillary diffusion fluxes are balanced to respect the capillary pressure and total flux continuity conditions.
Then, we considered the 2-D problem. Thus, we heuristically extended the two-phase gravity current model developed by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) to the case of a current beneath a semi-permeable layer. The saturation in the current is imposed by the capillary pressure and the buoyant flux continuity conditions at the current layer interface. The
![]() $\text{CO}_{2}$
migration is therefore described by a single transport equation and the brine movement is disregarded. The numerical simulations of the system have been performed using DuMu
$\text{CO}_{2}$
migration is therefore described by a single transport equation and the brine movement is disregarded. The numerical simulations of the system have been performed using DuMu
![]() $^{x}$
, an open-source simulator for the flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). First, we demonstrated that for a given ratio of the layer width to the domain width, there is a threshold value of the imposed
$^{x}$
, an open-source simulator for the flow and transport processes in porous media developed by the University of Stuttgart (Flemisch et al.
Reference Flemisch, Darcis, Erbertseder, Faigle, Lauser, Mosthaf, Müthing, Nuske, Tatomir and Wolff2011). First, we demonstrated that for a given ratio of the layer width to the domain width, there is a threshold value of the imposed
![]() $\text{CO}_{2}$
saturation at the bottom of the domain, beyond which there is no steady state gravity current. An analytical estimation of this critical saturation value is proposed. Then, we compared our model to simulations in the capillary-free and gravity-dominant cases. In the gravity-dominant case, the agreement is good; the model correctly predicts the geometrical characteristics of the current and the extension of the interface region where
$\text{CO}_{2}$
saturation at the bottom of the domain, beyond which there is no steady state gravity current. An analytical estimation of this critical saturation value is proposed. Then, we compared our model to simulations in the capillary-free and gravity-dominant cases. In the gravity-dominant case, the agreement is good; the model correctly predicts the geometrical characteristics of the current and the extension of the interface region where
![]() $\text{CO}_{2}$
can flow into the layer, i.e. where the current height exceeds the entry pressure of the layer. In the capillary-free case, we showed that considering the total velocity in the flux at the interface significantly improves the estimation of the current characteristics. This is surprising for a counter-current flow, where the total velocity is zero in average. Nevertheless, our simulations of
$\text{CO}_{2}$
can flow into the layer, i.e. where the current height exceeds the entry pressure of the layer. In the capillary-free case, we showed that considering the total velocity in the flux at the interface significantly improves the estimation of the current characteristics. This is surprising for a counter-current flow, where the total velocity is zero in average. Nevertheless, our simulations of
![]() $\text{CO}_{2}$
migration in heterogeneous formations clearly indicate that in a counter-current flow or far from an injection well, the convective component of the total flux at the local interfaces of the formation plays a non-negligible role in the
$\text{CO}_{2}$
migration in heterogeneous formations clearly indicate that in a counter-current flow or far from an injection well, the convective component of the total flux at the local interfaces of the formation plays a non-negligible role in the
![]() $\text{CO}_{2}$
migration. However, in both cases the model becomes less accurate when the imposed
$\text{CO}_{2}$
migration. However, in both cases the model becomes less accurate when the imposed
![]() $\text{CO}_{2}$
saturation at the bottom of the domain, or equivalently the incoming
$\text{CO}_{2}$
saturation at the bottom of the domain, or equivalently the incoming
![]() $\text{CO}_{2}$
buoyant flux, increases. This saturation must be low enough, i.e. such that the associated buoyant flux is much smaller than its maximum value, to approximatively respect the hydrostatic equilibrium condition in the gravity current. In the gravity-dominant case the model applies whatever the ratio of the layer permeability to the matrix permeability. In the capillary-free case this ratio must be low, less than 0.1, in order to respect the low value condition on the imposed
$\text{CO}_{2}$
buoyant flux, increases. This saturation must be low enough, i.e. such that the associated buoyant flux is much smaller than its maximum value, to approximatively respect the hydrostatic equilibrium condition in the gravity current. In the gravity-dominant case the model applies whatever the ratio of the layer permeability to the matrix permeability. In the capillary-free case this ratio must be low, less than 0.1, in order to respect the low value condition on the imposed
![]() $\text{CO}_{2}$
saturation. As a matter of fact, this constraint on the ratio sets to low values the range of imposed saturation inside which a steady state gravity current can take place.
$\text{CO}_{2}$
saturation. As a matter of fact, this constraint on the ratio sets to low values the range of imposed saturation inside which a steady state gravity current can take place.
The most important implication of our model for the geological storage of
![]() $\text{CO}_{2}$
concerns the trapping efficiency of the geological reservoir. As we discussed in the introduction, the capillary trapping is the outcome of a hysteretic process. It takes place at the trailing edge of the
$\text{CO}_{2}$
concerns the trapping efficiency of the geological reservoir. As we discussed in the introduction, the capillary trapping is the outcome of a hysteretic process. It takes place at the trailing edge of the
![]() $\text{CO}_{2}$
plume during the imbibition phase, i.e. after injection has stopped (Doughty Reference Doughty2007; Hesse et al.
Reference Hesse, Orr and Tchelepi2008). If the reservoir is initially free of
$\text{CO}_{2}$
plume during the imbibition phase, i.e. after injection has stopped (Doughty Reference Doughty2007; Hesse et al.
Reference Hesse, Orr and Tchelepi2008). If the reservoir is initially free of
![]() $\text{CO}_{2}$
, i.e. before injection, the trapped mass gives the
$\text{CO}_{2}$
, i.e. before injection, the trapped mass gives the
![]() $\text{CO}_{2}$
initial residual saturation, and also new characteristic curves, if another injection takes place. This mass depends on the total volume of reservoir swept by the plume. When capillarity is neglected and layers are semi-permeable the plume should invade a large volume of the reservoir, much larger than if the layers are impermeable. According to Land’s model, used for instance by Juanes et al. (Reference Juanes, Spiteri, Orr and Blunt2006) for applications to
$\text{CO}_{2}$
initial residual saturation, and also new characteristic curves, if another injection takes place. This mass depends on the total volume of reservoir swept by the plume. When capillarity is neglected and layers are semi-permeable the plume should invade a large volume of the reservoir, much larger than if the layers are impermeable. According to Land’s model, used for instance by Juanes et al. (Reference Juanes, Spiteri, Orr and Blunt2006) for applications to
![]() $\text{CO}_{2}$
sequestration reservoirs, residual saturations slightly smaller than the imposed saturations considered here (0.10–0.15) are expected in the 2-D layer matrix reservoir. When capillarity is taken into account and layers are perfect capillary barriers Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) showed that, compared to the capillary-free case, capillary diffusion can decrease by a factor of 2 the fraction of
$\text{CO}_{2}$
sequestration reservoirs, residual saturations slightly smaller than the imposed saturations considered here (0.10–0.15) are expected in the 2-D layer matrix reservoir. When capillarity is taken into account and layers are perfect capillary barriers Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) showed that, compared to the capillary-free case, capillary diffusion can decrease by a factor of 2 the fraction of
![]() $\text{CO}_{2}$
trapped in the gravity current. If the layers are imperfect capillary barriers, i.e.
$\text{CO}_{2}$
trapped in the gravity current. If the layers are imperfect capillary barriers, i.e.
![]() $\text{CO}_{2}$
can overcome locally the barrier, the use of a numerical code becomes a necessity to assess this efficiency. The other trapping mechanism, dissolution, should also be enhanced by the presence of semi-permeable layers as its importance depends on the contact volume between
$\text{CO}_{2}$
can overcome locally the barrier, the use of a numerical code becomes a necessity to assess this efficiency. The other trapping mechanism, dissolution, should also be enhanced by the presence of semi-permeable layers as its importance depends on the contact volume between
![]() $\text{CO}_{2}$
and brine.
$\text{CO}_{2}$
and brine.
Lastly, we would like to emphasize that our results may be easily applied to the problem of groundwater contamination by DNAPL (Dense Non Aqueous Phase Liquid) or LNAPL (Light Non aqueous Phase Liquid). The physical problems are identical to that of
![]() $\text{CO}_{2}$
: (i) the DNAPL migrates downwards, whereas the LNAPL upwards, both of which driven by the difference in the density with the aquifer interstitial water; and (ii) the heterogeneities of a subsurface aquifer are frequently of the semi-permeable type (Helmig Reference Helmig1997).
$\text{CO}_{2}$
: (i) the DNAPL migrates downwards, whereas the LNAPL upwards, both of which driven by the difference in the density with the aquifer interstitial water; and (ii) the heterogeneities of a subsurface aquifer are frequently of the semi-permeable type (Helmig Reference Helmig1997).
Acknowledgements
This study was supported by the project H-CUBE (Hydrodynamics, Heterogeneity, and Homogenization) of the French National Agency of Research (ANR).
Appendix A
In this appendix we provide several theoretical elements that support the extension to semi-permeable layers of the two-phase gravity current model of Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) exposed in § 4.
First, let us neglect capillarity and consider a 1-D vertical column filled with two homogeneous porous media: a permeable matrix and a semi-permeable layer of height
![]() $\unicode[STIX]{x1D6FF}$
located at the centre of the column. The absolute permeabilities of the matrix and the layer are respectively
$\unicode[STIX]{x1D6FF}$
located at the centre of the column. The absolute permeabilities of the matrix and the layer are respectively
![]() $k^{+}$
and
$k^{+}$
and
![]() $k^{-}$
. A constant saturation
$k^{-}$
. A constant saturation
![]() $S_{i}$
is imposed at the bottom of the column initially filled with brine (same configuration as in § 3) and flow is counter-current. Following the discussion of § 3, and more generally the results exposed in (Hayek et al.
Reference Hayek, Mouche and Mügler2009), we see that if
$S_{i}$
is imposed at the bottom of the column initially filled with brine (same configuration as in § 3) and flow is counter-current. Following the discussion of § 3, and more generally the results exposed in (Hayek et al.
Reference Hayek, Mouche and Mügler2009), we see that if
![]() $S_{i}<S_{M}$
, where
$S_{i}<S_{M}$
, where
![]() $S_{M}$
is the saturation at which the buoyant flux is maximum (figure 13), the plume can cross the layer and the steady state saturation in the layer
$S_{M}$
is the saturation at which the buoyant flux is maximum (figure 13), the plume can cross the layer and the steady state saturation in the layer
![]() $S_{l}$
is given by the buoyant flux continuity,
$S_{l}$
is given by the buoyant flux continuity,
![]() $G^{-}(S_{l})=G^{+}(S_{i})$
where
$G^{-}(S_{l})=G^{+}(S_{i})$
where
![]() $G^{+}$
and
$G^{+}$
and
![]() $G^{-}$
are the buoyant flux functions of the matrix and the layer respectively (2.17). Flux continuity shows also that the saturation at steady state above the layer is
$G^{-}$
are the buoyant flux functions of the matrix and the layer respectively (2.17). Flux continuity shows also that the saturation at steady state above the layer is
![]() $S_{i}$
. We assume here that
$S_{i}$
. We assume here that
![]() $S_{i}$
is lower than the Welge saturation,
$S_{i}$
is lower than the Welge saturation,
![]() $S_{W}\approx 0.4$
here, so that the saturations in the lower and upper parts part of the column are described as shock waves (Hayek et al.
Reference Hayek, Mouche and Mügler2009). If
$S_{W}\approx 0.4$
here, so that the saturations in the lower and upper parts part of the column are described as shock waves (Hayek et al.
Reference Hayek, Mouche and Mügler2009). If
![]() $S_{i}>S_{M}$
all the incoming flux cannot penetrate into the layer and an unsteady accumulation takes place beneath the lower interface of the layer. Again, flux continuity shows that the saturation is
$S_{i}>S_{M}$
all the incoming flux cannot penetrate into the layer and an unsteady accumulation takes place beneath the lower interface of the layer. Again, flux continuity shows that the saturation is
![]() $S_{2}$
in the accumulation zone,
$S_{2}$
in the accumulation zone,
![]() $S_{M}$
in the layer and
$S_{M}$
in the layer and
![]() $S_{1}$
above the layer where
$S_{1}$
above the layer where
![]() $G^{+}(S_{1})=G^{+}(S_{2})=G^{-}(S_{M})\;(S_{1}<S_{2})$
(figure 13). The width of the accumulation zone increases with time and the front of this zone is described as a shock travelling downwards. One must note that when
$G^{+}(S_{1})=G^{+}(S_{2})=G^{-}(S_{M})\;(S_{1}<S_{2})$
(figure 13). The width of the accumulation zone increases with time and the front of this zone is described as a shock travelling downwards. One must note that when
![]() $k^{-}\rightarrow 0$
,
$k^{-}\rightarrow 0$
,
![]() $S_{2}\rightarrow 1$
,
$S_{2}\rightarrow 1$
,
![]() $S_{1}\rightarrow 0$
and
$S_{1}\rightarrow 0$
and
![]() $S_{l}=S_{M}$
. From the counter-current flow condition,
$S_{l}=S_{M}$
. From the counter-current flow condition,
![]() $\boldsymbol{q}_{t}=0$
, it is easy to obtain the pressure gradient in the column
$\boldsymbol{q}_{t}=0$
, it is easy to obtain the pressure gradient in the column
where
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}(S)=k_{r\unicode[STIX]{x1D6FC}}(S)/\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
is the mobility of fluid
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}(S)=k_{r\unicode[STIX]{x1D6FC}}(S)/\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
is the mobility of fluid
![]() $\unicode[STIX]{x1D6FC}$
(
$\unicode[STIX]{x1D6FC}$
(
![]() $\unicode[STIX]{x1D6FC}=nw,w$
). After integration, the pressure in the accumulation zone is
$\unicode[STIX]{x1D6FC}=nw,w$
). After integration, the pressure in the accumulation zone is
where
![]() $p_{0}(z)$
is a pressure depending on
$p_{0}(z)$
is a pressure depending on
![]() $z$
only and
$z$
only and
![]() $h(t)$
is the thickness of the accumulation zone at time
$h(t)$
is the thickness of the accumulation zone at time
![]() $t$
. This thickness linearly increases with time with a velocity
$t$
. This thickness linearly increases with time with a velocity
![]() $G^{+}(S_{2})/S_{2}$
.
$G^{+}(S_{2})/S_{2}$
.
If we now introduce a second dimension to the problem, i.e. the vertical 1-D column becomes the 2-D system described in § 4, the accumulation can spread laterally, the velocity of the shock travelling downwards in one dimension tends to zero and the excess of influx is balanced by a spreading flux beneath the layer. We assume that the physics of this 2-D problem can be approximated as a vertical 1-D problem where saturations are governed by buoyant flux continuity conditions at the two interfaces between the matrix and layer and a 1-D spreading problem along the horizontal axis governed by the horizontal pressure gradient in the accumulation zone, i.e. the gravity current. As the saturation is constant along the vertical of the accumulation zone the spreading flow rate may be written
When
![]() $k^{-}\rightarrow 0$
,
$k^{-}\rightarrow 0$
,
![]() $p\rightarrow \left[\unicode[STIX]{x1D711}(S_{i})-\unicode[STIX]{x1D70C}_{nw}\right]gh/\unicode[STIX]{x1D707}_{nw}$
. This expression is different of the classical gravity current pressure because the brine and the
$p\rightarrow \left[\unicode[STIX]{x1D711}(S_{i})-\unicode[STIX]{x1D70C}_{nw}\right]gh/\unicode[STIX]{x1D707}_{nw}$
. This expression is different of the classical gravity current pressure because the brine and the
![]() $\text{CO}_{2}$
are in movement; the two fluids cannot be in the hydrostatic equilibrium. When
$\text{CO}_{2}$
are in movement; the two fluids cannot be in the hydrostatic equilibrium. When
![]() $S_{i}\approx 0$
one can approximate
$S_{i}\approx 0$
one can approximate
![]() $p\simeq \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gh/\unicode[STIX]{x1D707}_{nw}$
which is the classical expression of the gravity current pressure. In our 2-D gravity current model for a semi-permeable layer,
$p\simeq \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gh/\unicode[STIX]{x1D707}_{nw}$
which is the classical expression of the gravity current pressure. In our 2-D gravity current model for a semi-permeable layer,
![]() $S_{i}$
is small,
$S_{i}$
is small,
![]() $S_{i}\approx 0.1$
, and
$S_{i}\approx 0.1$
, and
![]() $k^{-}/k^{+}\ll 1$
which leads to a value of
$k^{-}/k^{+}\ll 1$
which leads to a value of
![]() $S_{2}$
close to one. Therefore, we assume, as a first approximation, that the previous expression of the gravity current pressure can be used. It is worth to remark that the values of the gravity current saturation simulated with DuMu
$S_{2}$
close to one. Therefore, we assume, as a first approximation, that the previous expression of the gravity current pressure can be used. It is worth to remark that the values of the gravity current saturation simulated with DuMu
![]() $^{x}$
for semi permeable layers of permeability
$^{x}$
for semi permeable layers of permeability
![]() $k^{-}/k^{+}=0.1$
and
$k^{-}/k^{+}=0.1$
and
![]() $0.25$
(§ 4) are in good agreement with their respective
$0.25$
(§ 4) are in good agreement with their respective
![]() $S_{2}$
values.
$S_{2}$
values.
When capillarity is taken into account and the physical parameters of the 2-D problem are such that the layer is a capillary barrier (§ 5.2) the model of Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) applies if
![]() $S_{i}$
is small,
$S_{i}$
is small,
![]() $\simeq 0.1$
. This constraint, which is the same as in the capillary-free case treated previously, must be introduced to approximatively respect the hydrostatic equilibrium condition in each phase. For this same reason
$\simeq 0.1$
. This constraint, which is the same as in the capillary-free case treated previously, must be introduced to approximatively respect the hydrostatic equilibrium condition in each phase. For this same reason
![]() $S_{i}$
must also be small when the layer is not a capillary barrier. According to the notations of (§ 3.1) the flux continuity condition at the lower matrix–layer interface is
$S_{i}$
must also be small when the layer is not a capillary barrier. According to the notations of (§ 3.1) the flux continuity condition at the lower matrix–layer interface is
where
![]() $D(S)=N_{c}\sqrt{k^{+}}\unicode[STIX]{x1D6EC}(S)J_{s}^{\prime }$
is the capillary diffusion coefficient (3.4). When
$D(S)=N_{c}\sqrt{k^{+}}\unicode[STIX]{x1D6EC}(S)J_{s}^{\prime }$
is the capillary diffusion coefficient (3.4). When
![]() $S_{i}\rightarrow 0$
the case of an impermeable layer described by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) is recovered. Figure 21 shows a comparison between the 1-D steady state saturations computed using a home-made code and the model. The system is the 1-D column filled with the piecewise homogeneous porous medium studied in § 3. We see that the model converges to the numerical solution when
$S_{i}\rightarrow 0$
the case of an impermeable layer described by Golding et al. (Reference Golding, Neufeld, Hesse and Huppert2011) is recovered. Figure 21 shows a comparison between the 1-D steady state saturations computed using a home-made code and the model. The system is the 1-D column filled with the piecewise homogeneous porous medium studied in § 3. We see that the model converges to the numerical solution when
![]() $S_{i}\rightarrow 0$
and the error is low when
$S_{i}\rightarrow 0$
and the error is low when
![]() $S_{i}$
is close to, or smaller than
$S_{i}$
is close to, or smaller than
![]() $0.1$
. This figure also illustrates the equality given in (A 4): the diffusive flux at the interface given by the model underestimates the numerical one.
$0.1$
. This figure also illustrates the equality given in (A 4): the diffusive flux at the interface given by the model underestimates the numerical one.

Figure 21. Piecewise homogeneous porous medium column. Saturation distributions predicted by the model and computed with a home-made code for four values of the imposed saturation
![]() $S_{i}$
.
$S_{i}$
.