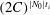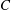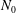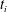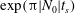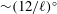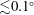1. Introduction
Examples of imploding gases include inertial confinement fusion (ICF) capsules (Atzeni & Meyer-ter-Vehn Reference Atzeni and Meyer-ter-Vehn2004), sonoluminescent bubbles (Suslick & Flannigan Reference Suslick and Flannigan2008) and core-collapse supernovae (Janka Reference Janka2012). The hydrodynamic stability of these flows is an important issue, as perturbations of sufficient amplitude can drain the energy driving the implosion, and the breakdown of symmetry, even for small amplitudes, can have important diagnostic/observational effects (e.g. Murphy Reference Murphy2014). Stability analyses of an imploding gas are significantly complicated by the time-dependent mean flow, and homologous flow (i.e. flow in which fluid elements share a common time-dependent scaling, the Hubble flow being a prime example) is a useful idealization that allows some analytical progress to be made. Such a study was performed for core-collapse supernovae by Goldreich & Weber (Reference Goldreich and Weber1980), who claim stability, but their results have recently been revisited by Cao & Lou (Reference Cao and Lou2009, Reference Cao and Lou2010), who claim instability. Chu (Reference Chu1996) applied the analysis of Goldreich & Weber (Reference Goldreich and Weber1980) to a sonoluminescing bubble and also claimed stability. The extensive body of work on the stability of ICF implosions has focused almost exclusively on interfacial instability, with little attention being given to the stability of the gas (see, however, Greenspan & Benney Reference Greenspan and Benney1963; Mjolsness & Ruppel Reference Mjolsness and Ruppel1978; Cook et al. Reference Cook, McQuillan, Takagi and Stephens2000). At the same time, hot-spot turbulence has recently received attention as a potential source of yield degradation in ICF capsules (Thomas & Kares Reference Thomas and Kares2012; Cerjan, Springer & Sepke Reference Cerjan, Springer and Sepke2013; Clark et al. Reference Clark, Hinkel, Eder, Jones, Haan, Hammel, Marinak, Milovich, Robey, Suter and Town2013; Gatu et al. Reference Gatu Johnson, Casey, Frenje, Li, Sguin, Petrasso, Ashabranner, Bionta, LePape, McKernan, Mackinnon, Kilkenny, Knauer and Sangster2013), and the origin of these vortical flows, if present, remains unclear. Basko & Murakami (Reference Basko and Murakami1998) considered the possibility of buoyancy instability in self-similar implosions but did not perform a formal stability analysis.
The purpose of this work is to clarify some of these issues by performing a stability analysis that complements previous work. By solving the initial value problem (Lai & Goldreich Reference Lai and Goldreich2000), rather than decomposing perturbations into radial modes, I am able to obtain results that are more physically transparent than those of previous authors, including a precise stability criterion. The following assumptions are made: (i) the implosion is externally driven rather than driven by gravity; (ii) dissipative effects are ignored (this is almost certainly unrealistic for ICF capsules and bubbles, but it permits isolation of the instability driving mechanism); and (iii) perturbations are assumed to be short-wavelength, incompressive and elongated in the direction of the implosion. I shall refer to this final approximation as the oblate limit, and it is perhaps the most useful new result to come out of this work, as it allows for significant analytical progress to be made in a problem that must otherwise be treated numerically. Under these assumptions, I demonstrate that homologously imploding ideal gases are essentially governed by the Schwarzschild criterion for buoyant stability (Schwarzschild Reference Schwarzschild1992), with a slight modification due to compression.
The basic equations and mean flow are outlined in § 2, the stability analysis is given in § 3, and § 4 summarizes and discusses applications.
2. Basic equations and mean flow
The fundamental equations used are the continuity equation, Euler’s equation and the first law of thermodynamics for adiabatic flow:
Here
![]() ${\it\rho}$
,
${\it\rho}$
,
![]() $\boldsymbol{v}$
,
$\boldsymbol{v}$
,
![]() $p$
and
$p$
and
![]() $s$
are the mass density, velocity, pressure and entropy of the gas and
$s$
are the mass density, velocity, pressure and entropy of the gas and
![]() $\text{d}/\text{d}t=\partial /\partial t+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}$
is the Lagrangian derivative following a fluid element (e.g. Landau & Lifshitz Reference Landau and Lifshitz1987). I will assume throughout an ideal-gas equation of state,
$\text{d}/\text{d}t=\partial /\partial t+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}$
is the Lagrangian derivative following a fluid element (e.g. Landau & Lifshitz Reference Landau and Lifshitz1987). I will assume throughout an ideal-gas equation of state,
![]() $p=({\it\gamma}-1){\it\rho}C_{v}T$
, where
$p=({\it\gamma}-1){\it\rho}C_{v}T$
, where
![]() ${\it\gamma}$
,
${\it\gamma}$
,
![]() $C_{v}$
and
$C_{v}$
and
![]() $T$
are the adiabatic index, specific heat and temperature of the gas. For this equation of state,
$T$
are the adiabatic index, specific heat and temperature of the gas. For this equation of state,
![]() $s=\ln (p{\it\rho}^{-{\it\gamma}})$
to within a constant factor; this expression will be used in what follows to define the entropy.
$s=\ln (p{\it\rho}^{-{\it\gamma}})$
to within a constant factor; this expression will be used in what follows to define the entropy.
Fluid elements in a homologous flow obey the relationship
![]() $r(t,a)=r(0,a)h(t)=ar_{01}h(t)$
, where
$r(t,a)=r(0,a)h(t)=ar_{01}h(t)$
, where
![]() $r$
is the spatial coordinate in the direction of the mean flow and the Lagrangian label for a fluid element is
$r$
is the spatial coordinate in the direction of the mean flow and the Lagrangian label for a fluid element is
![]() $a\equiv r(0,a)/r_{01}$
. For a spherical flow,
$a\equiv r(0,a)/r_{01}$
. For a spherical flow,
![]() $r(0,a)$
is the field of radial positions for all the fluid elements at
$r(0,a)$
is the field of radial positions for all the fluid elements at
![]() $t=0$
and
$t=0$
and
![]() $r_{01}\equiv r(0,1)$
is the outer radius of the gas at
$r_{01}\equiv r(0,1)$
is the outer radius of the gas at
![]() $t=0$
; this implies that the scale factor
$t=0$
; this implies that the scale factor
![]() $h(t)$
is normalized to unity at
$h(t)$
is normalized to unity at
![]() $t=0$
, i.e.
$t=0$
, i.e.
![]() $h(0)\equiv 1$
. The velocity field associated with homologous flow is
$h(0)\equiv 1$
. The velocity field associated with homologous flow is
![]() $v_{r}(t,a)=ar_{01}{\dot{h}}(t)=r(t,a){\dot{h}}/h$
, where an overdot denotes a time derivative. Mass and entropy conservation under spherical adiabatic homologous flow imply
$v_{r}(t,a)=ar_{01}{\dot{h}}(t)=r(t,a){\dot{h}}/h$
, where an overdot denotes a time derivative. Mass and entropy conservation under spherical adiabatic homologous flow imply
![]() ${\it\rho}(t,a)={\it\rho}_{0}(a)/h^{3}$
and
${\it\rho}(t,a)={\it\rho}_{0}(a)/h^{3}$
and
![]() $p(t,a)=p_{0}(a)/h^{3{\it\gamma}}$
, where a zero subscript denotes a spatial profile at
$p(t,a)=p_{0}(a)/h^{3{\it\gamma}}$
, where a zero subscript denotes a spatial profile at
![]() $t=0$
, and Euler’s equation becomes
$t=0$
, and Euler’s equation becomes
where the plus (minus) sign is associated with a decelerating (accelerating) implosion and
![]() $t_{c}$
is a characteristic time scale.
$t_{c}$
is a characteristic time scale.
For
![]() ${\it\gamma}=5/3$
and
${\it\gamma}=5/3$
and
![]() ${\dot{h}}_{0}=0$
, the time-dependent portion of expression (2.2) yields the well-known Kidder implosions (Kidder Reference Kidder1974; Atzeni & Meyer-ter-Vehn Reference Atzeni and Meyer-ter-Vehn2004)
${\dot{h}}_{0}=0$
, the time-dependent portion of expression (2.2) yields the well-known Kidder implosions (Kidder Reference Kidder1974; Atzeni & Meyer-ter-Vehn Reference Atzeni and Meyer-ter-Vehn2004)
For
![]() ${\dot{h}}_{0}\neq 0$
, an additional solution to (2.2) valid for any
${\dot{h}}_{0}\neq 0$
, an additional solution to (2.2) valid for any
![]() ${\it\gamma}$
is (Goldreich & Weber Reference Goldreich and Weber1980)
${\it\gamma}$
is (Goldreich & Weber Reference Goldreich and Weber1980)
 $$\begin{eqnarray}h(t)=\left(1-\sqrt{\frac{[3{\it\gamma}-1]^{2}}{6[{\it\gamma}-1]}}\frac{t}{t_{c}}\right)^{2/(3{\it\gamma}-1)}.\end{eqnarray}$$
$$\begin{eqnarray}h(t)=\left(1-\sqrt{\frac{[3{\it\gamma}-1]^{2}}{6[{\it\gamma}-1]}}\frac{t}{t_{c}}\right)^{2/(3{\it\gamma}-1)}.\end{eqnarray}$$
This solution, while valid only for accelerating implosions, is useful for assessing the impact of the gas equation of state. Following Atzeni & Meyer-ter-Vehn (Reference Atzeni and Meyer-ter-Vehn2004), accelerating solutions are defined as starting out from
![]() $t=0$
, so that they evolve from
$t=0$
, so that they evolve from
![]() $h=1$
to
$h=1$
to
![]() $h=C^{-1}$
, where
$h=C^{-1}$
, where
![]() $C\equiv r_{\mathit{initial}}/r_{\mathit{final}}$
is the convergence factor, i.e. the ratio of initial to final sizes. The decelerating solution, on the other hand (the Kidder implosion with the
$C\equiv r_{\mathit{initial}}/r_{\mathit{final}}$
is the convergence factor, i.e. the ratio of initial to final sizes. The decelerating solution, on the other hand (the Kidder implosion with the
![]() $+$
sign), is defined as stagnating at
$+$
sign), is defined as stagnating at
![]() $t=0$
, so that its implosion phase evolves from
$t=0$
, so that its implosion phase evolves from
![]() $h=C$
to
$h=C$
to
![]() $h=1$
.
$h=1$
.
Aside from the equation of state, the space-dependent portion of (2.2) is the only constraint on the spatial profile of the mean gas quantities. This allows for a significant amount of flexibility in setting up various mean flow profiles. An analytical model that mimics the hot spot of an ICF implosion during deceleration (this is likely to be a good approximation for a collapsing bubble as well) is given by
where the gas quantities have been normalized to their value at
![]() $a_{p}$
(the location of the density peak; see figure 1). Both
$a_{p}$
(the location of the density peak; see figure 1). Both
![]() $a_{p}$
and
$a_{p}$
and
![]() ${\it\sigma}$
can be regarded as free parameters of the model, and can be alternatively expressed in terms of ratios of physical quantities. The characteristic time scale in this case is
${\it\sigma}$
can be regarded as free parameters of the model, and can be alternatively expressed in terms of ratios of physical quantities. The characteristic time scale in this case is
![]() $t_{c}=\sqrt{{\it\gamma}}r_{01}{\it\sigma}/c_{0p}$
, where
$t_{c}=\sqrt{{\it\gamma}}r_{01}{\it\sigma}/c_{0p}$
, where
![]() $c_{0p}$
is the sound speed at
$c_{0p}$
is the sound speed at
![]() $a_{p}$
. The square of the Brunt–Väisälä, or buoyancy, frequency,
$a_{p}$
. The square of the Brunt–Väisälä, or buoyancy, frequency,
is useful for assessing buoyant stability (Johnson & Gammie Reference Johnson and Gammie2005). For homologous flow,
![]() $N^{2}=N_{0}^{2}h^{1-3{\it\gamma}}$
, and for the hot-spot configuration described above,
$N^{2}=N_{0}^{2}h^{1-3{\it\gamma}}$
, and for the hot-spot configuration described above,
Mean flow profiles for the hot-spot configuration are shown in figure 1.
3. Stability analysis
For an equilibrium configuration (
![]() $\boldsymbol{v}=0$
), it is well known that the local dispersion relation for short-wavelength incompressive modes governed by (2.1a−c
) is
$\boldsymbol{v}=0$
), it is well known that the local dispersion relation for short-wavelength incompressive modes governed by (2.1a−c
) is
where
![]() ${\it\omega}$
is the wave frequency and
${\it\omega}$
is the wave frequency and
![]() $k_{\bot }$
and
$k_{\bot }$
and
![]() $k_{r}$
are wavenumbers perpendicular and parallel to the mean gradients (see e.g. Johnson & Gammie Reference Johnson and Gammie2005). It can be seen from expression (3.1) that
$k_{r}$
are wavenumbers perpendicular and parallel to the mean gradients (see e.g. Johnson & Gammie Reference Johnson and Gammie2005). It can be seen from expression (3.1) that
![]() $N^{2}<0$
denotes instability;
$N^{2}<0$
denotes instability;
![]() $N^{2}>0$
is the Schwarzschild criterion for buoyant stability (Schwarzschild Reference Schwarzschild1992). The buoyancy frequency can be rewritten as
$N^{2}>0$
is the Schwarzschild criterion for buoyant stability (Schwarzschild Reference Schwarzschild1992). The buoyancy frequency can be rewritten as
where
![]() $g\equiv \text{d}v_{r}/\text{d}t$
is the acceleration and
$g\equiv \text{d}v_{r}/\text{d}t$
is the acceleration and
![]() $c_{s}$
is the mean sound speed. It can be seen from this expression that configurations with ‘order-over-disorder’ (
$c_{s}$
is the mean sound speed. It can be seen from this expression that configurations with ‘order-over-disorder’ (
![]() $\partial s/\partial r<0$
) are buoyantly unstable. If density gradients dominate, a ‘heavy-over-light’ configuration is unstable (
$\partial s/\partial r<0$
) are buoyantly unstable. If density gradients dominate, a ‘heavy-over-light’ configuration is unstable (
![]() $\partial {\it\rho}/\partial r>0$
), whereas if temperature gradients dominate, a ‘cold-over-hot’ configuration is unstable (
$\partial {\it\rho}/\partial r>0$
), whereas if temperature gradients dominate, a ‘cold-over-hot’ configuration is unstable (
![]() $\partial T/\partial r<0$
). The former situation represents Rayleigh–Taylor instability, and the latter represents thermal convection; in general, buoyancy instability depends upon the mean entropy gradient. Because fluid elements evolve adiabatically, and the relationship between entropy and density depends upon
$\partial T/\partial r<0$
). The former situation represents Rayleigh–Taylor instability, and the latter represents thermal convection; in general, buoyancy instability depends upon the mean entropy gradient. Because fluid elements evolve adiabatically, and the relationship between entropy and density depends upon
![]() ${\it\gamma}$
, the stability criterion in general depends upon the compressibility of the fluid. Notice that, in the limit
${\it\gamma}$
, the stability criterion in general depends upon the compressibility of the fluid. Notice that, in the limit
![]() $gL_{{\it\rho}}\ll c_{s}^{2}$
, where
$gL_{{\it\rho}}\ll c_{s}^{2}$
, where
![]() $L_{{\it\rho}}=(\partial \ln {\it\rho}/\partial r)^{-1}$
is the density gradient length scale, the growth rate is independent of
$L_{{\it\rho}}=(\partial \ln {\it\rho}/\partial r)^{-1}$
is the density gradient length scale, the growth rate is independent of
![]() ${\it\gamma}$
and reduces to the short-wavelength limit of the classical Rayleigh–Taylor growth rate when the effects of density gradient stabilization are included (e.g. Betti et al.
Reference Betti, Goncharov, McCrory and Verdon1998). For the hot-spot configuration described above, it can be seen from figure 1 that the entire gas region and most of the shell is buoyantly unstable during deceleration.
${\it\gamma}$
and reduces to the short-wavelength limit of the classical Rayleigh–Taylor growth rate when the effects of density gradient stabilization are included (e.g. Betti et al.
Reference Betti, Goncharov, McCrory and Verdon1998). For the hot-spot configuration described above, it can be seen from figure 1 that the entire gas region and most of the shell is buoyantly unstable during deceleration.
For a spherically symmetric mean flow (
![]() $\boldsymbol{v}=v_{r}\hat{\boldsymbol{r}}$
), perturbations can be decomposed into spherical harmonics
$\boldsymbol{v}=v_{r}\hat{\boldsymbol{r}}$
), perturbations can be decomposed into spherical harmonics
![]() $Y_{\ell m}({\it\theta},{\it\phi})$
, and the resulting equations are
$Y_{\ell m}({\it\theta},{\it\phi})$
, and the resulting equations are
where a prime denotes a fluctuation,
![]() $v_{\bot }^{\prime }$
is the component of the velocity fluctuation parallel to
$v_{\bot }^{\prime }$
is the component of the velocity fluctuation parallel to
![]() $\boldsymbol{{\rm\nabla}}Y_{\ell m}$
,
$\boldsymbol{{\rm\nabla}}Y_{\ell m}$
,
![]() $s^{\prime }=p^{\prime }/p-{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
is the entropy fluctuation, and
$s^{\prime }=p^{\prime }/p-{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
is the entropy fluctuation, and
![]() $\ell$
is a Legendre mode number (Lai & Goldreich Reference Lai and Goldreich2000). The third velocity component decouples from the other variables and will not be considered here. Short-wavelength, low-frequency fluctuations satisfy
$\ell$
is a Legendre mode number (Lai & Goldreich Reference Lai and Goldreich2000). The third velocity component decouples from the other variables and will not be considered here. Short-wavelength, low-frequency fluctuations satisfy
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\approx 0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\approx 0$
and
![]() $s^{\prime }\approx -{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
(the Boussinesq approximation for buoyancy-driven flows (Johnson & Gammie Reference Johnson and Gammie2005)). This reduces the perturbed continuity equation to the incompressive condition. It is important to note that the gas remains compressible; the incompressive condition applies only to the fluctuations.
$s^{\prime }\approx -{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
(the Boussinesq approximation for buoyancy-driven flows (Johnson & Gammie Reference Johnson and Gammie2005)). This reduces the perturbed continuity equation to the incompressive condition. It is important to note that the gas remains compressible; the incompressive condition applies only to the fluctuations.
Notice from expression (3.1) that the growth rate of local modes in an equilibrium configuration is largest for modes with
![]() $k_{r}\ll k_{\bot }$
. This suggests the additional approximation of restricting the analysis to modes with
$k_{r}\ll k_{\bot }$
. This suggests the additional approximation of restricting the analysis to modes with
![]() $\partial /\partial r\ll \ell /r$
, i.e. modes that are sufficiently elongated in the radial direction that their radial variation can be neglected. I shall refer to this (along with the incompressive condition) as the oblate limit, and the modes thus isolated as oblate modes. This approximation considerably simplifies the analysis while retaining the essential physics. In the oblate limit, which amounts to neglecting the pressure perturbation in (3.4), the linear equations reduce to the set of coupled ordinary differential equations
$\partial /\partial r\ll \ell /r$
, i.e. modes that are sufficiently elongated in the radial direction that their radial variation can be neglected. I shall refer to this (along with the incompressive condition) as the oblate limit, and the modes thus isolated as oblate modes. This approximation considerably simplifies the analysis while retaining the essential physics. In the oblate limit, which amounts to neglecting the pressure perturbation in (3.4), the linear equations reduce to the set of coupled ordinary differential equations
with
![]() $s^{\prime }=-{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
. The first term on the right-hand side of (3.6a
) represents angular momentum conservation: vortical modes spin faster (slower) under compression (expansion). The second term represents the baroclinic production of vorticity: entropy fluctuations spin up due to the baroclinic torque applied to them by the mean pressure gradient. The perturbed entropy equation represents the fact that, in the presence of a mean entropy gradient, entropy fluctuations evolve to compensate for mean entropy changes. An entropy fluctuation that moves up the mean entropy gradient, for example (to a region of higher mean entropy), must decrease in magnitude in order for total entropy to be conserved. This can increase or decrease the magnitude of the baroclinic term in the perturbed Euler equation.
$s^{\prime }=-{\it\gamma}{\it\rho}^{\prime }/{\it\rho}$
. The first term on the right-hand side of (3.6a
) represents angular momentum conservation: vortical modes spin faster (slower) under compression (expansion). The second term represents the baroclinic production of vorticity: entropy fluctuations spin up due to the baroclinic torque applied to them by the mean pressure gradient. The perturbed entropy equation represents the fact that, in the presence of a mean entropy gradient, entropy fluctuations evolve to compensate for mean entropy changes. An entropy fluctuation that moves up the mean entropy gradient, for example (to a region of higher mean entropy), must decrease in magnitude in order for total entropy to be conserved. This can increase or decrease the magnitude of the baroclinic term in the perturbed Euler equation.
One can see the connection between (3.6a
) and the vorticity equation as follows. The dominant vorticity component for oblate modes is the one perpendicular to both
![]() $\hat{\boldsymbol{r}}$
and
$\hat{\boldsymbol{r}}$
and
![]() $\boldsymbol{{\rm\nabla}}Y_{lm}$
; in axisymmetry, it is the only non-zero component and is given by
$\boldsymbol{{\rm\nabla}}Y_{lm}$
; in axisymmetry, it is the only non-zero component and is given by
where the approximation is valid for oblate modes and
![]() $P_{\ell }$
is a Legendre polynomial. The non-radial velocity of an oblate eddy is much smaller than its radial velocity fluctuation (this follows from
$P_{\ell }$
is a Legendre polynomial. The non-radial velocity of an oblate eddy is much smaller than its radial velocity fluctuation (this follows from
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\approx 0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\approx 0$
and
![]() $\ell /r\gg \partial /\partial r$
), which implies that its vorticity is dominated by radial motion in a frame moving with the mean flow. Appendix A of Johnson (Reference Johnson2014) derives the perturbed vorticity equation under the Boussinesq approximation; in spherical geometry and axisymmetry, the
$\ell /r\gg \partial /\partial r$
), which implies that its vorticity is dominated by radial motion in a frame moving with the mean flow. Appendix A of Johnson (Reference Johnson2014) derives the perturbed vorticity equation under the Boussinesq approximation; in spherical geometry and axisymmetry, the
![]() ${\it\phi}$
component of expression (A4) of Johnson (Reference Johnson2014) (there is a sign error in front of the baroclinic term in that reference) is
${\it\phi}$
component of expression (A4) of Johnson (Reference Johnson2014) (there is a sign error in front of the baroclinic term in that reference) is
Using the approximation in (3.7), one can readily show that (3.8) is equivalent to (3.6a ).
Using the mean flow expression
![]() $\text{d}\,\!\ln ({\it\rho}r^{2})/\text{d}t=-\partial v_{r}/\partial r$
and recalling that the Lagrangian derivative commutes with
$\text{d}\,\!\ln ({\it\rho}r^{2})/\text{d}t=-\partial v_{r}/\partial r$
and recalling that the Lagrangian derivative commutes with
![]() $a$
derivatives but not
$a$
derivatives but not
![]() $r$
derivatives, equations (3.6) can be combined to give
$r$
derivatives, equations (3.6) can be combined to give
The only assumptions regarding the mean flow that have been made in deriving this equation are an ideal-gas equation of state and radial adiabatic flow. This equation therefore governs oblate modes in any flow satisfying these conditions. It is shown in appendix A that (3.9) also applies to flows with cylindrical and planar symmetry. For
![]() $v_{r}=0$
, it reduces to the dispersion relation (3.1) with
$v_{r}=0$
, it reduces to the dispersion relation (3.1) with
![]() $k_{r}=0$
.
$k_{r}=0$
.

Figure 2. Growth factor as a function of mode number for the profile shown in figure 1 and a stagnating Kidder implosion/explosion (with
![]() $C=10$
), showing results from the full linear code (solid) and the analytical oblate limit (dotted).
$C=10$
), showing results from the full linear code (solid) and the analytical oblate limit (dotted).
For Kidder implosions, the solutions to (3.9) have the form
![]() $s^{\prime }\propto \exp (-\text{i}\int {\it\omega}\,\text{d}t)$
, with
$s^{\prime }\propto \exp (-\text{i}\int {\it\omega}\,\text{d}t)$
, with
![]() ${\it\omega}^{2}=N^{2}$
; this demonstrates that the stability of Kidder implosions is governed by the Schwarzschild criterion. The full solution is given by
${\it\omega}^{2}=N^{2}$
; this demonstrates that the stability of Kidder implosions is governed by the Schwarzschild criterion. The full solution is given by
and
![]() $L_{s0}\equiv r_{01}(\partial s_{0}/\partial a)^{-1}$
is the entropy gradient length scale at
$L_{s0}\equiv r_{01}(\partial s_{0}/\partial a)^{-1}$
is the entropy gradient length scale at
![]() $t=0$
. In these expressions, all quantities with a zero subscript can be regarded as functions of
$t=0$
. In these expressions, all quantities with a zero subscript can be regarded as functions of
![]() $a$
, since for oblate modes each fluid element evolves with time independently of all the others. For
$a$
, since for oblate modes each fluid element evolves with time independently of all the others. For
![]() $N_{0}^{2}=0$
, entropy fluctuations are conserved and
$N_{0}^{2}=0$
, entropy fluctuations are conserved and
![]() $v_{r}^{\prime }=v_{r0}^{\prime }/h$
(for
$v_{r}^{\prime }=v_{r0}^{\prime }/h$
(for
![]() ${\it\rho}_{0}^{\prime }=0$
), reflecting the conservation of angular momentum as the gas is compressed.
${\it\rho}_{0}^{\prime }=0$
), reflecting the conservation of angular momentum as the gas is compressed.
An implosion takes place over a finite time scale, such that the impact of unstable fluctuations on the mean flow depends upon both their initial amplitude and how much they are amplified over the course of the implosion. Expression (3.10) or (3.11) can be used to obtain an estimate of the growth factor when
![]() $N_{0}^{2}<0$
:
$N_{0}^{2}<0$
:
The growth factor for the decelerating solution takes into account the explosion phase that follows the implosion phase in the Kidder stagnating solution (i.e.
![]() $h$
evolving from
$h$
evolving from
![]() $C$
to 1 and then back to
$C$
to 1 and then back to
![]() $C$
), since the gas is unstable both before and after stagnation. The same expressions apply to the amplification of vorticity fluctuations.
$C$
), since the gas is unstable both before and after stagnation. The same expressions apply to the amplification of vorticity fluctuations.
Growth factors for a representative fluid element (
![]() $a=0.7$
) undergoing a decelerating Kidder implosion/explosion are shown in figure 2 as a function of Legendre mode number
$a=0.7$
) undergoing a decelerating Kidder implosion/explosion are shown in figure 2 as a function of Legendre mode number
![]() $\ell$
. These results were obtained with a Lagrangian code that solves the full set of linear equations (3.3)–(3.5), where the radial profile of the initial entropy fluctuation was a Gaussian with a width 10 % of the outer radius. It can be seen from figure 2 that oblate modes are the fastest-growing modes and that fairly large values of
$\ell$
. These results were obtained with a Lagrangian code that solves the full set of linear equations (3.3)–(3.5), where the radial profile of the initial entropy fluctuation was a Gaussian with a width 10 % of the outer radius. It can be seen from figure 2 that oblate modes are the fastest-growing modes and that fairly large values of
![]() $\ell$
are required to reach the oblate limit (
$\ell$
are required to reach the oblate limit (
![]() $\ell \gtrsim 100$
). Figure 3 shows the evolution of the peak vorticity for
$\ell \gtrsim 100$
). Figure 3 shows the evolution of the peak vorticity for
![]() $\ell =30$
in both the linear code and a two-dimensional version of the Lagrangian hydrodynamics code Kull (Rathkopf Reference Rathkopf, Miller, Owen, Stuart, Zika, Eltgroth, Madsen, McCandless, Nowak, Nemanic, Gentile and Keen2000) at various grid resolutions. These results indicate that a resolution of
$\ell =30$
in both the linear code and a two-dimensional version of the Lagrangian hydrodynamics code Kull (Rathkopf Reference Rathkopf, Miller, Owen, Stuart, Zika, Eltgroth, Madsen, McCandless, Nowak, Nemanic, Gentile and Keen2000) at various grid resolutions. These results indicate that a resolution of
![]() ${\sim}30$
zones per wavelength is required to accurately capture the amplification of vorticity under an implosion in a numerical simulation.
${\sim}30$
zones per wavelength is required to accurately capture the amplification of vorticity under an implosion in a numerical simulation.

Figure 3. Peak vorticity as a function of time for the profile given by expressions (2.5)–(2.6) (with
![]() ${\it\sigma}=0.25$
and
${\it\sigma}=0.25$
and
![]() $a_{p}=1$
), a stagnating Kidder implosion/explosion (with
$a_{p}=1$
), a stagnating Kidder implosion/explosion (with
![]() $C=10$
) and
$C=10$
) and
![]() $\ell =30$
. Shown are results from two-dimensional Kull calculations at several grid resolutions (solid, labelled by zones per wavelength), along with results from the linear code (dotted).
$\ell =30$
. Shown are results from two-dimensional Kull calculations at several grid resolutions (solid, labelled by zones per wavelength), along with results from the linear code (dotted).
For implosions whose trajectory is given by expression (2.4), the solutions to (3.9) again have the form
![]() $s^{\prime }\propto \exp (-\text{i}\!\int {\it\omega}\,\text{d}t)$
, where here
$s^{\prime }\propto \exp (-\text{i}\!\int {\it\omega}\,\text{d}t)$
, where here
and
![]() $D\equiv \partial v_{r}/\partial r$
is the dilatation. These solutions can equivalently be expressed as
$D\equiv \partial v_{r}/\partial r$
is the dilatation. These solutions can equivalently be expressed as
![]() $s^{\prime }\propto h^{{\it\beta}}$
, where
$s^{\prime }\propto h^{{\it\beta}}$
, where
where
![]() $\mathit{Ri}_{c}\equiv N^{2}/D^{2}$
is a compressive Richardson number. It can be seen that instability (
$\mathit{Ri}_{c}\equiv N^{2}/D^{2}$
is a compressive Richardson number. It can be seen that instability (
![]() ${\it\omega}_{i}>0$
, where
${\it\omega}_{i}>0$
, where
![]() ${\it\omega}_{i}$
is the imaginary part of
${\it\omega}_{i}$
is the imaginary part of
![]() ${\it\omega}$
) corresponds to
${\it\omega}$
) corresponds to
![]() ${\it\beta}_{r}<0$
, where
${\it\beta}_{r}<0$
, where
![]() ${\it\beta}_{r}$
is the real part of the negative branch of
${\it\beta}_{r}$
is the real part of the negative branch of
![]() ${\it\beta}$
(for an implosion, a quantity that grows with time decays with
${\it\beta}$
(for an implosion, a quantity that grows with time decays with
![]() $h$
).
$h$
).
For
![]() ${\it\gamma}=5/3$
,
${\it\gamma}=5/3$
,
![]() ${\it\beta}=\pm \sqrt{-\mathit{Ri }_{c}}=\pm \sqrt{-N_{0}^{2}t_{c}^{2}}$
, which is real for
${\it\beta}=\pm \sqrt{-\mathit{Ri }_{c}}=\pm \sqrt{-N_{0}^{2}t_{c}^{2}}$
, which is real for
![]() $N_{0}^{2}<0$
. For a monatomic gas, then, the stability of these implosions is also governed by the Schwarzschild criterion. For
$N_{0}^{2}<0$
. For a monatomic gas, then, the stability of these implosions is also governed by the Schwarzschild criterion. For
![]() ${\it\gamma}<5/3$
, however, the system is unconditionally unstable as a result of the additional growth due to compression. For
${\it\gamma}<5/3$
, however, the system is unconditionally unstable as a result of the additional growth due to compression. For
![]() ${\it\Delta}^{2}<0$
, i.e.
${\it\Delta}^{2}<0$
, i.e.
![]() $\mathit{Ri}_{c}>([5-3{\it\gamma}]/4)^{2}$
, the fluctuations have an oscillatory component with an amplitude that increases slowly with time. For
$\mathit{Ri}_{c}>([5-3{\it\gamma}]/4)^{2}$
, the fluctuations have an oscillatory component with an amplitude that increases slowly with time. For
![]() ${\it\Delta}^{2}>0$
, the growth is purely a power law in time, and increases with decreasing
${\it\Delta}^{2}>0$
, the growth is purely a power law in time, and increases with decreasing
![]() $\mathit{Ri}_{c}$
. The critical
$\mathit{Ri}_{c}$
. The critical
![]() $\mathit{Ri}_{c}$
above which oscillations appear varies between 0 for
$\mathit{Ri}_{c}$
above which oscillations appear varies between 0 for
![]() ${\it\gamma}=5/3$
and
${\it\gamma}=5/3$
and
![]() $1/4$
for
$1/4$
for
![]() ${\it\gamma}=1$
. This is reminiscent of the Richardson criterion for the stability of a stratified shear flow (Miles Reference Miles1961; Chimonas Reference Chimonas1970), with shear replaced by dilatation. In this case the transition is not between stability and instability, but rather simply between the presence and absence of oscillations.
${\it\gamma}=1$
. This is reminiscent of the Richardson criterion for the stability of a stratified shear flow (Miles Reference Miles1961; Chimonas Reference Chimonas1970), with shear replaced by dilatation. In this case the transition is not between stability and instability, but rather simply between the presence and absence of oscillations.
The complete linear solution for oblate modes under implosions satisfying expression (2.4) is
where
![]() $\mathscr{E}$
is the specific energy of the fluctuations (kinetic plus potential),
$\mathscr{E}$
is the specific energy of the fluctuations (kinetic plus potential),
![]() ${\it\xi}_{r}^{\prime }=-L_{s}s^{\prime }$
is the fluctuating radial fluid displacement,
${\it\xi}_{r}^{\prime }=-L_{s}s^{\prime }$
is the fluctuating radial fluid displacement,
![]() ${\it\omega}_{r}$
is the real part of
${\it\omega}_{r}$
is the real part of
![]() ${\it\omega}$
, and an overbar denotes an angular average. An estimate of the growth factor for the fluctuations in this case can be made from (3.16) or (3.17):
${\it\omega}$
, and an overbar denotes an angular average. An estimate of the growth factor for the fluctuations in this case can be made from (3.16) or (3.17):
 $$\begin{eqnarray}\mathscr{G}\sim C^{-{\it\beta}_{r}}\sim \left\{\begin{array}{@{}ll@{}}C^{\sqrt{-\mathit{Ri }_{c}}} & \text{for }\mathit{Ri}_{c}\ll -1,\\ C^{(5-3{\it\gamma})/2} & \text{for }\mathit{Ri}_{c}=0,\\ C^{(5-3{\it\gamma})/4} & \text{for }\mathit{Ri}_{c}>0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{G}\sim C^{-{\it\beta}_{r}}\sim \left\{\begin{array}{@{}ll@{}}C^{\sqrt{-\mathit{Ri }_{c}}} & \text{for }\mathit{Ri}_{c}\ll -1,\\ C^{(5-3{\it\gamma})/2} & \text{for }\mathit{Ri}_{c}=0,\\ C^{(5-3{\it\gamma})/4} & \text{for }\mathit{Ri}_{c}>0.\end{array}\right.\end{eqnarray}$$
4. Summary and discussion
By isolating incompressive modes that are elongated in the direction of the mean flow (oblate modes), the following conclusions are drawn regarding the stability of homologously imploding ideal gases: (i) monatomic gases are governed by the Schwarzschild criterion for buoyant stability; (ii) owing to the time-dependent nature of the mean flow, the growth is power law rather than exponential in time; (iii) additional growth occurs due to the conservation of angular momentum as vortices are compressed; and (iv) gases with
![]() ${\it\gamma}<5/3$
are weakly unstable due to this additional growth mechanism even when the flow is otherwise buoyantly stable. As pointed out by Cao & Lou (Reference Cao and Lou2009), the reason that Goldreich & Weber (Reference Goldreich and Weber1980) and Chu (Reference Chu1996) do not find instability is that they assume an isentropic background and ignore vorticity and entropy fluctuations; either of these assumptions precludes the development of buoyancy instability.
${\it\gamma}<5/3$
are weakly unstable due to this additional growth mechanism even when the flow is otherwise buoyantly stable. As pointed out by Cao & Lou (Reference Cao and Lou2009), the reason that Goldreich & Weber (Reference Goldreich and Weber1980) and Chu (Reference Chu1996) do not find instability is that they assume an isentropic background and ignore vorticity and entropy fluctuations; either of these assumptions precludes the development of buoyancy instability.
The short-wavelength nature of the most unstable modes coupled with the compression of the mean flow makes this instability challenging to capture in numerical calculations. Figure 3 indicates that accurately capturing the growth of vorticity under an implosion requires a resolution of the order of 30 zones per wavelength; this translates to an angular resolution of
![]() $360^{\circ }/(30\ell )=12^{\circ }/\ell$
. Capturing the fastest-growing modes (
$360^{\circ }/(30\ell )=12^{\circ }/\ell$
. Capturing the fastest-growing modes (
![]() $\ell \gtrsim 100$
) therefore requires an angular resolution
$\ell \gtrsim 100$
) therefore requires an angular resolution
![]() ${\lesssim}0.1^{\circ }$
. For an Eulerian code, high convergence ratios impose severe constraints on the resolution in the direction of the mean flow. Seeding buoyancy instability in the gas can occur in two ways: vorticity fluctuations can be transported there by shocks rippled from drive asymmetry or interfacial perturbations, or small-amplitude entropy fluctuations can be present initially in the gas. Even a sufficiently resolved calculation that is initialized without ambient density or temperature fluctuations may not capture this instability properly.
${\lesssim}0.1^{\circ }$
. For an Eulerian code, high convergence ratios impose severe constraints on the resolution in the direction of the mean flow. Seeding buoyancy instability in the gas can occur in two ways: vorticity fluctuations can be transported there by shocks rippled from drive asymmetry or interfacial perturbations, or small-amplitude entropy fluctuations can be present initially in the gas. Even a sufficiently resolved calculation that is initialized without ambient density or temperature fluctuations may not capture this instability properly.
Finally, for ICF implosions and sonoluminescent bubbles, the growth at large
![]() $\ell$
is likely to be reduced by conduction and viscosity (Atzeni & Meyer-ter-Vehn Reference Atzeni and Meyer-ter-Vehn2004; Weber et al.
Reference Weber, Clark, Cook, Busby and Robey2014). These effects have been neglected here for several reasons. (i) As with classical stability analyses, a better understanding is gained if the effects driving the instability are isolated first, and stabilizing effects are added afterwards. (ii) There are uncertainties associated with conduction and viscosity models, and it is useful to know what instabilities are lurking in the background in their absence. (iii) The analytic results obtained here in the adiabatic limit provide physical insight and are useful for code verification. Self-similar solutions have been obtained previously with non-adiabatic effects (Basko & Murakami Reference Basko and Murakami1998; Sanz et al.
Reference Sanz, Garnier, Cherfils, Masse and Temporal2005), although the adiabatic profiles in figure 1 are remarkably similar to the actual profiles in an ICF implosion (compare figure 1 with figure 3.11 of Atzeni & Meyer-ter-Vehn (Reference Atzeni and Meyer-ter-Vehn2004)). Dissipation affects small scales; in reality the amplification in figure 2 will fall off at high mode numbers. At the same time, figure 2 indicates that potentially significant growth can occur even for moderate
$\ell$
is likely to be reduced by conduction and viscosity (Atzeni & Meyer-ter-Vehn Reference Atzeni and Meyer-ter-Vehn2004; Weber et al.
Reference Weber, Clark, Cook, Busby and Robey2014). These effects have been neglected here for several reasons. (i) As with classical stability analyses, a better understanding is gained if the effects driving the instability are isolated first, and stabilizing effects are added afterwards. (ii) There are uncertainties associated with conduction and viscosity models, and it is useful to know what instabilities are lurking in the background in their absence. (iii) The analytic results obtained here in the adiabatic limit provide physical insight and are useful for code verification. Self-similar solutions have been obtained previously with non-adiabatic effects (Basko & Murakami Reference Basko and Murakami1998; Sanz et al.
Reference Sanz, Garnier, Cherfils, Masse and Temporal2005), although the adiabatic profiles in figure 1 are remarkably similar to the actual profiles in an ICF implosion (compare figure 1 with figure 3.11 of Atzeni & Meyer-ter-Vehn (Reference Atzeni and Meyer-ter-Vehn2004)). Dissipation affects small scales; in reality the amplification in figure 2 will fall off at high mode numbers. At the same time, figure 2 indicates that potentially significant growth can occur even for moderate
![]() $\ell$
. Definitive conclusions regarding the application of this analysis to ICF and sonoluminescent bubbles will require a more faithful representation of both the mean flow and the dissipation. This, as well as application to astrophysical gases, will be pursued in future studies.
$\ell$
. Definitive conclusions regarding the application of this analysis to ICF and sonoluminescent bubbles will require a more faithful representation of both the mean flow and the dissipation. This, as well as application to astrophysical gases, will be pursued in future studies.
Acknowledgements
I thank D. Clark, O. Hurricane, K. Mikaelian, O. Schilling and the referees for their comments. This work was performed under the auspices of Lawrence Livermore National Security, LLC (LLNS) under contract number DE-AC52-07NA27344.
Appendix A. Results for cylindrical and planar symmetry
A complete set of homologous solutions can also be derived for flows with cylindrical and planar symmetry. In general, mass and entropy conservation for homologous adiabatic flow imply
![]() ${\it\rho}(t,a)={\it\rho}_{0}(a)/h^{n}$
and
${\it\rho}(t,a)={\it\rho}_{0}(a)/h^{n}$
and
![]() $p(t,a)=p_{0}(a)/h^{n{\it\gamma}}$
, where
$p(t,a)=p_{0}(a)/h^{n{\it\gamma}}$
, where
![]() $n=1$
, 2 or 3 for planar, cylindrical or spherical symmetry, and the time-dependent portion of (2.2) is
$n=1$
, 2 or 3 for planar, cylindrical or spherical symmetry, and the time-dependent portion of (2.2) is
![]() $h^{n{\it\gamma}-n+1}\ddot{h}=\pm t_{c}^{-2}$
. All of the above results for the mean spatial profiles remain valid if
$h^{n{\it\gamma}-n+1}\ddot{h}=\pm t_{c}^{-2}$
. All of the above results for the mean spatial profiles remain valid if
![]() $r$
is interpreted as the spatial coordinate in the direction of the mean flow. Expression (2.3) for the Kidder implosion remains valid for
$r$
is interpreted as the spatial coordinate in the direction of the mean flow. Expression (2.3) for the Kidder implosion remains valid for
![]() ${\it\gamma}=1+2/n$
, and the generalization of (2.4) is
${\it\gamma}=1+2/n$
, and the generalization of (2.4) is
valid for
![]() ${\dot{h}}_{0}t_{c}=-\sqrt{2/(n{\it\gamma}-n)}$
. Both the buoyancy frequency and the dilatation have the time dependence
${\dot{h}}_{0}t_{c}=-\sqrt{2/(n{\it\gamma}-n)}$
. Both the buoyancy frequency and the dilatation have the time dependence
![]() $N\propto D\propto h^{(n-n{\it\gamma}-2)/2}$
.
$N\propto D\propto h^{(n-n{\it\gamma}-2)/2}$
.
Equations (3.6) for the perturbations remain valid in all three geometries, and imply
where
![]() $r_{0}=r(0,a)$
. Using the mean flow relation
$r_{0}=r(0,a)$
. Using the mean flow relation
![]() $\text{d}\ln ({\it\rho}r^{n-1})/\text{d}t=-\partial v_{r}/\partial r$
, this leads to (3.9). The solutions for a Kidder implosion, equations (3.10) and (3.11), are therefore valid for all three geometries (provided
$\text{d}\ln ({\it\rho}r^{n-1})/\text{d}t=-\partial v_{r}/\partial r$
, this leads to (3.9). The solutions for a Kidder implosion, equations (3.10) and (3.11), are therefore valid for all three geometries (provided
![]() ${\it\gamma}=1+2/n$
). Expressions (3.16) and (3.17) generalize to
${\it\gamma}=1+2/n$
). Expressions (3.16) and (3.17) generalize to