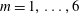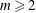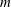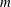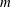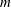1 Introduction
The instability of two-dimensional flat-bottom circular flows with stepwise vorticity profiles around a rigid cylinder (island) was investigated by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013). It was shown that the instability of azimuthal mode
![]() $m$
may lead to the emission of
$m$
may lead to the emission of
![]() $m$
vortex dipoles. Rabinovich, Kizner & Flierl (Reference Rabinovich, Kizner and Flierl2018) (referenced below as RKF) considered flows with stepwise potential vorticity (PV) profiles around a circular island, introducing the so-called beta-cone model, in which the beta effect is caused by conical bottom topography, i.e. by the background PV with a radial profile. The stability/instability conditions were established for circular flows with zero net vorticity. In the present paper we take as the initial flows some of the unstable configurations found in RKF, and study their time evolution numerically, our aim being to explore possible evolution scenarios. The parameters of the initial flow are fitted so as to ensure that one or another azimuthal mode is most unstable.
$m$
vortex dipoles. Rabinovich, Kizner & Flierl (Reference Rabinovich, Kizner and Flierl2018) (referenced below as RKF) considered flows with stepwise potential vorticity (PV) profiles around a circular island, introducing the so-called beta-cone model, in which the beta effect is caused by conical bottom topography, i.e. by the background PV with a radial profile. The stability/instability conditions were established for circular flows with zero net vorticity. In the present paper we take as the initial flows some of the unstable configurations found in RKF, and study their time evolution numerically, our aim being to explore possible evolution scenarios. The parameters of the initial flow are fitted so as to ensure that one or another azimuthal mode is most unstable.
The experience with dipoles on a beta plane (e.g. Hesthaven, Lynov & Nycander Reference Hesthaven, Lynov and Nycander1993) prompts the idea that the conical beta effect will not allow the dipoles to move too far from the original flow, but rather will make them turn back after a time. Another possibility is that the emitted dipoles may settle on a constant-background-PV line (a circle) and travel around the island in a quasi-steady manner. In this paper, we show that both outcomes in fact do occur at mild slopes.
Flows possessing circular symmetry were investigated by many authors, who mostly used the shallow-water model, where the free-surface elevation is not negligible (contrary to our assumption). For example, spiral gravity waves were found to emerge around a cylindrical seamount (Longuet-Higgins Reference Longuet-Higgins1967). Trapping of gravity waves was found to be possible under certain conditions (Longuet-Higgins Reference Longuet-Higgins1967, Reference Longuet-Higgins1969; Rhines Reference Rhines1969; Longuet-Higgins Reference Longuet-Higgins1970). A natural question would be, what the form of barotropic waves round a circular island on a beta cone could be, and whether trapping can occur in our case. We will show that these issues are essential for understanding the evolution of unstable flows.
In § 2, an outline of the beta-cone model and the basic-state flow is given, followed by a presentation of the numerical method used. The results of the simulations for weak slopes are discussed in § 3, where the focus is on the trajectories of the dipoles emitted due to the flow instability. The mechanism of the dipole formation is not discussed here because, qualitatively, it is identical to that in the flat-bottom case. In § 4 we explore some of the basic properties of Rossby waves in the barotropic beta-cone model to be used in the subsequent sections. Steep-slope effects on the flow are presented in § 5, where the role of the relatively strong Rossby waves is discussed. It is shown that strong beta effect prevents the emission of dipoles and brings the flow to a new quasi-stationary state. In § 6 we discuss the case of an intermediate slope. It is shown that the weak mode-1 instability leads first to some shift and deformation of the two PV rings, and at a later stage, to erosion of the inner ring due to filamentation. No dipole lobes emerge in this case. For higher modes, the dipoles formed due to the instability stay in the proximity of the island. A special case of the mode-2 instability is examined in detail, where the topographic Rossby waves have a strong impact on the emitted dipoles. In this case, the beta effect causes the reversal of an initially counterclockwise flow.

Figure 1. Typical profiles of the basic-flow potential vorticity
![]() $\bar{Q}$
(dashed, blue) and the azimuthal velocity
$\bar{Q}$
(dashed, blue) and the azimuthal velocity
![]() $\bar{V}$
(solid, red) for
$\bar{V}$
(solid, red) for
![]() $\unicode[STIX]{x1D6FD}=-0.1,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
$\unicode[STIX]{x1D6FD}=-0.1,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
![]() $R_{2}=4$
(positive
$R_{2}=4$
(positive
![]() $\unicode[STIX]{x1D6E4}_{1}$
and negative
$\unicode[STIX]{x1D6E4}_{1}$
and negative
![]() $\unicode[STIX]{x1D6E4}_{2}$
).
$\unicode[STIX]{x1D6E4}_{2}$
).
2 Problem statement and methods
2.1 Topographic beta cone. The basic flow
Here we repeat briefly the presentation of the problem statement given in an earlier publication of ours (RKF). Before turning to simulations, we consider an inviscid barotropic flow around a cylindrical island, assuming the bottom outside the island to have a constant radial slope, so that the depth increases linearly offshore. Under the quasi-geostrophic approximation and the rigid-lid condition at the sea surface, the flow is two-dimensional. In the polar coordinates
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D703}$
, the radial and azimuthal components of the velocity,
$\unicode[STIX]{x1D703}$
, the radial and azimuthal components of the velocity,
![]() $u$
and
$u$
and
![]() $v$
respectively, can be expressed in terms of a streamfunction
$v$
respectively, can be expressed in terms of a streamfunction
![]() $\unicode[STIX]{x1D713}$
as
$\unicode[STIX]{x1D713}$
as
The potential vorticity in this model is defined as
where
![]() $\unicode[STIX]{x1D701}$
is the relative vorticity,
$\unicode[STIX]{x1D701}$
is the relative vorticity,
![]() $\unicode[STIX]{x1D6FD}=\text{const}.$
is proportional to the slope, and is negative by definition for an island in the northern hemisphere. The inviscid flow is governed by the PV conservation equation,
$\unicode[STIX]{x1D6FD}=\text{const}.$
is proportional to the slope, and is negative by definition for an island in the northern hemisphere. The inviscid flow is governed by the PV conservation equation,
The basic flow is given by two uniform-PV rings (figure 1). The inner ring is bounded by the rigid contour
![]() $r=R$
, where the flow vanishes, and the liquid contour
$r=R$
, where the flow vanishes, and the liquid contour
![]() $r=R_{1}$
; the outer ring is bounded by the liquid contours
$r=R_{1}$
; the outer ring is bounded by the liquid contours
![]() $r=R_{1}$
and
$r=R_{1}$
and
![]() $r=R_{2}$
, where
$r=R_{2}$
, where
![]() $R<R_{1}<R_{2}$
. Outside the outer ring, the basic PV is equal to
$R<R_{1}<R_{2}$
. Outside the outer ring, the basic PV is equal to
![]() $\unicode[STIX]{x1D6FD}r$
. Denoting the PV of the basic flow by
$\unicode[STIX]{x1D6FD}r$
. Denoting the PV of the basic flow by
![]() $\bar{Q}$
, and the PV in the inner and outer rings by
$\bar{Q}$
, and the PV in the inner and outer rings by
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
, respectively, we write
$\unicode[STIX]{x1D6E4}_{2}$
, respectively, we write
 $$\begin{eqnarray}\displaystyle \bar{Q}(r)=\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x1D6E4}_{1},\quad R\leqslant r<R_{1}\quad \\ \unicode[STIX]{x1D6E4}_{2},\quad R_{1}\leqslant r<R_{2}\quad \\ \unicode[STIX]{x1D6FD}r,\quad r\geqslant R_{2}.\quad \end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{Q}(r)=\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x1D6E4}_{1},\quad R\leqslant r<R_{1}\quad \\ \unicode[STIX]{x1D6E4}_{2},\quad R_{1}\leqslant r<R_{2}\quad \\ \unicode[STIX]{x1D6FD}r,\quad r\geqslant R_{2}.\quad \end{array}\right. & & \displaystyle\end{eqnarray}$$
The condition for zero net vorticity imposes a relation between
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
,
$\unicode[STIX]{x1D6E4}_{2}$
,
The linear stability analysis of this basic flow can be found in RKF. Now we investigate numerically the nonlinear evolution of unstable flows. Moreover, for our simulations, we choose parameters
![]() $R_{1}$
,
$R_{1}$
,
![]() $R_{2}$
,
$R_{2}$
,
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6E4}_{1}$
so as to guarantee that a given azimuthal mode
$\unicode[STIX]{x1D6E4}_{1}$
so as to guarantee that a given azimuthal mode
![]() $m$
be most unstable among other modes.
$m$
be most unstable among other modes.
From this point on, we regard all the variables and constants to be non-dimensional, thus normalized, while keeping the designations unchanged. In this normalization, the radius of the rigid contour is taken as the length scale; the absolute value of PV in the inner ring serves as the scale for the potential and relative vorticity, and its inverse, as the (advective) time scale. So,
![]() $R=1$
in non-dimensional units, and
$R=1$
in non-dimensional units, and
![]() $\unicode[STIX]{x1D6E4}_{1}$
can be either +1 or
$\unicode[STIX]{x1D6E4}_{1}$
can be either +1 or
![]() $-1$
. The range of non-dimensional
$-1$
. The range of non-dimensional
![]() $\unicode[STIX]{x1D6FD}$
that will be explored is
$\unicode[STIX]{x1D6FD}$
that will be explored is
![]() $-0.5\leqslant \unicode[STIX]{x1D6FD}\leqslant 0$
(see RKF).
$-0.5\leqslant \unicode[STIX]{x1D6FD}\leqslant 0$
(see RKF).
2.2 Method of numerical simulations
We conduct high-Reynolds-number simulations employing the coefficient-form partial differential equation package of the COMSOL software based on the finite-element method. The vorticity-diffusion term
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}Q$
is added to the right-hand side part of equation (2.4) in order to maintain numerical stability, the magnitude of the non-dimensional kinematic viscosity coefficient
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}Q$
is added to the right-hand side part of equation (2.4) in order to maintain numerical stability, the magnitude of the non-dimensional kinematic viscosity coefficient
![]() $\unicode[STIX]{x1D708}$
being chosen by trial and error (see below). The resulting coupled system composed of equation (2.3) and the equation of PV evolution (i.e. equation (2.4) supplemented with the diffusion term) is solved as an initial-value problem in a two-dimensional
$\unicode[STIX]{x1D708}$
being chosen by trial and error (see below). The resulting coupled system composed of equation (2.3) and the equation of PV evolution (i.e. equation (2.4) supplemented with the diffusion term) is solved as an initial-value problem in a two-dimensional
![]() $(r,\unicode[STIX]{x1D703})$
rectangular grid,
$(r,\unicode[STIX]{x1D703})$
rectangular grid,
![]() $1<r<30$
and
$1<r<30$
and
![]() $0<\unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}$
. The unknown variables are the streamfunction
$0<\unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}$
. The unknown variables are the streamfunction
![]() $\unicode[STIX]{x1D713}$
and the relative vorticity
$\unicode[STIX]{x1D713}$
and the relative vorticity
![]() $\unicode[STIX]{x1D701}$
, which is related to
$\unicode[STIX]{x1D701}$
, which is related to
![]() $Q$
via equation (2.2). We apply the periodicity conditions at
$Q$
via equation (2.2). We apply the periodicity conditions at
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $\unicode[STIX]{x1D703}=2\unicode[STIX]{x03C0}$
and the no-slip conditions at both radial boundaries by setting
$\unicode[STIX]{x1D703}=2\unicode[STIX]{x03C0}$
and the no-slip conditions at both radial boundaries by setting
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}r=\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at
$\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}r=\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at
![]() $r=30$
, and
$r=30$
, and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}r=0$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}r=0$
and
![]() $\unicode[STIX]{x1D713}=0$
at
$\unicode[STIX]{x1D713}=0$
at
![]() $r=1$
. The integration in time is performed with an implicit second-order backward-difference scheme whose absolute tolerance is
$r=1$
. The integration in time is performed with an implicit second-order backward-difference scheme whose absolute tolerance is
![]() $10^{-5}$
and employing fourth-order integration for the rectangular Lagrangian elements used (for details see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013).
$10^{-5}$
and employing fourth-order integration for the rectangular Lagrangian elements used (for details see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013).
The computational domain,
![]() $30\times 2\unicode[STIX]{x03C0}$
in size, is divided into two or three subdomains. The first, fine-grid domain,
$30\times 2\unicode[STIX]{x03C0}$
in size, is divided into two or three subdomains. The first, fine-grid domain,
![]() $1\leqslant r<1.5$
with the mesh size of
$1\leqslant r<1.5$
with the mesh size of
![]() $0.05\times 0.03$
, is set off in order to be able to resolve the viscous boundary layer that may form next to the cylinder. The second is the main domain
$0.05\times 0.03$
, is set off in order to be able to resolve the viscous boundary layer that may form next to the cylinder. The second is the main domain
![]() $1.5\leqslant r<20$
with the mesh size of
$1.5\leqslant r<20$
with the mesh size of
![]() $0.1\times 0.03$
. In both domains,
$0.1\times 0.03$
. In both domains,
![]() $\unicode[STIX]{x1D708}$
is set to be
$\unicode[STIX]{x1D708}$
is set to be
![]() $10^{-4}$
. The third domain,
$10^{-4}$
. The third domain,
![]() $20\leqslant r\leqslant 30$
, is set off optionally as a wave absorbing layer in the cases where the reflection of waves from the outer boundary might be considerable. Here the mesh size is
$20\leqslant r\leqslant 30$
, is set off optionally as a wave absorbing layer in the cases where the reflection of waves from the outer boundary might be considerable. Here the mesh size is
![]() $0.1\times 0.03$
and the viscosity coefficient increases parabolically from
$0.1\times 0.03$
and the viscosity coefficient increases parabolically from
![]() $\unicode[STIX]{x1D708}=10^{-4}$
at
$\unicode[STIX]{x1D708}=10^{-4}$
at
![]() $r=20$
to
$r=20$
to
![]() $\unicode[STIX]{x1D708}=10$
at
$\unicode[STIX]{x1D708}=10$
at
![]() $r=30$
. This numerical setup implies about
$r=30$
. This numerical setup implies about
![]() $3\times 10^{6}$
degrees of freedom, consuming about 12 GB of memory. The adequacy of the chosen grid and values of
$3\times 10^{6}$
degrees of freedom, consuming about 12 GB of memory. The adequacy of the chosen grid and values of
![]() $\unicode[STIX]{x1D708}$
was confirmed by a few dozens of test runs with various dimensions of the three regions and mesh sizes in them, the tests proving that further increase of resolution would not lead to an essentially higher accuracy of results, especially, taking into account the computational cost of each run and the risk of the appearance of the grid instability in finer grids.
$\unicode[STIX]{x1D708}$
was confirmed by a few dozens of test runs with various dimensions of the three regions and mesh sizes in them, the tests proving that further increase of resolution would not lead to an essentially higher accuracy of results, especially, taking into account the computational cost of each run and the risk of the appearance of the grid instability in finer grids.
The absorbing-layer approach was chosen due to the lack of proper boundary conditions that could totally prevent reflection (e.g. Israeli & Orszag Reference Israeli and Orszag1981; Durran Reference Durran2013). We examined boundary conditions suggested by various authors (e.g. Orlanski Reference Orlanski1976; Rasch Reference Rasch1986; Higdon Reference Higdon1994) and found them to be ineffective on the beta cone, since Rossby waves are dispersive (see § 4), and the frequencies of the waves radiated during the flow evolution cannot be known in advance. Due to the spiral shape of the Rossby waves on a beta cone (§ 4), their strength, when they arrive at the absorbing layer, does not monotonically depend on
![]() $\unicode[STIX]{x1D6FD}$
, but reaches a maximum at some intermediate
$\unicode[STIX]{x1D6FD}$
, but reaches a maximum at some intermediate
![]() $\unicode[STIX]{x1D6FD}$
. This is because at a given
$\unicode[STIX]{x1D6FD}$
. This is because at a given
![]() $m$
, the smaller is
$m$
, the smaller is
![]() $\unicode[STIX]{x1D6FD}$
, the slower is the wave propagation, while the higher is
$\unicode[STIX]{x1D6FD}$
, the slower is the wave propagation, while the higher is
![]() $\unicode[STIX]{x1D6FD}$
, the stronger is the winding of the wave fronts (§§ 4 and 5), so at considerable distances from the island the radial propagation of the waves is weak again. We found the introduction of the absorbing layer to be helpful at
$\unicode[STIX]{x1D6FD}$
, the stronger is the winding of the wave fronts (§§ 4 and 5), so at considerable distances from the island the radial propagation of the waves is weak again. We found the introduction of the absorbing layer to be helpful at
![]() $\unicode[STIX]{x1D6FD}$
ranging from
$\unicode[STIX]{x1D6FD}$
ranging from
![]() $\unicode[STIX]{x1D6FD}=-0.1$
to
$\unicode[STIX]{x1D6FD}=-0.1$
to
![]() $\unicode[STIX]{x1D6FD}=-0.35$
.
$\unicode[STIX]{x1D6FD}=-0.35$
.
In each simulation, the vorticity production next to the inner wall is negligible at the beginning stage, because the basic velocity profile goes to zero nearly linearly as
![]() $r\rightarrow 1$
(figure 1). Only when the originally two-ring PV field breaks into separate vortex patches (dipoles) does the fine-structure vortex production (due to the formation and subsequent separation of the viscous boundary layer) become visible in the vicinity of the rigid wall. This process was investigated in detail by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013), who compared the results of flat-bottom high-Reynolds-number simulations with those obtained using a contour-surgery code in the absence of viscosity and found that, for reasonable thicknesses of the PV rings, the large-scale dynamics in the two cases was nearly indistinguishable. Aside of the inner wall, in the regions with no sharp PV gradients, the diffusion term is, on average, smaller by two orders of magnitude than the advection terms in the equation of PV evolution; so one may speak of the local PV conservation here. Clearly, in the areas where sharp PV gradients occur, the diffusion term is higher, and viscosity causes some smoothing in the PV field. This happens to the PV jumps at
$r\rightarrow 1$
(figure 1). Only when the originally two-ring PV field breaks into separate vortex patches (dipoles) does the fine-structure vortex production (due to the formation and subsequent separation of the viscous boundary layer) become visible in the vicinity of the rigid wall. This process was investigated in detail by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013), who compared the results of flat-bottom high-Reynolds-number simulations with those obtained using a contour-surgery code in the absence of viscosity and found that, for reasonable thicknesses of the PV rings, the large-scale dynamics in the two cases was nearly indistinguishable. Aside of the inner wall, in the regions with no sharp PV gradients, the diffusion term is, on average, smaller by two orders of magnitude than the advection terms in the equation of PV evolution; so one may speak of the local PV conservation here. Clearly, in the areas where sharp PV gradients occur, the diffusion term is higher, and viscosity causes some smoothing in the PV field. This happens to the PV jumps at
![]() $r=R_{1}$
and
$r=R_{1}$
and
![]() $r=R_{2}$
, and to thin filaments emerging during the flow evolution. Sufficiently thin filaments may be erased by viscosity; note that a somewhat similar erasing of thin filaments takes place in contour surgery simulations.
$r=R_{2}$
, and to thin filaments emerging during the flow evolution. Sufficiently thin filaments may be erased by viscosity; note that a somewhat similar erasing of thin filaments takes place in contour surgery simulations.
As for the initial condition, in order to get a reasonable machine time for the evolution of linear instability of the flow, we add a random perturbation to the basic PV field in the form of Gaussian noise. This random noise with zero mean and the standard deviation of
![]() $10^{-5}$
is applied on the entire computational grid. The noise is smaller by at least three orders of magnitude than the relative vorticity of the basic flow in the sense of the
$10^{-5}$
is applied on the entire computational grid. The noise is smaller by at least three orders of magnitude than the relative vorticity of the basic flow in the sense of the
![]() $l^{2}$
-norm calculated on the grid. An alternative initial perturbation consisting in a small deformation of the liquid contours bounding the PV rings (see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013) is applied only once (§ 3), just to ensure that the
$l^{2}$
-norm calculated on the grid. An alternative initial perturbation consisting in a small deformation of the liquid contours bounding the PV rings (see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013) is applied only once (§ 3), just to ensure that the
![]() $m$
-fold symmetry expected to hold in the case of an unstable mode
$m$
-fold symmetry expected to hold in the case of an unstable mode
![]() $m$
, is maintained long enough; this enables us to observe the almost symmetric quasi-periodic movement of the vortices that are generated due to the instability.
$m$
, is maintained long enough; this enables us to observe the almost symmetric quasi-periodic movement of the vortices that are generated due to the instability.
To check the global effect of vorticity diffusion and wave radiation/absorption on the flow evolution, we computed the integrals that are known to be invariant in ideal fluid, namely, the angular momentum, the energy and the potential enstrophy, and followed the rate of change per unit time in each of these integrals. As noted above (§ 2.1), the unit time corresponds to the advective time scale, which is generally much shorter than the diffusive time scale (except for the absorbing layer where the viscosity coefficient is high), so the rates of change are expected to be small as long as the wave field in the domain
![]() $20<r<30$
is weak.
$20<r<30$
is weak.
In almost all of our simulations, the angular momentum is conserved to quite a high degree of accuracy, the change per unit time being under
![]() $0.01\,\%$
. However, in the simulation with a clockwise basic flow at a moderate bottom slope (described in § 6.3), where the growing instability induces intense radial radiation of Rossby waves, the escaping waves carry a considerable amount of the angular momentum, transmitting it from the main flow to the absorption domain. As a result, by
$0.01\,\%$
. However, in the simulation with a clockwise basic flow at a moderate bottom slope (described in § 6.3), where the growing instability induces intense radial radiation of Rossby waves, the escaping waves carry a considerable amount of the angular momentum, transmitting it from the main flow to the absorption domain. As a result, by
![]() $t=1000$
, next to the island, a counterclockwise flow forms, and the overall angular momentum, which is positive at the beginning, becomes negative.
$t=1000$
, next to the island, a counterclockwise flow forms, and the overall angular momentum, which is positive at the beginning, becomes negative.
Prominent changes in energy and potential enstrophy occur predominantly when the instability enters its nonlinear stage, i.e. when structural changes of the flow begin. At this stage, which, depending on the initial conditions, culminates within approximately
![]() $50$
to
$50$
to
![]() $150$
time units, strong filamentation, boundary-layer formation and the separation of the latter from the rigid wall make the viscous dissipation of vorticity especially effective. During this stage, in all of our simulations except that mentioned in the previous paragraph, the energy usually decreases by approximately
$150$
time units, strong filamentation, boundary-layer formation and the separation of the latter from the rigid wall make the viscous dissipation of vorticity especially effective. During this stage, in all of our simulations except that mentioned in the previous paragraph, the energy usually decreases by approximately
![]() $0.25\,\%$
per unit time. After that, the flow develops rather adiabatically with slow energy dissipation, about
$0.25\,\%$
per unit time. After that, the flow develops rather adiabatically with slow energy dissipation, about
![]() $0.08\,\%$
per unit time. In the simulation described in § 6.3, where the effect of wave radiation/absorption is strong, the energy decrease by
$0.08\,\%$
per unit time. In the simulation described in § 6.3, where the effect of wave radiation/absorption is strong, the energy decrease by
![]() $t=150$
is approximately
$t=150$
is approximately
![]() $1.13\,\%$
per unit time.
$1.13\,\%$
per unit time.
When dealing with the enstrophy, we follow the excess potential enstrophy, i.e. the integral of
![]() $(\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}r)^{2}/2-(\unicode[STIX]{x1D6FD}r)^{2}/2$
. Here too the fastest decrease (usually up to
$(\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}r)^{2}/2-(\unicode[STIX]{x1D6FD}r)^{2}/2$
. Here too the fastest decrease (usually up to
![]() $0.55\,\%$
per unit time) occurs during the stage, in which structural changes in the flow begin; later on the decrease is much slower, approximately
$0.55\,\%$
per unit time) occurs during the stage, in which structural changes in the flow begin; later on the decrease is much slower, approximately
![]() $0.2\,\%$
per unit time. We attribute the observed fact that the decrease of the excess enstrophy is faster than that of the energy to the well-known phenomenon of inverse energy cascade from small scales to large scales in two-dimensional flows (e.g. Vallis Reference Vallis2017). In contrast, the potential enstrophy cascades downscale, where it is more effectively dissipated by viscosity. The only exception from these observations is represented by the simulation discussed in § 6.3, in which the effect of Rossby-wave radiation is dominant.
$0.2\,\%$
per unit time. We attribute the observed fact that the decrease of the excess enstrophy is faster than that of the energy to the well-known phenomenon of inverse energy cascade from small scales to large scales in two-dimensional flows (e.g. Vallis Reference Vallis2017). In contrast, the potential enstrophy cascades downscale, where it is more effectively dissipated by viscosity. The only exception from these observations is represented by the simulation discussed in § 6.3, in which the effect of Rossby-wave radiation is dominant.
3 Beta effect at weak slopes. Trajectories of emitted dipoles
As is known, in the flat-bottom case, the
![]() $m$
-mode instability of a barotropic flow around an island may lead to the emission of
$m$
-mode instability of a barotropic flow around an island may lead to the emission of
![]() $m$
dipoles for
$m$
dipoles for
![]() $m\geqslant 2$
(Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013). At weak slopes, namely at
$m\geqslant 2$
(Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013). At weak slopes, namely at
![]() $\unicode[STIX]{x1D6FD}$
of order 0.01, the instability is expected to evolve basically in the same way, as long as the topographic background vorticity
$\unicode[STIX]{x1D6FD}$
of order 0.01, the instability is expected to evolve basically in the same way, as long as the topographic background vorticity
![]() $\unicode[STIX]{x1D6FD}r$
appearing in (2.2) is negligible compared to the vorticity
$\unicode[STIX]{x1D6FD}r$
appearing in (2.2) is negligible compared to the vorticity
![]() $\unicode[STIX]{x1D701}$
. In fact, the linear stability analysis carried out in RKF showed no significant difference between the stability/instability regions in the parameter space for
$\unicode[STIX]{x1D701}$
. In fact, the linear stability analysis carried out in RKF showed no significant difference between the stability/instability regions in the parameter space for
![]() $m\geqslant 2$
between the flat-bottom case and the weak-slope case.
$m\geqslant 2$
between the flat-bottom case and the weak-slope case.

Figure 2. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
$\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
![]() $R_{2}=4$
, where mode 2 is most unstable. Red/blue colours mark positive/negative vorticity; grey, the island. Time is specified in non-dimensional units at the upper-left corner of each panel.
$R_{2}=4$
, where mode 2 is most unstable. Red/blue colours mark positive/negative vorticity; grey, the island. Time is specified in non-dimensional units at the upper-left corner of each panel.
The flow evolution in the presence of a weak slope is shown in figure 2 for the case of
![]() $\unicode[STIX]{x1D6FD}=-0.01$
,
$\unicode[STIX]{x1D6FD}=-0.01$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=1$
,
$\unicode[STIX]{x1D6E4}_{1}=1$
,
![]() $R_{1}=2.5$
and
$R_{1}=2.5$
and
![]() $R_{2}=4$
, where mode 2 is most linearly unstable (compared to other modes). In figure 2, as well as in the following figures, the highest colour density is determined by the maximum/minimum of vorticity in each panel separately. As anticipated, the instability results in the emission of two dipoles. Just after the emission, the dipoles move in an outward–counterclockwise direction, owing to the fact that here the positive-vorticity part of a dipole is more concentrated and is a little stronger (in terms of relative vorticity) than the negative one. Thus, the negative vortex has a tendency to wrap around the more compact positive vortex and move counterclockwise. As a dipole increases its distance from the cylinder, the counterclockwise component in the dipole movement increases, thus limiting the distance by a maximum of the order
$R_{2}=4$
, where mode 2 is most linearly unstable (compared to other modes). In figure 2, as well as in the following figures, the highest colour density is determined by the maximum/minimum of vorticity in each panel separately. As anticipated, the instability results in the emission of two dipoles. Just after the emission, the dipoles move in an outward–counterclockwise direction, owing to the fact that here the positive-vorticity part of a dipole is more concentrated and is a little stronger (in terms of relative vorticity) than the negative one. Thus, the negative vortex has a tendency to wrap around the more compact positive vortex and move counterclockwise. As a dipole increases its distance from the cylinder, the counterclockwise component in the dipole movement increases, thus limiting the distance by a maximum of the order
![]() $10$
(more specifically,
$10$
(more specifically,
![]() $8.4$
for the centroid of the positive-vorticity part of the dipole and
$8.4$
for the centroid of the positive-vorticity part of the dipole and
![]() $11.3$
for the centroid of the negative-vorticity part). From this moment,
$11.3$
for the centroid of the negative-vorticity part). From this moment,
![]() $t\approx 88$
, the dipole begins moving back to the cylinder, reaching the latter at
$t\approx 88$
, the dipole begins moving back to the cylinder, reaching the latter at
![]() $t\approx 140$
. The evolution goes in an essentially centrally symmetric manner. The mechanism that makes the dipole go back is explained below in this section.
$t\approx 140$
. The evolution goes in an essentially centrally symmetric manner. The mechanism that makes the dipole go back is explained below in this section.
Upon reaching the cylinder, the two dipoles collide, exchange their partners, and at
![]() $t\approx 190$
, two new dipoles emerge. This time, due to wave radiation, dissipation and filamentation, the dipoles are weaker than previously, so they move a lesser distance from the origin (about
$t\approx 190$
, two new dipoles emerge. This time, due to wave radiation, dissipation and filamentation, the dipoles are weaker than previously, so they move a lesser distance from the origin (about
![]() $5$
at
$5$
at
![]() $t\approx 220$
), return back to the cylinder, and collide again. This behaviour exhibits a quasi-periodic tendency and lasts for four quasi-periods until
$t\approx 220$
), return back to the cylinder, and collide again. This behaviour exhibits a quasi-periodic tendency and lasts for four quasi-periods until
![]() $t\approx 560$
. The fifth cycle is never observed, since in the first four cycles, the dipoles lose too much energy and are no longer strong enough to survive the collision. They eventually disintegrate; the two positive-vorticity parts attach to the cylinder, moving together counterclockwise and causing a generally counterclockwise velocity field around the cylinder. The two negative-vorticity parts are drifted by this flow and unite in a ring that encircles the cylinder and the positive-vorticity ring around it. Eventually, due to the viscosity and wave radiation, the negative vorticity spreads out (
$t\approx 560$
. The fifth cycle is never observed, since in the first four cycles, the dipoles lose too much energy and are no longer strong enough to survive the collision. They eventually disintegrate; the two positive-vorticity parts attach to the cylinder, moving together counterclockwise and causing a generally counterclockwise velocity field around the cylinder. The two negative-vorticity parts are drifted by this flow and unite in a ring that encircles the cylinder and the positive-vorticity ring around it. Eventually, due to the viscosity and wave radiation, the negative vorticity spreads out (
![]() $t=968$
).
$t=968$
).

Figure 3. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
$\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
![]() $R_{2}=2$
, where mode 4 is most unstable. Positive-vorticity patches are labelled by the numbers 1, 2, 3 and 4; negative-vorticity patches are labelled by the letters A, B, C and D. Colours and notations as in figure 2.
$R_{2}=2$
, where mode 4 is most unstable. Positive-vorticity patches are labelled by the numbers 1, 2, 3 and 4; negative-vorticity patches are labelled by the letters A, B, C and D. Colours and notations as in figure 2.

Figure 4. Second-cycle trajectories (from
![]() $t=350$
to
$t=350$
to
![]() $t=550$
) of the four dipoles shown in figure 3. Dashed line (blue) indicates the trajectories of the negative-vorticity vortices (the points of local minima of relative vorticity); dotted line (red), positive-vorticity vortices; solid line (purple), the middle points between the minimum and maximum in each dipole.
$t=550$
) of the four dipoles shown in figure 3. Dashed line (blue) indicates the trajectories of the negative-vorticity vortices (the points of local minima of relative vorticity); dotted line (red), positive-vorticity vortices; solid line (purple), the middle points between the minimum and maximum in each dipole.

Figure 5. Meandering of the four dipoles in the simulation at
![]() $\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
$\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
![]() $R_{2}=1.88$
, where mode 4 is most unstable. The vorticity field at times 280, 440 and 900; dashed line (purple) indicates the final circular orbit taken by the dipoles at
$R_{2}=1.88$
, where mode 4 is most unstable. The vorticity field at times 280, 440 and 900; dashed line (purple) indicates the final circular orbit taken by the dipoles at
![]() $t\geqslant 900$
. Other colours as in figure 2.
$t\geqslant 900$
. Other colours as in figure 2.
The tendency to quasi-periodicity is seen even better in the case of the mode-4 instability. This is illustrated by figure 3, in which the evolution of the flow corresponding to four full quasi-periods is shown. In contrast to the rest of simulations, to make the dynamics simpler, here we initiate the growth of instability by applying a small, order
![]() $10^{-5}$
mode-4 deformation of the liquid boundaries of the initially circular PV rings, exactly as was done by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013). Starting from the second row in figure 3, a new cycle begins in any next row. Each cycle includes the dipoles receding from the island, their swinging and returning to the island’s vicinity. To identify the vorticity patches, in the middle panel of each row, the positive-vorticity patches are labelled by the numbers 1, 2, 3 and 4, and the negative-vorticity ones by the letters A, B, C and D. At first (times
$10^{-5}$
mode-4 deformation of the liquid boundaries of the initially circular PV rings, exactly as was done by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013). Starting from the second row in figure 3, a new cycle begins in any next row. Each cycle includes the dipoles receding from the island, their swinging and returning to the island’s vicinity. To identify the vorticity patches, in the middle panel of each row, the positive-vorticity patches are labelled by the numbers 1, 2, 3 and 4, and the negative-vorticity ones by the letters A, B, C and D. At first (times
![]() $48,136$
and
$48,136$
and
![]() $172$
), the vortex couples are 1–A, 2–B, 3–C and 4–D. These couples remain coherent until approximately
$172$
), the vortex couples are 1–A, 2–B, 3–C and 4–D. These couples remain coherent until approximately
![]() $t=306$
(third row), when the first collision of the dipoles with the cylinder occurs. Starting from this collision, any new period begins with ‘exchange of partners’, i.e. with the formation of a new dipole (any positive-vorticity patch is now coupled with a different negative-vorticity patch). This quasi-periodic motion lasts until
$t=306$
(third row), when the first collision of the dipoles with the cylinder occurs. Starting from this collision, any new period begins with ‘exchange of partners’, i.e. with the formation of a new dipole (any positive-vorticity patch is now coupled with a different negative-vorticity patch). This quasi-periodic motion lasts until
![]() $t\approx 2460$
(the two last periods are not shown in the figure). Figure 4 shows the trajectories of the four dipoles during the second cycle that lasted approximately from
$t\approx 2460$
(the two last periods are not shown in the figure). Figure 4 shows the trajectories of the four dipoles during the second cycle that lasted approximately from
![]() $t=350$
to
$t=350$
to
![]() $t=450$
.
$t=450$
.
Figure 5 illustrates the behaviour of dipoles in another simulation, where
![]() $\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
$\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=1.5$
and
![]() $R_{2}=1.88$
. In this case, the four emitted dipoles make a swing (
$R_{2}=1.88$
. In this case, the four emitted dipoles make a swing (
![]() $t\approx 280$
), but do not reach the cylinder again. Instead, they meander about a circle, whose radius is approximately 8.5, and gradually settle symmetrically on this orbit travelling in a quasi-steady manner. This behaviour is similar to that of modons on a conventional beta plane, where
$t\approx 280$
), but do not reach the cylinder again. Instead, they meander about a circle, whose radius is approximately 8.5, and gradually settle symmetrically on this orbit travelling in a quasi-steady manner. This behaviour is similar to that of modons on a conventional beta plane, where
![]() $Q=\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}y$
and, at
$Q=\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}y$
and, at
![]() $\unicode[STIX]{x1D6FD}>0$
, steady translation of a modon is permitted in the positive direction of the
$\unicode[STIX]{x1D6FD}>0$
, steady translation of a modon is permitted in the positive direction of the
![]() $x$
-axis, i.e. eastward. If the modon’s axis is tilted at an acute angle (whether positive or negative) relative to the
$x$
-axis, i.e. eastward. If the modon’s axis is tilted at an acute angle (whether positive or negative) relative to the
![]() $x$
-axis, the modon meanders, while travelling predominantly eastward. Due to the Rossby-wave radiation (and possible viscous dissipation), the modon relaxes in an almost steady eastward translational movement. An initially northwest- or southwest-going beta-plane modon (obtuse tilt angle) either makes a turn in a predominantly eastward direction ending up in a quasi-steady state, or disintegrates in the course of the turn. This behaviour of the beta-plane modons was discussed in a number of publications (e.g. Hesthaven et al.
Reference Hesthaven, Lynov and Nycander1993; Velasco Fuentes & van Heijst Reference Velasco Fuentes and van Heijst1994). In this context, the beta-cone model differs from the beta-plane model by the fact that, on a beta cone, the steady-state trajectories are circles rather than straight lines (with the tilt angle being defined relative to a tangent line to a circle), and by the presence of the inner rigid boundary, where the returning dipoles meet. On a beta plane, a steady dipole moves with the higher PV to its left, i.e. opposite to the direction of the phase velocity of the Rossby waves. Similarly, on a beta cone, the permitted direction of steady dipoles is counterclockwise (as shown in figure 5), opposite to the clockwise direction of radiating Rossby waves (see § 4.1).
$x$
-axis, the modon meanders, while travelling predominantly eastward. Due to the Rossby-wave radiation (and possible viscous dissipation), the modon relaxes in an almost steady eastward translational movement. An initially northwest- or southwest-going beta-plane modon (obtuse tilt angle) either makes a turn in a predominantly eastward direction ending up in a quasi-steady state, or disintegrates in the course of the turn. This behaviour of the beta-plane modons was discussed in a number of publications (e.g. Hesthaven et al.
Reference Hesthaven, Lynov and Nycander1993; Velasco Fuentes & van Heijst Reference Velasco Fuentes and van Heijst1994). In this context, the beta-cone model differs from the beta-plane model by the fact that, on a beta cone, the steady-state trajectories are circles rather than straight lines (with the tilt angle being defined relative to a tangent line to a circle), and by the presence of the inner rigid boundary, where the returning dipoles meet. On a beta plane, a steady dipole moves with the higher PV to its left, i.e. opposite to the direction of the phase velocity of the Rossby waves. Similarly, on a beta cone, the permitted direction of steady dipoles is counterclockwise (as shown in figure 5), opposite to the clockwise direction of radiating Rossby waves (see § 4.1).

Figure 6. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=2.5$
and
$\unicode[STIX]{x1D6FD}=-0.01,\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=2.5$
and
![]() $R_{2}=4$
, where mode 2 is most unstable. Colours and notations as in figure 2.
$R_{2}=4$
, where mode 2 is most unstable. Colours and notations as in figure 2.
Figure 6 illustrates the development of the flow, with the same values of
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
as in figure 2, but this time with the basic flow going in the opposite direction (i.e. for the case of
$R_{2}$
as in figure 2, but this time with the basic flow going in the opposite direction (i.e. for the case of
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
). Again, mode 2 is most unstable here, and the process of formation of the two centrally symmetric dipoles is similar to that in the case of
$\unicode[STIX]{x1D6E4}_{1}=-1$
). Again, mode 2 is most unstable here, and the process of formation of the two centrally symmetric dipoles is similar to that in the case of
![]() $\unicode[STIX]{x1D6E4}_{1}=+1$
. This time the dipoles are emitted in the outward–clockwise direction, since now the negative-vorticity lobe is the more concentrated and strong one. When the dipoles leave the immediate neighbourhood of the cylinder, the beta effect becomes significant; as a result, the two dipoles swing around, and equalize so as to align themselves to the counterclockwise direction, and then, after some meandering (like that shown in figure 5), continue moving in an approximately circular trajectory. Figuratively, one may say that the dipoles find the proper direction (counterclockwise) and the ‘proper latitude’ (i.e. the value of the background vorticity) to move in a quasi-stationary manner.
$\unicode[STIX]{x1D6E4}_{1}=+1$
. This time the dipoles are emitted in the outward–clockwise direction, since now the negative-vorticity lobe is the more concentrated and strong one. When the dipoles leave the immediate neighbourhood of the cylinder, the beta effect becomes significant; as a result, the two dipoles swing around, and equalize so as to align themselves to the counterclockwise direction, and then, after some meandering (like that shown in figure 5), continue moving in an approximately circular trajectory. Figuratively, one may say that the dipoles find the proper direction (counterclockwise) and the ‘proper latitude’ (i.e. the value of the background vorticity) to move in a quasi-stationary manner.
The two scenarios presented in figures 2 and 6 differ markedly from each other because the directions in which the dipoles are emitted are different. The direction of the azimuthal component of the velocity of the emitted dipole right after the formation of the latter depends on the direction of the basic flow. Thus the dipoles’ propagation may be generally aligned or misaligned with the permitted direction of the orbital movement of a steady-state dipole.
When the basic flow is counterclockwise (figure 2), the dipole movement is unsteady, but its main direction corresponds to that of a steady-state dipole. The loop in the dipole’s trajectory is explained by the fact that distancing from the origin has different effect on the dipole counterparts: due to the beta effect, the positive (in the relative-vorticity sense) vortex enhances, while the negative one weakens; this causes the change in the dipole’s direction. On the way back to the cylinder, the beta effect on the two vortices is opposite to the above-described. Close to the cylinder, the neighbouring dipoles exchange their partners, and a new cycle of the process begins, though at a reduced intensity, which is due to the viscous dissipation, Rossby-wave radiation and filamentation.
In figure 6 the initial flow is clockwise. The dipoles are emitted almost radially and then, because now the negative vortex is more compact than the positive one, a dipole gains a clockwise velocity direction. Therefore, at the beginning, the dipole motion is not aligned with the permitted steady-state direction. When the dipoles leave the close neighbourhood of the cylinder, the beta effect becomes significant, and they swing around, tending to fit the steady-state direction of motion as observed in figure 6 at
![]() $t\geqslant 460$
. During this highly unsteady swing, the Rossby-wave radiation is strong and may lead to the dipoles’ breakdown. In fact, the settling of dipoles in a quasi-stationary (and almost circular) trajectory is not a common outcome in our simulations with
$t\geqslant 460$
. During this highly unsteady swing, the Rossby-wave radiation is strong and may lead to the dipoles’ breakdown. In fact, the settling of dipoles in a quasi-stationary (and almost circular) trajectory is not a common outcome in our simulations with
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
. In most of the simulations, the counterclockwise swing of the dipoles results in their disintegration.
$\unicode[STIX]{x1D6E4}_{1}=-1$
. In most of the simulations, the counterclockwise swing of the dipoles results in their disintegration.
4 Waves on the beta cone
When
![]() $\unicode[STIX]{x1D6FD}$
is large enough, the topographic Rossby waves produced by a non-stationary flow become important, playing a major role in the evolution of the flow. Here we present the basic theory of steadily propagating Rossby waves on the beta cone (§ 4.1), and also discuss the waves in the exterior region associated with growing perturbations of the flow (§ 4.2). The wave–flow interaction observed in the simulations is examined in the subsequent sections.
$\unicode[STIX]{x1D6FD}$
is large enough, the topographic Rossby waves produced by a non-stationary flow become important, playing a major role in the evolution of the flow. Here we present the basic theory of steadily propagating Rossby waves on the beta cone (§ 4.1), and also discuss the waves in the exterior region associated with growing perturbations of the flow (§ 4.2). The wave–flow interaction observed in the simulations is examined in the subsequent sections.
4.1 Steadily propagating waves
It is well known that in barotropic flows the beta effect (sloping bottom in our case) makes possible the development of Rossby waves. We are about to determine the shape of the wave fronts and the dispersion relation for the steadily propagating linear Rossby waves on the beta cone. In a frame of reference that rotates with the angular velocity equal to the azimuthal phase velocity of a wave, the latter is stationary. Therefore, in what follows, we refer to steadily propagating waves as to stationary waves. The linearized form of equation (2.4) with the account of (2.2) is:
Considering a free linear wave at a sufficient distance from the island, we seek a solution to the pair of equations (2.3) and (4.1) with separable variables in the form
![]() $\unicode[STIX]{x1D713}=F(r)\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
. This is a wave with a constant azimuthal phase velocity
$\unicode[STIX]{x1D713}=F(r)\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
. This is a wave with a constant azimuthal phase velocity
![]() $\unicode[STIX]{x1D714}/m$
(
$\unicode[STIX]{x1D714}/m$
(
![]() $\unicode[STIX]{x1D714}$
is real, since only stationary waves are discussed in this section). The wavenumber
$\unicode[STIX]{x1D714}$
is real, since only stationary waves are discussed in this section). The wavenumber
![]() $m$
must be an integer due to periodicity in
$m$
must be an integer due to periodicity in
![]() $\unicode[STIX]{x1D703}$
of the solution. The function
$\unicode[STIX]{x1D703}$
of the solution. The function
![]() $F(r)$
may be complex, and can be written as
$F(r)$
may be complex, and can be written as
![]() $F(r)=|F(r)|\text{e}^{\text{i}\arg [F(r)]}$
. Therefore, the streamfunction is
$F(r)=|F(r)|\text{e}^{\text{i}\arg [F(r)]}$
. Therefore, the streamfunction is
![]() $\unicode[STIX]{x1D713}=|F(r)|\text{e}^{\text{i}\{\arg [F(r)]+m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t\}}$
, and its argument is
$\unicode[STIX]{x1D713}=|F(r)|\text{e}^{\text{i}\{\arg [F(r)]+m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t\}}$
, and its argument is
![]() $\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},t)=\arg (\unicode[STIX]{x1D713})=\arg (F(r))+m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t$
. Lines of constant
$\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},t)=\arg (\unicode[STIX]{x1D713})=\arg (F(r))+m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t$
. Lines of constant
![]() $\unicode[STIX]{x1D719}$
are the lines at which the wave phase is constant; the wavevector is
$\unicode[STIX]{x1D719}$
are the lines at which the wave phase is constant; the wavevector is
(e.g. Whitham Reference Whitham1961; Pedlosky Reference Pedlosky2013). For the chosen form of solution, equation (4.1) yields,
Introduction of the variable
![]() $\sqrt{r}$
reduces equation (4.3) to the Bessel equation, the behaviour of the solution to (4.3) being dependent on the sign of
$\sqrt{r}$
reduces equation (4.3) to the Bessel equation, the behaviour of the solution to (4.3) being dependent on the sign of
![]() $\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}$
.
Consider first the case where
![]() $\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}>0$
. The general solution to (4.3) in this case is a superposition of the Hankel functions of order
$\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}>0$
. The general solution to (4.3) in this case is a superposition of the Hankel functions of order
![]() $2m$
,
$2m$
,
Since
![]() $\unicode[STIX]{x1D6FD}<0$
, such Rossby waves can travel only clockwise (
$\unicode[STIX]{x1D6FD}<0$
, such Rossby waves can travel only clockwise (
![]() $\unicode[STIX]{x1D714}<0$
). The asymptotic behaviour of solutions (4.4) at
$\unicode[STIX]{x1D714}<0$
). The asymptotic behaviour of solutions (4.4) at
![]() $\unicode[STIX]{x1D6FD}mr/\unicode[STIX]{x1D714}\gg 1$
is
$\unicode[STIX]{x1D6FD}mr/\unicode[STIX]{x1D714}\gg 1$
is
(Abramowitz & Stegun Reference Abramowitz and Stegun1964). The energy density of the waves is
![]() $(|v|^{2}+|u|^{2})/2$
, which by virtue of (2.1), (4.5) and (4.6), decreases asymptotically as
$(|v|^{2}+|u|^{2})/2$
, which by virtue of (2.1), (4.5) and (4.6), decreases asymptotically as
![]() $1/r^{5/2}$
with increasing
$1/r^{5/2}$
with increasing
![]() $r$
; hence the waves have finite energy. We note that for real topography, the depth levels out again after some distance from the island. So, formally, the infinite beta-cone model will not be applicable. We, however, may assume that this occurs far enough from the island, so the asymptotic behaviour in the framework of the beta-cone model still can be applied (see RKF for a detailed discussion of the limit
$r$
; hence the waves have finite energy. We note that for real topography, the depth levels out again after some distance from the island. So, formally, the infinite beta-cone model will not be applicable. We, however, may assume that this occurs far enough from the island, so the asymptotic behaviour in the framework of the beta-cone model still can be applied (see RKF for a detailed discussion of the limit
![]() $r\rightarrow \infty$
in the beta-cone model).
$r\rightarrow \infty$
in the beta-cone model).
According to (4.2), (4.5) and (4.6), the asymptotic (as
![]() $r\rightarrow \infty$
) wave vectors, which are perpendicular to the wavefronts, are
$r\rightarrow \infty$
) wave vectors, which are perpendicular to the wavefronts, are
where
![]() $k_{r1,2}$
and
$k_{r1,2}$
and
![]() $k_{\unicode[STIX]{x1D703}1,2}$
are the radial and azimuthal wavenumbers. Therefore the asymptotic dispersion relation for each of the two waves is
$k_{\unicode[STIX]{x1D703}1,2}$
are the radial and azimuthal wavenumbers. Therefore the asymptotic dispersion relation for each of the two waves is
Notice that in equation (4.8) only
![]() $k_{r1,2}$
are functions of
$k_{r1,2}$
are functions of
![]() $r$
, while
$r$
, while
![]() $\unicode[STIX]{x1D714}$
,
$\unicode[STIX]{x1D714}$
,
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D6FD}$
are constants.
$\unicode[STIX]{x1D6FD}$
are constants.
Consider a mode-
![]() $m$
wave packet, with the radial wavenumber components close to
$m$
wave packet, with the radial wavenumber components close to
![]() $k_{r}$
. The packet is composed of either waves having the form of
$k_{r}$
. The packet is composed of either waves having the form of
![]() $\unicode[STIX]{x1D713}_{1}$
(equation (4.5)) or waves having the form of
$\unicode[STIX]{x1D713}_{1}$
(equation (4.5)) or waves having the form of
![]() $\unicode[STIX]{x1D713}_{2}$
(equation (4.6)). The group velocity of each kind of packet is readily found from (4.8) (e.g. Whitham Reference Whitham1961; Pedlosky Reference Pedlosky2013),
$\unicode[STIX]{x1D713}_{2}$
(equation (4.6)). The group velocity of each kind of packet is readily found from (4.8) (e.g. Whitham Reference Whitham1961; Pedlosky Reference Pedlosky2013),
where
![]() $\boldsymbol{c}_{g1}$
and
$\boldsymbol{c}_{g1}$
and
![]() $\boldsymbol{c}_{g2}$
correspond to the packet composed of the waves
$\boldsymbol{c}_{g2}$
correspond to the packet composed of the waves
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D713}_{2}$
, respectively. The radial components of the group velocities
$\unicode[STIX]{x1D713}_{2}$
, respectively. The radial components of the group velocities
![]() $\boldsymbol{c}_{g1}$
and
$\boldsymbol{c}_{g1}$
and
![]() $\boldsymbol{c}_{g2}$
, that is, the velocities at which energy is transferred radially by the packet, are opposite in sign; namely, the packet of the first kind transfers energy radially outwards, while the wave packet of the second kind, inwards. The waves that are emitted by the unstable flow must obey the radiation condition, according to which energy cannot arrive from outside. These waves are represented by
$\boldsymbol{c}_{g2}$
, that is, the velocities at which energy is transferred radially by the packet, are opposite in sign; namely, the packet of the first kind transfers energy radially outwards, while the wave packet of the second kind, inwards. The waves that are emitted by the unstable flow must obey the radiation condition, according to which energy cannot arrive from outside. These waves are represented by
![]() $\unicode[STIX]{x1D713}_{1}$
. The other solution,
$\unicode[STIX]{x1D713}_{1}$
. The other solution,
![]() $\unicode[STIX]{x1D713}_{2}$
, represents a wave that brings energy from outside. Such a solution might be relevant, for example, when the domain in which the flow is considered has a distant external circular boundary, at which the waves of the first kind, represented by
$\unicode[STIX]{x1D713}_{2}$
, represents a wave that brings energy from outside. Such a solution might be relevant, for example, when the domain in which the flow is considered has a distant external circular boundary, at which the waves of the first kind, represented by
![]() $\unicode[STIX]{x1D713}_{1}$
, can be reflected. Theoretically, this is not our case. That is why, in the simulations, where an external boundary is introduced for technical reasons and where the reflection can be efficient, we apply the absorption-layer approach (§ 2.2).
$\unicode[STIX]{x1D713}_{1}$
, can be reflected. Theoretically, this is not our case. That is why, in the simulations, where an external boundary is introduced for technical reasons and where the reflection can be efficient, we apply the absorption-layer approach (§ 2.2).

Figure 7. Properties of Rossby waves on the beta cone, for
![]() $m=2$
and
$m=2$
and
![]() $\unicode[STIX]{x1D6FD}=-0.1$
. (a) Dispersion relation, frequency versus the radial wavenumber at
$\unicode[STIX]{x1D6FD}=-0.1$
. (a) Dispersion relation, frequency versus the radial wavenumber at
![]() $r=3$
. The exact relation described by equation (4.12) (solid line, red) and the asymptotic relation described by equation (4.8) (dashed line, blue). (b) Vorticity distribution for
$r=3$
. The exact relation described by equation (4.12) (solid line, red) and the asymptotic relation described by equation (4.8) (dashed line, blue). (b) Vorticity distribution for
![]() $\unicode[STIX]{x1D714}=-0.03$
at
$\unicode[STIX]{x1D714}=-0.03$
at
![]() $3<r<12$
(colours as in figure 2), thin solid lines mark the asymptotic wave fronts determined by equation (4.13). (c) Typical ray trajectory of a wave packet for
$3<r<12$
(colours as in figure 2), thin solid lines mark the asymptotic wave fronts determined by equation (4.13). (c) Typical ray trajectory of a wave packet for
![]() $\unicode[STIX]{x1D714}=-0.03$
at
$\unicode[STIX]{x1D714}=-0.03$
at
![]() $10<r<240$
; the scale is 20 times the scale in (b), the small cross designates the origin.
$10<r<240$
; the scale is 20 times the scale in (b), the small cross designates the origin.
Below in this section we consider in detail only the waves propagating outwards (the properties of the inward-going waves are then easily deduced). The dispersion relation (4.8) was found by using the asymptotic expansion of the Hankel functions in equations (4.5) and (4.6). However, the exact dispersion relation can be easily calculated by representing the Hankel function of the first kind appearing in (4.5) as
![]() $H_{2m}^{(1)}=|H_{2m}^{(1)}|\text{e}^{\text{i}\unicode[STIX]{x1D6E9}_{2m}}$
. In the case of
$H_{2m}^{(1)}=|H_{2m}^{(1)}|\text{e}^{\text{i}\unicode[STIX]{x1D6E9}_{2m}}$
. In the case of
![]() $\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}>0$
, which is under consideration now,
$\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}>0$
, which is under consideration now,
where
![]() $J_{2m}$
and
$J_{2m}$
and
![]() $Y_{2m}$
are the
$Y_{2m}$
are the
![]() $2m$
-order Bessel functions of the first and second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). Accordingly, by differentiating the right-hand side of (4.11) (see (4.2)) and using the identity
$2m$
-order Bessel functions of the first and second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). Accordingly, by differentiating the right-hand side of (4.11) (see (4.2)) and using the identity
![]() $J_{2m}(x)\,\text{d}Y_{2m}(x)/\text{d}x-Y_{2m}(x)\,\text{d}J_{2m}(x)/\text{d}x=2/\unicode[STIX]{x03C0}x$
, we arrive at the exact dispersion relation for Rossby waves on a beta cone,
$J_{2m}(x)\,\text{d}Y_{2m}(x)/\text{d}x-Y_{2m}(x)\,\text{d}J_{2m}(x)/\text{d}x=2/\unicode[STIX]{x03C0}x$
, we arrive at the exact dispersion relation for Rossby waves on a beta cone,
The main characteristics of the beta-cone Rossby waves are illustrated in figure 7 for the case of
![]() $m=2$
and
$m=2$
and
![]() $\unicode[STIX]{x1D6FD}=-0.1$
. Figure 7(a) presents the dispersion relation (4.12) for the example of
$\unicode[STIX]{x1D6FD}=-0.1$
. Figure 7(a) presents the dispersion relation (4.12) for the example of
![]() $r=3$
(solid line). The dashed line is the dispersion curve according to equation (4.8), which holds in the asymptotic limit
$r=3$
(solid line). The dashed line is the dispersion curve according to equation (4.8), which holds in the asymptotic limit
![]() $r\gg \unicode[STIX]{x1D714}/m\unicode[STIX]{x1D6FD}$
, far from the origin. The asymptotic dispersion relation approaches the exact relation in the limit of small frequencies
$r\gg \unicode[STIX]{x1D714}/m\unicode[STIX]{x1D6FD}$
, far from the origin. The asymptotic dispersion relation approaches the exact relation in the limit of small frequencies
![]() $\unicode[STIX]{x1D714}$
, or high radial wavenumbers, as can be seen in the figure.
$\unicode[STIX]{x1D714}$
, or high radial wavenumbers, as can be seen in the figure.
According to equation (4.5) the fronts
![]() $\unicode[STIX]{x1D719}=\text{const.}$
of the outward-propagating wave
$\unicode[STIX]{x1D719}=\text{const.}$
of the outward-propagating wave
![]() $\unicode[STIX]{x1D713}_{1}$
in the asymptotic regime
$\unicode[STIX]{x1D713}_{1}$
in the asymptotic regime
![]() $r\gg \unicode[STIX]{x1D714}/m\unicode[STIX]{x1D6FD}$
are the lines
$r\gg \unicode[STIX]{x1D714}/m\unicode[STIX]{x1D6FD}$
are the lines
where
![]() $\unicode[STIX]{x1D6F7}$
is an arbitrary constant ranging from
$\unicode[STIX]{x1D6F7}$
is an arbitrary constant ranging from
![]() $0$
to
$0$
to
![]() $2\unicode[STIX]{x03C0}$
. By choosing different values of
$2\unicode[STIX]{x03C0}$
. By choosing different values of
![]() $\unicode[STIX]{x1D6F7}$
we determine different phases; geometrically, these lines are spirals on the
$\unicode[STIX]{x1D6F7}$
we determine different phases; geometrically, these lines are spirals on the
![]() $(r,\unicode[STIX]{x1D703})$
-plane. In figure 7(b), where the distribution of vorticity,
$(r,\unicode[STIX]{x1D703})$
-plane. In figure 7(b), where the distribution of vorticity,
![]() $\text{Re}(\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713})$
, is shown, the solid lines mark the fronts obtained by varying the right-hand side of (4.13) with a constant step for the case of
$\text{Re}(\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713})$
, is shown, the solid lines mark the fronts obtained by varying the right-hand side of (4.13) with a constant step for the case of
![]() $m=2$
,
$m=2$
,
![]() $\unicode[STIX]{x1D6FD}=-0.1$
and
$\unicode[STIX]{x1D6FD}=-0.1$
and
![]() $\unicode[STIX]{x1D714}=-0.03$
. In accordance with equation (4.13), the spirals get wider with growing
$\unicode[STIX]{x1D714}=-0.03$
. In accordance with equation (4.13), the spirals get wider with growing
![]() $r$
; with increasing
$r$
; with increasing
![]() $|\unicode[STIX]{x1D6FD}|$
, the spirals get denser, their curvature (understood as the rate of change of a unit tangent vector along the curve) increasing.
$|\unicode[STIX]{x1D6FD}|$
, the spirals get denser, their curvature (understood as the rate of change of a unit tangent vector along the curve) increasing.
To find the path
![]() $(r_{g}(t),\unicode[STIX]{x1D703}_{g}(t))$
of the wave packet, the ray-tracing equations are invoked (Pedlosky Reference Pedlosky2013). These equations state that the wave packet propagates with the group velocity, i.e.
$(r_{g}(t),\unicode[STIX]{x1D703}_{g}(t))$
of the wave packet, the ray-tracing equations are invoked (Pedlosky Reference Pedlosky2013). These equations state that the wave packet propagates with the group velocity, i.e.
Using (4.9), the solution to (4.14) gives the following trajectory of the wave packet, which is the trajectory of the energy flux,
where the constant
![]() $r_{0}$
is determined by the initial location of the wave packet. A typical trajectory is shown in figure 7(c), for the case of
$r_{0}$
is determined by the initial location of the wave packet. A typical trajectory is shown in figure 7(c), for the case of
![]() $m=2$
,
$m=2$
,
![]() $\unicode[STIX]{x1D6FD}=-0.1$
and
$\unicode[STIX]{x1D6FD}=-0.1$
and
![]() $\unicode[STIX]{x1D714}=-0.03$
. The central radial wavenumber of the wave packet,
$\unicode[STIX]{x1D714}=-0.03$
. The central radial wavenumber of the wave packet,
![]() $k_{r1}$
, decreases with increasing
$k_{r1}$
, decreases with increasing
![]() $r$
(equation (4.7)). This implies that the average distance between adjacent crests grows as the packet advances in the radial direction.
$r$
(equation (4.7)). This implies that the average distance between adjacent crests grows as the packet advances in the radial direction.
For the inward-propagating wave
![]() $\unicode[STIX]{x1D713}_{2}$
, the vorticity distribution and the trajectory can be obtained as mirror images of those of
$\unicode[STIX]{x1D713}_{2}$
, the vorticity distribution and the trajectory can be obtained as mirror images of those of
![]() $\unicode[STIX]{x1D713}_{1}$
shown in figure 7(b,c). The azimuthal direction of an inward-propagating wave is still clockwise.
$\unicode[STIX]{x1D713}_{1}$
shown in figure 7(b,c). The azimuthal direction of an inward-propagating wave is still clockwise.
We now change to the case of
![]() $\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}<0$
, i.e. where
$\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D714}<0$
, i.e. where
![]() $\unicode[STIX]{x1D714}>0$
. A general solution to (4.3) is a linear combination of the modified Bessel functions
$\unicode[STIX]{x1D714}>0$
. A general solution to (4.3) is a linear combination of the modified Bessel functions
![]() $I_{2m}$
and
$I_{2m}$
and
![]() $K_{2m}$
. For the solution to be limited as
$K_{2m}$
. For the solution to be limited as
![]() $r\rightarrow \infty$
,
$r\rightarrow \infty$
,
![]() $I_{2m}$
should be omitted, so the streamfunction is
$I_{2m}$
should be omitted, so the streamfunction is
where the subscript
![]() $E$
is added to emphasize that this is an edge-wave solution that drops exponentially with increasing distance from the island. Asymptotically, as
$E$
is added to emphasize that this is an edge-wave solution that drops exponentially with increasing distance from the island. Asymptotically, as
![]() $r\rightarrow \infty$
, relation (4.16) becomes
$r\rightarrow \infty$
, relation (4.16) becomes
so this edge wave has a characteristic radial length scale (above which its amplitude decreases by more than a factor of
![]() $e$
) of
$e$
) of
![]() $|\unicode[STIX]{x1D714}/4m\unicode[STIX]{x1D6FD}|$
. It propagates only counterclockwise and has the highest amplitude at the rigid boundary.
$|\unicode[STIX]{x1D714}/4m\unicode[STIX]{x1D6FD}|$
. It propagates only counterclockwise and has the highest amplitude at the rigid boundary.
The edge-wave solution given by formulae (4.16) and (4.17) has no radial wave pattern, i.e. is a strictly azimuthal wave, and dies out rapidly as
![]() $r\rightarrow \infty$
. Therefore, it is suited to describe the far field (periphery) of counterclockwise steadily rotating highly localized centrally symmetric vortex configurations, say, of a number of dipoles moving in a circular orbit (§ 3), as well as of the multipoles and of the hexagonal flow discussed in the next section (cf. Kizner, Khvoles & McWilliams Reference Kizner, Khvoles and McWilliams2007). This distinction between the clockwise propagation of Rossby waves and the allowed counterclockwise steady rotation (around the island) of localized vortex structures on a beta cone is fundamental, exactly as is the distinction between the westward propagation of Rossby waves and the eastward movement of modons on the beta plane (see also Kizner et al.
Reference Kizner, Khvoles and McWilliams2007, where a similar distinction for the gamma-plane model was discussed). In what follows, the clockwise propagating Rossby waves will also be termed ‘radiating’ waves.
$r\rightarrow \infty$
. Therefore, it is suited to describe the far field (periphery) of counterclockwise steadily rotating highly localized centrally symmetric vortex configurations, say, of a number of dipoles moving in a circular orbit (§ 3), as well as of the multipoles and of the hexagonal flow discussed in the next section (cf. Kizner, Khvoles & McWilliams Reference Kizner, Khvoles and McWilliams2007). This distinction between the clockwise propagation of Rossby waves and the allowed counterclockwise steady rotation (around the island) of localized vortex structures on a beta cone is fundamental, exactly as is the distinction between the westward propagation of Rossby waves and the eastward movement of modons on the beta plane (see also Kizner et al.
Reference Kizner, Khvoles and McWilliams2007, where a similar distinction for the gamma-plane model was discussed). In what follows, the clockwise propagating Rossby waves will also be termed ‘radiating’ waves.
Equation (4.3) admits solutions also in the case of
![]() $\unicode[STIX]{x1D6FD}=0$
. The streamfunction in this case is proportional to
$\unicode[STIX]{x1D6FD}=0$
. The streamfunction in this case is proportional to
![]() $r^{-m}\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
, so the solution may be interpreted as a strictly azimuthal wave whose fronts are lines of constant
$r^{-m}\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
, so the solution may be interpreted as a strictly azimuthal wave whose fronts are lines of constant
![]() $\unicode[STIX]{x1D703}$
. These harmonic (zero-vorticity) waves are similar in shape to the edge waves discussed above, but decay slower as
$\unicode[STIX]{x1D703}$
. These harmonic (zero-vorticity) waves are similar in shape to the edge waves discussed above, but decay slower as
![]() $r\rightarrow \infty$
and may propagate both clockwise and counterclockwise. Such solutions are suitable for the description of the exterior fields around steadily rotating vortex patterns on the
$r\rightarrow \infty$
and may propagate both clockwise and counterclockwise. Such solutions are suitable for the description of the exterior fields around steadily rotating vortex patterns on the
![]() $f$
-plane (Kizner & Khvoles Reference Kizner and Khvoles2004a
,Reference Kizner and Khvoles
b
; Kizner et al.
Reference Kizner, Khvoles and McWilliams2007).
$f$
-plane (Kizner & Khvoles Reference Kizner and Khvoles2004a
,Reference Kizner and Khvoles
b
; Kizner et al.
Reference Kizner, Khvoles and McWilliams2007).
4.2 Growing perturbations in the exterior region
During the development of instability of the basic flow, the PV perturbations at the outer contour grow with time. Therefore, a growing perturbation, i.e. a growing wave, is forced in the outer region, at
![]() $r>R_{2}$
. This wave may be represented in the form
$r>R_{2}$
. This wave may be represented in the form
![]() $\unicode[STIX]{x1D713}=F(r)\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
, as in § 4.1, but with a non-real
$\unicode[STIX]{x1D713}=F(r)\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}$
, as in § 4.1, but with a non-real
![]() $\unicode[STIX]{x1D714}$
. We define
$\unicode[STIX]{x1D714}$
. We define
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $g$
to be the real and the imaginary parts of
$g$
to be the real and the imaginary parts of
![]() $\unicode[STIX]{x1D714}$
, i.e.
$\unicode[STIX]{x1D714}$
, i.e.
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70E}+g\text{i}$
. So, the azimuthal frequency of the wave is
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70E}+g\text{i}$
. So, the azimuthal frequency of the wave is
![]() $\unicode[STIX]{x1D70E}$
and its growth rate is
$\unicode[STIX]{x1D70E}$
and its growth rate is
![]() $g$
. In the case of growing instability,
$g$
. In the case of growing instability,
![]() $g$
is positive.
$g$
is positive.
Equation (4.3) holds also if
![]() $\unicode[STIX]{x1D714}$
is complex, its two solutions being given by (4.4). Since
$\unicode[STIX]{x1D714}$
is complex, its two solutions being given by (4.4). Since
![]() $1/\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D70E}-g\text{i})/(\unicode[STIX]{x1D70E}^{2}+g^{2})$
, we get
$1/\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D70E}-g\text{i})/(\unicode[STIX]{x1D70E}^{2}+g^{2})$
, we get
 $$\begin{eqnarray}\displaystyle \sqrt{-\frac{1}{\unicode[STIX]{x1D714}}}\equiv \unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FF}\text{i}=\frac{1}{\sqrt{2}}\sqrt{\sqrt{\frac{1}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}-\frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}+\text{i}\frac{1}{\sqrt{2}}\sqrt{\sqrt{\frac{1}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}+\frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}.\qquad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-\frac{1}{\unicode[STIX]{x1D714}}}\equiv \unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FF}\text{i}=\frac{1}{\sqrt{2}}\sqrt{\sqrt{\frac{1}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}-\frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}+\text{i}\frac{1}{\sqrt{2}}\sqrt{\sqrt{\frac{1}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}+\frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70E}^{2}+g^{2}}}.\qquad & & \displaystyle\end{eqnarray}$$
Here we consider only the wave propagating outwards, i.e.
![]() $\unicode[STIX]{x1D713}_{1}$
(equation (4.4)), and for simplicity deal with its asymptotic form (at
$\unicode[STIX]{x1D713}_{1}$
(equation (4.4)), and for simplicity deal with its asymptotic form (at
![]() $|\unicode[STIX]{x1D6FD}|mr/|\unicode[STIX]{x1D714}|\gg 1$
), given by equation (4.5) (an exact solution describing the perturbation in the exterior region was given by RKF). By plugging the first of equalities (4.18) into (4.5), we get the asymptotic form of the unsteady wave,
$|\unicode[STIX]{x1D6FD}|mr/|\unicode[STIX]{x1D714}|\gg 1$
), given by equation (4.5) (an exact solution describing the perturbation in the exterior region was given by RKF). By plugging the first of equalities (4.18) into (4.5), we get the asymptotic form of the unsteady wave,
The solution (4.19) dies out rapidly as
![]() $r\rightarrow \infty$
, as does the stationary edge-wave solution (4.17), yet it has also a radial wave pattern like the stationary radiating-wave solution (4.5). According to equation (4.19) the fronts
$r\rightarrow \infty$
, as does the stationary edge-wave solution (4.17), yet it has also a radial wave pattern like the stationary radiating-wave solution (4.5). According to equation (4.19) the fronts
![]() $\unicode[STIX]{x1D719}=\text{const.}$
of the outward-propagating wave
$\unicode[STIX]{x1D719}=\text{const.}$
of the outward-propagating wave
![]() $\unicode[STIX]{x1D713}_{1}$
in the asymptotic regime
$\unicode[STIX]{x1D713}_{1}$
in the asymptotic regime
![]() $r\gg |\unicode[STIX]{x1D714}|/m\unicode[STIX]{x1D6FD}$
are the lines
$r\gg |\unicode[STIX]{x1D714}|/m\unicode[STIX]{x1D6FD}$
are the lines
where
![]() $\unicode[STIX]{x1D6F7}$
is an arbitrary constant ranging from
$\unicode[STIX]{x1D6F7}$
is an arbitrary constant ranging from
![]() $0$
to
$0$
to
![]() $2\unicode[STIX]{x03C0}$
. Being forced by the growing perturbation at the outer PV step, this wave may propagate either clockwise or counterclockwise depending on the forcing, and in any case its asymptotic fronts (determined by equation (4.20) for
$2\unicode[STIX]{x03C0}$
. Being forced by the growing perturbation at the outer PV step, this wave may propagate either clockwise or counterclockwise depending on the forcing, and in any case its asymptotic fronts (determined by equation (4.20) for
![]() $r\rightarrow \infty$
) are spirals unwinding in the same direction as in stationary radiating waves. A typical vorticity field of this wave and its fronts are plotted in figure 8(a). By virtue of (4.19), the parameter
$r\rightarrow \infty$
) are spirals unwinding in the same direction as in stationary radiating waves. A typical vorticity field of this wave and its fronts are plotted in figure 8(a). By virtue of (4.19), the parameter
![]() $\unicode[STIX]{x1D6FF}$
represents the rate of spatial decay of the wave, in the sense that the wave’s characteristic radial length scale is
$\unicode[STIX]{x1D6FF}$
represents the rate of spatial decay of the wave, in the sense that the wave’s characteristic radial length scale is
![]() $1/4m|\unicode[STIX]{x1D6FD}|\unicode[STIX]{x1D6FF}^{2}$
, while the parameter
$1/4m|\unicode[STIX]{x1D6FD}|\unicode[STIX]{x1D6FF}^{2}$
, while the parameter
![]() $\unicode[STIX]{x1D6FE}$
characterizes the curvature of the spirals. From now on, we term
$\unicode[STIX]{x1D6FE}$
characterizes the curvature of the spirals. From now on, we term
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
the curvature of the spirals and the rate of spatial decay the wave, respectively. The profiles of
$\unicode[STIX]{x1D6FF}$
the curvature of the spirals and the rate of spatial decay the wave, respectively. The profiles of
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
as functions of
$\unicode[STIX]{x1D6FF}$
as functions of
![]() $g/|\unicode[STIX]{x1D70E}|$
are shown in figure 8(b), for the two possible propagation directions of the perturbations, for
$g/|\unicode[STIX]{x1D70E}|$
are shown in figure 8(b), for the two possible propagation directions of the perturbations, for
![]() $\unicode[STIX]{x1D70E}>0$
and
$\unicode[STIX]{x1D70E}>0$
and
![]() $\unicode[STIX]{x1D70E}<0$
.
$\unicode[STIX]{x1D70E}<0$
.

Figure 8. Properties of growing waves on the beta cone for
![]() $m=2$
and
$m=2$
and
![]() $\unicode[STIX]{x1D6FD}=-0.1$
. (a) Vorticity distribution for
$\unicode[STIX]{x1D6FD}=-0.1$
. (a) Vorticity distribution for
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70E}$
+
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70E}$
+
![]() $g\text{i}=0.03+0.05$
i at
$g\text{i}=0.03+0.05$
i at
![]() $3<r<12$
(colours as in figure 2), and the asymptotic wave fronts determined by equation (4.20) (marked by solid lines). (b) The curvature of the spirals,
$3<r<12$
(colours as in figure 2), and the asymptotic wave fronts determined by equation (4.20) (marked by solid lines). (b) The curvature of the spirals,
![]() $\unicode[STIX]{x1D6FE}$
, and the rate of spatial decay of the wave,
$\unicode[STIX]{x1D6FE}$
, and the rate of spatial decay of the wave,
![]() $\unicode[STIX]{x1D6FF}$
, as functions of the ratio
$\unicode[STIX]{x1D6FF}$
, as functions of the ratio
![]() $g/|\unicode[STIX]{x1D70E}|$
of the growth rate
$g/|\unicode[STIX]{x1D70E}|$
of the growth rate
![]() $g$
and the magnitude of the angular phase velocity
$g$
and the magnitude of the angular phase velocity
![]() $|\unicode[STIX]{x1D70E}|$
. The dotted line (blue) represents
$|\unicode[STIX]{x1D70E}|$
. The dotted line (blue) represents
![]() $\unicode[STIX]{x1D6FE}$
(at
$\unicode[STIX]{x1D6FE}$
(at
![]() $\unicode[STIX]{x1D70E}<0$
) or
$\unicode[STIX]{x1D70E}<0$
) or
![]() $\unicode[STIX]{x1D6FF}$
(at
$\unicode[STIX]{x1D6FF}$
(at
![]() $\unicode[STIX]{x1D70E}>0$
), and the solid line (red),
$\unicode[STIX]{x1D70E}>0$
), and the solid line (red),
![]() $\unicode[STIX]{x1D6FF}$
(at
$\unicode[STIX]{x1D6FF}$
(at
![]() $\unicode[STIX]{x1D70E}<0$
) or
$\unicode[STIX]{x1D70E}<0$
) or
![]() $\unicode[STIX]{x1D6FE}$
(at
$\unicode[STIX]{x1D6FE}$
(at
![]() $\unicode[STIX]{x1D70E}>0$
).
$\unicode[STIX]{x1D70E}>0$
).
It is instructive to examine the properties of a non-stationary wave when the growth rate is close to zero (yet the phase velocity of the perturbation is not zero). This corresponds to the case where any of the flow parameters (such as
![]() $R_{1},R_{2}$
or
$R_{1},R_{2}$
or
![]() $\unicode[STIX]{x1D6FD}$
) is close to its bifurcation value, which distinguishes between stable and unstable regimes (see RKF for a discussion on the bifurcation due to variation in
$\unicode[STIX]{x1D6FD}$
) is close to its bifurcation value, which distinguishes between stable and unstable regimes (see RKF for a discussion on the bifurcation due to variation in
![]() $\unicode[STIX]{x1D6FD}$
). Near the bifurcation point,
$\unicode[STIX]{x1D6FD}$
). Near the bifurcation point,
![]() $g^{2}\ll \unicode[STIX]{x1D70E}^{2}$
, so we may evaluate
$g^{2}\ll \unicode[STIX]{x1D70E}^{2}$
, so we may evaluate
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
to the first order in
$\unicode[STIX]{x1D6FF}$
to the first order in
![]() $g/\unicode[STIX]{x1D70E}$
from (4.18). We discriminate two cases according to the rotation direction of the unstable perturbation.
$g/\unicode[STIX]{x1D70E}$
from (4.18). We discriminate two cases according to the rotation direction of the unstable perturbation.
When the perturbation propagates clockwise (
![]() $\unicode[STIX]{x1D70E}<0$
), we get
$\unicode[STIX]{x1D70E}<0$
), we get
(see also figure 8
b). Substitution of (4.21) in (4.19) shows that in the limit
![]() $g\rightarrow 0$
the non-stationary wave (4.19) matches the stationary radiating Rossby wave (4.5). Since
$g\rightarrow 0$
the non-stationary wave (4.19) matches the stationary radiating Rossby wave (4.5). Since
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
as
$\unicode[STIX]{x1D6FF}\rightarrow 0$
as
![]() $g\rightarrow 0$
, near the bifurcation point the spatial extent of the wave gets wider; thus, energy can be drained to regions distant from the uniform-PV rings.
$g\rightarrow 0$
, near the bifurcation point the spatial extent of the wave gets wider; thus, energy can be drained to regions distant from the uniform-PV rings.
When the perturbation propagates counterclockwise (i.e.
![]() $\unicode[STIX]{x1D70E}>0$
), we get
$\unicode[STIX]{x1D70E}>0$
), we get
(see also figure 8
b). Substitution of (4.22) in (4.19) shows that, in the limit of
![]() $g\rightarrow 0$
, the growing wave (4.19) matches the stationary edge wave (4.17). Since
$g\rightarrow 0$
, the growing wave (4.19) matches the stationary edge wave (4.17). Since
![]() $\unicode[STIX]{x1D6FF}\rightarrow 1/\sqrt{\unicode[STIX]{x1D70E}}\neq 0$
as
$\unicode[STIX]{x1D6FF}\rightarrow 1/\sqrt{\unicode[STIX]{x1D70E}}\neq 0$
as
![]() $g\rightarrow 0$
, so this is not the case of radiating instability. Close to the bifurcation point, when instability shows up, the wave is localized in the island’s vicinity with a characteristic radial length scale of
$g\rightarrow 0$
, so this is not the case of radiating instability. Close to the bifurcation point, when instability shows up, the wave is localized in the island’s vicinity with a characteristic radial length scale of
![]() $|\unicode[STIX]{x1D70E}/4m\unicode[STIX]{x1D6FD}|$
.
$|\unicode[STIX]{x1D70E}/4m\unicode[STIX]{x1D6FD}|$
.
Based on the abovesaid and following Talley (Reference Talley1983), Kamenkovich & Pedlosky (Reference Kamenkovich and Pedlosky1996) and RKF, we identify the growing waves as radiating or trapped, according to the structure of the contiguous stationary wave, which can be either alternating in the radial direction, as in (4.5), or evanescent as in (4.17). Thus, regarding the general expression for the non-stationary wave (4.19), the case of
![]() $\unicode[STIX]{x1D70E}<0$
(
$\unicode[STIX]{x1D70E}<0$
(
![]() $\unicode[STIX]{x1D70E}>0$
) will be referred to as radiating (trapped) wave. We note that for
$\unicode[STIX]{x1D70E}>0$
) will be referred to as radiating (trapped) wave. We note that for
![]() $\unicode[STIX]{x1D6FD}>0$
, the propagation directions of the radiating and trapped waves are opposite to those at
$\unicode[STIX]{x1D6FD}>0$
, the propagation directions of the radiating and trapped waves are opposite to those at
![]() $\unicode[STIX]{x1D6FD}<0$
, and the non-stationary waves change their identification as radiating or trapped accordingly.
$\unicode[STIX]{x1D6FD}<0$
, and the non-stationary waves change their identification as radiating or trapped accordingly.
Growing perturbations may also occur on the
![]() $f$
-plane (i.e. where
$f$
-plane (i.e. where
![]() $\unicode[STIX]{x1D6FD}=0$
). In this case one cannot take directly the limit of
$\unicode[STIX]{x1D6FD}=0$
). In this case one cannot take directly the limit of
![]() $\unicode[STIX]{x1D6FD}\rightarrow 0$
in relation (4.19), since the latter is valid only for
$\unicode[STIX]{x1D6FD}\rightarrow 0$
in relation (4.19), since the latter is valid only for
![]() $|\unicode[STIX]{x1D6FD}|mr/|\unicode[STIX]{x1D714}|\gg 1$
. Instead, the limit
$|\unicode[STIX]{x1D6FD}|mr/|\unicode[STIX]{x1D714}|\gg 1$
. Instead, the limit
![]() $\unicode[STIX]{x1D6FD}\rightarrow 0$
can be taken in the expressions (4.4) or (4.16) using their Laurent-series expansion around zero (see e.g. RKF). The growing wave is then
$\unicode[STIX]{x1D6FD}\rightarrow 0$
can be taken in the expressions (4.4) or (4.16) using their Laurent-series expansion around zero (see e.g. RKF). The growing wave is then
![]() $\unicode[STIX]{x1D713}|_{\unicode[STIX]{x1D6FD}=0}=r^{-m}e^{gt}\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70E}t)}$
. Clearly, this wave carries no vorticity and has no spirality, contrary to the case of
$\unicode[STIX]{x1D713}|_{\unicode[STIX]{x1D6FD}=0}=r^{-m}e^{gt}\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70E}t)}$
. Clearly, this wave carries no vorticity and has no spirality, contrary to the case of
![]() $\unicode[STIX]{x1D6FD}\neq 0$
.
$\unicode[STIX]{x1D6FD}\neq 0$
.
5 Beta effect at steep slopes. Formation of quasi-steady patterns
5.1 Phase locking of growing perturbations

Figure 9. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.3$
,
$\unicode[STIX]{x1D6FD}=-0.3$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=1$
,
$\unicode[STIX]{x1D6E4}_{1}=1$
,
![]() $R_{1}=2.5$
and
$R_{1}=2.5$
and
![]() $R_{2}=4$
, where mode 2 is most unstable. Colours and notations are as in figure 2. Solid white arrow (
$R_{2}=4$
, where mode 2 is most unstable. Colours and notations are as in figure 2. Solid white arrow (
![]() $t=90$
) designates the propagation direction of the perturbation in the shape of the PV rings. Dotted black arrow designates the propagation direction of the wave in the exterior region.
$t=90$
) designates the propagation direction of the perturbation in the shape of the PV rings. Dotted black arrow designates the propagation direction of the wave in the exterior region.

Figure 10. Temporal evolution of the mode-2 waves on the inner and outer liquid contours
![]() $r=R_{1}=2.5$
and
$r=R_{1}=2.5$
and
![]() $r=R_{2}=4$
, and in the exterior region at
$r=R_{2}=4$
, and in the exterior region at
![]() $r=6$
and
$r=6$
and
![]() $r=10$
. (a) Amplitude (logarithmic scale); the dashed black line indicates the theoretically estimated growth rate (only the slope of this line is meaningful). (b) Phase. The flow parameters as in figure 9.
$r=10$
. (a) Amplitude (logarithmic scale); the dashed black line indicates the theoretically estimated growth rate (only the slope of this line is meaningful). (b) Phase. The flow parameters as in figure 9.
While at weak slopes (
![]() $\unicode[STIX]{x1D6FD}=-0.01$
) the beta effect is well pronounced only at relatively large distances (§ 3), at steeper slopes it becomes visible already in the region where formation of dipoles is expected to begin, i.e. next to the outer PV ring. Figure 9 shows the evolution of a counterclockwise flow at
$\unicode[STIX]{x1D6FD}=-0.01$
) the beta effect is well pronounced only at relatively large distances (§ 3), at steeper slopes it becomes visible already in the region where formation of dipoles is expected to begin, i.e. next to the outer PV ring. Figure 9 shows the evolution of a counterclockwise flow at
![]() $\unicode[STIX]{x1D6FD}=-0.3,R_{1}=2.5$
and
$\unicode[STIX]{x1D6FD}=-0.3,R_{1}=2.5$
and
![]() $R_{2}=4$
, where the gravest unstable mode is
$R_{2}=4$
, where the gravest unstable mode is
![]() $m=2$
. Until about
$m=2$
. Until about
![]() $t=30$
, the deformation of the vorticity rings is similar to that in the flat-bottom case (see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013) as well as in the weak-slope case (figures 2 and 4). However, at
$t=30$
, the deformation of the vorticity rings is similar to that in the flat-bottom case (see Kizner et al.
Reference Kizner, Makarov, Kamp and van Heijst2013) as well as in the weak-slope case (figures 2 and 4). However, at
![]() $\unicode[STIX]{x1D6FD}=-0.3$
, the closed flow does not emit any dipoles, and remains organized in a two-ring pattern.
$\unicode[STIX]{x1D6FD}=-0.3$
, the closed flow does not emit any dipoles, and remains organized in a two-ring pattern.
When the flow is unstable, the growing perturbation of the shape of the outer liquid contour forces the development of a spiral wave outside this contour, in the region where originally the velocity was zero. In the linear approximation, one may talk of the development of a wave just at
![]() $r>R_{2}$
, while the perturbations in the shapes of the liquid contours can be interpreted as two Rossby waves that develop just at the basic PV discontinuity contours,
$r>R_{2}$
, while the perturbations in the shapes of the liquid contours can be interpreted as two Rossby waves that develop just at the basic PV discontinuity contours,
![]() $r=R_{1}$
and
$r=R_{1}$
and
![]() $r=R_{2}$
. As known for parallel flows, the growth of the waves developing on the PV discontinuities is caused by their phase locking (see e.g. Heifetz, Bishop & Alpert Reference Heifetz, Bishop and Alpert1999; Vallis Reference Vallis2017). This is also observed in our simulations for the case of circular flows. Figure 10 shows the amplitude and phase of the azimuthal mode-2 Fourier component (denoted by
$r=R_{2}$
. As known for parallel flows, the growth of the waves developing on the PV discontinuities is caused by their phase locking (see e.g. Heifetz, Bishop & Alpert Reference Heifetz, Bishop and Alpert1999; Vallis Reference Vallis2017). This is also observed in our simulations for the case of circular flows. Figure 10 shows the amplitude and phase of the azimuthal mode-2 Fourier component (denoted by
![]() $\hat{\unicode[STIX]{x1D701}}_{2}$
) of the vorticity field at
$\hat{\unicode[STIX]{x1D701}}_{2}$
) of the vorticity field at
![]() $r=R_{1}=2.5$
and
$r=R_{1}=2.5$
and
![]() $r=R_{2}=4$
(i.e. where the basic-PV jumps occur), and in the exterior region at the circles
$r=R_{2}=4$
(i.e. where the basic-PV jumps occur), and in the exterior region at the circles
![]() $r=6$
and
$r=6$
and
![]() $r=10$
. As expected, after some period that takes for mode 2 to get established (but while the perturbation is still small), the stage of exponential growth of the amplitudes of the waves begins (figure 10
a) being accompanied by phase locking (figure 10
b). Here, that a third wave exists at
$r=10$
. As expected, after some period that takes for mode 2 to get established (but while the perturbation is still small), the stage of exponential growth of the amplitudes of the waves begins (figure 10
a) being accompanied by phase locking (figure 10
b). Here, that a third wave exists at
![]() $r>R_{2}$
, outside the contours
$r>R_{2}$
, outside the contours
![]() $r=R_{1}$
and
$r=R_{1}$
and
![]() $r=R_{2}$
, the phase locking occurs between the three waves. This stage lasts as long as the nonlinearity is reasonably small.
$r=R_{2}$
, the phase locking occurs between the three waves. This stage lasts as long as the nonlinearity is reasonably small.
According to the results of our linear stability analysis (RKF), at the chosen values of the governing parameters
![]() $\unicode[STIX]{x1D6FD}=-0.3,R_{1}=2.5$
, and
$\unicode[STIX]{x1D6FD}=-0.3,R_{1}=2.5$
, and
![]() $R_{2}=4$
, the mode-2 perturbation must run counterclockwise with the angular frequency
$R_{2}=4$
, the mode-2 perturbation must run counterclockwise with the angular frequency
![]() $\unicode[STIX]{x1D70E}\approx 0.07$
, the growth rate being
$\unicode[STIX]{x1D70E}\approx 0.07$
, the growth rate being
![]() $g\approx 0.053$
. Therefore, at the quasi-linear stage of the instability growth, the perturbation induced in the exterior region and having a spiral shape propagates counterclockwise as well; this can be observed in figure 10, where at
$g\approx 0.053$
. Therefore, at the quasi-linear stage of the instability growth, the perturbation induced in the exterior region and having a spiral shape propagates counterclockwise as well; this can be observed in figure 10, where at
![]() $40\leqslant t\leqslant 100$
, the gradients of the almost straight lines correspond well to the theoretically estimated values of
$40\leqslant t\leqslant 100$
, the gradients of the almost straight lines correspond well to the theoretically estimated values of
![]() $g$
indicated in figure 10(a) by a dashed line (only its slope makes sense).
$g$
indicated in figure 10(a) by a dashed line (only its slope makes sense).
At a later, nonlinear stage, when the perturbations actually do not grow, a Rossby wave behaving in a quasi-stationary manner develops in the exterior region. Since the exterior PV field has a radially alternating pattern, we are dealing here with a radiating wave which can propagate only clockwise. This is confirmed by the negative gradients of the phase at
![]() $r=6$
and
$r=6$
and
![]() $r=10$
when
$r=10$
when
![]() $t>110$
(figure 10
b). As the energy flux goes outwards (according to the typical ray trajectory in figure 7
c), distant parts of the spirals become more pronounced with the passage of time (
$t>110$
(figure 10
b). As the energy flux goes outwards (according to the typical ray trajectory in figure 7
c), distant parts of the spirals become more pronounced with the passage of time (
![]() $t=140$
in figure 9).
$t=140$
in figure 9).

Figure 11. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.35$
,
$\unicode[STIX]{x1D6FD}=-0.35$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
,
$\unicode[STIX]{x1D6E4}_{1}=-1$
,
![]() $R_{1}=2.3$
and
$R_{1}=2.3$
and
![]() $R_{2}=3$
, where mode 3 is most unstable. Colours and notations as in figure 2.
$R_{2}=3$
, where mode 3 is most unstable. Colours and notations as in figure 2.
5.2 Prevention of dipole emission. Pattern formation
As seen in figure 9, the developing mode-2 instability manifests itself first in making the two PV rings somewhat oval (
![]() $t=90$
). If the slope were weaker, this might end up in the formation of two dipoles (as was the case of beta
$t=90$
). If the slope were weaker, this might end up in the formation of two dipoles (as was the case of beta
![]() $\unicode[STIX]{x1D6FD}=-0.01$
in figure 2). Such a tendency can be observed e.g. at
$\unicode[STIX]{x1D6FD}=-0.01$
in figure 2). Such a tendency can be observed e.g. at
![]() $t=110$
, but the detachment of the PV lobes does not occur. We attribute this fact to the strong beta effect, namely, to the smoothing of the external boundary of the outer PV ring by the clockwise flow associated with the quasi-steady radiating Rossby wave that establishes in the exterior region (see § 5.1).
$t=110$
, but the detachment of the PV lobes does not occur. We attribute this fact to the strong beta effect, namely, to the smoothing of the external boundary of the outer PV ring by the clockwise flow associated with the quasi-steady radiating Rossby wave that establishes in the exterior region (see § 5.1).
Here, instability does not lead to the emergence of dipoles; instead, the sticking of the main vorticity ‘mass’ to the cylinder at a sufficiently high
![]() $\unicode[STIX]{x1D6FD}$
makes possible the formation of a new, multipolar configuration. Whether this new pattern is long lived or transient depends on the direction of its rotation. For example, as figure 11 suggests, at
$\unicode[STIX]{x1D6FD}$
makes possible the formation of a new, multipolar configuration. Whether this new pattern is long lived or transient depends on the direction of its rotation. For example, as figure 11 suggests, at
![]() $\unicode[STIX]{x1D6FD}=-0.35,\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=2.3$
and
$\unicode[STIX]{x1D6FD}=-0.35,\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=2.3$
and
![]() $R_{2}=3$
, where mode 3 is the most unstable one, the flow passes through a state that resembles a rotating vortex quadrupole (Kizner & Khvoles Reference Kizner and Khvoles2004a
; Kizner et al.
Reference Kizner, Khvoles and McWilliams2007; Trieling, van Heijst & Kizner Reference Trieling, van Heijst and Kizner2010). The direction of the quadrupole rotation is the same as that of the radiating Rossby waves in the exterior, i.e. clockwise; this entails its disintegration at a later stage (see § 4.1).
$R_{2}=3$
, where mode 3 is the most unstable one, the flow passes through a state that resembles a rotating vortex quadrupole (Kizner & Khvoles Reference Kizner and Khvoles2004a
; Kizner et al.
Reference Kizner, Khvoles and McWilliams2007; Trieling, van Heijst & Kizner Reference Trieling, van Heijst and Kizner2010). The direction of the quadrupole rotation is the same as that of the radiating Rossby waves in the exterior, i.e. clockwise; this entails its disintegration at a later stage (see § 4.1).

Figure 12. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.5$
,
$\unicode[STIX]{x1D6FD}=-0.5$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
,
$\unicode[STIX]{x1D6E4}_{1}=-1$
,
![]() $R_{1}=4$
and
$R_{1}=4$
and
![]() $R_{2}=4.6$
, where mode 6 is most unstable. Colours and notations are as in figure 2.
$R_{2}=4.6$
, where mode 6 is most unstable. Colours and notations are as in figure 2.
Vorticity strips start emerging at approximately
![]() $t=90$
, becoming best pronounced at
$t=90$
, becoming best pronounced at
![]() $t\approx 110$
and then gradually merging (at
$t\approx 110$
and then gradually merging (at
![]() $t\approx 140$
). The emergence of the strips can be explained through filamentation and interaction between the vorticity lobes that were generated due to the instability. As the quadrupolar configuration rotates clockwise around the island, each of the positive-vorticity patches emits a tail, and the end of the tail becomes a thin filament (
$t\approx 140$
). The emergence of the strips can be explained through filamentation and interaction between the vorticity lobes that were generated due to the instability. As the quadrupolar configuration rotates clockwise around the island, each of the positive-vorticity patches emits a tail, and the end of the tail becomes a thin filament (
![]() $t=60$
). This filament is caught by the next closest positive-vorticity patch, which travels much faster than the filament. The filament, therefore, rolls over this next patch and its own tail (
$t=60$
). This filament is caught by the next closest positive-vorticity patch, which travels much faster than the filament. The filament, therefore, rolls over this next patch and its own tail (
![]() $t=90$
). This way, because of the close proximity of the vorticity patches, each of them catches the filaments emitted by another. Since the large PV patches rotate synchronously and the filaments move primarily in the azimuthal direction, they eventually arrange in a number of distinct strips.
$t=90$
). This way, because of the close proximity of the vorticity patches, each of them catches the filaments emitted by another. Since the large PV patches rotate synchronously and the filaments move primarily in the azimuthal direction, they eventually arrange in a number of distinct strips.
This clockwise-rotating quadrupolar configuration has traits common with the non-local modon on a beta plane. A non-local modon is a dipole travelling in the direction in which stationary Rossby waves propagate, i.e. westward on a conventional beta plane (with the background PV increasing northward). This is an unstable core of a nonlinear wave that may be described by a formal steady-state solution (Berson & Kizner Reference Berson and Kizner2002). The instability develops especially slow if the perturbations do not break the dipole’s antisymmetry about the
![]() $x$
-axis. In this case, a filament grows slowly in the modon’s wake, being the main cause of the instability growth. In the same sense, the observed quadrupole in figure 11 is non-local, which is indicated by the presence of the long waves surrounding it. The quadrupole’s components only rotate and nearly do not move radially, which is in analogy with keeping the antisymmetry by a non-local modon. As distinct from a non-local modon on the beta plane, here the filament emitted by one vortex is absorbed by the next one; this increases to some extent the lifespan of the quadrupole.
$x$
-axis. In this case, a filament grows slowly in the modon’s wake, being the main cause of the instability growth. In the same sense, the observed quadrupole in figure 11 is non-local, which is indicated by the presence of the long waves surrounding it. The quadrupole’s components only rotate and nearly do not move radially, which is in analogy with keeping the antisymmetry by a non-local modon. As distinct from a non-local modon on the beta plane, here the filament emitted by one vortex is absorbed by the next one; this increases to some extent the lifespan of the quadrupole.
The unsteadiness of the clockwise 3-fold symmetric pattern manifests itself in the radiation of relatively strong Rossby waves emitted within the time interval from
![]() $t=40$
to
$t=40$
to
![]() $t=240$
. By
$t=240$
. By
![]() $t=400$
, a nearly circular clockwise flow with some residues of the 3-fold symmetry arises near the island, and by
$t=400$
, a nearly circular clockwise flow with some residues of the 3-fold symmetry arises near the island, and by
![]() $t=800$
the flow fully stabilizes in a circularly symmetric state. Unlike the basic state at
$t=800$
the flow fully stabilizes in a circularly symmetric state. Unlike the basic state at
![]() $t=0$
, now the PV in the rings is not homogeneous, and the rings are wider: the negative vorticity occurs in the range
$t=0$
, now the PV in the rings is not homogeneous, and the rings are wider: the negative vorticity occurs in the range
![]() $1<r<2.47$
, and the positive vorticity, in the range
$1<r<2.47$
, and the positive vorticity, in the range
![]() $2.47<r<4.5$
. Further, due to viscosity, the vorticity rings continue increasing their width.
$2.47<r<4.5$
. Further, due to viscosity, the vorticity rings continue increasing their width.
An example of emergence of a steady-state
![]() $m$
-fold pattern is shown in figure 12. Here the slope is considerably steeper (
$m$
-fold pattern is shown in figure 12. Here the slope is considerably steeper (
![]() $\unicode[STIX]{x1D6FD}=-0.5$
) and the outer PV ring is much thinner than the inner one;
$\unicode[STIX]{x1D6FD}=-0.5$
) and the outer PV ring is much thinner than the inner one;
![]() $\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=4,R_{2}=4.6$
, and mode 6 is the gravest unstable mode. The mode-6 instability generates six negative-vorticity lobes. But the strong Rossby waves gradually smooth away the negative-vorticity protuberances and filaments, thus making the outer boundary of the flow nearly circular. Since the 6-fold symmetric pattern rotates counterclockwise, that is, oppositely to the propagation direction of the radiating beta-cone Rossby waves, it may be steady (see § 4.1). Indeed, the simulations show that this pattern lasts until the end of the simulation,
$\unicode[STIX]{x1D6E4}_{1}=-1,R_{1}=4,R_{2}=4.6$
, and mode 6 is the gravest unstable mode. The mode-6 instability generates six negative-vorticity lobes. But the strong Rossby waves gradually smooth away the negative-vorticity protuberances and filaments, thus making the outer boundary of the flow nearly circular. Since the 6-fold symmetric pattern rotates counterclockwise, that is, oppositely to the propagation direction of the radiating beta-cone Rossby waves, it may be steady (see § 4.1). Indeed, the simulations show that this pattern lasts until the end of the simulation,
![]() $t=1000$
.
$t=1000$
.
In the last three simulations (figures 9–12) the absorbing-layer approach (§ 2.2) was used. Due to the relatively large values of
![]() $\unicode[STIX]{x1D6FD}$
, the Rossby waves emitted by the main flow were not negligible; thus, without the absorbing layer, the reflection from the outer boundary of the computational domain might have been significant.
$\unicode[STIX]{x1D6FD}$
, the Rossby waves emitted by the main flow were not negligible; thus, without the absorbing layer, the reflection from the outer boundary of the computational domain might have been significant.
Considering the results presented in §§ 3 and 5 we see that the bottom slope has a significant effect on the flow evolution only when the term
![]() $\unicode[STIX]{x1D6FD}r$
appearing in equation (2.2) is comparable in magnitude with the relative vorticity
$\unicode[STIX]{x1D6FD}r$
appearing in equation (2.2) is comparable in magnitude with the relative vorticity
![]() $\unicode[STIX]{x1D701}$
. In § 3, we considered basic flows with the maximal radius of the outer PV ring being 4 or less, and
$\unicode[STIX]{x1D701}$
. In § 3, we considered basic flows with the maximal radius of the outer PV ring being 4 or less, and
![]() $\unicode[STIX]{x1D6FD}=-0.01$
. So at the external boundary of the outer PV ring the term
$\unicode[STIX]{x1D6FD}=-0.01$
. So at the external boundary of the outer PV ring the term
![]() $\unicode[STIX]{x1D6FD}r$
was of order 0.04, which is really small compared to the relative vorticity of the flow (order 1 in the rings). The topographic effect in these simulations became noticeable only when the dipoles moved a considerable distance away from the island. In contrast, in the basic flows considered in the present section,
$\unicode[STIX]{x1D6FD}r$
was of order 0.04, which is really small compared to the relative vorticity of the flow (order 1 in the rings). The topographic effect in these simulations became noticeable only when the dipoles moved a considerable distance away from the island. In contrast, in the basic flows considered in the present section,
![]() $\unicode[STIX]{x1D6FD}R_{2}$
was of order 1 or higher, i.e. comparable with the relative vorticity in the rings; so, the topographic effect was significant already in close proximity of the island and not at far distances, and the bottom slope serves as a strong stabilizing factor in this case. These observations suggest that, along with
$\unicode[STIX]{x1D6FD}R_{2}$
was of order 1 or higher, i.e. comparable with the relative vorticity in the rings; so, the topographic effect was significant already in close proximity of the island and not at far distances, and the bottom slope serves as a strong stabilizing factor in this case. These observations suggest that, along with
![]() $\unicode[STIX]{x1D6FD}$
itself, the parameter
$\unicode[STIX]{x1D6FD}$
itself, the parameter
![]() $\unicode[STIX]{x1D6FD}R_{2}$
determines the type of evolution. Thus, when
$\unicode[STIX]{x1D6FD}R_{2}$
determines the type of evolution. Thus, when
![]() $\unicode[STIX]{x1D6FD}R_{2}\ll 1$
, we regard the slope as weak, while at
$\unicode[STIX]{x1D6FD}R_{2}\ll 1$
, we regard the slope as weak, while at
![]() $\unicode[STIX]{x1D6FD}R_{2}$
of order 1 or higher, the slope can be regarded as steep. In the next section we consider the evolution of unstable flows over moderate slopes, i.e. in the cases where
$\unicode[STIX]{x1D6FD}R_{2}$
of order 1 or higher, the slope can be regarded as steep. In the next section we consider the evolution of unstable flows over moderate slopes, i.e. in the cases where
![]() $\unicode[STIX]{x1D6FD}R_{2}$
is smaller than one, but not by an order of magnitude.
$\unicode[STIX]{x1D6FD}R_{2}$
is smaller than one, but not by an order of magnitude.
6 Beta effect at moderate slopes
6.1 Mode-1 instability

Figure 13. Mode-1 instability at
![]() $\unicode[STIX]{x1D6FD}=-0.1$
,
$\unicode[STIX]{x1D6FD}=-0.1$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
,
$\unicode[STIX]{x1D6E4}_{1}=-1$
,
![]() $R_{1}=2$
and
$R_{1}=2$
and
![]() $R_{2}=8$
. (a) Profiles of the basic-flow potential vorticity
$R_{2}=8$
. (a) Profiles of the basic-flow potential vorticity
![]() $\bar{Q}$
(dashed, blue), azimuthal velocity
$\bar{Q}$
(dashed, blue), azimuthal velocity
![]() $\bar{V}$
(solid, red) and vorticity
$\bar{V}$
(solid, red) and vorticity
![]() $\bar{\unicode[STIX]{x1D701}}$
(double, green). (b) Evolution of the vorticity field. Colours and notations as in figure 2. (c) Evolution of the PV field: magenta marks the outer-ring PV and blue, the inner-ring and the exterior PV. Notations as in figure 2.
$\bar{\unicode[STIX]{x1D701}}$
(double, green). (b) Evolution of the vorticity field. Colours and notations as in figure 2. (c) Evolution of the PV field: magenta marks the outer-ring PV and blue, the inner-ring and the exterior PV. Notations as in figure 2.
As explained in RKF, the mode-1 instability emerges in the presence of bottom topography only. Because of this special character, and for the completeness of the discussion on the possible evolution scenarios, we briefly present in this section our results related to the mode-1 instability.
According to our simulations, at weak slopes (when
![]() $\unicode[STIX]{x1D6FD}$
is of order 0.01) the mode-1 instabilities do not develop to large scales, and this is due to the low growth rate of the perturbation. The waves at the liquid contours grow at such a long time scale, that the tendency of viscosity to diffuse them manages to cease their growth to a noticeable magnitude. Therefore, the flow remains relatively close to its basic configuration (but with a smoothed radial PV profile).
$\unicode[STIX]{x1D6FD}$
is of order 0.01) the mode-1 instabilities do not develop to large scales, and this is due to the low growth rate of the perturbation. The waves at the liquid contours grow at such a long time scale, that the tendency of viscosity to diffuse them manages to cease their growth to a noticeable magnitude. Therefore, the flow remains relatively close to its basic configuration (but with a smoothed radial PV profile).
Figure 13 illustrates the evolution of the flow in the case of
![]() $\unicode[STIX]{x1D6FD}=-0.1$
,
$\unicode[STIX]{x1D6FD}=-0.1$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
,
$\unicode[STIX]{x1D6E4}_{1}=-1$
,
![]() $R_{1}=2$
and
$R_{1}=2$
and
![]() $R_{2}=8$
, when mode 1 is unstable. The basic flow (figure 13
a) is composed of two rings, whose PVs are
$R_{2}=8$
, when mode 1 is unstable. The basic flow (figure 13
a) is composed of two rings, whose PVs are
![]() $-1$
(inner ring) and
$-1$
(inner ring) and
![]() $-0.517$
(outer ring). The relative vorticity changes sign inside the outer ring, at
$-0.517$
(outer ring). The relative vorticity changes sign inside the outer ring, at
![]() $r=5.18$
, and, watching the evolution of the relative vorticity (figure 13
b) might be somewhat misleading. This is why we present here also the evolution of the PV (figure 13
c). As might be seen in this figure, no dipoles (or neighbouring positive- and negative-vorticity lobes) emerge due to the mode-1 instability, which fact sets this case apart from the above-considered scenarios with
$r=5.18$
, and, watching the evolution of the relative vorticity (figure 13
b) might be somewhat misleading. This is why we present here also the evolution of the PV (figure 13
c). As might be seen in this figure, no dipoles (or neighbouring positive- and negative-vorticity lobes) emerge due to the mode-1 instability, which fact sets this case apart from the above-considered scenarios with
![]() $m\geqslant 2$
(§§ 3 and 5). The two PV patches remain clearly distinguishable until at least
$m\geqslant 2$
(§§ 3 and 5). The two PV patches remain clearly distinguishable until at least
![]() $t=560$
, when strong filamentation of the inner patch begins. During the first stage of the instability development, the centres of PV mass of the two rings become a little shifted and the shapes of the rings deformed. The instability manifests itself most clearly in the change undergone by the inner ring (
$t=560$
, when strong filamentation of the inner patch begins. During the first stage of the instability development, the centres of PV mass of the two rings become a little shifted and the shapes of the rings deformed. The instability manifests itself most clearly in the change undergone by the inner ring (
![]() $510\leqslant t\leqslant 560$
). This corresponds to the observation made in the flat-bottom case by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013), who noted that in the case where the inner ring is thin relative to the outer ring, the outer ring undergoes only minor deformations. In our simulation, however, unlike the flat-bottom case, the inner ring separates from the island at approximately
$510\leqslant t\leqslant 560$
). This corresponds to the observation made in the flat-bottom case by Kizner et al. (Reference Kizner, Makarov, Kamp and van Heijst2013), who noted that in the case where the inner ring is thin relative to the outer ring, the outer ring undergoes only minor deformations. In our simulation, however, unlike the flat-bottom case, the inner ring separates from the island at approximately
![]() $t=600$
and becomes a thin filament wandering inside the outer ring. At a later stage, the growing instability leads to erosion of the inner ring due to the emergence of additional filaments (
$t=600$
and becomes a thin filament wandering inside the outer ring. At a later stage, the growing instability leads to erosion of the inner ring due to the emergence of additional filaments (
![]() $t=730$
); here, signs of chaotic advection can be noticed.
$t=730$
); here, signs of chaotic advection can be noticed.
6.2 Instabilities of mode
 $m\geqslant 2$
$m\geqslant 2$

Figure 14. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.1,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
$\unicode[STIX]{x1D6FD}=-0.1,\unicode[STIX]{x1D6E4}_{1}=1,R_{1}=2.5$
and
![]() $R_{2}=4$
, where mode 2 is most unstable. Colours and notations as in figure 2.
$R_{2}=4$
, where mode 2 is most unstable. Colours and notations as in figure 2.
The evolution of mode-2 instability in the case of a counterclockwise flow over an intermediate slope (
![]() $\unicode[STIX]{x1D6FD}=-0.1$
) is shown in figure 14. In this case, a structure forms, reminiscent of the vortex tripole revealed in laboratory experiments (van Heijst & Kloosterziel Reference van Heijst and Kloosterziel1989; Kloosterziel & van Heijst Reference Kloosterziel and van Heijst1991) and in numerical simulations (Carton, Flierl & Polvani Reference Carton, Flierl and Polvani1989; Carton & Legras Reference Carton and Legras1994; Morel & Carton Reference Morel and Carton1994); similar semi-analytical solutions on the
$\unicode[STIX]{x1D6FD}=-0.1$
) is shown in figure 14. In this case, a structure forms, reminiscent of the vortex tripole revealed in laboratory experiments (van Heijst & Kloosterziel Reference van Heijst and Kloosterziel1989; Kloosterziel & van Heijst Reference Kloosterziel and van Heijst1991) and in numerical simulations (Carton, Flierl & Polvani Reference Carton, Flierl and Polvani1989; Carton & Legras Reference Carton and Legras1994; Morel & Carton Reference Morel and Carton1994); similar semi-analytical solutions on the
![]() $f$
-plane were described by Kizner & Khvoles (Reference Kizner and Khvoles2004a
,Reference Kizner and Khvoles
b
), and on the and
$f$
-plane were described by Kizner & Khvoles (Reference Kizner and Khvoles2004a
,Reference Kizner and Khvoles
b
), and on the and
![]() $\unicode[STIX]{x1D6FE}$
-plane by Kizner et al. (Reference Kizner, Khvoles and McWilliams2007). The positive- and negative-vorticity lobes develop by
$\unicode[STIX]{x1D6FE}$
-plane by Kizner et al. (Reference Kizner, Khvoles and McWilliams2007). The positive- and negative-vorticity lobes develop by
![]() $t=100$
and form two dipoles, whose positive-vorticity parts stay attached to the island. The negative-vorticity parts of the dipoles, being weaker in value and less compact compared to their positive-vorticity partners, become thinner with time and break into filaments that eventually spread out (due to viscosity) around the positive-vorticity core.
$t=100$
and form two dipoles, whose positive-vorticity parts stay attached to the island. The negative-vorticity parts of the dipoles, being weaker in value and less compact compared to their positive-vorticity partners, become thinner with time and break into filaments that eventually spread out (due to viscosity) around the positive-vorticity core.
In figure 15, the flow evolution at the same slope (
![]() $\unicode[STIX]{x1D6FD}=-0.1$
) is shown. Here
$\unicode[STIX]{x1D6FD}=-0.1$
) is shown. Here
![]() $\unicode[STIX]{x1D6E4}_{1}=+1$
,
$\unicode[STIX]{x1D6E4}_{1}=+1$
,
![]() $R_{1}=1.5$
and
$R_{1}=1.5$
and
![]() $R_{2}=2$
. Now not only the gravest unstable mode is higher (
$R_{2}=2$
. Now not only the gravest unstable mode is higher (
![]() $m=4$
), but also the area of each ring is smaller than in figure 14. In this case, four dipoles are emitted due to the instability of the basic flow. Compared to the weak-slope case (figure 2), the dipoles travel a shorter distance from the origin (approximately 3 by
$m=4$
), but also the area of each ring is smaller than in figure 14. In this case, four dipoles are emitted due to the instability of the basic flow. Compared to the weak-slope case (figure 2), the dipoles travel a shorter distance from the origin (approximately 3 by
![]() $t=70$
) before they start coming back to the cylinder. Close to the cylinder, where the four dipoles collide, spiral vorticity patterns emerge due to the relatively high magnitude of
$t=70$
) before they start coming back to the cylinder. Close to the cylinder, where the four dipoles collide, spiral vorticity patterns emerge due to the relatively high magnitude of
![]() $\unicode[STIX]{x1D6FD}$
; these are the radiating Rossby waves discussed in § 4.
$\unicode[STIX]{x1D6FD}$
; these are the radiating Rossby waves discussed in § 4.

Figure 15. Evolution of the vorticity field at
![]() $\unicode[STIX]{x1D6FD}=-0.1$
,
$\unicode[STIX]{x1D6FD}=-0.1$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=1$
,
$\unicode[STIX]{x1D6E4}_{1}=1$
,
![]() $R_{1}=1.5$
and
$R_{1}=1.5$
and
![]() $R_{2}=2$
, where mode 4 is most unstable. Colours and notations as in figure 2.
$R_{2}=2$
, where mode 4 is most unstable. Colours and notations as in figure 2.

Figure 16. Evolution of the vorticity at
![]() $\unicode[STIX]{x1D6FD}=-0.1$
,
$\unicode[STIX]{x1D6FD}=-0.1$
,
![]() $\unicode[STIX]{x1D6E4}_{1}=-1$
,
$\unicode[STIX]{x1D6E4}_{1}=-1$
,
![]() $R_{1}=1.5$
and
$R_{1}=1.5$
and
![]() $R_{2}=2$
, where mode 2 is most unstable. Colours and notations as in figure 2.
$R_{2}=2$
, where mode 2 is most unstable. Colours and notations as in figure 2.

Figure 17. Radial profiles of the flow shown in figure 16. (a) The initial (basic) PV profile
![]() $\bar{Q}$
(blue), the azimuthally averaged vorticity profile
$\bar{Q}$
(blue), the azimuthally averaged vorticity profile
![]() $\hat{\unicode[STIX]{x1D701}}$
at
$\hat{\unicode[STIX]{x1D701}}$
at
![]() $t=600$
(green) and the azimuthally averaged PV profile
$t=600$
(green) and the azimuthally averaged PV profile
![]() $\hat{\unicode[STIX]{x1D701}}+\unicode[STIX]{x1D6FD}r$
at
$\hat{\unicode[STIX]{x1D701}}+\unicode[STIX]{x1D6FD}r$
at
![]() $t=600$
(red). (b) The initial (basic) azimuthal velocity profile
$t=600$
(red). (b) The initial (basic) azimuthal velocity profile
![]() $\bar{V}$
(blue), and the azimuthally averaged velocity profile
$\bar{V}$
(blue), and the azimuthally averaged velocity profile
![]() $\hat{v}$
at
$\hat{v}$
at
![]() $t=600$
(red). Parameters as in figure 16.
$t=600$
(red). Parameters as in figure 16.
6.3 Inversion of the near-island flow at mode-2 instability
As we saw, a weak slope affects the paths followed by the emitted dipoles (§ 3), while at sufficiently steep slopes, dipoles are not emitted at all (§ 4). Moderate slopes with initially clockwise flows offer a new situation, where the dipoles are emitted, yet are subject to strong interaction with the Rossby waves.
Figure 16 shows the evolution of an initially clockwise flow (
![]() $\unicode[STIX]{x1D6E4}=-1$
) in the case of
$\unicode[STIX]{x1D6E4}=-1$
) in the case of
![]() $\unicode[STIX]{x1D6FD}=-0.1$
, with liquid boundaries at
$\unicode[STIX]{x1D6FD}=-0.1$
, with liquid boundaries at
![]() $R_{1}=2.5$
and
$R_{1}=2.5$
and
![]() $R_{2}=4$
. At the initial stage, mode 2 is most unstable, and two dipoles begin forming (
$R_{2}=4$
. At the initial stage, mode 2 is most unstable, and two dipoles begin forming (
![]() $t=146$
). Since the initial flow is clockwise, the azimuthal component of the dipoles’ movement at the beginning is clockwise; this is opposite to the direction permitted for steady-state dipoles. Therefore, at approximately
$t=146$
). Since the initial flow is clockwise, the azimuthal component of the dipoles’ movement at the beginning is clockwise; this is opposite to the direction permitted for steady-state dipoles. Therefore, at approximately
![]() $t=158$
, the dipoles cease moving clockwise, and also slow down moving away from the cylinder. In the subsequent highly unsteady stage, the dipoles swing around, tending to fit the steady-state direction.
$t=158$
, the dipoles cease moving clockwise, and also slow down moving away from the cylinder. In the subsequent highly unsteady stage, the dipoles swing around, tending to fit the steady-state direction.
So far this is similar to the observed behaviour of the dipoles presented in § 3, figure 6. However, now the emerged dipoles (
![]() $t=146$
), while making a swing in their tendency to align themselves to the counterclockwise direction (see § 3), are drifted and obliterated by the relatively strong Rossby waves (
$t=146$
), while making a swing in their tendency to align themselves to the counterclockwise direction (see § 3), are drifted and obliterated by the relatively strong Rossby waves (
![]() $t=158$
to
$t=158$
to
![]() $220$
). Two new quasi-dipolar structures tend to form close to the cylinder (
$220$
). Two new quasi-dipolar structures tend to form close to the cylinder (
![]() $t=158$
); the negative-vorticity parts of these quasi-dipoles emerge from the negative-vorticity parts of the strong Rossby waves at the cylinder’s vicinity (the waves are clearly seen at
$t=158$
); the negative-vorticity parts of these quasi-dipoles emerge from the negative-vorticity parts of the strong Rossby waves at the cylinder’s vicinity (the waves are clearly seen at
![]() $t=158$
as vorticity spirals at the background). At later times, the new negative-vorticity regions get erased by the waves, while the region of pronounced positive vorticity reorganizes into a ring enveloping the cylinder. By
$t=158$
as vorticity spirals at the background). At later times, the new negative-vorticity regions get erased by the waves, while the region of pronounced positive vorticity reorganizes into a ring enveloping the cylinder. By
![]() $t=600$
, an outer, negative vorticity ring is formed. A two-ring structure is observed in the PV distribution too (the vorticity and PV profiles are shown in figure 17
a). Thus, the resulting flow is predominantly counterclockwise, i.e. opposite to the initial flow (figure 17
b).
$t=600$
, an outer, negative vorticity ring is formed. A two-ring structure is observed in the PV distribution too (the vorticity and PV profiles are shown in figure 17
a). Thus, the resulting flow is predominantly counterclockwise, i.e. opposite to the initial flow (figure 17
b).
Even though the resulting state at
![]() $t=600$
is not steady but rather undergoes minor changes in the PV field, it can be regarded as converging to some stable steady state. This stability is confirmed by the fact that the azimuthally averaged PV profile at
$t=600$
is not steady but rather undergoes minor changes in the PV field, it can be regarded as converging to some stable steady state. This stability is confirmed by the fact that the azimuthally averaged PV profile at
![]() $t\geqslant 600$
is a monotonically decreasing function of
$t\geqslant 600$
is a monotonically decreasing function of
![]() $r$
(figure 17
a), which fits the Rayleigh stability criterion (RKF).
$r$
(figure 17
a), which fits the Rayleigh stability criterion (RKF).
7 Conclusion
We studied numerically the evolution of unstable circular flows around an island, with the sea depth increasing offshore. The bottom slope, which is assumed constant, causes topographic beta effect (with
![]() $\unicode[STIX]{x1D6FD}<0$
). The flow is assumed to have zero total circulation and to be composed of two uniform-PV rings. Depending on the sign of the PV in the inner ring, the flow near the island is either counterclockwise, or clockwise.
$\unicode[STIX]{x1D6FD}<0$
). The flow is assumed to have zero total circulation and to be composed of two uniform-PV rings. Depending on the sign of the PV in the inner ring, the flow near the island is either counterclockwise, or clockwise.
At low
![]() $\unicode[STIX]{x1D6FD}$
(of order 0.01 in dimensionless units), in the near-island region, the beta effect upon a counterclockwise flow is negligible. Accordingly, as in the flat-bottom case, if mode
$\unicode[STIX]{x1D6FD}$
(of order 0.01 in dimensionless units), in the near-island region, the beta effect upon a counterclockwise flow is negligible. Accordingly, as in the flat-bottom case, if mode
![]() $m\geqslant 2$
is most unstable,
$m\geqslant 2$
is most unstable,
![]() $m$
dipoles are emitted outwards. However, when the dipoles recede considerably from the origin, the beta effect is no longer negligible: it forces the dipoles to turn back to the cylinder. Here they collide, and, by exchanging partners, rearrange into
$m$
dipoles are emitted outwards. However, when the dipoles recede considerably from the origin, the beta effect is no longer negligible: it forces the dipoles to turn back to the cylinder. Here they collide, and, by exchanging partners, rearrange into
![]() $m$
new dipoles that run away from the cylinder and then return again. Due to filamentation, viscous dissipation and wave radiation, this quasi-periodic process weakens, and ceases in the end. Another possible outcome is meandering and gradual symmetrical settling of
$m$
new dipoles that run away from the cylinder and then return again. Due to filamentation, viscous dissipation and wave radiation, this quasi-periodic process weakens, and ceases in the end. Another possible outcome is meandering and gradual symmetrical settling of
![]() $m$
dipoles in a circular orbit around the island, in which they move counterclockwise.
$m$
dipoles in a circular orbit around the island, in which they move counterclockwise.
When the initial flow is clockwise (and
![]() $\unicode[STIX]{x1D6FD}$
is still of order 0.01), the dipoles are emitted with a velocity component in the clockwise direction, which is opposite to the direction permitted for steady-state dipoles. Therefore, the emitted dipoles tend to turn counterclockwise and often disintegrate as a result. But when they manage to make the swing without breaking, they can eventually settle in a circular orbit, in which they move counterclockwise.
$\unicode[STIX]{x1D6FD}$
is still of order 0.01), the dipoles are emitted with a velocity component in the clockwise direction, which is opposite to the direction permitted for steady-state dipoles. Therefore, the emitted dipoles tend to turn counterclockwise and often disintegrate as a result. But when they manage to make the swing without breaking, they can eventually settle in a circular orbit, in which they move counterclockwise.
With increasing steepness of the slope, the radial distance travelled by the emitted dipoles shortens. When the magnitude of
![]() $\unicode[STIX]{x1D6FD}$
is high enough (
$\unicode[STIX]{x1D6FD}$
is high enough (
![]() $\unicode[STIX]{x1D6FD}$
of order 0.3 or higher), the dipole emission is prevented. A new flow pattern may form, possessing the
$\unicode[STIX]{x1D6FD}$
of order 0.3 or higher), the dipole emission is prevented. A new flow pattern may form, possessing the
![]() $m$
-fold symmetry, where
$m$
-fold symmetry, where
![]() $m$
is the number of the gravest unstable mode. The pattern may be steady or intermediate, depending on its rotation direction. If it rotates counterclockwise, it may be steady; otherwise, Rossby waves are emitted and, finally, a circular flow forms.
$m$
is the number of the gravest unstable mode. The pattern may be steady or intermediate, depending on its rotation direction. If it rotates counterclockwise, it may be steady; otherwise, Rossby waves are emitted and, finally, a circular flow forms.
For an initially counterclockwise flow at intermediate slopes (
![]() $\unicode[STIX]{x1D6FD}=-0.1$
), the dipoles may be emitted to a short distance before returning back to the cylinder, otherwise they stay attached to the island, but only with their strongest vorticity parts. In the case that the basic flow is clockwise, the emitted dipoles manage to travel some short distance offshore before being affected by the strong Rossby waves. The effect of the Rossby waves on the PV field is so significant that, eventually, the flow assumes the opposite direction relative to the original flow. At intermediate slopes, instability of mode 1 leads first to some shifting and distortion of the rings, and eventually to erosion of the inner ring due to filamentation.
$\unicode[STIX]{x1D6FD}=-0.1$
), the dipoles may be emitted to a short distance before returning back to the cylinder, otherwise they stay attached to the island, but only with their strongest vorticity parts. In the case that the basic flow is clockwise, the emitted dipoles manage to travel some short distance offshore before being affected by the strong Rossby waves. The effect of the Rossby waves on the PV field is so significant that, eventually, the flow assumes the opposite direction relative to the original flow. At intermediate slopes, instability of mode 1 leads first to some shifting and distortion of the rings, and eventually to erosion of the inner ring due to filamentation.
Closed flows around islands have been observed around Iceland, Taiwan, the islands of Kuril Chain (Shtokman Reference Shtokman1966) and the Pribilof islands (Kowalik & Stabeno Reference Kowalik and Stabeno1999). These closed flows may be induced by inertial and subinertial oscillations, reinforced by waves trapped by the sloping topography, or generated by winds (Longuet-Higgins Reference Longuet-Higgins1967, Reference Longuet-Higgins1969; Shtokman Reference Shtokman1966; Brink Reference Brink1999; Dyke Reference Dyke2005). It is expected that, being adapted to non-circular islands, some of the results presented above might become relevant to these kinds of flows. Apart from the currents around islands, after minor modification, the beta-cone concept can be applied to the treatment of flows in the presence of conical beta effect in a planetary scale, namely, of the Antarctic Circumpolar Current. These issues will be considered separately elsewhere.
Acknowledgements
This research was supported by the US–Israel Science Foundation (BSF), grant no. 2014206. The authors thank the anonymous referees for helpful comments on the manuscript. The contribution of M.R. to this article is part of his work towards a PhD degree.