1. Introduction
The dynamics of spherical gaseous detonations is controlled by small modifications of its inner structure which is thin compared to the radius. The direct-initiation process is a typical example of such a sensitivity, see Clavin & Denet (Reference Clavin and Denet2020). For large activation energy, a critical radius larger than the detonation thickness by two orders of magnitude has been identified by He & Clavin (Reference He and Clavin1994), illustrating a quasi-steady curvature-induced quenching of spherical detonations. Direct numerical simulations have confirmed such a large critical radius but they also show that strong unsteadiness of the inner-detonation structure is involved in the trajectories ‘propagation velocity vs radius’, especially near criticality, see He & Clavin (Reference He and Clavin1994), He (Reference He1996), Eckett, Quirk & Shepherd (Reference Eckett, Quirk and Shepherd2000) and Ng & Lee (Reference Ng and Lee2003). Investigating successful initiation far from the critical radius (supercritical regime) and neglecting the small gradient of the burnt-gas flow, Clavin & Denet (Reference Clavin and Denet2020) have shown that, near the CJ regime, unsteadiness is produced by the upstream-running compressible mode which controls the delayed response of the detonation structure to the burnt-gas flow. The analysis was performed in the limit of small heat release which provides us with a systematic framework for studying the problem which is one of two time scales.
The present paper is an extension of the Clavin & Denet (Reference Clavin and Denet2020) analysis to the critical dynamics in a spherical geometry. The objective is to elucidate further the mechanism responsible for the complex dynamics observed near criticality in direct numerical simulations, namely re-ignition after a quasi-quenching of the detonation with a propagation velocity decreasing well below the CJ velocity accompanied by a substantial increase of the reaction-zone thickness, called sometimes ‘decoupling of the reaction from the lead shock’. The problem is investigated here by an asymptotic analysis in the limit of small heat release, including unsteadiness, curvature and the gradient of the burnt-gas flow (rarefaction wave) at the exit of the reaction zone. The gradient of the rarefaction flow, which is small at the scale of the detonation thickness, plays, however, an important role in the critical dynamics; it controls the dynamics of the sonic point inside the rarefaction wave behind the reaction wave. Our attention will be limited to stable or weakly unstable detonations.
In the limit of small heat release, the Mach number is everywhere close to unity, ![]() $0<M-1 \ll 1$, and the problem reduces to a single equation for the flow. In a preliminary step, an analytical solution is obtained for the rarefaction wave behind a detonation treated as a discontinuity. Near the detonation front, the solution presents the same local properties as in ordinary spherical detonations approaching the CJ regime. For example, the decrease rate at the front is given by the curvature of the flow, as in Liñán, Kurdyumov & Sanchez (Reference Li nan, Kurdyumov and Sanchez2012) in the limit of large Mach number. The analytical solution of the burnt-gas flow is used as the external solution of the unsteady inner structure of curved detonations. The latter is analysed with the same formalism as in Clavin & Denet (Reference Clavin and Denet2020). A combination of matched asymptotic method and numerical study of the asymptotic equation is then used for improving our understanding of the phenomenon. When the detonation velocity is larger than the planar CJ velocity the detonation is overdrive and the sonic point is outside the inner structure of the reaction wave. Near the critical threshold of direct initiation, the propagation velocity of the lead shock first decreases below the CJ velocity and the unsteady regime is still overdriven. The dynamics of the sonic point (sonic condition of the flow relative to the lead shock) then controls the subsequent critical dynamics that leads to either sustained detonation propagation or detonation failure. In that respect, the gradient of the burnt-gas flow, even small, plays an important role, and analytical solutions for the rarefaction wave behind the reaction wave are quite useful.
$0<M-1 \ll 1$, and the problem reduces to a single equation for the flow. In a preliminary step, an analytical solution is obtained for the rarefaction wave behind a detonation treated as a discontinuity. Near the detonation front, the solution presents the same local properties as in ordinary spherical detonations approaching the CJ regime. For example, the decrease rate at the front is given by the curvature of the flow, as in Liñán, Kurdyumov & Sanchez (Reference Li nan, Kurdyumov and Sanchez2012) in the limit of large Mach number. The analytical solution of the burnt-gas flow is used as the external solution of the unsteady inner structure of curved detonations. The latter is analysed with the same formalism as in Clavin & Denet (Reference Clavin and Denet2020). A combination of matched asymptotic method and numerical study of the asymptotic equation is then used for improving our understanding of the phenomenon. When the detonation velocity is larger than the planar CJ velocity the detonation is overdrive and the sonic point is outside the inner structure of the reaction wave. Near the critical threshold of direct initiation, the propagation velocity of the lead shock first decreases below the CJ velocity and the unsteady regime is still overdriven. The dynamics of the sonic point (sonic condition of the flow relative to the lead shock) then controls the subsequent critical dynamics that leads to either sustained detonation propagation or detonation failure. In that respect, the gradient of the burnt-gas flow, even small, plays an important role, and analytical solutions for the rarefaction wave behind the reaction wave are quite useful.
The analysis also clarifies the question raised by Taylor (Reference Taylor1950a) concerning the self-similar solution of the rarefaction flow behind a spherical CJ detonation, obtained by Zeldovich (Reference Zeldovich1942) and Taylor (Reference Taylor1950a) in the limit of large Mach number. The detonation being treated as a discontinuity, the radial rate of change of the flow becomes infinite on the detonation front. According to Taylor (Reference Taylor1950a), it is unlikely that this result would be true if the modification of the inner structure is taken into account (non-zero detonation thickness). To address this question, a self-similar solution is derived in the present article for the CJ detonation moving with a propagation Mach number larger than unity by a small amount ![]() $0<M-1 \ll 1$ (small heat release). Amazingly, the new self-similar solution is qualitatively similar to that obtained in the opposite limit
$0<M-1 \ll 1$ (small heat release). Amazingly, the new self-similar solution is qualitatively similar to that obtained in the opposite limit ![]() $M\gg 1$; the gradient of the flow is also infinite on the front. However, this self-similar CJ flow is quite different from the unsteady flow behind an overdriven detonation approaching the CJ regime. The transitory flow, bridging the gap between the two flows, is obtained by a numerical solution of the asymptotic equation and is re-constructed by combining method of characteristics and analytical solutions. We will then see to what extent the self-similar flow is meaningful when the inner structure is taken into account.
$M\gg 1$; the gradient of the flow is also infinite on the front. However, this self-similar CJ flow is quite different from the unsteady flow behind an overdriven detonation approaching the CJ regime. The transitory flow, bridging the gap between the two flows, is obtained by a numerical solution of the asymptotic equation and is re-constructed by combining method of characteristics and analytical solutions. We will then see to what extent the self-similar flow is meaningful when the inner structure is taken into account.
The paper is organized as follows. The first part of the paper in §§ 2 and 3 is devoted to the rarefaction wave in a spherical geometry in the limit ![]() $0<M-1\ll 1$. The two-time-scale nature of this flow is discussed in § 2.1. The self-similar solution behind a spherical CJ detonation treated as a discontinuity is obtained in § 2.2. The unsteady rarefaction wave behind an overdriven detonation is presented in § 2.3. The transitory flow describing the transition from the overdriven regime to the self-similar CJ solution is obtained in § 3 for a detonation treated as a discontinuity. The rest of the paper is devoted to the study of the dynamics near criticality when the modifications to the inner structure are taken into account. The formulation of the problem and the method of solution are presented in § 4.1. The asymptotic analysis of overdriven detonations near the CJ regime is performed in § 4.2. The critical dynamics is discussed in § 5 where the numerical results are presented. Conclusions and perspectives are given in § 6.
$0<M-1\ll 1$. The two-time-scale nature of this flow is discussed in § 2.1. The self-similar solution behind a spherical CJ detonation treated as a discontinuity is obtained in § 2.2. The unsteady rarefaction wave behind an overdriven detonation is presented in § 2.3. The transitory flow describing the transition from the overdriven regime to the self-similar CJ solution is obtained in § 3 for a detonation treated as a discontinuity. The rest of the paper is devoted to the study of the dynamics near criticality when the modifications to the inner structure are taken into account. The formulation of the problem and the method of solution are presented in § 4.1. The asymptotic analysis of overdriven detonations near the CJ regime is performed in § 4.2. The critical dynamics is discussed in § 5 where the numerical results are presented. Conclusions and perspectives are given in § 6.
Five appendices are added. The jump conditions across a detonation treated as a discontinuity are recalled in Appendix A. The linear acoustic wave in a spherical geometry is briefly recalled in Appendix B and compared with the nonlinear structure of the rarefaction wave for ![]() $0<M-1\ll 1$. Technical details are presented in Appendix C, including the calculation of the motion of the sonic point in the rarefaction wave. The decay of an inert spherical shock wave freely propagating in open space is presented in Appendix D. The C-shaped curve of the steady-state approximation is briefly revisited in Appendix E, extending the previous analysis to a non-uniform flow of burnt gas.
$0<M-1\ll 1$. Technical details are presented in Appendix C, including the calculation of the motion of the sonic point in the rarefaction wave. The decay of an inert spherical shock wave freely propagating in open space is presented in Appendix D. The C-shaped curve of the steady-state approximation is briefly revisited in Appendix E, extending the previous analysis to a non-uniform flow of burnt gas.
2. Rarefaction wave behind a detonation treated as a discontinuity
In principle, gaseous detonations could be treated as a discontinuity if the length scale of the burnt-gas flow is larger than the detonation thickness, namely for a radius large enough in a spherical geometry. Even though the discontinuous model is not relevant for the critical dynamics, the unsteady solution of the rarefaction wave is first analysed with this model in the limit of small heat release. This is a useful preliminary step providing us with the external solution of the solution including the modification of the inner structure.
2.1. Two-time-scale analysis of the rarefaction wave
In the limit of small heat release, the flow of burnt gas close to the detonation front is controlled by a single equation, which corresponds to (6.6) of Clavin & Denet (Reference Clavin and Denet2020) by setting the reaction rate equal to zero. In this section, we show that this equation can be extended throughout the rarefaction wave. For that purpose we study the problem of fluid mechanics behind a supersonic discontinuity in the limit of a propagation velocity larger than the sound speed by a small amount. Denoting ![]() $\gamma$,
$\gamma$, ![]() $a$,
$a$, ![]() $p$ and
$p$ and ![]() $u$ the ratio of specific heat, the isentropic speed of sound, the pressure and the gas velocity (relative to the laboratory frame where the uncompressed gas is at rest), an inert compressible flow in a spherical geometry is governed by two hyperbolic equations
$u$ the ratio of specific heat, the isentropic speed of sound, the pressure and the gas velocity (relative to the laboratory frame where the uncompressed gas is at rest), an inert compressible flow in a spherical geometry is governed by two hyperbolic equations
where ![]() $r$ is the radius and
$r$ is the radius and ![]() $t$ the time, see Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012) and Clavin & Denet (Reference Clavin and Denet2020). For a detonation treated as a discontinuity, the pressure
$t$ the time, see Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012) and Clavin & Denet (Reference Clavin and Denet2020). For a detonation treated as a discontinuity, the pressure ![]() $p$ and the gas velocity
$p$ and the gas velocity ![]() $u$ on the detonation front
$u$ on the detonation front ![]() $r=r_f(t)$ are given in terms of the propagation velocity
$r=r_f(t)$ are given in terms of the propagation velocity ![]() $\mathcal {D}(t)$ by the conservation equations recalled in Appendix A, see (A1)–(A6),
$\mathcal {D}(t)$ by the conservation equations recalled in Appendix A, see (A1)–(A6),
where ![]() $M(t)\equiv \mathcal {D}(t)/a$ is the Mach number and the subscript
$M(t)\equiv \mathcal {D}(t)/a$ is the Mach number and the subscript ![]() $u$ identifies the constant properties upstream from the front. Written in the reference frame attached to the front equations (2.1) read
$u$ identifies the constant properties upstream from the front. Written in the reference frame attached to the front equations (2.1) read
 \begin{equation} \left. \begin{gathered} x\equiv r-r_f(t)\leqslant0, \quad \textrm{d}r_f(t)/\textrm{d}t=\mathcal{D}(t)\\ \frac{1}{\gamma p}\left[\frac{\partial}{\partial t}+(u\pm a-\mathcal{D})\frac{\partial}{\partial x}\right ]p \pm\frac{1}{a}\left[\frac{\partial}{\partial t}+(u\pm a-\mathcal{D})\frac{\partial}{\partial x}\right ]u={-} 2\frac{u}{r_f(t)+x}. \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} x\equiv r-r_f(t)\leqslant0, \quad \textrm{d}r_f(t)/\textrm{d}t=\mathcal{D}(t)\\ \frac{1}{\gamma p}\left[\frac{\partial}{\partial t}+(u\pm a-\mathcal{D})\frac{\partial}{\partial x}\right ]p \pm\frac{1}{a}\left[\frac{\partial}{\partial t}+(u\pm a-\mathcal{D})\frac{\partial}{\partial x}\right ]u={-} 2\frac{u}{r_f(t)+x}. \end{gathered} \right\} \end{equation} In the limit of small heat release ![]() $q_m/c_p T_u \equiv \epsilon ^2 \ll 1$, where
$q_m/c_p T_u \equiv \epsilon ^2 \ll 1$, where ![]() $q_m $ and
$q_m $ and ![]() $c_p $ are respectively the heat release and the specific heat per unit mass and
$c_p $ are respectively the heat release and the specific heat per unit mass and ![]() $T_u$ is the initial temperature of the unburnt gaseous mixture, the velocity of the planar CJ wave in steady state is slightly higher than the sound speed, see (A2),
$T_u$ is the initial temperature of the unburnt gaseous mixture, the velocity of the planar CJ wave in steady state is slightly higher than the sound speed, see (A2),
and attention is focused on detonations sufficiently close to the CJ regime
In the limit ![]() $\epsilon \ll 1$,
$\epsilon \ll 1$, ![]() $0<(M-1)=O(\epsilon )$, according to (A1)–(A6), the gas velocity is smaller than the speed of sound
$0<(M-1)=O(\epsilon )$, according to (A1)–(A6), the gas velocity is smaller than the speed of sound ![]() $u/a=O(\epsilon )$ at the front. The condition for which a weak shock wave
$u/a=O(\epsilon )$ at the front. The condition for which a weak shock wave ![]() $0<(M-1)\ll 1$ can be considered as a discontinuity is discussed in Clavin & Williams (Reference Clavin and Williams2002). According to (2.2a,b), the relative pressure variation is as small as
$0<(M-1)\ll 1$ can be considered as a discontinuity is discussed in Clavin & Williams (Reference Clavin and Williams2002). According to (2.2a,b), the relative pressure variation is as small as ![]() $u/a$ and the variation of
$u/a$ and the variation of ![]() $(1/\gamma )\delta p/ p-u/a$ is even smaller, of order
$(1/\gamma )\delta p/ p-u/a$ is even smaller, of order ![]() $(M-1)u/a$,
$(M-1)u/a$, ![]() $(1/\gamma )\delta p/ p-u/a=O(\epsilon ^2)$. The variation of the speed of sound is also of order
$(1/\gamma )\delta p/ p-u/a=O(\epsilon ^2)$. The variation of the speed of sound is also of order ![]() $\epsilon ^2$
$\epsilon ^2$ ![]() $\delta a/a=O(\epsilon ^2)$. Neglecting terms of order
$\delta a/a=O(\epsilon ^2)$. Neglecting terms of order ![]() $\epsilon ^2$, the variation of
$\epsilon ^2$, the variation of ![]() $a$ is negligible, and the isentropic relation
$a$ is negligible, and the isentropic relation ![]() $(1/\gamma )\delta p/ p\approx u/a$ holds at the front, up to the second order in the perturbation analysis for
$(1/\gamma )\delta p/ p\approx u/a$ holds at the front, up to the second order in the perturbation analysis for ![]() $\epsilon \ll 1$ under the conditions (2.4a,b) and (2.5) for which the relative jump of entropy across the detonation front is of order
$\epsilon \ll 1$ under the conditions (2.4a,b) and (2.5) for which the relative jump of entropy across the detonation front is of order ![]() $\epsilon ^2$. Then, the rarefaction wave is a quasi-transonic flow which can be analysed by a two-time-scale analysis.
$\epsilon ^2$. Then, the rarefaction wave is a quasi-transonic flow which can be analysed by a two-time-scale analysis.
It was known long ago that the rarefaction wave ![]() $u(r,t)$ behind a spherical detonation is delimited by a weak discontinuity at the radius
$u(r,t)$ behind a spherical detonation is delimited by a weak discontinuity at the radius ![]() $r_0(t)$ of a core of stagnant gas (
$r_0(t)$ of a core of stagnant gas (![]() $r_0<r_f$) which grows with the speed of sound
$r_0<r_f$) which grows with the speed of sound
The flow ![]() $u$ is oriented in the same direction as the propagation
$u$ is oriented in the same direction as the propagation ![]() $\mathcal {D}>0$,
$\mathcal {D}>0$, ![]() $u\geqslant 0$, and is increasing monotonically from zero at
$u\geqslant 0$, and is increasing monotonically from zero at ![]() $r=r_0(t)$ to a value (at the detonation front
$r=r_0(t)$ to a value (at the detonation front ![]() $r_f$) smaller than the speed of sound by a factor
$r_f$) smaller than the speed of sound by a factor ![]() $\epsilon$, so that the ordering
$\epsilon$, so that the ordering ![]() $u/a=O(\epsilon )$ holds throughout the rarefaction wave. The equations of the two characteristics
$u/a=O(\epsilon )$ holds throughout the rarefaction wave. The equations of the two characteristics ![]() $\mathcal {C}_{\pm }$ in (2.3) involve two differential operators
$\mathcal {C}_{\pm }$ in (2.3) involve two differential operators
The scalars ![]() $I_+\equiv (1/\gamma )\delta p/p + u/a$ and
$I_+\equiv (1/\gamma )\delta p/p + u/a$ and ![]() $I_-\equiv (1/\gamma )\delta p/p - u/a$ that are transported by upstream running characteristic
$I_-\equiv (1/\gamma )\delta p/p - u/a$ that are transported by upstream running characteristic ![]() $\mathcal {C}_{+}$ and downstream running characteristic
$\mathcal {C}_{+}$ and downstream running characteristic ![]() $\mathcal {C}_{-}$ respectively, are modified by the flow divergence on the right-hand side of (2.3) whose order of magnitude is
$\mathcal {C}_{-}$ respectively, are modified by the flow divergence on the right-hand side of (2.3) whose order of magnitude is ![]() $\epsilon a/r$,
$\epsilon a/r$,
Under the conditions (2.4a,b) and (2.5), the flow with respect to the front is quasi-transonic, ![]() $\mathcal {D}-u=O(\epsilon a)$. The propagation velocity
$\mathcal {D}-u=O(\epsilon a)$. The propagation velocity ![]() $V_-\equiv u-a-\mathcal {D} < 0$ of the downstream-running characteristics
$V_-\equiv u-a-\mathcal {D} < 0$ of the downstream-running characteristics ![]() $\mathcal {C}_-$ is approximately
$\mathcal {C}_-$ is approximately ![]() $-a$ throughout the rarefaction wave. (We use here the same convention as in Clavin & Williams Reference Clavin and Williams2002; upstream-running (downstream-running) characterizes a propagation towards the shock (the core of stagnation gas) in the frame attached to the front.) Near the detonation front where the flow relative to the front is subsonic
$-a$ throughout the rarefaction wave. (We use here the same convention as in Clavin & Williams Reference Clavin and Williams2002; upstream-running (downstream-running) characterizes a propagation towards the shock (the core of stagnation gas) in the frame attached to the front.) Near the detonation front where the flow relative to the front is subsonic ![]() $\mathcal {D}-u \leqslant a$ (overdriven regime), the characteristic
$\mathcal {D}-u \leqslant a$ (overdriven regime), the characteristic ![]() $\mathcal {C}_+$ is upstream running
$\mathcal {C}_+$ is upstream running ![]() $V_+=a-(\mathcal {D}-u)>0$. But a sonic point appears when
$V_+=a-(\mathcal {D}-u)>0$. But a sonic point appears when ![]() $u$ decreases since
$u$ decreases since ![]() $V_+=0$ when
$V_+=0$ when ![]() $\mathcal {D}-u=a$. Therefore the characteristic
$\mathcal {D}-u=a$. Therefore the characteristic ![]() $\mathcal {C}_+$ becomes downstream running (
$\mathcal {C}_+$ becomes downstream running (![]() $V_+<0$) behind the sonic point, which stands close to the front because we consider propagation regimes of the detonation that are close to the CJ regime which is characterized by the sonic condition at the detonation front. Then, the transport of
$V_+<0$) behind the sonic point, which stands close to the front because we consider propagation regimes of the detonation that are close to the CJ regime which is characterized by the sonic condition at the detonation front. Then, the transport of ![]() $I_-$ by
$I_-$ by ![]() $\mathcal {C}_-$ from the sonic point to
$\mathcal {C}_-$ from the sonic point to ![]() $r_0$ is quasi-instantaneous compared to the slow transport of
$r_0$ is quasi-instantaneous compared to the slow transport of ![]() $I_+$ by
$I_+$ by ![]() $\mathcal {C}_+$,
$\mathcal {C}_+$, ![]() $\vert V_+ \vert /a = O(\epsilon )$,
$\vert V_+ \vert /a = O(\epsilon )$, ![]() $\vert V_- \vert /a \approx 1$. Anticipating that the thickness of the rarefaction wave
$\vert V_- \vert /a \approx 1$. Anticipating that the thickness of the rarefaction wave ![]() $\Delta r\equiv (r_f-r_0 )$ is smaller than the detonation radius
$\Delta r\equiv (r_f-r_0 )$ is smaller than the detonation radius ![]() $\Delta r/r_f=O(\epsilon )$, see § 2.2, the modification of
$\Delta r/r_f=O(\epsilon )$, see § 2.2, the modification of ![]() $I_-$ by the geometrical effect during the transit time
$I_-$ by the geometrical effect during the transit time ![]() $\Delta r/a$ of
$\Delta r/a$ of ![]() $\mathcal {C}_-$ is of order
$\mathcal {C}_-$ is of order ![]() $\epsilon \Delta r/r_f =O(\epsilon ^2)$ and can be neglected. Then, to leading order in the limit
$\epsilon \Delta r/r_f =O(\epsilon ^2)$ and can be neglected. Then, to leading order in the limit ![]() $\epsilon \ll 1$, the isentropic relation of acoustics
$\epsilon \ll 1$, the isentropic relation of acoustics ![]() $(1/\gamma )\delta p/p=u/a$, which is valid inside the detonation structure in the limit of small heat release, holds throughout the rarefaction wave
$(1/\gamma )\delta p/p=u/a$, which is valid inside the detonation structure in the limit of small heat release, holds throughout the rarefaction wave ![]() $u\ll a$,
$u\ll a$, ![]() $u/\epsilon a=O(1)$. Then, neglecting the short time delay and the small flow modification (of order
$u/\epsilon a=O(1)$. Then, neglecting the short time delay and the small flow modification (of order ![]() $\epsilon ^2 a$) introduced by the fastest downstream-running mode and retaining only the slow time scale, the leading order of the flow
$\epsilon ^2 a$) introduced by the fastest downstream-running mode and retaining only the slow time scale, the leading order of the flow ![]() $u( r,t)$ is controlled by a single equation corresponding to the simple wave associated with
$u( r,t)$ is controlled by a single equation corresponding to the simple wave associated with ![]() $\mathcal {C}_+$,
$\mathcal {C}_+$,
2.2. Self-similar rarefaction wave behind a spherical CJ detonation
Generally speaking, when the modification to the inner structure of the leading front is ignored (zero detonation thickness), a self-similar solution exists when a finite amount of energy is deposited quasi-instantaneously by a quasi-punctual external source at the centre because there are no length and time scales in the problem. This is the case for the blast wave of Sedov (Reference Sedov1946) and Taylor (Reference Taylor1950b) and the rarefaction wave of Zeldovich (Reference Zeldovich1942) and Taylor (Reference Taylor1950a) behind a CJ detonation, obtained in the limit of large Mach number ![]() $M\gg 1$, see, for example, Clavin & Searby (Reference Clavin and Searby2016). We show below that, in the opposite limit of small heat release
$M\gg 1$, see, for example, Clavin & Searby (Reference Clavin and Searby2016). We show below that, in the opposite limit of small heat release ![]() $M_{o_{CJ}}-1\ll 1$, there is also a self-similar solution for the rarefaction wave behind a CJ detonation, which is qualitatively similar to the self-similar solution of Zeldovich (Reference Zeldovich1942) and Taylor (Reference Taylor1950a). The difference concerns mainly the extension of the self-similar rarefaction wave which is small compared to the radius of the detonation in the limit
$M_{o_{CJ}}-1\ll 1$, there is also a self-similar solution for the rarefaction wave behind a CJ detonation, which is qualitatively similar to the self-similar solution of Zeldovich (Reference Zeldovich1942) and Taylor (Reference Taylor1950a). The difference concerns mainly the extension of the self-similar rarefaction wave which is small compared to the radius of the detonation in the limit ![]() $M_{o_{CJ}}- 1\ll 1$.
$M_{o_{CJ}}- 1\ll 1$.
2.2.1. Formulation
Consider the spherical detonation propagating with the constant CJ velocity ![]() $\mathcal {D}_{o_{CJ}}\approx (1+\epsilon )a$ in the limit (2.4a,b)
$\mathcal {D}_{o_{CJ}}\approx (1+\epsilon )a$ in the limit (2.4a,b) ![]() $\epsilon \ll 1$. According to the conservation equations (A1)–(A6), the boundary condition at the front takes the form
$\epsilon \ll 1$. According to the conservation equations (A1)–(A6), the boundary condition at the front takes the form
Dividing by ![]() $\epsilon a$ and introducing the non-dimensional flow of order unity in the limit
$\epsilon a$ and introducing the non-dimensional flow of order unity in the limit ![]() $\epsilon \ll 1$,
$\epsilon \ll 1$, ![]() $v (x, t)\equiv u/(\epsilon a)$,
$v (x, t)\equiv u/(\epsilon a)$, ![]() $v\in [0, 1]$, (2.10a–c) yields
$v\in [0, 1]$, (2.10a–c) yields
where (2.4a,b) has been used. This suggests rescaling the distance from the front by using the new space variable ![]() $\eta \equiv x/\epsilon$, so that (2.11a,b) and (2.13) read
$\eta \equiv x/\epsilon$, so that (2.11a,b) and (2.13) read
The downstream relation (2.6a–c) is automatically fulfilled at ![]() $\eta =\eta _0(t) \equiv [r_0(t)-r_f(t)]/\epsilon$ since the relations
$\eta =\eta _0(t) \equiv [r_0(t)-r_f(t)]/\epsilon$ since the relations ![]() $v(\eta _0(t), t)=0$ and
$v(\eta _0(t), t)=0$ and ![]() $\text {d} v(\eta _0(t), t)/\text {d} t =0$ are verified by (2.14a,b),
$\text {d} v(\eta _0(t), t)/\text {d} t =0$ are verified by (2.14a,b), ![]() $v=0:\partial v/\partial t- a\partial v/\partial \eta =0$, yielding
$v=0:\partial v/\partial t- a\partial v/\partial \eta =0$, yielding ![]() $\text {d}\eta _0(t)/\text {d} t= -a$, so that, using (2.4a,b)
$\text {d}\eta _0(t)/\text {d} t= -a$, so that, using (2.4a,b) ![]() $\text {d}r_f/\text {d} t=(1+\epsilon )a$, one gets
$\text {d}r_f/\text {d} t=(1+\epsilon )a$, one gets ![]() $\text {d} r_0/\text {d} t=a$.
$\text {d} r_0/\text {d} t=a$.
Introducing the two lengths ![]() $r_{fi}$ and
$r_{fi}$ and ![]() $r_{0i}$ characterizing the initial condition
$r_{0i}$ characterizing the initial condition ![]() $t=0$,
$t=0$,
with ![]() $\epsilon \vert \eta _{0i} \vert$ being the initial thickness of the rarefaction wave, we will show below that a self-similar solution of (2.14a,b) exists in the limit
$\epsilon \vert \eta _{0i} \vert$ being the initial thickness of the rarefaction wave, we will show below that a self-similar solution of (2.14a,b) exists in the limit ![]() $\epsilon \ll 1$ if the initial thickness of the rarefaction wave
$\epsilon \ll 1$ if the initial thickness of the rarefaction wave ![]() $r_{fi}-r_{0i}$ is smaller than the initial radius of the detonation
$r_{fi}-r_{0i}$ is smaller than the initial radius of the detonation ![]() $r_{fi}$ by a factor
$r_{fi}$ by a factor ![]() $\epsilon$, as it is the case in the linear solution presented in Appendix B.1,
$\epsilon$, as it is the case in the linear solution presented in Appendix B.1,
To leading order, the denominator ![]() $r=r_f+\epsilon \eta$ on the right-hand side of (2.14a,b) can be replaced by
$r=r_f+\epsilon \eta$ on the right-hand side of (2.14a,b) can be replaced by ![]() $r_0(t)$ throughout the rarefaction wave
$r_0(t)$ throughout the rarefaction wave ![]() $r_0(t)\leqslant r\leqslant r_f(t)$ since, according to (2.17a–c),
$r_0(t)\leqslant r\leqslant r_f(t)$ since, according to (2.17a–c), ![]() $r_f(t)=r_0(t)+\epsilon at-\epsilon \eta _{0i}$ so that
$r_f(t)=r_0(t)+\epsilon at-\epsilon \eta _{0i}$ so that ![]() $r_f(t)=(1+\epsilon )r_0(t)+O(\epsilon r_{0i})$. Therefore, replacing the time variable
$r_f(t)=(1+\epsilon )r_0(t)+O(\epsilon r_{0i})$. Therefore, replacing the time variable ![]() $t$ by a time-like variable
$t$ by a time-like variable ![]() $\nu \equiv r_0(t)=at+r_{0i}$ whose dimension is a length, (2.14a,b) for the flow
$\nu \equiv r_0(t)=at+r_{0i}$ whose dimension is a length, (2.14a,b) for the flow ![]() $v( \eta , \nu )$ takes the form of a Burgers-like equation, free from parameter, in which the local viscous dissipation is replaced by a global (linear) damping rate on the right-hand side,
$v( \eta , \nu )$ takes the form of a Burgers-like equation, free from parameter, in which the local viscous dissipation is replaced by a global (linear) damping rate on the right-hand side,
where
The parameter ![]() $r_{0i}$ in the definition of the time-like variable
$r_{0i}$ in the definition of the time-like variable ![]() $\nu$ can be eliminated by a change of time origin.
$\nu$ can be eliminated by a change of time origin.
2.2.2. Infinite gradient of the flow on the front. Self-similar solution
As in the self-similar solution of Zeldovich (Reference Zeldovich1942) and Taylor (Reference Taylor1950a) obtained in the opposite limit of large Mach number ![]() $\mathcal {D}_{o_{CJ}}/a \gg 1$, the solution of (2.18) is singular on the detonation front where the gradient of the flow becomes infinite. The flow being constant on the front
$\mathcal {D}_{o_{CJ}}/a \gg 1$, the solution of (2.18) is singular on the detonation front where the gradient of the flow becomes infinite. The flow being constant on the front ![]() $v=1$, the unsteady term
$v=1$, the unsteady term ![]() $\partial v/\partial \nu$ in (2.18) is negligible around
$\partial v/\partial \nu$ in (2.18) is negligible around ![]() $\eta =0^-$ so that the steady-state approximation holds near the detonation front
$\eta =0^-$ so that the steady-state approximation holds near the detonation front ![]() $(v-1){\partial v}/{\partial \eta }\approx - {1}/{\nu }$
$(v-1){\partial v}/{\partial \eta }\approx - {1}/{\nu }$
 \begin{equation} 1-v= \sqrt {\frac{2}{\nu}(-\eta)}, \quad 1-\frac{u}{\epsilon a}= \sqrt {\frac{2[r_f(t)-r]}{\epsilon(at+r_{0i})}}, \end{equation}
\begin{equation} 1-v= \sqrt {\frac{2}{\nu}(-\eta)}, \quad 1-\frac{u}{\epsilon a}= \sqrt {\frac{2[r_f(t)-r]}{\epsilon(at+r_{0i})}}, \end{equation}
the time derivative ![]() $\partial v /\partial \nu \vert _{\eta =0^-} =\sqrt {-2\eta }/(2\nu ^{3/2})$ being negligible in a boundary layer at the front
$\partial v /\partial \nu \vert _{\eta =0^-} =\sqrt {-2\eta }/(2\nu ^{3/2})$ being negligible in a boundary layer at the front ![]() $\vert \partial v /\partial \nu \vert _{\eta =0^-} \ll 1/\nu$,
$\vert \partial v /\partial \nu \vert _{\eta =0^-} \ll 1/\nu$,
The divergence of the flow gradient on the front of a spherical CJ detonation ![]() $\partial v /\partial \eta \vert _{\eta =0^-} \propto 1/(-\eta )^{1/2}$ is a consequence of the sonic condition
$\partial v /\partial \eta \vert _{\eta =0^-} \propto 1/(-\eta )^{1/2}$ is a consequence of the sonic condition ![]() $\eta =0: \,v-1=0,\ \forall t$.
$\eta =0: \,v-1=0,\ \forall t$.
The self-similar solution of (2.18) is obtained by looking for a solution in the form
After multiplication by ![]() $1/V^2$, (2.23) takes the form
$1/V^2$, (2.23) takes the form ![]() $\text {d} [(1+z)/V]/\text {d} z+(1/V)\text {d} V/\text {d} z =0$, then, the solution
$\text {d} [(1+z)/V]/\text {d} z+(1/V)\text {d} V/\text {d} z =0$, then, the solution ![]() $V(z)$ satisfying the boundary condition at
$V(z)$ satisfying the boundary condition at ![]() $z=0$ is the root of a transcendental equation
$z=0$ is the root of a transcendental equation
According to this equation, the radius ![]() $r=r_0(t)$ of the spherical core of stagnant gas
$r=r_0(t)$ of the spherical core of stagnant gas ![]() $V=0$ corresponds to
$V=0$ corresponds to ![]() $z=-1$. Therefore,
$z=-1$. Therefore, ![]() $r_0(t)$ and
$r_0(t)$ and ![]() $r_f(t)$ are linked by the relation
$r_f(t)$ are linked by the relation
in agreement with the assumption (2.17a–c) in the limit of small heat release (2.4a,b), which finally takes the more restrictive form
in a consistent way with ![]() $r_f(t)\approx (1+\epsilon ) at+r_{fi}$ and
$r_f(t)\approx (1+\epsilon ) at+r_{fi}$ and ![]() $r_0(t)=at+r_{0i}$ yielding (2.26) for
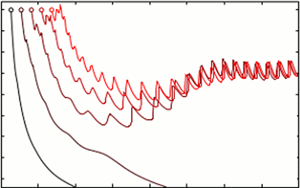
$r_0(t)=at+r_{0i}$ yielding (2.26) for ![]() $z=-1$. The velocity profile of the self-similar rarefaction wave is plotted in figure 1. Close to the detonation front
$z=-1$. The velocity profile of the self-similar rarefaction wave is plotted in figure 1. Close to the detonation front ![]() $z\approx 0$, namely for
$z\approx 0$, namely for ![]() $V= 1+\delta V$ with
$V= 1+\delta V$ with ![]() $\vert \delta V\vert \ll 1$,
$\vert \delta V\vert \ll 1$, ![]() $\ln V\approx \delta V-\delta V^2/2+\cdots$,
$\ln V\approx \delta V-\delta V^2/2+\cdots$, ![]() $V\ln V \approx -1+(\delta V)^2/2+\cdots$ so that (2.24) yields
$V\ln V \approx -1+(\delta V)^2/2+\cdots$ so that (2.24) yields ![]() $(\delta V)^2/2 +z\approx 0$ and the relation (2.20a,b) is recovered for
$(\delta V)^2/2 +z\approx 0$ and the relation (2.20a,b) is recovered for ![]() $\vert z\vert \ll 1$,
$\vert z\vert \ll 1$, ![]() $V\approx 1-\sqrt {-2z}$. At the radius of the stagnant core, the root of (2.24) goes to zero
$V\approx 1-\sqrt {-2z}$. At the radius of the stagnant core, the root of (2.24) goes to zero ![]() $\lim _{z=-1} V=0^+$ with a zero gradient
$\lim _{z=-1} V=0^+$ with a zero gradient ![]() $\text {d} V/\text {d} z\vert _{z=-1} =0$, as shown by taking the limit
$\text {d} V/\text {d} z\vert _{z=-1} =0$, as shown by taking the limit ![]() $V\to 0^+$ of the derivative of (2.24)
$V\to 0^+$ of the derivative of (2.24) ![]() $\text {d} (V\ln V)/\text {d} z-\text {d}V/\text {d} z+1=0$ leading to
$\text {d} (V\ln V)/\text {d} z-\text {d}V/\text {d} z+1=0$ leading to ![]() $\lim _{V\to 0^+}(\text {d}V/\text {d} z)=-2/\ln V\to 0^+$.
$\lim _{V\to 0^+}(\text {d}V/\text {d} z)=-2/\ln V\to 0^+$.

Figure 1. Solution of (2.23)–(2.24) representing the self-similar rarefaction flow behind the front of a spherical CJ detonation considered as a discontinuity for small heat release ![]() $(\mathcal {D}_{o_{CJ}}-a)/a\approx \epsilon \ll 1$. The reduced flow
$(\mathcal {D}_{o_{CJ}}-a)/a\approx \epsilon \ll 1$. The reduced flow ![]() $v= u(r,t)/\epsilon a$ is plotted vs the reduced distance from the front
$v= u(r,t)/\epsilon a$ is plotted vs the reduced distance from the front ![]() $z= (r-r_f(t) )/\epsilon r_{0}(t)$ with
$z= (r-r_f(t) )/\epsilon r_{0}(t)$ with ![]() $r_f(t)=\mathcal {D}_{o_{CI}}t+r_{fi}$,
$r_f(t)=\mathcal {D}_{o_{CI}}t+r_{fi}$, ![]() $r_0(t)=at+r_{0i}$ and, according to (2.26),
$r_0(t)=at+r_{0i}$ and, according to (2.26), ![]() $r_{fi} = (1+\epsilon )r_{0i}$.
$r_{fi} = (1+\epsilon )r_{0i}$.
To conclude the rarefaction wave behind a spherical CJ detonation sustained by a small heat release (![]() $M_{o_{CJ}}-1\approx \epsilon \ll 1$) is similar to the self-similar solution for
$M_{o_{CJ}}-1\approx \epsilon \ll 1$) is similar to the self-similar solution for ![]() $M_{o_{CJ}}\gg 1$. The only difference is quantitative; the extension of the rarefaction wave is smaller than the detonation radius
$M_{o_{CJ}}\gg 1$. The only difference is quantitative; the extension of the rarefaction wave is smaller than the detonation radius ![]() $r_f(t)$ by a factor
$r_f(t)$ by a factor ![]() $M_{o_{CJ}}-1$,
$M_{o_{CJ}}-1$, ![]() $(r_f-r_0)/r_f\approx (M_{o_{CJ}}-1)/M_{o_{CJ}}$ for small heat release while
$(r_f-r_0)/r_f\approx (M_{o_{CJ}}-1)/M_{o_{CJ}}$ for small heat release while ![]() $(r_f-r_0)/r_f=1/2$ for
$(r_f-r_0)/r_f=1/2$ for ![]() $M_{o_{CJ}}\gg 1$.
$M_{o_{CJ}}\gg 1$.
2.3. Rarefaction wave behind an overdriven detonation considered as a discontinuity
Within the framework of the discontinuous model the decay of the propagation velocity of an overdriven detonation ![]() $\mathcal {D}(\tau )$ in a spherical geometry to the planar Chapmann–Jouguet velocity
$\mathcal {D}(\tau )$ in a spherical geometry to the planar Chapmann–Jouguet velocity ![]() $\mathcal {D}_{o_{CJ}}$ occurs systematically after a finite time and at a finite radius. In this section, we derive an analytical expression for the rarefaction wave behind an overdriven detonation treated as a discontinuity approaching the CJ velocity, in the limit
$\mathcal {D}_{o_{CJ}}$ occurs systematically after a finite time and at a finite radius. In this section, we derive an analytical expression for the rarefaction wave behind an overdriven detonation treated as a discontinuity approaching the CJ velocity, in the limit ![]() $\epsilon \ll 1$. The subsequent relaxation to the self-similar solution is discussed in § 3.
$\epsilon \ll 1$. The subsequent relaxation to the self-similar solution is discussed in § 3.
2.3.1. Formulation
As already mentioned, there is no length (or time) scale in the direct-initiation problem with the discontinuous model. However, in view of bridging the gap with the study in the second part of this manuscript, it is useful to introduce the non-dimensional space and time variables ![]() $\xi$ and
$\xi$ and ![]() $\tau$ as well as the reduced flow field
$\tau$ as well as the reduced flow field ![]() $\mu (\xi ,\tau )$ that are of order unity inside the unsteady (and curved) inner structure of the detonation in the limit (2.4a,b)–(2.5)
$\mu (\xi ,\tau )$ that are of order unity inside the unsteady (and curved) inner structure of the detonation in the limit (2.4a,b)–(2.5)
where ![]() $l$ is the detonation thickness and
$l$ is the detonation thickness and ![]() $1/t_r=a/l$ the reaction rate at the Neumann state,
$1/t_r=a/l$ the reaction rate at the Neumann state,
For clarity, the results will be written with the two types of variables. Introducing the reduced radius ![]() $\tilde {r}_f(\tau )$ and propagation velocity
$\tilde {r}_f(\tau )$ and propagation velocity ![]() $\dot {\alpha }_\tau (\tau )$
$\dot {\alpha }_\tau (\tau )$
(2.10a–c) reduces to (6.6) in Clavin & Denet (Reference Clavin and Denet2020) without the reaction term
where
see Appendix C.1. In (2.31), ![]() $\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ is associated with the initial position of the front
$\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ is associated with the initial position of the front ![]() $r_{fi} \equiv r_f(0)$. The sonic condition with respect to the front
$r_{fi} \equiv r_f(0)$. The sonic condition with respect to the front ![]() $(\mathcal {D}-u)= a$ corresponds to
$(\mathcal {D}-u)= a$ corresponds to ![]() $(\mu -\dot {\alpha }_\tau )=0$, and a subsonic condition
$(\mu -\dot {\alpha }_\tau )=0$, and a subsonic condition ![]() $(\mathcal {D}-u) < a$ corresponds to
$(\mathcal {D}-u) < a$ corresponds to ![]() $(\mu -\dot {\alpha }_\tau )>0$ while
$(\mu -\dot {\alpha }_\tau )>0$ while ![]() $(\mu -\dot {\alpha }_\tau )<0$ characterizes a supersonic flow relative to the detonation front. The decay of the detonation velocity to the CJ velocity corresponds to
$(\mu -\dot {\alpha }_\tau )<0$ characterizes a supersonic flow relative to the detonation front. The decay of the detonation velocity to the CJ velocity corresponds to ![]() $\dot {\alpha }_\tau \to 0^+$ and
$\dot {\alpha }_\tau \to 0^+$ and ![]() $\mu _f \to 0^+$.
$\mu _f \to 0^+$.
As already mentioned, the radius ![]() $r=r_0(\tau )$ of the spherical core of stagnant gas
$r=r_0(\tau )$ of the spherical core of stagnant gas ![]() $u(r_0(\tau ), \tau )=0$
$u(r_0(\tau ), \tau )=0$
is a weak discontinuity of the flow moving at the speed of sound ![]() $\text {d} r_0(t)/\text {d} t=a$. Introducing the reduced thickness of the rarefaction wave
$\text {d} r_0(t)/\text {d} t=a$. Introducing the reduced thickness of the rarefaction wave ![]() $\vert \xi _0(\tau ) \vert$
$\vert \xi _0(\tau ) \vert$
the weak discontinuity is recovered in (2.31) at ![]() $\xi =\xi _0(\tau )$ where
$\xi =\xi _0(\tau )$ where ![]() ${\partial \mu }/{\partial \tau }\vert _{\xi =\xi _0^+} -(1+\dot {\alpha }_\tau ) {\partial \mu }/{\partial \xi }\vert _{\xi =\xi _0^+}=0$ and
${\partial \mu }/{\partial \tau }\vert _{\xi =\xi _0^+} -(1+\dot {\alpha }_\tau ) {\partial \mu }/{\partial \xi }\vert _{\xi =\xi _0^+}=0$ and ![]() $\mu =-1$ by differentiating the last expression in (2.34),
$\mu =-1$ by differentiating the last expression in (2.34), ![]() $\text {d} \mu (\xi _0(\tau ),\tau )/\text {d} \tau =\partial \mu /\partial \tau \vert _{\xi =\xi _0^+}+(\text {d} \xi _0/\text {d}\tau )\partial \mu /\partial \xi \vert _{\xi =\xi _0^+}$
$\text {d} \mu (\xi _0(\tau ),\tau )/\text {d} \tau =\partial \mu /\partial \tau \vert _{\xi =\xi _0^+}+(\text {d} \xi _0/\text {d}\tau )\partial \mu /\partial \xi \vert _{\xi =\xi _0^+}$ ![]() $=0$ yielding
$=0$ yielding
which corresponds effectively to ![]() $\text {d} r_0/\text {d} t=a$ that is
$\text {d} r_0/\text {d} t=a$ that is ![]() $\text {d} (r_0- r_f)/\text {d} t=a-\mathcal {D}$ with, according to (2.4a,b) and (2.30a,b),
$\text {d} (r_0- r_f)/\text {d} t=a-\mathcal {D}$ with, according to (2.4a,b) and (2.30a,b), ![]() $(a-\mathcal {D})=-\epsilon a(1+\dot {\alpha }_\tau )$. When the order of magnitude of
$(a-\mathcal {D})=-\epsilon a(1+\dot {\alpha }_\tau )$. When the order of magnitude of ![]() $\dot {\alpha }_\tau$ is not larger than unity in the limit
$\dot {\alpha }_\tau$ is not larger than unity in the limit ![]() $\epsilon \to 0$,
$\epsilon \to 0$, ![]() $(\mathcal {D}-a)/a =O( \epsilon )$, (2.35a,b) shows that the thickness of the rarefaction wave
$(\mathcal {D}-a)/a =O( \epsilon )$, (2.35a,b) shows that the thickness of the rarefaction wave ![]() $r_f(t)-r_0(t)$ increases with a velocity of order
$r_f(t)-r_0(t)$ increases with a velocity of order ![]() $\epsilon a$ smaller than the speed of sound by a factor
$\epsilon a$ smaller than the speed of sound by a factor ![]() $\epsilon$. Considering
$\epsilon$. Considering ![]() $\tau =O(1)$ in the limit of small heat release,
$\tau =O(1)$ in the limit of small heat release, ![]() $\lim _{\epsilon \to 0}\epsilon \xi _0=0$, (2.32a,b) yields
$\lim _{\epsilon \to 0}\epsilon \xi _0=0$, (2.32a,b) yields ![]() $\lim _{\epsilon \to 0} \tilde {r}_{f}=\tau +\tilde {r}_{fi}$, so that, to leading order, (2.31) reduces to
$\lim _{\epsilon \to 0} \tilde {r}_{f}=\tau +\tilde {r}_{fi}$, so that, to leading order, (2.31) reduces to
Rescaling the non-dimensional length ![]() $\xi$ and time
$\xi$ and time ![]() $\tau$ with
$\tau$ with ![]() $\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$,
$\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$,
(2.35a,b)–(2.36) take a form free from parameter
 \begin{equation}
\frac{\partial \mu}{\partial \tilde{\tau}} + [ \mu
-\dot{\alpha}_\tau(\tilde{\tau})]\frac {\partial
\mu}{\partial \tilde{\xi}}
={-}\frac{(1+\mu)}{\tilde{\tau}+1}, \quad \frac{\text{d}
\tilde{\xi}_0}{\text{d}\tilde{\tau}}={-}[1+\dot{\alpha}_\tau(\tilde{\tau})].
\end{equation}
\begin{equation}
\frac{\partial \mu}{\partial \tilde{\tau}} + [ \mu
-\dot{\alpha}_\tau(\tilde{\tau})]\frac {\partial
\mu}{\partial \tilde{\xi}}
={-}\frac{(1+\mu)}{\tilde{\tau}+1}, \quad \frac{\text{d}
\tilde{\xi}_0}{\text{d}\tilde{\tau}}={-}[1+\dot{\alpha}_\tau(\tilde{\tau})].
\end{equation} Once a general solution of (2.38a,b) is known, the dynamics of the front ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ is obtained by a boundary condition at the front. For the discontinuous model, the instantaneous flow of burned gas at the front, denoted by
$\dot {\alpha }_\tau (\tilde {\tau })$ is obtained by a boundary condition at the front. For the discontinuous model, the instantaneous flow of burned gas at the front, denoted by ![]() $\mu _f(\tilde {\tau })\equiv \mu (\tilde {\xi }=0,\tilde {\tau })$, is given by the conservation of mass, momentum and energy in Appendix A, leading to express
$\mu _f(\tilde {\tau })\equiv \mu (\tilde {\xi }=0,\tilde {\tau })$, is given by the conservation of mass, momentum and energy in Appendix A, leading to express ![]() $\mu _f(\tilde {\tau })$ in terms of
$\mu _f(\tilde {\tau })$ in terms of ![]() $\dot {\alpha }_\tau (\tilde {\tau })$
$\dot {\alpha }_\tau (\tilde {\tau })$
Equations (2.38a,b) and (2.39) represent an eigenvalue problem in which the unknown function ![]() $\dot {\alpha }_{\tau }(\tilde {\tau })$ appears in the boundary condition (2.39) and in (2.38a,b).
$\dot {\alpha }_{\tau }(\tilde {\tau })$ appears in the boundary condition (2.39) and in (2.38a,b).
2.3.2. Simplified formulation near the CJ velocity
The formulation gets simpler when attention is focused on the end of the detonation decay when the velocity is close to the CJ velocity,
Expanding (A1)–(A2) for small values of ![]() $( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a$ yields the well-known square root relation between the flow of burnt gas at the front
$( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a$ yields the well-known square root relation between the flow of burnt gas at the front ![]() ${u_b}(t)$ and the detonation velocity
${u_b}(t)$ and the detonation velocity ![]() $\mathcal {D}(\tau )$ near the CJ regime
$\mathcal {D}(\tau )$ near the CJ regime ![]() ${u_b}/{\epsilon a}\approx 1+\sqrt {2( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a}$, obtained by the relation
${u_b}/{\epsilon a}\approx 1+\sqrt {2( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a}$, obtained by the relation ![]() $( {M_{o_{CJ}}-M_{o_{CJ}}^{-1}})^2/({M-M^{-1}})^2 \approx 1\text {--}2( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a$ in (A1). Then the boundary condition at the front simplifies to
$( {M_{o_{CJ}}-M_{o_{CJ}}^{-1}})^2/({M-M^{-1}})^2 \approx 1\text {--}2( \mathcal {D}- \mathcal {D}_{o_{CJ}} )/\epsilon a$ in (A1). Then the boundary condition at the front simplifies to
where ![]() $u_{fi}$ and
$u_{fi}$ and ![]() $\mu _{fi}$ denote the initial value of
$\mu _{fi}$ denote the initial value of ![]() $u_{f}(\tau )$ and
$u_{f}(\tau )$ and ![]() $\mu _{f}(\tau )\equiv {u_{fi}}/{\epsilon a}-1$ with
$\mu _{f}(\tau )\equiv {u_{fi}}/{\epsilon a}-1$ with ![]() $u_{fi}>\epsilon a$. The term
$u_{fi}>\epsilon a$. The term ![]() $[\mu -\dot {\alpha }_\tau (\tilde {\tau })]$ can then be replaced by
$[\mu -\dot {\alpha }_\tau (\tilde {\tau })]$ can then be replaced by ![]() $\mu$ in (2.36) because the flow field in the rarefaction wave increases monotonically with the radius, from
$\mu$ in (2.36) because the flow field in the rarefaction wave increases monotonically with the radius, from ![]() $u=0$ at
$u=0$ at ![]() $r=r_0$ to a positive value
$r=r_0$ to a positive value ![]() $u_f$ on the front (
$u_f$ on the front (![]() $r=r_f$),
$r=r_f$), ![]() $\mu \in [-1, \mu _f]$, with, according to (2.40a,b)–(2.41a,b),
$\mu \in [-1, \mu _f]$, with, according to (2.40a,b)–(2.41a,b), ![]() $0\leqslant \dot {\alpha }_\tau \ll \mu _f \ll 1$ so that
$0\leqslant \dot {\alpha }_\tau \ll \mu _f \ll 1$ so that ![]() $\dot {\alpha }_\tau ( \tau ) \ll \vert \mu (\xi , \tau ) \vert$
$\dot {\alpha }_\tau ( \tau ) \ll \vert \mu (\xi , \tau ) \vert$ ![]() $\forall \xi \in [\xi _0,\, 0]$. Under the condition (2.40a,b), the unknown velocity of the front
$\forall \xi \in [\xi _0,\, 0]$. Under the condition (2.40a,b), the unknown velocity of the front ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ does not appear explicitly anymore on the left-hand side of (2.38a,b) which reduces to the Burgers-like equation in (2.18),
$\dot {\alpha }_\tau (\tilde {\tau })$ does not appear explicitly anymore on the left-hand side of (2.38a,b) which reduces to the Burgers-like equation in (2.18),
the unknown function being the flow at the front ![]() $\mu _f(\tilde {\tau }) \equiv u_f(\tilde {\tau })/\epsilon a -1$.
$\mu _f(\tilde {\tau }) \equiv u_f(\tilde {\tau })/\epsilon a -1$.
As we shall see in § 3.1, the solution ![]() $\mu (\tilde {\xi }, \tilde {\tau })$ of (2.43) reaches the self-similar CJ solution (2.23)–(2.24) in the long-time limit if the initial thickness of the rarefaction wave scales as (2.17a–c),
$\mu (\tilde {\xi }, \tilde {\tau })$ of (2.43) reaches the self-similar CJ solution (2.23)–(2.24) in the long-time limit if the initial thickness of the rarefaction wave scales as (2.17a–c), ![]() $\vert \tilde {\xi }_{0i}\vert =O(1)$ in the limit
$\vert \tilde {\xi }_{0i}\vert =O(1)$ in the limit ![]() $\epsilon \to 0$. Notice that (2.43), divided by
$\epsilon \to 0$. Notice that (2.43), divided by ![]() $r_{fi}$, yields (2.18) for
$r_{fi}$, yields (2.18) for ![]() $v=\mu +1$, the difference with the CJ problem being the boundary condition on the front (
$v=\mu +1$, the difference with the CJ problem being the boundary condition on the front (![]() $\tilde {\xi }=0$) which now involves an unknown flow
$\tilde {\xi }=0$) which now involves an unknown flow ![]() $\mu _f(\tilde {\tau })\ne 0$,
$\mu _f(\tilde {\tau })\ne 0$, ![]() $v(\eta =0, \nu ) \ne 1$.
$v(\eta =0, \nu ) \ne 1$.
2.3.3. Analytical solutions
The rarefaction wave behind a spherical detonation is a nonlinear solution of the Euler equations, which cannot be described by a linearized approximation, even if the flow velocity is smaller than the speed of sound as it is the case in the limit of small heat release. By comparison, the linear solution is briefly recalled in Appendix B. Equations (2.38a,b) and (2.43) have analytical solutions ![]() $\mu (\tilde {\xi }, \tilde {\tau })$ which provide us with an expression of the unsteady flow on the front
$\mu (\tilde {\xi }, \tilde {\tau })$ which provide us with an expression of the unsteady flow on the front ![]() $\mu _f(\tilde {\tau })= \mu (0, \tilde {\tau })$ in terms of the unknown function
$\mu _f(\tilde {\tau })= \mu (0, \tilde {\tau })$ in terms of the unknown function ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ which, according to (2.30a,b), represents the propagation velocity of the front
$\dot {\alpha }_\tau (\tilde {\tau })$ which, according to (2.30a,b), represents the propagation velocity of the front ![]() $\mathcal {D}(t)$. The dynamics of the front
$\mathcal {D}(t)$. The dynamics of the front ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ is then obtained in a second step through the boundary condition on the front. For example, the Rankine–Hugoniot condition yields the relaxation of a pure shock freely propagating in a spherical geometry which is derived in Appendix D. The end of the decay of an overdriven detonation, treated as a discontinuity, is obtained from (2.43) by using the boundary condition (2.41a,b).
$\dot {\alpha }_\tau (\tilde {\tau })$ is then obtained in a second step through the boundary condition on the front. For example, the Rankine–Hugoniot condition yields the relaxation of a pure shock freely propagating in a spherical geometry which is derived in Appendix D. The end of the decay of an overdriven detonation, treated as a discontinuity, is obtained from (2.43) by using the boundary condition (2.41a,b).
Analytical solutions of (2.38a,b) are obtained in the form of separated variables,
Introducing the notation ![]() $B'\equiv \text {d} B/\text {d} \tilde {\eta }$ and
$B'\equiv \text {d} B/\text {d} \tilde {\eta }$ and ![]() $\dot {A}\equiv \text {d} A/\text {d} \tilde {\tau }$,
$\dot {A}\equiv \text {d} A/\text {d} \tilde {\tau }$, ![]() ${\partial \mu }/{\partial \tilde {\tau }}=\dot {A}+(1+\dot {\alpha }_\tau )AB'$,
${\partial \mu }/{\partial \tilde {\tau }}=\dot {A}+(1+\dot {\alpha }_\tau )AB'$, ![]() $\mu {\partial \mu }/{\partial \tilde {\xi }}=(AB-\dot {\alpha }_\tau )AB'$, the unknown function
$\mu {\partial \mu }/{\partial \tilde {\xi }}=(AB-\dot {\alpha }_\tau )AB'$, the unknown function ![]() $\dot {\alpha }(\tilde {\tau })$ disappears from the equations for
$\dot {\alpha }(\tilde {\tau })$ disappears from the equations for ![]() $A(\tilde {\tau })$ and
$A(\tilde {\tau })$ and ![]() $B(\tilde {\eta })$, yielding
$B(\tilde {\eta })$, yielding
the second equation being obtained after division by ![]() $A^2 B$. The left-hand side of the second equation in (2.45) is a function of
$A^2 B$. The left-hand side of the second equation in (2.45) is a function of ![]() $\tilde {\tau }$ only, while the right-hand side is a function of
$\tilde {\tau }$ only, while the right-hand side is a function of ![]() $\tilde {\eta }$. Therefore, the two sides should be equal to the same constant yielding an ordinary differential equation for
$\tilde {\eta }$. Therefore, the two sides should be equal to the same constant yielding an ordinary differential equation for ![]() $A(\tilde {\tau })$ and
$A(\tilde {\tau })$ and ![]() $B(\tilde {\eta })$ respectively
$B(\tilde {\eta })$ respectively
The constant ![]() $k$ has to be obtained by an initial condition. Integration of the second equation is straightforward leading to a uniform gradient (straight profile of the flow). Introducing the initial value
$k$ has to be obtained by an initial condition. Integration of the second equation is straightforward leading to a uniform gradient (straight profile of the flow). Introducing the initial value ![]() $\tau =0: A=A_i$, the solution of the first equation is,
$\tau =0: A=A_i$, the solution of the first equation is,
the first term on the right-hand side being the general solution of the homogeneous equation and the second term a particular solution. Solutions of (2.43) then take the form
 \begin{gather} \mu(\tilde{\xi}, \tilde{\tau})= \frac{k[\tilde{\xi}-\tilde{\xi}_0(\tilde{\tau})]}{(1+\tilde{\tau})[A_i^{{-}1}+k\ln(1+\tilde{\tau})]}-1 \end{gather}
\begin{gather} \mu(\tilde{\xi}, \tilde{\tau})= \frac{k[\tilde{\xi}-\tilde{\xi}_0(\tilde{\tau})]}{(1+\tilde{\tau})[A_i^{{-}1}+k\ln(1+\tilde{\tau})]}-1 \end{gather} \begin{gather}\tilde{\xi}=0:\quad \mu_f( \tilde{\tau})= \frac{-k\tilde{\xi}_0(\tilde{\tau})}{(1+\tilde{\tau})[A_i^{{-}1}+k\ln(1+\tilde{\tau})]}-1, \quad \tilde{\tau}=0: 1+\mu_{fi}={-}k\tilde{\xi}_{0i}A_i, \end{gather}
\begin{gather}\tilde{\xi}=0:\quad \mu_f( \tilde{\tau})= \frac{-k\tilde{\xi}_0(\tilde{\tau})}{(1+\tilde{\tau})[A_i^{{-}1}+k\ln(1+\tilde{\tau})]}-1, \quad \tilde{\tau}=0: 1+\mu_{fi}={-}k\tilde{\xi}_{0i}A_i, \end{gather}
where the initial values ![]() $\mu _{fi}$ and
$\mu _{fi}$ and ![]() $\tilde {\xi }_{0i}$ have been used,
$\tilde {\xi }_{0i}$ have been used, ![]() $\tilde {\tau }=0: \mu _f=\mu _{fi},\,\tilde {\xi }_0=\tilde {\xi }_{0i}$. Eliminating
$\tilde {\tau }=0: \mu _f=\mu _{fi},\,\tilde {\xi }_0=\tilde {\xi }_{0i}$. Eliminating ![]() $A_i$ in favour of
$A_i$ in favour of ![]() $\mu _{fi}$,
$\mu _{fi}$, ![]() $A_i^{-1}=-k\tilde {\xi }_{0i}/(1+\mu _{fi})$, the constant
$A_i^{-1}=-k\tilde {\xi }_{0i}/(1+\mu _{fi})$, the constant ![]() $k$ is also eliminated from the expressions of
$k$ is also eliminated from the expressions of ![]() $\mu (\tilde {\xi }, \tilde {\tau })$ and
$\mu (\tilde {\xi }, \tilde {\tau })$ and ![]() $\mu _f( \tilde {\tau })$, leading to a two-parameter family of solutions involving the parameters
$\mu _f( \tilde {\tau })$, leading to a two-parameter family of solutions involving the parameters ![]() $\mu _{fi}$ and
$\mu _{fi}$ and ![]() $\tilde {\xi }_{0i}$,
$\tilde {\xi }_{0i}$,
 \begin{gather}\mu_f( \tilde{\tau})= \frac{- \tilde{\xi}_{0}(\tilde{\tau})}{(1+\tilde{\tau})[\theta_i+\ln(1+\tilde{\tau})]}-1, \quad \tilde{\xi}_0(\tilde{\tau})={-} \left[\tilde{\tau}+\int_0^{\tilde{\tau}}\dot{\alpha}_\tau(\tilde{\tau}')\text{d} \tilde{\tau}'\right]+\tilde{\xi}_{0i}. \end{gather}
\begin{gather}\mu_f( \tilde{\tau})= \frac{- \tilde{\xi}_{0}(\tilde{\tau})}{(1+\tilde{\tau})[\theta_i+\ln(1+\tilde{\tau})]}-1, \quad \tilde{\xi}_0(\tilde{\tau})={-} \left[\tilde{\tau}+\int_0^{\tilde{\tau}}\dot{\alpha}_\tau(\tilde{\tau}')\text{d} \tilde{\tau}'\right]+\tilde{\xi}_{0i}. \end{gather}
These expressions for the flow field are solutions to (2.38a,b) and also to (2.43) when ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ is small. Notice that the unknown function
$\dot {\alpha }_\tau (\tilde {\tau })$ is small. Notice that the unknown function ![]() $\dot {\alpha }_\tau (\tilde {\tau })$ appears only through
$\dot {\alpha }_\tau (\tilde {\tau })$ appears only through ![]() $\tilde {\xi }_0(\tilde {\tau })$. Written with the original variables, denoting
$\tilde {\xi }_0(\tilde {\tau })$. Written with the original variables, denoting ![]() $u_f(t)$ the flow on the front,
$u_f(t)$ the flow on the front, ![]() $u_{fi}$ its initial value (
$u_{fi}$ its initial value (![]() $t=0$),
$t=0$), ![]() $r_{fi}$ the initial radius of the front and
$r_{fi}$ the initial radius of the front and ![]() $\mathcal {D}_i>\mathcal {D}(t)$ the initial detonation velocity, (2.50a,b)–(2.51a,b), using the definition in (2.28)
$\mathcal {D}_i>\mathcal {D}(t)$ the initial detonation velocity, (2.50a,b)–(2.51a,b), using the definition in (2.28) ![]() $1+\mu =u/\epsilon a$, take the form
$1+\mu =u/\epsilon a$, take the form
where ![]() $u_{fi}/a=(r_{fi}-r_{0i})/(r_{0i}\theta _i)$. Self-consistency of the asymptotic analysis in the limit
$u_{fi}/a=(r_{fi}-r_{0i})/(r_{0i}\theta _i)$. Self-consistency of the asymptotic analysis in the limit ![]() $\epsilon \to 0$
$\epsilon \to 0$ ![]() $u_{fi}/a=O(\epsilon )$ is ensured by the scaling
$u_{fi}/a=O(\epsilon )$ is ensured by the scaling
Under the condition (2.42), the integral term can be neglected in the expression (2.51a,b) of ![]() $\tilde {\xi }_0$, so that (2.54) reduces to (2.25)
$\tilde {\xi }_0$, so that (2.54) reduces to (2.25) ![]() $(r_{f}(t)-r_{0}(t))/\epsilon \,r_{0}(t)=1$ for
$(r_{f}(t)-r_{0}(t))/\epsilon \,r_{0}(t)=1$ for ![]() $\tilde {\xi }_{0i}=-1$.
$\tilde {\xi }_{0i}=-1$.
Notice also that ![]() $\mu (\tilde {\xi }, \tilde {\tau })$ in (2.50a,b)–(2.53a,b) can be written in the same form as the self-similar solution of (2.18),
$\mu (\tilde {\xi }, \tilde {\tau })$ in (2.50a,b)–(2.53a,b) can be written in the same form as the self-similar solution of (2.18), ![]() $v=[z+\mathcal {A}(\nu )]/\mathcal {B}(\nu )$ with
$v=[z+\mathcal {A}(\nu )]/\mathcal {B}(\nu )$ with ![]() $z=\eta /\nu$,
$z=\eta /\nu$, ![]() $\mathcal {B}(\nu )=(\theta _i+\ln \nu )$ and
$\mathcal {B}(\nu )=(\theta _i+\ln \nu )$ and ![]() $\mathcal {A}(\nu )=[r_f(t)-r_0(t)]/\epsilon r_0(t)$ which reduces to
$\mathcal {A}(\nu )=[r_f(t)-r_0(t)]/\epsilon r_0(t)$ which reduces to ![]() $\mathcal {A}(\nu )=1-(1+\tilde {\xi }_{0i})/\nu$ for
$\mathcal {A}(\nu )=1-(1+\tilde {\xi }_{0i})/\nu$ for ![]() $\dot {\alpha }_\tau \ll 1$ and
$\dot {\alpha }_\tau \ll 1$ and ![]() $\mathcal {A}(\nu )=1$ for
$\mathcal {A}(\nu )=1$ for ![]() $\tilde {\xi }_{0i}=-1$.
$\tilde {\xi }_{0i}=-1$.
2.3.4. Simplified expression of the rarefaction flow near the CJ regime
According to (2.50a,b) and/or (2.52a–c), the gradient of the flow is uniform and decreases monotonically with the time. According to (2.51a,b) and/or (2.53a,b) the flow velocity on the front also decreases and the planar CJ velocity is reached at finite time ![]() $t_t$
$t_t$
However, at ![]() $t-t_t=0^-$, the flow field (2.50a,b)–(2.53a,b) is different from the self-similar rarefaction wave behind a CJ wave (2.22)–(2.24) plotted in figure 1. We will show in § 3.1 that the relaxation of the flow towards the CJ rarefaction wave occurs progressively for
$t-t_t=0^-$, the flow field (2.50a,b)–(2.53a,b) is different from the self-similar rarefaction wave behind a CJ wave (2.22)–(2.24) plotted in figure 1. We will show in § 3.1 that the relaxation of the flow towards the CJ rarefaction wave occurs progressively for ![]() $t>t_t$ after a sudden and sharp transition of the flow gradient on the front at
$t>t_t$ after a sudden and sharp transition of the flow gradient on the front at ![]() $t=t_t$.
$t=t_t$.
At the end of the decay, ![]() $\vert \dot {\alpha }_{\tau }\vert \ll 1$, (2.51a,b) where the integral term
$\vert \dot {\alpha }_{\tau }\vert \ll 1$, (2.51a,b) where the integral term ![]() $\int _0^{\tilde {\tau }}\dot {\alpha }_\tau (\tilde {\tau }')\,\text {d} \tilde {\tau }'$ is neglected (initial condition close to the CJ velocity), introducing
$\int _0^{\tilde {\tau }}\dot {\alpha }_\tau (\tilde {\tau }')\,\text {d} \tilde {\tau }'$ is neglected (initial condition close to the CJ velocity), introducing ![]() $\mu _f(\tilde {\tau }_t)=0$, leads to a transcendental equation for
$\mu _f(\tilde {\tau }_t)=0$, leads to a transcendental equation for ![]() $\tilde {\tau }_t$ in terms of
$\tilde {\tau }_t$ in terms of ![]() $\tilde {\xi }_{0i}$ and
$\tilde {\xi }_{0i}$ and ![]() $\mu _{fi}$
$\mu _{fi}$
 \begin{align} \int_0^{\tau_t}\dot{\alpha}_\tau( \tau')\text{d} \tau'\ll \tau_t,\quad \mu_f(\tilde{\tau}_t)=0 \Rightarrow \tilde{\tau}_t - \tilde{\xi}_{0i}= (1+\tilde{\tau}_t)\left[ -\frac{\tilde{\xi}_{0i}}{(1+\mu_{fi})}+\ln(1+\tilde{\tau}_t)\right ], \end{align}
\begin{align} \int_0^{\tau_t}\dot{\alpha}_\tau( \tau')\text{d} \tau'\ll \tau_t,\quad \mu_f(\tilde{\tau}_t)=0 \Rightarrow \tilde{\tau}_t - \tilde{\xi}_{0i}= (1+\tilde{\tau}_t)\left[ -\frac{\tilde{\xi}_{0i}}{(1+\mu_{fi})}+\ln(1+\tilde{\tau}_t)\right ], \end{align}
which has a single positive root which is small for ![]() $\mu _{fi} \ll 1$ whatever
$\mu _{fi} \ll 1$ whatever ![]() $\tilde {\xi }_{0i}<0$, see Appendix C.2. This root yields a simple expression of
$\tilde {\xi }_{0i}<0$, see Appendix C.2. This root yields a simple expression of ![]() $\tilde {\tau }_t$ (and/or
$\tilde {\tau }_t$ (and/or ![]() $t_t$) in terms of the initial value of the flow at the front
$t_t$) in terms of the initial value of the flow at the front
obtained from the Taylor expansion of (2.56a,b) when the quadratic terms ![]() $\tilde {\tau }_t^2$ are neglected. Limiting our attention to
$\tilde {\tau }_t^2$ are neglected. Limiting our attention to ![]() $0\leqslant t \leqslant t_t$,
$0\leqslant t \leqslant t_t$, ![]() $0\leqslant \tilde {\tau }=O(\tilde {\tau }_t)$, quadratic terms
$0\leqslant \tilde {\tau }=O(\tilde {\tau }_t)$, quadratic terms ![]() $\tilde {\tau }^2=(a t/r_{fi})^2$ are negligible, and a Taylor expansion of (2.50a,b)–(2.51a,b) in powers of
$\tilde {\tau }^2=(a t/r_{fi})^2$ are negligible, and a Taylor expansion of (2.50a,b)–(2.51a,b) in powers of ![]() $\tilde {\tau }_t\approx \mu _{fi}\ll 1$, limited to first order, yields
$\tilde {\tau }_t\approx \mu _{fi}\ll 1$, limited to first order, yields
 \begin{equation} 0\leqslant \tilde{\tau}\leqslant \tilde{\tau}_t\ll 1: \quad\mu \approx \frac{\tilde{\xi}}{(-\tilde{\xi}_{0i})}\left[1+\tilde{\tau}_t-\left (1+\frac{1}{-\tilde{\xi}_{0i}}\right )\tilde{\tau} \right ]+ \tilde{\tau}_t-\tilde{\tau}, \quad \vert\tilde{\xi}_{0i}\vert=O(1). \end{equation}
\begin{equation} 0\leqslant \tilde{\tau}\leqslant \tilde{\tau}_t\ll 1: \quad\mu \approx \frac{\tilde{\xi}}{(-\tilde{\xi}_{0i})}\left[1+\tilde{\tau}_t-\left (1+\frac{1}{-\tilde{\xi}_{0i}}\right )\tilde{\tau} \right ]+ \tilde{\tau}_t-\tilde{\tau}, \quad \vert\tilde{\xi}_{0i}\vert=O(1). \end{equation}
The downstream condition at the weak discontinuity, ![]() $\xi =\xi _0(\tilde {\tau }) : \mu =-1$ with
$\xi =\xi _0(\tilde {\tau }) : \mu =-1$ with ![]() $\tilde {\xi }_0=-\tilde {\tau }+\tilde {\xi }_{0i}$ in (2.43), is recovered at the first order of the Taylor expansion of (2.58) in the form
$\tilde {\xi }_0=-\tilde {\tau }+\tilde {\xi }_{0i}$ in (2.43), is recovered at the first order of the Taylor expansion of (2.58) in the form ![]() $\tilde {\xi }_0/(-\tilde {\xi }_{0i})=-1-\tilde {\tau }/(-\tilde {\xi }_{0i})$. According to (2.42) and (2.57), there is a boundary layer near the detonation front where the flow (2.58) takes an even simpler form at the end of the decay
$\tilde {\xi }_0/(-\tilde {\xi }_{0i})=-1-\tilde {\tau }/(-\tilde {\xi }_{0i})$. According to (2.42) and (2.57), there is a boundary layer near the detonation front where the flow (2.58) takes an even simpler form at the end of the decay ![]() $0\leqslant \tilde {\tau }\leqslant \tilde {\tau }_t\ll 1$
$0\leqslant \tilde {\tau }\leqslant \tilde {\tau }_t\ll 1$
 \begin{gather} -\tilde{\xi}\equiv \frac{(r_f-r)}{\epsilon r_{fi}}=O(\tilde{\tau}_t), \quad \tilde{\tau}_t\approx \mu_{fi}= \sqrt{\frac{2(\mathcal{D}_i-\mathcal{D}_{o_{CI}})}{\epsilon a}}\ll 1, \end{gather}
\begin{gather} -\tilde{\xi}\equiv \frac{(r_f-r)}{\epsilon r_{fi}}=O(\tilde{\tau}_t), \quad \tilde{\tau}_t\approx \mu_{fi}= \sqrt{\frac{2(\mathcal{D}_i-\mathcal{D}_{o_{CI}})}{\epsilon a}}\ll 1, \end{gather} \begin{gather}\mu(\tilde{\xi}, \tilde{\tau})\approx \frac{\tilde{\xi}}{-\tilde{\xi}_{0i}}-(\tilde{\tau}-\tilde{\tau}_t), \quad \mu_f(\tilde{\tau})\approx (\tilde{\tau}_t-\tilde{\tau}), \end{gather}
\begin{gather}\mu(\tilde{\xi}, \tilde{\tau})\approx \frac{\tilde{\xi}}{-\tilde{\xi}_{0i}}-(\tilde{\tau}-\tilde{\tau}_t), \quad \mu_f(\tilde{\tau})\approx (\tilde{\tau}_t-\tilde{\tau}), \end{gather}
obtained when terms of second order ![]() $\tilde {\tau }_t^2$ are neglected. This leads to
$\tilde {\tau }_t^2$ are neglected. This leads to
 \begin{align} \frac{\partial \mu(\tilde{\xi}, \tilde{\tau})}{\partial \tilde{\tau}} \approx{-}1, \quad \left.\frac{\partial u(r, t)}{\partial r}\right\vert_{r=r_f} \approx \frac{a}{r_f},\quad \frac{1}{\epsilon a}\frac{ \text{d} u_f(t)}{\text{d} t}\approx{-}\frac{a}{ r_{f}} \Rightarrow \frac{\text{d} u_f(t)}{\text{d} t}\approx{-}a\frac{u_f}{ r_{f}}, \end{align}
\begin{align} \frac{\partial \mu(\tilde{\xi}, \tilde{\tau})}{\partial \tilde{\tau}} \approx{-}1, \quad \left.\frac{\partial u(r, t)}{\partial r}\right\vert_{r=r_f} \approx \frac{a}{r_f},\quad \frac{1}{\epsilon a}\frac{ \text{d} u_f(t)}{\text{d} t}\approx{-}\frac{a}{ r_{f}} \Rightarrow \frac{\text{d} u_f(t)}{\text{d} t}\approx{-}a\frac{u_f}{ r_{f}}, \end{align}
where ![]() $r_{fi}$ has been replaced by
$r_{fi}$ has been replaced by ![]() $r_f$ in the denominators since
$r_f$ in the denominators since ![]() $r_f-r_{fi}=O(\epsilon r_{f})$. The terms of order
$r_f-r_{fi}=O(\epsilon r_{f})$. The terms of order ![]() $\epsilon$ being neglected in (2.43), retaining the small term
$\epsilon$ being neglected in (2.43), retaining the small term ![]() $(\tilde {\tau }_t-\tilde {\tau })$ which is of order
$(\tilde {\tau }_t-\tilde {\tau })$ which is of order ![]() $\tilde {\tau }_t\approx \mu _{fi}\equiv (u_{fi}/ \epsilon a)-1$, is meaningful in (2.60a,b) in an intermediate asymptotic limit
$\tilde {\tau }_t\approx \mu _{fi}\equiv (u_{fi}/ \epsilon a)-1$, is meaningful in (2.60a,b) in an intermediate asymptotic limit ![]() $\epsilon \ll \sqrt {2(\mathcal {D}_i-\mathcal {D}_{o_{CJ}})/\epsilon a}\ll 1$.
$\epsilon \ll \sqrt {2(\mathcal {D}_i-\mathcal {D}_{o_{CJ}})/\epsilon a}\ll 1$.
The last equation in (2.62a–c) corresponds to the closure assumption used in Clavin & Denet (Reference Clavin and Denet2020) who neglected the small gradient of the flow at the exit of the reaction zone. This equation is indeed quite general close to the CJ regime and was derived previously in the opposite limit ![]() $M_{o_{CJ}}\gg 1$ by Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012). This can be seen in (2.9)–(2.10a–c); because of the transonic character of the burnt gas flow near the detonation,
$M_{o_{CJ}}\gg 1$ by Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012). This can be seen in (2.9)–(2.10a–c); because of the transonic character of the burnt gas flow near the detonation, ![]() $u+a-\mathcal {D} \ll 1$, the term involving the gradient of the flow on the left-hand side becomes negligible near the detonation front, the unsteady term being balanced by the divergence of the flow
$u+a-\mathcal {D} \ll 1$, the term involving the gradient of the flow on the left-hand side becomes negligible near the detonation front, the unsteady term being balanced by the divergence of the flow ![]() $-a u/r$. More precisely in the limit of small heat release, using
$-a u/r$. More precisely in the limit of small heat release, using ![]() $\mathcal {D}_{o_{CJ}}-a\approx \epsilon a$,
$\mathcal {D}_{o_{CJ}}-a\approx \epsilon a$, ![]() $\mathcal {D} -a=\epsilon a (1+\dot {\alpha }_\tau )\approx \epsilon a$,
$\mathcal {D} -a=\epsilon a (1+\dot {\alpha }_\tau )\approx \epsilon a$, ![]() $u_f=O(\epsilon a)$,
$u_f=O(\epsilon a)$, ![]() $\mu =u/\epsilon a-1$, see (2.28), and, according to (2.62a–c),
$\mu =u/\epsilon a-1$, see (2.28), and, according to (2.62a–c), ![]() $\partial u/\partial r\vert _{r=r_f}\approx a/r_f$ with (2.57)
$\partial u/\partial r\vert _{r=r_f}\approx a/r_f$ with (2.57) ![]() $\mu _f<\mu _{fi}\ll 1$, the gradient term on the left-hand side of (2.10a–c) is shown to be smaller than the curvature term
$\mu _f<\mu _{fi}\ll 1$, the gradient term on the left-hand side of (2.10a–c) is shown to be smaller than the curvature term ![]() $au/r$ on the right-hand side by a factor
$au/r$ on the right-hand side by a factor ![]() $\epsilon$,
$\epsilon$,
As we shall see, this small gradient of the rarefaction flow cannot be ignored in the critical dynamics studied in § 4 because it controls the instantaneous position of the sonic point inside the rarefaction wave.
3. Transitory flow for the discontinuous model
The way the rarefaction wave (2.50a,b) reaches the self-similar solution behind the CJ wave (2.22)–(2.23) after ![]() $t_t$, is presented in this section for
$t_t$, is presented in this section for ![]() $M_{o_{CJ}}-1\ll 1$. The transition is similar to that described by Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012) in the opposite limit
$M_{o_{CJ}}-1\ll 1$. The transition is similar to that described by Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012) in the opposite limit ![]() $M_{o_{CJ}}\gg 1$.
$M_{o_{CJ}}\gg 1$.
3.1. Abrupt transition of the flow on the front
Both the flows (2.50a,b) and (2.22)–(2.23) vanish at the radius of the spherical core of stagnant gas but the gradient of the flow is uniform and finite in the former while it is infinite on the detonation front in the latter, see figure 1. The sonic condition of (2.50a,b) (relative to the detonation front) which is located at finite distance behind the detonation front for ![]() $t<t_t$, reaches the front at
$t<t_t$, reaches the front at ![]() $t=t_t$. Within the framework of the discontinuous model, the velocity of the burnt gas relative to the lead shock cannot become smaller than the sound speed on the detonation front. According to (2.41a,b)–(2.42), neither
$t=t_t$. Within the framework of the discontinuous model, the velocity of the burnt gas relative to the lead shock cannot become smaller than the sound speed on the detonation front. According to (2.41a,b)–(2.42), neither ![]() $\dot {\alpha }_t(t)$ nor
$\dot {\alpha }_t(t)$ nor ![]() $\mu _f(t)$ can become negative; they should vanish simultaneously at
$\mu _f(t)$ can become negative; they should vanish simultaneously at ![]() $t=t_t$ and stay equal to zero at later times
$t=t_t$ and stay equal to zero at later times ![]() $t>t_t$
$t>t_t$
Therefore, the decrease of ![]() $u_f(t)$ with a quasi-constant deceleration rate (2.61a,b) for
$u_f(t)$ with a quasi-constant deceleration rate (2.61a,b) for ![]() $t\leqslant t_t$ stops suddenly at
$t\leqslant t_t$ stops suddenly at ![]() $t=t_t$ since
$t=t_t$ since ![]() $u_f$ stays constant after
$u_f$ stays constant after ![]() $t_t$. A jump of deceleration of the flow is thus produced at
$t_t$. A jump of deceleration of the flow is thus produced at ![]() $t=t_t$ on the detonation front
$t=t_t$ on the detonation front
 \begin{equation} \left.\frac{1}{\epsilon a}\frac{\text{d} u_f}{\text{d} t}\right\vert^{t_t^+}_{t_t^-}=\frac{a}{r_f(t_t)}, \quad \left.\frac{\text{d} \mu_f}{\text{d} \tilde{\tau} }\right\vert^{\tilde{\tau}_t^+}_{\tilde{\tau}_t^-}=\frac{r_{fi}}{r_f(t_t)}\approx 1. \end{equation}
\begin{equation} \left.\frac{1}{\epsilon a}\frac{\text{d} u_f}{\text{d} t}\right\vert^{t_t^+}_{t_t^-}=\frac{a}{r_f(t_t)}, \quad \left.\frac{\text{d} \mu_f}{\text{d} \tilde{\tau} }\right\vert^{\tilde{\tau}_t^+}_{\tilde{\tau}_t^-}=\frac{r_{fi}}{r_f(t_t)}\approx 1. \end{equation} However, the trajectory in the phase space of velocity–radius “![]() $\mathcal {D}$-
$\mathcal {D}$-![]() $r_f$” is tangent to the axis
$r_f$” is tangent to the axis ![]() $\mathcal {D}=\mathcal {D}_{o_{CJ}}$ at
$\mathcal {D}=\mathcal {D}_{o_{CJ}}$ at ![]() $t=t_t$, as shown by (2.41a,b)
$t=t_t$, as shown by (2.41a,b) ![]() $\dot {\alpha }_\tau = \mu ^2_f(\tau )/2$ by using (2.61a,b)
$\dot {\alpha }_\tau = \mu ^2_f(\tau )/2$ by using (2.61a,b) ![]() $\mu _f \approx {a(t_t-t)}{ r_{fi}}$
$\mu _f \approx {a(t_t-t)}{ r_{fi}}$
 \begin{align}
&\epsilon\ll1, (t-t_t) \to 0^-: \quad
[\mathcal{D}(t)-\mathcal{D}_{o_{CJ}}]/a \to (\epsilon
/2)[(t-t_t )a/r_{fi}]^2, \nonumber\\
&\text{d} r_f/\text{d}
t\approx \mathcal{D}_{o_{CJ}}=a(1+\epsilon), \quad
(\mathcal{D}-\mathcal{D}_{o_{CJ}})/a \to (\epsilon
/2)(r_f-r_{f}(t_t) )^2/r_{fi}^2,
\end{align}
\begin{align}
&\epsilon\ll1, (t-t_t) \to 0^-: \quad
[\mathcal{D}(t)-\mathcal{D}_{o_{CJ}}]/a \to (\epsilon
/2)[(t-t_t )a/r_{fi}]^2, \nonumber\\
&\text{d} r_f/\text{d}
t\approx \mathcal{D}_{o_{CJ}}=a(1+\epsilon), \quad
(\mathcal{D}-\mathcal{D}_{o_{CJ}})/a \to (\epsilon
/2)(r_f-r_{f}(t_t) )^2/r_{fi}^2,
\end{align}
the last relation being valid near the CJ regime ![]() $0\leqslant \mathcal {D}-\mathcal {D}_{o_{CJ}}\ll \mathcal {D}_{o_{CJ}}$ in the limit of small heat release
$0\leqslant \mathcal {D}-\mathcal {D}_{o_{CJ}}\ll \mathcal {D}_{o_{CJ}}$ in the limit of small heat release ![]() $(\mathcal {D}_{o_{CJ}}-a)/a= \epsilon \ll 1$. The jumps in (3.2a,b) and the tangency of the trajectories at
$(\mathcal {D}_{o_{CJ}}-a)/a= \epsilon \ll 1$. The jumps in (3.2a,b) and the tangency of the trajectories at ![]() $t=t_t$ are consequences of the discontinuous model and are no longer valid when small modification of the inner structure of the detonation is taken into account.
$t=t_t$ are consequences of the discontinuous model and are no longer valid when small modification of the inner structure of the detonation is taken into account.
3.2. Transitory regime. An analytical study
The transitory flow between the transition from the straight profile (2.50a,b) for ![]() $\tilde {\tau }\leqslant \tilde {\tau }_t$ to the self-similar solution (2.22)–(2.24), denoted
$\tilde {\tau }\leqslant \tilde {\tau }_t$ to the self-similar solution (2.22)–(2.24), denoted ![]() $\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ in the following, is solution of (2.43) for a flow velocity at the front kept equal to its CJ value after
$\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ in the following, is solution of (2.43) for a flow velocity at the front kept equal to its CJ value after ![]() $t_t$
$t_t$
This flow is equal to (2.50a,b) (with ![]() $\mu _{fi}>0$) when
$\mu _{fi}>0$) when ![]() $t < t_t$,
$t < t_t$,
 \begin{equation} \tilde{\tau} \approx \tilde{\tau}_t^{-}, \quad \tilde{\xi}_{0}(\tilde{\tau}_t)\leqslant \tilde{\xi}\leqslant0:\quad \mu^{(tr)}(\tilde{\xi}, \tilde{\tau}_t)= \frac{\tilde{\xi}}{- \tilde{\xi}_{0i}+\tilde{\tau}_t}=\frac{\tilde{\xi}}{-\tilde{\xi}_0(\tilde{\tau}_t)}, \end{equation}
\begin{equation} \tilde{\tau} \approx \tilde{\tau}_t^{-}, \quad \tilde{\xi}_{0}(\tilde{\tau}_t)\leqslant \tilde{\xi}\leqslant0:\quad \mu^{(tr)}(\tilde{\xi}, \tilde{\tau}_t)= \frac{\tilde{\xi}}{- \tilde{\xi}_{0i}+\tilde{\tau}_t}=\frac{\tilde{\xi}}{-\tilde{\xi}_0(\tilde{\tau}_t)}, \end{equation}
where the simplified expression (2.58) has been used by introducing (2.56a,b)–(2.57) into (2.50a,b) neglecting the quadratic terms ![]() $\tilde {\tau }^2_t$. Equation (3.5) says simply that the transitory flow at
$\tilde {\tau }^2_t$. Equation (3.5) says simply that the transitory flow at ![]() $\tilde {\tau }=\tilde {\tau }_t$ has a straight profile corresponding to the reduced thickness
$\tilde {\tau }=\tilde {\tau }_t$ has a straight profile corresponding to the reduced thickness ![]() $\vert \tilde {\xi }_0(\tilde {\tau }_t)\vert$ of the rarefaction wave. Simultaneously with the jump of deceleration (3.2a,b), the flow gradient on the detonation front, which is finite for
$\vert \tilde {\xi }_0(\tilde {\tau }_t)\vert$ of the rarefaction wave. Simultaneously with the jump of deceleration (3.2a,b), the flow gradient on the detonation front, which is finite for ![]() $\tilde {\tau }<\tilde {\tau }_t$, jumps at
$\tilde {\tau }<\tilde {\tau }_t$, jumps at ![]() $\tilde {\tau }=\tilde {\tau }_t$ to become infinite at
$\tilde {\tau }=\tilde {\tau }_t$ to become infinite at ![]() $\tilde {\tau }=\tilde {\tau }_t^+$ and stays infinite afterwards
$\tilde {\tau }=\tilde {\tau }_t^+$ and stays infinite afterwards ![]() $\tilde {\tau }>\tilde {\tau }_t$
$\tilde {\tau }>\tilde {\tau }_t$
 \begin{equation} \tilde{\tau}=\tilde{\tau}_t^-{\ll} 1:\left. \frac{\partial \mu}{\partial \tilde{\xi}}\right\vert_{\tilde{\xi}=0^-}=\frac{1}{-\tilde{\xi}_0(\tilde{\tau}_t)}, \quad \tilde{\tau}>\tilde{\tau}_t: \lim_{\tilde{\xi}\to 0^-}\frac{\partial \mu^{(tr)}}{\partial \tilde{\xi}}\approx \frac{1}{\sqrt{-2\tilde{\xi}}}. \end{equation}
\begin{equation} \tilde{\tau}=\tilde{\tau}_t^-{\ll} 1:\left. \frac{\partial \mu}{\partial \tilde{\xi}}\right\vert_{\tilde{\xi}=0^-}=\frac{1}{-\tilde{\xi}_0(\tilde{\tau}_t)}, \quad \tilde{\tau}>\tilde{\tau}_t: \lim_{\tilde{\xi}\to 0^-}\frac{\partial \mu^{(tr)}}{\partial \tilde{\xi}}\approx \frac{1}{\sqrt{-2\tilde{\xi}}}. \end{equation}
These expressions are obtained by the same method as in § 2.2.2 for the self-similar CJ solution (2.22)–(2.23). Recalling that no boundary condition is used on the front to derive (2.50a,b)–(2.51a,b), this flow is still solution of (2.43) for ![]() $\tilde {\tau }>\tilde {\tau }_t$ when
$\tilde {\tau }>\tilde {\tau }_t$ when ![]() $\mu _f(\tilde {\tau })$ decreases below zero. The corresponding flow, denoted
$\mu _f(\tilde {\tau })$ decreases below zero. The corresponding flow, denoted ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ from now on, takes the form
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ from now on, takes the form
 \begin{align} \tilde{\tau}_t\approx \mu_{fi}\ll 1,\quad \tilde{\tau}\geqslant\tilde{\tau}_t,\quad \mu^{(wd)}(\tilde{\xi}, \tilde{\tau})\approx \frac{\tilde{\xi}+\tilde{\tau}-\tilde{\xi}_{0i}}{(1+\tilde{\tau})[-\tilde{\xi}_{0i}/(1+\tilde{\tau}_t)+\ln(1+\tilde{\tau})]}-1, \end{align}
\begin{align} \tilde{\tau}_t\approx \mu_{fi}\ll 1,\quad \tilde{\tau}\geqslant\tilde{\tau}_t,\quad \mu^{(wd)}(\tilde{\xi}, \tilde{\tau})\approx \frac{\tilde{\xi}+\tilde{\tau}-\tilde{\xi}_{0i}}{(1+\tilde{\tau})[-\tilde{\xi}_{0i}/(1+\tilde{\tau}_t)+\ln(1+\tilde{\tau})]}-1, \end{align}
where, neglecting the quadratic terms ![]() $\tilde {\tau }^2_t$, the flow at
$\tilde {\tau }^2_t$, the flow at ![]() $\tau =\tau _t$ is given in (3.5),
$\tau =\tau _t$ is given in (3.5), ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau }_t)=\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau }_t)$. The instantaneous position of the weak discontinuity corresponding to (3.7a–c),
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau }_t)=\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau }_t)$. The instantaneous position of the weak discontinuity corresponding to (3.7a–c), ![]() $\tilde {\xi }=\tilde {\xi }_0(\tilde {\tau })$:
$\tilde {\xi }=\tilde {\xi }_0(\tilde {\tau })$: ![]() $1+\mu ^{(wd)}(\tilde {\xi }_0, \tilde {\tau }_t)=0$, takes the form
$1+\mu ^{(wd)}(\tilde {\xi }_0, \tilde {\tau }_t)=0$, takes the form
Equation (3.7a–c) cannot represent the transitory flow nearby the detonation front for ![]() $\tilde {\tau } > \tilde {\tau }_t:$
$\tilde {\tau } > \tilde {\tau }_t:$ ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })\ne \mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ since
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })\ne \mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ since ![]() $\mu ^{(tr)}(0,\tilde {\tau })=0$ while
$\mu ^{(tr)}(0,\tilde {\tau })=0$ while ![]() $\mu ^{(wd)}(0,\tilde {\tau })<0\ \forall \,\tilde {\tau } > \tilde {\tau }_t$. However, (3.7a–c) still represents the transitory flow at a distance from the front large enough, as explained now by the method of characteristics.
$\mu ^{(wd)}(0,\tilde {\tau })<0\ \forall \,\tilde {\tau } > \tilde {\tau }_t$. However, (3.7a–c) still represents the transitory flow at a distance from the front large enough, as explained now by the method of characteristics.
The singular perturbation (3.6a,b), which is generated instantaneously at ![]() $\tilde {\tau }=\tilde {\tau }_t$ on the front, induces a disturbance which is transported downstream with the velocity
$\tilde {\tau }=\tilde {\tau }_t$ on the front, induces a disturbance which is transported downstream with the velocity ![]() $\mu ^{(tr)}$ by the mode
$\mu ^{(tr)}$ by the mode ![]() $\mathcal {C}_+$ (downstream running for
$\mathcal {C}_+$ (downstream running for ![]() $\tilde {\tau }>\tilde {\tau }_t$ since
$\tilde {\tau }>\tilde {\tau }_t$ since ![]() $\mu ^{(tr)}\leqslant 0$). According to (3.4), the characteristic curves
$\mu ^{(tr)}\leqslant 0$). According to (3.4), the characteristic curves ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau })$
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau })$
corresponds to the following equation for the flow velocity transported by ![]() $\mathcal {C}^+$
$\mathcal {C}^+$
 \begin{equation}
\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})\equiv
\mu^{(tr)}(\tilde{\xi}_{_{\,\mathcal{C}_+}}(\tilde{\tau}),
\tilde{\tau} ),\quad \frac{\text{d}
\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})}{\text{d}
\tilde{\tau}}={-}\frac{1+\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})}{\tilde{\tau}
+1}.
\end{equation}
\begin{equation}
\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})\equiv
\mu^{(tr)}(\tilde{\xi}_{_{\,\mathcal{C}_+}}(\tilde{\tau}),
\tilde{\tau} ),\quad \frac{\text{d}
\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})}{\text{d}
\tilde{\tau}}={-}\frac{1+\mu^{(tr)}_{_{\,\mathcal{C}_+}}(\tilde{\tau})}{\tilde{\tau}
+1}.
\end{equation}
Denoting ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$ the characteristic curve leaving the front (
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$ the characteristic curve leaving the front (![]() $\tilde {\xi }=0$) at
$\tilde {\xi }=0$) at ![]() $\tilde {\tau }=\tilde {\tau }'\geqslant \tilde {\tau }_t$, integration of (3.10a,b) from
$\tilde {\tau }=\tilde {\tau }'\geqslant \tilde {\tau }_t$, integration of (3.10a,b) from ![]() $\tilde {\tau } =\tilde {\tau }': \mu ^{(tr)}_{_{\,\mathcal {C}_+}}(\tilde {\tau }')=0$ yields the flow velocity transported by this characteristic in the form
$\tilde {\tau } =\tilde {\tau }': \mu ^{(tr)}_{_{\,\mathcal {C}_+}}(\tilde {\tau }')=0$ yields the flow velocity transported by this characteristic in the form
Integrating (3.9) from ![]() $\tau =\tau ':$
$\tau =\tau ':$ ![]() $\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }', \tilde {\tau }')=0$ using (3.11), then determines the characteristic curves
$\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }', \tilde {\tau }')=0$ using (3.11), then determines the characteristic curves ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$
All these characteristics leave the front slowly since their velocity is zero at the front (![]() $\xi =0$)
$\xi =0$) ![]() $\mu ^{(tr)}(0,\tilde {\tau }')=0$,
$\mu ^{(tr)}(0,\tilde {\tau }')=0$, ![]() $\partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')/\partial \tilde {\tau }\vert _{\tilde {\tau }=\tilde {\tau }'}=0$
$\partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')/\partial \tilde {\tau }\vert _{\tilde {\tau }=\tilde {\tau }'}=0$ ![]() $\forall \tilde {\tau }'\geqslant \tilde {\tau }_t$. They all reach the same velocity in the long-time limit,
$\forall \tilde {\tau }'\geqslant \tilde {\tau }_t$. They all reach the same velocity in the long-time limit, ![]() $\lim _{\tilde {\tau } \to \infty } \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')/\partial \tilde {\tau }=-1$. Moreover, in agreement with the fact that no shock can be created when the flow
$\lim _{\tilde {\tau } \to \infty } \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')/\partial \tilde {\tau }=-1$. Moreover, in agreement with the fact that no shock can be created when the flow ![]() $u(r,t)$ increases in space in the direction of the flow,
$u(r,t)$ increases in space in the direction of the flow, ![]() $\partial u/\partial r >0$, these characteristic curves do not cross each other. This is checked by noticing that the modulus of their velocity satisfies the following relation
$\partial u/\partial r >0$, these characteristic curves do not cross each other. This is checked by noticing that the modulus of their velocity satisfies the following relation ![]() $\tilde {\tau }_1' >\tilde {\tau }_2' \Rightarrow \vert \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_1')/\partial \tilde {\tau }\vert <\vert \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_2')/\partial \tilde {\tau }\vert$, see figure 2. Therefore, the trajectory
$\tilde {\tau }_1' >\tilde {\tau }_2' \Rightarrow \vert \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_1')/\partial \tilde {\tau }\vert <\vert \partial \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_2')/\partial \tilde {\tau }\vert$, see figure 2. Therefore, the trajectory ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ associated with the characteristic curve leaving the front at the earliest time
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ associated with the characteristic curve leaving the front at the earliest time ![]() $\tilde {\tau }'=\tilde {\tau }_t$ is, according to (3.13),
$\tilde {\tau }'=\tilde {\tau }_t$ is, according to (3.13),
with, according to (3.11), the following expression of the flow which is transported
In other words, ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ is the equation of the leading edge of the disturbance resulting from keeping equal to zero the front velocity
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ is the equation of the leading edge of the disturbance resulting from keeping equal to zero the front velocity ![]() $\tilde {\xi }=0:$
$\tilde {\xi }=0:$ ![]() $\mu ^{(tr)}=0$
$\mu ^{(tr)}=0$ ![]() $\forall \tilde {\tau }>\tilde {\tau }_t$. Ahead of this leading edge, the flow
$\forall \tilde {\tau }>\tilde {\tau }_t$. Ahead of this leading edge, the flow ![]() $\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ is equal to the ‘unperturbed’ flow (3.7a–c),
$\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ is equal to the ‘unperturbed’ flow (3.7a–c),

Figure 2. Example of three characteristic curves ![]() $\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$ for
$\tilde {\xi }=\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }')$ for ![]() $\tilde {\tau }'=\tilde {\tau }_t$,
$\tilde {\tau }'=\tilde {\tau }_t$, ![]() $\tilde {\tau }'=\tilde {\tau }'_2$ and
$\tilde {\tau }'=\tilde {\tau }'_2$ and ![]() $\tilde {\tau }'=\tilde {\tau }'_1$ with
$\tilde {\tau }'=\tilde {\tau }'_1$ with ![]() $\tilde {\tau }_t<\tau '_2<\tau '_1$. In the dashed region
$\tilde {\tau }_t<\tau '_2<\tau '_1$. In the dashed region ![]() $\tilde {\xi }\leqslant \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$, the transitory flow is equal to the unperturbed flow (3.7a–c) (straight profile whose slope is decreasing to zero)
$\tilde {\xi }\leqslant \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$, the transitory flow is equal to the unperturbed flow (3.7a–c) (straight profile whose slope is decreasing to zero) ![]() $\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })=\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$.
$\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })=\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$.
The junction point at which ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ is equal to (3.16)
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ is equal to (3.16)
 \begin{equation} \frac{\tilde{\xi}(\tilde{\tau})+\tilde{\tau}-\tilde{\xi}_{0i}}{-\tilde{\xi}_{0i}/(1+\tilde{\tau}_t)+\ln(1+\tilde{\tau})}=\tilde{\tau}_t+1 \Rightarrow \tilde{\xi}(\tilde{\tau})={-}\tilde{\tau} +(\tilde{\tau}_t+1)\ln(1+\tilde{\tau})\quad \forall\, \tilde{\xi}_{0i}, \end{equation}
\begin{equation} \frac{\tilde{\xi}(\tilde{\tau})+\tilde{\tau}-\tilde{\xi}_{0i}}{-\tilde{\xi}_{0i}/(1+\tilde{\tau}_t)+\ln(1+\tilde{\tau})}=\tilde{\tau}_t+1 \Rightarrow \tilde{\xi}(\tilde{\tau})={-}\tilde{\tau} +(\tilde{\tau}_t+1)\ln(1+\tilde{\tau})\quad \forall\, \tilde{\xi}_{0i}, \end{equation}
corresponds effectively to the characteristics (3.14) when the quadratic terms ![]() $\tilde {\tau }^2_t$ are neglected as it should be.
$\tilde {\tau }^2_t$ are neglected as it should be.
Strictly speaking, this point does not reach the core of stagnant gas (3.8) ![]() $\tilde {\xi }_0(\tilde {\tau })$ in the long-time limit,
$\tilde {\xi }_0(\tilde {\tau })$ in the long-time limit, ![]() $\lim _{\tilde {\tau }\to \infty }\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)- \tilde {\xi }_0(\tilde {\tau })\approx \ln \tilde {\tau }$. However, this is true in the sense of the self-similar analysis when using the self-similar variable
$\lim _{\tilde {\tau }\to \infty }\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)- \tilde {\xi }_0(\tilde {\tau })\approx \ln \tilde {\tau }$. However, this is true in the sense of the self-similar analysis when using the self-similar variable ![]() $z_{_{\,\mathcal {C}_+}}(\tilde {\tau })\equiv [r_{_{\,\mathcal {C}_+}}(t)-r_f(t)]/\epsilon r_0(t) \approx \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)/(-\tilde {\tau })$, yielding, according to (3.15)
$z_{_{\,\mathcal {C}_+}}(\tilde {\tau })\equiv [r_{_{\,\mathcal {C}_+}}(t)-r_f(t)]/\epsilon r_0(t) \approx \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)/(-\tilde {\tau })$, yielding, according to (3.15)
To conclude, the transitory flow ![]() $\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ is composed of two parts. The part corresponding to
$\mu ^{(tr)}(\tilde {\xi }, \tilde {\tau })$ is composed of two parts. The part corresponding to ![]() $\tilde {\xi } \leqslant \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ is the straight profile
$\tilde {\xi } \leqslant \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$ is the straight profile ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ in (3.7a–c) whose slope is uniform and decreases to zero
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ in (3.7a–c) whose slope is uniform and decreases to zero ![]() $\lim _{\tilde {\tau }\to \infty }(1+\tilde {\tau })^{-1}[-\tilde {\xi }_{0i}/(1+\tilde {\tau }_t)+\ln (1+\tilde {\tau })]^{-1}=0$. The transitory flow has a curved shape in the range
$\lim _{\tilde {\tau }\to \infty }(1+\tilde {\tau })^{-1}[-\tilde {\xi }_{0i}/(1+\tilde {\tau }_t)+\ln (1+\tilde {\tau })]^{-1}=0$. The transitory flow has a curved shape in the range ![]() $\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)\leqslant \tilde {\xi }\leqslant 0$, joining the straight solution
$\tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)\leqslant \tilde {\xi }\leqslant 0$, joining the straight solution ![]() $\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ at
$\mu ^{(wd)}(\tilde {\xi }, \tilde {\tau })$ at ![]() $\tilde {\xi } = \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$, while the slope is infinite at the front (
$\tilde {\xi } = \tilde {\xi }_{_{\,\mathcal {C}_+}}(\tilde {\tau }, \tilde {\tau }_t)$, while the slope is infinite at the front (![]() $\tilde {\xi }=0$). The evolution of the rarefaction wave is sketched in figure 3 where the theoretical expressions for the coordinates (position and flow velocity at time
$\tilde {\xi }=0$). The evolution of the rarefaction wave is sketched in figure 3 where the theoretical expressions for the coordinates (position and flow velocity at time ![]() $t$) of the point of junction with the straight profile are given.
$t$) of the point of junction with the straight profile are given.

Figure 3. Sketch of the transitory flow, plotted in a universal form for ![]() $\tilde {\xi }_{0i}=-1$ and
$\tilde {\xi }_{0i}=-1$ and ![]() $\tilde {\tau }_t\approx \mu _{fi}\ll 1$,
$\tilde {\tau }_t\approx \mu _{fi}\ll 1$, ![]() $\tilde {\tau }_t$ being the cross-over time (2.56a,b). The bold curve in black is the rarefaction wave
$\tilde {\tau }_t$ being the cross-over time (2.56a,b). The bold curve in black is the rarefaction wave ![]() $u^{(tr)}/\epsilon a= 1+\mu ^{(tr)}$ behind a detonation treated as a discontinuity, after the cross-over time
$u^{(tr)}/\epsilon a= 1+\mu ^{(tr)}$ behind a detonation treated as a discontinuity, after the cross-over time ![]() $\tilde {\tau }>\tilde {\tau }_t$. The slope is infinite at the front and the profile is straight away from the front where
$\tilde {\tau }>\tilde {\tau }_t$. The slope is infinite at the front and the profile is straight away from the front where ![]() $\mu ^{(tr)}=\mu ^{(wd)}$. Expressed in terms of the space variable
$\mu ^{(tr)}=\mu ^{(wd)}$. Expressed in terms of the space variable ![]() $\tilde {\xi }/(-\tilde {\xi }_0)=[r-r_f(t)]/[r_f(t)-r_0(t)]$,
$\tilde {\xi }/(-\tilde {\xi }_0)=[r-r_f(t)]/[r_f(t)-r_0(t)]$, ![]() $-\tilde {\xi }_0(\tilde {\tau })=\tilde {\tau }+1$, the profile of the transitory flow is parameter free, provided the time is measured by
$-\tilde {\xi }_0(\tilde {\tau })=\tilde {\tau }+1$, the profile of the transitory flow is parameter free, provided the time is measured by ![]() $(1+\tilde {\tau })/(1+\tilde {\tau }_t)$. The bold points are the time dependent radius and flow velocity of the junction point where the transitory flow
$(1+\tilde {\tau })/(1+\tilde {\tau }_t)$. The bold points are the time dependent radius and flow velocity of the junction point where the transitory flow ![]() $\mu ^{(tr)}$ matches
$\mu ^{(tr)}$ matches ![]() $\mu ^{wd}$ in (3.7a–c). The coloured straight lines represent the rarefaction wave (2.50a,b) of the overdriven detonations before the velocity reaches the planar CJ velocity
$\mu ^{wd}$ in (3.7a–c). The coloured straight lines represent the rarefaction wave (2.50a,b) of the overdriven detonations before the velocity reaches the planar CJ velocity ![]() $\tilde {\tau } < \tilde {\tau }_t$, the red one being just before the transition to CJ,
$\tilde {\tau } < \tilde {\tau }_t$, the red one being just before the transition to CJ, ![]() $\tilde {\tau } -\tilde {\tau }_t=0^-$.
$\tilde {\tau } -\tilde {\tau }_t=0^-$.
These theoretical results are fully confirmed by the numerical solution of (3.4)–(3.5). An example of numerical result is shown in figure 4. When the result is plotted with a space coordinate reduced by the thickness of the CJ rarefaction wave, the numerical analysis shows that the transitory flow and the self-similar CJ solution are quasi-identical in the range between the detonation front and the junction point travelling with the characteristic ![]() $\mathcal {C}_+$ issued from the front at
$\mathcal {C}_+$ issued from the front at ![]() $t=t_t$ at which the front reaches the CJ velocity. Outside this range, the numerical result shows a straight profile down to the stagnant core, in full agreement with (3.7a–c). The trajectory of the junction point between the two parts of the transitory flow corresponds exactly to the theoretical result plotted in figure 3.
$t=t_t$ at which the front reaches the CJ velocity. Outside this range, the numerical result shows a straight profile down to the stagnant core, in full agreement with (3.7a–c). The trajectory of the junction point between the two parts of the transitory flow corresponds exactly to the theoretical result plotted in figure 3.

Figure 4. Numerical solution (solid line) of (3.4)–(3.5), describing the transitory flow ![]() $u^{(tr)}/\epsilon a = 1+\mu ^{(tr)}$ for
$u^{(tr)}/\epsilon a = 1+\mu ^{(tr)}$ for ![]() $\tilde {\tau }-\tilde {\tau }_t=3$, using the non-dimensional radius, reduced by the thickness of the rarefaction wave. The dotted line is the self-similar rarefaction flow (2.23)–(2.25) behind the spherical CJ detonation, which is reached in the long-time limit
$\tilde {\tau }-\tilde {\tau }_t=3$, using the non-dimensional radius, reduced by the thickness of the rarefaction wave. The dotted line is the self-similar rarefaction flow (2.23)–(2.25) behind the spherical CJ detonation, which is reached in the long-time limit ![]() $\tilde {\tau }-\tilde {\tau }_t\to \infty$. The dashed straight line is (3.7a–c) for
$\tilde {\tau }-\tilde {\tau }_t\to \infty$. The dashed straight line is (3.7a–c) for ![]() $\tilde {\tau }-\tilde {\tau }_t=3$. The trajectory of the point at the junction of the numerical solution of (3.4)–(3.5) and the straight profile (3.7a–c) is in full agreement with the theoretical prediction (3.12)–(3.18). To summarize, the numerical solution of (3.4)–(3.5) is found to be exactly the straight profile (3.7a–c) below the junction while, in the range between the front and the junction point, there is no noticeable difference between the numerical solution of (3.4)–(3.5) and the self-similar solution (2.23)–(2.25).
$\tilde {\tau }-\tilde {\tau }_t=3$. The trajectory of the point at the junction of the numerical solution of (3.4)–(3.5) and the straight profile (3.7a–c) is in full agreement with the theoretical prediction (3.12)–(3.18). To summarize, the numerical solution of (3.4)–(3.5) is found to be exactly the straight profile (3.7a–c) below the junction while, in the range between the front and the junction point, there is no noticeable difference between the numerical solution of (3.4)–(3.5) and the self-similar solution (2.23)–(2.25).
4. Direct initiation of detonation
Modification to the inner structure influences drastically the dynamics of a spherical detonation. In contrast to the discontinuous model, detonation failure is observed when the detonation velocity reaches the CJ velocity for the first time at a too small radius (however, larger than the detonation thickness). Moreover, during successful initiation of a stable detonation, the CJ velocity is no longer reached abruptly. The critical dynamics is analysed here in the limit of small heat release.
4.1. Detonation model and method of solution
The reduced variables of order unity governing the structure and the dynamics of the inner structure in the limit of small heat release ![]() $\epsilon \to 0$ are
$\epsilon \to 0$ are ![]() $\xi =O(1)$ and
$\xi =O(1)$ and ![]() $\tau =O(1)$ in (2.27a–c) where
$\tau =O(1)$ in (2.27a–c) where ![]() $r_{fi}$ is the initial radius of the detonation at
$r_{fi}$ is the initial radius of the detonation at ![]() $\tau =0$. According to (2.36)–(2.37a–c), the link of
$\tau =0$. According to (2.36)–(2.37a–c), the link of ![]() $\xi$,
$\xi$, ![]() $\tau$ with
$\tau$ with ![]() $\tilde {\xi }\equiv \xi /\tilde {r}_{fi}$ and
$\tilde {\xi }\equiv \xi /\tilde {r}_{fi}$ and ![]() $\tilde {\tau }=\tau /\tilde {r}_{fi}$ is through the parameter
$\tilde {\tau }=\tau /\tilde {r}_{fi}$ is through the parameter ![]() $\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ of order unity in the limit
$\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ of order unity in the limit ![]() $\epsilon \to 0$.
$\epsilon \to 0$.
As in Clavin & Denet (Reference Clavin and Denet2020), we will use the detonation model of Clavin & Williams (Reference Clavin and Williams2002), obtained by an asymptotic analysis in the limit of small heat release, coupled to the Newtonian approximation neglecting the compressional heating in the reaction zone where the chemical energy is released (after the induction period),
The Rankine–Hugoniot conditions (A3)–(A5) in the limit (4.1) take the form,
where ![]() $\mathcal {E}$ is the activation energy governing the induction length, and
$\mathcal {E}$ is the activation energy governing the induction length, and ![]() $b=O(1)$ is its reduced form. A first simplification concerns the temperature and the mass fraction of species which, to leading order in the limit (4.1), are solutions of the steady-state version of the conservation equations of energy and mass, satisfying the Rankine–Hugoniot conditions at the lead shock, see the original article Clavin & Williams (Reference Clavin and Williams2002) recalled in § B.1 of Clavin & Denet (Reference Clavin and Denet2018). The unsteady distribution of the rate of heat release
$b=O(1)$ is its reduced form. A first simplification concerns the temperature and the mass fraction of species which, to leading order in the limit (4.1), are solutions of the steady-state version of the conservation equations of energy and mass, satisfying the Rankine–Hugoniot conditions at the lead shock, see the original article Clavin & Williams (Reference Clavin and Williams2002) recalled in § B.1 of Clavin & Denet (Reference Clavin and Denet2018). The unsteady distribution of the rate of heat release ![]() $\omega (\xi , \tau )$ can then be expressed in terms of the unsteady detonation velocity and the distribution in steady state,
$\omega (\xi , \tau )$ can then be expressed in terms of the unsteady detonation velocity and the distribution in steady state, ![]() $\omega (\xi , \tau )= \bar \omega (\xi , \dot {\alpha }_\tau (\tau ))$. Focusing our attention on propagation velocity close enough to the CJ velocity,
$\omega (\xi , \tau )= \bar \omega (\xi , \dot {\alpha }_\tau (\tau ))$. Focusing our attention on propagation velocity close enough to the CJ velocity, ![]() $y(\tau )\equiv b\dot {\alpha }_\tau (\tau )=O(1)$, the unsteady distribution of reaction rate takes the form
$y(\tau )\equiv b\dot {\alpha }_\tau (\tau )=O(1)$, the unsteady distribution of reaction rate takes the form ![]() $\omega (\xi , \tau )= \bar \omega (\xi , y(\tau ))$ which will be denoted simply
$\omega (\xi , \tau )= \bar \omega (\xi , y(\tau ))$ which will be denoted simply ![]() $\omega (\xi ,y)$ in the following. For the sake of simplicity we will use here the scaling law assuming that the distribution of reaction rate is fully governed by the induction length. Introducing the distribution of the planar CJ wave
$\omega (\xi ,y)$ in the following. For the sake of simplicity we will use here the scaling law assuming that the distribution of reaction rate is fully governed by the induction length. Introducing the distribution of the planar CJ wave ![]() $\omega _{o_{CJ}}(\xi )$, the reaction-rate distribution
$\omega _{o_{CJ}}(\xi )$, the reaction-rate distribution ![]() $\omega (\xi , y)$ then takes the form
$\omega (\xi , y)$ then takes the form
The chemical kinetics thus appears only through the activation energy ![]() $b$ and the CJ distribution
$b$ and the CJ distribution ![]() $\omega _{o_{CJ}}(\xi )$.
$\omega _{o_{CJ}}(\xi )$.
In order to further simplify the presentation, the same bounded-thickness model for the inner structure of the planar CJ detonation as in (3.15)–(3.17b) of Clavin & Denet (Reference Clavin and Denet2020) will be used,
so that, in the limit of small heat release, the structure of the flow in the planar CJ wave (![]() $y=0$)
$y=0$) ![]() $\mu _{o_{CJ}}(\xi )$ is solution to
$\mu _{o_{CJ}}(\xi )$ is solution to
According to (4.4a,b) and (4.5a,b) the exit of the reaction zone ![]() $\xi =\xi _b(\tau )$ of the unsteady inner structure of the spherical combustion wave is
$\xi =\xi _b(\tau )$ of the unsteady inner structure of the spherical combustion wave is
describing a substantial increase of the reaction-wave thickness when the velocity decreases below the CJ velocity ![]() $y<0$. However, for a reduced detonation velocity of order unity
$y<0$. However, for a reduced detonation velocity of order unity ![]() $\vert y\vert =O(1)$, the thickness of the detonation is of the same order of magnitude as in the planar CJ wave,
$\vert y\vert =O(1)$, the thickness of the detonation is of the same order of magnitude as in the planar CJ wave, ![]() $\text {e}^{-y}=O(1)$ in the limit
$\text {e}^{-y}=O(1)$ in the limit ![]() $\epsilon \to 0$. The variation of
$\epsilon \to 0$. The variation of ![]() $y$ is bounded from below since a supersonic velocity
$y$ is bounded from below since a supersonic velocity ![]() $\mathcal {D} \geqslant a$ implies
$\mathcal {D} \geqslant a$ implies ![]() $\dot {\alpha }_\tau \equiv (\mathcal {D}-\mathcal {D}_{o_{CJ}})/\epsilon a =(\mathcal {D}-a)/\epsilon a-1\geqslant -1$ so that
$\dot {\alpha }_\tau \equiv (\mathcal {D}-\mathcal {D}_{o_{CJ}})/\epsilon a =(\mathcal {D}-a)/\epsilon a-1\geqslant -1$ so that ![]() $y\equiv b \dot {\alpha }_\tau \geqslant -b$. In fact, according to the well-known chemical-kinetics quenching in combustion, occurring at a cross-over temperature for which the recombination reactions become faster than the chain-branching reactions, the rate of heat release vanishes earlier. In real combustion, this cross-over temperature
$y\equiv b \dot {\alpha }_\tau \geqslant -b$. In fact, according to the well-known chemical-kinetics quenching in combustion, occurring at a cross-over temperature for which the recombination reactions become faster than the chain-branching reactions, the rate of heat release vanishes earlier. In real combustion, this cross-over temperature ![]() $T_c$ at which the reaction rate decreases sharply and the induction time increases strongly is typically
$T_c$ at which the reaction rate decreases sharply and the induction time increases strongly is typically ![]() $T_c \approx 1000\ \textrm {K}$ in ordinary condition while the Neumann temperature of a CJ wave is approximately
$T_c \approx 1000\ \textrm {K}$ in ordinary condition while the Neumann temperature of a CJ wave is approximately ![]() $T_{No{CJ}}\approx 2000\ \textrm {K}$, see Sanchez & Williams (Reference Sanchez and Williams2014) and Clavin & Searby (Reference Clavin and Searby2016). Considering that ordinary combustion cannot proceed below
$T_{No{CJ}}\approx 2000\ \textrm {K}$, see Sanchez & Williams (Reference Sanchez and Williams2014) and Clavin & Searby (Reference Clavin and Searby2016). Considering that ordinary combustion cannot proceed below ![]() $T_c$ with
$T_c$ with ![]() $T_{No{CJ}} -T_c \approx (T_{No{CJ}} -T_u)/2$, a chemical quenching is assumed to be produced in the limit of small heat release for
$T_{No{CJ}} -T_c \approx (T_{No{CJ}} -T_u)/2$, a chemical quenching is assumed to be produced in the limit of small heat release for ![]() $y=y_c$ with typically
$y=y_c$ with typically ![]() $y_c= - b/2$. Then, the following condition is added to (4.4a,b)–(4.5a,b)
$y_c= - b/2$. Then, the following condition is added to (4.4a,b)–(4.5a,b)
The reaction being quenched below ![]() $y\leqslant y_c$, detonation fails systematically as soon as the detonation velocity decreases below the lower bound
$y\leqslant y_c$, detonation fails systematically as soon as the detonation velocity decreases below the lower bound ![]() $y_c$.
$y_c$.
Another key simplification of the limit (4.1) concerns the two-time-scale nature of the dynamics which, to a lesser extent, characterizes also real detonations. To leading order in the limit (4.1), following the reasoning used in § 2.1, the unsteady flow inside the inner structure of a spherical detonation is governed by a single equation corresponding to (2.36) plus an additional term on the right-hand side associated with the reaction rate
with, according to (2.30a,b)–(2.32a,b),
The key point which is used to obtain (4.10) is that the variations of pressure and flow velocity across the inner structure of the reaction wave are identical to leading order in the limit (4.1), ![]() ${\rm \pi} =\mu +1$ where
${\rm \pi} =\mu +1$ where ![]() ${\rm \pi} \equiv (1/\epsilon \mu )$,
${\rm \pi} \equiv (1/\epsilon \mu )$, ![]() $\ln (p/p_u) \approx u/a$, see Clavin & Williams (Reference Clavin and Williams2002) and also § B.1 of Clavin & Denet (Reference Clavin and Denet2018) and § 3.1 of Clavin & Denet (Reference Clavin and Denet2020) for a spherical geometry. The boundary condition at the lead shock (4.11) is the Rankine–Hugoniot relation (4.2a,b)–(4.3a,b) obtained from (A5)–(A6) for
$\ln (p/p_u) \approx u/a$, see Clavin & Williams (Reference Clavin and Williams2002) and also § B.1 of Clavin & Denet (Reference Clavin and Denet2018) and § 3.1 of Clavin & Denet (Reference Clavin and Denet2020) for a spherical geometry. The boundary condition at the lead shock (4.11) is the Rankine–Hugoniot relation (4.2a,b)–(4.3a,b) obtained from (A5)–(A6) for ![]() $M-1=\epsilon (1+y/b)$. The last term on the right-hand side of (4.10) is the damping rate (2.36)
$M-1=\epsilon (1+y/b)$. The last term on the right-hand side of (4.10) is the damping rate (2.36) ![]() $(l/a)(u/r)$ due to the divergence of the burnt-gas flow near the front for
$(l/a)(u/r)$ due to the divergence of the burnt-gas flow near the front for ![]() $r_f\gg l$ in a spherical geometry,
$r_f\gg l$ in a spherical geometry, ![]() $u/r\approx u/r_f$.
$u/r\approx u/r_f$.
When attention is focused on the inner structure, ![]() $\xi =O(1)$, the time-dependent velocity of the lead shock
$\xi =O(1)$, the time-dependent velocity of the lead shock ![]() $y(\tau )$ is obtained as an eigenfunction of the system (4.10)–(4.11) plus a boundary condition at the exit of the reaction zone. In contrast to Clavin & Denet (Reference Clavin and Denet2020) where, considering the burnt-gas flow as uniform, the decelerating flow
$y(\tau )$ is obtained as an eigenfunction of the system (4.10)–(4.11) plus a boundary condition at the exit of the reaction zone. In contrast to Clavin & Denet (Reference Clavin and Denet2020) where, considering the burnt-gas flow as uniform, the decelerating flow ![]() $\mu _b(\tau )$, solution to
$\mu _b(\tau )$, solution to ![]() $\text {d} \mu _b/\text {d} \tau \approx -(1+\mu _b)/\tilde {r}_f$, was imposed in the burnt gas
$\text {d} \mu _b/\text {d} \tau \approx -(1+\mu _b)/\tilde {r}_f$, was imposed in the burnt gas ![]() $\xi =-\text {e}^{-y}$, the solution of (4.10)–(4.11) will be matched now with the non-uniform flow of the rarefaction wave, solution to the inert version (2.36) of (4.10), denoted
$\xi =-\text {e}^{-y}$, the solution of (4.10)–(4.11) will be matched now with the non-uniform flow of the rarefaction wave, solution to the inert version (2.36) of (4.10), denoted ![]() $\mu ^{ext}( \xi , \tau )$ from now on. In overdriven regimes, this external flow field
$\mu ^{ext}( \xi , \tau )$ from now on. In overdriven regimes, this external flow field ![]() $\mu ^{ext}( \xi , \tau )$ is given by the analytical expressions (2.50a,b)–(2.51a,b), as discussed now.
$\mu ^{ext}( \xi , \tau )$ is given by the analytical expressions (2.50a,b)–(2.51a,b), as discussed now.
4.2. Overdriven regimes. Splitting and matching
The burnt-gas flow at the exit of the reaction zone of a supersonic reaction wave in the overdriven regime is, by definition, subsonic relative to the lead shock, ![]() $\mathcal {D}-u_b < a \Leftrightarrow \mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )>y(\tau )/b$. The sonic point
$\mathcal {D}-u_b < a \Leftrightarrow \mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )>y(\tau )/b$. The sonic point ![]() $\xi =\xi _s(\tau )$,
$\xi =\xi _s(\tau )$, ![]() $\mu ^{ext}(\xi _s(\tau ), \tau )=y(\tau )/b$, is located inside the rarefaction flow, behind the inner structure of the combustion wave. Overdriven regimes are then characterized by the relations
$\mu ^{ext}(\xi _s(\tau ), \tau )=y(\tau )/b$, is located inside the rarefaction flow, behind the inner structure of the combustion wave. Overdriven regimes are then characterized by the relations
the last inequality being in agreement with a rarefaction flow of inert gas which is an increasing function of the radius ![]() $\partial \mu ^{ext}/\partial \xi >0$. The larger the overdrive factor
$\partial \mu ^{ext}/\partial \xi >0$. The larger the overdrive factor ![]() $\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y(\tau )/b>0$ is, the larger is the distance between the sonic point and the exit of the reaction zone.The characteristic
$\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y(\tau )/b>0$ is, the larger is the distance between the sonic point and the exit of the reaction zone.The characteristic ![]() $\mathcal {C}_+$ of (2.36) is downstream running (towards the weak discontinuity
$\mathcal {C}_+$ of (2.36) is downstream running (towards the weak discontinuity ![]() $\xi =\xi _0<0$) behind the sonic point (
$\xi =\xi _0<0$) behind the sonic point (![]() $\xi <\xi _s$,
$\xi <\xi _s$, ![]() $\mu ^{ext} < y/b)$) while it is upstream running (towards the lead shock
$\mu ^{ext} < y/b)$) while it is upstream running (towards the lead shock ![]() $\xi =0$) for
$\xi =0$) for ![]() $\xi >\xi _s$,
$\xi >\xi _s$, ![]() $\mu ^{ext}>y/b$, see figure 5. Then, under the condition (4.13a–c), modifications of the inner structure of the combustion wave cannot influence the rarefaction flow in the burnt gas, which is still given by (2.50a,b)–(2.51a,b),
$\mu ^{ext}>y/b$, see figure 5. Then, under the condition (4.13a–c), modifications of the inner structure of the combustion wave cannot influence the rarefaction flow in the burnt gas, which is still given by (2.50a,b)–(2.51a,b),
where ![]() $\tilde {r}_f(\tau )$ is the reduced radius (4.12). Introducing the notation
$\tilde {r}_f(\tau )$ is the reduced radius (4.12). Introducing the notation
the function ![]() $\mu _f^{ext}(\tau )$ is, according to (2.51a,b),
$\mu _f^{ext}(\tau )$ is, according to (2.51a,b),
 \begin{equation} \mu^{ext}_f(\tau) = \frac{\tau \left[1+Y(\tau)\right ]+(-\tilde{\xi}_{0i})\tilde{r}_{fi}}{ \tilde{r}_f(\tau)[(-\tilde{\xi}_{0i})/(1+\mu^{ext}_{fi})+\ln(\tilde{r}_f/\tilde{r}_{fi})]}-1. \end{equation}
\begin{equation} \mu^{ext}_f(\tau) = \frac{\tau \left[1+Y(\tau)\right ]+(-\tilde{\xi}_{0i})\tilde{r}_{fi}}{ \tilde{r}_f(\tau)[(-\tilde{\xi}_{0i})/(1+\mu^{ext}_{fi})+\ln(\tilde{r}_f/\tilde{r}_{fi})]}-1. \end{equation}
The external flow ![]() $\mu ^{ext}(\xi , \tau )$ is a linear function of the radius (straight shape) with a slope decreasing monotonically to zero, regardless of the time-dependent velocity of the front
$\mu ^{ext}(\xi , \tau )$ is a linear function of the radius (straight shape) with a slope decreasing monotonically to zero, regardless of the time-dependent velocity of the front ![]() $y(\tau )$. The dependence of
$y(\tau )$. The dependence of ![]() $\mu _f^{ext}(\tau )$ on the past of the unknown solution
$\mu _f^{ext}(\tau )$ on the past of the unknown solution ![]() $y(\tau )$ through the integral
$y(\tau )$ through the integral ![]() $Y(\tau )$ comes from the increase of the thickness of the rarefaction wave with the time,
$Y(\tau )$ comes from the increase of the thickness of the rarefaction wave with the time, ![]() $-\xi _0(\tau )\equiv {[r_f(\tau )-r_0(\tau )]}/{l}$,
$-\xi _0(\tau )\equiv {[r_f(\tau )-r_0(\tau )]}/{l}$, ![]() $-\text {d}\xi _{0}/\text {d} \tau = 1+y/b$, see (2.34)–(2.35a,b). At large radius and close to the CJ velocity the external flow takes the simplified form (C12), reminiscent of (2.61a,b). To summarize, for overdriven regimes, the boundary condition in the burnt gas of the solution of (4.10) is (4.14)
$-\text {d}\xi _{0}/\text {d} \tau = 1+y/b$, see (2.34)–(2.35a,b). At large radius and close to the CJ velocity the external flow takes the simplified form (C12), reminiscent of (2.61a,b). To summarize, for overdriven regimes, the boundary condition in the burnt gas of the solution of (4.10) is (4.14)

Figure 5. Sketch of the flow in an overdriven regime with ![]() $0 < y/b < \mu ^{ext}_{f}$,
$0 < y/b < \mu ^{ext}_{f}$, ![]() $\mu ^{ext}(\xi _{s},0)=y/b$
$\mu ^{ext}(\xi _{s},0)=y/b$ ![]() $<\mu ^{ext}_{f}$,
$<\mu ^{ext}_{f}$, ![]() $\xi _{s}<-\text {e}^{-y}$. The distances plotted on the horizontal and vertical axis correspond to the simplified expressions (C12),
$\xi _{s}<-\text {e}^{-y}$. The distances plotted on the horizontal and vertical axis correspond to the simplified expressions (C12), ![]() $\tau _t$ corresponding to the time at which
$\tau _t$ corresponding to the time at which ![]() $\mu ^{ext}_{f}=0$.
$\mu ^{ext}_{f}=0$.
Introducing the decomposition
and subtracting (2.36) from (4.10)
the dynamics of the lead shock ![]() $y(\tau )$ during the decay of a combustion wave in the overdriven regime corresponds to the eigenfunction of the following problem
$y(\tau )$ during the decay of a combustion wave in the overdriven regime corresponds to the eigenfunction of the following problem
where ![]() $\mu ^{ext}(\xi , \tau )$ is given in (4.15) and
$\mu ^{ext}(\xi , \tau )$ is given in (4.15) and ![]() $\tau _s$ denotes the time at which the overdriven regime is no longer verified. The boundary conditions at
$\tau _s$ denotes the time at which the overdriven regime is no longer verified. The boundary conditions at ![]() $\xi =0$ and at
$\xi =0$ and at ![]() $\xi = -\text {e}^{-y(\tau )}$ are respectively the Rankine–Hugoniot relation (4.11) and (4.18).
$\xi = -\text {e}^{-y(\tau )}$ are respectively the Rankine–Hugoniot relation (4.11) and (4.18).
Typically, ![]() $\xi _s(\tau )$ increases when
$\xi _s(\tau )$ increases when ![]() $y(\tau )$ decreases, see § 5.1, so that the sonic point approaches the end of the reaction
$y(\tau )$ decreases, see § 5.1, so that the sonic point approaches the end of the reaction ![]() $\xi _b(\tau )=-\text {e}^{-y}$. As soon as the sonic point crosses the exit of the reaction zone,
$\xi _b(\tau )=-\text {e}^{-y}$. As soon as the sonic point crosses the exit of the reaction zone, ![]() $\tau \geqslant \tau _s$,
$\tau \geqslant \tau _s$, ![]() $\xi _s(\tau _s)=-\text {e}^{-y(\tau _s)}$,
$\xi _s(\tau _s)=-\text {e}^{-y(\tau _s)}$, ![]() $\mu ^{ext}(\xi _s,\tau )=y/b$, the propagation regime is no more overdriven; the external flow which is still solution of (2.38a,b) in the burnt gas
$\mu ^{ext}(\xi _s,\tau )=y/b$, the propagation regime is no more overdriven; the external flow which is still solution of (2.38a,b) in the burnt gas ![]() $\xi <-\text {e}^{-y(\tau )}$, is influenced by the disturbances emitted from the reactive transonic flow and transported downstream (towards the weak discontinuity
$\xi <-\text {e}^{-y(\tau )}$, is influenced by the disturbances emitted from the reactive transonic flow and transported downstream (towards the weak discontinuity ![]() $\xi =\xi _0<0$) by the characteristic
$\xi =\xi _0<0$) by the characteristic ![]() $\mathcal {C}_+$. Then, for
$\mathcal {C}_+$. Then, for ![]() $\tau > \tau _s$,
$\tau > \tau _s$, ![]() $\xi _s(\tau )>-\text {e}^{-y(\tau )}$, the boundary condition (4.19) is no longer valid and the rarefaction wave is no longer represented accurately by the analytical expression (4.15) everywhere in the burnt gas. In other words, soon after
$\xi _s(\tau )>-\text {e}^{-y(\tau )}$, the boundary condition (4.19) is no longer valid and the rarefaction wave is no longer represented accurately by the analytical expression (4.15) everywhere in the burnt gas. In other words, soon after ![]() $\tau _s$, the rarefaction flow behind the end of the reaction (
$\tau _s$, the rarefaction flow behind the end of the reaction (![]() $\xi <-\text {e}^{-y(\tau )}$) is modified by the heat which is released in the region delimited by the end of the reaction and the sonic point (
$\xi <-\text {e}^{-y(\tau )}$) is modified by the heat which is released in the region delimited by the end of the reaction and the sonic point (![]() $-\text {e}^{-y}\leqslant \xi \leqslant \xi _s$). However, as in the discontinuous model in § 3.2, see figures 3 and 4, the solution (4.15) is recovered downstream until the arrival of the disturbance transported by the characteristic
$-\text {e}^{-y}\leqslant \xi \leqslant \xi _s$). However, as in the discontinuous model in § 3.2, see figures 3 and 4, the solution (4.15) is recovered downstream until the arrival of the disturbance transported by the characteristic ![]() $\mathcal {C}_+$. The subsequent dynamics for
$\mathcal {C}_+$. The subsequent dynamics for ![]() $\tau \geqslant \tau _s$ should then be analysed by the numerical solution of (4.10)–(4.11) using an initial condition at
$\tau \geqslant \tau _s$ should then be analysed by the numerical solution of (4.10)–(4.11) using an initial condition at ![]() $\tau = \tau _s$ given by the solution of the eigenvalue problem (4.22)–(4.23).
$\tau = \tau _s$ given by the solution of the eigenvalue problem (4.22)–(4.23).
4.3. Initial condition
In a real initiation process the trajectory of the lead shock is fully determined by the strong blast wave (inert flow) which is generated initially by a quasi-punctual and quasi-instantaneous deposit of external energy at the centre. According to the self-similar solution of Sedov (Reference Sedov1946) and Taylor (Reference Taylor1950b), this strong blast wave depends only on the amount of energy which is deposited, see the discussion of Liñán et al. (Reference Li nan, Kurdyumov and Sanchez2012) for more details. Such an initial stage corresponds to a large Mach number which is beyond the scope of the asymptotic analysis in the limit ![]() $0 < M-1\ll 1$. The critical condition of initiation will be investigated in the present article by a parametric study of the initial conditions of the solution of (4.10)–(4.17). Three parameters of order unity in the limit
$0 < M-1\ll 1$. The critical condition of initiation will be investigated in the present article by a parametric study of the initial conditions of the solution of (4.10)–(4.17). Three parameters of order unity in the limit ![]() $\epsilon \to 0$ are involved at
$\epsilon \to 0$ are involved at ![]() $\tau =0$; the initial radius
$\tau =0$; the initial radius ![]() $\tilde {r}_{fi}\equiv \epsilon {r_{fi}}/{l}$, the initial thickness of the rarefaction wave
$\tilde {r}_{fi}\equiv \epsilon {r_{fi}}/{l}$, the initial thickness of the rarefaction wave ![]() $-\tilde {\xi }_{0i}\equiv (r_{fi}-r_{0i})/\epsilon r_{fi}>0$ and a positive parameter
$-\tilde {\xi }_{0i}\equiv (r_{fi}-r_{0i})/\epsilon r_{fi}>0$ and a positive parameter ![]() $\mu ^{ext}_{fi}$. The initial propagation velocity
$\mu ^{ext}_{fi}$. The initial propagation velocity ![]() $y_i=b(\mathcal {D}_i-\mathcal {D}_{o_{CJ}})/\epsilon a$ is related to the above-mentioned parameters through the inner structure of the detonation. Our attention will be focused on the initial velocity of weakly overdriven detonations close to the CJ velocity, typically
$y_i=b(\mathcal {D}_i-\mathcal {D}_{o_{CJ}})/\epsilon a$ is related to the above-mentioned parameters through the inner structure of the detonation. Our attention will be focused on the initial velocity of weakly overdriven detonations close to the CJ velocity, typically ![]() $y_i/b=0.15\text {--}0.5$ and on an initial extension of the rarefaction wave much larger than the detonation thickness, as in real initiation processes near criticality
$y_i/b=0.15\text {--}0.5$ and on an initial extension of the rarefaction wave much larger than the detonation thickness, as in real initiation processes near criticality
The numerical integration of (4.10)–(4.11) is initialized at ![]() $\tau =0$ by igniting the exothermal reaction in the inert flow (4.15)
$\tau =0$ by igniting the exothermal reaction in the inert flow (4.15)
 \begin{equation} \tau=0: \quad \mu^{ext}( \xi)=\frac{ (1+\mu^{ext}_{fi})}{(-\tilde{\xi}_{0i})\tilde{r}_{fi}}\,\xi+ \mu_{fi}^{ext}\quad \text{with} \ \mu_{fi}^{ext}>0, \end{equation}
\begin{equation} \tau=0: \quad \mu^{ext}( \xi)=\frac{ (1+\mu^{ext}_{fi})}{(-\tilde{\xi}_{0i})\tilde{r}_{fi}}\,\xi+ \mu_{fi}^{ext}\quad \text{with} \ \mu_{fi}^{ext}>0, \end{equation}
leading quickly, on a time scale shorter than unity, to the structure (4.13a–c) of an overdriven regime sketched in figure 5, ![]() $\mathcal {D}-u_b < a \Leftrightarrow \mu _{fi}^{ext}(-\text {e}^{-y_i})-y_i/b > 0$. For
$\mathcal {D}-u_b < a \Leftrightarrow \mu _{fi}^{ext}(-\text {e}^{-y_i})-y_i/b > 0$. For ![]() $\mu _{fi}^{ext}$ large enough, the initial detonation velocity is larger than the CJ velocity
$\mu _{fi}^{ext}$ large enough, the initial detonation velocity is larger than the CJ velocity ![]() $y_i>0$. As explained at the beginning of § 4.2, the rarefaction flow of burnt gas (4.15)–(4.17) is not perturbed by the heat release since the regime is overdriven.
$y_i>0$. As explained at the beginning of § 4.2, the rarefaction flow of burnt gas (4.15)–(4.17) is not perturbed by the heat release since the regime is overdriven.
5. Discussion of the critical dynamics
As discussed in Clavin & Denet (Reference Clavin and Denet2020), the case of large activation energy leading to strongly overdriven detonations is difficult and is left for future works. Within the framework of the detonation model (4.4a,b)–(4.9) in the limit of small heat release, the threshold of the longitudinal instability corresponds to a critical activation energy ![]() $b=b_c$ of order unity,
$b=b_c$ of order unity, ![]() $b_c=O(1)$, for example
$b_c=O(1)$, for example ![]() $b_c=1.27$ for the distribution
$b_c=1.27$ for the distribution ![]() $\omega _{o_{CJ}}(\xi )$ used in Clavin & Denet (Reference Clavin and Denet2018). Therefore, focusing our attention on marginally stable and/or unstable detonations (
$\omega _{o_{CJ}}(\xi )$ used in Clavin & Denet (Reference Clavin and Denet2018). Therefore, focusing our attention on marginally stable and/or unstable detonations (![]() $b$ of order unity), the curvature-induced quenching which is described in the quasi-steady approximation for
$b$ of order unity), the curvature-induced quenching which is described in the quasi-steady approximation for ![]() $b\gg 1$ in Appendix E cannot provide an accurate picture of detonation failure. However, we will see that the order of magnitude of the critical radius is correctly predicted.
$b\gg 1$ in Appendix E cannot provide an accurate picture of detonation failure. However, we will see that the order of magnitude of the critical radius is correctly predicted.
5.1. Slowdown mechanism of overdriven waves. Failure and successful initiation
Consider initial conditions for which the propagation velocity crosses the planar CJ velocity for the first time at ![]() $\tau =\tau _t$,
$\tau =\tau _t$, ![]() $y(\tau _t)=0$,
$y(\tau _t)=0$, ![]() $-\text {e}^{-y(\tau _t)}=-1$, with a radius small enough and an overdrive factor
$-\text {e}^{-y(\tau _t)}=-1$, with a radius small enough and an overdrive factor ![]() $\mu ^{ext}(-1, \tau _t)>0$ large enough so that the flow at the exit of the reaction zone continues to be subsonic (relative to the lead shock) well below the planar CJ velocity,
$\mu ^{ext}(-1, \tau _t)>0$ large enough so that the flow at the exit of the reaction zone continues to be subsonic (relative to the lead shock) well below the planar CJ velocity, ![]() $y<0:$
$y<0:$ ![]() $\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y/b>0$. According to (2.50a,b)–(2.51a,b), the sonic point inside the rarefaction flow of burnt gas behind an overdriven detonation moves towards the reaction zone when the acceleration
$\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y/b>0$. According to (2.50a,b)–(2.51a,b), the sonic point inside the rarefaction flow of burnt gas behind an overdriven detonation moves towards the reaction zone when the acceleration ![]() $\vert {\textrm {d}y}/\text {d} \tau \vert$ is not too large (
$\vert {\textrm {d}y}/\text {d} \tau \vert$ is not too large (![]() ${\textrm {d}y}/\text {d} \tau <0$), more precisely when the decrease rate of
${\textrm {d}y}/\text {d} \tau <0$), more precisely when the decrease rate of ![]() $1+{y(\tau )}/{b}>0$ is smaller than the damping rate by the curvature
$1+{y(\tau )}/{b}>0$ is smaller than the damping rate by the curvature
see (C17). The exit of the reaction zone ![]() $\xi =-\text {e}^{-y}$ moving in the opposite direction when
$\xi =-\text {e}^{-y}$ moving in the opposite direction when ![]() $y$ decreases, the overdrive factor
$y$ decreases, the overdrive factor ![]() $\mu ^{ext}(-\text {e}^{-y(\tau )},\tau )-y(\tau )/b>0$ decreases and the sonic point can catch the exit of the inner structure of the reaction wave at a later time.
$\mu ^{ext}(-\text {e}^{-y(\tau )},\tau )-y(\tau )/b>0$ decreases and the sonic point can catch the exit of the inner structure of the reaction wave at a later time.
The curvature term on the right-hand side of (4.10) influences the inner structure of the reaction wave and also the burnt-gas flow at the exit of the reaction zone, see (4.19). These two mechanisms have an opposite effect on the dynamics of the lead shock, as shown by the following rough arguments. Considering a constant flow (subsonic/shock) at the exit of the reaction zone, the solution of (4.10)–(4.11) describes the dynamics of an overdriven wave which is isolated from the external world. In the context of direct initiation, for a velocity ![]() $y<0$ well below the CJ wave, namely for
$y<0$ well below the CJ wave, namely for ![]() $\vert y\vert$ not small, the flow
$\vert y\vert$ not small, the flow ![]() $\mu (\xi ,\tau )$ in the inner structure of the combustion wave is fully out of equilibrium. Then, if the CJ wave is stable, the nonlinear relaxation towards equilibrium is expected to correspond to an increase of
$\mu (\xi ,\tau )$ in the inner structure of the combustion wave is fully out of equilibrium. Then, if the CJ wave is stable, the nonlinear relaxation towards equilibrium is expected to correspond to an increase of ![]() $y$, especially if the overdrive factor is small since the equilibrium would correspond to
$y$, especially if the overdrive factor is small since the equilibrium would correspond to ![]() $y\approx 0$. Therefore, the decay of
$y\approx 0$. Therefore, the decay of ![]() $y$ should be associated with the rarefaction-wave-induced flow at the exit of the reaction zone
$y$ should be associated with the rarefaction-wave-induced flow at the exit of the reaction zone ![]() $\mu ^{ext}(-\text {e}^{-y}, \tau )$. The corresponding response of the inner structure for adjusting the propagation velocity
$\mu ^{ext}(-\text {e}^{-y}, \tau )$. The corresponding response of the inner structure for adjusting the propagation velocity ![]() $y$ is thus delayed by the transit time of the characteristics
$y$ is thus delayed by the transit time of the characteristics ![]() $\mathcal {C}^+$
$\mathcal {C}^+$ ![]() $\xi =\xi _c(\tau , \tau ')$ leaving the end of the reaction
$\xi =\xi _c(\tau , \tau ')$ leaving the end of the reaction ![]() $\xi =-\text {e}^{-y(\tau )}$ at time
$\xi =-\text {e}^{-y(\tau )}$ at time ![]() $\tau$ to reach the point
$\tau$ to reach the point ![]() $\xi >-\text {e}^{-y}$ at a later time
$\xi >-\text {e}^{-y}$ at a later time ![]() $\tau '>\tau$. According to the left-hand side of the hyperbolic equation (4.10), the corresponding delay
$\tau '>\tau$. According to the left-hand side of the hyperbolic equation (4.10), the corresponding delay ![]() $\Delta \tau _{+}(\xi ,\tau )$,
$\Delta \tau _{+}(\xi ,\tau )$, ![]() $\tau '=\tau +\Delta \tau _{+}$, takes the form,
$\tau '=\tau +\Delta \tau _{+}$, takes the form,
reflecting the complexity of the dynamics since the delay (5.5) depends on the future of the inner structure ![]() $\mu (\xi ,\tau ')$,
$\mu (\xi ,\tau ')$, ![]() $y(\tau ')$,
$y(\tau ')$, ![]() $\tau '=\tau +\Delta \tau _+$. Except for the integral term
$\tau '=\tau +\Delta \tau _+$. Except for the integral term ![]() $Y(\tau )$, which is negligible in (4.17), the decay of the velocity
$Y(\tau )$, which is negligible in (4.17), the decay of the velocity ![]() $y(\tau )$ of an overdriven wave can be considered as slaved by the decreasing rate of the rarefaction flow
$y(\tau )$ of an overdriven wave can be considered as slaved by the decreasing rate of the rarefaction flow ![]() $\mu ^{ext}(-\text {e}^{-y}, \tau )$ but with the time delay
$\mu ^{ext}(-\text {e}^{-y}, \tau )$ but with the time delay ![]() $\Delta \tau _{+}(0,\tau )$ introduced by the characteristics
$\Delta \tau _{+}(0,\tau )$ introduced by the characteristics ![]() $\mathcal {C}_+$ travelling from the exit of the reaction zone to the lead shock.
$\mathcal {C}_+$ travelling from the exit of the reaction zone to the lead shock.
This is true up to a time ![]() $\tau =\tau _s$ at which the sonic point catches the exit of the inner structure
$\tau =\tau _s$ at which the sonic point catches the exit of the inner structure ![]() $\mu ^{ext}(-\text {e}^{-y(\tau _s)},\tau )=y(\tau _s)/b$ (sonic condition). When the sonic condition approaches the end of the reaction
$\mu ^{ext}(-\text {e}^{-y(\tau _s)},\tau )=y(\tau _s)/b$ (sonic condition). When the sonic condition approaches the end of the reaction ![]() $\mu ^{ext}({-\text {e}^{-y}})=y/b$ the denominator on the right-hand side of (5.5) approaches zero at the lower bound of the integral,
$\mu ^{ext}({-\text {e}^{-y}})=y/b$ the denominator on the right-hand side of (5.5) approaches zero at the lower bound of the integral, ![]() $\partial \xi _c(\tau , \tau ')/\partial \tau '\vert _{\tau '=\tau }\to 0^+$, see (5.3)–(5.4a,b), so that the time delay
$\partial \xi _c(\tau , \tau ')/\partial \tau '\vert _{\tau '=\tau }\to 0^+$, see (5.3)–(5.4a,b), so that the time delay ![]() $\Delta \tau _{+}(0,\tau )$ which is introduced by the response of the inner structure increases strongly. Keeping in mind that the time delay becomes infinite for a CJ wave in steady state when the burnt-gas flow is uniform,
$\Delta \tau _{+}(0,\tau )$ which is introduced by the response of the inner structure increases strongly. Keeping in mind that the time delay becomes infinite for a CJ wave in steady state when the burnt-gas flow is uniform, ![]() $\Delta \tau _{+}(0,\tau )\to \infty$ see § C.3 of Clavin & Denet (Reference Clavin and Denet2020), a slowdown of the velocity decay
$\Delta \tau _{+}(0,\tau )\to \infty$ see § C.3 of Clavin & Denet (Reference Clavin and Denet2020), a slowdown of the velocity decay ![]() $y(\tau )$ should occur when the sonic point
$y(\tau )$ should occur when the sonic point ![]() $\xi _s(\tau )$ approaches the end of the reaction
$\xi _s(\tau )$ approaches the end of the reaction ![]() $-\text {e}^{-y(\tau )}$ since the time delay of the response becomes much larger than the characteristic time of the forcing term responsible for the decay, namely the inverse of the decreasing rate of the rarefaction flow
$-\text {e}^{-y(\tau )}$ since the time delay of the response becomes much larger than the characteristic time of the forcing term responsible for the decay, namely the inverse of the decreasing rate of the rarefaction flow ![]() $\mu ^{ext}(\xi ,\tau )$. Therefore, the derivative
$\mu ^{ext}(\xi ,\tau )$. Therefore, the derivative ![]() ${\textrm {d}y}/\text {d}\tau$ approaches
${\textrm {d}y}/\text {d}\tau$ approaches ![]() $0$ for
$0$ for ![]() $y(\tau )<0$ (local minimum below the CJ velocity), and the decay of the propagation velocity is stopped.
$y(\tau )<0$ (local minimum below the CJ velocity), and the decay of the propagation velocity is stopped.
Consider the case for which this occurs when the propagation velocity is larger than the lower bound ![]() $y_c$ corresponding to the chemical-kinetics quenching
$y_c$ corresponding to the chemical-kinetics quenching ![]() $y_c < y(\tau _s) < 0$. Then, as soon as
$y_c < y(\tau _s) < 0$. Then, as soon as ![]() $\xi _s(\tau )+\text {e}^{-y(\tau )}$ crosses zero, the domain of the inner structure corresponding to
$\xi _s(\tau )+\text {e}^{-y(\tau )}$ crosses zero, the domain of the inner structure corresponding to ![]() $\xi \geqslant \xi _s({\tau })>-\text {e}^{-y(\tau )}$ becomes isolated from the rarefaction wave and thus from its damping rate. In other words the driving mechanism of the decay is switched off. As said earlier, the state of the flow inside the inner-detonation structure being out of equilibrium, a nonlinear relaxation process toward the stable CJ regime starts, so that the velocity
$\xi \geqslant \xi _s({\tau })>-\text {e}^{-y(\tau )}$ becomes isolated from the rarefaction wave and thus from its damping rate. In other words the driving mechanism of the decay is switched off. As said earlier, the state of the flow inside the inner-detonation structure being out of equilibrium, a nonlinear relaxation process toward the stable CJ regime starts, so that the velocity ![]() $y$ increases after
$y$ increases after ![]() $\tau _s$ for ending with a success of initiation. We will come back to the slowdown mechanism in § 5.2. Notice, however, that, for a large activation energy
$\tau _s$ for ending with a success of initiation. We will come back to the slowdown mechanism in § 5.2. Notice, however, that, for a large activation energy ![]() $b$, the success of initiation is not guarantee when the sonic point approaches the exit of the reaction zone because of a possible mechanism of curvature-induced quenching, similar to that in Appendix E. This case is not considered here and is left for future works.
$b$, the success of initiation is not guarantee when the sonic point approaches the exit of the reaction zone because of a possible mechanism of curvature-induced quenching, similar to that in Appendix E. This case is not considered here and is left for future works.
In any case, a detonation failure will be produced by the chemical-kinetics quenching (4.9) if the latter occurs before the sonic condition ![]() $y(\tau _s)\leqslant y_c<0$. Another possibility is that the condition in (5.1) is not verified by the initial conditions so that the sonic point could never catch the exit of the reaction zone. This will be investigated in future works.
$y(\tau _s)\leqslant y_c<0$. Another possibility is that the condition in (5.1) is not verified by the initial conditions so that the sonic point could never catch the exit of the reaction zone. This will be investigated in future works.
5.2. Numerical results
In order to illustrate the asymptotic analysis, preliminary numerical solutions of (4.10)–(4.12) are presented with the scaling law (4.4a,b), using the re-scaled distribution ![]() $\omega _{o_{CJ}}(\xi )$,
$\omega _{o_{CJ}}(\xi )$, ![]() $\int _{-1}^0\omega _{o_{CJ}}(\xi )\,\text {d}\xi =1$, of the three-step kinetic scheme (B16)–(B18) in Clavin & Denet (Reference Clavin and Denet2018) whose instability threshold corresponds to
$\int _{-1}^0\omega _{o_{CJ}}(\xi )\,\text {d}\xi =1$, of the three-step kinetic scheme (B16)–(B18) in Clavin & Denet (Reference Clavin and Denet2018) whose instability threshold corresponds to ![]() $b=1.27$. Two values of the reduced activation energy will be considered;
$b=1.27$. Two values of the reduced activation energy will be considered; ![]() $b=1$ for a stable CJ wave and
$b=1$ for a stable CJ wave and ![]() $b=2$ for a weakly unstable CJ wave. Typical results of a parametric study of the trajectories in the plane
$b=2$ for a weakly unstable CJ wave. Typical results of a parametric study of the trajectories in the plane ![]() $y-\tilde {r}_f$ are presented for an initial thickness of the rarefaction wave
$y-\tilde {r}_f$ are presented for an initial thickness of the rarefaction wave ![]() $30$ times larger than the detonation thickness,
$30$ times larger than the detonation thickness, ![]() $-\tilde {\xi }_{0i}\tilde {r}_{fi}\equiv (r_{fi}-r_{0i})/l=30$, by varying the initial radius
$-\tilde {\xi }_{0i}\tilde {r}_{fi}\equiv (r_{fi}-r_{0i})/l=30$, by varying the initial radius ![]() $\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ in the range
$\tilde {r}_{fi}\equiv \epsilon r_{fi}/l$ in the range ![]() $0.3-3.5$ for an initial velocity
$0.3-3.5$ for an initial velocity ![]() $y_i$ in the range 0.25–0.5.
$y_i$ in the range 0.25–0.5.
Successful initiation and detonation failure are shown in figure 6 for a stable case, ![]() $b=1$,
$b=1$, ![]() $y_i=0.25$ and
$y_i=0.25$ and ![]() $y_c=-0.5$ (chemical-kinetics quenching). A weakly unstable case for
$y_c=-0.5$ (chemical-kinetics quenching). A weakly unstable case for ![]() $b=2$,
$b=2$, ![]() $y_i=0.5$ and
$y_i=0.5$ and ![]() $y_c=-1$ is presented in figure 7. The results for such marginally unstable and stable detonations are similar, except for a nonlinear oscillation superimposed on the trajectories. For such moderate values of
$y_c=-1$ is presented in figure 7. The results for such marginally unstable and stable detonations are similar, except for a nonlinear oscillation superimposed on the trajectories. For such moderate values of ![]() $b$, detonation failure is produced by the chemical-kinetics quenching. This is clearly shown by decreasing the lower bound
$b$, detonation failure is produced by the chemical-kinetics quenching. This is clearly shown by decreasing the lower bound ![]() $y_c$ associated with the chemical-kinetics quenching. For example, considering the case
$y_c$ associated with the chemical-kinetics quenching. For example, considering the case ![]() $b=1$ and
$b=1$ and ![]() $y_c=-0.8$, a successful initiation is observed in figure 8 for
$y_c=-0.8$, a successful initiation is observed in figure 8 for ![]() $\tilde {r}_{fi}=0.5$ which corresponds to a detonation failure for
$\tilde {r}_{fi}=0.5$ which corresponds to a detonation failure for ![]() $y_c=-0.5$ in figure 6.
$y_c=-0.5$ in figure 6.

Figure 8. Numerical integration of (4.10)–(4.11) for a stable detonation ![]() $b=1$ for
$b=1$ for ![]() $y_c=-0.8$ and
$y_c=-0.8$ and ![]() $\tilde {r}_{fi}=0.5$, showing a successful initiation. The profiles of the reduced flow velocity
$\tilde {r}_{fi}=0.5$, showing a successful initiation. The profiles of the reduced flow velocity ![]() $u(\xi , \tau )/\epsilon a$ are plotted in (a) at different times. The trajectory
$u(\xi , \tau )/\epsilon a$ are plotted in (a) at different times. The trajectory ![]() $y(\tilde {r}_f)$ is plotted in (b). The full points denote the exit of the reaction zone and the open circles in (a) are the sonic points (relative to the lead shock).
$y(\tilde {r}_f)$ is plotted in (b). The full points denote the exit of the reaction zone and the open circles in (a) are the sonic points (relative to the lead shock).
The slowdown mechanism, discussed in § 5.1, leading to a minimum of propagation velocity well below the planar CJ velocity ![]() $y<0$, is clearly observed when the sonic point
$y<0$, is clearly observed when the sonic point ![]() $\xi =\xi _s(\tau )$ approaches the end of the reaction
$\xi =\xi _s(\tau )$ approaches the end of the reaction ![]() $\xi =-\text {e}^{y(\tau )}$, see figures 8 and 13 where the minimum
$\xi =-\text {e}^{y(\tau )}$, see figures 8 and 13 where the minimum ![]() $y\approx -0.71$ is reached at
$y\approx -0.71$ is reached at ![]() $\tau \approx 3$. During the subsequent re-acceleration of the propagation velocity
$\tau \approx 3$. During the subsequent re-acceleration of the propagation velocity ![]() $y(\tau )$ for
$y(\tau )$ for ![]() $\tau > 3$, the position of the sonic point inside the inner structure stays close to the end of the reaction, as in the solution of a steady and weakly curved CJ detonation with large activation energy, but, here the flow in the inner-detonation structure is out of equilibrium, as already mentioned. Notice that the minimum of propagation velocity
$\tau > 3$, the position of the sonic point inside the inner structure stays close to the end of the reaction, as in the solution of a steady and weakly curved CJ detonation with large activation energy, but, here the flow in the inner-detonation structure is out of equilibrium, as already mentioned. Notice that the minimum of propagation velocity ![]() $y(\tau )$ occurs just before the sonic point catches the exit of the inner structure of the reaction wave. This means that the external damping rate is balanced by the internal mechanism of re-acceleration for a small overdrive factor
$y(\tau )$ occurs just before the sonic point catches the exit of the inner structure of the reaction wave. This means that the external damping rate is balanced by the internal mechanism of re-acceleration for a small overdrive factor ![]() $\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y(\tau )/b>0$, a little bit before
$\mu ^{ext}(-\text {e}^{-y(\tau )}, \tau )-y(\tau )/b>0$, a little bit before ![]() $\tau _s$ for which the sonic condition is obtained
$\tau _s$ for which the sonic condition is obtained ![]() $\mu ^{ext}(-\text {e}^{-y(\tau _s)}, \tau )-y(\tau _s)/b=0$. Notice also that the minimum of
$\mu ^{ext}(-\text {e}^{-y(\tau _s)}, \tau )-y(\tau _s)/b=0$. Notice also that the minimum of ![]() $y(\tau )$ corresponds to a non-dimensional radius
$y(\tau )$ corresponds to a non-dimensional radius ![]() $\tilde {r}_f/b$ of order unity as for the critical radius of the C-shaped curve obtained by the quasi-steady state approximation, see Appendix E.
$\tilde {r}_f/b$ of order unity as for the critical radius of the C-shaped curve obtained by the quasi-steady state approximation, see Appendix E.
Inside the induction zone where the heat release is negligible, ![]() $\omega \approx 0$, the curvature term on the right-hand side of (4.10) makes the instantaneous distribution of the flow decreasing when approaching the lead shock,
$\omega \approx 0$, the curvature term on the right-hand side of (4.10) makes the instantaneous distribution of the flow decreasing when approaching the lead shock, ![]() $\partial \mu /\partial \xi <0$. Then, the distribution
$\partial \mu /\partial \xi <0$. Then, the distribution ![]() $\mu (\xi , \tau )$ presents a maximum inside the inner structure of the reaction wave, clearly shown in figures 8(a) and 10. The corresponding peak of pressure was observed in direct numerical simulations and was considered by Ng & Lee (Reference Ng and Lee2003) to be the driving mechanism of the re-acceleration of the wave leading to the detonation initiation in the critical regime. The flow velocity decreasing in space in the direction of propagation, formation of shock waves is possible inside the induction zone. This is observed in the numerical solutions of (4.10)–(4.12) during the increase of the detonation velocity for trajectories whose minimum of
$\mu (\xi , \tau )$ presents a maximum inside the inner structure of the reaction wave, clearly shown in figures 8(a) and 10. The corresponding peak of pressure was observed in direct numerical simulations and was considered by Ng & Lee (Reference Ng and Lee2003) to be the driving mechanism of the re-acceleration of the wave leading to the detonation initiation in the critical regime. The flow velocity decreasing in space in the direction of propagation, formation of shock waves is possible inside the induction zone. This is observed in the numerical solutions of (4.10)–(4.12) during the increase of the detonation velocity for trajectories whose minimum of ![]() $y$ is just above the lower bound (chemical-kinetics quenching) when the latter is small,
$y$ is just above the lower bound (chemical-kinetics quenching) when the latter is small, ![]() $0<(\mathcal {D}-a)/\epsilon a\equiv 1+y/b \approx 0^+$,
$0<(\mathcal {D}-a)/\epsilon a\equiv 1+y/b \approx 0^+$, ![]() $y+b\ll b$. This occurs for initial radius small enough, see for example the trajectory corresponding to
$y+b\ll b$. This occurs for initial radius small enough, see for example the trajectory corresponding to ![]() $\tilde {r}_{fi}=0.3$ in figure 9. The physical relevance of a detonation velocity becoming so close to
$\tilde {r}_{fi}=0.3$ in figure 9. The physical relevance of a detonation velocity becoming so close to ![]() $y=-b$ is questionable since it corresponds to a cross-over temperature for the chemical-kinetics quenching close to the initial temperature, since typically in real detonations the chemical-kinetics quenching corresponds to
$y=-b$ is questionable since it corresponds to a cross-over temperature for the chemical-kinetics quenching close to the initial temperature, since typically in real detonations the chemical-kinetics quenching corresponds to ![]() $y_c=-b/2$, see the paragraph above (4.9). The phenomenon of shock formation during the re-acceleration was also observed in the direct numerical simulations of Ng & Lee (Reference Ng and Lee2003) for a one-step kinetic rate law in a planar geometry. This question deserves more work.
$y_c=-b/2$, see the paragraph above (4.9). The phenomenon of shock formation during the re-acceleration was also observed in the direct numerical simulations of Ng & Lee (Reference Ng and Lee2003) for a one-step kinetic rate law in a planar geometry. This question deserves more work.

Figure 9. Numerical integration of (4.10)–(4.11) for stable detonation, ![]() $b=1$ and
$b=1$ and ![]() $y_c=-0.8$. The trajectory corresponding to
$y_c=-0.8$. The trajectory corresponding to ![]() $\tilde {r}_{fi}=0.1$ describes a failure of initiation
$\tilde {r}_{fi}=0.1$ describes a failure of initiation ![]() $y(\tau )\to -1$ and that corresponding to
$y(\tau )\to -1$ and that corresponding to ![]() $\tilde {r}_{fi}=0.3$ is a successful initiation with jumps during the increase of the detonation velocity resulting from the formation of shock waves in the induction zone, as explained in the text.
$\tilde {r}_{fi}=0.3$ is a successful initiation with jumps during the increase of the detonation velocity resulting from the formation of shock waves in the induction zone, as explained in the text.
Comparison between the numerical solution and the asymptotic analysis shows a very good agreement, confirming the validity and relevance of both numerical method and analytical solution. Solving numerically (4.10)–(4.12) for an initial condition (4.25), down to the radius of the core of stagnant gas ![]() $\xi =\xi _0(\tau )$ where
$\xi =\xi _0(\tau )$ where ![]() $u=0$, a straight part of the numerical solution is observed. The latter fits with an excellent accuracy the theoretical expression
$u=0$, a straight part of the numerical solution is observed. The latter fits with an excellent accuracy the theoretical expression ![]() $\mu ^{ext}(\xi ,\tau )$ in (4.15)–(4.17) for either successful initiation or failure, see figures 10 and 11. Moreover, the theoretical result (4.17) with
$\mu ^{ext}(\xi ,\tau )$ in (4.15)–(4.17) for either successful initiation or failure, see figures 10 and 11. Moreover, the theoretical result (4.17) with ![]() $Y=0$ fits also with a good accuracy the numerical result. This could be quite helpful for further theoretical analyses.
$Y=0$ fits also with a good accuracy the numerical result. This could be quite helpful for further theoretical analyses.
Moreover, the numerical solution of successful initiation clarifies the question raised long ago by Taylor (Reference Taylor1950a) concerning the link between the self-similar solution and the trajectory ‘detonation velocity vs radius’ for a successful initiation when the inner structure of the reaction wave is taken into account. A first indication is given by the instantaneous profiles of the burnt-gas flow behind the reaction zone in figure 10 for ![]() $\tau \geqslant 7$ showing similitudes with the discontinuous model in figure 4. The self-similar profile of figure 1 is recovered by the numerical result in the long-time limit
$\tau \geqslant 7$ showing similitudes with the discontinuous model in figure 4. The self-similar profile of figure 1 is recovered by the numerical result in the long-time limit ![]() $\tilde {\tau }\equiv \tau /\tilde {r}_{fi}\gg -\tilde {\xi }_{0i}$ when the reduced flow
$\tilde {\tau }\equiv \tau /\tilde {r}_{fi}\gg -\tilde {\xi }_{0i}$ when the reduced flow ![]() $\mu (\xi ,\tau )+1$ is plotted vs the self-similar variable (2.25)
$\mu (\xi ,\tau )+1$ is plotted vs the self-similar variable (2.25) ![]() $[r-r_f(t)]/[r_f(t)-r_0(t)] \equiv$
$[r-r_f(t)]/[r_f(t)-r_0(t)] \equiv$ ![]() $\tilde {\xi }/(-\tilde {\xi }_{0})$ with
$\tilde {\xi }/(-\tilde {\xi }_{0})$ with ![]() $\tilde {\xi }_{0}=-\tilde {\tau } +\tilde {\xi }_{0i}$. This is shown in figure 12. According to the zoom in figure 13, the slope
$\tilde {\xi }_{0}=-\tilde {\tau } +\tilde {\xi }_{0i}$. This is shown in figure 12. According to the zoom in figure 13, the slope ![]() $\partial \mu /\partial \xi \vert _{\xi =-\text {e}^{-y}}$, which is initially small (at the scale of the detonation thickness
$\partial \mu /\partial \xi \vert _{\xi =-\text {e}^{-y}}$, which is initially small (at the scale of the detonation thickness ![]() $\xi =O(1)$) in the overdriven regimes, increases when the sonic point gets into the inner structure, so that the flow gradient becomes infinite at the scale of the thickness of the rarefaction wave which increases linearly with the time.
$\xi =O(1)$) in the overdriven regimes, increases when the sonic point gets into the inner structure, so that the flow gradient becomes infinite at the scale of the thickness of the rarefaction wave which increases linearly with the time.

Figure 12. Numerical solutions at different times compared to the self-similar solution of (2.23)–(2.24) (dotted line) representing the self-similar rarefaction flow behind the front of a spherical CJ detonation considered as a discontinuity for small heat release ![]() $(\mathcal {D}_{o_{CJ}}-a)/a\approx \epsilon \ll 1$. The reduced flow
$(\mathcal {D}_{o_{CJ}}-a)/a\approx \epsilon \ll 1$. The reduced flow ![]() $v=\text u(r,t)/\epsilon a$ is plotted vs the reduced distance from the front
$v=\text u(r,t)/\epsilon a$ is plotted vs the reduced distance from the front ![]() $z= (r-r_f(t) )/\epsilon r_{0}(t)$ with
$z= (r-r_f(t) )/\epsilon r_{0}(t)$ with ![]() $r_f(t)=\mathcal {D}_{o_{CI}}t+r_{fi}$,
$r_f(t)=\mathcal {D}_{o_{CI}}t+r_{fi}$, ![]() $r_0(t)=at+r_{0i}$ and, according to (2.26),
$r_0(t)=at+r_{0i}$ and, according to (2.26), ![]() $r_{fi} = (1+\epsilon )r_{0i}$. Because of the finite thickness of the reaction zone
$r_{fi} = (1+\epsilon )r_{0i}$. Because of the finite thickness of the reaction zone ![]() $\text {e}^{-y}$ the origin of space variable has been shifted in the figure.
$\text {e}^{-y}$ the origin of space variable has been shifted in the figure.

Figure 13. Zoom of the velocity profiles for the same parameters as in figure 10 for later time. The sonic point is out of the picture at ![]() $\tau =3$.
$\tau =3$.
6. Conclusion and perspectives
The critical dynamics of the direct initiation of detonation is studied in the limit of small heat release reducing the problem to solve a single hyperbolic equation. This limit emphasizes the two-time-scale nature of the problem which also characterizes real detonations when the condition at the exit of the reaction zone is nearly sonic. The simplification comes from a flow Mach number differing from unity by a small amount everywhere. In real detonations near the CJ regime, this is true at the end of the reaction zone, but not close to the lead shock. Concerning the trajectories of the lead shock in direct initiation, the limit of small heat release introduces differences that are mainly quantitative, except for the overshoot during the re-acceleration phase which is sometimes observed in direct numerical simulations. Useful results of the asymptotic limit are the analytical expressions of the rarefaction flow for both discontinuous model of detonation and combustion waves whose inner structure is unsteady. Amazingly, these asymptotic solutions present the same characteristic properties as those of the flow in the opposite limit of a large Mach number of propagation. This confirms the relevance of the limit of small heat release for improving our understanding of the detonation dynamics.
The evolution of the sonic point (sonic condition relatively to the lead shock) inside the rarefaction wave is then found to be the key element of the overall dynamics. Due to the increase of the time delay by the response of the detonation inner structure to the burnt-gas flow, a slowdown mechanism is identified when the sonic point, located initially in the burnt gas away from the reaction wave (overdriven regimes), approaches the exit of the reaction zone. This mechanism explains the behaviour of the trajectories ‘propagation velocity vs radius’ observed near criticality in direct numerical simulations of successful initiation. The detonation velocity decreases well below the CJ velocity like for a failure and reaches a minimum associated with the onset of the sonic condition. This deceleration phase is followed by a re-acceleration back to the CJ regime corresponding to an isolated combustion wave whose inner structure is out of equilibrium. During this nonlinear relaxation, the sonic point stays inside the inner structure of the combustion wave, close to the end of the reaction zone. Failure is produced if the detonation velocity decreases so much that the chemical-kinetics quenching occurs in overdriven regimes when the sonic point is still in the burnt gas behind the exit of the reaction zone. This depends on the radius at which the velocity of the overdriven detonation crosses the CJ velocity for the first time; the smaller the radius, the stronger the damping rate and the detonation is more likely. Another outcome of the asymptotic analysis is to indicate how the self-similar CJ solution for the rarefaction wave is reached in the long-time limit, showing a behaviour similar to the discontinuous model.
Due to the difficulty pointed out in Clavin & Denet (Reference Clavin and Denet2020) for strongly unstable detonations in the limit of small heat release using the scaling law (4.4a,b), attention was limited in this article to a reduced activation energy of order unity ![]() $b=O(1)$. This prevents us seeing whether or not the curvature-induced quenching which is predicted without multiple-step chemistry (no cross-over temperature) by a quasi-steady approximation for large
$b=O(1)$. This prevents us seeing whether or not the curvature-induced quenching which is predicted without multiple-step chemistry (no cross-over temperature) by a quasi-steady approximation for large ![]() $b$, can also occur in the unsteady regime after the sonic point has caught the end of the reaction. Notice, however, that the radius at the minimum of velocity is of same order of magnitude as the quasi-steady critical radius. Future works will be devoted to this question. This should be performed with an unsteady reaction rate different from the scaling law (4.4a,b). More generally, improvements of the asymptotic analysis in the limit of small heat release will be sought to provide a better quantitative accuracy with real detonations. Another point which deserves more investigation is the re-ignition by shock waves observed when the minimum velocity is very low.
$b$, can also occur in the unsteady regime after the sonic point has caught the end of the reaction. Notice, however, that the radius at the minimum of velocity is of same order of magnitude as the quasi-steady critical radius. Future works will be devoted to this question. This should be performed with an unsteady reaction rate different from the scaling law (4.4a,b). More generally, improvements of the asymptotic analysis in the limit of small heat release will be sought to provide a better quantitative accuracy with real detonations. Another point which deserves more investigation is the re-ignition by shock waves observed when the minimum velocity is very low.
In this paper the analysis of the critical dynamics is limited to a spherical geometry. The result of plane or cylindrical detonations cannot be conjectured by dimensional arguments, the analysis has to be reconsidered from the beginning. The dynamics of the sonic point inside the rarefaction wave is expected to also play an essential role.
Acknowledgements
Long-standing enlightening discussions with A. Liñan have motivated this work.
Funding
Partial financial support of Agence National de la Recherche (contract ANR-18-CE05-0030) is acknowledged.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Conditions in the burnt gas behind the detonation front
The conditions behind a detonation treated as a discontinuity is obtained by the conservation of mass, momentum and energy across a planar detonation in quasi-steady state. They can be put in the form, see Clavin & Searby (Reference Clavin and Searby2016),
 \begin{gather} M \geqslant M_{o_{CJ}}>1: 1-\frac{\rho_u}{\rho_b} = \frac{1}{\gamma+1 }\frac{(M^2-1)}{M^2}\left[1+\sqrt{1-\left( \frac{M_{o_{CJ}}-M_{o_{CJ}}^{{-}1}}{M-M^{{-}1}}\right)^2} \right], \end{gather}
\begin{gather} M \geqslant M_{o_{CJ}}>1: 1-\frac{\rho_u}{\rho_b} = \frac{1}{\gamma+1 }\frac{(M^2-1)}{M^2}\left[1+\sqrt{1-\left( \frac{M_{o_{CJ}}-M_{o_{CJ}}^{{-}1}}{M-M^{{-}1}}\right)^2} \right], \end{gather}
where ![]() $\rho$ is the density, the subscripts
$\rho$ is the density, the subscripts ![]() $u$ and
$u$ and ![]() $b$ denote respectively the fresh mixture and the burnt gas,
$b$ denote respectively the fresh mixture and the burnt gas, ![]() $Q\propto q_m/c_pT_u$ is the reduced heat release and
$Q\propto q_m/c_pT_u$ is the reduced heat release and ![]() $M\equiv \mathcal {D}/a_u$ is the propagation Mach number. The square root is zero for the CJ regime corresponding to the sonic condition in the burnt gas
$M\equiv \mathcal {D}/a_u$ is the propagation Mach number. The square root is zero for the CJ regime corresponding to the sonic condition in the burnt gas ![]() $M=M_{o_{CJ}}:$
$M=M_{o_{CJ}}:$ ![]() $u_{bo_{CJ}}=\mathcal {D}_{o_{CJ}}-a_{bo_{CJ}}$ with
$u_{bo_{CJ}}=\mathcal {D}_{o_{CJ}}-a_{bo_{CJ}}$ with ![]() $a_{bo_{CJ}}=\sqrt {\gamma p_{bo_{CJ}}/\rho _{bo_{CJ}}}$. According to the last equation in (A2), the CJ Mach number is close to unity in the limit of small heat release,
$a_{bo_{CJ}}=\sqrt {\gamma p_{bo_{CJ}}/\rho _{bo_{CJ}}}$. According to the last equation in (A2), the CJ Mach number is close to unity in the limit of small heat release, ![]() $0<(M_{o_{CJ}}-1)\ll 1$. For weakly overdriven regimes
$0<(M_{o_{CJ}}-1)\ll 1$. For weakly overdriven regimes ![]() $0<(M-M_{o_{CJ}})/M_{o_{CJ}}\ll 1$ the square root in (A1) is small so that the propagation Mach number is also close to unity
$0<(M-M_{o_{CJ}})/M_{o_{CJ}}\ll 1$ the square root in (A1) is small so that the propagation Mach number is also close to unity ![]() $0<(M-1)\ll 1$ for small heat release and the flow velocity in the laboratory frame is much smaller than the sound speed
$0<(M-1)\ll 1$ for small heat release and the flow velocity in the laboratory frame is much smaller than the sound speed ![]() ${u_b}/{a_u}=O(M-1)$. However, the rarefaction wave is not a spherical acoustic wave even though it is a linear function of the radius behind a weakly overdriven detonation
${u_b}/{a_u}=O(M-1)$. However, the rarefaction wave is not a spherical acoustic wave even though it is a linear function of the radius behind a weakly overdriven detonation ![]() $M>M_{o{CJ}}$, as shown § 2.3, while the rarefaction wave behind a spherical CJ detonation investigated in § 2.2 is quite different.
$M>M_{o{CJ}}$, as shown § 2.3, while the rarefaction wave behind a spherical CJ detonation investigated in § 2.2 is quite different.
The Rankine–Hugoniot conditions at the Neumann state of an inert shock correspond to (A1)–(A2) when the square root on the right-hand side of (A1) is set equal to unity,
where the subscript ![]() $N$ denotes the Neumann state.
$N$ denotes the Neumann state.
Appendix B. Linear solution
A linear solution of the small flow behind a spherical detonation, treated as a discontinuity in the limit of small heat release (![]() $0 < M_{o_{CJ}}-1\ll 1$), is performed here. By comparison with the development in § 2, the purpose is to stress the nonlinear character of the rarefaction wave when approaching the CJ regime.
$0 < M_{o_{CJ}}-1\ll 1$), is performed here. By comparison with the development in § 2, the purpose is to stress the nonlinear character of the rarefaction wave when approaching the CJ regime.
B.1. Spherical acoustic wave
Let us first briefly recall the acoustic waves in a spherical geometry. The linear version of the isentropic Euler equations yields
where ![]() $(\rho -\bar \rho _b)/\bar \rho _b \ll 1$ with
$(\rho -\bar \rho _b)/\bar \rho _b \ll 1$ with ![]() $\bar \rho _b$ and
$\bar \rho _b$ and ![]() $a=a_b\approx a_u$ constant. Introducing the potential
$a=a_b\approx a_u$ constant. Introducing the potential ![]() $\varphi$, (B1) yield
$\varphi$, (B1) yield
where
in a spherical geometry. Introducing the function ![]() $f(r,t)$, and looking for the solution in the form
$f(r,t)$, and looking for the solution in the form ![]() $\varphi = f/r$,
$\varphi = f/r$,
the flow expressed in terms of the non-dimensional the transit time is
where ![]() $f'_1(\eta )$ and
$f'_1(\eta )$ and ![]() $f'_2(\eta )$ denote the derivative of
$f'_2(\eta )$ denote the derivative of ![]() $f_1(\eta )$ and
$f_1(\eta )$ and ![]() $f_2(\eta )$,
$f_2(\eta )$, ![]() $f'_1(\eta )\equiv \text {d} f_1(\eta )/\text {d}\eta$,
$f'_1(\eta )\equiv \text {d} f_1(\eta )/\text {d}\eta$, ![]() $f'_2(\eta )\equiv \text {d} f_2(\eta )/\text {d}\eta$, the unknown functions
$f'_2(\eta )\equiv \text {d} f_2(\eta )/\text {d}\eta$, the unknown functions ![]() $f_1(\eta )$ and
$f_1(\eta )$ and ![]() $f_2(\eta )$ being determined by the boundary conditions.
$f_2(\eta )$ being determined by the boundary conditions.
Consider the flow behind a supersonic front ![]() $r=r_f(t)$ propagating with the velocity
$r=r_f(t)$ propagating with the velocity ![]() $\mathcal {D}(t)= \text {d} r_f/\text {d}t$,
$\mathcal {D}(t)= \text {d} r_f/\text {d}t$, ![]() $M(t)=\mathcal {D}(t)/a>1$. Denoting
$M(t)=\mathcal {D}(t)/a>1$. Denoting ![]() $u_b(t)$ and
$u_b(t)$ and ![]() $\rho _b(t)$ the flow velocity and the density on the lead front and introducing the notations
$\rho _b(t)$ the flow velocity and the density on the lead front and introducing the notations ![]() $r_f(t) =r_f(t)/a$,
$r_f(t) =r_f(t)/a$, ![]() $\text {d} r_f/\text {d} t =M(t)$
$\text {d} r_f/\text {d} t =M(t)$
the boundary conditions at the front take the form
 \begin{gather} \frac{1}{ r_{f}(t)}\left[\frac{\dot{F}_1(t)}{1-M(t)}+\frac{\dot{F}_2(t)}{1+M(t)} \right]= \frac{\delta{\rho_b}(t)}{\bar \rho_b} \equiv\frac{ \left(\rho_b(t)-\bar \rho_b\right)}{\bar \rho_ b}, \end{gather}
\begin{gather} \frac{1}{ r_{f}(t)}\left[\frac{\dot{F}_1(t)}{1-M(t)}+\frac{\dot{F}_2(t)}{1+M(t)} \right]= \frac{\delta{\rho_b}(t)}{\bar \rho_b} \equiv\frac{ \left(\rho_b(t)-\bar \rho_b\right)}{\bar \rho_ b}, \end{gather} \begin{gather}\frac{1}{ r_{f}(t)}\left[\frac{\dot{F}_1(t)}{1-M(t)}-\frac{\dot{F}_2(t)}{1+M(t)} \right]+ \frac{F_1(t)+F_2(t)}{ r^2_{f}(t)}= \frac{{u_b}(t)}{a}, \end{gather}
\begin{gather}\frac{1}{ r_{f}(t)}\left[\frac{\dot{F}_1(t)}{1-M(t)}-\frac{\dot{F}_2(t)}{1+M(t)} \right]+ \frac{F_1(t)+F_2(t)}{ r^2_{f}(t)}= \frac{{u_b}(t)}{a}, \end{gather}
where ![]() $\rho _b$ and
$\rho _b$ and ![]() ${u_b}/{a}$ are expressed in terms of the propagation Mach number
${u_b}/{a}$ are expressed in terms of the propagation Mach number ![]() $M(t)$ through (A1)–(A2). The radius at which the flow vanishes
$M(t)$ through (A1)–(A2). The radius at which the flow vanishes ![]() $u(r_0(t),t)=0$,
$u(r_0(t),t)=0$, ![]() $\text {d} u/\text {d} r\vert _{r-r_0=0^+}>0$ should be a weak discontinuity,
$\text {d} u/\text {d} r\vert _{r-r_0=0^+}>0$ should be a weak discontinuity,
B.2. Solution
We look for the linear solution for the flow behind a CJ regime in a spherical geometry treated as a discontinuity propagating with the constant velocity of the planar wave in steady state ![]() $\mathcal {D}=\mathcal {D}_{oCJ}$ (constant Mach number
$\mathcal {D}=\mathcal {D}_{oCJ}$ (constant Mach number ![]() $M=M_{o_{CJ}}\equiv \mathcal {D}_{o_{CJ}}/a>1$)
$M=M_{o_{CJ}}\equiv \mathcal {D}_{o_{CJ}}/a>1$)
According to (A1) and (A2) for the square root =0, the right-hand side of (B9) and (B10) are constant,
Taking ![]() $\bar \rho _b=\rho _{bo_{CJ}}$, the right-hand side of (B9) is zero,
$\bar \rho _b=\rho _{bo_{CJ}}$, the right-hand side of (B9) is zero,
For small heat release ![]() $\epsilon \equiv (M_{o_{CJ}}-1) \ll 1$,
$\epsilon \equiv (M_{o_{CJ}}-1) \ll 1$, ![]() $u_{bo_{CJ}}/{a}\ll 1 \Rightarrow u/{a}\ll 1$, the linear solution (B5)–(B6) with (B9)–(B10) satisfying the boundary conditions (B13)–(B14) is
$u_{bo_{CJ}}/{a}\ll 1 \Rightarrow u/{a}\ll 1$, the linear solution (B5)–(B6) with (B9)–(B10) satisfying the boundary conditions (B13)–(B14) is
 \begin{gather} r_0(t)\leqslant r\leqslant r_{fo_{CJ}}:\frac{u( r, t)}{u_{bo_{CJ}}}=\left[ 1-\frac{1}{M_{o_{CJ}}^2-1}\left(\frac{ r_{fo_{CJ}}^2(t)}{ r^2}-1 \right)\right], \, r\leqslant r_0(t): u=0, \end{gather}
\begin{gather} r_0(t)\leqslant r\leqslant r_{fo_{CJ}}:\frac{u( r, t)}{u_{bo_{CJ}}}=\left[ 1-\frac{1}{M_{o_{CJ}}^2-1}\left(\frac{ r_{fo_{CJ}}^2(t)}{ r^2}-1 \right)\right], \, r\leqslant r_0(t): u=0, \end{gather}
where, according to (A1), ![]() ${u_{bo_{CJ}}}/{a}=(M_{o_{CJ}}^2-1)M_{o_{CJ}}^{-1}/(\gamma +1)$. The solution also satisfies the downstream condition (B11) of a weak discontinuity provided
${u_{bo_{CJ}}}/{a}=(M_{o_{CJ}}^2-1)M_{o_{CJ}}^{-1}/(\gamma +1)$. The solution also satisfies the downstream condition (B11) of a weak discontinuity provided ![]() $r_0(t)\equiv a\,t+ {r_{foi}}/{M_{o_{CJ}}}$
$r_0(t)\equiv a\,t+ {r_{foi}}/{M_{o_{CJ}}}$
the last relation being valid to leading order in the limit ![]() $\epsilon \to 0$,
$\epsilon \to 0$, ![]() $(\gamma -1) \to 0$. Therefore, the thickness of the rarefaction wave
$(\gamma -1) \to 0$. Therefore, the thickness of the rarefaction wave ![]() $r_{fo_{CJ}}-r_0$ increases also linearly with the time
$r_{fo_{CJ}}-r_0$ increases also linearly with the time
The calculation proceeds as follows. Using (B11) and (B14) integration of (B9) yields
where ![]() $A'$ is a constant. In order to save the notation the subscript
$A'$ is a constant. In order to save the notation the subscript ![]() $o_{CJ}$ has been omitted in
$o_{CJ}$ has been omitted in ![]() $M_{o_{CJ}}$ which is replaced by
$M_{o_{CJ}}$ which is replaced by ![]() $M$. Adding (B9) and (B10) yields a differential equation for
$M$. Adding (B9) and (B10) yields a differential equation for ![]() $F_1(t)$ when
$F_1(t)$ when ![]() $F_2(t)$ is eliminated by using (B19)
$F_2(t)$ is eliminated by using (B19)
where ![]() $A=(1-M^2)A'/(2M)$ is constant. Equation (B20) is easily integrated
$A=(1-M^2)A'/(2M)$ is constant. Equation (B20) is easily integrated
where ![]() $B$ is another constant and
$B$ is another constant and ![]() $F_2(t)$ is obtained from (B19). According to (B7)–(B8),
$F_2(t)$ is obtained from (B19). According to (B7)–(B8), ![]() $f_1(t- r)$ and
$f_1(t- r)$ and ![]() $f_2(t+ r)$ are obtained from
$f_2(t+ r)$ are obtained from ![]() $F_1(t)$ and
$F_1(t)$ and ![]() $F_2(t)$ by the substitution
$F_2(t)$ by the substitution ![]() $t\to [(t- r)+ r_{fi}]/(1-M)$ and
$t\to [(t- r)+ r_{fi}]/(1-M)$ and ![]() $t\to [(t+ r)+ r_{fi}]/(1+M)$ respectively,
$t\to [(t+ r)+ r_{fi}]/(1+M)$ respectively,
The constants ![]() $A$ and
$A$ and ![]() $B$ disappear from (B6) leading to (B16).
$B$ disappear from (B6) leading to (B16).
Because of the sonic condition at the front this linear solution is not self-consistent since the nonlinear terms are essential near the sonic condition as discussed now.
B.3. Inconsistency of the linear approximation behind a CJ detonation
The flow (B15) is effectively small for ![]() $r_0(t)\leqslant r \leqslant r_{fo_{CJ}}(t)$ when the heat release is small
$r_0(t)\leqslant r \leqslant r_{fo_{CJ}}(t)$ when the heat release is small
because the flow increases from ![]() $0$ to its value at the leading edge of the rarefaction wave
$0$ to its value at the leading edge of the rarefaction wave ![]() ${u_{bo_{CJ}}}$ which is, according to (B13), smaller than the sound speed
${u_{bo_{CJ}}}$ which is, according to (B13), smaller than the sound speed ![]() ${u_{bo_{CJ}}}/{a}\approx \epsilon$
${u_{bo_{CJ}}}/{a}\approx \epsilon$
Inside the rarefaction wave, ![]() $r_0(t)\leqslant r \leqslant r_{fo_{CJ}}(t)$,
$r_0(t)\leqslant r \leqslant r_{fo_{CJ}}(t)$, ![]() $r/r_0(t)-1=O(\epsilon )$, to leading order in the limit
$r/r_0(t)-1=O(\epsilon )$, to leading order in the limit ![]() $\epsilon \ll 1$, the velocity profile is linear since, according to (B25)–(B18)
$\epsilon \ll 1$, the velocity profile is linear since, according to (B25)–(B18)
neglecting terms of order ![]() $\epsilon ^2$, one has
$\epsilon ^2$, one has
The physical interpretation is simple, the numerator on the right-hand side of (B29) describes a propagation at the speed of sound while the denominator is the geometrical damping in a spherical geometry. The linear solution (B29) is different from the self-similar solution in figure 1. It is also different from the rarefaction wave (2.52a–c)–(2.53a,b), even though they are both linear in space. The flow (B29) is effectively solution of the linear version of (2.9) for ![]() $u\ll a$ and
$u\ll a$ and ![]() $r_f(t)-r_0(t)=\epsilon r_0(t)$,
$r_f(t)-r_0(t)=\epsilon r_0(t)$, ![]() $r\approx r_0(t)$,
$r\approx r_0(t)$,
as verified by the general solution of (B30) for the initial condition ![]() $u(r,t=0)=u_i(r)$,
$u(r,t=0)=u_i(r)$, ![]() $u=u_i(r-at) r_{0i}/r_0(t)$, leading to (B29) if the initial flow increases linearly in space
$u=u_i(r-at) r_{0i}/r_0(t)$, leading to (B29) if the initial flow increases linearly in space ![]() $u_i(r)=a\,(r-r_{0i})/r_{0i}$. The inconsistency of the linear solution (B29) is pointed out by computing the nonlinear term
$u_i(r)=a\,(r-r_{0i})/r_{0i}$. The inconsistency of the linear solution (B29) is pointed out by computing the nonlinear term ![]() $u{\partial u}/{\partial r}=a^2(r-r_0)/r_0^2=au/r_0$ which has the same order of magnitude as the right-hand side. This illustrates that the nonlinear term
$u{\partial u}/{\partial r}=a^2(r-r_0)/r_0^2=au/r_0$ which has the same order of magnitude as the right-hand side. This illustrates that the nonlinear term ![]() $u\partial u/\partial r$ plays an essential role in the transonic flow relative to the front.
$u\partial u/\partial r$ plays an essential role in the transonic flow relative to the front.
Appendix C. Details of calculation
C.1. Equation (2.31)
Using the notations (2.28), (2.10a–c) takes the form
This is (2.31).
C.2. Solution to (2.56a,b)
Attention is focused on
and one considers the positive solution ![]() $\tau _t>0$. Equation (2.56a,b) can be put in the form
$\tau _t>0$. Equation (2.56a,b) can be put in the form
 \begin{equation} \tilde{\tau}_t\left [ 1-\frac{\vert \tilde{\xi}_{0i}\vert}{1+\mu_{fi}} \right ]+\vert\tilde{\xi}_{0i}\vert\frac{\mu_{fi}}{(1+\mu_{fi})}= (1+\tilde{\tau}_t)\ln(1+\tilde{\tau}_t). \end{equation}
\begin{equation} \tilde{\tau}_t\left [ 1-\frac{\vert \tilde{\xi}_{0i}\vert}{1+\mu_{fi}} \right ]+\vert\tilde{\xi}_{0i}\vert\frac{\mu_{fi}}{(1+\mu_{fi})}= (1+\tilde{\tau}_t)\ln(1+\tilde{\tau}_t). \end{equation}
A graphical representation of the solution is plotted in figure 14 showing that ![]() $\tilde {\tau }_t\ll 1$ if
$\tilde {\tau }_t\ll 1$ if ![]() $0<\mu _{fi}\ll 1$. To leading order, a Taylor expansion in powers of
$0<\mu _{fi}\ll 1$. To leading order, a Taylor expansion in powers of ![]() $\tilde {\tau }_t$ then leads to
$\tilde {\tau }_t$ then leads to
which is also right for ![]() $\tilde {\xi }_{0i}=-1$ that is, according to the definition (2.37a–c), for
$\tilde {\xi }_{0i}=-1$ that is, according to the definition (2.37a–c), for ![]() $(r_{fi}-r_{0i}) =\epsilon r_{0i}$ which is valid in the self-similar solution of the CJ detonation (2.26). In this particular case, (C6) yields
$(r_{fi}-r_{0i}) =\epsilon r_{0i}$ which is valid in the self-similar solution of the CJ detonation (2.26). In this particular case, (C6) yields
C.3. Simplified expression for the external flow
Discarding the integral term ![]() $Y(\tau )/b=O(y_i/b)$, the time scale of the external flow (4.15) is larger than the response of the inner structure of the detonation by a factor
$Y(\tau )/b=O(y_i/b)$, the time scale of the external flow (4.15) is larger than the response of the inner structure of the detonation by a factor ![]() $\tilde {r}_{fi}$. According to (2.57), the time
$\tilde {r}_{fi}$. According to (2.57), the time ![]() $\tau _t$, solution to the equation
$\tau _t$, solution to the equation ![]() $\mu _f^{ext}(\tau _t)=0$, is close to
$\mu _f^{ext}(\tau _t)=0$, is close to ![]() $\mu ^{ext}_{fi}\tilde {r}_{fi}$ if
$\mu ^{ext}_{fi}\tilde {r}_{fi}$ if ![]() $\mu ^{ext}_{fi}$ is sufficiently smaller than unity,
$\mu ^{ext}_{fi}$ is sufficiently smaller than unity,
Consider a large radius ![]() $\tilde {r}_{fi}$ and an initial propagation velocity close to the CJ velocity as in (2.42), for which
$\tilde {r}_{fi}$ and an initial propagation velocity close to the CJ velocity as in (2.42), for which
so that the time ![]() $\tau _t\approx \tilde {r}_{fi}\mu ^{ext}_{fi}$ is larger than the characteristic time of the linear response of the inner structure which is of order unity, but
$\tau _t\approx \tilde {r}_{fi}\mu ^{ext}_{fi}$ is larger than the characteristic time of the linear response of the inner structure which is of order unity, but ![]() $\tilde {\tau }_t\equiv \tau _t/\tilde {r}_{fi}\approx \mu ^{ext}_{fi}\ll 1$ is small. For a lapse of time
$\tilde {\tau }_t\equiv \tau _t/\tilde {r}_{fi}\approx \mu ^{ext}_{fi}\ll 1$ is small. For a lapse of time ![]() $\tau$ of the same order as
$\tau$ of the same order as ![]() $\tau _t$, using (4.12),
$\tau _t$, using (4.12),
the instantaneous reduced curvature ![]() $1/\tilde {r}_f$ does not vary much and can be considered as a constant in (4.10). Under the condition (C10), the thickness of the boundary layer (2.59a,b)
$1/\tilde {r}_f$ does not vary much and can be considered as a constant in (4.10). Under the condition (C10), the thickness of the boundary layer (2.59a,b) ![]() $\Delta \vert \tilde {\xi }\vert \approx \mu ^{ext}_{fi}$,
$\Delta \vert \tilde {\xi }\vert \approx \mu ^{ext}_{fi}$, ![]() $\Delta \vert \xi \vert = O(\mu ^{ext}_{fi}\tilde {r}_{fi})$, is larger than the thickness of the inner structure which is of order unity for
$\Delta \vert \xi \vert = O(\mu ^{ext}_{fi}\tilde {r}_{fi})$, is larger than the thickness of the inner structure which is of order unity for ![]() $\text {e}^{-y}=O(1)$, so that the outer flow of an overdriven detonation reduces to (2.60a,b),
$\text {e}^{-y}=O(1)$, so that the outer flow of an overdriven detonation reduces to (2.60a,b),
with a length scale larger than the detonation thickness by a factor ![]() $\tilde {r}_{fi}\vert \tilde {\xi }_{0i} \vert$ and a time scale larger than the response time of the inner structure by a factor
$\tilde {r}_{fi}\vert \tilde {\xi }_{0i} \vert$ and a time scale larger than the response time of the inner structure by a factor ![]() $\tilde {r}_{fi}\gg 1$.
$\tilde {r}_{fi}\gg 1$.
C.4. Motion of the sonic point
In overdriven regimes, the position of the sonic point ![]() $\xi =\xi _s(\tau )$ is related to the evolution of the detonation velocity
$\xi =\xi _s(\tau )$ is related to the evolution of the detonation velocity ![]() $y(\tau )/b$. Introducing the relation
$y(\tau )/b$. Introducing the relation ![]() $\mu ^{ext}(\xi _s(\tau ), \tau )=y(\tau )/b$ into(4.15) and using (4.17) yields
$\mu ^{ext}(\xi _s(\tau ), \tau )=y(\tau )/b$ into(4.15) and using (4.17) yields
 \begin{equation} \left. \begin{gathered} 1+\frac{y(\tau)}{b}=\frac{ \xi_s(\tau)}{\tilde{r}_{f}(\tau)[(-\tilde{\xi}_{0i})/(1+\mu^{ext}_{fi})+\ln(\tilde{r}_f/\tilde{r}_{fi})]}+ (1+\mu_f^{ext}( \tau)),\\ \left [1+\frac{y(\tau)}{b}\right ]\left [\tilde{r}_{f}(\tau))\frac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right ]= \xi_s(\tau)+\tau \left[1+Y(\tau)\right ]+(-\tilde{\xi}_{0i})\tilde{r}_{fi}. \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} 1+\frac{y(\tau)}{b}=\frac{ \xi_s(\tau)}{\tilde{r}_{f}(\tau)[(-\tilde{\xi}_{0i})/(1+\mu^{ext}_{fi})+\ln(\tilde{r}_f/\tilde{r}_{fi})]}+ (1+\mu_f^{ext}( \tau)),\\ \left [1+\frac{y(\tau)}{b}\right ]\left [\tilde{r}_{f}(\tau))\frac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right ]= \xi_s(\tau)+\tau \left[1+Y(\tau)\right ]+(-\tilde{\xi}_{0i})\tilde{r}_{fi}. \end{gathered} \right\} \end{equation}
According to (4.12), the relation ![]() $\tilde {r}_f(\tau )=\tau + \tilde {r}_{fi}$ leads to
$\tilde {r}_f(\tau )=\tau + \tilde {r}_{fi}$ leads to
 \begin{equation}
\xi_s(\tau)= \begin{cases} \dfrac{y(\tau)}{b}\left[(\tau+\tilde{r}_{fi})\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right],\\
\tau\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-\tau-\dfrac{1}{b}\displaystyle\int^\tau_0y(\tau')\text{d}\tau'+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi}),\\
\tilde{r}_{fi}\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-(-\tilde{\xi}_{0i})\tilde{r}_{fi}.
\end{cases}
\end{equation}
\begin{equation}
\xi_s(\tau)= \begin{cases} \dfrac{y(\tau)}{b}\left[(\tau+\tilde{r}_{fi})\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right],\\
\tau\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-\tau-\dfrac{1}{b}\displaystyle\int^\tau_0y(\tau')\text{d}\tau'+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi}),\\
\tilde{r}_{fi}\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-(-\tilde{\xi}_{0i})\tilde{r}_{fi}.
\end{cases}
\end{equation}
Using ![]() $\text {d} [\tilde {r}_f\ln (\tilde {r}_f/\tilde {r}_{fi})]/\text {d} \tau =\ln (\tilde {r}_f/\tilde {r}_{fi})+1$, derivation of (C14) yields
$\text {d} [\tilde {r}_f\ln (\tilde {r}_f/\tilde {r}_{fi})]/\text {d} \tau =\ln (\tilde {r}_f/\tilde {r}_{fi})+1$, derivation of (C14) yields
 \begin{equation}
\frac{\text{d}\xi_s}{\text{d}\tau}= \begin{cases}
\dfrac{1}{b} \dfrac{{\textrm{d}y}}{\text{d} \tau}\left
[(\tau+\tilde{r}_{fi})\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\ \dfrac{y(\tau)}{b}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})+1\right
],\\
\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-1-\dfrac{y}{b}+\ln(\tilde{r}_f/\tilde{r}_{fi})+1,
\end{cases}
\end{equation}
\begin{equation}
\frac{\text{d}\xi_s}{\text{d}\tau}= \begin{cases}
\dfrac{1}{b} \dfrac{{\textrm{d}y}}{\text{d} \tau}\left
[(\tau+\tilde{r}_{fi})\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\tilde{r}_{f}\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\ \dfrac{y(\tau)}{b}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})+1\right
],\\
\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}-1-\dfrac{y}{b}+\ln(\tilde{r}_f/\tilde{r}_{fi})+1,
\end{cases}
\end{equation}to give
 \begin{equation}
\frac{\text{d}\xi_s}{\text{d}\tau}=
\begin{cases}\dfrac{1}{b}
\dfrac{{\textrm{d}y}}{\text{d} \tau}\tilde{r}_{f}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\ \dfrac{y(\tau)}{b}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\
\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi}),
\end{cases}
\end{equation}
\begin{equation}
\frac{\text{d}\xi_s}{\text{d}\tau}=
\begin{cases}\dfrac{1}{b}
\dfrac{{\textrm{d}y}}{\text{d} \tau}\tilde{r}_{f}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\ \dfrac{y(\tau)}{b}\left
[\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})\right
],\\
\dfrac{(-\tilde{\xi}_{0i})}{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi}),
\end{cases}
\end{equation}yielding
 \begin{equation} \frac{1}{(-\tilde{\xi}_{0i})/{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})}\frac{\text{d}\xi_s}{\text{d}\tau}= \tilde{r}_{f} \frac{1}{b} \frac{{\textrm{d}y}}{\text{d} \tau} +\left[1+\frac{y(\tau)}{b}\right ]. \end{equation}
\begin{equation} \frac{1}{(-\tilde{\xi}_{0i})/{(1+\mu^{ext}_{fi})}+\ln(\tilde{r}_f/\tilde{r}_{fi})}\frac{\text{d}\xi_s}{\text{d}\tau}= \tilde{r}_{f} \frac{1}{b} \frac{{\textrm{d}y}}{\text{d} \tau} +\left[1+\frac{y(\tau)}{b}\right ]. \end{equation}
The coefficient of ![]() ${\text {d}\xi _s}/{\text {d}\tau }$ on the left-hand side being positive, the sign of
${\text {d}\xi _s}/{\text {d}\tau }$ on the left-hand side being positive, the sign of ![]() ${\text {d}\xi _s}/{\text {d}\tau }$ is the same as
${\text {d}\xi _s}/{\text {d}\tau }$ is the same as ![]() $\tilde {r}_{f}\text {d}[1+{y(\tau )}/{b} ]/\text {d} \tau + [1+{y(\tau )}/{b} ]$ on the right-hand side.
$\tilde {r}_{f}\text {d}[1+{y(\tau )}/{b} ]/\text {d} \tau + [1+{y(\tau )}/{b} ]$ on the right-hand side.
Appendix D. Relaxation of spherical shock waves in open space
Introducing the reduced propagation velocity ![]() $\dot {\alpha }_{\tau }$ defined in (2.30a,b),
$\dot {\alpha }_{\tau }$ defined in (2.30a,b), ![]() $1+\dot {\alpha }_{\tau }\approx (\mathcal {D}-a)/\epsilon a$, the relaxation of an inert shock wave in spherical geometry corresponds to
$1+\dot {\alpha }_{\tau }\approx (\mathcal {D}-a)/\epsilon a$, the relaxation of an inert shock wave in spherical geometry corresponds to
Therefore, the end of the decay cannot be described by the approximation ![]() $\vert \dot {\alpha }_\tau \vert \ll 1$ used in (2.40a,b). At the Neumann state (
$\vert \dot {\alpha }_\tau \vert \ll 1$ used in (2.40a,b). At the Neumann state (![]() $\xi =0$), the flow is subsonic with respect to the shock
$\xi =0$), the flow is subsonic with respect to the shock ![]() $(\mathcal {D}-u_f)\leqslant a$, and, according to the Rankine–Hugoniot condition for
$(\mathcal {D}-u_f)\leqslant a$, and, according to the Rankine–Hugoniot condition for ![]() $(\mathcal {D}-a)/a \ll 1$, the boundary condition at the shock front reads
$(\mathcal {D}-a)/a \ll 1$, the boundary condition at the shock front reads ![]() $u_f\approx 2(\mathcal {D} -a)$ see (A1)-(A2) for
$u_f\approx 2(\mathcal {D} -a)$ see (A1)-(A2) for ![]() $Q=0$, which, using
$Q=0$, which, using ![]() $\mu +1\equiv u/\epsilon a$ in (2.28), corresponds to
$\mu +1\equiv u/\epsilon a$ in (2.28), corresponds to ![]() $\mu _f=1+2\dot {\alpha }_\tau$. Focusing attention on an initial velocity
$\mu _f=1+2\dot {\alpha }_\tau$. Focusing attention on an initial velocity ![]() $\mathcal {D}_i>a$ close to the sound speed, the function
$\mathcal {D}_i>a$ close to the sound speed, the function ![]() $\mathcal {D}(t)$ is decreasing monotonically from an initial value
$\mathcal {D}(t)$ is decreasing monotonically from an initial value ![]() $(\mathcal {D}_i-a)/a \ll 1$ to
$(\mathcal {D}_i-a)/a \ll 1$ to ![]() $a$. This is an eigenvalue problem consisting in determining the decreasing function
$a$. This is an eigenvalue problem consisting in determining the decreasing function ![]() $\dot {\alpha }_\tau (\tilde {\tau }) \to -1$ (
$\dot {\alpha }_\tau (\tilde {\tau }) \to -1$ (![]() $\mu _f(\tilde {\tau }) \to -1$), solution of
$\mu _f(\tilde {\tau }) \to -1$), solution of
satisfying the boundary condition
for a given initial condition
The flow of the rarefaction wave decreases from its Neumann value at the shock to ![]() $u=0$ when the distance from the shock increases, so that the instantaneous flow field
$u=0$ when the distance from the shock increases, so that the instantaneous flow field ![]() $\mu ( \tilde {\xi }, \tilde {\tau })$ decreases from
$\mu ( \tilde {\xi }, \tilde {\tau })$ decreases from ![]() $1+ 2 \dot {\alpha }_\tau (\tilde {\tau })$ at
$1+ 2 \dot {\alpha }_\tau (\tilde {\tau })$ at ![]() $\tilde {\xi }=0$ to
$\tilde {\xi }=0$ to ![]() $\mu =-1$ at
$\mu =-1$ at ![]() $\tilde {\xi }=\tilde {\xi }_0(\tilde {\tau })<0$ corresponding to the radius of the sphere of quiescent gas (
$\tilde {\xi }=\tilde {\xi }_0(\tilde {\tau })<0$ corresponding to the radius of the sphere of quiescent gas (![]() $u=0$). This point is a weak discontinuity propagating with the speed of the sound in the laboratory frame, according to (2.34),
$u=0$). This point is a weak discontinuity propagating with the speed of the sound in the laboratory frame, according to (2.34),
since ![]() $\text {d} \tilde {\xi }_0/\text {d}\tilde {\tau }=\text {d} \xi _0/\text {d} \tau$. As before, (D5) is automatically satisfied by the solution of (D2) which reduces to
$\text {d} \tilde {\xi }_0/\text {d}\tilde {\tau }=\text {d} \xi _0/\text {d} \tau$. As before, (D5) is automatically satisfied by the solution of (D2) which reduces to ![]() ${\partial \mu }/{\partial \tilde {\tau }} - ( 1 +\dot {\alpha }_\tau ) {\partial \mu }/{\partial \tilde {\xi }} = 0$ at
${\partial \mu }/{\partial \tilde {\tau }} - ( 1 +\dot {\alpha }_\tau ) {\partial \mu }/{\partial \tilde {\xi }} = 0$ at ![]() $\mu =-1$. Notice that the scalar field
$\mu =-1$. Notice that the scalar field ![]() $[\mu (\tilde {\xi }, \tilde {\tau })-\dot {\alpha }_\tau (\tilde {\tau })]$ decreases from a positive value
$[\mu (\tilde {\xi }, \tilde {\tau })-\dot {\alpha }_\tau (\tilde {\tau })]$ decreases from a positive value ![]() $1+\dot {\alpha }_{\tau }$ at the shock
$1+\dot {\alpha }_{\tau }$ at the shock ![]() $\tilde {\xi }=0$ to a negative value
$\tilde {\xi }=0$ to a negative value ![]() $-(1+\dot {\alpha }_{\tau })$ at
$-(1+\dot {\alpha }_{\tau })$ at ![]() $\tilde {\xi }_0(\tilde {\tau })<0$ so that there should be a sonic point (relative to the shock) inside the rarefaction wave at the point where
$\tilde {\xi }_0(\tilde {\tau })<0$ so that there should be a sonic point (relative to the shock) inside the rarefaction wave at the point where ![]() $(\mu -\dot {\alpha }_\tau )=0 \Leftrightarrow (\mathcal {D}-u)=a$.
$(\mu -\dot {\alpha }_\tau )=0 \Leftrightarrow (\mathcal {D}-u)=a$.
Equation (D2) has solutions in the same form as (2.44a–d) and (2.46a,b)–(2.48) are still valid since ![]() $\dot {\alpha }_\tau$ is eliminated from (2.45) when using
$\dot {\alpha }_\tau$ is eliminated from (2.45) when using ![]() ${\partial \mu }/{\partial \tilde {\tau }}=\dot {A}+(1+\dot {\alpha }_\tau )AB'$ and
${\partial \mu }/{\partial \tilde {\tau }}=\dot {A}+(1+\dot {\alpha }_\tau )AB'$ and ![]() $(\mu -\dot {\alpha }_\tau ) {\partial \mu }/{\partial \tilde {\xi }}=(AB-1-\dot {\alpha }_\tau )AB'$. Then, following the same development as in (2.46a,b)–(2.49), the solution to (D2),
$(\mu -\dot {\alpha }_\tau ) {\partial \mu }/{\partial \tilde {\xi }}=(AB-1-\dot {\alpha }_\tau )AB'$. Then, following the same development as in (2.46a,b)–(2.49), the solution to (D2), ![]() $\mu (\tilde {\xi }, \tilde {\tau })$ and
$\mu (\tilde {\xi }, \tilde {\tau })$ and ![]() $\mu _f(\tilde {\tau })$, expressed in terms of
$\mu _f(\tilde {\tau })$, expressed in terms of ![]() $\tilde {\xi }_0(\tilde {\tau })$ and the initial values
$\tilde {\xi }_0(\tilde {\tau })$ and the initial values ![]() $\tilde {\xi }_{0i}$ and
$\tilde {\xi }_{0i}$ and ![]() $\mu _{fi}$, take the same form as (2.50a,b)–(2.51a,b), obtained without using the boundary condition at the front. Using the boundary condition (D3) at the front and (D5) in the form
$\mu _{fi}$, take the same form as (2.50a,b)–(2.51a,b), obtained without using the boundary condition at the front. Using the boundary condition (D3) at the front and (D5) in the form
the expression of ![]() $\mu _f(\tilde {\tau })$ in (2.51a,b) yields an ordinary differential equation for
$\mu _f(\tilde {\tau })$ in (2.51a,b) yields an ordinary differential equation for ![]() $\tilde {\xi }_0(\tilde {\tau })$
$\tilde {\xi }_0(\tilde {\tau })$
 \begin{equation} \frac{1}{\tilde{\xi}_0(\tilde{\tau})} \frac{\text{d} \tilde{\xi}_0(\tilde{\tau})}{\text{d} \tilde{\tau}}= \frac{1}{2(1+\tilde{\tau})[\theta_i+\ln(1+\tilde{\tau})]},\quad \textrm{where}\ \theta_i\equiv{-} \frac{\tilde{\xi}_{0i}}{(1+\mu_{fi})}>0. \end{equation}
\begin{equation} \frac{1}{\tilde{\xi}_0(\tilde{\tau})} \frac{\text{d} \tilde{\xi}_0(\tilde{\tau})}{\text{d} \tilde{\tau}}= \frac{1}{2(1+\tilde{\tau})[\theta_i+\ln(1+\tilde{\tau})]},\quad \textrm{where}\ \theta_i\equiv{-} \frac{\tilde{\xi}_{0i}}{(1+\mu_{fi})}>0. \end{equation}This equation can be integrated by considering the integral
obtained by the change of variable ![]() $Y=\ln (1+\tilde {\tau }')$ leading to
$Y=\ln (1+\tilde {\tau }')$ leading to
 \begin{equation} \tilde{\xi}_0(\tilde{\tau})/\tilde{\xi}_{0i}=\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}, \Rightarrow \frac{\text{d} \tilde{\xi}_0}{\text{d} \tilde{\tau}}=\frac{\tilde{\xi}_{0i}}{2}\frac{1}{\theta_i(1+\tilde{\tau})\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}}. \end{equation}
\begin{equation} \tilde{\xi}_0(\tilde{\tau})/\tilde{\xi}_{0i}=\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}, \Rightarrow \frac{\text{d} \tilde{\xi}_0}{\text{d} \tilde{\tau}}=\frac{\tilde{\xi}_{0i}}{2}\frac{1}{\theta_i(1+\tilde{\tau})\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}}. \end{equation}
Putting together (D6) and (D9) provides us with the propagation velocity ![]() $\dot {\alpha }_\tau (\tilde {\tau })$
$\dot {\alpha }_\tau (\tilde {\tau })$
 \begin{equation} 1+\dot{\alpha}_\tau(\tilde{\tau}) = \frac{-\tilde{\xi}_{0i}/2}{\theta_i(1+\tilde{\tau})\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}} \end{equation}
\begin{equation} 1+\dot{\alpha}_\tau(\tilde{\tau}) = \frac{-\tilde{\xi}_{0i}/2}{\theta_i(1+\tilde{\tau})\sqrt {1+\frac{1}{\theta_i}\ln(1+\tilde{\tau})}} \end{equation}showing a relaxation toward the sound speed in the long-time limit in the form
Appendix E. Steady-state approximation for large activation energy
The quasi-steady approximation pointed out a curvature-induced quenching which is worth comparing with the unsteady trajectories. The steady-state approximation is not expected to be an accurate approximation in the direct initiation of spherical gaseous detonation, because the unsteady terms are of the same order of magnitude as the curvature term, see the discussion in Clavin & Denet (Reference Clavin and Denet2020). In this appendix the quasi-steady approximation of the inner structure is revisited in the limit of small heat release for large activation energy when the unsteady gradient of the burnt-gas flow of overdriven detonations is taken into account. Then, when the unsteady term on the left-hand side of (4.21) is neglected, the problem reduces to
Equations (E1)–(E2) correspond to a better quasi-steady approximation than in Clavin & Denet (Reference Clavin and Denet2020), because here, the unsteady effect of the external flow is retained, assuming a steady-state approximation only for the inner structure of the overdriven detonation. Equation (E1) can be written
and its integration from the end of the reaction zone where, according to (4.23) or (E2) ![]() $\xi =-\text {e}^{-y}$:
$\xi =-\text {e}^{-y}$: ![]() $\mu =\mu ^{ext}$ (
$\mu =\mu ^{ext}$ (![]() $\hat \mu =0$), leads to
$\hat \mu =0$), leads to
Then, the boundary condition on the lead shock in (4.11) or (E2), ![]() $\xi =0: \mu =1+2y(\tau )/b$,
$\xi =0: \mu =1+2y(\tau )/b$, ![]() $\mu ^{ext} =\mu ^{ext}_f(\tau )$,
$\mu ^{ext} =\mu ^{ext}_f(\tau )$, ![]() $\mu _{o_{CJ}}=1$, provides us with an implicit relation for
$\mu _{o_{CJ}}=1$, provides us with an implicit relation for ![]() $y(\tau )$ involving the solution
$y(\tau )$ involving the solution ![]() $\hat \mu (\xi , \tau )$
$\hat \mu (\xi , \tau )$
A closed equation relating ![]() $y(\tau )$ and
$y(\tau )$ and ![]() $\mu ^{ext}_f(\tau )$ is obtained for a large activation energy
$\mu ^{ext}_f(\tau )$ is obtained for a large activation energy ![]() $b\gg 1$, since
$b\gg 1$, since ![]() $\hat \mu (\xi , \tau )$ can be replaced by
$\hat \mu (\xi , \tau )$ can be replaced by ![]() $\mu _{o_{CJ}}(\xi \text {e}^{y})$ in the integral term
$\mu _{o_{CJ}}(\xi \text {e}^{y})$ in the integral term
as shown now. Looking for a solution corresponding to ![]() $y$ of order unity and
$y$ of order unity and ![]() $\tilde {r}_f$ of order
$\tilde {r}_f$ of order ![]() $b$,
$b$, ![]() $r_{fi}/l=O(b/\epsilon )$, one is led to consider
$r_{fi}/l=O(b/\epsilon )$, one is led to consider ![]() $(\mu ^{ext}_f)^2=O(1/b)$ in (E6). This is consistent with the simplified expression (C12) of the rarefaction wave behind a overdriven detonation
$(\mu ^{ext}_f)^2=O(1/b)$ in (E6). This is consistent with the simplified expression (C12) of the rarefaction wave behind a overdriven detonation
leading to
Then, the zeroth-order ![]() $\hat \mu _o(\xi ', \tau )$ of
$\hat \mu _o(\xi ', \tau )$ of ![]() $\hat \mu (\xi ', \tau )$ in the limit
$\hat \mu (\xi ', \tau )$ in the limit ![]() $b\gg 1$ can be used in the integral term on the right-hand side of (E5). This zeroth-order solution
$b\gg 1$ can be used in the integral term on the right-hand side of (E5). This zeroth-order solution ![]() $\hat \mu _o(\xi ', \tau )$ is solution to the steady version of (4.21)–(4.23) when the terms smaller than unity are neglected,
$\hat \mu _o(\xi ', \tau )$ is solution to the steady version of (4.21)–(4.23) when the terms smaller than unity are neglected,
yielding, according to (4.6a,b)-(4.7a–c), ![]() $\hat \mu _o(\xi ',\tau )=\mu _{o_{CJ}}(\xi ' \text {e}^{y(\tau )})$. This leads to the transcendental equation for
$\hat \mu _o(\xi ',\tau )=\mu _{o_{CJ}}(\xi ' \text {e}^{y(\tau )})$. This leads to the transcendental equation for ![]() $y$ in (E6) which, neglecting the term
$y$ in (E6) which, neglecting the term ![]() $\mu ^{ext}_f$ on the left-hand side in front of unity, can be written in the form
$\mu ^{ext}_f$ on the left-hand side in front of unity, can be written in the form
and ![]() $b[\mu ^{ext}_f(\tau )]^2=O(1)$, see (C11) and (E7), the integral
$b[\mu ^{ext}_f(\tau )]^2=O(1)$, see (C11) and (E7), the integral ![]() $\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '$ being close to
$\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '$ being close to ![]() $1/2$. Using (4.12)
$1/2$. Using (4.12) ![]() $\tilde {r}_f\approx \tau +\tilde {r}_{fi}$ and the simplified expression
$\tilde {r}_f\approx \tau +\tilde {r}_{fi}$ and the simplified expression ![]() $\mu _{f}^{ext}(\tau )$ in (E7) to eliminate
$\mu _{f}^{ext}(\tau )$ in (E7) to eliminate ![]() $\tau$ in favour of
$\tau$ in favour of ![]() $x$, (E10) yields the leading order in the limit
$x$, (E10) yields the leading order in the limit ![]() $b\gg 1$ of the quasi-steady trajectories in the phase space ‘velocity–radius’
$b\gg 1$ of the quasi-steady trajectories in the phase space ‘velocity–radius’ ![]() $y-x$. Using the substitutions
$y-x$. Using the substitutions ![]() $\sqrt {b/2}\,\mu ^{ext}_f \to \sqrt {b/2}\,\mu _b\equiv m_b$ and
$\sqrt {b/2}\,\mu ^{ext}_f \to \sqrt {b/2}\,\mu _b\equiv m_b$ and ![]() $\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '\to 1+\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '$, (E10) takes the same form as (7.1a) in Clavin & Denet (Reference Clavin and Denet2020) and the trajectories have a form similar to figure 1 ibid. with a definition of
$\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '\to 1+\int _{-1}^0\mu _{o_{CJ}}(\xi ')\,\text {d}\xi '$, (E10) takes the same form as (7.1a) in Clavin & Denet (Reference Clavin and Denet2020) and the trajectories have a form similar to figure 1 ibid. with a definition of ![]() $x$ which differs by a factor of order unity, compare (4.20a,b) ibid. with (E10). In particular, the critical radius
$x$ which differs by a factor of order unity, compare (4.20a,b) ibid. with (E10). In particular, the critical radius ![]() $r_f^*$ at the turning point (
$r_f^*$ at the turning point (![]() $y=-1$,
$y=-1$, ![]() $x=\text {e}$) of the C-shaped curve ‘CJ velocity–radius’, obtained from (E10) for
$x=\text {e}$) of the C-shaped curve ‘CJ velocity–radius’, obtained from (E10) for ![]() $b[\mu ^{ext}_f(\tau )]^2= 0$, is
$b[\mu ^{ext}_f(\tau )]^2= 0$, is
while it was ![]() ${r_f^*}/{l}= ({b}/{\epsilon })\,\text {e} [1+ \int _{-1}^{0}\mu _{o_{CJ}}(\xi ')\,\text {d}\xi ' ]$ in (4.20c) of Clavin & Denet (Reference Clavin and Denet2020) where the gradient of the burnt-gas flow was ignored. In any case the critical radius corresponds to a non-dimensional radius
${r_f^*}/{l}= ({b}/{\epsilon })\,\text {e} [1+ \int _{-1}^{0}\mu _{o_{CJ}}(\xi ')\,\text {d}\xi ' ]$ in (4.20c) of Clavin & Denet (Reference Clavin and Denet2020) where the gradient of the burnt-gas flow was ignored. In any case the critical radius corresponds to a non-dimensional radius ![]() $\tilde {r}_f/b$ of order unity.
$\tilde {r}_f/b$ of order unity.