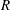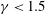1 Introduction
The electroconvection phenomenon, which exhibits complex temporal and spatial patterns, has been widely investigated by many researchers in the past few decades. Most of the research works have been focused on a sandwich set-up with two parallel flat plates and a thin layer of nematic liquid crystal in the middle. In the presence of an applied electric field perpendicular to the flat plates, spatial free charges can be induced in the liquid crystal due to the anisotropic nature of liquid crystal molecules. Then, the nonlinearity of the coupled electrohydrodynamic system can result in many convective patterns (such as normal rolls, oblique rolls or travelling rolls, etc.) in the liquid crystal layer of this sandwich configuration (Cross & Hohenberg Reference Cross and Hohenberg1993; Kramer & Pesch Reference Kramer and Pesch1995; Buka et al. Reference Buka, Éber, Pesch and Kramer2007).
However, due to the existence of two plates, the resulting convective flow in the liquid crystal of the sandwich set-up is highly three-dimensional, which makes the analysis very complicated. To remove the influence of the two plates, Faetti, Fronzoni & Rolla (Reference Faetti, Fronzoni and Rolla1983) came up with another set-up with liquid crystal suspended on a rectangular boundary, and the electroconvection phenomenon was then investigated in this suspended liquid crystal thin film where the flow motion could be approximately viewed as two-dimensional. They observed the formation of vortex patterns with certain spatial periodicity in the liquid crystal film when AC or DC voltage was applied. In this suspended film set-up, the free charges are mainly induced by a surface charge mechanism instead of anisotropy of the liquid crystal molecules. Subsequently, a series of research works have been carried out with respect to the electroconvection problem in a suspended liquid crystal film system. A highly two-dimensional system was realized by Morris, Bruyn & May (Reference Morris, Bruyn and May1990) by using smectic liquid crystal instead of nematic liquid crystal in their suspended thin film, since smectic layering can further constrain the flow of the third dimension and help to reduce the thickness variation of the film. In the experiment, they found that both DC and AC coupled set-ups can result in similar instability phenomena. Tsai, Daya & Morris (Reference Tsai, Daya and Morris2004) changed the experimental set-up from a long (very-large-aspect-ratio) rectangular film (Faetti et al. Reference Faetti, Fronzoni and Rolla1983; Morris et al. Reference Morris, Bruyn and May1990) to an annular shaped thin film. Therefore, the one-dimensional periodicity of the problem is perfectly retained and at the same time the aspect ratio of the set-up can be adjusted by changing the radius of the inner or outer circle. Using this set-up, they investigated the aspect ratio dependence of turbulent electroconvection. Daya, Deyirmenjian & Morris (Reference Daya, Deyirmenjian and Morris1999) applied additional Couette shear to the annular thin film set-up by rotating the inner edge of the film, so another control parameter, the rotational Reynolds number, was added into the system. They found that this additional control parameter can help to adjust the neutral stability boundary of the system. Further investigations were carried out on this annular system with or without Couette shear by direct numerical simulation (Tsai et al. Reference Tsai, Daya, Deyirmenjian and Morris2007; Tsai, Morris & Daya Reference Tsai, Morris and Daya2008). More flow visualization results of this electroconvection phenomenon have been revealed in these numerical studies.
Thus far, a great deal of effort has been put into research on electroconvection in suspended liquid crystal films. However, to simplify the problem, one-dimensional periodicity has been introduced in most of the previous experiments either by making the rectangular film very slender (large aspect ratio) or by using an annular shaped set-up and correspondingly assuming a certain wavenumber along one direction in the analysis. In the current work, a complete two-dimensional global stability analysis is carried out on the rectangular liquid crystal film. Instability of the electrohydrodynamic system with different aspect ratios is discussed. The development of a two-dimensional flow pattern on the liquid film as the aspect ratio varies is investigated through stability analysis. Moreover, to validate the results obtained from stability analysis, the convective flow on the film is quantitatively measured through a particle image velocimetry (PIV) experiment.
2 Experimental set-up
In the experiment, a liquid crystal film is suspended on a rectangular frame which is set up using two conductive molybdenum wires and two insulated nylon wires, as shown in figure 1. The diameters of the molybdenum wires and nylon wires are both 0.1 mm. The dimensions
![]() $d$
and
$d$
and
![]() $L$
vary in the ranges 2–6 mm and 3–14 mm respectively. The liquid crystal is 4’-n-octylbiphenyl-4-carbonitrile (8CB) (99 %, J&K Scientific) and the experimental temperature of the liquid film area is kept at
$L$
vary in the ranges 2–6 mm and 3–14 mm respectively. The liquid crystal is 4’-n-octylbiphenyl-4-carbonitrile (8CB) (99 %, J&K Scientific) and the experimental temperature of the liquid film area is kept at
![]() $34\,^{\circ }\text{C}$
, so that the liquid crystal can stay in the nematic phase (Sharma, MacDonald & Iannacchione Reference Sharma, MacDonald and Iannacchione2006). The average thickness of the film is
$34\,^{\circ }\text{C}$
, so that the liquid crystal can stay in the nematic phase (Sharma, MacDonald & Iannacchione Reference Sharma, MacDonald and Iannacchione2006). The average thickness of the film is
![]() $\bar{s}=25~\unicode[STIX]{x03BC}\text{m}$
, the conductivity of the liquid crystal is
$\bar{s}=25~\unicode[STIX]{x03BC}\text{m}$
, the conductivity of the liquid crystal is
![]() $\unicode[STIX]{x1D70E}=5\times 10^{-8}(\unicode[STIX]{x03A9}^{-1}~\text{m}^{-1})$
, the viscosity is
$\unicode[STIX]{x1D70E}=5\times 10^{-8}(\unicode[STIX]{x03A9}^{-1}~\text{m}^{-1})$
, the viscosity is
![]() $\unicode[STIX]{x1D702}=0.1~\text{kg}~(\text{s}~\text{m})^{-1}$
and the mass density is
$\unicode[STIX]{x1D702}=0.1~\text{kg}~(\text{s}~\text{m})^{-1}$
and the mass density is
![]() $\unicode[STIX]{x1D70C}=1.0\times 10^{3}~\text{kg}~\text{m}^{-3}$
(Morris, Bruyn & May Reference Morris, Bruyn and May1991; Patrício et al.
Reference Patrício, Leal, Pinto, Boto and Cidade2012). Here, the average thickness of the film is estimated by the value of the volume of the liquid crystal used to make the film divided by the area of the film. A DC voltage is applied between the molybdenum wires to drive the liquid film to move. To measure the flow field in the liquid film, a PIV experiment is carried out. In the experiment, fluorescent particles with diameters of
$\unicode[STIX]{x1D70C}=1.0\times 10^{3}~\text{kg}~\text{m}^{-3}$
(Morris, Bruyn & May Reference Morris, Bruyn and May1991; Patrício et al.
Reference Patrício, Leal, Pinto, Boto and Cidade2012). Here, the average thickness of the film is estimated by the value of the volume of the liquid crystal used to make the film divided by the area of the film. A DC voltage is applied between the molybdenum wires to drive the liquid film to move. To measure the flow field in the liquid film, a PIV experiment is carried out. In the experiment, fluorescent particles with diameters of
![]() $1{-}2~\unicode[STIX]{x03BC}\text{m}$
are added to the liquid crystal film to track the motion of the fluid. To ensure the uniformity of the tracking particles in the film, the fluorescent particles are premixed with the liquid crystal using an ultrasonic mixer at a temperature of
$1{-}2~\unicode[STIX]{x03BC}\text{m}$
are added to the liquid crystal film to track the motion of the fluid. To ensure the uniformity of the tracking particles in the film, the fluorescent particles are premixed with the liquid crystal using an ultrasonic mixer at a temperature of
![]() $50\,^{\circ }\text{C}$
before the experiment. A pulsed Nd : YAG laser with an energy of
$50\,^{\circ }\text{C}$
before the experiment. A pulsed Nd : YAG laser with an energy of
![]() $200~\text{mJ}$
and a frequency of 5 Hz is used to excite the fluorescence of the particles, and flow field images are captured by a CCD camera with a resolution of
$200~\text{mJ}$
and a frequency of 5 Hz is used to excite the fluorescence of the particles, and flow field images are captured by a CCD camera with a resolution of
![]() $2456\times 2058$
. In this work, all of the results obtained from PIV measurements are averaged results of 100 flow field images.
$2456\times 2058$
. In this work, all of the results obtained from PIV measurements are averaged results of 100 flow field images.
In previous experimental work, researchers used liquid crystal in the smectic phase instead of the nematic phase to make thin
![]() $(10^{-2}{-}10^{-1}~\unicode[STIX]{x03BC}\text{m})$
and stable film (Morris et al.
Reference Morris, Bruyn and May1990; Becker et al.
Reference Becker, Ried, Stannarius and Stegemeyer1997), which is a very good two-dimensional system. However, in the current PIV experiment, fluorescent tracking particles with diameters of
$(10^{-2}{-}10^{-1}~\unicode[STIX]{x03BC}\text{m})$
and stable film (Morris et al.
Reference Morris, Bruyn and May1990; Becker et al.
Reference Becker, Ried, Stannarius and Stegemeyer1997), which is a very good two-dimensional system. However, in the current PIV experiment, fluorescent tracking particles with diameters of
![]() $1{-}2~\unicode[STIX]{x03BC}\text{m}$
have to be evenly distributed in the liquid crystal film. Thus, we have to make a film with a thickness of tens of microns using nematic liquid crystal to realize the PIV measurements, although the thickness variation of a nematic liquid crystal film could affect the two-dimensionality of the system, as can be noted in figure 1. As reported by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983), two different types of flow patterns can be observed in a suspended nematic liquid crystal film, which are named as the domain mode and the vortex mode respectively. The domain mode results from a Carr–Helfrich mechanism in the anisotropic phase of the nematic liquid crystal, while the vortex mode is mainly driven by a surface charge mechanism. In this work, only the vortex mode (vortical flow pattern) is investigated and discussed.
$1{-}2~\unicode[STIX]{x03BC}\text{m}$
have to be evenly distributed in the liquid crystal film. Thus, we have to make a film with a thickness of tens of microns using nematic liquid crystal to realize the PIV measurements, although the thickness variation of a nematic liquid crystal film could affect the two-dimensionality of the system, as can be noted in figure 1. As reported by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983), two different types of flow patterns can be observed in a suspended nematic liquid crystal film, which are named as the domain mode and the vortex mode respectively. The domain mode results from a Carr–Helfrich mechanism in the anisotropic phase of the nematic liquid crystal, while the vortex mode is mainly driven by a surface charge mechanism. In this work, only the vortex mode (vortical flow pattern) is investigated and discussed.

Figure 1. Experimental set-up.
3 Linear stability analysis
The current analysis is based on a physical model similar to the ones proposed in previous works (Melcher & Taylor Reference Melcher and Taylor1969; Daya, Morris & Bruyn Reference Daya, Morris and Bruyn1997; Feiz, Namin & Amjadi Reference Feiz, Namin and Amjadi2015). It is assumed that the fluid motion in the liquid crystal film is restrained in two dimensions, which means that the convection in the third dimension inside the film is neglected. Due to the electric potential difference between the liquid crystal film surface and the surrounding air, free charges are induced at the surface of the film near the electrodes with the same signs, and they move in the film under the effects of fluid convection and the electric field induced by the electrodes. On the other hand, electric force resulting from distributed charges drives motion of fluids. Finally, a certain flow pattern could result in the liquid film after this coupling effect between the electric and flow fields has converged to a stable state. According to the above physical assumptions, this 2D coupling system can be described by the charge continuity equation and the incompressible Navier–Stokes equation, and they can be written in dimensionless form as follows:
where
![]() $q_{s}$
denotes the surface charge density,
$q_{s}$
denotes the surface charge density,
![]() $\boldsymbol{E}_{\boldsymbol{s}}$
is the electric field intensity projection on the liquid film,
$\boldsymbol{E}_{\boldsymbol{s}}$
is the electric field intensity projection on the liquid film,
![]() $\boldsymbol{u}$
is the fluid velocity and
$\boldsymbol{u}$
is the fluid velocity and
![]() $\unicode[STIX]{x1D713}$
is the stream function. Since the controlling equations are written in two-dimensional form, all of the material parameters are given in areal form as
$\unicode[STIX]{x1D713}$
is the stream function. Since the controlling equations are written in two-dimensional form, all of the material parameters are given in areal form as
![]() $\unicode[STIX]{x1D702}_{s}=\unicode[STIX]{x1D702}s$
,
$\unicode[STIX]{x1D702}_{s}=\unicode[STIX]{x1D702}s$
,
![]() $\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}s$
and
$\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}s$
and
![]() $\unicode[STIX]{x1D70E}_{s}=\unicode[STIX]{x1D70E}s$
, where
$\unicode[STIX]{x1D70E}_{s}=\unicode[STIX]{x1D70E}s$
, where
![]() $s$
is the thickness of the film. In (3.1) and (3.2), lengths and times are non-dimensionalized by
$s$
is the thickness of the film. In (3.1) and (3.2), lengths and times are non-dimensionalized by
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D700}_{0}d/\unicode[STIX]{x1D70E}s$
respectively, and the characteristic charge density is set as
$\unicode[STIX]{x1D700}_{0}d/\unicode[STIX]{x1D70E}s$
respectively, and the characteristic charge density is set as
![]() $\unicode[STIX]{x1D700}_{0}U/d$
, where
$\unicode[STIX]{x1D700}_{0}U/d$
, where
![]() $\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
$\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
![]() $d$
is the distance between the two electrodes and
$d$
is the distance between the two electrodes and
![]() $U$
is the potential drop between the two electrodes. The two dimensionless parameters,
$U$
is the potential drop between the two electrodes. The two dimensionless parameters,
![]() $P$
and
$P$
and
![]() $R$
, are analogous to the Prandtl number and Rayleigh number in the Rayleigh–Bénard convection problem, and are as defined below:
$R$
, are analogous to the Prandtl number and Rayleigh number in the Rayleigh–Bénard convection problem, and are as defined below:
Moreover, the surface charge
![]() $q_{s}$
and electric potential
$q_{s}$
and electric potential
![]() $\unicode[STIX]{x1D719}$
are coupled through the 3D Laplace equation,
$\unicode[STIX]{x1D719}$
are coupled through the 3D Laplace equation,
![]() $\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D719}=0$
, with boundary condition
$\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D719}=0$
, with boundary condition
![]() $q_{s}=-2(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}z)|_{z=0^{+}}$
(
$q_{s}=-2(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}z)|_{z=0^{+}}$
(
![]() $z$
is the normal direction of the liquid film surface) according to the Maxwell equation expressed in the 3D domain above the liquid crystal film. In this work, stability analysis is carried out with respect to the equilibrium state of the static liquid film with static charge distribution when DC voltage is applied on the electrodes. Thus, the base state of the fluid flow is
$z$
is the normal direction of the liquid film surface) according to the Maxwell equation expressed in the 3D domain above the liquid crystal film. In this work, stability analysis is carried out with respect to the equilibrium state of the static liquid film with static charge distribution when DC voltage is applied on the electrodes. Thus, the base state of the fluid flow is
![]() $\boldsymbol{u}=0$
everywhere. To calculate the base state of the charge density distribution
$\boldsymbol{u}=0$
everywhere. To calculate the base state of the charge density distribution
![]() $q_{s}$
, a linear electric potential drop is assumed between the two electrodes and the 3D Laplace equation is numerically solved using the second-order central difference method. To validate the computational results, the charge density distribution along a line in the middle of the film is taken to compare with the 2D analytical solution, as given by Daya et al. (Reference Daya, Morris and Bruyn1997). Moreover, to test the grid convergence, two different sets of grids (
$q_{s}$
, a linear electric potential drop is assumed between the two electrodes and the 3D Laplace equation is numerically solved using the second-order central difference method. To validate the computational results, the charge density distribution along a line in the middle of the film is taken to compare with the 2D analytical solution, as given by Daya et al. (Reference Daya, Morris and Bruyn1997). Moreover, to test the grid convergence, two different sets of grids (
![]() $30\times 40\times 10$
and
$30\times 40\times 10$
and
![]() $50\times 100\times 20$
, which in the 2D liquid film are
$50\times 100\times 20$
, which in the 2D liquid film are
![]() $20\times 30$
and
$20\times 30$
and
![]() $40\times 90$
respectively) are used in the computation. In the validation test, the film aspect ratio is set as
$40\times 90$
respectively) are used in the computation. In the validation test, the film aspect ratio is set as
![]() $\unicode[STIX]{x1D6FE}=2$
(
$\unicode[STIX]{x1D6FE}=2$
(
![]() $\unicode[STIX]{x1D6FE}=L/d$
, where
$\unicode[STIX]{x1D6FE}=L/d$
, where
![]() $L$
is the distance between the two insulated wires, as shown in figure 1). As shown in figure 2, the computed charge density distribution matches with the analytical solution very well and it does not vary with grid density. Therefore, in the remainder of the paper, a grid of
$L$
is the distance between the two insulated wires, as shown in figure 1). As shown in figure 2, the computed charge density distribution matches with the analytical solution very well and it does not vary with grid density. Therefore, in the remainder of the paper, a grid of
![]() $30\times 40\times 10$
is used in all of the computations.
$30\times 40\times 10$
is used in all of the computations.

Figure 2. Comparison of the analytical solution (Daya et al. Reference Daya, Morris and Bruyn1997) and the current computations for surface charge distribution.
In the stability analysis, small perturbations with temporal growth are assumed and superimposed onto base physical quantities as follows:
where
![]() $\unicode[STIX]{x1D719}_{0}$
,
$\unicode[STIX]{x1D719}_{0}$
,
![]() $q_{s0}$
,
$q_{s0}$
,
![]() $\unicode[STIX]{x1D713}_{0}$
are base state physical quantities and
$\unicode[STIX]{x1D713}_{0}$
are base state physical quantities and
![]() $\unicode[STIX]{x1D719}_{1}$
,
$\unicode[STIX]{x1D719}_{1}$
,
![]() $q_{s1}$
,
$q_{s1}$
,
![]() $\unicode[STIX]{x1D713}_{1}$
are spatial distributions of small perturbations;
$\unicode[STIX]{x1D713}_{1}$
are spatial distributions of small perturbations;
![]() $\unicode[STIX]{x1D706}$
is the temporal growth rate of perturbations. Since the base state for the current analysis is the static equilibrium of the liquid crystal film, we have
$\unicode[STIX]{x1D706}$
is the temporal growth rate of perturbations. Since the base state for the current analysis is the static equilibrium of the liquid crystal film, we have
![]() $\unicode[STIX]{x1D713}_{0}=0$
everywhere, and
$\unicode[STIX]{x1D713}_{0}=0$
everywhere, and
![]() $\unicode[STIX]{x1D719}_{0}$
and
$\unicode[STIX]{x1D719}_{0}$
and
![]() $q_{s0}$
can be solved from the 3D Laplace equation, as described previously. By substituting these perturbed quantities into the controlling equations (3.1) and (3.2) and neglecting higher-order term, linearized equations are obtained as follows:
$q_{s0}$
can be solved from the 3D Laplace equation, as described previously. By substituting these perturbed quantities into the controlling equations (3.1) and (3.2) and neglecting higher-order term, linearized equations are obtained as follows:
Since the surface charge
![]() $q_{s1}$
and electric potential
$q_{s1}$
and electric potential
![]() $\unicode[STIX]{x1D719}_{1}$
are also coupled by the linear Laplace equation, as mentioned previously, we use the following procedure (Feiz et al.
Reference Feiz, Namin and Amjadi2015) to relate these two quantities. First, we give an electric potential distribution
$\unicode[STIX]{x1D719}_{1}$
are also coupled by the linear Laplace equation, as mentioned previously, we use the following procedure (Feiz et al.
Reference Feiz, Namin and Amjadi2015) to relate these two quantities. First, we give an electric potential distribution
![]() $\unicode[STIX]{x1D719}_{1ij}$
, so that
$\unicode[STIX]{x1D719}_{1ij}$
, so that
![]() $\unicode[STIX]{x1D719}_{1ij}=1$
at the
$\unicode[STIX]{x1D719}_{1ij}=1$
at the
![]() $(i,j)$
grid point in the liquid film and
$(i,j)$
grid point in the liquid film and
![]() $\unicode[STIX]{x1D719}_{1ij}=0$
at the rest of the grid points. Then, a corresponding surface charge distribution
$\unicode[STIX]{x1D719}_{1ij}=0$
at the rest of the grid points. Then, a corresponding surface charge distribution
![]() $q_{sij}(x,y)$
can be solved from the 3D Laplace equation with a boundary condition of
$q_{sij}(x,y)$
can be solved from the 3D Laplace equation with a boundary condition of
![]() $q_{s}=-2(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}z)|_{z=0^{+}}$
. This routine is repeated for all
$q_{s}=-2(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}z)|_{z=0^{+}}$
. This routine is repeated for all
![]() $(i,j)$
grid points of the liquid film. Finally, for any given electric potential distribution
$(i,j)$
grid points of the liquid film. Finally, for any given electric potential distribution
![]() $\unicode[STIX]{x1D719}_{1}$
, the corresponding surface charge distribution can be superimposed as
$\unicode[STIX]{x1D719}_{1}$
, the corresponding surface charge distribution can be superimposed as
![]() $q_{s1}(x,y)=\sum _{i,j}\unicode[STIX]{x1D719}_{1}(x_{ij},y_{ij})q_{sij}(x,y)$
. By substituting this relationship into (3.8) and (3.9) and using a second-order central difference scheme to discretize spatial derivatives, finally an eigenvalue problem can be formed. The boundary conditions of this eigenvalue problem are given (Traoré & Pérez Reference Traoré and Pérez2012) as shown in figure 3.
$q_{s1}(x,y)=\sum _{i,j}\unicode[STIX]{x1D719}_{1}(x_{ij},y_{ij})q_{sij}(x,y)$
. By substituting this relationship into (3.8) and (3.9) and using a second-order central difference scheme to discretize spatial derivatives, finally an eigenvalue problem can be formed. The boundary conditions of this eigenvalue problem are given (Traoré & Pérez Reference Traoré and Pérez2012) as shown in figure 3.

Figure 3. Boundary conditions for stability analysis.
Eigenvalues with positive real parts (
![]() $\unicode[STIX]{x1D706}_{R}>0$
) indicate instability of the system, and the corresponding eigenvectors represent unstable spatial modes for the electric and fluid fields.
$\unicode[STIX]{x1D706}_{R}>0$
) indicate instability of the system, and the corresponding eigenvectors represent unstable spatial modes for the electric and fluid fields.
4 Results and discussion
In the electroconvection problem of a suspended liquid crystal film, as the applied voltage (or the dimensionless parameter
![]() $R$
) exceeds a critical value, the static equilibrium of the system is broken and the liquid film starts to move following a certain vortical pattern. This phenomenon has been widely reported in previous work with different film geometries (Faetti et al.
Reference Faetti, Fronzoni and Rolla1983; Morris et al.
Reference Morris, Bruyn and May1990; Tsai et al.
Reference Tsai, Daya and Morris2004). In the current experiment, using the PIV technique, the flow patterns on rectangular liquid films of different aspect ratios are obtained, and the resulting vortical motion is observed to vary with the film aspect ratio
$R$
) exceeds a critical value, the static equilibrium of the system is broken and the liquid film starts to move following a certain vortical pattern. This phenomenon has been widely reported in previous work with different film geometries (Faetti et al.
Reference Faetti, Fronzoni and Rolla1983; Morris et al.
Reference Morris, Bruyn and May1990; Tsai et al.
Reference Tsai, Daya and Morris2004). In the current experiment, using the PIV technique, the flow patterns on rectangular liquid films of different aspect ratios are obtained, and the resulting vortical motion is observed to vary with the film aspect ratio
![]() $\unicode[STIX]{x1D6FE}$
, as shown in figure 4. Moreover, flow velocity data obtained from the current PIV experiment are substituted into (3.1) to calculate the corresponding electric potential distributions. The calculated electric potential distributions are also plotted in figure 4, and the applied linear electric potential drop between the two electrodes is subtracted from the results.
$\unicode[STIX]{x1D6FE}$
, as shown in figure 4. Moreover, flow velocity data obtained from the current PIV experiment are substituted into (3.1) to calculate the corresponding electric potential distributions. The calculated electric potential distributions are also plotted in figure 4, and the applied linear electric potential drop between the two electrodes is subtracted from the results.

Figure 4. Convective patterns obtained from the PIV experiment under different aspect ratios. The left-hand side shows the flow patterns, while the right-hand side shows the patterns of the electric potential (calculated from the measured flow field): (a)
![]() $U=1012$
V,
$U=1012$
V,
![]() $\unicode[STIX]{x1D6FE}=0.73$
; (b)
$\unicode[STIX]{x1D6FE}=0.73$
; (b)
![]() $U=818$
V,
$U=818$
V,
![]() $\unicode[STIX]{x1D6FE}=1.72$
; (c)
$\unicode[STIX]{x1D6FE}=1.72$
; (c)
![]() $U=1014$
V,
$U=1014$
V,
![]() $\unicode[STIX]{x1D6FE}=2.03$
; (d)
$\unicode[STIX]{x1D6FE}=2.03$
; (d)
![]() $U=808$
V,
$U=808$
V,
![]() $\unicode[STIX]{x1D6FE}=3.28$
.
$\unicode[STIX]{x1D6FE}=3.28$
.
As shown in figure 4, the number of vortices distributed along the
![]() $x$
direction increases from 1 to 4 as the aspect ratio of the liquid film increases from 0.76 to 3.28. Similar vortex patterns are also obtained from stability analysis. Stability analysis is carried out at the same aspect ratios as those set in the experiment, and the unstable eigenmodes for the flow and electric fields are extracted and plotted in figure 5. As shown in figure 5, the obtained unstable eigenmodes match with the experimental results qualitatively well, and they both reveal a trend of an increasing number of vortices as the aspect ratio of the film increases.
$x$
direction increases from 1 to 4 as the aspect ratio of the liquid film increases from 0.76 to 3.28. Similar vortex patterns are also obtained from stability analysis. Stability analysis is carried out at the same aspect ratios as those set in the experiment, and the unstable eigenmodes for the flow and electric fields are extracted and plotted in figure 5. As shown in figure 5, the obtained unstable eigenmodes match with the experimental results qualitatively well, and they both reveal a trend of an increasing number of vortices as the aspect ratio of the film increases.

Figure 5. Unstable eigenmodes obtained from numerical stability analysis under different aspect ratios. The left-hand side shows the flow patterns, while the right-hand side shows the patterns of the electric potential: (a)
![]() $R=R_{c}=171.1$
,
$R=R_{c}=171.1$
,
![]() $\unicode[STIX]{x1D6FE}=0.73$
; (b)
$\unicode[STIX]{x1D6FE}=0.73$
; (b)
![]() $R=R_{c}=119.3$
,
$R=R_{c}=119.3$
,
![]() $\unicode[STIX]{x1D6FE}=1.72$
; (c)
$\unicode[STIX]{x1D6FE}=1.72$
; (c)
![]() $R=R_{c}=119.5$
,
$R=R_{c}=119.5$
,
![]() $\unicode[STIX]{x1D6FE}=2.03$
; (d)
$\unicode[STIX]{x1D6FE}=2.03$
; (d)
![]() $R=R_{c}=119.3$
,
$R=R_{c}=119.3$
,
![]() $\unicode[STIX]{x1D6FE}=3.28$
.
$\unicode[STIX]{x1D6FE}=3.28$
.
Through stability analysis, the critical
![]() $R$
number (
$R$
number (
![]() $R_{c}$
) is calculated for films with different aspect ratios, and the variation of
$R_{c}$
) is calculated for films with different aspect ratios, and the variation of
![]() $R_{c}$
with respect to the film aspect ratio (
$R_{c}$
with respect to the film aspect ratio (
![]() $\unicode[STIX]{x1D6FE}$
) is investigated. As shown in figure 6, the critical
$\unicode[STIX]{x1D6FE}$
) is investigated. As shown in figure 6, the critical
![]() $R$
number decreases almost exponentially with the film aspect ratio for roughly
$R$
number decreases almost exponentially with the film aspect ratio for roughly
![]() $\unicode[STIX]{x1D6FE}<1.5$
, and then the variation becomes slow until
$\unicode[STIX]{x1D6FE}<1.5$
, and then the variation becomes slow until
![]() $\unicode[STIX]{x1D6FE}\approx 2.5$
, where
$\unicode[STIX]{x1D6FE}\approx 2.5$
, where
![]() $R_{c}$
starts to increase slightly. Moreover, the flow patterns of the unstable eigenmodes are extracted at different aspect ratios, and boundaries that separate different flow patterns are marked as dashed lines in the plot. As shown in figure 6, the flow pattern boundaries all appear at local maxima of the
$R_{c}$
starts to increase slightly. Moreover, the flow patterns of the unstable eigenmodes are extracted at different aspect ratios, and boundaries that separate different flow patterns are marked as dashed lines in the plot. As shown in figure 6, the flow pattern boundaries all appear at local maxima of the
![]() $R_{c}$
–
$R_{c}$
–
![]() $\unicode[STIX]{x1D6FE}$
curve, especially for the low-aspect-ratio region. Similar characteristics of variation of
$\unicode[STIX]{x1D6FE}$
curve, especially for the low-aspect-ratio region. Similar characteristics of variation of
![]() $R_{c}$
and the flow pattern with respect to the aspect ratio of the rectangular boundary have been reported in computational work by Pérez et al. (Reference Pérez, Vázquez, Wu and Traoré2014), although the geometry of their problem was sandwich shaped and unipolar injection was the driving mechanism in their physical model. Moreover, with an annular geometry, Daya et al. (Reference Daya, Deyirmenjian and Morris1999) also found that
$R_{c}$
and the flow pattern with respect to the aspect ratio of the rectangular boundary have been reported in computational work by Pérez et al. (Reference Pérez, Vázquez, Wu and Traoré2014), although the geometry of their problem was sandwich shaped and unipolar injection was the driving mechanism in their physical model. Moreover, with an annular geometry, Daya et al. (Reference Daya, Deyirmenjian and Morris1999) also found that
![]() $R_{c}$
varies faster at low radius ratios, and local maxima of the
$R_{c}$
varies faster at low radius ratios, and local maxima of the
![]() $R_{c}$
curve indicate transition between adjacent flow patterns.
$R_{c}$
curve indicate transition between adjacent flow patterns.

Figure 6. Variation of the critical
![]() $R$
number with respect to the film aspect ratio.
$R$
number with respect to the film aspect ratio.

Figure 7. The flow pattern variation process as the film aspect ratio increases: (a)
![]() $R=R_{c}=143.75$
,
$R=R_{c}=143.75$
,
![]() $\unicode[STIX]{x1D6FE}=1.25$
; (b)
$\unicode[STIX]{x1D6FE}=1.25$
; (b)
![]() $R=R_{c}=121.43$
,
$R=R_{c}=121.43$
,
![]() $\unicode[STIX]{x1D6FE}=1.89$
; (c)
$\unicode[STIX]{x1D6FE}=1.89$
; (c)
![]() $R=R_{c}=121.91$
,
$R=R_{c}=121.91$
,
![]() $\unicode[STIX]{x1D6FE}=1.96$
; (d)
$\unicode[STIX]{x1D6FE}=1.96$
; (d)
![]() $R=R_{c}=121.67$
,
$R=R_{c}=121.67$
,
![]() $\unicode[STIX]{x1D6FE}=1.99$
.
$\unicode[STIX]{x1D6FE}=1.99$
.
A closer observation of the stability analysis results reveals the whole process of flow pattern variation. As shown in figure 7, when the aspect ratio of the film increases from 1.25 (close to the first flow pattern boundary), vortices start to be stretched gradually in the
![]() $x$
direction. Until
$x$
direction. Until
![]() $\unicode[STIX]{x1D6FE}=1.89$
, when vortices are maximumly stretched and the growth of vortices in the
$\unicode[STIX]{x1D6FE}=1.89$
, when vortices are maximumly stretched and the growth of vortices in the
![]() $x$
direction stops, a new flow structure starts to appear at one side of the film. As the aspect ratio further increases, this newly emerging flow structure gradually grows into the third vortex with similar dimensions to the other two. Due to the growth of the third vortex, the other two vortices are squeezed in the
$x$
direction stops, a new flow structure starts to appear at one side of the film. As the aspect ratio further increases, this newly emerging flow structure gradually grows into the third vortex with similar dimensions to the other two. Due to the growth of the third vortex, the other two vortices are squeezed in the
![]() $x$
direction and their lateral dimension decreases until the third vortex grows to a similar size to them.
$x$
direction and their lateral dimension decreases until the third vortex grows to a similar size to them.
In our experiment, it is also observed that the convective pattern shown on the film is not stable at some aspect ratios. At these aspect ratios, the number of vortices in the flow pattern switches from
![]() $m$
to
$m$
to
![]() $m+1$
intermittently. A similar phenomenon has been reported in the earlier work by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983) and Mao et al. (Reference Mao, Bruyn, Daya and Morris1996) for rectangular films with large aspect ratios (
$m+1$
intermittently. A similar phenomenon has been reported in the earlier work by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983) and Mao et al. (Reference Mao, Bruyn, Daya and Morris1996) for rectangular films with large aspect ratios (
![]() $\unicode[STIX]{x1D6FE}>3$
). They observed that the flow pattern is very stable when the lateral dimension (
$\unicode[STIX]{x1D6FE}>3$
). They observed that the flow pattern is very stable when the lateral dimension (
![]() $x$
direction) of the film is close to a multiple of the spatial period of the vortex pattern; otherwise, the flow pattern becomes less stable and vortex structures are created or destroyed at the ends of the film. In the current work, we reinvestigate this problem by stability analysis. In the stability analysis, as the
$x$
direction) of the film is close to a multiple of the spatial period of the vortex pattern; otherwise, the flow pattern becomes less stable and vortex structures are created or destroyed at the ends of the film. In the current work, we reinvestigate this problem by stability analysis. In the stability analysis, as the
![]() $R$
number further increases beyond the critical value, a new unstable eigenmode can appear at a certain point (second critical
$R$
number further increases beyond the critical value, a new unstable eigenmode can appear at a certain point (second critical
![]() $R$
number,
$R$
number,
![]() $R_{c2}$
). This new unstable flow mode has one more vortex than the previous mode and is always the dominant mode (with larger
$R_{c2}$
). This new unstable flow mode has one more vortex than the previous mode and is always the dominant mode (with larger
![]() $\unicode[STIX]{x1D706}_{R}$
), as shown in figure 8. Usually, this new unstable flow mode is not expected to be observed in the experiment because when the applied DC voltage is increased gradually in the experiment, the liquid film has already started to move when the voltage crosses the first critical value, and the base flow for the second stability analysis is no longer static. In this sense, the new unstable flow mode obtained here is spurious and we can only observe one type of flow pattern in the experiment. However, if this second critical voltage (
$\unicode[STIX]{x1D706}_{R}$
), as shown in figure 8. Usually, this new unstable flow mode is not expected to be observed in the experiment because when the applied DC voltage is increased gradually in the experiment, the liquid film has already started to move when the voltage crosses the first critical value, and the base flow for the second stability analysis is no longer static. In this sense, the new unstable flow mode obtained here is spurious and we can only observe one type of flow pattern in the experiment. However, if this second critical voltage (
![]() $U_{c2}$
) is very close to the first critical value (
$U_{c2}$
) is very close to the first critical value (
![]() $U_{c}$
), the new unstable mode can behave like a parallel mode of the previous mode and the flow pattern with one more vortex can appear in the experiment if the applied voltage is slightly perturbed. When this happens, the flow pattern shown on the film becomes less stable, as observed in the current experiment and earlier work (Faetti et al.
Reference Faetti, Fronzoni and Rolla1983; Mao et al.
Reference Mao, Bruyn, Daya and Morris1996). In other words, two adjacent linearly unstable modes can indicate instability of the resulting nonlinear flow pattern. In the current analysis, the ratio of the second critical
$U_{c}$
), the new unstable mode can behave like a parallel mode of the previous mode and the flow pattern with one more vortex can appear in the experiment if the applied voltage is slightly perturbed. When this happens, the flow pattern shown on the film becomes less stable, as observed in the current experiment and earlier work (Faetti et al.
Reference Faetti, Fronzoni and Rolla1983; Mao et al.
Reference Mao, Bruyn, Daya and Morris1996). In other words, two adjacent linearly unstable modes can indicate instability of the resulting nonlinear flow pattern. In the current analysis, the ratio of the second critical
![]() $R$
number to the first critical value (
$R$
number to the first critical value (
![]() $R_{c2}/R_{c}$
) is calculated from stability analysis for different aspect ratios, as plotted in figure 9. As can be observed from figure 9, the minima of the
$R_{c2}/R_{c}$
) is calculated from stability analysis for different aspect ratios, as plotted in figure 9. As can be observed from figure 9, the minima of the
![]() $R_{c2}/R_{c}$
curve are very close to 1 (
$R_{c2}/R_{c}$
curve are very close to 1 (
![]() $1<R_{c2}/R_{c}<1.005$
), and they all coincide with the flow pattern boundaries as marked in figure 6. This indicates that the flow pattern shown on the film tends to be less stable when the aspect ratio of the rectangular film is close to the flow pattern boundaries. This is expectable since at these boundaries, the flow pattern is in transition and hence unstable. Similar mode transition behaviour has also been observed in other eletroconvection or hydrodynamic systems with finite aspect ratios. In an experimental work on sheared annular electroconvection, Daya, Deyirmenjian & Morris (Reference Daya, Deyirmenjian and Morris2002) observed a convective pattern transition as the
$1<R_{c2}/R_{c}<1.005$
), and they all coincide with the flow pattern boundaries as marked in figure 6. This indicates that the flow pattern shown on the film tends to be less stable when the aspect ratio of the rectangular film is close to the flow pattern boundaries. This is expectable since at these boundaries, the flow pattern is in transition and hence unstable. Similar mode transition behaviour has also been observed in other eletroconvection or hydrodynamic systems with finite aspect ratios. In an experimental work on sheared annular electroconvection, Daya, Deyirmenjian & Morris (Reference Daya, Deyirmenjian and Morris2002) observed a convective pattern transition as the
![]() $R$
number was tuned up or down from the critical value
$R$
number was tuned up or down from the critical value
![]() $R_{c}$
. Binks & Mullin (Reference Binks and Mullin1997) reported a mode selection behaviour between six-cell and eight-cell flow patterns in electroconvection within a small-aspect-ratio cell. Pfister et al. (Reference Pfister, Schmidt, Cliffe and Mullin1988) also observed transition between different bifurcation branches in Taylor–Couette flow in a very short annulus.
$R_{c}$
. Binks & Mullin (Reference Binks and Mullin1997) reported a mode selection behaviour between six-cell and eight-cell flow patterns in electroconvection within a small-aspect-ratio cell. Pfister et al. (Reference Pfister, Schmidt, Cliffe and Mullin1988) also observed transition between different bifurcation branches in Taylor–Couette flow in a very short annulus.

Figure 8. Unstable eigenmodes at the first and second critical
![]() $R$
numbers with an aspect ratio of
$R$
numbers with an aspect ratio of
![]() $\unicode[STIX]{x1D6FE}=1.94$
: (a)
$\unicode[STIX]{x1D6FE}=1.94$
: (a)
![]() $R=R_{c}=121.67$
,
$R=R_{c}=121.67$
,
![]() $\unicode[STIX]{x1D706}_{R}=446.76$
; (b)
$\unicode[STIX]{x1D706}_{R}=446.76$
; (b)
![]() $R=R_{c2}=124.08$
,
$R=R_{c2}=124.08$
,
![]() $\unicode[STIX]{x1D706}_{R}=85.02$
; (c)
$\unicode[STIX]{x1D706}_{R}=85.02$
; (c)
![]() $R=R_{c2}=124.08$
,
$R=R_{c2}=124.08$
,
![]() $\unicode[STIX]{x1D706}_{R}=15.98$
.
$\unicode[STIX]{x1D706}_{R}=15.98$
.

Figure 9. The variation of
![]() $R_{c2}/R_{c}$
with respect to the film aspect ratio.
$R_{c2}/R_{c}$
with respect to the film aspect ratio.
As the aspect ratio of the film decreases below 1, flow patterns with distributions in the
![]() $y$
direction can also be obtained from stability analysis, as shown in figure 10. This flow structure development along the
$y$
direction can also be obtained from stability analysis, as shown in figure 10. This flow structure development along the
![]() $y$
direction is not as regulated as that in the
$y$
direction is not as regulated as that in the
![]() $x$
direction. A multiple-vortex pattern as observed in the
$x$
direction. A multiple-vortex pattern as observed in the
![]() $x$
direction cannot be obtained in the
$x$
direction cannot be obtained in the
![]() $y$
direction. Moreover, these flow patterns with very low aspect ratios cannot be observed from the current experiment and have not been reported in any previous experimental works. As can be noted in figure 10, the critical
$y$
direction. Moreover, these flow patterns with very low aspect ratios cannot be observed from the current experiment and have not been reported in any previous experimental works. As can be noted in figure 10, the critical
![]() $R$
numbers are extremely high compared with those calculated under larger aspect ratios (as shown in figure 6). Therefore, the driving voltages for these liquid films with small aspect ratios are very high, which makes experiment unrealizable.
$R$
numbers are extremely high compared with those calculated under larger aspect ratios (as shown in figure 6). Therefore, the driving voltages for these liquid films with small aspect ratios are very high, which makes experiment unrealizable.

Figure 10. Flow patterns obtained from stability analysis for very small aspect ratios: (a)
![]() $R=R_{c}=10385.8$
,
$R=R_{c}=10385.8$
,
![]() $\unicode[STIX]{x1D6FE}=0.10$
; (b)
$\unicode[STIX]{x1D6FE}=0.10$
; (b)
![]() $R=R_{c}=4205.8$
,
$R=R_{c}=4205.8$
,
![]() $\unicode[STIX]{x1D6FE}=0.15$
; (c)
$\unicode[STIX]{x1D6FE}=0.15$
; (c)
![]() $R=R_{c}=1224.1$
,
$R=R_{c}=1224.1$
,
![]() $\unicode[STIX]{x1D6FE}=0.25$
.
$\unicode[STIX]{x1D6FE}=0.25$
.
5 Conclusions
In this work, the electroconvection problem of a suspended liquid crystal film with a rectangular boundary was investigated. Global stability analysis was carried out to extract the resulting flow patterns on the film for different aspect ratios when the applied DC voltage reached critical values. The obtained flow patterns were well validated by PIV experiment. The variation of the critical voltage (
![]() $R$
number) with respect to the film aspect ratio was also obtained in the stability analysis. It was found that the critical voltage (
$R$
number) with respect to the film aspect ratio was also obtained in the stability analysis. It was found that the critical voltage (
![]() $R$
number) decreases almost exponentially fast in the low-aspect-ratio region (
$R$
number) decreases almost exponentially fast in the low-aspect-ratio region (
![]() $\unicode[STIX]{x1D6FE}<1.5$
), and then the variation becomes very slow. Moreover, the variation process of the flow pattern on the film as the aspect ratio gradually increases was described using stability analysis results. In the current experiment, the flow pattern was observed to be unstable at certain aspect ratios, as mentioned in earlier works by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983) and Mao et al. (Reference Mao, Bruyn, Daya and Morris1996). This phenomenon was explained by the occurrence of parallel unstable eigenmodes in the stability analysis. The flow structure development along the vertical direction (
$\unicode[STIX]{x1D6FE}<1.5$
), and then the variation becomes very slow. Moreover, the variation process of the flow pattern on the film as the aspect ratio gradually increases was described using stability analysis results. In the current experiment, the flow pattern was observed to be unstable at certain aspect ratios, as mentioned in earlier works by Faetti et al. (Reference Faetti, Fronzoni and Rolla1983) and Mao et al. (Reference Mao, Bruyn, Daya and Morris1996). This phenomenon was explained by the occurrence of parallel unstable eigenmodes in the stability analysis. The flow structure development along the vertical direction (
![]() $y$
direction) was also obtained in the stability analysis for small aspect ratios (
$y$
direction) was also obtained in the stability analysis for small aspect ratios (
![]() $\unicode[STIX]{x1D6FE}<1$
).
$\unicode[STIX]{x1D6FE}<1$
).
Acknowledgements
This research is supported by Shanghai Yangfan Plan (no. 14YF1400200), Shanghai Chenguang Plan (no. 13CG01) and Fudan’s Undergraduate Research Opportunities Program (no. 15101). The authors acknowledge T. Xu from Beijing MicroVec Ltd. for his guidance and help in the PIV experiment. The authors are also grateful to Professor L. Zhou, Professor C. Tian, Professor Y. Wu and Professor J. Xu for their interesting discussions, and would like to thank A. Li for her help in the experimental set-up.