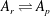1 Introduction
Mathematical modelling of chemically reacting gas mixtures within continuum theories usually relies upon models that comprise the conservation laws of mass, momentum and energy of the mixture, and an additional balance law that describes the progress of the reaction by tracking the rate of change of product concentration, driven by the reaction rate. These models are, on the one hand, well founded in molecular gas theory. On the other hand, they are mathematically tractable and provide a good description of real processes. This classical approach is well explained in seminal works (Hirschfelder et al. Reference Hirschfelder, Curtiss and Bird1954; Courant & Friedrichs Reference Courant and Friedrichs1977; Zel’dovich & Raizer Reference Zel’dovich and Raizer2002), as well as in more recent monographs devoted to combustion and detonation problems (Fickett Reference Fickett1985; Williams Reference Williams1985; Lee Reference Lee2008).
Versatile problems that appear in the detonation processes are both physically interesting and mathematically demanding. Physical aspects and various approaches that emerge in their study are well documented (Fickett Reference Fickett1985; Williams Reference Williams1985; Lee Reference Lee2008). On the other hand, the mathematical complexity of the detonation problem motivated the construction of model equations, like the one proposed by Majda (Reference Majda1981). It retained the basic features of the detonation process utilizing a reactive Burgers equation analogue. Such a model was analysed for the solution properties (Razani Reference Razani2002), as well as for the stability of the detonations (Liu & Yu Reference Liu and Yu1999; Szepessy Reference Szepessy1999; Lyng & Zumbrun Reference Lyng and Zumbrun2004). The existence of a solution for the complete set of detonation equations (Euler equations and reaction progress equation) was studied by Gardner (Reference Gardner1983) and Hesaaraki & Razani (Reference Hesaaraki and Razani2001). A then up-to-date review, comprising the detonation structure, was given by Clavin (Reference Clavin2004). Meanwhile, certain new aspects of detonation waves emerged within the continuum framework, e.g. radial propagation (Kasimov & Korneev Reference Kasimov and Korneev2014), multi-dimensional self-sustained detonations (Faria, Kasimov & Rosales Reference Faria, Kasimov and Rosales2015) and decay of plane detonation waves (Clavin & Denet Reference Clavin and Denet2018), so that detonation processes still remain in focus. Apart from the continuum approach, detonation problems were also analysed using the kinetic theory of gases as a starting point, and deriving macroscopic models as moment equations of distribution functions. In this approach the system was usually closed at Euler level (Conforto et al. Reference Conforto, Monaco, Schürrer and Ziegler2003, Reference Conforto, Groppi, Monaco and Spiga2004; Carvalho & Soares Reference Carvalho and Soares2012; Marques Junior et al. Reference Marques Junior, Soares, Bianchi and Kremer2015), leading to hyperbolic systems of balance laws (the exception is Conforto, Monaco & Ricciardello (Reference Conforto, Monaco and Ricciardello2014), where the closure was done at Navier–Stokes level). Finally, the intricacy of the numerical computation of detonation profiles due to the scale disparity brings additional difficulties. The computations should be carefully performed in order to obtain reliable results (see Bdzil & Stewart Reference Bdzil and Stewart2007; Cael et al. Reference Cael, Ng, Bates, Nikiforakis and Short2009).
The continuum models mentioned above can be enriched if one digs deeper into the structure of the medium. One of the simplest, and conceptually reasonable, ways is to take into account the information about the constituents by extending the list of state variables that describe the medium. In fact, this is the aim of the mixture theory developed within the framework of extended thermodynamics (Müller & Ruggeri Reference Müller and Ruggeri1998, pp. 79–104). In fact, in this approach, the state of the mixture is described by the fields of mass density, velocity and temperature of each constituent (Ruggeri & Simić Reference Ruggeri and Simić2007; Ruggeri Reference Ruggeri2009). This choice of state variables, and appropriate governing equations, enables more sophisticated modelling and acquiring more information about non-equilibrium processes. Moreover, this model for mixtures possesses two main features of extended thermodynamic models: it is dissipative, and it is hyperbolic. Nevertheless, it can be put within the classical framework either by means of Maxwellian iteration (Ruggeri & Simić Reference Ruggeri and Simić2009, Reference Ruggeri and Simić2017), or directly (Gouin & Ruggeri Reference Gouin and Ruggeri2008).
1.1 Assumptions and the aim of the paper
The aim of this paper is to propose a variant of the Zel’dovich–von Neumann–Döring (ZND) detonation model within the framework of multi-temperature extended thermodynamics of mixtures, and to investigate the detonation wave structure problem. In this approach the basic assumptions of the ZND model will be retained: the flow is assumed to be one-dimensional, the shock is described by a non-reactive jump discontinuity, and the chemical reaction occurs in a finite reaction zone following the shock front. Finally, the study will be concerned with overdriven detonations that propagate with a speed greater than the Chapman–Jouguet one. To that end, certain generalizations of the standard ZND model will be made. First, it will be assumed that the chemical reaction is reversible, restricting the analysis to the simplest possible mechanism, represented by
with only two constituents – reactants (
![]() $r$
) and products (
$r$
) and products (
![]() $p$
) of the forward reaction. This representation includes the symmetric reaction
$p$
) of the forward reaction. This representation includes the symmetric reaction
![]() $A_{1}+A_{1}\rightleftharpoons A_{2}+A_{2}$
, which has been considered in previous works about detonation and linear stability (see Carvalho & Soares Reference Carvalho and Soares2012; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015). Reaction (1.1) can also represent an inelastic transition of a polyatomic molecule from one energy state to another energy state and, in this case,
$A_{1}+A_{1}\rightleftharpoons A_{2}+A_{2}$
, which has been considered in previous works about detonation and linear stability (see Carvalho & Soares Reference Carvalho and Soares2012; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015). Reaction (1.1) can also represent an inelastic transition of a polyatomic molecule from one energy state to another energy state and, in this case,
![]() $A_{r}$
and
$A_{r}$
and
![]() $A_{p}$
denote two different energetic components of the same gas. Second, the rather restrictive assumption of local thermodynamic equilibrium will be replaced with a set of new assumptions about the constituents and their dynamics, at both molecular and macroscopic scale:
$A_{p}$
denote two different energetic components of the same gas. Second, the rather restrictive assumption of local thermodynamic equilibrium will be replaced with a set of new assumptions about the constituents and their dynamics, at both molecular and macroscopic scale:
(i) the molecular masses are equal,
 $m_{r}=m_{p}=m$
;
$m_{r}=m_{p}=m$
;(ii) the molecular diameters are equal,
 $d_{r}=d_{p}=d$
;
$d_{r}=d_{p}=d$
;(iii) the binding (formation) energies of the molecules are different,
 $\unicode[STIX]{x1D716}_{r}\neq \unicode[STIX]{x1D716}_{p}$
;
$\unicode[STIX]{x1D716}_{r}\neq \unicode[STIX]{x1D716}_{p}$
;(iv) during elastic collisions, molecules have monatomic-like behaviour, and both constituents will be modelled as hard spheres;
(v) the ratios of specific heats are equal,
 $\unicode[STIX]{x1D6FE}_{r}=\unicode[STIX]{x1D6FE}_{p}=\unicode[STIX]{x1D6FE}=5/3$
;
$\unicode[STIX]{x1D6FE}_{r}=\unicode[STIX]{x1D6FE}_{p}=\unicode[STIX]{x1D6FE}=5/3$
;(vi) the macroscopic state of the constituents is described by the fields of mass density
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
, velocity
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
, velocity
 $\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}$
and temperature
$\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}$
and temperature
 $T_{\unicode[STIX]{x1D6FC}}$
, with
$T_{\unicode[STIX]{x1D6FC}}$
, with
 $\unicode[STIX]{x1D6FC}=r,p$
; and
$\unicode[STIX]{x1D6FC}=r,p$
; and(vii) the constituents are assumed to be Eulerian fluids, and thus the viscosity and heat conductivity of the constituents do not influence the detonation structure and are not taken into account.
The physical motivation for the choice of chemical reaction (1.1) and the set of assumptions (i)–(vii) is to capture, in the simplest possible setting, the scenario that is typical for overdriven detonations. Namely, in the analysis of pathological detonations, Sharpe (Reference Sharpe1999), and also Khokhlov (Reference Khokhlov1989), mentioned that overdriven detonations have continuous but non-monotonic profiles, in which the turning point corresponds to the state with maximum heat release. So far, the simplest type of chemical reaction that allows this kind of behaviour is the two-step reaction
![]() $A\rightarrow B\rightarrow C$
, where the first reaction is exothermic, while the second one is endothermic. In a recent paper, Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015) used a reversible reaction of the kind (1.1), but did not comply with the expected behaviour of the state variables in overdriven detonations. Our aim is to bring into play the thermal non-equilibrium through the multi-temperature assumption, and to show that the standard overdriven detonation scenario is possible in (1.1) due to different temperatures of the constituents.
$A\rightarrow B\rightarrow C$
, where the first reaction is exothermic, while the second one is endothermic. In a recent paper, Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015) used a reversible reaction of the kind (1.1), but did not comply with the expected behaviour of the state variables in overdriven detonations. Our aim is to bring into play the thermal non-equilibrium through the multi-temperature assumption, and to show that the standard overdriven detonation scenario is possible in (1.1) due to different temperatures of the constituents.
1.2 Discussion of the assumptions
Assumptions (i) and (vi) are the most important ones for the generalizations in our model. Assumption (i), although it seems counter to our intentions for generalization, is a direct consequence of the mass conservation in chemical reaction (1.1). It induces a kind of singular behaviour of the mixture, since the molecules of the constituents cannot be distinguished in a mechanical sense due to their equal masses. This observation will be summarized as the basic assumption, and it will simplify the model – the difference of the velocities will be disregarded and a single-velocity model will be considered. On the other hand, assumption (vi) introduces the multi-velocity and multi-temperature structure into the model. This structure is already embedded into the rational thermodynamics of mixtures (see Truesdell Reference Truesdell1984, pp. 219–236), and has become fundamental in the extended thermodynamic theory of mixtures (Ruggeri & Simić Reference Ruggeri and Simić2007) and the kinetic theory of reactive mixtures (Bisi, Martalò & Spiga Reference Bisi, Martalò and Spiga2011, Reference Bisi, Martalò and Spiga2013; Murugesan, Sirmas & Radulescu Reference Murugesan, Sirmas and Radulescu2017). Furthermore, it is of macroscopic kind, but at the same time it goes deeply into the structure of matter and resonates with molecular assumptions, thus reflecting the primary aim of extended thermodynamics – to bridge the gap between the macro- and meso-scales. In the context of chemically reactive mixtures, it aims to describe the internal energy transfer from reactants to products of the reaction, or vice versa, and the corresponding opposite kinetic energy transfer. Such an assumption has been proved to be reasonable when the constituents have large discrepancies in molecular masses, and thus considerably different internal energies (temperatures) (see Bird Reference Bird1968; Kosuge, Aoki & Takata Reference Kosuge, Aoki and Takata2001; Madjarević, Ruggeri & Simić Reference Madjarević, Ruggeri and Simić2014). This observation came from studies in which non-reactive mixtures were analysed, and mutual interactions between the constituents were of purely mechanical nature. Our model will bring another novelty by applying the multi-temperature assumption to chemical interactions as well: the reaction rate for the reversible chemical reaction will be enriched with terms that take into account the constituents’ temperatures. It will be shown that this generalization, in conjunction with large initial discrepancy of concentrations of the constituents, will be sufficient to drive the constituents’ temperatures apart within the detonation wave. In such a way, we shall be in a position to prove that the difference of the temperatures, driven by the chemical reaction, influences the structure of the detonation profile.
Although our study is concerned with the relation of the multi-temperature assumption to the detonation profile, it does not have the aim to cover all the involved aspects and possible consequences. It will be shown in the discussion that it can be legitimately applied to multi-step chemical reactions or to other complex chemical processes, and used to describe both the structure of pathological detonation waves (Fickett & Davis Reference Fickett and Davis1979; Sharpe Reference Sharpe1999) and the effects resulting from the competing exothermic and endothermic reactions. In particular, in conjunction with reversible chemical reactions, it predicts the appearance of the non-monotonic profiles expected in the case of overdriven detonations, which we shall deal with in this paper.
Furthermore, the multi-temperature assumption may be related not only to different kinetic temperatures of the constituents, but also to different degrees of freedom of polyatomic molecules through vibrational temperature, as well as to different phases.
In particular, with regard to the multi-temperature formalisms applied to treat detonation, we quote, in particular, the relevant work about the modelling, structure and other aspects of detonation solutions in two-phase reactive flows (Powers, Stewart & Krier Reference Powers, Stewart and Krier1990a ,Reference Powers, Stewart and Krier b ) and the important contributions about the non-equilibrium effects in gaseous detonation systems resulting from the interplay between vibrational relaxation and chemical reactions (Taylor, Kessler & Oran Reference Taylor, Kessler and Oran2013; Shi et al. Reference Shi, Shen, Zhang, Zhang and Wena2017).
1.3 Structure of the paper
The paper is organized as follows. In §§ 2 and 3 we shall provide a proper background for the modelling of ZND detonation waves. Section 2 will review the basic aspects of the multi-temperature model for a binary reactive mixture, while § 3 will explain the main features of the steady ZND detonation waves in the context of reversible chemical reactions. Section 4 will contain the formulation of the steady detonation problem and the reduction of the model based upon the basic assumption regarding diffusion. After that, qualitative aspects of the reacting flow profiles will be analysed, which include the equilibrium state and the existence of non-monotonic profiles. In § 5 continuous multi-temperature steady reacting flow profiles are computed numerically for overdriven detonations, and compared with appropriate single-temperature profiles. Since the solution of the detonation problem depends on several parameters, their influence will be thoroughly analysed. It will be shown that, for certain values of the parameters, the multi-temperature model yields qualitatively different detonation profile in comparison to the single-temperature one. For other values of the parameters, the qualitative picture is the same. Nevertheless, the influence of two temperatures in the model is inevitable in the structure of the profiles. The paper ends with a summary and some possible studies to be considered as a continuation of our paper.
2 The multi-temperature model of reactive binary mixture
The framework for the detonation wave structure problem with reversible chemical reaction in a binary mixture will be the multi-temperature (MT) model developed within extended thermodynamics (Ruggeri & Simić Reference Ruggeri and Simić2007). A similar model was recently applied to the description of flame structures (Brini Reference Brini2009). The main feature of the model is the introduction of the velocities and the temperatures of the constituents, with the aim of capturing non-equilibrium effects in the simplest possible constitutive framework. Although it may seem quite unusual to extend the list of state variables of a macroscopic model in such a way, it resonates with the appropriate models derived within the kinetic theory of gases (Goldman & Sirovich Reference Goldman and Sirovich1967), and thus goes along with the main intention of rational extended thermodynamics (Müller & Ruggeri Reference Müller and Ruggeri1998) to bridge the gap between the macroscopic and mesoscopic levels of description. The rationale for this approach in detonation problems comes from the fact that chemical reactions are processes that could drive the medium out of equilibrium, in a chemical sense, as well as in mechanical and thermal senses.
2.1 Governing equations
The main modelling assumption is that each constituent of the mixture obeys the same balance laws as a single fluid, but mutual interaction of the constituents must be taken into account (Truesdell Reference Truesdell1984). The governing equations for an
![]() $n$
-component mixture (
$n$
-component mixture (
![]() $\unicode[STIX]{x1D6FC}=1,\ldots ,n$
) then read (see Ruggeri & Simić Reference Ruggeri and Simić2007):
$\unicode[STIX]{x1D6FC}=1,\ldots ,n$
) then read (see Ruggeri & Simić Reference Ruggeri and Simić2007):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x2202}t}+\text{div}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}},\\ \displaystyle \frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}})}{\unicode[STIX]{x2202}t}+\text{div}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}\otimes \boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}})=\boldsymbol{m}_{\unicode[STIX]{x1D6FC}},\\ \displaystyle \frac{\unicode[STIX]{x2202}(\frac{1}{2}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}v_{\unicode[STIX]{x1D6FC}}^{2}+\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}})}{\unicode[STIX]{x2202}t}+\text{div}\{({\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}v_{\unicode[STIX]{x1D6FC}}^{2}+\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}})\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}+\boldsymbol{q}_{\unicode[STIX]{x1D6FC}}\}=e_{\unicode[STIX]{x1D6FC}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x2202}t}+\text{div}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}},\\ \displaystyle \frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}})}{\unicode[STIX]{x2202}t}+\text{div}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}\otimes \boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}})=\boldsymbol{m}_{\unicode[STIX]{x1D6FC}},\\ \displaystyle \frac{\unicode[STIX]{x2202}(\frac{1}{2}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}v_{\unicode[STIX]{x1D6FC}}^{2}+\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}})}{\unicode[STIX]{x2202}t}+\text{div}\{({\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}v_{\unicode[STIX]{x1D6FC}}^{2}+\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}})\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}}\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}+\boldsymbol{q}_{\unicode[STIX]{x1D6FC}}\}=e_{\unicode[STIX]{x1D6FC}},\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
,
![]() $\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}$
and
$\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}}$
are the mass density, the velocity and the internal energy of the
$\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D6FC}}$
are the mass density, the velocity and the internal energy of the
![]() $\unicode[STIX]{x1D6FC}$
-constituent,
$\unicode[STIX]{x1D6FC}$
-constituent,
![]() $\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D64F}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\boldsymbol{q}_{\unicode[STIX]{x1D6FC}}$
are the stress tensor and the heat flux, while the source terms
$\boldsymbol{q}_{\unicode[STIX]{x1D6FC}}$
are the stress tensor and the heat flux, while the source terms
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
,
![]() $\boldsymbol{m}_{\unicode[STIX]{x1D6FC}}$
and
$\boldsymbol{m}_{\unicode[STIX]{x1D6FC}}$
and
![]() $e_{\unicode[STIX]{x1D6FC}}$
take into account the mutual interactions of the constituents. Moreover,
$e_{\unicode[STIX]{x1D6FC}}$
take into account the mutual interactions of the constituents. Moreover,
![]() $v_{\unicode[STIX]{x1D6FC}}=|\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}|$
and similar notations are adopted for other velocities from here on. It is an axiom of the mixture theory that conservation laws of mass, momentum and energy of the whole mixture must hold, imposing the following constraints on the source terms:
$v_{\unicode[STIX]{x1D6FC}}=|\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}|$
and similar notations are adopted for other velocities from here on. It is an axiom of the mixture theory that conservation laws of mass, momentum and energy of the whole mixture must hold, imposing the following constraints on the source terms:
In accordance with our assumption (vii), the stress tensor and the heat flux will be reduced to
where
![]() $\unicode[STIX]{x1D644}$
is the unit tensor.
$\unicode[STIX]{x1D644}$
is the unit tensor.
For the sake of brevity we shall omit the general analysis of the MT model of mixtures, which can be found elsewhere (Ruggeri & Simić Reference Ruggeri and Simić2007; Madjarević & Simić Reference Madjarević and Simić2013; Madjarević et al. Reference Madjarević, Ruggeri and Simić2014). Instead, the case of a binary reactive mixture will be presented. The governing equations consist of conservation laws of mass, momentum and energy for the mixture, and balance laws of mass, momentum and energy for one constituent (Ruggeri & Simić Reference Ruggeri and Simić2007). Since it is common practice in simple modelling of chemical reactions to monitor the behaviour of the product of the forward reaction, we decided to include the balance laws for the product in the governing equations, so that they read:
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{1}{2}\unicode[STIX]{x1D70C}z\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)^{2}+\unicode[STIX]{x1D70C}z\unicode[STIX]{x1D700}_{p}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{div}\left\{\left(\frac{1}{2}\unicode[STIX]{x1D70C}z\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)^{2}+\unicode[STIX]{x1D70C}z\unicode[STIX]{x1D700}_{p}+p_{p}\right)\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)\right\}=e_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{1}{2}\unicode[STIX]{x1D70C}z\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)^{2}+\unicode[STIX]{x1D70C}z\unicode[STIX]{x1D700}_{p}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{div}\left\{\left(\frac{1}{2}\unicode[STIX]{x1D70C}z\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)^{2}+\unicode[STIX]{x1D70C}z\unicode[STIX]{x1D700}_{p}+p_{p}\right)\left(\boldsymbol{v}+\frac{\boldsymbol{J}}{\unicode[STIX]{x1D70C}z}\right)\right\}=e_{p}.\end{eqnarray}$$
Here the following quantities are introduced:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{r}+\unicode[STIX]{x1D70C}_{p}\quad \text{mass density of the mixture,}\\ \displaystyle z=\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}\quad \text{concentration of the products,}\\ \displaystyle \boldsymbol{v}=\frac{1}{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}\boldsymbol{v}_{r}+\unicode[STIX]{x1D70C}_{p}\boldsymbol{v}_{p})\quad \text{mean velocity of the mixture,}\\ \displaystyle p=p_{r}+p_{p}\quad \text{total pressure of the mixture,}\\ \displaystyle \boldsymbol{J}=\unicode[STIX]{x1D70C}_{p}\boldsymbol{u}_{p}=-\unicode[STIX]{x1D70C}_{r}\boldsymbol{u}_{r}\quad \text{diffusion flux vector,}\\ \displaystyle \boldsymbol{u}_{\unicode[STIX]{x1D6FC}}=\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\boldsymbol{v}\;(\unicode[STIX]{x1D6FC}=r,p)\quad \text{diffusion velocities,}\\ \displaystyle \unicode[STIX]{x1D700}_{I}=\frac{1}{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}\unicode[STIX]{x1D700}_{r}+\unicode[STIX]{x1D70C}_{p}\unicode[STIX]{x1D700}_{p})\quad \text{intrinsic (thermal) internal energy density of the mixture,}\\ \displaystyle \unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}_{I}+\frac{1}{2\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}u_{r}^{2}+\unicode[STIX]{x1D70C}_{p}u_{p}^{2})\quad \text{internal energy density of the mixture,}\end{array}\right\}\quad \qquad\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{r}+\unicode[STIX]{x1D70C}_{p}\quad \text{mass density of the mixture,}\\ \displaystyle z=\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}\quad \text{concentration of the products,}\\ \displaystyle \boldsymbol{v}=\frac{1}{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}\boldsymbol{v}_{r}+\unicode[STIX]{x1D70C}_{p}\boldsymbol{v}_{p})\quad \text{mean velocity of the mixture,}\\ \displaystyle p=p_{r}+p_{p}\quad \text{total pressure of the mixture,}\\ \displaystyle \boldsymbol{J}=\unicode[STIX]{x1D70C}_{p}\boldsymbol{u}_{p}=-\unicode[STIX]{x1D70C}_{r}\boldsymbol{u}_{r}\quad \text{diffusion flux vector,}\\ \displaystyle \boldsymbol{u}_{\unicode[STIX]{x1D6FC}}=\boldsymbol{v}_{\unicode[STIX]{x1D6FC}}-\boldsymbol{v}\;(\unicode[STIX]{x1D6FC}=r,p)\quad \text{diffusion velocities,}\\ \displaystyle \unicode[STIX]{x1D700}_{I}=\frac{1}{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}\unicode[STIX]{x1D700}_{r}+\unicode[STIX]{x1D70C}_{p}\unicode[STIX]{x1D700}_{p})\quad \text{intrinsic (thermal) internal energy density of the mixture,}\\ \displaystyle \unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}_{I}+\frac{1}{2\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70C}_{r}u_{r}^{2}+\unicode[STIX]{x1D70C}_{p}u_{p}^{2})\quad \text{internal energy density of the mixture,}\end{array}\right\}\quad \qquad\end{eqnarray}$$
and
where
![]() $g_{\unicode[STIX]{x1D6FC}}$
are dynamic enthalpies.
$g_{\unicode[STIX]{x1D6FC}}$
are dynamic enthalpies.
To close the system of equations (2.4)–(2.9), one has to introduce constitutive assumptions about pressure and internal energy density, as well as to determine the structure of the source terms. The latter is dictated by the general principles of extended thermodynamics – Galilean invariance and the entropy principle. Galilean invariance determines the velocity dependence of source terms (Ruggeri & Simić Reference Ruggeri and Simić2007):
where
![]() $\hat{\unicode[STIX]{x1D70F}}_{p}$
,
$\hat{\unicode[STIX]{x1D70F}}_{p}$
,
![]() $\hat{\boldsymbol{m}}_{p}$
and
$\hat{\boldsymbol{m}}_{p}$
and
![]() $\hat{e}_{p}$
denote velocity-independent mass, momentum and energy production rate, respectively. Information about the chemical reaction is contained in the source term
$\hat{e}_{p}$
denote velocity-independent mass, momentum and energy production rate, respectively. Information about the chemical reaction is contained in the source term
![]() $\unicode[STIX]{x1D70F}_{p}$
of the mass balance law (2.7). Nevertheless, it is reflected in all other source terms as well, due to Galilean invariance (2.12). The entropy principle imposes a further restriction on the source terms by requiring that every thermodynamic process is compatible with an entropy inequality. Its consequences will be discussed in the sequel.
$\unicode[STIX]{x1D70F}_{p}$
of the mass balance law (2.7). Nevertheless, it is reflected in all other source terms as well, due to Galilean invariance (2.12). The entropy principle imposes a further restriction on the source terms by requiring that every thermodynamic process is compatible with an entropy inequality. Its consequences will be discussed in the sequel.
2.2 Constitutive assumptions and the state variables
Since viscosity and heat conductivity are not taken into account in our model, the constitutive assumptions are related to thermal and caloric equations of state. We shall restrict our study to a binary mixture of ideal gases that consists of reactants and products. As we are analysing the simplest possible model of a reversible chemical reaction,
![]() $A_{r}\rightleftharpoons A_{p}$
, according to assumption (i) the masses of the constituents ought to be equal due to mass conservation,
$A_{r}\rightleftharpoons A_{p}$
, according to assumption (i) the masses of the constituents ought to be equal due to mass conservation,
![]() $m_{r}=m_{p}=m$
. Consequently, the equations of state have the following form:
$m_{r}=m_{p}=m$
. Consequently, the equations of state have the following form:
where
![]() $k$
is the Boltzmann constant,
$k$
is the Boltzmann constant,
![]() $c_{v\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FC}})$
are the specific heats at constant volume and
$c_{v\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FC}})$
are the specific heats at constant volume and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}}$
are the binding energies. Assuming
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}}$
are the binding energies. Assuming
![]() $c_{vp}=c_{vr}=c_{v}=\text{const.}$
, and
$c_{vp}=c_{vr}=c_{v}=\text{const.}$
, and
![]() $\unicode[STIX]{x1D716}_{r}=c_{v}T_{0}$
, the internal energies take the form:
$\unicode[STIX]{x1D716}_{r}=c_{v}T_{0}$
, the internal energies take the form:
where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{p}-\unicode[STIX]{x1D716}_{r}$
, and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{p}-\unicode[STIX]{x1D716}_{r}$
, and
![]() $c_{v}=k/(m(\unicode[STIX]{x1D6FE}-1))$
in accordance with assumption (v).
$c_{v}=k/(m(\unicode[STIX]{x1D6FE}-1))$
in accordance with assumption (v).
The temperatures of the constituents are not equal in general, and we have to introduce the average (mean) temperature of the mixture as a global variable. Following Gouin & Ruggeri (Reference Gouin and Ruggeri2008) and Ruggeri & Simić (Reference Ruggeri and Simić2009), we shall define the average temperature using the definition of the intrinsic part of the internal energy density:
where we have taken into account the relations
![]() $\unicode[STIX]{x1D70C}_{p}=\unicode[STIX]{x1D70C}z$
and
$\unicode[STIX]{x1D70C}_{p}=\unicode[STIX]{x1D70C}z$
and
![]() $\unicode[STIX]{x1D70C}_{r}=\unicode[STIX]{x1D70C}(1-z)$
. It is also convenient to introduce the difference of temperatures,
$\unicode[STIX]{x1D70C}_{r}=\unicode[STIX]{x1D70C}(1-z)$
. It is also convenient to introduce the difference of temperatures,
as a state variable, which also serves as a measure of thermal non-equilibrium. In such a way, the temperatures of the constituents can be expressed in terms of
![]() $z$
,
$z$
,
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D6E9}$
, as follows:
$\unicode[STIX]{x1D6E9}$
, as follows:
The total pressure
![]() $p$
and the intrinsic internal energy density
$p$
and the intrinsic internal energy density
![]() $\unicode[STIX]{x1D700}_{I}$
of the mixture can be expressed in terms of
$\unicode[STIX]{x1D700}_{I}$
of the mixture can be expressed in terms of
![]() $T$
:
$T$
:
where we have taken into account assumption (v), that is,
![]() $\unicode[STIX]{x1D6FE}_{p}=\unicode[STIX]{x1D6FE}_{r}=\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}_{p}=\unicode[STIX]{x1D6FE}_{r}=\unicode[STIX]{x1D6FE}$
.
Having in mind the structure of the governing equations (2.4)–(2.9), we may fix the set of state variables. Although the first choice is usually
![]() $(\unicode[STIX]{x1D70C},\boldsymbol{v},T,\unicode[STIX]{x1D70C}_{p},\boldsymbol{v}_{p},T_{p})$
, using the relations given above, we shall adopt
$(\unicode[STIX]{x1D70C},\boldsymbol{v},T,\unicode[STIX]{x1D70C}_{p},\boldsymbol{v}_{p},T_{p})$
, using the relations given above, we shall adopt
![]() $\boldsymbol{U}=(\unicode[STIX]{x1D70C},\boldsymbol{v},T,z,\boldsymbol{J},\unicode[STIX]{x1D6E9})$
.
$\boldsymbol{U}=(\unicode[STIX]{x1D70C},\boldsymbol{v},T,z,\boldsymbol{J},\unicode[STIX]{x1D6E9})$
.
2.3 The source terms
In our model, the source terms describe the mutual interactions between the constituents. Their structure, compatible with entropy inequality, was determined by Ruggeri & Simić (Reference Ruggeri and Simić2007) when a non-reactive mixture is considered. However, the extended thermodynamics has its limits and the phenomenological coefficients cannot be determined within its framework. Instead, one has either to take into account experimental results, or to make a link with a more refined approach (e.g. kinetic theory) to determine them (see Madjarević & Simić Reference Madjarević and Simić2013; Madjarević et al. Reference Madjarević, Ruggeri and Simić2014). We shall proceed in the latter way.
2.3.1 The reaction rate
For the reactive mixture considered in this paper, the reaction rate is obtained from the kinetic theory; more precisely, from the Boltzmann equation for chemically reactive mixtures, assuming reactive differential cross-sections with activation energy, and a particular form of the velocity distribution functions in order to obtain an approximate solution to the reactive kinetic equations. Since we are considering an MT mixture, an appropriate form for such an input function should be a Maxwellian distribution in the constituent rest frame,
where
![]() $c_{\unicode[STIX]{x1D6FC}}=|\boldsymbol{c}_{\unicode[STIX]{x1D6FC}}|$
,
$c_{\unicode[STIX]{x1D6FC}}=|\boldsymbol{c}_{\unicode[STIX]{x1D6FC}}|$
,
![]() $\boldsymbol{c}_{\unicode[STIX]{x1D6FC}}$
being the molecular velocity of each constituent, and
$\boldsymbol{c}_{\unicode[STIX]{x1D6FC}}$
being the molecular velocity of each constituent, and
![]() $n_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}/m$
the constituent number density. However, the evaluation of the collision integrals applying to the input functions (2.19) becomes a very difficult task and the computations lead to intractable expressions. To overcome such difficulty we approximate function (2.19) through an expansion at the first order around a Maxwellian in the mixture rest frame with temperature
$n_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}/m$
the constituent number density. However, the evaluation of the collision integrals applying to the input functions (2.19) becomes a very difficult task and the computations lead to intractable expressions. To overcome such difficulty we approximate function (2.19) through an expansion at the first order around a Maxwellian in the mixture rest frame with temperature
![]() $T$
and mean velocity
$T$
and mean velocity
![]() $v$
:
$v$
:
 $$\begin{eqnarray}\displaystyle G_{\unicode[STIX]{x1D6FC}} & = & \displaystyle n_{\unicode[STIX]{x1D6FC}}\left(\frac{m}{2\unicode[STIX]{x03C0}kT}\right)^{3/2}\exp \left(-\frac{m}{2kT}(c_{\unicode[STIX]{x1D6FC}}-v)^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left[1+\frac{m}{kT}\mathop{\sum }_{i=1}^{3}(c_{\unicode[STIX]{x1D6FC}i}-v_{i})(v_{\unicode[STIX]{x1D6FC}i}-v_{i})+\left(\frac{m}{2kT}(c_{\unicode[STIX]{x1D6FC}}-v)^{2}-\frac{3}{2}\right)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{\unicode[STIX]{x1D6FC}} & = & \displaystyle n_{\unicode[STIX]{x1D6FC}}\left(\frac{m}{2\unicode[STIX]{x03C0}kT}\right)^{3/2}\exp \left(-\frac{m}{2kT}(c_{\unicode[STIX]{x1D6FC}}-v)^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left[1+\frac{m}{kT}\mathop{\sum }_{i=1}^{3}(c_{\unicode[STIX]{x1D6FC}i}-v_{i})(v_{\unicode[STIX]{x1D6FC}i}-v_{i})+\left(\frac{m}{2kT}(c_{\unicode[STIX]{x1D6FC}}-v)^{2}-\frac{3}{2}\right)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}\right].\end{eqnarray}$$
Here
![]() $(v_{\unicode[STIX]{x1D6FC}i}-v_{i})$
and
$(v_{\unicode[STIX]{x1D6FC}i}-v_{i})$
and
![]() $(c_{\unicode[STIX]{x1D6FC}i}-v_{i})$
represent the spatial components of the diffusion velocity and of the peculiar velocity, respectively, and
$(c_{\unicode[STIX]{x1D6FC}i}-v_{i})$
represent the spatial components of the diffusion velocity and of the peculiar velocity, respectively, and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}=(T_{\unicode[STIX]{x1D6FC}}-T)/T$
is the normalized temperature difference. The input function (2.20) represents a linearization of the Maxwellian distribution (2.19), with respect to the diffusion velocity and temperature difference.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}=(T_{\unicode[STIX]{x1D6FC}}-T)/T$
is the normalized temperature difference. The input function (2.20) represents a linearization of the Maxwellian distribution (2.19), with respect to the diffusion velocity and temperature difference.
Adopting reactive differential cross-sections with activation energy, and taking into account the indistinguishability of the colliding particles, the reaction rate for the mass concentration
![]() $z$
of the products results in (Kremer, Bianchi & Soares Reference Kremer, Bianchi and Soares2007)
$z$
of the products results in (Kremer, Bianchi & Soares Reference Kremer, Bianchi and Soares2007)
 $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D70F}}_{p} & = & \displaystyle 2\frac{\unicode[STIX]{x1D70C}^{2}}{m}\sqrt{\frac{\unicode[STIX]{x03C0}kT}{m}}d^{2}\exp \left(-\frac{\unicode[STIX]{x1D716}_{f}}{kT}\right)\left[(1-z)^{2}-z^{2}\exp \left(\frac{\unicode[STIX]{x1D716}_{f}-\unicode[STIX]{x1D716}_{b}}{kT}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(1-z)^{2}\left(\frac{\unicode[STIX]{x1D716}_{f}}{kT}+\frac{1}{2}\right)\unicode[STIX]{x1D6E5}_{r}-(1-z)^{2}\left(\frac{\unicode[STIX]{x1D716}_{b}}{kT}+\frac{1}{2}\right)\unicode[STIX]{x1D6E5}_{p}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D70F}}_{p} & = & \displaystyle 2\frac{\unicode[STIX]{x1D70C}^{2}}{m}\sqrt{\frac{\unicode[STIX]{x03C0}kT}{m}}d^{2}\exp \left(-\frac{\unicode[STIX]{x1D716}_{f}}{kT}\right)\left[(1-z)^{2}-z^{2}\exp \left(\frac{\unicode[STIX]{x1D716}_{f}-\unicode[STIX]{x1D716}_{b}}{kT}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(1-z)^{2}\left(\frac{\unicode[STIX]{x1D716}_{f}}{kT}+\frac{1}{2}\right)\unicode[STIX]{x1D6E5}_{r}-(1-z)^{2}\left(\frac{\unicode[STIX]{x1D716}_{b}}{kT}+\frac{1}{2}\right)\unicode[STIX]{x1D6E5}_{p}\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D716}_{f}$
and
$\unicode[STIX]{x1D716}_{f}$
and
![]() $\unicode[STIX]{x1D716}_{b}$
denote the forward and the backward activation energies of the chemical reaction. The reaction rate (2.21) shows a second-order form, in the sense that it depends explicitly on the square of the product concentration
$\unicode[STIX]{x1D716}_{b}$
denote the forward and the backward activation energies of the chemical reaction. The reaction rate (2.21) shows a second-order form, in the sense that it depends explicitly on the square of the product concentration
![]() $z$
and of the reactant concentration
$z$
and of the reactant concentration
![]() $(1-z)$
. This is a direct consequence of the fact that it was derived from the Boltzmann equation with binary reactive encounters. A detailed account of other aspects of the mathematical modelling of reactive flows may be found in Giovangigli (Reference Giovangigli1999).
$(1-z)$
. This is a direct consequence of the fact that it was derived from the Boltzmann equation with binary reactive encounters. A detailed account of other aspects of the mathematical modelling of reactive flows may be found in Giovangigli (Reference Giovangigli1999).
The thermodynamic equilibrium condition, chemical and thermal, corresponds to
![]() $\hat{\unicode[STIX]{x1D70F}}_{p}=0$
and, therefore, we will have thermodynamic equilibrium if
$\hat{\unicode[STIX]{x1D70F}}_{p}=0$
and, therefore, we will have thermodynamic equilibrium if
where
![]() ${\mathcal{Q}}=\unicode[STIX]{x1D716}_{f}-\unicode[STIX]{x1D716}_{b}=-2m\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
is the reaction heat. The last condition in (2.22) represents the law of mass action of the model and gives a constraint on the chemical equilibrium values of the product concentration
${\mathcal{Q}}=\unicode[STIX]{x1D716}_{f}-\unicode[STIX]{x1D716}_{b}=-2m\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
is the reaction heat. The last condition in (2.22) represents the law of mass action of the model and gives a constraint on the chemical equilibrium values of the product concentration
![]() $z$
and mixture temperature
$z$
and mixture temperature
![]() $T$
.
$T$
.
2.3.2 The momentum production rate
The momentum production rate in a binary mixture has the form:
where
![]() $\unicode[STIX]{x1D713}_{pp}$
is a phenomenological coefficient related to the relaxation time
$\unicode[STIX]{x1D713}_{pp}$
is a phenomenological coefficient related to the relaxation time
![]() $\unicode[STIX]{x1D70F}_{D}$
for diffusion. By linearizing the source term in the neighbourhood of the local equilibrium state, and taking into account the definition of the diffusion flux, one obtains
$\unicode[STIX]{x1D70F}_{D}$
for diffusion. By linearizing the source term in the neighbourhood of the local equilibrium state, and taking into account the definition of the diffusion flux, one obtains
2.3.3 The energy production rate
The energy production rate in a binary mixture reads
where
![]() $\unicode[STIX]{x1D703}_{pp}$
is a phenomenological coefficient related to the relaxation time
$\unicode[STIX]{x1D703}_{pp}$
is a phenomenological coefficient related to the relaxation time
![]() $\unicode[STIX]{x1D70F}_{T}$
for the temperature. By linearizing the source term in the neighbourhood of the local equilibrium state, and using the difference of temperatures
$\unicode[STIX]{x1D70F}_{T}$
for the temperature. By linearizing the source term in the neighbourhood of the local equilibrium state, and using the difference of temperatures
![]() $\unicode[STIX]{x1D6E9}$
as non-equilibrium variable, one obtains
$\unicode[STIX]{x1D6E9}$
as non-equilibrium variable, one obtains
In expressions (2.24) and (2.26), the relaxation times
![]() $\unicode[STIX]{x1D70F}_{D}$
and
$\unicode[STIX]{x1D70F}_{D}$
and
![]() $\unicode[STIX]{x1D70F}_{T}$
, which are part of the phenomenological coefficients, cannot be determined by the methods of extended thermodynamics. It was shown in Madjarević & Simić (Reference Madjarević and Simić2013) and Madjarević et al. (Reference Madjarević, Ruggeri and Simić2014), using the arguments of kinetic theory, that the relaxation times for diffusion and temperature can be related to diffusivity of the binary mixture. In our notation, the diffusivity
$\unicode[STIX]{x1D70F}_{T}$
, which are part of the phenomenological coefficients, cannot be determined by the methods of extended thermodynamics. It was shown in Madjarević & Simić (Reference Madjarević and Simić2013) and Madjarević et al. (Reference Madjarević, Ruggeri and Simić2014), using the arguments of kinetic theory, that the relaxation times for diffusion and temperature can be related to diffusivity of the binary mixture. In our notation, the diffusivity
![]() $D$
for the hard-sphere model reads:
$D$
for the hard-sphere model reads:
Taking into account that
![]() $m_{p}=m_{r}=m$
, the relaxation times reduce to the following simple form:
$m_{p}=m_{r}=m$
, the relaxation times reduce to the following simple form:
Note that
![]() $\unicode[STIX]{x1D70F}_{T}>\unicode[STIX]{x1D70F}_{D}$
, which is a typical result of kinetic theory.
$\unicode[STIX]{x1D70F}_{T}>\unicode[STIX]{x1D70F}_{D}$
, which is a typical result of kinetic theory.
2.4 The basic assumption and reduced form of the governing equations
Equations (2.4)–(2.9), with the source terms given by (2.21), (2.24) and (2.26), constitute a complete set of governing equations for a chemically reacting MT binary mixture. In their derivation we exploited all the simplifying assumptions mentioned in the introduction. However, it was mentioned that assumption (i) implies further simplifications. It is appropriate at this stage to introduce the basic assumption that will imply the reduction of the system of governing equations, and simplification of the remaining ones.
2.4.1 The basic assumption
Since reactants and products have equal molecular masses,
![]() $m_{r}=m_{p}=m$
, the molecules of the constituents are indistinguishable in a mechanical sense. Therefore, the diffusion of the constituents can be ignored and the momentum balance law (2.8) can be dropped from the list of governing equations.
$m_{r}=m_{p}=m$
, the molecules of the constituents are indistinguishable in a mechanical sense. Therefore, the diffusion of the constituents can be ignored and the momentum balance law (2.8) can be dropped from the list of governing equations.
The basic assumption is a consequence of the simplicity of the chemical reaction (1.1). The fact that the masses of the constituents are equal implies that one cannot distinguish the molecules of reactants and products during mechanical collisions. As a consequence, the mean (macroscopic) velocities of the constituents are equal,
![]() $\boldsymbol{v}_{r}=\boldsymbol{v}_{p}=\boldsymbol{v}$
, and the diffusion velocities vanish,
$\boldsymbol{v}_{r}=\boldsymbol{v}_{p}=\boldsymbol{v}$
, and the diffusion velocities vanish,
![]() $\boldsymbol{u}_{r}=\boldsymbol{u}_{p}=\mathbf{0}$
, as well as the diffusion flux,
$\boldsymbol{u}_{r}=\boldsymbol{u}_{p}=\mathbf{0}$
, as well as the diffusion flux,
![]() $\boldsymbol{J}=\mathbf{0}$
. However, the mean energies of the constituents may not be equal, which implies thermal non-equilibrium,
$\boldsymbol{J}=\mathbf{0}$
. However, the mean energies of the constituents may not be equal, which implies thermal non-equilibrium,
![]() $T_{r}\neq T_{p}$
, and chemical reaction may play a role in their approach to equilibrium. The MT assumption is in this case motivated by the presence of chemical reaction, rather than the difference of masses as in previous studies (Ruggeri & Simić Reference Ruggeri and Simić2009; Madjarević & Simić Reference Madjarević and Simić2013; Madjarević et al.
Reference Madjarević, Ruggeri and Simić2014).
$T_{r}\neq T_{p}$
, and chemical reaction may play a role in their approach to equilibrium. The MT assumption is in this case motivated by the presence of chemical reaction, rather than the difference of masses as in previous studies (Ruggeri & Simić Reference Ruggeri and Simić2009; Madjarević & Simić Reference Madjarević and Simić2013; Madjarević et al.
Reference Madjarević, Ruggeri and Simić2014).
2.4.2 The reduced form of the governing equations
As a consequence of the basic assumption, the set of governing equations reduces to five equations, namely (2.4)–(2.7) and (2.9), for the state variables
![]() $\boldsymbol{U}=(\unicode[STIX]{x1D70C},\boldsymbol{v},T,z,\unicode[STIX]{x1D6E9})$
, with production terms
$\boldsymbol{U}=(\unicode[STIX]{x1D70C},\boldsymbol{v},T,z,\unicode[STIX]{x1D6E9})$
, with production terms
![]() $\hat{\unicode[STIX]{x1D70F}}_{p}$
and
$\hat{\unicode[STIX]{x1D70F}}_{p}$
and
![]() $\hat{e}_{p}$
given by expressions (2.21) and (2.26).
$\hat{e}_{p}$
given by expressions (2.21) and (2.26).
The reduced set of equations describes the evolution of the considered binary reactive mixture, in a regime of thermal and chemical non-equilibrium in which diffusion, heat conduction and viscosity are not taken into account. Such a set of equations is the one considered in the sequel to define the mathematical setting for the determination of the detonation wave solutions.
3 Steady ZND detonation waves
In this section we follow the classical ZND model, advanced by Zel’dovich, von Neumann and Döring (see Fickett Reference Fickett1985; Williams Reference Williams1985; Lee Reference Lee2008), for a one-dimensional detonation wave, and propose its generalization taking into account the reversibility of the chemical reaction and the MT assumption.
The configuration of the ZND detonation wave consists of a plane, non-reactive shock wave propagating with constant speed
![]() $s$
in the direction orthogonal to the singular surface, followed by a finite reaction zone where the chemical reaction takes place and eventually reaches equilibrium.
$s$
in the direction orthogonal to the singular surface, followed by a finite reaction zone where the chemical reaction takes place and eventually reaches equilibrium.
The spatial structure of the steady detonation wave is determined by solving two different problems in a convenient parametric space. The first problem is purely algebraic and consists in determining the post-shock state – the von Neumann state
![]() $N$
– as the solution to the non-reactive jump Rankine–Hugoniot conditions. The second problem is the initial value problem for the determination of the continuous reacting flow in the reaction zone, with initial data at the von Neumann state. The final state
$N$
– as the solution to the non-reactive jump Rankine–Hugoniot conditions. The second problem is the initial value problem for the determination of the continuous reacting flow in the reaction zone, with initial data at the von Neumann state. The final state
![]() $S$
, at the end of the reaction zone, can be obtained either from the second problem, as the state of the continuous reacting flow for which the reactive mixture reaches the chemical and thermal equilibrium, or from a Rankine–Hugoniot analysis combined with the equilibrium condition, chemical and thermal.
$S$
, at the end of the reaction zone, can be obtained either from the second problem, as the state of the continuous reacting flow for which the reactive mixture reaches the chemical and thermal equilibrium, or from a Rankine–Hugoniot analysis combined with the equilibrium condition, chemical and thermal.
In what follows we refer the governing equations to the frame attached to the shock wave, and establish the analytic part of the modelling.
3.1 Governing equations in the moving frame
According to the ZND model, we shall assume that the wave moves in the
![]() $x$
-direction, from left to right, and that the flow is one-dimensional,
$x$
-direction, from left to right, and that the flow is one-dimensional,
![]() $\boldsymbol{v}=(v,0,0)$
. The wave configuration is supposed to be steady in the shock-attached frame, and we introduce the steady variable
$\boldsymbol{v}=(v,0,0)$
. The wave configuration is supposed to be steady in the shock-attached frame, and we introduce the steady variable
![]() $\unicode[STIX]{x1D709}$
and the relative velocity
$\unicode[STIX]{x1D709}$
and the relative velocity
![]() $u$
of the mixture with respect to the shock front:
$u$
of the mixture with respect to the shock front:
In the steady frame attached to the shock wave, the reaction zone extends from
![]() $x_{0}$
to
$x_{0}$
to
![]() $x_{S}$
, where
$x_{S}$
, where
![]() $x_{0}$
represents the location of the shock front. The state just behind the shock, located at
$x_{0}$
represents the location of the shock front. The state just behind the shock, located at
![]() $x=x_{0}$
, is the von Neumann state
$x=x_{0}$
, is the von Neumann state
![]() $N$
, where the chemical reaction is triggered, and the one located at
$N$
, where the chemical reaction is triggered, and the one located at
![]() $x=x_{S}$
, at the end of the reaction zone, is the final steady state
$x=x_{S}$
, at the end of the reaction zone, is the final steady state
![]() $S$
, where the mixture reaches chemical and thermal equilibrium. Ahead of the shock front, that is, for
$S$
, where the mixture reaches chemical and thermal equilibrium. Ahead of the shock front, that is, for
![]() $x>x_{0}$
, the quiescent mixture is at rest in its initial state
$x>x_{0}$
, the quiescent mixture is at rest in its initial state
![]() $I$
, where the rate of the chemical reaction is completely negligible.
$I$
, where the rate of the chemical reaction is completely negligible.
Assuming steady, one-dimensional travelling wave structure of the detonation wave, in which the vector of state variables
![]() $\boldsymbol{U}=(\unicode[STIX]{x1D70C},u,T,z,\unicode[STIX]{x1D6E9})$
depends on a single independent variable, say
$\boldsymbol{U}=(\unicode[STIX]{x1D70C},u,T,z,\unicode[STIX]{x1D6E9})$
depends on a single independent variable, say
![]() $\boldsymbol{U}(\unicode[STIX]{x1D709})=\boldsymbol{U}(x-st)$
, the governing equations are transformed into a set of ordinary differential equations:
$\boldsymbol{U}(\unicode[STIX]{x1D709})=\boldsymbol{U}(x-st)$
, the governing equations are transformed into a set of ordinary differential equations:
The source terms
![]() $\hat{\unicode[STIX]{x1D70F}}_{p}$
and
$\hat{\unicode[STIX]{x1D70F}}_{p}$
and
![]() $\hat{e}_{p}$
are used in linearized form (2.21) and (2.26), respectively. Formally, the governing equations of the standard ZND detonation waves are (3.2)–(3.5). Here, they are extended with (3.6), which describes the profile of the temperature difference
$\hat{e}_{p}$
are used in linearized form (2.21) and (2.26), respectively. Formally, the governing equations of the standard ZND detonation waves are (3.2)–(3.5). Here, they are extended with (3.6), which describes the profile of the temperature difference
![]() $\unicode[STIX]{x1D6E9}$
.
$\unicode[STIX]{x1D6E9}$
.
3.2 Algebraic analysis of the detonation wave
As the first step, the algebraic part of the problem will be studied. It will outline the basic structure of the detonation wave, including the important notion of equilibrium Hugoniot curve, peculiar for reversible chemical reactions.
3.2.1 Rankine–Hugoniot conditions
The governing equations of conservative type, equations (3.2)–(3.4), lead to the well-known algebraic Rankine–Hugoniot (RH) conditions that relate a state behind the shock wave to the initial state ahead the shock. Such conditions connect the fluxes of the conserved quantities across the wave front, and are given by
where
![]() $\unicode[STIX]{x1D70C}_{0}$
and
$\unicode[STIX]{x1D70C}_{0}$
and
![]() $p_{0}$
are the mass density and pressure at the unperturbed initial state. Moreover,
$p_{0}$
are the mass density and pressure at the unperturbed initial state. Moreover,
![]() $z_{0}=0$
and
$z_{0}=0$
and
![]() $\unicode[STIX]{x1D6E9}_{0}=0$
at the initial state. Additionally we have assumed that the initial state is at rest, so that
$\unicode[STIX]{x1D6E9}_{0}=0$
at the initial state. Additionally we have assumed that the initial state is at rest, so that
![]() $v_{0}=0$
and
$v_{0}=0$
and
![]() $u_{0}=-s$
. For each fixed value of the detonation velocity
$u_{0}=-s$
. For each fixed value of the detonation velocity
![]() $s$
, the corresponding von Neumann and equilibrium states can be determined from the RH conditions (3.7)–(3.9), with additional proper conditions, as will be explained in the sequel. Introducing the specific volume of the mixture,
$s$
, the corresponding von Neumann and equilibrium states can be determined from the RH conditions (3.7)–(3.9), with additional proper conditions, as will be explained in the sequel. Introducing the specific volume of the mixture,
![]() $\unicode[STIX]{x1D708}=1/\unicode[STIX]{x1D70C}$
, the states
$\unicode[STIX]{x1D708}=1/\unicode[STIX]{x1D70C}$
, the states
![]() $(\unicode[STIX]{x1D708},p)$
in the reaction zone, compatible with a strong detonation wave (Lee Reference Lee2008), are characterized as a function of the product concentration
$(\unicode[STIX]{x1D708},p)$
in the reaction zone, compatible with a strong detonation wave (Lee Reference Lee2008), are characterized as a function of the product concentration
![]() $z$
, with the shock speed
$z$
, with the shock speed
![]() $s$
as parameter, by
$s$
as parameter, by
where
![]() $\unicode[STIX]{x1D6F6}(z)$
is defined by
$\unicode[STIX]{x1D6F6}(z)$
is defined by
In the derivation of (3.10) we used the state equations (2.18); see Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015) for a detailed analysis.
3.2.2 Von Neumann state
The von Neumann state is the state just behind the shock wave. Since the passage of the mixture through the shock front is a non-reactive process, the progress variable remains constant through the shock and the temperature difference does not change. Accordingly,
![]() $z=0$
and
$z=0$
and
![]() $\unicode[STIX]{x1D6E9}=0$
at the von Neumann state. Therefore, the state
$\unicode[STIX]{x1D6E9}=0$
at the von Neumann state. Therefore, the state
![]() $N$
can be obtained as the non-trivial solution to the RH conditions (3.7)–(3.9) complemented by the conditions
$N$
can be obtained as the non-trivial solution to the RH conditions (3.7)–(3.9) complemented by the conditions
![]() $z=0$
and
$z=0$
and
![]() $\unicode[STIX]{x1D6E9}=0$
. Equivalently, the state
$\unicode[STIX]{x1D6E9}=0$
. Equivalently, the state
![]() $N$
can be obtained directly from conditions (3.10), together with the vanishing conditions for
$N$
can be obtained directly from conditions (3.10), together with the vanishing conditions for
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D6E9}$
, that is
$\unicode[STIX]{x1D6E9}$
, that is
3.2.3 Continuous reacting flow
The reacting flow in the reaction zone describes the continuous evolution of the mixture from the von Neumann state
![]() $N$
, say at
$N$
, say at
![]() $\unicode[STIX]{x1D709}=0$
, to the final state
$\unicode[STIX]{x1D709}=0$
, to the final state
![]() $S$
, say at
$S$
, say at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{S}$
, due to the chemical reaction and thermal equilibration. From the mathematical point of view, the ordinary differential equations (3.2)–(3.6) have to be solved for the fields
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{S}$
, due to the chemical reaction and thermal equilibration. From the mathematical point of view, the ordinary differential equations (3.2)–(3.6) have to be solved for the fields
![]() $\unicode[STIX]{x1D70C},~u,~T,~z$
and
$\unicode[STIX]{x1D70C},~u,~T,~z$
and
![]() $\unicode[STIX]{x1D6E9}$
, with initial conditions at the state
$\unicode[STIX]{x1D6E9}$
, with initial conditions at the state
![]() $N$
.
$N$
.
3.2.4 Equilibrium final state
The final state
![]() $S$
at the end of the reaction zone represents the state for which the reactive mixture reaches chemical and thermal equilibrium. It can be determined from expressions (3.10) with
$S$
at the end of the reaction zone represents the state for which the reactive mixture reaches chemical and thermal equilibrium. It can be determined from expressions (3.10) with
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D6E9}$
satisfying the equilibrium conditions (2.22). Therefore,
$\unicode[STIX]{x1D6E9}$
satisfying the equilibrium conditions (2.22). Therefore,
![]() $S$
is characterized by expressions (3.10) together with
$S$
is characterized by expressions (3.10) together with
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}=0,\quad \left(\frac{1+s^{2}}{\unicode[STIX]{x1D6FE}+1}+s^{2}\unicode[STIX]{x1D6F6}(z)\right)\left(\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}\frac{1+s^{2}}{\displaystyle s^{2}}-\unicode[STIX]{x1D6F6}(z)\right)=-\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{\displaystyle \ln \left(\frac{1-z}{z}\right)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}=0,\quad \left(\frac{1+s^{2}}{\unicode[STIX]{x1D6FE}+1}+s^{2}\unicode[STIX]{x1D6F6}(z)\right)\left(\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}\frac{1+s^{2}}{\displaystyle s^{2}}-\unicode[STIX]{x1D6F6}(z)\right)=-\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{\displaystyle \ln \left(\frac{1-z}{z}\right)},\end{eqnarray}$$
where we have used
![]() $\unicode[STIX]{x1D6F6}(z)$
defined by (3.11). Observe that the second condition in (3.13) represents the law of mass action given in (2.22) parametrized by the shock velocity
$\unicode[STIX]{x1D6F6}(z)$
defined by (3.11). Observe that the second condition in (3.13) represents the law of mass action given in (2.22) parametrized by the shock velocity
![]() $s$
.
$s$
.
Additionally, since the state
![]() $S$
represents the end point of the continuous reacting flow, in which the mixture reaches equilibrium and all state variables become constant, it can be obtained by integrating equations (3.2)–(3.6) from
$S$
represents the end point of the continuous reacting flow, in which the mixture reaches equilibrium and all state variables become constant, it can be obtained by integrating equations (3.2)–(3.6) from
![]() $\unicode[STIX]{x1D709}=0$
to
$\unicode[STIX]{x1D709}=0$
to
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{S}$
for which all the production rates vanish, as predicted by the equilibrium conditions (2.22) or (3.13).
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{S}$
for which all the production rates vanish, as predicted by the equilibrium conditions (2.22) or (3.13).
3.2.5 Chapman–Jouguet state
The Chapman–Jouguet state (CJ) is a particular final state obtained for the minimum admissible value of the shock velocity
![]() $s$
, say
$s$
, say
![]() $s_{j}$
. Since it is an equilibrium final state, equilibrium conditions (3.13) must be satisfied. Therefore, the
$s_{j}$
. Since it is an equilibrium final state, equilibrium conditions (3.13) must be satisfied. Therefore, the
![]() $CJ$
state is the final state of a strong detonation for which
$CJ$
state is the final state of a strong detonation for which
![]() $p/p_{0}$
is minimum and
$p/p_{0}$
is minimum and
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D708}_{0}$
is maximum, see (3.10). This corresponds to having
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D708}_{0}$
is maximum, see (3.10). This corresponds to having
![]() $\unicode[STIX]{x1D6F6}(z)=0$
(see Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015). Accordingly, we determine the
$\unicode[STIX]{x1D6F6}(z)=0$
(see Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015). Accordingly, we determine the
![]() $CJ$
velocity
$CJ$
velocity
![]() $s_{j}$
and the corresponding product concentration
$s_{j}$
and the corresponding product concentration
![]() $z_{j}$
by solving the equilibrium conditions (3.13), together with condition
$z_{j}$
by solving the equilibrium conditions (3.13), together with condition
![]() $\unicode[STIX]{x1D6F6}(z)=0$
. The
$\unicode[STIX]{x1D6F6}(z)=0$
. The
![]() $CJ$
state is then obtained from (3.10) for
$CJ$
state is then obtained from (3.10) for
![]() $z=z_{j}$
and
$z=z_{j}$
and
![]() $s=s_{j}$
.
$s=s_{j}$
.
3.2.6 Hugoniot diagram
The detonation solution can be represented in the
![]() $(\unicode[STIX]{x1D708},p)$
-plane through the Hugoniot diagram (Fickett Reference Fickett1985; Lee Reference Lee2008; Conforto et al.
Reference Conforto, Monaco and Ricciardello2014; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015) straightly connected to the RH conditions (3.7)–(3.9). As shown in figure 1, this is a qualitative representation of the solution in terms of Rayleigh lines and Hugoniot curves for fixed product concentration, as well as in terms of the equilibrium Hugoniot curve, which constitutes an important ingredient when the chemical reaction is reversible and the reactive mixture reaches a final equilibrium state (Lee Reference Lee2008; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015).
$(\unicode[STIX]{x1D708},p)$
-plane through the Hugoniot diagram (Fickett Reference Fickett1985; Lee Reference Lee2008; Conforto et al.
Reference Conforto, Monaco and Ricciardello2014; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015) straightly connected to the RH conditions (3.7)–(3.9). As shown in figure 1, this is a qualitative representation of the solution in terms of Rayleigh lines and Hugoniot curves for fixed product concentration, as well as in terms of the equilibrium Hugoniot curve, which constitutes an important ingredient when the chemical reaction is reversible and the reactive mixture reaches a final equilibrium state (Lee Reference Lee2008; Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015).

Figure 1. Hugoniot diagram showing unreacted (
![]() $z=0$
) and complete reaction (
$z=0$
) and complete reaction (
![]() $z=1$
) Hugoniot curves (solid black curves), Hugoniot curve corresponding to a fixed
$z=1$
) Hugoniot curves (solid black curves), Hugoniot curve corresponding to a fixed
![]() $z_{eq}$
value (solid grey curve), equilibrium Hugoniot curve (dashed curve) and Rayleigh lines (solid black straight lines).
$z_{eq}$
value (solid grey curve), equilibrium Hugoniot curve (dashed curve) and Rayleigh lines (solid black straight lines).
For fixed values of the material properties, say the specific heat ratio
![]() $\unicode[STIX]{x1D6FE}$
, the binding energy difference
$\unicode[STIX]{x1D6FE}$
, the binding energy difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
and the activation energy
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
and the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
, each Rayleigh line gathers all states obtained for a fixed value of the wave velocity
$\unicode[STIX]{x1D716}_{f}$
, each Rayleigh line gathers all states obtained for a fixed value of the wave velocity
![]() $s$
corresponding to mass and momentum conservation. Each Hugoniot curve for fixed product concentration collects all states along which the total energy of the mixture is preserved. On the other hand, the equilibrium Hugoniot curve accommodates all final equilibrium states for fixed values of the material properties. The necessity for the equilibrium Hugoniot curve comes from the fact that we analyse a reversible chemical reaction. Such a curve is the locus of all thermal and chemical equilibrium states, parametrized by the wave velocity
$s$
corresponding to mass and momentum conservation. Each Hugoniot curve for fixed product concentration collects all states along which the total energy of the mixture is preserved. On the other hand, the equilibrium Hugoniot curve accommodates all final equilibrium states for fixed values of the material properties. The necessity for the equilibrium Hugoniot curve comes from the fact that we analyse a reversible chemical reaction. Such a curve is the locus of all thermal and chemical equilibrium states, parametrized by the wave velocity
![]() $s$
.
$s$
.
In the Hugoniot diagram, we highlight two items, namely the
![]() $CJ$
state, corresponding to the tangency point of the Rayleigh line to the equilibrium Hugoniot curve, and the equilibrium final state
$CJ$
state, corresponding to the tangency point of the Rayleigh line to the equilibrium Hugoniot curve, and the equilibrium final state
![]() $(\unicode[STIX]{x1D708}_{eq},p_{eq})$
for a fixed value of
$(\unicode[STIX]{x1D708}_{eq},p_{eq})$
for a fixed value of
![]() $s$
(
$s$
(
![]() $s\geqslant s_{j}$
), obtained as the intersection point of the corresponding Rayleigh line with the equilibrium Hugoniot curve.
$s\geqslant s_{j}$
), obtained as the intersection point of the corresponding Rayleigh line with the equilibrium Hugoniot curve.
For the considered value
![]() $s>s_{j}$
, we also plot in figure 1 the fixed-concentration Hugoniot curve obtained for the corresponding value
$s>s_{j}$
, we also plot in figure 1 the fixed-concentration Hugoniot curve obtained for the corresponding value
![]() $z=z_{eq}$
(solid grey curve). The equilibrium state
$z=z_{eq}$
(solid grey curve). The equilibrium state
![]() $(\unicode[STIX]{x1D708}_{eq},p_{eq})$
for such
$(\unicode[STIX]{x1D708}_{eq},p_{eq})$
for such
![]() $s>s_{j}$
, point
$s>s_{j}$
, point
![]() $S$
in figure 1, is then the intersection of three curves: the corresponding Rayleigh line, the equilibrium Hugoniot curve, and the
$S$
in figure 1, is then the intersection of three curves: the corresponding Rayleigh line, the equilibrium Hugoniot curve, and the
![]() $z=z_{eq}$
Hugoniot curve. Although in figure 1 it seems that the latter two curves almost coincide, they do not and they must be distinguished.
$z=z_{eq}$
Hugoniot curve. Although in figure 1 it seems that the latter two curves almost coincide, they do not and they must be distinguished.
4 Continuous reacting flow – qualitative analysis
Certain features of the MT ZND detonation waves can be revealed by a qualitative analysis. On the one hand, a hierarchy of models can be established and the MT model gradually simplifies to the standard ZND model. On the other hand, certain properties of the solution, peculiar for MT models, can also be recognized.
4.1 Steady detonation equations and hierarchy of the models
The governing equations (3.2)–(3.6) will be written in dimensionless form using the following scaled variables (subscript
![]() $0$
refers to the unperturbed initial state in front of the shock wave):
$0$
refers to the unperturbed initial state in front of the shock wave):
 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D70C}}=\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{0}},\quad \tilde{u} =\frac{u}{\displaystyle \sqrt{\frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}}},\quad \tilde{T}=\frac{T}{T_{0}},\quad \tilde{\unicode[STIX]{x1D6E9}}=\frac{\unicode[STIX]{x1D6E9}}{T_{0}},\quad \unicode[STIX]{x0394}\tilde{\unicode[STIX]{x1D716}}=\frac{\,\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\,}{\displaystyle \frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \tilde{\unicode[STIX]{x1D716}}_{f}=\frac{\,\unicode[STIX]{x1D716}_{f}\,}{\displaystyle \frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \tilde{\unicode[STIX]{x1D709}}=\frac{\unicode[STIX]{x1D709}}{\displaystyle \unicode[STIX]{x1D70F}_{0}\sqrt{\frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}}},\phantom{\mathop{\sum }_{\sum }}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D70C}}=\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{0}},\quad \tilde{u} =\frac{u}{\displaystyle \sqrt{\frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}}},\quad \tilde{T}=\frac{T}{T_{0}},\quad \tilde{\unicode[STIX]{x1D6E9}}=\frac{\unicode[STIX]{x1D6E9}}{T_{0}},\quad \unicode[STIX]{x0394}\tilde{\unicode[STIX]{x1D716}}=\frac{\,\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\,}{\displaystyle \frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \tilde{\unicode[STIX]{x1D716}}_{f}=\frac{\,\unicode[STIX]{x1D716}_{f}\,}{\displaystyle \frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}},\quad \tilde{\unicode[STIX]{x1D709}}=\frac{\unicode[STIX]{x1D709}}{\displaystyle \unicode[STIX]{x1D70F}_{0}\sqrt{\frac{p_{0}}{\unicode[STIX]{x1D70C}_{0}}}},\phantom{\mathop{\sum }_{\sum }}\end{eqnarray}$$
where the reference time
![]() $\unicode[STIX]{x1D70F}_{0}$
is given by
$\unicode[STIX]{x1D70F}_{0}$
is given by
Although the choice (4.2) is taken for convenience,
![]() $\unicode[STIX]{x1D70F}_{0}$
and relaxation times
$\unicode[STIX]{x1D70F}_{0}$
and relaxation times
![]() $\unicode[STIX]{x1D70F}_{D}$
and
$\unicode[STIX]{x1D70F}_{D}$
and
![]() $\unicode[STIX]{x1D70F}_{T}$
(2.28) can be related to the so-called collision time scale, i.e. the mean free time of particles between collisions in equilibrium (Bardos, Golse & Levermore Reference Bardos, Golse and Levermore1993). Omitting, for brevity, the tilde in the quantities (4.1), the dimensionless governing equations of the steady detonation are as follows:
$\unicode[STIX]{x1D70F}_{T}$
(2.28) can be related to the so-called collision time scale, i.e. the mean free time of particles between collisions in equilibrium (Bardos, Golse & Levermore Reference Bardos, Golse and Levermore1993). Omitting, for brevity, the tilde in the quantities (4.1), the dimensionless governing equations of the steady detonation are as follows:
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\left(\frac{1}{2}\unicode[STIX]{x1D70C}zu^{2}+\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D70C}z\left(T+(1-z)\unicode[STIX]{x1D6E9}\right)-\unicode[STIX]{x1D70C}z\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\right)u\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x1D70F}_{0}}{\unicode[STIX]{x1D70F}_{T}}\frac{1}{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D70C}z(1-z)\unicode[STIX]{x1D6E9}+\tilde{\unicode[STIX]{x1D70F}}_{p}\frac{u^{2}}{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\left(\frac{1}{2}\unicode[STIX]{x1D70C}zu^{2}+\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D70C}z\left(T+(1-z)\unicode[STIX]{x1D6E9}\right)-\unicode[STIX]{x1D70C}z\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\right)u\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x1D70F}_{0}}{\unicode[STIX]{x1D70F}_{T}}\frac{1}{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D70C}z(1-z)\unicode[STIX]{x1D6E9}+\tilde{\unicode[STIX]{x1D70F}}_{p}\frac{u^{2}}{2},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D70F}}_{p} & = & \displaystyle \unicode[STIX]{x1D70C}^{2}\sqrt{T}\exp \left(-\frac{\unicode[STIX]{x1D716}_{f}}{T}\right)\left\{(1-z)^{2}-z^{2}\exp \left(-\frac{2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{T}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.(1-z)^{2}\left[\frac{\unicode[STIX]{x1D716}_{f}}{T}+\frac{1}{2}+(1-z)\frac{2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{T}\right]\frac{\unicode[STIX]{x1D6E9}}{T}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D70F}}_{p} & = & \displaystyle \unicode[STIX]{x1D70C}^{2}\sqrt{T}\exp \left(-\frac{\unicode[STIX]{x1D716}_{f}}{T}\right)\left\{(1-z)^{2}-z^{2}\exp \left(-\frac{2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{T}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.(1-z)^{2}\left[\frac{\unicode[STIX]{x1D716}_{f}}{T}+\frac{1}{2}+(1-z)\frac{2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}}{T}\right]\frac{\unicode[STIX]{x1D6E9}}{T}\right\}\end{eqnarray}$$
and
The governing equations consist of the conservation laws (4.3)–(4.5) of mass, momentum and energy for the mixture, and the balance laws (4.6) and (4.7) of mass and energy for the product. The balance law of momentum for the product is dropped from the set of governing equations in accordance with the basic assumption.
4.1.1 Governing equations solved with respect to first derivatives
The governing equations (4.3)–(4.7) can be solved with respect to first derivatives:
This form will be useful for the analysis of certain qualitative aspects of the solutions.
4.1.2 Hierarchy of the models
In § 5 we shall provide a comparative analysis of the detonation profiles obtained by the solutions to (4.3)–(4.7), with those obtained through the solutions to the simpler models. This analysis will be achieved through the hierarchy of models obtained through the simplification of the reaction rate (4.8). Namely,
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}$
can be split into a single-temperature (ST) part
$\tilde{\unicode[STIX]{x1D70F}}_{p}$
can be split into a single-temperature (ST) part
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
, which does not depend on
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
, which does not depend on
![]() $\unicode[STIX]{x1D6E9}$
, and an MT part
$\unicode[STIX]{x1D6E9}$
, and an MT part
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
, which depends on
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
, which depends on
![]() $\unicode[STIX]{x1D6E9}$
, as follows:
$\unicode[STIX]{x1D6E9}$
, as follows:
where
In such a way the following hierarchy of the models can be obtained and analysed in the sequel:
- (MT)
the MT model is described by the system (4.3)–(4.7), with the complete reaction rate term (4.8);
- (qMT)
the quasi-MT model consists of the same equations (4.3)–(4.7) as for the MT model, but with simplified reaction rate
 $\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
that does not take into account the contribution of the different temperatures; and
$\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
that does not take into account the contribution of the different temperatures; and- (ST)
the ST model consists of (4.3)–(4.6), assumes that the reaction rate
 $\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
and assumes a common temperature for both constituents throughout the whole process – this model, along with reversible chemical reaction, corresponds to the model studied in (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015).
$\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
and assumes a common temperature for both constituents throughout the whole process – this model, along with reversible chemical reaction, corresponds to the model studied in (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015).
4.2 Properties of the solution
The analysis of MT detonation waves possesses certain particular features which distinguish it from the standard analysis based upon reactive Euler equations. Such features will be qualitatively analysed in the sequel.
4.2.1 Equilibrium state
As mentioned above, the MT model of the steady detonation wave describes a continuous solution that connects the von Neumann state
![]() $\boldsymbol{U}_{N}$
with the equilibrium one
$\boldsymbol{U}_{N}$
with the equilibrium one
![]() $\boldsymbol{U}_{eq}$
. Thus, we analyse the boundary value problem for (4.3)–(4.7) in a (formally) unbounded domain
$\boldsymbol{U}_{eq}$
. Thus, we analyse the boundary value problem for (4.3)–(4.7) in a (formally) unbounded domain
![]() $\unicode[STIX]{x1D709}\in [0,\infty )$
, with the following boundary data:
$\unicode[STIX]{x1D709}\in [0,\infty )$
, with the following boundary data:
where
![]() $\unicode[STIX]{x1D709}_{S}$
denotes the value of the steady variable at which the process terminates. Note that condition (4.19) leads to a necessary condition for equilibrium.
$\unicode[STIX]{x1D709}_{S}$
denotes the value of the steady variable at which the process terminates. Note that condition (4.19) leads to a necessary condition for equilibrium.
Statement 1. If the system (4.3)–(4.7) is in an equilibrium state characterized by relations (4.19), then the state variables obey the following relations:
Proof. The terminal condition (4.19) implies that production terms in governing equations (4.6) and (4.7) vanish in equilibrium. In particular, the equilibrium condition for (4.6) implies that the reaction rate vanishes,
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}=0$
, which provides a relation between equilibrium values
$\tilde{\unicode[STIX]{x1D70F}}_{p}=0$
, which provides a relation between equilibrium values
![]() $z_{eq}$
,
$z_{eq}$
,
![]() $T_{eq}$
and
$T_{eq}$
and
![]() $\unicode[STIX]{x1D6E9}_{eq}$
. However, the equilibrium condition for (4.7) requires simultaneous vanishing of the reaction rate
$\unicode[STIX]{x1D6E9}_{eq}$
. However, the equilibrium condition for (4.7) requires simultaneous vanishing of the reaction rate
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}$
and the temperature difference
$\tilde{\unicode[STIX]{x1D70F}}_{p}$
and the temperature difference
![]() $\unicode[STIX]{x1D6E9}$
, which leads to
$\unicode[STIX]{x1D6E9}$
, which leads to
![]() $\unicode[STIX]{x1D6E9}_{eq}=0$
. As a consequence, we have
$\unicode[STIX]{x1D6E9}_{eq}=0$
. As a consequence, we have
so that the ST part
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
of the reaction rate vanishes independently, implying the law of mass action
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
of the reaction rate vanishes independently, implying the law of mass action
which completes the proof.
Having in mind the analysis developed in § 3, it becomes obvious that the terminal state of the system has to be the equilibrium one, i.e.
![]() $\boldsymbol{U}(\unicode[STIX]{x1D709}_{S})=\boldsymbol{U}_{S}=\boldsymbol{U}_{eq}$
, where the equilibrium state is uniquely determined by the intersection of the Rayleigh line and the equilibrium Hugoniot curve, together with the independent condition
$\boldsymbol{U}(\unicode[STIX]{x1D709}_{S})=\boldsymbol{U}_{S}=\boldsymbol{U}_{eq}$
, where the equilibrium state is uniquely determined by the intersection of the Rayleigh line and the equilibrium Hugoniot curve, together with the independent condition
![]() $\unicode[STIX]{x1D6E9}_{S}=\unicode[STIX]{x1D6E9}_{eq}=0$
. The additional condition (4.20b
) is peculiar for the MT model and has to be considered with particular attention, as will be shown in the sequel.
$\unicode[STIX]{x1D6E9}_{S}=\unicode[STIX]{x1D6E9}_{eq}=0$
. The additional condition (4.20b
) is peculiar for the MT model and has to be considered with particular attention, as will be shown in the sequel.
4.2.2 Non-monotonic detonation profiles
Further qualitative analysis will be based upon twofold characterization of the equilibrium state, given by the terminal condition (4.19). A distinguished role in this analysis will be played by the temperature difference
![]() $\unicode[STIX]{x1D6E9}$
. To facilitate the formulation of the forthcoming statements, we shall introduce the following notation for the state variables:
$\unicode[STIX]{x1D6E9}$
. To facilitate the formulation of the forthcoming statements, we shall introduce the following notation for the state variables:
In the case of reversible chemical reaction, typical ZND detonation profiles are monotonic (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), except in the neighbourhood of the Chapman–Jouguet solution, the solution that connects the von Neumann state
![]() $N$
with the Chapman–Jouguet state
$N$
with the Chapman–Jouguet state
![]() $CJ$
. However, equilibrium conditions (4.20) of the MT model imply the possibility of occurrence of non-monotonic profiles. The existence of such profiles will be demonstrated first through a qualitative analysis. It will then be confirmed by numerical computation in the next section.
$CJ$
. However, equilibrium conditions (4.20) of the MT model imply the possibility of occurrence of non-monotonic profiles. The existence of such profiles will be demonstrated first through a qualitative analysis. It will then be confirmed by numerical computation in the next section.
Statement 2 (Crossing condition).
Assume that there exists
![]() $\unicode[STIX]{x1D709}_{C}\in (0,\infty )$
such that the state vector
$\unicode[STIX]{x1D709}_{C}\in (0,\infty )$
such that the state vector
![]() $\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{C})=(\unicode[STIX]{x1D70C}_{C},u_{C},T_{C},z_{C})$
satisfies the equilibrium condition (4.20a
), i.e.
$\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{C})=(\unicode[STIX]{x1D70C}_{C},u_{C},T_{C},z_{C})$
satisfies the equilibrium condition (4.20a
), i.e.
![]() $z_{C}=z_{eq}$
,
$z_{C}=z_{eq}$
,
![]() $T_{C}=T_{eq}$
. Then, the following two cases are possible: either
$T_{C}=T_{eq}$
. Then, the following two cases are possible: either
(i)
 $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})=\unicode[STIX]{x1D6E9}_{C}=\unicode[STIX]{x1D6E9}_{eq}=0$
and the equilibrium state is reached at
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})=\unicode[STIX]{x1D6E9}_{C}=\unicode[STIX]{x1D6E9}_{eq}=0$
and the equilibrium state is reached at
 $\unicode[STIX]{x1D709}_{C}=\unicode[STIX]{x1D709}_{S}$
; or
$\unicode[STIX]{x1D709}_{C}=\unicode[STIX]{x1D709}_{S}$
; or(ii)
 $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
, which implies
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
, which implies
 $\text{d}\boldsymbol{U}(\unicode[STIX]{x1D709}_{C})/\text{d}\unicode[STIX]{x1D709}\neq \mathbf{0}$
, and the process will continue for
$\text{d}\boldsymbol{U}(\unicode[STIX]{x1D709}_{C})/\text{d}\unicode[STIX]{x1D709}\neq \mathbf{0}$
, and the process will continue for
 $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{C}$
.
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{C}$
.
Proof. If
![]() $z_{C}$
and
$z_{C}$
and
![]() $T_{C}$
satisfy the equilibrium condition (4.20a
), i.e. the law of mass action, then
$T_{C}$
satisfy the equilibrium condition (4.20a
), i.e. the law of mass action, then
![]() $\unicode[STIX]{x1D70C}_{C}$
and
$\unicode[STIX]{x1D70C}_{C}$
and
![]() $u_{C}$
are uniquely determined by (3.10) and (3.7) for the fixed value of
$u_{C}$
are uniquely determined by (3.10) and (3.7) for the fixed value of
![]() $s$
. Moreover,
$s$
. Moreover,
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}(z_{C},T_{C},\unicode[STIX]{x1D6E9}_{C})=0$
. In case (i) it is obvious that the equilibrium state is reached, since both equilibrium conditions (4.20) are satisfied. In case (ii),
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}(z_{C},T_{C},\unicode[STIX]{x1D6E9}_{C})=0$
. In case (i) it is obvious that the equilibrium state is reached, since both equilibrium conditions (4.20) are satisfied. In case (ii),
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
implies
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
implies
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}(\unicode[STIX]{x1D709}_{C})=\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}(z_{C},T_{C},\unicode[STIX]{x1D6E9}_{C})\neq 0$
. Consequently, by a simple inspection of the system (4.10)–(4.14), one may conclude that
$\tilde{\unicode[STIX]{x1D70F}}_{p}(\unicode[STIX]{x1D709}_{C})=\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}(z_{C},T_{C},\unicode[STIX]{x1D6E9}_{C})\neq 0$
. Consequently, by a simple inspection of the system (4.10)–(4.14), one may conclude that
![]() $\text{d}\boldsymbol{U}(\unicode[STIX]{x1D709}_{C})/\text{d}\unicode[STIX]{x1D709}\neq \mathbf{0}$
, which completes the proof.
$\text{d}\boldsymbol{U}(\unicode[STIX]{x1D709}_{C})/\text{d}\unicode[STIX]{x1D709}\neq \mathbf{0}$
, which completes the proof.
The crossing condition has a simple interpretation. If the state variables
![]() $\boldsymbol{U}^{ST}$
satisfy the law of mass action (4.20a
), and lie on the Rayleigh line and the equilibrium Hugoniot curve simultaneously, the ST part of the reaction rate will vanish,
$\boldsymbol{U}^{ST}$
satisfy the law of mass action (4.20a
), and lie on the Rayleigh line and the equilibrium Hugoniot curve simultaneously, the ST part of the reaction rate will vanish,
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}(\unicode[STIX]{x1D709}_{C})=0$
. However, if
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}(\unicode[STIX]{x1D709}_{C})=0$
. However, if
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
, the process is not terminated, since the derivatives of the state variables do not yet vanish, and the curve
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{C})\neq 0$
, the process is not terminated, since the derivatives of the state variables do not yet vanish, and the curve
![]() $\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
only crosses the equilibrium values at
$\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
only crosses the equilibrium values at
![]() $\unicode[STIX]{x1D709}_{C}$
. This motivates the denomination crossing condition. Its importance lies in the fact that it may occur for certain values of the parameters, in contrast to the standard ST case.
$\unicode[STIX]{x1D709}_{C}$
. This motivates the denomination crossing condition. Its importance lies in the fact that it may occur for certain values of the parameters, in contrast to the standard ST case.
Statement 3 (Local extremum).
Assume that there exists
![]() $\unicode[STIX]{x1D709}_{E}\in (0,\infty )$
such that the derivative of the state vector
$\unicode[STIX]{x1D709}_{E}\in (0,\infty )$
such that the derivative of the state vector
![]() $\boldsymbol{U}^{ST}$
vanishes,
$\boldsymbol{U}^{ST}$
vanishes,
![]() $\text{d}\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=(0,0,0,0)$
. Then, the following two cases are possible: either
$\text{d}\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=(0,0,0,0)$
. Then, the following two cases are possible: either
(i)
 $\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=0$
, which implies
$\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=0$
, which implies
 $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})=0$
, and the equilibrium state is reached at
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})=0$
, and the equilibrium state is reached at
 $\unicode[STIX]{x1D709}_{E}=\unicode[STIX]{x1D709}_{S}$
, or
$\unicode[STIX]{x1D709}_{E}=\unicode[STIX]{x1D709}_{S}$
, or(ii)
 $\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}\neq 0$
, which implies
$\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}\neq 0$
, which implies
 $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})\neq 0$
, and the process will continue for
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})\neq 0$
, and the process will continue for
 $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{E}$
.
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{E}$
.
Proof. If
![]() $\text{d}\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=(0,0,0,0)$
at some point
$\text{d}\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=(0,0,0,0)$
at some point
![]() $\unicode[STIX]{x1D709}_{E}\in (0,\infty )$
, then from (4.10)–(4.13) one obtains
$\unicode[STIX]{x1D709}_{E}\in (0,\infty )$
, then from (4.10)–(4.13) one obtains
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}(\unicode[STIX]{x1D709}_{E})=0$
. However, this condition is not sufficient for equilibrium since it only determines one relation between all the state variables
$\tilde{\unicode[STIX]{x1D70F}}_{p}(\unicode[STIX]{x1D709}_{E})=0$
. However, this condition is not sufficient for equilibrium since it only determines one relation between all the state variables
![]() $\boldsymbol{U}$
. If case (i) is valid,
$\boldsymbol{U}$
. If case (i) is valid,
![]() $\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=0$
, from (4.14) it follows that
$\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}=0$
, from (4.14) it follows that
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})=0$
, and the system reaches the equilibrium state at
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})=0$
, and the system reaches the equilibrium state at
![]() $\unicode[STIX]{x1D709}_{E}=\unicode[STIX]{x1D709}_{S}$
. If case (ii) is valid,
$\unicode[STIX]{x1D709}_{E}=\unicode[STIX]{x1D709}_{S}$
. If case (ii) is valid,
![]() $\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}\neq 0$
implies
$\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})/\text{d}\unicode[STIX]{x1D709}\neq 0$
implies
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})\neq 0$
from (4.14), and the process is not terminated, but continues for
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709}_{E})\neq 0$
from (4.14), and the process is not terminated, but continues for
![]() $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{E}$
.
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{E}$
.
As a conclusion of the analysis of non-monotonic profiles, one fundamental remark has to be given. Either in the case of crossing the equilibrium state (statement 2), or in the case of local extremum (statement 3), the main driving agent for continuation of the process is the temperature difference of the constituents.
4.2.3 Quasi-multi-temperature behaviour
In § 3 we defined the qMT model as the one consisting of (4.3)–(4.7), or equivalently (4.10)–(4.14), but with a simplified reaction rate
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
. Note that such a reaction rate does not depend on
$\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
. Note that such a reaction rate does not depend on
![]() $\unicode[STIX]{x1D6E9}$
, but only on the
$\unicode[STIX]{x1D6E9}$
, but only on the
![]() $\boldsymbol{U}^{ST}$
state vector. This fact has a simple consequence that will be exploited in our numerical computations.
$\boldsymbol{U}^{ST}$
state vector. This fact has a simple consequence that will be exploited in our numerical computations.
Statement 4. Assume that the reaction rate has the form
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
. Then (4.3)–(4.6), or equivalently (4.10)–(4.13), have the same structure as in the ST case and completely determine the solution for
$\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
. Then (4.3)–(4.6), or equivalently (4.10)–(4.13), have the same structure as in the ST case and completely determine the solution for
![]() $\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
. Equation (4.7), or equivalently (4.14), is decoupled from the rest of the system and serves for the determination of
$\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
. Equation (4.7), or equivalently (4.14), is decoupled from the rest of the system and serves for the determination of
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709})$
once the ST part of the model is solved.
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709})$
once the ST part of the model is solved.
Proof. It is sufficient to note that the differential part of the system (4.3)–(4.6) has the same structure as in the ST case (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), and thus does not depend on
![]() $\unicode[STIX]{x1D6E9}$
. If moreover
$\unicode[STIX]{x1D6E9}$
. If moreover
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
, then this part of the system has the ST structure, independent of
$\tilde{\unicode[STIX]{x1D70F}}_{p}=\tilde{\unicode[STIX]{x1D70F}}_{p}^{ST}$
, then this part of the system has the ST structure, independent of
![]() $\unicode[STIX]{x1D6E9}$
, the same as the one in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015). Therefore, the complete system (4.3)–(4.7) decouples into an ST part (4.3)–(4.6), which determines the behaviour of
$\unicode[STIX]{x1D6E9}$
, the same as the one in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015). Therefore, the complete system (4.3)–(4.7) decouples into an ST part (4.3)–(4.6), which determines the behaviour of
![]() $\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
, and an MT part (4.7), which tracks the evolution of
$\boldsymbol{U}^{ST}(\unicode[STIX]{x1D709})$
, and an MT part (4.7), which tracks the evolution of
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709})$
. The proof is then complete.
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D709})$
. The proof is then complete.
5 Continuous reacting flow profiles
The profiles of a continuous reacting flow can be determined numerically, by solving an appropriate initial value problem, as discussed in § 3.2. Namely, the governing equations of the problem are (4.3)–(4.7), for
![]() $\unicode[STIX]{x1D709}\in (0,+\infty )$
, and the initial data are taken as
$\unicode[STIX]{x1D709}\in (0,+\infty )$
, and the initial data are taken as
 $$\begin{eqnarray}\boldsymbol{U}(0)=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}(0)\\ u(0)\\ T(0)\\ z(0)\\ \unicode[STIX]{x1D6E9}(0)\end{array}\right)=\left(\begin{array}{@{}c@{}}\displaystyle \frac{4M_{0}^{2}}{3+M_{0}^{2}}\\ \displaystyle \sqrt{\unicode[STIX]{x1D6FE}}\,\frac{3+M_{0}^{2}}{4M_{0}}\\ \displaystyle \frac{1}{16}\left(14-\frac{3}{M_{0}^{2}}+5M_{0}^{2}\right)\\ 0\\ 0\end{array}\right)=\boldsymbol{U}_{N},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{U}(0)=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}(0)\\ u(0)\\ T(0)\\ z(0)\\ \unicode[STIX]{x1D6E9}(0)\end{array}\right)=\left(\begin{array}{@{}c@{}}\displaystyle \frac{4M_{0}^{2}}{3+M_{0}^{2}}\\ \displaystyle \sqrt{\unicode[STIX]{x1D6FE}}\,\frac{3+M_{0}^{2}}{4M_{0}}\\ \displaystyle \frac{1}{16}\left(14-\frac{3}{M_{0}^{2}}+5M_{0}^{2}\right)\\ 0\\ 0\end{array}\right)=\boldsymbol{U}_{N},\end{eqnarray}$$
where
![]() $\boldsymbol{U}_{N}$
stands for the von Neumann state. By
$\boldsymbol{U}_{N}$
stands for the von Neumann state. By
![]() $M_{0}=u_{0}/c_{0}$
we denote the Mach number in the unperturbed initial state in front of the shock, with
$M_{0}=u_{0}/c_{0}$
we denote the Mach number in the unperturbed initial state in front of the shock, with
![]() $c_{0}=\sqrt{\unicode[STIX]{x1D6FE}p_{0}/\unicode[STIX]{x1D70C}_{0}}$
being the adiabatic speed of sound. It will be convenient to express the Mach number in an alternative form, for the sake of comparison with the results presented in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015):
$c_{0}=\sqrt{\unicode[STIX]{x1D6FE}p_{0}/\unicode[STIX]{x1D70C}_{0}}$
being the adiabatic speed of sound. It will be convenient to express the Mach number in an alternative form, for the sake of comparison with the results presented in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015):
where
![]() $s_{j}$
is the dimensionless steady detonation wave velocity at the
$s_{j}$
is the dimensionless steady detonation wave velocity at the
![]() $CJ$
state, and
$CJ$
state, and
![]() $f$
is the so-called overdrive degree. For reasons that will become apparent in the sequel, a subsequent analysis of the reacting flow profiles will be restricted to overdriven detonations,
$f$
is the so-called overdrive degree. For reasons that will become apparent in the sequel, a subsequent analysis of the reacting flow profiles will be restricted to overdriven detonations,
![]() $f>1$
, for which
$f>1$
, for which
![]() $s>s_{j}$
and the equilibrium state lies on the strong branch of the equilibrium Hugoniot curve (see figure 1).
$s>s_{j}$
and the equilibrium state lies on the strong branch of the equilibrium Hugoniot curve (see figure 1).
To avoid singularities in numerical computations, we have to adopt a small value of the initial concentration of the product at the von Neumann state. Thus, we shall assume
![]() $z(0)=0.01$
in all the computations. Other possible singularities do not interfere with numerical simulations. In particular, we have
$z(0)=0.01$
in all the computations. Other possible singularities do not interfere with numerical simulations. In particular, we have
![]() $\unicode[STIX]{x1D70C}>0$
and
$\unicode[STIX]{x1D70C}>0$
and
![]() $u>0$
, and thus
$u>0$
, and thus
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $u$
do not create any singularity; moreover,
$u$
do not create any singularity; moreover,
![]() $z<1$
, since the chemical reaction is reversible, and no other singularity arises from
$z<1$
, since the chemical reaction is reversible, and no other singularity arises from
![]() $z$
. Finally, since we analyse only the overdriven detonations, the flow in the reaction zone is subsonic and
$z$
. Finally, since we analyse only the overdriven detonations, the flow in the reaction zone is subsonic and
![]() $u^{2}<\unicode[STIX]{x1D6FE}T$
throughout the flow.
$u^{2}<\unicode[STIX]{x1D6FE}T$
throughout the flow.
The latter singularity, corresponding to the sonic condition
![]() $u^{2}=\unicode[STIX]{x1D6FE}T$
, is rather delicate and has to be treated with care. When the detonation process comprises an exothermic reaction followed by an endothermic one, there is a possibility for a pathological detonation to occur (Fickett & Davis Reference Fickett and Davis1979). There is a point within the profile where the flow becomes sonic, and the detonation is unsupported and ends up on the weak branch of the equilibrium Hugoniot curve (see § 3.1 in Sharpe (Reference Sharpe1999) for a comprehensive analysis). In this case, the flow described by the model (4.3)–(4.7) will reach the singularity at the sonic point. For that reason, the analysis is restricted to overdriven detonations, while the other possibilities will be outlined in the final section.
$u^{2}=\unicode[STIX]{x1D6FE}T$
, is rather delicate and has to be treated with care. When the detonation process comprises an exothermic reaction followed by an endothermic one, there is a possibility for a pathological detonation to occur (Fickett & Davis Reference Fickett and Davis1979). There is a point within the profile where the flow becomes sonic, and the detonation is unsupported and ends up on the weak branch of the equilibrium Hugoniot curve (see § 3.1 in Sharpe (Reference Sharpe1999) for a comprehensive analysis). In this case, the flow described by the model (4.3)–(4.7) will reach the singularity at the sonic point. For that reason, the analysis is restricted to overdriven detonations, while the other possibilities will be outlined in the final section.
The terminal, i.e. the equilibrium, state is determined by condition (4.19) for
![]() $\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{S}$
. In the numerical computations, we perform the analysis on a finite domain
$\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{S}$
. In the numerical computations, we perform the analysis on a finite domain
![]() $\unicode[STIX]{x1D709}\in [0,\unicode[STIX]{x1D709}^{\ast }]$
,
$\unicode[STIX]{x1D709}\in [0,\unicode[STIX]{x1D709}^{\ast }]$
,
![]() $\unicode[STIX]{x1D709}^{\ast }\leqslant \unicode[STIX]{x1D709}_{S}$
, taking
$\unicode[STIX]{x1D709}^{\ast }\leqslant \unicode[STIX]{x1D709}_{S}$
, taking
![]() $\unicode[STIX]{x1D709}^{\ast }$
in such a way that the state variables reach the neighbourhood of the equilibrium state with sufficient accuracy. We shall not go for the determination of the position
$\unicode[STIX]{x1D709}^{\ast }$
in such a way that the state variables reach the neighbourhood of the equilibrium state with sufficient accuracy. We shall not go for the determination of the position
![]() $\unicode[STIX]{x1D709}_{S}$
of the equilibrium state, since it can be determined only approximately and the result depends on the accuracy proposed beforehand.
$\unicode[STIX]{x1D709}_{S}$
of the equilibrium state, since it can be determined only approximately and the result depends on the accuracy proposed beforehand.
The basic modelling novelty, i.e. the introduction of multiple temperatures, influences neither the von Neumann state nor the terminal equilibrium state. It may be reflected only in the reacting flow profiles. This is a consequence of the fact that von Neumann and equilibrium states are determined through the solution of the appropriate RH conditions and the vanishing of production terms, respectively, which both include the vanishing of the temperature difference, as described in § 3.2. The aim of the numerical computation of the reacting profiles is to analyse the influence of the temperature difference on its structure. It is important to note that the model (4.3)–(4.7) together with initial data (5.1) contains three parameters: the forward activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
, the overdrive degree
$\unicode[STIX]{x1D716}_{f}$
, the overdrive degree
![]() $f$
, and the binding energy difference
$f$
, and the binding energy difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
(or the reaction heat
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
(or the reaction heat
![]() ${\mathcal{Q}}=-2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
). Our aim is to analyse the influence of these parameters on the structure of the continuous reacting flow, and to compare these results with those presented in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), i.e. with ST profiles. Note that in view of statement 4, there is no need for a comparison with qMT profiles, since they are the same as ST ones. In figures 2–6, the steady variable
${\mathcal{Q}}=-2\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
). Our aim is to analyse the influence of these parameters on the structure of the continuous reacting flow, and to compare these results with those presented in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), i.e. with ST profiles. Note that in view of statement 4, there is no need for a comparison with qMT profiles, since they are the same as ST ones. In figures 2–6, the steady variable
![]() $\unicode[STIX]{x1D709}$
is given on a logarithmic scale and the state variables
$\unicode[STIX]{x1D709}$
is given on a logarithmic scale and the state variables
![]() $u$
,
$u$
,
![]() $p$
and
$p$
and
![]() $T$
are given in units of their corresponding values
$T$
are given in units of their corresponding values
![]() $u_{N}$
,
$u_{N}$
,
![]() $p_{N}$
and
$p_{N}$
and
![]() $T_{N}$
at the von Neumann state.
$T_{N}$
at the von Neumann state.
5.1 Case 1: Influence of
 $\unicode[STIX]{x1D716}_{f}$
on the profile
$\unicode[STIX]{x1D716}_{f}$
on the profile
First we consider the influence of the activation energy of the forward reaction
![]() $\unicode[STIX]{x1D716}_{f}$
on the structure of the continuous reacting flow profile. This is the case in which the MT assumption strongly reveals its influence and leads to completely new results in a qualitative sense. It is well known (Lee Reference Lee2008) that the activation energy is strictly related to the temperature sensitivity of the chemical reaction. To compare our results with (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), we adopted the same values of the parameters:
$\unicode[STIX]{x1D716}_{f}$
on the structure of the continuous reacting flow profile. This is the case in which the MT assumption strongly reveals its influence and leads to completely new results in a qualitative sense. It is well known (Lee Reference Lee2008) that the activation energy is strictly related to the temperature sensitivity of the chemical reaction. To compare our results with (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), we adopted the same values of the parameters:
Numerically computed profiles are presented in figure 2, for both MT and ST models.
For lower values of
![]() $\unicode[STIX]{x1D716}_{f}$
, one can observe two qualitatively different types of profiles. The first one (
$\unicode[STIX]{x1D716}_{f}$
, one can observe two qualitatively different types of profiles. The first one (
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
) is non-monotonic – it contains a crossing point with the state
$\unicode[STIX]{x1D716}_{f}=2.0$
) is non-monotonic – it contains a crossing point with the state
![]() $\boldsymbol{U}_{eq}^{ST}$
, as indicated by statement 2, as well as at least one local extremum, as described in statement 3. This does not occur in the ST case at all. Moreover, it can be observed that the MT profiles are driven out of the von Neumann state faster than the ST ones, and this fact can be attributed to the presence of MT part
$\boldsymbol{U}_{eq}^{ST}$
, as indicated by statement 2, as well as at least one local extremum, as described in statement 3. This does not occur in the ST case at all. Moreover, it can be observed that the MT profiles are driven out of the von Neumann state faster than the ST ones, and this fact can be attributed to the presence of MT part
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
in the reaction rate.
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
in the reaction rate.
When the activation energy is increased (
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
), the profiles become monotonic, like in the ST case. There is still, however, a difference between the MT and ST profiles: the MT profiles are driven out of the von Neumann state faster than the ST ones, but the ST profiles are steeper than the MT ones. Obviously, there exists a threshold value of the activation energy
$\unicode[STIX]{x1D716}_{f}=10.0$
), the profiles become monotonic, like in the ST case. There is still, however, a difference between the MT and ST profiles: the MT profiles are driven out of the von Neumann state faster than the ST ones, but the ST profiles are steeper than the MT ones. Obviously, there exists a threshold value of the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
which separates the non-monotonic profiles from monotonic ones. This issue will be tackled in the sequel.
$\unicode[STIX]{x1D716}_{f}$
which separates the non-monotonic profiles from monotonic ones. This issue will be tackled in the sequel.
As in Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), for very large values of the activation energy (
![]() $\unicode[STIX]{x1D716}_{f}=30.0$
), the reaction rate is considerably smaller (see (4.8)) and the profile is much wider – the equilibrium state is reached at
$\unicode[STIX]{x1D716}_{f}=30.0$
), the reaction rate is considerably smaller (see (4.8)) and the profile is much wider – the equilibrium state is reached at
![]() $\unicode[STIX]{x1D709}_{eq}\approx 10^{6}$
. Both MT and ST profiles are monotonic and have a similar behaviour as in the previous case. However, the difference between the state variables in the MT and ST cases is much less pronounced, e.g.
$\unicode[STIX]{x1D709}_{eq}\approx 10^{6}$
. Both MT and ST profiles are monotonic and have a similar behaviour as in the previous case. However, the difference between the state variables in the MT and ST cases is much less pronounced, e.g.
![]() $z^{MT}(\unicode[STIX]{x1D709})-z^{ST}(\unicode[STIX]{x1D709})<10^{-3}$
throughout the profile. For these reasons, the profiles obtained for
$z^{MT}(\unicode[STIX]{x1D709})-z^{ST}(\unicode[STIX]{x1D709})<10^{-3}$
throughout the profile. For these reasons, the profiles obtained for
![]() $\unicode[STIX]{x1D716}_{f}=30.0$
are not displayed in the whole range of
$\unicode[STIX]{x1D716}_{f}=30.0$
are not displayed in the whole range of
![]() $\unicode[STIX]{x1D709}$
, but just in the range that is significant for the first two cases.
$\unicode[STIX]{x1D709}$
, but just in the range that is significant for the first two cases.

Figure 2. Influence of
![]() $\unicode[STIX]{x1D716}_{f}$
on the reacting flow: profiles of
$\unicode[STIX]{x1D716}_{f}$
on the reacting flow: profiles of
![]() $z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for different values of
$z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for different values of
![]() $\unicode[STIX]{x1D716}_{f}$
.
$\unicode[STIX]{x1D716}_{f}$
.
The analysis of the temperature profiles of the constituents sheds new light on the MT phenomenon. In the case of non-reactive mixtures, it is usually related to the fact that constituents have disparate masses. In our problem the masses of reactants and products are equal by assumption,
![]() $m_{r}=m_{p}=m$
. Nevertheless, there is a temperature difference that cannot be ignored. A careful examination of the profiles, presented in figure 3, reveals that there appears an immediate temperature drop of the product temperature right behind the von Neumann state. This result suggests that the main reason for sustained thermal non-equilibrium between the constituents is not the mass difference, but the chemical reaction and the huge initial difference in the concentration of the constituents.
$m_{r}=m_{p}=m$
. Nevertheless, there is a temperature difference that cannot be ignored. A careful examination of the profiles, presented in figure 3, reveals that there appears an immediate temperature drop of the product temperature right behind the von Neumann state. This result suggests that the main reason for sustained thermal non-equilibrium between the constituents is not the mass difference, but the chemical reaction and the huge initial difference in the concentration of the constituents.

Figure 3. Influence of
![]() $\unicode[STIX]{x1D716}_{f}$
on the reacting flow: profiles of
$\unicode[STIX]{x1D716}_{f}$
on the reacting flow: profiles of
![]() $T(\unicode[STIX]{x1D709})$
,
$T(\unicode[STIX]{x1D709})$
,
![]() $T_{r}(\unicode[STIX]{x1D709})$
and
$T_{r}(\unicode[STIX]{x1D709})$
and
![]() $T_{p}(\unicode[STIX]{x1D709})$
obtained with the MT model for two different values of
$T_{p}(\unicode[STIX]{x1D709})$
obtained with the MT model for two different values of
![]() $\unicode[STIX]{x1D716}_{f}$
:
$\unicode[STIX]{x1D716}_{f}$
:
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
(a) and
$\unicode[STIX]{x1D716}_{f}=2.0$
(a) and
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
(b).
$\unicode[STIX]{x1D716}_{f}=10.0$
(b).
As a final remark, we would like to compare the non-monotonic profiles that appear in our model with the non-monotonic profiles in the standard model for ZND detonation waves. Namely, in the standard model, the non-monotonic temperature profiles appear for large values of the activation energy, and they are preceded by a longer induction zone and have steeper profiles (see Lee Reference Lee2008, pp. 77–78). Other state variables have monotonic profiles. The main difference between our model and the standard one is the reversibility of the chemical reaction and the MT assumption. They are both properly taken into account in the reaction rate (2.21), and its subsequent dimensionless forms. In contrast to the standard model, the non-monotonic profiles in our case appear in all the state variables and for small values of the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
. Therefore, it seems that reversibility and thermal non-equilibrium (
$\unicode[STIX]{x1D716}_{f}$
. Therefore, it seems that reversibility and thermal non-equilibrium (
![]() $\unicode[STIX]{x1D6E9}\neq 0$
) play the crucial role in generating non-monotonic profiles through their appearance in the reaction rate. It must be emphasized that the scope of this remark is restricted to ZND detonation waves, and that we do not tend to cover processes like Rayleigh flow, in which non-monotonic temperature profiles occur as well.
$\unicode[STIX]{x1D6E9}\neq 0$
) play the crucial role in generating non-monotonic profiles through their appearance in the reaction rate. It must be emphasized that the scope of this remark is restricted to ZND detonation waves, and that we do not tend to cover processes like Rayleigh flow, in which non-monotonic temperature profiles occur as well.
5.2 Case 2: Influence of
 $f$
on the profile
$f$
on the profile
The influence of the overdrive degree
![]() $f$
on the continuous reacting profiles is analysed for the following values of the parameters:
$f$
on the continuous reacting profiles is analysed for the following values of the parameters:
and the results are presented in figure 4. As expected, different values of
![]() $f$
lead to different terminal equilibrium states. However, there is no qualitative difference between the profiles – only non-monotonic profiles appear. This leads to the conclusion that the major influence on the qualitative structure of the profile still comes from the activation energy
$f$
lead to different terminal equilibrium states. However, there is no qualitative difference between the profiles – only non-monotonic profiles appear. This leads to the conclusion that the major influence on the qualitative structure of the profile still comes from the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
, rather than from the overdrive degree
$\unicode[STIX]{x1D716}_{f}$
, rather than from the overdrive degree
![]() $f$
. This is a consequence of the fact that the activation energy is strictly related to the temperature sensitivity of the chemical reaction.
$f$
. This is a consequence of the fact that the activation energy is strictly related to the temperature sensitivity of the chemical reaction.

Figure 4. Influence of
![]() $f$
on the reacting flow: profiles of
$f$
on the reacting flow: profiles of
![]() $z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for different values of
$z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for different values of
![]() $f$
.
$f$
.
In the present analysis we took the value
![]() $f=1.08$
with the aim to mimic the behaviour of the Chapman–Jouguet solution. It can be observed in the temperature profile illustrated in figure 4 that there occurs a temperature drop in the profile. A similar result has been obtained in (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), where it was attributed to the prevalence of backward reaction (which is endothermic) for
$f=1.08$
with the aim to mimic the behaviour of the Chapman–Jouguet solution. It can be observed in the temperature profile illustrated in figure 4 that there occurs a temperature drop in the profile. A similar result has been obtained in (Marques Junior et al.
Reference Marques Junior, Soares, Bianchi and Kremer2015), where it was attributed to the prevalence of backward reaction (which is endothermic) for
![]() $f=1.0$
. However, this phenomenon appears also for
$f=1.0$
. However, this phenomenon appears also for
![]() $f>1.0$
and yet has to be analysed carefully.
$f>1.0$
and yet has to be analysed carefully.
5.3 Case 3: Influence of
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the profile
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the profile
In Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), the influence of the binding energy difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
was not analysed at all. Nevertheless, in the context of MT ZND detonation waves, it is of interest to pay attention to the impact of this parameter on the reacting profiles, since it is related to the reaction heat. In fact, higher values of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
was not analysed at all. Nevertheless, in the context of MT ZND detonation waves, it is of interest to pay attention to the impact of this parameter on the reacting profiles, since it is related to the reaction heat. In fact, higher values of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
indicate more violent chemical reactions. Although
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
indicate more violent chemical reactions. Although
![]() $s_{j}$
varies with
$s_{j}$
varies with
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
, we kept the overdrive degree
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
, we kept the overdrive degree
![]() $f$
fixed in all the computations. However, we computed the profiles for two different values of
$f$
fixed in all the computations. However, we computed the profiles for two different values of
![]() $\unicode[STIX]{x1D716}_{f}$
, so that the final set of parameter values is
$\unicode[STIX]{x1D716}_{f}$
, so that the final set of parameter values is
and the results are presented in figures 5 and 6, for
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
and
$\unicode[STIX]{x1D716}_{f}=2.0$
and
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
, respectively.
$\unicode[STIX]{x1D716}_{f}=10.0$
, respectively.
It may be observed in figure 5 that for
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
all the computed profiles in the MT model are non-monotonic, regardless of the value of
$\unicode[STIX]{x1D716}_{f}=2.0$
all the computed profiles in the MT model are non-monotonic, regardless of the value of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
. This means that the influence of a low level of activation energy opens the door to non-monotonic profiles, without any regard to the heat of reaction.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
. This means that the influence of a low level of activation energy opens the door to non-monotonic profiles, without any regard to the heat of reaction.

Figure 5. Influence of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the reacting flow: profiles of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the reacting flow: profiles of
![]() $z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for
$z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
and different values of
$\unicode[STIX]{x1D716}_{f}=2.0$
and different values of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
.
However, figure 6 reveals that, for
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
, the value
$\unicode[STIX]{x1D716}_{f}=10.0$
, the value
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=1.0$
yields monotonic MT profiles, whereas higher values of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=1.0$
yields monotonic MT profiles, whereas higher values of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
yield non-monotonic profiles. Therefore, when the activation energy is high, the reaction has to be sufficiently violent in order to produce non-monotonic profiles. Moreover, by a continuity argument we may expect that there exists a threshold value of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
yield non-monotonic profiles. Therefore, when the activation energy is high, the reaction has to be sufficiently violent in order to produce non-monotonic profiles. Moreover, by a continuity argument we may expect that there exists a threshold value of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
which separates monotonic MT profiles from non-monotonic ones and this aspect will be analysed in the sequel.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
which separates monotonic MT profiles from non-monotonic ones and this aspect will be analysed in the sequel.

Figure 6. Influence of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the reacting flow: profiles of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
on the reacting flow: profiles of
![]() $z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for
$z(\unicode[STIX]{x1D709}),~u(\unicode[STIX]{x1D709}),~p(\unicode[STIX]{x1D709}),~T(\unicode[STIX]{x1D709})$
obtained with the MT model (black) and ST model (grey), for
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
and different values of
$\unicode[STIX]{x1D716}_{f}=10.0$
and different values of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
.
5.4 General remark on overdriven detonations
In view of the analysis related to the Hugoniot diagram (figure 1), and the detailed explanation of pathological and overdriven detonations, it may be observed that non-monotonic profiles of overdriven detonations exactly follow the scenario given by Khokhlov (Reference Khokhlov1989) and Sharpe (Reference Sharpe1999). They pass through the point in which (4.20a
) is satisfied, reach the turning point, and then converge to the equilibrium state. This behaviour is predicted in § 4 in the qualitative analysis of non-monotonic profiles. As already mentioned in the analysis of case 1, in the ST ZND model with reversible reaction, studied by Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), this behaviour cannot be obtained, but only the monotonic one. Therefore, the MT assumption appears to be a crucial modelling assumption for capturing the non-monotonic behaviour. In particular, for a certain range of values of the parameters, the single reversible reaction (1.1) in conjunction with the MT assumption yield the same qualitative behaviour in the case of overdriven detonation as the two-step reactions
![]() $A\rightarrow B\rightarrow C$
with an endothermic phase following the exothermic one.
$A\rightarrow B\rightarrow C$
with an endothermic phase following the exothermic one.
It is also interesting to relate the turning points in the state space and the corresponding heat release. In the MT ZND model, taking into account (2.18b
), the heat release is
![]() $Q=z\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
. The turning point in overdriven detonations corresponds to the maximum heat release (see Sharpe Reference Sharpe1999). Consequently, one has
$Q=z\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
. The turning point in overdriven detonations corresponds to the maximum heat release (see Sharpe Reference Sharpe1999). Consequently, one has
and this implies
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}=0$
(see (4.10)–(4.14)), which corresponds to the local extremum in our study. However, there remains a qualitative difference between the overdriven detonations in the MT ZND detonation model with a single reversible reaction, and the same detonations in the two-step model – in the former case there appear more than one local extremum in the profile. This will remain an open question for future studies.
$\tilde{\unicode[STIX]{x1D70F}}_{p}=0$
(see (4.10)–(4.14)), which corresponds to the local extremum in our study. However, there remains a qualitative difference between the overdriven detonations in the MT ZND detonation model with a single reversible reaction, and the same detonations in the two-step model – in the former case there appear more than one local extremum in the profile. This will remain an open question for future studies.
5.5 Qualitative analysis of the reaction rate
The analysis in case 3 to a certain extent confirms the observation already given in case 1 – the major influence on the qualitative behaviour of the continuous reacting profile comes from the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
. However, the heat of reaction
$\unicode[STIX]{x1D716}_{f}$
. However, the heat of reaction
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
becomes important, and actually decisive, when the activation energy is large and suppresses the non-monotonic behaviour.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
becomes important, and actually decisive, when the activation energy is large and suppresses the non-monotonic behaviour.
These findings can be supported by the qualitative analysis of the reaction rate
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
already given in (4.17) by
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
already given in (4.17) by
For
![]() $\unicode[STIX]{x1D716}_{f}$
small enough, the reaction rate
$\unicode[STIX]{x1D716}_{f}$
small enough, the reaction rate
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
is large enough to induce the crossing condition and appearance of a local extremum, i.e. the appearance of non-monotonic profiles. When
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
is large enough to induce the crossing condition and appearance of a local extremum, i.e. the appearance of non-monotonic profiles. When
![]() $\unicode[STIX]{x1D716}_{f}$
is increased, the exponential factor in
$\unicode[STIX]{x1D716}_{f}$
is increased, the exponential factor in
![]() $\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
is dominant and suppresses the non-monotonic behaviour. However, this may be changed if some other parameter, like
$\tilde{\unicode[STIX]{x1D70F}}_{p}^{MT}$
is dominant and suppresses the non-monotonic behaviour. However, this may be changed if some other parameter, like
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
, becomes sufficiently large to prevail and re-establish the non-monotonic profiles. That is what exactly happened in case 3.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
, becomes sufficiently large to prevail and re-establish the non-monotonic profiles. That is what exactly happened in case 3.
5.6 Threshold in the parameter space
The main difference between MT and ST ZND detonation waves lies in the fact that in the MT case there appear two qualitatively different configurations of continuous reacting profiles – non-monotonic and monotonic ones. The non-monotonic behaviour of state variables is directly related to the MT assumption, since both crossing condition and local extremum are consequences of thermal non-equilibrium,
![]() $\unicode[STIX]{x1D6E9}\neq 0$
. However, the parametric analysis revealed that the activation energy
$\unicode[STIX]{x1D6E9}\neq 0$
. However, the parametric analysis revealed that the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
has a major influence on the qualitative behaviour. Therefore, we performed a thorough numerical analysis of the profiles with the aim to determine the threshold in parameter space separating the non-monotonic from the monotonic ones.
$\unicode[STIX]{x1D716}_{f}$
has a major influence on the qualitative behaviour. Therefore, we performed a thorough numerical analysis of the profiles with the aim to determine the threshold in parameter space separating the non-monotonic from the monotonic ones.
Figure 7 presents the threshold in the
![]() $(\unicode[STIX]{x1D716}_{f},f)$
-plane for the fixed value of the reaction heat,
$(\unicode[STIX]{x1D716}_{f},f)$
-plane for the fixed value of the reaction heat,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=1.0$
. It reveals that a threshold exists separating two classes of profiles. It may be observed that the threshold value of the activation energy
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}=1.0$
. It reveals that a threshold exists separating two classes of profiles. It may be observed that the threshold value of the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
increases with the increase of the overdrive degree
$\unicode[STIX]{x1D716}_{f}$
increases with the increase of the overdrive degree
![]() $f$
, and this relation is approximately linear. The threshold values are the same for all the state variables
$f$
, and this relation is approximately linear. The threshold values are the same for all the state variables
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $u$
and
$u$
and
![]() $z$
, but they differ for
$z$
, but they differ for
![]() $T$
– there occurs a temperature drop phenomenon for small values of the overdrive degree
$T$
– there occurs a temperature drop phenomenon for small values of the overdrive degree
![]() $f\geqslant 1.0$
(up to
$f\geqslant 1.0$
(up to
![]() $f\approx 1.1$
). This is indicated in the threshold graph by a narrow dark grey region at the bottom that corresponds to the non-monotonic profiles, but it is related to a temperature drop which occurs in the ST case as well. For other state variables
$f\approx 1.1$
). This is indicated in the threshold graph by a narrow dark grey region at the bottom that corresponds to the non-monotonic profiles, but it is related to a temperature drop which occurs in the ST case as well. For other state variables
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $u$
and
$u$
and
![]() $z$
, this region should be regarded as light grey.
$z$
, this region should be regarded as light grey.

Figure 7. Threshold behaviour in the
![]() $(\unicode[STIX]{x1D716}_{f},f)$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables; non-monotonic profiles of the temperature
$(\unicode[STIX]{x1D716}_{f},f)$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables; non-monotonic profiles of the temperature
![]() $T$
(dark grey region).
$T$
(dark grey region).
Figure 8 presents the threshold in the
![]() $(\unicode[STIX]{x0394}\unicode[STIX]{x1D716},f)$
-plane for the fixed value of the activation energy,
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D716},f)$
-plane for the fixed value of the activation energy,
![]() $\unicode[STIX]{x1D716}_{f}=10.0$
. Numerical analysis showed that the threshold in this case is not linear, and that there is an upper bound for
$\unicode[STIX]{x1D716}_{f}=10.0$
. Numerical analysis showed that the threshold in this case is not linear, and that there is an upper bound for
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
for which the monotonic profiles appear. Also, the peculiar region of solely temperature non-monotonic profiles is found like in the previous case. It has to be noted that our analysis was performed for the value of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}$
for which the monotonic profiles appear. Also, the peculiar region of solely temperature non-monotonic profiles is found like in the previous case. It has to be noted that our analysis was performed for the value of
![]() $\unicode[STIX]{x1D716}_{f}$
for which two kinds of profiles exist; e.g. for
$\unicode[STIX]{x1D716}_{f}$
for which two kinds of profiles exist; e.g. for
![]() $\unicode[STIX]{x1D716}_{f}=2.0$
there exist only non-monotonic profiles in the region of parameter space in our study.
$\unicode[STIX]{x1D716}_{f}=2.0$
there exist only non-monotonic profiles in the region of parameter space in our study.

Figure 8. Threshold behaviour in the
![]() $(\unicode[STIX]{x0394}\unicode[STIX]{x1D716},f)$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables; non-monotonic profiles of the temperature
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D716},f)$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables; non-monotonic profiles of the temperature
![]() $T$
(dark grey region).
$T$
(dark grey region).
Finally, figure 9 presents the threshold in the
![]() $(\unicode[STIX]{x1D716}f,\unicode[STIX]{x0394}\unicode[STIX]{x1D716})$
-plane for the fixed value of the overdrive degree,
$(\unicode[STIX]{x1D716}f,\unicode[STIX]{x0394}\unicode[STIX]{x1D716})$
-plane for the fixed value of the overdrive degree,
![]() $f=1.5$
. Like in the first case, the threshold is approximately linear, and there is a lower bound for the activation energy
$f=1.5$
. Like in the first case, the threshold is approximately linear, and there is a lower bound for the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
for the existence of monotonic profiles. However, since
$\unicode[STIX]{x1D716}_{f}$
for the existence of monotonic profiles. However, since
![]() $f>1.1$
there is no region in the parameter space in which only temperature non-monotonic profiles appear.
$f>1.1$
there is no region in the parameter space in which only temperature non-monotonic profiles appear.

Figure 9. Threshold behaviour in the
![]() $(\unicode[STIX]{x1D716}f,\unicode[STIX]{x0394}\unicode[STIX]{x1D716})$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables.
$(\unicode[STIX]{x1D716}f,\unicode[STIX]{x0394}\unicode[STIX]{x1D716})$
-plane: non-monotonic profiles (white region) and monotonic profiles (light grey region) of all state variables.
6 Summary and forthcoming problems
In this work, we proposed a variant of the ZND detonation model for a chemically reactive mixture with the aim to study the non-equilibrium effects in the detonation wave. The standard ZND model is generalized in two aspects: (i) following Marques Junior et al. (Reference Marques Junior, Soares, Bianchi and Kremer2015), we introduced the reversible chemical reaction, and (ii) we considered a multi-temperature (MT) model for the gaseous mixture established within the framework of extended thermodynamics with the reaction rate derived from the kinetic theory.
One of the essential elements of the ZND detonation model is the finite length reaction zone following the shock wave, where the transformation of the mixture constituents to the detonation products occurs, due to the explosive chemical reaction and consequent energy release. The non-equilibrium effects in this zone determine the structure of the detonation wave solution and the model proposed in this paper allows us to capture many of these non-equilibrium effects, in particular those of thermal nature.
In fact, the MT model of the reactive mixture, combined with a detailed second-order rate law deduced from the kinetic theory, provides a comprehensive description of the detonation solution in terms of the underlying parameters in the detonation process, namely the overdrive degree, activation energy and chemical reaction heat. In particular, the MT model seems to be appropriate to describe the effects due to the transfer of internal energy from reactants to products of the reaction, or vice versa, and to the opposite transfer of kinetic energy. As an outcome, the one-step reversible chemical reaction together with the MT assumption provide a simple framework that properly describes steady overdriven detonations, and yields qualitatively the same results as a two-step reaction.
The main results obtained with the new model are of qualitative and quantitative nature, alike. Qualitatively, the introduction of the MT assumption in the reaction rate implied non-zero temperature difference within the profile and the possible existence of non-monotonic detonation profiles. The latter is a consequence of the more complex equilibrium condition, which, apart from the law of mass action, requires the equilibration of the constituents’ temperatures. However, the monotonicity of the detonation profile strongly depends on the underlying parameters mentioned above, which required a thorough quantitative analysis. By numerical computation, it was shown that the activation energy
![]() $\unicode[STIX]{x1D716}_{f}$
has the major influence on the monotonicity: lower values of the activation energy allow the appearance of non-monotonic profiles, whereas higher values suppress them. This result motivated the computation of the threshold in a pertinent parameter space, which separates monotonic from non-monotonic profiles. It appeared that the threshold value of
$\unicode[STIX]{x1D716}_{f}$
has the major influence on the monotonicity: lower values of the activation energy allow the appearance of non-monotonic profiles, whereas higher values suppress them. This result motivated the computation of the threshold in a pertinent parameter space, which separates monotonic from non-monotonic profiles. It appeared that the threshold value of
![]() $\unicode[STIX]{x1D716}_{f}$
increases with the increase of the overdrive degree
$\unicode[STIX]{x1D716}_{f}$
increases with the increase of the overdrive degree
![]() $f$
. Furthermore, a quantitative analysis showed that the temperatures of the constituents were driven apart by the chemical reaction, supported by the large discrepancy in initial concentrations of the constituents. Even in the quasi-MT case, in which the MT part of the reaction rate is not taken into account, there appears a temperature difference within the profiles.
$f$
. Furthermore, a quantitative analysis showed that the temperatures of the constituents were driven apart by the chemical reaction, supported by the large discrepancy in initial concentrations of the constituents. Even in the quasi-MT case, in which the MT part of the reaction rate is not taken into account, there appears a temperature difference within the profiles.
In our opinion, the inclusion of the MT phenomenon in the mathematical model enhances the description of the detonation profiles of the ZND type. It reveals certain substantially new aspects of the solution that were not captured with the single-temperature (ST) model. Since the MT phenomenon is the hallmark of thermal non-equilibrium in gaseous mixtures, we expect that its influence on the processes in reactive mixtures still has to be thoroughly studied. This opens the perspective for further applications of the MT model. In particular, it may be proved to be a key tool in the following problems:
(i) to investigate the stability of the detonation wave and the effects of the chemistry on stability;
(ii) to extend the MT approach to detonation and linear stability in a quaternary mixture with a bimolecular reversible reaction;
(iii) to describe in more detail the structure of detonation profiles, in particular the transition from the induction zone to the reaction zone;
(iv) to study pathological detonations, or other non-ideal configurations of detonation waves; and
(v) to study the spherical and cylindrical MT ZND detonations.
These are the planned topics of our future studies on detonation and stability. Some of them represent challenging problems, and additional tools will certainly be required. However, we believe that the MT model proposed here can contribute to a comprehensive analysis of the problems and, in particular, to a good description of the effects of chemistry on the detonation structure and propagation of instabilities. For example, when multi-step chemical reactions or other complex chemical mechanisms are involved in the detonation process, the thermal effects due to the coexisting exothermic and endothermic reactions or due to other dissipative processes have a great influence on the structure of the detonation wave and the MT model can be used to capture these effects.
Acknowledgements
This work was supported (D.M. and S.S.) by the Ministry of Education, Science and Technological Development, Republic of Serbia, through the project ‘Mechanics of nonlinear and dissipative systems – contemporary models, analysis and applications’, Project No. ON174016, and (A.J.S.) by the Portuguese Funds FCT, Portugal Project UID/MAT/00013/2013.