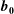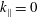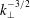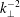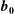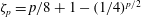1. Introduction
One of the most striking features of strong hydrodynamic (HD) turbulence is the presence of both a complex chaotic spatial/temporal behaviour and a remarkable degree of coherence. The small-scale correlations of turbulent motion are known to show significant deviations from the Gaussian statistics usually expected in systems with a large number of degrees of freedom (She, Jackson & Orszag Reference She, Jackson and Orszag1988). This phenomenon, known as intermittency, has been the subject of much research and controversy since its first experimental observation in 1949 (Batchelor & Townsend Reference Batchelor and Townsend1949). It still challenges any tentative rigorous analytical description from first principles (i.e. the Navier–Stokes equations). Intermittency can be measured by means of the probability density function (PDF) of the velocity differences between two points separated by a distance
$\boldsymbol{\ell }$
. In the presence of intermittency, PDFs develop increasingly stretched and fatter tails when
$\boldsymbol{\ell }$
decreases within the inertial range, showing the increasing probability of large extreme events. This non-self-similarity of PDFs in HD reflects the fact that the energy dissipation of turbulent fluctuations is not space-filling but concentrated in very intense vorticity filaments (Douady, Couder & Brachet Reference Douady, Couder and Brachet1991).
Recently, growing attention has been given to the study of intermittency in the weak turbulence (WT) regime (Falcon, Fauve & Laroche Reference Falcon, Fauve and Laroche2007). WT is the study of the long-time statistical behaviour of a sea of weakly interacting nonlinear dispersive waves, for which a natural asymptotic closure may be obtained. The energy transfer between waves occurs mostly among resonant sets of waves, and the resulting energy distribution, far from a thermodynamic equilibrium, is characterized by a wide power-law spectrum that can be derived exactly (Nazarenko Reference Nazarenko2011). WT is a very common natural phenomenon, studied, for example, in nonlinear optics (Dyachenko et al. Reference Dyachenko, Newell, Pushkarev and Zakharov1992), superfluid helium and processes of Bose–Einstein condensation (Lvov, Nazarenko & West Reference Lvov, Nazarenko and West2003), rotating fluids (Galtier Reference Galtier2003; Mininni & Pouquet Reference Mininni and Pouquet2010) and space plasmas (Galtier Reference Galtier2006). Intermittency has been observed in situations where coherent structures such as sea foam (Newell & Zakharov Reference Newell and Zakharov1992) or freak ocean waves (Janssen Reference Janssen2003) are present. In these particular examples, intermittency is linked to the breakdown of the weak nonlinearity assumption induced by the WT dynamics itself and therefore cannot be considered as an intrinsic property of this regime. A priori, intermittency seems to be at odds with classical WT theory (Zakharov, L’Vov & Falkovich Reference Zakharov, L’Vov and Falkovich1992) because of the random phase approximation, which allows the asymptotic closure and resultant derivation of the WT equations. For example, in fast rotating HD turbulence (i.e. weak inertial wave turbulence) a self-similar behaviour is found from structure functions both numerically and experimentally (van Bokhoven et al. Reference van Bokhoven, Clercx, van Heijst and Trieling2009; Mininni & Pouquet Reference Mininni and Pouquet2010). In this case, vorticity filaments are aligned with the rotation axis, which means, in particular, that the presence of structures is not necessarily indicative of intermittency. The classical WT theory has been extended to the case of random amplitudes (with phases and amplitudes statistically independent), and with the introduction of generating functions the time evolution equation for the PDF of the amplitudes has been derived for three- and four-wave processes (Choi, Lvov & Nazarenko Reference Choi, Lvov and Nazarenko2004; Nazarenko Reference Nazarenko2011). When wave breaking is present, intermittency is predicted with the tail of the PDF arbitrarily far from the exponential distribution required by the Gaussian form. This type of intermittency in Fourier space has been observed numerically and experimentally (Lvov, Nazarenko & Pokorni Reference Lvov, Nazarenko and Pokorni2006; Denissenko, Lukaschuk & Nazarenko Reference Denissenko, Lukaschuk and Nazarenko2007).
Weak magnetohydrodynamic (MHD) turbulence differs significantly from other WT cases because of the remarkable role played by the 2D modes, for which
$k_{\Vert }=0$
(
$\boldsymbol{k}$
is the wavevector in Fourier space and the subscript
$\Vert$
indicates the component of
$\boldsymbol{k}$
parallel to the guide field
$\boldsymbol{b}_{\mathbf{0}}$
). Since Alfvén waves have frequencies
${\it\omega}_{k}^{\pm }=\pm k_{\Vert }v_{A}$
(with
$v_{A}$
the Alfvén speed) and only counter-propagating waves can interact, the three-wave resonance condition,
${\it\omega}_{k_{1}}^{+}+{\it\omega}_{k_{2}}^{-}={\it\omega}_{k_{3}}^{\pm }$
and
$\boldsymbol{k}_{1}+\boldsymbol{k}_{2}=\boldsymbol{k}_{3}$
, implies that at least one mode must have
$k_{\Vert }=0$
(Shebalin, Matthaeus & Montgomery Reference Shebalin, Matthaeus and Montgomery1983; Ng & Bhattacharjee Reference Ng and Bhattacharjee1996), which corresponds analytically to the appearance of a
${\it\delta}(k_{\Vert })$
function (Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000). Thus, this mode acts as a catalyst for the nonlinear interactions. The situation is different for other systems, such as rotating turbulence, where the WT theory does not allow such 2D–3D mode interactions. Such interactions are nevertheless possible, and possibly non-negligible, but their origins are different (Scott Reference Scott2014). The 2D MHD mode is not a wave but rather a form of 2D condensate with a characteristic Alfvén time
${\it\tau}_{A}\sim 1/(k_{\Vert }v_{A})=+\infty$
, and cannot be treated by WT. The standard way to overcome this complication has been to assume that the
$k_{\Vert }$
spectrum of Alfvén waves is continuous across
$k_{\Vert }=0$
. Under this assumption, a
$k_{\bot }^{-2}$
energy spectrum was predicted analytically in the simplest case of zero cross-helicity with a direct cascade towards small scales (Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000, Reference Galtier, Nazarenko, Newell and Pouquet2002). This prediction has been confirmed observationally (Saur et al.
Reference Saur, Politano, Pouquet and Matthaeus2002) and numerically (Bigot, Galtier & Politano Reference Bigot, Galtier and Politano2008b
; Boldyrev & Perez Reference Boldyrev and Perez2009). Note, however, the inherent difficulty, when using a finite periodic numerical box, in smoothly approaching
$k_{\Vert }=0$
, due to discretization of modes, and obtaining a contribution of the three-wave resonance condition equivalent to a pure
${\it\delta}(k_{\Vert })$
function.
In this article, we investigate weak MHD turbulence through high-resolution 3D numerical simulations. We use higher-order statistical tools to demonstrate the presence of intermittency in the cascade direction and show that this property can be understood via a log-Poisson law where the influence of the 2D modes, which belong to strong turbulence, is included. As far as we know, this is the first time that intermittency results for MHD have been shown in the WT regime.
2. Numerical set-up
The incompressible MHD equations in the presence of a uniform magnetic field
$\boldsymbol{b}_{\mathbf{0}}$
read:
$$\begin{eqnarray}\partial _{t}\boldsymbol{z}^{\pm }\mp b_{0}\partial _{\Vert }\boldsymbol{z}^{\pm }+\boldsymbol{z}^{\mp }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\,\boldsymbol{z}^{\pm }=-\boldsymbol{{\rm\nabla}}P_{\ast }+{\it\nu}_{3}{\it\Delta}^{3}\boldsymbol{z}^{\pm },\end{eqnarray}$$
where
$\boldsymbol{z}^{\pm }=\boldsymbol{v}\pm \boldsymbol{b}$
(with
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{z}^{\pm }=0$
) are the fluctuating Elsässer fields,
$\boldsymbol{v}$
the plasma flow velocity,
$\boldsymbol{b}$
the normalized magnetic field (
$\boldsymbol{b}\rightarrow \sqrt{{\it\mu}_{0}{\it\rho}_{0}}\,\boldsymbol{b}$
, with
${\it\rho}_{0}$
a constant density and
${\it\mu}_{0}$
the magnetic permeability),
$P_{\ast }$
the total (magnetic plus kinetic) pressure and
${\it\nu}_{3}$
the hyperviscosity (a unit magnetic Prandtl number is taken). The MHD model offers a powerful description of large-scale astrophysical plasmas, including solar/stellar winds, accretion flows around black holes and intracluster plasmas in clusters of galaxies (Biskamp Reference Biskamp2003). Most often such plasmas are turbulent, with an incompressible energetically dominant component, and embedded in a large-scale magnetic field.
Equation (2.1) is computed using the pseudo-spectral solver TURBO (Teaca et al.
Reference Teaca, Verma, Knaepen and Carati2009; Meyrand & Galtier Reference Meyrand and Galtier2012) with periodic boundary conditions in all three directions. The nonlinear terms are partially de-aliased using a phase-shift method. Two situations will be considered: the full equations (case A) with
$1536^{2}\times 128$
collocation points (while the resolution in the parallel direction is coarser – since the parallel cascade is negligible – the computation box has a dimensional aspect ratio equal to one in real space) and the case where the interactions with the 2D modes are artificially reduced (case B; same spatial resolution as case A). In case B the reduction is obtained by imposing
$\hat{\boldsymbol{v}}(k_{\bot },k_{\Vert }=0)=\hat{\boldsymbol{b}}(k_{\bot },k_{\Vert }=0)=0$
at each time step (where
$\hat{~}$
denotes the Fourier transform). Note that it does not entirely preclude interactions between the 2D modes (
$k_{\Vert }=0$
) and other wave modes (
$k_{\Vert }>0$
). Indeed, as this is a pseudo-spectral simulation, during computation in real space of the nonlinear term (which happens at each iteration), the 2D modes might be fed by wave modes. Thus we cannot exclude totally (although it is certainly relatively small) the effect of the 2D modes on the nonlinear dynamics. The initial state consists of isotropic magnetic and velocity field fluctuations with random phases, such that the total cross-helicity is zero, and the kinetic and magnetic energies are equal to
$1/2$
and localized at the largest scales of the system (mostly wavenumbers
$k\in [2,4]$
are initially excited). There is no external forcing and we fix
${\it\nu}_{3}=4\times 10^{-15}$
and
$b_{0}=20$
. Note that the use of hyperviscosity might influence the intermittency properties by reducing them when the degree of hyperviscosity increases (Spyksma, Magcalas & Campbell Reference Spyksma, Magcalas and Campbell2012). Our analysis is systematically made at a time when the mean dissipation rate reaches its maximum, which corresponds to
$t_{\ast }=2196{\it\tau}_{A}$
with
${\it\tau}_{A}=1/(3b_{0})$
(this value is taken because energy is maximum at
$k_{\Vert }=3$
). An important parameter for our simulations is the ratio
${\it\chi}$
between the Alfvén wave time and the nonlinear time, i.e.
$$\begin{eqnarray}{\it\chi}\sim \frac{k_{\bot }|\boldsymbol{z}_{\bot }|}{k_{\Vert }b_{0}},\end{eqnarray}$$
which must be small (
${\it\chi}\ll 1$
) in the WT regime (thus the 2D modes do not belong to this regime). We have checked that this condition is satisfied in the range of scales where WT is studied (in fact
${\it\chi}<0.03$
for every wavenumber (
$k_{\bot },k_{\Vert }$
) with
$k_{\Vert }\neq 0$
). Note that the initial energies of the 2D modes are taken to be zero in order to favour a dynamics dominated by wave modes. With our (isotropic) initial conditions, anisotropy will develop such that energy will fill the Fourier space with, in particular,
$k_{\bot }\gg k_{\Vert }$
. This development is independent of the aspect ratio of the numerical box.
3. Results
Figure 1(a) shows a snapshot of the magnetic field modulus in a section perpendicular to
$\boldsymbol{b}_{\mathbf{0}}$
for case A. The large-scale coherent structures are mostly the signature of the initial condition, whereas the incoherent small-scale structures are produced by the nonlinear dynamics and the direct energy cascade. It is thought that the presence of such patchy structures is a signature of the weak MHD turbulence regime (we have checked that they are not present in case B). A close-up of the current density modulus is also given (figure 1
b). It reveals a hierarchy of current sheets, which are the dominant dissipative structures. Interestingly, we also see the formation of less intense filaments.
Figure 1. (a) Snapshot of the magnetic field modulus (on a linear scale) in a section perpendicular to
$\boldsymbol{b}_{\mathbf{0}}$
(case A). (b) Close-up of the current density modulus (on a logarithmic scale) corresponding to the marked (square) region in (a). The line integral convolution technique (Cabral & Leedom Reference Cabral and Leedom1993) reveals a hierarchy of current sheets as well as the formation of less intense filaments.
We shall quantify the turbulence statistics by introducing the bi-dimensional axisymmetric Elsässer energy spectra
$E^{\pm }(k_{\bot },k_{\Vert })$
, which are linked to the Elsässer energies
${\mathcal{E}}^{\pm }=\langle {\boldsymbol{z}^{\pm }}^{2}\rangle /2$
of the system (
$\langle \,\rangle$
denotes an integration over the physical space) by the double integral
${\mathcal{E}}^{\pm }=\iint E^{\pm }(k_{\bot },k_{\Vert })\text{d}k_{\bot }\text{d}k_{\Vert }$
. Figure 2 shows the results for case A. In order to improve the statistics the spectrum
$E^{+}$
is plotted after an integration from
$k_{\Vert }=1$
to 50 (red curve). In this way we suppress the contribution of the 2D modes and limit the cumulative contribution of the dissipative parallel scales, which can eventually alter the scaling law at the smallest scales. A spectrum compatible with the WT prediction in
$k_{\bot }^{-2}$
is clearly observed (see inset). Hence, this observation and the small value of
${\it\chi}$
(not shown) may be considered as a clear signature of WT. In addition, we plot the spectrum
$E^{-}$
for the 2D modes (black curve) in order to show that it behaves very differently, possessing a flat spectrum. The spectrum
$E^{-}$
(or
$E^{+}$
in the latter case) behaves similarly, as is expected for zero cross-helicity. Note that the
$-2$
spectrum appears only after a transition in which the scaling is shallower (
${\sim}\!-3/2$
). A possible interpretation of this transition is that, in order to emerge, WT needs a sufficient amount of resonant triadic interactions (otherwise one can fall in the discrete WT regime (Nazarenko Reference Nazarenko2011)), which can be found only at sufficiently small scales.
Figure 2. Transverse wavenumber Elsässer energy spectra,
$\int _{1}^{50}E^{+}(k_{\bot },k_{\Vert })\text{d}k_{\Vert }$
(red) and
$E^{-}(k_{\bot },k_{\Vert }=0)$
(black) for case A. The former spectrum is also shown when it is compensated by
$k_{\bot }^{2}$
(inset). The wavelet spectrum from the sampled slices (see text) is also shown (blue). The shaded area corresponds to the scales for which the intermittency study is conducted.
The detection of the WT regime can also be made directly from the wavenumber–frequency spectrum. In order to do this, during a time window around
$t_{\ast }$
, we follow the magnetic energy fluctuations in Fourier space at a given
$k_{\bot }$
(
$=64$
to be in the inertial range) and for
$k_{\Vert }$
between 0 and
$\pm 64$
. Then, we perform a time-Fourier transform of these signals and build the dispersion relation
${\it\omega}(k_{\Vert })$
. The result is shown in figure 3. As we can see, the signal is mainly concentrated near the linear dispersion relation of the Alfvén wave, confirming that the waves are weakly nonlinear. The weak nonlinear effects manifest themselves in a broadening of the (
${\it\omega},k_{\Vert }$
)-distribution with respect to the
${\it\omega}=2k_{\Vert }b_{0}$
curve. This result suggests that we are not in the discrete regime of WT (Nazarenko Reference Nazarenko2011). Importantly, we also see the contribution of coherent structures which correspond to a band at constant low frequency. Interestingly the same kind of observation has been made in the context of Bose–Einstein condensates (Nazarenko & Onorato Reference Nazarenko and Onorato2007).
Figure 3. Wavenumber–frequency spectrum of the magnetic energy fluctuations at
$k_{\bot }=64$
. The colour map is normalized to the maximal value of the spectrum at each fixed
$k_{\Vert }$
. Note the presence of a factor
$1/2$
in the frequency normalization because the energy (square of a field) is used.
We use wavelet coefficients to define the Elsässer field increments, denoted by
${\it\delta}z^{\pm }(\boldsymbol{x},\boldsymbol{\ell }_{\bot })$
, between two points separated by a vector
$\boldsymbol{\ell }_{\bot }$
transverse to
$\boldsymbol{b}_{\mathbf{0}}$
. For more details on the wavelet method used and the justifications for using it please refer to Kiyani et al. (Reference Kiyani, Chapman, Sahraoui, Hnat, Fauvarque and Khotyaintsev2013). Intermittency can be investigated through the PDFs of these increments for different spatial lags
$\ell _{\bot }$
. We do not report an intermittency analysis for vector separations along
$\boldsymbol{b}_{\mathbf{0}}$
because the corresponding range of scales is too narrow. The results from this analysis are shown in figure 4. For case A (a), strong intermittency is revealed through the development of more extended and heavier tails at a shorter distance
$\ell _{\bot }$
. The result is drastically different when the interaction with the 2D modes is artificially reduced (case B, b) – in this case intermittency is strongly reduced, with PDFs approaching closer to a Gaussian form. Removing the interactions between the 2D modes and other wave modes is equivalent theoretically to removing the three-wave resonant interactions which support the WT dynamics. Therefore, what we see in case B is mainly the result of the non-resonant (including quasi-resonant) triadic interactions, which are asymptotically negligible in the pure regime of WT (the contribution of four-wave resonances can be discarded because it leads theoretically to a steep
$-7/3$
spectrum (Sridhar & Goldreich Reference Sridhar and Goldreich1994) that is not observed – see below).
Figure 4. PDFs of the Elsässer field increments (given by the wavelet coefficients)
${\it\delta}z^{+}$
for case A (a) and B (b), and for four distances
$\ell _{\bot }$
(
$L_{0}$
is the size of the numerical box) corresponding to the circles inside the shaded area in figure 2. The PDFs are shifted vertically for clarity.
We further analyse intermittency through the symmetric structure functions:
$$\begin{eqnarray}S_{p}=\langle ({\it\delta}z^{+})^{p/2}\rangle \langle ({\it\delta}z^{-})^{p/2}\rangle =C_{p}\ell _{\bot }^{{\it\zeta}(\,p)},\end{eqnarray}$$
where
${\it\zeta}(\,p)$
are the scaling exponents that are to be measured in the inertial range (homogeneous axisymmetric turbulence is assumed) and
$C_{p}$
are some constants. The unusual definition (3.1) for the structure functions is related to the exact solution of the WT equations, which involves a power-law relation for the product of the Elsässer spectra. This information will be used below to develop a WT intermittency model. The study is conducted on several transverse planes and the fluctuations at different scales
$\ell _{\bot }$
are calculated using the undecimated discrete wavelet transform detailed in Kiyani et al. (Reference Kiyani, Chapman, Sahraoui, Hnat, Fauvarque and Khotyaintsev2013); a 12-point wavelet was chosen to overcome the limitations of normal two-point structure functions. Utilizing the periodic boundary conditions of the simulation allows us to construct large contiguously sampled signals in each plane; the ensemble of fluctuations is then constructed from a union of all the fluctuations generated from the signal in each of the planes. This ensures that we have a large sample to form our statistics. Figure 5 shows that case A is characterized by strong intermittency such that
${\it\zeta}(\,p)$
cannot be fitted with a trivial (linear) law, nor by the MHD log-Poisson model previously derived (Müller, Biskamp & Grappin Reference Müller, Biskamp and Grappin2003, equation (3)) when
$g=2$
(hereafter MBG-weak) or
$g=4$
(hereafter MBG-IK), which correspond respectively to weak (Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000) and strong (Kraichnan Reference Kraichnan1965) turbulence (with
${\it\delta}z\sim \ell _{\bot }^{1/g}$
). We also report the scaling exponents for case B, which behave differently as a result of the
$k_{\Vert }=0$
modes being removed. Interestingly, for case B, the data follow the same curvature as the strong MHD turbulence model (MBG-IK) and, as can be seen from the value of
${\it\zeta}(2)$
, are compatible with a
$k_{\bot }^{-3/2}$
spectrum. Note that in this case elongated structures (current sheets) are also present. Also, the origin of the
$-2$
scaling found in case A seems not to be linked to any field discontinuities (since then we should probably get a
$k_{\bot }^{-2}$
spectrum for case B).
Figure 5. Scaling exponents
${\it\zeta}(\,p)$
for cases A and B with a superimposed plot of the log-Poisson model (equation (3.4)) for
$C_{0}=1.08$
. The models MBG-weak and MBG-IK are also plotted (see details in text) for comparison. The errors quoted correspond to one standard error of the parameter fits.
We want to build a model that fits the exact solution of WT (energy spectrum in
$k_{\bot }^{-2}$
), which in physical space implies
${\it\zeta}(2)=1$
. Even if this power-law relation between the Fourier and physical spaces is not mathematically exact, it is clearly observed in figure 5 and can be considered as an excellent constraint for the intermittency model. Following the original development (She & Leveque Reference She and Leveque1994) we then define:
$$\begin{eqnarray}S_{p}=C_{p}\langle {\it\varepsilon}^{p/2}\rangle \ell _{\bot }^{p/2},\end{eqnarray}$$
where
$\langle {\it\varepsilon}\rangle$
is the mean dissipation rate of energy and
$\langle {\it\varepsilon}^{p/2}\rangle \sim \ell _{\bot }^{{\it\mu}_{p/2}}$
. The latter relation is the so-called refined similarity hypothesis (Kolmogorov Reference Kolmogorov1962). The log-Poisson distribution for the dissipation leads to the general relation (She & Leveque Reference She and Leveque1994; Biskamp Reference Biskamp2003):
$$\begin{eqnarray}{\it\mu}_{m}={\it\mu}(m)=-m{\it\Delta}+C_{0}(1-{\it\beta}^{m}),\end{eqnarray}$$
where
${\it\Delta}$
and
${\it\beta}$
are linked to the co-dimension
$C_{0}$
of the dissipative structures such that
$C_{0}={\it\Delta}/(1-{\it\beta})$
. We shall consider the co-dimension as a free parameter that will be estimated directly from the data. The system is closed by defining the value of
${\it\Delta}$
, which is related to the dissipation of the most singular structures, such that
$\ell _{\bot }^{-{\it\Delta}}\sim E_{\infty }/{\it\tau}_{\infty }$
, where
$E_{\infty }$
is the energy dissipated in these most singular structures and
${\it\tau}_{\infty }\sim \ell /v_{\ell }$
is the associated time scale.
${\it\Delta}$
may be obtained by considering the following remarks. Weak MHD turbulence behaves very differently from isotropic MHD, because in the former case the regime is driven at leading order by three-wave resonant interactions, with the scattering of two of these waves on a 2D/third mode. (In fact, weak MHD turbulence is not applied in a thin layer around
$k_{\Vert }=0$
(Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000) where strong turbulence may be expected.) These 2D modes are also important in characterizing dissipative structures (see figure 1): these structures, which look like vorticity/current sheets, are strongly elongated along the parallel direction and are therefore mainly localized around the
$k_{\Vert }=0$
plane in Fourier space. If we assume that the dynamics of the 2D modes are similar to the dynamics of two-dimensional strong turbulence, then it seems appropriate to consider that the time scale entering in the intermittency relation may be determined by (Biskamp Reference Biskamp2003)
$v_{\ell }\sim \ell _{\bot }^{1/4}$
, hence the value
${\it\Delta}=3/4$
. Note that the importance of the 2D modes on intermittency has already been emphasized in figure 4, where the PDFs are closer to a Gaussian when the interactions with them are greatly reduced. Taking all this into account, from (3.1) to (3.3) we finally obtain the intermittency model:
$$\begin{eqnarray}{\it\zeta}(\,p)=\frac{p}{8}+C_{0}-C_{0}\left(1-\frac{3}{4C_{0}}\right)^{p/2}.\end{eqnarray}$$
The plot for this model is superimposed in figure 5(top, red line) for a fractal co-dimension
$C_{0}=1.08$
, which is the value that best fits the data (a nonlinear least-squares regression is used). The model fits the numerical simulation perfectly, thus we may infer that weak MHD turbulence is mainly characterized by vorticity/current sheets. Note that the parameter
${\it\beta}$
in this model measures the degree of intermittency: non-intermittent turbulence corresponds to
${\it\beta}=1$
, whereas the limit
${\it\beta}=0$
represents an extremely intermittent state in which the dissipation is concentrated in one singular structure. According to the value obtained here,
${\it\beta}\simeq 1/4$
(with
$C_{0}\simeq 1$
), we might conclude that weak MHD turbulence appears more intermittent than strong isotropic MHD turbulence, for which
${\it\beta}=1/3$
.
4. Conclusion
This work presents numerical simulations of weak MHD turbulence. The key novel result in this work is that, for the first time, strong intermittency is shown to exist in such weakly interacting systems. The intermittency, as manifested in the statistical scaling exponents
${\it\zeta}(\,p)$
, is modelled with a log-Poisson law that provides excellent agreement with the results from the simulations. This model, which is a based on the She–Leveque type intermittency model (She & Leveque Reference She and Leveque1994) with additional physical insight from WT, allows one to make statements regarding the topology of the structures responsible for the intermittency directly from the behaviour of the
${\it\zeta}(\,p)$
function. In the case of our work, where the 2D modes play a central role via the dissipative structures, the model shows that the topology of these structures is very much like parallel sheets. Our results are important with respect to the interpretation of plasma turbulence observations and provide objective insights into the typically heated discussions on what constitutes turbulence in systems such as plasmas, which host a rich variety of waves and instabilities and at the same time are inherently nonlinear. The results of our work confirm that the quintessential signature of turbulence in the form of intermittency is not simply a property of strong turbulence, but may also be found in a medium where WT is present (Nazarenko Reference Nazarenko2011). Incompressible MHD is a unique example in WT because its dynamics, and so its existence, depends on the 2D modes. Since the 2D modes via the resonance interactions are responsible for intermittency, we can conclude that intermittency will always be found in weak MHD turbulence.
An illustration of the potential impact of our results can be seen in solar physics, where intermittency has been reported from a study of the magnetic field in active regions of the solar photosphere(Abramenko et al. Reference Abramenko, Yurchyshyn, Wang, Spirock and Goode2002), and where it is known that a strong guide field is present, as indicated by the presence of coronal loops. This intermittency could potentially be interpreted as a signature of the presence of a weak MHD turbulence regime instead of a strong regime. This interpretation also has a strong impact on coronal heating modelling (Bigot, Galtier & Politano Reference Bigot, Galtier and Politano2008a ).
In conclusion, contrary to common belief, the presence of intermittency in MHD turbulence is not necessarily a proxy of strong turbulence – our results show that intermittency alone cannot be the sole discriminator between weak and strong MHD turbulence regimes.
Acknowledgements
We thank one of the anonymous referees for his comments about the discrete WT regime. The computing resources for this research were made available through the UKMHD Consortium facilities, funded by STFC grant number ST/H008810/1. This work was granted access to the HPC resources of [CCRT/CINES/IDRIS] under the 2012 allocation [x2012046736] made by GENCI. R.M. acknowledges financial support from the French National Research Agency (ANR) contract 10-JCJC-0403. K.H.K. acknowledges financial support from the ANR-JC project THESOW. S.G. acknowledges Université Paris-Sud.
