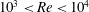1 Introduction
The flow around aerodynamic bodies undergoing rapid variation in angle of attack exhibits stalling behaviour that differs from the steady case. This dynamic stall is characterised by the separation of flow from near the leading edge and the development of a strong vortex originating from the shear layer at the point of separation (McCroskey, Carr & McAlister Reference McCroskey, Carr and McAlister1976; McCroskey Reference McCroskey1982; Carr Reference Carr1988). The ubiquity of such unsteady separating flows means that a more in-depth understanding of the processes governing dynamic stall would be advantageous to a variety of applications. Highly manoeuvrable aircraft, for example, are susceptible to leading-edge stall during high-pitch-rate manoeuvres (Lang & Francis Reference Lang and Francis1985), and the oscillatory relative velocity experienced by helicopter rotor blades (Ham & Garelick Reference Ham and Garelick1968; Harris & Pruyn Reference Harris and Pruyn1968) or wind turbines (Larsen, Nielsen & Krenk Reference Larsen, Nielsen and Krenk2007; Ferreira et al. Reference Ferreira, van Kuik, van Bussel and Scarano2009; Buchner, Smits & Soria Reference Buchner, Smits and Soria2014; Buchner et al. Reference Buchner, Lohry, Martinelli, Soria and Smits2015a ; Buchner, Soria & Smits Reference Buchner, Soria and Smits2015b ) can induce similar flow behaviour. In general, flow separation and stall is thought of as an operationally deleterious phenomenon; it can, for example, be a source of inefficiency, or can cause structural vibration or produce noise. Its existence in nature, however, shows that this is not always the case. Bird and insect flight utilise the leading-edge vortex created by dynamic stall to provide high instantaneous suction for acceleration and manoeuvring purposes (Ellington et al. Reference Ellington, Van den Berg, Willmott and Thomas1996; Shyy et al. Reference Shyy, Lian, Tang, Viieru and Liu2008), and there has been recent interest in applying observations from nature to the development of micro air vehicles utilising unsteady propulsion (Ol, Eldredge & Wang Reference Ol, Eldredge and Wang2009b ).
The behaviour of such flows is nonlinear and highly complex, with significant variation as a result of relatively small changes in conditions. As such, developing a fundamental understanding of the physical processes governing dynamic stall is challenging. Nevertheless, the potentially broad practical applications of dynamic stall motivate the need for a more thorough phenomenological understanding of its governing physics before practical manipulation can be fully realised. One question that may be posited, and that has been insufficiently addressed in the literature to date, is that of Reynolds number dependence.
Much of the work on Reynolds number effects has been performed with a view to applications in fighter jet manoeuvrability and helicopter rotor dynamics and is therefore conducted at high Reynolds numbers or for high Mach numbers. Of the literature that does exist at relatively low Reynolds number, such as that of Baik et al. (Reference Baik, Bernal, Granlund and Ol2012), the focus has been on the practicalities (from an applied engineering perspective) of force production. Such studies have mostly failed to find any significant variation with Reynolds number above a threshold of order
$O(10^{3})$
. This is because the forces, in the simplest analysis, scale with the circulation bound to the airfoil as well as the added-mass effect due to airfoil acceleration, neither of which are directly a function of Reynolds number (Brennen Reference Brennen1982; Anderson Reference Anderson2011), but depend only on the velocity differential across the shear layer at the point of separation (Buchner et al.
Reference Buchner, Smits and Soria2014, Reference Buchner, Soria and Smits2015b
). This shear layer strength is not a function of Reynolds number, and indeed it has been shown that the dimensionless circulation contained within the large-scale two-dimensional vortex structures associated with dynamic stall does not depend on Reynolds number (Buchner & Soria Reference Buchner and Soria2014). Baik & Bernal (Reference Baik and Bernal2012) present counter-evidence for pitching and plunging airfoils with Reynolds number of order
$O(10^{4})$
. They present evidence of variation in force production with Reynolds number in the range 10 000–30 000, despite no variation in the mean flow field being observed. That article is unclear as to the reason why there is a Reynolds number dependence in the forces produced, but provides some evidence of turbulent transition in the separated flow at approximately
$Re=10\,000$
.
The majority of the effort in studying Reynolds number effects has been focused on laminar–turbulent transition in the boundary layer and its effect on the incipient stages preceding the massive leading-edge separation that characterises dynamic stall, while relatively little attention has been paid to the effect of Reynolds number on the post-stall coherent structures, such as the leading-edge vortex. The work of Shreck, Faller & Robinson (Reference Shreck, Faller and Robinson2002), for example, falls into this category, using shear stress sensors placed in the vicinity of the leading edge to show small but consistent variation in the initial flow reversal angle with Reynolds number in the range
$4.8\times 10^{4}\leqslant Re\leqslant 1.92\times 10^{5}$
. This effect is shown to be coupled with the variation in boundary layer transition location measured in Shreck, Faller & Helin (Reference Shreck, Faller and Helin1998). No conclusions are drawn regarding the behaviour of the post-stall flow field. Ol et al. (Reference Ol, Bernal, Kang and Shyy2009a
) state that, although the Reynolds number has an effect on the size of the laminar separation bubble before stall occurs, there appears to be only a very limited effect of Reynolds number on the post-stall behaviour. The work of Ramesh et al. (Reference Ramesh, Gopalarathnam, Granlund, Ol and Edwards2014) empirically indicates that Reynolds number plays a role in affecting the total suction that may be maintained at the leading edge before boundary layer separation occurs; again, no conclusion is made regarding the effect of Reynolds number on the flow after separation has occurred. The surface pressure measurements on a pitching airfoil of Robinson & Wissler (Reference Robinson and Wissler1988) and of Conger & Ramaprian (Reference Conger and Ramaprian1994) agree that the effect of Reynolds number is confined to the magnitude of the pressure coefficient peak at the leading edge, and that this effect is only very minor.
Studies such as these have led to a conventional wisdom that Reynolds number is of minor importance to dynamic stall, with its effects being primarily confined to the pre- or incipient stages of stall. There exists, however, a dearth of data relating to the Reynolds number dependence of the post-stall flow field behaviour. For the post-stall behaviour, this assumption of Reynolds number independence has been insufficiently validated and there remain questions as to the behaviour of the flow as it evolves beyond the initial boundary layer separation and dynamic stall vortex rollup.
One of the primary effects of increasing Reynolds number in any flow is a transition to an unstable, turbulent, three-dimensional state. Three-dimensional, three-component velocity data from the tomographic particle image velocimetry (PIV) experiments of Buchner et al. (Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012) reveal the existence of three-dimensional substructure in a dynamic stall vortex at
$Re=7500$
as it convects past the trailing edge of a pitching plate, and into the wake region. The observations consist of significant spanwise velocities in the dynamic stall vortex core, as well as vortex filaments associated with, and azimuthally wrapped about, the dynamic stall vortex. An example of such a structure encircling the dynamic stall vortex as it convects into the wake is illustrated by isosurfaces of
$Q$
-criterion in figure 1(b), taken from Buchner et al. (Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012). The free-stream direction is from left to right and the trailing-edge position is indicated by a red arrow. The large-eddy simulations of Garmann & Visbal (Reference Garmann and Visbal2011) show a similar development of the three-dimensional structure within a dynamic stall vortex system, and show that the rate at which this three-dimensionality develops is highly dependent on Reynolds number. At
$Re=5000$
, the flow in Garmann & Visbal’s study is predominantly two-dimensional throughout the majority of the plate’s upstroke, with strong three-dimensional structures appearing only upon growth and shedding of the secondary and tertiary vorticity (figure 1
a). At this Reynolds number, the three-dimensional substructure is highly organised, consisting primarily of vortex filaments azimuthally aligned about the perimeter of the dynamic stall vortex. In contrast, at
$Re=40\,000$
, the three-dimensional substructure is much finer in scale, less clearly organised and it appears much more rapidly at the beginning of dynamic stall than at the lower Reynolds number. Similar transitional behaviour is observed numerically by Visbal (Reference Visbal2009) for flow over a plunging airfoil at Reynolds numbers between
$Re=10\,000$
and
$Re=60\,000$
. Neither Garmann & Visbal (Reference Garmann and Visbal2011), Buchner et al. (Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012) nor Visbal (Reference Visbal2009) explore the development and Reynolds number dependence of this substructure in a quantifiable way.
Figure 1. Isosurfaces of
$Q$
-criterion showing the evolution of three-dimensional structure in the form of azimuthally oriented vortex filaments in a dynamic stall vortex. (a) The large-eddy simulations of Garmann & Visbal (Reference Garmann and Visbal2011) at
$Re=5000$
, with two different motion smoothing parameters (Eldredge, Chengjie & Ol Reference Eldredge, Chengjie and Ol2009), and (b) the tomographic PIV measurements of Buchner et al. (Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012) at
$Re=7500$
, experimentally confirming the existence of three-dimensional structures of this type. In each case the free stream is from left to right. The tomographic PIV measurement covers only the wake region, with a red arrow marking the trailing-edge location.
Understanding the organised three-dimensional substructure of the dynamic stall vortex, and the physical processes leading to this structure, is important because it is these features that are precursors to the transition to fully turbulent flow. Such turbulent structures take their energy from the mean velocity gradient through the production term,
$\langle u_{i}^{\prime }u_{j}^{\prime }\rangle \unicode[STIX]{x2202}U_{i}/\unicode[STIX]{x2202}x_{j}$
, of the turbulent kinetic energy equation and thus must affect the mean evolution of the dynamic stall vortex. The present study investigates the existence of such features, and seeks to quantify their appearance and evolution, as well as providing a physical explanation for the production of such structures in the dynamic stall vortex system.
2 Problem description
The flow studied here results from a non-periodic rapid pitch–hold–return manoeuvre of a flat plate. Upon completion of the motion sequence, the plate is held steady to allow the generated structures associated with flow separation to convect and evolve downstream. In studying a single, non-periodic, pitch–hold–return motion, a single dynamic stall event can be observed in isolation.
The two primary parameters relevant to this flow are the Reynolds number, based on the chord of the pitching plate
$$\begin{eqnarray}\displaystyle Re_{c}=\frac{U_{\infty }c}{\unicode[STIX]{x1D708}}, & & \displaystyle\end{eqnarray}$$
and the dimensionless pitch rate, by which the airfoil motion may be characterised, defined as
$$\begin{eqnarray}\displaystyle K_{c}=\frac{c\dot{\unicode[STIX]{x1D703}}}{2U_{\infty }}, & & \displaystyle\end{eqnarray}$$
where
$\dot{\unicode[STIX]{x1D703}}$
is the steady angular velocity of the flat plate,
$U_{\infty }$
the free-stream velocity and
$c$
the chord length.
Figure 2. Pitch-ramp motion profile used in the experiments, with temporal locations of phase-ensemble measurements marked.
The plate kinematics chosen for this experiment dictate that the plate pitches about an axis coincident with its leading edge at a constant dimensionless rate of
$K_{c}=0.7$
to a maximum pitch angle of
$\unicode[STIX]{x1D703}=40^{\circ }$
, holds steady for
$0.1T$
(where
$T$
is the time taken to complete the movement) and returns to the zero-pitch-angle position at the same dimensionless rate. Figure 2 illustrates the kinematics used in the present study. This motion was chosen to fit within a canonical framework developed by the AIAA Low Reynolds Discussion Group (now the ‘Massively Separated Flows Discussion Group’) (Ol et al.
Reference Ol, Altman, Eldredge, Garmann and Lian2010). There is a wealth of literature on pure pitch-ramp cases, but in subsequently returning to zero pitch angle the current motion profile provides a richer test case, with the opportunity to study a wider range of transient phenomena. The pause time at the maximum pitch-up position is largely motivated by experimental limitations to the pitch control mechanism, but also serves to separate out the effects of pitch cessation and the beginning of the pitch-down motion.
Angular acceleration of the plate is sufficiently high such that the time taken to accelerate to within 99 % of the constant pitch rate
$K_{c}=0.7$
is approximately two orders of magnitude less than the
${\sim}O(0.5{-}1.0T)$
time scale of the dynamic stall vortex formation. Using the definition of Eldredge et al. (Reference Eldredge, Chengjie and Ol2009), the motion smoothing parameter is
$a\sim O(100)$
. The motion may thus be considered a perfect pitch ramp. Koochesfahani & Smiljanovski (Reference Koochesfahani and Smiljanovski1992, Reference Koochesfahani and Smiljanovski1993) showed that the initial acceleration rate served primarily to delay or bring forward the production of circulation but had no significant effect on the flow structures themselves, once produced. The computations of Gendrich, Koochesfahani & Visbal (Reference Gendrich, Koochesfahani and Visbal1995) support this conclusion.
Selection of plate kinematics and free-stream flow properties is based on the desire to produce data relevant to bio-inspired flight. The dimensionless rate of
$K_{c}=0.7$
is in the range to be expected for birds and insects during rapid perching and accelerative manoeuvres (Ol et al.
Reference Ol, Eldredge and Wang2009b
), while the Reynolds numbers tested cover the range of typical flight Reynolds numbers experienced by small birds and large insects (Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008). Measurements are presented for chord-based Reynolds numbers
$Re_{c}=1500$
, 2500, 4000, 5000, 7500 and 10 000. This Reynolds number range is relevant to the design of unsteadily propelled micro air vehicles (MAVs), but is also of particular fundamental physical interest, as there is evidence that the unsteady separating flow is transitional or exhibits highly organised turbulence in this range (Garmann & Visbal Reference Garmann and Visbal2011; Buchner et al.
Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012).
3 Experiment
Experiments were performed to examine the structure and evolution of the flow structures arising due to the pitching motion described in the previous section. Results from three experimental databases are discussed. All three experiments were performed under identical conditions, but differ in the orientation of the measurement domain over which PIV velocity data are acquired, and the facility in which the experiments were performed.
Figure 3. Arrangement of measurement domains relative to pitching plate and primary flow structures. (a) HT_XZ experiment, (b) VT_XZ experiment, and (c) relative placement of all measurement domains. Coordinate system as indicated, with a right-handed Cartesian coordinate system used.
Two-component, two-dimensional (2C-2D) time-resolved velocity data from PIV were acquired in a plane normal to the surface of the pitching plate, aligned with the
$X$
–
$Y$
coordinate plane, and spanwise equidistant from the walls of the water tunnel test section. The basic two-dimensional vortex structures produced by the pitching plate can be observed in this plane. Complete details of this
$X$
–
$Y$
plane experiment are described in Buchner & Soria (Reference Buchner and Soria2014). The spanwise variation of the basic two-dimensional flow was measured by performing planar 2C-2D PIV in an
$X$
–
$Z$
oriented plane parallel to the resting position of the plate (figure 3). By measuring in this plane, an axially oriented slice of the leading-edge dynamic stall vortex is observed. Two experimental databases in this plane orientation are available, differing in the height,
$\unicode[STIX]{x0394}h$
, of the measurement plane above the suction surface of the plate. The measurement domain in one instance is positioned at
$\unicode[STIX]{x0394}h=0.10c$
such that it captures an area of flow in the region between the plate’s surface and the core of the dynamic stall vortex, whilst in the other instance the measurement plane cuts directly through the core of the leading-edge dynamic stall vortex at
$\unicode[STIX]{x0394}h=0.30c$
. It has been observed by Buchner & Soria (Reference Buchner and Soria2014) that the leading-edge vortex core convects downstream at an approximately constant
$\unicode[STIX]{x0394}h\approx 0.3c$
after
$t/T\approx 1.00$
. The
$\unicode[STIX]{x0394}h=0.30c$
measurement is conducted in a vertical water tunnel facility (VT) at the Laboratory for Turbulence Research in Aerospace and Combustion (LTRAC), with symmetric no-slip spanwise end boundary conditions, while the
$\unicode[STIX]{x0394}h=0.10c$
experiment is performed in the LTRAC horizontal water tunnel (HT) under the same kinematic and scaling parameters but with asymmetric spanwise end boundary conditions. The horizontal water tunnel is an open channel such that one end of the pitching plate apparatus terminates perpendicularly to a no-slip wall, but the other end intersects a free surface. In each case, the test section is five chord lengths wide. It will be shown that the form of and range of scales inhabited by the three-dimensional structure in the leading-edge dynamic stall vortex system are not significantly affected by the end boundary conditions for the experiments performed. The use of two separate tunnels serves to confirm that the phenomena observed are not facility-dependent. It must be acknowledged, however, that experimental boundary conditions imposed by the testing facilities have not been completely eliminated from the experiments, and this should be kept in mind if making inferences about the truly infinite-span case.
To maintain succinctness, each experiment shall henceforth be abbreviated according to the relevant facility and plane of measurement. Cases VT_XY, VT_XZ and HT_XZ refer to experiments in the vertical tunnel and free surface horizontal channel, and in the
$X$
–
$Y$
and
$X$
–
$Z$
Cartesian planes, respectively. The conditions tested by each experiment are listed in table 1.
Table 1. Conditions of the experiment.
The airfoil used in the experiments is a flat plate with circular rounded leading and trailing edges, constructed of carbon fibre, and with a thickness-to-chord ratio of 2.3 %. Plate kinematics are controlled by a Parker–Hannifin AT6400 Indexer and Rorze RD-023MS motor driver, programmed using Motion Architect 6000 software. The drive motor microstepping resolution is
$80\,000$
steps per revolution, allowing smooth motion with no measurable vibration. The positional error due to control system response and the finite stiffness of the pitching plate were determined via a correlative procedure outlined in Buchner & Soria (Reference Buchner and Soria2014). It was shown that the deviation from the commanded motion was strictly less than
$1.8^{\circ }$
, with an uncertainty of
$\pm 0.27^{\circ }$
, which occurred due to overshoot at the cessation of motion. The overshoot increased in magnitude with Reynolds number, but remains small compared to the pitch amplitude. The measured motion profiles at
$Re=1500$
and
$Re=10\,000$
are shown in figure 4.
Table 2. Imaging parameters in each experiment.
Figure 4. Pitch-ramp motion profile used in the experiments (measured values).
Each experiment has a unique optical image acquisition set-up, with details given in table 2. The
$X$
–
$Y$
plane experiment (case VT_XY) provides time-resolved data, with 100 image pairs being acquired during the pitch motion period and 217 samples taken at each dimensionless time,
$t/T$
. Two PCO DiMax cameras were used in this experiment, one at high resolution capturing flow separation at the leading edge, and the other at lower resolution in the wake region. Only data from the high-resolution leading-edge camera are presented here. This camera has a
$2016\times 2016$
pixel complementary metal oxide semiconductor (CMOS) sensor, with the physical size of each pixel being
$11~\unicode[STIX]{x03BC}\text{m}\times 11~\unicode[STIX]{x03BC}\text{m}$
. In each
$X$
–
$Z$
plane experiment, phase-locked data are collected only at the phases marked A, B, C and D in figure 2, corresponding to dimensionless times
$t/T=0.76$
,
$1.00$
,
$1.50$
and
$2.00$
. A single ImperX Bobcat digital charge-coupled device (CCD) camera was used in the experiment HT_XZ. The camera has a
$4904\times 3280$
pixel high-resolution sensor array and each pixel is
$7.4~\unicode[STIX]{x03BC}\text{m}$
square. Images are acquired with a spatial resolution of
$0.039~\text{px}~\unicode[STIX]{x03BC}\text{m}^{-1}$
. Two PCO4000 cameras were used in the vertical tunnel experiment (VT_XZ), and the velocity fields are stitched together to provide a continuous measurement across the width of the tunnel test section with a spatial resolution of
$0.024~\text{px}~\unicode[STIX]{x03BC}\text{m}^{-1}$
. Each PCO4000 camera has a sensor size of
$4008\times 2672$
pixels, and a physical pixel size of
$9~\unicode[STIX]{x03BC}\text{m}\times 9~\unicode[STIX]{x03BC}\text{m}$
. Each camera is fitted with a 100 mm focal length Zeiss lens.
An in-house-developed iterative and adaptive multigrid cross-correlation parallelised digital particle image velocimetry (MCCDPIV) algorithm (Soria Reference Soria1996) is used for cross-correlation of particle image pairs. The accuracy and uncertainty of this algorithm for 2C-2D PIV image cross-correlation is assessed in Soria (Reference Soria1996) and Soria, Cater & Kostas (Reference Soria, Cater and Kostas1999). The random error associated with the PIV cross-correlation algorithm is approximately
$0.06$
pixels. Given that the standard error of the mean statistics reduces with the square root of the sample size, the standard error for each experiment is 0.18 %, 0.14 % and 0.05 % of the free-stream velocity in the VT_XY, VT_XZ and HT_XZ experiments, respectively. Derivative quantities such as vorticity tend to have higher uncertainty associated with their measurement. As outlined by Buchner & Soria (Reference Buchner and Soria2014), the uncertainty in the instantaneous vorticity in these experiments using the MCCDPIV algorithm is
$c\unicode[STIX]{x1D714}/U_{\infty }=7.8$
, with a standard error of the mean vorticity estimate of
$0.19$
. The final interrogation window (IW) sizes for the VT_XY, VT_XZ and HT_XZ experiments are 20, 32 and 48 pixels, respectively. The interrogation windows are overlapped such that the spacing of the resultant vector fields are 0.74 %, 0.67 % and 0.41 % of the respective chord length in each case. The relevant PIV processing parameters used in each experiment are given in table 3. In each case, image intensities are spatially homogenised using a sliding mean filter, and background reflections are removed via ensemble mean image subtraction. Bright reflections and regions with insufficient lighting are digitally masked.
Several validation procedures are applied to reduce the incidence of spurious, non-physical, vectors. A maximum particle displacement criterion is imposed, followed by a local dynamic mean operator test (Raffel et al.
Reference Raffel, Willert, Wereley and Kompenhans2007) on a
$3\times 3$
neighbourhood of vectors. Correlation quality is increased through application of an eight-point Hart filter, as well as a local
$\unicode[STIX]{x1D712}^{2}$
test utilising 13 points. Vectors resulting from a peak correlation coefficient less than
$0.6$
are rejected. Any vectors invalidated by these criteria are replaced via mean vector interpolation from nearest neighbours.
Table 3. Processing parameters in each experiment.
4 Results and discussion
4.1 Two-dimensional base flow
When a plate pitches rapidly to high angle of attack, the boundary layer separates from its surface and vortices are formed at both the leading and trailing edges. The strength of these vortices grows with time as circulation is continually added from the points of separation until each vortex sheds and convects away from the plate’s surface. This process is documented in detail by Buchner & Soria (Reference Buchner and Soria2014). Figure 5 illustrates the evolution of the basic two-dimensional flow by contours of ensemble-averaged vorticity derived from the PIV measurements. The fields are at
$Re=10\,000$
at selected times
$t/T=0.225$
, 0.45, 0.775 and 1.00. Every fourth velocity vector is given. Both the pitch-up and pitch-down motions produce a series of small vortices from the trailing edge, which interact and convect downstream, forming a jet of fluid downwards in the wake. At the leading edge, which is fixed in space, circulation accumulates in a tight leading-edge dynamic stall vortex, whose interaction with the no-slip condition at the suction surface of the plate subsequently produces secondary vorticity opposite in sign to the primary dynamic stall vortex.
Figure 5. Ensemble-averaged vorticity fields at
$Re=10\,000$
: (a–d)
$t/T=0.225$
, 0.45, 0.775 and 1.00.
This article focuses on the behaviour of the leading-edge dynamic stall vortex only. The morphology of the dynamic stall vortex is illustrated in detail in figure 6, with a comparison between
$Re=1500$
and
$Re=10\,000$
. During its formation, the dynamic stall vortex interacts with the no-slip boundary condition at the surface of the plate. This interaction induces secondary vorticity between the primary dynamic stall vortex and the plate’s surface, which is illustrated in figure 6 in red. During the return stroke of the plate, there is a rapid growth in the strength and extent of the secondary vorticity. This vorticity is opposite in sign to the primary vortex, and has been previously observed in similar flows (e.g. Soria et al.
Reference Soria, New, Lim and Parker2003; Ol Reference Ol2009; Buchner et al.
Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012). Eslam Panah, Akkala & Buchholz (Reference Eslam Panah, Akkala and Buchholz2015) concluded that this no-slip interaction and production of secondary vorticity plays a key role in regulating the leading-edge vortex strength.
It is during the plate’s return stroke that this small secondary region of opposite vorticity peels off from the plate’s suction surface and begins to envelop the primary dynamic stall vortex from the upstream side. Significant variation is observed at this point in the behaviour of this vorticity as a function of Reynolds number. At low Reynolds number, some fraction of the secondary vortex separates from the bulk and begins to orbit the primary dynamic stall vortex. Figure 6(a) shows just this behaviour, with the clockwise orbit of the secondary vorticity at this point in time halfway complete. The separation occurs at roughly
$t/T=0.55$
, coinciding with the re-acceleration of the plate in the return stroke. The orbiting component rejoins the bulk secondary vorticity after completing a single revolution. At higher Reynolds numbers of
$4000$
,
$5000$
and above, this effect is observed to weaken (see Buchner & Soria Reference Buchner and Soria2014, figures 13 and 14), and the secondary vorticity tends instead to remain coherent, slowly spreading about the periphery of the primary dynamic stall vortex from the upstream side.
Figure 6. Spanwise-normalised vorticity (
$c\unicode[STIX]{x1D714}_{z}/U_{\infty }$
) distribution in the vicinity of the leading edge at
$t/T=0.76$
for (a)
$Re=1500$
and (b)
$Re=10\,000$
. Diagrams are presented in coordinates aligned with the pitching plate, and the free-stream direction is from (a) to (b).
These flow features form the two-dimensional basic flow from which three-dimensional features may evolve, a process that is explored in subsequent sections.
4.2 A centrifugal instability
A centrifugally unstable rotating flow develops vortex filaments oriented azimuthally about the primary unstable vortex, and with a short wavelength in the axial direction (Williamson Reference Williamson1996). These are often referred to as ‘streamwise vortices’ or ‘rib vortices’ (Wu et al. Reference Wu, Sheridan, Soria and Welsh1994); or, when occurring in a boundary layer over a curved surface, as ‘Görtler vortices’ (Görtler Reference Görtler1954). The strongly rotational nature of the current flow suggests that centrifugal instabilities may play a role, and indeed the three-dimensional structure identified by Garmann & Visbal (Reference Garmann and Visbal2011) and Buchner et al. (Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012) associated with the leading-edge dynamic stall vortex appears to take a form consistent with the existence of such a centrifugal instability.
Rayleigh (Reference Rayleigh1917) developed a criterion for the identification of centrifugally unstable flow for the case of axisymmetric inviscid rotating flows with closed streamlines. Rayleigh’s criterion states that for instability to occur the angular momentum of the fluid must decrease with radial distance from the centre of rotation. The leading-edge vortex in the current experiment is however exposed to an asymmetric strain field imposed due to the no-slip boundary condition at the surface of the plate. The problem of determining the stability characteristics of the flow thus requires an analysis applicable to generalised two-dimensional base flows where the perturbation and growth of a three-dimensional centrifugal instability do not occur symmetrically about the axis of the revolving fluid. Sipp & Jacquin (Reference Sipp and Jacquin2000) provide such a criterion as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}=2(R^{-1}\Vert \boldsymbol{u}\Vert +\unicode[STIX]{x1D6FA})(\unicode[STIX]{x1D714}_{z}+2\unicode[STIX]{x1D6FA})<0, & & \displaystyle\end{eqnarray}$$
where
$R$
is the algebraic radius of curvature of the unstable streamline, defined by Theisel (Reference Theisel1995) as
$$\begin{eqnarray}\displaystyle R=\Vert \boldsymbol{u}\Vert ^{3}(u^{2}v_{x}-v^{2}u_{y})^{-1}. & & \displaystyle\end{eqnarray}$$
This modification to the Rayleigh criterion is valid for generalised two-dimensional base flows and, unlike the earlier formulation of Bayly (Reference Bayly1988), accounts for the Coriolis force due to constructing the equations of motion in a frame rotating with the fluid with angular velocity
$\unicode[STIX]{x1D6FA}$
. In the current experiment the angular velocity
$\unicode[STIX]{x1D6FA}$
of the reference frame is equal to the pitch rate of the plate,
$\dot{\unicode[STIX]{x1D703}}$
.
The non-axisymmetric Rayleigh criterion reveals that areas of centrifugal instability exist about the perimeter of the leading-edge vortex core, especially in the neighbourhood of the secondary vortex. These regions are indicated in figure 7 by grey shading. As outlined by Rayleigh (Reference Rayleigh1917), centrifugal instability arises because of the need for a rotating flow to satisfy conservation of both kinetic energy and angular momentum. In (4.1), a mismatch between the signs of the vorticity and streamline curvature causes a centrifugally unstable condition such that, for both of these quantities to be conserved, rotation begins about the azimuthal streamlines. It is the interaction between the counter-rotating primary and secondary dynamic stall vortices that yields instability in this flow.
Figure 7. Centrifugal instability in the leading-edge dynamic stall vortex system. Examples at
$t/T=1.00$
for (a)
$Re=1500$
, (b)
$Re=5000$
and (c)
$Re=10\,000$
. Regions susceptible to centrifugal instability, as defined by
$\unicode[STIX]{x1D6FD}<0$
per (4.1), are shaded grey. Blue and red contour lines, respectively, represent negative and positive spanwise vorticity and are spaced at
$c\unicode[STIX]{x1D714}_{z}/U_{\infty }=10$
intervals.
Being a second-order derivative quantity, the modified Rayleigh criterion (4.1) is subject to noise, but it is clear from figure 7 that the leading-edge vortex is bounded by a region of instability with, in particular, the existence of a strong negative region of the Rayleigh criterion in the region directly upstream of the leading-edge vortex. This is the region of genesis of three-dimensionality in the leading-edge vortex, and matches the region in which significant three-dimensional structure has been observed to develop most strongly both experimentally (Buchner et al. Reference Buchner, Buchmann, Kilany, Atkinson and Soria2012) and computationally (Garmann & Visbal Reference Garmann and Visbal2011).
The theoretical linear growth rate of a centrifugal instability in the inviscid limit, and for vanishingly small axial wavelengths, can be estimated for these flows by the real part of the square root of the negative of the Rayleigh criterion
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{c}=\sqrt{-\unicode[STIX]{x1D6FD}}\in \mathbb{R}. & & \displaystyle\end{eqnarray}$$
The maximum growth rate for the centrifugal instability of the leading-edge vortex occurs in the region bounded by the leading-edge vortex and the secondary vorticity and is plotted in units of radians per second in figure 8 against dimensionless time,
$t/T$
, for Reynolds numbers
$1500$
,
$5000$
,
$7500$
and
$10\,000$
. These values were computed from the temporally resolved data of the case VT_XY. Uncertainty in the measurement of the growth rate, due to velocity measurement uncertainty, is represented by the shaded areas. The growth rate curves collapse well with the scaling
$\hat{\unicode[STIX]{x1D70E}}_{c}=c\unicode[STIX]{x1D70E}_{c}/U_{\infty }$
, except in a temporal window towards the end of the pitching cycle, within which there remains a trend of increasing dimensionless growth rate with Reynolds number. Growth-rate curves for
$Re=2500$
and
$4000$
follow the same behaviour, but are omitted for clarity.
A separate, phase-averaged experiment was conducted under the same conditions as experimental case HT_XZ, and symbols representing the growth rate calculated from these data are shown in figure 8(b) for
$Re=5000{-}10\,000$
. These results match the case VT_XY growth-rate results within the error estimate, indicating that these results are repeatable and insensitive to spanwise end boundary conditions.
Figure 8. Growth rate of the centrifugal instability against dimensionless time, showing increasing growth rate with Reynolds number for
$Re=1500$
,
$5000$
,
$7500$
and
$10\,000$
. (a) Dimensional quantities, and (b) normalised by the chord length and free-stream velocity. Shading indicates the growth-rate error estimate.
Four distinct temporal domains can be observed in the behaviour of the scaled growth-rate curves given in figure 8(b). These are delineated in the figure as (i), (ii), (iii) and (iv). During the initial stages of the plate’s pitch-up motion, region (i), the leading-edge vortex is small and close to the plate’s leading edge, making estimation of any unstable growth rate inaccurate. Data are not presented in this region. Region (ii) encompasses the latter stages of the plate’s pitch-up motion, and significant variability may be observed in the instability growth rate. During this time, multiple small discrete vortices are formed, which subsequently merge into the primary dynamic stall structure. This rapidly changing topology drives the fluctuations in centrifugal growth rate seen during this period. The curves are, however, seen to collapse with Reynolds number within the amplitude of this variability. During the third temporal domain, region (iii), approximately corresponding with the return pitch motion of the plate, the collapse with Reynolds number is incomplete, suggesting that the instability is more persistent at higher Reynolds numbers, and we may expect to see this impact the three-dimensional arrangement of the flow during this latter part of the pitching cycle. Subsequent to cessation of the plate’s pitching motion, region (iv), the growth rate is experimentally indistinguishable from zero.
Figure 9. Phase-averaged (a,b) and root-mean-square (c,d) streamwise velocity component. Values at
$y=0.3c$
; (a,c)
$Re=1500$
and (b,d)
$Re=10\,000$
.
Figure 10. Phase-averaged and root-mean-square streamwise velocity component, for
$t/T=0.76$
(a,b) and
$t/T=1.00$
(c,d). Values at
$y=0.3c$
; (a,c)
$Re=1500$
and (b,d)
$Re=10\,000$
.
4.3 Spanwise measurements
To investigate the impact of the centrifugal instability on the three-dimensional arrangement of the leading-edge vortex system, velocity data are required over the spanwise dimension. Experiments were performed in the
$X$
–
$Z$
plane for this purpose, as described in § 3, allowing the direct observation of any spanwise variability.
Figure 9 shows the ensemble average and root mean square (r.m.s.) of the streamwise velocity component in the plane of measurement for case VT_XZ, plotted against the streamwise coordinate. The large negative streamwise phase-averaged velocity values in figure 9(a,b) confirm the position of this measurement plane within the leading-edge vortex core, slightly below its centre. In both the
$Re=1500$
and
$Re=10\,000$
cases the peak reverse streamwise flow occurs at
$t/T=1.00$
and is of order
$O(1)$
. As time progresses, the peak reverse streamwise flow location travels aftwards with the passage of the leading-edge vortex, passing the trailing edge by
$t/T=2.00$
. As the dynamic stall vortex passes, the velocity field re-establishes a value close to
$\bar{u}/U_{\infty }=1$
. Given the large velocity gradients near the vortex core, the mean velocity observed in the
$X$
–
$Z$
measurement plane is quite sensitive to small variations in the core location relative to the
$X$
–
$Z$
measurement plane and in the morphology of the leading-edge vortex. For example, a clear difference between the early-time (
$t/T=0.76$
) streamwise phase-averaged velocity profiles at each Reynolds number is observed. The positive peak at
$x/c\approx 0.3$
is a result of the more complex flow field at
$Re=1500$
illustrated in figure 6(a). The switch in sign between
$t/T=0.76$
and
$t/T=1.00$
relates to the movement of the secondary vorticity out of the
$X$
–
$Z$
measurement plane as it completes its orbit around the primary leading-edge vortex.
Despite the sensitivity of the mean streamwise velocity to the precise relative placement of the
$X$
–
$Z$
measurement plane and leading-edge dynamic stall vortex core, the r.m.s. values given in figure 9(c,d) are instructive in providing an understanding of the dynamic stall vortex’s structure. This is especially true away from the vortex’s core location, where the velocity gradients in the
$y$
-direction are lower and the observed velocities are thus less sensitive to the measurement plane’s location. In general, the r.m.s of the streamwise velocity component in the
$X$
–
$Z$
measurement plane displays three peaks. This is especially true at early times. In order of increasing streamwise position, the locations of the three peaks correspond to the upstream edge, core and downstream edge of the leading-edge vortex system. At higher Reynolds numbers, illustrated in figure 9(b,d) for
$Re=10\,000$
, the downstream peak is less prominently separated from the core peak. The upstream peak, however, remains distinct from the core and under scaling by the free-stream velocity is of greater magnitude, reaching
$\sqrt{u^{\prime }u^{\prime }}/U_{\infty }\approx 0.65$
, compared to
$\sqrt{u^{\prime }u^{\prime }}/U_{\infty }\approx 0.20$
at
$t/T=0.76$
in the
$Re=1500$
case.
A comparison of the VT_XZ case data in the
$X$
–
$Z$
plane with that from the VT_XY case is necessary to ensure consistency between the experiments and to assess the level of variability across the
$Z$
-span. Figure 10 directly compares the streamwise velocity component from the
$X$
–
$Y$
plane measurement with that taken from the
$X$
–
$Z$
plane, averaged across the
$Z$
-span of the measurement. A comparison of the r.m.s. of the streamwise velocity component is also made. The curves for mean and r.m.s. of the streamwise velocity component generally follow the same pattern in each experiment, with variability in the
$Z$
direction accounting for discrepancies between the curves of up to approximately 10 %–15 % of the maximum mean velocity value. That these discrepancies are small leads us to conclude that the experiments are comparable and that spanwise statistical variability in the VT_XZ experiment is small compared to the maximum flow velocities.
The vorticity fields shown in figure 11 provide some insight into the arrangement of the flow within the dynamic stall vortex at smaller scales. The figure represents the
$X$
–
$Z$
plane at
$\unicode[STIX]{x0394}h=0.3c$
, from the VT_XZ experiment. The contours depict instantaneous through-plane vorticity,
$c\unicode[STIX]{x1D714}_{y}/U_{\infty }$
, at
$t/T=0.76$
for three Reynolds numbers,
$Re=1500$
,
$5000$
and
$10\,000$
. The core of the dynamic stall vortex lies at approximately
$x/c=0.3$
, and the free-stream direction is from top to bottom. In each of the higher Reynolds number measurements (figure 11
b,c), a spanwise band of positive and negative fluctuating vorticity may be seen upstream of the vortex core. This feature does not appear at
$Re=1500$
(figure 11
a), in which case it may be observed that the flow’s arrangement is dramatically different. At
$Re=1500$
, the dynamic stall vortex substructure appears dominated by larger-scale features, with a size of the order of the vortex radius.
Small-scale features are also seen within the dynamic stall vortex core at
$Re=5000$
and
$Re=10\,000$
. The region dominated by fluctuating vorticity in these figures is smaller for the higher Reynolds number case. At
$Re=5000$
, there appears to be a region of strong fluctuation immediately downstream of the dynamic stall vortex core, at approximately
$0.5<x/c<0.6$
. This is consistent with the more distinct downstream r.m.s. peak in figure 10(a), compared to the
$Re=10\,000$
measurement in figure 10(b).
Figure 11. Instantaneous normalised vorticity fields. Case VT_XZ at
$t/T=0.77$
and
$\unicode[STIX]{x0394}h=0.3c$
, for (a)
$Re=1500$
, (b)
$Re=5000$
and (c)
$Re=10\,000$
.
The
$\unicode[STIX]{x0394}h=0.1c$
measurement plane (case HT_XZ) allows the visualisation of the region of the flow between the dynamic stall vortex core and the surface of the pitching plate. Such an instantaneous velocity field captured at
$t/T=1.00$
at
$Re=7500$
is represented in figure 12. Shading of blue through red indicates the magnitude of the velocity in the spanwise direction. It is clear that some phenomenon exists wherein positive, and subsequently negative, regions of spanwise velocity are arranged alternating in the spanwise direction. The spanwise velocity fluctuations manifest over a broad range of scales, and would be consistent with the existence of vortices lying parallel to, and intersecting, the measurement plane.
Overlaid on the colour map are contour lines of normalised through-plane vorticity,
$c\unicode[STIX]{x1D714}_{y}/U_{\infty }$
. The arrangement of vorticity in this instantaneous field differs from the arrangement of the spanwise velocity component fluctuations. Vortices are seen intersecting the plane of measurement upstream of the dynamic stall vortex core, consistent with the vorticity fields in figure 11. As with the spanwise velocity component fluctuations, these occur on a range of scales. There is relatively little through-plane vortex activity in the region between the vortex core and the plate (
$0.2<x/c<0.5$
) but rather activity is restricted almost exclusively to the more upstream region.
Figure 12. Instantaneous velocity field at
$Re=7500$
, case HT_XZ at
$t/T=1.00$
. The
$Y$
-coordinate is
$y=0.1c$
. Colours represent spanwise velocity, and solid black lines represent normalised through-plane vorticity contours.
Figure 13. (a) Illustration of the structure of the leading-edge dynamic stall vortex, showing the relative position of each spanwise
$X$
–
$Z$
measurement plane and coloured contours representing spanwise vorticity measured at
$Re=10\,000$
and
$t/T=1.00$
. The key features visible in each measurement plane are illustrated in (b) for
$\unicode[STIX]{x0394}h=0.1c$
and (c) for
$\unicode[STIX]{x0394}h=0.3c$
.
The measurements in figures 11 and 12 suggest a general three-dimensional arrangement consisting of vortices lying in the
$\unicode[STIX]{x0394}h=0.1c$
plane, which are wrapped azimuthally around the upstream side of the dynamic stall vortex intersecting both the
$\unicode[STIX]{x0394}h=0.1c$
and
$\unicode[STIX]{x0394}h=0.3c$
planes. This substructure arrangement might be expected in the case of a centrifugal instability of the leading-edge dynamic stall vortex (Görtler Reference Görtler1954; Williamson Reference Williamson1996; Canals & Pawlak Reference Canals and Pawlak2011), and thus supports the results of the inviscid Rayleigh analysis discussed in § 4.2 for Reynolds numbers above approximately 4000. There is some evidence that these vortex filaments also exist at the downstream bound of the dynamic stall vortex, perhaps as a continuation of the azimuthally wrapped filaments observed on the upstream edge. This is made most clear at intermediate Reynolds numbers by the downstream fluctuating vorticity in figure 11(b). Illustrations are provided in figure 13 depicting the salient features in each plane of measurement.
4.4 Scale decomposition via wavelet analysis
4.4.1 Method
The non-periodic, statistically non-stationary nature of the current experiment presents a challenge in attempting to quantify the scale-dependent features of the flow. Fourier analysis and other related methods may not be used. In decomposing a signal into sinusoidal functions, these methods necessitate an assumption of signal periodicity over the domain of measurement, thus discarding information regarding non-periodic, unsteady features of the flow. The wavelet transform provides a method by which non-periodic signals can be decomposed into a finite series of basis functions at various scales without loss of spatio-temporal information. Wavelet decomposition was applied to the present experimental dataset.
Wavelet analysis decomposes a signal using a localised, non-periodic basis function, called the wavelet function, which forms an orthogonal basis for the signal. The well-proven Daubechies wavelet construction (Daubechies Reference Daubechies1988) is chosen for this study due to its common use and simplicity of implementation. The Daubechies wavelet has also previously been applied to turbulent flows, both computationally and experimentally (see e.g. Qian & Weiss Reference Qian and Weiss1993; Katul & Parlange Reference Katul and Parlange1994; Weng & Lau Reference Weng and Lau1994; Li et al. Reference Li, Takei, Ochi, Saito and Horii1999). The wavelet decomposition function,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(x)=\mathop{\sum }_{k=0}^{N-1}(-1)^{k}c_{k}\unicode[STIX]{x1D719}(2x+k-N+1), & & \displaystyle\end{eqnarray}$$
is derived by taking differences, as described in Newland (Reference Newland1995), from a scaling function,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}(x)=\mathop{\sum }_{k=0}^{N-1}c_{k}\unicode[STIX]{x1D719}(2x-k),\quad N\text{ even}, & & \displaystyle\end{eqnarray}$$
which has the basic property that it may be dilated horizontally along the decomposition dimension,
$x$
, without loss of similarity. Additionally,
$\unicode[STIX]{x1D719}(x)$
will be orthogonal to itself in any translated position
$\unicode[STIX]{x1D719}(x-m)$
, where
$m$
is an integral value. The decomposition dimension may be spatial, or temporal, and in the present study is defined spatially. This scaling function achieves its dilative qualities through its self-referential construction wherein
$\unicode[STIX]{x1D719}(x)$
is dependent on values of
$\unicode[STIX]{x1D719}$
in the neighbourhood of
$x$
. The terms,
$c_{k}$
, in (4.4) and (4.5) are scalar coefficients, the selection of which must necessarily satisfy certain strict conditions in order for the wavelet expansion to form an accurate representation of the original signal, as outlined in Strang & Fix (Reference Strang and Fix1973) and Strang (Reference Strang1989).
A family of Daubechies wavelet bases is built by varying the number of coefficients used. An error analysis was performed on the accuracy of reconstruction of discrete velocity fields representing the dynamic stall obtained from 2C-2D PIV data. It is found that the r.m.s. error,
$\unicode[STIX]{x1D716}$
, of the reconstructed signal from the original is generally less than 1 % of the flow velocity, but with a minimum error using a Daubechies wavelet with 16 coefficients (figure 14
a). The resulting D16 wavelet function is shown in figure 14(b), with the range over which the function is defined normalised to unity.
Figure 14. Numerical reconstruction error (a), and the Daubechies D16 wavelet basis function (b).
The discrete wavelet transform is sequentially mapped in two spatial dimensions using Mallat’s pyramid algorithm (Mallat Reference Mallat1989). High-pass,
$\boldsymbol{H}_{j}$
, and low-pass,
$\boldsymbol{L}_{j}$
, filters, based on the coefficients of the scaling and wavelet functions, are applied to the velocity field, and the resulting approximation coefficients downsampled before further filtering is applied.
For a signal of length
$L_{0}$
, the wavelet transform can be calculated using Mallat’s filter cascade with
$J$
levels. If
$\boldsymbol{a}^{J}=f(\boldsymbol{x})$
, where
$\boldsymbol{a}^{J}$
represents the initial choice of approximation coefficients, then for
$j=J,(J-1),\ldots ,1$
the low- and high-pass filters can be applied as per (4.6) to successive approximation coefficients to distil the coefficients of each scale from the original signal:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\boldsymbol{a}^{j-1}=\boldsymbol{L}_{j}\boldsymbol{a}^{j},\\ \boldsymbol{b}^{j-1}=\boldsymbol{H}_{j}\boldsymbol{a}^{j}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The detail coefficients
$\boldsymbol{b}^{j}$
represent the decomposition of the signal at each scale,
$j$
.
The 2C-2D PIV data are padded to ensure a signal of size
$2^{m}\times 2^{n}$
samples, where
$m$
and
$n$
are positive integral values. The resulting multi-resolution scale decomposition consists of nine separate scales.
The signal can be reconstructed, once the desired filtering and/or modification has been performed in wavelet space, using the reverse process as in (4.7):
$$\begin{eqnarray}\displaystyle \boldsymbol{a}^{j}=\boldsymbol{L}_{j}^{\text{T}}\boldsymbol{a}^{j-1}+\boldsymbol{H}_{j}^{\text{T}}\boldsymbol{b}^{j-1}. & & \displaystyle\end{eqnarray}$$
If the process is completed for
$j=1,2,\ldots ,J$
, then
$\boldsymbol{a}^{J}=\hat{f}(\boldsymbol{x})$
, where
$\hat{f}(\boldsymbol{x})$
is the fully reconstructed velocity field. If it is desired that only a subset of the original velocity field’s composition is represented, then the range of scales,
$j$
, can be restricted. The physical spatial wavelength range to which each scale relates can be approximated by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{j}=\frac{L_{0}}{2j}, & & \displaystyle\end{eqnarray}$$
where
$L_{0}$
is the size of the measurement domain, and
$j$
is the scale number, ranging from 0 through
$(J-1)$
. The minimum measurable wavelength depends on the ratio of physical spatial resolution and the sample length of the measurement. This comparison must, however, be approached with caution: scale and wavelength are not entirely synonymous, as no assumption of periodicity is made by the wavelet transform. The characteristic length scales for each level of the multi-resolution analysis for the present data are given in table 4.
Table 4. Characteristic length scales for the multi-resolution wavelet analysis.
Figure 15. Multi-resolution scale reconstruction by wavelets. Scales 2–5 (top to bottom) at
$Re=7500$
,
$t/T=1.00$
, displaying details of spanwise variation in vortex substructure. Red colouring represents the streamwise velocity, while spanwise velocity is represented by the blue contours. Data are taken from (a) case VT_XZ and (b) case HT_XZ, at
$\unicode[STIX]{x0394}h=0.3c$
and
$\unicode[STIX]{x0394}h=0.1c$
, respectively.
4.4.2 Reconstructed scales
Over the set of nine scales reconstructed from the phase ensemble data, there exist significant variations in both structural arrangement and energy content by scale. Scale 0, a constant, represents a spatial mean of the velocity field, while increasing scale number implies diminishing feature size. Each one of these scale reconstructions represents features of the flow that vary over a length scale of the order given by table 4. Mean-square maps of selected reconstructed scales are presented in figure 15 to show regions of the flow in which fluctuations of each velocity component exist at each characteristic length scale. The examples shown are for the flow at
$Re=7500$
and
$t/T=1.00$
. The colour map represents the streamwise velocity component, while the line contours represent the spanwise velocity component. The free-stream direction is from top to bottom. The largest scale is at the top, with progressively smaller scales placed beneath. The largest and the very smallest scales show nothing of relevance to the present investigation and are not illustrated: scales 0 and 1 are larger than the diameter of the dynamic stall vortex, and scales 7 and 8 are small and dominated by measurement noise. Scales 2–6 illustrate the most interesting aspects of the present flow. Axes on the left side represent reconstructed scales from the vertical tunnel experiment (case VT_XZ) at
$\unicode[STIX]{x0394}h=0.3c$
, while axes on the right side represent the same scale reconstructions from the horizontal tunnel experiment (case HT_XZ) closer to the pitching plate surface at
$\unicode[STIX]{x0394}h=0.1c$
.
The bulk rotation of the dynamic stall vortex induces negative streamwise velocities between the vortex core and plate’s suction surface. The large region of high-magnitude streamwise velocity in scale 2 at the
$\unicode[STIX]{x0394}h=0.1c$
measurement plane is related to this. It is not seen in the
$\unicode[STIX]{x0394}h=0.3c$
measurement plane, which lies closer to the vortex axis. Similarly, a difference between the measurement planes may be observed at scale 3; the
$\unicode[STIX]{x0394}h=0.1c$
plane intersects the secondary vorticity upstream of the primary dynamic stall vortex, and the imprint of this feature may be seen in the reconstruction of this scale, whereas it does not appear in the
$\unicode[STIX]{x0394}h=0.3c$
plane. Spanwise variation is observed to be minimal in the secondary vorticity, with fluctuation in the streamwise velocity component dominating, which indicates that at this scale the secondary vorticity is primarily two-dimensional.
Figure 16. Temporal evolution of scale 4 at
$Re=7500$
, from case HT_XZ data: (a–d)
$t/T=0.76$
,
$1.00$
,
$1.50$
and
$2.00$
. Red colouring represents the streamwise velocity, while spanwise velocity is represented by the blue contours.
Despite the inhomogeneous, transient nature of the flow, the wavelet analysis reveals that periodic content does exist in the spanwise direction at scales 4 and 5, that is, at characteristic length scales,
$\unicode[STIX]{x1D706}$
of
$0.15c{-}0.2c$
. This spanwise periodicity is seen in both measurement planes, with fluctuating velocities of the order of
$0.25U_{\infty }$
in both the streamwise and spanwise components. In the VT_XZ case, where the measurement plane lies coincident with the dynamic stall vortex core, the primary feature at these scales is a region of spanwise-periodic fluctuation in the streamwise velocity component at the upstream boundary of the dynamic stall vortex. This feature also figures prominently in the scales reconstructed from the HT_XZ case data, closer to the wall. Significantly, this short-period spanwise periodicity lies in the region one would expect to see short-period spanwise periodic structures arising from the centrifugal instability shown in previous sections. In the measurement plane at
$\unicode[STIX]{x0394}h=0.1c$
, other features also become apparent. There exists a strong spanwise periodicity in the fluctuating spanwise velocity component directly between the leading-edge vortex core and the pitching plate’s surface. The magnitude of this feature appears to be of the same order as the upstream fluctuations in streamwise velocity, as well as inhabiting the same range of scales, and is consistent with the instantaneous structure shown in figure 12 as well as the structural hypothesis illustrated in figure 13.
The way in which these features evolve with time can be seen in figure 16, which illustrates the fluctuating streamwise and spanwise velocity components at scale 4 for
$t/T=0.76$
,
$1.00$
,
$1.50$
and
$2.00$
. The figure shows only Reynolds number
$Re=7500$
. It can be seen that the spanwise-periodic variability upstream of the dynamic stall vortex core begins early, prior to
$t/T=0.76$
, and continues to strengthen until
$t/T=1.50$
. Some weakening of this feature is seen in the
$t/T=2.00$
map, as the dynamic stall vortex system passes out of the measurement domain.
Figure 17 provides some insight into the dependence of this three-dimensional leading-edge vortex substructure on Reynolds number. Velocity reconstructions are presented at scale number 4, at phase
$t/T=1.00$
, for each of the Reynolds numbers measured,
$Re=1500$
to
$Re=10\,000$
. Data are taken from the VT_XZ measurement case. The spanwise-periodic fluctuation in the streamwise velocity component upstream of the vortex system appears strongly at Reynolds number
$Re=4000$
and above, but only faint signs of its presence can be seen at
$Re=1500$
and
$Re=2500$
. This is consistent with the changes in vortex substructure observed between the different Reynolds numbers in figure 11.
This variation of the substructure with Reynolds number can be seen even more clearly when plotting the through-plane normalised vorticity,
$c\unicode[STIX]{x1D714}_{y}/U_{\infty }$
, reconstructed at scale number 4. Two Reynolds numbers are chosen and the early-time evolution of the flow is illustrated in figure 18. At
$Re=5000$
, the three-dimensional spanwise periodicity associated with the centrifugal instability is clear from
$t/T=0.76$
, whereas at
$Re=1500$
there is no clear organised fluctuation at this scale early in the flow’s evolution. At
$t/T=1.00$
, upon completion of the plate’s pitching motion, similar spanwise periodicity is observed in the lower Reynolds number case, but this is intermittent. What this demonstrates is that, although the dynamic stall vortex system appears to develop significant three-dimensionality due to centrifugal instability at Reynolds numbers above approximately 2500–4000, the flow is potentially susceptible to such instability even below these Reynolds numbers.
Figure 17. Reconstruction of scale 4, at
$t/T=1.00$
for all Reynolds numbers, from case VT_XZ data: (a–f)
$Re=1500$
, 2500, 4000, 5000, 7500 and 10 000. Red colouring represents the streamwise velocity, while spanwise velocity is represented by the blue contours.
Figure 18. Early-time temporal
$\unicode[STIX]{x1D714}_{y}$
evolution of scale number 4 at (a)
$Re=1500$
and (b)
$Re=5000$
. Data taken from VT_XZ case.
4.4.3 Energy content
The energy content of the decomposed scales shows the relative dominance of coherent structures at each of the scales. The mean scale-based energy is plotted in figure 19 as a percentage of the total energy in the flow. Data are presented for each of the
$t/T$
phases measured, and the error bars represent the energy variance across the measurement ensemble.
Figure 19. Mean energy content by scale, from the wavelet multi-resolution analysis.
At
$t/T=0.76$
, the scale-specific energy content distribution is very similar over the upper end of the Reynolds number range, with little difference between
$Re=4000$
and
$Re=10\,000$
. The lower Reynolds number decomposition however, at
$Re=1500$
, reveals a bias towards the lower scale numbers (large-scale features), consistent with the observation of delayed substructure development at the smaller scales. By
$t/T=1.00$
this discrepancy has diminished, and the scale decomposition of energy in the flow remains invariant across the measured Reynolds number range after this time. It may also be observed that, by
$t/T=1.00$
, significantly higher variability has developed in the scale-dependent energy content of the
$Re=1500$
ensemble than in the higher Reynolds number cases. This can be suggestive of variation in the development of the three-dimensional vortex substructure at low Reynolds number, consistent with the observations in figure 18(a).
4.5 Instability spectral content
The flow currently under scrutiny is neither spatially nor temporally periodic, necessitating the application of wavelet analysis described in the previous section (§ 4.4). The results of that wavelet analysis, however, indicate that the flow does actually appear highly periodic and consistent across the spanwise direction, over the range of scales relevant to the apparent centrifugal instability. This is the case despite the unavoidable existence of spanwise no-slip end boundary conditions in the experimental facility. Observing this, a Fourier decomposition in the spanwise direction (and only the spanwise direction) may be justified. The limited, discretised, scale resolution of the wavelet analysis can thus be overcome, for spanwise periodic content.
Figure 20. Spanwise one-dimensional premultiplied power spectral density of the streamwise velocity component, calculated for each streamwise position, for (a)
$Re=1500$
, (b)
$Re=5000$
and (c)
$Re=10\,000$
at
$t/T=0.77$
. The leading-edge position is indicated by the thin grey line at
$x=0$
.
Figure 20 compares the premultiplied spanwise one-dimensional power spectral density functions of the fluctuating streamwise velocity, at
$t/T=0.76$
between
$Re=1500$
, 5000 and 10 000. The free-stream direction is from top to bottom, and the vertical line towards the left of the axes indicates the leading-edge position.
In each case, there exists a strong, but broad, spectrum peak in the vicinity of the leading edge, upstream of the dynamic stall vortex, and another broad peak in the core region of the leading-edge vortex, at
$x/c\approx 0.3$
. Despite normalising the spectra by the square of the free-stream velocity, the magnitude of both peaks is greater at higher Reynolds number, indicating the effect of Reynolds number on the level of turbulent fluctuation in the leading-edge vortex system. The general form of these spectra is the same if the spanwise velocity component is chosen instead.
The spatial frequency content of the velocity spectra varies with Reynolds number. At both
$Re=5000$
and
$Re=10\,000$
, the upstream spectrum peak lies in the approximate range
$k_{z}c=10{-}50$
radians per chord, but at lower Reynolds number, at
$Re=1500$
, it appears weaker and shifted to lower spatial frequencies by approximately a decade. The upstream spectrum also has a long tail extending to spatial frequencies comparable to the peak at higher Reynolds numbers. Like the upstream spectral peak, the core spectral peak also appears weakened and shifted by approximately a decade towards lower spatial frequencies in the
$Re=1500$
data, consistent with the larger-scale structures observed in the lower Reynolds number velocity fields.
A third spectral peak appears in the streamwise velocity component spectra at the downstream bound of the leading-edge vortex. This downstream peak is never completely distinct from the peak within the leading-edge vortex core, and does not appear at all at
$Re=1500$
or
$Re=2500$
. It can most clearly be seen at intermediate Reynolds numbers (illustrated here by the
$Re=5000$
case) but it becomes less distinct from the core as the Reynolds number is increased beyond 5000 towards the maximum values tested at
$Re=10\,000$
. The downstream spectral peak occurs at a spatial frequency range similar to that in the upstream spectral peak.
As the flow evolves, the spectral peak in the leading-edge vortex core reduces in magnitude at all Reynolds numbers tested. At
$Re=1500$
, the core spectral peak decays in magnitude in the
$k_{z}c=1{-}6$
radians per chord spatial frequency range, but increases in magnitude in the higher
$k_{z}c=10{-}50$
radians per chord range between
$t/T=0.76$
and
$t/T=1.00$
. The growth in this frequency range in the vortex core is accompanied by a growth in the magnitude of the upstream spectral peak at
$Re=1500$
, and a similar upward shift in spatial frequency range. At the higher Reynolds numbers, the upstream spectral peak persists strongly through
$t/T=1.00$
before decaying in magnitude as the leading-edge vortex system convects downstream.
Figure 21. Spanwise one-dimensional power spectral density of vorticity in the instability region upstream of the dynamic stall vortex: (a–f)
$Re=1500$
, 2500, 4000, 5000, 7500 and 10 000.
Performing a single spanwise power spectral density calculation on the through-plane vorticity component,
$\unicode[STIX]{x1D714}_{y}$
, in the region of the upstream peak, the plots in figure 21 may be produced. The general form of these spectra is a broad peak in the range
$k_{z}c=20{-}50$
radians per chord, diminishing with time. The significant difference with Reynolds number is a delay in the development of this peak at Reynolds numbers below
$Re=5000$
, and a reduced peak magnitude at these Reynolds numbers. The spatial frequency space inhabited by this peak is consistent with the wavelet analysis and is typical of what may be expected from a short-wave centrifugal instability. The delayed and reduced behaviour at the lower Reynolds numbers is consistent with the observations of delayed substructure growth seen in the wavelet multi-resolution reconstruction and energy analysis.
Figure 22. Peak energy (a) and frequency (b) of the spanwise instability as a function of Reynolds number and time.
Plotting the peak energy of the spanwise spectra as a function of time and Reynolds number (figure 22
a), the delayed development of the centrifugal instability at low Reynolds numbers is clearly seen. There is, however, little variation with Reynolds number above
$Re=4000$
. The spatial frequency at which the three-dimensional structure occurs (figure 22
b) reduces with time, demonstrating an energy shift towards longer wavelengths from approximately
$40$
radians per chord to
$20$
radians per chord at
$t/T=2.00$
. The peak energy of the instability decays also by a factor of approximately five over this time.
5 Summary and conclusions
A nominally two-dimensional, non-periodic, dynamic stall event has been produced experimentally, and studied quantitatively using particle image velocimetry. In the Reynolds number range
$Re=1500$
to
$Re=10\,000$
, organised three-dimensional flow features have been shown to exist, associated with the leading-edge dynamic stall vortex. It is suggested that this is due to the presence of a centrifugal instability affecting this flow. The arrangement of the three-dimensional substructure is consistent with the presence of a centrifugal instability, comprising short-period spanwise periodic vortex filaments around the periphery of the dynamic stall vortex core. It has been shown that these structures exist for Reynolds numbers above approximately 4000. At lower Reynolds numbers, the short-period spanwise periodicity develops more slowly, and is preceded by a vortex substructure dominated by larger-scale features.
The three-dimensional vortex substructure has been quantified as a function of both time and Reynolds number using a multi-resolution wavelet decomposition. The most energetic three-dimensional features inhabit a range of scales with characteristic lengths between 10 % and 15 % of the chord length. Comparing results of multiple experiments demonstrates no observable effect of variations in the spanwise end boundary conditions either on the general arrangement of the dynamic stall vortex substructure, or on the range of scales at which the three-dimensional features appear.
The wavelet decomposition of the velocities within the leading-edge vortex system suggests the vortex substructure to be spanwise-invariant for the range of length scales inhabited by the centrifugal instability, justifying the use of Fourier analysis in the spanwise direction. Spanwise power spectra show a broad spectral peak relating to this phenomenon, in the spatial frequency range 20–50 radians per chord, with a temporal energy shift towards larger wavelengths and a diminishing energy content after the completion of motion of the plate. The spanwise spectra are consistent with the delayed appearance of small-scale structure at low Reynolds numbers.
Acknowledgements
This research was sponsored by the Air Force Research Laboratory, under grant number FA2386-09-1-4091. The US Government is authorised to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon. This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. Some experimental materials were kindly provided by AAI Aerosonde.
