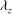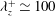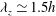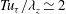1 Introduction
Townsend (Reference Townsend1961, Reference Townsend1976) originally introduced the concept of the ‘attached eddy’ to describe the energy-containing motions (i.e. coherent structures) populating the logarithmic region of wall-bounded turbulent flows. Given the length scale of the logarithmic region, the size of the energy-containing motions there would be proportional to the distance of their centre from the wall. This implies that, at least some parts of the energy-containing motions would reach the wall, and, in this sense, they are expected to be ‘attached’ to the wall. Under the assumption that these energy-containing motions in the logarithmic region (i.e. attached eddies) are statistically self-similar to one another, Townsend (Reference Townsend1976) theoretically predicted that turbulence intensity of the wall-parallel velocity components would exhibit a logarithmic wall-normal dependence as the mean-velocity profile does. The original theory of Townsend (Reference Townsend1976) has been significantly refined over a number of years by Perry and coworkers (e.g. Perry & Chong Reference Perry and Chong1982; Perry, Henbest & Chong Reference Perry, Henbest and Chong1986; Perry & Marusic Reference Perry and Marusic1995; Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005, among many others), who have elaborated to develop a self-consistent model predicting the statistics of wall-bounded turbulent flows with a structural model of the attached eddy in the form of a hairpin or
${\it\Lambda}$
vortex. Especially, these authors further predicted and verified the emergence of
$k_{x}^{-1}$
law in the spectra of wall-parallel velocity components (
$k_{x}$
is the streamwise wavenumber), which would be linked to the logarithmic wall-normal dependence of turbulence intensity of these velocity components (Perry & Chong Reference Perry and Chong1982).
A growing body of evidence, which supports the theoretical predictions made with the attached eddy hypothesis, has emerged, especially over the last decade. The logarithmic growth of the near-wall streamwise turbulence intensity with the Reynolds number is an example of this, as it would be given by extending Townsend’s prediction to the near-wall region (Marusic & Kunkel Reference Marusic and Kunkel2003). The linear growth of the spanwise integral length scale with the distance from the wall has also been understood as another important evidence (Tomkins & Adrian Reference Tomkins and Adrian2003; del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2004; Monty et al. Reference Monty, Stewart, Williams and Chong2007), as this indicates that the spanwise size of the energy-containing motions in the logarithmic region is proportional to the distance from the wall. Lastly, the logarithmic dependence of turbulence intensity of the wall-parallel velocity components has recently been indeed confirmed at sufficiently high Reynolds numbers (Jiménez & Hoyas Reference Jiménez and Hoyas2008; Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Orlandi, Bernardini & Pirozzoli Reference Orlandi, Bernardini and Pirozzoli2015), suggesting that the energy-containing motions in wall-bounded turbulent flow would indeed be organised in the form of Townsend’s attached eddies.
Very recently, the first author of the present study managed to compute the statistics of the attached eddies at a given length scale with a numerical experiment performed at moderate Reynolds numbers (
$Re_{{\it\tau}}\simeq 1000{-}2000$
where
$Re_{{\it\tau}}$
is the friction Reynolds number) (Hwang Reference Hwang2015). Built upon the linearly growing nature of the spanwise integral length scale with the distance from the wall, the numerical experiment is designed to isolate the energy-containing motions only at a given spanwise length scale using their ‘self-sustaining nature’ (Hwang & Cossu Reference Hwang and Cossu2010c
, Reference Hwang and Cossu2011). The isolated self-sustaining energy-containing motions were found to be self-similar with respect to their spanwise length scale, and their statistical structures were remarkably similar to those of the attached eddies, demonstrating the existence of Townsend’s attached eddies as energy-containing motions in wall-bounded turbulent flows. It was also shown that the single attached eddy is composed of two distinct elements, one of which is a long streaky motion and the other is a relatively compact streamwise vortical structure. At the considered Reynolds numbers, the size and the wall-normal location of the former streaky motion, the major carrier of the streamwise turbulence intensity, are roughly self-similar along
$$\begin{eqnarray}y\simeq 0.1{\it\lambda}_{z}\quad \text{and}\quad {\it\lambda}_{x}\simeq 10{\it\lambda}_{z},\end{eqnarray}$$
where
$y$
is the wall-normal direction,
${\it\lambda}_{x}$
the streamwise length scale and
${\it\lambda}_{z}$
the spanwise length scale, while those of the latter vortical structure, carrying all the velocity components, also self-similarly scale with
$$\begin{eqnarray}y\simeq 0.5\sim 0.7{\it\lambda}_{z}\quad \text{and}\quad {\it\lambda}_{x}\simeq 2\sim 3{\it\lambda}_{z}.\end{eqnarray}$$
The scaling also reveals that the smallest attached eddy, given with
${\it\lambda}_{z}^{+}\simeq 100$
, is a near-wall coherent motion in the form of a near-wall streak and with several quasi-streamwise vortices aligned to it (Hwang Reference Hwang2013), while the largest one, given with
${\it\lambda}_{z}\simeq 1.5h$
in a turbulence channel with the half-height
$h$
, is an outer motion composed of a very-large-scale motion (VLSM) and with several large-scale motions (LSMs) aligned to it (Hwang Reference Hwang2015). The attached eddies at intermediate length scales, the size of which is proportional to their distance from the wall, are also in the form of a long streak and several quasi-streamwise vortices, and contribute to the logarithmic region by filling the gap caused by the separation between the inner and outer length scales. It should be mentioned that this scenario incorporates all the coherent structures currently known and exhibits the behaviour consistent with the spectra of all the velocities and Reynolds stress (including
$k_{x}^{-1}$
spectra), providing an integrated description for the coherent structures within the attached eddy scenario (for further details, see also Hwang Reference Hwang2015).
The present study is an extension of the work by Hwang (Reference Hwang2015), and, in particular, it is aimed to explore the ‘dynamics’ of the self-sustaining attached eddies and its relevance to the corresponding motions in a fully turbulent environment. For this purpose, in the present study we consider the smallest computational box which allows for the self-sustaining mechanism of each of the attached eddies (i.e. the minimal unit). We then examine the detailed physical processes in the minimal unit by comparing them with those under fully developed turbulence. Particular emphasis of the present study is given to relating the self-sustaining process of the attached eddies with the dynamical behaviour often referred to as ‘bursting’ in the logarithmic and outer regions (Flores & Jiménez Reference Flores and Jiménez2010). To this end, we introduce two additional numerical experiments, designed to examine the physical processes composing the self-sustaining process of the attached eddies in the logarithmic and outer regions.
The paper is organised as follows. In § 2, we briefly introduce the numerical methods of extracting self-sustaining attached eddies at a given spanwise length scale (see also Hwang Reference Hwang2015, for further details). A careful observation of the instantaneous flow field is then followed in § 3 with examination of auto- and cross-correlation functions of several flow variables of interest. Especially in this section, we show that the bursting in the logarithmic and outer regions is likely a consequence of the self-sustaining process of the attached eddies. In § 4, a comprehensive discussion on the self-sustaining mechanism of the attached eddies is given with the two numerical experiments mentioned. The paper finally concludes in § 5.
2 Numerical experiment
2.1 Computation of self-sustaining attached eddies
We consider a turbulent channel, in which we denote
$x$
,
$y$
and
$z$
as the streamwise, wall-normal and spanwise directions, respectively. The upper and lower walls are set to be at
$y=0$
and
$y=2h$
, respectively, where
$h$
is the half-height of the channel. The numerical experiment in the present study is performed using the Navier–Stokes solver in our previous studies (Hwang & Cossu Reference Hwang and Cossu2010c
, Reference Hwang and Cossu2011; Hwang Reference Hwang2013, Reference Hwang2015). In this solver, the streamwise and spanwise directions are discretised using the Fourier–Galerkin method with the 2/3 rule, and the wall-normal direction is discretised using a second-order central difference scheme. Time integration is performed semi-implicitly using the Crank–Nicolson method for the terms with wall-normal derivatives and a third-order low-storage Runge–Kutta method for the rest of the terms. The computations are performed by imposing a constant volume flux across the channel.
As mentioned, the present numerical experiment is largely based on the previous work by Hwang (Reference Hwang2015) (the reader is strongly recommended to refer to this paper in which the numerical technique introduced in this section is fully verified). In turbulent channel flow, the spanwise length scale exhibits a linear growth with the distance from the wall (i.e.
$y$
) in the range from
${\it\lambda}_{z}^{+}\simeq 100$
to
${\it\lambda}_{z}\simeq 1.5h$
(del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004). The spanwise spectra of the streamwise velocity clearly reveal this feature, and are approximately aligned along
$y\sim 0.1{\it\lambda}_{z}$
(del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004; Hwang Reference Hwang2015). The key idea of Hwang (Reference Hwang2015) is to design a numerical simulation only for the energy-containing motions at a prescribed spanwise length
${\it\lambda}_{z}={\it\lambda}_{z,0}$
between
${\it\lambda}_{z}^{+}\simeq 100$
and
${\it\lambda}_{z}\simeq 1.5h$
by artificially removing the motions at the other spanwise length scales (i.e.
${\it\lambda}_{z}\neq {\it\lambda}_{z,0}$
).
First, the removal of the motions, the spanwise size of which is larger than the prescribed spanwise length
${\it\lambda}_{z,0}$
(i.e.
${\it\lambda}_{z}>{\it\lambda}_{z,0}$
) is implemented by setting the size of the spanwise computational domain
$L_{z}$
to be identical to the prescribed spanwise length scale
${\it\lambda}_{z,0}$
(i.e.
$L_{z}={\it\lambda}_{z,0}$
), while keeping a sufficiently long streamwise domain
$L_{x}$
. However, even in such a computational domain, the motions at
${\it\lambda}_{z}>{\it\lambda}_{z,0}$
are not completely removed, as a spurious motion, uniform along the spanwise direction, would still survive (Hwang Reference Hwang2013). This spurious motion is subsequently removed by taking the approach in Hwang (Reference Hwang2013) which explicitly filters out the spanwise uniform components by setting the right-hand side of the discretised momentum equation at each Runge–Kutta substep as follows:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\widehat{\text{RHS}}_{x}(y;k_{x}\neq 0,k_{z}=0)=0,\\ \widehat{\text{RHS}}_{y}(y;k_{x}\neq 0,k_{z}=0)=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where the RHS
$_{i}$
the right-hand side of
$i$
-component of the discretized momentum equation,
$~\widehat{\cdot }~$
denotes Fourier-transformed state in
$x$
and
$z$
directions and
$k_{x}$
and
$k_{z}$
are the streamwise and spanwise wavenumbers, respectively. We note that this technique is only aimed at removing the two-dimensional spurious motion populating the
$x$
–
$y$
plane, thus no action is taken for
$\widehat{\text{RHS}}_{z}$
(for further details, see also Hwang Reference Hwang2013).
Once the motions at
${\it\lambda}_{z}>{\it\lambda}_{z,0}$
are removed, the motions at
${\it\lambda}_{z}<{\it\lambda}_{z,0}$
are subsequently quenched using an over-damped large-eddy simulation (LES) (Hwang & Cossu Reference Hwang and Cossu2010c
; Hwang Reference Hwang2013, Reference Hwang2015). For the given scope of the present study, it is very important for the residual stress model of the LES not to generate any possible energy transfer to the resolved quantity. Therefore, as in Hwang (Reference Hwang2015), we consider the static Smagorinsky model in which the residual stress is modelled in a purely diffusive form:
$$\begin{eqnarray}\tilde{{\it\tau}}_{ij}-\frac{{\it\delta}_{ij}}{3}\tilde{{\it\tau}}_{kk}=-2{\it\nu}_{t}\tilde{\unicode[STIX]{x1D61A}}_{ij},\end{eqnarray}$$
with
$$\begin{eqnarray}{\it\nu}_{t}=(C_{s}\tilde{{\it\Delta}})^{2}\tilde{\mathscr{S}}\mathscr{D},\end{eqnarray}$$
where
$\tilde{\cdot }$
denotes the filtered quantity,
$\unicode[STIX]{x1D61A}_{ij}$
the strain rate tensor,
$C_{s}$
the Smagorinsky constant,
$\tilde{{\it\Delta}}=(\tilde{{\it\Delta}}_{1}\tilde{{\it\Delta}}_{2}\tilde{{\it\Delta}}_{3})^{1/3}$
the nominal filter width,
$\tilde{\mathscr{S}}=(2\tilde{\unicode[STIX]{x1D61A}}_{ij}\tilde{\unicode[STIX]{x1D61A}}_{ij})^{1/2}$
the norm of the strain rate tensor and
$\mathscr{D}=1-\exp [-(y^{+}/A^{+})^{3}]$
is the van Driest damping function (Härtel & Kleiser Reference Härtel and Kleiser1998). The removal of the motions at
${\it\lambda}_{z}<{\it\lambda}_{z,0}$
is subsequently carried out by increasing
$C_{s}$
with the increment
${\rm\Delta}C_{s}=0.05$
until we isolate the self-sustaining motions at
${\it\lambda}_{z}={\it\lambda}_{z,0}$
. We note that this approach is equivalent to increasing the filter width of LES without losing actual resolution (Mason & Cullen Reference Mason and Cullen1986). Finally, it should be mentioned that this approach itself does not strongly depend on the choice of the eddy viscosity model (Hwang & Cossu Reference Hwang and Cossu2010c
, Reference Hwang and Cossu2011).
The smallest computational domain, which allows for survival of the isolated self-sustaining attached eddies at a given spanwise length scale
${\it\lambda}_{z,0}$
(i.e. the minimal unit), is then sought. Since the spanwise size of the target attached eddies determines the spanwise computational domain
$L_{z}$
(i.e.
$L_{z}={\it\lambda}_{z,0}$
), only the size of the streamwise computational domain
$L_{x}$
needs to be examined by gradually reducing it from a sufficiently large value. Such a search of the minimal unit of the self-sustaining attached eddies at a given spanwise length scale was previously performed in Hwang & Cossu (Reference Hwang and Cossu2010c
) with the present over-damped LES, but without the filtering (2.1). In the present study, we therefore repeat this search again to check any possible effect of (2.1). It has been found that the filtering (2.1) does not significantly affect the size of the minimal unit, resulting in the following streamwise computational domain size for the self-sustaining attached eddies at
${\it\lambda}_{z,0}=L_{z}$
:
$$\begin{eqnarray}L_{x}=2L_{z}.\end{eqnarray}$$
In the present study, all the simulations are performed by keeping with this aspect ratio of the computational domain (see also table 1). We note that the use of this minimal streamwise computational domain is not a great limitation of the present study, as the minimal domain is found not to significantly change the second-order statistics of the isolated self-sustaining attached eddies at
${\it\lambda}_{z,0}=L_{z}$
. A detailed discussion on this issue is given in appendix B where the second-order statistics of the attached eddies with the minimal unit are compared with those with a long streamwise domain in Hwang (Reference Hwang2015). Finally, it should be mentioned that the filtering of the uniform motion along the streamwise direction, such as (2.1) for the spanwise direction, is not implemented. As we shall see in §§ 3 and 4, the streamwise uniform Fourier mode in the minimal unit mainly resolves the long streaky motion observed in a long computational domain. Indeed, we will see that the streamwise uniform Fourier mode is strongly correlated with the streaky motion (see § 3), and inhibition of the related physical process destroys the self-sustaining process in the minimal unit (see § 4).
Table 1. Simulation parameters in the present study. Here,
$Re_{m}$
is the Reynolds number based on the bulk velocity and
$T_{avg}$
is the time interval for the average. In the names of the simulations,
$L$
indicates ‘logarithmic’,
$O$
‘outer’ and
$S$
‘self-sustaining’.
The simulation parameters of the present study are summarised in table 1, where six different simulations are considered at two different Reynolds numbers (
$Re_{{\it\tau}}\simeq 950$
and
$Re_{{\it\tau}}\simeq 1800$
). For each computational domain, we consider a pair of simulations for the purpose of comparison. One is with
$C_{s}=0.05$
, the value known to provide the best statistics compared to that of direct numerical simulations (DNS) (Härtel & Kleiser Reference Härtel and Kleiser1998) and is performed to track the attached eddies with background turbulence, and the other is with an increased
$C_{s}$
and is to study the attached eddies surviving only through the self-sustaining mechanism. Typical spatial grid spacing of the simulations is set to be in the range of
${\rm\Delta}x^{+}=50{-}70$
,
${\rm\Delta}y_{\text{min}}^{+}=1{-}2$
and
${\rm\Delta}z^{+}=20{-}30$
, in order to properly resolve the near-wall motions. We note that this grid spacing is finer than that in Hwang (Reference Hwang2015) where the numerical technique applied here is fully verified with very long
$L_{x}$
. Finally, it should be mentioned that significantly long average times (
$T_{avg}$
) are considered to ensure sufficient convergence of the time correlation functions introduced in § 3. The convergence of the correlation functions have also been checked by doubling
$T_{avg}$
, but it is not significantly improved.
2.2 Validation and preliminary test
To verify the present LES, a reference simulation for
$C_{s}=0.05$
without applying (2.1) is first performed with the domain of
$O950$
: i.e. the minimal unit for the outer attached eddies (Hwang & Cossu Reference Hwang and Cossu2010c
). Figure 1 shows the mean-velocity profile and turbulent velocity fluctuations of the reference simulation. The statistics of the simulation show reasonable agreement with those of DNS by del Álamo et al. (Reference del Álamo, Jiménez, Zandonade and Moser2004), consistent with Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) who reported the effect of the computational domain size on the statistics. As discussed in § 2.1, the present numerical experiment also implements the filtering action (2.1) unlike the ordinary minimal box simulation which only considers a spatially confined computation box. Therefore, the statistics of the simulation for
$C_{s}=0.05$
with (2.1) is also checked (the dashed line in figure 1). Although the filtering (2.1) a little distorts the mean-velocity profile and the velocity fluctuations roughly for
$y^{+}>150$
(
$y>0.15h$
), it does not yield significant change overall in the statistics. Further inspection is performed by computing the time correlation functions of interest defined in § 3, and reveals that the filtering (2.1) does not significantly change the dynamical process in the considered computational domain. For further details, the reader refers to appendix A where a detailed comparison of the computed time correlation functions is made.
Figure 1. (a) Mean-velocity profile and (b) turbulent velocity fluctuations of the reference simulation: ——,
$O950$
without the filtering (2.1); – – – –,
$O950$
; – - – - –, DNS at
$Re_{{\it\tau}}=934$
(del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004).
Figure 2. Normalised second-order statistics of the attached eddies, scaled with the given spanwise length
$L_{z}$
: (a) streamwise velocity,
$y=0.3L_{z}$
; (b) wall-normal velocity,
$y=0.4L_{z}$
; (c) spanwise velocity,
$y=0.4L_{z}$
; (d) Reynolds stress,
$y=0.2L_{z}$
. Here, – – – –, from
$Re_{{\it\tau}}\simeq 950$
(
$SL950a$
,
$SL950b$
); ——, from
$Re_{{\it\tau}}\simeq 1800$
(
$SL1800a$
,
$SL1800b$
,
$SL1800c$
).
The only difference between the present numerical experiment and that in Hwang (Reference Hwang2015) is the streamwise size of the computational domain. To ensure that the change of the streamwise computational domain does not affect the self-similar nature of the computed attached eddies, the statistics of the attached eddies, obtained by implementing the technique in § 2.1, are also reported. Figure 2 shows the normalised second-order statistics of the simulations in which the attached eddies at the given spanwise length scale are isolated (i.e. the simulations tagged with ‘
$S$
’ in table 1). The computed statistics of the attached eddies are approximately self-similar with respect to their spanwise length scale
$L_{z}$
below certain wall-normal locations: the streamwise velocity fluctuation is self-similar roughly below
$y\simeq 0.3L_{z}$
(figure 2
a), the wall-normal and the spanwise velocity fluctuations are below
$y\simeq 0.4L_{z}$
(figure 2
b,c) and the Reynolds stress is below
$y\simeq 0.2L_{z}$
(figure 2
d). Above these wall-normal locations, the second-order statistics depend on the box size, as in Hwang (Reference Hwang2015). However, we note that the non-self-similar part of the fluctuations above these wall-normal locations is merely a fluctuation induced by the self-similar part in the wall-normal locations supposed to be ‘empty’, due to the absence of the motions larger than the attached eddies of interest (for further discussion, see also Hwang Reference Hwang2013, Reference Hwang2015). Finally, it should be mentioned that the second-order statistics of the wall-parallel velocity components show non-negligibly large contributions to the region close to the wall (figure 2
a,c), whereas those of the wall-normal velocity and the Reynolds stress are fairly small (figure 2
b,d): for example, at
$y=0.05L_{z}$
, the normalised streamwise and the spanwise velocity fluctuations are respectively approximately 0.98 and 0.68 times their maxima, whereas the wall-normal velocity and Reynolds stress are respectively found to be approximately 0.28 and 0.45 times their maxima. This is essentially due to the impermeability condition caused by the presence of the wall, and is exactly as in the statistical structure of the single attached eddy hypothesised by Townsend (Reference Townsend1976).
3 Results
3.1 The largest attached eddies: large-scale and very-large-scale motions
We first explore the temporal evolution of the largest attached eddies (i.e. the energy-containing motions at
${\it\lambda}_{z}=1.5h$
) in the minimal unit (
$O950$
and
$SO950$
in table 1). As discussed in Hwang (Reference Hwang2015), the largest attached eddy is composed of a VLSM (outer streaky motion) and LSMs (outer streamwise vortical structures) aligned with it. In a large computational domain, the VLSM is typically featured to be a long structure mainly carrying a large amount of the streamwise turbulent kinetic energy, and this is quite similar to the behaviour of the streaks in the near-wall region (Hwang Reference Hwang2015). Therefore, in the outer minimal unit, in which only single VLSM would be resolved mainly by zero streamwise wavenumber due to its long length (i.e.
$k_{x}=0$
; see also figure 6), its temporal evolution would be well tracked by
$$\begin{eqnarray}E_{u}=\frac{1}{2V_{h}}\int _{{\it\Omega}_{h}}u^{2}~\text{d}V,\end{eqnarray}$$
where
$u$
is the streamwise velocity fluctuation,
${\it\Omega}_{h}$
the lower (or upper) half of the computational domain of interest and
$V_{h}$
the volume of the half of the computational domain.
On the contrary, the LSM is a relatively short structure given with its streamwise length scale at
${\it\lambda}_{x}\simeq 3{-}4h$
. The structure at this length is identical to that often postulated as a hairpin vortex packet by Adrian and coworkers (Adrian Reference Adrian2007). This structure is relatively isotropic, compared to the VLSM which mostly carries the streamwise velocity fluctuation, in the sense that it contains all the velocity components (Hwang Reference Hwang2015). It is important to mention that this structure was found to share a number of statistical similarities with quasi-streamwise vortex in the near-wall region (Hwang Reference Hwang2015). This suggests that the LSMs would likely to be quasi-streamwise vortical structures in the outer region, although they are much more disorganised due to small-scale turbulence associated with cascade and turbulent dissipation (Jiménez Reference Jiménez2012). It should be mentioned that this view is consistent with del Álamo et al. (Reference del Álamo, Jiménez, Zandonade and Moser2006) who called this structure the ‘tall-attached vortex cluster’. Since the VLSM carries very little wall-normal or spanwise turbulent kinetic energy, in the minimal unit, the LSMs would be well characterised by either
$$\begin{eqnarray}E_{v}=\frac{1}{2V_{h}}\int _{{\it\Omega}_{h}}v^{2}~\text{d}V,\end{eqnarray}$$
or
$$\begin{eqnarray}E_{w}=\frac{1}{2V_{h}}\int _{{\it\Omega}_{h}}w^{2}~\text{d}V,\end{eqnarray}$$
where
$v$
and
$w$
are the wall-normal and spanwise velocity fluctuations, respectively. Later, we shall see that these two variables are indeed strongly correlated to each other (figure 5
c,d). Here, it should also be pointed out that the use of the primitive variables in characterising the quasi-streamwise vortical structure instead of enstrophy or streamwise vorticity is intentionally introduced to track their behaviour more precisely. Given the significant amount of small-scale turbulence associated with energy cascade and turbulent dissipation in the logarithmic and the outer regions, the variables such as enstrophy or streamwise vorticity would not faithfully represent the large-scale organised vortical structure. Indeed, Jiménez (Reference Jiménez2012) recently showed that such variables carry dominant energy around turbulent dissipation length scales.
Figure 3. Time evolution of the flow field of
$O950$
: (a) time trace of
$E_{u}^{+}$
(solid) and
$E_{v}^{+}$
(dashed); (b) magnification of (a) for
$tu_{{\it\tau}}/h\in [158,164]$
; (c–f) the corresponding flow visualisation at
$tu_{{\it\tau}}/h=159,160.2,160.9,162$
. In (c–f), the red and blue iso surfaces indicate
$u^{+}=-3.2$
and
$v^{+}=1.4$
, respectively.
A set of the flow fields of
$O950$
, in which the largest attached eddies are contained with other smaller-scale turbulent motions, are first examined. Figure 3 shows the time trace of
$E_{u}$
and
$E_{v}$
, and the corresponding evolution of the flow field in time. Both
$E_{u}$
and
$E_{v}$
show large-scale temporal oscillations with a time scale roughly at
$Tu_{{\it\tau}}/h\simeq 2{-}5$
(figure 3
a). This is exactly the feature known as ‘bursting’ by Flores & Jiménez (Reference Flores and Jiménez2010). A careful observation reveals that
$E_{u}$
and
$E_{v}$
oscillate with a certain phase difference: for example, at
$tu_{{\it\tau}}/h=159$
,
$E_{v}$
is around the local maximum while
$E_{u}$
being at fairly low-energy state (figure 3
b), and, at
$tu_{{\it\tau}}/h=160.2$
,
$E_{v}$
reaches the local minimum whereas
$E_{u}$
becomes considerably larger (figure 3
b). Visualisation of the corresponding flow fields in figure 3(c–f) suggests that this is likely due to the interactive dynamics between the VLSM (streak) and the LSMs (streamwise vortical structures). At
$tu_{{\it\tau}}/h=159$
(figure 3
c), the flow field exhibits a few fairly strong large-scale
$v$
structures, which would be a part composing the LSMs in the minimal unit. On the other hand,
$u$
structures in the flow field are fairly weak at this time, and they appear to be collectively gathered around the
$v$
structures. At
$tu_{{\it\tau}}/h=160.2$
(figure 3
d), the
$v$
structures become considerably weakened whereas the
$u$
structures are significantly amplified, forming a strong streaky structure extending over the entire streamwise domain. This amplification of the streaky structure appears to be a consequence of the ejection of the streamwise momentum by the strong
$v$
structures observed at
$tu_{{\it\tau}}/h=159$
(figure 3
c), clearly reminiscent of the ‘lift-up’ effect predicted by previous theoretical studies (del Álamo & Jiménez Reference del Álamo and Jiménez2006; Cossu, Pujals & Depardon Reference Cossu, Pujals and Depardon2009; Pujals et al.
Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010b
). The amplified streaky structure subsequently meanders along the streamwise direction (figure 3
$e$
). This process eventually leads to regeneration of new
$v$
structures with the breakdown of the streaky motion (figure 3
$f$
).
Figure 4. Time evolution of the flow field of
$SO950$
: (a) time trace of
$E_{u}^{+}$
(solid) and
$E_{v}$
(dashed); (b) magnification of (a) for
$tu_{{\it\tau}}/h\in [564,572]$
; (c–f) the corresponding flow visualisation at
$tu_{{\it\tau}}/h=565,568.5,569.3,570$
. In (c–f), the red and blue iso surfaces indicate
$u^{+}=-4$
and
$v^{+}=1.5$
, respectively.
Qualitatively the same behaviour is observed in the over-damped simulation
$SO950$
, in which only the energy-containing motions at
${\it\lambda}_{z}=1.5h$
are isolated by replacing all the smaller-scale motions with a crude eddy viscosity given with the increased
$C_{s}$
. Figure 4 shows the time trace of
$E_{u}$
and
$E_{v}$
, and the corresponding evolution of the flow field of
$SO950$
. As in
$O950$
(figure 3
a), both
$E_{u}$
and
$E_{v}$
exhibit temporal oscillations with the time scale at
$Tu_{{\it\tau}}/h=2{-}5$
(figure 4
a). In this case, a more prominent phase difference is observed between the oscillations of
$E_{u}$
and
$E_{v}$
(figure 4
a,b), presumably because the smaller-scale surrounding turbulent motions are removed in
$SO950$
. However, this could also be partially due to the increased oscillation amplitude of
$E_{u}$
in
$SO950$
, which has previously been shown to be an artefact caused either by the crude eddy viscosity itself or by the lack of the energy-containing motions in the near-wall and logarithmic regions (Hwang Reference Hwang2015). Not surprisingly, the flow fields of
$SO950$
are composed of much smoother structures than those of
$O950$
(figure 4
c–f). However, the temporal evolution of the
$u$
and
$v$
structures of
$SO950$
are remarkably similar to that of
$O950$
: the
$v$
structures significantly amplify the streaky
$u$
structure via the lift-up effect (figure 4
c,d); the amplified streaky
$u$
motion subsequently meanders along the streamwise direction (figure 4
$e$
); the
$v$
structures are finally regenerated with breakdown of the streaky
$u$
motion (figure 4
$f$
).
To statistically quantify this cyclic dynamical process, auto- and cross-correlations of several variables of interest are computed. It is also useful to introduce two additional variables, such that:
$$\begin{eqnarray}E_{0}=\int _{{\it\Omega}_{y,h}}|\hat{u} (y;k_{x},k_{z})|^{2}+|\hat{v}(y;k_{x},k_{z})|^{2}+|{\hat{w}}(y;k_{x},k_{z})|^{2}~\text{d}y,\end{eqnarray}$$
for
$k_{x}=0$
and
$k_{z}=2{\rm\pi}/L_{z}$
, and
$$\begin{eqnarray}E_{1}=\int _{{\it\Omega}_{y,h}}|\hat{u} (y;k_{x},k_{z})|^{2}+|\hat{v}(y;k_{x},k_{z})|^{2}+|{\hat{w}}(y;k_{x},k_{z})|^{2}~\text{d}y,\end{eqnarray}$$
for
$k_{x}=2{\rm\pi}/L_{x}$
and
$k_{z}=2{\rm\pi}/L_{z}$
. Here,
$\hat{\cdot }$
denotes the Fourier-transformed state in the
$x$
and
$z$
directions, and
${\it\Omega}_{y,h}$
is the lower (or upper) half of the wall-normal domain. We note that, in (3.2),
$E_{0}$
is introduced to compute the energy of the streamwise uniform component of the motions at
${\it\lambda}_{z}=1.5h$
, while
$E_{1}$
is to compute the energy of the first streamwise Fourier component, which would measure the meandering motion observed in figures 3 and 4. The correlation functions are defined as
$$\begin{eqnarray}C_{ij}({\it\tau})=\frac{\langle E_{i}(t+{\it\tau})E_{j}(t)\rangle }{\sqrt{\langle {E_{i}}^{2}(t)\rangle }\sqrt{\langle {E_{j}}^{2}(t)\rangle }},\end{eqnarray}$$
where
$i,j=u,v,w,0,1$
and
$\langle \cdot \rangle$
indicates average in time. In the present study, all the correlation functions are computed by averaging the lower and upper half-channels.
Figure 5. Time correlation functions of (a,c)
$O950$
and (b,d)
$SO950$
. In (a,b), ——,
$C_{uu}({\it\tau})$
; – – – –,
$C_{vv}({\it\tau})$
; – - – - –,
$C_{ww}({\it\tau})$
. In (c,d), ——,
$C_{uv}({\it\tau})$
; – – – –,
$C_{uw}({\it\tau})$
; – - – - –,
$C_{vw}({\it\tau})$
.
Figure 5 shows the correlation functions computed with
$E_{u}$
,
$E_{v}$
and
$E_{w}$
from
$O950$
and
$SO950$
. In the case of
$O950$
, all the auto-correlations decay to zero at
$|{\it\tau}u_{{\it\tau}}/h|\simeq 1{-}2$
, although
$C_{uu}$
tends to drop a little more slowly than
$C_{vv}$
and
$C_{ww}$
(figure 5
a). The size of the time interval, in which the auto-correlations remain positive, is
$Tu_{{\it\tau}}/h\simeq 2{-}4$
, and this roughly corresponds to the single period of the temporal oscillation of
$E_{u}$
and
$E_{v}$
(figure 3
a). The cross-correlation
$C_{uv}$
of
$O950$
also reveals that there is indeed a phase difference between
$E_{u}$
and
$E_{v}$
(figure 5
c): the peak of
$C_{uv}$
is located at
${\it\tau}u_{{\it\tau}}/h\simeq -0.6$
, indicating that
$E_{u}$
statistically reaches its local extremum approximately
${\rm\Delta}{\it\tau}u_{{\it\tau}}/h\simeq 0.6$
before
$E_{v}$
reaches its local extremum. On the other hand,
$E_{v}$
and
$E_{w}$
are found to be strongly correlated to each other:
$C_{vw}({\it\tau}=0)\simeq 0.7$
and
$C_{uw}$
also exhibits a peak at
${\it\tau}u_{{\it\tau}}/h\simeq -0.6$
as
$C_{uv}$
does (figure 5
c).
Qualitatively the same behaviour is observed in the correlation functions of
$SO950$
in which only the energy-containing motions at
${\it\lambda}_{z}\simeq 1.5h$
are isolated (figure 5
b,d). All the auto-correlations drop to zero near
$|{\it\tau}u_{{\it\tau}}/h|\simeq 1.5{-}2$
(figure 5
b), resulting in the time interval of positive auto-correlation to be
$Tu_{{\it\tau}}/h\simeq 4$
. As for
$O950$
, this time scale reasonably well quantifies a single period of the temporal oscillations of
$E_{u}$
and
$E_{v}$
(figure 4
a). The phase difference between
$E_{u}$
and
$E_{v}$
is also seen in
$C_{uv}$
of
$SO950$
(figure 5
d) which shows the peak at
${\it\tau}u_{{\it\tau}}/h\simeq -1.7$
. Finally,
$E_{v}$
and
$E_{w}$
are also found to be strongly correlated to each other, as seen in
$C_{vw}$
(figure 5
d).
Figure 6. Time correlation functions of (a,c)
$O950$
and (b,d)
$SO950$
. In (a,b), ——,
$C_{00}({\it\tau})$
; – – – –,
$C_{11}({\it\tau})$
; – - – - –,
$C_{01}({\it\tau})$
. In (c,d), ——,
$C_{0u}({\it\tau})$
; – – – –,
$C_{0v}({\it\tau})$
; – - – - –,
$C_{1v}({\it\tau})$
.
The correlation functions with
$E_{0}$
and
$E_{1}$
are also presented in figure 6. The auto- and cross-correlations obtained only with
$E_{0}$
and
$E_{1}$
(i.e.
$C_{00}$
,
$C_{11}$
and
$C_{01}$
) are given in figure 6(a,b). The correlation functions of
$O950$
show fairly similar behaviour to those of
$SO950$
:
$C_{00}$
and
$C_{11}$
of
$O950$
exhibit similar time scales to those of
$SO950$
, and
$C_{01}$
of both
$O950$
and
$SO950$
has a phase difference between
$E_{0}$
and
$E_{1}$
with
${\rm\Delta}{\it\tau}u_{{\it\tau}}/h=1$
. The phase difference between
$E_{0}$
and
$E_{1}$
implies that the streamwise uniform motion occurs first and the meandering motion follows, as in the instantaneous fields shown in figures 3 and 4. Here, it is interesting to note that the time scale of
$C_{11}$
(
$Tu_{{\it\tau}}/h\simeq 2$
) appears to be much smaller than that of
$C_{00}$
as well as that of
$C_{uu}$
,
$C_{vv}$
and
$C_{ww}$
(
$Tu_{{\it\tau}}/h\simeq 4$
; see also figure 5
a,b). This suggests that the meandering motion of the streak (figures 5
c and 6
c), which would be characterised by
$E_{1}$
, is a rapid process which persists only for roughly half of the bursting period.
Cross-correlations are further computed by also considering
$E_{u}$
,
$E_{v}$
and
$E_{w}$
, as shown in figure 6(c,d). The correlation
$C_{0u}$
shows that
$E_{0}$
and
$E_{u}$
are strongly correlated to each other in both
$O950$
and
$SO950$
, indicating that the streamwise uniform mode (
$k_{x}=0$
) at
${\it\lambda}_{z}=1.5h$
well represents the streaky motion (i.e. VLSM) in the minimal unit. This feature can also be confirmed from
$C_{0v}$
of
$O950$
and
$SO950$
, which behaves very similarly to
$C_{uv}$
(figure 5
c,d). Finally, the peak of
$C_{1v}$
for both
$O950$
and
$SO950$
is found roughly at
${\it\tau}u_{{\it\tau}}/h\simeq -1$
. This indicates that the meandering motion of the streak statistically appears before the vortical structures (LSMs) are fully amplified, consistent with the instantaneous flow fields given in figures 3 and 4.
Despite many qualitative similarities between the dynamical behaviours of the energy-containing motions in
$O950$
and
$SO950$
, it should be pointed out that the correlation functions of the two simulations (
$O950$
and
$SO950$
) are not quantitatively the same, although this is not very surprising given the aggressive nature of the present numerical experiment: for example, the time intervals of
$C_{vv}>0$
and
$C_{ww}>0$
of
$O950$
are smaller than those of
$SO950$
(figure 5
a,b), and the peak locations of
$C_{uv}$
,
$C_{uw}$
and
$C_{0v}$
of
$O950$
are a little different from those of
$SO950$
(figures 5
c,d, 6
c,d). Apparently, these differences could stem from two possible origins: one is that
$E_{u}$
,
$E_{v}$
and
$E_{w}$
of
$O950$
contain the effect of the surrounding smaller-scale turbulent motions, and the other is that the dynamical behaviour of the motions in
$SO950$
is probably a little distorted by the artificially increased eddy viscosity of
$SO950$
. The issue of which of the two more dominantly yields the differences could be clarified by further inspecting
$C_{00}$
,
$C_{11}$
and
$C_{01}$
(figure 6
a,b), as they are, in a way, obtained by applying cutoff filters to both of
$O950$
and
$SO950$
. It appears that the correlation functions of
$O950$
are not exactly the same as those of
$SO950$
, suggesting that increasing
$C_{s}$
a little distorts the motions at
${\it\lambda}_{z}=1.5h$
. However, the times scales of these correlation functions for
$O950$
do not appear to be significantly different from those for
$SO950$
. This implies that the correlation functions obtained with
$E_{u}$
,
$E_{v}$
and
$E_{w}$
of
$O950$
do not precisely represent the dynamical behaviour of the largest attached eddies at
${\it\lambda}_{z}=1.5h$
due to the contribution by the surrounding smaller-scale turbulent fluctuations.
3.2 The attached eddies in the logarithmic region
Now, we consider the attached eddies in the logarithmic region. As shown in § 2.2, the attached eddies in the logarithmic region generate a self-similar statistical structure with respect to the spanwise length scale
${\it\lambda}_{z,0}~(=L_{z})$
. This self-similar part, which contains the essential physical process of the energy-containing motions in the logarithmic region, appears mainly below
$y\simeq 0.3{-}0.4L_{z}$
(figure 2). To trace the dynamical behaviour of this self-similar part more precisely, the definitions of
$E_{u}$
,
$E_{v}$
,
$E_{w}$
,
$E_{0}$
and
$E_{1}$
given in (3.1) and (3.2) are a little modified, so that the wall-normal domain of the integration becomes only
$[0,2/3L_{z}]$
. We note that this new definition is still consistent with (3.1), as the wall-normal domain of the integration becomes
$[0,1]$
for
$L_{z}=1.5h$
, which is the spanwise length scale of the VLSM and the LSM.
Inspection of the instantaneous flow fields of all the simulations in the logarithmic region (see also table 1) reveals that basically the same dynamical process occurs in the attached eddies, given with streaks and quasi-streamwise vortical structures, at each of the spanwise length scales belonging to the logarithmic region: i.e. amplification of the streaks by the quasi-streamwise vortical structures, subsequent meandering of the streaks along the streamwise direction and breakdown of the streaks with regeneration of the quasi-streamwise vortical structures. To avoid repetition of the same discussion given in § 3.1, here we only report auto- and cross-correlation functions of the simulations concerning the logarithmic region with a focus on the scaling of the computed correlation functions.
Figure 7. Auto-correlation functions: (a,b)
$C_{uu}({\it\tau})$
; (c,d)
$C_{vv}({\it\tau})$
; (e,f)
$C_{11}({\it\tau})$
. In (a,c,e), ——
$L950a$
; – – – –
$L950b$
; – - – - –
$L1800a$
; –
$\cdot \cdot$
–
$\cdot \cdot$
–
$L1800b$
;
$\cdots \cdots$
$L1800c$
, while, in (b,d,f), ——
$LS950a$
; – – – –
$LS950b$
; – - – - –
$LS1800a$
; –
$\cdot \cdot$
–
$\cdot \cdot$
–
$LS1800b$
;
$\cdots \cdots$
$LS1800c$
.
Figure 7 shows auto-correlations obtained from all the simulations concerning the energy-containing motions in the logarithmic region. All the correlation functions from both full (figure 7
a,c,e) and over-damped simulations (figure 7
b,d,f) scale fairly well with the spanwise size of the attached eddies
$L_{z}~(={\it\lambda}_{z,0})$
, suggesting that the attached eddies in the minimal unit are ‘dynamically’ self-similar with respect to the spanwise size. The auto-correlation functions
$C_{uu}$
and
$C_{vv}$
in figure 7(a–d) reach zero at
${\it\tau}u_{{\it\tau}}/L_{z}\simeq \pm 1$
, indicating that the single period of the self-sustaining process would be roughly given by
$Tu_{{\it\tau}}/L_{z}\simeq 2$
. As in the case of the outer attached eddies,
$C_{11}$
, which characterises the time scale of the meandering motion of the streak, is found to have much shorter time scale
$Tu_{{\it\tau}}/L_{z}\simeq 1$
than that of
$C_{uu}$
and
$C_{vv}$
.
Figure 8. Cross-correlation functions: (a,b)
$C_{uv}({\it\tau})$
; (c,d)
$C_{vw}({\it\tau})$
; (e,f)
$C_{1v}({\it\tau})$
. In (a,c,e), ——
$L950a$
; – – – –
$L950b$
; – - – - –
$L1800a$
; –
$\cdot \cdot$
–
$\cdot \cdot$
–
$L1800b$
;
$\cdots \cdots$
$L1800c$
, while, in (b,d,f), ——
$SL950a$
; – – – –
$SL950b$
; – - – - –
$SL1800a$
; –
$\cdot \cdot$
–
$\cdot \cdot$
–
$SL1800b$
;
$\cdots \cdots$
$SL1800c$
.
Figure 8 shows several cross-correlations obtained from the same simulations. The cross-correlation
$C_{uv}$
of both full (figure 8
a) and over-damped simulations (figure 8
b) exhibits a phase difference between
$E_{u}$
and
$E_{v}$
(or
$E_{w}$
), similar to that of the simulations concerning the outer-scaling motions (figure 5
c,d). A strong correlation between
$E_{v}$
and
$E_{w}$
is also observed in the motions in the logarithmic region, similarly to those in the outer region (figure 8
c,d). Finally, the cross-correlation
$C_{1v}$
also confirms that amplification of
$E_{v}$
appears a little after
$E_{1}$
is amplified, indicating that the vortical structures in the logarithmic region are regenerated after the meandering motion (figure 8
e,f).
4 Discussion
Thus far, we have explored the dynamical behaviour of the attached eddies in the logarithmic and outer regions. The attached eddies in the minimal unit exhibit relatively large-scale temporal oscillations, ‘bursting’ as reported by Flores & Jiménez (Reference Flores and Jiménez2010). The bursting is also observed in the over-damped simulations, in which the attached eddies only at the given spanwise length scale survive through their self-sustaining mechanisms. The qualitatively good comparison of instantaneous flow fields and correlation functions between the full and the over-damped simulations suggests that the bursting is presumably the reflection of the self-sustaining process of the attached eddies with the characteristic turnover time scale given by:
$$\begin{eqnarray}\frac{Tu_{{\it\tau}}}{{\it\lambda}_{z}}\simeq 2,\end{eqnarray}$$
where
${\it\lambda}_{z}$
is the spanwise size of the given attached eddies, which corresponds to the spanwise domain size of the minimal unit
$L_{z}$
. Here, we note that if the spanwise length scale is chosen as
${\it\lambda}_{z}^{+}\simeq 100$
, (4.1) gives
$T^{+}\simeq 200$
, the well-known bursting period of the near-wall coherent structures in the minimal unit (Hamilton, Kim & Waleffe Reference Hamilton, Kim and Waleffe1995; Jiménez et al.
Reference Jiménez, Kawahara, Simens, Nagata and Shiba2005). On the other hand, if
${\it\lambda}_{z}=1.5h$
is considered, (4.1) yields
$Tu_{{\it\tau}}/h\simeq 3$
, which roughly corresponds to the bursting time scale of the largest attached eddies composed of VLSMs and LSMs (see § 3.1). The attached eddies the spanwise size of which is between
${\it\lambda}_{z}^{+}=100$
and
${\it\lambda}_{z}=1.5h$
burst in a self-similar manner with the time scale given by (4.1) (see § 3.2). We note that if
${\it\lambda}_{z}=3y$
is chosen, the time scale given in (4.1) becomes consistent with the bursting time scale of
$Tu_{{\it\tau}}/y\simeq 6$
reported by Flores & Jiménez (Reference Flores and Jiménez2010) who extracted this time scale from a direct numerical simulation, and, interestingly,
${\it\lambda}_{z}=3y$
corresponds well to the scaling
$y\simeq 0.3{-}0.4{\it\lambda}_{z}$
, below which the computed statistics of the isolated attached eddies are found to be self-similar (see also figure 2).
In the present study, it is also shown that the self-sustaining process of the attached eddies involves its two dynamically interconnected structural elements: one is the long streaky motion extending over the entire streamwise domain of the minimal unit (figure 6 c,d), and the other is the vortical structure which would be statistically in the form of quasi-streamwise vortices given the strong correlation between the wall-normal and spanwise velocities (figures 5 c,d and 8 c,d). The interactive dynamics between the two elements appears to be the backbone of the self-sustaining process of the attached eddies in the logarithmic and the outer regions, and is remarkably similar to that in the near-wall region (Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002). It should be pointed out, however, that this should not be very surprising, given the fact that the near-wall motion in the form of the near-wall streak and the quasi-streamwise vortices would simply be the smallest attached eddy (Hwang Reference Hwang2015).
Figure 9. A schematic diagram of self-sustaining process of the attached eddies (originally proposed by Hamilton et al. (Reference Hamilton, Kim and Waleffe1995) for the near-wall motions). The diagram incorporates the streak transient growth proposed by Schoppa & Hussain (Reference Schoppa and Hussain2002) for the near-wall motions as well as the Orr mechanism proposed by Jiménez (Reference Jiménez2013, Reference Jiménez2015). Here,
$u_{s}$
denotes the streamwise velocity given with the amplified streaks.
Figure 9 is a schematic diagram of the self-sustaining process of the attached eddies at a given spanwise length scale proposed in the present study based on the observations made in the previous section. This schematic diagram is originally from Hamilton et al. (Reference Hamilton, Kim and Waleffe1995), and, here, we further incorporate several previous contributions in this context (Schoppa & Hussain Reference Schoppa and Hussain2002; Jiménez Reference Jiménez2013, Reference Jiménez2015). The streaks are amplified via the ‘lift-up’ effect by which the streamwise vortical structures transfer energy of the mean shear to streaks (figures 3 c,d and 4 c,d). The amplified streaks then undergo ‘rapid’ meandering or oscillatory motion in the streamwise direction via streak instability or transient growth (see also § 3.2; Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002; Park, Hwang & Cossu Reference Park, Hwang and Cossu2011). The quasi-streamwise vortical structures are finally regenerated with breakdown of the streak via linear and/or nonlinear mechanisms (Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002; Jiménez Reference Jiménez2013, Reference Jiménez2015). In order to provide more solid evidence on the existence of these physical processes, we now introduce two additional numerical experiments, designed to examine the lift-up effect (the left branch from streamwise vortical structures to streaks in figure 9) and the streak meandering and regeneration of the streamwise vortical structures (the right and lower branches from streaks to streamwise vortical structures in figure 9), respectively.
4.1 Streak amplification: lift-up effect
The ‘lift-up’ effect has been very well understood as the robust mechanism for generation of the streaky motions both in transitional (Ellingsen & Palm Reference Ellingsen and Palm1975; Landahl Reference Landahl1980; Gustavsson Reference Gustavsson1991; Butler & Farrell Reference Butler and Farrell1992; Reddy & Henningson Reference Reddy and Henningson1993; Schmid & Henningson Reference Schmid and Henningson2001) and turbulent flows (Landahl Reference Landahl1990; Butler & Farrell Reference Butler and Farrell1993; Kim & Lim Reference Kim and Lim2000; Chernyshenko & Baig Reference Chernyshenko and Baig2005; del Álamo & Jiménez Reference del Álamo and Jiménez2006; Cossu et al. Reference Cossu, Pujals and Depardon2009; Pujals et al. Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010a ,Reference Hwang and Cossu b ; Willis, Hwang & Cossu Reference Willis, Hwang and Cossu2010). From a vortex dynamical viewpoint, it simply represents tilting of the streamwise vortices by mean shear: i.e.
$$\begin{eqnarray}\frac{\text{D}{\it\omega}_{y}}{\text{D}t}\sim \frac{\text{d}U}{\text{d}y}{\it\omega}_{x},\end{eqnarray}$$
where
$\text{D}/\text{D}t$
is the material time derivative,
${\it\omega}_{x}$
and
${\it\omega}_{y}$
are the streamwise and wall-normal vorticities, respectively. The ‘lift-up’ effect is an important origin of the ‘non-normality’ of the linearised Navier–Stokes operator, leading to a large amplification of an initial condition as well as a body forcing containing a significant amount of the wall-normal velocity component. Therefore, the non-modal stability analysis (Schmid & Henningson Reference Schmid and Henningson2001; Schmid Reference Schmid2007), which quantifies the amplification mechanism of the stable linearised Navier–Stokes operator, has been a popular methodology of most of the previous investigations. However, direct relevance of the ‘lift-up’ effect to fully developed turbulence has been very rarely shown, except by Kim & Lim (Reference Kim and Lim2000) who demonstrated its importance on the near-wall turbulence at a low Reynolds number by performing a direct numerical simulation without the off-diagonal term of the Orr–Sommerfeld–Squire operator representing (4.2).
The goal of this section is to demonstrate that the ‘lift-up’ effect is the essential part of the self-sustaining process of the attached eddies in the logarithmic and outer regions with a similar approach of Kim & Lim (Reference Kim and Lim2000). To this end, we modify their approach to suppress the lift-up effect only at a prescribed spanwise length scale. In the minimal unit, the streak amplification by the lift-up effect is found to be dominant at infinitely long streamwise wavelength (figure 6
c,d). To artificially suppress this lift-up effect at zero streamwise wavenumber (
$k_{x}=0$
), the following modified streamwise momentum equation is solved with the minimal unit:
$$\begin{eqnarray}\displaystyle \frac{\partial \bar{u}}{\partial t}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\bar{u}-\left([\hat{v}\text{e}^{\text{i}k_{z}z}+\hat{v}^{\ast }\text{e}^{-\text{i}k_{z}z}]|_{(k_{x},k_{z})=(0,2{\rm\pi}/L_{z})}\right)\frac{\text{d}\overline{U}}{\text{d}y}=-\frac{1}{{\it\rho}}\frac{\partial p}{\partial x}+({\it\nu}+{\it\nu}_{T}){\rm\nabla}^{2}\bar{u}, & & \displaystyle\end{eqnarray}$$
where the superscript
$^{\ast }$
denotes the complex conjugate,
$\bar{u}$
is the streamwise velocity and
$\overline{U}$
is the streamwise velocity averaged along the streamwise and spanwise directions at each time. In (4.3), the energy extraction mechanism from the mean shear
$\overline{U}$
by the wall-normal velocity (i.e. lift-up effect) is now artificially eliminated for the streamwise uniform streaky motions (
$k_{x}=0$
) at
${\it\lambda}_{z}=L_{z}$
by adding the third term on the left-hand side. We also note that this is equivalent to removing the off-diagonal term of the Orr–Sommerfeld–Squire operator for
$k_{x}=0$
and
$k_{z}=\pm 2{\rm\pi}/L_{z}$
, as in the approach by Kim & Lim (Reference Kim and Lim2000) whose numerical solver is written in the wall-normal velocity and vorticity form.
Figure 10. Time trace of
$E_{u}$
and
$E_{v}$
of
$SO950$
. At
$tU_{e}/h=7500$
(
$U_{e}$
is the centreline velocity of the laminar velocity profile with the same volume flux), the streamwise momentum equation is replaced by (4.3). Here,
$E_{u}$
and
$E_{v}$
are normalised with
$U_{e}$
.
The designed numerical experiment is first performed with
$SO950$
in which only the largest attached eddies sustain themselves without any smaller-scale turbulent motions. Figure 10 shows time trace of
$E_{u}$
and
$E_{v}$
. Initially, a normal
$SO950$
simulation is performed, yielding the non-trivial fluctuations of
$E_{u}$
and
$E_{v}$
via the self-sustaining process. At
$tU_{e}/h=7500$
(
$U_{e}$
is the centreline velocity of the laminar velocity profile with the same volume flux), the streamwise momentum equation is replaced by (4.3). Immediately after this time,
$E_{u}$
, which characterises the temporal evolution of the streak (the VLSM in this case), very rapidly decays, indicating that the streaky motion is very quickly destroyed by implementing (4.3) (figure 10
a). We note that, in
$tU_{e}/h\in [7500,7600]$
, this decay of
$E_{u}$
appears to be even faster than
$E_{v}$
, finally resulting in complete suppression of the self-sustaining process in
$SO950$
. The very rapid destruction of the streaky motion by implementing (4.3) is consistently observed with a few other initial conditions. This clearly suggests that the amplification of the long streaky motion is indeed governed by the ‘lift-up’ effect, consistent with a number of previous theoretical predictions along this line (del Álamo & Jiménez Reference del Álamo and Jiménez2006; Pujals et al.
Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010b
).
Figure 11. One-dimensional spanwise wavenumber spectra of (a,b) the streamwise and (c,d) the wall-normal velocities: (a,c)
$O950$
; (b,d)
$O950$
with (4.3). Here, the spectra are normalised with
$U_{e}$
for the purpose of comparison.
Figure 12. One-dimensional streamwise wavenumber spectra of (a,b) the streamwise and (c,d) the wall-normal velocities: (a,c)
$O950$
; (b,d)
$O950$
with (4.3). Here, the spectra are normalised with
$U_{e}$
for the purpose of comparison.
The numerical experimentation with (4.3) is also applied to
$O950$
in which the largest attached eddies are resolved with turbulent motions at other length scales. Not surprisingly,
$O950$
is not completely suppressed by (4.3), as the self-sustaining mechanisms at other scales would still be undisturbed. In figure 11, we compare the spanwise wavenumber spectra of
$O950$
(figure 11
a,c) with those of
$O950$
with (4.3) (figure 11
b,d). The streamwise velocity spectra of
$O950$
with (4.3) clearly show a significant amount of reduction of the streamwise turbulent kinetic energy at
${\it\lambda}_{z}=1.5h$
compared to those of
$O950$
(figure 11
a,b), indicating that the streaky motion at
${\it\lambda}_{z}=1.5h$
(VLSM) under full turbulence is also destroyed by inhibiting the lift-up effect. This also appears to yield reduction of the wall-normal turbulent kinetic energy at
${\it\lambda}_{z}=1.5h$
for
$y>0.5h$
(figure 11
c,d), as this length scale corresponds to that of the streamwise vortical structures involved in the self-sustaining process at
${\it\lambda}_{z}=1.5h$
(see also (1.1c,d
) with
${\it\lambda}_{z}=1.5h$
). However, it is quite interesting to note that the wall-normal turbulent kinetic energy at other spanwise wavelengths, particularly the ones near
${\it\lambda}_{z}\simeq 0.75h$
, appears to be significantly amplified with the removal of the streaky motions at
${\it\lambda}_{z}=1.5h$
, and generates additional energy even at
${\it\lambda}_{z}=1.5h$
. This suggests that the non-trivial scale interactions exist between the attached eddies at neighbouring length scales, although the detailed investigation of this issue is beyond the scope of the present study. Inspection of the streamwise wavenumber spectra shown in figure 12 also allows us to reach the same conclusion. Since (4.3) only applies to the streamwise uniform streaky motion (i.e.
$k_{x}=0$
), the spectra of the streamwise velocity show only a little change (figure 12
a,b). However, with the destruction of the streaky motions uniform along the streamwise direction, the spectra of the wall-normal velocity at
${\it\lambda}_{x}\simeq 3h$
show a considerable amount of reduction of energy for
$y>0.5h$
(figure 12
c,d), indicating that the streamwise vortical structures associated with the self-sustaining process at
${\it\lambda}_{z}=1.5h$
are destroyed. We note that the increased energy at
${\it\lambda}_{x}\simeq 1.5h$
in the streamwise wavenumber spectra of the wall-normal velocity should be associated with the increased energy of the wall-normal velocity near
${\it\lambda}_{z}\simeq 0.75h$
(figure 12
d).
Finally, it has been robustly found that suppressing the lift-up effect through (4.3) yields a considerable amount of turbulent skin-friction reduction, as reported in table 2 showing that the smaller the computational box is, the larger the drag reduction achieved. A considerable amount of turbulent skin-friction reduction by suppressing the lift-up effect here suggests that generation of turbulent skin-friction at high Reynolds numbers would be associated with the momentum transfer to the wall by the self-sustaining processes of the attached eddies in the logarithmic and outer region. This result also indicates that applying a linear flow control, e.g. with the approaches in Kim & Bewley (Reference Kim and Bewley2007), to relatively large-scale attached eddies would be a promising strategy for turbulent drag reduction. Despite many interesting further issues, a detailed investigation on the relation between turbulent skin friction and the self-sustaining process (or lift-up effect) in the logarithmic and outer regions is beyond the scope of the present study and is currently a subject of on-going investigation.
4.2 Streak breakdown and regeneration of streamwise vortical structures
In contrast to the ‘lift-up’ effect which has been an issue in a number of previous studies, the breakdown of amplified streaks and the subsequent regeneration of the streamwise vortical structures (see figure 9) have been much less studied, even for the near-wall motions. In the case of the near-wall motions, which would be the smallest attached eddies (Hwang Reference Hwang2015), the amplified streak typically experiences a rapid sinuous meandering or oscillatory motion before the streamwise vortices are generated (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002). This sinuous meandering motion is a consequence of the streak instability or transient growth (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002), although, in practice, distinguishing one from another appears to be almost impossible, given the fact that both of the processes are basically a consequence of the interaction with the same sinuous-mode instability (Hœpffner, Brandt & Henningson Reference Hœpffner, Brandt and Henningson2005). It should also be mentioned that the sinuous mode instability essentially originates from the ‘spanwise shear’ generated by the amplified streak (i.e.
$\partial u_{s}/\partial z$
where
$u_{s}$
is the streamwise velocity with the amplified streak; see also Park & Huerre (Reference Park and Huerre1995), Cossu & Brandt (Reference Cossu and Brandt2002), Hœpffner et al. (Reference Hœpffner, Brandt and Henningson2005), Park et al. (Reference Park, Hwang and Cossu2011)). It is therefore physically not meaningful to analyse this process using the approaches based on the linearised Navier–Stokes equation around ‘mean shear’, as the equation does not carry any relevant physics relating to this mechanism.
The sinuous meandering motion of the amplified streak feeds a small amount of the streamwise vortical structures, and they are subsequently amplified via nonlinear mechanisms (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002). Hamilton et al. (Reference Hamilton, Kim and Waleffe1995) proposed that wall-normal advection of the streamwise vortices would be the leading nonlinear regeneration mechanism based on a minimal Couette flow simulation (
$\text{D}{\it\omega}_{x}/\text{D}t\sim v\partial {\it\omega}_{x}/\partial y$
; figure 9). On the other hand, with a minimal channel flow simulation, Schoppa & Hussain (Reference Schoppa and Hussain2002) showed that stretching of the streamwise vortices by the streamwise meandering (or wavy) motion caused by the streak instability or transient growth would play an important role in this process (
$\text{D}{\it\omega}_{x}/\text{D}t\sim {\it\omega}_{x}\partial u/\partial x$
; figure 9). More recently, Jiménez (Reference Jiménez2013, Reference Jiménez2015) proposed that the Orr mechanism, a process by which the wall-normal velocity takes energy from the mean shear, also appears to play a role in this process especially for the motions in the logarithmic and outer regions. At this moment, it is quite difficult to convincingly argue which of the mechanisms would be dominant or most important among the three, especially for the generation of the streamwise vortical structures in the logarithmic and outer regions. However, it does not appear that solely the Orr mechanism (Jiménez Reference Jiménez2013, Reference Jiménez2015), which merely concerns the amplification of the wall-normal velocity only, would play a dominant role, given the strong correlation between the wall-normal and spanwise velocities (figures 5
c,d and 8
c,d).
Table 2. Skin-friction reduction
${\rm\Delta}C_{f}$
by suppressing the lift-up effect with (4.3).
Figure 13. Time trace of
$E_{u}$
and
$E_{v}$
of
$SO950$
. At
$tU_{e}/h=7500$
, (4.4) is applied. Here,
$E_{u}$
and
$E_{v}$
are normalised with
$U_{e}$
.
In the present study, it has been found that the rapid sinuous meandering motion of the amplified streak and the subsequent generation of the streamwise vortical structures are also robust features of the self-sustaining processes in the logarithmic and outer regions (figures 3
c, 4
c, 6
c,d, and 8
e,f). This suggests that the streak instability, which was previously analysed by Park et al. (Reference Park, Hwang and Cossu2011) for the outer attached eddies using the Floquet theory, or transient growth would also be an important process associated with the subsequent generation of the streamwise vortical structures. It is worth mentioning that this process is intricately tangled with the subsequent nonlinear amplification of the streamwise vortical structures, especially via the vortex stretching mechanism proposed by Schoppa & Hussain (Reference Schoppa and Hussain2002), as the vortical structures take the energy required for the amplification from the meandering (or wavy) streaky motion (i.e.
$\partial u_{s}/\partial x$
).
Given this observation, it is very tempting to postulate that the streak meandering motion, presumably caused by the streak instability or transient growth, would play a crucial role in regeneration of the streamwise vortical structures. The goal of this section is to examine this mechanism. For this purpose, here, we introduce a numerical experiment which artificially damps the sinuous meandering motion of the amplified streak. Since the streak meandering motion is dominant at
${\it\lambda}_{x}\simeq L_{x}$
in the minimal unit (figures 3
c and 4
d), we implement a damping of this wave component by modifying the right-hand side of the discretised streamwise momentum equation at each Runge–Kutta substep, such that:
$$\begin{eqnarray}\widehat{\text{RHS}}_{x}\left(y;k_{x}=\frac{2{\rm\pi}}{L_{x}},k_{z}=\pm \frac{2{\rm\pi}}{L_{z}}\right)\rightarrow {\it\mu}\widehat{\text{RHS}}_{x}\left(y;k_{x}=\frac{2{\rm\pi}}{L_{x}},k_{z}=\pm \frac{2{\rm\pi}}{L_{z}}\right),\end{eqnarray}$$
where
${\it\mu}$
is a factor which should be
${\it\mu}<1$
for damping. Here, we again stress that this technique is implemented only to the streamwise momentum equation to only suppress the meandering motion of
$u$
.
The damping technique (4.4) is applied to both
$O950$
and
$SO950$
by considering a few different
${\it\mu}~(=0.85,0.90,0.95)$
. However, the results are found to be qualitatively independent of the choice of
${\it\mu}$
, thus the results only for
${\it\mu}=0.95$
are reported in the present study. Figure 13 shows time trace of
$E_{u}$
and
$E_{v}$
of
$SO950$
in which (4.4) is applied at
$tU_{e}/h=7500$
. Immediately after (4.4) is applied,
$E_{v}$
decays very quickly. Examination with a few other initial conditions reveals that this behaviour is qualitatively independent of the initial condition, suggesting that the streak meandering motion observed in
$SO950$
is indeed directly involved in generation of the streamwise vortical structures. In
$SO950$
, both
$E_{u}$
and
$E_{v}$
eventually decay to zero after application of (4.4), but, in this case, it is quite interesting to note that
$E_{u}$
persists for a substantially long time. This certainly differs from the behaviour of
$E_{u}$
observed after applying (4.3) (compare figure 13
a with 10
a), implying that the lift-up effect is a very strong amplification process of the streamwise velocity (or streak) even with a small amplitude of the vortical structures.
Figure 14. One-dimensional spanwise wavenumber spectra of (a,b) the streamwise and (c,d) the wall-normal velocities: (a,c)
$O950$
; (b,d)
$O950$
with (4.4). Here, the spectra are normalised with
$U_{e}$
for the purpose of comparison.
Figure 15. One-dimensional streamwise wavenumber spectra of (a,b) the streamwise and (c,d) the wall-normal velocities: (a,c)
$O950$
; (b,d)
$O950$
with (4.4). Here, the spectra are normalised with
$U_{e}$
for the purpose of comparison.
The damping technique (4.4) is also applied to
$O950$
. The streamwise and spanwise wavenumber spectra of the streamwise and the wall-normal velocity are compared with those of
$O950$
, as respectively reported in figures 14 and 15. Consistent with the case of
$SO950$
, application of (4.4) to
$O950$
yields significant reduction of the wall-normal turbulent kinetic energy at
${\it\lambda}_{z}=1.5h$
(figure 14
c,d), despite the increase of the streamwise turbulent kinetic energy in the spanwise wavenumber spectra (figure 14
a,b; see also the next paragraph for a further discussion). The streamwise wavenumber spectra of the wall-normal turbulent kinetic energy also clearly exhibits a significant amount of reduction of the energy at
${\it\lambda}_{x}=3h$
(figure 15
c,d), indicating that the artificial damping of the streak meandering motion significantly destroys the generation mechanism of the streamwise vortical structures at this wavelength.
Despite the consistent result with
$SO950$
, in
$O950$
, application of (4.4) does not appear to completely destroy the structures at
${\it\lambda}_{z}=1.5h$
. Although the streamwise wavenumber spectra of the streamwise velocity show a large diminishing of the energy at
${\it\lambda}_{z}=1.5h$
(figure 15
a,b), confirming that (4.4) indeed inhibits the meandering motion of the streak at this wavelength, the increase of the streamwise turbulent kinetic energy in the spanwise wavenumber spectra (figure 14
b) imply that the streamwise uniform streaky motion (i.e.
$k_{x}=0$
mode in the minimal unit) is amplified on average. This also appears to be consistent with little change of the skin-friction drag, despite the significant destruction of the vortical structures at
${\it\lambda}_{x}=3h$
.
The intensification of the energy of the streamwise uniform motion is surprising, at least to us, given the complete suppression of the self-sustaining process in
$SO950$
. The increase of the energy of the streamwise uniform motion might be explained by the lack of a proper breakdown mechanism through the streak instability or transient growth artificially suppressed, as weaker vortices could also sustain stronger streaks which can breakdown at shorter streamwise wavelengths with the elevated breakdown threshold. However, the persisting streaky motion even with the damaged breakdown mechanism can also suggest that there may exist some additional feeding mechanisms of the streamwise vortical structures. Currently, we do not have a precise understanding of these mechanisms, although they might be from scale interaction or from the Orr-mechanism proposed by Jiménez (Reference Jiménez2013, Reference Jiménez2015). However, in any case, the result of the present numerical experiment directly supports the notion that the streak instability (or transient growth) and the following nonlinear vortex stretching of the streamwise vortical structures play a crucial role in the formation of the vortical structures in the logarithmic and the outer regions as well as in the determination of their streamwise length scale (Schoppa & Hussain Reference Schoppa and Hussain2002; Park et al.
Reference Park, Hwang and Cossu2011; Hwang Reference Hwang2015).
5 Concluding remarks
Thus far, we have investigated the self-sustaining process of the energy-containing motions in the logarithmic and outer regions (the attached eddies) by examining their dynamical behaviour in the minimal unit. The present study is summarised as follow:
-
(i) The attached eddies at a given spanwise length scale in the minimal unit exhibit a statistically recurrent dynamical behaviour which has been called ‘bursting’ (Flores & Jiménez Reference Flores and Jiménez2010). The bursting is also observed in the over-damped simulations in which the attached eddies survive only through their self-sustaining mechanisms, and is remarkably similar to that in the full simulations, indicating that the bursting is the reflection of the self-sustaining process of the attached eddies. For the attached eddies at the given spanwise length scale
${\it\lambda}_{z}$
, the time period of the bursting (i.e. the self-sustaining process) is found to scale with
$Tu_{{\it\tau}}/{\it\lambda}_{z}\simeq 2$
, suggesting that the statistically self-similar attached eddies in the logarithmic region (Hwang Reference Hwang2015) are also ‘dynamically’ self-similar. -
(ii) It is shown that the self-sustaining process of the attached eddies in the logarithmic and outer regions is very similar to that of the near-wall motions (Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002), which would be the smallest attached eddies (Hwang Reference Hwang2015). The attached eddies in the minimal unit in the logarithmic and outer regions, composed of two elements, the streak and the streamwise vortical structures, sustain themselves through the interactive dynamics between the two: (a) the streak is significantly amplified by the streamwise vortical structures via the lift-up effect; (b) the amplified streak subsequently experiences very rapid meandering motion along the streamwise direction; and (c) the meandering streaks breakdown with regeneration of new streamwise vortical structures.
-
(iii) To provide more convincing evidence on the existence of the proposed self-sustaining process in the logarithmic and outer regions, two numerical experiments are further performed. One is to artificially suppress the lift-up effect by modifying the technique introduced by Kim & Lim (Reference Kim and Lim2000), and the other is to artificially damp out the streak meandering motion, which would probably be a consequence of the streak instability or transient growth (Park et al. Reference Park, Hwang and Cossu2011). It is shown that the artificial suppression of the lift-up effect inhibits the amplification of the streak and subsequently suppresses the self-sustaining process of the attached eddies. Also, the artificial inhibition of the streak meandering motions destroy the generation of the streamwise vortical structures, significantly affecting the self-sustaining process. The numerical experiments also reveal that there are non-trivial scale interactions among the attached eddies.
The importance of the present study probably lies in the identification of the self-sustaining process of the energy-containing motions in the logarithmic and outer regions, given in the form of Townsend’s attached eddies. The existence of the self-sustaining process in these regions, which appears to be basically the same as that of the near-wall region, would provide some evidence on the relevance of the so-called ‘exact coherent structures’ at high Reynolds numbers: i.e. the exact solutions of the Navier–Stokes equation in the form of unstable stationary/travelling waves and relative periodic orbits (e.g., Nagata Reference Nagata1990; Kawahara & Kida Reference Kawahara and Kida2001; Waleffe Reference Waleffe2001; Faisst & Eckhardt Reference Faisst and Eckhardt2003; Wedin & Kerswell Reference Wedin and Kerswell2004; Jiménez et al. Reference Jiménez, Kawahara, Simens, Nagata and Shiba2005). At low Reynolds numbers, these solutions have been shown to form a skeleton of the basin of attraction of turbulent solutions in phase space (e.g., Gibson, Halcrow & Cvitanovic Reference Gibson, Halcrow and Cvitanovic2008), and their discovery has played a crucial role in recent advancement on understanding bypass transition and low Reynolds number turbulence. It should be mentioned that the exact coherent structure, typically given in the form of a wavy streak and flanked streamwise vortices, physically represents the self-sustaining process given in figure 9 (e.g., Waleffe Reference Waleffe2003). This therefore suggests that the attached eddies in the logarithmic and outer regions, which bear such a self-sustaining process, would be linked to the exact coherent structures at high Reynolds numbers at least to some extent.
Nevertheless, it is not yet clear how much such dynamical-system-based approaches could be extended further especially for describing the dynamics of coherent structures in high Reynolds number wall turbulence. Perhaps, one of the most important challenges would be description of the complex scale interactions between the self-sustaining structures at different length scales. In fact, the dynamical-system-based approaches implicitly assume that turbulence is a chaos occurring in a finite dimensional nonlinear system. Unfortunately, turbulence is, however, a chaos occurring in a spatially extended system, the dimension of which is virtually infinite, and is inherently a multi-scale phenomenon involving daunting scale interactions. Given this difficulty, the full suitability of the dynamical system approach especially to high Reynolds number turbulence is yet an open question, although the approach may enlighten at least some important aspects of turbulence.
Acknowledgements
Y.H. gratefully acknowledges Professor J. Jiménez for sharing his paper (Jiménez Reference Jiménez2015) before its publication. This work was partially supported by the Engineering and Physical Science Research Council (EPSRC) in the UK (EP/N019342/1).
Appendix A. Effect of the filtering (2.1) on time correlation functions
As mentioned, all the simulations of the present study are performed with the filtering technique (2.1) which removes the two-dimensional spurious motions populating the
$x$
–
$y$
plane in the spanwise minimal unit simulations; for further details, the reader is also referred to Hwang (Reference Hwang2013) in which a detailed discussion on this spurious motion is given. In figure 16, a set of time correlation functions of
$O950$
without (2.1) are compared with those of
$O950$
. All the presented correlation functions of
$O950$
without (2.1) show good agreement with those of
$O950$
, except
$C_{uv}({\it\tau})$
. It appears that
$C_{uv}({\it\tau})$
of
$O950$
without (2.1) is a little larger than that of
$O950$
, although the peak location of
$C_{uv}({\it\tau})$
itself shows good agreement. However, this may have been expected in a way, given the nature of the filtering technique (2.1) which removes the streamwise and wall-normal motions in the
$x$
–
$y$
plane. Overall good agreement of the correlation functions from the two simulations suggests that application of (2.1) does not significantly affect the motions in
$O950$
, as in our previous studies (Hwang Reference Hwang2013, Reference Hwang2015).
Figure 16. Time correlation functions of (a)
$O950$
without (2.1) and (b)
$O950$
. Here, ——,
$C_{uu}({\it\tau})$
; – – – –,
$C_{vv}({\it\tau})$
; – - – - –,
$C_{uv}({\it\tau})$
; –
$\cdot \cdot$
–
$\cdot \cdot$
–,
$C_{vw}({\it\tau})$
.
Figure 17. Comparison of the second-order statistics of the self-sustaining attached eddies in the minimal unit (
$SL1800c$
in the present study) with those in the long streamwise domain (
$L1800c$
in Hwang Reference Hwang2015): (a) the streamwise, wall-normal and spanwise velocities; (b) Reynolds stress. Here, ——,
$SL1800c$
in the present study; – – – –,
$L1800c$
in Hwang (Reference Hwang2015).
Appendix B. Comparison of statistics between attached eddies in the minimal and long computational domains
Here, we compare the statistics of the self-sustaining attached eddies in the minimal streamwise domain (
$L_{x}=2L_{z}$
;
$SL1800c$
in the present study) with those in a long streamwise domain (
$L_{x}=8{\rm\pi}h$
;
$L1800c$
in Hwang Reference Hwang2015). We note that the two simulations share the same spanwise computational domain size,
$L_{z}=0.75h$
, although the resolution of the present study is a little finer than that in Hwang (Reference Hwang2015). Except this, all the simulation parameters of the two simulations are identical to each other. Figure 17 shows the second-order statistics of
$SL1800c$
in the present study and those of
$L1800c$
in Hwang (Reference Hwang2015). The second-order statistics obtained with the streamwise minimal domain tend to generate larger velocity fluctuations and Reynolds stress in the region relatively close to the wall, except the streamwise velocity fluctuation showing a non-trivial difference. However, overall, the second-order statistics with the streamwise minimal domain do not considerably deviate from those with the long domain, indicating that the minimal domain does not significantly distort the second-order statistics of the interest. It should mentioned that qualitatively the same behaviour is observed in all the other minimal unit simulations in the present study in comparison to those with sufficiently long computational domains in Hwang (Reference Hwang2015).
