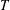1 Introduction
One of the most powerful mathematical tools used to address problems in hydrodynamic stability is the method of linear normal mode perturbation theory (Drazin & Reid Reference Drazin and Reid1981). Normal modes are readily computed for steady parallel background flows and, using Floquet theory, for temporally periodic flows. For a time-varying background flow, one can compute normal modes with meaningful interpretation if their evolution is sufficiently fast that the background may be assumed to be ‘frozen’ in time. Relatively recent developments in computational power have allowed non-parallel base states to be considered. One successful approach is to assume that underlying periodicity remains (e.g. see Klaassen & Peltier Reference Klaassen and Peltier1991; Caulfield & Peltier Reference Caulfield and Peltier2000), which continues to allow efficient spectral methods to be used. Alternatively, the concept of an unstable mode has been generalised to a ‘global mode’ (see the reviews of Huerre & Monkewitz Reference Huerre and Monkewitz1990; Chomaz Reference Chomaz2005) for base flows that lack translational invariance in any of the relevant coordinate directions. However, it is now appreciated that normal mode stability theory is by no means always able to describe the correct onset of perturbation growth or even the existence of instability in a broad class of flows including the classical problem of pressure-driven pipe flow, for which the transition to turbulence occurs despite the absence of any linear instabilities.
There has been an explosion of research attempting to describe perturbation growth in terms of ‘non-modal instabilities’ that result from the underlying non-normality of the linearised Navier–Stokes operator (see the reviews of Chomaz Reference Chomaz2005; Schmid Reference Schmid2007). One robust method, known as ‘direct–adjoint looping’ (DAL), is particularly well suited to the identification of transient ‘optimal’ perturbations to generic time-varying base flows (e.g. Schmid Reference Schmid2007; Arratia, Caulfield & Chomaz Reference Arratia, Caulfield and Chomaz2013; Luchini & Bottaro Reference Luchini and Bottaro2014). This method has a particular attraction when the base flow is varying sufficiently rapidly so that the abovementioned ‘frozen in time’ assumption is not valid, as normal modal analyses are formally inappropriate for the examination of infinitesimal perturbations that develop on such a relatively rapidly evolving basic state. The DAL method has typically been applied to consideration of perturbation growth in numerically simulated flows. The work presented here is the first demonstration of the efficacy of the method applied to observations in laboratory experiments of instability growing on a rapidly varying base flow.
In finite-volume axisymmetric gravity current experiments in which dense fluid (for example salty water) is released from a hollow cylindrical lock into a less dense (for example fresh water) ambient, the lock fluid is observed to spread as an expanding annulus (Hallworth et al.
Reference Hallworth, Huppert, Phillips and Sparks1996). However, a different structure is observed in axisymmetric intrusion experiments in which the two-layer ambient has equal upper- and lower-layer depths and the lock fluid has the average ambient density. In such a ‘vertically symmetric’ flow, the intrusion still spreads radially when released from a cylindrical lock. However, its front loses coherence as a result of growing quasi-periodic azimuthal disturbances which result in the lock fluid advancing as radially extending spokes (Sutherland & Nault Reference Sutherland and Nault2007). The results of one such experiment, illustrated in figure 1, show the azimuthal wavenumber associated with the spoke structure to lie around
$m=12$
.
Figure 1. (a) Top view snapshot taken 8.5 s after extraction of the cylindrical lock released a vertically symmetric intrusive gravity current (adapted from figure 2(c) of Sutherland & Nault Reference Sutherland and Nault2007). (b) Circular time series constructed from intensities recorded around a circle of radius 32 cm, as indicated by the dashed line in (a). (c) Magnitude of azimuthal Fourier coefficients computed from the light-intensity time series in (b) averaged for times between 8 s and 12 s. Here, the wavenumbers 0 and 1 have been set to zero to remove biases in intensity due to dye and uneven overhead lighting, which was towards one side of the tank. While there is still a non-trivial signal at azimuthal wavenumbers of
$m=2$
and 3 as a secondary consequence of these biases, the strongest peak, which occurs at an azimuthal wavenumber of
$m=12$
, is associated with the radially extending spokes.
Of course, disordered motions are introduced in the immediate vicinity of the cylindrical lock when it is extracted. If this alone were responsible for perturbations that evolve to form the observed radial spokes, then one would expect these structures to also develop for a bottom-propagating current, which is further prone to instability as a result of viscous stresses where it contacts the bottom boundary (Simpson Reference Simpson1972). That the radial spoke structure is not observed in the bottom-propagating current therefore suggests that the particular structure of the vertically symmetric intruding base flow is prone to a specific different kind of perturbation growth intimately related to the evolving structure of the base flow.
Because the azimuthal disturbances evolve on the same time scale as the slumping of the fluid from the lock into the intrusion, this problem is not amenable to a normal mode stability analysis, but is extremely well suited to the DAL method. In § 2, from the azimuthal perturbation equations we derive the appropriate adjoint perturbation equations relative to a natural inner product which defines an appropriate total perturbation energy norm. We also describe how this pair of equations is employed in the DAL method to identify ‘optimal’ perturbations exhibiting maximal total perturbation energy gain. Its numerical implementation is described in § 3, wherein it is applied specifically to examine azimuthal disturbances to an axisymmetric base flow which simulates the collapse of fluid from a cylindrical lock to form an intrusion at a density interface. We find that the optimal perturbation that extracts energy from the base flow at the fastest rate has azimuthal wavenumber consistent with, although somewhat larger than, that of the spokes observed in experiments. We draw our conclusions in § 4, and briefly consider possible future directions.
2 Theory
We are interested in the evolution of fully three-dimensional perturbations on a time-evolving axisymmetric basic state that simulates the sudden release of a cylinder of uniform-density fluid into an approximately two-layer ambient. Before describing the use of an appropriate DAL method, we describe the equations and the numerical approach used to simulate the evolution of the axisymmetric base flow.
2.1 Axisymmetric simulations
The Navier–Stokes equations for stratified Boussinesq flow are given in terms of the total density,
$\unicode[STIX]{x1D71A}$
, and velocity,
$\boldsymbol{u}=(\boldsymbol{u},\boldsymbol{v},\boldsymbol{w})\equiv (\boldsymbol{u}_{r},\boldsymbol{u}_{\unicode[STIX]{x1D703}},\boldsymbol{u}_{z})$
,
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}=-\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\frac{1}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x1D735}\boldsymbol{p}-\frac{g}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x1D71A}\hat{z}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u},\\ \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D71A}=-\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D71A}+\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D71A},\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0.\end{array}\right\}\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D70C}_{00}$
is the characteristic density,
$g$
is the gravitational acceleration,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D705}$
is the diffusivity of the density.
Under the assumption that the flow is axisymmetric, the momentum equations may be recast in terms of the azimuthal component of vorticity,
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D735}\times \boldsymbol{u})\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D703}}$
, to obtain
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}{\unicode[STIX]{x2202}t}=-Ur\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(\frac{\unicode[STIX]{x1D701}}{r}\right)-W\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}{\unicode[STIX]{x2202}z}+\frac{g}{\unicode[STIX]{x1D70C}_{00}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}r}+\unicode[STIX]{x1D708}\left(\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}}{r^{2}}\right).\end{eqnarray}$$
Here,
$U\equiv U(r,z,t)$
and
$W\equiv W(r,z,t)$
are the radial and vertical velocity components respectively, and
$\bar{\unicode[STIX]{x1D70C}}\equiv \bar{\unicode[STIX]{x1D70C}}(r,z,t)$
is the difference in density between the total and the background hydrostatically balanced density
$\unicode[STIX]{x1D70C}_{0}(z)$
.
Similarly, the axisymmetric form of the internal energy equation is
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}=-U\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}r}-W\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}z}-W\frac{\text{d}\unicode[STIX]{x1D70C}_{0}}{\text{d}z}+\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\bar{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
These equations are solved using finite-difference methods on a staggered grid (McMillan & Sutherland Reference McMillan and Sutherland2010). At each time step, the streamfunction,
$\unicode[STIX]{x1D6F9}$
, is determined from
$\unicode[STIX]{x1D701}$
by inverting the following equation:
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F9}-\frac{\unicode[STIX]{x1D6F9}}{r^{2}}=-\unicode[STIX]{x1D701}.\end{eqnarray}$$
This inversion is done by performing a Fourier–Bessel transform to (2.4), inverting the resulting algebraic matrix equation, and inverse transforming. Given
$\unicode[STIX]{x1D6F9}$
, the velocity components can then be found using
$$\begin{eqnarray}U=-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}z}\quad \text{and}\quad W=\frac{1}{r}\frac{\unicode[STIX]{x2202}r\,\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}r}.\end{eqnarray}$$
The simulation is initialised by assuming an approximately two-layer ambient stratification such that
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{0}(z)=\unicode[STIX]{x1D70C}_{00}+\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}(1-\tanh [(z-z_{0})/\unicode[STIX]{x1D70E}])/2,\end{eqnarray}$$
in which
$0\leqslant z\leqslant H$
and
$z_{0}=H/2$
. Here,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
is the density difference between the lower and upper layers and
$\unicode[STIX]{x1D70E}$
is the half-thickness of the interface. The initial density perturbation corresponds to uniform density in the lock of radius
$R_{c}$
, such that
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}(r,z,t=0)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}\tanh [(z-z_{0})/\unicode[STIX]{x1D70E}]/2, & r\leqslant R_{c},\\ 0, & r>R_{c}.\end{array}\right.\end{eqnarray}$$
This simulation describes the time evolution of a doubly symmetric intrusion, since the ambient fluid is prescribed with equal upper- and lower-layer depths and the density of the lock fluid is the average ambient density. Furthermore, consistently with the initial conditions for lock-release experiments, the initial velocity in the domain is set everywhere to zero,
$U=W=0$
. Since we wish, as much as possible, to replicate the conditions of the experiment shown in figure 1, we set
$H=10$
cm,
$\unicode[STIX]{x1D70E}=0.25$
cm and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=0.0548~\text{g}~\text{cm}^{-3}$
. As sensitivity tests, simulations were also run with thinner and thicker interfaces, as prescribed by
$\unicode[STIX]{x1D70E}=0.1$
cm and 0.5 cm respectively. The viscosity is taken to be that of water. Expecting that diffusivity does not play an important role in the development of axisymmetric instabilities, we set
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D708}$
. The simulation results in figure 2 show the evolution of a passive tracer field in which the concentration,
$C$
, is set to unity in the lock and zero elsewhere. As the simulation advances in time, the concentration field is advected by the computed velocity field.
Figure 2. Snapshots of the passive tracer field at times
$t=~0$
(a) and 2 s (b) determined from a fully nonlinear simulation restricted to be axisymmetric of fluid collapsing into two-layer ambient with interface thickness
$\unicode[STIX]{x1D70E}=0.25$
cm.
Immediately after the start of the simulation, the lock fluid collapses and the intrusion front advances radially along the interface of thickness
$\unicode[STIX]{x1D70E}=0.25$
cm at mid-depth in the domain. After 2 s (figure 2
b), the lock fluid is drawn into a vortex dipole with a counterclockwise vortex in the upper layer and a clockwise vortex in the lower layer. This symmetric evolution is clearly different from the one that would occur for a bottom-propagating current, supporting our hypothesis that the particular structure of such a base flow may lead to a new class of growing perturbations. We store the
$U$
,
$W$
and
$\bar{\unicode[STIX]{x1D70C}}$
fields at regular time steps. It is upon the evolution of these base flow fields that we wish to evaluate the susceptibility of the axisymmetric flow to optimal perturbations with non-trivial azimuthal structure.
2.2 Perturbation equations
We now consider the linearised evolution equations for perturbations superimposed on the time-evolving axisymmetric base flow described above. The total velocity and density fields may be written as
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{u}=\boldsymbol{U}(r,z,t)+\boldsymbol{u}(r,\unicode[STIX]{x1D703},z,t),\\ \unicode[STIX]{x1D754}=[\unicode[STIX]{x1D70C}_{0}(z)+\bar{\unicode[STIX]{x1D70C}}(r,z,t)]+\unicode[STIX]{x1D70C}(r,\unicode[STIX]{x1D703},z,t),\end{array}\right\}\end{eqnarray}$$
in which
$\boldsymbol{u}$
and
$\unicode[STIX]{x1D70C}$
represent the perturbation velocity and density respectively.
Substituting (2.8) into (2.1) and neglecting terms that are nonlinear in perturbation variables, we obtain
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}u=-U\unicode[STIX]{x2202}_{r}u-W\unicode[STIX]{x2202}_{z}u-\unicode[STIX]{x2202}_{r}Uu-\unicode[STIX]{x2202}_{z}Uw-\frac{1}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x2202}_{r}p+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}u,\\ \displaystyle \unicode[STIX]{x2202}_{t}w=-U\unicode[STIX]{x2202}_{r}w-W\unicode[STIX]{x2202}_{z}w-\unicode[STIX]{x2202}_{r}Wu-\unicode[STIX]{x2202}_{z}Ww-\frac{1}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x2202}_{z}p-\frac{g}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}w,\\ \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70C}=-U\unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D70C}-W\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D70C}-\unicode[STIX]{x2202}_{r}\bar{\unicode[STIX]{x1D70C}}u-\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{0}+\bar{\unicode[STIX]{x1D70C}})w+\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D70C}.\end{array}\right\}\end{eqnarray}$$
For an incompressible fluid, the pressure field satisfies
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}p=-2\unicode[STIX]{x1D70C}_{00}\left[\unicode[STIX]{x2202}_{r}U\unicode[STIX]{x2202}_{r}u+\unicode[STIX]{x2202}_{z}U\unicode[STIX]{x2202}_{r}w+\unicode[STIX]{x2202}_{r}W\unicode[STIX]{x2202}_{z}u+\unicode[STIX]{x2202}_{z}W\unicode[STIX]{x2202}_{z}w+\frac{1}{r^{2}}Uu\right]-g\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D70C}.\end{eqnarray}$$
Because
$\boldsymbol{U}\equiv (U,W)$
is independent of the azimuthal angle,
$\unicode[STIX]{x1D703}$
, and azimuthal velocity,
$V$
, the right-hand sides of (2.9) and (2.10) do not involve the perturbation azimuthal velocity,
$v$
. Azimuthal perturbations influence these fields only through the
$\unicode[STIX]{x1D703}$
derivatives in the Laplacian on the left-hand side of the pressure equation (2.10). For this system, the perturbation azimuthal velocity is effectively slaved to the other two time-evolving velocity components, and is determined directly from them through the incompressibility condition,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
.
Equations (2.9) may be thought of as a propagator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)$
of the state variable
$q(t)=(\boldsymbol{u}(t),\unicode[STIX]{x1D70C}(t))$
from its initial values at
$t=0$
to some target time,
$T$
, so that (see Arratia et al. (Reference Arratia, Caulfield and Chomaz2013) for more details)
$$\begin{eqnarray}q(T)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)q(0),\end{eqnarray}$$
in which the sub-index
$\unicode[STIX]{x1D706}$
represents the parameters of the flow under consideration. We are interested in identifying the perturbations that exhibit the largest total perturbation energy gain. For stratified flows, as discussed in more detail in Kaminski, Caulfield & Taylor (Reference Kaminski, Caulfield and Taylor2014), it is natural to consider the total perturbation energy, i.e. the sum of the perturbation kinetic energy and the perturbation potential energy densities, here defined as
$$\begin{eqnarray}E(\unicode[STIX]{x1D706},t)=\frac{1}{2}|\boldsymbol{u}|^{2}+\frac{gD}{{2\unicode[STIX]{x1D70C}_{00}}^{2}}|\unicode[STIX]{x1D70C}|^{2}=\frac{1}{2}\langle q(t),q(t)\rangle ,\end{eqnarray}$$
in which
$D$
is a characteristic depth scale for the stratification and
$\unicode[STIX]{x1D706}$
represents any relevant flow parameters. Such a total energy is a natural norm for the state variable
$q(t)$
, associated with an appropriate inner product, here denoted with angled brackets. For our problem, the natural choice of the scale
$D$
is the half-depth,
$\unicode[STIX]{x1D70E}$
, of the interface between the upper and lower layers along which the intrusion is expected to propagate, as defined in (2.6).
Therefore, for a given target time
$T$
, we are interested in optimising the gain
${\mathcal{G}}(\unicode[STIX]{x1D706},T)$
, defined as
$$\begin{eqnarray}\displaystyle {\mathcal{G}}(\unicode[STIX]{x1D706},T)\equiv \frac{E(\unicode[STIX]{x1D706},T)}{E(\unicode[STIX]{x1D706},0)} & = & \displaystyle \frac{\langle q(T),q(T)\rangle }{\langle q(0),q(0)\rangle }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\langle \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)q(0),\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)q(0)\rangle }{\langle q(0),q(0)\rangle }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\langle q(0),\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}^{\dagger }(T)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)q(0)\rangle }{\langle q(0),q(0)\rangle }.\end{eqnarray}$$
$\dagger$
denotes the adjoint propagator (relative to this particular inner product), such that 
$$\begin{eqnarray}\langle q^{\dagger },\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}q\rangle =\langle \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}^{\dagger }q^{\dagger },q\rangle\end{eqnarray}$$
for all appropriately smooth ‘direct’ state variables
$q$
and adjoint state variables
$q^{\dagger }$
.
The adjoint propagator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}^{\dagger }(T)$
may be thought of as the propagator of adjoint equations from
$T$
to 0 (Luchini & Bottaro Reference Luchini and Bottaro2014), which can be determined straightforwardly in this particular flow to be
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x2202}_{t}\boldsymbol{u}^{\dagger }=-\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\dagger }+(\unicode[STIX]{x1D735}\boldsymbol{U})\boldsymbol{u}^{\dagger }+gD(\unicode[STIX]{x1D735}\bar{\unicode[STIX]{x1D70C}})\unicode[STIX]{x1D70C}^{\dagger }-{\displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{00}}}\unicode[STIX]{x1D735}p^{\dagger }-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}^{\dagger },\\ \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70C}^{\dagger }=-\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{\dagger }+(\unicode[STIX]{x1D70C}_{00}/D)w^{\dagger }-\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D70C}^{\dagger }\end{array}\right\}\end{eqnarray}$$
for adjoint perturbation ‘velocity’
$\boldsymbol{u}^{\dagger }$
and ‘density’
$\unicode[STIX]{x1D70C}^{\dagger }$
. This field
$\boldsymbol{u}^{\dagger }$
is naturally incompressible, imposed by the adjoint ‘pressure’
$p^{\dagger }$
, which satisfies
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x1D6FB}^{2}p^{\dagger }=-\frac{1}{r}\unicode[STIX]{x2202}_{r}(r\unicode[STIX]{x1D701}w^{\dagger })+\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D701}u^{\dagger })+\frac{g}{\unicode[STIX]{x1D70C}_{00}}{\unicode[STIX]{x1D70C}^{\dagger }}_{z}+gD\left[\frac{1}{r}\unicode[STIX]{x2202}_{r}(r\bar{\unicode[STIX]{x1D70C}}_{r}\unicode[STIX]{x1D70C}^{\dagger })+\unicode[STIX]{x2202}_{z}(\bar{\unicode[STIX]{x1D70C}}_{z}\unicode[STIX]{x1D70C}^{\dagger })\right].\end{eqnarray}$$
As in (2.9) and (2.10), these equations decouple from the adjoint perturbation azimuthal velocity component
$v^{\dagger }$
. Azimuthal disturbances to
$u^{\dagger }$
,
$w^{\dagger }$
and
$\unicode[STIX]{x1D70C}^{\dagger }$
are imposed through the
$\unicode[STIX]{x1D703}$
dependence of the Laplacian acting on
$p^{\dagger }$
on the left-hand side of (2.16). It is clear that these equations also depend on the time-dependent base flow given by
$\boldsymbol{U}$
and
$\bar{\unicode[STIX]{x1D70C}}$
. The boundary conditions for the adjoint state variable
$q^{\dagger }$
are the same as for the direct state variable
$q$
. Due to integration by parts, which is at the heart of the determination of the adjoint propagator relative to the chosen inner product, the adjoint equations are well posed when integrated backwards in time. Furthermore, as is apparent from (2.13), the appropriate ‘initial’ condition for the adjoint equations is that
$q^{\dagger }(T)=q(T)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(T)q(0)$
.
Although the direct propagator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
is not self-adjoint, it is clear that the combination ‘loop’ of the direct (forward) propagator and the adjoint (backward) propagator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}^{\dagger }\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
is self-adjoint. Remembering that we are interested in determining the perturbation that attains the maximum gain,
$$\begin{eqnarray}{\mathcal{G}}_{max}(\unicode[STIX]{x1D706},T)=\max _{q(0)}\{{\mathcal{G}}(\unicode[STIX]{x1D706},T)\},\end{eqnarray}$$
where the maximisation is over all choices of initial conditions
$q(0)$
, it is apparent from (2.13c
) that we wish to determine the eigenmode of the operator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}^{\dagger }\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
with the largest (inevitably real) eigenvalue. Since we are only interested in this optimal perturbation, we iterate to determine this ‘optimal’ eigenmode, essentially by repeating the direct–adjoint loop until the structure of the initial state variable
$q(0)$
changes negligibly, thus being identified as the optimal initial perturbation.
3 Numerical implementation
We apply this power-iteration version of the (linearised) DAL method to examine the azimuthal perturbations observed in the cylindrical lock-release intrusive gravity current experiment shown in figure 1. As described in § 2.1, we calculate the time-varying base flow
$U$
,
$W$
and
$\overline{\unicode[STIX]{x1D70C}}$
using an axisymmetric direct numerical simulation. In most cases, we choose the target time for our optimisation to be
$T=2$
s, the time over which the azimuthally periodic perturbation structure was first observed to develop in the experiment. However, we have also examined optimal perturbations occurring in a target time
$T=1.5$
s, as it is to be expected that perturbations associated with different wavenumbers are favoured at different stages of the base flow evolution.
The initial ‘guess’ for the perturbation fields
$u$
,
$w$
and
$\unicode[STIX]{x1D70C}$
is random noise in the Fourier–Bessel decomposition of each field, such that the magnitude of the noise is inversely proportional to the vertical and radial wavenumber. This noise field is then inverse transformed into real space and multiplied by
$r^{2}\exp (-r^{2}/\unicode[STIX]{x1D6FF}^{2})$
so that the noise is zero at the origin and greatest at
$r=\sqrt{2}\unicode[STIX]{x1D6FF}$
, mimicking the experimental initial condition where the fluid is inevitably most turbulent locally where the cylindrical gate is extracted. We set the length scale
$\unicode[STIX]{x1D6FF}=5$
, so that the peak magnitude of the noise occurs at a location close to the lock radius,
$R_{c}=6$
cm. In most of the simulations results presented here, we further impose vertical symmetry of the noise about the midplane, as we hypothesise that the globally most strongly growing initial perturbation has such a symmetry, and so imposing this symmetry in the initial guess aids the convergence of the power-iteration algorithm. As discussed below, we test this hypothesis by relaxing the imposition of this symmetry in one suite of calculations. It is important to remember that the DAL method only identifies local extrema of the objective functional, and so it is necessary to investigate how sensitive any calculated results are to variation in the structure of the initial ‘guess’.
As the problem of optimising gain is linear, and we are fundamentally interested in the structure (in particular the azimuthal wavenumber) of the initial perturbation with the largest gain, we normalise the perturbation every time the iteration goes once around a complete direct–adjoint loop. Such normalisation also ensures that accuracy in the calculation is retained even in circumstances where there is substantial gain. We find that an appropriate way to achieve this normalisation is to divide the perturbation fields
$u$
,
$w$
and
$\unicode[STIX]{x1D70C}$
by a constant chosen so that the volume-integrated initial perturbation kinetic energy per unit azimuthal angle is
$$\begin{eqnarray}E_{k0}\equiv \iint \frac{1}{2}(u^{2}+w^{2})r\,\text{d}r\,\text{d}z=1.\end{eqnarray}$$
We do not include the azimuthal component
$v$
explicitly in this scaling for two reasons. First, as mentioned above,
$v$
is effectively ‘slaved’ to the other two velocity components through the incompressibility condition. Second, it does not appear in the leading-order perturbation energy equation even when the base flow has non-zero velocity.
Since the problem of interest is linear in the perturbation variables, it is possible to identify the optimal perturbation for each choice of the azimuthal wavenumber
$m$
independently using power iteration of the DAL method as described above. As is apparent from the governing equations (2.9) with (2.10), the base flow
$U$
,
$W$
and
$\bar{\unicode[STIX]{x1D70C}}$
in general varies with time. We integrate the perturbation equations over the interval
$[0,T]$
in steps of 0.0125 s. Similarly to the situation considered by Arratia et al. (Reference Arratia, Caulfield and Chomaz2013), we find that it is satisfactory to save the base flow at a relatively long period of 0.1 s, and linearly interpolate between these different saved values of the base flow fields to construct an appropriate approximation to the base flow at each of the time steps of the direct and adjoint codes, which we integrate in steps of 0.0125 s.
For this particular problem, the power-iteration method converges quite rapidly: after only three loops (each consisting of forward time-stepping the direct perturbation equations followed by backward time-stepping the adjoint equations), the perturbation
$u$
,
$w$
and
$\unicode[STIX]{x1D70C}$
fields change by a very small amount in subsequent direct–adjoint loops. The converged results of the DAL method give the perturbations with the largest gain in time
$T$
of the total perturbation energy, generally defined by the volume integral of (2.12). However, because the base flow has no azimuthal component, the decoupling of
$v$
from the evolution equations, as in (2.9) and (2.10), shows that the leading-order dominant contribution to the volume-integrated perturbation energy per unit mass and azimuthal angle is
$$\begin{eqnarray}E_{f}\equiv \iint \left[Uu+Ww+\frac{g}{\unicode[STIX]{x1D70C}_{00}}\unicode[STIX]{x1D70C}z\right]r\,\text{d}r\,\text{d}z,\end{eqnarray}$$
in which the terms involving the square of perturbation variables are considered to be negligible. The expression for
$E_{f}$
, which is not positive definite, effectively represents the change in the total energy, including perturbations and the background energy associated with the
$r$
-,
$z$
- and
$t$
-dependent background flow. Thus, if
$E_{f}$
is positive, the perturbed system has more energy than the background alone. In reality, such an apparent energy gain comes at the expense of an equivalent reduction in the energy of the background flow. However, in our linear treatment of the perturbation problem, we assume that the perturbations are small and so neglect formally the influence of this energy extraction by the developing perturbation on the evolution of the background flow itself.
In considering the evolution of perturbations with fixed azimuthal wavenumber
$m$
, a particular iteration was considered to be adequately converged for our purposes when this quantity
$E_{f}$
varied by less than 1 % from the previous iteration. Since
$E_{f}$
as defined in (3.2) is the dominant contribution to the perturbation energy, we expect perturbations with the largest value of this particular quantity to be observable in a laboratory experiment, and so we determine the predicted azimuthal wavenumber by identifying for which value of
$m$
the optimal perturbation has the largest value of
$E_{f}$
at the target time
$T$
.
Figure 3. Structure of the vertical velocity perturbation associated with maximal total perturbation energy gain over the time interval
$[0,T=2~\text{s}]$
with
$m=16$
azimuthal wavenumber at times (a) 0 and (b) 2 s for the DAL calculation initialised in the first pass with vertically symmetric noise, and at times (c) 0 and (d) 2 s for the calculation initialised with random noise and no vertical symmetry imposed. The time-evolving two-dimensional base flow is provided from the axisymmetric simulation for which the passive tracer field at the start and end times is shown in figure 2.
Figure 4. Variation with azimuthal wavenumber
$m$
of
$E_{f}$
as defined in (3.2) for optimal initial perturbations computed in five scenarios, as indicated in the legend. Here,
$T$
denotes the end time of the optimisation interval,
$\unicode[STIX]{x1D70E}$
is the thickness of the ambient interface defined implicitly by (2.6), and ‘asym’ refers to the noise around the model lock having no vertical symmetry at the start of the DAL computation.
In figure 3, we plot the initial (
$t=0$
) and final (
$t=T$
) states of the vertical velocity
$w$
of the converged optimal perturbation when the azimuthal wavenumber is set at the value
$m=16$
. As in figure 2, the optimisation is performed for a background state simulating an axisymmetric intrusion propagating along an interface of thickness
$\unicode[STIX]{x1D70E}=0.25$
cm, with optimal perturbations computed between
$t=0$
and the target time of
$T=2$
s.
The vertical velocity fields shown in figure 3(a,b) are computed by performing the DAL method starting in the first pass with an initial condition of vertically symmetric noise. By the start of the third pass, the looping procedure has converged on an optimal initial structure that has even vertical symmetry in
$w$
about the midplane. Although not shown here, at the start and final time the radial component
$u$
of the velocity field also has the same sign above and below the height of the interface at the midplane. The azimuthal velocity field
$v$
is (unsurprisingly) weaker at
$t=0$
, but also exhibits somewhat higher mode vertical structure. At the end time, all three components of the perturbation velocity field have comparable magnitudes, with significant amplitude only near the head of the intrusion. Through comparison of figures 2 and 3(a,b), it is apparent that as the base flow lock fluid collapses to form an intrusion, the mode-2 optimal perturbation is swept right into the heart of the evolving intrusion head, and the vertical velocity perturbation, although appreciably smaller in area, is significantly amplified by the strong toroidal vorticity stretching occurring in the vicinity of the spreading intrusion head.
As already noted, the DAL method only identifies local extrema of the cost functional, so it is important to test whether the optimal perturbation that is identified depends strongly on the choice of initial guess. We find that this is indeed the case. In figure 3(c,d), we plot the vertical velocity field for the optimal initial perturbation with the same azimuthal wavenumber
$m=16$
and its structure at the target time
$T=2$
s, computed without imposing vertical symmetry in the initial noise guess in the DAL method. In this case, it is evident that the DAL method converges to an optimal perturbation that has odd vertical symmetry in the vertical velocity field. As we show next, such odd perturbations are globally subdominant, in that the peak energy gain across all values of
$m$
appears to be associated with initial perturbations exhibiting even symmetry, consistent with our hypothesis.
The amplification of the perturbation energy is a strong function of azimuthal wavenumber, as shown in figure 4. This figure plots the variation of
$E_{f}$
with
$m$
in five different circumstances determined by the value of the optimisation target time,
$T$
, the value of the interface thickness,
$\unicode[STIX]{x1D70E}$
, prescribed for the ambient stratification used by the azimuthally symmetric simulations, and by the vertical structure of the initial noise. In the case with
$\unicode[STIX]{x1D70E}=0.25$
cm and
$T=2$
s, the optimal initial perturbation with the largest value of
$E_{f}$
at
$t=2$
s occurs for azimuthal wavenumber
$m=16$
. This is the disturbance with structure at
$t=0$
and 2 s shown in figure 3. Indeed, this appears to be close to the minimum wavenumber for perturbation growth: for wavenumbers less than
$m=15$
,
$E_{f}$
actually decreases for the ‘optimal’ perturbations with
$T=2$
, suggesting that lower wavenumbers are stable in the sense that the disturbances can only give up energy to the time-evolving basic state. Furthermore, the variation of
$E_{f}$
with
$m$
appears to be strongly peaked at
$m=16$
, suggesting the possibility of strong mode selection.
Somewhat unsurprisingly, the peak azimuthal wavenumber does depend upon the choice of the target time
$T$
and the value of
$\unicode[STIX]{x1D70E}$
used to prescribe the interface thickness in our axisymmetric simulations. Fixing the optimisation time at
$T=2$
s, we find a larger and sharper peak in
$E_{f}$
as a function of
$m$
if the interface is assumed to be sharper with
$\unicode[STIX]{x1D70E}=0.1$
cm (see figure 4). In this case, and also in the case with a thicker interface having
$\unicode[STIX]{x1D70E}=0.5$
cm, the disturbance with peak energy has azimuthal wavenumber
$m=17$
. For the thicker interface, we see that the scale selection is much weaker, with a broader range of wavenumbers with comparable final energy gain. Similar lack of a clear peak in gain also occurs when we consider a shorter target time of
$T=1.5$
s, in which case the peak gain (at
$m=25$
) is smaller than the peak gain predicted when
$T=2$
s.
As already noted, we also investigate whether the imposed symmetry of the initial noise field affects the structure of the initial perturbation identified by the power iteration. In another sequence of analyses, marked with diamonds in figure 4, we impose no vertical symmetry on the noise field used as a first guess. For this case, we once again find that the final energy of the optimal mode is largest for
$m=17$
, but this is not as strongly peaked as in the corresponding case with vertical symmetry imposed on the noise field. The peak value of the gain across all wavenumbers is smaller compared with the calculations with symmetrised noise, but there are wavenumbers where the predicted gain is larger for the perturbation for this suite of calculations.
Interestingly, for all cases with initial vertically asymmetric noise, the predicted optimal initial perturbations have approximately an odd symmetry, demonstrating that the fully random noise field is converging to a different local maximum of energy gain, associated with a qualitatively different type of initial perturbation. In figure 3(c,d), we show an example of this different type of initial perturbation and its final form at the target time
$T=2$
s. Such odd perturbations prove to be globally subdominant to the even perturbations found by initialisation with the symmetric noise field, as is apparent in figure 4, giving support to our hypothesis that the most preferred form of perturbation has the imposed up–down symmetry. In all cases, the final energy of the optimal perturbation is essentially negligible for
$m<10$
.
Although the azimuthal wavenumber of the optimal mode with peak energy does not agree precisely with the experimental observation of
$m\simeq 12$
, this prediction is undoubtedly consistent with the experiments, suggesting as it does a preference for a high azimuthal wavenumber in the perturbations that can grow on such strongly time-varying base flows. Indeed, it is not entirely unsurprising that there is some discrepancy for at least two reasons. First, the base flow that we consider does not correspond in all respects to the experimental flow. For example, we have shown that the peak energy of the optimal perturbation can vary somewhat depending upon the initial noise, and interface thickness as well as the target time for optimisation. Second, the DAL method utilised here is inherently linear, and there is no rigorous reason why the observed nonlinear structures, fundamentally modifying the ‘base flow’, at a given time instant correspond to the linear perturbations, formally infinitesimal at all times relative to the base flow, which are predicted to have the largest gain relative to some energetic measure. Nevertheless, the DAL method has managed to predict key aspects of the observed azimuthally periodic perturbations, confirming that this approach may be usefully applied to examine instabilities occurring in other rapidly evolving experimental flows.
4 Conclusions
In this paper, we have derived the forward (direct) and backward (adjoint) linear operators describing the evolution of azimuthally periodic perturbations on an axisymmetric arbitrarily rapidly evolving stratified flow corresponding to a slumping intruding gravity current. We have demonstrated the useful application of the recently developed DAL method to this flow, motivated by previously unexplained experimental observations of high-azimuthal-wavenumber perturbations in the form of ‘spokes’ developing on such a flow at finite amplitude. We have found that, at least within a linear framework, the DAL method typically converges rapidly, for all wavenumbers we consider, suggesting that at any given wavenumber there is a preferred spatial structure that exhibits a gain significantly larger than other azimuthally periodic perturbations with the same wavenumber. This suggests that there is a good chance that the predicted ‘optimal’ perturbation might actually be observed in the laboratory.
Using an appropriate measure of the total perturbation energy gain, we have found that the range of strongly growing initial perturbations have azimuthal wavenumbers only moderately larger than the peak azimuthal wavenumber observed in experiments, and certainly consistent considering the possible differences between the numerically considered base flow and the actual experimental flow. It is important to remember that the base flow that we consider does not correspond in all respects to the experimental flow. For example, we have shown that the peak energy of the optimal perturbation can vary somewhat depending upon the initial noise, and interface thickness as well as the target time for optimisation. We find that perturbations with an even symmetry in the vertical velocity are predicted to exhibit the largest gain across all choices of azimuthal wavenumber. Nevertheless, although not entirely conclusive, the comparison suggests that the observed azimuthally periodic spoke structure is the nonlinear manifestation of an ‘optimal’ perturbation whose growth inherently relies upon the ‘rapid’ evolution of the base flow.
In this sense, the DAL method applied to a rapidly evolving base flow presented here reveals a phenomenon often attributed to classical normal mode analysis of steady base flows, namely that the experimentally observed periodicity of a nonlinear structure can be associated with the wavelength of an infinitesimal perturbation that is the ‘most unstable’ in some appropriately defined sense. It is of great interest to investigate whether this association is fortuitous, or whether there is some deeper and more generic connection between the growth of ‘optimal’ perturbations and nonlinear saturated states. Here, we have presented evidence that a hybrid-numerical approach using the DAL method provides a foundation upon which to consider this issue. As three-dimensional time-resolved experimental data become more available due to advances in data acquisition and assimilation, we hypothesise that the method presented here, and its nonlinear generalisation (Kerswell, Pringle & Willis Reference Kerswell, Pringle and Willis2014), will be the key approaches that allow the development of an understanding of perturbation growth in rapidly varying fluid flows.
