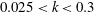1 Introduction
Under attached flow conditions, the classical low-order approach to estimate the unsteady lift response of an airfoil is unsteady thin-airfoil theory. Unsteady thin-airfoil theory uses potential flow to represent an airfoil by its camber line only. For an airfoil of small camber, singularities are distributed on the
![]() $x$
-axis in such a way that the induced velocity fulfils the kinematic boundary condition at the camber line. Every change in inflow conditions and every movement of the airfoil camber line alter the singularity distribution and thereby the bound vorticity on the airfoil. According to Kelvin’s circulation theorem, a change of bound vorticity leads to a shedding of vorticity in the wake. The shed wake vorticity, in turn, induces a velocity on the airfoil surface, such that a new kinematic boundary condition has to be fulfilled. This causes a change in the bound vorticity and thereby a change of the tangential velocity on the airfoil surface. The tangential velocity is related to the static pressure through Bernoulli’s equation, integrally responsible for the airfoil lift. Hence, the wake vorticity alters the unsteady lift of the airfoil compared with quasisteady conditions. Depending on the order of approximation of the kinematic boundary condition, solutions of different complexities can be derived. Expressing the induced velocity in terms of Fourier series and retaining only linear terms yields first-order transfer functions. First-order transfer functions for technically relevant flow scenarios were derived in the 1930s. Theodorsen (Reference Theodorsen1935) derived the first-order transfer function of an airfoil in pure harmonic oscillation. Sears (Reference Sears1938) derived the first-order transfer function of an airfoil entering a sinusoidal vertical gust. These first-order transfer functions, known as the Theodorsen and Sears functions, are commonly used in the engineering community (see Dowell Reference Dowell2014). Higher-order transfer functions model additional physical phenomena. In transonic flows, a compression shock causes a spatially non-constant stationary velocity field. Numerous second-order solutions accounting for this scenario exist. For subsonic flows, little attention has been attributed to the influence of a non-constant stationary velocity field on the dynamic airfoil response. Goldstein & Atassi (Reference Goldstein and Atassi1976) and Atassi (Reference Atassi1984) modelled the influence of the acceleration on the suction side of a lift-producing airfoil on an oncoming vertical gust: the gust is distorted, causing a dependence of the fluctuating lift on the gust wavenumber in the direction perpendicular to the airfoil.
$x$
-axis in such a way that the induced velocity fulfils the kinematic boundary condition at the camber line. Every change in inflow conditions and every movement of the airfoil camber line alter the singularity distribution and thereby the bound vorticity on the airfoil. According to Kelvin’s circulation theorem, a change of bound vorticity leads to a shedding of vorticity in the wake. The shed wake vorticity, in turn, induces a velocity on the airfoil surface, such that a new kinematic boundary condition has to be fulfilled. This causes a change in the bound vorticity and thereby a change of the tangential velocity on the airfoil surface. The tangential velocity is related to the static pressure through Bernoulli’s equation, integrally responsible for the airfoil lift. Hence, the wake vorticity alters the unsteady lift of the airfoil compared with quasisteady conditions. Depending on the order of approximation of the kinematic boundary condition, solutions of different complexities can be derived. Expressing the induced velocity in terms of Fourier series and retaining only linear terms yields first-order transfer functions. First-order transfer functions for technically relevant flow scenarios were derived in the 1930s. Theodorsen (Reference Theodorsen1935) derived the first-order transfer function of an airfoil in pure harmonic oscillation. Sears (Reference Sears1938) derived the first-order transfer function of an airfoil entering a sinusoidal vertical gust. These first-order transfer functions, known as the Theodorsen and Sears functions, are commonly used in the engineering community (see Dowell Reference Dowell2014). Higher-order transfer functions model additional physical phenomena. In transonic flows, a compression shock causes a spatially non-constant stationary velocity field. Numerous second-order solutions accounting for this scenario exist. For subsonic flows, little attention has been attributed to the influence of a non-constant stationary velocity field on the dynamic airfoil response. Goldstein & Atassi (Reference Goldstein and Atassi1976) and Atassi (Reference Atassi1984) modelled the influence of the acceleration on the suction side of a lift-producing airfoil on an oncoming vertical gust: the gust is distorted, causing a dependence of the fluctuating lift on the gust wavenumber in the direction perpendicular to the airfoil.
Relatively few experimental works have been performed on the frequency-dependent unsteady lift response under attached flow conditions. For the case of an oscillating airfoil, experimental investigations were performed in the 1940s and 1950s (Silverstein & Joyner Reference Silverstein and Joyner1939; Reid Reference Reid1940; Bratt Reference Bratt1945; Halfman Reference Halfman1952; Rainey Reference Rainey1957). Quantitative and qualitative agreement in amplitude and phase of Theodorsen’s first-order transfer function and the experimentally derived transfer functions was not found in any of the experiments. For the case of a stationary airfoil entering a sinusoidal vertical gust, even less experimental verification has been performed. Larose (Reference Larose1999) and Hatanaka & Tanaka (Reference Hatanaka and Tanaka2002) compared the admittance of bridge decks submitted to turbulent inflow with the Sears function. Both authors observed an increase of the dynamic lift amplitude with increasing frequency, while the Sears function predicts a decrease of the dynamic lift response due to the damping effect of the wake. A systematic investigation of an airfoil submitted to a sinusoidal vertical gust of distinct frequencies and amplitudes, however, is still missing.
In this study, we derive experimental transfer functions for the load response of an oscillating airfoil in a stationary air stream and a stationary airfoil in a fluctuating air stream. The magnitudes of the experimental transfer functions are compared with the magnitudes of the theoretical transfer functions. As the first-order Theodorsen and Sears functions build on thin-airfoil assumptions, an experimental set-up that is assumed to fulfil these assumptions is chosen: the airfoil has a Clark Y profile (11.7 % maximal thickness and 3.5 % maximal camber). It is placed at small angles of attack and submitted to small perturbations. By increasing the mean angle of attack and perturbation heights, the limitations of applicability of the first-order transfer functions are investigated.
2 Experimental set-up
The two transfer functions are examined in two experimental set-ups. The oscillating airfoil is investigated in the TU Darmstadt open-return wind tunnel, comprising a pitch–plunge rig. The stationary airfoil encountering a sinusoidal vertical gust is investigated in the University of Oldenburg active-grid wind tunnel. An overview of the experimental set-ups is given below; a more detailed description of both set-ups can be found in Cordes (Reference Cordes2016).
2.1 Oscillating airfoil
Figure 1 shows a schematic of the experimental set-up of the TU Darmstadt open-return wind tunnel: a two-dimensional airfoil is oscillated in a steady flow, using a pitch–plunge rig. The airfoil has a Clark Y section, a chord length of
![]() $c=0.12~\text{m}$
, a span of
$c=0.12~\text{m}$
, a span of
![]() $s=0.45~\text{m}$
and is mounted horizontally in a wind tunnel, covering the entire wind tunnel width. The wind tunnel has a closed test section of
$s=0.45~\text{m}$
and is mounted horizontally in a wind tunnel, covering the entire wind tunnel width. The wind tunnel has a closed test section of
![]() $0.45~\text{m}\times 0.45~\text{m}$
. A pitch–plunge rig, consisting of two linear actuators, is installed underneath the test section. The airfoil is mounted on the actuator pistons via aluminium adapters. The airfoil is oscillated around its leading edge at a mean angle of attack
$0.45~\text{m}\times 0.45~\text{m}$
. A pitch–plunge rig, consisting of two linear actuators, is installed underneath the test section. The airfoil is mounted on the actuator pistons via aluminium adapters. The airfoil is oscillated around its leading edge at a mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
in a pure pitch motion
$\unicode[STIX]{x1D6FC}_{m}$
in a pure pitch motion
![]() $\unicode[STIX]{x1D6FC}_{p}=\widehat{\unicode[STIX]{x1D6FC}}_{p}\sin (2\unicode[STIX]{x03C0}ft)$
of amplitude
$\unicode[STIX]{x1D6FC}_{p}=\widehat{\unicode[STIX]{x1D6FC}}_{p}\sin (2\unicode[STIX]{x03C0}ft)$
of amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
and frequency
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
and frequency
![]() $f$
, while the inflow velocity
$f$
, while the inflow velocity
![]() $U_{\infty }$
is kept constant. The dynamic pitch angle
$U_{\infty }$
is kept constant. The dynamic pitch angle
![]() $\unicode[STIX]{x1D6FC}_{p}$
is obtained from the position of the linear actuators and can be calculated with an uncertainty of
$\unicode[STIX]{x1D6FC}_{p}$
is obtained from the position of the linear actuators and can be calculated with an uncertainty of
![]() $u_{\unicode[STIX]{x1D6FC}_{p}}=\pm 8\times 10^{-2\circ }$
. The airfoil is equipped with three pressure taps at both the suction and pressure sides, to measure the pressure difference at three chord wise positions,
$u_{\unicode[STIX]{x1D6FC}_{p}}=\pm 8\times 10^{-2\circ }$
. The airfoil is equipped with three pressure taps at both the suction and pressure sides, to measure the pressure difference at three chord wise positions,
![]() $x/c=0.06$
, 0.11 and 0.14. Each pressure tap is connected to an HCL miniature pressure transducer. The coefficient of the pressure difference
$x/c=0.06$
, 0.11 and 0.14. Each pressure tap is connected to an HCL miniature pressure transducer. The coefficient of the pressure difference
![]() $C_{\unicode[STIX]{x0394}p}$
between the suction and pressure sides is obtained from
$C_{\unicode[STIX]{x0394}p}$
between the suction and pressure sides is obtained from
![]() $C_{\unicode[STIX]{x0394}p}=C_{p,SS}-C_{p,DS}$
, with an uncertainty of
$C_{\unicode[STIX]{x0394}p}=C_{p,SS}-C_{p,DS}$
, with an uncertainty of
![]() $u_{C_{\unicode[STIX]{x0394}p}}=\pm 4\times 10^{-2}$
.
$u_{C_{\unicode[STIX]{x0394}p}}=\pm 4\times 10^{-2}$
.

Figure 1. Side view of the experimental set-up of the pitching airfoil in a steady air stream.
For each parameter set (
![]() $U_{\infty }$
,
$U_{\infty }$
,
![]() $\unicode[STIX]{x1D6FC}_{m}$
,
$\unicode[STIX]{x1D6FC}_{m}$
,
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
and
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
and
![]() $f$
), a phase averaged
$f$
), a phase averaged
![]() $C_{\unicode[STIX]{x0394}p}$
from approximately 15 continuously performed pitch cycles is derived. Damping effects in the pressure taps, tubes and sensors which cause a phase lag and a reduction of the pressure signal amplitude are accounted for by an additional dynamic calibration.
$C_{\unicode[STIX]{x0394}p}$
from approximately 15 continuously performed pitch cycles is derived. Damping effects in the pressure taps, tubes and sensors which cause a phase lag and a reduction of the pressure signal amplitude are accounted for by an additional dynamic calibration.
2.2 Sinusoidal vertical gust
Figure 2 shows a schematic of the experimental set-up in the University of Oldenburg wind tunnel: a stationary two-dimensional airfoil is submitted to a fluctuating inflow, generated by means of an active grid. The active grid allows the generation of sinusoidal modulated turbulent inflow conditions. The modulation is homogeneous
![]() $y$
-direction perpendicular to the profile. The resulting flow, from now on referred to as sinusoidal vertical gust
$y$
-direction perpendicular to the profile. The resulting flow, from now on referred to as sinusoidal vertical gust
![]() $v_{g}=\widehat{v}_{g}\sin (2\unicode[STIX]{x03C0}f)$
, comprises a variable amplitude
$v_{g}=\widehat{v}_{g}\sin (2\unicode[STIX]{x03C0}f)$
, comprises a variable amplitude
![]() $\widehat{v}_{g}$
and variable frequency
$\widehat{v}_{g}$
and variable frequency
![]() $f$
. More information about the active grid and its performance is given by Knebel, Kittel & Peinke (Reference Knebel, Kittel and Peinke2011). By varying either the inflow velocity
$f$
. More information about the active grid and its performance is given by Knebel, Kittel & Peinke (Reference Knebel, Kittel and Peinke2011). By varying either the inflow velocity
![]() $U_{\infty }$
or the frequency
$U_{\infty }$
or the frequency
![]() $f$
, velocity perturbations of different wavelengths
$f$
, velocity perturbations of different wavelengths
![]() $\unicode[STIX]{x1D706}=f/U_{\infty }$
are obtained. The velocity perturbations lead to a fluctuating gust angle
$\unicode[STIX]{x1D706}=f/U_{\infty }$
are obtained. The velocity perturbations lead to a fluctuating gust angle
![]() $\unicode[STIX]{x1D6FC}_{g}=\widehat{\unicode[STIX]{x1D6FC}}_{g}\sin (2\unicode[STIX]{x03C0}f)$
on the airfoil with a reduced frequency
$\unicode[STIX]{x1D6FC}_{g}=\widehat{\unicode[STIX]{x1D6FC}}_{g}\sin (2\unicode[STIX]{x03C0}f)$
on the airfoil with a reduced frequency
![]() $k=\unicode[STIX]{x03C0}fc/U_{\infty }=\unicode[STIX]{x03C0}c/\unicode[STIX]{x1D706}$
. A two-dimensional airfoil with a Clark Y profile, a chord length of
$k=\unicode[STIX]{x03C0}fc/U_{\infty }=\unicode[STIX]{x03C0}c/\unicode[STIX]{x1D706}$
. A two-dimensional airfoil with a Clark Y profile, a chord length of
![]() $c=0.18~\text{m}$
and a span of
$c=0.18~\text{m}$
and a span of
![]() $s=0.8~\text{m}$
is mounted vertically at a mean angle of attack mean
$s=0.8~\text{m}$
is mounted vertically at a mean angle of attack mean
![]() $\unicode[STIX]{x1D6FC}_{m}$
approximately
$\unicode[STIX]{x1D6FC}_{m}$
approximately
![]() $\unicode[STIX]{x0394}x=1.1~\text{m}$
behind the active grid on a wind tunnel balance. The wind tunnel balance allows measurement of the lift
$\unicode[STIX]{x0394}x=1.1~\text{m}$
behind the active grid on a wind tunnel balance. The wind tunnel balance allows measurement of the lift
![]() $L$
with an uncertainty due to the accuracy of the force balance components of
$L$
with an uncertainty due to the accuracy of the force balance components of
![]() $u_{L}=\pm 0.12~\text{N}$
. The fluctuating angle of attack
$u_{L}=\pm 0.12~\text{N}$
. The fluctuating angle of attack
![]() $\unicode[STIX]{x1D6FC}_{g}$
was measured prior to the airfoil experiments in the empty wind tunnel at the airfoil leading-edge position (
$\unicode[STIX]{x1D6FC}_{g}$
was measured prior to the airfoil experiments in the empty wind tunnel at the airfoil leading-edge position (
![]() $x=0$
,
$x=0$
,
![]() $y=0$
,
$y=0$
,
![]() $z=h/2$
) by cross wires and a Dantec Streamline anemometer with an estimated uncertainty of
$z=h/2$
) by cross wires and a Dantec Streamline anemometer with an estimated uncertainty of
![]() $u_{\unicode[STIX]{x1D6FC}_{g}}=\pm 0.2^{\circ }$
.
$u_{\unicode[STIX]{x1D6FC}_{g}}=\pm 0.2^{\circ }$
.

Figure 2. Top view of the experimental set-up of the fixed airfoil encountering a sinusoidal vertical gust.
For each parameter combination (
![]() $\unicode[STIX]{x1D6FC}_{m}$
,
$\unicode[STIX]{x1D6FC}_{m}$
,
![]() $U_{\infty }$
,
$U_{\infty }$
,
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
and
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
and
![]() $f$
), a phase averaged lift response of approximately 200 cycles is derived.
$f$
), a phase averaged lift response of approximately 200 cycles is derived.
3 Transfer functions
Traditionally, transfer functions relate an input to an output signal. Here, the input signal is the fluctuating flow and the output signal is the airfoil lift response
![]() $L_{dyn}$
. Adopting the approach of the theoretically derived first-order transfer functions, the dynamic airfoil response is not related to the fluctuating flow but to the corresponding quasisteady lift response
$L_{dyn}$
. Adopting the approach of the theoretically derived first-order transfer functions, the dynamic airfoil response is not related to the fluctuating flow but to the corresponding quasisteady lift response
![]() $L_{qs}$
of the airfoil, which corresponds to a normalization of the transfer function
$L_{qs}$
of the airfoil, which corresponds to a normalization of the transfer function
![]() $h$
:
$h$
:
The transfer function
![]() $h$
is a complex function of the reduced frequency
$h$
is a complex function of the reduced frequency
![]() $k$
and comprises both magnitude and phase information. For purely harmonic excitations and responses, the magnitude corresponds to the ratio of the dynamic and quasisteady lift amplitudes,
$k$
and comprises both magnitude and phase information. For purely harmonic excitations and responses, the magnitude corresponds to the ratio of the dynamic and quasisteady lift amplitudes,
For values of
![]() $\widehat{h}<1$
, the dynamic lift is smaller than its quasisteady value. The argument of the transfer function represents the phase between the input and output signals,
$\widehat{h}<1$
, the dynamic lift is smaller than its quasisteady value. The argument of the transfer function represents the phase between the input and output signals,
For negative values of
![]() $\unicode[STIX]{x1D711}$
, the load response leads the excitation, while for positive values of
$\unicode[STIX]{x1D711}$
, the load response leads the excitation, while for positive values of
![]() $\unicode[STIX]{x1D711}$
, the load response lags the excitation. First-order transfer functions are functions of the reduced frequency
$\unicode[STIX]{x1D711}$
, the load response lags the excitation. First-order transfer functions are functions of the reduced frequency
![]() $k$
only. They are independent of the mean angle of attack
$k$
only. They are independent of the mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
and the perturbation amplitude. The perturbation amplitude corresponds to the pitch amplitude
$\unicode[STIX]{x1D6FC}_{m}$
and the perturbation amplitude. The perturbation amplitude corresponds to the pitch amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
in the case of the Theodorsen function and to the gust amplitude
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
in the case of the Theodorsen function and to the gust amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
in the case of the Sears function.
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
in the case of the Sears function.
3.1 Oscillating airfoil
The lift force is not directly accessible in the present experimental set-up. The coefficient of the pressure difference on the airfoil leading edge
![]() $C_{\unicode[STIX]{x0394}p}$
serves as an estimator for the lift, as proposed by Gaunaa & Andersen (Reference Gaunaa and Andersen2009). A closed-form first-order transfer function for the unsteady pressure distribution is given by Mateescu & Abdo (Reference Mateescu and Abdo2003). The unsteady pressure distribution is an intermediate result of the unsteady lift response, and integration of Mateescus and Abdo’s solution yields the Theodorsen function. It is assumed that validation of a first-order solution of the unsteady pressure is equivalent to validation of the Theodorsen function of the total lift. The transfer function of the coefficient of the pressure difference
$C_{\unicode[STIX]{x0394}p}$
serves as an estimator for the lift, as proposed by Gaunaa & Andersen (Reference Gaunaa and Andersen2009). A closed-form first-order transfer function for the unsteady pressure distribution is given by Mateescu & Abdo (Reference Mateescu and Abdo2003). The unsteady pressure distribution is an intermediate result of the unsteady lift response, and integration of Mateescus and Abdo’s solution yields the Theodorsen function. It is assumed that validation of a first-order solution of the unsteady pressure is equivalent to validation of the Theodorsen function of the total lift. The transfer function of the coefficient of the pressure difference
![]() $h_{C_{\unicode[STIX]{x0394}p}}$
is defined as
$h_{C_{\unicode[STIX]{x0394}p}}$
is defined as
The magnitude
![]() $\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
relates the amplitude of the coefficient of the dynamic pressure difference
$\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
relates the amplitude of the coefficient of the dynamic pressure difference
![]() $\widehat{C}_{\unicode[STIX]{x0394}p,dyn}$
to its quasisteady counterpart
$\widehat{C}_{\unicode[STIX]{x0394}p,dyn}$
to its quasisteady counterpart
![]() $\widehat{C}_{\unicode[STIX]{x0394}p,qs}$
,
$\widehat{C}_{\unicode[STIX]{x0394}p,qs}$
,
The quasisteady value
![]() $\widehat{C}_{\unicode[STIX]{x0394}p,qs}$
is obtained by
$\widehat{C}_{\unicode[STIX]{x0394}p,qs}$
is obtained by
where
![]() $\unicode[STIX]{x2202}C_{\unicode[STIX]{x0394}p,qs}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
is the slope of the coefficient of the pressure difference in the region of attached flow, derived from quasisteady reference measurements, and
$\unicode[STIX]{x2202}C_{\unicode[STIX]{x0394}p,qs}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
is the slope of the coefficient of the pressure difference in the region of attached flow, derived from quasisteady reference measurements, and
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
is the amplitude of the pitching angle of attack. In the dynamic experiments, a purely sinusoidal excitation is realized. This corresponds to
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
is the amplitude of the pitching angle of attack. In the dynamic experiments, a purely sinusoidal excitation is realized. This corresponds to
The amplitude
![]() $\widehat{C}_{\unicode[STIX]{x0394}p,dyn}$
and phase
$\widehat{C}_{\unicode[STIX]{x0394}p,dyn}$
and phase
![]() $\unicode[STIX]{x1D711}$
with respect to the pitching angle of attack
$\unicode[STIX]{x1D711}$
with respect to the pitching angle of attack
![]() $\unicode[STIX]{x1D6FC}_{p}$
are directly derived from phase averaged dynamic pressure measurements.
$\unicode[STIX]{x1D6FC}_{p}$
are directly derived from phase averaged dynamic pressure measurements.
3.2 Sinusoidal vertical gust
In this experimental set-up, the lift force is directly accessible, and the experimental transfer function
![]() $h_{L}$
is
$h_{L}$
is
Here,
![]() $h_{L}$
corresponds to the Sears function. As above, the magnitude
$h_{L}$
corresponds to the Sears function. As above, the magnitude
![]() $\widehat{h}_{L}$
relates the dynamic lift amplitude to the corresponding quasisteady lift amplitude,
$\widehat{h}_{L}$
relates the dynamic lift amplitude to the corresponding quasisteady lift amplitude,
The quasisteady lift amplitude
![]() $\widehat{L}_{qs}$
is the product of the quasisteady lift curve slope and the amplitude of the oncoming gust,
$\widehat{L}_{qs}$
is the product of the quasisteady lift curve slope and the amplitude of the oncoming gust,
The amplitude of the dynamic lift
![]() $\widehat{L}_{dyn}$
and phase
$\widehat{L}_{dyn}$
and phase
![]() $\unicode[STIX]{x1D711}$
are derived from phase averaged dynamic lift measurements, such that
$\unicode[STIX]{x1D711}$
are derived from phase averaged dynamic lift measurements, such that
As the gust travels over the airfoil with
![]() $U_{\infty }$
, a reference point for the determination of the phase
$U_{\infty }$
, a reference point for the determination of the phase
![]() $\unicode[STIX]{x1D711}$
between the gust angle
$\unicode[STIX]{x1D711}$
between the gust angle
![]() $\unicode[STIX]{x1D6FC}_{g}$
and the dynamic lift response
$\unicode[STIX]{x1D6FC}_{g}$
and the dynamic lift response
![]() $L_{dyn}$
has to be chosen. In the experiments, this reference point is set at the airfoil leading edge, as the preliminarily performed hotwire measurements are taken at this position. In the derivation of first-order transfer functions, the phase reference is traditionally set at the airfoil mid chord. This is accounted for by an additional phase shift of the Sears function.
$L_{dyn}$
has to be chosen. In the experiments, this reference point is set at the airfoil leading edge, as the preliminarily performed hotwire measurements are taken at this position. In the derivation of first-order transfer functions, the phase reference is traditionally set at the airfoil mid chord. This is accounted for by an additional phase shift of the Sears function.
4 Steady results
Figure 3 shows steady reference measurements of the coefficient of the pressure difference
![]() $C_{\unicode[STIX]{x0394}p,qs}$
(oscillating airfoil experiment) and the lift
$C_{\unicode[STIX]{x0394}p,qs}$
(oscillating airfoil experiment) and the lift
![]() $L_{qs}$
(sinusoidal vertical gust experiment), from which the quasisteady responses are derived. Both measured variables have a similar dependence on the mean angle of attack
$L_{qs}$
(sinusoidal vertical gust experiment), from which the quasisteady responses are derived. Both measured variables have a similar dependence on the mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
. This confirms the assumption that the coefficient of the pressure difference
$\unicode[STIX]{x1D6FC}_{m}$
. This confirms the assumption that the coefficient of the pressure difference
![]() $C_{\unicode[STIX]{x0394}p}$
at the airfoil leading edge is a good estimator for the total lift
$C_{\unicode[STIX]{x0394}p}$
at the airfoil leading edge is a good estimator for the total lift
![]() $L$
. In the region of attached flow,
$L$
. In the region of attached flow,
![]() $C_{\unicode[STIX]{x0394}p}$
and
$C_{\unicode[STIX]{x0394}p}$
and
![]() $L$
are proportional to
$L$
are proportional to
![]() $\unicode[STIX]{x1D6FC}_{m}$
. This is the angle of attack range in which first-order transfer functions are supposed to be valid.
$\unicode[STIX]{x1D6FC}_{m}$
. This is the angle of attack range in which first-order transfer functions are supposed to be valid.

Figure 3. Quasisteady reference measurements of the lift
![]() $L_{qs}$
(sinusoidal vertical gust experiment) and the coefficient of the pressure difference
$L_{qs}$
(sinusoidal vertical gust experiment) and the coefficient of the pressure difference
![]() $C_{\unicode[STIX]{x0394}p,qs}$
(oscillating airfoil experiment), exemplarily shown for
$C_{\unicode[STIX]{x0394}p,qs}$
(oscillating airfoil experiment), exemplarily shown for
![]() $U_{\infty }=15~\text{m}~\text{s}^{-1}$
. The region of attached flow is highlighted with a grey background.
$U_{\infty }=15~\text{m}~\text{s}^{-1}$
. The region of attached flow is highlighted with a grey background.
5 Unsteady results: oscillating airfoil
Figure 4 shows the influence of the mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
(figure 4
a) and the pitching amplitude
$\unicode[STIX]{x1D6FC}_{m}$
(figure 4
a) and the pitching amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
(figure 4
b) on the experimental transfer function of the pressure difference
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
(figure 4
b) on the experimental transfer function of the pressure difference
![]() $\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the pitching airfoil. Experimental values are compared with a first-order solution given by Mateescu & Abdo (Reference Mateescu and Abdo2003), which integrally yields the Theodorsen function.
$\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the pitching airfoil. Experimental values are compared with a first-order solution given by Mateescu & Abdo (Reference Mateescu and Abdo2003), which integrally yields the Theodorsen function.

Figure 4. The magnitude
![]() $\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the transfer function of the coefficient of the pressure difference
$\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the transfer function of the coefficient of the pressure difference
![]() $C_{\unicode[STIX]{x0394}p}$
. The airfoil is pitched continuously around its leading edge at the indicated mean angle of attack
$C_{\unicode[STIX]{x0394}p}$
. The airfoil is pitched continuously around its leading edge at the indicated mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
and pitch amplitude
$\unicode[STIX]{x1D6FC}_{m}$
and pitch amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
. An inflow velocity of
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
. An inflow velocity of
![]() $U_{\infty }=15~\text{m}~\text{s}^{-1}$
and pitching frequencies in the range
$U_{\infty }=15~\text{m}~\text{s}^{-1}$
and pitching frequencies in the range
![]() $1~\text{Hz}<f<12~\text{Hz}$
yield reduced frequencies in the range
$1~\text{Hz}<f<12~\text{Hz}$
yield reduced frequencies in the range
![]() $0.025<k<0.3$
. Experimental values, represented by marker symbols, are compared with a first-order solution given by Mateescu and Abdo. (a) Variation of
$0.025<k<0.3$
. Experimental values, represented by marker symbols, are compared with a first-order solution given by Mateescu and Abdo. (a) Variation of
![]() $\unicode[STIX]{x1D6FC}_{m}$
;
$\unicode[STIX]{x1D6FC}_{m}$
;
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}=4^{\circ }$
. (b) Variation of
$\widehat{\unicode[STIX]{x1D6FC}}_{p}=4^{\circ }$
. (b) Variation of
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
;
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
;
![]() $\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
.
$\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
.
A significant dependence of the experimental transfer function on the mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
is observed. At
$\unicode[STIX]{x1D6FC}_{m}$
is observed. At
![]() $\unicode[STIX]{x1D6FC}_{m}=-4^{\circ }$
, the experimental and theoretical values agree best. This is the angle of attack that produces zero mean pressure difference
$\unicode[STIX]{x1D6FC}_{m}=-4^{\circ }$
, the experimental and theoretical values agree best. This is the angle of attack that produces zero mean pressure difference
![]() $C_{\unicode[STIX]{x0394}p,qs}=0$
under quasisteady conditions. With increasing
$C_{\unicode[STIX]{x0394}p,qs}=0$
under quasisteady conditions. With increasing
![]() $\unicode[STIX]{x1D6FC}_{m}$
, the difference between the experimental and theoretical values increases. At the highest mean angle of attack of
$\unicode[STIX]{x1D6FC}_{m}$
, the difference between the experimental and theoretical values increases. At the highest mean angle of attack of
![]() $\unicode[STIX]{x1D6FC}_{m}=+8^{\circ }$
, significant differences are observed between the experimental values and the theoretical predictions. At this mean angle of attack, the total angle of attack
$\unicode[STIX]{x1D6FC}_{m}=+8^{\circ }$
, significant differences are observed between the experimental values and the theoretical predictions. At this mean angle of attack, the total angle of attack
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m}+\unicode[STIX]{x1D6FC}_{p}$
exceeds the static stall angle during every pitch cycle. The magnitudes
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m}+\unicode[STIX]{x1D6FC}_{p}$
exceeds the static stall angle during every pitch cycle. The magnitudes
![]() $\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the experimental and theoretical values show opposite frequency dependence and approach different values for
$\widehat{h}_{C_{\unicode[STIX]{x0394}p}}$
of the experimental and theoretical values show opposite frequency dependence and approach different values for
![]() $k\rightarrow 0$
.
$k\rightarrow 0$
.
From figure 4(b), we find that the pitching amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{p}$
has no influence on the transfer function. This is in accordance with linear theory and in good agreement with the findings of Halfman (Reference Halfman1952) for a harmonically pitching NACA 0012 airfoil.
$\widehat{\unicode[STIX]{x1D6FC}}_{p}$
has no influence on the transfer function. This is in accordance with linear theory and in good agreement with the findings of Halfman (Reference Halfman1952) for a harmonically pitching NACA 0012 airfoil.
6 Unsteady results: sinusoidal vertical gust
Figure 5 shows the influence of the mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
(figure 5
a) and the gust amplitude
$\unicode[STIX]{x1D6FC}_{m}$
(figure 5
a) and the gust amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
(figure 5
b) on the magnitude of the experimental transfer function of the lift
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
(figure 5
b) on the magnitude of the experimental transfer function of the lift
![]() $\widehat{h}_{L}$
of an airfoil encountering a sinusoidal vertical gust. Experimental values are compared with the magnitude of the Sears function.
$\widehat{h}_{L}$
of an airfoil encountering a sinusoidal vertical gust. Experimental values are compared with the magnitude of the Sears function.

Figure 5. The magnitude
![]() $\widehat{h}_{L}$
of the transfer function of the lift
$\widehat{h}_{L}$
of the transfer function of the lift
![]() $L$
. The airfoil is submitted to a fluctuating inflow of gust amplitude
$L$
. The airfoil is submitted to a fluctuating inflow of gust amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
with a gust frequency of
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
with a gust frequency of
![]() $f=5~\text{Hz}$
. The free stream velocity is varied in the range
$f=5~\text{Hz}$
. The free stream velocity is varied in the range
![]() $10~\text{m}~\text{s}^{-1}<U_{\infty }<25~\text{m}~\text{s}^{-1}$
, yielding different reduced frequencies
$10~\text{m}~\text{s}^{-1}<U_{\infty }<25~\text{m}~\text{s}^{-1}$
, yielding different reduced frequencies
![]() $k$
. Experimental values, indicated by marker symbols, are compared with the Sears function. (a) Variation of
$k$
. Experimental values, indicated by marker symbols, are compared with the Sears function. (a) Variation of
![]() $\unicode[STIX]{x1D6FC}_{m}$
;
$\unicode[STIX]{x1D6FC}_{m}$
;
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}=2.7^{\circ }$
. (b) Variation of
$\widehat{\unicode[STIX]{x1D6FC}}_{g}=2.7^{\circ }$
. (b) Variation of
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
;
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
;
![]() $\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
.
$\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
.
The experimental
![]() $\widehat{h}_{L}$
increases with increasing reduced frequency
$\widehat{h}_{L}$
increases with increasing reduced frequency
![]() $k$
, while the Sears function predicts the inverse. This behaviour is observed for all parameter combinations, regardless of whether the total angle of attack
$k$
, while the Sears function predicts the inverse. This behaviour is observed for all parameter combinations, regardless of whether the total angle of attack
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m}+\unicode[STIX]{x1D6FC}_{g}$
stays completely in the attached flow region or exceeds the static stall angle cyclically. The mean angle of attack
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m}+\unicode[STIX]{x1D6FC}_{g}$
stays completely in the attached flow region or exceeds the static stall angle cyclically. The mean angle of attack
![]() $\unicode[STIX]{x1D6FC}_{m}$
and the gust amplitude
$\unicode[STIX]{x1D6FC}_{m}$
and the gust amplitude
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}$
have no significant influence on
$\widehat{\unicode[STIX]{x1D6FC}}_{g}$
have no significant influence on
![]() $\widehat{h}_{L}$
.
$\widehat{h}_{L}$
.
For
![]() $\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
and
$\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
and
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}=5^{\circ }$
, additional experiments are carried out: the reduced frequency of the oncoming gust is varied by changing the gust frequency
$\widehat{\unicode[STIX]{x1D6FC}}_{g}=5^{\circ }$
, additional experiments are carried out: the reduced frequency of the oncoming gust is varied by changing the gust frequency
![]() $2~\text{Hz}<f<6~\text{Hz}$
in steps of
$2~\text{Hz}<f<6~\text{Hz}$
in steps of
![]() $\unicode[STIX]{x0394}f=1~\text{Hz}$
at five different free stream velocity values
$\unicode[STIX]{x0394}f=1~\text{Hz}$
at five different free stream velocity values
![]() $U_{\infty }$
. Figure 6 shows the magnitude
$U_{\infty }$
. Figure 6 shows the magnitude
![]() $\widehat{h}_{L}$
of the experimental transfer function for these parameter combinations. The experimental values of
$\widehat{h}_{L}$
of the experimental transfer function for these parameter combinations. The experimental values of
![]() $\widehat{h}_{L}$
fall in line, regardless of whether
$\widehat{h}_{L}$
fall in line, regardless of whether
![]() $U_{\infty }$
or
$U_{\infty }$
or
![]() $f$
is varied to change the reduced frequency
$f$
is varied to change the reduced frequency
![]() $k$
. This indicates that
$k$
. This indicates that
![]() $k$
is the right parameter to describe the problem. The Sears function fails to capture the experimental values in terms of frequency dependence and limiting values. A different approach to model the unsteady lift response of an airfoil encountering a sinusoidal vertical gust as a function of
$k$
is the right parameter to describe the problem. The Sears function fails to capture the experimental values in terms of frequency dependence and limiting values. A different approach to model the unsteady lift response of an airfoil encountering a sinusoidal vertical gust as a function of
![]() $k$
is provided by Atassi (Reference Atassi1984). Atassi’s theory is nonlinear in the steady flow and linear in the dynamic perturbation. For an airfoil with zero thickness, Atassi (Reference Atassi1984) separates the effects of mean angle of attack, camber and transverse gust number, and shows their contribution to the total response function, which is obtained as a sum of the individual effects. Employing Atassi’s model with the parameters corresponding to the experimental set-up (
$k$
is provided by Atassi (Reference Atassi1984). Atassi’s theory is nonlinear in the steady flow and linear in the dynamic perturbation. For an airfoil with zero thickness, Atassi (Reference Atassi1984) separates the effects of mean angle of attack, camber and transverse gust number, and shows their contribution to the total response function, which is obtained as a sum of the individual effects. Employing Atassi’s model with the parameters corresponding to the experimental set-up (
![]() $\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
, camber
$\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
, camber
![]() $\unicode[STIX]{x1D702}=3.5\,\%$
, transverse wavenumber corresponding to wind tunnel width) yields the presented plots.
$\unicode[STIX]{x1D702}=3.5\,\%$
, transverse wavenumber corresponding to wind tunnel width) yields the presented plots.

Figure 6. The magnitude
![]() $\widehat{h}_{L}$
of the transfer function of the lift
$\widehat{h}_{L}$
of the transfer function of the lift
![]() $L$
. At
$L$
. At
![]() $\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
, the airfoil is submitted to a fluctuating inflow with a gust amplitude of
$\unicode[STIX]{x1D6FC}_{m}=2^{\circ }$
, the airfoil is submitted to a fluctuating inflow with a gust amplitude of
![]() $\widehat{\unicode[STIX]{x1D6FC}}_{g}=5.5^{\circ }$
. The reduced frequency
$\widehat{\unicode[STIX]{x1D6FC}}_{g}=5.5^{\circ }$
. The reduced frequency
![]() $k$
is varied by varying the gust frequency
$k$
is varied by varying the gust frequency
![]() $f$
in the range
$f$
in the range
![]() $2~\text{Hz}<f<6~\text{Hz}$
at constant free stream velocity
$2~\text{Hz}<f<6~\text{Hz}$
at constant free stream velocity
![]() $10~\text{m}~\text{s}^{-1}<U_{\infty }<20~\text{m}~\text{s}^{-1}$
. Experimental values, indicated by marker symbols, are compared with the first-order solution by Sears (Reference Sears1938) and a second-order solution by Atassi (Reference Atassi1984).
$10~\text{m}~\text{s}^{-1}<U_{\infty }<20~\text{m}~\text{s}^{-1}$
. Experimental values, indicated by marker symbols, are compared with the first-order solution by Sears (Reference Sears1938) and a second-order solution by Atassi (Reference Atassi1984).
Contrary to Sears’ first-order transfer function, which does not capture the experimental results, Atassi’s solution captures the experimental data well in terms of frequency dependence and limiting values.
7 Discussion and conclusions
In the case of the oscillating airfoil (Theodorsen function), experimental results agree reasonably well with theory if the airfoil is oscillated around small mean angles of attack. The unsteady load response is independent of the perturbation amplitude, which is in good agreement with theory. With increasing mean angle of attack, the frequency dependence is inverted and the limiting value for
![]() $k\rightarrow 0$
falls below 1. It can be concluded, that the Theodorsen function is a good approximation of the unsteady load response of an oscillating airfoil, if the assumptions leading to thin-airfoil theory (small mean angle of attack, attached flow) are fulfilled.
$k\rightarrow 0$
falls below 1. It can be concluded, that the Theodorsen function is a good approximation of the unsteady load response of an oscillating airfoil, if the assumptions leading to thin-airfoil theory (small mean angle of attack, attached flow) are fulfilled.
In the case of a fixed airfoil encountering a sinusoidal vertical gust (Sears function), the experimental results are not in agreement with the theoretical predictions. The experimental values are uninfluenced by the gust amplitude and the mean angle of attack. It is also irrelevant whether the reduced frequency is changed by changing the gust frequency or the inflow velocity. For all investigated parameter combinations, the unsteady lift amplitude increases with increasing reduced frequency, while the Sears function predicts the inverse. All experimentally derived transfer functions approach limiting values
![]() $h_{L}(k\rightarrow 0)<1$
, while the quasisteady value of the Sears function is
$h_{L}(k\rightarrow 0)<1$
, while the quasisteady value of the Sears function is
![]() $S(k=0)=1$
. The observed discrepancy between experimental and theoretic results is very similar to the observations for the oscillating airfoil under high mean angles of attack. The Sears function appears to be more sensitive to the physical reason that causes experimental values to deviate from the Theodorsen function at high mean angles of attack. This physical reason might be the distortion of the steady velocity field by the presence of an airfoil. Assumptions comprised in first-order theory allow the superposition of partial solutions to obtain a global solution of the flow field. This entails that the oncoming velocity perturbation is completely uninfluenced by the presence of the airfoil. In the experiment, we found this approximation to be violated when we tried to measure the fluctuating angle of attack at the airfoil leading edge with the airfoil present in the test section. A theory accounting for the presence of the airfoil by a distortion of the steady flow field is the second-order closed-form transfer function by Atassi (Reference Atassi1984). Experimental results show good agreement with this second-order theory.
$S(k=0)=1$
. The observed discrepancy between experimental and theoretic results is very similar to the observations for the oscillating airfoil under high mean angles of attack. The Sears function appears to be more sensitive to the physical reason that causes experimental values to deviate from the Theodorsen function at high mean angles of attack. This physical reason might be the distortion of the steady velocity field by the presence of an airfoil. Assumptions comprised in first-order theory allow the superposition of partial solutions to obtain a global solution of the flow field. This entails that the oncoming velocity perturbation is completely uninfluenced by the presence of the airfoil. In the experiment, we found this approximation to be violated when we tried to measure the fluctuating angle of attack at the airfoil leading edge with the airfoil present in the test section. A theory accounting for the presence of the airfoil by a distortion of the steady flow field is the second-order closed-form transfer function by Atassi (Reference Atassi1984). Experimental results show good agreement with this second-order theory.
It can be concluded that for the present experimental set-up the Sears functions is not a suitable tool to approximate the unsteady lift response, although the experimental set-up meets the assumptions usually required when applying thin-airfoil theory. Hence, the Sears function should be applied with caution. The Sears function still lacks a systematic verification in terms of frequency dependence. In future work, experiments with flat thin plates should be carried out, further approaching thin-airfoil assumptions. For flow situations corresponding to the current set-up (airfoil with thickness and camber), the second-order transfer function by Atassi appears to be a more appropriate approach.
Acknowledgements
The present investigations were performed in the DFG PAK 780 project. The authors gratefully acknowledge the German Research Foundation (DFG) for funding the studies.