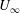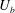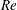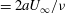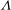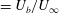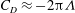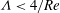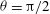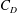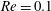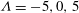1. Introduction
The modification of the flow past a body due to a uniform blowing or sucking component is of fundamental importance in many areas of engineering. For example, a through-surface flux is introduced to cool turbine blades or modify the force acting on lifting surfaces or can be generated by a phase change (e.g. evaporation).
Dukowicz (Reference Dukowicz1982) derived a closed-form expression for the drag force acting on a blowing/sucking sphere at low Reynolds numbers which retrieves Stokes’ (Reference Stokes1851) solution for
${\it\Lambda}=0$
. For strongly sucking flows, the flow is irrotational in the far field and the drag force reduces to what is expected by a global momentum analysis. At a Reynolds number of
$Re=1$
, the difference between the full numerical results and Dukowicz’s solution is approximately 10 % in the drag coefficient for blowing flows (Cliffe & Lever Reference Cliffe and Lever1985).
For the case of a cylinder, the complexity of the analysis is increased by the requirement of a far-field or Oseen correction (see the discussion by Stokes (Reference Stokes1851)). The study of the force on a cylinder at low
$Re$
has been developed over the last 100 years, and it is worth pointing out some of the historical elements, as they provide a guide to the different ways in which we could treat the problem in this paper. Later editions of Lamb’s book ‘Hydrodynamics’ include a discussion of the flow past a cylinder at low
$Re$
(Lamb Reference Lamb1932, p. 614, 1911). The technique Lamb employed attracted criticism in the 1960s because it was not a rigorous asymptotic analysis. The construction technique that Lamb employed is reasonably accurate, giving predictions for the drag coefficient up to
$Re=1$
that are within 5 % of the full solution. Lamb’s (Reference Lamb1911) technique follows that of Oseen, introducing a correction (advective) term to account for the far-field flow, but it is simpler as it makes use of a transformational split that is not extendable to the problem in this paper. While a matched asymptotic solution is mathematically rigorous and can account for the full inertia term, the series expansion method by Dennis & Shimshoni (Reference Dennis and Shimshoni1965) is just as powerful and accurate, though far less elegant mathematically.
The purpose of this paper is to examine the low-Reynolds-number flow past a cylinder which has a through-surface component and to develop an understanding of the influence of
$Re$
and
${\it\Lambda}$
on the drag force. The leading-order solution is calculated using a construction technique, which has the advantage of being simple. The fidelity of this approach is tested with comparisons against full numerical solutions. The mathematical model is described in § 2. Approximate solutions are developed in the limit of
${\it\Lambda}=0$
and strongly sucking flows and described in § 3. A comparison between predictions and numerical solutions is shown in § 4.
2. Mathematical model
We consider a cylinder of radius
$a$
fixed at the origin and set in a uniform flow. To account for the far field at low Reynolds numbers, the Oseen approximation is applied which uses a linear approximation for the inertia term so that
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}\approx U_{\infty }\partial \boldsymbol{u}/\partial x$
, where
$U_{\infty }$
is the far-field velocity. We are interested in examining the flow past a cylinder with a through-surface flow so that the radial blow component is included, and therefore seek to determine the leading-order solution to
$$\begin{eqnarray}{\it\rho}\left(U_{\infty }\frac{\partial \boldsymbol{u}}{\partial x}+\frac{U_{b}a}{r}\frac{\partial \boldsymbol{u}}{\partial r}\right)=-\boldsymbol{{\rm\nabla}}p+{\it\mu}{\rm\nabla}^{2}\boldsymbol{u},\end{eqnarray}$$
where
${\it\mu}$
is the dynamic viscosity,
${\it\rho}$
is the density and
$U_{b}$
is the blow velocity. The boundary conditions imposed on the flow are
$$\begin{eqnarray}(u_{r},u_{{\it\theta}})=(U_{b},0)\end{eqnarray}$$
at the surface of the cylinder (at
$r=a$
) and
$$\begin{eqnarray}(u_{r},u_{{\it\theta}})\rightarrow (U_{\infty }\cos {\it\theta},-U_{\infty }\sin {\it\theta})\end{eqnarray}$$
in the far field (as
$r\rightarrow \infty$
).
2.1. Defining equations
A vorticity–stream function (
${\it\omega}$
–
${\it\psi}$
) method of solution is employed (see Batchelor Reference Batchelor1967, appendix 2), where the velocity and vorticity fields are defined by
$$\begin{eqnarray}u_{r}=\frac{1}{r}\frac{\partial {\it\psi}}{\partial {\it\theta}},\quad u_{{\it\theta}}=-\frac{\partial {\it\psi}}{\partial r},\quad {\it\omega}=-\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial {\it\psi}}{\partial r}\right)-\frac{1}{r^{2}}\frac{\partial ^{2}{\it\psi}}{\partial {\it\theta}^{2}}.\end{eqnarray}$$
The boundary conditions (2.2) impose significant constraints on the velocity near the boundary, mainly because
$\partial u_{{\it\theta}}/\partial {\it\theta}=\partial u_{r}/\partial {\it\theta}=0$
. This means that
$$\begin{eqnarray}\left.{\it\omega}=\frac{\partial u_{{\it\theta}}}{\partial r}\right|_{r=a}\end{eqnarray}$$
and
$$\begin{eqnarray}\left.\frac{\partial u_{r}}{\partial r}\right|_{r=a}=-\frac{U_{b}}{a}\end{eqnarray}$$
(where mass conservation was used in (2.6)). From (2.1), the vorticity equation is
$$\begin{eqnarray}U_{\infty }\frac{\partial {\it\omega}}{\partial x}+\frac{U_{b}a}{r}\frac{\partial {\it\omega}}{\partial r}={\it\nu}{\rm\nabla}^{2}{\it\omega}.\end{eqnarray}$$
Our starting point is quite similar to that of Lamb (Reference Lamb1932) and involves expressing the vorticity field
$\tilde{{\it\omega}}$
(
$=2a{\it\omega}/U_{\infty }$
) as
$$\begin{eqnarray}\tilde{{\it\omega}}=\text{e}^{(Re/4)\tilde{r}\cos {\it\theta}}P,\end{eqnarray}$$
giving
$$\begin{eqnarray}\frac{Re^{2}}{8}{\it\Lambda}\frac{1}{\tilde{r}}\cos {\it\theta}P+\frac{Re}{2}\frac{{\it\Lambda}}{\tilde{r}}\frac{\partial P}{\partial \tilde{r}}+\left(\frac{Re}{4}\right)^{2}P=\tilde{{\rm\nabla}}^{2}P,\end{eqnarray}$$
where
$Re=2aU_{\infty }/{\it\nu}$
and
$\tilde{r}=r/a$
. Following Dukowicz (Reference Dukowicz1982), we seek the leading-order symmetric solution, which is of the form
$$\begin{eqnarray}P=P_{1}(\tilde{r})\sin {\it\theta},\end{eqnarray}$$
where
$P_{1}$
satisfies
$$\begin{eqnarray}P_{1}^{\prime \prime }+\frac{P_{1}^{\prime }}{\tilde{r}}(1-2{\it\beta})-\left(\left(\frac{Re}{4}\right)^{2}+\frac{1}{\tilde{r}^{2}}\right)P_{1}=0,\end{eqnarray}$$
where
${\it\beta}=Re\,{\it\Lambda}/4$
. This is valid provided that
$Re^{2}|{\it\Lambda}|\ll 1$
and for
${\it\beta}\rightarrow -\infty$
because the flow is symmetric about
${\it\theta}={\rm\pi}/2$
, but not for
${\it\beta}\rightarrow \infty$
. The solution that satisfies
$P_{1}\rightarrow 0$
as
$\tilde{r}\rightarrow \infty$
is
$$\begin{eqnarray}P_{1}=C_{1}\tilde{r}^{{\it\beta}}K_{(1+{\it\beta}^{2})^{1/2}}(Re\,\tilde{r}/4).\end{eqnarray}$$
The stream function,
${\it\psi}$
, can be constructed by writing it as the sum of the known blowing and free-stream components, together with a component to be determined. As such we write
$$\begin{eqnarray}{\it\psi}=U_{\infty }a({\it\Lambda}{\it\theta}+\tilde{r}\sin {\it\theta}+f_{1}\sin {\it\theta}).\end{eqnarray}$$
Substitution of (2.13) into (2.4) gives
$$\begin{eqnarray}f_{1}^{\prime \prime }+\frac{f_{1}^{\prime }}{r}-\frac{f_{1}}{r^{2}}=-\frac{1}{{\rm\pi}}\int _{0}^{{\rm\pi}}\sin {\it\theta}\tilde{{\it\omega}}\,\text{d}{\it\theta}=-\frac{1}{2{\rm\pi}}P_{1}(\tilde{r})\int _{0}^{2{\rm\pi}}\text{e}^{(Re\,\tilde{r}/4)\cos {\it\theta}}\sin ^{2}{\it\theta}\,\text{d}{\it\theta}.\end{eqnarray}$$
The boundary conditions for
$f_{1}$
are
$$\begin{eqnarray}f_{1}(1)=-1,\quad f_{1}^{\prime }(1)=-1,\quad \lim _{\tilde{r}\rightarrow \infty }f_{1}(\tilde{r})=0.\end{eqnarray}$$
The right-hand side of (2.14) is defined as
$C_{1}p_{1}(\tilde{r})$
, where
$$\begin{eqnarray}p_{1}(\tilde{r})=-\tilde{r}^{{\it\beta}}\frac{J_{1}(\text{i}Re\,\tilde{r}/4)}{\text{i}Re\,\tilde{r}/4}K_{(1+{\it\beta}^{2})^{1/2}}(Re\,\tilde{r}/4).\end{eqnarray}$$
We can solve (2.14) exactly by writing
$f_{1}=\tilde{r}g_{1}$
, which transforms the ordinary differential equation to
$$\begin{eqnarray}\frac{\text{d}(\tilde{r}^{3}g_{1}^{\prime })}{\text{d}\tilde{r}}=C_{1}p_{1}(\tilde{r})\tilde{r}^{2}.\end{eqnarray}$$
The boundary conditions on
$g_{1}$
are
$g_{1}(1)=-1$
,
$g_{1}^{\prime }(1)=0$
and
$g_{1}\rightarrow 0$
as
$\tilde{r}\rightarrow \infty$
. Integrating twice, we find two results. The first is that
$$\begin{eqnarray}f_{1}=C_{1}\tilde{r}\left(-\frac{1}{2\tilde{r}^{2}}G(1)-\int _{\infty }^{\tilde{r}}G(\tilde{r})\tilde{r}^{-3}\,\text{d}\tilde{r}\right),\end{eqnarray}$$
where
$$\begin{eqnarray}G(\tilde{r})=\int _{\tilde{r}}^{\infty }p_{1}(\tilde{r})\tilde{r}^{2}\,\text{d}\tilde{r}.\end{eqnarray}$$
The second result (which ensures that the far-field boundary condition is satisfied) is
$$\begin{eqnarray}C_{1}=\frac{2}{\displaystyle \int _{1}^{\infty }p_{1}(\tilde{r})\,\text{d}\tilde{r}}.\end{eqnarray}$$
The integrand scales as
$\tilde{r}^{{\it\beta}-2}$
in the far field (using
$K_{n}(z)\sim \text{exp}(-z)/z^{1/2}$
and
$J_{1}(\text{i}z)\sim \text{exp}(z)/z^{1/2}$
) and so the integral converges when
$-\infty <{\it\beta}<1$
.
2.2. Diagnostics
The pressure and viscous drag coefficients for characterizing the force on a cylinder are
$$\begin{eqnarray}C_{P}=\int _{0}^{2{\rm\pi}}\left(\frac{1}{Re}\frac{\partial \tilde{{\it\omega}}}{\partial \tilde{r}}-\frac{1}{2}{\it\Lambda}\tilde{{\it\omega}}\right)\sin {\it\theta}\,\text{d}{\it\theta},\quad C_{{\it\nu}}=-\frac{1}{Re}\int _{0}^{2{\rm\pi}}\tilde{{\it\omega}}\sin {\it\theta}\,\text{d}{\it\theta},\end{eqnarray}$$
which is an extension of the relationship given by Dennis & Shimshoni (Reference Dennis and Shimshoni1965) to include a through-surface flow. On substituting (2.8), (2.10), (2.12) into (2.21),
$$\begin{eqnarray}\displaystyle \hspace{-8.0pt}\left.\begin{array}{@{}c@{}}\displaystyle C_{P}=-C_{1}\frac{{\rm\pi}}{Re}\left(({\it\beta}+(1+{\it\beta}^{2})^{1/2})K_{(1+{\it\beta}^{2})^{1/2}}(Re/4)+\frac{Re}{4}K_{(1+{\it\beta}^{2})^{1/2}-1}(Re/4)\right),\\ \displaystyle C_{{\it\nu}}=-C_{1}\frac{{\rm\pi}}{Re}K_{(1+{\it\beta}^{2})^{1/2}}(Re/4).\quad \end{array}\!\!\!\right\} & & \displaystyle\end{eqnarray}$$
The ratio of the viscous drag to the total drag coefficient is
$$\begin{eqnarray}\frac{C_{{\it\nu}}}{C_{D}}=\frac{1}{{\it\beta}+(1+{\it\beta}^{2})^{1/2}+1+\displaystyle \frac{Re}{4}\displaystyle \frac{K_{(1+{\it\beta}^{2})^{1/2}-1}(Re/4)}{K_{(1+{\it\beta}^{2})^{1/2}}(Re/4)}},\end{eqnarray}$$
where
$C_{D}=C_{P}+C_{{\it\nu}}$
. Since
$Re$
is small,
$C_{{\it\nu}}/C_{D}$
is effectively a function of
$Re\,{\it\Lambda}$
. It should be noted that (2.23) does not depend on
$C_{1}$
.
3. Approximate solutions
We present a leading-order solution to (2.14) which will then be used to understand two limits: (a) the no-blow case where the result reduces to Lamb’s (Reference Lamb1911) original solution and (b) strongly sucking flows.
3.1. No-blow case (
${\it\Lambda}=0$
)
The purpose here is to retrieve Lamb’s solution for the no-blow case. When
${\it\Lambda}=0$
,
$p_{1}$
can be expressed exactly as
$$\begin{eqnarray}p_{1}=-K_{1}(Re\,\tilde{r}/4)\frac{J_{1}(\text{i}Re\,\tilde{r}/4)}{\text{i}Re\,\tilde{r}/4}.\end{eqnarray}$$
Using the substitution
$z=Re\,\tilde{r}/4$
, the integral in (2.20) can be written as
$$\begin{eqnarray}\int _{1}^{\infty }p_{1}\,\text{d}\tilde{r}=\frac{4}{Re}\int _{Re/4}^{\infty }K_{1}(z)\frac{J_{1}(\text{i}z)}{\text{i}z}\,\text{d}z=\frac{4}{Re}\int _{Re/4}^{\infty }K_{1}(z)\left(\frac{1}{2}+\mathop{\sum }_{n=1}^{\infty }\frac{z^{2n}}{2^{2n+1}n!(n+1)!}\right)\,\text{d}z,\end{eqnarray}$$
such that
$$\begin{eqnarray}\int _{1}^{\infty }p_{1}\,\text{d}\tilde{r}=\frac{2}{Re}\left(K_{0}(Re/4)+\mathop{\sum }_{n=1}^{\infty }\int _{Re/4}^{\infty }\frac{z^{2n}K_{1}(z)}{2^{2n}n!(n+1)!}\,\text{d}z\right).\end{eqnarray}$$
In the limit of
$Re\ll 1$
, the lower limit is close to zero and it can be shown, using (A 4), that
$$\begin{eqnarray}\mathop{\sum }_{n=1}^{\infty }\int _{0}^{\infty }\frac{z^{2n}K_{1}(z)}{2^{2n}n!(n+1)!}\,\text{d}z=\frac{1}{2},\end{eqnarray}$$
such that
$$\begin{eqnarray}C_{1}=\frac{Re}{\frac{1}{2}+K_{0}(Re/4)}.\end{eqnarray}$$
The drag coefficient corresponding to (3.5) is
$$\begin{eqnarray}C_{D}=-\frac{2{\rm\pi}}{\frac{1}{2}+K_{0}(Re/4)}\left(K_{1}(Re/4)+\frac{Re}{8}K_{0}(Re/4)\right)\cong -\frac{8{\rm\pi}}{Re(\frac{1}{2}+K_{0}(Re/4))},\end{eqnarray}$$
where use was made of (A 2). Now, Lamb (Reference Lamb1932, p. 616) derived the following expression for vorticity:
$$\begin{eqnarray}{\it\omega}=C\text{e}^{(\tilde{r}Re/4)\cos {\it\theta}}\frac{\partial }{\partial y}K_{0}(Re\,\tilde{r}/4)=-\frac{C}{a}\frac{Re}{4}\text{e}^{(\tilde{r}Re/4)\cos {\it\theta}}K_{1}(Re\,\tilde{r}/4)\sin {\it\theta},\end{eqnarray}$$
which is the same expression as that derived here from the vorticity equation. (It should be noted that there is a typographical error in Lamb’s vorticity expression, where
$\text{e}^{kz}$
should read
$\text{e}^{kx}$
; the correct analysis is given in Lamb (Reference Lamb1911) except for the typographical error of ‘sphere’ which should be ‘cylinder’ after equation (54).) A higher-order expansion of the stream function was determined,
$$\begin{eqnarray}C=\frac{2U_{\infty }}{\frac{1}{2}+K_{0}(Re/4)},\end{eqnarray}$$
or equivalently
$$\begin{eqnarray}C_{D}=-\frac{8{\rm\pi}}{Re\left(\frac{1}{2}+K_{0}(Re/4)\right)}.\end{eqnarray}$$
Therefore, the general expression for the drag coefficient agrees exactly with Lamb’s expression as
$Re\rightarrow 0$
(the difference for
$Re=1$
is less than 1 %).
3.2. Strongly sucking flow (
$-{\it\Lambda}\gg 1$
)
For strongly sucking flows where
$|{\it\beta}|\gg 1$
and
${\it\beta}<0$
, we can write
$$\begin{eqnarray}\frac{\displaystyle \int _{1}^{\infty }p_{1}\,\text{d}\tilde{r}}{K_{(1+{\it\beta}^{2})^{1/2}}(Re/4)}=-\frac{1}{2}\left(\frac{4}{Re}\right)^{{\it\beta}+1}\int _{Re/4}^{\infty }z^{{\it\beta}}\frac{K_{(1+{\it\beta}^{2})^{1/2}}(z)}{K_{(1+{\it\beta}^{2})^{1/2}}(Re/4)}\,\text{d}z\cong \frac{1}{2({\it\beta}-(1+{\it\beta}^{2})^{1/2}+1)},\end{eqnarray}$$
which can be substituted into (2.22), giving a drag coefficient of
$$\begin{eqnarray}C_{D}\approx -\frac{4{\rm\pi}}{Re}({\it\beta}+(1+{\it\beta}^{2})^{1/2}+1)({\it\beta}-(1+{\it\beta}^{2})^{1/2}+1).\end{eqnarray}$$
This reduces to
$$\begin{eqnarray}C_{D}\approx -2{\rm\pi}{\it\Lambda}.\end{eqnarray}$$
This approximation is appropriate when
$|{\it\beta}|\geqslant 1$
or
${\it\Lambda}<-4/Re$
(so that the asymptotic approximation is valid). Equation (3.12) agrees with a global momentum analysis when the far-field downstream flow is irrotational, which was derived by Pankhurst & Thwaites (Reference Pankhurst and Thwaites1953, appendix I) for high-
$Re$
flows. This is to be expected because in both cases, the boundary layer is thin compared with the size of the cylinder.
4. Numerical results
4.1. Solution technique
The Navier–Stokes equation was numerically solved using a finite-element method that employs a characteristic-based split (CBS) methodology (see Zienkiewicz, Taylor & Nithiarasu Reference Zienkiewicz, Taylor and Nithiarasu2005). The ACEsim code has been validated for two-dimensional flows (e.g. Nicolle & Eames Reference Nicolle and Eames2011; Klettner & Eames Reference Klettner and Eames2012). For low
$Re$
, White (Reference White1945) suggests a domain width of 2000
$a$
for the no-blow case to be unaffected by boundedness. As the influence of boundedness is increased for strong blowing/sucking, the domain width was increased to 20 000
$a$
for the two cases of
$|{\it\Lambda}|=5$
.
4.2. Results
Figure 1(a) shows the drag coefficient as a function of
${\it\Lambda}$
for
$Re=0.1$
. Good agreement is found between the analytical results and full numerical simulations. The asymptotic limit for strongly sucking flows (
$C_{D}\approx -2{\rm\pi}{\it\Lambda}$
) is confirmed for
$Re=1$
. Figure 1(b) shows the fraction of the total force due to viscous stresses for
$Re=0.1$
. For small
$|{\it\Lambda}|$
(
$\ll 1$
), the influence of blowing and sucking is symmetric on the drag force. For strongly sucking flows, the drag force increases linearly with
$|{\it\Lambda}|$
because the viscous stresses near the wall scale as
${\it\mu}|{\it\Lambda}|U_{\infty }/a$
. For strongly blowing flows,
$C_{D}\rightarrow 0$
because the vorticity is blown off the surface of the cylinder. Therefore, the influence of the through-surface flow is asymmetric on the drag force at large
${\it\Lambda}$
. For
${\it\beta}>0$
, the range of validity of the analysis was determined to be
${\it\beta}<1$
or
${\it\Lambda}<4/Re$
using a scaling analysis.
Figure 1. A comparison between the theoretical predictions and full numerical calculations of (a)
$C_{D}$
and (b)
$C_{{\it\nu}}/C_{D}$
as functions of
${\it\Lambda}$
and
${\it\Lambda}Re$
respectively. In (a,b) the dot-dashed and full curves correspond to the predictions (2.22), (2.23) for
$Re=1,0.1$
respectively and the full numerical simulations for
$Re=0.1$
are represented by crosses. The numerical results of Dennis & Shimshoni (Reference Dennis and Shimshoni1965) are plotted as red circles for the no-blow case. The blue line is the strongly sucking solution,
$C_{D}=-2{\rm\pi}{\it\Lambda}$
, given in Pankhurst & Thwaites (Reference Pankhurst and Thwaites1953, appendix I).
5. Conclusion
We identified the gap of low-Reynolds-number flow past a cylinder with a through-surface flow, and studied this problem using a analytical technique that identifies the leading-order component to the vorticity field. For the case of
${\it\Lambda}=0$
and
$Re\rightarrow 0$
, we retrieve Lamb’s (Reference Lamb1911) result for the drag force. For strongly sucking flows, where the flow is irrotational outside the thin boundary layer, the asymptotic result
$C_{D}\approx -2{\rm\pi}{\it\Lambda}$
is recovered. The agreement between the analytical results and the full numerical solutions is good for
$Re=0.1$
.
Appendix A. Useful relationships for
$K_{n}$
We list the recurrent and asymptotic relationships that are used in this paper.
$$\begin{eqnarray}\displaystyle \frac{\text{d}K_{n}}{\text{d}z}=-K_{n-1}(z)-\frac{n}{z}K_{n}(z). & & \displaystyle\end{eqnarray}$$
The expansion for
$K_{1}$
is
$$\begin{eqnarray}\displaystyle K_{1}(z)=\frac{1}{z}+\frac{z}{2}\log \left(\frac{z}{2}\right)+\cdots \,. & & \displaystyle\end{eqnarray}$$
When the argument
$n\gg 1$
,
$$\begin{eqnarray}\displaystyle K_{n}(z)\cong \frac{{\it\Gamma}(n)}{2}\left(\frac{z}{2}\right)^{-n}. & & \displaystyle\end{eqnarray}$$
Another useful formula is
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }z^{m}K_{n}(z)\,\text{d}z=2^{m-1}{\it\Gamma}\left(\frac{n+m+1}{2}\right){\it\Gamma}\left(\frac{m+1-n}{2}\right). & & \displaystyle\end{eqnarray}$$
