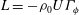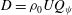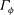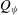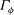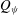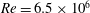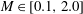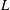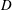1. Introduction
A body moving through a viscous fluid will experience a reaction force (and moment) due to its generated flow. This is the central problem of aero- and hydrodynamics. Ever since the birth of modern aerodynamics, great efforts have been made to find various force formulae and their underlying physical mechanisms. In this paper we consider the lift
$L$
and drag
$D$
exerted on a stationary body by a two-dimensional steady flow in the
$(x,y)$
-plane with the orthonormal basis
$(\boldsymbol{e}_{x},\boldsymbol{e}_{y})$
. At upstream infinity the flow has uniform velocity
$\boldsymbol{U}=U\boldsymbol{e}_{x}$
and constant properties denoted by suffix 0. Then when the flow is incompressible and irrotational with
$\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{{\rm\nabla}}{\it\phi}$
, we have
$D=0$
and the famous Kutta–Joukowski lift formula (K–J formula for short)
$$\begin{eqnarray}\displaystyle L=-{\it\rho}_{0}U{\it\Gamma}_{{\it\phi}},\quad {\it\Gamma}_{{\it\phi}}=\oint _{C}\boldsymbol{{\rm\nabla}}{\it\phi}\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l, & & \displaystyle\end{eqnarray}$$
which was first derived rigorously and published by Joukowski (Reference Jowkowski1906). (See Ackroyd, Axcell & Ruban (Reference Ackroyd, Axcell and Ruban2001), this book contains half-dozen English translations of the key papers that pioneered the modern science of flight, such as Kutta (Reference Kutta1902) and Joukowski (Reference Jowkowski1906).) Here,
$C$
is an arbitrarily chosen contour surrounding the airfoil with unit tangent vector
$\boldsymbol{t}$
. The circulation
${\it\Gamma}_{{\it\phi}}$
will be positive if counted counterclockwise, which of course is independent of the size and shape of
$C$
due to the kinematic nature of
$\boldsymbol{{\rm\nabla}}{\it\phi}$
(to see this, one only needs to take another contour
$C^{\prime }$
also enclosing the airfoil, and insert a cut
$AB$
to connect
$C$
and
$C^{\prime }$
; then
${\it\Gamma}_{{\it\phi}}$
along the single loop
$C+AB+C^{\prime }+BA$
in the counterclockwise direction is always zero). When the body is an airfoil with a sharp trailing edge where the Kutta condition is imposed (Kutta Reference Kutta1902), (1.1) has served as the very basis of classic steady aerodynamics, which states that the lift exerted on the body is solely determined by the circulation
${\it\Gamma}_{{\it\phi}}$
.
Due to the extreme simplicity and clear physical implication of (1.1), extending the application range of (1.1) has been of great theoretical and practical interest. The first step was to generalize (1.1) to viscous incompressible flow with high Reynolds number or small viscosity, such as water/air flow. Bryant, Williams & Taylor (Reference Bryant, Williams and Taylor1926) and Filon (Reference Filon1926) were among the first to check the validity of (1.1) for such flows. Assuming a large Reynolds number and a thin wake layer, Taylor obtained formulae for the lift and drag,
$$\begin{eqnarray}\displaystyle L=-{\it\rho}_{0}U{\it\Gamma}_{C},\quad {\it\Gamma}_{C}=\oint _{C}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l=\int _{S}{\it\omega}\,\text{d}S, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D=\int _{W}(P_{0}-P)\,\text{d}y,\quad P=p+\frac{1}{2}{\it\rho}_{0}|\boldsymbol{u}|^{2}, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{u}^{\prime }$
is the total velocity,
${\bf\omega}={\it\omega}\boldsymbol{e}_{z}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}$
is the vorticity and subscript
$0$
denotes the value at the uniform incoming flow. While (1.2c,d
) indicates clearly that the drag exerted on the body is exactly the total-pressure loss of the fluid in the wake, (1.2a,b
) needs some careful interpretation.
First, unlike (1.1), the lift-generating circulation
${\it\Gamma}_{C}$
is defined by the total disturbance velocity
$\boldsymbol{u}^{\prime }=\boldsymbol{u}-\boldsymbol{U}$
rather than its potential part only. This difference has seldom been discussed but is important for physical understanding and practical application. Since any vector field with proper continuity and smoothness can be decomposed into a longitudinal (irrotational) field and a transversal (solenoidal) field (not uniquely in general), namely the Helmholtz decomposition, the disturbance velocity field
$\boldsymbol{u}^{\prime }$
can always be written formally as
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }=\boldsymbol{u}_{{\it\phi}}+\boldsymbol{u}_{{\it\psi}}\equiv \boldsymbol{{\rm\nabla}}{\it\phi}+\boldsymbol{{\rm\nabla}}\times {\bf\psi}. & & \displaystyle\end{eqnarray}$$
Here,
${\it\phi}$
and
${\bf\psi}$
are called the velocity potential of the longitudinal field and the vortical stream function of the transversal field, respectively, which should be distinguished from the potential and stream function of the whole disturbance velocity
$\boldsymbol{u}^{\prime }$
in two-dimensional flow. In particular, in two dimensions we have
${\bf\psi}={\it\psi}\boldsymbol{e}_{z}$
such that
$\boldsymbol{u}_{{\it\psi}}=\boldsymbol{{\rm\nabla}}{\it\psi}\times \boldsymbol{e}_{z}$
, which degenerates to a single constant outside the boundary layers and vortical wake where the vorticity
${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}_{{\it\psi}}$
is non-zero. Furthermore, Lagerstrom, Cole & Trilling (Reference Lagerstrom, Cole and Trilling1949) and Wu (Reference Wu1956) have proved (without and with heat conduction, respectively) that a linearized viscous compressible flow including
$\boldsymbol{u}^{\prime }$
can be completely and uniquely split into longitudinal and transversal parts. Thus, in our case, the kinematic decomposition (1.3) is uniquely determined in the whole flow domain. Then, with
${\it\Gamma}_{{\it\phi}}$
defined in (1.1),
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{C}={\it\Gamma}_{{\it\phi}}+{\it\Gamma}_{{\it\psi}},\quad {\it\Gamma}_{{\it\psi}}=\oint _{C}\boldsymbol{u}_{{\it\psi}}\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l=-\oint _{C}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\psi}\,\text{d}l, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{n}$
is the unit normal vector pointing out of contour
$C$
with
$\boldsymbol{e}_{z}\times \boldsymbol{t}=-\boldsymbol{n}$
. The vortical wake may have a non-negligible effect on
${\it\Gamma}_{{\it\psi}}$
and hence on
${\it\Gamma}_{C}$
. Here, it is of crucial importance to stress that, unlike the independence of
${\it\Gamma}_{{\it\phi}}$
on the choice of
$C$
, as argued in the context of (1.1), generically
${\it\Gamma}_{{\it\psi}}$
depends on the choice of
$C$
.
Second, in steady viscous flow the vortical wake has to extend to downstream infinity, so any contour
$C$
must cut the wake, making
${\it\Gamma}_{{\it\psi}}$
and hence
${\it\Gamma}_{C}$
dependent on
$C$
in general. But Taylor points out that (i) the intersection of
$C$
and the wake has to be a vertical line (‘wake line’, denoted by
$W$
) with normal
$\boldsymbol{n}=\boldsymbol{e}_{x}$
, to ensure the force caused by the loss of total pressure in the wake does not affect lift; and (ii) with this choice of
$W$
, the net vorticity flux through
$W$
must vanish, i.e.
$$\begin{eqnarray}\displaystyle \int _{W}u{\it\omega}\,\text{d}y=0, & & \displaystyle\end{eqnarray}$$
thus
${\it\Gamma}_{C}$
is conditionally independent of the shape and size of
$C$
, supporting the experimental results obtained by Bryant and Williams in the same 1926 paper, with Taylor being a coauthor (Bryant et al.
Reference Bryant, Williams and Taylor1926). We call these conditions the first and second Taylor criteria, respectively. They ensure that
${\it\Gamma}_{{\it\psi}}=0$
and
${\it\Gamma}_{{\it\phi}}$
is replaceable by
${\it\Gamma}_{C}$
. Thus, (1.2a,b
) and (1.1) are consistent. For reasons to be explained in § 2.3, we call (1.2a,b
) a testable lift formula.
It is worth mentioning that the important condition (1.5) has been further elaborated by a few authors under the boundary-layer approximation, as reviewed by Sears (Reference Sears1956). Recently, the wake-layer behaviour has been analysed by Liu et al. (Reference Liu, Wu, Zhu, Zou and Liu2015) under the same approximation, see also Wu, Ma & Zhou (Reference Wu, Ma and Zhou2015, pp. 290–292), who re-derived (1.5) along with a further result
$$\begin{eqnarray}\displaystyle \int _{W}{\it\omega}\,\text{d}y=0, & & \displaystyle\end{eqnarray}$$
and found that (1.5) is necessary not only for
${\it\Gamma}_{C}$
to be independent of
$C$
but also for (1.2a,b
) itself to hold. While the validity of (1.5) for a time-averaged separated flow at large angles of attack is questionable, later in § 4.4 we shall show that (1.6) holds in the linear far field no matter whether the Reynolds number is large or not.
Then, in the work of Filon (Reference Filon1926) (independent of Taylor’s work) and later of Imai (Reference Imai1951) based on the far-field Oseen equations, the validity of the testable lift formula (1.2a,b
) was also confirmed when
$C$
recedes to infinity, and (1.2c,d
) takes an apparently kinematic and hence more general form, as an inflow contour integral of the normal component of the transversal velocity
$\boldsymbol{u}_{{\it\psi}}$
:
$$\begin{eqnarray}\displaystyle D={\it\rho}_{0}UQ_{{\it\psi}},\quad Q_{{\it\psi}}=-\oint _{C}\boldsymbol{u}_{{\it\psi}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}l=-\oint _{C}\boldsymbol{{\rm\nabla}}{\it\psi}\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l. & & \displaystyle\end{eqnarray}$$
Like the case of
${\it\Gamma}_{{\it\phi}}$
, owing to the kinematic nature of
${\it\psi}$
being the stream function of the solenoidal velocity constituent
$\boldsymbol{u}_{{\it\psi}}$
,
$Q_{{\it\psi}}$
is also independent of the choice of
$C$
.
Since
$\boldsymbol{u}_{{\it\psi}}$
is not observable, as will be explained in § 2.3, however, Filon’s drag formula (1.7) has seldom been mentioned in the aerodynamics community. In contrast, Wu, Ma & Zhou (Reference Wu, Ma and Zhou2006, p. 630) have proved that if only the leading-order term is retained, then Taylor’s drag formula (1.2c,d
) can be expressed solely in terms of the vorticity
$$\begin{eqnarray}D\simeq -{\it\rho}_{0}U\int _{W}y{\it\omega}\,\text{d}y,\end{eqnarray}$$
which is physically observable. On the other hand, since
${\it\psi}$
or
$\boldsymbol{u}_{{\it\psi}}$
is significant only in the boundary layer and wake, by using the boundary-layer or free shear-layer assumption
$\partial /\partial y\gg \partial /\partial x$
and integrating (1.7) by parts, we can also obtain (1.8). Thus we call (1.8) the testable version of Filon’s formula (1.7).
Naturally, the next relevant extension would be for viscous and compressible flow (N–S flow for short). Towards this goal, and within two dimensions, among others, Heaslet & Lomax (Reference Heaslet, Lomax and Sear1954, p. 145) have shown that the K–J formula (1.1) holds for subsonic and supersonic flows within the linear potential-flow theory. Finn & Gilbarg (Reference Finn and Gilbarg1957, Reference Finn and Gilbarg1958) have proved that (1.1) also holds rigorously for subsonic nonlinear potential flow, but with
$D=0$
. Subsequently Lagerstrom (Reference Lagerstrom1964, pp. 34–38) argued the validity of (1.2a,b
) for viscous compressible flow based on some plausible assumptions. Recently, by taking a Reynolds-averaged Navier–Stokes (RANS) simulation of steady flow over a NACA-0012 airfoil, Mele & Tognaccini (Reference Mele and Tognaccini2014) have found that the values of computed lift at
$M=0.7$
and 1.2 are in agreement with the prediction of (1.2a,b
). However, their data were too sparse to be conclusive. But, as for Filon’s drag formula (1.7), there has been almost no progress at all. In view of this situation, more theoretical and numerical studies in this direction are required.
In this paper we present a profound confirmation of the universal validity of Joukowski’s original lift formula (1.1) and Filon’s drag formula (1.7) for Navier–Stokes (N–S) flow by both theoretical and numerical analyses. We show in § 2 that these formulae remain at least formally effective for two-dimensional steady N–S flow over a wide range of the Mach number, if the contour
$C$
therein is sufficiently large to lie in the far field where the N–S equations can be linearized. These formulae have been further expressed by the jumps of
${\it\phi}$
and
${\it\psi}$
, which are called the Joukowski–Filon formulae. The physical causes and behaviours of these jumps are briefly commented upon, along with a discussion of multiple circulations. A rigorous theoretical proof of (1.1) and (1.7) is given in § 3 using the fundamental solutions of the linearized N–S equations, which enables us to state this innovative result as the Joukowski–Filon theorem. Next, the far-field structures of the compressible flow are studied analytically in § 4, along with estimates of the minimum distance of the linear far field from the body and some discussions on the decay of the vortical circulation. Furthermore, justifications of the testable lift formula (1.2a,b
) and the testable drag formula (1.8) are also given, which together are called the testable Joukowski–Filon formulae.
The neat Joukowski–Filon theorem, however, is not yet a complete aerodynamic theory. The universality of the theorem comes at the expense of lacking rich and valuable physical mechanisms in the near field, so it reveals little on the specific values
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
at different Mach numbers. On the other hand, since the testable Joukowski–Filon formulae are linearly dependent on the vorticity, they should also be valid for statistically stationary flow. Therefore, in § 5 we present our careful RANS simulation, which strongly supports our theory, reveals the Mach-number dependence of
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
, and enhances our understanding of the Joukowski–Filon theorem through relevant physical mechanisms. There is also some discussion about the implications of these theoretical–numerical results. Conclusions are given in § 6. To be self-contained, the fundamental-solution theory of Lagerstrom et al. (Reference Lagerstrom, Cole and Trilling1949) for two-dimensional steady linearized N–S equations is given in appendix A. Appendix B gives some of the detailed algebra used in developing our theory for the longitudinal velocity field.
2. Far-field force formulae and their implications
Let
$\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{u}^{\prime }$
be the total velocity field. At far field, as
$r=\sqrt{x^{2}+y^{2}}\rightarrow \infty$
, the disturbance velocity
$\boldsymbol{u}^{\prime }$
is weak enough to be linearized. This approach was successfully taken by Joukowski (Reference Jowkowski1906), and has been followed by other authors (Bryant et al.
Reference Bryant, Williams and Taylor1926; Filon Reference Filon1926; Imai Reference Imai1951; Finn & Gilbarg Reference Finn and Gilbarg1957). Like (1.3) for velocity, the key physics underlying the far-field expansion can be identified by the decomposition of linearized fluid motion in terms of its fundamental dynamic and thermodynamic processes: the transverse shearing process characterized by vorticity
${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}$
, and the longitudinal process characterized by the dilatation
${\it\vartheta}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}$
, pressure
$p$
and appropriate thermodynamic variables.
Before proceeding, for the purpose of clarity, we first review the general compressible N–S equation and formulae for the total force. The Cauchy motion equation (without an external body force) reads
$$\begin{eqnarray}\frac{\partial }{\partial t}({\it\rho}\boldsymbol{u})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{u}\boldsymbol{u})=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F},\end{eqnarray}$$
where for a Newtonian fluid the stress tensor
$\unicode[STIX]{x1D64F}$
is given by the Cauchy–Poisson constitutive equation, of which a convenient form is the triple decomposition given by Wu et al. (Reference Wu, Ma and Zhou2006, p. 53):
$$\begin{eqnarray}\unicode[STIX]{x1D64F}=-(p-{\it\mu}_{{\it\theta}}{\it\vartheta})\unicode[STIX]{x1D644}+2{\it\mu}{\it\bf\Omega}-2{\it\mu}\unicode[STIX]{x1D63D}.\end{eqnarray}$$
Here,
$$\begin{eqnarray}{\it\bf\Omega}={\textstyle \frac{1}{2}}[\boldsymbol{{\rm\nabla}}\boldsymbol{u}-(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}}]\quad \text{with }{\it\bf\Omega}=-{\it\bf\Omega}^{\text{T}}\end{eqnarray}$$
is the vorticity tensor or spin tensor,
$$\begin{eqnarray}\unicode[STIX]{x1D63D}={\it\vartheta}\unicode[STIX]{x1D644}-(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}}\quad \text{with }\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D63D}=\mathbf{0}\end{eqnarray}$$
is the surface strain-rate tensor (superscript
$\text{T}$
denotes transpose), and
${\it\mu}$
and
${\it\mu}_{{\it\theta}}={\it\zeta}+4{\it\mu}/3$
(with
${\it\zeta}$
being the bulk viscosity) are the shear viscosity and longitudinal viscosity, respectively. If the Stokes hypothesis is used then
${\it\zeta}=0$
. For laminar flow
${\it\mu}$
depends on temperature
$T(\boldsymbol{x},t)$
and for viscous turbulent flow we assume a turbulent viscosity
${\it\mu}_{t}(\boldsymbol{x},t)$
. Thus, for both flows we may set
${\it\mu}={\it\mu}(\boldsymbol{x},t)$
to represent the molecular viscosity or
${\it\mu}_{t}$
, or the sum of both. Then, let
${\it\Pi}=p-{\it\mu}_{{\it\theta}}{\it\vartheta}$
be the normal stress and substitute (2.2) into (2.1), the Navier–Stokes equation reads (Wu et al.
Reference Wu, Ma and Zhou2006, p. 55)
$$\begin{eqnarray}\frac{\partial }{\partial t}({\it\rho}\boldsymbol{u})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{u}\boldsymbol{u})=-\boldsymbol{{\rm\nabla}}{\it\Pi}-\boldsymbol{{\rm\nabla}}\times ({\it\mu}{\bf\omega})-2\boldsymbol{{\rm\nabla}}{\it\mu}\boldsymbol{\cdot }\unicode[STIX]{x1D63D},\end{eqnarray}$$
with the last term being the resistance force of iso-viscosity surfaces to their deformation.
On the other hand, the surface stress can be written as
$$\begin{eqnarray}\boldsymbol{t}\equiv \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}=-{\it\Pi}\boldsymbol{n}+{\bf\tau}+\boldsymbol{t}_{s},\end{eqnarray}$$
where
${\bf\tau}={\it\mu}{\bf\omega}\times \boldsymbol{n}$
is the shear stress and (Wu et al.
Reference Wu, Ma and Zhou2006, pp. 23, 53)
$$\begin{eqnarray}\boldsymbol{t}_{s}=-2{\it\mu}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D63D}=2{\it\mu}(\boldsymbol{n}\times \boldsymbol{{\rm\nabla}})\times \boldsymbol{u}\end{eqnarray}$$
is the viscous resistance of the fluid surface to its motion and deformation. It vanishes at stationary
$\partial B$
due to velocity adherence. Then, for two-dimensional steady N–S flow, the total force exerted on the body
$B$
can be expressed by a control-contour integral:
$$\begin{eqnarray}\displaystyle \boldsymbol{F} & \equiv & \displaystyle -\oint _{\partial B}(-{\it\Pi}\boldsymbol{n}+{\bf\tau})\,\text{d}l\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\frac{\text{D}}{\text{D}t}\int _{S_{f}}{\it\rho}\boldsymbol{u}\,\text{d}S+\oint _{C}(-{\it\Pi}\boldsymbol{n}+{\bf\tau}+\boldsymbol{t}_{s})\,\text{d}l\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\oint _{C}[({\it\Pi}\boldsymbol{n}+{\it\rho}\boldsymbol{u}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n})-({\bf\tau}+\boldsymbol{t}_{s})]\,\text{d}l,\end{eqnarray}$$
$\partial B$
is the boundary of body,
$C$
is an arbitrary control contour enclosing the body, and
$S_{f}$
is the area of fluid enclosed by
$C$
.
2.1. Joukowski–Filon formulae
Hereafter we assume
$C$
lies in a sufficiently far field where the flow can be linearized. In the linearization one always splits a variable into its constant reference value (which in the present problem is the value in uniform incoming flow) and a disturbance, and assumes the latter is small. For example,
$$\begin{eqnarray}\displaystyle & (\boldsymbol{u},{\it\rho},p,{\it\mu},k)=(\boldsymbol{U},{\it\rho}_{0},p_{0},{\it\mu}_{0},k_{0})+(\boldsymbol{u}^{\prime },{\it\rho}^{\prime },p^{\prime },{\it\mu}^{\prime },k^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{|\boldsymbol{u}^{\prime }|}{U_{0}},\frac{|{\it\rho}^{\prime }|}{{\it\rho}_{0}},\frac{|p^{\prime }|}{p_{0}},\frac{{\it\mu}^{\prime }}{{\it\mu}_{0}},\frac{k^{\prime }}{k_{0}}=O({\it\epsilon}),\quad {\it\epsilon}\ll 1, & \displaystyle\end{eqnarray}$$
$({\it\vartheta},|{\bf\omega}|)=O({\it\epsilon})$
. In particular, the transport coefficients, such as shear viscosity
${\it\mu}$
and heat conductivity
$k$
, are approximated by their constant values in the uniform incoming flow, since products such as
${\it\mu}^{\prime }{\bf\omega}$
and
${\it\mu}_{{\it\theta}}^{\prime }{\it\vartheta}$
, etc., are all of
$O({\it\epsilon}^{2})$
and negligible. Of course, for turbulent flow
${\it\mu}_{0}$
should be the reference eddy viscosity
${\it\mu}_{t0}\gg {\it\mu}_{0}$
. Having said this, below we drop the suffix
$0$
of constant transport coefficients.
Now, by (2.9), for steady flow the N–S equation (2.5) is linearized to
$$\begin{eqnarray}{\it\rho}_{0}\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }=-\boldsymbol{{\rm\nabla}}{\it\Pi}-{\it\mu}\boldsymbol{{\rm\nabla}}\times {\bf\omega}.\end{eqnarray}$$
Here, the disturbance velocity field
$\boldsymbol{u}^{\prime }$
can be uniquely split into a longitudinal field and a transversal field (Lagerstrom et al.
Reference Lagerstrom, Cole and Trilling1949, pp. 27–35),
$$\begin{eqnarray}\displaystyle {\it\rho}_{0}\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\phi} & = & \displaystyle -\boldsymbol{{\rm\nabla}}{\it\Pi},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\rho}_{0}\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{{\it\psi}} & = & \displaystyle -{\it\mu}\boldsymbol{{\rm\nabla}}\times {\bf\omega},\end{eqnarray}$$
$$\begin{eqnarray}{\it\rho}_{0}\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\phi}={\it\Pi}_{0}-{\it\Pi}.\end{eqnarray}$$
On the other hand, for constant
${\it\mu}$
we have
$$\begin{eqnarray}\oint _{C}\boldsymbol{t}_{s}\,\text{d}l=2{\it\mu}\oint _{C}(\boldsymbol{n}\times \boldsymbol{{\rm\nabla}})\times \boldsymbol{u}^{\prime }\,\text{d}l=\mathbf{0}\end{eqnarray}$$
and by using the exact continuity equation
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{u})=0$
and omitting higher-order terms we obtain
$$\begin{eqnarray}\displaystyle \oint _{C}{\it\rho}\boldsymbol{u}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}l=\oint _{C}{\it\rho}_{0}(\boldsymbol{{\rm\nabla}}{\it\phi}+\boldsymbol{u}_{{\it\psi}})\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}l. & & \displaystyle\end{eqnarray}$$
Thus, the linearized version of (2.8c ) is
$$\begin{eqnarray}\displaystyle \frac{1}{{\it\rho}_{0}}\boldsymbol{F}=\boldsymbol{U}\times \oint _{C}\boldsymbol{n}\times \boldsymbol{{\rm\nabla}}{\it\phi}\,\text{d}l-\boldsymbol{U}\boldsymbol{\cdot }\oint _{C}\boldsymbol{n}\boldsymbol{u}_{{\it\psi}}\,\text{d}l+{\it\nu}\oint _{C}{\bf\omega}\times \boldsymbol{n}\,\text{d}l, & & \displaystyle\end{eqnarray}$$
where the longitudinal equation (2.12) has been used. It remains to transform the shear stress
${\it\mu}{\bf\omega}\times \boldsymbol{n}$
by the transverse equation (2.11b
), which in two dimensions reads (
${\bf\omega}={\it\omega}\boldsymbol{e}_{z}$
)
$$\begin{eqnarray}\displaystyle \boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{{\it\psi}}=-{\it\nu}\boldsymbol{{\rm\nabla}}{\it\omega}\times \boldsymbol{e}_{z},\quad {\it\nu}={\it\mu}/{\it\rho}_{0}. & & \displaystyle\end{eqnarray}$$
The asymptotic behaviour of
$\boldsymbol{u}_{{\it\psi}}=(\partial {\it\psi}/\partial y,-\partial {\it\psi}/\partial x)$
is known (e.g. Galdi Reference Galdi1994, p. 223):
$$\begin{eqnarray}\displaystyle \left|\frac{\partial {\it\psi}}{\partial y}\right| & = & \displaystyle \left\{\begin{array}{@{}ll@{}}O(r^{-1/2}) & \text{for }\boldsymbol{x}\in \text{the wake},\\ O(r^{-1/2-{\it\epsilon}_{1}}) & \text{for }\boldsymbol{x}\notin \text{the wake},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left|\frac{\partial {\it\psi}}{\partial x}\right| & = & \displaystyle O(r^{-1/2-{\it\epsilon}_{2}}),\end{eqnarray}$$
${\it\epsilon}_{1},{\it\epsilon}_{2}>0$
as
$r\rightarrow \infty$
. Now, since 
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{U}\times \boldsymbol{u}_{{\it\psi}})=\boldsymbol{U}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}_{{\it\psi}}-\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{{\it\psi}}=-\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{{\it\psi}},\end{eqnarray}$$
(2.16) can be recast to
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{U}\times \boldsymbol{u}_{{\it\psi}})=\boldsymbol{{\rm\nabla}}\times ({\it\nu}{\bf\omega}),\end{eqnarray}$$
so that
$$\begin{eqnarray}\displaystyle \boldsymbol{U}\times \boldsymbol{u}_{{\it\psi}}={\it\nu}{\bf\omega}+\boldsymbol{{\rm\nabla}}{\it\eta} & & \displaystyle\end{eqnarray}$$
for some scalar function
${\it\eta}$
. But in two dimensions
$\boldsymbol{{\rm\nabla}}{\it\eta}\equiv \mathbf{0}$
, since the other terms in (2.20) are in the
$\boldsymbol{e}_{z}$
-direction. Thus, we obtain
$$\begin{eqnarray}\displaystyle {\it\nu}{\bf\omega}\times \boldsymbol{n}=(\boldsymbol{U}\times \boldsymbol{u}_{{\it\psi}})\times \boldsymbol{n}=\boldsymbol{u}_{{\it\psi}}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{U}-\boldsymbol{U}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{u}_{{\it\psi}}. & & \displaystyle\end{eqnarray}$$
Now, substituting (2.21) into (2.15) yields immediately
$$\begin{eqnarray}\displaystyle \boldsymbol{F}={\it\rho}_{0}\boldsymbol{U}\times \boldsymbol{e}_{z}{\it\Gamma}_{{\it\phi}}+{\it\rho}_{0}\boldsymbol{U}Q_{{\it\psi}}, & & \displaystyle\end{eqnarray}$$
where the circulation
${\it\Gamma}_{{\it\phi}}$
due to the longitudinal field and the inflow
$Q_{{\it\psi}}$
due to the transverse field are defined in (1.1) and (1.7), respectively. Thus, like viscous incompressible flow, lift and drag are also determined by the two scalars
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
given by (1.1) and (1.7). Note that the transversal circulation
${\it\Gamma}_{{\it\psi}}$
gives no contribution to the lift; thus it is (1.1) rather than (1.2a,b
) that is the exact counterpart of the incompressible version of lift in the far-field analysis. On the one hand, while for incompressible flow
$Q_{{\it\psi}}$
just describes the linearized version of the total-pressure loss, for compressible flow it may contain multiple mechanisms. On the other hand, from the derivation of (2.22), it seems that (2.22) is valid only when the integral contour
$C$
lies in the linear far field. However, as was argued in § 1 for incompressible flow, since
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
are independent of the shape and size of
$C$
, and
${\it\phi}$
and
${\it\psi}$
are regular everywhere except at the origin, once (2.22) has been proved for the linearized far field, it must also be true for a near-field or arbitrary integral contour
$C$
enclosing the body.
We now cast (2.22) to a neater and more symmetric form. Since our space is two-dimensional and the flow domain is doubly connected, as potentials rather than directly observable physical quantities,
${\it\phi}$
and
${\it\psi}$
can be multi-valued, having jumps
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
defined by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}f(x,y)\unicode[STIX]{x27E7}=\oint _{C}\,\text{d}f=f(x<0,+0)-f(x<0,-0)+f(x>0,-0)-f(x>0,+0),\qquad & & \displaystyle\end{eqnarray}$$
where for simplicity we have let the discontinuity be along the
$x$
-axis, although it may be shifted to anywhere without affecting the value of the jump. Therefore, the component form of (2.22) reads
$$\begin{eqnarray}\displaystyle & \displaystyle L=-{\it\rho}_{0}U{\it\Gamma}_{{\it\phi}}=-{\it\rho}_{0}U\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D={\it\rho}_{0}UQ_{{\it\psi}}=-{\it\rho}_{0}U\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
is well known,
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
seems to be new and follows from the integral of
$\boldsymbol{t}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\psi}$
along the segment of
$C$
that cuts the vortical-flow region, i.e. the wake. Equation (2.24b
) and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
are of no less importance than (2.24a
) and
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
, and we call them the Joukowski–Filon formulae (J–F formulae for short).
A rigorous theoretical proof of (2.22) or (2.24) will be given in § 3 by using the fundamental solutions of the linearized N–S equations for viscous compressible flows. However, for viscous flow the form of the set of equations (2.24) looks somewhat peculiar and requires a thorough interpretation of its mathematical and physical implications. We do this in the rest of this section.
2.2. Physical cause and behaviour of jumps
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
Write
$$\begin{eqnarray}\displaystyle {\it\phi}={\it\phi}_{m}+{\it\phi}_{s},\quad {\it\psi}={\it\psi}_{m}+{\it\psi}_{s}, & & \displaystyle\end{eqnarray}$$
where subscripts
$m$
and
$s$
denote multi-valued and single-valued, respectively. Then in a free space
$S_{\infty }$
and in polar coordinates
$(r,{\it\theta})$
, the solution of the Laplace equation
${\rm\nabla}^{2}f=0$
which is finite as
$r\rightarrow \infty$
has the familiar far-field Taylor expansion (e.g. Batchelor Reference Batchelor1967, § 2.10)
$$\begin{eqnarray}\displaystyle f(\boldsymbol{x})=\frac{{\it\kappa}}{2{\rm\pi}}{\it\theta}+c_{i}\frac{\partial }{\partial x_{i}}(\log r)+c_{ij}\frac{\partial ^{2}}{\partial x_{i}\partial x_{j}}(\log r)+\cdots \,. & & \displaystyle\end{eqnarray}$$
Here, we have dropped an arbitrary constant and assumed no point source of mass;
${\it\kappa}=\unicode[STIX]{x27E6}f\unicode[STIX]{x27E7}$
is the cyclic constant in a doubly connected flow domain, so that
$f-({\it\kappa}/2{\rm\pi}){\it\theta}$
is single-valued and of
$O(r^{-1})$
as
$r\rightarrow \infty$
. Now, by (1.3),
${\it\phi}$
and
${\it\psi}$
are solutions of the Poisson equations
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}{\it\phi}={\it\vartheta},\quad {\rm\nabla}^{2}{\it\psi}=-{\it\omega}, & & \displaystyle\end{eqnarray}$$
respectively, under proper boundary conditions. However, solving (2.27) for multi-valued
${\it\phi}$
and
${\it\psi}$
is as yet a non-trivial issue and beyond the concern of this paper. Our interest here is the physical cause of the same kind of jumps,
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
.
Actually, these jumps may or may not appear in a doubly connected flow domain, depending on whether the body-induced physical disturbance field is only partly or completely inside the domain. To see this, consider first the motion of a lift-producing body in
$S_{\infty }$
with the fluid otherwise at rest. Assume the body starts motion at
$t=0$
in
$S_{\infty }$
and then becomes a constant translation with velocity
$-\boldsymbol{U}$
. Evidently, at any finite
$t>0$
with
$t\leqslant T<\infty$
,
$S_{\infty }$
always contains the whole disturbance field created by the body, including both the body-carried disturbance at the current time
$t$
and the starting disturbance formed right after
$t=0$
that keeps moving to far downstream, as well as any possible connection between the two. This flow in
$S_{\infty }$
is inherently unsteady. It has been proved by Liu et al. (Reference Liu, Wu, Shi and Zhu2014a
) that, in both two and three dimensions and at any
$t<\infty$
, there are two positive parameters
$a,b>0$
such that
${\bf\omega}$
and
${\it\vartheta}$
decay as
$O(\text{e}^{-ar^{2}})$
and
$O(\text{e}^{-br})$
as
$|\boldsymbol{x}|\rightarrow \infty$
, respectively. Thus they can be considered physically compact or confined in a finite domain
$S$
(ignoring their exponentially decaying tails; cf. Saffman (Reference Saffman1992, p. 1)). The total vorticity (or total circulation in two dimensions) in
$S_{\infty }$
is identically zero, and hence no jump of
${\it\phi}$
and
${\it\psi}$
can occur. In this case, Liu et al. (Reference Liu, Wu, Shi and Zhu2014a
) have proved that
${\it\phi}$
must be single-valued and uniquely determined by the piecewise continuous
$({\it\omega},{\it\vartheta})$
-field via (2.27). The reasoning applies equally to
${\it\psi}$
. Indeed, if
$C$
encloses the entire vorticity field then evidently
$Q_{{\it\psi}}=0.$
In contrast, the domain where the flow is considered steady (viewed in body-fixed frame of reference), denoted by
$S_{st}$
, is obviously a subspace of
$S_{\infty }$
, which inevitably cuts off the starting disturbance once that has moved to sufficiently far downstream as
$t\rightarrow T$
for any
$T<\infty$
, such that its influence on the flow in
$S_{st}$
is negligible. But the total-circulation conservation theorem no longer holds in
$S_{st}$
. Conceptually, one may conceive that the topology of vortical flow in the complement subspace
$S_{\infty }-S_{st}$
is continued to the second branch of a double-branched
$S_{st}$
, which in the single-branched physical space leaves jumps of
${\it\phi}$
and
${\it\psi}$
as its only signature:
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
measure the total amount and spreading of the vorticity outside
$S_{st}$
, respectively. While the former does not depend on any specific
${\it\omega}$
-distribution that may even shrink to a point vortex, the latter does. These two jumps provide mutually complementary information. In fact, they may also occur if the flow in
$S_{st}$
becomes unsteady, as long as part of the vortical wake is cut off. Note that since the steady flow in
$S_{st}$
is nothing other than a part of the uniquely determined flow field in
$S_{\infty }$
, the uniqueness of
$({\it\phi}_{s},{\it\psi}_{s})$
in
$S_{st}$
is also ensured.
Having made the above observations, the behaviour of
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}={\it\Gamma}_{{\it\phi}}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}=-Q_{{\it\psi}}$
are also clear. They are both independent of
$C$
because
$\boldsymbol{u}_{{\it\phi}}$
is curl-free and
$\boldsymbol{u}_{{\it\psi}}$
is divergence-free, as was argued in § 1 for incompressible flow. This is consistent with the fact that, in contrast to
$({\it\phi}_{s},{\it\psi}_{s})$
, as a contour-integral effect the jumps
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
remain invariant with respect to
$r$
, as indicated by (2.26). Therefore,
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
can be determined well by linear far-field theory. Once this is done, (2.24) will hold exactly, independent of the size and shape of
$C$
.
2.3. Multiple circulations and their observability
Ever since Taylor’s lift formula (1.2a,b
), for viscous flow several different circulations
${\it\Gamma}_{C}$
,
${\it\Gamma}_{{\it\phi}}$
and
${\it\Gamma}_{{\it\psi}}$
have appeared, as seen from (1.4). Some of them are physically observable, and some are not. A quantity is said to be physically observable if it can be directly tested either experimentally or computationally. For any contour
$C$
enclosing area
$S$
, since
$$\begin{eqnarray}{\it\Gamma}_{C}=\oint _{C}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l=\int _{S}{\it\omega}\,\text{d}S=\oint _{C}\boldsymbol{u}_{{\it\psi}}\boldsymbol{\cdot }\boldsymbol{t}\,\text{d}l={\it\Gamma}_{{\it\psi}},\end{eqnarray}$$
both
${\it\Gamma}_{C}$
and
${\it\Gamma}_{{\it\psi}}$
are observable. But in a general viscous flow
${\it\Gamma}_{{\it\phi}}$
is not, unless either
$S$
is entirely inside the flow domain
$S_{f}$
and away from the body
$B$
so that
${\it\Gamma}_{{\it\phi}}=\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}=0$
, which is also the case if we introduce a cut to connect
${\it\Sigma}$
and
$\partial B$
so that
$S_{f}$
becomes singly connected, or
${\it\Gamma}_{{\it\psi}}=0$
in a certain asymptotic sense. On the other hand, as the ‘circulation’ of an auxiliary vortical velocity
$\boldsymbol{u}_{{\it\psi}}^{\bot }\equiv \boldsymbol{e}_{z}\times \boldsymbol{u}_{{\it\psi}}=\boldsymbol{{\rm\nabla}}{\it\psi}$
,
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}=-Q_{{\it\psi}}$
is generally not observable, unless either, as said above,
$C$
encloses the entire vortical-flow region including starting vortex, so that
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}=0$
, or
$Q_{{\it\psi}}$
approaches a fixed value in an asymptotical sense.
An immediate consequence of the above observation is that the great generality and exactness of the J–F formulae (2.24) comes at the expense of being not physically testable, and therefore they are not directly useful in applied aerodynamics. Therefore, after proving (2.24) in § 3, we still have to proceed to find when
${\it\Gamma}_{{\it\phi}}$
can be replaced by
${\it\Gamma}_{C}$
and
$Q_{{\it\psi}}$
replaced by proper integrals of an observable vortical variable. This will be done in § 4, also by using the fundamental solutions of the far-field linearized N–S equations. The results are then testable numerically, as will be given in § 5. More importantly, they further reveal the quantitative behaviours of far-field flow in different Mach-number regimes. But it will be seen that the expense of using observable quantities only to express lift and drag is that the testable formulae hold only when
$C$
is located at a sufficiently far field.
It should be stressed that physically non-testable quantities are still meaningful and of great value because they can be thoroughly theoretically analysed. In fact, our far-field theory to be presented in §§ 3 and 4 is heavily based on a study of the behaviours of
${\it\phi}$
and
${\it\psi}$
, which directly leads to the discovery of testable lift and drag formulae.
3. Joukowski–Filon theorem
In § 2.1, the Joukowski–Filon formulae (2.24) are derived under the assumption that a regular linearized far field does exist for viscous compressible flow. But whether such a field indeed exists still needs a proof. Lagerstrom (Reference Lagerstrom1964, p. 36) has pointed out that the linearization is feasible for viscous flow over a finite body, as we are concerned with here, but not necessarily so if either of these restrictions is removed. This assertion is not yet a rigorously proved theorem. In this section we provide a constructive proof by finding analytically the non-trivial and regular solution of
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
in the linear far field from subsonic to supersonic flows. This finding enables us to state (2.24) as a theorem. In § 4 we shall further find analytically the detailed behaviour of different components of far-field velocity, and thereby identify the key flow structures that lead to these jumps.
3.1. Fundamental solutions of linearized steady N–S equations
The conventional strategy for seeking out far-field flow solutions is to carry out separation of variables or to take the Fourier transform of velocity in the circumferential direction, and thereby obtain a series of approximate velocities, of which the first two coefficients are related to the drag and lift. This has been done by Filon (Reference Filon1926), Imai (Reference Imai1951), and Chadwick (Reference Chadwick1998), among others, for viscous incompressible flow. However, this approach involves very lengthy algebra and cannot fully determine all the coefficients, although the governing equation is already linearized (Oseen equation for incompressible flow). As a result, extending the same strategy to compressible flow would involve much more tedious algebra. Additional difficulty may occur since the governing equation for the longitudinal field (dilatation, pressure, entropy, etc.) in viscous compressible flow is a third-order parabolic equation, whose general solution is not yet known. To avoid these disadvantages, therefore, in this section we adopt a different strategy. As will be shown below, in addition to supporting and sharpening the results in § 2, the present section has its own theoretical merit as a short-cut alternative strategy to conventional far-field theories based on series expansion.
For an observer in the very far field, a body moving through a fluid appears as a singular point, and its action on the fluid appears as an impulse force. In this case the far-field disturbance flow is sufficiently weak and may well be governed by linearized N–S equations. Note that to calculate the impulse force there is no need to solve these equations under specified boundary conditions. Rather, it suffices to directly use the fundamental solution of the linearized steady N–S equations in free space. This is the basic idea in the study of linear differential equations, which will be called fundamental-solution theory and has been demonstrated by Lagerstrom (Reference Lagerstrom1964, pp. 75–81) for incompressible flow. The same strategy has been used by Liu et al. (Reference Liu, Wu, Shi and Zhu2014a
) in deriving the aforementioned asymptotic behaviour of the unsteady
$({\bf\omega},{\it\vartheta})$
-field in
$S_{\infty }$
.
Fortunately, the desired fundamental solutions have already been given by Lagerstrom et al. (Reference Lagerstrom, Cole and Trilling1949) for a different purpose (to obtain approximate solutions of flat-plate boundary layers and friction drag thereon), without considering heat conduction. The extension of these fundamental solutions to include heat conduction is straightforward if the viscosities and heat conductivity are assumed small (Mao, Shi & Wu Reference Mao, Shi and Wu2010; Mao Reference Mao2011). Specifically, let
${\it\nu}_{{\it\theta}}={\it\mu}_{{\it\theta}}/{\it\rho}_{0}$
be the longitudinal kinematic viscosity,
${\it\gamma}=c_{p}/c_{v}$
be the ratio of specific heats, and
${\it\alpha}$
be the heat diffusion coefficient, then it suffices to replace
${\it\nu}_{{\it\theta}}$
by
${\it\nu}_{{\it\theta}}+({\it\gamma}-1){\it\alpha}$
, which is called as the ‘diffusivity of sound’ (Lighthill Reference Lighthill, Batchelor and Davies1956, p. 263). It was also shown by Mao and coworkers that, if there is no strong heat addition, the entropy variation caused by the flow is a higher-order term in the far field, and hence we may omit it in the following development.
With these facts in mind, the linearized N–S equation (2.10) can be further simplified with the assumption
$p=p({\it\rho})$
. Introduce (primed) disturbance quantities by
$$\begin{eqnarray}\boldsymbol{u}=U\boldsymbol{e}_{x}+\boldsymbol{u}^{\prime },\quad {\it\rho}={\it\rho}_{0}(1+{\it\rho}^{\prime }),\end{eqnarray}$$
so that the steady momentum and continuity equations are
$$\begin{eqnarray}\displaystyle & U\partial _{x}\boldsymbol{u}^{\prime }-{\it\nu}_{{\it\theta}}\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }+{\it\nu}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}^{\prime })+c^{2}\boldsymbol{{\rm\nabla}}{\it\rho}^{\prime }=\boldsymbol{f}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }+U\partial _{x}{\it\rho}^{\prime }=0, & \displaystyle\end{eqnarray}$$
$c$
is the speed of sound and
$\boldsymbol{f}$
represents an external body force, which in our case is the force exerted on the fluid by the body. In the near-field formulation
$\boldsymbol{f}$
could have a compact distribution in
$(\boldsymbol{x},t)$
-space as used by Saffman (Reference Saffman1992, p. 51), but below it will be idealized as a
${\it\delta}$
-function of
$\boldsymbol{x}$
, i.e. 
$$\begin{eqnarray}\boldsymbol{f}=-\!\left(\begin{array}{@{}c@{}}D\\ L\\ \end{array}\right)\frac{{\it\delta}(\boldsymbol{x})}{{\it\rho}_{0}},\end{eqnarray}$$
where
$D$
and
$L$
are the drag and lift exerted on the body, and the full-space integral of
${\it\delta}(\boldsymbol{x})$
is unity:
$$\begin{eqnarray}\int {\it\delta}(\boldsymbol{x})\,\text{d}\boldsymbol{x}=1.\end{eqnarray}$$
Denote by
$\boldsymbol{G}$
the fundamental solution of (3.2) for
$\boldsymbol{u}^{\prime }$
, of which the derivation and expression are given in appendix A. Then the far field
$\boldsymbol{u}^{\prime }$
can be written as
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x})=\int \boldsymbol{G}(\boldsymbol{x},{\bf\xi})\boldsymbol{\cdot }\boldsymbol{f}({\bf\xi})\,\text{d}{\bf\xi}. & & \displaystyle\end{eqnarray}$$
Note that
$\boldsymbol{G}$
can also be split into longitudinal and transversal parts,
$$\begin{eqnarray}\boldsymbol{G}(\boldsymbol{x},{\bf\xi})=\boldsymbol{G}_{{\it\phi}}(\boldsymbol{x},{\bf\xi})+\boldsymbol{G}_{{\it\psi}}(\boldsymbol{x},{\bf\xi}),\end{eqnarray}$$
so the longitudinal and transversal velocities defined by (1.3) now read
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{{\it\phi}} & = & \displaystyle \boldsymbol{{\rm\nabla}}{\it\phi}(\boldsymbol{x})=\int \boldsymbol{G}_{{\it\phi}}(\boldsymbol{x},{\bf\xi})\boldsymbol{\cdot }\boldsymbol{f}({\bf\xi})\,\text{d}{\bf\xi},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{{\it\psi}} & = & \displaystyle \boldsymbol{{\rm\nabla}}\times {\bf\psi}=\int \boldsymbol{G}_{{\it\psi}}(\boldsymbol{x},{\bf\xi})\boldsymbol{\cdot }\boldsymbol{f}({\bf\xi})\,\text{d}{\bf\xi}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{G}_{{\it\phi}}(\boldsymbol{x},0) & = & \displaystyle \frac{1}{2{\rm\pi}U}\int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{\text{i}l}\left(\begin{array}{@{}cc@{}}-l^{2} & \text{i}l\partial _{y}\\ \text{i}l\partial _{y} & \partial _{y}^{2}\end{array}\right)\frac{\exp \left(-|y|\sqrt{l^{2}-\displaystyle \frac{U^{2}l^{2}}{c^{2}+\text{i}{\it\nu}_{{\it\theta}}Ul}}\right)}{2\sqrt{l^{2}-\displaystyle \frac{U^{2}l^{2}}{c^{2}+\text{i}{\it\nu}_{{\it\theta}}Ul}}}\,\text{d}l,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{G}_{{\it\psi}}(\boldsymbol{x},0) & = & \displaystyle -\frac{1}{2{\rm\pi}U}\int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{\text{i}l}\left(\begin{array}{@{}cc@{}}-\partial _{y}^{2} & \text{i}l\partial _{y}\\ \text{i}l\partial _{y} & l^{2}\end{array}\right)\frac{\exp \left(-|y|\sqrt{l^{2}+\displaystyle \frac{\text{i}Ul}{{\it\nu}}}\right)}{2\sqrt{l^{2}+\displaystyle \frac{\text{i}Ul}{{\it\nu}}}}\,\text{d}l.\end{eqnarray}$$
It should be stressed that these two formulae indicate that although the governing equations of the longitudinal and transversal processes can be completely decoupled, their solutions cannot, except for very special cases, since generically a body force can cause both longitudinal and transversal disturbances (cf. Saffman Reference Saffman1992, p. 52). This is indeed true in our case, where
$\boldsymbol{f}$
represents the force exerted by a solid body that includes all possible couplings of different processes on the body surface and in the nonlinear flow regions. Even if the entire disturbance flow field is sufficiently weak and can be linearized, the boundary coupling between
${\bf\omega}$
and
${\it\Pi}$
still exists for viscous flow and is responsible for the key mechanism of boundary vorticity creation, which was first revealed by Lighthill (Reference Lighthill and Rosenhead1963) and is well known today (e.g. Wu et al.
Reference Wu, Ma and Zhou2006, pp. 138–144).
Compared to dealing with the disturbance velocity
$\boldsymbol{u}^{\prime }$
directly, we find it sometimes more convenient to deal with the velocity potential
${\it\phi}$
and the vortical stream function
${\it\psi}$
. By substituting (3.3) and (3.8) into (3.7) and integrating the results with all the integral constants dropped for simplicity, we can obtain
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}=\frac{L{\it\phi}_{l}+D{\it\phi}_{d}}{2{\rm\pi}{\it\rho}_{0}U}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\psi}=\frac{L{\it\psi}_{l}+D{\it\psi}_{d}}{2{\rm\pi}{\it\rho}_{0}U}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{l}=\text{sgn}\,y\int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{2\text{i}l}\text{e}^{-|y|\sqrt{(1-M^{2})l^{2}+\text{i}(({\it\nu}_{{\it\theta}}M^{4})/U)l^{3}}}\,\text{d}l, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{d}=-\int _{-\infty }^{\infty }\text{e}^{\text{i}lx}\frac{\text{e}^{-|y|\sqrt{(1-M^{2})l^{2}+\text{i}(({\it\nu}_{{\it\theta}}M^{4})/U)l^{3}}}}{2\sqrt{(1-M^{2})l^{2}+\text{i}\displaystyle \frac{{\it\nu}_{{\it\theta}}M^{4}}{U}l^{3}}}\,\text{d}l & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\psi}_{l}=\int _{-\infty }^{\infty }\text{e}^{\text{i}lx}\frac{\text{e}^{-|y|\sqrt{l^{2}+2\text{i}kl}}}{2\sqrt{l^{2}+2\text{i}kl}}\,\text{d}l,\quad k=\frac{U}{2{\it\nu}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\psi}_{d}=\text{sgn}\,y\int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{2\text{i}l}\text{e}^{-|y|\sqrt{l^{2}+2\text{i}kl}}\,\text{d}l, & \displaystyle\end{eqnarray}$$
$l$
and
$d$
denoting the possible contributions of lift and drag to
${\it\phi}$
and
${\it\psi}$
, respectively.
Remarks.
Obviously, the transverse part of the solution described by
${\it\psi}_{l}$
and
${\it\psi}_{d}$
is independent of the Mach number and has the same behaviour for incompressible flow. But the longitudinal part described by
${\it\phi}_{l}$
and
${\it\phi}_{d}$
depends explicitly on the Mach number, as seen from their common key factor
$$\begin{eqnarray}\displaystyle (1-M^{2})l^{2}+\text{i}\frac{{\it\nu}_{{\it\theta}}M^{4}}{U}l^{3} & & \displaystyle\end{eqnarray}$$
in the Fourier space. As shown in appendix B, this factor takes different leading-order forms for subsonic, transonic, and supersonic flows, leading to different structures of the linear far field. In general, the velocity potential
${\it\phi}_{l}$
and
${\it\phi}_{d}$
cannot be integrated exactly, but can be expressed only by contour integrals, say (B 3), which can be directly proved to be finite everywhere except at the singular origin. This fact indicates that the linearized far field indeed exists for compressible flow, which is true even for inviscid subsonic flow, but only for viscous transonic and supersonic flows.
3.2. Joukowski–Filon theorem
With the above preparations, we can state the following innovative theorem, named after the discoverers of (1.1) and (1.7), which is solely due to the double-connection of flow domain and flow steadiness:
The Joukowski–Filon theorem.
For a two-dimensional steady viscous flow of compressible fluid over a rigid body, the lift and drag exerted on the body can be solely determined by the jumps of the velocity potential and vortical stream function given by (2.24a ) and (2.24b ), respectively.
Proof. First, since jumps can be located anywhere by choosing appropriate integral constants in
${\it\phi}$
and
${\it\psi}$
, for simplicity we have dropped all these constants, implying that the jumps must lie on the
$x$
-axis as defined by (2.23). But setting
$y=0$
removes any explicit role of the viscosities and Mach number from (3.11) and (3.12), making
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
formally independent of
$Re$
and
$M$
. This simplifies our analysis significantly.
Second, by comparing the structures of the velocity potential
${\it\phi}_{l}$
and
${\it\phi}_{d}$
generated by lift and drag, respectively, it is easy to confirm that only
${\it\phi}_{l}$
may have a possible discontinuity. Thus we can ignore
${\it\phi}_{d}$
, and by setting
$y=\pm 0$
in (3.11a
) we obtain
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}(x,\pm 0)=\pm \int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{2\text{i}l}\,\text{d}l=\pm \frac{{\rm\pi}}{2}\text{sgn}\,x, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \text{sgn}\,x=\left\{\begin{array}{@{}ll@{}}+1 & \text{if }x>0,\\ -1 & \text{if }x<0.\end{array}\right. & & \displaystyle\end{eqnarray}$$
Since this is the only possible jump of
${\it\phi}_{l}$
and
${\it\phi}_{d}$
, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}{\it\phi}_{l}\unicode[STIX]{x27E7}=-2{\rm\pi},\quad \unicode[STIX]{x27E6}{\it\phi}_{d}\unicode[STIX]{x27E7}=0. & & \displaystyle\end{eqnarray}$$
Similarly, by setting
$y=\pm 0$
in (3.12b
) we have
$$\begin{eqnarray}\displaystyle {\it\psi}_{d}(x,\pm 0)=\pm \int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{2\text{i}l}\,\text{d}l=\pm \frac{{\rm\pi}}{2}\text{sgn}\,x, & & \displaystyle\end{eqnarray}$$
which is also the only possible jump in
${\it\psi}_{l}$
and
${\it\psi}_{d}$
:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}{\it\psi}_{l}\unicode[STIX]{x27E7}=0,\quad \unicode[STIX]{x27E6}{\it\psi}_{d}\unicode[STIX]{x27E7}=-2{\rm\pi}. & & \displaystyle\end{eqnarray}$$
Therefore, by substituting (3.16) into (3.9) and (3.18) into (3.10), (2.24) follows at once.
Third, as argued in § 2.2, both
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
are independent of
$r$
as well as the size and shape of the contour
$C$
. Finally, the observation made at the beginning of this section has ensured the existence of the linearized far field from subsonic flow all the way to supersonic flow. Thus the proof is completed.
Remarks.
-
(1) It is well known that the classic linearized Oseen equation is a uniformly effective far-field asymptotic approximation at any Reynolds number. Similarly, the derivation of (2.24) in § 2.1 and the fundamental solutions of
${\it\phi}$
and
${\it\psi}$
in § 3.1 impose no limitation on the magnitude of viscosities or Reynolds number. Therefore, the Joukowski–Filon formulae (2.24) are also uniformly effective at any Reynolds number. -
(2) Although
${\it\phi}$
,
${\it\psi}$
,
$\boldsymbol{u}_{{\it\phi}}$
and
$\boldsymbol{u}_{{\it\psi}}$
are non-observable, once well established, the Joukowski–Filon theorem immediately converts the jumps
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
to observable quantities in a generalized sense: they are just equivalent to the lift and drag (divided by
${\it\rho}_{0}U$
) obtained by any experiments or computations!
In the above proof we did not appeal to any specific behaviour of
${\it\phi}$
and
${\it\psi}$
. This approach makes the proof concise and general, but leaves the relevant physical mechanisms of lift and drag obscure. Thus, to explore the underlying physics we still have to directly analyse the disturbance velocity. We do this in the next section.
4. Far-field flow structures and testable Joukowski–Filon formulae
In this section, the Joukowski–Filon theorem will be proved again by directly considering the disturbance velocity, in particular for the lift formula of the supersonic flow. A preliminary discussion of near-sonic flow, the estimates for the distance of the linear far field from the body, and the far-field decay of vortical circulation will also be given. Finally, testable forms of the J–F formulae will be given, which, of course, are physically testable and practically applicable but valid only in the linear far field.
4.1. Vortical stream function and transverse velocity
The vortical stream function generated by the lift
${\it\psi}_{l}$
is independent of Mach number and considered first. Equation (3.12a
) can be integrated exactly by shifting the integral contour to
$\text{Im}\,l=-k$
, i.e.
$$\begin{eqnarray}\displaystyle {\it\psi}_{l} & = & \displaystyle \int _{-\infty }^{\infty }\text{e}^{\text{i}lx}\frac{\text{e}^{-|y|\sqrt{l^{2}+2\text{i}kl}}}{2\sqrt{l^{2}+2\text{i}kl}}\,\text{d}l=\text{e}^{kx}\int _{\text{i}k-\infty }^{\text{i}k+\infty }\text{e}^{\text{i}nx}\frac{\text{e}^{-|y|\sqrt{n^{2}+k^{2}}}}{2\sqrt{n^{2}+k^{2}}}\,\text{d}n\nonumber\\ \displaystyle & = & \displaystyle \text{e}^{kx}\int _{-\infty }^{\infty }\text{e}^{\text{i}nx}\frac{\text{e}^{-|y|\sqrt{n^{2}+k^{2}}}}{2\sqrt{n^{2}+k^{2}}}\,\text{d}n=\text{e}^{kx}\text{K}_{0}(kr),\end{eqnarray}$$
where
$r=\sqrt{x^{2}+y^{2}}$
and
$\text{K}_{0}$
is the modified Bessel function of the second kind of order zero, which has the following useful properties
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}z}\text{K}_{0}(z)=-\text{K}_{1}(z),\quad \text{K}_{0}(z)\sim \sqrt{\frac{{\rm\pi}}{2z}}\text{e}^{-z}\left(1-\frac{1}{8z}+\cdots \!\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}z}(z\text{K}_{1})=-z\text{K}_{0},\quad \text{K}_{1}(z)\sim \sqrt{\frac{{\rm\pi}}{2z}}\text{e}^{-z}\left(1+\frac{3}{8z}+\cdots \!\right). & & \displaystyle\end{eqnarray}$$
In general the integral in (3.12b
) cannot be integrated explicitly except for special cases, say low-Reynolds-number flow with
$k\ll 1$
. In this case (3.12b
) approximates to
$$\begin{eqnarray}\displaystyle {\it\psi}_{d}\approx \text{sgn}\,y\int _{-\infty }^{\infty }\frac{\text{e}^{\text{i}lx}}{2\text{i}l}\text{e}^{-|yl|}\,\text{d}l=\text{sgn}\,y\arctan \left(\frac{x}{|y|}\right), & & \displaystyle\end{eqnarray}$$
of which the jump is
$-2{\rm\pi}$
, being consistent with (3.18). But for high-Reynolds-number flow, which is our main concern, such a simple function is no longer available. Instead, we consider its derivatives and the results are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\psi}_{d}}{\partial x}=-\frac{\partial {\it\psi}_{l}}{\partial y}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\psi}_{d}}{\partial y}=\frac{\partial {\it\psi}_{l}}{\partial x}-2k{\it\psi}_{l}, & \displaystyle\end{eqnarray}$$
${\it\psi}_{l}$
and
${\it\psi}_{d}$
, see (3.12).
Collecting the above results, for any impulse-force-induced flow the transversal velocity
$\boldsymbol{u}_{{\it\psi}}=(\partial {\it\psi}/\partial y,-\partial {\it\psi}/\partial x)$
is
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\psi}}{\partial y}=-\frac{kD\text{e}^{kx}}{2{\rm\pi}{\it\rho}_{0}U}\left[\text{K}_{0}(kr)+\frac{x}{r}\text{K}_{1}(kr)\right]-\frac{kL\text{e}^{kx}}{2{\rm\pi}{\it\rho}_{0}U}\frac{y}{r}\text{K}_{1}(kr), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\partial {\it\psi}}{\partial x}=-\frac{kD\text{e}^{kx}}{2{\rm\pi}{\it\rho}_{0}U}\frac{y}{r}\text{K}_{1}(kr)-\frac{kL\text{e}^{kx}}{2{\rm\pi}{\it\rho}_{0}U}\left[\text{K}_{0}(kr)-\frac{x}{r}\text{K}_{1}(kr)\right] & \displaystyle\end{eqnarray}$$
${\it\omega}$
is 
$$\begin{eqnarray}{\it\omega}=-2k\frac{\partial {\it\psi}}{\partial x}=-\frac{k^{2}D\text{e}^{kx}}{{\rm\pi}{\it\rho}_{0}U}\frac{y}{r}\text{K}_{1}(kr)-\frac{k^{2}L\text{e}^{kx}}{{\rm\pi}{\it\rho}_{0}U}\left[\text{K}_{0}(kr)-\frac{x}{r}\text{K}_{1}(kr)\right].\end{eqnarray}$$
Note that (4.5) and (4.6) are valid at any Mach number provided that the linearized far field has been reached.
Recalling the definition of inflow
$Q_{{\it\psi}}$
and the divergence-free condition
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}_{{\it\psi}}=0$
, the result of
$Q_{{\it\psi}}$
obtained from the contour integral along an arbitrary loop
$C$
is equivalent to that along a circular contour, i.e.
$$\begin{eqnarray}Q_{{\it\psi}}\equiv -\oint _{C}\boldsymbol{u}_{{\it\psi}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}l=-\int _{0}^{2{\rm\pi}}\boldsymbol{u}_{{\it\psi}}\boldsymbol{\cdot }\boldsymbol{n}r\text{d}{\it\theta}.\end{eqnarray}$$
Substituting (4.5) into (4.39) and denoting
$z=kr$
yields
$$\begin{eqnarray}\displaystyle Q_{{\it\psi}} & = & \displaystyle \frac{zD}{2{\rm\pi}{\it\rho}_{0}U}\left[\text{K}_{0}(z)\int _{0}^{2{\rm\pi}}\text{e}^{z\cos {\it\theta}}\cos {\it\theta}\,\text{d}{\it\theta}+\text{K}_{1}(z)\int _{0}^{2{\rm\pi}}\text{e}^{z\cos {\it\theta}}\,\text{d}{\it\theta}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{zL}{2{\rm\pi}{\it\rho}_{0}U}\text{K}_{0}(z)\int _{0}^{2{\rm\pi}}\text{e}^{z\cos {\it\theta}}\sin {\it\theta}\,\text{d}{\it\theta},\end{eqnarray}$$
where the second line vanishes identically. The integrals of the first line are exactly the definition of the modified Bessel function of the first kind,
$$\begin{eqnarray}\displaystyle \text{I}_{0}(z) & = & \displaystyle \frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\text{e}^{z\cos {\it\theta}}\,\text{d}{\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{I}_{1}(z) & = & \displaystyle \frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\text{e}^{z\cos {\it\theta}}\cos {\it\theta}\,\text{d}{\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}[\text{I}_{1}(z)\text{K}_{0}(z)+\text{I}_{0}(z)\text{K}_{1}(z)]=\frac{1}{z}.\end{eqnarray}$$
By substituting this identity into (4.8), the J–F drag formula (2.24b ) follows immediately.
4.2. Velocity potential and longitudinal velocity
To obtain as much information as possible from these integrals, we make a case-by-case analysis for different Mach-number regimes. For clarity, only the main results are listed here, with detailed algebra given in appendix B.
4.2.1. Subsonic flow
For the subsonic flow, the velocity potential
${\it\phi}_{l}$
and
${\it\phi}_{d}$
are given by (B 8), i.e.
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}=\text{sgn}\,y\arctan \left(\frac{x}{{\it\beta}|y|}\right),\quad {\it\beta}=\sqrt{1-M^{2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\phi}_{d}=\frac{1}{2{\it\beta}}\ln (x^{2}+{\it\beta}^{2}y^{2}). & & \displaystyle\end{eqnarray}$$
Furthermore, by setting
$y=\pm 0$
in (4.11) we obtain
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}(x,\pm 0)=\pm \frac{{\rm\pi}}{2}\text{sgn}\,x, & & \displaystyle\end{eqnarray}$$
which, of course, is identical to (3.14) and confirms our previous proof. Note that the above results are exactly the theory of inviscid subsonic flow (Finn & Gilbarg Reference Finn and Gilbarg1957), of which the circulation and the origin of the lift are well known.
4.2.2. Supersonic flow
For the supersonic flow, the velocity potential
${\it\phi}_{l}$
and
${\it\phi}_{d}$
are given by (B 11) and (B 17), i.e.
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{l}=\frac{{\rm\pi}}{2}\text{sgn}\,y\,\text{erf}\left(\frac{x-B|y|}{2\sqrt{{\it\Lambda}B|y|}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{d}=-\frac{{\rm\pi}}{2B}\text{erf}\left(\frac{x-B|y|}{2\sqrt{{\it\Lambda}B|y|}}\right), & \displaystyle\end{eqnarray}$$
$\text{erf}(\cdot )$
is defined by (B 12) and 
$$\begin{eqnarray}B^{2}=M^{2}-1>0,\quad {\it\Lambda}\equiv \frac{{\it\nu}_{{\it\theta}}M^{4}}{2B^{2}U}\ll 1.\end{eqnarray}$$
Similarly, by setting
$y=\pm 0$
we obtain
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}(x,\pm 0)=\pm \frac{{\rm\pi}}{2}\text{sgn}\,x, & & \displaystyle\end{eqnarray}$$
which, of course, is identical to (3.14) and confirms our previous proof. However, since the J–F lift formula is new in supersonic flow, we prove this formula again by directly considering the disturbance velocity.
With the help of (3.9) and (4.13), the longitudinal velocity components can be approximated by (retaining only the leading term)
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}}{\partial x} & {\approx} & \displaystyle \frac{\text{sgn}\,y}{4{\rm\pi}{\it\rho}_{0}UB}(BL-\text{sgn}\,yD)\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{(x-B|y|)^{2}}{4{\it\Lambda}B|y|}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}}{\partial y} & {\approx} & \displaystyle -\frac{1}{4{\rm\pi}{\it\rho}_{0}U}(BL-\text{sgn}\,yD)\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{(x-B|y|)^{2}}{4{\it\Lambda}B|y|}\right].\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial {\it\phi}}{\partial y}=-\text{sgn}\,yB\frac{\partial {\it\phi}}{\partial x}.\end{eqnarray}$$
As pointed out by Lagerstrom et al. (Reference Lagerstrom, Cole and Trilling1949, p. 96), just like inviscid Mach waves, the resultant disturbance of the longitudinal wave is normal to the Mach line. For supersonic flow the far field can be regarded as asymptotically inviscid with
${\it\Lambda}\rightarrow 0$
. As seen from (4.16a
) and (4.16b
),
$(\partial {\it\phi}/\partial x,\partial {\it\phi}/\partial y)\rightarrow 0$
, except for the narrow region where
$x-B|y|\cong 0$
. As a result, the circulation is contributed only by the velocity across the Mach line. Furthermore, since the disturbance velocity along the Mach line
$x-B|y|=0$
is zero, we need only to consider the contribution of the normal velocity across the Mach line. This is indeed true, as can be seen more clearly below.
Denote the Mach angle temporarily by
${\it\theta}$
, such that
$$\begin{eqnarray}\sin {\it\theta}=\text{sgn}\,y\frac{1}{M}.\end{eqnarray}$$
Then the normal velocity across the Mach line is
$$\begin{eqnarray}\displaystyle u_{n}^{\pm } & = & \displaystyle -\frac{\partial {\it\phi}}{\partial x}\sin {\it\theta}+\frac{\partial {\it\phi}}{\partial y}\cos {\it\theta}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{M(D\,\text{sgn}\,y-BL)}{4{\rm\pi}{\it\rho}_{0}BU}\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{(x-B|y|)^{2}}{4{\it\Lambda}B|y|}\right],\end{eqnarray}$$
$+$
and
$-$
denote the upper and lower Mach lines, respectively, and the normal distance away from the Mach line is 
$$\begin{eqnarray}n^{\pm }=-x\sin {\it\theta}+y\cos {\it\theta}=-\text{sgn}\,y\frac{x-B|y|}{M}.\end{eqnarray}$$
Define the circulation across the upper and lower Mach lines as
$$\begin{eqnarray}{\it\Gamma}_{{\it\phi}}^{\pm }\equiv \int _{-{\it\delta}}^{{\it\delta}}u_{n}\,\text{d}n^{\pm },\end{eqnarray}$$
where
${\it\delta}$
is the half-width of the Mach-line region, which of course is very small and for our purpose can be regarded as a small fixed number. Substituting (4.20) and (4.21) into (4.22) yields
$$\begin{eqnarray}{\it\Gamma}_{{\it\phi}}^{\pm }=-\frac{ML}{4{\rm\pi}{\it\rho}_{0}U}\int _{-{\it\delta}}^{{\it\delta}}\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{M^{2}n^{2}}{4{\it\Lambda}B|y|}\right]\,\text{d}n,\end{eqnarray}$$
where the total contribution of
$D$
is identically zero due to its symmetric property, see (4.20).
Finally, we replace variable
$n$
by
${\it\xi}=Mn/2\sqrt{{\it\Lambda}B|y|}$
, so for fixed
$n={\it\delta}$
we obtain
$$\begin{eqnarray}{\it\xi}=\frac{M{\it\delta}}{2\sqrt{{\it\Lambda}B|y|}}\rightarrow \infty \quad \text{as }{\it\Lambda}\rightarrow 0.\end{eqnarray}$$
Thus (4.23) can be written as
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\phi}}^{\pm }=-\frac{L}{2\sqrt{{\rm\pi}}{\it\rho}_{0}U}\int _{-\infty }^{\infty }\text{e}^{-{\it\xi}^{2}}\,\text{d}{\it\xi}=-\frac{L}{2{\it\rho}_{0}U}. & & \displaystyle\end{eqnarray}$$
Therefore, since
${\it\Gamma}_{{\it\phi}}={\it\Gamma}_{{\it\phi}}^{+}+{\it\Gamma}_{{\it\phi}}^{-}$
, the J–F lift formula (2.24a
) for supersonic flow follows. Note that in this case
${\it\Lambda}$
has no explicit effect.
4.2.3. Near-sonic flow
For near-sonic flow only some particular integrals have been obtained, of which the most important results are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}(x,0)=\left(\frac{{\rm\pi}U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{1/2}\frac{\text{sgn}\,x-1}{2\sqrt{|x|}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}(0,y)=-\left(\frac{U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{2/3}\frac{\sqrt{3}\text{G}(\frac{4}{3})}{|y|^{1/3}}, & \displaystyle\end{eqnarray}$$
$\text{G}(\cdot )$
is the Gamma function defined by (B 21). The result of (4.26a
) is consistent with that of the leading term obtained by inviscid and nonlinear transonic far-field theory (e.g. Cole & Cook Reference Cole and Cook1986, p. 207). This also confirms our early assertion that the linearized near-sonic far field does exist, but only for viscous flow.
By comparing the results of (B 22) and (4.26b
) we note that
$\boldsymbol{{\rm\nabla}}{\it\phi}_{d}$
rather than
$\boldsymbol{{\rm\nabla}}{\it\phi}_{l}$
dominates
$\boldsymbol{u}_{{\it\phi}}$
in the near-sonic far field, while for the subsonic and supersonic far fields both are dominant. Of utmost importance is that
$\boldsymbol{{\rm\nabla}}{\it\phi}_{d}$
decays extremely slow as
$O(r^{-1/3})$
, which makes the linearized far field for sonic flow almost beyond reach numerically in the
$y$
-direction, in particular in the drag calculation.
4.3. Distance of the linear far field from the body
We now use the preceding solutions of the linear equations to predict how large the minimum distance
$r_{m}$
from the body should be for them to become exact, which can then be tested by a numerical study. In this way, the existence of the linear far field can be checked more concretely. The estimate is based on a simple requirement that the order of magnitude of the relevant disturbance velocity constituents, after being non-dimensionalized, is not larger than unity. As a familiar example, for small-
$Re$
incompressible Stokes flow with drag coefficient
$C_{d}\sim Re^{-1}$
(e.g. Lagerstrom Reference Lagerstrom1964, p. 83), we have
$r_{m}=O(Re^{-1})$
; then the far field with
$r>\text{const.}/Re$
, one should turn to the Oseen equation. It is then straightforward to find the following estimates, where the Reynolds numbers as well as the coefficients of lift and drag,
$C_{l}$
and
$C_{d}$
, are defined in the conventional way:
-
(i) Transversal far field: by (4.5), we have
(4.27a )
$$\begin{eqnarray}\displaystyle & \displaystyle r_{m}=O\left(\frac{C_{d}^{2}Re}{16{\rm\pi}}\right)\quad \text{independent of }M. & \displaystyle\end{eqnarray}$$
-
(ii) Longitudinal far field, subsonic: by (4.11) we have
(4.27b )
$$\begin{eqnarray}\displaystyle & \displaystyle r_{m}=O\left(\frac{C_{l}}{4{\rm\pi}{\it\beta}}\right). & \displaystyle\end{eqnarray}$$
-
(iii) Longitudinal far field, supersonic: by (4.16) we have
(4.27c )where
$$\begin{eqnarray}\displaystyle & \displaystyle r_{m}=\left\{\begin{array}{@{}ll@{}}\displaystyle O\left(\frac{C_{d}^{2}Re_{{\it\theta}}}{24{\rm\pi}BM^{4}}\right) & \text{if }B<1,\\ \displaystyle O\left(\frac{B^{3}C_{l}^{2}Re_{{\it\theta}}}{24{\rm\pi}M^{4}}\right) & \text{if }B\geqslant 1,\end{array}\right. & \displaystyle\end{eqnarray}$$
$Re_{{\it\theta}}$
is the Reynolds number based on the longitudinal viscosity
${\it\nu}_{{\it\theta}}$
.
-
(iv) Longitudinal far field, near sonic: by (4.26), we have
(4.27d )
$$\begin{eqnarray}\displaystyle & \displaystyle r_{m}=O\left(\frac{C_{d}^{3}Re_{{\it\theta}}^{2}}{16{\rm\pi}^{3}}\right). & \displaystyle\end{eqnarray}$$
Clearly, different dominant dynamic processes and flow structures at different Mach-number regimes result in vastly different linear far-field locations, with a variety of dependences on
$C_{l}$
or
$C_{d}$
,
$Re$
or
$Re_{{\it\theta}}$
, and
$M$
. Of these distances the linear
$\boldsymbol{u}_{{\it\phi}}$
-field for near-sonic flow is the farthest from the body. It should be stressed that, because
$\boldsymbol{u}_{{\it\phi}}$
and
$\boldsymbol{u}_{{\it\psi}}$
coexist in the same momentum equation and have to be balanced, one should determine the location of the linear far field by the larger
$r_{m}$
of
$\boldsymbol{u}_{{\it\phi}}$
and
$\boldsymbol{u}_{{\it\psi}}$
, and similarly that of the
$x$
- and
$y$
-components of each constituent.
Since the viscous linear far field does exist for compressible flow (including subsonic, transonic, and supersonic flow), it will be seen in § 5 that all these estimates are numerically confirmed.
4.4. Far-field decay of vortical circulation
For compressible viscous flow, if
$W$
intersects shock waves that can also generate vorticity as boundary layers do, then the second Taylor criterion can no longer be satisfied. Thus, to make (1.2a,b
) valid in the general case, we should let
$C$
include all vorticity sources, and
$W$
, the downstream face of
$C$
, lie in the linearized far field. We call this requirement the generalized Taylor second criterion. With this and the first Taylor criteria satisfied, we find that
${\it\Gamma}_{{\it\psi}}$
always decreases to zero exponentially as the wake line position
$x=X_{W}\rightarrow \infty$
.
In particular, since
$\boldsymbol{u}_{{\it\psi}}$
is significant only at the wake line with
$\boldsymbol{n}=\boldsymbol{e}_{x}$
, and vanishes exponentially elsewhere, and
${\it\omega}=-2k\partial {\it\psi}/\partial x$
in the linearized region, from the second expression of (1.4) we have, for arbitrary
$X_{W}$
,
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\psi}}=-\int _{W}\frac{\partial {\it\psi}}{\partial x}\,\text{d}y=\frac{1}{2k}\int _{W}{\it\omega}\,\text{d}y. & & \displaystyle\end{eqnarray}$$
Now, there are two ways to prove
$\int {\it\omega}\,\text{d}y=0$
. The first one is based on near-wake analysis and presented by Liu et al. (Reference Liu, Wu, Zhu, Zou and Liu2015). The second one uses the fundamental solution to calculate (4.28) directly, which provides more information. By substituting (4.6) into (4.28) and using (4.5), we obtain
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\psi}}=-\frac{k\text{e}^{kx}L}{{\rm\pi}{\it\rho}_{0}U}\int _{0}^{\infty }\left[\text{K}_{0}(kr)-\frac{x}{r}\text{K}_{1}(kr)\right]\,\text{d}y, & & \displaystyle\end{eqnarray}$$
where the term involving drag
$D$
is identically zero, due to it being anti-symmetric about the
$x$
-axis, and for simplicity we have taken the infinite wake plane. Denoting
$\tilde{x}=kx,{\tilde{y}}=ky$
and
$\tilde{r}=kr$
, and then integrating by parts, (4.29) can be further reduced to
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\psi}}=-\frac{\tilde{x}\text{e}^{\tilde{x}}L}{{\rm\pi}{\it\rho}_{0}U}\left[\tilde{x}\int _{1}^{\infty }\sqrt{z^{2}-1}\text{K}_{1}(\tilde{x}z)\,\text{d}z-\int _{1}^{\infty }\frac{\text{K}_{1}(\tilde{x}z)}{\sqrt{z^{2}-1}}\,\text{d}z\right]. & & \displaystyle\end{eqnarray}$$
Define
$$\begin{eqnarray}J(\tilde{x},n)\equiv \int _{1}^{\infty }(z^{2}-1)^{n-1}\text{K}_{1}(\tilde{x}z)\,\text{d}z,\end{eqnarray}$$
of which the integral is well known and the result is
$$\begin{eqnarray}J(\tilde{x},n)=\text{G}(n)2^{n-1}\tilde{x}^{-n}\text{K}_{1-n}(\tilde{x}).\end{eqnarray}$$
This reduces (4.30) to
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\psi}}=-\frac{2^{1/2}\tilde{x}^{1/2}\text{e}^{\tilde{x}}L}{{\rm\pi}{\it\rho}_{0}U}\left[\text{G}\left(\frac{3}{2}\right)\text{K}_{-1/2}(\tilde{x})-\frac{1}{2}\text{G}\left(\frac{1}{2}\right)\text{K}_{1/2}(\tilde{x})\right]. & & \displaystyle\end{eqnarray}$$
Since
$$\begin{eqnarray}\displaystyle \text{K}_{-n}(z)=\text{K}_{n}(z),\quad \text{G}(x+1)=x\text{G}(x), & & \displaystyle\end{eqnarray}$$
then we have
$$\begin{eqnarray}\displaystyle {\it\Gamma}_{{\it\psi}}=0,\quad \text{or equivalently},\quad \int _{W}{\it\omega}\,\text{d}y=0, & & \displaystyle\end{eqnarray}$$
the same as (1.6) but derived without using the boundary-layer approximation.
Following these discussions, therefore, the generically non-observable
${\it\Gamma}_{{\it\phi}}$
becomes observable when it is used to measure the total vorticity in
$S_{st}$
:
$$\begin{eqnarray}\displaystyle \lim _{X_{W}\rightarrow \infty }{\it\Gamma}_{C}={\it\Gamma}_{{\it\phi}}=\int _{S_{st}}{\it\omega}\,\text{d}S, & & \displaystyle\end{eqnarray}$$
which is independent of the precise location of
$W$
, as ensured by the generalized Taylor criteria.
4.5. Testable Joukowski–Filon formulae
Although the remarks following the Joukowski–Filon theorem indicated that
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
have become observable quantities, this is evidently still not satisfied if the integrands of
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
are not observable. We thus need to find the circumstances in which these integrands can be replaced by physically observable variables. Now the preceding analyses of the flow behaviour have revealed that the required circumstance is the linear far field, of which the existence has been confirmed by the estimates made in § 4.3. Therefore, we are now ready to derive a pair of testable Joukowski–Filon formulae, which are stated first:
The testable Joukowski–Filon formulae.
For a two-dimensional steady viscous flow of compressible fluid over a rigid body, the lift and drag exerted on the body are given by
$$\begin{eqnarray}\displaystyle L=-{\it\rho}_{0}U{\it\Gamma}_{C},\quad {\it\Gamma}_{C}=\int _{S}{\it\omega}\,\text{d}S, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D={\it\rho}_{0}UQ_{W},\quad Q_{W}=-\int _{W}y{\it\omega}\,\text{d}y, & & \displaystyle\end{eqnarray}$$
respectively, where
$W$
is the downstream face of the outer boundary of
$S$
, which is perpendicular to the incoming flow and lies in the linear far field.
In the following, we call (4.37) the testable J–F formulae (TJ–F formulae for short). Obviously, (4.37) is the same as (1.2a,b ), and (4.37c,d ) is also exactly the same as the far-field profile drag formula (1.8) for incompressible flow, indicating the compressibility effect such as entropy gradient does not enter the far-field drag formula. Note, however, no small-viscosity assumption was made in deriving (4.37), and hence, like (2.24), they are valid in a wide Reynolds-number range as well.
To derive (4.37) we note that, first, from (2.24a ) and (1.4) the lift formula can be written as
$$\begin{eqnarray}L=-{\it\rho}_{0}U{\it\Gamma}_{C}+{\it\rho}_{0}U{\it\Gamma}_{{\it\psi}},\end{eqnarray}$$
where the last term can be regarded as a correction term. Of course, this correction term is strongly dependent on the choice of the contour
$C$
, which vanishes if the generalized Taylor criteria are satisfied, as proved in § 4.4.
Second, substituting (4.6) into the second equation of (4.37c,d ) yields
$$\begin{eqnarray}\displaystyle Q_{W}=\frac{2\tilde{x}^{2}\text{e}^{\tilde{x}}D}{{\rm\pi}{\it\rho}_{0}U}\int _{1}^{\infty }\sqrt{z^{2}-1}\text{K}_{1}(\tilde{x}z)\,\text{d}z=\frac{2D}{{\rm\pi}{\it\rho}_{0}U}\tilde{x}^{2}\text{e}^{\tilde{x}}J\left(\tilde{x},\frac{3}{2}\right), & & \displaystyle\end{eqnarray}$$
which by (4.32) becomes
$$\begin{eqnarray}\displaystyle Q_{W}=\frac{D}{{\rm\pi}{\it\rho}_{0}U}2^{1/2}\text{G}\left(\frac{1}{2}\right)\tilde{x}^{1/2}\text{e}^{\tilde{x}}\text{K}_{1/2}(\tilde{x}). & & \displaystyle\end{eqnarray}$$
Then since
$$\begin{eqnarray}\displaystyle \text{K}_{1/2}(z)=\sqrt{\frac{{\rm\pi}}{2z}}\text{e}^{-z},\quad \text{G}\left(\frac{1}{2}\right)=\sqrt{{\rm\pi}}, & & \displaystyle\end{eqnarray}$$
(4.37c,d ) follows immediately, which is independent of the Mach number and is valid provided that the generalized Taylor criteria are satisfied.
It has been mentioned in § 2.3 that the expense of replacing the non-testable formulae by testable formulae is that one can no longer enjoy the arbitrariness of the contour
$C$
. The error introduced by this replacement vanishes as
$C$
recedes to infinity. Here, a closer observation of the validity range of (4.37a,b
) and (4.37c,d
) is desired.
Physically, the validity of (4.37a,b
) relies simply on the smallness of
${\it\Gamma}_{{\it\psi}}$
, which by (4.28) is proportional to the vorticity integral along the wake plane. On the other hand, the validity of (4.37c,d
) requires that in the far field the source of drag comes solely from the wake, including all vorticity generated by boundary layers and shock waves. Only if this generalized Taylor second criterion is satisfied, can the drag be precisely expressed by the
$y$
-moment of the vorticity integral along
$W$
. Consequently, although in principle to ensure the validity of both (4.37a,b
) and (4.37c,d
) the linear far field of the whole flow should be reached, their realizations may sometimes be considerably different and easier. Indeed, in calculating
${\it\Gamma}_{C}$
the vorticities at the upper and lower half-planes both usually have extremely small magnitudes compared to those in the boundary layer or wake shear layer, where
${\it\omega}$
has different signs that can cancel each other in the integral along
$W$
, so that (4.37a,b
) can be valid even when the linear far field for the whole flow has not yet been reached. In contrast, however, in calculating
$Q_{W}$
this sign difference of vorticity becomes enhancement of the integrand due to taking the
$y$
-moment, and hence to ensure its validity the linear far field of the whole flow has to be reached. This contrast between calculations of lift and drag is especially strong for near-sonic flow, as seen from (4.27d
) and § 5.3, where at high Reynolds number the linear far field can hardly be reached numerically, making (4.37c,d
) ineffective. Furthermore, the above difference between the TJ–F lift formula and the drag formula makes the former measurable in an experiment such as that made by Bryant et al. (Reference Bryant, Williams and Taylor1926), but the latter difficult since its validity requires the integral contour to lie totally in the linear far field where the magnitude of the vorticity is small.
In fact, (4.37c,d
) is not the only possible testable drag formula. Suppose that
$|\boldsymbol{{\rm\nabla}}{\it\phi}_{d}|\ll |\boldsymbol{u}_{{\it\psi}}|$
in the wake, which is valid for subsonic and supersonic flows, as indicated by (4.5), (4.11) and (4.16), one may replace
$\boldsymbol{u}_{{\it\psi}}$
by
$\boldsymbol{u}^{\prime }$
in (2.24b
) and replace
$C$
by a far wake line
$W$
, confined only on the wake domain. Our numerical tests (figure not shown) indicate that this replacement indeed works well for subsonic and supersonic flows, but behaves worse than (4.37c,d
) for high-transonic flow since
$\boldsymbol{{\rm\nabla}}{\it\phi}_{d}$
decays extremely slow, as predicted by (4.26). On the other hand, the concept of wake boundary is very fuzzy, which makes the results of this possible testable drag formula to a certain extent artificial. Thus we prefer to use (4.37c,d
) as our testable drag formula.
5. Numerical study and physical discussions
As argued at the end of § 1, the Joukowski–Filon theorem alone is not yet a complete aerodynamic theory. The strength of the theorem can be fully exploited only if its profound physical implications are revealed and enriched by near-field information. Therefore, a careful numerical study has been conducted, of which the aims are:
-
(i) to test the validity of the theory of §§ 2–4, especially the TJ–F formulae (4.37) as well as the predicted location of the linearized far field in a wide Mach-number range;
-
(ii) to provide quantitative information for
${\it\Gamma}_{C}$
and
$Q_{W}$
themselves; and -
(iii) to gain a thorough physical understanding of our major findings.
These tasks are reported in this section.
5.1. Numerical method and validation
Since the TJ–F formulae are solely and linearly dependent on the vorticity, they should also be valid for statistically stationary flow, which is the only possible way for the high-Reynolds-number flow with shocks and separation to be (time-averaged) steady. Thus we performed a RANS simulation of an RAE-2822 airfoil in steady viscous and compressible flow. But, in the RANS simulation a variable eddy viscosity is inevitably involved, which at the boundary of the computational domain may not be constant (nor accurately captured due to the coarse grid there), which is different from the conditions used in deriving the TJ–F formulae. Nevertheless, in these formulae the eddy viscosity does not appear explicitly, and our results show that a variable eddy viscosity has a negligibly small effect in testing the theoretical prediction.
In this section, quantities are made dimensionless by the airfoil chord length as well as the velocity
$U$
, density
${\it\rho}_{0}$
, and sound speed
$c$
of the uniform incoming flow. The Reynolds number, angles of attack, and incoming-flow Mach numbers are chosen as
$Re=6.5\times 10^{6},{\it\alpha}=2.31^{\circ }$
and
$5^{\circ }$
, and
$M\in [0.1,2.0]$
, with an interval 0.1, except for
$M\in [0.7,1.1]$
, where it is 0.05. The mesh number we adopted is
$1601\times 512$
in the circumferential and normal directions, respectively. The height of the first cell to the wall and the minimum streamwise spacing at the leading and trailing edges are
$5\times 10^{-6}$
and
$2\times 10^{-4}$
, respectively. The computational-domain size is as large as
$400$
in order to reach the linear far field. The initial condition is set as the free-stream quantities. The far-field boundary conditions are treated by local one-dimensional Riemann invariants, which were designed by Thomas & Salas (Reference Thomas and Salas1986) to study transonic flow over a body and extensively examined. It is found to be reliable for transonic flows over lifting airfoils and wings (e.g. Hafez & Wahba Reference Hafez and Wahba2007). No-slip and adiabatic conditions are applied on the airfoil surface.
The OpenCFD-EC2D-1.5.4 program developed by Professor X. L. Li of the Chinese Academy of Sciences is employed to solve the compressible Navier–Stokes equations. In this open-source software, these equations are solved by a finite-volume method, with the convective terms discretized by a third-order WENO (weighted essentially non-oscillatory) scheme for shock capture and the viscous terms by a second-order central difference. For temporal terms a first-order LU-SGS (lower–upper symmetric-Gauss–Seidel) method is used with a dimensionless time step
${\rm\Delta}t=10^{-4}$
. We assume constant
${\it\mu}$
and set
${\it\mu}_{{\it\theta}}=4{\it\mu}/3$
. The SA turbulence model is used for this RANS simulation.
Figure 1 compares the computed pressure coefficient,
$C_{p}=p/(({\it\rho}_{0}U^{2})/2)$
, over the airfoil with experimental data (Cook, McDonald & Firmin Reference Cook, McDonald and Firmin1979) at the same flow conditions. The agreement is good, indicating a validation of our scheme.
Figure 1. The pressure coefficient distribution of an RAE-2822 airfoil at
$Re=6.5\times 10^{6}$
,
$M=0.729$
,
${\it\alpha}=2.31^{\circ }$
. Solid line shows the numerical results and ● shows the experimental data from Cook et al. (Reference Cook, McDonald and Firmin1979).
It was found that, except for too large an integral contour
$C$
where the mesh is too sparse, or too small an integral contour where strong shock waves intersect it, the lift and drag coefficients computed from the general force formula (2.8c
) are in excellent agreement with that from the wall-stress integral (2.8a
) throughout the entire computed Mach-number range, with maximum relative error less than 1 % and 4 %, for the lift and drag coefficients, respectively (figure not shown). On the other hand, the independence of the result on mesh and time-step sizes has been checked for
$M=0.8$
(see table 1, where
$C_{l}$
and
$C_{d}$
are also calculated by (2.8c
) with a typical contour
$C$
). In all cases, the errors of lift and drag are very small.
Figure 2. Mach-number dependence of lift coefficients of an RAE-2822 airfoil at
$Re=6.5\times 10^{6}$
. Solid line shows results from the wall-stress integral. Results given by the TJ–F lift formula (4.37a,b
) with
${\it\Gamma}_{C}$
calculated along the contour with wake line position
$X_{W}$
. Dashed–dotted line,
$X_{W}=1$
; dashed–dotted–dotted line,
$X_{W}=2$
; short-dashed line,
$X_{W}=5$
. (a)
${\it\alpha}=2.31^{\circ }$
; (b)
${\it\alpha}=5.0^{\circ }$
.
Table 1. Validation of mesh size and time-step size at
$M=0.8$
. The lift and drag coefficients are computed by (2.8c
).
In the following, the mesh and time step sizes of case 1 and the TJ–F formulae (4.37) are adopted.
5.2. The Mach-number dependence of lift
Figure 2 shows a comparison of the Mach-number dependence of the lift coefficients, computed by the standard wall-stress integral (denoted by ‘stress integral’) and the TJ–F lift formula (4.37a,b
) (denoted by ‘K–J’), for different wake positions at two angles of attack. In both cases the lift coefficients are almost independent of the wake position
$X_{W}$
before they reach their maximum values, at which point some differences between the predictions of the wall-stress integral and (4.37a,b
) start to occur, finally decreasing as
$X_{W}$
increases. Below we make several physical observations.
First, the observed independence or dependence on
$X_{W}$
can be easily understood based on the concept of multiple circulations. In the subsonic regime, Taylor’s second criterion stated in § 1 ensures
${\it\Gamma}_{{\it\psi}}=0$
or
${\it\Gamma}_{C}={\it\Gamma}_{{\it\phi}}$
, so
$C_{l}$
is independent of
$X_{W}$
, as confirmed by figure 2. However, in transonic and supersonic flow, a shock wave may cause boundary-layer separation, with shear layers shedding into the wake in a non-symmetric manner on the upper and lower surfaces. Such shear layers may also arise due to shock–shock interactions. Thus Taylor’s second criterion is violated and the choice of
$X_{W}$
can strongly affect
${\it\Gamma}_{C}$
, as shown in figure 2. Without being aware of multiple circulation, this dependence on
$X_{W}$
might mislead one into thinking that (1.2a,b
) or (4.37a,b
) no longer hold once shocks appear; but we now see that the ‘error’ is actually caused by
${\it\Gamma}_{{\it\psi}}$
, for which the effect coexists with shocks, and it is this that makes
${\it\Gamma}_{C}$
dependent on
$X_{W}$
. Nevertheless, as long as the generalized second Taylor criterion is satisfied, (4.37a,b
) still holds in the linear far field, as Filon (Reference Filon1926) has proved for incompressible flow.
Second, the location of the linear far field (§ 4.3) estimated by (4.27) can now be checked. Since flow turbulence has almost died out at the far field (except in the wake), to make the estimate we can use the Reynolds number
$Re=O(10^{6})$
based on molecular viscosity; and, for subsonic and low-transonic flow we have
$C_{d}=O(10^{-3})$
(see figure 5 below). Thus by (4.27a
) we just need
$X_{W}=O(1)$
, which is confirmed by figure 2. However, for high-transonic and supersonic flow we have
$C_{d}=O(10^{-2})$
, so by (4.27a
) we have
$X_{W}=O(10^{2})$
, indicating that the linear far field is much farther away compared to that of subsonic flow. This is the origin of an appreciable error in using (4.37a,b
) with
$X_{W}=O(1)$
in supersonic flow. The effect of
${\it\Gamma}_{{\it\psi}}$
indeed disappears when we chose
$X_{W}=O(10^{2})$
. Having seen this, we consider the above agreement strong support for the validity of the basic lift formula (4.37a,b
). It is also confirmation of the existence of the linear far field of
$\boldsymbol{u}_{{\it\psi}}$
in the whole computed Mach-number range.
On the other hand, for near-sonic flow where
$C_{d}=O(10^{-1})$
, the prediction of (4.27d
) is
$r_{m}=O(10^{8})$
, which is far away from the reach of any finite-domain computation. Thus, the still perfectness of (4.37a,b
) for near-sonic flow is particularly impressive. As explained at the penultimate paragraph of § 4.5, the validity of (4.37a,b
) even before reaching the linear far field is due to cancellation of extremely weak vorticities with opposite signs behind the shock waves from the upper and lower half-planes (see figure 3).
Figure 3. Vorticity contour of an RAE-2822 airfoil at
$Re=6.5\times 10^{6},{\it\alpha}=2.31^{\circ }$
with shown range
${\it\omega}\in [-5.0,5.0]$
. Solid line indicates
${\it\omega}>0$
and dashed line indicates
${\it\omega}<0$
, with interval 0.53. (a)
$M=0.75$
,
${\it\omega}\times 10^{-4}\in (-4.9,1.2)$
; (b)
$M=0.85$
,
${\it\omega}\times 10^{-4}\in (-3.0,1.3)$
.
Third, a qualitative interpretation of the
$M$
-dependence of lift can be made. Consider the case at
${\it\alpha}=2.31^{\circ }$
as an example. As seen from figure 2(a), in the low-
$M$
range
${\it\Gamma}_{C}$
increases monotonically with
$M$
until a shock wave appears on the upper surface at a critical Mach number (see figures 3(a) and 4(a) for the vorticity and Mach contours at
$M=0.75$
, respectively). This confirms our preceding theoretical result that for subsonic flow the lift-generating mechanism is just a natural extension of that for incompressible flow, without a qualitative physical change. In contrast, once we enter the transonic regime, the shock cuts off
${\it\Gamma}_{C}$
suddenly to a much lower level, evidently due to the aforementioned strong shock-induced vorticity shedding into the wake. This dropping of
${\it\Gamma}_{C}$
then stops at
$M\approx 0.85$
due to the formation of a lower-surface shock which has at least the same strength as that of the upper surface (see figures 3(b) and 4(b) for the vorticity and Mach contours at
$M=0.85$
, respectively), which causes strong shedding of vorticity of the opposite sign and hence turns the
${\it\Gamma}_{C}$
–
$M$
curve into a new smooth supersonic stage.
Figure 4. Mach-number contour of an RAE-2822 airfoil at
$Re=6.5\times 10^{6},{\it\alpha}=2.31^{\circ }$
. Solid line indicates
$M\geqslant 1$
and dashed line indicates
$M<1$
, with interval 0.05. (a)
$M=0.75$
; (b)
$M=0.85$
.
5.3. The Mach-number dependence of drag
Unlike the lift, for which we have
${\it\Gamma}_{C}={\it\Gamma}_{{\it\phi}}$
for subsonic flow, since Filon’s drag formula (1.7) or (2.24b
) is solely expressed in terms of non-observable
$\boldsymbol{u}_{{\it\psi}}$
or
${\it\psi}$
, it has seldom been cited and never been tested in the aerodynamics community. In contrast, quite a few testable approximate far-field drag formulae, which are mathematically rigorous, have been designed and are in use. Equation (4.37c,d
) is new for viscous compressible flow and will be tested here for the first time.
Figure 5 shows the comparison of the Mach-number dependence of the drag coefficients, computed by the wall-stress integral and the TJ–F drag formula (4.37c,d
) (denoted by ‘Filon’). The agreement is again excellent in the subsonic and supersonic regimes, as well as most of the transonic regime (
$0.7<M<1.3$
for
${\it\alpha}=2.31^{\circ }$
). Note that the figure only displays the results for three large values of
$X_{W}$
; however, at most calculated Mach numbers
$X_{W}$
can be much nearer to the trailing edge such that it still gives the desired agreement, as long as it satisfies with the minimum
$r_{m}$
predicted in § 4.3 (test plots not shown).
Figure 5. Mach-number dependence of drag coefficients of an RAE-2822 airfoil at
$Re=6.5\times 10^{6}$
. Solid line shows results from the wall-stress integral. Results given by the TJ–F drag formula (4.37c,d
) with
$Q_{W}$
calculated along the wake line whose position is
$X_{W}$
. Dashed–dotted line,
$X_{W}=50$
; dashed–dotted–dotted line,
$X_{W}=100$
; short-dashed line,
$X_{W}=400$
. (a)
${\it\alpha}=2.31^{\circ }$
; (b)
${\it\alpha}=5.0^{\circ }$
.
An obvious disagreement between the stress integral and the prediction of (4.37c,d
) occurs at
$M\in (1.0,1.1)$
, which can hardly be improved by increasing
$X_{W}$
since the linear far field for this case recedes to as far as
$r_{m}=O(10^{8})$
. Although the vorticities behind the shock waves are still weak, their effect is enhanced in the
$y$
-moment integral. In this situation, as explained at the penultimate paragraph of § 4.5, (4.37c,d
) is valid only if the linear far field has been truly reached.
Having said this, let us turn to some specific physical issues. First, like the case of lift, for subsonic flow the independence of
$Q_{W}$
from
$X_{W}$
is ensured by the fact that all vorticity comes from the boundary layers, which form a roughly defined parabolic wake zone. Even for a low-transonic flow with
$M<1$
, with some shocks (see figures 3 and 4), because the supersonic regions are confined to the vicinity of the body surface, the shock-generated vorticity is also confined to that parabolic wake. This is confirmed by our numerical tests with
$X_{W}=5$
(figure not shown), showing that perfect agreement between (4.37c,d
) and the stress integral can be reached for
$M<1$
(all the way to the maximum
$C_{d}$
and slightly further). At the supersonic side, with
$M\geqslant 1.2$
, a similar independence of
$Q_{W}$
from
$X_{W}$
reappears, but this requires
$X_{W}=O(10^{2})$
, as estimated by (4.27a
). The difference between the results from the stress integral and (4.37c,d
) reduces as
$M$
increases. These observations, along with those on the lift, indicate that our computational domain has reached the entire linearized far field from low-speed to low-transonic flow, and for supersonic flow.
Second, a qualitative interpretation of the Mach-number dependence of drag can be made. Consider again the case of
${\it\alpha}=2.31^{\circ }$
as an example. In the low-
$M$
range the drag is very low and almost constant, with
$C_{d}\approx 8.4\times 10^{-3}$
. This is a typical characteristic of streamlined bodies in subsonic flow due to the dominance of the skin-friction drag. As
$M$
increases from 0.7 to 0.9, shocks appear and
$C_{d}$
increases sharply from
$9.0\times 10^{-3}$
to 0.124 due to the wave drag. But, unlike the lift, in the far field the wave drag is not directly measured by
$\boldsymbol{{\rm\nabla}}{\it\phi}_{d}$
but by the contribution of the shock-generated vorticity moment in (4.37c,d
). There, since transonic shocks may extend very far in the
$y$
-direction, although the vorticity behind the shocks is weak, its
$y$
-moment can be of the same order of magnitude as, or even larger than, that of the attached boundary layers and associated wake shear layer, where
${\it\omega}$
has high peaks but a small
$y$
-extension. Unlike the lift, the sharp increase of the drag does not stop at
$M=0.85$
, but continues until the shocks reach the trailing edge at
$M=0.9$
. Thereafter
$C_{d}$
decreases smoothly as
$M$
increases, since the shocks at the trailing edge become more and more oblique, reducing the shock-generated vorticity moment.
Finally, why the near-sonic linear far field recedes so far in the
$y$
-direction can now be physically understood. As shocks start to appear in the transonic flow, their curvature will generate a vorticity field which, though very weak, may have very large extension in the
$y$
-direction. Therefore, far downstream what one sees is a sudden lateral expansion of a single wake as the incoming velocity increases from
$M<1$
to
$M=1$
. This wide wake is full of vorticity coming from both boundary layers and shocks.
Figure 6. Far-field view of the disturbance pressure contours of an RAE-2822 airfoil at
$Re=6.5\times 10^{6},M=1.4,{\it\alpha}=2.31^{\circ }$
. Solid line is
$p^{\prime }>0$
and dashed line is
$p^{\prime }<0$
. (a) Numerical result. (b) Analytical solution calculated by (2.12) with
$Re=100$
to make the narrow Mach-line strips distinguishable.
5.4. The universality of the Joukowski–Filon theorem
The beauty and value of the J–F formulae (2.24) and TJ–F formulae (4.37) are their extreme neatness and broad validity over a wide Mach-number range. They provide a universal and yet exact framework for understanding the physically representative quantities of lift and drag, which are just a pair of far-field contour integrals
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
, respectively. For complex compressible flows,
${\it\Gamma}_{{\it\phi}}$
and
$Q_{{\it\psi}}$
serve as two encompassing parameters that can contain all the net effects of various flow processes, structures and their interactions on lift and drag.
Although the linearized N–S equations can be split into a longitudinal process and a transversal process, both lift and drag have their origin in the transversal process. On the one hand, while
${\it\Gamma}_{{\it\phi}}$
is associated only with a potential flow, it is still ‘induced’ by a point-like vortex generated by the point-like body located at
$\boldsymbol{x}=\mathbf{0}$
, a picture that holds for both subsonic and supersonic flows. Interestingly, while the distribution of
$\boldsymbol{{\rm\nabla}}{\it\phi}$
is smooth in subsonic flow, it becomes almost singular in supersonic flow, concentrated in the narrow neighbourhood of a pair of Mach-line bundles of opposite families, which are the degenerated form of shocks emitted from the body. Figure 6 shows this situation, where the analytical solution is calculated using the linearized Bernoulli integral (2.12), with
${\it\phi}_{x}$
given by (4.16a
) and
${\it\mu}_{{\it\theta}}{\rm\nabla}^{2}{\it\phi}$
omitted, in which
$L$
and
$D$
are determined by the numerical results. If the Mach lines are symmetric with respect to the
$x$
-axis, we obtain
${\it\Gamma}_{{\it\phi}}^{+}=-{\it\Gamma}_{{\it\phi}}^{-}$
and no lift exists. Thus, it is the Mach-line asymmetry that causes a lift for supersonic flow, but once again that asymmetry is eventually ‘induced’ by the point-like vortex.
On the other hand, the underlying physical mechanism behind the validity of the TJ–F drag formula is that all vorticity in the wake line, lying in the linear far field, can be regarded as wake vorticity, which is confined to a finite region. This is due to advection of vorticity being much stronger than its diffusion for large Reynolds numbers. Roughly speaking, as vorticity generated by both the boundary layer and shocks is advected downstream, it also diffuses mainly along the direction perpendicular to the main stream. Since the gradient of the vorticity generated by the boundary layer is much larger than that generated by shocks, in subsonic and supersonic flows the former diffuses much more rapidly than the latter and will eventually overcome the latter. As a result, the origins of vorticities in the wake line are no longer distinguishable. This is why the TJ–F formula is valid. However, in near-sonic flow the transverse scale of the vorticity generated by shocks is so large that it can hardly be overcome by the vorticity diffused from shear layers in any finite-domain simulation. This invalidates the TJ–F formula in the narrow range of
$M\approx 1$
.
For viscous compressible flow, this physical picture is consistent with a near-field force formula given by Wu & Wu (Reference Wu and Wu1993), see also Liu et al. (Reference Liu, Shi, Zhu, Su, Zou and Wu2014b
), where
$\boldsymbol{F}$
is dominated by the domain integral of a moment of
${\rm\nabla}^{2}({\it\mu}{\bf\omega})$
for both two- and three-dimensional flows. However, if one traces the primary origin of the transversal vorticity field all the way to the body surface, then one again finds the longitudinal field, because it is the tangent pressure gradient that is the dynamic cause of the vorticity generation (Liu et al.
Reference Liu, Wu, Zhu, Zou and Liu2015).
Finally, the neatness and broad validity of (4.37a,b
) and (4.37c,d
) are possible because many specific near-field flow structures decay sufficiently fast as
$X_{W}\rightarrow \infty$
. But it is these structures that determine the specific Mach-number dependence of lift and drag for each specific flow, and enable one to identify the detailed physical mechanisms responsible for the forces. These are evidently of crucial importance in engineering applications, and can be found only from detailed near-field flow data and explained by relevant diagnostic theories, such as that reported in Liu et al. (Reference Liu, Shi, Zhu, Su, Zou and Wu2014b
).
6. Conclusions and discussions
This paper studies the total lift and drag experienced by a body moving with constant velocity through a two-dimensional, externally unbounded, viscous and compressible fluid at rest at infinity, both theoretically and numerically. Our major findings are summarized as follows.
-
(1) Based on far-field linearized Navier–Stokes equations and the Helmholtz decomposition of the disturbance velocity field
$\boldsymbol{u}^{\prime }=\boldsymbol{u}_{{\it\phi}}+\boldsymbol{u}_{{\it\psi}}$
, it is found that the lift and drag are exactly and universally given by a pair of Joukowski–Filon formulae (J–F formulae for short) (2.24), expressed as the contour integrals of
$\boldsymbol{u}_{{\it\phi}}=\boldsymbol{{\rm\nabla}}{\it\phi}$
and
$\boldsymbol{u}_{{\it\psi}}=\boldsymbol{{\rm\nabla}}{\it\psi}\times \boldsymbol{e}_{z}$
, or the jumps
${\it\Gamma}_{{\it\phi}}=\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$Q_{{\it\psi}}=-\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
, respectively. These formulae are independent of the incoming-flow Mach number
$M$
and Reynolds number
$Re$
as the direct consequences of the unique kinematic features of two-dimensional, steady and viscous external flow. First, because it is two-dimensional, the flow domain is doubly connected, permitting the velocity potentials
${\it\phi}$
and
${\it\psi}$
both to be multi-valued and have jumps. Second, the steadiness means that the flow domain must exclude some wake vorticity that leads to non-zero jumps
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
as the kinematic measure of lift and drag. Third, because of viscosity and the vortical wake, the circulation
${\it\Gamma}_{C}$
has two constituents,
${\it\Gamma}_{{\it\phi}}$
and
${\it\Gamma}_{{\it\psi}}$
. -
(2) A complete far-field linearized theory is developed analytically. Its first role is to give a rigorous proof of the J–F formulae, so that the result can be stated as the Joukowski–Filon theorem. Owing to the pure kinematic nature,
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}_{{\it\phi}}=\mathbf{0}$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}_{{\it\psi}}=0$
, once the theorem is proved in the linear far field the J–F formulae are also independent of the shape and size of the integration contour
$C$
surrounding the body. To the authors’ knowledge, this is the first time that it has been discovered that the classic and fundamental aerodynamic theorems of Joukowski and Filon for incompressible flow can be exactly carried over all the way to supersonic flow, without any change in form. -
(3) The second role of the theory is to clarify the dominant flow structures, such as shear layers and shock waves, responsible for the lift and drag in different ranges of
$M$
, and thereby to make specific estimates of the minimum distances of the linear far field to the body in different Mach-number ranges. This includes the most critical case with
$M\approx 1$
, but for which the viscous linear field is too far away to be reached by any finite-domain numerical simulation. -
(4) Because velocity potentials are not physically observable quantities, the integrands of the J–F formulae are not directly testable. The key to making them testable is to find the condition at which
${\it\Gamma}_{{\it\psi}}\rightarrow 0$
. This is the third role of the theory, leading to a testable version of the J–F formulae (TJ–F formulae for short). They are also independent of
$M$
and
$Re$
, but hold only in the linear far field. They approach the universal J–F formulae asymptotically as the integration contour recedes to infinity. -
(5) A careful RANS simulation of typical airfoil flow is performed. It confirms directly the TJ–F formulae along with their behaviour predicted by the theory, as well as the predicted minimum distance of the linear far field. Except for near-sonic flow, for which the linear far field is too remote, the excellent numerical agreement between the predicted lift and drag using the TJ–F formulae and using the wall-stress integrals can be considered as strong support for the exact and universal J–F formulae. Based on near-field flow data, the numerical results are able to reveal the underlying physical mechanisms behind the Mach-number dependence of lift and drag, and thereby enhance the understanding of the Joukowski–Filon theorem.
-
(6) Both the universal J–F formulae and far-field TJ–F formulae reveal that the origin of aerodynamic forces in viscous compressible flow is in a transversal process. This is evident for the drag, and also true for the lift, since even
${\it\Gamma}_{{\it\phi}}$
in (2.24a
) can be viewed as ‘induced’ by a point-like vortex at the origin. In subsonic flow the vortex induces a smooth field surrounding the body, while in supersonic flow it induces the asymmetry of a pair of Mach-line bundles emitted from the body. Compared to other dynamic–thermodynamic fields generated by the body, such as shocks, expansions, temperature gradients (and associated variable viscosities), entropy increments, etc., the vorticity extends the farthest downstream and is the only signature of disturbed flow observable at a remote wake line. Perhaps only the very remote lateral extension of the longitudinal process in near-sonic flow could be comparable to the downstream extension of vorticity. However, the ultimate origin of the vorticity field is still the dynamic coupling of the longitudinal and transverse processes at solid walls and curved shocks.
The specific values of
$\unicode[STIX]{x27E6}{\it\phi}\unicode[STIX]{x27E7}$
and
$\unicode[STIX]{x27E6}{\it\psi}\unicode[STIX]{x27E7}$
are beyond the scope of the formulae themselves, but are the synthetic effects of various complex dynamic fields generated by the body motion. Therefore, it is believed that a rational combination of the universal J–F formulae and aerodynamic force theories in terms of special near-field flows (e.g. Liu et al.
Reference Liu, Shi, Zhu, Su, Zou and Wu2014b
) can provide a powerful means for the development of modern high-speed aerodynamics at a fundamental level, especially for complex flows with coupled multiple dynamic and thermodynamic processes.
As shown in § 2.1, the inherent nature of linearized analysis is such that it retains only constant reference values for all transport coefficients, such as viscosities and heat conductivity. This feature imposes a limitation in applying the theory to a linearized turbulent far field, since the best one could do is, as mentioned in § 2.1, to use a constant reference eddy viscosity
${\it\mu}_{t0}$
that is approximately
$O(10^{3}){\it\mu}_{0}$
. However, our RANS simulation indicates that, qualitatively (data not shown here, which may not be accurate enough due to the sparse grid in the far field), turbulence occurs mainly in the vortical wake with a non-negligible varying eddy viscosity
${\it\mu}_{t}(\boldsymbol{x})$
, but
${\it\mu}_{t}(\boldsymbol{x})$
is not significantly larger than the molecular viscosity near the shocks. This varying-
${\it\mu}_{t}$
effect cannot be captured by the linearized theory although it is applicable to statistically steady flow. Consequently, the minimum distance of the linearized transverse far field would be significantly shortened by a large
${\it\mu}_{t0}$
, which may explain the perfectness of the TJ–F formula (4.37c,d
) in the subsonic region; but since
${\it\mu}_{t}(\boldsymbol{x})$
remains of the same order of magnitude as the laminar viscosity near the shocks in the far field, the minimum distance of the linearized longitudinal turbulent far field may not be significantly shortened, especially for near-sonic flow.
Acknowledgements
This work was supported by NSFC (grant nos 10921202, 11472016). The numerical computation was partially performed on TianHe-1(A) at the National Supercomputer Center in Tianjin. The authors are very grateful to Professors F. Liu, W.-D. Su, Y.-P. Shi, T.-S. Liu and X.-L. Li, and Mrs S.-F. Zou and A.-K. Gao for very valuable discussions. Our special thanks go to Dr P. R. Spalart and all the anonymous referees whose comments and suggested new references have led to the clarification of some key issues.
Appendix A. Fundamental solution of the linearized N–S equations
This appendix highlights the derivation of the fundamental solution of (3.2) for
$\boldsymbol{u}^{\prime }$
in two-dimensional steady flow, obtained by Lagerstrom et al. (Reference Lagerstrom, Cole and Trilling1949, pp. 172–175, 182–193).
Denote the Fourier transform and inverse transform of (3.2) in the
$x$
-direction as
$$\begin{eqnarray}\widetilde{f}(l,y)=\int _{-\infty }^{\infty }\text{e}^{-\text{i}lx}f(x,y)\,\text{d}x,\quad f(x,y)=\frac{1}{2{\rm\pi}}\int _{-\infty }^{\infty }\text{e}^{\text{i}lx}\widetilde{f}(l,y)\,\text{d}l.\end{eqnarray}$$
Now the equations in (3.2) are transformed to (upon eliminating
$\widetilde{{\it\rho}}$
)
$$\begin{eqnarray}(a\unicode[STIX]{x1D648}_{1}-b\unicode[STIX]{x1D648}_{2}-k^{2}\unicode[STIX]{x1D644})\boldsymbol{\cdot }\widetilde{\boldsymbol{u}}=-\widetilde{\boldsymbol{f}},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle a={\it\nu}_{{\it\theta}}+\frac{c^{2}}{\text{i}lU},\quad b={\it\nu},\quad k^{2}=\text{i}lU & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D648}_{1}=\left(\begin{array}{@{}cc@{}}-l^{2} & \text{i}l\partial _{y}\\ \text{i}l\partial _{y} & \partial _{y}^{2}\end{array}\right),\quad \unicode[STIX]{x1D648}_{2}=\left(\begin{array}{@{}cc@{}}-\partial _{y}^{2} & \text{i}l\partial _{y}\\ \text{i}l\partial _{y} & l^{2}\end{array}\right). & & \displaystyle\end{eqnarray}$$
To find the fundamental solution of (A 2) the following theorem is very useful:
Theorem 1. If
$\unicode[STIX]{x1D648}_{1}$
and
$\unicode[STIX]{x1D648}_{2}$
are two linear differential matrix operators such that
$$\begin{eqnarray}\unicode[STIX]{x1D648}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D648}_{2}=\unicode[STIX]{x1D648}_{2}\boldsymbol{\cdot }\unicode[STIX]{x1D648}_{1}=\mathbf{0},\quad \unicode[STIX]{x1D648}_{1}-\unicode[STIX]{x1D648}_{2}=L\unicode[STIX]{x1D644},\end{eqnarray}$$
where
$\unicode[STIX]{x1D644}$
is the unit matrix and
$L$
is a scalar linear differential operator, then the fundamental solution
$\boldsymbol{G}(\boldsymbol{x},{\bf\xi})$
of (A 2) is given by
$$\begin{eqnarray}\boldsymbol{G}(\boldsymbol{x},{\bf\xi})=\frac{1}{k^{2}}\left(\unicode[STIX]{x1D648}_{1}g_{\sqrt{k^{2}/a}}-\unicode[STIX]{x1D648}_{2}g_{\sqrt{k^{2}/b}}\right),\end{eqnarray}$$
where
$g_{{\it\beta}}(x,{\it\xi})$
is the fundamental solution of the scalar operator
$L-{\it\beta}^{2}$
.
Now, since
$L=\partial _{y}^{2}-l^{2}$
, of which the fundamental solution
$g_{{\it\beta}}$
with far-field decaying condition is
$$\begin{eqnarray}g_{{\it\beta}}=\frac{\text{e}^{-|y|\sqrt{{\it\beta}^{2}+l^{2}}}}{2\sqrt{{\it\beta}^{2}+l^{2}}},\quad \text{Re}\sqrt{{\it\beta}^{2}+l^{2}}>0,\end{eqnarray}$$
then the fundamental solution of (A 2) comes from (A 5) and (A 6) directly, which we denote as
$\widetilde{\boldsymbol{G}}$
,
$$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{G}}(l,y)=\frac{1}{k^{2}}\left[\unicode[STIX]{x1D648}_{1}\frac{\exp \left(-|y|\displaystyle \sqrt{\frac{k^{2}}{a}+l^{2}}\right)}{\displaystyle 2\sqrt{\frac{k^{2}}{a}+l^{2}}}-\unicode[STIX]{x1D648}_{2}\frac{\exp \left(-|y|\displaystyle \sqrt{\frac{k^{2}}{b}+l^{2}}\right)}{\displaystyle 2\sqrt{\frac{k^{2}}{b}+l^{2}}}\right]. & & \displaystyle\end{eqnarray}$$
Transforming back to the physical space, we obtain
$$\begin{eqnarray}\boldsymbol{G}=\int _{-\infty }^{\infty }\left[\unicode[STIX]{x1D648}_{1}\frac{\exp \left(-|y|\displaystyle \sqrt{\frac{k^{2}}{a}+l^{2}}\right)}{\displaystyle 2\sqrt{\frac{k^{2}}{a}+l^{2}}}-\unicode[STIX]{x1D648}_{2}\frac{\exp \left(-|y|\displaystyle \sqrt{\frac{k^{2}}{b}+l^{2}}\right)}{\displaystyle 2\sqrt{\frac{k^{2}}{b}+l^{2}}}\right]\frac{\text{e}^{\text{i}lx}\,\text{d}l}{2{\rm\pi}k^{2}},\end{eqnarray}$$
with
$a,b,k^{2}$
and
$\unicode[STIX]{x1D648}_{1},\unicode[STIX]{x1D648}_{2}$
being given by (A 3a–c
) and (A 3d,e
), respectively.
Appendix B. Far-field longitudinal velocity components
We give detailed algebra for the derivation of the far-field longitudinal velocity
$\boldsymbol{{\rm\nabla}}{\it\phi}$
from its Fourier transform (3.11). The basic idea in studying the integrals therein is to choose appropriate integral contours to ensure the far-field decaying condition. Denote
$$\begin{eqnarray}(1-M^{2})l^{2}+\text{i}\frac{{\it\nu}_{{\it\theta}}M^{4}}{U}l^{3}=A\text{e}^{-\text{i}{\it\theta}},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle A^{2}=\left[1+\left(\frac{M^{4}}{1-M^{2}}\frac{{\it\nu}_{{\it\theta}}l}{U}\right)^{2}\right](1-M^{2})^{2}l^{4}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tan {\it\theta}=\frac{M^{4}}{1-M^{2}}\frac{{\it\nu}_{{\it\theta}}l}{U}. & \displaystyle\end{eqnarray}$$
${\it\phi}_{l}$
given by (3.11a
) can be written as 
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}=\text{sgn}\,y\int _{0}^{\infty }\text{e}^{-|y|A^{1/2}\cos ({\it\theta}/2)}\sin \left(xl-|y|A^{1/2}\sin \frac{{\it\theta}}{2}\right)\frac{\text{d}l}{l}. & & \displaystyle\end{eqnarray}$$
But since the integral in (3.11b ) is not convergent, we consider its derivatives instead. In fact, due to the identity
$$\begin{eqnarray}\frac{\partial {\it\phi}_{d}}{\partial y}=\frac{\partial {\it\phi}_{l}}{\partial x},\end{eqnarray}$$
only
$\partial {\it\phi}_{d}/\partial x$
has to be considered, that is
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}=\int _{0}^{\infty }\text{e}^{-|y|A^{1/2}\cos ({\it\theta}/2)}\sin \left(xl-|y|A^{1/2}\sin \frac{{\it\theta}}{2}-\frac{{\it\theta}}{2}\right)\frac{l\text{d}l}{A^{1/2}}. & & \displaystyle\end{eqnarray}$$
Note that the above results are valid only for small viscosity. However, contrary to the subsonic flow
$1-M^{2}>0$
, where the viscosity can be omitted and the results are the corresponding potential flow, for
$1-M^{2}\leqslant 0$
the viscosity can never be omitted, otherwise
${\it\theta}={\rm\pi}$
and the disturbance can never die out. This simple observation stresses the vital role of viscosity in sonic and supersonic flows, which is the key mechanism for the shock waves to be weakened and die out eventually.
B.1. Subsonic flow
For subsonic flow, we have
$$\begin{eqnarray}A^{1/2}\approx {\it\beta}l,\quad \frac{{\it\theta}}{2}\approx {\it\lambda}l,\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\beta}^{2}=1-M^{2}>0,\quad {\it\lambda}\equiv \frac{{\it\nu}_{{\it\theta}}M^{4}}{2{\it\beta}^{2}U}\ll 1.\end{eqnarray}$$
Substituting (B 4) into (B 3a ) gives
$$\begin{eqnarray}\displaystyle {\it\phi}_{l} & = & \displaystyle \text{sgn}\,y\int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\sin (xl-{\it\lambda}{\it\beta}|y|l^{2})\frac{\text{d}l}{l}\nonumber\\ \displaystyle & = & \displaystyle \text{sgn}\,y\int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\sin (xl)\frac{\text{d}l}{l}-{\it\lambda}{\it\beta}y\int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\cos (xl)l\,\text{d}l\nonumber\\ \displaystyle & = & \displaystyle \text{sgn}\,y\arctan \left(\frac{x}{{\it\beta}|y|}\right)+\frac{{\it\lambda}{\it\beta}y(x^{2}-{\it\beta}^{2}y^{2})}{(x^{2}+{\it\beta}^{2}y^{2})^{2}}.\end{eqnarray}$$
Similarly, by substituting (B 4) into (B 3c ) we can obtain
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{d}}{\partial x} & = & \displaystyle \int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\sin [(x-{\it\lambda})l-{\it\lambda}{\it\beta}|y|l^{2}]\frac{\text{d}l}{{\it\beta}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\sin [(x-{\it\lambda})l]\frac{\text{d}l}{{\it\beta}}-{\it\lambda}|y|\int _{0}^{\infty }\text{e}^{-{\it\beta}|y|l}\cos (xl)l^{2}\,\text{d}l\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{{\it\beta}}\frac{x-{\it\lambda}}{(x-{\it\lambda})^{2}+{\it\beta}^{2}y^{2}}+\text{sgn}\,y\frac{2{\it\lambda}}{{\it\beta}}\frac{{\it\beta}^{2}y^{2}(3x^{2}-{\it\beta}^{2}y^{2})}{(x^{2}+{\it\beta}^{2}y^{2})^{3}}.\end{eqnarray}$$
Evidently, the above results include incompressible flow as a special case with
$M={\it\lambda}=0$
and
${\it\beta}=1$
. They can also be regarded as a first-order viscous modification of inviscid subsonic flow if terms proportional to
${\it\lambda}$
are retained. Furthermore, since the terms involving
${\it\nu}_{{\it\theta}}$
are all proportional to
$r^{-2}$
for subsonic flow, as seen in (B 6) and (B 7), they of course make no contribution to the circulation as
$r\rightarrow \infty$
or
${\it\nu}_{{\it\theta}}\rightarrow 0$
. Thus we may simply set
${\it\nu}_{{\it\theta}}=0$
to obtain
$$\begin{eqnarray}\displaystyle {\it\phi}_{l} & = & \displaystyle \text{sgn}\,y\arctan \left(\frac{x}{{\it\beta}|y|}\right),\quad {\it\beta}=\sqrt{1-M^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\phi}_{d}=\frac{1}{2{\it\beta}}\ln (x^{2}+{\it\beta}^{2}y^{2}). & & \displaystyle\end{eqnarray}$$
Note that although the original form of
${\it\phi}_{d}$
, i.e. (3.11b
), is not convergent, the derivatives of (B 8c
) are identical to those of (3.11b
). Thus (B 8c
) can be regarded as the finite part of (3.11b
).
B.2. Supersonic flow
For supersonic flow, we have
$$\begin{eqnarray}A^{1/2}\approx Bl,\quad \frac{{\it\theta}}{2}\approx \frac{{\rm\pi}}{2}-{\it\Lambda}l,\end{eqnarray}$$
where
$$\begin{eqnarray}B^{2}=M^{2}-1>0,\quad {\it\Lambda}\equiv \frac{{\it\nu}_{{\it\theta}}M^{4}}{2B^{2}U}\ll 1.\end{eqnarray}$$
Substituting (B 9) into (B 3a ) we have
$$\begin{eqnarray}\displaystyle {\it\phi}_{l} & = & \displaystyle \text{sgn}\,y\int _{0}^{\infty }\text{e}^{-{\it\Lambda}B|y|l^{2}}\sin [(x-B|y|)l]\frac{\text{d}l}{l}\nonumber\\ \displaystyle & = & \displaystyle \frac{{\rm\pi}}{2}\text{sgn}\,y\,\text{erf}\left(\frac{x-B|y|}{2\sqrt{{\it\Lambda}B|y|}}\right),\end{eqnarray}$$
where
$\text{erf}(\cdot )$
is the error function defined by
$$\begin{eqnarray}\text{erf}(z)=\frac{2}{\sqrt{{\rm\pi}}}\int _{0}^{z}\text{e}^{-t^{2}}\,\text{d}t.\end{eqnarray}$$
Similarly, for
$\partial {\it\phi}_{d}/\partial x$
we have
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{d}}{\partial x} & = & \displaystyle -\int _{0}^{\infty }\text{e}^{-{\it\Lambda}B|y|l^{2}}\cos [(x+{\it\Lambda}-B|y|)l]\frac{\text{d}l}{B}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2B}\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{(x+{\it\Lambda}-B|y|)^{2}}{4{\it\Lambda}B|y|}\right]\end{eqnarray}$$
and due to (B 3b ) and (B 11) we have
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{d}}{\partial y}=\frac{\partial {\it\phi}_{l}}{\partial x}=\frac{\text{sgn}\,y}{2}\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\exp \left[-\frac{(x-B|y|)^{2}}{4{\it\Lambda}B|y|}\right]. & & \displaystyle\end{eqnarray}$$
Note that the viscosity can cause the maximum longitudinal disturbance velocity induced by the drag (not by the lift) to lie not exactly along the Mach line but to have a displacement
${\it\Lambda}$
away from it. However, since in most cases
${\it\Lambda}\ll 1$
, we can omit this infinitesimal displacement effect. With this in mind, (B 13) can be integrated to yield
$$\begin{eqnarray}\displaystyle {\it\phi}_{d} & = & \displaystyle {\it\phi}_{d}(-\infty ,y)-\frac{1}{2B}\sqrt{\frac{{\rm\pi}}{{\it\Lambda}B|y|}}\int _{-\infty }^{x}\exp \left[-\frac{({\it\xi}-B|y|)^{2}}{4{\it\Lambda}B|y|}\right]\text{d}{\it\xi}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle {\it\phi}_{d}(-\infty ,y)-\frac{{\rm\pi}}{2B}\text{erf}\,\left(\frac{x-B|y|}{2\sqrt{{\it\Lambda}B|y|}}\right)+\frac{{\rm\pi}}{2B}.\end{eqnarray}$$
$y$
-derivative of (B 16) and compare the result with (B 14), then
${\it\phi}_{d}$
can be simply denoted as 
$$\begin{eqnarray}\displaystyle {\it\phi}_{d}=-\frac{{\rm\pi}}{2B}\text{erf}\,\left(\frac{x-B|y|}{2\sqrt{{\it\Lambda}B|y|}}\right), & & \displaystyle\end{eqnarray}$$
which gives the same leading term of the velocity field.
B.3. Near-sonic flow
For near-sonic flow we have
$$\begin{eqnarray}\displaystyle A\approx \frac{{\it\nu}_{{\it\theta}}M^{4}}{U}l^{3},\quad {\it\theta}\approx \frac{{\rm\pi}}{2}. & & \displaystyle\end{eqnarray}$$
Then the velocity potential
${\it\phi}_{l}$
, (B 3a
), can be written as
$$\begin{eqnarray}\displaystyle {\it\phi}_{l}=\text{sgn}\,y\int _{0}^{\infty }\text{e}^{-|y|M^{2}\sqrt{{\it\nu}_{{\it\theta}}/(2U)}l^{3/2}}\sin \left(xl-|y|M^{2}\sqrt{\frac{{\it\nu}_{{\it\theta}}}{2U}}l^{3/2}\right)\frac{\text{d}l}{l}, & & \displaystyle\end{eqnarray}$$
of which the integral always exists, but only for special cases can it be integrated to yield analytical results. In particular, we have
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{l}(x,\pm 0)=\pm \frac{{\rm\pi}}{2}\text{sgn}\,x, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}_{l}(x,y)=\left[\text{G}\left(\frac{2}{3}\right)\left(\frac{U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{1/3}\frac{x}{|y|^{2/3}}-\frac{{\rm\pi}}{6}\right]\text{sgn}\,y,\quad |x|\ll 1, & \displaystyle\end{eqnarray}$$
$\text{G}(\cdot )$
is the Gamma function defined by 
$$\begin{eqnarray}\text{G}(z)=\int _{0}^{\infty }t^{z-1}\text{e}^{-t}\,\text{d}t.\end{eqnarray}$$
From (B 20) we can see that
${\it\phi}_{l}$
decreases from
${\rm\pi}/2$
to
$-{\rm\pi}/2$
for
$y>0$
as
$x$
increases from
$-\infty$
to
$+\infty$
, while
${\it\phi}_{l}(0,y)$
retains a constant value
$-{\rm\pi}/6$
even for
$y\rightarrow \infty$
. These results suggest a very slow decay of
$\partial {\it\phi}_{l}/\partial x$
. Indeed, we have
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{l}}{\partial x}(0,y)=\text{G}\left(\frac{2}{3}\right)\left(\frac{U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{1/3}\frac{\text{sgn}\,y}{|y|^{2/3}}. & & \displaystyle\end{eqnarray}$$
On the other hand, for the longitudinal velocity generated by the drag, we have
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}=\left(\frac{U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{1/2}\int _{0}^{\infty }\text{e}^{-|y|M^{2}\sqrt{{\it\nu}_{{\it\theta}}/(2U)}l^{3/2}}\sin \left(xl-|y|M^{2}\sqrt{\frac{{\it\nu}_{{\it\theta}}}{2U}}l^{3/2}-\frac{{\rm\pi}}{4}\right)\frac{\text{d}l}{l^{1/2}}.\qquad & & \displaystyle\end{eqnarray}$$
In particular, we have
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}(x,0)=\left(\frac{{\rm\pi}U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{1/2}\frac{\text{sgn}\,x-1}{2\sqrt{|x|}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\phi}_{d}}{\partial x}(0,y)=-\left(\frac{U}{{\it\nu}_{{\it\theta}}M^{4}}\right)^{2/3}\frac{\sqrt{3}\text{G}\left(\frac{4}{3}\right)}{|y|^{1/3}}. & \displaystyle\end{eqnarray}$$
