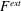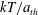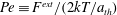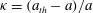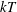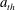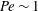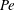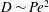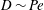1 Introduction
Self-diffusion in colloidal dispersions can be hindered or enhanced by entropic and hydrodynamic forces. In a quiescent solvent, thermal forces acting on a single colloid induce a random walk with variance characterized by the Stokes–Einstein diffusivity:
$D_{a}=kT/6{\rm\pi}{\it\eta}a$
(Einstein Reference Einstein1906). Here,
$a$
is the particle radius,
$kT$
is the thermal energy and
${\it\eta}$
is the solvent viscosity. The Stokes–Einstein diffusivity describes the maximum random walk that thermal forces alone can generate. The presence of other colloids weakens diffusive Brownian displacements hydrodynamically and entropically. The former, hydrodynamic hindrance, occurs via a reduction in the particle mobility: individual displacements in the random walk are diminished as the wandering particle entrains other nearby no-slip surfaces. The latter, entropic hindrance, arises during long-time self-diffusion, which has been previously described as ‘cell jumping’ (Stillinger & Weber Reference Stillinger and Weber1982; Zwanzig Reference Zwanzig1983) and ‘cage hopping’ (Rallison & Hinch Reference Rallison and Hinch1986), during which structural distortion further impedes particle motion. In consequence, equilibrium self-diffusion is a monotonically decreasing function of volume fraction
${\it\phi}$
, eventually approaching zero upon reaching the maximum packing fraction
${\it\phi}_{m}$
(Kops-Werkhoven & Fijnaut Reference Kops-Werkhoven and Fijnaut1982; van Megen, Underwood & Snook Reference van Megen, Underwood and Snook1986; van Megen & Underwood Reference van Megen and Underwood1989; Brady Reference Brady1994). One may expect, then, that the hindrance of colloidal self-diffusion grows more pronounced as the dispersion becomes more dense. Such is not the case in the presence of external forces.
Imposed flows and forces act to enhance diffusion and dispersion, and this flow-induced migration may become more pronounced with increasing volume fraction. This behaviour plays a central role in many biological and industrial suspensions: platelet migration toward artery walls (Tangelder et al.
Reference Tangelder, Teirlinck, Slaaf and Reneman1985); red blood cells localizing near the centreline of capillaries (Fåhræus & Lindqvist Reference Fåhræus and Lindqvist1931); and mixing in fluidized-bed reactors, for example. The particle-scale transport processes underlying these applications are well characterized; for example, shearing flow can resuspend settled particles, even in the presence weak inertial forces (Leighton & Acrivos Reference Leighton and Acrivos1986, Reference Leighton and Acrivos1987a
,Reference Leighton and Acrivos
b
; Acrivos, Mauri & Fan Reference Acrivos, Mauri and Fan1993); pressure-driven tube and pipe flows can lead to margination (Kumar, Henríquez Rivera & Graham Reference Kumar, Henríquez Rivera and Graham2014) or particle concentration toward the tube centre (Phillips et al.
Reference Phillips, Armstrong, Brown, Graham and Abbott1992; Zhang & Acrivos Reference Zhang and Acrivos1994). Measurement of such diffusion produced insight regarding the combined influence of flow and particle interaction: Eckstein, Bailey & Shapiro (Reference Eckstein, Bailey and Shapiro1977) measured shear-induced migration and found that diffusion in the velocity-gradient direction that scales as
$D\sim a^{2}\dot{{\it\gamma}}$
, where
$a$
is the particle radius and
$\dot{{\it\gamma}}$
is the shear rate. Leighton & Acrivos (Reference Leighton and Acrivos1987a
) found a similar advective scaling
$a^{2}\dot{{\it\gamma}}$
of the shear-induced self-diffusion in concentrated colloidal suspensions, and additionally determined that the volume fraction dependence should scale as
$D\sim {\it\phi}^{2}$
, revealing the role of three-sphere interactions for permanent displacements.
In the present study we identify that the unifying feature in systems in which self-diffusion is not hindered but enhanced is a transition from particle motion dominated by stochastic processes (thermal forces) to particle motion defined by deterministic forces (external flow), which in turn influence suspension symmetry. The interplay between deterministic flows and non-hydrodynamic forces dictate the magnitude and shape of the distorted, non-equilibrium structure. Suspensions subjected to strong deterministic forces develop a pronounced non-equilibrium microstructure, which may exhibit varying degrees of structural symmetry. When hydrodynamic forces are the only microscopic forces involved, a suspension may be highly distorted from equilibrium though the structure is spherically symmetric about any given particle, as in the case of extensional (Batchelor & Green Reference Batchelor and Green1972) and sedimentation (Batchelor Reference Batchelor1982) flows. Non-hydrodynamic forces prevent the formation of such a spherically symmetric structure – evidence that flow-reversibility for deterministic relative trajectories has been destroyed.
When entropic forces exert even a weak influence, strong deterministic forces and flow can produce a pronounced non-equilibrium configuration, which can in turn lead to gradient-driven diffusion. Gadala-Maria & Acrivos (Reference Gadala-Maria and Acrivos1980) first hypothesized the development of asymmetric flow-induced structure in sheared non-colloidal suspensions, in an effort to explain a long-time decrease in the steady-state shear viscosity. Leighton & Acrivos (Reference Leighton and Acrivos1987a
) identified the origin of this behaviour as shear-induced particle migration. Recognizing that particle trajectories should be flow-reversible even for three-particle and higher encounters, they proposed that particle roughness is required to drive non-colloids irreversibly off their trajectories which, in shear flow, destroy closed orbits (Arp & Mason Reference Arp and Mason1977). The resultant loss of fore–aft symmetry leads to entropic dispersion (Eckstein et al.
Reference Eckstein, Bailey and Shapiro1977; Leighton & Acrivos Reference Leighton and Acrivos1987a
; da Cunha & Hinch Reference da Cunha and Hinch1996; Brady & Morris Reference Brady and Morris1997). Surface roughness in a strongly sheared dispersion thus induces entropic shear-induced diffusion in the directions along and transverse to flow:
$D\sim a^{2}\dot{{\it\gamma}}{\it\phi}$
in all directions (da Cunha & Hinch Reference da Cunha and Hinch1996; Brady & Morris Reference Brady and Morris1997). Weak thermal motion plays an identical role to surface roughness and, for perfectly smooth particles, breaks the fore–aft symmetry of relative trajectories, inducing transverse dispersion of the same magnitude as longitudinal entropic dispersion (Brady & Morris Reference Brady and Morris1997). Thus, pronounced asymmetry of the suspension microstructure accompanies strong diffusion enhancement. However, the degree of structural asymmetry is not mirrored by diffusional anisotropy: only an
$O(1)$
prefactor differentiates diffusion along and transverse to shear flow.
Hydrodynamic diffusion is another important example of enhanced self-diffusion in shear flow, distinct from the entropic dispersion discussed above in that it does not require broken fore–aft interaction symmetry. Hydrodynamic diffusion can arise from velocity fluctuations, one source of which is variable-duration encounters (Acrivos et al.
Reference Acrivos, Batchelor, Hinch, Koch and Mauri1992; Wang, Mauri & Acrivos Reference Wang, Mauri and Acrivos1996). Longitudinal flow-induced diffusion can arise even in the absence of non-hydrodynamic (e.g. interparticle and thermal) forces; Acrivos et al. (Reference Acrivos, Batchelor, Hinch, Koch and Mauri1992) showed that even in the pure hydrodynamic limit, the longitudinal component of shear-induced self-diffusion (parallel to the flow direction) scales as
$O({\it\phi}\ln {\it\phi}^{-1})$
. The authors ascribe this diffusion to hydrodynamic interactions between pairs of particle pairs that are widely separated. In contrast, the fore–aft symmetry of pairwise particle encounters prevents net displacements in the directions normal to flow. As a result, shear-induced self-diffusion in either the velocity gradient or vorticity directions is imperceptible in the so-called ‘pure hydrodynamic limit’ (Wang et al.
Reference Wang, Mauri and Acrivos1996; Brady & Morris Reference Brady and Morris1997), where the frequency of three-body and higher interactions scales as
${\it\phi}^{2}$
. Three-body interactions are thus essential for net fore–aft migration in the directions transverse to flow. The anisotropy of the diffusion tensor in sheared non-colloids thus diverges in the dilute limit, in contrast to the
$O(1)$
anisotropy observed in strongly sheared suspensions interacting via long-range interparticle repulsion.
Anisotropic hydrodynamic diffusion in a symmetric, non-equilibrium microstructure also arises in sedimentation of non-colloids. The strength of this anisotropy depends, as it does in shear flow, on the role played by non-hydrodynamic forces and concentration. For example, in moderately concentrated dispersions,
$0.05\leqslant {\it\phi}\leqslant 0.15$
, diffusive migration in the flow direction is nearly twice that in the direction transverse to gravity (Nicolai et al.
Reference Nicolai, Herzhaft, Hinch, Oger and Guazzelli1995). As the suspension becomes dilute, anisotropy becomes more pronounced. Indeed, while vertical hydrodynamic dispersion has been observed in suspensions as dilute as
$0.025\leqslant {\it\phi}\leqslant 0.10$
, transverse dispersion is nearly imperceptible owing to the reversibility of Stokes-flow trajectories (Ham & Homsy Reference Ham and Homsy1988). The dilute experiments of Ham & Homsy showed that the vertical hydrodynamic dispersivity scales advectively as the mean sedimentation velocity
$\langle \boldsymbol{U}\rangle$
and the particle size
$a$
, while transverse diffusion is imperceptible. Only when three-body interactions play a role can transverse diffusion emerge in sedimentation of smooth non-colloids, but simple pair interactions can produce longitudinal hydrodynamic diffusion.
Overall then, the only requirement for enhanced diffusion is a non-equilibrium microstructure – which may or may not be symmetric. The strength and character of the diffusion depends on the relative importance of hydrodynamic and non-hydrodynamic forces, specifically on their influence on particle trajectories and structural symmetry. Surprisingly perhaps, as a non-equilibrium microstructure gains symmetry, diffusive anisotropy becomes more pronounced. A powerful tool for understanding this behaviour is the connection between the analysis of particle pair trajectories and that of microstructural evolution and their clear connections to transport processes. Sedimentation is ideal for exposing this connection: whereas isolated particle pairs sediment in tandem in monodisperse suspensions, polydispersity – either in density or size – produces relative motion. Indeed,
$O({\it\phi})$
corrections in the sedimentation velocity and diffusion can arise from simple pairwise interactions of smooth non-colloids (Batchelor Reference Batchelor1982, Reference Batchelor1983).
Falling-ball rheometry is a particularly revealing example of polydisperse sedimentation, where a heavy sphere sediments through a collection of neutrally buoyant background particles, and its mean and fluctuating motion are utilized to infer rheological properties of the suspension. When all such particles are non-colloids, the falling ball accumulates bath particles (on average) in a radially symmetric distribution about its surface (Batchelor Reference Batchelor1982) hindering the average fall speed but also inducing velocity fluctuations. The
$O({\it\phi})$
correction to the average and variance of sedimentation speed have been computed as a function of ball size for the pure hydrodynamic limit (Batchelor Reference Batchelor1982; Batchelor & Wen Reference Batchelor and Wen1982; Davis & Hill Reference Davis and Hill1992); a non-equilibrium Stokes–Einstein relation between these viscosity and diffusivity corrections was recently established by Hoh & Zia (Reference Hoh and Zia2015). The presence of finite surface roughness produces transverse diffusion as well that scales as
$O({\it\phi})$
(Davis Reference Davis1992; da Cunha & Hinch Reference da Cunha and Hinch1996), showing that the degree of diffusional anisotropy is intimately tied to the interaction range of interparticle forces. Experimental observations support these predictions of anisotropy, size effects and concentration dependence (Nicolai, Peysson & Guazzelli Reference Nicolai, Peysson and Guazzelli1996; Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998). However, the trajectory analysis utilized in such theory bars the analytical examination of the role played by stochastic forces, e.g. Brownian motion and roughness, on such differences. More broadly, understanding of the influence of entropic forces on diffusion can contribute to emerging questions regarding the role of particle roughness in suspension rheology. The presence of even very weak thermal motion transforms falling-ball rheometry to its colloidal analogue, active microrheology.
The focus of the present work is to discover the role played by entropic and hydrodynamic forces in force-induced diffusion in suspensions of hydrodynamically interacting colloids, utilizing active microrheology, where the ‘falling ball’ is now a colloidal ‘probe’ particle. The theoretical framework for active microrheology in dilute suspensions is well established (Squires & Brady Reference Squires and Brady2005; Khair & Brady Reference Khair and Brady2006; Zia & Brady Reference Zia and Brady2010, Reference Zia and Brady2012, Reference Zia and Brady2013; Swan & Zia Reference Swan and Zia2013). The mean motion of the probe is utilized to infer the viscosity of the suspension (Squires & Brady Reference Squires and Brady2005; Khair & Brady Reference Khair and Brady2006; Zia & Brady Reference Zia and Brady2013; Swan & Zia Reference Swan and Zia2013). Fluctuations in probe motion are enhanced by flow, producing anisotropic force-induced diffusion, studied previously by Zia & Brady (Reference Zia and Brady2010) in the absence of hydrodynamic interactions. Recently Hoh & Zia (Reference Hoh and Zia2015) showed that accounting for the effects of hydrodynamic interactions on probe fluctuations gives, in the absence of thermal motion, hydrodynamic diffusion that recovers the results of Davis & Hill (Reference Davis and Hill1992) for falling-ball rheometry. Recently, Zia & Brady (Reference Zia and Brady2012) showed that a non-equilibrium imbalance between fluctuation and dissipation (viscous drag and entropic force-induced diffusion) leads to suspension stress; we thus expect the qualitative role played by hydrodynamic interactions on these two fundamental quantities to lead to insights in the evolution of suspension stress. In particular, one can unify observations of hydrodynamic and entropic diffusion in the many types of flows described above by viewing them through the lens of microrheology.
The remainder of this paper is organized as follows: in § 2, the model system of a probe forced through an unbounded, dilute colloidal dispersion is presented, with a brief review of the relevant two-body hydrodynamic functions. A model for the interparticle force that adjusts the minimum approach distance, and thus the strength of hydrodynamic interactions between particles, is given in § 2.2. The Smoluchowski framework that governs the microstructure is derived in § 3, for both mean and fluctuating contributions, which are interpreted as an apparent microviscosity and effective probe diffusivity, respectively. Evaluation of flow-induced diffusivity requires solution of the Smoluchowski equation, governing the mean and fluctuating suspension microstructure, which evolves with probe forcing strength
$\mathit{Pe}$
and the range of interparticle repulsions
${\it\kappa}$
; these are presented in § 3.2, and the results are given in § 4. Comparison of our results to macroscopic flow-induced migration, including simple shear, sedimentation and falling-ball rheometry, is made in § 5. The study is concluded with a summary in § 6.
2 Model system
We consider a collection of
$N_{b}$
rigid, spherical, colloidal bath particles of hydrodynamic radius
$a$
dispersed homogeneously throughout a volume
$V$
of Newtonian solvent of density
${\it\rho}$
and dynamic viscosity
${\it\eta}$
. In the absence of external forces, the colloids take on an equilibrium arrangement defined by a balance of Brownian and interparticle forces,
$\boldsymbol{F}^{B}$
and
$\boldsymbol{F}^{P}$
, respectively. A constant external force
$\boldsymbol{F}^{\mathit{ext}}$
drives a ‘probe’ particle, also a rigid sphere of radius
$a$
, through the dispersion, disrupting the equilibrium configuration by setting fluid and particles into motion. The characteristic velocity
$U$
of probe motion sets the Reynolds number:
$\mathit{Re}\equiv {\it\rho}Ua/{\it\eta}\ll 1$
, so the fluid mechanics is governed by the Stokes equations. The volume fraction
${\it\phi}\equiv (4{\rm\pi}a^{3}/3)N_{b}/V\ll 1$
, and thus pair interactions, set the suspension behaviour. We adopt a relative coordinate system centred on the probe located at a position
$\boldsymbol{z}$
where at any time
$t$
a bath particle may be found at a position
$\boldsymbol{r}$
relative to the probe (figure 1). Hydrodynamic coupling during pairwise interactions set particle motion and are given by well-known pair-mobility functions, which we briefly review next.
Figure 1. The microrheology model system with tuneable interparticle interaction range.
2.1 Two-body hydrodynamics
In the absence of an ambient flow field, the translational velocity
$\boldsymbol{U}_{{\it\alpha}}$
of particle
${\it\alpha}$
in Stokes flow is a linear combination of the hydrodynamic drag forces
$\boldsymbol{F}_{{\it\beta}}^{H}$
on each particle
${\it\beta}$
in the suspension (Kim & Karrila Reference Kim and Karrila1991). The hydrodynamic mobility tensor
$\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}$
defines the strength of coupling between the velocity of particle
${\it\alpha}$
and the hydrodynamic drag on particle
${\it\beta}$
. The velocity of particle
${\it\alpha}\in \{1,2\}$
in a two-sphere geometry is
$$\begin{eqnarray}\boldsymbol{U}_{{\it\alpha}}=-\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{H}-\unicode[STIX]{x1D648}_{{\it\alpha}2}^{UF}\boldsymbol{\cdot }\boldsymbol{F}_{2}^{H}.\end{eqnarray}$$
For two identical spheres of hydrodynamic radius
$a$
, the hydrodynamic mobility tensor
$\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}$
has the tensorial form
$$\begin{eqnarray}\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}=\frac{1}{6{\rm\pi}{\it\eta}a}[x_{{\it\alpha}{\it\beta}}^{a}(r/a)\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+y_{{\it\alpha}{\it\beta}}^{a}(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})],\end{eqnarray}$$
where
$r=|\boldsymbol{r}|$
is the distance between particle centres,
$\hat{\boldsymbol{r}}=\boldsymbol{r}/r$
is the unit vector parallel to the line of centres and
$\unicode[STIX]{x1D644}$
is the second-rank identity tensor. The scalar mobility functions
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
describe the hydrodynamic coupling between particle motion and hydrodynamic drag parallel and transverse to the line of centres, respectively. The configuration geometry completely defines the hydrodynamic mobility tensors. For same-sized particles,
$\unicode[STIX]{x1D648}_{11}^{UF}=\unicode[STIX]{x1D648}_{22}^{UF}$
and
$\unicode[STIX]{x1D648}_{12}^{UF}=\unicode[STIX]{x1D648}_{21}^{UF}$
. In addition,
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
are fully characterized by the dimensionless centre-to-centre separation
$r/a$
. Methods to compute these pair mobilities in unbounded suspensions as functions of
$r/a$
are well known (Jeffrey & Onishi Reference Jeffrey and Onishi1984; Kim & Karrila Reference Kim and Karrila1991).
Relative motion arising from an external force on the probe (particle 1) is characterized by the difference between the probe self-mobility
$\unicode[STIX]{x1D648}_{11}^{UF}$
and the entrained particle mobility
$\unicode[STIX]{x1D648}_{21}^{UF}$
, which may be expressed as a linear combination of the functions
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D648}_{11}^{UF}-\unicode[STIX]{x1D648}_{21}^{UF}=\frac{1}{6{\rm\pi}{\it\eta}a}[(x_{11}^{a}(r/a)-x_{21}^{a}(r/a))\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}(r/a)-y_{21}^{a}(r/a))(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})].\end{eqnarray}$$
The same linear combinations of
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
appear in the relative translational diffusion tensor
$\unicode[STIX]{x1D63F}_{r}$
:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63F}_{r} & \equiv & \displaystyle kT(\unicode[STIX]{x1D648}_{22}^{UF}-\unicode[STIX]{x1D648}_{12}^{UF}-\unicode[STIX]{x1D648}_{21}^{UF}+\unicode[STIX]{x1D648}_{11}^{UF}),\nonumber\\ \displaystyle & = & \displaystyle 2D_{a}[(x_{11}^{a}(r/a)-x_{21}^{a}(r/a))\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}(r/a)-y_{21}^{a}(r/a))(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})],\end{eqnarray}$$
where
$D_{a}=kT/6{\rm\pi}{\it\eta}a$
is the diffusivity of a particle of radius
$a$
in pure solvent. For same-sized particles, the relative mobility in (2.3) is equivalent to the relative diffusion in (2.4): Brownian flux is simply relative motion arising from equal and opposite thermal forces on particles 1 and 2 (Batchelor Reference Batchelor1976, Reference Batchelor1982). In this work, we follow the notation of Batchelor (Reference Batchelor1982) to express relative motion and relative diffusion compactly by the scalar functions
$G(r/a)$
and
$H(r/a)$
, the couplings along and transverse to the line of centres, respectively:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}_{r}=2D_{a}[G(r/a)\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+H(r/a)(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})].\end{eqnarray}$$
Hydrodynamic drag
$\boldsymbol{F}_{{\it\beta}}^{H}$
on a particle
${\it\beta}$
in Stokes flow is exactly balanced by non-hydrodynamic forces e.g. external forces
$\boldsymbol{F}_{{\it\beta}}^{\mathit{ext}}$
, thermal/Brownian forces
$\boldsymbol{F}_{{\it\beta}}^{B}$
or interparticle forces
$\boldsymbol{F}_{{\it\beta}}^{P}$
. Interparticle forces are defined by specific interaction potentials and dictate how closely the probe and bath particle can approach one another, consequently influencing the strength of hydrodynamic interactions between them and the strength with which they entrain one another. The role of interparticle forces is discussed next.
2.2 Interparticle forces and the excluded-annulus model
The central focus of this work is to elucidate the influence hydrodynamic and entropic forces exert on force-induced diffusion. Hydrodynamic interactions cannot be adjusted independently of non-hydrodynamic forces: as interparticle entrainment strengthens, some microscale transport processes are activated while others are suppressed. For example, Brownian flux toward relatively more mobile configurations emerges in the presence of radial mobility gradients, while interparticle flux is dampened owing to weaker relative radial mobility at contact. Contributions to mean and fluctuating probe motion from each of these forces can be interrogated by adjusting the proximity with which the no-slip surfaces of the probe and bath particle can approach one another. The excluded-annulus model (Russel Reference Russel1984) facilitates the systematic tuning of hydrodynamic interaction strength by introducing a ‘contact surface’ at
$r=r_{\mathit{min}}$
, the minimum allowable separation between the probe and bath particle centres. When
$r_{\mathit{min}}\gg 2a$
, the hydrodynamic surfaces are always widely separated and hydrodynamic entrainment is negligible. In this limit, the force-induced diffusion should approach that computed by Zia & Brady (Reference Zia and Brady2010), dominated by interparticle contributions in the absence of hydrodynamic interactions. The opposite limit,
$r_{\mathit{min}}\sim 2a$
, permits no-slip surfaces to approach closely. For
$r_{\mathit{min}}/2a\rightarrow 1$
, force-induced diffusion comprises predominantly hydrodynamic and Brownian contributions.
The excluded-annulus model defines the interparticle potential as
$$\begin{eqnarray}V(r)=\left\{\begin{array}{@{}ll@{}}0,\quad & r\geqslant r_{\mathit{min}},\\ \infty ,\quad & r<r_{\mathit{min }},\end{array}\right.\end{eqnarray}$$
where
$V(r)$
is made dimensionless by the thermal energy. The interparticle force acting on a particle
${\it\beta}$
is derivable from this conservative potential,
$\boldsymbol{F}_{{\it\beta}}^{P}=-kT\,\boldsymbol{{\rm\nabla}}_{{\it\beta}}V$
, where the derivative is taken with respect to the absolute position
$\boldsymbol{x}_{{\it\beta}}$
of the particle. Additional frictional or other dissipative interparticle forces could be incorporated into this model in a straightforward manner, as done in prior studies of hydrodynamic diffusion of rough, non-colloidal spheres (Davis Reference Davis1992).
The flux of particle
${\it\beta}$
due to Brownian diffusion is identical to that generated by an equivalent ‘thermodynamic’ force
$\boldsymbol{F}_{{\it\beta}}^{B}=-kT\boldsymbol{{\rm\nabla}}_{{\it\beta}}\ln P_{2}$
(Batchelor Reference Batchelor1972). In the absence of external forces and ambient flow, the suspension adopts an equilibrium Boltzmann distribution
$P_{2}^{\mathit{eq}}(\boldsymbol{r})\sim \exp (-V(\boldsymbol{r})/kT)$
, in which interparticle and Brownian flux balance. From the interaction potential defined in (2.6), one can show that the equilibrium distribution
$P_{2}^{\mathit{eq}}$
is uniform and independent of
$\boldsymbol{z}$
and
$\boldsymbol{r}$
in all accessible configurations
$(r\geqslant r_{\mathit{min}})$
with the excluded-annulus potential.
The annular volume defined by
$r_{\mathit{min}}$
describes a region excluded from particle approach and may extend beyond the particle no-slip surface. The range of such interparticle repulsion,
$r_{\mathit{min}}=2a_{\mathit{th}}$
, can be set by e.g. surface asperities, electrostatic repulsion or grafted polymer hairs, among others, which extend particle size to a thermodynamic or steric radius
$a_{\mathit{th}}$
. The range of this repulsion dictates the degree to which hydrodynamic interactions influence particle motion and suspension rheology; for this reason, we define a dimensionless repulsion distance
${\it\kappa}$
as a measure of the strength of hydrodynamic interactions,
$$\begin{eqnarray}{\it\kappa}=\frac{a_{\mathit{th}}-a}{a}.\end{eqnarray}$$
The hard-sphere repulsion can vary as
$0\leqslant {\it\kappa}<\infty$
, corresponding to the strongest possible hydrodynamic interactions when
${\it\kappa}$
is zero and to negligibly weak hydrodynamic interactions when
${\it\kappa}\rightarrow \infty$
, i.e. for long-range repulsion. Long-range hydrodynamic interactions dampen particle motion when
${\it\kappa}\sim 1$
, and lubrication interactions become important for small excluded-annulus thicknesses
${\it\kappa}\ll 1$
.
3 Theoretical framework
In prior work by Zia & Brady (Reference Zia and Brady2010) and Hoh & Zia (Reference Hoh and Zia2015), expressions for force-induced diffusivity were developed from the perspective of probe flux. The former defined force-induced diffusion and studied it in the absence of hydrodynamic interactions; the latter examined force-induced diffusion in hydrodynamically interacting particles in the absence of Brownian motion. In this section, we create a comprehensive model that combines the physics of both studies to obtain a complete picture of force-induced diffusivity for colloidal, hydrodynamically interacting particles.
3.1 Flux- and flow-induced diffusivity
Probe motion through the dispersion distorts the mean and fluctuating microstructure, with many possible distorted arrangements. The pair-probability density
$P_{2}(\boldsymbol{z},\boldsymbol{r};t)$
represents the likelihood of any arrangement
$\{\boldsymbol{z},\boldsymbol{r}\}$
of the probe and a bath particle at time
$t$
. The particle probability flux
$\boldsymbol{j}_{{\it\alpha}}\equiv \boldsymbol{U}_{{\it\alpha}}P_{2}(\boldsymbol{z},\boldsymbol{r};t)$
describes the evolution of microstructural configuration owing to the translational motion of particle
${\it\alpha}$
. The velocity
$\boldsymbol{U}_{{\it\alpha}}$
of particle
${\it\alpha}$
is expressed in (2.1) as a linear combination of hydrodynamic drag forces on the probe and bath particle. The hydrodynamic drag
$\boldsymbol{F}_{{\it\beta}}^{H}$
must exactly balance all non-hydrodynamic forces acting on particle
${\it\beta}$
, which, in the present study, comprise Brownian, interparticle and external forces,
$\boldsymbol{F}_{{\it\beta}}^{B}$
,
$\boldsymbol{F}_{{\it\beta}}^{P}$
and
$\boldsymbol{F}_{{\it\beta}}^{\mathit{ext}}$
, respectively. Brownian and interparticle forces act on all particles in the suspension, while the external force acts only on the probe (particle 1). The external force on the probe drives the system from equilibrium by inducing net particle motion
$\boldsymbol{U}_{{\it\alpha}}$
, which advects pair density as defined by the flux
$\boldsymbol{j}_{{\it\alpha}}$
:
$$\begin{eqnarray}\boldsymbol{j}_{{\it\alpha}}=\left[\unicode[STIX]{x1D63F}_{{\it\alpha}1}\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}\right)-(\unicode[STIX]{x1D63F}_{{\it\alpha}2}-\unicode[STIX]{x1D63F}_{{\it\alpha}1})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\right]P_{2},\end{eqnarray}$$
where
$\unicode[STIX]{x1D63F}_{{\it\alpha}{\it\beta}}\equiv kT\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}$
and the operators
$\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}$
and
$\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}$
are gradients taken with respect to the relative coordinates
$\{\boldsymbol{z},\boldsymbol{r}\}$
. In (3.1), only the non-equilibrium pair probability
$P_{2}(\boldsymbol{z},\boldsymbol{r};t)$
explicitly depends on the probe position
$\boldsymbol{z}$
; all other quantities depend only on the relative geometry
$\boldsymbol{r}$
.
Mean and fluctuating motions can be interpreted as microviscosity and microdiffusivity, respectively (Zia & Brady Reference Zia and Brady2010). These contributions are easily identified upon taking the Fourier transform of the flux with respect to probe position:
$$\begin{eqnarray}\tilde{\boldsymbol{j}}_{1}=\unicode[STIX]{x1D63F}_{11}(\boldsymbol{r})\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)\tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)+(\unicode[STIX]{x1D63F}_{11}(\boldsymbol{r})-\unicode[STIX]{x1D63F}_{21}(\boldsymbol{r}))\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\tilde{P}_{2},\end{eqnarray}$$
where
$\tilde{\boldsymbol{j}}_{1}$
and
$\tilde{P_{2}}$
are the Fourier transforms of the probe flux and pair-probability density, respectively, and
$\boldsymbol{k}$
is the wave vector.
The long-time self-diffusion is determined by many encounters with bath particles, so the flux
$\tilde{\boldsymbol{j}}$
is averaged over all pair configurations:
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \,\tilde{\boldsymbol{j}}_{1}\rangle =(\boldsymbol{U}_{S}-\text{i}\boldsymbol{k}D_{a})\tilde{P}_{1}+\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)\tilde{P}_{2}\,\text{d}\boldsymbol{r}+\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\tilde{P}_{2}\,\text{d}\boldsymbol{r},\qquad & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{U}_{S}=\boldsymbol{F}^{\mathit{ext}}/6{\rm\pi}{\it\eta}a$
is the Stokes velocity of the probe through pure solvent,
$\unicode[STIX]{x1D63F}_{a}=kT/6{\rm\pi}{\it\eta}a\,\unicode[STIX]{x1D644}$
is the bare diffusivity of the probe and
$\tilde{P}_{1}(\boldsymbol{k};t)\equiv \int \tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)\,\text{d}\boldsymbol{r}$
represents the Fourier-transformed probe probability density. The first term on the right-hand side of (3.3) represents the probe flux through the solvent. The second term represents how the average presence of bath particles reduces the probe self-mobility from its motion through pure solvent, consequently altering mean and fluctuating probe trajectory. The final term represents how the interparticle and Brownian flux dissipate microstructural gradients and drive the suspension toward equilibrium. The arrangement of bath particles about the probe is necessary to evaluate these integrals. Thus, the structure function
$g_{\boldsymbol{k}}(\boldsymbol{k},\boldsymbol{r};t)$
is defined as (Zia & Brady Reference Zia and Brady2010):
$$\begin{eqnarray}\tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)\equiv n_{b}g_{\boldsymbol{k}}(\boldsymbol{k},\boldsymbol{r};t)\tilde{P}_{1}(\boldsymbol{k};t),\end{eqnarray}$$
where
$n_{b}=3{\it\phi}/(4{\rm\pi}a^{3})$
is the number density of bath particles.
The mean and fluctuating motion of the probe after many encounters with bath particles occurs over large distances and long times, corresponding to small wave vectors
$\boldsymbol{k}$
. Expansion of the structure function
$g_{\boldsymbol{k}}$
in small
$\boldsymbol{k}$
gives
$$\begin{eqnarray}g_{\boldsymbol{k}}(\boldsymbol{r},\boldsymbol{k};t)=g(\boldsymbol{r};t)+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{d}(\boldsymbol{r};t)+O(|\boldsymbol{k}|^{2}),\end{eqnarray}$$
where
$\text{i}$
is the imaginary unit. The right-hand side of (3.5) contains both the mean particle configuration,
$g(\boldsymbol{r};t)$
, which describes the likelihood of finding a bath particle at
$\boldsymbol{r}$
with which to interact, and a probability-weighted displacement, or fluctuation field,
$\boldsymbol{d}(\boldsymbol{r};t)$
which gives the strength and direction of ‘kicks’ from probe–bath interactions.
The small-
$\boldsymbol{k}$
expansion (3.5) of the structure function is substituted into (3.3) to yield the ensemble-averaged probe flux:
$$\begin{eqnarray}\displaystyle \langle \tilde{\boldsymbol{j}}_{1}\rangle & = & \displaystyle \left\{\boldsymbol{U}_{a}+n_{b}\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)g\,\text{d}\boldsymbol{r}+n_{b}\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g\,\text{d}\boldsymbol{r}\right\}\tilde{P}_{1}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}\boldsymbol{k}\boldsymbol{\cdot }\left\{\unicode[STIX]{x1D63F}_{a}+n_{b}\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left[g\unicode[STIX]{x1D644}-\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)\boldsymbol{d}\right]\text{d}\boldsymbol{r}-n_{b}\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}\,\text{d}\boldsymbol{r}\right\}\tilde{P}_{1},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D63F}_{r}$
was defined in (2.4). Note that the dot product with the wave vector
$\boldsymbol{k}$
in the above expression is performed with the second index of the term in braces. The first quantity in braces in (3.6) represents the mean motion of the probe averaged over all bath particle configurations, which we define as the effective translational velocity
$\boldsymbol{U}^{\mathit{eff}}$
:
$$\begin{eqnarray}\boldsymbol{U}^{\mathit{eff}}\equiv \boldsymbol{U}_{a}+n_{b}\left\{\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)g\,\text{d}\boldsymbol{r}+\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g\,\text{d}\boldsymbol{r}\right\}.\end{eqnarray}$$
The second term in braces in (3.6) represents the fluctuations of the probe averaged over all bath particle configurations, which we define as the effective long-time self-diffusivity
$\unicode[STIX]{x1D63F}^{\mathit{eff}}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{eff}}\equiv \unicode[STIX]{x1D63F}_{a}+n_{b}\left\{\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left[g\unicode[STIX]{x1D644}-\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)\boldsymbol{d}\right]\text{d}\boldsymbol{r}-\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}\,\text{d}\boldsymbol{r}\right\}.\end{eqnarray}$$
As expected, the effective velocity and effective long-time self-diffusivity approach their corresponding values in pure solvent,
$\boldsymbol{U}_{a}$
and
$\unicode[STIX]{x1D63F}_{a}$
, in the limit where the number density
$n_{b}$
of bath particles approaches zero. The two integrals in both the expressions for the effective translational velocity and the effective long-time self-diffusivity explicitly preserve the effects of bath particles on probe motion. The first integrals in both expressions average the hydrodynamic reduction in the probe particle self-mobility due to the nearby presence of a bath particle over all possible configurations. The second integrals in each equation describe how gradients in the microstructure and probability-weighted displacement field create an entropic restoring force, driving the dispersion back toward an equilibrium configuration.
We pause to connect theory to physical measurements. To obtain the viscosity and diffusion tensor, the only quantity which must be measured is the total displacement of the probe over time. The mean and diffusive probe motion described by (3.7) and (3.8) can be measured in experiments by tracking probe motion and, from this, one can compute the average speed as
$\langle U\rangle =\text{d}\langle x\rangle /\text{d}t$
. The average speed is then utilized to obtain the microviscosity via the relation
$$\begin{eqnarray}\frac{{\it\eta}^{\mathit{micro}}}{{\it\eta}}=\frac{6{\rm\pi}{\it\eta}a}{F^{\mathit{ext}}}\langle U\rangle ,\end{eqnarray}$$
where
$F^{\mathit{ext}}$
is a constant external force applied to the probe and
${\it\eta}^{\mathit{micro}}$
is the microviscosity (Squires & Brady Reference Squires and Brady2005; Khair & Brady Reference Khair and Brady2006). From the total and mean displacement one may then compute the microdiffusivity as
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{micro}}=\frac{1}{2}\frac{\text{d}}{\text{d}t}\langle \boldsymbol{x}^{\prime }(t)\boldsymbol{x}^{\prime }(t)\rangle ,\end{eqnarray}$$
where
$\boldsymbol{x}^{\prime }(t)\equiv \boldsymbol{x}(t)-\langle \boldsymbol{x}(t)\rangle$
is the displacement from the mean as a function of time and the angle brackets signify an average over several realizations (Zia & Brady Reference Zia and Brady2010). Detailed knowledge of the embedding material is not required.
We place our focus on the extent to which the external force changes probe diffusion; it is thus instructive to separate the effective diffusivity into equilibrium and non-equilibrium contributions. To this end, we write the microstructure
$g(\boldsymbol{r})$
and the displacement field
$\boldsymbol{d}(\boldsymbol{r})$
each in terms of the equilibrium value in the absence of external forcing,
$g^{\mathit{eq}}(\boldsymbol{r})$
and
$\boldsymbol{d}^{\mathit{eq}}(\boldsymbol{r})$
, and the departure from equilibrium arising from the external force,
$g^{\mathit{neq}}(\boldsymbol{r})$
and
$\boldsymbol{d}^{\mathit{neq}}(\boldsymbol{r})$
:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle g(\boldsymbol{r})=g^{\mathit{eq}}(\boldsymbol{r})+g^{\mathit{neq}}(\boldsymbol{r}),\\ \displaystyle \boldsymbol{d}(\boldsymbol{r})=\boldsymbol{d}^{\mathit{eq}}(\boldsymbol{r})+\boldsymbol{d}^{\mathit{neq}}(\boldsymbol{r}).\end{array}\right\}\end{eqnarray}$$
For a dilute dispersion, the equilibrium microstructure
$g^{\mathit{eq}}(\boldsymbol{r})$
is uniform and equal to unity for all separations
$r\geqslant r_{\mathit{min}}$
. From the definitions in (3.11), the effective long-time self-diffusivity
$\unicode[STIX]{x1D63F}^{\mathit{eff}}$
may be separated into equilibrium
$\unicode[STIX]{x1D63F}^{\mathit{eq}}$
and force-induced terms
$\unicode[STIX]{x1D63F}^{\mathit{flow}}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{eff}}=\unicode[STIX]{x1D63F}^{\mathit{eq}}+\unicode[STIX]{x1D63F}^{\mathit{flow}},\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{eq}}\equiv \unicode[STIX]{x1D63F}_{a}+n_{b}\left\{\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\,\text{d}\boldsymbol{r}-\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}^{\mathit{eq}}\,\text{d}\boldsymbol{r}\right\},\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{flow}}\equiv n_{b}\left\{\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left[g^{\mathit{neq}}\unicode[STIX]{x1D644}-\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)\boldsymbol{d}^{\mathit{neq}}\right]\text{d}\boldsymbol{r}-\int \frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}^{\mathit{neq}}\,\text{d}\boldsymbol{r}\right\}.\end{eqnarray}$$
Equation (3.13) shows that the equilibrium long-time self-diffusivity of the probe particle is the sum of its diffusivity in pure solvent
$\unicode[STIX]{x1D63F}_{a}$
plus two corrections arising from the bath particles: the first describes reduction in probe motion owing to the presence of the equilibrium microstructure; the second describes isotropic displacements of the probe that are entropic in origin, driving the probe to more mobile configurations. Note that the first integral contributes both to the short-time and long-time self-diffusivity of the probe particle as no configurational changes need to occur – this contribution is strictly hydrodynamic in character. The second integral contributes only to the long-time self-diffusivity as the probe and bath particle displace one another from entropically, changing the particle configuration.
Force-induced diffusion depends on both the mean and fluctuating microstructure,
$g(\boldsymbol{r})$
and
$\boldsymbol{d}(\boldsymbol{r})$
. The first term in (3.14) for the force-induced diffusivity shows that distortion of the microstructure further hinders the probe as the suspension force thickens. However, the non-equilibrium probability-weighted displacement field and its gradient enhance the diffusive spread: interactions with bath particles deflect and scatter the probe particle from its intended trajectory. The expressions governing the microstructure
$g(\boldsymbol{r})$
and probability-weighted displacement field
$\boldsymbol{d}(\boldsymbol{r})$
are presented next.
3.2 Microstructure and fluctuation field
The mean and fluctuating suspension microstructure are governed by the Smoluchowski equation, which reads, at the pair level,
$$\begin{eqnarray}\frac{\partial P_{2}(\boldsymbol{z},\boldsymbol{r};t)}{\partial t}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}\boldsymbol{\cdot }\boldsymbol{j}_{1}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }(\boldsymbol{j}_{2}-\boldsymbol{j}_{1})=0.\end{eqnarray}$$
Expressions for the probe flux vector
$\boldsymbol{j}_{1}$
and the relative flux vector
$\boldsymbol{j}_{2}-\boldsymbol{j}_{1}$
for identical spheres follow from (3.1):
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{j}_{1}=\unicode[STIX]{x1D63F}_{11}\boldsymbol{\cdot }\left[\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}P_{2}-\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}P_{2}\right]+\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}P_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{j}_{2}-\boldsymbol{j}_{1}=-\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\left[\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}P_{2}-\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}P_{2}\right]-\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}P_{2}. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D63F}_{11}=kT\unicode[STIX]{x1D648}_{11}^{UF}$
and the relative translational diffusion tensor is given by
$\unicode[STIX]{x1D63F}_{r}=2kT(\unicode[STIX]{x1D648}_{11}^{UF}-\unicode[STIX]{x1D648}_{12}^{UF})$
.
The choice of interparticle potential restricts the radial component of relative particle velocity to be outward at contact:
$\hat{\boldsymbol{r}}\boldsymbol{\cdot }(\boldsymbol{U}_{2}-\boldsymbol{U}_{1})\geqslant 0$
. Particles can approach no closer than the minimum approach distance
$r_{\mathit{min}}$
defined by the excluded annulus. Traditionally, the constraint of no overlap of the excluded annuli is enforced in the Smoluchowski framework as zero relative flux at every point of contact on the minimum approach surface. Recently, Hoh & Zia (Reference Hoh and Zia2015) showed that in the non-colloidal limit, this boundary condition must be approached with care. The naive approach of simply assuming interparticle flux can be replaced by zero hydrodynamic mobility at contact gives an apparent ‘sink’ of particle fluctuations. To resolve this apparent failure to conserve probability in the analytical solution, one must recognize that the no-flux condition requires the balancing flux of the hard-sphere force, even in the pure hydrodynamics limit, as shown by Hoh & Zia (Reference Hoh and Zia2015). In the present study of colloidal active microrheology, the finite strength of thermal forces counteracts the advective influx of bath particle density, automatically enforcing the no-flux boundary condition at
$r_{\mathit{min}}$
.
The expressions for the probe self-flux and the relative flux (3.16) are substituted into the pair Smoluchowski equation (3.15). Its Fourier transform reads
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial \tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)}{\partial t}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\left[\unicode[STIX]{x1D63F}_{11}\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)\tilde{P}_{2}+\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\tilde{P}_{2}\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }\left[\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)\tilde{P}_{2}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\tilde{P}_{2}\right]=0.\end{eqnarray}$$
Insertion of
$\tilde{P}_{2}$
(3.4) gives, at steady state and to leading order in the concentration of bath particles,
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\boldsymbol{k}\boldsymbol{\cdot }\left[(\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)g+\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }\left[\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g\right]=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }\left[\frac{1}{2}\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}-\text{i}\boldsymbol{k}\right)g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g\right]=0\quad \text{at}~r=2a, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g\rightarrow 1\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{r}\sim a,\quad \unicode[STIX]{x1D63F}_{a},\unicode[STIX]{x1D63F}_{11}\sim D_{a},\quad \unicode[STIX]{x1D63F}_{r}\sim 2D_{a},\quad \boldsymbol{F}^{\mathit{ext}}\sim F^{\mathit{ext}}.\end{eqnarray}$$
Variables and operators are henceforth dimensionless unless otherwise noted. The expansion (3.5) is inserted into (3.16); from the resulting expression the terms of order zero in the wave vector govern the steady microstructure
$g$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}g]=0\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g\rightarrow 1\quad \text{as}~r\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$Pe=F^{\mathit{ext}}/2kT/a_{\mathit{th}}$
. Alternatively, the Péclet number can be interpreted as a ratio of time scales: 
$$\begin{eqnarray}\mathit{Pe}=\frac{F^{\mathit{ext}}}{2kT/a_{\mathit{th}}}=\frac{{\it\tau}_{\mathit{diff}}}{{\it\tau}_{\mathit{adv}}},\end{eqnarray}$$
where the advective time scale
${\it\tau}_{\mathit{adv}}=a_{\mathit{th}}/U_{S}$
gives the time required for a particle of size
$a_{\mathit{th}}$
and translational velocity
$U_{S}$
to move a distance given by its thermodynamic size. The diffusive time scale
${\it\tau}_{\mathit{diff}}=a_{\mathit{th}}^{2}/2D_{a}$
gives the time over which a particle will explore an area set by its entropic size.
The terms proportional to
$\boldsymbol{k}$
govern the probability-weighted fluctuation field:
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Pe}(\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D644})\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+{\textstyle \frac{1}{2}}[\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}g+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\unicode[STIX]{x1D63F}_{r}g)]-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}]=0,\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }[-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D63F}_{r}g+Pe\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}]=0\quad \text{at}~r=2,\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{d}\rightarrow 0\quad \text{as}~r\rightarrow \infty ,\qquad & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D63F}_{11}$
is given by the mobility functions: 
$$\begin{eqnarray}\unicode[STIX]{x1D63F}_{11}=x_{11}^{a}\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+y_{11}^{a}(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}).\end{eqnarray}$$
The detailed solutions for the microstructure and the fluctuation field as a function of both
$\mathit{Pe}$
and
${\it\kappa}$
are described next.
4 Results
The theoretical framework presented in § 3 provides the methodology for computing microrheological quantities, e.g. the suspension viscosity and probe diffusion, from the mean and fluctuating suspension microstructure. The microstructural solutions are presented next in § 4.1. The effective and force-induced probe diffusion are then computed from the mean and fluctuating microstructure, and are presented in § 4.2.
4.1 The fluctuation field
The Smoluchowski equations (3.20) and (3.22) derived in the previous section govern the mean and fluctuating suspension microstructure, respectively, where steady-state behaviour develops under a competition between multiple forces: external, Brownian, interparticle and hydrodynamic. The Péclet number sets the strength of the external force and the dimensionless repulsion distance
${\it\kappa}\equiv (a_{\mathit{th}}-a)/a$
sets the strength of hydrodynamic interactions. The structure, and subsequently the rheology, exhibit parametric dependence on
${\it\kappa}$
and
$\mathit{Pe}$
. In this section, we present solutions for the fluctuating microstructure
$\boldsymbol{d}(\boldsymbol{r};\mathit{Pe},{\it\kappa})$
for asymptotically strong and weak forcing and hydrodynamics, followed by numerical solution for arbitrary
$\mathit{Pe}$
and
${\it\kappa}$
. We begin with the equilibrium case.
4.1.1 Equilibrium fluctuations:
$\mathit{Pe}\equiv 0$
A balance of interparticle and thermal forces in the absence of external forcing
$(\mathit{Pe}\equiv 0)$
defines the equilibrium microstructure. For dilute dispersions interacting via an excluded-annulus interparticle potential, the equilibrium mean microstructure is uniform for all accessible configurations, i.e.
$g^{\mathit{eq}}(r\geqslant 2)=1$
. The equation governing fluctuations in the equilibrium microstructure
$\boldsymbol{d}^{\mathit{eq}}(\boldsymbol{r})$
follows from substituting
$\mathit{Pe}=0$
and
$g=g^{\mathit{eq}}=1$
into the Smoluchowski equation (3.22).
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{d}^{\mathit{eq}}]={\textstyle \frac{1}{2}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }[-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D63F}_{r}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{d}^{\mathit{eq}}]=0\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{d}^{\mathit{eq}}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$\boldsymbol{r}$
; thus the equilibrium fluctuation field has the form
$\boldsymbol{d}^{\mathit{eq}}=d_{0}(r)\hat{\boldsymbol{r}}$
. The ordinary differential equation for
$d_{0}(r)$
is as follows: 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G(s)\frac{\text{d}d_{0}}{\text{d}r}\right]-2H(s)d_{0}=+\frac{1}{2}r^{2}W(s), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}d_{0}}{\text{d}r}=+\frac{1}{2}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{0}\rightarrow 0\quad \text{as}~r\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$G$
,
$H$
and
$W$
are functions of the hydrodynamic centre-to-centre separation
$s\equiv (1+{\it\kappa})r$
, and we have introduced the definition 
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}\equiv W(s)\hat{\boldsymbol{r}}=\left[{\displaystyle \frac{2}{r}}(G(s)-H(s))+\frac{\text{d}G}{\text{d}r}\right]\hat{\boldsymbol{r}}\end{eqnarray}$$
for the divergence of the relative mobility. With the substitution
$d_{0}(r)=-f_{1}(r)/2$
into (4.1a
), the system governing the linear-response perturbation to the steady microstructure
$f_{1}(r)$
is identically recovered (cf. Khair & Brady (Reference Khair and Brady2006) equations (4.8a–c)). Thus, for a given excluded-annulus thickness
${\it\kappa}$
, the
$O(1)$
displacement field
$d_{0}(r)$
is everywhere equal to the first perturbation to the suspension microstructure
$f_{1}(r)$
scaled by
$-1/2$
.
We note that
$d_{0}(r)$
is everywhere negative, and thus fluctuations induced by the equilibrium microstructure entropically hinder probe diffusion, regardless of the strength of hydrodynamic interactions. This can be understood as follows. Equilibrium probe fluctuations
$\boldsymbol{d}^{\mathit{eq}}(\boldsymbol{r})=\hat{\boldsymbol{r}}d_{0}(r)$
are directed along the line of centres with a bath particle. Positive and negative values of
$d_{0}(r)$
correspond to entropically enhanced and hindered diffusion, respectively: the sign denotes whether fluctuations tend to scatter the particle outward from its current location (positive
$d_{0}$
) or push the probe position back toward the origin (negative
$d_{0}$
). The equilibrium fluctuation field is proportional to the negative of the linear-response distortion from equilibrium,
$d_{0}(r)=-f_{1}(r)/2$
(a finding we will utilize to show that the microrheology model generalizes the Stokes–Einstein relation in § 4.2.1). The linear-response distortion from equilibrium
$f_{1}(r)$
is everywhere positive, indicating that bath particle accumulation and depletion at weak forcing occur upstream and downstream of the probe, respectively. Thus, equilibrium fluctuations from probe–bath interactions are restoring in nature. A bath particle centred at
$\boldsymbol{r}$
will ‘kick’ the probe entropically away from it, hindering the random walk of the probe. Such inward kicks arise both via hard-sphere repulsion at the minimum approach distance and via deterministic Brownian drift to separate particles along their line of centres. Details given in appendix A show that the magnitude of equilibrium fluctuations,
$d_{0}(r)$
, decreases for all values of
$r$
as no-slip surfaces are permitted to approach each other more closely (or, equivalently, as the repulsion range
${\it\kappa}$
setting entropic size decreases). With a weakening fluctuation field, entropic hindrance lessens, corresponding to a smaller disparity between the short- and long-time self-diffusion when hydrodynamic interactions are strong.
4.1.2 Fluctuations at weak forcing:
$\mathit{Pe}\ll 1$
In the limit of weak external forcing,
$\mathit{Pe}\ll 1$
, thermal agitation easily dissipates disturbances created by the translating probe, and the distortion to the equilibrium microstructure is weak, suitable for expansion of the microstructure and deflection field in
$\mathit{Pe}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle g_{0}(\boldsymbol{r};\mathit{Pe}\ll 1)=1+\mathit{Pe}\,\hat{\boldsymbol{F}}\boldsymbol{\cdot }\hat{\boldsymbol{r}}f_{1}(r)+\mathit{Pe}^{2}\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }[\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}f_{2}(r)+\unicode[STIX]{x1D644}\,h_{2}(r)]+\cdots , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{d}(\boldsymbol{r};\mathit{Pe}\ll 1) & = & \displaystyle \hat{\boldsymbol{r}}d_{0}(r)+\mathit{Pe}\,\hat{\boldsymbol{F}}\boldsymbol{\cdot }[\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}d_{1}(r)+\unicode[STIX]{x1D644}\,c_{1}(r)]\nonumber\\ \displaystyle & & \displaystyle +\,\mathit{Pe}^{2}\,\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }[\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\,d_{2}(r)+\hat{\boldsymbol{r}}\unicode[STIX]{x1D644}\,2c_{2}(r)+\unicode[STIX]{x1D644}\hat{\boldsymbol{r}}\,b_{2}(r)]+\cdots .\end{eqnarray}$$
These expressions are substituted into the Smoluchowski equation governing the microstructure (3.20) and the fluctuation field (3.22). A coupled system of equations for the radial functions
$f_{1}(r),f_{2}(r)$
, etc. is obtained by matching orders of
$\mathit{Pe}$
and Legendre polynomials. The details of this system of equations, the numerical solution method and results for the radial functions are given in appendix A. At
$O(\mathit{Pe})$
, the non-equilibrium fluctuation field is monopolar and quadrupolar. Dipole character in the fluctuation field is required for entropic diffusion: net fluctuations oriented toward or away from
$\boldsymbol{z}$
result in entropic hindrance or enhancement, respectively. Thus, the contributions
$d_{1}(r)$
and
$c_{1}(r)$
to the fluctuation field do not result in entropic diffusion. However, as will be shown in § 4.2.2, the
$O(\mathit{Pe})$
fluctuation field contributes to hydrodynamic diffusion.
The
$O(\mathit{Pe})$
fluctuation field suggests the first signs of anisotropy. The projection of the fluctuation field along the line of forcing, the longitudinal fluctuation field,
$d^{\Vert }(\boldsymbol{r})$
is:
$$\begin{eqnarray}d^{\Vert }(\boldsymbol{r})=d_{0}(r)\cos {\it\theta}+\mathit{Pe}[d_{1}(r)\cos ^{2}{\it\theta}+c_{1}(r)]+O(\mathit{Pe}^{2}).\end{eqnarray}$$
The transverse fluctuation field
$d^{\bot }(\boldsymbol{r})$
is the projection of the fluctuation field normal to the line of forcing, modulo the azimuthal dependence. That is,
$\boldsymbol{d}\boldsymbol{\cdot }\boldsymbol{e}_{x}=d^{\bot }(\boldsymbol{r})\cos {\it\varphi}$
and
$\boldsymbol{d}\boldsymbol{\cdot }\boldsymbol{e}_{y}=d^{\bot }(\boldsymbol{r})\sin {\it\varphi}$
, where
${\it\varphi}$
is the azimuthal angle measured from the positive
$x$
-axis toward the positive
$y$
-axis. Through
$O(\mathit{Pe})$
, the transverse fluctuation field is:
$$\begin{eqnarray}d^{\bot }(\boldsymbol{r})=d_{0}(r)\sin {\it\theta}+\mathit{Pe}[d_{1}(r)\cos {\it\theta}\sin {\it\theta}]+O(\mathit{Pe}^{2}).\end{eqnarray}$$
Inspection of
$d^{\Vert }(\boldsymbol{r})$
and
$d^{\bot }(\boldsymbol{r})$
reveals that the perturbation function
$c_{1}(r)$
contributes only to longitudinal fluctuations, while the perturbation function
$d_{1}(r)$
contributes equally to both projections. This disparity will be shown to lead to anisotropy in the force-induced diffusion in § 4.2.2.
The expansion of the fluctuation field becomes singular at
$O(\mathit{Pe}^{2})$
. Thus, (4.5) must be matched to an outer solution at radial distances
${\it\rho}\equiv \mathit{Pe}\,r=O(1)$
where advection still matters. The details are given in appendix A, where it is shown that the outer solution does not contribute to flow-induced diffusion until
$O(\mathit{Pe}^{4})$
. We will show in § 4.2.2 that
$d_{2}(r)$
,
$c_{2}(r)$
and
$b_{2}(r)$
of the inner solution dominate the entropic (thermal and interparticle) contributions to force-induced diffusion. We briefly look ahead to the effect of these functions on the diffusion. The flow-induced fluctuations that contribute entropically (via interparticle and thermal forces) to probe diffusion occur at
$O(\mathit{Pe}^{2})$
. Like the equilibrium fluctuation field, positive and negative values of
$d_{2}(r)$
,
$c_{2}(r)$
and
$b_{2}(r)$
would correspond to entropic diffusion enhancement and hindrance, respectively. In appendix A, the perturbation function
$c_{2}(r)$
is shown to contribute only to longitudinal probe diffusion, while the functions
$b_{2}(r)$
and
$d_{2}(r)$
contribute to probe diffusion in all directions. The
$O(\mathit{Pe}^{2})$
perturbation functions
$c_{2}(r)$
and
$b_{2}(r)$
are everywhere positive and enhance probe diffusion at
$O(\mathit{Pe}^{2})$
. In addition, the functions
$b_{2}(r)$
and
$c_{2}(r)$
are very similar, but not identical to one another. Because
$c_{2}(r)$
is weighted by a factor of 2 in the perturbation expansion for the fluctuation field, the ratio of longitudinal to transverse entropic probe diffusion should be approximately 3 : 1 by inspection of the perturbation expansion. This 3 : 1 ratio is evident in figure 4, where the green triangles and the blue diamonds represent the entropic contributions to flow-induced diffusion at
$O(\mathit{Pe}^{2})$
. The sum of the entropic contributions reflects this approximate 3 : 1 ratio between longitudinal and transverse probe diffusion.
To summarize, the weakly nonlinear fluctuation fields exhibit anisotropy at
$O(\mathit{Pe})$
, the first deviation from the equilibrium fluctuation field (and thus we expect flow-induced diffusion to be anisotropic), and becomes singular at
$O(\mathit{Pe}^{2})$
. The outer solution contributes to force-induced diffusion which scales as
$\mathit{Pe}^{4}$
, so only the inner solution is needed.
4.1.3 Fluctuations in the ‘pure hydrodynamic’ limit:
$\mathit{Pe}^{-1}=0,{\it\kappa}=0$
The infinite-
$\mathit{Pe}$
limit,
$Pe^{-1}\equiv 0$
, distinct from
$Pe\gg 1$
, was studied by Hoh & Zia (Reference Hoh and Zia2015), who found that in the absence of any Brownian motion or particle roughness, longitudinal fluctuations are enhanced by flow. The key aspects of the study relevant to the present investigation are summarized here. In this limit, Brownian motion is absent and the particles are smooth, so the microstructure is governed by advection alone. As shown by Batchelor (Reference Batchelor1982), the solution for the mean microstructure
$g(\boldsymbol{r})$
is spherically symmetric. The relative radial mobility governs the slowdown of bath particles relative to the probe as they approach; the slower dynamics manifest microstructurally as relative accumulation of bath particles. Batchelor’s solution is written here in terms of the relative mobility functions
$G$
and
$H$
:
$$\begin{eqnarray}g(r)=\frac{1}{G(r)}\exp \left[\int _{r}^{\infty }\frac{2}{{\it\xi}}\left(1-\frac{H({\it\xi})}{G({\it\xi})}\right)\text{d}{\it\xi}\right].\end{eqnarray}$$
The spherically symmetric microstructure gives the microviscosity as
$$\begin{eqnarray}{\it\eta}_{i}^{H}=-\int _{2}^{\infty }g({\it\xi})[x_{11}^{a}({\it\xi})+2y_{11}^{a}({\it\xi})-3]{\it\xi}^{2}\,\text{d}{\it\xi},\end{eqnarray}$$
which is Newtonian and, for same-sized probe and bath particles, is equal to 2.52.
This limit was approached from the colloidal framework (Hoh & Zia Reference Hoh and Zia2015) by letting
$\mathit{Pe}$
grow large, permitting formation of a diffusive boundary layer at contact that shrinks as
$\mathit{Pe}^{-1}$
, during which the microviscosity force thickens to this limiting infinite-
$\mathit{Pe}$
Newtonian plateau (Khair & Brady Reference Khair and Brady2006). This plateau is not reached as long as the boundary layer persists, i.e. microstructural asymmetry is required for non-Newtonian rheology. Khair & Brady (Reference Khair and Brady2006) found that particle density in the diffusive boundary layer scales as
$\mathit{Pe}^{0.799}$
, giving force thickening as
${\it\eta}_{i}=A-B\mathit{Pe}^{-0.201}$
, and showing that Batchelor’s ‘outer’ solution fully defines the infinite-
$\mathit{Pe}$
Newtonian plateau, while the extent of force thickening is governed by the ‘inner’ solution. A naive first approach for force-induced diffusion in the
$\mathit{Pe}\gg 1$
limit for hydrodynamically interacting particles would follow their approach and determine the corresponding ‘outer’ and ‘inner’ solutions for the fluctuation field.
Taking such an approach to the
$\mathit{Pe}\gg 1$
limit for microstructural fluctuations, Hoh & Zia (Reference Hoh and Zia2015) determined the longitudinal and transverse fluctuation fields as governed by advection alone. The transverse fluctuation field is a single spherical harmonic,
$$\begin{eqnarray}d^{\bot }(\boldsymbol{r})=d_{1}^{\bot }(r)P_{1}^{1}(\cos {\it\theta}),\end{eqnarray}$$
where
$P_{n}^{m}(\cos {\it\theta})$
is the associated Legendre polynomial with argument
$\cos {\it\theta}$
of degree
$n$
and order
$m$
. The longitudinal fluctuation field comprises an infinitude of odd Legendre polynomial modes:
$$\begin{eqnarray}d^{\Vert }(\boldsymbol{r})=\mathop{\sum }_{n\,\mathit{odd}}d_{n}^{\Vert }(r)P_{n}(\cos {\it\theta}),\end{eqnarray}$$
where
$P_{n}(\cos {\it\theta})$
is the Legendre polynomial with argument
$\cos {\it\theta}$
of degree
$n$
. The radial dependence of the degree-one spherical harmonics gives for longitudinal fluctuations (Hoh & Zia Reference Hoh and Zia2015):
$$\begin{eqnarray}d_{1}^{\Vert }(r)=\left(\frac{2}{r}\right)^{2}\frac{1}{L(r)}\int _{r}^{\infty }\left(\frac{z}{2}\right)^{2}[x_{11}^{a}(z)+2y_{11}^{a}(z)-3]g(z)\,\text{d}z,\end{eqnarray}$$
and for transverse fluctuations,
$$\begin{eqnarray}d_{1}^{\bot }(r)=\left(\frac{r}{2}\right)g(r)\sqrt{g(r)L(r)}\int _{r}^{\infty }\left(\frac{2}{z}\right)\frac{x_{11}^{a}(z)-y_{11}^{a}(z)}{L(z)\sqrt{g(z)L(z)}}\,\text{d}z.\end{eqnarray}$$
Unlike the mean microstructure, the longitudinal fluctuations in (4.12) cannot be matched to leading order to the inner solution governed by a balance of advection and radial diffusion. The naive approach predicts zero longitudinal and transverse flow-induced diffusion even in the limit
$\mathit{Pe}^{-1}\equiv 0$
. This apparent paradox is resolved by careful enforcement of the no-flux boundary condition, recognizing that non-hydrodynamic forces, including the rigidity of the probe and entropic forces, must be accounted for in this analytical model, both playing a role even in the pure hydrodynamic limit (Hoh & Zia Reference Hoh and Zia2015). Doing so properly captures fluctuations in the pure hydrodynamic limit, which are enhanced by flow, recovering precisely the theoretical results of Davis & Hill (Reference Davis and Hill1992) for macroscopic falling-ball rheometry, and the matching experimental observations of Abbott et al. (Reference Abbott, Graham, Mondy and Brenner1998).
The transition of longitudinal probe diffusion from hindered to enhanced evidently takes place at some strength of forcing and strength of hydrodynamic interactions between the two asymptotic limits studied thus far, and requires numerical study of the intervening, finite-
$\mathit{Pe}$
region.
4.1.4 Arbitrary strength of forcing and hydrodynamic interactions
We now turn our attention to the evolution of the fluctuation field under arbitrary strength of forcing and hydrodynamic interactions, via numerical solution of the Smoluchowski equation utilizing a second-order finite difference scheme (details are given in appendix B). Of particular interest is the region of reversal from hindrance (in the linear-response regime) to enhancement (for stronger forcing). A sweep across
$\mathit{Pe}$
and
${\it\kappa}$
will reveal when – and why – diffusive fluctuations in probe motion transition from hindering to enhancing as probe forcing grows, and how it depends on the range of interparticle repulsion.
Contour plots for the longitudinal and transverse fluctuation fields are shown in figure 2. At equilibrium
$(\mathit{Pe}=0)$
, fluctuations are dipolar, where both longitudinal and transverse fluctuations push inward. This equilibrium dipole dominates the fluctuation field when external forcing is present but weak because the first non-equilibrium fluctuations (monopolar and quadrupolar) are
$O(Pe)$
weaker. The transition from entropically hindering fluctuations to enhancing fluctuations occurs at
$\mathit{Pe}\sim 1$
. This is visually evident in the contour plots in panel (a) for
$Pe=1$
, where regions that were red (blue) for
$Pe<1$
are now blue (red); that is, the fluctuation field changes sign, indicating when fluctuations are oriented inward (hindering) or outward (entropically enhancing). As forcing grows stronger, moving to the right in each row of each panel, a boundary layer and wake structure emerge, indicating that the strongest deflections occur due to interactions very near the probe. In panel (a), fore–aft asymmetry of longitudinal fluctuations becomes quite pronounced for strong forcing, with the strongest kicks from the upstream face of the probe. In panel (b), deflections mirrored across the line of external force are equal in magnitude but opposite in sign. For
$Pe\leqslant 1$
, these red and blue regions indicate that a transverse kick always tends to push the probe back toward the line of forcing, hindering scattering. The reversal from hindered to enhanced deflections is evident by
$Pe=5$
, where red and blue have switched sides, and deflections always tend to scatter the probe off its mean path.
Figure 2. Contour plots of the fluctuation field around a (black) excluded volume for probe driven to the right, with fluctuations (a) along and (b) transverse to the line of the external force for a range of
$Pe$
and strength of hydrodynamics
${\it\kappa}$
. The colour scheme for the
$Pe=0$
column indicates equivalent probability of a kick in the positive or negative direction. For
$Pe\neq 0$
, the colour scheme is as follows: In (a), red regions correspond to high probability of a strong kick that scatters the probe; blue corresponds to weak kicks of low probability. In (b), for
$Pe\neq 0$
, red indicates high probability of strong kicks in the positive
$y$
direction; blue indicates high probability of strong kicks in the negative
$y$
direction; i.e. the depth of colour indicates the strength of a transverse kick away from the line of probe forcing.
The strength of hydrodynamic interactions also exerts a ‘direct’ influence on the fluctuation field, particularly as the external force grows. Three values of
${\it\kappa}$
are shown in the three rows in each of panels (a) and (b) in figure 2; moving down any given column shows that stronger hydrodynamic interactions lead to a wider, more diffuse boundary layer structure which remains attached to the probe farther along its downstream face. This behaviour owes its origin to the monotonic decrease of the relative mobility functions
$G$
and
$H$
with decreasing surface separation
$r$
, which illustrates that hydrodynamic coupling slows relative particle motion. For a given value of
$Pe$
, these slower dynamics weaken the accumulation of structure, as well as its fluctuations, and impede probe–bath particle separation on the downstream face of the probe, narrowing the wake structure as hydrodynamic interactions grow stronger. However, this direct effect of apparent reduced relative mobility is not the full picture.
Hydrodynamic interactions provide a mechanism for particle scattering – distinct from entropic scattering. As the probe hydrodynamically entrains bath particles, its motion slows compared to its Stokes velocity
$U_{S}$
through pure solvent. The duration of time over which the probe entrains a bath particle depends on how closely the two can approach one another – which is set by the range of interparticle repulsion,
${\it\kappa}$
. In consequence, probe velocity fluctuates as the probe moves comparatively fast through pure solvent pockets and more slowly when towing a nearby bath particle along. We note that the entrainment trajectory perspective reveals a key aspect of hydrodynamically induced fluctuations: it accompanies spherically symmetric microstructure. Hiding in the mean and fluctuation microstructure, at any value of
$Pe$
and
${\it\kappa}$
, is a spherically symmetric microstructure, as one of many harmonics. The strength of this harmonic dictates the strength of hydrodynamic scattering. That hydrodynamic deflection can arise from spherically symmetric structure stands in stark contrast to entropically enhanced deflections, which are induced by dipolar – asymmetric – structure.
To summarize, at weak forcing, the longitudinal and transverse fluctuation fields are qualitatively and quantitatively similar for all strengths
${\it\kappa}$
of hydrodynamic interactions, where an
$O(1)$
equilibrium diffusive dipole dominates the fluctuation field; in the next section it will be shown that this acts to entropically hinder probe diffusion. As the strength of external forcing
$\mathit{Pe}$
increases, the upstream fluctuations compress into a boundary layer region, while downstream, fluctuations extend into a wake. When no-slip surfaces are able to approach one another closely,
${\it\kappa}\ll 1$
, a stronger external force is required to compress the boundary layer. This is a direct consequence of lubrication interactions slowing particle dynamics, and more energy is required to squeeze the fluid out between the probe and a bath particle in the upstream compression region. In addition, the dipole moment of the fluctuation field changes sign with increasing
$\mathit{Pe}$
for all strengths
${\it\kappa}$
of hydrodynamic interaction. We will see that the sign of the dipole moment is indicative of whether probe diffusion is entropically hindered or enhanced relative to Brownian diffusion through pure solvent. However, we will also see that hydrodynamic diffusion is the dominant mechanism for force-induced diffusion at large
$\mathit{Pe}$
and small
${\it\kappa}$
. Predicting whether hydrodynamic diffusion is hindered or enhanced is not easily inferred from a qualitative examination of the fluctuation field: as discussed above, multiple spherical harmonics contribute directly (the presence of bath particles induces velocity fluctuations from
$\boldsymbol{U}_{S}$
) and indirectly (hydrodynamic force thickening of the apparent microviscosity implies a reduction in short-time self-diffusion). A clearer picture of hydrodynamic diffusion is obtained when all contributions to
$\unicode[STIX]{x1D63F}^{\mathit{flow}}$
are computed and examined as functions of forcing strength and hydrodynamic interactions, which is taken up in the next section.
4.2 Effective probe diffusion
Having established the mean and fluctuating suspension microstructure, here we compute the effective and force-induced probe diffusion, as they vary with the strength of hydrodynamic interactions
${\it\kappa}$
and the strength of the external force
$\mathit{Pe}$
. The results are separated into four sections: equilibrium diffusion, weakly nonlinear diffusion, hydrodynamic diffusion in the infinite-
$Pe$
limit and diffusion over a sweep through arbitrary strengths of forcing and hydrodynamic interactions.
4.2.1 Equilibrium diffusion and the Stokes–Einstein relation
The contributions of bath particles to the equilibrium long-time self-diffusivity, given by (3.13), can be divided into hydrodynamic, Brownian and interparticle contributions, as follows:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{eq}}=\unicode[STIX]{x1D63F}_{a}+\unicode[STIX]{x1D63F}^{\mathit{eq},H}+\unicode[STIX]{x1D63F}^{\mathit{eq},B}+\unicode[STIX]{x1D63F}^{\mathit{eq},P},\end{eqnarray}$$
where each contribution (in dimensional form) is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{eq},H}=D^{\mathit{eq},H}\unicode[STIX]{x1D644}=n_{b}\int _{r\geqslant r_{\mathit{min}}}(\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\,\text{d}\boldsymbol{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{eq},B}=D^{\mathit{eq},B}\unicode[STIX]{x1D644}=n_{b}\int _{r\geqslant r_{\mathit{min}}}\frac{1}{2}\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}\boldsymbol{d}^{\mathit{eq}}\,\text{d}\boldsymbol{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{eq},P}=D^{\mathit{eq},P}\unicode[STIX]{x1D644}=n_{b}\oint _{r=r_{\mathit{min}}}\frac{1}{2}\hat{\boldsymbol{r}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}\boldsymbol{d}^{\mathit{eq}}\,\text{d}\boldsymbol{r}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D^{\mathit{eq},H}=D_{a}{\it\phi}_{\mathit{th}}\int _{2}^{\infty }(x_{11}^{a}(s)+2y_{11}^{a}(s)-3)r^{2}\,\text{d}r, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D^{\mathit{eq},B}=D_{a}{\it\phi}_{\mathit{th}}\int _{2}^{\infty }W(s)d_{0}(r)r^{2}\,\text{d}r, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D^{\mathit{eq},P}=D_{a}{\it\phi}_{\mathit{th}}4G(r=2)d_{0}(2). & \displaystyle\end{eqnarray}$$
$G(r=2)$
in (4.16) is the relative mobility function evaluated at thermodynamic contact (i.e. at
$r=2$
, corresponding to a dimensionless separation
$s=2(1+{\it\kappa})$
), and describes how readily interparticle forces induce relative motion of two particles in thermodynamic contact. For a thin excluded annulus
$({\it\kappa}\ll 1)$
, the relative radial mobility
$G$
vanishes linearly as the surface separation
${\it\kappa}$
when the thermodynamic and hydrodynamic radii are coincident.
Figure 3. (a) Bath particle contributions to the equilibrium long-time self-diffusivity
$\unicode[STIX]{x1D63F}^{\mathit{eq}}=(D_{a}+D^{\mathit{eq},H}+D^{\mathit{eq},B}+D^{\mathit{eq},P})\unicode[STIX]{x1D644}$
as a function of the excluded-annulus thickness
${\it\kappa}$
as computed in this work from (4.16). (b) The
$O({\it\phi}_{\mathit{th}})$
intrinsic microviscosity in the limit
$\mathit{Pe}\rightarrow 0$
((b) only, from Khair & Brady (Reference Khair and Brady2006), with permission).
The hydrodynamic, Brownian and interparticle contributions to the equilibrium long-time self-diffusivity are plotted in figure 3(a). All three are negative for all
${\it\kappa}$
, indicating that the equilibrium distribution of bath particles always hinders probe diffusion. As hydrodynamic interactions become weak (
${\it\kappa}\rightarrow \infty$
), hindrance of long-time self-diffusion is entropic, arising from collisions at the thermodynamic surface. In this limit, the diffusivity approaches
$D_{a}(1-2{\it\phi}_{\mathit{th}})$
, recovering the entropic hindrance of a particle diffusing in a dilute dispersion in the absence of hydrodynamic interactions (Batchelor Reference Batchelor1976; Zia & Brady Reference Zia and Brady2010). As the strength of hydrodynamic interactions grows (
${\it\kappa}$
decreases), the interparticle contributions weaken as the relative motion during collisions weakens. This reduced self-mobility, combined with Brownian flux toward less hindered configurations, causes the hydrodynamic and Brownian contributions to grow with decreasing
${\it\kappa}$
. The total hindrance approaches a local minimum for an excluded-annulus thickness
${\it\kappa}\approx 0.6$
. Particles could thus be designed to diffuse maximally at a given volume fraction
${\it\phi}_{\mathit{th}}$
, by setting a range of interparticle repulsion of the order of a particle radius. As lubrication interactions become important, the total hindrance again increases, reaching a limiting value of
$D_{a}(1-2.1{\it\phi}_{\mathit{th}})$
consistent with passive diffusion in hydrodynamically interacting suspensions (Batchelor Reference Batchelor1976; Rallison & Hinch Reference Rallison and Hinch1986).
A comparison between the
$O({\it\phi})$
reduction in the equilibrium probe diffusion and the corresponding increase in the
$\mathit{Pe}\rightarrow 0$
microviscosity reveals that the Stokes–Einstein equation is valid in suspensions – not just continuum solvents – when measured via single-particle motion:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\mathit{eq}}=\frac{kT}{6{\rm\pi}{\it\eta}(1+{\it\eta}_{i}^{0}{\it\phi}_{\mathit{th}})a}\unicode[STIX]{x1D644}+O({\it\phi}_{\mathit{th}}^{2}).\end{eqnarray}$$
This is shown graphically in figures 3(a) and 3(b), the latter showing the
$O({\it\phi}_{\mathit{th}})$
microviscosity (Khair & Brady Reference Khair and Brady2006). The two data sets match identically such that plotting them together would overlay the curves exactly on one another. This agreement gives the precise connection of fluctuation and dissipation that cannot be achieved in the corresponding limit of shear flow, where the Einstein correction
${\it\eta}(1+5/2{\it\phi})$
does not capture the diffusive motion of a single particle but rather the response of the suspension as a continuum to a bulk shearing flow. Near equilibrium, whether a particle moves in response to an instantaneous stochastic or deterministic force, the resultant impulse is dissipated in identical fashion by the equilibrium suspension microstructure.
In summary, the equilibrium microstructure always hinders probe diffusion. The extent of hindrance varies non-monotonically with the range of interparticle repulsion (the strength of hydrodynamic interactions)
${\it\kappa}$
. With long-range repulsion,
${\it\kappa}\rightarrow \infty$
the hindrance is purely entropic: collisions at the thermodynamic radii result in fluctuations oriented radially inward, driving the probe toward the origin
$\boldsymbol{z}$
. When the excluded annulus is thin and configurations with nearly touching hydrodynamic surfaces are permitted, Brownian drift down mobility gradients replaces collision scattering. This drift is a weaker source of hindrance than interparticle collisions; thus entropic hindrance is weaker. However, direct hydrodynamic hindrance emerges, further reducing both the short- and long-time self-diffusion of the probe.
4.2.2 Weak forcing: the first effect of flow
The flow-induced self-diffusivity
$\unicode[STIX]{x1D63F}^{\mathit{flow}}$
given by (3.14) can be separated into hydrodynamic, Brownian and interparticle contributions as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{flow},H}=n_{b}\int (\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a})\boldsymbol{\cdot }\left[g^{\mathit{neq}}\unicode[STIX]{x1D644}-\left(\frac{\boldsymbol{F}^{\mathit{ext}}}{kT}\right)\boldsymbol{d}^{\mathit{neq}}\right]\text{d}\boldsymbol{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{flow},B}=n_{b}\int _{r\geqslant r_{\mathit{min}}}\frac{1}{2}\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}\boldsymbol{d}^{\mathit{neq}}\,\text{d}\boldsymbol{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\mathit{flow},P}=n_{b}\oint _{r=r_{\mathit{min}}}\frac{1}{2}\hat{\boldsymbol{r}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}\boldsymbol{d}^{\mathit{neq}}\,\text{d}\boldsymbol{r}. & \displaystyle\end{eqnarray}$$
$Pe$
grows, owing to monotonic force thickening of viscosity with
$Pe$
(Khair & Brady Reference Khair and Brady2006). Insertion of (4.4) into (4.18a
) shows that this is a weakly nonlinear effect: 
$$\begin{eqnarray}\displaystyle & & \displaystyle D_{a}{\it\phi}_{\mathit{th}}\mathit{Pe}^{2}\int _{r\geqslant 2}\left\{\left[\frac{1}{5}(3x_{11}^{a}+2y_{11}^{a}-5)f_{2}(r)+(x_{11}^{a}+2y_{11}^{a}-3)h_{2}(r)\right]\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\left[\frac{1}{5}(x_{11}^{a}+4y_{11}^{a}-5)f_{2}(r)+(x_{11}^{a}+2y_{11}^{a}-3)h_{2}(r)\right](\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})\right\}r^{2}\,\text{d}r.\end{eqnarray}$$
This expression confirms that the mean microstructure serves only to reduce probe diffusion, regardless of the strength of hydrodynamic interactions, when forcing is weak. A discussion of the detailed contributions of the structure functions
$f_{2}(r)$
and
$h_{2}(r)$
is given in appendix A.
The second contribution in (4.18a
) to flow-induced diffusion arises from non-equilibrium fluctuations,
$\boldsymbol{d}^{\mathit{neq}}$
. Insertion of the small-
$\mathit{Pe}$
fluctuation field (4.5) into (4.18a
) gives the leading-order direct effect of hydrodynamics at weak forcing:
$$\begin{eqnarray}\displaystyle & & \displaystyle -2D_{a}{\it\phi}_{\mathit{th}}\mathit{Pe}^{2}\int _{r\geqslant 2}\left\{\left[\frac{1}{5}(3x_{11}^{a}+2y_{11}^{a}-5)d_{1}(r)+(x_{11}^{a}+2y_{11}^{a}-3)c_{1}(r)\right]\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\left[\frac{1}{5}(x_{11}^{a}-y_{11}^{a})d_{1}(r)\right](\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})\right\}r^{2}\,\text{d}r.\end{eqnarray}$$
Evaluation of the coefficients in expression (4.20) reveals two important facts: first, it produces strongly anisotropic diffusion, and second, fluctuations hinder diffusion for all strengths of hydrodynamics when forcing is weak. A detailed discussion of the contribution of the coefficients
$c_{1}$
and
$d_{1}$
is given in the appendix A.
The Brownian contribution to the diffusivity, (4.18b
), owes its origin to the configuration-dependent mobility function that drives preferential drift toward relatively more mobile particle arrangements. Insertion of the small-
$\mathit{Pe}$
fluctuation field (4.5) into (4.18b
) gives the leading-order Brownian contribution to flow-induced diffusion at weak forcing:
$$\begin{eqnarray}\displaystyle & \displaystyle D_{a}{\it\phi}_{\mathit{th}}\mathit{Pe}^{2}\!\!\int _{r\geqslant 2}r^{2}W(r)\!\left[\left(\frac{3}{5}d_{2}(r)+2c_{2}(r)+b_{2}(r)\!\right)\!\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}+\left(\frac{1}{5}d_{2}(r)+b_{2}(r)\!\right)\!(\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})\right]\!\text{d}r. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In contrast to the hydrodynamic contribution, non-equilibrium Brownian forces enhance diffusion, regardless of the strength of hydrodynamic interactions.
The interparticle contribution, (4.18c
), arises due to collisions with the non-equilibrium arrangement of bath particles that scatter the probe. Insertion of the small-
$\mathit{Pe}$
fluctuation field (4.5) into (4.18c
) gives the leading-order interparticle contribution to flow-induced diffusion for weak external forcing:
$$\begin{eqnarray}\displaystyle & \displaystyle 4D_{a}{\it\phi}_{\mathit{th}}\mathit{Pe}^{2}G({\it\kappa})[({\textstyle \frac{3}{5}}d_{2}(2)+2c_{2}(2)+b_{2}(2))\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}+({\textstyle \frac{1}{5}}d_{2}(2)+b_{2}(2))(\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})].\qquad & \displaystyle\end{eqnarray}$$
As with the Brownian contribution, which is also entropic in origin, the interparticle force serves to enhance probe diffusion – regardless of the strength of hydrodynamic interactions.
Each of the three contributions – hydrodynamic, Brownian and interparticle – are plotted in figure 4, where they are separated into longitudinal (4
a) and transverse (4
b) diffusion, and are plotted as a function of the strength of hydrodynamic interactions,
${\it\kappa}$
. The hydrodynamic diffusion is anisotropic, and always negative: it hinders diffusion regardless of the strength of hydrodynamics. The hindrance is strongest when the repulsion distance vanishes; this effect weakens as the repulsion range
${\it\kappa}$
grows and no-slip surfaces are kept farther apart by longer-ranged interparticle forces.
Figure 4. The longitudinal (a) and transverse (b) components of the flow-induced diffusion in the limit of weak forcing
$(\mathit{Pe}\ll 1)$
as a function of the dimensionless repulsion distance
${\it\kappa}$
. Here, the flow-induced diffusion is normalized by the isolated probe diffusivity
$D_{a}$
, the thermodynamic volume fraction of bath particles
${\it\phi}_{\mathit{th}}$
and
$Pe^{2}$
.
The Brownian and interparticle contributions are both positive for all ranges of repulsion
${\it\kappa}$
. While both contributions arise due to entropic effects, Brownian disturbance flows are solvent-mediated and become weaker as
${\it\kappa}$
grows. In contrast, the growing excluded volume produces monotonically increasing interparticle diffusion.
The total low-
$Pe$
flow-induced diffusion decreases as hydrodynamic interactions grow stronger. That is, hydrodynamic interactions suppress diffusion when external forcing is weak. In the limit of strong hydrodynamics,
${\it\kappa}\rightarrow 0$
, the left end of the axes, the Brownian contribution dominates with diffusion driven primarily by variation in the relative radial mobility. In the opposite limit of large
${\it\kappa}$
(weak hydrodynamics), interparticle contributions dominate, because hydrodynamic surfaces are widely separated, and relative mobility during a collision is high. The transition from one limit to the other shows the smooth evolution in the roles of hydrodynamic, Brownian and interparticle forces. The diffusion is anisotropic for all strengths of hydrodynamic interactions: the strength of longitudinal relative to transverse diffusion is approximately 3 : 1 ratio for all ranges of interparticle repulsion.
In summary, flow enhancement of diffusion is
$O(\mathit{Pe}^{2})$
, compared to passive Brownian diffusion of a tracer in a suspension – but overall is still hindered compared to Brownian diffusion in a pure solvent. The enhancement arises due to entropic scattering alone, and competes with the suppressive effect of hydrodynamic diffusion. Both interparticle collisions and Brownian drift contribute to entropic enhancement of diffusion, with the former playing a more dominant role: collisions at the excluded annulus are more effective than Brownian drift at scattering the probe, shown by the monotonic increase in the total flow-induced diffusion in all directions with increasing excluded-annulus thickness
${\it\kappa}$
. The flow-induced diffusion is anisotropic, showing that the structure is asymmetric but only weakly so due to the entropic nature of particle scattering.
4.2.3 Hydrodynamic diffusion and Stokes-flow reversibility:
$\mathit{Pe}^{-1}\equiv 0$
,
${\it\kappa}=0$
Here we move to the opposite limit of strong forcing and strong hydrodynamics, where Brownian motion plays no role at all. Force-induced diffusion in this limit was studied in our recent work, which we briefly summarize here for completeness (Hoh & Zia Reference Hoh and Zia2015). In this pure hydrodynamics limit,
$\mathit{Pe}^{-1}\equiv 0$
and
${\it\kappa}\rightarrow 0$
, that is, no Brownian motion and full hydrodynamics. This regime is, in essence, falling-ball rheometry, for which detailed solutions for hydrodynamic diffusion via trajectory analysis are well known (Davis & Hill Reference Davis and Hill1992). We found via microrheology that the probe undergoes purely hydrodynamic longitudinal diffusion:
$$\begin{eqnarray}D_{\Vert }^{\mathit{flow}}=1.26aU_{S}{\it\phi},\end{eqnarray}$$
and the transverse hydrodynamic diffusion is identically zero, owing to the fore–aft symmetry of Stokes flow relative trajectories, in excellent agreement with the trajectory analysis theory of Davis & Hill, who predicted vertical diffusion
$D_{\Vert }^{\mathit{flow}}=1.33aU_{S}{\it\phi}$
, and the falling-ball experiments of Abbott et al. (Reference Abbott, Graham, Mondy and Brenner1998), who measured vertical diffusion
$D_{\Vert }^{\mathit{flow}}=1.20aU_{S}{\it\phi}^{1.08}$
. However, analysis of probe fluctuation in the corresponding limit utilizing the microrheology framework leads to several important outcomes.
The first outcome is that the microrheology approach enables extension to finite
$Pe$
, i.e. where Brownian motion matters, a regime that cannot be modelled via deterministic trajectory analysis. This is of particular interest in the study of actively forced colloidal particles – the subject of the present study. Because the Péclet number can be defined in terms of the Stokes velocity as
$\mathit{Pe}\equiv a_{\mathit{th}}U_{S}/2D_{a}$
, our approach allowed us to recast the hydrodynamic longitudinal diffusion (4.25) in terms of the Stokes–Einstein diffusion:
$$\begin{eqnarray}D_{\Vert }^{\mathit{flow}}=2.52\mathit{Pe}\,D_{a}{\it\phi},\end{eqnarray}$$
showing the advective scaling of flow-induced diffusion when external forcing is strong. In the next section, we will show how this limit of hydrodynamic diffusion is approached asymptotically as described by (4.24).
In addition, the trajectory analysis approach cannot predict the emergence of transverse diffusion with weak thermal motion. In contrast, the microrheology model developed here captures thermodynamic forces (and particle roughness) and shows that even very weak Brownian motion produces asymmetry within the diffusive boundary layer, leading to entropic diffusion. We will see in the next section that transverse flow-induced diffusion is indeed weak when hydrodynamics and external forcing are strong, but it does not vanish entirely.
Perhaps the most important outcome of studying the pure hydrodynamics limit from a microrheological perspective is that it reveals a precise balance between fluctuation (force-induced diffusion) and dissipation (apparent microviscosity) in far from equilibrium suspensions:
$$\begin{eqnarray}D_{\Vert }^{\mathit{flow}}={\textstyle \frac{1}{2}}{\it\eta}_{i}^{H}aU_{S}{\it\phi}=1.26aU_{S}{\it\phi};\end{eqnarray}$$
that is, diffusion and drag arise from a common microstructural origin even far from equilibrium.
4.2.4 Arbitrary strength of flow and hydrodynamics,
$\mathit{Pe}$
and
${\it\kappa}$
In this section, the flow-induced diffusion is presented for the full range of external forcing and strength of hydrodynamic interactions. For any non-zero and finite value of
$Pe$
, Brownian motion destroys structural symmetry; even when Brownian motion is very weak,
$Pe\gg 1$
, structural asymmetry leads to non-Newtonian rheology. Here we conduct a sweep from
$0\leqslant Pe\leqslant 1000$
and
$10^{-5}\leqslant {\it\kappa}<\infty$
, utilizing the fluctuation field results presented in § 4.1.4. The longitudinal and transverse components of the flow-induced diffusion are plotted individually in figure 5. To illustrate qualitative differences between the dependence of the longitudinal and transverse components on changes in hydrodynamics strength
${\it\kappa}$
, two rows are shown: in the top row,
${\it\kappa}\geqslant 0.4$
, corresponds to long-ranged interparticle repulsion. In the bottom row (c,d),
${\it\kappa}\leqslant 0.4$
, corresponds to stronger hydrodynamic interactions.
Figure 5. The longitudinal and transverse components of the flow-induced diffusivity as a function of the forcing strength
$Pe$
, for several values of
${\it\kappa}=(a_{th}-a)/a$
. Top row (a,b): long-range repulsion,
${\it\kappa}\geqslant 0.4$
, with (a) longitudinal and (b) transverse diffusion. Bottom row (c,d): stronger hydrodynamic interactions,
${\it\kappa}\leqslant 0.4$
, with (c) longitudinal and (d) transverse diffusion.
Beginning with the top row, the longitudinal and transverse diffusion are plotted in 5(a) and 5(b), respectively, as a function of
$\mathit{Pe}$
, where a family of curves is shown in each plot for
$0.4\leqslant {\it\kappa}<\infty$
. Starting with weak hydrodynamic interactions,
${\it\kappa}\rightarrow \infty$
, flow-induced diffusion is enhanced owing entirely to entropic scattering. As hydrodynamics grow stronger (progressively lighter curves), relative motion (via both advection and diffusion) becomes more difficult. The radial relative mobility
$G(s)$
decreases more rapidly than transverse relative motion
$H(s)$
, particularly when lubrication interactions start to play a role. That is, it becomes easier for a bath particle to pass around the probe than to approach it and, in consequence, trajectories are deflected around the probe, resulting in fewer collisions between probe and bath particles. This ‘collision shielding’ is the primary origin of the change in particle interactions and microstructure that leads to suppression of flow-induced diffusion.
Collision shielding can be quantified by measuring the collision frequency, estimated as the maximum value of the pair-distribution function at probe–bath particle contact, and tracking how it evolves with the strength of hydrodynamic interactions. This measure of collision frequency is plotted in figure 6(a), where the number of collisions
$g^{\mathit{max}}\equiv \max (g(\boldsymbol{r};\mathit{Pe},{\it\kappa}))$
along the axis of forcing is plotted as a function of strength of hydrodynamics,
$0.1\leqslant {\it\kappa}\leqslant 10$
and is divided by
$Pe$
to give number of collisions per advective step. Scaling
$g^{\mathit{max}}$
by
$\mathit{Pe}$
gives a sensitive measure of the variation in collision frequency with the strength of hydrodynamic interactions, owing to the dependence of particle density inside the boundary layer on the strength of hydrodynamic interactions. In their absence
$g(2)\sim \mathit{Pe}$
(Squires & Brady Reference Squires and Brady2005), giving way to sublinear scaling as hydrodynamic interactions grow strong (Khair & Brady Reference Khair and Brady2006); thus a division by
$Pe$
clearly reveals decreased collision frequency as hydrodynamics grow stronger. This trend is clearly seen in the plot: when the repulsion range is small (left end of the plot, strong hydrodynamics),
$g^{\mathit{max}}/\mathit{Pe}$
is relatively small. Physically, fewer bath particles make contact with the probe at the minimum approach distance. Fewer collisions means less entropic scattering at large
$\mathit{Pe}$
and, in turn, weakened diffusion.
Figure 6. (a) The maximum value
$g^{\mathit{max}}\equiv \max (g(\boldsymbol{r};\mathit{Pe},{\it\kappa}))$
of the pair-distribution function at large
$\mathit{Pe}$
, i.e. when Brownian motion is present but weak, normalized on
$\mathit{Pe}$
, plotted as a function of repulsion range
${\it\kappa}$
. Its value is an estimate for the frequency of particle collisions at the thermodynamic surfaces. (b–e) Illustration of the collision-shielding effect, shown here for
$\mathit{Pe}^{-1}\equiv 0$
with (b)
${\it\kappa}=10$
; (c)
${\it\kappa}=1$
; (d)
${\it\kappa}=0.1$
; (e)
${\it\kappa}=0.0001$
; solid lines are bath particle approach trajectories. Trajectories that collide at the thermodynamic surface are shaded grey. Trajectories deflected by hydrodynamic interactions are curved; some make contact (grey region); some do not (white region). As
${\it\kappa}$
decreases, fewer collisions occur, suppressing entropic scattering. Panels (b–e) from Hoh & Zia (Reference Hoh and Zia2015), with permission.
This behaviour can be understood by examining pair trajectories which highlight the collision shielding that occurs when particle encounters are deflected by hydrodynamic interactions, as discussed in our recent work (Hoh & Zia Reference Hoh and Zia2015). These trajectories are reproduced in figure 6(b–e), showing the two types of particle encounters: collisions and deflections. Collisions are encounters in which particle contact occurs, and does so at the surface of the excluded annulus. Deflections are encounters in which a particle trajectory is deflected by hydrodynamic interactions; this is collision shielding. Fluctuations can arise from collisions only (
${\it\kappa}\rightarrow \infty$
), deflection only (
$\mathit{Pe}^{-1}=0$
,
${\it\kappa}=0$
) or a combination of the two. The extent to which such collisions are avoided is set by the size of the excluded annulus; as
${\it\kappa}$
shrinks, hydrodynamic interactions more effectively prevent contact. When
${\it\kappa}$
is finite, longitudinal and transverse scattering can still occur due to both entropic and hydrodynamic encounters, where the relative influence of the two scattering mechanisms is a sensitive function of
${\it\kappa}$
, as illustrated in figure 5.
Returning to the flow-induced diffusion in figure 5, the decrease in the force-induced diffusion with increasing strength of hydrodynamics when
${\it\kappa}\geqslant 0.4$
(top row, a and b) shows that entropic scattering diminishes in the presence of hydrodynamic interactions, owing to shielding of the probe from collisions with bath particles. In the regime of larger
${\it\kappa}$
, entropic scattering is the primary mode of diffusion and thus its suppression by collision shielding gives rise to quantitative weakening of both longitudinal and transverse diffusion in figure 5(a,b). However, as hydrodynamic interactions grow even stronger,
${\it\kappa}\leqslant 0.4$
(c,d), a more nuanced picture emerges.
In the bottom row of figure 5, plots (c,d), the interparticle repulsion distance is
${\it\kappa}\leqslant 0.4$
, where lubrication interactions are accessible. The longitudinal and transverse flow-induced diffusion are plotted in (c) and (d), respectively, and again a family of curves is shown, now corresponding to
$0.00001\leqslant {\it\kappa}\leqslant 0.4$
. For weak forcing, the left end of the plots, strengthening hydrodynamic coupling exerts only a quantitative effect. However, for stronger forcing, an interesting transition emerges. Flow-induced diffusion in this regime transitions from entropic to hydrodynamic in origin, owing to the increased role played by hydrodynamic interactions. That is, for
$\mathit{Pe}\gtrsim 1$
, the value
${\it\kappa}\approx 0.4$
signifies a marked qualitative transition in the anisotropy of the diffusion tensor. As indicated by the arrow pointing in the opposite direction, a reversal in the effect of hydrodynamic interactions emerges: when
${\it\kappa}<0.4$
, decreases in
${\it\kappa}$
lead to increased longitudinal diffusion only – but continued decrease in the transverse diffusion (cf. figure 5
c,d). This is a reversal in the trend seen in (a), where for
${\it\kappa}\geqslant 0.4$
, decreasing
${\it\kappa}$
results in a reduction in the force-induced diffusion in all directions (cf. figure 5
a,b). This can be understood microstructurally as follows.
Lubrication interactions become important for
${\it\kappa}\lesssim 0.1$
. Collision-shielding continues to dampen transverse force-induced diffusion in this limit: fewer relative trajectories coincide with the minimum approach surface at
$r_{\mathit{min}}$
. The reversibility of Stokes flow dictates that transverse force-induced diffusion at
$O({\it\phi}_{\mathit{th}})$
vanishes in the dual limits
$\mathit{Pe}\rightarrow \infty$
and
${\it\kappa}=0$
, the so-called ‘pure hydrodynamic’ limit. The entropic effects of finite thermal motion or an excluded-volume surface offset from the hydrodynamic radii both act to break the fore–aft symmetry of relative trajectories. Thus, interparticle or Brownian forces are necessary for perceptible transverse force-induced diffusion of
$O({\it\phi}_{\mathit{th}})$
. However, the longitudinal force-induced diffusion increases for small
${\it\kappa}$
owing to the direct effect of hydrodynamic interactions: when the probe entrains a bath particle, its velocity deviates from its Stokes velocity
$U_{S}$
. Randomness in the background bath particle distribution thence leads to velocity fluctuations. The probe moves relatively faster through solvent pockets and relatively slower when dragging a nearby bath particle along with it.
These microscopic dynamics lead to a non-monotonic dependence of longitudinal diffusion on the strength of hydrodynamics. One can draw analogy to the equilibrium behaviour, where same competition between entropic and hydrodynamic effects led to a minimum value of diffusion at the same value of
${\it\kappa}$
. In both cases, at the point at which entropic scattering diminishes, the effects of hydrodynamic entrainment on scattering become important. However, the transverse force-induced diffusion decreases monotonically as
${\it\kappa}$
decreases. In consequence, the anisotropy of the flow-induced diffusion grows dramatically as
${\it\kappa}$
decreases, i.e. as hydrodynamic interactions grow stronger. The anisotropy becomes more pronounced at strong forcing with very short-ranged interparticle repulsions, growing from
$O(1)$
when dominated by entropic scattering to
$O(\mathit{Pe})$
when hydrodynamic diffusion is the dominant mechanism.
The transition from entropic to hydrodynamic diffusion is highlighted in figure 7 where each of the individual contributions to flow-induced diffusion – hydrodynamic, Brownian and interparticle – is plotted in two limits, weak and strong hydrodynamics,
${\it\kappa}\rightarrow \infty$
and
${\it\kappa}\rightarrow 0$
, respectively. In this figure, the flow-induced diffusivity is normalized by the bare diffusivity
$D_{a}$
, the thermodynamic volume fraction of bath particles
${\it\phi}_{\mathit{th}}$
and forcing
$\mathit{Pe}$
. In the limit of weak hydrodynamic interactions, the force-induced diffusion is purely entropic in origin regardless of the strength of external forcing: probe and bath particle collisions at the excluded annulus scatter the probe from its intended trajectory. In the opposite limit of strong hydrodynamics, force-induced diffusion at weak forcing is purely entropic in origin. Brownian drift pushes the probe away from the distorted microstructure toward relatively more mobile configurations. With strong external forcing, the velocity fluctuations set by hydrodynamic entrainment of bath particles take over as the dominant scattering mechanism. The approach to the infinite-
$\mathit{Pe}$
limiting value of the force-induced diffusivity
$D_{\Vert }^{\mathit{flow}}=2.52D_{a}\mathit{Pe}{\it\phi}$
described by (4.24), is slow: the asymmetric microstructure (the diffusive boundary layer) persists even when external forcing is many orders of magnitude stronger than the thermal force. Figure 7 illustrates the fact that by
$\mathit{Pe}=10^{3}$
that the hydrodynamic contribution in the strong hydrodynamic limit has reached a value of
$D_{\Vert }^{\mathit{flow}}\approx 1.65D_{a}\mathit{Pe}{\it\phi}$
and is continuing to climb slowly toward the asymptotic value of
$D_{\Vert }^{\mathit{flow}}=2.52D_{a}\mathit{Pe}{\it\phi}$
.
Figure 7. The hydrodynamic, interparticle and Brownian contributions to
$D_{\Vert }^{\mathit{flow}}$
as a function of
$\mathit{Pe}$
in the limits of weak hydrodynamic interactions
$({\it\kappa}\rightarrow \infty )$
and strong hydrodynamic interactions
$({\it\kappa}\rightarrow 0)$
. Diffusion (a) along and (b) transverse to the line of external force.
The transverse force-induced diffusion normalized by
$\mathit{Pe}$
is plotted in figure 7(b). Transverse diffusion, when normalized by the strength of external forcing, describes the variance in the trajectory observed on the scale of advective motion; namely, how the displacements transverse to the applied force compare to the net translation in the forcing direction. When the interparticle repulsion distance
${\it\kappa}$
is small, transverse diffusion approaches zero when normalized by
$\mathit{Pe}$
, indicating a vanishing variance in the probe trajectory normal to the external force on the scale of advective motion. However, small surface asperities,
${\it\kappa}>0$
, produce transverse entropic diffusion which scales as
$$\begin{eqnarray}D_{\bot }^{\mathit{flow}}\sim G(2(1+{\it\kappa}))\mathit{Pe}^{{\it\delta}}D_{a}{\it\phi}_{\mathit{th}},\end{eqnarray}$$
where the contact value of the relative radial mobility,
$G(2(1+{\it\kappa}))\sim {\it\kappa}$
, shows how readily relative motion occurs at the excluded annulus from a collision, and
$\mathit{Pe}^{{\it\delta}}$
represents the magnitude of the asymmetry within the diffusive boundary layer, where the exponent
${\it\delta}$
approaches 0.799 in the limit of short-ranged interparticle repulsion and strong forcing. As expected, transverse flow-induced diffusion is indeed weak when hydrodynamics and external forcing are strong, but it does not vanish entirely until the limit in which particles are smooth and Brownian motion is absent.
With infinitesimal but non-zero Brownian motion, such a fluctuation field leads to a Brownian contribution to the transverse force-induced diffusion which would scale as
$D_{a}{\it\phi}$
, which is
$O(\mathit{Pe})$
smaller than (and hence imperceptible compared to) the leading-order hydrodynamic contributions to the longitudinal force-induced diffusion. To observe Brownian motion in the strong forcing limit, the time scale for diffusion becomes increasingly long relative to the advective time scale. That is, one would have to wait an infinite amount of time to diffuse; one must wait the same amount of time to observe a Brownian step as to observe a transverse force-induced diffusion step.
While it is satisfying that the behaviour at large
$\mathit{Pe}$
and
${\it\kappa}\rightarrow 0$
asymptotes toward that of the pure hydrodynamic limit (i.e. enhancement of longitudinal and suppression of transverse fluctuations as
$\mathit{Pe}$
grows asymptotically large), the novel intermediate regime results presented here afford several new insights. First, the result that hydrodynamic interactions suppress fluctuations at small
$\mathit{Pe}$
emerges clearly as a result of the colloidal approach. In addition, the numerical value of the particle roughness
${\it\kappa}$
that triggers the transition from hindered to enhanced diffusion can be identified, suggesting a frequency and strength of collisions required to appreciably break the fore–aft symmetry of relative Stokes flow trajectories. Interestingly, three-body and higher interactions for perfectly smooth particles can lead to transverse displacements and perhaps can be interpreted through the lens of dilute theory as an effective roughness
${\it\kappa}$
. Finally, just as the limits
$\mathit{Pe}=0$
and
$\mathit{Pe}^{-1}=0$
give Newtonian rheology and the colloidal approach can recover these limits, the intervening behaviour – shear thinning and shear thickening for mean motion, flow-induced diffusion for fluctuations – are of significant rheological interest.
5 Comparisons to ‘macro’ rheology: shear, sedimentation and falling-ball rheometry
In the absence of hydrodynamic interactions, flow-induced diffusion enhances particle scattering entropically. Morris & Brady (Reference Morris and Brady1996) determined the long-time self-diffusivity in a weakly sheared
$(\mathit{Pe}\ll 1)$
dilute dispersion of non-hydrodynamically interacting colloids:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}_{\infty ,\mathit{macro}}^{s}({\it\kappa}\rightarrow \infty )=D_{a}[(1-2{\it\phi})\unicode[STIX]{x1D644}+{\textstyle \frac{46}{15}}{\it\phi}\mathit{Pe}\hat{\unicode[STIX]{x1D640}}+0.65{\it\phi}\mathit{Pe}^{3/2}\unicode[STIX]{x1D644}+O({\it\phi}^{2},{\it\phi}\mathit{Pe}^{2})].\end{eqnarray}$$
A particle diffuses with its bare diffusivity in solvent
$D_{a}\unicode[STIX]{x1D644}$
, minus the entropic hindrance
$2D_{a}{\it\phi}\unicode[STIX]{x1D644}$
from the equilibrium distribution of colloids (Lekkerkerker & Dhont Reference Lekkerkerker and Dhont1984; Rallison & Hinch Reference Rallison and Hinch1986), plus an
$O({\it\phi}\mathit{Pe})$
enhancement valid for any general linear flow, where
$\hat{\unicode[STIX]{x1D640}}$
is the rate of strain tensor of the imposed flow made dimensionless on the strain rate
$\dot{{\it\gamma}}$
. In active microrheology, the probe is towed through an otherwise quiescent dispersion of background bath particles,
$\hat{\unicode[STIX]{x1D640}}\equiv \unicode[STIX]{x1D7EC}$
; thus there can be no
$O({\it\phi}\mathit{Pe})$
diffusion enhancement in active microrheology. Additionally, the form of the isotropic
$O({\it\phi}\mathit{Pe}^{3/2})$
diffusion enhancement in (5.1) is specific only to simple shear – neither microstructural disturbances nor diffusion enhancement of
$O(\mathit{Pe}^{3/2})$
are observed in active microrheology. Indeed, in their study of force-induced diffusion of non-hydrodynamically interacting colloids, Zia & Brady (Reference Zia and Brady2010) computed long-time self-diffusivity of a weakly forced microrheological probe to leading order in
$\mathit{Pe}$
in the limit of weak forcing:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}_{\infty ,\mathit{micro}}^{s}({\it\kappa}\rightarrow \infty )=D_{a}[(1-2{\it\phi})\unicode[STIX]{x1D644}+{\it\phi}\mathit{Pe}^{2}({\textstyle \frac{184}{45}}\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}+{\textstyle \frac{44}{15}}\unicode[STIX]{x1D644})].\end{eqnarray}$$
Though the scaling in
$Pe$
of macroscopic shear-induced and microscopic force-induced diffusion differs quantitatively when thermal forces are strong, both are entropic in origin and arise from distorted (non-equilibrium) suspension microstructures.
Hydrodynamic interactions exert a twofold impact on flow-induced diffusion: interaction between no-slip surfaces decreases average particle mobility, while pairwise entrainment causes the (configuration dependent) velocity to fluctuate (somewhat analogously to velocity fluctuations due to hard-sphere collisions). We interpret this weaker particle mobility as apparent hydrodynamic shear thickening and, equivalently, reduced short- and long-time self-diffusion. Hydrodynamically, the apparent viscosity of sheared colloidal dispersions is known to shear thicken monotonically as a function of
$\mathit{Pe}$
(Bergenholtz, Brady & Vicic Reference Bergenholtz, Brady and Vicic2002). For weak imposed flow, however, shear thinning is observed: the entropic contributions to the apparent viscosity dominate at low
$\mathit{Pe}$
. For simple shear, Morris & Brady (Reference Morris and Brady1996) found that hydrodynamic interactions between particles reduce the
$O({\it\phi}\mathit{Pe})$
diffusion enhancement and introduce anisotropy at
$O({\it\phi}\mathit{Pe}^{3/2})$
:
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D63F}_{\infty ,\mathit{macro}}^{s}({\it\kappa}\rightarrow 0)\nonumber\\ \displaystyle & & \displaystyle \quad =D_{a}[(1-2.07{\it\phi})\unicode[STIX]{x1D644}+0.30{\it\phi}\mathit{Pe}\hat{\unicode[STIX]{x1D640}}+(0.13\unicode[STIX]{x1D644}+\mathscr{D}^{h}+\mathscr{D}^{p}){\it\phi}\mathit{Pe}^{3/2}+O({\it\phi}^{2},{\it\phi}\mathit{Pe}^{2})],\qquad\end{eqnarray}$$
where
$\mathscr{D}^{h}$
and
$\mathscr{D}^{p}$
are the contributions from the homogeneous and particular solutions, respectively, for the leading-order microstructural disturbance in the outer region where advection and diffusion balance, which occurs at particle separations
$R\sim \mathit{Pe}^{1/2}=O(1)r$
. As was the case for negligible hydrodynamic interactions, the
$O({\it\phi}\mathit{Pe})$
diffusion enhancement in (5.3) holds for all general linear flows, but the form of the
$O({\it\phi}\mathit{Pe}^{3/2})$
contribution is specific for simple shear flows.
In active microrheology, for strong hydrodynamics the outer region in which advection and diffusion balance occurs at even larger separations
$R\sim \mathit{Pe}^{1}r=O(1)$
. In this outer region, the leading-order disturbances to the mean
$g^{\mathit{neq}}(R)$
and fluctuating
$\boldsymbol{d}^{\mathit{neq}}(R)$
microstructure scale as
$\mathit{Pe}^{3}$
and
$\mathit{Pe}^{2}$
, respectively. The reduction in the probe self-diffusivity due to the presence of a bath particle,
$\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D63F}_{a}$
, and the divergence of the relative diffusivity,
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}_{r}$
, scale as
$\mathit{Pe}^{4}R^{-4}$
and
$\mathit{Pe}^{5}R^{-5}$
in this outer region, respectively. Thus, all hydrodynamic and Brownian contributions to force-induced diffusion from the outer solution are
$O(\mathit{Pe}^{4})$
small, indicating that the leading-order
$O(\mathit{Pe}^{2})$
force-induced diffusion is determined solely from the inner region. Here, thermal motion dominates microstructural evolution. The predominant role of hydrodynamics is the indirect effect: the apparent microviscosity force thickens and the diffusion enhancement weakens.
The opposite limit of strong flow (weak thermal forces) reveals the crucial role of interparticle forces on determining non-Newtonian rheology and diffusion enhancement. For a strongly sheared suspension, Brady & Morris (Reference Brady and Morris1997) utilize a ‘radial balance approximation’ to find a long-time self-diffusivity,
$(\mathit{Pe}^{-1}\equiv 0)$
, where interparticle interactions are governed by short-ranged excluded-annulus repulsions offset slightly from the hydrodynamic radius, with a scaling
$$\begin{eqnarray}\unicode[STIX]{x1D63F}_{\infty ,\mathit{macro}}^{s}(\mathit{Pe}\gg 1,{\it\kappa}\rightarrow 0)\sim \dot{{\it\gamma}}a^{2}{\it\kappa}^{0.22}{\it\phi}.\end{eqnarray}$$
The contributions in the velocity and velocity-gradient directions were found by Brady and Morris to be identical, i.e.
$D_{11}=D_{22}$
. The only non-zero ‘off-diagonal’ diffusivity component in simple shear is
$D_{12}=D_{21}$
: off-diagonal components involving the vorticity direction can be shown to be zero via symmetry arguments. da Cunha & Hinch (Reference da Cunha and Hinch1996) employ trajectory analyses for rough spheres to show that the hydrodynamic diffusion for spheres with dimensionless surface roughness given by
${\it\epsilon}\equiv {\it\kappa}$
is approximately linear in the scaling
${\it\epsilon}^{0.4374}(\ln (1/{\it\epsilon})+1.347)^{-0.7012}$
in the range
$10^{-4}\leqslant {\it\epsilon}\leqslant 10^{-3}$
. The discrepancy in scales arises partially from approximations required for each of the different solution methods. Regardless of the solution method, both show persistence of
$O({\it\phi})$
diffusion in all directions from an excluded annulus of non-zero thickness.
Heavy particles sedimenting in Stokes flow under gravity exhibit an overall reduction in settling velocity, with the nature of the hindrance dependent on the underlying suspension microstructure. Hindered settling reduces the sedimentation velocity proportional to
$U_{S}{\it\phi}^{1/3}$
for cubic lattices (Hasimoto Reference Hasimoto1959) and proportional to
$U_{S}{\it\phi}$
for randomly arranged dispersions (Batchelor Reference Batchelor1972). In addition to hindered mean fall speed, hydrodynamic dispersion in the direction of body forces has been observed in suspensions as dilute as
$0.025\leqslant {\it\phi}\leqslant 0.10$
(Ham & Homsy Reference Ham and Homsy1988): in their experiments, vertical hydrodynamic dispersivity was observed to scale advectively, by the mean sedimentation velocity
$\langle \boldsymbol{U}\rangle$
and the particle size
$a$
. In our study, we determined the order-
${\it\phi}$
longitudinal probe diffusivity to scale as
$D_{a}\mathit{Pe}$
in the corresponding strong hydrodynamic limit. Converting to advective quantities, the
$O({\it\phi})$
longitudinal force-induced diffusion is proportional to
$aU_{S}$
, consistent with the findings of Ham and Homsy.
For dilute dispersions, the fore–aft symmetry of relative pair trajectories in Stokes flow prevents velocity variance transverse to mean motion. At moderate volume fraction, three-body and higher-order interactions break symmetry and induce perceptible horizontal dispersivity in non-Brownian suspensions. Anisotropy favours dispersion in the direction of gravity, with vertical fluctuations observed to be nearly twice horizontal fluctuations for semidilute dispersions where
$0.05\leqslant {\it\phi}\leqslant 0.15$
(Nicolai et al.
Reference Nicolai, Herzhaft, Hinch, Oger and Guazzelli1995). Koch & Shaqfeh (Reference Koch and Shaqfeh1991) showed that three-body and higher-order interactions lead to a so-called ‘screening’ mechanism, which one might extend to suggest that the longitudinal force-induced probe diffusion could decrease in the moderately concentrated regime with increasing volume fraction: the presence of a third particle can destabilize the tandem motion of a probe entraining a bath particle directly along the axis of forcing, reducing the duration of the entrainment event.
The dual limits of asymptotically weak thermal motion
$(\mathit{Pe}^{-1}\equiv 0)$
and a vanishingly thin excluded annulus
$({\it\kappa}\equiv 0)$
defines the ‘pure hydrodynamic’ limit, a highly singular regime studied in detail in our recent work (Hoh & Zia Reference Hoh and Zia2015) where we compared it to macroscopic falling-ball rheometry (Davis & Hill Reference Davis and Hill1992; Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998). In this regime, force-induced diffusion is scaled on advective quantities, namely the Stokes velocity
$U_{S}$
and the hydrodynamic probe radius
$a$
. Physically, diffusion proportional to
$aU_{S}{\it\phi}$
is perceptible diffusion on the scale of deterministic motion: the mean-squared displacement from the fluctuating motion is comparable to the square of the net displacement itself. Force-induced diffusion that scales as
$D_{a}$
is imperceptible relative to the mean motion in the limit
$\mathit{Pe}^{-1}\equiv 0$
.
6 Summary and concluding remarks
We have quantified the effects of hydrodynamic interactions on the fluctuating motion of a microrheological probe and on its long-time self-diffusion, utilizing a statistical mechanics framework to formulate the mean and fluctuating contributions to the probe probability flux, which then reveal the probe velocity and effective diffusivity. The Smoluchowski equation conserves bath particle probability density and defines governing equations for the mean and fluctuating suspension microstructure, as it evolves with flow strength
$\mathit{Pe}$
and range of interparticle repulsion (strength of hydrodynamic interactions), set by the excluded-annulus parameter
${\it\kappa}$
. The Smoluchowski equations for the mean and fluctuating microstructures were solved analytically in the limits of weak and strong forcing, and numerically in between. It was shown that hydrodynamic, Brownian and interparticle forces act to hinder equilibrium probe diffusivity and enhance the flow-induced diffusion away from equilibrium.
Bath particle contributions to the equilibrium probe self-diffusion comprise hydrodynamic (short time) and entropic (long time) hindrances. For a dilute colloidal suspension, the overall reduction in probe self-diffusion is linear in
${\it\phi}_{\mathit{th}}$
, the volume fraction of bath particles based on their thermodynamic or excluded-volume size. When interparticle repulsion is long ranged (
${\it\kappa}\gg 1$
) the hydrodynamic no-slip surfaces of the probe and bath particle are widely separated. In this weak hydrodynamics limit, the reduction in probe self-diffusion is entirely entropic: bath particle collisions at the minimum approach surface
$r_{\mathit{min}}$
impede the random walk of the probe uniformly in all directions. The equilibrium probe self-diffusion in this limit approaches
$D_{a}(1-2{\it\phi}_{\mathit{th}})$
, in agreement with prior studies of entropically hindered diffusion (Lekkerkerker & Dhont Reference Lekkerkerker and Dhont1984; Rallison & Hinch Reference Rallison and Hinch1986; Zia & Brady Reference Zia and Brady2010). When interparticle repulsion is short ranged (
${\it\kappa}\ll 1$
) the no-slip surfaces are permitted to approach one another closely. In this strong hydrodynamics limit, the equilibrium distribution of no-slip surfaces reduces the short-time self-diffusion of the probe as
$D_{a}(1-1.83{\it\phi}_{\mathit{th}})$
. The hydrodynamic reduction in the short-time self-diffusion acts in conjunction with Brownian drift to entropically hinder the long-time self-diffusion of
$D_{a}(1-2.1{\it\phi}_{\mathit{th}})$
. The strong hydrodynamics limit agrees with the findings of Batchelor (Reference Batchelor1983) for hindered diffusion of sedimenting spheres.
We propose that a perhaps more precise view of this process of equilibrium hindrance is that long-time self-diffusion produces local density fluctuations which are in turn smoothed by Brownian drift. Brownian drift, initially described by Ermak & McCammon (Reference Ermak and McCammon1978) and Fixman (Reference Fixman1978), effectively drives particles toward less hindered configurations. We have shown that these temporary local mobility gradients introduce deterministic character to otherwise stochastic motion. This deterministic motion arises at the expense of weakened long-time self-diffusion.
Brownian drift scales with the thermal energy
$kT$
, with the divergence of the relative mobility
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D648}^{UF}$
, when made dimensionless, setting the strength of deterministic forces. One could interpret this quantity as a sort of ‘thermal’ Péclet number. As
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D648}^{UF}$
is a vector field, the Péclet number is thus configuration dependent. In the absence of external forces, it measures the deterministic response to a density fluctuation in the microstructure. It is a maximum when two particles are in contact, but the pairwise mobility functions reveal that this quantity is never greater than unity. We showed that this leads to hindrance of diffusive motion, and that deterministic forces must be larger than thermal forces for diffusive probe scattering to be enhanced. In another interpretation, a fixed energy
$kT$
is imparted by the suspension to any given test particle. In the absence of other particles, the entirety of this energy acts to maximize the random walk of the test particle. In the presence of other particles however, part of this thermal energy is utilized to drive a closely spaced pair apart, deterministically, leaving less energy to produce variance in particle position. The proportion of energy supporting deterministic motion versus stochastic motion is, in a sense, a purely thermal
$\mathit{Pe}$
.
The utility of active microrheology in connecting probe fluctuations to energy dissipation is first apparent in the linear-response regime. Through active microrheology, the equilibrium probe self-diffusion is related to the linear-response apparent microviscosity via the Stokes–Einstein relation. We showed that, modulo a constant, the Smoluchowski equations governing the equilibrium fluctuation field and the linear-response mean microstructure are identical for all excluded-annulus parameters. Equivalency of the linear-response microstructure and equilibrium fluctuation field implies that the bath particle contributions to both the equilibrium long-time self-diffusion of the probe and the linear-response apparent microviscosity are identical for all strengths of hydrodynamic interactions. This must be so: active microrheology is the measurement by which one can extend the fluctuation-dissipation relation to suspensions. The probe–bath interactions that dissipate energy from a deterministic external force
$\boldsymbol{F}^{\mathit{ext}}$
via Stokes drag are identical to the interactions that hinder probe fluctuations and diffusion from thermal forces.
Asymptotic expansions of the mean and fluctuating microstructure in
$\mathit{Pe}$
revealed that the first contributions to force-induced probe diffusion scale as
$D_{a}\mathit{Pe}^{2}{\it\phi}_{\mathit{th}}$
for all strengths of hydrodynamic interactions. Entropic contributions (Brownian and interparticle) to force-induced diffusion arise from dipolar fluctuation fields. Positive and negative dipole moments in the fluctuation field correspond respectively to displacements oriented radially outward, enhancing diffusion by driving the probe away from its current position in all directions, and radially inward, hindering the random walk of the probe. Both the analytical and numerical solution reveal this approximate 3 : 1 anisotropy in the force-induced diffusion holds for all strengths of hydrodynamic interactions, at low
$\mathit{Pe}$
.
Also in this weakly nonlinear regime, the hydrodynamic contributions to force-induced diffusion at
$O(\mathit{Pe}^{2})$
were found to be more nuanced than entropic fluctuations. An apparently more viscous suspension dissipates more energy from an external force and impedes probe motion; consequently, the indirect effect of hydrodynamic interactions on force-induced diffusion is a reduction due to hydrodynamic force thickening. These contributions are fully dictated by the mean microstructure: isotropic accumulations of bath particles (monopolar disturbances) and redistribution of bath particles from the sides to the front and back of the probe (quadrupolar disturbances) lead to force thickening in the apparent microviscosity and, subsequently, hindered diffusion. The direct effect of hydrodynamic interactions comes from natural variations in the suspension: the probe moves relatively faster through solvent pockets, while it slows down when entraining a nearby bath particle. Diffusive (stochastic) trajectories arise from such velocity fluctuations, so the direct effect of hydrodynamics is to enhance probe diffusion. When the external forcing is weak compared to thermal motion, the probe cannot entrain a bath particle for too long before Brownian drift separates the pair. Thus, the direct entrainment effect does not last long enough to counteract the
$O(\mathit{Pe}^{2})$
force thickening in the apparent microviscosity. The overall effect of hydrodynamic interactions at weak external forcing dampens force-induced diffusion, and the trend is monotonic in the range of interparticle interactions
$r_{\mathit{min}}$
: diffusion enhancement weakens as the no-slip surfaces are permitted to approach one another more closely.
The limit
$\mathit{Pe}\gg 1$
corresponds to external forcing much greater than thermal forces. For finite
${\it\kappa}$
, the no-slip surfaces of the probe and bath particle are permitted to approach closer to one another. Force-induced diffusion weakens with decreasing
${\it\kappa}$
for
${\it\kappa}\gtrsim 0.4$
, corresponding to a ‘collision-shielding’ effect: the frequency of entropic collisions at the minimum approach distance decreases as long-ranged hydrodynamic interactions deflect relative trajectories away from the thermodynamic surfaces. Lubrication interactions become important for
${\it\kappa}\lesssim 0.4$
. Collision shielding continues to dampen transverse force-induced diffusion in this limit as fewer relative trajectories coincide with the minimum approach surface at
$r_{\mathit{min}}$
. The reversibility of Stokes flow dictates that transverse force-induced diffusion at
$O({\it\phi})$
vanishes in the dual limits
$\mathit{Pe}^{-1}=0$
and
${\it\kappa}=0$
, the so-called ‘pure hydrodynamic’ limit as confirmed in our recent work (Hoh & Zia Reference Hoh and Zia2015) and shown for falling-ball rheometry (Davis & Hill Reference Davis and Hill1992). The entropic effects of finite thermal motion or an excluded-volume surface offset from the hydrodynamic radii both act to break the fore–aft symmetry of relative trajectories. Thus, interparticle or Brownian forces are necessary for perceptible transverse force-induced diffusion of
$O({\it\phi})$
. The longitudinal force-induced diffusion increases for small
${\it\kappa}$
because of the direct effect of hydrodynamic interactions: when the probe entrains a bath particle, its speed deviates from its Stokes velocity
$U_{S}$
. Random variation of the background bath particle distribution leads to velocity fluctuations. The probe moves relatively faster through solvent pockets and relatively slower when dragging a nearby bath particle along with it. Longitudinal force-induced diffusion is thus non-monotonic in the range of interparticle repulsions, so the degree of anisotropy in force-induced diffusion becomes more pronounced with very short-ranged interparticle repulsions.
Connections were made to the non-Newtonian ‘macro’rheology of colloidal dispersions, which is intimately tied to asymmetry in suspension microstructures (Brady & Morris Reference Brady and Morris1997; Bergenholtz et al.
Reference Bergenholtz, Brady and Vicic2002). The same holds true for microrheology: the evolution of asymmetric boundary layer and wake structures accompanies force thinning and subsequently force thickening in the apparent microviscosity (Khair & Brady Reference Khair and Brady2006). In the absence of entropic (Brownian and interparticle) forces, these asymmetric structures cannot form. Instead, bath particle accumulation is spherically symmetric about the probe (Batchelor Reference Batchelor1982) and the apparent microviscosity is Newtonian, depending only on the relative size of the probe compared to the bath particles (Davis & Hill Reference Davis and Hill1992; Almog & Brenner Reference Almog and Brenner1997). Interparticle and Brownian forces are thus sources of non-Newtonian rheology and force-induced diffusion. These entropic forces act to break fore–aft symmetry of relative probe–bath trajectories by hindering the ability of bath particles to approach the probe. Thermal forces lead to Brownian drift, which is purely repulsive: the probe and bath particle tend toward more mobile configurations as dictated by the divergence of the relative mobility, which is monotonic in the radial separation
$r$
. Likewise, hard-sphere repulsions offset from the hydrodynamic radius act to filter incoming bath particle density, pushing the particles off of the trajectory defined by hydrodynamics alone. Entropic forces thus break Stokes-flow symmetry by causing bath particles to pass the probe farther from the line of forcing than the approach on the upstream face. It is this symmetry breaking that leads to appreciable transverse force-induced diffusion. Indeed, perceptible
$O({\it\phi})$
transverse diffusion has been observed experimentally in falling-ball rheometry (Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998), where surface roughness has been proposed as one possible source of transverse diffusion (Davis Reference Davis1992).
Looking forward, the interparticle force need not be purely repulsive or conservative, two factors which could lead to surprising changes in rheology and diffusion, particularly in the limit of very weak Brownian motion. The former, attractive interparticle forces, break symmetry inversely to excluded-annulus repulsions: bath particles would be pulled off of relative trajectories closer to the probe, and would exit downstream to the probe along trajectories closer to the line of forcing than their approach. Attractive forces could thus shift the spherically symmetric microstructure to have a wake of relative bath particle accumulation, with relative depletions in front of the probe. The latter, dissipative or frictional interparticle forces, could lead to apparent force thickening even in the absence of thermal forces. The rate of frictional energy dissipation is a function of the energy input; for microrheology, the energy input is simply the applied external force. Thus, with larger energy inputs, bath particles near contact would dissipate more energy. A larger external force would not then proportionately increase the mean motion of the probe as predicted by a Newtonian viscosity and Stokes drag, precisely the definition of apparent force thickening. Fortunately, the theoretical framework developed in this work is easily extended to both of these cases and can verify the above predictions.
Future work can address such a range of interparticle forces, connecting with, for example, diffusive migration in colloidal gels (Zia, Landrum & Russel Reference Zia, Landrum and Russel2014) along with the effects of unequal sizes of bath particle probe. A small probe forced through a dilute dispersion of larger colloids will be slowed down more significantly during entrainment events, so the magnitude of velocity variations should increase with increasing relative bath particle size. Conversely, the velocity of a large probe forced through a dilute dispersion of small bath particles will not fluctuate as greatly when entraining a bath particle, and so the suspension resembles an effective continuum. However, the criterion for applying a dilute theory approach is more stringent for large probes:
${\it\phi}\ll b/a$
where
$b$
and
$a$
are the bath and probe radii, respectively (Zia & Brady Reference Zia and Brady2010). We expect a monotonic increase in the force-induced diffusion with increasing relative size of the bath particles, converging on the falling-ball rheometry predictions of Davis & Hill (Reference Davis and Hill1992) in the absence of thermal motion.
Finally, moving beyond the dilute limit, the fore–aft symmetry of pairwise trajectories is broken owing to long-ranged hydrodynamic interactions with the rest of the suspension. Thus, each pairwise encounter between the probe and a bath particle should impart some transverse displacement, even when
${\it\phi}$
is somewhat dilute. The dilute theory in this study can be extended to more concentrated suspensions by determining the effective transverse ‘irreversibility’ per encounter, or an equivalent value of the dimensionless repulsion distance
${\it\kappa}$
that faithfully captures the amount by which fore–aft symmetry is broken per pairwise encounter. Perceptible transverse force-induced diffusion in more concentrated, hydrodynamically interacting systems could be extended from the dilute theory in this study by interpreting curves with a larger
${\it\kappa}$
. Indeed, our preliminary Stokesian dynamics simulations of active microrheology have shown that the transverse force-induced diffusion of hard spheres in semi-dilute to concentrated dispersions collapses onto the dilute theory predictions of particles with effective roughness
${\it\kappa}$
of
$O(0.1)$
(Su, Chu & Zia Reference Su, Chu and Zia2015a
; Su et al.
Reference Su, Gu, Hoh and Zia2015b
).
Appendix A. Low Péclet perturbation expansion
Here we present the method for numerically solving the low Péclet fluctuation field
$\boldsymbol{d}$
. The method follows that of Khair & Brady (Reference Khair and Brady2006) for the steady microstructure at low Péclet number in active microrheology, and we extend it to the fluctuation field. We solve the Smoluchowski equations when
$\mathit{Pe}\ll 1$
for the steady microstructure
$g(\boldsymbol{r})$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}g]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}g]=0\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g\rightarrow 1\quad \text{as}~r\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$\boldsymbol{d}(\boldsymbol{r})$
: 
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Pe}(\unicode[STIX]{x1D63F}_{11}-\unicode[STIX]{x1D644})\boldsymbol{\cdot }\hat{\boldsymbol{F}}g+{\textstyle \frac{1}{2}}[\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}g+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\unicode[STIX]{x1D63F}_{r}g)]-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[\mathit{Pe}\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}]=\mathbf{0},\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{r}}\boldsymbol{\cdot }[-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D63F}_{r}g+Pe\,\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}+\unicode[STIX]{x1D63F}_{r}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{d}]=\mathbf{0}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{d}\rightarrow \mathbf{0}\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$g(\boldsymbol{r})$
and fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
may be expanded in the Péclet number: 
$$\begin{eqnarray}\displaystyle & \displaystyle g_{0}(\boldsymbol{r};\mathit{Pe}\ll 1)=1+\mathit{Pe}\,\hat{\boldsymbol{F}}\boldsymbol{\cdot }\hat{\boldsymbol{r}}f_{1}(r)+\mathit{Pe}^{2}\,\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }(\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}f_{2}(r)+\unicode[STIX]{x1D644}h_{2}(r))+\cdots , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{d}(\boldsymbol{r};\mathit{Pe}\ll 1) & = & \displaystyle \hat{\boldsymbol{r}}d_{0}(r)+\mathit{Pe}\,\hat{\boldsymbol{F}}\boldsymbol{\cdot }(\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}d_{1}(r)+\unicode[STIX]{x1D644}c_{1}(r))\nonumber\\ \displaystyle & & \displaystyle +\,\mathit{Pe}^{2}\,\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }(\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}d_{2}(r)+\hat{\boldsymbol{r}}\unicode[STIX]{x1D644}2c_{2}(r)+\unicode[STIX]{x1D644}\hat{\boldsymbol{r}}b_{2}(r))+\cdots .\end{eqnarray}$$
The ordinary differential equation and boundary conditions governing
$f_{1}(r)$
are obtained by substituting (A 3) into (A 1) and grouping terms of
$O(\mathit{Pe})$
and angular dependence
$\hat{\boldsymbol{F}}\boldsymbol{\cdot }\hat{\boldsymbol{r}}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}f_{1}}{\text{d}r}\right]-2Hf_{1}=-r^{2}W, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}f_{1}}{\text{d}r}=-1\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}\rightarrow 0\quad \text{as}~r\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$W\equiv \text{d}G/\text{d}r+2(G-H)/r$
describes the radial component of the divergence of the relative mobility. The ordinary differential equation and boundary conditions governing
$f_{2}(r)$
are obtained by substituting (A 3) into (A 1) and grouping terms of
$O(\mathit{Pe}^{2})$
and angular dependence
$\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}$
: 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}f_{2}}{\text{d}r}\right]-6Hf_{2}=-r^{2}Wf_{1}-r^{2}G\frac{\text{d}f_{1}}{\text{d}r}+rHf_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}f_{2}}{\text{d}r}=-f_{1}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{2}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$h_{2}(r)$
are obtained by substituting (A 3) into (A 1) and grouping spherically symmetric terms of
$O(\mathit{Pe}^{2})$
: 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}h_{2}}{\text{d}r}\right]=-2Hf_{2}-rHf_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}h_{2}}{\text{d}r}=0\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle h_{2}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$d_{0}(r)$
are obtained by substituting (A 3) and (A 4) into (A 2) and grouping terms of
$O(\mathit{Pe}^{0})$
and angular dependence
$\hat{\boldsymbol{r}}$
: 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}d_{0}}{\text{d}r}\right]-2Hd_{0}=+\frac{1}{2}r^{2}W, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}d_{0}}{\text{d}r}=+\frac{1}{2}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{0}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$d_{0}(r)=-f_{1}(r)/2$
in (A 8), shows that the system governing
$f_{1}$
(equation (A 5)) is identically recovered. Thus, the
$O(\mathit{Pe}^{0})$
displacement field
$d_{0}(r)$
for a given value of the excluded-annulus thickness
${\it\kappa}$
is everywhere equal to the first perturbation to the suspension microstructure
$f_{1}(r)$
multiplied by
$-1/2$
. The differential equation and boundary conditions governing
$d_{1}(r)$
and
$c_{1}(r)$
are obtained by substituting (A 3) and (A 4) into (A 2) and grouping terms of
$O(\mathit{Pe}^{1})$
and angular dependence
$\hat{\boldsymbol{F}}\boldsymbol{\cdot }\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}$
and
$\hat{\boldsymbol{F}}$
, respectively. For
$d_{1}(r)$
, this gives 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}d_{1}}{\text{d}r}\right]-6Hd_{1}=r^{2}Wf_{1}+\frac{3}{2}\left(r^{2}G\frac{\text{d}f_{1}}{\text{d}r}-rHf_{1}\right)+r^{2}(x_{11}^{a}-y_{11}^{a}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}d_{1}}{\text{d}r}=+f_{1}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{1}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$c_{1}(r)$
, we find: 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}c_{1}}{\text{d}r}\right]=-2Hd_{1}+\frac{3}{2}rHf_{1}+r^{2}(y_{11}^{a}-1), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}c_{1}}{\text{d}r}=0\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle c_{1}\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
The singular nature of the perturbation expansion emerges at
$O(\mathit{Pe}^{2})$
for the fluctuation field. The far-field boundary conditions for the displacement field functions
$d_{2}(r)$
,
$c_{2}(r)$
and
$b_{2}(r)$
do not decay to zero as
$r\rightarrow \infty$
but rather approach constant values of
$d_{2}^{\infty }$
,
$c_{2}^{\infty }$
and
$b_{2}^{\infty }$
, respectively which match to the outer solution, which in turn decays to zero at infinite separation. The differential equation and boundary conditions governing
$d_{2}(r)$
,
$c_{2}(r)$
, and
$b_{2}(r)$
are thus:
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}d_{2}}{\text{d}r}\right]-12Hd_{2} & = & \displaystyle -r^{2}Wd_{1}-r^{2}G\frac{\text{d}d_{1}}{\text{d}r}+2rHd_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}r^{2}Wf_{2}+r^{2}G\frac{\text{d}f_{2}}{\text{d}r}-2rHf_{2}+r^{2}(x_{11}^{a}-y_{11}^{a})f_{1},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}d_{2}}{\text{d}r}=+\frac{1}{2}f_{2}-d_{1}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{2}\rightarrow d_{2}^{\infty }\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$c_{2}(r)$
, we find: 
$$\begin{eqnarray}\displaystyle 2\left(\frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}c_{2}}{\text{d}r}\right]-2Hc_{2}\right) & = & \displaystyle -4Hd_{2}-r^{2}Wc_{1}-r^{2}G\frac{\text{d}c_{1}}{\text{d}r}-rHd_{1}\nonumber\\ \displaystyle & & \displaystyle +\,2rHf_{2}+r^{2}(y_{11}^{a}-1)f_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}c_{2}}{\text{d}r}=-\frac{1}{2}c_{1}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle c_{2}\rightarrow c_{2}^{\infty }\quad \text{as}~r\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$b_{2}(r)$
, 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}r}\left[r^{2}G\frac{\text{d}b_{2}}{\text{d}r}\right]-2Hb_{2}=-2Hd_{2}-rHd_{1}+\frac{1}{2}r^{2}Wh_{2}+r^{2}G\frac{\text{d}h_{2}}{\text{d}r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}b_{2}}{\text{d}r}=\frac{1}{2}h_{2}\quad \text{at}~r=2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{2}\rightarrow b_{2}^{\infty }\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G=1-\frac{3}{2(1+{\it\kappa})}r^{-1}+O(r^{-3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H=1-\frac{3}{4(1+{\it\kappa})}r^{-1}+O(r^{-3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle W=\frac{15}{2(1+{\it\kappa})^{4}}r^{-5}+O(r^{-7}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle x_{11}^{a}-y_{11}^{a}=-\frac{15}{4(1+{\it\kappa})^{4}}r^{-4}+O(r^{-6}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y_{11}^{a}-1=O(r^{-6}). & \displaystyle\end{eqnarray}$$
$f_{1}(r)$
gives, to
$O(r^{-4})$
: 
$$\begin{eqnarray}\displaystyle f_{1}(r\gg 2) & = & \displaystyle f_{1}^{\infty }r^{-2}\nonumber\\ \displaystyle & & \displaystyle +\left[\frac{3}{8(1+{\it\kappa})}r^{-3}+\frac{9}{20(1+{\it\kappa})^{2}}r^{-4}\right]\left(3f_{1}^{\infty }-\frac{5}{(1+{\it\kappa})^{3}}\right)+O(r^{-5}).\qquad\end{eqnarray}$$
The far field requires an adjustable parameter
$f_{1}^{\infty }$
denoting the leading-order dipole strength. Far-field expressions may be found in a similar manner for the remaining steady microstructure and fluctuation field perturbation functions.
The microstructure and deflection field can then be obtained numerically for all separations
$r$
utilizing the ode45 solver in Matlab. The scalar mobility functions
$G$
,
$H$
,
$W$
,
$x_{11}^{a}$
and
$y_{11}^{a}$
are evaluated numerically: for separation distances
$(1+{\it\kappa})r\geqslant 1.01$
, the twin-multipole expansions of Jeffrey & Onishi (Reference Jeffrey and Onishi1984) are evaluated through the first 300 terms, while for separation distances
$(1+{\it\kappa})r<1.01$
the lubrication approximations from Kim & Karrila (Reference Kim and Karrila1991) are utilized.
In the absence of hydrodynamic interactions
$({\it\kappa}\rightarrow \infty )$
at asymptotically small Péclet, the fluctuation field
$\boldsymbol{d}$
has the analytical solution found by Zia & Brady (Reference Zia and Brady2010):
$$\begin{eqnarray}\displaystyle \boldsymbol{d}(\boldsymbol{r};\mathit{Pe}\ll 1) & = & \displaystyle \hat{\boldsymbol{r}}(-2r^{-2})+\mathit{Pe}\,\hat{\boldsymbol{F}}\boldsymbol{\cdot }\left(\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\left[3r^{-1}-{\textstyle \frac{28}{3}}r^{-3}\right]+\unicode[STIX]{x1D644}\left[-{\textstyle \frac{7}{3}}r^{-1}+{\textstyle \frac{28}{9}}r^{-3}\right]\right)\nonumber\\ \displaystyle & & \displaystyle +\,\mathit{Pe}^{2}\,\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\boldsymbol{ : }\left(\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\left[-{\textstyle \frac{5}{4}}+{\textstyle \frac{26}{3}}r^{-2}-{\textstyle \frac{44}{3}}r^{-4}\right]+\hat{\boldsymbol{r}}\unicode[STIX]{x1D644}\left[{\textstyle \frac{13}{6}}-{\textstyle \frac{272}{45}}r^{-2}+{\textstyle \frac{88}{15}}r^{-4}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D644}\hat{\boldsymbol{r}}\left[{\textstyle \frac{5}{4}}-{\textstyle \frac{14}{5}}r^{-2}+{\textstyle \frac{44}{15}}r^{-4}\right]\right)+\cdots .\end{eqnarray}$$
These analytical solutions, along with the numerical solutions for the steady microstructure and deflection field for finite excluded-annulus thicknesses
${\it\kappa}$
, are plotted in figures 8–10. These numerical solutions for the steady microstructure and fluctuation field in the perturbation expansions are required to compute the equilibrium hindrance
$\unicode[STIX]{x1D63F}^{\mathit{eq}}$
and the asymptotic
$O(\mathit{Pe}^{2})$
behaviour of the force-induced diffusivity
$\unicode[STIX]{x1D63F}^{\mathit{flow}}$
for weak forcing.
Figure 8. (a) The
$O(\mathit{Pe})$
microstructure perturbation function
$f_{1}(r)$
, and (b) the
$O(\mathit{Pe}^{2})$
microstructure perturbation functions
$f_{2}(r)$
and (c)
$h_{2}(r)$
plotted as functions of
$r$
for several values of the excluded-annulus thickness
${\it\kappa}=(a_{\mathit{th}}-a)/a$
. Curves darken with increasing
${\it\kappa}$
. The dashed curves are the limiting behaviour as
${\it\kappa}\rightarrow \infty$
.
Figure 9. (a) The
$O(1)$
fluctuation field perturbation function
$d_{0}(r)$
, and (b) the
$O(\mathit{Pe})$
fluctuation field perturbation functions
$d_{1}(r)$
and (c)
$c_{1}(r)$
plotted as functions of
$r$
for several values of the excluded-annulus thickness
${\it\kappa}=(a_{\mathit{th}}-a)/a$
. Curves darken with increasing
${\it\kappa}$
. The dashed curves are the limiting behaviour as
${\it\kappa}\rightarrow \infty$
.
Figure 10. The
$O(\mathit{Pe}^{2})$
deflection field functions
$d_{2}(r)$
(a),
$c_{2}(r)$
(b), and
$b_{2}(r)$
(c) plotted as functions of
$r$
for several values of the excluded-annulus thickness
${\it\kappa}=(a_{\mathit{th}}-a)/a$
. Curves darken with increasing
${\it\kappa}$
. The dashed curves are the limiting behaviour as
${\it\kappa}\rightarrow \infty$
.
As shown in figure 8, the microstructural perturbation function
$h_{2}(r)$
is positive for all excluded-annulus thicknesses. Positive values of
$h_{2}(r)$
indicate spherically symmetric accumulation of bath particle density at
$O(\mathit{Pe}^{2})$
. The probe experiences an
$O(1)$
reduction in its self-mobility from the presence of a bath particle, so the overall hydrodynamic force thickening effect is the product of the
$O(\mathit{Pe}^{2})$
bath particle accumulation and the
$O(1)$
reduction in probe speed per bath particle encounter. The perturbation function
$f_{2}$
simply reflects additional accumulation or depletion of bath particle density preferentially along the line of forcing; negative values of
$f_{2}$
imply additional
$O(\mathit{Pe}^{2})$
depletion of particles along the line of forcing relative to the regions transverse to the line of forcing. This preferential depletion of particles along the axis of forcing leads to anisotropic diffusion. However, of these two effects, the hindering monopolar effect dominates owing to a slightly larger scalar prefactor. This
$h_{2}$
prefactor is identical in both the longitudinal (
$\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
) and transverse (
$(\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})$
) terms in (4.19); that is, the hindrance is isotropic.
The
$O(\mathit{Pe}^{2})$
accumulation of bath particle density hinders longitudinal and transverse diffusion isotropically, as the contribution described by
$h_{2}(r)$
in (4.19) is identical for both the
$\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
and
$(\unicode[STIX]{x1D644}-\hat{\boldsymbol{F}}\hat{\boldsymbol{F}})$
components. Slight anisotropy is evident in the flow-induced diffusion from the redistribution of bath particles from the axis of forcing to the sides of the probe as described by
$f_{2}(r)$
. At the level of bath particle redistribution, transverse diffusion is affected more strongly by the probe mobility normal to the line of centres
$y_{11}^{a}(r)$
while longitudinal diffusion depends more strongly on the probe mobility along the line of centres
$x_{11}^{a}(r)$
.
Appendix B. Finite difference method
Computation of the effective probe diffusion
$\unicode[STIX]{x1D63F}^{\mathit{eff}}$
for arbitrary strength of forcing
$Pe$
and hydrodynamics
${\it\kappa}$
requires numerical solution of (3.20) and (3.22) governing the mean microstructure
$g$
and the fluctuation field
$\boldsymbol{d}$
. To carry this out, we employ a second-order finite difference solution of the Smoluchowski equation. To illustrate this method, we present here the finite difference scheme applied to the longitudinal fluctuation field. The numerical method for determining the transverse fluctuation field is identical. For
$\mathit{Pe}>1$
, radial gradients in the microstructure and fluctuation field become appreciable and require careful treatment. The radial coordinate is stretched via the transformation
$y=\mathit{Pe}(r-2)$
to concentrate grid points in this region as a boundary layer forms. In a spherical polar coordinate system with the polar angle
${\it\theta}$
measured from
$\boldsymbol{F}^{\mathit{ext}}$
(cf. figure 1), the Smoluchowski equation for the steady microstructure
$g$
is expressed in terms of
$y$
and
${\it\theta}$
as:
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathit{Pe}\,W(s)\cos {\it\theta}g+\mathit{Pe}^{2}\,G(s)\cos {\it\theta}\frac{\partial g}{\partial y}-\mathit{Pe}\,H(s)\frac{\sin {\it\theta}}{r}\frac{\partial g}{\partial {\it\theta}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,G(s)\left(\mathit{Pe}^{2}\frac{\partial ^{2}g}{\partial y^{2}}+\mathit{Pe}\left[\frac{2}{r}+\frac{\text{d}\ln G}{\text{d}r}\right]\frac{\partial g}{\partial y}\right)+\frac{H(s)}{r^{2}}\left(\frac{\partial ^{2}g}{\partial {\it\theta}^{2}}+\cot {\it\theta}\frac{\partial g}{\partial {\it\theta}}\right)=0,\qquad\end{eqnarray}$$
where
$s\equiv (1+{\it\kappa})r$
. The corresponding boundary conditions are:
$$\begin{eqnarray}\displaystyle & \displaystyle \cos {\it\theta}g+\frac{\partial g}{\partial y}=0\quad \text{at}~y=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g\rightarrow 1\quad \text{as}~y\rightarrow \infty . & \displaystyle\end{eqnarray}$$
$d^{\Vert }$
is expressed in terms of
$y$
and
${\it\theta}$
as: 
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathit{Pe}\,W(s)\cos {\it\theta}d^{\Vert }+\mathit{Pe}^{2}\,G(s)\cos {\it\theta}\frac{\partial d^{\Vert }}{\partial y}-\mathit{Pe}\,H(s)\frac{\sin {\it\theta}}{r}\frac{\partial d^{\Vert }}{\partial {\it\theta}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,G(s)\left(\mathit{Pe}^{2}\frac{\partial ^{2}d^{\Vert }}{\partial y^{2}}+\mathit{Pe}\left[\frac{2}{r}+\frac{\text{d}\ln G}{\text{d}r}\right]\frac{\partial d^{\Vert }}{\partial y}\right)+\frac{H(s)}{r^{2}}\left(\frac{\partial ^{2}d^{\Vert }}{\partial {\it\theta}^{2}}+\cot {\it\theta}\frac{\partial d^{\Vert }}{\partial {\it\theta}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{W(s)}{2}\cos {\it\theta}g+\mathit{Pe}\,G(s)\cos {\it\theta}\frac{\partial g}{\partial y}-H(s)\frac{\sin {\it\theta}}{r}\frac{\partial g}{\partial {\it\theta}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathit{Pe}\,((x_{11}^{a}(s)-y_{11}^{a}(s))\cos ^{2}{\it\theta}+(y_{11}^{a}(s)-1))g,\end{eqnarray}$$
with boundary conditions:
$$\begin{eqnarray}\displaystyle & \displaystyle \cos {\it\theta}d^{\Vert }+\frac{\partial d^{\Vert }}{\partial y}=\mathit{Pe}^{-1}\frac{1}{2}\cos {\it\theta}g\quad \text{at}~y=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d^{\Vert }\rightarrow 0\quad \text{as}~y\rightarrow \infty . & \displaystyle\end{eqnarray}$$
The semi-infinite domain
$y\in [0,+\infty )$
is mapped to the finite domain
$t\in [0,1]$
via the transform:
$$\begin{eqnarray}t=\exp \left(-\left[{\it\omega}+\frac{1-{\it\omega}}{1+y}\right]y\right),\end{eqnarray}$$
where the distribution of grid points in real space
$y$
are tuned using the adjustable parameter
${\it\omega}$
. The Smoluchowski equations for the steady microstructure and fluctuation field are discretized with a central difference scheme.
For prescribed values of the excluded-annulus parameter
${\it\kappa}\equiv r_{\mathit{min}}/2a-1$
and the strength of forcing
$\mathit{Pe}\equiv F^{\mathit{ext}}a(1+{\it\kappa})/2kT$
the discretized Smoluchowski equation for the steady microstructure
$g$
is first solved for a given discretization in
$t$
and
${\it\theta}$
– in this article we present results with 1200 uniformly spaced grid points in
${\it\theta}$
and 1200 logarithmically spaced grid points in
$t$
. The solution for
$g$
is obtained utilizing the LaPack iterative banded solver in Matlab. The partial derivatives
$\partial g/\partial {\it\theta}$
and
$\partial g/\partial t$
are then evaluated numerically at each point in the grid to determine the forcing function on the right-hand side of the Smoluchowski equation for the fluctuation field
$d^{\Vert }$
. The Smoluchowski equation for the fluctuation field
$d^{\Vert }$
is then solved on an identical grid to the steady microstructure
$g$
for the same values of
$\mathit{Pe}$
and
${\it\kappa}$
. These solutions for
$g$
and
$d^{\Vert }$
, along with the hydrodynamic mobility functions, comprise the integrands for the equilibrium and flow-induced diffusion
$D_{\Vert }^{\mathit{flow}}$
, which are integrated numerically over the entire domain outside of the probe’s excluded volume utilizing first-degree Newton–Cotes quadrature.
