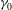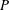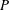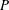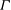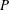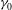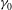1. Introduction
First developed by Zakharov (e.g. Zakharov, L’vov & Falkovich Reference Zakharov, L’vov and Falkovich1992), weak-turbulence theory (WTT) aims at describing the steady-state statistical property of an ensemble of waves in weakly nonlinear interactions (see also Newell & Rumpf Reference Newell and Rumpf2011). In the wavenumber
$k$
domain, the WTT steady-state analytical solution yields a power-law inertial-range spectrum
$I_{{\it\eta}}\sim k^{{\it\alpha}}$
with a constant energy flux
$P$
from large forcing scales to small dissipative scales. Over the years, this result has found applications in various physical contexts including plasma physics (e.g. Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2002), optics (e.g. Dyachenko et al.
Reference Dyachenko, Newell, Pushkarev and Zakharov1992), internal waves (e.g. Lvov, Polzin & Tabak Reference Lvov, Polzin and Tabak2004), surface gravity and capillary waves (e.g. Zakharov & Filonenko Reference Zakharov and Filonenko1966, Reference Zakharov and Filonenko1967). As a representative physical system with three-wave resonant interactions, capillary wave turbulence has been the subject of many investigations. In addition to the fundamental interest of this problem, an accurate representation of capillary waves on water surface is also important in understanding the air–sea interaction (e.g. Csanady Reference Csanady2001) and remote sensing of the ocean (e.g. Martin Reference Martin2014).
Under stationary state, the inertial range of a capillary wave spectrum can be obtained by solving the kinetic equation (Zakharov & Filonenko Reference Zakharov and Filonenko1967; Stiassnie, Agnon & Shemer Reference Stiassnie, Agnon and Shemer1991; Pushkarev & Zakharov Reference Pushkarev and Zakharov2000). Two of the inherent assumptions in these works are that nonlinear wave interactions are not suppressed by discreteness in wavenumber, i.e. the finite-box effect (e.g. Pushkarev & Zakharov Reference Pushkarev and Zakharov2000) is neglected, and, to make the equation solvable, the assumption that dissipation does not exist within the inertial range. This yields a closed-form WTT solution:
$$\begin{eqnarray}I_{{\it\eta}}(k)=2{\rm\pi}C\frac{P^{1/2}{\it\rho}^{1/4}}{{\it\sigma}^{3/4}}k^{-19/4},\end{eqnarray}$$
where
${\it\sigma}$
is the surface tension coefficient,
${\it\rho}$
is the fluid density,
$C$
is a proportional constant and
$P$
measures the (constant) energy flux from large to small scales. Here,
$I_{{\it\eta}}(k)$
is defined as (e.g. Zakharov & Filonenko Reference Zakharov and Filonenko1967)
$$\begin{eqnarray}\langle \hat{{\it\eta}}_{\boldsymbol{k}}\hat{{\it\eta}}_{\boldsymbol{k}^{\prime }}^{\ast }\rangle =I_{{\it\eta}}(k){\it\delta}(\boldsymbol{k}-\boldsymbol{k}^{\prime }),\end{eqnarray}$$
with the angle brackets denoting ensemble average and
$\hat{{\it\eta}}_{\boldsymbol{k}}=1/(2{\rm\pi})\iint _{-\infty }^{\infty }{\it\eta}_{\boldsymbol{r}}\text{e}^{-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}\,\text{d}\boldsymbol{r}$
being the Fourier transform of surface elevation
${\it\eta}_{\boldsymbol{r}}\equiv {\it\eta}(x,y)$
. The term
$I_{{\it\eta}}(k)$
, as defined in (1.2), is shown in Pan & Yue (Reference Pan and Yue2014) to be (proportional to) the energy density spectrum of
${\it\eta}$
(e.g. Phillips Reference Phillips1985). For sufficiently high nonlinearity, (1.1) has been confirmed experimentally in terms of the scalings
$I_{{\it\eta}}\sim k^{-19/4}$
(e.g. Falcon, Laroche & Fauve Reference Falcon, Laroche and Fauve2007; Xia, Shats & Punzmann Reference Xia, Shats and Punzmann2010) and
$I_{{\it\eta}}\sim P^{1/2}$
(Deike, Berhanu & Falcon Reference Deike, Berhanu and Falcon2014a
). Numerically, the scaling of
$I_{{\it\eta}}\sim k^{-19/4}$
is recovered in a number of independent studies (e.g. Pushkarev & Zakharov Reference Pushkarev and Zakharov1996, Reference Pushkarev and Zakharov2000; Deike et al.
Reference Deike, Daniel, Berhanu and Falcon2014b
; Pan & Yue Reference Pan and Yue2014). Pan & Yue (Reference Pan and Yue2014) provide a detailed investigation of (1.1), extending the verification of the
$I_{{\it\eta}}\sim P^{1/2}$
scaling over a broad range of
$P$
.
While there are many investigations of the weak turbulence in the stationary regime where energy input is balanced by energy dissipation, freely decaying capillary wave turbulence is much less studied. A notable exception is the theoretical work of Falkovich, Shapiro & Shtilman (Reference Falkovich, Shapiro and Shtilman1995), where the decaying spectrum is considered in the framework of the kinetic equation. Under the WTT assumptions, the unsteady solution of the kinetic equation yields a time-varying spectral amplitude inversely proportional to time, and a power-law spectrum within an inertial range of fixed width that decays with constant spectral slope
${\it\alpha}=-19/4$
:
$$\begin{eqnarray}I_{{\it\eta}}(k,t)\sim k^{-19/4}t^{-1},\quad \text{for }t>t^{0},\end{eqnarray}$$
where
$t^{0}$
is the initial time of the evolution of the power-law spectrum. The total energy is obtained in Falkovich et al. (Reference Falkovich, Shapiro and Shtilman1995) by analytical integration of (1.3) in
$k$
, to yield
$E(t)\sim t^{-1}$
.
In physically realistic situations, finite-box effect is always present, and dissipation exists over broad scales. The validity of (1.3) under these effects must be checked by experimental and numerical studies. While there is no numerical investigation of this problem, experimental investigations show that, during the decay, the inertial range varies, with the cutoff wavenumber
$k_{c}$
moving towards lower
$k$
as time increases (Kolmakov et al.
Reference Kolmakov, Levchenko, Brazhnikov, Mezhov-Deglin, Silchenko and McClintock2004; Deike, Berhanu & Falcon Reference Deike, Berhanu and Falcon2012; Deike, Bacri & Falcon Reference Deike, Bacri and Falcon2013). The spectral slope
${\it\alpha}$
is, in general, found to be time-varying (e.g. Miquel & Mordant Reference Miquel and Mordant2011; Deike et al.
Reference Deike, Bacri and Falcon2013, Reference Deike, Berhanu and Falcon2014a
), depending on the nonlinearity level and viscosity of the fluid. The time decay of the modal amplitudes obtained in all experiments is exponential, rather than
$t^{-1}$
. In terms of the total energy
$E(t)$
, the only direct measurement is that of Deike et al. (Reference Deike, Berhanu and Falcon2012), which also shows an exponential decay, in disagreement with the theory (notwithstanding possible effects of gravity waves on the energy measurement which may affect the direct comparison). It is postulated that at least some of these apparent discrepancies can be attributed to the inherent assumptions underlying (1.3) (e.g. Kolmakov et al.
Reference Kolmakov, Levchenko, Brazhnikov, Mezhov-Deglin, Silchenko and McClintock2004; Miquel & Mordant Reference Miquel and Mordant2011; Deike et al.
Reference Deike, Bacri and Falcon2013). This leaves the modification of (1.3) under finite-box effect and broad-scale dissipation an open issue.
The broad-scale dissipation present in the actual physics is especially important for decaying turbulence, as it enhances unsteadiness by allowing a faster spectral energy variation at broad scales. Yet it introduces an extra dynamics into the weak-turbulence problem. Deike et al. (Reference Deike, Berhanu and Falcon2014a
) show, for stationary turbulence, that dissipation within the inertial range results in a non-constant inter-modal energy transfer. This is in contrast to WTT which postulates and obtains a constant energy flux
$P$
transferring energy across
$k$
from large to small scales. The variation of energy transfer in
$k$
affects the experimental (or numerical) quantification of
$P$
. For the case of stationary-state forced turbulence, earlier measurements of
$P$
(e.g. Falcon et al.
Reference Falcon, Laroche and Fauve2007; Xia et al.
Reference Xia, Shats and Punzmann2010) rely on the assumption that
$P$
is equal to the total energy input rate, or equivalently the total rate of dissipation
${\it\Gamma}$
. The obtained results are in apparent disagreement with the WTT scaling of
$I_{{\it\eta}}\sim P^{1/2}$
. This controversy is later shown to be resolvable (Deike et al.
Reference Deike, Berhanu and Falcon2014a
), in a limited range of nonlinearity, by defining
$P$
as the average of the inter-modal energy transfer over the entire inertial range. In decaying turbulence with broad-scale dissipation, the inter-modal energy transfer is further affected by the unsteadiness of the spectrum, and an effective way to evaluate
$P$
is not available.
The complexities associated with the unsteadiness in the decaying turbulence, broad-scale dissipation and finite-box effect, inevitably present in realistic physical experiments, are closely coupled. The general problem is difficult, and there is still not a clear elucidation, especially in the context of direct numerical investigation, of the underlying dynamics. In particular, it would be desirable to obtain a modified form of (1.3) (or (1.1)) for the spectral evolution, as well as that for
$E(t)$
, applicable to the general physical problem of decaying capillary wave turbulence. Physically, the role of unsteadiness in the spectrum evolution and dynamics, the time dependence of the spectral slope
${\it\alpha}(t)$
, as well as its inherent connection to the wave field and dissipation magnitude, remain unknown. These are the focus of the present work.
We perform direct numerical simulation of decaying capillary wave turbulence implementing the nonlinear primitive Euler equations. We consider low Bond number such that the influence of gravity is neglected. The problem we solve is a substantial generalization of Pan & Yue (Reference Pan and Yue2014), where realistic broad-scale dissipation is included in the context of decaying turbulence. In contrast to Pan & Yue (Reference Pan and Yue2014), we also simulate the evolving spectrum for a long enough time scale to investigate the time-varying dynamics. Our results replicate those from experiments on a power-law spectrum with exponential modal decay, as well as monochromatic decrease of
$k_{c}$
and variation of
${\it\alpha}$
during the decay. Along with the evolution of the spectrum (
$\partial I_{{\it\eta}}/\partial t\neq 0$
), the broad-scale dissipation results in variation of the energy transfer,
${\mathcal{J}}(k,t)$
, along
$k$
. This substantially complicates the evaluation of the energy flux
$P$
. We propose a novel and effective way to obtain
$P$
, by integrating the modal energy balance equation along
$k$
, thus incorporating both effects of unsteadiness and non-constant inter-model energy transfer
${\mathcal{J}}$
. The obtained results on
$P$
are shown to be consistent with the framework of Pushkarev & Zakharov (Reference Pushkarev and Zakharov2000) and Pan & Yue (Reference Pan and Yue2014) in terms of the scaling
$I_{{\it\eta}}\sim P^{1/2}$
. By considering energy dissipated at broad scales, we also show that the total energy dissipation rate
${\it\Gamma}$
can be significantly higher than
$P$
, which settles the previous debate on the measurement of
$P$
by assuming the equivalence of the two (Falcon et al.
Reference Falcon, Laroche and Fauve2007; Xia et al.
Reference Xia, Shats and Punzmann2010).
Based on our simulations, we are able to describe the time-dependent power-law spectrum within the inertial range [
$k_{b},k_{c}(t)$
] in an explicit general form:
$$\begin{eqnarray}I_{{\it\eta}}(k,t)=I^{0}k^{{\it\alpha}^{0}-A(t-t^{0})}\text{e}^{-B(t-t^{0})},\quad \text{for }k_{b}<k<k_{c}(t)\text{ and }t>t^{0},\end{eqnarray}$$
where
$I^{0}$
and
${\it\alpha}^{0}$
are respectively the spectral amplitude and slope at
$t=t^{0}$
,
$k_{b}$
is the (almost) constant wavenumber above which the power-law spectrum is established and
$k_{c}(t)$
is the spectral location where the spectrum departs from the power law (1.4);
$A$
and
$B$
are functions of
${\it\gamma}_{0}$
only.
Equation (1.4) is shown to fit our numerical data obtained over the ranges of dissipation magnitude, spectral amplitude (nonlinearity) and evolution time that can be obtained by our simulation. For sufficiently high initial nonlinearity,
${\it\alpha}^{0}\approx -19/4$
. While
$A({\it\gamma}_{0})$
represents the time-varying rate of the spectral slope
${\it\alpha}(t)={\it\alpha}^{0}-A(t-t^{0})$
, we show that the value of
${\it\alpha}$
at a given
$t$
can be solely related to the nonlinearity level of the spectrum at that time, irrespective of
${\it\gamma}_{0}$
. The evolution of energy
$E_{I}(t)$
within the inertial range is shown to be well predicted by the analytical integration of (1.4).
2. Numerical formulation
We consider isotropic decaying capillary wave turbulence in the context of potential flow (velocity potential
${\it\phi}(x,y,z,t)$
), in terms of the primitive Euler evolution equations (e.g. Zakharov Reference Zakharov1968) for the surface elevation
${\it\eta}(x,y,t)$
and surface velocity potential
${\it\psi}(x,y,t)\equiv {\it\phi}(x,y,{\it\eta},t)$
:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}_{t}=-\boldsymbol{{\rm\nabla}}{\it\eta}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\psi}+(1+\boldsymbol{{\rm\nabla}}{\it\eta}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\eta}){\it\phi}_{z}|_{{\it\eta}}+F^{-1}[{\it\gamma}_{k}{\it\eta}_{\boldsymbol{k}}],\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\psi}_{t}=-\frac{1}{2}\boldsymbol{{\rm\nabla}}{\it\psi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\psi}+\frac{1}{2}(1+\boldsymbol{{\rm\nabla}}{\it\eta}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\eta}){\it\phi}_{z}|_{{\it\eta}}^{2}+\frac{{\it\sigma}}{{\it\rho}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\frac{\boldsymbol{{\rm\nabla}}{\it\eta}}{\sqrt{1+|\boldsymbol{{\rm\nabla}}{\it\eta}|^{2}}}+F^{-1}[{\it\gamma}_{k}{\it\psi}_{\boldsymbol{k}}],\quad & \displaystyle\end{eqnarray}$$
$F^{-1}$
is the inverse Fourier transform and
${\it\gamma}_{k}\equiv {\it\gamma}(k)=-{\it\gamma}_{0}k^{2}$
is applied on all
$k$
, modelling the broad-scale viscous dissipation at the free surface (e.g. Deike et al.
Reference Deike, Berhanu and Falcon2014a
).
We numerically integrate (2.1) and (2.2) in time with the high-order spectral (HOS) method (refer to Pan & Yue (Reference Pan and Yue2014) for a validation of the method). The simulation starts from an initial isotropic wave field with arbitrary spectral energy distribution. After sufficient time, an inertial-range power-law spectrum forms due to nonlinear wave interactions. Our objective is to study the decay of this spectrum until the physics reaches a purely dissipative regime, i.e. we focus on the spectrum with an inertial range longer than a critical value (in practice,
${\gtrsim}0.3$
decade). To obtain a broad range of energy variation, we choose an initial state specified by a JONSWAP spectrum (the inertial-range results are not sensitive to the specific choice of the initial spectrum), with effective steepness
${\it\beta}=k_{p}H_{s}/2=0.25$
(with
$k_{p}$
being the peak wavenumber and
$H_{s}$
the significant wave height), which is the highest nonlinearity that can be modelled by the HOS method.
Simulations are carried out on a periodic domain with
$256\times 256$
grid points (
$k_{max}=256$
) with a
$2/3$
dealiasing rule. The peak wavenumber
$k_{p}=10k_{0}$
, with
$k_{0}$
being the fundamental wavenumber of the domain. Up to third-order nonlinearity is included to allow interactions of both three and four waves (cf. Pushkarev & Zakharov Reference Pushkarev and Zakharov1996; Pan & Yue Reference Pan and Yue2014). We define the normalized dissipation coefficient
$\widehat{{\it\gamma}}_{0}\equiv {\it\gamma}_{0}k_{p}^{2}/{\it\omega}_{p}$
, where
${\it\omega}_{p}=\sqrt{{\it\sigma}k_{p}^{3}/{\it\rho}}$
is the angular frequency corresponding to
$k_{p}$
. A power-law spectrum can be obtained in our simulation for
$\widehat{{\it\gamma}}_{0}\in (0.5\times 10^{-5},3.0\times 10^{-5})$
. This range is limited above by the dominance of dissipation over nonlinear interaction and below by the inherent numerical instability associated with the growth of short waves. Results for selected values of
$\widehat{{\it\gamma}}_{0}=0.8\times 10^{-5}$
,
$1.6\times 10^{-5}$
and
$2.4\times 10^{-5}$
are presented.
Figure 1. A typical decay of the power-law spectrum for
$\widehat{{\it\gamma}}_{0}=1.6\times 10^{-5}$
. The spectra from top to bottom are realized at
$t/T_{p}=600$
(
${\it\alpha}=-4.8$
,
$t/T_{p}=2100$
(
${\it\alpha}=-5.7$
,
$t/T_{p}=3600$
(
${\it\alpha}=-6.7$
and
$t/T_{p}=5100$
(
${\it\alpha}=-7.5$
, where
$T_{p}=2{\rm\pi}/{\it\omega}_{p}$
. For reference, the power-law (——) and exponential (– – –) fits of the spectra within [
$k_{b}$
,
$k_{c}$
] and [
$k_{c}$
,
$k_{max}$
] respectively, as well as values of
$k_{c}$
(▫) are indicated. Inset: variation of
$k_{c}$
(▫) with
$t$
, and the linear fit (——) with
$R^{2}=0.96$
.
3. Results
Figure 1 shows a typical decay of the spectrum
$I_{{\it\eta}}$
after the power-law inertial range is established. This plot is a representative of all our results, where the evolving spectrum features a power-law range within [
$k_{b},k_{c}(t)$
] (with
$k_{b}\approx 1.5k_{p}$
) and an exponential range within [
$k_{c}(t),k_{max}$
]. In practice (with sufficiently wide [
$k_{b},k_{c}$
]),
$k_{c}$
is obtained from the intersection of the power-law
$I_{{\it\eta}}\sim k^{{\it\alpha}}$
and exponential
$I_{{\it\eta}}\sim \exp ({\it\beta}k)$
fits of the numerical data. Physically,
$k_{c}$
corresponds to the spectral location at which the time scales of nonlinear interaction and viscous dissipation are balanced (Kolmakov et al.
Reference Kolmakov, Levchenko, Brazhnikov, Mezhov-Deglin, Silchenko and McClintock2004; Deike et al.
Reference Deike, Daniel, Berhanu and Falcon2014b
). As the spectrum decays,
$k_{c}$
decreases monotonically (cf. Kolmakov et al.
Reference Kolmakov, Levchenko, Brazhnikov, Mezhov-Deglin, Silchenko and McClintock2004). This decrease is found to be approximately linear with
$t$
for all our cases (see figure 1 inset). Within the power-law range, it is clear that
$I_{{\it\eta}}\sim k^{{\it\alpha}}$
where
${\it\alpha}={\it\alpha}(t)$
. As the spectrum evolves,
${\it\alpha}$
decreases as the negative power-law spectral slope steepens. This phenomenon, also observed in the simulation without dissipation in the inertial range (Pan & Yue Reference Pan and Yue2014), is concluded to be due to the finite-box effect. This is a phenomenon where nonlinear wave interactions are suppressed due to the discreteness in
$k$
(and nonlinear resonance broadening is insufficient to overcome it) (e.g. Pushkarev & Zakharov Reference Pushkarev and Zakharov2000). It results in a steeper spectrum at lower nonlinearity, as evidenced also from gravity wave turbulence (e.g. Denissenko, Lukaschuk & Nazarenko Reference Denissenko, Lukaschuk and Nazarenko2007).
Figure 2 plots
$I_{{\it\eta}}(k_{j},t)$
as a function of time for different values of
$k_{j}\in [k_{b},k_{max}]$
. Regardless of whether
$k_{j}$
is in the power-law range,
$I_{{\it\eta}}(t;k_{j})$
decays exponentially (cf. Deike et al.
Reference Deike, Berhanu and Falcon2012, Reference Deike, Bacri and Falcon2013) with
$I_{{\it\eta}}(k,t)\sim \exp (-{\it\xi}t)$
, where
${\it\xi}={\it\xi}(k)$
. As a fixed
$k_{j}$
goes from below to above
$k_{c}(t)$
(due to the time variation of
$k_{c}(t)$
),
${\it\xi}$
decreases slightly, as evidenced by the change of slope of
$I_{{\it\eta}}(t;k_{j})$
beyond
$t$
when
$k_{c}(t)$
becomes smaller than
$k_{j}$
(for example the
$k_{j}/k_{0}=24$
, 32 curves in the figure, while
${\it\xi}$
is constant for
$k_{j}=16k_{0}<k_{c}(t)$
and
$k_{j}=45k_{0}>k_{c}(t)$
for the time range plotted).
Figure 2. Evolution of
$I_{{\it\eta}}(t;k_{j})$
for four select modes
$k_{j}/k_{0}=16$
(○), 24 (▫), 32 (▵) and 45 (▿). For reference, linear curve fits for
$k_{j}$
less (——) or greater (– – –) than
$k_{c}(t)$
are plotted.
The modal decay rate
${\it\xi}(k)$
as a function of
$k$
is plotted in figure 3. For comparison, the modal dissipation rate
${\it\gamma}_{{\it\nu}}(k)=2|{\it\gamma}(k)|$
is also shown. In general,
${\it\xi}(k)\neq {\it\gamma}_{{\it\nu}}(k)$
due to the inter-modal energy transfer. For a given
${\it\gamma}_{0}$
, there is a wavenumber
$k_{{\it\gamma}}$
above which
${\it\xi}(k)<{\it\gamma}_{{\it\nu}}(k)$
, indicating a transition to a regime where more energy is dissipated by
${\it\gamma}_{0}$
than can be explained by the decrease in
$I_{{\it\eta}}$
. This can be elucidated by considering the modal energy balance:
$$\begin{eqnarray}\frac{\partial \mathscr{E}}{\partial t}+\frac{\partial {\mathcal{J}}}{\partial k}=-{\it\gamma}_{{\it\nu}}\mathscr{E}\;,\end{eqnarray}$$
where
$\mathscr{E}(k,t)={\it\sigma}k^{3}I_{{\it\eta}}(k)/(2{\rm\pi})$
is the modal energy density. As
$\partial \mathscr{E}/\partial t=-{\it\xi}\mathscr{E}$
,
$\partial {\mathcal{J}}/\partial k$
can be explicitly evaluated as
$\partial {\mathcal{J}}/\partial k=({\it\xi}-{\it\gamma}_{{\it\nu}})\mathscr{E}$
. In the subregime
$k<k_{{\it\gamma}}$
, we have
${\it\xi}\approx {\it\gamma}_{{\it\nu}}$
and
$\partial {\mathcal{J}}/\partial k\approx 0$
(see figure 3), and the energy flux can be approximated by a constant, say,
$P_{{\it\gamma}}\equiv {\mathcal{J}}|_{k=k_{{\it\gamma}}}$
. In this wavenumber regime, the framework of WTT is recovered with (constant) energy flux
$P=P_{{\it\gamma}}$
. For
$k>k_{{\it\gamma}}$
,
${\it\xi}<{\it\gamma}_{{\it\nu}}$
and
$\partial {\mathcal{J}}/\partial k<0$
, showing that the energy transferred by
$P_{{\it\gamma}}$
is absorbed in this regime. Using this physical argument,
$P_{{\it\gamma}}$
can be evaluated by
$$\begin{eqnarray}P_{{\it\gamma}}=\int _{k_{{\it\gamma}}}^{k_{max}}({\it\gamma}_{{\it\nu}}-{\it\xi})\mathscr{E}(k)\,\text{d}k.\end{eqnarray}$$
Figure 4 shows the variation of
$P_{{\it\gamma}}^{1/2}$
as a function of the spectral evolution characterized by the spectral amplitude at the reference wavenumber
$k_{b}$
,
$I_{{\it\eta}}(t;k_{b})/I_{{\it\eta}}(t^{0};k_{b})$
. We observe that the dependence of
$I_{{\it\eta}}\sim P_{{\it\gamma}}^{1/2}$
resembles closely that obtained in Pan & Yue (Reference Pan and Yue2014) for
$P$
in the context of WTT. The deviations from the WTT theoretical scaling for decreasing amplitude in both cases reflect the presence of the finite-box effect. Since
$I_{{\it\eta}}(t;k_{b})\sim \exp (-{\it\xi}t)$
, we obtain
$P_{{\it\gamma}}\sim \exp (-2{\it\xi}t)$
. The total energy dissipation rate, calculated as
$$\begin{eqnarray}{\it\Gamma}=\int _{0}^{k_{max}}{\it\gamma}_{{\it\nu}}\mathscr{E}\,\text{d}k,\end{eqnarray}$$
is also plotted in figure 4, showing that in general
${\it\Gamma}>P_{{\it\gamma}}$
. This explains the significant overprediction of
$P$
using
${\it\Gamma}$
(or equivalently by using energy input in forcing turbulence) in previous work (Falcon et al.
Reference Falcon, Laroche and Fauve2007; Xia et al.
Reference Xia, Shats and Punzmann2010).
The impact of the unsteady effect on the evaluation of
$P_{{\it\gamma}}$
can be seen from (3.2); it tends to reduce
$P_{{\it\gamma}}$
. The relative importance of the unsteady effect can be characterized by a parameter
${\mathcal{Z}}$
:
$$\begin{eqnarray}{\mathcal{Z}}\equiv \frac{\displaystyle \int _{k>k_{{\it\gamma}}}{\it\xi}\mathscr{E}\,\text{d}k}{\displaystyle \int _{k>k_{{\it\gamma}}}{\it\gamma}_{{\it\nu}}\mathscr{E}\,\text{d}k}.\end{eqnarray}$$
The parameter
${\mathcal{Z}}$
is plotted in figure 4, showing that
${\mathcal{Z}}=0.6{-}0.7$
(in general, also a function of
${\it\gamma}_{0}$
). This illustrates the significant unsteady effect for this problem, in contrast to our previous work for quasi-stationary turbulence (Pan & Yue Reference Pan and Yue2014) where, in theory,
${\mathcal{Z}}=0$
(in the actual numerics,
${\mathcal{Z}}=0.1{-}0.2$
(Pan & Yue Reference Pan and Yue2014)).
Figure 3. Normalized modal decay rate
$\hat{{\it\xi}}(k)\equiv {\it\xi}(k)/{\it\gamma}_{{\it\nu},p}$
(
$\hat{{\it\gamma}}_{{\it\nu}}(k)=2|{\it\gamma}(k)|/{\it\gamma}_{{\it\nu},p}$
(——) and variation of energy transfer
$(\partial {\mathcal{J}}/\partial k)/(\mathscr{E}{\it\gamma}_{{\it\nu},p})$
(
$k$
at a certain time
$t/T_{p}=2100$
, where
${\it\gamma}_{{\it\nu},p}\equiv {\it\gamma}_{{\it\nu}}(k_{p})$
. The linear fit within the inertial range
${\it\xi}=A\ln k+B$
(– – –), and locations of
$k_{{\it\gamma}}$
(●) and
$k_{c}$
(▫) are indicated. Inset: values of
$|R|=|B/A|$
(▫) and
$A/{\it\gamma}_{{\it\nu},p}$
(○) for different values of
$\widehat{{\it\gamma}}_{0}$
.
Figure 4. Normalized energy flux
$\widehat{P}_{{\it\gamma}}\equiv P_{{\it\gamma}}/({\it\sigma}{\it\omega}_{p})$
(
$\widehat{{\it\Gamma}}\equiv {\it\Gamma}/({\it\sigma}{\it\omega}_{p})$
(
${\mathcal{Z}}$
(
$I_{{\it\eta}}(t;k_{b})/I_{{\it\eta}}(t^{0};k_{b})$
. The WTT scaling
$I_{{\it\eta}}\sim P^{1/2}$
is indicated (– – –).
Equation (1.4) is equivalent to
$$\begin{eqnarray}I_{{\it\eta}}(k,t)=I^{0}k^{{\it\alpha}^{0}}\exp (-{\it\xi}(k)(t-t^{0})),\end{eqnarray}$$
where
${\it\xi}=A\,\text{ln}\,k+B$
, which describes the exponential modal decay with rate
${\it\xi}(k)$
from an initial power-law spectrum
$I^{0}k^{{\it\alpha}^{0}}$
, as evidenced from figures 1 and 2. The linear dependence of
${\it\xi}$
and
$\ln k$
is confirmed in figure 3. Indeed, this is an algebraic requirement for the spectrum to maintain power-law form in the evolution. Since
${\it\xi}$
is not a function of time in the power-law range (cf. figure 2),
$A$
and
$B$
are constants (and functions of
${\it\gamma}_{0}$
only).
The explicit time dependence of the spectral slope
${\it\alpha}(t)$
can be factored out in (1.4) to obtain
$$\begin{eqnarray}{\it\alpha}=\frac{1}{\ln k+R}\left(\ln \frac{I_{{\it\eta}}(k)}{I^{0}}+R{\it\alpha}^{0}\right)\!,\quad R\equiv B/A.\end{eqnarray}$$
While
$A$
and
$B$
are functions of
${\it\gamma}_{0}$
, we find that the value of
$R$
(see figure 3 inset) remains almost constant over the range of
${\it\gamma}_{0}$
we consider. Equation (3.6) thus shows that, even though the evolutional rates of
${\it\alpha}(t)$
and
$I_{{\it\eta}}(t;k)$
depend on the magnitude of dissipation, the instantaneous
${\it\alpha}$
is uniquely related to the spectral magnitude (nonlinearity), independent of
${\it\gamma}_{0}$
. Physically, this states that the development of the spectral slope within the inertial range is governed by nonlinear wave interactions (only), i.e. local effects of dissipation are removed by faster nonlinear interactions. To further validate this, we plot in figure 5 the spectral slope
${\it\alpha}$
as a function of
$I_{{\it\eta}}(k_{b})$
for all values of
${\it\gamma}_{0}$
that we consider. Indeed, all of the data collapse to the curve described by (3.6). The value of
${\it\alpha}\approx -19/4$
, corresponding to WTT (see (1.1)), is achieved at the highest nonlinearity (
$I_{{\it\eta}}(k_{b})$
) that can be modelled by the HOS method. In a recent experiment with a much broader range of dissipation magnitude (varying over a factor of 100) (Deike et al.
Reference Deike, Berhanu and Falcon2014a
),
${\it\alpha}$
is found to be different between the regimes of high and low dissipation. The result may also depend on the specific form of dissipation considered (cf. Deike et al.
Reference Deike, Berhanu and Falcon2012; Miquel, Alexakis & Mordant Reference Miquel, Alexakis and Mordant2014). The underlying physics for broader ranges of dissipation magnitude and nonlinearity level requires further investigation.
Figure 5. Spectral slope
$|{\it\alpha}|$
as a function of
$I_{{\it\eta}}(k_{b})$
for
${\it\gamma}_{0}=0.8\times 10^{-5}$
(○),
$1.6\times 10^{-5}$
(▫) and
$2.4\times 10^{-5}$
(▵). Scatter of the data is caused by the fluctuations of the spectra. Equation (3.6) is indicated (– – –).
If dissipation is absent in the power-law range (and
${\mathcal{Z}}\rightarrow 0$
), the decay of the total energy
$E$
can be related to the (constant) nonlinear energy flux
$P$
to obtain
$E\sim t^{-1}$
(Falkovich et al.
Reference Falkovich, Shapiro and Shtilman1995). Indeed, this relation can be derived by direct integration of the equation
$\text{d}E/\text{d}t=-{\it\Gamma}=-P\sim -E^{2}$
(since
$I_{{\it\eta}}\sim P^{1/2}$
), where the assumption of
$P={\it\Gamma}$
is needed. In the present context of broad-scale dissipation,
${\it\Gamma}>P_{{\it\gamma}}\sim P$
and the
$t^{-1}$
scaling does not hold. We focus on the power-law range and define
$E_{I}\sim \iint _{k_{b}}^{k_{c}}k^{2}I_{{\it\eta}}(k)\,\text{d}\boldsymbol{k}$
. Substitution of (1.4) (or equivalently (3.5)) gives
$$\begin{eqnarray}E_{I}(t)\sim \frac{\exp (-B(t-t^{0}))}{4+{\it\alpha}(t)}(k_{c}(t)^{4+{\it\alpha}(t)}-k_{b}^{4+{\it\alpha}(t)}).\end{eqnarray}$$
Figure 6 plots the evolution of
$E_{I}$
with time, comparing the numerical data with (3.7). Agreement is achieved over two decades of
$E_{I}$
for the range of
${\it\gamma}_{0}$
we consider. This consolidates the effectiveness of (1.4) in representing the decaying spectrum, and provides a simple form in approximating
$E_{I}(t)$
.
Figure 6. Variations of energy
$E_{I}/E_{I}^{0}$
(where
$E_{I}^{0}$
is the inertial-range spectral energy at
$t=t^{0}$
) with time from predictions of (3.7) (——) and numerical data for
${\it\gamma}_{0}=0.8\times 10^{-5}$
(▫),
$1.6\times 10^{-5}$
(○) and
$2.4\times 10^{-5}$
(▿).
4. Conclusion
We present a direct numerical investigation of freely decaying capillary wave turbulence with broad-scale dissipation of magnitude
${\it\gamma}_{0}$
. The problem we consider is an extension of WTT (Zakharov & Filonenko Reference Zakharov and Filonenko1967; Falkovich et al.
Reference Falkovich, Shapiro and Shtilman1995) where the turbulence is allowed to evolve freely in the presence of physically realistic dissipation and finite-box effect. Our simulation results are consistent with evidence from physical experiments, in terms of the shortening of the power-law range and the steepening of the spectral slope
${\it\alpha}$
during the decay (e.g. Kolmakov et al.
Reference Kolmakov, Levchenko, Brazhnikov, Mezhov-Deglin, Silchenko and McClintock2004; Miquel & Mordant Reference Miquel and Mordant2011; Deike et al.
Reference Deike, Berhanu and Falcon2012, Reference Deike, Bacri and Falcon2013). Based on our numerical findings, we obtain a simple model, (1.4), describing the evolution of the power-law spectrum in the form of exponential modal decay from an initial spectrum. The rate of modal decrease in time,
${\it\xi}(k)$
, is shown to be given by
${\it\xi}(k)=A\ln k+B$
, with
$A$
and
$B$
depending only on
${\it\gamma}_{0}$
. Over the range of dissipation magnitude that can be obtained using our direct simulation, the instantaneous spectral slope
${\it\alpha}$
during the evolution is found to depend only on the nonlinearity of the spectrum at that time, irrespective of
${\it\gamma}_{0}$
. The decay of energy within the inertial range obtained from (1.4) is also shown to approximate well those obtained from simulations. These findings are in contrast to the theoretical result (Falkovich et al.
Reference Falkovich, Shapiro and Shtilman1995) without broad-scale dissipation and finite-box effect, underscoring the importance of these effects in the actual physical problem. Relative to WTT, broad-scale dissipation and unsteadiness here result in a non-constant inter-modal energy transfer
${\mathcal{J}}$
in the inertial range, which requires an alternative quantification of the energy flux
$P$
. Within a subrange
$k<k_{{\it\gamma}}$
of our inertial range, we find that
$\partial {\mathcal{J}}/\partial k\approx 0$
, so that the energy flux can be approximated by a constant
$P=P_{{\it\gamma}}={\mathcal{J}}|_{k=k_{{\it\gamma}}}$
. In this subrange, the framework of (stationary) WTT is obtained, and we recover the WTT scaling
$I_{{\it\eta}}\sim P_{{\it\gamma}}^{1/2}$
(e.g. Pushkarev & Zakharov Reference Pushkarev and Zakharov2000; Pan & Yue Reference Pan and Yue2014). The present results describing decaying capillary wave turbulence are expected to hold in other weak-turbulence systems with broad-scale dissipation.
Acknowledgement
This research is supported financially by grants from the Office of Naval Research.
