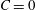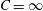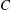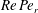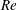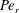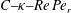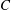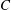1 Introduction
The rheology of, and orientation dynamics in, suspensions of anisotropic particles is relevant to an immense array of scenarios, both fundamental and applied, with length scales ranging from the microscopic to the geological (Mueller, Llewellin & Mader Reference Mueller, Llewellin and Mader2011; Caro et al.
Reference Caro, Pedley, Schroter and Seed2012; Hogan et al.
Reference Hogan, Tian, Brown, Westbrook, Heymsfield and Eastment2012; Masaeli et al.
Reference Masaeli, Sollier, Amini, Mao, Camacho, Doshi, Mitragotri, Alexeev and Carlo2012; Amini, Lee & Carlo Reference Amini, Lee and Carlo2014), and the particle geometry varying between extremes of disk- and fibre-shaped morphologies (van Olphen Reference van Olphen1963; Derakhshandeh et al.
Reference Derakhshandeh, Kerekes, Hatzikiriakos and Bennington2011; Mueller et al.
Reference Mueller, Llewellin and Mader2011; Caro et al.
Reference Caro, Pedley, Schroter and Seed2012). In contrast to suspensions of spheres, anisotropic particle suspensions exhibit a rich array of equilibrium and non-equilibrium phases owing to the additional orientational degree of freedom at the microstructural level (Vroege & Lekkerkerker Reference Vroege and Lekkerkerker1992; Brown & Rennie Reference Brown and Rennie2001; Michot et al.
Reference Michot, Bihannic, Maddi, Funari, Baravian, Levitz and Davison2006; Lekkerkerker & Vroege Reference Lekkerkerker and Vroege2012). Transitions in orientational order, usually at high volume fractions, are often accompanied by abrupt changes in transport characteristics (Larson Reference Larson1988; Claeys & Brady Reference Claeys and Brady1993). A spheroid serves as a canonical anisotropic particle, its aspect ratio being the microstructural parameter. The rheology of a suspension of spheroids is sensitively dependent on the underlying orientation distribution. A fundamental result of Stokesian hydrodynamics is that an isolated non-Brownian spheroid in simple shear flow rotates indefinitely along any of a one-parameter family of spherical ellipses (Jeffery orbits) (Jeffery Reference Jeffery1922; Kim & Karrila Reference Kim and Karrila1991). The parameter, the orbit constant
$C$
, takes values between 0 and
$\infty$
. The existence of Jeffery orbits implies that the long-time orientation distribution remains crucially dependent on the initial conditions. The non-convergence to a unique steady state leads to an indeterminate rheology. The indeterminacy is a consequence of Stokes flow reversibility, which leads to closed streamlines or pathlines in other situations, with profound implications for the relevant microscale transport processes (Batchelor & Green Reference Batchelor and Green1972a
,Reference Batchelor and Green
b
; Kao, Cox & Mason Reference Kao, Cox and Mason1977; Subramanian & Brady Reference Subramanian and Brady2006; Subramanian & Koch Reference Subramanian and Koch2006a
,Reference Subramanian and Koch
b
, Reference Subramanian and Koch2007; Krishnamurthy Reference Krishnamurthy2014).
For spheroids larger than approximately 10 microns in low-viscosity media, inertia is expected to play a dominant role in eliminating the aforementioned indeterminacy. In recent work (Einarsson et al.
Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015; Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2016), a weak inertial drift across Jeffery orbits was found to stabilize a unique orbit for neutrally buoyant spheroids with aspect ratios (
$\unicode[STIX]{x1D705}$
) greater than approximately 0.14. The orientation dynamics underwent a bifurcation for (oblate) spheroids with
$\unicode[STIX]{x1D705}<0.14$
, owing to a sign reversal of the drift, leading to a pair of stable Jeffery orbits, corresponding to tumbling (
$C=\infty$
) and spinning (
$C=0$
) motions, separated by an unstable repeller (see figure 1). The steady-state partitioning of orientations between these two orbits is uniquely determined only by stochastic fluctuations, and the case of rotary Brownian motion (thermal orientation fluctuations) was analysed in some detail (Dabade et al.
Reference Dabade, Marath and Subramanian2016). In § 2, we show that the steady-state orientation distribution, resulting from a balance of an inertial drift and rotary Brownian motion, has a thermodynamic interpretation. The bifurcation in the orientation dynamics in the presence of rotary Brownian motion, identified in Dabade et al. (Reference Dabade, Marath and Subramanian2016), has analogies to a thermodynamic phase transition, the orbit constant playing the role of an orientational order parameter. The original pair of Jeffery orbits (
$C=0$
and
$C=\infty$
), smeared out by thermal fluctuations, may be regarded as spinning and tumbling phases, and comprise the small- and large-
$C$
branches of a two-phase envelope ending in a critical point. The three-dimensional parameter space characterizing this ‘tumbling–spinning transition’ has a one-to-one correspondence with the familiar thermodynamic description of the one-component phase transition. Specifically,
$\unicode[STIX]{x1D705}$
and
$C$
are analogous to the pressure and specific volume respectively, while an appropriate non-dimensional shear rate plays the role of an inverse non-equilibrium temperature. However, the time required to attain a steady state becomes exceedingly large deep within the two-phase envelope. Hence, later in § 2, we analyse the time-dependent orientation distribution for different initial conditions, and show that the finite-time evolution in the two-phase envelope is characterized by a pronounced hysteresis, leading to the suspension viscosity being sensitively dependent on the precise shear history. We also propose a precise experimental protocol to observe this hysteresis. We summarize our findings in § 3, where we also argue that the tumbling–spinning hysteresis should be observable in more general circumstances.
Figure 1. Jeffery orbits (green), the constant-
$C$
trajectories of the spheroid orientation vector on the unit sphere, are plotted for oblate spheroids of aspect ratios (a) 0.12 and (c) 0.05. In each case, the repeller (red), a Jeffery orbit at leading order, divides the unit sphere into basins of attractions corresponding to the tumbling (
$C=\infty$
) and spinning (
$C=0$
) orbits. The inertial trajectories (black), shown in (b) and (d) for the same aspect ratios, start on either side of the repeller and spiral away towards the limiting orbits.
2 The spheroid orientation distribution: results and interpretation
The non-dimensional equation governing the orientation distribution
$\unicode[STIX]{x1D6FA}(\boldsymbol{p})$
, where the unit vector
$\boldsymbol{p}$
denotes the spheroid orientation, is given by
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}_{\boldsymbol{p}}\boldsymbol{\cdot }[(\dot{\boldsymbol{p}}_{\mathit{jeff}}+Re\,\dot{\boldsymbol{p}}_{i})\unicode[STIX]{x1D6FA}]=\frac{1}{Pe_{r}}\unicode[STIX]{x1D6FB}_{\boldsymbol{p}}^{2}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
The second term on the left-hand side is the combined drift due to convection along a Jeffery orbit at leading order (Kim & Karrila Reference Kim and Karrila1991) and the
$O(Re)$
inertial convection derived in Dabade et al. (Reference Dabade, Marath and Subramanian2016). Here,
$Re=\unicode[STIX]{x1D70C}_{f}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$
is the microscale Reynolds number based on the spheroid semi-major axis
$L$
,
$\unicode[STIX]{x1D70C}_{f}$
and
$\unicode[STIX]{x1D707}$
are the fluid density and viscosity, and
$\dot{\unicode[STIX]{x1D6FE}}^{-1}$
, the inverse shear rate, is the time scale of the simple shear flow (
$\unicode[STIX]{x1D735}\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}\mathbf{1}_{y}\mathbf{1}_{x}$
). The Laplacian in (2.1) denotes orientational diffusion driven by Brownian couples, and is inversely proportional to the rotary Péclet number defined as
$Pe_{r}=[kT{\mathcal{M}}(\unicode[STIX]{x1D705})]^{-1}\dot{\unicode[STIX]{x1D6FE}}$
, where
$kT$
is the thermal energy unit and
${\mathcal{M}}(\unicode[STIX]{x1D705})$
is the aspect-ratio-dependent mobility associated with transverse rotation (Kim & Karrila Reference Kim and Karrila1991).
In the absence of inertia and Brownian motion, equation (2.1) takes the form
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}t}+\frac{1}{h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\left(\frac{h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FA}}{(\unicode[STIX]{x1D705}^{2}+1)}\right)=0\end{eqnarray}$$
in orbit-aligned coordinates
$(C,\unicode[STIX]{x1D70F})$
,
$\unicode[STIX]{x1D70F}$
being the orbit phase that satisfies
$\text{d}\unicode[STIX]{x1D70F}/\text{d}t=\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D705}^{2}+1)$
(Leal & Hinch Reference Leal and Hinch1971), with
$\dot{\boldsymbol{p}}_{\mathit{jeff}}=h_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D705}^{2}+1)\hat{\unicode[STIX]{x1D749}}$
,
$\hat{\unicode[STIX]{x1D749}}$
being the unit tangent vector to a Jeffery orbit. In (2.2),
$h_{C}$
and
$h_{\unicode[STIX]{x1D70F}}$
are the metric factors corresponding to the
$C$
and
$\unicode[STIX]{x1D70F}$
coordinate lines, and
$\unicode[STIX]{x1D6FC}$
is the angle between
$\hat{\unicode[STIX]{x1D749}}$
and
$\hat{\boldsymbol{C}}$
, the latter being the unit vector along the
$C$
coordinate. The convective operator in (2.2) does not lead to a unique steady state. Every initial condition, except one, leads to a different time-dependent orientation distribution. The dependence on time is periodic since the initial condition is merely convected around with the Jeffery angular velocity. As is evident from (2.2), the exceptional initial condition that leads to a time-independent
$\unicode[STIX]{x1D6FA}$
must be of the form
$\unicode[STIX]{x1D6FA}\propto 1/(h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC})$
, where the proportionality allows for a multiplicative factor that is an arbitrary function of
$C$
alone, this corresponding to the distribution across orbits.
Experiments on anisotropic particle suspensions invariably involve a slight polydispersity in the particle aspect ratio (Okagawa, Cox & Mason Reference Okagawa, Cox and Mason1973; Ennis, Okagawa & Mason Reference Ennis, Okagawa and Mason1978; Ivanov, Van de Ven & Mason Reference Ivanov, Van de Ven and Mason1982). It turns out that the phase mixing due to the differential rotations induced by this polydispersity leads to all of the time-dependent solutions of (2.2) converging to the aforementioned steady state on a time scale that is
$O(1/\unicode[STIX]{x1D70E})$
for aspect ratios of order unity. Here,
$\unicode[STIX]{x1D70E}$
is the standard deviation of the aspect-ratio distribution. However, the polydispersity-induced phase mixing only leads to a steady-state distribution along a Jeffery orbit, and leaves the initial distribution across orbits unchanged at leading order.
The distribution across orbits, which is indeterminate at leading order, is determined over a much longer time scale, the smaller of
$O((\dot{\unicode[STIX]{x1D6FE}}Re)^{-1})$
or
$O(\dot{\unicode[STIX]{x1D6FE}}^{-1}Pe_{r})$
(as shown later, for certain combinations of
$Re$
,
$Pe_{r}$
and
$\unicode[STIX]{x1D705}$
, the actual time scale can be exponentially larger than the nominal estimates given), from a balance of inertia and Brownian motion. The relative importance of the latter two mechanisms is determined by
$Re\,Pe_{r}(\propto \dot{\unicode[STIX]{x1D6FE}}^{2})$
. In the regime corresponding to
$Re\ll 1$
,
$Pe_{r}\gg 1$
, with
$Re\,Pe_{r}$
arbitrary, equation (2.1), with the addition of a slight polydispersity, may be solved using a multiple scales analysis (Subramanian & Brady Reference Subramanian and Brady2004). If
$h(\unicode[STIX]{x1D705},\bar{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D70E})$
is the probability density characterizing the aspect-ratio distribution, so that
$\unicode[STIX]{x1D70E}^{2}=\int (\unicode[STIX]{x1D705}-\bar{\unicode[STIX]{x1D705}})^{2}h(\unicode[STIX]{x1D705},\bar{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D70E})\,\text{d}\unicode[STIX]{x1D705}$
,
$\bar{\unicode[STIX]{x1D705}}$
being the mean aspect ratio, with
$\unicode[STIX]{x1D70E}\ll \bar{\unicode[STIX]{x1D705}}$
, the expression for
$\bar{\unicode[STIX]{x1D6FA}}=\int \unicode[STIX]{x1D6FA}h(\unicode[STIX]{x1D705},\bar{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D70E})\,\text{d}\unicode[STIX]{x1D705}$
may be obtained with the aid of the expansion
$\bar{\unicode[STIX]{x1D6FA}}=\bar{\unicode[STIX]{x1D6FA}}_{0}+Re\bar{\unicode[STIX]{x1D6FA}}_{1}$
(
$Re\bar{\unicode[STIX]{x1D6FA}}_{1}\ll \bar{\unicode[STIX]{x1D6FA}}_{0}$
) and the ansatz
$\bar{\unicode[STIX]{x1D6FA}}_{0}=f(C,t_{2})g(C,\unicode[STIX]{x1D70F},t_{1};\unicode[STIX]{x1D70E})$
. Here,
$\bar{\unicode[STIX]{x1D6FA}}$
is the orientation probability density corresponding to a spheroid with the mean aspect ratio
$\bar{\unicode[STIX]{x1D705}}$
, and
$t_{1}=t$
(corresponding to Stokesian convection and polydispersity) and
$t_{2}=Re\,t$
(corresponding to inertia or Brownian motion when
$Re\,Pe_{r}$
is
$O(1)$
) are the dimensionless fast and slow time scales. It is shown in the supplementary material available at https://doi.org/10.1017/jfm.2016.779 that the equations governing
$\bar{\unicode[STIX]{x1D6FA}}_{0}$
and
$\bar{\unicode[STIX]{x1D6FA}}_{1}$
take the forms
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D6FA}_{0}}}{\unicode[STIX]{x2202}t_{1}^{2}}+\frac{1}{h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC}}\left(B(\bar{\unicode[STIX]{x1D705}})\frac{\unicode[STIX]{x1D70E}^{2}}{2t_{1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{0}}-A^{2}(\bar{\unicode[STIX]{x1D705}})\frac{\unicode[STIX]{x1D70E}^{2}}{2}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{o}^{2}}\right)(\bar{\unicode[STIX]{x1D6FA}_{0}}h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D6FA}}_{1}}{\unicode[STIX]{x2202}t_{1}^{2}}+\frac{1}{h_{C}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC}}\left(B(\bar{\unicode[STIX]{x1D705}})\frac{\unicode[STIX]{x1D70E}^{2}}{2t_{1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{0}}-A^{2}(\bar{\unicode[STIX]{x1D705}})\frac{\unicode[STIX]{x1D70E}^{2}}{2}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{o}^{2}}\right)(\bar{\unicode[STIX]{x1D6FA}_{1}}h_{C}\,h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2t_{1}}\left(\frac{1}{Re\,Pe_{r}}\unicode[STIX]{x1D6FB}_{\boldsymbol{p}}^{2}\bar{\unicode[STIX]{x1D6FA}}_{0}-\unicode[STIX]{x1D735}_{\boldsymbol{p}}\boldsymbol{\cdot }[\dot{\boldsymbol{p}}_{i}\bar{\unicode[STIX]{x1D6FA}}_{0}]-\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D6FA}_{0}}}{\unicode[STIX]{x2202}t_{2}}\right),\end{eqnarray}$$
where
$B(\bar{\unicode[STIX]{x1D705}})=(\bar{\unicode[STIX]{x1D705}}^{3}-3\bar{\unicode[STIX]{x1D705}})/(1+\bar{\unicode[STIX]{x1D705}}^{2})^{3}$
and
$A(\bar{\unicode[STIX]{x1D705}})=(1-\bar{\unicode[STIX]{x1D705}}^{2})/(1+\bar{\unicode[STIX]{x1D705}}^{2})^{2}$
. In (2.3)–(2.4),
$\unicode[STIX]{x1D70F}_{0}=\unicode[STIX]{x1D70F}-(\bar{\unicode[STIX]{x1D705}}/(\bar{\unicode[STIX]{x1D705}}^{2}+1))t_{1}$
, where
$\unicode[STIX]{x1D70F}_{0}$
denotes the (fictitious) initial phase calculated from the current phase (of a spheroid of aspect ratio
$\unicode[STIX]{x1D705}$
) using the Jeffery angular velocity of the spheroid with the mean aspect ratio. Equation (2.4) shows that the phase mixing has a diffusive character (with
$t_{1}^{2}$
as the relevant time variable), with the diffusivity being given by
$D=((1-\bar{\unicode[STIX]{x1D705}}^{2})^{2}/(1+\bar{\unicode[STIX]{x1D705}}^{2})^{4})(\unicode[STIX]{x1D70E}^{2}/2)$
. Using the ansatz above for
$\bar{\unicode[STIX]{x1D6FA}}_{0}$
, with
$g(C,\unicode[STIX]{x1D70F},t_{1};\unicode[STIX]{x1D70E})=1/(h_{c}h_{\unicode[STIX]{x1D70F}}\sin \unicode[STIX]{x1D6FC})$
, and applying a secularity constraint to preclude an algebraically growing term in
$\bar{\unicode[STIX]{x1D6FA}}_{1}$
on the
$t_{1}$
scale, one obtains the following equation for the distribution across the orbits
$f(C,t_{2})$
:
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t_{2}}+\frac{1}{Re}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C}\left[\left(Re\unicode[STIX]{x0394}C_{i}-\frac{\unicode[STIX]{x1D712}_{2}}{2Pe_{r}C}\right)f\right]=\frac{1}{Re\,Pe_{r}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C}\left(\frac{\unicode[STIX]{x1D712}_{1}}{2}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}C}\right).\end{eqnarray}$$
The second term on the left-hand side of (2.5) denotes the combination of the
$O(Pe_{r}^{-1})$
Brownian and the
$O(Re)$
inertial drifts,
$Re\unicode[STIX]{x0394}C_{i}$
being the inertia-induced change in
$C$
over a Jeffery period (Dabade et al.
Reference Dabade, Marath and Subramanian2016), while the right-hand side denotes orientational diffusion with a
$C$
-dependent diffusivity, and
$\unicode[STIX]{x1D712}_{1}=((\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}^{2}+C^{2}(7/2+s(1/4\unicode[STIX]{x1D705}^{2})+\unicode[STIX]{x1D705}^{2}/4)+C^{4}(\unicode[STIX]{x1D705}^{2}+1))$
and
$\unicode[STIX]{x1D712}_{2}=((-\unicode[STIX]{x1D705}^{2}+1)/\unicode[STIX]{x1D705}^{2}+C^{2}(6-(7/2+1/4\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}/4))+2C^{4}(\unicode[STIX]{x1D705}^{2}+1))$
. The one-dimensional drift–diffusion formulation, together with no-flux conditions that arise from symmetry constraints at
$C=0$
and
$C=\infty$
, implies that the steady-state solution of (2.5), given by Dabade et al. (Reference Dabade, Marath and Subramanian2016),
$$\begin{eqnarray}f_{s}(C)=N\exp \left[-Re\,Pe_{r}\int ^{C}\left(\frac{{\displaystyle \frac{\unicode[STIX]{x1D712}_{2}}{Re\,Pe_{r}C^{\prime }}}-2\unicode[STIX]{x0394}C_{i}(C^{\prime };\unicode[STIX]{x1D705})}{\unicode[STIX]{x1D712}_{1}}\right)\text{d}C^{\prime }\right],\end{eqnarray}$$
is an equilibrium of the Boltzmann form,
$N$
being a normalization constant. It should be noted that the form arises because the drift in the one-dimensional formulation resulting from the multiple scale formalism can always be written as the gradient of a potential, and does not point to a conservative system; there can evidently be no conserved energy-like quantity in the non-equilibrium strong-shear scenario under consideration. Thus,
$(Re\,Pe_{r})^{-1}$
in (2.6) is the
$kT$
-equivalent, and the function multiplying it may be interpreted as an effective potential
$U(C;\unicode[STIX]{x1D705},Re\,Pe_{r})$
. Inertia and Brownian motion cause any initial Jeffery-orbit distribution to slide down to the potential minima, this tendency being balanced by the
$O(Re\,Pe_{r})^{-1}$
diffusive fluctuations in
$C$
due to Brownian motion alone.
The potential
$U(C;\unicode[STIX]{x1D705},Re\,Pe_{r})$
exhibits a rather complicated dependence on
$\unicode[STIX]{x1D705}$
and
$Re\,Pe_{r}$
. In order to develop the thermodynamic analogy, we first focus on a particular value,
$Re\,Pe_{r}=70\,000$
, to illustrate the variation in the nature of
$U$
with changing
$\unicode[STIX]{x1D705}$
. In figure 2(b–f), we have plotted the potential
$U(C;\unicode[STIX]{x1D705},70\,000)$
as well as the associated steady state
$f_{s}(C)$
(not normalized for purposes of illustration) for various aspect ratios. With increasing aspect ratio, the potential starts off as one having a single minimum close to
$C/(C+1)=1$
, changes to one with a pair of minima separated by a maximum (a double-well structure) over an intermediate range of aspect ratios, and for sufficiently large aspect ratios, reverts to one with a single minimum that is now close to
$C/(C+1)=0$
. The potential minima at each
$\unicode[STIX]{x1D705}$
may be regarded as phases in a manner similar to the free energy minima in thermodynamic systems. In figure 2(a), we therefore track the potential extrema in the
$\unicode[STIX]{x1D705}{-}C$
plane, leading to the S-shaped extremum locus for
$Re\,Pe_{r}=70\,000$
. It should be noted that, for the chosen
$Re\,Pe_{r}$
, the pair of minima have equal magnitudes at
$\unicode[STIX]{x1D705}=0.019$
.
Figure 2. (a) The extremum locus for
$Re\,Pe_{r}$
of 70 000; the potential has a double-welled structure in the range
$0.009<\unicode[STIX]{x1D705}<0.11$
. (b–f) The potential (dashed) and steady-state distribution
$f_{s}(C)$
(solid) for various aspect ratios.
Figure 3. (a) The extrema loci, together with dashed tie lines, for various values of
$Re\,Pe_{r}$
. (b) The potential curves (
$U$
) for values of
$Re\,Pe_{r}$
just above and below 70 000. (c,d) The two-phase envelope in the
$\unicode[STIX]{x1D705}$
–
$C$
and
$Re\,Pe_{r}$
–
$C$
planes respectively.
One now repeats the above exercise for other values of
$Re\,Pe_{r}$
, and the loci of the potential extrema for various values of
$Re\,Pe_{r}$
are given in figure 3(a). In the limit
$Re\,Pe_{r}\ll 1$
,
$Pe_{r}\gg 1$
, when Brownian motion alone controls the distribution across Jeffery orbits,
$U(C;\unicode[STIX]{x1D705},Re\,Pe_{r})$
has a single minimum regardless of
$\unicode[STIX]{x1D705}$
, and this minimum moves to progressively larger values of
$C$
with decreasing
$\unicode[STIX]{x1D705}$
(see
$Re\,Pe_{r}=0$
in figure 3
a). For the oblate spheroids of interest with
$\unicode[STIX]{x1D705}<1$
, this minimum lies in the vicinity of the tumbling mode, and the corresponding
$f_{s}(C)$
was originally derived in Leal & Hinch (Reference Leal and Hinch1971). The emergence of an inertial drift with increasing
$Re\,Pe_{r}$
leads to a broadening of the minimum until, for sufficiently large
$Re\,Pe_{r}$
,
$U(C;\unicode[STIX]{x1D705},Re\,Pe_{r})$
transitions to a double-welled structure, if the aspect ratio of the spheroid is below a critical value. This transition is due to the bidirectional nature of the inertial drift. The critical
$\unicode[STIX]{x1D705}$
is a function of
$Re\,Pe_{r}$
, approaching a maximum of 0.14 in the deterministic limit (
$Re\,Pe_{r}\rightarrow \infty$
), with the pair of minima asymptoting to the spinning (
$C=0$
) and tumbling (
$C=\infty$
) modes, and the intermediate maximum approaching the
$\unicode[STIX]{x1D705}$
-dependent repeller in figure 1. For a given multivalued locus, a horizontal dashed line is drawn at the
$\unicode[STIX]{x1D705}$
for which the two potential minima have equal magnitudes, in analogy with thermodynamic tie lines (see figure 3
b). The small-
$C$
and large-
$C$
minima that it connects may be identified respectively with ‘spinning’ and ‘tumbling’ phases that coexist at the particular
$\unicode[STIX]{x1D705}$
and
$Re\,Pe_{r}$
. This leads to a phase diagram with a two-phase (tumbling–spinning) envelope that ends in a critical point,
$(C,\unicode[STIX]{x1D705},Re\,Pe_{r})\equiv (3.1,0.0665,1150)$
. The projections of the phase diagram in the
$\unicode[STIX]{x1D705}{-}C$
and
$Re\,Pe_{r}{-}C$
planes are shown in figures 3(c) and 3(d) respectively. The constant-
$Re\,Pe_{r}$
loci in figure 3(c) may be regarded as isotherm analogues, the non-dimensional inverse shear rate squared,
$(Re\,Pe_{r})^{-1}$
, being the non-equilibrium temperature equivalent. Tie lines in figure 3(a) replace the intermediate non-monotonic (and, in the one-component case, thermodynamically inaccessible) portion of the isotherms in the range
$1150<Re\,Pe_{r}<\infty$
. Interestingly, figure 3(c) includes, on one hand, the infinite-temperature isotherm calculated in Leal & Hinch (Reference Leal and Hinch1971); on the other hand, the two-phase envelope is also finite in extent, being bounded below by the zero-temperature isotherm at
$\unicode[STIX]{x1D705}=0.0126$
. The latter is a piecewise linear curve defined by
$C=0,\unicode[STIX]{x1D705}>0.0126$
;
$0<C<\infty ,\unicode[STIX]{x1D705}=0.0126$
;
$C=\infty ,\unicode[STIX]{x1D705}<0.0126$
, and implies a discontinuous transition from a suspension of spinning spheroids to tumbling ones across
$\unicode[STIX]{x1D705}=0.0126$
in the limit
$Re\,Pe_{r}\rightarrow \infty$
(Dabade et al.
Reference Dabade, Marath and Subramanian2016)! Thus, in this limit, the orbit-constant distribution is a delta function at either
$C=0$
or
$C=\infty$
, except for
$\unicode[STIX]{x1D705}=0.0126$
, when it comprises a pair of delta functions at both of the aforementioned
$C$
values.
Figure 4. The three-dimensional phase diagram in
$C$
–
$\unicode[STIX]{x1D705}$
–
$Re\,Pe_{r}$
coordinates. The tumbling–spinning envelope ending in a critical point is shown as red-dashed lines.
The phase diagrams in figure 3(a–d) arise from a one-dimensional description of the orientation dynamics along the
$C$
coordinate, and for
$\unicode[STIX]{x1D705}\ll 1$
, this requires
$Pe_{r}\gg \unicode[STIX]{x1D705}^{-3}$
(Hinch & Leal Reference Hinch and Leal1972). When
$Pe_{r}$
is
$O(\unicode[STIX]{x1D705}^{-3})$
or smaller, Brownian rotations affect the orientation distribution both across and along Jeffery orbits, close to the gradient–vorticity plane, and a reduced description requires first determining the full orientation distribution on the unit sphere.
The tumbling–spinning transition identified above has a striking similarity to the coil–stretch transition of high-molecular-weight polymers in extension-dominated flows (De Gennes Reference De Gennes1974; Hinch Reference Hinch1974). Intrachain hydrodynamic interactions sharpen the transition from the coiled to the stretched configuration, with increasing flow strength (characterized by a Deborah number
$De=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D70F}_{r}$
,
$\unicode[STIX]{x1D70F}_{r}$
being the longest relaxation time), so as to render it discontinuous. The discontinuous transition implies a hysteresis, and coiled and stretched states (produced by varying deformation histories) can coexist at a given
$De$
for times much longer than
$\unicode[STIX]{x1D70F}_{r}$
(Schroeder, Shaqfeh & Chu Reference Schroeder, Shaqfeh and Chu2004). The coexistence, and approach in select scenarios to a bimodal equilibrium, have been verified in single-molecule experiments (Schroeder et al.
Reference Schroeder, Babcock, Shaqfeh and Chu2003) and simulations (Beck & Shaqfeh Reference Beck and Shaqfeh2006) respectively. The coiled and stretched states may be identified with the aforementioned tumbling and spinning phases respectively, with the average polymer extension in a coarse-grained description,
$De$
and the polymer molecular weight being analogous to
$C$
,
$\unicode[STIX]{x1D705}$
and
$Re\,Pe_{r}$
respectively. A tentative phase diagram in the
$\text{extension}{-}De$
plane, the analogue of figure 3(c), appears in Schroeder et al. (Reference Schroeder, Babcock, Shaqfeh and Chu2003).
The hysteretic orientation dynamics of thin oblate spheroids is better understood in the three-dimensional
$\unicode[STIX]{x1D705}{-}C{-}Re\,Pe_{r}$
space in figure 4. The region of multiple extrema in figure 3(a) now defines a binodal volume, and the shaded regions define a smaller spinodal volume confined between the inflection-point loci of the double-welled potentials. The binodal volume shrinks with decreasing
$Re\,Pe_{r}$
, vanishing at
$Re\,Pe_{r}=1150$
(the vertical plane, with
$\log (Re\,Pe_{r})/(\log (Re\,Pe_{r})+1)=0.876$
, passing through the critical point). Unlike the thermodynamic case, there is no equation of state that constrains
$\unicode[STIX]{x1D705}$
to be a certain function of
$Re\,Pe_{r}$
and
$C$
, and all points within the hysteretic binodal volume remain accessible (this remains true for the polymeric case). The analogue of spinodal dynamics corresponds to the evolution of
$f(C)$
from an initial condition (
$f_{0}(C)$
) peaked close to the potential maximum, while the analogue of the nucleation-growth route ensues for an initial condition peaked outside the inflection-point interval. Figure 5(a) shows the rapid evolution for
$Re\,Pe_{r}=3\times 10^{5}$
, starting from a narrow Gaussian at the potential maximum, into a bimodal distribution peaked at the potential minima. In figure 5(b), for an initial Gaussian adjacent to the small-
$C$
potential minimum, the distribution remains unimodal, and a second peak is ‘nucleated’ at much later times via a barrier-hopping process. The time-dependent viscosities for the aforementioned evolutions are shown in figure 5(c). The viscosity for the spinodal case changes quickly, on account of peak splitting, in contrast to the slow evolution of the viscosity for the initial condition in the hysteretic region outside the spinodal volume.
Figure 5. The evolutions starting from localized Gaussians (magenta) peaked at the maximum (a) and adjacent to the small-
$C$
minimum (b) of the potential (red);
$\unicode[STIX]{x1D705}=0.016$
,
$Re\,Pe_{r}=3\times 10^{5}$
. The
$f_{s}(C)$
in each case is shown as a blue curve. The dashed line corresponds to the instant ((a)
$6.5\times 10^{-4}D_{r}^{-1}$
and (b)
$6.1\times 10^{-3}D_{r}^{-1}$
) at which a tumbling peak first appears. (c) Corresponding evolutions of the scaled viscosities (see § 2 of the supplementary material for the details of the evaluation of viscosity) (a) black and (b) red (
$\unicode[STIX]{x1D702}_{0}$
and
$\unicode[STIX]{x1D702}_{s}$
are the initial and steady-state values).
Figure 6. (a) Intrinsic viscosity evolutions for the quenches identified in the text (the inset shows the evolution for step 2 of the second quench). (b) The quasi-steady distributions at
$Re\,Pe_{r}=2\times 10^{5}$
. The second quench leads to a greater fraction of spinning spheroids, and therefore a higher viscosity.
The generation of the localized Gaussian profiles above requires an external field. However, an isotropic orientation distribution can be readily generated by initial mixing. The
$f_{0}(C)$
corresponding to this well-mixed state is given by
$(C\unicode[STIX]{x1D705}E[-(C^{2}(\unicode[STIX]{x1D705}^{2}-1))/(C^{2}+1)])/(\unicode[STIX]{x03C0}\sqrt{C^{2}+1}(\unicode[STIX]{x03C0}C^{2}\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x03C0}))$
, where
$E$
is the complete elliptic integral of the second kind. For this
$f_{0}(C)$
, a signature of the hysteresis is the sensitive dependence of the viscosity in the binodal volume to the precise shear rate history. To illustrate this dependence, we consider a pair of ‘quenches’ applied to an isotropic suspension of spheroids with
$\unicode[STIX]{x1D705}=0.04$
. In the first single-step quench, the suspension is sheared at an
$Re\,Pe_{r}$
of
$2\times 10^{5}$
. In the second quench, the suspension is first sheared at an
$Re\,Pe_{r}$
of 25 000 until a steady state (achieved at a time
$t_{eq}$
), and
$Re\,Pe_{r}$
is then increased to the aforementioned value of
$2\times 10^{5}$
. The evolution of the viscosities is plotted in figure 6(a). In the first quench, the distribution, and thence the viscosity, settles down to a quasi-steady state arising from the partitioning of
$f_{0}(C)$
across the potential maximum, followed by local equilibration in the spinning and tumbling wells. In the second quench, the viscosity evolves quickly to its steady-state value in the first step due to the lower
$Re\,Pe_{r}$
. In the second step, it evolves to a different quasi-steady state that corresponds to a partitioning of the steady state for
$Re\,Pe_{r}=25\,000$
. The true steady states are inaccessible for both the first quench and the second step of the second quench, due to the exceedingly large barrier-hopping times. (Kramer’s theory gives the barrier-hopping scale as
$((4\unicode[STIX]{x03C0}Re\,Pe_{r})/(\unicode[STIX]{x1D712}_{1}|_{C_{max}}(f^{\prime \prime }|_{C_{max}}f^{\prime \prime }|_{C_{min}})^{1/2}))\exp (Re\,Pe_{r}\unicode[STIX]{x0394}U)$
(Chandrasekhar Reference Chandrasekhar1943), where
$\unicode[STIX]{x0394}U$
is the potential difference between the lower minimum (
$C_{min}$
) and the central maximum (
$C_{max}$
).) The pair of quasi-steady states, at
$Re\,Pe_{r}=2\times 10^{5}$
, are shown in figure 6(b), and represent a viscosity contrast of approximately 3.8. In terms of actual experimental parameters, the quenches above may be achieved in a time of approximately 3 h, by shearing oblate spheroids of
$L\sim 10~\unicode[STIX]{x03BC}\text{m}$
in an aqueous medium with the maximum shear rate needed to achieve
$Re\,Pe_{r}=2\times 10^{5}$
, this being
$900~\text{s}^{-1}$
(a 10 % polydispersity is sufficient to achieve the separation of time scales required for (2.5) to describe the orientation dynamics and the resulting viscosity variation). Much higher viscosity contrasts are obtainable from ‘spin-rich’ initial conditions, but, as indicated above, these require the imposition of external fields (Okagawa & Mason Reference Okagawa and Mason1974; Ennis et al.
Reference Ennis, Okagawa and Mason1978).
The focus above was on a thermodynamic interpretation of the tumbling–spinning transition, and on the hysteresis characterizing the finite-time orientation dynamics of inertial spheroids in shearing flows in the presence of thermal fluctuations. Inertia and Brownian motion are somewhat incompatible in terms of the relevant particle size ranges. Thus, the convergence to a unique long-time equilibrium, consistent with the thermodynamic picture in figure 3, may require unrealistically long times, especially for spheroids large enough for the inertial drift to be significant. The rheological signature of the hysteresis – a multivalued shear viscosity at a given shear rate (
$Re\,Pe_{r}$
), as in figure 6, should, however, be measurable.
3 Conclusions
The thermodynamic interpretation of the steady-state orientation distribution in a dilute suspension of spheroids, and the associated hysteresis discussed in the latter half of § 2, arises due to the combined effect of a bistable potential induced by nonlinearity and stochasticity. The bidirectionality of the inertial drift, in fact, persists at finite
$Re$
(Rosén et al.
Reference Rosén, Einarsson, Nordmark, Aidun, Lundell and Mehlig2015). Other sources of nonlinearity and stochasticity should lead to similar behaviour. Athermal orientation fluctuations arising from hydrodynamic interactions should control the tumbling–spinning transition at higher volume fractions (
$nL^{3}$
). Each such interaction changes
$C$
by a finite amount, and the resulting relaxation is non-local in orientation space, being governed by a Boltzmann equation
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t}+Re\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C}(\unicode[STIX]{x0394}C_{i}f) & = & \displaystyle nL^{3}\int \,\text{d}C^{\prime }\int \,\text{d}\boldsymbol{r}_{\bot }y\int \,\text{d}{\hat{C}}\,\text{d}{\hat{C}}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \times \,[f({\hat{C}})f({\hat{C}}^{\prime }){\mathcal{K}}({\hat{C}},{\hat{C}}^{\prime }|C,C^{\prime };\boldsymbol{r}_{\bot })-f(C)f(C^{\prime })]\end{eqnarray}$$
for small
$nL^{3}$
when pair interactions drive the fluctuations. The scattering kernel
${\mathcal{K}}$
in (3.1) relates the pre-(
$[{\hat{C}},{\hat{C}}^{\prime }]$
) and post-(
$[C,C^{\prime }]$
) interaction orbit-constant pairs, and
$\text{d}\boldsymbol{r}_{\bot }$
denotes the differential interaction cross-section. (Unlike the traditional Boltzmann formulation, in the coarse-grained orbit-constant-based description, the pre- and post-interaction variables do not bear a one-to-one correspondence (the pair interaction is also a function of the Jeffery phases), and the probabilistic relation between the two is appropriately described by a scattering kernel.) It should be noted that
$Re(nL^{3})^{-1}$
in (3.1) is the analogue of
$Re\,Pe_{r}$
in (2.5). Although an analysis based on (3.1) is difficult due to
${\mathcal{K}}$
not being known (Dabade et al.
Reference Dabade, Marath and Subramanian2016), this might nevertheless be the most convenient experimental route, with the hysteretic time scale capable of being tuned to modest values by varying the volume fraction, rendering both short-time dynamics and long-time orientational equilibria observable. Fluid viscoelasticity in either steady (Leal Reference Leal1975) or large-amplitude oscillatory shear (Harlen & Koch Reference Harlen and Koch1997; Leahy et al.
Reference Leahy, Cheng, Ong, Liddell-Watson and Cohen2013) is an alternate (experimentally) more accessible source of nonlinearity, and the ratio of normal stress differences (besides
$De$
) (Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2015) may allow one to additionally tune the nature of the nonlinear drift. The existence of multiple steady states as a function of the particular initial orientation has, in fact, already been observed in experiments (Petrich et al.
Reference Petrich, Chaouche, Koch and Cohen2000) involving oscillatory shear flow of a dilute suspension of fibres in a dilute polymer solution, although the role of stochastic orientation fluctuations remains unexplored. It is also worth mentioning that the thermodynamic interpretation, based on the steady-state orientation distribution, has a larger regime of validity than the hysteretic dynamics analysed in the latter half of § 2. While the analysis of the time-dependent orientation distribution in § 2 relies on the effects of phase mixing due to a finite aspect-ratio polydispersity, the phase diagrams given in figures 3 and 4 remain valid even for a perfectly monodisperse suspension of spheroids (provided that
$Pe_{r}\gg \unicode[STIX]{x1D705}^{-3}$
). It should be noted that, in this limit, Brownian motion alone acts to redistribute orientations both along and across orbits starting from the initial condition. Since these processes occur on comparable time scales of
$O(Pe_{r}\unicode[STIX]{x1D705}^{2})$
for thin oblate spheroids (
$\unicode[STIX]{x1D705}\ll 1$
), there is no longer the separation of time scales needed for (2.5) to be valid.
While figures 3 and 4 bear a striking resemblance to the equilibrium phase diagram (and its projections onto different planes) of a single-component system, there are important differences that need to be pointed out. In the thermodynamic case, the system is macroscopic, consisting of an enormous number (
$N_{A}\sim O(10^{23})$
) of microscopic entities. An overwhelming fraction of all possible microstates correspond to the average value of the relevant macroscopic property (say, density), and the fluctuations about this average value are negligibly small, being
$O(N_{A}^{-1/2})$
. For the tumbling–spinning transition examined here, there is no such distinction between micro- and macro-states, since the thermodynamic equivalence is drawn with a single spheroid. Thus, except in the limit of large
$Re\,Pe_{r}$
, the phases identified based on the
$C$
corresponding to the peak value of the orbit-constant distribution have a finite spread about the maximum. Further, the phase space for a single spheroid is the unit sphere, and this is unlike the spatially extended ensemble typical of thermodynamic systems. As a result, there is no notion of diverging correlation lengths or times in the vicinity of the critical point. These peculiar features are also inherent to the single polymer molecule which exhibits a coil–stretch transition, and thus the tumbling–spinning and coil–stretch transitions bear a closer connection to each other than either of them to the thermodynamics of a one-component system.
The tumbling–spinning transition highlights an interesting connection between suspension rheology and polymer physics. Much like the coil–stretch transition for polymer solutions (Larson Reference Larson2005; Shaqfeh Reference Shaqfeh2005), the tumbling–spinning transition endows an inertial suspension of thin oblate spheroids with a memory that far exceeds the nominal microstructural relaxation times. This memory is likely to significantly influence the suspension stress response in inhomogeneous shearing flows, since the viscosities corresponding to different (Lagrangian) shear rate histories can differ by a large amount due to the large difference in the dissipation associated with spinning and tumbling spheroids. Non-hydrodynamic forces, including Brownian motion, have been known to play a subtle role in determining the strong-shear rheology of spherical particle suspensions at high volume fractions (Brady & Morris Reference Brady and Morris1997; Cheng et al. Reference Cheng, Mccoy, Israelachvili and Cohen2011). In contrast, the tumbling–spinning transition points to the subtle role played by Brownian motion in determining the rheology of anisotropic particle suspensions at much lower volume fractions. Furthermore, in being a simpler system with far fewer degrees of freedom when compared with high-molecular-weight polymers, a sheared suspension of anisotropic particles may serve as a model system for the study of hysteretic dynamics in complex fluid systems.
The numerical solutions of (2.5) are obtained using the finite-element method which is implemented on Freefem
$++$
(Hecht Reference Hecht2012).
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2016.779.
