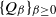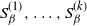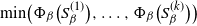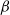1. Introduction
It is well known that Markov chains targeting multimodal distributions, such as those that appear in mixture models, will often mix very slowly. Of course, some algorithms are still faster than others, and the present paper is motivated by the problem of comparing different MCMC (Markov chain Monte Carlo) algorithms in this ‘highly multimodal’ regime. We provide a step in this direction by finding some simple sufficient conditions under which we can find an explicit formula for the spectral gap for MCMC algorithms on multimodal target distributions. To be slightly more precise, we consider a sequence of Markov transition kernels 
$\{Q_{\beta}\}_{\beta \geq 0}$ with state space 
$\Omega$ partitioned into pieces 
$\Omega = \sqcup_{i=1}^{k} S_{\beta}^{(i)}$. One of our main results, Lemma 2, gives sufficient conditions under which the spectral gap 
$\lambda_{\beta}$ of 
$Q_{\beta}$ is asymptotically given by the worst-case conductance 
$\Phi_{\min}(\beta) = \min\big(\Phi_{\beta}\big(S_{\beta}^{(1)}\big), \ldots, \Phi_{\beta}\big(S_{\beta}^{(k)}\big)\big)$, in the sense
\begin{equation} \lim_{\beta \rightarrow \infty} \frac{\log\!(\lambda_{\beta})}{\log\!(\Phi_{\min}(\beta))} = 1.\end{equation}
The main heuristic behind our calculations is that, in the highly multimodal regime, a Markov chain with strongly multimodal stationary distribution will mix within its starting mode before travelling between modes. When this occurs, we say that the Markov chain exhibits metastable behaviour, and the mixing properties of the Markov chain are often determined by the rate of transition between modes at stationarity (see, e.g., [Reference Bovier and Den Hollander2] and the references therein for an introduction to metastability). As a prototypical example, we consider the simple mixture of two Gaussians,
\begin{equation} \pi_{\sigma} = \frac{1}{2} \mathcal{N}\big(\!-1,\sigma^{2}\big) + \frac{1}{2} \mathcal{N}\big(1,\sigma^{2}\big) ,\end{equation}
for 
$\sigma > 0$. When 
$\sigma$ is close to 0, the usual tuning heuristic for the random walk Metropolis–Hastings (MH) algorithms (see, e.g., [Reference Roberts, Gelman and Gilks19]) suggests using a proposal distribution with standard deviation on the order of 
$\sigma$, such as
\begin{equation*}K_{\sigma}(x,\cdot) = \mathcal{N}(x,\sigma^{2}).\end{equation*}
Informally, an MH chain 
$\{X_{t}\}_{t \geq 0}$ with proposal distribution 
$K_{\sigma}$, target distribution 
$\pi_{\sigma}$, and initial point 
$X_{0} \in [\!-2,-0.5]$ in one of the modes will evolve according to the following three stages:
1. For t very small, the law of the chain
$X_t$, $\mathcal{L}(X_{t})$, will depend quite strongly on the starting point $X_{0}$.-
2. For
$\sigma^{-1} \ll t \ll \text{e}^{c_{1} \sigma^{-2}}$ and $c_{1} > 0$ small, the chain will have mixed very well on its first mode and is very unlikely to have ever left the interval $(\!-\infty, -0.1)$, so that
for some
\begin{equation*}\| \mathcal{L}(X_{t}) - \mathcal{N}\big(\!-1,\sigma^{2}\big) \|_{\text{TV}} \ll \text{e}^{-c_{2} \sigma^{-1}}\end{equation*}
$c_{2} > 0$. Note that $\mathcal{L}(X_{t})$ is close to $\mathcal{N}\big(\!-1,\sigma^{2}\big)$, which is not its stationary measure $\pi_{\sigma}$.
-
3. For
$t \gg \text{e}^{c_{3} \sigma^{-2}}$, the chain will have mixed well on the entire state space in the sense that
for some
\begin{equation*}\| \mathcal{L}(X_{t}) - \pi_{\sigma} \|_{\text{TV}} \ll \text{e}^{-c_{3} \sigma^{-1}}\end{equation*}
$c_{3} > 0$.
In the context of this example, the main result of our work is a straightforward way to verify that there is a sharp transition around 
$t \approx \text{e}^{\frac{1}{2} \sigma^{-2}}$, so that we may take 
$c_{1} = c_{3} = \frac{1}{2}$ in this heuristic description (see Theorems 1 and 2 for a precise statement). In the notation of (1.1), we can take the parameter 
$\beta$ that indexes our chains to be equal to 
$\sigma^{-1}$. We view 
$\beta$ as indexing ‘how multimodal’ a chain is, while in this particular example 
$\sigma^{-1}$ measures both the width of each mode and how well separated they are.
We believe that these scaling exponents 
$c_{1},c_{3}$ are natural ways to measure performance in the highly multimodal regime, as they seem to capture the most important differences in algorithm performance; see our companion paper [Reference Mangoubi, Pillai and Smith11] for further discussion of this point and relationships to the literature on optimal scaling and lifted Markov chains.
1.1. Related work
Our work is closely related to two large pieces of the Markov chain literature: decomposition bounds (see, e.g., [Reference Jerrum, Son, Tetali and Vigoda5, Reference Madras and Randall10, Reference Pillai and Smith17, Reference Woodard, Schmidler and Huber23, Reference Woodard, Schmidler and Huber24]) and metastability bounds (see, e.g., the popular books [Reference Bovier and Den Hollander2, Reference Olivieri and Vares16] and the references within the recent articles [Reference Beltrán and Landim1, Reference Landim6]). It is far beyond the scope of the present article to give a comprehensive survey. Instead, we describe the small gap in the literature that the present article fills.
Our main goal was to find sufficient conditions for metastability that are both easy to verify for typical statistical examples, and still give an asymptotically exact formula for the spectral gap. Such bounds would allow a (relatively) simple way to compare the asymptotic performance of different algorithms. Despite the size of the literature on metastability, we were not able to find results that met both of these criteria.
Much of the existing work on decomposition bounds applies to examples from statistics in a straightforward way ([Reference Woodard, Schmidler and Huber23, Reference Woodard, Schmidler and Huber24] are both applied in this context, but the other references above can be extended to this setting as well). However, because the resulting bound involves a product of two terms that can be small, it is not straightforward to use these bounds to actually compute the asymptotics of the spectral gap—we merely obtain bounds.
The existing work from the metastability community tends to give much sharper bounds, and many results on metastability can be used to compute the asymptotics of the spectral gap. However, these results are typically not aimed at a statistical audience, and they can be difficult to apply to the Markov chains that appear in computational statistics. Most Markov chains used in this setting are discrete-time chains on unbounded, continuous state spaces; they are also typically geometrically ergodic but not uniformly ergodic. To our knowledge, the most recent large-scale text on metastability [Reference Bovier and Den Hollander2] does not directly give bounds on any Markov chains in this setting. Other recent surveys also seem to omit this setting.
Of course, this does not mean that the ideas in the book (and the larger literature on metastability) cannot be applied at all. Some of the classical approaches to metastability can be extended to this setting without much difficulty, but the methods that seem simplest to extend are based on assumptions that seem difficult to verify for statistical examples. For example, approaches based on the analysis of ‘typical’ trajectories between modes may require a detailed understanding of these trajectories, and it is usually quite difficult to compute these trajectories.
Our results allow the computation of the asymptotics of the spectral gap, and the assumptions are stated in terms that should be familiar to the statistics community. In particular, our assumption about control of the tails is stated in terms of control of hitting times and a Lyapunov condition, which are quite similar to conditions in the dominant drift-and-minorization approach to convergence analysis of Markov chains in statistics [Reference Meyn and Tweedie15, Reference Rosenthal21]. While the basic idea of metastability is not new, we believe that such ‘in-between’ results are a useful compromise that focuses on the most relevant properties for comparison of Markov chains targeting multimodal distributions that arise in a statistical context. Although our introduction focuses on a simple Metropolis–Hastings algorithm with a one-dimensional stationary measure based on Gaussians, the main conditions we study here are also fairly easy to verify for a wide variety of other Markov chains. Towards the end of this paper we illustrate metastability with a simple example related to a high-dimensional Gibbs-like sampler for the problem of estimating the volume of a set, and our companion paper [Reference Mangoubi, Pillai and Smith11] uses our main result to prove metastability for the Hamiltonian Monte Carlo algorithm in a mixture setting.
1.2. Guide to the paper
In Section 2 we review the basic notation and definitions, and also provide some simple bounds. Our main results on metastability are presented in Section 3. Finally, we give an illustrative one-dimensional Gaussian application in Section 4 and an illustrative high-dimensional Gibbs-like sampler in Section 5.
2. Preliminaries
2.1. Basic notation
Throughout the remainder of the paper we denote by 
$\pi$ the smooth density function of a probability distribution on a convex subset of 
$\mathbb{R}^{d}$. We denote by 
$\mathcal{L}(X)$ the distribution of a random variable X. Similarly, if 
$\mu$ is a probability measure, we write ‘
$X \sim \mu$’ for ‘X has distribution 
$\mu$’. We use 
$\mathbb{P}[{\cdot}]$ and 
$\mathbb{E}[{\cdot}]$ to denote probabilities and expectations. We will often consider a Markov chain 
$\{X_{t}\}_{t \geq 0}$ sampled from a transition kernel L and with initial distribution 
$X_{0} \sim \mu$; when we wish to emphasize the role of the starting distribution, we will write 
$\mathbb{P}_{\mu}[{\cdot}]$ and 
$\mathbb{E}_{\mu}[{\cdot}]$. In a slight abuse of notation, we write 
$\mathbb{P}_{x}[{\cdot}]$ and 
$\mathbb{E}_{x}[{\cdot}]$ in the special case that 
$\mu$ is a point mass concentrated at 
$x \in \Omega$.
For two nonnegative functions or sequences f,g, we write 
$f = O(g)$ as shorthand for the statement: there exist constants 
$0 < C_{1},C_{2} < \infty$ such that, for all 
$x > C_{1}$, 
$f(x) \leq C_{2} \, g(x)$. We write 
$f = \Omega(g)$ for 
$g = O(\,f)$, and we write 
$f = \Theta(g)$ if both 
$f= O(g)$ and 
$g=O(\,f)$. Relatedly, we write 
$f = o(g)$ as shorthand for the statement: 
$\lim_{x \rightarrow \infty} \frac{f(x)}{g(x)} = 0$. Finally, we write 
$f = \tilde{O}(g)$ if there exist constants 
$0 < C_{1},C_{2}, C_{3} < \infty$ such that, for all 
$x > C_{1}$, 
$f(x) \leq C_{2} \, g(x) \log\!(x)^{C_{3}}$, and write 
$f = \tilde{\Omega}(g)$ for 
$g = \tilde{O}(\,f)$. As shorthand, we say that a function f is ‘bounded by a polynomial’ if there exists a polynomial g such that 
$f = O(g)$.
2.2. Cheeger’s inequality and the spectral gap
We recall the basic definitions used to measure the efficiency of MCMC algorithms. Let L be a reversible transition kernel with unique stationary distribution 
$\mu$ on 
$\mathbb{R}^{d}$. It is common to view L as an operator from 
$L_{2}(\pi)$ to itself via the formula
\begin{equation*}(L f)(x) = \int_{y \in \mathbb{R}^{d}} L(x,\text{d} y) f(y).\end{equation*}
The constant function is always an eigenfunction of this operator, with eigenvalue 1. We define the space 
$W^{\perp} = \big\{ f \in L_{2}(\mu) : \int_{x} f(x) \mu(\text{d} x) = 0 \big\}$ of functions that are orthogonal to the constant function, and denote by 
$L^{\perp}$ the restriction of the operator L to the space 
$W^{\perp}$. We then define the spectral gap 
$\rho$ of L by the formula
\begin{equation*}\rho = 1 - \sup \big\{ |\lambda| : \lambda \in \text{Spectrum}(L^{\perp}) \big\},\end{equation*}
where Spectrum refers to the usual spectrum of an operator. If 
$L^{\perp}$ has a largest eigenvalue 
$|\lambda|$ (for example, if L is a matrix of a finite-state-space Markov chain), then 
$\rho = 1-| \lambda |$.
Cheeger’s inequality [Reference Cheeger and Gunning3, Reference Lawler and Sokal7] provides bounds for the spectral gap in terms of the ability of L to move from any set to its complement in a single step. This ability is measured by the conductance 
$\Phi$, which is defined by the pair of equations
\begin{align*} \Phi & = \inf_{S \in \mathcal{A} \, : \, 0 < \mu(S)
< \frac{1}{2}} \Phi(S) , \\[2pt] \Phi(S) & = \frac{ \int_{x} \mathbbm{1}\{x \in S\} L(x,S^{\text{c}}) \mu(\text{d} x)}{\mu(S) },\end{align*}
where 
$\mathcal{A}= \mathcal{A}(\mathbb{R}^{d})$ denotes the usual collection of Lebesgue-measurable subsets of 
$\mathbb{R}^{d}$. Cheeger’s inequality for reversible Markov chains, first proved in [Reference Lawler and Sokal7], gives
\begin{equation} \frac{\Phi^2}{2} \leq \rho \leq 2 \Phi.\end{equation}
2.3. Traces and hitting times
We recall some standard definitions related to Markov processes.
Definition 1. (Trace and restriction chains.) Let L be the transition kernel of a reversible ergodic Markov chain on state space 
$\Omega$ with stationary measure 
$\mu$, and let 
$S \subset \Omega$ be a measurable subset with 
$\mu(S) > 0$. Let 
$\{X_{t}\}_{t \geq 0}$ be a Markov chain evolving according to L, and iteratively define
\begin{eqnarray*}c_{0} & = \inf \{t \geq 0\,{:}\, X_{t} \in S \} , \\[2pt]c_{i+1} & = \inf \{t > c_{i} \,{:}\, X_{t} \in S \}.\end{eqnarray*}
Then 
$\hat{X}_{t} = X_{c_{t}}$, 
$t \geq 0$, is the trace of 
$\{X_{t}\}_{t \geq 0}$ on S. Note that 
$\{\hat{X}_{t}\}_{t \geq 0}$ is a Markov chain with state space S, and so this procedure also defines a transition kernel with state space S. We call this kernel the trace of the kernel L on S.
Similarly, define the restriction 
$\mu |_{S}$ of 
$\mu$ to S by
\begin{equation*}\mu |_{S}(A) = \frac{\mu(S \cap A)}{\mu(S)}\end{equation*}
for measurable 
$A \subset \Omega$. Define the restriction 
$L|_{S}$ of L to S to be the Metropolis–Hastings kernel with proposal distribution L and target distribution 
$\mu |_{S}$, that is, the transition kernel given by 
$L |_{S}(x,A) = L(x,A)$ for all 
$x \in S$ and measurable 
$A \subset S \backslash \{ x\}$, and by 
$L |_{S}(x,\{x\}) = L(x,\{x\}) + L(x,S^{\text{c}})$. We call 
$L |_{S}$ the restriction of the kernel L to S.
We note that both the trace and restriction kernels are defined here purely to help us write conditions that are easier to verify in practice. In particular, although 
$L |_{S}$ is a Metropolis–Hastings kernel, we do not assume in any sense that the kernel L itself is a practical Metropolis–Hastings algorithm in statistics.
Definition 2. (Hitting time.) Let 
$\{X_{t}\}_{t \geq 0}$ be a Markov chain with initial point 
$X_{0} = x$ and let S be a measurable set. Then 
$\tau_{x,S} = \inf \{t \geq 0\,{:}\, X_{t} \in S\}$ is called the hitting time of S from x. When the starting point 
$X_{0} = x$ is already fixed, we sometimes use the shorthand 
$\tau_{S}$.
3. Generic metastability bounds
Denote by 
$\{Q_{\beta}\}_{\beta \geq 0}$ the transition kernels of a collection of reversible ergodic Markov chains with stationary measures 
$\{ \pi_{\beta}\}_{ \beta \geq 0}$ on common state space 
$\Omega$, which we take to be a convex subset of 
$\mathbb{R}^d$. Throughout the remainder of the paper we will always use the subscript 
$\beta$ to indicate which chain is being used; for example, 
$\Phi_{\beta}(S)$ is the conductance of the set S with respect to the chain 
$Q_{\beta}$, 
$\rho_{\beta}$ is the spectral gap of 
$Q_{\beta}$, and so on.
Our two main results are:
-
1. In Lemma 1, we fix a set
$S \subset \Omega$ and give sufficient conditions for the worst-case hitting time of $S^{\text{c}}$ from S to be bounded by the average-case hitting time $\Phi_{\beta}(S)$. -
2. In Lemma 2, we consider sufficient conditions on the entire partition
$S^{(1)},\ldots,S^{(k)}$ to ensure that the spectral gap of $Q_{\beta}$ is approximately equal to the worst-case conductance $\min_{1 \leq i \leq k} \Phi_{\beta}(S^{(i)})$.
3.1. Metastability and hitting times
The main point of our first set of assumptions is to guarantee that the Markov chain cannot get ‘stuck’ for a long time before mixing within a mode S. Fix 
$S \subset \Omega$ with 
$\inf_{\beta \geq 0} \pi_{\beta}(S) \equiv c_{1} > 0$. We will also define a sequence of sets 
$G_{\beta}, B_{\beta}, W_{\beta} \subset S$ indexed by 
$\beta \geq 0$ that satisfy 
$G_{\beta} \subset W_{\beta}$ and 
$B_{\beta} \subset W_{\beta}^{\text{c}} \cap S$.
In the following assumption we think of the set 
$G_{\beta}$ as the points that are ‘deep within’ the mode S, the points 
$B_{\beta}$ as the points that are ‘far in the tails’ of the target distribution, and the ‘covering set’ 
$W_{\beta}$ as a way of separating these two regions. To help with intuition, a reasonable choice of these sets in the special case of the mixture of Gaussians in (1.2) is illustrated in Figure 1. These sets are 
$S = (\!-\infty,0)$, 
$G_{\beta} = (\!-\sigma^{-9},0)$, 
$W_{\beta} = (\!-\sigma^{-10},0)$, and 
$B_{\beta} = (\!-\infty,-\sigma^{-10}]$. Note that Figure 1 shows two collections of these sets. The first covers S; the second is associated with 
$S^{\text{c}}$, which is needed by Lemma 2 below. Also note that, as this example suggests, there is a great deal of flexibility in designing these sets; changing, e.g., 9 to 
$11.3$ and 10 to 
$11.7$ in these definitions would not substantially change our analysis.
Figure 1. A cartoon plot of the target density 
$f_{\sigma}$ with the regions illustrated. Note that we have substantially compressed the regions so that they are all visible; in a scale drawing, 
$B_{\beta}$ would not be visible.
Our assumptions are as follows.
Assumptions 1. We assume the following all hold for 
$\beta > \beta_{0}$ sufficiently large:
-
1. Small conductance: There exists some
$c > 0$ such that $\Phi_{\beta}(S) \leq \text{e}^{-c \beta}$. -
2. Rapid mixing within
$G_{\beta}$: Let $\hat{Q}_{\beta}$ be the restriction of $Q_{\beta}$ to S. There exists some function $r_{1}$ bounded by a polynomial such that
(3.1)
\begin{equation} \sup_{x \in G_{\beta}} \big\| \hat{Q}_{\beta}^{r_{1}(\beta)}(x,\cdot) - \pi_{\beta} |_{S}(\cdot) \big\|_{\text{TV}} \leq \beta^{-2} \Phi_{\beta}(S).\end{equation}
-
3. Never stuck in
$W_{\beta}\backslash G_{\beta}$: There exists some function $r_{2}$ bounded by a polynomial such that
\begin{equation*} \sup_{x \in W_{\beta}\backslash G_{\beta}} \mathbb{P}_{x}[\tau_{ G_{\beta} \cup S^{\text{c}}} > r_{2}(\beta)] \leq \beta^{-2} \Phi_{\beta}(S).\end{equation*}
-
4. Never hitting
$W_{\beta}^{\text{c}}$: We have
(3.2)
\begin{equation} \sup_{x \in G_{\beta} } \mathbb{P}_{x}\big[\tau_{W_{\beta}^{\text{c}}}
< \min\!( r_{1}(\beta) + r_{2}(\beta) + 1, \tau_{S^{\text{c}}})\big] \leq \Phi_{\beta}(S)^{4}.\end{equation}
It is important to note that the first inequality in (3.2) is strict; one use of this assumption is to check that 
$\tau_{W_{\beta}^{\text{c}}} = \tau_{S^{\text{c}}}$ occurs with high probability for ‘typical’ starting points in 
$G_{\beta}$.
Remark 1. As is common in the metastable literature, there are a wide variety of tweaks to these assumptions that would give similar results. For example, it is possible to get a very similar result if we replace the chain 
$\hat{Q}_{\beta}$ by another chain that closely approximates the dynamics of 
$Q_{\beta}$ on S (e.g. the trace of 
$Q_{\beta}$ on S rather than the restriction), at some small cost in checking that periodicity does not pose a problem. Similarly, the power 4 appearing in (3.2) could be decreased at some small cost to the other constants appearing in this assumption.
Under these assumptions, we have the following conclusion.
Lemma 1. (Hitting times and conductance.) Let Assumptions 1 hold, and fix a point x that is in 
$G_{\beta} $ for all 
$\beta > \beta_{0}(x)$ sufficiently large. Then, for all 
$\epsilon > 0$,
\begin{equation*}\mathbb{P}_{x} \left[ \frac{\log\!(\tau_{S^{\text{c}}})}{-\log\!(\Phi_{\beta}(S))} > 1 + \epsilon \right] = o(1).\end{equation*}
Proof. Fix 
$p \in W_{\beta}$, and define 
$T = T(\beta) = r_{1}(\beta) + r_{2}(\beta) + 1$. Throughout the following argument we denote by 
$\{X_{t}\}_{t \geq 0}$ a Markov chain sampled from 
$Q_{\beta}$ (with starting point indicated by subscripts). We then calculate:
\begin{align*}\mathbb{P}_{p}[\tau_{S^{\text{c}}} \leq T ] &\geq \inf_{q \in G_{\beta}} \mathbb{P}_{q}[\tau_{S^{\text{c}}} \leq r_{1}(\beta) + 1] - \mathbb{P}_{p}[\tau_{G_{\beta} \cup S^{\text{c}}} > r_{2}(\beta)] \\[3pt] &\geq \mathbb{P}_{\pi_{\beta} |_{S}}[X_{1} \in S^{\text{c}}] - \sup_{q \in G_{\beta}} \big\| \hat{Q}_{\beta}^{r_{1}(\beta)}(q,\cdot) - \pi_{\beta} |_{S}(\cdot) \big\|_{\text{TV}} - \mathbb{P}_{p}[\tau_{ G_{\beta} \cup S^{\text{c}}} > r_{2}(\beta)] \\[3pt]&= \Phi_{\beta}(S) - \sup_{q \in G_{\beta}} \big\| \hat{Q}_{\beta}^{r_{1}(\beta)}(q,\cdot) - \pi_{\beta} |_{S}(\cdot) \big\|_{\text{TV}} - \mathbb{P}_{p}[\tau_{ G_{\beta} \cup S^{\text{c}}} > r_{2}(\beta)],\end{align*}
where the first inequality follows from using the Markov property at the stopping time 
$\min\!(\tau_{G_{\beta} \cup S^{\text{c}}},r_{2}(\beta))$, and the second is the triangle inequality (for the total variation metric on distributions). Applying Assumptions 1.2 and 1.3, the two negative terms in this expression are both bounded by 
$\beta^{-2} \Phi_{\beta}(S)$. This implies that
\begin{equation} \mathbb{P}_{p}[\tau_{S^{\text{c}}} \leq T] \geq \Phi_{\beta}(S)\big(1 - 2 \beta^{-2}\big).\end{equation}
If we also have 
$p \in G_{\beta} \subset W_{\beta}$, then applying Assumption 1.4 gives
\begin{equation} \mathbb{P}_{p}[\tau_{W_{\beta}^{\text{c}}}
< \min\!(T, \tau_{p,S^{\text{c}}})] \leq \Phi_{\beta}(S)^{4}.\end{equation}
We now iteratively apply (3.3) and (3.4) to control the behaviour of 
$\{X_{t}\}_{t \geq 0}$ over longer time intervals. More precisely, for all 
$k \in \mathbb{N}$ and starting points 
$p \in G_{\beta}$,
\begin{align*}& \mathbb{P}_{p}[\tau_{S^{\text{c}}} > kT] = \\[3pt] & \qquad \mathbb{P}_{p}[\tau_{S^{\text{c}}} > kT | \tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}] \mathbb{P}_{p}[ \tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta} ] \\[3pt]& \qquad + \mathbb{P}_{p}[\tau_{S^{\text{c}}} > kT | \tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}^{\text{c}} ] \mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}^{\text{c}} ] \\[3pt]& \quad \leq \mathbb{P}_{p}[\tau_{S^{\text{c}}} > kT | \tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}] \mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T] \\[3pt]& \qquad + \mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}^{\text{c}}] \\[3pt]& \quad \leq (1 - \Phi_{\beta}(S)(1 - 2 \beta^{-2})) \mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T] + \mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T, \, X_{(k-1)T} \in W_{\beta}^{\text{c}}] \\[3pt]& \quad \leq (1 - \Phi_{\beta}(S)(1 - 2 \beta^{-2}))\mathbb{P}_{p}[\tau_{S^{\text{c}}} > (k-1)T] + k\Phi_{\beta}(S)^{4}, \end{align*}
where (3.3) is used in the second-last line and (3.4) is used in the last line. Iterating and collecting terms, this gives
\begin{equation} \mathbb{P}_{p}[\tau_{S^{\text{c}}} > kT] \leq \big(1 - \Phi_{\beta}(S)\big(1 - 2 \beta^{-2}\big)\big)^{k} + k^{2} \Phi_{\beta}(S)^{4}.\end{equation}
Fix any 
$\epsilon > 0$ and take 
$k = \lceil \beta \Phi_{\beta}(S)^{-1} \rceil$. By Assumption 1.1 and the fact that 
$r_{1},r_{2}$ are bounded by polynomials,
\begin{equation*}k T = \lceil \beta \Phi_{\beta}(S)^{-1} \rceil (r_{1}(\beta) + r_{2}(\beta) + 1) \leq \Phi_{\beta}(S)^{-1} (5 \beta (r_{1}(\beta) + r_{2}(\beta))) \leq \Phi_{\beta}(S)^{-1-\epsilon} ,\end{equation*}
for all 
$\beta > \beta_{0}(\epsilon)$ sufficiently large. Fix x as in the statement of the lemma; we can use this bound on kT along with (3.5) to conclude that
\begin{align*}\mathbb{P}_{x}\bigg[ \frac{\log\!(\tau_{S^{\text{c}}})}{-\log\!(\Phi_{\beta}(S))} > 1 + \epsilon\bigg] &= \mathbb{P}_{x}[\tau_{S^{\text{c}}} > \Phi_{\beta}(S)^{-1 - \epsilon}] \\[3pt] & \leq \mathbb{P}_{x}[\tau_{S^{\text{c}}} > k T] \\[3pt] &\leq \big(1 - \Phi_{\beta}(S)\big(1 - 2 \beta^{-2}\big)\big)^{k} + k^{2} \Phi_{\beta}(S)^{4} = o(1).\end{align*}
This completes the proof of the lemma.
3.2. Metastability and spectral gaps
If we can partition the state space of a Markov chain into a collection of sets 
$S^{(1)},\ldots,S^{(k)}$ satisfying Assumptions 1, we typically expect the spectral gap of the Markov chain to be entirely determined by the typical transition rates between these sets. However, we must rule out a few possible sources of bad behaviour:
-
1. Very slow mixing in the ‘tails’ of the distribution could have an impact on the spectral gap.
-
2. A typical transition from one mode could land far out in the tails of the mode being entered, causing the walk to get ‘stuck’.
-
3. The transitions between modes might exhibit near-periodic behaviour, even if the Markov chain is not exactly periodic.
-
4. There might be metastability among collections of modes. For example, there might be some
$I \subset \{1,2,\ldots,k\}$ for which $\Phi_{\beta}(\cup_{i \in I} S^{(i)})$ is much smaller than $\min_{1 \leq i \leq k} \Phi_{\beta}(S^{(i)})$.
Although detailed discussion of metastability is beyond the scope of the present paper, the first three types of behaviour can all cause the spectral gap to be very different from the prediction given by our metastability heuristic. The fourth behaviour simply says that you have chosen the ‘wrong’ partition of the state space, and that you should check the conditions again after joining several pieces of the partition together.
The following assumptions rule out these new complications.
Assumptions 2. Let 
$\Omega = \sqcup_{i=1}^{k} S^{(i)}$ be a partition of 
$\Omega$ into k pieces. Set 
${\Phi _{\min }} = \min ({\Phi _\beta }({S^{(1)}})), \ldots ,{\Phi _\beta }({S^{(k)}}))$ and 
$\Phi_{\max} = \max(\Phi_{\beta}(S^{(1)}), \ldots, \Phi_{\beta}(S^{(k)}))$. We assume the following.
-
1. Metastability of sets: Each set
$S^{(i)}$ satisfies Assumptions 1 (with $\Phi_{\beta}(S)$ replaced by $\Phi_{\max}$ in Assumption 1.1 and replaced by $\Phi_{\min}$ in Assumptions 1.2–4). We use the superscript (i) to extend the notation of that assumption in the obvious way. -
2. Lyapunov control of tails: Denote by
$B_{r}(x)$ the ball of radius $r > 0$ around a point $x \in \Omega$. Assume there exist $0 < m, M < \infty$ satisfying
Assume there exist a collection of privileged points
\begin{equation*} \cup_{i=1}^{k} W_{\beta}^{(i)} \subset B_{M}(0), \qquad B_{m}(0) \subset \cup_{i=1}^{k} G_{\beta}^{(i)}.\end{equation*}
$s_{i} \in G_{\beta}^{(i)}$ such that the function $V_{\beta}(x) = \exp\{\beta \min_{1 \leq i \leq k} \| x - s_{i} \|\}$ satisfies
for all
\begin{equation*} (Q_{\beta} V_{\beta})( x) \leq \bigg(1 - \frac{1}{r_{3}(\beta)}\bigg) V_{\beta}( x) + r_{4} \text{e}^{\ell \beta}\end{equation*}
$x \in \Omega$, where $r_{3}, r_{4}$ are bounded by polynomials and $0 \leq \ell < m$.
-
3. Never hitting
$W_{\beta}^{\text{c}}$: We have the following variant of (3.2):
(3.6)
\begin{eqnarray} \sup_{x \in \cup_{i=1}^{k} G_{\beta}^{(i)}} \mathbb{P}\Big[\tau_{x, \big(\cup_{i=1}^{k}W_{\beta}^{(i)}\big)^{\text{c}}}
< \Phi_{\min}^{-2}\Big] &\leq \Phi_{\min}^{4}.\end{eqnarray}
-
4. Non-periodicity: For all
$1 \leq i \neq j \leq k$,
(3.7)
\begin{eqnarray} \inf_{\beta} \inf_{x \in S^{(i)} } Q_{\beta}(x,S^{(i)}) & \equiv c_{2}^{(i)} > 0, \end{eqnarray}
(3.8)
\begin{eqnarray}\sup_{x \in S^{(i)}} Q_{\beta}\big(x,S^{(j)} \backslash G_{\beta}^{(j)}\big) &
< \Phi_{\min}^{4}.\end{eqnarray}
-
5. Connectedness: There exists some
$r_{5}$ bounded by a polynomial such that the graph with vertex set $\{1,2,\ldots,k\}$ and edge set
(3.9)is connected.
\begin{equation} \left\{ (i,j)\,{:}\,\min \left( \inf_{x \in S^{(i)}} \mathbb{P}\big[X_{\tau_{x,(S^{(i)})^{\text{c}}}} \in S^{(j)}\big], \inf_{x \in S^{(j)}} \mathbb{P}\big[X_{\tau_{x,(S^{(j)})^{\text{c}}}} \in S^{(i)}\big]\right) \geq r_{5}(\beta) \right \}\end{equation}
Lemma 2. (Spectral gap and conductance.) Let Assumptions 2 hold. Denote by 
$\lambda_{\beta}$ and 
$\Phi_{\beta}$ the spectral gap and conductance of 
$Q_{\beta}$. Then
\begin{equation} \lim_{\beta \rightarrow \infty} \frac{\log\!(\lambda_{\beta})}{\log\!(\Phi_{\min})} = \lim_{\beta \rightarrow \infty} \frac{\log\!(\Phi_{\beta})}{\log\!(\Phi_{\min})} = 1.\end{equation}
Proof. Define the candidate ‘small set’ 
$R = \cup_{i=1}^{k} G_{\beta}^{(i)}$.
For convenience, we define 
$T_{\max} = T_{\max}(\beta) \equiv \Phi_{\min}^{-1.5}$ to be the longest timescale of interest in this problem; we note that any mixing behaviour should occur on this timescale, while on the other hand there should be no entrances to the ‘bad’ set 
$W \equiv \big(\cup_{i=1}^{k} W_{\beta}^{(i)}\big)^{\text{c}}$. In order to reduce notational clutter, we will frequently use q with a subscript to refer to a function that is bounded by a polynomial and whose specific values are not of interest.
We will begin by estimating the mixing rate of 
$Q_{\beta}$ for Markov chains started at points 
$x,y \in R$. We do this by coupling Markov chains 
$\{X_{t}\}_{t =0}^{T_{\max}}$, 
$\{Y_{t}\}_{t =0}^{T_{\max}}$ started at 
$X_{0} = x$, 
$Y_{0} = y$ for some 
$x,y \in R$ and trying to force them to collide. (Note that the Markov chains are only defined up until this ‘maximal time’ 
$T_{\max}$.) This saves us from having to either explicitly write 
$\min\!(\cdot, T_{\max})$, or add extremely small terms that correspond to the probability that various times exceed 
$T_{\max}$, in essentially all of the following calculations. This choice has virtually no other impact. Roughly speaking, we will make the following two calculations:
-
1. If we run the two chains independently, the time it takes for them to both be in
$G_{\beta}^{(i)}$, for the same i simultaneously, is not too much larger than the conjectured relaxation time $\Phi_{\min}^{-1}$. -
2. If we run two chains started on the same good set
$G_{\beta}^{(i)}$, the two chains will couple long before either one transitions from $G_{\beta}^{(i)}$ to another mode.
We now give some further details, following this sketch. Let 
$x,y \in R$.
Part 1: Time to be in same good set simultaneously. We will run the chains independently until the first time 
$\psi_{1} = \inf \big\{t \geq 0\,{:}\, \text{there exists } 1 \leq i \leq k \text{ such that } X_{t}, Y_{t} \in G_{\beta}^{(i)} \big\}$ that they are both in the same ‘good’ part of the partition. Define 
$\psi_{2} = \inf \big\{t \geq 0\,{:}\, \text{there exists } 1 \leq i \leq k\break \text{such that } X_{t}, Y_{t} \in S^{(i)} \big\}$, the first time that 
$\{X_{t}\}$, 
$\{Y_{t}\}$ are both in the same part of our partition. For convenience, set 
$c_{2} = \min\!(c_{2}^{(1)}, \ldots, c_{2}^{(k)}, 0.5)$.
Let 
$1 \leq a,b \leq k$ satisfy 
$x \in G_{\beta}^{(a)}$, 
$y \in G_{\beta}^{(b)}$ and let G be the connected graph whose existence is guaranteed in (3.9). Since G is a connected graph on k vertices, there is a path 
$\gamma$ in G from a to b of length 
$|\gamma| \leq k-1$. We next consider the event 
$\mathcal{E}$ that, the first 
$|\gamma|$ times that 
$\{X_{t}\}_{t \geq 0}$ or 
$\{Y_{t}\}_{t \geq 0}$ changes parts of the partition, they go towards each other along the path 
$\gamma$. By (3.9), 
$\mathbb{P}[\mathcal{E}] \geq r_{5}(\beta)^{k-1}$.
Bounding the amount of time spent in each part of the partition along this path by (3.5) and (3.7), this implies that
\begin{equation} \mathbb{P}\big[\psi_{2} \leq q_{1}(\beta) \Phi_{\min}^{-1}\big] \geq \frac{1}{2} c_{2} r_{5}(\beta)^{k-1}\end{equation}
for some function 
$q_{1}$ that is bounded by a polynomial. By (3.8),
\begin{equation*}\mathbb{P}[\psi_{1} = \psi_{2}] \geq 1- T_{\max} \Phi_{\min}^{4} \geq 1 - \Phi_{\min}^{2}.\end{equation*}
Combining this with (3.11),
\begin{align}\mathbb{P}\big[\psi_{1} \leq q_{1}(\beta) \Phi_{\min}^{-1}\big] &\geq \mathbb{P}\big[\psi_{2} \leq q_{1}(\beta) \Phi_{\min}^{-1}\big] - \mathbb{P}[\psi_{1} \neq \psi_{2}]\nonumber\\[3pt] &\geq \frac{1}{2} c_{2} r_{5}(\beta)^{k-1} - \Phi_{\min}^{2} \equiv \frac{1}{q_{2}(\beta)}, \end{align}
where we note that 
$q_{2}$ is bounded by a polynomial.
Part 2: Mixing from same good set. If 
$\psi_{1} \geq T_{\max} - r_{1}(\beta)$, continue to evolve 
$\{X_{t}\}_{t \geq 0}$, 
$\{Y_{t}\}_{t \geq 0}$ independently. Otherwise, let 
$1 \leq i \leq k$ satisfy 
$X_{\psi_{1}}, \, Y_{\psi_{1}} \in S^{(i)}$. We then let 
$\{ \hat{X}_{t} \}_{t \geq 0}$, 
$\{ \hat{Y}_{t} \}_{t \geq 0}$ be Markov chains evolving according to the Metropolis–Hastings kernel with proposal distribution 
$Q_{\beta}$ and target distribution 
$\pi_{\beta} |_{S^{(i)}}$. We give these chains initial points 
$\hat{X}_{0} = X_{\psi_{1}}$, 
$\hat{Y}_{0} = Y_{\psi_{1}}$ and couple them according to a maximal 
$r_{1}(\beta)$-step coupling (that is, a coupling that maximizes 
$\mathbb{P}[\hat{X}_{r_{1}(\beta)} = \hat{Y}_{r_{1}(\beta)}]$; such a coupling is known to exist [Reference Griffeath4]).
We next observe that the following informal algorithm gives a valid coupling of the Markov chains 
$\{X_{t}\}_{t = \psi_{1}}^{\psi_{1} + r_{1}(\beta)}$, 
$\{\hat{X}_{t}\}_{t = 0}^{r_{1}(\beta)}$:
-
1. Run the full Markov chain
$\{X_{t}\}_{t = \psi_{1}}^{\psi_{1} + r_{1}(\beta)}$ according to $Q_{\beta}$. -
2. For all
$t < \tau_{\text{bad}} \equiv \inf \{s\,{:}\,X_{\psi_{1} + s} \notin S^{(i)} \}$, set $\hat{X}_{t} = X_{\psi_{1} + t}$. -
3. If
$ \tau_{\text{bad}} < r_{1}(\beta)$, continue to evolve $\{\hat{X}_{s}\}_{s=\tau_{\text{bad}}}^{r_{1}(\beta)}$ independently of $\{X_{t}\}_{t=0}^{r_{1}(\beta)}$. (Note that the particular choice made in this third step will not influence the analysis—we could make any measurable choice here.)
We couple the pair of chains 
$\{X_{t}\}_{t = \psi_{1}}^{\psi_{1} + r_{1}(\beta)}$, 
$\{\hat{X}_{t}\}_{t = 0}^{r_{1}(\beta)}$ this way, and we couple 
$\{Y_{t}\}_{t = \psi_{1}}^{\psi_{1} + r_{1}(\beta)}$, 
$\{\hat{Y}_{t}\}_{t = 0}^{r_{1}(\beta)}$ analogously. Under these couplings, we have
\begin{align*}\mathbb{P}[X_{\psi_{1} + r_{1}(\beta)} \neq Y_{\psi_{1} + r_{1}(\beta)}] & \leq \mathbb{P}[\hat{X}_{r_{1}(\beta)} \neq \hat{Y}_{r_{1}(\beta)}] + \mathbb{P}[X_{\psi_{1} + r_{1}(\beta)} \neq \hat{X}_{r_{1}(\beta)}] \\[3pt]& \quad + \mathbb{P}[Y_{\psi_{1} + r_{1}(\beta)} \neq \hat{Y}_{r_{1}(\beta)}] \\[3pt]&\leq \beta^{-2} \Phi_{\max} + 2 \Phi_{\min}^{4},\end{align*}
where the first term is bounded by (3.1) and the last two terms are bounded by (3.6).
Combining this with (3.12), we conclude that
\begin{equation} \mathbb{P}[X_{T_{1}} = Y_{T_{1}}] = (1 -o(1)),\end{equation}
where 
$T_{1} = \lceil q_{1}(\beta) \Phi_{\min}^{-1} + r_{1}(\beta) \rceil$.
This completes the proof of our two-stage analysis, as (3.13) gives a useful minorization bound for 
$x,y \in R$. Note that (3.13) is very close to a minorization condition in the sense of [Reference Rosenthal21] for the small set R. Applying the closely related Lemma A.11 of [Reference Mangoubi and Smith12] (see also [Reference Mangoubi and Smith13]), the minorization bound (3.13), and the drift bound in Assumptions 2.2, we find
\begin{equation*}\| Q_{\beta}^{t}(x,\cdot) - \pi_{\beta}(\cdot) \|_{\text{TV}} \leq M(\beta,x) \exp\bigg\{-\frac{t \Phi_{\min}}{q_{4}(\beta)}\bigg\},\end{equation*}
where 
$q_{4}(\cdot) \geq 1$ and, for each x, 
$M(\cdot,x)$ is bounded by a polynomial.
By Theorem 2.1 of [Reference Roberts and Rosenthal20], this implies that
\begin{equation} \lambda_{\beta} \geq \frac{\Phi_{\min}}{q_{4}(\beta)}.\end{equation}
By (2.1), the conductance 
$\Phi_{\beta}$ of 
$Q_{\beta}$ satisfies
\begin{equation} \lambda_{\beta} \leq 2 \Phi_{\beta} \leq 2 \Phi_{\min}.\end{equation}
Combining (3.14) and (3.15), we conclude that
\begin{equation*} \frac{\Phi_{\min}}{q_{4}(\beta)} \leq \frac{\Phi_{\beta}}{q_{4}(\beta)}, \qquad \lambda_{\beta} \leq 2 \Phi_{\min} \leq 2 \Phi_{\beta}.\end{equation*}
This immediately implies the limit in (3.10), completing the proof of the lemma.
4 Application to mixtures of Gaussians
We define the usual random walk Metropolis algorithm.
Definition 3. (Random walk Metropolis algorithm.) The transition kernel K of the random walk Metropolis algorithm with step size 
$\sigma > 0$ and target distribution 
$\pi$ on 
$\mathbb{R}^{d}$ with density 
$\rho$ is given by the following algorithm for sampling 
$X \sim K(x,\cdot)$:
-
1. Sample
$\epsilon_{1} \sim \mathcal{N}(0,\sigma^{2})$ and $U_{1} \sim \text{Unif}[0,1]$. -
2. If
set
\begin{equation*}U
< \frac{\rho(x + \epsilon_{1})}{\rho(x)},\end{equation*}
$X = x + \epsilon_{1}$, otherwise set $X=x$.
For 
$\sigma > 0$, define the mixture distribution
\begin{equation*} \pi_{\sigma} = \frac{1}{2} \mathcal{N}(\!-1,\sigma^{2}) + \frac{1}{2} \mathcal{N}(1,\sigma^{2})\end{equation*}
and denote its density by 
$f_{\sigma}$. Let 
$K_{\sigma}$ be the kernel from Definition 3 with step size 
$\sigma$ and target distribution 
$\pi_{\sigma}$.
Denote by 
$\lambda_{\sigma}$ the relaxation time of 
$K_{\sigma}$ (the reciprocal of the spectral gap of 
$K_\sigma$), and denote by 
$\Phi_{\sigma} = \Phi(K_{\sigma}, (\!-\infty,0))$ the Cheeger constant associated with kernel 
$K_{\sigma}$ and set 
$(\!-\infty,0)$.
We will state our two main results about this walk; the proofs are deferred until both results have been stated. First, we have an asymptotic formula for the Cheeger constant.
Theorem 1. The Cheeger constant 
$\Phi_{\sigma}$ satisfies
\begin{equation} \lim_{\sigma \rightarrow 0} (\!-2 \sigma^{2}) \, \log\!(\Phi_{\sigma}) = 1.\end{equation}
For fixed 
$x \in (\!-\infty,0)$, let 
$\{X_{t}^{(\sigma)}\}_{t \in \mathbb{N}}$ be a Markov chain with transition kernel 
$K_{\sigma}$ and initial point 
$X_{1}^{(\sigma)} = x$. Define the hitting time 
$\tau_{x}^{(\sigma)} = \inf \{ t > 0\,{:}\,X_{t}^{(\sigma)} \notin (\!-\infty,0)\}$.
We also have the following estimate of the spectral gap and the hitting time.
Theorem 2. For all 
$\epsilon > 0$ and fixed 
$x \in (\!-\infty,0)$, the hitting time 
$\tau_{x}^{(\sigma)}$ satisfies
\begin{equation*} \lim_{\sigma \rightarrow 0} \mathbb{P}\bigg[\frac{\log\!\big(\tau_{x}^{(\sigma)}\big)}{\log\!(\Phi_{\sigma})}
< 1 + \epsilon\bigg] = 1\end{equation*}
and the relaxation time satisfies
\begin{equation*} \lim_{\sigma \rightarrow 0} \frac{\log\!(\lambda_{\sigma})}{\log\!(\Phi_{\sigma})} = \lim_{\sigma \rightarrow 0} \frac{\log\!(\lambda_{\sigma})}{\log\!(\Phi(K_{\sigma}))} = 1.\end{equation*}
Remark 2. This result implies that the Cheeger constant 
$\Phi(K_{\sigma})$ of 
$K_{\sigma}$ is close to the bottleneck ratio 
$\Phi_{\sigma} = \Phi(K_{\sigma}, (\!-\infty,0))$ associated with the set 
$(\!-\infty,0)$, at least for 
$\sigma$ very small. The set 
$(\!-\infty,0)$ is of course a natural guess for the set with the ‘worst’ conductance, though we do not know of any simple argument that would actually prove this. In some sense this is the motivation for the approach taken in this paper: it can be very hard to guess a good partition, even in a very simple example!
We begin by proving Theorem 1.
Proof of Theorem 1. Let 
$\{X_{t}\}_{t \geq 0}$ be a Markov chain with transition kernel 
$K_{\sigma}$, started at 
$X_{0} \sim \pi_{\sigma}$, and drawn according to the stationary distribution. Denote by 
$\phi_{\sigma}$ the density of the Gaussian with variance 
$\sigma^{2}$. Defining the set 
$\mathcal{E} = \{X_{0} < -\sigma^{-1} \} \cup \{|X_{1} - X_{0}| > \sigma^{-1} \}$, we have
\begin{align*}\mathbb{P}[\{X_{0}
< 0\} \cap \{\, X_{1} > 0\} \cap \mathcal{E}^{\text{c}}] &\leq \int_{-\sigma^{-1}}^{0} \int_{0}^{\sigma^{-1}} f_{\sigma}(x) \phi_{\sigma}(y-x) \, \text{d} x \, \text{d} y \\[4pt]& \leq 2\int_{-\sigma^{-1}}^{0} \int_{0}^{\sigma^{-1}} \phi_{\sigma}(1+x) \phi_{\sigma}(y-x) \, \text{d} x \, \text{d} y \\[4pt]&= \frac{2}{\pi \sigma^{2}}\!\!\int_{-\sigma^{-1}}^{0} \int_{0}^{\sigma^{-1}} \!\!\!\!\!\!\!\! \exp\bigg\{-\frac{1}{2 \sigma^{2}}( (1+x)^{2} + (y-x)^{2})\bigg\} \text{d} x \, \text{d} y \\[4pt]&\leq \frac{2}{\pi \sigma^{2}} \int_{-\sigma^{-1}}^{0} \int_{0}^{\sigma^{-1}} \text{e}^{-\frac{1}{2 \sigma^{2}}} = \frac{2}{\pi \sigma^{4}} \text{e}^{-\frac{1}{2 \sigma^{2}}}.\end{align*}
We also have the simple bound
\begin{align*}\mathbb{P}[\mathcal{E}] &\leq \mathbb{P}[X_{0}
< - \sigma^{-1}] + \mathbb{P}[|X_{1} - X_{0} | > \sigma^{-1}] \\[4pt]&\leq 2 \int_{-\infty}^{-\sigma^{-1}} \phi_{\sigma}(x) \, \text{d} x + 2 \int_{\sigma^{-1}}^{\infty} \phi_{\sigma}(x) \, \text{d} x \\[4pt]&\leq \frac{4}{\sqrt{2 \pi} \sigma} \exp\bigg\{-\frac{(\sigma^{-1}-1)^{2}}{2 \sigma^{2}}\bigg\} \leq \frac{4}{\sqrt{2 \pi} \sigma} \text{e}^{-\frac{1}{3} \sigma^{-3}},\end{align*}
where the last inequality holds for all 
$\sigma$ sufficiently small. Putting these two bounds together, we have, for all 
$\sigma > 0$ sufficiently small,
\begin{equation*}\mathbb{P}[X_{0}
< 0, \, X_{1} > 0] \leq \frac{1}{\pi \sigma^{4}} \text{e}^{-\frac{1}{2 \sigma^{2}}} + \frac{4}{\sqrt{2 \pi} \sigma} \text{e}^{-\frac{1}{3} \sigma^{-3}}.\end{equation*}
Taking logs, this immediately proves that 
$\lim_{\sigma \rightarrow 0} (\!-2 \sigma^{2}) \, \log\!(\Phi_{\sigma}) \leq 1$, the desired upper bound on the left-hand side of (4.1). To prove the lower bound on this quantity, begin by defining the intervals 
$I_{\sigma} = (\!-2 \sigma^{20}, - \sigma^{20})$ and 
$J_{\sigma} = (\sigma^{10},2 \sigma^{10})$. Since 
$\sigma^{20} \ll \sigma^{10}$ for 
$\sigma$ small, we have, for sufficiently small 
$\sigma > 0$,
\begin{equation*}\inf_{x \in I_{\sigma}, y \in J_{\sigma}} \frac{f_{\sigma}(y)}{f_{\sigma}(x)} \geq 1.\end{equation*}
Informally, this means that any proposed step from 
$I_{\sigma}$ to 
$J_{\sigma}$ will be accepted. Thus, letting 
$Y \sim \mathcal{N}(0,\sigma^{2})$ be independent of 
$X_{1}$, we have
\begin{align*}\mathbb{P}[X_{0}
< 0, X_{1} > 0] &\geq \mathbb{P}[ X_{0} \in I_{\sigma}, X_{1} \in J_{\sigma}] \\[3pt]&\geq \mathbb{P}[X_{0} \in I_{\sigma}] \inf_{x \in I_{\sigma}} \mathbb{P}[ X_{0} + Y \in J_{\sigma} \, | \, X_{0} = x] \\[3pt]&\geq \left(\frac{\sigma^{20}}{4 \sqrt{2 \pi}\,} \text{e}^{-\frac{1}{2 \sigma^{2}}} \right) \times \left( \frac{\sigma^{10}}{4 \sqrt{2 \pi}\,} \right),\end{align*}
where the last inequality holds for all 
$\sigma > 0$ sufficiently small. Taking logs, this proves that 
$\lim_{\sigma \rightarrow 0} (\!-2 \sigma^{2}) \, \log\!(\Phi_{\sigma}) \geq 1$, completing the proof of (4.1).
Proof of Theorem 2. We defer some of the longer exact calculations in this proof to Appendix A, retaining here the key steps that might be used to prove similar metastability results for other Markov chains. To prove Theorem 2, it is enough to verify Assumptions 1 and 2 for the sets 
$S^{(1)} = (\!-\infty,0)$ and 
$S^{(2)} = [0,\infty)$, with the decomposition of 
$S^{(1)}$ into 
$G_{\beta}^{(1)} = (\!-\sigma^{-9},0)$, 
$W_{\beta}^{(1)} = (\!-\sigma^{-10},0)$, 
$B_{\beta}^{(1)} = (\!-\infty, -\sigma^{-10})$, and 
$G_{\beta}^{(2)}$, 
$W_{\beta}^{(2)}$, and 
$B_{\beta}^{(2)}$ defined analogously (see Figure 1). Note that Assumption 1.1 follows immediately from (4.1), which we have already proved.
Denote by 
$\hat{K}_{\sigma}$ the Metropolis–Hastings transition kernel on 
$(\!-\infty,0)$ that has as its proposal kernel 
$K_{\sigma}$ and as its target distribution the density 
$\hat{\rho}_{\sigma}(x) = 2 f_{\sigma}(x)$, 
$x \in (\!-\infty,0)$.
We begin by proving some stronger Lyapunov-like bounds for 
$K_{\sigma}$ and 
$\hat{K}_{\sigma}$.
Lemma 3. Let 
$V_{\sigma}(x) = \text{e}^{\sigma^{-1} \min\!(\|x - 1\|, \|x+1\|)}$. Then there exist 
$0 < \alpha \leq 1$, 
$0 \leq M,C < \infty$ such that, for all 
$K \in \{K_{\sigma}, \hat{K}_{\sigma}\}$ and 
$x \in (\!-\infty,-M \sigma)$,
\begin{equation} (K V_{\sigma})(x) \leq (1 - \alpha) V_{\sigma}(x) + C.\end{equation}
Furthermore, Assumption 2.2 holds.
Proof. The proof is deferred to Appendix A.
We next check the main condition.
Theorem 3. With notation as above, Assumption 1.2 is satisfied.
Proof. We begin with a weak estimate of mixing from within a good set.
Lemma 4. Fix 
$0 < \delta < \frac{1}{20}$. With notation as above, there exist some constants 
$0 < a_{1}, A_{1} < \infty$ such that
\begin{equation} \sup_{-\sigma^{-11} < x,y
< -\delta} \big\| \hat{K}_{\sigma}^{T}(x,\cdot) - \hat{K}_{\sigma}^{T}(y,\cdot) \big\|_{\text{TV}} \leq A_{1} \text{e}^{-a_{1} \sigma^{-1}}\end{equation}
for 
$T > A_{1} \sigma^{-a_{1}}$.
Proof. The proof is deferred to Appendix A.
Note that this bound is not good enough for our conclusions, since our upper bound 
$\text{e}^{-a_{1} \sigma^{-1}}$ is still very large compared to the conductance of interest. We improve the bound by iterating it several times.
Lemma 5. Fix 
$0 < \delta < \frac{1}{20}$. There exist constants 
$0 < a_{2},A_{2} < \infty$ depending only on 
$\delta$ such that
\begin{equation} \sup_{-\sigma^{-9} < x,y
< -\delta} \big\| \hat{K}_{\sigma}^{S}(x,\cdot) - \hat{K}_{\sigma}^{S}(y,\cdot) \big\|_{\text{TV}} \leq A_{2} \text{e}^{-a_{2} \sigma^{-5}}\end{equation}
for 
$S = \lceil A_{2} \sigma^{-a_{2}} \rceil$. Furthermore, there exist constants 
$0 < a_{3}, A_{3} < \infty$ such that
\begin{equation} \sup_{x \in (\!-\delta,0)} \mathbb{P}[ \tau_{x,(\!-\delta,0)^{\text{c}}}
< A_{3} \sigma^{-a_{3}}] \geq 1- \text{e}^{-\sigma^{-10}}.\end{equation}
Proof. The proof is deferred to Appendix A.
Fix 
$\delta = 0.01$. Combining (4.4) with the bound in (4.5) on the length of excursions above 
$- \delta$ completes the proof of the Theorem 3.
Lemma 6. With notation as above, Assumptions 1.3, 1.4, and 2.3 hold.
Proof. These all follow immediately from Lemma 3 and the definition of our partition.
Next, note that Assumption 2.1 holds by the symmetry of 
$S^{(1)}, S^{(2)}$ and the fact that we have already checked Assumptions 1.
Thus, it remains only to check Assumption 2.4.
Lemma 7. With notation as above, Assumption 2.4 holds.
Proof. It is immediately clear that 
$K_{\sigma}(x,(\!-\infty,x]) \geq \frac{1}{2}$ for all 
$x \in \mathbb{R}$, which implies (3.7). Standard Gaussian inequalities imply that 
$\sup_{x < 0} K_{\sigma}(x,(\sigma^{10},\infty)) \leq \text{e}^{-\sigma^{9}}$ for 
$\sigma < \sigma_{0}$ sufficiently small. Combining this with (4.1) completes the proof of (3.8).
Since we have verified all the assumptions of Lemmas 1 and 2, applying them completes the proof of Theorem 2.
5. Application to sampling from high-dimensional sets
We give an example with a very different flavour from that in Section 4: an analysis of multimodality in a simple Gibbs-like walk for sampling from the uniform distribution on a high-dimensional set. To keep the analysis as simple and easy-to-read as possible, we consider a very simple situation; we briefly discuss some generalizations in Remark 4.
We begin by defining a simple variant of the hit-and-run sampler introduced in [Reference Turchin22]. Roughly speaking, this algorithm proceeds by choosing a random direction at every step and sampling uniformly along this line. More precisely, denote by 
$\lambda$ the Lebesgue measure on 
$\mathbb{R}^{d}$ and fix an open set 
$\mathcal{C} \subset \mathbb{R}^{d}$ with 
$0 < \lambda(\mathcal{C}) < \infty$. We define the associated sampler L with target distribution equal to the uniform distribution on 
$\mathcal{C}$ by the following algorithm for sampling 
$X \sim L(x,\cdot)$:
-
1. Sample v uniformly on the unit sphere
$\{ y \in \mathbb{R}^{n}\,{:}\, \| y \| = 1\}$. -
2. Define
$\ell' = \{ x + sv\,{:}\,s \in \mathbb{R}^{n} \} \cap \mathcal{C}$. Note that $\ell'$ is a union of line segments and includes x; let $\ell$ be the connected component of $\ell'$ that contains x. -
3. Return
$X \sim \text{Unif}(\ell)$.
We now set up the main problem. Roughly speaking, we will check that this algorithm exhibits metastability when 
$\mathcal{C}$ is the union of two moderately rounded sets that have small intersection. A concrete family of such sets is given in Example 1.
Proceeding more formally, fix constants 
$r,R \in \mathbb{R}$ such that 
$0<r<R$, and 
$\Delta >0$. Let 
$\hat{\textsf{A}}_1, \hat{\textsf{A}}_2, \ldots \subseteq \mathbb{R}^{d}$ and 
$\hat{\textsf{K}}_1, \hat{\textsf{K}}_2, \ldots \subseteq \mathbb{R}^{d}$ be two sequences of convex bodies. Suppose that, for each 
$\beta \in \mathbb{N}$, the convex bodies 
$\hat{\textsf{A}}_\beta$ and 
$\hat{\textsf{K}}_\beta$ each contain a (possibly different) ball of radius r, and are each contained in a (possibly different) ball of radius R. For each 
$\beta \in \mathbb{N}$, we define 
$\textsf{A}_\beta \coloneqq \hat{\textsf{A}}_\beta + B(0,\Delta)$ and 
$\textsf{K}_\beta \coloneqq \hat{\textsf{K}}_\beta + B(0,\Delta)$, where ‘
$+$’ denotes the Minkowski sum. Finally, let 
$\mathcal{C}_{\beta} = \textsf{A}_{\beta} \cup \textsf{K}_{\beta}$, and let 
$Q_{\beta}$ be the hit-and-run sampler associated with the set 
$\mathcal{C}_{\beta}$.
For 
$c > 0$ and 
$S \subset \mathbb{R}^{d}$, we define the c-interior of S by 
$S^{(\!-c)} = \{x \in \mathbb{R}^{d}\,{:}\, \inf_{y \notin S} \| x - y \| > c \}$.
We assume the following conditions on our sequences of convex bodies 
$\hat{\textsf{A}}_1, \hat{\textsf{A}}_2, \ldots \subseteq \mathbb{R}^{d}$ and 
$\hat{\textsf{K}}_1, \hat{\textsf{K}}_2, \ldots \subseteq \mathbb{R}^{d}$ in order to guarantee metastability.
Assumptions 3. We assume:
-
1. There exists a measurable set
$S \subset \mathbb{R}^{d}$ such that, for all $\beta \in \mathbb{N}$,
\begin{align*} \textsf{K}_{\beta} \cap S &\subseteq \textsf{A}_{\beta} \cap S , \\[3pt] \textsf{A}_{\beta} \cap S^{\text{c}} & \subseteq \textsf{K}_{\beta} \cap S^{\text{c}} , \\[3pt] \textsf{A}_{\beta}^{\big(\!-\frac{1}{80 \sqrt{d}\,} \Delta\big)} &\subset S , \\[3pt] \textsf{K}_{\beta}^{\big(\!-\frac{1}{80 \sqrt{d}\,} \Delta\big)} &\subset S^{\text{c}} . \end{align*}
-
2. Define the function
which is just the conductance of the set
\begin{equation*} f(\beta) \coloneqq \frac{1}{\lambda(S \cap \mathcal{C}_{\beta})} \int_{S \cap \mathcal{C}_{\beta}} Q_{\beta}(x, S^{\text{c}}) \, \text{d} x,\end{equation*}
$S \cap \mathcal{C}_{\beta}$ for the kernel $Q_{\beta}$. There exist constants $c_{1},c_{2},c_{3} > 0$ such that $\text{e}^{-c_{1} \beta^{c_{2}}} < f(\beta) \leq \text{e}^{-c_{3}\beta}$ for all $\beta \in \mathbb{N}$.
The main result of this section is the following theorem.
Theorem 4. Fix sequences of convex sets satisfying Assumptions 3, and let 
$Q_{\beta}$ be the associated hit-and-run transition kernel. The spectral gap 
$\rho_{\beta}$ and conductance 
$\Phi_{\beta}$ of 
$Q_{\beta}$ satisfy
\begin{equation*} \lim_{\beta \rightarrow \infty} \frac{\log\!(\rho_{\beta})}{\log\!(\Phi_{\beta}(S))} = 1.\end{equation*}
Example 1. As a concrete example, for any 
$\Delta < \frac{1}{10}$, consider the 
$\Delta$-rounded simplex 
$\mathcal{D} = \{x \in \mathbb{R}^d\,{:}\, x[i] \geq 0 \text{ for all } i\in [d] \text{ and } \|x\|_1 \leq 1 \} + B(0, \Delta)$. For all 
$\alpha \geq 0$, let 
$\textsf{A}^\alpha = \alpha \textbf{1} + \mathcal{D}$, where 
$\textbf{1} = (1,\ldots, 1)^\top$ is the all-ones vector. Let 
$\textsf{K}^\alpha = -\textsf{A}^\alpha$, and let 
$\mathcal{C}^\alpha = \textsf{A}^\alpha \cup \textsf{K}^\alpha$. Note that these sets are clearly contained, for example, in the ball of radius 
$R=2$ around the origin, and contain, for example, the ball of radius 
$r= \frac{1}{2d^{2}}$ around 
$(\frac{1}{2d},\ldots,\frac{1}{2d})$.
We next check that this sequence satisfies Assumptions 3 for some appropriate choice of 
$\alpha = \alpha(\beta)$. Let S be the half-plane 
$S = \{x \in \mathbb{R}^d\,{:}\, \textbf{1}^\top x \geq 0\}$. Define the function
\begin{equation*} F(\alpha) \coloneqq \frac{1}{\lambda(S \cap \textsf{A}^{\alpha})} \int_{S \cap \textsf{A}^{\alpha}} L^\alpha(x, S^{\text{c}}) \,\text{d} x,\end{equation*}
where 
$L^\alpha$ is the hit-and-run sampler associated with the set 
$\mathcal{C}^\alpha$.
We note that F is clearly continuous, strictly monotone decreasing on 
$[0,\Delta]$, and satisfies 
$f(0) > 0$ and 
$F(\Delta) = 0$. Thus, there exists a monotone increasing function 
$g\,{:}\, [0,\infty) \mapsto [0,\Delta]$ that satisfies 
$\text{e}^{-c_{1} x^{c_{2}}} < F(g(\beta)) \leq \text{e}^{-c_{3}x}$ for some 
$c_{1},c_{2},c_{3} > 0$ and all 
$\beta \in [0,\infty)$.
Define 
$\textsf{A}_\beta\coloneqq \textsf{A}^{g(\beta)}$, 
$\textsf{K}_\beta\coloneqq \textsf{K}^{g(\beta)}$, and 
$\mathcal{C}_\beta = \mathcal{C}^{g(\beta)} = \textsf{A}^{g(\beta)} \cup \textsf{K}^{g(\beta)}$ for all 
$\beta \in \mathbb{N}$ (see Figure 2). Then the sequence 
$\mathcal{C}_1, \mathcal{C}_2, \ldots$ satisfies the assumptions of Theorem 4.
Figure 2. The convex sets 
$\textsf{A}_\beta$ and 
$\textsf{K}_\beta$, and their union 
$\mathcal{C}_\beta = \textsf{A}_\beta \cup \textsf{K}_\beta$, considered in Example 1. Theorem 4 implies metastability of the hit-and-run Markov chain on the uniform distribution on the sets 
$\mathcal{C}_\beta$ as 
$\beta \rightarrow \infty$.
Remark 3. Note that we did not need to explicitly compute either 
$\Phi_{\beta}(S)$ or 
$\rho_{\beta}$ here! For this particular example, estimating 
$\Phi_{\beta}(S)$ is likely not too difficult, but in more complicated examples this can be useful.
Remark 4. In Theorem 4, we held the ambient dimension d, the radii of the contained and containing balls r, R, and the amount of ‘rounding’ 
$\Delta$ as constant for simplicity. We point out here that the proof of Theorem 4 more or less goes through for many sequences of convex bodies even when these constants are allowed to change (and indeed even when the amount of rounding 
$\Delta$ is 0). Essentially the only serious difficulty comes from the step at which we check that the mixing time of the walk restricted to each part of the partition is small. In the proof of Theorem 4, we checked this by invoking Corollary 1.2 of [Reference Lovász and Vempala9], the strongest result in this area that we are aware of. This theorem has basically two requirements for the sequence of convex bodies 
$\mathcal{K}_{\beta}$:
-
1. Denote by
$R_{\beta}$ the radius of the smallest ball containing $\mathcal{K}_{\beta}$, $r_{\beta}$ the radius of the largest ball contained in $\mathcal{K}_{\beta}$, and $d_{\beta}$ its dimension. Then $\frac{R_{\beta} d_{\beta}}{r_{\beta}}$ cannot grow more than polynomially quickly in $\beta$. -
2. From any starting point, the hit-and-run kernel must jump at least some non-negligible distance with non-negligible probability, in a sense made formal by (B.4).
The first condition is often trivial to verify. The second condition seems trivial in moderate dimension, and is guaranteed by having a fixed dimension d and degree of rounding 
$\Delta >0$. It can hold even as d goes to infinity and 
$\Delta = 0$, but it turns out to be more complicated in higher dimensions. We can see the basic difficulty quite clearly by considering the cube 
$[0,1]^{n}$: if a hit-and-run walk is started at the origin, it will stay there until the proposed direction v has components that are either all positive or all negative. This has probability 
$2^{-(n-1)}$, so on average the walk will not move at all for something on the order of 
$2^{n}$ steps. Thus, although the walk mixes in polynomial time started from the point 
$(0.5,0.5,\ldots,0.5)$, the worst-case mixing time is 
$\Omega(2^{n})$. Thus, the worst-case mixing time can be quite bad for sequences of convex bodies with growing dimensions.
There is a large literature on dealing with ‘corners’ in high-dimensional bodies (with some discussion in [Reference Lovász and Vempala9] itself), but a detailed discussion is far beyond the scope of the present article. For this reason, we limit ourselves to convex bodies (such as 
$\Delta$-rounded convex bodies) where it is easy to see that the walk gets ‘far’ from the boundary within a few steps with high probability.
Proof of Theorem 4. We verify the conditions in Assumptions 2 for the partition 
$S \sqcup S^{\text{c}}$ of 
$\Omega$, with trivial choice of sets 
$G_{\beta} = W_{\beta} \equiv S$, 
$B_{\beta} = \emptyset$.
Going down the list quickly, we look at the referenced parts of Assumptions 1:
-
1. This follows from the fact that
$\text{e}^{-c_{1} \beta^{c_{2}}} < f(\beta) \leq \text{e}^{-c_{3}\beta}$ for all $\beta \in \mathbb{N}$. -
2. Checking this is the main difficulty in proving the theorem. This follows from applying Lemma 8 in Appendix B with the choice
$\epsilon = \beta^{-2} \Phi_{\beta}(S)$; note that the result is polynomial in $\beta$ because of the assumption that $\Phi_{\beta}(S) \geq \text{e}^{-c_{1} \beta^{c_{2}}}$ for some $c_{1},c_{2} > 0$. -
3.
$W_{\beta} \cup B_{\beta} \backslash G_{\beta} = \emptyset$, so this is immediate. -
4. For the same reason as part 3, this is immediate.
We then verify the remaining parts of Assumptions 2:
-
1. This just refers to the parts of Assumptions 1 checked above.
-
2. Since
$\Omega$ is compact, this is clear. -
3. Again, since
$W_{\beta} \cup B_{\beta} \backslash G_{\beta} = \emptyset$, this is immediate. -
4. By the symmetry of the problem, (3.7) holds with constant at least
$\frac{1}{2}$. The inequality (3.8) follows again from the fact that $W_{\beta} \cup B_{\beta} \backslash G_{\beta} = \emptyset$. -
5. Since our partition has only two parts, this is immediate.
Having checked Assumptions 2, the result follows from an application of Lemma 2.
Appendix A. Technical bounds from the proof of Theorem 2
We prove some technical lemmas that occur in the proof of Theorem 2.
Proof of Lemma 3. Let 
$a = a_{\sigma}$ be the unique local minimum of 
$f_{\sigma}$ in the interval 
$(\!-2, -0.5)$—it is clear one such exists for all 
$\sigma > \sigma_{0}$ sufficiently large, and that 
$a_{\sigma}$ is within distance 
$O\big(\text{e}^{-\frac{1}{3 \sigma^{2}}}\big)$ of 
$-1$). Let 
$Q_{\sigma}$ be the transition kernel given in Definition 3 with step size 
$\sigma$ and target distribution 
$\mathcal{N}(a,4\sigma^{2})$. Let 
$L_{\sigma}(x) = \text{e}^{-\sigma^{-1} \|x-1\|}$. By a standard computation (e.g. keeping track of the constants in the proof of Theorem 3.2 of [Reference Mengersen and Tweedie14]), there exist 
$0 < \alpha \leq 1$ and 
$0 \leq C < \infty$ such that 
$(Q_{\sigma} L_{\sigma})(x) \leq (1-\alpha)L(x) + C$ for all 
$x \in \mathbb{R}$ and 
$Q \in \{Q_{\sigma}, \hat{Q}_{\sigma}\}$. Next, observe that
\begin{equation*}\inf_{x \in (\!-\infty,-10 \sigma)} \frac{\text{d}^{2}}{\text{d} x^{2}} -\log\!(\,f_{\sigma}(x)) \geq \frac{1}{8 \sigma^{2}}.\end{equation*}
In particular, 
$f_{\sigma}$ is strongly log-concave on the interval 
$(\!-\infty,-10 \sigma)$ with the same parameter as the density of 
$\mathcal{N}(a,4\sigma^{2})$. Thus, if we fix 
$M > 0$ and 
$x \in (\!-\infty,-M \sigma)$ and let 
$X \sim K_{\sigma}(x,\cdot)$, we have, for 
$K \in \{K_{\sigma}, \hat{K}_{\sigma}\}$,
\begin{align}(K V_{\sigma})(x) &\leq (Q_{\sigma} L_{\sigma})(x) + \mathbb{E}[V_{\sigma}(X) \mathbbm{1}_{X > -10 \sigma}]\nonumber\\[3pt] &\leq (1 -\alpha) L_{\sigma}(x) + C + \mathbb{E}[V_{\sigma}(X) \mathbbm{1}_{X > -10 \sigma}]\nonumber\\[3pt] &= (1 -\alpha) V_{\sigma}(x) + C + \mathbb{E}[V_{\sigma}(X) \mathbbm{1}_{X > -10 \sigma}]. \end{align}
Let 
$Y \sim \mathcal{N}(0,\sigma^{2})$. As 
$M \rightarrow \infty$, for 
$K = \hat{K}_{\sigma}$ we can then bound the last term by
\begin{equation} \mathbb{E}[V_{\sigma}(X) \mathbbm{1}_{X > -10 \sigma}] \leq V_{\sigma}(x) \mathbb{E}[\text{e}^{\sigma^{-1}Y} \mathbbm{1}_{x+ Y \in [\!-10\sigma,0] }] = (1+o(1)) V_{\sigma}(x).\end{equation}
Combining (A.1) and (A.2) completes the proof of (4.2) in the case 
$K = \hat{K}_{\sigma}$. In the case 
$K = K_{\sigma}$, we replace (A.4) by the similar bound
\begin{align*}\mathbb{E}[V_{\sigma}(X) \mathbbm{1}_{X > -10 \sigma}] & \leq V_{\sigma}(x) \mathbb{E}[\text{e}^{\sigma^{-1}Y} \mathbbm{1}_{x+ Y \in [\!-10\sigma,10 \sigma] }] + V_{\sigma}(x) \mathbb{P}[x+Y > 10 \sigma] \\[3pt] & = (1+o(1)) V_{\sigma}(x)\end{align*}
to obtain the same conclusion.
Finally, Assumption 2.2 immediately follows from (4.2) in the case 
$K = K_{\sigma}$ and the trivial inequality 
$\sup_{|x| \leq M \sigma} (K_{\sigma} V_{\sigma})(x) \leq \text{e}^{\sigma^{-3}}$ for any fixed M and all 
$\sigma < \sigma_{0} = \sigma_{0}(A)$ sufficiently small.
Proof of Lemma 4. Fix 
$\alpha, C$ as in Lemma 3 and let 
$\mu$ be the uniform distribution on the interval 
$I = [\!-1-\frac{10 C}{\alpha} \sigma, -1 + \frac{10 C}{\alpha} \sigma]$. We note that 
$\hat{K}_{\sigma}$ inherits the following minorization condition from the standard Gaussian:
\begin{equation} \inf_{x \in I} \inf_{J \subset I} \hat{K}_{\sigma}(x,J) \geq \epsilon \mu(J)\end{equation}
for some 
$\epsilon > 0$ that does not depend on 
$\sigma$.
Fix 
$-\sigma^{-10} < x,y < -\delta$. Applying the popular ‘drift-and-minorization’ bound in Section 10 of [Reference Meyn and Tweedie15], using the ‘drift’ bound in (4.2) and the ‘minorization’ bound in (A.3) gives a bound of the form
\begin{equation} \sup_{-\sigma^{-10} < x,y < -\delta} \big\| \hat{K}_{\sigma}^{T}(x,\cdot) - \hat{K}_{\sigma}^{T}(y,\cdot) \big\|_{\text{TV}} \leq B_{1} \text{e}^{-b_{1} \sigma^{-1}} + 2 \sup_{-\sigma^{-10} < x < -\delta} \mathbb{P}[\tau_{x, (\!-M \sigma,\infty)}
< t]\end{equation}
for all 
$T > B_{1} \sigma^{-b_{1}}$, where 
$0 < b_{1}, B_{1}$ are constants that do not depend on 
$\sigma$. Note that the second term on the right-hand side, which does not appear in [Reference Meyn and Tweedie15], represents the possibility that a Markov chain ever escapes from the set 
$(\!-\infty,-M \sigma)$ on which the drift bound (4.2) holds.
Fix 
$-\sigma^{-10} < x < -\delta$ and let 
$\{X_{t}\}_{t \geq 0}$ be a Markov chain with transition kernel 
$\hat{K}_{\sigma}$ and starting point 
$X_{0} = x$. Let 
$\tau = \inf \{t \geq 0\,{:}\,X_{t} > -M \sigma \}$. By (4.2), we have, for all 
$t \in \mathbb{N}$, 
$\mathbb{E}[V_{\sigma}(X_{t}) \mathbbm{1}_{\tau \geq t-1}] \leq (1-\alpha)^{t} V_{\sigma}(X_{0}) + \frac{C}{\alpha}$. Thus, by Markov’s inequality,
\begin{eqnarray*}\mathbb{P}[\tau \leq t] &\leq \text{e}^{-\sigma^{-1} (\!-M \sigma + 1)} \sum\limits_{s=0}^{t} \bigg((1-\alpha)^{t} V_{\sigma}(X_{0}) + \frac{C}{\alpha}\bigg) \\[3pt] &\leq t \, \text{e}^{-\sigma^{-1} (\!-M \sigma + 1)} \bigg(\text{e}^{\sigma^{-1} (\!-\delta+1)} + \frac{C}{\alpha}\bigg).\end{eqnarray*}
Combining this with (A.4) completes the proof of the lemma.
Proof of Lemma 5. We denote by 
$\{X_{t}\}_{t \geq 0}$ a Markov chain with transition kernel 
$\hat{K}_{\sigma}$ and some starting point 
$X_{0} = x$. To improve on the bound in Lemma 4, we must control what can occur when coupling does not happen quickly. There are two possibilities to control: the possibility that 
$\{X_{t}\}_{t \geq 0}$ goes above 
$- \delta$, and the possibility that it goes below 
$-\sigma^{-10}$. The latter is easier to control; by (4.2) and Markov’s inequality, for all 
$\epsilon > 0$ there exist constants 
$c_{1} = c_{1}(\epsilon), C_{1} = C_{1}(\epsilon) > 0$ such that
\begin{align}\sup_{|X_{0}| \leq \sigma^{-\beta}} \mathbb{P}\left[\min_{1 \leq t \leq \text{e}^{\sigma^{-\beta}}} X_{t}
< -\sigma^{-\beta - \epsilon}\right] &\leq \text{e}^{\sigma^{-\beta}} \, \sup_{|X_{1}| \leq \sigma^{-\beta}} \sup_{1 \leq t \leq \text{e}^{\sigma^{-\beta}}} \frac{\mathbb{E}[\text{e}^{|X_{t}|}]}{\text{e}^{\sigma^{-\beta - \epsilon}}}\nonumber\\[3pt] &\leq \text{e}^{\sigma^{-\beta}} \left( \frac{\text{e}^{\sigma^{-\beta}} + \alpha^{-1} C}{\text{e}^{\sigma^{-\beta - \epsilon}}} \right)\nonumber\\[3pt] &\leq C_{1} \text{e}^{-c_{1} \sigma^{-\beta - \epsilon}} \end{align}
uniformly in 
$\beta \geq 1$.
The possibility that 
$\{X_{t} \}_{t \geq 0}$ goes above 
$- \delta$ cannot be controlled in the same way, because it does not have negligible probability on the timescale of interest. Instead, we use the fact that 
$X_{t}$ will generally exit the interval 
$(\!- \delta, 0)$ fairly quickly, often to the interval 
$(\!-\infty, - \delta)$.
To see this, fix 
$x \in (\!- \delta, 0)$ and let 
$\{X_{t}\}_{t \geq 0}$ have starting point 
$X_{0} = x$. Next, let 
$\{\epsilon_{t}\}_{t \geq 1}$ be a sequence of independent and identically distributed 
$\mathcal{N}(0,\sigma^{2})$ random variables and let 
$Y_{t} = X_{0} + \sum_{s=1}^{t} \epsilon_{t}$. For 
$I \subset \mathbb{R}$, let 
$\psi_{x,I} = \inf \{t \geq 0\,{:}\, Y_{t} \in I\}$ be the hitting time of I for the Markov chain 
$\{Y_{t}\}_{t \geq 0}$. Observing the forward mapping representation of 
$K_{\sigma}$ in Definition 3, and that 
$f_{\sigma}$ is monotone on 
$(\!- \delta, 0)$, it is clear that we can couple 
$\{X_{t}\}_{t \geq 0}$, 
$\{Y_{t}\}_{t \geq 0}$ so that
\begin{equation} X_{t} \leq Y_{t} \text{ for all } 0 \leq t \leq \min\!(\tau_{x,(\!-\delta,0)^{\text{c}}}, \psi_{x,(\!-\delta,0)^{\text{c}}}).\end{equation}
But, by standard calculations for a simple random walk,
\begin{equation} \sup_{x \in (\!-\delta,0)} \mathbb{P}[\psi_{x,(\!-\delta,0)^{\text{c}}} > C_{2} \sigma^{-c_{2}}] \leq \sigma^{2}, \qquad \inf_{x \in (\!-\delta,0)} \mathbb{P}[Y_{\psi_{x,(\!-\delta,0)^{\text{c}}}}
< -\delta] > C_{3} \sigma\end{equation}
for some constants 
$c_{2}, C_{2}, C_{3}$ that do not depend on 
$\sigma$. (To see the first inequality in (A.7), note that a direct calculation for Gaussians gives 
$\sup_{x \in (\!-\delta,0)} \mathbb{P}[\psi_{x,(\!-\delta,0)^{\text{c}}} > C_{2}' \sigma^{-c_{2}'}] >\break C_{2}'' > 0$ for some 
$C_{2}', c_{2}' C_{2}'' > 0$; applying the strong Markov property to iterate this bound as in the proof of (3.5) gives the desired conclusion. The second inequality in (A.7) follows from the observation that 
$\mathbb{P}[Y_{1} > C_{3}' \sigma] > C_{3}'' > 0$ for some constants 
$C_{3}', C_{3}'' > 0$ and then the well-known ‘gambler’s ruin’ calculation (see, e.g., Section 10.14.4 of [Reference Resnick18]).)
Combining (A.7) with (A.6) and noting that 
$\{X_{t}\}_{t \geq 0}$ never exits 
$(\!-\infty,0)$ by construction, we find
\begin{equation*}\sup_{x \in (\!-\delta,0)} \mathbb{P}[ \tau_{x,(\!-\delta,0)^{\text{c}}}
< C_{2} \sigma^{-c_{2}}] \geq C_{3} \sigma - \sigma^{2} = C_{3}(\sigma) (1 - o(1)).\end{equation*}
Noting that these bounds are uniform over the starting point 
$X_{0} \in (\!-\delta,0)$, we find, for 
$k \in \mathbb{N}$, 
$\sup_{x \in (\!-\delta,0)} \mathbb{P}[ \tau_{x,(\!-\delta,0)^{\text{c}}} < k \,C_{2} \sigma^{-c_{2}}] \geq 1 - (1 - C_{3}(\sigma) - \sigma^{2})^{k}$. Taking k very large (
$k > \sigma^{-12}$ suffices) gives 
$\sup_{x \in (\!-\delta,0)} \mathbb{P}[ \tau_{x,(\!-\delta,0)^{\text{c}}} < C_{4} \sigma^{-c_{4}}] \geq 1- \text{e}^{-\sigma^{-10}}$ for some constants 
$0 \leq c_{4}, C_{4} < \infty$, which is exactly (4.5).
Combining the bound (4.3) on the mixing of 
$\hat{K}_{\sigma}$ on 
$(\!-\sigma^{-11},-\delta)$ with the bound (A.5) on the possibility of excursions below 
$-\sigma^{-11}$ and the bound (4.5) on the length of excursions above 
$- \delta$ completes the proof of the lemma.
Appendix B. Technical bounds from the proof of Theorem 4
We obtain the required bound on the mixing time, which is essentially a corollary of [Reference Lovász and Vempala9, Theorem 1.1].
Lemma 8. Fix sequences of convex sets satisfying Assumptions 3, and denote by 
$L_{\beta}$ the hit-and-run kernel on 
$\mathcal{C}_{\beta} \cap S = \textsf{A}_{\beta} \cap S$, with stationary measure 
$\pi_{\beta}$ the uniform distribution on this set. Then there exists some constant 
$0 < C < \infty$ that does not depend on 
$\beta$ (though depending on d) such that, for all 
$\epsilon > 0$ and all 
$T > C \log\!(\epsilon^{-1})$, 
$\sup_{x \in \mathcal{C}_{\beta} \cap S} \| L_{\beta}^{T}(x,\cdot) - \pi_{\beta}(\cdot) \|_{\text{TV}} \leq \epsilon$.
Proof. For 
$0 < \delta < 0.15$, define 
$\textsf{A}_{\beta,\delta} = \{x \in \textsf{A}_{\beta} \cap S\,{:}\, \inf_{y \notin \textsf{A}_{\beta} \cap S} \|x-y\| < \delta \}$ to be the points at least distance 
$\delta$ from the boundary of 
$\textsf{A}_{\beta} \cap S$. Recall from [Reference Lovász and Vempala9, Corollary 1.2] that 
$\sup_{x \in \textsf{A}_{\beta, \delta}} \| L_{\beta}^{t}(x,\cdot) - \pi_{\beta}(\cdot) \|_{\text{TV}} \leq 0.25$ for all 
$t > C_{1}(\delta) \equiv 4 \times 10^{11} n^{3} \frac{\textsf{R}^2}{\textsf{r}^2} \log\!(4 \delta^{-1})$.
Applying the Markov property and then this bound (together with the well-known fact that TV distance to stationarity decays exponentially quickly, as shown, e.g., in [Reference Levin, Peres and Wilmer8, Lemmas 4.11, 4.12], we have, for all 
$t_{1},t_{2} \in \mathbb{N}$,
\begin{align}\sup_{x \in \textsf{A}_{\beta} \cap S} \big\| L_{\beta}^{t_{1} + t_{2}}(x,\cdot) - \pi_{\beta}(\cdot) \big\|_{\text{TV}} &\leq \sup_{x \in \textsf{A}_{\beta} \cap S} \mathbb{P}_{x}[\tau_{\textsf{A}_{\beta,\delta}} > t_{1}] + \sup_{x \in \textsf{A}_{\beta,\delta}} \big\| L_{\beta}^{t_{2}}(x,\cdot) - \pi_{\beta}(\cdot) \big\|_{\text{TV}} \nonumber\\[3pt]
&\leq \sup_{x \in \textsf{A}_{\beta} \cap S} \mathbb{P}_{x}[\tau_{\textsf{A}_{\beta,\delta}} > t_{1}] + 2^{- \big\lfloor \frac{t_{2}}{C_{1}} \big\rfloor}. \end{align}
Fix any point 
$x \in \textsf{A}_{\beta}$. We now consider the hit-and-run step defined by sampling v uniformly on the 
$(d-1)$-dimensional unit sphere, setting 
$\ell = \{ x + sv \,{:}\, s \in \mathbb{R}^{d} \} \cap \textsf{A}_{\beta}$, and sampling 
$X \sim \text{Unif}(\ell)$. Recall that 
$\textsf{A}_\beta \coloneqq \hat{\textsf{A}}_\beta + B(0,\Delta)$ is the Minkowski sum of a convex body with a ball of radius 
$\Delta$. This implies that x lies on the surface of some ball 
$\mathfrak{B} \subseteq \textsf{A}_\beta$, where 
$\mathfrak{B}$ has radius 
$\frac{1}{2}\Delta$. Denote by 
$n_{x}$ the normal vector to the tangent plane of 
$\mathfrak{B}$ at x, and let 
$v^{\perp}$ be the component of v in the direction of 
$n_{x}$. Since the vector v which determines the hit-and-run step is uniformly distributed on the 
$(d-1)$-dimensional unit sphere, standard concentration inequalities for the uniform distribution on the sphere imply that
\begin{equation*} \mathbb{P}\bigg[\| v^{\perp} \| \geq \frac{1}{3 \sqrt{d}\,}\bigg] \geq \frac{1}{2}.\end{equation*}
It is an exercise in two-dimensional Euclidean geometry to check that, when 
$\| v^{\perp} \| \geq \frac{1}{3 \sqrt{d}\,}$, there exists some 
$z \in \ell$ such that 
$B_{\frac{1}{20 \sqrt{d}\,}}(z) \subseteq \mathfrak{B} \subseteq \textsf{A}_\beta$ (see Figure B1(a) for a picture proof of this fact). Denote by 
$\mathcal{E}$ the event that there exists 
$z \in \ell\,{:}\, B_{\frac{1}{20 \sqrt{d}\,}}(z) \subseteq \mathfrak{B} \subseteq \textsf{A}_\beta$; we have shown that
\begin{equation} \mathbb{P}[\mathcal{E}] \geq \frac{1}{2}.\end{equation}
Figure B1. An illustration of the convex geometry in the proof of Lemma 8.
We now continue by analysing the distribution of X on the event 
$\mathcal{E}$, and fix the 
$z \in \ell$ whose existence is guaranteed as above. We note that 
$\mathcal{E}$ depends only on v. Let a,b be the two intersection points of 
$\ell$ with the convex body 
$\textsf{A}_\beta$, and consider the convex hull 
$\Gamma = \text{Convex}\big(\{a\} \cup \{b\} \cup B_{\frac{1}{20 \sqrt{d}\,} \Delta}(z)\big) \subset \textsf{A}_\beta$ of these two points and the ball 
$B_{\frac{1}{20 \sqrt{d}\,} \Delta}(z)$. Let m be the midpoint of the line segment [z, a], and let M be the midpoint of the line [z, b]. Since the convex hull 
$\Gamma$ consists of the union of two prisms which share a base consisting of a 
$(d-1)$-dimensional ball of radius 
$\frac{1}{20 \sqrt{d}\,} \Delta$ centred at the point z, we can see that all the points on the lines [z, m] and [z, M] are in the 
$\frac{1}{40 \sqrt{d}\,}\Delta$-interior of 
$\Gamma \subseteq \textsf{A}_\beta$; see Figure 3(b). On the event 
$\mathcal{E}$, then,
\begin{equation*}\mathbb{P} \left[ X \in \textsf{A}_{\beta}^{\big(\!-\frac{1}{40 \sqrt{d}\,}\Delta\big)} \, \big| \, \mathcal{E} \right] \geq \mathbb{P}[X \in [z,m] \cup [z,M] \mid \mathcal{E}] \geq \frac{1}{2}.\end{equation*}
Combining this with (B.2), we have shown that
\begin{equation} \mathbb{P} \left[X \in \textsf{A}_{\beta}^{\big(\!-\frac{1}{40 \sqrt{d}\,}\Delta\big)}\right] \geq \frac{1}{4}.\end{equation}
Now, our assumption that 
$\textsf{K}_{\beta} \cap S \subseteq \textsf{A}_{\beta} \cap S$ implies that 
$\mathcal{C}_\beta \cap S = \textsf{A}_{\beta} \cap S$. Moreover, by another one of our assumptions, S contains the 
$\frac{1}{80 \sqrt{d}\,}\Delta$-interior of 
$\textsf{A}_{\beta}$. Therefore, applying (B.3) gives
\begin{equation} \inf_{x} L_{\alpha}\left(x,\mathcal{C}_{\beta, \frac{1}{80 \sqrt{d}\,}\Delta}\right) \geq \frac{1}{4}.\end{equation}
Applying this to (B.1) with the choice 
$\delta = \frac{1}{80 \sqrt{d}\,}\Delta$, we find
\begin{equation*}\sup_{x \in \mathcal{C}_{\beta} \cap S} \big\| L_{\beta}^{t_{1} + t_{2}}(x,\cdot) - \pi_{\beta}(\cdot) \big\|_{\text{TV}} \leq \left(1 - \frac{1}{4}\right)^{t_{1}} + 2^{- \big\lfloor \frac{t_{2}}{C_{1}} \big\rfloor}.\end{equation*}
Choosing 
$t_{1} = \big\lceil \frac{\log\!(\epsilon)}{\log\!(1-\frac{1}{4})} \big\rceil$ and 
$t_{2} = \frac{\log\!(\epsilon)}{2 C_{1}\big(\frac{1}{80 \sqrt{d}\,}\Delta\big)}$ gives
\begin{align*}\sup_{x \in \mathcal{C}_{\beta} \cap S} \big\| L_{\beta}^{t_{1} + t_{2}}(x,\cdot) - \pi_{\beta}(\cdot) \big\|_{\text{TV}} \leq \epsilon. \\[-40pt] \end{align*}
Acknowledgements
We would like to thank Neil Shephard and Gareth Roberts for some questions about multimodal distributions and helpful comments on initial results.
NSP gratefully acknowledges the support of ONR. AS was supported by an NSERC Discovery grant. OM was supported by NSF-dms 1312831, by an NSERC Discovery grant, and by a Canadian Statistical Sciences Institute (CANSSI) Postdoctoral Fellowship.
