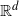1. Introduction
Random graphs are a powerful tool for modeling real-world large networks such as the internet [Reference Albert, Jeong and Barabási1], telecommunication networks [Reference Haenggi, Andrews, Baccelli, Dousse and Franceschetti21], social networks [Reference Newman, Watts and Strogatz33], neural networks [Reference Lago-Fernández, Huerta, Corbacho and Sigüenza28], transportation networks [Reference Kaluza, Kölzsch, Gastner and Blasius25], financial systems [Reference Cont, Moussa and Bastos e Santos10], and many more (see e.g. [Reference Newman32] and [Reference Van Der Hofstad39] for overviews). The idea is to overcome the intractability of a given network, for example because of its size, by mimicking its most interesting features with a probabilistic model. In particular, three main characteristics have been highlighted in the recent literature that are often observed in real life (see e.g. [Reference Candellero and Fountoulakis8], [Reference Heydenreich, Hulshof and Jorritsma22], and [Reference Jacob and Mörters23]).
• Scale-free property. A graph is said to exhibit the scale-free property if the degree (i.e. the number of neighbors) of its vertices follows a power law. This results in the presence of hubs, i.e. nodes with a very high degree.
• Small-world property. When sampling two vertices at random, their graph distance (the minimum number of edges to cross to go from one vertex to the other) is typically of logarithmic order on the total number of nodes. If the nodes of the graph are embedded in a metric space, for example in
 $\mathbb{R}^d$, this translates into saying that two nodes at Euclidean distance D are with high probability at graph distance
$\mathbb{R}^d$, this translates into saying that two nodes at Euclidean distance D are with high probability at graph distance  $\textrm{O}(\!\log D)$.
$\textrm{O}(\!\log D)$.• High clustering coefficient. When two vertices share a common neighbor, there is a ‘high’ probability that they are linked, too.
These properties are of great importance when studying, for example, the spread of information or infections (see e.g. [Reference Pastor-Satorras and Vespignani35], [Reference Moore and Newman31], [Reference Coupechoux and Lelarge11], and [Reference Riley, Eames, Isham, Mollison and Trapman36]) or other related random processes on the network (such as first passage percolation [Reference Komjáthy and Lodewijks27], the Ising model [Reference Barrat and Weigt3], or random walks [Reference Heydenreich, Hulshof and Jorritsma22]). Unfortunately, classical models of random graphs do not exhibit these three properties at once. Just to give a few examples, the Erdős–Rényi model has only the small-world property, the Chung–Lu [Reference Chung and Lu9], Norros–Reittu [Reference Norros and Reittu34], and preferential attachment [Reference Barabási and Albert2] models are scale-free and small-world, but all have vanishing clustering coefficient as the number of nodes tends to infinity. As a rule of thumb, one can think that regular, nearest-neighbor lattices have high clustering but long distances, while classic random graphs have low clustering and small distances. The Watts–Strogatz network [Reference Watts and Strogatz40] was one of the first attempts to ‘artificially’ build a random graph that boasts high clustering and the small-world property, but it lacks the scale-free property.
Spatial random graphs, i.e. graphs whose vertices are embedded in some metric space, offer a possible solution to the shortcomings of classical models. While in the physics literature they have been quite extensively studied (see [Reference Barthélemy4] for a broad review of the topic), very few models have been analyzed in a fully rigorous mathematical fashion. Among those which exhibit or are conjectured to exhibit the three properties mentioned above, we mention the hyperbolic random graph [Reference Gugelmann, Panagiotou and Peter20], the spatial preferential attachment model [Reference Jacob and Mörters23], the geometric inhomogeneous random graph [Reference Bringmann, Keusch and Lengler7], the age-dependent random connection model [Reference Gracar, Grauer, Lüchtrath and Mörters19], and scale-free percolation.
Scale-free percolation was introduced by Deijfen, van der Hofstad, and Hooghiemstra [Reference Deijfen, van der Hofstad and Hooghiemstra13], and can be considered a combination of long-range percolation (see e.g. [Reference Berger5] and [Reference Biskup6]) and inhomogeneous random graphs such as the Norros–Reittu model. The vertices of the graph lie on the ![]() $\mathbb{Z}^d$ lattice and random weights
$\mathbb{Z}^d$ lattice and random weights ![]() $\{W_x\}_{x\in\mathbb{Z}^d}$ are assigned independently to each of them. The distribution of the weights follows a power law: we have
$\{W_x\}_{x\in\mathbb{Z}^d}$ are assigned independently to each of them. The distribution of the weights follows a power law: we have ![]() $P(W>w)=w^{-(\tau-1)}L(w)$ for some
$P(W>w)=w^{-(\tau-1)}L(w)$ for some ![]() $\tau>1$ and an L function slowly varying at infinity. Finally, any two vertices
$\tau>1$ and an L function slowly varying at infinity. Finally, any two vertices ![]() $x,y\in\mathbb{Z}^d$ are linked by an unoriented edge with probability
$x,y\in\mathbb{Z}^d$ are linked by an unoriented edge with probability
where ![]() $\lambda, \alpha>0$ are two parameters of the model and
$\lambda, \alpha>0$ are two parameters of the model and ![]() $\|\cdot\|$ is the Euclidean distance. Deprez, Hazra, and Wüthrich [Reference Deprez, Hazra and Wüthrich15] argued that scale-free percolation is a suitable model, for example, for the interbank network presented in [Reference Soramäki, Bech, Arnold, Glass and Beyeler37]. Deprez and Wüthrich [Reference Deprez and Wüthrich14] introduced the continuous-space counterpart of scale-free percolation, where the vertices of the graph are sampled according to a homogeneous Poisson point process of intensity
$\|\cdot\|$ is the Euclidean distance. Deprez, Hazra, and Wüthrich [Reference Deprez, Hazra and Wüthrich15] argued that scale-free percolation is a suitable model, for example, for the interbank network presented in [Reference Soramäki, Bech, Arnold, Glass and Beyeler37]. Deprez and Wüthrich [Reference Deprez and Wüthrich14] introduced the continuous-space counterpart of scale-free percolation, where the vertices of the graph are sampled according to a homogeneous Poisson point process of intensity ![]() ${\nu}>0$ in
${\nu}>0$ in ![]() $\mathbb{R}^d$. On the one hand, this additional source of randomness makes the model more flexible and possibly more suitable for applications to real-world networks. On the other hand, technical difficulties emerge, especially when dealing with fixed configurations of the point process. The probability of linking two vertices is the same as in [Reference Deijfen, van der Hofstad and Hooghiemstra13], but Deprez and Wüthrich prefer to restrict to a Pareto distribution for the weight distribution:
$\mathbb{R}^d$. On the one hand, this additional source of randomness makes the model more flexible and possibly more suitable for applications to real-world networks. On the other hand, technical difficulties emerge, especially when dealing with fixed configurations of the point process. The probability of linking two vertices is the same as in [Reference Deijfen, van der Hofstad and Hooghiemstra13], but Deprez and Wüthrich prefer to restrict to a Pareto distribution for the weight distribution: ![]() $P(W>w)= w^{-(\tau-1)}$ for
$P(W>w)= w^{-(\tau-1)}$ for ![]() $w\geq 1$ (note that in the present paper we have chosen to stick to the notation of [Reference Deijfen, van der Hofstad and Hooghiemstra13]). We point out that the results appearing in [Reference Deprez and Wüthrich14] are annealed, that is, obtained after integration against the underlying Poisson point process.
$w\geq 1$ (note that in the present paper we have chosen to stick to the notation of [Reference Deijfen, van der Hofstad and Hooghiemstra13]). We point out that the results appearing in [Reference Deprez and Wüthrich14] are annealed, that is, obtained after integration against the underlying Poisson point process.
Both the original scale-free percolation model of [Reference Deijfen, van der Hofstad and Hooghiemstra13] and the continuum scale-free percolation of [Reference Deprez and Wüthrich14] share the following features. If ![]() $\alpha\leq d$ or
$\alpha\leq d$ or ![]() $\gamma\,:\!=\alpha(\tau-1)/d\leq 1$, then the nodes of the graph have almost surely infinite degree. If instead
$\gamma\,:\!=\alpha(\tau-1)/d\leq 1$, then the nodes of the graph have almost surely infinite degree. If instead ![]() $\min\{\alpha,(\tau-1)\alpha\}>d$, then the degree of the vertices follows a power law of index
$\min\{\alpha,(\tau-1)\alpha\}>d$, then the degree of the vertices follows a power law of index ![]() $\gamma$ (hence the graph has the scale-free property). Now let
$\gamma$ (hence the graph has the scale-free property). Now let ![]() $\lambda_c$ be the percolation threshold of the graph, that is, the value such that for
$\lambda_c$ be the percolation threshold of the graph, that is, the value such that for ![]() $\lambda<\lambda_c$ all the connected components of the graph are finite and for
$\lambda<\lambda_c$ all the connected components of the graph are finite and for ![]() $\lambda>\lambda_c$ there exists almost surely a (unique) infinite connected component. Assume
$\lambda>\lambda_c$ there exists almost surely a (unique) infinite connected component. Assume ![]() $\min\{\alpha,(\tau-1)\alpha\}>d$. Then, again for both models, the following holds: for
$\min\{\alpha,(\tau-1)\alpha\}>d$. Then, again for both models, the following holds: for ![]() $d\geq 2$, if
$d\geq 2$, if ![]() $\gamma\in(1,2)$ then
$\gamma\in(1,2)$ then ![]() $\lambda_c=0$, while if
$\lambda_c=0$, while if ![]() $\gamma>2$ then
$\gamma>2$ then ![]() $\lambda_c\in(0,\infty)$; for
$\lambda_c\in(0,\infty)$; for ![]() $d=1$, if
$d=1$, if ![]() $\gamma\in(1,2)$ then
$\gamma\in(1,2)$ then ![]() $\lambda_c=0$, if
$\lambda_c=0$, if ![]() $\gamma>2$ and
$\gamma>2$ and ![]() $\alpha\in(1,2]$ then
$\alpha\in(1,2]$ then ![]() $\lambda_c\in(0,\infty)$, and if
$\lambda_c\in(0,\infty)$, and if ![]() $\min\{\alpha,(\tau-1)\alpha\}>2$ then
$\min\{\alpha,(\tau-1)\alpha\}>2$ then ![]() $\lambda_c=\infty$. Once the percolation properties have been established, one can talk about graph distances (for the discrete-space model the results on percolation and distances of [Reference Deijfen, van der Hofstad and Hooghiemstra13] have been complemented in [Reference Deprez, Hazra and Wüthrich15]). The graph distance between two nodes x and y belonging to the same connected component of the graph is the minimum number of edges that one has to cross to go from x to y. Assume again
$\lambda_c=\infty$. Once the percolation properties have been established, one can talk about graph distances (for the discrete-space model the results on percolation and distances of [Reference Deijfen, van der Hofstad and Hooghiemstra13] have been complemented in [Reference Deprez, Hazra and Wüthrich15]). The graph distance between two nodes x and y belonging to the same connected component of the graph is the minimum number of edges that one has to cross to go from x to y. Assume again ![]() $\min\{\alpha,(\tau-1)\alpha\}>d$. Again for both models, when the vertex degrees have infinite variance (corresponding to
$\min\{\alpha,(\tau-1)\alpha\}>d$. Again for both models, when the vertex degrees have infinite variance (corresponding to ![]() $\gamma\in(1,2)$), the graph distance between two points belonging to the infinite component of the graph grows like the
$\gamma\in(1,2)$), the graph distance between two points belonging to the infinite component of the graph grows like the ![]() $\log\log$ of their Euclidean distance (in this case the graph is said to exhibit the ultra-small-world property). When the vertex degrees have finite variance (
$\log\log$ of their Euclidean distance (in this case the graph is said to exhibit the ultra-small-world property). When the vertex degrees have finite variance (![]() $\gamma >2$) and
$\gamma >2$) and ![]() $\lambda>\lambda_c$, two cases are possible: if
$\lambda>\lambda_c$, two cases are possible: if ![]() $\alpha\in(d,2d)$, then the graph distance of two points at Euclidean distance D grows roughly as
$\alpha\in(d,2d)$, then the graph distance of two points at Euclidean distance D grows roughly as ![]() $(\!\log D)^\Delta$ for some constant
$(\!\log D)^\Delta$ for some constant ![]() $\Delta>0$ still not precisely known (small-world property); if
$\Delta>0$ still not precisely known (small-world property); if ![]() $\alpha>2d$ the graph distance is bounded from below by a constant times the Euclidean distance. We point out that the regime where the degrees have infinite variance (
$\alpha>2d$ the graph distance is bounded from below by a constant times the Euclidean distance. We point out that the regime where the degrees have infinite variance (![]() $\gamma\in(1,2)$ in our case) is usually the relevant one for applications (see e.g. [Reference Albert, Jeong and Barabási1] and [Reference Jeong, Tombor, Albert, Oltvai and Barabási24]).
$\gamma\in(1,2)$ in our case) is usually the relevant one for applications (see e.g. [Reference Albert, Jeong and Barabási1] and [Reference Jeong, Tombor, Albert, Oltvai and Barabási24]).
1.1. Our contribution
In the present paper we aim to prove quenched results for scale-free percolation in continuous space, that is, statements that hold for almost every realization ![]() $\eta$ of the underlying Poisson point process. This is one of the main differences from [Reference Deprez and Wüthrich14]: taking the annealed measure therein allows the authors to calculate relevant quantities explicitly. Unfortunately, in most cases, annealed properties give little information about a given configuration
$\eta$ of the underlying Poisson point process. This is one of the main differences from [Reference Deprez and Wüthrich14]: taking the annealed measure therein allows the authors to calculate relevant quantities explicitly. Unfortunately, in most cases, annealed properties give little information about a given configuration ![]() $\eta$. Say, for example, that the degree distribution has an exponentially decaying tail for half of the realizations of the Poisson point process, and a heavy tail for the other half. The annealed result would still state that the degree distribution is heavy-tailed, yet half of the simulations would behave otherwise! Besides their mathematical interest, quenched results are therefore also important because they guarantee that a simulation of the graph will always exhibit a given feature. Another difference from [Reference Deprez and Wüthrich14] is that we assume more general distributions for the weights, not restricting to Pareto.
$\eta$. Say, for example, that the degree distribution has an exponentially decaying tail for half of the realizations of the Poisson point process, and a heavy tail for the other half. The annealed result would still state that the degree distribution is heavy-tailed, yet half of the simulations would behave otherwise! Besides their mathematical interest, quenched results are therefore also important because they guarantee that a simulation of the graph will always exhibit a given feature. Another difference from [Reference Deprez and Wüthrich14] is that we assume more general distributions for the weights, not restricting to Pareto.
We start by analyzing the tail of the degree distribution. The regime of parameters that ensures infinite degree for all the vertices slightly improves those of [Reference Deijfen, van der Hofstad and Hooghiemstra13] and [Reference Deprez and Wüthrich14]; see Theorem 2.1 and Remark 2.2. More interesting is the case of finite degrees. In [Reference Deprez and Wüthrich14], under the condition of weights that follow a Pareto distribution, it was possible to calculate the whole distribution of the annealed degree of a vertex just by integrating over the Poisson measure. While there is clearly no chance that this works for all the vertices of the graph for a fixed configuration ![]() $\eta$, we show that the behavior of the tail of the degree of all vertices is the same (hence the graph is scale-free). More precisely, we show (see Theorem 2.2) that for almost every
$\eta$, we show that the behavior of the tail of the degree of all vertices is the same (hence the graph is scale-free). More precisely, we show (see Theorem 2.2) that for almost every ![]() $\eta$ the following holds: for all
$\eta$ the following holds: for all ![]() $x\in\eta$ there exists a slowly varying function
$x\in\eta$ there exists a slowly varying function ![]() $\ell(\!\cdot\!)=\ell(\cdot,\eta,x)$ such that the probability that
$\ell(\!\cdot\!)=\ell(\cdot,\eta,x)$ such that the probability that ![]() $D_x$, the degree of x, is bigger than some
$D_x$, the degree of x, is bigger than some ![]() $s>0$ is equal to
$s>0$ is equal to ![]() $\ell(s)s^{-\gamma}$, where
$\ell(s)s^{-\gamma}$, where ![]() $\gamma \,:\!=\alpha(\tau-1)/d$. Our proof follows the strategy of [Reference Deijfen, van der Hofstad and Hooghiemstra13] rather than that of [Reference Deprez and Wüthrich14], but a major difference emerges already when calculating the expectation of the degree of a vertex given the value
$\gamma \,:\!=\alpha(\tau-1)/d$. Our proof follows the strategy of [Reference Deijfen, van der Hofstad and Hooghiemstra13] rather than that of [Reference Deprez and Wüthrich14], but a major difference emerges already when calculating the expectation of the degree of a vertex given the value ![]() $w>0$ of its weight. While in [Reference Deijfen, van der Hofstad and Hooghiemstra13] it is shown by direct computation that the expectation is equal up to a constant to
$w>0$ of its weight. While in [Reference Deijfen, van der Hofstad and Hooghiemstra13] it is shown by direct computation that the expectation is equal up to a constant to ![]() $\xi w^{d/\alpha}$ for an explicit
$\xi w^{d/\alpha}$ for an explicit ![]() $\xi>0$, in our case there is a correction of the order
$\xi>0$, in our case there is a correction of the order ![]() $w^{d/(2\alpha)}$ that accounts for the fluctuations of the Poisson point process (see Proposition 3.3). We apply concentration inequalities in combination with the so-called Campbell theorem to achieve this result. With some further effort we prove that the result holds for all the points of
$w^{d/(2\alpha)}$ that accounts for the fluctuations of the Poisson point process (see Proposition 3.3). We apply concentration inequalities in combination with the so-called Campbell theorem to achieve this result. With some further effort we prove that the result holds for all the points of ![]() $\eta$ at once.
$\eta$ at once.
We then move to the clustering coefficient of the graph, which was not studied in either [Reference Deijfen, van der Hofstad and Hooghiemstra13] or [Reference Deprez and Wüthrich14]. For a given graph, the local clustering coefficient ![]() ${\textrm{CC}}(x)$ of a node x is given by
${\textrm{CC}}(x)$ of a node x is given by ![]() $\Delta_x$, the number of triangles with a vertex in x (i.e. triplets of edges of the form (x, y), (y, z), (z, x)), divided by
$\Delta_x$, the number of triangles with a vertex in x (i.e. triplets of edges of the form (x, y), (y, z), (z, x)), divided by ![]() $D_x(D_x-1)/2$. This second quantity represents the number of ‘possible’ triangles with a vertex in x, also called open triangles. The averaged clustering coefficient of a finite graph is the average of
$D_x(D_x-1)/2$. This second quantity represents the number of ‘possible’ triangles with a vertex in x, also called open triangles. The averaged clustering coefficient of a finite graph is the average of ![]() ${\textrm{CC}}(x)$ over all its vertices (there is also a notion of global clustering coefficient that we do not analyze here). For an infinite graph like ours, we define the averaged clustering coefficient as the limit (if it exists) for
${\textrm{CC}}(x)$ over all its vertices (there is also a notion of global clustering coefficient that we do not analyze here). For an infinite graph like ours, we define the averaged clustering coefficient as the limit (if it exists) for ![]() $n\to\infty$ of
$n\to\infty$ of ![]() ${\textrm{CC}}_n$, where
${\textrm{CC}}_n$, where ![]() ${\textrm{CC}}_n$ is the average of the local clustering coefficients of the vertices inside the d-dimensional box of side-length n centered at the origin. We show that
${\textrm{CC}}_n$ is the average of the local clustering coefficients of the vertices inside the d-dimensional box of side-length n centered at the origin. We show that ![]() ${\textrm{CC}}_n$ is self-averaging (a similar property has been recently proved in [Reference Stegehuis, van Der Hofstad and van Leeuwaarden38] for the hyperbolic random graph when the number of nodes goes to infinity; see also [Reference Fountoulakis, van der Hoorn, Müller and Schepers18]), so that its limit exists and is almost surely equal to the expectation of the local clustering coefficient of the origin 0 obtained under the Palm measure associated with the Poisson point process with a point added at 0 (see Theorem 2.3). We also show that this quantity is strictly positive (high clustering coefficient). The proof consists in dividing the box of size n into mesoscopic boxes of side-length
${\textrm{CC}}_n$ is self-averaging (a similar property has been recently proved in [Reference Stegehuis, van Der Hofstad and van Leeuwaarden38] for the hyperbolic random graph when the number of nodes goes to infinity; see also [Reference Fountoulakis, van der Hoorn, Müller and Schepers18]), so that its limit exists and is almost surely equal to the expectation of the local clustering coefficient of the origin 0 obtained under the Palm measure associated with the Poisson point process with a point added at 0 (see Theorem 2.3). We also show that this quantity is strictly positive (high clustering coefficient). The proof consists in dividing the box of size n into mesoscopic boxes of side-length ![]() $m<n$. We then approximate the clustering coefficient of each m-box by a truncated clustering coefficient that does not take into account either vertices that are close to the border of the boxes or vertices touched by edges that connect different m-boxes. In so doing, we obtain independent truncated clustering coefficients in each mesoscopic box and we can use the law of large numbers as
$m<n$. We then approximate the clustering coefficient of each m-box by a truncated clustering coefficient that does not take into account either vertices that are close to the border of the boxes or vertices touched by edges that connect different m-boxes. In so doing, we obtain independent truncated clustering coefficients in each mesoscopic box and we can use the law of large numbers as ![]() $n\to\infty$. In decorrelating the clustering coefficient of each m-box, we must control the correlation of the local clustering coefficient of vertices lying in different m-boxes. To do so, we use a second moment approach in combination with the Slivnyak–Mecke theorem. It is interesting to note that the positivity of the clustering coefficient does not depend on the local connectivity properties of the graph or on
$n\to\infty$. In decorrelating the clustering coefficient of each m-box, we must control the correlation of the local clustering coefficient of vertices lying in different m-boxes. To do so, we use a second moment approach in combination with the Slivnyak–Mecke theorem. It is interesting to note that the positivity of the clustering coefficient does not depend on the local connectivity properties of the graph or on ![]() ${\nu}$; see Remark 2.4. We believe that the mesoscopic boxes approach might also be applied to the original scale-free percolation model of [Reference Deijfen, van der Hofstad and Hooghiemstra13] to prove positivity of the clustering coefficient.
${\nu}$; see Remark 2.4. We believe that the mesoscopic boxes approach might also be applied to the original scale-free percolation model of [Reference Deijfen, van der Hofstad and Hooghiemstra13] to prove positivity of the clustering coefficient.
Positivity of the clustering coefficient was proved for a related model, the geometric inhomogeneous random graph (GIRG), in [Reference Bringmann, Keusch and Lengler7]; see [Reference Komjáthy and Lodewijks27] for a comparison with scale-free percolation. We briefly stress the differences from our work. First of all, the GIRG is a finite-volume model, so the clustering coefficient is always well-defined and no limiting procedure is needed. Secondly, the methods of proof used in [Reference Bringmann, Keusch and Lengler7] (namely, Le Cam’s theorem and an Azuma-type inequality with error event) do not apply in our setting, since the problem of dealing with an infinite number of random variables cannot be overcome. Furthermore, these techniques guarantee only results that hold with high probability, and not almost surely. Finally, in addition to showing that the clustering coefficient is positive, we also show a self-averaging property and an exact formula for the clustering coefficient.
We point out that, at least under the hypothesis of Pareto weights, the results on percolation and graph distances presented in the Introduction have annealed probability equal to 1; see [Reference Deprez and Wüthrich14, Theorems 3.2 and 3.6]. Hence they also hold in the quenched sense (see Remark 2.1 for a comparison between our parameters and those of [Reference Deprez and Wüthrich14]). It follows that under the right range of parameters, scale-free percolation in continuous space fulfills, for almost every realization of the Poisson point process ![]() $\eta$, all the three properties presented in the Introduction (scale-free, small-world, and positive clustering coefficient), almost surely. This suggests that the model is a good candidate for modeling real spatial networks. We believe, for example, that it encloses the main features of the cattle trading network in France (see [Reference Dutta, Ezanno and Vergu16]), which was the original motivation for our work. The nodes of the graph are given by farms, assembling centers and cattle markets in the country (for a total of about
$\eta$, all the three properties presented in the Introduction (scale-free, small-world, and positive clustering coefficient), almost surely. This suggests that the model is a good candidate for modeling real spatial networks. We believe, for example, that it encloses the main features of the cattle trading network in France (see [Reference Dutta, Ezanno and Vergu16]), which was the original motivation for our work. The nodes of the graph are given by farms, assembling centers and cattle markets in the country (for a total of about ![]() $200\,000$ holdings), so that the hypothesis of vertices placed according to a Poisson point process reflects the geographic irregularities in a more realistic way than
$200\,000$ holdings), so that the hypothesis of vertices placed according to a Poisson point process reflects the geographic irregularities in a more realistic way than ![]() $\mathbb{Z}^d$. An undirected edge is placed between two holdings if there has been at least a transaction between the two during a given time window. It has been observed that the degree of the nodes on yearly aggregated data follows a power law of index
$\mathbb{Z}^d$. An undirected edge is placed between two holdings if there has been at least a transaction between the two during a given time window. It has been observed that the degree of the nodes on yearly aggregated data follows a power law of index ![]() $\gamma\simeq 1.3$ which is quite stable over different years (
$\gamma\simeq 1.3$ which is quite stable over different years (![]() $\pm0.1$). Note that this falls into the interesting regime of infinite variance of the degrees. Likewise, the network exhibits a high clustering coefficient and a small diameter (about 15, which is close to the logarithm of the total number of nodes). Comprehension of the topology of this network might be of paramount importance when studying the possible outbreak of an infection in the cattle population.
$\pm0.1$). Note that this falls into the interesting regime of infinite variance of the degrees. Likewise, the network exhibits a high clustering coefficient and a small diameter (about 15, which is close to the logarithm of the total number of nodes). Comprehension of the topology of this network might be of paramount importance when studying the possible outbreak of an infection in the cattle population.
1.2. Structure of the paper
We will introduce the model and some notation in Section 2.1. We will present the main results on the degree distribution (Theorem 2.1 and Theorem 2.2) and on the clustering coefficient (Theorem 2.3) in Sections 2.2 and 2.3. We deal with the proof of the infinite-degree case in Section 3.1 and of the finite-degree case in Section 3.2. Section 4 is dedicated to the proof of the positivity of the clustering coefficient. In Appendix A we recall the Campbell and Slivnyak–Mecke theorems.
2. Model and main results
2.1. The model
Scale-free percolation in continuous space is a random variable on the space of all simple spatial undirected random graphs with vertices in ![]() $\mathbb{R}^d$. To construct an instance of the graph
$\mathbb{R}^d$. To construct an instance of the graph ![]() $G=(V,E)$ we proceed in three steps.
$G=(V,E)$ we proceed in three steps.
• We sample the nodes V of the graph according to a homogeneous Poisson point process in
 $\mathbb{R}^d$ of intensity
$\mathbb{R}^d$ of intensity  ${\nu}>0$. We let P denote its law and let E denote the expectation with respect to P. A configuration of the point process will be denoted by
${\nu}>0$. We let P denote its law and let E denote the expectation with respect to P. A configuration of the point process will be denoted by  $\eta\in(\mathbb{R}^d)^{\mathbb{N}}$.
$\eta\in(\mathbb{R}^d)^{\mathbb{N}}$.-
• We assign to each vertex
 $x\in\eta$ a random weight
$x\in\eta$ a random weight  $W_x>0$. The weights are independent and identically distributed (i.i.d.) with law P. The distribution function F associated with P is regularly varying at infinity with exponent
$W_x>0$. The weights are independent and identically distributed (i.i.d.) with law P. The distribution function F associated with P is regularly varying at infinity with exponent  $\tau-1$, that is,
where
$\tau-1$, that is,
where \begin{equation*} 1-F(w)=P(W>w)=w^{-(\tau-1)}L(w),\end{equation*}
\begin{equation*} 1-F(w)=P(W>w)=w^{-(\tau-1)}L(w),\end{equation*}
 $ L(\!\cdot\!)$ is a function that is slowly varying at
$ L(\!\cdot\!)$ is a function that is slowly varying at  $+\infty$.
$+\infty$.
-
• We finally draw the edges E of the random graph via a percolation process. For every pair of points
 $x,y\in\eta$ with weights
$x,y\in\eta$ with weights  $W_x,W_y$, the undirected edge (x, y) is present with probability
(1)where
$W_x,W_y$, the undirected edge (x, y) is present with probability
(1)where \begin{equation}1-{\textrm{e}}^{{-{{W_x W_y}/{\|x-y\|^{\alpha}}}}} ,\end{equation}
\begin{equation}1-{\textrm{e}}^{{-{{W_x W_y}/{\|x-y\|^{\alpha}}}}} ,\end{equation}
 $\|\cdot\|$ denotes the Euclidean norm in
$\|\cdot\|$ denotes the Euclidean norm in  $\mathbb{R}^d$ and
$\mathbb{R}^d$ and  $\alpha>0$ is a parameter. When two vertices x, y are connected by an edge we write
$\alpha>0$ is a parameter. When two vertices x, y are connected by an edge we write  $x\leftrightarrow y$ (if they are not connected we write
$x\leftrightarrow y$ (if they are not connected we write  $x\not\leftrightarrow y$). For the event that a vertex x is connected to some other point in a region
$x\not\leftrightarrow y$). For the event that a vertex x is connected to some other point in a region  $A\subseteq\mathbb{R}^d$, we write
$A\subseteq\mathbb{R}^d$, we write  $x\leftrightarrow A$.
$x\leftrightarrow A$.
Remark 2.1. In [Reference Deprez and Wüthrich14] an additional parameter ![]() $\lambda>0$ appears in the definition of the linking probabilities:
$\lambda>0$ appears in the definition of the linking probabilities: ![]() $p_{x,y}=1-\exp\{-\lambda W_xW_y\|x-y\|^{-\alpha}\}$. In this paper we prefer to fix
$p_{x,y}=1-\exp\{-\lambda W_xW_y\|x-y\|^{-\alpha}\}$. In this paper we prefer to fix ![]() $\lambda=1$ without loss of generality. Indeed, having parameters
$\lambda=1$ without loss of generality. Indeed, having parameters ![]() $\lambda=\tilde\lambda$ and
$\lambda=\tilde\lambda$ and ![]() ${\nu}=\tilde{\nu}$ in the model presented in [Reference Deprez and Wüthrich14] is completely equivalent to choosing
${\nu}=\tilde{\nu}$ in the model presented in [Reference Deprez and Wüthrich14] is completely equivalent to choosing ![]() ${\nu}=\tilde{\nu} \tilde\lambda^{d/\alpha}$ in our case.
${\nu}=\tilde{\nu} \tilde\lambda^{d/\alpha}$ in our case.
For a given realization ![]() $\eta$ of the Poisson point process we will often perform the last two steps at once under the quenched law
$\eta$ of the Poisson point process we will often perform the last two steps at once under the quenched law ![]() $ P^\eta$, with
$ P^\eta$, with ![]() $E^\eta$ denoting the associated expectation. This is the law of the graph once we have fixed
$E^\eta$ denoting the associated expectation. This is the law of the graph once we have fixed ![]() $\eta$. We write
$\eta$. We write ![]() $\mathbb{P}$ for the annealed law of the graph, i.e.
$\mathbb{P}$ for the annealed law of the graph, i.e. ![]() $\mathbb{P}=\textrm{P}\times P^\eta$, and
$\mathbb{P}=\textrm{P}\times P^\eta$, and ![]() $\mathbb{E}$ for the corresponding expectation. For
$\mathbb{E}$ for the corresponding expectation. For ![]() $x\in\mathbb{R}^d$, we let
$x\in\mathbb{R}^d$, we let ![]() $\textrm{P}_x$ indicate the law of the Poisson point process conditioned on having a point in x; analogously, for
$\textrm{P}_x$ indicate the law of the Poisson point process conditioned on having a point in x; analogously, for ![]() $x,y\in\mathbb{R}^d$, the measure
$x,y\in\mathbb{R}^d$, the measure ![]() $\textrm{P}_{x,y}$ is obtained by conditioning on having one point in x and one in y. We will not enter into the details of (n-fold) Palm measures, but we point out that in both cases the conditioning does not influence the rest of the Poisson point process; see e.g. [Reference Daley and Vere-Jones12, Chapter 13]. Consequently we will let
$\textrm{P}_{x,y}$ is obtained by conditioning on having one point in x and one in y. We will not enter into the details of (n-fold) Palm measures, but we point out that in both cases the conditioning does not influence the rest of the Poisson point process; see e.g. [Reference Daley and Vere-Jones12, Chapter 13]. Consequently we will let ![]() $\mathbb{P}_x =\textrm{P}_x\times P^\eta=\textrm{P}\times P^{\eta\cup \{x\}}$ be the law of the graph conditioned on having a point at
$\mathbb{P}_x =\textrm{P}_x\times P^\eta=\textrm{P}\times P^{\eta\cup \{x\}}$ be the law of the graph conditioned on having a point at ![]() $x\in\mathbb{R}^d$ and
$x\in\mathbb{R}^d$ and ![]() $\mathbb{E}_x$ the associated expectation. Analogously we will write
$\mathbb{E}_x$ the associated expectation. Analogously we will write ![]() $\mathbb{P}_{x,y}=\textrm{P}_{x,y}\times P^\eta=\textrm{P}\times P^{\eta\cup \{x\}\cup\{y\}}$ and
$\mathbb{P}_{x,y}=\textrm{P}_{x,y}\times P^\eta=\textrm{P}\times P^{\eta\cup \{x\}\cup\{y\}}$ and ![]() $\mathbb{E}_{x,y}$ for the expectation with respect to
$\mathbb{E}_{x,y}$ for the expectation with respect to ![]() $\mathbb{P}_{x,y}$.
$\mathbb{P}_{x,y}$.
We let 0 denote the origin of ![]() $\mathbb{R}^d$. We let
$\mathbb{R}^d$. We let ![]() $B_n$ be the d-dimensional box of side-length
$B_n$ be the d-dimensional box of side-length ![]() $n>0$ centered at 0. We let
$n>0$ centered at 0. We let ![]() $V_n=V_n(\eta)$ be the set of points of
$V_n=V_n(\eta)$ be the set of points of ![]() $\eta$ that are in
$\eta$ that are in ![]() $B_n$ and let
$B_n$ and let ![]() $N_n=N_n(\eta)$ be their number. Finally,
$N_n=N_n(\eta)$ be their number. Finally, ![]() $\mathcal{B}_r(x)$ denotes the Euclidean ball of radius
$\mathcal{B}_r(x)$ denotes the Euclidean ball of radius ![]() $r>0$ centered at
$r>0$ centered at ![]() $x\in\mathbb{R}^d$.
$x\in\mathbb{R}^d$.
2.2. Results on the degree
For each ![]() $x\in\eta$ we let
$x\in\eta$ we let ![]() $D_x\,:\!=\#\{y\in\eta\colon y\leftrightarrow x\}$ be the degree of a vertex x in the random graph, i.e. the random variable counting the number of neighbors of x. We start by showing that for certain values of the parameters the graph is almost surely degenerate, in the sense that all of its vertices have infinite degree.
$D_x\,:\!=\#\{y\in\eta\colon y\leftrightarrow x\}$ be the degree of a vertex x in the random graph, i.e. the random variable counting the number of neighbors of x. We start by showing that for certain values of the parameters the graph is almost surely degenerate, in the sense that all of its vertices have infinite degree.
Theorem 2.1. Suppose one of the following conditions is satisfied:
(a)
 $\alpha\leq d$,
$\alpha\leq d$,-
(b)
 $E[W^{d/\alpha}]=\infty$.
$E[W^{d/\alpha}]=\infty$.
Then, for ![]() $\textrm{P}$-almost every
$\textrm{P}$-almost every ![]() $\eta$,
$\eta$, ![]() $P^\eta$-almost surely all points in
$P^\eta$-almost surely all points in ![]() $\eta$ have infinite degree.
$\eta$ have infinite degree.
Remark 2.2. Note that condition (b) in Theorem 2.1 is implied in particular by
(bʹ) the weight distribution satisfies
for some \begin{equation*}1-F(w)\geq c\,w^{-(\tau-1)}\end{equation*}
\begin{equation*}1-F(w)\geq c\,w^{-(\tau-1)}\end{equation*}
 $c>0$ and
$c>0$ and  $\tau>1$ such that
$\tau>1$ such that  $\gamma\,:\!=\alpha(\tau-1)/d\leq 1$.
$\gamma\,:\!=\alpha(\tau-1)/d\leq 1$.
This stronger condition is the one appearing in [Reference Deijfen, van der Hofstad and Hooghiemstra13].
We point out that the proof of Theorem 2.1 follows immediately from the analogous result of [Reference Deprez and Wüthrich14] when the weights have a Pareto distribution. We will provide an alternative proof that, besides covering more general distribution functions F, serves as a warm-up for the kind of techniques we will use more intensively later on, based on Campbell’s theorem.
We move to the analysis of the regime where the degree of the nodes is almost surely finite. In this case, we show that for almost all ![]() $\eta$ the graph is scale-free and the degree of all points follows a power law with the same exponent.
$\eta$ the graph is scale-free and the degree of all points follows a power law with the same exponent.
Theorem 2.2. Suppose that ![]() $\alpha>d$ and
$\alpha>d$ and ![]() $\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every
$\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every ![]() $\eta$, we have that
$\eta$, we have that ![]() $s^\gamma P^\eta(D_x>s)$ is slowly varying for each
$s^\gamma P^\eta(D_x>s)$ is slowly varying for each ![]() $x\in\eta$. That is, there exists a slowly varying function
$x\in\eta$. That is, there exists a slowly varying function ![]() $\ell(\!\cdot\!)=\ell(\cdot,\eta,x)$ such that
$\ell(\!\cdot\!)=\ell(\cdot,\eta,x)$ such that
Remark 2.3. The slowly varying function in (2) clearly has to depend on x and ![]() $\eta$. However, it is not clear whether all the
$\eta$. However, it is not clear whether all the ![]() $\ell$ have the same asymptotic behavior. That is, with our proof it is not possible to say whether, for P-almost every
$\ell$ have the same asymptotic behavior. That is, with our proof it is not possible to say whether, for P-almost every ![]() $\eta$ and
$\eta$ and ![]() $\eta'$, and for all
$\eta'$, and for all ![]() $x\in\eta$ and
$x\in\eta$ and ![]() $x'\in\eta'$, we have
$x'\in\eta'$, we have ![]() $\ell(s,\eta,x)/\ell(s,\eta',x')\to 1$ as
$\ell(s,\eta,x)/\ell(s,\eta',x')\to 1$ as ![]() $s\to\infty$.
$s\to\infty$.
2.3. Results on the clustering coefficient
The average clustering coefficient is usually defined for finite graphs as the average of the local clustering coefficients. More precisely, for a finite undirected graph ![]() $\mathcal{G}=(\mathcal{V},\mathcal{E})$ and a node
$\mathcal{G}=(\mathcal{V},\mathcal{E})$ and a node ![]() $x\in \mathcal{V}$, we define the local clustering coefficient at x as
$x\in \mathcal{V}$, we define the local clustering coefficient at x as
where ![]() $\Delta_x$ is the number of closed triangles in the graph that have x as one of their vertices (a closed triangle is a triplet of edges in
$\Delta_x$ is the number of closed triangles in the graph that have x as one of their vertices (a closed triangle is a triplet of edges in ![]() $\mathcal{E}$ of the type
$\mathcal{E}$ of the type ![]() $\{(y,z), (z,w), (w,y)\}$), with the convention that
$\{(y,z), (z,w), (w,y)\}$), with the convention that ![]() ${\textrm{CC}}(x)$ is 0 if
${\textrm{CC}}(x)$ is 0 if ![]() $D_x$ is equal to 0 or 1. The quantity
$D_x$ is equal to 0 or 1. The quantity ![]() $D_x(D_x-1)/2$ can be interpreted as the number of open triangles in x (an open triangle in a vertex z is a pair of edges of the kind
$D_x(D_x-1)/2$ can be interpreted as the number of open triangles in x (an open triangle in a vertex z is a pair of edges of the kind ![]() $\{(y,z),(z,w)\}$, without any requirement for the presence of the third edge that would close the triangle), so
$\{(y,z),(z,w)\}$, without any requirement for the presence of the third edge that would close the triangle), so ![]() ${\textrm{CC}}(x)$ takes values in [0,1]. The averaged clustering coefficient of the graph
${\textrm{CC}}(x)$ takes values in [0,1]. The averaged clustering coefficient of the graph ![]() $\mathcal{G}$ is
$\mathcal{G}$ is
Clearly also ![]() ${\textrm{CC}_{\textrm{av}}}(\mathcal{G})$ takes values in [0,1]. It is not completely obvious what the definition of averaged clustering coefficient should be for an infinite graph. We say that an infinite spatial graph
${\textrm{CC}_{\textrm{av}}}(\mathcal{G})$ takes values in [0,1]. It is not completely obvious what the definition of averaged clustering coefficient should be for an infinite graph. We say that an infinite spatial graph ![]() $\mathcal{G}=(\mathcal{V},\mathcal{E})$ embedded in
$\mathcal{G}=(\mathcal{V},\mathcal{E})$ embedded in ![]() $\mathbb{R}^d$ with all vertices having finite degree has averaged clustering coefficient
$\mathbb{R}^d$ with all vertices having finite degree has averaged clustering coefficient ![]() ${\textrm{CC}_{\textrm{av}}}(\mathcal{G})$ if the following limit exists:
${\textrm{CC}_{\textrm{av}}}(\mathcal{G})$ if the following limit exists:
(we work with integers for simplicity). It is possible to construct infinite graphs for which this limit does not exist. We also note that this definition is in principle different from considering the limit of the clustering coefficients of the subgraphs of ![]() $\mathcal{G}$ obtained by considering only vertices in
$\mathcal{G}$ obtained by considering only vertices in ![]() $B_n$, since
$B_n$, since ![]() ${\textrm{CC}}(x)$ also takes into account the edges connecting points that lie out of
${\textrm{CC}}(x)$ also takes into account the edges connecting points that lie out of ![]() $B_n$.
$B_n$.
Going back to our model, we will let
be the random variable describing the averaged clustering coefficient inside the box of side n. Note that under the assumptions ![]() $\alpha >d$ and
$\alpha >d$ and ![]() $\gamma >1$, for P-almost every
$\gamma >1$, for P-almost every ![]() $\eta$, all the nodes
$\eta$, all the nodes ![]() $x\in\eta$ have finite degree,
$x\in\eta$ have finite degree, ![]() $P^\eta$-almost surely (see Theorem 2.2). Thus, the
$P^\eta$-almost surely (see Theorem 2.2). Thus, the ![]() $\textrm{CC}(x)$ are well-defined and finite, except perhaps on a set of measure 0. Our main result of this section states that the averaged clustering coefficient of the scale-free percolation in continuous space exists, is self-averaging, and is strictly positive.
$\textrm{CC}(x)$ are well-defined and finite, except perhaps on a set of measure 0. Our main result of this section states that the averaged clustering coefficient of the scale-free percolation in continuous space exists, is self-averaging, and is strictly positive.
Theorem 2.3. Suppose that ![]() $\alpha>d$ and
$\alpha>d$ and ![]() $\gamma\,:\!=\alpha(\tau-1)/d>1$. For P-almost all configurations
$\gamma\,:\!=\alpha(\tau-1)/d>1$. For P-almost all configurations ![]() $\eta$, the average clustering coefficient exists
$\eta$, the average clustering coefficient exists ![]() $ P^\eta$-almost surely and does not depend on
$ P^\eta$-almost surely and does not depend on ![]() $\eta$. It is given by
$\eta$. It is given by
Remark 2.4. Going through the proof of Theorem 2.3, it is plausible that the positivity of the clustering coefficient does not depend on the local properties of the graph or on ![]() ${\nu}$, as one might have thought. For example, we can set to 0 the probability of connecting two points that are at distance smaller than some
${\nu}$, as one might have thought. For example, we can set to 0 the probability of connecting two points that are at distance smaller than some ![]() $R>0$ and leave (1) for points at distance larger than R. Then we would still have that the associated n-truncated clustering coefficient
$R>0$ and leave (1) for points at distance larger than R. Then we would still have that the associated n-truncated clustering coefficient ![]() $\tilde{\textrm{CC}}_n$ converges almost surely to
$\tilde{\textrm{CC}}_n$ converges almost surely to ![]() $\mathbb{E}_0[\tilde{\textrm{CC}}(0)]$, with
$\mathbb{E}_0[\tilde{\textrm{CC}}(0)]$, with ![]() $\tilde {\textrm{CC}}(0)$ the corresponding local clustering coefficient. At the same time,
$\tilde {\textrm{CC}}(0)$ the corresponding local clustering coefficient. At the same time, ![]() $\mathbb{E}_0[\tilde {\textrm{CC}}(0)]$ would still be strictly positive for any
$\mathbb{E}_0[\tilde {\textrm{CC}}(0)]$ would still be strictly positive for any ![]() $R>0$ by arguments similar to those in the proof of Theorem 2.3.
$R>0$ by arguments similar to those in the proof of Theorem 2.3.
3. Degree
In both the infinite- and finite-degree cases, for convenience we will first prove the properties of the degree of the vertices via an auxiliary random variable under ![]() $ P^\eta$. We call it
$ P^\eta$. We call it ![]() $D_0$ with a slight abuse of notation, since P-almost surely the origin 0 does not belong to
$D_0$ with a slight abuse of notation, since P-almost surely the origin 0 does not belong to ![]() $\eta$. It is convenient, though, to imagine having a further point in the origin and treating it like all the other points of the graph, so that when we talk about
$\eta$. It is convenient, though, to imagine having a further point in the origin and treating it like all the other points of the graph, so that when we talk about ![]() $D_0$ we can think of
$D_0$ we can think of ![]() $ P^\eta$ as being replaced by
$ P^\eta$ as being replaced by ![]() $ P^{\eta\cup \{0\}}$. In a second moment we will transpose the properties of
$ P^{\eta\cup \{0\}}$. In a second moment we will transpose the properties of ![]() $D_0$ to the degree of the other vertices.
$D_0$ to the degree of the other vertices.
3.1. Infinite degree
In this section we prove Theorem 2.1. We start with the following proposition about ![]() $D_0$.
$D_0$.
Proposition 3.1. If conditions (a) or (b) in Theorem 2.1 are satisfied, then for P-almost all ![]() $\eta$ we have
$\eta$ we have ![]() $P^\eta(D_0=\infty)=1 .$
$P^\eta(D_0=\infty)=1 .$
Proof of Proposition 3.1. The statement will be proved by showing that, for each value ![]() $w>0$ of the weight in 0 and for P-almost every
$w>0$ of the weight in 0 and for P-almost every ![]() $\eta$, the following sum is infinite:
$\eta$, the following sum is infinite:
where the expectation on the right-hand side is taken with respect to W. Indeed, if we condition on the value of ![]() $W_0$, the presence of each edge (0,x) becomes independent from the others. We can therefore use the second Borel–Cantelli lemma to imply that there are infinitely many points in the configuration
$W_0$, the presence of each edge (0,x) becomes independent from the others. We can therefore use the second Borel–Cantelli lemma to imply that there are infinitely many points in the configuration ![]() $\eta$ connected to 0. By Campbell’s theorem (see Theorem A.1), the above sum is infinite for almost every
$\eta$ connected to 0. By Campbell’s theorem (see Theorem A.1), the above sum is infinite for almost every ![]() $\eta$ if the following integral is
$\eta$ if the following integral is
However, in view of the inequality ![]() $1-{\textrm{e}}^{-u}\geq(u\wedge 1)/2$ for
$1-{\textrm{e}}^{-u}\geq(u\wedge 1)/2$ for ![]() $u \geq0$, it is enough to show the divergence of the integral
$u \geq0$, it is enough to show the divergence of the integral
By first applying Tonelli’s theorem and then passing to polar coordinates, we can rewrite the right-hand side of (3) as
where ![]() $\sigma(S_{d-1})$ denotes the surface area of the
$\sigma(S_{d-1})$ denotes the surface area of the ![]() $(d-1)$-sphere of radius 1. The last integral is divergent for
$(d-1)$-sphere of radius 1. The last integral is divergent for ![]() $\alpha\leq d$, so case (a) is proved.
$\alpha\leq d$, so case (a) is proved.
When instead ![]() $\alpha>d$, we note that the integral inside the expectation is finite and we can continue the manipulation, obtaining
$\alpha>d$, we note that the integral inside the expectation is finite and we can continue the manipulation, obtaining
for some constant ![]() $c>0$. The last expression is again infinite under the assumptions of case (b).
$c>0$. The last expression is again infinite under the assumptions of case (b).
Proof of Theorem 2.1. In view of the Proposition 3.1 we know that the set of ![]() $\eta$ for which
$\eta$ for which ![]() $\smash{\sum_{x\in\eta} P^\eta(0\leftrightarrow x \mid W_0=w)=\infty}$ has P-measure 1. Take an
$\smash{\sum_{x\in\eta} P^\eta(0\leftrightarrow x \mid W_0=w)=\infty}$ has P-measure 1. Take an ![]() $\eta$ in this set and any point
$\eta$ in this set and any point ![]() $y\in\eta$. We have
$y\in\eta$. We have
 \[\sum_{x\in\eta\setminus\lbrace y\rbrace} P^\eta(y\leftrightarrow x \mid W_y=w)=\sum_{x\in\eta\setminus\lbrace y\rbrace} P^\eta(0\leftrightarrow x \mid W_0=w)\dfrac{E [1-{\textrm{e}}^{-wW\|x-y\|^{-\alpha}}]}{E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]}=\infty ,\]
\[\sum_{x\in\eta\setminus\lbrace y\rbrace} P^\eta(y\leftrightarrow x \mid W_y=w)=\sum_{x\in\eta\setminus\lbrace y\rbrace} P^\eta(0\leftrightarrow x \mid W_0=w)\dfrac{E [1-{\textrm{e}}^{-wW\|x-y\|^{-\alpha}}]}{E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]}=\infty ,\]
since the fraction goes to 1 as ![]() $\|x\|$ goes to infinity. By Borel–Cantelli this shows that y also has infinite degree
$\|x\|$ goes to infinity. By Borel–Cantelli this shows that y also has infinite degree ![]() $ P^\eta$-almost surely. Since there is a countable number of points in
$ P^\eta$-almost surely. Since there is a countable number of points in ![]() $\eta$, we are done.
$\eta$, we are done.
3.2. Polynomial degree
As in the previous section we will first prove a statement about the random variable ![]() $D_0$. The proof of Theorem 2.2 will be inferred as a consequence.
$D_0$. The proof of Theorem 2.2 will be inferred as a consequence.
Proposition 3.2. Suppose that ![]() $\alpha>d$ and
$\alpha>d$ and ![]() $\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every
$\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every ![]() $\eta$, there exists a slowly varying function
$\eta$, there exists a slowly varying function ![]() $\ell(\!\cdot\!)=\ell(\cdot,\eta)$ such that
$\ell(\!\cdot\!)=\ell(\cdot,\eta)$ such that
The strategy for demonstrating Proposition 3.2 follows the lines of the proof of Theorem 2.2 in [Reference Deijfen, van der Hofstad and Hooghiemstra13], which in turn follows [Reference Yukich41]. Analogously to Proposition 2.3 of [Reference Deijfen, van der Hofstad and Hooghiemstra13], we first analyze the properties of the expectation of the degree of a point conditional to its weight ![]() $w>0$. One of the main problems when dealing with vertices that are randomly distributed in space is the following: while in scale-free percolation on the lattice one can show by direct computations that the expectation of the degree is equal to a constant times
$w>0$. One of the main problems when dealing with vertices that are randomly distributed in space is the following: while in scale-free percolation on the lattice one can show by direct computations that the expectation of the degree is equal to a constant times ![]() $w^{d/\alpha}$, in the continuous-space case one has to finely control the fluctuations of the degree due to the irregularity of the point process. We show that these fluctuations are of order smaller than
$w^{d/\alpha}$, in the continuous-space case one has to finely control the fluctuations of the degree due to the irregularity of the point process. We show that these fluctuations are of order smaller than ![]() $w^{d/2\alpha}\log w$.
$w^{d/2\alpha}\log w$.
Proposition 3.3. Suppose that ![]() $\alpha>d$ and
$\alpha>d$ and ![]() $\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every realization
$\gamma\,:\!=\alpha(\tau-1)/d>1$. Then, for P-almost every realization ![]() $\eta$, we have
$\eta$, we have
with ![]() $c_0\,:\!=v_d\Gamma(1-d/\alpha)E[W^{d/\alpha}]$. Here
$c_0\,:\!=v_d\Gamma(1-d/\alpha)E[W^{d/\alpha}]$. Here ![]() $v_d$ indicates the volume of the d-dimensional unitary ball,
$v_d$ indicates the volume of the d-dimensional unitary ball, ![]() $\Gamma(\!\cdot\!)$ is the gamma function, and the constant in
$\Gamma(\!\cdot\!)$ is the gamma function, and the constant in ![]() $\textrm{O}(\!\cdot\!)$ is uniformly bounded in
$\textrm{O}(\!\cdot\!)$ is uniformly bounded in ![]() $\eta$ from below and above.
$\eta$ from below and above.
Proof of Proposition 3.3. We let ![]() $Z_w=Z_w(\eta)\,:\!=E^\eta[D_0 \mid W_0=w]$ and note that
$Z_w=Z_w(\eta)\,:\!=E^\eta[D_0 \mid W_0=w]$ and note that ![]() $Z_w$ is a random variable that depends only on the Poisson process. Since
$Z_w$ is a random variable that depends only on the Poisson process. Since ![]() $D_0=\sum_{x\in\eta}\mathds 1_{\{{0\leftrightarrow x}\}}$, we can use Campbell’s theorem (see (27) in Theorem A.1) applied to the function
$D_0=\sum_{x\in\eta}\mathds 1_{\{{0\leftrightarrow x}\}}$, we can use Campbell’s theorem (see (27) in Theorem A.1) applied to the function ![]() $f(x)\,:\!=E[1-{\textrm{e}}^{-wW/\|x\|^\alpha}]$, to explicitly compute
$f(x)\,:\!=E[1-{\textrm{e}}^{-wW/\|x\|^\alpha}]$, to explicitly compute
For the second equality we used Fubini and then made the change of variables ![]() $y=x(wW)^{-1/\alpha}$. The constant
$y=x(wW)^{-1/\alpha}$. The constant ![]() $c_0$ is the one appearing in the statement of the theorem; it is obtained by passing to polar coordinates and then using integration by parts. We can instead use (28) in order to calculate the variance
$c_0$ is the one appearing in the statement of the theorem; it is obtained by passing to polar coordinates and then using integration by parts. We can instead use (28) in order to calculate the variance ![]() $ \textrm{V}$:
$ \textrm{V}$:
To see the last equality it is sufficient to make the change of variables ![]() $y=xw^{-1/\alpha}$. We also note that
$y=xw^{-1/\alpha}$. We also note that ![]() $c_1\leq c_0$ because the expectation inside the integral is smaller than 1, so the variance has to be smaller than the expectation.
$c_1\leq c_0$ because the expectation inside the integral is smaller than 1, so the variance has to be smaller than the expectation.
We will show that for P-almost every ![]() $\eta$ we have
$\eta$ we have
which implies (5). We will only show the upper bound, the lower bound being very similar. Let ![]() $\theta>0$. We use the exponential Chebyshev inequality to bound
$\theta>0$. We use the exponential Chebyshev inequality to bound
 \begin{align}\textrm{P}(Z_w - \textrm{E}[Z_w]\geq \sqrt{\textrm{V}(Z_w)}\log w)&=\textrm{P}({\textrm{e}}^{\theta Z_w }\geq {\textrm{e}}^{\theta ( \sqrt{\textrm{V}(Z_w)}\log w + \textrm{E}[Z_w])})\nonumber\\*&\leq \exp\{-\theta (\sqrt{\textrm{V}(Z_w)}\log w+\textrm{E}[Z_w])+\log \textrm{E}[{\textrm{e}}^{\theta Z_w}]\} .\end{align}
\begin{align}\textrm{P}(Z_w - \textrm{E}[Z_w]\geq \sqrt{\textrm{V}(Z_w)}\log w)&=\textrm{P}({\textrm{e}}^{\theta Z_w }\geq {\textrm{e}}^{\theta ( \sqrt{\textrm{V}(Z_w)}\log w + \textrm{E}[Z_w])})\nonumber\\*&\leq \exp\{-\theta (\sqrt{\textrm{V}(Z_w)}\log w+\textrm{E}[Z_w])+\log \textrm{E}[{\textrm{e}}^{\theta Z_w}]\} .\end{align}
Campbell’s theorem in its exponential form (see (26)) applied to the function ![]() $f(x)\,:\!=\theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]$ gives
$f(x)\,:\!=\theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]$ gives
If we restrict to values of ![]() $\theta$ smaller than 1, a third-order Taylor expansion shows that
$\theta$ smaller than 1, a third-order Taylor expansion shows that
 \begin{align*}&\exp\{\theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]\}-1\\*&\quad \leq \theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}] +\dfrac{ \theta^2}{2} E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]^2 + \textrm{O}(\theta^3 E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]) ,\end{align*}
\begin{align*}&\exp\{\theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]\}-1\\*&\quad \leq \theta E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}] +\dfrac{ \theta^2}{2} E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]^2 + \textrm{O}(\theta^3 E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]) ,\end{align*}
where we used the trivial bound ![]() $E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]\leq 1$ for the last term. Integrating over x in the above inequality and in view of the expressions for the expectation (6) and the variance (7) of
$E[1-{\textrm{e}}^{-wW\|x\|^{-\alpha}}]\leq 1$ for the last term. Integrating over x in the above inequality and in view of the expressions for the expectation (6) and the variance (7) of ![]() $Z_w$, we obtain
$Z_w$, we obtain
Inserting this estimate back into (8) yields, for all ![]() $\theta\in[0,1]$,
$\theta\in[0,1]$,
In particular, by choosing ![]() $\theta=\log w/\sqrt{\textrm{V}(Z_w)}$, we obtain for w large enough
$\theta=\log w/\sqrt{\textrm{V}(Z_w)}$, we obtain for w large enough
If we consider the sequence ![]() $w_n=n$, we see that the quantity on the right-hand side of (9) is summable in n and Borel–Cantelli tells us that
$w_n=n$, we see that the quantity on the right-hand side of (9) is summable in n and Borel–Cantelli tells us that
The random variable ![]() $Z_w$ is increasing in w, so that
$Z_w$ is increasing in w, so that ![]() $Z_{\lfloor w\rfloor} \leq Z_w\leq Z_{\lfloor w\rfloor+1}$. Moreover, in view of (6) and (7), we see that the sequences
$Z_{\lfloor w\rfloor} \leq Z_w\leq Z_{\lfloor w\rfloor+1}$. Moreover, in view of (6) and (7), we see that the sequences ![]() $\textrm{E}(Z_n), \sqrt{\textrm{V}(Z_n)}$ and
$\textrm{E}(Z_n), \sqrt{\textrm{V}(Z_n)}$ and ![]() $\log n$ all satisfy
$\log n$ all satisfy
We can thus conclude that
 \begin{align*} \limsup_{n\to \infty}\dfrac{Z_w-\textrm{E}(Z_w)}{\sqrt{\textrm{V}(Z_w)}\log w}&\leq \limsup_{n\to\infty}\dfrac{Z_{\lfloor w\rfloor +1}-\textrm{E}(Z_{\lfloor w\rfloor}\!)}{\sqrt{\textrm{V}(Z_{\lfloor w \rfloor})}\log \lfloor w \rfloor}\\*&=\limsup_{n\to\infty}\dfrac{Z_{\lfloor w\rfloor +1}-\textrm{E}(Z_{\lfloor w\rfloor+1}\!)}{\sqrt{\textrm{V}(Z_{\lfloor w \rfloor+1})}\log (\lfloor w \rfloor+1)}\\*&\leq 1 .\end{align*}
\begin{align*} \limsup_{n\to \infty}\dfrac{Z_w-\textrm{E}(Z_w)}{\sqrt{\textrm{V}(Z_w)}\log w}&\leq \limsup_{n\to\infty}\dfrac{Z_{\lfloor w\rfloor +1}-\textrm{E}(Z_{\lfloor w\rfloor}\!)}{\sqrt{\textrm{V}(Z_{\lfloor w \rfloor})}\log \lfloor w \rfloor}\\*&=\limsup_{n\to\infty}\dfrac{Z_{\lfloor w\rfloor +1}-\textrm{E}(Z_{\lfloor w\rfloor+1}\!)}{\sqrt{\textrm{V}(Z_{\lfloor w \rfloor+1})}\log (\lfloor w \rfloor+1)}\\*&\leq 1 .\end{align*}
Proof of Proposition 3.2. We let ![]() $Y_w$ be the random variable describing the value of
$Y_w$ be the random variable describing the value of ![]() $D_0$ conditioned on the event
$D_0$ conditioned on the event ![]() $\{W_0=w\}$:
$\{W_0=w\}$:
We split the integral
where
![]() $c_0$ being the same constant appearing in (5). We point out that this definition is slightly different from the equivalent appearing in [Reference Deijfen, van der Hofstad and Hooghiemstra13, eq. (2.11)] in order to control the fluctuations of the expected degree of 0. Since
$c_0$ being the same constant appearing in (5). We point out that this definition is slightly different from the equivalent appearing in [Reference Deijfen, van der Hofstad and Hooghiemstra13, eq. (2.11)] in order to control the fluctuations of the expected degree of 0. Since ![]() $P^\eta(D_0>s)$ is a monotone function, (4) follows if we can prove that
$P^\eta(D_0>s)$ is a monotone function, (4) follows if we can prove that
on a dense set of points (see [Reference Feller17, Section VIII.8]). We claim that ![]() $A_1(s)=A_1(\eta,s)$ does not contribute to the regular variation of
$A_1(s)=A_1(\eta,s)$ does not contribute to the regular variation of ![]() $P^\eta(D_0>s)$ for P-almost all
$P^\eta(D_0>s)$ for P-almost all ![]() $\eta$, that is,
$\eta$, that is,
We will show how to get (13) at the end of the proof. Thanks to (13), we see that in order to prove (12) it is enough to verify that, for ![]() $s\in(0,\infty)$,
$s\in(0,\infty)$,
On the one hand, for all ![]() $t>0$ we clearly have
$t>0$ we clearly have
On the other hand, for all ![]() $\varepsilon>0$ we have
$\varepsilon>0$ we have
 \begin{align*}A_2(t)&\geq 1-F((1+\varepsilon)m(t))-\int_{(1+\varepsilon)m(t)}^\infty P^\eta(Y_w\leq t)\,\textrm{d}F(w)\nonumber\\*&\geq(1-F((1+\varepsilon)m(t))(1+\textrm{o}_t(1)) .\end{align*}
\begin{align*}A_2(t)&\geq 1-F((1+\varepsilon)m(t))-\int_{(1+\varepsilon)m(t)}^\infty P^\eta(Y_w\leq t)\,\textrm{d}F(w)\nonumber\\*&\geq(1-F((1+\varepsilon)m(t))(1+\textrm{o}_t(1)) .\end{align*}
For the last line, we used the following fact. By (5), ![]() $E^\eta[Y_{w}]>t(1+\varepsilon d/2\alpha)$ for all
$E^\eta[Y_{w}]>t(1+\varepsilon d/2\alpha)$ for all ![]() $w\geq (1+\varepsilon)m(t)$ when t is sufficiently large (depending on
$w\geq (1+\varepsilon)m(t)$ when t is sufficiently large (depending on ![]() $\eta$); this allows us to use the Chebyshev inequality and bound, uniformly in
$\eta$); this allows us to use the Chebyshev inequality and bound, uniformly in ![]() $w>(1+\varepsilon)m(t)$,
$w>(1+\varepsilon)m(t)$,
where ![]() $V^\eta$ represents the variance with respect to
$V^\eta$ represents the variance with respect to ![]() $ P^\eta$ and the second inequality follows from the fact that
$ P^\eta$ and the second inequality follows from the fact that ![]() $Y_w$ is a sum of independent indicator functions.
$Y_w$ is a sum of independent indicator functions.
Putting it all together and using the fact that ![]() $\lim_{t\to\infty}m(st)/m(t)=s^{\alpha/d}$, we obtain
$\lim_{t\to\infty}m(st)/m(t)=s^{\alpha/d}$, we obtain
as we wanted to prove.
We now only need to show (13). We start by upper-bounding ![]() $A_1(s)$ by
$A_1(s)$ by
 \begin{align} &P^\eta(Y_{m(s)}>s) \notag \\* &\quad =P^\eta\biggl(\sum_{y\in\eta}\mathds 1_{\{{y\leftrightarrow 0}\}}-E^\eta[\mathds 1_{\{{y\leftrightarrow 0}\}} \mid W_0=m(s)]>s-E^\eta[Y_{m(s)}] \mid W_0=m(s)\biggr).\end{align}
\begin{align} &P^\eta(Y_{m(s)}>s) \notag \\* &\quad =P^\eta\biggl(\sum_{y\in\eta}\mathds 1_{\{{y\leftrightarrow 0}\}}-E^\eta[\mathds 1_{\{{y\leftrightarrow 0}\}} \mid W_0=m(s)]>s-E^\eta[Y_{m(s)}] \mid W_0=m(s)\biggr).\end{align}
Taking s sufficiently large and thanks to Proposition 3.3, we can make ![]() $s-E^\eta[Y_{m(s)}]$ positive, allowing us to apply Bernstein’s inequality. We obtain
$s-E^\eta[Y_{m(s)}]$ positive, allowing us to apply Bernstein’s inequality. We obtain
where for the first term in the denominator of the exponent we used the inequality
Since
we get ![]() $A_1(s)\leq {\textrm{e}}^{-\log^4s/4}$ and (13) is proved.
$A_1(s)\leq {\textrm{e}}^{-\log^4s/4}$ and (13) is proved.
Proof of Theorem 2.2. Take any ![]() $x\in\eta$. We first prove a lower bound on
$x\in\eta$. We first prove a lower bound on ![]() $ P^\eta(D_x>s)$. First of all we claim that
$ P^\eta(D_x>s)$. First of all we claim that
where ![]() $c(x,\eta)\,:\!=(1+\|x\|/\|y\|)^{-\alpha}$ and
$c(x,\eta)\,:\!=(1+\|x\|/\|y\|)^{-\alpha}$ and ![]() $y\in\eta$ is the closest point to the origin in
$y\in\eta$ is the closest point to the origin in ![]() $\eta$. In order to prove the claim we write
$\eta$. In order to prove the claim we write
Since the indicator functions in the first sum are mutually independent under ![]() $ P^\eta(\cdot \mid W_x=w)$ and those in the second sum are mutually independent under
$ P^\eta(\cdot \mid W_x=w)$ and those in the second sum are mutually independent under ![]() $ P^\eta(\cdot \mid W_0=c(x,\eta)\cdot w)$, it will be sufficient to show that, for all
$ P^\eta(\cdot \mid W_0=c(x,\eta)\cdot w)$, it will be sufficient to show that, for all ![]() $z\in\eta\setminus \{x\}$,
$z\in\eta\setminus \{x\}$,
since this ensures that ![]() $D_x\geq D_0-1$ stochastically. We calculate
$D_x\geq D_0-1$ stochastically. We calculate
 \begin{align*} P^\eta(\mathds 1_{\{{x\leftrightarrow z}\}}=1 \mid W_x=w)&=E[1-{\textrm{e}}^{-wW_z\|z-x\|^{-\alpha} }]\\*&\geq E[1-{\textrm{e}}^{-c(x,\eta)\cdot w W_z\|z\|^{-\alpha} }]\\*&= P^\eta(\mathds 1_{\{{0\leftrightarrow z}\}}=1 \mid W_0=c(x,\eta)\cdot w) ,\end{align*}
\begin{align*} P^\eta(\mathds 1_{\{{x\leftrightarrow z}\}}=1 \mid W_x=w)&=E[1-{\textrm{e}}^{-wW_z\|z-x\|^{-\alpha} }]\\*&\geq E[1-{\textrm{e}}^{-c(x,\eta)\cdot w W_z\|z\|^{-\alpha} }]\\*&= P^\eta(\mathds 1_{\{{0\leftrightarrow z}\}}=1 \mid W_0=c(x,\eta)\cdot w) ,\end{align*}
where for the inequality we used the fact that ![]() $\|z-x\|/\|z\|\leq (\|y\|+\|x\|)/\|y\|$.
$\|z-x\|/\|z\|\leq (\|y\|+\|x\|)/\|y\|$.
Thanks to the claim we can now bound
 \begin{align*} P^\eta(D_x>s)&=\int_0^\infty P^\eta(D_x>s \mid W_x=w)\,\textrm{d}F(w)\\*&\geq \int_0^\infty P^\eta(D_0>s+1 \mid W_0=c(x,\eta)\cdot w )\,\textrm{d}F(w) .\end{align*}
\begin{align*} P^\eta(D_x>s)&=\int_0^\infty P^\eta(D_x>s \mid W_x=w)\,\textrm{d}F(w)\\*&\geq \int_0^\infty P^\eta(D_0>s+1 \mid W_0=c(x,\eta)\cdot w )\,\textrm{d}F(w) .\end{align*}
If the weights simply follow a Pareto distribution with exponent ![]() $\tau$, then with a change of variables
$\tau$, then with a change of variables ![]() $u=c(x,\eta)\cdot w$ we would obtain
$u=c(x,\eta)\cdot w$ we would obtain ![]() $ P^\eta(D_x>s)\geq c(x,\eta)^{\tau-1} P^\eta(D_0>s+1)$, and we would be done thanks to Proposition 3.2. In the general case we have to proceed as in the proof of Proposition 3.2 by splitting the integral on the right-hand side of the last display into the integral between 0 and
$ P^\eta(D_x>s)\geq c(x,\eta)^{\tau-1} P^\eta(D_0>s+1)$, and we would be done thanks to Proposition 3.2. In the general case we have to proceed as in the proof of Proposition 3.2 by splitting the integral on the right-hand side of the last display into the integral between 0 and ![]() $m(s)/c(x,\eta)$ plus the integral between
$m(s)/c(x,\eta)$ plus the integral between ![]() $m(s)/c(x,\eta)$ and
$m(s)/c(x,\eta)$ and ![]() $+\infty$, where m(s) is defined in (11). We call the first part
$+\infty$, where m(s) is defined in (11). We call the first part ![]() $\tilde A_1(s)$ and the second part
$\tilde A_1(s)$ and the second part ![]() $\tilde A_2(s)$ similarly to (10). Following step by step what we did in the proof of Proposition 3.2 (see (15) and below), we note that
$\tilde A_2(s)$ similarly to (10). Following step by step what we did in the proof of Proposition 3.2 (see (15) and below), we note that
which does not contribute to the regular variation of the sum. Finally (see (14) and the argument below) we have that ![]() $\lim_{t\to\infty}\tilde A_2(st)/\tilde A_2(t)=s^{-\gamma}$, since
$\lim_{t\to\infty}\tilde A_2(st)/\tilde A_2(t)=s^{-\gamma}$, since ![]() $\tilde A_2(t)$ is upper-bounded by
$\tilde A_2(t)$ is upper-bounded by ![]() $1-F(m(t)/c(x,\eta))$ and lower-bounded by
$1-F(m(t)/c(x,\eta))$ and lower-bounded by ![]() $1-F((1+\varepsilon)m(t)/c(x,\eta))$ minus a negligible term. We therefore conclude that there exists a slowly varying function
$1-F((1+\varepsilon)m(t)/c(x,\eta))$ minus a negligible term. We therefore conclude that there exists a slowly varying function ![]() $\ell_1(\!\cdot\!)=\ell_1(\cdot,x,\eta)$ such that
$\ell_1(\!\cdot\!)=\ell_1(\cdot,x,\eta)$ such that
An upper bound ![]() $ P^\eta(D_x>s)\leq \ell_2(s)s^{-\gamma}$ for some other slowly varying function
$ P^\eta(D_x>s)\leq \ell_2(s)s^{-\gamma}$ for some other slowly varying function ![]() $\ell_2=\ell_2(x,\eta)$ can be obtained in a completely similar way. These two bounds yield the desired result.
$\ell_2=\ell_2(x,\eta)$ can be obtained in a completely similar way. These two bounds yield the desired result.
4. Clustering coefficient
The idea for the proof of Theorem 2.3 consists in approximating ![]() ${\textrm{CC}}_n$ with the sum of independent random variables in order to use the standard law of large numbers.
${\textrm{CC}}_n$ with the sum of independent random variables in order to use the standard law of large numbers.
First of all we divide ![]() $\mathbb{R}^d$ into disjoint mesoscopic boxes of side-length
$\mathbb{R}^d$ into disjoint mesoscopic boxes of side-length ![]() $m>0$, one of which is centered at the origin (the superposition of the sides of the boxes is of no importance). For a point
$m>0$, one of which is centered at the origin (the superposition of the sides of the boxes is of no importance). For a point ![]() $x\in\mathbb{R}^d$ we let
$x\in\mathbb{R}^d$ we let ![]() $Q_m(x)$ be the unique m-box containing x. We also fix
$Q_m(x)$ be the unique m-box containing x. We also fix ![]() $\delta>0$ small and divide each of the boxes
$\delta>0$ small and divide each of the boxes ![]() $Q_m$ as
$Q_m$ as ![]() $Q_m=\overline Q_m\cup \partial Q_m$, where
$Q_m=\overline Q_m\cup \partial Q_m$, where
are the interior points of the box and ![]() $\partial Q_m=\partial Q_{m,\delta}\,:\!=Q_m\setminus \overline Q_m$ is the
$\partial Q_m=\partial Q_{m,\delta}\,:\!=Q_m\setminus \overline Q_m$ is the ![]() $\delta$-frame of the box. For a realization of our graph
$\delta$-frame of the box. For a realization of our graph ![]() $G=(V,E)$ and a point
$G=(V,E)$ and a point ![]() $x\in V$, we define
$x\in V$, we define
 \begin{align*}\widehat{\textrm{CC}}^m(x)=\widehat{\textrm{CC}}^{m,\delta}(x)\,:\!=\begin{cases}0 &\text{if }x\in\partial Q_m(x),\\0 &\text{if }x\leftrightarrow Q_m^c(x),\\{\textrm{CC}}(x)&\text{otherwise.}\end{cases}\end{align*}
\begin{align*}\widehat{\textrm{CC}}^m(x)=\widehat{\textrm{CC}}^{m,\delta}(x)\,:\!=\begin{cases}0 &\text{if }x\in\partial Q_m(x),\\0 &\text{if }x\leftrightarrow Q_m^c(x),\\{\textrm{CC}}(x)&\text{otherwise.}\end{cases}\end{align*}
For ![]() $n\geq m$ we finally define the
$n\geq m$ we finally define the ![]() $(m,\delta)$-truncated clustering coefficient as
$(m,\delta)$-truncated clustering coefficient as
The idea is now to approximate ![]() ${\textrm{CC}}_n$ by
${\textrm{CC}}_n$ by ![]() $\widehat{\textrm{CC}}_n^m$, to show that
$\widehat{\textrm{CC}}_n^m$, to show that ![]() $\widehat{\textrm{CC}}_n^m$ converges thanks to the law of large numbers to
$\widehat{\textrm{CC}}_n^m$ converges thanks to the law of large numbers to ![]() $\mathbb{E}[\widehat{\textrm{CC}}_m^m]$ and that this value is close to the desired
$\mathbb{E}[\widehat{\textrm{CC}}_m^m]$ and that this value is close to the desired ![]() $\mathbb{E}_0[{\textrm{CC}}(0)]$. This is formalized in the next three statements, which are valid under the hypothesis of Theorem 2.3.
$\mathbb{E}_0[{\textrm{CC}}(0)]$. This is formalized in the next three statements, which are valid under the hypothesis of Theorem 2.3.
Proposition 4.1. ![]() $\mathbb{P}$-almost surely we have
$\mathbb{P}$-almost surely we have
for some constants ![]() $c_1,\,c_2>0$ that may depend on d,
$c_1,\,c_2>0$ that may depend on d, ![]() $ \alpha$, E[W], and
$ \alpha$, E[W], and ![]() $\nu$, but that do not depend on either m or
$\nu$, but that do not depend on either m or ![]() $\delta$.
$\delta$.
Lemma 4.1. ![]() $\mathbb{P}$-almost surely we have
$\mathbb{P}$-almost surely we have
Lemma 4.2. There exist constants ![]() $c_1,c_2>0$ that may depend on d,
$c_1,c_2>0$ that may depend on d, ![]() $\alpha$, E[W], and
$\alpha$, E[W], and ![]() $\nu$, but that do not depend on either m or
$\nu$, but that do not depend on either m or ![]() $\delta$, such that
$\delta$, such that
The proofs of Lemmas 4.1 and 4.2 are pretty straightforward and are collected in Section 4.1. The proof of Proposition 4.1 is much more involved and is the object of Section 4.2. We are now able to prove Theorem 2.3.
Proof of Theorem 2.3. The convergence of ![]() ${\textrm{CC}}_n$ to
${\textrm{CC}}_n$ to ![]() $\mathbb{E}_0[{\textrm{CC}}(0)]$ can be obtained by putting together the results of Proposition 4.1 and Lemmas 4.1 and 4.2, and letting first
$\mathbb{E}_0[{\textrm{CC}}(0)]$ can be obtained by putting together the results of Proposition 4.1 and Lemmas 4.1 and 4.2, and letting first ![]() $m\to\infty$ and then
$m\to\infty$ and then ![]() $\delta\to0$.
$\delta\to0$.
We now need only prove that ![]() $\mathbb{E}_0[{\textrm{CC}}(0)]>0\,$. Write
$\mathbb{E}_0[{\textrm{CC}}(0)]>0\,$. Write ![]() $\mathcal{B}$ for
$\mathcal{B}$ for ![]() $\mathcal{B}_1(0)$ and consider the following events:
$\mathcal{B}_1(0)$ and consider the following events:
 \begin{align*}\mathcal{E}_1\,&=\lbrace \#(\eta\cap \mathcal{B})=2\rbrace ,\\*\mathcal{E}_2\,&=\lbrace \text{the points in } (\eta\cup\{0\}) \cap \mathcal{B} \text{ form a clique} \rbrace ,\\*\mathcal{E}_3\,&= \lbrace0 \text{ has no neighbors outside } \mathcal{B}\rbrace .\end{align*}
\begin{align*}\mathcal{E}_1\,&=\lbrace \#(\eta\cap \mathcal{B})=2\rbrace ,\\*\mathcal{E}_2\,&=\lbrace \text{the points in } (\eta\cup\{0\}) \cap \mathcal{B} \text{ form a clique} \rbrace ,\\*\mathcal{E}_3\,&= \lbrace0 \text{ has no neighbors outside } \mathcal{B}\rbrace .\end{align*}
Under the event ![]() $\mathcal{E}_1\cap\mathcal{E}_2\cap\mathcal{E}_3$, the local clustering coefficient of the origin is 1. Therefore
$\mathcal{E}_1\cap\mathcal{E}_2\cap\mathcal{E}_3$, the local clustering coefficient of the origin is 1. Therefore
Given the value of ![]() $W_0$, the events
$W_0$, the events ![]() $\mathcal{E}_1\cap\mathcal{E}_2$ and
$\mathcal{E}_1\cap\mathcal{E}_2$ and ![]() $\mathcal{E}_3$ are independent. Hence
$\mathcal{E}_3$ are independent. Hence
In order to bound from below the second of the probabilities in the integral, we note that
and we subsequently apply Jensen’s inequality and Campbell’s theorem, thus obtaining
 \begin{align*}\mathbb{P}_0(\mathcal{E}_3\mid W_0=w)&=\textrm{E}_0\Biggl[ \prod_{x\in \eta\cap \mathcal{B}^c}E[{\textrm{e}}^{-{{w W_x}/{\|x\|^\alpha}}}] \Biggr]\\*&\geq \exp\Biggl\{-\textrm{E}_0\Biggl[\sum_{x\in \eta\cap \mathcal{B}^c}\dfrac{w E[W_y]}{\|y\|^\alpha}\Biggr]\Biggr\}\\*&={\textrm{e}}^{-cE[W]w{\nu} }\end{align*}
\begin{align*}\mathbb{P}_0(\mathcal{E}_3\mid W_0=w)&=\textrm{E}_0\Biggl[ \prod_{x\in \eta\cap \mathcal{B}^c}E[{\textrm{e}}^{-{{w W_x}/{\|x\|^\alpha}}}] \Biggr]\\*&\geq \exp\Biggl\{-\textrm{E}_0\Biggl[\sum_{x\in \eta\cap \mathcal{B}^c}\dfrac{w E[W_y]}{\|y\|^\alpha}\Biggr]\Biggr\}\\*&={\textrm{e}}^{-cE[W]w{\nu} }\end{align*}
for some ![]() $c>0$ that does not depend on w, where
$c>0$ that does not depend on w, where ![]() $\textrm{E}_0$ is the expectation with respect to
$\textrm{E}_0$ is the expectation with respect to ![]() $\textrm{P}_0$. Since
$\textrm{P}_0$. Since ![]() $\mathbb{P}_0(\mathcal{E}_1\cap\mathcal{E}_2 \mid W_0=w)$ is uniformly bounded from below by a constant when
$\mathbb{P}_0(\mathcal{E}_1\cap\mathcal{E}_2 \mid W_0=w)$ is uniformly bounded from below by a constant when ![]() $w\geq 1$, and since
$w\geq 1$, and since ![]() ${P(W\geq 1)> 0}$, we obtain
${P(W\geq 1)> 0}$, we obtain ![]() $\mathbb{E}_0[{\textrm{CC}}(0)]>0\,$.
$\mathbb{E}_0[{\textrm{CC}}(0)]>0\,$.
4.1. Proofs of the lemmas
Proof of Lemma 4.1. We write ![]() $n=mq+r$, with
$n=mq+r$, with ![]() $q\in \mathbb{N}$ and
$q\in \mathbb{N}$ and ![]() $0\leq r<m$. We let
$0\leq r<m$. We let ![]() $Q(1),...,Q({q^d})$ be the
$Q(1),...,Q({q^d})$ be the ![]() $q^d$-boxes of side-length m fully contained in
$q^d$-boxes of side-length m fully contained in ![]() $B_n$ and
$B_n$ and ![]() $H=\bigl(\bigcup_{j}Q(j)\bigr)^c$. We also define
$H=\bigl(\bigcup_{j}Q(j)\bigr)^c$. We also define
Then
 \begin{equation*}\widehat{\textrm{CC}}^m_n=\biggl(\dfrac{mq}{n}\biggr)^d\dfrac{1}{q^d}\sum_{j=1}^{q^d}X(j)+\dfrac{1}{\nu n^d}\sum_{x\in H\cap V_n}\widehat{\textrm{CC}}^m(x) .\end{equation*}
\begin{equation*}\widehat{\textrm{CC}}^m_n=\biggl(\dfrac{mq}{n}\biggr)^d\dfrac{1}{q^d}\sum_{j=1}^{q^d}X(j)+\dfrac{1}{\nu n^d}\sum_{x\in H\cap V_n}\widehat{\textrm{CC}}^m(x) .\end{equation*}
Since the X(j) are i.i.d. random variables (note that the overlap of the Q-boxes does not represent a problem: as their intersection is a set of Lebesgue measure 0, with probability 1 there will not be any point lying in their intersection) with finite ![]() $\mathbb{P}$-expectation, as n goes to infinity, the first summand on the right-hand side converges
$\mathbb{P}$-expectation, as n goes to infinity, the first summand on the right-hand side converges ![]() $\mathbb{P}$-almost surely to
$\mathbb{P}$-almost surely to ![]() $\mathbb{E}[X(1)]=\mathbb{E}[\widehat{\textrm{CC}}^m_m]$ by translation invariance. The second summand converges almost surely to 0 since
$\mathbb{E}[X(1)]=\mathbb{E}[\widehat{\textrm{CC}}^m_m]$ by translation invariance. The second summand converges almost surely to 0 since ![]() $\widehat{\textrm{CC}}^m(x)\leq 1$ and the number of points in
$\widehat{\textrm{CC}}^m(x)\leq 1$ and the number of points in ![]() $H\cap V_n$ follows a Poisson distribution with parameter
$H\cap V_n$ follows a Poisson distribution with parameter ![]() $n^d-(mq)^d=\textrm{O}(n^{d-1})$.
$n^d-(mq)^d=\textrm{O}(n^{d-1})$.
Proof of Lemma 4.2. By the Slivnyak–Mecke theorem (see Theorem A.2) with ![]() $n=1$ we have
$n=1$ we have
where we used translation invariance for the last equality. On the other hand,
where
Since ![]() $W_m$ follows a Poisson law of parameter
$W_m$ follows a Poisson law of parameter ![]() $(1-(1-2\delta)^d){\nu} m^d$,
$(1-(1-2\delta)^d){\nu} m^d$, ![]() $\mathbb{E}[W_m]/({\nu} m^d)$ is smaller than
$\mathbb{E}[W_m]/({\nu} m^d)$ is smaller than ![]() $2d\delta$. The fact that
$2d\delta$. The fact that ![]() $\mathbb{E}[U_m]/({\nu} m^d)$ is bounded from above by
$\mathbb{E}[U_m]/({\nu} m^d)$ is bounded from above by ![]() $c (\delta m)^{d-\alpha}$ will be proved in Proposition 4.2. Putting it all together we obtain
$c (\delta m)^{d-\alpha}$ will be proved in Proposition 4.2. Putting it all together we obtain
4.2 Proof of Proposition 4.1
We begin with an elementary lemma.
Lemma 4.3. For P-almost all ![]() $\eta$ there exists
$\eta$ there exists ![]() $ \bar n\in\mathbb{N}$ such that, for all
$ \bar n\in\mathbb{N}$ such that, for all ![]() $n\geq \bar n$,
$n\geq \bar n$,
Proof. For a Poisson random variable X of parameter ![]() $\mu>0$, the bound
$\mu>0$, the bound ![]() $P(|X-\mu|>\varepsilon)< 2\exp\{-\varepsilon^2/(4\mu)\}$ holds for all
$P(|X-\mu|>\varepsilon)< 2\exp\{-\varepsilon^2/(4\mu)\}$ holds for all ![]() $0<\varepsilon<\mu$; see e.g. [Reference Mitzenmacher and Upfal29, Theorem 5.4]. Since under P the number of points falling in
$0<\varepsilon<\mu$; see e.g. [Reference Mitzenmacher and Upfal29, Theorem 5.4]. Since under P the number of points falling in ![]() $B_n$ follows a Poisson distribution of parameter
$B_n$ follows a Poisson distribution of parameter ![]() ${\nu} n^d$, the conclusion follows by a simple Borel–Cantelli argument (in fact it is possible to improve the statement further).
${\nu} n^d$, the conclusion follows by a simple Borel–Cantelli argument (in fact it is possible to improve the statement further).
Proof of Proposition 4.1. For simplicity we will consider a sequence of n of the form ![]() $n=qm$, where
$n=qm$, where ![]() $q\in\mathbb{N}$. It is in fact highly plausible that for all other n of the form
$q\in\mathbb{N}$. It is in fact highly plausible that for all other n of the form ![]() $n=qm+r$ with
$n=qm+r$ with ![]() $r\in[0,m)$, what happens in the area
$r\in[0,m)$, what happens in the area ![]() $B_n\setminus B_{qm}$ is negligible in the limit
$B_n\setminus B_{qm}$ is negligible in the limit ![]() $n\to\infty$. We bound
$n\to\infty$. We bound
 \begin{align}|{\textrm{CC}}_n-\widehat{\textrm{CC}}_n^m|&=\biggl|\dfrac{1}{N_n}-\dfrac{1}{{\nu} n^d}\biggr|\sum_{x\in V_n}{\textrm{CC}}(x)+\dfrac{1}{{\nu} n^d}\biggl(\sum_{x\in V_n}{\textrm{CC}}(x)-\widehat{\textrm{CC}}^m(x)\biggr)\nonumber\\*&\leq \biggl|1-\dfrac{N_n}{{\nu} n^d}\biggr|+\dfrac{1}{{\nu} n^d}(W_n+U_n) ,\end{align}
\begin{align}|{\textrm{CC}}_n-\widehat{\textrm{CC}}_n^m|&=\biggl|\dfrac{1}{N_n}-\dfrac{1}{{\nu} n^d}\biggr|\sum_{x\in V_n}{\textrm{CC}}(x)+\dfrac{1}{{\nu} n^d}\biggl(\sum_{x\in V_n}{\textrm{CC}}(x)-\widehat{\textrm{CC}}^m(x)\biggr)\nonumber\\*&\leq \biggl|1-\dfrac{N_n}{{\nu} n^d}\biggr|+\dfrac{1}{{\nu} n^d}(W_n+U_n) ,\end{align}
where
and
The first summand in (16) tends ![]() $\mathbb{P}$-almost surely to 0 as
$\mathbb{P}$-almost surely to 0 as ![]() $n\to \infty$ by Lemma 4.3. We then note that under
$n\to \infty$ by Lemma 4.3. We then note that under ![]() $\mathbb{P}$ the random variable
$\mathbb{P}$ the random variable ![]() $W_n$ has a Poisson distribution of parameter
$W_n$ has a Poisson distribution of parameter ![]() $(1 - {(1 - 2\delta )^d})v{n^d}$, which can be dominated by a Poisson distribution of parameter
$(1 - {(1 - 2\delta )^d})v{n^d}$, which can be dominated by a Poisson distribution of parameter ![]() $ 2d\delta{\nu} n^d$. Reasoning as in the the proof of Lemma 4.3, it is possible to show that, for all n large enough,
$ 2d\delta{\nu} n^d$. Reasoning as in the the proof of Lemma 4.3, it is possible to show that, for all n large enough, ![]() $W_n$ is smaller than
$W_n$ is smaller than ![]() $4d\delta {\nu} n^d$, for example, so
$4d\delta {\nu} n^d$, for example, so ![]() $\limsup_{n\to\infty}n^{-d}W_n\leq c_1{\delta}$.
$\limsup_{n\to\infty}n^{-d}W_n\leq c_1{\delta}$.
It remains to show that ![]() $\mathbb{P}$-almost surely.
$\mathbb{P}$-almost surely.
Assume for now that there exists a constant ![]() $c>0$ such that the following estimates hold:
$c>0$ such that the following estimates hold:
where ![]() $\mathbb{V}$ denotes the variance with respect to
$\mathbb{V}$ denotes the variance with respect to ![]() $\mathbb{P}$. The proof of these two bounds will be postponed to Proposition 4.2 below. By the Chebyshev inequality,
$\mathbb{P}$. The proof of these two bounds will be postponed to Proposition 4.2 below. By the Chebyshev inequality,
for some ![]() $\tilde c>0$. We would like to finish the proof via Borel–Cantelli, but the right-hand side of the last display is not summable in n. Nevertheless
$\tilde c>0$. We would like to finish the proof via Borel–Cantelli, but the right-hand side of the last display is not summable in n. Nevertheless ![]() $U_n$ is an increasing sequence, so we can proceed as follows. Recall that
$U_n$ is an increasing sequence, so we can proceed as follows. Recall that ![]() $n=qm$. By taking the sequence
$n=qm$. By taking the sequence ![]() $n_k\,:\!=2^km$, we have
$n_k\,:\!=2^km$, we have
which is summable in k. Hence there exists almost surely a ![]() $\bar k$ such that
$\bar k$ such that ![]() $U_{n_k}\leq 2c\,{n_k}^d(\delta m)^{d-\alpha}$ for all
$U_{n_k}\leq 2c\,{n_k}^d(\delta m)^{d-\alpha}$ for all ![]() $k\geq \bar k$. Now take any
$k\geq \bar k$. Now take any ![]() $n>2^{\bar k}m$ and let K be the integer such that
$n>2^{\bar k}m$ and let K be the integer such that ![]() $2^Km\leq n<2^{K+1}m$. By monotonicity we get
$2^Km\leq n<2^{K+1}m$. By monotonicity we get
and (17) follows.
Proposition 4.2. There exists a constant ![]() $c>0$ such that
$c>0$ such that
where ![]() $\mathbb{V}$ denotes the variance with respect to
$\mathbb{V}$ denotes the variance with respect to ![]() $\mathbb{P}$.
$\mathbb{P}$.
Proof of Proposition 4.2. Let ![]() $Q(1),\ldots,Q(q^d)$ be the boxes of side-length m contained in
$Q(1),\ldots,Q(q^d)$ be the boxes of side-length m contained in ![]() $B_n$. For the expectation we have
$B_n$. For the expectation we have
 \begin{align}\mathbb{E}[U_n]&=\mathbb{E}\Biggl[\sum_{j=1}^{q^d}\sum_{x\in \overline Q(j)\cap\eta}\mathds 1_{\{{x\leftrightarrow(Q_m(x))^c}\}}\Biggr]\nonumber\\*&= q^d\mathbb{E}\Biggl[ \mathbb{E}\Biggl[ \sum_{x\in V_{m(1-2\delta)}} \mathds 1_{\{{x\leftrightarrow B_m^c}\}} \biggm| V_m \Biggr] \Biggr]\notag \\*&\leq q^d \mathbb{E}[ N_{m(1-2\delta)}\mathbb{P}_0(0\leftrightarrow B_{\delta m}^c) ] .\end{align}
\begin{align}\mathbb{E}[U_n]&=\mathbb{E}\Biggl[\sum_{j=1}^{q^d}\sum_{x\in \overline Q(j)\cap\eta}\mathds 1_{\{{x\leftrightarrow(Q_m(x))^c}\}}\Biggr]\nonumber\\*&= q^d\mathbb{E}\Biggl[ \mathbb{E}\Biggl[ \sum_{x\in V_{m(1-2\delta)}} \mathds 1_{\{{x\leftrightarrow B_m^c}\}} \biggm| V_m \Biggr] \Biggr]\notag \\*&\leq q^d \mathbb{E}[ N_{m(1-2\delta)}\mathbb{P}_0(0\leftrightarrow B_{\delta m}^c) ] .\end{align}
In the second equality we used the translation invariance of the model and then the tower property of expectation by conditioning on the position of the points of the Poisson process inside ![]() $B_m$. For the inequality we upper-bounded the probability that a point
$B_m$. For the inequality we upper-bounded the probability that a point ![]() $x\in V_{m(1-2\delta)}$ is connected to the exterior of
$x\in V_{m(1-2\delta)}$ is connected to the exterior of ![]() $B_m$ by the probability that, under the Palm measure, the origin is connected to some point in
$B_m$ by the probability that, under the Palm measure, the origin is connected to some point in ![]() $B_{\delta m}^c$ (since for each
$B_{\delta m}^c$ (since for each ![]() $x\in V_{m(1-2\delta)}$ all the points in
$x\in V_{m(1-2\delta)}$ all the points in ![]() $B_m^c$ are outside a box of side
$B_m^c$ are outside a box of side ![]() $\delta m$ centered at x). We estimate this probability as follows:
$\delta m$ centered at x). We estimate this probability as follows:
 \begin{align}\mathbb{P}_0(0\leftrightarrow B_{\delta m}^c)&=1-\mathbb{E}_0\Biggl[ \prod_{y\in V\setminus V_{\delta m}}E[{\textrm{e}}^{-{{W_0W_y}/{\|y\|^\alpha}}}\mid W_0] \Biggr]\nonumber\\*&\leq 1-\exp\Biggl\{-\mathbb{E}_{0}\Biggl[\sum_{y\in V\setminus V_{\delta m}}\dfrac{W_0E[W_y]}{\|y\|^\alpha}\Biggr]\Biggr\} \notag \\&\leq \int_{y\in B_{\delta m}^c}\dfrac{E[W]^2}{\|y\|^{\alpha}}\,\textrm{d} y \notag \\*&= c'(\delta m)^{d-\alpha}\end{align}
\begin{align}\mathbb{P}_0(0\leftrightarrow B_{\delta m}^c)&=1-\mathbb{E}_0\Biggl[ \prod_{y\in V\setminus V_{\delta m}}E[{\textrm{e}}^{-{{W_0W_y}/{\|y\|^\alpha}}}\mid W_0] \Biggr]\nonumber\\*&\leq 1-\exp\Biggl\{-\mathbb{E}_{0}\Biggl[\sum_{y\in V\setminus V_{\delta m}}\dfrac{W_0E[W_y]}{\|y\|^\alpha}\Biggr]\Biggr\} \notag \\&\leq \int_{y\in B_{\delta m}^c}\dfrac{E[W]^2}{\|y\|^{\alpha}}\,\textrm{d} y \notag \\*&= c'(\delta m)^{d-\alpha}\end{align}
for some ![]() $c'>0$ that does not depend on either m or
$c'>0$ that does not depend on either m or ![]() $\delta$. In the first line we used the fact that, conditioned on the weight of point 0, the presence of connections between 0 and the other points of the Poisson point process becomes independent. For the second line we applied Jensen’s inequality twice. For the third line we first used the inequality
$\delta$. In the first line we used the fact that, conditioned on the weight of point 0, the presence of connections between 0 and the other points of the Poisson point process becomes independent. For the second line we applied Jensen’s inequality twice. For the third line we first used the inequality ![]() $1-{\textrm{e}}^{-x}\leq x$ for
$1-{\textrm{e}}^{-x}\leq x$ for ![]() $x>0$, then we applied Campbell’s theorem (see Theorem A). Finally we used polar coordinates in order to evaluate the integral. Plugging this back into (20), we obtain (18).
$x>0$, then we applied Campbell’s theorem (see Theorem A). Finally we used polar coordinates in order to evaluate the integral. Plugging this back into (20), we obtain (18).
We move to the variance of ![]() $U_n$. For
$U_n$. For ![]() $x\in \eta$ we set
$x\in \eta$ we set
so that ![]() $U_n=\sum_{x\in V_n}A(x)$. Note that by the Slivnyak–Mecke theorem (see Theorem A.2) we have
$U_n=\sum_{x\in V_n}A(x)$. Note that by the Slivnyak–Mecke theorem (see Theorem A.2) we have
On the other hand we can write
 \begin{equation}\mathbb{V}(U_n)=\mathbb{E}[U_n^2]-\mathbb{E}[U_n]^2=\mathbb{E}[U_n]+\mathbb{E}\Biggl[\sum_{x\neq y\in V_n}A(x)A(y)\Biggr]-\mathbb{E}[U_n]^2 .\end{equation}
\begin{equation}\mathbb{V}(U_n)=\mathbb{E}[U_n^2]-\mathbb{E}[U_n]^2=\mathbb{E}[U_n]+\mathbb{E}\Biggl[\sum_{x\neq y\in V_n}A(x)A(y)\Biggr]-\mathbb{E}[U_n]^2 .\end{equation}
Now applying Theorem A.2 to the function
we can evaluate the second summand on the right-hand side:
 \begin{align}\mathbb{E}\Biggl[\sum_{x\neq y\in V_n}A(x)A(y)\Biggr]&={\nu}^2\int_{B_n}\int_{B_n}\mathbb{E}_{x,y}[A(x)A(y)]\,\textrm{d}x\,\textrm{d}y\notag\\*&={\nu}^2\int_{B_n}\int_{B_n}C(x,y)\,\textrm{d}x\,\textrm{d}y+{\mathbb{E}[U_n]}^2+{\nu}^2R ,\end{align}
\begin{align}\mathbb{E}\Biggl[\sum_{x\neq y\in V_n}A(x)A(y)\Biggr]&={\nu}^2\int_{B_n}\int_{B_n}\mathbb{E}_{x,y}[A(x)A(y)]\,\textrm{d}x\,\textrm{d}y\notag\\*&={\nu}^2\int_{B_n}\int_{B_n}C(x,y)\,\textrm{d}x\,\textrm{d}y+{\mathbb{E}[U_n]}^2+{\nu}^2R ,\end{align}
where
and R is the rest given by
Note that for ![]() $y\in Q_m(x)$ we have
$y\in Q_m(x)$ we have ![]() $\mathbb{E}_{x,y}[A(x)]=\mathbb{E}_{x}[A(x)]$. For
$\mathbb{E}_{x,y}[A(x)]=\mathbb{E}_{x}[A(x)]$. For ![]() $y\not\in Q_m(x)$,
$y\not\in Q_m(x)$,
for some ![]() ${\tilde c_1}>0$. For the first inequality we used the fact that for
${\tilde c_1}>0$. For the first inequality we used the fact that for ![]() $A(x)=1$, the point x has to be connected to y (which gives the second addendum) or to any other point outside
$A(x)=1$, the point x has to be connected to y (which gives the second addendum) or to any other point outside ![]() $Q_m(x)$ (first addendum), and in this second case the presence of y in the point process plays no role. This, together with the bound
$Q_m(x)$ (first addendum), and in this second case the presence of y in the point process plays no role. This, together with the bound
yields
We now only need to bound the correlation C(x, y). We introduce the event
The random variables A(x) and A(y) are independent under the event ![]() $\mathcal{E}(x,y)$. Therefore
$\mathcal{E}(x,y)$. Therefore
 \begin{align}C(x,y)&\leq \mathbb{E}_{x,y}[A(x)|\mathcal{E}(x,y)] \mathbb{E}_{x,y}[A(y)|\mathcal{E}(x,y)]\mathbb{P}(\mathcal{E}(x,y))\notag\\*&\quad\, +\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)-\mathbb{E}_{x,y}[A(x)]\mathbb{E}_{x,y}[A(y)]\nonumber\\&\leq \mathbb{E}_{x,y}[A(x)]\mathbb{E}_{x,y}[A(y)]\biggl(\dfrac{1}{\mathbb{P}_{x,y}(\mathcal{E}(x,y))}-1\biggr)+\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)\nonumber\\*&\leq \mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)\biggl(\dfrac{1}{\mathbb{P}_{x,y}(\mathcal{E}(x,y))}+1\biggr) ,\end{align}
\begin{align}C(x,y)&\leq \mathbb{E}_{x,y}[A(x)|\mathcal{E}(x,y)] \mathbb{E}_{x,y}[A(y)|\mathcal{E}(x,y)]\mathbb{P}(\mathcal{E}(x,y))\notag\\*&\quad\, +\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)-\mathbb{E}_{x,y}[A(x)]\mathbb{E}_{x,y}[A(y)]\nonumber\\&\leq \mathbb{E}_{x,y}[A(x)]\mathbb{E}_{x,y}[A(y)]\biggl(\dfrac{1}{\mathbb{P}_{x,y}(\mathcal{E}(x,y))}-1\biggr)+\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)\nonumber\\*&\leq \mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)\biggl(\dfrac{1}{\mathbb{P}_{x,y}(\mathcal{E}(x,y))}+1\biggr) ,\end{align}
where in the second line we used the inequality ![]() $\mathbb{E}_{x,y}[W|Z]\leq \mathbb{E}_{x,y}[W]/\mathbb{P}_{x,y}(Z)$ and in the last line we just bounded
$\mathbb{E}_{x,y}[W|Z]\leq \mathbb{E}_{x,y}[W]/\mathbb{P}_{x,y}(Z)$ and in the last line we just bounded ![]() $\mathbb{E}_{x,y}[A(x)]$ and
$\mathbb{E}_{x,y}[A(x)]$ and ![]() $\mathbb{E}_{x,y}[A(y)]$ by 1. We also observe that
$\mathbb{E}_{x,y}[A(y)]$ by 1. We also observe that
 \begin{align}\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)&\leq \mathbb{P}_{x,y}(x\leftrightarrow \mathcal{B}_{\|x-y\|/2}(x))+\mathbb{P}_{x,y}(y\leftrightarrow \mathcal{B}_{\|x-y\|/2}(y))\nonumber\\*&\leq \mathbb{P}_{x,y}(x\leftrightarrow y)+2\mathbb{P}_{0}(0\leftrightarrow \mathcal{B}_{\|x-y\|/2}(0))\notag\\*&\leq {\tilde c_5}\,\|x-y\|^{d-\alpha}\end{align}
\begin{align}\mathbb{P}_{x,y}(\mathcal{E}(x,y)^c)&\leq \mathbb{P}_{x,y}(x\leftrightarrow \mathcal{B}_{\|x-y\|/2}(x))+\mathbb{P}_{x,y}(y\leftrightarrow \mathcal{B}_{\|x-y\|/2}(y))\nonumber\\*&\leq \mathbb{P}_{x,y}(x\leftrightarrow y)+2\mathbb{P}_{0}(0\leftrightarrow \mathcal{B}_{\|x-y\|/2}(0))\notag\\*&\leq {\tilde c_5}\,\|x-y\|^{d-\alpha}\end{align}
for some ![]() ${\tilde c_5}>0$, where the last inequality can be obtained as in (21). From (24) and (25) it follows that whenever we consider
${\tilde c_5}>0$, where the last inequality can be obtained as in (21). From (24) and (25) it follows that whenever we consider ![]() $x,y\in\mathbb{R}^d$ such that, for example,
$x,y\in\mathbb{R}^d$ such that, for example, ![]() ${\tilde c_5}\,\|x-y\|^{d-\alpha}\leq 1/2$, we get
${\tilde c_5}\,\|x-y\|^{d-\alpha}\leq 1/2$, we get ![]() $C(x,y)\leq {\tilde c_6}\,\|x-y\|^{d-\alpha}$. Hence, setting
$C(x,y)\leq {\tilde c_6}\,\|x-y\|^{d-\alpha}$. Hence, setting ![]() ${r}\,:\!=(2{\tilde c_5})^{1/(\alpha-d)}$, we can bound
${r}\,:\!=(2{\tilde c_5})^{1/(\alpha-d)}$, we can bound
for some constant ![]() $c>0$. The proof is finished by putting together (22), (18), (23), and this last estimate.
$c>0$. The proof is finished by putting together (22), (18), (23), and this last estimate.
Appendix A. Campbell and Slivnyak–Mecke theorems
In this section we present versions of Campbell’s theorem and of the so-called extended Slivnyak–Mecke theorem in the simple case of a homogeneous Poisson point process. For a version of Theorem A.1 similar to the one presented here, see [Reference Kingman26, Section 3.2]. For a simple proof of Theorem A.2, see [Reference Moller and Waagepetersen30, Theorem 13.3]. More complete and general versions of these theorems in the framework of Palm theory can be found in [Reference Daley and Vere-Jones12, Chapter 13].
Theorem A.1. (Campbell theorem, homogeneous case.) Let ![]() $\eta$ be a homogeneous Poisson point process on
$\eta$ be a homogeneous Poisson point process on ![]() $\mathbb{R}^d$ with intensity
$\mathbb{R}^d$ with intensity ![]() ${\nu}$ under measure P, with E the associated expectation. Let
${\nu}$ under measure P, with E the associated expectation. Let ![]() $f\colon \mathbb{R}^d\to\mathbb{R}$ be a measurable function. The random sum
$f\colon \mathbb{R}^d\to\mathbb{R}$ be a measurable function. The random sum ![]() $S=\sum_{x\in\eta} f(x)$ is absolutely convergent with probability one if and only if
$S=\sum_{x\in\eta} f(x)$ is absolutely convergent with probability one if and only if
If the previous integral is finite, then we have
for any complex ![]() $\theta$ such that the integral on the right-hand side converges. Moreover,
$\theta$ such that the integral on the right-hand side converges. Moreover,
and if the last integral is finite, then
where V is the (possibly infinite) variance with respect to P.
Theorem A.2. (Extended Slivnyak–Mecke theorem.) Let ![]() $\eta$ be a homogeneous Poisson point process on
$\eta$ be a homogeneous Poisson point process on ![]() $\mathbb{R}^d$ with intensity
$\mathbb{R}^d$ with intensity ![]() ${\nu}$ under measure P, with E the associated expectation. For
${\nu}$ under measure P, with E the associated expectation. For ![]() $n\in\mathbb{N}$ and for any positive function
$n\in\mathbb{N}$ and for any positive function ![]() $f\colon (\mathbb{R}^d)^n\times (\mathbb{R}^d)^{\mathbb{N}}\to[0,\infty)$,
$f\colon (\mathbb{R}^d)^n\times (\mathbb{R}^d)^{\mathbb{N}}\to[0,\infty)$,
 \begin{equation*}\textrm{E}\Biggl[\sum_{x_1,\dots, x_n\in\eta}^{\neq} f(x_1,\dots,x_n;\,\eta\setminus\{x_1,\dots,x_n\})\Biggr]={\nu}^n\int_{\mathbb{R}^d}\dots\int_{\mathbb{R}^d} \textrm{E}[f(x_1,\dots,x_n;\,\eta)]\,\textrm{d}x_1\ldots\textrm{d}x_n ,\end{equation*}
\begin{equation*}\textrm{E}\Biggl[\sum_{x_1,\dots, x_n\in\eta}^{\neq} f(x_1,\dots,x_n;\,\eta\setminus\{x_1,\dots,x_n\})\Biggr]={\nu}^n\int_{\mathbb{R}^d}\dots\int_{\mathbb{R}^d} \textrm{E}[f(x_1,\dots,x_n;\,\eta)]\,\textrm{d}x_1\ldots\textrm{d}x_n ,\end{equation*}
where the ![]() $\neq$ sign over the sum means that
$\neq$ sign over the sum means that ![]() $x_1,\dots,x_n$ are pairwise distinct.
$x_1,\dots,x_n$ are pairwise distinct.
Acknowledgements
We thank three anonymous referees for helping us to improve the original manuscript. The second author would like to thank Quentin Berger for useful discussions. This work was carried out with financial support of the French Research Agency (ANR), project ANR-16-CE32-0007-01 (CADENCE).