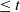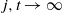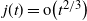1. Introduction
Let
$(\xi_i, \eta_i)_{i\in\mathbb{N}}$
be independent copies of a random vector
$(\xi, \eta)$
with arbitrarily dependent and almost surely (a.s.) strictly positive components. Let
$S\,:\!=\, (S_i)_{i\geq 0}$
denote the zero-delayed random walk with increments
$\xi_i$
for
$i\in\mathbb{N}$
, that is,
$S_0\,:\!=\, 0$
and
$S_i\,:\!=\, \xi_1+\cdots+\xi_i$
for
$i\in\mathbb{N}$
. Define
\begin{equation*}T_i\,:\!=\, S_{i-1}+\eta_i,\quad i\in \mathbb{N}.\end{equation*}
The sequence
$T\,:\!=\, (T_i)_{i\in\mathbb{N}}$
is called a perturbed random walk (PRW for short).
Classical renewal theory is an area of applied probability dealing with non-decreasing random walks S and various derived processes such as the following.
The renewal process
$(R(t))_{t\geq 0}$
defined by
\begin{equation*}R(t)\,:\!=\, \sum_{i\geq 1}\mathbb{1}_{\{S_i\leq t\}},\quad t\geq 0.\end{equation*}
The first passage time process
$(\nu(t))_{t\geq 0}$
defined by (1.1)
\begin{equation}\nu(t)\,:\!=\, \inf\{i\in\mathbb{N}\colon S_i>t\},\quad t\geq 0.\end{equation}
The undershoot
$t-S_{\nu(t)-1}$
, the overshoot
$S_{\nu(t)}-t$
, and others.
A good overview of renewal theory can be found in [Reference Asmussen2], [Reference Gut12], and [Reference Resnick25] and the more recent accounts [Reference Iksanov14] and [Reference Mitov and Omey20]. A survey of various results for PRWs T (with not necessarily positive
$\xi$
and
$\eta$
) and, in particular, counterparts of some renewal-theoretic results can be found in the book [Reference Iksanov14]. An incomplete list of more recent papers addressing various aspects of the PRWs includes [Reference Alsmeyer, Iksanov and Marynych1], [Reference Duchamps, Pitman and Tang9], [Reference Iksanov, Pilipenko and Samoilenko17], [Reference Pitman and Tang22], [Reference Pitman and Yakubovich23], and [Reference Rashytov24].
We proceed by recalling the construction of a general branching process (a.k.a. a Crump–Mode–Jagers branching process) in the special case in which it is generated by T. At time 0 there is one individual, the ancestor. The ancestor produces offspring (the first generation) with birth times given by the points of T. The first generation produces second-generation individuals. The shifts of birth times of the second generation individuals with respect to their mothers’ birth times are distributed according to copies of T, and for different mothers these copies are independent. The second generation produces the third one, and so on. All individuals act independently of each other. See Figure 1 for an illustration.
Figure 1. A general branching process generated by T. Superscripts indicate generation numbers. The shifts of birth times of the second generation individuals with respect to their mothers’ birth times are distributed according to independent copies of T. For instance,
$T_7^{(2)}-T_2^{(1)}$
,
$T_9^{(2)}-T_2^{(1)}$
, and
$T_8^{(2)}-T_2^{(1)}$
are distributed as the first three smallest elements of T. Note that, in general,
$T=(T_k)_{k\in\mathbb{N}}$
is not monotone due to the perturbations. For example,
$T_2>T_3$
because
$\eta_2>\xi_2+\eta_3$
.
Clearly the random sequence
$T^{(j)}$
defined by the birth times in the jth generation of the process (
$j\geq 2$
) is much more complicated than the perturbed random walk
$T^{(1)}=T$
defining the birth times in the first generation. It is natural to call
$(T^{(j)})_{j\geq 2}$
an iterated perturbed random walk on a general branching process tree. If
$\eta=\xi$
a.s., in which case
$T=S$
a.s., the term iterated random walk on a general branching process tree may be used for the corresponding sequence
$(S^{(j)})_{j\geq 2}$
. This should not be confused with iterated renewal processes treated in [Reference Sen27]. In this paper we initiate a systematic study of
$T^{(j)}$
for
$j\geq 2$
and its derived processes, our primary purpose being to obtain counterparts of the classical renewal-theoretic results.
Now we introduce notation to be used throughout the paper. Put
$N(t)\,:\!=\, \sum_{i\geq 1}\mathbb{1}_{\{T_i\leq t\}}$
and
$V(t)\,:\!=\, \mathbb{E} N(t)$
for
$t\in\mathbb{R}$
. As usual, we shall write
$x_{+}$
for
$\max(x,0)$
. Since
$\eta_i$
is independent of
$S_{i-1}$
, it is clear that
\begin{equation}V(t)=\mathbb{E} U((t-\eta)_{+})=(U\ast G)(t)=\int_{[0,\,t]}U(t-y)\,{\textrm{d}} G(y),\quad t\geq 0.\end{equation}
where, for
$t\in\mathbb{R}$
,
$U(t)\,:\!=\, \mathbb{E} \nu(t)=\sum_{i\geq 0}\mathbb{P}\{S_i\leq t\}$
is the renewal function and
$G(t)=\mathbb{P}\{\eta\leq t\}$
. Note that
$U(t)=V(t)=G(t)=0$
for
$t<0$
. Here and in what follows, we let
$u \ast v$
denote the Lebesgue–Stieltjes convolution of two functions u and v of locally bounded variation. We also use the notation
$u^{\ast(j)}$
,
$j\in\mathbb{N}$
, for the jth convolution power of u.
For
$t\geq 0$
and
$j\in\mathbb{N}$
, we let
$N_j(t)$
denote the number of jth-generation individuals with birth times
$\leq t$
and put
$V_j(t)\,:\!=\, \mathbb{E} N_j(t)$
. Then
$N_1(t)=N(t)$
,
$V_1(t)=V(t)$
and
\begin{equation*}V_j(t)=(V_{j-1}\ast V)(t)=\int_{[0,\,t]} V_{j-1}(t-y)\,{\textrm{d}} V(y),\quad j\geq 2,\ t\geq 0.\end{equation*}
For example, in Figure 1 we have
$N_1(t)=N(t)=3$
and
$N_2(t)=7$
. For
$r\in\mathbb{N}$
, let
$N_{j-1}^{(r)}(t)$
be the number of successors in the jth generation with birth times within
$[T_r,t+T_r]$
of the first generation individual with birth time
$T_r$
. By the branching property,
$\bigl(N_{j-1}^{(1)}(t)\bigr)_{t\geq 0}$
,
$\bigl(N_{j-1}^{(2)}(t)\bigr)_{t\geq 0},\ldots$
are independent copies of
$N_{j-1}$
that are also independent of T. The basic decomposition that sheds light on the properties of
$N_j\,:\!=\, (N_j(t))_{t\geq 0}$
and also demonstrates its recursive structure is
\begin{equation*} N_j(t)=\sum_{r\geq 1}N^{(r)}_{j-1}(t-T_r)\mathbb{1}_{\{T_r\leq t\}},\quad j\geq 2,\ t\geq 0.\end{equation*}
Further, let
$T^{(j-1)}\,:\!=\, \big(T^{(j-1)}_r\big)_{r\geq 1}$
be some enumeration of birth times in the
$(j-1)$
th generation; let
$\smash{N_{1,j}^{(r)}(t)}$
be the number of children in the jth generation with birth times within
$\smash{\big[T^{(j-1)}_r,t+T^{(j-1)}_r\big]}$
of the
$(j-1)$
th-generation individual with birth time
$T^{(j-1)}_r$
. Again, by the branching property,
$\bigl(N_{1,j}^{(1)}(t)\bigr)_{t\geq 0}$
,
$\bigl(N_{1,j}^{(2)}(t)\bigr)_{t\geq 0},\ldots$
are independent copies of
$(N(t))_{t\geq 0}$
that are also independent of
$T^{(j-1)}$
. With these ingredients we can write another recursive decomposition of
$N_j$
as follows:
\begin{equation*}N_j(t)=\sum_{r\geq 1}N^{(r)}_{1,j}\big(t-T^{(j-1)}_r\big)\mathbb{1}_{\{T^{(j-1)}_r\leq t\}},\quad j\geq 2,\ t\geq 0.\end{equation*}
Note that, for
$j\geq 2$
,
$N_j$
is a particular instance of a random process with immigration at random times (the term was introduced in [Reference Dong and Iksanov8]; see also [Reference Iksanov and Rashytov15]).
Our motivation for introducing the iterated perturbed random walks is at least threefold.
-
(1) For each integer
$j\geq 2$
, the sequence
$T^{(j)}$
and the process
$N_j$
are a natural generalization of the perturbed random walk T and the counting process
$(N(t))_{t\geq 0}$
. It is interesting to investigate the extent to which the renewal-theoretic properties of T and (N(t)) are inherited by
$T^{(j)}$
and
$N_j$
. Thus the activity undertaken in the present article can be thought of as the development of renewal theory for the iterated perturbed random walks. -
(2) The sequence
$\big(T^{(j)}\big)_{j\in\mathbb{N}}$
is a particular instance of a branching random walk in which the first generation point process is
$(N(t))_{t\geq 0}$
, the counting process of a perturbed random walk. Alternatively – and this is our preferred viewpoint – for
$j\in\mathbb{N}$
,
$T^{(j)}$
can be interpreted as the sequence of birth times in the jth generation of a general branching process. Therefore the results of the present article contribute towards better understanding of how the births occur within a particular generation. Being of intrinsic interest for the theory of general branching processes, this information also sheds light on the organization of levels (the sets of vertices located at the same distance from the root) of some random trees (e.g. random recursive trees and binary search trees) that can be constructed as family trees of general branching processes stopped at suitable random times. We refer to [Reference Holmgren and Janson13] for more details and examples of embeddable random trees. -
(3) Renewal theory for perturbed random walks is an inevitable ingredient for investigation of nested occupancy scheme in random environment generated by stick-breaking. Referring to [Reference Buraczewski, Dovgay and Iksanov6] and [Reference Iksanov, Marynych and Samoilenko16] for more details, we only mention that the latter scheme is a generalization of the classical Karlin infinite balls-in-boxes occupancy scheme [Reference Gnedin, Hansen and Pitman11, Reference Karlin19].Unlike the Karlin scheme, in which the collection of boxes is unique, there is a nested hierarchy of boxes, and the hitting probabilities of boxes are defined in terms of iterated stick-breaking. Assuming that n balls have been thrown, let
$K_n(j)$
denote the number of occupied boxes in the jth level, which is the basic object of interest. It turns out that whenever
$j=j_n={\textrm{o}}\big((\log n)^{1/2}\big)$
(the case of fixed j is included), the distributional behavior of
$K_n(j)$
as
$n\to\infty$
is the same as that of
$N_j(\log n)$
, when the underlying perturbed random walk T is appropriately chosen.
We call the jth generation early, intermediate, or late depending on whether j is fixed,
$j=j(t)\to\infty$
and
$j(t)={\textrm{o}}(t)$
as
$t\to\infty$
, or
$j=j(t)$
is of order t. In view of Proposition 2.1 below, there are no other regimes because
$N_j(t)=0$
a.s. for large enough t whenever
$j=j(t)$
grows faster than t. Assume for the time being that j is a late generation and that T is a collection of random points, not necessarily the perturbed random walk. Nevertheless we retain the notation
$N_j$
and
$V_j$
. In this case the asymptotic behavior of
$V_j$
and
$N_j$
is well understood. For instance, a delicate counterpart of the key renewal theorem for
$V_j$
, which includes both a version of the elementary renewal theorem and a version of Blackwell’s theorem, can be found in Theorem A of [Reference Biggins4]. For the corresponding a.s. result for
$N_j$
, see Theorem B of the same paper and Theorem 4 of [Reference Biggins5]. A strong law of large numbers for
$N_j(bj)$
for appropriate
$b>0$
is given in formula (1.1) of [Reference Biggins4]. From these and other results of this flavor it follows that
$N_j$
forgets what was happening in the early history and particularly in the first generation. The behavior of
$N_j$
is universal for a wide class of input processes (responsible for the first generation). It is driven by limit theorems available for general branching processes, such as convergence of the Biggins martingales, large deviations, etc.
While the present paper deals with some intermediate generations, the early generations, which admit a much simpler analysis, are treated in a separate paper [Reference Iksanov, Rashytov and Samoilenko18]. The behavior of the iterated perturbed random walks in the early and intermediate generations is very different from that in the late generations. When j is a non-late generation, the process
$N_j$
inherits, for the most part, the properties of N, in a modified form. This statement is confirmed by counterparts of the elementary renewal theorem (Theorems 2.1 and 2.2), the key renewal theorem (Theorem 2.3), and Blackwell’s theorem (Corollary 2.1), which are our main results. As far as early generations are concerned, the claim is justified by results obtained in [Reference Iksanov, Rashytov and Samoilenko18].
The remainder of the paper is structured as follows. Our main findings are formulated in Section 2 and then proved in Section 3. Also, Section 2 contains two previously known results concerning
$N_j$
and
$V_j$
. To our knowledge, all the results presented in this paper form the state of the art as far as the intermediate generations of the iterated perturbed random walks are concerned. Finally, the Appendix collects the proofs of some auxiliary results.
2. Results
2.1. Height of a confined general branching process tree
For
$t\geq 0$
, put
\begin{equation*}H(t)\,:\!=\, \inf\{j\in\mathbb{N}\colon N_j(t)=0\}\end{equation*}
and note that
$N_j(t)=0$
a.s. for all
$j\geq H(t)$
. We call the variable H(t) the height of a general branching process tree generated by a perturbed random walk T and confined to the strip [0, t].
Proposition 2.1. For each
$t\geq 0$
,
$H(t)<\infty$
a.s. Furthermore,
\begin{equation}\lim_{t\to\infty}\dfrac{H(t)}{t}=\dfrac{1}{\gamma}\in (0,\infty)\quad\textit{a.s.},\end{equation}
where
$\gamma\,:\!=\, \sup\{z>0\colon \mu(z)<1\}$
and
\begin{equation*}\mu(z)\,:\!=\, \inf_{s>0}\biggl({\textrm{e}}^{zs}\dfrac{\mathbb{E} {\textrm{e}}^{-s\eta}}{1-\mathbb{E} {\textrm{e}}^{-s\xi}}\biggr)\quad\textit{for $z>0$.}\end{equation*}
Proof. By assumption,
$\mathbb{P}\{\eta=0\}=0$
. This entails
\begin{equation*} \lim_{s\to\infty}\dfrac{\mathbb{E} {\textrm{e}}^{-s\eta}}{1-\mathbb{E} {\textrm{e}}^{-s\xi}}=0 \end{equation*}
and thereupon
\begin{equation*}\lim_{z\to 0+}\mu(z)=0.\end{equation*}
Also,
\begin{equation*}\lim_{z\to\infty}\mu(z)=\lim_{s\to 0+}\dfrac{\mathbb{E} {\textrm{e}}^{-s\eta}}{1-\mathbb{E} {\textrm{e}}^{-s\xi}}=\infty.\end{equation*}
This shows that
$\gamma\in (0,\infty)$
.
Recall that, for
$n\in\mathbb{N}$
,
$\big(T_r^{(n)}\big)_{r\in\mathbb{N}}$
denotes some enumeration of birth times in the nth generation of the general branching process. Put
$B(n)\,:\!=\, \inf_{r\geq 1} T_r^{(n)}$
. By the famous Biggins result [Reference Biggins3, corollary on p. 635],
\begin{equation}\lim_{n\to\infty}\dfrac{B(n)}{n}=\gamma\quad\text{a.s.}\end{equation}
Since, for
$n\in\mathbb{N}$
and
$t>0$
,
$\{H(t)>n\}=\{B(n)\leq t\}$
and, according to (2.2),
$\lim_{n\to\infty}B(n)=+\infty$
a.s., we infer
$H(t)<\infty$
a.s.
Finally, we have
$B(H(t))>t\geq B(H(t)-1)$
a.s. The left-hand inequality ensures that
$\lim_{t\to\infty}H(t)=+\infty$
a.s., which together with (2.2) proves (2.1) with the help of a standard sandwich argument.
Proposition 2.1 implies, in particular, that if
\begin{equation*}\liminf_{t\to\infty}\dfrac{j(t)}{t}>\gamma^{-1},\end{equation*}
then there exists an a.s. finite
$t_0>0$
such that
$N_{j(t)}(t)=0$
for all
$t\geq t_0$
. This observation justifies our classification of generations (early, intermediate, late). Furthermore, the analysis of
$N_{j}$
for the late generations can be restricted to the range in which
$j=j(t)$
grows no faster than
$\gamma^{-1}t$
as
$t\to\infty$
.
It is seldom possible to find the constant
$\gamma$
explicitly. Here is one happy exception. Let
$(\xi,\eta)=(|\!\log W|, |\!\log(1-W)|)$
, where W has a uniform distribution on
$[0,\,1]$
. The distribution of the sequence
$\big({\textrm{e}}^{-T_i}\big)_{i\in\mathbb{N}}$
is known as the Griffiths–Engen–McCloskey distribution with parameter 1. In this case,
$\mu(z)={\textrm{e}} z$
for
$z>0$
, which gives
$\gamma={\textrm{e}}^{-1}$
.
2.2. Counterparts of the elementary renewal theorem for intermediate generations
The simplest result of renewal theory, called the elementary renewal theorem, tells us that
\begin{equation*}U(t)=\sum_{i\geq 0}\mathbb{P}\{S_i\leq t\} \sim \dfrac{t}{{\tt m}},\quad t\to\infty,\end{equation*}
where
${\tt m}\,:\!=\, \mathbb{E} \xi<\infty$
; see for instance Theorem 3.3.3 of [Reference Resnick25]. Here and below, the notation
$f(t)\sim g(t)$
means that the ratio
$f(t)/g(t)$
tends to 1 as
$t\to\infty$
.
From (1.2) it follows that, without any assumptions on
$\eta$
,
\begin{equation*} V(t) \sim \dfrac{t}{{\tt m}},\quad t\to\infty.\end{equation*}
This is a counterpart of the elementary renewal theorem for the perturbed random walks.
In this section we state two results on the first-order behavior of the convolution powers
$V_j$
of V. Our first result, Theorem 2.1, deals with ‘early intermediate’ generations satisfying
$j=j(t)\to\infty$
and
$j(t)={\textrm{o}}(t^{1/2})$
as
$t\to\infty$
, as well as early generations. At this point we stress that even though both Theorem 2.1 and Theorem 2.2 hold true for early generations, the assumptions of these theorems are too restrictive as far as early generations are concerned. We refer to the companion article [Reference Iksanov, Rashytov and Samoilenko18] for a proper version of the elementary renewal theorem in early generations. Recall the standard notation
$x\wedge y=\min (x,y)$
for
$x,y\in\mathbb{R}$
.
Theorem 2.1. Assume that either
-
(i)
$\mathbb{E}\xi^2<\infty$
and
$\mathbb{E}\eta<\infty$
or -
(ii)
$\mathbb{E}\xi^2=\infty$
,
$\mathbb{P}\{\xi>t\}={\textrm{O}}(t^{-r})$
and
$\mathbb{E}(\eta\wedge t)={\textrm{O}}\big(t^{2-r}\big)$
for some
$r\in (1,\,2)$
, as
$t\to\infty$
.
Then, for any integer-valued function
$j=j(t)$
satisfying
$j(t)={\textrm{o}}\big(t^{(r-1)/2}\big)$
as
$t\to\infty$
, where we put
$r=2$
if conditions
$\textrm{(i)}$
prevail,
\begin{equation*} V_j(t) \sim \dfrac{t^j}{{\tt m}^j j!},\quad t\to\infty.\end{equation*}
Here
${\tt m}=\mathbb{E}\xi<\infty$
.
Remark 2.1. The condition
$\mathbb{E}\xi^r<\infty$
for some
$r\in(1,2)$
is clearly sufficient for
$\mathbb{P}\{\xi>t\}={\textrm{O}}(t^{-r})$
. Further, the condition
$\mathbb{E}\eta^{r-1}<\infty$
is sufficient for
$\mathbb{E}(\eta\wedge t)={\textrm{O}}\big(t^{2-r}\big)$
,
$t\to\infty$
. This follows from
\begin{align*}\mathbb{E}(\eta\wedge t)&=\int_0^t \mathbb{P}\{\eta>y\}\,{\textrm{d}} y\\&\leq \int_0^t \biggl(\dfrac{t}{y}\biggr)^{2-r}\mathbb{P}\{\eta>y\}\,{\textrm{d}} y\\&\leq t^{2-r}\int_0^\infty y^{r-2}\mathbb{P}\{\eta>y\}\,{\textrm{d}} y\\&=(r-1)^{-1}\mathbb{E}\eta^{r-1}t^{2-r}.\end{align*}
Note that part (i) of Theorem 2.1 has already been obtained via a slightly different argument in formula (4.6) of [Reference Buraczewski, Dovgay and Iksanov6].
Next we give a fairly surprising result which shows that the convolution power
$V_j$
exhibits a phase transition in the generations j satisfying
$j=j(t)\sim \textrm{const.}\cdot t^{1/2}$
as
$t\to\infty$
. Here further moment and smoothness assumptions seem to be indispensable. In particular, we assume that the distribution of
$\xi$
is spread out, which means that some convolution power of the distribution function
$t\mapsto \mathbb{P}\{\xi\leq t\}$
has an absolutely continuous component.
Theorem 2.2. Assume that the distribution of
$\xi$
is spread out, that
$\mathbb{E} \xi^3<\infty$
and
$\mathbb{E} \eta^2<\infty$
. Then, for any integer-valued function
$j=j(t)$
satisfying
$j(t)={\textrm{o}}(t^{2/3})$
as
$t\to\infty$
,
\begin{equation*}V_j(t) \sim \dfrac{t^j}{{\tt m}^j j!}\exp\biggl(\dfrac{\gamma_0{\tt m}j^2}{t}\biggr),\quad t\to\infty,\end{equation*}
where
\begin{equation}\gamma_0\,:\!=\, \int_{[0,\,\infty)}{\textrm{d}} (V(y)-{\tt m}^{-1}y)=\lim_{t\to\infty}(V(t)-{\tt m}^{-1}t)=\dfrac{\mathbb{E}\xi^2}{2{\tt m}^2}-\dfrac{\mathbb{E}\eta}{{\tt m}}\end{equation}
may be positive, negative, or zero.
Remark 2.2. Assume that
$(\xi, \eta)=(|\!\log W|, |\!\log(1-W)|)$
, where W is a random variable having uniform distribution on [0, 1]. Then both
$\xi$
and
$\eta$
have the exponential distribution of unit mean. Therefore
\begin{equation*}V(t)=\sum_{i\geq 1}\mathbb{P}\{S_{i-1}+\eta_i \leq t\}=\sum_{i\geq 1}\mathbb{P}\{S_{i} \leq t\}=U(t)-1=t,\quad t\geq 0,\end{equation*}
where the last equality follows from
$U(t)=t+1$
for
$t\geq 0$
; see for instance the bottom of page 211 of [Reference Resnick25]. Thus
$V(t)=t$
for
$t\geq 0$
and
\begin{equation*}V_j(t)=\int_0^t V_{j-1}(y)\,{\textrm{d}} y=\dfrac{t^j}{j!},\quad j\geq 2,\ t\geq 0,\end{equation*}
where the last equality follows by induction. This is in line with the asymptotics provided by Theorem 2.2, for, in this case,
$\gamma_0=0$
and
${\tt m}=1$
.
2.3. Counterparts of the key renewal theorem and Blackwell’s theorem for intermediate generations
We start by recalling a few standard notions of renewal theory.
Let
$d>0$
. The distribution of
$\xi$
is d-lattice if it is concentrated on the set
$(dn)_{n\in\mathbb{N}_0}$
and not concentrated on the set
$(d_1n)_{n\in\mathbb{N}_0}$
for any
$d_1>d$
, where
$\mathbb{N}_0\,:\!=\, \mathbb{N}\cup \{0\}$
. The distribution of
$\xi$
is non-lattice if it is not d-lattice for any
$d>0$
.
A function
$f\colon [0,\infty)\to [0,\infty)$
is called directly Riemann integrable (dRi) on
$[0,\infty)$
if
-
(a)
$\overline{\sigma}(h)<\infty$
for each
$h>0$
, and -
(b)
$\lim_{h\to 0+} \big(\overline{\sigma}(h)-\underline{\sigma}(h)\big)=0$
, where
\begin{equation*}\overline{\sigma}(h)\,:\!=\, h\sum_{n\geq 1}\sup_{(n-1)h\leq y < nh} f(y)\quad \text{and}\quad \underline{\sigma}(h)\,:\!=\, h\sum_{n\geq 1}\inf_{(n-1)h\leq y<nh}f(y).\end{equation*}
Blackwell’s theorem is the most important and complicated result of renewal theory. Here is its formulation (see e.g. Theorem 1.10 of [Reference Mitov and Omey20]). Recall that U denotes the renewal function.
Proposition 2.2. Let
${\tt m}=\mathbb{E}\xi<\infty$
. If the distribution of
$\xi$
is non-lattice, then, for any fixed
$h>0$
,
\begin{equation*}\lim_{t\to\infty}(U(t+h)-U(t))=\dfrac{h}{{\tt m}}.\end{equation*}
If the distribution of
$\xi$
is d-lattice, then, for any fixed positive integer n,
\begin{equation*}\lim_{t\to\infty}(U(t+dn)-U(t))=\dfrac{dn}{{\tt m}}.\end{equation*}
If
${\tt m}=\infty$
, then both limits are equal to
$0$
.
Thus Blackwell’s theorem reads a bit differently for non-lattice and lattice distributions, which justifies the necessity of distinguishing between these types of distribution. The same dichotomy is also needed for the key renewal theorem; see for instance Theorem 1.12 of [Reference Mitov and Omey20].
In renewal theory the key renewal theorem is usually obtained as a corollary to Blackwell’s theorem; see for instance [Reference Resnick25, pp. 241–242]. We proceed differently by first proving a counterpart of the key renewal theorem (Theorem 2.3) and then obtain a counterpart of Blackwell’s theorem (Corollary 2.1) as a corollary.
Theorem 2.3. Let
$f\colon [0,\infty)\to [0,\infty)$
be a directly Riemann integrable function on
$[0,\infty)$
. Assume that either
$\textrm{(a)}$
or
$\textrm{(b)}$
below holds true.
-
(a) The distribution of
$\xi$
is non-lattice, the conditions of Theorem 2.1 hold and
$j(t)={\textrm{o}}\big(t^{(r-1)/2}\big)$
as
$t\to\infty$
, with the same
$r\in(1,2]$
as in Theorem 2.1. -
(b) The conditions of Theorem 2.2 hold and
$j(t)={\textrm{o}}(t^{2/3})$
as
$t\to\infty$
.
Then
\begin{equation*} (f\ast V_j)(t)=\int_{[0,\,t]}f(t-y)\,{\textrm{d}} V_j(y) \sim \biggl(\dfrac{1}{{\tt m}}\int_0^\infty f(y)\,{\textrm{d}} y\biggr) V_{j-1}(t),\quad t\to\infty,\end{equation*}
where
${\tt m}=\mathbb{E}\xi<\infty$
, and
$V_{j-1}(t)$
on the right-hand side can be replaced with
$t^{j-1}/(m^{j-1} (j-1)!)$
in the case
$\textrm{(a)}$
, or with
$t^{j-1}/(m^{j-1} (j-1)!)\exp(\gamma_0{\tt m}j^2/t)$
in the case
$\textrm{(b)}$
.
Remark 2.3. In part (b) of Theorem 2.3, one of the assumptions, coming from Theorem 2.2, is that the distribution of
$\xi$
is spread out. We note that every spread out distribution is non-lattice but not vice versa. To justify the second claim, observe that the distribution concentrated at points 1 and
$\sqrt{2}$
is non-lattice but not spread out.
Upon taking
$f(y)=\mathbb{1}_{[0,\,h)}(y)$
in Theorem 2.3, we immediately obtain the following.
Corollary 2.1. Let
$h>0$
be fixed. Under the assumptions of Theorem 2.3,
\begin{equation*} V_j(t+h)-V_j(t) \sim \dfrac{h}{m}V_{j-1}(t),\quad t\to\infty.\end{equation*}
2.4. Some previously known results
In this section we collect two previously known facts concerning the asymptotic behavior of
$N_j$
in the intermediate generations. They are borrowed from [Reference Iksanov, Marynych and Samoilenko16] and stated here for completeness and the reader’s convenience. We write
${\overset{{\textrm{f.d.d.}}}\longrightarrow}$
to denote weak convergence of finite-dimensional distributions.
Theorem 2.4. (Multivariate central limit theorem for
$(N_j(t))_{t\geq 0}$
.)Assume that
${\tt s}^2={\textrm{Var}}\,\xi\in (0,\infty)$
and
$\mathbb{E} \eta<\infty$
. Let
$j=j(t)$
be any positive integer-valued function satisfying
$j(t)\to \infty$
and
$j(t)={\textrm{o}}(t^{1/2})$
as
$t\to\infty$
. Then, as
$t\to\infty$
,
\begin{equation}\biggl(\dfrac{\lfloor j(t)\rfloor^{1/2}(\lfloor j(t)u\rfloor-1)!}{({\tt s}^2{\tt m}^{-2\lfloor j(t)u\rfloor-1}t^{2\lfloor j(t)u\rfloor-1})^{1/2}}\bigl(N_{\lfloor j(t)u\rfloor}(t)-V_{\lfloor j(t)u \rfloor}(t)\bigr)\biggr)_{u>0}{\overset{{\textrm{f.d.d.}}}\longrightarrow} \biggl(\int_{[0,\,\infty)}{\textrm{e}}^{-uy}{\textrm{d}} B(y)\biggr)_{u>0},\end{equation}
where
$(B(v))_{v\geq 0}$
is a standard Brownian motion.
According to Proposition 3.1 and Theorems 3.2 and 3.3 of [Reference Buraczewski, Dovgay and Iksanov6], the centering
$V_{\lfloor j(t)u \rfloor}(t)$
in (2.4) can be replaced by its leading term
\begin{equation*}t^{\lfloor j(t)u \rfloor}/\big((\lfloor j(t)u \rfloor)!{\tt m}^{\lfloor j(t)u \rfloor}\big),\end{equation*}
provided that
$j(t)={\textrm{o}}(t^{1/3})$
. For functions
$t\mapsto j(t)$
which grow faster, this is not always the case. Plainly, the possibility/impossibility of such a replacement is justified by the second-order behavior of
$V_j$
. It should come as no surprise that second-order results for
$V_j$
require more restrictive assumptions on the distributions of
$\xi$
and
$\eta$
than the corresponding first-order results. The following proposition, which is concerned with the rate of convergence in the elementary renewal theorem for
$V_j$
, was proved in Proposition 8.1 of [Reference Iksanov, Marynych and Samoilenko16].
Proposition 2.3. Assume that the distribution of
$\xi$
has an absolutely continuous component, that
$\mathbb{E} {\textrm{e}}^{\beta_1\xi}<\infty$
,
$\mathbb{E} {\textrm{e}}^{\beta_2\eta}<\infty$
for some
$\beta_1,\beta_2>0$
, and
\begin{equation*}\gamma_0=\dfrac{\mathbb{E}\xi^2}{2{\tt m}^2}-\dfrac{\mathbb{E} \eta}{{\tt m}}>0.\end{equation*}
Then
\begin{equation}V_j(t)-\dfrac{t^j}{j!{\tt m}^j} \sim \dfrac{\gamma_0 jt^{j-1}}{(j-1)!{\tt m}^{j-1}},\quad t\to\infty ,\end{equation}
whenever
$j=j(t)={\textrm{o}}\big(t^{1/2}\big)$
as
$t\to\infty$
(j is allowed to be fixed).
Formula (2.5) can be thought of as a generalization of formulae (2.3) and (3.2). These provide the second-order behavior of the functions V and U, respectively.
3. Proofs
3.1. Preparatory results
Recall that U denotes the renewal function for
$(S_n)_{n\in\mathbb{N}_0}$
. According to Lorden’s inequality, which holds whenever
$\mathbb{E}\xi^2<\infty$
,
\begin{equation}U(t)-{\tt m}^{-1}t \leq c_0,\quad t\geq 0,\end{equation}
where
$c_0\,:\!=\, \mathbb{E} \xi^2/{\tt m}^2$
and
${\tt m}=\mathbb{E}\xi<\infty$
. See [Reference Carlsson and Nerman7] for an elegant proof. We also note that
\begin{equation}\lim_{t\to\infty}(U(t)-{\tt m}^{-1}t)=\dfrac{\mathbb{E}\xi^2}{2{\tt m}^2}\end{equation}
provided that the distribution of
$\xi$
is non-lattice and
$\mathbb{E}\xi^2<\infty$
; see for instance Example 3.10.3 of [Reference Resnick25]. Further, by Wald’s identity (see [Reference Asmussen2, Proposition A10.2(a)]) and the definition of
$\nu(t)$
given in (1.1),
$t\leq \mathbb{E} S_{\nu(t)}={\tt m} \mathbb{E}\nu(t)={\tt m}U(t)$
. Thus
\begin{equation}U(t)\geq {\tt m}^{-1}t,\quad t\geq 0.\end{equation}
Since
$V(t)\leq U(t)$
for
$t\geq 0$
, we infer that
\begin{equation*} V(t)-{\tt m}^{-1}t \leq c_0,\quad t\geq 0.\end{equation*}
On the other hand, assuming that
$\mathbb{E}\eta<\infty$
(whereas the assumption
$\mathbb{E}\xi^2<\infty$
is not needed here),
\begin{align}V(t)-{\tt m}^{-1}t&=\int_{[0,\,t]}(U(t-y)-{\tt m}^{-1}(t-y))\,{\textrm{d}} G(y)-{\tt m}^{-1} \int_0^t (1-G(y))\,{\textrm{d}} y\notag\\[4pt]&\geq-{\tt m}^{-1}\int_0^t (1-G(y))\,{\textrm{d}} y\notag\\[4pt]&\geq -{\tt m}^{-1}\mathbb{E}\eta,\end{align}
using
$U(t)\geq {\tt m}^{-1}t$
. Thus we have shown that, under the assumptions
$\mathbb{E}\xi^2<\infty$
and
$\mathbb{E}\eta<\infty$
,
\begin{equation*} \big|V(t)-{\tt m}^{-1}t\big|\leq c_L,\quad t\geq 0,\end{equation*}
where
$c_L=\max(c_0, {\tt m}^{-1}\mathbb{E}\eta)$
.
Let
$u,v,w\colon \mathbb{R}\mapsto \mathbb{R}$
be functions of locally bounded variation. Since the Lebesgue–Stieltjes convolution
$u\ast v(t)=\int_\mathbb{R} u(t-y)\,{\textrm{d}} v(y)$
for
$t\in\mathbb{R}$
will be used frequently in what follows, we recall its elementary properties, which follow immediately from the definition.
Commutativity.
$u\ast v =v\ast u$
.
Associativity.
$(u\ast v)\ast w = u\ast(v\ast w)$
.
Distributivity.
$(u+v)\ast w=(u\ast w) +(v\ast w)$
.
Existence of the identity. If
$z(t)=\mathbb{1}_{[0,\infty)}(t)$
, then
$u\ast z=z\ast u = u$
. Thus the function z is the identity with respect to the Lebesgue–Stieltjes convolution.
Further properties of the convolution operation can be found in Section 3.2 of [Reference Resnick25] or Section 1.3.1 of [Reference Rudin26].
3.2. Results on convolution powers of functions of linear growth and proofs of Theorems 2.1 and 2.2
The results presented here are concerned with the following purely analytic problem. Assume that a non-decreasing function f exhibits linear growth, that is,
$f(t) \sim at$
as
$t\to\infty$
for some
$a>0$
. Then, for fixed
$j\in\mathbb{N}$
,
\begin{equation*}f^{\ast(j)}(t) \sim \dfrac{a^j t^j}{j!},\quad t\to\infty.\end{equation*}
Imposing various assumptions on the behavior of
$f(t)-at$
, we shall extend these asymptotics to the case when
$j=j(t)$
diverges to infinity as
$t\to\infty$
.
Proposition 3.1. Let
$f\colon \mathbb{R}\to [0,\,\infty)$
be a non-decreasing right-continuous function vanishing on the negative half-line and satisfying
\begin{equation}f(t)=at+{\textrm{O}}(t^{\alpha}),\quad t\to\infty\end{equation}
for some
$a>0$
and
$\alpha\in [0,1)$
. Then, for any integer-valued function
$j=j(t)$
such that
$j(t)={\textrm{o}}(t^{(1-\alpha)/2})$
as
$t\to\infty$
,
\begin{equation*}f_j(t)\,:\!=\, f^{\ast(j)}(t) \sim \dfrac{a^j t^j}{j!},\quad t\to\infty.\end{equation*}
Proof. According to (3.5) there exists
$C\geq 1$
such that
\begin{equation}-C(t+1)^{\alpha} \leq f(t)-at \leq C(t+1)^{\alpha},\quad t\geq 0.\end{equation}
For
$j\in\mathbb{N}$
and
$t\geq 0$
, put
\begin{equation*}r_j(t)\,:\!=\, \int_{[0,\,t]}f_j(t-y)\,{\textrm{d}} (f(y)-ay)=\int_{[0,\,t]}(f(t-y)-a(t-y))\,{\textrm{d}} f_{j}(y)\end{equation*}
and note that
\begin{equation*}f_j(t)=r_{j-1}(t)+a\int_0^t f_{j-1}(y)\,{\textrm{d}} y,\quad j\geq 2,\ t\geq 0.\end{equation*}
By virtue of (3.6), we conclude that
\begin{equation*}|r_j(t)|\leq C(t+1)^{\alpha}f_j(t),\quad j\in\mathbb{N},\ t\geq 0.\end{equation*}
Using this bound and mathematical induction, we obtain
\begin{equation}W_j^{-}(t)\leq f_j(t)\leq W_j^{+}(t),\quad j\in\mathbb{N},\ t\geq 0,\end{equation}
where
$W_j^{\pm}$
is defined recursively by
$W_0^{\pm}(t)\,:\!=\, 1$
and
\begin{equation*}W_j^{\pm}(t)=\biggl(\pm C(t+1)^{\alpha}W^{\pm}_{j-1}(t)+a\int_{0}^t W_{j-1}^{\pm}(y)\,{\textrm{d}} y\biggr)_{+},\quad j\in\mathbb{N},\ t\geq 0.\end{equation*}
Here we recall that
$x_{+}=\max(x,0)$
, and note that taking the non-negative part is only relevant for
$W_j^{-}$
ensuring its non-negativity, whereas it can be omitted for
$W_j^+$
.
It remains to show that
\begin{equation}W_j^{\pm}(t) \sim \dfrac{a^j t^j}{j!},\quad t\to\infty.\end{equation}
To this end, we first prove by induction that
\begin{equation}W_j^{+}(t)\leq \dfrac{a^j t^j}{j!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(t+1)^{\alpha(j-i)+i}}{i!},\quad j\in\mathbb{N},\ t\geq 0.\end{equation}
Whereas for
$j=1$
this follows immediately because
$W_1^{+}(t)=C(t+1)^{\alpha}+at$
, the induction step works as follows:
\begin{align*} &W_{j+1}^+(t)\\ &\quad \leq C(t+1)^{\alpha}\biggl(\dfrac{a^j t^j}{j!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(t+1)^{\alpha(j-i)+i}}{i!}\biggr)\\&\quad \quad\, +a\int_0^{t}\biggl(\dfrac{a^j y^j}{j!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(y+1)^{\alpha(j-i)+i}}{i!}\biggr)\,{\textrm{d}} y\\&\quad \leq \sum_{i=0}^{j}\binom{j}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!}+\dfrac{a^{j+1}t^{j+1}}{(j+1)!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^{i+1}C^{j-i}}{i!}\dfrac{(t+1)^{\alpha(j-i)+i+1}}{\alpha(j-i)+i+1}\\&\quad \leq \dfrac{a^{j+1}t^{j+1}}{(j+1)!}+\sum_{i=0}^{j}\binom{j}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^{i+1}C^{j-i}}{(i+1)!}(t+1)^{\alpha(j-i)+i+1}\\&\quad = \dfrac{a^{j+1}t^{j+1}}{(j+1)!}+\sum_{i=0}^{j}\binom{j}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!}+\sum_{i=1}^{j}\binom{j}{i-1}\dfrac{a^iC^{j+1-i}}{i!}(t+1)^{\alpha(j+1-i)+i}\\&\quad = \dfrac{a^{j+1}t^{j+1}}{(j+1)!}+\sum_{i=0}^{j}\binom{j+1}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!},\end{align*}
using the binomial identity
$\binom{j}{i}+\binom{j}{i-1}=\binom{j+1}{i}$
for the last step. Further, using
$j(t)={\textrm{o}}(t)$
, we obtain
\begin{align*}\dfrac{j!}{a^j t^j}\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(t+1)^{\alpha(j-i)+i}}{i!}&\sim\dfrac{j!}{a^j (t+1)^j}\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(t+1)^{\alpha(j-i)+i}}{i!}\\&\leq \sum_{i=0}^{j-1}\biggl(\dfrac{j!}{i!}\biggr)^{2}\biggl(\dfrac{C}{a}\biggr)^{j-i}(t+1)^{(1-\alpha)(i-j)}\\& \leq \sum_{i=0}^{j-1}\big(j^{j-i}\big)^2\big(Ca^{-1}\big)^{j-i}(t+1)^{(1-\alpha)(i-j)}\\&\leq \sum_{i\geq 1} \biggl(\dfrac{Ca^{-1} j^2}{(t+1)^{1-\alpha}}\biggr)^i\\&=\dfrac{Ca^{-1} j^2}{(t+1)^{1-\alpha}}\biggl(1-\dfrac{Ca^{-1} j^2}{(t+1)^{1-\alpha}}\biggr)^{-1}.\end{align*}
Thus, in view of the assumption
$j(t)={\textrm{o}}(t^{(1-\alpha)/2})$
, we have
\begin{equation}\limsup_{t\to\infty}\dfrac{j!}{a^j t^j}W_j^{+}(t)\leq 1.\end{equation}
We use similar reasoning to prove that
\begin{equation}W_j^{-}(t)\geq \biggl(\dfrac{a^j t^j}{j!}-\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(t+1)^{\alpha(j-i)+i}}{i!}\biggr)_{+},\quad j\in\mathbb{N},\ t\geq 0.\end{equation}
While (3.11) is obviously true for
$j=1$
, we obtain with the help of induction, for
$j\geq 2$
,
\begin{align*}W_{j+1}^-(t)&\geq -C(t+1)^{\alpha}W_{j}^{-}(t)+a\int_0^t W_{j}^{-}(y)\,{\textrm{d}} y\\&\geq -C (t+1)^\alpha W_{j}^{+}(t)+a\int_0^t W_{j}^{-}(y)\,{\textrm{d}} y\\&\geq -C(t+1)^{\alpha}W_{j}^{+}(t)+a\int_0^t \biggl(\dfrac{a^j y^j}{j!}-\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^iC^{j-i}(y+1)^{\alpha(j-i)+i}}{i!}\biggr)\,{\textrm{d}} y\\&\geq -C(t+1)^{\alpha}\biggl(\dfrac{a^j t^j}{j!}+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^iC^{j-i}(t+1)^{\alpha(j-i)+i}}{i!}\biggr)\\&\quad\, +a\int_0^t \biggl(\dfrac{a^j y^j}{j!}-\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^i C^{j-i}(y+1)^{\alpha(j-i)+i}}{i!}\biggr)\,{\textrm{d}} y\\&\geq \dfrac{a^{j+1}t^{j+1}}{(j+1)!}-\biggl(\sum_{i=0}^{j}\binom{j}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!} \\&\quad\,+\sum_{i=0}^{j-1}\binom{j}{i}\dfrac{a^{i+1}C^{j-i}}{i!}\int_0^t (y+1)^{\alpha(j-i)+i}{\textrm{d}} y\biggr)\\&\geq \dfrac{a^{j+1}t^{j+1}}{(j+1)!}-\sum_{i=0}^{j}\binom{j+1}{i}\dfrac{a^i C^{j+1-i}(t+1)^{\alpha(j+1-i)+i}}{i!}.\end{align*}
We have used (3.7) and (3.9) for the second and fourth inequalities, respectively. Since
$W_{j+1}^-$
is non-negative, we arrive at (3.11). Thus
\begin{equation}\liminf_{t\to\infty}\dfrac{j!}{a^j t^j}W_j^{-}(t)\geq 1.\end{equation}
Combining (3.10) and (3.12) yields (3.8), thereby finishing the proof of Proposition 3.1.
Proof of Theorem 2.1. It is enough to show that the function V satisfies all the assumptions of Proposition 3.1 with
$a={\tt m}^{-1}$
and
$\alpha=2-r$
, where
$r=2$
in case (i). We first prove that
\begin{equation}U(t)={\tt m}^{-1}t+{\textrm{O}}(t^{2-r}),\quad t\to\infty.\end{equation}
Case (i). In this case (3.13) follows from (3.3) and Lorden’s inequality (3.1).
Case (ii). Let
$S_0^\ast$
be a random variable with distribution
\begin{equation*}\mathbb{P}\{S_0^\ast\in{\textrm{d}} x\}={\tt m}^{-1}\mathbb{P}\{\xi>x\}\mathbb{1}_{(0,\infty)}(x)\,{\textrm{d}} x.\end{equation*}
Note that, by formula (2) of [Reference Carlsson and Nerman7],
\begin{equation}\mathbb{E} U(t-S_0^\ast)={\tt m}^{-1}t,\quad t\geq 0.\end{equation}
Then
\begin{equation*}U(t)-{\tt m}^{-1}t=\int_{[0,\,t]}\mathbb{P}\{S_0^\ast>t-y\}\,{\textrm{d}} U(y) \sim {\tt m}^{-1}\int_0^t \mathbb{P}\{S_0^\ast>y\}\,{\textrm{d}} y,\quad t\to\infty,\end{equation*}
where the equality is simply (3.14), and the asymptotic relation follows from Theorem 4 of [Reference Sgibnev28]. The cited theorem applies because
$\mathbb{E}\xi^2=\infty$
entails
$\mathbb{E} S_0^\ast=\infty$
. Observe that
\begin{equation*}\mathbb{P}\{S_0^\ast>t\}={\tt m}^{-1}\int_t^{\infty} \mathbb{P}\{\xi>y\}\,{\textrm{d}} y={\textrm{O}}\big(t^{-(r-1)}\big)\quad \text{as $t\to\infty$,}\end{equation*}
as a consequence of
$\mathbb{P}\{\xi>t\}={\textrm{O}}(t^{-r})$
. In view of this we infer that
\begin{equation*}U(t)-{\tt m}^{-1}t \sim {\tt m}^{-1}\int_0^t \mathbb{P}\{S_0^\ast>y\}\,{\textrm{d}} y={\textrm{O}}\big(t^{2-r}\big),\quad t\to\infty,\end{equation*}
and thereupon (3.13).
It remains to check that under the assumption
$\mathbb{E}(\eta\wedge t)={\textrm{O}}\big(t^{2-r}\big)$
as
$t\to\infty$
,
\begin{equation}V(t)={\tt m}^{-1}t+{\textrm{O}}\big(t^{2-r}\big),\quad t\to\infty.\end{equation}
Since
$\int_0^t (1-G(y))\,{\textrm{d}} y=\mathbb{E} (\eta \wedge t)$
, an equivalent form of the equality in (3.4) is
\begin{equation*}V(t)-{\tt m}^{-1}t=\int_{[0,\,t]}\big(U(t-y)-{\tt m}^{-1}(t-y)\big)\,{\textrm{d}} G(y)-{\tt m}^{-1}\mathbb{E} (\eta\wedge t).\end{equation*}
With this relation at hand, (3.15) follows because each summand is
${\textrm{O}}(t^{2-r})$
by (3.13) and the assumption of the theorem, respectively.
The next result provides asymptotics of convolution powers
$f^{\ast(j)}$
for
$j=j(t)$
which may grow faster than
$t^{1/2}$
under the assumption that the function
$|f(t)-at|$
has a finite total variation and satisfies an additional integrability assumption. We shall use the convention that, for a function
$x\colon \mathbb{R}\to\mathbb{R}$
,
$x^{\ast(0)}(t)=\mathbb{1}_{[0,\infty)}(t)$
,
$t\in\mathbb{R}$
. Also, we shall write
$\mathcal{V}_I(x)$
for the total variation of x on the (possibly infinite) interval I. Finally, if x is a function of a finite total variation on
$[a,\,b]$
,
$-\infty\leq a<b\leq\infty$
and y is a measurable function on I, we stipulate that
\begin{equation*}\int_{[a,\,b]} y(t)|{\textrm{d}} x(t)|=\int_{[a,\,b]} y(t)\,{\textrm{d}} (\mathcal{V}_{[a,\,t]}(x)),\end{equation*}
where the integral on the right-hand side is understood in the Lebesgue–Stieltjes sense.
Proposition 3.2. Let
$f\colon \mathbb{R}\mapsto [0,\,\infty)$
be a non-decreasing right-continuous function vanishing on the negative half-line. Assume that the function
$\varepsilon$
defined by
\begin{equation}\varepsilon(t)\,:\!=\, f(t)-at,\quad t\geq 0,\end{equation}
for some
$a>0$
, satisfies
\begin{equation}\int_{[0,\,\infty)}y|{\textrm{d}} \varepsilon(y)|<\infty.\end{equation}
Then, for any integer-valued function
$j=j(t)$
such that
$j(t)={\textrm{o}}\big(t^{2/3}\big)$
as
$t\to\infty$
,
\begin{equation}f_j(t)\,:\!=\, f^{\ast(j)}(t) \sim \dfrac{a^j t^j}{j!}\exp\biggl(\dfrac{\gamma_0 j^2}{a t}\biggr),\quad t\to\infty,\end{equation}
where
\begin{equation*}\gamma_0\,:\!=\, \int_{[0,\,\infty)}{\textrm{d}} \varepsilon(y)=\lim_{t\to\infty}(f(t)-at). \end{equation*}
Proof. The function
$\varepsilon$
, as the difference of two non-decreasing functions, has a finite total variation on every finite interval. In particular, (3.17) entails
\begin{equation*}\int_{[0,\,\infty)}|{\textrm{d}} \varepsilon(y)|\leq \int_{[0,\,1)}|{\textrm{d}} \varepsilon(y)|+\int_{[1,\,\infty)}y|{\textrm{d}} \varepsilon(y)|<\infty.\end{equation*}
Thus
$\varepsilon$
has a finite total variation on
$[0,\infty)$
. Write
\begin{equation*}\int_0^{\infty}|\varepsilon(y)-\gamma_0|{\textrm{d}} y=\int_0^{\infty}\bigg|\int_{(y,\,\infty)}{\textrm{d}} \varepsilon(z)\bigg|{\textrm{d}} y\leq \int_0^{\infty}\int_{(y,\,\infty)}|{\textrm{d}} \varepsilon(z)|{\textrm{d}} y=\int_{[0,\,\infty)}y|{\textrm{d}} \varepsilon(y)|<\infty,\end{equation*}
using integration by parts for the last equality. Hence (3.17) implies that
\begin{equation}\int_0^\infty |\varepsilon(y)-\gamma_0|{\textrm{d}} y<\infty.\end{equation}
Now we modify (3.16) in a neighborhood of the origin, so that the essential properties of
$\varepsilon$
given by (3.17) and (3.19) are preserved. Put
\begin{equation}f(t)=(at+\gamma_0)_++\widetilde{\varepsilon}(t)\,:\!= \ell(t)+\widetilde{\varepsilon}(t),\quad t\in\mathbb{R}.\end{equation}
Note that both summands can be non-zero in a bounded left neighborhood of the origin, yet
\begin{equation*} \int_{\mathbb{R}}|\widetilde{\varepsilon}(y)|{\textrm{d}} y<\infty\quad\text{and}\quad \int_{\mathbb{R}}|y| |{\textrm{d}} \widetilde{\varepsilon}(y)|<\infty\end{equation*}
because
$t\mapsto \varepsilon(t)-\gamma_0-\widetilde{\varepsilon}(t)$
has a bounded support. The advantage of (3.20) is justified by two facts:
-
(i) a simple formula for the convolution powers of
$\ell$
, namely (3.21)
\begin{equation}\ell^{\ast(j)}(t)=\dfrac{(at+\gamma_0 j)^j_{+}}{j!},\quad j\in\mathbb{N},\ t\in\mathbb{R},\end{equation}
-
(ii) the function
$\widetilde{\varepsilon}$
decays sufficiently fast and, as such, is asymptotically negligible in the sense that
$\ell^{\ast(j)}(t)\sim f^{\ast(j)}(t)$
as
$t\to\infty$
.
To check (3.21) we use mathematical induction. Whereas the formula is trivial for
$j=1$
, the induction step works as follows: for
$t\geq -a^{-1}\gamma_0(j+1)$
,
\begin{align*}\ell^{\ast(j+1)}(t)&=\int_{\mathbb{R}}\dfrac{(a(t-y)+\gamma_0 j)^j_{+}}{j!}{\textrm{d}} \ell(y)\\&=a\int_{-\gamma_0 a^{-1}}^{t+j\gamma_0 a^{-1}}\dfrac{(a(t-y)+\gamma_0 j)^j}{j!}{\textrm{d}} y\\&=\int_0^{at+\gamma_0(j+1)}\dfrac{z^j}{j!}{\textrm{d}} z\\&=\dfrac{(at+\gamma_0(j+1))^{j+1}}{(j+1)!},\end{align*}
and
$\ell^{\ast(j+1)}(t)=0$
for
$t<-a^{-1}\gamma_0(j+1)$
.
As far as point (ii) is concerned, using (3.20), commutativity and distributivity of the Lebesgue–Stieltjes convolution yields
\begin{equation*}f^{\ast(j)}(t)=\ell^{\ast(j)}(t)+\sum_{k=0}^{j-1}\binom{j}{k}(\ell^{\ast(k)}\ast\widetilde{\varepsilon}^{\ast(j-k)})(t),\quad t\in \mathbb{R}.\end{equation*}
We are going to show that the second summand is asymptotically negligible with respect to
$\ell^{\ast(j)}(t)$
whenever
$j(t)={\textrm{o}}\big(t^{2/3}\big)$
. Assume this has already been done. Then (3.18) follows immediately because, for large enough t,
\begin{equation*}f^{\ast(j)}(t) = \ell^{\ast(j)}(t) = \dfrac{a^jt^j}{j!}\biggl(1+\dfrac{\gamma_0 j}{at}\biggr)^j = \dfrac{a^jt^j}{j!}\exp\biggl(j\log \biggl(1+\dfrac{\gamma_0j}{at}\biggr)\biggr).\end{equation*}
The right-hand side is asymptotically equivalent to
\begin{equation*}\dfrac{a^jt^j}{j!}\exp\biggl(\dfrac{\gamma_0 j^2}{at}\biggr)\end{equation*}
whenever
$j=j(t)={\textrm{o}}\big(t^{2/3}\big)$
as
$t\to\infty$
.
Passing to the analysis of
\begin{equation*}R_j(t)\,:\!=\, \sum_{k=0}^{j-1}\binom{j}{k}(\ell^{\ast(k)}\ast\widetilde{\varepsilon}^{\ast(j-k)})(t),\quad t\geq 0 ,\end{equation*}
we first check that
\begin{equation}\mathcal{V}_{\mathbb{R}}(\ell\ast \widetilde{\varepsilon})\leq \widetilde{C}<\infty\end{equation}
for an absolute constant
$C>0$
. For
$t\in\mathbb{R}$
,
\begin{equation*}(\ell\ast\widetilde{\varepsilon})(t)=\int_{\mathbb{R}}\widetilde{\varepsilon}(t-y)\,{\textrm{d}} \ell(y)=a\int_{-a^{-1}\gamma_0}^\infty \widetilde{\varepsilon}(t-y)\,{\textrm{d}} y=a\int_{-\infty}^{t+a^{-1}\gamma_0}\widetilde{\varepsilon}(y)\,{\textrm{d}} y.\end{equation*}
Thus (3.22) holds with
$\widetilde{C}\,:\!=\, a\int_{\mathbb{R}}|\widetilde{\varepsilon}(y)|{\textrm{d}} y$
. Put
\begin{equation*}g_{i,j}(t)\,:\!=\, \mathcal{V}_{(-\infty,\,t]}\big(\ell^{\ast(i)} \ast \widetilde{\varepsilon}^{\ast(j)}\big),\quad i,j\in\mathbb{N}_0,\ t\in\mathbb{R}.\end{equation*}
Then, for
$i,j\in\mathbb{N}$
, taking into account commutativity of the Lebesgue–Stieltjes convolution, we infer that
\begin{align*}g_{i,j}(t)&=\mathcal{V}_{(-\infty,\,t]}((\ell^{\ast(i-1)} \ast \widetilde{\varepsilon}^{\ast(j-1)})\ast (\ell\ast \widetilde{\varepsilon}))\\&\leq \mathcal{V}_{(-\infty,\,t]}(\ell^{\ast(i-1)} \ast \widetilde{\varepsilon}^{\ast(j-1)})\mathcal{V}_{(-\infty,\,t]} (\ell\ast \widetilde{\varepsilon})\\&\leq \mathcal{V}_{(-\infty,\,t]}(\ell^{\ast(i-1)} \ast \widetilde{\varepsilon}^{\ast(j-1)})\mathcal{V}_{\mathbb{R}} (\ell\ast \widetilde{\varepsilon})\\&\leq \widetilde{C}g_{i-1,j-1}(t),\quad t\in\mathbb{R}.\end{align*}
Here we have used the fact that the total variation of the convolution of two functions is bounded by the product of their total variations; see Theorem 1.3.2(c) of [Reference Rudin26]. Iterating this inequality, we conclude that
\begin{align}|R_j(t)|&\leq \sum_{k=0}^{j-1}\binom{j}{k}g_{k,j-k}(t)\notag\\&\leq \sum_{k\leq j/2}\binom{j}{k}\widetilde{C}^k g_{0,j-2k}(t)+\sum_{j/2<k<j}\binom{j}{k}\widetilde{C}^{j-k} g_{2k-j,0}(t),\quad t\in\mathbb{R}.\end{align}
Note that
\begin{equation*}g_{0,j-2k}(t)\leq \mathcal{V}_{\mathbb{R}}\big(\widetilde{\varepsilon}^{\ast(j-2k)}\big)\leq \big(\mathcal{V}_{\mathbb{R}}(\widetilde{\varepsilon})\big)^{j-2k}\leq \widetilde{C}_1^{j-2k}\quad\text{for } \widetilde{C}_1\,:\!=\, \int_{\mathbb{R}}|{\textrm{d}} \widetilde{\varepsilon}(y)|<\infty.\end{equation*}
Therefore the first sum on the right-hand side of (3.23) satisfies
\begin{align*}\sum_{k\leq j/2}\binom{j}{k}\widetilde{C}^k g_{0,j-2k}(t)&\leq \sum_{k\leq j/2}\binom{j}{k}\widetilde{C}^k\widetilde{C}^{j-2k}_1\\&\leq \big(\widetilde{C}\widetilde{C}_1^{-1}+\widetilde{C}_1\big)^j\\&={\textrm{o}}\biggl(\dfrac{a^jt^j}{j!}\biggl(1+\dfrac{\gamma_0 j}{at}\biggr)^j\biggr),\quad t\to\infty,\end{align*}
for
$b^j=b^{j(t)}$
grows more slowly than
\begin{equation*}\dfrac{a^jt^j}{j!}\biggl(1+\dfrac{\gamma_0 j}{at}\biggr)^j\quad\text{as $t\to\infty$}\end{equation*}
for an arbitrary finite constant
$b>0$
. Now we analyze the second sum on the right-hand side of (3.23):
\begin{align*}\sum_{j/2<k<j}\binom{j}{k}\widetilde{C}^{j-k} g_{2k-j,0}(t)&=\sum_{j/2<k<j}\binom{j}{k}\widetilde{C}^{j-k}\mathcal{V}_{(-\infty,\,t]}\big(\ell^{\ast(2k-j)}\big)\\&=\sum_{j/2<k<j}\binom{j}{k}\widetilde{C}^{j-k}\ell^{\ast(2k-j)}(t)\\&=\sum_{j/2<k<j}\binom{j}{k}\widetilde{C}^{j-k}\dfrac{(at +\gamma_0(2k-j))^{2k-j}}{(2k-j)!}\\&=\sum_{1\leq k<j/2}\binom{j}{k}\widetilde{C}^{k}\dfrac{(at +\gamma_0(j-2k))^{j-2k}}{(j-2k)!}.\end{align*}
Here the second equality follows from monotonicity of
$\ell$
and the third equality holds for t large enough. It is important for what follows that, for
$k<j/2$
and
$t>0$
,
\begin{equation*}\dfrac{(at +\gamma_0(j-2k))^{j-2k}}{(j-2k)!}\leq \dfrac{a^{j-2k}t^{j-2k}}{(j-2k)!}\exp\biggl(\dfrac{\gamma_0 (j-2k)^2}{at}\biggr).\end{equation*}
Case
$\gamma_0\geq 0$
. We obtain, for
$t>0$
,
\begin{align*}\sum_{1\leq k<j/2}\binom{j}{k}\widetilde{C}^{k}\dfrac{(at +\gamma_0(j-2k))^{j-2k}}{(j-2k)!}&\leq \exp\biggl(\dfrac{\gamma_0 j^2}{at}\biggr)\sum_{1\leq k<j/2}\binom{j}{k}\widetilde{C}^{k}\dfrac{a^{j-2k}t^{j-2k}}{(j-2k)!}\\&=\dfrac{a^jt^j}{j!}\exp\biggl(\dfrac{\gamma_0 j^2}{at}\biggr)\sum_{1\leq k<j/2}\dfrac{(j!)^2}{(j-k)!(j-2k)!}\dfrac{1}{k!}\dfrac{\widetilde{C}^{k}}{a^{2k}t^{2k}}\\&\leq \dfrac{a^jt^j}{j!}\exp\biggl(\dfrac{\gamma_0 j^2}{at}\biggr)\sum_{k\geq 1}j^{3k}\dfrac{1}{k!}\dfrac{\widetilde{C}^{k}}{a^{2k}t^{2k}}\\&=\dfrac{a^jt^j}{j!}\exp\biggl(\dfrac{\gamma_0 j^2}{at}\biggr)\biggl(\exp\biggl(\dfrac{\widetilde{C}j^3}{a^2t^2}\biggr)-1\biggr).\end{align*}
The last factor converges to zero whenever
$j=j(t)={\textrm{o}}\big(t^{2/3}\big)$
, whence the claim.
Case
$\gamma_0<0$
. Arguing in the same vein, it is enough to check that
\begin{equation*}\sum_{1\leq k<j/2}\dfrac{1}{k!}\biggl(\dfrac{\widetilde{C}j^3}{a^2t^2}\biggr)^k\exp\biggl(\dfrac{\gamma_0(j-2k)^2}{at}\biggr)={\textrm{o}}\biggl(\exp\biggl(\dfrac{\gamma_0j^2}{at}\biggr)\biggr),\quad t\to\infty ,\end{equation*}
which is equivalent to
\begin{equation*}I_t\,:\!=\, \sum_{1\leq k<j/2}\dfrac{1}{k!}\biggl(\dfrac{\widetilde{C}j^3}{a^2t^2}\biggr)^k\exp\biggl(\dfrac{4|\gamma_0|k(j-k)}{at}\biggr)={\textrm{o}}(1),\quad t\to\infty.\end{equation*}
Invoking the inequality
\begin{equation*}\exp\biggl(\dfrac{4|\gamma_0|k(j-k)}{at}\biggr)\leq \exp(4|\gamma_0|a^{-1}k)\end{equation*}
for
$1\leq k<j$
and large enough t, we infer that
\begin{equation*}I_t\leq \sum_{1\leq k<j/2}\dfrac{1}{k!}\biggl(\dfrac{\widetilde{C}j^3\exp(4|\gamma_0|a^{-1})}{a^2t^2}\biggr)^k\leq\exp\biggl(\dfrac{\widetilde{C}j^3}{a^2t^2}\exp(4|\gamma_0|a^{-1})\biggr)-1 \to 0,\quad t\to\infty.\end{equation*}
The proof of Proposition 3.2 is complete.
Proof of Theorem 2.2. We intend to apply Proposition 3.2 with
$f=V$
,
$a={\tt m}^{-1}$
. To this end, it is enough to check that, under the assumptions of Theorem 2.2,
\begin{equation*}\int_{[0,\,\infty)}y\big|{\textrm{d}} (V(y)-{\tt m}^{-1}y)\big|<\infty.\end{equation*}
Recall that
$V=U\ast G$
, and let Id denote the identity function on
$[0,\infty)$
, that is,
$\textrm{Id}(t)\,:\!=\, t_{+}=t\mathbb{1}_{[0,\infty)}(t)$
for
$t\in\mathbb{R}$
. Then
\begin{equation*}V-{\tt m}^{-1}\textrm{Id}=(U-{\tt m}^{-1}\textrm{Id})\ast G-{\tt m}^{-1}(\textrm{Id}\ast (1-G)).\end{equation*}
Using this and integration by parts yields
\begin{align*}\int_{[0,\,\infty)}y|{\textrm{d}} (V(y)-{\tt m}^{-1}y)|&=-\int_{[0,\,\infty)}y{\textrm{d}} \mathcal{V}_{[y,\,\infty)}(V-{\tt m}^{-1}\textrm{Id})\\[4pt]&=\int_{[0,\,\infty)}\mathcal{V}_{[y,\,\infty)}(V-{\tt m}^{-1}\textrm{Id})\,{\textrm{d}} y\\[4pt]&\leq \int_{[0,\,\infty)}\mathcal{V}_{[y,\,\infty)}(U-{\tt m}^{-1}\textrm{Id})\,{\textrm{d}} y+{\tt m}^{-1}\int_{[0,\,\infty)}\mathcal{V}_{[y,\,\infty)}(\textrm{Id}\ast (1-G))\,{\textrm{d}} y\\[4pt]&=\int_{[0,\,\infty)}y|{\textrm{d}} (U(y)-{\tt m}^{-1}y)|+{\tt m}^{-1}\int_0^{\infty}\int_y^{\infty} (1-G(z))\,{\textrm{d}} z\,{\textrm{d}} y.\end{align*}
The first summand is finite by Remark 3.1.7(ii) of [Reference Frenk10], and the second is finite in view of the assumption
$\mathbb{E}\eta^2<\infty$
.
The explicit form of
$\gamma_0$
follows from the decomposition
\begin{equation*}V(t)-{\tt m}^{-1}t=\int_{[0,\,t]}(U(t-y)-{\tt m}^{-1}(t-y))\,{\textrm{d}} G(y)-{\tt m}^{-1}\int_{[0,\,t]}y{\textrm{d}} G(y)-{\tt m}^{-1}t(1-G(t)),\end{equation*}
in which the first summand converges to
$(2{\tt m}^2)^{-1}\mathbb{E}\xi^2$
by the dominated convergence theorem, (3.1) and (3.2), the second converges to
$-{\tt m}^{-1}\mathbb{E}\eta$
, and the third tends to zero as
$t\to\infty$
.
Finally, we give a general result on the behavior of
$f^{\ast(j)}$
for arbitrary
$j=j(t)={\textrm{o}}(t)$
. Unfortunately, this result can seldom be applied to the counting function V but is of independent interest and has at least two merits. On the one hand, it gives a probabilistic explanation of a rather mysterious appearance of the exponent in (3.18). On the other hand, it may be used for guessing the behavior of
$V_j$
for
$j=j(t)$
growing at least as fast as
$t^{2/3}$
.
Proposition 3.3. Let
$(\widetilde{S}_j)_{j\in\mathbb{N}_0}$
be a non-decreasing zero-delayed random walk with
$K(t)\,:\!=\, \mathbb{P}\{\widetilde{S}_1\leq t\}$
for
$t\in\mathbb{R}$
. Assume that, for some
$a>0$
,
\begin{equation*}f(t)=at-\int_0^t(1-K(y))\,{\textrm{d}} y,\quad t\geq 0.\end{equation*}
Then
\begin{equation*}f^{\ast(j)}(t)=\dfrac{\mathbb{E} \big(at-\widetilde{S}_j\big)_{+}^j}{j!},\quad j\in\mathbb{N},\ t\geq 0.\end{equation*}
In particular, if
$\mathbb{E} \widetilde{S}_1^2<\infty$
and
$j=j(t)={\textrm{o}}(t^{2/3})$
as
$t\to\infty$
, then (3.18)holds with
$\gamma_0=-\mathbb{E} \widetilde{S}_1$
.
Remark 3.1. In the setting of Proposition 3.3, assume that
$\mathbb{E} \widetilde{S}_1^3<\infty$
and
$j=j(t)={\textrm{o}}\big(t^{3/4}\big)$
as
$t\to\infty$
. Without going into details (which become rather technical), we state that
\begin{equation*}\mathbb{E}\big(at-\widetilde{S}_j\big)_+^j \sim a^jt^j\exp\big(\gamma_0 j^2/t+\big(\gamma_1/2-\gamma_0^2\big)j^3/t^2\big),\quad t\to\infty,\end{equation*}
where
$\gamma_0=-\mathbb{E} \widetilde{S}_1$
and
$\gamma_1\,:\!=\, \mathbb{E} \widetilde{S}_1^2$
.
3.3. Proof of Theorem 2.3
Our proof of Theorem 2.3 relies on counterparts for perturbed random walks of some standard renewal-theoretic results. We start by recalling that the renewal function U is subadditive, which means that
\begin{equation*}U(x+y)\leq U(x)+U(y),\quad x,y\in\mathbb{R}.\end{equation*}
This follows, for instance, from formula (5.7) of [Reference Gut12]. The counterpart of this inequality for the function V defined by
\begin{equation*}V(x)=\mathbb{E} N(x)=\sum_{i\geq 1}\mathbb{P}\{S_{i-1}+\eta_i\leq x\},\quad x\in\mathbb{R},\end{equation*}
is
\begin{equation}V(x+y)-V(x)\leq U(y),\quad x,y\in\mathbb{R}.\end{equation}
Indeed, for
$x,y\geq 0$
,
\begin{align} V(x+y)-V(x)&=\mathbb{E} (U(x+y-\eta)-U(x-\eta))\mathbb{1}_{\{\eta\leq x\}}+\mathbb{E} U(x+y-\eta)\mathbb{1}_{\{x<\eta\leq x+y\}}\notag \\ &\leq U(y)(\mathbb{P}\{\eta\leq x\}+\mathbb{P}\{x<\eta\leq x+y\}) \notag \\ &\leq U(y),\end{align}
using subadditivity and monotonicity of U for the penultimate inequality. If
$x,y<0$
, then both sides of (3.24) are zero. Finally, we use monotonicity of V to obtain the following: if
$x<0$
and
$y\geq 0$
, then
$V(x+y)-V(x)=V(x+y)\leq V(y)\leq U(y)$
, and if
$x\geq 0$
and
$y<0$
, then
$V(x+y)-V(x)\leq 0=U(y)$
.
Lemmas 3.1 and 3.2 below are counterparts for the function V of Blackwell’s theorem and the key renewal theorem, respectively. Observe that the presence of the
$\eta_i$
plays no role, and the results are of the same form as for renewal function U.
Lemma 3.1. Let
$h>0$
be any fixed number.
-
(a) Assume that the distribution of
$\xi$
is non-lattice and
${\tt m}=\mathbb{E}\xi<\infty$
. Then
\begin{equation*}\lim_{t\to\infty} (V(t+h)-V(t))={\tt m}^{-1}h.\end{equation*}
-
(b) Assume that
${\tt m}=\infty$
(the assumption that the distribution of
$\xi$
is non-lattice is not needed). Then (3.26)
\begin{equation}\lim_{t\to\infty} (V(t+h)-V(t))=0.\end{equation}
Lemma 3.2. Let
$f\colon \mathbb{R}\to \mathbb{R}$
be a dRi function on
$\mathbb{R}$
.
-
(a) Assume that
${\tt m}<\infty$
and that the distribution of
$\xi$
is non-lattice. Then
\begin{equation*}\lim_{t\to\infty} \int_{[0,\,\infty)} f(t-y)\,{\textrm{d}} V(y)= {\tt m}^{-1} \int_\mathbb{R} f(y)\,{\textrm{d}} y.\end{equation*}
-
(b) Assume that
${\tt m}=\infty$
(the assumption that the distribution of
$\xi$
is non-lattice is not needed). Then
\begin{equation*}\lim_{t\to\infty} \int_{[0,\,\infty)} f(t-y)\,{\textrm{d}} V(y)=0.\end{equation*}
If f is dRi on
$[0,\infty)$
or
$(-\infty, 0]$
, then the ranges of integration
$[0,\,\infty)$
and
$\mathbb{R}$
should be replaced with
$[0,\,t]$
and
$[0,\infty)$
or
$[t,\infty)$
and
$(-\infty, 0]$
, respectively.
The proofs of Lemmas 3.1 and 3.2 are postponed to Appendices B and C, respectively.
In some cases the precision of Lemma 3.2 is not needed. In this situation the following ‘light’ version, borrowed from Lemma 9.1 of [Reference Iksanov, Marynych and Samoilenko16], may suffice.
Lemma 3.3. Let
$f\colon \mathbb{R}\to [0,\infty)$
be a dRi function on
$\mathbb{R}$
. Then, for some
$r>0$
and all
$x\in\mathbb{R}$
,
\begin{equation}\int_{[0,\,\infty)} f(x-y)\,{\textrm{d}} V(y)\leq r.\end{equation}
If f is dRi on
$[0,\infty)$
or
$(-\infty, 0]$
, then the range of integration
$[0,\,\infty)$
should be replaced with
$[0,\,x]$
or
$[x,\infty)$
and then (3.27)holds for all
$x\geq 0$
or all
$x\leq 0$
, respectively.
Having Lemmas 3.1, 3.2, and 3.3 at our disposal, we are ready to prove Theorem 2.3.
Proof of Theorem 2.3. For
$t\geq 0$
, put
\begin{equation*} g(t)\,:\!=\, \int_{[0,\,t]}f(t-y)\,{\textrm{d}} V(y)\quad\text{and}\quad I\,:\!=\, {\tt m}^{-1}\int_0^\infty f(y)\,{\textrm{d}} y. \end{equation*}
By Lemma 3.2(a), given
$\varepsilon>0$
there exists
$t_0>0$
such that
$|g(t)-I|\leq \varepsilon$
whenever
$t\geq t_0$
. Also, by Lemma 3.3,
$g(t)\leq J$
for some
$J>0$
and all
$t\geq 0$
. Hence, for
$t\geq t_0$
, by the associativity
\begin{align} (f\ast V_j)(t)&=(f\ast (V\ast V_{j-1}))(t)\notag \\ &=(g\ast V_{j-1})(t)\notag\\&=\int_{[0,\,t]}g(t-y)\,{\textrm{d}} V_{j-1}(y)\notag\\&=\int_{[0,\,t-t_0]}g(t-y)\,{\textrm{d}} V_{j-1}(y)+\int_{(t-t_0,\,t]}g(t-y)\,{\textrm{d}} V_{j-1}(y)\notag\\&\leq (I+\varepsilon)V_{j-1}(t)+J (V_{j-1}(t)-V_{j-1}(t-t_0)).\end{align}
We claim that
\begin{equation}\lim_{t\to\infty}\dfrac{V_{j(t)-1}(t)-V_{j(t)-1}(t-t_0)}{V_{j(t)-1}(t)}=0.\end{equation}
Note that (3.29) is not a direct consequence of the elementary renewal theorem, for the theorem provides the asymptotics of
$V_{j(t-t_0)-1}(t-t_0)$
rather than
$V_{j(t)-1}(t-t_0)$
which is actually needed for (3.29). To prove (3.29), with the help of (3.24) we write
\begin{align*} 0&\leq V_{j(t)-1}(t)-V_{j(t)-1}(t-t_0)\\ &=\int_{[0,\,t]}(V(t-y)-V(t-t_0-y))\,{\textrm{d}} V_{j(t)-2}(y)\\ &\leq U(t_0)V_{j(t)-2}(t)\end{align*}
for all
$t\geq 0$
. Thus (3.29) follows from
\begin{equation*}\lim_{t\to\infty}\dfrac{V_{j(t)-2}(t)}{V_{j(t)-1}(t)}=0,\end{equation*}
which is a consequence of Theorems 2.1 and 2.2 applied with
$j=j(t)-1$
and
$j=j(t)-2$
.
Combining (3.28) and (3.29), we obtain
\begin{equation*}\limsup_{t\to\infty}\dfrac{(f\ast V_j)(t)}{V_{j-1}(t)}\leq I.\end{equation*}
The converse inequality for the limit inferior follows analogously. The remaining statements of Theorem 2.3 are secured by Theorems 2.1 and 2.2.
Appendix A. Proof of Proposition 3.3
Proof. Replacing K with
$t\mapsto K(at)$
, we can and do assume that
$a=1$
, that is,
$f(t)=\int_0^t K(y)\,{\textrm{d}} y$
or, for short,
$f=K\ast \textrm{Id}$
. Then, by the commutativity of the convolution,
\begin{equation*}f^{\ast(j)}(t)=\big((\textrm{Id})^{\ast(j)}\ast K^{\ast(j)}\big)(t)=\int_{[0,\,t]}\dfrac{(t-y)^j}{j!}{\textrm{d}} K^{\ast(j)}(y)=\dfrac{\mathbb{E} \big(t-\widetilde{S}_j\big)_{+}^j}{j!},\quad t\geq 0.\end{equation*}
If
$\mathbb{E} \widetilde{S}_1^2<\infty$
, then
$j=j(t)={\textrm{o}}\big(t^{2/3}\big)$
as
$t\to\infty$
implies that
\begin{equation*} \mathbb{E} \big(t-\widetilde{S}_j\big)_{+}^j \sim t^j\exp\biggl(\dfrac{\gamma_0j^2}{t}\biggr),\quad t\to\infty.\end{equation*}
This can be justified as follows. We first note that
$\gamma_0<0$
. Further, in the decomposition
\begin{equation}\mathbb{E}\biggl(1-\dfrac{\widetilde{S}_j}{t}\biggr)_{+}^j=\mathbb{E} \Big({\textrm{e}}^{j\log\big(1-\widetilde{S}_j/t\big)}\mathbb{1}_{\{\widetilde{S}_j\leq t/2\}}\Big)+\mathbb{E}\biggl(1-\dfrac{\widetilde{S}_j}{t}\biggr)_{+}^j\mathbb{1}_{\{\widetilde{S}_j\in (t/2,\,t)\}},\end{equation}
the second summand is bounded by
$2^{-j}$
and
\begin{equation*}2^{-j}={\textrm{o}}\biggl(\exp\biggl(\dfrac{\gamma_0j^2}{t}\biggr)\biggr)\quad\text{as $t\to\infty$}\end{equation*}
for
$j^2/t={\textrm{o}}(j)$
. The first summand in (A.1) can be bounded with the help of the inequalities
\begin{equation*}-x-x^2 \leq \log(1-x)\leq -x,\quad x\in [0,\,1/2]\quad\text{and}\quad 1-x\leq {\textrm{e}}^{-x},\quad x\in\mathbb{R}.\end{equation*}
Indeed, we obtain, for
$j\geq 4$
,
\begin{align*} \mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\biggl(1-\dfrac{j\widetilde{S}_j^2}{t^2}\biggr)&\leq \mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\biggl(1-\dfrac{j\widetilde{S}_j^2}{t^2}\biggr)\mathbb{1}_{\{\widetilde{S}_j\leq t/2\}}\\ &\leq \mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}{\textrm{e}}^{-j\widetilde{S}_j^2/t^2}\mathbb{1}_{\{\widetilde{S}_j\leq t/2\}}\\ &\leq \mathbb{E} ({\textrm{e}}^{j\log(1-\widetilde{S}_j/t)}\mathbb{1}_{\{\widetilde{S}_j\leq t/2\}})\\ &\leq \mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\mathbb{1}_{\{\widetilde{S}_j\leq t/2\}}\\ &\leq \mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}.\end{align*}
For
$\lambda\geq 0$
, put
$\phi(\lambda)\,:\!=\, \mathbb{E} {\textrm{e}}^{-\lambda\widetilde{S}_1}$
. In view of
$\mathbb{E}\widetilde{S}_1^2<\infty$
, we infer that
\begin{equation*}\mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}=\phi^j(j/t)=\biggl(1+\dfrac{\gamma_0 j}{t}+{\textrm{O}}\biggl(\dfrac{j^2}{t^2}\biggr)\biggr)^j.\end{equation*}
The right-hand side is asymptotically equivalent to
$\exp\big(\gamma_0 j^2/t\big)$
as
$t\to\infty$
under the assumption
$j=j(t)={\textrm{o}}\big(t^{2/3}\big)$
. Finally, the relation
\begin{equation*}\mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\biggl(\dfrac{j\widetilde{S}_j^2}{t^2}\biggr)={\textrm{o}}\Big(\mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\Big),\quad t\to\infty ,\end{equation*}
can be checked using the equality
\begin{equation*}\mathbb{E} {\textrm{e}}^{-j\widetilde{S}_j/t}\widetilde{S}_j^2=\dfrac{\partial^2}{\partial \lambda^2}(\phi^j (\lambda))\bigg|_{\lambda=j/t}\end{equation*}
in conjunction with the assumptions
$j=j(t)={\textrm{o}}\big(t^{2/3}\big)$
and
$\mathbb{E}\widetilde{S}_1^2<\infty$
.
Appendix B. Proof of Lemma 3.1
Proof of part (a). According to Blackwell’s theorem (Proposition 2.2),
\begin{equation}\lim_{t\to\infty}(U(t+h)-U(t))={\tt m}^{-1}h.\end{equation}
In view of (B.1),
\begin{equation*}\lim_{t\to\infty}(U(t+h-\eta)-U(t-\eta))\mathbb{1}_{\{\eta\leq t-t^{1/2}\}}={\tt m}^{-1}h\quad\text{a.s.}\end{equation*}
Recalling (3.24), we infer that
\begin{equation*}\lim_{t\to\infty}\mathbb{E} (U(t+h-\eta)-U(t-\eta))\mathbb{1}_{\{\eta\leq t-t^{1/2}\}}={\tt m}^{-1}h\end{equation*}
by Lebesgue’s dominated convergence theorem. Another appeal to (3.24) yields
\begin{equation*}\mathbb{E} (U(t+h-\eta)-U(t-\eta))\mathbb{1}_{\{t-t^{1/2}<\eta\leq t\}}\leq U(h)\mathbb{P}\big\{t-t^{1/2}<\eta\leq t\big\},\end{equation*}
and the right-hand side converges to 0 as
$t\to\infty$
. Finally, by monotonicity,
\begin{equation*}\mathbb{E} U(t+h-\eta)\mathbb{1}_{\{t<\eta\leq t+h\}}\leq U(h)\mathbb{P}\{t<\eta\leq t+h\},\end{equation*}
and the right-hand side converges to 0 as
$t\to\infty$
. Invoking the first equality in (3.25) with
$x=t$
and
$y=h$
completes the proof of part (a).
Proof of part (b). If the distribution of
$\xi$
is non-lattice, then, by Blackwell’s theorem,
\begin{equation}\lim_{t\to\infty}(U(t+h)-U(t))=0.\end{equation}
If the distribution of
$\xi$
is d-lattice, then, by Blackwell’s theorem (Proposition 2.2), (B.2) holds for
$h=nd$
,
$n\in\mathbb{N}$
. However, using monotonicity of U we can ensure that (B.2) holds for any fixed
$h>0$
in both non-lattice and lattice cases. With this at hand, repeating the proof of part (a) verbatim, we arrive at (3.26).
Appendix C. Proof of Lemma 3.2
Proof of part (a). We only prove the claim under the assumption that f is dRi on
$\mathbb{R}$
, which is equivalent to the fact that
$f_{+}$
and
$f_{-}$
(non-negative and non-positive parts of f) are dRi on
$\mathbb{R}$
. Thus we can and do assume that
$f\geq 0$
on
$\mathbb{R}$
. Obviously it is enough to show that
\begin{equation*}\lim_{t\to\infty} \int_{[0,\,t]} f(t-y)\,{\textrm{d}} V(y)= {\tt m}^{-1} \int_0^\infty f(y)\,{\textrm{d}} y\end{equation*}
and
\begin{equation*}\lim_{t\to\infty} \int_{(t,\,\infty)} f(t-y)\,{\textrm{d}} V(y)= {\tt m}^{-1} \int_{-\infty}^0 f(y)\,{\textrm{d}} y.\end{equation*}
The proof of the first relation with U replacing V can be found in [Reference Resnick25, pp. 241–242]. We only check the second limit relation by closely following the aforementioned proof. We proceed via three steps, successively complicating the structure of f.
Step 1. First suppose that
\begin{equation*}f(t)=\mathbb{1}_{[(n-1)h,\,nh)}(t),\quad t<0, \end{equation*}
for fixed non-positive integer n and
$h>0$
. Then
$f(t-y)=1$
if and only if
$y\in (t-nh,\,t-(n-1)h]$
, which entails
\begin{equation*}\int_{(t,\,\infty)}f(t-y)\,{\textrm{d}} V(y)=V(t-(n-1)h)-V(t-nh).\end{equation*}
By Lemma 3.1(a), the last difference tends to
${\tt m}^{-1}h$
as
$t\to\infty$
, thereby proving that
\begin{equation*}\lim_{t\to\infty} \int_{(t,\,\infty)}f(t-y)\,{\textrm{d}} V(y)={\tt m}^{-1}h={\tt m}^{-1}\int_{-\infty}^0 f(y)\,{\textrm{d}} y.\end{equation*}
Step 2. Now suppose that
\begin{equation*}f(t)=\sum_{n\leq 0} c_n\mathbb{1}_{[(n-1)h,\,nh)}(t),\quad t<0, \end{equation*}
where
$(c_n)_{n\leq 0}$
is a sequence of non-negative numbers satisfying
$\sum_{n\leq 0}c_n<\infty$
. An argument similar to that used in the previous step enables us to assert that
\begin{equation*} \int_{(t,\,\infty)}f(t-y)\,{\textrm{d}} V(y)=\sum_{n\leq 0}c_n(V(t-(n-1)h)-V(t-nh)). \end{equation*}
Using Lemma 3.1(a) in combination with (3.24), with the help of Lebesgue’s dominated convergence theorem, we infer that
\begin{equation*} \lim_{t\to\infty} \int_{(t,\,\infty)} f(t-y)\,{\textrm{d}} V(y)={\tt m}^{-1}h \sum_{n\leq 0} c_n={\tt m}^{-1}\int_{-\infty}^ 0 f(y)\,{\textrm{d}} y. \end{equation*}
Step 3. Now let f be an arbitrary non-negative dRi function on
$\mathbb{R}$
(in fact for the present proof it is enough for it to be dRi on
$(-\infty, 0)$
). For each
$h>0$
, put
\begin{equation*} \overline{f}_h(t)\,:\!=\, \sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\sup}\,f(y)\mathbb{1}_{[(n-1)h,\,nh)}(t),\quad t<0 ,\end{equation*}
and
\begin{equation*}\underline{f}_h(t)\,:\!=\, \sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\inf}\,f(y)\mathbb{1}_{[(n-1)h,\,nh)}(t), \quad t<0.\end{equation*}
By the definition of direct Riemann integrability,
\begin{equation*}\sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\sup}\,f(y)<\infty \quad \text{and}\quad \sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\inf}\,f(y)<\infty\end{equation*}
for each
$h>0$
. Thus the functions
$\overline{f}_h$
and
$\underline{f}_h$
have the same structure as the functions discussedin Step 2. According to the result of Step 2,
\begin{equation*}\lim_{t\to\infty} \int_{(t,\,\infty)}\overline{f}_h(t-y)\,{\textrm{d}} V(y)={\tt m}^{-1}h\sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\sup}\,f(y)\,:\!= {\tt m}^{-1}\overline{\sigma}(h)\end{equation*}
and
\begin{equation*}\lim_{t\to\infty} \int_{(t,\,\infty)}\underline{f}_h(t-y)\,{\textrm{d}} V(y)={\tt m}^{-1}h\sum_{n\leq 0}\underset{(n-1)h\leq y<nh}{\inf}\,f(y)\,:\!= {\tt m}^{-1}\underline{\sigma}(h)\end{equation*}
for all
$h>0$
. Since, for each
$h>0$
,
\begin{equation*}\underline{f}_h(t)\leq f(t)\leq \overline{f}_h(t),\quad t<0,\end{equation*}
it follows that
\begin{align*}{\tt m}^{-1}\underline{\sigma}(h)&=\underset{t\to\infty}{\lim\inf}\,\int_{(t,\,\infty)}\underline{f}_h(t-y)\,{\textrm{d}} V(y)\\&\leq \underset{t\to\infty}{\lim\inf}\,\int_{(t,\,\infty)} f(t-y)\,{\textrm{d}} V(y)\\&\leq \underset{t\to\infty}{\lim\sup}\,\int_{(t,\,\infty)}f(t-y)\,{\textrm{d}} V(y)\\&\leq \underset{t\to\infty}{\lim\sup}\,\int_{(t,\,\infty)}\overline{f}_h(t-y)\,{\textrm{d}} V(y)\\&={\tt m}^{-1}\overline{\sigma}(h).\end{align*}
We have
$\lim_{h\to 0+}\,(\overline{\sigma}(h)-\underline{\sigma}(h))=0$
by the definition of direct Riemann integrability. Also, it is known that
$\lim_{h\to 0+}\, \overline{\sigma}(h)=\int_{-\infty}^0 f(y)\,{\textrm{d}} y$
. Letting
$h\to 0+$
in the last chain of inequalities completes the proof of part (a).
Proof of part (b). Use part (b) of Lemma 3.1 in place of part (a) and proceed as above. This finishes the proof of Lemma 3.2.
Acknowledgements
We thank the anonymous referee for many useful suggestions which greatly improved the presentation of our results.
Funding information
The present work was supported by the National Research Foundation of Ukraine (project 2020.02/0014 ‘Asymptotic regimes of perturbed random walks: on the edge of modern and classical probability’).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
