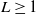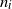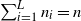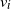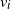1. Introduction
1.1. Motivation and related literature
In reliability engineering and system security, one of the most useful methods for enhancing the reliability characteristics of a system is to allocate redundant components to the system. The redundancy can be performed at the component level or the system level. In the former case some redundant components are connected to each component, while in the latter case the original coherent system fastens to some copies of itself. In a commonly used type of redundancy, called active redundancy, the original component and the redundant ones work simultaneously in parallel. In this case, the lifetime of the resulting parallel subsystem equals the maximum lifetime of the connected components. This strategy is mostly applied when replacement of the components during the operation time of the system is impossible. As redundancy allocation is a widely used method for improving the performance of products, numerous researchers have paid attention to developing the theories and applications of this subject. For example, Li and Ding [Reference Li and Ding21] investigated the allocation of active redundancies to a k-out-of-n system in which the lifetimes of independent components are stochastically ordered. You et al. [Reference You, Fang and Li32] studied k-out-of-n redundant systems with dependent components. Eryilmaz and Ucum [Reference Eryilmaz and Ucum8] determined the optimal number of spare components for a weighted k-out-of-n. Bayramoglu Kavlak [Reference Bayramoglu Kavlak2] investigated the reliability and the mean residual life functions of coherent systems with active redundancies at the component and system levels. Zhang [Reference Zhang34] investigated the optimal allocation of active redundancies for weighted k-out-of-n systems. Zhang et al. [Reference Zhang, Amini Seresht and Ding35] compared the component redundancy versus system redundancy for coherent systems with dependent and identically distributed components. Fang and Li [Reference Fang and Li12] studied the allocation of one active redundancy to coherent systems consisting of heterogeneous and statistically dependent components. Utilizing the minimal path decomposition, they proposed a necessary and sufficient condition identifying a better allocating strategy from two candidates. Fang and Li [Reference Fang and Li13] investigated allocating multiple matched active redundant components to coherent systems. Fang and Li [Reference Fang and Li14] studied the coherent systems with one active redundancy, using the minimal cut decomposition of the system. Torrado et al. [Reference Torrado, Arriaza and Navarro31] studied the redundancy allocation for a coherent system formed by modules, under different settings related to dependency and distribution of components. They stochastically compared the redundancies at the component level versus redundancies at the module level. Torrado [Reference Torrado30] considered a coherent system having possibly dependent subsystems in which the components are connected in parallel or in series. It is assumed that a number of possibly dependent components in each subsystem are randomly selected from a heterogeneous population. Torrado stochastically compared such systems with different numbers of components, based on majorization orders, and determined the optimal numbers of components in each subsystem such that the system reliability is maximized. In particular, she examined the results for series-parallel systems. The redundancy allocation in a series-parallel system has also been considered by some authors, among which we refer to Soltani et al. [Reference Soltani, Sadjadi and Tavakkoli-Moghaddam29], Karimi et al. [Reference Karimi, Niaki, Miriha, Ghare Hasanluo and Javanmard20], and Fang et al. [Reference Fang, Balakrishnan and Jin15].
It is worth noting that the redundant components can be added to the system as inactive (cold and warm standby) components. Systems with cold and warm standby redundancy have also been investigated in the reliability literature; see, for example, Eryilmaz [Reference Eryilmaz6], Finkelstein et al. [Reference Finkelstein, Hazra and Cha17], Shen et al. [Reference Shen, Hu and Ye28], and Behboudi et al. [Reference Behboudi, Borzadaran and Asadi3].
1.2. Survival signatures of coherent systems
The first main step to assess the reliability and stochastic characteristics of an n-component system is to get knowledge about the structure function of the system as well as the probability distribution of component lifetimes. In this regard, a useful concept for assessing the reliability of the system through the reliability of its components is the notion of survival signature. This concept is particularly significant for describing the structures of coherent systems with multiple types of components. Consider an n-component coherent system consisting of L different types, such that there are
![]() $n_i$
components from the ith type,
$n_i$
components from the ith type,
![]() $i=1,\ldots, L$
, and
$i=1,\ldots, L$
, and
![]() $\sum_{i=1}^L n_i=n$
. The reliability function of the system, at any time t, can be represented as follows:
$\sum_{i=1}^L n_i=n$
. The reliability function of the system, at any time t, can be represented as follows:
 \begin{align}\bar{F}_T(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\,\mathbb{P}(C_1(t)=l_1, \ldots, C_L(t)=l_L),\end{align}
\begin{align}\bar{F}_T(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\,\mathbb{P}(C_1(t)=l_1, \ldots, C_L(t)=l_L),\end{align}
where
![]() $C_i(t)$
denotes the number of components of type i working at time t, and
$C_i(t)$
denotes the number of components of type i working at time t, and
![]() $\Phi$
is called the survival signature and represents ‘the probability that the system is working when exactly
$\Phi$
is called the survival signature and represents ‘the probability that the system is working when exactly
![]() $l_i$
components of type i is working’; see Coolen and Coolen-Maturi [Reference Coolen and Coolen-Maturi4].
$l_i$
components of type i is working’; see Coolen and Coolen-Maturi [Reference Coolen and Coolen-Maturi4].
Suppose that the lifetimes of the components of the same type are exchangeable dependent and the lifetimes of the components of different types are dependent. Commonly, the dependency structure is modeled using a survival copula. In other words, if
![]() $T_j^{(i)}$
denotes the lifetime of the jth component from type i,
$T_j^{(i)}$
denotes the lifetime of the jth component from type i,
![]() $j=1, \ldots, n_i$
,
$j=1, \ldots, n_i$
,
![]() $i=1, \ldots, L$
, and
$i=1, \ldots, L$
, and
![]() $\bar{F}_i,\;i=1, \ldots, L$
denotes the common reliability function for the components of the ith type, then there is a survival copula
$\bar{F}_i,\;i=1, \ldots, L$
denotes the common reliability function for the components of the ith type, then there is a survival copula
![]() $\hat{C}$
such that the joint reliability of
$\hat{C}$
such that the joint reliability of
![]() $T_j^{(i)}$
can be written as
$T_j^{(i)}$
can be written as
 \begin{align}&\mathbb{P}\bigl( T_1^{(1)}>t_1^{(1)}, \ldots, T_{n_1}^{(1)}>t_{n_1}^{(1)}, \ldots, T_1^{(L)}>t_L^{(L)}, \ldots, T_{n_L}^{(L)}>t_{n_L}^{(L)}\bigr)\nonumber\\[5pt] &\quad = \hat{C}\bigl(\bar{F}_1\bigl(t_1^{(1)}\bigr), \ldots, \bar{F}_1\bigl(t_{n_1}^{(1)}\bigr), \ldots, \bar{F}_L\bigl(t_1^{(L)}\bigr), \ldots, \bar{F}_L\bigl(t_{n_L}^{(L)}\bigr)\bigr). \end{align}
\begin{align}&\mathbb{P}\bigl( T_1^{(1)}>t_1^{(1)}, \ldots, T_{n_1}^{(1)}>t_{n_1}^{(1)}, \ldots, T_1^{(L)}>t_L^{(L)}, \ldots, T_{n_L}^{(L)}>t_{n_L}^{(L)}\bigr)\nonumber\\[5pt] &\quad = \hat{C}\bigl(\bar{F}_1\bigl(t_1^{(1)}\bigr), \ldots, \bar{F}_1\bigl(t_{n_1}^{(1)}\bigr), \ldots, \bar{F}_L\bigl(t_1^{(L)}\bigr), \ldots, \bar{F}_L\bigl(t_{n_L}^{(L)}\bigr)\bigr). \end{align}
See, for example, Navarro [Reference Navarro24], Navarro et al. [Reference Navarro, Pellerey and Di Crescenzo25], and Fang and Li [Reference Fang and Li14]. In this case it can be shown that
 \begin{align}\bar{F}_T(t)&={\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L}\nonumber\\[5pt]&\quad \times\Phi(l_1,\ldots, l_L) \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{i_1+l_1},\underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{\bar{F}_L(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr),\end{align}
\begin{align}\bar{F}_T(t)&={\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L}\nonumber\\[5pt]&\quad \times\Phi(l_1,\ldots, l_L) \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{i_1+l_1},\underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{\bar{F}_L(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr),\end{align}
where
denotes the m repetitions of u; see Eryilmaz et al. [Reference Eryilmaz, Coolen and Coolen-Maturi9, Reference Eryilmaz, Coolen and Coolen-Maturi10]. If the components of the system are independent, then the representation (1.1) is converted to the following expression:
 \begin{align}\bar{F}_T(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\prod_{i=1}^L \binom{n_i}{l_i}[\bar{F}_i(t)]^{l_i} [{F}_i(t)]^{n_i-l_i}.\end{align}
\begin{align}\bar{F}_T(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\prod_{i=1}^L \binom{n_i}{l_i}[\bar{F}_i(t)]^{l_i} [{F}_i(t)]^{n_i-l_i}.\end{align}
Many authors have considered the reliability properties of a coherent system with multi-type components based on the survival signature, and for various applications. Among these we mention recent papers by Feng et al. [Reference Feng, Patelli, Beer and Coolen16], Samaniego and Navarro [Reference Samaniego and Navarro27], and Eryilmaz et al. [Reference Eryilmaz, Coolen and Coolen-Maturi9, Reference Eryilmaz, Coolen and Coolen-Maturi10]. Huang et al. [Reference Huang, Coolen and Coolen-Maturi19] used the notion of survival signature for the formulation of the reliability–redundancy allocation problem. They considered the objective function to maximize the system reliability under some constraints.
Zarezadeh and Asadi [Reference Zarezadeh and Asadi33] studied the reliability and preventive maintenance of coherent systems with multi-type components whose components are subject to failure according to multiple external shocks. Hashemi et al. [Reference Hashemi, Asadi and Zarezadeh18] proposed two maintenance strategies for optimal preservation of coherent systems consisting of independent multi-type components.
1.3. Contributions of this paper
This paper aims to study the optimal number of redundancy allocation to n-component coherent systems consisting of different components. It is assumed that the components of the system are dependent, where a given copula function models the dependency structure. We are interested in allocating
![]() $v_i$
active redundant components to each component of type i, under the constraint on the number of existing spare components. To get the optimal number of
$v_i$
active redundant components to each component of type i, under the constraint on the number of existing spare components. To get the optimal number of
![]() $v_i$
, we propose two cost-based functions. More precisely, the contributions of the paper are as follows.
$v_i$
, we propose two cost-based functions. More precisely, the contributions of the paper are as follows.
-
We propose a mean cost rate function in terms of the costs of renewing the failed components and the costs of refreshing the alive components at the time of the system failure. Then we find the optimal number of redundant components,
 $v_i$
, to be added to each component of type i, such that the proposed cost function is minimized.
$v_i$
, to be added to each component of type i, such that the proposed cost function is minimized. -
We introduce a mean cost rate function, relevant to an age replacement policy, in terms of the costs of renewing (refreshing) the failed (alive) components at the failure time of the system or at a predetermined time
 $\tau$
, whichever occurs first. Then the optimal values of
$\tau$
, whichever occurs first. Then the optimal values of
 $v_i$
are obtained, such that the suggested cost-based function achieves its minimum value.
$v_i$
are obtained, such that the suggested cost-based function achieves its minimum value. -
In the particular important case that the system is a series-parallel system, we provide the formulas for the proposed mean cost rate functions. Then we investigate the optimal number of the components for each parallel subsystem such that the proposed functions are minimized.
The derivations of the paper are extensions of the results of Eryilmaz [Reference Eryilmaz7], who investigated the optimal number of components in the case that the structure function is k-out-of-n with independent components.
1.4. Organization of the paper
The remainder of the paper is arranged as follows. In Section 2, using the settings of Section 1.2, we present the formulation of the system reliability function (1.3) in the case that
![]() $v_i$
components are added as active redundant to each component of type i,
$v_i$
components are added as active redundant to each component of type i,
![]() $i=1,\dots, L$
. Then, utilizing this formulation, a mean cost rate function is introduced at the time of the system failure. Next, a mean cost rate function is established based on the costs of replacing the system at its failure time or at a predetermined time
$i=1,\dots, L$
. Then, utilizing this formulation, a mean cost rate function is introduced at the time of the system failure. Next, a mean cost rate function is established based on the costs of replacing the system at its failure time or at a predetermined time
![]() $\tau$
, whichever occurs first. The expressions for the proposed mean cost rate functions are derived in terms of the reliability function (1.3). Some examples of coherent systems are presented to illustrate the applications of the proposed approaches; a 6-component system consisting of two types of dependent components, and an 8-component system composed of three types of components that are independent. The optimal number of redundant components, based on the proposed cost-based functions, are discussed for each system numerically. Section 3 is devoted to the particular case that the system is a series-parallel system. In Section 2 we provide the formulas for the proposed mean cost rate functions for such systems. Then we investigate the optimal number of the components for each parallel subsystem such that the proposed cost functions are minimized. The results of this section are numerically illustrated for a series-parallel system consisting of three parallel subsystems connected in series. Some concluding remarks in Section 4 finalize the paper. Detailed proofs are given in the Appendix.
$\tau$
, whichever occurs first. The expressions for the proposed mean cost rate functions are derived in terms of the reliability function (1.3). Some examples of coherent systems are presented to illustrate the applications of the proposed approaches; a 6-component system consisting of two types of dependent components, and an 8-component system composed of three types of components that are independent. The optimal number of redundant components, based on the proposed cost-based functions, are discussed for each system numerically. Section 3 is devoted to the particular case that the system is a series-parallel system. In Section 2 we provide the formulas for the proposed mean cost rate functions for such systems. Then we investigate the optimal number of the components for each parallel subsystem such that the proposed cost functions are minimized. The results of this section are numerically illustrated for a series-parallel system consisting of three parallel subsystems connected in series. Some concluding remarks in Section 4 finalize the paper. Detailed proofs are given in the Appendix.
2. Optimal number of redundant components
We consider an n-component coherent system consisting of multiple types of components with the following description. The system is built up of L types of components,
![]() $L\geq 1$
, such that there are
$L\geq 1$
, such that there are
![]() $n_i$
components of type i and
$n_i$
components of type i and
![]() $\sum_{i=1}^{L}n_i=n$
. We assume that the common reliability function of the components of type i is
$\sum_{i=1}^{L}n_i=n$
. We assume that the common reliability function of the components of type i is
![]() $\bar{F}_i(.)$
,
$\bar{F}_i(.)$
,
![]() $i=1,2,\dots,L$
. The lifetimes of the components of the same type are exchangeable dependent and the lifetimes of the components of different types are dependent. The assumed dependency structure is modeled by a survival copula given in (1.2). To increase the reliability of the system, we wish to add
$i=1,2,\dots,L$
. The lifetimes of the components of the same type are exchangeable dependent and the lifetimes of the components of different types are dependent. The assumed dependency structure is modeled by a survival copula given in (1.2). To increase the reliability of the system, we wish to add
![]() $v_i$
active redundancies to each component of type i,
$v_i$
active redundancies to each component of type i,
![]() $i=1,\ldots, L$
. Each original component in the system and its redundant components are assumed to be independent and identically distributed (i.i.d.). Let
$i=1,\ldots, L$
. Each original component in the system and its redundant components are assumed to be independent and identically distributed (i.i.d.). Let
![]() $T_R$
denote the lifetime of the system incorporated by redundant components. Because an original component and its redundant ones make a parallel subsystem, one can easily show that the reliability function of
$T_R$
denote the lifetime of the system incorporated by redundant components. Because an original component and its redundant ones make a parallel subsystem, one can easily show that the reliability function of
![]() $T_R$
at time t can be represented as follows:
$T_R$
at time t can be represented as follows:
 \begin{align*}\bar{F}_{T_R}(t)&={\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L} \nonumber\\[5pt]&\quad \times\Phi(l_1,\ldots, l_L)\hat{C}\Bigl(\underbrace{1-{F}_1^{v_1+1}(t)}_{i_1+l_1}, \underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{1-{F}_L^{v_L+1}(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr).\end{align*}
\begin{align*}\bar{F}_{T_R}(t)&={\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L} \nonumber\\[5pt]&\quad \times\Phi(l_1,\ldots, l_L)\hat{C}\Bigl(\underbrace{1-{F}_1^{v_1+1}(t)}_{i_1+l_1}, \underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{1-{F}_L^{v_L+1}(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr).\end{align*}
In the case of independence of all components, this representation reduces to
 \begin{align*}\bar{F}_{T_R}(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\prod_{i=1}^L \binom{n_i}{l_i}\bigl[1-{F}_i^{v_i+1}(t)\bigr]^{l_i}\bigl[{F}_i^{v_i+1}(t)\bigr]^{n_i-l_i}.\end{align*}
\begin{align*}\bar{F}_{T_R}(t)=\sum_{l_1=0}^{n_1}\!\cdots\!\sum_{l_L=0}^{n_L}\Phi(l_1,\ldots, l_L)\prod_{i=1}^L \binom{n_i}{l_i}\bigl[1-{F}_i^{v_i+1}(t)\bigr]^{l_i}\bigl[{F}_i^{v_i+1}(t)\bigr]^{n_i-l_i}.\end{align*}
The problem of interest in this redundancy strategy is to determine the optimal number of spares allocated to each component. In this paper our approach is to find v based on the minimization of a kind of cost criterion. In this regard we set up two mean cost rate functions to obtain the optimal number of redundant components. One of them is imposed based on the cost of the system failure, which depends on the number of failed components when a system failure occurs. The other one is defined based on an age replacement policy. In the next subsections, we describe these two functions with details.
Remark 2.1. Although the system considered above is described in the general case that the component lifetimes of the same type are exchangeable dependent and the lifetimes of the components of different types are dependent, in allocating the redundant components we assumed that in the constructed parallel subsystem the components are i.i.d. This assumption seems to be a restriction in some practical cases, but it should be noted that if we drop the i.i.d. assumption for the redundant components, the computation of the system reliability would be a challenging problem and potentially involve complex calculations. We believe that considering the problem of optimal redundancy under i.i.d. components in each subsystem, as is done in this paper, could be a first step towards solving the more general cases; see also Samaniego [Reference Samaniego26, pp. 76–77].
2.1. Cost function at system failure
Suppose that the system starts working at
![]() $t=0$
and fails at a random time after
$t=0$
and fails at a random time after
![]() $t=0$
. Assume that when the system fails we have a cost
$t=0$
. Assume that when the system fails we have a cost
![]() $c_i$
for each failed component of type i to replace it with a new one and a cost
$c_i$
for each failed component of type i to replace it with a new one and a cost
![]() $c_i^*$
for each unfailed component to refresh it so that it becomes as good as new, where we assume that
$c_i^*$
for each unfailed component to refresh it so that it becomes as good as new, where we assume that
![]() $c_i\geq c^*_i$
,
$c_i\geq c^*_i$
,
![]() $i=1, \ldots, L$
. Furthermore, we assume that
$i=1, \ldots, L$
. Furthermore, we assume that
![]() $c^{**}$
denotes the fixed overall cost for system failure. With
$c^{**}$
denotes the fixed overall cost for system failure. With
![]() $T_R$
as the lifetime of the system after redundancy, let the random variable
$T_R$
as the lifetime of the system after redundancy, let the random variable
![]() $X_i(T_R)$
denote the number of failed components of type i at the time of system failure,
$X_i(T_R)$
denote the number of failed components of type i at the time of system failure,
![]() $i=1,\dots,L$
. Then the mean cost rate function for a failed system is defined as
$i=1,\dots,L$
. Then the mean cost rate function for a failed system is defined as
where
![]() $\mathbf{v}=(v_1,\ldots, v_L)$
. The numerator is the expected cost of the system failure, and the denominator is the mean time to failure (MTTF) of the system, so
$\mathbf{v}=(v_1,\ldots, v_L)$
. The numerator is the expected cost of the system failure, and the denominator is the mean time to failure (MTTF) of the system, so
![]() $\mathrm{Cost}_1$
becomes the mean cost per unit of time. Note that in the system after redundancy, there are altogether
$\mathrm{Cost}_1$
becomes the mean cost per unit of time. Note that in the system after redundancy, there are altogether
![]() $n_i(v_i+1)$
components of type i,
$n_i(v_i+1)$
components of type i,
![]() $i=1,2, \ldots, L$
. The relation (2.1) can be rewritten in terms of the lifetime of the original system without any redundancy, T, as
$i=1,2, \ldots, L$
. The relation (2.1) can be rewritten in terms of the lifetime of the original system without any redundancy, T, as
 \begin{align}\mathrm{Cost}_1(\mathbf{v})&=\dfrac{\sum_{i=1}^Lc_i(v_i+1)\mathbb{E}(X_i(T))+\sum_{i=1}^L c_i^*(v_i+1)\mathbb{E}(n_i-X_i(T))+c^{**}}{\mathbb{E}(T_R)}\nonumber\\[5pt]&=\dfrac{\sum_{i=1}^L(c_i-c_i^*)(v_i+1)\mathbb{E}(X_i(T))+\sum_{i=1}^L c_i^*(v_i+1)n_i+c^{**}}{\mathbb{E}( T_R)}.\end{align}
\begin{align}\mathrm{Cost}_1(\mathbf{v})&=\dfrac{\sum_{i=1}^Lc_i(v_i+1)\mathbb{E}(X_i(T))+\sum_{i=1}^L c_i^*(v_i+1)\mathbb{E}(n_i-X_i(T))+c^{**}}{\mathbb{E}(T_R)}\nonumber\\[5pt]&=\dfrac{\sum_{i=1}^L(c_i-c_i^*)(v_i+1)\mathbb{E}(X_i(T))+\sum_{i=1}^L c_i^*(v_i+1)n_i+c^{**}}{\mathbb{E}( T_R)}.\end{align}
Lemma 2.1. The quantity
![]() $\mathbb{E}( X_i(T))$
in (2.2) can be expressed as follows:
$\mathbb{E}( X_i(T))$
in (2.2) can be expressed as follows:
 \begin{align*}&\mathbb{E}( X_i(T))\\[5pt] & =n_i\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{1}{\delta}\sum_{m_1=0}^{n_1}\!\cdots\! \sum_{m_i=0}^{n_i-1}\!\cdots\! \sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L)\\[5pt] & \quad \times \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\! \binom{n_L}{m_L} A_{\mathbf{m}}^{(i)}(t,\delta) \,{\mathrm{d}} t,\end{align*}
\begin{align*}&\mathbb{E}( X_i(T))\\[5pt] & =n_i\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{1}{\delta}\sum_{m_1=0}^{n_1}\!\cdots\! \sum_{m_i=0}^{n_i-1}\!\cdots\! \sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L)\\[5pt] & \quad \times \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\! \binom{n_L}{m_L} A_{\mathbf{m}}^{(i)}(t,\delta) \,{\mathrm{d}} t,\end{align*}
where
 \begin{align}A_{\mathbf{m}}^{(i)}(t,\delta)&=\mathbb{P}\bigl({T_1^{(1)}>t},\ldots,{T_{m_1}^{(1)}>t},{T_{m_1+1}^{(1)}\leq t},\ldots, {T_{n_1}^{(1)}\leq t}, \nonumber\\[5pt]&\quad \ldots, t<T_1^{(i)}\leq t+\delta, {T_2^{(i)}>t},\ldots,{T_{m_i+1}^{(i)}>t},{T_{m_i+2}^{(i)}\leq t},\ldots, {T_{n_i}^{(i)}\leq t}, \nonumber\\[5pt]&\quad \ldots, {T_1^{(L)}>t},\ldots,{T_{m_L}^{(L)}>t},{T_{m_L+1}^{(L)}\leq t},\ldots, {T_{n_L}^{(L)}\leq t}\bigr).\end{align}
\begin{align}A_{\mathbf{m}}^{(i)}(t,\delta)&=\mathbb{P}\bigl({T_1^{(1)}>t},\ldots,{T_{m_1}^{(1)}>t},{T_{m_1+1}^{(1)}\leq t},\ldots, {T_{n_1}^{(1)}\leq t}, \nonumber\\[5pt]&\quad \ldots, t<T_1^{(i)}\leq t+\delta, {T_2^{(i)}>t},\ldots,{T_{m_i+1}^{(i)}>t},{T_{m_i+2}^{(i)}\leq t},\ldots, {T_{n_i}^{(i)}\leq t}, \nonumber\\[5pt]&\quad \ldots, {T_1^{(L)}>t},\ldots,{T_{m_L}^{(L)}>t},{T_{m_L+1}^{(L)}\leq t},\ldots, {T_{n_L}^{(L)}\leq t}\bigr).\end{align}
Proof.
 \begin{align*} \mathbb{E}( X_i(T))&=\mathbb{E}\Biggl( \sum_{j=1}^{n_i}I\bigl(T_j^{(i)}\leq T\bigr)\Biggr)\\[5pt] &=\sum_{j=1}^{n_i}\mathbb{P}\bigl(T_j^{(i)}\leq T\bigr)=n_i\mathbb{P}\bigl(T_1^{(i)}\leq T\bigr)\\[5pt]&=n_i\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta\bigr)}{\delta} \,{\mathrm{d}} t,\end{align*}
\begin{align*} \mathbb{E}( X_i(T))&=\mathbb{E}\Biggl( \sum_{j=1}^{n_i}I\bigl(T_j^{(i)}\leq T\bigr)\Biggr)\\[5pt] &=\sum_{j=1}^{n_i}\mathbb{P}\bigl(T_j^{(i)}\leq T\bigr)=n_i\mathbb{P}\bigl(T_1^{(i)}\leq T\bigr)\\[5pt]&=n_i\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta\bigr)}{\delta} \,{\mathrm{d}} t,\end{align*}
where the third equality follows from the exchangeability of the components of type i,
![]() $i=1, \dots, L$
. By conditioning on the number of live components of each type, we obtain
$i=1, \dots, L$
. By conditioning on the number of live components of each type, we obtain
 \begin{align}&\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta, C_j(t)=m_j, j=1,\ldots, L \bigr) \nonumber\\& =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L) \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\nonumber\\[5pt]& \quad \times A_{\mathbf{m}}^{(i)}(t,\delta).\end{align}
\begin{align}&\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\mathbb{P}\bigl(T>t,t<T_1^{(i)}\leq t+\delta, C_j(t)=m_j, j=1,\ldots, L \bigr) \nonumber\\& =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L) \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\nonumber\\[5pt]& \quad \times A_{\mathbf{m}}^{(i)}(t,\delta).\end{align}
The last equality in (2.4) holds because the components of the same type have a common failure time distribution.![]()
In the following theorem, (2.3) is represented based on the survival copula of the component lifetimes.
Theorem 2.1. Using the inclusion–exclusion rule,
![]() $A_{\mathbf{m}}^{(i)}(t,\delta)$
can be represented as follows:
$A_{\mathbf{m}}^{(i)}(t,\delta)$
can be represented as follows:
 \begin{align*}&A_{\mathbf{m}}^{(i)}(t, \delta)\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times \biggl[\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-(m_1+j_1)},\ldots,\underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-(m_i+j_i+1)},\ldots,\underbrace{\bar{F}_L(t)}_{m_L+j_L}, \underbrace{1}_{n_L-(m_L+j_L)}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-(m_1+j_1)},\ldots,\underbrace{\bar{F}_i(t)}_{m_i+j_i},\bar{F}_i(t+\delta),\underbrace{1}_{n_i-(m_i+j_i+1)}, \ldots,\underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-(m_L+j_L)}\Bigr)\biggr].\end{align*}
\begin{align*}&A_{\mathbf{m}}^{(i)}(t, \delta)\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times \biggl[\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-(m_1+j_1)},\ldots,\underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-(m_i+j_i+1)},\ldots,\underbrace{\bar{F}_L(t)}_{m_L+j_L}, \underbrace{1}_{n_L-(m_L+j_L)}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-(m_1+j_1)},\ldots,\underbrace{\bar{F}_i(t)}_{m_i+j_i},\bar{F}_i(t+\delta),\underbrace{1}_{n_i-(m_i+j_i+1)}, \ldots,\underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-(m_L+j_L)}\Bigr)\biggr].\end{align*}
Proof. See Appendix A.![]()
Note that in the particular case of independence of all components, we get
 \begin{align}&\mathbb{E}( X_i(T))\nonumber\\[5pt] & =n_i\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L) \notag \\[5pt] & \quad \times \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\nonumber\\[5pt]& \quad \times\int_{0}^{\infty}\bar{F}_1^{m_1}(t)F_1^{n_1-m_1}(t)\!\cdots\!\bar{F}_i^{m_i}(t)F_i^{n_i-m_i-1}(t)\!\cdots\! \bar{F}_L^{m_L}(t)F_L^{n_L-m_L}(t) \,{\mathrm{d}} F_i(t).\end{align}
\begin{align}&\mathbb{E}( X_i(T))\nonumber\\[5pt] & =n_i\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\Phi(m_1,\ldots,m_{i-1},m_i+1,m_{i+1},\ldots, m_L) \notag \\[5pt] & \quad \times \binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\nonumber\\[5pt]& \quad \times\int_{0}^{\infty}\bar{F}_1^{m_1}(t)F_1^{n_1-m_1}(t)\!\cdots\!\bar{F}_i^{m_i}(t)F_i^{n_i-m_i-1}(t)\!\cdots\! \bar{F}_L^{m_L}(t)F_L^{n_L-m_L}(t) \,{\mathrm{d}} F_i(t).\end{align}
In order to minimize the mean cost rate function
![]() $\mathrm{Cost}_1(\mathbf{v})$
, we impose the constraint that there are at most
$\mathrm{Cost}_1(\mathbf{v})$
, we impose the constraint that there are at most
![]() $M_i$
components of type i as spares,
$M_i$
components of type i as spares,
![]() $i=1,\dots,L$
. This means that the number of the components that can be connected in parallel at the ith group satisfies the inequality
$i=1,\dots,L$
. This means that the number of the components that can be connected in parallel at the ith group satisfies the inequality
![]() $n_iv_i\leq M_i$
,
$n_iv_i\leq M_i$
,
![]() $i=1,\ldots, L$
. To determine the optimal values of
$i=1,\ldots, L$
. To determine the optimal values of
![]() $v_i$
, we do the following: for given values of
$v_i$
, we do the following: for given values of
![]() $n_i, c_i, c_i^*$
, and
$n_i, c_i, c_i^*$
, and
![]() $M_i$
,
$M_i$
,
![]() $i=1, \ldots, L$
, and
$i=1, \ldots, L$
, and
![]() $c^{**}$
, we evaluate
$c^{**}$
, we evaluate
![]() $\mathrm{Cost}_1(\mathbf{v})$
for all possible choices of
$\mathrm{Cost}_1(\mathbf{v})$
for all possible choices of
![]() $v_1, \ldots, v_L$
such that for all i,
$v_1, \ldots, v_L$
such that for all i,
![]() $n_iv_i\leq M_i$
. Then the optimal values of
$n_iv_i\leq M_i$
. Then the optimal values of
![]() $v_1, \ldots, v_L$
can be determined as the values for which the corresponding mean cost rate function
$v_1, \ldots, v_L$
can be determined as the values for which the corresponding mean cost rate function
![]() $\mathrm{Cost}_1(\mathbf{v})$
is minimum.
$\mathrm{Cost}_1(\mathbf{v})$
is minimum.
Remark 2.2. If the system has a k-out-of-n structure with independent components from multiple type components, then (2.5) reduces to the result of Eryilmaz [Reference Eryilmaz7]. This is so because for such systems the survival signature is obviously given by
 \begin{align*}\Phi(l_1,\ldots, l_L)=\begin{cases}1, & \sum_{j=1}^L l_j\geq k,\\0, & \text{otherwise,}\end{cases}\end{align*}
\begin{align*}\Phi(l_1,\ldots, l_L)=\begin{cases}1, & \sum_{j=1}^L l_j\geq k,\\0, & \text{otherwise,}\end{cases}\end{align*}
i.e. the system works if at least k components are alive.
2.2. Cost function based on preventive replacement
In this section we propose a kind of age replacement preventive maintenance policy for the system with multiple types of components described in Section 1.2. The policy of renewing the system performed by the operator is such that it is replaced at failure time or at a predetermined time
![]() $\tau$
, whichever occurs first. There are many papers on age replacement strategy; the interested reader can refer to Zhao et al. [Reference Zhao, Al-Khalifa, Hamouda and Nakagawa36], Ashrafi and Asadi [Reference Ashrafi and Asadi1], and Mizutani et al. [Reference Mizutani, Zhao and Nakagawa23], for example. Mannai and Gasmi [Reference Mannai and Gasmi22] found the optimal configuration of a k-out-of-n system so that the expected total costs of the system under some generalized age replacement policies are minimized.
$\tau$
, whichever occurs first. There are many papers on age replacement strategy; the interested reader can refer to Zhao et al. [Reference Zhao, Al-Khalifa, Hamouda and Nakagawa36], Ashrafi and Asadi [Reference Ashrafi and Asadi1], and Mizutani et al. [Reference Mizutani, Zhao and Nakagawa23], for example. Mannai and Gasmi [Reference Mannai and Gasmi22] found the optimal configuration of a k-out-of-n system so that the expected total costs of the system under some generalized age replacement policies are minimized.
Here, suppose that the operator has
![]() $M_i$
components of type i available as spares, and he/she decides to add
$M_i$
components of type i available as spares, and he/she decides to add
![]() $v_i$
components to each of the components of type i, where
$v_i$
components to each of the components of type i, where
![]() $n_iv_i\leq M_i$
. Under the implemented policy here, the aim is to find the optimal number of v such that the mean cost rate we impose below is minimized.
$n_iv_i\leq M_i$
. Under the implemented policy here, the aim is to find the optimal number of v such that the mean cost rate we impose below is minimized.
If the replacement occurs after the system failure, i.e.
![]() $T_R\leq \tau$
, then, considering the costs
$T_R\leq \tau$
, then, considering the costs
![]() $c_i$
,
$c_i$
,
![]() $c_i^*$
, and
$c_i^*$
, and
![]() $c^{**}$
as defined in the previous subsection, the average cost of renewing the system is obtained as
$c^{**}$
as defined in the previous subsection, the average cost of renewing the system is obtained as
 \begin{align*}M_1(\mathbf{v})&=\sum_{i=1}^L c_i \mathbb{E}( X_i(T_R)\mid T_R\leq \tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i(v_i+1)-X_i(T_R)\mid T_R\leq \tau)+c^{**}\nonumber\\[5pt]&=\sum_{i=1}^L (v_i+1)c_i \mathbb{E}( X_i(T)\mid T\leq\tau)+\sum_{i=1}^L (v_i+1)c^*_i \mathbb{E}( n_i-X_i(T)\mid T\leq\tau)+c^{**}\nonumber\\[5pt]&=\sum_{i=1}^L (c_i-c^*_i)(v_i+1) \mathbb{E}( X_i(T)\mid T\leq\tau)+\sum_{i=1}^L (v_i+1)c^*_i n_i+c^{**},\end{align*}
\begin{align*}M_1(\mathbf{v})&=\sum_{i=1}^L c_i \mathbb{E}( X_i(T_R)\mid T_R\leq \tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i(v_i+1)-X_i(T_R)\mid T_R\leq \tau)+c^{**}\nonumber\\[5pt]&=\sum_{i=1}^L (v_i+1)c_i \mathbb{E}( X_i(T)\mid T\leq\tau)+\sum_{i=1}^L (v_i+1)c^*_i \mathbb{E}( n_i-X_i(T)\mid T\leq\tau)+c^{**}\nonumber\\[5pt]&=\sum_{i=1}^L (c_i-c^*_i)(v_i+1) \mathbb{E}( X_i(T)\mid T\leq\tau)+\sum_{i=1}^L (v_i+1)c^*_i n_i+c^{**},\end{align*}
where T is the lifetime of the system before redundancy allocation.
If the system is replaced before failure, i.e.
![]() $T_R>\tau$
, then, by the costs
$T_R>\tau$
, then, by the costs
![]() $c_i$
and
$c_i$
and
![]() $c_i^*$
,
$c_i^*$
,
![]() $i=1, \ldots, L$
for renewing the failed components and refreshing the alive components of type i, respectively, the system will be as good as the new condition. Let
$i=1, \ldots, L$
for renewing the failed components and refreshing the alive components of type i, respectively, the system will be as good as the new condition. Let
![]() $N_i(\tau)$
be the number of failed components of type i on
$N_i(\tau)$
be the number of failed components of type i on
![]() $[0, \tau]$
. Then the average cost of renewing the system is defined as
$[0, \tau]$
. Then the average cost of renewing the system is defined as
 \begin{align*}M_2(\mathbf{v})&=\sum_{i=1}^L c_i \mathbb{E}( N_i(\tau)\mid T_R>\tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i(v_i+1))-N_i(\tau)\mid T_R>\tau)\nonumber\\[5pt]&=\sum_{i=1}^L (c_i-c^*_i)(v_i+1) \mathbb{E}( N_i(\tau)\mid T>\tau)+\sum_{i=1}^L (v_i+1)c^*_i n_i.\end{align*}
\begin{align*}M_2(\mathbf{v})&=\sum_{i=1}^L c_i \mathbb{E}( N_i(\tau)\mid T_R>\tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i(v_i+1))-N_i(\tau)\mid T_R>\tau)\nonumber\\[5pt]&=\sum_{i=1}^L (c_i-c^*_i)(v_i+1) \mathbb{E}( N_i(\tau)\mid T>\tau)+\sum_{i=1}^L (v_i+1)c^*_i n_i.\end{align*}
Consequently, the mean cost rate function of the system renewing at time
![]() $\min\!(\tau, T_R)$
is achieved as
$\min\!(\tau, T_R)$
is achieved as
where it is attained that
To compute (2.6), we need to calculate
![]() $\mathbb{E}( N_i(\tau)\mid T>\tau)$
and
$\mathbb{E}( N_i(\tau)\mid T>\tau)$
and
![]() $\mathbb{E}( X_i(T)\mid T\leq \tau)$
. For the first one, we have
$\mathbb{E}( X_i(T)\mid T\leq \tau)$
. For the first one, we have
 \begin{align}&\mathbb{E}( N_i(\tau)\mid T>\tau)\notag \\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_i=0}^{n_i} j_i \mathbb{P}(N_i(\tau)=j_i, T>\tau)\nonumber\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i \mathbb{P}(T>\tau \mid N_1(\tau)=j_1,\ldots, N_L(\tau)=j_L)\,\mathbb{P}(N_1(\tau)=j_1,\ldots, N_L(\tau)=j_L)\nonumber\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i \Phi(n_1-j_1,\ldots, n_L-j_L)\binom{n_1}{j_1}\!\cdots\! \binom{n_L}{j_L}B(\tau,j_1,\dots,j_L),\end{align}
\begin{align}&\mathbb{E}( N_i(\tau)\mid T>\tau)\notag \\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_i=0}^{n_i} j_i \mathbb{P}(N_i(\tau)=j_i, T>\tau)\nonumber\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i \mathbb{P}(T>\tau \mid N_1(\tau)=j_1,\ldots, N_L(\tau)=j_L)\,\mathbb{P}(N_1(\tau)=j_1,\ldots, N_L(\tau)=j_L)\nonumber\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i \Phi(n_1-j_1,\ldots, n_L-j_L)\binom{n_1}{j_1}\!\cdots\! \binom{n_L}{j_L}B(\tau,j_1,\dots,j_L),\end{align}
where
 \begin{align}B(\tau,j_1,\dots,j_L)&=\mathbb{P}\bigl(T_1^{(1)}\leq\tau, \ldots, T_{j_1}^{(1)}\leq\tau, T_{j_1+1}^{(1)}>\tau, \ldots, T_{n_1}^{(1)}>\tau, \nonumber\\[5pt]&\quad \ldots, T_1^{(L)}\leq\tau, \ldots, T_{j_L}^{(L)}\leq\tau, T_{j_L+1}^{(L)}>\tau, \ldots, T_{n_L}^{(L)}>\tau \bigr).\end{align}
\begin{align}B(\tau,j_1,\dots,j_L)&=\mathbb{P}\bigl(T_1^{(1)}\leq\tau, \ldots, T_{j_1}^{(1)}\leq\tau, T_{j_1+1}^{(1)}>\tau, \ldots, T_{n_1}^{(1)}>\tau, \nonumber\\[5pt]&\quad \ldots, T_1^{(L)}\leq\tau, \ldots, T_{j_L}^{(L)}\leq\tau, T_{j_L+1}^{(L)}>\tau, \ldots, T_{n_L}^{(L)}>\tau \bigr).\end{align}
Using a method similar to that used in Lemma 2.1, we can calculate
![]() $\mathbb{E}( X_i(T)\mid T\leq \tau)$
,
$\mathbb{E}( X_i(T)\mid T\leq \tau)$
,
![]() $i=1,\dots,L$
as follows:
$i=1,\dots,L$
as follows:
Now we can write
for which we have
 \begin{align*}&\mathbb{P}\bigl(s<T\leq \tau, s<T_1^{(i)}\leq s+\delta\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\;\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}\mathbb{P}\bigl(s<T\leq \tau\mid s<T_1^{(i)}\leq s+\delta, C_1(\tau)=l_1, \\[5pt] & \quad \ldots, C_i(\tau)=l_i, C_L(\tau)=l_L, C_1(s)=m_1,\ldots, C_i(s)=m_i,\ldots, C_L(s)=m_L\bigr) \, \\[5pt] & \quad \times \mathbb{P}\bigl(s<T_1^{(i)}\leq s+\delta,C_1(\tau)=l_1, \ldots, C_i(\tau)=l_i,C_L(\tau)=l_L, C_1(s)=m_1,\ldots, C_i(s)=m_i,\\[5pt] & \quad \ldots, C_L(s)=m_L)\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\;\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}[\Phi(m_1,\ldots, m_L)-\Phi(l_1,\ldots, l_L)]\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr]\nonumber\\[5pt]& \quad \times \binom{n_i-1}{m_i}\binom{m_i}{l_i}A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau),\end{align*}
\begin{align*}&\mathbb{P}\bigl(s<T\leq \tau, s<T_1^{(i)}\leq s+\delta\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\;\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}\mathbb{P}\bigl(s<T\leq \tau\mid s<T_1^{(i)}\leq s+\delta, C_1(\tau)=l_1, \\[5pt] & \quad \ldots, C_i(\tau)=l_i, C_L(\tau)=l_L, C_1(s)=m_1,\ldots, C_i(s)=m_i,\ldots, C_L(s)=m_L\bigr) \, \\[5pt] & \quad \times \mathbb{P}\bigl(s<T_1^{(i)}\leq s+\delta,C_1(\tau)=l_1, \ldots, C_i(\tau)=l_i,C_L(\tau)=l_L, C_1(s)=m_1,\ldots, C_i(s)=m_i,\\[5pt] & \quad \ldots, C_L(s)=m_L)\bigr)\nonumber\\[5pt] & =\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\;\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}[\Phi(m_1,\ldots, m_L)-\Phi(l_1,\ldots, l_L)]\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr]\nonumber\\[5pt]& \quad \times \binom{n_i-1}{m_i}\binom{m_i}{l_i}A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau),\end{align*}
where
 \begin{align}&A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\nonumber\\[5pt]& =\mathbb{P}\bigl(T_1^{(1)}>\tau, \ldots, T_{l_1}^{(1)}>\tau, s<T_{l_1+1}^{(1)}\leq \tau, \ldots, s<T_{m_1}^{(1)}\leq \tau, T_{m_1+1}^{(1)}\leq s,\ldots, T_{n_1}^{(1)}\leq s, \ldots,\nonumber \\[5pt] & \quad T_1^{(i)}>\tau, \ldots, T_{l_i}^{(i)}>\tau, s<T_{l_i+1}^{(i)}\leq\tau, \ldots, s<T_{m_i}^{(i)}\leq\tau, s<T_{m_i+1}^{(i)}\leq s+\delta,\notag \\[5pt] & \quad T_{m_i+2}^{(i)}\leq s,\ldots, T_{n_i}^{(i)}\leq s, \ldots, T_1^{(L)}>\tau, \ldots, T_{l_L}^{(L)}>\tau, s<T_{l_L+1}^{(L)}\leq \tau, \ldots, s<T_{m_L}^{(L)}\leq \tau, \notag \\[5pt] & \quad T_{m_L+1}^{(L)}\leq s,\ldots, T_{n_L}^{(L)}\leq s \bigr).\end{align}
\begin{align}&A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\nonumber\\[5pt]& =\mathbb{P}\bigl(T_1^{(1)}>\tau, \ldots, T_{l_1}^{(1)}>\tau, s<T_{l_1+1}^{(1)}\leq \tau, \ldots, s<T_{m_1}^{(1)}\leq \tau, T_{m_1+1}^{(1)}\leq s,\ldots, T_{n_1}^{(1)}\leq s, \ldots,\nonumber \\[5pt] & \quad T_1^{(i)}>\tau, \ldots, T_{l_i}^{(i)}>\tau, s<T_{l_i+1}^{(i)}\leq\tau, \ldots, s<T_{m_i}^{(i)}\leq\tau, s<T_{m_i+1}^{(i)}\leq s+\delta,\notag \\[5pt] & \quad T_{m_i+2}^{(i)}\leq s,\ldots, T_{n_i}^{(i)}\leq s, \ldots, T_1^{(L)}>\tau, \ldots, T_{l_L}^{(L)}>\tau, s<T_{l_L+1}^{(L)}\leq \tau, \ldots, s<T_{m_L}^{(L)}\leq \tau, \notag \\[5pt] & \quad T_{m_L+1}^{(L)}\leq s,\ldots, T_{n_L}^{(L)}\leq s \bigr).\end{align}
In the following theorem, the probabilities in (2.8) and (2.9) are represented based on the survival copula of component lifetimes.
Theorem 2.2. Using the inclusion–exclusion rule, we obtain the following expressions for
![]() $B(\tau,j_1,\dots,j_L)$
and
$B(\tau,j_1,\dots,j_L)$
and
![]() $A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)$
, respectively:
$A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)$
, respectively:
 \begin{align*}&B(\tau,j_1,\dots,j_L)\\[5pt]& ={\sum_{b_1=0}^{j_1}\!\cdots\!\sum_{b_L=0}^{j_L}}(\!-\!1)^{b_1+\cdots+ b_L}\binom{j_1}{b_1}\!\cdots\! \binom{j_L}{b_L} \hat{C}\Bigl(\underbrace{\bar{F}_1(\tau)}_{n_1-j_1+b_1},\underbrace{1}_{j_1-b_1},\ldots,\underbrace{\bar{F}_L(\tau)}_{n_L-j_L+b_L},\underbrace{1}_{j_L-b_L)}\Bigr)\end{align*}
\begin{align*}&B(\tau,j_1,\dots,j_L)\\[5pt]& ={\sum_{b_1=0}^{j_1}\!\cdots\!\sum_{b_L=0}^{j_L}}(\!-\!1)^{b_1+\cdots+ b_L}\binom{j_1}{b_1}\!\cdots\! \binom{j_L}{b_L} \hat{C}\Bigl(\underbrace{\bar{F}_1(\tau)}_{n_1-j_1+b_1},\underbrace{1}_{j_1-b_1},\ldots,\underbrace{\bar{F}_L(\tau)}_{n_L-j_L+b_L},\underbrace{1}_{j_L-b_L)}\Bigr)\end{align*}
and
 \begin{align*}&A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{\,j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times {\sum_{d_1=0}^{m_1-l_1}\!\cdots\!\sum_{d_i=0}^{m_i-l_i}\!\cdots\!\sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots + d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\ &\quad \times \biggl[\hat{C}\Bigl(\underbrace{\bar{F}_k(\tau)}_{l_k+d_k}, \underbrace{\bar{F}_k(s)}_{m_k-l_k+j_k-d_k}\!,\underbrace{1}_{n_k-m_k-j_k}\!\!,1 \leq k \leq L, k\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+j_i-d_i+1}\!, \underbrace{1}_{n_i-m_i-j_i-1}\Bigr)\\[5pt] &\quad -\hat{C}\Bigl(\underbrace{\bar{F}_k(\tau)}_{l_k+d_k}, \underbrace{\bar{F}_k(s)}_{m_k-l_k+j_k-d_k}\!,\underbrace{1}_{n_k-m_k-j_k}\!\!,1 \leq k \leq L, k\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+j_i-d_i}\!\!, \bar{F}_i(s+\delta), \!\underbrace{1}_{n_i-m_i-j_i-1} \Bigr)\biggr].\end{align*}
\begin{align*}&A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{\,j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times {\sum_{d_1=0}^{m_1-l_1}\!\cdots\!\sum_{d_i=0}^{m_i-l_i}\!\cdots\!\sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots + d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\ &\quad \times \biggl[\hat{C}\Bigl(\underbrace{\bar{F}_k(\tau)}_{l_k+d_k}, \underbrace{\bar{F}_k(s)}_{m_k-l_k+j_k-d_k}\!,\underbrace{1}_{n_k-m_k-j_k}\!\!,1 \leq k \leq L, k\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+j_i-d_i+1}\!, \underbrace{1}_{n_i-m_i-j_i-1}\Bigr)\\[5pt] &\quad -\hat{C}\Bigl(\underbrace{\bar{F}_k(\tau)}_{l_k+d_k}, \underbrace{\bar{F}_k(s)}_{m_k-l_k+j_k-d_k}\!,\underbrace{1}_{n_k-m_k-j_k}\!\!,1 \leq k \leq L, k\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+j_i-d_i}\!\!, \bar{F}_i(s+\delta), \!\underbrace{1}_{n_i-m_i-j_i-1} \Bigr)\biggr].\end{align*}
Proof. See Appendix B.![]()
Corollary 2.1. For the particular case of independent components, it can be deduced that
 \begin{align}\mathbb{E}( N_i(\tau)\mid T>\tau)=\dfrac{1}{\bar{F}(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i\Phi(n_1-j_1,\ldots, n_L-j_L)\prod_{l=1}^L \binom{n_l}{j_l}F_l^{j_l}(\tau)\bar{F}_l^{n_l-j_l}(\tau).\end{align}
\begin{align}\mathbb{E}( N_i(\tau)\mid T>\tau)=\dfrac{1}{\bar{F}(\tau)}\sum_{j_1=0}^{n_1}\!\cdots\!\sum_{j_L=0}^{n_L} j_i\Phi(n_1-j_1,\ldots, n_L-j_L)\prod_{l=1}^L \binom{n_l}{j_l}F_l^{j_l}(\tau)\bar{F}_l^{n_l-j_l}(\tau).\end{align}
Also, in this case we have
 \begin{align*}A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)&=\Biggl\{\prod_{j=1,j\neq i}^L F_j^{n_j-m_j}(s)[\bar{F}_j(\tau)-\bar{F}_j(s)]^{m_j-l_j}\bar{F}_j^{l_j}(\tau)\Biggr\}\\[5pt]&\quad \times[\bar{F}_i(s)-\bar{F}_i(s+\delta)]F_i^{n_i-m_i-1}(s)[\bar{F}_i(\tau)-\bar{F}_i(s)]^{m_i-l_i}\bar{F}_i^{l_i}(\tau),\end{align*}
\begin{align*}A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)&=\Biggl\{\prod_{j=1,j\neq i}^L F_j^{n_j-m_j}(s)[\bar{F}_j(\tau)-\bar{F}_j(s)]^{m_j-l_j}\bar{F}_j^{l_j}(\tau)\Biggr\}\\[5pt]&\quad \times[\bar{F}_i(s)-\bar{F}_i(s+\delta)]F_i^{n_i-m_i-1}(s)[\bar{F}_i(\tau)-\bar{F}_i(s)]^{m_i-l_i}\bar{F}_i^{l_i}(\tau),\end{align*}
which in turn implies that
 \begin{align} &\mathbb{E}( X_i(T)\mid T\leq \tau) \notag \\[5pt] & =\dfrac{n_i}{1-\bar{F}_{T}(\tau)}\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}[\Phi(m_1,\ldots, m_L)-\Phi(l_1,\ldots, l_L)]\nonumber\\[5pt]& \quad \times\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr] \binom{n_i-1}{m_i}\binom{m_i}{l_i}\notag \\[5pt]& \quad \times \int_{0}^{\tau}\Biggl\{\prod_{j=1,j\neq i}^L F_j^{n_j-m_j}(s)[\bar{F}_j(\tau)-\bar{F}_j(s)]^{m_j-l_j}\bar{F}_j^{l_j}(\tau)\Biggr\}\nonumber\\[5pt]& \quad \times F_i^{n_i-m_i-1}(s)[\bar{F}_i(\tau)-\bar{F}_i(s)]^{m_i-l_i}\bar{F}_i^{l_i}(\tau) \,{\mathrm{d}} F_i(s).\end{align}
\begin{align} &\mathbb{E}( X_i(T)\mid T\leq \tau) \notag \\[5pt] & =\dfrac{n_i}{1-\bar{F}_{T}(\tau)}\sum_{m_1=0}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=0}^{n_L}\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}[\Phi(m_1,\ldots, m_L)-\Phi(l_1,\ldots, l_L)]\nonumber\\[5pt]& \quad \times\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr] \binom{n_i-1}{m_i}\binom{m_i}{l_i}\notag \\[5pt]& \quad \times \int_{0}^{\tau}\Biggl\{\prod_{j=1,j\neq i}^L F_j^{n_j-m_j}(s)[\bar{F}_j(\tau)-\bar{F}_j(s)]^{m_j-l_j}\bar{F}_j^{l_j}(\tau)\Biggr\}\nonumber\\[5pt]& \quad \times F_i^{n_i-m_i-1}(s)[\bar{F}_i(\tau)-\bar{F}_i(s)]^{m_i-l_i}\bar{F}_i^{l_i}(\tau) \,{\mathrm{d}} F_i(s).\end{align}
It is worth noting that if the structure of the system is k-out-of-n whose components are independent, then (2.10) and (2.11) are reduced to the results that appeared in Eryilmaz [Reference Eryilmaz7].
For given values
![]() $n_i, c_i, c_i^*, M_i$
,
$n_i, c_i, c_i^*, M_i$
,
![]() $i=1,\ldots, L$
,
$i=1,\ldots, L$
,
![]() $c^{**}$
and
$c^{**}$
and
![]() $\tau$
, we aim to determine the optimal values of
$\tau$
, we aim to determine the optimal values of
![]() $v_i$
under the constraints
$v_i$
under the constraints
![]() $n_iv_i\leq M_i$
,
$n_iv_i\leq M_i$
,
![]() $ i=1, \ldots, L$
, such that the mean cost rate function
$ i=1, \ldots, L$
, such that the mean cost rate function
![]() $\mathrm{Cost}_2$
is minimized.
$\mathrm{Cost}_2$
is minimized.
In the following, we present two examples to examine the aforementioned theoretical results.
Example 2.1. Consider the system depicted in Figure 1, given in Feng et al. [Reference Feng, Patelli, Beer and Coolen16] and Eryilmaz et al. [Reference Eryilmaz, Coolen and Coolen-Maturi10]. The system consists of six components in which components 1, 2, and 5 are of type 1 and components 3, 4, and 6 are of type 2. The survival signature of the system is presented in Table 1. Assume that the dependency structure of the component lifetimes is modeled by a parametric family of copulas known as the Gumbel–Hougaard family, defined as
where
![]() $\alpha\geq 1$
is the dependency parameter in the family. The value
$\alpha\geq 1$
is the dependency parameter in the family. The value
![]() $\alpha=1$
corresponds to the independent condition. Let the component lifetimes of the two types follow exponential distributions with reliability functions
$\alpha=1$
corresponds to the independent condition. Let the component lifetimes of the two types follow exponential distributions with reliability functions
![]() $\bar{F}_i(t)={\mathrm{e}}^{-t\theta_i}$
, where we assume that
$\bar{F}_i(t)={\mathrm{e}}^{-t\theta_i}$
, where we assume that
![]() $\theta_1=0.2$
and
$\theta_1=0.2$
and
![]() $\theta_2=0.3$
. If there are
$\theta_2=0.3$
. If there are
![]() $M_1=9$
and
$M_1=9$
and
![]() $M_2=6$
components from type 1 and type 2, respectively, as spares, then
$M_2=6$
components from type 1 and type 2, respectively, as spares, then
![]() $v_1\in\{0,1,2,3\}$
and
$v_1\in\{0,1,2,3\}$
and
![]() $ v_2\in\{0,1,2\}$
. To find the optimal number of redundant components for each type, we use the following values for the replacement costs:
$ v_2\in\{0,1,2\}$
. To find the optimal number of redundant components for each type, we use the following values for the replacement costs:
![]() $c_1=3$
,
$c_1=3$
,
![]() $c_2=2$
,
$c_2=2$
,
![]() $c_1^*=1.5$
,
$c_1^*=1.5$
,
![]() $c_2^*=1$
, and
$c_2^*=1$
, and
![]() $ c^{**}=10$
. To compute the numerator of (2.2), we need to compute
$ c^{**}=10$
. To compute the numerator of (2.2), we need to compute
![]() $\mathbb{E}( X_i(T)), i=1, 2$
. From Lemma 2.1 and Theorem 2.1, we have
$\mathbb{E}( X_i(T)), i=1, 2$
. From Lemma 2.1 and Theorem 2.1, we have
 \begin{align*}&\mathbb{E}( X_1(T))=n_1\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{1}{\delta}\sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\Phi(m_1+1, m_2) \binom{n_1-1}{m_1}\binom{n_2}{m_2}A_{\mathbf{m}}^{(1)}(t,\delta) \,{\mathrm{d}} t,\end{align*}
\begin{align*}&\mathbb{E}( X_1(T))=n_1\int_{0}^{\infty} \lim_{\delta\rightarrow 0}\dfrac{1}{\delta}\sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\Phi(m_1+1, m_2) \binom{n_1-1}{m_1}\binom{n_2}{m_2}A_{\mathbf{m}}^{(1)}(t,\delta) \,{\mathrm{d}} t,\end{align*}
where
 \begin{align*}A_{\mathbf{m}}^{(1)}(t, \delta)&={\sum_{j_1=0}^{n_1-m_1-1} \sum_{j_2=0}^{n_2-m_2}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1}\binom{n_2-m_2}{j_2}} \\[5pt]&\quad \times \bigl[ {\mathrm{e}}^{-[(m_1+j_1+1)(t \theta_1)^{\alpha}+(m_2+j_2)(t \theta_2)^{\alpha}]^{1/\alpha}}-{\mathrm{e}}^{-[(m_1+j_1)(t \theta_1)^{\alpha}+((t+\delta)\theta_1)^{\alpha}+(m_2+j_2)(t \theta_2)^{\alpha}]^{1/\alpha}}\bigr].\end{align*}
\begin{align*}A_{\mathbf{m}}^{(1)}(t, \delta)&={\sum_{j_1=0}^{n_1-m_1-1} \sum_{j_2=0}^{n_2-m_2}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1}\binom{n_2-m_2}{j_2}} \\[5pt]&\quad \times \bigl[ {\mathrm{e}}^{-[(m_1+j_1+1)(t \theta_1)^{\alpha}+(m_2+j_2)(t \theta_2)^{\alpha}]^{1/\alpha}}-{\mathrm{e}}^{-[(m_1+j_1)(t \theta_1)^{\alpha}+((t+\delta)\theta_1)^{\alpha}+(m_2+j_2)(t \theta_2)^{\alpha}]^{1/\alpha}}\bigr].\end{align*}

Figure 1. The system in Example 2.1 with two types of components.
Table 1. Survival signature of the system in Figure 1.

Thus we get
 \begin{align*}&\mathbb{E}( X_1(T))\\[5pt] & =n_1 \sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\binom{n_1-1}{m_1}\binom{n_2}{m_2}\Phi(m_1+1, m_2)\\[5pt] & \quad \times \sum_{j_1=0}^{n_1-m_1-1} \sum_{j_2=0}^{n_2-m_2} (\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1}\binom{n_2-m_2}{j_2}\\[5pt]& \quad \times \theta_1^{\alpha}\bigl[(m_1+j_1+1)\theta_1^{\alpha}+(m_2+j_2)\theta_2^{\alpha}\bigr]^{-1}.\end{align*}
\begin{align*}&\mathbb{E}( X_1(T))\\[5pt] & =n_1 \sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\binom{n_1-1}{m_1}\binom{n_2}{m_2}\Phi(m_1+1, m_2)\\[5pt] & \quad \times \sum_{j_1=0}^{n_1-m_1-1} \sum_{j_2=0}^{n_2-m_2} (\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1}\binom{n_2-m_2}{j_2}\\[5pt]& \quad \times \theta_1^{\alpha}\bigl[(m_1+j_1+1)\theta_1^{\alpha}+(m_2+j_2)\theta_2^{\alpha}\bigr]^{-1}.\end{align*}
Similarly, we have
 \begin{align*}&\mathbb{E}( X_2(T))\\[5pt] & =n_2 \sum_{m_1=0}^{n_1}\sum_{m_2=0}^{n_2-1}\binom{n_1}{m_1}\binom{n_2-1}{m_2}\Phi(m_1, m_2+1)\\[5pt] & \quad\times \sum_{j_1=0}^{n_1-m_1} \sum_{j_2=0}^{n_2-m_2-1} (\!-\!1)^{j_1+ j_2}\binom{n_1-m_1}{j_1}\binom{n_2-m_2-1}{j_2}\\[5pt]& \quad \times\theta_2^{\alpha}\bigl[(m_1+j_1)\theta_1^{\alpha}+(m_2+j_2+1)\theta_2^{\alpha}\bigr]^{-1}.\end{align*}
\begin{align*}&\mathbb{E}( X_2(T))\\[5pt] & =n_2 \sum_{m_1=0}^{n_1}\sum_{m_2=0}^{n_2-1}\binom{n_1}{m_1}\binom{n_2-1}{m_2}\Phi(m_1, m_2+1)\\[5pt] & \quad\times \sum_{j_1=0}^{n_1-m_1} \sum_{j_2=0}^{n_2-m_2-1} (\!-\!1)^{j_1+ j_2}\binom{n_1-m_1}{j_1}\binom{n_2-m_2-1}{j_2}\\[5pt]& \quad \times\theta_2^{\alpha}\bigl[(m_1+j_1)\theta_1^{\alpha}+(m_2+j_2+1)\theta_2^{\alpha}\bigr]^{-1}.\end{align*}
Also, the denominator of (2.2) can be written as follows:
 \begin{align*} \mathbb{E}( T_R)&=\int_0^{\infty} \bar{F}_{T_R}(t) \,{\mathrm{d}} t\\[5pt] &={\sum_{l_1=0}^{n_1}\sum_{l_2=0}^{n_2}}\binom{n_1}{l_1} \binom{n_2}{l_2}\Phi(l_1, l_2){\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}}(\!-\!1)^{i_1+ i_2}\binom{n_1-l_1}{i_1} \binom{n_2-l_2}{i_2} \nonumber\\[5pt]&\quad \times\int_0^{\infty} {\mathrm{e}}^{- [(i_1+l_1)(\!-\!\ln(1-(1-\exp[-t \theta_1])^{v_1+1}))^{\alpha}+(i_2+l_2)(\!-\!\ln(1-(1-\exp[-t \theta_2])^{v_2+1}))^{\alpha} ]^{1/\alpha}} \,{\mathrm{d}} t,\end{align*}
\begin{align*} \mathbb{E}( T_R)&=\int_0^{\infty} \bar{F}_{T_R}(t) \,{\mathrm{d}} t\\[5pt] &={\sum_{l_1=0}^{n_1}\sum_{l_2=0}^{n_2}}\binom{n_1}{l_1} \binom{n_2}{l_2}\Phi(l_1, l_2){\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}}(\!-\!1)^{i_1+ i_2}\binom{n_1-l_1}{i_1} \binom{n_2-l_2}{i_2} \nonumber\\[5pt]&\quad \times\int_0^{\infty} {\mathrm{e}}^{- [(i_1+l_1)(\!-\!\ln(1-(1-\exp[-t \theta_1])^{v_1+1}))^{\alpha}+(i_2+l_2)(\!-\!\ln(1-(1-\exp[-t \theta_2])^{v_2+1}))^{\alpha} ]^{1/\alpha}} \,{\mathrm{d}} t,\end{align*}
which should be evaluated numerically by suitable softwares such as Mathematica. The values of
![]() $\mathrm{Cost}_1(\mathbf{v})$
for different combinations of
$\mathrm{Cost}_1(\mathbf{v})$
for different combinations of
![]() $v_1$
and
$v_1$
and
![]() $ v_2$
are presented in Table 2 for two values
$ v_2$
are presented in Table 2 for two values
![]() $\alpha=2$
(dependent components) and
$\alpha=2$
(dependent components) and
![]() $\alpha=1$
(independent components). It is seen that
$\alpha=1$
(independent components). It is seen that
![]() $v_1=2$
and
$v_1=2$
and
![]() $v_2=0$
are the optimal choices for the number of redundant components of types 1 and 2, respectively, under the criterion
$v_2=0$
are the optimal choices for the number of redundant components of types 1 and 2, respectively, under the criterion
![]() $\mathrm{Cost}_1$
in the case
$\mathrm{Cost}_1$
in the case
![]() $\alpha=2$
, and
$\alpha=2$
, and
![]() $v_1=3$
and
$v_1=3$
and
![]() $v_2=0$
are the optimal numbers in the case
$v_2=0$
are the optimal numbers in the case
![]() $\alpha=1$
.
$\alpha=1$
.
Table 2. The values of
![]() $\mathrm{Cost}_1(\mathbf{v})$
and
$\mathrm{Cost}_1(\mathbf{v})$
and
![]() $\mathrm{Cost}_2(\mathbf{v})$
in Example 2.1 in the case of dependent components
$\mathrm{Cost}_2(\mathbf{v})$
in Example 2.1 in the case of dependent components
![]() $(\alpha=2)$
and independent components
$(\alpha=2)$
and independent components
![]() $(\alpha=1)$
.
$(\alpha=1)$
.

Suppose that the described system is maintained under the aforementioned age replacement policy, where we assume that
![]() $\tau=2$
, i.e. the replacement time of the system is
$\tau=2$
, i.e. the replacement time of the system is
![]() $\min\!(T_R, 2)$
. From equations (2.7) and (2.8) the mean number of failed components of ith type at time
$\min\!(T_R, 2)$
. From equations (2.7) and (2.8) the mean number of failed components of ith type at time
![]() $\tau$
, before system failure, is evaluated by the following expression:
$\tau$
, before system failure, is evaluated by the following expression:
 \begin{align*}&\mathbb{E}( N_i(\tau)\mid T>\tau)\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\sum_{j_2=0}^{n_2} j_i \Phi(n_1-j_1, n_2-j_2)\binom{n_1}{j_1} \binom{n_2}{j_2}{\sum_{b_1=0}^{j_1}\sum_{b_2=0}^{j_2}}(\!-\!1)^{b_1+ b_2}\binom{j_1}{b_1} \binom{j_2}{b_2} \\[5pt]& \quad \times \exp\bigl[-\tau\bigl( \theta_1^{\alpha}(n_1-j_1+b_1)+\theta_2^{\alpha}(n_2-j_2+b_2) \bigr)^{1/\alpha}\bigr], \quad i=1, 2,\end{align*}
\begin{align*}&\mathbb{E}( N_i(\tau)\mid T>\tau)\\[5pt]& =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1}\sum_{j_2=0}^{n_2} j_i \Phi(n_1-j_1, n_2-j_2)\binom{n_1}{j_1} \binom{n_2}{j_2}{\sum_{b_1=0}^{j_1}\sum_{b_2=0}^{j_2}}(\!-\!1)^{b_1+ b_2}\binom{j_1}{b_1} \binom{j_2}{b_2} \\[5pt]& \quad \times \exp\bigl[-\tau\bigl( \theta_1^{\alpha}(n_1-j_1+b_1)+\theta_2^{\alpha}(n_2-j_2+b_2) \bigr)^{1/\alpha}\bigr], \quad i=1, 2,\end{align*}
where from (1.3) we get
 \begin{align*}\bar{F}_T(\tau)&={\sum_{l_1=0}^{n_1}\sum_{l_2=0}^{n_2}}{\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}}(\!-\!1)^{i_1+ i_1}\binom{n_1}{l_1} \binom{n_2}{l_2}\binom{n_1-l_1}{i_1} \binom{n_2-l_2}{i_2}\Phi(l_1, l_2)\nonumber\\[5pt]&\quad \times \exp\bigl[-\tau\bigl((i_1+l_1)\theta_1^{\alpha}+(i_2+l_2)\theta_2^{\alpha} \bigr)^{1/\alpha}\bigr].\end{align*}
\begin{align*}\bar{F}_T(\tau)&={\sum_{l_1=0}^{n_1}\sum_{l_2=0}^{n_2}}{\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}}(\!-\!1)^{i_1+ i_1}\binom{n_1}{l_1} \binom{n_2}{l_2}\binom{n_1-l_1}{i_1} \binom{n_2-l_2}{i_2}\Phi(l_1, l_2)\nonumber\\[5pt]&\quad \times \exp\bigl[-\tau\bigl((i_1+l_1)\theta_1^{\alpha}+(i_2+l_2)\theta_2^{\alpha} \bigr)^{1/\alpha}\bigr].\end{align*}
Next, for the mean number of failed components at the time of the system failure given that the system has failed before
![]() $\tau$
, we have
$\tau$
, we have
 \begin{align*}&\mathbb{E}( X_1(T)\mid T\leq \tau)\\[5pt]& =\dfrac{n_1}{1-\bar{F}_T(\tau)}\sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\sum_{l_1=0}^{m_1}\sum_{l_2=0}^{m_2}[\Phi(m_1, m_2)-\Phi(l_1, l_2)]\binom{n_1-1}{m_1}\binom{m_1}{l_1}\binom{n_2}{m_2}\binom{m_2}{l_2}\\& \quad \times {\sum_{j_1=0}^{n_1-m_1-1}\sum_{j_2=0}^{n_2-m_2}}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1} \binom{n_2-m_2}{j_2}\\[5pt] & \quad\times {\sum_{d_1=0}^{m_1-l_1}\sum_{d_2=0}^{m_2-l_2}}(\!-\!1)^{d_1+d_2}\binom{m_1-l_1}{d_1} \binom{m_2-l_2}{d_2}\\[5pt]& \quad \times \dfrac{\theta_1^{\alpha}\bigl[ {\mathrm{e}}^{-\tau((l_1+d_1)\theta_1^{\alpha}+(l_2+d_2)\theta_2^{\alpha} )^{1/\alpha}}- {\mathrm{e}}^{-\tau((m_1+j_1+1)\theta_1^{\alpha}+(m_2+j_2)\theta_2^{\alpha} )^{1/\alpha}}\bigr]}{(m_1-l_1+j_1-d_1+1)\theta_1^{\alpha}+(m_2-l_2+j_2-d_2)\theta_2^{\alpha}}\end{align*}
\begin{align*}&\mathbb{E}( X_1(T)\mid T\leq \tau)\\[5pt]& =\dfrac{n_1}{1-\bar{F}_T(\tau)}\sum_{m_1=0}^{n_1-1}\sum_{m_2=0}^{n_2}\sum_{l_1=0}^{m_1}\sum_{l_2=0}^{m_2}[\Phi(m_1, m_2)-\Phi(l_1, l_2)]\binom{n_1-1}{m_1}\binom{m_1}{l_1}\binom{n_2}{m_2}\binom{m_2}{l_2}\\& \quad \times {\sum_{j_1=0}^{n_1-m_1-1}\sum_{j_2=0}^{n_2-m_2}}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1-1}{j_1} \binom{n_2-m_2}{j_2}\\[5pt] & \quad\times {\sum_{d_1=0}^{m_1-l_1}\sum_{d_2=0}^{m_2-l_2}}(\!-\!1)^{d_1+d_2}\binom{m_1-l_1}{d_1} \binom{m_2-l_2}{d_2}\\[5pt]& \quad \times \dfrac{\theta_1^{\alpha}\bigl[ {\mathrm{e}}^{-\tau((l_1+d_1)\theta_1^{\alpha}+(l_2+d_2)\theta_2^{\alpha} )^{1/\alpha}}- {\mathrm{e}}^{-\tau((m_1+j_1+1)\theta_1^{\alpha}+(m_2+j_2)\theta_2^{\alpha} )^{1/\alpha}}\bigr]}{(m_1-l_1+j_1-d_1+1)\theta_1^{\alpha}+(m_2-l_2+j_2-d_2)\theta_2^{\alpha}}\end{align*}
and
 \begin{align*}&\mathbb{E}( X_2(T)\mid T\leq \tau)\\[5pt]& =\dfrac{n_2}{1-\bar{F}_T(\tau)}\sum_{m_1=0}^{n_1}\sum_{m_2=0}^{n_2-1}\sum_{l_1=0}^{m_1}\sum_{l_2=0}^{m_2}[\Phi(m_1, m_2)-\Phi(l_1, l_2)]\binom{n_1}{m_1}\binom{m_1}{l_1}\binom{n_2-1}{m_2}\binom{m_2}{l_2}\\& \quad \times {\sum_{j_1=0}^{n_1-m_1}\sum_{j_2=0}^{n_2-m_2-1}}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1}{j_1} \binom{n_2-m_2-1}{j_2} \\ & \quad\times {\sum_{d_1=0}^{m_1-l_1}\sum_{d_2=0}^{m_2-l_2}}(\!-\!1)^{d_1+d_2}\binom{m_1-l_1}{d_1} \binom{m_2-l_2}{d_2}\\[5pt]& \quad \times \dfrac{\theta_2^{\alpha}\bigl[ {\mathrm{e}}^{-\tau((l_1+d_1)\theta_1^{\alpha}+(l_2+d_2)\theta_2^{\alpha} )^{1/\alpha}}- {\mathrm{e}}^{-\tau((m_1+j_1)\theta_1^{\alpha}+(m_2+j_2+1)\theta_2^{\alpha} )^{1/\alpha}}\bigr]}{(m_1-l_1+j_1-d_1)\theta_1^{\alpha}+(m_2-l_2+j_2-d_2+1)\theta_2^{\alpha}}.\end{align*}
\begin{align*}&\mathbb{E}( X_2(T)\mid T\leq \tau)\\[5pt]& =\dfrac{n_2}{1-\bar{F}_T(\tau)}\sum_{m_1=0}^{n_1}\sum_{m_2=0}^{n_2-1}\sum_{l_1=0}^{m_1}\sum_{l_2=0}^{m_2}[\Phi(m_1, m_2)-\Phi(l_1, l_2)]\binom{n_1}{m_1}\binom{m_1}{l_1}\binom{n_2-1}{m_2}\binom{m_2}{l_2}\\& \quad \times {\sum_{j_1=0}^{n_1-m_1}\sum_{j_2=0}^{n_2-m_2-1}}(\!-\!1)^{j_1+ j_2}\binom{n_1-m_1}{j_1} \binom{n_2-m_2-1}{j_2} \\ & \quad\times {\sum_{d_1=0}^{m_1-l_1}\sum_{d_2=0}^{m_2-l_2}}(\!-\!1)^{d_1+d_2}\binom{m_1-l_1}{d_1} \binom{m_2-l_2}{d_2}\\[5pt]& \quad \times \dfrac{\theta_2^{\alpha}\bigl[ {\mathrm{e}}^{-\tau((l_1+d_1)\theta_1^{\alpha}+(l_2+d_2)\theta_2^{\alpha} )^{1/\alpha}}- {\mathrm{e}}^{-\tau((m_1+j_1)\theta_1^{\alpha}+(m_2+j_2+1)\theta_2^{\alpha} )^{1/\alpha}}\bigr]}{(m_1-l_1+j_1-d_1)\theta_1^{\alpha}+(m_2-l_2+j_2-d_2+1)\theta_2^{\alpha}}.\end{align*}
By substituting these results in (2.6), the mean cost rate of replacement strategy can be evaluated. In Table 2 the values of
![]() $\mathrm{Cost}_2(\mathbf{v})$
are calculated for different combinations of
$\mathrm{Cost}_2(\mathbf{v})$
are calculated for different combinations of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, for both dependent and independent situations. It follows from the results of the table that for
$v_2$
, for both dependent and independent situations. It follows from the results of the table that for
![]() $v_1=1$
and
$v_1=1$
and
![]() $v_2=0$
, the mean cost rate
$v_2=0$
, the mean cost rate
![]() $\mathrm{Cost}_2(\mathbf{v})$
is minimized, in both cases
$\mathrm{Cost}_2(\mathbf{v})$
is minimized, in both cases
![]() $\alpha=1,2$
.
$\alpha=1,2$
.
Table 3. The optimum values of
![]() $\mathbf{v}$
by minimizing
$\mathbf{v}$
by minimizing
![]() $\mathrm{Cost}_i(v_1,v_2)$
,
$\mathrm{Cost}_i(v_1,v_2)$
,
![]() $i=1,2$
, for different
$i=1,2$
, for different
![]() $\alpha$
in Example 2.1.
$\alpha$
in Example 2.1.

Table 4. The optimum values of
![]() $\mathbf{v}$
by minimizing
$\mathbf{v}$
by minimizing
![]() $\mathrm{Cost}_1$
for different costs in Example 2.1.
$\mathrm{Cost}_1$
for different costs in Example 2.1.

In order to investigate the robustness of our strategies concerning the model parameters, we calculate some numerical results based on these parameters. The results in Table 3 shows the effect of the dependency parameter
![]() $\alpha$
on the optimal values of
$\alpha$
on the optimal values of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, for different values of
$v_2$
, for different values of
![]() $\alpha$
. As can be seen, when
$\alpha$
. As can be seen, when
![]() $\alpha$
increases (i.e. we get far from independence), the number of redundant components decreases based on the objective function
$\alpha$
increases (i.e. we get far from independence), the number of redundant components decreases based on the objective function
![]() $\mathrm{Cost}_1(v_1,v_2)$
but remain unchanged under the
$\mathrm{Cost}_1(v_1,v_2)$
but remain unchanged under the
![]() $\mathrm{Cost}_2(v_1,v_2)$
. This makes sense since under more dependency the MTTF is increased and the need to spare components reduces. Also, it should be noted that the higher the
$\mathrm{Cost}_2(v_1,v_2)$
. This makes sense since under more dependency the MTTF is increased and the need to spare components reduces. Also, it should be noted that the higher the
![]() $\alpha$
, the lower the mean cost rates. To explore the sensitivity of the proposed models with respect to component costs,
$\alpha$
, the lower the mean cost rates. To explore the sensitivity of the proposed models with respect to component costs,
![]() $\mathbf{c}=(c_1,c_2)$
and
$\mathbf{c}=(c_1,c_2)$
and
![]() $\mathbf{c}^*=(c_1^*,c_2^*)$
, we have provided some numerical results in Table 4 for
$\mathbf{c}^*=(c_1^*,c_2^*)$
, we have provided some numerical results in Table 4 for
![]() $\alpha=2$
. In the top left panel of the table, we observe that for fixed values of
$\alpha=2$
. In the top left panel of the table, we observe that for fixed values of
![]() $c_1^*=1.5$
and
$c_1^*=1.5$
and
![]() $c_2^*=1$
, the increase in costs
$c_2^*=1$
, the increase in costs
![]() $c_1$
and
$c_1$
and
![]() $c_2$
results in a reduction in the number of optimal values of
$c_2$
results in a reduction in the number of optimal values of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. In the bottom left panel of the table, the costs
$v_2$
. In the bottom left panel of the table, the costs
![]() $c_i$
and
$c_i$
and
![]() $c^*_i$
,
$c^*_i$
,
![]() $i=1,2$
, of the two types are swapped. In this case, when the costs
$i=1,2$
, of the two types are swapped. In this case, when the costs
![]() $c_1^*$
and
$c_1^*$
and
![]() $c_2^*$
are fixed as
$c_2^*$
are fixed as
![]() $c_1^*=1$
and
$c_1^*=1$
and
![]() $c_2^*=1.5$
, we again observe that the increase in the costs
$c_2^*=1.5$
, we again observe that the increase in the costs
![]() $c_1$
and
$c_1$
and
![]() $c_2$
results in a decline in the number of optimal values of
$c_2$
results in a decline in the number of optimal values of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. In the top right panel of the table it can be seen that for fixed values of renewing failed components as
$v_2$
. In the top right panel of the table it can be seen that for fixed values of renewing failed components as
![]() $c_1=6, c_2=5.5$
, the decrease in the costs
$c_1=6, c_2=5.5$
, the decrease in the costs
![]() $c_1^*$
and
$c_1^*$
and
![]() $c_2^*$
results in an increase to the number of optimal values of
$c_2^*$
results in an increase to the number of optimal values of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. As shown in the bottom right panel, the same result holds by swapping the costs of the components of type 1 and type 2. It is seen that in all four parts of Table 4 the value of costs and the numbers of spare components are inversely related to each other. Table 5 shows the behavior of the number of redundant components from another point of view. In the left panel of the table we have kept
$v_2$
. As shown in the bottom right panel, the same result holds by swapping the costs of the components of type 1 and type 2. It is seen that in all four parts of Table 4 the value of costs and the numbers of spare components are inversely related to each other. Table 5 shows the behavior of the number of redundant components from another point of view. In the left panel of the table we have kept
![]() $c_2 (c^*_2)$
constant and have increased the values of
$c_2 (c^*_2)$
constant and have increased the values of
![]() $c_1 (c^*_1)$
. In fact, we have assumed that
$c_1 (c^*_1)$
. In fact, we have assumed that
![]() $c_1=\omega c_2$
and
$c_1=\omega c_2$
and
![]() $c_1^*=\omega c_2^*$
for
$c_1^*=\omega c_2^*$
for
![]() $\omega=1.5,2,3, \ldots, 10$
. As seen, when
$\omega=1.5,2,3, \ldots, 10$
. As seen, when
![]() $\omega$
increases the optimal value of the redundant component
$\omega$
increases the optimal value of the redundant component
![]() $v_1$
decreases and the optimal value of
$v_1$
decreases and the optimal value of
![]() $v_2$
increases. In the right panel of the table we exchange the costs of type 1 and type 2, i.e. we assume
$v_2$
increases. In the right panel of the table we exchange the costs of type 1 and type 2, i.e. we assume
![]() $c_2=\omega c_1$
and
$c_2=\omega c_1$
and
![]() $c_2^*=\omega c_1^*$
. In this case we observe no changes in the number of redundant components
$c_2^*=\omega c_1^*$
. In this case we observe no changes in the number of redundant components
![]() $v_1, v_2$
when
$v_1, v_2$
when
![]() $\omega$
increases.
$\omega$
increases.
Table 5. The optimum values of
![]() $\mathbf{v}$
by minimizing
$\mathbf{v}$
by minimizing
![]() $\mathrm{Cost}_1$
for different costs in Example 2.1.
$\mathrm{Cost}_1$
for different costs in Example 2.1.

In this example the distributions of the component lifetimes are ordered such that
![]() $\bar{F}_1(t)\geq \bar{F}_2(t)$
, for all
$\bar{F}_1(t)\geq \bar{F}_2(t)$
, for all
![]() $t>0$
, i.e. the reliability (and subsequently the MTTF) of the components of type 1 is more than type 2. Note that according to the system structure, it is revealed that the components of type 1 are generally in more critical positions than those of type 2. Hence one should intuitively expect that the optimal solution, according to the cost criterion, would be the case in which one allocates more components of type 1 than type 2.
$t>0$
, i.e. the reliability (and subsequently the MTTF) of the components of type 1 is more than type 2. Note that according to the system structure, it is revealed that the components of type 1 are generally in more critical positions than those of type 2. Hence one should intuitively expect that the optimal solution, according to the cost criterion, would be the case in which one allocates more components of type 1 than type 2.
To see whether this fact affects the number of
![]() $v_i$
, we let
$v_i$
, we let
![]() $\bar{F}_2^*(t)={\mathrm{e}}^{-0.07 t^{2}}$
,
$\bar{F}_2^*(t)={\mathrm{e}}^{-0.07 t^{2}}$
,
![]() $t>0$
, be the reliability function of the components of type 2. In this case the two reliability functions cross each other such that
$t>0$
, be the reliability function of the components of type 2. In this case the two reliability functions cross each other such that
![]() $\bar{F}_1(t)<\bar{F}_2^*(t)$
for
$\bar{F}_1(t)<\bar{F}_2^*(t)$
for
![]() $t<2.86$
and
$t<2.86$
and
![]() $\bar{F}_1(t)>\bar{F}_2^*(t)$
for
$\bar{F}_1(t)>\bar{F}_2^*(t)$
for
![]() $t>2.86$
. Note that the MTTF for components of type 2 in this new case is the same as the previous one. By fixing the other parameters as before, we get the results given in Table 6. We see that although the distributions cross each other, the optimal numbers of components in Table 6 are mostly the same as those in Table 3, perhaps since the MTTFs have not been changed in either case.
$t>2.86$
. Note that the MTTF for components of type 2 in this new case is the same as the previous one. By fixing the other parameters as before, we get the results given in Table 6. We see that although the distributions cross each other, the optimal numbers of components in Table 6 are mostly the same as those in Table 3, perhaps since the MTTFs have not been changed in either case.
Table 6. The optimum values of
![]() $\mathbf{v}$
by minimizing
$\mathbf{v}$
by minimizing
![]() $\mathrm{Cost}_1(v_1,v_2)$
, for different values of
$\mathrm{Cost}_1(v_1,v_2)$
, for different values of
![]() $\alpha$
in Example 2.1.
$\alpha$
in Example 2.1.

As a final point, to see the effect of the survival copula on the optimal numbers of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, we suppose that the dependency structure is followed by the Clayton copula with the following form:
$v_2$
, we suppose that the dependency structure is followed by the Clayton copula with the following form:
The parameter
![]() $\alpha$
manages the dependency degree of the copula, and the limiting case
$\alpha$
manages the dependency degree of the copula, and the limiting case
![]() $\alpha=0$
gives the independence. We obtain the optimal values of redundant components for some values of
$\alpha=0$
gives the independence. We obtain the optimal values of redundant components for some values of
![]() $\alpha$
in Table 7. As can be seen, by increasing
$\alpha$
in Table 7. As can be seen, by increasing
![]() $\alpha$
, the values of
$\alpha$
, the values of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
and also the mean cost rate show increase, which is in contradiction to the results in Table 3. Hence the output of the optimization problem strongly pertains to the functional structure of dependence, not only to the dependency parameter.
$v_2$
and also the mean cost rate show increase, which is in contradiction to the results in Table 3. Hence the output of the optimization problem strongly pertains to the functional structure of dependence, not only to the dependency parameter.
Table 7. The optimum values of
![]() $\mathbf{v}$
by minimizing
$\mathbf{v}$
by minimizing
![]() $\mathrm{Cost}_1(v_1,v_2)$
for different
$\mathrm{Cost}_1(v_1,v_2)$
for different
![]() $\alpha$
under the Clayton copula in Example 2.1.
$\alpha$
under the Clayton copula in Example 2.1.

In the following example we consider an 8-component system consisting of three types of components. For fixed values of
![]() $v_i$
, we minimize the function
$v_i$
, we minimize the function
![]() $\mathrm{Cost}_1$
and also the function
$\mathrm{Cost}_1$
and also the function
![]() $\mathrm{Cost}_2$
in the case that the replacement time of the unfailed system,
$\mathrm{Cost}_2$
in the case that the replacement time of the unfailed system,
![]() $\tau$
, is considered as the variable of interest.
$\tau$
, is considered as the variable of interest.
Example 2.2. Consider the system depicted in Figure 2, given in Huang et al. [Reference Huang, Coolen and Coolen-Maturi19]. The system has eight components from which three components (1, 2, and 3) are of type 1, three components (4, 5, and 7) are of type 2, and two components (6 and 8) are of type 3. The values of the system survival signature are computed in [Reference Huang, Coolen and Coolen-Maturi19], to which we refer the reader for the details.

Figure 2. The system in Example 2.2.
Suppose here that all the components are independent, where the components of type i have common Weibull reliability functions
![]() $\bar{F}_i(t)={\mathrm{e}}^{-\beta_i t^{\alpha_i}}$
,
$\bar{F}_i(t)={\mathrm{e}}^{-\beta_i t^{\alpha_i}}$
,
![]() $\alpha_i, \beta_i>0$
for
$\alpha_i, \beta_i>0$
for
![]() $i=1,2,3$
. In Table 8 we present the mean cost rate
$i=1,2,3$
. In Table 8 we present the mean cost rate
![]() $\mathrm{Cost}_1(v_1, v_2,v_3)$
for given values of
$\mathrm{Cost}_1(v_1, v_2,v_3)$
for given values of
![]() $\beta_1=3$
,
$\beta_1=3$
,
![]() $\beta_2=4$
,
$\beta_2=4$
,
![]() $ \beta_3=2$
,
$ \beta_3=2$
,
![]() $\alpha_1=2$
,
$\alpha_1=2$
,
![]() $\alpha_2=3$
,
$\alpha_2=3$
,
![]() $ \alpha_3=1$
when the cost parameters are
$ \alpha_3=1$
when the cost parameters are
![]() $c_1=1.5$
,
$c_1=1.5$
,
![]() $ c_2=1$
,
$ c_2=1$
,
![]() $c_3=2, c_1^*=0.75$
,
$c_3=2, c_1^*=0.75$
,
![]() $c_2^*=0.4$
,
$c_2^*=0.4$
,
![]() $c_3^*=1$
, and
$c_3^*=1$
, and
![]() $c^{**}=10$
. Assume that we have
$c^{**}=10$
. Assume that we have
![]() $M_1=7$
,
$M_1=7$
,
![]() $M_2=4$
, and
$M_2=4$
, and
![]() $M_3=5$
components from types 1, 2, and 3, respectively, as spares. Hence we can choose
$M_3=5$
components from types 1, 2, and 3, respectively, as spares. Hence we can choose
![]() $v_1\in \{0, 1, 2 \}$
,
$v_1\in \{0, 1, 2 \}$
,
![]() $v_2\in \{0, 1\}$
, and
$v_2\in \{0, 1\}$
, and
![]() $v_3\in \{0, 1, 2\}$
as the redundancy for each type, respectively.
$v_3\in \{0, 1, 2\}$
as the redundancy for each type, respectively.
Table 8. The values of
![]() $\mathrm{Cost}_1(\mathbf{v})$
and
$\mathrm{Cost}_1(\mathbf{v})$
and
![]() $\mathrm{Cost}_2(\mathbf{v})$
in Example 2.2.
$\mathrm{Cost}_2(\mathbf{v})$
in Example 2.2.

In the left panel of Table 8, the values of
![]() $\mathrm{Cost}_1$
are computed for different combinations of
$\mathrm{Cost}_1$
are computed for different combinations of
![]() $v_i$
. As can be seen, by adding
$v_i$
. As can be seen, by adding
![]() $v_1=0$
,
$v_1=0$
,
![]() $v_2=1$
, and
$v_2=1$
, and
![]() $ v_3=0$
as the redundant components to groups 1, 2, and 3, respectively, we get the minimum value for the mean cost rate
$ v_3=0$
as the redundant components to groups 1, 2, and 3, respectively, we get the minimum value for the mean cost rate
![]() $\mathrm{Cost}_1(v_1, v_2,v_3)$
.
$\mathrm{Cost}_1(v_1, v_2,v_3)$
.
Under the assumption that
![]() $\tau$
is the variable of interest, in the right panel of the table we have minimized
$\tau$
is the variable of interest, in the right panel of the table we have minimized
![]() $\mathrm{Cost}_2(v_1, v_2,v_3)$
in terms of
$\mathrm{Cost}_2(v_1, v_2,v_3)$
in terms of
![]() $\tau$
and have reported the optimum value of
$\tau$
and have reported the optimum value of
![]() $\tau$
, in the case that the values of
$\tau$
, in the case that the values of
![]() $v_i$
are kept fixed and known. It is observed that among all minimized values of
$v_i$
are kept fixed and known. It is observed that among all minimized values of
![]() $\mathrm{Cost}_2$
, the least value is obtained for the case that the number of redundant components are
$\mathrm{Cost}_2$
, the least value is obtained for the case that the number of redundant components are
![]() $v_1=0$
,
$v_1=0$
,
![]() $v_2=1$
, and
$v_2=1$
, and
![]() $ v_3=0$
, for which we have
$ v_3=0$
, for which we have
![]() $\tau=0.375$
.
$\tau=0.375$
.
3. Optimal number of components in series-parallel systems
An important subclass of coherent systems is the class of series-parallel systems. A series-parallel system is a series structure of L parallel subsystems,
![]() $L\geq 1$
; see e.g. Figure 3. The purpose here is to find the optimal number of the components in the lth parallel subsystem, under the condition that there are available
$L\geq 1$
; see e.g. Figure 3. The purpose here is to find the optimal number of the components in the lth parallel subsystem, under the condition that there are available
![]() $M_l$
components of type l, where the components in the lth subsystem are exchangeable dependent having common reliability function
$M_l$
components of type l, where the components in the lth subsystem are exchangeable dependent having common reliability function
![]() $\bar{F}_l$
,
$\bar{F}_l$
,
![]() $l=1,\ldots, L$
. Furthermore, suppose that the random failure times of the components of different types are dependent. The dependency structure in the system is built with a copula function
$l=1,\ldots, L$
. Furthermore, suppose that the random failure times of the components of different types are dependent. The dependency structure in the system is built with a copula function
![]() $\hat{C}$
, as described in Section 2. Under the mean cost rate criteria defined in Section 2, the problem of optimal allocation is to find the optimal values of
$\hat{C}$
, as described in Section 2. Under the mean cost rate criteria defined in Section 2, the problem of optimal allocation is to find the optimal values of
![]() $n_l$
for each subsystem so that (2.1) or (2.6) is minimized.
$n_l$
for each subsystem so that (2.1) or (2.6) is minimized.
In the following we provide the corresponding expressions for the cost-based functions in a series-parallel system. First note that for this system we have
 \begin{align*}\Phi(l_1,\ldots, l_L)=\begin{cases}1 & \text{for all $j\in\{1,\ldots,L\}\colon l_j\geq 1$,}\\[5pt]0 & \text{otherwise.}\end{cases}\end{align*}
\begin{align*}\Phi(l_1,\ldots, l_L)=\begin{cases}1 & \text{for all $j\in\{1,\ldots,L\}\colon l_j\geq 1$,}\\[5pt]0 & \text{otherwise.}\end{cases}\end{align*}
Hence from (1.3) we get
 \begin{align*}\bar{F}_T(t)&={\sum_{l_1=1}^{n_1}\!\cdots\!\sum_{l_L=1}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L}\nonumber\\[5pt]&\quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{i_1+l_1},\underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{\bar{F}_L(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr),\end{align*}
\begin{align*}\bar{F}_T(t)&={\sum_{l_1=1}^{n_1}\!\cdots\!\sum_{l_L=1}^{n_L}}{\sum_{i_1=0}^{n_1-l_1}\!\cdots\!\sum_{i_L=0}^{n_L-l_L}}(\!-\!1)^{i_1+\cdots+ i_L}\binom{n_1}{l_1}\!\cdots\! \binom{n_L}{l_L}\binom{n_1-l_1}{i_1}\!\cdots\! \binom{n_L-l_L}{i_L}\nonumber\\[5pt]&\quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{i_1+l_1},\underbrace{1}_{n_1-(i_1+l_1)},\ldots,\underbrace{\bar{F}_L(t)}_{i_L+l_L},\underbrace{1}_{n_L-(i_L+l_L) }\Bigr),\end{align*}
and in the special case of independent components, we derive from (1.4)
 \begin{align*}\bar{F}_T(t)=\prod_{l=1}^L (1-[1-\bar{F}_l(t)]^{n_l}).\end{align*}
\begin{align*}\bar{F}_T(t)=\prod_{l=1}^L (1-[1-\bar{F}_l(t)]^{n_l}).\end{align*}

Figure 3. A series-parallel system with three subsystems.
3.1. Cost function at system failure
In a similar manner to Section 2.1, the mean cost rate function for system failure is defined as
where
![]() $\mathbf{n}=(n_1,\ldots, n_L)$
, and
$\mathbf{n}=(n_1,\ldots, n_L)$
, and
 \begin{align}\mathbb{E}( X_i(T))=n_i \sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}\binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\int_{0}^{\infty}\lim_{\delta\rightarrow 0}\dfrac{A_{\mathbf{m}}^{(i)}(t,\delta)}{\delta} \,{\mathrm{d}} t,\end{align}
\begin{align}\mathbb{E}( X_i(T))=n_i \sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=0}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}\binom{n_1}{m_1}\!\cdots\! \binom{n_i-1}{m_i}\!\cdots\!\binom{n_L}{m_L}\int_{0}^{\infty}\lim_{\delta\rightarrow 0}\dfrac{A_{\mathbf{m}}^{(i)}(t,\delta)}{\delta} \,{\mathrm{d}} t,\end{align}
in which
![]() $A_{\mathbf{m}}^{(i)}(t,\delta)$
is introduced in (2.3). For the independent components, (3.2) reduces to the following expression:
$A_{\mathbf{m}}^{(i)}(t,\delta)$
is introduced in (2.3). For the independent components, (3.2) reduces to the following expression:
 \begin{align}\mathbb{E}( X_i(T))=n_i \int_0^{\infty} \prod_{l=1,l\neq i}^L (1-(1-\bar{F}_l(t))^{n_l}) \,{\mathrm{d}} F_{i}(t).\end{align}
\begin{align}\mathbb{E}( X_i(T))=n_i \int_0^{\infty} \prod_{l=1,l\neq i}^L (1-(1-\bar{F}_l(t))^{n_l}) \,{\mathrm{d}} F_{i}(t).\end{align}
If
![]() $L=1$
then the system becomes a parallel system with
$L=1$
then the system becomes a parallel system with
![]() $n_1$
components, and hence in this case
$n_1$
components, and hence in this case
![]() $\mathbb{E}( X_1(T))=n_1$
.
$\mathbb{E}( X_1(T))=n_1$
.
For the considered series-parallel system in which the components of subsystems are independent, Eryilmaz et al. [Reference Eryilmaz, Özkurt and Rekan11] gained a similar result for
![]() $\mathbb{E}( X_i(T))$
in (3.3). Subsequently, they found the optimal numbers of components in each subsystem based on the minimization of cost function (3.1) under the constraints on the total allotted cost for replacing failed components and the total allotted cost for rejuvenation of unfailed ones. Hence our results in this subsection may be considered as an extension of their work to the case of dependent components. Also, Dembinska and Eryilmaz [Reference Dembinska and Eryilmaz5] discussed a similar problem for the case that the lifetime distributions of components are discrete; in particular, they obtained some results for discrete phase-type distribution.
$\mathbb{E}( X_i(T))$
in (3.3). Subsequently, they found the optimal numbers of components in each subsystem based on the minimization of cost function (3.1) under the constraints on the total allotted cost for replacing failed components and the total allotted cost for rejuvenation of unfailed ones. Hence our results in this subsection may be considered as an extension of their work to the case of dependent components. Also, Dembinska and Eryilmaz [Reference Dembinska and Eryilmaz5] discussed a similar problem for the case that the lifetime distributions of components are discrete; in particular, they obtained some results for discrete phase-type distribution.
3.2. Cost function based on preventive replacement
The mean cost rate function of the system for age replacement at time
![]() $\min\!(\tau, T)$
is defined as
$\min\!(\tau, T)$
is defined as
where
 \begin{align*}M_1(\mathbf{n})=\sum_{i=1}^L c_i \mathbb{E}( X_i(T)\mid T\leq \tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i-X_i{(T)}\mid T\leq \tau)+c^{**}\end{align*}
\begin{align*}M_1(\mathbf{n})=\sum_{i=1}^L c_i \mathbb{E}( X_i(T)\mid T\leq \tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i-X_i{(T)}\mid T\leq \tau)+c^{**}\end{align*}
and
 \begin{align*}M_2(\mathbf{n})=\sum_{i=1}^L c_i \mathbb{E}( N_i{(\tau)}\mid T>\tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i-N_i{(\tau)}\mid T>\tau).\end{align*}
\begin{align*}M_2(\mathbf{n})=\sum_{i=1}^L c_i \mathbb{E}( N_i{(\tau)}\mid T>\tau)+\sum_{i=1}^L c^*_i \mathbb{E}( n_i-N_i{(\tau)}\mid T>\tau).\end{align*}
Using the formula for the survival signature of the series-parallel system, from the results given in Section 2.2, we get the following expressions:
 \begin{align*}\mathbb{E}( N_i(\tau)\mid T>\tau)=\dfrac{1}{\bar{F}(\tau)}\sum_{j_1=0}^{n_1-1}\!\cdots\!\sum_{j_L=0}^{n_L-1} j_i \binom{n_1}{j_1}\!\cdots\! \binom{n_L}{j_L}B(\tau, j_1,\dots,j_L)\end{align*}
\begin{align*}\mathbb{E}( N_i(\tau)\mid T>\tau)=\dfrac{1}{\bar{F}(\tau)}\sum_{j_1=0}^{n_1-1}\!\cdots\!\sum_{j_L=0}^{n_L-1} j_i \binom{n_1}{j_1}\!\cdots\! \binom{n_L}{j_L}B(\tau, j_1,\dots,j_L)\end{align*}
and for
![]() $n_i\geq 2$
$n_i\geq 2$
 \begin{align}&\mathbb{E}( X_i(T)\mid T\leq \tau)=\dfrac{n_i}{1-\bar{F}_T(\tau)} \Biggl[\sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=1}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}{\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}}\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr] \\[5pt]& \times\binom{n_i-1}{m_i}\binom{m_i}{l_i}\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}} s - \sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=1}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}{\sum_{l_1=1}^{m_1}\!\cdots\!\sum_{l_L=1}^{m_L}}\nonumber\\[5pt]& \quad\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr]\binom{n_i-1}{m_i}\binom{m_i}{l_i}\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}} s \Biggr].\end{align}
\begin{align}&\mathbb{E}( X_i(T)\mid T\leq \tau)=\dfrac{n_i}{1-\bar{F}_T(\tau)} \Biggl[\sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=1}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}{\sum_{l_1=0}^{m_1}\!\cdots\!\sum_{l_L=0}^{m_L}}\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr] \\[5pt]& \times\binom{n_i-1}{m_i}\binom{m_i}{l_i}\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}} s - \sum_{m_1=1}^{n_1}\!\cdots\!\sum_{m_i=1}^{n_i-1}\!\cdots\!\sum_{m_L=1}^{n_L}{\sum_{l_1=1}^{m_1}\!\cdots\!\sum_{l_L=1}^{m_L}}\nonumber\\[5pt]& \quad\Biggl[\prod_{j=1,j\neq i}^L\binom{n_j}{m_j}\binom{m_j}{l_j}\Biggr]\binom{n_i-1}{m_i}\binom{m_i}{l_i}\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}} s \Biggr].\end{align}
If
![]() $n_i=1$
then it is easily deduced that
$n_i=1$
then it is easily deduced that
Example 3.1. Consider a series-parallel system with
![]() $L=3$
subsystems and assume that there are
$L=3$
subsystems and assume that there are
![]() $M_1=2, M_2=3$
, and
$M_1=2, M_2=3$
, and
![]() $M_3=3$
components from types 1, 2, and 3, respectively, to construct the system. Suppose that the joint reliability function of the component lifetimes follow the multivariate Pareto model given by
$M_3=3$
components from types 1, 2, and 3, respectively, to construct the system. Suppose that the joint reliability function of the component lifetimes follow the multivariate Pareto model given by
 \begin{align*}&\mathbb{P}\bigl( T_1^{(1)}>t_1^{(1)}, \ldots, T_{n_1}^{(1)}>t_{n_1}^{(1)}, \ldots, T_1^{(L)}>t_L^{(L)}, \ldots, T_{n_L}^{(L)}>t_{n_L}^{(L)}\bigr)\\[5pt] &\quad =\Biggl[ 1+\theta_1\sum_{i=1}^{n_1}t_i^{(1)}+\cdots+\theta_L\sum_{i=1}^{n_L}t_i^{(L)} \Biggr]^{-\alpha} \end{align*}
\begin{align*}&\mathbb{P}\bigl( T_1^{(1)}>t_1^{(1)}, \ldots, T_{n_1}^{(1)}>t_{n_1}^{(1)}, \ldots, T_1^{(L)}>t_L^{(L)}, \ldots, T_{n_L}^{(L)}>t_{n_L}^{(L)}\bigr)\\[5pt] &\quad =\Biggl[ 1+\theta_1\sum_{i=1}^{n_1}t_i^{(1)}+\cdots+\theta_L\sum_{i=1}^{n_L}t_i^{(L)} \Biggr]^{-\alpha} \end{align*}
for
![]() $\theta_i>0, i=1, \ldots, L$
, and
$\theta_i>0, i=1, \ldots, L$
, and
![]() $\alpha>0$
. In fact the corresponding survival copula is
$\alpha>0$
. In fact the corresponding survival copula is
and the marginal reliability functions of the components in the subsystems are
![]() $\bar{F}_i(t)=(1+\theta_i t)^{-\alpha}$
,
$\bar{F}_i(t)=(1+\theta_i t)^{-\alpha}$
,
![]() $i=1,2, \ldots, L$
.
$i=1,2, \ldots, L$
.
First note that for the described system we have
 \begin{align*}&\int_{0}^{\infty}\lim_{\delta\rightarrow 0}\dfrac{A_{\mathbf{m}}^{(i)}(t,\delta)}{\delta} \,{\mathrm{d}} t\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt]& \quad \times \dfrac{\theta_i}{\theta_i(m_i+j_i+1)+\sum_{l=1, l\neq i}^{L}\theta_l(m_l+j_l)}.\end{align*}
\begin{align*}&\int_{0}^{\infty}\lim_{\delta\rightarrow 0}\dfrac{A_{\mathbf{m}}^{(i)}(t,\delta)}{\delta} \,{\mathrm{d}} t\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt]& \quad \times \dfrac{\theta_i}{\theta_i(m_i+j_i+1)+\sum_{l=1, l\neq i}^{L}\theta_l(m_l+j_l)}.\end{align*}
By replacing these expressions in (3.2),
![]() $\mathbb{E}( X_i(T))$
,
$\mathbb{E}( X_i(T))$
,
![]() $i=1, 2, 3$
are obtained.
$i=1, 2, 3$
are obtained.
Let
![]() ${\mathbf{\theta}}=(0.4, 0.2, 0.3)$
,
${\mathbf{\theta}}=(0.4, 0.2, 0.3)$
,
![]() $\mathbf{c}=(1.5, 2, 3)$
,
$\mathbf{c}=(1.5, 2, 3)$
,
![]() $\mathbf{c}^*=(0.3, 0.75, 1)$
,
$\mathbf{c}^*=(0.3, 0.75, 1)$
,
![]() $c^{**}=8$
, and
$c^{**}=8$
, and
![]() $\alpha=2$
. The values of the mean cost rate function
$\alpha=2$
. The values of the mean cost rate function
![]() $\mathrm{Cost}_3$
are obtained for all combinations of
$\mathrm{Cost}_3$
are obtained for all combinations of
![]() $n_1, n_2$
, and
$n_1, n_2$
, and
![]() $n_3$
, such that
$n_3$
, such that
![]() $n_1\in\{1, 2\}$
,
$n_1\in\{1, 2\}$
,
![]() $n_2\in\{1, 2, 3\}$
, and
$n_2\in\{1, 2, 3\}$
, and
![]() $n_3\in\{1,2,3\}$
. Also, under the age replacement strategy in
$n_3\in\{1,2,3\}$
. Also, under the age replacement strategy in
![]() $\tau=1$
, the values of mean cost rate function
$\tau=1$
, the values of mean cost rate function
![]() $\mathrm{Cost}_4$
are calculated for different values
$\mathrm{Cost}_4$
are calculated for different values
![]() $n_1$
,
$n_1$
,
![]() $n_2$
, and
$n_2$
, and
![]() $n_3$
.
$n_3$
.
Table 9. The values of
![]() $\mathrm{Cost}_3(\mathbf{n})$
and
$\mathrm{Cost}_3(\mathbf{n})$
and
![]() $\mathrm{Cost}_4(\mathbf{n})$
in Example 3.1.
$\mathrm{Cost}_4(\mathbf{n})$
in Example 3.1.

To compute
![]() $\mathrm{Cost}_4(\tau)$
, we use the following simplified expressions:
$\mathrm{Cost}_4(\tau)$
, we use the following simplified expressions:
 \begin{align*} &\mathbb{E}( N_i(\tau)\mid T>\tau)\\[5pt] & =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1-1}\sum_{j_2=0}^{n_2-1}\sum_{j_3=0}^{n_3-1} j_i \binom{n_1}{j_1} \binom{n_2}{j_2} \binom{n_3}{j_3}{\sum_{b_1=0}^{j_1}\sum_{b_2=0}^{j_2}\sum_{b_3=0}^{j_3}}(\!-\!1)^{b_1+ b_2+ b_L}\\[5pt]& \quad \binom{j_1}{b_1}\binom{j_2}{b_2}\binom{j_3}{b_3}[1+\theta_1\tau(n_1-j_1+b_1)+\theta_2\tau(n_2-j_2+b_2)+\theta_3\tau(n_3-j_3+b_3)]^{-\alpha},\end{align*}
\begin{align*} &\mathbb{E}( N_i(\tau)\mid T>\tau)\\[5pt] & =\dfrac{1}{\bar{F}_T(\tau)}\sum_{j_1=0}^{n_1-1}\sum_{j_2=0}^{n_2-1}\sum_{j_3=0}^{n_3-1} j_i \binom{n_1}{j_1} \binom{n_2}{j_2} \binom{n_3}{j_3}{\sum_{b_1=0}^{j_1}\sum_{b_2=0}^{j_2}\sum_{b_3=0}^{j_3}}(\!-\!1)^{b_1+ b_2+ b_L}\\[5pt]& \quad \binom{j_1}{b_1}\binom{j_2}{b_2}\binom{j_3}{b_3}[1+\theta_1\tau(n_1-j_1+b_1)+\theta_2\tau(n_2-j_2+b_2)+\theta_3\tau(n_3-j_3+b_3)]^{-\alpha},\end{align*}
for
![]() $i=1, 2, 3$
, where
$i=1, 2, 3$
, where
 \begin{align*}&\bar{F}_T(\tau)\\[5pt]& ={\sum_{l_1=1}^{n_1}\sum_{l_2=1}^{n_2}\sum_{l_3=1}^{n_3}}{\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}\sum_{i_3=0}^{n_3-l_3}}(\!-\!1)^{i_1+ i_2+ i_3}\binom{n_1}{l_1}\binom{n_2}{l_2}\binom{n_3}{l_3}\binom{n_1-l_1}{i_1}\binom{n_2-l_2}{i_2} \binom{n_3-l_3}{i_3}\nonumber\\[5pt]& \quad (1+\theta_1 \tau(i_1+l_1)+\theta_2 \tau(i_2+l_2)+\theta_3 \tau(i_3+l_3))^{-\alpha}.\end{align*}
\begin{align*}&\bar{F}_T(\tau)\\[5pt]& ={\sum_{l_1=1}^{n_1}\sum_{l_2=1}^{n_2}\sum_{l_3=1}^{n_3}}{\sum_{i_1=0}^{n_1-l_1}\sum_{i_2=0}^{n_2-l_2}\sum_{i_3=0}^{n_3-l_3}}(\!-\!1)^{i_1+ i_2+ i_3}\binom{n_1}{l_1}\binom{n_2}{l_2}\binom{n_3}{l_3}\binom{n_1-l_1}{i_1}\binom{n_2-l_2}{i_2} \binom{n_3-l_3}{i_3}\nonumber\\[5pt]& \quad (1+\theta_1 \tau(i_1+l_1)+\theta_2 \tau(i_2+l_2)+\theta_3 \tau(i_3+l_3))^{-\alpha}.\end{align*}
Also, we obtain
![]() $\mathbb{E}( X_i(T)\mid T\leq \tau), i=1, 2, 3$
by placing the following quantity in (3.4):
$\mathbb{E}( X_i(T)\mid T\leq \tau), i=1, 2, 3$
by placing the following quantity in (3.4):
 \begin{align*}&\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}}s \\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{\,j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times {\sum_{d_1=0}^{m_1-l_1}\!\cdots\!\sum_{d_i=0}^{m_i-l_i}\!\cdots\!\sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots + d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\[5pt]& \quad \times \dfrac{\theta_i\bigl[\bigl(1+\tau(\!\sum_{k=1}^L \theta_k(l_k+d_k)) \bigr)^{-\alpha}-\bigl(1+\tau(\theta_i(m_i+j_i+1)+\sum_{k=1, \neq i}^L \theta_k(m_k+j_k))\bigr)^{-\alpha}\bigr]}{\theta_i(m_i-l_i+j_i-d_i+1)+\sum_{k=1, \neq i}^L \theta_k(m_k-l_k+j_k-d_k)}.\end{align*}
\begin{align*}&\int_{0}^{\tau}\lim_{\delta\rightarrow 0}\dfrac{1}{\delta} A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau) \,{\mathrm{d}}s \\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\!\sum_{j_i=0}^{n_i-m_i-1}\!\cdots\!\sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{\,j_1+\cdots + j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\& \quad \times {\sum_{d_1=0}^{m_1-l_1}\!\cdots\!\sum_{d_i=0}^{m_i-l_i}\!\cdots\!\sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots + d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\[5pt]& \quad \times \dfrac{\theta_i\bigl[\bigl(1+\tau(\!\sum_{k=1}^L \theta_k(l_k+d_k)) \bigr)^{-\alpha}-\bigl(1+\tau(\theta_i(m_i+j_i+1)+\sum_{k=1, \neq i}^L \theta_k(m_k+j_k))\bigr)^{-\alpha}\bigr]}{\theta_i(m_i-l_i+j_i-d_i+1)+\sum_{k=1, \neq i}^L \theta_k(m_k-l_k+j_k-d_k)}.\end{align*}
The results are given in Table 9. It is seen from the results that based on the objective function
![]() $\mathrm{Cost}_3(.)$
the optimal series-parallel system has
$\mathrm{Cost}_3(.)$
the optimal series-parallel system has
![]() $n_1=2$
,
$n_1=2$
,
![]() $n_2=3$
,
$n_2=3$
,
![]() $n_3=2$
components. Since the reliability of type 2 is greater than the other two types, it is expected that more components for the second subsystem will lead to a reduction in the mean cost rate of system failure. Also,
$n_3=2$
components. Since the reliability of type 2 is greater than the other two types, it is expected that more components for the second subsystem will lead to a reduction in the mean cost rate of system failure. Also,
![]() $ n_1 = 2$
,
$ n_1 = 2$
,
![]() $n_2 = 2$
,
$n_2 = 2$
,
![]() $n_3 = 2 $
are the optimal number of components in the subsystems so as to minimize the average cost rate of the age replacement policy.
$n_3 = 2 $
are the optimal number of components in the subsystems so as to minimize the average cost rate of the age replacement policy.
4. Conclusions
In this paper we have studied the optimal number of redundancy allocation in an n-component coherent system consisting of heterogeneous components. We assumed that the system has been built up of L different types of components,
![]() $L\geq 1$
, where there are
$L\geq 1$
, where there are
![]() $n_i$
components of type i and
$n_i$
components of type i and
![]() $\sum_{i=1}^{L}n_i=n$
. We assumed that the components of the different types in the system are statistically dependent. The system reliability function was modeled by the notion of survival signature in terms of a given survival copula function. We further assumed
$\sum_{i=1}^{L}n_i=n$
. We assumed that the components of the different types in the system are statistically dependent. The system reliability function was modeled by the notion of survival signature in terms of a given survival copula function. We further assumed
![]() $M_i$
components available as spares for the components of type i. We investigated the number of active redundant components
$M_i$
components available as spares for the components of type i. We investigated the number of active redundant components
![]() $v_i$
,
$v_i$
,
![]() $n_iv_i\leq M_i$
, that can be added to each component of type i such that the imposed cost functions are minimized,
$n_iv_i\leq M_i$
, that can be added to each component of type i such that the imposed cost functions are minimized,
![]() $i=1,\dots, L$
. We first proposed a cost function in terms of the costs of renewing the failed components and the costs of refreshing the alive components at the time of the system failure. Subsequently, we proposed a cost-based function in terms of the costs of the renewing (refreshing) the failed (alive) components at the system failure time or at a predetermined time
$i=1,\dots, L$
. We first proposed a cost function in terms of the costs of renewing the failed components and the costs of refreshing the alive components at the time of the system failure. Subsequently, we proposed a cost-based function in terms of the costs of the renewing (refreshing) the failed (alive) components at the system failure time or at a predetermined time
![]() $\tau$
, whichever occurs first. In the last part of the paper, using the settings of the first part, we studied the particular case that the system is a series-parallel system. We derived the formulas for the proposed cost functions and used them to investigate the optimal number of the components in each parallel subsystem. The expressions for the proposed cost functions were derived using the mixture representation of the system reliability function based on the notion of survival signature. The results were examined numerically for some particular coherent systems. The proposed mean cost rate functions simultaneously consider the cost of the system and its MTTF (which is directly related to its reliability). Hence this optimization problem can be viewed as a bi-objective reliability–redundancy allocation problem but with a more comfortable setup. In this study we considered the general case that the components of the same group are exchangeable and the components of different groups and dependent. Although these assumptions are more realistic and hence increase the range of applications of our results, they obviously lead to greater complexity of the formulas. An even more realistic case is the situation that the components in each group are dependent in a more general sense than that of exchangeability. Developing results in this direction may be considered for future study. Here we assumed active redundancy for components. Allocating the other variants of spares, i.e. cold and warm standby, for coherent systems may be investigated as interesting problems for future studies.
$\tau$
, whichever occurs first. In the last part of the paper, using the settings of the first part, we studied the particular case that the system is a series-parallel system. We derived the formulas for the proposed cost functions and used them to investigate the optimal number of the components in each parallel subsystem. The expressions for the proposed cost functions were derived using the mixture representation of the system reliability function based on the notion of survival signature. The results were examined numerically for some particular coherent systems. The proposed mean cost rate functions simultaneously consider the cost of the system and its MTTF (which is directly related to its reliability). Hence this optimization problem can be viewed as a bi-objective reliability–redundancy allocation problem but with a more comfortable setup. In this study we considered the general case that the components of the same group are exchangeable and the components of different groups and dependent. Although these assumptions are more realistic and hence increase the range of applications of our results, they obviously lead to greater complexity of the formulas. An even more realistic case is the situation that the components in each group are dependent in a more general sense than that of exchangeability. Developing results in this direction may be considered for future study. Here we assumed active redundancy for components. Allocating the other variants of spares, i.e. cold and warm standby, for coherent systems may be investigated as interesting problems for future studies.
Appendix A. Proof of Theorem 2.1
Define the events M,
![]() $N^c$
, and
$N^c$
, and
![]() $L^C$
as follows:
$L^C$
as follows:
 \begin{align*}M&\equiv\bigl\{{T_1^{(1)}>t},\ldots,{T_{m_1}^{(1)}>t},{T_2^{(i)}>t},\ldots,{T_{m_i+1}^{(i)}>t},{T_1^{(L)}>t},\ldots,{T_{m_L}^{(L)}>t} \bigr\},\\[5pt]N^c &\equiv\bigl\{{T_{m_1+1}^{(1)}<t},\ldots, {T_{n_1}^{(1)}<t}, {T_{m_i+2}^{(i)}<t},\ldots, {T_{n_i}^{(i)}<t}, {T_{m_L+1}^{(L)}<t},\ldots, {T_{n_L}^{(L)}<t} \bigr\},\\[5pt]L^c &\equiv\bigl\{t<T_1^{(i)}<t+\delta\bigr\}.\end{align*}
\begin{align*}M&\equiv\bigl\{{T_1^{(1)}>t},\ldots,{T_{m_1}^{(1)}>t},{T_2^{(i)}>t},\ldots,{T_{m_i+1}^{(i)}>t},{T_1^{(L)}>t},\ldots,{T_{m_L}^{(L)}>t} \bigr\},\\[5pt]N^c &\equiv\bigl\{{T_{m_1+1}^{(1)}<t},\ldots, {T_{n_1}^{(1)}<t}, {T_{m_i+2}^{(i)}<t},\ldots, {T_{n_i}^{(i)}<t}, {T_{m_L+1}^{(L)}<t},\ldots, {T_{n_L}^{(L)}<t} \bigr\},\\[5pt]L^c &\equiv\bigl\{t<T_1^{(i)}<t+\delta\bigr\}.\end{align*}
Then
![]() $A_{\mathbf{m}}^{(i)}(t, \delta)$
is equal to the following:
$A_{\mathbf{m}}^{(i)}(t, \delta)$
is equal to the following:
Evidently we have
and
Note that we can write
Therefore we can easily see that
 \begin{align*}&\mathbb{P}(M\cap N)\\[5pt] & =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l} {\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}} \binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\ & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align*}
\begin{align*}&\mathbb{P}(M\cap N)\\[5pt] & =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l} {\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}} \binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\ & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align*}
If we subtract
![]() $\mathbb{P}(M)$
from both sides of this equation, then we have
$\mathbb{P}(M)$
from both sides of this equation, then we have
 \begin{align}&\mathbb{P}(M\cap N)-\mathbb{P}(M)\nonumber\\[5pt] & =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l} {\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}} \binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L} \\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\[5pt]& \quad -\biggl[\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1},\underbrace{1}_{n_1-m_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+1},\underbrace{1}_{n_i-m_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L},\underbrace{1}_{n_L-m_L}\Bigr)\biggr]\nonumber\\& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align}
\begin{align}&\mathbb{P}(M\cap N)-\mathbb{P}(M)\nonumber\\[5pt] & =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l} {\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}} \binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L} \\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\[5pt]& \quad -\biggl[\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1},\underbrace{1}_{n_1-m_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+1},\underbrace{1}_{n_i-m_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L},\underbrace{1}_{n_L-m_L}\Bigr)\biggr]\nonumber\\& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align}
Similarly we have
 \begin{align*}&\mathbb{P}(M\cap N \cap L)\nonumber\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr),\nonumber\end{align*}
\begin{align*}&\mathbb{P}(M\cap N \cap L)\nonumber\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr),\nonumber\end{align*}
 \begin{align} &\mathbb{P}(M\cap N \cap L)-\mathbb{P}(M\cap L)\nonumber\\[5pt]& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align}
\begin{align} &\mathbb{P}(M\cap N \cap L)-\mathbb{P}(M\cap L)\nonumber\\[5pt]& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{j_1+\cdots +j_L=l}{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\nonumber\\[5pt]& ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\nonumber\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr).\end{align}
Then, replacing (A.2) and (A.3) in (A.1), we have
 \begin{align*} &A_{\mathbf{m}}^{(i)}(t, \delta)\\[5pt] & =-{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt] & \quad +{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt] & ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \biggl[ \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\biggr] .\end{align*}
\begin{align*} &A_{\mathbf{m}}^{(i)}(t, \delta)\\[5pt] & =-{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt] & \quad +{\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L+1}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt] & ={\sum_{j_1=0}^{n_1-m_1}\!\cdots\! \sum_{j_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{j_L=0}^{n_L-m_L}}(\!-\!1)^{j_1+\cdots +j_L}\binom{n_1-m_1}{j_1}\!\cdots\! \binom{n_i-m_i-1}{j_i}\!\cdots\!\binom{n_L-m_L}{j_L}\\[5pt] & \quad \times \biggl[ \hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i+1},\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_1(t)}_{m_1+j_1},\underbrace{1}_{n_1-m_1-j_1},\ldots, \underbrace{\bar{F}_i(t)}_{m_i+j_i}, \bar{F}_i(t+\delta),\underbrace{1}_{n_i-m_i-j_i-1}, \ldots, \underbrace{\bar{F}_L(t)}_{m_L+j_L},\underbrace{1}_{n_L-m_L-j_L}\Bigr)\biggr] .\end{align*}
Appendix B. Proof of Theorem 2.2
Let us define the following events:
 \begin{align*} M&\equiv\bigl\{T_1^{(j)}>\tau, \ldots, T_{l_j}^{(j)}>\tau, T_{l_j+1}^{(j)}>s, \ldots, T_{m_j}^{(j)}>s,1 \leq j \leq L, j\neq i,\\[5pt]& \quad\ T_1^{(i)}>\tau, \ldots, T_{l_i}^{(i)}>\tau, T_{l_i+1}^{(i)}>s, \ldots, T_{m_i+1}^{(i)}>s\bigr\},\\[5pt] N^c&\equiv\bigl\{ T_{m_j+1}^{(j)}<s,\ldots, T_{n_j}^{(j)}<s, 1 \leq j \leq L, j\neq i, T_{m_i+2}^{(i)}<s,\ldots, T_{n_i}^{(i)}<s \bigr\},\\[5pt] L^c&\equiv\bigl\{T_{l_j+1}^{(j)}<\tau, \ldots, T_{m_j}^{(j)}<\tau, 1 \leq j \leq L, \bigr\},\\[5pt]K^c&\equiv\bigl\{T_{m_i+1}^{(i)}<s+\delta \bigr\}.\end{align*}
\begin{align*} M&\equiv\bigl\{T_1^{(j)}>\tau, \ldots, T_{l_j}^{(j)}>\tau, T_{l_j+1}^{(j)}>s, \ldots, T_{m_j}^{(j)}>s,1 \leq j \leq L, j\neq i,\\[5pt]& \quad\ T_1^{(i)}>\tau, \ldots, T_{l_i}^{(i)}>\tau, T_{l_i+1}^{(i)}>s, \ldots, T_{m_i+1}^{(i)}>s\bigr\},\\[5pt] N^c&\equiv\bigl\{ T_{m_j+1}^{(j)}<s,\ldots, T_{n_j}^{(j)}<s, 1 \leq j \leq L, j\neq i, T_{m_i+2}^{(i)}<s,\ldots, T_{n_i}^{(i)}<s \bigr\},\\[5pt] L^c&\equiv\bigl\{T_{l_j+1}^{(j)}<\tau, \ldots, T_{m_j}^{(j)}<\tau, 1 \leq j \leq L, \bigr\},\\[5pt]K^c&\equiv\bigl\{T_{m_i+1}^{(i)}<s+\delta \bigr\}.\end{align*}
Hence
 \begin{align}& A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\notag \\[5pt] & =\mathbb{P}(M\cap N^c \cap L^c \cap K^c)\nonumber\\[5pt] & =\mathbb{P}(M)-\mathbb{P}(M\cap N)-\mathbb{P}(M\cap L)-\mathbb{P}(M \cap K)+\mathbb{P}(M \cap N \cap L)+\mathbb{P}(M \cap N \cap K)\nonumber\\[5pt]& \quad +\mathbb{P}(M \cap K \cap L)-\mathbb{P}(M \cap N \cap L \cap K).\end{align}
\begin{align}& A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\notag \\[5pt] & =\mathbb{P}(M\cap N^c \cap L^c \cap K^c)\nonumber\\[5pt] & =\mathbb{P}(M)-\mathbb{P}(M\cap N)-\mathbb{P}(M\cap L)-\mathbb{P}(M \cap K)+\mathbb{P}(M \cap N \cap L)+\mathbb{P}(M \cap N \cap K)\nonumber\\[5pt]& \quad +\mathbb{P}(M \cap K \cap L)-\mathbb{P}(M \cap N \cap L \cap K).\end{align}
It can be easily shown that
 \begin{align*} \mathbb{P}(M)&= \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j},\underbrace{1}_{n_j-m_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+1},\underbrace{1}_{n_i-m_i-1}\Bigr),\\[5pt]\mathbb{P}(M \cap K)&=\mathbb{P}\bigl(M\cap \bigl\{ T_{m_i+1}^{(i)}>s+\delta \} \bigr\}\bigr)\\[5pt]&=\hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i}, \bar{F}_i(s+\delta),\underbrace{1}_{n_i-m_i-1}\Bigr).\end{align*}
\begin{align*} \mathbb{P}(M)&= \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j},\underbrace{1}_{n_j-m_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+1},\underbrace{1}_{n_i-m_i-1}\Bigr),\\[5pt]\mathbb{P}(M \cap K)&=\mathbb{P}\bigl(M\cap \bigl\{ T_{m_i+1}^{(i)}>s+\delta \} \bigr\}\bigr)\\[5pt]&=\hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i}, \bar{F}_i(s+\delta),\underbrace{1}_{n_i-m_i-1}\Bigr).\end{align*}
Note also that the event N (the complement of
![]() $N^c$
) can be represented as
$N^c$
) can be represented as
Thus we get
 \begin{align*}&\mathbb{P}(M \cap N)\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr),\end{align*}
\begin{align*}&\mathbb{P}(M \cap N)\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr),\end{align*}
and hence
 \begin{align*}&\mathbb{P}(M \cap N)-\mathbb{P}(M)\\[5pt]& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& ={\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}(\!-\!1)^{r_1+\cdots +r_L+1}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\end{align*}
\begin{align*}&\mathbb{P}(M \cap N)-\mathbb{P}(M)\\[5pt]& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& ={\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}(\!-\!1)^{r_1+\cdots +r_L+1}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt] & \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j}, 1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\end{align*}
and
 \begin{align*}&\mathbb{P}(M \cap N \cap K)\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap K).\end{align*}
\begin{align*}&\mathbb{P}(M \cap N \cap K)\\[5pt]& =\sum_{l=1}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap K).\end{align*}
Similarly, we have
Therefore we get
 \begin{align*}\mathbb{P}(M \cap L)&=\sum_{y=1}^{\sum_{j=1}^L (m_j -l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\[5pt]&\quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j-d_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i-d_i+1}, \underbrace{1}_{n_i-m_i-1}\Bigr)\end{align*}
\begin{align*}\mathbb{P}(M \cap L)&=\sum_{y=1}^{\sum_{j=1}^L (m_j -l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\[5pt]&\quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j-d_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i-d_i+1}, \underbrace{1}_{n_i-m_i-1}\Bigr)\end{align*}
and
 \begin{align*}&\mathbb{P}(M \cap L \cap K)\\[5pt]& =\sum_{l=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+r_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j-r_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+r_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i-r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-1}\Bigr).\end{align*}
\begin{align*}&\mathbb{P}(M \cap L \cap K)\\[5pt]& =\sum_{l=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+r_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j-r_j},\underbrace{1}_{n_j-m_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+r_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i-r_i},\bar{F}_i{(s+\delta)}, \underbrace{1}_{n_i-m_i-1}\Bigr).\end{align*}
Also, after some manipulations, one can verify that
![]() $\mathbb{P}(M \cap N \cap L)$
and
$\mathbb{P}(M \cap N \cap L)$
and
![]() $\mathbb{P}(M \cap N \cap L \cap K)$
, respectively, can be written as
$\mathbb{P}(M \cap N \cap L \cap K)$
, respectively, can be written as
 \begin{align*}&\mathbb{P}(M \cap N \cap L)\\[5pt]& =\sum_{l=1}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}( M \cap L)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad\times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& \quad +\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i}\Bigr) \\[5pt]& \quad+\mathbb{P}(M \cap L)\end{align*}
\begin{align*}&\mathbb{P}(M \cap N \cap L)\\[5pt]& =\sum_{l=1}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}( M \cap L)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad\times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& \quad +\sum_{l=0}^{n-\sum_{i=1}^L m_i -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\[5pt]& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1},\underbrace{1}_{n_i-m_i-r_i}\Bigr) \\[5pt]& \quad+\mathbb{P}(M \cap L)\end{align*}
and
 \begin{align*}&\mathbb{P}(M \cap N \cap L \cap K)\\[5pt]& =\sum_{l=1}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap L \cap K) \\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& \quad +\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap L \cap K).\end{align*}
\begin{align*}&\mathbb{P}(M \cap N \cap L \cap K)\\[5pt]& =\sum_{l=1}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=1}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap L \cap K) \\& =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\& \quad +\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\\[5pt]& \quad +\mathbb{P}(M \cap L \cap K).\end{align*}
Finally, by replacing the obtained expressions in (B.1), we have
 \begin{align*} &A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\\[5pt] & =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\\& \quad \!\cdots\!\binom{n_L-m_L}{r_L}\times\sum_{y=0}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& \quad -\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr) \\& ={\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}(\!-\!1)^{r_1+\cdots +r_L}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots +d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \biggl[ \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j}\!,\underbrace{1}_{n_j-m_j-r_j}\!\!,1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i}\!,\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\!\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j}\!,\underbrace{1}_{n_j-m_j-r_j}\!\!,1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i}\!\!,\bar{F}_i{(s+\delta)},\!\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\biggr].\end{align*}
\begin{align*} &A_{\mathbf{m}, \mathbf{l}}^{(i)}(s,s+\delta, \tau)\\[5pt] & =\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\\& \quad \!\cdots\!\binom{n_L-m_L}{r_L}\times\sum_{y=0}^{\sum_{j=1}^L (m_j-l_j)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i},\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\& \quad -\sum_{l=0}^{n-\sum_{j=1}^L m_j -1}(\!-\!1)^{l+1}\underset{r_1+\cdots +r_L=l}{\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times\sum_{y=0}^{\sum_{i=1}^L (m_i-l_i)}(\!-\!1)^{y+1}\underset{d_1+\cdots +d_L=y}{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j},\underbrace{1}_{n_j-m_j-r_j},1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i},\bar{F}_i{(s+\delta)},\underbrace{1}_{n_i-m_i-r_i-1}\Bigr) \\& ={\sum_{r_1=0}^{n_1-m_1}\!\cdots\! \sum_{r_i=0}^{n_i-m_i-1}\!\cdots\! \sum_{r_L=0}^{n_L-m_L}}(\!-\!1)^{r_1+\cdots +r_L}\binom{n_1-m_1}{r_1}\!\cdots\! \binom{n_i-m_i-1}{r_i}\!\cdots\!\binom{n_L-m_L}{r_L}\\& \quad \times{\sum_{d_1=0}^{m_1-l_1}\!\cdots\! \sum_{d_L=0}^{m_L-l_L}}(\!-\!1)^{d_1+\cdots +d_L}\binom{m_1-l_1}{d_1}\!\cdots\! \binom{m_L-l_L}{d_L}\\& \quad \times \biggl[ \hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j}\!,\underbrace{1}_{n_j-m_j-r_j}\!\!,1 \leq j \leq L, j\neq i,\underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i+1-d_i}\!,\underbrace{1}_{n_i- m_i-r_i-1}\Bigr)\\[5pt]& \quad -\hat{C}\Bigl(\underbrace{\bar{F}_j(\tau)}_{l_j+d_j},\!\underbrace{\bar{F}_j(s)}_{m_j-l_j+r_j-d_j}\!,\underbrace{1}_{n_j-m_j-r_j}\!\!,1 \leq j \leq L, j\neq i, \underbrace{\bar{F}_i(\tau)}_{l_i+d_i}, \!\underbrace{\bar{F}_i(s)}_{m_i-l_i+r_i-d_i}\!\!,\bar{F}_i{(s+\delta)},\!\underbrace{1}_{n_i-m_i-r_i-1}\Bigr)\biggr].\end{align*}
Acknowledgements
We would like to thank the Associate Editor and two anonymous referees for their constructive comments and suggestions, which led to improvements in the presentation of the paper.
Funding information
Asadi’s research work was performed in IPM Isfahan branch and was in part supported by a grant from IPM (no. 1400620212).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.