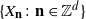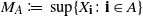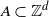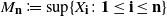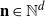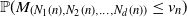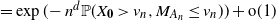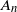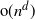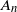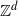1. Introduction
Let us consider a d-dimensional stationary random field
![]() $\{X_\textbf{n} \colon \textbf{n}\in{\mathbb Z}^d\}$
with its partial maxima
$\{X_\textbf{n} \colon \textbf{n}\in{\mathbb Z}^d\}$
with its partial maxima
defined for finite
![]() $A\subset{\mathbb Z}^d$
. We also put
$A\subset{\mathbb Z}^d$
. We also put
![]() $M_{\textbf{j},\textbf{n}} := \sup \{ X_\textbf{i} \colon \textbf{j} \leq \textbf{i} \leq \textbf{n}\}$
and
$M_{\textbf{j},\textbf{n}} := \sup \{ X_\textbf{i} \colon \textbf{j} \leq \textbf{i} \leq \textbf{n}\}$
and
![]() $M_{\textbf{n}} := M_{\mathbf{1},\textbf{n}}$
for
$M_{\textbf{n}} := M_{\mathbf{1},\textbf{n}}$
for
![]() $\textbf{j},\textbf{n}\in{\mathbb Z}^d$
. The goal is to study the asymptotic behaviour of
$\textbf{j},\textbf{n}\in{\mathbb Z}^d$
. The goal is to study the asymptotic behaviour of
![]() ${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n)$
as
${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n)$
as
![]() $n\to\infty$
, for
$n\to\infty$
, for
![]() $\{v_n\}\subset \mathbb{R}$
and
$\{v_n\}\subset \mathbb{R}$
and
![]() $\textbf{N}(n)\to\pmb{\infty}$
coordinate-wise.
$\textbf{N}(n)\to\pmb{\infty}$
coordinate-wise.
In the case
![]() $d=1$
, when
$d=1$
, when
![]() $\{X_n\colon n\in\mathbb{Z}\}$
is a stationary sequence, the well-known result of O’Brien [Reference O’Brien17, Theorem 2.1] states that under a broad class of circumstances
$\{X_n\colon n\in\mathbb{Z}\}$
is a stationary sequence, the well-known result of O’Brien [Reference O’Brien17, Theorem 2.1] states that under a broad class of circumstances
holds for some
![]() $p(n)\to\infty$
satisfying
$p(n)\to\infty$
satisfying
![]() $p(n)= {\text{o}}(n)$
. For m-dependent
$p(n)= {\text{o}}(n)$
. For m-dependent
![]() $\{X_n\}$
we can set
$\{X_n\}$
we can set
![]() $p(n):= m$
in formula (1.1), as Newell [Reference Newell16] shows. It follows that the extremal index
$p(n):= m$
in formula (1.1), as Newell [Reference Newell16] shows. It follows that the extremal index
![]() $\theta$
for
$\theta$
for
![]() $\{X_n\}$
, defined by Leadbetter [Reference Leadbetter14], equals
$\{X_n\}$
, defined by Leadbetter [Reference Leadbetter14], equals
where
![]() $p(n)=m$
in the m-dependent case. More generally, we can put
$p(n)=m$
in the m-dependent case. More generally, we can put
![]() $p(n)=m$
in (1.2) whenever condition
$p(n)=m$
in (1.2) whenever condition
![]() $D^{(m+1)}(v_n)$
, introduced by Chernick, Hsing, and McCormick [Reference Chernick, Hsing and McCormick5], is satisfied.
$D^{(m+1)}(v_n)$
, introduced by Chernick, Hsing, and McCormick [Reference Chernick, Hsing and McCormick5], is satisfied.
We recall that the extremal index
![]() $\theta\in[0,1]$
is interpreted as the reciprocal of the mean number of high threshold exceedances in a cluster. Formula (1.2) for
$\theta\in[0,1]$
is interpreted as the reciprocal of the mean number of high threshold exceedances in a cluster. Formula (1.2) for
![]() $\theta$
may be treated as an answer to the question: Asymptotically, what is the probability that a given element of a cluster of large values is its last element on the right?
$\theta$
may be treated as an answer to the question: Asymptotically, what is the probability that a given element of a cluster of large values is its last element on the right?
Looking for formulas analogous to (1.1) and (1.2) for arbitrary
![]() $d\in\mathbb{N_+}$
, one can try to answer the properly formulated d-dimensional version of the above question. This point is realized in Sections 3 and 4. In Section 3 we prove the main result, Theorem 3.1. We establish that in a general setting the approximation
$d\in\mathbb{N_+}$
, one can try to answer the properly formulated d-dimensional version of the above question. This point is realized in Sections 3 and 4. In Section 3 we prove the main result, Theorem 3.1. We establish that in a general setting the approximation
holds with
![]() $A(\textbf{p}(n)) \subset \{\textbf{j} \in {\mathbb Z}^d \colon -\textbf{p}(n) \leq \textbf{j} \leq \textbf{p}(n)\}$
defined by (2.6),
$A(\textbf{p}(n)) \subset \{\textbf{j} \in {\mathbb Z}^d \colon -\textbf{p}(n) \leq \textbf{j} \leq \textbf{p}(n)\}$
defined by (2.6),
![]() $\textbf{N}(n)$
fulfilling (2.1), and
$\textbf{N}(n)$
fulfilling (2.1), and
![]() $\textbf{p}(n)\to\pmb{\infty}$
satisfying
$\textbf{p}(n)\to\pmb{\infty}$
satisfying
![]() $\textbf{p}(n)= {\text{o}}(\textbf{N}(n))$
and some other rate of growth conditions. For
$\textbf{p}(n)= {\text{o}}(\textbf{N}(n))$
and some other rate of growth conditions. For
![]() $d=1$
we have
$d=1$
we have
![]() $A(p(n))=\{1,2,\ldots, p(n)\}$
and formula (1.3) simplifies to (1.1). Corollary 3 provides the local mixing condition (3.7) equivalent to the fact that (1.3) holds with
$A(p(n))=\{1,2,\ldots, p(n)\}$
and formula (1.3) simplifies to (1.1). Corollary 3 provides the local mixing condition (3.7) equivalent to the fact that (1.3) holds with
![]() $\textbf{p}(n):= (m,m,\ldots,m)$
. Section 4 is devoted to considerations concerning the notion of the extremal index for random fields. Formula (4.2), being a generalization of (1.2), and its simplified version (4.3) for fields fulfilling (3.7) are proposed there. In Section 6 the results from Sections 3 and 4 are used to describe the asymptotics of partial maxima for the moving maximum field.
$\textbf{p}(n):= (m,m,\ldots,m)$
. Section 4 is devoted to considerations concerning the notion of the extremal index for random fields. Formula (4.2), being a generalization of (1.2), and its simplified version (4.3) for fields fulfilling (3.7) are proposed there. In Section 6 the results from Sections 3 and 4 are used to describe the asymptotics of partial maxima for the moving maximum field.
In Section 5 we focus on m-dependent fields and present a corollary of the main theorem generalizing the aforementioned Newell’s formula [Reference Newell16]. We also compare the obtained result with the limit theorem for m-dependent fields proved by Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12, Theorem 2.1].
The present paper provides a d-dimensional generalization of O’Brien’s formula (1.1) with a handy and immediate conclusion for m-dependent fields. Another general theorem by Turkman [Reference Turkman19, Theorem 1] is not really applicable in the m-dependent case. A recent result obtained independently by Ling [Reference Ling15, Lemma 3.2] is a special case of Theorem 3.1. Other theorems on the topic were given for some subclasses of weakly dependent fields: in the two-dimensional Gaussian setting by French and Davis [Reference French and Davis9]; for two-dimensional moving maxima and moving averages by Basrak and Tafro [Reference Basrak and Tafro3]; for m-dependent and max-m-approximable fields by Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12]; for regularly varying fields by Wu and Samorodnitsky [Reference Wu and Samorodnitsky20]. The proof of Theorem 3.1 presented in the paper, although achieved independently, is similar to proofs of [Reference French and Davis9, Lemma 4] and [Reference Ling15, Lemma 3.2].
2. Preliminaries
An element
![]() $\textbf{n}\in{\mathbb Z}^d$
is often denoted by
$\textbf{n}\in{\mathbb Z}^d$
is often denoted by
![]() $(n_1,n_2,\ldots,n_d)$
and
$(n_1,n_2,\ldots,n_d)$
and
![]() $\|\textbf{n}\|$
is its sup norm. We write
$\|\textbf{n}\|$
is its sup norm. We write
![]() $\textbf{i}\leq \textbf{j}$
and
$\textbf{i}\leq \textbf{j}$
and
![]() $\textbf{n}\to\pmb{\infty}$
whenever
$\textbf{n}\to\pmb{\infty}$
whenever
![]() $i_l\leq j_l$
and
$i_l\leq j_l$
and
![]() $n_l\to\infty$
, respectively, for all
$n_l\to\infty$
, respectively, for all
![]() $l\in\{1,2,\ldots, d\}$
. We put
$l\in\{1,2,\ldots, d\}$
. We put
![]() $\mathbf{0}:= (0,0,\ldots,0)$
,
$\mathbf{0}:= (0,0,\ldots,0)$
,
![]() $\mathbf{1}:= (1,1,\ldots,1)$
, and
$\mathbf{1}:= (1,1,\ldots,1)$
, and
![]() $\pmb{\infty}:= (\infty,\infty,\ldots,\infty)$
.
$\pmb{\infty}:= (\infty,\infty,\ldots,\infty)$
.
In our considerations
![]() $\{X_{\textbf{n}} \colon \textbf{n}\in{\mathbb Z}^d\}$
is a d-dimensional stationary random field. We ask for the asymptotics of
$\{X_{\textbf{n}} \colon \textbf{n}\in{\mathbb Z}^d\}$
is a d-dimensional stationary random field. We ask for the asymptotics of
![]() ${\mathbb{P}}(M_{\textbf{N}(n)}\leq v_n)$
as
${\mathbb{P}}(M_{\textbf{N}(n)}\leq v_n)$
as
![]() $n\to\infty$
, for
$n\to\infty$
, for
![]() $\textbf{N} = \{\textbf{N}(n) \colon n\in{\mathbb N}\}\subset{\mathbb N}^d$
, such that
$\textbf{N} = \{\textbf{N}(n) \colon n\in{\mathbb N}\}\subset{\mathbb N}^d$
, such that
and
![]() $\{v_n \colon n\in{\mathbb N}\} \subset {\mathbb R}$
.
$\{v_n \colon n\in{\mathbb N}\} \subset {\mathbb R}$
.
We are interested in weakly dependent fields. We assume that
is satisfied for some
![]() $r_n\to\infty$
and all
$r_n\to\infty$
and all
![]() $k_n\to\infty$
such that
$k_n\to\infty$
such that
![]() $k_n= {\text{o}}(r_n)$
, with
$k_n= {\text{o}}(r_n)$
, with
Applying the classical fact (see e.g. O’Brien [Reference O’Brien17])
we obtain that (2.2) implies
Above,
![]() $p_l(n)= {\text{o}}(N_l(n))$
for
$p_l(n)= {\text{o}}(N_l(n))$
for
![]() $l\in\{1,2,\ldots,d\}$
, which we denote by
$l\in\{1,2,\ldots,d\}$
, which we denote by
![]() $\textbf{p}(n)= {\text{o}}(\textbf{N}(n))$
.
$\textbf{p}(n)= {\text{o}}(\textbf{N}(n))$
.
Remark 2.1. For
![]() $d=1$
, weak dependence in the sense of (2.2) is ensured by any of the following conditions: Leadbetter’s
$d=1$
, weak dependence in the sense of (2.2) is ensured by any of the following conditions: Leadbetter’s
![]() $D(v_n)$
, O’Brien’s
$D(v_n)$
, O’Brien’s
![]() $\text{AIM}(v_n)$
, or Jakubowski’s
$\text{AIM}(v_n)$
, or Jakubowski’s
![]() $B_1(v_n)$
; see [Reference Leadbetter14], [Reference O’Brien17], and [Reference Jakubowski10]. For
$B_1(v_n)$
; see [Reference Leadbetter14], [Reference O’Brien17], and [Reference Jakubowski10]. For
![]() $d\in{\mathbb N}_+$
the considered property follows, for example, from condition
$d\in{\mathbb N}_+$
the considered property follows, for example, from condition
![]() $B_1^{\textbf{N}}(v_n)$
introduced by Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła13]. In particular, m-dependent fields are weakly dependent; see Section 5. A similar notion of weak dependence was investigated by Ling [Reference Ling15, Lemma 3.1].
$B_1^{\textbf{N}}(v_n)$
introduced by Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła13]. In particular, m-dependent fields are weakly dependent; see Section 5. A similar notion of weak dependence was investigated by Ling [Reference Ling15, Lemma 3.1].
Let
![]() $\preccurlyeq$
be an arbitrary total order on
$\preccurlyeq$
be an arbitrary total order on
![]() ${\mathbb Z}^d$
which is translation-invariant, that is,
${\mathbb Z}^d$
which is translation-invariant, that is,
![]() $\textbf{i} \preccurlyeq \textbf{j}$
implies
$\textbf{i} \preccurlyeq \textbf{j}$
implies
![]() $\textbf{i} + \textbf{k} \preccurlyeq \textbf{j} + \textbf{k}$
. An example of such an order is the lexicographic order:
$\textbf{i} + \textbf{k} \preccurlyeq \textbf{j} + \textbf{k}$
. An example of such an order is the lexicographic order:
We will write
![]() $\textbf{i} \prec \textbf{j}$
whenever
$\textbf{i} \prec \textbf{j}$
whenever
![]() $\textbf{i} \preccurlyeq \textbf{j}$
and
$\textbf{i} \preccurlyeq \textbf{j}$
and
![]() $\textbf{i}\neq\textbf{j}$
. For technical requirements in further sections, we define the set
$\textbf{i}\neq\textbf{j}$
. For technical requirements in further sections, we define the set
![]() $A(\textbf{p})\subset {\mathbb Z}^d$
for each
$A(\textbf{p})\subset {\mathbb Z}^d$
for each
![]() $\textbf{p}\in{\mathbb N}^d$
as follows:
$\textbf{p}\in{\mathbb N}^d$
as follows:
3. Main theorem
In the following the main result of the paper is presented. The asymptotic behaviour of
![]() ${\mathbb{P}}(M_{\textbf{N}(n)}\leq v_n)$
as
${\mathbb{P}}(M_{\textbf{N}(n)}\leq v_n)$
as
![]() $n\to\infty$
, for weakly dependent
$n\to\infty$
, for weakly dependent
![]() $\{X_{\textbf{n}}\}$
and for
$\{X_{\textbf{n}}\}$
and for
![]() $\{\textbf{N}(n)\}$
and
$\{\textbf{N}(n)\}$
and
![]() $\{v_n\}$
as in Section 2, is described.
$\{v_n\}$
as in Section 2, is described.
Theorem 3.1. Let
![]() $\{X_\textbf{n}\}$
satisfy (2.2) for some
$\{X_\textbf{n}\}$
satisfy (2.2) for some
![]() $r_n\to\infty$
and all
$r_n\to\infty$
and all
![]() $k_n\to\infty$
such that
$k_n\to\infty$
such that
![]() $k_n={\text{o}}(r_n)$
. If
$k_n={\text{o}}(r_n)$
. If
then, for every
![]() $\{k_n\}$
as above, we obtain
$\{k_n\}$
as above, we obtain
with
![]() $\textbf{p}(n)$
and
$\textbf{p}(n)$
and
![]() $A(\textbf{p}(n))$
given by (2.3) and (2.6), respectively.
$A(\textbf{p}(n))$
given by (2.3) and (2.6), respectively.
Remark 3.1. If (2.2) holds for some
![]() $k_n\to\infty$
, then (3.1) is implied by the condition
$k_n\to\infty$
, then (3.1) is implied by the condition
This follows from (2.5) and the inequality
The proof of the theorem generalizes the reasoning proposed by O’Brien [Reference O’Brien17, Theorem 2.1] for sequences. A way of dividing the event
![]() $\{M_{\textbf{p}(n)} > v_n\}$
into
$\{M_{\textbf{p}(n)} > v_n\}$
into
![]() $p^*(n):= p_1(n)p_2(n)\cdots p_d(n)$
mutually exclusive events determined by
$p^*(n):= p_1(n)p_2(n)\cdots p_d(n)$
mutually exclusive events determined by
![]() $\preccurlyeq$
(which are similar in some sense) plays a key role in the proof. An analogous technique was used by French and Davis [Reference French and Davis9, Lemma 4] in the two-dimensional Gaussian case. Recently, Ling [Reference Ling15, Lemma 3.1] expanded their result to some non-Gaussian fields. In both papers the authors restrict themselves to the lexicographic order on
$\preccurlyeq$
(which are similar in some sense) plays a key role in the proof. An analogous technique was used by French and Davis [Reference French and Davis9, Lemma 4] in the two-dimensional Gaussian case. Recently, Ling [Reference Ling15, Lemma 3.1] expanded their result to some non-Gaussian fields. In both papers the authors restrict themselves to the lexicographic order on
![]() ${\mathbb Z}^2$
.
${\mathbb Z}^2$
.
Proof of Theorem 3.1
. Let the assumptions of the theorem be satisfied. Then (2.5) holds. Dividing the set
![]() $\{M_{\textbf{p}(n)} > v_n\}$
into
$\{M_{\textbf{p}(n)} > v_n\}$
into
![]() $p^*(n)=p_1(n)p_2(n)\cdots p_d(n)$
disjoint sets and applying monotonicity and stationarity, we obtain
$p^*(n)=p_1(n)p_2(n)\cdots p_d(n)$
disjoint sets and applying monotonicity and stationarity, we obtain
 \begin{align*} {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)& = \sum_{\mathbf{1}\leq \textbf{j} \leq \textbf{p}(n)} {\mathbb{P}}(X_\textbf{j} > v_n, X_{\textbf{i}} \leq v_n\ \text{for all}\ \textbf{i} \succ \textbf{j}\ \text{such that}\ \mathbf{1} \leq \textbf{i} \leq \textbf{p}(n) )\\& \geq \sum_{\mathbf{1}\leq \textbf{j} \leq \textbf{p}(n)} {\mathbb{P}} (X_\textbf{j} > v_n, X_{\textbf{i}} \leq v_n\ \text{ for all }\ \textbf{i} \in A(\textbf{p}(n))+\textbf{j} ) \\& = p^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n ),\end{align*}
\begin{align*} {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)& = \sum_{\mathbf{1}\leq \textbf{j} \leq \textbf{p}(n)} {\mathbb{P}}(X_\textbf{j} > v_n, X_{\textbf{i}} \leq v_n\ \text{for all}\ \textbf{i} \succ \textbf{j}\ \text{such that}\ \mathbf{1} \leq \textbf{i} \leq \textbf{p}(n) )\\& \geq \sum_{\mathbf{1}\leq \textbf{j} \leq \textbf{p}(n)} {\mathbb{P}} (X_\textbf{j} > v_n, X_{\textbf{i}} \leq v_n\ \text{ for all }\ \textbf{i} \in A(\textbf{p}(n))+\textbf{j} ) \\& = p^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n ),\end{align*}
which, combined with (2.5) and the fact that
![]() $k_n^dp^*(n) \sim n^d$
, gives
$k_n^dp^*(n) \sim n^d$
, gives
In the second step of the proof we will show that the reverse inequality to (3.4) also holds. It is sufficient to consider the case
![]() ${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n) \to \gamma$
for
${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n) \to \gamma$
for
![]() $\gamma \in [0,1]$
, and we do so. Since
$\gamma \in [0,1]$
, and we do so. Since
![]() $\gamma=0$
is excluded by assumption (3.1) and for
$\gamma=0$
is excluded by assumption (3.1) and for
![]() $\gamma =1$
the proven inequality is obvious, we focus on
$\gamma =1$
the proven inequality is obvious, we focus on
![]() $\gamma\in(0,1)$
. Let us choose
$\gamma\in(0,1)$
. Let us choose
![]() $\{t_n\}\subset{\mathbb N}_+$
so that
$\{t_n\}\subset{\mathbb N}_+$
so that
![]() $t_n\to\infty$
and
$t_n\to\infty$
and
![]() $t_n={\text{o}}(k_n)$
. Put
$t_n={\text{o}}(k_n)$
. Put
Since
![]() $t_n= {\text{o}}(r_n)$
, (2.5) holds with
$t_n= {\text{o}}(r_n)$
, (2.5) holds with
![]() $k_n$
replaced by
$k_n$
replaced by
![]() $t_n$
and
$t_n$
and
![]() $\textbf{p}(n)$
replaced by
$\textbf{p}(n)$
replaced by
![]() $\textbf{s}(n)$
. Also,
$\textbf{s}(n)$
. Also,
![]() $\textbf{p}(n) = {\text{o}}(\textbf{s}(n))$
and
$\textbf{p}(n) = {\text{o}}(\textbf{s}(n))$
and
![]() $\textbf{s}(n)= {\text{o}}(\textbf{N}(n))$
. Moreover, for the sets
$\textbf{s}(n)= {\text{o}}(\textbf{N}(n))$
. Moreover, for the sets
and
we obtain
 \begin{align*}\dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)}& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n) - {\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)} \\[6pt]& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)} - 1\\& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{ {\text{o}}(s^*(n)/p^*(n)) \cdot {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)} - 1\\& = \dfrac{1+{\text{o}}(1)}{{\text{o}}(1)} \cdot \dfrac{t_n^d {\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{k_n^d {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)} - 1.\end{align*}
\begin{align*}\dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)}& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n) - {\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)} \\[6pt]& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{{\mathbb{P}}(M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n)} - 1\\& = \dfrac{{\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{ {\text{o}}(s^*(n)/p^*(n)) \cdot {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)} - 1\\& = \dfrac{1+{\text{o}}(1)}{{\text{o}}(1)} \cdot \dfrac{t_n^d {\mathbb{P}}(M_{\textbf{s}(n)} > v_n)}{k_n^d {\mathbb{P}}(M_{\textbf{p}(n)} > v_n)} - 1.\end{align*}
Applying (2.5) twice, we get
and consequently
Now, observe that
 \begin{align*}{\mathbb{P}} (M_{\textbf{s}(n)} > v_n) & = {\mathbb{P}} (M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n) + {\mathbb{P}} (M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n) \\& = {\mathbb{P}} (M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n) (1+ {\text{o}}(1))\\& \leq \sum_{\textbf{j} \in C(\textbf{p}(n), \textbf{s}(n))} {\mathbb{P}} (X_{\mathbf{j}} > v_n, M_{A(\textbf{p}(n)) + \textbf{j}} \leq v_n) \cdot (1+ {\text{o}}(1))\\& \leq s^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n) (1+ {\text{o}}(1)),\end{align*}
\begin{align*}{\mathbb{P}} (M_{\textbf{s}(n)} > v_n) & = {\mathbb{P}} (M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n) + {\mathbb{P}} (M_{B(\textbf{p}(n), \textbf{s}(n))} > v_n) \\& = {\mathbb{P}} (M_{\textbf{s}(n)} > v_n, M_{B(\textbf{p}(n), \textbf{s}(n))} \leq v_n) (1+ {\text{o}}(1))\\& \leq \sum_{\textbf{j} \in C(\textbf{p}(n), \textbf{s}(n))} {\mathbb{P}} (X_{\mathbf{j}} > v_n, M_{A(\textbf{p}(n)) + \textbf{j}} \leq v_n) \cdot (1+ {\text{o}}(1))\\& \leq s^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n) (1+ {\text{o}}(1)),\end{align*}
by property (3.5), subadditivity and monotonicity of probability, and by stationarity of the field
![]() $\{X_{\textbf{n}}\}$
. Applying (2.5) with
$\{X_{\textbf{n}}\}$
. Applying (2.5) with
![]() $(k_n, \textbf{p}(n))$
replaced by
$(k_n, \textbf{p}(n))$
replaced by
![]() $(t_n, \textbf{s}(n))$
and the fact that
$(t_n, \textbf{s}(n))$
and the fact that
![]() $t_n^d s^*(n) \sim n^d$
, we conclude that
$t_n^d s^*(n) \sim n^d$
, we conclude that
 \begin{align}{\mathbb{P}} (M_{\textbf{N}(n)}\leq v_n) & \geq \exp (\!-t_n^d s^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n) (1+ {\text{o}}(1))) + {\text{o}}(1)\notag \\&= \exp (\!-n^d {\mathbb{P}}(X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n)) + {\text{o}}(1).\end{align}
\begin{align}{\mathbb{P}} (M_{\textbf{N}(n)}\leq v_n) & \geq \exp (\!-t_n^d s^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n) (1+ {\text{o}}(1))) + {\text{o}}(1)\notag \\&= \exp (\!-n^d {\mathbb{P}}(X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))} \leq v_n)) + {\text{o}}(1).\end{align}
Since inequalities (3.4) and (3.6) are both satisfied, the proof is complete.
Theorem 3.1 immediately yields the following generalization of the result established by Chernick, Hsing, and McCormick [Reference Chernick, Hsing and McCormick5, Proposition 1.1] for
![]() $d=1$
. Assumption (3.7) given below is a multidimensional counterpart of the local mixing condition
$d=1$
. Assumption (3.7) given below is a multidimensional counterpart of the local mixing condition
![]() $D^{(m+1)}(v_n)$
defined in [Reference Chernick, Hsing and McCormick5] for sequences and it is satisfied by m-dependent fields, for example (see Section 5.1).
$D^{(m+1)}(v_n)$
defined in [Reference Chernick, Hsing and McCormick5] for sequences and it is satisfied by m-dependent fields, for example (see Section 5.1).
Corollary 3.1. Let the assumptions of Theorem 3.1 be satisfied. Then
if and only if
where
![]() $k_n\to\infty$
is such that
$k_n\to\infty$
is such that
![]() $k_n = {\text{o}}(r_n)$
.
$k_n = {\text{o}}(r_n)$
.
We point out that Corollary 3.1 reforms a faulty formula for m-dependent fields proposed by Ferreira and Pereira [Reference Ferreira and Pereira8, Proposition 2.1]; see [Reference Jakubowski and Soja-Kukieła12, Example 5.5]. We also suggest comparing the above condition (3.7) with assumption
![]() $D^{\prime\prime}(v_n, \mathcal{B}_n,\mathcal{V})$
proposed by Pereira, Martins, and Ferreira [Reference Pereira, Martins and Ferreira18, Definition 3.1].
$D^{\prime\prime}(v_n, \mathcal{B}_n,\mathcal{V})$
proposed by Pereira, Martins, and Ferreira [Reference Pereira, Martins and Ferreira18, Definition 3.1].
Remark 3.2. There exists a close relationship between Theorem 3.1 and compound Poisson approximations in the spirit of Arratia, Goldstein, and Gordon [Reference Arratia, Goldstein and Gordon1, Section 4.2.1]. The random variable
with the expectation
![]() ${\lambda^{(1)}_n}:= N^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n ) $
, estimates the number of clusters of exceedances over
${\lambda^{(1)}_n}:= N^*(n) {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n ) $
, estimates the number of clusters of exceedances over
![]() $v_n$
in the set
$v_n$
in the set
![]() $\{\textbf{k} \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
, and we have
$\{\textbf{k} \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
, and we have
Remark 3.3. It is worth noting that translation-invariant linear orders on the set of indices
![]() ${\mathbb Z}^d$
play a significant role in considerations (by Basrak and Planinić [Reference Basrak and Planinić4], Wu and Samorodnitsky [Reference Wu and Samorodnitsky20]) on the extremes of regularly varying fields.
${\mathbb Z}^d$
play a significant role in considerations (by Basrak and Planinić [Reference Basrak and Planinić4], Wu and Samorodnitsky [Reference Wu and Samorodnitsky20]) on the extremes of regularly varying fields.
4. Extremal index
In this part we use the results given in Section 3 to establish formulas (4.2) and (4.3) for the extremal index
![]() $\theta$
for random fields. We refer to Choi [Reference Choi6] or Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12] for definitions and some considerations on the extremal index in the multidimensional setting.
$\theta$
for random fields. We refer to Choi [Reference Choi6] or Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12] for definitions and some considerations on the extremal index in the multidimensional setting.
Here we present a method for calculating the number
![]() $\theta\in[0,1]$
satisfying
$\theta\in[0,1]$
satisfying
whenever such a
![]() $\theta$
exists. Let us observe that according to (2.4) we have
$\theta$
exists. Let us observe that according to (2.4) we have
and, moreover, Theorem 3.1 yields
for
![]() $\textbf{N}(n)$
,
$\textbf{N}(n)$
,
![]() $v_n$
and
$v_n$
and
![]() $\textbf{p}(n)$
satisfying appropriate assumptions. Hence, provided that
$\textbf{p}(n)$
satisfying appropriate assumptions. Hence, provided that
condition (4.1) is satisfied if and only if
Formula (4.2), allowing computation of extremal indices
![]() $\theta$
for random fields, is a multidimensional generalization of (1.2). In the special case when assumption (3.7) is satisfied, it is easy to show that formula (4.2) simplifies to the following:
$\theta$
for random fields, is a multidimensional generalization of (1.2). In the special case when assumption (3.7) is satisfied, it is easy to show that formula (4.2) simplifies to the following:
The above formulas are in line with the interpretation of
![]() $\theta$
as the reciprocal of the mean number of high threshold exceedances in a cluster. Indeed, they answer the question: What is the asymptotic probability that a given element of a cluster is the distinguished element of the cluster?, where the distinguished element in a cluster is the greatest one with respect to the order
$\theta$
as the reciprocal of the mean number of high threshold exceedances in a cluster. Indeed, they answer the question: What is the asymptotic probability that a given element of a cluster is the distinguished element of the cluster?, where the distinguished element in a cluster is the greatest one with respect to the order
![]() $\preccurlyeq$
. This identification of a unique representative for each cluster is called declustering, declumping, or anchoring, and has much in common with compound Poisson approximations (see e.g. [Reference Arratia, Goldstein and Gordon1], [Reference Barbour and Chryssaphinou2], and [Reference Basrak and Planinić4]).
$\preccurlyeq$
. This identification of a unique representative for each cluster is called declustering, declumping, or anchoring, and has much in common with compound Poisson approximations (see e.g. [Reference Arratia, Goldstein and Gordon1], [Reference Barbour and Chryssaphinou2], and [Reference Basrak and Planinić4]).
Remark 4.1. Formula (4.2) justifies the following definition of the runs estimator
![]() $\hat{\theta}^R_{\textbf{N}(n)}$
for the extremal index
$\hat{\theta}^R_{\textbf{N}(n)}$
for the extremal index
![]() $\theta$
:
$\theta$
:
where
![]() $S_n$
is the number of exceedances over
$S_n$
is the number of exceedances over
![]() $v_n$
in the set
$v_n$
in the set
![]() $\{\textbf{k}\in{\mathbb Z}^d \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
.
$\{\textbf{k}\in{\mathbb Z}^d \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
.
5. Maxima of m-dependent fields
In this section we focus on m-dependent fields. We recall that
![]() $\{X_\textbf{n}\}$
is m-dependent for some
$\{X_\textbf{n}\}$
is m-dependent for some
![]() $m\in{\mathbb N} $
if the families
$m\in{\mathbb N} $
if the families
![]() $\{X_{\textbf{i}}\colon \textbf{i}\in U \}$
and
$\{X_{\textbf{i}}\colon \textbf{i}\in U \}$
and
![]() $\{X_{\textbf{j}} \colon \textbf{j}\in V\}$
are independent for all pairs of finite sets
$\{X_{\textbf{j}} \colon \textbf{j}\in V\}$
are independent for all pairs of finite sets
![]() $ U , V \subset{\mathbb Z}^d$
satisfying
$ U , V \subset{\mathbb Z}^d$
satisfying
![]() $\min \{\|\textbf{i}-\textbf{j}\| \colon \textbf{i}\in U ,\,\textbf{j}\in V \} > m$
.
$\min \{\|\textbf{i}-\textbf{j}\| \colon \textbf{i}\in U ,\,\textbf{j}\in V \} > m$
.
Let us assume that
![]() $\{X_{\textbf{n}}\}$
is m-dependent and satisfies (3.1) for some sequence
$\{X_{\textbf{n}}\}$
is m-dependent and satisfies (3.1) for some sequence
![]() $\{v_n\}\subset{\mathbb R} $
. Then it is easy to show that condition (3.3) holds too (see [Reference Jakubowski and Soja-Kukieła12, Remark 4.2]). Below, we present two methods that can be used to calculate the limit of
$\{v_n\}\subset{\mathbb R} $
. Then it is easy to show that condition (3.3) holds too (see [Reference Jakubowski and Soja-Kukieła12, Remark 4.2]). Below, we present two methods that can be used to calculate the limit of
![]() ${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n)$
. A direct connection between them can be given and we illustrate it in the case
${\mathbb{P}}(M_{\textbf{N}(n)} \leq v_n)$
. A direct connection between them can be given and we illustrate it in the case
![]() $d=2$
.
$d=2$
.
5.1. First method
The first of the methods is a consequence of the main result presented in the paper. Since the field
![]() $\{X_{\textbf{n}}\}$
is m-dependent, it satisfies (2.2) for each
$\{X_{\textbf{n}}\}$
is m-dependent, it satisfies (2.2) for each
![]() $k_n\to\infty$
such that
$k_n\to\infty$
such that
![]() $k_n= {\text{o}}(r_n)$
, for some
$k_n= {\text{o}}(r_n)$
, for some
![]() $r_n\to\infty$
(see e.g. [Reference Jakubowski and Soja-Kukieła12]). Moreover, the inequality
$r_n\to\infty$
(see e.g. [Reference Jakubowski and Soja-Kukieła12]). Moreover, the inequality
 \begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_{n} \geq M_{A((m,m,\ldots,m))}, M_{A(\textbf{p}(n)) \backslash A((m,m,\ldots,m))} > v_n ) \\& \qquad \leq n^d \sum_{\textbf{i} \in A(\textbf{p}(n)), \|\textbf{i}\| > m} {\mathbb{P}}(X_{\mathbf{0}} > v_{n}, X_{\textbf{i}} > v_{n})\\& \qquad = n^d \sum_{\textbf{i} \in A(\textbf{p}(n)), \|\textbf{i}\| > m} {\mathbb{P}}(X_{\mathbf{0}} > v_{n}){\mathbb{P}}(X_{\textbf{i}} > v_{n})\\& \qquad \leq n^d \cdot \dfrac{n^d}{k_n^d} \cdot {\mathbb{P}}(X_{\mathbf{0}} > v_{n})^2 (1+ {\text{o}}(1))\end{align*}
\begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_{n} \geq M_{A((m,m,\ldots,m))}, M_{A(\textbf{p}(n)) \backslash A((m,m,\ldots,m))} > v_n ) \\& \qquad \leq n^d \sum_{\textbf{i} \in A(\textbf{p}(n)), \|\textbf{i}\| > m} {\mathbb{P}}(X_{\mathbf{0}} > v_{n}, X_{\textbf{i}} > v_{n})\\& \qquad = n^d \sum_{\textbf{i} \in A(\textbf{p}(n)), \|\textbf{i}\| > m} {\mathbb{P}}(X_{\mathbf{0}} > v_{n}){\mathbb{P}}(X_{\textbf{i}} > v_{n})\\& \qquad \leq n^d \cdot \dfrac{n^d}{k_n^d} \cdot {\mathbb{P}}(X_{\mathbf{0}} > v_{n})^2 (1+ {\text{o}}(1))\end{align*}
holds with the right-hand side tending to zero by (3.3). From Corollary 3.1, we obtain
5.2. Second method
The second formula comes from Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12, Theorem 2.1]. It states that we have
under the above assumptions on
![]() $\{X_{\textbf{n}}\}$
. This result is a consequence of the Bonferroni-type inequality from Jakubowski and Rosiński [Reference Jakubowski and Rosiński11, Theorem 2.1].
$\{X_{\textbf{n}}\}$
. This result is a consequence of the Bonferroni-type inequality from Jakubowski and Rosiński [Reference Jakubowski and Rosiński11, Theorem 2.1].
5.3. Comparison
For
![]() $d=1$
both of the formulas simplify to the well-known result of Newell [Reference Newell16]:
$d=1$
both of the formulas simplify to the well-known result of Newell [Reference Newell16]:
Each of them allows us to describe the asymptotic behaviour of maxima on the base of tail properties of joint distribution of a fixed finite dimension. To apply the first method, one uses the distribution of the
![]() $(1 + ((2m+1)^d-1)/2)$
-element family
$(1 + ((2m+1)^d-1)/2)$
-element family
To involve the second method, we use the distribution of the
![]() $(m+1)^d$
-element family
$(m+1)^d$
-element family
![]() $\{X_{\textbf{n}}\colon \mathbf{0} \leq \textbf{n} \leq (m,m,\ldots,m)\}$
.
$\{X_{\textbf{n}}\colon \mathbf{0} \leq \textbf{n} \leq (m,m,\ldots,m)\}$
.
Below, a link between the two formulas is described in two ways: a more conceptual one, and one that is shorter but perhaps less intuitive. To avoid annoying technicalities, we focus on
![]() $d=2$
.
$d=2$
.
5.3.1 First approach: counting clusters
Our aim is to calculate the number of clusters of exceedances over
![]() $v_n$
in the window
$v_n$
in the window
![]() $W:= \{\textbf{k}\in{\mathbb Z}^2 \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
in two different ways and obtain, as a consequence, the equivalence of (5.1) and (5.2).
$W:= \{\textbf{k}\in{\mathbb Z}^2 \colon \mathbf{1} \leq \textbf{k} \leq \textbf{N}(n)\}$
in two different ways and obtain, as a consequence, the equivalence of (5.1) and (5.2).
Let the random set
![]() $J_n$
be given as
$J_n$
be given as
![]() $J_n:= \{\textbf{k}\in W \colon X_{\textbf{k}}>v_n\}$
and let
$J_n:= \{\textbf{k}\in W \colon X_{\textbf{k}}>v_n\}$
and let
![]() $\leftrightarrow$
be the equivalence relation on
$\leftrightarrow$
be the equivalence relation on
![]() $J_n$
, defined as follows:
$J_n$
, defined as follows:
 \begin{gather*} \textbf{i} \leftrightarrow \textbf{j} \ {\text{whenever there exist}\ {l\in\mathbb{N}}\ \text{and}\ {\textbf{k}_0,\textbf{k}_1, \ldots, \textbf{k}_l,\textbf{k}_{l+1}\in J_n, \textbf{k}_0=\textbf{i}, \textbf{k}_{l+1}=\textbf{j}}} \\ {\text{such that} }\ \max_{0\leq h\leq l}\|\textbf{k}_{h+1}-\textbf{k}_h\| \leq m,\end{gather*}
\begin{gather*} \textbf{i} \leftrightarrow \textbf{j} \ {\text{whenever there exist}\ {l\in\mathbb{N}}\ \text{and}\ {\textbf{k}_0,\textbf{k}_1, \ldots, \textbf{k}_l,\textbf{k}_{l+1}\in J_n, \textbf{k}_0=\textbf{i}, \textbf{k}_{l+1}=\textbf{j}}} \\ {\text{such that} }\ \max_{0\leq h\leq l}\|\textbf{k}_{h+1}-\textbf{k}_h\| \leq m,\end{gather*}
for
![]() $\textbf{i},\textbf{j}\in J_n$
. We define a cluster as an equivalence class of
$\textbf{i},\textbf{j}\in J_n$
. We define a cluster as an equivalence class of
![]() $\leftrightarrow$
and obtain the partition
$\leftrightarrow$
and obtain the partition
![]() $\mathcal{C}_n:= J_n/ _{\leftrightarrow}$
of
$\mathcal{C}_n:= J_n/ _{\leftrightarrow}$
of
![]() $J_n$
into
$J_n$
into
![]() $\Lambda_n:= \# \mathcal{C}_n$
clusters. We put
$\Lambda_n:= \# \mathcal{C}_n$
clusters. We put
 \begin{gather*}\lambda_n := {\mathbb{E}} (\Lambda_n),\quad\mathcal{C}^{\prime}_n:= \Bigl\{C\in\mathcal{C}_n \colon \max_{\textbf{i}, \textbf{j} \in C}\|\textbf{i}-\textbf{j}\| \leq m\Bigr\},\\\mathcal{C}^{\prime\prime}_{n}:= \mathcal{C}_n \backslash \mathcal{C}^{\prime}_n,\quad\Lambda^{\prime}_n:= \#\mathcal{C}^{\prime}_n,\quad\lambda^{\prime}_n:= {\mathbb{E}} (\Lambda^{\prime}_n).\end{gather*}
\begin{gather*}\lambda_n := {\mathbb{E}} (\Lambda_n),\quad\mathcal{C}^{\prime}_n:= \Bigl\{C\in\mathcal{C}_n \colon \max_{\textbf{i}, \textbf{j} \in C}\|\textbf{i}-\textbf{j}\| \leq m\Bigr\},\\\mathcal{C}^{\prime\prime}_{n}:= \mathcal{C}_n \backslash \mathcal{C}^{\prime}_n,\quad\Lambda^{\prime}_n:= \#\mathcal{C}^{\prime}_n,\quad\lambda^{\prime}_n:= {\mathbb{E}} (\Lambda^{\prime}_n).\end{gather*}
Let
![]() $\Lambda^{(1)}_n$
and
$\Lambda^{(1)}_n$
and
![]() $\lambda^{(1)}_n$
, associated with the method presented in Section 5.1, be defined as in Remark 3.2 with
$\lambda^{(1)}_n$
, associated with the method presented in Section 5.1, be defined as in Remark 3.2 with
![]() $\textbf{p} (n):= (m,m)$
. Recall that we have
$\textbf{p} (n):= (m,m)$
. Recall that we have
Analogously (see [Reference Jakubowski and Soja-Kukieła12, Remark 2.2]) we define
![]() $\Lambda^{(2)}_n$
and
$\Lambda^{(2)}_n$
and
![]() $\lambda^{(2)}_n$
related to the method from Section 5.2 as follows:
$\lambda^{(2)}_n$
related to the method from Section 5.2 as follows:
 \begin{align*}\Lambda^{(2)}_n &:= \sum_{\textbf{k} \in W}\sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}},\\
\lambda^{(2)}_n &:= {\mathbb{E}} (\Lambda^{(2)}_n) = N^*(n) \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} {\mathbb{P}}(M_{\pmb{\varepsilon}, (m,m)} > v_n).\end{align*}
\begin{align*}\Lambda^{(2)}_n &:= \sum_{\textbf{k} \in W}\sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}},\\
\lambda^{(2)}_n &:= {\mathbb{E}} (\Lambda^{(2)}_n) = N^*(n) \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} {\mathbb{P}}(M_{\pmb{\varepsilon}, (m,m)} > v_n).\end{align*}
Assume that
![]() $C\in\mathcal{C}^{\prime}_n$
. Let
$C\in\mathcal{C}^{\prime}_n$
. Let
and suppose we have
![]() $M_{B(C,m) \backslash C} \leq v_n$
(which is obviously satisfied in the typical case
$M_{B(C,m) \backslash C} \leq v_n$
(which is obviously satisfied in the typical case
![]() $B(C,m)\subset W$
). Observe that for such C we have
$B(C,m)\subset W$
). Observe that for such C we have
and
where
and
![]() $\textbf{k}(C)$
satisfies the condition
$\textbf{k}(C)$
satisfies the condition
We will show that each of the following equalities holds:
This will entail the condition
![]() $\lambda_n=\lambda^{\prime}_n + {\text{o}}(1) = \lambda^{(1)}_n +{\text{o}}(1) = \lambda^{(2)}_n +{\text{o}}(1)$
and complete this section.
$\lambda_n=\lambda^{\prime}_n + {\text{o}}(1) = \lambda^{(1)}_n +{\text{o}}(1) = \lambda^{(2)}_n +{\text{o}}(1)$
and complete this section.
To show (5.5), observe that the event
![]() $\{\# \mathcal{C}^{\prime\prime}_n = l\}$
, for
$\{\# \mathcal{C}^{\prime\prime}_n = l\}$
, for
![]() $l\in\mathbb{N}_+$
, implies that there exist pairs
$l\in\mathbb{N}_+$
, implies that there exist pairs
![]() $\textbf{j}(i,a), \textbf{j}(i,b) \in J_n$
, for
$\textbf{j}(i,a), \textbf{j}(i,b) \in J_n$
, for
![]() $i\in\{1,2,\ldots,l\}$
, such that
$i\in\{1,2,\ldots,l\}$
, such that
![]() $m < \|\textbf{j}(i,a) - \textbf{j}(i,b)\|\leq 2m$
holds for each i and
$m < \|\textbf{j}(i,a) - \textbf{j}(i,b)\|\leq 2m$
holds for each i and
![]() $\|\textbf{j}(i_1,c_1)-\textbf{j}(i_2,c_2)\| > m$
is satisfied for
$\|\textbf{j}(i_1,c_1)-\textbf{j}(i_2,c_2)\| > m$
is satisfied for
![]() $i_1\neq i_2$
and
$i_1\neq i_2$
and
![]() $c_1, c_2\in\{a,b\}$
. Thus we have
$c_1, c_2\in\{a,b\}$
. Thus we have
Since
by (3.3), we obtain
and finally
![]() $\delta_n={\text{o}}(1)$
.
$\delta_n={\text{o}}(1)$
.
Before we establish (5.6) and (5.7), we will give an upper bound for the probability that a fixed
![]() $\textbf{k}\in W$
belongs to a large cluster. Note that we have
$\textbf{k}\in W$
belongs to a large cluster. Note that we have
 \begin{align}& {\mathbb{P}} (\textbf{k} \in C \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag\\[6pt] & \qquad = {\mathbb{P}} (\textbf{k} \in C \text{ and } \|\textbf{j}-\textbf{k}\|\leq m \text{ for all }\textbf{j}\in C, \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag\\[6pt] & \qquad\quad\, + {\mathbb{P}} (\textbf{k} \in C \text{ and } \|\textbf{j}-\textbf{k}\|> m \text{ for some }\textbf{j}\in C, \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag \\[6pt] & \qquad \leq {\mathbb{P}} (\|\textbf{i} - \textbf{k}\| \leq m \text{ and } \|\textbf{j} - \textbf{k}\|\leq m \text{ and } \|\textbf{i} - \textbf{j}\|>m, \text{ for some }\textbf{i},\textbf{j}\in J_n) \notag\\[6pt] &\qquad\quad\, + {\mathbb{P}} (\textbf{k} \in J_n \text{ and } m<\|\textbf{k}-\textbf{j}\|\leq 2m \text{ for some }\textbf{j} \in J_n) \notag\\[6pt] &\qquad \leq ((2m+1)^4 + ((4m+1)^2 - (2m+1)^2)) {\mathbb{P}}(X_{\mathbf{0}} > v_n)^2 = a(m){\mathbb{P}}(X_{\mathbf{0}} > v_n)^2\end{align}
\begin{align}& {\mathbb{P}} (\textbf{k} \in C \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag\\[6pt] & \qquad = {\mathbb{P}} (\textbf{k} \in C \text{ and } \|\textbf{j}-\textbf{k}\|\leq m \text{ for all }\textbf{j}\in C, \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag\\[6pt] & \qquad\quad\, + {\mathbb{P}} (\textbf{k} \in C \text{ and } \|\textbf{j}-\textbf{k}\|> m \text{ for some }\textbf{j}\in C, \text{ for some } C\in\mathcal{C}_n^{\prime\prime}) \notag \\[6pt] & \qquad \leq {\mathbb{P}} (\|\textbf{i} - \textbf{k}\| \leq m \text{ and } \|\textbf{j} - \textbf{k}\|\leq m \text{ and } \|\textbf{i} - \textbf{j}\|>m, \text{ for some }\textbf{i},\textbf{j}\in J_n) \notag\\[6pt] &\qquad\quad\, + {\mathbb{P}} (\textbf{k} \in J_n \text{ and } m<\|\textbf{k}-\textbf{j}\|\leq 2m \text{ for some }\textbf{j} \in J_n) \notag\\[6pt] &\qquad \leq ((2m+1)^4 + ((4m+1)^2 - (2m+1)^2)) {\mathbb{P}}(X_{\mathbf{0}} > v_n)^2 = a(m){\mathbb{P}}(X_{\mathbf{0}} > v_n)^2\end{align}
with
![]() $a(m):= (2m+1)^4 + 4m(3m+1)$
.
$a(m):= (2m+1)^4 + 4m(3m+1)$
.
Applying observation (5.3), property (5.8) and taking into account estimation errors for clusters situated near the edges of the window W, we obtain
 \begin{align*}\delta_n^{(1)} & = {\mathbb{E}} \biggl|\sum_{\textbf{k} \in W} \bigl(\mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime}_n, M_{\textbf{k} + A(m,m)}\leq v_n \}}+ \mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime\prime}_n , M_{\textbf{k} + A(m,m)}\leq v_n\}}\bigr) - \Lambda^{\prime}_n \biggr|\\& \leq {\mathbb{E}}\biggl|\sum_{C\in\mathcal{C}^{\prime}_n} \sum_{\textbf{k}\in C} \mathbb{I}_{\{M_{\textbf{k} + A(m,m)}\leq v_n\}} - \Lambda^{\prime}_n\biggr|+ {\mathbb{E}} \biggl(\sum_{\textbf{k} \in W} \mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime\prime}_n \}}\biggr)\\& \leq 2m(N_1(n)+N_2(n)) {\mathbb{P}}(X_{\mathbf{0}} > v_n)+ a(m)N^*(n){\mathbb{P}}(X_{\mathbf{0}} > v_n)^2,\end{align*}
\begin{align*}\delta_n^{(1)} & = {\mathbb{E}} \biggl|\sum_{\textbf{k} \in W} \bigl(\mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime}_n, M_{\textbf{k} + A(m,m)}\leq v_n \}}+ \mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime\prime}_n , M_{\textbf{k} + A(m,m)}\leq v_n\}}\bigr) - \Lambda^{\prime}_n \biggr|\\& \leq {\mathbb{E}}\biggl|\sum_{C\in\mathcal{C}^{\prime}_n} \sum_{\textbf{k}\in C} \mathbb{I}_{\{M_{\textbf{k} + A(m,m)}\leq v_n\}} - \Lambda^{\prime}_n\biggr|+ {\mathbb{E}} \biggl(\sum_{\textbf{k} \in W} \mathbb{I}_{\{\textbf{k} \in \bigcup \mathcal{C}^{\prime\prime}_n \}}\biggr)\\& \leq 2m(N_1(n)+N_2(n)) {\mathbb{P}}(X_{\mathbf{0}} > v_n)+ a(m)N^*(n){\mathbb{P}}(X_{\mathbf{0}} > v_n)^2,\end{align*}
which combined with assumption (3.3) implies (5.6). Quite similarly, using (5.4) instead of (5.3) and writing
![]() $\bar{W}:= \{\textbf{k}\in {\mathbb Z}^2 \colon \mathbf{1}-(m,m) \leq \textbf{k} \leq \textbf{N}(n)\}$
, we conclude that
$\bar{W}:= \{\textbf{k}\in {\mathbb Z}^2 \colon \mathbf{1}-(m,m) \leq \textbf{k} \leq \textbf{N}(n)\}$
, we conclude that
 \begin{align*}\delta_n^{(2)}& \leq {\mathbb{E}} \biggl| \sum_{\textbf{k}\in \bar{W} } \mathbb{I}_{\{\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime}_n \}} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}} - \Lambda^{\prime}_n\biggr| \\& \quad\, + {\mathbb{E}} \biggl(\sum_{\textbf{k}\in\bar{W}\backslash W} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} \bigl| (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}}\bigr|\biggr) \\& \quad\, + 2{\mathbb{E}} \biggl(\sum_{\textbf{k}\in W} \mathbb{I}_{\{\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime\prime}_n \}} \biggr)\\& \leq {\mathbb{E}}\biggl| \sum_{C\in \mathcal{C}^{\prime}_n} \sum_{\textbf{k}\in \bar{C}} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}} - \Lambda^{\prime}_n \biggr|\\& \quad\, + \sum_{\textbf{k}\in\bar{W}\backslash W} (2m+1){\mathbb{P}}(X_{\mathbf{0}} > v_n) + 2N^*(n){\mathbb{P}} (\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime\prime}_n)\\& \leq 2m(2m+1)(N_1(n)+N_2(n)){\mathbb{P}}(X_\mathbf{0}>v_n)\\& \quad\, + m(2m + 1)(N_1(n) + N_2(n) + m){\mathbb{P}}(X_\mathbf{0} > v_n) + 2(m + 1)^2a(m)N^*(n){\mathbb{P}}(X_\mathbf{0} > v_n)^2.\end{align*}
\begin{align*}\delta_n^{(2)}& \leq {\mathbb{E}} \biggl| \sum_{\textbf{k}\in \bar{W} } \mathbb{I}_{\{\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime}_n \}} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}} - \Lambda^{\prime}_n\biggr| \\& \quad\, + {\mathbb{E}} \biggl(\sum_{\textbf{k}\in\bar{W}\backslash W} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} \bigl| (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}}\bigr|\biggr) \\& \quad\, + 2{\mathbb{E}} \biggl(\sum_{\textbf{k}\in W} \mathbb{I}_{\{\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime\prime}_n \}} \biggr)\\& \leq {\mathbb{E}}\biggl| \sum_{C\in \mathcal{C}^{\prime}_n} \sum_{\textbf{k}\in \bar{C}} \sum_{\pmb{\varepsilon}\in\{0,1\}^2} (\!-1)^{\varepsilon_1 + \varepsilon_2} \mathbb{I}_{\{M_{\textbf{k}+\pmb{\varepsilon}, \textbf{k} + (m,m)} > v_n\}} - \Lambda^{\prime}_n \biggr|\\& \quad\, + \sum_{\textbf{k}\in\bar{W}\backslash W} (2m+1){\mathbb{P}}(X_{\mathbf{0}} > v_n) + 2N^*(n){\mathbb{P}} (\textbf{k}\in\bar{C} \text{ for some }C\in\mathcal{C}^{\prime\prime}_n)\\& \leq 2m(2m+1)(N_1(n)+N_2(n)){\mathbb{P}}(X_\mathbf{0}>v_n)\\& \quad\, + m(2m + 1)(N_1(n) + N_2(n) + m){\mathbb{P}}(X_\mathbf{0} > v_n) + 2(m + 1)^2a(m)N^*(n){\mathbb{P}}(X_\mathbf{0} > v_n)^2.\end{align*}
Since the right-hand side tends to zero by (3.3), property (5.7) follows.
5.3.2. Second approach: direct verification
In this part we assume that
![]() $\preccurlyeq$
is the lexicographic order on
$\preccurlyeq$
is the lexicographic order on
![]() ${\mathbb Z}^2$
. Let us note that
${\mathbb Z}^2$
. Let us note that
 \begin{align*}& {\mathbb{P}} (M_{{(0,0)},(m,m)} > v_n) - {\mathbb{P}} (M_{(1,0),(m,m)} > v_n) - {\mathbb{P}} (M_{(0,1),(m,m)} > v_n) + {\mathbb{P}} (M_{(1,1),(m,m)} > v_n) \\[6pt] & \qquad = {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n) \\[6pt] & \qquad\quad\, - {\mathbb{P}} (M_{(0,1), (0,m){}} > v_n, M_{(1,0),(m,0)} >v_n, M_{(1,1), (m,m)} \leq v_n)\end{align*}
\begin{align*}& {\mathbb{P}} (M_{{(0,0)},(m,m)} > v_n) - {\mathbb{P}} (M_{(1,0),(m,m)} > v_n) - {\mathbb{P}} (M_{(0,1),(m,m)} > v_n) + {\mathbb{P}} (M_{(1,1),(m,m)} > v_n) \\[6pt] & \qquad = {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n) \\[6pt] & \qquad\quad\, - {\mathbb{P}} (M_{(0,1), (0,m){}} > v_n, M_{(1,0),(m,0)} >v_n, M_{(1,1), (m,m)} \leq v_n)\end{align*}
is true with
![]() $R((p_1,p_2)):= A((p_1,p_2))\cap {\mathbb N}^2$
, where on the left-hand side of the equation the sum of probabilities from (5.2) for
$R((p_1,p_2)):= A((p_1,p_2))\cap {\mathbb N}^2$
, where on the left-hand side of the equation the sum of probabilities from (5.2) for
![]() $d=2$
appears. Next, let us look at the exponent in (5.1) and observe that
$d=2$
appears. Next, let us look at the exponent in (5.1) and observe that
 \begin{align*}& {\mathbb{P}} (X_{(0,0)} > v_n,M_{A((m,m))} \leq v_n) \\& \qquad = {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n) \\& \qquad\quad\, - {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-m),(m,-1)} > v_n)\end{align*}
\begin{align*}& {\mathbb{P}} (X_{(0,0)} > v_n,M_{A((m,m))} \leq v_n) \\& \qquad = {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n) \\& \qquad\quad\, - {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-m),(m,-1)} > v_n)\end{align*}
and, moreover, the second summand of the right-hand side satisfies
 \begin{align*}& {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-m),(m,-1)} > v_n) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-l),(m,-l)} > v_n, M_{(1,-l+1), (m,-1)} \leq v_n) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,0)} >\! v_n, M_{R((m,m-l))} \leq v_n, M_{(1,-l),(m,-l)} > v_n, M_{(1,-l+1), (m,-1)} \leq v_n) + {\text{o}}(n^{-2}) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,l)} > v_n, M_{(0,l) + R((m,m-l))} \leq v_n, M_{(1,0),(m,0)} > v_n, M_{(1,1), (m,l-1)} \leq v_n) + {\text{o}}(n^{-2}) \\& \qquad = {\mathbb{P}} (M_{(0,1), (0,m)} > v_n, M_{(1,0),(m,0)} >v_n, M_{(1,1), (m,m)} \leq v_n ) + {\text{o}}(n^{-2}) .\end{align*}
\begin{align*}& {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-m),(m,-1)} > v_n) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,0)} > v_n, M_{R((m,m))} \leq v_n, M_{(1,-l),(m,-l)} > v_n, M_{(1,-l+1), (m,-1)} \leq v_n) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,0)} >\! v_n, M_{R((m,m-l))} \leq v_n, M_{(1,-l),(m,-l)} > v_n, M_{(1,-l+1), (m,-1)} \leq v_n) + {\text{o}}(n^{-2}) \\& \qquad = \sum_{l=1}^{m} {\mathbb{P}} (X_{(0,l)} > v_n, M_{(0,l) + R((m,m-l))} \leq v_n, M_{(1,0),(m,0)} > v_n, M_{(1,1), (m,l-1)} \leq v_n) + {\text{o}}(n^{-2}) \\& \qquad = {\mathbb{P}} (M_{(0,1), (0,m)} > v_n, M_{(1,0),(m,0)} >v_n, M_{(1,1), (m,m)} \leq v_n ) + {\text{o}}(n^{-2}) .\end{align*}
In the above statement, probabilities of mutually exclusive events are summed up, and m-dependence, assumption (3.3), and stationarity are applied. Finally, we obtain
Summarizing, we have confirmed that both presented methods lead to the same result.
Remark 5.1. The above reasoning for m-dependent fields can also be applied in the general setting. Suppose that formula (1.3), with
![]() $\preccurlyeq$
the lexicographic order on
$\preccurlyeq$
the lexicographic order on
![]() ${\mathbb Z}^2$
, describes the asymptotics of partial maxima of the stationary field
${\mathbb Z}^2$
, describes the asymptotics of partial maxima of the stationary field
![]() $\{X_\textbf{n} \colon \textbf{n}\in{\mathbb Z}^2\}$
. Then
$\{X_\textbf{n} \colon \textbf{n}\in{\mathbb Z}^2\}$
. Then
holds if and only if
![]() $\{X_\textbf{n}\}$
satisfies the following condition:
$\{X_\textbf{n}\}$
satisfies the following condition:
 \begin{equation}\sum_{l=1}^{p_2(n)} {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{U_l(\textbf{p} (n))} > v_n, M_{V_l(\textbf{p} (n))} > v_n, M_{W_l(\textbf{p} (n))} \leq v_n) = {\text{o}}(n^{-2}),\end{equation}
\begin{equation}\sum_{l=1}^{p_2(n)} {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{U_l(\textbf{p} (n))} > v_n, M_{V_l(\textbf{p} (n))} > v_n, M_{W_l(\textbf{p} (n))} \leq v_n) = {\text{o}}(n^{-2}),\end{equation}
where
 \begin{align*}U_l(\textbf{p}) & := \{0,\ldots, p_1\} \times \{p_2-l+1, \ldots, p_2\},\\[3pt] V_l(\textbf{p}) & := \{1,\ldots, p_1\} \times \{-l\},\\[3pt] W_l(\textbf{p}) & := A(\textbf{p}) \cap ({\mathbb Z}\times \{-l+1,\ldots, p_2-l\}).\end{align*}
\begin{align*}U_l(\textbf{p}) & := \{0,\ldots, p_1\} \times \{p_2-l+1, \ldots, p_2\},\\[3pt] V_l(\textbf{p}) & := \{1,\ldots, p_1\} \times \{-l\},\\[3pt] W_l(\textbf{p}) & := A(\textbf{p}) \cap ({\mathbb Z}\times \{-l+1,\ldots, p_2-l\}).\end{align*}
Formula (5.9) generalizes (5.2). In the present section we have used the fact that m-dependent fields satisfy (5.10) with
![]() $\textbf{p}(n):= (m,m)$
.
$\textbf{p}(n):= (m,m)$
.
6. Example: moving maxima
Below, we use the results from Sections 3 and 4 to describe the asymptotics of partial maxima for the moving maximum field. We note that approaches to the problem using different methods can be found in Basrak and Tafro [Reference Basrak and Tafro3] or Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12]. In the first paper compound Poisson point process approximation is applied, while in the second paper the authors combine a Bonferroni-like inequality and max-m-approximability.
In the following,
![]() $\{Z_\textbf{n}\}$
is an array of independent, identically distributed random variables satisfying
$\{Z_\textbf{n}\}$
is an array of independent, identically distributed random variables satisfying
for some index
![]() $\alpha >0$
and slowly varying function L, and
$\alpha >0$
and slowly varying function L, and
We define
and
![]() $v_n:= a_n v$
with fixed
$v_n:= a_n v$
with fixed
![]() $v>0$
. Then
$v>0$
. Then
Let us consider the moving maximum field
![]() $\{X_\textbf{n}\}$
defined as
$\{X_\textbf{n}\}$
defined as
where
![]() $c_\textbf{j}\in{\mathbb R}$
, not all equal to zero, satisfy
$c_\textbf{j}\in{\mathbb R}$
, not all equal to zero, satisfy
From Cline [Reference Cline7, Lemma 2.2] it follows that the field
![]() $\{X_\textbf{n}\}$
is well-defined and
$\{X_\textbf{n}\}$
is well-defined and
 \begin{align}\lim_{x\to\infty}\dfrac{{\mathbb{P}}(X_\mathbf{0}>x)}{{\mathbb{P}}(|Z_\mathbf{0}|>x)}& = \lim_{x\to\infty}\dfrac{{\mathbb{P}} (\sup_{\textbf{j}\in{\mathbb Z} ^d}c_\textbf{j} Z_{\textbf{j}}>x) }{{\mathbb{P}}(|Z_\mathbf{0}|>x)} \notag \\& = \lim_{x\to\infty}\dfrac{\sum_{\textbf{j}\in{\mathbb Z}^d} {\mathbb{P}}(c_\textbf{j} Z_{\textbf{j}}>x)}{{\mathbb{P}}(|Z_\mathbf{0}|>x)} \notag \\& = p \sum_{c_\textbf{j} > 0} c_\textbf{j} ^\alpha+ q \sum_{c_\textbf{j} < 0} |c_\textbf{j} |^\alpha{,}\end{align}
\begin{align}\lim_{x\to\infty}\dfrac{{\mathbb{P}}(X_\mathbf{0}>x)}{{\mathbb{P}}(|Z_\mathbf{0}|>x)}& = \lim_{x\to\infty}\dfrac{{\mathbb{P}} (\sup_{\textbf{j}\in{\mathbb Z} ^d}c_\textbf{j} Z_{\textbf{j}}>x) }{{\mathbb{P}}(|Z_\mathbf{0}|>x)} \notag \\& = \lim_{x\to\infty}\dfrac{\sum_{\textbf{j}\in{\mathbb Z}^d} {\mathbb{P}}(c_\textbf{j} Z_{\textbf{j}}>x)}{{\mathbb{P}}(|Z_\mathbf{0}|>x)} \notag \\& = p \sum_{c_\textbf{j} > 0} c_\textbf{j} ^\alpha+ q \sum_{c_\textbf{j} < 0} |c_\textbf{j} |^\alpha{,}\end{align}
with
![]() $q:= 1-p$
.
$q:= 1-p$
.
Since the moving maximum field is
![]() $\max$
-m-approximable, there exists a phantom distribution function for
$\max$
-m-approximable, there exists a phantom distribution function for
![]() $\{X_\textbf{n}\}$
(see Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12]) and hence the field is weakly dependent in the sense of (2.2). We will apply Theorem 3.1, with
$\{X_\textbf{n}\}$
(see Jakubowski and Soja-Kukieła [Reference Jakubowski and Soja-Kukieła12]) and hence the field is weakly dependent in the sense of (2.2). We will apply Theorem 3.1, with
![]() $\preccurlyeq$
being the lexicographic order on
$\preccurlyeq$
being the lexicographic order on
![]() ${\mathbb Z}^d$
, to describe the asymptotics of partial maxima. Let us observe that the exponent in (3.2) satisfies
${\mathbb Z}^d$
, to describe the asymptotics of partial maxima. Let us observe that the exponent in (3.2) satisfies
 \begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n) \\& \qquad = n^d{\mathbb{P}}\biggl(\bigcup_{\textbf{j}\in{\mathbb Z}^d} \{c_\textbf{j} Z_\textbf{j} > v_n \}, \bigcap_{\textbf{k}\in{\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\} \biggr)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\biggl( c_\textbf{j} Z_\textbf{j} > v_n , \bigcap_{\textbf{k}\in{\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\biggl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}), \bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}} \Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) {\mathbb{P}} \biggl(\bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1),\end{align*}
\begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n) \\& \qquad = n^d{\mathbb{P}}\biggl(\bigcup_{\textbf{j}\in{\mathbb Z}^d} \{c_\textbf{j} Z_\textbf{j} > v_n \}, \bigcap_{\textbf{k}\in{\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\} \biggr)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\biggl( c_\textbf{j} Z_\textbf{j} > v_n , \bigcap_{\textbf{k}\in{\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\biggl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}), \bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1)\\& \qquad = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}} \Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) {\mathbb{P}} \biggl(\bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) + {\text{o}}(1),\end{align*}
as
![]() $n\to\infty$
, where the second equality follows from (6.2) combined with the choice of
$n\to\infty$
, where the second equality follows from (6.2) combined with the choice of
![]() $\{v_n\}$
and the last equality is a consequence of the independence of
$\{v_n\}$
and the last equality is a consequence of the independence of
![]() $Z_\textbf{j}$
for
$Z_\textbf{j}$
for
![]() $\textbf{j}\in{\mathbb Z}^d$
. Note that we have
$\textbf{j}\in{\mathbb Z}^d$
. Note that we have
 \begin{align*}{\mathbb{P}}\biggl(\bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) & \geq {\mathbb{P}}\biggl(\bigcap_{\textbf{k} \in {\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) \\& \geq {\mathbb{P}} (M_{A(\textbf{p}(n))}\leq v_n) \\& \geq 1- {\text{o}}(n^d){\mathbb{P}}(X_{\mathbf{0}} >v_n) \\& = 1 + {\text{o}}(1).\end{align*}
\begin{align*}{\mathbb{P}}\biggl(\bigcap_{\textbf{k} \neq \textbf{j}} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) & \geq {\mathbb{P}}\biggl(\bigcap_{\textbf{k} \in {\mathbb Z}^d} \Bigl\{\max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{k} - \textbf{i}} Z_\textbf{k}) \leq v_n\Bigr\}\biggr) \\& \geq {\mathbb{P}} (M_{A(\textbf{p}(n))}\leq v_n) \\& \geq 1- {\text{o}}(n^d){\mathbb{P}}(X_{\mathbf{0}} >v_n) \\& = 1 + {\text{o}}(1).\end{align*}
Moreover, for
![]() $p_{\min}(n):= \min \{p_l(n) \colon 1\leq l\leq d\}$
and for
$p_{\min}(n):= \min \{p_l(n) \colon 1\leq l\leq d\}$
and for
![]() $q(n) \in {\mathbb N}$
chosen so that
$q(n) \in {\mathbb N}$
chosen so that
it follows that
 \begin{align*}& \biggl| n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr)- n^d \sum_{\textbf{j}\in{\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) \biggr| \\& \qquad \leq n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n, \sup_{\mathbf{0} \prec \textbf{i} \notin A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr)\\& \qquad \leq n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n, \sup_{\|\textbf{i} \| > p_{\min}(n)} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr)\\& \qquad \leq n^d\sum_{\|\textbf{j}\| \leq q(n)} {\mathbb{P}}\Bigl(\sup_{\|\textbf{i} \| > p_{\min}(n)} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr) + n^d \sum_{\|\textbf{j}\| > q(n)} {\mathbb{P}}( c_\textbf{j} Z_\textbf{j} > v_n)\\& \qquad \leq {n^d}(2 q(n)+1)^d {\mathbb{P}}\Bigl(\sup_{\|\textbf{i} \| > p_{\min}(n)/2} (c_{\textbf{i}} Z_{\mathbf{0}}) > v_n \Bigr) + n^d \sum_{\|\textbf{j}\| > q(n)} {\mathbb{P}}( c_\textbf{j} Z_\textbf{j} > v_n){.}\end{align*}
\begin{align*}& \biggl| n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \max_{\textbf{i}\in A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr)- n^d \sum_{\textbf{j}\in{\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) \biggr| \\& \qquad \leq n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n, \sup_{\mathbf{0} \prec \textbf{i} \notin A(\textbf{p}(n))} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr)\\& \qquad \leq n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n, \sup_{\|\textbf{i} \| > p_{\min}(n)} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr)\\& \qquad \leq n^d\sum_{\|\textbf{j}\| \leq q(n)} {\mathbb{P}}\Bigl(\sup_{\|\textbf{i} \| > p_{\min}(n)} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j}) > v_n \Bigr) + n^d \sum_{\|\textbf{j}\| > q(n)} {\mathbb{P}}( c_\textbf{j} Z_\textbf{j} > v_n)\\& \qquad \leq {n^d}(2 q(n)+1)^d {\mathbb{P}}\Bigl(\sup_{\|\textbf{i} \| > p_{\min}(n)/2} (c_{\textbf{i}} Z_{\mathbf{0}}) > v_n \Bigr) + n^d \sum_{\|\textbf{j}\| > q(n)} {\mathbb{P}}( c_\textbf{j} Z_\textbf{j} > v_n){.}\end{align*}
The first summand on the right-hand side tends to zero due to the choice of q(n) and the second summand tends to zero by properties (6.1), (6.2), and the definition of
![]() $v_n$
. We conclude that
$v_n$
. We conclude that
 \begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n) \\&\qquad = \biggl(n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) + {\text{o}}(1)\biggr) (1+ {\text{o}}(1)) + {\text{o}}(1).\end{align*}
\begin{align*}& n^d {\mathbb{P}} (X_{\mathbf{0}} > v_n, M_{A(\textbf{p}(n))}\leq v_n) \\&\qquad = \biggl(n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr) + {\text{o}}(1)\biggr) (1+ {\text{o}}(1)) + {\text{o}}(1).\end{align*}
To complete the above calculation, it is sufficient to observe that
 \begin{align*}n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr)& = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_{\mathbf{0}} > v_n \geq \sup_{\textbf{i} \prec \textbf{j}} (c_{\textbf{i}} Z_{\mathbf{0}})\Bigr)\\& = n^d {\mathbb{P}}\Bigl(\sup_{\textbf{j} \in {\mathbb Z}^d} (c_\textbf{j} Z_{\mathbf{0}}) > v_n\Bigr) \\& \to (p(c^+)^{\alpha} + q(c^-)^{\alpha})v^{-\alpha},\end{align*}
\begin{align*}n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_\textbf{j} > v_n \geq \sup_{\mathbf{0} \prec \textbf{i}} (c_{\textbf{j} - \textbf{i}} Z_\textbf{j})\Bigr)& = n^d \sum_{\textbf{j} \in {\mathbb Z}^d} {\mathbb{P}}\Bigl( c_\textbf{j} Z_{\mathbf{0}} > v_n \geq \sup_{\textbf{i} \prec \textbf{j}} (c_{\textbf{i}} Z_{\mathbf{0}})\Bigr)\\& = n^d {\mathbb{P}}\Bigl(\sup_{\textbf{j} \in {\mathbb Z}^d} (c_\textbf{j} Z_{\mathbf{0}}) > v_n\Bigr) \\& \to (p(c^+)^{\alpha} + q(c^-)^{\alpha})v^{-\alpha},\end{align*}
with
![]() $c^+:= \max_{\textbf{i} \in{\mathbb Z} ^d}\max\{c_\textbf{i},0\}$
and
$c^+:= \max_{\textbf{i} \in{\mathbb Z} ^d}\max\{c_\textbf{i},0\}$
and
![]() $c^-:= \max_{\textbf{i} \in{\mathbb Z} ^d} \max\{-c_\textbf{i},0\}$
. By (3.2) we obtain
$c^-:= \max_{\textbf{i} \in{\mathbb Z} ^d} \max\{-c_\textbf{i},0\}$
. By (3.2) we obtain
Applying formula (4.2) and property (6.2), we calculate the extremal index of
![]() $\{X_\textbf{n}\}$
as follows:
$\{X_\textbf{n}\}$
as follows:
whenever the denominator is positive, which is the only interesting case.
Acknowledgements
The author would like to thank the referees and the associate editor for comments and suggestions which improved the manuscript significantly.